Ax = b ; b = b 1 b 2. a 11 a 12 a 1n a 21 a 22 a 2n. b m. a m1 a m2 a mn
|
|
|
- Alfonso Nicoletti
- 5 anni fa
- Visualizzazioni
Transcript
1 SISTEMI LINERI Consideriamo il seguente sistema di m equazioni lineare nelle n incognite,,, n : a + a + + a n n = b >< a + a + + a n n = b = >: a m + a m + + a mn n = b m tale sistema può essere scritto in forma matriciale come segue: = b dove = n ; b = b b b m ; = a a a n a a a n a m a m a mn Se m = n, ossia il numero di equazioni è uguale al numero delle incognite e la matrice è quadrata, il sistema lineare si dice quadrato Iniziamo lo studio dei sistemi lineari partendo proprio dai sistemi quadrati SISTEMI LINERI QUDRTI Per risolvere il sistema lineare quadrato = b operiamo in modo analogo a come si procede con le equazioni lineari del tipo a = b, dove, se a =, la soluzione è data da = (a) b = b a Infatti, se det () = jj =, esiste la matrice inversa di, che indichiamo con Segue che la soluzione del sistema è = = b Sviluppando il prodotto matrice per vettore b, ci accorgiamo che jb j jb j n = jj dove B i, con i = ; :::; n, è la matrice ottenuta sostituendo alla i-esima colonna di il vettore dei termini noti b: bbiamo dimostrato il seguente teorema: jb n j B : = b; a ; :::; a n B : = a ; b; :::; a n B n : = a ; a ; :::; b Theorem (di Cramer) Dato il sistema = b con matrice nn, b R n vettore dei termini noti (assegnato) e R n vettore delle incognite Se det () = il sistema ha una e una sola soluzione (e si dice determinato) data da: = b -> () i = det (B i) det () dove B i è la matrice ottenuta sostituendo la i-esima colonna di con il vettore dei termini noti
2 Questi sistemi per cui sappiamo calcolare la soluzione tramire la Regola di Cramer, meritano una denominazione particolare: De nition (Sistema di Cramer) Dato il sistema quadrato = b esso si dice di Cramer se det () = Eample Consideriamo il seguente sistema < + n = + n = : + = scrivo il sistema in forma matriciale z } { z } { z } { = Nel risolverlo, prima controllare che sia un sistema di Cramer, appurato ciò calcolo la soluzione con la regola di Cramer: [Step ] det () = =, il sistema è di Cramer; [Step ] Trovo la soluzione con la regola di Cramer Consideriamo = a ; a ; a, dove a = ; a = ; a = b Il metodo di Cramer ci richiede di calcolare: det b; a ; a = det a ; b; a = det a ; a ; b = = = = la soluzione è dunque ossia = det b; a ; a det () = det a ; b; a det () = det a ; a ; b = det () = = =
3 Eercise Risolvere i seguenti sistemi lineari quadrati utilizzando la regola di Cramer: + = = < : >< >: = + + = + = = + + = + = + = Siamo in grado di risolvere i sistemi di Cramer Passiamo ora a trattare la classe dei sistemi omogenei, ossia i sistemi = b con b = vettore nullo, che non necessariamente fanno parte del club ristretto dei sistemi di Cramer SISTEMI LINERI OMOGENEI Risolvere un sistema omogeneo (non necessariamente quadrato) = equivale a trovare i valori,,, n per cui a + a + ::: + a n n = R m () Sappiamo che se i vettori colonna di, vale a dire a, a,, a n, sono linearmente indipendenti, allora l unico modo per avere soddisfatta l equazione () è ssare = = ::: = n = che equivale a dire che l unica soluzione del sistema = è = R n l contrario, se i vettori colonna di sono linearmente dipendenti, allora (per de nizione di dipendenza linare) esiste,,, n, non tutti nulli, = n = = che soddisfano () Ciò signi ca che il sistema = ammette almeno una soluzione non banale Ma se è tale per cui =, allora R, abbiamo che: ( ) {z} = = ovvero, tutti i vettori v =, con R, sono soluzione del sistema (le soluzioni sono in nite) l insieme dei vettori soluzione è un sottospazio vettoriale di R n de nito come segue In particolare, V = fv : v = g Per studiarne la dimensione di V, possiamo ragionare come segue Sappiamo che il sistema omogeneo = può essere scritto in modo equivalente come segue a + a + ::: + a n n = R m
4 Supponiamo che i primi k (< n) vettori a ; :::; a k siano tra loro linearmente indipendenti (se così non fosse riordinarli in modo che i primi k siano tra loro linearmente indipendenti), mentre i restanti n k dipendono linearmente dai primi k, ossia posso ssare ad arbitrio k+ ; :::; n e ancora ottenere, scegliendo,, k in modo consono che a + ::: + a k k = a k k+ ::: a n n ma dalla scelta arbitraria di k+ ; :::; n, ottengo n k vettori linearmente indipendenti di R n Segue che la dim (V ) = n k e si dice che esistono n k soluzioni per indicare che la soluzione dipendende da come scelgo i "parametri" k+ ; :::; n Per de nizione, sappiamo che il rango di ci indica il numero di righe e colonne di linearmente indipendenti, segue che dim (V ) = n rango () Summary Ricapitoliamo sui sistemi omogenei: Un sistema omogeneo = ha sempre almeno una soluzione, ovvero la soluzione banale = se è di Cramer (sistema quadrato e det () = ), ha un unica soluzione, ossia il vettore nullo (soluzione banale) se non è di Cramer, allora l insime delle soluzioni del sistema costituisce un sottospazio vettoriale di dimensione dim (V ) = n rango () Come trovare V (sottospazio vettoriale insieme soluzione di = )? Solution Dato rango () = k, scegliere (a piacere) k righe di tra loro linearmente indipendenti ed eliminare le restanti m k Otteniamo (), matrice con k righe linearmetne indipendenti Costruire la matrice () accostando k vettori colonna linearmente indipendenti di () (scelti a piacere) e costruire b () come b meno i restanti vettori colonna di () moltiplicati per le rispettive incognite bbiamo ora il sistema () () = b () dove () è il vettore contenente le sole incognite di relative ai vettori colonna di () utilizzati per costruire () Tale sistema è di Cramer (per costruzione) nelle sole incognite contenute in () (le incognite non contenute in () le considero come parametri) e posso risolverlo con la regola di Cramer Le soluzioni trovare saranno funzioni delle n k, dove k = rango (), variabili (non contenute in () ) che ho considerato come parametri, ossia esistono n k soluzioni pplichiamo la procedura ad un esempio concreto Eample Consideriamo il seguente sistema: z } { z } { z } { = trovo che det () = e rango () =, ossia una riga di è linearmente dipendenti dalle restanti Noto ad esempio che l ultima riga di si può ottenere dalla seconda sottratta la prima (terza riga = seconda riga - prima riga), questo signi ca che soddisfatte le prime due righe, la terza è automaticamente soddisfatta Elimino la terza riga e ottengo z } () z } { b { z () } { = b
5 un sistema equivalente a quello di partenza (ricordarsi che solo per sistemi omogenei, se () è ottenuta eliminando da una riga linearmente dipendente dalle restanti, allora i due sistemi () = e = sono equivalenti, ossia hanno lo stesso insieme di soluzioni) che può essere riscritto come segue: + + = Noto che il vettore è linearmente dipendente dagli altri due (allo stesso tempo avrei potuto scegliere il primo (il secondo) vettore essendo anch esso linearmente dipendente dai restanti, in questo caso avrei ottenuto la soluzione in funzione di ( )) Porto a destra: + = () z } { z } { z } { > = b () e mi riconduco ad un sistema di Cramer (non omogeneo) nelle sole variabili e, () = b (), che risolvo utilizzando la regola di Cramer: = = vale a dire, ssato = in modo arbitrario, il vettore soluzione di = b è L insieme soluzione è V = < : 9 = : R ; Risolvere il sistema eliminando la prima riga invece della terza e veri care che l insieme soluzione sia sempre lo stesso
6 Eercise Trovare l insieme soluzione V (sottospazio vettoriale) per i seguenti sistemi omogenei: = 9 = = = questo punto sappiamo risolvere tutti i sistemi omogenei e i sistemi di Cramer non omogenei Passiamo allora ai sistemi non omogenei che non sono (necessariamente) di Cramer, per i quali non sappiamo ancora trovarne la soluzione SISTEMI LINERI NON OMOGENEI bbiamo visto che per i sistemi omogenei esiste sempre almeno una soluzione, ossia il vettore nullo Ciò non è vero per i sistemi non omogenei Per questi sistemi la soluzione può esistere ed essere unica (sistemi determinati), può esistere ed essere in numero maggiore di uno o meglio in nite (sistemi indeterminati), non esistere (sistemi impossibili) In particolare, il seguente teorema ci dice quando un sistema lineare (qualsiasi) ha almeno una soluzione: Theorem 9 (di Rouché-Capelli) Condizione necessaria e su ciente a nché il sistema di m equazioni in n incognite = b abbia soluzione è che rango()=rango(jb) Remark Il teorema ci dice se il sistema lineare ha almeno una soluzione, ma non ci indica quante Remark Nota che trovare una soluzione di = b equivale a trovare dei coe cienti, tali per cui la combinazione lineare dei vettori colonna di per tali coe cienti mi restituisce il vettore dei termini noti b Ma perché questo sia possibile, b deve essere linearmente dipendente dai vettori colonna di, ossia rango () = rango (jb) Ciò equivale a dire che il sistema = b, con := a ; a ; :::; a n, ha soluzione se e solo se b span a ; a ; :::; a n Grazie al teorema di Rouché-Capelli siamo in grado di capire se un sistema lineare ha almeno una soluzione, ossia se il sistema è risolubile ppurato che un sistema lineare è risolubile, cerchiamo ora di capire quante soluzioni esistono e come ottenerle Per quanti care il numero di soluzioni di un sistema lineare risolubile, ci viene in aiuto il seguente teorema: Theorem Se = b, con b =, sistema di m equazioni in n incognite, ammette una soluzione, le soluzioni del sistema sono i vettori in R n del tipo + con = Pertanto il sistema non omogeneo ha n r soluzioni con r = rango ()
7 Remark Notare che l insieme delle soluzioni di una sistema lineare non omogeneo non costituiscono un sottospazio vettoriale Quest ultimo teorema ci permette di discutere i sistemi lineari Eample Discutere il seguente sistema lineare al variare del parametro : + = det () = (k + ) k + k = k + k = k (k + ) = % k = & k = Se k = e k = il sistema è di Cramer Esiste un unica soluzione Se k =, rango () = = rango (jb) = Non esistono soluzioni Se k =, rango () = rango (jb) = Il sistema ha soluzioni questo punto ci resta da capire come calcolare le soluzioni per sistemi non omogenei che non sono di Cramer L idea è sempre la stessa Dobbiamo trattare alcune variabili come parametri e ricondurci ad un sistema che è di Cramer per quelle variabili che non sono considerate come parametri Ovviamente dobbiamo assicurarci che rango() = rango(jb) ppurato ciò, possiamo procedere come segue: Se rango() < m, signi ca che ci sono delle righe di che sono linearmente dipendenti dalle altre Le isoliamo e le eliminiamo, eliminiamo inoltre le componenti di b corrispondenti Ottengo la matrice () e il vettore dei termini noti b (), ossia il sistema equivalente () = b () Per costruzione rango () è uguale al numero di righe di () Il sistema () = b (), con () := a (); ; a (); ; :::; a ();n, può anche essere scritto come: a (); + a (); + ::: + a ();n n = b () Essendo rango () = k, esistono k vettori colonna di () linearmente indipendenti, mentre i restanti n k sono dipendenti dai primi Isolo k vettori linearmente indipendenti a sinistra dell equazione (supponiamo che siano i primi k) e i restanti gli "porto" a destra del segno di uguale: a (); + a (); + ::: + a ();k k = b () a ();k+ k+ ::: a ();n n e costruisco la matrice () come matrice dei k vettori colonna linearmente indipendenti di () che ho isolato, mentre il nuovo vettore dei termini noti lo de nisco come segue: b () = b () a ()k+ k+ ::: a ()n n questo punto ho un sistema che è di Cramer nelle variabili,,, k : () () = b () che risolvo con il metodo di Cramer La soluzione dipenderà da k+,, n, ossia esistono n k soluzioni
8 Eample Trovare la soluzione del seguente sistema in n= incognite e m= equazioni: z } { z } { z } { = utilizzando la regola di Kronecker e dopo essermi calcolato diversi minori di, scopro che rango () = = rango (jb) Questo signi ca che il sistema ammette soluzioni e in (lo stesso in jb) esistono -= righe che possono essere espresse come combinazione lineare delle restanti, ossia esistono equazioni (delle ) che sono automaticamente soddisfatte una volta soddisfatte le restanti due d esempio, noto che riga = riga - riga, riga = riga + volte riga e riga = (-)*riga Posso, eliminare le ultime tre equazioni e ricondurmi ad un sistema equivalente in equazioni e incognite: z } () z } { { = b () b z } { a questo punto, noto che le prime colonne di sono due vettori linearmente indipendenti, mentre le restanti due colonne di sono due vettori linearmente dipendenti dai primi due Riscrivo il sistema nelle sole incognite e, trattando e come fossero parametri: z } () { () b z } { z () } { + = + () () = b () è un sistema di Cramer, che risolvo utilizzando la regola di Cramer: = + = + le soluzioni trovate dipendono da e, ossia sono Eercise Trovare le soluzioni dei seguenti sistemi: = = = = 9
9 Eample Dato il seguente sistema = Noto che rango () = rango (jb) =, ossia esistono due equazioni del sistema che sono automaticamente soddisfatte una volta veri cate le restanti tal proposito, indicare quale dei seguenti sistemi è equivalente a quello dato: La risposta è semplice, solo il terzo Infatti, nel primo ho eliminato due righe di (meglio di jb) che sono linearmente indipendenti da quelle non eliminate Stessa cosa nel secondo caso = = = lla ne di queste note sulle lezioni relative ai sistemi lineari, possiamo riassumere quanto segue: Summary Sia = b un sistema in n incognite con m equazioni: [] Se rango () < rango (jb), il sistema è privo di soluzioni; [] Se rango () < rango (jb) = n, il sistema ha un unica soluzione; [] Se rango () = rango (jb) < n, il sistema ha in nite soluzioni 9
A titolo di esempio proponiamo la risoluzione del sistema sia con il metodo della matrice inversa sia con il metodo di Cramer.
 ) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
Manlio Bordoni. APPUNTI SULLA RAPPRESENTAZIONE DEI SOTTOSPAZI VETTORIALI DI R n I MODO. v 11. v n1
 Manlio Bordoni APPUNTI SULLA RAPPRESENTAZIONE DEI SOTTOSPAZI VETTORIALI DI R n I MODO Sia dato un insieme di generatori v v =,, v k = v n di W : questo vuol dire che ogni vettore w W si scrive come combinazione
Manlio Bordoni APPUNTI SULLA RAPPRESENTAZIONE DEI SOTTOSPAZI VETTORIALI DI R n I MODO Sia dato un insieme di generatori v v =,, v k = v n di W : questo vuol dire che ogni vettore w W si scrive come combinazione
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
Argomento 13 Sistemi lineari
 Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
I sistemi lineari di n equazioni in n incognite
 I sistemi lineari I sistemi lineari di n equazioni in n incognite I sistemi lineari di n equazioni in n incognite, sono formati da equazioni di primo grado, in cui le incognite hanno tutte esponente uguale
I sistemi lineari I sistemi lineari di n equazioni in n incognite I sistemi lineari di n equazioni in n incognite, sono formati da equazioni di primo grado, in cui le incognite hanno tutte esponente uguale
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito B 3/05/005 A. A. 004 005 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito B 3/05/005 A. A. 004 005 ) Risolvere il seguente sistema
Esercitazione 6 - Soluzione
 Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Note per il corso di Geometria Corso di laurea in Ing. Edile/Architettura. 4 Sistemi lineari. Metodo di eliminazione di Gauss Jordan
 Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
Corso di Geometria BIAR, BSIR Esercizi 3: soluzioni
 Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Rango e teorema di Rouché-Capelli Esercizio. Calcolare il rango di ciascuna delle seguenti matrici: ( ) ( ) ( ) A =, A =, A =, A 4 = ( ). a a a Soluzione.
Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Rango e teorema di Rouché-Capelli Esercizio. Calcolare il rango di ciascuna delle seguenti matrici: ( ) ( ) ( ) A =, A =, A =, A 4 = ( ). a a a Soluzione.
Introduzione soft alla matematica per l economia e la finanza. Marta Cardin, Paola Ferretti, Stefania Funari
 Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
Federica Gregorio e Cristian Tacelli
 1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
1. Sistemi di equazioni lineari. 1.1 Considerazioni preliminari
 1. Sistemi di equazioni lineari 1.1 Considerazioni preliminari I sistemi lineari sono sistemi di equazioni di primo grado in più incognite. Molti problemi di matematica e fisica portano alla soluzione
1. Sistemi di equazioni lineari 1.1 Considerazioni preliminari I sistemi lineari sono sistemi di equazioni di primo grado in più incognite. Molti problemi di matematica e fisica portano alla soluzione
Pagine di Algebra lineare. di premessa al testo Pagine di Geometria di Sara Dragotti. Parte terza: SISTEMI LINEARI
 Pagine di Algebra lineare di premessa al testo Pagine di Geometria di Sara Dragotti Parte terza: SISTEMI LINEARI 1. Definizioni Dato un campo K ed m 1 polinomi su K in n indeterminate di grado non superiore
Pagine di Algebra lineare di premessa al testo Pagine di Geometria di Sara Dragotti Parte terza: SISTEMI LINEARI 1. Definizioni Dato un campo K ed m 1 polinomi su K in n indeterminate di grado non superiore
Sistemi Lineari. Andrea Galasso
 Sistemi Lineari Andrea Galasso Esercizi svolti Teorema. (Rouché-Capelli. Un sistema lineare Ax = b ammette soluzioni se e solo se il rango della matrice dei coefficienti A è uguale al rango della matrice
Sistemi Lineari Andrea Galasso Esercizi svolti Teorema. (Rouché-Capelli. Un sistema lineare Ax = b ammette soluzioni se e solo se il rango della matrice dei coefficienti A è uguale al rango della matrice
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016.
 Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
Sistemi II. Sistemi II. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
SISTEMI LINEARI MATRICI E SISTEMI 1
 MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
Corso di Geometria BIAR, BSIR Esercizi 4: soluzioni
 Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Esercizio. Sono dati i seguenti sistemi lineari omogenei nelle incognite x, y, z: { x + y z = x + y z = x + y z = S : x y + z =, S :, S 3 : x 3y =,
Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Esercizio. Sono dati i seguenti sistemi lineari omogenei nelle incognite x, y, z: { x + y z = x + y z = x + y z = S : x y + z =, S :, S 3 : x 3y =,
Analisi matematica Esercizi di Algebra Lineare: Parte I.
 Analisi matematica Esercizi di Algebra Lineare Parte I. March,. Calcolo vettoriale in R. Dati u v calcolare 8 z SOLUZIONI u + v u + v v u z u+ v+ z (u z) uv zu zuv juj ju vj jv zj vers (u) vers ( v) vers
Analisi matematica Esercizi di Algebra Lineare Parte I. March,. Calcolo vettoriale in R. Dati u v calcolare 8 z SOLUZIONI u + v u + v v u z u+ v+ z (u z) uv zu zuv juj ju vj jv zj vers (u) vers ( v) vers
SISTEMI LINEARI. x 2y 2z = 0. Svolgimento. Procediamo con operazioni elementari di riga sulla matrice del primo sistema: 1 1 1 3 1 2 R 2 R 2 3R 0 4 5.
 SISTEMI LINEARI Esercizi Esercizio. Risolvere, se possibile, i seguenti sistemi: x y z = 0 x + y + z = 3x + y + z = 0 x y = 4x + z = 0, x y z = 0. Svolgimento. Procediamo con operazioni elementari di riga
SISTEMI LINEARI Esercizi Esercizio. Risolvere, se possibile, i seguenti sistemi: x y z = 0 x + y + z = 3x + y + z = 0 x y = 4x + z = 0, x y z = 0. Svolgimento. Procediamo con operazioni elementari di riga
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI
 SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
Sistemi Lineari. Elisabetta Colombo. Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 200-20 2 a di o.0 4 Capelli Rango o Caratterisca : definizioni a di o.0 Un equazione nelle n incognite x,..., x n della forma dove
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 200-20 2 a di o.0 4 Capelli Rango o Caratterisca : definizioni a di o.0 Un equazione nelle n incognite x,..., x n della forma dove
Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta. Metodi per il calcolo del rango di una matrice
 Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta Versione del 21/12/07 Metodi per il calcolo del rango di una matrice Sia A M m,n (K). Denotiamo con A (i) la riga i-ma di A, i {1,..., m}.
Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta Versione del 21/12/07 Metodi per il calcolo del rango di una matrice Sia A M m,n (K). Denotiamo con A (i) la riga i-ma di A, i {1,..., m}.
Sistemi d equazioni lineari
 Introduzione Introduzione Sia dato il seguente sistema d equazioni: S S S S Come si risolve un sistema... come si risolve? Lezione 25.wpd 08/01/2011 XXV - 1 Lezione 25.wpd 08/01/2011 XXV - 2 Introduzione
Introduzione Introduzione Sia dato il seguente sistema d equazioni: S S S S Come si risolve un sistema... come si risolve? Lezione 25.wpd 08/01/2011 XXV - 1 Lezione 25.wpd 08/01/2011 XXV - 2 Introduzione
0.1 Complemento diretto
 1 0.1 Complemento diretto Dato U V, un complemento diretto di U é un sottospazio W V tale che U W = {0} U + W = V cioé la somma di U con il suo complemento diretto é diretta, e dá tutto lo spazio vettoriale
1 0.1 Complemento diretto Dato U V, un complemento diretto di U é un sottospazio W V tale che U W = {0} U + W = V cioé la somma di U con il suo complemento diretto é diretta, e dá tutto lo spazio vettoriale
Lezione 10: Teorema di Rouchè-Capelli e la classificazione dei sistemi lineari
 Lezione 10: Teorema di Rouchè-Capelli e la classificazione dei sistemi lineari In questa lezione ci dedicheremo a studiare a fondo quali proprietà della matrice dei coefficienti di un sistema (e della
Lezione 10: Teorema di Rouchè-Capelli e la classificazione dei sistemi lineari In questa lezione ci dedicheremo a studiare a fondo quali proprietà della matrice dei coefficienti di un sistema (e della
Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite
 3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
Soluzioni. Foglio 1. Rette e piani. n x + c = 0. (1)
 Soluzioni Foglio 1. Rette e piani. Esercizio 1. Se n è la normale al piano, sia c = n x 0. Dimostriamo prima che se x π, allora x soddisfa Si ha Sostituendo dentro (1) si ottiene n x + c = 0. (1) x = x
Soluzioni Foglio 1. Rette e piani. Esercizio 1. Se n è la normale al piano, sia c = n x 0. Dimostriamo prima che se x π, allora x soddisfa Si ha Sostituendo dentro (1) si ottiene n x + c = 0. (1) x = x
Sistemi lineari 1 / 12
 Sistemi lineari 1 / 12 Sistemi lineari 2 / 12 Ricordiamo che cosa è un sistema lineare con m equazioni in n incognite (m,n N, m,n 1): a 11 x 1 + +a 1n x n = b 1 a 21 x 1 + +a 2n x n = b 2, (1).. a m1 x
Sistemi lineari 1 / 12 Sistemi lineari 2 / 12 Ricordiamo che cosa è un sistema lineare con m equazioni in n incognite (m,n N, m,n 1): a 11 x 1 + +a 1n x n = b 1 a 21 x 1 + +a 2n x n = b 2, (1).. a m1 x
Il teorema di Rouché-Capelli
 Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
SISTEMI LINEARI. x y + 2t = 0 2x + y + z t = 0 x z t = 0 ; S 3 : ; S 5x 2y z = 1 4x 7y = 3
 SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
MATEMATICA. a.a. 2014/ Sistemi di equazioni lineari
 MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
Note sull algoritmo di Gauss
 Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Esempio. L immagine di f è l insieme dei vettori w = (w 1, w 2 ) R 2 che hanno w 1 = w 2. Quindi:
 Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
SISTEMI LINEARI, METODO DI GAUSS
 SISTEMI LINEARI, METODO DI GAUSS Abbiamo visto che un sistema di m equazioni lineari in n incognite si può rappresentare in forma matriciale come A x = b dove: A è la matrice di tipo (m, n) dei coefficienti
SISTEMI LINEARI, METODO DI GAUSS Abbiamo visto che un sistema di m equazioni lineari in n incognite si può rappresentare in forma matriciale come A x = b dove: A è la matrice di tipo (m, n) dei coefficienti
Esercizi sui sistemi di equazioni lineari.
 Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Esercizi svolti. risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale
 Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Argomento 13 Sistemi lineari
 Sistemi lineari: definizioni Argomento 3 Sistemi lineari I Un equazione nelle n incognite x,,x n della forma c x + + c n x n = b ove c,,c n sono numeri reali (detti coefficienti) eb è un numero reale (detto
Sistemi lineari: definizioni Argomento 3 Sistemi lineari I Un equazione nelle n incognite x,,x n della forma c x + + c n x n = b ove c,,c n sono numeri reali (detti coefficienti) eb è un numero reale (detto
r 2 r 2 2r 1 r 4 r 4 r 1
 SPAZI R n 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x, y, z)
SPAZI R n 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x, y, z)
0.1 Soluzioni esercitazione IV, del 28/10/2008
 1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
il determinante che si ottiene da A, sopprimendo la i - esima riga e la j - esima colonna. Si definisce complemento algebrico dell'elemento a ij
 Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
ALGEBRA LINEARE PARTE III
 DIEM sez Matematica Finanziaria Università degli studi di Genova Dicembre 200 Indice PREMESSA 2 GENERALITA 2 RAPPRESENTAZIONE DI UN SISTEMA LINEARE IN FORMA MATRI- CIALE 2 3 SOLUZIONE DI SISTEMI LINEARI
DIEM sez Matematica Finanziaria Università degli studi di Genova Dicembre 200 Indice PREMESSA 2 GENERALITA 2 RAPPRESENTAZIONE DI UN SISTEMA LINEARE IN FORMA MATRI- CIALE 2 3 SOLUZIONE DI SISTEMI LINEARI
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) 2 settembre 2013 Tema A
 Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) settembre 013 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Modulo di Geometria e Algebra Lineare (vecchio programma) settembre 013 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
ESERCIZI SULLE MATRICI
 ESERCIZI SULLE MATRICI Consideriamo il sistema lineare a, x + a, x + + a,n x n = b a, x + a, x + + a,n x n = b a m, x + a m, x + + a m,n x n = b m di m equazioni in n incognite che ha a, a,n A = a m, a
ESERCIZI SULLE MATRICI Consideriamo il sistema lineare a, x + a, x + + a,n x n = b a, x + a, x + + a,n x n = b a m, x + a m, x + + a m,n x n = b m di m equazioni in n incognite che ha a, a,n A = a m, a
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Risoluzione di sistemi lineari
 Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
Sistemi di equazioni lineari
 Sistemi di equazioni lineari Siano X 1,, X n indeterminate Un equazione lineare (o di primo grado) nelle incognite X 1,, X n a coefficienti nel campo K è della forma a 1 X 1 + + a n X n = b, a i, b K,
Sistemi di equazioni lineari Siano X 1,, X n indeterminate Un equazione lineare (o di primo grado) nelle incognite X 1,, X n a coefficienti nel campo K è della forma a 1 X 1 + + a n X n = b, a i, b K,
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari
 Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Argomenti trattati nella settimana novembre Il libro cui faccio riferimento, se non specificato altrimenti, è Lang, Algebra lineare
 Argomenti trattati nella settimana 23-27 novembre 2009 Il libro cui faccio riferimento, se non specificato altrimenti, è Lang, Algebra lineare 1 Sistemi lineari; 2 applicazioni lineari; Sistemi lineari;
Argomenti trattati nella settimana 23-27 novembre 2009 Il libro cui faccio riferimento, se non specificato altrimenti, è Lang, Algebra lineare 1 Sistemi lineari; 2 applicazioni lineari; Sistemi lineari;
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 5. Rango
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
Esercizi di Matematica di Base Scienze biologiche e Scienze e Tecnologie dell Ambiente
 Esercizi di Matematica di Base Scienze biologiche e Scienze e Tecnologie dell Ambiente Dati i vettori di R (i) Calcolare il prodotto scalare v w, (ii) Stabilire se v e w sono ortogonali, (ii) Stabilire
Esercizi di Matematica di Base Scienze biologiche e Scienze e Tecnologie dell Ambiente Dati i vettori di R (i) Calcolare il prodotto scalare v w, (ii) Stabilire se v e w sono ortogonali, (ii) Stabilire
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
PROBLEMA. Costruire matrici quadrate contenute. Fare i determinanti delle matrici quadrate contenute in A
 A = PROBLEMA 0 1 2 7 2 5 3 0 (2 4) Costruire matrici quadrate contenute in A (possibili solo matrici quadrate 2 2 e 1 1) Fare i determinanti delle matrici quadrate contenute in A Questo porta al concetto
A = PROBLEMA 0 1 2 7 2 5 3 0 (2 4) Costruire matrici quadrate contenute in A (possibili solo matrici quadrate 2 2 e 1 1) Fare i determinanti delle matrici quadrate contenute in A Questo porta al concetto
8 novembre Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
12 gennaio Commenti esame di geometria - Ing. gestionale - a.a
 Questo documento riporta commenti, approfondimenti o metodi di soluzione alternativi per alcuni esercizi dell esame Ovviamente alcuni esercizi potevano essere risolti utilizzando metodi ancora diversi
Questo documento riporta commenti, approfondimenti o metodi di soluzione alternativi per alcuni esercizi dell esame Ovviamente alcuni esercizi potevano essere risolti utilizzando metodi ancora diversi
ESERCIZI PROPOSTI. det A = = per cui il sistema si può risolvere applicando le formule di Cramer, cioè: dove: = =
 ESERCIZI PROPOSTI Risolvere i seguenti sistemi lineari )-0), utilizzando, dove possibile, sia il metodo di Cramer sia quello della matrice inversa, dopo aver analizzato gli esempi a)-d): 2x + + 4z 5 a)
ESERCIZI PROPOSTI Risolvere i seguenti sistemi lineari )-0), utilizzando, dove possibile, sia il metodo di Cramer sia quello della matrice inversa, dopo aver analizzato gli esempi a)-d): 2x + + 4z 5 a)
x 1 x 2 x 3 x 4 x 3 x 1 + x 3
 a.a. -6 Esercizi. Applicazioni lineari. Soluzioni. Sia : R 4 R 4 l applicazione lineare data da e siano dati i sottospazi + x ( x ) = +, + x 4 + x 4 U = span{, } W = span{, }. (i) Determinare ker e dire
a.a. -6 Esercizi. Applicazioni lineari. Soluzioni. Sia : R 4 R 4 l applicazione lineare data da e siano dati i sottospazi + x ( x ) = +, + x 4 + x 4 U = span{, } W = span{, }. (i) Determinare ker e dire
Rango di una matrice e teorema di Rouché-Capelli
 Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
LEZIONE 5. AX = 0 m,1.
 LEZIONE 5 5 isoluzione di sistemi Supponiamo che AX = B sia un sistema di equazioni lineari Ad esso associamo la sua matrice completa (A B Per quanto visto nella precedente lezione, sappiamo di poter trasformare,
LEZIONE 5 5 isoluzione di sistemi Supponiamo che AX = B sia un sistema di equazioni lineari Ad esso associamo la sua matrice completa (A B Per quanto visto nella precedente lezione, sappiamo di poter trasformare,
a + 2b + c 3d = 0, a + c d = 0 c d
 SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
1 Caratteristica di una matrice
 Università Bergamo Primo anno Ingegneria Geometria e Algebra Lineare Anno accademico 207208 Domande su: Caratteristica una matrice; sottospazi vettoriali, basi e mensione; sistemi lineari. Caratteristica
Università Bergamo Primo anno Ingegneria Geometria e Algebra Lineare Anno accademico 207208 Domande su: Caratteristica una matrice; sottospazi vettoriali, basi e mensione; sistemi lineari. Caratteristica
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE (esercitazione del 18 gennaio 2011)
 Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE (esercitazione del 18 gennaio 2011) ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE (esercitazione del 18 gennaio 2011) ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola
GEOMETRIA I Prima Prova Intermedia 3 Novembre 2017
 Corso di Laurea in Fisica GEOMETRIA I Prima Prova Intermedia Novembre 017 Cognome: Nome: Matricola: PARTE 1 Test a risposta multipla Una ed una sola delle quattro affermazioni è corretta. Indicarla con
Corso di Laurea in Fisica GEOMETRIA I Prima Prova Intermedia Novembre 017 Cognome: Nome: Matricola: PARTE 1 Test a risposta multipla Una ed una sola delle quattro affermazioni è corretta. Indicarla con
Spazi vettoriali. Indipendenza lineare.
 Spazi vettoriali Indipendenza lineare Nel piano vettoriale G 2, fissato un punto O ed identificati i vettori con i segmenti orientati con origine in O, informalmente si puo dire che che due vettori sono
Spazi vettoriali Indipendenza lineare Nel piano vettoriale G 2, fissato un punto O ed identificati i vettori con i segmenti orientati con origine in O, informalmente si puo dire che che due vettori sono
Esercizi di ripasso: geometria e algebra lineare.
 Esercizi di ripasso: geometria e algebra lineare. Esercizio. Sia r la retta passante per i punti A(2,, 3) e B(,, 2) in R 3. a. Scrivere l equazione cartesiana del piano Π passante per A e perpendicolare
Esercizi di ripasso: geometria e algebra lineare. Esercizio. Sia r la retta passante per i punti A(2,, 3) e B(,, 2) in R 3. a. Scrivere l equazione cartesiana del piano Π passante per A e perpendicolare
Appunti su Indipendenza Lineare di Vettori
 Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Istituzioni di Matematica I. Esercizi su sistemi lineari. & % x + y " #z = "1 & '#x " y+ z =1
 Istituzioni di Matematica I Esercizi su sistemi lineari Esempio. Dire per quali valori di λ R il sistema x " y+ z = 2 % x + y " z = " x " y+ z = ha una sola soluzione, per quali nessuna, per quali infinite
Istituzioni di Matematica I Esercizi su sistemi lineari Esempio. Dire per quali valori di λ R il sistema x " y+ z = 2 % x + y " z = " x " y+ z = ha una sola soluzione, per quali nessuna, per quali infinite
Sistemi lineari. a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2 : : : a m1 x 1 + a m2 x 2 +..
 Sistemi lineari: definizioni Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto termine
Sistemi lineari: definizioni Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto termine
LeLing12: Ancora sui determinanti.
 LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
Geometria BAER I canale Foglio esercizi 3
 Geometria BAER I canale Foglio esercizi 3 Esercizio. Discutere le soluzioni del seguente sistema lineare nelle incognite,, z al variare del parametro k. 3 + kz = k k + 3z = k k + z = Soluzione: Il determinante
Geometria BAER I canale Foglio esercizi 3 Esercizio. Discutere le soluzioni del seguente sistema lineare nelle incognite,, z al variare del parametro k. 3 + kz = k k + 3z = k k + z = Soluzione: Il determinante
Sistemi lineari. a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2 : : : a m1 x 1 + a m2 x 2 +..
 Sistemi lineari: definizioni Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto termine
Sistemi lineari: definizioni Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto termine
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA
 CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI 4 GEOMETRIA 2008/09 Esercizio 4.1 (5.10). Dati i vettori di R 3 : v 1 (1, 1, 2), v 2 (2, 4, 6), v 3 ( 1, 2, 5), v 4 (1, 1, 10) determinare
CORSO DI LAUREA IN INGEGNERIA EDILE/ARCHITETTURA FOGLIO DI ESERCIZI 4 GEOMETRIA 2008/09 Esercizio 4.1 (5.10). Dati i vettori di R 3 : v 1 (1, 1, 2), v 2 (2, 4, 6), v 3 ( 1, 2, 5), v 4 (1, 1, 10) determinare
1 Esercizi 13. 3x + λy + 2z = 0 (1 λ)x + 5y + 3z = 0 3x + 2y + z = 0
 1 Esercizi 13 1. Discutere le soluzioni del sistema seguente al variare del parametro λ R. 3x + λy + 2z 0 (1 λ)x + 5y + 3z 0 3x + 2y + z 0 Soluzione. Si tratta di un SLO 3 3 e sappiamo che tale sistema
1 Esercizi 13 1. Discutere le soluzioni del sistema seguente al variare del parametro λ R. 3x + λy + 2z 0 (1 λ)x + 5y + 3z 0 3x + 2y + z 0 Soluzione. Si tratta di un SLO 3 3 e sappiamo che tale sistema
Istituzioni di Matematiche Modulo A (ST)
 Istituzioni di Matematiche Modulo A (ST V II foglio di esercizi ESERCIZIO. Nei seguenti sistemi lineari, discutere l insieme delle soluzioni al variare del parametro t, o dei parametri t e τ, in R. 5 x
Istituzioni di Matematiche Modulo A (ST V II foglio di esercizi ESERCIZIO. Nei seguenti sistemi lineari, discutere l insieme delle soluzioni al variare del parametro t, o dei parametri t e τ, in R. 5 x
Ingegneria Gestionale - Corso di Analisi II e Algebra anno accademico 2008/2009
 Ingegneria Gestionale - Corso di Analisi II e Algebra anno accademico 28/29 Dire se le seguenti proposizioni sono vere o false: ESERCITAZIONE. Proposizione Vera Falsa f : R R 4 rk(f f : R 4 R rk(f f :
Ingegneria Gestionale - Corso di Analisi II e Algebra anno accademico 28/29 Dire se le seguenti proposizioni sono vere o false: ESERCITAZIONE. Proposizione Vera Falsa f : R R 4 rk(f f : R 4 R rk(f f :
ANALISI MATEMATICA. Informazioni utili alla preparazione della prova parziale: Conoscere:
 ANALISI MATEMATICA 3 a prova parziale del 03-04-2017 Regole di comportamento: Il tempo a disposizione per la prova parziale è di un'ora e trenta minuti. Dotarsi esclusivamente di penna nera o blu, matita
ANALISI MATEMATICA 3 a prova parziale del 03-04-2017 Regole di comportamento: Il tempo a disposizione per la prova parziale è di un'ora e trenta minuti. Dotarsi esclusivamente di penna nera o blu, matita
I. Foglio di esercizi su vettori linearmente dipendenti e linearmente indipendenti. , v 2 = α v 1 + β v 2 + γ v 3. α v 1 + β v 2 + γ v 3 = 0. + γ.
 ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
Veri ca di Matematica sulle matrici [1]
![Veri ca di Matematica sulle matrici [1] Veri ca di Matematica sulle matrici [1]](/thumbs/69/60779192.jpg) Veri ca di Matematica sulle matrici []. Si considerino le matrici A e de nite da 5 A = 2 3 7 5 4 7 3 A ; = 5 6 7 alcolare det(a), det(); la matrice somma = A + ; la matrice prodotto D = A. 6 7 2 2 2 3
Veri ca di Matematica sulle matrici []. Si considerino le matrici A e de nite da 5 A = 2 3 7 5 4 7 3 A ; = 5 6 7 alcolare det(a), det(); la matrice somma = A + ; la matrice prodotto D = A. 6 7 2 2 2 3
Esercizi svolti. delle matrici
 Esercizi svolti. astratti. Si dica se l insieme delle coppie reali (x, y) soddisfacenti alla relazione x + y è un sottospazio vettoriale di R La risposta è sì, perchè l unica coppia reale che soddisfa
Esercizi svolti. astratti. Si dica se l insieme delle coppie reali (x, y) soddisfacenti alla relazione x + y è un sottospazio vettoriale di R La risposta è sì, perchè l unica coppia reale che soddisfa
VETTORI E MATRICI. Ing. Nicola Cappuccio 2014 U.F.5 ELEMENTI SCIENTIFICI ED ELETTRONICI APPLICATI AI SISTEMI DI TELECOMUNICAZIONI
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
LEZIONE 3. a + b + 2c + e = 1 b + d + g = 0 3b + f + 3g = 2. a b c d e f g
 LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
Soluzioni del Foglio 2 I sistemi lineari
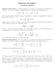 Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
Un sistema di equazioni lineari ( o brevemente un sistema lineare) di m equazioni in n incognite, si presenta nella forma:
 SISTEMI LINEARI Un sistema di equazioni lineari ( o brevemente un sistema lineare) di m equazioni in n incognite, si presenta nella forma: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x n =
SISTEMI LINEARI Un sistema di equazioni lineari ( o brevemente un sistema lineare) di m equazioni in n incognite, si presenta nella forma: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x n =
MATRICI. Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: a 2 m. a n m) i j R, 1 i n, 1 j m.
 MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
RANGO DI UNA MATRICE ρ(a)
 RANGO DI UNA MATRICE (A) a,... a A M M am,... a, n mn, K É il massimo ordine di un minore estratto con determinante non nullo. Equivalentemente è il massimo numero di righe (colonne) linearmente indipendenti.
RANGO DI UNA MATRICE (A) a,... a A M M am,... a, n mn, K É il massimo ordine di un minore estratto con determinante non nullo. Equivalentemente è il massimo numero di righe (colonne) linearmente indipendenti.
24 giugno Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a COGNOME... NOME... N. MATRICOLA...
 4 giugno 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore.
4 giugno 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore.
Inversa. Inversa. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 00-0, http://users.mat.unimi.it/users/colombo/programmabio.html e 3 con i Matrici inverse di matrici quadrate e con i Sia A una
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 00-0, http://users.mat.unimi.it/users/colombo/programmabio.html e 3 con i Matrici inverse di matrici quadrate e con i Sia A una
Esercitazione N.2. Sistemi lineari con parametro. di sistemi lineari con parametro. La regola di Cramer Discussione e risoluzione
 Esercitaione N. maro 7 Sistemi lineari con parametro La regola di Cramer Discussione e risoluione di sistemi lineari con parametro sistemi lineari omogenei Rosalba Barattero ESERCIZIO. Sistema di Cramer
Esercitaione N. maro 7 Sistemi lineari con parametro La regola di Cramer Discussione e risoluione di sistemi lineari con parametro sistemi lineari omogenei Rosalba Barattero ESERCIZIO. Sistema di Cramer
Prima di risolverli, è necessario prevedere se ci saranno soluzioni e, eventualmente, quante saranno.
 Sistemi lineari Prima di risolverli, è necessario prevedere se ci saranno soluzioni e, eventualmente, quante saranno. La discussione di un sistema si imposta in questo modo: 1 studiare il rango della matrice
Sistemi lineari Prima di risolverli, è necessario prevedere se ci saranno soluzioni e, eventualmente, quante saranno. La discussione di un sistema si imposta in questo modo: 1 studiare il rango della matrice
Compito di MD 13 febbraio 2014
 Compito di MD 13 febbraio 2014 IMPORTANTE: Non si possono consultare libri e appunti. Non si possono usare calcolatrici, computer o altri dispositivi elettronici. Non si può scrivere con il lapis. Motivare
Compito di MD 13 febbraio 2014 IMPORTANTE: Non si possono consultare libri e appunti. Non si possono usare calcolatrici, computer o altri dispositivi elettronici. Non si può scrivere con il lapis. Motivare
Note sui sistemi lineari
 Note sui sistemi lineari Sia K un campo e siano m e n due numeri interi positivi. Sia A M(m n, K) e sia b K m. Consideriamo il sistema lineare Ax = b nell incognita x K n (o, se preferite, nelle incognite
Note sui sistemi lineari Sia K un campo e siano m e n due numeri interi positivi. Sia A M(m n, K) e sia b K m. Consideriamo il sistema lineare Ax = b nell incognita x K n (o, se preferite, nelle incognite
La riduzione a gradini e i sistemi lineari (senza il concetto di rango)
 CAPITOLO 4 La riduzione a gradini e i sistemi lineari (senza il concetto di rango) Esercizio 4.1. Risolvere il seguente sistema non omogeneo: 2x+4y +4z = 4 x z = 1 x+3y +4z = 3 Esercizio 4.2. Risolvere
CAPITOLO 4 La riduzione a gradini e i sistemi lineari (senza il concetto di rango) Esercizio 4.1. Risolvere il seguente sistema non omogeneo: 2x+4y +4z = 4 x z = 1 x+3y +4z = 3 Esercizio 4.2. Risolvere
Sistemi di equazioni lineari
 Sistemi di equazioni lineari I sistemi di equazioni si incontrano in natura in molti problemi di vita reale. Per esempio, prendiamo in considerazione una bevanda a base di uova, latte e succo d arancia.
Sistemi di equazioni lineari I sistemi di equazioni si incontrano in natura in molti problemi di vita reale. Per esempio, prendiamo in considerazione una bevanda a base di uova, latte e succo d arancia.
