G. Parmeggiani, 17/5/2018 Algebra Lineare, a.a. 2017/2018, numero di MATRICOLA PARI
|
|
|
- Giacinto Ferraro
- 5 anni fa
- Visualizzazioni
Transcript
1 G Parmeggiani, 17/5/2018 Algebra Lineare, aa 2017/2018, Scuola di Scienze - Corsi di laurea: Studenti: Statistica per l economia e l impresa Statistica per le tecnologie e le scienze numero di MATRICOLA PARI Nota 3: Calcolo di determinanti Sia A una matrice quadrata di ordine n Il determinante di A è un numero che dipende da A Esso si indica con il simbolo det(a, oppure Det(A Impariamo a calcolarlo, cominciando con i casi n = 1, 2, 3 Il caso n=1 Se A = a 11, è Det(A = a11 a11 a Il caso n=2 Se A =, è Det(A = a a 21 a 11 a 22 a a Esempio 1 Il determinante di A = 2 3 è Det(A = = 10 = a11 a Abbiamo detto che Det = a a 21 a 11 a 22 a a 21 Osserviamo che 22 a 11 a 22 = a 11 ( Det a 22 = = a 11 ( 1 (la somma degli indici di a11 Det a 22 = e = a 11 ( 1 (la somma degli indici di a 11 il determinante della matrice che si ottiene da A sopprimendo la 1 a riga e la 1 a colonna di A = ( il determinante della matrice che si ottiene da A = a 11 ( 1 (la somma degli indici di a 11 sopprimendo la riga e la colonna in cui si trova a 11 a a 21 = a ( Det a 21 = = a ( 1 (la somma degli indici di a Det a 21 = = a ( 1 (la somma degli indici di a il determinante della matrice che si ottiene da A sopprimendo la 1 a riga e la 2 a colonna di A = ( il determinante della matrice che si ottiene da A = a ( 1 (la somma degli indici di a sopprimendo la riga e la colonna in cui si trova a Indicando con i simboli C 11 C la matrice che si ottiene da A sopprimendo la 1 a riga e la 1 a colonna, la matrice che si ottiene da A sopprimendo la 1 a riga e la 2 a colonna, 1
2 ed inoltre abbiamo: A 11 = ( DetC 11, A = ( DetC, a11 a Det = a a 21 a 11 A 11 + a A 22 Si tenga a mente ( che a 11 ed a sono gli elementi della 1 a riga di A a11 a Quindi se A = a 21 a 22 ( (1 mettere in evidenza gli elementi della 1 a a11 a riga di A: a 21 a 22, quello che abbiamo fatto per calcolare Det(A è stato: (2 per ciascuna posizione (1, j della 1 a riga di A (posto (1, 1 e posto (1, 2 costruire la matrice C 1j (ottenuta sopprimendo da A la 1 a riga e la j esima colonna di A, calcolare Det(C 1j, calcolare ( 1 1+j, calcolare A 1j = ( 1 1+j Det(C 1j, (3 calcolare il prodotto ( A a 11 a 11 A Il caso n=3 Sia A = a 11 a a 13 a 21 a 22 a 23 Per calcolare Det(A procediamo come nel a 31 a 32 a 33 caso n = 2 a 11 a a 13 (1 Mettiamo in evidenza gli elementi della 1 a riga di A: a 21 a 22 a 23 a 31 a 32 a 33 (2 per ciascuna posizione (1, j della 1 a riga di A (posto (1, 1, posto (1, 2 e posto (1, 3 costruiamo la matrice C 1j (ottenuta sopprimendo da A la 1 a riga e la j esima colonna di A: ( a22 a C 11 = 23 a21 a, C a 32 a = 23 a21, C 33 a 31 a 13 = 33 a 31 a 22 a 32 calcoliamo Det(C 1j, usando il caso n = 2, ossia il caso precedente a quello che stiamo analizzando ora (che è n = 3: a22 a DetC 11 = Det 23 = a a 32 a 22 a 33 a 23 a 32, ( 33 a21 a DetC = Det 23 = a a 31 a 21 a 33 a 23 a 31, ( 33 a21 a DetC 13 = Det 22 = a a 31 a 21 a 32 a 22 a 31, 32, 2
3 calcoliamo ( 1 1+j : ( = 1, ( = 1, ( = 1, calcoliamo A 1j = ( 1 1+j Det(C 1j : A 11 = ( DetC 11 = a 22 a 33 a 23 a 32, A = ( DetC = (a 21 a 33 a 23 a 31, A 13 = ( DetC 13 = a 21 a 32 a 22 a 31 (3 Il determinante di A è il prodotto Det a 11 a a 13 a 21 a 22 a 23 = a 11 a a 13 A 11 A = a 11 A 11 + a A + a 13 A 13 = a 31 a 32 a 33 A 13 = a 11 ( DetC 11 + a ( DetC + a 13 ( DetC 13 Esempio 2 Calcoliamo il determinante della matrice A = In questo caso abbiamo per cui DetA a 11 = 3, a = 2, a 13 = 1, C 11 =, C 6 3 =, C =, = 3( Det + ( 2( Det + 1( Det = 2 6 = 3( ( 2( 1(0 8 + (0 2 = 3( = = 81 Quello che abbiamo fatto è quindi: (a per le matrici 1 1 porre Det ( a 11 = a11, (b dare una formula che permetta di calcolare il determinante delle matrici 2 2 sapendo come calcolare il determinante delle matrici 1 1, ossia dare una formula che permetta di calcolare il determinante delle matrici nel caso n = 2 sapendo come calcolare il determinante delle matrici nel caso precedente, cioè il caso n = 1 (si veda il punto (a, (c dare una formula che permetta di calcolare il determinante delle matrici 3 3 sapendo come calcolare il determinante delle matrici 2 2, ossia dare una formula che permetta di calcolare il determinante delle matrici nel caso n = 3 sapendo come calcolare il determinante delle matrici nel caso precedente, cioè il caso n = 2 (si veda il punto (b Procediamo quindi allo stesso modo, dando una formula che permetta di calcolare il determinante delle matrici n n sapendo come calcolare il determinante delle matrici 3
4 (n 1 (n 1, ossia dare una formula che permetta di calcolare il determinante delle matrici nel caso n sapendo come calcolare il determinante delle matrici nel caso precedente, cioè il caso n 1 Sia dunque A = a ij una matrice n n definizione: Cominciamo con il dare la seguente Def 1 Per ogni 1 i n e 1 j n si chiama matrice complementare dell elemento a ij od anche matrice complementare di posto (i,j in A, e si indica con il simbolo C ij, la matrice che si ottiene da A sopprimendo la i-esima riga e la j-esima colonna Dunque C ij è una matrice (n 1 (n 1 1 i Esempio 3 Se A = 1 + i i 0 5i 1 4i, allora 7 + 2i i 14i 1 i i i 0 5i 1 4i 7 + 2i i 14i 1 i i i 0 1 4i = C 24; 7 + 2i 34 14i togliendo la 2 a riga e la 4 a colonna 1 i i i 0 5i 1 4i 7 + 2i i 14i 1 i i i i = C 35 togliendo la 3 a riga e la 5 a colonna 4
5 Def 2 Per ogni 1 i n e 1 j n si chiama cofattore di posto (i,j di A, e si indica con il simbolo A ij, il numero A ij = ( 1 i+j Det (C ij, dove C ij è la matrice complementare di posto (i, j in A Si ha: Formula del determinante di una matrice sviluppato rispetto alla 1 a riga se A = ( a ij è una matrice n n allora DetA = a 11 A 11 + a A + + a 1,n 1 A 1,n 1 + a 1n A 1n dove A 11, A,, A 1,n 1, A 1n sono i cofattori di A di posti (1, 1, (1, 2,, (1, n 1, (1, n (ossia i posti della 1 a riga rispettivamente Esempio 4 Calcoliamo il determinante della matrice A = Usando la formula dello sviluppo del determinante rispetto alla 1 a riga di A abbiamo: DetA = 1 A 11 + ( 5 A + 0 A A 14 = A 11 5A + 3A 14 Dobbiamo quindi calcolare A 11, A ed A 14 A = ( Det = = Det = = 2( Det ( Det ( Det 0 0 = 7 5 = 2( (0 0 = 20, 5
6 A A 14 = ( Det = = Det = = (6( Det ( Det = (6( ( 10 0 = ( = 100, = ( Det = = Det = = (6( Det ( Det ( Det ( Det 2 0 = = 1 7 = (6(0 0 2( 10 0 = 2( 10 = 20 Dunque otteniamo: DetA = A 11 5A + 3A 14 = ( 20 = 580 Si puó dimostrare il seguente Teorema Sia A una matrice n n Allora, fissato i {1,, n} si ha che a i1 A i1 +a i2 A i2 + +a i,n 1 A i,n 1 +a in A in = a 11 A 11 +a A + +a 1,n 1 A 1,n 1 +a 1n A 1n, ossia che ( DetA = a i1 A i1 + a i2 A i2 + + a i,n 1 A i,n 1 + a in A in ( si chiama lo sviluppo di Laplace del determinante di A rispetto alla i- esima riga di A 6
7 Quindi, per calcolare il determinante di una matrice A, si puó partire mettendo in evidenza gli elementi di una riga qualunque, e non necessariamente la 1 a, come abbiamo fatto fino ad ora a11 a Esempio 5 Sia A = una matrice 2 2 Sviluppiamo il determinante a 21 a 22 di A rispetto alla 2 a riga di A: mettiamo in evidenza gli elementi della 2 a riga di A: a11 a, a 21 a 22 C 21 è la matrice che si ottiene da A togliendo la 2 a riga e la 1 a colonna, quindi C 21 = ( a ; C22 è la matrice che si ottiene da A togliendo la 2 a riga e la 2 a colonna, quindi C 22 = ( a 11 Allora a 21 A 21 + a 22 A 22 = a 21 ( DetC 21 + a 22 ( DetC 22 = = a 21 Det ( a + a22 Det ( a 11 = a21 a + a 22 a 11 = = a 11 a 22 a a 21 dà lo stesso risultato che abbiamo ottenuto partendo dalla 1 a riga Conviene quindi sviluppare il determinante rispetto alla riga che contiene piú zeri Esempio 6 Riconsideriamo la matrice dell Esempio 4, A = , e calcoliamo il suo determinante rispetto alla 3 a riga (che contiene due zeri Allora DetA = ( 2( Det ( Det Calcoliamo separatamente Det e Det Per entrambe queste matrici 3 3 non è conveniente calcolare il determinante rispetto alla 3 a riga, ma è indifferente scegliere la 1 a o la 2 a Per fare esercizio scegliamo in entrambi i casi la 2 a riga: 7
8 5 0 3 Det = 2( Det = 2(0 15 4( 25 0 = = 130 Det = 6( Det = 6( (5 0 = = ( Det ( Det 5 0 = = 1 5 Quindi Det(A = ( ( = 580 (lo stesso numero che avevamo ottenuto sviluppando il determinante rispetto alla 1 a riga Cosí come si puó sviluppare il determinante di una matrice rispetto ad una qualunque sua riga, lo si puó sviluppare rispetto ad una qualunque sua colonna, dal momento che vale il seguente Teorema Sia A una matrice n n Allora, fissati j {1,, n} e si ha che ( DetA = a 1j A 1j + a 2j A 2j + + a n 1,j A n 1,j + a nj A nj ( si chiama lo sviluppo di Laplace del determinante di A rispetto alla j-esima colonna di A Conviene quindi sviluppare il determinante rispetto alla riga oppure alla colonna che contiene piú zeri Esempio 7 Riconsideriamo la matrice degli Esempi 4 e 6, A = , e calcoliamo il suo determinante rispetto alla 3 a colonna (che contiene tre zeri Allora DetA = 0 ( Det ( Det ( Det ( Det = = 5Det
9 1 5 3 Calcoliamo Det 6 2 4, ad esempio rispetto alla 2 a colonna: Det = = ( 5( Det ( Det = ( 5( 1( (2 + 6 = = ( Det 1 3 = 6 4 quindi Det(A = ( = 580 (si noti che è lo stesso numero che abbiamo ottenuto sviluppando il determinante rispetto alla 1 a oppure alla 3 a riga Proprietà del determinante Sia A una matrice n n (1 Se A ha una riga (risp una colonna nulla, oppure se A ha due righe (risp due colonne uguali, allora Det(A = 0 (2 Se A è la matrice che si ottiene da A mediante lo scambio di due righe (risp due colonne allora Det(A = Det(A (3 Se A è la matrice che si ottiene da A sommando ad una riga (risp ad una colonna di A un altra riga (risp un altra colonna di A moltiplicata per un numero c, allora Det(A =Det(A (4 Se A è la matrice che si ottiene da A moltiplicando una riga (risp una colonna di A per un numero c, allora Det(A = cdet(a (5 Det(A T =Det(A (6 Se B è un altra matrice n n allora Det(AB=Det(A Det(B (7 A è non singolare se e solo se Det(A 0, e se A è non singolare si ha Det(A 1 = 1 Det(A NB Per quanto riguarda ( la proprietà (7, si ricordi che avevamo già osservato che a b una matrice 2 2 A = è non singolare se e solo se il numero ad bc 0, e c d tale numero è proprio Det(A 9
10 Esercizio Si provi che il determinante di una matrice triangolare superiore (risp inferiore è il prodotto degli elementi diagonali Sia T una matrice n n triangolare superiore (la dimostrazione è simile per le matrici triangolari inferiori: Chiamiamo: t 11 0 t t 33 T = t 44 O 0 t nn T 1 la matrice che si ottiene da T sopprimendo la 1 a riga e la 1 a colonna (T 1 è triangolare superiore (n 1 (n 1: t 22 0 t t 44 T 1 =, O 0 t nn T 2 la matrice che si ottiene da T 1 sopprimendo la 1 a riga e la 1 a colonna (T 2 è triangolare superiore (n 2 (n 2: t 33 0 t 44 T 2 =, O t nn e cosí via per ogni k = 2,, n 1 chiamiamo T k la matrice che si ottiene da T k 1 sopprimendo la 1 a riga e la 1 a colonna T k è una matrice triangolare superiore (n k (n k Sviluppiamo il determinante di T ripetto alla 1 a colonna di T: DetT = t 11 ( DetT 1 = t 11 DetT 1 10
11 Sviluppiamo il determinante di T 1 ripetto alla 1 a colonna di T 1 : DetT = t 11 DetT 1 = t 11 (t 22 ( DetT 2 = t 11 t 22 DetT 2 Cosí procedendo otteniamo: DetT = t 11 t 22 DetT 2 = = t 11 t 22 t 33 DetT 3 = = t 11 t 22 t 33 t 44 DetT 4 = = = = t 11 t 22 t n 1,n 1 DetT n 1 = = t 11 t 22 t n 1,n 1 Det ( t nn = = t 11 t 22 t n 1,n 1 t nn In particolare da ció segue: Il determinante di una matrice diagonale è il prodotto degli elementi diagonali, poichè le matrici diagonali sono particolari matrici triangolari superiori Esercizio Si ha: Sia A una matrice n n Si provi che per ogni scalare c si ha: Det(cA = c n Det(A Det(cA = Det((cI n A = Det(cI n Det(A Poichè ci n è una matrice scalare n n, in particolare una matrice diagonale, per l esercizio precedente si ha che Det(cI n = prodotto degli elementi diagonali di ci n Tali elementi sono tutti uguali a c, ed il loro prodotto ha n fattori (perchè ci n è n n, dunque Det(cI n = c n, per cui Det(cA = c n Det(A 11
, è Det(A) = a 11 a 22 a 12 a 21. ( il determinante della matrice che si ottiene da A. la 1 a riga e la 2 a colonna di A
 G Parmeggiani, 2/12/2013 Algebra Lineare 1 A, corso di laurea SGI, aa 2013/2014 Nota 4: Calcolo di determinanti Sia A una matrice quadrata di ordine n Il determinante di A è un numero che dipende da A
G Parmeggiani, 2/12/2013 Algebra Lineare 1 A, corso di laurea SGI, aa 2013/2014 Nota 4: Calcolo di determinanti Sia A una matrice quadrata di ordine n Il determinante di A è un numero che dipende da A
Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Trieste, Padova
 ALGEBRA LINEARE I A PER SCIENZE STATISTICHE, A.A. 8/9, GEMMA PARMEGGIANI Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Trieste, 63 353 Padova Programma del corso. Nota
ALGEBRA LINEARE I A PER SCIENZE STATISTICHE, A.A. 8/9, GEMMA PARMEGGIANI Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Trieste, 63 353 Padova Programma del corso. Nota
ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, SGI, A.A. 2010/2011, GEMMA PARMEGGIANI
 ALGEBRA LINEARE I A PER SCIENZE STATISTICHE, SGI, A.A. /, GEMMA PARMEGGIANI Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Trieste, 63 353 Padova Programma del corso.
ALGEBRA LINEARE I A PER SCIENZE STATISTICHE, SGI, A.A. /, GEMMA PARMEGGIANI Università degli Studi di Padova Dipartimento di Matematica Pura e Applicata via Trieste, 63 353 Padova Programma del corso.
ALGEBRA LINEARE I (A) per Scienze Statistiche, SGI, a.a. 2014/2015
 ALGEBRA LINEARE I (A) per Scienze Statistiche, SGI, a.a. 4/5 Gemma Parmeggiani Università degli Studi di Padova Dipartimento di Matematica via Trieste 63 353 Padova Programma del corso. Nota : Osservazioni
ALGEBRA LINEARE I (A) per Scienze Statistiche, SGI, a.a. 4/5 Gemma Parmeggiani Università degli Studi di Padova Dipartimento di Matematica via Trieste 63 353 Padova Programma del corso. Nota : Osservazioni
VETTORI E MATRICI. Ing. Nicola Cappuccio 2014 U.F.5 ELEMENTI SCIENTIFICI ED ELETTRONICI APPLICATI AI SISTEMI DI TELECOMUNICAZIONI
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
ALGEBRA LINEARE I (A) PER SCIENZE STATISTICHE, SGI, A.A. 2013/2014, GEMMA PARMEGGIANI
 ALGEBRA LINEARE I A PER SCIENZE STATISTICHE, SGI, A.A. 3/4, GEMMA PARMEGGIANI Università degli Studi di Padova Dipartimento di Matematica via Trieste, 63 353 Padova Programma del corso. Nota : Matrici
ALGEBRA LINEARE I A PER SCIENZE STATISTICHE, SGI, A.A. 3/4, GEMMA PARMEGGIANI Università degli Studi di Padova Dipartimento di Matematica via Trieste, 63 353 Padova Programma del corso. Nota : Matrici
Matrici. Prof. Walter Pugliese
 Matrici Prof. Walter Pugliese Le matrici Una matrice è un insieme di numeri reali organizzati in righe e colonne. Se n è il numero delle righe e m e il numero delle colonne si dice che la matrice è di
Matrici Prof. Walter Pugliese Le matrici Una matrice è un insieme di numeri reali organizzati in righe e colonne. Se n è il numero delle righe e m e il numero delle colonne si dice che la matrice è di
Determinante. Elisabetta Colombo. Determinante. Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico ,
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, 1 n=2 2 3 con le 4 n=2 n=2 con le Ad ogni matrice quadrata A = (a ij ) j=1...n i=1...n di ordine n si può associare
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, 1 n=2 2 3 con le 4 n=2 n=2 con le Ad ogni matrice quadrata A = (a ij ) j=1...n i=1...n di ordine n si può associare
Matrici quadrate particolari
 Matrici quadrate particolari Sia A Mn(K) una matrice quadrata. Gli elementi (a 1,1, a 2,2,, a n,n ) costituiscono la diagonale principale di A. Gli elementi (a 1,n, a 2,n-1,, a n-1,2, a n,1 ) costituiscono
Matrici quadrate particolari Sia A Mn(K) una matrice quadrata. Gli elementi (a 1,1, a 2,2,, a n,n ) costituiscono la diagonale principale di A. Gli elementi (a 1,n, a 2,n-1,, a n-1,2, a n,1 ) costituiscono
Anno 4 Matrice inversa
 Anno 4 Matrice inversa 1 Introduzione In questa lezione parleremo della matrice inversa di una matrice quadrata: definizione metodo per individuarla Al termine della lezione sarai in grado di: descrivere
Anno 4 Matrice inversa 1 Introduzione In questa lezione parleremo della matrice inversa di una matrice quadrata: definizione metodo per individuarla Al termine della lezione sarai in grado di: descrivere
Argomento 12 Matrici
 Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
I determinanti. a11 a A = 12 a 21 a 22
 I determinanti. Queste note, basate sugli appunti delle lezioni, riepilogano rapidamente la definizione e le proprietà del determinante. Vengono inoltre illustrati i metodi di calcolo e alcune dimostrazioni.
I determinanti. Queste note, basate sugli appunti delle lezioni, riepilogano rapidamente la definizione e le proprietà del determinante. Vengono inoltre illustrati i metodi di calcolo e alcune dimostrazioni.
MATRICI e DETERMINANTI. Prof.ssa Maddalena Dominijanni
 MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
Il determinante. Calcolo del determinante di matrici particolari. matrici di ordine 2: sia. a11 a A = allora
 Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Sui determinanti e l indipendenza lineare di vettori
 Sui determinanti e l indipendenza lineare di vettori 1 Si dice che m vettori v 1, v 2,,v m di R n sono linearmente indipendenti, se una loro combinazione lineare può dare il vettore nullo solo se i coefficienti
Sui determinanti e l indipendenza lineare di vettori 1 Si dice che m vettori v 1, v 2,,v m di R n sono linearmente indipendenti, se una loro combinazione lineare può dare il vettore nullo solo se i coefficienti
LEZIONE i i 3
 LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE i 0 3 Le sottomatrici 2 2 di A sono. 1 2 i i 3. Invece (
 LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
1 se k = r i. 0 altrimenti. = E ij (c)
 Facoltà di Scienze Statistiche, Algebra Lineare A, G.Parmeggiani LEZIONE 5 Matrici elementari e loro inverse Si fissi m un numero naturale. Per ogni i, j m con i j siano E ij (c) (ove c è uno scalare )
Facoltà di Scienze Statistiche, Algebra Lineare A, G.Parmeggiani LEZIONE 5 Matrici elementari e loro inverse Si fissi m un numero naturale. Per ogni i, j m con i j siano E ij (c) (ove c è uno scalare )
MATRICI. 1. Esercizi
 MATICI Esercizio Siano A = 0, B = Esercizi 2, C = 0 2 2 Calcolare: a2a B; b3a + 2B 4C; c 2A + B + 2C 2B; d3b + 2(2A C (A + B + 2C isolvere, se possibile: ( 3X + 2(A X + B + 2(C + 2X = 0; (2 4A + 2(B +
MATICI Esercizio Siano A = 0, B = Esercizi 2, C = 0 2 2 Calcolare: a2a B; b3a + 2B 4C; c 2A + B + 2C 2B; d3b + 2(2A C (A + B + 2C isolvere, se possibile: ( 3X + 2(A X + B + 2(C + 2X = 0; (2 4A + 2(B +
Il prodotto tra matrici non è commutativo. Nelle notazioni precedenti, ponendo n = p e m = q si hanno:
 L anello delle matrici Esempio. Siano A = [ ] 0 1 3 0 2 1, B = 1 2 0 0 1 2 3 4, 1 0 calcolare AB e BA. Osservazioni Siano A Mat m,n (K) e B Mat p,q (K). Il prodotto AB è definito se n = p. Si ha AB Mat
L anello delle matrici Esempio. Siano A = [ ] 0 1 3 0 2 1, B = 1 2 0 0 1 2 3 4, 1 0 calcolare AB e BA. Osservazioni Siano A Mat m,n (K) e B Mat p,q (K). Il prodotto AB è definito se n = p. Si ha AB Mat
CORSO DI GEOMETRIA DETERMINANTE A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
G. Parmeggiani, 29/3/2018 Algebra Lineare, a.a. 2017/2018, numero di MATRICOLA PARI. Svolgimento degli Esercizi per casa 4
 G. Parmeggiani, 29/3/2018 Algebra Lineare, a.a. 2017/2018, Scuola di Scienze - Corsi di laurea: Studenti: Statistica per l economia e l impresa Statistica per le tecnologie e le scienze numero di MARICOLA
G. Parmeggiani, 29/3/2018 Algebra Lineare, a.a. 2017/2018, Scuola di Scienze - Corsi di laurea: Studenti: Statistica per l economia e l impresa Statistica per le tecnologie e le scienze numero di MARICOLA
MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI
 MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI LE MATRICI DEFINIZIONE: Una matrice è un insieme di numeri disposti su righe e colonne. 1 3 7 M = 2 5 1 M è
MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI LE MATRICI DEFINIZIONE: Una matrice è un insieme di numeri disposti su righe e colonne. 1 3 7 M = 2 5 1 M è
Equivalentemente, le colonne di A sono linearmente indipendenti se e solo se
 Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
DETERMINANTE DI MATRICI QUADRATE
 DETERMINANTE DI MATRICI QUADRATE Definizioni e Proprietà 12 Novembre 2015 Pietro Pennestrì pennestri1694905@studentiuniroma1it Università di Roma Sapienza SOMMARIO 1 Introduzione 11 Cenni Storici 12 Definizione
DETERMINANTE DI MATRICI QUADRATE Definizioni e Proprietà 12 Novembre 2015 Pietro Pennestrì pennestri1694905@studentiuniroma1it Università di Roma Sapienza SOMMARIO 1 Introduzione 11 Cenni Storici 12 Definizione
determinante della sottomatrice ottenuta da A cancellando la i-esima riga e la j-esima colonna
 Data una matrice quadrata A di ordine n si definisce minore complementare m ij dell elemento generico a ij della matrice A il determinante della sottomatrice ottenuta da A cancellando la i-esima riga e
Data una matrice quadrata A di ordine n si definisce minore complementare m ij dell elemento generico a ij della matrice A il determinante della sottomatrice ottenuta da A cancellando la i-esima riga e
ALGEBRA LINEARE PARTE II
 DIEM sez. Matematica Finanziaria Marina Resta Università degli studi di Genova Dicembre 005 Indice PREMESSA INVERSA DI UNA MATRICE DETERMINANTE. DETERMINANTE DI MATRICI ELEMENTARI................. MATRICI
DIEM sez. Matematica Finanziaria Marina Resta Università degli studi di Genova Dicembre 005 Indice PREMESSA INVERSA DI UNA MATRICE DETERMINANTE. DETERMINANTE DI MATRICI ELEMENTARI................. MATRICI
MATRICI. Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: a 2 m. a n m) i j R, 1 i n, 1 j m.
 MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
Determinante. Sia M(n, n, K) lo spazio delle matrici quadrate n n a coefficienti in un campo K, vogliamo provare il seguente Teorema:
 Determinante 1 Proprieta Sia M(n, n, K) lo spazio delle matrici quadrate n n a coefficienti in un campo K, vogliamo provare il seguente Teorema: Theorem 1.1 Esiste un unica mappa F dallo spazio delle matrici
Determinante 1 Proprieta Sia M(n, n, K) lo spazio delle matrici quadrate n n a coefficienti in un campo K, vogliamo provare il seguente Teorema: Theorem 1.1 Esiste un unica mappa F dallo spazio delle matrici
ha come obiettivo quello di costruire a partire da A una matrice U, m n, che abbia il
 Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 6 Eliminazione di Gauss con scambi di righe Sia A O una matrice m n. Abbiamo illustrato nella Lezione 5 un algoritmo che ha come
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 6 Eliminazione di Gauss con scambi di righe Sia A O una matrice m n. Abbiamo illustrato nella Lezione 5 un algoritmo che ha come
A =, c d. d = ad cb. c d A =
 Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
LeLing12: Ancora sui determinanti.
 LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
= elemento che compare nella seconda riga e quinta colonna = -4 In generale una matrice A di m righe e n colonne si denota con
 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti su m righe e n colonne. I numeri che compaiono nella tabella si dicono elementi della matrice. La loro individuazione
Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti su m righe e n colonne. I numeri che compaiono nella tabella si dicono elementi della matrice. La loro individuazione
Algebra Lineare Ingegneria Chimica Anno Accademico 2018/19
 Algebra Lineare Ingegneria Chimica Anno Accademico 2018/19 Caboara Lezione 26 Novembre 2018 Esercizio 1. Risolvere il sistema 3x + 2y z = 1 x y + z = 3 x + y + 2z = 0 usando la regola di Cramer Costruiamo
Algebra Lineare Ingegneria Chimica Anno Accademico 2018/19 Caboara Lezione 26 Novembre 2018 Esercizio 1. Risolvere il sistema 3x + 2y z = 1 x y + z = 3 x + y + 2z = 0 usando la regola di Cramer Costruiamo
LEZIONE 4. Le sottomatrici 2 2 di A sono. Invece ( 1 3 non è sottomatrice di A.
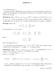 LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
il determinante che si ottiene da A, sopprimendo la i - esima riga e la j - esima colonna. Si definisce complemento algebrico dell'elemento a ij
 Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Si noti che la matrice trasposta A ha lo stesso determinante. Questa proprietà è generale;
 Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe.
![Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe. Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe.](/thumbs/100/147138366.jpg) Matrici triangolari [Abate, 32] Definizione Una matrice A = a ij ) R m,n si dice triangolare superiore se a ij = 0 per ogni i > j; triangolare inferiore se a ij = 0 per ogni i < j Lezioni 05 e 06 Una matrice
Matrici triangolari [Abate, 32] Definizione Una matrice A = a ij ) R m,n si dice triangolare superiore se a ij = 0 per ogni i > j; triangolare inferiore se a ij = 0 per ogni i < j Lezioni 05 e 06 Una matrice
Determinanti. Definizione ed esempi. Definizione ed esempi. Proprietà dei determinanti Rango di matrici
 Introduzione S S S Rango di matrici Si dice sottomatrice d'una matrice data la matrice ottenuta selezionando un certo numero di righe e di colonne della matrice iniziale. Lezione 24.wpd 08/01/2011 XXIV
Introduzione S S S Rango di matrici Si dice sottomatrice d'una matrice data la matrice ottenuta selezionando un certo numero di righe e di colonne della matrice iniziale. Lezione 24.wpd 08/01/2011 XXIV
Matematica II,
 Matematica II,.05.04 Diamo qui la nozione di determinante di una matrice quadrata, le sue prime proprieta, e ne deriviamo una caratterizzazione delle matrici non singolari e una formula per l inversa di
Matematica II,.05.04 Diamo qui la nozione di determinante di una matrice quadrata, le sue prime proprieta, e ne deriviamo una caratterizzazione delle matrici non singolari e una formula per l inversa di
MATRICI E SISTEMI LINEARI
 MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
Il determinante. a11 a A = 12 a 21 a 22
 Il determinante Queste note, basate sugli appunti delle lezioni, riepilogano rapidamente la definizione e le proprietà del determinante Vengono inoltre illustrati i metodi di calcolo e alcune dimostrazioni
Il determinante Queste note, basate sugli appunti delle lezioni, riepilogano rapidamente la definizione e le proprietà del determinante Vengono inoltre illustrati i metodi di calcolo e alcune dimostrazioni
RIDUZIONE E RANGO , C = 2 5 1
 MATRICI E SISTEMI RIDUZIONE E RANGO Riduzione di matrici (definizioni, trasformazioni elementari). Calcolo del rango e dell inversa (metodo di Gauss, metodo di Gauss-Jordan). 3 4 Esercizio Ridurre per
MATRICI E SISTEMI RIDUZIONE E RANGO Riduzione di matrici (definizioni, trasformazioni elementari). Calcolo del rango e dell inversa (metodo di Gauss, metodo di Gauss-Jordan). 3 4 Esercizio Ridurre per
Geometria BIAR Esercizi 2
 Geometria BIAR 0- Esercizi Esercizio. a Si consideri il generico vettore v b R c (a) Si trovi un vettore riga x (x, y, z) tale che x v a (b) Si trovi un vettore riga x (x, y, z) tale che x v kb (c) Si
Geometria BIAR 0- Esercizi Esercizio. a Si consideri il generico vettore v b R c (a) Si trovi un vettore riga x (x, y, z) tale che x v a (b) Si trovi un vettore riga x (x, y, z) tale che x v kb (c) Si
Determinante e rango
 1 DETERMINANTE DI UNA MATRICE 1 III-3 Determinante e rango Indice 1 Determinante di una matrice 1 2 Calcolo della matrice inversa 6 3 Calcolo del rango 8 4 Soluzioni degli esercizi 12 1 Determinante di
1 DETERMINANTE DI UNA MATRICE 1 III-3 Determinante e rango Indice 1 Determinante di una matrice 1 2 Calcolo della matrice inversa 6 3 Calcolo del rango 8 4 Soluzioni degli esercizi 12 1 Determinante di
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI
 CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # GEOMETRIA E ALGEBRA 009/0 Esercizio.. Dati i vettori di R : v (,, ), v (, 4, 6), v (,, 5), v 4 (,, 0) determinare se v 4 è combinazione
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # GEOMETRIA E ALGEBRA 009/0 Esercizio.. Dati i vettori di R : v (,, ), v (, 4, 6), v (,, 5), v 4 (,, 0) determinare se v 4 è combinazione
( ) TEORIA DELLE MATRICI. A. Scimone a.s pag 1
 . Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
. Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
1. Proprietà della somma di matrici. 1. (A + B) + C = A + (B + C) qualunque. 2. A + B = B + A qualunque siano le matrici
 Matrici R. Notari 1 1. Proprietà della somma di matrici 1. (A + B) + C = A + (B + C) qualunque siano le matrici A, B, C Mat(m, n; K). 2. A + B = B + A qualunque siano le matrici A, B Mat(m, n; K). 3. Sia
Matrici R. Notari 1 1. Proprietà della somma di matrici 1. (A + B) + C = A + (B + C) qualunque siano le matrici A, B, C Mat(m, n; K). 2. A + B = B + A qualunque siano le matrici A, B Mat(m, n; K). 3. Sia
Esercizi di Algebra Lineare Determinanti
 Esercizi di Algebra Lineare Determinanti Anna M. Bigatti 3-6 dicembre 2012 Calcolo del determinante Proposizione 1. Alcune proprietà dei determinanti: (a) Il determinante del prodotto è il prodotto dei
Esercizi di Algebra Lineare Determinanti Anna M. Bigatti 3-6 dicembre 2012 Calcolo del determinante Proposizione 1. Alcune proprietà dei determinanti: (a) Il determinante del prodotto è il prodotto dei
1 1 2 Il complemento algebrico dell'elemento a 3 2 = 0 è C 2,3 = ( 1) = 1. a j i C i,j. Valutiamo i complementi algebrici C 3,2, C 3,3 :
 Esercizi di Geometria 1 1. Si calcoli il determinante della seguente matrice, utilizzando il metodo di Laplace: 1 2 3 B = 2 1 3 0 4 1 Richiamo Sia A = (a j i ) i,j {1...n} matrice in M n (C). Allora, per
Esercizi di Geometria 1 1. Si calcoli il determinante della seguente matrice, utilizzando il metodo di Laplace: 1 2 3 B = 2 1 3 0 4 1 Richiamo Sia A = (a j i ) i,j {1...n} matrice in M n (C). Allora, per
Giuseppe Accascina. Note del corso di Geometria e Algebra
 Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 26-27 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 26-27 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
MATRICI E OPERAZIONI
 MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
Giuseppe Accascina. Note del corso di Geometria e Algebra
 Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 27-28 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 27-28 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Introduzione all algebra delle matrici. Appunti a cura di Lara Ercoli
 Introduzione all algebra delle matrici ppunti a cura di Lara Ercoli Indice Definizioni 3. Matrici particolari............................ 4 2 Operazioni con le matrici 8 2. Somma di matrici.............................
Introduzione all algebra delle matrici ppunti a cura di Lara Ercoli Indice Definizioni 3. Matrici particolari............................ 4 2 Operazioni con le matrici 8 2. Somma di matrici.............................
Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche. Appunti del corso di Matematica
 Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 19 - Determinante Anno Accademico 2015/2016 M. Tumminello,
Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 19 - Determinante Anno Accademico 2015/2016 M. Tumminello,
1 Determinante di una matrice 1. 2 Calcolo della matrice inversa 7. 3 Calcolo del rango 8. 4 Soluzioni degli esercizi 12. n! = n.
 1 DETERMINANTE DI UNA MATRICE 1 Determinante e rango Indice 1 Determinante di una matrice 1 2 Calcolo della matrice inversa 7 3 Calcolo del rango 8 4 Soluzioni degli esercizi 12 1 Determinante di una matrice
1 DETERMINANTE DI UNA MATRICE 1 Determinante e rango Indice 1 Determinante di una matrice 1 2 Calcolo della matrice inversa 7 3 Calcolo del rango 8 4 Soluzioni degli esercizi 12 1 Determinante di una matrice
Esercitazione 6 - Soluzione
 Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
PROBLEMA. Costruire matrici quadrate contenute. Fare i determinanti delle matrici quadrate contenute in A
 A = PROBLEMA 0 1 2 7 2 5 3 0 (2 4) Costruire matrici quadrate contenute in A (possibili solo matrici quadrate 2 2 e 1 1) Fare i determinanti delle matrici quadrate contenute in A Questo porta al concetto
A = PROBLEMA 0 1 2 7 2 5 3 0 (2 4) Costruire matrici quadrate contenute in A (possibili solo matrici quadrate 2 2 e 1 1) Fare i determinanti delle matrici quadrate contenute in A Questo porta al concetto
Lezione 4 - Esercitazioni di Algebra e Geometria - Anno accademico
 Trasformazioni elementari sulle matrici Data una matrice A K m,n definiamo su A le seguenti tre trasformazioni elementari: T : scambiare tra loro due righe (o due colonne) di A; T : sommare ad una riga
Trasformazioni elementari sulle matrici Data una matrice A K m,n definiamo su A le seguenti tre trasformazioni elementari: T : scambiare tra loro due righe (o due colonne) di A; T : sommare ad una riga
PreCorso di Matematica - PCM Corso M-Z
 PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
Elementi di Algebra Matriciale. (richiami)
 Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
Metodi per la risoluzione di sistemi lineari
 Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
Metodi per la risoluzione di sistemi lineari
 Metodi per la risoluzione di sistemi lineari 1 Sistemi di equazioni lineari 1.1 Determinante di matrici quadrate Ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante della matrice
Metodi per la risoluzione di sistemi lineari 1 Sistemi di equazioni lineari 1.1 Determinante di matrici quadrate Ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante della matrice
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
Corso di Matematica e Statistica 3 Algebra delle matrici. Una tabella rettangolare: la matrice. Una tabella rettangolare: la matrice
 Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Def. 1. Si chiamano operazioni elementari sulle righe di A le tre seguenti operazioni:
 Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 5 Operazioni elementari sulle righe di una matrice Sia A una matrice m n. Def. 1. Si chiamano operazioni elementari sulle righe
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, G.Parmeggiani LEZIONE 5 Operazioni elementari sulle righe di una matrice Sia A una matrice m n. Def. 1. Si chiamano operazioni elementari sulle righe
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
Metodi e Modelli per l Ottimizzazione Combinatoria Problema dell assegnamento e matrici totalmente unimodulari
 Metodi e Modelli per l Ottimizzazione Combinatoria Problema dell assegnamento e matrici totalmente unimodulari L. De Giovanni G. Zambelli 1 Problema dell assegnamento Sia dato un grafo non orientato bipartito
Metodi e Modelli per l Ottimizzazione Combinatoria Problema dell assegnamento e matrici totalmente unimodulari L. De Giovanni G. Zambelli 1 Problema dell assegnamento Sia dato un grafo non orientato bipartito
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
1. [15 punti] Calcolare il rango della seguente matrice a coefficienti reali: ( 1/2) 1 (1/2)
![1. [15 punti] Calcolare il rango della seguente matrice a coefficienti reali: ( 1/2) 1 (1/2) 1. [15 punti] Calcolare il rango della seguente matrice a coefficienti reali: ( 1/2) 1 (1/2)](/thumbs/101/152415317.jpg) Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE del 17 febbraio 011 ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola in alto a destra
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE del 17 febbraio 011 ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola in alto a destra
MATRICI E SISTEMI LINEARI
 1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
Metodi Matematici per l Economia anno 2017/2018 Gruppo B
 Metodi Matematici per l Economia anno 2017/2018 Gruppo B Docente: Giacomo Dimarco Dipartimento di Matematica e Informatica Università di Ferrara https://sites.google.com/a/unife.it/giacomo-dimarco-home-page/
Metodi Matematici per l Economia anno 2017/2018 Gruppo B Docente: Giacomo Dimarco Dipartimento di Matematica e Informatica Università di Ferrara https://sites.google.com/a/unife.it/giacomo-dimarco-home-page/
x n i sima pos. x, y = x T y = x i y i R. i=1
 1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
Esercitazione di Matematica su matrici e sistemi lineari
 Esercitazione di Matematica su matrici e sistemi lineari Notazioni: deta, A T =trasposta di A, A 1 =inversa di A. 1. Si considerino le matrici A, B, C, D denite da 1 0 5 1 A = 0, B = 0 0, C = 0 1 0 6 1
Esercitazione di Matematica su matrici e sistemi lineari Notazioni: deta, A T =trasposta di A, A 1 =inversa di A. 1. Si considerino le matrici A, B, C, D denite da 1 0 5 1 A = 0, B = 0 0, C = 0 1 0 6 1
08 - Matrici, Determinante e Rango
 Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 08 - Matrici, Determinante e Rango Anno Accademico 2013/2014 D.
Università degli Studi di Palermo Facoltà di Economia CdS Sviluppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 08 - Matrici, Determinante e Rango Anno Accademico 2013/2014 D.
Esercitazioni di Algebra e Geometria
 Esercitazioni di Algebra e Geometria Anno Accademico 2010 2011 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.30
Esercitazioni di Algebra e Geometria Anno Accademico 2010 2011 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.30
Corso di Geometria BIAR, BSIR Esercizi 2: soluzioni
 Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
Argomento 13 Sistemi lineari
 Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Per esempio, una matrice 4 4 triangolare alta ha la forma. 0 a. mentre una matrice di ordine 4 triangolare bassa è del tipo
 Matrici triangolari Prima di esporre il metodo LU per la risoluzione di sistemi lineari, introduciamo la nozione di matrice triangolare Ci limiteremo al caso di matrici quadrate anche se l estensione a
Matrici triangolari Prima di esporre il metodo LU per la risoluzione di sistemi lineari, introduciamo la nozione di matrice triangolare Ci limiteremo al caso di matrici quadrate anche se l estensione a
SISTEMI LINEARI. x y + 2t = 0 2x + y + z t = 0 x z t = 0 ; S 3 : ; S 5x 2y z = 1 4x 7y = 3
 SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
Esercitazioni di Algebra e Geometria
 Esercitazioni di Algebra e Geometria Anno Accademico 2011 2012 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.00
Esercitazioni di Algebra e Geometria Anno Accademico 2011 2012 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.00
Algebra lineare. Laboratorio di programmazione e calcolo CdL in Chimica. Pierluigi Amodio
 Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Esercitazione di Calcolo Numerico 1 22 Aprile Determinare la fattorizzazione LU della matrice a 1 1 A = 3a 2 a 2a a a 2 A =
 Esercitazione di Calcolo Numerico 22 Aprile 29. Determinare la fattorizzazione LU della matrice a A = 3a 2 a 2a a a 2 ed utilizzarla per calcolare il det(a). 2. Calcolare il determinante della matrice
Esercitazione di Calcolo Numerico 22 Aprile 29. Determinare la fattorizzazione LU della matrice a A = 3a 2 a 2a a a 2 ed utilizzarla per calcolare il det(a). 2. Calcolare il determinante della matrice
Sistemi II. Sistemi II. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Lezione 11. Somma di matrici Prodotto di una matrice per uno scalare Prodotto di matrici Determinante Sistemi lineari in forma matriciale
 Lezione Somma di matrici Prodotto di una matrice per uno scalare Prodotto di matrici Determinante Sistemi lineari in forma matriciale Matrici. Somma Date due matrici n x m, A = A ij e B = B ij, con i =,,,
Lezione Somma di matrici Prodotto di una matrice per uno scalare Prodotto di matrici Determinante Sistemi lineari in forma matriciale Matrici. Somma Date due matrici n x m, A = A ij e B = B ij, con i =,,,
a.a MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI
 aa 2012-2013 MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI 1 Sistemi di equazioni lineari Definizione 11 i Un equazione lineare nelle indeterminate (o incognite X 1,, X 1 m a coefficienti interi (o razionali,
aa 2012-2013 MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI 1 Sistemi di equazioni lineari Definizione 11 i Un equazione lineare nelle indeterminate (o incognite X 1,, X 1 m a coefficienti interi (o razionali,
Applicazioni eliminazione di Gauss
 Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
Definizione 1. Una matrice n m a coefficienti in K é una tabella del tipo. ... K m, detto vettore riga i-esimo, ed a im
 APPUNTI ed ESERCIZI su matrici, rango e metodo di eliminazione di Gauss Corso di Laurea in Chimica, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 23 Aprile 2010 Matrici, rango e metodo
APPUNTI ed ESERCIZI su matrici, rango e metodo di eliminazione di Gauss Corso di Laurea in Chimica, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 23 Aprile 2010 Matrici, rango e metodo
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE (esercitazione del 18 gennaio 2011)
 Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE (esercitazione del 18 gennaio 2011) ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE (esercitazione del 18 gennaio 2011) ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola
Sistemi Lineari. Andrea Galasso
 Sistemi Lineari Andrea Galasso Esercizi svolti Teorema. (Rouché-Capelli. Un sistema lineare Ax = b ammette soluzioni se e solo se il rango della matrice dei coefficienti A è uguale al rango della matrice
Sistemi Lineari Andrea Galasso Esercizi svolti Teorema. (Rouché-Capelli. Un sistema lineare Ax = b ammette soluzioni se e solo se il rango della matrice dei coefficienti A è uguale al rango della matrice
Algebra matriciale. Un algebra è un sistema di segni in cui sono definite delle operazioni Algebra scalare Algebra dei vettori Algebra matriciale
 Algebra matriciale Algebra Un algebra è un sistema di segni in cui sono definite delle operazioni Algebra scalare Algebra dei vettori Algebra matriciale In algebra matriciale un numero è chiamato scalare
Algebra matriciale Algebra Un algebra è un sistema di segni in cui sono definite delle operazioni Algebra scalare Algebra dei vettori Algebra matriciale In algebra matriciale un numero è chiamato scalare
1 Introduzione alle matrici quadrate 2 2 a coefficienti in R.
 1 Introduzione alle matrici quadrate 2 2 a coefficienti in R Per introdurre il concetto di matrice, a 2 righe e 2 colonne, iniziamo col considerare griglie o tabelle di numeri Gli elementi della griglia,
1 Introduzione alle matrici quadrate 2 2 a coefficienti in R Per introdurre il concetto di matrice, a 2 righe e 2 colonne, iniziamo col considerare griglie o tabelle di numeri Gli elementi della griglia,
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
2x 5y +4z = 3 x 2y + z =5 x 4y +6z = A =
 Esercizio 1. Risolvere il sistema lineare 2x 5y +4z = x 2y + z =5 x 4y +6z =10 (1) Soluz. La matrice dei coefficienti è 1 4 6, calcoliamone il rango. Il determinante di A è (applico la regola di Sarrus):
Esercizio 1. Risolvere il sistema lineare 2x 5y +4z = x 2y + z =5 x 4y +6z =10 (1) Soluz. La matrice dei coefficienti è 1 4 6, calcoliamone il rango. Il determinante di A è (applico la regola di Sarrus):
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI
 SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
