Matematica. Corso integrato di. per le scienze naturali ed applicate. Materiale integrativo. Paolo Baiti 1 Lorenzo Freddi 1
|
|
|
- Claudio Costantini
- 5 anni fa
- Visualizzazioni
Transcript
1 Corso integrato di Matematica per le scienze naturali ed applicate Materiale integrativo Paolo Baiti 1 Lorenzo Freddi 1 1 Dipartimento di Matematica e Informatica, Università di Udine, via delle Scienze 6, 331 Udine, Italy ([baiti freddi]@dimi.uniud.it
2 Capitolo aggiuntivo 9 Funzioni di due o più variabili Sia D un sottoinsieme non vuoto di R n. Una funzione f : D R (x 1,...,x n f(x 1,...,x n è una funzione reale di n variabili reali Funzioni di n variabili Funzioni di due variabili. Esempi e grafici Se n = allora f è una funzione reale di variabili reali. Per rappresentarne il grafico, cioè l insieme G = {(x, y, z D R : z = f(x, y} si usa generalmente un riferimento cartesiano ortogonale di assi x, y, z. Esempio 9.1. La funzione definita su R da f(x, y = x + y
3 FUNZIONI DI DUE VARIABILI. ESEMPI E GRAFICI 3 ha grafico contenuto tutto nel semispazio delle z. Si ha f(, = e f(x, y > (x, y. Le intersezioni del grafico con i piani paralleli al piano xy (di equazione z = cioè i piani z = c sono insiemi vuoti se c <, il solo punto (, se c = e circonferenze di raggio c se c > (di equazione x + y = c. Le intersezioni con i piani x = e y = sono parabole di equazione z = y e z = x, rispettivamente. Con queste informazioni si può fare un disegno approssimativo del grafico che rappresenta un superficie nello spazio detta paraboloide. f(,= z z=c z=x z=y x +y =c y x Esempio 9.. La funzione definita su R da f(x, y = x y invece non si annulla in un solo punto; l insieme dei punti in cui si annulla (cioè l intersezione del grafico con il piano z = è infatti costituito dalla coppie (x, y tali che x y =. Poiché x y = (x y(x + y, per la legge di annullamento del prodotto, questo insieme consiste dei grafici delle due rette di equazione y = x e y = x (vedi figura 9.. Le intersezioni con i piani x = e y = sono invece le parabole di equazione rispettivamente z = y e z = x. Le intersezioni con i piani z = c sono invece iperboli di equazione x y = c: vedi figure 9. e 9.. Il grafico che si ottiene è una superficie detta paraboloide iperbolico, rappresentata in figura 9..
4 4CAPITOLO AGGIUNTIVO 9. FUNZIONI DI DUE O PIÙ VARIABILI Paraboloide iperbolico: restrizione a [, ] [, ] Paraboloide iperbolico: intersezione col piano z = Intersezione col piano z = Intersezione col piano z = Limiti Sia f : D R con D sottoinsieme di R n. Una definizione di limite per x x ci è già nota nel caso in cui n = 1, D è un intervallo e x vi appartiene o è un suo estremo. Se si considera ad esempio la definizione 14.4, si osserva che essa non si estende in maniera ovvia al caso in cui, x R n, perché in R n non sappiamo quale significato attribuire al simbolo < utilizzato nella definizione. Tuttavia, come abbiamo visto ad esempio
5 LIMITI 5 nell esercizio 1.4, la definizione di limite lim f(x = l, x x si può scrivere in altre forme equivalenti, tra cui, nel caso l R, la seguente: per ogni ε > esiste δ > tale che x D, < x x < δ f(x l < ε. Questo scritto ha senso anche in R n se alle barrette del valore assoluto diamo il significato di modulo di vettori di R n, purché il dominio D soddisfi ad una opportuna condizione (come del resto succedeva in R. Osserviamo ora che l insieme {x R n : x x < δ ε } = = {(x 1,...,x n R n : (x1 x (x n x n < δ ε } che per n = 1 era un intervallo aperto di centro x, quando n = rappresenta la parte interna di un cerchio e per n = 3 la parte interna di una palla. Il ruolo degli intervalli è quindi ora giocato dalle palle aperte di centro x e raggio δ, cioè dagli insiemi B δ (x = {x R n : x x < δ} = = {(x 1, x,...,x n R n : (x 1 x (x n x n < δ }. Nel caso n = le palle B δ (x sono i cerchi pieni di centro x e raggio δ privati del bordo, mentre se n = 3 sono le sfere piene di centro x e raggio δ private della superficie sferica esterna. La definizione di limite per funzioni di n variabili si ottiene allora semplicemente sostituendo le palle agli intervalli. Definizione 9.3. Sia D un sottoinsieme di R n e x R n con la proprietà che in ogni palla aperta di centro x cada almeno un punto di D diverso da x. Si dice che lim f(x = l R x x se per ogni ε > esiste δ > tale che x D, < x x < δ f(x l < ε, o, equivalentemente, se per ogni ε > esiste δ > tale che f(x l < ε per ogni x B δ (x D \ {x }.
6 6CAPITOLO AGGIUNTIVO 9. FUNZIONI DI DUE O PIÙ VARIABILI Osservazione 9.4. Un punto x che soddisfa l ipotesi che ogni palla aperta di centro x contiene almeno un punto di D diverso da x si dice un punto di accumulazione per D. Si osservi che questa ipotesi è il minimo che si debba richiedere per essere sicuri che per ogni ε > esiste almeno un punto x D tale che < x x < δ (per far si, cioè, che x possa tendere ad x. Nel calcolo dei limiti di funzioni di più variabili valgono le stesse regole algebriche che valevano per i limiti di funzioni di una sola variabile, ma i casi di indeterminazione sono, generalmente, più difficili da trattare, come mostrano gli esempi seguenti. Esempio 9.5. La funzione f(x, y = x4 + y 4 x + y è definita su D = R \ {(, }. Il punto (x, y = (, è di accumulazione per D, ed ha quindi senso porsi il problema dell esistenza del limite x 4 + y 4 lim (x,y (, x + y. Numeratore e denominatore tendono a e quindi il limite si presenta in forma indeterminata. Si può però osservare che e che e quindi x4 + y 4 x + y = x x + y x + x x + y 1, y x + y 1 x4 + y 4 x + y x + y y x + y y Poiché il secondo membro tende a zero per (x, y (, allora, per confronto, anche il limite di f(x, y è zero. Si può osservare che la definizione di limite è soddisfatta prendendo δ ε = ε. Esempio 9.6. La funzione f(x, y = { 1 se xy = altrimenti
7 CONTINUITÀ 7 è definita su R (disegnarne il grafico e si può quindi considerare il limite lim f(x, y, (x,y (, ma questo limite non esiste perché ogni palla di centro (, contiene sia punti in cui la funzione vale sia punti in cui vale 1 e la differenza f(x l non può allora essere resa minore di (per esempio ε = 1/ per nessun valore di δ ε. Continuità La definizione di funzione continua in un punto è del tutto analoga a quella già data nel caso di una sola variabile. Definizione 9.7. Una funzione f : D R si dice continua in un punto di accumulazione x D se risulta lim x x f(x = f(x. Se il punto x D non è di accumulazione per D (cioè è un punto isolato allora si assume per definizione che f sia continua in x. f si dice continua in un insieme D se è continua in ogni punto di D. Esempio 9.8. La funzione f(x, y = x 4 + y 4 x + y se (x, y (, se (x, y = (, è continua in ogni punto di R e in particolare è continua in (, (vedi Esempio 9.5. Esercizio 9.9. Mostrare che x 1. lim (x,y (, x + y = ; x. lim non esiste; (x,y (, x + y xy 3. lim (x,y (, x + y + xy = ; 4. lim (x,y (, xy log x + y =.
8 8CAPITOLO AGGIUNTIVO 9. FUNZIONI DI DUE O PIÙ VARIABILI Derivate parziali di funzioni di variabili Sia f una funzione il cui dominio contenga una palla aperta di centro (x, y e sia R il suo raggio. In particolare allora f è definita anche in ogni punto del tipo (x + h, y qualunque sia h R tale che h < R. Definizione 9.1. Se esiste finito il limite (9.1 lim h f(x + h, y h allora si dice che f è derivabile parzialmente rispetto ad x nel punto (x, y e il valore del limite si chiama derivata parziale di f rispetto ad x nel punto (x, y e si denota usualmente col simbolo f x (x, y. Si osservi che il limite (9.1 è un limite usuale di una funzione della sola variabile h R. Per indicare la derivata parziale rispetto ad x si usano spesso anche altri simboli tra cui f x (x, y, D x f(x, y, x f(x, y. Si definisce analogamente la derivata parziale rispetto ad y nel punto (x, y come il limite (se esiste ed è finito e si denota con il simbolo f(x, y + h lim h h f y (x, y o altri simboli analoghi a quelli usati per la derivata parziale rispetto ad x. In conseguenza della definizione le regole di calcolo per la derivata parziale rispetto ad x (o ad y sono le stesse che valevano per le funzioni di una sola variabile, considerando l altra variabile come una costante.
9 GRADIENTE 9 Esempio La funzione f(x, y = x + y. è definita su R ed ha derivate parziali f x (x, y = x f y x + y, (x, y = y x + y che sono definite per ogni (x, y (,. Nel punto (, la funzione non è derivabile parzialmente né rispetto ad x né rispetto ad y. Esercizio 9.1. Calcolare, dove esistono, le derivate parziali delle funzioni seguenti. 1. f(x, y = arctan(y/x;. f(x, y = x4 + y x + y ; 3. f(x, y = xy x + y + xy ; 4. f(x, y = { 1 se xy = altrimenti. R 1. Il dominio di f è R \ {(,y : y R}. Si ha entrambe definite sul dominio di f. f x (x,y = y x + y f y (x,y = x x + y. Gradiente Sia f una funzione di due variabili derivabile parzialmente in un punto (x, y. Il vettore delle derivate parziali f(x, y = si chiama gradiente di f nel punto (x, y. ( f x (x, y, f y (x, y
10 1CAPITOLO AGGIUNTIVO 9. FUNZIONI DI DUE O PIÙ VARIABILI Significato geometrico del gradiente Quando è diverso da (, il vettore gradiente individua la direzione di massima pendenza del grafico della funzione. Derivate di ordine superiore Se una funzione ammette derivate parziali in tutti i punti di un dominio D allora possiamo considerare le derivate parziali come funzioni di D in R (x, y f x (x, y (x, y f y (x, y. Se a loro volta queste funzioni ammettono derivate parziali in un punto (x, y D ( f (x, y, x x ( f (x, y, x y ( f (x, y y x y ( f (x, y y allora queste ultime sono le derivate parziali seconde di f in (x, y e si indicano con i simboli x (x, y, x y (x, y, y x (x, y, y (x, y. Esempio Calcoliamo le derivate parziali seconde della funzione f(x, y = arctan(y/x. Si ha ( (x, y = x x y (x, y = ( x y x + y x y = f ( x x x + y y x = f ( y y x + y = xy (x + y = xy (x + y = y x (x + y y x + y = y x (x + y.
11 DERIVATE DI ORDINE SUPERIORE 11 Il fatto che le derivate seconde miste risultino uguali non è una particolarità della funzione considerata, ma è una proprietà comune a tutte le funzioni che hanno derivate seconde miste continue, come afferma il seguente teorema di inversione dell ordine di derivazione. Teorema (di Schwarz Se una funzione ammette entrambe le derivate seconde miste in una palla di centro un punto (x, y e se queste sono continue nel punto (x, y allora si ha x y (x, y = f y x (x, y. Mostriamo con un esempio che il teorema non è vero se le derivate seconde miste non sono continue. Esempio La funzione f(x, y = x 3 y xy 3 x + y se (x, y (, se (x, y = (, ammette derivate seconde miste nel punto (, e si ha (, = 1, x y f (, = 1. y x È infatti facile calcolare le derivate parziali prime in tutti i punti diversi da (, e si ha f x = x4 y + 4x y 3 y 5 (x + y f y = x + 4y x 3 x 5 y4 (x + y e possono essere calcolate in (, utilizzando la definizione e analogamente f f(h, f(, (, = lim = x h h f f(, h f(, (, = lim =. y h h
12 1CAPITOLO AGGIUNTIVO 9. FUNZIONI DI DUE O PIÙ VARIABILI Anche le derivate seconde miste in (, possono essere calcolate usando la definizione y x (, = y (f f x (, h f x (, h 5 x(, = lim = lim h h h h 5 = 1 e l altra si calcola analogamente. In tutti i punti diversi da (, le derivate seconde miste si possono calcolare invece usando le usuali regole di derivazione, e si può poi controllare che non sono continue in (,, anche se questa verifica non è necessaria perché se fossero continue allora, per il teorema di Schwarz sull inversione dell ordine di derivazione, dovrebbero essere uguali. Esercizio Mostrare che la funzione { y f(x, y arctan(x/y se y se y = ammette derivate seconde miste nel punto (, ma non sono uguali. Matrice Hessiana Così come le derivate parziali costituiscono un vettore, le derivate seconde possono essere considerate gli elementi di una matrice Hf(x, y = x (x f, y x y (x, y y x (x, y y (x, y detta matrice Hessiana di f nel punto (x, y, e si denota anche col simbolo f(x. Derivate parziali di funzioni di n variabili La definizione di derivata parziale rispetto ad una delle due variabili si può estendere facilmente a funzioni di 3 o più variabili. Sia f una funzione il cui dominio sia un sottoinsieme D di R n contenente una palla aperta di centro x = (x 1,...,xn e sia R il suo raggio. In particolare allora f è definita anche in ogni punto del tipo qualunque sia h tale che h < R. (x 1,...,x i + h,...,x n
13 PROBLEMI DI MASSIMO E DI MINIMO 13 Definizione Se esiste finito il limite f(x 1 lim,...,xi + h,...,xn f(x h h allora si dice che f è derivabile parzialmente rispetto ad x i nel punto x e il valore del limite si chiama derivata parziale di f rispetto ad x i nel punto x e si denota usualmente col simbolo f x i (x. Se f è derivabile parzialmente rispetto ad ogni variabile in un punto x il vettore ( f (x, f (x,..., f (x x 1 x x n si chiama gradiente di f in x. Analogamente a quanto fatto per le funzioni di due variabili si possono considerare, se esistono le derivate seconde f x i x j che costituiscono gli elementi di una matrice quadrata n n Hf(x = detta matrice Hessiana di f nel punto x. ( (x x i x j ij Massimi e minimi locali Definizione Problemi di massimo e di minimo Sia D R n e f : D R. Un punto x D si dice di massimo locale (o relativo per f su D se esiste una palla di centro x, B δ (x, tale che f(x f(x x B δ (x D, e si dice di minimo locale (o relativo se esiste una palla di centro x, B δ (x, tale che f(x f(x x B δ (x D.
14 14CAPITOLO AGGIUNTIVO 9. FUNZIONI DI DUE O PIÙ VARIABILI Definizione Un punto x D si dice interno a D se esiste una palla di centro x tutta contenuta in D. Condizione necessaria Teorema 9.. (dei punti critici Sia D R n, f : D R e x un punto di massimo o di minimo locale per f interno a D. Se esiste il gradiente di f nel punto x allora f(x = (,..., cioè tutte le derivate parziali prime in x sono nulle. Dimostrazione Basta osservare che il punto x è un punto di massimo o di minimo locale per le restrizioni di f alle rette di R n passanti per x e parallele agli assi coordinati, e utilizzare l analogo teorema (di Fermat dimostrato per le funzioni di una sola variabile. I punti in cui si annulla il gradiente si dicono critici o stazionari. Condizione sufficiente per le funzioni di variabili Teorema 9.1. (Criterio della matrice Hessiana Sia D R, f : D R una funzione con derivate parziali seconde continue e (x, y un punto interno a D. Se risulta allora f(x, y = e det Hf(x, y > i se f xx (x, y > il punto è di minimo locale; ii se f xx (x, y < il punto è di massimo locale. Se invece det Hf(x, y < allora il punto non è né di massimo né di minimo (si dice in tal caso che è un punto di sella. Osservazione 9.. Il teorema non dice nulla sul caso det Hf(x, y =
15 PROBLEMI DI MASSIMO E DI MINIMO 15 nel quale, infatti, può accadere che il punto sia di massimo o di minimo o anche di sella. Si considerino ad esempio le funzioni f(x, y = x y, f(x, y = x y, f(x, y = x 3 y. Esercizio 9.3. Determinare massimi e minimi locali delle funzioni seguenti 1. f(x, y = x + y ;. f(x, y = x y ; 3. f(x, y = x y xy; 4. f(x, y = x + xy ; 5. f(x, y = y 3y x + x 3 ; 6. f(x, y = (y x (x + y + y. Il criterio della matrice Hessiana è estendibile a funzioni di più di variabili, ma guardare il determinante della matrice Hessiana non è più sufficiente. Si può dare una condizione generale, ma di verifica meno facile. In particolare, se x è critico, una condizione sufficiente affinché sia di minimo è che la matrice Hessiana in x sia definita positiva, cioè Hf(x v, v > v R n \ {} dive Hf(x v è il prodotto righe per colonne della matrice Hf(x con il vettore colonna v. Se invece risulta Hf(x v, v < v R n \ {} cioè l Hessiana in x è definita negativa, allora x è un punto di massimo.
Matematica. Corso integrato di. per le scienze naturali ed applicate. Materiale integrativo.
 Corso integrato di Matematica per le scienze naturali ed applicate Materiale integrativo http://www.dimi.uniud.it/biomat/ Paolo Baiti 1 Lorenzo Freddi 1 1 Dipartimento di Matematica e Informatica, Università
Corso integrato di Matematica per le scienze naturali ed applicate Materiale integrativo http://www.dimi.uniud.it/biomat/ Paolo Baiti 1 Lorenzo Freddi 1 1 Dipartimento di Matematica e Informatica, Università
Modulo 5 Funzioni di piú variabili. A. Scanu
 Modulo 5 Funzioni di piú variabili A. Scanu 1 1 Generalitá In questo modulo studieremo funzioni di piú di una variabile cioé del tipo f : R n R m con n, m 1. In particolare prenderemo in considerazione
Modulo 5 Funzioni di piú variabili A. Scanu 1 1 Generalitá In questo modulo studieremo funzioni di piú di una variabile cioé del tipo f : R n R m con n, m 1. In particolare prenderemo in considerazione
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Estremi. 5. Determinare le dimensioni di una scatola rettangolare di volume v assegnato, che abbia la superficie minima.
 Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
Estremi 1. Determinare gli estremi relativi di f(x, y) = e x (x 1)(y 1) + (y 1).. Determinare gli estremi relativi di f(x, y) = y (y + 1) cos x. 3. Determinare gli estremi relativi di f(x, y) = xye x +y..
UNIVERSITÀ DI ROMA TOR VERGATA. Analisi Matematica II per Ingegneria Prof. C. Sinestrari
 UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte (sintetiche) ai quesiti degli esercizi del 12.X.2018 1. (a) Ω è aperto, Ω = {0, 1, 2}, Ω = Ω, Ω = [0, 1]
UNIVERSITÀ DI ROMA TOR VERGATA Analisi Matematica II per Ingegneria Prof. C. Sinestrari Risposte (sintetiche) ai quesiti degli esercizi del 12.X.2018 1. (a) Ω è aperto, Ω = {0, 1, 2}, Ω = Ω, Ω = [0, 1]
Massimi e minimi relativi in R n
 Massimi e minimi relativi in R n Si consideri una funzione f : A R, con A R n, e sia x A un punto interno ad A. Definizione: si dice che x è un punto di massimo relativo per f se B(x, r) A tale che f(y)
Massimi e minimi relativi in R n Si consideri una funzione f : A R, con A R n, e sia x A un punto interno ad A. Definizione: si dice che x è un punto di massimo relativo per f se B(x, r) A tale che f(y)
Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Bacchelli - a.a. 2010/2011.
 Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Baccelli - a.a. 2010/2011. 06 - Derivate, differenziabilità, piano tangente, derivate di ordine superiore. Riferimenti: R.Adams, Calcolo
Appunti sul corso di Complementi di Matematica mod. Analisi prof. B.Baccelli - a.a. 2010/2011. 06 - Derivate, differenziabilità, piano tangente, derivate di ordine superiore. Riferimenti: R.Adams, Calcolo
R. Capone Analisi Matematica Calcolo Differenziale Funzioni di due variabili
 Richiami teorici Sia una funzione di due variabili definita in un insieme A e sia un punto interno ad A. Se R è un dominio regolare di centro e di dimensioni e la funzione della sola variabile x, risulta
Richiami teorici Sia una funzione di due variabili definita in un insieme A e sia un punto interno ad A. Se R è un dominio regolare di centro e di dimensioni e la funzione della sola variabile x, risulta
Matematica. Corso integrato di. per le scienze naturali ed applicate. Materiale integrativo. Paolo Baiti 1 Lorenzo Freddi 1
 Corso integrato di Matematica per le scienze naturali ed applicate Materiale integrativo Paolo Baiti 1 Lorenzo Freddi 1 1 Dipartimento di Matematica e Informatica, Università di Udine, via delle Scienze
Corso integrato di Matematica per le scienze naturali ed applicate Materiale integrativo Paolo Baiti 1 Lorenzo Freddi 1 1 Dipartimento di Matematica e Informatica, Università di Udine, via delle Scienze
,, con 2. S oppure se x
 Deinizioni preliminari Alcuni elementi sull ottimizzazione di unzioni in due variabili Si deinisce intorno di raggio centro in r un punto S con e si indica con I r R / S R il cerchio di raggio r e r con
Deinizioni preliminari Alcuni elementi sull ottimizzazione di unzioni in due variabili Si deinisce intorno di raggio centro in r un punto S con e si indica con I r R / S R il cerchio di raggio r e r con
ESERCIZI SU MASSIMI E MINIMI DI FUNZIONI IN PIÙ VARIABILI. m(x, y, z) = (2x 2 + y 2 )e x2 y 2, f(x, y) = (y x 2 )(y x2. f(x, y) = x 3 + (x y) 2,
 ESERCIZI SU MASSIMI E MINIMI DI FUNZIONI IN PIÙ VARIABILI VALENTINA CASARINO Esercizi per il corso di Analisi Matematica, (Ingegneria Gestionale, dell Innovazione del Prodotto, Meccanica e Meccatronica,
ESERCIZI SU MASSIMI E MINIMI DI FUNZIONI IN PIÙ VARIABILI VALENTINA CASARINO Esercizi per il corso di Analisi Matematica, (Ingegneria Gestionale, dell Innovazione del Prodotto, Meccanica e Meccatronica,
Insiemi di numeri reali
 Capitolo 1 1.1 Elementi di teoria degli insiemi Se S è una totalità di oggetti x, si dice che S è uno spazio avente gli elementi x. Se si considerano alcuni elementi di S si dice che essi costituiscono
Capitolo 1 1.1 Elementi di teoria degli insiemi Se S è una totalità di oggetti x, si dice che S è uno spazio avente gli elementi x. Se si considerano alcuni elementi di S si dice che essi costituiscono
Mauro Sassetti. Calcolo differenziale ed integrale. per funzioni di due variabili reali.
 Mauro Sassetti Calcolo differenziale ed integrale per funzioni di due variabili reali. Breve esposizione dei principali risultati. Parte prima : Calcolo differenziale 1. Generalità 1.1 L insieme R come
Mauro Sassetti Calcolo differenziale ed integrale per funzioni di due variabili reali. Breve esposizione dei principali risultati. Parte prima : Calcolo differenziale 1. Generalità 1.1 L insieme R come
Soluzione. Il dominio E consiste nella parte di spazio contenuta nella sfera ma esterna al cono rappresentata in Figura 1. Infatti
 Esercizio 1 (G. Ziglio). (6 punti) Calcolare il volume della porzione di spazio E interna alla sfera di equazione x 2 + y 2 + z 2 = 1 ed esterna al cono di equazione z 2 = x 2 + y 2 E = (x, y, z) R x 2
Esercizio 1 (G. Ziglio). (6 punti) Calcolare il volume della porzione di spazio E interna alla sfera di equazione x 2 + y 2 + z 2 = 1 ed esterna al cono di equazione z 2 = x 2 + y 2 E = (x, y, z) R x 2
ESERCIZIO SVOLTO N 1 ESERCIZIO SVOLTO N 2. Determinare e rappresentare graficamente il dominio della funzione
 ESERCIZIO SVOLTO N 1 Determinare e rappresentare graficamente il dominio della funzione f(x, y) = y 2 x 2 Trovare gli eventuali punti stazionari e gli estremi di f Il dominio della funzione è dato da dom
ESERCIZIO SVOLTO N 1 Determinare e rappresentare graficamente il dominio della funzione f(x, y) = y 2 x 2 Trovare gli eventuali punti stazionari e gli estremi di f Il dominio della funzione è dato da dom
Esercitazione n 6. Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (b)f(x, y) = 4y 4 16x 2 y + x
 Esercitazione n 6 1 Massimi e minimi di funzioni di più variabili Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (a)f(x, y) = x 3 + y 3 + xy (b)f(x, y) = 4y 4 16x
Esercitazione n 6 1 Massimi e minimi di funzioni di più variabili Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (a)f(x, y) = x 3 + y 3 + xy (b)f(x, y) = 4y 4 16x
FUNZIONI DI DUE VARIABILI REALI. f(x, y) = ax + by + c. f(x, y) = x 2 + y 2
 0.1 FUNZIONI DI DUE VARIABILI REALI Sia A R 2. Una applicazione f : A R si chiama funzione reale di due variabili reali ESEMPI: 1. La funzione affine di due variabili reali: 2. f(x, y) = ax + by + c f(x,
0.1 FUNZIONI DI DUE VARIABILI REALI Sia A R 2. Una applicazione f : A R si chiama funzione reale di due variabili reali ESEMPI: 1. La funzione affine di due variabili reali: 2. f(x, y) = ax + by + c f(x,
CORSO DI LAUREA IN INFORMATICA ANALISI MATEMATICA I MODULO, I E II MODULO, II MODULO II PROVA SCRITTA DI GENNAIO 2006: SOLUZIONI
 CORSO DI LAUREA IN INFORMATICA ANALISI MATEMATICA I MODULO, I E II MODULO, II MODULO II PROVA SCRITTA DI GENNAIO 2006: SOLUZIONI Notiamo che lo studio delle funzioni assegnate f,..., f 4 si riduce a considerare
CORSO DI LAUREA IN INFORMATICA ANALISI MATEMATICA I MODULO, I E II MODULO, II MODULO II PROVA SCRITTA DI GENNAIO 2006: SOLUZIONI Notiamo che lo studio delle funzioni assegnate f,..., f 4 si riduce a considerare
Estremi relativi (liberi) per campi scalari
 Estremi relativi (liberi) per campi scalari Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Estremi relativi (liberi) Analisi Matematica B 1 / 60 Punti
Estremi relativi (liberi) per campi scalari Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Estremi relativi (liberi) Analisi Matematica B 1 / 60 Punti
ANALISI B alcuni esercizi proposti
 ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
ANALISI B alcuni esercizi proposti G.P. Leonardi Parte II 1 Limiti e continuità per funzioni di 2 variabili Esercizio 1.1 Calcolare xy log(1 + x ) lim (x,y) (0,0) 2x 2 + 5y 2 Esercizio 1.2 Studiare la
Istituzioni di Matematiche Modulo B (SG)
 Istituzioni di Matematiche Modulo B (SG) II foglio di esercizi ESERCIZIO 1. Per ciascuna funzione f(, ) calcolare le derivate parziali f (, ) e f (, ) e determinare il relativo dominio di definizione.
Istituzioni di Matematiche Modulo B (SG) II foglio di esercizi ESERCIZIO 1. Per ciascuna funzione f(, ) calcolare le derivate parziali f (, ) e f (, ) e determinare il relativo dominio di definizione.
DERIVATE SUCCESSIVE E MATRICE HESSIANA
 FUNZIONI DI DUE VARIABILI 1 DERIVATE SUCCESSIVE E MATRICE HESSIANA Derivate parziali seconde e matrice hessiana. Sviluppo di Taylor del secondo ordine. Punti stazionari. Punti di massimo o minimo (locale
FUNZIONI DI DUE VARIABILI 1 DERIVATE SUCCESSIVE E MATRICE HESSIANA Derivate parziali seconde e matrice hessiana. Sviluppo di Taylor del secondo ordine. Punti stazionari. Punti di massimo o minimo (locale
Svolgimento. f y (x, y) = 8 y 2 x. 1 x 2 y = 0. y 2 x = 0. (si poteva anche ricavare la x dalla seconda equazione e sostituire nella prima)
 Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 2013-2014 (dott.ssa Vita Leonessa) Esercizi svolti: Ricerca di massimi e minimi di funzioni a
Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 2013-2014 (dott.ssa Vita Leonessa) Esercizi svolti: Ricerca di massimi e minimi di funzioni a
I teoremi della funzione inversa e della funzione implicita
 I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;
![a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [; a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;](/thumbs/69/60588320.jpg) ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
Simmetrie e quadriche
 Appendice A Simmetrie e quadriche A.1 Rappresentazione e proprietà degli insiemi nel piano Una delle prime difficoltà che si incontrano nell impostare il calcolo di un integrale doppio consiste nel rappresentare
Appendice A Simmetrie e quadriche A.1 Rappresentazione e proprietà degli insiemi nel piano Una delle prime difficoltà che si incontrano nell impostare il calcolo di un integrale doppio consiste nel rappresentare
Punti di massimo o di minimo per funzioni di n variabili reali
 Punti di massimo o di minimo per funzioni di n variabili reali Dati f : A R n R ed X 0 A, X 0 si dice : punto di minimo assoluto se X A, f ( x ) f ( X 0 ) punto di massimo assoluto se X A, f ( x ) f (
Punti di massimo o di minimo per funzioni di n variabili reali Dati f : A R n R ed X 0 A, X 0 si dice : punto di minimo assoluto se X A, f ( x ) f ( X 0 ) punto di massimo assoluto se X A, f ( x ) f (
Analisi Matematica 2 Funzioni di due o piú variabili
 Analisi Matematica 2 Funzioni di due o piú variabili Monica Marras - Universita di Cagliari mmarras@unica.it Monica Marras - Universita di Cagliari CCS Ingegneria Meccanica e Ingegneria Chimica mmarras@unica.it
Analisi Matematica 2 Funzioni di due o piú variabili Monica Marras - Universita di Cagliari mmarras@unica.it Monica Marras - Universita di Cagliari CCS Ingegneria Meccanica e Ingegneria Chimica mmarras@unica.it
Analisi Matematica IV modulo Soluzioni prova scritta preliminare n. 1
 Analisi Matematica IV modulo Soluzioni prova scritta preliminare n. 1 Corso di laurea in Matematica, a.a. 2005-2006 27 aprile 2006 1. Disegnare approssimativamente nel piano (x, y) l insieme x 4 6xy 2
Analisi Matematica IV modulo Soluzioni prova scritta preliminare n. 1 Corso di laurea in Matematica, a.a. 2005-2006 27 aprile 2006 1. Disegnare approssimativamente nel piano (x, y) l insieme x 4 6xy 2
1. Richiami. v = x 2 + y 2.
 Gli elementi del prodotto cartesiano 1 Richiami R 2 = x, y R} sono detti vettori Ogni vettore v è una coppia ordinata ed i numeri reali x e y sono detti le componenti di v In particolare si denota con
Gli elementi del prodotto cartesiano 1 Richiami R 2 = x, y R} sono detti vettori Ogni vettore v è una coppia ordinata ed i numeri reali x e y sono detti le componenti di v In particolare si denota con
Corso di laurea: Ingegneria aerospaziale e meccanica Programma di Fondamenti di Analisi Matematica II a.a. 2013/14 Docente: Fabio Paronetto
 Corso di laurea: Ingegneria aerospaziale e meccanica Programma di Fondamenti di Analisi Matematica II a.a. 2013/14 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo
Corso di laurea: Ingegneria aerospaziale e meccanica Programma di Fondamenti di Analisi Matematica II a.a. 2013/14 Docente: Fabio Paronetto Gli argomenti denotati con un asterisco tra parentesi (e solo
Alcune nozioni di calcolo differenziale
 Alcune nozioni di calcolo differenziale G. Mastroeni, M. Pappalardo 1 Limiti per funzioni di piu variabili Supporremo noti i principali concetti algebrici e topologici relativi alla struttura dello spazio
Alcune nozioni di calcolo differenziale G. Mastroeni, M. Pappalardo 1 Limiti per funzioni di piu variabili Supporremo noti i principali concetti algebrici e topologici relativi alla struttura dello spazio
Analisi Matematica 2
 Analisi Matematica 2 Differenziabilità per funzioni di due variabili Differenziabilità per funzioni di due variabili CCS Ingegneria Meccanica e Ingegneria Chimica 1 / 26 Differenziabilitá Data la funzione
Analisi Matematica 2 Differenziabilità per funzioni di due variabili Differenziabilità per funzioni di due variabili CCS Ingegneria Meccanica e Ingegneria Chimica 1 / 26 Differenziabilitá Data la funzione
Funzioni implicite - Esercizi svolti
 Funzioni implicite - Esercizi svolti Esercizio. È data la funzione di due variabili F (x, y) = y(e y + x) log x. Verificare che esiste un intorno I in R del punto di ascissa x 0 = sul quale è definita
Funzioni implicite - Esercizi svolti Esercizio. È data la funzione di due variabili F (x, y) = y(e y + x) log x. Verificare che esiste un intorno I in R del punto di ascissa x 0 = sul quale è definita
Istituzioni di Matematiche terza parte
 Istituzioni di Matematiche terza parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 35 index Il concetto di limite 1 Il
Istituzioni di Matematiche terza parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 35 index Il concetto di limite 1 Il
Esempio di grafico di una funzione reale di due variabili reali
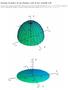 Esempio di grafico di una funzione reale di due variabili reali In questo lucido è rappresentato il grafico della funzione reale di due variabili reali definita da: f(x, y) = 1 x y, in particolare in alto
Esempio di grafico di una funzione reale di due variabili reali In questo lucido è rappresentato il grafico della funzione reale di due variabili reali definita da: f(x, y) = 1 x y, in particolare in alto
Analisi Matematica 2. Continuità, derivabilità e differenziabilità
 Docente: E. G. Casini Università degli Studi dell Insubria DIPATIMENTO DI SCIENZA E ALTA TECNOLOGIA Corso di Studio in Matematica e Fisica Analisi Matematica ichiami di Teoria ed Esercizi con Svolgimento
Docente: E. G. Casini Università degli Studi dell Insubria DIPATIMENTO DI SCIENZA E ALTA TECNOLOGIA Corso di Studio in Matematica e Fisica Analisi Matematica ichiami di Teoria ed Esercizi con Svolgimento
Massimi e minimi vincolati
 Massimi e minimi vincolati Data una funzione G C 1 (D), dove D è un aperto di R 2, sappiamo bene dove andare a cercare gli eventuali punti di massimo e minimo relativi. Una condizione necessaria affinché
Massimi e minimi vincolati Data una funzione G C 1 (D), dove D è un aperto di R 2, sappiamo bene dove andare a cercare gli eventuali punti di massimo e minimo relativi. Una condizione necessaria affinché
ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA
 ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA Prova scritta del 6 giugno 2004: soluzioni ESERCIZIO - Data la funzione f) 3 2 4 + 27 + 9 2 ) /3 4 + 27, + 9 si chiede
ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA Prova scritta del 6 giugno 2004: soluzioni ESERCIZIO - Data la funzione f) 3 2 4 + 27 + 9 2 ) /3 4 + 27, + 9 si chiede
Analisi Matematica II Corso di Ingegneria Gestionale Compito del f(x, y) = e (x3 +x) y
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--7 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 8--7 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
1 Ampliamento del piano e coordinate omogenee
 1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
Quick calculus Capitolo 1 Il problema della tangente
 Quick calculus Capitolo 1 Il problema della tangente Introduzione Ricavare una retta tangente ad una curva di secondo grado come un circonferenza o una parabola, è un problema che si risolve facilmente.
Quick calculus Capitolo 1 Il problema della tangente Introduzione Ricavare una retta tangente ad una curva di secondo grado come un circonferenza o una parabola, è un problema che si risolve facilmente.
ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE
 ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE 1 Funzioni libere I punti stazionari di una funzione libera di più variabili si ottengono risolvendo il sistema di equazioni
ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE 1 Funzioni libere I punti stazionari di una funzione libera di più variabili si ottengono risolvendo il sistema di equazioni
Esercizi su estremi vincolati e assoluti
 Esercizi su estremi vincolati e assoluti Esercizio 1. di sul quadrato Determinare i punti di minimo e di massimo (e i relativi valori di minimo e massimo) assoluto f(x, y) = x cos(πy) Q = [0, 1] [0, 1].
Esercizi su estremi vincolati e assoluti Esercizio 1. di sul quadrato Determinare i punti di minimo e di massimo (e i relativi valori di minimo e massimo) assoluto f(x, y) = x cos(πy) Q = [0, 1] [0, 1].
1 Note ed esercizi risolti a ricevimento
 1 Note ed esercizi risolti a ricevimento Nota 1. Il polinomio di Taylor della funzione f x, y) due variabili), del secondo ordine, nel punto x 0, y 0 ), è P 2 x, y) = f x 0, y 0 ) + f x x 0, y 0 ) x x
1 Note ed esercizi risolti a ricevimento Nota 1. Il polinomio di Taylor della funzione f x, y) due variabili), del secondo ordine, nel punto x 0, y 0 ), è P 2 x, y) = f x 0, y 0 ) + f x x 0, y 0 ) x x
Il teorema di Lagrange e la formula di Taylor
 Il teorema di Lagrange e la formula di Taylor Il teorema del valor medio di Lagrange, valido per funzioni reali di una variabile reale, si estende alle funzioni reali di più variabili. Come si vedrà, questo
Il teorema di Lagrange e la formula di Taylor Il teorema del valor medio di Lagrange, valido per funzioni reali di una variabile reale, si estende alle funzioni reali di più variabili. Come si vedrà, questo
2. I numeri reali e le funzioni di variabile reale
 . I numeri reali e le funzioni di variabile reale Introduzione Il metodo comunemente usato in Matematica consiste nel precisare senza ambiguità i presupposti, da non cambiare durante l elaborazione dei
. I numeri reali e le funzioni di variabile reale Introduzione Il metodo comunemente usato in Matematica consiste nel precisare senza ambiguità i presupposti, da non cambiare durante l elaborazione dei
APPUNTI DI MATEMATICA: I limiti e la continuità Le derivate. Prof. ssa Prenol R.
 APPUNTI DI MATEMATICA: I iti e la continuità Le derivate Prof. ssa Prenol R. INTERVALLI e INTORNI Definizione di intervallo: è un sottoinsieme di numeri reali e può essere - ilitato: graficamente viene
APPUNTI DI MATEMATICA: I iti e la continuità Le derivate Prof. ssa Prenol R. INTERVALLI e INTORNI Definizione di intervallo: è un sottoinsieme di numeri reali e può essere - ilitato: graficamente viene
Limiti di funzioni di due variabili
 Limiti di funzioni di due variabili Definizione 1 Sia f : A R 2 R e x 0 = (x 0, y 0 ) punto di accumulazione di A. Diciamo che se e solo se Diciamo che se e solo se f(x) = f(x, y) = L x x 0 (x,y) (x 0,y
Limiti di funzioni di due variabili Definizione 1 Sia f : A R 2 R e x 0 = (x 0, y 0 ) punto di accumulazione di A. Diciamo che se e solo se Diciamo che se e solo se f(x) = f(x, y) = L x x 0 (x,y) (x 0,y
Massimi e minimi vincolati
 Massimi e minimi vincolati Vedremo tra breve un metodo per studiare il problema di trovare il minimo e il massimo di una funzione su di un sottoinsieme dello spazio ambiente che non sia un aperto. Abbiamo
Massimi e minimi vincolati Vedremo tra breve un metodo per studiare il problema di trovare il minimo e il massimo di una funzione su di un sottoinsieme dello spazio ambiente che non sia un aperto. Abbiamo
1. Funzioni implicite
 1. Funzioni implicite 1.1 Il caso scalare Sia X R 2 e sia f : X R. Una funzione y : (a, b) R si dice definita implicitamente dall equazione f(x, y) = 0 in (a, b) quando: 1. (x, y(x)) X x (a, b); 2. f(x,
1. Funzioni implicite 1.1 Il caso scalare Sia X R 2 e sia f : X R. Una funzione y : (a, b) R si dice definita implicitamente dall equazione f(x, y) = 0 in (a, b) quando: 1. (x, y(x)) X x (a, b); 2. f(x,
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA
 ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
Ottimizzazione vincolata
 Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
ESERCIZI DI METODI QUANTITATIVI PER L ECONOMIA DIP. DI ECONOMIA E MANAGEMENT DI FERRARA A.A. 2016/2017. Ottimizzazione libera
 ESERCIZI DI METODI QUANTITATIVI PER L ECONOMIA DIP. DI ECONOMIA E MANAGEMENT DI FERRARA A.A. 2016/2017 Ottimizzazione libera Esercizio 1. Si determinino, se esistono, gli estremi delle seguenti funzioni
ESERCIZI DI METODI QUANTITATIVI PER L ECONOMIA DIP. DI ECONOMIA E MANAGEMENT DI FERRARA A.A. 2016/2017 Ottimizzazione libera Esercizio 1. Si determinino, se esistono, gli estremi delle seguenti funzioni
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/0/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/0/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/0/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/0/03) Università di Verona - Laurea in Biotecnologie
Teorema delle Funzioni Implicite
 Teorema delle Funzioni Implicite Sia F una funzione di due variabili definita in un opportuno dominio D di R 2. Consideriamo l equazione F (x, y) = 0, questa avrà come soluzioni coppie di valori (x, y)
Teorema delle Funzioni Implicite Sia F una funzione di due variabili definita in un opportuno dominio D di R 2. Consideriamo l equazione F (x, y) = 0, questa avrà come soluzioni coppie di valori (x, y)
Corso di Geometria BIAR, BSIR Esercizi 10: soluzioni
 Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
Corso di Geometria 2010-11 BIAR, BSIR Esercizi 10: soluzioni 1 Geometria dello spazio Esercizio 1. Dato il punto P 0 = ( 1, 0, 1) e il piano π : x + y + z 2 = 0, determinare: a) Le equazioni parametriche
= 2x 2λx = 0 = 2y 2λy = 0
 ESERCIZI SULLA OTTIMIZZAZIONE VINCOLATA ESERCIZIO Determinare i punti di massimo e minimo di f x, y = x y soggetta al vincolo x + y = Il vincolo è chiuso e limitato (circonferenza di raggio ) e la funzione
ESERCIZI SULLA OTTIMIZZAZIONE VINCOLATA ESERCIZIO Determinare i punti di massimo e minimo di f x, y = x y soggetta al vincolo x + y = Il vincolo è chiuso e limitato (circonferenza di raggio ) e la funzione
NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE
 NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE ROBERTO GIAMBÒ 1. DEFINIZIONI E PRIME PROPRIETÀ In queste note saranno presentate alcune proprietà principali delle funzioni convesse di una variabile
NOTE SULLE FUNZIONI CONVESSE DI UNA VARIABILE REALE ROBERTO GIAMBÒ 1. DEFINIZIONI E PRIME PROPRIETÀ In queste note saranno presentate alcune proprietà principali delle funzioni convesse di una variabile
Coordinate Cartesiane nel Piano
 Coordinate Cartesiane nel Piano O = (0,0) origine degli assi x ascissa, y ordinata sistemi monometrici: stessa unità di misura sui due assi x, y sistemi dimetrici: unità di misura diverse sui due assi
Coordinate Cartesiane nel Piano O = (0,0) origine degli assi x ascissa, y ordinata sistemi monometrici: stessa unità di misura sui due assi x, y sistemi dimetrici: unità di misura diverse sui due assi
Limiti di funzioni di una variabile
 Capitolo 6 Limiti di funzioni di una variabile 6.1 Limiti all infinito La definizione di ite data per le successioni si può immediatamente trasportare al caso di una funzione definita in un qualunque insieme
Capitolo 6 Limiti di funzioni di una variabile 6.1 Limiti all infinito La definizione di ite data per le successioni si può immediatamente trasportare al caso di una funzione definita in un qualunque insieme
DERIVATA DI UNA FUNZIONE REALE. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR.
 DERIVATA DI UNA FUNZIONE REALE 1. Definizioni. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR. DEFINIZIONE 1. Sia x 0 un elemento di I. Per ogni x (I \ {x 0 }) consideriamo
DERIVATA DI UNA FUNZIONE REALE 1. Definizioni. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR. DEFINIZIONE 1. Sia x 0 un elemento di I. Per ogni x (I \ {x 0 }) consideriamo
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti) 2 settembre 2008 Tema A
 Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti 2 settembre 28 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
Università degli Studi di Bergamo Matematica II (5 e 7,5 crediti 2 settembre 28 Tema A Tempo a disposizione: 2 ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio va iniziato all inizio
FUNZIONI REALI DI DUE VARIABILI REALI
 FUNZIONI REALI DI DUE VARIABILI REALI DEFINIZIONE VARIABILI Una funione f, associa ad ogni una coppia ordinata di numeri reali,, appartenente ad un sottoinsieme S del piano, uno e un solo numero reale.
FUNZIONI REALI DI DUE VARIABILI REALI DEFINIZIONE VARIABILI Una funione f, associa ad ogni una coppia ordinata di numeri reali,, appartenente ad un sottoinsieme S del piano, uno e un solo numero reale.
Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile
 Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 41 1 Derivata
Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 41 1 Derivata
Massimi e minimi vincolati
 Massimi e minimi vincolati Sia f una funzione differenziabile, definita su un aperto A di R N. Se K è un sottoinsieme chiuso e limitato di A, per il teorema di Weierstrass f assume massimo e minimo su
Massimi e minimi vincolati Sia f una funzione differenziabile, definita su un aperto A di R N. Se K è un sottoinsieme chiuso e limitato di A, per il teorema di Weierstrass f assume massimo e minimo su
2. Funzioni reali di più variabili reali
 Corso di Laurea in Ingegneria delle Telecomunicazioni - A.A.2001-2002 Traccia del corso di Analisi Matematica L-B 2. Funzioni reali di più variabili reali Riferimenti. Minnaja:Matematica Due, par.3.1-3.4
Corso di Laurea in Ingegneria delle Telecomunicazioni - A.A.2001-2002 Traccia del corso di Analisi Matematica L-B 2. Funzioni reali di più variabili reali Riferimenti. Minnaja:Matematica Due, par.3.1-3.4
Matematica e Statistica
 Matematica e Statistica Prova d esame (08/0/0) Università di Verona - Laurea in Biotecnologie - A.A. 0/ Tema A Matematica e Statistica Prova di MATEMATICA (08/0/0) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (08/0/0) Università di Verona - Laurea in Biotecnologie - A.A. 0/ Tema A Matematica e Statistica Prova di MATEMATICA (08/0/0) Università di Verona - Laurea in Biotecnologie
Fissiamo nello spazio un sistema di riferimento cartesiano ortogonale O, x, y, z, u.
 Fissiamo nello spazio un sistema di riferimento cartesiano ortogonale O, x, y, z, u. Definizione Una quadriche è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee
Fissiamo nello spazio un sistema di riferimento cartesiano ortogonale O, x, y, z, u. Definizione Una quadriche è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee
Esercitazione n 5. 1 Limiti e continuità di funzioni in più variabili. Esercizio 1: Si verifichi che la funzione f definita per ogni (x, y) R 2 da
 Esercitazione n 5 1 Limiti e continuità di funzioni in più variabili Esercizio 1: Si verifici ce la funzione f definita per ogni (, y) R 2 da { 4 y 4 se (, y) (0, 0) f(, y) = 2 +y 2 0 se (, y) = (0, 0)
Esercitazione n 5 1 Limiti e continuità di funzioni in più variabili Esercizio 1: Si verifici ce la funzione f definita per ogni (, y) R 2 da { 4 y 4 se (, y) (0, 0) f(, y) = 2 +y 2 0 se (, y) = (0, 0)
1. Richiami. v = x 2 + y 2.
 Gli elementi del prodotto cartesiano 1. Richiami R 2 = x, y R} sono detti vettori. Ogni vettore v è una coppia ordinata ed i numeri reali x e y sono detti le componenti di v. In particolare si denota con
Gli elementi del prodotto cartesiano 1. Richiami R 2 = x, y R} sono detti vettori. Ogni vettore v è una coppia ordinata ed i numeri reali x e y sono detti le componenti di v. In particolare si denota con
Corso di Geometria BIAR, BSIR Esercizi 4: soluzioni
 Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Esercizio. Sono dati i seguenti sistemi lineari omogenei nelle incognite x, y, z: { x + y z = x + y z = x + y z = S : x y + z =, S :, S 3 : x 3y =,
Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Esercizio. Sono dati i seguenti sistemi lineari omogenei nelle incognite x, y, z: { x + y z = x + y z = x + y z = S : x y + z =, S :, S 3 : x 3y =,
Prima parte: DOMINIO E INSIEMI DI LIVELLO
 FUNZIONI DI DUE VARIABILI 1 Prima parte: DOMINIO E INSIEMI DI LIVELLO Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia insiemi aperti, chiusi, limitati, convessi, connessi
FUNZIONI DI DUE VARIABILI 1 Prima parte: DOMINIO E INSIEMI DI LIVELLO Domini e disequazioni in due variabili. Insiemi di livello. Elementi di topologia insiemi aperti, chiusi, limitati, convessi, connessi
10 - Applicazioni del calcolo differenziale
 Università degli Studi di Palermo Facoltà di Economia CdS Sviuppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 10 - Applicazioni del calcolo differenziale Anno Accademico 2015/2016
Università degli Studi di Palermo Facoltà di Economia CdS Sviuppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 10 - Applicazioni del calcolo differenziale Anno Accademico 2015/2016
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017
 Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
Tutorato di Complementi di Analisi Matematica e Statistica Parte di Analisi 6 e 10 aprile 2017 Esercizi: serie di potenze e serie di Taylor 1 Date le serie di potenze a.) n=2 ln(n) n 3 (x 5)n b.) n=2 ln(n)
Matematica e Statistica
 Matematica e Statistica Prova d esame (25/09/203) Università di Verona - Laurea in Biotecnologie - A.A. 202/3 Matematica e Statistica Prova di MATEMATICA (25/09/203) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (25/09/203) Università di Verona - Laurea in Biotecnologie - A.A. 202/3 Matematica e Statistica Prova di MATEMATICA (25/09/203) Università di Verona - Laurea in Biotecnologie
(a) Le derivate parziali f x. f y = x2 + 2xy + 3 si annullano contemporaneamente in (1, 2) e ( 1, 2). Le derivate seconde di f valgono.
 Esercizio 1 Si consideri la funzione f(x, y) = x 2 y + xy 2 + y (a) Determinare i punti di massimo e minimo relativo e di sella del grafico di f. (b) Determinare i punti di massimo e minimo assoluto di
Esercizio 1 Si consideri la funzione f(x, y) = x 2 y + xy 2 + y (a) Determinare i punti di massimo e minimo relativo e di sella del grafico di f. (b) Determinare i punti di massimo e minimo assoluto di
variabili. se i limiti esistono e si chiamano rispettivamente derivata parziale rispetto ad x e rispetto ad y.
 Funzioni di più variabili Derivate parziali Qui saranno considerate soltanto funzioni di due variabili, ma non c è nessuna difficoltà ad estendere le nuove nozioni a funzioni di n ( > variabili ( Definizione:
Funzioni di più variabili Derivate parziali Qui saranno considerate soltanto funzioni di due variabili, ma non c è nessuna difficoltà ad estendere le nuove nozioni a funzioni di n ( > variabili ( Definizione:
Richiami di matematica
 corso di Economia Politica I (sede di San Benedetto del Tronto) Nota Lo scopo di queste pagine è sostanzialmente quello di richiamare l attenzione degli studenti su alcuni strumenti analitici utili per
corso di Economia Politica I (sede di San Benedetto del Tronto) Nota Lo scopo di queste pagine è sostanzialmente quello di richiamare l attenzione degli studenti su alcuni strumenti analitici utili per
y (b) f(x, y) = y log x sin x (c) f(x, y) = tan y (d) f(x, y) = e x y (f) f(x, y) = cos(x 2 + y 2 )
 FUNZIONI DI PIÙ VARIABILI. Siano date le seguenti funzioni: (a) f(x, y) = 3x + y (c) h(x, y) = x y (b) g(x, y) = xy (d) k(x, y) = x + y Determinare e disegnare nel piano cartesiano il dominio delle funzioni
FUNZIONI DI PIÙ VARIABILI. Siano date le seguenti funzioni: (a) f(x, y) = 3x + y (c) h(x, y) = x y (b) g(x, y) = xy (d) k(x, y) = x + y Determinare e disegnare nel piano cartesiano il dominio delle funzioni
Matematica e Statistica
 Matematica e Statistica Prova d esame (26/06/203) Università di Verona - Laurea in Biotecnologie - A.A. 202/3 Matematica e Statistica Prova di MATEMATICA (26/06/203) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (26/06/203) Università di Verona - Laurea in Biotecnologie - A.A. 202/3 Matematica e Statistica Prova di MATEMATICA (26/06/203) Università di Verona - Laurea in Biotecnologie
Analisi Matematica T_2 (prof.g.cupini) A.A CdL Ingegneria Automaz./Energ.Elettrica - Univ.Bologna REGISTRO DELLE LEZIONI
 Analisi Matematica T_2 (prof.g.cupini) A.A.2014-2015 - CdL Ingegneria Automaz./Energ.Elettrica - Univ.Bologna REGISTRO DELLE LEZIONI Lu, 23 febbraio 2015 Presentazione del corso. Curve parametriche: definizione.
Analisi Matematica T_2 (prof.g.cupini) A.A.2014-2015 - CdL Ingegneria Automaz./Energ.Elettrica - Univ.Bologna REGISTRO DELLE LEZIONI Lu, 23 febbraio 2015 Presentazione del corso. Curve parametriche: definizione.
COMPITO IN CLASSE DI MATEMATICA Funzioni di due variabili Classe 5ª D. Fila A
 Esercizio 1 Determinare il dominio della seguente funzione: COMPITO IN CLASSE DI MATEMATICA Funzioni di due variabili Classe 5ª D Fila A (a) f (, ln( + 4 Esercizio Calcolare le derivate parziali delle
Esercizio 1 Determinare il dominio della seguente funzione: COMPITO IN CLASSE DI MATEMATICA Funzioni di due variabili Classe 5ª D Fila A (a) f (, ln( + 4 Esercizio Calcolare le derivate parziali delle
1. Riconoscere la natura delle coniche rappresentate dalle seguenti equazioni e disegnarle:
 Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 204-205 (dott.ssa Vita Leonessa) Esercizi proposti n. 3: Funzioni a due variabili. Riconoscere
Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 204-205 (dott.ssa Vita Leonessa) Esercizi proposti n. 3: Funzioni a due variabili. Riconoscere
Soluzioni del compito di Istituzioni di Matematiche/Matematica per Chimica F45 e F5X (10/2/11)
 Soluzioni del compito di Istituzioni di Matematiche/Matematica per Chimica F5 e F5X (//). La funzione f(x) = x 3x x + (a) èdefinita purché l argomento della radice sia non negativo cioè perx 3x : quindi
Soluzioni del compito di Istituzioni di Matematiche/Matematica per Chimica F5 e F5X (//). La funzione f(x) = x 3x x + (a) èdefinita purché l argomento della radice sia non negativo cioè perx 3x : quindi
Istituzioni di Matematiche terza parte
 Istituzioni di Matematiche terza parte anno acc. 2013/2014 Univ. degli Studi di Milano D.Bambusi, C.Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 45 index Il concetto di ite 1 Il
Istituzioni di Matematiche terza parte anno acc. 2013/2014 Univ. degli Studi di Milano D.Bambusi, C.Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 45 index Il concetto di ite 1 Il
Funzioni reali di 2 variabili reali
 Funzioni reali di 2 variabili reali Sono funzioni del tipo: f :domf R 2 R Ad ogni punto P =(x, y) di un sottoinsieme dom f P =(x, y) f (P )=f (x, y) di R 2 associano un numero reale f (P )=f (x, y). Se
Funzioni reali di 2 variabili reali Sono funzioni del tipo: f :domf R 2 R Ad ogni punto P =(x, y) di un sottoinsieme dom f P =(x, y) f (P )=f (x, y) di R 2 associano un numero reale f (P )=f (x, y). Se
Matematica e Statistica
 Matematica e Statistica Prova d Esame (04/0/00) Università di Verona - Laurea in Biotecnologie - A.A. 009/0 Matematica e Statistica Prova d Esame di MATEMATICA (04/0/00) Università di Verona - Laurea in
Matematica e Statistica Prova d Esame (04/0/00) Università di Verona - Laurea in Biotecnologie - A.A. 009/0 Matematica e Statistica Prova d Esame di MATEMATICA (04/0/00) Università di Verona - Laurea in
Istituzioni di Matematiche seconda parte
 Istituzioni di Matematiche seconda parte anno acc. 2010/2011 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 26 index 1 2 Continuità Cristina Turrini
Istituzioni di Matematiche seconda parte anno acc. 2010/2011 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 26 index 1 2 Continuità Cristina Turrini
Richiami sugli insiemi numerici
 Richiami sugli insiemi numerici denota l insieme vuoto cioè l insieme privo di elementi. N = {1, 2, 3,...} denota l insieme dei numeri naturali. Z = {..., 2, 1, 0, 1, 2,...} denota l insieme dei numeri
Richiami sugli insiemi numerici denota l insieme vuoto cioè l insieme privo di elementi. N = {1, 2, 3,...} denota l insieme dei numeri naturali. Z = {..., 2, 1, 0, 1, 2,...} denota l insieme dei numeri
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile
 Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di Bari) Analisi Matematica
Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di Bari) Analisi Matematica
12 gennaio Commenti esame di geometria - Ing. gestionale - a.a
 Questo documento riporta commenti, approfondimenti o metodi di soluzione alternativi per alcuni esercizi dell esame Ovviamente alcuni esercizi potevano essere risolti utilizzando metodi ancora diversi
Questo documento riporta commenti, approfondimenti o metodi di soluzione alternativi per alcuni esercizi dell esame Ovviamente alcuni esercizi potevano essere risolti utilizzando metodi ancora diversi
Forme differenziali lineari e loro integrazione
 Forme differenziali lineari e loro integrazione Integrazione di una forma differenziale in due variabili Siano L(, ) e ( ) consideriamo l espressione M, due funzioni definite e continue in un insieme connesso
Forme differenziali lineari e loro integrazione Integrazione di una forma differenziale in due variabili Siano L(, ) e ( ) consideriamo l espressione M, due funzioni definite e continue in un insieme connesso
Topologia, continuità, limiti in R n
 Topologia, continuità, limiti in R n Ultimo aggiornamento: 18 febbraio 2017 1. Preliminari Prima di iniziare lo studio delle funzioni di più variabili, in generale funzioni di k variabili e a valori in
Topologia, continuità, limiti in R n Ultimo aggiornamento: 18 febbraio 2017 1. Preliminari Prima di iniziare lo studio delle funzioni di più variabili, in generale funzioni di k variabili e a valori in
Analisi Matematica II Corso di Ingegneria Gestionale Compito del A
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del -7-5 - A Esercizio ( punti Data la funzione f(x, y = x + y + 4xy 8x 4y + 4 i trovare tutti i punti critici e, se possibile, caratterizzarli
Analisi Matematica II Corso di Ingegneria Gestionale Compito del -7-5 - A Esercizio ( punti Data la funzione f(x, y = x + y + 4xy 8x 4y + 4 i trovare tutti i punti critici e, se possibile, caratterizzarli
Teoremi di Fermat, Rolle, Lagrange, Cauchy, de l Hôpital
 Teoremi di Fermat, Rolle, Lagrange, Cauchy, de l Hôpital Copyright c 2007 Pasquale Terrecuso Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Teoremi
Teoremi di Fermat, Rolle, Lagrange, Cauchy, de l Hôpital Copyright c 2007 Pasquale Terrecuso Tutti i diritti sono riservati. E vietata la riproduzione, anche parziale, senza il consenso dell autore. Teoremi
IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero
 IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero Il teorema degli zeri è fondamentale per determinare se una funzione continua in un intervallo chiuso [ a ; b ] si annulla in almeno un punto interno
IL TEOREMA DEGLI ZERI Una dimostrazione di Ezio Fornero Il teorema degli zeri è fondamentale per determinare se una funzione continua in un intervallo chiuso [ a ; b ] si annulla in almeno un punto interno
Università di Trieste Facoltà d Ingegneria. Esercitazioni per la preparazione della prova scritta di Matematica 3 Dott.
 Università di Trieste Facoltà d Ingegneria. Esercitazioni per la preparazione della prova scritta di Matematica 3 Dott. Franco Obersnel Lezione : struttura di IR n, prodotto scalare, distanza e topologia.
Università di Trieste Facoltà d Ingegneria. Esercitazioni per la preparazione della prova scritta di Matematica 3 Dott. Franco Obersnel Lezione : struttura di IR n, prodotto scalare, distanza e topologia.
