UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
|
|
|
- Marcellina Lombardi
- 5 anni fa
- Visualizzazioni
Transcript
1 UNIVERITÀ DEGLI TUDI DI TERAMO FACOLTÀ DI CIENZE POLITICHE CORO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED AICURATIVA I Parziale - Compito A 5/4/5 A. A. 4 5 ) Risolvere la seguente disequazione razionale intera di primo grado: 7 x 8x 5 + x > + Iniziamo con il trasportare al primo membro tutti i termini che compaiono al secondo membro: 7 x 8x 5 (*) + x > Determiniamo il minimo comune multiplo: 7 x + x 68x 5 6 > Moltiplichiamo ambo i membri per 6, ovvero per il minimo comune multiplo: 7 x + x 68x 5> volgiamo i calcoli: 5 x + x 6+ 6x 5> Raccogliamo i termini simili: 5x 5> emplifichiamo ambo i membri della disequazione per 5: x > La disequazione data (*), pertanto, ammette la seguente soluzione: x > { x } = >
2 ) Risolvere la seguente disequazione razionale intera di secondo grado: x x+ x+ ( )( ) Iniziamo con il trasportare al primo membro tutti i termini che compaiono al secondo membro: x x+ x+ ( )( ) Eseguiamo il prodotto e sviluppiamo il quadrato del binomio: 4x + x6x x + x+ 4 Eliminiamo la parentesi tonda cambiando di segno: 4x + x6xx x 4 Determiniamo il minimo comune multiplo: 6x + 8x4x4x 4x 4 Moltiplichiamo ambo i membri per 4, ovvero per il minimo comune multiplo: 6x + 8x4x4x 4x Raccogliamo i termini simili: (*) x x criviamo l equazione associata alla disequazione (*): x x = Troviamo le soluzioni dell equazione associata utilizzando la formula risolutiva ridotta: b b ± ac ± ( ) ( ) ± + 56 x, = = = = a ± 56 ± 6 = =
3 Ne segue, quindi: 6 6 x = = = x = = = 6 Allora la (*), e di conseguenza la disequazione assegnata, ammette soluzioni, ovvero è positiva, per valori esterni alle due radici appena determinate: x, x 6 6 = x, x 6 ) Risolvere la seguente disequazione razionale fratta: x+ x x x+ 5 Iniziamo con il trasportare al primo membro tutti i termini che compaiono al secondo membro: x+ x 4 (*) + x x+ 5 Determiniamo il minimo comune multiplo: 5 x+ x+ + 5 x x+ 5 x x 4 x x+ volgiamo i calcoli: ( )( ) 5( x )( x+ ) ( x + x+ x+ ) + ( x + x x ) ( x x x+ ) ( x + xx ) ( x )( x+ ) 5 da cui: 5x + x+ 5x+ + 5x + x 5x 5x + 5x+ x4x 8x+ 4x+ 8 5 x x+ ( )( )
4 Raccogliamo i termini simili: (**) + + 9x x 8 ( x )( x+ ) 5 Prima di studiare la disequazione occorre determinare il suo campo di esistenza, ovvero bisogna trovare quei valori della x per i quali il denominatore non si annulla: 5 sempre 5( x )( x + ) x x x + x La (**) allora è equivalente al seguente sistema (numeratore e denominatore devono essere discordi!!!): 9x + x+ 8 5( x )( x+ ) > tudiamo la prima disequazione del sistema: (***) 9x + x+ 8 Cambiamo il segno ad ambo i membri ed invertiamo il verso della disequazione: () 9x x8 Dividiamo per ambo i membri della disequazione: x 7x6 criviamo ora l equazione associata: x 7x 6 = le cui soluzioni sono date da: x, b± b ac 7± ± + ± ± = = = = = a Ne segue, quindi: x 7 4 = = = x = = = 6 6 cioè la () è soddisfatta per valori esterni alle due radici.
5 Allora la (***) ammette soluzioni, ovvero è negativa, dove la () è soddisfatta, ossia per valori esterni alle due radici appena determinate: x, x = x, x 6 tudiamo ora la seconda disequazione del sistema: 5 x x+ > (****) ( )( ) criviamo ora l equazione associata, dividendo ambo i membri per 5: x x+ = ( )( ) le cui soluzioni sono date da: ( x ) ( x ) = x = + = x4 = Allora la (****) ammette soluzioni, ovvero è positiva, per valori esterni alle due radici appena determinate: x<, x> { } = x <, x>
6 Le soluzioni della (*) si ottengono, quindi, riportando in un unico grafico le soluzioni ed, facendo il prodotto dei segni e considerando le soluzioni negative (bisogna tenere in considerazione il verso della disequazione assegnata!!!): I dis. II dis = x<, x<, x 4) Calcolare il determinante della seguente matrice: 5 A = 4 Essendo A una matrice quadrata di ordine 4, risulta possibile calcolare il suo determinante utilizzando il metodo di Laplace, sviluppandolo rispetto alla seconda o terza o quarta riga (è più conveniente scegliere una di tali righe in quanto in ciascuna vi è un elemento nullo, a differenza della prima riga costituita da elementi non nulli!!!). Consideriamo, ad esempio, la terza riga (i conti sono più semplici poiché gli elementi non nulli sono tutti uguali ad!!!). Per la regola dei segni otteniamo: + 5 A = + + 4
7 Calcoliamo ora il determinante di A: det A=+ + = = = = = = =5 4+ =45 =48 Dunque: det A = 48 5) Date le seguenti matrici: 4 A = 5 B = 4 6 dire se sono moltiplicabili e, in caso affermativo, calcolare la matrice prodotto AB oppure BA. In primo luogo osserviamo che la matrice A ha odine e la matrice B ha ordine. Poiché il numero delle colonne della matrice A, ovvero, è uguale al numero delle righe della matrice B, ovvero, ne segue che è possibile eseguire il prodotto AB e, moltiplicando le due matrici righe per colonne, risulta: 4 + ( ) + ( ) ( ) ( ) AB = 5 ( ) ( ) 5 4 ( ) ( ) = + + = + ( ) ( ) ( ) 4+ 6 ( ) =
8 Dunque: AB = è la matrice prodotto di ordine (il numero delle sue righe è pari a quello delle righe di A ed il numero delle sue colonne è uguale a quello delle colonne di B). apendo che il prodotto tra matrici non è commutativo, dobbiamo vedere se è anche possibile svolgere il prodotto BA. Osserviamo, a riguardo, che il numero delle colonne della matrice B, ovvero, non è uguale al numero delle righe della matrice A, ovvero, motivo per cui non risulta affatto possibile eseguire il prodotto BA.
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERITÀ DEGLI TUDI DI TERAMO FACOLTÀ DI CIENZE POLITICHE CORO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED AICURATIVA I Parziale - Compito C 5//5 A. A. 5 ) Risolvere la seguente disequazione razionale
UNIVERITÀ DEGLI TUDI DI TERAMO FACOLTÀ DI CIENZE POLITICHE CORO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED AICURATIVA I Parziale - Compito C 5//5 A. A. 5 ) Risolvere la seguente disequazione razionale
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERITÀ DEGLI TUDI DI TERAMO FACOLTÀ DI CIENZE POLITICHE CORO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED AICURATIVA I Parziale - Compito B 5/4/5 A. A. 4 5 ) Risolvere la seguente disequazione razionale
UNIVERITÀ DEGLI TUDI DI TERAMO FACOLTÀ DI CIENZE POLITICHE CORO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED AICURATIVA I Parziale - Compito B 5/4/5 A. A. 4 5 ) Risolvere la seguente disequazione razionale
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
( ) ( ) ( ) 0 ( ) ( ) ( ) disequazione razionale intera di I grado. isolvere la seguente disequazione. razionale intera di I grado
 > isolvere la seguente isolvere la seguente disequazione disequazione razionale intera di I grado razionale intera di I grado rasportiamo tutti i termini del secondo membro al primo membro ambiandoli di
> isolvere la seguente isolvere la seguente disequazione disequazione razionale intera di I grado razionale intera di I grado rasportiamo tutti i termini del secondo membro al primo membro ambiandoli di
3x + x 5x = x = = 4 + 3x ; che equivale, moltiplicando entrambi i membri per 2, a risolvere. 4x + 6 x = 4 + 3x.
 1 Soluzioni esercizi 1.1 Equazioni di 1 e grado Risolvere le seguenti equazioni di 1 grado: 1) 3x 5x = 1 x. Abbiamo: 3x + x 5x = 1 + x = 1 + 4 x = 5. ) x + 3 x = + 3x. Facciamo il m.c.m. : 4x + 6 x = 4
1 Soluzioni esercizi 1.1 Equazioni di 1 e grado Risolvere le seguenti equazioni di 1 grado: 1) 3x 5x = 1 x. Abbiamo: 3x + x 5x = 1 + x = 1 + 4 x = 5. ) x + 3 x = + 3x. Facciamo il m.c.m. : 4x + 6 x = 4
5. EQUAZIONI e DISEQUAZIONI
 5. EQUAZIONI e DISEQUAZIONI 1. Per ognuna delle affermazioni seguenti, indicare se e vera o falsa, motivando la risposta (a) L equazione di primo grado (1 2)x = 2 ha soluzione x = 2(1+ 2). V F (b) La disequazione
5. EQUAZIONI e DISEQUAZIONI 1. Per ognuna delle affermazioni seguenti, indicare se e vera o falsa, motivando la risposta (a) L equazione di primo grado (1 2)x = 2 ha soluzione x = 2(1+ 2). V F (b) La disequazione
Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 4 Novembre Trinomi di secondo grado
 Esercitazioni di Matematica Generale AA 016/017 Pietro Pastore Lezione del 4 Novembre 016 Trinomi di secondo grado Possiamo usare le soluzioni dell equazione di secondo grado per scomporre il trinomio
Esercitazioni di Matematica Generale AA 016/017 Pietro Pastore Lezione del 4 Novembre 016 Trinomi di secondo grado Possiamo usare le soluzioni dell equazione di secondo grado per scomporre il trinomio
A titolo di esempio proponiamo la risoluzione del sistema sia con il metodo della matrice inversa sia con il metodo di Cramer.
 ) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
Esercizi sulle Disequazioni
 Esercizi sulle Disequazioni Esercizio Trovare le soluzioni delle seguenti disequazioni:.).).).) ).) ) ).).7) 8.8).) Esercizio Trovare le soluzioni delle seguenti disequazioni tratte dal secondo parziale
Esercizi sulle Disequazioni Esercizio Trovare le soluzioni delle seguenti disequazioni:.).).).) ).) ) ).).7) 8.8).) Esercizio Trovare le soluzioni delle seguenti disequazioni tratte dal secondo parziale
Frazioni algebriche. Osserviamo che un espressione di questo tipo si ottiene talvolta quando ci si propone di ottenere il quoziente di due monomi.
 Frazioni algebriche 14 14.1 Definizione di frazione algebrica Diamo la seguente definizione: Definizione 14.1. Si definisce frazione algebrica un espressione del tipo A B polinomi. dove A e B sono Osserviamo
Frazioni algebriche 14 14.1 Definizione di frazione algebrica Diamo la seguente definizione: Definizione 14.1. Si definisce frazione algebrica un espressione del tipo A B polinomi. dove A e B sono Osserviamo
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA AZIENDALE CORSO DI LAUREA IN STATISTICA Prof. Franco EUGENI Prof.ssa Daniela TONDINI Parziale n. - Compito II A.
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA AZIENDALE CORSO DI LAUREA IN STATISTICA Prof. Franco EUGENI Prof.ssa Daniela TONDINI Parziale n. - Compito II A.
Disequazioni - ulteriori esercizi proposti 1
 Disequazioni - ulteriori esercizi proposti Trovare le soluzioni delle seguenti disequazioni o sistemi di disequazioni:. 5 4 >. 4. < 4. 4 9 5. 9 > 6. > 7. < 8. 5 4 9. > > 4. < 4. < > 9 4 Non esitate a comunicarmi
Disequazioni - ulteriori esercizi proposti Trovare le soluzioni delle seguenti disequazioni o sistemi di disequazioni:. 5 4 >. 4. < 4. 4 9 5. 9 > 6. > 7. < 8. 5 4 9. > > 4. < 4. < > 9 4 Non esitate a comunicarmi
DISEQUAZIONI DI SECONDO GRADO
 DISEQUAZIONI DI SECONDO GRADO Esercizio - -8 - - - - - - Esercizio L equazione non ha soluzioni e quindi la parabola non interseca l asse delle ascisse - - - - - Pertanto la parabola, avendo la concavità
DISEQUAZIONI DI SECONDO GRADO Esercizio - -8 - - - - - - Esercizio L equazione non ha soluzioni e quindi la parabola non interseca l asse delle ascisse - - - - - Pertanto la parabola, avendo la concavità
MATEMATICA EQUAZIONI FRATTE, DI SECONDO GRADO O SUPERIORE GSCATULLO
 MATEMATICA EQUAZIONI FRATTE, DI SECONDO GRADO O SUPERIORE GSCATULLO Equazioni fratte, di secondo grado o superiore Le equazioni di secondo grado Un equazione è di secondo grado se si può scrivere nella
MATEMATICA EQUAZIONI FRATTE, DI SECONDO GRADO O SUPERIORE GSCATULLO Equazioni fratte, di secondo grado o superiore Le equazioni di secondo grado Un equazione è di secondo grado se si può scrivere nella
Corso di Geometria BIAR, BSIR Esercizi 2: soluzioni
 Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
CORSO ZERO DI MATEMATICA
 UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA EQUAZIONI E DISEQUAZIONI DI SECONDO GRADO Dr. Erasmo Modica erasmo@galois.it EQUAZIONI DI SECONDO GRADO Definizione: Dicesi
UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA EQUAZIONI E DISEQUAZIONI DI SECONDO GRADO Dr. Erasmo Modica erasmo@galois.it EQUAZIONI DI SECONDO GRADO Definizione: Dicesi
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA III Parziale - Compito C 6/5/5 A. A. 4 5 ) Studiare la seguente funzione polinomiale:
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA III Parziale - Compito C 6/5/5 A. A. 4 5 ) Studiare la seguente funzione polinomiale:
Disequazioni fratte. Una disequazione in cui l'incognita compare a denominatore si chiama fratta o frazionaria.
 1 Disequazioni fratte Una disequazione in cui l'incognita compare a denominatore si chiama fratta o frazionaria. Prima di affrontare le disequazioni fratte, ricordiamo il procedimento che utilizziamo per
1 Disequazioni fratte Una disequazione in cui l'incognita compare a denominatore si chiama fratta o frazionaria. Prima di affrontare le disequazioni fratte, ricordiamo il procedimento che utilizziamo per
Anno Scolastico 2014/15 - Classe 1D Verifica di matematica dell 11 Maggio Soluzioni degli esercizi. 2(x 2) 2(x 1) + 2 = 3x
 Anno Scolastico 2014/15 - Classe 1D Verifica di matematica dell 11 Maggio 2015 - Soluzioni degli esercizi Risolvere le seguenti equazioni. Dove è necessario, scrivere le condizioni di accettabilità e usarle
Anno Scolastico 2014/15 - Classe 1D Verifica di matematica dell 11 Maggio 2015 - Soluzioni degli esercizi Risolvere le seguenti equazioni. Dove è necessario, scrivere le condizioni di accettabilità e usarle
DISEQUAZIONI DI SECONDO GRADO. Le disequazioni di secondo grado intere si presentano nella forma (o equivalgono ad essa):
 P. \ Disequazioni di secondo grado Maggio 0 Copyright-I.S. DISEQUAZIONI DI SECONDO GRADO DISEQUAZIONI INTERE DI SECONDO GRADO Le disequazioni di secondo grado intere si presentano nella forma (o equivalgono
P. \ Disequazioni di secondo grado Maggio 0 Copyright-I.S. DISEQUAZIONI DI SECONDO GRADO DISEQUAZIONI INTERE DI SECONDO GRADO Le disequazioni di secondo grado intere si presentano nella forma (o equivalgono
Precorso di Matematica
 UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTA DI ARCHITETTURA Precorso di Matematica Anna Scaramuzza Anno Accademico 2005-2006 4-10 Ottobre 2005 INDICE 1. ALGEBRA................................. 3 1.1 Equazioni
UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTA DI ARCHITETTURA Precorso di Matematica Anna Scaramuzza Anno Accademico 2005-2006 4-10 Ottobre 2005 INDICE 1. ALGEBRA................................. 3 1.1 Equazioni
Equazioni di primo grado ad un incognita
 Equazioni di primo grado ad un incognita Identità Si dice IDENTITÀ un uguaglianza fra due espressioni letterali che è verificata per ogni valore attribuito alle lettere. 2a = 2a è un identità a = 3 2 3
Equazioni di primo grado ad un incognita Identità Si dice IDENTITÀ un uguaglianza fra due espressioni letterali che è verificata per ogni valore attribuito alle lettere. 2a = 2a è un identità a = 3 2 3
Identità ed equazioni
 Matematica e-learning - Identità ed equazioni Prof. erasmo@galois.it A.A. 2009/2010 1 Generalità sulle equazioni Si consideri un uguaglianza tra due espressioni algebriche A = B Se si sostituiscono al
Matematica e-learning - Identità ed equazioni Prof. erasmo@galois.it A.A. 2009/2010 1 Generalità sulle equazioni Si consideri un uguaglianza tra due espressioni algebriche A = B Se si sostituiscono al
x 2 + (x+4) 2 = 20 Alle equazioni di secondo grado si possono applicare i PRINCIPI di EQUIVALENZA utilizzati per le EQUAZIONI di PRIMO GRADO.
 EQUAZIONI DI SECONDO GRADO Un'equazione del tipo x 2 + (x+4) 2 = 20 è un'equazione DI SECONDO GRADO IN UNA INCOGNITA. Alle equazioni di secondo grado si possono applicare i PRINCIPI di EQUIVALENZA utilizzati
EQUAZIONI DI SECONDO GRADO Un'equazione del tipo x 2 + (x+4) 2 = 20 è un'equazione DI SECONDO GRADO IN UNA INCOGNITA. Alle equazioni di secondo grado si possono applicare i PRINCIPI di EQUIVALENZA utilizzati
Elementi sulle diseguaglianze tra numeri relativi
 Elementi sulle diseguaglianze tra numeri relativi Dati due numeri disuguali a e b risulta a>b oppure ao oppure a-b
Elementi sulle diseguaglianze tra numeri relativi Dati due numeri disuguali a e b risulta a>b oppure ao oppure a-b
Monomi L insieme dei monomi
 Monomi 10 10.1 L insieme dei monomi Definizione 10.1. Un espressione letterale in cui numeri e lettere sono legati dalla sola moltiplicazione si chiama monomio. Esempio 10.1. L espressione nelle due variabili
Monomi 10 10.1 L insieme dei monomi Definizione 10.1. Un espressione letterale in cui numeri e lettere sono legati dalla sola moltiplicazione si chiama monomio. Esempio 10.1. L espressione nelle due variabili
I. Foglio di esercizi su vettori linearmente dipendenti e linearmente indipendenti. , v 2 = α v 1 + β v 2 + γ v 3. α v 1 + β v 2 + γ v 3 = 0. + γ.
 ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
La domanda che ci si deve porre innanzitutto per iniziare a risolvere questa disequazione è la seguente:
 Disequazioni: caso generale Consideriamo ora la risoluzione di disequazioni che presentino al suo interno valori assoluti e radici. Cercheremo di stabilire con degli esempio delle linee guida per la risoluzione
Disequazioni: caso generale Consideriamo ora la risoluzione di disequazioni che presentino al suo interno valori assoluti e radici. Cercheremo di stabilire con degli esempio delle linee guida per la risoluzione
MATRICI E OPERAZIONI
 MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
Le disequazioni frazionarie (o fratte)
 Le disequazioni frazionarie (o fratte) Una disequazione si dice frazionaria (o fratta) se l'incognita compare al denominatore. Esempi di disequazioni fratte sono: 0 ; ; < 0 ; ; Come per le equazioni fratte,
Le disequazioni frazionarie (o fratte) Una disequazione si dice frazionaria (o fratta) se l'incognita compare al denominatore. Esempi di disequazioni fratte sono: 0 ; ; < 0 ; ; Come per le equazioni fratte,
MATEMATICA SCOMPOSIZIONE E FRAZIONE ALGEBRICHE GSCATULLO
 MATEMATICA SCOMPOSIZIONE E FRAZIONE ALGEBRICHE GSCATULLO 1 Scomposizione e frazioni algebriche Scomposizione in Fattori Scomporre in fattori un polinomio significa scriverlo sotto forma di un prodotto
MATEMATICA SCOMPOSIZIONE E FRAZIONE ALGEBRICHE GSCATULLO 1 Scomposizione e frazioni algebriche Scomposizione in Fattori Scomporre in fattori un polinomio significa scriverlo sotto forma di un prodotto
Disequazioni di secondo grado
 Disequazioni di secondo grado Una disequazione di secondo grado è una disequazione del tipo (oppure a b c o a b c ) a b c oppure a b c I) Cominciamo considerando disequazioni in cui a Esempio Consideriamo
Disequazioni di secondo grado Una disequazione di secondo grado è una disequazione del tipo (oppure a b c o a b c ) a b c oppure a b c I) Cominciamo considerando disequazioni in cui a Esempio Consideriamo
Esercizi sui sistemi di equazioni lineari.
 Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
LE EQUAZIONI DI SECONDO GRADO
 LE EQUAZIONI DI SECONDO GRADO Definizione: un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza, si può scrivere nella forma, detta normale: ax + bx + c 0!!!!!con!a 0 Le lettere
LE EQUAZIONI DI SECONDO GRADO Definizione: un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza, si può scrivere nella forma, detta normale: ax + bx + c 0!!!!!con!a 0 Le lettere
ANALISI MATEMATICA PER IL CdL IN INFORMATICA ESERCIZI SULLE DISEQUAZIONI
 ANALISI MATEMATICA PER IL CdL IN INFORMATICA ESERCIZI SULLE DISEQUAZIONI Risolvere le seguenti disequazioni: ( 1 ) x < x + 1 1) 4x + 4 x ) x + 1 > x 4x x 10 ) x 4 x 5 4x + > ; 4) ; 5) 0; ) x 1 x + 1 x
ANALISI MATEMATICA PER IL CdL IN INFORMATICA ESERCIZI SULLE DISEQUAZIONI Risolvere le seguenti disequazioni: ( 1 ) x < x + 1 1) 4x + 4 x ) x + 1 > x 4x x 10 ) x 4 x 5 4x + > ; 4) ; 5) 0; ) x 1 x + 1 x
Precorso di Matematica Maria Margherita Obertino Università degli Studi di Torino Di.S.A.F.A.
 Precorso di Matematica Maria Margherita Obertino Università degli Studi di Torino Di.S.A.F.A. Scomposizione dei polinomi in fattori primi ( 2.4 del testo) Equazioni di primo grado ( 3.1 del testo) Equazioni
Precorso di Matematica Maria Margherita Obertino Università degli Studi di Torino Di.S.A.F.A. Scomposizione dei polinomi in fattori primi ( 2.4 del testo) Equazioni di primo grado ( 3.1 del testo) Equazioni
EQUAZIONI, DISEQUAZIONI E SISTEMI
 EQUAZIONI, DISEQUAZIONI E SISTEMI RICHIAMI DI TEORIA Definizione: sia f una funzione reale di variabile reale. Gli elementi del dominio di f su cui la funzione assume valore nullo costituiscono l' insieme
EQUAZIONI, DISEQUAZIONI E SISTEMI RICHIAMI DI TEORIA Definizione: sia f una funzione reale di variabile reale. Gli elementi del dominio di f su cui la funzione assume valore nullo costituiscono l' insieme
Radicali. 2.1 Radici. Il simbolo
 Radicali. Radici.. Radici quadrate Ricordiamo che il quadrato di un numero reale a è il numero che si ottiene moltiplicando a per se stesso. Il quadrato di un numero è sempre un numero non negativo; numeri
Radicali. Radici.. Radici quadrate Ricordiamo che il quadrato di un numero reale a è il numero che si ottiene moltiplicando a per se stesso. Il quadrato di un numero è sempre un numero non negativo; numeri
DOMINIO E IMMAGINE DI UNA FUNZIONE REALE DI VARIABILE REALE
 OMINIO E IMMAGINE I UNA FUNZIONE REALE I VARIABILE REALE La prima operazione che dobbiamo fare quando ci accingiamo a studiare una funzione (per poterne poi determinare il grafico) è quella di individuare
OMINIO E IMMAGINE I UNA FUNZIONE REALE I VARIABILE REALE La prima operazione che dobbiamo fare quando ci accingiamo a studiare una funzione (per poterne poi determinare il grafico) è quella di individuare
francesca fattori speranza - versione febbraio 2018 EQUAZIONI DI SECONDO GRADO E SUPERIORE INTERE E FRATTE a) Intere
 francesca fattori speranza - versione febbraio 018 EQUAZIONI DI SECONDO GRADO E SUPERIORE INTERE E FRATTE a) Intere a x + bx + c = 0, a, b, c sono numeri reali a 0 a n x n + a n 1 x n 1 +... + a 1 x +
francesca fattori speranza - versione febbraio 018 EQUAZIONI DI SECONDO GRADO E SUPERIORE INTERE E FRATTE a) Intere a x + bx + c = 0, a, b, c sono numeri reali a 0 a n x n + a n 1 x n 1 +... + a 1 x +
TEMI D ESAME DI ANALISI MATEMATICA I
 TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
ESERCIZI SULLE DISEQUAZIONI I
 ESERCIZI SULLE DISEQUAZIONI I Risolvere le seguenti disequazioni: 1 1) { x < x + 1 4x + 4 x ) { x + 1 > x 4x x 10 ) x 4 x 5 4x + > ; 4) ; 5) x 1 x + 1 x + 1 0 ) x > x 0 7) x > 4x + 1; 8) 4 5 x 1 < 1 x
ESERCIZI SULLE DISEQUAZIONI I Risolvere le seguenti disequazioni: 1 1) { x < x + 1 4x + 4 x ) { x + 1 > x 4x x 10 ) x 4 x 5 4x + > ; 4) ; 5) x 1 x + 1 x + 1 0 ) x > x 0 7) x > 4x + 1; 8) 4 5 x 1 < 1 x
ESERCIZI IN PIÙ I NUMERI COMPLESSI
 ESERCIZI IN PIÙ I NUMERI COMPLESSI L equazione x x 0 non ha soluzioni nell insieme dei numeri reali; infatti, applicando la formula ridotta, si ottiene x, 3. Interpretando come numero immaginario, cioè
ESERCIZI IN PIÙ I NUMERI COMPLESSI L equazione x x 0 non ha soluzioni nell insieme dei numeri reali; infatti, applicando la formula ridotta, si ottiene x, 3. Interpretando come numero immaginario, cioè
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
Definizione: Due equazioni si dicono equivalenti se ammettono le stesse soluzioni.
 Facoltà di Medicina e Chirurgia Corso Zero di Matematica Gruppi: MC-MF3 / PS-MF3 II Lezione EQUAZIONI E SISTEMI Dr. E. Modica erasmo@galois.it www.galois.it IDENTITÀ ED EQUAZIONI Si consideri un uguaglianza
Facoltà di Medicina e Chirurgia Corso Zero di Matematica Gruppi: MC-MF3 / PS-MF3 II Lezione EQUAZIONI E SISTEMI Dr. E. Modica erasmo@galois.it www.galois.it IDENTITÀ ED EQUAZIONI Si consideri un uguaglianza
1 Funzioni algebriche fratte
 1 Funzioni algebriche fratte 1.1 Esercizio svolto y = x 1 x 11x + 10 (generalizzazione) La funzione è del tipo y = f(x) g(x) con f(x) e g(x) polinomi reali in x. Per determinare il dominio D della funzione
1 Funzioni algebriche fratte 1.1 Esercizio svolto y = x 1 x 11x + 10 (generalizzazione) La funzione è del tipo y = f(x) g(x) con f(x) e g(x) polinomi reali in x. Per determinare il dominio D della funzione
LE EQUAZIONI LINEARI LE IDENTITA ( )( ) 5. a Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a
 LE EQUAZIONI LINEARI 1 LE IDENTITA a b = ( a + b)( a b) () 1 a = a + a ( ) ( a + b) = a + ab + b () 3 Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a b = ( a+ b)( a b) È sempre vera qualunque
LE EQUAZIONI LINEARI 1 LE IDENTITA a b = ( a + b)( a b) () 1 a = a + a ( ) ( a + b) = a + ab + b () 3 Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a b = ( a+ b)( a b) È sempre vera qualunque
Equazioni di primo grado
 Equazioni di primo grado 15 15.1 Identità ed equazioni Analizziamo le seguenti proposizioni: a ) cinque è uguale alla differenza tra sette e due ; b ) la somma di quattro e due è uguale a otto ; c ) il
Equazioni di primo grado 15 15.1 Identità ed equazioni Analizziamo le seguenti proposizioni: a ) cinque è uguale alla differenza tra sette e due ; b ) la somma di quattro e due è uguale a otto ; c ) il
1. Denotando con I(x 0, r) l intorno sulla retta reale di centro x 0 R e raggio r 0, si considerino i 3 insiemi
 Matematica generale: svolgimento compito del 2 maggio 22 Tutte le risposte vanno motivate: rispondere solo si, no, o dare soltanto il risultato non basta. Gli esercizi e 2 vanno svolti perfettamente prima
Matematica generale: svolgimento compito del 2 maggio 22 Tutte le risposte vanno motivate: rispondere solo si, no, o dare soltanto il risultato non basta. Gli esercizi e 2 vanno svolti perfettamente prima
ESERCITAZIONE 11 : EQUAZIONI E DISEQUAZIONI
 ESERCITAZIONE 11 : EQUAZIONI E DISEQUAZIONI e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: Martedi 16-18 Dipartimento di Matematica, piano terra, studio 126 18 Dicembre 2012 Esercizio
ESERCITAZIONE 11 : EQUAZIONI E DISEQUAZIONI e-mail: tommei@dm.unipi.it web: www.dm.unipi.it/ tommei Ricevimento: Martedi 16-18 Dipartimento di Matematica, piano terra, studio 126 18 Dicembre 2012 Esercizio
raggruppiamo il quadrato di binomio dividiamo per 0 effettuiamo i calcoli a secondo membro Distinguiamo i tre casi: 2 ± 2 ; 2 = 0 ; + si ottiene, =
 Equazioni di II grado Equazione di II grado completa Un equazione di II grado è un equazione che, ridotta a forma normale, è del tipo ++=0 con 0. Per risolverla occorre calcolare il discriminante dell
Equazioni di II grado Equazione di II grado completa Un equazione di II grado è un equazione che, ridotta a forma normale, è del tipo ++=0 con 0. Per risolverla occorre calcolare il discriminante dell
a x 2 + b x + c Scomposizione del trinomio (se possibile) Risolvere l equazione Disegnare la parabola associata Risolvere la disequazione
 OPERAZIONI CON TRINOMI DI II GRADO a x 2 + b x + c Risolvere l equazione Scomposizione del trinomio (se possibile) Disegnare la parabola associata Risolvere la disequazione Completamento di un quadrato
OPERAZIONI CON TRINOMI DI II GRADO a x 2 + b x + c Risolvere l equazione Scomposizione del trinomio (se possibile) Disegnare la parabola associata Risolvere la disequazione Completamento di un quadrato
Risolvere le seguenti disequazioni
 Risolvere le seguenti disequazioni 1. x 4x x 4 > 0 Innanzi tutto il denominatore deve essere non nullo, quindi l insieme di definizione (o campo d esistenza) è x ±. Se decomponiamo sia numeratore che denominatore,
Risolvere le seguenti disequazioni 1. x 4x x 4 > 0 Innanzi tutto il denominatore deve essere non nullo, quindi l insieme di definizione (o campo d esistenza) è x ±. Se decomponiamo sia numeratore che denominatore,
3 Dispense di Matematica per il primo anno dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore Frazioni Algebriche
 3 Dispense di Matematica per il primo anno dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore Frazioni Algebriche 100 Per l esercitazioni on-line visita le pagine : www.chihapauradellamatematica.org
3 Dispense di Matematica per il primo anno dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore Frazioni Algebriche 100 Per l esercitazioni on-line visita le pagine : www.chihapauradellamatematica.org
il determinante che si ottiene da A, sopprimendo la i - esima riga e la j - esima colonna. Si definisce complemento algebrico dell'elemento a ij
 Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
L1 L2 L3 L4. Esercizio. Infatti, osserviamo che p non può essere un multiplo di 3 perché è primo. Pertanto, abbiamo solo due casi
 Sia p 5 un numero primo. Allora, p è sempre divisibile per 4. Scriviamo p (p ) (p + ). Ora, p 5 è primo e, quindi, dispari. Dunque, p e p + sono entrambi pari. Facciamo vedere anche che uno tra p e p +
Sia p 5 un numero primo. Allora, p è sempre divisibile per 4. Scriviamo p (p ) (p + ). Ora, p 5 è primo e, quindi, dispari. Dunque, p e p + sono entrambi pari. Facciamo vedere anche che uno tra p e p +
Equazioni di secondo grado Prof. Walter Pugliese
 Equazioni di secondo grado Prof. Walter Pugliese La forma normale di un equazione di secondo grado Un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza già studiati per le
Equazioni di secondo grado Prof. Walter Pugliese La forma normale di un equazione di secondo grado Un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza già studiati per le
1 Disquazioni di primo grado
 1 Disquazioni di primo grado 1 1 Disquazioni di primo grado Si assumono assodate le regole per la risoluzione delle equazioni lineari Ricordando che una disuguaglianza è una scrittura tra due espressioni
1 Disquazioni di primo grado 1 1 Disquazioni di primo grado Si assumono assodate le regole per la risoluzione delle equazioni lineari Ricordando che una disuguaglianza è una scrittura tra due espressioni
Equazioni e disequazioni. M.Simonetta Bernabei, Horst Thaler
 Equazioni e disequazioni M.Simonetta Bernabei, Horst Thaler A(x)=0 x si chiama incognita dell equazione. Se oltre all incognita non compaiono altre lettere l equazione si dice numerica, altrimenti letterale.
Equazioni e disequazioni M.Simonetta Bernabei, Horst Thaler A(x)=0 x si chiama incognita dell equazione. Se oltre all incognita non compaiono altre lettere l equazione si dice numerica, altrimenti letterale.
Disequazioni di II grado
 Disequazioni di II grado Scomposizione di un trinomio di 2 grado La scomposizione del trinomio di 2 grado ax 2 + bx + c dipende dal discriminante. Se questo è positivo esistono radici reali e distinte
Disequazioni di II grado Scomposizione di un trinomio di 2 grado La scomposizione del trinomio di 2 grado ax 2 + bx + c dipende dal discriminante. Se questo è positivo esistono radici reali e distinte
Precorso di Matematica
 Precorso di Matematica Lezione 4 Andrea Susa PROPRIETÀ GENERALI DISEQUAZIONI 1 Proprietà disuguaglianze Siano,,, allora valgono le seguenti proprietà se
Precorso di Matematica Lezione 4 Andrea Susa PROPRIETÀ GENERALI DISEQUAZIONI 1 Proprietà disuguaglianze Siano,,, allora valgono le seguenti proprietà se
Equazioni frazionarie e letterali
 Equazioni frazionarie e letterali 17 17.1 Equazioni di grado superiore al primo riducibili al primo grado Nel capitolo 15 abbiamo affrontato le equazioni di primo grado. Adesso consideriamo le equazioni
Equazioni frazionarie e letterali 17 17.1 Equazioni di grado superiore al primo riducibili al primo grado Nel capitolo 15 abbiamo affrontato le equazioni di primo grado. Adesso consideriamo le equazioni
ESERCIZI SVOLTI DI RIEPILOGO SU EQUAZIONI E DISEQUAZIONI IRRAZIONALI ALCUNI CONCETTI DI BASE SU EQUAZIONI E DISEQUAZIONI IRRAZIONALI
 ESERCIZI SVOLTI DI RIEPILOGO SU EQUAZIONI E DISEQUAZIONI IRRAZIONALI ALCUNI CONCETTI DI BASE SU EQUAZIONI E DISEQUAZIONI IRRAZIONALI EQUAZIONI IRRAZIONALI Una equazione si definisce irrazionale quando
ESERCIZI SVOLTI DI RIEPILOGO SU EQUAZIONI E DISEQUAZIONI IRRAZIONALI ALCUNI CONCETTI DI BASE SU EQUAZIONI E DISEQUAZIONI IRRAZIONALI EQUAZIONI IRRAZIONALI Una equazione si definisce irrazionale quando
UNITÀ 4. DISEQUAZIONI E SISTEMI DI DISEQUAZIONI 1. Generalità e definizioni sulle disequazioni. 2. I principi di equivalenza delle disequazioni. 3.
 UNITÀ. DISEQUAZIONI E SISTEMI DI DISEQUAZIONI. Generalità e definizioni sulle diquazioni.. I principi di equivalenza delle diquazioni.. Diquazioni di primo grado.. Diquazioni con più fattori di primo grado..
UNITÀ. DISEQUAZIONI E SISTEMI DI DISEQUAZIONI. Generalità e definizioni sulle diquazioni.. I principi di equivalenza delle diquazioni.. Diquazioni di primo grado.. Diquazioni con più fattori di primo grado..
INTEGRALI INDEFINITI e DEFINITI Esercizi risolti
 INTEGRALI INDEFINITI e DEFINITI Esercizi risolti E data la funzione f( = (a Provare che la funzione F ( = + arcsin è una primitiva di f( sull intervallo (, (b Provare che la funzione G( = + arcsin π è
INTEGRALI INDEFINITI e DEFINITI Esercizi risolti E data la funzione f( = (a Provare che la funzione F ( = + arcsin è una primitiva di f( sull intervallo (, (b Provare che la funzione G( = + arcsin π è
Le disequazioni di primo grado. Prof. Walter Pugliese
 Le disequazioni di primo grado Prof. Walter Pugliese Concetto di disequazione Consideriamo la seguente disuguaglianza: 2x 3 < 5 + x Procedendo per tentativi, attribuiamo alla lettera x alcuni valori e
Le disequazioni di primo grado Prof. Walter Pugliese Concetto di disequazione Consideriamo la seguente disuguaglianza: 2x 3 < 5 + x Procedendo per tentativi, attribuiamo alla lettera x alcuni valori e
Prontuario degli argomenti di Algebra
 Prontuario degli argomenti di Algebra NUMERI RELATIVI Un numero relativo è un numero preceduto da un segno + o - indicante la posizione rispetto ad un punto di riferimento a cui si associa il valore 0.
Prontuario degli argomenti di Algebra NUMERI RELATIVI Un numero relativo è un numero preceduto da un segno + o - indicante la posizione rispetto ad un punto di riferimento a cui si associa il valore 0.
Metodi per la risoluzione di sistemi lineari
 Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
Metodi per la risoluzione di sistemi lineari Sistemi di equazioni lineari. Rango di matrici Come è noto (vedi [] sez.0.8), ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante
ESERCIZI SUL DOMINIO DI UNA FUNZIONE A UNA VARIABILE REALE. Le FUNZIONI RAZIONALI INTERE (i polinomi) hanno come insieme di definizione R.
 ESERCIZI SUL DOMINIO DI UNA FUNZIONE A UNA VARIABILE REALE PREMESSA Ai fini dello studio di una funzione la prima operazione da compiere è quella di determinare il suo dominio, ovvero l' insieme valori
ESERCIZI SUL DOMINIO DI UNA FUNZIONE A UNA VARIABILE REALE PREMESSA Ai fini dello studio di una funzione la prima operazione da compiere è quella di determinare il suo dominio, ovvero l' insieme valori
1 Fattorizzazione di polinomi
 1 Fattorizzazione di polinomi Polinomio: un polinomio di grado n nella variabile x, è dato da p(x) = a n x n + a n 1 x n 1 + + a 1 x + a 0 con a n 0, a 0 è detto termine noto, a k è detto coefficiente
1 Fattorizzazione di polinomi Polinomio: un polinomio di grado n nella variabile x, è dato da p(x) = a n x n + a n 1 x n 1 + + a 1 x + a 0 con a n 0, a 0 è detto termine noto, a k è detto coefficiente
Disequazioni. 3 Liceo Scientifico 3 Liceo Scientifico sez. Scienze Applicate A.S. 2016/2017 Prof. Andrea Pugliese
 Disequazioni 3 Liceo Scientifico 3 Liceo Scientifico sez. Scienze Applicate A.S. 2016/2017 Prof. Andrea Pugliese Definizione ed esempi Date due espressioni algebriche A e B contenenti numeri e lettere
Disequazioni 3 Liceo Scientifico 3 Liceo Scientifico sez. Scienze Applicate A.S. 2016/2017 Prof. Andrea Pugliese Definizione ed esempi Date due espressioni algebriche A e B contenenti numeri e lettere
Soluzioni della verifica scritta 1 B Scientifico 24/01/2009
 Soluzioni della verifica scritta 1 B Scientifico 4/01/009 Esercizio 1. Il polinomio x +x 4 5 xy + y non èordinatoné rispetto a x nè rispetto a y. E completo rispetto a y ma non rispetto a x. Nonè omogeneo.
Soluzioni della verifica scritta 1 B Scientifico 4/01/009 Esercizio 1. Il polinomio x +x 4 5 xy + y non èordinatoné rispetto a x nè rispetto a y. E completo rispetto a y ma non rispetto a x. Nonè omogeneo.
r 2 r 2 2r 1 r 4 r 4 r 1
 SPAZI R n 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x, y, z)
SPAZI R n 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x, y, z)
Equazioni e disequazioni algebriche. Soluzione. Si tratta del quadrato di un binomio. Si ha pertanto. (x m y n ) 2 = x 2m 2x m y n + y 2n
 Si tratta del quadrato di un binomio. Si ha pertanto (x m y n ) 2 = x 2m 2x m y n + y 2n 4. La divisione (x 3 3x 2 + 5x 2) : (x 2) ha Q(x) = x 2 x + 3 e R = 4 Dalla divisione tra i polinomi risulta (x
Si tratta del quadrato di un binomio. Si ha pertanto (x m y n ) 2 = x 2m 2x m y n + y 2n 4. La divisione (x 3 3x 2 + 5x 2) : (x 2) ha Q(x) = x 2 x + 3 e R = 4 Dalla divisione tra i polinomi risulta (x
www.matematicamente.it Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di 2 grado 1
 www.matematicamente.it Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado 1 Verifica di matematica, classe II liceo scientifico Equazioni di secondo grado, equazioni frazionarie,
www.matematicamente.it Verifica classe II liceo scientifico: equazioni, disequazioni, problemi di grado 1 Verifica di matematica, classe II liceo scientifico Equazioni di secondo grado, equazioni frazionarie,
EQUAZIONI DI II GRADO
 RICHIAMI SULLE EQUAZIONI DI PRIMO E SECONDO GRADO PROF.SSA ROSSELLA PISCOPO Indice 1 EQUAZIONI DI I GRADO --------------------------------------------------------------------------------------------------
RICHIAMI SULLE EQUAZIONI DI PRIMO E SECONDO GRADO PROF.SSA ROSSELLA PISCOPO Indice 1 EQUAZIONI DI I GRADO --------------------------------------------------------------------------------------------------
Sistemi II. Sistemi II. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
1 Identità ed equazioni
 1 Identità ed equazioni Consideriamo l uguaglianza espressa dalla seguente frase: Trova un numero tale che il suo doppio sommato con se stesso sia uguale al suo triplo. x > 2x + x = 3x La relazione: 2x
1 Identità ed equazioni Consideriamo l uguaglianza espressa dalla seguente frase: Trova un numero tale che il suo doppio sommato con se stesso sia uguale al suo triplo. x > 2x + x = 3x La relazione: 2x
Esercitazioni di Matematica
 Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
3. (Da Medicina 2003) Moltiplicando i due membri di un'equazione per il numero -1, le soluzioni dell'equazione che si ottiene:
 1 EQUAZIONI 1. (Da Veterinaria 2006) L equazione di secondo grado che ammette per soluzioni x1 = 3 e x2 = -1/ 2 è: a) 2x 2 + (2 3-2)x - 6 = 0 b) 2x 2 - (2 3-2)x - 6 = 0 c) 2x 2 - (2 3-2)x + 6 = 0 d) 2x
1 EQUAZIONI 1. (Da Veterinaria 2006) L equazione di secondo grado che ammette per soluzioni x1 = 3 e x2 = -1/ 2 è: a) 2x 2 + (2 3-2)x - 6 = 0 b) 2x 2 - (2 3-2)x - 6 = 0 c) 2x 2 - (2 3-2)x + 6 = 0 d) 2x
Disequazioni di secondo grado
 Disequazioni di secondo grado.1 Risoluzione delle disequazioni di secondo grado Una disequazione di secondo grado si presenta in una delle seguenti forme: a + b + c > 0; a + b + c 0; a + b + c < 0; a +
Disequazioni di secondo grado.1 Risoluzione delle disequazioni di secondo grado Una disequazione di secondo grado si presenta in una delle seguenti forme: a + b + c > 0; a + b + c 0; a + b + c < 0; a +
MATRICI e DETERMINANTI. Prof.ssa Maddalena Dominijanni
 MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
Verifica di matematica, classe II liceo scientifico sistemi, problemi con sistemi, radicali, equiestensione. risolvere con il metodo di Cramer
 Verifica di matematica, classe II liceo scientifico sistemi, problemi con sistemi, radicali, equiestensione 1. 5 x y x 3y 1 risolvere con il metodo di Cramer. x 1 3 y y x 3 risolvere con il metodo di riduzione
Verifica di matematica, classe II liceo scientifico sistemi, problemi con sistemi, radicali, equiestensione 1. 5 x y x 3y 1 risolvere con il metodo di Cramer. x 1 3 y y x 3 risolvere con il metodo di riduzione
ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE
 ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE 1 Funzioni libere I punti stazionari di una funzione libera di più variabili si ottengono risolvendo il sistema di equazioni
ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE 1 Funzioni libere I punti stazionari di una funzione libera di più variabili si ottengono risolvendo il sistema di equazioni
Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 21 Novembre Logaritmi e Proprietà
 Esercitazioni di Matematica Generale A.A. 016/017 Pietro Pastore Lezione del 1 Novembre 016 Logaritmi e Proprietà Quando scriviamo log a b = c che leggiamo logaritmo in base a di b uguale a c, c è l esponente
Esercitazioni di Matematica Generale A.A. 016/017 Pietro Pastore Lezione del 1 Novembre 016 Logaritmi e Proprietà Quando scriviamo log a b = c che leggiamo logaritmo in base a di b uguale a c, c è l esponente
Punti di massimo o di minimo per funzioni di n variabili reali
 Punti di massimo o di minimo per funzioni di n variabili reali Dati f : A R n R ed X 0 A, X 0 si dice : punto di minimo assoluto se X A, f ( x ) f ( X 0 ) punto di massimo assoluto se X A, f ( x ) f (
Punti di massimo o di minimo per funzioni di n variabili reali Dati f : A R n R ed X 0 A, X 0 si dice : punto di minimo assoluto se X A, f ( x ) f ( X 0 ) punto di massimo assoluto se X A, f ( x ) f (
4. Determina le misure dei tre lati x, y, z di un triangolo sapendo che il perimetro è 53cm, inoltre
 www.matematicamente.it Verifica II liceo scientifico: Sistemi, Radicali, Equiestensione 1 Verifica di matematica, classe II liceo scientifico Sistemi, problemi con sistemi, radicali, equiestensione 1.
www.matematicamente.it Verifica II liceo scientifico: Sistemi, Radicali, Equiestensione 1 Verifica di matematica, classe II liceo scientifico Sistemi, problemi con sistemi, radicali, equiestensione 1.
Metodi per la risoluzione di sistemi lineari
 Metodi per la risoluzione di sistemi lineari 1 Sistemi di equazioni lineari 1.1 Determinante di matrici quadrate Ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante della matrice
Metodi per la risoluzione di sistemi lineari 1 Sistemi di equazioni lineari 1.1 Determinante di matrici quadrate Ad ogni matrice quadrata A è associato un numero reale det(a) detto determinante della matrice
Argomento 13 Sistemi lineari
 Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
QUINTO APPELLO DEL CORSO DI ANALISI MATEMATICA CORSO DI LAURA IN INFORMATICA, A.A. 2017/18 23 LUGLIO 2018 CORREZIONE. x 4 f(x) = x 2 + x 2
 QUINTO APPELLO DEL CORSO DI ANALISI MATEMATICA CORSO DI LAURA IN INFORMATICA, A.A. 27/8 23 LUGLIO 28 CORREZIONE Esercizio ) Considerate la funzione f definita da f(x) = x 2 + x 2. Trovatene il dominio
QUINTO APPELLO DEL CORSO DI ANALISI MATEMATICA CORSO DI LAURA IN INFORMATICA, A.A. 27/8 23 LUGLIO 28 CORREZIONE Esercizio ) Considerate la funzione f definita da f(x) = x 2 + x 2. Trovatene il dominio
Le equazioni lineari
 Perchè bisogna saper risolvere delle equazioni? Perché le equazioni servono a risolvere dei problemi! Le equazioni lineari Un problema è una proposizione che richiede di determinare i valori di alcune
Perchè bisogna saper risolvere delle equazioni? Perché le equazioni servono a risolvere dei problemi! Le equazioni lineari Un problema è una proposizione che richiede di determinare i valori di alcune
Disequazioni goniometriche
 Appunti di Matematica Disequazioni goniometriche Disequazioni goniometriche elementari a) Riprendiamo gli esempi che abbiamo fatto per le equazioni trasformandoli in disequazioni: sen Le soluzioni saranno:
Appunti di Matematica Disequazioni goniometriche Disequazioni goniometriche elementari a) Riprendiamo gli esempi che abbiamo fatto per le equazioni trasformandoli in disequazioni: sen Le soluzioni saranno:
Il determinante. Calcolo del determinante di matrici particolari. matrici di ordine 2: sia. a11 a A = allora
 Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Soluzioni del Foglio 2 I sistemi lineari
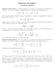 Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )( ) ( )( ) ( )( )
 SOLUZIONI II ALLENAMENTO REGIONALE TEMATICO VENERDÌ 4 DICEMBRE 08 Quesito Siano due numeri interi primi tra loro tali che quanto vale? Sviluppando l espressione si ottiene quindi e e la soluzione è Quesito
SOLUZIONI II ALLENAMENTO REGIONALE TEMATICO VENERDÌ 4 DICEMBRE 08 Quesito Siano due numeri interi primi tra loro tali che quanto vale? Sviluppando l espressione si ottiene quindi e e la soluzione è Quesito
DISEQUAZIONI FRATTE di SECONDO GRADO
 DISEQUAZIOI FRATTE di SECODO GRADO Si tratta di disequazioni che contengono delle frazioni algebriche e che hanno, a numeratore e/o a denominatore, dei polinomi di secondo grado. Il metodo per risolverle
DISEQUAZIOI FRATTE di SECODO GRADO Si tratta di disequazioni che contengono delle frazioni algebriche e che hanno, a numeratore e/o a denominatore, dei polinomi di secondo grado. Il metodo per risolverle
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
MATEMATICA PROPEDEUTICA PER LO STUDIO DELLE FUNZIONI GSCATULLO
 MATEMATICA PROPEDEUTICA PER LO STUDIO DELLE FUNZIONI GSCATULLO 1 Propedeutica alle Funzioni Premessa Questo documento vuole essere una preparazione per lo studio delle funzioni, comprendendo tutte quelle
MATEMATICA PROPEDEUTICA PER LO STUDIO DELLE FUNZIONI GSCATULLO 1 Propedeutica alle Funzioni Premessa Questo documento vuole essere una preparazione per lo studio delle funzioni, comprendendo tutte quelle
