Generalizzazioni del Teorema di Weierstrass
|
|
|
- Valentino Sacco
- 5 anni fa
- Visualizzazioni
Transcript
1 Capitolo 2 Generalizzazioni del Teorema di Weierstrass Il principale riferimento bibliografico per questa lezione è il testo di Checcucci, Tognoli, Vesentini [1]. Introduzione Supponiamo che X = R n. È noto (teorema di Weierstrass) che se K è un sottoinsieme compatto di R n e f : K R è una funzione continua allora f ha massimo e minimo. In effetti se si guarda alla dimostrazione del teorema di Weierstrass con le successioni ci si accorge che, se ci si accontenta di provare l esistenza del minimo, cosa a cui siamo maggiormente interessati, la condizione di continuità x n x può essere sostituita con la più debole lim f(x n) = f(x) n x n x lim inf n f(x n) f(x). Per l esistenza del minimo non è dunque necessario che la funzione sia continua, ma basta che sia semicontinua inferiormente. A pensarci bene, non serve nemmeno che il dominio di f sia compatto, ma basta che siano relativamente compatti gli insiemi di sottolivello (e il dominio di f essere anche tutto R n ), cioè che f sia coerciva. Questo succede, ad esempio, se f : R n R e lim x f(x) = +. Poichè siamo interessati a casi in cui X è uno spazio di funzioni e quindi uno spazio topologico più generale di R n (molto spesso si tratterà di uno spazio metrico) introdurremo le nozioni di semicontinuità e di coercività in ambito più generale. Preliminari topologici Sia (X, τ) uno spazio topologico. Dato un punto x X denoteremo con U (x) la famiglia di tutti gli intorni di X. Definizione 2.1 (Primo assioma di numerabilità (N 1 )) Si dice che X soddisfa al primo assioma di numerabilità se ogni punto di x ammette un sistema fondamentale di intorni numerabile (cioè una famiglia numerabile di intorni di x tale che ogni intorno di x contiene un intorno della famiglia). 7
2 8 CAPITOLO 2. GENERALIZZAZIONI DEL TEOREMA DI WEIERSTRASS Definizione 2.2 (Secondo assioma di numerabilità (N 2 )) Si dice che X soddisfa al secondo assioma di numerabilità, o che è a base numerabile, se esiste una base di aperti numerabile per la topologia di X (cioè esiste una famiglia numerabile di aperti tale che ogni altro aperto è unione di aperti della famiglia). Si potrebbe dimostrare che N 2 N 1. Osservazione 2.3 Gli spazi metrici soddisfano il primo assioma di numerabilità. In genere uno spazio metrico non soddisfa il secondo assioma di numerabilità (esempio R con la topologia discreta) a meno che non si ponga che sia separabile cioè che contenga un sottoinsieme numerabile denso. È questo il caso degli spazi metrici compatti che vedremo nella prossima sezione. In ogni caso, gli spazi metrici separabili soddisfano entrambi gli assiomi di numerabilità. Compattezza Sia X uno spazio topologico e Y X (anche eventualmente Y = X). {A i } i I di sottoinsiemi di X si dice un ricoprimento di Y se A i Y. Se ciascuno degli A i è aperto si parla di ricoprimento aperto. i I Una famiglia Definizione 2.4 Y si dice compatto se ogni ricoprimento aperto {A i } i I di Y ammette un sottoricoprimento finito, cioè esiste un sottoinsieme finito di indici J I tale che i J A i Y. Osservazione 2.5 Se Y è compatto in X rispetto ad una topologia τ allora resta compatto anche in ogni topologia più debole (cioè meno fine). Proposizione 2.6 I sottoinsiemi compatti di R n con la topologia euclidea sono tutti e soli quelli chiusi e limitati. È subito visto che questa proprietà non è soddisfatta in tutti gli spazi topologici. Per esempio, in uno spazio X costituito da almeno due punti con la topologia banale un punto è un sottoinsieme compatto ma non chiuso (il complementare non è aperto). Negli spazi metrici le cose vanno un po meglio, nel senso che vale una delle due implicazioni del teorema precedente. Precisamente: Proposizione 2.7 Sia X uno spazio metrico e K X. limitato. K compatto K chiuso e È importante però rilevare che il viceversa in generale non è vero nemmeno negli spazi metrici dove i compatti sono caratterizzati dal fatto di essere completi e totalmente limitati (per ogni ε > 0 sono contenuti in un unione finita di palle di raggio ε) che sono condizioni più forti della chiusura e della limitatezza. Tuttavia come vedremo gli spazi metrici sono meglio degli altri almeno per il fatto che la compattezza è caratterizzabile sequenzialmente nello stesso modo di R n. Definizione 2.8 Y si dice sequenzialmente compatto se da ogni successione di elementi di Y è possibile estrarre una sottosuccessione convergente in Y. Tra compattezza e compattezza sequenziale non vale, in generale, alcuna delle due implicazioni. Tuttavia le due nozioni coincidono negli spazi metrici.
3 9 Teorema 2.9 Sia X uno spazio metrico e Y X. Y è compatto se e solo se è sequenzialmente compatto. Dimostrazione (schema) Sia (y n ) una successione di elementi di Y. Se i suoi valori costituiscono un insieme finito allora esiste una sottosuccessione costante convergente a uno dei valori della successione che è ovviamente un punto di Y. Se l insieme dei valori della successione è infinito, usando il fatto che gli spazi metrici soddisfano il primo assioma di numerabilità si dimostra, come nel teorema di Bolzano-Weierstrass, che la successione ha almeno un punto di accumulazione. La conclusione segue dal fatto che K è chiuso. È più complicata e gioca un ruolo essenziale il fatto che uno spazio metrico compatto è separabile, e quindi soddisfa anche il secondo assioma di numerabilità. Osservazione 2.10 Se K è un sottoinsieme compatto di uno spazio topologico X allora K è uno spazio topologico compatto per la topologia indotta da X. Ne consegue che ogni proprietà stabilita per gli spazi topologici compatti si può applicare anche a tutti i sottoinsiemi compatti riguardandoli come spazi topologici compatti con la topologia di sottospazio. Proposizione 2.11 Ogni sottoinsieme chiuso di uno spazio topologico compatto è compatto. Dimostrazione Sia X compatto e C un sottoinsieme chiuso. Sia {A i } i I una famiglia di aperti tali che C i I A i. Il complementare C è aperto e si ha X = C C ( i I A i ) C. Poichè X è compatto esiste J I finito tale che X ( j J A j ) C. Ne segue che e pertanto C è compatto. C j J A j La proprietà dell intersezione finita Definizione 2.12 Si dice che una famiglia {B i } i I ha la proprietà dell intersezione finita se per ogni sottoinsieme finito J di I l intersezione j J B j è non vuota. Con la proprietà dell intersezione finita si può dare la seguente caratterizzazione degli insiemi compatti. Teorema 2.13 Sia X uno spazio topologico. X è compatto se e solo se ogni famiglia di chiusi di X che abbia la proprietà dell intersezione finita ha un intersezione non vuota. Dimostrazione ( ) Sia {C i } una famiglia di chiusi di X con la proprietà dell intersezione finita e poniamo per assurdo che i I C i =.
4 10 CAPITOLO 2. GENERALIZZAZIONI DEL TEOREMA DI WEIERSTRASS Allora X = ( i I C i ) = i I C i. Poichè X è compatto allora esiste J finito tale che vale a dire X = j J C J, j J C J = contro la proprietà dell intersezione finita. ( ) Sia {A i } i I un ricoprimento aperto di X. Allora, posto C i = A i per ogni i I, si ha che {C i } i I è una famiglia di chiusi tale che i I C i = ( i I A i ) =. Per ipotesi dunque la famiglia {C i } i I non ha la proprietà dell intersezione finita. Ma allora esiste un sottoinsieme finito J di I tale che j J C j = e quindi j J A j = ( j J C j ) = X. Allora {A j } j J è un sottoricoprimento finito e X risulta compatto per l arbitrarietà del ricoprimento {A i } i I. Semicontinuità Definiamo R = R { } {+ }. In R considereremo sempre la topologia in cui gli intorni sono definiti come in R ed in più un intorno di è qualunque sottoinsieme di R contenente un intervallo del tipo [, a[, un intorno di + è qualunque sottoinsieme di R contenente un intervallo del tipo ]b, + ]. Definizione 2.14 Una funzione f : X R si dice semicontinua inferiormente se f 1 (]c, + ]) = {x X : f(x) > c} è aperto in X (o equivalentemente se l insieme di sottolivello {x X : f(x) c} è chiuso) per ogni c R; semicontinua eriormente se f 1 ([, c[) = {x X : f(x) < c} è aperto in X per ogni a R. Esempio 2.15 Le funzioni caratteristiche di aperti sono semicontinue inferiormente, mentre le funzioni caratteristiche di chiusi sono semicontinue eriormente. Esempio 2.16 Sia S un sottoinsieme di X. Si chiama funzione indicatrice di S la funzione { 0 se x S χ (x) = S + se x X \ S Le funzioni indicatrici di aperti sono semicontinue eriormente, mentre le funzioni indicatrici di chiusi sono semicontinue inferiormente. Ricordiamo che una funzione è continua se le controimmagini degli aperti di R sono aperti in X. Il seguente teorema è di agevole dimostrazione se si usa il fatto, non banale, che ogni aperto di R si può scrivere come unione di intervalli aperti di R (quindi compresi quelli del tipo [, a[ e ]b, + ]), cioè gli intervalli aperti costituiscono una base per la topologia di R. Proposizione 2.17 f è continua se e solo se è semicontinua eriormente e inferiormente.
5 11 Dimostrazione La necessità è banale. Proviamo la sufficienza, cioè poniamo che f sia semicontinua eriormente ed inferiormente e dimostriamo che è continua. Sia A un insieme aperto di R, allora A = γ I J γ dove J γ sono intervalli aperti del tipo ]α γ, β γ [, ]α γ, + ] o [, β γ [. Dimostriamo che f 1 (A) è aperto. Poiché f 1 (A) = f 1( ) γ I J γ = γ I f 1( ) J γ, e, poiché in conseguenzea delle ipotesi di semicontinuità ciascuno degli insiemi f 1( ) J γ è aperto (in particolare si usa il fatto che f 1 (]α, β[) = f 1 (]α, + ][) f 1 ([, β[)), allora f 1 (A) è aperto perché è unione di insiemi aperti. Dal momento che, fissato c, {x X : f(x) > c} è aperto in X se e solo se per ogni x X tale che f(x) > c esiste un intorno U di x tale che f(y) > c per ogni y U, è naturale porre la seguente definizione. Definizione 2.18 Una funzione f : X R si dice semicontinua inferiormente nel punto x se e solo se per ogni c R tale che f(x) > c esiste un intorno U di x tale che f(y) > c per ogni y U. Esercizio 2.19 Scrivere, in analogia con la precedente, la definizione di funzione semicontinua eriormente in un punto x. Chiaramente, f è s.c.i. in X se e solo se f è s.c.i. in x per ogni x X. Teorema 2.20 Una funzione f : X R è semicontinua inferiormente nel punto x se e solo se (2.1) f(x) inf f(y) = f(x) lim inf y x Dimostrazione Ricordiamo che, per definizione, lim inf f(y) = y x f(y) lim inf f(y). inf f(y), \{x} quindi l uguaglianza e la seconda disuguaglianza sono immediate. Supponiamo che f sia semicontinua inferiormente, e dimostriamo la prima. A tal scopo, preso un arbitrario ε > 0 sia c = f(x) ε. Allora, per la definizione 2.18, esiste un intorno U di x tale che e si ha quindi, a maggior ragione inf f(y) f(x) ε inf f(y) f(x) ε e la disuguaglianza cercata si ottiene ora passando al limite per ε 0. poniamo che f soddisfi la condizione f(x) e sia c R tale che f(x) > c. Allora c < inf f(y), inf f(y) y x Viceversa, e pertanto esiste U U (x) tale che inf f(y) > c, da cui f(y) > c per ogni y U, e quindi per la definizione 2.18 f è semicontinua inferiormente in x.
6 12 CAPITOLO 2. GENERALIZZAZIONI DEL TEOREMA DI WEIERSTRASS Osservazione 2.21 Osservato che allora si ha sempre che inf f(y) f(x) = f(x), f(x) inf f(y), e quindi la prima disuguaglianza in (2.1) è in realtà un uguaglianza. Semicontinuità sequenziale Definizione 2.22 Una funzione f : X R si dice sequenzialmente semicontinua inferiormente in un punto x X se 1 f(x) lim inf n f(x n) per ogni x n x. È facile verificare, utilizzando il Teorema 2.20 che la semicontinuità implica la semicontinuità sequenziale. Il viceversa, che non vale in generale (vedi Dal Maso [2], Example 1.6), è però vero negli spazi topologici che soddisfano il primo assioma di numerabilità e quindi negli spazi metrici. Vale cioè il seguente teorema. Teorema 2.23 Sia X uno spazio topologico soddisfacente al primo assioma di numerabilità. Una funzione f : X R è semicontinua inferiormente in x 0 X se e solo se f è sequenzialmente semicontinua inferiormente in x 0 X. Dimostrazione Dimostriamo la necessità lasciando la sufficienza, che come già detto vale anche se X non soddisfa al primo assioma di numerabilità, per esercizio. Supponiamo dunque che f sia sequenzialmente semicontinua inferiormente in x 0 X e poniamo per assurdo che non sia semicontinua inferiormente, cioè che esista c < f(x 0 ) tale che per ogni U U(x) esiste y U tale che f(y) c. Sia (U n ) un sistema fondamentale numerabile di intorni di x 0 tale che U n+1 U n per ogni n N. Per quanto osservato sopra, per ogni n N esiste y n U n tale che Allora y n x 0 in X e si ha f(y n ) c. lim inf n f(y n) c < f(x 0 ), contro la semicontinuità inferiore sequenziale. Le seguenti proprietà delle funzioni semicontinue inferiormente sono elementari e seguono direttamente dalle definizioni. Proposizione 2.24 Sia {f i } i I una famiglia di funzioni s.c.i. (rispettivamente seq. s.c.i.) definite su X. Si ha che la funzione f(x) = f i (x) è s.c.i. (rispettivamente seq. s.c.i.); i I se I è finito allora la funzione g(x) = f i (x) è s.c.i. (rispettivamente seq. s.c.i.). i I Proposizione 2.25 Se f e g sono s.c.i. (rispettivamente seq. s.c.i.) e se f + g è ben definita, allora f + g è s.c.i. (rispettivamente seq. s.c.i.). 1 Ricordiamo che lim inf n f(xn) := inf f(x k) = lim inf f(x k). n N k n n k n
7 BIBLIOGRAFIA 13 Applicazioni a problemi di minimo Teorema 2.26 (Weierstrass). Assumiamo che 1. f sia semicontinua inferiormente su X; 2. K sia compatto e chiuso. Allora esiste il minimo di f su K. Sia X un spazio topologico, K X e f : X R Dimostrazione (Caso sequenziale) Diamo la dimostrazione dapprima nel caso in cui X è uno spazio metrico così si possono usare le caratterizzazioni sequenziali della semicontinuità e della compattezza. Sia (x n ) una successione minimizzante, cioè una successione di punti di U tale che lim f(x n) = inf f n K (dimostrare per esercizio che una successione siffatta esiste sempre, usando le proprietà dell estremo inferiore). Poichè K è compatto, esiste (x nk ) tale che x nk x K, ma f è semicontinua inferiormente, quindi f(x) lim inf f(x n k ) = lim f(x n) = inf f. k n K da cui segue che x è un punto di minimo. Dimostrazione (Caso generale) Se f è la costante + non c è nulla da provare. Altrimenti si ha inf{f(x) : x K} = M < + Poichè f è s.c.i. allora per ogni t l insieme C t := {x K : f(x) t} = K {x X : f(x) t} è un sottoinsieme chiuso di K (come intersezione di due chiusi; qui si usa l ipotesi: K chiuso) e quindi è compatto; per t > M è anche non vuoto. La famiglia di chiusi {C t } t>m essendo monotona crescente rispetto all inclusione, gode della proprietà dell intersezione finita e quindi, siccome K è compatto, non può essere vuoto l insieme {x K : f(x) t} = {x K : f(x) M}. Bibliografia t>m [1] V. Checcucci, A. Tognoli, and E. Vesentini, Lezioni di topologia generale, Feltrinelli, Milano, [2] G. Dal Maso, An introduction to γ-convergence, Birkhäuser, Boston, 1993.
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale
 4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
Geometria Superiore Esercizi 1 (da consegnare entro... )
 Geometria Superiore Esercizi 1 (da consegnare entro... ) In questi esercizi analizziamo il concetto di paracompattezza per uno spazio topologico e vediamo come questo implichi l esistenza di partizioni
Geometria Superiore Esercizi 1 (da consegnare entro... ) In questi esercizi analizziamo il concetto di paracompattezza per uno spazio topologico e vediamo come questo implichi l esistenza di partizioni
SPAZI METRICI. Uno spazio metrico X con metrica d si indica con il simbolo (X, d). METRICI 1
 SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
Esistenza di funzioni continue non differenziabili in alcun punto
 UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
TOPOLOGIE. Capitolo 2. 2.1 Spazi topologici
 Capitolo 2 TOPOLOGIE Ogni spazio che si considera in gran parte della matematica e delle sue applicazioni è uno spazio topologico di qualche tipo: qui introduciamo in generale le nozioni di base della
Capitolo 2 TOPOLOGIE Ogni spazio che si considera in gran parte della matematica e delle sue applicazioni è uno spazio topologico di qualche tipo: qui introduciamo in generale le nozioni di base della
A i è un aperto in E. i=1
 Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
INDICAZIONI PER LA RICERCA DEGLI ASINTOTI VERTICALI
 2.13 ASINTOTI 44 Un "asintoto", per una funzione y = f( ), è una retta alla quale il grafico della funzione "si avvicina indefinitamente", "si avvicina di tanto quanto noi vogliamo", nel senso precisato
2.13 ASINTOTI 44 Un "asintoto", per una funzione y = f( ), è una retta alla quale il grafico della funzione "si avvicina indefinitamente", "si avvicina di tanto quanto noi vogliamo", nel senso precisato
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8. Cognome:... Nome:... Matricola:...
 Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
TOPOLOGIA ALBERTO SARACCO
 TOPOLOGIA ALBERTO SARACCO Abstract. Le presenti note saranno il più fedeli possibile a quanto detto a lezione. I testi consigliati sono Jänich [1], Kosniowski [2] e Singer- Thorpe [3]. Un ottimo libro
TOPOLOGIA ALBERTO SARACCO Abstract. Le presenti note saranno il più fedeli possibile a quanto detto a lezione. I testi consigliati sono Jänich [1], Kosniowski [2] e Singer- Thorpe [3]. Un ottimo libro
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
FUNZIONI CONTINUE - ESERCIZI SVOLTI
 FUNZIONI CONTINUE - ESERCIZI SVOLTI 1) Verificare che x è continua in x 0 per ogni x 0 0 ) Verificare che 1 x 1 x 0 è continua in x 0 per ogni x 0 0 3) Disegnare il grafico e studiare i punti di discontinuità
FUNZIONI CONTINUE - ESERCIZI SVOLTI 1) Verificare che x è continua in x 0 per ogni x 0 0 ) Verificare che 1 x 1 x 0 è continua in x 0 per ogni x 0 0 3) Disegnare il grafico e studiare i punti di discontinuità
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
1.1. Spazi metrici completi
 SPAZI METRICI: COMPLETEZZA E COMPATTEZZA Note informali dalle lezioni 1.1. Spazi metrici completi La nozione di convergenza di successioni è centrale nello studio degli spazi metrici. In particolare è
SPAZI METRICI: COMPLETEZZA E COMPATTEZZA Note informali dalle lezioni 1.1. Spazi metrici completi La nozione di convergenza di successioni è centrale nello studio degli spazi metrici. In particolare è
5. La teoria astratta della misura.
 5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
Convessità e derivabilità
 Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
Equazioni differenziali ordinarie
 Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
Appunti di Complementi di Matematica. Jacobo Pejsachowicz (a cura di Nathan Quadrio)
 Appunti di Complementi di Matematica Jacobo Pejsachowicz (a cura di Nathan Quadrio) 1 Indice 1 Cenni della teoria degli insiemi 4 1.1 Classi ed insiemi........................... 4 1.2 Operazioni fra gli
Appunti di Complementi di Matematica Jacobo Pejsachowicz (a cura di Nathan Quadrio) 1 Indice 1 Cenni della teoria degli insiemi 4 1.1 Classi ed insiemi........................... 4 1.2 Operazioni fra gli
Limiti e continuità di funzioni reali di una variabile
 di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
Gli asintoti di una funzione sono rette, quindi possono essere: rette verticali o rette orizzontali o rette oblique.
 Asintoti Gli asintoti di una funzione sono rette, quindi possono essere: rette verticali o rette orizzontali o rette oblique. Asintoti verticali Sia 0 punto di accumulazione per dom(f). La retta = 0 è
Asintoti Gli asintoti di una funzione sono rette, quindi possono essere: rette verticali o rette orizzontali o rette oblique. Asintoti verticali Sia 0 punto di accumulazione per dom(f). La retta = 0 è
3.1 Successioni. R Definizione (Successione numerica) E Esempio 3.1 CAPITOLO 3
 CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 2011/2012
 Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
OGNI SPAZIO VETTORIALE HA BASE
 1 Mimmo Arezzo OGNI SPAZIO VETTORIALE HA BASE CONVERSAZIONE CON ALCUNI STUDENTI DI FISICA 19 DICEMBRE 2006 2 1 Preliminari Definizione 1.0.1 Un ordinamento parziale (o una relazione d ordine parziale)
1 Mimmo Arezzo OGNI SPAZIO VETTORIALE HA BASE CONVERSAZIONE CON ALCUNI STUDENTI DI FISICA 19 DICEMBRE 2006 2 1 Preliminari Definizione 1.0.1 Un ordinamento parziale (o una relazione d ordine parziale)
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
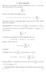 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
19. Inclusioni tra spazi L p.
 19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
Appunti di Analisi convessa. Paolo Acquistapace
 Appunti di Analisi convessa Paolo Acquistapace 6 dicembre 2012 Indice 1 Spazi vettoriali topologici 4 1.1 Insiemi convessi.......................... 4 1.2 Funzionale di Minkowski..................... 6
Appunti di Analisi convessa Paolo Acquistapace 6 dicembre 2012 Indice 1 Spazi vettoriali topologici 4 1.1 Insiemi convessi.......................... 4 1.2 Funzionale di Minkowski..................... 6
Una ricetta per il calcolo dell asintoto obliquo. Se f(x) è asintotica a mx+q allora abbiamo f(x) mx q = o(1), da cui (dividendo per x) + o(1), m =
 Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Massimi e minimi vincolati in R 2 - Esercizi svolti
 Massimi e minimi vincolati in R 2 - Esercizi svolti Esercizio 1. Determinare i massimi e minimi assoluti della funzione f(x, y) = 2x + 3y vincolati alla curva di equazione x 4 + y 4 = 1. Esercizio 2. Determinare
Massimi e minimi vincolati in R 2 - Esercizi svolti Esercizio 1. Determinare i massimi e minimi assoluti della funzione f(x, y) = 2x + 3y vincolati alla curva di equazione x 4 + y 4 = 1. Esercizio 2. Determinare
Università degli Studi di Catania A.A. 2012-2013. Corso di laurea in Ingegneria Industriale
 Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
PROVA DI VERIFICA DEL 24/10/2001
 PROVA DI VERIFICA DEL 24/10/2001 [1] Il prodotto di due numeri non nulli è maggiore di zero se: a. il loro rapporto è maggiore di zero, b. il loro rapporto è minore di zero, c. il loro rapporto è uguale
PROVA DI VERIFICA DEL 24/10/2001 [1] Il prodotto di due numeri non nulli è maggiore di zero se: a. il loro rapporto è maggiore di zero, b. il loro rapporto è minore di zero, c. il loro rapporto è uguale
ANALISI non Lineare. Diego Averna
 ANALISI non Lineare Ovvero: presentazione di Analisi non Lineare Diego Averna Dipartimento di Matematica e Informatica Facoltà di Scienze MM.FF.NN. Via Archirafi, 34-90123 Palermo (Italy) diego.averna@unipa.it
ANALISI non Lineare Ovvero: presentazione di Analisi non Lineare Diego Averna Dipartimento di Matematica e Informatica Facoltà di Scienze MM.FF.NN. Via Archirafi, 34-90123 Palermo (Italy) diego.averna@unipa.it
Proprietà metriche di R. Funzioni da R in R. Funzioni continue da R in R. Limiti di funzioni da R in R.
 Università di Trieste - Facoltà d'ingegneria Corsi di Laurea in Ingegneria Chimica, Elettrica, Elettronica, dei Materiali Programma del corso di Analisi Matematica I Anno Accademico 1999-2000 Prof. Pierpaolo
Università di Trieste - Facoltà d'ingegneria Corsi di Laurea in Ingegneria Chimica, Elettrica, Elettronica, dei Materiali Programma del corso di Analisi Matematica I Anno Accademico 1999-2000 Prof. Pierpaolo
Sulla monotonia delle funzioni reali di una variabile reale
 Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Problemi di approssimazione per operatori positivi in spazi adattati
 UNIVERSITÀ DEGLI STUDI DI BARI Dottorato di Ricerca in Matematica XV Ciclo A.A. 2002 2003 Tesi di Dottorato Problemi di approssimazione per operatori positivi in spazi adattati Presentata da Mirella CAPPELLETTI
UNIVERSITÀ DEGLI STUDI DI BARI Dottorato di Ricerca in Matematica XV Ciclo A.A. 2002 2003 Tesi di Dottorato Problemi di approssimazione per operatori positivi in spazi adattati Presentata da Mirella CAPPELLETTI
Lo Spettro primo di un anello. Carmelo Antonio Finocchiaro
 Lo Spettro primo di un anello Carmelo Antonio Finocchiaro 2 Indice 1 Lo spettro primo di un anello: introduzione 5 1.1 Le regole del gioco................................ 5 1.2 Prime definizioni e risultati
Lo Spettro primo di un anello Carmelo Antonio Finocchiaro 2 Indice 1 Lo spettro primo di un anello: introduzione 5 1.1 Le regole del gioco................................ 5 1.2 Prime definizioni e risultati
Definizione DEFINIZIONE
 Definizione Funzione reale di due variabili reali Indichiamo con R 2 l insieme di tutti i vettori bidimensionali. Dato un sottoinsiemed R 2, una funzione f: D R è una legge che assegna a ogni punto (x,
Definizione Funzione reale di due variabili reali Indichiamo con R 2 l insieme di tutti i vettori bidimensionali. Dato un sottoinsiemed R 2, una funzione f: D R è una legge che assegna a ogni punto (x,
Esercitazioni di statistica
 Esercitazioni di statistica Misure di associazione: Indipendenza assoluta e in media Stefania Spina Universitá di Napoli Federico II stefania.spina@unina.it 22 ottobre 2014 Stefania Spina Esercitazioni
Esercitazioni di statistica Misure di associazione: Indipendenza assoluta e in media Stefania Spina Universitá di Napoli Federico II stefania.spina@unina.it 22 ottobre 2014 Stefania Spina Esercitazioni
G. Pareschi ALGEBRE DI BOOLE. 1. Algebre di Boole
 G. Pareschi ALGEBRE DI BOOLE 1. Algebre di Boole Nel file precedente abbiamo incontrato la definizione di algebra di Boole come reticolo: un algebra di Boole e un reticolo limitato, complementato e distributivo.
G. Pareschi ALGEBRE DI BOOLE 1. Algebre di Boole Nel file precedente abbiamo incontrato la definizione di algebra di Boole come reticolo: un algebra di Boole e un reticolo limitato, complementato e distributivo.
Indice. 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo... 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità...
 Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
SIMULAZIONE TEST ESAME - 1
 SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
Riconoscere e formalizzare le dipendenze funzionali
 Riconoscere e formalizzare le dipendenze funzionali Giorgio Ghelli 25 ottobre 2007 1 Riconoscere e formalizzare le dipendenze funzionali Non sempre è facile indiduare le dipendenze funzionali espresse
Riconoscere e formalizzare le dipendenze funzionali Giorgio Ghelli 25 ottobre 2007 1 Riconoscere e formalizzare le dipendenze funzionali Non sempre è facile indiduare le dipendenze funzionali espresse
ALGEBRA I: CARDINALITÀ DI INSIEMI
 ALGEBRA I: CARDINALITÀ DI INSIEMI 1. CONFRONTO DI CARDINALITÀ E chiaro a tutti che esistono insiemi finiti cioè con un numero finito di elementi) ed insiemi infiniti. E anche chiaro che ogni insieme infinito
ALGEBRA I: CARDINALITÀ DI INSIEMI 1. CONFRONTO DI CARDINALITÀ E chiaro a tutti che esistono insiemi finiti cioè con un numero finito di elementi) ed insiemi infiniti. E anche chiaro che ogni insieme infinito
Le funzioni reali di variabile reale
 Prof. Michele Giugliano (Gennaio 2002) Le funzioni reali di variabile reale ) Complementi di teoria degli insiemi. A) Estremi di un insieme numerico X. Dato un insieme X R, si chiama maggiorante di X un
Prof. Michele Giugliano (Gennaio 2002) Le funzioni reali di variabile reale ) Complementi di teoria degli insiemi. A) Estremi di un insieme numerico X. Dato un insieme X R, si chiama maggiorante di X un
Problemi di ottimizzazione in teoria del trasporto e applicazioni
 Università di Pisa Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Matematica A. A. 2001/02 Tesi di Laurea Problemi di ottimizzazione in teoria del trasporto e applicazioni Candidato
Università di Pisa Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Matematica A. A. 2001/02 Tesi di Laurea Problemi di ottimizzazione in teoria del trasporto e applicazioni Candidato
ALCUNE APPLICAZIONI DEL CALCOLO DIFFERENZIALE
 ALCUNE APPLICAZIONI DEL CALCOLO DIFFERENZIALE Sia I un intervallo di R e siano a = inf(i) R { } e b = sup(i) R {+ }; i punti di I diversi dagli estremi a e b, ( e quindi appartenenti all intervallo aperto
ALCUNE APPLICAZIONI DEL CALCOLO DIFFERENZIALE Sia I un intervallo di R e siano a = inf(i) R { } e b = sup(i) R {+ }; i punti di I diversi dagli estremi a e b, ( e quindi appartenenti all intervallo aperto
VARIABILI ALEATORIE CONTINUE
 VARIABILI ALEATORIE CONTINUE Se X è una variabile aleatoria continua, la probabilità che X assuma un certo valore x fissato è in generale zero, quindi non ha senso definire una distribuzione di probabilità
VARIABILI ALEATORIE CONTINUE Se X è una variabile aleatoria continua, la probabilità che X assuma un certo valore x fissato è in generale zero, quindi non ha senso definire una distribuzione di probabilità
Il Teorema di Fritz John: tre differenti approcci
 Università degli Studi di Milano Bicocca FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI Corso di Laurea Triennale in Matematica Il Teorema di Fritz John: tre differenti approcci Tesi di Laurea in Matematica
Università degli Studi di Milano Bicocca FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI Corso di Laurea Triennale in Matematica Il Teorema di Fritz John: tre differenti approcci Tesi di Laurea in Matematica
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
21. Studio del grafico di una funzione: esercizi
 1. Studio del grafico di una funzione: esercizi Esercizio 1.6. Studiare ciascuna delle seguenti funzioni in base allo schema di pagina 194, eseguendo anche il computo della derivata seconda e lo studio
1. Studio del grafico di una funzione: esercizi Esercizio 1.6. Studiare ciascuna delle seguenti funzioni in base allo schema di pagina 194, eseguendo anche il computo della derivata seconda e lo studio
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Successioni e serie di funzioni
 Successioni e serie di funzioni A. Albanese, A. Leaci, D. Pallara In questa dispensa generalizzeremo la trattazione delle successioni e delle serie al caso in cui i termini delle stesse siano non numeri
Successioni e serie di funzioni A. Albanese, A. Leaci, D. Pallara In questa dispensa generalizzeremo la trattazione delle successioni e delle serie al caso in cui i termini delle stesse siano non numeri
0.1 Esercizi calcolo combinatorio
 0.1 Esercizi calcolo combinatorio Esercizio 1. Sia T l insieme dei primi 100 numeri naturali. Calcolare: 1. Il numero di sottoinsiemi A di T che contengono esattamente 8 pari.. Il numero di coppie (A,
0.1 Esercizi calcolo combinatorio Esercizio 1. Sia T l insieme dei primi 100 numeri naturali. Calcolare: 1. Il numero di sottoinsiemi A di T che contengono esattamente 8 pari.. Il numero di coppie (A,
Corso di Analisi Matematica. Funzioni continue
 a.a. 203/204 Laurea triennale in Informatica Corso di Analisi Matematica Funzioni continue Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
a.a. 203/204 Laurea triennale in Informatica Corso di Analisi Matematica Funzioni continue Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
Parte 2. Metodi Matematici per la Meccanica Quantistica. Spazi di pre-hilbert e spazi di Hilbert. Gianpiero CATTANEO
 Parte Metodi Matematici per la Meccanica Quantistica Spazi di pre-hilbert e spazi di Hilbert Gianpiero CATTANEO 10 giugno 008 Indice I - Spazi con Prodotto Interno e Spazi di Hilbert 5 1 Spazi con Prodotto
Parte Metodi Matematici per la Meccanica Quantistica Spazi di pre-hilbert e spazi di Hilbert Gianpiero CATTANEO 10 giugno 008 Indice I - Spazi con Prodotto Interno e Spazi di Hilbert 5 1 Spazi con Prodotto
F (x) = f(x) per ogni x I. Per esempio:
 Funzioni Primitive (Integrali Indefiniti) (l.v.) Pur essendo un argomento che fa parte del Calcolo Differenziale, molti autori inseriscono funzioni primitive nel capitolo sul Calcolo Integrale, in quanto
Funzioni Primitive (Integrali Indefiniti) (l.v.) Pur essendo un argomento che fa parte del Calcolo Differenziale, molti autori inseriscono funzioni primitive nel capitolo sul Calcolo Integrale, in quanto
Funzioni periodiche. Una funzione si dice periodica di periodo T se T > 0 è il più piccolo numero reale positivo tale che
 Funzioni periodiche Una funzione si dice periodica di periodo T se T > 0 è il più piccolo numero reale positivo tale che -T T In ogni intervallo di ampiezza pari a T il grafico di tale funzione si ripete.
Funzioni periodiche Una funzione si dice periodica di periodo T se T > 0 è il più piccolo numero reale positivo tale che -T T In ogni intervallo di ampiezza pari a T il grafico di tale funzione si ripete.
La logica modale e la dimostrazione dell esistenza di Dio di Gödel. LOGICA MODALE
 La logica modale e la dimostrazione dell esistenza di Dio di Gödel. In alcuni giornali ho letto che di recente ci sono stati diversi studi che hanno riportato alla ribalta la dimostrazione dell esistenza
La logica modale e la dimostrazione dell esistenza di Dio di Gödel. In alcuni giornali ho letto che di recente ci sono stati diversi studi che hanno riportato alla ribalta la dimostrazione dell esistenza
FUNZIONI CONVESSE. + e x 0
 FUNZIONI CONVESSE Sia I un intervallo aperto di R (limitato o illimitato) e sia f(x) una funzione definita in I. Dato x 0 I, la retta r passante per il punto P 0 (x 0, f(x 0 )) di equazione y = f(x 0 )
FUNZIONI CONVESSE Sia I un intervallo aperto di R (limitato o illimitato) e sia f(x) una funzione definita in I. Dato x 0 I, la retta r passante per il punto P 0 (x 0, f(x 0 )) di equazione y = f(x 0 )
Ottimizzazione non Vincolata
 Dipartimento di Informatica e Sitemistica Università di Roma Corso Dottorato Ingegneria dei Sistemi 15/02/2010, Roma Outline Ottimizzazione Non Vincolata Introduzione Ottimizzazione Non Vincolata Algoritmi
Dipartimento di Informatica e Sitemistica Università di Roma Corso Dottorato Ingegneria dei Sistemi 15/02/2010, Roma Outline Ottimizzazione Non Vincolata Introduzione Ottimizzazione Non Vincolata Algoritmi
Due dimostrazioni alternative nella teoria di Ramsey
 Due dimostrazioni alternative nella teoria di Ramsey 28 Marzo 2007 Introduzione Teoria di Ramsey: sezione della matematica a metà tra la combinatoria e la teoria degli insiemi. La questione tipica è quella
Due dimostrazioni alternative nella teoria di Ramsey 28 Marzo 2007 Introduzione Teoria di Ramsey: sezione della matematica a metà tra la combinatoria e la teoria degli insiemi. La questione tipica è quella
Capitolo 5: Macchine di Turing e calcolabilitá secondo Turing
 Capitolo 5: Macchine di Turing e calcolabilitá secondo Turing 1 Macchina di Turing (MDT ) Un dispositivo che accede a un nastro (potenzialmente) illimitato diviso in celle contenenti ciascuna un simbolo
Capitolo 5: Macchine di Turing e calcolabilitá secondo Turing 1 Macchina di Turing (MDT ) Un dispositivo che accede a un nastro (potenzialmente) illimitato diviso in celle contenenti ciascuna un simbolo
Introduzione alla programmazione lineare. Mauro Pagliacci
 Introduzione alla programmazione lineare Mauro Pagliacci c Draft date 25 maggio 2010 Premessa In questo fascicolo sono riportati gli appunti dalle lezioni del corso di Elaborazioni automatica dei dati
Introduzione alla programmazione lineare Mauro Pagliacci c Draft date 25 maggio 2010 Premessa In questo fascicolo sono riportati gli appunti dalle lezioni del corso di Elaborazioni automatica dei dati
APPENDICE NOZIONI BASE E VARIE
 pag. 131 Appendice: Nozioni base e varie G. Gerla APPENDICE NOZIONI BASE E VARIE 1. Funzioni e relazioni di equivalenza Questi appunti sono rivolti a persone che abbiano già una conoscenza elementare della
pag. 131 Appendice: Nozioni base e varie G. Gerla APPENDICE NOZIONI BASE E VARIE 1. Funzioni e relazioni di equivalenza Questi appunti sono rivolti a persone che abbiano già una conoscenza elementare della
Insiemi di livello e limiti in più variabili
 Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
Analisi funzionale. Riccarda Rossi Lezione 9
 Riarda Rossi Lezione 9 Caratterizzazione della onvergenza debole in L p (Ω) Siano 1 < p < e {f n}, f L p (Ω): allora f n f in L p (Ω) Teorema di ompattezza debole in L p (Ω) Teorema Siano 1 < p < e {f
Riarda Rossi Lezione 9 Caratterizzazione della onvergenza debole in L p (Ω) Siano 1 < p < e {f n}, f L p (Ω): allora f n f in L p (Ω) Teorema di ompattezza debole in L p (Ω) Teorema Siano 1 < p < e {f
Politecnico di Milano Corso di Analisi e Geometria 1. Federico Lastaria federico.lastaria@polimi.it
 Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@poi.it Primi teoremi di caclolo differenziale Ottobre 2010. Indice 1 Funzioni derivabili su un intervallo 1 1.1
Politecnico di Milano Corso di Analisi e Geometria 1 Federico Lastaria federico.lastaria@poi.it Primi teoremi di caclolo differenziale Ottobre 2010. Indice 1 Funzioni derivabili su un intervallo 1 1.1
Corso di Analisi Matematica. Successioni e serie numeriche
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
+ P a n n=1 + X. a n = a m 3. n=1. m=4. Per poter dare un significato alla somma (formale) di infiniti termini, ricorriamo al seguente procedimento:
 Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Successioni di funzioni reali
 E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
Massimi e minimi vincolati
 Massimi e minimi vincolati In problemi di massimo e minimo vincolato viene richiesto di ricercare massimi e minimi di una funzione non definita su tutto R n, ma su un suo sottoinsieme proprio. Esempio:
Massimi e minimi vincolati In problemi di massimo e minimo vincolato viene richiesto di ricercare massimi e minimi di una funzione non definita su tutto R n, ma su un suo sottoinsieme proprio. Esempio:
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
LEZIONE 31. B i : R n R. R m,n, x = (x 1,..., x n ). Allora sappiamo che è definita. j=1. a i,j x j.
 LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
Misure e funzioni a variazione limitata
 Capitolo 2 Misure e funzioni a variazione limitata 2.1 Richiami di teoria della misura e integrazione Sia un insieme non vuoto e sia F una σ-algebra su, cioè una famiglia di sottoinsiemi di che gode delle
Capitolo 2 Misure e funzioni a variazione limitata 2.1 Richiami di teoria della misura e integrazione Sia un insieme non vuoto e sia F una σ-algebra su, cioè una famiglia di sottoinsiemi di che gode delle
Appunti del corso di Probabilità e Processi Stocastici
 Appunti del corso di Probabilità e Processi Stocastici in continua revisione e aggiornamento Michele Gianfelice Dipartimento di Matematica Università della Calabria Campus di Arcavacata Ponte Pietro Bucci
Appunti del corso di Probabilità e Processi Stocastici in continua revisione e aggiornamento Michele Gianfelice Dipartimento di Matematica Università della Calabria Campus di Arcavacata Ponte Pietro Bucci
Quesiti di Analisi Matematica A
 Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
I appello - 24 Marzo 2006
 Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Parte 6. Applicazioni lineari
 Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
COGNOME e NOME: FIRMA: MATRICOLA:
 Anno Accademico 203/ 204 Corsi di Analisi Matematica I (Proff A Villani e F Faraci) Prova d Esame del giorno 6 febbraio 204 Prima prova scritta (compito A) Non sono consentiti formulari, appunti, libri
Anno Accademico 203/ 204 Corsi di Analisi Matematica I (Proff A Villani e F Faraci) Prova d Esame del giorno 6 febbraio 204 Prima prova scritta (compito A) Non sono consentiti formulari, appunti, libri
Funzioni in più variabili
 Funzioni in più variabili Corso di Analisi 1 di Andrea Centomo 27 gennaio 2011 Indichiamo con R n, n 1, l insieme delle n-uple ordinate di numeri reali R n4{(x 1, x 2,,x n ), x i R, i =1,,n}. Dato X R
Funzioni in più variabili Corso di Analisi 1 di Andrea Centomo 27 gennaio 2011 Indichiamo con R n, n 1, l insieme delle n-uple ordinate di numeri reali R n4{(x 1, x 2,,x n ), x i R, i =1,,n}. Dato X R
Capitolo 4. Funzioni continue e limiti. 4.1 Intorni
 Capitolo 4 Funzioni continue e iti In questo capitolo definiremo la nozione di funzione continua e ne studieremo le proprietà fondamentali. Introdurremo inoltre l operazione fondamentale dell analisi infinitesimale,
Capitolo 4 Funzioni continue e iti In questo capitolo definiremo la nozione di funzione continua e ne studieremo le proprietà fondamentali. Introdurremo inoltre l operazione fondamentale dell analisi infinitesimale,
EQUAZIONI non LINEARI
 EQUAZIONI non LINEARI Francesca Pelosi Dipartimento di Matematica, Università di Roma Tor Vergata CALCOLO NUMERICO e PROGRAMMAZIONE http://www.mat.uniroma2.it/ pelosi/ EQUAZIONI non LINEARI p.1/44 EQUAZIONI
EQUAZIONI non LINEARI Francesca Pelosi Dipartimento di Matematica, Università di Roma Tor Vergata CALCOLO NUMERICO e PROGRAMMAZIONE http://www.mat.uniroma2.it/ pelosi/ EQUAZIONI non LINEARI p.1/44 EQUAZIONI
Lezione 6. Divisibilità e divisori. Teorema di divisione euclidea. Algoritmo delle divisioni successive.
 Lezione 6 Prerequisiti: L'insieme dei numeri interi. Lezione 5. Divisibilità e divisori. Teorema di divisione euclidea. Algoritmo delle divisioni successive. Questa è la prima lezione dedicata all'anello
Lezione 6 Prerequisiti: L'insieme dei numeri interi. Lezione 5. Divisibilità e divisori. Teorema di divisione euclidea. Algoritmo delle divisioni successive. Questa è la prima lezione dedicata all'anello
Capitolo 1 ANALISI COMPLESSA
 Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Calcolo differenziale Test di autovalutazione
 Test di autovalutazione 1. Sia f : R R iniettiva, derivabile e tale che f(1) = 3, f (1) = 2, f (3) = 5. Allora (a) (f 1 ) (3) = 1 5 (b) (f 1 ) (3) = 1 2 (c) (f 1 ) (1) = 1 2 (d) (f 1 ) (1) = 1 3 2. Sia
Test di autovalutazione 1. Sia f : R R iniettiva, derivabile e tale che f(1) = 3, f (1) = 2, f (3) = 5. Allora (a) (f 1 ) (3) = 1 5 (b) (f 1 ) (3) = 1 2 (c) (f 1 ) (1) = 1 2 (d) (f 1 ) (1) = 1 3 2. Sia
Registro dell'insegnamento
 Registro dell'insegnamento Anno accademico 2015/2016 Prof. MATTEO FOCARDI Settore inquadramento MAT/05 - ANALISI MATEMATICA REGISTRO Scuola Scienze della Salute Umana NON CHIUSO Dipartimento Matematica
Registro dell'insegnamento Anno accademico 2015/2016 Prof. MATTEO FOCARDI Settore inquadramento MAT/05 - ANALISI MATEMATICA REGISTRO Scuola Scienze della Salute Umana NON CHIUSO Dipartimento Matematica
Esame di Analisi Matematica prova scritta del 23 settembre 2013
 Esame di Analisi Matematica prova scritta del 23 settembre 2013 1. Determinare dominio, limiti significativi, intervalli di monotonia della funzione f (x) = (2x + 3) 2 e x/2 e tracciarne il grafico. In
Esame di Analisi Matematica prova scritta del 23 settembre 2013 1. Determinare dominio, limiti significativi, intervalli di monotonia della funzione f (x) = (2x + 3) 2 e x/2 e tracciarne il grafico. In
CONVESSITÀ NELLA GEOMETRIA DEL TAXI DI MINKOWSKI
 CONVESSITÀ NELLA GEOMETRIA DEL TAXI DI MINKOWSKI ELISABETTA AVIZZANO NICOLETTA CAPOTORTO CHIARA CEROCCHI GIORGIO CICCARELLA IVAN COLAVITA EMANUELE DI CARO SERENA NUNZIATA AMANDA PISELLI ANDREA PIEPOLI
CONVESSITÀ NELLA GEOMETRIA DEL TAXI DI MINKOWSKI ELISABETTA AVIZZANO NICOLETTA CAPOTORTO CHIARA CEROCCHI GIORGIO CICCARELLA IVAN COLAVITA EMANUELE DI CARO SERENA NUNZIATA AMANDA PISELLI ANDREA PIEPOLI
1. Intorni di un punto. Punti di accumulazione.
 1. Intorni di un punto. Punti di accumulazione. 1.1. Intorni circolari. Assumiamo come distanza di due numeri reali x e y il numero non negativo x y (che, come sappiamo, esprime la distanza tra i punti
1. Intorni di un punto. Punti di accumulazione. 1.1. Intorni circolari. Assumiamo come distanza di due numeri reali x e y il numero non negativo x y (che, come sappiamo, esprime la distanza tra i punti
Elementi di topologia della retta
 Elementi di topologia della retta nome insieme definizione l insieme è un concetto primitivo che si accetta come intuitivamente noto secondo George Cantor, il padre della teoria degli insiemi: Per insieme
Elementi di topologia della retta nome insieme definizione l insieme è un concetto primitivo che si accetta come intuitivamente noto secondo George Cantor, il padre della teoria degli insiemi: Per insieme
Lezioni di Ottimizzazione
 Lezioni di Ottimizzazione Italo Capuzzo Dolcetta Flavia Lanzara Dipartimento di Matematica Guido Castelnuovo Sapienza Università di Roma A.A. 2007-2008 Ultimo aggiornamento: October 5, 2007 1 Indice 1
Lezioni di Ottimizzazione Italo Capuzzo Dolcetta Flavia Lanzara Dipartimento di Matematica Guido Castelnuovo Sapienza Università di Roma A.A. 2007-2008 Ultimo aggiornamento: October 5, 2007 1 Indice 1
Geometria Superiore. A.A. 2014/2015 CdL in Matematica Università degli Studi di Salerno. March 2, 2015
 Geometria Superiore A.A. 2014/2015 CdL in Matematica Università degli Studi di Salerno Luca Vitagliano March 2, 2015 Programma Prerequisiti. Spazi affini. Anelli commutativi con unità. Ideali. Anelli quoziente.
Geometria Superiore A.A. 2014/2015 CdL in Matematica Università degli Studi di Salerno Luca Vitagliano March 2, 2015 Programma Prerequisiti. Spazi affini. Anelli commutativi con unità. Ideali. Anelli quoziente.
x log(x) + 3. f(x) =
 Università di Bari, Corso di Laurea in Economia e Commercio Esame di Matematica per l Economia L/Z Dr. G. Taglialatela 03 giugno 05 Traccia dispari Esercizio. Calcolare Esercizio. Calcolare e cos log d
Università di Bari, Corso di Laurea in Economia e Commercio Esame di Matematica per l Economia L/Z Dr. G. Taglialatela 03 giugno 05 Traccia dispari Esercizio. Calcolare Esercizio. Calcolare e cos log d
Se x* e punto di minimo (locale) per la funzione nell insieme Ω, Ω = { x / g i (x) 0 i I, h j (x)= 0 j J } lo e anche per F(x) = f o (x) + c x x 2
 NLP -OPT 1 CONDIZION DI OTTIMO [ Come ricavare le condizioni di ottimo. ] Si suppone x* sia punto di ottimo (minimo) per il problema min f o (x) con vincoli g i (x) 0 i I h j (x) = 0 j J la condizione
NLP -OPT 1 CONDIZION DI OTTIMO [ Come ricavare le condizioni di ottimo. ] Si suppone x* sia punto di ottimo (minimo) per il problema min f o (x) con vincoli g i (x) 0 i I h j (x) = 0 j J la condizione
