EH. Equazioni di Hamilton
|
|
|
- Pasquale Nicolosi
- 5 anni fa
- Visualizzazioni
Transcript
1 EH. Equazioni di Hamilton Iniziamo questo capitolo con un osservazione di carattere preliminare. Consideriamo, per esempio, un sistema differenziale costituito da N equazioni ciascuna del secondo ordine, in forma normale: y h = f h (x, y l, y l), h, l = 1, 2,, N Evidentemente è sempre possibile abbassare l ordine delle equazioni dal secondo al primo, introducendo delle nuove variabili z h uguali alle derivate prime di y h. Si ottiene allora un sistema di 2N equazioni differenziali, ciascuna del primo ordine, equivalente al sistema da cui siamo partiti: y h = z h z h = f h (x, y l, z l ) Si dice allora, che si è passati da una formulazione del secondo ordine ad una formulazione del primo ordine. Questo metodo, qui illustrato mediante un esempio, è del tutto generale e può essere utilizzato per abbassare di un unità l ordine delle equazioni di qualsiasi sistema differenziale dal quale si voglia partire. Osserviamo che l abbassamento dell ordine delle equazioni che compongono un sistema differenziale richiede l introduzione di tante nuove variabili quante sono le variabili incognite del sistema di partenza e il raddoppio del numero di equazioni del sistema, per cui nel suo complesso l ordine del sistema differenziale rimane immutato. Non esiste un unico modo di scegliere le nuove variabili per effettuare la riduzione dell ordine delle equazioni di un sistema. Questo risulta chiaro, in quanto, dopo aver effettuato l abbassamento dell ordine delle equazioni
2 equazioni di Hamilton 151 del sistema nel modo indicato, è sempre lecita un ulteriore trrasformazione regolare di variabili, che lascia immutato l ordine delle equazioni. Formulazione del primo ordine delle equazioni del moto Considerando le equazioni del moto di Lagrange, nella forma in cui esiste la lagrangiana, sappiamo che costituiscono un sistema di equazioni differenziali, ciascuna del secondo ordine, riducibile in forma normale, se si fa eccezione di quei casi degeneri in cui la matrice dell energia cinetica è semidefinita positiva. Si dice, allora che la formulazione lagrangiana del problema del moto di una sistema olonomo è una formulazione del secondo ordine. E possibile passare dalla formulazione del secondo ordine del problema del moto ad una formulazione del primo ordine, introducendo tante nuove variabili quante sono le derivate prime rispetto al tempo dei parametri lagrangiani. Otteniamo così il sistema: q h = v h d dt L v h L q h = 0 (EH.1) Le variabili (q h, v h ) (q h, q h ) si dicono variabili lagrangiane. Come si è osservato prima, però, la scelta delle variabili non è univoca e si può ottenere un sistema di equazioni differenziali equivalente a quello di partenza, a condizione che l ulteriore trasformazione di variabili che si effettua, sia regolare. In particolare una scelta di variabili significativa è quella che utilizza, anzichè le variabili lagrangiane, le variabili (q h, p h ) che vengono dette variabili hamiltoniane o variabili canoniche, dove le nuove variabili: p h = L q h (EH.2)
3 152 A. Strumia, Meccanica razionale sono dette momenti coniugati o momenti canonici. Con questa scelta il sistema assume la forma normale. La regolarità della trasformazione: (q h, v h ) (q h, p h ) è garantita dalla non singolarità della matrice jacobiana della trasformazione: J δ hk 0 p h q k in tutti i punti dello spazio delle variabili (q h, v h ). Condizione che è garantita dalla regolarità della trasformazione che coinvolge le sole variabili che vengono modificate: p h v k v p che equivale a richiedere che il sistema lagrangiano sia riducibile in forma normale: p h det(j ) = det v k = det 2 L v h v k 0, (EH.3) Notiamo che supposto che il potenziale sia ordinario, oppure che l eventuale potenziale generalizzato sia lineare in q, tale condizione equivale alla non singolarità della matrice dell energia cinetica in tutti i punti dello spazio degli eventi nei quali la matrice è definita. Ed essendo la matrice dell energia cinetica definita positiva, questo equivale alla convessità della funzione rispetto alle variabili lagrangiane.
4 equazioni di Hamilton 153 Trasformate di Legendre Il tipo di trasformazione che ci interessa esaminare è ben nota e prende il nome di trasformazione di Legendre. Essa si può caratterizzare nel modo seguente. Consideriamo una funzione differenziabile: f : A R, A R N di classe C (2) almeno. Denotiamo con x (x h ) gli elementi di A e definiamo una seconda funzione: In maniera tale che: g : A A R g(x h, y h ) = x h y h f(x h ) (EH.4) Notiamo che x e y sono variabili indipendenti. Per come è stata definita, la g è essa pure differenziabile e della stessa classe della f. Tra tutte le possibili funzioni del tipo g vogliamo indagare se esiste, e a quali condizioni, una funzione g che sia indipendente da x. Imporre l indipendenza della g da x equivale a richiedere che in ogni punto del dominio sia soddisfatta la condizione: ϕ k (x h, y h ) = y k f x k = 0 (EH.5) che rappresenta un vincolo per le variabili x, y. La funzione g(y h ) = x h y h f(x h ) (EH.6)
5 154 A. Strumia, Meccanica razionale così caratterizzata prende il nome di trasformata di Legendre della f. Per calcolare le derivate parziali della f rispetto a x h, e rispettivamente della g rispetto a y h, le variabili x h e y h vanno trattate come variabili condizionate. Questo significa che differenziando entrambi i membri della (EH.6), in forza del vincolo (EH.5) tra le variabili, si ha: dg = d(x h y h ) df + λ k dϕ k dove sono stati introdotti i moltiplicatori di Lagrange λ k. Sviluppando si ha: g dy h = x h dy h + y h dx h f ϕ k ϕ k dx h + λ k dx h + λ k dy h y h x h x h y h dal momento che la condizione (EH.5) comporta: dϕ k = 0 Data l arbitrarietà di dx h e dy h seguono le condizioni: g y h = x h + λ k ϕ k y h, f x h = y h + λ k ϕ k x h Tenendo conto del vincolo (EH.5) otteniamo i seguenti risultati: g y h = x h, f x h = y h, λ k = 0 a condizione che: ϕ k det x h = det 2 f 0, x h x k x A (EH.7)
6 equazioni di Hamilton 155 Essendo tale matrice non singolare non può avere autovalori nulli e quindi λ k = 0; diversamente esisterebbe un autovettore associato ad un autovalore nullo. Osserviamo anche che la richiesta che la matrice hessiana della f sia non singolare su tutto il dominio A equivale a richiedere che la forma quadratica: 2 f x h x k v h v k 0 sia non nulla per ogni v, in ogni punto di A. Ma se tale forma quadratica non si annulla (essendo f di classe C (2) ) essa ha lo stesso segno in tutto il dominio A, ad esempio, è sempre positiva; allora la condizione equivale a richiedere che la funzione f sia convessa su tutto A. Osserviamo che questa condizione di convessità è anche la condizione che rende legittimo il cambiamento di variabili x y in tutto il dominio A. Possiamo allora passare dalla formulazione di un problema nelle variabili x alla formulazione dello stesso problema nelle variabili y facendo entrare in gioco la trasformata di Legendre g che dipende solo da y in luogo della f che dipende da x. Equazioni di Hamilton L applicazione della trasformazione di Legendre: v p al sistema delle equazioni del moto (EH.1) comporta l introduzione della trasformata di Legendre della lagrangiana: H = v h p h L (EH.8)
7 156 A. Strumia, Meccanica razionale che prende il nome di funzione di Hamilton o hamiltoniana, la quale dipende da p invece che da v, oltre che, naturalmente dalle variabili q che non vengono coinvolte nella trasformazione, ed eventualmente dal tempo: H(q h, p h, t) = v h p h L(q h, v h, t) Si ha allora, in base ai risultati del paragrafo precedente: H p h = v h, L v h = p h (EH.9) Dobbiamo poi tenere conto che le funzioni H e L dipendono anche da q, t e quindi, grazie alla (EH.8) si ha: H = L, q h q h H t = L t (EH.10) Introducendo i risultati (EH.9) e (EH.10) nel sistema di equazioni del primo ordine (EH.1) otteniamo le equazioni di Hamilton o equazioni canoniche: q h = H p h, ṗ h = H q h (EH.11) Osserviamo che l equivalenza tra la formulazione lagrangiana e la formulazione hamiltoniana delle equazioni del moto, è garantita a condizione che il sistema delle equazioni del moto dal quale si parte sia riducibile in forma normale. Per sistemi non riducibili in forma normale le due formulazioni non si equivalgono, per cui possono esistere sistemi meccanici che ammettono la trattazione lagrangiana e non quella hamiltoniana o viceversa.
8 equazioni di Hamilton 157 Integrale generale e integrali particolari del moto Si estendono, come al solito, anche per le equazioni di Hamilton i concetti di integrale generale del moto e di integrale particolare del moto. Si dice integrale generale del moto l integrale generale del sistema delle equazioni canoniche, cioè la famiglia delle 2N soluzioni del sistema (EH.11), caratterizzata da 2N costanti, tante quanto è l ordine del sistema differenziale. L integrale generale si può rappresentare come: q h = q h (t, c 1, c 2,, c 2N ) p h = p h (t, c 1, c 2,, c 2N ) (EH.12) Si dice integrale particolare del moto un integrale particolare del sistema differenziale delle equazioni canoniche, cioè una delle soluzioni che si ottiene assegnando un valore particolare a ciascuna delle 2N costanti c 1, c 2,, c 2N, ovvero assegnando le condizioni iniziali per le variabili canoniche q h, p h. Integrale primo del moto Una funzione: ψ = ψ(q 1, q 2,, q N, p 1, p 2,, p N, t) si dice integrale primo del moto quando, sostituendo in essa alle variabili q h, p h le funzioni q h (t), p h (t) che rappresentano un integrale particolare del moto, la funzione ψ assume un valore costante nel tempo: ψ(q 1 (t), q 2 (t),, q N (t), p 1 (t), p 2 (t),, p N (t), t) = C, t
9 158 A. Strumia, Meccanica razionale Il valore della costante può essere calcolato facilmente utilizzando le condizioni iniziali, grazie al fatto che ψ mantiene in ogni istante il valore iniziale. Coordinate cicliche o ignorabili Una coordinata canonica q h si dice coordinata ciclica o ignorabile, per un sistema governato dall hamiltoniana H, se non compare nell hamiltoniana, ma compare solamente il suo momento coniugato p h. Di conseguenza dalle equazioni di Hamilton si ottiene: ṗ h = 0 p h = costante Ad ogni coordinata ciclica viene quindi a corrispondere un integrale primo del moto. Notiamo che se una coordinata q h è ciclica per la lagrangiana, essa risulta ciclica anche per l hamiltoniana e viceversa. Infatti si ha: H q h = L q h = 0 Parentesi di Poisson e integrali primi del moto Consideriamo una funzione differenziabile delle variabili canoniche ed eventualmente del tempo: ψ = ψ(q l, p l, t) E ci domandiamo a quali condizioni questa funzione può essere un integrale primo del moto. A questo scopo dobbiamo richiedere che:
10 equazioni di Hamilton 159 dψ dt (q l, p l, t) = ψ q h + ψ ṗ h + ψ q h p h t = 0 Eliminando q h, ṗ h mediante le equazioni di Hamilton ricaviamo: dψ dt (q l, p l, t) = ψ H ψ H + ψ q h p h p h q h t = 0 Introducendo le parentesi di Poisson definite, per ogni coppia di funzioni differenziabili delle variabili hamiltoniane f, g ed eventualmente del tempo, come: [f, g] = f q h g p h f p h g q h (EH.13) si può riscrivere: dψ dt (q l, p l, t) = [ψ, H] + ψ t = 0 Osserviamo, in particolare, che quando la funzione ψ non dipende esplicitamente dal tempo, cioè si ha: ψ t = 0 la condizione affinchè una funzione delle sole variabili canoniche sia un integrale primo del moto si riduce a richiedere che si annulli la sua parentesi di Poisson con l hamiltoniana: dψ dt (q l, p l ) = [ψ, H] = 0
11 160 A. Strumia, Meccanica razionale Si osserva ancora che qualora la funzione ψ sia l hamiltoniana stessa si ha: dh dt = [H, H] + H t = H t = 0 L hamiltoniana, dunque, risulta essere un integrale primo del moto se e solo se non dipende esplicitamente dal tempo. Grazie alla seconda delle (EH.10) sappiamo che questo equivale a richiedere che la lagrangiana non dipenda esplicitamente del tempo. Facendo uso delle parentesi di Poisson è possibile riscrivere in una nuova forma le equazioni canoniche. Si ha infatti: q h = [q h, H] ṗ h = [p h, H] (EH.14) Questa forma ha il vantaggio di eliminare il segno negativo, dando un aspetto simmetrico alle equazioni. Hamiltoniana L hamiltoniana è stata definita come trasformata di Legendre della lagrangiana mediante la (EH.8) che possiamo riscrivere in termini delle usuali notazioni: H = q h p h L essendo: L = T + U
12 equazioni di Hamilton 161 Per calcolare esplicitamente l espressione di H ricordiamo che l energia cinetica di un sistema olonomo si può scrivere nella forma: dove: T = T 0 + T 1 + T 2 T 0 = d, T 1 = b h q h, T 2 = 1 2 a hk q h q k E il potenziale (generalizzato) si può scrivere: Allora abbiamo: U = U 0 + U 1, U 0 = g, U 1 = f h q h Quindi: p h = a hk q k + b h + f h Segue: q h p h = a hk q h q k + b h q h + f h q h = 2T 2 + T 1 + U 1 H = T 2 T 0 U 0 (EH.15) A questo stesso risultato si può giungere anche facendo uso della formula di Eulero per le funzioni omogenee di grado n: x i f x i = n f (EH.16)
13 162 A. Strumia, Meccanica razionale essendo f = f(x i ) una funzione omogenea, a valori reali, di grado n delle variabili x i. Nel nostro caso le funzioni T 2, T 1, T 0 sono omogenee nelle variabili q h di gradi rispettivi 2, 1, 0, e le funzioni U1, U 0 sono funzioni omogenee delle stesse variabili di gradi rispettivi 1, 0. Di conseguenza si ottiene: E quindi: q h p h = q h L q h = 2 T 2 + T 1 + U 1 H = q h p h L = 2 T 2 + T 1 + U 1 (T 2 + T 1 + T 0 + U 1 + U 0 ) = T 2 T 0 U 0 Quando i vincoli sono indipendenti dal tempo, come è stato evidenziato nel capitolo relativo alla cinematica delle masse, abbiamo che: T 0 = 0, T 1 = 0 = T = T 2 Di conseguenza l espressione dell hamiltoniana si specializza come: H = T U 0 (EH.17) Come conseguenza abbiamo il seguente risultato: Quando i vincoli sono indipendenti dal tempo e il potenziale è ordinario, cioè le forze sono conservative, l hamiltoniana coincide con l energia meccanica del sistema ed è un integrale primo del moto. Infatti se il potenziale è ordinario si ha U = U 0 e la (EH.17) diviene: H = T U = T + V = E (EH.18)
14 equazioni di Hamilton 163 Inoltre, essendo i vincoli indipendenti dal tempo, sia T che U non dipendono dal tempo, perciò H non dipende esplicitamente dal tempo ed è quindi un integrale primo del moto, che coincide con l integrale primo dell energia. L hamiltoniana viene perciò considerata come una funzione che generalizza il concetto di energia meccanica. Formulazione mista: funzione di Routh Si chiama funzione di Routh la trasformata di Legendre ridotta alle prime M, con M < N variabili: R = M h=1 q h p h L (EH.19) Una simile funzione si comporta come un hamiltoniana rispetto alle prime M coordinate generalizzate q h e come una lagrangiana rispetto alle restanti N M coordinate. Essa viene a dipendere, infatti dalle variabili nel modo seguente: R = R(q 1, q 2, q N, p 1, p 2,, p M, q M+1, q M+2,, q N, t) Le equazioni del moto del sistema sono allora date da un sistema misto di equazioni di Hamilton e di equazioni di Lagrange: q h = R p h ṗ h = R q h, h = 1, 2, M (EH.20) d dt R q h R q h = 0, h = M + 1, M + 2,, N
15 164 A. Strumia, Meccanica razionale Un formulazione mista di questo tipo può essere particolarmente conveniente quando le prime M variabili sono cicliche, perchè, in questo caso i primi M momenti coniugati sono già determinati, in quanto sono integrali primi del moto e la funzione di Routh viene a dipendere, durante il moto, da M costanti e solo dalle ultime N M coordinate lagrangiane, dalle loro derivate prime e dal tempo, come se il problema avesse N M gradi di libertà: R = R(q M + 1, q N, p 1 (0),, p M (0), q M+1,, q N, t) Quindi il sistema delle N M equazioni di tipo lagrangiano risulta disaccoppiato.
Equazioni di Hamilton
 Equazioni di Hamilton Osservazione di carattere preliminare Consideriamo un sistema differenziale costituito da N equazioni ciascuna del secondo ordine, in forma normale: y h = f h (x, y l, y l), h, l
Equazioni di Hamilton Osservazione di carattere preliminare Consideriamo un sistema differenziale costituito da N equazioni ciascuna del secondo ordine, in forma normale: y h = f h (x, y l, y l), h, l
Richiami di Meccanica Classica
 Richiami di Meccanica Classica Corso di Fisica Matematica 3 (seconda parte), a.a. 2016/17 G. Gaeta 18/4/2017 Questa dispensa, che va vista in connessione a quella sul principio variazionale e la formulazione
Richiami di Meccanica Classica Corso di Fisica Matematica 3 (seconda parte), a.a. 2016/17 G. Gaeta 18/4/2017 Questa dispensa, che va vista in connessione a quella sul principio variazionale e la formulazione
Metodi multiscala per le fasi condensate
 p. 1/2 Metodi multiscala per le fasi condensate Cenni di meccanica razionale - II Antonino Polimeno antonino.polimeno@unipd.it Università degli Studi di Padova Dipartimento di Scienze Chimiche p. 2/2 Lagrange
p. 1/2 Metodi multiscala per le fasi condensate Cenni di meccanica razionale - II Antonino Polimeno antonino.polimeno@unipd.it Università degli Studi di Padova Dipartimento di Scienze Chimiche p. 2/2 Lagrange
EL. Equazioni di Lagrange
 EL. Equazioni di Lagrange Abbiamo seguito, finora, un certo parallelismo fra il modo di trattare la statica e la dinamica: siamo riusciti a stabilire, per il punto materiale, la condizione di equilibrio
EL. Equazioni di Lagrange Abbiamo seguito, finora, un certo parallelismo fra il modo di trattare la statica e la dinamica: siamo riusciti a stabilire, per il punto materiale, la condizione di equilibrio
7.9 Il caso vincolato: vincoli di disuguaglianza
 7.9 Il caso vincolato: vincoli di disuguaglianza Il problema con vincoli di disuguaglianza: g i (x) 0, i = 1,..., p, (51) o, in forma vettoriale: g(x) 0, può essere trattato basandosi largamente su quanto
7.9 Il caso vincolato: vincoli di disuguaglianza Il problema con vincoli di disuguaglianza: g i (x) 0, i = 1,..., p, (51) o, in forma vettoriale: g(x) 0, può essere trattato basandosi largamente su quanto
SO. Stabilità e piccole oscillazioni
 SO. Stabilità e piccole oscillazioni L argomento della stabilità, nato nell ambito della meccanica, ai fini di fornire dei criteri matematici per formalizzare la nozione intuitiva di stabilità di una configurazione
SO. Stabilità e piccole oscillazioni L argomento della stabilità, nato nell ambito della meccanica, ai fini di fornire dei criteri matematici per formalizzare la nozione intuitiva di stabilità di una configurazione
FORMALISMO LAGRANGIANO PER SISTEMI VINCOLATI (Schema del contenuto delle lezioni e riferimenti bibliografici)
 FORMALISMO LAGRANGIANO PER SISTEMI VINCOLATI (Schema del contenuto delle lezioni e riferimenti bibliografici) 1. Vincoli e principio di D Alembert (vd. Fasano Marmi cap 1 (o anche Dell Antonio cap. 6,
FORMALISMO LAGRANGIANO PER SISTEMI VINCOLATI (Schema del contenuto delle lezioni e riferimenti bibliografici) 1. Vincoli e principio di D Alembert (vd. Fasano Marmi cap 1 (o anche Dell Antonio cap. 6,
TC. Trasformazioni canoniche
 TC. Trasformazioni canoniche Funzione generatrice Consideriamo le equazioni di Hamilton: q h = H, ṗ h = H (TC.1) per le variabili canoniche q h, p h, relative ad un hamiltoniana generica H(q h, p h, t),
TC. Trasformazioni canoniche Funzione generatrice Consideriamo le equazioni di Hamilton: q h = H, ṗ h = H (TC.1) per le variabili canoniche q h, p h, relative ad un hamiltoniana generica H(q h, p h, t),
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Edile ed Edile/Architettura. Geometria Proiettiva Docente F.
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Edile ed Edile/Architettura Geometria Proiettiva Docente F. Flamini CONICHE PROIETTIVE: Classificazione e forme canoniche proiettive Si
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Edile ed Edile/Architettura Geometria Proiettiva Docente F. Flamini CONICHE PROIETTIVE: Classificazione e forme canoniche proiettive Si
Università degli Studi di Roma La Sapienza
 Università degli Studi di Roma La Sapienza Dipartimento di Informatica e Sistemistica A. Ruberti Proff. Gianni Di Pillo and Laura Palagi Note per il corso di OTTIMIZZAZIONE (a.a. 2007-08) Dipartimento
Università degli Studi di Roma La Sapienza Dipartimento di Informatica e Sistemistica A. Ruberti Proff. Gianni Di Pillo and Laura Palagi Note per il corso di OTTIMIZZAZIONE (a.a. 2007-08) Dipartimento
Estremi liberi. (H x, x) x 2 (1) F (x) =
 Estremi liberi Allo scopo di ottenere delle condizioni sufficienti affinchè un punto stazionario sia un estremante, premettiamo alcuni risultati riguardanti le proprietà delle forme quadratiche. Sia H
Estremi liberi Allo scopo di ottenere delle condizioni sufficienti affinchè un punto stazionario sia un estremante, premettiamo alcuni risultati riguardanti le proprietà delle forme quadratiche. Sia H
Sistemi dinamici-parte 2 Parentesi di Poisson e trasformazioni canoniche
 Sistemi dinamici-parte 2 Parentesi di e trasformazioni AM Cherubini 11 Maggio 2007 1 / 25 Analogamente a quanto fatto per i sistemi lagrangiani occorre definire, insieme alla struttura del sistema, anche
Sistemi dinamici-parte 2 Parentesi di e trasformazioni AM Cherubini 11 Maggio 2007 1 / 25 Analogamente a quanto fatto per i sistemi lagrangiani occorre definire, insieme alla struttura del sistema, anche
DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA
 DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA Sia dato un sistema con vincoli lisci, bilaterali e FISSI. Ricaviamo, dall equazione simbolica della dinamica, il teorema
DEDUZIONE DEL TEOREMA DELL'ENERGIA CINETICA DELL EQUAZIONE SIMBOLICA DELLA DINAMICA Sia dato un sistema con vincoli lisci, bilaterali e FISSI. Ricaviamo, dall equazione simbolica della dinamica, il teorema
Polinomio di Taylor del secondo ordine per funzioni di due variabili
 Esercitazioni del 15 aprile 2013 Polinomio di Taylor del secondo ordine per funzioni di due variabili Sia f : A R 2 R una funzione di classe C 2. Fissato un p unto (x 0, y 0 A consideriamo il seguente
Esercitazioni del 15 aprile 2013 Polinomio di Taylor del secondo ordine per funzioni di due variabili Sia f : A R 2 R una funzione di classe C 2. Fissato un p unto (x 0, y 0 A consideriamo il seguente
Le derivate parziali
 Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Sia f(x, y) una funzione definita in un insieme aperto A R 2 e sia P 0 = x 0, y 0 un punto di A. Essendo A un aperto, esiste un intorno I(P 0, δ) A. Preso un punto P(x, y) I(P 0, δ), P P 0, possiamo definire
Punti di massimo o di minimo per funzioni di n variabili reali
 Punti di massimo o di minimo per funzioni di n variabili reali Dati f : A R n R ed X 0 A, X 0 si dice : punto di minimo assoluto se X A, f ( x ) f ( X 0 ) punto di massimo assoluto se X A, f ( x ) f (
Punti di massimo o di minimo per funzioni di n variabili reali Dati f : A R n R ed X 0 A, X 0 si dice : punto di minimo assoluto se X A, f ( x ) f ( X 0 ) punto di massimo assoluto se X A, f ( x ) f (
Allora esistono δ > 0 e σ > 0 tali che. f(x, y) = 0; (2) la funzione ϕ : ]x 0 δ, x 0 + δ [ R, y = ϕ(x), è derivabile e.
![Allora esistono δ > 0 e σ > 0 tali che. f(x, y) = 0; (2) la funzione ϕ : ]x 0 δ, x 0 + δ [ R, y = ϕ(x), è derivabile e. Allora esistono δ > 0 e σ > 0 tali che. f(x, y) = 0; (2) la funzione ϕ : ]x 0 δ, x 0 + δ [ R, y = ϕ(x), è derivabile e.](/thumbs/96/129204172.jpg) 16 42 Funzioni implicite Il seguente teorema fornisce una condizione sufficiente affinché, data un equazione della forma f(x, ) = 0, sia possibile determinare come funzione della x Teo 11 (Teorema della
16 42 Funzioni implicite Il seguente teorema fornisce una condizione sufficiente affinché, data un equazione della forma f(x, ) = 0, sia possibile determinare come funzione della x Teo 11 (Teorema della
19 Marzo Equazioni differenziali.
 19 Marzo 2019 Equazioni differenziali. Definizione 1. Si chiama equazione differenziale una relazione che coinvolge una o più derivate di una funzione incognita y(x), la funzione stessa, funzioni di x
19 Marzo 2019 Equazioni differenziali. Definizione 1. Si chiama equazione differenziale una relazione che coinvolge una o più derivate di una funzione incognita y(x), la funzione stessa, funzioni di x
0.1 Forme quadratiche
 0.1. FORME QUADRATICHE 1 0.1 Forme quadratiche In questa sezione possiamo applicare il Teorema degli Assi Principali per giustificare alcune fatti che sono stati utilizzati nella riduzione a forma canonica
0.1. FORME QUADRATICHE 1 0.1 Forme quadratiche In questa sezione possiamo applicare il Teorema degli Assi Principali per giustificare alcune fatti che sono stati utilizzati nella riduzione a forma canonica
Compito del 14 giugno 2004
 Compito del 14 giugno 004 Un disco omogeneo di raggio R e massa m rotola senza strisciare lungo l asse delle ascisse di un piano verticale. Il centro C del disco è collegato da una molla di costante elastica
Compito del 14 giugno 004 Un disco omogeneo di raggio R e massa m rotola senza strisciare lungo l asse delle ascisse di un piano verticale. Il centro C del disco è collegato da una molla di costante elastica
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica. Corso di Geometria ed Algebra Docente F. Flamini
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica Corso di Geometria ed Algebra Docente F. Flamini Capitolo IV - 3: Teorema Spettrale degli operatori autoaggiunti e Teorema
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica Corso di Geometria ed Algebra Docente F. Flamini Capitolo IV - 3: Teorema Spettrale degli operatori autoaggiunti e Teorema
Compito di gennaio 2001
 Compito di gennaio 001 Un asta omogenea A di massa m e lunghezza l è libera di ruotare attorno al proprio estremo mantenendosi in un piano verticale All estremità A dell asta è saldato il baricentro di
Compito di gennaio 001 Un asta omogenea A di massa m e lunghezza l è libera di ruotare attorno al proprio estremo mantenendosi in un piano verticale All estremità A dell asta è saldato il baricentro di
EQUAZIONI DI LAGRANGE E STAZIONARIETÀ DEL POTENZIALE
 EQUAZIONI DI LAGRANGE E STAZIONARIETÀ DEL POTENZIALE Equazioni di Lagrange in forma non conservativa Riprendiamo l equazione simbolica della dinamica per un sistema olonomo a vincoli perfetti nella forma
EQUAZIONI DI LAGRANGE E STAZIONARIETÀ DEL POTENZIALE Equazioni di Lagrange in forma non conservativa Riprendiamo l equazione simbolica della dinamica per un sistema olonomo a vincoli perfetti nella forma
FM210 / MA - Secondo scritto ( )
 FM10 / MA - Secondo scritto (6-7-017) Esercizio 1. Un asta rigida omogenea di lunghezza l e massa M è vincolata a muoversi su un piano verticale di coordinate x-y (con l asse x orizzontale e l asse y verticale,
FM10 / MA - Secondo scritto (6-7-017) Esercizio 1. Un asta rigida omogenea di lunghezza l e massa M è vincolata a muoversi su un piano verticale di coordinate x-y (con l asse x orizzontale e l asse y verticale,
Equazioni differenziali
 Equazioni differenziali Generalità sulle equazioni differenziali ordinarie del primo ordine Si chiama equazione differenziale ordinaria[ ] del primo ordine un equazione nella quale compare y = y e la sua
Equazioni differenziali Generalità sulle equazioni differenziali ordinarie del primo ordine Si chiama equazione differenziale ordinaria[ ] del primo ordine un equazione nella quale compare y = y e la sua
Le equazioni di Lagrange
 Prof. Ettore Pennestrì Dipartimento di Ingegneria dell Impresa Università Roma Tor Vergata Cenni di calcolo variazionale Testi consigliati per approfondimenti Lanczos, C, The Variational Principles of
Prof. Ettore Pennestrì Dipartimento di Ingegneria dell Impresa Università Roma Tor Vergata Cenni di calcolo variazionale Testi consigliati per approfondimenti Lanczos, C, The Variational Principles of
I teoremi della funzione inversa e della funzione implicita
 I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
I teoremi della funzione inversa e della funzione implicita Appunti per il corso di Analisi Matematica 4 G. Mauceri Indice 1 Il teorema della funzione inversa 1 Il teorema della funzione implicita 3 1
Le condizioni di Karush-Kuhn-Tucker
 Capitolo 9 Le condizioni di Karush-Kuhn-Tucker 9. Introduzione In questo capitolo deriveremo le condizioni necessarie di Karush-Kuhn-Tucker (KKT) per problemi vincolati in cui S è descritto da vincoli
Capitolo 9 Le condizioni di Karush-Kuhn-Tucker 9. Introduzione In questo capitolo deriveremo le condizioni necessarie di Karush-Kuhn-Tucker (KKT) per problemi vincolati in cui S è descritto da vincoli
7.4 Massimi e minimi vincolati. Moltiplicatori di Lagrange
 4 7.4 Massimi e minimi vincolati. Moltiplicatori di Lagrange Sia f (,,, n ) una funzione delle n variabili,,, n, supponiamo che esse non siano indipendenti, cioè che siano legate da p < n equazioni: ϕ(,,,
4 7.4 Massimi e minimi vincolati. Moltiplicatori di Lagrange Sia f (,,, n ) una funzione delle n variabili,,, n, supponiamo che esse non siano indipendenti, cioè che siano legate da p < n equazioni: ϕ(,,,
7.5 Il caso vincolato: preliminari
 7.5 Il caso vincolato: preliari Consideriamo ora il problema vincolato 3, che qui riscriviamo: fx gx 0 hx = 0, 13 con g : IR n IR p e h : IR n IR m, m n. Ricordiamo che F = {x IR n : gx 0, hx = 0}, denota
7.5 Il caso vincolato: preliari Consideriamo ora il problema vincolato 3, che qui riscriviamo: fx gx 0 hx = 0, 13 con g : IR n IR p e h : IR n IR m, m n. Ricordiamo che F = {x IR n : gx 0, hx = 0}, denota
Analisi Matematica III modulo Soluzioni della prova scritta preliminare n. 2
 Analisi Matematica III modulo Soluzioni della prova scritta preliminare n. Corso di laurea in Matematica, a.a. 003-004 17 dicembre 003 1. Si consideri la funzione f : R R definita da f(x, y) = x 4 y arctan
Analisi Matematica III modulo Soluzioni della prova scritta preliminare n. Corso di laurea in Matematica, a.a. 003-004 17 dicembre 003 1. Si consideri la funzione f : R R definita da f(x, y) = x 4 y arctan
Esercizi per Geometria II Geometria euclidea e proiettiva
 Esercizi per Geometria II Geometria euclidea e proiettiva Filippo F. Favale 8 aprile 014 Esercizio 1 Si consideri E dotato di un riferimento cartesiano ortonormale di coordinate (x, y) e origine O. Si
Esercizi per Geometria II Geometria euclidea e proiettiva Filippo F. Favale 8 aprile 014 Esercizio 1 Si consideri E dotato di un riferimento cartesiano ortonormale di coordinate (x, y) e origine O. Si
Cognome Nome Matricola Codice ESEMPIO 1
 Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
Cognome Nome Matricola Codice ESEMPIO 1 [1]. (***) Definizione di derivata di una funzione in un punto. Sia A R N ; sia a A; sia f : A R M ; sia f differenziabile in a; allora la derivata di f in a è...
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del f(x, y) = x 2 + 2y 2 x 3 y 3
 Analisi Matematica II Corso di Ingegneria Gestionale Compito A del 7-7-8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito A del 7-7-8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
II Università degli Studi di Roma
 Versione preliminare dicembre 200 TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 8. Quadriche in R 3. In questo paragrafo studiamo le quadriche in R 3. Definizione. Una
Versione preliminare dicembre 200 TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 8. Quadriche in R 3. In questo paragrafo studiamo le quadriche in R 3. Definizione. Una
Cinematica delle masse
 Cinematica delle masse CM. Cinematica delle masse In questo capitolo introduciamo i concetti di quantità di moto, momento della quantità di moto e di energia cinetica, e sviluppiamo i teoremi ad essi relativi,
Cinematica delle masse CM. Cinematica delle masse In questo capitolo introduciamo i concetti di quantità di moto, momento della quantità di moto e di energia cinetica, e sviluppiamo i teoremi ad essi relativi,
1 Ampliamento del piano e coordinate omogenee
 1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
Note sulle funzioni convesse/concave
 Note sulle funzioni convesse/concave 4th December 2008 1 Definizioni e proprietà delle funzioni convesse/concave. Definizione 1.1 Un insieme A IR n è detto convesso se per ogni x 1 e x 2 punti di A, il
Note sulle funzioni convesse/concave 4th December 2008 1 Definizioni e proprietà delle funzioni convesse/concave. Definizione 1.1 Un insieme A IR n è detto convesso se per ogni x 1 e x 2 punti di A, il
Statica. Basilio Bona. DAUIN-Politecnico di Torino. Basilio Bona (DAUIN-Politecnico di Torino) Statica / 16
 Statica Basilio Bona DAUIN-Politecnico di Torino 2008 Basilio Bona (DAUIN-Politecnico di Torino) Statica 2008 1 / 16 Statica - Introduzione La statica studia le relazioni di equilibrio e/o di equivalenza
Statica Basilio Bona DAUIN-Politecnico di Torino 2008 Basilio Bona (DAUIN-Politecnico di Torino) Statica 2008 1 / 16 Statica - Introduzione La statica studia le relazioni di equilibrio e/o di equivalenza
LEZIONE 23. ax 2 + bxy + cy 2 + dx + ey + f
 LEZIONE 23 23.1. Riduzione delle coniche a forma canonica. Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y a meno di costanti moltiplicative non nulle, diciamo
LEZIONE 23 23.1. Riduzione delle coniche a forma canonica. Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y a meno di costanti moltiplicative non nulle, diciamo
0.1 Spazi Euclidei in generale
 0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
0.1. SPAZI EUCLIDEI IN GENERALE 1 0.1 Spazi Euclidei in generale Sia V uno spazio vettoriale definito su R. Diremo, estendendo una definizione data in precedenza, che V è uno spazio vettoriale euclideo
Geometria A. Università degli Studi di Trento Corso di laurea in Matematica A.A. 2017/ Maggio 2018 Prova Intermedia
 Geometria A Università degli Studi di Trento Corso di laurea in Matematica A.A. 7/8 Maggio 8 Prova Intermedia Il tempo per la prova è di ore. Durante la prova non è permesso l uso di appunti e libri. Esercizio
Geometria A Università degli Studi di Trento Corso di laurea in Matematica A.A. 7/8 Maggio 8 Prova Intermedia Il tempo per la prova è di ore. Durante la prova non è permesso l uso di appunti e libri. Esercizio
Funzioni implicite - Esercizi svolti
 Funzioni implicite - Esercizi svolti Esercizio. È data la funzione di due variabili F (x, y) = y(e y + x) log x. Verificare che esiste un intorno I in R del punto di ascissa x 0 = sul quale è definita
Funzioni implicite - Esercizi svolti Esercizio. È data la funzione di due variabili F (x, y) = y(e y + x) log x. Verificare che esiste un intorno I in R del punto di ascissa x 0 = sul quale è definita
Funzioni di n variabili a valori vettoriali
 Funzioni di n variabili a valori vettoriali Ultimo aggiornamento: 22 maggio 2018 1 Differenziale per funzioni da R n in R k Una funzione F : A R n R k può essere vista come una k-upla di funzioni scalari
Funzioni di n variabili a valori vettoriali Ultimo aggiornamento: 22 maggio 2018 1 Differenziale per funzioni da R n in R k Una funzione F : A R n R k può essere vista come una k-upla di funzioni scalari
Compito di gennaio 2005
 Compito di gennaio 2005 In un piano verticale, si consideri il vincolo mobile costituito da una semicirconferenza di raggio R e centro C, i cui estremi A e B possono strisciare lungo l asse delle ascisse:
Compito di gennaio 2005 In un piano verticale, si consideri il vincolo mobile costituito da una semicirconferenza di raggio R e centro C, i cui estremi A e B possono strisciare lungo l asse delle ascisse:
Parte 12b. Riduzione a forma canonica
 Parte 2b. Riduzione a forma canonica A. Savo Appunti del Corso di Geometria 202-3 Indice delle sezioni. Coniche, 2. Esempio di riduzione, 4 3. Teoremi fondamentali, 6 4. Come determinare l equazione canonica,
Parte 2b. Riduzione a forma canonica A. Savo Appunti del Corso di Geometria 202-3 Indice delle sezioni. Coniche, 2. Esempio di riduzione, 4 3. Teoremi fondamentali, 6 4. Come determinare l equazione canonica,
Appunti di Geometria - 2
 Appunti di Geometria - Samuele Mongodi - s.mongodi@sns.it Cambi di base e applicazioni lineari Richiami Sia V uno spazio vettoriale di dimensione n sul campo K, con base assegnata e,..., e n } (ad esempio
Appunti di Geometria - Samuele Mongodi - s.mongodi@sns.it Cambi di base e applicazioni lineari Richiami Sia V uno spazio vettoriale di dimensione n sul campo K, con base assegnata e,..., e n } (ad esempio
1. Funzioni implicite
 1. Funzioni implicite 1.1 Il caso scalare Sia X R 2 e sia f : X R. Una funzione y : (a, b) R si dice definita implicitamente dall equazione f(x, y) = 0 in (a, b) quando: 1. (x, y(x)) X x (a, b); 2. f(x,
1. Funzioni implicite 1.1 Il caso scalare Sia X R 2 e sia f : X R. Una funzione y : (a, b) R si dice definita implicitamente dall equazione f(x, y) = 0 in (a, b) quando: 1. (x, y(x)) X x (a, b); 2. f(x,
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Tabella 1: Best 5 out of 6 es.1 es.2 es.3 es.4 es.5 es.6 somma Meccanica Razionale 1: Scritto Generale
 Tabella 1: Best 5 out of 6 es.1 es.2 es.3 es.4 es.5 es.6 somma 5 5 5 5 5 5 30 Meccanica Razionale 1: Scritto Generale 02.02.2011 Cognome e nome:....................................matricola:......... 1.
Tabella 1: Best 5 out of 6 es.1 es.2 es.3 es.4 es.5 es.6 somma 5 5 5 5 5 5 30 Meccanica Razionale 1: Scritto Generale 02.02.2011 Cognome e nome:....................................matricola:......... 1.
Matematica Finanziaria 29 novembre 2000
 Matematica Finanziaria 29 novembre 2000 Ottimizzazione. Cognome Nome FILA A ESERCIZIO 1: Gestione del rischio a) Ricavare l espressione del vettore dei coe cienti nella tecnica dei minimi quadrati. b)
Matematica Finanziaria 29 novembre 2000 Ottimizzazione. Cognome Nome FILA A ESERCIZIO 1: Gestione del rischio a) Ricavare l espressione del vettore dei coe cienti nella tecnica dei minimi quadrati. b)
Analisi Matematica II - INGEGNERIA Gestionale - B 20 luglio 2017 Cognome: Nome: Matricola:
 Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
Analisi Matematica II - INGEGNERIA Gestionale - B luglio 7 Cognome: Nome: Matricola: IMPORTANTE: Giustificare tutte le affermazioni e riportare i calcoli essenziali Esercizio [8 punti] Data la matrice
Note sull algoritmo di Gauss
 Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
LUISS Laurea specialistica in Economia e Finanza Anno Accademico 2010/2011
 LUISS Laurea specialistica in Economia e Finanza Anno Accademico 1/11 Corso di Metodi Matematici per la Finanza Prof. Fausto Gozzi, Dr. Davide Vergni Soluzioni esercizi 4,5,6 esame scritto del 13/9/11
LUISS Laurea specialistica in Economia e Finanza Anno Accademico 1/11 Corso di Metodi Matematici per la Finanza Prof. Fausto Gozzi, Dr. Davide Vergni Soluzioni esercizi 4,5,6 esame scritto del 13/9/11
II Università degli Studi di Roma
 Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
Sistemi di equazioni differenziali
 Capitolo 5 Sistemi di equazioni differenziali Molti problemi sono governati non da una singola equazione differenziale, ma da un sistema di più equazioni. Ad esempio questo succede se si vuole descrivere
Capitolo 5 Sistemi di equazioni differenziali Molti problemi sono governati non da una singola equazione differenziale, ma da un sistema di più equazioni. Ad esempio questo succede se si vuole descrivere
Corso di Geometria Meccanica, Elettrotecnica Esercizi 11: soluzioni
 Corso di Geometria 0- Meccanica Elettrotecnica Esercizi : soluzioni Esercizio Scrivere la matrice canonica di ciascuna delle seguenti trasformazioni lineari del piano: a) Rotazione di angolo π b) Rotazione
Corso di Geometria 0- Meccanica Elettrotecnica Esercizi : soluzioni Esercizio Scrivere la matrice canonica di ciascuna delle seguenti trasformazioni lineari del piano: a) Rotazione di angolo π b) Rotazione
Il vettore velocità angolare (avendo scelto θ come in Figura) si scrive come:
 9 Moti rigidi notevoli In questo capitolo consideriamo alcuni esempi particolarmente significativi di moto di un sistema rigido. Quelle che seguono sono applicazioni delle equazioni cardinali di un sistema
9 Moti rigidi notevoli In questo capitolo consideriamo alcuni esempi particolarmente significativi di moto di un sistema rigido. Quelle che seguono sono applicazioni delle equazioni cardinali di un sistema
Analisi 4 - SOLUZIONI (compito del 29/09/2011)
 Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
FUNZIONI DI DUE VARIABILI REALI. f(x, y) = ax + by + c. f(x, y) = x 2 + y 2
 0.1 FUNZIONI DI DUE VARIABILI REALI Sia A R 2. Una applicazione f : A R si chiama funzione reale di due variabili reali ESEMPI: 1. La funzione affine di due variabili reali: 2. f(x, y) = ax + by + c f(x,
0.1 FUNZIONI DI DUE VARIABILI REALI Sia A R 2. Una applicazione f : A R si chiama funzione reale di due variabili reali ESEMPI: 1. La funzione affine di due variabili reali: 2. f(x, y) = ax + by + c f(x,
Esercitazioni di Geometria A: curve algebriche
 Esercitazioni di Geometria A: curve algebriche 24-25 maggio 2016 Esercizio 1 Sia P 2 il piano proiettivo complesso munito delle coordinate proiettive (x 0 : x 1 : x 2 ). Sia r la retta proiettiva di equazione
Esercitazioni di Geometria A: curve algebriche 24-25 maggio 2016 Esercizio 1 Sia P 2 il piano proiettivo complesso munito delle coordinate proiettive (x 0 : x 1 : x 2 ). Sia r la retta proiettiva di equazione
Φ D 2 L. k > 0. M O=A s. sistema (che è rappresentato in figura ). Infine, vogliamo calcolare le reazioni vincolari sul sistema.
 Esercizio 1. Un sistema materiale è costituito da una lamina piana omogenea di massa M e lato L e da un asta AB di lunghezza l e massa m. La lamina scorre con un lato sull asse x ed è soggetta a una forza
Esercizio 1. Un sistema materiale è costituito da una lamina piana omogenea di massa M e lato L e da un asta AB di lunghezza l e massa m. La lamina scorre con un lato sull asse x ed è soggetta a una forza
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti)
 Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
I. Foglio di esercizi su vettori linearmente dipendenti e linearmente indipendenti. , v 2 = α v 1 + β v 2 + γ v 3. α v 1 + β v 2 + γ v 3 = 0. + γ.
 ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE
 ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE 1 Funzioni libere I punti stazionari di una funzione libera di più variabili si ottengono risolvendo il sistema di equazioni
ESERCITAZIONE SUI PUNTI STAZIONARI DI FUNZIONI LIBERE E SULLE FUNZIONI OMOGENEE 1 Funzioni libere I punti stazionari di una funzione libera di più variabili si ottengono risolvendo il sistema di equazioni
11 Piccole oscillazioni attorno a posizioni stabili
 11 Piccole oscillazioni attorno a posizioni stabili Consideriamo un sistema con l gradi di libertà descrivibile mediante le coordinate lagrangiane (q 1,..., q l ). Supponiamo che i vincoli siano lisci
11 Piccole oscillazioni attorno a posizioni stabili Consideriamo un sistema con l gradi di libertà descrivibile mediante le coordinate lagrangiane (q 1,..., q l ). Supponiamo che i vincoli siano lisci
1 Sistemi Dinamici Esercizio del Parziale del 29/11/2010
 1 Sistemi Dinamici Esercizio del Parziale del 29/11/2010 Si consideri il sistema dinamico con { ẋ = y ẏ = d U(x) U(x) = 2 ( x 2 3 x + 4 ) e x/2. (2) 1. Tracciare qualitativamente le curve di fase del sistema
1 Sistemi Dinamici Esercizio del Parziale del 29/11/2010 Si consideri il sistema dinamico con { ẋ = y ẏ = d U(x) U(x) = 2 ( x 2 3 x + 4 ) e x/2. (2) 1. Tracciare qualitativamente le curve di fase del sistema
Modellistica dei Manipolatori Industriali 01BTT Esame del 18/02/2002 Soluzione
 Modellistica dei Manipolatori Industriali BTT Esame del 8/2/22 Soluzione Sistemi di riferimento e cinematica di posizione In Figura a) il manipolatore è stato ridisegnato per mettere in evidenza variabili
Modellistica dei Manipolatori Industriali BTT Esame del 8/2/22 Soluzione Sistemi di riferimento e cinematica di posizione In Figura a) il manipolatore è stato ridisegnato per mettere in evidenza variabili
ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA
 ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA Prova scritta del 6 giugno 2004: soluzioni ESERCIZIO - Data la funzione f) 3 2 4 + 27 + 9 2 ) /3 4 + 27, + 9 si chiede
ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA Prova scritta del 6 giugno 2004: soluzioni ESERCIZIO - Data la funzione f) 3 2 4 + 27 + 9 2 ) /3 4 + 27, + 9 si chiede
4 Autovettori e autovalori
 4 Autovettori e autovalori 41 Cambiamenti di base Sia V uno spazio vettoriale tale che dim V n Si è visto in sezione 12 che uno spazio vettoriale ammette basi distinte, ma tutte con la medesima cardinalità
4 Autovettori e autovalori 41 Cambiamenti di base Sia V uno spazio vettoriale tale che dim V n Si è visto in sezione 12 che uno spazio vettoriale ammette basi distinte, ma tutte con la medesima cardinalità
Esercizi sui sistemi di equazioni lineari.
 Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Richiami di algebra delle matrici a valori reali
 Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 2 Secondo compito in itinere 30 Giugno 2016
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Giugno 6 Cognome: Nome: Matricola: Es.: 9 punti Es.: 9 punti Es.: 6 punti Es.4: 9 punti Totale. Si consideri
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Giugno 6 Cognome: Nome: Matricola: Es.: 9 punti Es.: 9 punti Es.: 6 punti Es.4: 9 punti Totale. Si consideri
Prova Scritta di Robotica II
 Prova Scritta di Robotica II 10 Giugno 009 Esercizio 1 Ricavare l espressione della matrice d inerzia Bq per il robot planare PRP mostrato in figura. Per i = 1,, 3, siano: m i = massa del braccio i; I
Prova Scritta di Robotica II 10 Giugno 009 Esercizio 1 Ricavare l espressione della matrice d inerzia Bq per il robot planare PRP mostrato in figura. Per i = 1,, 3, siano: m i = massa del braccio i; I
Analisi Matematica II Corso di Ingegneria Gestionale Compito del y 2
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 15--18 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 15--18 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Geometria delle masse
 Geometria delle masse BA. Baricentri Per la trattazione riguardante i baricentri non ci è più sufficiente considerare i corpi come insiemi di punti geometrici, ma abbiamo bisogno di introdurre una nuova
Geometria delle masse BA. Baricentri Per la trattazione riguardante i baricentri non ci è più sufficiente considerare i corpi come insiemi di punti geometrici, ma abbiamo bisogno di introdurre una nuova
Dinamica dei Sistemi Multicorpo Esempi di reti elettriche
 Dinamica dei Sistemi Multicorpo Esempi di reti elettriche Basilio Bona Dipartimento di Automatica e Informatica Politecnico di Torino basilio.bona@polito.it Internal Report: DAUIN/BB/2005/09.01 Versione:
Dinamica dei Sistemi Multicorpo Esempi di reti elettriche Basilio Bona Dipartimento di Automatica e Informatica Politecnico di Torino basilio.bona@polito.it Internal Report: DAUIN/BB/2005/09.01 Versione:
Massimi e minimi vincolati
 Massimi e minimi vincolati Data una funzione G C 1 (D), dove D è un aperto di R 2, sappiamo bene dove andare a cercare gli eventuali punti di massimo e minimo relativi. Una condizione necessaria affinché
Massimi e minimi vincolati Data una funzione G C 1 (D), dove D è un aperto di R 2, sappiamo bene dove andare a cercare gli eventuali punti di massimo e minimo relativi. Una condizione necessaria affinché
Applicazioni lineari tra spazi euclidei. Cambi di base.
 pplicazioni lineari tra spazi euclidei. Cambi di base. Esercizio. Data la seguente applicazione lineare f : R R : f(x, y, z) = (x z, x + y, y + z), scrivere la matrice B, rappresentativa di f rispetto
pplicazioni lineari tra spazi euclidei. Cambi di base. Esercizio. Data la seguente applicazione lineare f : R R : f(x, y, z) = (x z, x + y, y + z), scrivere la matrice B, rappresentativa di f rispetto
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
Analisi Matematica II Corso di Ingegneria Gestionale Compito del xy + 2x + 2y + 2xy + 2x + 2y + sin
 Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Analisi Matematica II Corso di Ingegneria Gestionale Compito del 9--8 - È obbligatorio consegnare tutti i fogli, anche la brutta e il testo. - Le risposte senza giustificazione sono considerate nulle.
Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 Totale
 Es. 1 Es. 2 Es. Es. 4 Es. 5 Totale Analisi e geometria 2 rimo Appello Docente: 17 luglio 29 Cognome: Nome: Matricola: Tutte le risposte devono essere motivate. Gli esercizi vanno svolti su questi fogli,
Es. 1 Es. 2 Es. Es. 4 Es. 5 Totale Analisi e geometria 2 rimo Appello Docente: 17 luglio 29 Cognome: Nome: Matricola: Tutte le risposte devono essere motivate. Gli esercizi vanno svolti su questi fogli,
Soluzioni del Foglio 2 I sistemi lineari
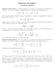 Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
Forme differenziali lineari e loro integrazione
 Forme differenziali lineari e loro integrazione Integrazione di una forma differenziale in due variabili Siano L(, ) e ( ) consideriamo l espressione M, due funzioni definite e continue in un insieme connesso
Forme differenziali lineari e loro integrazione Integrazione di una forma differenziale in due variabili Siano L(, ) e ( ) consideriamo l espressione M, due funzioni definite e continue in un insieme connesso
Massimi e minimi vincolati
 Massimi e minimi vincolati Vedremo tra breve un metodo per studiare il problema di trovare il minimo e il massimo di una funzione su di un sottoinsieme dello spazio ambiente che non sia un aperto. Abbiamo
Massimi e minimi vincolati Vedremo tra breve un metodo per studiare il problema di trovare il minimo e il massimo di una funzione su di un sottoinsieme dello spazio ambiente che non sia un aperto. Abbiamo
Equazioni differenziali del 2 ordine Prof. Ettore Limoli. Sommario. Equazione differenziale omogenea a coefficienti costanti
 Equazioni differenziali del 2 ordine Prof. Ettore Limoli Sommario Equazione differenziale omogenea a coefficienti costanti... 1 Equazione omogenea di esempio... 2 Equazione differenziale non omogenea a
Equazioni differenziali del 2 ordine Prof. Ettore Limoli Sommario Equazione differenziale omogenea a coefficienti costanti... 1 Equazione omogenea di esempio... 2 Equazione differenziale non omogenea a
Fondamenti di Analisi Matematica 2 - a.a. 2016/2017 Primo appello
 Fondamenti di Analisi Matematica 2 - a.a. 216/217 Primo appello Esercizi senza svolgimento - Tema 1 Ω = { x, y, z) R 3 : 4x 2 + y 2 + z 2 1, z }. x = ρ/2) sen ϕ cos ϑ, 1. y = ρ sen ϕ sen ϑ, ρ [, 1], ϕ
Fondamenti di Analisi Matematica 2 - a.a. 216/217 Primo appello Esercizi senza svolgimento - Tema 1 Ω = { x, y, z) R 3 : 4x 2 + y 2 + z 2 1, z }. x = ρ/2) sen ϕ cos ϑ, 1. y = ρ sen ϕ sen ϑ, ρ [, 1], ϕ
2 2 2 A = Il Det(A) = 2 quindi la conica è non degenere, di rango 3.
 Studio delle coniche Ellisse Studiare la conica di equazione 2x 2 + 4xy + y 2 4x 2y + 2 = 0. Per prima cosa dobbiamo classificarla. La matrice associata alla conica è: 2 2 2 A = 2 2 2 Il DetA = 2 quindi
Studio delle coniche Ellisse Studiare la conica di equazione 2x 2 + 4xy + y 2 4x 2y + 2 = 0. Per prima cosa dobbiamo classificarla. La matrice associata alla conica è: 2 2 2 A = 2 2 2 Il DetA = 2 quindi
1. Lunedì 2/10/2017, ore: 2(2) Introduzione e presentazione del corso. Richiami: equazioni cardinali della dinamica.
 Registro delle lezioni di MECCANICA 2 Corso di Laurea in Matematica 8 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: 19 dicembre 2017 1. Lunedì 2/10/2017, 9 11. ore: 2(2) Introduzione
Registro delle lezioni di MECCANICA 2 Corso di Laurea in Matematica 8 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: 19 dicembre 2017 1. Lunedì 2/10/2017, 9 11. ore: 2(2) Introduzione
Prof. Giuseppe Scippa [EQUAZIONI DIFFERENZIALI] Sintesi dei principali tipi dei equazioni differenziali.
![Prof. Giuseppe Scippa [EQUAZIONI DIFFERENZIALI] Sintesi dei principali tipi dei equazioni differenziali. Prof. Giuseppe Scippa [EQUAZIONI DIFFERENZIALI] Sintesi dei principali tipi dei equazioni differenziali.](/thumbs/98/136949441.jpg) 2015 Prof. Giuseppe Scippa [EQUAZIONI DIFFERENZIALI] Sintesi dei principali tipi dei equazioni differenziali. EQUAZIONI DIFFERENZIALI ( pag. 2088) Si chiama equazione differenziale un equazione che ha
2015 Prof. Giuseppe Scippa [EQUAZIONI DIFFERENZIALI] Sintesi dei principali tipi dei equazioni differenziali. EQUAZIONI DIFFERENZIALI ( pag. 2088) Si chiama equazione differenziale un equazione che ha
Analisi Matematica 2 (Corso di Laurea in Informatica)
 COGNOME NOME Matr. Firma dello studente A Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. Firma dello studente A Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
Matematica. Corso integrato di. per le scienze naturali ed applicate. Materiale integrativo.
 Corso integrato di Matematica per le scienze naturali ed applicate Materiale integrativo http://www.dimi.uniud.it/biomat/ Paolo Baiti 1 Lorenzo Freddi 1 1 Dipartimento di Matematica e Informatica, Università
Corso integrato di Matematica per le scienze naturali ed applicate Materiale integrativo http://www.dimi.uniud.it/biomat/ Paolo Baiti 1 Lorenzo Freddi 1 1 Dipartimento di Matematica e Informatica, Università
CAPITOLO 14. Quadriche. Alcuni esercizi di questo capitolo sono ripetuti in quanto risolti in maniera differente.
 CAPITOLO 4 Quadriche Alcuni esercizi di questo capitolo sono ripetuti in quanto risolti in maniera differente. Esercizio 4.. Stabilire il tipo di quadrica corrispondente alle seguenti equazioni. Se si
CAPITOLO 4 Quadriche Alcuni esercizi di questo capitolo sono ripetuti in quanto risolti in maniera differente. Esercizio 4.. Stabilire il tipo di quadrica corrispondente alle seguenti equazioni. Se si
ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA
 ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA Prova scritta del 2 luglio 2004: soluzioni Data la funzione f() = 3 2 2 arctan + 0, si chiede di: a) calcolare il dominio
ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA Prova scritta del 2 luglio 2004: soluzioni Data la funzione f() = 3 2 2 arctan + 0, si chiede di: a) calcolare il dominio
A Analisi Matematica 2 (Corso di Laurea in Informatica) Simulazione compito d esame
 COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
COGNOME NOME Matr. Firma dello studente A Analisi Matematica (Corso di Laurea in Informatica) Simulazione compito Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
Esercizi sulle coniche (prof.ssa C. Carrara)
 Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle da un altra angolazione.. Determinare
Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle da un altra angolazione.. Determinare
Un quaternione è un numero complesso con quattro componenti anziché due. Si scrive così :
 Un quaternione è un numero complesso con quattro componenti anziché due. Si scrive così : Q = q r + q i i + q j j + q k k ove le quantità q sono numeri reali e i, j e k sono tre unità immaginarie. Quando
Un quaternione è un numero complesso con quattro componenti anziché due. Si scrive così : Q = q r + q i i + q j j + q k k ove le quantità q sono numeri reali e i, j e k sono tre unità immaginarie. Quando
