32 Capitolo 2. Radicali Esercizi dei singoli paragrafi ; ; ; , , 3 25, 100, 125; 216; 8 27 ;
|
|
|
- Martino Palmieri
- 5 anni fa
- Visualizzazioni
Transcript
1 Cpitolo Rdicli Esercizi Esercizi dei singoli prgrfi - Rdici Determin le seguenti rdici qudrte rzionli qundo è possibile clcolrle) m ) n ) o ) 0, 0 0, 09 0, , Determin le seguenti rdici qudrte rzionli qundo è possibile clcolrle) 0, , 0 0, Senz usre l clcoltrice determin per ciscun delle seguenti rdici qudrte il vlore pprossimto /0:,, 7,,, 7 Estri le seguenti rdici di espressioni letterli, fcendo ttenzione l vlore ssoluto + + x + x Senz usre l clcoltrice determin per ciscun delle seguenti rdici cubiche il vlore pprossimto /0:,, 7, 00,, 0 ) Determin le seguenti rdici se esistono ) Determin le seguenti rdici se esistono 0, 00 0,
2 Sezione Esercizi ) Determin le seguenti rdici se esistono 0, , ) Determin le seguenti rdici se esistono , ) Determin le seguenti rdici se esistono x + x x - Condizioni di esistenz ) Determin le condizioni di esistenz dei seguenti rdicli x + x x + x y xy x y x + x x x x ) Determin le condizioni di esistenz dei seguenti rdicli x x + ) + x x + x + x ) ) x + x + x + x + x + x + x x x ) Determin le condizioni di esistenz dei seguenti rdicli x x + y y + ) x x b x ) x )x + ) x + x x x x + + x 9
3 Cpitolo Rdicli ) Determin le condizioni di esistenz dei seguenti rdicli b b xx ) x x + y + xy m + m xx + ) + + ) b ) Determin le condizioni di esistenz dei seguenti rdicli x x + x x - Potenze esponente rzionle x x + x x + x + Clcol le seguenti potenze con esponente rzionle xx + )x + ) x + x x + x 9 ) 9 ) 7 7 ) Clcol le seguenti potenze con esponente rzionle 9 ) ) 7 ) 9 0, 00) 0, 0, 0, 00 0, ) Trsform le seguenti espressioni in form di potenz con esponente frzionrio 7 )
4 Sezione Esercizi 9 ) Trsform nell form rdicle le seguenti espressioni + ) ) + ) + + ) 0 Scrivi in ordine crescente i seguenti numeri: 0, , 0, ) 0, 0, ) 0,, 0 0, 0, Semplificzione di rdici Trsform i seguenti rdicli pplicndo l proprietà invrintiv = 9 = = = = = Trsform i seguenti rdicli pplicndo l proprietà invrintiv = = 7 7 =, > 0 =, > 0 7 = x + x + = 7 ) Semplific i seguenti rdicli ) Semplific i seguenti rdicli 9 ) Semplific i seguenti rdicli ) ) Semplific i seguenti rdicli ) ) + ) 0 0 0
5 Cpitolo Rdicli 7 ) Semplific i seguenti rdicli 0 9 9x y b 9 x y 9 x y) 0 b 0 0 b 0 x y x ) Semplific i seguenti rdicli + ) 9 7 b x + ) 9 ) Semplific i seguenti rdicli x + x x + 9x + 9x y 0,00x y 9 0 b b c 7 c+b) b x x x + x + x b ++ 9 x + x + x + x 0 ) Semplific i seguenti rdicli x x + x + x + ) x x + 9) x + x + 9) x + x) b x +x y)+) x+y+x+y b 7 x +x +x+) [ ] Semplific i seguenti rdicli n n n n n n n n n 7 n n n n n n+ n+ x y b x 0 - Moltipliczione e divisione di rdici ) Esegui le seguenti moltipliczioni e divisioni di rdicli ) 0 : : 9 :
6 Sezione Esercizi 7 ) Esegui le seguenti moltipliczioni e divisioni di rdicli : : 9 ) Esegui le seguenti moltipliczioni e divisioni di rdicli ) : 9 : + 0 e) 0 : + + [ ] Esegui le seguenti operzioni le lettere rppresentno numeri reli positivi) 9 b b : x x : x 9 b : b : ) Esegui le seguenti operzioni le lettere rppresentno numeri reli positivi) x xy y x + ) : x b : + b x +x +b b : x +x +b b 7 ) Esegui le seguenti operzioni le lettere rppresentno numeri reli positivi) ++ + x+ x + : 9 x x+ : x x +x b + b + xy y x : x + y ) Esegui le seguenti operzioni le lettere rppresentno numeri reli positivi) : b ) b : ) ++ x x+ x x +b b b +b b 9 ) Esegui le seguenti operzioni le lettere rppresentno numeri reli positivi) b+b +b) xy x x y +b) x b + b xy + y x : x y x xy x+y
7 Cpitolo Rdicli - Portre un fttore sotto il segno di rdice 0 ) Trsport dentro l rdice i fttori esterni m ) n ) o ) p ) q ) 9 r ) + ) ) Trsport dentro l rdice i fttori esterni, discutendo i csi letterli x x x x ) x ) x x +x 7 - Portre un fttore fuori dl segno di rdice x x x +x x x x x ) Semplific i rdicli portndo fuori i fttori possibili ttenzione l vlore ssoluto) 0 0 0, m ) 7 n ) 0 o ) p ) 0 ) Semplific i rdicli portndo fuori i fttori possibili ttenzione l vlore ssoluto) m ) n ) o ) p ) ) Semplific i rdicli portndo fuori i fttori possibili ttenzione l vlore ssoluto) x y b b c d 9 x 9 b x x 7 x b 7 7 b b c 7
8 Sezione Esercizi 9 ) Semplific i rdicli portndo fuori i fttori possibili ttenzione l vlore ssoluto) + x x x 7 x b c 9 b c 7 x b c d 7 b b Potenz di rdice e rdice di rdice ) Esegui le seguenti potenze di rdici ) ) ) ) ) ) ) ) ) ) ) ) m ) ) n ) ) o ) ) p ) 9 9 ) 7 ) Esegui le seguenti potenze di rdici ) ) ) ) ) ) ) ) ) b b ) b ) ) b ) Esegui le seguenti rdici di rdici 0 9 ) Esegui le seguenti rdici di rdici b + ) ) b) + b) b +b 9 - Somm di rdicli 0 ) Esegui le seguenti operzioni con i rdicli ) + 7 [ 7 )]
9 0 Cpitolo Rdicli ) Esegui le seguenti operzioni con i rdicli ) ) Esegui le seguenti operzioni con i rdicli ) ) ) Esegui le seguenti operzioni con i rdicli b + 0, b b + b b b x x x + x + x x b + + b b + + b x x + 0, 7 + ) Esegui le seguenti operzioni con i rdicli b 7 b b + xy + x y + xy x + y) ) Esegui le seguenti operzioni con i rdicli + ) + ) ) ) ) + ) ) ) + ) ) + ) ) + ) ) ) ) ) Esegui le seguenti operzioni con i rdicli + ) ) ) + ) 7 ) ) ) + + ) ) + ) + + ) ) 7 ) Esegui le seguenti operzioni con i rdicli + ) ) + ) + ) 9 ) [ + ) )] + ) + 9) + ) + : + )
10 Sezione Esercizi ) + + ) + ) ) ) Esegui le seguenti operzioni con i rdicli + ) ) + ) ) 7) ) x ) x + x) x + x) x + x)x x) + + ) ) 9 ) Esegui le seguenti operzioni con i rdicli x + y) x y) ) ) + ) + ) + ) + ) + ) ) ) + ) + 7 ) ) [ + ) + ] ) + + ) 7 ) ) + ) + ) ) + ) 0 Esegui le seguenti operzioni con i rdicli x ) + x + ) x ) ) + ) ) 0 + 7) x y + x 7y 7 ) 7 + ) 7x + x 7 ) Esegui le seguenti operzioni con i rdicli b b b b b : b b b x + xy y y y x y + ) ) + ) ) + b b b b b : b b b) ) Esegui le seguenti operzioni con i rdicli b b b +b 9b b b b 9 b+b b x y x+y +b b x +xy+y x y
11 Cpitolo Rdicli : + x x+ x x+ x x + ) Esegui le seguenti operzioni con i rdicli + +) +) +) ) + b + +b b b ) b b + b+) x y x x ) y + y x y y x y b b b b ) : b b ++ b b + b+b b ) ++ x +xy+y x+ x x +x+9 x+y x ) Esegui le seguenti operzioni con i rdicli x x x+ x +x+ x x+ x x+ : x +x + x +x y y xy +xy x+ y y x y y + + y y x ) y + +) + : + ) 7 b+b xy +b) x x y +b) x + x x + x + x : y+) y x x b + b [ ] Esegui le seguenti operzioni con i rdicli + +) +) +) ) ) + 9 +) : 9 ) +) + + ) 7 ) y + : y y +y +y+ y ) + : [ ] Esegui le seguenti operzioni con i rdicli x + xy y y y x y x +xy+y + x y x x y + x + x y + x y ++9
12 Sezione Esercizi x y + x x y + y x x+ + x x+ + xy y x x y x x y + y x y ) x y x x+ ) x 7 ) Esegui trsformndo i rdicli in potenze con esponente frzionrio : 7 7 : b b b b b : b b b 0 - Rzionlizzzione del denomintore di un frzione ) Rzionlizz i seguenti rdicli Rzionlizz i seguenti rdicli x x x 70 ) Rzionlizz i seguenti rdicli x x x x x x ) Rzionlizz i seguenti rdicli b +b x y x y x x+ 7 Rzionlizz i seguenti rdicli
13 Cpitolo Rdicli 7 ) Rzionlizz i seguenti rdicli b b b b b 9b 7b c x x b c x y+ xy xy 9 9 x [ ] Rzionlizz i seguenti rdicli x x+ x+ y x x y +b + b x y x+y 7 Rzionlizz i seguenti rdicli x x x+ xx+) b) + b b ) Rzionlizz i seguenti rdicli + b b + b + b b + b b b+b + b - Rdicli doppi 77 ) b deve essere un qudrto perfetto per pplicre l formul di trsformzione ) b deve essere un qudrto perfetto per pplicre l formul di trsformzione
14 Sezione Esercizi 79 b deve essere un qudrto perfetto per pplicre l formul di trsformzione Equzioni, disequzioni, sistemi 7 0 ) Risolvi le seguenti equzioni coefficienti irrzionli x = x = x = x = + x = x ) x = x + = x + + )x = ) ) Risolvi le seguenti equzioni coefficienti irrzionli x x = x x x + ) = x + x+ + x+ = x x + x x+ x+ = x + ) x + ) = ) Risolvi le seguenti equzioni coefficienti irrzionli x x = x x ) x = + xx ) x x + x 0 0x = + x x = 0 ) Risolvi le seguenti disequzioni coefficienti irrzionli x + < x + ) + x) < x + > 0 x ) < x + ) x x ) Risolvi i seguenti sistemi di disequzioni coefficienti irrzionli { x )x < { x ) > x x ) > x ) ) Risolvi i seguenti sistemi di equzioni coefficienti irrzionli { x + y = x + y = { x = y x + = y + { x + y = x y = x+ ) = y + x y =
15 Cpitolo Rdicli ) Risolvi i seguenti sistemi di equzioni coefficienti irrzionli { x + y = x y = { x + y = x + y = { x y = x + y = 0 { x y = x + y = { x + y = x y = 7 ) Risolvi i seguenti sistemi di equzioni coefficienti irrzionli { x + y = x + y = { x y = 7 x + y = 0 { x + y = x + y = { x y = x y = ) Risolvi i seguenti sistemi di equzioni coefficienti irrzionli { x y = x + y = { x + y = x + y = 0 { x + y = 0 x + y = { x + y = x + y = 9 ) Risolvi i seguenti sistemi di equzioni coefficienti irrzionli { x y = 0 x + 9y = 0 { x + y = x y = { x y = x y = 0 Esercizi di riepilogo 90 Vero o Flso? È dto un qudrto di lto Il suo perimetro è in numero irrzionle V F L su re è un numero irrzionle V F 9 Vero o Flso? È dto un rettngolo di bse e ltezz il suo perimetro è un numero irrzionle V F l su re è un numero rzionle V F il perimetro non esiste perché non si sommno rzionli con irrzionli V F l misur del perimetro è un numero si rzionle che irrzionle V F 9 Vero o Flso? Un tringolo rettngolo h i cteti lunghi rispettivmente cm e cm l ipotenus h come misur un numero rzionle V F il perimetro è un numero irrzionle V F
16 Sezione Esercizi 7 l re è un numero irrzionle V F 9 Vero o Flso? È dto un qudrto di lto + l misur dell digonle è un numero irrzionle V F l re è un numero irrzionle V F 9 Vero o Flso? È dto un rettngolo di bse e ltezz il perimetro è un numero irrzionle V F l re è un numero irrzionle V F l misur dell digonle è un numero irrzionle V F il qudrto dell misur del perimetro è un numero irrzionle V F 9 Un tringolo rettngolo h un cteto lungo 7 cm Determin, se esiste, un possibile misur dell ltro cteto in modo che quest si un numero irrzionle e che l ipotenus si, invece, un numero rzionle 9 Perché l uguglinz ) = è fls? 97 Determin il vlore di verità delle seguenti ffermzioni l rdice terz del triplo di è ugule d dti due numeri reli positivi, il quoziente delle loro rdici qudrte è ugule ll rdice qudrt del quoziente il doppio dell rdice qudrt di è ugule ll rdice qudrt del qudruplo di dti due numeri reli positivi, l somm delle loro rdici cubiche è ugule ll rdice cubic dell loro somm l rdice cubic di è l metà dell rdice cubic di dti un numero rele positivo, l rdice qudrt dell su rdice cubic è ugule ll rdice cubic dell su rdice qudrt sommndo due rdicli letterli simili si ottiene un rdicle che h l stess prte letterle dei rdicli dti 9 Riscrivi in ordine crescente i rdicli,,, 99 Verific che il numero irrzionle 7 pprtiene ll intervllo ) e rppresentlo sull sse dei numeri reli 00 Dti i numeri α = 0 ) 0 + ) + 7 7) 7 7) e β = + ) ) +, quli ffermzioni sono vere? sono entrmbi irrzionli solo α è irrzionle α è minore di β α è mggiore di β β è irrzionle negtivo 0 Le misure rispetto l cm dei lti di un rettngolo sono i numeri reli l = 7 e l = ) : Determinre l misur del perimetro e dell digonle del rettngolo 0 Se x è positivo e diverso d, l espressione E = x x+ : ugule : x + x+ è
17 Cpitolo Rdicli x x x x 0 0 Stbilire se l seguente ffermzione è ver o fls Per tutte le coppie, b) di numeri reli positivi con = b, l espressione E = + b + b +b b + b b h il numertore doppio del denomintore 0 Clcol il vlore delle seguenti espressioni letterli per i vlori indicti delle lettere x + per x = x + per x = x + x per x = x + x per x = 0 Trsform in un rdicle di indice 9 il seguente rdicle x + ) per x = b b : b + b + +b b + 0 ) Risolvi le seguenti equzioni x + + x + = x+ +x x + x+ 07 Per qule vlore di k il sistem linere è determinto? x = { x + k )y = x + y = k 0 L insieme di soluzioni dell disequzione )x < 0 è: x 0 x 0 x > 0 x < 0 R 09 Dt l espressione E = che l rendono positiv 0 Dt l funzione fx) = x+ x+ x determin il suo dominio riscrivi l funzione rzionlizzndo il denomintore clcol f) per quli vlori di x si h fx) > 0? risolvi l equzione fx) = 0 + +) +, stbilire se esistono vlori di Risposte b), h), i) 0 7 e), h) b), d), h) 9 c), e) 0,, i) 0 d) +, e) +, f) x
18 Sezione Esercizi 9 ) x R, b) x, c) x >, d) y 0, f)x > ) x, d), i) ) < x, e) b < b > b) 0 x x >, e) < < 0 > ) x R, d) x R, g) < x < x > 0, i) x > 0, f) 7 ), f), i) c) 7, g) 9 ) + ) + c), e) 0, i) b), d), h) ), e), g) 00 b), d), e) 9, g) 7 ), e) b x, i) y ) x + ), e) b, i) 9 b) + x, f), h) b + 0 c), d) x, h) x b x+ b) 9, e) n, i)x ), d) 0, i) c) 7, e) 7, h) b), d), e) 0, h)
19 0 Cpitolo Rdicli b), c)b, e) b) x+) x ), c) b, e) x) +x)+x ) 7 b) +)+) ) ), c) x )x+) x )x+), f) x y xy +b ) b, d) +) 7 ) 7, e) x+ x x+) 9 ) +b x 0 ), g), o) b) x 7, g) ) ) 0, b) 9, c), d), k) 0 b) 97, g) e) b, C E b >= 0 b) x x, C E x x, i) + + ) d), l), p) 9 7 j) b h) 9 f) + b), C E > b 0 c), f) 7, g) + ), h) 7 7 c), j) ) 0, b) 0, c) +, d) +, e) 7, f) 0 ) b, b) + b) b ) 9 b b
20 Sezione Esercizi e) +, f) 7, g) 9 +, h) 9, i) +, j) 7 i) 0 +, l) + 7 i) + f) 9, k) ) x y, g) c) b 7, h) b e) +, f) x x+) ) +), b) b ) b +, c) y, d) b+) bb ), e) ), f) x+y x+ ) x, c) y ) y +, d), e) 0 b 0 +b), f) ) x x+ x ), b) 7 +), c), d) y, e) +) ), f) + ) y) y x y, b) +x) x x + xy + y, c), d) x+y) xy x y, e) + ) 7 ), b), c) 9 9, d) b 7 d), h), j) 70 c) 7 c) x 7 b) b +, l) 9, d), e), f) 7 d) + 77 d) d) + 0 e), f), g), h)
21 Cpitolo Rdicli ), b) + 0, c) + ), e), f) 7 + ) ) +, b), c) +7 0, d) 0 9 ) x <, b) x > ), b) 0 ), c) x >, d) x <, e) x < x < ) ), b) ), c) + ), d) + ) ) ), b) ), c) 0 0, d) R, e) + ) 7 ), b) ), c) + ), d) ) ) + ), b) ), c) ), d) 9 ) R, b) ), c) ) 0 ), b) )
Sezione Esercizi ; ; ; 1 4. f ) 13 + g ) , 100, 125; f ) 216; 8 27 ; ; e ) g ) 0; h )
 Sezione Esercizi Esercizi Esercizi dei singoli prgrfi - Rdici Determin le seguenti rdici qudrte rzionli (qundo è possiile clcolrle) 00 l ) m ) n ) o ) 0,0 0,0 0,000 0, Determin le seguenti rdici qudrte
Sezione Esercizi Esercizi Esercizi dei singoli prgrfi - Rdici Determin le seguenti rdici qudrte rzionli (qundo è possiile clcolrle) 00 l ) m ) n ) o ) 0,0 0,0 0,000 0, Determin le seguenti rdici qudrte
I radicali. Cos è un radicale? ESERCIZIO 2.1. Determina le C.E. dei seguenti radicali e delle seguenti espressioni contenenti radicali.
 I rdicli Cos è un rdicle? Il simbolo si chim rdicle e si legge rdice ennesim di. - n si chim indice dell rdice e deve essere un numero nturle mggiore di zero. Qundo l indice si sottintende e il rdicle
I rdicli Cos è un rdicle? Il simbolo si chim rdicle e si legge rdice ennesim di. - n si chim indice dell rdice e deve essere un numero nturle mggiore di zero. Qundo l indice si sottintende e il rdicle
Radicali. Definizioni Variazioni di radicali Operazioni Razionalizzazione Radicali doppi Potenze con esponente razionale Esercizi
 Rdicli Definizioni Vrizioni di rdicli Operzioni Rzionlizzzione Rdicli doppi Potenze con esponente rzionle Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni n L espressione è comunemente dett rdice
Rdicli Definizioni Vrizioni di rdicli Operzioni Rzionlizzzione Rdicli doppi Potenze con esponente rzionle Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni n L espressione è comunemente dett rdice
IL CALCOLO LETTERALE: I MONOMI Conoscenze. per a = - 2 vale:
 IL CALCOLO LETTERALE: I MONOMI Conoscenze. Complet.. Un espressione letterle è.... Per clcolre il vlore numerico di un espressione letterle isogn...... c. Non si possono ssegnre lle lettere che compiono
IL CALCOLO LETTERALE: I MONOMI Conoscenze. Complet.. Un espressione letterle è.... Per clcolre il vlore numerico di un espressione letterle isogn...... c. Non si possono ssegnre lle lettere che compiono
IL CALCOLO LETTERALE: I MONOMI Conoscenze. per a = - 2 vale:
 IL CALCOLO LETTERALE: I MONOMI Conoscenze. Complet.. Un espressione letterle è un scrittur in cui compiono operzioni tr numeri rppresentti, tutti o in prte, d lettere. Per clcolre il vlore numerico di
IL CALCOLO LETTERALE: I MONOMI Conoscenze. Complet.. Un espressione letterle è un scrittur in cui compiono operzioni tr numeri rppresentti, tutti o in prte, d lettere. Per clcolre il vlore numerico di
RECUPERO EQUAZIONI E DISEQUAZIONI CON COEFFICIENTI IRRAZIONALI
 I NUMERI REALI E I RADICALI Recupero RECUPERO EQUAZIONI E DISEQUAZIONI CON COEFFICIENTI IRRAZIONALI COMPLETA Risolvi l disequzione ( ). ( ) ( ) ( ) Elimin le prentesi clcolndo il prodotto. Applic l regol
I NUMERI REALI E I RADICALI Recupero RECUPERO EQUAZIONI E DISEQUAZIONI CON COEFFICIENTI IRRAZIONALI COMPLETA Risolvi l disequzione ( ). ( ) ( ) ( ) Elimin le prentesi clcolndo il prodotto. Applic l regol
I.S.I. E. Fermi - Lucca Istituto Tecnico settore Tecnologico
 Anno scolstico / Progrmm di MATEMATICA Clsse : B Insegnnte : Ghilrducci Pol I.S.I. E. Fermi - Lucc Istituto Tecnico settore Tecnologico Equzioni e disequzioni di primo grdo : Equzioni intere frtte e letterli
Anno scolstico / Progrmm di MATEMATICA Clsse : B Insegnnte : Ghilrducci Pol I.S.I. E. Fermi - Lucc Istituto Tecnico settore Tecnologico Equzioni e disequzioni di primo grdo : Equzioni intere frtte e letterli
Scheda per il recupero 2
 Sched A Ripsso Sched per il recupero Numeri rzionli e introduzione i numeri reli Definizioni principli DOMANDE RISPOSTE ESEMPI Che cos è un frzione? Qundo un frzione si dice ridott i minimi termini? Un
Sched A Ripsso Sched per il recupero Numeri rzionli e introduzione i numeri reli Definizioni principli DOMANDE RISPOSTE ESEMPI Che cos è un frzione? Qundo un frzione si dice ridott i minimi termini? Un
n volte m volte n+m volte n volte n volte n volte } = a n + n + n = a n m
 Corso di Potenzimento.. 009/010 1 Potenze e Rdicli Dto un numero positivo, negtivo o nullo e un numero intero positivo n, si definisce potenz di se ed esponente n il prodotto di n fttori tutti uguli d
Corso di Potenzimento.. 009/010 1 Potenze e Rdicli Dto un numero positivo, negtivo o nullo e un numero intero positivo n, si definisce potenz di se ed esponente n il prodotto di n fttori tutti uguli d
ISTITUTO DI ISTRUZIONE SUPERIORE E.FERMI Anno scolastico: 2016/17. Istituto tecnico settore tecnologico. Classe II H
 ISTITUTO DI ISTRUZIONE SUPERIORE E.FERMI Anno scolstico: /7 Progrmm di mtemtic Istituto tecnico settore tecnologico. Clsse II H Disequioni di primo grdo sistemi di disequioni e disequioni frtte. Segno
ISTITUTO DI ISTRUZIONE SUPERIORE E.FERMI Anno scolstico: /7 Progrmm di mtemtic Istituto tecnico settore tecnologico. Clsse II H Disequioni di primo grdo sistemi di disequioni e disequioni frtte. Segno
X X Y 2 1 0,5 0,25 Y 0,25 1 2,25 4. Disegna i grafici delle rette rappresentate dalle seguenti equazioni
 Funzioni Consider le seguenti telle e stilisci se e sono direttmente proporzionli, inversmente proporzionli o se vi è un proporzionlità qudrtic. Scrivi l espressione nlitic delle funzioni e rppresentle
Funzioni Consider le seguenti telle e stilisci se e sono direttmente proporzionli, inversmente proporzionli o se vi è un proporzionlità qudrtic. Scrivi l espressione nlitic delle funzioni e rppresentle
Calcolo letterale. 1) Operazioni con i monomi. a) La moltiplicazione. b) La divisione. c) Risolvi le seguenti espressioni con i monomi.
 Clcolo letterle. ) Operzioni con i monomi. ) L moltipliczione. ) L divisione. c) Risolvi le seguenti espressioni con i monomi. ) I polinomi. ) Clcol le seguenti somme di polinomi. ) Applic l proprietà
Clcolo letterle. ) Operzioni con i monomi. ) L moltipliczione. ) L divisione. c) Risolvi le seguenti espressioni con i monomi. ) I polinomi. ) Clcol le seguenti somme di polinomi. ) Applic l proprietà
Programma di matematica Prof.ssa Tacchi Lucia Anno scolastico 2017/2018 classe I A
 Isi E. Fermi Lucc Progrmm di mtemtic Prof.ss Tcchi Luci nno scolstico 7/8 clsse I Gli insiemi numerici i numeri nturli i numeri interi i numeri rzionli ssoluti i reltivi. Potenze nche con esponente intero
Isi E. Fermi Lucc Progrmm di mtemtic Prof.ss Tcchi Luci nno scolstico 7/8 clsse I Gli insiemi numerici i numeri nturli i numeri interi i numeri rzionli ssoluti i reltivi. Potenze nche con esponente intero
Istituto Tecnico Industriale E.Fermi Programma di matematica classe II I Anno scolastico 2017/2018
 Istituto Tecnico Industrile E.Fermi Progrmm di mtemtic clsse II I Anno scolstico / Insegnnte : Mrco Cmi Divisione tr due polinomi : Regol di Ruffini. Teorem del resto. Scomposiione di un polinomio con
Istituto Tecnico Industrile E.Fermi Progrmm di mtemtic clsse II I Anno scolstico / Insegnnte : Mrco Cmi Divisione tr due polinomi : Regol di Ruffini. Teorem del resto. Scomposiione di un polinomio con
ISTITUTO DI ISTRUZIONE SUPERIORE E.FERMI Anno scolastico: 2017/18. Istituto tecnico settore tecnologico. Classe II H
 ISTITUTO DI ISTRUZIONE SUPERIORE E.FERMI Anno scolstico: 7/8 Istituto tecnico settore tecnologico. Clsse II H Progrmm di mtemtic Equioni di primo grdo prmetriche. Disequioni di primo grdo sistemi di disequioni
ISTITUTO DI ISTRUZIONE SUPERIORE E.FERMI Anno scolstico: 7/8 Istituto tecnico settore tecnologico. Clsse II H Progrmm di mtemtic Equioni di primo grdo prmetriche. Disequioni di primo grdo sistemi di disequioni
Isi E.Fermi Programma di matematica classe II L. Anno scolastico 2017/2018
 Isi E.Fermi Progrmm di mtemtic clsse II L Prof.ss Tcchi Luci Anno scolstico / Ripsso: Polinomi ed operioni con essi. Prodotti notevoli. Scomposiioni. Frioni lgeriche. Equioni di primo grdo intere letterli
Isi E.Fermi Progrmm di mtemtic clsse II L Prof.ss Tcchi Luci Anno scolstico / Ripsso: Polinomi ed operioni con essi. Prodotti notevoli. Scomposiioni. Frioni lgeriche. Equioni di primo grdo intere letterli
2 x = 64 (1) L esponente (x) a cui elevare la base (2) per ottenere il numero 64 è detto logaritmo (logaritmo in base 2 di 64), indicato così:
 Considerimo il seguente problem: si vuole trovre il numero rele tle che: = () L esponente () cui elevre l bse () per ottenere il numero è detto ritmo (ritmo in bse di ), indicto così: In prticolre in questo
Considerimo il seguente problem: si vuole trovre il numero rele tle che: = () L esponente () cui elevre l bse () per ottenere il numero è detto ritmo (ritmo in bse di ), indicto così: In prticolre in questo
{ } 3 [ ] [ ] [ ] [ ] Esercizi per il precorso ( )( ) Prof. Margherita Fochi. 1.- Esercizi sui polinomi. + x. x R. ( )( ) + R. ( )( )( ) a.
![{ } 3 [ ] [ ] [ ] [ ] Esercizi per il precorso ( )( ) Prof. Margherita Fochi. 1.- Esercizi sui polinomi. + x. x R. ( )( ) + R. ( )( )( ) a. { } 3 [ ] [ ] [ ] [ ] Esercizi per il precorso ( )( ) Prof. Margherita Fochi. 1.- Esercizi sui polinomi. + x. x R. ( )( ) + R. ( )( )( ) a.](/thumbs/59/42788277.jpg) Prof. Mrgherit Fochi Esercizi per il precorso.- Esercizi sui polinomi Semplificre le seguenti espressioni utilizzndo i prodotti notevoli:. ) ) ) ) ) 8 [ ] 8. ) ) ) ) ] [. ) ) ) [ ] { } y y y y y [ ] 8
Prof. Mrgherit Fochi Esercizi per il precorso.- Esercizi sui polinomi Semplificre le seguenti espressioni utilizzndo i prodotti notevoli:. ) ) ) ) ) 8 [ ] 8. ) ) ) ) ] [. ) ) ) [ ] { } y y y y y [ ] 8
Polo Scientifico Tecnico Professionale Settore Tecnico E.Fermi Programma di matematica classe II D e indicazioni per il recupero
 Polo Scientifico Tecnico Professionle Settore Tecnico E.Fermi Progrmm di mtemtic clsse II D e indicioni per il recupero Anno scolstico / Frioni lgeriche e reltive operioni. Le funioni polinomili. Il Teorem
Polo Scientifico Tecnico Professionle Settore Tecnico E.Fermi Progrmm di mtemtic clsse II D e indicioni per il recupero Anno scolstico / Frioni lgeriche e reltive operioni. Le funioni polinomili. Il Teorem
ISTITUTO TECNICO INDUSTRIALE "E. FERMI" LUCCA
 ISTITUTO TECNICO INDUSTRIALE "E. FERMI" LUCCA Anno Scolstico / Progrmm di MATEMATICA svolto dll clsse second se. A INSEGNANTE: MUSUMECI LUCIANA Divisione tr due polinomi.regol di Ruffini. Teorem del resto.
ISTITUTO TECNICO INDUSTRIALE "E. FERMI" LUCCA Anno Scolstico / Progrmm di MATEMATICA svolto dll clsse second se. A INSEGNANTE: MUSUMECI LUCIANA Divisione tr due polinomi.regol di Ruffini. Teorem del resto.
Esercizi estivi per la classe seconda
 Esercii estivi per l clsse second ) Risolvere le seguenti disequioni: [nessun soluione] R f) R i) l) n) ) Risolvere i seguenti sistemi di disequioni: ) Risolvi i seguenti sistemi con il metodo di sostituione:,,,
Esercii estivi per l clsse second ) Risolvere le seguenti disequioni: [nessun soluione] R f) R i) l) n) ) Risolvere i seguenti sistemi di disequioni: ) Risolvi i seguenti sistemi con il metodo di sostituione:,,,
LICEO SCIENTIFICO CLASSICO SCIENZE UMANE MARCONI DELPINO
 LICEO SCIENTIFICO CLASSICO SCIENZE UMANE MARCONI DELPINO RECUPERO ESTIVO PER LE CLASSI ^D- E SCIENTIFICO Argomenti d rivedere: I QUADRIMESTRE: ) Equzioni di secondo grdo e relzioni tr coefficienti e rdici
LICEO SCIENTIFICO CLASSICO SCIENZE UMANE MARCONI DELPINO RECUPERO ESTIVO PER LE CLASSI ^D- E SCIENTIFICO Argomenti d rivedere: I QUADRIMESTRE: ) Equzioni di secondo grdo e relzioni tr coefficienti e rdici
Il calcolo letterale
 Appunti di Mtemtic Il clcolo letterle Finor imo studito gli insiemi numerici espressioni numeriche. Ν, Ζ, Q, R ed operto con numeri In mtemtic però è molto importnte sper operre con le lettere e sviluppre
Appunti di Mtemtic Il clcolo letterle Finor imo studito gli insiemi numerici espressioni numeriche. Ν, Ζ, Q, R ed operto con numeri In mtemtic però è molto importnte sper operre con le lettere e sviluppre
B8. Equazioni di secondo grado
 B8. Equzioni di secondo grdo B8.1 Legge di nnullmento del prodotto Spendo che b0 si può dedurre che 0 oppure b0. Quest è l legge di nnullmento del prodotto. Pertnto spendo che (-1) (+)0 llor dovrà vlere
B8. Equzioni di secondo grdo B8.1 Legge di nnullmento del prodotto Spendo che b0 si può dedurre che 0 oppure b0. Quest è l legge di nnullmento del prodotto. Pertnto spendo che (-1) (+)0 llor dovrà vlere
ISTITUTO DI ISTRUZIONE SUPERIORE E.FERMI
 I ISTITUTO DI ISTRUZIONE SUPERIORE E.FERMI Anno scolstico -7 MATEMATICA Clsse E Istituto tecnico tecnologico Progrmm svolto Insegnnte : Ptrii Consni ALGEBRA: Regol di Ruffini. Teorem del resto. Scomposiione
I ISTITUTO DI ISTRUZIONE SUPERIORE E.FERMI Anno scolstico -7 MATEMATICA Clsse E Istituto tecnico tecnologico Progrmm svolto Insegnnte : Ptrii Consni ALGEBRA: Regol di Ruffini. Teorem del resto. Scomposiione
Il calcolo letterale
 Il clcolo letterle Finor imo studito gli insiemi numerici espressioni numeriche. Ν, Ζ, Q, R ed operto con numeri In mtemtic però è molto importnte sper operre con le lettere e sviluppre le regole di quello
Il clcolo letterle Finor imo studito gli insiemi numerici espressioni numeriche. Ν, Ζ, Q, R ed operto con numeri In mtemtic però è molto importnte sper operre con le lettere e sviluppre le regole di quello
Appunti di Matematica 1 - I polinomi - Polinomi. I vari monomi che compongono il polinomio si chiamano termini del polinomio.
 ppunti di Mtemtic Polinomi Un polinomio è un somm lgeric di monomi. ; c sono polinomi. ; I vri monomi che compongono il polinomio si chimno termini del polinomio. Un monomio può nche essere considerto
ppunti di Mtemtic Polinomi Un polinomio è un somm lgeric di monomi. ; c sono polinomi. ; I vri monomi che compongono il polinomio si chimno termini del polinomio. Un monomio può nche essere considerto
Corso di Analisi: Algebra di Base. 4^ Lezione. Radicali. Proprietà dei radicali. Equazioni irrazionali. Disequazioni irrazionali. Allegato Esercizi.
 Corso di Anlisi: Algebr di Bse ^ Lezione Rdicli. Proprietà dei rdicli. Equzioni irrzionli. Disequzioni irrzionli. Allegto Esercizi. RADICALI : Considerto un numero rele ed un numero intero positivo n,
Corso di Anlisi: Algebr di Bse ^ Lezione Rdicli. Proprietà dei rdicli. Equzioni irrzionli. Disequzioni irrzionli. Allegto Esercizi. RADICALI : Considerto un numero rele ed un numero intero positivo n,
Anno 2. Potenze di un radicale e razionalizzazione
 Anno Potenze di un rdicle e rzionlizzzione Introduzione In quest lezione impreri utilizzre le ultime due tipologie di operzioni sui rdicli, cioè l potenz di un rdicle e l rdice di un rdicle. Successivmente
Anno Potenze di un rdicle e rzionlizzzione Introduzione In quest lezione impreri utilizzre le ultime due tipologie di operzioni sui rdicli, cioè l potenz di un rdicle e l rdice di un rdicle. Successivmente
Il calcolo letterale
 Progetto Mtemtic in Rete Il clcolo letterle Finor imo studito gli insiemi numerici (espressioni numeriche). Ν, Ζ, Q, R ed operto con numeri In mtemtic però è molto importnte sper operre con le lettere
Progetto Mtemtic in Rete Il clcolo letterle Finor imo studito gli insiemi numerici (espressioni numeriche). Ν, Ζ, Q, R ed operto con numeri In mtemtic però è molto importnte sper operre con le lettere
I S I E. Fermi - Lucca Istituto Tecnico settore Tecnologico
 I S I E. Fermi - Lucc Istituto Tecnico settore Tecnologico Anno scolstico / Progrmm di MATEMATICA Clsse : II C Insegnnte : Podestà Tiin Divisione tr due polinomi.regol di Ruffini. Teorem del resto. Scomposiione
I S I E. Fermi - Lucc Istituto Tecnico settore Tecnologico Anno scolstico / Progrmm di MATEMATICA Clsse : II C Insegnnte : Podestà Tiin Divisione tr due polinomi.regol di Ruffini. Teorem del resto. Scomposiione
LE FRAZIONI ALGEBRICHE
 LE FRAZIONI ALGEBRICHE 9 Per ricordre H Un frzione lgebric eá un frzione che h l numertore e l denomintore dei polinomi; ess h quindi significto per tutti i vlori reli delle lettere che in ess compiono
LE FRAZIONI ALGEBRICHE 9 Per ricordre H Un frzione lgebric eá un frzione che h l numertore e l denomintore dei polinomi; ess h quindi significto per tutti i vlori reli delle lettere che in ess compiono
Appunti di Matematica 1 - I polinomi - Polinomi. I vari monomi che compongono il polinomio si chiamano termini del polinomio.
 ppunti di Mtemtic Polinomi Un polinomio è un somm lgebric di monomi. Esempio: b ; y y ; b c sono polinomi. I vri monomi che compongono il polinomio si chimno termini del polinomio. Un monomio può nche
ppunti di Mtemtic Polinomi Un polinomio è un somm lgebric di monomi. Esempio: b ; y y ; b c sono polinomi. I vri monomi che compongono il polinomio si chimno termini del polinomio. Un monomio può nche
ISTITUTO TECNICO INDUSTRIALE "E. Fermi" LUCCA Anno Scolastico 2017/2018 Programma di MATEMATICA classe prima Sez. G Insegnante: MUSUMECI LUCIANA
 ISTITUTO TENIO INDUSTILE "E. Fermi" LU nno Solstio / Progrmm di MTEMTI lsse prim Sez. G Insegnnte MUSUMEI LUIN Gli insiemi ppresentzione di un insieme. I sottoinsiemi. Le operzioni on gli insiemi unione
ISTITUTO TENIO INDUSTILE "E. Fermi" LU nno Solstio / Progrmm di MTEMTI lsse prim Sez. G Insegnnte MUSUMEI LUIN Gli insiemi ppresentzione di un insieme. I sottoinsiemi. Le operzioni on gli insiemi unione
Scheda Sei ESPONENZIALI E LOGARITMI. 0,+. Inoltre valgono le
 Sched Sei ESPONENZIALI E LOGARITMI L funzione esponenzile Assegnto un numero rele >0, si dice funzione esponenzile in bse l funzione Grfici dell funzione esponenzile Se = l funzione esponenzile è costnte:
Sched Sei ESPONENZIALI E LOGARITMI L funzione esponenzile Assegnto un numero rele >0, si dice funzione esponenzile in bse l funzione Grfici dell funzione esponenzile Se = l funzione esponenzile è costnte:
Unità Didattica N 3 Le inequazioni. Unità Didattica N 3 Le inequazioni
 9 ) Proprietà delle disuguglinze fr numeri reli reltivi ) Inequzioni e loro proprietà ) Inequzioni rzionli intere di primo grdo d un incognit 4) Segno del trinomio di secondo grdo : T = c 5) Inequzioni
9 ) Proprietà delle disuguglinze fr numeri reli reltivi ) Inequzioni e loro proprietà ) Inequzioni rzionli intere di primo grdo d un incognit 4) Segno del trinomio di secondo grdo : T = c 5) Inequzioni
Unità Didattica N 02. I concetti fondamentali dell aritmetica
 1 Unità Didttic N 0 I concetti fondmentli dell ritmetic 01) Il concetto di potenz 0) Proprietà delle potenze 0) L nozione di rdice ritmetic 0) Multipli e divisori di un numero 05) Criteri di divisibilità
1 Unità Didttic N 0 I concetti fondmentli dell ritmetic 01) Il concetto di potenz 0) Proprietà delle potenze 0) L nozione di rdice ritmetic 0) Multipli e divisori di un numero 05) Criteri di divisibilità
Equazioni. Definizioni e concetti generali. Incognita: Lettera (di solito X) alla quale e possibile sostituire dei valori numerici
 Equzioni Prerequisiti Scomposizioni polinomili Clcolo del M.C.D. e del m.c.m. tr polinomi P(X) = 0, con P(X) polinomio di grdo qulsisi Definizioni e concetti generli Incognit: Letter (di solito X) ll qule
Equzioni Prerequisiti Scomposizioni polinomili Clcolo del M.C.D. e del m.c.m. tr polinomi P(X) = 0, con P(X) polinomio di grdo qulsisi Definizioni e concetti generli Incognit: Letter (di solito X) ll qule
Classi IIC IID - IIE - IIH
 stituto Professionle di Stto per l ndustri e l Artiginto Gincrlo Vlluri Clssi C D - E - H ALUNNO CLASSE ESEGU TUTT GL ESERCZ SU UN FOGLO PROTOCOLLO O UN QUADERNO. Ulteriore ripsso e recupero nche nei siti
stituto Professionle di Stto per l ndustri e l Artiginto Gincrlo Vlluri Clssi C D - E - H ALUNNO CLASSE ESEGU TUTT GL ESERCZ SU UN FOGLO PROTOCOLLO O UN QUADERNO. Ulteriore ripsso e recupero nche nei siti
Istituto Professionale di Stato per l Industria e l Artigianato Giancarlo Vallauri. Classe I H
 Istituto Professionle di Stto per l Industri e l Artiginto Gincrlo Vlluri Clsse I H ALUNNO CLASSE Ulteriore ripsso e recupero nche nei siti www.vlluricrpi.it (dip. mtemtic recupero). In vcnz si può trovre
Istituto Professionle di Stto per l Industri e l Artiginto Gincrlo Vlluri Clsse I H ALUNNO CLASSE Ulteriore ripsso e recupero nche nei siti www.vlluricrpi.it (dip. mtemtic recupero). In vcnz si può trovre
Classi IV C IV E ALUNNO CLASSE LEGGI UNO DEI SEGUENTI TESTI. Istituto Professionale di Stato per l Industria e l Artigianato Giancarlo Vallauri
 Per informzioni, consigli, problemi robbypit@tin.it Istituto Professionle di Stto per l Industri e l Artiginto Gincrlo Vlluri Clssi IV C IV E.s. 0/0 ALUNNO CLASSE ESEGUI TUTTI GLI ESERCIZI SU UN FOGLIO
Per informzioni, consigli, problemi robbypit@tin.it Istituto Professionle di Stto per l Industri e l Artiginto Gincrlo Vlluri Clssi IV C IV E.s. 0/0 ALUNNO CLASSE ESEGUI TUTTI GLI ESERCIZI SU UN FOGLIO
Esercizi svolti Limiti. Prof. Chirizzi Marco.
 Cpitolo II Limiti delle funzioni di un vribile Esercizi svolti Limiti Prof. Chirizzi rco www.elettrone.ltervist.org 1) Verificre che risult: = Dobbimo provre che per ogni ε positivo, rbitrrimente piccolo,
Cpitolo II Limiti delle funzioni di un vribile Esercizi svolti Limiti Prof. Chirizzi rco www.elettrone.ltervist.org 1) Verificre che risult: = Dobbimo provre che per ogni ε positivo, rbitrrimente piccolo,
UNITA 13. GLI ESPONENZIALI
 UNITA. GLI ESPONENZIALI. Le potenze con esponente intero, rzionle e rele.. Le proprietà delle potenze.. Equzioni esponenzili che si riconducono ll stess bse. 4. L funzione esponenzile. 5. Il grfico dell
UNITA. GLI ESPONENZIALI. Le potenze con esponente intero, rzionle e rele.. Le proprietà delle potenze.. Equzioni esponenzili che si riconducono ll stess bse. 4. L funzione esponenzile. 5. Il grfico dell
Esercizi di consolidamento
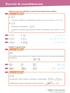 Esercizi di consolidmento Stilisci per quli vlori delle lettere le seguenti frzioni lgeriche hnno significto. esercizio guidto. L frzione h significto se il denomintore è diverso d zero e ciò ccde se 6¼
Esercizi di consolidmento Stilisci per quli vlori delle lettere le seguenti frzioni lgeriche hnno significto. esercizio guidto. L frzione h significto se il denomintore è diverso d zero e ciò ccde se 6¼
1 Equazioni e disequazioni di secondo grado
 UNIVERSITÀ DEGLI STUDI DI ROMA LA SAPIENZA - Fcoltà di Frmci e Medicin - Corso di Lure in CTF 1 Equzioni e disequzioni di secondo grdo Sino 0, b e c tre numeri reli noti, risolvere un equzione di secondo
UNIVERSITÀ DEGLI STUDI DI ROMA LA SAPIENZA - Fcoltà di Frmci e Medicin - Corso di Lure in CTF 1 Equzioni e disequzioni di secondo grdo Sino 0, b e c tre numeri reli noti, risolvere un equzione di secondo
Principali proprietà delle operazioni
 Principli proprietà delle operzioni Proprietà commuttiv dell ddizione + b b +,b N Proprietà commuttiv dell moltipliczione b b,b N Proprietà distributiv dell moltipliczione (b + c) (b + c) b + c (b c) (b
Principli proprietà delle operzioni Proprietà commuttiv dell ddizione + b b +,b N Proprietà commuttiv dell moltipliczione b b,b N Proprietà distributiv dell moltipliczione (b + c) (b + c) b + c (b c) (b
Le frazioni algebriche
 Le frzioni lgeriche Definizione se A e B sono due polinomi e B è diverso dl polinomio nullo, B A viene dett frzione lgeric. Esempio sono esempi di frzioni lgeriche. NOTA ogni monomio o polinomio può essere
Le frzioni lgeriche Definizione se A e B sono due polinomi e B è diverso dl polinomio nullo, B A viene dett frzione lgeric. Esempio sono esempi di frzioni lgeriche. NOTA ogni monomio o polinomio può essere
POTENZA CON ESPONENTE REALE
 PRECORSO DI MATEMATICA VIII Lezione ESPONENZIALI E LOGARITMI E. Modic mtemtic@blogscuol.it www.mtemtic.blogscuol.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero rele > 0 ed un numero rele qulunque,
PRECORSO DI MATEMATICA VIII Lezione ESPONENZIALI E LOGARITMI E. Modic mtemtic@blogscuol.it www.mtemtic.blogscuol.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero rele > 0 ed un numero rele qulunque,
Le frazioni algebriche
 Progetto Mtemtic in Rete - Frzioni lgeriche - Le frzioni lgeriche Definizione se A e B sono due polinomi e B è diverso dl polinomio nullo, B A viene dett frzione lgeric. Esempio sono esempi di frzioni
Progetto Mtemtic in Rete - Frzioni lgeriche - Le frzioni lgeriche Definizione se A e B sono due polinomi e B è diverso dl polinomio nullo, B A viene dett frzione lgeric. Esempio sono esempi di frzioni
Matematica C3, Algebra 2
 Mtemtic C Algebr Relese 0.0 www.mtemticmente.it Mrch 0 Contents Numeri reli. Di numeri nturli i numeri irrzionli................................. Numeri reli.................................................
Mtemtic C Algebr Relese 0.0 www.mtemticmente.it Mrch 0 Contents Numeri reli. Di numeri nturli i numeri irrzionli................................. Numeri reli.................................................
, x 2. , x 3. è un equazione nella quale le incognite appaiono solo con esponente 1, ossia del tipo:
 Sistemi lineri Un equzione linere nelle n incognite x 1, x 2, x,, x n è un equzione nell qule le incognite ppiono solo con esponente 1, ossi del tipo: 1 x 1 + 2 x 2 + x +!+ n x n = b con 1, 2,,, n numeri
Sistemi lineri Un equzione linere nelle n incognite x 1, x 2, x,, x n è un equzione nell qule le incognite ppiono solo con esponente 1, ossi del tipo: 1 x 1 + 2 x 2 + x +!+ n x n = b con 1, 2,,, n numeri
I RADICALI. H La misura di un segmento non eá sempre esprimibile mediante un numero razionale; per esempio, se un
 I RADICALI Per ricordre H L misur di un segmento non eá semre esrimiile medinte un numero rzionle er esemio, se un qudrto h lto unitrio, l misur dell su digonle, che eá, non eá rzionle. Per misurre occorre
I RADICALI Per ricordre H L misur di un segmento non eá semre esrimiile medinte un numero rzionle er esemio, se un qudrto h lto unitrio, l misur dell su digonle, che eá, non eá rzionle. Per misurre occorre
Equazioni di 2 grado. Definizioni Equazioni incomplete Equazione completa Relazioni tra i coefficienti della equazione e le sue soluzioni Esercizi
 Equzioni di grdo Definizioni Equzioni incomplete Equzione complet Relzioni tr i coefficienti dell equzione e le sue soluzioni Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni Un equzione è: Un uguglinz
Equzioni di grdo Definizioni Equzioni incomplete Equzione complet Relzioni tr i coefficienti dell equzione e le sue soluzioni Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni Un equzione è: Un uguglinz
Materia: MATEMATICA Data: 5/04/2005
 Mteri: MATEMATICA Dt: 5/4/25 L disequzione e' un disuguglinz che e' verifict per certi intervlli di vlori Ad esempio l disequzione x - 4 e' verifict per tutti i vlori dell x mggiori di 4, cioè se l posto
Mteri: MATEMATICA Dt: 5/4/25 L disequzione e' un disuguglinz che e' verifict per certi intervlli di vlori Ad esempio l disequzione x - 4 e' verifict per tutti i vlori dell x mggiori di 4, cioè se l posto
). Poiché tale funzione è una parabola, il suo
 PROBLEMA ) Il rggio dell circonferenz di centro B vri tr i vlori: x b) ( x x ) ( PQCR) = ( ABC) ( APR) ( BPQ) = ( x) x = + 8 6 8 I vlori di x che rendono minim o mssim l funzione rendono, rispettivmente,
PROBLEMA ) Il rggio dell circonferenz di centro B vri tr i vlori: x b) ( x x ) ( PQCR) = ( ABC) ( APR) ( BPQ) = ( x) x = + 8 6 8 I vlori di x che rendono minim o mssim l funzione rendono, rispettivmente,
Compiti delle vacanze di matematica CLASSE 4BS a.s. 2014/2015
 Compiti delle vcnze di mtemtic CLASSE 4BS.s. 014/01 - PER GLI STUDENTI CON ESAME A SETTEMBRE ( e consiglito chi h vuto difficoltà durnte l nno scolstico) : Studire gli rgomenti ffrontti durnte l nno svolgere
Compiti delle vcnze di mtemtic CLASSE 4BS.s. 014/01 - PER GLI STUDENTI CON ESAME A SETTEMBRE ( e consiglito chi h vuto difficoltà durnte l nno scolstico) : Studire gli rgomenti ffrontti durnte l nno svolgere
CORSO ZERO DI MATEMATICA
 UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA ESPONENZIALI E LOGARITMI Dr. Ersmo Modic ersmo@glois.it www.glois.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero
UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA ESPONENZIALI E LOGARITMI Dr. Ersmo Modic ersmo@glois.it www.glois.it POTENZA CON ESPONENTE REALE Definizione: Dti un numero
j Verso la scuola superiore +l calcolo letterale Monomi Polinomi e prodotti notevoli Equazioni
 j Verso l suol superiore +l lolo letterle Monomi Polinomi e prodotti notevoli Equzioni Monomi Il monomio x 4 y è simile : x 4 y 5 +x 4 y x y Due monomi sono simili se hnno l prte letterle ugule e, siome
j Verso l suol superiore +l lolo letterle Monomi Polinomi e prodotti notevoli Equzioni Monomi Il monomio x 4 y è simile : x 4 y 5 +x 4 y x y Due monomi sono simili se hnno l prte letterle ugule e, siome
LAVORO PER IL RECUPERO DEL DEBITO MATEMATICA CLASSI 3 S.M. DA CONSEGNARE IL PRIMO GIORNO DI ATTIVITA DI SPORTELLO
 LAVORO PER IL RECUPERO DEL DEBITO MATEMATICA CLAI.M. DA CONEGNARE IL PRIMO GIORNO DI ATTIVITA DI PORTELLO DEVI RIOLVERE PRIMA DI TUTTO I PROBLEMI E GLI EERCIZI QUI ELENCATI. TERMINATI QUETI, RIOLVI ALCUNI
LAVORO PER IL RECUPERO DEL DEBITO MATEMATICA CLAI.M. DA CONEGNARE IL PRIMO GIORNO DI ATTIVITA DI PORTELLO DEVI RIOLVERE PRIMA DI TUTTO I PROBLEMI E GLI EERCIZI QUI ELENCATI. TERMINATI QUETI, RIOLVI ALCUNI
Corso Integrato: Matematica e Statistica. Corso di Matematica (6 CFU)
 Corso di Lure in Scienze e Tecnologie Agrrie Corso Integrto: Mtemtic e Sttistic Modulo: Mtemtic (6 CFU) (4 CFU Lezioni + CFU Esercitzioni) Corso di Lure in Tutel e Gestione del territorio e del Pesggio
Corso di Lure in Scienze e Tecnologie Agrrie Corso Integrto: Mtemtic e Sttistic Modulo: Mtemtic (6 CFU) (4 CFU Lezioni + CFU Esercitzioni) Corso di Lure in Tutel e Gestione del territorio e del Pesggio
{ 1, 2,3, 4,5,6,7,8,9,10,11,12, }
 Lezione 01 Aritmetic Pgin 1 di 1 I numeri nturli I numeri nturli sono: 0,1,,,4,5,6,7,8,,10,11,1, L insieme dei numeri nturli viene indicto col simbolo. } { 0,1,,, 4,5,6,7,8,,10,11,1, } L insieme dei numeri
Lezione 01 Aritmetic Pgin 1 di 1 I numeri nturli I numeri nturli sono: 0,1,,,4,5,6,7,8,,10,11,1, L insieme dei numeri nturli viene indicto col simbolo. } { 0,1,,, 4,5,6,7,8,,10,11,1, } L insieme dei numeri
E U Q A U Z A I Z O I N O I N DI SE S C E O C N O DO
 EQUAZIONI DI ECONDO GRADO Riepilogo delle soluzioni in bse l segno di < φ : b > : b b Prof I voi, EQUAZIONI DI ECONDO GRADO EQUAZIONI PURE DI ECONDO GRADO : EEMPI ) ) ) 7 7 ) > φ (impossibile) ) impossibil
EQUAZIONI DI ECONDO GRADO Riepilogo delle soluzioni in bse l segno di < φ : b > : b b Prof I voi, EQUAZIONI DI ECONDO GRADO EQUAZIONI PURE DI ECONDO GRADO : EEMPI ) ) ) 7 7 ) > φ (impossibile) ) impossibil
COGNOME..NOME CLASSE.DATA
 COGNOME..NOME CLASSE.DATA FUNZIONE ESPONENZIALE - VERIFICA OBIETTIVI Sper definire un funzione esponenzile. Sper rppresentre un funzione esponenzile. Sper individure le crtteristiche del grfico di un funzione
COGNOME..NOME CLASSE.DATA FUNZIONE ESPONENZIALE - VERIFICA OBIETTIVI Sper definire un funzione esponenzile. Sper rppresentre un funzione esponenzile. Sper individure le crtteristiche del grfico di un funzione
x + 0 (occorrerà tenere conto del segno del coeff. e, qualora x tenda a, della parità o disparità dell esponente)
 . LIMITI DI FUNZIONI ALGEBRICHE (POLINOMI, RAPPORTI DI POLINOMI, RADICALI) L definizione generle di funzione lgebric non è semplicissim, e non voglimo occuprcene qui. Comunque, sono lgebriche, fr l ltro,
. LIMITI DI FUNZIONI ALGEBRICHE (POLINOMI, RAPPORTI DI POLINOMI, RADICALI) L definizione generle di funzione lgebric non è semplicissim, e non voglimo occuprcene qui. Comunque, sono lgebriche, fr l ltro,
Alcune mosse che utilizzano le proprietà delle operazioni in N
 Operzioni in N Proprietà commuttiv dell ddizione + b b +,b N Proprietà ssocitiv dell ddizione ( + b) + c + (b + c) + b + c,b,c N Proprietà invrintiv dell sottrzione b ( + c) (b + c) b ( c) (b c),b,c N,b,c
Operzioni in N Proprietà commuttiv dell ddizione + b b +,b N Proprietà ssocitiv dell ddizione ( + b) + c + (b + c) + b + c,b,c N Proprietà invrintiv dell sottrzione b ( + c) (b + c) b ( c) (b c),b,c N,b,c
Valore del parametro Tipo di Equazione Soluzioni Equazione di I grado x = 4. Equazione Spuria x 1 = 0 x 2 = 5 Equazione Completa con < 0
 Equzioni letterli di II grdo Un equzione letterle di II grdo è un equzione che contiene, oltre l letter che rppresent l incognit dell equzione, ltre lettere, dette prmetri, che rppresentno numeri ben determinti,
Equzioni letterli di II grdo Un equzione letterle di II grdo è un equzione che contiene, oltre l letter che rppresent l incognit dell equzione, ltre lettere, dette prmetri, che rppresentno numeri ben determinti,
436 Capitolo 17. Equazioni frazionarie e letterali Equazioni di grado superiore al primo riducibili al primo grado
 46 Cpitolo 7 Equzioni frzionrie e letterli 74 Esercizi 74 Esercizi dei singoli prgrfi 7 - Equzioni di grdo superiore l primo riducibili l primo grdo 7 ( ) Risolvere le seguenti equzioni riconducendole
46 Cpitolo 7 Equzioni frzionrie e letterli 74 Esercizi 74 Esercizi dei singoli prgrfi 7 - Equzioni di grdo superiore l primo riducibili l primo grdo 7 ( ) Risolvere le seguenti equzioni riconducendole
RACCOLTA DI ESERCIZI PER I CORSI PRELIMINARI
 RACCOLTA DI ESERCIZI PER I CORSI PRELIMINARI PROPRIETÀ DEI NUMERI INTERI, SCOMPOSIZIONI, ECC.. Se A è ugule e B è ugule, qunto vlgono m.c.m. ed M.C.D. dei numeri A e B? 0 e. Se si moltiplicno due numeri
RACCOLTA DI ESERCIZI PER I CORSI PRELIMINARI PROPRIETÀ DEI NUMERI INTERI, SCOMPOSIZIONI, ECC.. Se A è ugule e B è ugule, qunto vlgono m.c.m. ed M.C.D. dei numeri A e B? 0 e. Se si moltiplicno due numeri
- Appunti di Matematica 1 Licei Umanistici - - I polinomi - Polinomi
 Polinomi Un polinomio è un somm lgeric di monomi. Esempio: ; c sono polinomi. ; I vri monomi che compongono il polinomio si chimno termini del polinomio. Un monomio può nche essere considerto come un polinomio
Polinomi Un polinomio è un somm lgeric di monomi. Esempio: ; c sono polinomi. ; I vri monomi che compongono il polinomio si chimno termini del polinomio. Un monomio può nche essere considerto come un polinomio
2 Numeri reali. M. Simonetta Bernabei & Horst Thaler
 2 Numeri reli M. Simonett Bernei & Horst Thler Numeri interi positivi o Nturli 0 1 2 3 4 Con i numeri Nturli è sempre possiile fre l ddizione e l moltipliczione p.es.: 5+2 = 7; 3*4 = 12; m non sempre l
2 Numeri reli M. Simonett Bernei & Horst Thler Numeri interi positivi o Nturli 0 1 2 3 4 Con i numeri Nturli è sempre possiile fre l ddizione e l moltipliczione p.es.: 5+2 = 7; 3*4 = 12; m non sempre l
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2002 Sessione ordinaria
 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO Sessione ordinri Il cndidto risolv uno dei due problemi e 5 dei quesiti in cui si rticol il questionrio. PROBLEMA In un pino, riferito d un sistem
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO Sessione ordinri Il cndidto risolv uno dei due problemi e 5 dei quesiti in cui si rticol il questionrio. PROBLEMA In un pino, riferito d un sistem
Unità 3 Metodi particolari per il calcolo di reti
 Unità 3 Metodi prticolri per il clcolo di reti 1 Cos c è nell unità Metodi prticolri per il clcolo di reti con un solo genertore Prtitore di tensione Prtitore di corrente Metodi di clcolo di reti con più
Unità 3 Metodi prticolri per il clcolo di reti 1 Cos c è nell unità Metodi prticolri per il clcolo di reti con un solo genertore Prtitore di tensione Prtitore di corrente Metodi di clcolo di reti con più
1 Espressioni polinomiali
 1 Espressioni polinomili Un monomio è un espressione letterle in un vribile x che contiene un potenz inter (non negtiv, cioè mggiori o uguli zero) di x moltiplict per un numero rele: x n AD ESEMPIO: sono
1 Espressioni polinomili Un monomio è un espressione letterle in un vribile x che contiene un potenz inter (non negtiv, cioè mggiori o uguli zero) di x moltiplict per un numero rele: x n AD ESEMPIO: sono
MATEMATICA Classe Prima
 Liceo Clssico di Treiscce Esercizi per le vcnze estive 0 MATEMATICA Clsse Prim Cpitolo Numeri nturli Primi ogni pgin del cpitolo Cpitolo Numeri nturli Primi ogni pgin del cpitolo Per gli llievi promossi
Liceo Clssico di Treiscce Esercizi per le vcnze estive 0 MATEMATICA Clsse Prim Cpitolo Numeri nturli Primi ogni pgin del cpitolo Cpitolo Numeri nturli Primi ogni pgin del cpitolo Per gli llievi promossi
COMPITI PER LE VACANZE ESTIVE DALLA SECONDA ALLA TERZA
 COMPITI PER LE VACANZE ESTIVE DALLA SECONDA ALLA TERZA PROBLEMI DI APPLICAZIONE DELL'ALGEBRA ALLA GEOMETRIA ) Inscrivere in un semicirconferenz di dimetro r un rettngolo ABCD vente il lto AB sul dimetro
COMPITI PER LE VACANZE ESTIVE DALLA SECONDA ALLA TERZA PROBLEMI DI APPLICAZIONE DELL'ALGEBRA ALLA GEOMETRIA ) Inscrivere in un semicirconferenz di dimetro r un rettngolo ABCD vente il lto AB sul dimetro
U.D. N 13 Le inequazioni ad una incognita
 Unità Didttic N Le inequzioni d un incognit 5 U.D. N Le inequzioni d un incognit 0) Proprietà delle disuguglinze fr numeri reli reltivi 0) Inequzioni e loro proprietà 0) Inequzioni rzionli intere di primo
Unità Didttic N Le inequzioni d un incognit 5 U.D. N Le inequzioni d un incognit 0) Proprietà delle disuguglinze fr numeri reli reltivi 0) Inequzioni e loro proprietà 0) Inequzioni rzionli intere di primo
Equazioni 1 grado. Definizioni Classificazione Risoluzione Esercizi
 Equzioni grdo Definizioni Clssificzione Risoluzione Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni Prendimo in esme le due espressioni numeriche 8 entrmbe sono uguli 7, e l scrittur si chim uguglinz
Equzioni grdo Definizioni Clssificzione Risoluzione Esercizi Mteri: Mtemtic Autore: Mrio De Leo Definizioni Prendimo in esme le due espressioni numeriche 8 entrmbe sono uguli 7, e l scrittur si chim uguglinz
DISCIPLINA* RIPASSO UNITA 1 UNITA 2 UNITA 3 UNITA 4 UNITA 5 UNITA 6
 All. Anno Scolstico 6-7 Clsse Bl DISCIPLINA* Mtemtic DOCENTE; Giovnn Frre Testo in dozione: L. Ssso l Mtemtic colori edizione zzurr Primo biennio ed. De Agostini- Petrini RIPASSO le frzioni lgebriche:
All. Anno Scolstico 6-7 Clsse Bl DISCIPLINA* Mtemtic DOCENTE; Giovnn Frre Testo in dozione: L. Ssso l Mtemtic colori edizione zzurr Primo biennio ed. De Agostini- Petrini RIPASSO le frzioni lgebriche:
I S I E. Fermi - Lucca Istituto Tecnico settore Tecnologico
 I S I E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Podestà Tizin Gli insiemi numerii I numeri nturli, i numeri interi, i numeri rzionli. ddizione, sottrzione,
I S I E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Podestà Tizin Gli insiemi numerii I numeri nturli, i numeri interi, i numeri rzionli. ddizione, sottrzione,
I S I E. Fermi - Lucca Istituto Tecnico settore Tecnologico
 I S I E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Podestà Tizin Gli insiemi numerii I numeri nturli, i numeri interi, i numeri rzionli. ddizione, sottrzione,
I S I E. Fermi - Lu Istituto Tenio settore Tenologio nno solstio / Progrmm di MTEMTI lsse I Insegnnte Podestà Tizin Gli insiemi numerii I numeri nturli, i numeri interi, i numeri rzionli. ddizione, sottrzione,
Esponenziali e logaritmi
 Esponenzili e ritmi ESPONENZIALI Potenze con esponente rele L potenz è definit: se > 0, per ogni R se 0, per tutti e soli gli R se < 0, per tutti e soli gli Z Sono definite: ( ) ( ) ( ) 7 7 Non sono definite:
Esponenzili e ritmi ESPONENZIALI Potenze con esponente rele L potenz è definit: se > 0, per ogni R se 0, per tutti e soli gli R se < 0, per tutti e soli gli Z Sono definite: ( ) ( ) ( ) 7 7 Non sono definite:
ESPONENZIALI E LOGARITMI
 ESPONENZIALI E LOGARITMI RICHIAMI DI TEORIA dom f Im f grfico Funzioni esponenzili y=^ con > Funzioni esponenzili y=^ con
ESPONENZIALI E LOGARITMI RICHIAMI DI TEORIA dom f Im f grfico Funzioni esponenzili y=^ con > Funzioni esponenzili y=^ con
0x3 0x5 2 R. Sistemi di disequazioni. Esercizio no.1. Esercizio no.2. Esercizio no.3. Esercizio no.4. Esercizio no.5. Esercizio no.6. Esercizio no.
 Edutecnic.it Sistemi di disequzioni Sistemi di disequzioni Esercizio no. Esercizio no. Esercizio no. ) ) Esercizio no. ) ) 9 ) Soluzione pg. [ ] Soluzione pg. [ ] Soluzione pg. 9 Soluzione pg. Esercizio
Edutecnic.it Sistemi di disequzioni Sistemi di disequzioni Esercizio no. Esercizio no. Esercizio no. ) ) Esercizio no. ) ) 9 ) Soluzione pg. [ ] Soluzione pg. [ ] Soluzione pg. 9 Soluzione pg. Esercizio
Anno 1. Numeri reali: proprietà e applicazioni di uso comune
 Anno Numeri reli: proprietà e ppliczioni di uso comune Introduzione L insieme dei numeri rzionli è composto d numeri che si ottengono dl rpporto tr due numeri interi. Tle rpporto, o frzione, è sempre ssociile
Anno Numeri reli: proprietà e ppliczioni di uso comune Introduzione L insieme dei numeri rzionli è composto d numeri che si ottengono dl rpporto tr due numeri interi. Tle rpporto, o frzione, è sempre ssociile
Esercizi di Analisi Matematica
 Università degli Studi di Udine Anno Accdemico 07/8 Diprtimento di Scienze Mtemtic, Informtiche e Fisiche Corsi di Lure in Informtic e in IBW Esercizi di Anlisi Mtemtic Esercizi del 7 ottobre 07. Nell
Università degli Studi di Udine Anno Accdemico 07/8 Diprtimento di Scienze Mtemtic, Informtiche e Fisiche Corsi di Lure in Informtic e in IBW Esercizi di Anlisi Mtemtic Esercizi del 7 ottobre 07. Nell
equazioni e disequazioni
 T Cpitolo equzioni e disequzioni Disequzioni e princìpi di equivlenz Le disuguglinze sono enunciti fr espressioni che confrontimo medinte le seguenti relzioni d ordine: (minore), (mggiore), # (minore o
T Cpitolo equzioni e disequzioni Disequzioni e princìpi di equivlenz Le disuguglinze sono enunciti fr espressioni che confrontimo medinte le seguenti relzioni d ordine: (minore), (mggiore), # (minore o
Maturità scientifica, corso di ordinamento, sessione ordinaria 2000-2001
 Mtemtic per l nuov mturità scientific A. Bernrdo M. Pedone Mturità scientific, corso di ordinmento, sessione ordinri 000-001 PROBLEMA 1 Si consideri l seguente relzione tr le vribili reli x, y: 1 1 1 +
Mtemtic per l nuov mturità scientific A. Bernrdo M. Pedone Mturità scientific, corso di ordinmento, sessione ordinri 000-001 PROBLEMA 1 Si consideri l seguente relzione tr le vribili reli x, y: 1 1 1 +
Calendario Boreale (EUROPA) 2014 QUESITO 1
 www.mtefili.it Clendrio Borele (EUROPA) 204 QUESITO Si determini, se esiste, un cono circolre retto tle che il suo volume e l su superficie totle bbino lo stesso vlore numerico. Indichimo con r il rggio
www.mtefili.it Clendrio Borele (EUROPA) 204 QUESITO Si determini, se esiste, un cono circolre retto tle che il suo volume e l su superficie totle bbino lo stesso vlore numerico. Indichimo con r il rggio
Risoluzione verifica di matematica 3C del 17/12/2013
 Problem 1 Risoluzione verific di mtemtic C del 17/1/01 Si clcolno le intersezioni tr le rette generiche del fscio proprio y x y 1, risolvendo il sistem: x y 1 y mx Si ottengono i punti di coordinte espresse
Problem 1 Risoluzione verific di mtemtic C del 17/1/01 Si clcolno le intersezioni tr le rette generiche del fscio proprio y x y 1, risolvendo il sistem: x y 1 y mx Si ottengono i punti di coordinte espresse
MODALITA DIVALUTAZIONE DEGLI STUDENTI CON CARENZE NEL SECONDO QUADRIMESTRE ESITO SOSPESO MATEMATICA BIENNIO. Coordinatrice: Prof. ANTONINA CASTANIOTTO
 LICEO SCIENTICO STATALE LEONARDO DA VINCI GENOVA.s.04-5 MODALITA DIVALUTAZIONE DEGLI STUDENTI CON CARENZE NEL SECONDO QUADRIMESTRE ESITO SOSPESO MATEMATICA BIENNIO Coordintrice: Prof. ANTONINA CASTANIOTTO
LICEO SCIENTICO STATALE LEONARDO DA VINCI GENOVA.s.04-5 MODALITA DIVALUTAZIONE DEGLI STUDENTI CON CARENZE NEL SECONDO QUADRIMESTRE ESITO SOSPESO MATEMATICA BIENNIO Coordintrice: Prof. ANTONINA CASTANIOTTO
Verifica 10 ESPONENZIALI E LOGARITMI
 Verific 0 SPONNZIALI LOGARITMI TST I FIN APITOLO Qule delle seguenti figure non rppresent un funzione? A È dt l funzione f : R R, descritt dll legge 4. Qunto vle l immgine di 0? A 0... 4. 4. L funzione
Verific 0 SPONNZIALI LOGARITMI TST I FIN APITOLO Qule delle seguenti figure non rppresent un funzione? A È dt l funzione f : R R, descritt dll legge 4. Qunto vle l immgine di 0? A 0... 4. 4. L funzione
KIT ESTIVO MATEMATICA A.S. 2015/16 CLASSI SECONDE IeFP OPERATORE GRAFICO
 ZENALE e BUTIINONE KIT ESTIVO MATEMATICA A.S. 0/ CLASSI SECONDE IeFP OPERATORE GRAFICO Al fine di tenere in llenmento le ilità mtemtihe propedeutihe ll lsse terz, onsiglimo lo svolgimento piere di eserizi
ZENALE e BUTIINONE KIT ESTIVO MATEMATICA A.S. 0/ CLASSI SECONDE IeFP OPERATORE GRAFICO Al fine di tenere in llenmento le ilità mtemtihe propedeutihe ll lsse terz, onsiglimo lo svolgimento piere di eserizi
Appunti di Matematica 4 - Triangoli qualsiasi - Triangoli qualsiasi
 Tringoli qulsisi Considerimo un tringolo qulsisi ABC e dottimo l seguente notzione: nel vertice A l ngolo è α, nel vertice B β, nel vertice C γ e indichimo con il lto opposto d A, con b quello opposto
Tringoli qulsisi Considerimo un tringolo qulsisi ABC e dottimo l seguente notzione: nel vertice A l ngolo è α, nel vertice B β, nel vertice C γ e indichimo con il lto opposto d A, con b quello opposto
Disequazioni di secondo grado
 Disequzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Disequzioni i seono gro Cpitolo Risoluzione lgeri Verifi per l lsse seon COGNOME............................... NOME............................. Clsse.................................... Dt...............................
Appunti di Matematica 1 - Numeri razionali - I numeri razionali. Le frazioni
 Appunti di Mtemtic I numeri rzionli Le frzioni Definimo un frzione come il rpporto di due numeri interi cioè n n, d Ζ con d 0 d in cui il numero scritto sopr ll line di frzione viene chimto numertore e
Appunti di Mtemtic I numeri rzionli Le frzioni Definimo un frzione come il rpporto di due numeri interi cioè n n, d Ζ con d 0 d in cui il numero scritto sopr ll line di frzione viene chimto numertore e
Antonella Greco, Rosangela Mapelli. E-Matematica. E-Book di Matematica per il triennio. Volume 1
 Antonell Greco, Rosngel Mpelli E-Mtemtic E-Book di Mtemtic per il triennio Volume COPIA SAGGIO Cmpione grtuito fuori commercio d esclusivo uso dei docenti Grmond 009 Tutti i diritti riservti Vi Tevere,
Antonell Greco, Rosngel Mpelli E-Mtemtic E-Book di Mtemtic per il triennio Volume COPIA SAGGIO Cmpione grtuito fuori commercio d esclusivo uso dei docenti Grmond 009 Tutti i diritti riservti Vi Tevere,
Introduzione alle disequazioni algebriche
 Introduzione lle disequzioni lgebriche Giovnni decide di fre ttività fisic e chiede informzioni due plestre. Un plestr privt chiede un quot d iscrizione nnu di 312, più 2 per ogni ingresso. L plestr comunle
Introduzione lle disequzioni lgebriche Giovnni decide di fre ttività fisic e chiede informzioni due plestre. Un plestr privt chiede un quot d iscrizione nnu di 312, più 2 per ogni ingresso. L plestr comunle
