APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
|
|
|
- Fabio Giuliani
- 5 anni fa
- Visualizzazioni
Transcript
1 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine di a A è indicato con f (a). A è detto dominio di f e B codominio di f. Se f : A B è un applicazione, chiamiamo immagine di f il sottoinsieme di B costituito dalle immagini di tutti gli elementi di A e scriviamo: Im f = {b B a A tale che f (a) = b}. Un applicazione f : A B si dice suriettiva se Im f = B, cioè se ogni elemento b B è immagine di qualche elemento a A. 2 / 57
2 Un applicazione f : A B si dice iniettiva se per ogni x, y A, con x y, si ha f (x) f (y), cioè se f associa ad elementi distinti di A elementi distinti di B. Equivalentemente, se f è iniettiva si ha: f (x) = f (y) x = y. Un applicazione si dice biettiva (o corrispondenza biunivoca) se è sia iniettiva che suriettiva. Dato un insieme A, l applicazione i A : A A definita da i A (a) = a per ogni a A si chiama applicazione identica su A. i A è un applicazione sia iniettiva che suriettiva, cioè è biettiva. 3 / 57
3 Date due applicazioni f : A B e g : B C, chiamiamo applicazione composta di f e g (o composizione di f e g) l applicazione g f : A C definita da: (g f )(a) = g(f (a)) a A. Se f : A B è un applicazione biettiva, l applicazione che associa ad ogni elemento di B l unico elemento di A da cui proviene mediante f è detta applicazione inversa di f e si indica con f 1 : B A. Per ogni b B f 1 (b) = a, dove a è l unico elemento di A tale che f (a) = b. 4 / 57
4 OPERAZIONI SU INSIEMI Importanti esempi di applicazioni sono le operazioni su un insieme. Dati due insiemi A e B chiamiamo prodotto cartesiano di A e B, e scriviamo A B, l insieme costituito dalle coppie ordinate aventi il primo elemento in A e il secondo in B, cioè: A B = {(a, b) a A, b B}. Si pone A A = A 2 e il piano cartesiano si identifica con R 2. Un operazione definita su un insieme A è un applicazione A A A. L immagine di una coppia (a, b) è indicata con a b. 5 / 57
5 Proprietà delle operazioni su un insieme Un operazione su un insieme G è: 1. associativa se (a b) c = a (b c), per ogni a, b, c G 2. commutativa se a b = b a per ogni a, b G. Sia G un insieme su cui è definita un operazione. Un elemento e G è detto elemento unità o elemento neutro se per ogni a G si ha a e = e a = a. Sia G un insieme su cui è definita un operazione che ammette l elemento neutro e. Un elemento a G si dice invertibile se esiste a G tale che a a = a a = e. 6 / 57
6 STRUTTURE ALGEBRICHE Si definisce struttura algebrica un insieme non vuoto su cui siano definite una o più operazioni. Sono strutture algebriche: GRUPPI, ANELLI e CAMPI. Sia G un insieme su cui è definita un operazione. Diremo che (G, ) è un gruppo se: 1. è associativa 2. esiste l elemento neutro e 3. ogni elemento è invertibile. Se vale la proprietà commutativa, il gruppo è detto abeliano. 7 / 57
7 Sia A un insieme su cui sono definite sue operazioni, che indichiamo con + e. (A, +, ) è un anello se: 1. (A, +) è un gruppo abeliano 2. è associativa 3. per ogni a, b, c A si ha: a (b + c) = a b + a c (a + b) c = a c + b c. Se (A, ) è commutativo, l anello è detto commutativo. Un anello commutativo (A, +, ) con l unità, ovvero dotato dell elemento neutro 1 rispetto all operazione, è detto campo se ogni elemento non nullo è invertibile. 8 / 57
8 LE MATRICI Un importante esempio di struttura algebrica su cui si basano le tecniche dell'algebra lineare è quello delle matrici.
9 Sia k un campo. Una tabella del tipo: a 11 a a 1n a 21 a a 2n A = a m1 a m2... a mn dove gli a ij k si dice matrice di tipo m n su k. L insieme delle matrici m n su k si indica con k m,n. (a 11, a 12,..., a 1n ), (a 21, a 22,..., a 2n ),...,(a m1, a m2,..., a mn ) sono m n-uple di elementi di k dette righe della matrice. (a 11, a 21,..., a m1 ), (a 12, a 22,..., a m2 ),...,(a 1n, a 2n,..., a mn ) sono n m-uple di elementi di k dette colonne della matrice. 28 / 57
10 Una matrice si indica anche con A = (a ij ) 1 i m o A = (a ij ) o ancora: A = R 1 R 2... R m ( o A = 1 j n C 1 C 2... C n ). Se m = n, la matrice A si dirà quadrata di ordine n. Una matrice quadrata A k n,n si dice diagonale se a ij = 0 per i j, cioè: A = a a a nn. 29 / 57
11 Sia A = (a ij ) k m,n. Si chiama trasposta di A la matrice di k n,m ottenuta scambiando a ij con a ji per ogni i, j, cioè t A = (a ji ). Proposizione Sia A k m,n. Allora: 1. t ( t A) = A 2. t (A + B) = t A + t B. Una matrice A è detta simmetrica se t A = A. È detta antisimmetrica se t A = A. 36 / 57
12 1. Somma OPERAZIONI NELL'INSIEME DELLE MATRICI Siano A = (a ij ) e B = (b ij ) matrici di k m,n. Diremo somma tra A e B la matrice: A + B = (a ij + b ij ), i = 1,..., m, j = 1,..., n, cioè la matrice ottenuta sommando gli elementi di A e di B che stanno nella stessa riga e colonna. Proposizione k m,n è un gruppo abeliano rispetto alla somma.
13 2. Prodotto per uno scalare (o prodotto esterno) Dotiamo k m,n di un prodotto esterno. Se b K e A = (a ij ) k m,n, poniamo: b A = (b a ij ), cioè: a 11 a a 1n b a 11 b a b a 1n a 21 a a 2n b = b a 21 b a b a 2n a m1 a m2... a mn b a m1 b a m2... b a mn 30 / 57
14 3. Prodotto tra matrici Siano A = (a ij ) k m,n e B = (b ij ) k n,p. Definiamo il prodotto righe per colonne A B k m,p la matrice così ottenuta: A B = (c ij ), i = 1,..., m, j = 1,..., p, con c ij = a i1 b 1j + a i2 b 2j + + a in b nj. L elemento di posto i, j è la somma dei prodotti degli elementi della i-esima riga di A per gli elementi della j-esima colonna di B. 37 / 57
15 Determinante di una matrice Il determinante di una matrice è un numero e si definisce solo per le matrici quadrate, cioè quelle che hanno lo stesso numero di righe e di colonne. Sia A = ( a11 a 12 a 21 a 22 una matrice quadrata di ordine 2. Allora il determinante di A, che si indica con det A o A, è il numero: det A = A = a 11 a 12 a 21 a 22 ) = a 11a 22 a 12 a / 57
16 Sia A = a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 una matrice quadrata di ordine 3. Il determinante di A è il numero: A = a 11 a 22 a 33 +a 12 a 23 a 31 +a 13 a 21 a 32 a 13 a 22 a 31 a 12 a 21 a 33 a 11 a 23 a 32. Ci sono due metodi mnemonici, dovuti a Sarrus, per ricordare la regola: a 11 a 12 a 13 a 11 a 12 a 13 A = a 21 a 22 a 23 a 21 a 22 a 23 a 31 a 32 a 33 a 31 a 32 a 33 A = a 11 a 12 a 13 a 11 a 12 a 21 a 22 a 23 a 21 a 22 a 31 a 32 a 33 a 31 a 32 a 11 a 12 a 13 a 11 a 12 a 21 a 22 a 23 a 21 a 22 a 31 a 32 a 33 a 31 a / 57
17 Per calcolare il determinante di una matrice quadrata di ordine superiore a 3 abbiamo bisogno della seguente definizione: Sia A = (a ij ) una matrice quadrata di ordine n. Diremo complemento algebrico di posto (i, j), e si indica con A ij, il prodotto di ( 1) i+j e del determinante della matrice quadrata di ordine n 1 ottenuta da A sopprimendo la i-esima riga e la j-esima colonna. 40 / 57
18 Il seguente risultato ci fornisce una regola di calcolo per il determinante di una matrice di ordine n. Teorema (Primo teorema di Laplace) Sia A = (a ij ) una matrice quadrata di ordine n. La somma dei prodotti degli elementi di una riga (o colonna) per i rispettivi complementi algebrici è uguale al determinante di A, cioè: A = ( A = n a ij A ij j=1 n a ij A ij i=1 i = 1,..., n j = 1,..., n ) Il risultato che si ottiene non dipende dalla particolare riga o colonna scelta.
19 Teorema (Secondo teorema di Laplace) Sia A = (a ij ) una matrice quadrata di ordine n. La somma dei prodotti degli elementi di una riga (o colonna) per i complementi algebrici di un altra riga o (colonna) è uguale a 0, cioè: n a ij A hj = 0 j=1 ( n a ij A ik i=1 i h j k ) 41 / 57
20 Proposizione Sia A k n,n. 1. A = t A. 2. Se una riga (o colonna) di A è nulla = A = Se A è una matrice ottenuta da A scambiando due sue righe (o colonne) A = A. 4. Se due righe (o colonne) di A sono uguali = A = Se la riga R i di A è del tipo R i = R i + R i, allora: A = R 1. R i + R i. R n = R 1. R i. R n + R 1. R i. R n. 42 / 57 Proprietà dei determinanti
21 6. Se la colonna C i di A è del tipo C i = C i + C i, allora: A = C 1... C i + C i... C n = = C 1... C i... C n + C1... C i... C n. 7. Sia λ k. Allora: R 1. λr i. R n R 1. = λ R i. R n e C1... λc i... C n = λ C1... C i... C n 8. Se A ha due righe (o colonne) proporzionali = A = / 57
22 Teorema (Teorema di Binet) Siano A, B k n,n. Allora il determinante della matrice A B è il prodotto dei determinanti delle due matrici, cioè: A B = A B. La matrice quadrata I = kn,n è detta matrice identica di ordine n. Essa è tale che, se A k n,n, allora: A I = I A = A.
23 Matrice inversa Una matrice A k n,n è detta invertibile se esiste una matrice B k n,n tale che: A B = B A = I. B è detta matrice inversa di A e si indica anche con A 1. Sia A k n,n. Chiamiamo matrice aggiunta di A la matrice A a avente in ogni posto (i, j) il complemento algebrico di posto (i, j): A a = (A ij ). Teorema Una matrice A k n,n è invertibile A 0. In tal caso, la matrice inversa di A è: A 1 = 1 t A a. A DIMOSTRAZIONE. 49 / 57
24 Rango di una matrice Sia A = (a ij ) una matrice m n. Chiamiamo minore di ordine k estratto da A il determinante di una matrice k k ottenuta con gli elementi comuni a k righe e k colonne di A. Sia A una matrice m n. Chiamiamo rango di A, che indichiamo con ρ(a), l ordine massimo di un minore non nullo. Osservazione Dire che ρ(a) = r significa dire che esiste un minore non nullo di ordine r e che tutti i minori di ordine r + 1 sono nulli. 45 / 57
25 Riduzione per righe e calcolo del rango Una matrice A = (a ij ) si dice ridotta per righe (o colonne) se in ogni riga (o colonna) non nulla esiste un elemento a hk = 0 tale che a jk = 0 per ogni j > h, cioè al di sotto del quale vi sono solo zeri (o a hj = 0 per ogni j > k, cioè alla destra del quale compaiono solo zeri). Gli elementi a hk 0 (uno per ogni riga non nulla) sono detti speciali. Sia A k m,n una matrice e Siano R 1,..., R m le sue righe. La riduzione per righe permette di passare da una matrice A ad una matrice A ridotta per righe, in modo che ρ(a) = ρ(a ). Le operazioni, dette elementari, sulla matrice A che consentono di non alterare il suo rango sono: scambio di due righe moltiplicazione di una riga per uno scalare non nullo, cioè R i λr i sostituzione di una riga con la somma della riga stessa e di un multiplo di un altra riga, cioè R i R i + λr j. 46 / 57
26 Il numero delle righe non nulle di una matrice ridotta è uguale al suo rango. Quindi, per calcolare il rango di una matrice A è sufficiente ridurla e calcolare il rango della matrice ridotta così ottenuta. 48 / 57
27 SISTEMI LINEARI Un sistema lineare è un insieme di m equazioni lineari in n incognite a coefficienti in un campo k. Si parlerà di sistema lineare m n: a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2... a m1 x 1 + a m2 x a mn x n = b m, con a ij, b h k. Gli a ij vengono detti coefficienti delle incognite e i b h termini noti. x 1,..., x n sono le n incognite. 50 / 57
28 Si considerano le matrici: a 11 a a 1n a 21 a a 2n A = a m1 a m2... a mn B = b 1 b 2... b m km,1, e A B = km,n, X = x 1 x 2... x n kn,1, a 11 a a 1n b 1 a 21 a a 2n b km,n+1 a m1 a m2... a mn b m La matrice A è detta matrice dei coefficienti o matrice incompleta, B matrice (o colonna) dei termini noti, X matrice o colonna delle incognite e A B matrice completa. Osserviamo che il sistema lineare si può scrivere nella forma AX = B. 51 / 57
29 Sia AX = B un sistema lineare di tipo m n. Diremo soluzione del sistema lineare un elemento (α 1, α 2,..., α n ) k n tale che, posto: α = si abbia A α = B., cioè sostituendo α i ad ognixi i per i = 1,..., n vengono soddisfatte tutte le equazioni. α 1 α 2... α n Un sistema lineare si dice impossibile se non ammette alcuna soluzione, possibile se ammette almeno una soluzione. Quando il sistema ammette un unica soluzione è detto determinato e, quando ne ammette più di una, è detto indeterminato. 52 / 57
30 Condizioni di risolubilità di un sistema lineare Un risultato fondamentale nella teoria dei sistemi lineari è il Teorema di Rouchè - Capelli che descrive le condizioni di risolubilità di un sistema lineare, ma non fornisce un metodo per trovarne le soluzioni. Teorema (Teorema di Rouchè-Capelli I) Un sistema lineare AX = B di tipo m n è possibile ρ(a) = ρ(a B). (DIMOSTRAZIONE NELLE PROSSIME LEZIONI) Quindi se il rango di A è minore del rango di A B, allora il sistema è incompatibile. Nel caso di uguaglianza il sistema è compatibile, ovvero può essere determinato oppure indeterminato. 54 / 57
31 Sia AX = B un sistema lineare nelle n incognite x 1,..., x n. r incognite x i1,..., x ir si dicono libere se possono assumere valori arbitrari (cioè liberi) in funzione dei quali sono determinati i valori delle incognite del sistema x 1,..., x n. Teorema (Teorema di Rouchè-Capelli II) Sia AX = B sistema lineare di tipo m n e sia ρ(a) = ρ(a B) = r. Allora il sistema ha n r incognite libere e diciamo che il sistema ammette n r soluzioni (ovvero il sistema è indeterminato con n-r incognite libere). Quindi se: - r = n il sistema è determinato (non ci sono incognite libere) - r < n il sistema è indeterminato con n-r incognite libere
32 Risoluzione di sistemi lineari con il metodo di riduzione Due sistemi lineari AX = B e A X = B in n incognite si dicono equivalenti se hanno le stesse soluzioni. Metodo di riduzione Sia AX = B un sistema lineare m n. Riducendo per righe la matrice completa A B, in modo che gli elementi speciali compaiano in A, otteniamo un sistema lineare A X = B equivalente a quello di partenza, ma con la matrice A ridotta. A questo punto risolvere il sistema lineare A X = B è semplice: si procede per sostituzione dal basso verso l alto, ricavando di volta in volta l incognita corrispondente all elemento speciale. 53 / 57
33 Risoluzione di sistemi lineari con il metodo di Cramer Teorema (Teorema di Cramer) Un sistema lineare AX = B di tipo n n è determinato A 0. In tal caso, considerate le matrici: b 1 a a 1n a 11 b 1... a 1n b 2 a a 2n B 1 = , B a 21 b 2... a 2n 2 = , b n a n2... a nn a n1 b n... a nn a 11 a b 1 a 21 a b 2 B n = ,... a n1 a n2... b n la soluzione del sistema è: ( B1 A, B 2 A,..., B ) n. A DIMOSTRAZIONE. 55 / 57
34 Se: Sistemi omogenei B = allora il sistema lineare AX = B è detto omogeneo. Banalmente in questo caso si ha ρ(a) = ρ(a B) e il sistema ammette sempre una soluzione, che è (0, 0,..., 0). Questa è detta soluzione banale Proprietà Un sistema lineare omogeneo AX = 0 di tipo m n ha soluzioni non banali ρ(a) < n. Quindi se il rango di A r è minore di n il sistema ammette infinite soluzioni con n-r incognite libere. Se r = n allora il sistema ammette solo la soluzione banale. 56 / 57
35 Matrici invertibili a destra e a sinistra
36
37
Testi consigliati e contatti
 Testi consigliati e contatti P.Bonacini, M. G. Cinquegrani, L. Marino, Algebra lineare: esercizi svolti, Cavallotto Edizioni, Catania P. Bonacini, M. G. Cinquegrani, L. Marino, Geometria analitica: esercizi
Testi consigliati e contatti P.Bonacini, M. G. Cinquegrani, L. Marino, Algebra lineare: esercizi svolti, Cavallotto Edizioni, Catania P. Bonacini, M. G. Cinquegrani, L. Marino, Geometria analitica: esercizi
Testi consigliati e orario di ricevimento
 Testi consigliati e orario di ricevimento P. Bonacini, M. G. Cinquegrani, L. Marino, Algebra lineare: esercizi svolti, Cavallotto Edizioni, Catania P. Bonacini, M. G. Cinquegrani, L. Marino, Geometria
Testi consigliati e orario di ricevimento P. Bonacini, M. G. Cinquegrani, L. Marino, Algebra lineare: esercizi svolti, Cavallotto Edizioni, Catania P. Bonacini, M. G. Cinquegrani, L. Marino, Geometria
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari
 Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Le matrici. Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1.
 Le matrici Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1. Siano m, n N\{0}. Una matrice m n a coefficienti in K è una tabella di m n elementi di K disposti
Le matrici Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1. Siano m, n N\{0}. Una matrice m n a coefficienti in K è una tabella di m n elementi di K disposti
( ) TEORIA DELLE MATRICI. A. Scimone a.s pag 1
 . Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
. Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
A =, c d. d = ad cb. c d A =
 Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
MATRICI E SISTEMI LINEARI
 MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
Corso di Matematica e Statistica 3 Algebra delle matrici. Una tabella rettangolare: la matrice. Una tabella rettangolare: la matrice
 Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
Esempio. L immagine di f è l insieme dei vettori w = (w 1, w 2 ) R 2 che hanno w 1 = w 2. Quindi:
 Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
Anno Accademico 2015/2016
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2015/2016 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2015/2016 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe.
![Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe. Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe.](/thumbs/100/147138366.jpg) Matrici triangolari [Abate, 32] Definizione Una matrice A = a ij ) R m,n si dice triangolare superiore se a ij = 0 per ogni i > j; triangolare inferiore se a ij = 0 per ogni i < j Lezioni 05 e 06 Una matrice
Matrici triangolari [Abate, 32] Definizione Una matrice A = a ij ) R m,n si dice triangolare superiore se a ij = 0 per ogni i > j; triangolare inferiore se a ij = 0 per ogni i < j Lezioni 05 e 06 Una matrice
MATRICI E SISTEMI LINEARI
 1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
GEOMETRIA 1 prima parte
 GEOMETRIA 1 prima parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 44 index Relazioni in un insieme 1 Relazioni in un insieme 2 Gruppi,
GEOMETRIA 1 prima parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 44 index Relazioni in un insieme 1 Relazioni in un insieme 2 Gruppi,
Federica Gregorio e Cristian Tacelli
 1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
Nozioni e notazioni: concetti primitivi di insieme, elemento ed appartenenza.
 Geometria I lezione del 30 settembre 2013 Presentazione del corso. Nozioni e notazioni: concetti primitivi di insieme, elemento ed appartenenza. Insiemi numerici: i numeri naturali, gli interi, i numeri
Geometria I lezione del 30 settembre 2013 Presentazione del corso. Nozioni e notazioni: concetti primitivi di insieme, elemento ed appartenenza. Insiemi numerici: i numeri naturali, gli interi, i numeri
Il prodotto tra matrici non è commutativo. Nelle notazioni precedenti, ponendo n = p e m = q si hanno:
 L anello delle matrici Esempio. Siano A = [ ] 0 1 3 0 2 1, B = 1 2 0 0 1 2 3 4, 1 0 calcolare AB e BA. Osservazioni Siano A Mat m,n (K) e B Mat p,q (K). Il prodotto AB è definito se n = p. Si ha AB Mat
L anello delle matrici Esempio. Siano A = [ ] 0 1 3 0 2 1, B = 1 2 0 0 1 2 3 4, 1 0 calcolare AB e BA. Osservazioni Siano A Mat m,n (K) e B Mat p,q (K). Il prodotto AB è definito se n = p. Si ha AB Mat
Elementi di Algebra Lineare Il determinante
 Elementi di Algebra Lineare Cristina Turrini UNIMI - 2015/2016 Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 17 index 1 2 Sottomatrici e minori Cristina Turrini (UNIMI - 2015/2016)
Elementi di Algebra Lineare Cristina Turrini UNIMI - 2015/2016 Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 17 index 1 2 Sottomatrici e minori Cristina Turrini (UNIMI - 2015/2016)
Sistemi di equazioni lineari
 Sistemi di equazioni lineari Siano X 1,, X n indeterminate Un equazione lineare (o di primo grado) nelle incognite X 1,, X n a coefficienti nel campo K è della forma a 1 X 1 + + a n X n = b, a i, b K,
Sistemi di equazioni lineari Siano X 1,, X n indeterminate Un equazione lineare (o di primo grado) nelle incognite X 1,, X n a coefficienti nel campo K è della forma a 1 X 1 + + a n X n = b, a i, b K,
a.a MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI
 aa 2012-2013 MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI 1 Sistemi di equazioni lineari Definizione 11 i Un equazione lineare nelle indeterminate (o incognite X 1,, X 1 m a coefficienti interi (o razionali,
aa 2012-2013 MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI 1 Sistemi di equazioni lineari Definizione 11 i Un equazione lineare nelle indeterminate (o incognite X 1,, X 1 m a coefficienti interi (o razionali,
VETTORI E MATRICI. Ing. Nicola Cappuccio 2014 U.F.5 ELEMENTI SCIENTIFICI ED ELETTRONICI APPLICATI AI SISTEMI DI TELECOMUNICAZIONI
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
Note per il corso di Geometria Corso di laurea in Ing. Edile/Architettura. 4 Sistemi lineari. Metodo di eliminazione di Gauss Jordan
 Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
Anno Accademico 2016/2017
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2016/2017 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2016/2017 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Algebra lineare. Laboratorio di programmazione e calcolo CdL in Chimica. Pierluigi Amodio
 Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI
 SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
il determinante che si ottiene da A, sopprimendo la i - esima riga e la j - esima colonna. Si definisce complemento algebrico dell'elemento a ij
 Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016.
 Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
PreCorso di Matematica - PCM Corso M-Z
 PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
Elementi di Algebra Lineare Applicazioni lineari
 Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 50 index Applicazioni lineari 1 Applicazioni lineari
Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 50 index Applicazioni lineari 1 Applicazioni lineari
Esercitazioni di Algebra e Geometria
 Esercitazioni di Algebra e Geometria Anno Accademico 2011 2012 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.00
Esercitazioni di Algebra e Geometria Anno Accademico 2011 2012 Dott.ssa Elisa Pelizzari e-mail elisa.peli@libero.it Esercitazioni: lunedì 14.30 16.30 venerdì 14.30 16.30 Ricevimento studenti: venerdì 13.00
1. Sistemi di equazioni lineari. 1.1 Considerazioni preliminari
 1. Sistemi di equazioni lineari 1.1 Considerazioni preliminari I sistemi lineari sono sistemi di equazioni di primo grado in più incognite. Molti problemi di matematica e fisica portano alla soluzione
1. Sistemi di equazioni lineari 1.1 Considerazioni preliminari I sistemi lineari sono sistemi di equazioni di primo grado in più incognite. Molti problemi di matematica e fisica portano alla soluzione
Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta. Metodi per il calcolo del rango di una matrice
 Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta Versione del 21/12/07 Metodi per il calcolo del rango di una matrice Sia A M m,n (K). Denotiamo con A (i) la riga i-ma di A, i {1,..., m}.
Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta Versione del 21/12/07 Metodi per il calcolo del rango di una matrice Sia A M m,n (K). Denotiamo con A (i) la riga i-ma di A, i {1,..., m}.
MATRICI. Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: a 2 m. a n m) i j R, 1 i n, 1 j m.
 MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
4. Richiami: sistemi lineari e matrici
 4 Richiami: sistemi lineari e matrici Vettori 4a Combinazioni lineari Indichiamo con R n l insieme delle n-uple ordinate di elementi di R, { } R n := x = (x 1, x 2,, x n ) x i R, i = 1,,n Si dice che x
4 Richiami: sistemi lineari e matrici Vettori 4a Combinazioni lineari Indichiamo con R n l insieme delle n-uple ordinate di elementi di R, { } R n := x = (x 1, x 2,, x n ) x i R, i = 1,,n Si dice che x
APPUNTI DI ALGEBRA LINEARE
 APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
Anno Accademico 2017/2018
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2017/2018 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2017/2018 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
MATEMATICA. a.a. 2014/ Sistemi di equazioni lineari
 MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
VETTORI E MATRICI. De nizione 1 Chiamiamo vettore x una n-pla ordinata di numeri reali. x 1 x 2. x n
 VETTORI E MATRICI De nizione 1 Chiamiamo vettore x una n-pla ordinata di numeri reali x 1 x. x n 5 L insieme di tutti i vettori con n componenti reali si indica con R n :I numeri reali si possono pensare
VETTORI E MATRICI De nizione 1 Chiamiamo vettore x una n-pla ordinata di numeri reali x 1 x. x n 5 L insieme di tutti i vettori con n componenti reali si indica con R n :I numeri reali si possono pensare
Si noti che la matrice trasposta A ha lo stesso determinante. Questa proprietà è generale;
 Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Argomento 13 Sistemi lineari
 Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Matrici e sistemi. Geometria. Matrici e operazioni tra matrici. Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante
 Geometria Matrici e sistemi Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante 2 2006 Politecnico di Torino 1 Matrici e sistemi Matrici: definizione e notazioni Somma e
Geometria Matrici e sistemi Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante 2 2006 Politecnico di Torino 1 Matrici e sistemi Matrici: definizione e notazioni Somma e
Introduzione all algebra delle matrici. Appunti a cura di Lara Ercoli
 Introduzione all algebra delle matrici ppunti a cura di Lara Ercoli Indice Definizioni 3. Matrici particolari............................ 4 2 Operazioni con le matrici 8 2. Somma di matrici.............................
Introduzione all algebra delle matrici ppunti a cura di Lara Ercoli Indice Definizioni 3. Matrici particolari............................ 4 2 Operazioni con le matrici 8 2. Somma di matrici.............................
3 Soluzione di sistemi lineari
 3 Soluzione di sistemi lineari Prima di addentrarci nello studio dei metodi numerici, è doveroso introdurre le matrici e alcune strutture particolari di matrici nonchè alcuni concetti fondamentali quali
3 Soluzione di sistemi lineari Prima di addentrarci nello studio dei metodi numerici, è doveroso introdurre le matrici e alcune strutture particolari di matrici nonchè alcuni concetti fondamentali quali
Il teorema di Rouché-Capelli
 Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Corso introduttivo pluridisciplinare Matrici e sistemi lineari
 Corso introduttivo pluridisciplinare Matrici e sistemi lineari anno acc. 2013/2014 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano Corso introduttivo pluridisciplinare 1 / 30
Corso introduttivo pluridisciplinare Matrici e sistemi lineari anno acc. 2013/2014 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano Corso introduttivo pluridisciplinare 1 / 30
Argomento 12 Matrici
 Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
Metodi Matematici per l Economia anno 2017/2018 Gruppo B
 Metodi Matematici per l Economia anno 2017/2018 Gruppo B Docente: Giacomo Dimarco Dipartimento di Matematica e Informatica Università di Ferrara https://sites.google.com/a/unife.it/giacomo-dimarco-home-page/
Metodi Matematici per l Economia anno 2017/2018 Gruppo B Docente: Giacomo Dimarco Dipartimento di Matematica e Informatica Università di Ferrara https://sites.google.com/a/unife.it/giacomo-dimarco-home-page/
2x 5y +4z = 3 x 2y + z =5 x 4y +6z = A =
 Esercizio 1. Risolvere il sistema lineare 2x 5y +4z = x 2y + z =5 x 4y +6z =10 (1) Soluz. La matrice dei coefficienti è 1 4 6, calcoliamone il rango. Il determinante di A è (applico la regola di Sarrus):
Esercizio 1. Risolvere il sistema lineare 2x 5y +4z = x 2y + z =5 x 4y +6z =10 (1) Soluz. La matrice dei coefficienti è 1 4 6, calcoliamone il rango. Il determinante di A è (applico la regola di Sarrus):
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
Determinanti. Definizione ed esempi. Definizione ed esempi. Proprietà dei determinanti Rango di matrici
 Introduzione S S S Rango di matrici Si dice sottomatrice d'una matrice data la matrice ottenuta selezionando un certo numero di righe e di colonne della matrice iniziale. Lezione 24.wpd 08/01/2011 XXIV
Introduzione S S S Rango di matrici Si dice sottomatrice d'una matrice data la matrice ottenuta selezionando un certo numero di righe e di colonne della matrice iniziale. Lezione 24.wpd 08/01/2011 XXIV
Corso di Geometria BIAR, BSIR Esercizi 2: soluzioni
 Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
LEZIONE Equazioni matriciali. Negli Esempi e si sono studiati più sistemi diversi AX 1 = B 1, AX 2 = R m,n, B = (b i,h ) 1 i m
 LEZIONE 4 41 Equazioni matriciali Negli Esempi 336 e 337 si sono studiati più sistemi diversi AX 1 = B 1, AX 2 = B 2,, AX p = B p aventi la stessa matrice incompleta A Tale tipo di problema si presenta
LEZIONE 4 41 Equazioni matriciali Negli Esempi 336 e 337 si sono studiati più sistemi diversi AX 1 = B 1, AX 2 = B 2,, AX p = B p aventi la stessa matrice incompleta A Tale tipo di problema si presenta
CORSO DI GEOMETRIA DETERMINANTE A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
MATRICI e DETERMINANTI. Prof.ssa Maddalena Dominijanni
 MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
Note sull algoritmo di Gauss
 Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Terminiamo gli esercizi dell ultima lezione. (LUCIDI) Calcolare, se possibile, AC, CA, CH e HC. (LUCIDI)
 Terminiamo gli esercizi dell ultima lezione. (LUCIDI) Esempi Calcolare, se possibile, AC, CA, CH e HC. (LUCIDI) Osservazioni per le matrici quadrate a) Data A M n (K) è possibile definire ricorsivamente
Terminiamo gli esercizi dell ultima lezione. (LUCIDI) Esempi Calcolare, se possibile, AC, CA, CH e HC. (LUCIDI) Osservazioni per le matrici quadrate a) Data A M n (K) è possibile definire ricorsivamente
LEZIONE 3. a + b + 2c + e = 1 b + d + g = 0 3b + f + 3g = 2. a b c d e f g
 LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
Ettore Panella Algebra delle matrici e Sistemi lineari 1 MATRICI. Si definisce matrice un insieme ordinato di numeri disposti su righe e colonne.
 Ettore Panella Algebra delle matrici e Sistemi lineari 1 MATRICI Si definisce matrice un insieme ordinato di numeri disposti su righe e colonne. 1-3 4 5 7 0 La precedente è una matrice 2 3 costituita da
Ettore Panella Algebra delle matrici e Sistemi lineari 1 MATRICI Si definisce matrice un insieme ordinato di numeri disposti su righe e colonne. 1-3 4 5 7 0 La precedente è una matrice 2 3 costituita da
Matrici quadrate particolari
 Matrici quadrate particolari Sia A Mn(K) una matrice quadrata. Gli elementi (a 1,1, a 2,2,, a n,n ) costituiscono la diagonale principale di A. Gli elementi (a 1,n, a 2,n-1,, a n-1,2, a n,1 ) costituiscono
Matrici quadrate particolari Sia A Mn(K) una matrice quadrata. Gli elementi (a 1,1, a 2,2,, a n,n ) costituiscono la diagonale principale di A. Gli elementi (a 1,n, a 2,n-1,, a n-1,2, a n,1 ) costituiscono
Capitolo 3 Matrici. Marco Robutti. Facoltà di ingegneria Università degli studi di Pavia. Anno accademico
 Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
ALGEBRA LINEARE PARTE III
 DIEM sez Matematica Finanziaria Università degli studi di Genova Dicembre 200 Indice PREMESSA 2 GENERALITA 2 RAPPRESENTAZIONE DI UN SISTEMA LINEARE IN FORMA MATRI- CIALE 2 3 SOLUZIONE DI SISTEMI LINEARI
DIEM sez Matematica Finanziaria Università degli studi di Genova Dicembre 200 Indice PREMESSA 2 GENERALITA 2 RAPPRESENTAZIONE DI UN SISTEMA LINEARE IN FORMA MATRI- CIALE 2 3 SOLUZIONE DI SISTEMI LINEARI
Sistemi di equazioni lineari
 Sistemi di equazioni lineari A. Bertapelle 25 ottobre 212 Cos è un sistema lineare? Definizione Un sistema di m equazioni lineari (o brevemente sistema lineare) nelle n incognite x 1,..., x n, a coefficienti
Sistemi di equazioni lineari A. Bertapelle 25 ottobre 212 Cos è un sistema lineare? Definizione Un sistema di m equazioni lineari (o brevemente sistema lineare) nelle n incognite x 1,..., x n, a coefficienti
Istituzioni di Matematiche prima parte
 Istituzioni di Matematiche prima parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano Istituzioni di Matematiche 1 / 33 index Generalità sugli insiemi 1 Generalità
Istituzioni di Matematiche prima parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano Istituzioni di Matematiche 1 / 33 index Generalità sugli insiemi 1 Generalità
ESEMPIO DI SISTEMA LINEARE CON SOLUZIONE. Esercizio Si consideri il sistema di equazioni lineari dipendente da un parametro λ R:
 ESEMPIO DI SISTEMA LINEARE CON SOLUZIONE Esercizio Si consideri il sistema di equazioni lineari dipendente da un parametro λ R: x 1 + x = 0 6x 1 + (λ + )x + x 3 + x 4 = 1 x 1 4x + (λ + 1)x 3 + 6x 4 = 3
ESEMPIO DI SISTEMA LINEARE CON SOLUZIONE Esercizio Si consideri il sistema di equazioni lineari dipendente da un parametro λ R: x 1 + x = 0 6x 1 + (λ + )x + x 3 + x 4 = 1 x 1 4x + (λ + 1)x 3 + 6x 4 = 3
SISTEMI LINEARI. x y + 2t = 0 2x + y + z t = 0 x z t = 0 ; S 3 : ; S 5x 2y z = 1 4x 7y = 3
 SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 3. Sistemi di equazioni lineari
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
= elemento che compare nella seconda riga e quinta colonna = -4 In generale una matrice A di m righe e n colonne si denota con
 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti su m righe e n colonne. I numeri che compaiono nella tabella si dicono elementi della matrice. La loro individuazione
Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti su m righe e n colonne. I numeri che compaiono nella tabella si dicono elementi della matrice. La loro individuazione
LEZIONE 5. AX = 0 m,1.
 LEZIONE 5 5 isoluzione di sistemi Supponiamo che AX = B sia un sistema di equazioni lineari Ad esso associamo la sua matrice completa (A B Per quanto visto nella precedente lezione, sappiamo di poter trasformare,
LEZIONE 5 5 isoluzione di sistemi Supponiamo che AX = B sia un sistema di equazioni lineari Ad esso associamo la sua matrice completa (A B Per quanto visto nella precedente lezione, sappiamo di poter trasformare,
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni 2. MATRICI
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 2 MATRICI Siano m, n N \ {0}, sia K un campo Una matrice m n a coefficienti in K è una
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 2 MATRICI Siano m, n N \ {0}, sia K un campo Una matrice m n a coefficienti in K è una
Algebra delle matrici
 Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Elementi di Algebra Matriciale. (richiami)
 Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
Istituzioni di Matematiche prima parte
 Istituzioni di Matematiche prima parte anno acc. 2014/2015 Univ. Studi di Milano E.Frigerio, C.Turrini (Univ. Studi di Milano Istituzioni di Matematiche 1 / 30 index Generalità sugli insiemi 1 Generalità
Istituzioni di Matematiche prima parte anno acc. 2014/2015 Univ. Studi di Milano E.Frigerio, C.Turrini (Univ. Studi di Milano Istituzioni di Matematiche 1 / 30 index Generalità sugli insiemi 1 Generalità
Istituzioni di Matematiche sesta parte
 Istituzioni di Matematiche sesta parte anno acc. 2013/2014 Univ. Studi di Milano D.Bambusi, C.Turrini (Univ. Studi di Milano Istituzioni di Matematiche 1 / 27 index Matrici e operazioni tra matrici 1 Matrici
Istituzioni di Matematiche sesta parte anno acc. 2013/2014 Univ. Studi di Milano D.Bambusi, C.Turrini (Univ. Studi di Milano Istituzioni di Matematiche 1 / 27 index Matrici e operazioni tra matrici 1 Matrici
I sistemi lineari di n equazioni in n incognite
 I sistemi lineari I sistemi lineari di n equazioni in n incognite I sistemi lineari di n equazioni in n incognite, sono formati da equazioni di primo grado, in cui le incognite hanno tutte esponente uguale
I sistemi lineari I sistemi lineari di n equazioni in n incognite I sistemi lineari di n equazioni in n incognite, sono formati da equazioni di primo grado, in cui le incognite hanno tutte esponente uguale
Sistemi Lineari. Elisabetta Colombo. Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 200-20 2 a di o.0 4 Capelli Rango o Caratterisca : definizioni a di o.0 Un equazione nelle n incognite x,..., x n della forma dove
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 200-20 2 a di o.0 4 Capelli Rango o Caratterisca : definizioni a di o.0 Un equazione nelle n incognite x,..., x n della forma dove
Contenuti aggiuntivi su matrici e determinanti, Dimostrazioni del Capitolo 3
 Contenuti aggiuntivi su matrici e determinanti, Dimostrazioni del Capitolo 3 Dimostrazione 310 Sia W = L(C A ) K Osserviamo che S è una base di W Infatti S è indipendente, inoltre ogni vettore di W dipende
Contenuti aggiuntivi su matrici e determinanti, Dimostrazioni del Capitolo 3 Dimostrazione 310 Sia W = L(C A ) K Osserviamo che S è una base di W Infatti S è indipendente, inoltre ogni vettore di W dipende
Lezione Risoluzione di sistemi
 Lezione Risoluzione di sistemi Sia AX = B un sistema di equazioni lineari, con la sua matrice completa associate (A B) Per la Proposizione sappiamo di poter trasformare con operazioni elementari di riga
Lezione Risoluzione di sistemi Sia AX = B un sistema di equazioni lineari, con la sua matrice completa associate (A B) Per la Proposizione sappiamo di poter trasformare con operazioni elementari di riga
Lezione 11. Somma di matrici Prodotto di una matrice per uno scalare Prodotto di matrici Determinante Sistemi lineari in forma matriciale
 Lezione Somma di matrici Prodotto di una matrice per uno scalare Prodotto di matrici Determinante Sistemi lineari in forma matriciale Matrici. Somma Date due matrici n x m, A = A ij e B = B ij, con i =,,,
Lezione Somma di matrici Prodotto di una matrice per uno scalare Prodotto di matrici Determinante Sistemi lineari in forma matriciale Matrici. Somma Date due matrici n x m, A = A ij e B = B ij, con i =,,,
LEZIONE 1 C =
 LEZIONE 1 11 Matrici a coefficienti in R Definizione 111 Siano m, n Z positivi Una matrice m n a coefficienti in R è un insieme di mn numeri reali disposti su m righe ed n colonne circondata da parentesi
LEZIONE 1 11 Matrici a coefficienti in R Definizione 111 Siano m, n Z positivi Una matrice m n a coefficienti in R è un insieme di mn numeri reali disposti su m righe ed n colonne circondata da parentesi
Sistemi II. Sistemi II. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Soluzioni del Foglio 2 I sistemi lineari
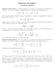 Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
LEZIONE i i 3
 LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
M.P. Cavaliere ELEMENTI DI MATEMATICA E LOGICA MATEMATICA DISCRETA STRUTTURE ALGEBRICHE
 M.P. Cavaliere ELEMENTI DI MATEMATICA E LOGICA MATEMATICA DISCRETA STRUTTURE ALGEBRICHE Operazioni in un insieme Sia A un insieme non vuoto; una funzione f : A A A si dice operazione binaria (o semplicemente
M.P. Cavaliere ELEMENTI DI MATEMATICA E LOGICA MATEMATICA DISCRETA STRUTTURE ALGEBRICHE Operazioni in un insieme Sia A un insieme non vuoto; una funzione f : A A A si dice operazione binaria (o semplicemente
LEZIONE i 0 3 Le sottomatrici 2 2 di A sono. 1 2 i i 3. Invece (
 LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Richiami di algebra delle matrici a valori reali
 Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Esercizi svolti. risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale
 Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Matematica discreta 1 [145016]
![Matematica discreta 1 [145016] Matematica discreta 1 [145016]](/thumbs/94/119285443.jpg) Facoltà di Scienze Matematiche, Fisiche e Naturali anno accademico 2008/09 Registro dell'attività didattica Matematica discreta 1 [145016] Attività didattica: Attività didattica [codice] Corso di studio
Facoltà di Scienze Matematiche, Fisiche e Naturali anno accademico 2008/09 Registro dell'attività didattica Matematica discreta 1 [145016] Attività didattica: Attività didattica [codice] Corso di studio
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Lezione Determinanti
 Lezione 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Lezione 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Sistemi lineari - Parte Seconda - Esercizi
 Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
Esercitazione 6 - Soluzione
 Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Geometria e Algebra. Ingegneria dell Informazione
 Geometria e Algebra Ingegneria dell Informazione 2013 2014 Rocco Chirivì Dipartimento di Matematica e Fisica Università del Salento rocco.chirivi@unisalento.it www.dmf.unisalento.it/persone/chirivi Modalità
Geometria e Algebra Ingegneria dell Informazione 2013 2014 Rocco Chirivì Dipartimento di Matematica e Fisica Università del Salento rocco.chirivi@unisalento.it www.dmf.unisalento.it/persone/chirivi Modalità
Appunti di Algebra Lineare per il Corso di Istituzioni di Matematica. Davide Fermi
 Appunti di Algebra Lineare per il Corso di Istituzioni di Matematica Davide Fermi Novembre 213 Indice.1 Introduzione...................................... 1.2 Vettori in R n.....................................
Appunti di Algebra Lineare per il Corso di Istituzioni di Matematica Davide Fermi Novembre 213 Indice.1 Introduzione...................................... 1.2 Vettori in R n.....................................
