4. Analisi dei segnali periodici e serie di Fourier
|
|
|
- Lorenzo Marino
- 8 anni fa
- Visualizzazioni
Transcript
1 4. Analisi dei segnali periodici e serie di Forier Joseph Forier Nel so lavoro fondamentale del 187 Théorie analytiqe de la chaler, Jean Baptiste Joseph 1 La vita di Forier, oltre ad essere pittosto criosa e travagliata, offre interessanti spnti di riflessione, se la confrontiamo con i nostri giorni. Nono di 1 fratelli, rimasto orfano a 1 anni, iniziò ad interessarsi intensamente... di matematica all età di 13 anni: qattordicenne si stdiò i corposi 6 volmi del Cors de mathématiqes di Bézot e il corso Mécaniqe en général di Bosst, ricevendone n premio l anno sccessivo. La sa formazione si divideva tra l ideale della conqista delle vette del sapere scientifico a 1 anni osserva in na lettera che a qella stessa età ormai Newton e Pascal avevano ragginto l immortalità con le loro scoperte e gli ideali di gistizia e di gaglianza per na società migliore, la casa più grande e nobile per la qale chinqe potesse spendersi. Sperato con varie traversie tra ci la prigione con condanna alla ghigliottina il periodo del terrore, a 7 anni iniziò ad insegnare al Collège de France e sccessivamente all École Polytechniqe, dove incontrò e freqentò Lagrange, Laplace, Monge, Carnot, tra i più significativi esponenti della matematica francese del tempo e non solo francese, ovviamente... A 3 anni partecipò alla spedizione in Egitto con Napoleone, svolgendovi n importante rolo di fondatore e organizzatore delle locali istitzioni scolastiche e archeologiche; al ritorno in Francia, invece di riprendere la freqentazione accademica, f nominato da Napoleone prefetto a Grenoble, dove ancora na volta la sa amministrazione f molto attiva ed efficiente. Ormai 36 enne iniziò ad occparsi della trasmissione del calore e dopo 3 anni completò il lavoro Théorie analytiqe de la chaler che lo ha reso celebre nel 187. Benché le idee presentate fossero notevolmente originali ed innovative, la gistificazione matematica presentava qalche difficoltà non risolta s ci i matematici continarono a lavorare per i de secoli sccessivi... e solo dopo 1 anni f eletto alla Académie des Sciences, che pbblicò finalmente la sa opera nel 18. Gli ltimi anni di vita frono solo scientificamente, qesta volta movimentati da varie discssioni con colleghi che intendevano sminire o attribirsi i meriti e le scoperte di Forier: da qesto solo pnto di vista, la nostra civiltà non è molto cambiata
2 4. ANALISI DEI SEGNALI PERIODICI E SERIE DI FOURIER 4- Forier comprese che ogni segnale T-periodico pò essere ottento come sovrapposizione di infiniti segnali trigonometrici, ognno dei qali associato ad na freqenza mltipla della freqenza fondamentale f 1/T. Qesta lezione fornisce na semplice introdzione a qesta fondamentale scoperta. Abbiamo già visto che i segnali trigonometrici reali associati ad na freqenza ω πf sono caratterizzati da con ω t a ω cosωt+b ω sinωt ρ ω cosωt+θ ω û ω e iωt +û ω e iωt, 4.1 û ω û ω c ω a ω ib ω, ρ ω a ω ib ω û ω û ω, θ ω Arga ib Argû ω Argû ω. 4.a 4.b 4.c Le freqenze in gioco, che devono essere mltiple di ω π/t, saranno del tipo ω kω πkf e dipenderanno qindi dall intero k N; i rispettivi coefficienti saranno indicati con a k,b k,ρ k,θ k,û k,û k. Ci aspettiamo qindi na rappresentazione t a + + a k coskω t+b k sinkω t ρ + + ρ k coskω t+θ k û + û k e ikωt +û k e ikωt k û k e ikωt. 4.3a 4.3b 4.3c Notazione Commento a?. Il termine costante nelle 4.3a,b,c a ρ û viene indicato facendo comparire il fattore a denominatore per conservare l identità 4.a tra i coefficienti a k,b k,ρ k,û k anche per k. Per qanto visto, la scelta di na delle tre forme 4.3a,b,c è irrilevante ai fini dello svilppo della teoria: ogni risltato pò essere facilmente convertito da na all altra grazie alle 4.a,b,c: per semplicità ed eleganza dei calcoli, noi privilegeremo la rappresentazione complessa 4.3c. Natralmente la teoria matematica soggiacente al discorso precedente non è così semplice, coinvolgendo serie di infiniti segnali. Riassmiamo le qestioni principali in ordine di difficoltà: Tre problemi fondamentali dell analisi di Forier Notazione Polinomi trigonometrici. Assegnato n periodo T ed n vettore α α k, k N,...,N, di coefficienti complessi, indicheremo con P αt il segnale P αt : α k e ikωt. 4.4 Problema 4.1 Identificazione dei coefficienti Spponiamo di sapere a priori che il segnale T-periodico sia la sintesi di n nmero finito di segnali trigonometrici, cioè t P α t Come determinare i coefficienti α α k in fnzione di? α k e ikωt. 4.5
3 4. ANALISI DEI SEGNALI PERIODICI E SERIE DI FOURIER 4-3 Problema 4. Migliore approssimazione Spponiamo che il segnale T-periodico sia generico : in generale, esso non sarà ottenibile come sovrapposizione di n nmero finito di segnali trigonometrici che forniscono sempre n segnale contino e derivabile infinite volte!. Di consegenza, ogni rappresentazione di come n polinomio trigonometrico P α è sempre affetta da n errore Err α : t P α t+err α t α k e ikωt +Err α t. 4.6 L errore Err α t : t P α t t α k e ikωt 4.7 è esso stesso n segnale dipendente dal tempo che dipende ovviamente dalla scelta dei coefficienti α α k. Ci piacerebbe trovare i coefficienti α α k che rendono l errore il più piccolo possibile in n senso ancora da precisare!. Come scegliere i coefficienti α α k? Problema 4.3 Analisi e sintesi di segnali arbitrari Spponiamo di aver già risolto i problemi precedenti e di aver individato i cosiddetti coefficienti di Forier α k û k in modo da minimizzare l errore 4.7. Sono vere, e in qale senso, le formle 4.3a,b,c? Sarà vero che, qando N tende a +, l errore ottimale Err N di 4.7 che, come vedremo, dipenderà solo dal nmero N dei coefficienti coinvolti tende a? La risposta ai problemi precedenti è codificata nella nozione di prodotto scalare tra de segnali, che stdiamo nella prossima sezione. 4.1 Prodotti scalari e sistemi ortogonali di segnali Richiamiamo innanzittto la nozione astratta di prodotto scalare che è stata stdiata nei corsi di geometria e algebra lineare. Definizione 4.4 Prodotto scalare di segnali Sia V SD no spazio vettoriale di segnali. Un prodotto scalare di segnali in V è na applicazione che ad ogni coppia di segnali,v V associa n nmero complesso v C con qeste proprietà: Linearità in ciascn argomento +v w w + v w, v +w v + w λ v λ v, λv λ v,v,w V,,v V, λ C. 4.8 Simmetria hermitiana v v,v V. 4.9 semipositività. 4.1 La seminorma associata al prodotto scalare è definita da :, Richiami Disgaglianza triangolare e disgaglianza di Schwarz. La norma associata ad n prodotto scalare soddisfa qeste de fondamentali disgaglianze: +v + v,v V, 4.1 v v,v V. 4.13
4 4. ANALISI DEI SEGNALI PERIODICI E SERIE DI FOURIER 4-4 Definizione 4.5 Sistemi ortogonali e ortonormali di segnali De elementi, v V si dicono ortogonali se v Un sistema di segnali E {...e N,e N+1,...,e 1,e,e 1,e,...,e N,... } di no spazio vettoriale V SD si dice ortogonale se eh ek se h k; ek e k ek > h,k Z Il sistema E si dice ortonormale se, oltre ad essere ortogonale, la norma dei soi elementi è nitaria, cioè eh ek se h k; ek e k ek 1 h,k Z Lemma 4.6 Norma della somma e Teorema di Pitagora Siano,v de segnali nello spazio vettoriale V; si ha +v +Re v + v In particolare, se, v sono ortogonali allora +v + v Dimostrazione La 4.17 è n semplice calcolo: +v +v +v + v + v + v v + v + v + v. Definizione 4.7 Prodotto scalare tra de segnali periodici Il prodotto scalare di de segnali complessi periodici e limitati,v B T,+ è definito da v : tvtdt 1 T tvt dt Definizione 4.8 Media, Energia Media o Potenza e scarto qadratico medio La media di n segnale periodico limitato B T,+ è definita da : 1 tdt 1 T t dt. 4. L energia media, o potenza, di n segnale periodico limitato B T,+ è il qadrato della norma di ed è definita da P[] : t dt 1 T t dt. 4.1 Se,v B T,+ sono de segnali T-periodici, il loro scarto qadratico medio è l energia media della differenza v, cioè P[ v] v v t vt dt. 4. Nota La potenza non è che la media del segnale o, eqivalentemente, il prodotto scalare di con se stesso Poiché si lavora spesso con segnali complessi è fondamentale sare il modlo all interno del qadrato che definisce la potenza. Per non sbagliare, conviene lasciarlo indicato anche qando il segnale è reale. Analogamente, qando si lavora con segnali reali, si potrebbe eliminare il simbolo di conigio nella definizione 4.19; sempre per evitare errori, conviene però indicarlo in ogni caso.
5 4. ANALISI DEI SEGNALI PERIODICI E SERIE DI FOURIER 4-5 Esercizio Se na fnzione v è T-periodica e integrabile, allora la sa media come la sa potenza pò essere calcolata in ogni intervallo di ampiezza T, poiché l integrale t +T t vtdt non dipende dal pnto t R. Qindi t +T t tdt, +T t dt. t t È facile poi controllare che la media e la potenza non cambiano se si calcolano gli integrali s intervalli di lnghezza mltipla intera del periodo. Esercizio La media e la potenza sono invarianti per rescaling: se è T-periodico e v R ω[] v /ω vtdt ω /ω ωtdt 1 sds, P[v] P[]. T T Esercizio Mostrare che se è limitato e periodico non importa qale sia il periodo Nel caso della potenza si ottiene lim T + P[] lim T + tdt lim T + t dt lim T + t dt. 4.3 T t dt. 4.4 T L integrale E[] : lim t dt 4.5 T + T viene chiamato anche energia del segnale. Per n segnale periodico non nllo l energia è sempre + ; la qantità fisicamente significativa rimane dnqe l energia media per nità di tempo, la potenza appnto. Esercizio Siano c ωt : cosωt, s ωt : sinωt, e ωt : e iωt. Calcolare, per ω, Cosa cambia per ω? c ω s ω e ω, c ω s ω 1, eω Identificazione dei coefficienti di Forier Riprendiamo ora il primo e più semplice problema introdotto all inizio di qesta lezione. L identificazione dei coefficienti α k nel problema 4.1 è na consegenza delle segenti formle, che vengono chiamate relazioni di ortogonalità dei segnali trigonometrici. Ricordiamo che la media di n segnale periodico è stata definita in 4.8 Lemma 4.9 Media e ortogonalità dei segnali trigonometrici Per ω R si ha e iωt dt eiωt 1 iωt In particolare, se ω kω πk T se ω,, k Z, allora e ikωt { 1 se k, se k. e iωt dt 1 se ω Finalmente, se k,h Z, i segnali trigonometrici risltano T-periodici e si ha { e ikω t e ihωt e ik hωt 1 se k h, se k h. 4.8
6 4. ANALISI DEI SEGNALI PERIODICI E SERIE DI FOURIER 4-6 Corollario 4.1 Ortonormalità del sistema di Forier Nello spazio vettoriale B T,+ dei segnali T-periodici, il sistema è ortonormale. E : { e ikωt : k Z }, ω : π T, 4.9 Corollario 4.11 Identificazione dei coefficienti Se n segnale ammette la rappresentazione 4.5 allora i coefficienti α k sono nivocamente determinati e sono dati da α k û k : e ikω t t+t i coefficienti û k vengono chiamati coefficienti di Forier di. t te ikωt dt; 4.3 Dimostrazione Per non confonderci, cambiamo l indice di sommatoria in 4.5 in h: t h N α h e ihω t e moltiplichiamo scalarmente! l identità per e ikω t : grazie alla linearità del prodotto scalare e poiché la somma è finita, otteniamo e ikω t h N α h e ihω t e ikω t h N α h e ihω t e ikω t α k, dove abbiamo sfrttato il fatto che ttti i termini della sommatoria, eccettato qello di posto k, sono nlli grazie alle relazioni di ortogonalità 4.8. Le corrispondenti proprietà per le fnzioni trigonometriche reali sono date da Corollario 4.1 Ortogonalità dei segnali trigonometrici reali Se k, h N si ha coskω t coshω t 1 se k h >, 1 se k h, 4.31 se k h, sinkω t sinhω t { 1 se k h >, 4.3 altrimenti, coskω t sinhω t Dimostrazione Basta svilppare la 4.8 in parte reale e parte immaginaria: coskω t coshω t + sinkω t sinhω t, sinkω t coshω t coskω t sinhω t, scambiare h con h e sommare le identità corrispondenti. Prendendo la parte reale e la parte immaginaria di 4.3 si ottiene Corollario 4.13 Coefficienti a k e b k Se è n polinomio trigonometrico del tipo t α N + α k coskω t+β k sinkω t
7 4. ANALISI DEI SEGNALI PERIODICI E SERIE DI FOURIER 4-7 allora i coefficienti α k,β k sono nivocamente determinati e sono dati da α k a k : coskω t β k b k : sinkω t t+t t t+t t tcoskω tdt tsinkω tdt Nota I coefficienti di posto k. Nel caso k si ha a ρ û t +T t tdt; 4.35 il coefficiente di posto è qindi la media integrale di. b è invece sempre nllo, la serie dei seni parte dall indice 1. Lemma 4.14 Potenza di n polinomio trigonometrico Se il segnale è la sintesi di n nmero finito di segnali trigonometrici t a N + a k coskω t+b k sinkω t ρ N + ρ k coskω t+θ k û + û k e ikωt +û k e ikωt û k e ikωt 4.36a 4.36b 4.36c allora la sa potenza è data da P[] t+t t dt a t 4 ρ û k. a k + b k ρ k 4.36d Dimostrazione Basta svilppare il calcolo diretto: P[] û k e ikω t h N û h e ihω t û k e ikω t û h e ihω t h N û k û h e ikω t e ihω t h, û h û k h û k. Commento Un teorema di Pitagora per le potenze. In generale se n segnale è la sovrapposizione di segnali k è falso che la potenza di sia la somma delle potenze dei singoli k così come è falso in generale che il
8 4. ANALISI DEI SEGNALI PERIODICI E SERIE DI FOURIER 4-8 qadrato di na somma sia gale alla somma dei qadrati!. Qesta proprietà rislta sorprendentemente verificata se gli addendi k û k e ikω t sono segnali trigonometrici: infatti û k e ikω t û k, 4.37 cioè la potenza della somma di segnali trigonometrici è la somma delle potenze. Qesta proprietà è na consegenza diretta delle relazioni di ortogonalità 4.8 e ne gistifica il nome. Torniamo al Corollario 4.11: l espressione 4.3 che definisce i coefficienti di Forier ha perfettamente senso anche se non è n polinomio trigonometrico, basta che sia limitato, T-periodico, e misrabile, cioè n elemento di B T,+. Convenzione Misrabilità dei segnali. Per non appesantire lteriormente l esposizione, salvo lteriori precisazioni, d ora in avanti spporremo sempre che ttti i segnali che incontreremo siano misrabili. Poniamo qindi la segente definizione: Definizione 4.15 Coefficienti di Forier Sia B T,+ ; i coefficienti di Forier di sono dati da û k : e ikωt t+t per ogni intero N N, l N-esimo polinomio di Forier di è dato da ˆP N t : t te ikωt dt; 4.38 û k e ikωt Rimane da capire qale rolo giocano i coefficienti di Forier per n segnale arbitrario: è qanto verrà discsso nel prossimo paragrafo. 4.3 Il problema della migliore approssimazione. Fissato n intero positivo N che misrerà qanti termini e relativi coefficienti siamo disposti a spendere per approssimare il segnale, in generale non potrà essere rappresentato esattamente come sovrapposizione di N+1 segnali trigonometrici aventi freqenze comprese tra Nω e Nω. Comnqe noi scegliamo i coefficienti α α k, k N,..., 1,,1,...,N, sostitendo a la somma P α t α k e ikωt 4.4 noi commettiamo n errore; qesto errore pò essere rappresentato come il segnale che rislta dalla differenza di con P α, cioè Err α t : t P α t t α k e ikωt Natralmente na bona scelta dei coefficienti α α k corrisponde al fatto che il segnale Err α sia piccolo : qale criterio tilizzare, però, per misrare qanto è piccolo Err α? Una delle nmerose scelte possibili è qella di richiedere che sia piccola la potenza di Err α, cioè lo scarto qadratico medio E α : P[Err α ] P[ P α ] t+t N P Pα α t α k e ikωt dt. 4.4 t
9 4. ANALISI DEI SEGNALI PERIODICI E SERIE DI FOURIER 4-9 Qesto nmero dipende in definitiva dai coefficienti α α k : ebbene, il prossimo risltato mostra che se scegliamo α k esattamente pari al coefficiente di Forier û k di, l errore E α è il più piccolo possibile. Qesta fondamentale proprietà, che gistifica il rolo privilegiato dei coefficienti di Forier, si esprime anche dicendo che qesti individano la miglior approssimazione del segnale in termini di n segnale trigonometrico P α. Teorema 4.16 Errore di miglior approsimazione Sia B T,+, P α il polinomio trigonometrico associato 4.4 ai coefficienti α α k, k N,...,N, e sia ˆP N il corrispondente polinomio associato ai coefficienti di Forier ˆP N t : û k e ikωt, û k : e ikω t t+t t te ikωt dt Si ha: [ E α P[ P α ] P ˆP N] + α k û k In particolare l errore E α è minimo qando l ltima sommatoria di destra in 4.44 si annlla, cioè per α k û k e in tal caso coincide con lo scarto qadratico medio tra e il so N-esimo polinomio di Forier ÊN P [ ˆP ] N. Teorema 4.17 Disgaglianza di Bessel Sia B T,+ e sia ˆP N il corrispondente polinomio associato ai coefficienti di Forier ˆP N t : û k e ikωt, û k : e ikω t t +T t te ikωt dt Allora [ Ê N P ˆP N] t+t t N t û k e ikωt dt P[] P[ˆPN ] P[] In particolare si ottiene la disgaglianza di Bessel û k ] P[ˆPN û k P[] t+t t t dt Dimostrazione Osserviamo innanzittto na importante proprietà: se P α è n polinomio trigonometrico di grado N allora ˆP N P α Infatti, svilppando i calcoli si ottiene P α α k e ikω t h N grazie al Lemma Analogamente ˆPN P α û h e ihω t α k e ikω t h, α k e ikω t û h α k e ihω t e ikω t û k α k, 4.49 û k α k. 4.5 In particolare, scegliendo α k û k, cioè P α ˆP N, ˆPN ˆPN ˆPN ] ˆPN P[ˆPN. 4.51
10 4. ANALISI DEI SEGNALI PERIODICI E SERIE DI FOURIER 4-1 A qesto pnto si ha facilmente [ P ˆP N] Ricordando la 4.36d si conclde. ˆP N ˆPN + ˆPN ˆPN ˆPN ˆPN. ˆPN ˆPN La dimostrazione del Teorema 4.16 sege direttamente da qesta semplice decomposizione: P α ˆP N ˆPN + P α e, grazie alla 4.48, ˆP N ˆPN P α 4.5 da ci, per il teorema di Pitagora 4.18 [ P[ P α ] P ˆP N] [ˆPN ] +P P α ÊN + α k û k. 4.4 Proprietà elementari dei coefficienti di Forier Linearità Se,v sonodesegnalicicorrispondonoicoefficientidiforierû k,a k,b k eˆv k,a k,b k, allora al segnale +v corrispondono i coefficienti û k + ˆv k,a k +a k,b k +b k. In simboli } û k +v û k + ˆv k v ˆv k Segnali reali Se è reale allora û k û k. Si dice anche che la sccessione û k è hermitiana. Invarianza rispetto a cambiamenti di scala Se è T-periodica e λ > è il fattore di cambiamento di scala, la fnzione vt : R λ []t λt è T/λ-periodica e i coefficienti di Forier di v sono gli stessi di qelli di : Infatti, con la sostitzione s : λt, û k R λ [] û k ˆv k λ T /λ λte πi k T λt dt 1 T se πi k T s ds û k. Riflessione Se vt t è ottento per riflessione rispetto all origine dei tempi si inverte l ordine temporale, allora ˆv k û k, cioè Se è reale, in termini dei coefficienti a k,b k si ha û k t û k a k,b k t a k, b k. 4.56
11 4. ANALISI DEI SEGNALI PERIODICI E SERIE DI FOURIER 4-11 Parità e disparità Se è pari cioè t t allora Se è dispari cioè t t allora {û k û k, b k. {û k û k, a k. Ritardi Dato n segnale SR e n ritardo τ, abbiamo indicato con S τ [] il corrispondente segnale ritardato di τ vt S τ []t : t τ. I coefficienti di Forier di v : S τ [] risltano modlati per n esponenziale complesso di freqenza fondamentale pari a τ/t o plsazione τω, cioè û k ˆv k e iωτk û k È ovvio che n ritardo di n intero periodo o di soi mltipli interi non comporta alcna effettiva modlazione, essendo τ/t intero; più interessante osservare che n ritardo di mezzo periodo cambia alternativamente solo il segno dei coefficienti τ : T/ ˆv k 1 k û k. Modlazione Modlare n segnale significa moltiplicarlo per n segnale esponenziale del tipo e iαt, α R. Evidentemente, se si richiede che la modlazione mantenga la T-periodicità il coefficiente α dovrà essere n mltiplo intero n della plsazione fondamentale ω ; posto qindi vt : e inωt t si ha ˆv k û k n. Da qesta formla si dedce facilmente che vt : cosnω tt ˆv k 1 ] [û k n +û k+n, vt : sinnω tt ˆv k 1 ] [û k n û k+n. i Serie e trasformata di Forier Come vedremo nelle prossime lezioni, la trasformata di Forier di n segnale v B, + viene definita dall integrale ˆvf : + vte πif t dt, 4.58 e per alcni segnali particolarmente importanti il so valore si pò trovare s opportne tavole. Qeste tavole forniscono n asilio di calcolo anche per le serie di Forier; ecco la semplice procedra, nel caso di n segnale B T,+ : Si fissa n intervallo t,t +T di lnghezza pari al periodo tipicamente T/,T/ e a partire da si costrisce il novo segnale { t se t t,t +T, vt : t1 t,t +T 4.59 altrimenti. Nel caso dell intervallo simmetrico T/,T/ si ha vt trectt/t.
12 4. ANALISI DEI SEGNALI PERIODICI E SERIE DI FOURIER 4-1 Si calcola la trasformata di Forier di v definita dalla formla 4.58 e si ottiene n novo segnale ˆvf che dipende dalla freqenza f. Ovviamente il metodo è vantaggioso se il segnale v si trova facilmente a partire dalle tavole! I coefficienti di Forier di si ottengono dividendo per T i valori della trasformata ˆv campionata a passo f : 1 T : in formle û k : 1 T ˆvkf 1 T ˆv k T 4.6 Esercizio Dimostrare le formle precedenti. 4.5 Convergenza in energia delle serie di Forier Cosa significa che n segnale pò essere rappresentato dalla sovrapposizione cioè dalla serie di infiniti segnali, come nelle 4.3a,b,c? Ovviamente, dal pnto di vista nmerico, non è possibile trattare la somma di infiniti termini poiché ogni manipolazione digitale dei segnali deve fare intervenire necessariamente solo n nmero finito di addendi: ad esempio, nel caso della rappresentazione esponenziale 4.3c, proprio i polinomi ˆP N t : û k e ikωt a N + a k coskω t+b k sinkω t 4.61 che abbiamo considerato nella lezione precedente. Qesti ltimi fanno intervenire M : N + 1 termini in posizione simmetrica rispetto all indice k : ciò che si pò ragionevolmente sperare è che qando si sceglie N abbastanza grande la rappresentazione tramite ˆP N sia abbastanza accrata, cioè l errore tra il segnale originale e ˆP N sia piccolo. Abbiamo già visto che l errore Êrr N t : t ˆP N t 4.6 è esso stesso n segnale, cioè dipende dal tempo t e che il modo più comodo di misrarne la grandezza qando si ha a che fare con l analisi di Forier è qello di considerarne la potenza Ê N : P[Êrr N ] t+t È natrale pertanto introdrre la segente definizione: t t ˆP N t dt Definizione 4.18 Convergenza in energia Diciamo che la serie di Forier k û k e ikωt converge in energia al segnale qando lo scarto qadratico medio 4.63 tra e l N-esimo polinomio di Forier 4.61 tende a qando N tende a +. In simboli lim N + t+t t N t û k e ikωt dt L so di somme simmetriche è gistificato dall identità 4.61 con la rappresentazione trigonometrica tramite i coefficienti a k e b k ; si noti che se il segnale è reale nella somma 4.61 sono coinvolti N +1 coefficienti reali, in qanto i coefficienti û k e û k sono l no il conigato dell altro.
13 4. ANALISI DEI SEGNALI PERIODICI E SERIE DI FOURIER 4-13 Teorema 4.19 Le serie di Forier del segnale converge a Ogni segnale B T,+ ammette lo svilppo in serie di Forier nel senso della convergenza in energia 4.18: t û k e ikωt ρ + + ρ k coskω t+θ k k a + + a k coskω t+b k sinkω t, dove i coefficienti di Forier sono nivocamente determinati da 4.65 t+t û k t+t t te ikωt dt, a k tcoskω tdt, b k t { ûk û k a k ib k ρ k e iθ k, t+t ρ k a k ±ib k, θ k Arga k ib k t tsinkω tdt, per k Commento L avverbio nivocamente del precedente ennciato significa che se na qalnqe serie del tipo4.65 converge in energia ad n segnale, allora necessariamente i coefficienti û k,a k,b k sono determinati dall espressione In altre parole, il corollario 4.11 vale qalnqe sia il segnale. Teorema 4. Identità di Parseval Se,v sono de segnali in B T,+ con coefficienti di Forier û k,a k,b k, ˆv k,a k,b k rispettivamente, allora valgono le identità P[] t+t v t+t t t dt t tvtdt k k û k a û kˆv k a a a k +b k, 4.67 ak a k +b k b k Commento A differenza della 4.65, che coinvolge infiniti segnali, le de serie 4.67 e 4.68 sono più semplicemente serie nmeriche, la prima delle qali è oltrettto a termini non negativi. Fa parte dell ennciato del teorema garantire che qeste serie sono convergenti. È facile constatare che la 4.67 è n caso particolare della 4.68, ottento scegliendo v. Esercizio Considerando le somme parziali, verificare, indipendentemente dall ennciato del teorema, che le de serie in 4.68 coincidono. Esercizio Mostrare che 4.67 è na diretta consegenza del Teorema 4.19 e dell identità Esercizio Ripetendo lo stesso procedimento sato nella dimostrazione del Lemma 4.14, dimostrare la 4.68 qando e v sono de polinomi trigonometrici qindi le serie che intervengono in 4.68 sono in realtà somme finite. 4.6 Convergenza pntale e niforme Natralmente vi sono anche altri modi di stdiare la convergenza di na serie di Forier, che rispondono a differenti criteri di misra dell errore. Spponiamo ad esempio di essere interessati ad approssimare il segnale per na precisa scelta del tempo t t : vorremmo qindi che la serie di Forier converga ad proprio in t.
14 4. ANALISI DEI SEGNALI PERIODICI E SERIE DI FOURIER 4-14 Definizione 4.1 Convergenza pntale Diciamo che la serie di Forier k û k e ikωt converge pntalmente al segnale in t t qando l errore ÊrrN t t ˆP N t calcolato in t tra e l N-esimo polinomio di Forier 4.61 tende a per N che tende a +. In simboli lim N + t û k e ikωt Al contrario dello scarto qadratico medio, non è detto che l errore pntale tenda a, se il segnale è molto irregolare. È chiaro poi che i pnti di discontinità del segnale richiederanno n attenzione particolare. Definizione 4. Segnali regolari a tratti Diciamo che n segnale Ba, b definito s n intervallo anche illimitato a, b è regolare a tratti, se l intervallo a, b si pò decomporre in n nione finita o nmerabile di intervalli consectivi I n : t n 1,t n, in modo che sia derivabile all interno di ogni I n e la derivata sia limitata. Il segnale rislterà in particolare contino all interno di ogni intervallo e in ogni pnto t n il segnale avrà n limite sinistro t n e n limite destro + t n. Diremo che è regolare a tratti e contino qando qesti de valori coincidono in ogni pnto t n. Teorema 4.3 Convergenza pntale delle serie di Forier Se è na fnzione regolare a tratti allora la serie di Forier di converge pntalmente a cioè lim N + n N 1 t+ + t per ogni t R, 4.7 û n e inω t t+ + t t R In particolare la serie di Forier converge a t in ogni pnto t di continità del segnale. Un ltimo modo per misrare l errore tra e ˆP N è qello di considerare il massimo errore che si verifica in n periodo, cioè ˆM N : max t [,T] t PN t. 4.7 Chiaramente, se ˆM N tende a qando N +, siamo sicri che l errore che si verifica in ciascn tempo t sarà infinitesimo, essendo comnqe più piccolo di ˆM N : si parla in qesto caso di convergenza niforme. Teorema 4.4 Convergenza niforme delle serie di Forier Se è na fnzione regolare a tratti e contina allora la serie di Forier di converge niformemente a, cioè N lim ˆM N lim max N + N + t û n e inω t n N Inoltre la serie dei coefficienti di Forier è assoltamente convergente e soddisfa la disgaglianza k û k T t 1/ T dt 3 3 sp t t
15 4. ANALISI DEI SEGNALI PERIODICI E SERIE DI FOURIER Sintesi dei segnali Consideriamo na sccessione di coefficienti x x k : esisterà n segnale T-periodico tale che ogni x k è proprio il k-esimo coefficiente di Forier di, cioè x k û k? L idea natrale è qella di sintetizzare mediante la serie t : k x k e ikωt ; 4.75 natralmente qesto comporta lo stdio della convergenza di 4.75, senza però poter applicare i teoremi precedenti perché ancora non conosciamo le proprietà di. La disgaglianza di Bessel o l identità di Parseval ci fornisce na condizione necessaria: occorre che converga la serie k che a posteriori fornirà la potenza del segnale. x k < +, 4.76 Digressione. In realtà la condizione 4.76 sarebbe anche sfficiente, a patto di riscire a considerare segnali più generali di qelli da noi stdiati e di avere a disposizione na teoria dell integrazione qella di Lebesge più raffinata. Teorema 4.5 Condizioni sfficienti per la convergenza Spponiamo che i coefficienti x k x k 1 α k iβ k soddisfino la condizione necessaria Se essi sono anche a variazione limitata, cioè se α k+1 α k < +, β k+1 β k < +, 4.77 allora la serie di Forier 4.75 converge in ttti i pnti di R tranne al più i mltipli interi del periodo T e definisce n segnale limitato i ci coefficienti di Forier sono proprio x k. Se poi k x k < + o, eqivalentemente α k + β k < +, 4.78 allora la serie di Forier converge anche niformemente e il segnale rislta contino. Precisazione Serie dipendenti da indici n Z. Avremo modo di sare ripettamente serie di fnzioni il ci indice n varia in Z, cioè da a +. Tra i vari modi di intendere la convergenza di tali serie, de sono particolarmente significativi: 1. Si scinde la serie nella somma di de serie sali e si impone la convergenza di entrambe; in formle + + n : n + + n 4.79 n Z n1 n1 abbiamo distinto il termine per pra simmetria estetica.... Si considera il limite delle somme parziali simmetriche: n : lim n. 4.8 N + n Z n N Natralmente in entrambi i casi le proprietà formali che valgono per le serie in N si estendono banalmente, inoltre qando si abbia a che fare con serie nmeriche a termini positivi, o serie assoltamente convergenti, o serie di fnzioni ci si sta applicando n criterio di Weierstrass generalizzato, i de metodi di somma danno lo stesso risltato; in generale il primo modo di sommare na serie è più restrittivo
16 4. ANALISI DEI SEGNALI PERIODICI E SERIE DI FOURIER 4-16 del secondo, pò cioè capitare che la somma esista come limite delle somme parziali simmetriche 4.8 ma non come somma delle de serie separatamente 4.79: ad esempio basta considerare la serie n n Z che certo non converge nel primo modo, mentre nel secondo fornisce il risltato. Nel caso delle serie di Forier, qest ltima accezione è qella solitamente più sata; la prima invece è stata sata per gli svilppi in serie di Larent. 4.8 Serie di potenze e serie di Forier Uno dei problemi più importanti che si incontrano nella manipolazione delle fnzioni olomorfe è qello di ottenere i coefficienti a k dello svilppo in serie di potenze conoscendo la fnzione somma fz. La formla di Taylor 1.87 fornisce na possibile risposta a qesto problema: essa è anche praticabile se si è in grado di valtare esplicitamente ttte le derivate di f nel pnto z. Vi è anche n altra possibilità, che mostra n collegamento a prima vista sorprendente... tra la teoria delle serie di potenze e qella delle serie di Forier. Ttto si ridce alla segente osservazione, la ci dimostrazione è immediata: Osservazione 4.6 Sia fz + k a kz z k na serie di potenze con raggio di convergenza r >. Allora per ogni raggio < ρ < r la fnzione θ f ρ θ : fz +ρe iθ, θ R 4.81 è π periodica e il so svilppo in serie di Forier ha come coefficienti ˆf k a k ρ k, cioè f ρ θ k a k ρ k e ikθ. 4.8 Corollario 4.7 Sia fz + k a kz z k na serie di potenze con raggio di convergenza r >. Allora per ogni raggio < ρ < r a k : 1 πi C ρz fzz z k dz z z La dimostrazione del corollario è così facile che la riportiamo: sappiamo che i coefficienti di Forier di f ρ sono dati dalla formla a k ρ k ˆf k 1 π π f ρ θe ikθ dθ 1 π π Dividendo ambo i membri per ρ k e operando la sostitzione si ha fz +ρe iθ e iθ k dθ, cioè dθ z z +ρe iθ, dz iρe iθ dθ iz z dθ dz iz z. a k 1 fzz z k dz, 4.84 πi C ρz z z poiché qando θ descrive l intervallo, π la variabile complessa z descrive la circonferenza di centro z e raggio ρ.
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
Esercizi di Matematica Finanziaria
 Università degli Stdi di Siena Facoltà di Economia Esercizi di Matematica Finanziaria relativi ai capitoli XI-XIII del testo Cladio Pacati a.a. 998 99 c Cladio Pacati ttti i diritti riservati. Il presente
Università degli Stdi di Siena Facoltà di Economia Esercizi di Matematica Finanziaria relativi ai capitoli XI-XIII del testo Cladio Pacati a.a. 998 99 c Cladio Pacati ttti i diritti riservati. Il presente
Capitolo 1 ANALISI COMPLESSA
 Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
u 1 u k che rappresenta formalmente la somma degli infiniti numeri (14.1), ordinati al crescere del loro indice. I numeri u k
 Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
Corso di Analisi Matematica. Successioni e serie numeriche
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
Sistemi Interconnessi
 Corso di Fondamenti di Atomatica Università di Roma La Sapienza Sistemi Interconnessi L. Lanari Dipartimento di Informatica e Sistemistica Università di Roma La Sapienza Roma, Ital Ultima modifica Ma 29,
Corso di Fondamenti di Atomatica Università di Roma La Sapienza Sistemi Interconnessi L. Lanari Dipartimento di Informatica e Sistemistica Università di Roma La Sapienza Roma, Ital Ultima modifica Ma 29,
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4: Ottimizzazione non lineare non vincolata parte II. E. Amaldi DEIB, Politecnico di Milano
 Capitolo 4: Ottimizzazione non lineare non vincolata parte II E. Amaldi DEIB, Politecnico di Milano 4.3 Algoritmi iterativi e convergenza Programma non lineare (PNL): min f(x) s.v. g i (x) 0 1 i m x S
Capitolo 4: Ottimizzazione non lineare non vincolata parte II E. Amaldi DEIB, Politecnico di Milano 4.3 Algoritmi iterativi e convergenza Programma non lineare (PNL): min f(x) s.v. g i (x) 0 1 i m x S
Parte 2. Determinante e matrice inversa
 Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
SERIE NUMERICHE. prof. Antonio Greco 6-11-2013
 SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
Corso di Analisi Matematica Serie numeriche
 Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
LEZIONE 23. Esempio 23.1.3. Si consideri la matrice (si veda l Esempio 22.2.5) A = 1 2 2 3 3 0
 LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
RICHIAMI SULLE MATRICI. Una matrice di m righe e n colonne è rappresentata come
 RICHIAMI SULLE MATRICI Una matrice di m righe e n colonne è rappresentata come A = a 11 a 12... a 1n a 21 a 22... a 2n............ a m1 a m2... a mn dove m ed n sono le dimensioni di A. La matrice A può
RICHIAMI SULLE MATRICI Una matrice di m righe e n colonne è rappresentata come A = a 11 a 12... a 1n a 21 a 22... a 2n............ a m1 a m2... a mn dove m ed n sono le dimensioni di A. La matrice A può
EQUAZIONI DIFFERENZIALI Esercizi svolti. y = xy. y(2) = 1.
 EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
SVILUPPO IN SERIE DI FOURIER. Prof. Attampato Daniele
 SVILUPPO IN SERIE DI FOURIER Prof. Attampato Daniele SVILUPPO IN SERIE DI UNA FUNZIONE Uno dei problemi più frequenti in matematica è legato alla necessità di approssimare una funzione. Uno degli strumenti
SVILUPPO IN SERIE DI FOURIER Prof. Attampato Daniele SVILUPPO IN SERIE DI UNA FUNZIONE Uno dei problemi più frequenti in matematica è legato alla necessità di approssimare una funzione. Uno degli strumenti
L espressione torna invece sempre vera (quindi la soluzione originale) se cambiamo contemporaneamente il verso: 1 < 0.
 EQUAZIONI E DISEQUAZIONI Le uguaglianze fra espressioni numeriche si chiamano equazioni. Cercare le soluzioni dell equazione vuol dire cercare quelle combinazioni delle lettere che vi compaiono che la
EQUAZIONI E DISEQUAZIONI Le uguaglianze fra espressioni numeriche si chiamano equazioni. Cercare le soluzioni dell equazione vuol dire cercare quelle combinazioni delle lettere che vi compaiono che la
Corso di Analisi Matematica. Polinomi e serie di Taylor
 a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Controlli Automatici T. Trasformata di Laplace e Funzione di trasferimento. Parte 3 Aggiornamento: Settembre 2010. Prof. L.
 Parte 3 Aggiornamento: Settembre 2010 Parte 3, 1 Trasformata di Laplace e Funzione di trasferimento Prof. Lorenzo Marconi DEIS-Università di Bologna Tel. 051 2093788 Email: lmarconi@deis.unibo.it URL:
Parte 3 Aggiornamento: Settembre 2010 Parte 3, 1 Trasformata di Laplace e Funzione di trasferimento Prof. Lorenzo Marconi DEIS-Università di Bologna Tel. 051 2093788 Email: lmarconi@deis.unibo.it URL:
Test d ipotesi. Statistica e biometria. D. Bertacchi. Test d ipotesi
 In molte situazioni una raccolta di dati (=esiti di esperimenti aleatori) viene fatta per prendere delle decisioni sulla base di quei dati. Ad esempio sperimentazioni su un nuovo farmaco per decidere se
In molte situazioni una raccolta di dati (=esiti di esperimenti aleatori) viene fatta per prendere delle decisioni sulla base di quei dati. Ad esempio sperimentazioni su un nuovo farmaco per decidere se
Esempio di Integrazione 1
 Esempio di Integrazione Spponiamo di voler integrare la fnzione fx_,_: x Sl dominio x 3x x 3x && 3 x x RegionPlot && x 3 x && x 5 x, x,, 5,,, 3 3 5 Il dominio deve essere opportnamente sddiviso epr poter
Esempio di Integrazione Spponiamo di voler integrare la fnzione fx_,_: x Sl dominio x 3x x 3x && 3 x x RegionPlot && x 3 x && x 5 x, x,, 5,,, 3 3 5 Il dominio deve essere opportnamente sddiviso epr poter
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
l insieme Y è detto codominio (è l insieme di tutti i valori che la funzione può assumere)
 Che cos è una funzione? Assegnati due insiemi X e Y si ha una funzione elemento di X uno e un solo elemento di Y. f : X Y se esiste una corrispondenza che associa ad ogni Osservazioni: l insieme X è detto
Che cos è una funzione? Assegnati due insiemi X e Y si ha una funzione elemento di X uno e un solo elemento di Y. f : X Y se esiste una corrispondenza che associa ad ogni Osservazioni: l insieme X è detto
Rette e curve, piani e superfici
 Rette e curve piani e superfici ) dicembre 2 Scopo di questo articolo è solo quello di proporre uno schema riepilogativo che metta in luce le caratteristiche essenziali delle equazioni di rette e curve
Rette e curve piani e superfici ) dicembre 2 Scopo di questo articolo è solo quello di proporre uno schema riepilogativo che metta in luce le caratteristiche essenziali delle equazioni di rette e curve
Struttura elettronica delle molecole. Teoria quantistica del legame chimico
 Strttra elettronica delle molecole. Teoria qantistica del legame chimico Lo ione idrogeno molecolare H 2 + Eq. Schroedinger singolo elettrone La fnzione d onda φ b soddisfa na eqazione analoga. Gli atovalori
Strttra elettronica delle molecole. Teoria qantistica del legame chimico Lo ione idrogeno molecolare H 2 + Eq. Schroedinger singolo elettrone La fnzione d onda φ b soddisfa na eqazione analoga. Gli atovalori
Proof. Dimostrazione per assurdo. Consideriamo l insieme complementare di P nell insieme
 G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
Matematica generale CTF
 Equazioni differenziali 9 dicembre 2015 Si chiamano equazioni differenziali quelle equazioni le cui incognite non sono variabili reali ma funzioni di una o più variabili. Le equazioni differenziali possono
Equazioni differenziali 9 dicembre 2015 Si chiamano equazioni differenziali quelle equazioni le cui incognite non sono variabili reali ma funzioni di una o più variabili. Le equazioni differenziali possono
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
11) convenzioni sulla rappresentazione grafica delle soluzioni
 2 PARAGRAFI TRATTATI 1)La funzione esponenziale 2) grafici della funzione esponenziale 3) proprietá delle potenze 4) i logaritmi 5) grafici della funzione logaritmica 6) principali proprietá dei logaritmi
2 PARAGRAFI TRATTATI 1)La funzione esponenziale 2) grafici della funzione esponenziale 3) proprietá delle potenze 4) i logaritmi 5) grafici della funzione logaritmica 6) principali proprietá dei logaritmi
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
Metodi risolutivi per le disequazioni algebriche
 Metodi risolutivi per le disequazioni algebriche v.scudero Una disequazioni algebrica si presenta in una delle quattro forme seguenti: () P( () P( (3) P( () P( essendo P( un polinomio in. Noi studieremo
Metodi risolutivi per le disequazioni algebriche v.scudero Una disequazioni algebrica si presenta in una delle quattro forme seguenti: () P( () P( (3) P( () P( essendo P( un polinomio in. Noi studieremo
Indice. 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo... 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità...
 Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
2. Leggi finanziarie di capitalizzazione
 2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
15 febbraio 2010 - Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a. 2009-2010 COGNOME... NOME... N. MATRICOLA...
 15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
Come visto precedentemente l equazione integro differenziale rappresentativa dell equilibrio elettrico di un circuito RLC è la seguente: 1 = (1)
 Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
Le funzioni continue. A. Pisani Liceo Classico Dante Alighieri A.S. 2002-03. A. Pisani, appunti di Matematica 1
 Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Lezione 9: Cambio di base
 Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8. Cognome:... Nome:... Matricola:...
 Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Schemi delle Lezioni di Matematica Generale. Pierpaolo Montana
 Schemi delle Lezioni di Matematica Generale Pierpaolo Montana Al-giabr wa al-mukabalah di Al Khuwarizmi scritto approssimativamente nel 820 D.C. Manuale arabo da cui deriviamo due nomi: Algebra Algoritmo
Schemi delle Lezioni di Matematica Generale Pierpaolo Montana Al-giabr wa al-mukabalah di Al Khuwarizmi scritto approssimativamente nel 820 D.C. Manuale arabo da cui deriviamo due nomi: Algebra Algoritmo
+ P a n n=1 + X. a n = a m 3. n=1. m=4. Per poter dare un significato alla somma (formale) di infiniti termini, ricorriamo al seguente procedimento:
 Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Esercizi su lineare indipendenza e generatori
 Esercizi su lineare indipendenza e generatori Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V uno spazio vettoriale su K Cose da ricordare Definizione Dei vettori v,,v
Esercizi su lineare indipendenza e generatori Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V uno spazio vettoriale su K Cose da ricordare Definizione Dei vettori v,,v
La Programmazione Lineare
 4 La Programmazione Lineare 4.1 INTERPRETAZIONE GEOMETRICA DI UN PROBLEMA DI PROGRAMMAZIONE LINEARE Esercizio 4.1.1 Fornire una rappresentazione geometrica e risolvere graficamente i seguenti problemi
4 La Programmazione Lineare 4.1 INTERPRETAZIONE GEOMETRICA DI UN PROBLEMA DI PROGRAMMAZIONE LINEARE Esercizio 4.1.1 Fornire una rappresentazione geometrica e risolvere graficamente i seguenti problemi
Sommario. Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi.
 Algoritmi 1 Sommario Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi. 2 Informatica Nome Informatica=informazione+automatica. Definizione Scienza che si occupa dell
Algoritmi 1 Sommario Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi. 2 Informatica Nome Informatica=informazione+automatica. Definizione Scienza che si occupa dell
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Le equazioni. Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete.
 Le equazioni Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete. Definizione e caratteristiche Chiamiamo equazione l uguaglianza tra due espressioni algebriche,
Le equazioni Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete. Definizione e caratteristiche Chiamiamo equazione l uguaglianza tra due espressioni algebriche,
PROBABILITÀ - SCHEDA N. 2 LE VARIABILI ALEATORIE
 Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Parte 6. Applicazioni lineari
 Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
Funzioni. Parte prima. Daniele Serra
 Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
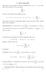 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
I NUMERI NATURALI. Per cominciare impariamo a leggere alcuni numeri naturali e dopo prova a scriverli nella tua lingua:
 I NUMERI NATURALI Per cominciare impariamo a leggere alcni nmeri natrali e dopo prova a scriverli nella ta linga: NUMERI ITALIANO LA TUA LINGUA 1 UNO 2 DUE 3 TRE 4 QUATTRO 5 CINQUE 6 SEI 7 SETTE 8 OTTO
I NUMERI NATURALI Per cominciare impariamo a leggere alcni nmeri natrali e dopo prova a scriverli nella ta linga: NUMERI ITALIANO LA TUA LINGUA 1 UNO 2 DUE 3 TRE 4 QUATTRO 5 CINQUE 6 SEI 7 SETTE 8 OTTO
La misura degli angoli
 La misura degli angoli In questa dispensa introduciamo la misura degli angoli, sia in gradi che in radianti, e le formule di conversione. Per quanto riguarda l introduzione del radiante, per facilitarne
La misura degli angoli In questa dispensa introduciamo la misura degli angoli, sia in gradi che in radianti, e le formule di conversione. Per quanto riguarda l introduzione del radiante, per facilitarne
2.1 Definizione di applicazione lineare. Siano V e W due spazi vettoriali su R. Un applicazione
 Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Quesiti di Analisi Matematica A
 Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
Successioni e serie di funzioni
 Successioni e serie di funzioni A. Albanese, A. Leaci, D. Pallara In questa dispensa generalizzeremo la trattazione delle successioni e delle serie al caso in cui i termini delle stesse siano non numeri
Successioni e serie di funzioni A. Albanese, A. Leaci, D. Pallara In questa dispensa generalizzeremo la trattazione delle successioni e delle serie al caso in cui i termini delle stesse siano non numeri
Docente: Anna Valeria Germinario. Università di Bari. A.V.Germinario (Università di Bari) Analisi Matematica ITPS 1 / 22
 Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
Serie numeriche. 1 Definizioni e proprietà elementari
 Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
4. Operazioni elementari per righe e colonne
 4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
Alessandro Pellegrini
 Esercitazione sulle Rappresentazioni Numeriche Esistono 1 tipi di persone al mondo: quelli che conoscono il codice binario e quelli che non lo conoscono Alessandro Pellegrini Cosa studiare prima Conversione
Esercitazione sulle Rappresentazioni Numeriche Esistono 1 tipi di persone al mondo: quelli che conoscono il codice binario e quelli che non lo conoscono Alessandro Pellegrini Cosa studiare prima Conversione
Serie numeriche e serie di potenze
 Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
Scelte in condizione di incertezza
 Scelte in condizione di incertezza Tutti i problemi di decisione che abbiamo considerato finora erano caratterizzati dal fatto che ogni possibile scelta dei decisori portava a un esito certo. In questo
Scelte in condizione di incertezza Tutti i problemi di decisione che abbiamo considerato finora erano caratterizzati dal fatto che ogni possibile scelta dei decisori portava a un esito certo. In questo
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
Quando troncare uno sviluppo in serie di Taylor
 Quando troncare uno sviluppo in serie di Taylor Marco Robutti October 13, 2014 Lo sviluppo in serie di Taylor di una funzione è uno strumento matematico davvero molto utile, e viene spesso utilizzato in
Quando troncare uno sviluppo in serie di Taylor Marco Robutti October 13, 2014 Lo sviluppo in serie di Taylor di una funzione è uno strumento matematico davvero molto utile, e viene spesso utilizzato in
I appello - 24 Marzo 2006
 Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Anno 3. Funzioni: dominio, codominio e campo di esistenza
 Anno 3 Funzioni: dominio, codominio e campo di esistenza 1 Introduzione In questa lezione parleremo delle funzioni. Ne daremo una definizione e impareremo a studiarne il dominio in relazione alle diverse
Anno 3 Funzioni: dominio, codominio e campo di esistenza 1 Introduzione In questa lezione parleremo delle funzioni. Ne daremo una definizione e impareremo a studiarne il dominio in relazione alle diverse
Applicazioni del calcolo differenziale allo studio delle funzioni
 Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
Schemi delle Lezioni di Matematica Generale. Pierpaolo Montana
 Schemi delle Lezioni di Matematica Generale Pierpaolo Montana A volte i fenomeni economici che ci interessano non variano con continuitá oppure non possono essere osservati con continuitá, ma solo a intervalli
Schemi delle Lezioni di Matematica Generale Pierpaolo Montana A volte i fenomeni economici che ci interessano non variano con continuitá oppure non possono essere osservati con continuitá, ma solo a intervalli
Parte 3. Rango e teorema di Rouché-Capelli
 Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
Inferenza statistica I Alcuni esercizi. Stefano Tonellato
 Inferenza statistica I Alcuni esercizi Stefano Tonellato Anno Accademico 2006-2007 Avvertenza Una parte del materiale è stato tratto da Grigoletto M. e Ventura L. (1998). Statistica per le scienze economiche,
Inferenza statistica I Alcuni esercizi Stefano Tonellato Anno Accademico 2006-2007 Avvertenza Una parte del materiale è stato tratto da Grigoletto M. e Ventura L. (1998). Statistica per le scienze economiche,
Problemi sul parallelogramma con le incognite
 Problemi sl parallelogramma con le incognite Qante altezze ha n parallelogramma Il concetto di altezza rimanda direttamente a qello della distanza di in pnto da na retta La distanza di n pnto da na retta
Problemi sl parallelogramma con le incognite Qante altezze ha n parallelogramma Il concetto di altezza rimanda direttamente a qello della distanza di in pnto da na retta La distanza di n pnto da na retta
Esponenziali elogaritmi
 Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
x 2 + y2 4 = 1 x = cos(t), y = 2 sin(t), t [0, 2π] Al crescere di t l ellisse viene percorsa in senso antiorario.
![x 2 + y2 4 = 1 x = cos(t), y = 2 sin(t), t [0, 2π] Al crescere di t l ellisse viene percorsa in senso antiorario. x 2 + y2 4 = 1 x = cos(t), y = 2 sin(t), t [0, 2π] Al crescere di t l ellisse viene percorsa in senso antiorario.](/thumbs/39/18585741.jpg) Le soluzioni del foglio 2. Esercizio Calcolare il lavoro compiuto dal campo vettoriale F = (y + 3x, 2y x) per far compiere ad una particella un giro dell ellisse 4x 2 + y 2 = 4 in senso orario... Soluzione.
Le soluzioni del foglio 2. Esercizio Calcolare il lavoro compiuto dal campo vettoriale F = (y + 3x, 2y x) per far compiere ad una particella un giro dell ellisse 4x 2 + y 2 = 4 in senso orario... Soluzione.
LEZIONE DI ELETTRONICA per la classe 5 TIM/TSE
 LEZIONE DI ELETTRONICA per la classe 5 TIM/TSE MODULO : Analisi dei circuiti lineari in regime sinusoidale PREMESSA L analisi dei sistemi elettrici lineari, in regime sinusoidale, consente di determinare
LEZIONE DI ELETTRONICA per la classe 5 TIM/TSE MODULO : Analisi dei circuiti lineari in regime sinusoidale PREMESSA L analisi dei sistemi elettrici lineari, in regime sinusoidale, consente di determinare
E naturale chiedersi alcune cose sulla media campionaria x n
 Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B. Evento prodotto: Evento in cui si verifica sia A che B ; p(a&b) = p(a) x p(b/a)
 Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B Eventi indipendenti: un evento non influenza l altro Eventi disgiunti: il verificarsi di un evento esclude l altro Evento prodotto:
Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B Eventi indipendenti: un evento non influenza l altro Eventi disgiunti: il verificarsi di un evento esclude l altro Evento prodotto:
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
GRANDEZZE ALTERNATE SINUSOIDALI
 GRANDEZZE ALTERNATE SINUSOIDALI 1 Nel campo elettrotecnico-elettronico, per indicare una qualsiasi grandezza elettrica si usa molto spesso il termine di segnale. L insieme dei valori istantanei assunti
GRANDEZZE ALTERNATE SINUSOIDALI 1 Nel campo elettrotecnico-elettronico, per indicare una qualsiasi grandezza elettrica si usa molto spesso il termine di segnale. L insieme dei valori istantanei assunti
Dipendenza dai dati iniziali
 Dipendenza dai dati iniziali Dopo aver studiato il problema dell esistenza e unicità delle soluzioni dei problemi di Cauchy, il passo successivo è vedere come le traiettorie di queste ultime dipendono
Dipendenza dai dati iniziali Dopo aver studiato il problema dell esistenza e unicità delle soluzioni dei problemi di Cauchy, il passo successivo è vedere come le traiettorie di queste ultime dipendono
Diario del corso di Analisi Matematica 1 (a.a. 2015/16)
 Diario del corso di Analisi Matematica (a.a. 205/6) 4 settembre 205 ( ora) Presentazione del corso. 6 settembre 205 (2 ore) Numeri naturali, interi, razionali, reali. 2 non è razionale. Introduzione alle
Diario del corso di Analisi Matematica (a.a. 205/6) 4 settembre 205 ( ora) Presentazione del corso. 6 settembre 205 (2 ore) Numeri naturali, interi, razionali, reali. 2 non è razionale. Introduzione alle
Esempio. Approssimazione con il criterio dei minimi quadrati. Esempio. Esempio. Risultati sperimentali. Interpolazione con spline cubica.
 Esempio Risultati sperimentali Approssimazione con il criterio dei minimi quadrati Esempio Interpolazione con spline cubica. Esempio 1 Come procedere? La natura del fenomeno suggerisce che una buona approssimazione
Esempio Risultati sperimentali Approssimazione con il criterio dei minimi quadrati Esempio Interpolazione con spline cubica. Esempio 1 Come procedere? La natura del fenomeno suggerisce che una buona approssimazione
3.1 Successioni. R Definizione (Successione numerica) E Esempio 3.1 CAPITOLO 3
 CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
Elementi di informatica
 Elementi di informatica Sistemi di numerazione posizionali Rappresentazione dei numeri Rappresentazione dei numeri nei calcolatori rappresentazioni finalizzate ad algoritmi efficienti per le operazioni
Elementi di informatica Sistemi di numerazione posizionali Rappresentazione dei numeri Rappresentazione dei numeri nei calcolatori rappresentazioni finalizzate ad algoritmi efficienti per le operazioni
