Un sistema di equazioni lineari ( o brevemente un sistema lineare) di m equazioni in n incognite, si presenta nella forma:
|
|
|
- Iolanda Ventura
- 5 anni fa
- Visualizzazioni
Transcript
1 SISTEMI LINEARI Un sistema di equazioni lineari ( o brevemente un sistema lineare) di m equazioni in n incognite, si presenta nella forma: a x + a 2 x a n x n = b a 2 x + a 22 x a 2n x n = b 2.. a m x + a m2 x a mn x n = b m Le incognite sono x, x 2,, x n e i termini noti sono b, b 2,, b m. Un sistema lineare di m equazioni in n incognite può appartenere ad una ed una sola delle seguenti categorie: sistema possibile : questo a sua volta presenta due possibilità: una sola soluzione costituita da una n pla di valori o infinite soluzioni dipendenti ciascuna da uno o più parametri, soluzioni che si possono determinare dando opportuni valori ai parametri. sistema impossibile: non esistono soluzioni comuni alle varie equazioni. Ci proponiamo, oltre che di imparare a risolvere un sistema lineare, anche di imparare a discuterlo, cioè a scoprire a priori (quindi senza doverlo risolvere), se è risolubile o no, e quante sono le sue soluzioni. Al biennio avete imparato a risolvere semplici sistemi lineari con vari metodi, che si basano tutti sull idea di fondo che è quella di trovare un sistema che abbia le stesse soluzioni di quello dato ma sia scritto in una forma più semplice. DEFINIZIONE. Due sistemi lineari di m equazioni in n incognite si dicono equivalenti se hanno le stesse soluzioni, cioè se ogni n pla che è soluzione dell uno lo è anche dell altro. x + y = Ad esempio i sistemi 2x y = 0 x = y = 2x x = y = 2 sono equivalenti, come si verifica facilmente. Un ottima tecnica per risolvere un sistema lineare è quella di trovare un sistema equivalente a quello dato ma con una struttura più semplice. Per farlo vediamo prima come un sistema può essere scritto in forma matriciale. Il sistema di m equazioni in n incognite scritto sopra corrisponde a: Ax = b, dove A è la matrice dei coefficienti, x è la matrice delle incognite ( o vettore colonna), b è la matrice dei termini noti. a a 2 a n x b a a 2 a n b a 2 a 22 a 2n a 2 a 22 a 2n b A = [ x = [ b = [ C = [ 2 a m a m2 a mn x n b m a m a m2 a mn b m E anche importante la matrice C, detta matrice completa, costruita a partire dalla A accostandole a destra la colonna dei termini noti: possiamo anche scrivere C = [A B. Se b = 0 allora il sistema si dice omogeneo. In generale il sistema Ax = 0 si dice sistema omogeneo associato al sistema Ax = b.
2 . I SISTEMI DI CRAMER Prima di affrontare la risoluzione di un sistema lineare qualunque, ci soffermiamo su un caso particolare notevole, quello di un sistema di n equazioni in n incognite, la cui matrice A è invertibile. Si chiama sistema di Cramer. Ax = b, con A matrice n n, deta 0 Poiché il deta 0, esiste la matrice inversa A. Moltiplichiamo a sinistra entrambi i membri dell equazione per A e otteniamo: Regola di Cramer: Un sistema di n equazioni in n incognite Ax = b la cui matrice dei coefficienti abbia determinante diverso da zero ha come unica soluzione la n-upla di numeri reali x, x 2,., x n data dalle seguenti formule x = deta deta x 2 = deta 2 deta x = deta deta A Ax = A b Applico la proprietà associativa della moltiplicazione tra matrici ed eseguo il prodotto A A. Il prodotto di una matrice per la sua inversa dà la matrice identica, quindi: I x = A b. Quindi si trova l unica soluzione x = A b del sistema lineare assegnato. Nel caso ad esempio di un sistema di tre equazioni in tre incognite, effettuando esplicitamente il prodotto di A A 2 A A = [ A det (A) 2 A 22 A 2 per b si ottiene, ad esempio per x la seguente espressione: A A 2 A x = deta (A b + A 2 b 2 + A b ) b a 2 a che non è altro che il prodotto di per il determinante della matrice [ b deta 2 a 22 a 2, ottenuta dalla matrice b a 2 a A sostituendo la prima colonna con i termini noti. Si riconosce in questo modo di procedere la ben nota regola di Cramer che avete visto al biennio. x n = deta n deta essendo A, A 2,.., A n le matrici ottenute da A sostituendo rispettivamente la prima, la seconda, la terza colonna, ecc. con il vettore b dei termini noti. Esempio: 2x + x 2 = 0 x x 2 = 0 A = [ 2 deta = b = [ 0 Scriviamo la matrice inversa: A = [ 2 x = A b = [ 2 [ 0 = [
3 Applichiamo ora la regola di Cramer su esposta, come al biennio: x = x 2 = det [ 0 = = det [ 2 0 = = 2. TRASFORMAZIONI LINEARI Definizione: Una funzione f: R n R m si dice lineare se è additiva e omogenea, ovvero se gode delle seguenti proprietà: f (x + y) = f(x) + f (y) f(kx) = k f(x) x, y R n ( proprietà di additività) k R, x R n ( proprietà di omogeneità) Le due proprietà sopra scritte si possono compendiare nell unica condizione: f (k x + k 2 y) = k f(x) + k 2 f (y) k, k 2 R, x, y R n Inoltre se f è lineare, f(0) = 0 Teorema di rappresentazione delle funzioni lineari: Una funzione f: R n R m è lineare se e solo se f(x) = A x, dove A è una matrice di m righe per n colonne.. CASO GENERALE DI SISTEMA LINEARE Torniamo a considerare in generale il sistema Ax = b, essendo A una matrice di m righe per n colonne qualunque, e sia Ax = 0 il sistema omogeneo associato. Se x 0 è una soluzione del sistema di partenza, e x è un altra sua soluzione, è subito visto che x x 0 è soluzione del sistema omogeneo associato. Infatti: Ax = b e Ax 0 = b allora A(x x 0 ) = 0. Allo stesso modo si vede che se y è una soluzione di Ax = 0, allora x 0 + y è soluzione di Ax = b. Possiamo allora enunciare la seguente proposizione: Proposizione: le soluzioni di un sistema lineare si ottengono tutte sommando una sua soluzione particolare con la soluzione generale di un sistema omogeneo associato. Per risolvere un sistema occorre dunque affrontare una duplice questione:. Vedere se esiste una soluzione particolare x 0 del sistema stesso ( in caso contrario il sistema non ammette alcuna soluzione) 2. Dare un procedimento per trovare una soluzione generale del sistema omogeneo associato.
4 Esaminiamo la prima questione: la condizione affinché esista una soluzione x 0 del sistema Ax = b, tale cioè che Ax 0 = b, è che il vettore b appartenga all immagine della trasformazione lineare f rappresentata dal sistema. In pratica il vettore b deve poter essere scritto come combinazione lineare delle colonne di A. Ciò equivale a dire che le due matrici completa (C) e incompleta (A ) del sistema: a a 2 a n a a 2 a n b a 2 a 22 a 2n a 2 a 22 a 2n b A = [ C = [ 2 a m a m2 a mn a m a m2 a mn b m abbiano lo stesso rango. Teorema di Rouché-Capelli: Un sistema lineare Ax = b ha soluzioni se e soltanto se la matrice incompleta A e la matrice completa C hanno lo stesso rango. Per esaminare la seconda questione non daremo un procedimento generale, ma useremo degli esempi. Dato un sistema lineare, procederemo alla sua risoluzione in quattro passi: passo 0: scrittura matriciale passo : applicazione del Teorema di Rouchè Capelli ( per stabilire s il sistema è possibile oppure no) passo 2: predisposizione del sistema all utilizzo della regola di Cramer passo : applicazione della regola di Cramer ESEMPIO. Sia dato il seguente sistema: x + y + z = x y + 2z = 0 x + y + 4z = Passo 0: A = [ 2 b = [ 0 C = [ Passo : trovo il rango di A e il rango di C. Calcolo deta = 0. Allora il rango di A non è. Vedo che al suo interno c è il minore [ che ha determinante -2, pertanto il rango di A è 2. Considero ora la matrice completa C: al suo interno c è lo stesso minore di prima, quindi r(c) 2. Orlo il minore [ con la quarta colonna e l ultima riga e ottengo la matrice [ 0 che ha determinante 2. Pertanto il rango di C è. Per il Teorema di Rouché Capelli il sistema è impossibile. 0 ESEMPIO 2. Sia dato il seguente sistema:
5 x + y + z = x y + 2z = 0 x + y + 4z = 2 Passo 0: A = [ 2 b = [ 0 C = [ Passo : r(a) = 2 ( visto prima). r(c) 2 perché det [ = 2 0 Orlo la matrice [ utilizzando l ultima colonna e l ultima riga ottenendo la matrice [ 0, il 2 cui determinante è 0. Orlo la matrice utilizzando la terza colonna, e ottengo [ 2 il cui determinante 4 è di nuovo 0. Pertanto r(c) = 2. Per il Teorema di Rouché Capelli il sistema è possibile. Passo 2. Predispongo il sistema all utilizzo della regola di Cramer. Scrivo il sistema formato solo dalle prime due equazioni ( perché faccio riferimento al minore non singolare [ ), e porto al secondo membro di ogni equazione i termini con l incognita z: Passo : Utilizzo la regola di Cramer x = det (A ) x + y = z x y = 2z det [ z deta = 2z det [ = y = det (A z det [ 2) deta = 2z = z + 2z 2 2z + z 2 = 2 2 z = z Al variare di z le infinite soluzioni del sistema sono le terne ( z; + z; z) Il che equivale a dire che una soluzione particolare del sistema è ad esempio la terna ( ; ; 0) ottenuta 2 2 ponendo z = 0, e una soluzione generale del sistema omogeneo associato è ( z; z; z). 2 2 Poiché le soluzioni del sistema si ottengono in funzione del valore di un parametro, in questo caso z, si dice che il sistema ha soluzioni. ESEMPIO. Sia dato il seguente sistema: x y + w + = 0 y 2z + w = 0 6x y + 2z + w + 2 = 0
6 Passo 0. 0 A = [ b = [ 0 C = [ Passo. Calcolo il rango A. Intanto individuo un minore di ordine 2 non singolare: [ il cui determinante è. 0 Quindi r(a) 2. 0 Quindi orlo il minore con la terza colonna e ottengo [ 0 2 il cui determinante è Allora orlo il minore con la quarta colonna e ottengo [ 0 il cui determinante è 0. 6 Allora r(a) = 2. Per calcolare il rango di C posso orlare il minore di ordine 2 con la quinta colonna e ottengo [ il cui determinante è 0. Quindi, non avendo altre possibilità di orlatura, si conclude che r(c) = 2. Per il teorema di Rouché Capelli il sistema è possibile. Passo. Predispongo il sistema all utilizzo della regola di Cramer. x y + w + = 0 y 2z + w = 0 x y = w y = 2z w Passo 4. Risolvo il sistema con la regola di Cramer. x = det(a det [ w ) deta = 2z w det [ = 0 w + 2z w y = det(a 2 ) w det [ deta = 0 2z w = = 6z w 2z 2w = 2z w = 2 z 2 w Le soluzioni del sistema sono le quaterne ordinate ( 2 z 2 w ; 2z w; z; w ). Poiché le soluzioni si trovano al variare di due parametri, si dice che il sistema ha 2 soluzioni.
7 4. METODO DI ELIMINAZIONE DI GAUSS Equivalenza di matrici. Si chiamano operazioni elementari sulle righe (rispettivamente sulle colonne) di una matrice le seguenti operazioni i) scambio di due righe (colonne); ii) moltiplicazione di una riga (colonna) per una costante k 0 iii) sostituzione di una riga (colonna) con la somma della riga (colonna) stessa con un altra moltiplicata per una costante k. Due matrici A e B si dicono equivalenti per righe (rispettivamente per colonne) se B si ottiene da A eseguendo un numero finito di operazioni elementari sulle righe (colonne). Scriveremo che A B. È facile dimostrare che se A B allora B A e che se A B e B C allora A C, cioè che la relazione è una relazione di equivalenza. Ed è importante il Teorema. Se le matrici complete di due sistemi lineari sono equivalenti per righe allora i sistemi sono equivalenti, cioè hanno le stesse soluzioni Vediamo ora, su un esempio, come si possa utilizzare il precedente teorema per la risoluzione di un sistema lineare. Consideriamo il seguente sistema: La matrice completa è: C = [ x + y + z t = 2x + y + z + t = 2 x y z = 0 x + y + z t = Se sommiamo alla II riga di C la prima moltiplicata per 2, alla II la I moltiplicata per ed alla IV la I moltiplicata per otteniamo: [ Ora se in questa nuova matrice sommiamo alla III riga la seconda moltiplicata per 2 troviamo [ Infine se sommiamo alla IV riga la II moltiplicata per 2 9 risulta [
8 Quest ultima matrice ottenuta mediante operazioni elementari sulla matrice C è ad essa equivalente, e quindi in virtù del teorema sopra esposto il sistema di partenza è equivalente al sistema: che è palesemente impossibile. x + y + z t = y z + 5t = 0 9t = 0 = 6/9 In questo esempio abbiamo ridotto la matrice A ad una matrice equivalente più semplice nel senso precisato dalla seguente definizione. Definizione. Una matrice A di tipo m n di elemento generico a ij si dice ridotta (per righe) se in ogni riga che non contiene solo zeri esiste un elemento a ij 0 tale che per ogni k con i < k m si ha a kj = 0. Il procedimento illustrato è sempre possibile in quanto sussiste il seguente teorema: Teorema. Sia A una matrice qualsiasi, allora esiste una matrice B ridotta per righe equivalente alla A. Presentiamo a questo punto il metodo di eliminazione di Gauss, che si basa sul seguente teorema: Teorema (di Gauss). Se un sistema lineare è ottenuto da un altro con una delle seguenti operazioni: i) scambio di due equazioni ii) moltiplicazione di ambo i membri di un equazione per una costante non nulla iii) un equazione è sostituita dalla somma di sé stessa con un multiplo di un altra allora i due sistemi hanno le stesse soluzioni. Lo illustriamo mediante alcuni esempi. ESEMPIO. x = 9 Sia dato il seguente sistema: x + 5x 2 2x = 2 x + 2x 2 = Possiamo effettuare le seguenti operazioni: i) scambiamo la prima riga con la terza: ii) moltiplichiamo la prima riga per : x + 2x 2 = x + 5x 2 2x = 2 x = 9 x + 6x 2 = 9 x + 5x 2 2x = 2 x = 9
9 iii) aggiungiamo la prima riga moltiplicata per alla seconda: x + 6x 2 = 9 x 2 2x = x = 9 Ormai il sistema è risolto: dalla terza equazione si ha x =, x 2 = e x =. L algoritmo di Gauss funziona anche quando il numero delle equazioni è diverso dal numero delle incognite cioè quando m n. Vediamolo nei prossimi esempi. ESEMPIO 2. Sia dato il seguente sistema: x + y = 2x + y = 2x + 2y = 2 in cui m > n. Aggiungendo alla seconda ed alla terza riga la prima moltiplicata per 2 si ha il sistema equivalente x + y = 5y = 5 4y = 4 A questo punto è già chiaro che l unica soluzione è x = 2 e y =. In ogni caso, proseguendo l algoritmo si può aggiungere alla terza riga la seconda moltiplicata per 4 5 ottenendo: x + y = 5y = 5 0 = 0 L ultima uguaglianza è un identità, a riprova del fatto che le equazioni sono ridondanti. Nel caso in cui il sistema fosse impossibile procedendo con l algoritmo si arriva ad una contraddizione. ESEMPIO. Sia dato il seguente sistema: x + y = 2x + y = 2x + 2y = 0 Sempre aggiungendo alla seconda ed alla terza riga la prima moltiplicata per 2 si ha il sistema equivalente x + y = 5y = 5 4y = 2 a questo punto, però, aggiungendo alla terza riga la seconda moltiplicata per 4 si ottiene: 5 x + y = 5y = 5 0 = 2
10 Quindi una palese contraddizione: possiamo concludere dunque che il sistema dato non ammette soluzioni, o, come più comunemente ma meno propriamente si dice, è impossibile. Un sistema lineare può anche avere infinite soluzioni: ESEMPIO 4. x + y = 4 Consideriamo il sistema 2x + 2y = 8 Applicando l algoritmo di Gauss (moltiplicando la prima riga per - e sommandola alla seconda) si ottiene il sistema: x + y = 4 0 = 0 equivalente a quello dato, da cui si vede che la seconda equazione è inutile, quindi la soluzione è data da tutte le infinite coppie di numeri che hanno come somma 4, che possiamo scrivere, ad esempio, come x = t e y = 4 t. In particolare nei casi in cui il numero di equazioni è uguale al numero di incognite il metodo di Gauss viene applicato per ridurre la matrice dei coefficienti a una matrice triangolare. Illustriamolo nel caso di un sistema di tre equazioni in tre incognite. Dato il sistema: a x + a 2 x 2 + a x = b a 2 x + a 22 x 2 + a 2 x = b 2 a x + a 2 x 2 + a x = b moltiplichiamo la prima equazione per a 2 e la seconda equazione per a e sottraiamole tra loro. L equazione che così si ottiene non ha più il termine in x. Analogamente moltiplichiamo la prima equazione per a e la terza per a e quindi sottraiamole: l equazione che così si ottiene è anch essa priva del termine in x. Con queste due operazioni abbiamo trasformato il sistema in un altro equivalente nel quale la seconda e la terza equazione non contengono l incognita x : a x + a 2 x 2 + a x = b a 22 x 2 + a 2 x = b 2 a 2 x 2 + a x = b A questo punto moltiplichiamo la seconda equazione per a 2 e la terza equazione per a 22 e sottraiamole: l equazione che così si ottiene non ha più neanche l incognita x 2 : si tratta di un equazione nella sola incognita x. A questo punto il sistema si presenta nella forma detta a matrice triangolare superiore: a x + a 2 x 2 + a x = b a 22 x 2 + a 2 x = b 2 a x = b Dalla terza equazione, almeno se a 0 è possibile ricavare x = b a. Se ne sostituisce il valore nella seconda e da essa, almeno se a 22 0, si ricava x 2. Trovate x 2 e x, si sostituiranno nella prima equazione dalla quale, almeno se a 0, si ricava x.
11 Il metodo di Gauss consente quindi di formulare il seguente teorema: Teorema. Ogni sistema di n equazioni con n incognite, con matrice dei coefficienti a determinante diverso da 0, può essere trasformato in un sistema a matrice triangolare superiore. ESEMPIO 5. Risolviamo il seguente sistema col metodo della triangolazione: x + x 2 + x = x 2x 2 + 4x = 2x x 2 x = 4 Moltiplichiamo la prima riga per e sottraiamola dalla seconda. Otteniamo x 2 + x = 2. Analogamente moltiplichiamo la prima equazione per 2 e sottraiamola dalla terza, e otteniamo x 2 5x = 2 Il sistema risulta così trasformato nel sistema equivalente: x + x 2 + x = x 2 + x = 2 x 2 5x = 2 Moltiplichiamo ora la seconda equazione per e la terza per e sottraiamo membro a membro ottenendo: 62x = 62 Quindi il sistema può riscriversi in forma triangolare superiore in questo modo: x + x 2 + x = x 2 + x = 2 x = Da cui risalendo e sostituendo via via a catena, si ottiene x 2 = e x =. Provate ora a risolvere lo stesso sistema col metodo di Cramer. Quale ritenete sia il metodo più conveniente?
Argomento 13 Sistemi lineari
 Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Note sull algoritmo di Gauss
 Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
SISTEMI LINEARI. x y + 2t = 0 2x + y + z t = 0 x z t = 0 ; S 3 : ; S 5x 2y z = 1 4x 7y = 3
 SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito B 3/05/005 A. A. 004 005 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito B 3/05/005 A. A. 004 005 ) Risolvere il seguente sistema
I sistemi lineari di n equazioni in n incognite
 I sistemi lineari I sistemi lineari di n equazioni in n incognite I sistemi lineari di n equazioni in n incognite, sono formati da equazioni di primo grado, in cui le incognite hanno tutte esponente uguale
I sistemi lineari I sistemi lineari di n equazioni in n incognite I sistemi lineari di n equazioni in n incognite, sono formati da equazioni di primo grado, in cui le incognite hanno tutte esponente uguale
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
Note per il corso di Geometria Corso di laurea in Ing. Edile/Architettura. 4 Sistemi lineari. Metodo di eliminazione di Gauss Jordan
 Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
Sistemi di equazioni lineari
 Sistemi di equazioni lineari Siano X 1,, X n indeterminate Un equazione lineare (o di primo grado) nelle incognite X 1,, X n a coefficienti nel campo K è della forma a 1 X 1 + + a n X n = b, a i, b K,
Sistemi di equazioni lineari Siano X 1,, X n indeterminate Un equazione lineare (o di primo grado) nelle incognite X 1,, X n a coefficienti nel campo K è della forma a 1 X 1 + + a n X n = b, a i, b K,
A titolo di esempio proponiamo la risoluzione del sistema sia con il metodo della matrice inversa sia con il metodo di Cramer.
 ) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Sistemi Lineari. Elisabetta Colombo. Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 200-20 2 a di o.0 4 Capelli Rango o Caratterisca : definizioni a di o.0 Un equazione nelle n incognite x,..., x n della forma dove
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 200-20 2 a di o.0 4 Capelli Rango o Caratterisca : definizioni a di o.0 Un equazione nelle n incognite x,..., x n della forma dove
SISTEMI LINEARI, METODO DI GAUSS
 SISTEMI LINEARI, METODO DI GAUSS Abbiamo visto che un sistema di m equazioni lineari in n incognite si può rappresentare in forma matriciale come A x = b dove: A è la matrice di tipo (m, n) dei coefficienti
SISTEMI LINEARI, METODO DI GAUSS Abbiamo visto che un sistema di m equazioni lineari in n incognite si può rappresentare in forma matriciale come A x = b dove: A è la matrice di tipo (m, n) dei coefficienti
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016.
 Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
Registro Lezioni di Algebra lineare del 15 e 16 novembre 2016 Di seguito si riporta il riassunto degli argomenti svolti; i riferimenti sono a parti del Cap8 Elementi di geometria e algebra lineare Par5
ALGEBRA LINEARE PARTE III
 DIEM sez Matematica Finanziaria Università degli studi di Genova Dicembre 200 Indice PREMESSA 2 GENERALITA 2 RAPPRESENTAZIONE DI UN SISTEMA LINEARE IN FORMA MATRI- CIALE 2 3 SOLUZIONE DI SISTEMI LINEARI
DIEM sez Matematica Finanziaria Università degli studi di Genova Dicembre 200 Indice PREMESSA 2 GENERALITA 2 RAPPRESENTAZIONE DI UN SISTEMA LINEARE IN FORMA MATRI- CIALE 2 3 SOLUZIONE DI SISTEMI LINEARI
Sistemi lineari. a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2 : : : a m1 x 1 + a m2 x 2 +..
 Sistemi lineari: definizioni Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto termine
Sistemi lineari: definizioni Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto termine
Sistemi lineari. a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2 : : : a m1 x 1 + a m2 x 2 +..
 Sistemi lineari: definizioni Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto termine
Sistemi lineari: definizioni Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto termine
Esercizi sui sistemi di equazioni lineari.
 Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
1. Sistemi di equazioni lineari. 1.1 Considerazioni preliminari
 1. Sistemi di equazioni lineari 1.1 Considerazioni preliminari I sistemi lineari sono sistemi di equazioni di primo grado in più incognite. Molti problemi di matematica e fisica portano alla soluzione
1. Sistemi di equazioni lineari 1.1 Considerazioni preliminari I sistemi lineari sono sistemi di equazioni di primo grado in più incognite. Molti problemi di matematica e fisica portano alla soluzione
Introduzione soft alla matematica per l economia e la finanza. Marta Cardin, Paola Ferretti, Stefania Funari
 Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
Introduzione soft alla matematica per l economia e la finanza Marta Cardin, Paola Ferretti, Stefania Funari Capitolo Sistemi di equazioni lineari.8 Il Teorema di Cramer Si consideri un generico sistema
Applicazioni eliminazione di Gauss
 Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI
 SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
Federica Gregorio e Cristian Tacelli
 1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
3x 2 = 6. 3x 2 x 3 = 6
 Facoltà di Scienze Statistiche, Algebra Lineare 1 A, GParmeggiani LEZIONE 7 Sistemi lineari Scrittura matriciale di un sistema lineare Def 1 Un sistema di m equazioni ed n incognite x 1, x 2, x n, si dice
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, GParmeggiani LEZIONE 7 Sistemi lineari Scrittura matriciale di un sistema lineare Def 1 Un sistema di m equazioni ed n incognite x 1, x 2, x n, si dice
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari
 Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
MATEMATICA. a.a. 2014/ Sistemi di equazioni lineari
 MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
MATEMATICA a.a. 2014/15 8. Sistemi di equazioni lineari SISTEMI LINEARI Si definisce sistema lineare un sistema di p equazioni di primo grado in q incognite. a11x1 + a12 x2 +... + a1 qxq = k1 a21x1 + a22x2
Istituzioni di Matematiche sesta parte
 Istituzioni di Matematiche sesta parte anno acc. 2013/2014 Univ. Studi di Milano D.Bambusi, C.Turrini (Univ. Studi di Milano Istituzioni di Matematiche 1 / 27 index Matrici e operazioni tra matrici 1 Matrici
Istituzioni di Matematiche sesta parte anno acc. 2013/2014 Univ. Studi di Milano D.Bambusi, C.Turrini (Univ. Studi di Milano Istituzioni di Matematiche 1 / 27 index Matrici e operazioni tra matrici 1 Matrici
LEZIONE 2. ( ) a 1 x 1 + a 2 x a n x n = b, ove a j, b R sono fissati.
 LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
Il teorema di Rouché-Capelli
 Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite
 3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
3 Sistemi lineari 3 Generalità Si consideri il sistema a coefficienti reali di m equazioni lineari in n incognite ovvero, in forma matriciale, a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n x
MATRICI E SISTEMI LINEARI
 1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
Istituzioni di Matematiche prima parte
 Istituzioni di Matematiche prima parte anno acc. 2014/2015 Univ. Studi di Milano E.Frigerio, C.Turrini (Univ. Studi di Milano Istituzioni di Matematiche 1 / 30 index Generalità sugli insiemi 1 Generalità
Istituzioni di Matematiche prima parte anno acc. 2014/2015 Univ. Studi di Milano E.Frigerio, C.Turrini (Univ. Studi di Milano Istituzioni di Matematiche 1 / 30 index Generalità sugli insiemi 1 Generalità
Esercitazione 6 - Soluzione
 Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
il determinante che si ottiene da A, sopprimendo la i - esima riga e la j - esima colonna. Si definisce complemento algebrico dell'elemento a ij
 Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Istituzioni di Matematiche prima parte
 Istituzioni di Matematiche prima parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano Istituzioni di Matematiche 1 / 33 index Generalità sugli insiemi 1 Generalità
Istituzioni di Matematiche prima parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano Istituzioni di Matematiche 1 / 33 index Generalità sugli insiemi 1 Generalità
Sistemi II. Sistemi II. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Sistemi di equazioni lineari
 Sistemi di equazioni lineari A. Bertapelle 25 ottobre 212 Cos è un sistema lineare? Definizione Un sistema di m equazioni lineari (o brevemente sistema lineare) nelle n incognite x 1,..., x n, a coefficienti
Sistemi di equazioni lineari A. Bertapelle 25 ottobre 212 Cos è un sistema lineare? Definizione Un sistema di m equazioni lineari (o brevemente sistema lineare) nelle n incognite x 1,..., x n, a coefficienti
Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe.
![Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe. Matrici triangolari [Abate, 3.2] Lezioni 05 e 06. Determinante di una matrice triangolare [Abate, es. 9.3] Matrici ridotte per righe.](/thumbs/100/147138366.jpg) Matrici triangolari [Abate, 32] Definizione Una matrice A = a ij ) R m,n si dice triangolare superiore se a ij = 0 per ogni i > j; triangolare inferiore se a ij = 0 per ogni i < j Lezioni 05 e 06 Una matrice
Matrici triangolari [Abate, 32] Definizione Una matrice A = a ij ) R m,n si dice triangolare superiore se a ij = 0 per ogni i > j; triangolare inferiore se a ij = 0 per ogni i < j Lezioni 05 e 06 Una matrice
Geometria BIAR Esercizi 2
 Geometria BIAR 0- Esercizi Esercizio. a Si consideri il generico vettore v b R c (a) Si trovi un vettore riga x (x, y, z) tale che x v a (b) Si trovi un vettore riga x (x, y, z) tale che x v kb (c) Si
Geometria BIAR 0- Esercizi Esercizio. a Si consideri il generico vettore v b R c (a) Si trovi un vettore riga x (x, y, z) tale che x v a (b) Si trovi un vettore riga x (x, y, z) tale che x v kb (c) Si
La riduzione a gradini e i sistemi lineari (senza il concetto di rango)
 CAPITOLO 4 La riduzione a gradini e i sistemi lineari (senza il concetto di rango) Esercizio 4.1. Risolvere il seguente sistema non omogeneo: 2x+4y +4z = 4 x z = 1 x+3y +4z = 3 Esercizio 4.2. Risolvere
CAPITOLO 4 La riduzione a gradini e i sistemi lineari (senza il concetto di rango) Esercizio 4.1. Risolvere il seguente sistema non omogeneo: 2x+4y +4z = 4 x z = 1 x+3y +4z = 3 Esercizio 4.2. Risolvere
0.1 Complemento diretto
 1 0.1 Complemento diretto Dato U V, un complemento diretto di U é un sottospazio W V tale che U W = {0} U + W = V cioé la somma di U con il suo complemento diretto é diretta, e dá tutto lo spazio vettoriale
1 0.1 Complemento diretto Dato U V, un complemento diretto di U é un sottospazio W V tale che U W = {0} U + W = V cioé la somma di U con il suo complemento diretto é diretta, e dá tutto lo spazio vettoriale
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 3. Sistemi di equazioni lineari
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Esercizi svolti. risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale
 Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Rango di una matrice e teorema di Rouché-Capelli
 Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
SISTEMI LINEARI MATRICI E SISTEMI 1
 MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
Corso di Geometria BIAR, BSIR Esercizi 3: soluzioni
 Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Rango e teorema di Rouché-Capelli Esercizio. Calcolare il rango di ciascuna delle seguenti matrici: ( ) ( ) ( ) A =, A =, A =, A 4 = ( ). a a a Soluzione.
Corso di Geometria - BIAR, BSIR Esercizi : soluzioni Rango e teorema di Rouché-Capelli Esercizio. Calcolare il rango di ciascuna delle seguenti matrici: ( ) ( ) ( ) A =, A =, A =, A 4 = ( ). a a a Soluzione.
2x 5y +4z = 3 x 2y + z =5 x 4y +6z = A =
 Esercizio 1. Risolvere il sistema lineare 2x 5y +4z = x 2y + z =5 x 4y +6z =10 (1) Soluz. La matrice dei coefficienti è 1 4 6, calcoliamone il rango. Il determinante di A è (applico la regola di Sarrus):
Esercizio 1. Risolvere il sistema lineare 2x 5y +4z = x 2y + z =5 x 4y +6z =10 (1) Soluz. La matrice dei coefficienti è 1 4 6, calcoliamone il rango. Il determinante di A è (applico la regola di Sarrus):
Equazioni di primo grado
 Equazioni di primo grado 15 15.1 Identità ed equazioni Analizziamo le seguenti proposizioni: a ) cinque è uguale alla differenza tra sette e due ; b ) la somma di quattro e due è uguale a otto ; c ) il
Equazioni di primo grado 15 15.1 Identità ed equazioni Analizziamo le seguenti proposizioni: a ) cinque è uguale alla differenza tra sette e due ; b ) la somma di quattro e due è uguale a otto ; c ) il
CORSI DI LAUREA IN MATEMATICA E FISICA. Esercizio 1.1. Risolvere graficamente e algebricamente i seguenti sistemi di due equazioni in due incognite:
 CORS D LAUREA N MATEMATCA E FSCA FOGLO D ESERCZ # 1 GEOMETRA 1 Esercizio 1.1. Risolvere graficamente e algebricamente i seguenti sistemi di due equazioni in due incognite: 2x + y = 4 x 2y = 6 x + 3y =
CORS D LAUREA N MATEMATCA E FSCA FOGLO D ESERCZ # 1 GEOMETRA 1 Esercizio 1.1. Risolvere graficamente e algebricamente i seguenti sistemi di due equazioni in due incognite: 2x + y = 4 x 2y = 6 x + 3y =
LEZIONE 3. a + b + 2c + e = 1 b + d + g = 0 3b + f + 3g = 2. a b c d e f g
 LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
LE EQUAZIONI LINEARI LE IDENTITA ( )( ) 5. a Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a
 LE EQUAZIONI LINEARI 1 LE IDENTITA a b = ( a + b)( a b) () 1 a = a + a ( ) ( a + b) = a + ab + b () 3 Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a b = ( a+ b)( a b) È sempre vera qualunque
LE EQUAZIONI LINEARI 1 LE IDENTITA a b = ( a + b)( a b) () 1 a = a + a ( ) ( a + b) = a + ab + b () 3 Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a b = ( a+ b)( a b) È sempre vera qualunque
Corso di Geometria BIAR, BSIR Esercizi 2: soluzioni
 Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
CORSI DI LAUREA IN MATEMATICA E FISICA
 CORSI DI LAUREA IN MATEMATICA E FISICA FOGLIO DI ESERCIZI # 6 GEOMETRIA 1 Esercizio 6.1 (Esercizio 5.1). Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Per esempio il vettore
CORSI DI LAUREA IN MATEMATICA E FISICA FOGLIO DI ESERCIZI # 6 GEOMETRIA 1 Esercizio 6.1 (Esercizio 5.1). Scrivere un vettore w R 3 linearmente dipendente dal vettore v ( 1, 9, 0). Per esempio il vettore
Geometria BAER PRIMO CANALE Foglio esercizi 1
 Geometria BAER PRIMO CANALE Foglio esercizi 1 Esercizio 1. Risolvere le seguenti equazioni lineari nelle variabili indicate trovando una parametrizzazione dell insieme delle soluzioni. a) x + 5y = nelle
Geometria BAER PRIMO CANALE Foglio esercizi 1 Esercizio 1. Risolvere le seguenti equazioni lineari nelle variabili indicate trovando una parametrizzazione dell insieme delle soluzioni. a) x + 5y = nelle
A =, c d. d = ad cb. c d A =
 Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Dipendenza e indipendenza lineare
 Dipendenza e indipendenza lineare Luciano Battaia Questi appunti () ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia campus
Dipendenza e indipendenza lineare Luciano Battaia Questi appunti () ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia campus
0.1 Soluzioni esercitazione IV, del 28/10/2008
 1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
VETTORI E MATRICI. Ing. Nicola Cappuccio 2014 U.F.5 ELEMENTI SCIENTIFICI ED ELETTRONICI APPLICATI AI SISTEMI DI TELECOMUNICAZIONI
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
Sistemi lineari 1 / 12
 Sistemi lineari 1 / 12 Sistemi lineari 2 / 12 Ricordiamo che cosa è un sistema lineare con m equazioni in n incognite (m,n N, m,n 1): a 11 x 1 + +a 1n x n = b 1 a 21 x 1 + +a 2n x n = b 2, (1).. a m1 x
Sistemi lineari 1 / 12 Sistemi lineari 2 / 12 Ricordiamo che cosa è un sistema lineare con m equazioni in n incognite (m,n N, m,n 1): a 11 x 1 + +a 1n x n = b 1 a 21 x 1 + +a 2n x n = b 2, (1).. a m1 x
( 5) 2 = = = +1
 1 IDENTITA ED EQUAZIONI Consideriamo la seguente uguaglianza: ( 2x + 3) 2 = 4x 2 +12x + 9 Diamo alcuni valori arbitrari all incognita x e vediamo se l uguaglianza risulta vera. Per x = 1 si avrà: ( 2 1+
1 IDENTITA ED EQUAZIONI Consideriamo la seguente uguaglianza: ( 2x + 3) 2 = 4x 2 +12x + 9 Diamo alcuni valori arbitrari all incognita x e vediamo se l uguaglianza risulta vera. Per x = 1 si avrà: ( 2 1+
Equivalentemente, le colonne di A sono linearmente indipendenti se e solo se
 Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta. Metodi per il calcolo del rango di una matrice
 Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta Versione del 21/12/07 Metodi per il calcolo del rango di una matrice Sia A M m,n (K). Denotiamo con A (i) la riga i-ma di A, i {1,..., m}.
Note per le esercitazioni di Geometria 1 a.a. 2007/08 A. Lotta Versione del 21/12/07 Metodi per il calcolo del rango di una matrice Sia A M m,n (K). Denotiamo con A (i) la riga i-ma di A, i {1,..., m}.
r 2 r 2 2r 1 r 4 r 4 r 1
 SPAZI R n 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x, y, z)
SPAZI R n 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x, y, z)
1 1, { x1 2x 2 + x 3 = 0 2x 2 8x 3 = 1 x 1 x 4 = = 0
 a.a. 5-6 Esercizi. Sistemi lineari. Soluzioni.. Determinare quali delle quaterne, 3,, sono soluzioni del sistema di tre equazioni in 4 incognite { x x + x 3 = x 8x 3 = x x 4 =. Sol. Sostituendo ad x, x,
a.a. 5-6 Esercizi. Sistemi lineari. Soluzioni.. Determinare quali delle quaterne, 3,, sono soluzioni del sistema di tre equazioni in 4 incognite { x x + x 3 = x 8x 3 = x x 4 =. Sol. Sostituendo ad x, x,
Esercizi Di Geometria 1 (BAER) Canale 1 Da consegnare Lunedi 26 Ottobre
 Esercizi Di Geometria 1 (BAER) Canale 1 Da consegnare Lunedi 26 Ottobre SETTIMANA 4 (19 25 Ottobre) Matrici elementari Gli esercizi sono presi dal libro Intorduction to Linear Algebra di Serge Lang. Esercizio
Esercizi Di Geometria 1 (BAER) Canale 1 Da consegnare Lunedi 26 Ottobre SETTIMANA 4 (19 25 Ottobre) Matrici elementari Gli esercizi sono presi dal libro Intorduction to Linear Algebra di Serge Lang. Esercizio
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Esempio Date a = (1, 2, 3) e b = (4, 5, 6), calcolare. 2(a + b) 3(2a b).
 Matematica II, 26.02.04 Passiamo ora a considerare l insieme R 3 = {(x, x 2, x 3 ); x, x 2, x 3 R}, costituito dalle terne ordinate di numeri reali. Ciascuna terna puo essere pensata come un unica entita,
Matematica II, 26.02.04 Passiamo ora a considerare l insieme R 3 = {(x, x 2, x 3 ); x, x 2, x 3 R}, costituito dalle terne ordinate di numeri reali. Ciascuna terna puo essere pensata come un unica entita,
Istituzioni di Matematica I. Esercizi su sistemi lineari. & % x + y " #z = "1 & '#x " y+ z =1
 Istituzioni di Matematica I Esercizi su sistemi lineari Esempio. Dire per quali valori di λ R il sistema x " y+ z = 2 % x + y " z = " x " y+ z = ha una sola soluzione, per quali nessuna, per quali infinite
Istituzioni di Matematica I Esercizi su sistemi lineari Esempio. Dire per quali valori di λ R il sistema x " y+ z = 2 % x + y " z = " x " y+ z = ha una sola soluzione, per quali nessuna, per quali infinite
Corso di Matematica e Statistica 3 Algebra delle matrici. Una tabella rettangolare: la matrice. Una tabella rettangolare: la matrice
 Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
Sistemi lineari - Parte Seconda - Esercizi
 Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
Riassumiamo le proprietà dei numeri reali da noi utilizzate nel corso di Geometria.
 Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
Capitolo 2 Campi 2.1 Introduzione Studiamo ora i campi. Essi sono una generalizzazione dell insieme R dei numeri reali con le operazioni di addizione e di moltiplicazione. Nel secondo paragrafo ricordiamo
SISTEMI DI DUE EQUAZIONI IN DUE INCOGNITE
 SISTEMI DI DUE EQUAZIONI IN DUE INCOGNITE Un equazione di primo grado in una incognita del tipo, con ha: una sola soluzione (equazione determinata) se nessuna soluzione (equazione impossibile) se tutte
SISTEMI DI DUE EQUAZIONI IN DUE INCOGNITE Un equazione di primo grado in una incognita del tipo, con ha: una sola soluzione (equazione determinata) se nessuna soluzione (equazione impossibile) se tutte
Sistemi di equazioni lineari
 Sistemi di equazioni lineari I sistemi di equazioni si incontrano in natura in molti problemi di vita reale. Per esempio, prendiamo in considerazione una bevanda a base di uova, latte e succo d arancia.
Sistemi di equazioni lineari I sistemi di equazioni si incontrano in natura in molti problemi di vita reale. Per esempio, prendiamo in considerazione una bevanda a base di uova, latte e succo d arancia.
Operazioni tra matrici e n-uple
 CAPITOLO Operazioni tra matrici e n-uple Esercizio.. Date le matrici 0 4 e dati λ = 5, µ =, si calcoli AB, BA, A+B, B A, λa+µb. Esercizio.. Per ognuna delle seguenti coppie di matrici A, B e scalari λ,
CAPITOLO Operazioni tra matrici e n-uple Esercizio.. Date le matrici 0 4 e dati λ = 5, µ =, si calcoli AB, BA, A+B, B A, λa+µb. Esercizio.. Per ognuna delle seguenti coppie di matrici A, B e scalari λ,
Argomento 13 Sistemi lineari
 Sistemi lineari: definizioni Argomento 3 Sistemi lineari I Un equazione nelle n incognite x,,x n della forma c x + + c n x n = b ove c,,c n sono numeri reali (detti coefficienti) eb è un numero reale (detto
Sistemi lineari: definizioni Argomento 3 Sistemi lineari I Un equazione nelle n incognite x,,x n della forma c x + + c n x n = b ove c,,c n sono numeri reali (detti coefficienti) eb è un numero reale (detto
Appunti su Indipendenza Lineare di Vettori
 Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Appunti su Indipendenza Lineare di Vettori Claudia Fassino a.a. Queste dispense, relative a una parte del corso di Matematica Computazionale (Laurea in Informatica), rappresentano solo un aiuto per lo
Definizione: Due equazioni si dicono equivalenti se ammettono le stesse soluzioni.
 Facoltà di Medicina e Chirurgia Corso Zero di Matematica Gruppi: MC-MF3 / PS-MF3 II Lezione EQUAZIONI E SISTEMI Dr. E. Modica erasmo@galois.it www.galois.it IDENTITÀ ED EQUAZIONI Si consideri un uguaglianza
Facoltà di Medicina e Chirurgia Corso Zero di Matematica Gruppi: MC-MF3 / PS-MF3 II Lezione EQUAZIONI E SISTEMI Dr. E. Modica erasmo@galois.it www.galois.it IDENTITÀ ED EQUAZIONI Si consideri un uguaglianza
a + 2b + c 3d = 0, a + c d = 0 c d
 SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
Matematica per Chimica, Chimica Industriale e Scienze dei Materiali Primo appello 7/02/2012 Tema A
 Matematica per Chimica, Chimica Industriale e Scienze dei Materiali Primo appello 7/02/202 Tema A NOME:..................................................... COGNOME:.....................................................
Matematica per Chimica, Chimica Industriale e Scienze dei Materiali Primo appello 7/02/202 Tema A NOME:..................................................... COGNOME:.....................................................
AUTOVALORI, AUTOVETTORI, AUTOSPAZI
 AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
Corso introduttivo pluridisciplinare Matrici e sistemi lineari
 Corso introduttivo pluridisciplinare Matrici e sistemi lineari anno acc. 2013/2014 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano Corso introduttivo pluridisciplinare 1 / 30
Corso introduttivo pluridisciplinare Matrici e sistemi lineari anno acc. 2013/2014 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano Corso introduttivo pluridisciplinare 1 / 30
Lezioni di Algebra Lineare. II. Aritmetica delle matrici e eliminazione di Gauss. versione ottobre 2008
 versione ottobre 2008 Lezioni di Algebra Lineare II. Aritmetica delle matrici e eliminazione di Gauss Contenuto. 1. Somma di matrici e prodotto di una matrice per uno scalare 2. Prodotto di matrici righe
versione ottobre 2008 Lezioni di Algebra Lineare II. Aritmetica delle matrici e eliminazione di Gauss Contenuto. 1. Somma di matrici e prodotto di una matrice per uno scalare 2. Prodotto di matrici righe
Inversa. Inversa. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 00-0, http://users.mat.unimi.it/users/colombo/programmabio.html e 3 con i Matrici inverse di matrici quadrate e con i Sia A una
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 00-0, http://users.mat.unimi.it/users/colombo/programmabio.html e 3 con i Matrici inverse di matrici quadrate e con i Sia A una
Soluzioni del Foglio 2 I sistemi lineari
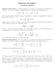 Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
Compito di MD 13 febbraio 2014
 Compito di MD 13 febbraio 2014 IMPORTANTE: Non si possono consultare libri e appunti. Non si possono usare calcolatrici, computer o altri dispositivi elettronici. Non si può scrivere con il lapis. Motivare
Compito di MD 13 febbraio 2014 IMPORTANTE: Non si possono consultare libri e appunti. Non si possono usare calcolatrici, computer o altri dispositivi elettronici. Non si può scrivere con il lapis. Motivare
Le matrici. A cura di Benedetta Noris, 17 aprile Cos è una matrice. 2 Rappresentazione di una matrice generica 2
 Le matrici A cura di Benedetta Noris, 17 aprile 2012 benedetta.noris1@unimib.it Indice 1 Cos è una matrice 1 2 Rappresentazione di una matrice generica 2 3 Somma di matrici e prodotto di una matrice per
Le matrici A cura di Benedetta Noris, 17 aprile 2012 benedetta.noris1@unimib.it Indice 1 Cos è una matrice 1 2 Rappresentazione di una matrice generica 2 3 Somma di matrici e prodotto di una matrice per
ESERCIZI SULLE MATRICI
 ESERCIZI SULLE MATRICI Consideriamo il sistema lineare a, x + a, x + + a,n x n = b a, x + a, x + + a,n x n = b a m, x + a m, x + + a m,n x n = b m di m equazioni in n incognite che ha a, a,n A = a m, a
ESERCIZI SULLE MATRICI Consideriamo il sistema lineare a, x + a, x + + a,n x n = b a, x + a, x + + a,n x n = b a m, x + a m, x + + a m,n x n = b m di m equazioni in n incognite che ha a, a,n A = a m, a
Risoluzione di sistemi lineari
 Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
Capitolo VI SISTEMI LINEARI
 Capitolo VI SISTEMI LINEARI 1 Concetti fondamentali 11 Definizione Un equazione in n incognite x 1,, x n a coefficienti in R si dice lineare se è della forma: a 1 x 1 + + a n x n = b con a i R e b R Una
Capitolo VI SISTEMI LINEARI 1 Concetti fondamentali 11 Definizione Un equazione in n incognite x 1,, x n a coefficienti in R si dice lineare se è della forma: a 1 x 1 + + a n x n = b con a i R e b R Una
Esercitazione di Calcolo Numerico 1 22 Aprile Determinare la fattorizzazione LU della matrice a 1 1 A = 3a 2 a 2a a a 2 A =
 Esercitazione di Calcolo Numerico 22 Aprile 29. Determinare la fattorizzazione LU della matrice a A = 3a 2 a 2a a a 2 ed utilizzarla per calcolare il det(a). 2. Calcolare il determinante della matrice
Esercitazione di Calcolo Numerico 22 Aprile 29. Determinare la fattorizzazione LU della matrice a A = 3a 2 a 2a a a 2 ed utilizzarla per calcolare il det(a). 2. Calcolare il determinante della matrice
PreCorso di Matematica - PCM Corso M-Z
 PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
ESERCIZI PROPOSTI. det A = = per cui il sistema si può risolvere applicando le formule di Cramer, cioè: dove: = =
 ESERCIZI PROPOSTI Risolvere i seguenti sistemi lineari )-0), utilizzando, dove possibile, sia il metodo di Cramer sia quello della matrice inversa, dopo aver analizzato gli esempi a)-d): 2x + + 4z 5 a)
ESERCIZI PROPOSTI Risolvere i seguenti sistemi lineari )-0), utilizzando, dove possibile, sia il metodo di Cramer sia quello della matrice inversa, dopo aver analizzato gli esempi a)-d): 2x + + 4z 5 a)
Tempo a disposizione. 90 minuti. 1 [6 punti] Dimostrare che, per ogni n N, n 1, vale la disuguaglianza:
![Tempo a disposizione. 90 minuti. 1 [6 punti] Dimostrare che, per ogni n N, n 1, vale la disuguaglianza: Tempo a disposizione. 90 minuti. 1 [6 punti] Dimostrare che, per ogni n N, n 1, vale la disuguaglianza:](/thumbs/72/66437341.jpg) Dipartimento di Matematica e Informatica Anno Accademico 05-06 Corso di Laurea in Informatica (L-) Prova in itinere di Matematica Discreta ( CFU) Febbraio 06 A Tempo a disposizione. 90 minuti [6 punti]
Dipartimento di Matematica e Informatica Anno Accademico 05-06 Corso di Laurea in Informatica (L-) Prova in itinere di Matematica Discreta ( CFU) Febbraio 06 A Tempo a disposizione. 90 minuti [6 punti]
