I.S.I.S.S. A. Giordano Venafro (IS) Appunti di Fisica n. 3
|
|
|
- Roberta Lombardo
- 5 anni fa
- Visualizzazioni
Transcript
1 I.S.I.S.S. A. Giordano Venafro (IS) 1 Fenomeni Magnetici prof. Valerio D Andrea VB ST - A.S. 2017/2018 Appunti di Fisica n. 3 In natura esiste un minerale che è in grado di attirare oggetti di ferro: la magnetite, un magnete naturale. Alcuni oggetti (es. ferro, nichel) a contatto con la magnetite vengono magnetizzati, cioé acquisiscono le stesse proprietà di un magnete (si chiamano ferromagnetici). Ogni magnete ha un polo nord e un polo sud, poli dello stesso tipo si attraggono, poli opposti si respingono. Se dividiamo un magnete in 2 ciascuno dei frammenti ha un polo nord e un polo sud: non posso avere un polo magnetico separato. La Terra è un magnete, i poli magnetici si trovano nelle regioni vicino i poli geografici opposti. 1.1 Campo Magnetico Ogni magnete genera nello spazio circostante un campo magnetico B (campo vettoriale). L unità di misura di B è il Tesla: 1 T=1 N/(1 A 1 m). Il campo prodotto da un magnete a barra è analogo al campo elettrico prodotto da un dipolo elettrico. Anche per B si definiscono le linee di campo: sono in ogni punto tangenti al campo magnetico B; escono dal polo nord ed entrano nel polo sud; hanno densità proporzionale all intensità del campo. 1.2 Forza tra Magneti e Correnti Oersted nel 1820 scoprì che un filo percorso da corrente genera un campo magnetico con le seguenti proprietà: le linee di campo sono circonferenze concentriche con il filo; il verso del campo si ottiene puntando il pollice nel verso della corrente, le altre dita si chiudono nel verso del campo. Nel 1821 Faraday osservò che un filo percorso da corrente subisce una forza se immerso in un campo magnetico. Questa forza è: sempre perpendicolare al piano formato da corrente e campo B; il verso è dato dalla regola della mano destra con pollice nel verso della corrente e indice nel verso di B. 1
2 1.3 Legge di Ampère Dopo le esperienze di Oersted e Faraday, Ampère verificò sperimentalmente che 2 fili percorsi da correnti esercitano una forza tra di loro, i fili si attraggono se la corrente ha lo stesso verso, si respingono se le correnti sono in verso opposto. La legge di Ampère afferma che questa forza tra fili rettilinei e paralleli è direttamente proporzionale alle correnti i 1 e i 2 e alla lunghezza l dei fili e inversamente proporzionale alla distanza d tra essi: F = µ 0 i 1 i 2 2π d l (1) dove µ 0 è la permeabilità magnetica del vuoto, costante che ha un valore fissato di: µ 0 = 4π 10 7 N/A 2 (2) questa valore è stato scelto per definire in modo operativo l Ampère: una corrente di 1 A che attraversa 2 fili, distanti 1 m, produce su ogni metro di lunghezza una forza: F = µ 0 i 1 i 2 2π d l = 4π 10 7 N/A 2 (1 A)(1 A) 2π 1 m 1 m = N. (3) 1.4 Forza Magnetica su un Filo percorso da Corrente Sperimentalmente si osserva che la forza che subisce un filo percorso da corrente è massima quando esso è disposto perpendicolarmente alle linee del campo B, mentre la forza è nulla se è parallelo. In generale questa forza si può scrivere: F = i l B (4) dove l è un vettore con modulo pari alla lunghezza e che segue il verso della corrente; il modulo della forza è: F = Bil sin α (5) dove α è l angolo compreso tra i vettori l e B. 1.5 Legge di Biot-Savart Consideriamo 2 fili rettilinei e paralleli percorsi da corrente i e i 1, sappiamo che il campo B prodotto da essi è perpendicolare ai fili, quindi uno dei fili genera sull altro una forza pari a (usiamo Eq. (4)): F = Bi 1 l. (6) La legge di Ampère Eq. (1) afferma che il modulo di questa forza è: F = µ 0 ii 1 2π d l (7) e eguagliando le 2 espressioni si può ricavare l espressione per il campo magnetico prodotto da un filo rettilineo: B = µ 0 i (8) 2π d questa è la legge di Biot-Savart, trovata sperimentalmente dai 2 fisici francesi nel
3 1.6 Campo Magnetico di una Spira e di un Solenoide Usando la legge di Biot-Savart si può trovare il campo magnetico di una spira circolare percorsa da corrente, in particolare sull asse della spira dove il campo è perpendicolare ad essa. Al centro della spira il campo magnetico è: B = µ 0 i (9) 2 R dove R è il raggio della spira; su un punto dell asse distante x dal centro della spira il campo è: B = µ 0 2 ir 2 (R2 + x 2 ) 3. (10) Un filo conduttore avvolto a elica è detto solenoide. Un solenoide molto lungo percorso da corrente produce un campo magnetico parallelo e uniforme all interno, praticamente nullo all esterno. Se N è il numero di spire e l è la lunghezza del solenoide, il campo all interno è dato dalla formula: Ni B = µ 0 (11) l 2 Forza di Lorentz Correnti elettriche sono soggette a forza magnetica, di conseguenza anche cariche elettriche in movimento se immerse in un campo magnetico B risentono della forza di Lorentz: F = q v B (12) dove v è la velocità della carica elettrica. Come nel caso dell Eq. (4), la forza è nulla se il moto è parallelo a B, è massimo se sono perpendicolari ed in generale il modulo della forza è: F = qvb sin α (13) dove α è l angolo compreso tra i vettori v e B. La direzione della forza è perpendicolare sia a v che B, mentre il verso è dato dalla regola della mano destra, applicata tenedo conto del segno della carica. 2.1 Moto di una Carica all interno di un Campo Magnetico Uniforme In generale la forza di Lorentz non può cambiare il modulo della velocità di una carica, modifica soltanto la sua direzione. Il caso può semplice è una carica che si muove perpendicolarmente ad un campo B uniforme. In questo caso il moto descritto dalla carica sarà un moto circolare uniforme con la forza di Lorentz che rappresenta la forza centripeta del moto: qvb = m v2 (14) r da questa equazione si puà ricavare il raggio del moto della carica nel campo magnetico: r = mv qb. (15) Velocità obliqua rispetto al campo B Se la velocità della carica ha una inclinazione qualsiasi rispetto alla direzione del campo B, si può studiare il moto scomponendo la velocità nella direzione perpendicolare e parallela a B: nella direzione parallela la forza di Lorentz è nulla, quindi si avrà un moto rettilineo uniforme; nella direzione perpendicolare la forza di Lorentz è F = qv B, si avrà un moto circolare. La combinazione dei 2 moti da origine ad una traiettoria ad elica cilindrica a passo costante, il raggio dell elica ha la stessa espressione di Eq. (15) sostituendo la velocità con v. 3
4 2.2 Effetto Hall Se poniamo una lamina conduttrice percorsa da corrente in un campo magnetico, le cariche inizieranno a muoversi a causa della forza di Lorentz. Se la corrente e il campo B sono perpendicolari, si crea una differenza di potenziale nella direzione trasversale, il cui segno dipende dai portatori di carica. Le cariche che vengono spostate creano un campo elettrico (con la relatica forza elettrica) che contrasta la forza di Lorentz. Ad un certo si crea una situazione di equilibrio: F E = F B qe = qvb (16) Se usiamo la relazione E = V H d (dove d è la larghezza della lamina), si può ricavare l espressione per la tensione di Hall V H : V H = dvb (17) quindi V H è direttamente proporzionale al campo magnetico. 3 Flusso del Campo Magnetico Si definisce il flusso del campo magnetico attraverso una superficie piana come: Φ S ( B) = B S = BS cos α (18) dove α è l angolo compreso tra B e S (nel caso di una superficie non piana devo fare una sommatoria dei flussi su ogni superficie piana). L unità di misura di Φ S ( B) è il Weber: Wb = T m 2. Il teorema di Gauss per il magnetismo afferma che il flusso del campo magnetico attraverso una superficie chiusa è uguale a zero: Φ Ω ( B) = 0. (19) Come abbiamo visto, il teorema di Gauss per il campo elettrico afferma invece che il flusso è proporzionale alla carica interna. L Eq. (19) esprime il fatto che non esistono cariche magnetiche isolate, per questo il Φ Ω ( B) è nullo (si può dimostrare il teorema nel caso del filo rettilineo). 4 Teorema di Ampère Si definisce la circuitazione del campo magnetico lungo una linea chiusa orientata con la somma dei prodotti scalari del campo per i vettori spostamento: Γ γ ( B) = i B i s i. (20) Il teorema di Ampère afferma che la circuitazione di B attraverso un qualunque cammino chiuso γ è proporzionale alla corrente concatenata con γ: Γ γ ( B) = µ 0 i con (21) risultato anche qui diverso dal campo elettrico dove la circuitazione è nulla. L Eq. (21) indica che il campo magnetico NON è conservativo. Per dimostrare il teorema di Ampère si considera il caso in cui il campo è prodotto da un filo rettilineo e γ è una circonferenza; usando la legge di Biot-Savart nell Eq. (20) e la lunghezza della circonferenza di ottiene l Eq. (21). 4
5 5 Proprietà Magnetiche dei Materiali In natura esistono 3 tipi di materiali con proprietà magnetiche diverse: materiali ferromagnetici (ferro, nichel cobalto), possono essere magnetizzate e sono fortemente attratti dai magneti; materiali paramagnetici, sono debolmente attratti dal campo magnetico; materiali diamagnetici, sono debolmente respinte dal campo magnetico. 5
IL CAMPO MAGNETICO FENOMENI MAGNETICI FONDAMENTALI CARATTERISTICHE DEL CAMPO MAGNETICO INDUZIONE ELETTROMAGNETICA
 IL CAMPO MAGNETICO FENOMENI MAGNETICI FONDAMENTALI CARATTERISTICHE DEL CAMPO MAGNETICO INDUZIONE ELETTROMAGNETICA MAGNETI E SOSTANZE FERROMAGNETICHE MAGNETI capaci di attirare oggetti di ferro naturali
IL CAMPO MAGNETICO FENOMENI MAGNETICI FONDAMENTALI CARATTERISTICHE DEL CAMPO MAGNETICO INDUZIONE ELETTROMAGNETICA MAGNETI E SOSTANZE FERROMAGNETICHE MAGNETI capaci di attirare oggetti di ferro naturali
Magnete. Campo magnetico. Fenomeni magnetici. Esempio. Esempio. Che cos è un magnete? FENOMENI MAGNETICI
 Magnete FENOMENI MAGNETICI Che cos è un magnete? Un magnete è un materiale in grado di attrarre pezzi di ferro Prof. Crosetto Silvio 2 Prof. Crosetto Silvio Quando si avvicina ad un pezzo di magnetite
Magnete FENOMENI MAGNETICI Che cos è un magnete? Un magnete è un materiale in grado di attrarre pezzi di ferro Prof. Crosetto Silvio 2 Prof. Crosetto Silvio Quando si avvicina ad un pezzo di magnetite
Elementi di Fisica 2CFU
 Elementi di Fisica 2CFU III parte - Elettromagnetismo Andrea Susa MAGNETISMO 1 Magnete Alcune sostanze naturali, come ad esempio la magnetite, hanno la proprietà di attirare pezzetti di ferro, e per questo
Elementi di Fisica 2CFU III parte - Elettromagnetismo Andrea Susa MAGNETISMO 1 Magnete Alcune sostanze naturali, come ad esempio la magnetite, hanno la proprietà di attirare pezzetti di ferro, e per questo
CAPITOLO 7 SORGENTI DEL CAMPO MAGNETICO LEGGE DI AMPERE PROPRIETÀ MAGNETICHE DELLA MATERIA
 CAPITOLO 7 SORGENTI DEL CAMPO MAGNETICO LEGGE DI AMPERE PROPRIETÀ MAGNETICHE DELLA MATERIA Elisabetta Bissaldi (Politecnico di Bari) - A.A. 2017-2018 2 Campo magnetico prodotto da una corrente Si consideri
CAPITOLO 7 SORGENTI DEL CAMPO MAGNETICO LEGGE DI AMPERE PROPRIETÀ MAGNETICHE DELLA MATERIA Elisabetta Bissaldi (Politecnico di Bari) - A.A. 2017-2018 2 Campo magnetico prodotto da una corrente Si consideri
Il campo magnetico. n I poli magnetici di nome contrario non possono essere separati: non esiste il monopolo magnetico
 Il campo magnetico n Le prime osservazioni dei fenomeni magnetici risalgono all antichità n Agli antichi greci era nota la proprietà della magnetite di attirare la limatura di ferro n Un ago magnetico
Il campo magnetico n Le prime osservazioni dei fenomeni magnetici risalgono all antichità n Agli antichi greci era nota la proprietà della magnetite di attirare la limatura di ferro n Un ago magnetico
Il magnetismo magnetismo magnetite
 Magnetismo Il magnetismo Fenomeno noto fin dall antichità. Il termine magnetismo deriva da Magnesia città dell Asia Minore dove si era notato che un minerale, la magnetite, attirava a sé i corpi ferrosi.
Magnetismo Il magnetismo Fenomeno noto fin dall antichità. Il termine magnetismo deriva da Magnesia città dell Asia Minore dove si era notato che un minerale, la magnetite, attirava a sé i corpi ferrosi.
IL CAMPO MAGNETICO. V Classico Prof.ssa Delfino M. G.
 IL CAMPO MAGNETICO V Classico Prof.ssa Delfino M. G. UNITÀ - IL CAMPO MAGNETICO 1. Fenomeni magnetici 2. Calcolo del campo magnetico 3. Forze su conduttori percorsi da corrente 4. La forza di Lorentz LEZIONE
IL CAMPO MAGNETICO V Classico Prof.ssa Delfino M. G. UNITÀ - IL CAMPO MAGNETICO 1. Fenomeni magnetici 2. Calcolo del campo magnetico 3. Forze su conduttori percorsi da corrente 4. La forza di Lorentz LEZIONE
S N S N S N N S MAGNETISMO
 MAGNETISMO Esistono forze che si manifestano tra particolari materiali (ad es. la magnetite, il ferro) anche privi di carica elettrica. Queste forze possono essere sia attrattive che repulsive, analogamente
MAGNETISMO Esistono forze che si manifestano tra particolari materiali (ad es. la magnetite, il ferro) anche privi di carica elettrica. Queste forze possono essere sia attrattive che repulsive, analogamente
Elettromagnetismo (4/6) Magnetismo Lezione 22, 18/12/2018, JW ,
 Elettromagnetismo (4/6) Magnetismo Lezione 22, 18/12/2018, JW 26.1-26.4, 26.6-26.7 1 1. Magneti permanenti Le estremità di una barretta magnetica corrispondono a poli opposti (detti polo nord e polo sud).
Elettromagnetismo (4/6) Magnetismo Lezione 22, 18/12/2018, JW 26.1-26.4, 26.6-26.7 1 1. Magneti permanenti Le estremità di una barretta magnetica corrispondono a poli opposti (detti polo nord e polo sud).
Il campo magnetico. Non esiste la carica magnetica (monopoli magnetici) Due modi per creare campi magnetici: elettromagnete:
 Il campo magnetico Non esiste la carica magnetica (monopoli magnetici) Due modi per creare campi magnetici: elettromagnete: correnti elettrici creano campo magnetici magneti permanenti (calamiti) ogni
Il campo magnetico Non esiste la carica magnetica (monopoli magnetici) Due modi per creare campi magnetici: elettromagnete: correnti elettrici creano campo magnetici magneti permanenti (calamiti) ogni
Unità 9. Il campo magnetico
 Unità 9 Il campo magnetico 1. La forza di Lorentz Se un fascio catodico è in un campo magnetico: La forza di Lorentz Gli elettroni risentono di una forza magnetica anche se non sono in un filo metallico;
Unità 9 Il campo magnetico 1. La forza di Lorentz Se un fascio catodico è in un campo magnetico: La forza di Lorentz Gli elettroni risentono di una forza magnetica anche se non sono in un filo metallico;
FENOMENI MAGNETICI NATURALI
 MAGNETISMO l Il magnetismo è una caratteristica di certi corpi, detti magneti, grazie alla quale essi esercitano una forza a distanza su sostanze come il ferro, attirandole. FENOMENI MAGNETICI NATURALI
MAGNETISMO l Il magnetismo è una caratteristica di certi corpi, detti magneti, grazie alla quale essi esercitano una forza a distanza su sostanze come il ferro, attirandole. FENOMENI MAGNETICI NATURALI
MAGNETISMO. Alcuni materiali (calamite o magneti) hanno la proprietà di attirare pezzetti di ferro (o cobalto, nickel e gadolinio).
 MAGNETISMO Alcuni materiali (calamite o magneti) hanno la proprietà di attirare pezzetti di ferro (o cobalto, nickel e gadolinio). Le proprietà magnetiche si manifestano alle estremità del magnete, chiamate
MAGNETISMO Alcuni materiali (calamite o magneti) hanno la proprietà di attirare pezzetti di ferro (o cobalto, nickel e gadolinio). Le proprietà magnetiche si manifestano alle estremità del magnete, chiamate
Calamite e fenomeni magnetici
 Campo magnetico Calamite e fenomeni magnetici Magnetite: scoperta dai Greci (ossido di ferro capace di attirare piccoli pezzettini di ferro) Materiali ferromagnetici: ferro, cobalto, nichel... se posti
Campo magnetico Calamite e fenomeni magnetici Magnetite: scoperta dai Greci (ossido di ferro capace di attirare piccoli pezzettini di ferro) Materiali ferromagnetici: ferro, cobalto, nichel... se posti
Fenomeni Magnetici. Campo Magnetico e Forza di Lorentz. Moto di cariche in campo magnetico. Momento e campo magnetico di una spira.
 Fenomeni Magnetici Campo Magnetico e Forza di Lorentz Moto di cariche in campo magnetico Momento e campo magnetico di una spira Legge di Ampère Solenoide Campo Magnetico I fenomeni magnetici possono essere
Fenomeni Magnetici Campo Magnetico e Forza di Lorentz Moto di cariche in campo magnetico Momento e campo magnetico di una spira Legge di Ampère Solenoide Campo Magnetico I fenomeni magnetici possono essere
CAMPO MAGNETICO Proprietà della magnetite (Fe 3 O 4 ): attira a sé materiali ferrosi o altre sostanze dette magnetiche Poli del magnete = parti in
 CAMPO MAGNETICO Proprietà della magnetite (Fe 3 O 4 ): attira a sé materiali ferrosi o altre sostanze dette magnetiche Poli del magnete = parti in cui si evidenzia tale proprietà Proprietà magnetiche possono
CAMPO MAGNETICO Proprietà della magnetite (Fe 3 O 4 ): attira a sé materiali ferrosi o altre sostanze dette magnetiche Poli del magnete = parti in cui si evidenzia tale proprietà Proprietà magnetiche possono
Unità 8. Fenomeni magnetici fondamentali
 Unità 8 Fenomeni magnetici fondamentali 1. La forza magnetica e le linee del campo magnetico Già ai tempi di Talete (VI sec. a.c.) era noto che la magnetite, un minerale di ferro, attrae piccoli oggetti
Unità 8 Fenomeni magnetici fondamentali 1. La forza magnetica e le linee del campo magnetico Già ai tempi di Talete (VI sec. a.c.) era noto che la magnetite, un minerale di ferro, attrae piccoli oggetti
CORSO DI BIOFISICA IL MATERIALE CONTENUTO IN QUESTE DIAPOSITIVE E AD ESCLUSIVO USO DIDATTICO PER L UNIVERSITA DI TERAMO
 CORSO DI IOFISICA IL MATERIALE CONTENUTO IN QUESTE DIAPOSITIVE E AD ESCLUSIVO USO DIDATTICO PER L UNIVERSITA DI TERAMO LE IMMAGINE CONTENUTE SONO STATE TRATTE DAL LIRO FONDAMENTI DI FISICA DI D. HALLIDAY,
CORSO DI IOFISICA IL MATERIALE CONTENUTO IN QUESTE DIAPOSITIVE E AD ESCLUSIVO USO DIDATTICO PER L UNIVERSITA DI TERAMO LE IMMAGINE CONTENUTE SONO STATE TRATTE DAL LIRO FONDAMENTI DI FISICA DI D. HALLIDAY,
P I P I 100W P R. eff. Veff. eff. eff
 esercizi 1 Uno stereo da 100 W per canale ha gli altoparlanti da 8 W. Calcolare i valori efficaci della corrente e tensione, a) al valore massimo della potenza b) quando il volume è abbassato ad una potenza
esercizi 1 Uno stereo da 100 W per canale ha gli altoparlanti da 8 W. Calcolare i valori efficaci della corrente e tensione, a) al valore massimo della potenza b) quando il volume è abbassato ad una potenza
Corrente elettrica. Marcello Borromeo corso di Fisica per Farmacia - Anno Accademico
 Corrente elettrica Sotto l effetto di un campo elettrico le cariche si possono muovere In un filo elettrico, se una carica dq attraversa una sezione del filo nel tempo dt abbiamo una corrente di intensità
Corrente elettrica Sotto l effetto di un campo elettrico le cariche si possono muovere In un filo elettrico, se una carica dq attraversa una sezione del filo nel tempo dt abbiamo una corrente di intensità
Filo percorso da corrente
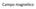 Campo magne*co Filo percorso da corrente Sperimentalmente si osserva che: un filo percorso da corrente genera intorno a se un campo magnetico le cui linee di forza sono concentriche al punto in cui passa
Campo magne*co Filo percorso da corrente Sperimentalmente si osserva che: un filo percorso da corrente genera intorno a se un campo magnetico le cui linee di forza sono concentriche al punto in cui passa
Campo magnetico terrestre
 Magnetismo Vicino a Magnesia, in Asia Minore, si trovava una sostanza capace di attrarre il ferro Due sbarrette di questo materiale presentano poli alle estremità, che si attraggono o si respingono come
Magnetismo Vicino a Magnesia, in Asia Minore, si trovava una sostanza capace di attrarre il ferro Due sbarrette di questo materiale presentano poli alle estremità, che si attraggono o si respingono come
MAGNETI E AZIONI MAGNETICHE DELLE CORRENTI
 MAGNETI E AZIONI MAGNETICHE DELLE CORRENTI In natura esistono corpi capaci di attrarre i materiali ferrosi: i magneti naturali. Un esempio di magnete naturale è la magnetite, che è un minerale da cui si
MAGNETI E AZIONI MAGNETICHE DELLE CORRENTI In natura esistono corpi capaci di attrarre i materiali ferrosi: i magneti naturali. Un esempio di magnete naturale è la magnetite, che è un minerale da cui si
ESERCIZI IL MAGNETISMO DOMANDE CALCOLI EFFETTI MAGNETICI DELL ELETTRICITÀ DOMANDE. Quanto vale α se sul filo agisce una forza di 4, N?
 20 test (30 minuti) TEST INTERATTIVI 1 IL MAGNETISMO 1 Descrivi almeno una analogia e una differenza tra cariche elettriche e poli magnetici. 2 Che cosa accade quando spezziamo in due parti un magnete?
20 test (30 minuti) TEST INTERATTIVI 1 IL MAGNETISMO 1 Descrivi almeno una analogia e una differenza tra cariche elettriche e poli magnetici. 2 Che cosa accade quando spezziamo in due parti un magnete?
Campo magne*co F B. Il verso della forza di deviazione è tale che i vettori F, v, B (in quest ordine) formano una terna destrorsa.
 Campo magne*co Il Magne*smo L esistenza di una forza capace di attirare particelle metalliche risale all antica città di Magnesia in Grecia. In quella città ricca di molte miniere di Ferro si osservarono
Campo magne*co Il Magne*smo L esistenza di una forza capace di attirare particelle metalliche risale all antica città di Magnesia in Grecia. In quella città ricca di molte miniere di Ferro si osservarono
Il campo magnetico. Le prime osservazioni dei fenomeni magnetici
 Il campo magnetico Le prime osservazioni dei fenomeni magnetici la magnetite (Fe 3 O 4 ) attira la limatura di ferro un ago magnetico libero di ruotare intorno ad un asse verticale si orienta con una delle
Il campo magnetico Le prime osservazioni dei fenomeni magnetici la magnetite (Fe 3 O 4 ) attira la limatura di ferro un ago magnetico libero di ruotare intorno ad un asse verticale si orienta con una delle
Il magnetismo. Il campo magnetico
 Il magnetismo Un magnete (o calamita) è un corpo che genera intorno a sé un campo di forza che attrae il ferro Un magnete naturale è un minerale contenente magnetite, il cui nome deriva dal greco "pietra
Il magnetismo Un magnete (o calamita) è un corpo che genera intorno a sé un campo di forza che attrae il ferro Un magnete naturale è un minerale contenente magnetite, il cui nome deriva dal greco "pietra
Il flusso del campo magnetico
 Il flusso del campo magnetico Il flusso del campo magnetico attraverso una superficie si definisce in modo analogo al flusso del campo elettrico. ( B) BScos Con α angolo compreso tra B e S. L unità di
Il flusso del campo magnetico Il flusso del campo magnetico attraverso una superficie si definisce in modo analogo al flusso del campo elettrico. ( B) BScos Con α angolo compreso tra B e S. L unità di
Lez. 20 Magnetismo. Prof. Giovanni Mettivier
 Lez. 20 Magnetismo Prof. Giovanni Mettivier 1 Dott. Giovanni Mettivier, PhD Dipartimento Scienze Fisiche Università di Napoli Federico II Compl. Univ. Monte S.Angelo Via Cintia, I-80126, Napoli mettivier@na.infn.it
Lez. 20 Magnetismo Prof. Giovanni Mettivier 1 Dott. Giovanni Mettivier, PhD Dipartimento Scienze Fisiche Università di Napoli Federico II Compl. Univ. Monte S.Angelo Via Cintia, I-80126, Napoli mettivier@na.infn.it
CAPITOLO 7 TEOREMA DI AMPERE
 CAPITOLO 7 DI 7.1 Prima legge elementare di Laplace Le correnti generano i campi magnetici. Per calcolare il campo magnetico prodotto da un filo percorso da corrente dobbiamo usare una procedura simile
CAPITOLO 7 DI 7.1 Prima legge elementare di Laplace Le correnti generano i campi magnetici. Per calcolare il campo magnetico prodotto da un filo percorso da corrente dobbiamo usare una procedura simile
CAPITOLO 6 CAMPI MAGNETICI
 CAPITOLO 6 6.1 Introduzione Come una bacchetta elettrizzata produce attorno a se un campo elettrico E così possiamo dire che un magnete produce un campo vettoriale che chiamiamo campo magnetico B. Le osservazioni
CAPITOLO 6 6.1 Introduzione Come una bacchetta elettrizzata produce attorno a se un campo elettrico E così possiamo dire che un magnete produce un campo vettoriale che chiamiamo campo magnetico B. Le osservazioni
Corrente elettrica. Marcello Borromeo corso di Fisica per Farmacia - Anno Accademico
 Corrente elettrica Sotto l effetto di un campo elettrico le cariche si possono muovere In un filo elettrico, se una carica dq attraversa una sezione del filo nel tempo dt abbiamo una corrente di intensità
Corrente elettrica Sotto l effetto di un campo elettrico le cariche si possono muovere In un filo elettrico, se una carica dq attraversa una sezione del filo nel tempo dt abbiamo una corrente di intensità
Interazioni di tipo magnetico II
 NGEGNERA GESTONALE corso di Fisica Generale Prof. E. Puddu nterazioni di tipo magnetico 1 Forza magnetica su una carica in moto Una particella di carica q in moto risente di una forza magnetica chiamata
NGEGNERA GESTONALE corso di Fisica Generale Prof. E. Puddu nterazioni di tipo magnetico 1 Forza magnetica su una carica in moto Una particella di carica q in moto risente di una forza magnetica chiamata
FENOMENI MAGNETICI NATURALI
 MAGNETISMO l Il magnetismo è una caratteristica di certi corpi, detti magneti, grazie alla quale essi esercitano una forza a distanza su sostanze come il ferro, attirandole. FENOMENI MAGNETICI NATURALI
MAGNETISMO l Il magnetismo è una caratteristica di certi corpi, detti magneti, grazie alla quale essi esercitano una forza a distanza su sostanze come il ferro, attirandole. FENOMENI MAGNETICI NATURALI
FENOMENI MAGNETICI NATURALI
 MAGNETISMO l Il magnetismo è una caratteristica di certi corpi, detti magneti, grazie alla quale essi esercitano una forza a distanza su sostanze come il ferro, attirandole. FENOMENI MAGNETICI NATURALI
MAGNETISMO l Il magnetismo è una caratteristica di certi corpi, detti magneti, grazie alla quale essi esercitano una forza a distanza su sostanze come il ferro, attirandole. FENOMENI MAGNETICI NATURALI
Esistono alcune sostanze che manifestano la capacità di attirare la limatura di ferro, in particolare, la magnetite
 59 Esistono alcune sostanze che manifestano la capacità di attirare la limatura di ferro, in particolare, la magnetite Questa proprietà non è uniforme su tutto il materiale, ma si localizza prevelentemente
59 Esistono alcune sostanze che manifestano la capacità di attirare la limatura di ferro, in particolare, la magnetite Questa proprietà non è uniforme su tutto il materiale, ma si localizza prevelentemente
Il campo magnetico. 1. Fenomeni magnetici 2. Calcolo del campo magnetico 3. Forze su conduttori percorsi da corrente 4. La forza di Lorentz
 Il capo agnetico 1. Fenoeni agnetici 2. Calcolo del capo agnetico 3. Forze su conduttori percorsi da corrente 4. La forza di Lorentz Prof. Giovanni Ianne 1/21 Fenoeni agnetici La agnetite è un inerale
Il capo agnetico 1. Fenoeni agnetici 2. Calcolo del capo agnetico 3. Forze su conduttori percorsi da corrente 4. La forza di Lorentz Prof. Giovanni Ianne 1/21 Fenoeni agnetici La agnetite è un inerale
SCHEDARIO: I FENOMENI MAGNETICI: IL CAMPO MAGNETICO
 SCHEDARO: ENOMEN MAGNETC: L CAMPO MAGNETCO 1. LE PRME OSSERVAZON GENERALTA Analogamente ai fenomeni elettrici anche i fenomeni magnetici furono osservati fino dall antichità. Già ai tempi dei Greci si
SCHEDARO: ENOMEN MAGNETC: L CAMPO MAGNETCO 1. LE PRME OSSERVAZON GENERALTA Analogamente ai fenomeni elettrici anche i fenomeni magnetici furono osservati fino dall antichità. Già ai tempi dei Greci si
Appunti di elettromagnetismo
 Appunti di elettromagnetismo Andrea Biancalana ottobre 1999 1 Magneti e correnti elettriche Magneti: esistono materiali che manifestano interazioni non-gravitazionali e non-elettriche; caratteristica dei
Appunti di elettromagnetismo Andrea Biancalana ottobre 1999 1 Magneti e correnti elettriche Magneti: esistono materiali che manifestano interazioni non-gravitazionali e non-elettriche; caratteristica dei
Campi magnetici generati da corrente
 Campi magnetici generati da corrente E noto che una particella carica in moto genera un campo magnetico nella zona circostante. Vediamo ora come calcolare il campo magnetico generato da una corrente. Suddividiamo
Campi magnetici generati da corrente E noto che una particella carica in moto genera un campo magnetico nella zona circostante. Vediamo ora come calcolare il campo magnetico generato da una corrente. Suddividiamo
Fisica Main Training Lorenzo Manganaro
 Fisica Main Training 2016-2017 Lorenzo Manganaro 1. Campo magnetico e Forza di Lorentz 2. Campo magnetico e corrente elettrica 3. Induzione elettromagnetica 4. Applicazioni 30 25 20 Veterinaria Ottica
Fisica Main Training 2016-2017 Lorenzo Manganaro 1. Campo magnetico e Forza di Lorentz 2. Campo magnetico e corrente elettrica 3. Induzione elettromagnetica 4. Applicazioni 30 25 20 Veterinaria Ottica
Interazioni di tipo magnetico II
 INGEGNERIA GESTIONALE corso di Fisica Generale Prof. E. Puddu Interazioni di tipo magnetico II 1 Forza magnetica su una carica in moto Una particella di carica q in moto risente di una forza magnetica
INGEGNERIA GESTIONALE corso di Fisica Generale Prof. E. Puddu Interazioni di tipo magnetico II 1 Forza magnetica su una carica in moto Una particella di carica q in moto risente di una forza magnetica
Magnetostatica. Indice. Mauro Saita Versione provvisoria. Novembre 2017.
 Magnetostatica Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria. Novembre 2017. Indice 1 Magnetismo 2 1.1 Forza magnetica e vettore induzione magnetica.................. 3 1.2 Esperimento
Magnetostatica Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria. Novembre 2017. Indice 1 Magnetismo 2 1.1 Forza magnetica e vettore induzione magnetica.................. 3 1.2 Esperimento
Esercizi di magnetismo
 Esercizi di magnetismo Fisica II a.a. 2003-2004 Lezione 16 Giugno 2004 1 Un riassunto sulle dimensioni fisiche e unità di misura l unità di misura di B è il Tesla : definisce le dimensioni [ B ] = [m]
Esercizi di magnetismo Fisica II a.a. 2003-2004 Lezione 16 Giugno 2004 1 Un riassunto sulle dimensioni fisiche e unità di misura l unità di misura di B è il Tesla : definisce le dimensioni [ B ] = [m]
Fenomenologia Forza magnetica su carica in moto e definizione di campo magnetico Forza magnetica su conduttore percorso da corrente
 CAMPO MAGNETICO Fenomenologia Forza magnetica su carica in moto e definizione di campo magnetico Forza magnetica su conduttore percorso da corrente INTERAZIONI MAGNETICHE Le proprietà magnetiche di alcuni
CAMPO MAGNETICO Fenomenologia Forza magnetica su carica in moto e definizione di campo magnetico Forza magnetica su conduttore percorso da corrente INTERAZIONI MAGNETICHE Le proprietà magnetiche di alcuni
CAMPO MAGNETICO E FORZA DI LORENTZ
 QUESITI 1 CAMPO MAGNETICO E FORZA DI LORENTZ 1. (Da Medicina e Odontoiatria 2013) Un cavo percorso da corrente in un campo magnetico può subire una forza dovuta al campo. Perché tale forza non sia nulla
QUESITI 1 CAMPO MAGNETICO E FORZA DI LORENTZ 1. (Da Medicina e Odontoiatria 2013) Un cavo percorso da corrente in un campo magnetico può subire una forza dovuta al campo. Perché tale forza non sia nulla
Nuova Forza. La forza Gravitazionale è attrattiva ed agisce su ogni MASSA La forza elettrica è attrattiva o repulsiva ed agisce sulle CARICHE
 Nuova orza La forza Gravitazionale è attrattiva ed agisce su ogni MASSA La forza elettrica è attrattiva o repulsiva ed agisce sulle CARICHE Come Agisce? Può essere attrattiva Un metallo (la magnetite)
Nuova orza La forza Gravitazionale è attrattiva ed agisce su ogni MASSA La forza elettrica è attrattiva o repulsiva ed agisce sulle CARICHE Come Agisce? Può essere attrattiva Un metallo (la magnetite)
DE MAGNETE. 1. Fino al 1820
 DE MAGNETE 1. Fino al 1820 Che i magneti esistano lo sanno anche i sassi fin dai tempi dei greci. In particolare è assodato che: come accade per l elettricità, esistono anche due tipi di magnetismo; ciò
DE MAGNETE 1. Fino al 1820 Che i magneti esistano lo sanno anche i sassi fin dai tempi dei greci. In particolare è assodato che: come accade per l elettricità, esistono anche due tipi di magnetismo; ciò
ELETTROTECNICA. Elettromagnetismo. Livello 13. Andrea Ros sdb
 ELETTROTECNICA Livello 13 Elettromagnetismo Andrea Ros sdb Livello 13 Elettromagnetismo Sezione 1 Campi magnetici e correnti elettriche Nel 1820 il fisico Oersted scoprì che il passaggio di una corrente
ELETTROTECNICA Livello 13 Elettromagnetismo Andrea Ros sdb Livello 13 Elettromagnetismo Sezione 1 Campi magnetici e correnti elettriche Nel 1820 il fisico Oersted scoprì che il passaggio di una corrente
2. Si pone una carica elettrica in prossimità di un filo percorso da corrente; cosa accadrà?
 1. Dei principali fenomeni dell elettromagnetismo può essere data una descrizione a diversi livelli ; in quale dei seguenti elenchi essi sono messi in ordine, dal più intuitivo al più astratto? (a) Forza,
1. Dei principali fenomeni dell elettromagnetismo può essere data una descrizione a diversi livelli ; in quale dei seguenti elenchi essi sono messi in ordine, dal più intuitivo al più astratto? (a) Forza,
LA V TLEGGE T O R I DI AMPERE g. bonomi fisica sperimentale (mecc., elettrom.) Introduzione
 Introduzione Un cannone elettromagnetico a rotaia spara un proiettile con una accelerazione molto elevata: da zero a 10 km/s in 1 ms; circa 5 x 10 6 g. Come si realizza una tale accelerazione? https://www.youtube.com/watch?v=wbxdef6oghe
Introduzione Un cannone elettromagnetico a rotaia spara un proiettile con una accelerazione molto elevata: da zero a 10 km/s in 1 ms; circa 5 x 10 6 g. Come si realizza una tale accelerazione? https://www.youtube.com/watch?v=wbxdef6oghe
Lezione 9 Forze e campi magnetici
 Lezione 9 Forze e campi magnetici 9.1 Forza di Lorentz Serway, Cap 22 Forza di Lorenz (particella carica) F = q v B Forza di Lorenz (filo rettilineo di lunghezza l percorso da corrente I) F = I l B Legge
Lezione 9 Forze e campi magnetici 9.1 Forza di Lorentz Serway, Cap 22 Forza di Lorenz (particella carica) F = q v B Forza di Lorenz (filo rettilineo di lunghezza l percorso da corrente I) F = I l B Legge
PROGRAMMA DI FISICA. CLASSE: 4^ SEZ.:A Scientifico
 Viale Papa Giovanni XXIII 25 10098 RIVOLI Tel. 0119586756 Fax 0119589270 Sede di SANGANO 10090 via San Giorgio, 10 Tel. e fax 0119087184 SCIENTIFICO LINGUISTICO SCIENZE UMANE ECONOMICO SOCIALE e-mail:
Viale Papa Giovanni XXIII 25 10098 RIVOLI Tel. 0119586756 Fax 0119589270 Sede di SANGANO 10090 via San Giorgio, 10 Tel. e fax 0119087184 SCIENTIFICO LINGUISTICO SCIENZE UMANE ECONOMICO SOCIALE e-mail:
Magnetismo. Fisica x Biologi 2017 Fabio Bernardini
 Magnetismo Il magnetismo entra nella nostra esperiemza a partire dalla bussola. Si può verificare che lʼorientamento dellʼago della bussola può essere modificato in due modi: avvicinando un magnete alla
Magnetismo Il magnetismo entra nella nostra esperiemza a partire dalla bussola. Si può verificare che lʼorientamento dellʼago della bussola può essere modificato in due modi: avvicinando un magnete alla
CAPITOLO 6 CAMPI MAGNETICI
 CAPITOLO 6 CAMPI MAGNETICI Elisabetta issaldi (Politecnico di ari) - A.A. 2017-2018 2 Interazione magnetica Magnetismo: proprietà osservata fin dall antichità in alcuni minerali (es. MAGNETITE) di attirare
CAPITOLO 6 CAMPI MAGNETICI Elisabetta issaldi (Politecnico di ari) - A.A. 2017-2018 2 Interazione magnetica Magnetismo: proprietà osservata fin dall antichità in alcuni minerali (es. MAGNETITE) di attirare
P I P I 100W P R. eff. Veff. eff. eff
 Uno stereo da 100 W per canale ha gli altoparlanti da 8 W. Calcolare i valori efficaci della corrente e tensione, a) al valore massimo della potenza b) quando il volume è abbassato ad una potenza di 1
Uno stereo da 100 W per canale ha gli altoparlanti da 8 W. Calcolare i valori efficaci della corrente e tensione, a) al valore massimo della potenza b) quando il volume è abbassato ad una potenza di 1
Riassunto lezione 11
 Riassunto lezione 11 Forza di Coloumb attrattiva o repulsiva F A B = 1 4 π ϵ 0 q A q B r 2 Consideriamo effetto di una carica sola campo elettrico: E Q = F Qq q = 1 4 π ϵ 0 Q r 2 ^u A B Come si rappresenta?
Riassunto lezione 11 Forza di Coloumb attrattiva o repulsiva F A B = 1 4 π ϵ 0 q A q B r 2 Consideriamo effetto di una carica sola campo elettrico: E Q = F Qq q = 1 4 π ϵ 0 Q r 2 ^u A B Come si rappresenta?
PROGETTO DI FISICA 2004/2005 CAMPO ELETTRICO E CAMPO MAGNETICO
 PROGETTO DI FISICA 2004/2005 CAMPO ELETTRICO E CAMPO MAGNETICO Autore Aleo Giacomo Luca 5H A.s. 2004/2005 1 ANALOGIE E DIFFERENZE 1) CAMPO ELETTRICO + + - - + + + + - + + + - + + + - + + + - - + + Corpo
PROGETTO DI FISICA 2004/2005 CAMPO ELETTRICO E CAMPO MAGNETICO Autore Aleo Giacomo Luca 5H A.s. 2004/2005 1 ANALOGIE E DIFFERENZE 1) CAMPO ELETTRICO + + - - + + + + - + + + - + + + - + + + - - + + Corpo
Per casa. [ 2, N, uscente]
![Per casa. [ 2, N, uscente] Per casa. [ 2, N, uscente]](/thumbs/77/75061402.jpg) p.273 libro Per casa Una carica di 0,5 μc viaggia in un campo magnetico di 0,15 T con velocità di 3 m/s in una direzione perpendicolare con il campo. Trovare intensità direzione e verso della forza che
p.273 libro Per casa Una carica di 0,5 μc viaggia in un campo magnetico di 0,15 T con velocità di 3 m/s in una direzione perpendicolare con il campo. Trovare intensità direzione e verso della forza che
Corso di fisica generale con elementi di fisica tecnica
 Corso di fisica generale con elementi di fisica tecnica Aniello (Daniele) Mennella Dipartimento di Fisica Secondo modulo Parte prima (fondamenti di elettromagnetismo) Lezione 3 Campi magnetici e forza
Corso di fisica generale con elementi di fisica tecnica Aniello (Daniele) Mennella Dipartimento di Fisica Secondo modulo Parte prima (fondamenti di elettromagnetismo) Lezione 3 Campi magnetici e forza
1. La forza di Lorentz. Se un fascio catodico è in un campo magnetico:
 Il campo magnetico 1. La forza di Lorentz Se un fascio catodico è in un campo magnetico: La forza di Lorentz Gli elettroni risentono di una forza magnetica anche se non sono in un filo metallico; l'importante
Il campo magnetico 1. La forza di Lorentz Se un fascio catodico è in un campo magnetico: La forza di Lorentz Gli elettroni risentono di una forza magnetica anche se non sono in un filo metallico; l'importante
CAPITOLO 6 CAMPI MAGNETICI
 CAPITOLO 6 CAMPI MAGNETICI Elisabetta issaldi (Politecnico di ari) - A.A. 2017-2018 2 Interazione magnetica Magnetismo: proprietà osservata fin dall antichità in alcuni minerali (es. MAGNETITE) di attirare
CAPITOLO 6 CAMPI MAGNETICI Elisabetta issaldi (Politecnico di ari) - A.A. 2017-2018 2 Interazione magnetica Magnetismo: proprietà osservata fin dall antichità in alcuni minerali (es. MAGNETITE) di attirare
MOTO DI UNA PARTICELLA IN UN CAMPO ELETTRICO
 MOTO DI UNA PARTICELLA IN UN CAMPO ELETTRICO Sappiamo che mettendo una carica positiva q chiamata carica di prova o carica esploratrice in un punto vicino all oggetto carico si manifesta un vettore campo
MOTO DI UNA PARTICELLA IN UN CAMPO ELETTRICO Sappiamo che mettendo una carica positiva q chiamata carica di prova o carica esploratrice in un punto vicino all oggetto carico si manifesta un vettore campo
FENOMENI MAGNETICI NATURALI
 MAGNETISMO l Il magnetismo è una caratteristica di certi corpi, detti magneti, grazie alla quale essi esercitano una forza a distanza su sostanze come il ferro, attirandole. FENOMENI MAGNETICI NATURALI
MAGNETISMO l Il magnetismo è una caratteristica di certi corpi, detti magneti, grazie alla quale essi esercitano una forza a distanza su sostanze come il ferro, attirandole. FENOMENI MAGNETICI NATURALI
FLUSSO E CIRCUITAZIONE DEL
 FLUSSO E CIRCUITAZIONE DEL CAMPO MAGNETICO PREMESSA Il concetto di campo elettromagnetico fu intuito da Faraday e precisato da Maxwell. Può essere espresso dicendo che la presenza di cariche elettriche
FLUSSO E CIRCUITAZIONE DEL CAMPO MAGNETICO PREMESSA Il concetto di campo elettromagnetico fu intuito da Faraday e precisato da Maxwell. Può essere espresso dicendo che la presenza di cariche elettriche
Storia delle scoperte del campo magnetico
 Storia delle scoperte del campo magnetico Prof. Daniele Ippolito Liceo Scientifico Amedeo di Savoia di Pistoia VI secolo a.c. Talete osserva che la magnetite, un minerale composto al 72% di ferro, estratto
Storia delle scoperte del campo magnetico Prof. Daniele Ippolito Liceo Scientifico Amedeo di Savoia di Pistoia VI secolo a.c. Talete osserva che la magnetite, un minerale composto al 72% di ferro, estratto
σ int =. σ est = Invece, se il guscio è collegato a massa, la superficie esterna si scarica e la densità di carica σ est è nulla. E =.
 Esercizio 1 a) Poiché la carica è interamente contenuta all interno di una cavità circondata da materiale conduttore, si ha il fenomeno dell induzione totale. Quindi sulla superficie interna della sfera
Esercizio 1 a) Poiché la carica è interamente contenuta all interno di una cavità circondata da materiale conduttore, si ha il fenomeno dell induzione totale. Quindi sulla superficie interna della sfera
Approfondimento. Forze magnetiche su fili percorsi da corrente: dipoli magnetici
 Approfondimento Forze magnetiche su fili percorsi da corrente: dipoli magnetici correnti elettriche e campi magnetici: le sorgenti del campo magnetico Principio di equivalenza di Ampere Proprietà magnetiche
Approfondimento Forze magnetiche su fili percorsi da corrente: dipoli magnetici correnti elettriche e campi magnetici: le sorgenti del campo magnetico Principio di equivalenza di Ampere Proprietà magnetiche
1 CIRCUITAZIONE E FLUSSO DEL CAMPO MAGNETICO. 2 Circuitazione di B: il teorema di Ampère
 CRCUTAZONE E FLUSSO DEL CAMPO MAGNETCO Abbiamo gia detto che per determinare completamente un campo vettoriale dobbiamo dare il valore della sua circuitazione ed il flusso del campo attraverso una superficie
CRCUTAZONE E FLUSSO DEL CAMPO MAGNETCO Abbiamo gia detto che per determinare completamente un campo vettoriale dobbiamo dare il valore della sua circuitazione ed il flusso del campo attraverso una superficie
Formulario. Entrante Uscente. Vettori Angolo tra l'asse e il vettore 1. Cinematica Equazioni della cinematica. Moti Moto periodico
 Formulario Entrante Uscente Vettori Angolo tra l'asse e il vettore sin cos. 2. 0. 2. 0 Cinematica Equazioni della cinematica Modulo dell'accelerazione centripeta Modulo della velocità nel moto circolare
Formulario Entrante Uscente Vettori Angolo tra l'asse e il vettore sin cos. 2. 0. 2. 0 Cinematica Equazioni della cinematica Modulo dell'accelerazione centripeta Modulo della velocità nel moto circolare
Scudo magnetico terrestre
 Hendrik Antoon Lorentz Nobel per la Fisica 1902 Il magnetismo Scudo magnetico terrestre magnetite TRATTO DA: I PROBLEMI DELLA FISICA- Cutnell, Johnson, Young, Standler Zanichelli editore L AMALDI PER I
Hendrik Antoon Lorentz Nobel per la Fisica 1902 Il magnetismo Scudo magnetico terrestre magnetite TRATTO DA: I PROBLEMI DELLA FISICA- Cutnell, Johnson, Young, Standler Zanichelli editore L AMALDI PER I
Campo magnetico B e correnti
 Campo magnetico B e correnti Dalle lezioni precedenti appare evidente che: corrente elettrica B corrente elettrica Pertanto è importante saper calcolare il campo magnetico a partire da una distribuzione
Campo magnetico B e correnti Dalle lezioni precedenti appare evidente che: corrente elettrica B corrente elettrica Pertanto è importante saper calcolare il campo magnetico a partire da una distribuzione
Induzione Elettromagnetica
 Induzione Elettromagnetica Abbiamo visto che una corrente elettrica produce sempre un campo magnetico. Un campo magnetico è in grado di produrre una corrente? (se sì esso produrrà anche una ddp ed un campo
Induzione Elettromagnetica Abbiamo visto che una corrente elettrica produce sempre un campo magnetico. Un campo magnetico è in grado di produrre una corrente? (se sì esso produrrà anche una ddp ed un campo
Campo magnetico e forza di Lorentz (I)
 Campo magnetico e forza di Lorentz (I) Fatti sperimentali (Oersted e Ampere) Legge di Gauss per il campo magnetico Forza di Lorentz Definizione del campo magnetico Magnetismo Noto fin dall antichita` (VI
Campo magnetico e forza di Lorentz (I) Fatti sperimentali (Oersted e Ampere) Legge di Gauss per il campo magnetico Forza di Lorentz Definizione del campo magnetico Magnetismo Noto fin dall antichita` (VI
df = I dl B df = dq v B
 Forza Magnetica su un conduttore Forza magnetica agente su un filo percorso da corrente Consideriamo un filo percorso da una corrente in presenza di un campo magnetico. Agirà una forza su ciascuna delle
Forza Magnetica su un conduttore Forza magnetica agente su un filo percorso da corrente Consideriamo un filo percorso da una corrente in presenza di un campo magnetico. Agirà una forza su ciascuna delle
Cose da sapere - elettromagnetismo
 Cose da sapere - elettromagnetismo In queste pagine c e` un riassunto di relazioni e risultati che abbiamo discusso e che devono essere conosciuti. Forza di Lorentz agente su una carica q in moto con velocita`
Cose da sapere - elettromagnetismo In queste pagine c e` un riassunto di relazioni e risultati che abbiamo discusso e che devono essere conosciuti. Forza di Lorentz agente su una carica q in moto con velocita`
Facoltà di Ingegneria Prova scritta di Fisica II - VO 15-Aprile-2003
 Facoltà di Ingegneria Prova scritta di Fisica II - VO 5-Aprile-003 Esercizio n. Un campo magnetico B è perpendicolare al piano individuato da due fili paralleli, cilindrici e conduttori, distanti l uno
Facoltà di Ingegneria Prova scritta di Fisica II - VO 5-Aprile-003 Esercizio n. Un campo magnetico B è perpendicolare al piano individuato da due fili paralleli, cilindrici e conduttori, distanti l uno
Cap 6.1- Campi magnetici
 Cap 6.1- Campi magnetici Cap 6.1- Campi magnetici Come una bacchetta elettrizzata produce attorno a se un campo elettrico E così possiamo dire che un magnete produce un campo vettoriale che chiamiamo campo
Cap 6.1- Campi magnetici Cap 6.1- Campi magnetici Come una bacchetta elettrizzata produce attorno a se un campo elettrico E così possiamo dire che un magnete produce un campo vettoriale che chiamiamo campo
LICEO SCIENTIFICO STATALE A. VALLISNERI Classe 5A 2 o periodo/ 1 a verifica scritta 6 febbraio Campo magnetico e suoi effetti
 LICEO SCIENTIFICO STATALE A. VALLISNERI Classe 5A 2 o periodo/ 1 a verifica scritta 6 febbraio 2012 Campo magnetico e suoi effetti Alunno:................................................ Domande a risposta
LICEO SCIENTIFICO STATALE A. VALLISNERI Classe 5A 2 o periodo/ 1 a verifica scritta 6 febbraio 2012 Campo magnetico e suoi effetti Alunno:................................................ Domande a risposta
La forza di Lorentz è: una forza conservativa. una forza radiale. una forza a distanza. tutte le le risposte precedenti.
 La forza di Lorentz è: una forza conservativa. una forza radiale. una forza a distanza. tutte le le risposte precedenti. 1 / 1 La forza di Lorentz è: una forza conservativa. una forza radiale. una forza
La forza di Lorentz è: una forza conservativa. una forza radiale. una forza a distanza. tutte le le risposte precedenti. 1 / 1 La forza di Lorentz è: una forza conservativa. una forza radiale. una forza
Le basi del magnetismo
 1 Le basi del magnetismo 1. enomeni magnetici elementari Così come l'ambra per i fenomeni elettrici, un'altra sostanza naturale, la magnetite, è all origine delle prime investigazioni dell'uomo sui fenomeni
1 Le basi del magnetismo 1. enomeni magnetici elementari Così come l'ambra per i fenomeni elettrici, un'altra sostanza naturale, la magnetite, è all origine delle prime investigazioni dell'uomo sui fenomeni
2. L unità di misura della costante k che compare nella legge di Coulomb è:
 Fatti sperimentali e loro descrizione fenomenologica 1 Vero o falso 2 Quesiti a risposta multipla 1. Si considerino due cariche elettriche, q 1 = +2 10 4 C e q 2 = 3 10 5 C, poste alla distanza d = 1,
Fatti sperimentali e loro descrizione fenomenologica 1 Vero o falso 2 Quesiti a risposta multipla 1. Si considerino due cariche elettriche, q 1 = +2 10 4 C e q 2 = 3 10 5 C, poste alla distanza d = 1,
1 Prove esami Fisica II
 1 Prove esami Fisica II Prova - 19-11-2002 Lo studente risponda alle seguenti domande: 1) Scrivere il teorema di Gauss (2 punti). 2) Scrivere, per un conduttore percorso da corrente, il legame tra la resistenza
1 Prove esami Fisica II Prova - 19-11-2002 Lo studente risponda alle seguenti domande: 1) Scrivere il teorema di Gauss (2 punti). 2) Scrivere, per un conduttore percorso da corrente, il legame tra la resistenza
Si ripetano i calcoli nel caso in cui la R2 si interrompe e nel caso in cui R2 vada in corto circuito.
 Dati i valori delle tre resistenze R1=25Ω R2=8Ω R3=14Ω e considerando una d.d.p. di 12 V tra A e, Calcolare a) la resistenza equivalente b) la corrente totale e la corrente che passa attraverso i rami
Dati i valori delle tre resistenze R1=25Ω R2=8Ω R3=14Ω e considerando una d.d.p. di 12 V tra A e, Calcolare a) la resistenza equivalente b) la corrente totale e la corrente che passa attraverso i rami
Quantità di Carica Elettrica
 ELETTROMAGNETISMO Quantità di Carica Elettrica Il concetto nasce dalla esperienza della attrazione e repulsione elettrostatica Un corpo è carico quando il numero di elettroni (Ne) e di protoni (Np) è differente
ELETTROMAGNETISMO Quantità di Carica Elettrica Il concetto nasce dalla esperienza della attrazione e repulsione elettrostatica Un corpo è carico quando il numero di elettroni (Ne) e di protoni (Np) è differente
FISICA. CdS Scienze Biologiche. Stefania Spagnolo. Dip. di Matematica e Fisica Ennio De Giorgi
 FISICA CdS Scienze Biologiche Stefania Spagnolo Dip. di Matematica e Fisica Ennio De Giorgi http://www.dmf.unisalento.it/~spagnolo stefania.spagnolo@le.infn.it (please, usate oggetto/subject: CdSBiologia)
FISICA CdS Scienze Biologiche Stefania Spagnolo Dip. di Matematica e Fisica Ennio De Giorgi http://www.dmf.unisalento.it/~spagnolo stefania.spagnolo@le.infn.it (please, usate oggetto/subject: CdSBiologia)
Campo magnetico e forza di Lorentz (II)
 Campo magnetico e forza di Lorentz (II) Moto di particelle cariche in un campo magnetico Seconda legge elementare di Laplace Principio di equivalenza di Ampere Effetto Hall Galvanometro Moto di una particella
Campo magnetico e forza di Lorentz (II) Moto di particelle cariche in un campo magnetico Seconda legge elementare di Laplace Principio di equivalenza di Ampere Effetto Hall Galvanometro Moto di una particella
Facoltà di Ingegneria Prova scritta di Fisica II - 23 Settembre Compito A Esercizio n.1 O Esercizio n. 2 O
 Facoltà di Ingegneria Prova scritta di Fisica II - 3 Settembre 003 - Compito A Esercizio n.1 Quattro cariche di uguale valore q, due positive e due negative, sono poste nei vertici di un quadrato di lato
Facoltà di Ingegneria Prova scritta di Fisica II - 3 Settembre 003 - Compito A Esercizio n.1 Quattro cariche di uguale valore q, due positive e due negative, sono poste nei vertici di un quadrato di lato
Liceo Scientifico Leonardo da Vinci Francesco Caracciolo La Grotteria V H 2004/2005 Elementi di cinematica ed elettromagnetismo
 Liceo Scientifico Leonardo da Vinci Francesco Caracciolo La Grotteria V H 004/005 Elementi di cinematica ed elettromagnetismo 1. Moto di una particella inserita in un campo elettrico: moto parabolico.
Liceo Scientifico Leonardo da Vinci Francesco Caracciolo La Grotteria V H 004/005 Elementi di cinematica ed elettromagnetismo 1. Moto di una particella inserita in un campo elettrico: moto parabolico.
ElettroMagnetismo Il campo magnetico
 FISICA ElettroMagnetismo Il campo magnetico Autore: prof. Pappalardo Vincenzo docente di Matematica e Fisica IL FLUSSO DEL CAMPO MAGNETICO Il flusso del campo magnetico B attraverso una superficie, si
FISICA ElettroMagnetismo Il campo magnetico Autore: prof. Pappalardo Vincenzo docente di Matematica e Fisica IL FLUSSO DEL CAMPO MAGNETICO Il flusso del campo magnetico B attraverso una superficie, si
Induzione magnetica 1
 l flusso concatenato nduzione magnetica 1 è solenoidale è definito il flusso di concatenato con una linea chiusa e orientata Φ () n d (verso della normale n indotto dalla percorrenza della linea secondo
l flusso concatenato nduzione magnetica 1 è solenoidale è definito il flusso di concatenato con una linea chiusa e orientata Φ () n d (verso della normale n indotto dalla percorrenza della linea secondo
L ELETTROMAGNETISMO. Dr. Daniele Di Gioacchino Istituto Nazionale di Fisica Nucleare Laboratori Nazionali di Frascati
 forza elettrica di Coulomb Campo elettrico L ELETTROMAGNETISMO Dr. Daniele Di Gioacchino Istituto Nazionale di Fisica Nucleare Laboratori Nazionali di Frascati Campo magnetico Campo magnetico di un filo
forza elettrica di Coulomb Campo elettrico L ELETTROMAGNETISMO Dr. Daniele Di Gioacchino Istituto Nazionale di Fisica Nucleare Laboratori Nazionali di Frascati Campo magnetico Campo magnetico di un filo
Prova Scritta Elettromagnetismo (a.a. 2018/19, S. Giagu/F. Lacava/F. Piacentini)
 Prova Scritta Elettromagnetismo - 8.6.09 a.a. 08/9, S. Giagu/F. Lacava/F. Piacentini) recupero primo esonero: risolvere l esercizio : tempo massimo.5 ore. recupero secondo esonero: risolvere l esercizio
Prova Scritta Elettromagnetismo - 8.6.09 a.a. 08/9, S. Giagu/F. Lacava/F. Piacentini) recupero primo esonero: risolvere l esercizio : tempo massimo.5 ore. recupero secondo esonero: risolvere l esercizio
Nome Cognome...Classe Data.. 1
 Esercitazione in preparazione al compito di fisica 1 Una spira rettangolare di filo di rame di lati, rispettivamente, di 2,0 cm e 4,0 cm è percorsa da 0,5 ma di corrente e viene immersa in un campo magnetico
Esercitazione in preparazione al compito di fisica 1 Una spira rettangolare di filo di rame di lati, rispettivamente, di 2,0 cm e 4,0 cm è percorsa da 0,5 ma di corrente e viene immersa in un campo magnetico
Conservazione della carica elettrica
 Elettrostatica La forza elettromagnetica è una delle interazioni fondamentali dell universo L elettrostatica studia le interazioni fra le cariche elettriche non in movimento Da esperimenti di elettrizzazione
Elettrostatica La forza elettromagnetica è una delle interazioni fondamentali dell universo L elettrostatica studia le interazioni fra le cariche elettriche non in movimento Da esperimenti di elettrizzazione
FISICA GENERALE II CdL in Scienza dei Materiali a.a. 2018/2019 Prof. Roberto Francini Programma del corso:
 FISICA GENERALE II CdL in Scienza dei Materiali a.a. 2018/2019 Prof. Roberto Francini Programma del corso: - Proprietà generali delle cariche elettriche - Cariche puntiformi e distribuzioni continue di
FISICA GENERALE II CdL in Scienza dei Materiali a.a. 2018/2019 Prof. Roberto Francini Programma del corso: - Proprietà generali delle cariche elettriche - Cariche puntiformi e distribuzioni continue di
Corso di fisica generale con elementi di fisica tecnica
 Corso di fisica generale con elementi di fisica tecnica Aniello (Daniele) Mennella Dipartimento di Fisica Secondo modulo Parte prima (fondamenti di elettromagnetismo) Lezione 3 Campi magnetici e forza
Corso di fisica generale con elementi di fisica tecnica Aniello (Daniele) Mennella Dipartimento di Fisica Secondo modulo Parte prima (fondamenti di elettromagnetismo) Lezione 3 Campi magnetici e forza
FISICA GENERALE T-2. Federico Fabiano. June 6, Esercitazione 5: Campo magnetico, legge di Laplace, forza magnetica su fili percorsi da corrente
 FISICA GENERALE T- Federico Fabiano June 6, 018 Esercitazione 5: Campo magnetico, legge di Laplace, forza magnetica su fili percorsi da corrente Problema 1. Una spira rettangolare si trova immersa in un
FISICA GENERALE T- Federico Fabiano June 6, 018 Esercitazione 5: Campo magnetico, legge di Laplace, forza magnetica su fili percorsi da corrente Problema 1. Una spira rettangolare si trova immersa in un
Campo magnetico e forza di Lorentz (I)
 Campo magnetico e forza di Lorentz (I) Fatti sperimentali (Oersted e Ampere) Legge di Gauss per il campo magnetico Forza di Lorentz Definizione del campo magnetico Magnetismo Noto fin dall antichita` (VI
Campo magnetico e forza di Lorentz (I) Fatti sperimentali (Oersted e Ampere) Legge di Gauss per il campo magnetico Forza di Lorentz Definizione del campo magnetico Magnetismo Noto fin dall antichita` (VI
Nuova Forza. La forza Gravitazionale è attrattiva ed agisce su ogni MASSA La forza elettrica è attrattiva o repulsiva ed agisce sulle CARICHE
 Nuova Forza La forza Gravitazionale è attrattiva ed agisce su ogni MASSA La forza elettrica è attrattiva o repulsiva ed agisce sulle CARICHE Come Agisce? Può essere attrattiva Un metallo (la magnetite)
Nuova Forza La forza Gravitazionale è attrattiva ed agisce su ogni MASSA La forza elettrica è attrattiva o repulsiva ed agisce sulle CARICHE Come Agisce? Può essere attrattiva Un metallo (la magnetite)
