GEOMETRIA 1 terza parte
|
|
|
- Ernesto Ferraro
- 4 anni fa
- Visualizzazioni
Transcript
1 GEOMETRIA 1 terza parte Cristina Turrini C. di L. in Fisica /2015 Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 1 / 32
2 index Applicazioni lineari 1 Applicazioni lineari 2 Nucleo e immagine di un applicazione 3 Isomorfismo di spazi vettoriali 4 La matrice rappresentativa Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 2 / 32
3 Applicazioni lineari Applicazioni lineari Siano V, W spazi vettoriali sullo stesso campo K. Consideriamo un applicazione f : V W. Si dice che f è lineare (o K-lineare) se u, v V, λ, µ K è: 1) f (u + v) = f (u) + f (v), cioè f conserva la somma o f è additiva; 2) f (λu) = λ f (u), cioè f è omogenea di I grado; (1) + 2)) è equivalente a ciascuna delle seguenti: 3) f (λu + µv) = λ f (u) + µ f (v), 3 ) f ( n i=1 λ iu i ) = n i=1 λ i f (u i ) u 1,..., u n, λ 1,..., λ n K. cioè f conserva le combinazioni lineari. Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 3 / 32
4 Applicazioni lineari Esempi di applicazioni lineari V spazio vettoriale, si può considerare l applicazione identica id V : V V; l applicazione identica è lineare. V, W, si può considerare 0 : V W, v 0 W. L applicazione nulla è lineare. sia V uno spazio vettoriale su K e B = {b 1,..., b n } una sua base (ordinata: qui e nel seguito parlando di base sottointenderemo sempre che lo sia); l applicazione definita da Φ B : V K n Φ B (v) = λ 1 λ λ n se v = λ 1 b 1 + λ 2 b λ n b n, è lineare. Φ B associa ad ogni vettore le sue componenti rispetto alla base B (dette anche coordinate nella base B). Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 4 / 32
5 Applicazioni lineari V = K n, W = K m, A Mat m,n (K), L A : K n K m, (prodotto riga per colonna) x A x L applicazione L A viene detta applicazione associata alla matrice A e, per le proprietà del prodotto riga per colonna, è lineare. Se A Mat m,n (K) e B Mat n,p (K), allora si hanno le applicazioni L A : K n K m e L B : K p K n per cui si può considerare la composizione L A L B : K p K m. Risulta L A L B = L A B cioè l applicazione composta L A L B è l applicazione associata alla matrice A B Mat m,p prodotto riga per colonna di A per B. Se I = I m Mat m è la matrice identica, allora L I : K m K m è l applicazione identica. Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 5 / 32
6 Applicazioni lineari Lo spazio delle applicazioni lineari Siano V e W spazi vettoriali sul campo K. Denotiamo con L(V, W) (o con Hom K (V, W) o Hom(V, W)) l insieme delle applicazioni lineari da V a W. Poniamo L(V, W) = {f : V W f è lineare} + : L(V, W) L(V, W) L(V, W) (f, g) f + g (f + g)(v) = f (v) + g(v) : K L(V, W) L(V, W) (λ, f ) λf (λf )(v) = λf (v) (definizioni puntuali di somma e di prodotto per uno scalare) L(V, W) con queste leggi di composizione è uno spazio vettoriale su K. Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 6 / 32
7 Applicazioni lineari Propriet`à elementari delle applicazioni lineari Siano V, W, Z spazi vettoriali sul campo K. 1) f (0 V ) = 0 W (infatti f (0 V ) = f (0 v) = 0 f (v) = 0 W ). 2) g : W Z. Se f, g sono lineari g f : V Z è lineare. (infatti g f (λu + µv) = g(f (λu + µv)) = g(λf (u) + µf (v)) = λg(f (u) + µg(f (v)) = λ g f (u) + µ g f (v)). 3) Se f è biunivoca, l applicazione inversa di f, f 1 : W V è lineare. (infatti si verifica che il vettore λf 1 (u ) + µf 1 (v ) è l inverso di λu + µv infatti f (λf 1 (u ) + µf 1 (v )) = λf (f 1 (u )) + µf (f 1 (v )) = λu + µv ). Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 7 / 32
8 Applicazioni lineari Teorema di esistenza e unicità TEOREMA - Siano V e W spazi vettoriali su K. Sia B = {b 1,..., b n } una base di V e siano w 1,..., w n W vettori comunque presi. Allora esiste una ed una sola applicazione lineare φ : V W tale che φ(b i ) = w i, i = 1,..., n Dimostrazione - Unicità. v V = B, v = α 1 b α n b n ( la scrittura è unica). Dobbiamo costruire f : V W con le condizioni richieste. Deve necessariamente essere: f (v) = f (α 1 b α n b n ) = α 1 f (b 1 ) + + α n f (b n ) = α 1 w α n w n. L unica possibile definizione è allora ( ) se v = α 1 b α n b n. f (v) = α 1 w α n w n Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 8 / 32
9 Applicazioni lineari Esistenza Si deve mostrare che l applicazione f definita in ( ) soddisfa le condizioni richieste dall enunciato. f è lineare. Infatti (ad esempio per l additività) se e allora quindi v = α 1 b α n b n. u = β 1 b β n b n, v + u = α 1 b α n b n + β 1 b β n b n = = (α 1 + β 1 )b (α n + β n )b n ; f (v + u) = (α 1 + β 1 )w (α n + β n )w n = f (v) + f (u). E analogamente per l omogeneità. f (b i ) = w i, i. Infatti b i = 0b b i + + 0b n f (b i ) = 1w i. Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 9 / 32
10 Applicazioni lineari Siano sempre V e W spazi vettoriali su K, con V f.g., dim V = n, e siano v 1,..., v k V, e w 1,..., w k W. PROBLEMA - Un applicazione lineare f : V W tale che v i w i i = 1,..., k esiste? È unica? Occorre distinguere due casi 1) Se {v 1,..., v k } è l.i., allora l applicazione f esiste, ma in generale non è unica. Infatti l insieme {v 1,..., v k } si può completare a una base, cioè v k+1,..., v n t.c. {v 1,..., v k, v k+1,..., v n } sia base di V. Presi arbitrariamente w k+1,... w n W, per il teorema di esistenza e unicità!f t.c. f (v 1 ) = w 1,... f (v k ) = w k, f (v k+1 ) = w k+1..., f (v n ) = w n Quest applicazione soddisfa le nostre richieste, ma i vettori w k+1,... w n possono essere scelti arbitrariamente in W quindi in generale f. Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 10 / 32
11 Applicazioni lineari 2) Se {v 1,..., v k } è l.d. allora l applicazione f in generale non esiste. Infatti, può esistere un applicazione lineare tale che f (v i ) = w i solo se le relazioni di dipendenza lineare tra i v i sussistono (con gli stessi coefficienti!) tra i w i. Ad esempio, se v 3 = v 1 v 2 f (v 3 ) = f (v 1 v 2 ) = f (v 1 ) f (v 2 ), cioè w 3 = w 1 w 2. Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 11 / 32
12 index Nucleo e immagine di un applicazione 1 Applicazioni lineari 2 Nucleo e immagine di un applicazione 3 Isomorfismo di spazi vettoriali 4 La matrice rappresentativa Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 12 / 32
13 Nucleo e immagine di un applicazione Nucleo e immagine di un applicazione lineare Siano V, W spazi vettoriali su un campo K e sia f : V W lineare. Si dice nucleo di f e si indica con ker(f ) l insieme dei vettori di V che hanno per immagine il vettore nullo. ker(f ) = {v V f (v) = 0 W } Si dice immagine di f e si indica con Im(f ) l usuale immagine dell applicazione. Im(f ) = {w W v V : f (v) = w} Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 13 / 32
14 Nucleo e immagine di un applicazione Proprietà a) ker(f ) V è un sottospazio. Infatti f (0 V ) = 0 W 0 V ker(f ); Inoltre, presi λ, µ K, u, v ker(f ) si ha f (λu+µv) = λf (u)+µf (v) = λ 0 W +µ 0 W = 0 W λu+µv ker(f ). b) Im(f ) W è un sottospazio (verificarlo). TEOREMA (caratterizzazione delle applicazioni lineari iniettive)- Siano V, W spazi vettoriali f.g. su un campo K, f : V W lineare. Sono equivalenti: i) f è iniettiva; ii) ker(f ) = {0 V } (ossia dim(ker(f )) = 0; iii) v 1,..., v n l.i. f (v 1 ),..., f (v n ) l.i. Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 14 / 32
15 Nucleo e immagine di un applicazione Dimostrazione i) ii) Se esistesse v 0 V tale che v ker(f ), si avrebbe f (v) = 0 W. Poichè però f (0 V ) = 0 W, verrebbe contraddetta l iniettività di f. ii) iii) v 1,..., v n V l.i. Dobbiamo dimostrare f (v 1 ),..., f (v n ) l.i. λ 1 f (v 1 ) + + λ n f (v n ) = 0 W f (λ 1 v λ n v n ) = 0 W λ 1 v λ n v n ker(f ) = {0 V } λ 1 v λ n v n = 0 V λ 1 = = λ n = 0 f (v 1 ),..., f (v n ) l.i. iii) i) Dobbiamo dimostrare che se f (v 1 ) = f (v 2 ) = w allora v 1 = v 2. f (v 1 v 2 ) = f (v 1 ) f (v 2 ) = w w = 0 W Se fosse v 1 v 2 0 V, sarebbe v 1 v 2 l.i. e f (v 1 v 2 ) = 0 W l.d.. Contro l ipotesi iii). Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 15 / 32
16 Nucleo e immagine di un applicazione TEOREMA (caratterizzazione delle applicazioni lineari suriettive)- Siano V, W spazi vettoriali f.g. su un campo K, f : V W lineare. Sono equivalenti: i) f è suriettiva; ii) dim(im(f )) = dim(w); iii) < v 1,..., v n >= V < f (v 1 ),..., f (v n ) >= W. (dimostrazione per esercizio). OSSERVAZIONE - In generale (se anche f non è suriettiva) si ha < v 1,..., v n >= V < f (v 1 ),..., f (v n ) >= Im(f ). OSSERVAZIONE - Abbiamo visto che le applicazioni lineari iniettive sono quelle che mutano insiemi di vettori l.i. in insiemi di vettori l.i. e che le applicazioni lineari suriettive sono quelle che mutano generatori di V in generatori di W. Ne segue che le applicazioni lineari biunivoche sono caratterizzate dal mutare basi in basi. Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 16 / 32
17 Nucleo e immagine di un applicazione Teorema della nullità + rango TEOREMA - Siano V, W spazi vettoriali f.g. su un campo K, e sia f : V W lineare. Si ha: ( ) dim(v) = dim(ker(f )) + dim(im(f )). Dimostrazione Anzitutto osserviamo che tutti gli spazi coinvolti dalla ( ) sono f.g. perchè sottospazi di spazi f.g.. Se Im(f ) = {0}, allora f è l applicazione nulla (f (v) = 0, v V) e quindi ker(f ) = V, per cui ( ) è verificata. Possiamo quindi supporre che Im(f ) {0}. Allora Im(f ) ammette una base. Sia {c 1,..., c k } una base di Im(f ). Si prendano (arbitrariamente) vettori b 1,..., b k in V tali che f (b i ) = c i, i = 1,..., k. Se ker(f ) {0}, si prende una base {a 1,..., a r } di ker(f ). Altrimenti non si prende nessun altro vettore. Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 17 / 32
18 Nucleo e immagine di un applicazione Dimostriamo che B = {a 1,..., a r, b 1,..., b k } è una base di V. Questo prova la ( ) perchè si ha dim(v) = r + k = dim(ker(f )) + dim(im(f )). B è l.i. Infatti sia ( ) α 1 a α r a r + β 1 b β k b k = 0. ( ) implica f (α 1 a α r a r + β 1 b β k b k ) = f (0) = 0, quindi 0 = f (α 1 a α r a r + β 1 b β k b k ) = α 1 f (a 1 ) + + α r f (a r ) + β 1 f (b 1 ) + + β k f (b k ) = β 1 c β k c k. Ma c 1,..., c k sono l.i. (base di Im(f )), quindi β 1 = = β k = 0, per cui diventa α 1 a α r a r = 0. Ma a 1,..., a r sono l.i. (base di ker(f )), per cui α 1 = = α r = 0. Pertanto tutti i coefficienti di ( ) sono necessariamente nulli, e quindi B è l.i.. Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 18 / 32
19 Nucleo e immagine di un applicazione < B >= V Sia v V. Dobbiamo mostrare che v si può scrivere come combinazione lineare dei vettori di B. Si ha f (v) Im(f ) =< c 1,..., c k >, quindi f (v) = γ 1 c 1 + +γ k c k = γ 1 f (b 1 )+ +γ k f (b k ) = f (γ 1 b 1 + +γ k b k ). Quindi f (v) f (γ 1 b γ k b k ) = f (v γ 1 b 1 γ k b k ) = 0. Pertanto v γ 1 b 1 γ k b k ker(f ) =< a 1,..., a r > e perciò v γ 1 b 1 γ k b k = δ 1 a δ r a r. In conclusione v = γ 1 b γ k b k + δ 1 a δ r a r. COROLLARIO - Sia f : V W lineare, con V, W f.g. e dim(v) = dim(w). Allora f è iniettiva se e solo se è suriettiva se e solo se è biunivoca. Dimostrazione f iniettiva se e solo se dim(ker(f )) = 0 se e solo se dim(v) = dim(im(f )) se e solo se dim(w) = dim(im(f )) se e solo se f suriettiva. Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 19 / 32
20 index Isomorfismo di spazi vettoriali 1 Applicazioni lineari 2 Nucleo e immagine di un applicazione 3 Isomorfismo di spazi vettoriali 4 La matrice rappresentativa Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 20 / 32
21 Isomorfismo di spazi vettoriali Endomorfismi, isomorfismi, automorfismi ESEMPI Un applicazione lineare biunivoca si dice isomorfismo. Un applicazione lineare da uno spazio in se stesso si dice endomorfismo. Un applicazione isomorfismo ed endomorfismo si dice automorfismo. 1 id V : V V è un automorfismo. 2 se A è una matrice quadrata m m, allora L A : K m K m è un endomorfismo. 3 se A è una matrice quadrata m m invertibile, allora L A : K m K m è un isomorfismo e l applicazione inversa di L A è (L A ) 1 = L A 1 (infatti si ha L A 1 L A = L A 1 A = L I = id). Siano V, W spazi vettoriali su un campo K. Si dice che V e W sono isomorfi, e si scrive V W, se esiste un isomorfismo f : V W. La relazione di isomorfismo è di equivalenza (verificarlo). Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 21 / 32
22 Isomorfismo di spazi vettoriali TEOREMA - Due spazi vettoriali f.g. V e W sullo stesso campo K sono isomorfi se e solo se hanno la stessa dimensione. Dimostrazione Se esiste un isomorfismo f : V W allora f trasforma una base di V in una base di W, quindi dim(v) = dim(w). Se dim(v) = dim(w) = n, allora, fissata una base B = {b 1, b 2,..., b n } l applicazione Φ B : V K n definita da Φ B (v) = λ 1 λ λ n se v = λ 1 b 1 + λ 2 b λ n b n, è un isomorfismo, da cui si deduce che V è isomorfo a K n. Analogamente si costruisce un isomorfismo Φ C : W K n. Di conseguenza (Φ C ) 1 Φ B : V W è pure un isomorfismo. Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 22 / 32
23 index La matrice rappresentativa 1 Applicazioni lineari 2 Nucleo e immagine di un applicazione 3 Isomorfismo di spazi vettoriali 4 La matrice rappresentativa Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 23 / 32
24 La matrice rappresentativa Proprietà della trasformazione L A Sia A Mat m,n (K), siano K n, K m spazi vettoriali. Abbiamo visto che si può costruire L A : K n K m lineare, x A x = y. Si ha: ker L A = {x K n : L A (x) = 0 K m } = {x K n : A x = 0} = {soluzioni del sistema omogeneo A x = 0}. α 11 x α 1n x n = 0. α m1 x α mn x n = 0 ImL A = {y K m : x K n : y = L A (x)} = {y K m : x : A x = y} = {termini noti che rendono risolubile il sistema riportato qui sotto} α 11 x α 1n x n = y 1. α m1 x α mn x n = y m Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 24 / 32
25 La matrice rappresentativa Sia {e 1,..., e n } la base standard di K n. Calcoliamo L A (e i ) Per esempio, per i = 1, α 11 α 1n α L A (e 1 ) = 21 α 2n..... α m1 α mn di A = Analogamente, L A (e i ) = i-esima colonna di A. α 11 α 21. α m1 e 1,..., e n = K n quindi L A (e 1 ),..., L A (e n ) = ImL A (generatori di K n sono mutati da L A in generatori di ImL A ), pertanto i vettori colonna di A sono generatori di ImL A. = A (1) = I colonna Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 25 / 32
26 La matrice rappresentativa Costruzione della matrice rappresentativa Siano V, W spazi vettoriali sul campo K, con dim V = n, dim W = m, e siano A = {a 1,..., a n } una base (ordinata) di V, e B = {b 1,..., b m } una base (ordinata) di W. Sia f : V W lineare; f è univocamente determinata da f (a 1 ),..., f (a n ) (teorema di esistenza e unicità): noti f (a 1 ),..., f (a n ) si può ricostruire f. Scriviamo i vettori f (a 1 ),..., f (a n ) W come combinazioni lineari dei vettori della base B : f (a 1 ) = α 11 b 1 + α 21 b α m1 b m f (a 2 ) = α 12 b 1 + α 22 b α m2 b m. f (a n ) = α 1n b 1 + α 2n b α mn b m Gli α ij sono univocamente determinati da f e la determinano univocamente. Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 26 / 32
27 La matrice rappresentativa Costruiamo la matrice A Mat m,n (K) le cui colonne sono le coordinate dei vettori f (a 2 ) nella base B: α 11 α 12 α 1n α A = 21 α 22 α 2n α m1 α m2 α mn Vogliamo dimostrare che f = L A. Consideriamo il diagramma f V W Φ A Φ B ( ) K n L A K m in cui Φ A denota l applicazione che ad ogni vettore di V associa le sue coordinate nella base A e Φ B quella che ad ogni vettore di W associa le sue coordinate nella base B. Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 27 / 32
28 La matrice rappresentativa Il quadrato ( ) commuta, ossia si ha ( ) L A Φ A = Φ B f. Trattandosi di applicazioni lineari, (per il teorema di esistenza e unicità) basta verificare l uguaglianza ( ) sui vettori di una base. Verifichiamola sui vettori della base A = {a 1,..., a n }. Ad esempio, per a 1, L A Φ A (a 1 ) = L A (e 1 ) = I colonna di A = α 11 α 21. α m1 Φ B f (a 1 ) = Φ B (α 11 b 1 + α 21 b α m1 b m ) = α 11 α 21. α m1. Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 28 / 32
29 La matrice rappresentativa In generale, L A (Φ A (a i )) = A (i) = i esima colonna di A Φ B (f (a i )) = A (i) = i esima colonna di A quindi L A Φ A = Φ B f. Ricapitolando: tutti gli spazi vettoriali f.g. sono del tipo K n ; tutte le applicazioni lineari tra spazi vettoriali f.g. sono del tipo L A. Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 29 / 32
30 La matrice rappresentativa L applicazione M A B Abbiamo visto che, dati due spazi vettoriali V e W di dimensioni rispettive n e m, e date le basi (ordinate) A e B di V e W rispett., ad una applicazione lineare f : V W può essere associata una matrice A tale che essenzialmente si abbia f = L A. La matrice A si dice associata ad f rispetto alle basi A e B o rappresentativa di f rispetto alle basi A e B e si scrive Abbiamo costruito un applicazione A = M A B (f ). M A B : L(V, W) Mat m,n, f A Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 30 / 32
31 La matrice rappresentativa Siano V, W e Z spazi vettoriali (su K) di dimensioni rispettive n, m e l, con basi rispettive A, B e C e siano f : V W e g : W Z applicazioni lineari. PROPRIETÀ (si omettono le dimostrazioni) M A B è un isomorfismo tra gli spazi vettoriali L(V, W) e Mat m,n. M A C (g f ) = M B C (g) M A B (f ), cioè alla composizione di applicazioni lineari corrisponde il prodotto riga per colonna delle matrici rappresentative. Nel caso m = n, V = W, A = B si ha M A B (id V ) = I m. Nel caso m = n, se f : V W è un isomorfismo, e f 1 : W V è l isomorfismo inverso, allora la matrice M A B (f ) è invertibile e si ha M A B (f ) 1 = M B A(f 1 ). Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 31 / 32
32 La matrice rappresentativa Conseguenza: se V è uno spazio vettoriale e A, B sono due sue basi, e f : V V è un endomorfismo, allora esiste una matrice invertibile N tale che ( ) M A A(f ) = N 1 M B B(f ) N. Infatti basta prendere N = M B A (id V) (verificarlo). Due matrici quadrate A, B Mat n si dicono simili se esiste una matrice invertibile N GL(n) tale che B = N 1 A N. La formula ( ) mostra che le matrici rapprentative rispetto a basi diverse di uno stesso endomorfismo sono matrici simili (si noti però che in entrambi i casi la base deve essere la stessa in dominio e codominio!). OSSERVAZIONE - Nel caso V = K n, W = K m e f = L A, con A Mat m,n, la matrice rappresentativa rispetto alle basi canoniche di L A è proprio A. Cristina Turrini (C. di L. in Fisica /2015) GEOMETRIA 1 32 / 32
Elementi di Algebra Lineare Applicazioni lineari
 Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2015/2016 Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 18 index Applicazioni lineari 1 Applicazioni lineari
Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2015/2016 Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 18 index Applicazioni lineari 1 Applicazioni lineari
GEOMETRIA 1 seconda parte
 GEOMETRIA 1 seconda parte Cristina Turrini C. di L. in Fisica - 2015/2016 Cristina Turrini (C. di L. in Fisica - 2015/2016) GEOMETRIA 1 1 / 52 index Applicazioni lineari 1 Applicazioni lineari 2 Nucleo
GEOMETRIA 1 seconda parte Cristina Turrini C. di L. in Fisica - 2015/2016 Cristina Turrini (C. di L. in Fisica - 2015/2016) GEOMETRIA 1 1 / 52 index Applicazioni lineari 1 Applicazioni lineari 2 Nucleo
GEOMETRIA 1 seconda parte
 GEOMETRIA 1 seconda parte Gilberto Bini - Cristina Turrini 2017/2018 Gilberto Bini - Cristina Turrini (2017/2018) GEOMETRIA 1 1 / 62 index Applicazioni lineari 1 Applicazioni lineari 2 Nucleo e immagine
GEOMETRIA 1 seconda parte Gilberto Bini - Cristina Turrini 2017/2018 Gilberto Bini - Cristina Turrini (2017/2018) GEOMETRIA 1 1 / 62 index Applicazioni lineari 1 Applicazioni lineari 2 Nucleo e immagine
Elementi di Algebra Lineare Applicazioni lineari
 Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 50 index Applicazioni lineari 1 Applicazioni lineari
Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 50 index Applicazioni lineari 1 Applicazioni lineari
Elementi di Algebra Lineare Spazi Vettoriali
 Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 41 index Spazi vettoriali
Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 41 index Spazi vettoriali
APPLICAZIONI LINEARI O OMOMORFISMI
 42 APPLICAZIONI LINEARI O OMOMORFISMI Definizione 9 Dati due spazi vettoriali U e V sullo stesso campo K, una applicazione f : U V è detta lineare o omomorfismo se soddisfa le seguenti due condizioni:
42 APPLICAZIONI LINEARI O OMOMORFISMI Definizione 9 Dati due spazi vettoriali U e V sullo stesso campo K, una applicazione f : U V è detta lineare o omomorfismo se soddisfa le seguenti due condizioni:
Elementi di Algebra Lineare Spazi Vettoriali
 Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2015/2016 Antonio Lanteri e Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 37 index Spazi vettoriali
Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2015/2016 Antonio Lanteri e Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 37 index Spazi vettoriali
Elementi di Algebra Lineare Spazi Vettoriali
 Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2017/2018 Antonio Lanteri e Cristina Turrini (UNIMI - 2017/2018) Elementi di Algebra Lineare 1 / 37 index Spazi vettoriali
Elementi di Algebra Lineare Spazi Vettoriali Antonio Lanteri e Cristina Turrini UNIMI - 2017/2018 Antonio Lanteri e Cristina Turrini (UNIMI - 2017/2018) Elementi di Algebra Lineare 1 / 37 index Spazi vettoriali
GEOMETRIA 1 seconda parte
 GEOMETRIA 1 seconda parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 40 index Spazi vettoriali 1 Spazi vettoriali 2 Sottospazi 3 Sistemi
GEOMETRIA 1 seconda parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 40 index Spazi vettoriali 1 Spazi vettoriali 2 Sottospazi 3 Sistemi
GEOMETRIA 1 Autovalori e autovettori
 GEOMETRIA 1 Autovalori e autovettori Gilberto Bini - Anna Gori - Cristina Turrini 2018/2019 Gilberto Bini - Anna Gori - Cristina Turrini (2018/2019) GEOMETRIA 1 1 / 28 index Matrici rappresentative "semplici"
GEOMETRIA 1 Autovalori e autovettori Gilberto Bini - Anna Gori - Cristina Turrini 2018/2019 Gilberto Bini - Anna Gori - Cristina Turrini (2018/2019) GEOMETRIA 1 1 / 28 index Matrici rappresentative "semplici"
GEOMETRIA 1 quarta parte
 GEOMETRIA 1 quarta parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 36 index Forme bilineari 1 Forme bilineari 2 Il caso reale: spazi
GEOMETRIA 1 quarta parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 36 index Forme bilineari 1 Forme bilineari 2 Il caso reale: spazi
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
PROGRAMMA del corso di. GEOMETRIA 1 - Algebra Lineare. Laurea Triennale in Matematica. Anno Accademico 2007/08. docente : Bruno Zimmermann
 PROGRAMMA del corso di GEOMETRIA 1 - Algebra Lineare Laurea Triennale in Matematica Anno Accademico 2007/08 docente : Bruno Zimmermann (Il presente programma è stato redatto sulla base degli appunti del
PROGRAMMA del corso di GEOMETRIA 1 - Algebra Lineare Laurea Triennale in Matematica Anno Accademico 2007/08 docente : Bruno Zimmermann (Il presente programma è stato redatto sulla base degli appunti del
Elementi di Algebra Lineare Spazi Vettoriali
 Elementi di Algebra Lineare Spazi Vettoriali Cristina Turrini UNIMI - 2018/2019 Cristina Turrini (UNIMI - 2018/2019) Elementi di Algebra Lineare 1 / 32 index Spazi vettoriali 1 Spazi vettoriali 2 Sottospazi
Elementi di Algebra Lineare Spazi Vettoriali Cristina Turrini UNIMI - 2018/2019 Cristina Turrini (UNIMI - 2018/2019) Elementi di Algebra Lineare 1 / 32 index Spazi vettoriali 1 Spazi vettoriali 2 Sottospazi
APPLICAZIONI LINEARI
 APPLICAZIONI LINEARI Fra le applicazioni definite tra spazi vettoriali sono particolarmente significative quelle che conservano le operazioni, dette applicazioni lineari. Definizione Siano V, W due k-s.v.
APPLICAZIONI LINEARI Fra le applicazioni definite tra spazi vettoriali sono particolarmente significative quelle che conservano le operazioni, dette applicazioni lineari. Definizione Siano V, W due k-s.v.
Esempio. L immagine di f è l insieme dei vettori w = (w 1, w 2 ) R 2 che hanno w 1 = w 2. Quindi:
 Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
Esercizi su applicazioni lineari. Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V,W,U spazi vettoriali su K.
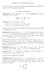 Esercizi su applicazioni lineari Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V,W,U spazi vettoriali su K. 1. Cose da ricordare Definizione 1.1. Una funzione f : V W si
Esercizi su applicazioni lineari Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V,W,U spazi vettoriali su K. 1. Cose da ricordare Definizione 1.1. Una funzione f : V W si
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia
 CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2015-16 Complementi ed Esercizi 1. AUTOVETTORI e AUTOVALORI di ENDOMORFISMI e MATRICI Una applicazione lineare avente per dominio e condominio lo stesso spazio vettoriale
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2015-16 Complementi ed Esercizi 1. AUTOVETTORI e AUTOVALORI di ENDOMORFISMI e MATRICI Una applicazione lineare avente per dominio e condominio lo stesso spazio vettoriale
Soluzione degli esercizi di algebra lineare (del 26 ottobre 2018)
 Soluzione degli esercizi di algebra lineare (del 26 ottobre 28) Esercizio. Siano V un K-spazio vettoriale con base B = (v,..., v n ) e W un K-spazio vettoriale con base C = (w,..., w m ), e sia f : V W
Soluzione degli esercizi di algebra lineare (del 26 ottobre 28) Esercizio. Siano V un K-spazio vettoriale con base B = (v,..., v n ) e W un K-spazio vettoriale con base C = (w,..., w m ), e sia f : V W
Algebra Lineare. a.a Gruppo A-H. Prof. P. Piazza Soluzioni del compito pomeridiano del 6/12/2004
 Algebra Lineare. a.a. 004-05. Gruppo A-H. Prof. P. Piazza Soluzioni del compito pomeridiano del 6/1/004 Esercizio 1. Siano V e W due spazi vettoriali e sia F : V W un isomorfismo (quindi F è lineare e
Algebra Lineare. a.a. 004-05. Gruppo A-H. Prof. P. Piazza Soluzioni del compito pomeridiano del 6/1/004 Esercizio 1. Siano V e W due spazi vettoriali e sia F : V W un isomorfismo (quindi F è lineare e
Matematica discreta 1 [145016]
![Matematica discreta 1 [145016] Matematica discreta 1 [145016]](/thumbs/94/119285443.jpg) Facoltà di Scienze Matematiche, Fisiche e Naturali anno accademico 2008/09 Registro dell'attività didattica Matematica discreta 1 [145016] Attività didattica: Attività didattica [codice] Corso di studio
Facoltà di Scienze Matematiche, Fisiche e Naturali anno accademico 2008/09 Registro dell'attività didattica Matematica discreta 1 [145016] Attività didattica: Attività didattica [codice] Corso di studio
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia
 CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2018-19 Complementi ed Esercizi APPLICAZIONI LINEARI Siano V e V spazi vettoriali sul campo K. Una applicazione L: V V si dice lineare se: 1 AL. L(v+w) = L(v) +
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2018-19 Complementi ed Esercizi APPLICAZIONI LINEARI Siano V e V spazi vettoriali sul campo K. Una applicazione L: V V si dice lineare se: 1 AL. L(v+w) = L(v) +
Soluzioni primi compitini - Geometria 1
 Soluzioni primi compitini - Geometria Caterina Vernieri Ottobre 7 Le soluzioni proposte non sono state riviste dai professori Soluzioni Primi Compitini - G I compitino 7//3 Esercizio Al variare di α R
Soluzioni primi compitini - Geometria Caterina Vernieri Ottobre 7 Le soluzioni proposte non sono state riviste dai professori Soluzioni Primi Compitini - G I compitino 7//3 Esercizio Al variare di α R
APPUNTI DI ALGEBRA LINEARE
 APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
Foglio di esercizi numero 2 Corso di Fondamenti di Algebra Lineare e Geometria Ingegneria Aerospaziale e Meccanica
 Foglio di esercizi numero 2 Corso di Fondamenti di Algebra Lineare e Geometria Ingegneria Aerospaziale e Meccanica Esercizio 1. Sia f l endomorfismo di R 4 definito nel modo seguente: f(x, y, z, w) = (w,
Foglio di esercizi numero 2 Corso di Fondamenti di Algebra Lineare e Geometria Ingegneria Aerospaziale e Meccanica Esercizio 1. Sia f l endomorfismo di R 4 definito nel modo seguente: f(x, y, z, w) = (w,
Anno Accademico 2017/2018
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2017/2018 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2017/2018 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Fondamenti di ALGEBRA LINEARE E GEOMETRIA
 Fondamenti di ALGEBRA LINEARE E GEOMETRIA Corso di laurea in Ingegneria Gestionale 2011-2012 Michel Lavrauw Dipartimento di Tecnica e Gestione dei Sistemi Industriali Università di Padova Lezione 15 Capitolo
Fondamenti di ALGEBRA LINEARE E GEOMETRIA Corso di laurea in Ingegneria Gestionale 2011-2012 Michel Lavrauw Dipartimento di Tecnica e Gestione dei Sistemi Industriali Università di Padova Lezione 15 Capitolo
Anno Accademico 2016/2017
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2016/2017 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2016/2017 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
0.1 Coordinate in uno spazio vettoriale
 0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
Matematica Discreta I
 Matematica Discreta I 5 Febbraio 8 TEMA A Esercizio Sia data la matrice A M (R) A = (i) Calcolare gli autovalori di A (ii) Determinare una base di R composta di autovettori di A (iii) Diagonalizzare la
Matematica Discreta I 5 Febbraio 8 TEMA A Esercizio Sia data la matrice A M (R) A = (i) Calcolare gli autovalori di A (ii) Determinare una base di R composta di autovettori di A (iii) Diagonalizzare la
Definizione 1 Una applicazione f : V W, con V, W spazi vettoriali sul campo K si dice lineare se conserva le combinazioni lineari:
 Applicazioni lineari Definizione Una applicazione f : V W, con V, W spazi vettoriali sul campo K si dice lineare se conserva le combinazioni lineari: f(αv + βv 2 ) = αf(v ) + βf(v 2 ) v, v 2 V, α, β K.
Applicazioni lineari Definizione Una applicazione f : V W, con V, W spazi vettoriali sul campo K si dice lineare se conserva le combinazioni lineari: f(αv + βv 2 ) = αf(v ) + βf(v 2 ) v, v 2 V, α, β K.
ENDOMORFISMI. NOTE DI ALGEBRA LINEARE
 ENDOMORFISMI. NOTE DI ALGEBRA LINEARE 2010-11 MARCO MANETTI: 15 GENNAIO 2011 1. Endomorfismi e sottospazi invarianti Definizione 1.1. Sia V uno spazio vettoriale su K. Un endomorfismo di V è una qualsiasi
ENDOMORFISMI. NOTE DI ALGEBRA LINEARE 2010-11 MARCO MANETTI: 15 GENNAIO 2011 1. Endomorfismi e sottospazi invarianti Definizione 1.1. Sia V uno spazio vettoriale su K. Un endomorfismo di V è una qualsiasi
LEZIONE 12. Y = f(x) = f( x j,1 f(e j ) = x j,1 A j = AX = µ A (X),
 LEZIONE 1 1.1. Matrice di un applicazione lineare. Verifichiamo ora che ogni applicazione lineare f: R n R m è della forma µ A per un unica A R m,n. Definizione 1.1.1. Per ogni j 1,..., n indichiamo con
LEZIONE 1 1.1. Matrice di un applicazione lineare. Verifichiamo ora che ogni applicazione lineare f: R n R m è della forma µ A per un unica A R m,n. Definizione 1.1.1. Per ogni j 1,..., n indichiamo con
GEOMETRIA 1 prima parte
 GEOMETRIA 1 prima parte Gilberto Bini - Cristina Turrini 2016/2017 Gilberto Bini - Cristina Turrini (2016/2017) GEOMETRIA 1 1 / 89 index Relazioni in un insieme 1 Relazioni in un insieme 2 Gruppi, anelli,
GEOMETRIA 1 prima parte Gilberto Bini - Cristina Turrini 2016/2017 Gilberto Bini - Cristina Turrini (2016/2017) GEOMETRIA 1 1 / 89 index Relazioni in un insieme 1 Relazioni in un insieme 2 Gruppi, anelli,
APPLICAZIONI LINEARI
 APPLICAZIONI LINEARI Esercizi Esercizio Date le seguenti applicazioni lineari f : R 2 R 3 definita da fx y = x 2y x + y x + y; 2 g : R 3 R 2 definita da gx y z = x + y x y; 3 h : Rx] 2 R 2 definita da
APPLICAZIONI LINEARI Esercizi Esercizio Date le seguenti applicazioni lineari f : R 2 R 3 definita da fx y = x 2y x + y x + y; 2 g : R 3 R 2 definita da gx y z = x + y x y; 3 h : Rx] 2 R 2 definita da
Applicazioni Lineari. Nota Bene: Questo materiale non deve essere considerato come sostituto delle lezioni.
 Politecnico di Torino. Applicazioni Lineari. Nota Bene: Questo materiale non deve essere considerato come sostituto delle lezioni. Argomenti: Basi e coordinate. Applicazioni lineari. Matrici come applicazioni
Politecnico di Torino. Applicazioni Lineari. Nota Bene: Questo materiale non deve essere considerato come sostituto delle lezioni. Argomenti: Basi e coordinate. Applicazioni lineari. Matrici come applicazioni
Nozioni e notazioni: concetti primitivi di insieme, elemento ed appartenenza.
 Geometria I lezione del 30 settembre 2013 Presentazione del corso. Nozioni e notazioni: concetti primitivi di insieme, elemento ed appartenenza. Insiemi numerici: i numeri naturali, gli interi, i numeri
Geometria I lezione del 30 settembre 2013 Presentazione del corso. Nozioni e notazioni: concetti primitivi di insieme, elemento ed appartenenza. Insiemi numerici: i numeri naturali, gli interi, i numeri
Autovalori e autovettori
 Autovalori e autovettori Definizione 1 (per endomorfismi). Sia V uno spazio vettoriale su di un campo K e f : V V un suo endomorfismo. Si dice autovettore per f ogni vettore x 0 tale che f(x) = λx, per
Autovalori e autovettori Definizione 1 (per endomorfismi). Sia V uno spazio vettoriale su di un campo K e f : V V un suo endomorfismo. Si dice autovettore per f ogni vettore x 0 tale che f(x) = λx, per
Geometria e Topologia I 18 maggio
 Geometria e Topologia I 18 maggio 2005 64 17 Mappe affini (17.1) Definizione. Siano X e Y due spazi affini sullo stesso campo K. Una funzione f : X Y si dice affine (anche, mappa affine o trasformazione
Geometria e Topologia I 18 maggio 2005 64 17 Mappe affini (17.1) Definizione. Siano X e Y due spazi affini sullo stesso campo K. Una funzione f : X Y si dice affine (anche, mappa affine o trasformazione
Rango di una matrice e teorema di Rouché-Capelli
 Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
GEOMETRIA 1 prima parte
 GEOMETRIA 1 prima parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 44 index Relazioni in un insieme 1 Relazioni in un insieme 2 Gruppi,
GEOMETRIA 1 prima parte Cristina Turrini C. di L. in Fisica - 2014/2015 Cristina Turrini (C. di L. in Fisica - 2014/2015) GEOMETRIA 1 1 / 44 index Relazioni in un insieme 1 Relazioni in un insieme 2 Gruppi,
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 5. Rango
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 5 Rango Definizione 1 Sia A M m,n (K) una matrice m n a coefficienti nel campo K Il rango
Appunti del corso di geometria 1. G. Bande
 Appunti del corso di geometria 1 G. Bande 21 febbraio 2011 2 Indice 1 Spazi vettoriali 5 1.0.1 Esempi di spazi vettoriali.................. 6 1.1 Sottospazi vettoriali......................... 7 1.1.1
Appunti del corso di geometria 1 G. Bande 21 febbraio 2011 2 Indice 1 Spazi vettoriali 5 1.0.1 Esempi di spazi vettoriali.................. 6 1.1 Sottospazi vettoriali......................... 7 1.1.1
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
Matrici simili, invarianti e decomposizione di matrici 1 / 14
 Matrici simili, invarianti e decomposizione di matrici 1 / 14 Applicazioni lineari 2 / 14 Se X = t [x 1,...,x n ] sono le coordinate di un generico vettore rispetto alla base canonica, possiamo assumere
Matrici simili, invarianti e decomposizione di matrici 1 / 14 Applicazioni lineari 2 / 14 Se X = t [x 1,...,x n ] sono le coordinate di un generico vettore rispetto alla base canonica, possiamo assumere
REGISTRO DELLE LEZIONI
 UNIVERSITA DEGLI STUDI DI GENOVA FACOLTA DI SCIENZE MATEMATICHE, FISICHE E NATURALI REGISTRO DELLE LEZIONI del Corso UFFICIALE di GEOMETRIA B tenute dal prof. Domenico AREZZO nell anno accademico 2006/2007
UNIVERSITA DEGLI STUDI DI GENOVA FACOLTA DI SCIENZE MATEMATICHE, FISICHE E NATURALI REGISTRO DELLE LEZIONI del Corso UFFICIALE di GEOMETRIA B tenute dal prof. Domenico AREZZO nell anno accademico 2006/2007
GEOMETRIA 1 ottava parte
 GEOMETRIA 1 ottava parte Cristina Turrini C. di L. in Fisica - 214/215 Cristina Turrini (C. di L. in Fisica - 214/215) GEOMETRIA 1 1 / 15 index 1 Cristina Turrini (C. di L. in Fisica - 214/215) GEOMETRIA
GEOMETRIA 1 ottava parte Cristina Turrini C. di L. in Fisica - 214/215 Cristina Turrini (C. di L. in Fisica - 214/215) GEOMETRIA 1 1 / 15 index 1 Cristina Turrini (C. di L. in Fisica - 214/215) GEOMETRIA
Forme bilineari simmetriche
 Forme bilineari simmetriche Qui il campo dei coefficienti è sempre R Definizione 1 Sia V uno spazio vettoriale Una forma bilineare su V è una funzione b: V V R tale che v 1, v 2, v 3 V b(v 1 + v 2, v 3
Forme bilineari simmetriche Qui il campo dei coefficienti è sempre R Definizione 1 Sia V uno spazio vettoriale Una forma bilineare su V è una funzione b: V V R tale che v 1, v 2, v 3 V b(v 1 + v 2, v 3
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 3. Sistemi di equazioni lineari
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Applicazioni lineari In questo Capitolo vogliamo esporre la teoria delle applicazioni lineari, argomento centrale dell algebra lineare.
 Capitolo 4 Applicazioni lineari In questo Capitolo vogliamo esporre la teoria delle applicazioni lineari, argomento centrale dell algebra lineare. 4.1 Concetto di applicazione lineare Cominciamo dalla
Capitolo 4 Applicazioni lineari In questo Capitolo vogliamo esporre la teoria delle applicazioni lineari, argomento centrale dell algebra lineare. 4.1 Concetto di applicazione lineare Cominciamo dalla
0.1 Coordinate in uno spazio vettoriale
 .1. COORDINATE IN UNO SPAZIO VETTORIALE 1.1 Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
.1. COORDINATE IN UNO SPAZIO VETTORIALE 1.1 Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
ENDOMORFISMI. ove B := (v 1,v 2,v 3 ). (1) Determinare gli autovalori di f e le relative molteplicità algebriche e geometriche.
 ENDOMORFISMI Esercizi Esercizio 1 Siano v 1 := T (1, 1, 1, 0), v 2 := T (0, 1, 2, 1), v 3 := T (0, 0, 1, 1) Consideriamo V := L(v 1,v 2,v 3 ) R 4 e sia f End R (V ) associato alla matrice A := MB B (f)
ENDOMORFISMI Esercizi Esercizio 1 Siano v 1 := T (1, 1, 1, 0), v 2 := T (0, 1, 2, 1), v 3 := T (0, 0, 1, 1) Consideriamo V := L(v 1,v 2,v 3 ) R 4 e sia f End R (V ) associato alla matrice A := MB B (f)
LEZIONE 21 [ ] D [ ] 1. k n. k m. k n,1 k m,1
![LEZIONE 21 [ ] D [ ] 1. k n. k m. k n,1 k m,1 LEZIONE 21 [ ] D [ ] 1. k n. k m. k n,1 k m,1](/thumbs/92/110228368.jpg) LEZIONE 21 21.1. Matrice di un applicazione lineare. Siano V e W spazi vettoriali su k = R, C finitamente generati e siano = (v 1,..., v n ) e = (w 1,..., w m ) basi di V e W rispettivamente. Come abbiamo
LEZIONE 21 21.1. Matrice di un applicazione lineare. Siano V e W spazi vettoriali su k = R, C finitamente generati e siano = (v 1,..., v n ) e = (w 1,..., w m ) basi di V e W rispettivamente. Come abbiamo
Esercizi di Geometria
 UNIVERSITÀ DEGLI STUDI DI TRENTO FACOLTÀ DI INGEGNERIA Marco Andreatta Luca Migliorini Gianluca Occhetta Davide Panizzolo Lorenza Tonetto Marina Avitabile Esercizi di Geometria Luglio 2000 2 1. Programma
UNIVERSITÀ DEGLI STUDI DI TRENTO FACOLTÀ DI INGEGNERIA Marco Andreatta Luca Migliorini Gianluca Occhetta Davide Panizzolo Lorenza Tonetto Marina Avitabile Esercizi di Geometria Luglio 2000 2 1. Programma
Argomenti trattati nella settimana novembre Il libro cui faccio riferimento, se non specificato altrimenti, è Lang, Algebra lineare
 Argomenti trattati nella settimana 23-27 novembre 2009 Il libro cui faccio riferimento, se non specificato altrimenti, è Lang, Algebra lineare 1 Sistemi lineari; 2 applicazioni lineari; Sistemi lineari;
Argomenti trattati nella settimana 23-27 novembre 2009 Il libro cui faccio riferimento, se non specificato altrimenti, è Lang, Algebra lineare 1 Sistemi lineari; 2 applicazioni lineari; Sistemi lineari;
Geometria I 2009-mag
 Geometria I 2009-mag-06 124 17 Mappe affini Cfr: Nacinovich, Cap V, 3 [3]. (17.1) Definizione. Siano X e Y due spazi affini sullo stesso campo K. Una funzione f : X Y si dice affine (anche, mappa affine
Geometria I 2009-mag-06 124 17 Mappe affini Cfr: Nacinovich, Cap V, 3 [3]. (17.1) Definizione. Siano X e Y due spazi affini sullo stesso campo K. Una funzione f : X Y si dice affine (anche, mappa affine
DIAGONALIZZAZIONE. M(f) =
 DIAGONALIZZAZIONE Esercizi Esercizio 1. Sia f End(R 3 ) associato alla matrice M(f) = 0 1 2 0. 2 (1) Determinare gli autovalori di f e le relative molteplicità. (2) Determinare gli autospazi di f e trovare,
DIAGONALIZZAZIONE Esercizi Esercizio 1. Sia f End(R 3 ) associato alla matrice M(f) = 0 1 2 0. 2 (1) Determinare gli autovalori di f e le relative molteplicità. (2) Determinare gli autospazi di f e trovare,
Fattorizzazione QR e matrici di Householder
 Fattorizzazione QR e matrici di Householder ottobre 009 In questa nota considereremo un tipo di fattorizzazione che esiste sempre nel caso di matrici quadrate non singolari ad entrate reali. Definizione
Fattorizzazione QR e matrici di Householder ottobre 009 In questa nota considereremo un tipo di fattorizzazione che esiste sempre nel caso di matrici quadrate non singolari ad entrate reali. Definizione
Esercizi Applicazioni Lineari
 Esercizi Applicazioni Lineari (1) Sia f : R 4 R 2 l applicazione lineare definita dalla legge f(x, y, z, t) = (x + y + z, y + z + t). (a) Determinare il nucleo di f, l immagine di f, una loro base e le
Esercizi Applicazioni Lineari (1) Sia f : R 4 R 2 l applicazione lineare definita dalla legge f(x, y, z, t) = (x + y + z, y + z + t). (a) Determinare il nucleo di f, l immagine di f, una loro base e le
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 19 GIUGNO 2012
 INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 19 GIUGNO 2012 MATTEO LONGO Esercizio 1. Al variare del parametro a R, si consideri l applicazione lineare L a : R R definita dalle
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 19 GIUGNO 2012 MATTEO LONGO Esercizio 1. Al variare del parametro a R, si consideri l applicazione lineare L a : R R definita dalle
NOTE DI ALGEBRA LINEARE v = a 1 v a n v n, w = b 1 v b n v n
 NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
NOTE DI ALGEBRA LINEARE 2- MM 9 NOVEMBRE 2 Combinazioni lineari e generatori Sia K un campo e V uno spazio vettoriale su K Siano v,, v n vettori in V Definizione Un vettore v V si dice combinazione lineare
Applicazioni lineari tra spazi euclidei. Cambi di base.
 pplicazioni lineari tra spazi euclidei. Cambi di base. Esercizio. Data la seguente applicazione lineare f : R R : f(x, y, z) = (x z, x + y, y + z), scrivere la matrice B, rappresentativa di f rispetto
pplicazioni lineari tra spazi euclidei. Cambi di base. Esercizio. Data la seguente applicazione lineare f : R R : f(x, y, z) = (x z, x + y, y + z), scrivere la matrice B, rappresentativa di f rispetto
ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5. Indice. 2. Esercizi 5
 ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5 Indice 1. Principali definizioni 1 2. Esercizi 5 Operazioni con le matrici 1. Principali definizioni Ricordiamo le principali definizioni legate alle matrici a coefficienti
ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5 Indice 1. Principali definizioni 1 2. Esercizi 5 Operazioni con le matrici 1. Principali definizioni Ricordiamo le principali definizioni legate alle matrici a coefficienti
Spazi affini e combinazioni affini.
 Spazi affini e combinazioni affini. Morfismi affini. Giorgio Ottaviani Abstract Introduciamo il concetto di combinazione affine in uno spazio affine, e in base a questo, ne caratterizziamo i sottospazi.
Spazi affini e combinazioni affini. Morfismi affini. Giorgio Ottaviani Abstract Introduciamo il concetto di combinazione affine in uno spazio affine, e in base a questo, ne caratterizziamo i sottospazi.
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari
 Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Prova scritta di geometria e algebra lineare del Esercizio 1 Sono dati il piano π e la retta r k in R 3 definiti da:
 Prova scritta di geometria e algebra lineare del 20.07.2017 Esercizio 1 Sono dati il piano π e la retta r k in R 3 definiti da: π : { x = 1 + t s y = t + 2s z = 2 + 2t + s con k costante reale assegnata.
Prova scritta di geometria e algebra lineare del 20.07.2017 Esercizio 1 Sono dati il piano π e la retta r k in R 3 definiti da: π : { x = 1 + t s y = t + 2s z = 2 + 2t + s con k costante reale assegnata.
Sistemi lineari e spazi vettoriali 1 / 14
 Sistemi lineari e spazi vettoriali 1 / 14 Sistemi lineari 2 / 14 Studieremo sistemi lineari costituiti da m equazioni in n incognite (m,n N, m,n 1): cioè a 11 x 1 + +a 1n x n = b 1 a 21 x 1 + +a 2n x n
Sistemi lineari e spazi vettoriali 1 / 14 Sistemi lineari 2 / 14 Studieremo sistemi lineari costituiti da m equazioni in n incognite (m,n N, m,n 1): cioè a 11 x 1 + +a 1n x n = b 1 a 21 x 1 + +a 2n x n
Federica Gregorio e Cristian Tacelli
 1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
1 Sistemi lineari Federica Gregorio e Cristian Tacelli Un sistema lineare m n (m equazioni in n incognite) è un insieme di equazioni lineari che devono essere soddisfatte contemporaneamente a 11 x 1 +
Appunti di Geometria - 2
 Appunti di Geometria - Samuele Mongodi - s.mongodi@sns.it Cambi di base e applicazioni lineari Richiami Sia V uno spazio vettoriale di dimensione n sul campo K, con base assegnata e,..., e n } (ad esempio
Appunti di Geometria - Samuele Mongodi - s.mongodi@sns.it Cambi di base e applicazioni lineari Richiami Sia V uno spazio vettoriale di dimensione n sul campo K, con base assegnata e,..., e n } (ad esempio
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni 2. MATRICI
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 2 MATRICI Siano m, n N \ {0}, sia K un campo Una matrice m n a coefficienti in K è una
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 2 MATRICI Siano m, n N \ {0}, sia K un campo Una matrice m n a coefficienti in K è una
GEOMETRIA 1 quarta parte
 GEOMETRIA 1 quarta parte Cristina Turrini C. di L. in Fisica - 2015/2016 Cristina Turrini (C. di L. in Fisica - 2015/2016) GEOMETRIA 1 1 / 76 index Forme bilineari 1 Forme bilineari 2 Il caso reale: spazi
GEOMETRIA 1 quarta parte Cristina Turrini C. di L. in Fisica - 2015/2016 Cristina Turrini (C. di L. in Fisica - 2015/2016) GEOMETRIA 1 1 / 76 index Forme bilineari 1 Forme bilineari 2 Il caso reale: spazi
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA
 Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
Esempi. In R 2, le coppia (2, 5) è combinazione lineare dei vettori (0, 1) e (1, 1). Infatti:
 Combinazioni lineari [Abate, 4.2] Sia V uno spazio vettoriale e v 1, v 2,..., v n dei vettori di V. Diremo che un vettore w V è combinazione lineare dei vettori v 1,..., v n se esistono a 1, a 2,..., a
Combinazioni lineari [Abate, 4.2] Sia V uno spazio vettoriale e v 1, v 2,..., v n dei vettori di V. Diremo che un vettore w V è combinazione lineare dei vettori v 1,..., v n se esistono a 1, a 2,..., a
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Edile ed Edile/Architettura. Complementi di Geometria Proiettiva Docente F.
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Edile ed Edile/Architettura Complementi di Geometria Proiettiva Docente F. Flamini POLARITA DEFINITA DA UNA CONICA 1 Spazio vettoriale duale.
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria Edile ed Edile/Architettura Complementi di Geometria Proiettiva Docente F. Flamini POLARITA DEFINITA DA UNA CONICA 1 Spazio vettoriale duale.
ii 1.20 Rango di una matrice Studio dei sistemi lineari Teoremi di Cramer e Rouché-Capelli......
 Indice Prefazione vii 1 Matrici e sistemi lineari 1 1.1 Le matrici di numeri reali................. 1 1.2 Nomenclatura in uso per le matrici............ 3 1.3 Matrici ridotte per righe e matrici ridotte
Indice Prefazione vii 1 Matrici e sistemi lineari 1 1.1 Le matrici di numeri reali................. 1 1.2 Nomenclatura in uso per le matrici............ 3 1.3 Matrici ridotte per righe e matrici ridotte
Corso di Laurea in Fisica. Geometria. a.a Canale 3 Prof. P. Piazza Magiche notazioni
 Corso di Laurea in Fisica. Geometria. a.a. 23-4. Canale 3 Prof. P. Piazza Magiche notazioni Siano V e W due spazi vettoriali e sia T : V W un applicazione lineare. Fissiamo una base B per V ed una base
Corso di Laurea in Fisica. Geometria. a.a. 23-4. Canale 3 Prof. P. Piazza Magiche notazioni Siano V e W due spazi vettoriali e sia T : V W un applicazione lineare. Fissiamo una base B per V ed una base
Registro dell insegnamento
 UNIVERSITÀ DEGLI STUDI Registro dell insegnamento Anno Accademico 2011/2012 Facoltà Ingegneria...................................... Insegnamento GEOMETRIA E ALGEBRA LINEARE.... Settore Mat03...........................................
UNIVERSITÀ DEGLI STUDI Registro dell insegnamento Anno Accademico 2011/2012 Facoltà Ingegneria...................................... Insegnamento GEOMETRIA E ALGEBRA LINEARE.... Settore Mat03...........................................
Anno Accademico 2015/2016
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2015/2016 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2015/2016 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
GE110 - Geometria 1. Prova in Itinere 2 27 Maggio 2010
 GE110 - Geometria 1 Prova in Itinere 2 27 Maggio 2010 COGNOME e NOME : Problema 1: Problema 2: Problema 3: 1 2 Problema 1. Nello spazio affine reale A 5 R si fissi il riferimento affine canonico, e siano
GE110 - Geometria 1 Prova in Itinere 2 27 Maggio 2010 COGNOME e NOME : Problema 1: Problema 2: Problema 3: 1 2 Problema 1. Nello spazio affine reale A 5 R si fissi il riferimento affine canonico, e siano
(V) (FX) L unione di due basi di uno spazio vettoriale è ancora una base dello spazio vettoriale.
 8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
Le risposte vanno giustificate con chiarezza. 1) Nello spazio vettoriale V delle matrici 2 2 a coefficienti reali, considera le matrici A 1 = , A 4 =
 Università degli Studi di Roma Tor Vergata. Corso di Laurea in Matematica Esame di Geometria 1 con Elementi di Storia Prof. F. Tovena 30 gennaio 2015 Le risposte vanno giustificate con chiarezza. 1 Nello
Università degli Studi di Roma Tor Vergata. Corso di Laurea in Matematica Esame di Geometria 1 con Elementi di Storia Prof. F. Tovena 30 gennaio 2015 Le risposte vanno giustificate con chiarezza. 1 Nello
CAPITOLO IV RISOLUZIONE DEI SISTEMI LINEARI COL METODO DEI DETERMINANTI
 CAPITOLO IV RISOLUZIONE DEI SISTEMI LINEARI COL METODO DEI DETERMINANTI 1. REGOLA DI CRAMER Sia S un sistema lineare di n ( 2) equazioni in n incognite su un campo K : a 11 x 1 + a 12 x 2 + + a 1n x n
CAPITOLO IV RISOLUZIONE DEI SISTEMI LINEARI COL METODO DEI DETERMINANTI 1. REGOLA DI CRAMER Sia S un sistema lineare di n ( 2) equazioni in n incognite su un campo K : a 11 x 1 + a 12 x 2 + + a 1n x n
Prima prova in itinere di Geometria (Corso di laurea in Fisica, Canali A-C e D-O) Prof. Barucci e Piccinni 29 novembre 2011
 Prima prova in itinere di Geometria (Corso di laurea in Fisica, Canali A-C e D-O) Prof Barucci e Piccinni 29 novembre 2011 a Scrivere subito canale, cognome e nome b Utilizzare questi fogli per le risposte
Prima prova in itinere di Geometria (Corso di laurea in Fisica, Canali A-C e D-O) Prof Barucci e Piccinni 29 novembre 2011 a Scrivere subito canale, cognome e nome b Utilizzare questi fogli per le risposte
Il Teorema Spettrale. 0.1 Applicazioni lineari simmetriche ed hermitiane
 0.1. APPLICAZIONI LINEARI SIMMETRICHE ED HERMITIANE 1 Il Teorema Spettrale In questa nota vogliamo esaminare la dimostrazione del Teorema Spettrale e studiare le sue conseguenze per quanto riguarda i prodotti
0.1. APPLICAZIONI LINEARI SIMMETRICHE ED HERMITIANE 1 Il Teorema Spettrale In questa nota vogliamo esaminare la dimostrazione del Teorema Spettrale e studiare le sue conseguenze per quanto riguarda i prodotti
SUPERFICI DI RIEMANN (settima parte) anno acc. 2008/2009
 (settima parte) anno acc. 2008/2009 Divisori molto ampi Sia X una superficie di Riemann compatta, D Div(X) un divisore su X e Φ D l applicazione associata. Si dice che D è molto ampio se Φ = Φ D è un immersione
(settima parte) anno acc. 2008/2009 Divisori molto ampi Sia X una superficie di Riemann compatta, D Div(X) un divisore su X e Φ D l applicazione associata. Si dice che D è molto ampio se Φ = Φ D è un immersione
Esercizi di MATEMATICA PER RCHITETTURA prima parte: Algebra Lineare e Geometria
 Esercizi di MATEMATICA PER RCHITETTURA prima parte: Algebra Lineare e Geometria Avvertenze In quanto segue tutti i vettori hanno il medesimo punto d origine O l origine dello spazio cartesiano. Possiamo
Esercizi di MATEMATICA PER RCHITETTURA prima parte: Algebra Lineare e Geometria Avvertenze In quanto segue tutti i vettori hanno il medesimo punto d origine O l origine dello spazio cartesiano. Possiamo
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica. Corso di Geometria ed Algebra Docente F. Flamini
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica Corso di Geometria ed Algebra Docente F. Flamini Capitolo IV - 3: Teorema Spettrale degli operatori autoaggiunti e Teorema
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica Corso di Geometria ed Algebra Docente F. Flamini Capitolo IV - 3: Teorema Spettrale degli operatori autoaggiunti e Teorema
4. Richiami: sistemi lineari e matrici
 4 Richiami: sistemi lineari e matrici Vettori 4a Combinazioni lineari Indichiamo con R n l insieme delle n-uple ordinate di elementi di R, { } R n := x = (x 1, x 2,, x n ) x i R, i = 1,,n Si dice che x
4 Richiami: sistemi lineari e matrici Vettori 4a Combinazioni lineari Indichiamo con R n l insieme delle n-uple ordinate di elementi di R, { } R n := x = (x 1, x 2,, x n ) x i R, i = 1,,n Si dice che x
Note per il corso di Geometria Corso di laurea in Ing. Edile/Architettura. 4 Sistemi lineari. Metodo di eliminazione di Gauss Jordan
 Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
Note per il corso di Geometria 2006-07 Corso di laurea in Ing. Edile/Architettura Sistemi lineari. Metodo di eliminazione di Gauss Jordan.1 Operazioni elementari Abbiamo visto che un sistema di m equazioni
A. Languasco - Esercizi Matematica B - 2. Spazi Vettoriali e Trasformazioni lineari 1
 A. Languasco - Esercizi Matematica B - 2. Spazi Vettoriali e Trasformazioni lineari 1 A: Spazi vettoriali e sottospazi Corso di Matematica B - Ingegneria Informatica Testi di Esercizi A1. Provare che l
A. Languasco - Esercizi Matematica B - 2. Spazi Vettoriali e Trasformazioni lineari 1 A: Spazi vettoriali e sottospazi Corso di Matematica B - Ingegneria Informatica Testi di Esercizi A1. Provare che l
Basi di spazi vettoriali di polinomi Consideriamo lo spazio vettoriale dei polinomi di grado al più 2 R 2 [x] = {ax 2 + bx + c; a, b, c R},
![Basi di spazi vettoriali di polinomi Consideriamo lo spazio vettoriale dei polinomi di grado al più 2 R 2 [x] = {ax 2 + bx + c; a, b, c R}, Basi di spazi vettoriali di polinomi Consideriamo lo spazio vettoriale dei polinomi di grado al più 2 R 2 [x] = {ax 2 + bx + c; a, b, c R},](/thumbs/101/148734730.jpg) Lezione del 03.04. Dopo avere svolto un esercizio in uno spazio vettoriale di polinomi, si è introdotto il concetto di applicazione lineare e l esempio fondamentale di applicazione lineare da uno spazio
Lezione del 03.04. Dopo avere svolto un esercizio in uno spazio vettoriale di polinomi, si è introdotto il concetto di applicazione lineare e l esempio fondamentale di applicazione lineare da uno spazio
Algebra Lineare - Autunno 2008
 Algebra Lineare - Autunno 2008 Kieran O Grady 1 29 Settembre: Vettori geometrici Segmenti orientati ed equipollenza. Vettori geometrici. Somma e prodotto per uno scalare: definizione e proprietà algebriche.
Algebra Lineare - Autunno 2008 Kieran O Grady 1 29 Settembre: Vettori geometrici Segmenti orientati ed equipollenza. Vettori geometrici. Somma e prodotto per uno scalare: definizione e proprietà algebriche.
10. Il gruppo Speciale Lineare SL(V )
 1 2 3 4 5 6 7 8 9 1 10. Il gruppo Speciale Lineare SL(V ) Siano F un campo e V uno spazio vettoriale di dimensione n su F. Indichiamo con GL(V ) l insieme delle applicazioni lineari biiettive di V in sé.
1 2 3 4 5 6 7 8 9 1 10. Il gruppo Speciale Lineare SL(V ) Siano F un campo e V uno spazio vettoriale di dimensione n su F. Indichiamo con GL(V ) l insieme delle applicazioni lineari biiettive di V in sé.
LAUREA IN INGEGNERIA CIVILE ED AMBIENTE-TERRITORIO Corso di Matematica 2 Padova TEMA n.1
 LAUREA IN INGEGNERIA CIVILE ED AMBIENTE-TERRITORIO Corso di Matematica Padova -8-8 TEMA n.1 PARTE 1. Quesiti preliminari Stabilire se le seguenti affermazioni sono vere o false giustificando brevemente
LAUREA IN INGEGNERIA CIVILE ED AMBIENTE-TERRITORIO Corso di Matematica Padova -8-8 TEMA n.1 PARTE 1. Quesiti preliminari Stabilire se le seguenti affermazioni sono vere o false giustificando brevemente
Corso di Laurea in Fisica. Geometria 1. a.a Gruppo B. Prof. P. Piazza Soluzioni compito a casa del 17/11/06 B =
 Corso di Laurea in Fisica. Geometria. a.a. 26-7. Gruppo B. Prof. P. Piazza Soluzioni compito a casa del 7//6 Soluzione esercizio. Sia B {e, e 2 } e sia B {v, v 2 }. La matrice B del cambiamento di base
Corso di Laurea in Fisica. Geometria. a.a. 26-7. Gruppo B. Prof. P. Piazza Soluzioni compito a casa del 7//6 Soluzione esercizio. Sia B {e, e 2 } e sia B {v, v 2 }. La matrice B del cambiamento di base
