AM2: Tracce delle lezioni- Settimana 12 SISTEMI DI EQUAZIONI DIFFERENZIALI LINEARI
|
|
|
- Agostino Mariani
- 4 anni fa
- Visualizzazioni
Transcript
1 AM2: Tracce delle lezioni- Settimana 12 SISTEMI DI EQUAZIONI DIFFERENZIALI LINEARI Sia A = (a ij ), i, j = 1,..., n matrice n n. Le soluzioni del sistema differenziale lineare di n equazioni nelle n incognite x i (t) ( ) ẋ = Ax, ovvero ẋ i (t) = a i1 x 1 (t) a in x n (t), i = 1,..., n sono definite per tutti i tempi. Segue da Ax ( ij a 2 ij ) 1 2 x e dalla Proposizione 3. NOTA. Lo stesso vale per sistemi lineari a coefficenti variabili e continui, cioé se a ij = a ij (t), a ij C(I), i, j, I intervallo in R. Infatti ogni sistema non autonomo, ove cioé il campo f C 1 (R n R, R n ) dipenda esplicitamente dalla variabile indipendente t, ovvero ogni sistema della forma ẋ(t) = f(x(t), t) t R si puó scrivere, equivalentemente, come sistema autonoma introducendo un nuovo campo ˆf C 1 (R n R, R n R) cosí definito ˆf(x 1,..., x n, x n+1 ) = (f 1 (x 1,..., x n, x n+1 ),..., f n (x 1,..., x n, x n+1 ), 1) Evidentemente, ẋ i (t) = f i (x 1 (t),..., x n (t), t), x i (t 0 ) = c i, i = 1,..., n ẋ i (t) = ˆf i (x 1 (t),..., x n (t), x n+1 (t)), i = 1,..., n, ẋ n+1 (t) = 1, x i (t 0 ) = x i, i = 1,..., n, x n+1 (t 0 ) = t 0. Proposizione 4 L insieme di tutte le soluzioni di ( ), cioé N := {x C 1 (R, R n ) : ẋ = Ax} é un sottospazio linare di C 1 (R, R n ) di dimensione n. Il fatto, evidente, che combinazioni lineari αx(t)+βy(t) di soluzioni sia ancora soluzione si traduce nella linearitá dell insieme delle soluzioni. Poi, dire che N ha dimensione n equivale a dire che 1
2 1. Esistono n soluzioni x i C 1 (R, R n ), i = 1,..., n linearmente indipendenti, cioé tali che 2. Le x i generano N, cioé c i x i (t) = 0 t c 1 = c 2 =... = c n = 0 x N, esistono costanti c 1,..., c n tali che x(t) = c i x i (t) = 0 t Basta prendere x i nel modo seguente: fissati n vettori v i R n linearmente indipendenti, x i é la soluzione di ( ) soddisfacente la condizione iniziale x i (0) = v i. Chiaramente le x i sono linearmente indipendenti. Poi, se x é soluzione, siano c i R tali che x(0) = n c i v i = n c i x i (0) e sia ˆx(t) := n c i x i (t). Siccome x e ˆx sono soluzioni dello stesso problema di Cauchy, allora x ˆx (per il Teorema di Picard). Definizione Un sistema di n soluzioni linearmente indipendenti x i di ( ) é sistema fondamentale per ( ) e X(t) = (x i,..., x n ) = (x i j(t)) i,j=1,...,n é matrice fondamentale. Se X(0) é la matrice identitá, cioé X(0) = (e 1,..., e n ) ovvero x i j(0) = δ ij, X é matrice principale. Notiamo che se x i é sistema fondamentale allora ogni soluzione x di ( ) si scrive come combinazione lineare delle x i : x(t) = c i x i (t), c i R ( Integrale Generale ) e, se X é matrice principale X(t)c, c = (c 1,..., c n ) é la soluzione del problema di Cauchy con condizione iniziale x(0) = c. Definizione. Siano x i, i = 1,..., n soluzioni di ( ) e X(t) := (x 1,..., x n ) = (x i j(t)) i,j=1,...,n. Allora W (t) := det X(t) é il determinante Wronskiano delle x i. Proposizione 5 Siano x i n soluzioni di ( ). Le seguenti affermazioni sono equivalenti: (i) x i é sistema fondamentale (ii) W (t) 0 t (iii) esiste t 0 tale che W (t 0 ) 0 2
3 Prova. (i) implica (ii). Infatti, se no, esiste t 0 tale che W (t 0 ) = 0 e quindi i vettori x i (t 0 ) sono linearmente dipendenti, cioé esistono costanti c i non tutte nulle tali che n c i x i (t 0 ) = 0. Ora, se ˆx(t) := n c i x i (t), ˆx é soluzione che si annulla in t 0, e quindi, per l unicitá della soluzione del problema di Cauchy, n c i x i (t) = ˆx 0, cioé le x i sono linearmente dipendenti. (ii) implica ovviamente (iii). (iii) implica (i). Infatti, se no, esistono c i tale che n c i x i (t) = 0 per tutti i t e quindi anche per t = t 0, contraddicendo il fatto che i vettori di R n dati da x i (t 0 ) sono lineamente indipendenti perché a determinante diverso da zero. NOTA. variabili. Quanto sopra continua a valere anche per sistemi lineari a coefficenti RIDUZIONE A FORMA CANONICA Sia e i, i = 1,..., n base canonica di R n. Sia D(λ 1,..., λ n ) := (λ 1 e 1,..., λ n e n ) (matrice diagonale avente λ 1,..., λ n come elementi sulla diagonale principale). Il (piú semplice) sistema differenziale ẋ = D(λ 1,..., λ n )x x(t) = ((x 1 (t),..., x n (t)) é formato dalle n equazioni disaccoppiate ẋ i = λ i x i, i = 1,..., n Il sistema ammette quindi le soluzioni x i = e λ it e i Queste soluzioni sono a Wronskiano diverso da zero e quindi formano un sistema fondamentale e ogni soluzione é della forma x = c i e λit e i = ( c 1 e λ1t,..., c n e λnt), c i R ( Integrale Generale ) Se A ha n autovalori reali distinti, allora A ha una base di autovettori v i R n, i = 1,..., n. Proviamo che l Integrale Generale del sistema ẋ = Ax si scrive c i e λit v i, c i R A tale scopo, introduciamo la matrice avente come colonne gli autovettori P := ( v 1,..., v n) = ( ) vj i 3 i,j=1,...,n
4 Siccome i vettori v i sono linearmente indipendenti, P é invertibile. dapprima che A si puó ricondurre alla forma canonica Verifichiamo Infatti, P 1 AP = (λ 1 e 1,..., λ n e n ) = D(λ 1,..., λ n ) P 1 APe i = P 1 Av i = λ i P 1 v i = λ i e i ovvero λ i e i é la i-esima colonna di P 1 AP. Ma allora, se ẋ = Ax e y := P 1 x, é x = Py e ẏ = P 1 ẋ e quindi ẏ = P 1 APy = D(λ 1,..., λ n )y e quindi y = n c i e λ it e i e quindi l integrale generale di ẋ = Ax si scrive appunto P ( n c i e λ it e i ) = n c i e λ it v i. Supponiamo adesso che A abbia ancora tutti autovalori distinti, ma che abbia q autovalori reali µ i, i = 1,..., q e 2p 2 autovalori complessi, q+2p = n (notiamo che se λ = α+iβ é autovalore complesso allora anche λ = α iβ lo é, perché A é matrice di numeri reali e quindi il suo polinomio caratteristico é a coefficenti reali). Siano λ j, λ j j = 1,..., p e µ i, i = 1,..., q gli autovalori complessi e, rispettivamente, reali, di A. A tali autovalori corrispondono n autovettori linearmente indipendenti, diciamo v j, v j, j = 1,..., p, u i, i = 1,..., q : notiamo che mentre u i R n, i v j sono vettori in C n (vettori a componenti complesse) e compaiono in coppie complesse coniugate giacché Av j = λ j v j Av j = λ j v j (la lineare indipendenza sussiste, nei fatti, in C n ). Posto ξ j := Rv j, η j := Iv j (ovvero v j = ξ j + iη j, ξ j, η j R n ), é Aξ j + iaη j = Av j = λ j v j = (α j + iβ j ) (ξ j + iη j ) = α j ξ j β j η j + i(β j ξ j + α j η j ) Sia ora Aξ j = α j ξ j β j η j, Aη j = β j ξ j + α j η j P := ( ξ 1, η 1,..., ξ p, η p, u 1,... u q) la matrice (n n reale) avente le prime 2p colonne formate dai vettori parte reale e coefficente dell immaginario degli autovettori corrispondenti ai λ i e le rimanenti q colonne formate dagli autovettori reali. Ovviamente tali vettori sono linearmente indipendenti e quindi P é invertibile. Mostriamo che P 1 AP = (α 1 e 1 β 1 e 2, β 1 e 1 + α 1 e 2,..., α p e p β p e p+1, β p e p + α p e p+1, µ 1 e 2p+1,..., µ q e n ) 4
5 (P 1 AP é qui, come altrove, descritta come n-upla di vettori colonna). É questa la forma canonica di A in presenza di autovalori distinti, reali o complessi. Verifichiamolo: P 1 APe 1 = P 1 Aξ 1 = P 1 ( α 1 ξ 1 β 1 η 1) = αe 1 β 1 e 2 P 1 APe 2 = P 1 Aη 1 = P 1 ( β 1 ξ 1 + α 1 η 1) = βe 1 + α 1 e 2 e cosí via fino alle colonne di posto 2p 1 e 2p. Per le rimanenti si trova invece P 1 APe 2p+i = µ i e 2p+i. Posto y = (x, ξ, η) R q R p R p, il sistema ẏ = P 1 APy si disaccoppia nelle q equazioni ẋ i = µ i x i i = 1,..., q e nei p sistemi 2 2 ξ j = α j ξ j β j η j, η j = β j ξ j + α j η j, ξ j, η j C 1 (R, R) j = 1,..., p Posto z j (t) := ξ j (t) + iη j (t), ż j := ξ j + i η j, il sistema si riscrive come che ha le soluzioni ż j = (α j + iβ j )z j z j = c exp(α j t + iβ j t) = ce α jt (cos β j t + i sin β j t), c C Prendendo c = 1, c = i otteniamo coppie di soluzioni in forma reale ξ j = e α jt cos β j t, η j = e α jt sin β j t, ξ j = e αt j sin β j t, η j = e α jt cos β j t Si ottiengono cosí 2p + q soluzioni che, come é immediato verficare, sono a Wronskiano diverso da zero e quindi formano un sistema fondamentale per il sistema in forma canonica e che, applicando P, fornisce un sistema fondamentale per il sistema dato ẋ = Ax. Piú in generale, se P é matrice invertibile e di ẏ = P 1 APy, allora c i Py i é Integrale Generale di ẋ = Ax. n c i y i é Integrale Generale Si tratta allora di trovare una matrice P che riduca A nella forma piú semplice possibile, la sua forma canonica. Cosí abbiamo proceduto nel caso diagonalizzabile. Si puó procedere in questo modo 5
6 anche quando, a causa della presenza di autovalori multipli, fosse impossibile diagonalizzare A (ricordiamo che anche in presenza di autovalori multipli A puó avere n autovettori linearmente indipendenti e quindi essere diagonalizzabile: é questo il caso se A é simmetrica). In tali casi la forma canonica risulterá peró piuttosto complicata (forme di Jordan). Ci limitiamo a considerare il caso A ha un solo autovalore, reale, cui corrisponde un unico autovettore. Cominciamo dalla situazione piú semplice, cioé n = 2. Sia dunque λ zero di molteplicitá 2 (molteplicitá algebrica di λ) del polinomio caratteristico di A, matrice 2 2. Se la molteplicitá geometrica di λ, ovvero dim (ker(a λi)) é uguale alla molteplicitá algebrica di λ (cioé é 2) cioé a λ corrispondono due autovettori linearmente indipendenti, allora A é, come sopra, diagonalizzabile. Supponiamo quindi che λ abbia un unico autovettore v. Ció implica che Im (A λj ) = {h R 2 : u R 2 tale che Au λu = h} é un sottospazio di dimensione 1: Im (A λj ) = {tu : t R} per qualche u 0. Di piú, Im (A λj ) = {tv : t R} Questo perché Au λu = tu Au (λ + t)u = 0 e quindi t = 0 ( λ é l unico autovalore!) e quindi u é un multiplo di v ( v é l unico autovettore!) Dunque esiste u tale che Au λu = v. In particolare, u Ker(A λi) 2 ed u si dice autovettore generalizzato. Sia ora P = (v, u) la matrice avente per colonne l autovettore e l autovettore generalizzato; ovviamente P é invertibile. Si ha P 1 APe 1 = P 1 Av = P 1 λv = λe 1 P 1 APe 2 = P 1 Au = P 1 (λu + v) = λe 2 + e 1 Dunque P 1 AP = (λe 1, e 1 + λe 2 ) É questa la forma canonica di A. Il sistema associato a P 1 AP é ẋ = λx + y, ẏ = λy 6
7 Una soluzione di tale sistema é y 0, x = e λt. Una seconda soluzione é y = e λt e quindi (xe λt ) = 1 e quindi x = te λt. Tali soluzioni sono a Wronskiano non nullo e quindi formano un sistema fondamentale. Dunque un sistema fondamentale per ẋ = Ax é dato da P ( e λt e 1 ) = e λt v, P ( te λt e 1 + e λt e 2 ) = te λt v + e λt u Argomenti analoghi si applicano al caso piú generale in cui la matrice n n A ha un unico autovalore λ ( avente quindi molteplicitá algebrica n) avente molteplicitá geometrica 1, cioé Au = λu ha una sola soluzione u 1 ( a meno di multipli). La proprietá chiave (che sussiste in effetti senza ipotesi sulla molteplicitá geometrica di λ e che diamo senza dimostrazione) é la seguente: 1. Una conseguenza di (!) é che (!) Ker (A λi) n = R n (!) Ker (A λi) k = Ker (A λi) k+1 Ker (A λi) k = R n Infatti, u Ker (A λi) k+2 0 = (A λi) k+2 (u) = (A λi) k+1 (Au λu) (A λi) k (Au λu) = 0 u Ker (A λi) k+1 = Ker (A λi) k. 2. Una conseguenza di dim [Ker (A λi)] = 1 é che (+) dim [ Ker (A λi) k+1] = dim [ Ker (A λi) k] + 1 se Ker (A λi) k é sottospazio proprio di Ker (A λi) k+1. Infatti, da segue u : (A λi) k+1 (u) = 0, (A λi) k (u) 0 0 = (A λi) k+1 (u) = (A λi) (A λi) k (u) (A λi) k (αu) = u 1 per qualche α 0. Ugualmente (A λi) k+1 (u) = 0 (A λi) k (βu) = u 1 per qualche β 0 e quindi αu + βu Ker (A λi) k. In particolare, da (!) e 1., segue che allora (+) vale per ogni k < n. 3. Una conseguenza di 2. é che (A λi) [ Ker (A λi) k+1] = Ker (A λi) k 7
8 Intanto, u Ker (A λi) k+1 (A λi) k (Au λu) = 0 cioé (A λi) [ Ker (A λi) k+1] Ker (A λi) k. Poi, usando 2., dim [Ker (A λi)] = 1 dim [ (A λi) ( Ker (A λi) k+1)] = = dim [ Ker (A λi) k+1] 1 = dim [ Ker (A λi) k] Da 3. segue che esiste u 2 tale che Au 2 λu 2 = u 1, e poi, iterando, per ogni k < n esiste u k+1 Ker (A λi) k+1 tale che Au k+1 λu k+1 = u k. Sia ora P = (u 1,..., u n ) la matrice avente per colonne l autovettore u 1 e gli k = 2,..., n. Siccome u k P 1 APe 1 = P 1 Au 1 = P 1 λu 1 = λe 1 P 1 APe k = P 1 Au k = P 1 (λu k + u k 1 ) = λe k + e k 1, concludiamo che P 1 AP = (λe 1, λe 2 + e 1,..., λe n + e n 1 ) autovettori generalizzati k = 2,..., n ove P 1 AP é descritta come riga di vettori colonna. É questa la forma canonica per A. Ora, il sistema differenziale associato a P 1 AP é ẏ 1 = λy 1 + y 2, ẏ 2 = λy 2 + y 3,..., ẏ n 1 = λy n 1 + y n, ẏ n = λy n Iterando il calcolo effettuato nel caso n = 2 troviamo per tale sistema le n soluzioni (e λt, 0, , 0) (te λt, e λt, 0, , 0) (t 2 e λt, te λt, e λt, 0,..., 0)... (t n 1 e λt, t n 2 e λt,......, e λt ) Tali n soluzioni hanno Wronskiano evidentemente diverso da zero e quindi formano un sistema fondamentale da cui, applicando P, si ottiene un sistema fondamentale per ẋ = Ax. Equazioni differenziali di ordine superiore 8
9 Consideriamo il problema di Cauchy: data f C 1 (R n R, R), t 0 R, trovare δ > 0 e y C n ((t 0 δ, t 0 + δ) tale che y (n) (t) = f(y(t), y (t),..., y (n 1) (t), t), t (t 0 δ, t 0 + δ) y(t 0 ) = c 0, y (t 0 ) = c 1, y (n 1) (t 0 ) = c n Se y é una soluzione, allora x 1 := y, x 2 := y,..., x n 1 := y (n 2), x n := y (n 1) risolve il sistema differenziale del primo ordine associato ẋ 1 = x 2, ẋ n 1 = x n, ẋ n = f(x 1,..., x n, t) insieme alla condizione iniziale x 1 (t 0 ) = c 0,..., x n (t 0 ) = c n. In particolare il problema di Cauchy dato ha al piú una soluzion, ed ha in effetti esattamente una soluzione ottenuta a partire dalla soluzione del problema di Cauchy per il sistema del primo ordine associato. Si estendono poi in modo ovvio i teoremi di esistenza globale validi per i sistemi del primo ordine. In particolare, se a j, j = 1,... n sono funzioni continue in I, l equazione lineare di ordine n (EDL) y (n) (t) + a 1 (t)y (n 1) (t) +..., a n (t)y(t) = 0 ha soluzioni definite in I e tali soluzioni formano un sottospazio lineare di dimensione n di C n (I). Una base di tale spazio, diciamo y 1,..., y n, si chiama Sistema Fondamentale. Un sistema di n soluzione é un sistema fondamentale se e solo se il Wronskiano W (t) := det ( y (i 1) j (t) ) i,j=1,...,n é diverso da zero per ogni t (equivalentemente: per qualche t). Se y j, j = 1,..., n é sistema fondamentale, allora le soluzioni di (EDL) sono tutte e sole le funzioni y = c 1 y c n y n, c j R Integrale Generale Se a j sono costanti, e se λ é uno zero reale di molteplicitá q di p(λ) := λ n + a 1 λ n a n polinomio caratteristico allora (EDL) ha le q soluzioni y 1 = e λt, y 2 = te λt,... y q = t q 1 e λt Se invece λ = α + iβ é uno zero complesso di molteplicitá p (e cosí pure λ) (EDL) ha le 2p soluzioni y 1 = e αt sin βt, y 2 = te αt sin βt,... y p = t p 1 e αt sin βt ŷ 1 = e αt cos βt, ŷ 2 = e αt cos βt,... ŷ p = t p 1 e αt cos βt Si ottiene in questo modo un sistema fondamentale. 9
AM210/ : Tracce delle lezioni- Settimana XI SISTEMI DI EQUAZIONI DIFFERENZIALI LINEARI
 AM21/214-15: Tracce delle lezioni- Settimana XI SISTEMI DI EQUAZIONI DIFFERENZIALI LINEARI Sia A = At = a ij t, a ij CR, i, j = 1,..., n matrice n n. Siccome, per ogni T > risulta Atx sup At x, le soluzioni
AM21/214-15: Tracce delle lezioni- Settimana XI SISTEMI DI EQUAZIONI DIFFERENZIALI LINEARI Sia A = At = a ij t, a ij CR, i, j = 1,..., n matrice n n. Siccome, per ogni T > risulta Atx sup At x, le soluzioni
AM210/ : Tracce delle lezioni- Settimana XII
 AM210/2013-14: Tracce delle lezioni- Settimana XII SISTEMI LINEARI A COEFFICENTI COSTANTI Esponenziale di una matrice, matrice principale. Siano, a ij R. Se A = (a ij i,j=1,...,n, é e A := n=0 A n n! :=
AM210/2013-14: Tracce delle lezioni- Settimana XII SISTEMI LINEARI A COEFFICENTI COSTANTI Esponenziale di una matrice, matrice principale. Siano, a ij R. Se A = (a ij i,j=1,...,n, é e A := n=0 A n n! :=
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
0 0 c. d 1. det (D) = d 1 d n ;
 Registro Lezione di Algebra lineare del 23 novembre 216 1 Matrici diagonali 2 Autovettori e autovalori 3 Ricerca degli autovalori, polinomio caratteristico 4 Ricerca degli autovettori, autospazi 5 Matrici
Registro Lezione di Algebra lineare del 23 novembre 216 1 Matrici diagonali 2 Autovettori e autovalori 3 Ricerca degli autovalori, polinomio caratteristico 4 Ricerca degli autovettori, autospazi 5 Matrici
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti)
 Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Sistemi differenziali 2 2: esercizi svolti. 1 Sistemi lineari Stabilità nei sistemi lineari
 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Stabilità nei sistemi lineari 14 1 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Gli esercizi contrassegnati con il simbolo * presentano
Sistemi differenziali : esercizi svolti 1 Sistemi lineari Stabilità nei sistemi lineari 14 1 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Gli esercizi contrassegnati con il simbolo * presentano
Autovalori, Autovettori, Diagonalizzazione.
 Autovalori Autovettori Diagonalizzazione Autovalori e Autovettori Definizione Sia V uno spazio vettoriale sul campo K = R o C e sia T : V V un endomorfismo Un vettore non nullo v V \ {O} si dice autovettore
Autovalori Autovettori Diagonalizzazione Autovalori e Autovettori Definizione Sia V uno spazio vettoriale sul campo K = R o C e sia T : V V un endomorfismo Un vettore non nullo v V \ {O} si dice autovettore
Autovalori e autovettori di una matrice quadrata
 Autovalori e autovettori di una matrice quadrata Data la matrice A M n (K, vogliamo stabilire se esistono valori di λ K tali che il sistema AX = λx ammetta soluzioni non nulle. Questo risulta evidentemente
Autovalori e autovettori di una matrice quadrata Data la matrice A M n (K, vogliamo stabilire se esistono valori di λ K tali che il sistema AX = λx ammetta soluzioni non nulle. Questo risulta evidentemente
- ciascun autovalore di T ha molteplicità geometrica uguale alla moltplicitaà algebrica.
 Lezioni del 14.05 e 17.05 In queste lezioni si sono svolti i seguenti argomenti. Ripresa del teorema generale che fornisce condizioni che implicano la diagonalizzabilità, indebolimento delle ipotesi, e
Lezioni del 14.05 e 17.05 In queste lezioni si sono svolti i seguenti argomenti. Ripresa del teorema generale che fornisce condizioni che implicano la diagonalizzabilità, indebolimento delle ipotesi, e
Corso di Laurea in Matematica - Esame di Geometria 1. Prova scritta del 7 settembre 2015
 Corso di Laurea in Matematica - Esame di Geometria 1 Prova scritta del 7 settembre 215 Cognome Nome Numero di matricola Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi. corretti, non
Corso di Laurea in Matematica - Esame di Geometria 1 Prova scritta del 7 settembre 215 Cognome Nome Numero di matricola Voto ATTENZIONE. Riportare lo svolgimento completo degli esercizi. corretti, non
1 Addendum su Diagonalizzazione
 Addendum su Diagonalizzazione Vedere le dispense per le definizioni di autovettorre, autovalore e di trasformazione lineare (o matrice) diagonalizzabile. In particolare, si ricorda che una condizione necessaria
Addendum su Diagonalizzazione Vedere le dispense per le definizioni di autovettorre, autovalore e di trasformazione lineare (o matrice) diagonalizzabile. In particolare, si ricorda che una condizione necessaria
Diagonalizzazione di matrici: autovalori, autovettori e costruzione della matrice diagonalizzante 1 / 13
 Diagonalizzazione di matrici: autovalori, autovettori e costruzione della matrice diagonalizzante 1 / 13 Matrici diagonali 2 / 13 Ricordiamo che una matrice quadrata si dice matrice diagonale se a ij =
Diagonalizzazione di matrici: autovalori, autovettori e costruzione della matrice diagonalizzante 1 / 13 Matrici diagonali 2 / 13 Ricordiamo che una matrice quadrata si dice matrice diagonale se a ij =
AUTOVALORI, AUTOVETTORI, AUTOSPAZI
 AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
Parte 8. Prodotto scalare, teorema spettrale
 Parte 8. Prodotto scalare, teorema spettrale A. Savo Appunti del Corso di Geometria 3-4 Indice delle sezioni Prodotto scalare in R n, Basi ortonormali, 4 3 Algoritmo di Gram-Schmidt, 7 4 Matrici ortogonali,
Parte 8. Prodotto scalare, teorema spettrale A. Savo Appunti del Corso di Geometria 3-4 Indice delle sezioni Prodotto scalare in R n, Basi ortonormali, 4 3 Algoritmo di Gram-Schmidt, 7 4 Matrici ortogonali,
Corso di Geometria Ing. Informatica e Automatica Test 1: soluzioni
 Corso di Geometria Ing. Informatica e Automatica Test : soluzioni k Esercizio Data la matrice A = k dipendente dal parametro k, si consideri il k sistema lineare omogeneo AX =, con X = x x. Determinare
Corso di Geometria Ing. Informatica e Automatica Test : soluzioni k Esercizio Data la matrice A = k dipendente dal parametro k, si consideri il k sistema lineare omogeneo AX =, con X = x x. Determinare
Autovettori e autovalori
 Autovettori e autovalori Definizione 1 Sia A Mat(n, n), matrice a coefficienti reali. Si dice autovalore di A un numero λ R tale che v 0 R n Av = λv. Ogni vettore non nullo v che soddisfa questa relazione
Autovettori e autovalori Definizione 1 Sia A Mat(n, n), matrice a coefficienti reali. Si dice autovalore di A un numero λ R tale che v 0 R n Av = λv. Ogni vettore non nullo v che soddisfa questa relazione
EQUAZIONI DIFFERENZIALI
 EQUAZIONI DIFFERENZIALI 1 Primo ordine - variabili separabili Sia dato il problema di Cauchy seguente: { y = a(x)b(y) Si proceda come segue y(x 0 ) = y 0 (1) Si calcolino le radici dell equazione b(y)
EQUAZIONI DIFFERENZIALI 1 Primo ordine - variabili separabili Sia dato il problema di Cauchy seguente: { y = a(x)b(y) Si proceda come segue y(x 0 ) = y 0 (1) Si calcolino le radici dell equazione b(y)
La forma normale di Schur
 La forma normale di Schur Dario A Bini, Università di Pisa 30 ottobre 2013 Sommario Questo modulo didattico contiene risultati relativi alla forma normale di Schur, alle sue proprietà e alle sue applicazioni
La forma normale di Schur Dario A Bini, Università di Pisa 30 ottobre 2013 Sommario Questo modulo didattico contiene risultati relativi alla forma normale di Schur, alle sue proprietà e alle sue applicazioni
Corso di Matematica Discreta. Anno accademico Appunti sulla diagonalizzazione.
 Corso di Matematica Discreta. Anno accademico 2008-2009 Appunti sulla diagonalizzazione. Autovalori e autovettori di un endomorfismo lineare. Sia T : V V una applicazione lineare da uno spazio vettoriale
Corso di Matematica Discreta. Anno accademico 2008-2009 Appunti sulla diagonalizzazione. Autovalori e autovettori di un endomorfismo lineare. Sia T : V V una applicazione lineare da uno spazio vettoriale
Sistemi di due equazioni differenziali del primo ordine a coefficienti costanti
 Sistemi i ue equazioni ifferenziali el primo orine a coefficienti costanti Enrico Schlesinger In questo paragrafo si risolve il sistema i equazioni ifferenziali x ax + by () y cx + y ove x e y sono ue
Sistemi i ue equazioni ifferenziali el primo orine a coefficienti costanti Enrico Schlesinger In questo paragrafo si risolve il sistema i equazioni ifferenziali x ax + by () y cx + y ove x e y sono ue
Esempio. L immagine di f è l insieme dei vettori w = (w 1, w 2 ) R 2 che hanno w 1 = w 2. Quindi:
 Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
Nucleo, immagine e loro proprietà [Abate, 5.2] Data una applicazione lineare f : V W, chiamiamo nucleo di f l insieme N(f) := { v V : f(v) = 0 W } Se S V è un sottoinsieme del dominio, indichiamo con f(s)
LEZIONE 12. v = α 1 v α n v n =
 LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
LEZIONE 12 12.1. Combinazioni lineari. Definizione 12.1.1. Sia V uno spazio vettoriale su k = R, C e v 1,..., v n V vettori fissati. Un vettore v V si dice combinazione lineare di v 1,..., v n se esistono
Applicazioni lineari simmetriche e forme quadratiche reali.
 Applicazioni lineari simmetriche e forme quadratiche reali 1 Applicazioni lineari simmetriche Consideriamo lo spazio IR n col prodotto scalare canonico X Y = t XY = x 1 y 1 + + x n y n Definizione Un applicazione
Applicazioni lineari simmetriche e forme quadratiche reali 1 Applicazioni lineari simmetriche Consideriamo lo spazio IR n col prodotto scalare canonico X Y = t XY = x 1 y 1 + + x n y n Definizione Un applicazione
Il Teorema Spettrale. 0.1 Applicazioni lineari simmetriche ed hermitiane
 0.1. APPLICAZIONI LINEARI SIMMETRICHE ED HERMITIANE 1 Il Teorema Spettrale In questa nota vogliamo esaminare la dimostrazione del Teorema Spettrale e studiare le sue conseguenze per quanto riguarda i prodotti
0.1. APPLICAZIONI LINEARI SIMMETRICHE ED HERMITIANE 1 Il Teorema Spettrale In questa nota vogliamo esaminare la dimostrazione del Teorema Spettrale e studiare le sue conseguenze per quanto riguarda i prodotti
ESAME DI GEOMETRIA. 6 febbraio 2002 CORREZIONE QUIZ
 ESAME DI GEOMETRIA 6 febbraio CORREZIONE QUIZ. La parte reale di ( + i) 9 è positiva. QUIZ Si può procedere in due modi. Un primo modo è osservare che ( + i) =i, dunque ( + i) 9 =(+i)(i) 4 = 4 ( + i) :
ESAME DI GEOMETRIA 6 febbraio CORREZIONE QUIZ. La parte reale di ( + i) 9 è positiva. QUIZ Si può procedere in due modi. Un primo modo è osservare che ( + i) =i, dunque ( + i) 9 =(+i)(i) 4 = 4 ( + i) :
Algebra lineare. {ax 2 + bx + c R 2 [x] : 2a + 3b = 1} a b c d. M(2, 2) : a + c + d = 2. a b. c d
![Algebra lineare. {ax 2 + bx + c R 2 [x] : 2a + 3b = 1} a b c d. M(2, 2) : a + c + d = 2. a b. c d Algebra lineare. {ax 2 + bx + c R 2 [x] : 2a + 3b = 1} a b c d. M(2, 2) : a + c + d = 2. a b. c d](/thumbs/104/162200055.jpg) Algebra lineare 1. Riconoscere se il seguente insieme costituisce uno spazio vettoriale. In caso affermativo trovarne la dimensione e una base. (R n [x] denota lo spazio dei polinomi nell indeterminata
Algebra lineare 1. Riconoscere se il seguente insieme costituisce uno spazio vettoriale. In caso affermativo trovarne la dimensione e una base. (R n [x] denota lo spazio dei polinomi nell indeterminata
Geometria Prova scritta, appello unico, sessione autunnale Corso di laurea in fisica A.A 2017/2018 Canali A C, e L Pa
 Geometria Prova scritta, appello unico, sessione autunnale Corso di laurea in fisica A.A 27/28 Canali A C, e L Pa Durata: 2 ore e 3 minuti Simone Diverio Alessandro D Andrea Paolo Piccinni 7 settembre
Geometria Prova scritta, appello unico, sessione autunnale Corso di laurea in fisica A.A 27/28 Canali A C, e L Pa Durata: 2 ore e 3 minuti Simone Diverio Alessandro D Andrea Paolo Piccinni 7 settembre
Diagonalizzabilità di endomorfismi
 Capitolo 16 Diagonalizzabilità di endomorfismi 16.1 Introduzione Nei capitoli precedenti abbiamo definito gli endomorfismi su uno spazio vettoriale E. Abbiamo visto che, dato un endomorfismo η di E, se
Capitolo 16 Diagonalizzabilità di endomorfismi 16.1 Introduzione Nei capitoli precedenti abbiamo definito gli endomorfismi su uno spazio vettoriale E. Abbiamo visto che, dato un endomorfismo η di E, se
4 Autovettori e autovalori
 4 Autovettori e autovalori 41 Cambiamenti di base Sia V uno spazio vettoriale tale che dim V n Si è visto in sezione 12 che uno spazio vettoriale ammette basi distinte, ma tutte con la medesima cardinalità
4 Autovettori e autovalori 41 Cambiamenti di base Sia V uno spazio vettoriale tale che dim V n Si è visto in sezione 12 che uno spazio vettoriale ammette basi distinte, ma tutte con la medesima cardinalità
Compito di Geometria e Algebra per Ing. Informatica ed Elettronica
 Compito di Geometria e Algebra per Ing Informatica ed Elettronica 17-02-2015 1) Sia f : R 4 R 3 la funzione lineare definita da f((x, y, z, t)) = ( x + y 2z + kt, x + y + t, 2x + y + z) (x, y, z, t) R
Compito di Geometria e Algebra per Ing Informatica ed Elettronica 17-02-2015 1) Sia f : R 4 R 3 la funzione lineare definita da f((x, y, z, t)) = ( x + y 2z + kt, x + y + t, 2x + y + z) (x, y, z, t) R
Per le risposte utilizza gli spazi predisposti. Quando richiesto, il procedimento va esposto brevemente, ma in maniera comprensibile.
 COGNOME............................... NOME..................................... Punti ottenuti Esame di geometria Scrivi cognome e nome negli spazi predisposti in ciascuno dei tre fogli. Per ogni domanda
COGNOME............................... NOME..................................... Punti ottenuti Esame di geometria Scrivi cognome e nome negli spazi predisposti in ciascuno dei tre fogli. Per ogni domanda
Definizione. Sia f : V V un endomorfismo e λ R. Se esiste v V non nullo tale che
 Autovalori ed autovettori [Abate, 131] Sia f : V V un endomorfismo e λ R Se esiste v V non nullo tale che f(v) = λv, diremo che λ è un autovalore di f e che v è un autovettore di f associato a λ Lezioni
Autovalori ed autovettori [Abate, 131] Sia f : V V un endomorfismo e λ R Se esiste v V non nullo tale che f(v) = λv, diremo che λ è un autovalore di f e che v è un autovettore di f associato a λ Lezioni
AM2: Tracce delle lezioni- X Settimana
 AM: Tracce delle lezioni- X Settimana EQUAZIONI DIFFERENZIALI ORDINARIE Equazioni differenziali lineari del I ordine Date le funzioni a(x), b(x) continue in (a, b) determinare, se esistono, le funzioni
AM: Tracce delle lezioni- X Settimana EQUAZIONI DIFFERENZIALI ORDINARIE Equazioni differenziali lineari del I ordine Date le funzioni a(x), b(x) continue in (a, b) determinare, se esistono, le funzioni
0.1 Condizione sufficiente di diagonalizzabilità
 0.1. CONDIZIONE SUFFICIENTE DI DIAGONALIZZABILITÀ 1 0.1 Condizione sufficiente di diagonalizzabilità È naturale porsi il problema di sapere se ogni matrice sia o meno diagonalizzabile. Abbiamo due potenziali
0.1. CONDIZIONE SUFFICIENTE DI DIAGONALIZZABILITÀ 1 0.1 Condizione sufficiente di diagonalizzabilità È naturale porsi il problema di sapere se ogni matrice sia o meno diagonalizzabile. Abbiamo due potenziali
Elementi di Algebra Lineare. Spazio Vettoriale (lineare)
 Elementi di Algebra Lineare Spazio Vettoriale (lineare) Uno spazio vettoriale su un corpo F è una quadrupla (X, F, +, ) costituita da: un insieme di elementi X, detti vettori, un corpo F, i cui elementi
Elementi di Algebra Lineare Spazio Vettoriale (lineare) Uno spazio vettoriale su un corpo F è una quadrupla (X, F, +, ) costituita da: un insieme di elementi X, detti vettori, un corpo F, i cui elementi
Parte 7. Autovettori e autovalori
 Parte 7. Autovettori e autovalori A. Savo Appunti del Corso di Geometria 23-4 Indice delle sezioni Endomorfismi, 2 Cambiamento di base, 3 3 Matrici simili, 6 4 Endomorfismi diagonalizzabili, 7 5 Autovettori
Parte 7. Autovettori e autovalori A. Savo Appunti del Corso di Geometria 23-4 Indice delle sezioni Endomorfismi, 2 Cambiamento di base, 3 3 Matrici simili, 6 4 Endomorfismi diagonalizzabili, 7 5 Autovettori
y = cos x y = (y ) 2 + c : giustifichino le due affermazioni. y = y y = y 2 y = y(1 y) y = xy Applicazioni Equazioni delle cinetica chimica:
 Corso di laurea in Chimica Industriale Matematica II A.A. 2015/2016 Argomenti delle lezioni Giovedí 3 marzo - 2 ore. Richiami sulle equazioni e sui metodi utilizzati nel risolverle. Equazioni differenziali.
Corso di laurea in Chimica Industriale Matematica II A.A. 2015/2016 Argomenti delle lezioni Giovedí 3 marzo - 2 ore. Richiami sulle equazioni e sui metodi utilizzati nel risolverle. Equazioni differenziali.
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica. Corso di Geometria ed Algebra Docente F. Flamini
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica Corso di Geometria ed Algebra Docente F. Flamini Capitolo IV - 3: Teorema Spettrale degli operatori autoaggiunti e Teorema
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria: Elettronica Corso di Geometria ed Algebra Docente F. Flamini Capitolo IV - 3: Teorema Spettrale degli operatori autoaggiunti e Teorema
Caso di A non regolare
 Caso di A non regolare December 2, 2 Una matrice A è regolare quando è quadrata e in corrispondenza di ogni autovalore di molteplicità algebrica m si ha una caduta di rango pari proprio a m Ovvero: rk
Caso di A non regolare December 2, 2 Una matrice A è regolare quando è quadrata e in corrispondenza di ogni autovalore di molteplicità algebrica m si ha una caduta di rango pari proprio a m Ovvero: rk
3. Elementi di Algebra Lineare.
 CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
Matrici simili. Matrici diagonalizzabili.
 Matrici simili. Matrici diagonalizzabili. Definizione (Matrici simili) Due matrici quadrate A, B si dicono simili se esiste una matrice invertibile P tale che B = P A P. () interpretazione: cambio di base.
Matrici simili. Matrici diagonalizzabili. Definizione (Matrici simili) Due matrici quadrate A, B si dicono simili se esiste una matrice invertibile P tale che B = P A P. () interpretazione: cambio di base.
Compiti di geometria & algebra lineare. Anno: 2004
 Compiti di geometria & algebra lineare Anno: 24 Anno: 24 2 Primo compitino di Geometria e Algebra 7 novembre 23 totale tempo a disposizione : 3 minuti Esercizio. [8pt.] Si risolva nel campo complesso l
Compiti di geometria & algebra lineare Anno: 24 Anno: 24 2 Primo compitino di Geometria e Algebra 7 novembre 23 totale tempo a disposizione : 3 minuti Esercizio. [8pt.] Si risolva nel campo complesso l
Esercizi di Geometria 1 - Foglio 3bis
 Esercizi di Geometria - Foglio 3bis Alessandro Rubin (alex.rubin@outlook.com) Si ringrazia Ricardo Tzantzoglou per il codice L A TEX condiviso dicembre 7 Esercizio. Sia f : V W un applicazione e G = {(v,
Esercizi di Geometria - Foglio 3bis Alessandro Rubin (alex.rubin@outlook.com) Si ringrazia Ricardo Tzantzoglou per il codice L A TEX condiviso dicembre 7 Esercizio. Sia f : V W un applicazione e G = {(v,
Equazioni Differenziali (4)
 Equazioni Differenziali (4) Esercizio 1 Risolvere il problema di Cauchy y = e y x + y x, y(1) = 1. Esercizio 2 Risolvere il problema di Cauchy y = 2y 1 x 2 + 1 x, y(0) = 0. Esercizio 3 Risolvere il problema
Equazioni Differenziali (4) Esercizio 1 Risolvere il problema di Cauchy y = e y x + y x, y(1) = 1. Esercizio 2 Risolvere il problema di Cauchy y = 2y 1 x 2 + 1 x, y(0) = 0. Esercizio 3 Risolvere il problema
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
Sistemi differenziali: esercizi svolti. 1 Sistemi lineari 2 2... 2 2 Sistemi lineari 3 3... 10
 Sistemi differenziali: esercizi svolti Sistemi lineari 2 2 2 2 Sistemi lineari 3 3 2 Sistemi differenziali: esercizi svolti Sistemi lineari 2 2 Gli esercizi contrassegnati con il simbolo * presentano un
Sistemi differenziali: esercizi svolti Sistemi lineari 2 2 2 2 Sistemi lineari 3 3 2 Sistemi differenziali: esercizi svolti Sistemi lineari 2 2 Gli esercizi contrassegnati con il simbolo * presentano un
Algebra lineare e geometria AA Appunti sul cambio di base in uno spazio vettoriale
 Algebra lineare e geometria AA. -7 Appunti sul cambio di base in uno spazio vettoriale Matrice di un applicazione lineare Siano V e W due spazi vettoriali su un campo K {R, C}, entrambi finitamente generati,
Algebra lineare e geometria AA. -7 Appunti sul cambio di base in uno spazio vettoriale Matrice di un applicazione lineare Siano V e W due spazi vettoriali su un campo K {R, C}, entrambi finitamente generati,
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia
 CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2015-16 Complementi ed Esercizi 1. AUTOVETTORI e AUTOVALORI di ENDOMORFISMI e MATRICI Una applicazione lineare avente per dominio e condominio lo stesso spazio vettoriale
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2015-16 Complementi ed Esercizi 1. AUTOVETTORI e AUTOVALORI di ENDOMORFISMI e MATRICI Una applicazione lineare avente per dominio e condominio lo stesso spazio vettoriale
LA DIAGONALIZZAZIONE. asdf. Polinomi di matrici. 30 January 2012
 asdf LA DIAGONALIZZAZIONE 30 January 2012 L'intento di questo articolo è di affrontare, si spera sempre nel modo più corretto e chiaro possibile, la trattazione di un argomento importante nell'ambito dell'algebra
asdf LA DIAGONALIZZAZIONE 30 January 2012 L'intento di questo articolo è di affrontare, si spera sempre nel modo più corretto e chiaro possibile, la trattazione di un argomento importante nell'ambito dell'algebra
ESEMPIO DI SISTEMA LINEARE CON SOLUZIONE. Esercizio Si consideri il sistema di equazioni lineari dipendente da un parametro λ R:
 ESEMPIO DI SISTEMA LINEARE CON SOLUZIONE Esercizio Si consideri il sistema di equazioni lineari dipendente da un parametro λ R: x 1 + x = 0 6x 1 + (λ + )x + x 3 + x 4 = 1 x 1 4x + (λ + 1)x 3 + 6x 4 = 3
ESEMPIO DI SISTEMA LINEARE CON SOLUZIONE Esercizio Si consideri il sistema di equazioni lineari dipendente da un parametro λ R: x 1 + x = 0 6x 1 + (λ + )x + x 3 + x 4 = 1 x 1 4x + (λ + 1)x 3 + 6x 4 = 3
TEORIA DEI SISTEMI ANALISI DEI SISTEMI LTI
 TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI ANALISI DEI SISTEMI LTI Ing. Cristian
TEORIA DEI SISTEMI Laurea Specialistica in Ingegneria Meccatronica Laurea Specialistica in Ingegneria Gestionale Indirizzo Gestione Industriale TEORIA DEI SISTEMI ANALISI DEI SISTEMI LTI Ing. Cristian
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
Autovalori e autovettori
 Autovalori e autovettori Definizione 1 (per endomorfismi). Sia V uno spazio vettoriale su di un campo K e f : V V un suo endomorfismo. Si dice autovettore per f ogni vettore x 0 tale che f(x) = λx, per
Autovalori e autovettori Definizione 1 (per endomorfismi). Sia V uno spazio vettoriale su di un campo K e f : V V un suo endomorfismo. Si dice autovettore per f ogni vettore x 0 tale che f(x) = λx, per
Algebra lineare e geometria AA Appunti sul cambio di base in uno spazio vettoriale
 Algebra lineare e geometria AA. 8-9 Appunti sul cambio di base in uno spazio vettoriale Matrice di un applicazione lineare Siano V e W due spazi vettoriali su un campo K {R, C}, entrambi finitamente generati,
Algebra lineare e geometria AA. 8-9 Appunti sul cambio di base in uno spazio vettoriale Matrice di un applicazione lineare Siano V e W due spazi vettoriali su un campo K {R, C}, entrambi finitamente generati,
Matematica per Chimica, Chimica Industriale e Scienze dei Materiali Primo appello 7/02/2012 Tema A
 Matematica per Chimica, Chimica Industriale e Scienze dei Materiali Primo appello 7/02/202 Tema A NOME:..................................................... COGNOME:.....................................................
Matematica per Chimica, Chimica Industriale e Scienze dei Materiali Primo appello 7/02/202 Tema A NOME:..................................................... COGNOME:.....................................................
Applicazioni lineari e diagonalizzazione. Esercizi svolti
 . Applicazioni lineari Esercizi svolti. Si consideri l applicazione f : K -> K definita da f(x,y) = x + y e si stabilisca se è lineare. Non è lineare. Possibile verifica: f(,) = 4; f(,4) = 6; quindi f(,4)
. Applicazioni lineari Esercizi svolti. Si consideri l applicazione f : K -> K definita da f(x,y) = x + y e si stabilisca se è lineare. Non è lineare. Possibile verifica: f(,) = 4; f(,4) = 6; quindi f(,4)
FM1 - Equazioni differenziali e meccanica. Il metodo di variazione delle costanti (Livia Corsi)
 Corso di laurea in Matematica - Anno Accademico 009/010 FM1 - Equazioni differenziali e meccanica Il metodo di variazione delle costanti (Livia Corsi Il metodo di variazione delle costanti è una tecnica
Corso di laurea in Matematica - Anno Accademico 009/010 FM1 - Equazioni differenziali e meccanica Il metodo di variazione delle costanti (Livia Corsi Il metodo di variazione delle costanti è una tecnica
Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare. Marco Robutti
 Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare Marco Robutti 5 Ottobre 2017 1 Introduzione Gli esercizi di questo capitolo riguardano i seguenti
Capitolo 8 Forme quadratiche e loro applicazioni Esercizi svolti Tutorato di geometria e algebra lineare Marco Robutti 5 Ottobre 2017 1 Introduzione Gli esercizi di questo capitolo riguardano i seguenti
Matematica Discreta I
 Matematica Discreta I 5 Febbraio 8 TEMA A Esercizio Sia data la matrice A M (R) A = (i) Calcolare gli autovalori di A (ii) Determinare una base di R composta di autovettori di A (iii) Diagonalizzare la
Matematica Discreta I 5 Febbraio 8 TEMA A Esercizio Sia data la matrice A M (R) A = (i) Calcolare gli autovalori di A (ii) Determinare una base di R composta di autovettori di A (iii) Diagonalizzare la
ENDOMORFISMI. ove B := (v 1,v 2,v 3 ). (1) Determinare gli autovalori di f e le relative molteplicità algebriche e geometriche.
 ENDOMORFISMI Esercizi Esercizio 1 Siano v 1 := T (1, 1, 1, 0), v 2 := T (0, 1, 2, 1), v 3 := T (0, 0, 1, 1) Consideriamo V := L(v 1,v 2,v 3 ) R 4 e sia f End R (V ) associato alla matrice A := MB B (f)
ENDOMORFISMI Esercizi Esercizio 1 Siano v 1 := T (1, 1, 1, 0), v 2 := T (0, 1, 2, 1), v 3 := T (0, 0, 1, 1) Consideriamo V := L(v 1,v 2,v 3 ) R 4 e sia f End R (V ) associato alla matrice A := MB B (f)
Forme bilineari e prodotti scalari
 Forme bilineari e prodotti scalari Il prodotto scalare standard di R n può anche essere scritto come un prodotto riga per colonna u, v R n = u t Iv dove I è la matrice identità. Possiamo generalizzare
Forme bilineari e prodotti scalari Il prodotto scalare standard di R n può anche essere scritto come un prodotto riga per colonna u, v R n = u t Iv dove I è la matrice identità. Possiamo generalizzare
APPLICAZIONI LINEARI O OMOMORFISMI
 42 APPLICAZIONI LINEARI O OMOMORFISMI Definizione 9 Dati due spazi vettoriali U e V sullo stesso campo K, una applicazione f : U V è detta lineare o omomorfismo se soddisfa le seguenti due condizioni:
42 APPLICAZIONI LINEARI O OMOMORFISMI Definizione 9 Dati due spazi vettoriali U e V sullo stesso campo K, una applicazione f : U V è detta lineare o omomorfismo se soddisfa le seguenti due condizioni:
CORSO DI LAUREA IN INGEGNERIA.
 CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 9 GEOMETRIA E ALGEBRA LINEARE 2012/13 Esercizio 9.1 (8.40). Sia T : R 2 R 3 l applicazione definita da T(x,y) = (2x,x y,2y), e siano B = {(1,0), (1,1)
CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 9 GEOMETRIA E ALGEBRA LINEARE 2012/13 Esercizio 9.1 (8.40). Sia T : R 2 R 3 l applicazione definita da T(x,y) = (2x,x y,2y), e siano B = {(1,0), (1,1)
1 Il polinomio minimo.
 Abstract Il polinomio minimo, così come il polinomio caratterisico, è un importante invariante per le matrici quadrate. La forma canonica di Jordan è un approssimazione della diagonalizzazione, e viene
Abstract Il polinomio minimo, così come il polinomio caratterisico, è un importante invariante per le matrici quadrate. La forma canonica di Jordan è un approssimazione della diagonalizzazione, e viene
Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di Geometria 1
 Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di Geometria 1 A.A. 28-29 - Docente: Prof. E. Sernesi Tutori: Andrea Abbate e Matteo Acclavio Soluzioni del tutorato numero 1 14
Università degli Studi Roma Tre - Corso di Laurea in Matematica Tutorato di Geometria 1 A.A. 28-29 - Docente: Prof. E. Sernesi Tutori: Andrea Abbate e Matteo Acclavio Soluzioni del tutorato numero 1 14
Esercitazione 6 - Soluzione
 Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
Anno Accademico 28-29 Corso di Algebra Lineare e Calcolo Numerico per Ingegneria Meccanica Esercitazione 6 - Soluzione Immagine, nucleo. Teorema di Rouché-Capelli. Esercizio Sia L : R 3 R 3 l applicazione
2. Fra tutti i rettangoli inscritti in una circonferenza, determinare quello di area massima.
 2. Fra tutti i rettangoli inscritti in una circonferenza, determinare quello di area massima. 3. Fra tutti i cilindri a base rotonda inscritti in una sfera, determinare quello di volume massimo. 4. Dimostrare
2. Fra tutti i rettangoli inscritti in una circonferenza, determinare quello di area massima. 3. Fra tutti i cilindri a base rotonda inscritti in una sfera, determinare quello di volume massimo. 4. Dimostrare
Matrice esponenziale e sistemi differenziali lineari a coefficienti costanti
 Matrice esponenziale e sistemi differenziali lineari a coefficienti costanti Matrice esponenziale Sia A R n,n una matrice quadrata n n Per definire l esponenziale di A, prendiamo spunto dall identità e
Matrice esponenziale e sistemi differenziali lineari a coefficienti costanti Matrice esponenziale Sia A R n,n una matrice quadrata n n Per definire l esponenziale di A, prendiamo spunto dall identità e
Sistemi lineari. Sia A R m n, x R n Ax = b è un vettore di m componenti. a m,1 x 1 + a m,2 x a m,n x n = b m
 1 Sistemi lineari. Sia A R m n, x R n Ax = b è un vettore di m componenti. Numero di operazioni per calcolare b: m n moltiplicazioni m (n 1) addizioni. a 1,1 x 1 + a 1,2 x 2 +... + a 1,n x n = b 1 a 2,1
1 Sistemi lineari. Sia A R m n, x R n Ax = b è un vettore di m componenti. Numero di operazioni per calcolare b: m n moltiplicazioni m (n 1) addizioni. a 1,1 x 1 + a 1,2 x 2 +... + a 1,n x n = b 1 a 2,1
Esercizi di ripasso: geometria e algebra lineare.
 Esercizi di ripasso: geometria e algebra lineare. Esercizio. Sia r la retta passante per i punti A(2,, 3) e B(,, 2) in R 3. a. Scrivere l equazione cartesiana del piano Π passante per A e perpendicolare
Esercizi di ripasso: geometria e algebra lineare. Esercizio. Sia r la retta passante per i punti A(2,, 3) e B(,, 2) in R 3. a. Scrivere l equazione cartesiana del piano Π passante per A e perpendicolare
SISTEMI DI EQUAZIONI DIFFERENZIALI LINEARI
 SISTEMI DI EQUAZIONI DIFFERENZIALI LINEARI DANIELE ANDREUCCI DIP. METODI E MODELLI, UNIVERSITÀ LA SAPIENZA VIA A.SCARPA 16, 161 ROMA, ITALY andreucci@dmmm.uniroma1.it 1. Lo spazio delle soluzioni Un sistema
SISTEMI DI EQUAZIONI DIFFERENZIALI LINEARI DANIELE ANDREUCCI DIP. METODI E MODELLI, UNIVERSITÀ LA SAPIENZA VIA A.SCARPA 16, 161 ROMA, ITALY andreucci@dmmm.uniroma1.it 1. Lo spazio delle soluzioni Un sistema
SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI
 SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI Generalità sui sistemi Sia xt, yt la soluzione del problema di Cauchy Posto vt = e xtyt, calcolare v x = 3x x = y = x y = 0 Sia x = 3x y y = x + y Scrivere
SISTEMI DI EQUAZIONI DIFFERENZIALI- ESERCIZI SVOLTI Generalità sui sistemi Sia xt, yt la soluzione del problema di Cauchy Posto vt = e xtyt, calcolare v x = 3x x = y = x y = 0 Sia x = 3x y y = x + y Scrivere
Lezioni di Algebra Lineare V. Autovalori e autovettori
 Lezioni di Algebra Lineare V. Autovalori e autovettori Versione novembre 2008 Contenuto 1. Cambiamenti di base 2. Applicazioni lineari, matrici e cambiamenti di base 3. Autovalori e autovettori 2 1. Cambiamenti
Lezioni di Algebra Lineare V. Autovalori e autovettori Versione novembre 2008 Contenuto 1. Cambiamenti di base 2. Applicazioni lineari, matrici e cambiamenti di base 3. Autovalori e autovettori 2 1. Cambiamenti
Corso di Laurea in Fisica. Geometria. a.a Prof. P. Piazza Soluzione compito a casa del 24/10/09
 Corso di Laurea in Fisica. Geometria. a.a. 29-. Prof. P. Piazza Soluzione compito a casa del 24//9 Soluzione esercizio. Siano A e B due matrici simmetriche e λ un numero reale. Dobbiamo mostrare che anche
Corso di Laurea in Fisica. Geometria. a.a. 29-. Prof. P. Piazza Soluzione compito a casa del 24//9 Soluzione esercizio. Siano A e B due matrici simmetriche e λ un numero reale. Dobbiamo mostrare che anche
Capitolo IX DIAGONALIZZAZIONE DI MATRICI SIMMETRICHE
 Capitolo IX DIAGONALIZZAZIONE DI MATRICI SIMMETRICHE 1. Matrici ortogonali Ricordiamo che, nel Cap. VII, abbiamo studiato le matrici di cambio di base in un R spazio vettoriale. In tale occasione, abbiamo
Capitolo IX DIAGONALIZZAZIONE DI MATRICI SIMMETRICHE 1. Matrici ortogonali Ricordiamo che, nel Cap. VII, abbiamo studiato le matrici di cambio di base in un R spazio vettoriale. In tale occasione, abbiamo
Geometria e algebra lineare (II parte) Bruno Martelli
 Geometria e algebra lineare (II parte) Bruno Martelli Dipartimento di Matematica, Largo Pontecorvo 5, 56127 Pisa, Italy E-mail address: martelli at dm dot unipi dot it versione: 7 marzo 2017 Indice Introduzione
Geometria e algebra lineare (II parte) Bruno Martelli Dipartimento di Matematica, Largo Pontecorvo 5, 56127 Pisa, Italy E-mail address: martelli at dm dot unipi dot it versione: 7 marzo 2017 Indice Introduzione
Equazioni di Stato: soluzione tramite la matrice esponenziale
 Equazioni di Stato: soluzione tramite la matrice esponenziale A. Laudani November 15, 016 Un po di Sistemi Consideriamo il problema di Cauchy legato allo stato della nostra rete elettrica {Ẋ(t) = A X(t)
Equazioni di Stato: soluzione tramite la matrice esponenziale A. Laudani November 15, 016 Un po di Sistemi Consideriamo il problema di Cauchy legato allo stato della nostra rete elettrica {Ẋ(t) = A X(t)
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 27 GIUGNO 2016
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 7 GIUGNO 06 MATTEO LONGO Ogni versione del compito contiene solo due tra i quattro esercizi 6-7-8-9. Esercizio. Considerare
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA CHIMICA E DEI MATERIALI 7 GIUGNO 06 MATTEO LONGO Ogni versione del compito contiene solo due tra i quattro esercizi 6-7-8-9. Esercizio. Considerare
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006. Matematica 2 (Analisi)
 Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
Universita degli Studi di Ancona Laurea in Ingegneria Meccanica ed Informatica a Distanza Anno Accademico 2005/2006 Matematica 2 (Analisi) Nome:................................. N. matr.:.................................
ESERCIZI DI MATEMATICA DISCRETA ANNO 2006/2007
 ESERCIZI DI MATEMATICA DISCRETA ANNO 6/7 //7 () Ridurre la seguente matrice ad una a scala ridotta utilizzando il metodo di Gauss-Jordan. Soluzione. () Determinare quante e quali sono le matrici a scala
ESERCIZI DI MATEMATICA DISCRETA ANNO 6/7 //7 () Ridurre la seguente matrice ad una a scala ridotta utilizzando il metodo di Gauss-Jordan. Soluzione. () Determinare quante e quali sono le matrici a scala
Matrici jordanizzabili
 Capitolo 17 Matrici jordanizzabili 17.1 Introduzione Abbiamo visto che non tutte le matrici sono simili a matrici diagonali. Mostreremo in questo capitolo che alcune matrici sono simili a matrici di Jordan.
Capitolo 17 Matrici jordanizzabili 17.1 Introduzione Abbiamo visto che non tutte le matrici sono simili a matrici diagonali. Mostreremo in questo capitolo che alcune matrici sono simili a matrici di Jordan.
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 17 SETTEMBRE 2012
 INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 7 SETTEMBRE 202 Esercizio. Sia V = R[X] 2 lo spazio vettoriale dei polinomi ax 2 + bx + c nella variabile X di grado al più 2 a coefficienti
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 7 SETTEMBRE 202 Esercizio. Sia V = R[X] 2 lo spazio vettoriale dei polinomi ax 2 + bx + c nella variabile X di grado al più 2 a coefficienti
(V) (FX) L unione di due basi di uno spazio vettoriale è ancora una base dello spazio vettoriale.
 8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
Equazioni differenziali lineari di ordine n
 Equazioni differenziali lineari di ordine n Si tratta di equazioni del tipo u (n) (t) + a 1 (t)u (n 1) (t) +... + a n 1 (t)u (t) + a n (t)u(t) = f(t), t I, (1) con n intero 2 ed I R intervallo reale, in
Equazioni differenziali lineari di ordine n Si tratta di equazioni del tipo u (n) (t) + a 1 (t)u (n 1) (t) +... + a n 1 (t)u (t) + a n (t)u(t) = f(t), t I, (1) con n intero 2 ed I R intervallo reale, in
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA
 Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
Cognome Nome Matricola FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA Ciarellotto, Esposito, Garuti Prova del 21 settembre 2013 Dire se è vero o falso (giustificare le risposte. Bisogna necessariamente rispondere
Prova scritta di Geometria 1 Docente: Giovanni Cerulli Irelli 20 Gennaio 2017
 Prova scritta di Geometria Docente: Giovanni Cerulli Irelli Gennaio 7 Esercizio. Si considerino i seguenti tre punti dello spazio euclideo: P :=, Q :=, R :=.. Dimostrare che P, Q ed R non sono collineari.
Prova scritta di Geometria Docente: Giovanni Cerulli Irelli Gennaio 7 Esercizio. Si considerino i seguenti tre punti dello spazio euclideo: P :=, Q :=, R :=.. Dimostrare che P, Q ed R non sono collineari.
Applicazioni lineari e diagonalizzazione
 Autovalori e autovettori Matrici associate a applicazioni lineari Endomorfismi semplici e matrici diagonalizzabili Prodotti scalari e Teorema Spettrale nel caso generale 2 2006 Politecnico di Torino 1
Autovalori e autovettori Matrici associate a applicazioni lineari Endomorfismi semplici e matrici diagonalizzabili Prodotti scalari e Teorema Spettrale nel caso generale 2 2006 Politecnico di Torino 1
Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 12/07/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI
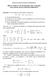 Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 12/07/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI Esercizio 1 Si consideri la conica affine d equazione 9x 2 + 6y 2 4xy 6x + 8y = 1 (1)
Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 12/07/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI Esercizio 1 Si consideri la conica affine d equazione 9x 2 + 6y 2 4xy 6x + 8y = 1 (1)
Elementi di Algebra Lineare
 Elementi di Algebra Lineare Corso di Calcolo Numerico, a.a. 2009/2010 Francesca Mazzia Dipartimento di Matematica Università di Bari 13 Marzo 2006 Francesca Mazzia (Univ. Bari) Elementi di Algebra Lineare
Elementi di Algebra Lineare Corso di Calcolo Numerico, a.a. 2009/2010 Francesca Mazzia Dipartimento di Matematica Università di Bari 13 Marzo 2006 Francesca Mazzia (Univ. Bari) Elementi di Algebra Lineare
ẋ + a 0 x = 0 (1) Dimostrazione. Risolvendo la (1) per separazione di variabili, troviamo x(t) = c 0 e a0t (2) φ :R S 1 ẍ + a 1 ẋ + a 0 x = 0 (3)
 Corso di laurea in Matematica - Anno Accademico 006/007 FM1 - Equazioni dierenziali e meccanica Il metodo della variazione delle costanti (Livia Corsi Il metodo della variazione delle costanti è una tecnica
Corso di laurea in Matematica - Anno Accademico 006/007 FM1 - Equazioni dierenziali e meccanica Il metodo della variazione delle costanti (Livia Corsi Il metodo della variazione delle costanti è una tecnica
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2012 Rossi Algebra Lineare 2012 1 / 59 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2012 Rossi Algebra Lineare 2012 1 / 59 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
Fondamenti di Algebra Lineare e Geometria TEMA A
 Fondamenti di Algebra Lineare e Geometria Ingegneria Aerospaziale ed Ingegneria dell Energia - Canale B Secondo Appello - luglio TEMA A Risolvere i seguenti esercizi motivando adeguatamente ogni risposta.
Fondamenti di Algebra Lineare e Geometria Ingegneria Aerospaziale ed Ingegneria dell Energia - Canale B Secondo Appello - luglio TEMA A Risolvere i seguenti esercizi motivando adeguatamente ogni risposta.
Anno Accademico 2016/2017
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2016/2017 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2016/2017 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
DIAGONALIZZAZIONE. M(f) =
 DIAGONALIZZAZIONE Esercizi Esercizio 1. Sia f End(R 3 ) associato alla matrice M(f) = 0 1 2 0. 2 (1) Determinare gli autovalori di f e le relative molteplicità. (2) Determinare gli autospazi di f e trovare,
DIAGONALIZZAZIONE Esercizi Esercizio 1. Sia f End(R 3 ) associato alla matrice M(f) = 0 1 2 0. 2 (1) Determinare gli autovalori di f e le relative molteplicità. (2) Determinare gli autospazi di f e trovare,
LEZIONE 16 A = Verifichiamo se qualcuna fra le entrate a di A è suo autovalore. determinare per quale entrata a di A risulta rk(a ai 2 ) 1.
 LEZIONE 16 16.1. Autovalori, autovettori ed autospazi di matrici. Introduciamo la seguente definizione. Definizione 16.1.1. Siano k = R, C e A k n,n. Un numero λ k si dice autovalore di A su k) se rka
LEZIONE 16 16.1. Autovalori, autovettori ed autospazi di matrici. Introduciamo la seguente definizione. Definizione 16.1.1. Siano k = R, C e A k n,n. Un numero λ k si dice autovalore di A su k) se rka
Forma canonica di Jordan
 Capitolo INTRODUZIONE Forma canonica di Jordan Siano λ i, per i =,, h, gli autovalori distinti della matrice A e siano r i i corrispondenti gradi di molteplicità all interno del polinomio caratteristico:
Capitolo INTRODUZIONE Forma canonica di Jordan Siano λ i, per i =,, h, gli autovalori distinti della matrice A e siano r i i corrispondenti gradi di molteplicità all interno del polinomio caratteristico:
DIAGONALIZZAZIONE E FORME QUADRATICHE / ESERCIZI PROPOSTI
 M.GUIDA, S.ROLANDO, 204 DIAGONALIZZAZIONE E FORME QUADRATICHE / ESERCIZI PROPOSTI L asterisco contrassegna gli esercizi più difficili o che possono considerarsi meno basilari. Autovalori, autospazi e diagonalizzazione
M.GUIDA, S.ROLANDO, 204 DIAGONALIZZAZIONE E FORME QUADRATICHE / ESERCIZI PROPOSTI L asterisco contrassegna gli esercizi più difficili o che possono considerarsi meno basilari. Autovalori, autospazi e diagonalizzazione
Algebra Lineare Autovalori
 Algebra Lineare Autovalori Stefano Berrone Sandra Pieraccini Dipartimento di Matematica Politecnico di Torino, Corso Duca degli Abruzzi 24, 10129, Torino, Italy e-mail: sberrone@calvino.polito.it sandra.pieraccini@polito.it
Algebra Lineare Autovalori Stefano Berrone Sandra Pieraccini Dipartimento di Matematica Politecnico di Torino, Corso Duca degli Abruzzi 24, 10129, Torino, Italy e-mail: sberrone@calvino.polito.it sandra.pieraccini@polito.it
Rango di una matrice e teorema di Rouché-Capelli
 Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
