Funzioni continue. Hynek Kovarik. Università di Brescia. Analisi Matematica 1
|
|
|
- Federica Di Gregorio
- 4 anni fa
- Visualizzazioni
Transcript
1 Funzioni continue Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 1 / 44
2 Funzioni continue Definizione Siano f : A R e x 0 A. Diciamo che f è CONTINUA in x 0 A se ε > 0 δ > 0 : x ]x 0 δ, x 0 + δ[ A f (x) f (x 0 ) < ε. Diciamo che f : A R è CONTINUA su A se f è continua in ogni punto di A. Interpretazine geometrica: a piccole variazioni di x, vicino a x 0, corrispondono piccole variazioni del valore f (x) (che rimane vicino a f (x 0 ).) Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 2 / 44
3 Esempi 1 La funzione f : x 1 x è continua su A = R \ {0} 2 La funzione f : x sin ( ) 1 è continua su A = R \ {0} x Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 3 / 44
4 Caratterizzazione della continuità mediante limite Teorema Dati f : A R e x 0 A, supponiamo che x 0 sia un punto di accumulazione per A. Allora f è continua in x 0 lim x x0 f (x) = f (x 0 ). Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 4 / 44
5 Caratterizzazione di continuità mediante successioni Teorema: Sia f : A R. Allora f è continua in x 0 {x n } A con x n x 0 si ha lim n f (x n) = f (x 0 ). Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 5 / 44
6 Esempio Usiamo il teorema precedente per dimostrare che la funzione ( ) 1 f (x) = cos, x R \ {0} x non ammette limite per x 0. Basta trovare due successioni {a n } e {b n } infinitesime e tali che Scegliamo, ad esempio, lim f (a n) lim f (b n). n n Si ha a n = lim f (a n) = 0, n 1 π 2 + 2πn, b n = 1 2πn. lim f (b n) = 1. n Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 6 / 44
7 Continuità e operazioni algebriche su funzioni Siano f, g : A R due funzioni continue e sia x 0 A. Allora, 1 le funzioni 2 Se allora f + g, f g sono continue in x 0. I intorno di x 0 tale che g(x) 0 x I, f g è continua in x 0. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 7 / 44
8 Conseguenza: - i polinomi; P(x) = a n x n + a n 1 x n a 1 x + a 0 sono funzioni continue in R. - le funzioni razionali; f (x) = P(x) Q(x), P, Q polinomi sono continue in ogni punto del loro dominio. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 8 / 44
9 Teorema Siano A, B R, f : A B, g : B R e x 0 A. Se f è continua in x 0 e g è continua in f (x 0 ) B allora g f è continua in x 0. Dimostrazione: Sia ε > 0. Siccome g è continua in f (x 0 ), esiste δ > 0 tale che y I δ (f (x 0 )) B : g(y) g(f (x 0 ) < ε. D altra parte, f è continua in x 0. Quindi esiste δ > 0 tale che x I δ (x 0 ) A : f (x) f (x 0 ) < ε. Scegliendo ε = δ e y = f (x) si ottiene da cui la tesi x I δ (x 0 ) A : g(f (x)) g(f (x 0 ) < ε, Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 9 / 44
10 Conseguenza: Se f : A R è continua su A, sin f (x), cos f (x), f (x), a f (x), log a f (x)(f (x) > 0), sono anch esse continue in A. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 10 / 44
11 Punti di discontinuità Classifichiamo i punti di discontinuità di una funzione f in queste 4 categorie: 1 punti di discontinuità eliminabile; 2 punti di infinito; 3 punti di discontinuità di tipo salto; 4 punti di discontinuità di seconda specie. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 11 / 44
12 1 Se lim x x0 f (x) = L R con L f (x 0 ), allora si dice che la funzione f presenta una DISCONTINUITÀ ELIMINABILE in x 0. N.B.: se f ha in x 0 un punto di discontinuità eliminabile, allora la funzione { f (x) se x dom f, x x 0 h(x) = L se x = x 0. è continua in x 0. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 12 / 44
13 Esempio f : R R f (x) = { 0 se x 0 1 se x = 0 ha in x 0 = 0 una discontinuità eliminabile. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 13 / 44
14 2 Se lim x x0 f (x) =, oppure se esistono i limiti destro e sinistro e (almeno) uno di questi è infinito (= + oppure = ), allora si dice che x 0 è PUNTO DI INFINITO. 3 Se i limiti destro e sinistro esistono in R ma sono differenti si dice che x 0 è PUNTO DI SALTO. 4 Se (almeno) uno dei due limiti destro o sinistro non esiste, allora si dice che x 0 presenta una DISCONTINUITÀ DI SECONDA SPECIE. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 14 / 44
15 Proprietà delle funzioni continue Definizione Sia A R e sia f : I R. Chiamiamo 1 estremo superiore di f, l estremo superiore dell insieme immagine di f, ossia sup f = sup{f (x) : x A}. A 2 massimo di f, il massimo di im(f ) max f = max{f (x) : x A}. A 3 Un punto x 0 in cui f (x 0 ) = max A f si dice punto di massimo per f e quindi vale f (x) f (x 0 ) x A. Attenzione!!!!! non confondere - punto di massimo per f - massimo di f (si dice anche valore di massimo di f ) Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 15 / 44
16 Definizione Sia A R e sia f : A R. Chiamiamo 1 estremo inferiore di f, l estremo inferiore dell insieme immagine di f, ossia inf A f = inf{f (x) : x A}. 2 minimo di f (o valore di minimo di f ), il minimo dell insieme immagine di f, ossia min A f = min{f (x) : x A} 3 Un punto x 0 in cui f (x 0 ) = min f si dice punto di minimo per f e quindi vale f (x 0 ) f (x) x A. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 16 / 44
17 Teorema di Weierstrass Sia f : [a, b] R continua su [a, b] intervallo chiuso e limitato. Allora f ammette almeno un punto di massimo e almeno un punto di minimo in [a, b], cioè x m, x M [a, b] : x [a, b] f (x m ) f (x) f (x M ). Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 17 / 44
18 Tutte le ipotesi del teorema sono fondamentali: se una di esse non è soddisfatta, la tesi è falsa: 1. Siano I = [0, 1[, f (x) = 2x + 1. f è continua su I, I è limitato ma non è chiuso. Notiamo che f ammette minimo su I : è x = 0, min I f = 1, f non ammette massimo: si ha sup I f = 3, che non viene assunto in alcun punto di I. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 18 / 44
19 2. Siano I = R, f (x) = arctan(x). I è illimitato, f non ha né punti di massimo, né punti di minimo su I. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 19 / 44
20 3. Siano I = [ 1, 1] e f : [ 1, 1] R data da { x 2 per x [ 1, 1] \ {0}, f (x) = 2 se x = 0. f non ha minimo, e inf f = 0. max f = 2 e 0 è l unico punto di massimo. In questo caso I = [ 1, 1] è chiuso e limitato, ma f non è continua. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 20 / 44
21 Corollario al teorema di Weierstrass Sia f : [a, b] R continua in [a, b]. Allora f è limitata. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 21 / 44
22 Teorema di Bolzano o degli zeri Sia f : [a, b] R una funzione continua in [a, b] tale che f (a)f (b) < 0. Allora esiste almeno un punto c (a, b) tale che f (c) = 0. Chiamiamo il punto c zero della funzione f. Osservazione: Il teorema assicura che f ammette almeno uno zero c, non ci dice nulla sull unicitàdi c. In generale, c non è unico! Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 22 / 44
23 Una conseguenza del teorema degli zeri Teorema (dei valori intermedi) Sia f : [a, b] R una funzione continua in [a, b]. Allora, f assume tutti i valori compresi tra min [a,b] f e max [a,b] f. In particolare, im(f ) è un intervallo. Dimostrazione: Siano x min e x max i punti di minimo e massimo e denotiamo m = min [a,b] f = f (x min), M = max [a,b] f = f (x max). Senza ledere la generalità possiamo supporre che x min < x max. Sia y (n, M). Dobbiamo dimostrare che esiste un c (a, b) tale che f (c) = y. (1) Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 23 / 44
24 Sia g(x) = f (x) y. Allora g(x min ) < 0 e g(x max ) > 0. Quindi il Teorema di Bolzano degli zeri applicato alla funzione g sull intervallo [x min, x max ] implica che esite c (x min, x max ) (a, b), tale che g(c) = 0. Da qui segue l equazione (1) e quindi la tesi. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 24 / 44
25 Funzioni continue invertibili Sia f : A R continua in A e iniettiva. Allora f è invertibile, con funzione inversa f 1 : im(f ) R. f 1 è continua in im(f )? Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 25 / 44
26 Esempio sia A = [0, 1] (2, 3] (unione di due intervalli) e sia f : A R data da { x se x [0, 1] f (x) = x 1 se x (2, 3]. Allora f è continua in A ma la sua inversa { f 1 : [0, 2] R, f 1 x se x [0, 1] (x) = x + 1 se x (1, 2]. è però una funzione discontinua in x = 1. Notiamo che A non è un intervallo, ma è l unione di due intervalli. Se invece A = I è un intervallo, la situazione cambia. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 26 / 44
27 Teorema: caratterizzazione delle funzioni continue invertibili Sia I un intervallo e sia f : I R una funzione continua su I. Allora f è invertibile f è strettamente monotona. Se f è strettamente monotona, allora la funzione inversa f 1 : im(f ) R è ancora monotona, con una monotonia dello stesso tipo di f. Domanda: essa è anche continua? Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 27 / 44
28 Teorema Siano I intervallo f : I R continua su I f : I R invertibile Allora f 1 : im(f ) R è continua. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 28 / 44
29 Confronto di funzioni Sia x 0 R e supponiamo che f, g siano due funzioni definite in un intorno di x 0. Supponiamo inoltre che esista il limite Definizione f (x) lim x x 0 g(x) = l R. 1 se l R, l 0, diciamo che f è dello stesso ordine di grandezza di g per x x 0 e scriviamo f (x) g(x) x x 0 2 se l = 1, diciamo che f è equivalemnte a g per x x 0 : f (x) g(x) x x 0 3 se l = 0, diciamo che f è trascurabile rispetto g per x x 0 : f (x) = o(g(x)) x x 0 Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 29 / 44
30 Le espressioni, e o ( o piccolo ) si chiamano i simboli di Landau. Esempio Per f (x) = sin x e g(x) = x si ha sin x x x 0 sin x = o(x) x ±. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 30 / 44
31 Proprietà di simboli di Landau Per x x 0 si ha 1 f (x) g(x) f (x) g(x) 2 f (x) g(x) f (x) = g(x) + o(g(x)) 3 λ R, λ 0 : f (x) = o(λg(x)) f (x) = o(g(x)) 4 λ R : f (x) = o(g(x)) λf (x) = o(g(x)) 5 f (x) = o(1) lim x x0 f (x) = 0 Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 31 / 44
32 Confronto di alcune funzioni elementari Per n, m N si ha 1 x n = o(x m ) x 0 n > m 2 x n = o(x m ) x ± n < m 3 x α = o(e x ) x + α R 4 e x = o( x α ) x α R 5 log x = o(x α ) x + α > 0 6 log x = o(x α ) x 0 + α > 0 Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 32 / 44
33 Proposizione Sia x 0 R e siano f, f, g e g tali che Se esistono i limiti allora f (x) f (x), g(x) g(x) x x 0. lim f (x) g(x) e lim x x 0 x x0 f (x) g(x), f (x) lim f (x) g(x) = lim f (x) g(x) e lim x x 0 x x0 x x0 g(x) = lim x x 0 f (x) g(x) Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 33 / 44
34 Esempio Siccome 1 cos x + sin x x x x x 0 log(1 + 2x) + x 2 2x + x 2 2x x 0, si ha 1 cos x + sin x lim x 0 log(1 + 2x) + x 2 = 1 2 Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 34 / 44
35 Infinitesimi Definizione Sia f : dom(f ) R e x 0 R punto di accumulazione per dom(f ). Se lim f (x) = 0, x x 0 si dice che f è infinitesima per x x 0. Definizione Siano f e ϕ due funzioni infinitesime per x x 0. Sia ϕ 0. Se esiste α > 0 tale che f (x) ϕ(x) α x x 0, allora α si dice l ordine di infinitesimo di f rispetto a ϕ per x x 0. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 35 / 44
36 Esempio La funzione f (x) = x 2 4x + 4 è infinitesima di ordine 2 rispetto a ϕ(x) = x 2 per x 2. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 36 / 44
37 Infiniti Definizione Sia f : dom(f ) R e x 0 R punto di accumulazione per dom(f ). Se lim f (x) = ± o lim f (x) = ±, x x 0 + x x 0 allora si dice che f è infinita per x x 0. Definizione Siano f e ϕ due funzioni infinite per x x 0. Sia ϕ 0. Se esiste α > 0 tale che f (x) ϕ(x) α x x 0, allora α si dice l ordine di infinito di f rispetto a ϕ per x x 0. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 37 / 44
38 Esempio La funzione f (x) = x 4 + x + 1 è infinita di ordine 2 rispetto a ϕ(x) = x per x +. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 38 / 44
39 Asintoti Definizione Sia f : A R definita in A = (a, + ) con a R. Se esistono m, q R tali che lim (f (x) mx q) = 0, (2) x + allora diciamo che la retta y = mx + q è asintoto destro della funzione f. Definizione Sia f : A R definita in A = (, a) con a R. Se esistono m, q R tali che lim (f (x) mx q) = 0, (3) x allora diciamo che la retta y = mx + q è asintoto sinistro della funzione f. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 39 / 44
40 Asintoti Definizione L asintoto y = mx + q si dice orizzontale se m = 0. obliquo se m 0. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 40 / 44
41 Asintoti Definizione Sia f : A R e sia x 0 un punto di accumulazione per A. Se lim f (x) = ± o lim f (x) = ±, x x 0 + x x 0 allora diciamo che la retta x = x 0 è asintoto verticale di f. Esempio La funzione tan : ( π/2, π/2) R ammette asintoti verticali in x 0 = π/2 e x 0 = π/2. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 41 / 44
42 Asintoti: calcolo di coefficienti m e q 1 Se esistono finiti i limiti f (x) lim =: l 1 e lim x + x (f (x) l 1x) =: l 2, x + allora f ammette asintoto destro y = mx + q con m = l 1 e q = l 2. 2 Analogamente, se esistono finiti i limiti f (x) lim =: l 1 e lim x x (f (x) l 1x) =: l 2, x allora f ammette asintoto sinistro y = mx + q con m = l 1 e q = l 2. Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 42 / 44
43 Esempio: Sia f : R R data da Vale f (x) = log(1 + e x ) + x 2 + x + 1 e f (x) log(e x (1 + e x )) + x lim = lim x + x x + x = lim x + 2x + log(1 + e x ) x = 2, lim (f (x) 2x) = lim x + (log(1 + x + ex ) x) + lim ( x 2 + x + 1 x) x + = lim x + (log(e x (1 + e x )) + = lim log(1 + x + e x ) + 1 }{{} 2 = 1 2. =0 lim x + x + 1 x 2 + x x) Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 43 / 44
44 Quindi f ammette asintoto destro y = 2x Analogamente si ha e f (x) x lim = lim x x x x = 1, lim (f (x) + x) = lim x log(1 + x ex ) }{{} =0 = lim x x + 1 x 2 + x + 1 x = Quindi f ammette asintoto sinistro y = x lim x ( x 2 + x x) lim x x 2x = 1 2 Hynek Kovarik (Università di Brescia) Funzioni continue Analisi Matematica 1 44 / 44
Limiti e continuità. Hynek Kovarik. Analisi A. Università di Brescia. Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68
 Limiti e continuità Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68 Cenni di topologia La nozione di intorno Sia x 0 R e r > 0.
Limiti e continuità Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi A 1 / 68 Cenni di topologia La nozione di intorno Sia x 0 R e r > 0.
Algebra dei limiti. quando l espressione a secondo membro è definita (non si hanno forme indeterminate), si ha. lim. f (x)
 Algebra dei limiti Teorema. Se lim f () = l R e lim g() = m R, allora, 0 0 quando l espressione a secondo membro è definita (non si hanno forme indeterminate), si ha lim (f () + g()) = lim f () + lim g()
Algebra dei limiti Teorema. Se lim f () = l R e lim g() = m R, allora, 0 0 quando l espressione a secondo membro è definita (non si hanno forme indeterminate), si ha lim (f () + g()) = lim f () + lim g()
 Limiti di funzioni all infinito (1) lim f(x) = λ R x K>0 : x > K f(x) λ < ε (2) lim f(x) = x M>0 >0 K>0 : x > K f(x) > M (3) lim f(x) = x M>0 >0 K>0 : x > K f(x) < < M Se f(x) è definita in un intorno
Limiti di funzioni all infinito (1) lim f(x) = λ R x K>0 : x > K f(x) λ < ε (2) lim f(x) = x M>0 >0 K>0 : x > K f(x) > M (3) lim f(x) = x M>0 >0 K>0 : x > K f(x) < < M Se f(x) è definita in un intorno
Calcolo differenziale II
 Calcolo differenziale II Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Derivate (II) Analisi Matematica 1 1 / 36 Massimi e minimi Definizione Sia A R, f
Calcolo differenziale II Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Derivate (II) Analisi Matematica 1 1 / 36 Massimi e minimi Definizione Sia A R, f
ANALISI 1 1 NONA/DECIMA LEZIONE Limiti notevoli di funzioni Funzioni continue
 ANALISI 1 1 NONA/DECIMA LEZIONE Limiti notevoli di funzioni Funzioni continue 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email: saccon@mail.dm.unipi.it web: http://www2.ing.unipi.it/
ANALISI 1 1 NONA/DECIMA LEZIONE Limiti notevoli di funzioni Funzioni continue 1 prof. Claudio Saccon, Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email: saccon@mail.dm.unipi.it web: http://www2.ing.unipi.it/
Limiti di funzioni. Hynek Kovarik. Università di Brescia. Analisi Matematica 1
 Limiti di funzioni Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi Matematica 1 1 / 38 Cenni di topologia La nozione di intorno
Limiti di funzioni Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Limiti e continuità Analisi Matematica 1 1 / 38 Cenni di topologia La nozione di intorno
Analisi Matematica 1 Quattordicesima lezione
 Analisi Matematica 1 Quattordicesima lezione prof. Claudio Saccon Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email: saccon@mail.dm.unipi.it web: http://www2.ing.unipi.it/ d6081/index.html
Analisi Matematica 1 Quattordicesima lezione prof. Claudio Saccon Dipartimento di Matematica Applicata, Via F. Buonarroti 1/C email: saccon@mail.dm.unipi.it web: http://www2.ing.unipi.it/ d6081/index.html
Successioni numeriche
 Successioni numeriche Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Successioni Analisi Matematica 1 1 / 48 Definizione Una successione a valori reali è
Successioni numeriche Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Successioni Analisi Matematica 1 1 / 48 Definizione Una successione a valori reali è
Nozioni di base - Quiz - 2
 Nozioni di base - Quiz - Rispondere ai seguenti quesiti (una sola risposta è corretta).. L insieme delle soluzioni della disequazione (a) (0, ) (, + ) (x ) log(x) x + 0 è: (b) [, ] (c) (d) (e) (, + ) (0,
Nozioni di base - Quiz - Rispondere ai seguenti quesiti (una sola risposta è corretta).. L insieme delle soluzioni della disequazione (a) (0, ) (, + ) (x ) log(x) x + 0 è: (b) [, ] (c) (d) (e) (, + ) (0,
Proprietà globali delle funzioni continue
 Limiti e continuità Teorema di esistenza degli zeri Teorema dei valori intermedi Teorema di Weierstrass Teoremi sulla continuità della funzione inversa 2 2006 Politecnico di Torino 1 Data una funzione
Limiti e continuità Teorema di esistenza degli zeri Teorema dei valori intermedi Teorema di Weierstrass Teoremi sulla continuità della funzione inversa 2 2006 Politecnico di Torino 1 Data una funzione
Analisi Matematica. Limiti di successioni numeriche e di funzioni
 a.a. 2014/2015 Laurea triennale in Informatica Analisi Matematica Limiti di successioni numeriche e di funzioni Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per
a.a. 2014/2015 Laurea triennale in Informatica Analisi Matematica Limiti di successioni numeriche e di funzioni Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per
Dimostrazione. Indichiamo con α e β (finiti o infiniti) gli estremi dell intervallo I. Poniamo
 C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
C.6 Funzioni continue Pag. 114 Dimostrazione del Corollario 4.25 Corollario 4.25 Sia f continua in un intervallo I. Supponiamo che f ammetta, per x tendente a ciascuno degli estremi dell intervallo, iti
Continuità di funzioni
 Continuità di funzioni Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva Università degli Studi di Padova Dipartimento di Matematica 2 novembre 2015 Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva
Continuità di funzioni Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva Università degli Studi di Padova Dipartimento di Matematica 2 novembre 2015 Annalisa Cesaroni, Paola Mannucci e Alvise Sommariva
Matematica: Continuità e calcolo dei limiti (Cap.7)
 Matematica: Continuità e calcolo dei limiti (Cap.7) Marco Dall Aglio LUISS University mdallaglio@luiss.it A.A. 2016-17 Dall Aglio (LUISS) Guerraggio Cap.7 A.A. 2016-17 1 / 24 Continuità in un punto Definizione
Matematica: Continuità e calcolo dei limiti (Cap.7) Marco Dall Aglio LUISS University mdallaglio@luiss.it A.A. 2016-17 Dall Aglio (LUISS) Guerraggio Cap.7 A.A. 2016-17 1 / 24 Continuità in un punto Definizione
Derivate. Hynek Kovarik. Analisi A. Università di Brescia. Hynek Kovarik (Università di Brescia) Derivate Analisi A 1 / 33
 Derivate Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Derivate Analisi A 1 / 33 Definizione: rapporto incrementale Sia f : domf R R. Dati x 1, x 2 domf con x 1 x
Derivate Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Derivate Analisi A 1 / 33 Definizione: rapporto incrementale Sia f : domf R R. Dati x 1, x 2 domf con x 1 x
Istituzioni di Matematiche terza parte
 Istituzioni di Matematiche terza parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 35 index Il concetto di limite 1 Il
Istituzioni di Matematiche terza parte anno acc. 2011/2012 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 35 index Il concetto di limite 1 Il
Istituzioni di Matematiche seconda parte
 Istituzioni di Matematiche seconda parte anno acc. 2010/2011 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 26 index 1 2 Continuità Cristina Turrini
Istituzioni di Matematiche seconda parte anno acc. 2010/2011 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 26 index 1 2 Continuità Cristina Turrini
DERIVATE. Rispondere ai seguenti quesiti. Una sola risposta è corretta. 1. Data la funzione f(x) =2+ x 7, quale delle seguente affermazioni èvera?
 DERIVATE Rispondere ai seguenti quesiti. Una sola risposta è corretta.. Data la funzione f(x) =+ x 7, quale delle seguente affermazioni èvera? (a) f(x) nonè derivabile in x =0 (b) f (0) = (c) f (0) = (d)
DERIVATE Rispondere ai seguenti quesiti. Una sola risposta è corretta.. Data la funzione f(x) =+ x 7, quale delle seguente affermazioni èvera? (a) f(x) nonè derivabile in x =0 (b) f (0) = (c) f (0) = (d)
Calcolo differenziale I
 Calcolo differenziale I Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Derivate Analisi Matematica 1 1 / 25 Definizione: rapporto incrementale Sia f : A
Calcolo differenziale I Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Derivate Analisi Matematica 1 1 / 25 Definizione: rapporto incrementale Sia f : A
Calcolo infinitesimale
 Calcolo infinitesimale L operazione di limite L operazione di limite ha lo scopo di descrivere il comportamento di una funzione nei pressi di un punto di accumulazione per il suo dominio. Limite finito
Calcolo infinitesimale L operazione di limite L operazione di limite ha lo scopo di descrivere il comportamento di una funzione nei pressi di un punto di accumulazione per il suo dominio. Limite finito
Infiniti e Infinitesimi
 Infiniti e Infinitesimi Infiniti e Infinitesimi Def. Una funzione f() si dice infinitesima per (o per ), punto di accumulazione per il dominio di f(), se: f ( ) ( oppure f ( ) ) Infiniti e Infinitesimi
Infiniti e Infinitesimi Infiniti e Infinitesimi Def. Una funzione f() si dice infinitesima per (o per ), punto di accumulazione per il dominio di f(), se: f ( ) ( oppure f ( ) ) Infiniti e Infinitesimi
Limiti e continuità Test di autovalutazione
 Test di autovalutazione 1. Si indichi con M(t) la mantissa di t. Il limite lim x 0 M(1 x ) non esiste (b) vale 1 (c) vale 0 è uguale a M(lim x 0 (1 x )). Sia a n una successione infinitesima e consideriamo
Test di autovalutazione 1. Si indichi con M(t) la mantissa di t. Il limite lim x 0 M(1 x ) non esiste (b) vale 1 (c) vale 0 è uguale a M(lim x 0 (1 x )). Sia a n una successione infinitesima e consideriamo
CONTINUITA. c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Limiti di funzioni - Funzioni continue cap3b.pdf 1
 CONTINUITA c Paola Gervasio - Analisi Matematica - A.A. 208/9 Limiti di funzioni - Funzioni continue cap3b.pdf Ricordiamo la definizione di limite lim 0 f () = l R: I ε (l), I δ ( 0 ) : dom(f ) I δ ( 0
CONTINUITA c Paola Gervasio - Analisi Matematica - A.A. 208/9 Limiti di funzioni - Funzioni continue cap3b.pdf Ricordiamo la definizione di limite lim 0 f () = l R: I ε (l), I δ ( 0 ) : dom(f ) I δ ( 0
Polinomi di Taylor. Hynek Kovarik. Analisi A. Università di Brescia. Hynek Kovarik (Università di Brescia) Polinomi di Taylor Analisi A 1 / 27
 Polinomi di Taylor Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Polinomi di Taylor Analisi A 1 / 27 Introduzione Sia f : I R e sia x 0 I. Problemi: come approssimare
Polinomi di Taylor Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Polinomi di Taylor Analisi A 1 / 27 Introduzione Sia f : I R e sia x 0 I. Problemi: come approssimare
6. Asintoti e continuità
 6. Asintoti e continuità Davide Catania davide.catania@unibs.it Esercitazioni di Analisi Matematica 1 Asintoti Continuità Asintoto orizzontale: la retta y = l è l asintoto orizzontale a + (o destro) di
6. Asintoti e continuità Davide Catania davide.catania@unibs.it Esercitazioni di Analisi Matematica 1 Asintoti Continuità Asintoto orizzontale: la retta y = l è l asintoto orizzontale a + (o destro) di
Funzioni di più variabli: dominio, limiti, continuità
 Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
Funzioni di più variabli: dominio, limiti, continuità
 Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
Funzioni di più variabli: dominio, limiti, continuità Riccarda Rossi Università di Brescia Analisi Matematica B Riccarda Rossi (Università di Brescia) Funzioni di più variabli Analisi Matematica B 1 /
Istituzioni di Matematiche terza parte
 Istituzioni di Matematiche terza parte anno acc. 2013/2014 Univ. degli Studi di Milano D.Bambusi, C.Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 45 index Il concetto di ite 1 Il
Istituzioni di Matematiche terza parte anno acc. 2013/2014 Univ. degli Studi di Milano D.Bambusi, C.Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 45 index Il concetto di ite 1 Il
Corso di Analisi Matematica. Comportamenti asintotici
 a.a. 2013/2014 Laurea triennale in Informatica Corso di Analisi Matematica Comportamenti asintotici Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
a.a. 2013/2014 Laurea triennale in Informatica Corso di Analisi Matematica Comportamenti asintotici Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
Serie di Fourier. Hynek Kovarik. Analisi Matematica 2. Università di Brescia
 Serie di Fourier Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Serie di Fourier Analisi Matematica 2 1 / 37 Polinomi trigonometrici Definizione Si dice
Serie di Fourier Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Serie di Fourier Analisi Matematica 2 1 / 37 Polinomi trigonometrici Definizione Si dice
ANALISI MATEMATICA I (Versione A) - 24 Novembre 2000 RISOLUZIONE. = 4x 2 + 8x 3 + o(x 3 )
 ANALISI MATEMATICA I (Versione A) - 4 Novembre 000 RISOLUZIONE ESERCIZIO 1. Data la funzione = (e x 1) log(1 + 4x ) : 1. Calcolare lo sviluppo di ordine 3 di MacLaurin di. Scriviamo gli sviluppi di ordine
ANALISI MATEMATICA I (Versione A) - 4 Novembre 000 RISOLUZIONE ESERCIZIO 1. Data la funzione = (e x 1) log(1 + 4x ) : 1. Calcolare lo sviluppo di ordine 3 di MacLaurin di. Scriviamo gli sviluppi di ordine
Punti di discontinuità
 Punti di discontinuità DEF. 15 Siano f una funzione reale di una variabile reale definita nel sottoinsieme X di R, x 0 un punto di X per esso di accumulazione. Se f non è continua in x 0, essa si dice
Punti di discontinuità DEF. 15 Siano f una funzione reale di una variabile reale definita nel sottoinsieme X di R, x 0 un punto di X per esso di accumulazione. Se f non è continua in x 0, essa si dice
Polinomi di Taylor. Hynek Kovarik. Università di Brescia. Analisi Matematica 1
 Polinomi di Taylor Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Polinomi di Taylor Analisi Matematica 1 1 / 18 Introduzione Sia f : I R e sia x 0 I. Problemi:
Polinomi di Taylor Hynek Kovarik Università di Brescia Analisi Matematica 1 Hynek Kovarik (Università di Brescia) Polinomi di Taylor Analisi Matematica 1 1 / 18 Introduzione Sia f : I R e sia x 0 I. Problemi:
23 INVERTIBILITÀ E CONTINUITÀ
 23 INVERTIBILITÀ E CONTINUITÀ Ricordiamo che se A, B sono insiemi e f : A B è una funzione iniettiva, ovvero a 1 a 2 = fa 1 ) fa 2 ), allora la relazione gb) = a fa) = b definisce una funzione g : Im f
23 INVERTIBILITÀ E CONTINUITÀ Ricordiamo che se A, B sono insiemi e f : A B è una funzione iniettiva, ovvero a 1 a 2 = fa 1 ) fa 2 ), allora la relazione gb) = a fa) = b definisce una funzione g : Im f
Corso di Analisi Matematica. Calcolo differenziale
 a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Calcolo differenziale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Calcolo differenziale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
Corso di Analisi Matematica Limiti di funzioni
 Corso di Analisi Matematica Limiti di funzioni Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 39 1 Definizione di ite 2 Il calcolo dei
Corso di Analisi Matematica Limiti di funzioni Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 39 1 Definizione di ite 2 Il calcolo dei
Funzioni Continue. se (e solo se) 0
 f : A R R A ' Funzioni Continue La funzione f si dice continua in f ( f ( se (e solo se A Ne seguono tre proprietà affinché f( sia continua in :. Devono esistere finiti il ite destro e sinistro di f( in.
f : A R R A ' Funzioni Continue La funzione f si dice continua in f ( f ( se (e solo se A Ne seguono tre proprietà affinché f( sia continua in :. Devono esistere finiti il ite destro e sinistro di f( in.
Funzioni derivabili (V. Casarino)
 Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
1. Calcolo Differenziale per funzioni di una variabile
 1. Calcolo Differenziale per funzioni di una variabile 1.1 Definizione di Derivata e prime proprietà Definizione 1.1 Sia f :]a, b[ R, x 0 ]a, b[. Allora esiste δ > 0 : x 0 + ]a, b[, 0 < < δ. Se esiste
1. Calcolo Differenziale per funzioni di una variabile 1.1 Definizione di Derivata e prime proprietà Definizione 1.1 Sia f :]a, b[ R, x 0 ]a, b[. Allora esiste δ > 0 : x 0 + ]a, b[, 0 < < δ. Se esiste
Gli intervalli di R. (a, b R, a b)
 Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
allora f (x) f (x 0 ) < ε D f R si dice continua, se è continua in ogni punto del suo dominio D. In simboli, D R è continua in x 0 D se:
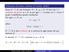 Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
Deinizione (Funzione continua (A.Cauchy, 180)) Siano D R una unzione, D R, x 0 D. Si dice che è continua nel punto x 0 D, se per ogni ε > 0 esiste un δ > 0 per il quale è soddisatta questa condizione:
7 Il Teorema di Bolzano - Weierstrass
 dimostrazione di (3.6). Supponiamo per esempio che f sia crescente e che x 0 < b Poniamo l + := inf f(x) x I,x 0
dimostrazione di (3.6). Supponiamo per esempio che f sia crescente e che x 0 < b Poniamo l + := inf f(x) x I,x 0
Analisi Matematica I DISEQUAZIONI Risposte Pagina Es. 1 Es. 2 Es. 3 Es. 4 Es. 5 1
 Analisi Matematica I DISEQUAZIONI Risposte Pagina Es. Es. Es. 3 Es. 4 Es. 5 AVVERTENZA: Scrivere le risposte scelte nello spazio in alto a destra. In ogni esercizio una sola risposta è corretta. Esercizio.
Analisi Matematica I DISEQUAZIONI Risposte Pagina Es. Es. Es. 3 Es. 4 Es. 5 AVVERTENZA: Scrivere le risposte scelte nello spazio in alto a destra. In ogni esercizio una sola risposta è corretta. Esercizio.
Confronto locale di funzioni Test di autovalutazione
 Test di autovalutazione 1. Per x 0: (a) x 3 = o(x 4 ) (b) x 4 = o(sin x 2 ) (c) x 3 x 3 + 1 (d) x 7 + x x 2 x 2. Il limite lim x 0 + (a) vale 0 (b) non esiste (c) vale 2 (d) è infinito 4x 3 x ln x tan
Test di autovalutazione 1. Per x 0: (a) x 3 = o(x 4 ) (b) x 4 = o(sin x 2 ) (c) x 3 x 3 + 1 (d) x 7 + x x 2 x 2. Il limite lim x 0 + (a) vale 0 (b) non esiste (c) vale 2 (d) è infinito 4x 3 x ln x tan
Equazioni differenziali
 Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 2 1 / 42 Equazioni differenziali Un equazione
Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 2 1 / 42 Equazioni differenziali Un equazione
DERIVATA DI UNA FUNZIONE REALE. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR.
 DERIVATA DI UNA FUNZIONE REALE 1. Definizioni. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR. DEFINIZIONE 1. Sia x 0 un elemento di I. Per ogni x (I \ {x 0 }) consideriamo
DERIVATA DI UNA FUNZIONE REALE 1. Definizioni. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR. DEFINIZIONE 1. Sia x 0 un elemento di I. Per ogni x (I \ {x 0 }) consideriamo
Serie di Taylor. Hynek Kovarik. Analisi Matematica 2. Università di Brescia
 Serie di Taylor Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Serie di Taylor Analisi Matematica 2 1 / 16 Serie di Taylor Il nostro obiettivo è di scrivere
Serie di Taylor Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Serie di Taylor Analisi Matematica 2 1 / 16 Serie di Taylor Il nostro obiettivo è di scrivere
Teorema di sostituzione o del limite di funzioni composte
 Teorema di sostituzione o del limite di funzioni composte Questo teorema serve per calcolare il limite di funzioni composte sfruttando limiti fondamentali o altri limiti già noti. TEOREMA. Se esiste lim
Teorema di sostituzione o del limite di funzioni composte Questo teorema serve per calcolare il limite di funzioni composte sfruttando limiti fondamentali o altri limiti già noti. TEOREMA. Se esiste lim
Esercizi svolti. a 2 x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.
 Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
LEZIONI Dispense a cura del docente Teorema degli Zeri e Teorema di Weierstrass.
 LEZIONI 8-9-0 Contents 8.4. Teorema degli Zeri e Teorema di Weierstrass 95 8.5. Ulteriori nozioni sui iti di funzioni. 0 8.6. Asintoto obliquo. 07 8.7. Funzione Inversa. Continuità della funzione inversa.
LEZIONI 8-9-0 Contents 8.4. Teorema degli Zeri e Teorema di Weierstrass 95 8.5. Ulteriori nozioni sui iti di funzioni. 0 8.6. Asintoto obliquo. 07 8.7. Funzione Inversa. Continuità della funzione inversa.
Successioni numeriche (II)
 Successioni numeriche (II) Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Successioni (II) Analisi A 1 / 52 Forme indeterminate associate a funzioni razionali fratte:
Successioni numeriche (II) Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Successioni (II) Analisi A 1 / 52 Forme indeterminate associate a funzioni razionali fratte:
Istituzioni di Matematiche quarta parte
 Istituzioni di Matematiche quarta parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 22 index Derivate 1 Derivate 2 Teoremi
Istituzioni di Matematiche quarta parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 22 index Derivate 1 Derivate 2 Teoremi
STUDIO di FUNZIONE. c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Studio di funzione cap6b.pdf 1
 STUDIO di FUNZIONE c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Studio di funzione cap6b.pdf 1 Punti di estremo: punto di massimo assoluto Def. Sia 0 dom(f) = D. Si dice che 0 è un punto di massimo
STUDIO di FUNZIONE c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Studio di funzione cap6b.pdf 1 Punti di estremo: punto di massimo assoluto Def. Sia 0 dom(f) = D. Si dice che 0 è un punto di massimo
Esercizi di Analisi Matematica 1, utili per la preparazione all esame scritto - Seconda parte SOLUZIONI
 Esercizi di Analisi Matematica Esercizi di Analisi Matematica, utili per la preparazione all esame scritto - Seconda parte SOLUZIONI Es. Per ognuna delle seguenti figure, dire se la curva nel piano cartesiano
Esercizi di Analisi Matematica Esercizi di Analisi Matematica, utili per la preparazione all esame scritto - Seconda parte SOLUZIONI Es. Per ognuna delle seguenti figure, dire se la curva nel piano cartesiano
7. Studio elementare di funzioni
 7. Studio elementare di funzioni Davide Catania davide.catania@unibs.it Esercitazioni di Analisi Matematica 1 Studio elementare di funzioni (1) Trova il dominio. data f (x) (2) Studia la simmetria e la
7. Studio elementare di funzioni Davide Catania davide.catania@unibs.it Esercitazioni di Analisi Matematica 1 Studio elementare di funzioni (1) Trova il dominio. data f (x) (2) Studia la simmetria e la
Facoltà di Scienze MFN, Università di Cagliari Analisi Matematica 1 (Informatica), a.a. 2007/08. Insiemi numerici: sup A, inf A
 Facoltà di Scienze MFN, Università di Cagliari Analisi Matematica 1 (Informatica, a.a. 2007/08 Esercizi: Parte 1 Insiemi numerici: sup A, inf A 1. Verificare se A, nel caso sia non vuoto, è limitato superiormente,
Facoltà di Scienze MFN, Università di Cagliari Analisi Matematica 1 (Informatica, a.a. 2007/08 Esercizi: Parte 1 Insiemi numerici: sup A, inf A 1. Verificare se A, nel caso sia non vuoto, è limitato superiormente,
A Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica) Simulazione compito d esame
 COGNOME NOME Matr. A Analisi Matematica (Corso di Laurea in Informatica e Bioinformatica) Firma dello studente Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
COGNOME NOME Matr. A Analisi Matematica (Corso di Laurea in Informatica e Bioinformatica) Firma dello studente Tempo: 3 ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni
Analisi Matematica (A L) Limiti di successioni numeriche e di funzioni
 a.a. 2015/2016 Laurea triennale in Informatica Analisi Matematica (A L) Limiti di successioni numeriche e di funzioni Nota: questo file differisce da quello proiettato in aula per la sola impaginazione.
a.a. 2015/2016 Laurea triennale in Informatica Analisi Matematica (A L) Limiti di successioni numeriche e di funzioni Nota: questo file differisce da quello proiettato in aula per la sola impaginazione.
D Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica)
 COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
Limiti di funzioni 1 / 41
 Limiti di funzioni 1 / 41 Comportamento agli estremi: operazione di ite 2 / 41 Sia f (x) una funzione definita su R e supponiamo di voler studiare l andamento della funzione agli estremi del dominio: x
Limiti di funzioni 1 / 41 Comportamento agli estremi: operazione di ite 2 / 41 Sia f (x) una funzione definita su R e supponiamo di voler studiare l andamento della funzione agli estremi del dominio: x
Università degli Studi di Palermo Facoltà di Economia. Dipartimento di Scienze Economiche, Aziendali e Statistiche. Appunti del corso di Matematica
 Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 07 - Continuità Anno Accademico 2015/2016 M. Tumminello,
Università degli Studi di Palermo Facoltà di Economia Dipartimento di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica 07 - Continuità Anno Accademico 2015/2016 M. Tumminello,
19 LIMITI FONDAMENTALI - II
 19 LIMITI FONDAMENTALI - II 3. Il ite che permette il calcolo di forme indeterminate in cui sono presenti funzioni logaritmiche è: log1 + = 1. La dimostrazione di questo ite si ha subito dal ite Esempio.
19 LIMITI FONDAMENTALI - II 3. Il ite che permette il calcolo di forme indeterminate in cui sono presenti funzioni logaritmiche è: log1 + = 1. La dimostrazione di questo ite si ha subito dal ite Esempio.
Nota: A meno che non sia specificato diversamente, si intende che i teoremi, lemmi, proposizioni sotto menzionati siano stati dimostrati a lezione.
 Programma di Analisi Matematica 1 (Canale ICM) svolto per lezioni - A. Languasco - C. Vagnoni 1 Nota: A meno che non sia specificato diversamente, si intende che i teoremi, lemmi, proposizioni sotto menzionati
Programma di Analisi Matematica 1 (Canale ICM) svolto per lezioni - A. Languasco - C. Vagnoni 1 Nota: A meno che non sia specificato diversamente, si intende che i teoremi, lemmi, proposizioni sotto menzionati
ESERCIZI E COMPLEMENTI DI ANALISI MATEMATICA: quinto foglio. A. Figà Talamanca
 ESERCIZI E COMPLEMENTI DI ANALISI MATEMATICA: quinto foglio A. Figà Talamanca 14 ottobre 2010 2 0.1 Ancora limiti di funzioni di variabile reale Esercizio 1 Sia f(x) = [sin x] definita nell insieme [0,
ESERCIZI E COMPLEMENTI DI ANALISI MATEMATICA: quinto foglio A. Figà Talamanca 14 ottobre 2010 2 0.1 Ancora limiti di funzioni di variabile reale Esercizio 1 Sia f(x) = [sin x] definita nell insieme [0,
Matematica 1 mod. A per Matematica Esempi di quiz
 Matematica 1 mod. A per Matematica Esempi di quiz 1. Sia x un numero reale. Allora x 3: è uguale a 3x 2. può essere diverso da 3x 2. è sempre un numero irrazionale. 2. Sia S l insieme delle soluzioni della
Matematica 1 mod. A per Matematica Esempi di quiz 1. Sia x un numero reale. Allora x 3: è uguale a 3x 2. può essere diverso da 3x 2. è sempre un numero irrazionale. 2. Sia S l insieme delle soluzioni della
Studio qualitativo del grafico di una funzione
 Studio qualitativo del grafico di una funzione Obiettivo: ottenere informazioni per descrivere qualitativamente l andamento del grafico di una funzione f campo di esistenza (cioè, l insieme di definizione)
Studio qualitativo del grafico di una funzione Obiettivo: ottenere informazioni per descrivere qualitativamente l andamento del grafico di una funzione f campo di esistenza (cioè, l insieme di definizione)
Limiti di funzioni. Mauro Saita Versione provvisoria. Ottobre 2015
 Limiti di funzioni Mauro Saita e-mail maurosaita@tiscalinet.it Versione provvisoria. Ottobre 2015 Indice 1 Limiti 2 1.1 Definizione di ite................................ 2 1.2 Alcuni teoremi sui iti..............................
Limiti di funzioni Mauro Saita e-mail maurosaita@tiscalinet.it Versione provvisoria. Ottobre 2015 Indice 1 Limiti 2 1.1 Definizione di ite................................ 2 1.2 Alcuni teoremi sui iti..............................
Soluzione: Per la proprietà di linearità delle sommatorie abbiamo S = A + B,
 Ingegneria Elettronica e Informatica Analisi Matematica a Foschi) Compito del 7.6.208. Calcola la parte intera della somma S definita dalla seguente sommatoria 02 S := 000 ) ) k + k. 2 00 k=2 Soluzione:
Ingegneria Elettronica e Informatica Analisi Matematica a Foschi) Compito del 7.6.208. Calcola la parte intera della somma S definita dalla seguente sommatoria 02 S := 000 ) ) k + k. 2 00 k=2 Soluzione:
LICEO CLASSICO ANDREA DA PONTEDERA
 ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classe 5A PROGRAMMA DI MATEMATICA svolto fino al 15 aprile (evidenziate in giallo le aggiunte rispetto al file precedente) Intervallo limitato
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classe 5A PROGRAMMA DI MATEMATICA svolto fino al 15 aprile (evidenziate in giallo le aggiunte rispetto al file precedente) Intervallo limitato
Per cominciare, osserviamo che f si ottiene traslando di 2, nella direzione negativa dell asse x, la funzione. g(x) = x e x
 Studi di funzione 1) Studiare la funzione definita da f(x) = x + e (x+). Per cominciare, osserviamo che f si ottiene traslando di, nella direzione negativa dell asse x, la funzione g(x) = x e x cioè abbiamo
Studi di funzione 1) Studiare la funzione definita da f(x) = x + e (x+). Per cominciare, osserviamo che f si ottiene traslando di, nella direzione negativa dell asse x, la funzione g(x) = x e x cioè abbiamo
Limiti e continuità. Teoremi sui limiti. Teorema di unicità del limite Teorema di permanenza del segno Teoremi del confronto Algebra dei limiti
 Limiti e continuità Teorema di unicità del ite Teorema di permanenza del segno Teoremi del confronto Algebra dei iti 2 2006 Politecnico di Torino 1 Se f(x) =` ` è unico Per assurdo, siano ` 6= `0 con f(x)
Limiti e continuità Teorema di unicità del ite Teorema di permanenza del segno Teoremi del confronto Algebra dei iti 2 2006 Politecnico di Torino 1 Se f(x) =` ` è unico Per assurdo, siano ` 6= `0 con f(x)
Limiti di funzioni e continuità
 Limiti di funzioni e continuità Paolo Montanari Appunti di Matematica Limiti di funzioni e continuità 1 Funzioni limitate La funzione f(x) è limitata superiormente se esiste un numero reale M tale che
Limiti di funzioni e continuità Paolo Montanari Appunti di Matematica Limiti di funzioni e continuità 1 Funzioni limitate La funzione f(x) è limitata superiormente se esiste un numero reale M tale che
Argomenti delle singole lezioni del corso di Analisi Matematica 1 (Laurea triennale di Matematica, A.A )
 Argomenti delle singole lezioni del corso di Analisi Matematica 1 (Laurea triennale di Matematica, A.A. 2018-19) NB. Le indicazioni bibliografiche si riferiscono al libro di testo. Lezione nr. 1, 1/10/2018.
Argomenti delle singole lezioni del corso di Analisi Matematica 1 (Laurea triennale di Matematica, A.A. 2018-19) NB. Le indicazioni bibliografiche si riferiscono al libro di testo. Lezione nr. 1, 1/10/2018.
ESERCIZI MATEMATICA GENERALE - Canale III Prof. A. Fabretti 1 A.A. 2009/2010
 ESERCIZI MATEMATICA GENERALE - Canale III Prof. A. Fabretti A.A. 2009/200 Limiti di funzione Calcolare i seguenti limiti ) 2) 3) 4) 5) 6) 6) lim 2 + 2 4 3 2 + 2 lim 2 + ( 3 2 ) lim log + 2 2 + ( 3 2 )
ESERCIZI MATEMATICA GENERALE - Canale III Prof. A. Fabretti A.A. 2009/200 Limiti di funzione Calcolare i seguenti limiti ) 2) 3) 4) 5) 6) 6) lim 2 + 2 4 3 2 + 2 lim 2 + ( 3 2 ) lim log + 2 2 + ( 3 2 )
Diario del Corso Analisi Matematica I e Analisi Matematica
 Diario del Corso Analisi Matematica I e Analisi Matematica 1. Martedì 2 ottobre 2012 Nozioni di Teoria degli Insiemi. Numeri Naturali, loro proprietà, modello geometrico, sommatoria. 2. Mercoledì 3 ottobre
Diario del Corso Analisi Matematica I e Analisi Matematica 1. Martedì 2 ottobre 2012 Nozioni di Teoria degli Insiemi. Numeri Naturali, loro proprietà, modello geometrico, sommatoria. 2. Mercoledì 3 ottobre
Soluzioni degli esercizi di Analisi Matematica I
 Soluzioni degli esercizi di Analisi Matematica I (Prof. Pierpaolo Natalini) Roberta Bianchini 30 ottobre 07 FOGLIO. Determinare il dominio e il segno della funzione ( ) f(x) = arccos x x + π/3.. Verificare
Soluzioni degli esercizi di Analisi Matematica I (Prof. Pierpaolo Natalini) Roberta Bianchini 30 ottobre 07 FOGLIO. Determinare il dominio e il segno della funzione ( ) f(x) = arccos x x + π/3.. Verificare
Istituzioni di Matematiche prima parte
 Istituzioni di Matematiche prima parte anno acc. 2010/2011 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 45 index Proprietà elementari dei sottoinsiemi
Istituzioni di Matematiche prima parte anno acc. 2010/2011 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 45 index Proprietà elementari dei sottoinsiemi
Limiti di funzioni reali e Funzioni continue. x b di ciascuna delle seguenti affermazioni se è vera o falsa.
 Limiti di funzioni reali e Funzioni continue 1. Sia f(x) definita in un intervallo I tale che f(x) + per x x 0 I. A. [f(x)] + per x x 0, dove [f(x)] è la parte intera di f(x). B. f(x) > 0 per ogni 0
Limiti di funzioni reali e Funzioni continue 1. Sia f(x) definita in un intervallo I tale che f(x) + per x x 0 I. A. [f(x)] + per x x 0, dove [f(x)] è la parte intera di f(x). B. f(x) > 0 per ogni 0
Corso di Laurea in Ingegneria, Settore Informazione (gruppi 2-3), A.A. 2007/2008 Docente: Antonio Ponno
 Programma del Corso di Matematica A Corso di Laurea in Ingegneria, Settore Informazione (gruppi 2-3), A.A. 2007/2008 Docente: Antonio Ponno Premessa (D) dopo un teorema o una proposizione citati sta ad
Programma del Corso di Matematica A Corso di Laurea in Ingegneria, Settore Informazione (gruppi 2-3), A.A. 2007/2008 Docente: Antonio Ponno Premessa (D) dopo un teorema o una proposizione citati sta ad
x x ' La funzione f si dice continua in x 0 se (e solo se) 0
 : A R R A ' Funzioni Continue La unzione si dice continua in ( ( se (e solo se A Ne seguono tre proprietà ainché ( sia continua in :. Devono esistere initi il ite destro e sinistro di ( in. Tali iti devono
: A R R A ' Funzioni Continue La unzione si dice continua in ( ( se (e solo se A Ne seguono tre proprietà ainché ( sia continua in :. Devono esistere initi il ite destro e sinistro di ( in. Tali iti devono
Matematica con elementi di Informatica
 Limiti e Funzioni Continue Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologia Farmaceutiche Anno
Limiti e Funzioni Continue Matematica con elementi di Informatica Tiziano Vargiolu Dipartimento di Matematica vargiolu@math.unipd.it Corso di Laurea Magistrale in Chimica e Tecnologia Farmaceutiche Anno
Funzioni continue di una variabile
 Università degli Studi di Palermo Facoltà di Economia Dip. di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica Generale Funzioni continue di una variabile Anno Accademico 2013/2014
Università degli Studi di Palermo Facoltà di Economia Dip. di Scienze Economiche, Aziendali e Statistiche Appunti del corso di Matematica Generale Funzioni continue di una variabile Anno Accademico 2013/2014
1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: c) x + 1 d)x sin x.
 Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
1 Analisi mat. I - Esercizi del 13/10/99
 Analisi mat. I - Esercizi del //99 ES. Delle seguenti funzioni determinare: il dominio l immagine gli eventuali asintoti l insieme dove sono continue e quali siano estendibili per continuita. Determinare
Analisi mat. I - Esercizi del //99 ES. Delle seguenti funzioni determinare: il dominio l immagine gli eventuali asintoti l insieme dove sono continue e quali siano estendibili per continuita. Determinare
LIMITI DI FUNZIONI. c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Limiti di funzioni cap3a.pdf 1
 LIMITI DI FUNZIONI c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Limiti di funzioni cap3a.pdf 1 Intorni Def. Siano 0 R e r R +. Chiamiamo intorno di centro 0 e raggio r l intervallo aperto e limitato
LIMITI DI FUNZIONI c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Limiti di funzioni cap3a.pdf 1 Intorni Def. Siano 0 R e r R +. Chiamiamo intorno di centro 0 e raggio r l intervallo aperto e limitato
Limiti e continuità. Limiti di funzioni
 Limiti e continuità Limite all ininito di una unzione Limite al inito di una unzione Continuità di una unzione Limite ininito al inito di una unzione Limiti laterali di una unzione Punti di discontinuità
Limiti e continuità Limite all ininito di una unzione Limite al inito di una unzione Continuità di una unzione Limite ininito al inito di una unzione Limiti laterali di una unzione Punti di discontinuità
del punto c (dove c può essere un numero reale oppure + ), escluso al più il punto
 C.4 Limiti Pag. 87 Dimostrazione del Teorema 3.27 Teorema 3.27 Sia f una funzione definita e monotona in un intorno destro I + (c) del punto c (dove c può essere un numero reale oppure ), escluso al più
C.4 Limiti Pag. 87 Dimostrazione del Teorema 3.27 Teorema 3.27 Sia f una funzione definita e monotona in un intorno destro I + (c) del punto c (dove c può essere un numero reale oppure ), escluso al più
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA
 ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
Prova parziale del corso Analisi Matematica e Geometria 13/12/2016. Tema D
 Università Iuav di Venezia Anno Accademico 2016-2017 CLT Architettura Costruzione Conservazione Prova parziale del corso Analisi Matematica e Geometria 13/12/2016 Tema D 1. Tutte e sole le primitive della
Università Iuav di Venezia Anno Accademico 2016-2017 CLT Architettura Costruzione Conservazione Prova parziale del corso Analisi Matematica e Geometria 13/12/2016 Tema D 1. Tutte e sole le primitive della
Limiti di funzioni 1 / 39
 Limiti di funzioni 1 / 39 Comportamento agli estremi: operazione di ite 2 / 39 Sia f (x) una funzione definita su R e supponiamo di voler studiare l andamento della funzione agli estremi del dominio: x
Limiti di funzioni 1 / 39 Comportamento agli estremi: operazione di ite 2 / 39 Sia f (x) una funzione definita su R e supponiamo di voler studiare l andamento della funzione agli estremi del dominio: x
Esercizi proposti. x b) f(x) = 2. Determinare i punti di non derivabilità delle funzioni
 Esercizi proposti 1. Calcolare la derivata prima f () per le seguenti funzioni: a) f() = c) f() = ( 1 + 1 b) f() = 1 arctan ) d) f() = cos ( ( + ) 5) e) f() = 1 + sin 1 f) f() = arcsin 1. Determinare i
Esercizi proposti 1. Calcolare la derivata prima f () per le seguenti funzioni: a) f() = c) f() = ( 1 + 1 b) f() = 1 arctan ) d) f() = cos ( ( + ) 5) e) f() = 1 + sin 1 f) f() = arcsin 1. Determinare i
Successioni numeriche
 Successioni numeriche Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Successioni Analisi A 1 / 35 Definizione Una successione a valori reali è una funzione f : N R
Successioni numeriche Hynek Kovarik Università di Brescia Analisi A Hynek Kovarik (Università di Brescia) Successioni Analisi A 1 / 35 Definizione Una successione a valori reali è una funzione f : N R
Diario del Corso Analisi Matematica I
 Diario del Corso Analisi Matematica I 1. Martedì 1 ottobre 2013 Presentazione del corso. Nozioni di Teoria degli Insiemi. Numeri Naturali, loro proprietà, rappresentazione geometrica, sommatoria, principio
Diario del Corso Analisi Matematica I 1. Martedì 1 ottobre 2013 Presentazione del corso. Nozioni di Teoria degli Insiemi. Numeri Naturali, loro proprietà, rappresentazione geometrica, sommatoria, principio
Analisi Matematica II
 Analisi Matematica II Limiti e continuità in R N Claudio Saccon 1 1 Dipartimento di Matematica, Via F. Buonarroti 1/C,56127 PISA email: claudio.sacconchiocciolaunipi.it sito web: http://pagine.dm.unipi.it/csblog1
Analisi Matematica II Limiti e continuità in R N Claudio Saccon 1 1 Dipartimento di Matematica, Via F. Buonarroti 1/C,56127 PISA email: claudio.sacconchiocciolaunipi.it sito web: http://pagine.dm.unipi.it/csblog1
1 Limiti e continuità per funzioni di una variabile
 1 Limiti e continuità per funzioni di una variabile Considerazioni introduttive Consideriamo la funzione f() = sin il cui dominio naturale è R\ {0}. Problema: non è possibile calcolare il valore di f per
1 Limiti e continuità per funzioni di una variabile Considerazioni introduttive Consideriamo la funzione f() = sin il cui dominio naturale è R\ {0}. Problema: non è possibile calcolare il valore di f per
Analisi Matematica 1 Soluzioni prova scritta n. 1
 Analisi Matematica Soluzioni prova scritta n Corso di laurea in Matematica, aa 008-009 5 giugno 009 Sia a n la successione definita per ricorrenza: a n+ 3 a n a 3 n, a 3 a n+ 3 a n a 3 n, a 3 a n+ 3 a
Analisi Matematica Soluzioni prova scritta n Corso di laurea in Matematica, aa 008-009 5 giugno 009 Sia a n la successione definita per ricorrenza: a n+ 3 a n a 3 n, a 3 a n+ 3 a n a 3 n, a 3 a n+ 3 a
