Appunti del corso di Probabilità e Processi Stocastici
|
|
|
- Marta Simonetti
- 8 anni fa
- Visualizzazioni
Transcript
1 Appunti del corso di Probabilità e Processi Stocastici in continua revisione e aggiornamento Michele Gianfelice Dipartimento di Matematica Università della Calabria Campus di Arcavacata Ponte Pietro Bucci - cubo 30B Arcavacata di ende CS gianfelice@mat.unical.it a.a. 2007/2008
2 Indice I Elementi di Calcolo delle Probabilità 3 1 Alcune nozioni di teoria della misura Insiemi misurabili Generalità sulle misure Misure positive Misure segnate Successioni di misure Convergenza forte Convergenza debole e dualità Misure di probabilità Spazi di Probabilità Convergenza in distanza variazionale Convergenza debole Applicazioni tra spazi misurabili e variabili aleatorie Stabilità della collezione delle v.a. rispetto alla topologia della convergenza puntuale Generalità sull attesa di una variabile aleatoria Disuguaglianza di Markov e sue generalizzazioni Funzione caratteristica di una variabile aleatoria Proprietà della funzione caratteristica di una v.a Problema dei momenti Attesa condizionata rispetto ad una sigma-algebra Attesa condizionata rispetto ad una v.a Versione regolare di una probabilità condizionata Attesa condizionata come operatore di proiezione su un sottospazio chiuso di L 2 Ω, F, P Proprietà dell attesa condizionata Estensione dell attesa condizionata a L 1 Ω, F, P Correlazione tra coppie d eventi Indipendenza stocastica ed ortogonalità tra sottospazi di L 2 Ω, F, P Convergenza di successioni di variabili aleatorie Convergenza quasi certa Convergenza in probabilità
3 2.3 Convergenza in media di ordine p Convergenza in distribuzione legge Metrizzabilità della convergenza debole Connessioni tra le varie nozioni di convergenza di successioni di v.a elazione tra convergenza in distribuzione e le altre nozioni di convergenza elazione tra convergenza in probabilità e le altre nozioni di convergenza elazione tra convergenza in media di ordine p e le altre nozioni di convergenza elazione tra convergenza P-q.c. e le altre nozioni di convergenza Martingale Martingale a tempo discreto Caratterizzazione e proprietà Convergenza Martingale indicizzate da un generico insieme totalmente ordinato Martingale inverse Martingale a tempo continuo II Introduzione alla teoria dei processi stocastici Variabili aleatorie gaussiane Vettori aleatori gaussiani Sistemi gaussiani
4 Parte I Elementi di Calcolo delle Probabilità 3
5 Capitolo 1 Alcune nozioni di teoria della misura 1.1 Insiemi misurabili Sia Ω un insieme e P Ω l insieme delle parti di Ω, A Ω sia A c := Ω\A. Definizione 1 Una collezione A d insiemi di Ω è detta algebra di Boole se: 1. Ω A ; 2. se A A allora A c A ; 3. se n N, A i A, i = 1,.., n, allora n i=1 A i A. Definizione 2 Un algebra di Boole A è detta σalgebra se, data {A n } n N numerabile d insiemi di Ω allora n N A n A. A una collezione Osservazione 3 Osserviamo che dalla precedente definizione segue che anche l intersezione numerabile di elementi di A appartiene ad A, poiché se n N A n A, dove n N, A n A, allora per definizione di algebra di Boole A n N A c n = n N Ac n, ma A c n A, n N. Inoltre notiamo che P Ω verifica tutti gli assiomi che definiscono una σalgebra, pertanto l insieme delle σalgebre non è vuoto. Teorema 4 Data una collezione G di sottoinsiemi di Ω esiste la più piccola σalgebra σ G contenente G e σ G è detta σalgebra generata da σ G. Dimostrazione: Sia I G la collezione di tutte le σalgebre di Ω contenenti G, allora σ G := B IG B. Esempio 1 Se Ω coincide con munito della topologia euclidea e G coincide con la collezione degli aperti di rispetto a tale topologia, σ G è detta σalgebra dei boreliani di e si denota col simbolo B. Esercizio 1 Dimostrare che se G = {, q]} q Q allora, σ G = B. 4
6 Definizione 5 Siano A e B due σalgebre d insiemi di Ω. Allora, se ogni elemento A di A è anche elemento di B diremo che A è contenuta in B, ovvero A B, il che permette di definire una relazione d ordine parziale tra σalgebre di sottoinsiemi di Ω. Osservazione 6 Dalla definizione precedente segue che ogni σalgebra A di sottoinsiemi di Ω è contenuta in P Ω e pertanto questa è detta σalgebra massimale. Definizione 7 Sia {A n } n N n N : P Ω una collezione numerabile d insiemi di Ω. Allora, se A n A n+1, {A n } n N è detta crescente, A := n N A n lim n A n e la collezione {A n } n N è detta accrescere a A, in simboli A n A. A n A n+1, {A n } n N è detta decrescente, A := n N A n lim n A n e la collezione {A n } n N è detta decrescere a A, in simboli A n A. Inoltre, una collezione numerabile d insiemi di Ω che sia crescente o decrescente è detta monotona. Definizione 8 Una collezione M di sottoinsiemi di Ω tale che, se {A n } n N M è una collezione monotona, allora A M è detta classe monotona di elementi di P Ω. Proposizione 9 Una σalgebra A di sottoinsiemi di Ω è una classe monotona. Dimostrazione: Se {A n } n N A è una successione crescente, allora A = n N A n A per definizione di σalgebra. Inoltre, considerando {A c n} n N, che è decrescente, si ha A c = c A c n = A n A, 1.1 n N ovvero che A è una classe monotona. Osservazione 10 Se G P Ω, dalla definizione di σalgebra generata da G, resta allora definita M G la classe monotona generata da G, ovvero la più piccola classe monotona contenente gli elementi di G. Teorema 11 Se B è un algebra di Boole, M B e σ B coincidono. Dimostrazione: σ B è una classe monotona, quindi σ B M B. D altra parte, se dato A P Ω n N A A; B := {B P Ω : A B, A B, A B M B}, 1.2 poiché le applicazioni,, : P Ω P Ω P Ω 1.3 5
7 sono simmetriche, B A A; B A A B; B. Inoltre, A P Ω, A A; B è una classe monotona, infatti, se {B n } n N A A; B è crescente decrescente, come pure {A B n } n N, mentre {A B n } n N, {A\B n } n N sono decrescenti crescenti, {B n \A} n N è crescente decrescente ed il loro limite è in M B, quindi lo è anche il limite di {A B n } n N. Siccome B M B, se A B allora, B B, B A A; B. Perciò B A A; B e A A; B M B. Tuttavia, B M B, se A B, A A B; B, ovvero B A B; B. Dunque, B, B M B, B B, B B, B B M B. Quindi, posto B = Ω, B M B implica B c M B, ovvero M B è un algebra di Boole. Siccome però se {A n } n N M B, {B n } n N tale che n N, B n := n k=0 A k è crescente lim n A n = lim n B n M B e dunque M B è una σalgebra, perciò M B σ B. Se A e B sono due σalgebre indichiamo con A B la σalgebra σ {A, B}, ovvero la quella generata dagli eventi di A e di B. Inoltre, se I è un insieme di indici e {B} i I una famiglia di σalgebre indicizzata da I poniamo i I B i la σalgebra generata dagli eventi degli elementi di {B} i I. Definizione 12 Dato un insieme Ω ed una σalgebra di suoi sottoinsiemi A, la coppia Ω, A è detta spazio misurabile. 1.2 Generalità sulle misure Misure positive Definizione 13 Sia E un insieme ed E un algebra di Boole di suoi sottoinsiemi. Una misura positiva finitamente additiva µ su E, E è un applicazione E A µ A che per ogni A, B E disgiunti, cioè A B =, µ A B = µ A + µ B. Definizione 14 Sia E un insieme ed E una σalgebra dei suoi sottoinsiemi. Una misura positiva µ su E, E è un applicazione E A µ A σadditiva, ovvero tale che, per ogni collezione numerabile {A n } n 1 di elementi di E i cui termini sono insiemi mutuamente disgiunti, cioè A i A j = se i j, µ n 1 A n = n 1 µ A n. Data una misura positiva µ su E, E, la terna E, E, µ è detta spazio di misura. Inoltre, sia E µ := {A E : A, A + E tale che A A A + e µ A + \A = 0}. 1.6 E µ E ed è una σalgebra, pertanto E µ è detta completamento di E µ rispetto a µ. Ne segue che µ si può estendere ad E µ ponendo A E µ, µ A = µ A e quindi considerare lo spazio di misura E, E µ, µ completamento di E, E, µ. Dunque, se E µ = E, E, E, µ è detto completo. Sia ora E uno spazio topologico di Haussdorff: 6
8 localmente compatto, ovvero tale che ogni punto di E ammette un intorno compatto; σcompatto o numerabile all infinito, ovvero tale che esiste una successione crescente di sottoinsiemi compatti di E, {K n } n 1 tali che n 1, K n K n+1, esaustiva di E, cioè E = n 1 K n. Data E = B E la σalgebra dei boreliani di E, ovvero quella generata dagli aperti di E, una misura positiva µ su E, B E è detta localmente finita se K E compatto, µ K <. Il teorema di adon-iesz afferma che esiste una corrispondenza biunivoca tra i funzionali lineari positivi sullo spazio lineare C 0 E delle funzioni continue a supporto compatto su E a valori reali ed un sottoinsieme M + E delle misure localmente finite positive su E, B E, dette misure di adon positive, che sono il completamento di restrizioni a E, B E di determinate misure definite su E, E, con E σalgebra contenente B E. In generale, se µ φ è una misura su E, E che origina da un funzionale positivo φ su C 0 E tramite la costruzione di adon- iesz, il completamento E, B E µφ, µ φ di E, B E, µ φ 0, con µ φ 0 restrizione a E, B E di µ φ, non coincide con E, E, µ φ. Ciò è però vero nel caso in cui E sia anche metrizzabile. Infatti in tal caso data una qualsiasi misura positiva µ 0 localmente finita su E, B E esiste una misura positiva di adon µ coincidente con µ 0 su E, B E. Inoltre, µ è regolare, ovvero B B E µ, ε > 0, C, A B E con C chiuso e A aperto, tali che C B A e µ A\C < ε Misure segnate Se E è metrizzabile e compatto, è uno spazio di Hausdorff compatto, quindi localmente compatto e σcompatto. Munendo C 0 E C E della norma, mediante la decomposizione di Jordan si può costruire lo spazio lineare M E delle misure di adon segnate che risulta essere in corrispondenza biunivoca con il duale di C E. Sia quindi E metrizzabile, localmente compatto e σcompatto. Consideriamo gli spazi lineari di funzioni reali su E : C 0 E, spazio delle funzioni continue a supporto compatto; C E, spazio delle funzioni continue nulle all, ovvero tali che ε > 0, K ε compatto tale che f x < ε x Kε; c E C b E, spazio delle funzioni continue limitate. Chiaramente, C 0 E C E C b E, valendo l uguaglianza se E è compatto. Munendo questi spazi della norma si ottengono altrettanti spazi normati tali che: C b E è di Banach; C E è un sottospazio chiuso di C b E ; C 0 E è denso in C E. 7
9 Tramite la compattificazione ad un punto di E, è possibile costruire un isomorfismo tra M Ė, con Ė compattificazione ad un punto di E, ed il sottoinsieme di M E delle misure di adon segnate finite M 1 E, il quale risulta essere in corrispondenza biunivoca con il duale di C E. 1.3 Successioni di misure Sia E metrizzabile, localmente compatto e σcompatto Convergenza forte Indicando con M 1,+ E il sottoinsieme di M 1 E collezione delle misure positive finite su E e definendo su M 1 E la norma µ M 1 := µ = µ + E + µ E, dove µ +, µ M 1,+ E sono gli elementi della decomposizione di Hahn-Jordan di µ M 1 E, {µ n } n 1 M 1 E converge fortemente a µ M 1 E, se converge in norma M Convergenza debole e dualità Per quanto appena esposto, è possibile allora definire la seguenti nozioni di convergenza debole: 1. {µ n } n 1 M E converge vagamente a µ M E, se f C 0 E, {µ n } n 1 converge a µ f, ovvero {µ n } n 1 converge nella topologia *-debole di C 0 E. 2. {µ n } n 1 M 1 E converge debolmente a µ M 1 E, se f C E, {µ n } n 1 converge a µ f, ovvero {µ n } n 1 converge nella topologia *-debole di C E. 3. {µ n } n 1 M 1 E converge strettamente a µ M 1 E, se f C b E, {µ n } n 1 converge a µ f. Vale il seguente diagramma di relazioni tra le nozioni di convergenza appena definite: convergenza in norma M 1 = convergenza stretta = convergenza debole = convergenza vaga. Definizione 15 Una misura µ M 1 E è detta tesa se ε > 0, K ε E compatto tale che µ K c ε < ε. Equivalentemente µ è tesa se il suo supporto è σcompatto, ovvero può essere rappresentato come unione al più numerabile di compatti. Definizione 16 Sia I un insieme di indici. Una famiglia di misure {µ i } i I M 1 E è detta tesa se ε > 0, K ε E compatto tale che i I, µ i K c ε < ε. Teorema 17 Sia {µ n } n 1 M 1 E. {µ n } n 1 converge debolmente se e solo se c > 0 ed un sottoinsieme D denso in C E tale che µ n M 1 c, n 1 e la successione {µ n g} n 1 converge g D. 8
10 Dimostrazione: L implicazione diretta nel caso generale è più difficile da dimostrare di quella in cui si suppone che c > 0 : µ n M 1 c, n 1. Poiché nel seguito si considereranno soltanto misure di probabilità, ci restingeremo a questo caso. Ovviamente se {µ n } n 1 converge debolmente la successione {µ n g} n 1 converge g D con D denso in C E. Inoltre, la palla di raggio c nella topologia debole di C E, che è isomorfo a M 1 E, è compatta, quindi, se µ è il limite di {µ n } n 1 nella topologia debole, µ M 1 c. La successione di funzionali lineari su C E {l n } n 1 tali che n 1, g C E, l n g := µ n g è uniformemente limitata ed equicontinua, infatti n 1, l n C E = µ n M 1 E c ; l n g f c g f, 1.7 inoltre è convergente su un sottoinsieme D denso in C E. Quindi, per il teorema di Ascoli-Arzelà, è convergente su tutto C E. Allora, l limite di {l n } n 1 definisce una misura di adon µ M 1 E e dunque {µ n } n 1 converge debolmente a µ. Teorema 18 Sia {µ n } n 1 M 1 E. {µ n } n 1 converge strettamente se solo se {µ n } n 1 converge debolmente e ε > 0, K ε E compatto e N ε > 0 tale che, n N ε, µ n K c ε < ε, ovvero la famiglia {µ n } n Nε+1 è tesa. Dimostrazione: {µ n } n 1 converge strettamente allora converge debolmente e, dall implicazione diretta del teorema precedente, c > 0 : µ n M 1 c, n 1. Quindi se {µ n } n 1 converge debolmente a µ allora µ E = µ M 1 c. Dunque, ε > 0, K ε : µ Kε c < ε. Allora, tramite 2 Ė, è possibile trovare f ε C b E : 0 < f ε 1 e supp f ε Kε, c Inoltre, N ε : n > N ε, µ n f ε µ f ε < ε 2. Pertanto, µ f ε µ K c ε < ε µ n f ε < µ f ε + ε 2 < µ K c ε + ε 2 < ε. 1.9 Poiché E è localmente compatto e σcompatto, Esiste una successione {H n } n 1 di sottoinsiemi compatti di E, esaustiva di E, tale che n 1, H n H n+1. Allora, sia n ε tale che H c n ε supp f ε. Si ha che n 1 µ n H c n ε µn f ε. Quindi, n > N ε, µ n H c n ε < ε. Dato ε > 0, sia K ε E compatto e N ε > 0 tale che, n N ε, µ n K c ε < ε. Se g C 0 E tale che g x = 1, x K ε, f C b E, f = gf + u con u tale che supp u K c ε. Quindi, n 1, µ n f = µ n fg + µ n u Poiché per ipotesi {µ n } n 1 converge debolmente, indicando con µ il suo limite, {µ n fg} n 1 converge a µ fg. Inoltre, µ n u u µ n K c ε ε f. 9
11 Teorema 19 Sia {µ n } n 1 M 1,+ E tale che {µ n } n 1 converge debolmente a µ e {µ n E} n 1 converge a µ E <. Allora {µ n } n 1 converge strettamente. Dimostrazione: Basta dimostrare che ε > 0, K ε E compatto e N ε > 0 tale che, n N ε, µ n K c ε < ε e la tesi segue dall implicazione inversa del teorema precedente. Dato ε > 0, sia K ε E compatto tale che µ n K c ε < ε e sia f C0 E tale che supp f K ε, 0 f 1 e µ f > µ M 1 ε. Sia N ε > 0 tale che, n N ε, Allora, µ n E µ n f + µ n K c ε, pertanto, µ n E µ E < ε, µ n f µ f < ε µ n K c ε µn E µ n f µ n E + µ f µ n f µ f µ n E µ E + 2ε Teorema 20 Sia E uno spazio metrico completo e separabile, allora ogni µ M 1 E è tesa. Dimostrazione: È sufficiente restringersi al caso in cui µ M1,+ E e µ E = 1. Poiché E è separabile, esiste una successione {B n k } k 1 di palle aperte di E di raggio 1 che ricopre E. Allora, n ε > 0 esiste N ε n tale che µ B n k N ε n k > 1 ε. Quindi, poiché E è completo, l insieme 2 n n 1 k N n ε B n k è totalmente limitato ed ha chiusura compatta K. Pertanto, ν K > 1 ε. Osservazione 21 Quest ultimo risultato è valido anche sotto le ipotesi più deboli per cui E sia topologicamente completo, ovvero E ammette una metrica equivalente rispetto a cui è compatto, e che µ sia separabile, ovvero abbia supporto separabile. In generale è sufficiente restringersi al caso in cui E sia uno spazio topologico polacco, ovvero omeomorfo ad uno spazio metrico completo separabile. Tuttavia in molte applicazioni si assume inoltre che E sia localmente compatto e σcompatto. La mancanza di questi due ultimi requisiti infatti non garantisce la possibilità di definire una misura finita per mezzo del teorema di adon-iesz, in quanto in tal caso ogni misura di finita su E, B E rappresenta un funzionale lineare continuo positivo su C 0 E ma il viceversa non è in genarale vero. Inoltre, C 0 E non è in generale denso in C E. 1.4 Misure di probabilità Definizione 22 Sia Ω, A uno spazio misurabile. Una misura positiva σadditiva P su Ω, A tale che P Ω = 1 è detta misura di probabilità su Ω, A. Osservazione 23 Una misura di probabilità ha le seguenti proprietà: 1. P = P Ω c = 0. 10
12 2. Se A, B A, A B, P B = P A + P B\A P A Se A, B A, P B A = P A\B + P B\A + P A B = P A + P B P A B 1.14 il che implica P A + P B, 1.15 P A i P A i i N 4. Se {A n } n N è crescente, allora P A = P lim A n = P A n = P A 0 A n \A n 1 n = P A 0 + n 1 n N i N P A n \A n 1 = P A 0 + n 1 Esercizio 2 Dimostrare che se {A n } n N è decrescente, allora P A = P lim A n = P A n = lim P A n n n n N n 1 P A n A n 1 = lim n P A n ed inoltre che, se A =, allora ciò è equivalente alla proprietà 2 della definizione di misura di probabilità Spazi di Probabilità Sia P E, E M +,1 E la collezione delle misure di probabilità su E, E. Scelta, µ P E, E, la terna E, E, µ è detta spazio di probabilità probabilizzato. Inoltre, se E µ è la σalgebra completamento di E rispetto a µ definita nella 1.6, ne segue che µ si può estendere a E µ e quindi considerare lo spazio di probabilità E, E µ, µ completamento di E, E, µ. Se E = E µ, E, E, µ è uno spazio di probabilità completo Convergenza in distanza variazionale Definizione 24 Sia E, E uno spazio misurabile, si definisce distanza in variazione tra due misure di probabilità µ, ν P E, E la quantità V ar µ ν := 1 2 sup µ A ν A A E Dunque, una successione di misure di probabilità {µ n } n 1 P E, E converge a µ in variazione se lim n V ar µ n µ = 0. 11
13 Osservazione 25 Se E è localmente compatto e σcompatto ed E = B E, ν 1, ν 2 P E V ar ν 1 ν 2 = 1 2 ν 2 ν 2 M Infatti, posto µ := ν 1 ν 2 M 1 E, gli elementi della cui decomposizione di Hahn-Jordan denotiamo con µ +, µ, poiché A B E si ha ν 1 A ν 2 A = ν 1 A c ν 2 A c, 1.20 µ M 1 = µ + E + µ E = ν 1 ν 2 A + ν 1 ν 2 A c 2 sup ν 1 A ν 2 A A BE Inoltre, A B E 2 ν 1 A ν 2 A = ν 1 A ν 2 A + ν 1 A c ν 2 A c 1.22 = µ + A + µ A + µ + A c + µ A c µ M 1. Dunque, in tal caso la nozione di convergenza in variazione equivale a quella di convergenza forte in M 1 E. Osservazione 26 Nel caso in cui E, B E =, B e µ, ν sono a.c. rispetto alla misura di Lebesgue, con densità rispettivamente f e g, µ ν M 1 = dx f x g x Analogamente se E è discreto e {µ i } i 1, {ν i } i 1 sono i valori assunti rispettivamente da µ e ν sugli atomi di E, µ ν M 1 = µ i ν i i Convergenza debole Teorema 27 Sia E sia uno spazio topologico polacco, localmente compatto e σcompatto. Una successione {µ n } n 1 P E converge vagamente se e solo se converge strettamente. Dimostrazione: Poiché C 0 E è denso in C E e n 1, µ n M 1 = 1, dall implicazione inversa del Teorema 17 segue che {µ n } n 1 converge debolmente a µ tale che µ E = 1 = µ n E Pertanto per il Teorema 19 si ha che {µ n } n 1 converge strettamente. 12
14 Osservazione 28 Se E è polacco, localmente compatto e σcompatto, per il precedente risultato la convergenza stretta di {µ n } n 1 P E è equivalente a quella vaga e quindi a quella debole. Pertanto nel linguaggio comune del Calcolo delle Probabilità e della Statistica Matematica tali nozioni di convergenza per le misure di probabilità vanno sotto il nome di convergenza debole. Definizione 29 Sia E sia uno spazio topologico polacco, localmente compatto e σcompatto. Una successione di misure di probabilità {P n } n 1 converge in generale ad una misura di probabilità P se, A B E tale che P A = 0, la successione numerica {P n A} n 1 converge a P A. Teorema 30 Sia E sia uno spazio topologico polacco, localmente compatto e σcompatto. Data una successione di misure di probabilità {P n } n 1, le seguenti affermazioni sono equivalenti: 1. {P n } n 1 converge debolmente a P; 2. lim n P n A P A A B E chiuso; 3. lim n P n A P A A B E aperto; 4. {P n } n 1 converge in generale a P. Dimostrazione: Sia ρ una metrica equivalente, A B E chiuso e f ε A x := ρ x, A 1 0, 1.26 ε A ε := {x E : f ε A x > 0} = {x E : ρ x, A < ε}, 1.27 con E x ρ x, A := inf y A ρ x, y +. Allora, poiché P n A = P n dx 1 A x P n dx f ε A x, 1.28 si ha lim n P n A lim n E E P n dx f ε A x = E Se A è aperto, A c è chiuso, perciò E P dx f ε A x P A ε P A ε 0 lim n P n A = lim n 1 P n A c = 1 lim n P n A c 1 P A c = P A Sia Å:= A\ A. Dato che per ipotesi P A = 0 e passando al complementare 3. 2., si ha lim n P n A lim n P n A P A = P A, 1.31 lim n P n A lim n P n Å P Å = P A Quindi, A B E tale che P A = 0, {P n A} n 1 converge a P A. 13
15 4. 1. Sia f C b E. Allora M > 0 : f M. Considerata la partizione T k := {t 0,.., t k } di [ M, M] tale che M = t 0 <.. < t k = M, k 1 e i = 0,.., k, t i / D con D := {t : P{x E : f x = t} 0} Sia B i := {x E : f x [t i, t i+1 }; dalla continuità di f segue che f 1 t i, t i+1 è aperto e B i f 1 {t i } f 1 {t i+1 }. Siccome t i / D, P B i = 0, perciò dalla 4. segue che Allora, E k 1 lim n i=0 k 1 t i P n B i = t i P B i P n dx f x P dx f x k 1 P E n dx f x t i P n B i E + i=1 k 1 k 1 + t i P n B i t i P B i + k 1 t i P B i P dx f x i=1 i=1 i=1 E 2 max t k 1 k 1 i+1 t i + t i P n B i t i P B i 0 i k 1 e la tesi segue dall arbitrarietà di T k. i=0 i=1 i=1 Definizione 31 Sia E, E uno spazio misurabile. Una collezione d insiemi K 0 E E è detta classe determinante se, date due misure di probabilità P e Q su E, E che soddisfano ne segue che sono identiche, ovvero P A = Q A, A E. P A = Q A, A K 0 E 1.35 Definizione 32 Sia E sia uno spazio topologico polacco, localmente compatto e σcompatto. Una collezione d insiemi K 1 E B E è detta classe determinante convergenza se, data una successione di misure di probabilità {P n } n 1 convergente a P si ha che se {P n A} n 1 convergente a P A, A K 1 E : P A = 0, allora {P n A} n 1 convergente a P A, A B E tale che P A = 0. Osservazione 33 Nel caso in cui E = n, 1 n <, dalla definizione di funzione di distribuzione di un vettore aleatorio data nella sezione seguente, la collezione degli insiemi K := { n i=1, x i ] : x 1,.., x n n } 1.36 risulta essere una classe determinante e per il Teorema 129 è anche una classe determinante convergenza. 14
16 Nel caso in cui E = N, K 0 N e K 1 N coincidono con la collezione degli insiemi cilindrici, ovvero la collezione di sottoinsiemi A di N per cui esistono n 1 e B B n K tali che, posto x = {x i } i N, A coincide con { x N : x 1,.., x n B }. Nel caso in cui E = C [0, 1] invece si può scegliere come K 0 C [0, 1] la collezione degli insiemi cilindrici, tuttavia K 1 C [0, 1] K 0 C [0, 1]. Infatti, se {P n } n 1 P C [0, 1] è la successione tale che n 1, P n := δ xnt con x n t := nt1 [0, 1 n ] t nt [ 1 n, 2 ] t 1.37 n e P := δ 0, allora, A K 0 C [0, 1], n 1, P n A = 0 o 1. Inoltre se P A = 0, {P n A} n 1 converge a P A, mentre se B := {x t C [0, 1] : x t 1 2 }, 1.38 B B C [0, 1] che coincide con la σalgebra generata dagli elementi di K 0 C [0, 1] e P B = P n B = 0, n 1, ma P B = 1. Quindi, {P n B} n 1 converge a P B. Definizione 34 Sia E sia uno spazio topologico polacco e I un insieme di indici. Una famiglia di misure di probabilità {P i } i I P E è detta relativamente compatta se ogni successione {P n } n 1 {P i } i I contiene una sottosuccessione debolmente convergente ad un elemento di P E. Teorema 35 di Prokhorov Sia E sia uno spazio topologico polacco e I un insieme di indici. Una famiglia di misure di probabilità {P i } i I P E è relativamente compatta se e solo se è tesa. Dimostrazione: Ci restringiamo al caso in cui E = che è anche localmente compatto e σcompatto. Se {P i } i I è relativamente compatta ma non tesa, ε > 0 tale che K compatto sup i I P i K c > ε. Da ciò segue che, n 1, sup i I P i n, n c sup P i [ n, n] c > ε 1.39 i I e quindi che n 1, P in {P i } i I per cui P in n, n c > ε. Dato che {P i } i I è relativamente compatta, da {P in } n 1 si può estrarre una sottosuccessione {P ink } k 1 debolmente convergente a Q P. Allora, per il Teorema 30, n 1, 0 < ε < lim k P ink n, n c Q n, n c, 1.40 ma poiché lim n Q n, n c = Q n 1 n, n c = 0 ciò è impossibile. 15
17 {P i } i I è tesa e {P n } n 1 {P i } i I. Sia {F n } n 1 la corrispondente successione di funzioni di distribuzione. Per il Teorema di Helly teorema 41 {F nk } k 1 {F n } n 1 ed una funzione di distribuzione generalizzata G tale che {F nk x} k 1 converge a G x, x C G. Scelto ε > 0, sia I ε = a ε, b ε ] tale che n 1, P n I c ε < ε, ovvero tale che P n I ε > 1 ε. Se a, b C G tali che a < a ε < b ε < b, allora 1 ε < P nk a ε, b ε ] P nk a, b] = F nk b F nk a k G b G a Inoltre, k 1, P nk, + = 1 da cui segue, passando al limite per k che G + G = 1. Siccome però G è una funzione di distribuzione generalizzata, 0 G G + 1, quindi G = 0 e G + = 1, ovvero G è una funzione di distribuzione. Perciò, dalla Definizione 42 segue che {F nk } k 1 converge in generale a G e quindi dal Teorema 129 segue che la successione associata di misure di probabilità {P nk } k 1 converge debolmente a Q, distribuzione di probabilità associata a G. Funzioni di distribuzione e convergenza in legge Sia E, B E =, B e P P. La funzione ha le seguenti proprietà: x F x := P, x] [0, 1] F è non decrescente, ovvero, x, y : x y, F x F y ; 2. lim x F x = 0 ; lim x F x = 1; 3. F è continua a destra, ovvero x, lim y x F y = F x, ed ammette limite a sinistra, ovvero x, lim y x F y = F x. Definizione 36 Ogni funzione F : che verifica le proprietà 1,2,3 precedentemente descritte è detta funzione di distribuzione. Teorema 37 di Carathéodory Sia Ω un insieme, A un algebra di Boole di suoi sottoinsiemi e sia µ 0 una misura σfinita su Ω, A. Allora, esiste un unica misura µ P Ω, σ A estensione di µ 0, ovvero tale che A A, µ A = µ 0 A. Teorema 38 Sia F una funzione di distribuzione. Esiste un unica misura di probabilità P su, B tale che a, b : a < b, Pa, b] = F b F a. 16
18 Dimostrazione: Sia A l algebra dei sottoinsiemi di generata da insiemi A che sono unioni disgiunte di intervalli del tipo a, b] con a, b : a < b, ovvero A := n a k, b k ], 1.43 k=1 e sia P 0 tale che A A P 0 A := n F b k F a k k=1 P 0 così definita è unica e finitamente additiva. esta da dimostrarne la σadditività e la tesi segue dal teorema di Carathéodory. A tal fine basta mostrare che P 0 è continua a, ovvero, che se {A n } n 1 è una successione decrescente a di insiemi di A, cioè tale che A n+1 A n e A, allora P 0 A n. Supponiamo innanzi tutto che n 1, A n [ N, N] con N <. Dato che F x è continua a destra ed ogni A n è somma finita d intervalli aperti a sinistra e chiusi a destra, n 1, ε > 0, B n A tale che B n A n e P 0 A n P 0 B n ε2 n. Siccome [ N, N] è compatto e n 1 A n = n 1 B n =, {[ N, N]\B n } n 1 è un ricoprimento aperto di [ N, N]. Allora, per il teorema di Heine-Borel si può estrarre un sottoricoprimento finito. Perciò, n 0 ε > 0 tale che [ N, N] = n 0 ε n=1 n 0 ε [ N, N]\Bn = [ N, N]\ ovvero n 0 ε n=1 B n =. Quindi, siccome A 1 A n0 ε, n 0 ε P 0 An0 ε = P0 A n0 ε\ B n + P 0 n=1 n=1 n 0 ε n=1 n=1 B n n=1 B n, n 0 ε n 0 ε = P 0 An0 ε\b n P 0 A n \B n 1.47 n 0 ε n=1 n 0 ε P 0 A n \B n ε n=1 2 n = ε 1 2 n 0ε+1 < ε, 1.48 ovvero lim n P 0 A n = 0. In generale è sufficiente scegliere ε > 0 un N ε > 0 tale che P 0 [ N ε, N ε] > 1 ε. Allora, poiché A n = [ N ε, N ε] A n [ N ε, N ε] c A n, P 0 A n P 0 [ N ε, N ε] A n + ε. Perciò, ripetendo lo stesso argomento precedente esposto per A n per [ N ε, N ε] A n, per n sufficientemente grande, si ottiene P 0 [ N ε, N ε] A n < ε da cui la tesi. Definizione 39 Una funzione G : tale che: 17
19 1. G è non decrescente, ovvero, x, y : x y, G x G y ; 2. lim x G x 0 ; lim x G x 1; 3. G è continua a destra, ovvero x, lim y x G y = G x. è detta funzione di distribuzione generalizzata. Ovviamente dalla definizione di funzione di distribuzione si ha che questa classe è contenuta in quella delle funzioni di distribuzione generalizzate. Definizione 40 Sia I un insieme di indici. Una famiglia di funzioni di distribuzione generalizzate {G i } i I su, è detta relativamente compatta se, {G n } n 1 {G i } i I, G {G i } i I ed una sottosuccessione {n k } k 1 {n} tale che, x C G, insieme dei punti di continuità di G, lim k G nk x = G x. Teorema 41 di Helly La classe delle funzioni di distribuzione generalizzate è sequenzialmente compatta. Dimostrazione: Sia {G n } n 1 una successione di funzioni generalizzate e T := {x 1, x 2,..} un sottoinsieme numerabile denso in. Dalla limitatezza della successione numerica {G n x 1 } n 1 segue che esiste {n 1 k } k 1 {n} tale che {G 1 n x 1 } k 1 ha limite g 1 per k. Allora, è k possibile estrarre da {n 1 k } k 1 una sottosuccessione {n 2 k } k 1 tale che {G 2 n x 2 } k 1 ha limite g 2 k per k e così via. In questo modo resta definita su T una funzione G T x tale che G T x i = g i e, considerando la successione diagonale {n k k } k 1, x i T, si ha lim k G k n x i = g i. Sia allora k x G x := inf{g T y : y T, y > x} G è non decrescente. Infatti, dato che gli elementi della successione {G n } n 1 sono funzioni non decrescenti, si ha che G k n x G k k n y, x, y T : x y e quindi, passando al k limite per k, ciò vale anche per G T. Dunque, dalla sua definizione si ha che G è non decrescente. G è continua a destra. Sia {x k } k 1 x e d := lim k G x k. Chiaramente, G x d, ma se fosse G x < d, per la definizione di G esisterebbe y T : x < y, G y < d. Quindi, poiché {x k } k 1 x, esisterebbe k y : k > k y, x < x k < y, dunque G x k G y < d che implica lim k G x k < d, contro l ipotesi che tale limite è proprio uguale a d. Pertanto G è una funzione di distribuzione generalizzata. x 0 C G, lim m G x m n 0 = G x 0. m Infatti, y T : y > x 0, esta da dimostrare che, lim m G n m m x 0 lim m G n m m y = G T y,
20 quindi lim m G x m n 0 inf{g T y : y T, y > x 0 } = G x m D altra parte sia x < y < x 0 con y T. Allora, G x G y = G T y = lim G y = lim m n m m mg y lim m n m mg x m n 0, 1.52 m ma se x x 0 si ha che G x 0 limm G x m n 0. Pertanto, se x 0 C G, G x m 0 = G x0, dunque G x 0 lim m G n m m x 0 lim G x m n 0 lim m m G x m m n 0 = G x m Definizione 42 Una successione di funzioni di distribuzione {F n } n 1 definite su converge in generale alla funzione di distribuzione F : se, x C F, insieme dei punti di continuità di F, la successione numerica {F n x} n 1 converge ad F x. In generale, sia n 1. Consideriamo lo spazio misurabile n, B n, se P n indica la collezione delle misure di probabilità su n, B n, P n P n. La funzione n n x = x 1,.., x n F x = F x 1,.., x n := P {y n : y i x i } [0, 1] 1.54 ha le seguenti proprietà: 1. lim xi F x 1,.., x n = 0 i = 1,.., n; 2. lim x F x = 1; 3. F è continua a destra in ogni argomento, ovvero i = 1,.., n, lim yi x i F x 1,.., x i 1, y, x i+1,.., x n = F x 1,.., x i 1, x i, x i+1,.., x n 1.55 e quindi collettivamente, cioè x n, lim y x F y = F x. Definizione 43 Ogni funzione F : n che verifica le proprietà 1,2,3 precedentemente descritte è detta funzione di distribuzione multivariata n-dimensionale. Nel caso unidimensionale F è detta funzione di distribuzione univariata. Se F su n, n 2,è una funzione di distribuzione, scelto i = 1,.., n, passando al limite per x i + nell espressione di F x 1,.., x n si ottiene una funzione di distribuzione F i : n 1, per cui, se y n 1 è tale che y j = x j, con j {1,.., n}\{i}, F i y 1,.., y n 1 = i=1 lim F x 1,.., x n x i + Nel linguaggio del Calcolo delle Probabilità e della Statistica, le F i sono dette funzioni di distribuzione marginali n 1-dimensionali della funzione di distribuzione F. 19
21 Osservazione 44 Allo stesso modo, scelto un sottoinsieme {i 1,.., i k } di k n 1 elementi in {1,.., n} la funzione F i1,..,i k : n k per cui, se y n k è tale che y j = x j, con j {1,.., n}\{i 1,.., i k }, F i1,..,i k y 1,.., y n k = lim F x 1,.., x n, 1.57 x i1,..,x ik +,..,+ è detta funzione di distribuzione marginale n 1-dimensionale della funzione di distribuzione F. Analogamente al caso delle funzioni di distribuzione univariate, il Teorema di Carathéodory implica il seguente risultato Teorema 45 Sia F una funzione di distribuzione multivariata n-dimensionale. Allora esiste un unica misura di probabilità P su n, B n tale che se i = 1,.., n ai,b i F n x 1,.., x n := F n x 1,.., x i 1, b i, x i+1,..x n F n x 1,.., x i 1, a i, x i+1,..x n, 1.58 n P n i=1a i, b i ] = ai,b i F n x 1,.., x n i=1 Nel seguito, considerato lo spazio di probabilità n, B n, P, n 1, per ogni funzione f a valori reali misurabile su n, B n tale che P dx f x 0 P dx f x 0 <, 1.60 n n porremo P dx f x = n df x f x. n 1.61 Caratterizzazione della convergenza debole tramite la trasformata di Fourier-Stieltjes della distribuzione di probabilità Funzione caratteristica di una distribuzione di probabilità su n, n 1 Definizione 46 Si definisce funzione caratteristica di una distribuzione di probabilità P P n la funzione n t ϕ t := P dx e it,x = df x e it,x C n n Dunque ϕ è la trasformata di Fourier-Stieltjes della funzione di distribuzione F che coincide con la trasformata di Fourier della densità di probabilità associata, se tale distribuzione di probabilità è assolutamente continua rispetto alla misura di Lebesgue su n. Qui di seguito ci restringeremo al caso delle funzioni di distribuzione univariate, tuttavia quanto esposto resta valido anche nel caso delle funzioni di distribuzione multivariate. 20
22 Teorema 47 di unicità Siano F e G due funzioni di distribuzione su tali che le funzioni carattesistiche delle distribuzioni di probabilità associate coincidono t. Allora anche F e G coincidono su tutto. Dimostrazione: Sia I un intervallo di e ε > 0, sia f ε x := 1 inf y I x y ε f ε è continua e f ε 1. Inoltre, ε > 0, N ε > 0 : N > N ε, I suppf ε [ N, N]. Poiché f ε N = f ε N = 0, per il teorema di Stone-Weierstrass, f ε può essere approssimata.uniformemente per mezzo di polinomi trigonometrici. Ovvero, esiste: una successione di funzioni {f ε N,n } n 1 della forma f ε N,n x = n k=0 a ke iπx k N ; un indice n N 1 e una successione {δ N } N 1 tale che δ N 0, per cui, per ogni n n N sup f ε N,n x f ε x < δ N ; x [ N,N] sup x f ε N,n x < Allora. poiché per ipotesi ε > 0, df x e itx = df x f ε N,n x = Dunque, N df x f ε x dg x f ε x = df x f ε x N N N f ε f ε N,n df x + f ε f ε N N,n dg x + N N N 2δ N + df x f ε N,n x 1 1 [ N,N] c x dg x e itx 1.65 dg x f ε N,n x N N df x f ε N,n x N dg x f ε x 1.67 N dg x f ε N,n x dg x f ε N,n x 1 1 [ N,N] c x 2δ N F N + F N G N + G N. Passando al limite per N si ha df x f ε x = dg x f ε x 1.68 che, per ε 0 implica df = dg per ogni intervallo I e quindi A B. I I 21
23 Teorema 48 formula d inversione Sia F una funzione di distribuzione su e ϕ la funzione caratteristica della distribuzione di probabilità associata. Allora: 1. a, b tale che a < b e F è continua in a e b, 1 F b F a = lim c 2π c c dt e ita e itb ϕ t it 2. Se ϕ L 1, F ha densità f x = 1 dte itx ϕ t π Dimostrazione: 1. Sia Poiché Inoltre, 1 t ψ c x = 1 2π 1 c 2π c dt e ita e itb ϕ t = 1 it 2π df x 1 2π c c c c dt e ita e itb e itx = it dt e ita e itb df x e itx = 1.71 it df x ψ c x. e ita e itb b e itx = it dxe itx b a, 1.72 a ψ c x = 1 c dt e ita e itb e itx c b a <. 2π it π è una funzione dispari, quindi c c c sin t x a sin t x b dt t = 1 cx a du sin u 2π cx a u 1 cx b du sin u 2π cx b u Ma la funzione y sin u du è continua in x e y e sin u du = π. Quindi, uniformemente in x u u x lim ψ c = 1 a,b + 1 δ{a} + δ {b} c 2 Sia ora P la misura di probabilità su, B associata a F, ovvero tale che a, b con a < b, P a, b] = F b F a. Per il teorema di Lebesgue della convergenza dominata, lim c df x ψ c x = df x ψ c x = P a, b + 1 P{a} + P{b} = F b F a + 1 F a F a + 1 F b F b 2 2 = F b + F b F a + F a
24 Ma se a e b sono punti di continuità di F, allora df x ψ c x = F b F a. lim c 2. Se ϕ L 1, sia f x la sua antitrasfomata di Fourier. Allora, f è uniformemente continua su e lim x + f x = lim x f x = 0. Dunque, f è integrabile su un intervallo finito di. Quindi, se < a < b < +, per il teorema di Fubini, b a dxf x = b a dx 1 2π c = lim dt 1 c c 2π dte itx ϕ t = e ita e itb ϕ t. it dt 2π ϕ t b a dxe itx 1.76 Se 1 c F b F a = lim dt e ita e itb ϕ t 1.77 c 2π c it e a e b sono punti di continuità di F, allora, x, F x = x dyf y 1.78 e poiché F è non decrescente e lim x F x = 1, f è sommabile, quindi la distribuzione di probabilità associata ad F è a.c. rispetto alla misura di Lebesgue. Dunque, la seconda affermazione del teorema segue dalla prima. Osservazione 49 La formula d inversione provvede ad un altra dimostrazione del teorema di unicità. Teorema 50 di Bochner-Khinchin Sia ϕ C ; C tale che ϕ 0 = 1. Condizione necessaria e sufficiente affinche ϕ sia la funzione caratteristica di una distribuzione di probabilità su, B è che la forma quadratica associata, ovvero n ϕ t i t j λ i λj, n 1, e {t i } n i=1, {λ i } n i=1 C, 1.79 sia definita positiva. i,j=1 Dimostrazione: Essendo la dimostrazione della sufficienza particolarmente complicata, dimostriamo solo l implicazione diretta. Se ϕ t = df x eitx allora, n 1, e {t i } n i=1, {λ i } n i=1 C, n df x e ixt i t j n 2 λ i λj = df x e itix λ i i,j=1 i=1 23
25 Teorema 51 di Pólya Se ϕ C è una funzione pari tale che: 1. ϕ t 0, t + ; 2. ϕ 0 = 1; 3. lim t ϕ t = 0; 4. ϕ è convessa su +, allora ϕ è una funzione caratteristica. Teorema 52 di Marcinkiewicz Se t P t C è un polinomio e ϕ = e P caratteristica, allora P ha al più grado 2. una funzione Convergenza debole di una successione di misure di probabilità su e convergenza puntuale della successione associata di funzioni caratteristiche Lemma 53 Sia {P n } n 1 P una successione tesa di misure di probabilità tale che ogni sua sottosuccessione debolmente convergente ammette lo stesso limite P P. Allora l intera successione {P n } n 1 converge debolmente a P. Dimostrazione: Se {P n } n 1 non converge debolmente a P, f C b tale che {E f n } n 1 non converge a E f. Quindi, ε > 0 e {n ε} {n} tale che En ε f E f ε > 0, però essendo {P k } k {n ε } tesa e dunque, per il teorema di Prokhorov, relativamente compatta, {n ε} {n ε} tale che {P k } k {n ε } converge debolmente a Q P. Ma, per ipotesi P = Q quindi {E f k } k {n ε } converge a E f contro l ipotesi En ε f E f ε. Lemma 54 Sia {P n } n 1 P una successione tesa di misure di probabilità e sia {ϕ n } n 1 la corrispondente successione di funzioni caratteristiche. Allora, {P n } n 1 converge debolmente se e solo se {ϕ n } n 1 converge puntualmente. Dimostrazione: Segue dalla definizione di convergenza stretta, considerando t le funzioni cos tx, sin tx. {P n } n 1 è tesa quindi, per il teorema di Prokhorov, {n } {n} tale che {P k } k {n } converge debolmente a P P. Se {P n } n 1 non converge debolmente a P, per il lemma precedente {n } {n } tale che {P k } k {n } converge debolmente a Q P. Poiché t, lim n ϕ n t allora, P dx e itx = lim ϕ n n t = lim ϕ n n t = Q dx e itx Quindi, per il teorema di unicità, P = Q, contro l ipotesi che P Q. 24
26 Lemma 55 Sia F una funzione di distribuzione e ϕ la funzione caratteristica associata. Allora c > 0 tale che, a > 0 [ ] E 1 [ 1 a, 1 c a dt 1 e ϕ t a ]c a Dimostrazione: Siccome Per teorema di Fubini 1 a a 0 a dt 1 e ϕ t = 1 a 0 = df x 1 e ϕ t = dt sin ax ax 0 df x cos tx, 1.83 df x 1 cos tx = df x 1 a inf 1 sin y y : y >1 y c 1 {x : x > 1a } df x. a 0 df x {x : ax >1} dt 1 cos tx 1.84 Teorema 56 di continuità Sia {F n } n 1 una successione di funzioni di distribuzione e sia {ϕ n } n 1 la corrispondente successione di funzioni caratteristiche. 1. Se {F n } n 1 converge in generale alla funzione di distribuzione F, allora {ϕ n } n 1 converge puntualmente a ϕ funzione caratteristica di F. 2. Se {ϕ n } n 1 converge puntualmente ed il limite ϕ è una funzione continua in t = 0, allora ϕ è la funzione caratteristica di una distribuzione di probabilità P e la successione {F n } n 1 converge in generale a F funzione di distribuzione associata a P. Dimostrazione: 1. Poiché per il Teorema 129 la convergenza in generale della successione {F n } n 1 è equivalente alla convergenza stretta delle distribuzioni di probabilità associate, considerando t le funzioni sin tx e cos tx si ha la tesi. 2. Sia {ϕ n } n 1 convergente puntualmente a ϕ continua in t = 0 e sia, n 1, P n la distribuzione di probabilità associata a F n. a > 0, per il lemma precedente P n [ 1 a, 1 a ]c c a dt [1 e ϕ a n t] 1.85 e per teorema di Lebesgue della convergenza dominata lim P n [ 1a, 1a n ]c c a a lim dt [1 e ϕ n t] = c n a 0 0 a 0 dt [1 e ϕ t]
27 Ma essendo ϕ continua in t = 0, ε > 0, a ε > 0 tale che n 1 P n [ 1 a ε, 1 a ε ] c ε Perciò la successione {P n } 1 è tesa, quindi, per il teorema di Prokhorov, relativamente compatta e, per i due precedenti lemmi, convergente debolmente a P P. Pertanto, t lim ϕ n t = lim P n dx e n n itx = P dx e itx, 1.88 ma per ipotesi, t, lim n ϕ n t = ϕ t. Quindi, t, ϕ t = P dx e itx Osservazione 57 La topologia della convergenza debole è metrizzabile, ciò verrà discusso per il caso delle misure su quando si tratterà la convergenza in distribuzione di successioni di variabili aleatorie. 26
28 1.5 Applicazioni tra spazi misurabili e variabili aleatorie Definizione 58 Data una coppia di spazi misurabili Ω, F e E, E, un applicazione X : Ω E è detta misurabile se X 1 E F, ovvero se B E, X 1 B F. Definizione 59 Sia Ω, F, P uno spazio di probabilità. Un applicazione misurabile ξ da Ω, F a, B è detta variabile aleatoria; Un applicazione misurabile ξ da Ω, F a n, B n è detto vettore aleatorio. In generale, una generica applicazione misurabile tra spazi misurabile è detta elemento aleatorio. Nel seguito supporremo che tutti gli elementi aleatori abbiano valori in uno spazio E polacco, localmente compatto e σcompatto, e dunque che P E := P E, B E M 1,+ E Osservazione 60 Inoltre, useremo l abbreviazione v.a. per indicare sia i vettori che le variabili aleatorie e, considerato lo spazio di probabilità n, B n, P, n 1, per ogni f misurabile su n, B n in sé tale che P dx f x 0 P dx f x 0 <, 1.91 n n porremo E f ξ := P dx f x = df x f x n n Definizione 61 Sia Ω, F, P uno spazio di probabilità, ξ una v.a. e η un vettore aleatorio n- dimensionale. La misura P ξ := P ξ 1 P è detta distribuzione di probabilità o legge della variabile aleatoria ξ e la funzione x F ξ x := P {ω Ω : ξ ω x} = P ξ, x] [0, 1] 1.93 è detta funzione di distribuzione o ripartizione della variabile aleatoria ξ. Allo stesso modo, P η := P η 1 P n è detta distribuzione di probabilità o legge della vettore aleatorio η e la funzione n n x 1,.., x n = x F η x = F η x 1,.., x n := P {ω Ω : η i ω x i } è detta funzione di distribuzione o ripartizione del vettore aleatorio η. 27 i=1 n = P η {y n : y i x i } [0, 1] i=1
29 1.5.1 Stabilità della collezione delle v.a. rispetto alla topologia della convergenza puntuale Definizione 62 Una successione di v.a. {ξ n } n 1 definite su Ω, F converge puntualmente se, ω Ω, la successione numerica {ξ n ω} n 1 è convergente. Se inoltre esiste ξ : Ω tale che, ω Ω, lim n ξ n ω = ξ ω, allora {ξ n ω} n 1 è detta convergere puntualmente a ξ. Teorema 63 Sia {ξ n } n 1 una successione di v.a. definite su Ω, F convergente puntualmente a ξ. Allora, ξ è una v.a.. Dimostrazione: Basta verificare che, c, {ω Ω : ξ ω < c} è misurabile. Tuttavia quest insieme coincide con l insieme M c := { ω Ω : ξ m ω < c 1 } F k k 1 n 1 m n Infatti, dato ω Ω, se ξ ω < c, esiste k 1 tale che ξ ω < c 1 k, ma poiché {ξ n ω } n 1 converge a ξ ω esiste n sufficientemente grande tale che m n, ξ m ω < c 1 k. Quindi, ω M c. Viceversa, se ω M c, allora esiste m 1 tale che m m, ξ m ω < c 1 k, per qualche k 1, cioè ξ ω < c. 1.6 Generalità sull attesa di una variabile aleatoria D ora in poi, laddove non espressamente specificato, considereremo Ω, F, P come spazio di probabilità completo, cioè tale che ogni sottoinsieme di un insieme trascurabile rispetto a P, ovvero di probabilità nulla, risulti misurabile. Sia ξ una v.a. positiva, data la successione di v.a. ξ n ω := n2 n k=1 k 1 2 n 1 ξ 1 [ k 1 2 n, k 2 n ω + n1 ξ 1 [n,+ ω, 1.95 ω Ω, n 1, si ha ξ n ω ξ n+1 ω ξ ω e {ξ n ω} n 1 converge ad ξ ω. Ponendo, n 1, E ξ n := n2 n k=1 k 1 2 n P { [ k 1 ω Ω : ξ ω 2, k } + np {ω Ω : ξ ω n}, 1.96 n 2 n dato che E ξ n E ξ n+1, limn E ξ n esiste ed eventualmente uguaglia +. Sia allora E ξ := lim n E ξ n Tale limite è detto valore atteso della variabile aleatoria ξ. Data una qualsiasi variabile aleatoria ξ, ponendo ξ + := ξ 0, ξ := ξ 0, ξ = ξ + ξ, il valore atteso di ξ, E ξ = E ξ + E ξ, risulta definito se E ξ + E ξ < + ed è finito se E ξ +, E ξ < +, ovvero se E ξ = E ξ + + E ξ < +. 28
30 Teorema 64 della convergenza monotona Sia Ω, F, P uno spazio di probabilità e su questo siano definite le v.a. η e ξ. Sia inoltre {ξ n } n 1 una successione di v.a. su Ω, F, P convergente puntualmente a ξ. 1. Se {ξ n } n 1 e η sono tali che E η > e n 1, si ha η ξ n ξ n+1 ξ, allora la successione numerica crescente {E ξ n } n 1 converge a E ξ. 2. Se {ξ n } n 1 e η sono tali che E η < e n 1, si ha η ξ n ξ n+1 ξ, allora la successione numerica decrescente {E ξ n } n 1 converge a E ξ. Dimostrazione: 1. Supponiamo dapprima che η 0. n 1, sia {ξ k n } k 1 una successione crescente di v.a. semplici convergenti puntualmente a ξ n. Allora, posto ζ 1 := ξ 1 1 e k 2, ζ k := max 1 n k ξ k n, si ha che {ζ k } k 1 è una successione crescente di funzioni semplici tali che k 1, ζ k = max 1 n k ξk n max ξ n = ξ k ξ n k Sia ζ := lim n ζ n. Poiché per 1 n k, ξ k n precedente disuguaglianza n 1 si ottiene ζ k, passando al limite per k dalla ξ n ζ ξ 1.99 ovvero ζ = ξ. Inoltre, siccome {ζ k } k 1 è una successione crescente di funzioni semplici E ξ = E ζ = lim n E ζ n lim n E ξ n D altra parte, poiché {ξ k } k 1 è crescente e n 1, ξ n ξ, segue lim n E ξ n E ξ dunque la tesi. Sia η è una generica v.a. tale che E η >. a Se E η =, allora n 1, E ξ n = dunque di conseguenza anche E ξ =. b Se E η <, allora E η < e la successione di v.a. {ξ n η} n 1 ha termini non negativi, è crescente e coverge puntualmente a ξ η. Percui, per quanto prima dimostrato, la successione numerica {E ξ n η} n 1 è a termini positivi, crescente e convergente a E ξ E η. Ma poiché E η < ciò implica che la successione numerica {E ξ n } n 1 è crescente e convergente a E ξ. 2. Considerando η, ξ e { ξ k } k 1 la tesi segue dal punto precedente. 29
31 1.6.1 Disuguaglianza di Markov e sue generalizzazioni Proposizione 65 Disuguaglianza di Markov Sia X una v.a. non negativa definita su Ω, F, P. λ > 0 vale P{ω Ω : X ω > λ} E X λ Dimostrazione: λ > 0 si ha E X = E X1 [0,λ] X + E X1 λ,+ X E X1 λ,+ X λe 1 λ,+ X = λp{ω Ω : X ω > λ}. Corollario 66 Se f è una funzione non negativa, strettamente crescente e X una v.a. definita su Ω, F, P. λ > 0 si ha E f X P{ω Ω : X ω > λ} f λ Dimostrazione: Poiché f è strettamente crescente P{ω Ω : X ω > λ} = P X 1 [λ, + = P X 1 {x : f x > f λ}, e siccome f è non negativa, dalla disuguaglianza di Markov segue P X 1 {x : f x > f λ} P X 1 dx f x f λ = E f X f λ. Osservazione 67 Disuguagluanza di Markov esponenziale Il precedente risultato implica che r, λ > 0, P{ω Ω : X ω > λ} e rλ E e rx Quindi P{ω Ω : X ω > λ} inf r>0 e rλ E e rx = e sup r>0 [rλ log EerX ] Corollario 68 Disuguaglianza di Chebichev Sia X una v.a. definita su Ω, F, P. ε > 0 vale P{ω Ω : X ω E X > ε} V ar X ε Dimostrazione: Si ponga Y := X E X e si applichi il corollario precedente considerando f = x 2. Esercizio 3 Dimostrare la disuguaglianza di Chebichev generalizzata P{ω Ω : X ω E X > ε} E X E X p ε p, p >
32 1.7 Funzione caratteristica di una variabile aleatoria Definizione 69 Si definisce funzione caratteristica di un v.a. ξ n definito sullo spazio di probabilità Ω, F, P, ϕ ξ t := P ξ dx e it,x = df ξ x e it,x = E e it,ξ n n la funzione caratteristica della distribuzione di probabilità P ξ P n Proprietà della funzione caratteristica di una v.a. Consideriamo il caso in cui ξ sia una v.a. su uno spazio di probabilità Ω, F, P, allora ϕ ξ t ha le seguenti proprietà: 1. ϕξ t ϕξ 0 = ϕ ξ t = ϕ ξ t. 3. ϕ ξ t è uniformemente continua in. Infatti, t, h, ϕξ t + h ϕ ξ t = E [ e it+hξ e itξ] E e ith quindi per il teorema di Lebesgue della convergenza dominata lim h 0 E e ihξ 1 = Se B B B df ξ = B df ξ, F ξ è detta simmetrica. Allora, ϕ ξ t F ξ è simmetrica. Infatti, se F ξ è simmetrica E [sin tx] = 0, perciò ϕ ξ t = E [cos tx]. Viceversa, poiché ϕ ξ t = ϕ ξ t = ϕ ξ t = ϕ ξ t, dal teorema di unicità si ha che ξ e ξ hanno la stessa funzione di distribuzione. 5. Se n 1 tale che E ξ n <, allora ϕ ξ C r, r n e ϕ ξ t = n k=0 ϕ k ξ 0 itk k! + o t Infatti, per la disuguaglianza di Lyapunov, r n, E ξ r 1 r E ξ n 1 n. Inoltre, [ ] ϕ ξ t + h ϕ ξ t = E e itξ eihξ 1 h h
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
5. La teoria astratta della misura.
 5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale
 4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
Università degli Studi di Catania A.A. 2012-2013. Corso di laurea in Ingegneria Industriale
 Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
A i è un aperto in E. i=1
 Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Esistenza di funzioni continue non differenziabili in alcun punto
 UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
19. Inclusioni tra spazi L p.
 19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
Limiti e continuità di funzioni reali di una variabile
 di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
di funzioni reali di una variabile Corso di Analisi Matematica - capitolo VI Facoltà di Economia, UER Maria Caterina Bramati Université Libre de Bruxelles ECARES 22 Novembre 2006 Intuizione di ite di funzione
u 1 u k che rappresenta formalmente la somma degli infiniti numeri (14.1), ordinati al crescere del loro indice. I numeri u k
 Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
SPAZI METRICI. Uno spazio metrico X con metrica d si indica con il simbolo (X, d). METRICI 1
 SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
Capitolo 4: Ottimizzazione non lineare non vincolata parte II. E. Amaldi DEIB, Politecnico di Milano
 Capitolo 4: Ottimizzazione non lineare non vincolata parte II E. Amaldi DEIB, Politecnico di Milano 4.3 Algoritmi iterativi e convergenza Programma non lineare (PNL): min f(x) s.v. g i (x) 0 1 i m x S
Capitolo 4: Ottimizzazione non lineare non vincolata parte II E. Amaldi DEIB, Politecnico di Milano 4.3 Algoritmi iterativi e convergenza Programma non lineare (PNL): min f(x) s.v. g i (x) 0 1 i m x S
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
16. Vari modi di convergenza delle successioni di funzioni reali misurabili.
 16. Vari modi di convergenza delle successioni di funzioni reali misurabili. L argomento centrale di questa ultima parte del corso è lo studio in generale della convergenza delle successioni negli spazi
16. Vari modi di convergenza delle successioni di funzioni reali misurabili. L argomento centrale di questa ultima parte del corso è lo studio in generale della convergenza delle successioni negli spazi
1 Convessità olomorfa
 1 Convessità olomorfa Esercizio 1 Sia f O(C n ) e sia X = {f = 0}; dimostrare che, per ogni K compatto di X, l inviluppo K O(Cn ) è contenuto in X. Esercizio 2 Fissato un reale δ (0, 2π), consideriamo
1 Convessità olomorfa Esercizio 1 Sia f O(C n ) e sia X = {f = 0}; dimostrare che, per ogni K compatto di X, l inviluppo K O(Cn ) è contenuto in X. Esercizio 2 Fissato un reale δ (0, 2π), consideriamo
G. Pareschi ALGEBRE DI BOOLE. 1. Algebre di Boole
 G. Pareschi ALGEBRE DI BOOLE 1. Algebre di Boole Nel file precedente abbiamo incontrato la definizione di algebra di Boole come reticolo: un algebra di Boole e un reticolo limitato, complementato e distributivo.
G. Pareschi ALGEBRE DI BOOLE 1. Algebre di Boole Nel file precedente abbiamo incontrato la definizione di algebra di Boole come reticolo: un algebra di Boole e un reticolo limitato, complementato e distributivo.
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
Funzioni. Parte prima. Daniele Serra
 Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Corso di Analisi Numerica
 Corso di Laurea in Ingegneria Informatica Corso di Analisi Numerica 8 - METODI ITERATIVI PER I SISTEMI LINEARI Lucio Demeio Dipartimento di Scienze Matematiche 1 Norme e distanze 2 3 4 Norme e distanze
Corso di Laurea in Ingegneria Informatica Corso di Analisi Numerica 8 - METODI ITERATIVI PER I SISTEMI LINEARI Lucio Demeio Dipartimento di Scienze Matematiche 1 Norme e distanze 2 3 4 Norme e distanze
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8. Cognome:... Nome:... Matricola:...
 Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
APPUNTI DI MATEMATICA ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1)
 ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1) Un insieme è una collezione di oggetti. Il concetto di insieme è un concetto primitivo. Deve esistere un criterio chiaro, preciso, non ambiguo, inequivocabile,
ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1) Un insieme è una collezione di oggetti. Il concetto di insieme è un concetto primitivo. Deve esistere un criterio chiaro, preciso, non ambiguo, inequivocabile,
Corso di Analisi Matematica Serie numeriche
 Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
Corso di Analisi Matematica. Successioni e serie numeriche
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
Serie numeriche. 1 Definizioni e proprietà elementari
 Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
l insieme Y è detto codominio (è l insieme di tutti i valori che la funzione può assumere)
 Che cos è una funzione? Assegnati due insiemi X e Y si ha una funzione elemento di X uno e un solo elemento di Y. f : X Y se esiste una corrispondenza che associa ad ogni Osservazioni: l insieme X è detto
Che cos è una funzione? Assegnati due insiemi X e Y si ha una funzione elemento di X uno e un solo elemento di Y. f : X Y se esiste una corrispondenza che associa ad ogni Osservazioni: l insieme X è detto
RICHIAMI SULLE MATRICI. Una matrice di m righe e n colonne è rappresentata come
 RICHIAMI SULLE MATRICI Una matrice di m righe e n colonne è rappresentata come A = a 11 a 12... a 1n a 21 a 22... a 2n............ a m1 a m2... a mn dove m ed n sono le dimensioni di A. La matrice A può
RICHIAMI SULLE MATRICI Una matrice di m righe e n colonne è rappresentata come A = a 11 a 12... a 1n a 21 a 22... a 2n............ a m1 a m2... a mn dove m ed n sono le dimensioni di A. La matrice A può
1.1. Spazi metrici completi
 SPAZI METRICI: COMPLETEZZA E COMPATTEZZA Note informali dalle lezioni 1.1. Spazi metrici completi La nozione di convergenza di successioni è centrale nello studio degli spazi metrici. In particolare è
SPAZI METRICI: COMPLETEZZA E COMPATTEZZA Note informali dalle lezioni 1.1. Spazi metrici completi La nozione di convergenza di successioni è centrale nello studio degli spazi metrici. In particolare è
Insiemi di livello e limiti in più variabili
 Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
Parte 2. Determinante e matrice inversa
 Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
VARIABILI ALEATORIE MULTIPLE E TEOREMI ASSOCIATI. Dopo aver trattato delle distribuzioni di probabilità di una variabile aleatoria, che
 VARIABILI ALATORI MULTIPL TORMI ASSOCIATI Fonti: Cicchitelli Dall Aglio Mood-Grabill. Moduli 6 9 0 del programma. VARIABILI ALATORI DOPPI Dopo aver trattato delle distribuzioni di probabilità di una variabile
VARIABILI ALATORI MULTIPL TORMI ASSOCIATI Fonti: Cicchitelli Dall Aglio Mood-Grabill. Moduli 6 9 0 del programma. VARIABILI ALATORI DOPPI Dopo aver trattato delle distribuzioni di probabilità di una variabile
SIMULAZIONE TEST ESAME - 1
 SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
Autovalori e Autovettori
 Daniela Lera Università degli Studi di Cagliari Dipartimento di Matematica e Informatica A.A. 2008-2009 Autovalori e Autovettori Definizione Siano A C nxn, λ C, e x C n, x 0, tali che Ax = λx. (1) Allora
Daniela Lera Università degli Studi di Cagliari Dipartimento di Matematica e Informatica A.A. 2008-2009 Autovalori e Autovettori Definizione Siano A C nxn, λ C, e x C n, x 0, tali che Ax = λx. (1) Allora
Convessità e derivabilità
 Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
Convessità e derivabilità Definizione 1 (convessità per funzioni derivabili) Sia f : (a, b) R derivabile su (a, b). Diremo che f è convessa o concava su (a, b) se per ogni 0 (a,b) il grafico di f sta tutto
2 FUNZIONI REALI DI VARIABILE REALE
 2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3.1 Successioni. R Definizione (Successione numerica) E Esempio 3.1 CAPITOLO 3
 CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
Esercizi svolti su serie di Fourier
 Esercizi svolti su serie di Fourier Esercizio. (Onda quadra. Determinare i coefficienti di Fourier della funzione x [, f(x = x [, prolungata a una funzione -periodica su R (d ora in poi denoteremo con
Esercizi svolti su serie di Fourier Esercizio. (Onda quadra. Determinare i coefficienti di Fourier della funzione x [, f(x = x [, prolungata a una funzione -periodica su R (d ora in poi denoteremo con
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 2011/2012
 Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
RELAZIONI BINARIE. Proprietà delle relazioni Data una relazione R, definita in un insieme non vuoto U, si hanno le seguenti proprietà :
 RELAZIONI INARIE Dati due insiemi non vuoti, A detto dominio e detto codominio, eventualmente coincidenti, si chiama relazione binaria (o corrispondenza) di A in, e si indica con f : A, (oppure R ) una
RELAZIONI INARIE Dati due insiemi non vuoti, A detto dominio e detto codominio, eventualmente coincidenti, si chiama relazione binaria (o corrispondenza) di A in, e si indica con f : A, (oppure R ) una
1 Insiemi e terminologia
 1 Insiemi e terminologia Assumeremo come intuitiva la nozione di insieme e ne utilizzeremo il linguaggio come strumento per studiare collezioni di oggetti. Gli Insiemi sono generalmente indicati con le
1 Insiemi e terminologia Assumeremo come intuitiva la nozione di insieme e ne utilizzeremo il linguaggio come strumento per studiare collezioni di oggetti. Gli Insiemi sono generalmente indicati con le
Equazioni differenziali ordinarie
 Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
Quesiti di Analisi Matematica A
 Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
Due dimostrazioni alternative nella teoria di Ramsey
 Due dimostrazioni alternative nella teoria di Ramsey 28 Marzo 2007 Introduzione Teoria di Ramsey: sezione della matematica a metà tra la combinatoria e la teoria degli insiemi. La questione tipica è quella
Due dimostrazioni alternative nella teoria di Ramsey 28 Marzo 2007 Introduzione Teoria di Ramsey: sezione della matematica a metà tra la combinatoria e la teoria degli insiemi. La questione tipica è quella
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
TOPOLOGIE. Capitolo 2. 2.1 Spazi topologici
 Capitolo 2 TOPOLOGIE Ogni spazio che si considera in gran parte della matematica e delle sue applicazioni è uno spazio topologico di qualche tipo: qui introduciamo in generale le nozioni di base della
Capitolo 2 TOPOLOGIE Ogni spazio che si considera in gran parte della matematica e delle sue applicazioni è uno spazio topologico di qualche tipo: qui introduciamo in generale le nozioni di base della
MATEMATICA DEL DISCRETO elementi di teoria dei grafi. anno acc. 2009/2010
 elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
elementi di teoria dei grafi anno acc. 2009/2010 Grafi semplici Un grafo semplice G è una coppia ordinata (V(G), L(G)), ove V(G) è un insieme finito e non vuoto di elementi detti vertici o nodi di G, mentre
Una ricetta per il calcolo dell asintoto obliquo. Se f(x) è asintotica a mx+q allora abbiamo f(x) mx q = o(1), da cui (dividendo per x) + o(1), m =
 Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Prodotto elemento per elemento, NON righe per colonne Unione: M R S
 Relazioni binarie Una relazione binaria può essere rappresentata con un grafo o con una matrice di incidenza. Date due relazioni R, S A 1 A 2, la matrice di incidenza a seguito di varie operazioni si può
Relazioni binarie Una relazione binaria può essere rappresentata con un grafo o con una matrice di incidenza. Date due relazioni R, S A 1 A 2, la matrice di incidenza a seguito di varie operazioni si può
TOPOLOGIA ALBERTO SARACCO
 TOPOLOGIA ALBERTO SARACCO Abstract. Le presenti note saranno il più fedeli possibile a quanto detto a lezione. I testi consigliati sono Jänich [1], Kosniowski [2] e Singer- Thorpe [3]. Un ottimo libro
TOPOLOGIA ALBERTO SARACCO Abstract. Le presenti note saranno il più fedeli possibile a quanto detto a lezione. I testi consigliati sono Jänich [1], Kosniowski [2] e Singer- Thorpe [3]. Un ottimo libro
Chiusura lineare. N.B. A può essere indifferentemente un insieme, finito o no, o un sistema. Es.1. Es.2
 Chiusura lineare Def. Sia A V (K) con A. Si dice copertura lineare (o chiusura lineare) di A, e si indica con L(A), l insieme dei vettori di V che risultano combinazioni lineari di un numero finito di
Chiusura lineare Def. Sia A V (K) con A. Si dice copertura lineare (o chiusura lineare) di A, e si indica con L(A), l insieme dei vettori di V che risultano combinazioni lineari di un numero finito di
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
Funzione reale di variabile reale
 Funzione reale di variabile reale Siano A e B due sottoinsiemi non vuoti di. Si chiama funzione reale di variabile reale, di A in B, una qualsiasi legge che faccia corrispondere, a ogni elemento A x A
Funzione reale di variabile reale Siano A e B due sottoinsiemi non vuoti di. Si chiama funzione reale di variabile reale, di A in B, una qualsiasi legge che faccia corrispondere, a ogni elemento A x A
Corso di Analisi Matematica. Funzioni continue
 a.a. 203/204 Laurea triennale in Informatica Corso di Analisi Matematica Funzioni continue Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
a.a. 203/204 Laurea triennale in Informatica Corso di Analisi Matematica Funzioni continue Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
Sui concetti di definizione, teorema e dimostrazione in didattica della matematica
 Liceo Scientifico Statale P. Paleocapa, Rovigo XX Settimana della Cultura Scientifica e Tecnologica 19 marzo 2010 Sui concetti di definizione, teorema e dimostrazione in didattica della matematica Prof.
Liceo Scientifico Statale P. Paleocapa, Rovigo XX Settimana della Cultura Scientifica e Tecnologica 19 marzo 2010 Sui concetti di definizione, teorema e dimostrazione in didattica della matematica Prof.
COGNOME e NOME: FIRMA: MATRICOLA:
 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti,
Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti,
Sulle funzioni di W 1,p (Ω) a traccia nulla
 Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
Appunti di Complementi di Matematica. Jacobo Pejsachowicz (a cura di Nathan Quadrio)
 Appunti di Complementi di Matematica Jacobo Pejsachowicz (a cura di Nathan Quadrio) 1 Indice 1 Cenni della teoria degli insiemi 4 1.1 Classi ed insiemi........................... 4 1.2 Operazioni fra gli
Appunti di Complementi di Matematica Jacobo Pejsachowicz (a cura di Nathan Quadrio) 1 Indice 1 Cenni della teoria degli insiemi 4 1.1 Classi ed insiemi........................... 4 1.2 Operazioni fra gli
E naturale chiedersi alcune cose sulla media campionaria x n
 Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
DOMINI A FATTORIZZAZIONE UNICA
 DOMINI A FATTORIZZAZIONE UNICA CORSO DI ALGEBRA, A.A. 2012-2013 Nel seguito D indicherà sempre un dominio d integrità cioè un anello commutativo con unità privo di divisori dello zero. Indicheremo con
DOMINI A FATTORIZZAZIONE UNICA CORSO DI ALGEBRA, A.A. 2012-2013 Nel seguito D indicherà sempre un dominio d integrità cioè un anello commutativo con unità privo di divisori dello zero. Indicheremo con
Lezione n. 2 (a cura di Chiara Rossi)
 Lezione n. 2 (a cura di Chiara Rossi) QUANTILE Data una variabile casuale X, si definisce Quantile superiore x p : X P (X x p ) = p Quantile inferiore x p : X P (X x p ) = p p p=0.05 x p x p Graficamente,
Lezione n. 2 (a cura di Chiara Rossi) QUANTILE Data una variabile casuale X, si definisce Quantile superiore x p : X P (X x p ) = p Quantile inferiore x p : X P (X x p ) = p p p=0.05 x p x p Graficamente,
Applicazioni lineari
 Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
4. Operazioni elementari per righe e colonne
 4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
4. Operazioni elementari per righe e colonne Sia K un campo, e sia A una matrice m n a elementi in K. Una operazione elementare per righe sulla matrice A è una operazione di uno dei seguenti tre tipi:
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
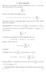 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
a) Osserviamo innanzi tutto che dev essere x > 0. Pertanto il dominio è ]0, + [. b) Poniamo t = log x. Innanzi tutto si ha:
![a) Osserviamo innanzi tutto che dev essere x > 0. Pertanto il dominio è ]0, + [. b) Poniamo t = log x. Innanzi tutto si ha: a) Osserviamo innanzi tutto che dev essere x > 0. Pertanto il dominio è ]0, + [. b) Poniamo t = log x. Innanzi tutto si ha:](/thumbs/28/12902483.jpg) ESERCIZIO - Data la funzione f (x) = (log x) 6 7(log x) 5 + 2(log x) 4, si chiede di: a) calcolare il dominio di f ; ( punto) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire
ESERCIZIO - Data la funzione f (x) = (log x) 6 7(log x) 5 + 2(log x) 4, si chiede di: a) calcolare il dominio di f ; ( punto) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire
Teoria degli insiemi
 Teoria degli insiemi pag 1 Easy Matematica di dolfo Scimone Teoria degli insiemi Il concetto di insieme si assume come primitivo, cioè non riconducibile a concetti precedentemente definiti. Sinonimi di
Teoria degli insiemi pag 1 Easy Matematica di dolfo Scimone Teoria degli insiemi Il concetto di insieme si assume come primitivo, cioè non riconducibile a concetti precedentemente definiti. Sinonimi di
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Dipendenza dai dati iniziali
 Dipendenza dai dati iniziali Dopo aver studiato il problema dell esistenza e unicità delle soluzioni dei problemi di Cauchy, il passo successivo è vedere come le traiettorie di queste ultime dipendono
Dipendenza dai dati iniziali Dopo aver studiato il problema dell esistenza e unicità delle soluzioni dei problemi di Cauchy, il passo successivo è vedere come le traiettorie di queste ultime dipendono
Successioni e serie di funzioni
 Successioni e serie di funzioni A. Albanese, A. Leaci, D. Pallara In questa dispensa generalizzeremo la trattazione delle successioni e delle serie al caso in cui i termini delle stesse siano non numeri
Successioni e serie di funzioni A. Albanese, A. Leaci, D. Pallara In questa dispensa generalizzeremo la trattazione delle successioni e delle serie al caso in cui i termini delle stesse siano non numeri
L espressione torna invece sempre vera (quindi la soluzione originale) se cambiamo contemporaneamente il verso: 1 < 0.
 EQUAZIONI E DISEQUAZIONI Le uguaglianze fra espressioni numeriche si chiamano equazioni. Cercare le soluzioni dell equazione vuol dire cercare quelle combinazioni delle lettere che vi compaiono che la
EQUAZIONI E DISEQUAZIONI Le uguaglianze fra espressioni numeriche si chiamano equazioni. Cercare le soluzioni dell equazione vuol dire cercare quelle combinazioni delle lettere che vi compaiono che la
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Anello commutativo. Un anello è commutativo se il prodotto è commutativo.
 Anello. Un anello (A, +, ) è un insieme A con due operazioni + e, dette somma e prodotto, tali che (A, +) è un gruppo abeliano, (A, ) è un monoide, e valgono le proprietà di distributività (a destra e
Anello. Un anello (A, +, ) è un insieme A con due operazioni + e, dette somma e prodotto, tali che (A, +) è un gruppo abeliano, (A, ) è un monoide, e valgono le proprietà di distributività (a destra e
LE FUNZIONI E LE LORO PROPRIETÀ
 LE FUNZIONI E LE LORO PROPRIETÀ LE FUNZIONI REALI DI VARIABILE REALE COSA SONO LE FUNZIONI Dati due sottoinsiemi A e B non vuoti di R, una FUNZIONE da A a B è una relazione che associa ad ogni numero reale
LE FUNZIONI E LE LORO PROPRIETÀ LE FUNZIONI REALI DI VARIABILE REALE COSA SONO LE FUNZIONI Dati due sottoinsiemi A e B non vuoti di R, una FUNZIONE da A a B è una relazione che associa ad ogni numero reale
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
NOME:... MATRICOLA:... Scienza dei Media e della Comunicazione, A.A. 2007/2008 Analisi Matematica 1, Esame scritto del 08.02.2008. x 1.
 NOME:... MATRICOLA:.... Scienza dei Media e della Comunicazione, A.A. 007/008 Analisi Matematica, Esame scritto del 08.0.008 Indicare per quali R vale la seguente diseguaglianza : + >. Se y - - è il grafico
NOME:... MATRICOLA:.... Scienza dei Media e della Comunicazione, A.A. 007/008 Analisi Matematica, Esame scritto del 08.0.008 Indicare per quali R vale la seguente diseguaglianza : + >. Se y - - è il grafico
2.1 Definizione di applicazione lineare. Siano V e W due spazi vettoriali su R. Un applicazione
 Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
Algebra Lineare e Geometria
 Algebra Lineare e Geometria Corso di Laurea in Ingegneria Elettronica A.A. 2013-2014 Prova d esame del 16/06/2014. 1) a) Determinare la matrice associata all applicazione lineare T : R 3 R 4 definita da
Algebra Lineare e Geometria Corso di Laurea in Ingegneria Elettronica A.A. 2013-2014 Prova d esame del 16/06/2014. 1) a) Determinare la matrice associata all applicazione lineare T : R 3 R 4 definita da
Funzioni. Capitolo 6. 6.1 Concetto di funzione e definizioni preliminari
 Capitolo 6 Funzioni 6. Concetto di funzione e definizioni preliminari Definizione 6. Dati due insiemi non vuoti D e C, si dice applicazione o funzione una qualsiasi legge (relazione) che associa ad ogni
Capitolo 6 Funzioni 6. Concetto di funzione e definizioni preliminari Definizione 6. Dati due insiemi non vuoti D e C, si dice applicazione o funzione una qualsiasi legge (relazione) che associa ad ogni
1.2 Funzioni, dominio, codominio, invertibilità elementare, alcune identità trigonometriche
 . Funzioni, dominio, codominio, invertibilità elementare, alcune identità trigonometriche Per le definizioni e teoremi si fa riferimento ad uno qualsiasi dei libri M.Bertsch - R.Dal Passo Lezioni di Analisi
. Funzioni, dominio, codominio, invertibilità elementare, alcune identità trigonometriche Per le definizioni e teoremi si fa riferimento ad uno qualsiasi dei libri M.Bertsch - R.Dal Passo Lezioni di Analisi
Moto uniforme sul toro bidimensionale
 4/3/06 Luigi Chierchia Moto uniforme sul toro bidimensionale 1. Il toro bidimensionale Denotiamo con R l insieme dei numeri reali e con Z l insieme dei numeri interi (con segno) {..., 2, 1, 0, 1, 2,...};
4/3/06 Luigi Chierchia Moto uniforme sul toro bidimensionale 1. Il toro bidimensionale Denotiamo con R l insieme dei numeri reali e con Z l insieme dei numeri interi (con segno) {..., 2, 1, 0, 1, 2,...};
ALGEBRA I: CARDINALITÀ DI INSIEMI
 ALGEBRA I: CARDINALITÀ DI INSIEMI 1. CONFRONTO DI CARDINALITÀ E chiaro a tutti che esistono insiemi finiti cioè con un numero finito di elementi) ed insiemi infiniti. E anche chiaro che ogni insieme infinito
ALGEBRA I: CARDINALITÀ DI INSIEMI 1. CONFRONTO DI CARDINALITÀ E chiaro a tutti che esistono insiemi finiti cioè con un numero finito di elementi) ed insiemi infiniti. E anche chiaro che ogni insieme infinito
1 Giochi a due, con informazione perfetta e somma zero
 1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
LEZIONE 31. B i : R n R. R m,n, x = (x 1,..., x n ). Allora sappiamo che è definita. j=1. a i,j x j.
 LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
Esercizi svolti. 1. Si consideri la funzione f(x) = 4 x 2. a) Verificare che la funzione F(x) = x 2 4 x2 + 2 arcsin x è una primitiva di
 Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
Parte 6. Applicazioni lineari
 Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
EQUAZIONI DIFFERENZIALI Esercizi svolti. y = xy. y(2) = 1.
 EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
Luigi Piroddi piroddi@elet.polimi.it
 Automazione industriale dispense del corso 10. Reti di Petri: analisi strutturale Luigi Piroddi piroddi@elet.polimi.it Analisi strutturale Un alternativa all analisi esaustiva basata sul grafo di raggiungibilità,
Automazione industriale dispense del corso 10. Reti di Petri: analisi strutturale Luigi Piroddi piroddi@elet.polimi.it Analisi strutturale Un alternativa all analisi esaustiva basata sul grafo di raggiungibilità,
