Indice. 1 Introduzione ai modelli lineari 2. 2 Dataset 3. 3 Il Modello 8. 4 In pratica Peso e percorrenza... 12
|
|
|
- Clemente Vaccaro
- 8 anni fa
- Visualizzazioni
Transcript
1 Indice 1 Introduzione ai modelli lineari 2 2 Dataset 3 3 Il Modello 8 4 In pratica Peso e percorrenza 12 1
2 Capitolo 1 Introduzione ai modelli lineari Quando si analizzano dei dati, spesso si vuole scoprire se esiste una particolare relazione tra essi A volte, in particolare, si vuole scoprire se una o più variabili in gioco dipendono dalle altre: y = f(x 1,, x p ; β), dove β sono dei parametri incogniti Se questa relazione fosse esatta non ci sarebbe nulla da studiare In realtà succede che y = f(x 1,, x p ; β) + ɛ In questa parte del corso studieremo la più semplice funzione f ovvero una funzione lineare nei parametri: y = β 0 + β 1 x + ɛ Perché la più semplice? 1 E facilmente interpretabile 2 E semplice da utilizzare 2
3 Capitolo 2 Dataset Iniziamo a vedere come si utilizza un modello di questo tipo su un dataset reale con l utilizzo del software R Per prima cosa dobbiamo caricare il dataset che utilizzeremo: autodat che potete trovare su Apriamo il file e vediamo che nella prima ci sono un file di questo si carica su R attraverso il comando > auto = readtable("autodat", header = TRUE) L oggetto auto è un data-frame e contiene le seguenti variabili: > names(auto) [1] "marca" "alimentazione" "aspirazione" "carrozzeria" [5] "trazione" "posizmotore" "distassi" "lunghezza" [9] "larghezza" "altezza" "peso" "cilindrata" [13] "compressione" "HP" "girimax" "percorrurbana" [17] "percorrstrada" "Ncilindri" per caricare ognuna di esse in memoria con il proprio nome dobbiamo utilizzare il comando: > attach(auto) 3
4 Potrebbe essere interessante stabilire se esiste una relazione tra la percorrenza urbana, il numero di kilometri che si fanno con un litro di carburante, e per esempio il peso Infatti possiamo immaginare che a parità di condizioni una pacchina più pesante consumi più di un altra più leggera Questo possiamo vederlo graficamente mettendo su un piano cartesiano le due variabili: sull ascissa mettiamo il peso e sull ordinata la percorrenza urbana, che d ora in poi chiamerò semplicemente percorrenza > plot(peso, percorrurbana) percorrurbana peso Figura 21: La percorrenza in funzione del peso 4
5 Ogni punto del grafico corrisponde ad una macchina Dal grafico si vede subito che aumentando il peso diminuisce la percorrenza Notiamo che c è un gruppo di punti che si discosta notevolmente dala parte restante del dataset In particolare questi punti hanno una percorrenza più alta e quindi un consumo più basso Questo può dipendere dal fatto che quel gruppo di macchine ha caratteristiche diverse rispetto alle altre Per scoprirlo possiamo estrarre quei punti singolarmente Per fare ciò possiamo utilizzare la funzione interattiva identify che permette di conoscere a quale riga del dataset corrisponde il punto semplicemente cliccandoci sopra con il mouse > plot(peso, percorrurbana) > v = identify(peso, percorrurbana) > v [1] A questo punto clicchiamo i punti che ci interessano e quando abbiamo finito clicchiamo con il pulsante destro sulla finestra grafica e scegliamo stop Vediamo per esempio che > alimentazione[v] [1] diesel diesel Levels: benz diesel Ovvero entrambe le macchine sono alimentate a diesel, che ha, come è noto, un consumo più basso rispetto alle macchine a benzina Ma è possibile anche fare grafici più sofisticati con R, in questo modo si ha un idea più chiara del dataset: 5
6 > plot(peso, percorrurbana, type = "n", ylab = "percorrenza urbana (km/litro)", + xlab = "peso") > d <- alimentazione == "benz" > points(peso[d], percorrurbana[d], col = 2, pch = 2) > points(peso[!d], percorrurbana[!d], col = 3, pch = 3) > legend(1550, 20, pch = c(2, 3), col = c(2, 3), legend = c("benzina", + "diesel")) percorrenza urbana (km/litro) benzina diesel peso Figura 22: La percorrenza in funzione del peso, differenze di alimentazione 6
7 in questo modo distinguiamo anche le macchine alimentate a benzina con le diesel E molto interessante confrontare anche più variabili insieme: > M = cbind(percorrurbana, cilindrata, Ncilindri, peso) > pairs(m, col = ifelse(d, 2, 3), pch = ifelse(d, 2, 3)) percorrurbana cilindrata Ncilindri peso Figura 23: Grafici incrociati 7
8 Capitolo 3 Il Modello Torniamo al nostro modello Immagiamo di avere un campione di n unità (per esempio n macchine) di cui sono disponibili per ogni unità alcune caratteristiche (la perccorrenza, il peso, etc) Siano x e y due caratteristiche, noi vogliamo studiare come si comporta la caratteristica y al variare di x Come già detto, l ipotesi più semplice che si può fare è quella di un modello lineare y = β 0 + β 1 x + ɛ, con β 0 e β 1 parametri incogniti Da un punto vista grafico y = β 0 + β 1 x è una retta con intercetta β 0 e coefficiente angolare β 1, il termine aggiuntivo ɛ è un errore In questo schema il nostro scopo è trovare la retta più vicina ai dati ovvero i valori β 0 e β 1 migliori Ma che vuol dire più vicina? E migliore in che senso? Per precisare meglio questi concetti 8
9 abbiamo bisogno di un struttura matematica più rigorosa Poniamo y 1 = β 0 + β 1 x 1 + ɛ 1 y i = β 0 + β 1 x i + ɛ i y n = β 0 + β 1 x n + ɛ n O meglio utilizzando una relazione matriciale: y = Xβ + ɛ dove y = y 1 y i X = 1 x 1 1 x i β = β 0 β 1 ɛ = ɛ 1 ɛ i y n 1 x n ɛ n Ora se poniamo ˆβ una stima di β, si ha per ogni x i che ŷ i = ˆβ 0 + ˆβ 1 x i e quindi ŷ = X ˆβ è la retta stimata Ora vogliamo minimizzare l errore che commettiamo approssimando i dati y i con i valori stimati ŷ i : a questo scopo per ogni i poniamo e i = y i ŷ i I valori e i vengono chiamati residui e rappresentano l errore commeso per ogni unità Abbiamo però bisogno di un errore globale che sintetizzi tutti gli errori contemporaneamente Ci sono vari modi per definire questo errore, il più utilizzato è sicuramente questo: n n D(β) = e 2 i = [y i β 0 + β 1 x i ] 2 i=1 i=1 9
10 La funzione D viene spesso chiamata devianza Per trovare il β migliore, come promesso all inizio, dobbiamo minimizzare questa funzione Questo è quello che si chiama criterio dei minimi quadrati Per andare avanti bisogna però fare alcune ipotesi sugli errori ɛ i, le ipotesi classiche sono quelle chiamate di omoschedasticità: E(ɛ i ) = 0 i = 1,, n V ar(ɛ i ) = σ 2 i = 1,, n Cov(ɛ i, ɛ j ) = 0 i, j = 1,, n i j Minimizzando la funzione D(β) otteniamo che ˆβ = ( X t X ) 1 X t y Utilizzando il valore trovato possiamo ottenere anche una stima del parametro incognito σ 2 : s 2 = D( ˆβ) n 2 s = D( ˆβ) n 2 Queste formule che avviamo costruito in un caso particolarmente semplice del modello lineare valgono in realtà più in generale Infatti possiamo immaginare che la variabili non dipenda da una sola caratteristica x ma da un certo numero di caratteristiche: x 1,, x p 1 : y = β 0 + β 1 x β p 1 x p 1 La formulazione del modello diventa a questo punto: y 1 = β 0 + β 1 x β p 1 x ip 1 + ɛ 1 y i = β 0 + β 1 x i1 + + β p 1 x ip 1 + ɛ i y n = β 0 + β 1 x n1 + + β p 1 x np 1 + ɛ n 10
11 Ma sempre nella forma matriciale y = Xβ + ɛ dove però a differenza di prima X = 1 x 11 x 1p 1 1 x i1 x ip 1 β = β 0 β 1 1 x n1 x np 1 β p 1 Il metodo dei minimi quadrati porta quindi a ˆβ = ( X t X ) 1 X t y da cui s 2 = D( ˆβ) n p s = D( ˆβ) n p 11
12 Capitolo 4 In pratica Analizziamo quindi il nostro dataset delle auto utilizzando il modello appena introdotto 41 Peso e percorrenza Possiamo a questo punto studiare la relazione tra peso e percorrenza Poniamo percorrenza = β 0 + β 1 peso + ɛ Per costruire tutte le stime che ci occorrono basta un solo semplice comando in R: lm > fit = lm(percorrurbana ~ peso) > fit Call: lm(formula = percorrurbana ~ peso) Coefficients: (Intercept) peso
13 Il nome lm sta per linear model e come vedete restituisce i coefficienti stimati: ˆβ0 (Intercept) e ˆβ 1 peso Ma il comando lm fa molto di più! Per ottenere una lista di tutti gli oggetti che restituisce dobbiamo dare > names(fit) [1] "coefficients" "residuals" "effects" "rank" [5] "fittedvalues" "assign" "qr" "dfresidual" [9] "xlevels" "call" "terms" "model" Tra le cose che restituisce lm troviamo i coefficienti stimati (coefficients), i residui (residuals), i valori stimati ŷ (fittedvalues) Graficamente il risultato è quello dato dalla figura 51 13
14 > plot(peso, percorrurbana) > abline(reg = fit, col = 2) percorrurbana peso Figura 41: Retta di regrssione e residui 14
15 In realtà informazioni più significative possono essere ricavate utilizzando il comando summary: > summary(fit) Call: lm(formula = percorrurbana ~ peso) Residuals: Min 1Q Median 3Q Max Coefficients: Estimate Std Error t value Pr(> t ) (Intercept) <2e-16 *** peso <2e-16 *** --- Signif codes: 0 *** 0001 ** 001 * Residual standard error: 1826 on 201 degrees of freedom Multiple R-Squared: 05748, Adjusted R-squared: F-statistic: 2717 on 1 and 201 DF, p-value: < 22e-16 Ma analizziamo meglio l output di summary Per prima cosa salviamolo e vediamo le informazione che contiene: > sfit = summary(fit) > names(sfit) [1] "call" "terms" "residuals" "coefficients" [5] "aliased" "sigma" "df" "rsquared" [9] "adjrsquared" "fstatistic" "covunscaled" 15
16 Partiamo dall inizio La prima cosa che vediamo è la formula del modello (Call) Poi ci sono delle informazioni sui residui (Residuals) come il minimo il massimo e quartili Il vettore di tutti i residui può essere ricavato in vari modi: > fit$residuals > sfit$residuals > residuals(fit) > residuals(sfit) Notiamo (dalla mediana e dai quartili) che i residui non sono simmetrici rispetto allo 0 Questo probabilmente dipende dal fatto che stiamo considerando contemporaneamente sia macchine a benzina che diesel Poi troviamo una tabella con i coefficienti stimati e altre utili informazioni (Coefficients) Prendiamo ad esempio la seconda riga: > sfit$coef[2, ] Estimate Std Error t value Pr(> t ) e e e e-39 Essa si riferisce al coefficiente della variabile peso, ovvero β 1 Il primo valore è la sua stima ( ˆβ 1 ), il secondo è il suo errore standard e il terzo il rapporto fra questi due che corrisponde al valore t oss del test di ipotesi β 1 = 0 Più questo valore è alto più è bassa la probabiltà di sbagliare rifiutando l ipotesi che β 1 = 0 (sotto l ipotesi aggiuntiva di normalità degli errori) Un altro indice di ciò è dato dalla P ( X > t ) (con X va normale standard) ovvero il quarto valore: in questo caso è un numero molto vicino a 0 che vuol dire che β 1 0 La componente peso è quindi significativa per il modello (sempre nel caso di normalità) Il valore Residual standard error è il valore che per noi è dato da σ e degrees of freedom è il valore n p della formula che corrisponde al numero di gradi di libertà della variabile Chi-quadro che se ne ricava (osserviamo che nel nostro caso p = 2) Per ottenere questi valori basta digitare 16
17 > sfit$sigma [1] > sfit$df[2] [1] 201 Nel summary troviamo anche il Multiple R-Squared calcolato attraverso la formula: R 2 = 1 (yi ŷ i ) 2 ( y i y i ) 2 = ( ŷ i y i ) 2 ( y i y i ) 2 = varianzione spiegata varianzione totale Il valore R 2 viene chiamato coefficiente di determinazione e indica la quota di variabilità che siamo riusciti ad interpretare utilizzando il modello Questo è un valore tra 0 e 1; nel nostro caso è 057 che indica un discreto grado di accostamento tra dati osservati e interpolati Per ricavare questo valore dobbiamo scrivere > sfit$rsquared [1] Notiamo che R 2 = ρ 2 = s2 xy s 2 xs 2 y ma i due fattori hano significati diversi: il primo è un indice della bontà di adattamento mentre il secondo (la correlazione al quadrato) è un indice di dipendenza tra x e y L ultima informazione che troviamo nel summary è la statistica F : F-statistic: questa verrà spiegata in seguito Osserviamo che anche se ad una prima analisi abbiamo dei risultati confortanti guardando meglio il grafico si vede che c è un intero gruppo di dati (le macchine diesel) che si discostano notevolmente dalla retta; possiamo quindi, almeno ad una prima analisi distinguere le due situazioni creando due modelli differenti 17
18 > fitb = lm(percorrurbana[d] ~ peso[d]) > fitd = lm(percorrurbana[!d] ~ peso[!d]) > plot(peso, percorrurbana, type = "n", ylab = "percorrenza urbana (km/litro)", + xlab = "peso") > points(peso[d], percorrurbana[d], col = 2, pch = 2) > points(peso[!d], percorrurbana[!d], col = 3, pch = 3) > legend(45, 20, pch = c(2, 3), col = c(2, 3), legend = c("benzina", + "diesel")) > abline(reg = fitb, col = 2, lty = 2) > abline(reg = fitd, col = 3, lty = 4) percorrenza urbana (km/litro) peso 18
19 In questo caso però notiamo che per valori estremi del peso nelle macchine a benzina il modello lineare non sembra funzionare bene 19
> d = alimentazione == "benz" > mean(percorr.urbana[!d]) - mean(percorr.urbana[d]) [1] 2.385627. > sd(percorr.urbana[d]) [1] 2.
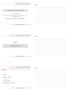
![> d = alimentazione == benz > mean(percorr.urbana[!d]) - mean(percorr.urbana[d]) [1] 2.385627. > sd(percorr.urbana[d]) [1] 2. > d = alimentazione == benz > mean(percorr.urbana[!d]) - mean(percorr.urbana[d]) [1] 2.385627. > sd(percorr.urbana[d]) [1] 2.](/thumbs/39/18486992.jpg) A questo punto vale la pena di soffermarci di più sull alimentazione. Intanto cerchiamo di indagare se l alimentazione è davvero un fattore significativo per la percorrenza come è luogo comune pensare.
A questo punto vale la pena di soffermarci di più sull alimentazione. Intanto cerchiamo di indagare se l alimentazione è davvero un fattore significativo per la percorrenza come è luogo comune pensare.
STATISTICA 1, metodi matematici e statistici Introduzione al linguaggio R Esercitazione 8: 27-05-2004
 esercitazione 8 p. 1/8 STATISTICA 1, metodi matematici e statistici Introduzione al linguaggio R Esercitazione 8: 27-05-2004 Luca Monno Università degli studi di Pavia luca.monno@unipv.it http://www.lucamonno.it
esercitazione 8 p. 1/8 STATISTICA 1, metodi matematici e statistici Introduzione al linguaggio R Esercitazione 8: 27-05-2004 Luca Monno Università degli studi di Pavia luca.monno@unipv.it http://www.lucamonno.it
Esercitazione Statistica Computazionale B Modelli di regressione lineare semplice Verifica di ipotesi - Analisi della varianza
 Esercitazione Statistica Computazionale B Modelli di regressione lineare semplice Verifica di ipotesi - Analisi della varianza 3 maggio 2005 Esercizio 1 Consideriamo l esempio del libro di testo Annette
Esercitazione Statistica Computazionale B Modelli di regressione lineare semplice Verifica di ipotesi - Analisi della varianza 3 maggio 2005 Esercizio 1 Consideriamo l esempio del libro di testo Annette
Capitolo 12 La regressione lineare semplice
 Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 12 La regressione lineare semplice Insegnamento: Statistica Corso di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara
Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 12 La regressione lineare semplice Insegnamento: Statistica Corso di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 8
 CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 8 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Test delle ipotesi sulla varianza In un azienda che produce componenti meccaniche, è stato
CORSO DI STATISTICA (parte 2) - ESERCITAZIONE 8 Dott.ssa Antonella Costanzo a.costanzo@unicas.it Esercizio 1. Test delle ipotesi sulla varianza In un azienda che produce componenti meccaniche, è stato
Laboratorio R Corso di Algebra e Modelli lineari (Anno Accademico 2011-12)
 Laboratorio R Corso di Algebra e Modelli lineari (Anno Accademico 011-1) REGRESSIONE LINEARE SEMPLICE OPEN STATISTICA 8.44 Per 8 settimanali, appartenenti alla medesima fascia di prezzo e presenti in edicola
Laboratorio R Corso di Algebra e Modelli lineari (Anno Accademico 011-1) REGRESSIONE LINEARE SEMPLICE OPEN STATISTICA 8.44 Per 8 settimanali, appartenenti alla medesima fascia di prezzo e presenti in edicola
FASCI DI RETTE. scrivere la retta in forma esplicita: 2y = 3x + 4 y = 3 2 x 2. scrivere l equazione del fascio di rette:
 FASCI DI RETTE DEFINIZIONE: Si chiama fascio di rette parallele o fascio improprio [erroneamente data la somiglianza effettiva con un fascio!] un insieme di rette che hanno tutte lo stesso coefficiente
FASCI DI RETTE DEFINIZIONE: Si chiama fascio di rette parallele o fascio improprio [erroneamente data la somiglianza effettiva con un fascio!] un insieme di rette che hanno tutte lo stesso coefficiente
SPC e distribuzione normale con Access
 SPC e distribuzione normale con Access In questo articolo esamineremo una applicazione Access per il calcolo e la rappresentazione grafica della distribuzione normale, collegata con tabelle di Clienti,
SPC e distribuzione normale con Access In questo articolo esamineremo una applicazione Access per il calcolo e la rappresentazione grafica della distribuzione normale, collegata con tabelle di Clienti,
Indice. 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo... 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità...
 Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Rette e curve, piani e superfici
 Rette e curve piani e superfici ) dicembre 2 Scopo di questo articolo è solo quello di proporre uno schema riepilogativo che metta in luce le caratteristiche essenziali delle equazioni di rette e curve
Rette e curve piani e superfici ) dicembre 2 Scopo di questo articolo è solo quello di proporre uno schema riepilogativo che metta in luce le caratteristiche essenziali delle equazioni di rette e curve
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Prof. Silvio Reato Valcavasia Ricerche. Il piano cartesiano
 Il piano cartesiano Per la rappresentazione di grafici su di un piano si utilizza un sistema di riferimento cartesiano. Su questo piano si rappresentano due rette orientate (con delle frecce all estremità
Il piano cartesiano Per la rappresentazione di grafici su di un piano si utilizza un sistema di riferimento cartesiano. Su questo piano si rappresentano due rette orientate (con delle frecce all estremità
Lezione n. 2 (a cura di Chiara Rossi)
 Lezione n. 2 (a cura di Chiara Rossi) QUANTILE Data una variabile casuale X, si definisce Quantile superiore x p : X P (X x p ) = p Quantile inferiore x p : X P (X x p ) = p p p=0.05 x p x p Graficamente,
Lezione n. 2 (a cura di Chiara Rossi) QUANTILE Data una variabile casuale X, si definisce Quantile superiore x p : X P (X x p ) = p Quantile inferiore x p : X P (X x p ) = p p p=0.05 x p x p Graficamente,
Statistica e biometria. D. Bertacchi. Variabili aleatorie. V.a. discrete e continue. La densità di una v.a. discreta. Esempi.
 Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
LABORATORIO-EXCEL N. 2-3 XLSTAT- Pro Versione 7 VARIABILI QUANTITATIVE
 LABORATORIO-EXCEL N. 2-3 XLSTAT- Pro Versione 7 VARIABILI QUANTITATIVE DESCRIZIONE DEI DATI DA ESAMINARE Sono stati raccolti i dati sul peso del polmone di topi normali e affetti da una patologia simile
LABORATORIO-EXCEL N. 2-3 XLSTAT- Pro Versione 7 VARIABILI QUANTITATIVE DESCRIZIONE DEI DATI DA ESAMINARE Sono stati raccolti i dati sul peso del polmone di topi normali e affetti da una patologia simile
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
lo 2 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000
 Capittol lo 2 Visualizzazione 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000 Nel primo capitolo sono state analizzate le diverse componenti della finestra di Word 2000: barra del titolo, barra dei menu,
Capittol lo 2 Visualizzazione 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000 Nel primo capitolo sono state analizzate le diverse componenti della finestra di Word 2000: barra del titolo, barra dei menu,
Prof.ssa Paola Vicard
 Questa nota consiste perlopiù nella traduzione (con alcune integrazioni) da Descriptive statistics di J. Shalliker e C. Ricketts, 2000, University of Plymouth Consideriamo i dati nel file esercizio10_dati.xls.
Questa nota consiste perlopiù nella traduzione (con alcune integrazioni) da Descriptive statistics di J. Shalliker e C. Ricketts, 2000, University of Plymouth Consideriamo i dati nel file esercizio10_dati.xls.
Validazione dei modelli Strumenti quantitativi per la gestione
 Validazione dei modelli Strumenti quantitativi per la gestione Emanuele Taufer Validazione dei modelli Il data set Auto I dati Il problema analizzato Validation set approach Diagramma a dispersione Test
Validazione dei modelli Strumenti quantitativi per la gestione Emanuele Taufer Validazione dei modelli Il data set Auto I dati Il problema analizzato Validation set approach Diagramma a dispersione Test
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Strumenti e metodi per la redazione della carta del pericolo da fenomeni torrentizi
 Versione 2.0 Strumenti e metodi per la redazione della carta del pericolo da fenomeni torrentizi Corso anno 2011 E. MANUALE UTILIZZO HAZARD MAPPER Il programma Hazard Mapper è stato realizzato per redarre,
Versione 2.0 Strumenti e metodi per la redazione della carta del pericolo da fenomeni torrentizi Corso anno 2011 E. MANUALE UTILIZZO HAZARD MAPPER Il programma Hazard Mapper è stato realizzato per redarre,
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Disegni di Ricerca e Analisi dei Dati in Psicologia Clinica. Rcmdr
 Disegni di Ricerca e Analisi dei Dati in Psicologia Clinica Rcmdr http://www.r-project.org http://qplab.psy.unipd.it Che cos è Rcmdr? Rcmdr è un pacchetto che possiamo scaricare dal CRAN e installare su
Disegni di Ricerca e Analisi dei Dati in Psicologia Clinica Rcmdr http://www.r-project.org http://qplab.psy.unipd.it Che cos è Rcmdr? Rcmdr è un pacchetto che possiamo scaricare dal CRAN e installare su
Analisi bivariata. Dott. Cazzaniga Paolo. Dip. di Scienze Umane e Sociali paolo.cazzaniga@unibg.it
 Dip. di Scienze Umane e Sociali paolo.cazzaniga@unibg.it Introduzione : analisi delle relazioni tra due caratteristiche osservate sulle stesse unità statistiche studio del comportamento di due caratteri
Dip. di Scienze Umane e Sociali paolo.cazzaniga@unibg.it Introduzione : analisi delle relazioni tra due caratteristiche osservate sulle stesse unità statistiche studio del comportamento di due caratteri
Inferenza statistica. Statistica medica 1
 Inferenza statistica L inferenza statistica è un insieme di metodi con cui si cerca di trarre una conclusione sulla popolazione sulla base di alcune informazioni ricavate da un campione estratto da quella
Inferenza statistica L inferenza statistica è un insieme di metodi con cui si cerca di trarre una conclusione sulla popolazione sulla base di alcune informazioni ricavate da un campione estratto da quella
Esercizi test ipotesi. Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010
 Esercizi test ipotesi Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Verifica delle ipotesi - Esempio quelli di Striscia la Notizia" effettuano controlli casuali per vedere se le pompe
Esercizi test ipotesi Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Verifica delle ipotesi - Esempio quelli di Striscia la Notizia" effettuano controlli casuali per vedere se le pompe
Analisi della performance temporale della rete
 Analisi della performance temporale della rete In questo documento viene analizzato l andamento nel tempo della performance della rete di promotori. Alcune indicazioni per la lettura di questo documento:
Analisi della performance temporale della rete In questo documento viene analizzato l andamento nel tempo della performance della rete di promotori. Alcune indicazioni per la lettura di questo documento:
4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI
 119 4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI Indice degli Argomenti: TEMA N. 1 : INSIEMI NUMERICI E CALCOLO
119 4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI Indice degli Argomenti: TEMA N. 1 : INSIEMI NUMERICI E CALCOLO
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in
 Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Esercitazione #5 di Statistica. Test ed Intervalli di Confidenza (per una popolazione)
 Esercitazione #5 di Statistica Test ed Intervalli di Confidenza (per una popolazione) Dicembre 00 1 Esercizi 1.1 Test su media (con varianza nota) Esercizio n. 1 Il calore (in calorie per grammo) emesso
Esercitazione #5 di Statistica Test ed Intervalli di Confidenza (per una popolazione) Dicembre 00 1 Esercizi 1.1 Test su media (con varianza nota) Esercizio n. 1 Il calore (in calorie per grammo) emesso
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
Esempio. Approssimazione con il criterio dei minimi quadrati. Esempio. Esempio. Risultati sperimentali. Interpolazione con spline cubica.
 Esempio Risultati sperimentali Approssimazione con il criterio dei minimi quadrati Esempio Interpolazione con spline cubica. Esempio 1 Come procedere? La natura del fenomeno suggerisce che una buona approssimazione
Esempio Risultati sperimentali Approssimazione con il criterio dei minimi quadrati Esempio Interpolazione con spline cubica. Esempio 1 Come procedere? La natura del fenomeno suggerisce che una buona approssimazione
Lezione 5. Argomenti. Premessa Vincolo di bilancio La scelta ottima del consumatore
 Lezione 5 Argomenti Premessa Vincolo di bilancio La scelta ottima del consumatore 5.1 PREESSA Nonostante le preferenze portino a desiderare quantità crescenti di beni, nella realtà gli individui non sono
Lezione 5 Argomenti Premessa Vincolo di bilancio La scelta ottima del consumatore 5.1 PREESSA Nonostante le preferenze portino a desiderare quantità crescenti di beni, nella realtà gli individui non sono
1. Scopo dell esperienza.
 1. Scopo dell esperienza. Lo scopo di questa esperienza è ricavare la misura di tre resistenze il 4 cui ordine di grandezza varia tra i 10 e 10 Ohm utilizzando il metodo olt- Amperometrico. Tale misura
1. Scopo dell esperienza. Lo scopo di questa esperienza è ricavare la misura di tre resistenze il 4 cui ordine di grandezza varia tra i 10 e 10 Ohm utilizzando il metodo olt- Amperometrico. Tale misura
Capitolo 4: Ottimizzazione non lineare non vincolata parte II. E. Amaldi DEIB, Politecnico di Milano
 Capitolo 4: Ottimizzazione non lineare non vincolata parte II E. Amaldi DEIB, Politecnico di Milano 4.3 Algoritmi iterativi e convergenza Programma non lineare (PNL): min f(x) s.v. g i (x) 0 1 i m x S
Capitolo 4: Ottimizzazione non lineare non vincolata parte II E. Amaldi DEIB, Politecnico di Milano 4.3 Algoritmi iterativi e convergenza Programma non lineare (PNL): min f(x) s.v. g i (x) 0 1 i m x S
Esame di Statistica del 17 luglio 2006 (Corso di Laurea Triennale in Biotecnologie, Università degli Studi di Padova).
 Esame di Statistica del 17 luglio 2006 (Corso di Laurea Triennale in Biotecnologie, Università degli Studi di Padova). Cognome Nome Matricola Es. 1 Es. 2 Es. 3 Es. 4 Somma Voto finale Attenzione: si consegnano
Esame di Statistica del 17 luglio 2006 (Corso di Laurea Triennale in Biotecnologie, Università degli Studi di Padova). Cognome Nome Matricola Es. 1 Es. 2 Es. 3 Es. 4 Somma Voto finale Attenzione: si consegnano
Carichiamo il segnale contenuto nel file ecg_es_20121128.mat
 Esercitazione su analisi segnale ECG Carichiamo il segnale contenuto nel file ecg_es_20121128.mat Il file contiene due variabili - dt, che vale 0.004 - ecg, che è vettore lungo 6500 campioni La frequenza
Esercitazione su analisi segnale ECG Carichiamo il segnale contenuto nel file ecg_es_20121128.mat Il file contiene due variabili - dt, che vale 0.004 - ecg, che è vettore lungo 6500 campioni La frequenza
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
RAPPRESENTAZIONE GRAFICA E ANALISI DEI DATI SPERIMENTALI CON EXCEL
 RAPPRESENTAZIONE GRAFICA E ANALISI DEI DATI SPERIMENTALI CON EXCEL 1 RAPPRESENTAZIONE GRAFICA Per l analisi dati con Excel si fa riferimento alla versione 2007 di Office, le versioni successive non differiscono
RAPPRESENTAZIONE GRAFICA E ANALISI DEI DATI SPERIMENTALI CON EXCEL 1 RAPPRESENTAZIONE GRAFICA Per l analisi dati con Excel si fa riferimento alla versione 2007 di Office, le versioni successive non differiscono
RELAZIONE TRA VARIABILI QUANTITATIVE. Lezione 7 a. Accade spesso nella ricerca in campo biomedico, così come in altri campi della
 RELAZIONE TRA VARIABILI QUANTITATIVE Lezione 7 a Accade spesso nella ricerca in campo biomedico, così come in altri campi della scienza, di voler studiare come il variare di una o più variabili (variabili
RELAZIONE TRA VARIABILI QUANTITATIVE Lezione 7 a Accade spesso nella ricerca in campo biomedico, così come in altri campi della scienza, di voler studiare come il variare di una o più variabili (variabili
Teoria delle code. Sistemi stazionari: M/M/1 M/M/1/K M/M/S
 Teoria delle code Sistemi stazionari: M/M/1 M/M/1/K M/M/S Fabio Giammarinaro 04/03/2008 Sommario INTRODUZIONE... 3 Formule generali di e... 3 Leggi di Little... 3 Cosa cerchiamo... 3 Legame tra N e le
Teoria delle code Sistemi stazionari: M/M/1 M/M/1/K M/M/S Fabio Giammarinaro 04/03/2008 Sommario INTRODUZIONE... 3 Formule generali di e... 3 Leggi di Little... 3 Cosa cerchiamo... 3 Legame tra N e le
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Metodi Stocastici per la Finanza
 Metodi Stocastici per la Finanza Tiziano Vargiolu vargiolu@math.unipd.it 1 1 Università degli Studi di Padova Anno Accademico 2011-2012 Lezione 6 Indice 1 Il metodo bootstrap 2 Esercitazione 3 Interpolazione
Metodi Stocastici per la Finanza Tiziano Vargiolu vargiolu@math.unipd.it 1 1 Università degli Studi di Padova Anno Accademico 2011-2012 Lezione 6 Indice 1 Il metodo bootstrap 2 Esercitazione 3 Interpolazione
Perché il logaritmo è così importante?
 Esempio 1. Perché il logaritmo è così importante? (concentrazione di ioni di idrogeno in una soluzione, il ph) Un sistema solido o liquido, costituito da due o più componenti, (sale disciolto nell'acqua),
Esempio 1. Perché il logaritmo è così importante? (concentrazione di ioni di idrogeno in una soluzione, il ph) Un sistema solido o liquido, costituito da due o più componenti, (sale disciolto nell'acqua),
Lezione 10: Il problema del consumatore: Preferenze e scelta ottimale
 Corso di Scienza Economica (Economia Politica) prof. G. Di Bartolomeo Lezione 10: Il problema del consumatore: Preferenze e scelta ottimale Facoltà di Scienze della Comunicazione Università di Teramo Scelta
Corso di Scienza Economica (Economia Politica) prof. G. Di Bartolomeo Lezione 10: Il problema del consumatore: Preferenze e scelta ottimale Facoltà di Scienze della Comunicazione Università di Teramo Scelta
La Programmazione Lineare
 4 La Programmazione Lineare 4.1 INTERPRETAZIONE GEOMETRICA DI UN PROBLEMA DI PROGRAMMAZIONE LINEARE Esercizio 4.1.1 Fornire una rappresentazione geometrica e risolvere graficamente i seguenti problemi
4 La Programmazione Lineare 4.1 INTERPRETAZIONE GEOMETRICA DI UN PROBLEMA DI PROGRAMMAZIONE LINEARE Esercizio 4.1.1 Fornire una rappresentazione geometrica e risolvere graficamente i seguenti problemi
SCHEDA M MOSAICI CLASSIFICARE CON LA SIMMETRIA
 SCHEDA M MOSAICI CLASSIFICARE CON LA SIMMETRIA Qui sotto avete una griglia, che rappresenta una normale quadrettatura, come quella dei quaderni a quadretti; nelle attività che seguono dovrete immaginare
SCHEDA M MOSAICI CLASSIFICARE CON LA SIMMETRIA Qui sotto avete una griglia, che rappresenta una normale quadrettatura, come quella dei quaderni a quadretti; nelle attività che seguono dovrete immaginare
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
STATISTICA 1, metodi matematici e statistici Introduzione al linguaggio R Esercitazione2: 04-03-2005
 esercitazione 2 p. 1/12 STATISTICA 1, metodi matematici e statistici Introduzione al linguaggio R Esercitazione2: 04-03-2005 Luca Monno Università degli studi di Pavia luca.monno@unipv.it http://www.lucamonno.it
esercitazione 2 p. 1/12 STATISTICA 1, metodi matematici e statistici Introduzione al linguaggio R Esercitazione2: 04-03-2005 Luca Monno Università degli studi di Pavia luca.monno@unipv.it http://www.lucamonno.it
Antonella Martinucci, Rossana Nencini, 2013 IL PESO. classe quarta
 Antonella Martinucci, Rossana Nencini, 2013 IL PESO classe quarta I bambini utilizzano spontaneamente il concetto di pesante? Collochiamo su un banco alcuni oggetti: penne matite gomme fogli scottex quaderni
Antonella Martinucci, Rossana Nencini, 2013 IL PESO classe quarta I bambini utilizzano spontaneamente il concetto di pesante? Collochiamo su un banco alcuni oggetti: penne matite gomme fogli scottex quaderni
Massimi e minimi vincolati di funzioni in due variabili
 Massimi e minimi vincolati di funzioni in due variabili I risultati principali della teoria dell ottimizzazione, il Teorema di Fermat in due variabili e il Test dell hessiana, si applicano esclusivamente
Massimi e minimi vincolati di funzioni in due variabili I risultati principali della teoria dell ottimizzazione, il Teorema di Fermat in due variabili e il Test dell hessiana, si applicano esclusivamente
Come costruire una distribuzione di frequenze per caratteri quantitativi continui
 Come costruire una distribuzione di frequenze per caratteri quantitativi continui Consideriamo i dati contenuti nel primo foglio di lavoro (quello denominato dati) del file esempio2.xls. I dati si riferiscono
Come costruire una distribuzione di frequenze per caratteri quantitativi continui Consideriamo i dati contenuti nel primo foglio di lavoro (quello denominato dati) del file esempio2.xls. I dati si riferiscono
FISICA. Le forze. Le forze. il testo: 2011/2012 La Semplificazione dei Testi Scolastici per gli Alunni Stranieri IPSIA A.
 01 In questa lezione parliamo delle forze. Parliamo di forza quando: spostiamo una cosa; solleviamo un oggetto; fermiamo una palla mentre giochiamo a calcio; stringiamo una molla. Quando usiamo (applichiamo)
01 In questa lezione parliamo delle forze. Parliamo di forza quando: spostiamo una cosa; solleviamo un oggetto; fermiamo una palla mentre giochiamo a calcio; stringiamo una molla. Quando usiamo (applichiamo)
NUOVA PROCEDURA COPIA ED INCOLLA PER L INSERIMENTO DELLE CLASSIFICHE NEL SISTEMA INFORMATICO KSPORT.
 NUOVA PROCEDURA COPIA ED INCOLLA PER L INSERIMENTO DELLE CLASSIFICHE NEL SISTEMA INFORMATICO KSPORT. Con l utilizzo delle procedure di iscrizione on line la società organizzatrice ha a disposizione tutti
NUOVA PROCEDURA COPIA ED INCOLLA PER L INSERIMENTO DELLE CLASSIFICHE NEL SISTEMA INFORMATICO KSPORT. Con l utilizzo delle procedure di iscrizione on line la società organizzatrice ha a disposizione tutti
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Statistica. Lezione 6
 Università degli Studi del Piemonte Orientale Corso di Laurea in Infermieristica Corso integrato in Scienze della Prevenzione e dei Servizi sanitari Statistica Lezione 6 a.a 011-01 Dott.ssa Daniela Ferrante
Università degli Studi del Piemonte Orientale Corso di Laurea in Infermieristica Corso integrato in Scienze della Prevenzione e dei Servizi sanitari Statistica Lezione 6 a.a 011-01 Dott.ssa Daniela Ferrante
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
PROCEDURA INVENTARIO DI MAGAZZINO di FINE ESERCIZIO (dalla versione 3.2.0)
 PROCEDURA INVENTARIO DI MAGAZZINO di FINE ESERCIZIO (dalla versione 3.2.0) (Da effettuare non prima del 01/01/2011) Le istruzioni si basano su un azienda che ha circa 1000 articoli, che utilizza l ultimo
PROCEDURA INVENTARIO DI MAGAZZINO di FINE ESERCIZIO (dalla versione 3.2.0) (Da effettuare non prima del 01/01/2011) Le istruzioni si basano su un azienda che ha circa 1000 articoli, che utilizza l ultimo
IL METODO PER IMPOSTARE E RISOLVERE I PROBLEMI DI FISICA (NB non ha nulla a che vedere con il metodo scientifico)
 IL METODO PER IMPOSTARE E RISOLVERE I PROBLEMI DI FISICA (NB non ha nulla a che vedere con il metodo scientifico) [nota: Nel testo sono riportate tra virgolette alcune domande che insegnanti e studenti
IL METODO PER IMPOSTARE E RISOLVERE I PROBLEMI DI FISICA (NB non ha nulla a che vedere con il metodo scientifico) [nota: Nel testo sono riportate tra virgolette alcune domande che insegnanti e studenti
Uso di base delle funzioni in Microsoft Excel
 Uso di base delle funzioni in Microsoft Excel Le funzioni Una funzione è un operatore che applicato a uno o più argomenti (valori, siano essi numeri con virgola, numeri interi, stringhe di caratteri) restituisce
Uso di base delle funzioni in Microsoft Excel Le funzioni Una funzione è un operatore che applicato a uno o più argomenti (valori, siano essi numeri con virgola, numeri interi, stringhe di caratteri) restituisce
Applicazioni lineari
 Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Si sa che la via più breve tra due punti è la linea retta. Ma vi siete mai chiesti, Qual è la via più breve tra tre punti? o tra quattro punti?
 Dov'è Moriart? Cerchiamo la via più breve con Mathcad Potete determinare la distanza più breve da tre punti e trovare Moriart? Si sa che la via più breve tra due punti è la linea retta. Ma vi siete mai
Dov'è Moriart? Cerchiamo la via più breve con Mathcad Potete determinare la distanza più breve da tre punti e trovare Moriart? Si sa che la via più breve tra due punti è la linea retta. Ma vi siete mai
Introduzione a ROOT. 1. Informazioni generali
 Introduzione a ROOT 1. Informazioni generali ROOT è un ambiente visualizzazione e trattamento dati interattivo sviluppato al CERN (si veda il sito ufficiale http://root.cern.ch interamente sviluppato in
Introduzione a ROOT 1. Informazioni generali ROOT è un ambiente visualizzazione e trattamento dati interattivo sviluppato al CERN (si veda il sito ufficiale http://root.cern.ch interamente sviluppato in
Nell esempio verrà mostrato come creare un semplice documento in Excel per calcolare in modo automatico la rata di un mutuo a tasso fisso conoscendo
 Nell esempio verrà mostrato come creare un semplice documento in Excel per calcolare in modo automatico la rata di un mutuo a tasso fisso conoscendo - la durata del mutuo in anni - l importo del mutuo
Nell esempio verrà mostrato come creare un semplice documento in Excel per calcolare in modo automatico la rata di un mutuo a tasso fisso conoscendo - la durata del mutuo in anni - l importo del mutuo
Funzioni. Funzioni /2
 Funzioni Una funzione f è una corrispondenza tra due insiemi A e B che a ciascun elemento di A associa un unico elemento di B. Si scrive: f : A B l'insieme A si chiama il dominio della funzione f, l'insieme
Funzioni Una funzione f è una corrispondenza tra due insiemi A e B che a ciascun elemento di A associa un unico elemento di B. Si scrive: f : A B l'insieme A si chiama il dominio della funzione f, l'insieme
Un modello matematico di investimento ottimale
 Un modello matematico di investimento ottimale Tiziano Vargiolu 1 1 Università degli Studi di Padova Liceo Scientifico Benedetti Venezia, giovedì 30 marzo 2011 Outline 1 Investimento per un singolo agente
Un modello matematico di investimento ottimale Tiziano Vargiolu 1 1 Università degli Studi di Padova Liceo Scientifico Benedetti Venezia, giovedì 30 marzo 2011 Outline 1 Investimento per un singolo agente
Regressione logistica. Strumenti quantitativi per la gestione
 Regressione logistica Strumenti quantitativi per la gestione Emanuele Taufer file:///c:/users/emanuele.taufer/dropbox/3%20sqg/classes/4a_rlg.html#(1) 1/25 Metodi di classificazione I metodi usati per analizzare
Regressione logistica Strumenti quantitativi per la gestione Emanuele Taufer file:///c:/users/emanuele.taufer/dropbox/3%20sqg/classes/4a_rlg.html#(1) 1/25 Metodi di classificazione I metodi usati per analizzare
Dovremmo a questo punto incominciare a vedere la suddivisione della nostra superficie.
 Vediamo ancora come lavorare sulle superfici attraverso la loro parametrizzazione, e suddivisione progressiva. Alcune volte in Grasshopper ci sono diversi modi per fare le stesse cose. Abbiamo visto il
Vediamo ancora come lavorare sulle superfici attraverso la loro parametrizzazione, e suddivisione progressiva. Alcune volte in Grasshopper ci sono diversi modi per fare le stesse cose. Abbiamo visto il
STATISTICA DESCRITTIVA SCHEDA N. 5: REGRESSIONE LINEARE
 STATISTICA DESCRITTIVA SCHEDA N. : REGRESSIONE LINEARE Nella Scheda precedente abbiamo visto che il coefficiente di correlazione fra due variabili quantitative X e Y fornisce informazioni sull esistenza
STATISTICA DESCRITTIVA SCHEDA N. : REGRESSIONE LINEARE Nella Scheda precedente abbiamo visto che il coefficiente di correlazione fra due variabili quantitative X e Y fornisce informazioni sull esistenza
Cosa dobbiamo già conoscere?
 Cosa dobbiamo già conoscere? Insiemistica (operazioni, diagrammi...). Insiemi finiti/numerabili/non numerabili. Perché la probabilità? In molti esperimenti l esito non è noto a priori tuttavia si sa dire
Cosa dobbiamo già conoscere? Insiemistica (operazioni, diagrammi...). Insiemi finiti/numerabili/non numerabili. Perché la probabilità? In molti esperimenti l esito non è noto a priori tuttavia si sa dire
LEZIONE n. 5 (a cura di Antonio Di Marco)
 LEZIONE n. 5 (a cura di Antonio Di Marco) IL P-VALUE (α) Data un ipotesi nulla (H 0 ), questa la si può accettare o rifiutare in base al valore del p- value. In genere il suo valore è un numero molto piccolo,
LEZIONE n. 5 (a cura di Antonio Di Marco) IL P-VALUE (α) Data un ipotesi nulla (H 0 ), questa la si può accettare o rifiutare in base al valore del p- value. In genere il suo valore è un numero molto piccolo,
tommaso.iacomino@gmail.com INTERNET EXPLORER Guida introduttiva CAPITOLO 1 Fig. 1
 INTERNET EXPLORER Guida introduttiva CAPITOLO 1 Fig. 1 IMPORTANTE: forse non visualizzate questa barra, se così fosse usiamo questa procedura: posizioniamo il cursore sulla parte vuota tasto destro del
INTERNET EXPLORER Guida introduttiva CAPITOLO 1 Fig. 1 IMPORTANTE: forse non visualizzate questa barra, se così fosse usiamo questa procedura: posizioniamo il cursore sulla parte vuota tasto destro del
Test statistici di verifica di ipotesi
 Test e verifica di ipotesi Test e verifica di ipotesi Il test delle ipotesi consente di verificare se, e quanto, una determinata ipotesi (di carattere biologico, medico, economico,...) è supportata dall
Test e verifica di ipotesi Test e verifica di ipotesi Il test delle ipotesi consente di verificare se, e quanto, una determinata ipotesi (di carattere biologico, medico, economico,...) è supportata dall
LEZIONE 31. B i : R n R. R m,n, x = (x 1,..., x n ). Allora sappiamo che è definita. j=1. a i,j x j.
 LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
Esercitazione n.2 Inferenza su medie
 Esercitazione n.2 Esercizio L ufficio del personale di una grande società intende stimare le spese mediche familiari dei suoi impiegati per valutare la possibilità di attuare un programma di assicurazione
Esercitazione n.2 Esercizio L ufficio del personale di una grande società intende stimare le spese mediche familiari dei suoi impiegati per valutare la possibilità di attuare un programma di assicurazione
LABORATORIO EXCEL XLSTAT 2008 SCHEDE 2 e 3 VARIABILI QUANTITATIVE
 Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) LABORATORIO EXCEL
Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) LABORATORIO EXCEL
0.1 Percorrenza e Cilindrata
 0.1 Percorrenza e Cilindrata Iniziamo ora un analisi leggermente più complessa basata sempre sui concetti appena introdotti. Innanzi tutto possiamo osservare, dal grafico ottenuto con il comando pairs,
0.1 Percorrenza e Cilindrata Iniziamo ora un analisi leggermente più complessa basata sempre sui concetti appena introdotti. Innanzi tutto possiamo osservare, dal grafico ottenuto con il comando pairs,
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
Matematica 1 - Corso di Laurea in Ingegneria Meccanica
 Matematica 1 - Corso di Laurea in Ingegneria Meccanica Esercitazione su massimi e minimi vincolati 9 dicembre 005 Esercizio 1. Considerare l insieme C = {(x,y) R : (x + y ) = x } e dire se è una curva
Matematica 1 - Corso di Laurea in Ingegneria Meccanica Esercitazione su massimi e minimi vincolati 9 dicembre 005 Esercizio 1. Considerare l insieme C = {(x,y) R : (x + y ) = x } e dire se è una curva
Guida all uso di Java Diagrammi ER
 Guida all uso di Java Diagrammi ER Ver. 1.1 Alessandro Ballini 16/5/2004 Questa guida ha lo scopo di mostrare gli aspetti fondamentali dell utilizzo dell applicazione Java Diagrammi ER. Inizieremo con
Guida all uso di Java Diagrammi ER Ver. 1.1 Alessandro Ballini 16/5/2004 Questa guida ha lo scopo di mostrare gli aspetti fondamentali dell utilizzo dell applicazione Java Diagrammi ER. Inizieremo con
E naturale chiedersi alcune cose sulla media campionaria x n
 Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
PROGRAMMA SVOLTO NELLA SESSIONE N.
 Università C. Cattaneo Liuc, Corso di Statistica, Sessione n. 1, 2014 Laboratorio Excel Sessione n. 1 Venerdì 031014 Gruppo PZ Lunedì 061014 Gruppo AD Martedì 071014 Gruppo EO PROGRAMMA SVOLTO NELLA SESSIONE
Università C. Cattaneo Liuc, Corso di Statistica, Sessione n. 1, 2014 Laboratorio Excel Sessione n. 1 Venerdì 031014 Gruppo PZ Lunedì 061014 Gruppo AD Martedì 071014 Gruppo EO PROGRAMMA SVOLTO NELLA SESSIONE
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Sistemi Informativi Territoriali. Map Algebra
 Paolo Mogorovich Sistemi Informativi Territoriali Appunti dalle lezioni Map Algebra Cod.735 - Vers.E57 1 Definizione di Map Algebra 2 Operatori locali 3 Operatori zonali 4 Operatori focali 5 Operatori
Paolo Mogorovich Sistemi Informativi Territoriali Appunti dalle lezioni Map Algebra Cod.735 - Vers.E57 1 Definizione di Map Algebra 2 Operatori locali 3 Operatori zonali 4 Operatori focali 5 Operatori
Elaborazione dei dati su PC Regressione Multipla
 21 Elaborazione dei dati su PC Regressione Multipla Analizza Regressione Statistiche Grafici Metodo di selezione Analisi dei dati 21.1 Introduzione 21.2 Regressione lineare multipla con SPSS 21.3 Regressione
21 Elaborazione dei dati su PC Regressione Multipla Analizza Regressione Statistiche Grafici Metodo di selezione Analisi dei dati 21.1 Introduzione 21.2 Regressione lineare multipla con SPSS 21.3 Regressione
Biblioteca di Cervia NOZIONI BASE DI INFORMATICA
 Biblioteca di Cervia NOZIONI BASE DI INFORMATICA NOZIONI DI INFORMATICA Il PC è composto solitamente di tre parti principali: - Il Case, ovvero il contenitore del cuore del computer, da qui si accende
Biblioteca di Cervia NOZIONI BASE DI INFORMATICA NOZIONI DI INFORMATICA Il PC è composto solitamente di tre parti principali: - Il Case, ovvero il contenitore del cuore del computer, da qui si accende
Indice Statistiche Univariate Statistiche Bivariate
 Indice 1 Statistiche Univariate 1 1.1 Importazione di un file.data.............................. 1 1.2 Medie e variabilità................................... 6 1.3 Distribuzioni di frequenze...............................
Indice 1 Statistiche Univariate 1 1.1 Importazione di un file.data.............................. 1 1.2 Medie e variabilità................................... 6 1.3 Distribuzioni di frequenze...............................
Parte I. Concetti preliminari. Statistica per la Neuropsicologia. Sommario. Notes. Notes. Notes. Davide Crepaldi
 MoMo Lab, Department of Psychology, University of Milano-Bicocca, Italy davide.crepaldi1@unimib.it Ospedale S. Antonio Abate 25 novembre 2011 Parte I Concetti preliminari Sommario Strumento e pensiero
MoMo Lab, Department of Psychology, University of Milano-Bicocca, Italy davide.crepaldi1@unimib.it Ospedale S. Antonio Abate 25 novembre 2011 Parte I Concetti preliminari Sommario Strumento e pensiero
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
CAPITOLO 8 LA VERIFICA D IPOTESI. I FONDAMENTI
 VERO FALSO CAPITOLO 8 LA VERIFICA D IPOTESI. I FONDAMENTI 1. V F Un ipotesi statistica è un assunzione sulle caratteristiche di una o più variabili in una o più popolazioni 2. V F L ipotesi nulla unita
VERO FALSO CAPITOLO 8 LA VERIFICA D IPOTESI. I FONDAMENTI 1. V F Un ipotesi statistica è un assunzione sulle caratteristiche di una o più variabili in una o più popolazioni 2. V F L ipotesi nulla unita
INTRODUZIONE AI CICLI
 www.previsioniborsa.net INTRODUZIONE AI CICLI _COSA SONO E A COSA SERVONO I CICLI DI BORSA. Partiamo dalla definizione di ciclo economico visto l argomento che andremo a trattare. Che cos è un ciclo economico?
www.previsioniborsa.net INTRODUZIONE AI CICLI _COSA SONO E A COSA SERVONO I CICLI DI BORSA. Partiamo dalla definizione di ciclo economico visto l argomento che andremo a trattare. Che cos è un ciclo economico?
Lezione 9: Cambio di base
 Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Test d ipotesi. Statistica e biometria. D. Bertacchi. Test d ipotesi
 In molte situazioni una raccolta di dati (=esiti di esperimenti aleatori) viene fatta per prendere delle decisioni sulla base di quei dati. Ad esempio sperimentazioni su un nuovo farmaco per decidere se
In molte situazioni una raccolta di dati (=esiti di esperimenti aleatori) viene fatta per prendere delle decisioni sulla base di quei dati. Ad esempio sperimentazioni su un nuovo farmaco per decidere se
Equazione della Circonferenza - Grafico di una Circonferenza - Intersezione tra Circonferenza e Retta
 Equazione della Circonferenza - Grafico di una Circonferenza - Intersezione tra Circonferenza e Retta Francesco Zumbo www.francescozumbo.it http://it.geocities.com/zumbof/ Questi appunti vogliono essere
Equazione della Circonferenza - Grafico di una Circonferenza - Intersezione tra Circonferenza e Retta Francesco Zumbo www.francescozumbo.it http://it.geocities.com/zumbof/ Questi appunti vogliono essere
1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario:
 Esempi di domande risposta multipla (Modulo II) 1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario: 1) ha un numero di elementi pari a 5; 2) ha un numero di elementi
Esempi di domande risposta multipla (Modulo II) 1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario: 1) ha un numero di elementi pari a 5; 2) ha un numero di elementi
