La serie numerica di Fibonacci
|
|
|
- Anna Maria Mariani
- 8 anni fa
- Visualizzazioni
Transcript
1 1 La serie numerica di Fibonacci il sistema di numerazione e sviluppo della natura 2 Nato a Pisa Fibonacci ( ) 1240) Visse la sua giovinezza in Algeria dove imparò le cifre indo-arabiche, elaborò l aritmetica l che conosciamo e introdusse lo 0. Risolse molti problemi matematici legati alla riproduzione e all evoluzione di un fenomeno 3 La successione si compone di una serie di numeri nella quale ognuno di essi è la somma dei due numeri precedenti Cos è? = = = = = =21 21.
2 4 Esempi di applicazione La riproduzione dei conigli In condizioni ideali una coppia di conigli è in grado di riprodursi già da un mese dopo la nascita. La femmina è in grado di generare una seconda coppia di conigli già un mese dopo l accoppiamento l con il maschio. Prendiamo una coppia di conigli e mettiamola in un recinto. Supponiamo che i nostri conigli non muoiano mai. Quante coppie di conigli ci sono dopo 1, 2, 3, 4, 5.. mesi? 5 Albero genealogico di un fuco In uno sciame di api ci sono le api (femmine) e i fuchi (maschi). Le api femmine si dividono in operaie e regine. Le api regine sono api operaie nutrite con pappa reale e, diversamente dalle operaie semplici, sono in grado di produrre uova. Le api femmine sono tutte generate dall unione dell ape regina con un fuco (uova fecondate) Le api maschio nascono dalle uova dell ape regina non fecondate. Quindi possiamo dire che le femmine hanno 2 genitori: l ape l regina e un fuco, mentre i fuchi hanno un solo genitore: l ape l regina. Quanti nonni, bisnonni, trisnonni hanno i fuchi? 6 La strada delle api Salire le scale giochini Alcuni giochini Costruisci il muretto Fai il dolce!
3 La 7 strada delle api Un ape per muoversi nel suo alveare può spostarsi solamente per celle contigue. Si contino quanti possibili itinerari ci sono per raggiungere la cella 1, quelli per raggiungere la cella 2, la 3..sapendo che l ape l deve sempre spostarsi da una cella con numero inferiore ad un altra con numero maggiore Per raggiungere la cella 1 1 Per raggiungere la cella 2 si può: andare direttamente in 2 tragitto Per raggiungere la cella 3 si può: Per raggiungere la cella 4 si può: TORNA INDIETRO N itinerari possibili 8 Costruisci il muretto Si hanno a disposizione un certo numero di mattoni tutti uguali aventi spessore pari alla metà dell altezza.. Per costruire un muretto i mattoni possono essere disposti o in verticale o in orizzontale in due file f come in figura. Avendo a disposizione 1, 2, Mattoni in quanti modi si può costruire tale muretto alto un mattone? n possibilità 1 mattone 1 2 mattoni 2 3 mattoni 3 4 mattoni 5 TORNA INDIETRO 5 mattoni 8 9 Salire le scale TORNA INDIETRO Gradini della scala Immaginiamo che per salire una rampa di scale sia possibile o salire un gradino per volta o al massimo due insieme. Se la scala è costituita da 1, 2,3.. scalini, in quanti modi diversi è possibile arrivare in cima? N possibilità (1+1, 1 da due gradini) 2 3 (1+1+1, 1+2, 2+1) 3 4 ( , 1+2+1, 2+1+1, 1+1+2, 2+2) 5 5 ( , , , , 2+2+1, 1+2+2, 2+1+2, ) 8
4 10 Fai il dolce! Un azienda produce solamente due tipi di dolci. Uno richiede un tempo si preparazione di 1 ora e l altro l di due ore. In base al tempo a disposizione si trovino le diverse possibilità di produzione dei due dolci Tempo in ore N pos. 1 (solo dolce1) 1 2 (dolce1+dolce1 o dolce2) 2 3 (d1+d1+d1 o d2+d1 o d1+d2) 3 4 (d1+d1+d1+d1 o d1+d2+d1 o d2+d1+d1 o d1+d1+d2 o d2+d2) 5 5 (d1+d1+d1+d1+d1 o d2+d1+d1+d1 o d1+d2+d2+d1 o d1+d1+d2+d1 o d1+d1+d1+d2 o d1+d2+d2 o d2+d1+d2 o d2+d2+d1) 8 TORNA INDIETRO 11 C è molto di più La successione di Fibonacci non è solamente un modello matematico per risolvere teorici problemi di evoluzione ma è ravvisabile in tutto ciò che ci circonda. E un caso? La Natura conosce la matematica? Il creato è regolato da una legge superiore? 12 in natura Piante Fiori Frutta Verdura Corpo umano Animali e altro
5 La 13 Nelle piante successione numerica di Fibonacci La ramificazione La ramificazione e il fogliame La fillotassi 14 La ramificazione delle piante Lo sviluppo di una pianta, ammesso che non venga potata o in qualche modo controllata da azioni esterne, avviene secondo fasi, di durata diversa, dipendenti dalla stagione e dalle condizioni climatiche in genere. Un tronco può dar vita ad un ramo solo se è maturo ovvero a partire dalla propria seconda fase di crescita. Inoltre, un tronco non potrà generare più di un ramo per ogni fase altrimenti rischierebbe di indebolire troppo la pianta compromettendone la salute. 15 La ramificazione delle piante Analogamente un ramo può generare solamente dalla seconda fase del proprio sviluppo e dar vita unicamente ad un ulteriore ramo per ogni fase. Lo schema in figura illustra schematicamente la crescita di una pianta e la ramificazione. In ogni fase di crescita è ravvisabile la serie di Fibonacci contando il numero di rami posseduti dalla pianta.
6 16 La ramificazione e il fogliame Un esempio di quanto precedentemente detto in merito alla ramificazione degli alberi e delle piante in genere è dato dalla pianta del biancospino In essa la serie di Fibonacci non solo è ravvisabile dal numero di rami presenti ad ogni fase della crescita della pianta ma anche dal numero delle foglie che la pianta stessa fa germogliare ogni qual volta si ramifica. 17 La fillotassi Molte piante mostrano i numeri di Fibonacci anche nella disposizione ione occupata dalle foglie intorno allo stelo. Osservando una pianta dall alto alto ci si accorge, infatti, che le foglie non sono disposte casualmente ma secondo una sorta di spirale: ogni foglia tende ad occupare una posizione tale da non nascondere le compagne sottostanti. Grazie a questo ordine ogni foglia può ricevere la quantità di luce sufficiente per compiere il proprio ciclo vitale regolarmente e l acqua l della pioggia può raggiungere rapidamente, attraverso lo stelo, le radici. Quando la pianta è provvista di molte foglie capita inevitabilmente che ci siano foglie dispose sopra ad altre. Il fatto curioso è che la spirare della disposizione delle foglie lungo uno stelo compie sempre un numero di giri intorno allo stelo stesso prima che una foglia si sovrapponga ad un altra pari ad un numero di Fibonacci (solitamente 5 o 8 ). E ancora: contando le foglie sistemate sullo stelo tra due che si sovrappongono.se ne trovano sempre una quantità pari ad un numero di Fibonacci 18 La fillotassi Circa il 90% delle piante presenta la disposizione delle foglie come descritto, e anche molte piante grasse tra le quali anche i cactus hanno le spine disposte seguendo la legge dei numeri di Fibonacci anche se non sempre è palesemente riscontrabile. P I A N T A D I G I R A S O L E
7 Esempi di piante grasse 19 I fiori 20 Anche i fiori presentano la successione di Fibonacci come ottimizzazione ottimizzazione del numero di petali posseduti. Esistono infatti pochissime specie di di fiori che non hanno un numero di petali pari ad un numero della successione di Fibonacci. Del resto resto è assai raro trovare un quadrifoglio! (4 non è un numero di Fibonacci) Una fucsia con 4 petali Un quadrifoglio I fiori 21 Alcuni esempi di fiori 1 petalo 2 petali 3 petali 5 petali 8 petali 13 petali 34 petali 55 petali petali
8 22 Gladioli Viola del pensiero Fiore di ibisco Alcuni fiori commestibili con un numero di petali pari ad un numero di Fibonacci Violette Borragine 23 Malva Fiore di zucca Calendula Pimpinella 24 I fiori La passiflora : esempio splendido di come i numeri di Fibonacci ricorrono anche nei fiori 2 insiemi di 5 foglioline verdi Sopra i sottilissimi petali viola- bianchi un insieme di 5 stami a forma di T, e sopra ancora altri 3 a forma di chiodi. DIETRO: 3 verdi foglioline che proteggono il germoglio 5 foglie verdi Altre 5 foglie verdi
9 25 I fiori Nelle margherite (ma anche nei girasoli ed altri fiori simili) al centro della corolla si possono notare semini disposti secondo due ordini di spirali: le spirali che si avvolgono in senso antiorario sono 21 e quelle in senso orario sono I fiori 27 La frutta Non potevano mancare i numeri di Fibonacci nella frutta: sezionando trasversalmente una noce, una banana, una mela, una pera si ottengono NOCE: 2 parti BANANA: 3 parti MELA: 5 parti
10 28 La frutta Osservando la buccia dell ananas si possono notare che le placche esagonali formano tre diverse tipologie di spirali che, con diverse inclinazioni, dalla base risalgono il frutto. 29 La frutta Analogamente anche una pigna è costituita da scaglie disposte lungo due insiemi di spirali come mostrato in figura, di 8 e 13 involuzioni 30 La verdura E gli ortaggi non sono da meno in quanto a sfoggiare i numeri di Fibonacci nelle sezioni o nelle spirali che descrivono la crescita del vegetale
11 31 Le verdure 32 Il corpo umano Anche l uomo l presenta i numeri di Fibonacci in numerosi elementi un naso, una bocca, due occhi, due orecchie, due braccia, cinque dita I denti? I denti non sono un numero di Fiboncacci! Le falangi della mano sono in proporzione tra loco come 2:3:5:8 33 Gli animali Alcuni esempi di animali di Fibonacci La forma del Nautilus si ottiene collegando semicirconferenze di diametro crescente pari ogni volta ad numero di Fibonacci
12 34 altro Uragano Linda Una Galassia Tutti i pianeti interni distano dal Sole nelle proporzioni della successione (Sole 1, Mercurio 1, Venere 2, Terra 3, Marte 5); e quelli esterni distano ugualmente da Giove (Giove 1, Saturno 1, Urano 2, Nettuno 3, Plutone 5); La successione di Fibonacci è intimamente legata alla spirale logaritmica, modello matematico che descrive una vastissima gamma di fenomeni a spirale 35 altro Un vastissimo numero di artisti, affascinati dalla successione di Fibonacci e dal suo riscontro nella creazione, sono stati ispirati nel creare alcune delle proprie opere, durante l arco l di secoli MUSICA: compositori come Bach, Bartók, Debussy,, Schubert, Satie, Beethoven, Mozart, ma anche molte Band contemporanee come i Mercury Rev, i Tools. ARTE FIGURATIVA: uno sposo dei numeri di Fibonacci è sicuramente Mario Merz, ma nei secoli molti sono coloro che nei propri quadri o nelle sculture hanno utilizzato questa successione per rappresentare la crescita e l evoluzione l della vita degli elementi rappresentati. Diversi Film Cinematografici sono ispirati a questi numeri Alcuni modelli finanziari che descrivono la crescita e l andamento l economico sono basati sulla successione di Fibonacci e tanto altro ancora Mario Merz Volo di Numeri Mole Antonelliana (Torino) 36 Compito Si realizzi un piatto ispirato ai numeri di Fibonacci e si compili una scheda tecnica evidenziando gli aspetti dove tale successione è presente In particolare non dovranno mancare: - nome ricetta - ingredienti (grammatura, numero, tipologia ) - attrezzature - tempi di preparazione e, eventualmente, di cottura - presentazione del piatto - breve descrizione sulla scelta di quanto sopra indicato in relazione ai numeri di Fibonacci e alla sua presenza in natura Si alleghino foto o quanto altro possa essere utile per una migliore valutazione del lavoro
La successione numerica di Fibonacci
 MATEMATICA E REALTA La successione numerica di Fibonacci il sistema di numerazione e sviluppo della natura Fibonacci (1170-1240) Nato a Pisa Visse la sua giovinezza in Algeria dove imparò le cifre indo-arabiche,
MATEMATICA E REALTA La successione numerica di Fibonacci il sistema di numerazione e sviluppo della natura Fibonacci (1170-1240) Nato a Pisa Visse la sua giovinezza in Algeria dove imparò le cifre indo-arabiche,
MA COME VIVE UN APE E QUALI SONO I SUOI COMPITI?
 MA COME VIVE UN APE E QUALI SONO I SUOI COMPITI? LE API VOLANDO DA UN FIORE ALL ALTRO RACCOLGONO IL NETTARE PRODOTTO DAI FIORI E LO UTILIZZANO PER FARE IL MIELE CHE SARA UNA PREZIOSA SCORTA DI CIBO PER
MA COME VIVE UN APE E QUALI SONO I SUOI COMPITI? LE API VOLANDO DA UN FIORE ALL ALTRO RACCOLGONO IL NETTARE PRODOTTO DAI FIORI E LO UTILIZZANO PER FARE IL MIELE CHE SARA UNA PREZIOSA SCORTA DI CIBO PER
Progressioni numeriche Successione di Fibonacci e sezione aurea
 Progressioni numeriche Successione di Fibonacci e sezione aurea Progetto Matematica e Statistica - Progetto Lauree Scientifiche Loredana Caso 1 Successioni numeriche 2 Una successione numerica è una sequenza
Progressioni numeriche Successione di Fibonacci e sezione aurea Progetto Matematica e Statistica - Progetto Lauree Scientifiche Loredana Caso 1 Successioni numeriche 2 Una successione numerica è una sequenza
LE PIANTE. acqua anidride carbonica
 Unità La foglia e la fotosintesi La foglia è la parte principale della pianta, perché nelle foglie la pianta produce il proprio cibo. luce solare acqua anidride carbonica clorofilla glucosio ossigeno Nella
Unità La foglia e la fotosintesi La foglia è la parte principale della pianta, perché nelle foglie la pianta produce il proprio cibo. luce solare acqua anidride carbonica clorofilla glucosio ossigeno Nella
Ricorsione. (da lucidi di Marco Benedetti)
 Ricorsione (da lucidi di Marco Benedetti) Funzioni ricorsive Dal punto di vista sintattico, siamo in presenza di una funzione ricorsiva quando all interno della definizione di una funzione compaiono una
Ricorsione (da lucidi di Marco Benedetti) Funzioni ricorsive Dal punto di vista sintattico, siamo in presenza di una funzione ricorsiva quando all interno della definizione di una funzione compaiono una
La spirale iperbolica: Fu descritta per la prima volta da Pierre Varignon (1654-1722). L equazione, espressa in coordinate polari, è del tipo:
 Esistono delle forme geometriche che sono in grado, per complessi fattori psicologici non del tutto chiariti, di comunicarci un senso d equilibrio, di gradimento e di benessere. Tra queste analizzeremo
Esistono delle forme geometriche che sono in grado, per complessi fattori psicologici non del tutto chiariti, di comunicarci un senso d equilibrio, di gradimento e di benessere. Tra queste analizzeremo
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
Interesse, sconto, ratei e risconti
 129 Interesse, sconto, ratei e risconti Capitolo 129 129.1 Interesse semplice....................................................... 129 129.1.1 Esercizio per il calcolo dell interesse semplice........................
129 Interesse, sconto, ratei e risconti Capitolo 129 129.1 Interesse semplice....................................................... 129 129.1.1 Esercizio per il calcolo dell interesse semplice........................
Statistica e biometria. D. Bertacchi. Variabili aleatorie. V.a. discrete e continue. La densità di una v.a. discreta. Esempi.
 Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
da 2 a 5 giocatori, dai 10 anni in su, durata 30 minuti
 da 2 a 5 giocatori, dai 10 anni in su, durata 30 minuti OBIETTIVO Il vincitore è colui che, dopo due round di gioco, delle sue 11 ordinazioni, ne ha consegnate il maggior numero. CONTENUTO DELLA SCATOLA
da 2 a 5 giocatori, dai 10 anni in su, durata 30 minuti OBIETTIVO Il vincitore è colui che, dopo due round di gioco, delle sue 11 ordinazioni, ne ha consegnate il maggior numero. CONTENUTO DELLA SCATOLA
PRIME LETTURE Materiali per leggere e fare insieme. con Il mondo del Signor Acqua. Gita alla fattoria di Agostino Traini
 PRIME LETTURE Materiali per leggere e fare insieme con Il mondo del Signor Acqua. Gita alla fattoria di Agostino Traini INDICAZIONI DIDATTICHE Agostino Traini Illustrazioni dell autore serie Il mondo del
PRIME LETTURE Materiali per leggere e fare insieme con Il mondo del Signor Acqua. Gita alla fattoria di Agostino Traini INDICAZIONI DIDATTICHE Agostino Traini Illustrazioni dell autore serie Il mondo del
Nascita e morte delle stelle
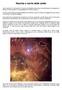 Nascita e morte delle stelle Se la materia che componeva l universo primordiale fosse stata tutta perfettamente omogenea e diffusa in modo uguale, non esisterebbero né stelle né pianeti. C erano invece
Nascita e morte delle stelle Se la materia che componeva l universo primordiale fosse stata tutta perfettamente omogenea e diffusa in modo uguale, non esisterebbero né stelle né pianeti. C erano invece
Capitolo 3 Riproduzione e trasmissione dei cromosomi
 Capitolo 3 Riproduzione e trasmissione dei cromosomi 3.1 Nelle cellule somatiche del topolino domestico vi sono 40 cromosomi. a. Quanti cromosomi riceve dal padre? b. Quanti autosomi sono presenti nel
Capitolo 3 Riproduzione e trasmissione dei cromosomi 3.1 Nelle cellule somatiche del topolino domestico vi sono 40 cromosomi. a. Quanti cromosomi riceve dal padre? b. Quanti autosomi sono presenti nel
Cittadinanza e Costituzione
 Cittadinanza e Costituzione Anno Scolastico 20010/11 Progetto di Cittadinanza e Costituzione Finalità Essere cittadini di un mondo in continuo cambiamento ha come premessa il conoscere e il porre in atto
Cittadinanza e Costituzione Anno Scolastico 20010/11 Progetto di Cittadinanza e Costituzione Finalità Essere cittadini di un mondo in continuo cambiamento ha come premessa il conoscere e il porre in atto
15. Antico gioco russo
 15. Antico gioco russo In un antico gioco russo, attraverso i risultati casuali ottenuti dall allacciamento di cordicelle, i giovani cercavano una previsione sul tipo di legame che si sarebbe instaurata
15. Antico gioco russo In un antico gioco russo, attraverso i risultati casuali ottenuti dall allacciamento di cordicelle, i giovani cercavano una previsione sul tipo di legame che si sarebbe instaurata
IL CICLO (RITMO) VITALE DELLA MUFFA
 IL CICLO (RITMO) VITALE DELLA MUFFA (Pezzo di formaggio ammuffito) Problema: cos è quest oggetto? Discussione dei bambini: osservazione, annusa mento e proposta di varie risposte, tra cui è formaggio con
IL CICLO (RITMO) VITALE DELLA MUFFA (Pezzo di formaggio ammuffito) Problema: cos è quest oggetto? Discussione dei bambini: osservazione, annusa mento e proposta di varie risposte, tra cui è formaggio con
LA DIFFERENZA un nodo da sciogliere. Un percorso ad ostacoli in classe prima e seconda
 LA DIFFERENZA un nodo da sciogliere Un percorso ad ostacoli in classe prima e seconda Sandra Taccetti, 2013 LE CRITICITÀ LA NOSTRA INTENZIONE E' QUELLA DI PROBLEMATIZZARE QUESTI PERCORSI PERCHE' NONOSTANTE
LA DIFFERENZA un nodo da sciogliere Un percorso ad ostacoli in classe prima e seconda Sandra Taccetti, 2013 LE CRITICITÀ LA NOSTRA INTENZIONE E' QUELLA DI PROBLEMATIZZARE QUESTI PERCORSI PERCHE' NONOSTANTE
Capitolo 4.2. Analisi tecnica: Fibonacci
 1 Capitolo 4.2 Analisi tecnica: Fibonacci 0 Contenuti ANALISI TECNICA: FIBONACCI L analisi di Fibonacci mira a identificare i potenziali livelli di supporto e di resistenza futuri basati sui trend dei
1 Capitolo 4.2 Analisi tecnica: Fibonacci 0 Contenuti ANALISI TECNICA: FIBONACCI L analisi di Fibonacci mira a identificare i potenziali livelli di supporto e di resistenza futuri basati sui trend dei
Università degli Studi di Ferrara - A.A. 2014/15 Dott. Valerio Muzzioli ORDINAMENTO DEI DATI
 ORDINAMENTO DEI DATI Quando si ordina un elenco (ovvero una serie di righe contenenti dati correlati), le righe sono ridisposte in base al contenuto di una colonna specificata. Distinguiamo due tipi di
ORDINAMENTO DEI DATI Quando si ordina un elenco (ovvero una serie di righe contenenti dati correlati), le righe sono ridisposte in base al contenuto di una colonna specificata. Distinguiamo due tipi di
Martina Zaminato Classe III A A.S. 2012/2013
 Martina Zaminato Classe III A A.S. 2012/2013 IL SOLE Tutti prima o poi si chiedono cosa sia il Sole, già da bambini chi non è stato incuriosito dalla nostra stella? Il Sole non è altro che una gigantesca
Martina Zaminato Classe III A A.S. 2012/2013 IL SOLE Tutti prima o poi si chiedono cosa sia il Sole, già da bambini chi non è stato incuriosito dalla nostra stella? Il Sole non è altro che una gigantesca
VEGETALI U N S O T U R I O L O P S I T T O S U N O D. Vegetali V5 I SEMI V1 V2 V3 V8 U1
 VEGETAL L P E U R S T Vegetali SEM V1 V2 V3 V8 U1 1 VEGETAL L P E U R S T SEM Quando un seme cade nel terreno può germogliare se trova le condizioni adatte. Esperienza 1: om è fatto un seme. Materiale
VEGETAL L P E U R S T Vegetali SEM V1 V2 V3 V8 U1 1 VEGETAL L P E U R S T SEM Quando un seme cade nel terreno può germogliare se trova le condizioni adatte. Esperienza 1: om è fatto un seme. Materiale
Il calcolo letterale per risolvere problemi e per dimostrare
 Il calcolo letterale per risolvere problemi e per dimostrare (si prevedono circa 25 ore di lavoro in classe) Nome e cognome dei componenti del gruppo che svolge le attività di gruppo di questa lezione
Il calcolo letterale per risolvere problemi e per dimostrare (si prevedono circa 25 ore di lavoro in classe) Nome e cognome dei componenti del gruppo che svolge le attività di gruppo di questa lezione
A COSA SERVE IL FUSTO? Il fusto si trova fuori dal terreno e serve a
 A COSA SERVE IL FUSTO? Il fusto si trova fuori dal terreno e serve a sostenere la pianta contenere i vasi in cui scorre la linfa Il fusto tende sempre a crescere verso l alto. Ci sono diversi tipi di fusto:
A COSA SERVE IL FUSTO? Il fusto si trova fuori dal terreno e serve a sostenere la pianta contenere i vasi in cui scorre la linfa Il fusto tende sempre a crescere verso l alto. Ci sono diversi tipi di fusto:
Gli strumenti della geografia
 Gli strumenti della geografia La geografia studia lo spazio, cioè i tanti tipi di luoghi e di ambienti che si trovano sulla Terra. La geografia descrive lo spazio e ci spiega anche come è fatto, come vivono
Gli strumenti della geografia La geografia studia lo spazio, cioè i tanti tipi di luoghi e di ambienti che si trovano sulla Terra. La geografia descrive lo spazio e ci spiega anche come è fatto, come vivono
per le persone in formazione del ramo di formazione e d esame <inserire il ramo>
 Commissione svizzera d esame per la formazione commerciale di base Esame finale di tirocinio per impiegati di commercio 2013 Serie 2013/01 - profilo B per le persone in formazione del ramo di formazione
Commissione svizzera d esame per la formazione commerciale di base Esame finale di tirocinio per impiegati di commercio 2013 Serie 2013/01 - profilo B per le persone in formazione del ramo di formazione
LA NATURA E LA SCIENZA
 LA NATURA E LA SCIENZA La NATURA è tutto quello che sta intorno a noi: le persone, gli animali, le piante, le montagne, il cielo, le stelle. e tante altre cose non costruite dall uomo. Lo studio di tutte
LA NATURA E LA SCIENZA La NATURA è tutto quello che sta intorno a noi: le persone, gli animali, le piante, le montagne, il cielo, le stelle. e tante altre cose non costruite dall uomo. Lo studio di tutte
Sommario. Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi.
 Algoritmi 1 Sommario Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi. 2 Informatica Nome Informatica=informazione+automatica. Definizione Scienza che si occupa dell
Algoritmi 1 Sommario Definizione di informatica. Definizione di un calcolatore come esecutore. Gli algoritmi. 2 Informatica Nome Informatica=informazione+automatica. Definizione Scienza che si occupa dell
Interesse, sconto, ratei e risconti
 TXT HTM PDF pdf P1 P2 P3 P4 293 Interesse, sconto, ratei e risconti Capitolo 129 129.1 Interesse semplice....................................................... 293 129.1.1 Esercizio per il calcolo dell
TXT HTM PDF pdf P1 P2 P3 P4 293 Interesse, sconto, ratei e risconti Capitolo 129 129.1 Interesse semplice....................................................... 293 129.1.1 Esercizio per il calcolo dell
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
SCHEDA TECNICA PER IL MONTAGGIO DELLE COPERTURE LA COPERTURA TOSCANA.
 SCHEDA TECNICA PER IL MONTAGGIO DELLE COPERTURE LA COPERTURA TOSCANA. La COPERTURATOSCANA, prodotta da COTTOREF, è composta da tre articoli fondamentali: tegole, coppi e colmi, oltre ad una serie di pezzi
SCHEDA TECNICA PER IL MONTAGGIO DELLE COPERTURE LA COPERTURA TOSCANA. La COPERTURATOSCANA, prodotta da COTTOREF, è composta da tre articoli fondamentali: tegole, coppi e colmi, oltre ad una serie di pezzi
Tempo Abilità Tipologie di lavoro contenuto/contenuti? Lavoro individuale, a coppie o di gruppo della visita aziendale. 1 settimana Leggere
 CONTENUTI DEL MODULO Gli alunni prima della visita aziendale cercano informazioni sulla loro impresa partner su internet o nella loro cerchia di conoscenze e predispongono su questa base il testo di un
CONTENUTI DEL MODULO Gli alunni prima della visita aziendale cercano informazioni sulla loro impresa partner su internet o nella loro cerchia di conoscenze e predispongono su questa base il testo di un
IL CAPOLUOGO AL MICROSCOPIO
 IL CAPOLUOGO AL MICROSCOPIO Il Servizio Statistica della Provincia di Mantova coltiva il progetto di costituire una banca dati provinciale di provenienza anagrafica che non vuole divenire una duplicazione
IL CAPOLUOGO AL MICROSCOPIO Il Servizio Statistica della Provincia di Mantova coltiva il progetto di costituire una banca dati provinciale di provenienza anagrafica che non vuole divenire una duplicazione
Economia Applicata ai sistemi produttivi. 06.05.05 Lezione II Maria Luisa Venuta 1
 Economia Applicata ai sistemi produttivi 06.05.05 Lezione II Maria Luisa Venuta 1 Schema della lezione di oggi Argomento della lezione: il comportamento del consumatore. Gli economisti assumono che il
Economia Applicata ai sistemi produttivi 06.05.05 Lezione II Maria Luisa Venuta 1 Schema della lezione di oggi Argomento della lezione: il comportamento del consumatore. Gli economisti assumono che il
CONOSCERE IL PROPRIO CORPO
 CONOSCERE IL PROPRIO CORPO Gli esseri viventi sono fatti di parti che funzionano assieme in modo diverso. Hanno parti diverse che fanno cose diverse. Il tuo corpo è fatto di molte parti diverse. Alcune
CONOSCERE IL PROPRIO CORPO Gli esseri viventi sono fatti di parti che funzionano assieme in modo diverso. Hanno parti diverse che fanno cose diverse. Il tuo corpo è fatto di molte parti diverse. Alcune
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
Tabella 7. Dado truccato
 0 ALBERTO SARACCO 4. Compiti a casa 7novembre 200 4.. Ordini di grandezza e calcolo approssimato. Esercizio 4.. Una valigia misura 5cm di larghezza, 70cm di lunghezza e 45cm di altezza. Quante palline
0 ALBERTO SARACCO 4. Compiti a casa 7novembre 200 4.. Ordini di grandezza e calcolo approssimato. Esercizio 4.. Una valigia misura 5cm di larghezza, 70cm di lunghezza e 45cm di altezza. Quante palline
FISICA. Le forze. Le forze. il testo: 2011/2012 La Semplificazione dei Testi Scolastici per gli Alunni Stranieri IPSIA A.
 01 In questa lezione parliamo delle forze. Parliamo di forza quando: spostiamo una cosa; solleviamo un oggetto; fermiamo una palla mentre giochiamo a calcio; stringiamo una molla. Quando usiamo (applichiamo)
01 In questa lezione parliamo delle forze. Parliamo di forza quando: spostiamo una cosa; solleviamo un oggetto; fermiamo una palla mentre giochiamo a calcio; stringiamo una molla. Quando usiamo (applichiamo)
Psicometria (8 CFU) Corso di Laurea triennale STANDARDIZZAZIONE
 Psicometria (8 CFU) Corso di Laurea triennale Un punteggio all interno di una distribuzione è in realtà privo di significato se preso da solo. Sapere che un soggetto ha ottenuto un punteggio x=52 in una
Psicometria (8 CFU) Corso di Laurea triennale Un punteggio all interno di una distribuzione è in realtà privo di significato se preso da solo. Sapere che un soggetto ha ottenuto un punteggio x=52 in una
FESTA DIDATTICA ALL ORTO BOTANICO
 FESTA DIDATTICA ALL ORTO BOTANICO Come funziona Le feste sono rivolte a bambini da 4 a 8 anni. La feste didattiche hanno una durata di 3 ore e prevedono la partecipazione di un massimo di 25 bambini. Abbiamo
FESTA DIDATTICA ALL ORTO BOTANICO Come funziona Le feste sono rivolte a bambini da 4 a 8 anni. La feste didattiche hanno una durata di 3 ore e prevedono la partecipazione di un massimo di 25 bambini. Abbiamo
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
La catena alimentare. Sommario
 La catena alimentare classe Istituto Comprensivo anno scolastico 2009/10 Sommario Che cos è la catena alimentare Il ciclo alimentare I produttori I consumatori primari I consumatori secondari I consumatori
La catena alimentare classe Istituto Comprensivo anno scolastico 2009/10 Sommario Che cos è la catena alimentare Il ciclo alimentare I produttori I consumatori primari I consumatori secondari I consumatori
UNIVERSITÀ DEGLI STUDI DI TERAMO
 UNIVERSITÀ DEGLI STUDI DI TERAMO CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA (Classe 7) Corso di Matematica per l Economia (Prof. F. Eugeni) TEST DI INGRESSO Teramo, ottobre 00 SEZIONE
UNIVERSITÀ DEGLI STUDI DI TERAMO CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA (Classe 7) Corso di Matematica per l Economia (Prof. F. Eugeni) TEST DI INGRESSO Teramo, ottobre 00 SEZIONE
(liberamente interpretato da http://www2.unipr.it/~bottarel/epi/homepage.html) SCHEDA ALUNNI. Descrizione dell attività:
 Pagina 1 di 11 (liberamente interpretato da http://www2.unipr.it/~bottarel/epi/homepage.html) SCHEDA ALUNNI Descrizione dell attività: Problema 1. Siamo nel 2060 ed ormai gli umani hanno colonizzato Marte.
Pagina 1 di 11 (liberamente interpretato da http://www2.unipr.it/~bottarel/epi/homepage.html) SCHEDA ALUNNI Descrizione dell attività: Problema 1. Siamo nel 2060 ed ormai gli umani hanno colonizzato Marte.
Probabilità discreta
 Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
REALTÀ E MODELLI SCHEDA DI LAVORO
 REALTÀ E MODELLI SCHEDA DI LAVORO Bagaglio a mano Le regole per il bagaglio a mano di diverse compagnie aeree stabiliscono che la valigia (o borsa) deve avere un peso massimo di 5 kg e che la somma dei
REALTÀ E MODELLI SCHEDA DI LAVORO Bagaglio a mano Le regole per il bagaglio a mano di diverse compagnie aeree stabiliscono che la valigia (o borsa) deve avere un peso massimo di 5 kg e che la somma dei
La scala maggiore. In questa fase è come se sapessimo il modo giusto di aprire la bocca per parlare ma non avessimo idea delle parole da dire
 La scala maggiore Ora che abbiamo dato un pò di cenni teorici e impostato sia la mano destra che la sinistra è venuto il momento di capire cosa suonare con il basso ( impresa ardua direi ), cioè quando
La scala maggiore Ora che abbiamo dato un pò di cenni teorici e impostato sia la mano destra che la sinistra è venuto il momento di capire cosa suonare con il basso ( impresa ardua direi ), cioè quando
Ulteriori problemi di fisica e matematica
 Facoltà di Medicina e Chirurgia Università degli Studi di Firenze Agosto 2010 Ulteriori problemi di fisica e matematica Giovanni Romano Perché un raggio di luce proveniente dal Sole e fatto passare attraverso
Facoltà di Medicina e Chirurgia Università degli Studi di Firenze Agosto 2010 Ulteriori problemi di fisica e matematica Giovanni Romano Perché un raggio di luce proveniente dal Sole e fatto passare attraverso
Genetica. Mendel e la genetica
 Genetica Le leggi dell ereditarietà di Mendel Ereditarietà e cromosomi Estensioni della genetica mendeliana Applicazioni della genetica Genoma umano Mendel e la genetica Mendel 81822-1884), un monaco di
Genetica Le leggi dell ereditarietà di Mendel Ereditarietà e cromosomi Estensioni della genetica mendeliana Applicazioni della genetica Genoma umano Mendel e la genetica Mendel 81822-1884), un monaco di
La Dignità. L unione si fonda sui valori indivisibili e universali di dignità, libertà, uguaglianza e solidarietà
 La Dignità L unione si fonda sui valori indivisibili e universali di dignità, libertà, uguaglianza e solidarietà Essa pone la persona al centro delle sue azioni istituendo la cittadinanza dell Unione e
La Dignità L unione si fonda sui valori indivisibili e universali di dignità, libertà, uguaglianza e solidarietà Essa pone la persona al centro delle sue azioni istituendo la cittadinanza dell Unione e
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
6. La Terra. Sì, la terra è la tua casa. Ma che cos è la terra? Vediamo di scoprire qualcosa sul posto dove vivi.
 6. La Terra Dove vivi? Dirai che questa è una domanda facile. Vivo in una casa, in una certa via, di una certa città. O forse dirai: La mia casa è in campagna. Ma dove vivi? Dove sono la tua casa, la tua
6. La Terra Dove vivi? Dirai che questa è una domanda facile. Vivo in una casa, in una certa via, di una certa città. O forse dirai: La mia casa è in campagna. Ma dove vivi? Dove sono la tua casa, la tua
La scala musicale e le alterazioni
 La scala musicale e le alterazioni Unità didattica di Educazione Musicale classe seconda Obiettivi del nostro lavoro Acquisire il concetto di scala musicale e di intervallo. Conoscere la struttura della
La scala musicale e le alterazioni Unità didattica di Educazione Musicale classe seconda Obiettivi del nostro lavoro Acquisire il concetto di scala musicale e di intervallo. Conoscere la struttura della
Energia potenziale elettrica e potenziale. In queste pagine R indicherà una regione in cui è presente un campo elettrostatico.
 Energia potenziale elettrica e potenziale 0. Premessa In queste pagine R indicherà una regione in cui è presente un campo elettrostatico. 1. La forza elettrostatica è conservativa Una o più cariche ferme
Energia potenziale elettrica e potenziale 0. Premessa In queste pagine R indicherà una regione in cui è presente un campo elettrostatico. 1. La forza elettrostatica è conservativa Una o più cariche ferme
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Attività di Educazione Ambientale per le SCUOLE DELL INFANZIA
 Attività di Educazione Ambientale per le SCUOLE DELL INFANZIA PRECISAZIONI: I percorsi sono consigliati per tutte le classi: varierà la specificità ed il grado di approfondimento del programma. La maggior
Attività di Educazione Ambientale per le SCUOLE DELL INFANZIA PRECISAZIONI: I percorsi sono consigliati per tutte le classi: varierà la specificità ed il grado di approfondimento del programma. La maggior
Alla ricerca dell algoritmo. Scoprire e formalizzare algoritmi.
 PROGETTO SeT Il ciclo dell informazione Alla ricerca dell algoritmo. Scoprire e formalizzare algoritmi. Scuola media Istituto comprensivo di Fagagna (Udine) Insegnanti referenti: Guerra Annalja, Gianquinto
PROGETTO SeT Il ciclo dell informazione Alla ricerca dell algoritmo. Scoprire e formalizzare algoritmi. Scuola media Istituto comprensivo di Fagagna (Udine) Insegnanti referenti: Guerra Annalja, Gianquinto
L osservatorio è collocato all interno del Parco pineta tra Saronno e Varese. Attorno ad esso troviamo un incredibile distesa di alberi.
 L osservatorio L osservatorio è collocato all interno del Parco pineta tra Saronno e Varese. Attorno ad esso troviamo un incredibile distesa di alberi. All interno troviamo la sala conferenze e i vari
L osservatorio L osservatorio è collocato all interno del Parco pineta tra Saronno e Varese. Attorno ad esso troviamo un incredibile distesa di alberi. All interno troviamo la sala conferenze e i vari
OSSERVAZIONI SISTEMATICHE DI RILEVAZIONE PRECOCE AREA DELL INTELLIGENZA NUMERICA
 OSSERVAZIONI SISTEMATICHE DI RILEVAZIONE PRECOCE AREA DELL INTELLIGENZA NUMERICA Potenziamento dell area dell intelligenza numerica Processi lessicali Denomina su richiesta i numeri fino a 10 (come si
OSSERVAZIONI SISTEMATICHE DI RILEVAZIONE PRECOCE AREA DELL INTELLIGENZA NUMERICA Potenziamento dell area dell intelligenza numerica Processi lessicali Denomina su richiesta i numeri fino a 10 (come si
Con il termine programma Teacch si intende l organizzazione dei servizi per persone autistiche realizzato nella Carolina del Nord, che prevede una
 IL PROGRAMMA TEACCH Con il termine programma Teacch si intende l organizzazione dei servizi per persone autistiche realizzato nella Carolina del Nord, che prevede una presa in carico globale in senso sia
IL PROGRAMMA TEACCH Con il termine programma Teacch si intende l organizzazione dei servizi per persone autistiche realizzato nella Carolina del Nord, che prevede una presa in carico globale in senso sia
SOMIGLIANZA TRA INDIVIDUI
 SOMIGLIANZA TRA INDIVIDUI Si riferisce alla possibilità di riconoscere delle caratteristiche fenotipiche comuni tra animali diversi, dovute alla loro parentela. PARENTELA Due individui si dicono parenti
SOMIGLIANZA TRA INDIVIDUI Si riferisce alla possibilità di riconoscere delle caratteristiche fenotipiche comuni tra animali diversi, dovute alla loro parentela. PARENTELA Due individui si dicono parenti
Tavoli e scrivanie di design per case ed uffici da sogno!
 Tavoli e scrivanie di design per case ed uffici da sogno! CuDriEc 24 novembre, 2015 Tavoli e scrivanie di design trasformano un ambiente. Un tavolo moderno, una scrivania di design, da soli arredano una
Tavoli e scrivanie di design per case ed uffici da sogno! CuDriEc 24 novembre, 2015 Tavoli e scrivanie di design trasformano un ambiente. Un tavolo moderno, una scrivania di design, da soli arredano una
Capitolo 3. L applicazione Java Diagrammi ER. 3.1 La finestra iniziale, il menu e la barra pulsanti
 Capitolo 3 L applicazione Java Diagrammi ER Dopo le fasi di analisi, progettazione ed implementazione il software è stato compilato ed ora è pronto all uso; in questo capitolo mostreremo passo passo tutta
Capitolo 3 L applicazione Java Diagrammi ER Dopo le fasi di analisi, progettazione ed implementazione il software è stato compilato ed ora è pronto all uso; in questo capitolo mostreremo passo passo tutta
PROVA DI MATEMATICA - Scuola Primaria - Classe Seconda - Fascicolo 1
 PROVA DI MATEMATICA - Scuola Primaria - Classe Seconda - Fascicolo 1 Rilevazione degli apprendimenti Anno Scolastico 2013 2014 PROVA DI MATEMATICA Scuola Primaria Classe Seconda Fascicolo 1 Spazio per
PROVA DI MATEMATICA - Scuola Primaria - Classe Seconda - Fascicolo 1 Rilevazione degli apprendimenti Anno Scolastico 2013 2014 PROVA DI MATEMATICA Scuola Primaria Classe Seconda Fascicolo 1 Spazio per
Algoritmi e diagrammi di flusso
 Algoritmi e diagrammi di flusso Un algoritmo può essere descritto come una sequenza finita ed ordinata di operazioni che descrivono la soluzione di un problema. Per sequenza finita si intende che un algoritmo
Algoritmi e diagrammi di flusso Un algoritmo può essere descritto come una sequenza finita ed ordinata di operazioni che descrivono la soluzione di un problema. Per sequenza finita si intende che un algoritmo
Appunti sulla Macchina di Turing. Macchina di Turing
 Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
Come visto precedentemente l equazione integro differenziale rappresentativa dell equilibrio elettrico di un circuito RLC è la seguente: 1 = (1)
 Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
LA MOLTIPLICAZIONE IN CLASSE SECONDA
 LA MOLTIPLICAZIONE IN CLASSE SECONDA Rossana Nencini, 2013 Le fasi del lavoro: 1. Proponiamo ai bambini una situazione reale di moltiplicazione: portiamo a scuola una scatola di biscotti (. ) e diamo la
LA MOLTIPLICAZIONE IN CLASSE SECONDA Rossana Nencini, 2013 Le fasi del lavoro: 1. Proponiamo ai bambini una situazione reale di moltiplicazione: portiamo a scuola una scatola di biscotti (. ) e diamo la
IDEE SOSTENIBILI IN MOVIMENTO: CON IL LUDOBUS LA SCIENZA SI TRASFORMA IN ESPERIENZA
 IDEE SOSTENIBILI IN MOVIMENTO: CON IL LUDOBUS LA SCIENZA SI TRASFORMA IN ESPERIENZA Il progetto In compagnia di tre amici, Elettra, Semino e Azzurro, andiamo a presentarvi le iniziative del progetto Idee
IDEE SOSTENIBILI IN MOVIMENTO: CON IL LUDOBUS LA SCIENZA SI TRASFORMA IN ESPERIENZA Il progetto In compagnia di tre amici, Elettra, Semino e Azzurro, andiamo a presentarvi le iniziative del progetto Idee
Calcolo del Valore Attuale Netto (VAN)
 Calcolo del Valore Attuale Netto (VAN) Il calcolo del valore attuale netto (VAN) serve per determinare la redditività di un investimento. Si tratta di utilizzare un procedimento che può consentirci di
Calcolo del Valore Attuale Netto (VAN) Il calcolo del valore attuale netto (VAN) serve per determinare la redditività di un investimento. Si tratta di utilizzare un procedimento che può consentirci di
Scopri il piano di Dio: Pace e vita
 Scopri il piano di : Pace e vita E intenzione di avere per noi una vita felice qui e adesso. Perché la maggior parte delle persone non conosce questa vita vera? ama la gente e ama te! Vuole che tu sperimenti
Scopri il piano di : Pace e vita E intenzione di avere per noi una vita felice qui e adesso. Perché la maggior parte delle persone non conosce questa vita vera? ama la gente e ama te! Vuole che tu sperimenti
La propagazione delle onde luminose può essere studiata per mezzo delle equazioni di Maxwell. Tuttavia, nella maggior parte dei casi è possibile
 Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
GUIDA RAPIDA PER LA COMPILAZIONE DELLA SCHEDA CCNL GUIDA RAPIDA PER LA COMPILAZIONE DELLA SCHEDA CCNL
 GUIDA RAPIDA BOZZA 23/07/2008 INDICE 1. PERCHÉ UNA NUOVA VERSIONE DEI MODULI DI RACCOLTA DATI... 3 2. INDICAZIONI GENERALI... 4 2.1. Non modificare la struttura dei fogli di lavoro... 4 2.2. Cosa significano
GUIDA RAPIDA BOZZA 23/07/2008 INDICE 1. PERCHÉ UNA NUOVA VERSIONE DEI MODULI DI RACCOLTA DATI... 3 2. INDICAZIONI GENERALI... 4 2.1. Non modificare la struttura dei fogli di lavoro... 4 2.2. Cosa significano
COSTRUIRE UN TEAM VINCENTE DENTRO E FUORI DAL CAMPO
 COSTRUIRE UN TEAM VINCENTE DENTRO E FUORI DAL CAMPO I punti chiave per la formazione e gestione del team di lavoro PARTE 1. Le differenze tra gruppo e squadra Come prima indicazione, consiglio di andare
COSTRUIRE UN TEAM VINCENTE DENTRO E FUORI DAL CAMPO I punti chiave per la formazione e gestione del team di lavoro PARTE 1. Le differenze tra gruppo e squadra Come prima indicazione, consiglio di andare
REGOLAMENTO FAENTINO L INIZIO. Il tavolo sarà composto da 4 giocatori dove ognuno gioca per sé stesso.
 REGOLAMENTO FAENTINO LE PEDINE Sono 144 così divise: Fiori x 4 (Est, Sud, Ovest, Nord) Stagioni x 4 (Est, Sud, Ovest, Nord) Dall 1 al 9 x 4 Scritti (detti anche caratteri) Dall 1 al 9 x 4 Canne (detti
REGOLAMENTO FAENTINO LE PEDINE Sono 144 così divise: Fiori x 4 (Est, Sud, Ovest, Nord) Stagioni x 4 (Est, Sud, Ovest, Nord) Dall 1 al 9 x 4 Scritti (detti anche caratteri) Dall 1 al 9 x 4 Canne (detti
Qui cade sua altezza
 Qui cade sua altezza Silvia Sbaragli N.R.D. Bologna DFA, SUPSI Locarno (Svizzera) Pubblicato in: Sbaragli S. (2010). Qui cade sua altezza. La Vita Scolastica. 18, 25-27. Nell insegnamento della matematica
Qui cade sua altezza Silvia Sbaragli N.R.D. Bologna DFA, SUPSI Locarno (Svizzera) Pubblicato in: Sbaragli S. (2010). Qui cade sua altezza. La Vita Scolastica. 18, 25-27. Nell insegnamento della matematica
SISTEMA di GESTIONE QUALITÀ Non Conformità ed Efficacia delle Azioni Correttive Preventive
 SISTEMA di GESTIONE QUALITÀ Non Conformità ed Efficacia delle Azioni Correttive Preventive Il sistema di gestione della qualità a cui mi riferisco è quello relativo alla norma ISO-9001:2000. Prima di entrare
SISTEMA di GESTIONE QUALITÀ Non Conformità ed Efficacia delle Azioni Correttive Preventive Il sistema di gestione della qualità a cui mi riferisco è quello relativo alla norma ISO-9001:2000. Prima di entrare
4 LA PALETTA È possibile «svuotare» la paletta spostando solo due segmenti. Sai dire come?
 GIOCHI MATEMATICI 1 CUORI, QUADRI, PICCHE E FIORI Riempi le caselle della griglia con i simboli,, e in modo che ogni simbolo compaia una sola volta in ogni riga e in ogni colonna. GIOCHI MATEMATICI 2 LA
GIOCHI MATEMATICI 1 CUORI, QUADRI, PICCHE E FIORI Riempi le caselle della griglia con i simboli,, e in modo che ogni simbolo compaia una sola volta in ogni riga e in ogni colonna. GIOCHI MATEMATICI 2 LA
ESSERE OPERATI DI CATARATTA
 DIPARTIMENTO CHIRURGICO SPECIALISTICO Unità Operativa di Oculistica Direttore: Prof. Paolo Perri ESSERE OPERATI DI CATARATTA OPUSCOLO INFORMATIVO PER I PAZIENTI Gentile Signora/e, questo opuscolo ha lo
DIPARTIMENTO CHIRURGICO SPECIALISTICO Unità Operativa di Oculistica Direttore: Prof. Paolo Perri ESSERE OPERATI DI CATARATTA OPUSCOLO INFORMATIVO PER I PAZIENTI Gentile Signora/e, questo opuscolo ha lo
IL TEMPO Pagine per l insegnante
 IL TEMPO Pagine per l insegnante Il tempo è una successione di avvenimenti, viene percepito grazie a mutamenti e ha una durata valutabile. A volte avvenimenti diversi accadono contemporaneamente; a volte
IL TEMPO Pagine per l insegnante Il tempo è una successione di avvenimenti, viene percepito grazie a mutamenti e ha una durata valutabile. A volte avvenimenti diversi accadono contemporaneamente; a volte
Ai Dirigenti degli STAPA CePICA LORO SEDI. Autoriproduzioni vivaistiche
 Ai Dirigenti degli STAPA CePICA LORO SEDI Autoriproduzioni vivaistiche Come è noto in base alla vigente normativa fitosanitaria il materiale di moltiplicazione può essere prodotto soltanto da Ditte vivaistiche,
Ai Dirigenti degli STAPA CePICA LORO SEDI Autoriproduzioni vivaistiche Come è noto in base alla vigente normativa fitosanitaria il materiale di moltiplicazione può essere prodotto soltanto da Ditte vivaistiche,
Esercitazione numeri
 Sapendo che 0 C corrispondono a 32 F e che -40 C corrispondono a -40 F, determina: 1) una formula che trasforma gradi Fahrenheit in gradi Celsius; 2) una formula che trasforma gradi Celsius in gradi Fahrenheit.
Sapendo che 0 C corrispondono a 32 F e che -40 C corrispondono a -40 F, determina: 1) una formula che trasforma gradi Fahrenheit in gradi Celsius; 2) una formula che trasforma gradi Celsius in gradi Fahrenheit.
Scuola Media Piancavallo 2
 LA CELLULA Una caratteristica di quasi tutti gli esseri viventi è quella di possedere una struttura più o meno complessa in cui parti diverse, gli organi, sono adatte a svolgere funzioni specifiche. Il
LA CELLULA Una caratteristica di quasi tutti gli esseri viventi è quella di possedere una struttura più o meno complessa in cui parti diverse, gli organi, sono adatte a svolgere funzioni specifiche. Il
Le obbligazioni: misure di rendimento Tassi d interesse, elementi di valutazione e rischio delle attività finanziarie
 Le obbligazioni: misure di rendimento Tassi d interesse, elementi di valutazione e rischio delle attività finanziarie Economia degli Intermediari Finanziari 29 aprile 2009 A.A. 2008-2009 Agenda 1. Il calcolo
Le obbligazioni: misure di rendimento Tassi d interesse, elementi di valutazione e rischio delle attività finanziarie Economia degli Intermediari Finanziari 29 aprile 2009 A.A. 2008-2009 Agenda 1. Il calcolo
La trasmissione dei caratteri ereditari. Le leggi di Mendel (1882-1884)
 La trasmissione dei caratteri ereditari Le leggi di Mendel (1882-1884) Le leggi di Mendel studiano la trasmissione di caratteri qualitativi prodotti da un singolo gene Procedimento sperimentale di Mendel
La trasmissione dei caratteri ereditari Le leggi di Mendel (1882-1884) Le leggi di Mendel studiano la trasmissione di caratteri qualitativi prodotti da un singolo gene Procedimento sperimentale di Mendel
LEZIONE: Pensiero Computazionale. Tempo della lezione: 45-60 Minuti. - Tempo di preparazione: 15 Minuti.
 3 LEZIONE: Pensiero Computazionale Tempo della lezione: 45-60 Minuti. - Tempo di preparazione: 15 Minuti. Obiettivo Principale: Introdurre il modello del Pensiero Computazionale come metodo per la risoluzione
3 LEZIONE: Pensiero Computazionale Tempo della lezione: 45-60 Minuti. - Tempo di preparazione: 15 Minuti. Obiettivo Principale: Introdurre il modello del Pensiero Computazionale come metodo per la risoluzione
Dio, il mondo e il Big- -Bang
 Dio, il mondo e il Big- -Bang come parlare di Dio creatore ome ha fatto Dio a fare il Mondo? Dio, i miracoli e le leggi della natura DIO e il Mondo Dio, Adamo ed Eva, e l evoluzione Dio o il Big Bang?
Dio, il mondo e il Big- -Bang come parlare di Dio creatore ome ha fatto Dio a fare il Mondo? Dio, i miracoli e le leggi della natura DIO e il Mondo Dio, Adamo ed Eva, e l evoluzione Dio o il Big Bang?
MOCA. Modulo Candidatura. http://www.federscacchi.it/moca. moca@federscacchi.it. [Manuale versione 1.0 marzo 2013]
![MOCA. Modulo Candidatura. http://www.federscacchi.it/moca. moca@federscacchi.it. [Manuale versione 1.0 marzo 2013] MOCA. Modulo Candidatura. http://www.federscacchi.it/moca. moca@federscacchi.it. [Manuale versione 1.0 marzo 2013]](/thumbs/25/5308947.jpg) MOCA Modulo Candidatura http://www.federscacchi.it/moca moca@federscacchi.it [Manuale versione 1.0 marzo 2013] 1/12 MOCA in breve MOCA è una funzionalità del sito web della FSI che permette di inserire
MOCA Modulo Candidatura http://www.federscacchi.it/moca moca@federscacchi.it [Manuale versione 1.0 marzo 2013] 1/12 MOCA in breve MOCA è una funzionalità del sito web della FSI che permette di inserire
SERVIZIO NAZIONALE DI VALUTAZIONE 2010 11
 SERVIZIO NAZIONALE DI VALUTAZIONE 2010 11 Le rilevazioni degli apprendimenti A.S. 2010 11 Gli esiti del Servizio nazionale di valutazione 2011 e della Prova nazionale 2011 ABSTRACT Le rilevazioni degli
SERVIZIO NAZIONALE DI VALUTAZIONE 2010 11 Le rilevazioni degli apprendimenti A.S. 2010 11 Gli esiti del Servizio nazionale di valutazione 2011 e della Prova nazionale 2011 ABSTRACT Le rilevazioni degli
Gestione ed analisi di base dati nell epidemiologia. delle malattie infettive
 Università degli Studi di Torino - Facoltà di Medicina Veterinaria Laboratorio di epidemiologia delle malattie infettive Scuola Specializzazione in Sanità Animale, Allevamento e Produzioni Zootecniche
Università degli Studi di Torino - Facoltà di Medicina Veterinaria Laboratorio di epidemiologia delle malattie infettive Scuola Specializzazione in Sanità Animale, Allevamento e Produzioni Zootecniche
Ragionamento spaziale visivo e percezione
 2 Ragionamento spaziale visivo e percezione Serie e analogie figurali! In alcune batterie di test psicoattitudinali sono ampiamente rappresentati i quesiti che propongono un elenco di figure: in alcuni
2 Ragionamento spaziale visivo e percezione Serie e analogie figurali! In alcune batterie di test psicoattitudinali sono ampiamente rappresentati i quesiti che propongono un elenco di figure: in alcuni
ASSOCIAZIONE ANFFAS ONLUS UDINE. presenta LA NOSTRA VISION. Questo documento è in versione facile da leggere
 ASSOCIAZIONE ANFFAS ONLUS UDINE presenta LA NOSTRA VISION Questo documento è in versione facile da leggere - Michele Bertotti - Chiara Billo - Elena Casarsa - Anna Latargia - Lucrezia Pittolo - Erika Pontelli
ASSOCIAZIONE ANFFAS ONLUS UDINE presenta LA NOSTRA VISION Questo documento è in versione facile da leggere - Michele Bertotti - Chiara Billo - Elena Casarsa - Anna Latargia - Lucrezia Pittolo - Erika Pontelli
63 7. Quale geometria per la computer grafica? 75 8. L omografia e l affinità nella digitalizzazione e georeferenziazione
 Indice 7 Presentazione 9 Premessa 11 Introduzione 13 1. Rilevamento ed oggetto 19 2. La stazione totale 23 3. La procedura generale 33 4. Dai punti al modello tridimensionale 45 5. Il modello tridimensionale
Indice 7 Presentazione 9 Premessa 11 Introduzione 13 1. Rilevamento ed oggetto 19 2. La stazione totale 23 3. La procedura generale 33 4. Dai punti al modello tridimensionale 45 5. Il modello tridimensionale
Cenni di geografia astronomica. Giorno solare e giorno siderale.
 Cenni di geografia astronomica. Tutte le figure e le immagini (tranne le ultime due) sono state prese dal sito Web: http://www.analemma.com/ Giorno solare e giorno siderale. La durata del giorno solare
Cenni di geografia astronomica. Tutte le figure e le immagini (tranne le ultime due) sono state prese dal sito Web: http://www.analemma.com/ Giorno solare e giorno siderale. La durata del giorno solare
Antonella Martinucci, Rossana Nencini, 2013 IL PESO. classe quarta
 Antonella Martinucci, Rossana Nencini, 2013 IL PESO classe quarta I bambini utilizzano spontaneamente il concetto di pesante? Collochiamo su un banco alcuni oggetti: penne matite gomme fogli scottex quaderni
Antonella Martinucci, Rossana Nencini, 2013 IL PESO classe quarta I bambini utilizzano spontaneamente il concetto di pesante? Collochiamo su un banco alcuni oggetti: penne matite gomme fogli scottex quaderni
In mostra la Biodiversità
 In mostra la Biodiversità Attività pratiche, curiose, ludiche per la Scuola e il grande pubblico Perchè conoscere provando è divertente Micromondo Insetti Millimondo Piante Micromondo Parlare di biodiversità
In mostra la Biodiversità Attività pratiche, curiose, ludiche per la Scuola e il grande pubblico Perchè conoscere provando è divertente Micromondo Insetti Millimondo Piante Micromondo Parlare di biodiversità
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
I.C. "L.DA VINCI" LIMBIATE CURRICOLO IN VERTICALE ANNO SCOLASTICO 2014/2015 GEOGRAFIA
 GEOGRAFIA Osservare gli spazi circostanti Saper distinguere sopra-sotto, davantidietro etc. svolgendo semplici percorsi sul foglio e attraverso giochi di psicomotricità (AL TERMINE DELLA SCUOLA DELL'INFANZIA)
GEOGRAFIA Osservare gli spazi circostanti Saper distinguere sopra-sotto, davantidietro etc. svolgendo semplici percorsi sul foglio e attraverso giochi di psicomotricità (AL TERMINE DELLA SCUOLA DELL'INFANZIA)
u 1 u k che rappresenta formalmente la somma degli infiniti numeri (14.1), ordinati al crescere del loro indice. I numeri u k
 Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
