Determinante, autovalori e autovettori
|
|
|
- Albana Castelli
- 4 anni fa
- Visualizzazioni
Transcript
1 Determinante, autovalori e autovettori Lorenzo Pareschi Dipartimento di Matematica, Universitá di Ferrara lorenzopareschi@unifeit Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 1 / 39
2 Determinante Definizione (Matrici di permutazione) Definiamo le matrici P rs, dette matrici di permutazione elementari, ottenute dalla matrice identità scambiando le righe r e s Esempio (Matrici di permutazione) Un esempio di matrice di permutazione a partire da I = è la seguente (r =2, s =3) P 23 = Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 2 / 39
3 Quindi P rs A è una matrice uguale ad A ma con le righe r ed s scambiate fra loro Analogamente AP rs è una matrice uguale ad A ma con le colonne r ed s scambiate fra loro Definizione (Determinante) Dato l insieme delle matrici quadrate di ordine n, a ogni matrice A di questo insieme associamo un numero che indicheremo con det(a), detto determinante di A, tale che 1 Se A è una matrice triangolare (superiore o inferiore), allora det(a) è uguale al prodotto degli elementi sulla diagonale 2 Se A e B sono due matrici quadrate di ordine n, det(ab) = det(a) det(b) 3 det(p rs )= 1 per ogni valore di r, s con r s Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 3 / 39
4 Proprietà del determinante 1 Se la matrice A ha due righe o due colonne uguali il determinante è nullo Dimostrazione Sia infatti P rs con r e s indici delle righe o colonne uguali Allora se le righe sono uguali P rsa = A, se invece le colonne sono uguali AP rs = A Nel primo caso avremo ossia det(a) =det(p rsa) =det(p rs)det(a) = det(a) Analogamente nell altro caso si ha det(a) = det(a) quindi det(a) =0 det(a) =det(ap rs) =det(a)det(p rs) = det(a) quindi det(a) =0 2 Dato α in R, det(αa) =α n det(a) Dimostrazione Infatti det(αa) =det(αia) =det(αi)det(a) =α n det(a) perché αi = diag(α,, α) e il determinante è dato dal prodotto degli elementi sulla diagonale, ossia α n Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 4 / 39
5 3 Se A è la matrice ottenuta moltiplicando tutti gli elementi di una riga (o di una colonna) di A per α allora det(a) =α det(a) Dimostrazione Per esempio sia A ottenuta moltiplicando la prima riga per α, allora A = αa 11 αa 12 αa 1n a 21 a 22 a 2n a n1 a n2 a nn = α A quindi det(a) =α det(a) 4 Se una riga o una colonna di A sono nulli, il determinante sarà nullo Dimostrazione Discende direttamente dalla proprietà precedente nel caso α =0 Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 5 / 39
6 5 Se una riga o una colonna di A è combinazione lineare delle altre allora il determinante è nullo Dimostrazione Per esempio indichiamo con A T j la riga j-esima che è combinazione lineare delle altre (per semplicità solo di quelle che la precedono) A T j = α 1A T 1 + α 2A T α j 1A T j 1 Moltiplicando ora la matrice A a sinistra per la matrice triangolare inferiore P = α 1 α 2 α j (colonna j) si ottiene la matrice PA in cui la riga j-esima è nulla Quindi 0=det(PA)=det(P )det(a) Ma det(p )=1e quindi necessariamente det(a) =0 (riga j) Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 6 / 39
7 6 Sia A non singolare Allora Dimostrazione segue Infatti da det(a 1 )= 1 det(a) AA 1 = A 1 A = I det(aa 1 )=det(a)det(a 1 )=det(i) =1 Esempio (Casi particolari matrici 2 2) Nel caso di una matrice 2 2 si può verificare direttamente che se ( ) a b A = c d allora det(a) =ad bc, verifica le tre proprietà che caratterizzano il determinante Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 7 / 39
8 Esempio (Casi particolari matrici 3 3) Nel caso di una matrice 3 3 si può verificare che se allora A = ( ) a1 a 2 a 3 b 1 b 2 b 3 c 1 c 2 c 3 det(a) =a 1 b 2 c 3 + a 2 b 3 c 1 + a 3 b 1 c 2 a 1 b 3 c 2 a 2 b 1 c 3 a 3 b 2 c 1 Un metodo pratico per ricordarsi la precedente formula è dato dalla regola delle diagonali illustrata di seguito a 1 a 2 a 3 a 1 a 2 b 1 b 2 b 3 b 1 b 2 regola delle diagonali c 1 c 2 c 3 c 1 c 2 dove i prodotti diagonali da sinistra a destra vanno considerati con il segno +, quelli da destra a sinistra con il segno Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 8 / 39
9 Esempio (Calcolo con la regola delle diagonali) Sovente si utilizza la notazione per indicare il determinante di una matrice Avremo quindi per matrici =1 4 2 ( 3) = 10 e nel caso di matrici = = Vedremo come l eliminazione di Gauss ci consentirá di calcolare il determinante per matrici di dimensioni maggiori Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 9 / 39
10 Autovalori e autovettori Uno dei problemi più importanti dell algebra lineare é rappresentato dal calcolo degli autovalori e autovettori di una matrice quadrata Nelle applicazioni tali quantità intervengono come assi preferenziali di rotazione, direzioni di maggior sforzo, frequenze di risonanza, ecc Definizione (Autovalore e autovettore) Sia A una matrice quadrata n n ad elementi reali Definiamo autovalore e rispettivamente autovettore della matrice A un numero λ ed un vettore u non nullo per cui Au = λu o equivalentemente (A λi)u =0 Dalla definizione precedente segue che u è una soluzione non nulla di un sistema lineare omogeneo di matrice A λi Au = λu Au λu =0 (A λi)u =0 Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 19 / 39
11 Osservazione Se u è un autovettore di A, tale è anche αu, con α numero reale o complesso non nullo A(αu) =α(au) =α(λu) =λ(αu) Ossia gli autovettori sono infiniti In particolare potremo sempre scegliere l autovettore unitario Infatti se u è un autovettore e u T u = c 2 0 allora v = u/c è un autovettore unitario v T v = 1 c 2 ut u = 1 c 2 c2 =1 Una proprietà (che non dimostreremo) utile al fine di controllare i risultati nel calcolo di autovalori (e autovettori) Proposizione La somma degli autovalori di una matrice A uguaglia la somma degli elementi sulla diagonale della matrice A Tale somma è detta traccia della matrice A Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 20 / 39
12 Determinante e sistemi lineari omogenei Sia ora A quadrata di tipo n n Il sistema lineare omogeneo Ax =0 ammette sempre la soluzione identicamente nulla x =0 In particolare se la soluzione é unica, allora tale soluzione coincide con x =0 Vale il seguente risultato Teorema Il sistema lineare omogeneo Ax =0, con A matrice quadrata ammette soluzione non nulla det(a) =0 Dimostrazione Dimostriamo solo l implicazione Se il sistema ammette una soluzione x =(x 1,,x n) 0allora indicate con A 1,,A n le colonne di A abbiamo Ax = x 1A x na n =0, con x i,i=1,,n non tutti nulli Dunque se x j 0possiamo scrivere A j = x1 A 1 xj 1 A j 1 xj+1 A j+1 xn A n x j x j x j x j Dalla proprietá 5 del determinante applicata alle colonne si ha det(a) =0 Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 21 / 39
13 Calcolo di autovalori e autovettori Sia ora A quadrata di tipo n n Vogliamo risolvere il problema del calcolo pratico di autovalori e autovettori affrontando il sistema lineare (A λi)u =0, con u non nullo Sappiamo che il calcolo di una soluzione non nulla u è possibile se e soltanto se det(a λi) =0 L equazione det(a λi) = A λi =0 è detta equazione caratteristica di A Più precisamente si calcola il determinante della matrice caratteristica a 11 λ a 12 a 13 a 1n a 21 a 22 λ a 23 a 2n A λi = a n1 a n2 a n3 a nn λ ottenuta da A sottraendo λ da ogni elemento della diagonale di A Si può dimostrare che det(a λi) è un polinomio di grado n in λ p A (λ) =det(a λi) =( 1) n λ n + c n 1 λ n c 1 λ + c 0 detto polinomio caratteristico Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 22 / 39
14 In pratica, quindi, per calcolare autovalori e autovettori dobbiamo: 1 determinare le radici del polinomio caratteristico p A (λ) =det(a λi) =0; 2 per ogni autovalore determinato al punto 1), risolvere il sistema lineare (A λi)u =0 per calcolare gli autovettori associati a λ La risoluzione del punto 1) rende il problema del calcolo degli autovalori molto difficile Evariste Galois ( ) ha infatti dimostrato che non esiste nessuna formula algebrica per calcolare le radici di un polinomio di grado n 5 Un caso particolarmente facile è il caso di matrici triangolari Abbiamo infatti Proposizione Se A è una matrice triangolare allora gli autovalori coincidono con gli elementi della diagonale Dimostrazione La dimostrazione del risultato è immediata, basta osservare che se la matrice triangolare ha dimensione n vale det(a λi) =(a 11 λ)(a 22 λ) (a nn λ) Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 23 / 39
15 In pratica, nel caso generale, solo per n =2la cosa è immediata, con la nota formula risolutiva di un equazione di secondo grado che implica λ 2 + bλ + c =0 λ = b ± b 2 4c 2 Per n =3la formula non è così diretta Se però si è in grado di indovinare una radice del polinomio, sia λ, allora si può scrivere con Ossia λ 3 + c 2 λ 2 + c 1 λ + c 0 =(λ λ )( λ 2 + b 1 λ + b 0 ) λ + b 1 = c 2, λ b 1 + b 0 = c 1, λ b 0 = c 0 b 1 = c 2 λ, b 0 = c 1 + λ (c 2 λ ) Il calcolo delle restanti due radici può quindi essere effettuato sul polinomio di grado due λ 2 + b 1 λ + b 0 =0 Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 24 / 39
16 Esempio (Autovalori e autovettori di matrici 2 2) Calcoliamo gli autovalori e autovettori di ( ) ( ) λ 7 A = A λi = λ A λi = (5 λ)(4 + λ)+14=λ 2 λ 6=(λ +2)(λ 3) = 0 implica che gli autovalori sono λ 1 = 2, λ 2 =3 a) λ 1 = 2 ( ) ( 7 7 x 0 (A λ 1 I)u = = 2 2)( y 0) (R 1 /7) 0 0 (R 2 2R 1 ) ossia y = s, x = s con s in R Gli autovettori hanno la forma u =( s, s) T Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 25 / 39
17 Esempio (continuazione) b) λ 2 =3 (A λ 2 I)u = ( ) ( 2 7 x 0 = 2 7)( y 0) /2 (R 1 /2) 0 0 (R 2 +2R 1 ) ossia y = s, x = 7s/2 con s in R Gli autovettori hanno la forma u =( 7s/2,s) Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 26 / 39
18 Esempio (Altre situazioni per matrici 2 2) Vediamo altre situazioni che si possono presentare nel caso di matrici 2 2 ( ) 2 3 A = A λi = λ λ =(2 λ)2 =0 λ =2, radice doppia ( ) ( 0 3 x 0 = 0 0)( y 0) (R 1 /3) 0 0 otteniamo y =0, x = s e quindi u =(s, 0) T Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 27 / 39
19 Esempio (continuazione) Consideriamo ora A = ( ) A λi = 1 λ λ =(1 λ)2 =0 λ =1, radice doppia ( ) ( 0 0 x 0 = 0 0)( y 0) otteniamo x = s, y = t Ogni vettore u =(s, t) T è un autovettore (ossia ogni vettore in R 2 ) Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 28 / 39
20 Esempio (Autovalori e autovettori di matrici 3 3) Vediamo ora il caso di matrici 3 3 ( 3 0 ) 0 A = A λi = 3 λ λ λ =(3 λ)(6 λ)( 5 λ)+2 15(3 λ) = =(3 λ)[(6 λ)( 5 λ)+30]=(3 λ)(λ 2 λ) =λ(3 λ)(λ 1) Gli autovalori sono quindi λ = 0, 3, 1 (la presenza dell autovalore nullo indica che det(a) =0) a) λ 1 =0 ( )( ) x y z = ( ) Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 29 / 39
21 Esempio (continuazione) quindi z = s, y = 1 3 s, x =0e u 1 = (R 1 /3) (R 2 +4R 1 ) (R 3 16R 1 ) /3 (R 2 /6) (R 3 +15R 2 ) ( 0, 1 3 s, s ) T autovettore Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 30 / 39
22 Esempio (continuazione) b) λ 2 =1 ( )( ) x y z quindi z = s, y = 2 5 s, x =0e u 2 = = ( ) (R 1 /2) (R 2 +4R 1 ) (R 3 16R 1 ) /5 (R 2 /5) (R 3 +15R 2 ) ( 0, 2 5 s, s ) T autovettore Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 31 / 39
23 Esempio (continuazione) c) λ 3 =3 ( )( ) x y z = ( ) (R 1 R 2 ) /4 1/2 (R 1 /( 4)) (R 2 16R 1 ) Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 32 / 39
24 Esempio (continuazione) 1 3/4 1/ (R 2 / 3) quindi z = s, y =0, x = 1 2 s e u 3 = ( ) T 1 s, 0,s autovettore 2 Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 33 / 39
25 Esempio (Altri casi matrici 3 3) ( ) A = A λi = λ λ λ =(4 λ)( λ)(3 λ) 4 4+2λ+2(4 λ)+4(3 λ) = λ λ 2 16λ =0 Proviamo a indovinare una radice del polinomio: λ =0no λ =1, 1 no λ =2si (λ 2)( λ 2 +5λ 6) = 0 λ 2,λ 3 = 5 ± = 5 ± 1 2 = { 3 Gli autovalori sono λ 1 =2,λ 2 =2,λ 3 =3, ossia l autovalore 2 ha molteplicità algebrica due 2 Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 34 / 39
26 Esempio (continuazione) a) λ =2 ( )( ) x y z = ( ) /2 (R 1 /2) (R 2 2R 1 ) (R 3 2R 1 ) quindi z = s, y = t, x = t 1 2 s ( Ogni vettore u = t 1 ) T 2 s, t, s è autovettore Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 35 / 39
27 Esempio (continuazione) b) λ =3 ( )( ) x y z = ( ) (R 2 2R 1 ) (R 3 2R 1 ) (R 3 2R 2 ) quindi z = s, y = s, x = s e u 3 =(s, s, s) T unico autovettore Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 36 / 39
28 Esercizi Esercizio Si calcolino i determinanti delle seguenti matrici (a) , (b) , (c) , (d) , (e) , (f) (g) , (h) Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 37 / 39
29 Esercizio Per ciascuna delle seguenti matrici (i) A = (ii) A = (iii) A = (iv) A = (vii) A = (v) A = calcolare i rispettivi autovalori e autovettori; (viii) A = (vi) A = Lorenzo Pareschi (Univ Ferrara) Determinante, autovalori e autovettori 39 / 39
Applicazioni eliminazione di Gauss
 Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof. F.Podestà, a.a
 APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
APPUNTI SULLA DIAGONALIZZAZIONE Corso Prof FPodestà, aa 003-004 Sia V uno spazio vettoriale e sia f : V V una applicazione lineare una tale applicazione da uno spazio vettoriale in se stesso è chiamata
3. Elementi di Algebra Lineare.
 CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari 3. Elementi di Algebra Lineare. 1 Sistemi lineari Sia A IR m n, x IR n di n Ax = b è un vettore di m componenti.
Sistemi lineari. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
Sistemi lineari Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utenti.unife.it/lorenzo.pareschi/ lorenzo.pareschi@unife.it Lorenzo Pareschi (Univ. Ferrara)
VETTORI E MATRICI. Ing. Nicola Cappuccio 2014 U.F.5 ELEMENTI SCIENTIFICI ED ELETTRONICI APPLICATI AI SISTEMI DI TELECOMUNICAZIONI
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
Elementi di Algebra Lineare
 Elementi di Algebra Lineare Corso di Calcolo Numerico, a.a. 2009/2010 Francesca Mazzia Dipartimento di Matematica Università di Bari 13 Marzo 2006 Francesca Mazzia (Univ. Bari) Elementi di Algebra Lineare
Elementi di Algebra Lineare Corso di Calcolo Numerico, a.a. 2009/2010 Francesca Mazzia Dipartimento di Matematica Università di Bari 13 Marzo 2006 Francesca Mazzia (Univ. Bari) Elementi di Algebra Lineare
MATRICI E SISTEMI LINEARI
 MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
MATRICI E SISTEMI LINEARI - PARTE I - Felice Iavernaro Dipartimento di Matematica Università di Bari 27 Febbraio 2006 Felice Iavernaro (Univ. Bari) Matrici e Sistemi lineari 27/02/2006 1 / 1 Definizione
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
LEZIONE i 0 3 Le sottomatrici 2 2 di A sono. 1 2 i i 3. Invece (
 LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
0.1 Condizione sufficiente di diagonalizzabilità
 0.1. CONDIZIONE SUFFICIENTE DI DIAGONALIZZABILITÀ 1 0.1 Condizione sufficiente di diagonalizzabilità È naturale porsi il problema di sapere se ogni matrice sia o meno diagonalizzabile. Abbiamo due potenziali
0.1. CONDIZIONE SUFFICIENTE DI DIAGONALIZZABILITÀ 1 0.1 Condizione sufficiente di diagonalizzabilità È naturale porsi il problema di sapere se ogni matrice sia o meno diagonalizzabile. Abbiamo due potenziali
Algebra lineare. Laboratorio di programmazione e calcolo CdL in Chimica. Pierluigi Amodio
 Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
1 Addendum su Diagonalizzazione
 Addendum su Diagonalizzazione Vedere le dispense per le definizioni di autovettorre, autovalore e di trasformazione lineare (o matrice) diagonalizzabile. In particolare, si ricorda che una condizione necessaria
Addendum su Diagonalizzazione Vedere le dispense per le definizioni di autovettorre, autovalore e di trasformazione lineare (o matrice) diagonalizzabile. In particolare, si ricorda che una condizione necessaria
LEZIONE i i 3
 LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Richiami di algebra delle matrici a valori reali
 Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Equivalentemente, le colonne di A sono linearmente indipendenti se e solo se
 Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Geometria Prova scritta, appello unico, sessione autunnale Corso di laurea in fisica A.A 2017/2018 Canali A C, e L Pa
 Geometria Prova scritta, appello unico, sessione autunnale Corso di laurea in fisica A.A 27/28 Canali A C, e L Pa Durata: 2 ore e 3 minuti Simone Diverio Alessandro D Andrea Paolo Piccinni 7 settembre
Geometria Prova scritta, appello unico, sessione autunnale Corso di laurea in fisica A.A 27/28 Canali A C, e L Pa Durata: 2 ore e 3 minuti Simone Diverio Alessandro D Andrea Paolo Piccinni 7 settembre
LEZIONE 4. Le sottomatrici 2 2 di A sono. Invece ( 1 3 non è sottomatrice di A.
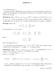 LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
x n i sima pos. x, y = x T y = x i y i R. i=1
 1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
Vettori e matrici. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Vettori e matrici Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utentiunifeit/lorenzopareschi/ lorenzopareschi@unifeit Lorenzo Pareschi Univ Ferrara
Vettori e matrici Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utentiunifeit/lorenzopareschi/ lorenzopareschi@unifeit Lorenzo Pareschi Univ Ferrara
MATRICI ORTOGONALI. MATRICI SIMMETRICHE E FORME QUADRATICHE
 DIAGONALIZZAZIONE 1 MATRICI ORTOGONALI. MATRICI SIMMETRICHE E FORME QUADRATICHE Matrici ortogonali e loro proprietà. Autovalori ed autospazi di matrici simmetriche reali. Diagonalizzazione mediante matrici
DIAGONALIZZAZIONE 1 MATRICI ORTOGONALI. MATRICI SIMMETRICHE E FORME QUADRATICHE Matrici ortogonali e loro proprietà. Autovalori ed autospazi di matrici simmetriche reali. Diagonalizzazione mediante matrici
MATRICI. Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: a 2 m. a n m) i j R, 1 i n, 1 j m.
 MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
ALGEBRA C. MALVENUTO
 ALGEBRA CANALE A-L ESAME SECONDA PARTE SECONDO ESONERO 27 GENNAIO 22 C. MALVENUTO Istruzioni. Completare subito la parte inferiore di questa pagina con il proprio nome, cognome e firma. Scrivere solamente
ALGEBRA CANALE A-L ESAME SECONDA PARTE SECONDO ESONERO 27 GENNAIO 22 C. MALVENUTO Istruzioni. Completare subito la parte inferiore di questa pagina con il proprio nome, cognome e firma. Scrivere solamente
AUTOVALORI, AUTOVETTORI, AUTOSPAZI
 AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
AUTOVALORI, AUTOVETTORI, AUTOSPAZI. Esercizi Esercizio. Sia f : R 3 R 3 l endomorfismo definito da f(x, y, z) = (x+y, y +z, x+z). Calcolare gli autovalori ed una base per ogni autospazio di f. Dire se
La forma normale di Schur
 La forma normale di Schur Dario A Bini, Università di Pisa 30 ottobre 2013 Sommario Questo modulo didattico contiene risultati relativi alla forma normale di Schur, alle sue proprietà e alle sue applicazioni
La forma normale di Schur Dario A Bini, Università di Pisa 30 ottobre 2013 Sommario Questo modulo didattico contiene risultati relativi alla forma normale di Schur, alle sue proprietà e alle sue applicazioni
Sistemi lineari. Sia A R m n, x R n Ax = b è un vettore di m componenti. a m,1 x 1 + a m,2 x a m,n x n = b m
 1 Sistemi lineari. Sia A R m n, x R n Ax = b è un vettore di m componenti. Numero di operazioni per calcolare b: m n moltiplicazioni m (n 1) addizioni. a 1,1 x 1 + a 1,2 x 2 +... + a 1,n x n = b 1 a 2,1
1 Sistemi lineari. Sia A R m n, x R n Ax = b è un vettore di m componenti. Numero di operazioni per calcolare b: m n moltiplicazioni m (n 1) addizioni. a 1,1 x 1 + a 1,2 x 2 +... + a 1,n x n = b 1 a 2,1
Corso di Geometria BIAR, BSIR Esercizi 2: soluzioni
 Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
Autovalori e autovettori di una matrice quadrata
 Autovalori e autovettori di una matrice quadrata Data la matrice A M n (K, vogliamo stabilire se esistono valori di λ K tali che il sistema AX = λx ammetta soluzioni non nulle. Questo risulta evidentemente
Autovalori e autovettori di una matrice quadrata Data la matrice A M n (K, vogliamo stabilire se esistono valori di λ K tali che il sistema AX = λx ammetta soluzioni non nulle. Questo risulta evidentemente
LeLing12: Ancora sui determinanti.
 LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
Soluzione della prova scritta di di Algebra lineare del 10 giugno Esercizio 1
 Soluzione della prova scritta di di Algebra lineare del 0 giugno 05 Esercizio (a) La matrice A che rappresenta f rispetto alle basi assegnate è la seguente: A = 0 0 0 (b) Applicando il metodo di Gauss
Soluzione della prova scritta di di Algebra lineare del 0 giugno 05 Esercizio (a) La matrice A che rappresenta f rispetto alle basi assegnate è la seguente: A = 0 0 0 (b) Applicando il metodo di Gauss
Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 27/09/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI
 Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 7/9/6 SOLUZIONE DEGLI ESERCIZI PROPOSTI Esercizio. Si consideri la quadrica affine C d equazione cartesiana xy + yz z + 4x =. ()
Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 7/9/6 SOLUZIONE DEGLI ESERCIZI PROPOSTI Esercizio. Si consideri la quadrica affine C d equazione cartesiana xy + yz z + 4x =. ()
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti)
 Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
Autovalori e autovettori, matrici simmetriche e forme quadratiche (cenni) (prof. M. Salvetti) April 14, 2011 (alcune note non complete sugli argomenti trattati: eventuali completamenti saranno aggiunti)
4 Autovettori e autovalori
 4 Autovettori e autovalori 41 Cambiamenti di base Sia V uno spazio vettoriale tale che dim V n Si è visto in sezione 12 che uno spazio vettoriale ammette basi distinte, ma tutte con la medesima cardinalità
4 Autovettori e autovalori 41 Cambiamenti di base Sia V uno spazio vettoriale tale che dim V n Si è visto in sezione 12 che uno spazio vettoriale ammette basi distinte, ma tutte con la medesima cardinalità
Diagonalizzabilità di endomorfismi
 Capitolo 16 Diagonalizzabilità di endomorfismi 16.1 Introduzione Nei capitoli precedenti abbiamo definito gli endomorfismi su uno spazio vettoriale E. Abbiamo visto che, dato un endomorfismo η di E, se
Capitolo 16 Diagonalizzabilità di endomorfismi 16.1 Introduzione Nei capitoli precedenti abbiamo definito gli endomorfismi su uno spazio vettoriale E. Abbiamo visto che, dato un endomorfismo η di E, se
Autovalori, Autovettori, Diagonalizzazione.
 Autovalori Autovettori Diagonalizzazione Autovalori e Autovettori Definizione Sia V uno spazio vettoriale sul campo K = R o C e sia T : V V un endomorfismo Un vettore non nullo v V \ {O} si dice autovettore
Autovalori Autovettori Diagonalizzazione Autovalori e Autovettori Definizione Sia V uno spazio vettoriale sul campo K = R o C e sia T : V V un endomorfismo Un vettore non nullo v V \ {O} si dice autovettore
Diagonalizzazione di matrici: autovalori, autovettori e costruzione della matrice diagonalizzante 1 / 13
 Diagonalizzazione di matrici: autovalori, autovettori e costruzione della matrice diagonalizzante 1 / 13 Matrici diagonali 2 / 13 Ricordiamo che una matrice quadrata si dice matrice diagonale se a ij =
Diagonalizzazione di matrici: autovalori, autovettori e costruzione della matrice diagonalizzante 1 / 13 Matrici diagonali 2 / 13 Ricordiamo che una matrice quadrata si dice matrice diagonale se a ij =
ALGEBRA LINEARE PARTE II
 DIEM sez. Matematica Finanziaria Marina Resta Università degli studi di Genova Dicembre 005 Indice PREMESSA INVERSA DI UNA MATRICE DETERMINANTE. DETERMINANTE DI MATRICI ELEMENTARI................. MATRICI
DIEM sez. Matematica Finanziaria Marina Resta Università degli studi di Genova Dicembre 005 Indice PREMESSA INVERSA DI UNA MATRICE DETERMINANTE. DETERMINANTE DI MATRICI ELEMENTARI................. MATRICI
A =, c d. d = ad cb. c d A =
 Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
=. Il vettore non è della forma λ, dunque non è un. 2. Il vettore 8 2 non è della forma λ 1
 a.a. 2005-2006 Esercizi. Autovalori e autovettori. Soluzioni. Sia A = e sia x =. Dire se x è autovettore di A. Se si dire per quale 8 autovalore. Sol. Si ha =. Il vettore non è della forma λ dunque 8 29
a.a. 2005-2006 Esercizi. Autovalori e autovettori. Soluzioni. Sia A = e sia x =. Dire se x è autovettore di A. Se si dire per quale 8 autovalore. Sol. Si ha =. Il vettore non è della forma λ dunque 8 29
Elementi di Algebra Matriciale. (richiami)
 Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
Lezione Determinanti
 Lezione 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Lezione 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Geometria BIAR Esercizi 2
 Geometria BIAR 0- Esercizi Esercizio. a Si consideri il generico vettore v b R c (a) Si trovi un vettore riga x (x, y, z) tale che x v a (b) Si trovi un vettore riga x (x, y, z) tale che x v kb (c) Si
Geometria BIAR 0- Esercizi Esercizio. a Si consideri il generico vettore v b R c (a) Si trovi un vettore riga x (x, y, z) tale che x v a (b) Si trovi un vettore riga x (x, y, z) tale che x v kb (c) Si
DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI
 DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI Nota. La descrizione di lezioni non ancora svolte si deve intendere come una previsione/pianificazione.
DIARIO DEL CORSO DI MATHEMATICS FOR DATA SCIENCE TRENTO, A.A. 2018/19 DOCENTI: ANDREA CARANTI, SIMONE UGOLINI Nota. La descrizione di lezioni non ancora svolte si deve intendere come una previsione/pianificazione.
1. [15 punti] Calcolare il rango della seguente matrice a coefficienti reali: ( 1/2) 1 (1/2)
![1. [15 punti] Calcolare il rango della seguente matrice a coefficienti reali: ( 1/2) 1 (1/2) 1. [15 punti] Calcolare il rango della seguente matrice a coefficienti reali: ( 1/2) 1 (1/2)](/thumbs/101/152415317.jpg) Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE del 17 febbraio 011 ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola in alto a destra
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE del 17 febbraio 011 ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola in alto a destra
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia
 CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2015-16 Complementi ed Esercizi 1. AUTOVETTORI e AUTOVALORI di ENDOMORFISMI e MATRICI Una applicazione lineare avente per dominio e condominio lo stesso spazio vettoriale
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2015-16 Complementi ed Esercizi 1. AUTOVETTORI e AUTOVALORI di ENDOMORFISMI e MATRICI Una applicazione lineare avente per dominio e condominio lo stesso spazio vettoriale
Endomorfismi e matrici simmetriche
 CAPITOLO Endomorfismi e matrici simmetriche Esercizio.. [Esercizio 5) cap. 9 del testo Geometria e algebra lineare di Manara, Perotti, Scapellato] Calcolare una base ortonormale di R 3 formata da autovettori
CAPITOLO Endomorfismi e matrici simmetriche Esercizio.. [Esercizio 5) cap. 9 del testo Geometria e algebra lineare di Manara, Perotti, Scapellato] Calcolare una base ortonormale di R 3 formata da autovettori
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Determinante. Sia M(n, n, K) lo spazio delle matrici quadrate n n a coefficienti in un campo K, vogliamo provare il seguente Teorema:
 Determinante 1 Proprieta Sia M(n, n, K) lo spazio delle matrici quadrate n n a coefficienti in un campo K, vogliamo provare il seguente Teorema: Theorem 1.1 Esiste un unica mappa F dallo spazio delle matrici
Determinante 1 Proprieta Sia M(n, n, K) lo spazio delle matrici quadrate n n a coefficienti in un campo K, vogliamo provare il seguente Teorema: Theorem 1.1 Esiste un unica mappa F dallo spazio delle matrici
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
CALCOLO NUMERICO. Francesca Mazzia. Calcolo degli autovalori. Dipartimento Interuniversitario di Matematica. Università di Bari
 CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari Calcolo degli autovalori 1 Calcolo degli autovalori Gli autovalore e gli autovettore di una matrice quadrata
CALCOLO NUMERICO Francesca Mazzia Dipartimento Interuniversitario di Matematica Università di Bari Calcolo degli autovalori 1 Calcolo degli autovalori Gli autovalore e gli autovettore di una matrice quadrata
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI
 CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # GEOMETRIA E ALGEBRA 009/0 Esercizio.. Dati i vettori di R : v (,, ), v (, 4, 6), v (,, 5), v 4 (,, 0) determinare se v 4 è combinazione
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # GEOMETRIA E ALGEBRA 009/0 Esercizio.. Dati i vettori di R : v (,, ), v (, 4, 6), v (,, 5), v 4 (,, 0) determinare se v 4 è combinazione
0.1 Coordinate in uno spazio vettoriale
 0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
0.. COORDINATE IN UNO SPAZIO VETTORIALE 0. Coordinate in uno spazio vettoriale Sia V uno spazio vettoriale di dimensione finita n costruito sul campo K. D ora in poi, ogni volta che sia fissata una base
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
Applicazioni lineari e diagonalizzazione
 Applicazioni lineari e diagonalizzazione Autospazi Autovettori e indipendenza lineare Diagonalizzabilità e autovalori 2 2006 Politecnico di Torino 1 Esempio (1/6) Utilizzando un esempio già studiato, cerchiamo
Applicazioni lineari e diagonalizzazione Autospazi Autovettori e indipendenza lineare Diagonalizzabilità e autovalori 2 2006 Politecnico di Torino 1 Esempio (1/6) Utilizzando un esempio già studiato, cerchiamo
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
Corso di Calcolo Numerico
 Corso di Laurea in Ingegneria Gestionale Sede di Fermo Corso di 7 - CALCOLO NUMERICO CON MATRICI Richiami teorici Operazioni fondamentali Siano A = {a ij } e B = {b ij }, i = 1,..., m, j = 1,..., n due
Corso di Laurea in Ingegneria Gestionale Sede di Fermo Corso di 7 - CALCOLO NUMERICO CON MATRICI Richiami teorici Operazioni fondamentali Siano A = {a ij } e B = {b ij }, i = 1,..., m, j = 1,..., n due
Esame di Geometria e Algebra Lineare Politecnico di Milano Ingegneria informatica Appello 10 Febbraio 2015 Cognome: Nome: Matricola:
 Esame di Geometria e Algebra Lineare Politecnico di Milano Ingegneria informatica Appello Febbraio 25 Cognome: Nome: Matricola: Tutte le risposte devono essere motivate Gli esercizi vanno svolti su questi
Esame di Geometria e Algebra Lineare Politecnico di Milano Ingegneria informatica Appello Febbraio 25 Cognome: Nome: Matricola: Tutte le risposte devono essere motivate Gli esercizi vanno svolti su questi
{Geometria per [Fisica e (Fisica e Astrofisica)]}
![{Geometria per [Fisica e (Fisica e Astrofisica)]} {Geometria per [Fisica e (Fisica e Astrofisica)]}](/thumbs/103/157763717.jpg) {Geometria per [Fisica e (Fisica e Astrofisica)]} Foglio 9 - Soluzioni Esercizio (facoltativo) Un quadrato magico reale di ordine n è una matrice di M n n (R) tale che sommando gli elementi di ogni sua
{Geometria per [Fisica e (Fisica e Astrofisica)]} Foglio 9 - Soluzioni Esercizio (facoltativo) Un quadrato magico reale di ordine n è una matrice di M n n (R) tale che sommando gli elementi di ogni sua
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE110 - Geometria 1 a.a Prova scritta del TESTO E SOLUZIONI
 UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE0 - Geometria a.a. 07-08 Prova scritta del 7-7-08 TESTO E SOLUZIONI Svolgere tutti gli esercizi.. Per R considerare il sistema lineare X
UNIVERSITÀ DEGLI STUDI ROMA TRE Corso di Laurea in Matematica GE0 - Geometria a.a. 07-08 Prova scritta del 7-7-08 TESTO E SOLUZIONI Svolgere tutti gli esercizi.. Per R considerare il sistema lineare X
CORSO DI GEOMETRIA DETERMINANTE A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
CORSO DI LAUREA IN INGEGNERIA.
 CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 9 GEOMETRIA E ALGEBRA LINEARE 2012/13 Esercizio 9.1 (8.40). Sia T : R 2 R 3 l applicazione definita da T(x,y) = (2x,x y,2y), e siano B = {(1,0), (1,1)
CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 9 GEOMETRIA E ALGEBRA LINEARE 2012/13 Esercizio 9.1 (8.40). Sia T : R 2 R 3 l applicazione definita da T(x,y) = (2x,x y,2y), e siano B = {(1,0), (1,1)
Il determinante. Calcolo del determinante di matrici particolari. matrici di ordine 2: sia. a11 a A = allora
 Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Lezioni di Algebra Lineare V. Autovalori e autovettori
 Lezioni di Algebra Lineare V. Autovalori e autovettori Versione novembre 2008 Contenuto 1. Cambiamenti di base 2. Applicazioni lineari, matrici e cambiamenti di base 3. Autovalori e autovettori 2 1. Cambiamenti
Lezioni di Algebra Lineare V. Autovalori e autovettori Versione novembre 2008 Contenuto 1. Cambiamenti di base 2. Applicazioni lineari, matrici e cambiamenti di base 3. Autovalori e autovettori 2 1. Cambiamenti
AUTOVALORI E AUTOVETTORI
 Capitolo 4 AUTOVALORI E AUTOVETTORI Abbiamo visto nel paragrafo 2.17 che la matrice associata ad una applicazione lineare f : R n R m dipende dalle basi scelte in R n e R m. Un problema interessante che
Capitolo 4 AUTOVALORI E AUTOVETTORI Abbiamo visto nel paragrafo 2.17 che la matrice associata ad una applicazione lineare f : R n R m dipende dalle basi scelte in R n e R m. Un problema interessante che
DIAGONALIZZAZIONE E FORME QUADRATICHE / ESERCIZI PROPOSTI
 M.GUIDA, S.ROLANDO, 204 DIAGONALIZZAZIONE E FORME QUADRATICHE / ESERCIZI PROPOSTI L asterisco contrassegna gli esercizi più difficili o che possono considerarsi meno basilari. Autovalori, autospazi e diagonalizzazione
M.GUIDA, S.ROLANDO, 204 DIAGONALIZZAZIONE E FORME QUADRATICHE / ESERCIZI PROPOSTI L asterisco contrassegna gli esercizi più difficili o che possono considerarsi meno basilari. Autovalori, autospazi e diagonalizzazione
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE (esercitazione del 18 gennaio 2011)
 Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE (esercitazione del 18 gennaio 2011) ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola
Università di Modena e Reggio Emilia Facoltà di Scienze MM.FF.NN. PROVA DI ALGEBRA LINEARE (esercitazione del 18 gennaio 2011) ISTRUZIONI PER LO SVOLGIMENTO. Scrivere cognome, nome, numero di matricola
RICHIAMI DI ALGEBRA LINEARE E NORME DI MATRICI E VETTORI. a 11 a 12 a 1n a 21 a 22 a 2n. a m1 a m2 a mn
 RICHIAMI DI ALGEBRA LINEARE E NORME DI MATRICI E VETTORI LUCIA GASTALDI 1. Matrici. Operazioni fondamentali. Una matrice A è un insieme di m n numeri reali (o complessi) ordinati, rappresentato nella tabella
RICHIAMI DI ALGEBRA LINEARE E NORME DI MATRICI E VETTORI LUCIA GASTALDI 1. Matrici. Operazioni fondamentali. Una matrice A è un insieme di m n numeri reali (o complessi) ordinati, rappresentato nella tabella
LEZIONE 16 A = Verifichiamo se qualcuna fra le entrate a di A è suo autovalore. determinare per quale entrata a di A risulta rk(a ai 2 ) 1.
 LEZIONE 16 16.1. Autovalori, autovettori ed autospazi di matrici. Introduciamo la seguente definizione. Definizione 16.1.1. Siano k = R, C e A k n,n. Un numero λ k si dice autovalore di A su k) se rka
LEZIONE 16 16.1. Autovalori, autovettori ed autospazi di matrici. Introduciamo la seguente definizione. Definizione 16.1.1. Siano k = R, C e A k n,n. Un numero λ k si dice autovalore di A su k) se rka
Prodotto scalare e matrici < PX,PY >=< X,Y >
 Prodotto scalare e matrici Matrici ortogonali Consideriamo in R n il prodotto scalare canonico < X,Y >= X T Y = x 1 y 1 + +x n y n. Ci domandiamo se esistono matrici P che conservino il prodotto scalare,
Prodotto scalare e matrici Matrici ortogonali Consideriamo in R n il prodotto scalare canonico < X,Y >= X T Y = x 1 y 1 + +x n y n. Ci domandiamo se esistono matrici P che conservino il prodotto scalare,
1 Il polinomio minimo.
 Abstract Il polinomio minimo, così come il polinomio caratterisico, è un importante invariante per le matrici quadrate. La forma canonica di Jordan è un approssimazione della diagonalizzazione, e viene
Abstract Il polinomio minimo, così come il polinomio caratterisico, è un importante invariante per le matrici quadrate. La forma canonica di Jordan è un approssimazione della diagonalizzazione, e viene
Matematica Discreta I
 Matematica Discreta I 5 Febbraio 8 TEMA A Esercizio Sia data la matrice A M (R) A = (i) Calcolare gli autovalori di A (ii) Determinare una base di R composta di autovettori di A (iii) Diagonalizzare la
Matematica Discreta I 5 Febbraio 8 TEMA A Esercizio Sia data la matrice A M (R) A = (i) Calcolare gli autovalori di A (ii) Determinare una base di R composta di autovettori di A (iii) Diagonalizzare la
Sistemi lineari - Parte Seconda - Esercizi
 Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
Si noti che la matrice trasposta A ha lo stesso determinante. Questa proprietà è generale;
 Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
I. Foglio di esercizi su vettori linearmente dipendenti e linearmente indipendenti. , v 2 = α v 1 + β v 2 + γ v 3. α v 1 + β v 2 + γ v 3 = 0. + γ.
 ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
ESERCIZI SVOLTI DI ALGEBRA LINEARE (Sono svolti alcune degli esercizi proposti nei fogli di esercizi su vettori linearmente dipendenti e vettori linearmente indipendenti e su sistemi lineari ) I. Foglio
il determinante che si ottiene da A, sopprimendo la i - esima riga e la j - esima colonna. Si definisce complemento algebrico dell'elemento a ij
 Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
1 2 1 x = Quando sapremo calcolare i determinanti potremo ricavare:
 5 NOVEMBRE 2009 Esempio: Risolviamo il sistema: 3x + 2y + 4z = 1 2x y + z = 0 x + 2y + 3z = 1 1 2 4 3 1 4 3 2 1 0 1 1 2 0 1 2 1 0 1 2 3 1 1 3 1 2 1 x =, y =, z = 3 2 4 3 2 4 3 2 4 2 1 1 2 1 1 2 1 1 1 2
5 NOVEMBRE 2009 Esempio: Risolviamo il sistema: 3x + 2y + 4z = 1 2x y + z = 0 x + 2y + 3z = 1 1 2 4 3 1 4 3 2 1 0 1 1 2 0 1 2 1 0 1 2 3 1 1 3 1 2 1 x =, y =, z = 3 2 4 3 2 4 3 2 4 2 1 1 2 1 1 2 1 1 1 2
Rango di una matrice e teorema di Rouché-Capelli
 Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Rango di una matrice e teorema di Rouché-Capelli Sappiamo che a una matrice m n, A, è associata l applicazione lineare L A : R n R m, L A (X) = AX, X R n. Definizione 1. Lo spazio nullo di A, N (A), è
Fondamenti di Matematica del discreto
 Fondamenti di Matematica del discreto M1 - Insiemi numerici 25 gennaio 2013 - Laurea on line Esercizio 1. Dire, motivando la risposta, se è possibile scrivere 3 come combinazione lineare di 507 e 2010,
Fondamenti di Matematica del discreto M1 - Insiemi numerici 25 gennaio 2013 - Laurea on line Esercizio 1. Dire, motivando la risposta, se è possibile scrivere 3 come combinazione lineare di 507 e 2010,
- ciascun autovalore di T ha molteplicità geometrica uguale alla moltplicitaà algebrica.
 Lezioni del 14.05 e 17.05 In queste lezioni si sono svolti i seguenti argomenti. Ripresa del teorema generale che fornisce condizioni che implicano la diagonalizzabilità, indebolimento delle ipotesi, e
Lezioni del 14.05 e 17.05 In queste lezioni si sono svolti i seguenti argomenti. Ripresa del teorema generale che fornisce condizioni che implicano la diagonalizzabilità, indebolimento delle ipotesi, e
SISTEMI LINEARI. x y + 2t = 0 2x + y + z t = 0 x z t = 0 ; S 3 : ; S 5x 2y z = 1 4x 7y = 3
 SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
Matrici simili. Matrici diagonalizzabili.
 Matrici simili. Matrici diagonalizzabili. Definizione (Matrici simili) Due matrici quadrate A, B si dicono simili se esiste una matrice invertibile P tale che B = P A P. () interpretazione: cambio di base.
Matrici simili. Matrici diagonalizzabili. Definizione (Matrici simili) Due matrici quadrate A, B si dicono simili se esiste una matrice invertibile P tale che B = P A P. () interpretazione: cambio di base.
Autovettori e autovalori
 Autovettori e autovalori Definizione 1 Sia A Mat(n, n), matrice a coefficienti reali. Si dice autovalore di A un numero λ R tale che v 0 R n Av = λv. Ogni vettore non nullo v che soddisfa questa relazione
Autovettori e autovalori Definizione 1 Sia A Mat(n, n), matrice a coefficienti reali. Si dice autovalore di A un numero λ R tale che v 0 R n Av = λv. Ogni vettore non nullo v che soddisfa questa relazione
Matematica per Chimica, Chimica Industriale e Scienze dei Materiali Primo appello 7/02/2012 Tema A
 Matematica per Chimica, Chimica Industriale e Scienze dei Materiali Primo appello 7/02/202 Tema A NOME:..................................................... COGNOME:.....................................................
Matematica per Chimica, Chimica Industriale e Scienze dei Materiali Primo appello 7/02/202 Tema A NOME:..................................................... COGNOME:.....................................................
Definizione 1. Una matrice n m a coefficienti in K é una tabella del tipo. ... K m, detto vettore riga i-esimo, ed a im
 APPUNTI ed ESERCIZI su matrici, rango e metodo di eliminazione di Gauss Corso di Laurea in Chimica, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 23 Aprile 2010 Matrici, rango e metodo
APPUNTI ed ESERCIZI su matrici, rango e metodo di eliminazione di Gauss Corso di Laurea in Chimica, Facoltà di Scienze MM.FF.NN., UNICAL (Dott.ssa Galati C.) Rende, 23 Aprile 2010 Matrici, rango e metodo
0 0 c. d 1. det (D) = d 1 d n ;
 Registro Lezione di Algebra lineare del 23 novembre 216 1 Matrici diagonali 2 Autovettori e autovalori 3 Ricerca degli autovalori, polinomio caratteristico 4 Ricerca degli autovettori, autospazi 5 Matrici
Registro Lezione di Algebra lineare del 23 novembre 216 1 Matrici diagonali 2 Autovettori e autovalori 3 Ricerca degli autovalori, polinomio caratteristico 4 Ricerca degli autovettori, autospazi 5 Matrici
Definizione. Sia f : V V un endomorfismo e λ R. Se esiste v V non nullo tale che
 Autovalori ed autovettori [Abate, 131] Sia f : V V un endomorfismo e λ R Se esiste v V non nullo tale che f(v) = λv, diremo che λ è un autovalore di f e che v è un autovettore di f associato a λ Lezioni
Autovalori ed autovettori [Abate, 131] Sia f : V V un endomorfismo e λ R Se esiste v V non nullo tale che f(v) = λv, diremo che λ è un autovalore di f e che v è un autovettore di f associato a λ Lezioni
Contenuti aggiuntivi su matrici e determinanti, Dimostrazioni del Capitolo 3
 Contenuti aggiuntivi su matrici e determinanti, Dimostrazioni del Capitolo 3 Dimostrazione 310 Sia W = L(C A ) K Osserviamo che S è una base di W Infatti S è indipendente, inoltre ogni vettore di W dipende
Contenuti aggiuntivi su matrici e determinanti, Dimostrazioni del Capitolo 3 Dimostrazione 310 Sia W = L(C A ) K Osserviamo che S è una base di W Infatti S è indipendente, inoltre ogni vettore di W dipende
( ) TEORIA DELLE MATRICI. A. Scimone a.s pag 1
 . Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
. Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
a.a MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI
 aa 2012-2013 MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI 1 Sistemi di equazioni lineari Definizione 11 i Un equazione lineare nelle indeterminate (o incognite X 1,, X 1 m a coefficienti interi (o razionali,
aa 2012-2013 MATEMATICA GENERALE: SISTEMI LINEARI E MATRICI 1 Sistemi di equazioni lineari Definizione 11 i Un equazione lineare nelle indeterminate (o incognite X 1,, X 1 m a coefficienti interi (o razionali,
Corso di Laurea in Fisica. Geometria. a.a Prof. P. Piazza Soluzione compito a casa del 24/10/09
 Corso di Laurea in Fisica. Geometria. a.a. 29-. Prof. P. Piazza Soluzione compito a casa del 24//9 Soluzione esercizio. Siano A e B due matrici simmetriche e λ un numero reale. Dobbiamo mostrare che anche
Corso di Laurea in Fisica. Geometria. a.a. 29-. Prof. P. Piazza Soluzione compito a casa del 24//9 Soluzione esercizio. Siano A e B due matrici simmetriche e λ un numero reale. Dobbiamo mostrare che anche
Elementi di Algebra Lineare Applicazioni lineari
 Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 50 index Applicazioni lineari 1 Applicazioni lineari
Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 50 index Applicazioni lineari 1 Applicazioni lineari
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2012 Rossi Algebra Lineare 2012 1 / 59 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2012 Rossi Algebra Lineare 2012 1 / 59 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
, è Det(A) = a 11 a 22 a 12 a 21. ( il determinante della matrice che si ottiene da A. la 1 a riga e la 2 a colonna di A
 G Parmeggiani, 2/12/2013 Algebra Lineare 1 A, corso di laurea SGI, aa 2013/2014 Nota 4: Calcolo di determinanti Sia A una matrice quadrata di ordine n Il determinante di A è un numero che dipende da A
G Parmeggiani, 2/12/2013 Algebra Lineare 1 A, corso di laurea SGI, aa 2013/2014 Nota 4: Calcolo di determinanti Sia A una matrice quadrata di ordine n Il determinante di A è un numero che dipende da A
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari
 Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Parte 7. Autovettori e autovalori
 Parte 7. Autovettori e autovalori A. Savo Appunti del Corso di Geometria 23-4 Indice delle sezioni Endomorfismi, 2 Cambiamento di base, 3 3 Matrici simili, 6 4 Endomorfismi diagonalizzabili, 7 5 Autovettori
Parte 7. Autovettori e autovalori A. Savo Appunti del Corso di Geometria 23-4 Indice delle sezioni Endomorfismi, 2 Cambiamento di base, 3 3 Matrici simili, 6 4 Endomorfismi diagonalizzabili, 7 5 Autovettori
Soluzione della seconda prova intermedia di Algebra lineare del 17 maggio Esercizio 1
 Soluzione della seconda prova intermedia di Algebra lineare del 17 maggio 2012 Esercizio 1 (a) Si calcola il polinomio caratteristico λ 2 1 p(λ) = det k 1 2k λ k 1 2 2 λ usando lo sviluppo di Laplace secondo
Soluzione della seconda prova intermedia di Algebra lineare del 17 maggio 2012 Esercizio 1 (a) Si calcola il polinomio caratteristico λ 2 1 p(λ) = det k 1 2k λ k 1 2 2 λ usando lo sviluppo di Laplace secondo
Geometria A. Università degli Studi di Trento Corso di laurea in Matematica A.A. 2017/ Maggio 2018 Prova Intermedia
 Geometria A Università degli Studi di Trento Corso di laurea in Matematica A.A. 7/8 Maggio 8 Prova Intermedia Il tempo per la prova è di ore. Durante la prova non è permesso l uso di appunti e libri. Esercizio
Geometria A Università degli Studi di Trento Corso di laurea in Matematica A.A. 7/8 Maggio 8 Prova Intermedia Il tempo per la prova è di ore. Durante la prova non è permesso l uso di appunti e libri. Esercizio
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
