Introduzione all analisi grafica
|
|
|
- Ambra Franchini
- 8 anni fa
- Visualizzazioni
Transcript
1 Edoardo Dotto Introduzione all analisi grafica Una nota didattica Palermo 2009
2 Il testo che segue è la stesura di alcune lezioni tenute nel corso di Disegno dell Architettura presso la Facoltà di Architettura dell Università di Catania con sede a Siracusa. I temi trattati - quello del potere che il disegno dispiega nell indagine della forma architettonica e del ruolo che esso ha nel costruire e precisare il pensiero progettuale - sono stati per me motivo di curiosità fin dall elaborazione della tesi di laurea. A tanti anni di interesse non è corrisposta un elaborazione sistematica degli argomenti, ma piuttosto, come si vedrà, una serie di riflessioni tenute insieme dall entusiasmo per come il disegno di architettura, lontano dall essere soltanto una congerie di tecniche e di procedure, sia connaturato all essenza del pensiero architettonico. Questa nota, più che cercare di esaurire l argomento, peraltro brillantemente affrontato da parecchi studiosi, vuole esclusivamente costituire un introduzione, necessariamente parziale, alla pratica dell analisi grafica e della consapevole rappresentazione dell architettura.
3 Introduzione all analisi grafica Una nota didattica La formazione scolastica che ciascuno di noi ha ricevuto, nella quasi totalità dei casi, ha privilegiato nettamente il linguaggio verbale rispetto a quello musicale o delle immagini. Probabilmente, data la straordinaria immediatezza e duttilità della parola, questa scelta ci ha permesso di comunicare fin dai primi anni di vita in modo rapido ed efficace. Purtroppo, molto spesso l ambito in cui si esercita il linguaggio verbale si rivela pervasivo e limita nettamente l uso di differenti forme di espressione. Nella scuola primaria, almeno fino a qualche decennio fa, era molto frequente che si proponessero agli scolari delle esperienze didattiche distanti dal mondo dei libri. Spesso si trattava di concerti, rappresentazioni teatrali o di passeggiate all aria aperta. A questa varietà di situazioni, dettata più da occasioni fortuite che da un progetto coerente, si contrapponeva una pratica costante: ciascuna esperienza andava raccontata «per iscritto», sotto forma di pensierini o di temino, a seconda delle età. Ciascuno era costretto quindi alla riduzione delle più varie esperienze al linguaggio verbale. Se in alcuni casi ciò era possibile senza grandi difficoltà, nel dovere tradurre le sensazioni visive o talvolta il ricordo preciso di alcuni passaggi musicali usando le parole, ci si scontrava con una serie di problemi che lasciavano immediatamente spazio alla retori- 3
4 ca più melensa. Usare le parole per raccontare la musica o le forme imponeva all immaginazione ed alla memoria una forzatura che spesso smorzava i preziosi entusiasmi infantili. Purtroppo però anche nel mondo degli adulti, le parole non sono il medium adatto ad ogni descrizione. Talvolta i racconti si rivelano inefficaci a rappresentare la realtà e di conseguenza si rischia di finire vittima di pericolosi fraintendimenti. Nonostante ciascuno di noi sia stato abituato all analisi - grammaticale, logica e sintattica - del linguaggio verbale, ne sperimentiamo spesso l inadeguatezza. Per lo studio e la rappresentazione dell architettura il mezzo linguistico più indicato, come è ovvio, è quello delle immagini, in primo luogo il disegno. Esso costituisce uno strumento di analisi molto potente e consente di esplorare compiutamente aspetti che il linguaggio verbale può soltanto sfiorare. Studiare l architettura attraverso il disegno significa utilizzare il linguaggio che è stato utilizzato per progettarla, significa quindi usare una chiave di accesso privilegiata per la comprensione della forma. Questo tipo di studio prende il nome di analisi grafica e può essere condotto non solo su disegni di rilievo e su disegni di progetto, ma a ben vedere anche su immagini di altro tipo come vedute, prospettive, disegni schematici. La pratica dell analisi grafica è di importanza cruciale per la formazione e la crescita di un architetto. Essa consente di studiare l architettura in modo approfondito, talvolta con esiti sorprendenti. Il tema dell analisi grafica è profondamente connaturato a quello della rappresentazione. Questo termine, come è noto, indica un azione - quella del rappresentare - che non può prescindere dalla drastica sintesi di alcuni aspetti che costituiscono la realtà rappresentata. Nell assistere ad una rappresentazione teatrale, ad esempio, ci rendiamo conto che l azione che si svolge sotto i nostri occhi è doverosamente una sintesi della realtà (solitamente immaginaria) cui 4
5 essa allude. Le azioni dei personaggi, ovviamente, sono illustrate soltanto nelle parti significative, quelle legate all incedere del racconto. Non li seguiremo, ad esempio, nei loro compiti domestici o di igiene personale, a meno che questo non comporti una ricaduta nell economia dell azione teatrale. Per fare un altro esempio, la fotografia di un architettura costituisce senza dubbio una rappresentazione di quell edificio. Essa però, della realtà tangibile, esclude un enorme quantità di aspetti, eliminando tra le altre cose, la tridimensionalità, la materialità e gli odori del luogo ritratto. Quasi sempre una forma d arte identifica anche un sistema di rappresentazione, di cui assume le regole, i limiti e le possibilità specifiche. In definitiva, ogni rappresentazione più che riproporre la realtà, ne determina una riduzione, una sintesi, un riepilogo, escludendo in modo spesso drastico le informazioni di cui è portatrice. Lo scrittore argentino Jorge Luis Borges, in uno dei suoi fulminanti racconti, chiarisce in modo straordinario come la sintesi sia un aspetto fondamentale della rappresentazione. Egli racconta di un re 1 che sprona i suoi cartografi a realizzare una topografia del regno, quanto più dettagliata possibile, portandoli, dopo parecchie stesure, a realizzare una carta in scala al vero, grande quanto al regno, distesa su di esso, scomoda ed ingombrante. Se nel rappresentare non si compiono le selezioni adeguate, la rappresentazione è quantomeno inutile ed inefficace. Come è ovvio non esiste, se non per aspetti macroscopici, un modo unico di selezionare gli aspetti più rilevanti della realtà, e quindi di rappresentarla. Ciascuno di noi, per così dire, di essa si forma una propria immagine, nella quale prevalgono aspetti cui è più sensibile o che semplicemente è in grado di comprendere e, di conseguenza, di comunicare efficacemente. La qualità del vedere è indissolubilmente legata alla dimensione culturale di chi guarda. Anche dal punto di vista neurologico, vede- 5
6 re è una funzione particolarmente complessa che coinvolge in modo contemporaneo più parti del cervello. Come, con un abile sintesi, Wim Wenders ci mostra nel suo straordinario film Fino alla fine del mondo 2 del oltre che in alcuni suoi scritti - vedere, capire e memorizzare sono operazioni che avvengono contemporaneamente, in relazione virtuosa tra loro. Più capiamo ciò che vediamo, più siamo in grado di imparare e di conseguenza più riusciamo a vedere con acutezza e precisione. Se capiamo quello che vediamo, infatti, l esperienza del vedere completa ed in qualche caso ristruttura il nostro sapere. Ma perché, potremmo chiederci, allora sono soltanto alcuni gli aspetti della realtà che colpiscono il nostro occhio, aggiungendosi alla nostra esperienza? In altri termini, in che modo si forma il nostro personale punto di vista? Gli studiosi del linguaggio hanno indagato in profondità le relazioni che intercorrono tra la nostra percezione del mondo e gli schemi linguistici che utilizziamo. Tra gli altri, Benjamin Lee Whorf - un allievo del grande linguista Edward Sapir - all inizio del Novecento ha mostrato come sia praticamente impossibile leggere la realtà se non attraverso i nostri schemi linguistici. Secondo Whorf «... il mondo si presenta come un flusso caleidoscopico di impressioni che deve essere organizzato dalle nostre menti, il che vuol dire che deve essere organizzato in larga misura dal sistema linguistico delle nostre menti» 3. Il sistema linguistico, infatti, non è soltanto uno strumento per riprodurre la realtà, esso, piuttosto, dà forma alle idee ed è addirittura «il programma e la guida dell attività mentale dell individuo». Per formulare e verificare e sue ipotesi Whorf ha studiato per parecchio tempo la lingua degli indiani americani Hopi. Nel corso delle sue ricerche ha notato come essi non conoscano i tempi verbali ed utilizzino, per comunicare eventi o azioni, esclusivamente una forma verbale che si riferisce nella maggior parte dei casi al 6
7 1. L idea di Storia nella quale agiamo ha una struttura analoga a quella di una retta orientata, in cui gli eventi si susseguono secondo un ordine scandito dall incedere del tempo. Ogni situazione è irripetibile. La cultura della Tradizione, invece ha uno schema ripetitivo, circolare, in cui gli eventi si ripropongono ciclicamente. tempo presente. Nel racconto di un fatto avvenuto in un lontano passato, l unica differenza rispetto ad uno recente è che il primo sarà reso in modo meno vivido, più vago, con meno dettagli e minore partecipazione emotiva. Se confrontiamo questa condizione con quella che emerge dall osservazione dei nostri tempi verbali, risulta subito evidente la nostra diversa percezione del tempo. In italiano, ad esempio, soltanto nel modo indicativo, coniughiamo ben cinque tempi passati (imperfetto, passato prossimo, passato remoto, trapassato prossimo e trapassato remoto), il presente e due tempi futuri. Il futuro anteriore, in particolare, che descrive un futuro in cui una certa azione sarà già stata compiuta, è davvero sintomatico della precisione con la quale intendiamo situare le azioni nel tempo. Il nostro modo di percepire il tempo, come si vede dalle strutture del nostro linguaggio (figura 1), è diametralmente opposto a quello degli indiani Hopi. Per loro il tempo si ripete ciclicamente, seguendo ritmi naturali, come l alternarsi del giorno e della notte o il fluire delle stagioni. Per noi il tempo si orienta drasticamente in una direzione che va dal passato al futuro, dal prima al dopo. Per loro il sapere è preservato dalla Tradizione, che è un ambito culturale in 7
8 cui le soluzioni ai problemi del vivere si sono rese omogenee. Il nostro ambito, invece è quello della Storia, in cui le novità tendono spesso ad escludere le pratiche desuete, in una continua ricerca di miglioramenti. Se la Tradizione conserva uno stato di equilibrio con la realtà circostante, la Storia deve inseguirlo di continuo. La nostra maniera di vedere il tempo si riverbera distintamente, tra l altro, in una serie di supporti per l organizzazione della nostra giornata. Si pensi, ad esempio, alle nostre agende, vere e proprie macchine del tempo in cui possiamo leggere la traccia delle nostre azioni passate e i nostri programmi futuri. Il nostro linguaggio ci predispone ad un preciso tipo di organizzazione del tempo e questo ci lega indissolubilmente a strumenti e pratiche con le quali strutturiamo le nostre giornate e la nostra vita. Roland Barthes a questo proposito asseriva che la lingua «è semplicemente fascista; il fascismo, infatti non è impedire di dire, ma obbligare a dire» 4. Egli lucidamente indicava così l enorme potere che il linguaggio ha sui pensieri e sul modo in cui possiamo organizzarli. Siamo legati l un l altro da una analoga capacità di vedere il mondo, veicolata direttamente dall uso del nostro linguaggio. Ad un limite evidente delle nostre opportunità di pensiero, insito nell adozione e nell uso di un linguaggio, corrisponde però la possibilità di condividere i nostri pensieri con quanti utilizzano la nostra stessa lingua. In altri termini, cediamo un po della nostra libertà in cambio della possibilità di comunicare facilmente ed efficacemente. Di questi meccanismi era ben consapevole anche lo scrittore inglese George Orwell il quale, in una straordinaria appendice del romanzo 1984, nel quale viene descritta una società estremamente repressiva, guidata da un fantomatico Grande fratello 5, riflette sui principi della cosiddetta Neolingua, cioè una lingua riformata, costruita appositamente per rendere più efficace il controllo sugli 8
9 individui, impedendo una reale autonomia di pensiero. Eliminando alcuni termini cruciali dal vocabolario e storpiando il significato di altri, è possibile consegnare alla collettività una lingua che non consente alcuna riflessione fluida e coerente sui temi della libertà e della volontà individuale. Ciascuna parola è un po come la scheda di un libro in una grande biblioteca. Una volta smarrita si perde persino coscienza dell esistenza del libro e lo si rende definitivamente inaccessibile, con tutto ciò che esso contiene. Dunque i nostri schemi mentali sono profondamente legati all immagine che ci formiamo della realtà. Il modo in cui la rappresentiamo (ed il linguaggio è un tipo di rappresentazione) non può facilmente travalicare i confini dei nostri modelli linguistici. L ambito della nostra individualità - che si mantiene comunque sorprendentemente vasto - si riduce ad uno scarto personale nell ampiezza dei nostri strumenti linguistici e nell uso originale di elementi della comunicazione condivisi nella collettività cui apparteniamo. Rappresentare quindi significa, all interno di schemi condivisi, selezionare le informazioni che della realtà consideriamo rilevanti e che siano in grado di restituire di essa un immagine coerente. Lo strumento che usiamo per rappresentare non è neutrale, ma ha esso stesso un forte gradiente analitico. Nel corso dell elaborazione della mia tesi di laurea ho voluto condurre su di me un piccolo esperimento. Ad una fase piuttosto avanzata della stesura del progetto, ho provato ad utilizzare, una per volta, le tecniche di disegno di tre architetti contemporanei. Ho provato a disegnare per alcuni giorni il mio progetto imitando Franco Purini, poi Alvaro Siza, poi Umberto Riva, alla stregua di un falsario, che deve riproporre fino ai dettagli più minuti le tecniche e gli stilemi dell autore che vuole replicare. Il progetto subiva ogni volta degli scantonamenti nella direzione in cui quel modo di 9
10 2. Un disegno che imita la grafia e gli stilemi formali di Franco Purini, un falso maldestro. Nell imitare questo modo di disegnare, mi sono trovato ad assumere, in modo involontario, alcuni schemi progettuali, analoghi a quelli del suo pensiero. Il linguaggio grafico che ho utilizzato non è neutrale: rende facili alcuni percorsi di progetto e ne allontana altri. Per questo motivo la scelta di uno specifico modo di disegnare deve essere sempre ponderato e consapevole. disegnare sembrava essere il più adatto. Imitando Purini (figura 2), il progetto si chiariva nell impianto generale, con scelte fondative nette ed evidenti. Disegnando come Siza, la struttura geometrica dell impianto si faceva più evidente e perdeva la sua rigidità iniziale. Disegnando come Riva, l attenzione si focalizzava sui dettagli, i materiali, la scala umana. Avveniva qualcosa di molto simile a ciò che viene descritto da Jean Genet, nel suo lavoro teatrale Le serve 6, in cui due domestiche approfittano dell assenza della padrona per provarne i vestiti ed usarne gli oggetti personali. Dopo un po ne assumono i modi, gli atteggiamenti, il comportamento ed il linguaggio, replicando di fatto, benché inconsapevolmente, gli schemi del suo pensiero. Tra gli strumenti adatti alla rappresentazione delle forme, ne esiste uno con cui la nostra cultura ha stabilito una relazione granitica, una sorta di patto di sangue, sugellato da una fedele e collaudata continuità: la geometria. Per capire quanto essa sia ormai connaturata al nostro modo di vedere basta osservare due opere dell artista anglosas- 10
11 3. Richard Long, Midsummer circles, Londra Le pietre, disposte sul pavimento in modo irregolare, vengono subito riconosciute come elementi di tre cerchi sul suolo. Gli schemi geometrici che abbiamo imparato a riconoscere fin dall infanzia influenzano la nostra capacità di comprendere e descrivere il mondo. 4. Richard Long, senza titolo, Inghilterra Guardando l immagine siamo portati a riconoscere tre circonferenze anche se non abbiamo alcuna esperienza dell andamento del terreno. L abitudine a discernere le forme geometriche è tale da spingerci in tempi molto rapidi ad ipotesi complesse sulla forma del suolo. sone Richard Long 7. La prima (figura 3) si intitola Midsummer Circles (Londra 1993), ed è costruita disponendo parecchie pietre di forma allungata secondo direzioni radiali lungo tre circonferenze. Dato che le pietre sono di misura diversa soltanto una faccia si trova allineata alla sagoma circolare. L effetto visivo è molto efficace. Benché non vi sia di fatto alcuna vera circonferenza (date le superfici scabre ed irregolari delle pietre) siamo immediatamente portati a riconoscerle. La forma della circonferenza è ormai connaturata al nostro modo di vedere e, quindi, sovrapponiamo lo schema che conosciamo ad una realtà che, a ben vedere ci sollecita con un immagine parecchio più 11
12 5. Una vignetta degli anni 40 di Carl Barks. Paperino, convinto, in seguito ad un feroce scherzo dei nipotini, di essere su di un isola deserta, scopre di essere stato ingannato. I cerchi concentrici sul terreno, che ricordano parecchie opere di Richard Long, sono per Paperino la prova inoppugnabile della presenza umana. complessa, irrisolta e complicata. Il nostro sistema linguistico-geometrico - potremmo dire - compie una sintesi rapida, mostrandoci una forma definita laddove in realtà vi sono soltanto parecchie pietre non squadrate. Nella seconda opera (figura 4), realizzata in Inghilterra nel 1967, si vedono tre circonferenze nette, bianche, che spiccano sulla superficie erbosa, tracciate disseminando una terra chiara. Ma anche in questo caso, se si osserva l immagine con occhio innocente, si vede che la forma del terreno e lo scorcio prospettico, rendono del tutto illegibili le forme circolari. I tre cerchi sono nella nostra mente, elaborati dalla nostra cultura, e li riconosciamo tenendo conto anche delle condizioni del terreno, di cui non abbiamo alcuna esperienza diretta. La nostra capacità di analisi e di sintesi si esprime in modo quasi autonomo. Ciascuna delle forme che percepiamo, anche inconsapevolmente, finisce con l essere interpretata attraverso i nostri schemi culturali e linguistici che ci restituiscono una rappresentazione coerente, anche se probabilmente opinabile, della realtà. Non vi è dubbio che per noi le forme geometriche assurgano ormai a segno e traccia dell intelligenza e della presenza umana (figura 5). Vitruvio, nell introduzione al Sesto Libro del De Architectura, narra del filosofo Aristippo che «gettato in seguito a 12
13 6. Nel film di Stanley Kubrick 2001: Odissea nello spazio, la scoperta del monolito nero ritrovato nel sottosuolo di Marte, pone agli scenziati inquietanti interrogativi sulla storia dell Universo e della vita intelligente. È difficile, infatti considerare un solido geometrico come opera del caso, piuttosto che della volontà cosciente. naufragio sulla spiaggia di Rodi, si accorse di alcune figure geometriche tracciate sopra la sabbia e, a quanto dicono, si rivolse ai suoi compagni esclamando: abbiamo buone speranze. Scorgo infatti tracce di presenza umana» 8. Nel racconto di Vitruvio è il segno geometrico, probabilmente una linea, a segnalare la presenza umana, più delle stesse orme del piede nudo o dei calzari. D altra parte nel film 2001: Odissea nello spazio, la versione cinematografica di Stanley Kubrick del romanzo di Artur C. Clarke 9, è il monolito (figura 6), un nettissimo impenetrabile parallelepipedo dalle origini misteriose, a rimandare ad una civiltà intelligente che deve averlo realizzato. Un manufatto geometrico, secondo il nostro sentire comune, non può essere opera del caso, ma soltanto prodotto dell attività consapevole dell intelligenza. Inoltre, siamo portati a riconoscere delle strutture geometriche anche in alcune forme naturali (che quindi sappiamo non essere prodotte dall intelligenza umana). Alcune piante, le cactacee in modo particolare, hanno una forma che si presta a questo tipo di interpretazione. Non possiamo asserire ad esempio che l Astrophitum Myriostigma abbia una struttura pentagonale, ma siamo fortemente orientati a riconoscerne e descriverne la forma in stretta analogia 13
14 7. L Astrophitum è una delle piante che in modo più evidente mostra una struttura intrinsecamente geometrica. Ma, dobbiamo chiederci, ne riconosciamo la struttura geometrica perché siamo in qualche modo allenati a farlo? In altri termini: è la nostra cultura che ci porta a interpretare la forma vegetale in questo modo preciso? 8. L esercizio di disegno di forme naturali risulta particolarmente utile se si cerca di estrarre dalle strutture complesse delle semplici leggi costitutive. Nel ridisegno di una conchiglia, ad esempio, sono soltanto alcune le viste che in qualche maniera ne svelano l organizzazione geometrica. Dopo averle individuate la forma si chiarisce. con la geometria del pentagono (figura 7). A rigor del vero, però, per riconoscere la struttura geometrica di una forma naturale dobbiamo osservarla da un punto di osservazione preciso, tale da esaltare la regolarità che cerchiamo. È quanto succede, ad esempio, se proviamo a disegnare una forma complessa, come quella di una conchiglia (figura 8). Osservata da punti di vista casuali essa si presenta come una forma criptica, priva di elementi gerarchicamente distinti. Se viene esaminata da una prospettiva precisa, invece, si chiarisce immediatamente non solo la struttura della sua forma ma anche, per così dire, la morfogenesi, il significato formale della sua crescita. 14
15 9. La forma intricata della Pirite cubica, uno dei minerali da cui si estrae il ferro, diviene immediatamente chiara se la si interpreta come l intersezione di parecchi cubi di diverse misure. Anche in questo caso è la nostra conoscenza della geometria a fornirci le categorie adatte per descrivere la forma in modo chiaro ed efficace. 10. In un disegno infantile possiamo trovare molti esempi del modo in cui il mondo circostante viene filtrato dalla conoscenza delle forme geometriche elementari che acquisiamo fin dai primi anni di vita. La complessità delle cose viene ridotta con disinvoltura e fantasia a pochi stilemi formali che apprendiamo soprattutto attraverso il gioco. L immagine confusa della pirite cubica (figura 9) diventa immediatamente chiara se pensiamo che si tratta di cubi di dimensioni diverse che si intersecano vicendevolmente. Anzi è molto facile che, abituati come siamo a riconoscere le forme geometriche, realizziamo questa semplificazione senza alcuno sforzo, spontaneamente. Molto probabilmente apprendiamo questa capacità di realizzare sintesi attraverso analogie con le forme geometriche nei primi anni di vita. Se osserviamo un disegno infantile (figura 10), ci rendiamo conto di come tra le tante forme che suggeriscono una diretta corrispondenza con figure geometriche (il sole come una circonferen- 15
16 11. Il rapporto tra due numeri consecutivi in una serie di Fibonacci, tende ad un numero irrazionale che è lo stesso che esprime il rapporto tra i due lati del rettangolo aureo. Esso mantiene la propria forma se vi si somma o vi si sottrae un quadrato. Molte regole di accrescimento in natura si basano su questa legge matematica. za, la casa composta di triangoli e rettangoli) ve ne siano altre, come la forma di un tronco d albero, in cui la forzatura cui sottoponiamo la realtà si mostra più evidente. La geometria è una sorta di filtro che interponiamo tra i nostri occhi ed il mondo. È uno schema che, esattamente come dice Whorf, consente di discernere, anche grossolanamente, gli elementi della realtà laddove altrimenti vi sarebbe soltanto «un flusso caleidoscopico di immagini». La nostra capacità di leggere il mondo e di interpretarlo facendo ricorso a delle forme che ad esso ci sembrano analoghe, non si può scindere dalla nostra creatività e dalla nostra attitudine ad immaginare. In entrambi i casi utilizziamo la nostra capacità di rappresentare. Se nel primo caso - raccontando il mondo esistente - facciamo riferimento all aspetto mimetico della rappresentazione, nel secondo caso - quando utilizziamo la nostra creativita ad esempio per progettare l architettura - ne applichiamo le immense possibilità poietiche 10. Gli schemi, anche quelli geometrici, attraverso i quali leggiamo la realtà, sono gli stessi di cui ci serviamo per dare ordine alla nostra immaginazione. Per dimostrarlo, basterebbe analizzare in modo approfondito - 16
17 12. Il Nautilus, tra tutte le conchiglie, è forse quella che in modo più chiaro mostra la corrispondenza tra una forma naturale e la regola di accrescimento basata sulla serie di Fibonacci e sul rettangolo aureo. Per Le Corbusier, che si interessò molto a questi temi, essa era una sorta di segno della presenza delle leggi geometriche in natura. purtroppo non in questa nota - l intreccio fitto tra il rapporto aureo (e quindi la serie di Fibonacci), la geometria del pentagono e del decagono e la struttura geometrica di alcune forme naturali. L eccezionale condizione matematica della serie di Fibonacci (ciascun numero è medio proporzionale tra quello che precede e quello che segue ed è somma dei due che precedono), si può sintetizzare nel rapporto che intercorre tra due numeri contigui (cioè il numero φ, irrazionale, che vale 0,618...) che è anche il rapporto tra i lati del cosiddetto rettangolo aureo (figura 11). Tale rettangolo gode di una proprietà unica, cioè quella di mantenere la propria forma, quindi il rapporto tra i lati, se ad esso si sottrae o si somma un quadrato. Nel mondo delle scienze naturali, ad esempio nello studio di piante e conchiglie, questo numero ha guidato la lettura della forma di parecchie specie. Nelle conchiglie non è raro che la struttura del guscio sia tale, infatti, da lasciare inalterata la forma complessiva della conchiglia nel corso dell accrescimento (figura 12). Pur con lo svilupparsi del mollusco, e quindi con il necessario accrescimento del guscio, la forma complessiva rimane identica, in modo tale che la conchiglia pur aumentando di volume si mantiene - potremmo dire - omotetica a se stessa. Nella maggior 17
18 13. L ovale centrale della pianta della biblioteca di Vienna, realizzata attorno al 1720 da J. B. Fischer Von Erlach, ha un rapporto tra le lunghezze degli assi uguale al numero aureo φ. È molto frequente che si applichino nel progetto gli stessi schemi che si è imparato a riconoscere nell interpretazione del mondo circostante. parte dei casi, le forme che hanno queste caratteristiche sono sempre intrinsecamente legate a rapporti aurei. Una tale convergenza tra aspetti desunti dall osservazione della natura e da intuizioni in campo esclusivamente matematico, non ha lasciato indifferenti artisti ed architetti, formati al disegno geometrico e consapevoli della struttura di pentagoni e decagoni, la cui costruzione si fonda sulla ricerca della parte aurea di un segmento. Fin dal periodo classico, infatti, alcuni templi sono disegnati nel rispetto del rapporto aureo, non solo in facciata. A Vienna nel Settecento, l architetto Johann Bernhard Fischer von Erlach usò un ovale aureo per delimitare l aula centrale della biblioteca cittadina 11 (figura 13). Le Corbusier negli anni Quaranta del secolo scorso, riflettendo sui legami tra il rapporto aureo, le misure del corpo umano e le posizioni che esso assume nello svolgere le varie attività, costruì un affascinante sistema armonico di lunghezze che consente di dimensionare in modo semplice mobili, oggetti, abitazioni e persino ambiti urbani 12 (figura 14). Uno schema astratto come quello della sezione aurea non solo riesce a guidarci con sicurezza nella lettura di forme naturali, ma può indirizzare la nostra creatività, disciplinando l invenzione attraverso 18
19 14. Tra il 1942 ed il 1948, Le Corbusier mise a punto un sistema di dimensioni armoniche, basate sulle misure del corpo umano e legate tra loro dalla legge matematica della serie di Fibonacci. Questo sistema di misura, il Modulor, venne trascritto in alcune tabelle ed in un nastro graduato, per potere essere utilizzato comodamente sia sul tavolo da disegno che in cantiere. Benché sia stato poco utilizzato, il Modulor costituisce ancora una lezione di armonia. regole condivise all interno della nostra cultura, che appartengono allo stesso linguaggio geometrico sul quale ci formiamo da molte generazioni. Questa condizione è comune a parecchie leggi geometriche, metodi di tracciamento e tecniche grafiche. Ciascuna di esse, nel costituire un modo per leggere il nostro ambiente, determina uno schema di pensiero che si manifesta in forme diverse nella nostra attività creativa. Se è vero che le forme che inventiamo sono quasi sempre un elaborazione, più o meno complessa, di ciò che abbiamo appreso e maturato nel corso della nostra formazione, allora è probabile che ogni volta che vogliamo studiare un architettura - attraverso il disegno magari - è necessario essere informati sugli schemi mentali, le conoscenze geometriche, le abitudini formali dell autore. In altre parole, dobbiamo conoscerne il linguaggio grafico e geometrico ed essere coscienti di quali strumenti, tecnici e concettuali, può avere usato per sviluppare il suo progetto. 19
20 15. La pianta della casa Goldenberg, progettata da Louis I. Kahn nel 1959, a prescindere dall immagine finale, ha una forma che è pienamente debitrice della geometria del quadrato. Oltre al cortile centrale, se ne leggono le diagonali ed alcuni frammenti del contorno più esterno. In una intervista alla rivista studentesca Perspecta, Kahn con alcuni schemi mostrò con chiarezza quale fosse la gerarchia degli elementi che costituiscono la casa, riferendoli sempre allo schema di base. La geometria, se usata con consapevolezza e con intelligenza, è uno strumento di controllo eccezionale per il progetto di architettura e nell opera di architetti come Kahn può diventare persino fonte di ispirazione poetica. Ovviamente non siamo in grado, il più delle volte, di analizzare un architettura conoscendo esattamente il repertorio tecnico dell autore, ma è possibile, confidando nel nostro buon senso, orientarci in modo responsabile. In altre parole, possiamo indagare le architetture utilizzando degli strumenti che reputiamo essere quantomeno pertinenti rispetto all ambito culturale in cui l autore ha maturato il suo progetto. Non avrebbe molto senso, ad esempio, utilizzare la geometria frattale per studiare l architettura romana e spiegarne la forma. A questo proposito è illuminante un intervista di Alberto Arbasino a Borges. Il primo, raffinato poliglotta, chiese a Borges in 20
21 16. I rapporti armonici fondamentali della musica greca derivano da teorie matematiche di ambito pitagorico. Essi sono stati utilizzati da pittori ed architetti, specie un età rinascimentale, per dare le giuste proporzioni agli spazi ed agli impianti architettonici, nella convinzione che le stesse qualità dell armonia sonora fossero percepibili visivamente. che lingua avrebbe preferito condurre l intervista. Il maestro argentino rispose con naturalezza che non lo sapeva, perchè non sapeva di quale argomento avrebbero parlato. Se si fosse discusso di poesia avrebbe preferito l italiano. Per discettare di teologia senza dubbio avrebbe utilizzato il tedesco mentre avrebbe riservato la lingua inglese a questioni più immanenti. In altri termini avrebbe scelto, fra quelle che conosceva, la lingua più pertinente all oggetto da trattare, lo strumento più accordato alla realtà da descrivere. Anche se disponiamo di strumenti ben più modesti di quelli messi in campo da Borges, il suo approccio è probabilmente il più efficace quando si vuole praticare consapevolmente l analisi dell architettura. La pianta della casa Goldenberg di Louis Kahn 13 (figura 15), ad esempio, è più legata alla struttura del quadrato di quanto non sia possibile immaginare ad una prima lettura. Se studiamo i progetti di Kahn tenendo ben presente la sua grande passione per la geometria piana elementare, abbiamo la possibilità di mettere nel campo dell analisi gli strumenti più adeguati ad una corretta lettura critica. Se invece vogliamo approfondire la conoscenza dell architettura di Leon Battista Alberti 14 (figure 16 e 17), ad esempio, non possiamo non tenere conto che egli, come molti suoi contemporanei, fece 21
22 17. Schemi armonici basati sul quadrato nel prospetto della chiesa di Santa Maria Novella a Firenze, realizzata da Leon Battista Alberti tra il 1456 ed il I tracciati geometrici sottesi alla definizione della forma costituiscono una sorta di trama invisibile su cui si dipana l organizzazione plastica della facciata. largo uso dei rapporti armonici 15, cioè di speciali rapporti numerici di origine pitagorica che, fin dal periodo classico, furono applicati sia al campo dell architettura che della musica. Il maestro del Razionalismo svizzero Alberto Sartoris, alla metà degli anni Ottanta, ormai anziano, rilasciò una straordinaria intervista sul suo modo di disegnare, sulle sue tecniche di progetto, sugli strumenti che utilizzava 16. A proposito del compasso disse delle parole illuminanti: «Il compasso mi fu molto utile. La curva ha una grande importanza nella mia architettura». A ben vedere questa frase, apparentemente innocente, colloca con nettezza e precisione il ruolo della geometria e degli strumenti da disegno. Sartoris pone sulla stessa linea di mira il compasso, cioè lo strumento, la curva, cioè la forma geometrica, e l architettura, cioè la forma costruita. La relazione che si determina è di assoluta contiguità, le tre realtà sono strettamente interrelate e, a ben vedere, nella pratica del progetto esse sono in qualche modo sincroniche, quasi come se fossero la stessa medesima cosa. Gli strumenti da disegno hanno una potenza enorme nel guidare la nostra immaginazione. Ci serviamo di strumenti che consentono con semplicità di tracciare delle forme, e li scegliamo perchè ci aiu- 22
23 18. La copertura del piccolo ingresso della Staatsgalerie di Stoccarda progettata da James Stirling, segue esattamente l inclinazione della squadretta. Lo strumento ha in qualche modo suggerito al progettista una soluzione. Siamo sempre consapevoli del fatto che gli strumenti che utilizziamo influiscono sulle nostre scelte? tino a disegnare proprio quelle forme e non altre. L evoluzione degli strumenti da disegno ha una stretta relazione con il mutare della forma architettonica e, benché questa storia incrociata sia ancora tutta da scrivere, le vicende degli ultimi decenni ci mostrano quanto sia fitto questo legame. La diffusione dei programmi di CAD nel mondo dell architettura ha infatti aperto nuove possibilità di disegno che hanno rapidamente tracciato nuove strade per l immaginazione, consentendo la progettazione e la realizzazione di forme letteralmente impensabili anche solo venti anni fa. Ma questo meccanismo si svolge anche al livello più minuto. James Stirling, ad esempio, nel progettare la piccola pensilina dell ingresso alla Staatsgalerie di Stoccarda 17 (figura 18), ne ha inclinato le falde di 30. Certamente anche un inclinazione di 29 o 31 gradi sarebbe stata accettabile sia dal punto di vista tecnico che formale ma, come è ovvio che sia, l architetto ha scelto un inclinazione trovata sulla sua squadra da disegno, affidandosi docilmente, come avviene il più delle volte, alla soluzione proposta dal suo strumento. Ovviamente, quanto più potente e complesso è lo strumento, tanto più intricata ed indistinguibile è l influenza che esso ha sulla creatività. Un moderno software per il disegno architettonico fornisce una 23
24 19. Le Corbusier nella lettera che scrive nel 1925 ad una sua committente, M.me Mayer, mostra l esito del suo progetto disegnando una assonometria ed alcune prospettive. La complessità spaziale del progetto è tale che una serie di piante e di sezioni non sarebbero state in grado di rendere appieno la qualità dell edificio. Le Corbusier preferisce quindi disegnare otto prospettive, in sequenza, dipanando una sorta di racconto cinematografico del percorso all interno della casa. In generale, il tipo di rappresentazione che utilizziamo va adeguato alle caratteristiche dell architettura che disegnamo. Operando in modo inconsapevole e casuale, rischiamo di non riuscire a comunicare la forma dell architettura. gamma sterminata di strumenti grafici innovativi, che talvolta non hanno un diretto corrispettivo nelle funzioni offerte dagli strumenti da disegno tradizionali. Generalmente si associa l analisi grafica alla ricerca ed al ridisegno delle geometrie sottese alla forma dell architettura. Gli schemi che si ottengono, che talvolta hanno un evidenza immediata ed una straordinaria capacità comunicativa, vengono sovrapposti a piante, prospetti o sezioni del progetto studiato. In alcuni casi fortunati si arriva a mostrare come a partire da geometrie elementari sapientemente com- 24
25 20. Una delle tavole tratte dal volume di August Choisy L art de batir chez les Romains, del L uso del assonometria militare dal basso si rivela in questo caso perfettamente adatta a mostrare contemporaneamente la pianta, lo spazio interno e la struttura dell architettura. La scelta opportuna del metodo di rappresentazione e della direzione di proiezione è un aspetto fondamentale della rappresentazione dell architettura ed in nessun caso può essere sottovalutato. binate si ottengano coerentemente forme complesse. In questi casi, gli esiti dell analisi grafica mostrano strette analogie con i disegni di progetto originali, nei quali talvolta si vede emergere la forma dal reticolo di linee determinato dalla trama geometrica che regge la pianta o il prospetto. Questo, però, non è l unico modo di affrontare l analisi grafica. Ciascun metodo di rappresentazione, a ben vedere, costituisce un modo fortemente orientato e parziale di descrivere un oggetto. Quello che una pianta racconta è profondamente diverso da quello che può comunicare una sezione. Un assonometria ed una prospettiva della stessa architettura ne mostrano aspetti molto diversi. Nella straordinaria lettera a madame Mayer di Le Corbusier 18 (figura 19), nella quale l architetto simula una passeggiata virtuale all interno della villa progettata, si trovano quasi soltanto prospettive a tratto lineare, acute ed efficaci. Probabilmente questo era il modo più adatto di analizzare e di mostrare l organizzazione spaziale dei volumi dell edificio utilizzando uno sguardo in soggettiva. D altra parte, ad esempio, le celebri assonometrie di Choisy 19 (figura 20) puntual- 25
26 21. Un immagine tratta dal taccuino duecentesco di Villard de Honnecourt. In parecchi casi gli schemi geometrici che Villard sovrappone alle immagini di animali appaiono del tutto insufficienti ad interpretarne la forma e ne forzano visibilmente la figura. Non sempre gli schemi più semplici sono adatti a descrivere fenomeni complessi. mente descrivono al contempo spazi e strutture dell architettura, specie nel caso di assonometrie iposcopiche. A seconda del tipo di analisi che si vuole condurre, si possono (e si devono!) scegliere modi diversi di rappresentare, quindi diverse maniere di esaltare o sottacere degli aspetti dell oggetto rappresentato. Occorre compiere delle scelte sul modo di raccontare un architettura che siano coerenti con le nostre intenzioni. Adottare un metodo di rappresentazione è come scegliere una lingua precisa. Significa trovarsi nella situazione di obbligo cui si riferisce Barthes, cioè scegliere una lingua la cui struttura influenza il nostro racconto in una precisa direzione. Per questo dobbiamo usare un metodo di rappresentazione che sia pertinente rispetto a quello che desideriamo mostrare. Dobbiamo scegliere la lingua più adatta, proprio come diceva Borges ad Arbasino. Molto spesso l analisi e la descrizione delle architetture si rifanno al criterio di massima semplicità. Più una descrizione, un modello di riferimento, una geometria di generazione appare semplice, immediata, lineare, più si è tentati di considerare questa rappresentazione come quella corretta. Purtroppo le cose non funzionano sempre così. Spesso troviamo delle regole semplici per interpretare le forme 26
27 22. I poliedri regolari. Sono soltanto cinque ed hanno per facce poligoni regolari. Sono il tetraedro, l esaedro (o cubo), l ottaedro, il dodecaedro e l icosaedro. Noti fin dall antichità, sono studiati nell ultimo libro degli Elementi di Euclide. Per la loro impenetrabile bellezza, in molti periodi della Storia, sono stati caricati di valori simbolici. perchè queste regole sono quelle che conosciamo meglio, che applichiamo con maggiore assiduità e su cui abbiamo basato la nostra formazione. Dobbiamo fare continuamente attenzione al modo in cui applichiamo gli strumenti dell analisi grafica. Come si è visto, i modelli che utilizziamo per descrivere la realtà influenzano in modo determinante il nostro modo di vedere. Talvolta la scelta di uno di essi forza così tanto la lettura delle cose da portare sia a travisamenti che addirittura ad errori paradossali. Tra i disegni del taccuino di Villard De Honnecourt 20, si trovano parecchie figure di animali (figura 21). Ad alcune di esse Villard sovrappone delle figure geometriche elementari, interpretando le forme naturali con l ausilio del linguaggio geometrico. Se in alcuni casi le geometrie descrivono con buona approssimazione animali e volti umani, in altri casi la sovrapposizione appare forzata, eccessiva ed inconcludente. La perfezione geometrica e la sua intrinseca semplicità, hanno - per così dire - un tale potere seduttivo anche sulle menti più brillanti, che talvolta pare che il desiderio di utilizzare la geometria come modello analitico possa addirittura offuscare le capacità di giudizio. Si veda il caso dei cinque poliedri regolari 21 (figura 22). In gioventù 27
28 23. Un immagine che mostra l ipotesi formulata da Keplero sulla distribuzione dei pianeti lungo circonferenze che appartengono a sfere inscritte e circoscritte ai poliedri regolari. Ovviamente questa ipotesi è del tutto priva di fondamento e non ha alcun valore scientifico, ma mostra con chiarezza quanto possa essere attraente un modello interpretativo della realtà basato su semplici considerazioni geometriche. Purtroppo la chiarezza e l eleganza di un ipotesi non ne garantiscono la veridicità. Keplero suggerì che la posizione reciproca dei pianeti del sistema solare potesse essere dettata dalla loro disposizione lungo le circonferenze massime di sei sfere concentriche, inscritte e circoscritte a dei solidi regolari di misura diversa 22. Anzi, a dire il vero, non solo avanzò l ipotesi, ma lo fece dicendo che avrebbe «dimostrato che Dio, nel creare l universo, aveva in mente i solidi regolari». Ovviamente l ipotesi del giovane Keplero era terribilmente azzardata e fuori di logica. Tra l altro il numero delle sfere celesti così ottenute non era uguale a quello dei pianeti allora conosciuti (figura 23). In questo caso emblematico il modello geometrico utilizzato per spiegare la realtà appariva talmente perfetto e convincente da ammaliare l intelletto perfino di un uomo come Keplero. Per inciso va detto che pochi anni dopo Keplero avrebbe seguito molto da vicino Tycho Brahe, il quale aveva raccolto una immensa quantità di dati desunti da attente osservazioni, che permisero a Keplero di formulare ipotesi scientifiche, seppure più complesse, di ben altra fondatezza. 28
29 24. Un immagine wireframe del progetto del museo Guggenheim di Bibao, di Frank O Gehry. I volumi non sono dei solidi semplici, parallelepipedi, prismi o porzioni di sfera, ma piuttosto dei corpi complessi, modellati, tra l altro, con l ausilio di potenti softwares. A quali risultati si può giungere se si cerca di interpretare questa architettura con gli strumenti della geometria elementare? Non sono forse necessari altri, più accordati strumenti di indagine? I solidi regolari sono presi in considerazione anche nel Timeo di Platone 23, e per questo motivo sono detti anche solidi platonici. A ciascuno di essi Platone accoppia un elemento della natura, la terra all esaedro, il fuoco al tetraedro, l acqua all ottaedro ed infine l aria all icosaedro. Dato che i solidi sono cinque e gli elementi soltanto quattro, al dodecaedro Platone associa una quinta essenza che non definisce compiutamente ma la cui esistenza è in qualche modo provata dall esistenza del quinto solido regolare. In altri termini, in questo caso, come anche nell ipotesi di Keplero, è il modello utilizzato per descrivere i fenomeni ad imporre dei ripensamenti sulla realtà. La tentazione di applicare un modello di analisi semplice ed apparentemente perfetto può portare a grandi confusioni nell esame della realtà. Se questi errori (o sviste) celebri sono state operati da menti di grande statura, noi, a maggior ragione, nello scegliere ed utilizzare i nostri schemi di analisi, nella comune pratica di studio dobbiamo impedire che le nostre ipotesi, benché eleganti, ci porti- 29
30 no a travisare la realtà in modo grossolano. La ricerca dei metodi da utilizzare nello studio di una specifica architettura quindi va compiuta con attenzione, nel tentativo di dotarci e servirci di uno strumento pertinente adatto al nostro scopo. La semplicità, talvolta, non è un criterio di scelta sufficiente. Come potremmo, con la geometria solida elementare e con le sole proiezioni ortogonali, descrivere compiutamente e comprendere a fondo ad esempio le forme delle architetture di Frank Gehry 24 (figura 24) o di Zaha Hadid? In definitiva l analisi grafica non prevede un procedimento univoco. I nostri modi di operare vanno selezionati in relazione all oggetto da studiare, basandoci sulla nostra cultura, la nostra esperienza ed eventualmente sul nostro intuito. L analisi grafica non si fonda su un percorso deduttivo, ma piuttosto ci obbliga ad usare i nostri strumenti spingendoci talvolta alla ricerca di regole inedite. Come si è detto, non è possibile sfuggire al condizionamento che i nostri schemi mentali ci impongono, perché è soltanto attraverso l uso che di essi facciamo che riusciamo a leggere ed organizzare la nostra esperienza della realtà. Ma rispetto a questa costrizione abbiamo un vantaggio, sappiamo che essa opera in noi continuamente e quindi possiamo esercitare la nostra libertà decidendo di guidare consapevolmente la nostra formazione. Sappiamo che ciò che studiamo ci influenza, ma possiamo scegliere liberamente cosa studiare, dotandoci, seppure lentamente, di strumenti articolati e sensibili, integrati con i nostri interessi. La scelta dei modi dell analisi è frutto di esperienza e di competenza e la sua qualità coincide senza mediazioni col nostro percorso formativo, con le nostre passioni, con le nostre capacità, affinandosi continuamente, in un percorso dialettico, senza fine. 30
31 Note 1 J. L. Borges, Del rigore nella scienza, in idem, L Artefice, Milano 1999, pp W. Wenders, L atto di vedere, Milano W. Wenders, Fino alla fine del Mondo, film, B. Lee Whorf, Linguaggio, pensiero e realtà, Torino 1977, pp R. Barthes, Lezione, Torino 1981, p G. Orwell, 1984, Milano 1973, pp J. Genet, Le serve, Milano AA. VV., Richard Long, catalogo (Roma 1994), Milano M. Vitruvio Pollione, De Architectura, Studio Tesi, Pordenone 1992, p S. Kubrick, 2001: Odissea nello spazio, film, A. C. Clarke, 2001: Odissea nello spazio, Milano 2008 (titolo originale: The Sentinel, 1948). 10 V. Ugo, Fondamenti della rappresentazione architettonica, Bologna 1994, pp J. Sedlmayr, J. B. Fischer von Erlach architetto, Milano 1996, p Le Corbusier, Il Modulor, Milano D. B. Brownlee, D. G. De Long, Louis Kahn: In the Realm of Architecture, New York 1991, p Su questi temi si veda il volume fondamentale di R. Wittkower, Principi architettonici nell età dell umanesimo, Torino Per una sintesi sul tema dei rapporti armonici, cfr. E. Dotto, Il disegno degli ovali armonici, Catania AA. VV., Alberto Sartoris. Opere , a cura di M. Cometa, Cefalù 1987, p J. Stirling, M. Wilford and Associates, La nuova Galleria di Stato a Stoccarda, a cura di M. Zardini, supplemento a «Casabella» n. 516, Milano, Settembre W. Boesiger, H. Girsberger, Le Corbusier , Bologna 1987, pp A. Choisy, L art de batir chez les Romains, Paris A. Erlande-Brandenbourg, R. Pernoud, J. Gimpel, R. Bechmann, Villard de Honnecourt. Disegni, Milano Sui poliedri regolari esistono parecchi studi di grande interesse. Tra i più adatti ad esplorare l argomento si segnala: M. Emmer, La perfezione visibile, Roma- Napoli W. R. Shea, La rivoluzione scientifica, in AA. VV., Storia delle scienze. Le scienze fisiche ed astronomiche, Torino 1992, p Platone, Timeo, a cura di G. Reale, Milano 1984, pp Frank O Gehry , numero monografico di «El croquis», n , Barcellona 1995, pp
32 Finito di stampare nel mese di dicembre 2009 presso la tipografia ZetaPrinting, Palermo.
Che cos è l intelligenza e come funzionano i test del Q.I.
 Che cos è l intelligenza e come funzionano i test del Q.I. Non esiste, al giorno d oggi, un parere unanime della comunità scientifica sulla definizione di intelligenza. In generale, potremmo dire che è
Che cos è l intelligenza e come funzionano i test del Q.I. Non esiste, al giorno d oggi, un parere unanime della comunità scientifica sulla definizione di intelligenza. In generale, potremmo dire che è
I libri di testo. Carlo Tarsitani
 I libri di testo Carlo Tarsitani Premessa Per accedere ai contenuti del sapere scientifico, ai vari livelli di istruzione, si usa comunemente anche un libro di testo. A partire dalla scuola primaria, tutti
I libri di testo Carlo Tarsitani Premessa Per accedere ai contenuti del sapere scientifico, ai vari livelli di istruzione, si usa comunemente anche un libro di testo. A partire dalla scuola primaria, tutti
I CAMPI DI ESPERIENZA
 I CAMPI DI ESPERIENZA IL SE E L ALTRO sviluppa il senso dell identità personale; riconosce ed esprime sentimenti e emozioni; conosce le tradizioni della famiglia, della comunità e della scuola, sviluppando
I CAMPI DI ESPERIENZA IL SE E L ALTRO sviluppa il senso dell identità personale; riconosce ed esprime sentimenti e emozioni; conosce le tradizioni della famiglia, della comunità e della scuola, sviluppando
Alla ricerca dell algoritmo. Scoprire e formalizzare algoritmi.
 PROGETTO SeT Il ciclo dell informazione Alla ricerca dell algoritmo. Scoprire e formalizzare algoritmi. Scuola media Istituto comprensivo di Fagagna (Udine) Insegnanti referenti: Guerra Annalja, Gianquinto
PROGETTO SeT Il ciclo dell informazione Alla ricerca dell algoritmo. Scoprire e formalizzare algoritmi. Scuola media Istituto comprensivo di Fagagna (Udine) Insegnanti referenti: Guerra Annalja, Gianquinto
Qui cade sua altezza
 Qui cade sua altezza Silvia Sbaragli N.R.D. Bologna DFA, SUPSI Locarno (Svizzera) Pubblicato in: Sbaragli S. (2010). Qui cade sua altezza. La Vita Scolastica. 18, 25-27. Nell insegnamento della matematica
Qui cade sua altezza Silvia Sbaragli N.R.D. Bologna DFA, SUPSI Locarno (Svizzera) Pubblicato in: Sbaragli S. (2010). Qui cade sua altezza. La Vita Scolastica. 18, 25-27. Nell insegnamento della matematica
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
ESERCITAZIONE OSSERVARE UN ALBERO
 L esercizio richiesto consiste nella scelta di un albero e il suo monitoraggio/racconto al fine di sviluppare l osservazione attenta come mezzo per la conoscenza del materiale vegetale. L esercitazione
L esercizio richiesto consiste nella scelta di un albero e il suo monitoraggio/racconto al fine di sviluppare l osservazione attenta come mezzo per la conoscenza del materiale vegetale. L esercitazione
CERTIFICAZIONE DELLE COMPETENZE ITALIANO
 CERTIFICAZIONE DELLE COMPETENZE ITALIANO Livello di base non raggiunto Non ha raggiunto tutte le competenze minime previste nel livello di base Riconosce ed utilizza le strutture linguistiche di base Comprende
CERTIFICAZIONE DELLE COMPETENZE ITALIANO Livello di base non raggiunto Non ha raggiunto tutte le competenze minime previste nel livello di base Riconosce ed utilizza le strutture linguistiche di base Comprende
Project Cycle Management
 Project Cycle Management Tre momenti centrali della fase di analisi: analisi dei problemi, analisi degli obiettivi e identificazione degli ambiti di intervento Il presente materiale didattico costituisce
Project Cycle Management Tre momenti centrali della fase di analisi: analisi dei problemi, analisi degli obiettivi e identificazione degli ambiti di intervento Il presente materiale didattico costituisce
MIND FITNESS STRETCH YOUR BRAIN WITH ART. MIND FITNESS 09 07 2015 Milano
 MIND FITNESS STRETCH YOUR BRAIN WITH ART DI FRONTE ALL OPERA D ARTE IMPARARE A LEGGERE UN SISTEMA COMPLESSO L arte contemporanea ci pone problemi inaspettati. Quando entriamo in un museo o in una galleria,
MIND FITNESS STRETCH YOUR BRAIN WITH ART DI FRONTE ALL OPERA D ARTE IMPARARE A LEGGERE UN SISTEMA COMPLESSO L arte contemporanea ci pone problemi inaspettati. Quando entriamo in un museo o in una galleria,
PROGETTO ACCOGLIENZA Classi prime Anno scolastico 2012/2013
 SCUOLA SECONDARIA DI PRIMO GRADO SIMONE DA CORBETTA PROGETTO ACCOGLIENZA Classi prime Anno scolastico 2012/2013 1 Introduzione Il progetto accoglienza nasce dalla convinzione che i primi mesi di lavoro
SCUOLA SECONDARIA DI PRIMO GRADO SIMONE DA CORBETTA PROGETTO ACCOGLIENZA Classi prime Anno scolastico 2012/2013 1 Introduzione Il progetto accoglienza nasce dalla convinzione che i primi mesi di lavoro
Corso di Laurea in Scienze della Formazione Primaria Università di Genova MATEMATICA Il
 Lezione 5:10 Marzo 2003 SPAZIO E GEOMETRIA VERBALE (a cura di Elisabetta Contardo e Elisabetta Pronsati) Esercitazione su F5.1 P: sarebbe ottimale a livello di scuola dell obbligo, fornire dei concetti
Lezione 5:10 Marzo 2003 SPAZIO E GEOMETRIA VERBALE (a cura di Elisabetta Contardo e Elisabetta Pronsati) Esercitazione su F5.1 P: sarebbe ottimale a livello di scuola dell obbligo, fornire dei concetti
Chiara Strada IMMAGINI SONORE LAVORO CON LISA
 Chiara Strada IMMAGINI SONORE LAVORO CON LISA Questo allegato si riferisce al precedente materiale della serie Tasti & Testi, intitolato Immagini Sonore, pubblicato a settembre come primo di quest anno
Chiara Strada IMMAGINI SONORE LAVORO CON LISA Questo allegato si riferisce al precedente materiale della serie Tasti & Testi, intitolato Immagini Sonore, pubblicato a settembre come primo di quest anno
SCUOLA PRIMARIA SCIENZE NATURALI E SPERIMENTALI. Competenza: 1. Comunicazione efficace Indicatore: 1.1 Comprensione
 SCUOLA PRIMARIA SCIENZE NATURALI E SPERIMENTALI Competenza: 1. Comunicazione efficace Indicatore: 1.1 Comprensione Descrittori Classe 1 Descrittori Classe 2 Descrittori Classe 3 Descrittori Classe 4 Descrittori
SCUOLA PRIMARIA SCIENZE NATURALI E SPERIMENTALI Competenza: 1. Comunicazione efficace Indicatore: 1.1 Comprensione Descrittori Classe 1 Descrittori Classe 2 Descrittori Classe 3 Descrittori Classe 4 Descrittori
La ricerca empirica in educazione
 La ricerca empirica in educazione Alberto Fornasari Docente di Pedagogia Sperimentale Dipartimento di Scienze della Formazione, Psicologia, Comunicazione Il ricercatore ha il compito di trovare relazioni
La ricerca empirica in educazione Alberto Fornasari Docente di Pedagogia Sperimentale Dipartimento di Scienze della Formazione, Psicologia, Comunicazione Il ricercatore ha il compito di trovare relazioni
Lezione n 2 L educazione come atto ermeneutico (2)
 Lezione n 2 L educazione come atto ermeneutico (2) Riprendiamo l analisi interrotta nel corso della precedente lezione b) struttura dialogica del fatto educativo Per rispondere a criteri ermenutici, l
Lezione n 2 L educazione come atto ermeneutico (2) Riprendiamo l analisi interrotta nel corso della precedente lezione b) struttura dialogica del fatto educativo Per rispondere a criteri ermenutici, l
Da dove nasce l idea dei video
 Da dove nasce l idea dei video Per anni abbiamo incontrato i potenziali clienti presso le loro sedi, come la tradizione commerciale vuole. L incontro nasce con una telefonata che il consulente fa a chi
Da dove nasce l idea dei video Per anni abbiamo incontrato i potenziali clienti presso le loro sedi, come la tradizione commerciale vuole. L incontro nasce con una telefonata che il consulente fa a chi
IMMAGINANDO QUELLO CHE NON SI VEDE
 Laboratorio in classe: tra forme e numeri GRUPPO FRAZIONI - CLASSI SECONDE DELLA SCUOLA PRIMARIA Docenti: Lidia Abate, Anna Maria Radaelli, Loredana Raffa. IMMAGINANDO QUELLO CHE NON SI VEDE 1. UNA FIABA
Laboratorio in classe: tra forme e numeri GRUPPO FRAZIONI - CLASSI SECONDE DELLA SCUOLA PRIMARIA Docenti: Lidia Abate, Anna Maria Radaelli, Loredana Raffa. IMMAGINANDO QUELLO CHE NON SI VEDE 1. UNA FIABA
PROMUOVERSI MEDIANTE INTERNET di Riccardo Polesel. 1. Promuovere il vostro business: scrivere e gestire i contenuti online» 15
 Indice Introduzione pag. 9 Ringraziamenti» 13 1. Promuovere il vostro business: scrivere e gestire i contenuti online» 15 1. I contenuti curati, interessanti e utili aiutano il business» 15 2. Le aziende
Indice Introduzione pag. 9 Ringraziamenti» 13 1. Promuovere il vostro business: scrivere e gestire i contenuti online» 15 1. I contenuti curati, interessanti e utili aiutano il business» 15 2. Le aziende
TEST DI ORIENTAMENTO PER LA SCELTA DELLA SCUOLA SUPERIORE
 TEST DI ORIENTAMENTO PER LA SCELTA DELLA SCUOLA SUPERIORE Scuola Italia via Italia n 10 - Roma studente Francesco M. classe III A N.B. Ricorda che quanto leggerai è totalmente riservato, vincolato dal
TEST DI ORIENTAMENTO PER LA SCELTA DELLA SCUOLA SUPERIORE Scuola Italia via Italia n 10 - Roma studente Francesco M. classe III A N.B. Ricorda che quanto leggerai è totalmente riservato, vincolato dal
LA GRAFICA E LA GEOMETRIA OPERATIVA
 LA GRAFICA E LA GEOMETRIA OPERATIVA La geometria operativa, contrariamente a quella descrittiva basata sulle regole per la rappresentazione delle forme geometriche, prende in considerazione lo spazio racchiuso
LA GRAFICA E LA GEOMETRIA OPERATIVA La geometria operativa, contrariamente a quella descrittiva basata sulle regole per la rappresentazione delle forme geometriche, prende in considerazione lo spazio racchiuso
Anno 2004/2005 CORSO SNES-CSI PER FORMATORI. Bologna, 3 dicembre 2005. Lara Rossin
 Anno 2004/2005 LA FIGURA DEL FORMATORE CSI -LE SUE PECULIARITÀ E LA SUA MISSION- CORSO SNES-CSI PER FORMATORI Bologna, 3 dicembre 2005 Lara Rossin 1 INTRODUZIONE Non si insegna e non si può insegnare,
Anno 2004/2005 LA FIGURA DEL FORMATORE CSI -LE SUE PECULIARITÀ E LA SUA MISSION- CORSO SNES-CSI PER FORMATORI Bologna, 3 dicembre 2005 Lara Rossin 1 INTRODUZIONE Non si insegna e non si può insegnare,
Appunti sulla Macchina di Turing. Macchina di Turing
 Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
FINESTRE INTERCULTURALI
 Scuola Classe 1C FINESTRE INTERCULTURALI DIARIO DI BORDO 2013 / 2014 IC Gandhi - Secondaria di primo grado Paolo Uccello Insegnante / materia Anelia Cassai/lettere Data Febbraio Durata 4h TITOLO DELLA
Scuola Classe 1C FINESTRE INTERCULTURALI DIARIO DI BORDO 2013 / 2014 IC Gandhi - Secondaria di primo grado Paolo Uccello Insegnante / materia Anelia Cassai/lettere Data Febbraio Durata 4h TITOLO DELLA
FINESTRE INTERCULTURALI
 Scuola Classe 1C FINESTRE INTERCULTURALI DIARIO DI BORDO 2013 / 2014 IC Gandhi - Secondaria di primo grado Paolo Uccello Insegnante / materia lettere Data Febbraio Durata 4h TITOLO DELLA FINESTRA INTERCULTURALE
Scuola Classe 1C FINESTRE INTERCULTURALI DIARIO DI BORDO 2013 / 2014 IC Gandhi - Secondaria di primo grado Paolo Uccello Insegnante / materia lettere Data Febbraio Durata 4h TITOLO DELLA FINESTRA INTERCULTURALE
UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA
 UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA Tutti gli anni, affrontando l argomento della divisibilità, trovavo utile far lavorare gli alunni sul Crivello di Eratostene. Presentavo ai ragazzi una
UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA Tutti gli anni, affrontando l argomento della divisibilità, trovavo utile far lavorare gli alunni sul Crivello di Eratostene. Presentavo ai ragazzi una
LA MOLTIPLICAZIONE IN CLASSE SECONDA
 LA MOLTIPLICAZIONE IN CLASSE SECONDA Rossana Nencini, 2013 Le fasi del lavoro: 1. Proponiamo ai bambini una situazione reale di moltiplicazione: portiamo a scuola una scatola di biscotti (. ) e diamo la
LA MOLTIPLICAZIONE IN CLASSE SECONDA Rossana Nencini, 2013 Le fasi del lavoro: 1. Proponiamo ai bambini una situazione reale di moltiplicazione: portiamo a scuola una scatola di biscotti (. ) e diamo la
II.f. Altre attività sull euro
 Altre attività sull euro II.f È consigliabile costruire modelli in carta o cartoncino di monete e banconote, e farli usare ai bambini in varie attività di classe fin dal primo o al più dal secondo anno.
Altre attività sull euro II.f È consigliabile costruire modelli in carta o cartoncino di monete e banconote, e farli usare ai bambini in varie attività di classe fin dal primo o al più dal secondo anno.
Le funzioni continue. A. Pisani Liceo Classico Dante Alighieri A.S. 2002-03. A. Pisani, appunti di Matematica 1
 Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
CIRCOLO DIDATTICO DI SAN MARINO Anno Scolastico 2013/2014
 CIRCOLO DIDATTICO DI SAN MARINO Anno Scolastico 2013/2014 RICERCA-AZIONE Insegnare per competenze: Lo sviluppo dei processi cognitivi Scuola Elementare Fiorentino DESCRIZIONE DELL ESPERIENZA Docente: Rosa
CIRCOLO DIDATTICO DI SAN MARINO Anno Scolastico 2013/2014 RICERCA-AZIONE Insegnare per competenze: Lo sviluppo dei processi cognitivi Scuola Elementare Fiorentino DESCRIZIONE DELL ESPERIENZA Docente: Rosa
Tesina per il corso di Psicotecnologie dell apprendimento per l integrazione delle disabilità
 Tesina per il corso di Psicotecnologie dell apprendimento per l integrazione delle disabilità ANALISI DEL TITOLO Per prima cosa cercheremo di analizzare e capire insieme il senso del titolo di questo lavoro:
Tesina per il corso di Psicotecnologie dell apprendimento per l integrazione delle disabilità ANALISI DEL TITOLO Per prima cosa cercheremo di analizzare e capire insieme il senso del titolo di questo lavoro:
Modulo didattico sulla misura di grandezze fisiche: la lunghezza
 Modulo didattico sulla misura di grandezze fisiche: la lunghezza Lezione 1: Cosa significa confrontare due lunghezze? Attività n 1 DOMANDA N 1 : Nel vostro gruppo qual è la matita più lunga? DOMANDA N
Modulo didattico sulla misura di grandezze fisiche: la lunghezza Lezione 1: Cosa significa confrontare due lunghezze? Attività n 1 DOMANDA N 1 : Nel vostro gruppo qual è la matita più lunga? DOMANDA N
CONSIGLI PER POTENZIARE L APPRENDIMENTO DELLA LINGUA
 CONSIGLI PER POTENZIARE L APPRENDIMENTO DELLA LINGUA Possiamo descrivere le strategie di apprendimento di una lingua straniera come traguardi che uno studente si pone per misurare i progressi nell apprendimento
CONSIGLI PER POTENZIARE L APPRENDIMENTO DELLA LINGUA Possiamo descrivere le strategie di apprendimento di una lingua straniera come traguardi che uno studente si pone per misurare i progressi nell apprendimento
Roberto Farnè Università di Bologna
 Roberto Farnè Università di Bologna Ora l apertura della parte scientifica a questi lavori, per capire innanzitutto il senso di questo appuntamento. Non abbiamo bisogno, nessuno di noi credo abbia bisogno
Roberto Farnè Università di Bologna Ora l apertura della parte scientifica a questi lavori, per capire innanzitutto il senso di questo appuntamento. Non abbiamo bisogno, nessuno di noi credo abbia bisogno
La valutazione nella didattica per competenze
 Nella scuola italiana il problema della valutazione delle competenze è particolarmente complesso, infatti la nostra scuola è tradizionalmente basata sulla trasmissione di saperi e saper fare ed ha affrontato
Nella scuola italiana il problema della valutazione delle competenze è particolarmente complesso, infatti la nostra scuola è tradizionalmente basata sulla trasmissione di saperi e saper fare ed ha affrontato
DIMENSIONI CRITERI INDICATORI
 Allegato 4 - Manerbio META EDUCATIVA: autonomia in ambito scolastico (classe 4/5 scuola primaria) DIMENSIONI CRITERI INDICATORI GESTIONALE OPERATIVA Uso degli strumenti Conoscere gli strumenti necessari
Allegato 4 - Manerbio META EDUCATIVA: autonomia in ambito scolastico (classe 4/5 scuola primaria) DIMENSIONI CRITERI INDICATORI GESTIONALE OPERATIVA Uso degli strumenti Conoscere gli strumenti necessari
IL CORPO, LA MENTE, LA COMUNICAZIONE
 IL CORPO, LA MENTE, LA COMUNICAZIONE. Sai che cosa è la propriocezione? SI SENTIRE TUTTE LE PARTI DEL PROPRIO CORPO IN TESTA. Quindi essere padrone delle singole parti del proprio corpo in ogni momento
IL CORPO, LA MENTE, LA COMUNICAZIONE. Sai che cosa è la propriocezione? SI SENTIRE TUTTE LE PARTI DEL PROPRIO CORPO IN TESTA. Quindi essere padrone delle singole parti del proprio corpo in ogni momento
63 7. Quale geometria per la computer grafica? 75 8. L omografia e l affinità nella digitalizzazione e georeferenziazione
 Indice 7 Presentazione 9 Premessa 11 Introduzione 13 1. Rilevamento ed oggetto 19 2. La stazione totale 23 3. La procedura generale 33 4. Dai punti al modello tridimensionale 45 5. Il modello tridimensionale
Indice 7 Presentazione 9 Premessa 11 Introduzione 13 1. Rilevamento ed oggetto 19 2. La stazione totale 23 3. La procedura generale 33 4. Dai punti al modello tridimensionale 45 5. Il modello tridimensionale
IDEE PER LO STUDIO DELLA MATEMATICA
 IDEE PER LO STUDIO DELLA MATEMATICA A cura del 1 LA MATEMATICA: perché studiarla??? La matematica non è una disciplina fine a se stessa poichè fornisce strumenti importanti e utili in molti settori della
IDEE PER LO STUDIO DELLA MATEMATICA A cura del 1 LA MATEMATICA: perché studiarla??? La matematica non è una disciplina fine a se stessa poichè fornisce strumenti importanti e utili in molti settori della
GIOCHI MATEMATICI PER LA SCUOLA SECONDARIA DI I GRADO ANNO SCOLASTICO 2011-2012
 GIOCHI MATEMATICI PER LA SCUOLA SECONDARIA DI I GRADO ANNO SCOLASTICO 2011-2012 L unità di Milano Città Studi del Centro matematita propone anche per l a.s. 2011-2012 una serie di problemi pensati per
GIOCHI MATEMATICI PER LA SCUOLA SECONDARIA DI I GRADO ANNO SCOLASTICO 2011-2012 L unità di Milano Città Studi del Centro matematita propone anche per l a.s. 2011-2012 una serie di problemi pensati per
Come valutare le caratteristiche aerobiche di ogni singolo atleta sul campo
 Come valutare le caratteristiche aerobiche di ogni singolo atleta sul campo Prima di organizzare un programma di allenamento al fine di elevare il livello di prestazione, è necessario valutare le capacità
Come valutare le caratteristiche aerobiche di ogni singolo atleta sul campo Prima di organizzare un programma di allenamento al fine di elevare il livello di prestazione, è necessario valutare le capacità
IL MANAGER COACH: MODA O REQUISITO DI EFFICACIA. Nelle organizzazioni la gestione e lo sviluppo dei collaboratori hanno una importanza fondamentale.
 IL MANAGER COACH: MODA O REQUISITO DI EFFICACIA Nelle organizzazioni la gestione e lo sviluppo dei collaboratori hanno una importanza fondamentale. Gestione e sviluppo richiedono oggi comportamenti diversi
IL MANAGER COACH: MODA O REQUISITO DI EFFICACIA Nelle organizzazioni la gestione e lo sviluppo dei collaboratori hanno una importanza fondamentale. Gestione e sviluppo richiedono oggi comportamenti diversi
Strategie e metodi per un apprendimento efficace
 Strategie e metodi per un apprendimento efficace In più di 100 anni, gli psicologi cognitivi dell apprendimento hanno sviluppato parecchie tecniche di studio: alcune accelerano l apprendimento, altre invece
Strategie e metodi per un apprendimento efficace In più di 100 anni, gli psicologi cognitivi dell apprendimento hanno sviluppato parecchie tecniche di studio: alcune accelerano l apprendimento, altre invece
IL PAESE QUATRICERCHIO
 Scuola dell infanzia di Santa Maria in Punta UNITÀ DI APPRENDIMENTO: IL PAESE QUATRICERCHIO UN MONDO DI FORME(prima parte) Comprendente: UDA CONSEGNA AGLI STUDENTI PIANO DI LAVORO GRIGLIA DI OSSERVAZIONE/RUBRICA
Scuola dell infanzia di Santa Maria in Punta UNITÀ DI APPRENDIMENTO: IL PAESE QUATRICERCHIO UN MONDO DI FORME(prima parte) Comprendente: UDA CONSEGNA AGLI STUDENTI PIANO DI LAVORO GRIGLIA DI OSSERVAZIONE/RUBRICA
Indice. 1 Il monitoraggio del progetto formativo --------------------------------------------------------------- 3. 2 di 6
 LEZIONE MONITORARE UN PROGETTO FORMATIVO. UNA TABELLA PROF. NICOLA PAPARELLA Indice 1 Il monitoraggio del progetto formativo --------------------------------------------------------------- 3 2 di 6 1 Il
LEZIONE MONITORARE UN PROGETTO FORMATIVO. UNA TABELLA PROF. NICOLA PAPARELLA Indice 1 Il monitoraggio del progetto formativo --------------------------------------------------------------- 3 2 di 6 1 Il
SCHEDA M MOSAICI CLASSIFICARE CON LA SIMMETRIA
 SCHEDA M MOSAICI CLASSIFICARE CON LA SIMMETRIA Qui sotto avete una griglia, che rappresenta una normale quadrettatura, come quella dei quaderni a quadretti; nelle attività che seguono dovrete immaginare
SCHEDA M MOSAICI CLASSIFICARE CON LA SIMMETRIA Qui sotto avete una griglia, che rappresenta una normale quadrettatura, come quella dei quaderni a quadretti; nelle attività che seguono dovrete immaginare
PROGETTAZIONE DISCIPLINARE DI DIPARTIMENTO
 Progettazione disciplinare di dipartimento Pag. 1 di 5 ANNO SCOLASTICO 2013-2014 PROGETTAZIONE DISCIPLINARE DI DIPARTIMENTO TECNOLOGIA classe prima FINALITA OBIETTIVI GENERALI Le finalità educative (obiettivi
Progettazione disciplinare di dipartimento Pag. 1 di 5 ANNO SCOLASTICO 2013-2014 PROGETTAZIONE DISCIPLINARE DI DIPARTIMENTO TECNOLOGIA classe prima FINALITA OBIETTIVI GENERALI Le finalità educative (obiettivi
Attività destinata a raccogliere e a catalogare documenti con l'obiettivo di farli conoscere e diffonderli.
 DOCUMENTAZIONE Attività destinata a raccogliere e a catalogare documenti con l'obiettivo di farli conoscere e diffonderli. Attività di elaborazione, raccolta, organizzazione e diffusione di documenti.
DOCUMENTAZIONE Attività destinata a raccogliere e a catalogare documenti con l'obiettivo di farli conoscere e diffonderli. Attività di elaborazione, raccolta, organizzazione e diffusione di documenti.
O P E N S O U R C E M A N A G E M E N T PILLOLE DI TEST COMPRENSIONE. w w w. o s m v a l u e. c o m
 O P E N S O U R C E M A N A G E M E N T PILLOLE DI TEST COMPRENSIONE w w w. o s m v a l u e. c o m COMPRENSIONE (RELAZIONI) Qualità generale delle relazioni. Capacità della persona di costruirsi relazioni
O P E N S O U R C E M A N A G E M E N T PILLOLE DI TEST COMPRENSIONE w w w. o s m v a l u e. c o m COMPRENSIONE (RELAZIONI) Qualità generale delle relazioni. Capacità della persona di costruirsi relazioni
LEZIONI CON I PAD Docente scuola secondaria IC Moglia Carla Casareggio Classi seconde 2014/2015 Proprietà triangoli e quadrilateri con Sketchometry
 LEZIONI CON I PAD Docente scuola secondaria IC Moglia Carla Casareggio Classi seconde 2014/2015 Proprietà triangoli e quadrilateri con Sketchometry La costruzione di figure geometriche al computer con
LEZIONI CON I PAD Docente scuola secondaria IC Moglia Carla Casareggio Classi seconde 2014/2015 Proprietà triangoli e quadrilateri con Sketchometry La costruzione di figure geometriche al computer con
PROCESSO DI INDICIZZAZIONE SEMANTICA
 PROCESSO DI INDICIZZAZIONE SEMANTICA INDIVIDUAZIONE DEI TEMI/CONCETTI SELEZIONE DEI TEMI/CONCETTI ESPRESSIONE DEI CONCETTI NEL LINGUAGGIO DI INDICIZZAZIONE TIPI DI INDICIZZAZIONE SOMMARIZZAZIONE INDICIZZAZIONE
PROCESSO DI INDICIZZAZIONE SEMANTICA INDIVIDUAZIONE DEI TEMI/CONCETTI SELEZIONE DEI TEMI/CONCETTI ESPRESSIONE DEI CONCETTI NEL LINGUAGGIO DI INDICIZZAZIONE TIPI DI INDICIZZAZIONE SOMMARIZZAZIONE INDICIZZAZIONE
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
PARTIAMO DA ALCUNE DOMANDE
 PARTIAMO DA ALCUNE DOMANDE Esiste l immagine del disabile intellettivo come persona adulta nella mia mente? Quali sono i maggiori ostacoli che i famigliari/ operatori incontrano nella costruzione di un
PARTIAMO DA ALCUNE DOMANDE Esiste l immagine del disabile intellettivo come persona adulta nella mia mente? Quali sono i maggiori ostacoli che i famigliari/ operatori incontrano nella costruzione di un
DALLA TESTA AI PIEDI
 PROGETTO EDUCATIVO DIDATTICO ANNUALE SCUOLA DELL INFANZIA A. MAGNANI BALIGNANO DALLA TESTA AI PIEDI ALLA SCOPERTA DEL NOSTRO CORPO Anno scolastico 2013-14 MOTIVAZIONI Il corpo è il principale strumento
PROGETTO EDUCATIVO DIDATTICO ANNUALE SCUOLA DELL INFANZIA A. MAGNANI BALIGNANO DALLA TESTA AI PIEDI ALLA SCOPERTA DEL NOSTRO CORPO Anno scolastico 2013-14 MOTIVAZIONI Il corpo è il principale strumento
LA TERAPIA DELLA RICONCILIAZIONE
 Premise 1 LA TERAPIA DELLA RICONCILIAZIONE Ci sono varie forme di riconciliazione, così come ci sono varie forme di terapia e varie forme di mediazione. Noi qui ci riferiamo alla riconciliazione con una
Premise 1 LA TERAPIA DELLA RICONCILIAZIONE Ci sono varie forme di riconciliazione, così come ci sono varie forme di terapia e varie forme di mediazione. Noi qui ci riferiamo alla riconciliazione con una
Psicologia dell orientamento scolastico e professionale. Indice
 INSEGNAMENTO DI PSICOLOGIA DELL ORIENTAMENTO SCOLASTICO E PROFESSIONALE LEZIONE I ORIENTAMENTO E PSICOLOGIA PROF.SSA ANNAMARIA SCHIANO Indice 1 L orientamento: significato e tipologie ---------------------------------------------------------------
INSEGNAMENTO DI PSICOLOGIA DELL ORIENTAMENTO SCOLASTICO E PROFESSIONALE LEZIONE I ORIENTAMENTO E PSICOLOGIA PROF.SSA ANNAMARIA SCHIANO Indice 1 L orientamento: significato e tipologie ---------------------------------------------------------------
I Solidi Regolari??-??- 2001
 I Solidi Regolari??-??- 2001 Cosa sono i Solidi Platonici 1 I Solidi Platonici sono solidi convessi delimitati da facce costitute da poligoni regolari tutti uguali tra loro. Un Solido di questo genere
I Solidi Regolari??-??- 2001 Cosa sono i Solidi Platonici 1 I Solidi Platonici sono solidi convessi delimitati da facce costitute da poligoni regolari tutti uguali tra loro. Un Solido di questo genere
L USO DELLA PNL IN AZIENDA: COME, QUANDO E PERCHE
 L USO DELLA PNL IN AZIENDA: COME, QUANDO E PERCHE LA SCIENZA Se si cerca programmazione neurolinguistica O PNL si hanno questi risultati ( tantissimi ) Definire la PNL, Programmazione Neuro Linguistica
L USO DELLA PNL IN AZIENDA: COME, QUANDO E PERCHE LA SCIENZA Se si cerca programmazione neurolinguistica O PNL si hanno questi risultati ( tantissimi ) Definire la PNL, Programmazione Neuro Linguistica
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Equilibrio bayesiano perfetto. Giochi di segnalazione
 Equilibrio bayesiano perfetto. Giochi di segnalazione Appunti a cura di Stefano Moretti, Silvia VILLA e Fioravante PATRONE versione del 26 maggio 2006 Indice 1 Equilibrio bayesiano perfetto 2 2 Giochi
Equilibrio bayesiano perfetto. Giochi di segnalazione Appunti a cura di Stefano Moretti, Silvia VILLA e Fioravante PATRONE versione del 26 maggio 2006 Indice 1 Equilibrio bayesiano perfetto 2 2 Giochi
UMAGO ARALDICA ATTRAVERSO GLI OCCHI DEL BAMBINO
 UMAGO ARALDICA ATTRAVERSO GLI OCCHI DEL BAMBINO Scuola materna italiana Girotondo Umago Educatrici: Jelena Mrak e Roberta Lakošeljac Umago, maggio 2016 PREMESSA Il concetto astratto di tempo è un concetto
UMAGO ARALDICA ATTRAVERSO GLI OCCHI DEL BAMBINO Scuola materna italiana Girotondo Umago Educatrici: Jelena Mrak e Roberta Lakošeljac Umago, maggio 2016 PREMESSA Il concetto astratto di tempo è un concetto
I.C. "L.DA VINCI" LIMBIATE CURRICOLO IN VERTICALE ANNO SCOLASTICO 2014/2015 GEOGRAFIA
 GEOGRAFIA Osservare gli spazi circostanti Saper distinguere sopra-sotto, davantidietro etc. svolgendo semplici percorsi sul foglio e attraverso giochi di psicomotricità (AL TERMINE DELLA SCUOLA DELL'INFANZIA)
GEOGRAFIA Osservare gli spazi circostanti Saper distinguere sopra-sotto, davantidietro etc. svolgendo semplici percorsi sul foglio e attraverso giochi di psicomotricità (AL TERMINE DELLA SCUOLA DELL'INFANZIA)
IT Questionario per formatori di insegnanti di lingue Analisi dei dati
 IT Questionario per formatori di insegnanti di lingue Analisi dei dati Tu 1. Al questionario hanno risposto sette formatori di insegnanti di lingue. 2. Sei formatori parlano l inglese, sei il francese,
IT Questionario per formatori di insegnanti di lingue Analisi dei dati Tu 1. Al questionario hanno risposto sette formatori di insegnanti di lingue. 2. Sei formatori parlano l inglese, sei il francese,
LA DISTRIBUZIONE DI PROBABILITÀ DEI RITORNI AZIONARI FUTURI SARÀ LA MEDESIMA DEL PASSATO?
 LA DISTRIBUZIONE DI PROBABILITÀ DEI RITORNI AZIONARI FUTURI SARÀ LA MEDESIMA DEL PASSATO? Versione preliminare: 25 Settembre 2008 Nicola Zanella E-Mail: n.zanella@yahoo.it ABSTRACT In questa ricerca ho
LA DISTRIBUZIONE DI PROBABILITÀ DEI RITORNI AZIONARI FUTURI SARÀ LA MEDESIMA DEL PASSATO? Versione preliminare: 25 Settembre 2008 Nicola Zanella E-Mail: n.zanella@yahoo.it ABSTRACT In questa ricerca ho
SCIENZE E TECNOLOGIA
 SCIENZE E TECNOLOGIA COMPETENZE Dimostra conoscenze scientifico-tecnologiche che gli consentono di analizzare dati e fatti della realtà e di verificare l'attendibilità delle analisi quantitative e statistiche
SCIENZE E TECNOLOGIA COMPETENZE Dimostra conoscenze scientifico-tecnologiche che gli consentono di analizzare dati e fatti della realtà e di verificare l'attendibilità delle analisi quantitative e statistiche
LINGUAGGI, CREATIVITA, ESPRESSIONE TECNOLOGIA - INFORMATICA
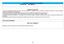 LINGUAGGI, CREATIVITA, ESPRESSIONE TECNOLOGIA - INFORMATICA FINALITA EDUCATIVE La tecnica è la struttura razionale del lavoro, cioè l uso consapevole e finalizzato di mezzi, materiali e procedimenti operativi
LINGUAGGI, CREATIVITA, ESPRESSIONE TECNOLOGIA - INFORMATICA FINALITA EDUCATIVE La tecnica è la struttura razionale del lavoro, cioè l uso consapevole e finalizzato di mezzi, materiali e procedimenti operativi
Classe seconda scuola primaria
 Classe seconda scuola primaria Il percorso di seconda cerca di approfondire le differenze tra le principali proprietà delle figure geometriche solide, in particolare il cubo, e di creare attività di osservazione
Classe seconda scuola primaria Il percorso di seconda cerca di approfondire le differenze tra le principali proprietà delle figure geometriche solide, in particolare il cubo, e di creare attività di osservazione
Emozione: Risposta affettiva a situazioni oggettive o a stati soggettivi che turbano profondamente la coscienza.
 Emozione: Risposta affettiva a situazioni oggettive o a stati soggettivi che turbano profondamente la coscienza. Le emozioni esercitano una forza incredibilmente potente sul comportamento umano. Le emozioni
Emozione: Risposta affettiva a situazioni oggettive o a stati soggettivi che turbano profondamente la coscienza. Le emozioni esercitano una forza incredibilmente potente sul comportamento umano. Le emozioni
Istruzioni per leggere bene. Istruzioni per leggere bene
 Istruzioni per leggere bene A cura di Silvana Loiero 1 La lettura orientativa La prima: farsi un idea generale La seconda: identificare le parti La terza: scorrere indici e sintesi La quarta: leggere rapidamente
Istruzioni per leggere bene A cura di Silvana Loiero 1 La lettura orientativa La prima: farsi un idea generale La seconda: identificare le parti La terza: scorrere indici e sintesi La quarta: leggere rapidamente
L uso e il significato delle regole (gruppo A)
 L uso e il significato delle regole (gruppo A) Regole organizzative: devono essere rispettare per far sì che la struttura possa funzionare e che si possa vivere in un contesto di rispetto reciproco; Regole
L uso e il significato delle regole (gruppo A) Regole organizzative: devono essere rispettare per far sì che la struttura possa funzionare e che si possa vivere in un contesto di rispetto reciproco; Regole
Presentazione. Obiettivi dell area «Modelli mentali»
 Presentazione In queste schede scoprirai alcuni meccanismi che si mettono in funzione quando cerchi di comprendere un testo. Un lettore esperto infatti è in grado di estrarre dal testo le informazioni
Presentazione In queste schede scoprirai alcuni meccanismi che si mettono in funzione quando cerchi di comprendere un testo. Un lettore esperto infatti è in grado di estrarre dal testo le informazioni
Archivi e Laboratorio Didattico. Descrizione di un modello
 Archivi e Laboratorio Didattico. Descrizione di un modello Antonio Brusa Università di Bari/Silsis di Pavia Milano, 19 ottobre 2006 Filottrano 17 aprile 2007 Fermo 29 gennaio 2008 I documenti omogenei:
Archivi e Laboratorio Didattico. Descrizione di un modello Antonio Brusa Università di Bari/Silsis di Pavia Milano, 19 ottobre 2006 Filottrano 17 aprile 2007 Fermo 29 gennaio 2008 I documenti omogenei:
Insegnare le abilità sociali con la carta a T. ins. Fabrizia Monfrino
 Insegnare le abilità sociali con la carta a T ins. Fabrizia Monfrino Scuola: I circolo di Giaveno (To) Classe: trasversale Anno scolastico: 2003/2004 Insegnare le abilità sociali con l uso della carta
Insegnare le abilità sociali con la carta a T ins. Fabrizia Monfrino Scuola: I circolo di Giaveno (To) Classe: trasversale Anno scolastico: 2003/2004 Insegnare le abilità sociali con l uso della carta
Memory Fitness TECNICHE DI MEMORIA
 Memory Fitness TECNICHE DI MEMORIA IL CERVELLO E LE SUE RAPPRESENTAZIONI Il cervello e le sue rappresentazioni (1/6) Il cervello e le sue rappresentazioni (2/6) Approfondiamo ora come possiamo ulteriormente
Memory Fitness TECNICHE DI MEMORIA IL CERVELLO E LE SUE RAPPRESENTAZIONI Il cervello e le sue rappresentazioni (1/6) Il cervello e le sue rappresentazioni (2/6) Approfondiamo ora come possiamo ulteriormente
PROGRAMMAZIONE DIDATTICA DI ARTE E IMMAGINE. Classi Prime
 PROGRAMMAZIONE DIDATTICA DI ARTE E IMMAGINE Classi Prime Progettazione annuale 1. Rilevazione dei livelli di partenza della classe ed individuazione delle competenze precedentemente acquisite. Profilo
PROGRAMMAZIONE DIDATTICA DI ARTE E IMMAGINE Classi Prime Progettazione annuale 1. Rilevazione dei livelli di partenza della classe ed individuazione delle competenze precedentemente acquisite. Profilo
ITALIANO PONTE TRA LE CULTURE NEL MEDITERRANEO
 ITALIANO PONTE TRA LE CULTURE NEL MEDITERRANEO 1 PERCHÉ CONOSCERE L ITALIANO È UN PLUSVALORE? 2 Perché conoscere l italiano è un plusvalore? Un esempio dal Marocco Malika Eddakhch- docente di italianistica
ITALIANO PONTE TRA LE CULTURE NEL MEDITERRANEO 1 PERCHÉ CONOSCERE L ITALIANO È UN PLUSVALORE? 2 Perché conoscere l italiano è un plusvalore? Un esempio dal Marocco Malika Eddakhch- docente di italianistica
PERCORSO. Per una trattazione completa degli aspetti geometrici dell'unità Didattica, cfr. articolo sui "percorsi"
 PERCORSO Le finalità di questa Unità Didattica sono strettamente intrecciate con gli obiettivi di apprendimento logico-linguistico e geometrico. Obiettivi logico-linguistici: Nel lavoro sul "percorso",
PERCORSO Le finalità di questa Unità Didattica sono strettamente intrecciate con gli obiettivi di apprendimento logico-linguistico e geometrico. Obiettivi logico-linguistici: Nel lavoro sul "percorso",
FISICA. Le forze. Le forze. il testo: 2011/2012 La Semplificazione dei Testi Scolastici per gli Alunni Stranieri IPSIA A.
 01 In questa lezione parliamo delle forze. Parliamo di forza quando: spostiamo una cosa; solleviamo un oggetto; fermiamo una palla mentre giochiamo a calcio; stringiamo una molla. Quando usiamo (applichiamo)
01 In questa lezione parliamo delle forze. Parliamo di forza quando: spostiamo una cosa; solleviamo un oggetto; fermiamo una palla mentre giochiamo a calcio; stringiamo una molla. Quando usiamo (applichiamo)
La mia autostima. Edizioni Erickson. Deborah Plummer. Dario Ianes Centro Studi Erickson Università di Bolzano www.darioianes.it
 Edizioni Erickson La mia autostima Dario Ianes Centro Studi Erickson Università di Bolzano www.darioianes.it Deborah Plummer Introduzione L immaginazione come strumento per il cambiamento Imagework: un
Edizioni Erickson La mia autostima Dario Ianes Centro Studi Erickson Università di Bolzano www.darioianes.it Deborah Plummer Introduzione L immaginazione come strumento per il cambiamento Imagework: un
insegnanti : Gabriella Balbo Anna Maria De Marchi Maria Cristina Giraldel
 insegnanti : Gabriella Balbo Anna Maria De Marchi Maria Cristina Giraldel BAMBINI COINVOLTI : 19 del gruppo rosa (D) 17 del gruppo giallo (C) INSEGNANTI RESPONSABILI : Balbo Gabriella Anna Maria De Marchi
insegnanti : Gabriella Balbo Anna Maria De Marchi Maria Cristina Giraldel BAMBINI COINVOLTI : 19 del gruppo rosa (D) 17 del gruppo giallo (C) INSEGNANTI RESPONSABILI : Balbo Gabriella Anna Maria De Marchi
GRUPPI DI INCONTRO per GENITORI
 Nell ambito delle attività previste dal servizio di Counseling Filosofico e di sostegno alla genitorialità organizzate dal nostro Istituto, si propone l avvio di un nuovo progetto per l organizzazione
Nell ambito delle attività previste dal servizio di Counseling Filosofico e di sostegno alla genitorialità organizzate dal nostro Istituto, si propone l avvio di un nuovo progetto per l organizzazione
PLIDA Progetto Lingua Italiana Dante Alighieri Certificazione di competenza in lingua italiana
 PLIDA Progetto Lingua Italiana Dante Alighieri Certificazione di competenza in lingua italiana giugno 2011 PARLARE Livello MATERIALE PER L INTERVISTATORE 2 PLIDA Progetto Lingua Italiana Dante Alighieri
PLIDA Progetto Lingua Italiana Dante Alighieri Certificazione di competenza in lingua italiana giugno 2011 PARLARE Livello MATERIALE PER L INTERVISTATORE 2 PLIDA Progetto Lingua Italiana Dante Alighieri
Disturbi Specifici dell Apprendimento
 Disturbi Specifici dell Apprendimento Nuove norme in materia di segnalazione Intervento al collegio del 07/05/2013 Prima della legge 170 Una serie di circolari che mirano all inclusione scolastica riconoscendo
Disturbi Specifici dell Apprendimento Nuove norme in materia di segnalazione Intervento al collegio del 07/05/2013 Prima della legge 170 Una serie di circolari che mirano all inclusione scolastica riconoscendo
SERVE ANCORA AVERE UN SISTEMA DI QUALITÀ CERTIFICATO?
 LA NUOVA ISO 9001 : 2008 SERVE ANCORA AVERE NEL 2009 UN SISTEMA DI QUALITÀ CERTIFICATO? Paolo Citti Ordinario Università degli Studi di Firenze Presidente AICQ Tosco Ligure 1 Si legge oggi sui giornali
LA NUOVA ISO 9001 : 2008 SERVE ANCORA AVERE NEL 2009 UN SISTEMA DI QUALITÀ CERTIFICATO? Paolo Citti Ordinario Università degli Studi di Firenze Presidente AICQ Tosco Ligure 1 Si legge oggi sui giornali
Plurilinguismo: dal mondo a casa nostra Poster 6
 1 Plurilingue?! Si, ma come? Spiegazioni Domande Risposte Corrette Note Non è assolutamente possibile dare una breve definizione scientifica che sia in grado di rendere la complessità del sistema di segni
1 Plurilingue?! Si, ma come? Spiegazioni Domande Risposte Corrette Note Non è assolutamente possibile dare una breve definizione scientifica che sia in grado di rendere la complessità del sistema di segni
COME PARLARE DI DISLESSIA IN CLASSE.
 COME PARLARE DI DISLESSIA IN CLASSE. UNA METAFORA PER SPIEGARE I DSA La psicologa americana ANIA SIWEK ha sviluppato in anni di pratica professionale un modo semplice ed efficace di spiegare i DSA ai bambini,
COME PARLARE DI DISLESSIA IN CLASSE. UNA METAFORA PER SPIEGARE I DSA La psicologa americana ANIA SIWEK ha sviluppato in anni di pratica professionale un modo semplice ed efficace di spiegare i DSA ai bambini,
Raccomandazione del Parlamento europeo 18/12/2006 CLASSE PRIMA COMPETENZE ABILITÀ CONOSCENZE. Operare con i numeri
 COMPETENZA CHIAVE MATEMATICA Fonte di legittimazione Raccomandazione del Parlamento europeo 18/12/2006 CLASSE PRIMA COMPETENZE ABILITÀ CONOSCENZE L alunno utilizza il calcolo scritto e mentale con i numeri
COMPETENZA CHIAVE MATEMATICA Fonte di legittimazione Raccomandazione del Parlamento europeo 18/12/2006 CLASSE PRIMA COMPETENZE ABILITÀ CONOSCENZE L alunno utilizza il calcolo scritto e mentale con i numeri
PROGRAMMAZIONE SCUOLA PRIMARIA - CLASSE TERZA
 CURRICOLO D ISTITUTO COMPRENDERE COMUNICARE RIFLETTERE RIELABORARE PROGRAMMAZIONE SCUOLA PRIMARIA - CLASSE TERZA AREA DEI LINGUAGGI (italiano, lingua inglese, musica, arte e immagine) TRAGUARDI PER LO
CURRICOLO D ISTITUTO COMPRENDERE COMUNICARE RIFLETTERE RIELABORARE PROGRAMMAZIONE SCUOLA PRIMARIA - CLASSE TERZA AREA DEI LINGUAGGI (italiano, lingua inglese, musica, arte e immagine) TRAGUARDI PER LO
S- magari si potrebbe dire la prima riga, la seconda riga UNITÀ DIDATTICA: TESTO POETICO. Obiettivi
 UNITÀ DIDATTICA: TESTO POETICO Obiettivi - Confrontare due testi poetici - Trovare le differenze e le somiglianze - Osservare le differenze e coglierne le caratteristiche. ATTIVITÀ L argomento presentato
UNITÀ DIDATTICA: TESTO POETICO Obiettivi - Confrontare due testi poetici - Trovare le differenze e le somiglianze - Osservare le differenze e coglierne le caratteristiche. ATTIVITÀ L argomento presentato
Project Cycle Management La programmazione della fase di progettazione esecutiva. La condivisione dell idea progettuale.
 Project Cycle Management La programmazione della fase di progettazione esecutiva. La condivisione dell idea progettuale. Il presente materiale didattico costituisce parte integrante del percorso formativo
Project Cycle Management La programmazione della fase di progettazione esecutiva. La condivisione dell idea progettuale. Il presente materiale didattico costituisce parte integrante del percorso formativo
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
COMUNICAZIONE E ASCOLTO NELLA COPPIA
 COMUNICAZIONE E ASCOLTO NELLA COPPIA Comunicare vuol dire scambiare informazioni legate a fatti o ad emozioni personali con un'altra persona. La vera comunicazione avviene quando uno riceve il messaggio
COMUNICAZIONE E ASCOLTO NELLA COPPIA Comunicare vuol dire scambiare informazioni legate a fatti o ad emozioni personali con un'altra persona. La vera comunicazione avviene quando uno riceve il messaggio
55820/2014 ----------------
 55820/2014 Data: 06 settembre 2014 Dove arriva la Bibbia? di Ilvo Diamanti 06 settembre 2014 Dalla ricerca «Gli italiani e la Bibbia» che viene presentata stasera al Festival letteratura di Mantova un
55820/2014 Data: 06 settembre 2014 Dove arriva la Bibbia? di Ilvo Diamanti 06 settembre 2014 Dalla ricerca «Gli italiani e la Bibbia» che viene presentata stasera al Festival letteratura di Mantova un
Presentazione delle prove ITALIANO. Alessia Mattei - Ricercatrice INVALSI 10 luglio 2014
 Presentazione delle prove ITALIANO Alessia Mattei - Ricercatrice INVALSI 10 luglio 2014 Cosa contiene il QdR Esplicita i punti di riferimento concettuali e i criteri operativi utilizzati nella costruzione
Presentazione delle prove ITALIANO Alessia Mattei - Ricercatrice INVALSI 10 luglio 2014 Cosa contiene il QdR Esplicita i punti di riferimento concettuali e i criteri operativi utilizzati nella costruzione
TECNOLOGIA - SCUOLA PRIMARIA
 TECNOLOGIA - SCUOLA PRIMARIA TRAGUARDI DI SVILUPPO DELLE COMPETENZE L alunno esplora e interpreta il mondo fatto dall uomo, individua le funzioni di un artefatto e di una semplice macchina, usa oggetti
TECNOLOGIA - SCUOLA PRIMARIA TRAGUARDI DI SVILUPPO DELLE COMPETENZE L alunno esplora e interpreta il mondo fatto dall uomo, individua le funzioni di un artefatto e di una semplice macchina, usa oggetti
Non cercate di soddisfare la vostra vanità, insegnando loro troppe cose. Risvegliate la loro curiosità.
 Non cercate di soddisfare la vostra vanità, insegnando loro troppe cose. Risvegliate la loro curiosità. E sufficiente aprire la mente, non sovraccaricarla. Mettetevi soltanto una scintilla. Se vi è della
Non cercate di soddisfare la vostra vanità, insegnando loro troppe cose. Risvegliate la loro curiosità. E sufficiente aprire la mente, non sovraccaricarla. Mettetevi soltanto una scintilla. Se vi è della
Istituto Comprensivo Cepagatti anno scolastico 2015-2016
 Finalità della Scuola del primo ciclo Compito fondamentale della scuola del primo ciclo d istruzione, che comprende la Scuola Primaria e la Scuola Secondaria di primo grado, è la promozione del pieno sviluppo
Finalità della Scuola del primo ciclo Compito fondamentale della scuola del primo ciclo d istruzione, che comprende la Scuola Primaria e la Scuola Secondaria di primo grado, è la promozione del pieno sviluppo
L apprendimento si verifica in un atmosfera sicura derivante dall aver formato solide relazioni interpersonali.
 L apprendimento si verifica in un atmosfera sicura derivante dall aver formato solide relazioni interpersonali. (Michael Grinder dopo aver osservato Carl Rogers). Prima che qualcuno si interessi a quello
L apprendimento si verifica in un atmosfera sicura derivante dall aver formato solide relazioni interpersonali. (Michael Grinder dopo aver osservato Carl Rogers). Prima che qualcuno si interessi a quello
NUMERI PER CONTARE GIOCARE
 ISTITUTO COMPRENSIVO DI NOTARESCO INFANZIA- NOTARESCO - G. VOMANO PAGLIARE - MORROD ORO A. S. 2016/19 PROGETTO DI FORMAZIONE NUMERI PER CONTARE NUMERI PER GIOCARE Approfondimento delle tematiche disciplinari
ISTITUTO COMPRENSIVO DI NOTARESCO INFANZIA- NOTARESCO - G. VOMANO PAGLIARE - MORROD ORO A. S. 2016/19 PROGETTO DI FORMAZIONE NUMERI PER CONTARE NUMERI PER GIOCARE Approfondimento delle tematiche disciplinari
