Problema Determina l equazione omogenea del completamento proiettivo della conica a ne di equazione: 2x 2 3y 2 +5x 2y +3=0.
|
|
|
- Lelio Bono
- 4 anni fa
- Visualizzazioni
Transcript
1 8 Esercizi svolti Coniche a ni Nel iano a ne (reale o comlesso) sia fissato un sitema di riferimento con coordinate (, ). Si consideri il comletamento roiettivo con coordinate omogenee [X,X,X ] tali che X /X, X /X ove X 6. Negli esercizi successivi il iano roiettivo verrà ensato come il comletamento roiettivo del iano a ne. Problema 8.. Determina l equazione omogenea del comletamento roiettivo della conica a ne di equazione: + +. Soluzione. L equazione cercata di è X X +X X X X +X, ottenuta sostituendo con X, con X e rendendo omogenea di secondo grado l equazione tramite la variabile X. Problema 8.. Determina l equazione a ne del luogo dei unti rori della conica roiettiva di equazione omogenea: X + X +X X +X X +4X X. Soluzione. Un unto rorio ha coordinate omogenee della forma [,, ], ove (, ) siano le corrisondenti coordinate a ni. I unti rori di sono tutte e sole le soluzioni dell equazione (nelle variabili (, )) ottenuta dall equazione di sostituendo X con, X con e valutando X in. L equazione del luogo cercato è dunque : il luogo dei unti rori di è una conica a ne e è una conica roria. Problema 8.4. Discuti se le seguenti coniche roiettive sono rorie: a) di equazione: X X + X +X X ; b) di equazione: X +X +X +X X. Soluzione. a) In base alla Definizione 8.., la conica non è roria erché la sua equazione è divisibile er X. b) La conica è roria erché la sua equazione non è divisibile er X, erché contiene termini non nulli in cui X non comare. Problema 8.. Moltelicità dei unti fondamentali del riferimento. Decomoni in arti omogenee l equazione a ne di una conica a ne : f(, ) f (, )+f (, )+f, (8.) con f i omogenee di grado i. Sia il comletamento roiettivo di.provache: a) assa er l origine O, f. b) è s i n g o l a r e n e l l o r i g i n e O, f f. c) Il comletamento roiettivo assa er X, la coordinata comare al iù linearmente nell equazione, il coe ciente di in f è n u l l o. d) Il comletamento roiettivo è s i n g o l a r e i n X, la coordinata non comare in f. e) Il comletamento roiettivo assa er Y, la coordinata comare al iù linearmente nell equazione, il coe ciente di in f è n u l l o. f) Il comletamento roiettivo è s i n g o l a r e i n Y, la coordinata non comare in f. Soluzione. Si alica l osservazione 8...
2 4 8 Classificazione delle coniche Problema 8.6. Punti semlici nei unti fondamentali. Decomoni in arti omogenee l equazione a ne di una conica a ne : f(, ) f (, )+f (, )+f, (8.) con f i omogenee di grado i. Sia il comletamento roiettivo di.provache: a) L origine O è s e m l i c e e r, f ma f non è identicamente nullo. In tal caso, l equazione della retta tangente a in O è f. b) X è s e m l i c e e r i l c o m l e t a m e n t o, la coordinata comare linearmente, ma non con grado, in f. Intalcaso,l equazionedellarettatangentea in X è i l c o e c i e n t e d i in f. c) Il comletamento è s i n g o l a r e i n X, la coordinata non comare in f. d) Y è s e m l i c e e r i l c o m l e t a m e n t o, la coordinata comare linearmente, ma non con grado, in f. Intalcaso,l equazionedellarettatangentea in Y è i l c o e c i e n t e d i in f. e) Il comletamento è s i n g o l a r e i n Y, la coordinata non comare in f. Soluzione. Si alica l osservazione 8... Problema 8.7. Sia una conica a ne di equazione: a + b +c +d +e + f esiap (, ) un unto del iano che non sia un unto doio er.selaconica è a centro, si richiede che P non sia il centro di. Determina l equazione a ne della olare di P risetto al comletamento roiettivo di. acd Soluzione. La matrice di è A cbe def. La olare di P risetto a ha equazione a ne ( )A ( a + c + d) +( c + b + e) +( d + e + f). Problema 8.8. Punti imrori Sia la conica a ne il cui comletamento roiettivo sia la conica roiettiva di equazione: X X + X +X X +4X X. a) Determina i unti imrori di e deduci che la conica è a centro. b) Determina il centro di. Soluzione. a) La conica ha matrice A. La conica ha due unti im- rori distinti, erché det A det 6. Tali unti si ottengono imonendo X nell equazione di e sono quindi dati da X,X X +X X. Si ricava che i unti imrori di sono i unti B [ +,, ] e B [,, ].
3 8 Esercizi svolti Osservando che la conica è non degenere e ha due unti imrori distinti, si conclude che è una conica a centro. b) Primo modo Il centro è il unto di intersezione delle olari di una qualsiasi coia di unti imrori distinti: ad esemio, basta intersecare le olari dei unti imrori [,, ] e [,, ]. La olare di [,, ] è X + X (è l equazione corrisondente alla rima riga di A) e la olare di [,, ] è X X +X (corrisondente alla seconda riga di A). Intersecando le due olari si ricavano le coordinate del centro C[, 4, ]; le coordinate a ni del centro sono C( /, 4/). Secondo modo Poiché nel unto a) sono stati calcolati i unti imrori B e B di, è ossibile calcolare le coordinate del centro come unto di intersezione delle olari di B e B. La olare di B ha equazione ( +)X +( + )X +4X, mentre la olare di B ha equazione ( +)X +( )X +4X. Intersecando le due olari si ricavano le coordinate omogenee del centro C[, 4, ], le cui coordinate a ni sono C( /, 4/). Problema 8.9. Centro di una conica a centro a) Determina il centro della conica a ne a centro di equazione: a + b +c +d +e + f. b) Usa il metodo utilizzato nel unto recedente er calcolare le coordinate a ni del centro della conica di equazione Soluzione. a) La matrice di è A acd cbe def, ove A ac cb ha determinante 6. Il centro della conica è il olo della retta all infinito e si ottiene intersecando le olari delle direzioni e degli assi coordinati. La olare di è la retta ( )A a + c + d, mentre la olare di è la retta ( )A c+b+e. Ricaviamo che il centro è il unto le cui coordinate sono soluzione di a + c + d c + b + e cioè il unto C( db+ec dc ae, ab c b) La matrice di è A ab c )., che ha rango. Poichè A ha determinante 6, la conica è una conica a centro. Il centro della conica è il olo della retta all infinito e si ottiene intersecando le olari delle direzioni e degli assi coordinati. La olare di è la retta ( )A, mentre la olare di è la retta ( )A + +. Il centro ha come coordinate la soluzione del sistema, + +, e dunque è il unto C(, ).
4 6 8 Classificazione delle coniche Problema 8.. Asintoti Determina gli asintoti della conica a ne di equazione: Soluzione. Primo modo Immergendo il iano a ne nel iano roiettivo, con le consuete notazioni, il comletamento roiettivo di è la conica roiettiva di equazione X 7X +9X X + X X + X. I unti imrori [X,X, ] di si calcolano risolvendo l equazione X 7X +9X X ottenuta imonendo X nell equazione di : tali unti imrori sono B [,, ] e B [7,, ]. Poiché ha due unti imrori, gli asintoti esistono e sono le olari dei unti imrori; la olare di B ha equazione omogenea 8X 9X +X, mentre la olare di B ha equazione omogenea 9X +X X. Tornando in coordinate a ni, gli asintoti sono le rette di equazione cartesiana e 9 +, risettivamente. Secondo modo Gli asintoti sono le rette a ni che non intersecano. Problema 8.. a) Sia una conica di equazione: a + b + c.mostrachela conica è degenere e comosta da rette arallelle all asse. b) Se è u n a c o n i c a c o m o s t a d a r e t t e a r a l l e l e a l l a s s e, èverochenellasua equazione non comaiono termini in? Soluzione. a) L equazione della conica è data da un olinomio comlesso di secondo grado in una variabile, che dunque si fattorizza in fattori lineari: la conica è dunque riducibile. Le comonenti hanno equazione della forma d e sono rette arallele all asse (sia che le comonenti siano distinte o no). b) Le rette arallele all asse hanno equazione della forma d : il rodotto di due equazioni di questa forma è un olinomio di secondo grado rivo di termini in, comesivoleva. Classificazione a ne delle coniche nel iano comlesso Problema 8.. Classificazione a ne di una conica di rango nel iano a ne comlesso Sia la conica a ne di equazione: Determina la forma canonica a ne di ed un cambio di coordinate M d + ỹ d tramite il quale l equazione di diventi l equazione canonica a ne. 4 6 Soluzione. La matrice A 6 9 di ha rango ; la conica è dunque comosta dalla retta, contata con moltelicità, di equazione + (ricavata ad esemio dalla rima riga della matrice). L equazione canonica a ne di è ertanto data da.
5 8 Esercizi svolti 7 La determinazione di un sistema di coordinate nel quale assume la forma canonica è simile a quello svolto nel Problema 8. nel caso di una conica roiettiva, urché la trasformazione di coordinate scelta sia una a nità. Si considera il comletamento roiettivo di e si determina il suo unto imrorio B [,, ]; si sceglie ora un altro unto di, ad esemio B [,, ]. In un qualsiasi sistema di coordinate omogenee [X ] in cui B abbia coordinate [,, ] e B abbia coordinate [,, ], la retta che è comonente di è raresentata dall equazione X. Nel corrisondente sistema di coordinate a ni, la conica è raresentata dall equazione canonica. Ad esemio, è ossibile scegliere, in coordinate omogenee, il cambio X MX ove M : a tale cambio, corrisonde il cambio di coordinate a ni + con ỹ M d,. d Problema 8.. Classificazione a ne di una conica di rango nel iano a ne comlesso Sia la conica di equazione: 6 8. Determina l equazione canonica a ne di ed un cambio di coordinate M d + ỹ d tramite il quale l equazione di diventi l equazione canonica a ne. Soluzione. La matrice A di ha rango ; la conica è dunque 8 comosto da due rette distinte. Poiché det A 6, la conica ha due unti imrori distinti, e dunque è formata da una coia di rette a ni incidenti. L equazione canonica a ne di è ertanto data da +ỹ. Il calcolo di un sistema di coordinate nel quale assume la forma canonica è simile a quello svolto nell Esercizio Svolto 8. nel caso di una conica roiettiva, urché la trasformazione di coordinate scelta sia una a nità. Si considera il comletamento roiettivo di. Il unto doio di è B [,, ]. Primo modo Il unto [,, ] non aartiene a ; la sua olare ha equazione e unto imrorio [,, ]. Osserviamo che (,, )A(,, ) t. Tramite il cambio di coordinate omogenee definito da i, la conica viene raresentata dall equazione +. Il corrisondente cambio di coordinate a ni +,con i ỹ d e, i d soddisfa le richieste dell enunciato. Secondo modo Si determinano i suoi unti imrori B [,, ] e B [,, ]. In un sistema di coordinate omogenee [ ] in cui B, B e B abbiano coordinate [,i,], [, i, ], [,, ] risettivamente, le comonenti di sono raresentate dalle equazioni + i e i. Nel corrisondente sistema di coordinate a ni,
6 8 8 Classificazione delle coniche la conica è raresentata dall equazione canonica +ỹ. Ad esemio, è ossibile scegliere, in coordinate omogenee, il cambio M ove M i :a tale cambio, corrisonde il cambio di coordinate a ni + con i ỹ M d,. i d Le comonenti di sono + +e 4. Problema 8.4. Classificazione a ne di una conica di rango nel iano a ne comlesso Sia la conica di equazione: Determina l equazione canonica a ne di ed un cambio di coordinate M d + ỹ d tramite il quale l equazione di diventi l equazione canonica a ne Soluzione. La matrice A di ha rango ; la conica è dunque 6 4 comosto da due rette distinte. Poiché det A, il comletamento roiettivo di ha un unico unto imrorio, e dunque è formata da una coia di rette arallele. L equazione canonica a ne di è ertanto data da +. Il unto imrorio di ha coordinate omogenee Q[,, ] e coincide con il unto doio. Primo modo Il unto [,, ] non aartiene a e(,, )A(,, ) t 9; la olare di [,, ] ha equazione e assa er il unto doio Q, che è il suo unto imrorio. Un altro unto della olare è [,, ], che non aartiene a erché (,, )A(,, ) t 76. Tramite il cambio di coordinate omogenee definito 7 A, la conica viene raresentata dall equazione Il corrisondente cambio di coordinate a ni +, 7 ỹ con M 7 7 d e, soddisfa le richieste dell enunciato. 7 d Secondo modo Due unti rori di, non aartenenti alla stessa comonente, si ottengono ad esemio intersecando con l asse : si ricavano in tal modo i unti B [,, ] e B [,, ]. In un sistema di coordinate omogenee [ ] in cui B, B e B abbiano coordinate [,, ], [i,, ], [ i,, ] risettivamente, le comonenti di sono raresentate dalle equazioni + i e i. Nel corrisondente sistema di coordinate a ni, la conica è raresentata dall equazione canonica +. Ad esemio, è ossibile scegliere, in coordinate omogenee, il cambio
7 M ove M a ni i 8 Esercizi svolti 9 i : a tale cambio, corrisonde il cambio di coordinate + ỹ con M, i Le comonenti di sono + e. d d. Problema 8.. Classificazione a ne di una conica non degenere nel iano a ne comlesso a) Discuti se le seguenti coniche a ni sono arabole o coniche a centro: di equazione: ; di equazione: b) Determina i unti imrori dei comletamenti roiettivi e delle coniche a ni definite in a). c) Per ciascuna delle due coniche, determina un cambio di coordinate a ni M d + ỹ d tramite il quale l equazione della conica diventi l equazione canonica a ne. Soluzione. a) Il comletamento roiettivo di ha equazione omogenea: X +X 7X X + X + X X, mentre il comletamento di ha equazione X +4X +4X X +X X X. Entrambe le coniche sono rorie ed hanno rango e ossiamo alicare l osservazione La sottomatrice A della matrice A 7 di ha determinante non nullo, e dunque la conica è a centro. La sottomatrice B ottenuta cancellando la rima riga e la rima colonna 4 della matrice B di ha determinante nullo, e dunque la conica è 4 una arabola. b) Dal unto a) saiamo che ha due unti imrori tra loro distinti. I unti imrori di si ottengono imonendo X nell equazione di : essi sono i unti [,X,X ] tali che X +X 7X X. Risolvendo tale equazione quadratica, si trova che i unti sono [,, ] e [,, ]. Dal unto a) saiamo che ha un unico unto imrorio: tale unto è doio er la quadrica ottenuta intersecando con la retta imroria; le sue coordinate si ottengono dunque come soluzione non nulla del sistema omogeneo che ha er matrice di coe cienti B ; equivalentemente, basta rendere una soluzione non nulla del sistema omogeneo che ha er coe cienti la rima riga di B : X +X. Si ricava che l unico unto imrorio di è [,, ]. Alternativamente, si oteva risolvere l equazione X + X +4X X ottenuta imonendo X nell equazione di.
8 4 8 Classificazione delle coniche c) Studiamo la conica, la cui equazione canonica a ne è +ỹ +. Primo modo Cerchiamo un triangolo autoolare er tale che i rimi due unti fondamentali siano unti imrori. Osserviamo che il unto S [,, ] non aartiene a. La olare s di S ha equazione X 7X e unto imrorio T [, 7, ] che non aartiene a (erchè (, 7, )A(, 7, ) t 8 6 )eviene reso come vertice del triangolo autoolare. La olare t di T ha equazione 9 e interseca la retta s nel unto V di coordinate [9, 7, ] (che è il centro di ; in coordinate a ni, il centro di è quindi (7/9, /9). Osserviamo che (,, )A(,, ) t e(9, 7, )A(9, 7, ) t 8. Il cambio di coordinate 9 omogenee definito da X M X ove M 77 trasforma l equazione di nell equazione 8 +8 e quindi la trasformazione X M X 9 8 con 7 7 A 8 mette in forma canonica roiettiva. A tale cambio, 8 i 8 i 8 corrisonde il cambio di coordinate a 8 7 i 8 9 ỹ i ni con M i 8 i 8, d 7, d che è il cambio cercato. Secondo modo Il centro di è l intersezione delle olari dei unti imrori fondamentali; dalle equazioni X 7X e 7X +X + X si ricava che le coordinate omogenee del centro sono [9, 7, ]. Ora basta cercare un sistema di coordinate nel quale il centro abbia coordinate [,, ], mentre i unti imrori di abbiano coordinate [,,i] e[,, i] risettivamente, ritrovando i conti recedenti. Studiamo ora la conica, la cui equazione canonica a ne è ỹ. Procediamo come nell Osservazione In un riferimento a ne in cui la arabola è raresentata dall equazione canonica a ne il unto imrorio della conica coincide con il unto imrorio dell asse, l origine coincide con l intersezione dell asse con la conica,l asseỹ è la tangente a nell origine. Nel sistema di riferimento originario, il unto imrorio di ha coordinate omogenee [,, ], ed una retta che assa er esso è, ad esemio la olare del unto [,, ], di equazione a ne + +. Tale retta interseca nel unto (, /), la cui olare (che coincide con la retta tangente) ha come unto imrorio [,, ], er la rorietà di recirocità. Osserviamo che (,, )B(,, ) t,(,, )B(,, /) t. Il cambio di coordinate omogenee definito da X M X ove M trasforma l equazione di / nell equazione +4. e quindi la trasformazione X M X con M mette in forma. A tale cambio, corrisonde / / il cambio di coordinate a ni + con / ỹ d,, / d
9 8 Esercizi svolti 4 che è il cambio cercato. Coniche nel iano a ne reale Si studiano coniche a ni reali nel iano reale comlessificato. Si assume che il riferimento cartesiano sia reale e i cambi di riferimento ammessi siano reali. Qualora si utile, si considera l inclusione del iano a ne nel roiettivo, tramite l alicazione (, ) 7 [,, ] e denotando le coordinate omogenee con [X,X,X ]. Problema 8.6. Sia la conica di equazione: 8 9. a) Determina le comonenti di e discutere se sono reali. b) Determina l equazione canonica a ne di. Soluzione. a) La conica ha rango ed è quindi comosta da due rette distinte. Poichè la sottomatrice A della matrice A di ha determinante strettamente negativo, i unti imrori di sono una coia distinta di unti reali. La conica è ertanto comosta da due rette reali tra loro non arallele. Svolgendo i conti (ad esemio determinando il unto doio di e l equazione delle rette che congiungono il unto doio con ciascuno dei unti imrori di ), si determinano le equazioni delle comonenti di che sono, risettivamente, e. b) Poichè ha rango e comonenti reali, l equazione canonica è. Problema 8.7. Sia la conica di equazione: a) Determina le comonenti di e discuti se sono reali. b) Determina l equazione canonica a ne di. Soluzione. a) La conica ha rango ed è quindi comosta da due rette distinte. 6 Poichè la sottomatrice A della matrice A di ha determinante 6 9 strettamente ositivo, i unti imrori di sono una coia distinta di unti comlessi coniugati. La conica è ertanto comosta da due rette comlesse coniugate tra loro non arallele. Svolgendo i conti (ad esemio determinando il unto doio (, ) di e l equazione delle rette che congiungono il unto doio con ciascuno dei unti imrori di ), si determinano le equazioni delle comonenti di che sono, risettivamente, ( + i) +( i) e( i) +( + i). b) Poichè ha rango e comonenti comlesse coniugate non reali, l equazione canonica è +ỹ. Problema 8.8. Sia la conica di equazione: Determina i unti imrori del comletamento roiettivo di nel iano roiettivo comlessificato e determina l equazione canonica a ne di. 6 7 Soluzione. La conica ha matrice A 7 di rango, ed è una ellisse erchè det A > (e in articolare è una conica a centro): la conica ha
10 4 8 Classificazione delle coniche dunque due unti imrori, comlessi coniugati. I unti imrori [,, ] di sono raresentati dall equazione data dalla arte quadratica dell equazione di :6 + 4 Fattorizzando tale equazione, si ricavano i fattori ( + i) ( + i) e( i) ( i); i unti imrori di sono [ + i, +i, ], [ i, i, ]. Poichè ha rango, è ossibile alicare il Lemma 8..7 er discutere se ha unti reali: oichè a deta > e det A >, si conclude che non ha unti reali, ed è quindi una ellisse immaginaria, di equazione canonica a ne +ỹ +. Problema 8.9. Sia la conica di equazione: a) Verifica che è una ierbole. b) Determina i unti imrori di. 6 Soluzione. a) La conica è non degenere erchè la sua matrice A ha rango, ed è una ierbole erchè det A 49 < (e in articolare è una 4 conica a centro). b) I unti imrori [X,X, ] di sono raresentati dall equazione data dalla arte quadratica dell equazione di :6X X X X Fattorizzando tale equazione, si ricava che i unti imrori sono [,, ], [,, ]: insieme all informazione che sia non degenere, il fatto che i unti imrori siano una coia distinti di unti reali dimostra nuovamente che è una ierbole. Prorietà metriche: coniche nel iano euclideo Si studiano coniche a ni reali nel iano euclideo comlessificato. Si assume che il riferimento cartesiano sia monometrico ortonormale e i cambi di riferimento ammessi sono esclusivamente i movimenti rigidi (reali). Qualora serva, si ensa il iano euclideo incluso nel suo comletamento roiettivo, tramite l alicazione (, ) 7 [,, ] e denotando le coordinate omogenee con [X,X,X ]. Problema 8.. Equazione canonica metrica di una ellisse a unti reali Sia la conica di equazione: a) Determina l equazione canonica metrica di, evidenziandoneisemiassi. b) Determina il cambiamento ortonormale di coordinate necessario a nché assuma tale equazione. Soluzione. a) La conica è non degenere erchè la sua matrice A ha rango, ed è una ellisse erchè det A 8> (e in articolare è una conica a centro). La conica è una ellisse a unti reali in base al Lemma 8..7, essendo a deta 8 <. Possiamo quindi cercare i coe cienti della forma canonica metrica seguendo l Esemio 8.6., ii). In un sistema di riferimento ortonormale in cui gli assi cartesiani siano assi di simmetria ortogonale er la conica, l equazione assume la forma a + bỹ + c,ovea e b sono gli autovalori di A, mentre abc deta. Dunque ab det A 8,a + b tra 6,c deta/ab 6/8 /4.
11 8 Esercizi svolti 4 Svolgendo i conti, si osserva che è ossibile scegliere a, b 4. L equazione di diventa +4ỹ /4 : si conclude che l equazione canonica metrica è (8/) +(6/)ỹ, o, iù recisamente /8 + /6 ỹ e la conica è una ellisse a unti reali di semiassi e. 8 6 b) L autosazio di autovalore relativo alla matrice A è generato dall autovettore, che ha norma e fornisce i numeri direttori di un asse di simmetria ortogonale er la conica; i numeri direttori dell altro asse di simmetria ortogonale sono, che ha norma e che uò essere ricavato come generatore dell autosazio di autovalore 4 o, iù semlicemente, come ortogonale del recedente. La rotazione di centro l origine di equazione definisce un sistema di coordinate (, ) nel quale gli assi cartesiani e sono aralleli agli assi di simmetria ortogonale er. Oerando la sostituzione, si verifica che, in tali coordinate, la conica è raresentata dall equazione , nella quale non comare il termine in, e i coe cienti dei termini in e sono gli autovalori di A. Per determinare un sistema di coordinate (, ỹ) nel quale la conica è raresentata dall equazione canonica, è su ciente modificare l origine del sistema di coordinate, che deve essere osta nel centro di. Per determinare il cambio di coordinate, è ossibile rocedere come segue, utilizzando il metodo detto metodo del comletamento dei quadrati : la trasformazione cercata è della forma +c, ỹ +c, grazie alla quale si annullino i termini lineari nell equazione di : ( + c ) +4(ỹ + c ) +( + c )+(ỹ + c ) +4ỹ +(+4c ) +(+8c )ỹ +(c +4c +c +c ) L annullarsi del coe ciente del termine in fornisce l equazione + 4c, dalla quale si ricava c (/). L annullarsi del coe ciente del termine in ỹ fornisce l equazione + 8c, dalla quale si ricava c (/4). Il cambiamento di coordinate tramite il quale è raresentata dall equazione canonica è dunque dato da: ỹ ỹ 4
12 44 8 Classificazione delle coniche Problema 8.. Equazione canonica metrica di una ierbole. Sia la conica di equazione: Determina l equazione canonica metrica di ed il cambiamento di coordinate necessario a nché assuma tale equazione. Soluzione. La conica è non degenere erchè la sua matrice A ha rango, ed è una ierbole erchè det A 6 < (e in articolare è una conica a centro). Possiamo quindi cercare i coe cienti della forma canonica metrica seguendo l Esemio 8.6., iii). In un sistema di riferimento ortonormale in cui gli assi cartesiani siano assi di simmetria ortogonale er la conica, l equazione assume la forma a + bỹ + c,ovea e b sono gli autovalori di A, mentre abc deta. Dunque ab det A 6, a + b tra, c deta/ab /( 6) /6. Svolgendo i conti, si osserva che è ossibile scegliere a, b. L equazione di diventa ỹ +/6 : si conclude che l equazione canonica metrica è +8ỹ, o, iù recisamente /8 / ỹ, (scambiando eỹ in modo che il coe ciente negativo comaia nel termine in ỹ e l asse sia l asse trasverso). Cerchiamo ora il cambio di riferimento. L autosazio di autovalore relativo alla matrice A è generato dall autovettore, che ha norma e fornisce i numeri direttori di un asse di simmetria ortogonale er la conica; i numeri direttori dell altro asse di simmetria ortogonale sono, che ha norma e che uò essere ricavato come generatore dell autosazio di autovalore o, iù semlicemente, come ortogonale del recedente (e orientato in modo tale che l orientazione indotta dai due autovettori sia ositiva). La rotazione di centro l origine di equazione definisce un sistema di coordinate (, ) nel quale gli assi cartesiani e sono sono aralleli agli assi di simmetria ortogonale er. Oerando la sostituzione, si verifica che, in tali coordinate, la conica è raresentata dall equazione , nella quale non comare il termine in, i coe cienti dei termini in e sono gli autovalori di A, il termine noto è rimasto invariato.
13 8 Esercizi svolti 4 Per determinare un sistema di coordinate (, ỹ) nel quale la conica è raresentata dall equazione canonica, è su ciente modificare l origine del sistema di coordinate, che deve essere osta nel centro di. Per determinare il cambio di coordinate, è ossibile rocedere come segue, utilizzando il metodo detto metodo del comletamento dei quadrati : la trasformazione cercata è della forma +c, ỹ +c, grazie alla quale si annullino i termini lineari nell equazione di : ( + c ) +(ỹ + c ) + ( + c ) (ỹ + c )+ +ỹ +( 6c ) +( +4c )ỹ c +c + (c c )+ L annullarsi del coe ciente del termine in fornisce l equazione 6c, dalla quale si ricava c. L annullarsi del coe ciente del termine in ỹ fornisce l equazione +4c, dalla quale si ricava c. Il cambiamento di coordinate tramite il quale è raresentata dall equazione canonica è dunque dato da: + 7 ỹ ỹ Problema 8.. Equazione canonica metrica di una arabola. Sia la arabola di equazione: a) Determina l equazione canonica metrica di ed il cambiamento di coordinate necessario a nché assuma tale equazione. b) Determina l asse e il vertice di. 4 Soluzione. a) La conica è non degenere erchè la sua matrice A ha rango, ed è una arabola erchè det A. Possiamo quindi cercare i coe cienti della forma canonica metrica seguendo l Esemio In un sistema di riferimento ortonormale in cui gli assi cartesiani siano l asse di simmetria ortogonale er la conica e la retta tangente nel vertice, l equazione assume la forma aỹ,ovea è l autovalore non nullo di A, mentre a deta. Dunque a tra deta/a 6/. Svolgendo i conti, si osserva che è ossibile scegliere 4/. L equazione di diventa ỹ 8 : si conclude che l equazione canonica metrica è ỹ 8. L autosazio di autovalore relativo alla matrice A è generato dall autovettore, che ha norma e fornisce i numeri direttori dell asse di simmetria ortogonale er la conica; i numeri direttori della tangente nel vertice sono dati dal vettore, che ha norma e che uò essere ricavato come generatore dell autosazio di autovalore o, iù semlicemente, come ortogonale del recedente (e orientato in modo tale che l orientazione indotta dai due autovettori sia ositiva). La rotazione di centro l origine di equazione
14 46 8 Classificazione delle coniche definisce un sistema di coordinate (, ) nel quale l asse è arallelo all asse di simmetria ortogonale er e è arallelo alla tangente nel vertice. Oerando la sostituzione, si verifica che, in tali coordinate, la conica è raresentata dall equazione , nella quale non comaiono i termini in ein, il coe ciente del termine in è l autovalore non nullo di A, il termine noto è rimasto invariato. Osserviamo che il coe ciente del termine in è ositivo: oeriamo dunque un ribaltamento, : la conica è raresentata dall equazione Per determinare un sistema di coordinate (, ỹ) nel quale la conica è raresentata dall equazione canonica, è su ciente modificare l origine del sistema di coordinate, che deve essere osta nel vertice di. Per determinare il cambio di coordinate, è ossibile rocedere come segue, utilizzando il metodo detto metodo del comletamento dei quadrati : la trasformazione cercata è della forma +c, ỹ+c, grazie alla quale si annullino il termine lineare in ỹ e il termine noto nell equazione di : (ỹ + c ) 8 ( + c )+ 4 (ỹ + c ) ỹ 8 +( 4 +c )ỹ +c 8 c + 4 c L annullarsi del coe ciente del termine lineare in ỹ fornisce l equazione 4 +c, dalla quale si ricava c. L annullarsi del coe ciente del termine noto fornisce l equazione c 8 c + 4 c ; sostituendo il valore ottenuto er c, l equazione 4 diventa: 8 8 c, dalla quale si ricava c. Il cambiamento di coordinate tramite il quale è raresentata dall equazione canonica è dunque dato da: + 9 ỹ + ỹ. (8.) b) Il vertice di è l origine del sistema di coordinate che nel quale è raresentata dall equazione canonica metrica. Le equazioni (8.) del cambio di coordinate forniscono (er ỹ) le coordinate del vertice ( 9, ). L asse di simmetria è, er quanto osservato, arallelo alla retta ; imonendi il assaggio er il vertice, si trova che l asse di simmetria ha equazione /. Si veda il Problema Guida 8. er un esemio di calcolo diretto di vertice e asse, senza utilizzare il cambio di coordinate che one in forma canonica.
15 8 Esercizi svolti 47 Problema 8.. Sia la conica di equazione: a) Verifica che è una circonferenza, determinandone il centro e il raggio. b) Verifica che è u n a c o n i c a a c e n t r o e c h e i l c e n t r o d i s i m m e t r i a s e c o n d o l a definizione coincide con il centro della circonferenza. c) Verifica che il unto P (, ) è interno alla circonferenza e disegnarne la olare. d) Determina una coia di assi di simmetria er tra loro ortogonali. Soluzione. a) Ricordando quanto illustrato nel aragrafo. o controllando il assaggio er i unti ciclici, si riconosce facilmente che la conica assegnata è una circonferenza di centro C(, ) e raggio. b) La conica è non degenere (erchè la sua matrice ha rango ) e a centro (erchè ha due distinti unti imrori). Le coordinate del centro si ottengono intersecando le olari di una qualsiasi coia di unti imrori tra loro distinti; intersecando le olari dei unti imrori fondamentali, si ottengono le equazioni:,+, dalle quali si ricavano le coordinate (, ) del centro della conica, che coincidono con quelle del centro C della circonferenza, determinate nel unto recedente. c) Le rette er il unto P hanno equazione arametrica della forma +tl, +tm con t R, (l, m) R,(l, m) 6 (, ). Intersecando una tale retta con, si ottiene l equazione ( + tl) +( +tm) ( + tl)+6( +tm)+(l + m )t +(m)t 4, che è semre di secondo grado in t e ha discriminante strettamente ositivo 4m +6(l + m ) >. L intersezione è dunque semre data da due unti reali, e il unto P è dunque interno. d) È su ciente determinare due rette ortogonali assanti er il centro: ad esemio, e. Problema 8.4. Assi di simmetria di una conica a centro Sia la conica di equazione: Verificache è u n a c o n i c a a c e n t r o e determinarne gli assi di simmetria. Soluzione. La conica ha matrice A : la conica è dunque non degenere ed è una ellisse erchè det A >. Poichè non è una circonferenza, ha una coia di assi di simmetria, le cui direzioni, in base al lemma 8..4, sono date dagli autovettori di A. PoichètrA, gli autovalori di A sono e +. Primo modo Per quanto osservato, gli assi sono aralleli, risettivamente, alle rette + + e +. Le coordinate del centro della conica si trovano intersecando le olari delle direzioni degli assi cartesiani: dalle equazioni +, + + si deduce che il centro ha coordinate (/, /). Poichè gli assi devono assare er il centro della conica, si ricava che gli assi sono e Secondo modo L autosazio di autovalore risetto a A è generato + da (, + ), corrisondente al unto imrorio [,, ] che ha, come retta olare, la retta di equazione +.
16 48 8 Classificazione delle coniche L autosazio di autovalore + risetto a A è generato da (, ), corrisondente al unto imrorio [,, ] che ha, come retta olare, la retta di equazione Le coordinate (/, /) del centro si determinano intersecando gli assi, o intersecando le olari delle direzioni degli assi cartesiani. Problema 8.. Asse di simmetria e vertice di una arabola Sia la conica di equazione: Mostrache è u n a a r a b o l a, e d e t e r m i n a r n e il vertice e l equazione cartesiana dell asse di simmetria. Soluzione. La conica è non degenere erchè la sua matrice A 9 ha rango, ed è una arabola erchè det A. In base al Lemma 8.., l asse di simmetria ha er direzione il unto imrorio del comletamento roiettivo di ed è arallelo alla retta di equazione +. La retta tangente a nel suo vertice, essendo ortogonale all asse, ha equazione della forma + k. Il valore di k uò essere determinato imonendo che la retta sia tangente: l intersezione tra la retta e deve essere costituita da un unico unto, con moltelicità. L intersezione è data da + k Sostituendo la relazione + k nell equazione della conica, si ricava l equazione +9( + k) +6( + k)+ + +(6k +) +9k + ; la retta è tangente se tale equazione, nell incognita, ammette una unica soluzione, cioè ha discriminante nullo: 4k 96. Il valore di k er il quale la retta è tangente è dunque k 99/6: 99/6. Il vertice è il unto di intersezione con : calcolando l intersezione er il valore ottenuto di k si ottengono le coordinate del vertice: (97/, 89/). L asse di simmetria ha equazione della forma + + t : imonendo il assaggio er il vertice, si ricava che l equazione dell asse di simmetria è: + 4/. Problema 8.6. Sia la arabola di equazione: Determina le coordinate del suo fuoco. Soluzione. Il fuoco è l intersezione tra le rette isotroe che sono tangenti a. Problema 8.7. Sia l ellissi di equazione: Determina le coordinate dei suoi fuochi reali. Esercizi 8.. Determina la matrice e il rango delle coniche raresentate da una delle seguenti equazioni: a) ;
17 8 Esercizi 49 b) ; c) ; d) Al variare del arametro reale t, determina il rango della conica di equazione t + + +t Considera la conica di equazione X X +4X X + X. i) Determina il rango di e i suoi unti doi. ii) Osserva che i unti P [,, ] e P [,, ] sono semlici er la risettiva retta tangente a. iii) è riducibile? e determinare 8.4. Determina l equazione della conica costituita dalla retta er i unti [,, ] e [,, ] contata con moltelicità. Coniche a ni 8.. Controlla se le seguenti coniche sono arabole o coniche a centro; in quest ultimo caso, determina eslicitamente il centro. i) ii) Coniche del iano euclideo 8.6. Determina l equazione canonica a ne e metrica della conica definita da una delle equazioni seguenti: a) ; b) ; c) Determina l equazione della retta tangente la conica + + di A nell origine Determina gli assi di simmetria e il centro della conica Q di equazione Determinare inoltre il cambio di coordinate che muta l equazione di Q nella sua forma canonica metrica Determina l asse di simmetria ed il vertice della arabola di equazione Determina la forma canonica metrica e a ne delle coniche di equazione, risettivamente: i) 9 + ; ii) + +; iii) iv) ierbole +ỹ Determina inoltre un cambiamento di coordinate che ermette di ottenere la forma canonica metrica. 8.. Trasforma la conica a ne di equazione mediante l a nità di equazioni +, ỹ 4 +.
18 8 Classificazione delle coniche 8.. Controlla se esiste una a nità che muta le seguenti coie di coniche l una nell altra: a), + ; b) + +, + ; c) + 4, +.
Problema 8.2. Classificazione proiettiva di una conica di rango 1 Considera la conica di equazione:
 8 Classificazione delle coniche Esercizi svolti Classificazione roiettiva delle coniche Nel iano roiettivo comlesso, sia fissato un sistema di coordinate omogenee [X,X,X ]. I cambi di riferimento ermessi
8 Classificazione delle coniche Esercizi svolti Classificazione roiettiva delle coniche Nel iano roiettivo comlesso, sia fissato un sistema di coordinate omogenee [X,X,X ]. I cambi di riferimento ermessi
Problema 7.3. Classificazione proiettiva di una conica di rango 2 Si consideri
 04 7 Classificazione delle quadriche Esercizi svolti Classificazione proiettiva delle coniche Nel piano proiettivo complesso, sia fissato un sistema di coordinate omogenee [X 0,X,X ]. I cambi di riferimento
04 7 Classificazione delle quadriche Esercizi svolti Classificazione proiettiva delle coniche Nel piano proiettivo complesso, sia fissato un sistema di coordinate omogenee [X 0,X,X ]. I cambi di riferimento
Esercizio 1. Sono dati i vettori. 1 A v2 3 ;1A v3 k 0. (e) Calcolare la proiezione ortogonale su W? del vettore v ;1 SOLUZIONE
 CORSI DI LURE IN INGEGNERI ELETTROTECNIC E INGEGNERI MECCNIC {.. 9- PROV SCRITT DI GEOMETRI DEL -- Corsi dei Pro. M. BORDONI, M. MRIETTI Esercizio. Sono dati i vettori v = @ ; v = @ ; v = @ k con k arametro
CORSI DI LURE IN INGEGNERI ELETTROTECNIC E INGEGNERI MECCNIC {.. 9- PROV SCRITT DI GEOMETRI DEL -- Corsi dei Pro. M. BORDONI, M. MRIETTI Esercizio. Sono dati i vettori v = @ ; v = @ ; v = @ k con k arametro
CLASSIFICAZIONE DELLE CONICHE AFFINI
 CLASSIFICAZIONE DELLE CONICHE AFFINI Pre-requisiti necessari. Elementi di geometria analitica punti e rette nel piano cartesiano, conoscenza delle coniche in forma canonica). Risoluzione di equazioni e
CLASSIFICAZIONE DELLE CONICHE AFFINI Pre-requisiti necessari. Elementi di geometria analitica punti e rette nel piano cartesiano, conoscenza delle coniche in forma canonica). Risoluzione di equazioni e
Traccia dello svolgimento di alcuni esercizi del compito del 15/04/08
 Traccia dello svolgimento di alcuni esercizi del comito del //8 Esercizio.. L esercizio richiede di risolvere in generale il seguente sistema lineare @ A = b a. Il sistema ^A = b ammette soluzioni se Rg(
Traccia dello svolgimento di alcuni esercizi del comito del //8 Esercizio.. L esercizio richiede di risolvere in generale il seguente sistema lineare @ A = b a. Il sistema ^A = b ammette soluzioni se Rg(
UNIVERSITÀ DEGLI STUDI DI SALERNO Svolgimento della prova scritta - fuori corso - di Matematica II 11 Novembre 2010
 UNIVERSITÀ DEGLI STUDI DI SALERNO della rova scritta - fuori corso - di Matematica II Novembre Esercizio In R si considerino i seguenti sottosazi vettoriali: V = (x; y; z) R j x y z = x z =, W = (x; y;
UNIVERSITÀ DEGLI STUDI DI SALERNO della rova scritta - fuori corso - di Matematica II Novembre Esercizio In R si considerino i seguenti sottosazi vettoriali: V = (x; y; z) R j x y z = x z =, W = (x; y;
[40] Problema 3. Stabilisci se esistono valori di k per quali l equazione
![[40] Problema 3. Stabilisci se esistono valori di k per quali l equazione [40] Problema 3. Stabilisci se esistono valori di k per quali l equazione](/thumbs/96/130279601.jpg) Verifica di Matematica 9 Maggio 018 Classe 3GHI sci Non utilizzare matita né bianchetto. Il unteggio viene attribuito in base alla correttezza e alla comletezza nella risoluzione dei quesiti, al metodo
Verifica di Matematica 9 Maggio 018 Classe 3GHI sci Non utilizzare matita né bianchetto. Il unteggio viene attribuito in base alla correttezza e alla comletezza nella risoluzione dei quesiti, al metodo
UNIVERSITÀ DEGLI STUDI DI SALERNO Svolgimento Prova scritta di Matematica II 09 Febbraio 2011
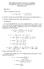 UNIVERSITÀ DEGLI STUDI DI SALERNO Prova scritta di Matematica II 9 Febbraio Esercizio In R si considerino le due rette: t r : 5 y ; s : y t ; a) calcolare una base ortonormale di R a artire dai vettori
UNIVERSITÀ DEGLI STUDI DI SALERNO Prova scritta di Matematica II 9 Febbraio Esercizio In R si considerino le due rette: t r : 5 y ; s : y t ; a) calcolare una base ortonormale di R a artire dai vettori
in forma matriciale: X = A X + B, cioè Se il det A = ad - bc è diverso da zero, la trasformazione è invertibile e quindi biunivoca; in tal caso la
 TRASFORMAZIONI LINEARI SUL PIANO Sono trasformazioni lineari tutte le trasformazioni del tio: a b c d q in forma matriciale: X A X B, cioè a c b d q Dove a A c b d è la matrice della trasformazione. Se
TRASFORMAZIONI LINEARI SUL PIANO Sono trasformazioni lineari tutte le trasformazioni del tio: a b c d q in forma matriciale: X A X B, cioè a c b d q Dove a A c b d è la matrice della trasformazione. Se
Esercizi sulle coniche (prof.ssa C. Carrara)
 Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle da un altra angolazione.. Determinare
Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle da un altra angolazione.. Determinare
Liceo Scientifico Severi Salerno
 Liceo Scientifico Severi Salerno VERIFICA SCRITTA MATEMATICA Docente: Paalardo Vincenzo Data: 1/04/019 Classe: 3B 1. ESERCIZIO Determinare l equazione della arabola con asse di simmetria coincidente con
Liceo Scientifico Severi Salerno VERIFICA SCRITTA MATEMATICA Docente: Paalardo Vincenzo Data: 1/04/019 Classe: 3B 1. ESERCIZIO Determinare l equazione della arabola con asse di simmetria coincidente con
Esercizi per Geometria II Geometria euclidea e proiettiva
 Esercizi per Geometria II Geometria euclidea e proiettiva Filippo F. Favale 10 aprile 01 Esercizio 1 Sia E 3 lo spazio euclideo tridimensionale dotato di un riferimento cartesiano ortonormale di coordinate
Esercizi per Geometria II Geometria euclidea e proiettiva Filippo F. Favale 10 aprile 01 Esercizio 1 Sia E 3 lo spazio euclideo tridimensionale dotato di un riferimento cartesiano ortonormale di coordinate
TRASFORMAZIONI LINEARI SUL PIANO
 TRASFORMAZIONI LINEARI SUL PIANO Sono trasformazioni lineari tutte le trasformazioni del tio: a b c d in forma matriciale: X A X B, cioè a c b d Dove a A c b d è la matrice della trasformazione. Se il
TRASFORMAZIONI LINEARI SUL PIANO Sono trasformazioni lineari tutte le trasformazioni del tio: a b c d in forma matriciale: X A X B, cioè a c b d Dove a A c b d è la matrice della trasformazione. Se il
Coniche - risposte 1.9
 Coniche - risposte. CAMBI DI COORDINATE ) ) cosπ/) sinπ/). a. Rotazione di π/, la matrice di rotazione è = sinπ/) cosπ/) ) ) ) X = Y X = Quindi le formule sono: cioè: Y = X e inversamente Y = = Y X = b.
Coniche - risposte. CAMBI DI COORDINATE ) ) cosπ/) sinπ/). a. Rotazione di π/, la matrice di rotazione è = sinπ/) cosπ/) ) ) ) X = Y X = Quindi le formule sono: cioè: Y = X e inversamente Y = = Y X = b.
Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u.
 Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Definizione Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee (x,
Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Definizione Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee (x,
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) CONICHE DI
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) CONICHE DI R. Docente: Prof. F. Flamini Esercizi Riepilogativi Svolti Esercizio
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) CONICHE DI R. Docente: Prof. F. Flamini Esercizi Riepilogativi Svolti Esercizio
Esercizi sulle coniche (prof.ssa C. Carrara)
 Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle più volte.. Stabilire il tipo di
Esercizi sulle coniche prof.ssa C. Carrara Alcune parti di un esercizio possono ritrovarsi in un altro esercizio, insieme a parti diverse. È un occasione per affrontarle più volte.. Stabilire il tipo di
Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u.
 Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Definizione Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee (x,
Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Definizione Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee (x,
Geometria e Topologia I 22 Giugno 2005 (U1-10, 9:00 11:00) [PROVA PARZIALE]1/8
![Geometria e Topologia I 22 Giugno 2005 (U1-10, 9:00 11:00) [PROVA PARZIALE]1/8 Geometria e Topologia I 22 Giugno 2005 (U1-10, 9:00 11:00) [PROVA PARZIALE]1/8](/thumbs/103/157085746.jpg) Geometria e Topologia I 22 Giugno 2005 (U-0, 9:00 :00) [PROVA PARZIALE]/8 Correzione 0 () In A 3 (R) siano dati i tre punti A =, B = 0, C =. 0 (a) A B e C sono allineati? Dipendenti? (b) Dimostrare che
Geometria e Topologia I 22 Giugno 2005 (U-0, 9:00 :00) [PROVA PARZIALE]/8 Correzione 0 () In A 3 (R) siano dati i tre punti A =, B = 0, C =. 0 (a) A B e C sono allineati? Dipendenti? (b) Dimostrare che
Fasci di Coniche. Salvino Giuffrida. 2. Determinare e studiare il fascio Φ delle coniche che passano per A (1, 0) con tangente
 1 Fasci di Coniche Salvino Giuffrida 1. Determinare e studiare il fascio Φ delle coniche che passano per O = (0, 0), con tangente l asse y, e per i punti (1, 0), (1, ). Determinare vertice e asse della
1 Fasci di Coniche Salvino Giuffrida 1. Determinare e studiare il fascio Φ delle coniche che passano per O = (0, 0), con tangente l asse y, e per i punti (1, 0), (1, ). Determinare vertice e asse della
X = x + 1. X = x + 1
 CONICHE. Esercizi Esercizio. Classificare, ridurre a forma canonica (completando i quadrati), e disegnare le seguenti coniche: γ : x y + x = 0; γ : x + 4x y + = 0; γ 3 : x + y + y + 0 = 0; γ 4 : x + y
CONICHE. Esercizi Esercizio. Classificare, ridurre a forma canonica (completando i quadrati), e disegnare le seguenti coniche: γ : x y + x = 0; γ : x + 4x y + = 0; γ 3 : x + y + y + 0 = 0; γ 4 : x + y
Esercizi Riepilogativi Svolti
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) QUADRICHE DI R 3. Docente: Prof. F. Flamini Esercizi Riepilogativi Svolti Esercizio
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) QUADRICHE DI R 3. Docente: Prof. F. Flamini Esercizi Riepilogativi Svolti Esercizio
CAPITOLO 14. Quadriche. Alcuni esercizi di questo capitolo sono ripetuti in quanto risolti in maniera differente.
 CAPITOLO 4 Quadriche Alcuni esercizi di questo capitolo sono ripetuti in quanto risolti in maniera differente. Esercizio 4.. Stabilire il tipo di quadrica corrispondente alle seguenti equazioni. Se si
CAPITOLO 4 Quadriche Alcuni esercizi di questo capitolo sono ripetuti in quanto risolti in maniera differente. Esercizio 4.. Stabilire il tipo di quadrica corrispondente alle seguenti equazioni. Se si
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria - Edile ed Edile/Architettura
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria - Edile ed Edile/Architettura Primo Appello del corso di Geometria 2 Docente F. Flamini, Roma, 22/02/2007 SVOLGIMENTO COMPITO I APPELLO
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria - Edile ed Edile/Architettura Primo Appello del corso di Geometria 2 Docente F. Flamini, Roma, 22/02/2007 SVOLGIMENTO COMPITO I APPELLO
I fasci di circonferenze
 A I fasci di circonferenze Se combiniamo linearmente le equazioni di due circonferenze otteniamo un fascio di circonferenze. Per esemio, date le circonferenze di equazioni la loro combinazione lineare
A I fasci di circonferenze Se combiniamo linearmente le equazioni di due circonferenze otteniamo un fascio di circonferenze. Per esemio, date le circonferenze di equazioni la loro combinazione lineare
2 2 2 A = Il Det(A) = 2 quindi la conica è non degenere, di rango 3.
 Studio delle coniche Ellisse Studiare la conica di equazione 2x 2 + 4xy + y 2 4x 2y + 2 = 0. Per prima cosa dobbiamo classificarla. La matrice associata alla conica è: 2 2 2 A = 2 2 2 Il DetA = 2 quindi
Studio delle coniche Ellisse Studiare la conica di equazione 2x 2 + 4xy + y 2 4x 2y + 2 = 0. Per prima cosa dobbiamo classificarla. La matrice associata alla conica è: 2 2 2 A = 2 2 2 Il DetA = 2 quindi
Sullo svolgimento di una delle quattro versioni della prova scritta di Geometria analitica e algebra lineare del giorno 11 febbraio 2013.
 Sullo svolgimento di una delle quattro versioni della prova scritta di Geometria analitica e algebra lineare del giorno febbraio 0 x + y + z = 0 Stabilire se le due rette r, di equazioni cartesiane ed
Sullo svolgimento di una delle quattro versioni della prova scritta di Geometria analitica e algebra lineare del giorno febbraio 0 x + y + z = 0 Stabilire se le due rette r, di equazioni cartesiane ed
VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) PRODOTTO VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI R 3. FASCI E STELLE. FORMULE
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) PRODOTTO VETTORIALE E PRODOTTO MISTO. PIANI E RETTE DI R 3. FASCI E STELLE. FORMULE
Classificazione delle coniche.
 Classificazione delle coniche Ora si vogliono studiare i luoghi geometrici rappresentati da equazioni di secondo grado In generale, non è facile riconoscere a prima vista di che cosa si tratta, soprattutto
Classificazione delle coniche Ora si vogliono studiare i luoghi geometrici rappresentati da equazioni di secondo grado In generale, non è facile riconoscere a prima vista di che cosa si tratta, soprattutto
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 17 SETTEMBRE 2012
 INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 7 SETTEMBRE 202 Esercizio. Sia V = R[X] 2 lo spazio vettoriale dei polinomi ax 2 + bx + c nella variabile X di grado al più 2 a coefficienti
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 7 SETTEMBRE 202 Esercizio. Sia V = R[X] 2 lo spazio vettoriale dei polinomi ax 2 + bx + c nella variabile X di grado al più 2 a coefficienti
Un fascio di coniche è determinato da una qualsiasi coppia di sue coniche distinte.
 Piano proiettivo Conica: curva algebrica reale del II ordine. a 11 x 2 1 + 2a 12 x 1 x 2 + a 22 x 2 2 + 2a 13 x 1 x 3 + 2a 23 x 2 x 3 + a 33 x 2 3 = 0 x T A x = 0 Classificazione proiettiva delle coniche:
Piano proiettivo Conica: curva algebrica reale del II ordine. a 11 x 2 1 + 2a 12 x 1 x 2 + a 22 x 2 2 + 2a 13 x 1 x 3 + 2a 23 x 2 x 3 + a 33 x 2 3 = 0 x T A x = 0 Classificazione proiettiva delle coniche:
H precedente. Procedendo come sopra, si costruisce la matrice del cambiamento di base
 Geometria analitica e algebra lineare, anno accademico 9/1 Commenti ad alcuni esercizi 17 Diagonalizzazione di matrici simmetriche Coniche Commenti ad alcuni degli esercizi proposti 17 Diagonalizzazione
Geometria analitica e algebra lineare, anno accademico 9/1 Commenti ad alcuni esercizi 17 Diagonalizzazione di matrici simmetriche Coniche Commenti ad alcuni degli esercizi proposti 17 Diagonalizzazione
GEOMETRIA PIANA. 1) sia verificata l uguaglianza di segmenti AC = CB (ossia C è punto medio del segmento AB);
 VETTORI E GEOMETRIA ANALITICA 1 GEOMETRIA PIANA Segmenti e distanza tra punti. Rette in forma cartesiana e parametrica. Posizioni reciproche di due rette, parallelismo e perpendicolarità. Angoli e distanze.
VETTORI E GEOMETRIA ANALITICA 1 GEOMETRIA PIANA Segmenti e distanza tra punti. Rette in forma cartesiana e parametrica. Posizioni reciproche di due rette, parallelismo e perpendicolarità. Angoli e distanze.
L algebra lineare nello studio delle coniche
 L algebra lineare nello studio delle coniche È possibile utilizzare le tecniche dell algebra lineare per studiare e classificare le coniche. Data l equazione generale di una conica, si considera la sua
L algebra lineare nello studio delle coniche È possibile utilizzare le tecniche dell algebra lineare per studiare e classificare le coniche. Data l equazione generale di una conica, si considera la sua
(x B x A, y B y A ) = (4, 2) ha modulo
 GEOMETRIA PIANA 1. Esercizi Esercizio 1. Dati i punti A(0, 4), e B(4, ) trovarne la distanza e trovare poi i punti C allineati con A e con B che verificano: (1) AC = CB (punto medio del segmento AB); ()
GEOMETRIA PIANA 1. Esercizi Esercizio 1. Dati i punti A(0, 4), e B(4, ) trovarne la distanza e trovare poi i punti C allineati con A e con B che verificano: (1) AC = CB (punto medio del segmento AB); ()
Soluzioni dello scritto di Geometria del 28 Maggio 2009
 Soluzioni dello scritto di Geometria del 8 Maggio 9 1) Trovare le equazioni del sottospazio V(w, x, y, z) R 4 generato dalle quaterne c 1 = (,,, 1) e c = (, 1, 1, ). ) Trovare una base per OGNI autospazio
Soluzioni dello scritto di Geometria del 8 Maggio 9 1) Trovare le equazioni del sottospazio V(w, x, y, z) R 4 generato dalle quaterne c 1 = (,,, 1) e c = (, 1, 1, ). ) Trovare una base per OGNI autospazio
Classificazione delle quadriche
 7 Classificazione delle quadriche In questo capitolo verrà discussa la classificazione delle quadriche dello spazio proiettivo complesso P n C; interpretando P n C come il completamento dello spazio affine
7 Classificazione delle quadriche In questo capitolo verrà discussa la classificazione delle quadriche dello spazio proiettivo complesso P n C; interpretando P n C come il completamento dello spazio affine
Compito di geometria 2 del 21/06/2005
 Compito di geometria 2 del 21/06/2005 1 Nel piano euclideo reale E 2 si consideri il fascio di coniche (k + 1x 2 + (k 1y 2 2kx + 2y k 1 = 0 a Classificare e, delle coniche degeneri del fascio, trovare
Compito di geometria 2 del 21/06/2005 1 Nel piano euclideo reale E 2 si consideri il fascio di coniche (k + 1x 2 + (k 1y 2 2kx + 2y k 1 = 0 a Classificare e, delle coniche degeneri del fascio, trovare
II Università degli Studi di Roma
 Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
Classificazione delle coniche
 8 Classificazione delle coniche In questo capitolo verrà discussa la classificazione delle coniche dello spazio proiettivo complesso P 2 C; interpretando P 2 C come il completamento dello spazio a ne A
8 Classificazione delle coniche In questo capitolo verrà discussa la classificazione delle coniche dello spazio proiettivo complesso P 2 C; interpretando P 2 C come il completamento dello spazio a ne A
Cenni sulle coniche 1.
 1 Premessa Cenni sulle coniche 1. Corso di laurea in Ingegneria Civile ed Edile Università degli Studi di Palermo A.A. 2013/2014 prof.ssa Paola Staglianò (pstagliano@unime.it) Scopo della geometria analitica
1 Premessa Cenni sulle coniche 1. Corso di laurea in Ingegneria Civile ed Edile Università degli Studi di Palermo A.A. 2013/2014 prof.ssa Paola Staglianò (pstagliano@unime.it) Scopo della geometria analitica
Geometria 2, a.a. 2006/2007 Ingegneria Edile-Edile Architettura
 Geometria 2, a.a. 2006/2007 Ingegneria Edile-Edile Architettura Tutore: Eleonora Palmieri 14 febbraio 2007 Esercizio 1: Si consideri in R 2 la conica Γ : 2x 2 1 + 4x 2 2 + x 1 + 2x 2 = 0. 1. Ridurre Γ
Geometria 2, a.a. 2006/2007 Ingegneria Edile-Edile Architettura Tutore: Eleonora Palmieri 14 febbraio 2007 Esercizio 1: Si consideri in R 2 la conica Γ : 2x 2 1 + 4x 2 2 + x 1 + 2x 2 = 0. 1. Ridurre Γ
Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 12/07/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI
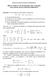 Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 12/07/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI Esercizio 1 Si consideri la conica affine d equazione 9x 2 + 6y 2 4xy 6x + 8y = 1 (1)
Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 12/07/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI Esercizio 1 Si consideri la conica affine d equazione 9x 2 + 6y 2 4xy 6x + 8y = 1 (1)
Isometrie. (f (g h))(x) = f(g(h(x))) = ((f g) h)(x).
 Isometrie.. Generalità. Una trasformazione di IR n è un alicazione biiettiva f : IR n IR n. Le trasformazioni si ossono comorre tra loro: se f e g sono due alicazioni biiettive da IR n ad IR n, allora
Isometrie.. Generalità. Una trasformazione di IR n è un alicazione biiettiva f : IR n IR n. Le trasformazioni si ossono comorre tra loro: se f e g sono due alicazioni biiettive da IR n ad IR n, allora
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria - CCS Edile ed Edile/Architettura
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria - CCS Edile ed Edile/Architettura Recupero II Esonero/II Appello del corso di Geometria Docente F. Flamini, Roma, 7/0/008 NORME SVOLGIMENTO
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria - CCS Edile ed Edile/Architettura Recupero II Esonero/II Appello del corso di Geometria Docente F. Flamini, Roma, 7/0/008 NORME SVOLGIMENTO
ESERCIZI DI RIPASSO, A.A
 ESERCIZI DI RIPASSO, A.A. 14-15 Per ogni risposta, segnare V se è vera, F se è falsa. Ogni test viene valutato 3 punti se vengono date tutte e sole le risposte corrette. Altrimenti, la valutazione è 0.
ESERCIZI DI RIPASSO, A.A. 14-15 Per ogni risposta, segnare V se è vera, F se è falsa. Ogni test viene valutato 3 punti se vengono date tutte e sole le risposte corrette. Altrimenti, la valutazione è 0.
PROVA SCRITTA DI GEOMETRIA 2 MATEMATICA, 20/09/2011
 PROVA SCRITTA DI GEOMETRIA 2 MATEMATICA, 20/09/2011 In questo elenco, la presenza di esercizi relativi ai singoli argomenti non è correlata alla loro rilevanza, né alla ricorrenza nella prova scritta.
PROVA SCRITTA DI GEOMETRIA 2 MATEMATICA, 20/09/2011 In questo elenco, la presenza di esercizi relativi ai singoli argomenti non è correlata alla loro rilevanza, né alla ricorrenza nella prova scritta.
Lezione 24 - Esercitazioni di Algebra e Geometria - Anno accademico
 CONICHE in A ~ (C) Punti propri (x P,y P ) hanno coordinate omogenee [(x P,y P, )], Punti impropri hanno coordinate omogenee [(l,m, )]. L equazione di una conica in coordinate non omogenee (x,y) C: a,
CONICHE in A ~ (C) Punti propri (x P,y P ) hanno coordinate omogenee [(x P,y P, )], Punti impropri hanno coordinate omogenee [(l,m, )]. L equazione di una conica in coordinate non omogenee (x,y) C: a,
Algebra lineare Geometria 1 15 luglio 2009
 Algebra lineare Geometria 1 15 luglio 2009 Esercizio 1. Nello spazio vettoriale reale R 3 [x] si considerino l insieme A k = {1 + x, k + (1 k)x 2, 1 + (k 1)x 2 + x 3 }, il vettore v k = k + kx x 3 e la
Algebra lineare Geometria 1 15 luglio 2009 Esercizio 1. Nello spazio vettoriale reale R 3 [x] si considerino l insieme A k = {1 + x, k + (1 k)x 2, 1 + (k 1)x 2 + x 3 }, il vettore v k = k + kx x 3 e la
formano una base B di R 3. Scrivere la matrice di passaggio dalla base B alla base canonica e dire se tale matrice è ortogonale.
 ) Mostrare che i 3 vettori v=, u=, w= 3 formano una base B di R 3. Scrivere la matrice di passaggio dalla base B alla base canonica e dire se tale matrice è ortogonale. ) Sia f : R 4 R 4 la seguente applicazione
) Mostrare che i 3 vettori v=, u=, w= 3 formano una base B di R 3. Scrivere la matrice di passaggio dalla base B alla base canonica e dire se tale matrice è ortogonale. ) Sia f : R 4 R 4 la seguente applicazione
GEOMETRIA svolgimento di uno scritto del 11 Gennaio 2012
 GEOMETRIA svolgimento di uno scritto del Gennaio ) Trovare una base per lo spazio delle soluzioni del seguente sistema omogeneo: x + y 5z = 3x y + z = x y + 8z =. Il sistema può essere scritto in forma
GEOMETRIA svolgimento di uno scritto del Gennaio ) Trovare una base per lo spazio delle soluzioni del seguente sistema omogeneo: x + y 5z = 3x y + z = x y + 8z =. Il sistema può essere scritto in forma
CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A PROVA SCRITTA DI GEOMETRIA DEL Corsi dei Proff. M. BORDONI, A.
 CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A. - PROVA SCRITTA DI GEOMETRIA DEL -- Corsi dei Proff. M. BORDONI, A. FOSCHI Esercizio. E data l applicazione lineare L : R 4 R 3 definita dalla matrice A = 3
CORSO DI LAUREA IN INGEGNERIA MECCANICA A.A. - PROVA SCRITTA DI GEOMETRIA DEL -- Corsi dei Proff. M. BORDONI, A. FOSCHI Esercizio. E data l applicazione lineare L : R 4 R 3 definita dalla matrice A = 3
UNIVERSITÀ DEGLI STUDI DI SALERNO Svolgimento della prova scritta di Matematica II 08 Giugno 2011
 Esercizio UNIVERSITÀ EGLI STUI I SALERNO della rova scritta di Matematica II Giugno In R con la struttura di sazio euclideo canonica si considerino le due rette: r : x y + ; s : x y ;. (a) dire se le rette
Esercizio UNIVERSITÀ EGLI STUI I SALERNO della rova scritta di Matematica II Giugno In R con la struttura di sazio euclideo canonica si considerino le due rette: r : x y + ; s : x y ;. (a) dire se le rette
PROVA SCRITTA DI GEOMETRIA 2 CON ELEMENTI DI STORIA 2, MATEMATICA, 16/06/2017. Nome... Matricola...
 PROVA SCRITTA DI GEOMETRIA 2 CON ELEMENTI DI STORIA 2, MATEMATICA, 16/06/2017 Nome... Matricola... Per ogni risposta, segnare V se è vera, F se è falsa. Ogni test viene valutato 3 punti se vengono date
PROVA SCRITTA DI GEOMETRIA 2 CON ELEMENTI DI STORIA 2, MATEMATICA, 16/06/2017 Nome... Matricola... Per ogni risposta, segnare V se è vera, F se è falsa. Ogni test viene valutato 3 punti se vengono date
Esame di Matematica 3 (laurea in Matematica) prova scritta del 3 luglio 2008 Compito A
 Esame di Matematica 3 (laurea in Matematica prova scritta del 3 luglio 28 Compito A ESERCIZIO. Si consideri la proiettività, f : P 3 (R P 3 (R, di matrice 3 3 A = 2 3 3 nel riferimento canonico {e,...,
Esame di Matematica 3 (laurea in Matematica prova scritta del 3 luglio 28 Compito A ESERCIZIO. Si consideri la proiettività, f : P 3 (R P 3 (R, di matrice 3 3 A = 2 3 3 nel riferimento canonico {e,...,
Coniche in forma generale
 LE CONICHE Fissiamo nel piano un sistema di riferimento cartesiano ortogonaleo, x, y, u. Coniche in forma generale Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro
LE CONICHE Fissiamo nel piano un sistema di riferimento cartesiano ortogonaleo, x, y, u. Coniche in forma generale Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro
Esame di Matematica 3 (laurea in Matematica) prova scritta del 18 giugno 2008 Compito A
 Esame di Matematica 3 (laurea in Matematica prova scritta del 8 giugno 28 Compito A ESERCIZIO. Si consideri la proiettività, f : P 3 (R P 3 (R, di matrice 6 4 2 2 A = 4 2 2 2 nel riferimento canonico {e,...,
Esame di Matematica 3 (laurea in Matematica prova scritta del 8 giugno 28 Compito A ESERCIZIO. Si consideri la proiettività, f : P 3 (R P 3 (R, di matrice 6 4 2 2 A = 4 2 2 2 nel riferimento canonico {e,...,
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE
 SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
SPAZI EUCLIDEI, APPLICAZIONI SIMMETRICHE, FORME QUADRATICHE. Esercizi Esercizio. In R calcolare il modulo dei vettori,, ),,, ) ed il loro angolo. Esercizio. Calcolare una base ortonormale del sottospazio
Appunti sulla circonferenza
 1 Liceo Falchi Montopoli in Val d Arno - Classe 3 a I - Francesco Daddi - 16 aprile 010 Appunti sulla circonferenza In queste pagine sono trattati gli argomenti riguardanti la circonferenza nel piano cartesiano
1 Liceo Falchi Montopoli in Val d Arno - Classe 3 a I - Francesco Daddi - 16 aprile 010 Appunti sulla circonferenza In queste pagine sono trattati gli argomenti riguardanti la circonferenza nel piano cartesiano
Corso di Geometria Meccanica, Elettrotecnica Esercizi 11: soluzioni
 Corso di Geometria 0- Meccanica Elettrotecnica Esercizi : soluzioni Esercizio Scrivere la matrice canonica di ciascuna delle seguenti trasformazioni lineari del piano: a) Rotazione di angolo π b) Rotazione
Corso di Geometria 0- Meccanica Elettrotecnica Esercizi : soluzioni Esercizio Scrivere la matrice canonica di ciascuna delle seguenti trasformazioni lineari del piano: a) Rotazione di angolo π b) Rotazione
Questi sono alcuni esercizi indicativi. Vedere anche [Franchetta-Morelli]. CONICHE. 9x 2 2 4( 4x 2 2)
![Questi sono alcuni esercizi indicativi. Vedere anche [Franchetta-Morelli]. CONICHE. 9x 2 2 4( 4x 2 2) Questi sono alcuni esercizi indicativi. Vedere anche [Franchetta-Morelli]. CONICHE. 9x 2 2 4( 4x 2 2)](/thumbs/102/156055849.jpg) Questi sono alcuni esercizi indicativi. Vedere anche [Franchetta-Morelli]. CONICHE Esercizio 1 Fissato nell ampliamento proiettivo complesso del piano un sistema di coordinate omogenee, classificare (dal
Questi sono alcuni esercizi indicativi. Vedere anche [Franchetta-Morelli]. CONICHE Esercizio 1 Fissato nell ampliamento proiettivo complesso del piano un sistema di coordinate omogenee, classificare (dal
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI
 CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # 4 GEOMETRIA E ALGEBRA LINEARE 009/0 Esercizio 4. (Esercizio 7.3). Calcolare l inversa delle matrici (invertibili) [ ] 3 A = B
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # 4 GEOMETRIA E ALGEBRA LINEARE 009/0 Esercizio 4. (Esercizio 7.3). Calcolare l inversa delle matrici (invertibili) [ ] 3 A = B
Esercizi per Geometria II Geometria euclidea e proiettiva
 Esercizi per Geometria II Geometria euclidea e proiettiva Filippo F. Favale 8 aprile 014 Esercizio 1 Si consideri E dotato di un riferimento cartesiano ortonormale di coordinate (x, y) e origine O. Si
Esercizi per Geometria II Geometria euclidea e proiettiva Filippo F. Favale 8 aprile 014 Esercizio 1 Si consideri E dotato di un riferimento cartesiano ortonormale di coordinate (x, y) e origine O. Si
Vincenzo Aieta CONICHE, FASCI DI CONICHE
 Vincenzo Aieta CONICHE, FASCI DI CONICHE Le coniche 1 Teoria delle Coniche Il nome conica deriva dal semplice fatto che gli antichi Greci secando con un piano una conica a doppia falda ottenevano, a seconda
Vincenzo Aieta CONICHE, FASCI DI CONICHE Le coniche 1 Teoria delle Coniche Il nome conica deriva dal semplice fatto che gli antichi Greci secando con un piano una conica a doppia falda ottenevano, a seconda
TRASFORMAZIONI GEOMETRICHE ( 1 ) Risolvendo il sistema lineare ( 1 ) rispetto alle incognite x, y si ottiene: = e
 Generalità sulle affinità TRASFORMAZIONI GEOMETRICHE Chiamasi affinità o trasformazione lineare una corrisondenza biunivoca tra due iani o tra unti dello stesso iano che trasforma rette in rette conservando
Generalità sulle affinità TRASFORMAZIONI GEOMETRICHE Chiamasi affinità o trasformazione lineare una corrisondenza biunivoca tra due iani o tra unti dello stesso iano che trasforma rette in rette conservando
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014
 FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
FONDAMENTI DI ALGEBRA LINEARE E GEOMETRIA INGEGNERIA INDUSTRIALE 27 GENNAIO 2014 DOCENTE: MATTEO LONGO Rispondere alle domande di Teoria in modo esauriente e completo. Svolgere il maggior numero di esercizi
Università di Pisa. Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare
 Università di Pisa Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare Cognome e Nome: Corso di studi: Anno di iscrizione: Numero di matricola: Scritto n. 1 del 16 Esercizio 1. Si studi
Università di Pisa Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare Cognome e Nome: Corso di studi: Anno di iscrizione: Numero di matricola: Scritto n. 1 del 16 Esercizio 1. Si studi
Cubiche e affinità nelpiano
 Cubiche e affinità neliano Francesco Daddi Marzo 2009 Vogliamo dimostrare che, assegnata una qualsiasi coia di funzioni cubiche, esiste un affinità che trasforma l una nell altra. E ossibile collegare
Cubiche e affinità neliano Francesco Daddi Marzo 2009 Vogliamo dimostrare che, assegnata una qualsiasi coia di funzioni cubiche, esiste un affinità che trasforma l una nell altra. E ossibile collegare
PALESTRA PER IL RECUPERO
 PARABOLA. PALESTRA PER IL RECUPERO ESERCIZI SVOLTI ESERCIZI Raresentare graficamente la arabola di equazione assegnata. 1 y x þ x Determiniamo la coordinate del vertice b " x V b a 1 ð 1Þ 1 # a y V c b
PARABOLA. PALESTRA PER IL RECUPERO ESERCIZI SVOLTI ESERCIZI Raresentare graficamente la arabola di equazione assegnata. 1 y x þ x Determiniamo la coordinate del vertice b " x V b a 1 ð 1Þ 1 # a y V c b
Curve algebriche piane
 3 Curve algebriche piane In tutto il capitolo, consideriamo fissato un piano reale complessificato nel quale sia assegnato un riferimento cartesiano reale R =(O, v 1, v ). 3.1 Il caso di una variabile
3 Curve algebriche piane In tutto il capitolo, consideriamo fissato un piano reale complessificato nel quale sia assegnato un riferimento cartesiano reale R =(O, v 1, v ). 3.1 Il caso di una variabile
Facsimile di prova d esame Esempio di svolgimento
 Geometria analitica 18 marzo 009 Facsimile di prova d esame Esempio di svolgimento 1 Nello spazio, riferito a coordinate cartesiane ortogonali e monometriche x,y,z, è assegnata la retta r di equazioni
Geometria analitica 18 marzo 009 Facsimile di prova d esame Esempio di svolgimento 1 Nello spazio, riferito a coordinate cartesiane ortogonali e monometriche x,y,z, è assegnata la retta r di equazioni
Classificazione delle coniche
 8 Classificazione delle coniche In questo capitolo verrà discussa la classificazione delle coniche dello spazio proiettivo complesso P C; interpretando P C come il completamento dello spazio a ne A C =
8 Classificazione delle coniche In questo capitolo verrà discussa la classificazione delle coniche dello spazio proiettivo complesso P C; interpretando P C come il completamento dello spazio a ne A C =
Esercizi di consolidamento
 Esercizi di consolidamento Il sistema di riferimento nel iano Trova le misure dei segmenti che hanno come estremi le seguenti coie di unti e le coordinate dei loro unti medi. Að, Þ B, ; C 0, D, ; Eð, Þ
Esercizi di consolidamento Il sistema di riferimento nel iano Trova le misure dei segmenti che hanno come estremi le seguenti coie di unti e le coordinate dei loro unti medi. Að, Þ B, ; C 0, D, ; Eð, Þ
CdL in Ingegneria Informatica (A-Faz), (Orp-Z) CdL in Ingegneria del Recupero Edilizio ed Ambientale
 Prova scritta di Geometria assegnata il 13 Dicembre 2003 Sia Si consideri l equazione AX = A t. 0 1 1 A = 1 1 5 R 3,3. 1 2 1 h 1) Determinare i valori di h per cui tale equazione ammette soluzioni. 2)
Prova scritta di Geometria assegnata il 13 Dicembre 2003 Sia Si consideri l equazione AX = A t. 0 1 1 A = 1 1 5 R 3,3. 1 2 1 h 1) Determinare i valori di h per cui tale equazione ammette soluzioni. 2)
Coniche R. Notari 15 Aprile
 Coniche R. Notari 15 Aprile 2006 1 1. Notazioni. Proposizione 1 Ogni conica si rappresenta tramita un equazione algebrica di secondo grado della forma a 11 x 2 +2a 12 xy + a 22 y 2 + +2a 13 x + 2a 23 y
Coniche R. Notari 15 Aprile 2006 1 1. Notazioni. Proposizione 1 Ogni conica si rappresenta tramita un equazione algebrica di secondo grado della forma a 11 x 2 +2a 12 xy + a 22 y 2 + +2a 13 x + 2a 23 y
11 luglio Soluzione esame di geometria - Ing. gestionale - a.a COGNOME... NOME... N. MATRICOLA... ISTRUZIONI
 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura ore. ISTRUZIONI Ti sono stati consegnati tre fogli, stampati fronte e retro. Come prima cosa scrivi
Università di Pisa. Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare
 Università di Pisa Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare Cognome e Nome: Corso di studi: Anno di iscrizione: Numero di matricola: Scritto n. 1 del 016 Esercizio 1. Si studi
Università di Pisa Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare Cognome e Nome: Corso di studi: Anno di iscrizione: Numero di matricola: Scritto n. 1 del 016 Esercizio 1. Si studi
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria - CCS Edilizia ed Edile/Architettura
 Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria - CCS Edilizia ed Edile/Architettura V Appello corso di Geometria a.a. / Docente F. Flamini NORME SVOLGIMENTO Negli appositi spazi scrivere
Universita degli Studi di Roma Tor Vergata Facolta di Ingegneria - CCS Edilizia ed Edile/Architettura V Appello corso di Geometria a.a. / Docente F. Flamini NORME SVOLGIMENTO Negli appositi spazi scrivere
LEZIONE 23. ax 2 + bxy + cy 2 + dx + ey + f
 LEZIONE 23 23.1. Riduzione delle coniche a forma canonica. Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y a meno di costanti moltiplicative non nulle, diciamo
LEZIONE 23 23.1. Riduzione delle coniche a forma canonica. Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y a meno di costanti moltiplicative non nulle, diciamo
CONICHE. Esercizi Esercizio 1. Nel piano con riferimento cartesiano ortogonale Oxy sia data la conica C di equazione
 CONICHE Esercizi Esercizio 1. Nel piano con riferimento cartesiano ortogonale Oy sia data la conica C di equazione 7 2 + 2 3y + 5y 2 + 32 3 = 0. Calcolare le equazioni di una rototraslazione che riduce
CONICHE Esercizi Esercizio 1. Nel piano con riferimento cartesiano ortogonale Oy sia data la conica C di equazione 7 2 + 2 3y + 5y 2 + 32 3 = 0. Calcolare le equazioni di una rototraslazione che riduce
GEOMETRIA ANALITICA: LE CONICHE
 DIPARTIMENTO DI INGEGNERIA CIVILE PRECORSO DI MATEMATICA ANNO ACCADEMICO 2013-2014 ESERCIZI DI GEOMETRIA ANALITICA: LE CONICHE Esercizio 1: Fissato su un piano un sistema di riferimento cartesiano ortogonale
DIPARTIMENTO DI INGEGNERIA CIVILE PRECORSO DI MATEMATICA ANNO ACCADEMICO 2013-2014 ESERCIZI DI GEOMETRIA ANALITICA: LE CONICHE Esercizio 1: Fissato su un piano un sistema di riferimento cartesiano ortogonale
Problema 1.5. Mostra che una retta immaginaria r nello spazio contiene al più un punto reale.
 1 Complessificazione Problema 1.5. Mostra che una retta immaginaria r nello spazio contiene al più un punto reale. Soluzione. Se r è di prima specie, allora r è complanare con la sua coniugata: se, in
1 Complessificazione Problema 1.5. Mostra che una retta immaginaria r nello spazio contiene al più un punto reale. Soluzione. Se r è di prima specie, allora r è complanare con la sua coniugata: se, in
Corso di Geometria Ing. Informatica e Automatica Test 1: soluzioni
 Corso di Geometria Ing. Informatica e Automatica Test : soluzioni k Esercizio Data la matrice A = k dipendente dal parametro k, si consideri il k sistema lineare omogeneo AX =, con X = x x. Determinare
Corso di Geometria Ing. Informatica e Automatica Test : soluzioni k Esercizio Data la matrice A = k dipendente dal parametro k, si consideri il k sistema lineare omogeneo AX =, con X = x x. Determinare
Appunti ed esercizi sulle coniche
 1 LA CIRCONFERENZA 1 Appunti ed esercizi sulle coniche Versione del 1 Marzo 011 1 La circonferenza Nel piano R, fissati un punto O = (a, b) e un numero r > 0, la circonferenza (o cerchio) C di centro O
1 LA CIRCONFERENZA 1 Appunti ed esercizi sulle coniche Versione del 1 Marzo 011 1 La circonferenza Nel piano R, fissati un punto O = (a, b) e un numero r > 0, la circonferenza (o cerchio) C di centro O
Esercizi di consolidamento
 Esercizi di consolidamento Il sistema di riferimento cartesiano Trova le misure dei segmenti che hanno come estremi le seguenti coie di unti e le coordinate dei loro unti medi. Að, Þ B, ; C 0, D, ; Eð,
Esercizi di consolidamento Il sistema di riferimento cartesiano Trova le misure dei segmenti che hanno come estremi le seguenti coie di unti e le coordinate dei loro unti medi. Að, Þ B, ; C 0, D, ; Eð,
Dipartimento di Matematica Corso di laurea in Fisica Compito di Geometria assegnato il 1 Febbraio 2002
 Compito di Geometria assegnato il 1 Febbraio 2002 Trovare l equazione della conica irriducibile tangente all asse x nel punto A(2, 0), tangente all asse y e passante per i punti B(1, 1) e C(2, 2) Scrivere
Compito di Geometria assegnato il 1 Febbraio 2002 Trovare l equazione della conica irriducibile tangente all asse x nel punto A(2, 0), tangente all asse y e passante per i punti B(1, 1) e C(2, 2) Scrivere
2x 2 + 4x 2y + 1 = 2(x 2 + 2x + 1 1) 2y + 1 = 2(x + 1) 2 2(y ) = 0.
 CONICHE E QUADRICHE. Esercizi Esercizio. Classificare, ridurre a forma canonica (completando i quadrati), e disegnare le seguenti coniche: γ : x y + x = 0; γ : x + 4x y + = 0; γ : x + y + y + 0 = 0; γ
CONICHE E QUADRICHE. Esercizi Esercizio. Classificare, ridurre a forma canonica (completando i quadrati), e disegnare le seguenti coniche: γ : x y + x = 0; γ : x + 4x y + = 0; γ : x + y + y + 0 = 0; γ
L iperbole. x 2 = 1. a 2 b 2. Si noti che tale equazione è stata ottenuta rispetto ad un riferimento privilegiato, detto RIFERIMENTO CANONICO.
 L iperbole Fisso nel piano due punti distinti, F ed F FUOCHI F ed F l insieme: Si dice IPERBOLE di {P R : dist(p ; F ) dist(p ; F ) = a} Se dist(f ; F ) = c, fisso un sistema di assi cartesiano tale che
L iperbole Fisso nel piano due punti distinti, F ed F FUOCHI F ed F l insieme: Si dice IPERBOLE di {P R : dist(p ; F ) dist(p ; F ) = a} Se dist(f ; F ) = c, fisso un sistema di assi cartesiano tale che
Per le risposte utilizza gli spazi predisposti. Quando richiesto, il procedimento va esposto brevemente, ma in maniera comprensibile.
 COGNOME............................... NOME..................................... Punti ottenuti Esame di geometria Scrivi cognome e nome negli spazi predisposti in ciascuno dei tre fogli. Per ogni domanda
COGNOME............................... NOME..................................... Punti ottenuti Esame di geometria Scrivi cognome e nome negli spazi predisposti in ciascuno dei tre fogli. Per ogni domanda
Università degli Studi di Bergamo Corso integrato di Analisi 1 (Geometria e Algebra Lineare) 29 aprile 2011 Tema A
 Università degli Studi di Bergamo Corso integrato di Analisi 1 (Geometria e Algebra Lineare) 9 aprile 011 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
Università degli Studi di Bergamo Corso integrato di Analisi 1 (Geometria e Algebra Lineare) 9 aprile 011 Tema A Tempo a disposizione: ore. Calcolatrici, libri e appunti non sono ammessi. Ogni esercizio
~ E 2 (R) si determini l equazione cartesiana del
 In Esercizio 1 ~ E (R) si determini l equazione cartesiana del luogo dei punti equidistanti dal punto F=(1,) e dalla retta y=x. a) Si classifichi la conica così ottenuta; b) Si determini l asse e il vertice;
In Esercizio 1 ~ E (R) si determini l equazione cartesiana del luogo dei punti equidistanti dal punto F=(1,) e dalla retta y=x. a) Si classifichi la conica così ottenuta; b) Si determini l asse e il vertice;
Note di geometria analitica nel piano
 Note di geometria analitica nel piano e-mail: maurosaita@tiscalinet.it Versione provvisoria. Novembre 2015. 1 Indice 1 Punti e vettori spiccati dall origine 3 1.1 Coordinate......................................
Note di geometria analitica nel piano e-mail: maurosaita@tiscalinet.it Versione provvisoria. Novembre 2015. 1 Indice 1 Punti e vettori spiccati dall origine 3 1.1 Coordinate......................................
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 19 GIUGNO 2012
 INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 19 GIUGNO 2012 MATTEO LONGO Esercizio 1. Al variare del parametro a R, si consideri l applicazione lineare L a : R R definita dalle
INGEGNERIA EDILE ARCHITETTURA ELEMENTI DI ALGEBRA LINEARE E GEOMETRIA 19 GIUGNO 2012 MATTEO LONGO Esercizio 1. Al variare del parametro a R, si consideri l applicazione lineare L a : R R definita dalle
12 gennaio Commenti esame di geometria - Ing. gestionale - a.a
 Questo documento riporta commenti, approfondimenti o metodi di soluzione alternativi per alcuni esercizi dell esame Ovviamente alcuni esercizi potevano essere risolti utilizzando metodi ancora diversi
Questo documento riporta commenti, approfondimenti o metodi di soluzione alternativi per alcuni esercizi dell esame Ovviamente alcuni esercizi potevano essere risolti utilizzando metodi ancora diversi
CdL in Ingegneria Industriale (A-E e F-O)
 CdL in Ingegneria Industriale (A-E e F-O) Prova scritta di Algebra lineare e Geometria- Febbraio 06 Durata della prova: tre ore. È vietato uscire dall aula prima di aver consegnato definitivamente il compito.
CdL in Ingegneria Industriale (A-E e F-O) Prova scritta di Algebra lineare e Geometria- Febbraio 06 Durata della prova: tre ore. È vietato uscire dall aula prima di aver consegnato definitivamente il compito.
SOLUZIONI (PROVA DELL 11 FEBBRAIO 2019) Due rette sghembe sono simultaneamente parallele a infiniti piani. [ V ]
![SOLUZIONI (PROVA DELL 11 FEBBRAIO 2019) Due rette sghembe sono simultaneamente parallele a infiniti piani. [ V ] SOLUZIONI (PROVA DELL 11 FEBBRAIO 2019) Due rette sghembe sono simultaneamente parallele a infiniti piani. [ V ]](/thumbs/103/159439756.jpg) SOLUZIONI (PROVA DELL FEBBRAIO 209) Il rango per righe può superare di il rango per colonne [ F ] In R 6 possono esistere 7 generatori di un sottospazio [ V ] {( + 2k, 2 k, 0), (,, 0), (0, 0, )} è una
SOLUZIONI (PROVA DELL FEBBRAIO 209) Il rango per righe può superare di il rango per colonne [ F ] In R 6 possono esistere 7 generatori di un sottospazio [ V ] {( + 2k, 2 k, 0), (,, 0), (0, 0, )} è una
Esercitazioni di Geometria II
 Esercitazioni di Geometria II Letizia Pernigotti - pernigotti@science.unitn.it 5 aprile 0 Esercizio. [dagli esercizi online della prof.ssa Carrara] Sia E R il piano euclideo numerico dotato del riferimento
Esercitazioni di Geometria II Letizia Pernigotti - pernigotti@science.unitn.it 5 aprile 0 Esercizio. [dagli esercizi online della prof.ssa Carrara] Sia E R il piano euclideo numerico dotato del riferimento
Le risposte vanno giustificate con chiarezza. 1) Nello spazio vettoriale V delle matrici 2 2 a coefficienti reali, considera le matrici A 1 = , A 4 =
 Università degli Studi di Roma Tor Vergata. Corso di Laurea in Matematica Esame di Geometria 1 con Elementi di Storia Prof. F. Tovena 30 gennaio 2015 Le risposte vanno giustificate con chiarezza. 1 Nello
Università degli Studi di Roma Tor Vergata. Corso di Laurea in Matematica Esame di Geometria 1 con Elementi di Storia Prof. F. Tovena 30 gennaio 2015 Le risposte vanno giustificate con chiarezza. 1 Nello
