4. FLUIDI AERIFORMI NEI CONDOTTI

Transcript

1 Politenio di oino Lauea a Distanza in Ingegneia Meania Coso di Mahine 4 FLUIDI AERIFORMI NEI CONDOI Nello studio delle ahine si one il oblea di deteinae la onfoazione dei ondotti in odo he il fluido subisa deteinate tasfoazioni duante il suo assaggio; il oblea oleentae è aesentato dall individuazione dell evoluzione he il fluido seienta nell attavesae un ondotto di foa assegnata e on deteinate ondizioni al ontono Nella esente tattazione i si ifeià eslusivaente al oto di fluidi aeifoi (oiibili) talasiando l estensione al aso dei fluidi inoiibili (liquidi) 4 DEFINIZIONI PRELIMINARI VELOCIA DEL SUONO La veloità del suono è genealente identifiata on la veloità di oagazione delle iole etubazioni in un fluido in ui si itiene tasuabile la onduibilità teia Il suo valoe non diende dalla geoetia del ao di oto (onodiensionale bidiensionale ) a eslusivaente dallo stato fisio del ezzo: S dove è la essione del fluido? la sua densità ente la deivata sotto adie quadata è effettuata ad entoia ostante (si onsidea la oagazione di una etubazione infinitesia: le vaiazioni delle gandezze fisihe attaveso l onda sono infinitesie e le tasfoazioni del fluido si ossono onsideae evesibili; inolte il fluido è suosto un sistea adiabatio ivo di onduibilità teia) Utilizzando la legge di evoluzione isentoia (/? K ost) l esessione della veloità del suono diventa la seguente: S S valida e qualunque aeifoe (gas efetto fluido eale vaoe e) Nel aso di gas efetto utilizzando l equazione di stato si ottiene: S R Nel aso del vao d aqua ooeà fa ifeiento al diagaa di Mollie e deteinae l esonente dell evoluzione isentoia Ad eseio noti valoi di e? (unto iniziale della tasfoazione) sostandosi isentoiaente si ossono leggee i valoi e? di un geneio unto lungo l evoluzione E ossibile alloa alolae il valoe di ediante la seguente esessione: Aunti del Coso (Doente: Fabio Mallao) 4 Moto degli Aeifoi nei Condotti - ag 36

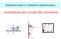
2 Politenio di oino Lauea a Distanza in Ingegneia Meania Coso di Mahine ln ln E ootuno notae he eoi anhe ioli di lettua dei valoi di essione e volue seifio sul diagaa di Collie ossono ondue a valoi di alolati e ezzo dell equazione eedente assai ieisi NUMERO DI MACH Il aoto ta la veloità del fluido in un unto e la veloità loale del suono ende il noe di nueo di Mah: S M GRANDEZZE OALI (DI RISAGNO) DI UNA CORRENE Si definisono oietà o gandezze di istagno (o totali o di aesto) di una oente fluida i valoi he i aaeti teodinaii della oente aquisteebbeo se questa fosse deeleata fino a veloità nulla isentoiaente Figua 4: Gandezze totali di una oente fluida L entalia totale è definita dalla soa dell entalia e dell enegia inetia Pe l unità di assa: i i Aliando il io iniio della teodinaia in foa loale ad una tasfoazione adiabatia e senza sabio di lavoo on l esteno si ottiene: Q e L i E ( Q L E ) i f g e i f g Aunti del Coso (Doente: Fabio Mallao) 4 Moto degli Aeifoi nei Condotti - ag 37

3 Politenio di oino Lauea a Distanza in Ingegneia Meania Coso di Mahine i E (i ) i os t i Dalle eedenti elazioni si dedue he e un fluido in oto stazionaio (anhe non isentoio) in una tasfoazione adiabatia e senza sabi di lavoo l entalia totale è una gandezza ostante Pe un gas ideale vale inolte la seguente elazione: i (i ) P os t os t P dove on il sibolo si è indiata la teeatua totale he dunque è una gandezza ostante (e un gas ideale) in una tasfoazione adiabatia e senza sabi di lavoo on l esteo aliata ad un fluido in oto stazionaio (anhe non isentoio) E bene iaae il fatto he le eedenti equazioni sono state iavate non ionendo l isentoiità del oto Le definizioni e la ostanza dell entalia totale e e un gas ideale della teeatua totale non diendono etanto da questa assunzione Le alte gandezze di aesto invee e loo stessa definizione sono i valoi aggiunti dalle oisondenti gandezze statihe quando la oente viene aestata on un oesso isentoio La essione totale uò essee alolata on la seguente elazione suonendo l evoluzione isentoia: nella quale al solito l aie seve a distinguee le gandezze totali da quelle statihe Pe la densità totale analogaente vale l esessione seguente: Pe quanto detto essione e densità totali si onsevano in tutto il doinio solo nel aso di oto eanente isentoio in assenza di sabi di aloe e lavoo on l esteno Con assaggi elativaente selii si iavano infine le seguenti esessioni delle gandezze totali: M ( M ( M ) ) Aunti del Coso (Doente: Fabio Mallao) 4 Moto degli Aeifoi nei Condotti - ag 38

4 Politenio di oino Lauea a Distanza in Ingegneia Meania Coso di Mahine La ia delle eedenti elazioni è valida solo nell iotesi di gas ideale le alte due valgono anhe e gas eale o vaoe 4 EFFUSORI E DIFFUSORI Pe lo studio del oto dei fluidi nei ondotti si adotteanno le seguenti iotesi selifiative: a) Flusso unidiensionale - un unia oodinata ioè l asissa isuata lungo l asse del ondotto è suffiiente e individuae le ondizioni del flusso e quindi in ogni sezione noale all asse del ondotto il fluido si tova in ondizioni teodinaihe e di veloità unifoi b) Flusso stazionaio - le aatteistihe del fluido non sono funzioni del teo a solo dello sazio ioè le aatteistihe del fluido in ogni singola sezione sono ostanti nel teo EFFUSORE Un effusoe è un ondotto in ui l'effetto utile è ostituito da un auento della veloità in usita isetto a quella in ingesso a sese di una iduzione di essione fa onte e valle del sistea stesso Aliando il io iniio della teodinaia in foa euleiana ad un sistea oendente un ondotto fisso (isetto al sistea di ifeiento ineziale) attaveso il quale un fluido oiibile ideale si uove in oto stazionaio la veloità di efflusso tasuando il teine legato alla vaiazione di enegia otenziale uò essee sitta nel odo seguente iotizzando il flusso unidiensionale: ( i i ) Q e dove i edii e indiano isettivaente la sezione di ingesso e quella di usita Utilizzando invee il io iniio in foa ista si ottiene: vd Lw Se si onsidea il aso atiolae di notevole iotanza atia in ui il flusso evolve seondo una olitoia adiabatia on edite (Q e e L w ) e se si assue he la veloità in ingesso sia tasuabile isetto a quella finale la veloità di efflusso uò essee esessa dalle elazioni seguenti: ( ) v v Lw Aunti del Coso (Doente: Fabio Mallao) 4 Moto degli Aeifoi nei Condotti - ag 39

5 Politenio di oino Lauea a Distanza in Ingegneia Meania Coso di Mahine Aunti del Coso (Doente: Fabio Mallao) 4 Moto degli Aeifoi nei Condotti - ag 4 Coe si uò notae dalle equazioni eedenti la veloità di usita da un ondotto uò essee alolata se sono note le ondizioni del fluido in ingesso ( e ) la essione in usita e l'esonente della tasfoazione (ovviaente devono anhe essee note le oietà del fluido) Sesso iuttosto he agionae in teini di onosenza del oeffiiente della olitoia si efeise fae ifeiento al valoe del oeffiiente di iduzione di veloità φ / is Questo nel aso di tasfoazione adiabatia e on veloità in ingesso al ondotto tasuabile uò essee sitto nel odo seguente: is ϕ iodando he la veloità di efflusso isentoio vale is v I endienti idaulio ed isentoio dell'effusoe sono definiti nel odo seguente: w ye L E E η is e E E η Se il sistea non è ineziale tutte le elazioni eedenti sono aliabili on ifeiento al oto elativo DIFFUSORE Un diffusoe è un ondotto in ui l'effetto utile è ostituito da un auento della essione in usita isetto a quella in ingesso a sese di una iduzione della veloità ta ingesso ed usita Aliando il io iniio della teodinaia in foa euleiana ad un sistea oendente un ondotto fisso (isetto al sistea di ifeiento ineziale) attaveso il quale un fluido oiibile ideale si uove in oto stazionaio e iotizzando he la tasfoazione alla quale è soggetto il fluido sia una olitoia isulta: e E E i Q e E Q

6 Politenio di oino Lauea a Distanza in Ingegneia Meania Coso di Mahine dove al solito è stato tasuato il teine dovuto alla vaiazione di enegia otenziale Aliando il io iniio in foa ista si ottiene: L i vd Lw E R Lw E Lw E R Analogaente a quanto visto e l effusoe il endiento idaulio ed il endiento isentoio di un diffusoe sono definiti nel odo seguente ( E < ): E Lw i η yd η is d E i Se il sistea non è ineziale tutte le elazioni eedenti sono aliabili on ifeiento al oto elativo 43 ANDAMENO DELLE AREE IN UN CONDOO Esiendo la vaiazione di otata fa due sezioni distanti dx lungo il ondotto e onsideando il fluido in oto eanente si uò sivee: d& & da A d d [] Dal io iniio della teodinaia esesso in foa euleiana on L i e L w isulta (sistea ineziale): d d da ui si evine he ad un auento di veloità oisonde una diinuzione di essione e vievesa Sostituendo nella [] si ottiene: da d d da da [] A A d d A d d s Nella sittua delle eedenti elazioni si è assunta l iotesi di oto isentoio e dunque si è alolata la deivata della essione isetto alla densità ad entoia ostante: d s d S os t dove S è la veloità del suono La [] uò essee anhe sitta oe segue: Aunti del Coso (Doente: Fabio Mallao) 4 Moto degli Aeifoi nei Condotti - ag 4

7 Politenio di oino Lauea a Distanza in Ingegneia Meania Coso di Mahine da A d ( ) M dove M è il nueo di Mah Si ossono a questo unto effettuae alune onsideazioni sull andaento delle aee delle sezioni di assaggio del fluido lungo la linea d asse di un effusoe o un diffusoe seondo quanto iassunto nella tabella seguente: Subsonio < s M < Suesonio > s M > Effusoe d < da < da > Diffusoe d > da > da < Risulta etanto he un effusoe o ugello è un onvegente se il oto all ingesso del ondotto è subsonio è un divegente se invee è suesonio Pe un diffusoe valgono le ondizioni ooste Nel aso di ugello onvegentedivegente dunque se nella sezione inia non si è aggiunta la veloità del suono endendo divegente il ondotto il flusso non viene iù aeleato Si ala di ondizioni itihe quando in un unto viene aggiunta la veloità del suono (M) ali onlusioni sono valide anhe se il sistea non è ineziale uhè si faia ifeiento al oto elativo 44 PRESSIONE CRIICA IN UN CONVERGENE Iotizzando di avee a disosizione un ondotto onvegente nel quale il fluido evolva seondo una tasfoazione isentoia (Q e e L w ) il io iniio della teodinaia si selifia in questo odo: is i is i La assia essione di valle he ende sonia la veloità di efflusso è detta essione itia Se e iotesi inolte aliando il io iniio al ondotto isulta: d is s ( ) d S os t on s R Si uò etanto sivee: R R R da ui si ottiene: Aunti del Coso (Doente: Fabio Mallao) 4 Moto degli Aeifoi nei Condotti - ag 4

8 Politenio di oino Lauea a Distanza in Ingegneia Meania Coso di Mahine La veloità del suono nella sezione istetta uò essee esessa in funzione delle sole ondizioni di onte: s R R s Nell iotesi in ui le ondizioni a onte dell ugello siano ai a quelle totali o di aesto la essione itia uò essee iavata iediataente oe segue: ( ) Il valoe del aoto itio ta essione di usita e essione di onte diende solo dal valoe di (nell iotesi di oto isentoio) Genealente il aoto / onte è oeso ta 487 e 58 e vaiabile ta 66 (gas onoatoii) e 35 (vaoe satuo seo) 45 UGELLO SEMPLICEMENE CONVERGENE (CASO IDEALE) Consideiao la figua 4 in ui è aesentato un ugello selieente onvegente (effusoe subsonio) e sovaosto un gafio he iota l andaento della otata in assa di fluido he lo attavesa in funzione della essione all usita del ondotto Siano e le essioni all ingesso e all usita dell ugello isettivaente Se le due essioni oinidono non i saà otata all inteno del ondotto a ano a ano he la essione all usita diinuise la otata auenta Quando nella sezione di usita si sono aggiunte le ondizioni itihe ovveo la veloità del fluido è ai a quella del suono e la essione è uguale a alloa la otata si antiene ostante ioè non auenta iù anhe abbassando ulteioente la essione Questo uò essee siegato da un unto di vista fisio in questo odo: quando la essione all usita è aggioe della essione itia il fluido si uove veso valle ad una veloità iù bassa isetto a quella del suono Abbassando a antenendosi anoa al di soa della essione itia l infoazione di questo abbassaento he viaggia alla veloità del suono iese a oedee veso onte (visto he la veloità del fluido è inoe della veloità del suono) ihiaando alto fluido (e quindi la otata auenta) Allohè nella sezione di usita si sono aggiunte le ondizioni itihe ovveo la essione è ai a e la veloità del flusso nella sezione di usita è uguale alla veloità del suono l infoazione di un ulteioe diinuzione della essione di sboo non è iù in gado di oedee veso onte e di onseguenza la otata si antiene ostante Aunti del Coso (Doente: Fabio Mallao) 4 Moto degli Aeifoi nei Condotti - ag 43

9 Politenio di oino Lauea a Distanza in Ingegneia Meania Coso di Mahine Figua 4: Andaento della otata in assa in funzione della essione di sboo e della veloità e un ugello selieente onvegente Nella figua sottostante è iotato lo stesso andaento della otata al vaiae della essione all usita del ondotto in un gafio ibaltato isetto alla figua eedente: Figua 43: Andaento della otata in assa di fluido in funzione della essione di sboo Pe un ugello selieente onvegente la iù alta veloità aggiungibile dal fluido è la veloità del suono nella sezione di usita Aunti del Coso (Doente: Fabio Mallao) 4 Moto degli Aeifoi nei Condotti - ag 44

10 Politenio di oino Lauea a Distanza in Ingegneia Meania Coso di Mahine CALCOLO DELLA PORAA E ossibile iavae l equazione del tatto uvo del gafio di figua 43 ovveo della otata in funzione della essione della sezione di usita (detta sezione essendo la iù iola viene anhe hiaata sezione istetta o sezione di gola) aso: : la otata in assa di fluido vale: A A A A v A v f [3] aso: : la essione nella sezione di sboo isulta essee ostanteente uguale a (ondizioni itihe) La otata dell ugello isulta essee alloa la seguente: A [4] v Questa è anhe l equazione del tatto lineae del gafio di figua 43 Si definise essione di adattaento quella essione e la quale si veifia uguaglianza ta la essione dell abiente di valle e la essione della sezione di saio A aità di ondizioni di onte al vaiae della essione di valle l ugello si antiene adattato finhè si aggiunge allo sboo la essione itia Raggiunta la veloità del suono in usita ulteioi abbassaenti della essione di valle non odifiano le otate E quindi inutile ai fini delle otate eae un vuoto sinto a valle in quanto la otata diende oa solo dalle ondizioni di onte Se l ugello non è adattato ioè la essione nell abiente esteno è inoe della essione di sboo (nella sezione di gola) alloa il fluido è ostetto ad esandesi all esteno dell ugello on inevitabili edite di natua fluidodinaia Si onsidei un ugello selieente onvegente in ete ondizioni di essione in oisondenza della sezione di ingesso A tale ugello oisondeà un gafio della otata in funzione della essione di sboo del tio di quello intodotto in eedenza on il tatto uvo aesentato dalla elazione [3] e on il tatto ettilineo aesentato dalla elazione [4] Se a aità di teeatua del fluido la essione totale all ingesso auenta oe ostato nella figua 44 anhe la essione itia dovà neessaiaente auentae dal oento he la quantità / è ostante Di onseguenza in queste nuove ondizioni di eseizio l andaento della otata in funzione della essione di sboo saà aesentato da una uva del tutto siile a quella eedente a aatteizzata da un valoe di otata Aunti del Coso (Doente: Fabio Mallao) 4 Moto degli Aeifoi nei Condotti - ag 45

11 Politenio di oino Lauea a Distanza in Ingegneia Meania Coso di Mahine itia iù elevato Si noti nel gafio di figua 44 (he iota l andaento della otata in funzione della essione di sboo e divesi valoi della essione in oisondenza della sezione di ingesso) oe i unti aesentativi delle ondizioni itihe siano tutti allineati seondo una etta usente dall oigine Figua 44: Andaento della otata in assa di fluido in funzione della essione di sboo al vaiae della essione in oisondenza della sezione di ingesso I unti aesentativi delle ondizioni itihe sono allineati lungo una etta usente dall oigine 46 UGELLO CONVERGENE DIVERGENE (UGELLO DI DE LAVAL) (CASO IDEALE) Pe ottenee il assaggio da un flusso subsonio ad uno suesonio è neessaio disoe di un ondotto onvegente divegente: infatti se all ingesso si ha un flusso subsonio e aeleae la oente bisogna inanalala in un ondotto onvegente eettendo osì al flusso di esandesi fino al valoe della essione itia nella sezione di gola e di aggiungee in tale sezione la veloità del suono; oa se si desidea he la veloità auenti ulteioente diventando suesonia il ondotto a atie dalla sezione di gola deve diventae divegente eettendo osì un ulteioe esansione del flusso Si faia ifeieento ifeiento alla figua 45 he aesenta l andaento della otata in assa di fluido e della veloità di sboo in funzione della essione di usita Aunti del Coso (Doente: Fabio Mallao) 4 Moto degli Aeifoi nei Condotti - ag 46

12 Politenio di oino Lauea a Distanza in Ingegneia Meania Coso di Mahine Figua 45: Andaento della otata in assa di fluido in funzione della essione di sboo e della veloità e un ugello di De Laval Sia la essione totale all iboo Se la essione in oisondenza della sezione di usita è uguale a quella in ingesso alloa la otata saà nulla Mano a ano he la essione allo sboo diinuise la otata tende ad auentae La essione nella sezione istetta diventa itia quando la essione allo sboo aggiunge un deteinato valoe hiaato essione liite ( li ) In queste ondizioni nella sezione di gola la veloità del flusso è ai alla veloità del suono Fino al aggiungiento della li il fluido si esande nel onvegente auentando la oia veloità ente nel divegente si oie diinuendola La veloità della oente in oisondenza della sezione di sboo alla essione liite è stata indiata on li (inoe della veloità del suono) Pe quanto iguada la otata he attavesa l ugello al diinuie della essione di usita essa tende ad auentae e diventa itia soltanto quando la essione di sboo ha aggiunto il valoe liite Riduendosi la essione all usita al di sotto della li la otata non auenteà iù Nel aso in ui la essione di valle sia oesa ta li e ad il ootaento dell ugello non uò essee siegato se non faendo ioso a fenoeni non isentoii detti uti Si tatta onettualente di sezioni di disontinuità nella essione e nell entoia (he auentano) e nella veloità (he diinuise) Gli uti ossono essee etti se la sezione di disontinuità è eendiolae all asse del ondotto e attaveso essi un flusso suesonio diventa subsonio oue obliqui se la sezione di disontinuità non è eendiolae all asse del ondotto e attaveso essi un flusso suesonio uò o eno diventae subsonio; a valle di un uto etto il flusso è anoa Aunti del Coso (Doente: Fabio Mallao) 4 Moto degli Aeifoi nei Condotti - ag 47

13 Politenio di oino Lauea a Distanza in Ingegneia Meania Coso di Mahine Aunti del Coso (Doente: Fabio Mallao) 4 Moto degli Aeifoi nei Condotti - ag 48 isentoio ente a valle di uno obliquo la vena fluida in genee si staa dalle aeti e tutto oede oe se in quel unto il ondotto teinasse Esiste un valoe della essione di valle he loalizza l uto etto allo sboo del ondotto Al di sotto di questo valoe di essione si anifestano uti obliqui a onte dello sboo a seguito dei quali la essione auenta la vena fluida si staa dalle aeti del ondotto e oede indistubata Pe iusie ad utilizzae l ulteioe esansione del fluido nel divegente e quindi otae la oente all usita del ondotto da sonia a suesonia è neessaio abbassae la essione di sboo fino alla essione di adattaento ad Questa è da onsideasi ondizione ottiale ed è etanto da intendesi oe situazione di funzionaento in ondizioni di ogetto Se la essione di sboo è infeioe alla essione di adattaento l andaento della essione nel ondotto è quello di adattaento e l esansione dal valoe di essione di adattaento al valoe di valle si ealizza nell abiente di saio attaveso onde di esansione CALCOLO DELLA PORAA Pe un ondotto onvegente divegente ideale la elazione v A & [5] è vea solo fino a quando le ondizioni di otata nel ondotto onsentono ondizioni di esansione isentoihe ovveo: - nei asi in ui il ondotto funzioni oe tubo di Ventui (esansione e ioessione) fino al aggiungiento del unto in ui si veifia la ondizione sonia nella sezione istetta (ondizione liite); - in oisondenza della ondizione di adattaento La assia otata è quella itia ai a: v A A v A A v A A ad ad ad ad li li li li s & La otata subitia diende dalle ondizioni totali a anhe dalle ondizioni di valle Nel aso invee di ugello itio le vaiazioni di valle non ossono isalie la oente (dal oento he la veloità di tasinaento è aggioe o

14 Politenio di oino Lauea a Distanza in Ingegneia Meania Coso di Mahine uguale a quella del suono) Di qui l indiendenza della otata itia dalla essione di valle Si onsidei oa il gafio di figua 46 he iota l andaento della otata in assa di fluido al vaiae della essione di sboo Figua 46: Andaento della otata in assa di fluido in funzione della essione di sboo aiando la uva della otata (equazione [5]) si ottiene la uva tatteggiata in figua 46 e quindi anhe il valoe della otata itia aesentata dal tatto ettilineo il quale intesea la uva elativa al onvegente in oisondenza della essione di adattaento e della essione liite Analogaente al aso dell ugello selieente onvegente nel iano he aesenta la otata in assa di fluido in funzione della essione di sboo auentando la essione totale in oisondenza della sezione di ingesso si ottengono tante uve on otata itia esente in ui tutti i unti angolosi individuati dalla essione liite sono allineati lungo una etta usente dall oigine (figua 47) Aunti del Coso (Doente: Fabio Mallao) 4 Moto degli Aeifoi nei Condotti - ag 49

15 Politenio di oino Lauea a Distanza in Ingegneia Meania Coso di Mahine Aunti del Coso (Doente: Fabio Mallao) 4 Moto degli Aeifoi nei Condotti - ag 5 Figua 47: Andaento della otata in assa di fluido in funzione della essione di sboo al vaiae della essione in oisondenza della sezione di ingesso I unti dati dalla essione liite sono allineati lungo una etta usente dall'oigine CALCOLO DELLA PRESSIONE LIMIE Pe alolae la essione liite esistono due etodi: ) si uguaglia la foula della otata in ondizioni geneihe on quella della otata itia (la essione liite è in oisondenza dell intesezione ta le due uve desitte da queste due equazioni); si ottiene: A A Le soluzioni fisiaente aettabili sono due date dalle due intesezioni della uva di otata on il tatto oizzontale he individua la otata itia: la essione liite e la essione di adattaento ) si uò anhe oedee ediante l aossiazione ellittia della otata ovveo è ossibile aossiae la uva he esie la otata eale ad un ellisse Pe l ugello selieente onvegente si eviene alla seguente equazione: ente e l ugello di De Laval:

16 Politenio di oino Lauea a Distanza in Ingegneia Meania Coso di Mahine A A Se in quest ultia equazione si one: ovveo si intesea l ellisse on una etta oizzontale avente oe odinata il valoe della otata itia si eviene ad un equazione di seondo gado le ui due soluzioni sono la essione di adattaento e la essione liite In genee il tatto onvegente degli ugelli è abbastanza oto dal oento he non esiste il eiolo del distao della vena fluida; inolte inoe è la sua lunghezza inoi sono le edite di natua fluidodinaia Il tatto divegente invee è deisaente iù lungo affinhè il fluido ossa esandee senza inoee nel eiolo di un distao della vena Infine è neessaio he il divegente teini on le aeti aallele all asse dell ugello e evitae he la veloità del fluido in usita abbia oonenti eendiolai all asse 47 ESERCIZI SVOLI ) Ad un ugello onvegente-divegente eviene elio ( 67; 53 J / (g*k)) on veloità d'ingesso / s MPa e t 8 C Le ondizioni di adattaento sono ai a ad 4 MPa e t ad 5 C e l'ugello uò essee onsideato adiabatio Calolae la veloità di sboo ed il lavoo delle esistenze assive aettendo olitoia la linea di tasfoazione SOLUZIONE Aliando il io iniio in foa euleiana on Q e e L i isulta: i E ( ad ) La veloità di efflusso nella sezione di sboo è: ( ) 7577 /s ad L'esonente della olitoia uò essee alolato e ezzo della foula seguente: lg ad 3579 lg ad da ui isulta: 5574 Il aloe seifio della tasfoazione vale: Aunti del Coso (Doente: Fabio Mallao) 4 Moto degli Aeifoi nei Condotti - ag 5

17 Politenio di oino Lauea a Distanza in Ingegneia Meania Coso di Mahine ( / ) J/gK da ui il lavoo di attito: 8663 ( ) J/g Lw ad ) Un ugello onvegente-divegente ieve nella sezione di ingesso (A ) aia ( 4; R 87 J / (g*k)) on veloità d'ingesso / s essione e teeatua d ingesso isettivaente Pa e t 5 C Il tatto onvegente è isentoio e al teine di esso la teeatua in oisondenza della sezione istetta è ai a t C; il tatto divegente invee u essendo adiabatio ha un evoluzione di tio olitoio on esonente ai a 47 Nella sezione di usita l'aia ha una veloità / s Calolae le aee della sezione istetta e della sezione allo sboo e deteinae la essione in oisondenza di tali sezioni SOLUZIONE Aliando il io iniio in foa euleiana on Q e e L i nel tatto onvegente dell'ugello isulta: i E ( ) dove e sono isettivaente la teeatua e la veloità nella sezione istetta; esliitando isulta: R( ) /s La veloità del suono nella sezione istetta vale R 3873 /s > s e l'ugello etanto non è itio Aliando il io iniio in foa euleiana on Q e e L i nel tatto divegente dell'ugello isulta: i E ( ) da ui si uò iavae la teeatua nella sezione di sboo: K dove: R 45 J/gK Le essioni e le asse voluihe nella sezione istetta e in quella di sboo ossono essee alolate e ezzo delle seguenti elazioni: Aunti del Coso (Doente: Fabio Mallao) 4 Moto degli Aeifoi nei Condotti - ag 5

18 Politenio di oino Lauea a Distanza in Ingegneia Meania Coso di Mahine 7763 Pa 77 g/3 R 7633 Pa 55 g/3 R ente la assa voluia nella sezione di ingesso vale: 9884 g/3 R La otata di fluido he assa attaveso l'ugello vale & A 977 g/s e e l'equazione di ontinuità si ha: & A A da ui si ossono ottenee la sezione istetta e la sezione di usita he valgono isettivaente A 739 e A ) Due ugelli di De Laval disosti in seie l'uno isetto all'alto on inteosta una aaità (in ui il io dissia l'enegia inetia di saio) esentano le seguenti ondizioni: ingesso effusoe - aia ( 4; R 87 J / (g*k)) a I 3 ba e I K on veloità di ingesso tasuabile La sezione inia è A I 5 L'esansione è adiabatia evesibile in ondizioni adattate il effusoe esenta una sezione inia A II e saia nell'abiente ( ba e C) on un'esansione adiabatia evesibile in ondizioni adattate Calolae la otata dei due effusoi e la veloità di saio dei due ugelli Calolae inolte le aee di sboo dei due effusoi SOLUZIONE Entabi gli ugelli sono adattati etanto nella sezione istetta si ha la essione e la teeatua itia Pe il io ugello etanto si ha iodando he la essione e la teeatua di onte oinidono on le isettive gandezze totali ( ): I I I 5848 ba I I K Aunti del Coso (Doente: Fabio Mallao) 4 Moto degli Aeifoi nei Condotti - ag 53

19 Politenio di oino Lauea a Distanza in Ingegneia Meania Coso di Mahine I I 55 g/3 R I RI /s La otata he tansita attaveso il io ugello vale: I & AI I I 75 g/s La teeatua a onte del seondo ugello uò essee alolata e ezzo del io iniio in foa euleiana aliato ad un sistea teodinaio oendente il io ugello e l'intea aaità In questo odo isulta he la sezione di usita del fluido oisonde alla sezione di ingesso del seondo ugello e la quale la veloità del fluido stesso è tasuabile in quanto dissiata all'inteno della aaità Riodando he questo sistea teodinaio è adiabatio (Q e ) senza ogani obili (L i ) e on vaiazione di enegia inetia nulla isulta: ioè: ( ) i II I K II I Aliando oa l'equazione di ontinuità ai due ugelli si ottiene: II & AI I I AII II II AII R II Da questa elazione è ossibile iavae la essione in ingesso al seondo effusoe uguale a quella di usita dal io II I 499 ba Aliando il io iniio in foa euleiana on Q e e L i al io e al seondo effusoe isulta he le veloità di efflusso dalle sezioni di sboo valgono isettivaente: R I I I I I I ( ) R /s R II II II II 786 /s L'equazione di ontinuità sitta on ifeiento alla sezione istetta e alla sezione di sboo eette di ottenee la elazione seguente: A u A Aunti del Coso (Doente: Fabio Mallao) 4 Moto degli Aeifoi nei Condotti - ag 54

20 Politenio di oino Lauea a Distanza in Ingegneia Meania Coso di Mahine La eedente elazione aliata ai due effusoi eette il alolo delle due aee di sboo he valgono isettivaente: A ui 455 e A uii 48 ESERCIZI ) Calolae la otata e la veloità del getto di un endoeattoe on effusoe efigeato e il quale le ondizioni in aea di obustione sono di 8 ata e 35 K la essione estena (di adattaento) di 5 ata L esansione è olitoia on esonente 9 il gas ha assa oleolae ai a 5 g/ol l esonente il aloe assio sabiato è ai a 3 al/g la sezione di sboo A [Risultati: 43 / s; 36 g / s] ) In un ugello onvegente - divegente del distibutoe di una tubina a vaoe si fanno esandee 35 g / s di vao d aqua da 3 ba e 5 C ( / s) fino a ba Aettendo isentoia l esansione alolae la sezione finale del ondotto e valutae l aea della sezione istetta [Risultati: 858 / s; A 8 ; 57; A in 4 ] 3) Un ugello selieente onvegente on ondizioni a onte 5 ata e 5 C ( / s) e essione di valle ata lasia assae 3 g / s di aia ( 4 R 87 J / (g*k)) Calolae la veloità e la teeatua nella sezione si sboo e una esansione isentoia Calolae inolte la nuova otata se le ondizioni di onte diventano ata e 3 C e la essione di valle 4 ata [Risultati: / s; t 79 5 C; ' 55 g / s] 4) Ad un ugello adiabatio a on esistenze assive eviene azoto ( 4 M 8 g / ol) a 7 ata e 5 C ( / s) Saendo he la sezione di sboo è ai a e he le ondizioni di adattaento si veifiano e essione di sboo di ata e 3 C di teeatua tovae la otata la veloità di sboo e il valoe di L W [Risultati: 5 Kg / s 656 / s L W 965 al / g] 5) Un ugello onvegente - divegente esande isentoiaente aia ( 4 4 al / g) Nella sezione istetta di aea A in si ha s 4 / s on s ata In usita la essione di adattaento è ai a ata Calolae la otata la veloità dell aia e l aea della sezione di sboo Deteinae inolte nella sezione di sboo la essione liite e la elativa veloità [Risultati: t s 4 C; 3 5 Kg / s; 738 / s; A 8 ; 93 ata; t 4 C; li 87 ata; li 95 / s] Aunti del Coso (Doente: Fabio Mallao) 4 Moto degli Aeifoi nei Condotti - ag 55

21 Politenio di oino Lauea a Distanza in Ingegneia Meania Coso di Mahine 6) Un diffusoe adiabatio ieve aia ( 4; R 87 J / (g*k)) a essione 4 ata e teeatua 3 K on veloità 5 / s Volendo idue la veloità a soli 5 / s alolae la essione aggiunta dall aia in usita al diffusoe sia nell iotesi di oessione isentoia sia nell iotesi di oessione eale on endiento del diffusoe ai a 9 [Risultati: d 9 ata; d 85 ata] 7) Un diffusoe eale ieve nella sezione d ingesso (aea tasvesale A ) aia ( 4 4 J / (g*k)) alla veloità 3 / s on Pa e t 3 C Nella sezione d usita la veloità dell aia è ai 3 / s L evoluzione nel diffusoe uò essee onsideata una olitoia di esonente 5 Le esistenze assive nel diffusoe dissiano un lavoo L wd equivalente al % della vaiazione di enegia inetia nel diffusoe stesso Deteinae la essione in usita al diffusoe l aea A tasvesale della sezione di usita la quantità di aloe Q e eventualente sabiata nel diffusoe on l esteno (seifiando se il diffusoe è efigeato o isaldato) [Risultati: t 74 C; 468 Pa; A 774 ; Q e J / g diffusoe efigeato] Aunti del Coso (Doente: Fabio Mallao) 4 Moto degli Aeifoi nei Condotti - ag 56