Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u.
|
|
|
- Baldassare Garofalo
- 4 anni fa
- Visualizzazioni
Transcript
1 Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Definizione Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee (x, y, t ) soddisfano un equazione di secondo grado omogenea nelle variabili x, y, t : a 11 x 2 + 2a12 x y + a 22 y 2 + 2a13 x t + 2a 23 y t + a 33 t 2 = 0. Per considerare i punti propri della conica teniamo conto del fatto che x = x t e y = y t. Allora, dividendo per t 2 : x 2 a 11 t 2 + 2a x y y 2 12 t t + a 22 t 2 + 2a x y 13 t + 2a 23 t + a 33 = 0 a 11 x 2 + 2a 12 xy + a 22 y 2 + 2a 13 x + 2a 23 y + a 33 = 0. Questa è l equazione della conica in forma non omogenea. 1 / 41
2 Ad ogni conica associamo la matrice simmetrica: a 11 a 12 a 13 B = a 12 a 22 a 23. a 13 a 23 a 33 Se poniamo: x = x y t e x = x y 1, allora l equazione della conica può essere scritta in forma compatta. La forma omogenea può essere scritta in questo modo: t x Bx = 0, mentre quella non omogenea in quest altro: t xbx = 0. 2 / 41
3 Definizione Se il polinomio a 11 x 2 + 2a 12 x y + a 22 y 2 + 2a 13 x t + 2a 23 y t + a 33 t 2 si spezza nel prodotto di due fattori lineari, distinti o meno, la conica si dice riducibile o spezzata ed i suoi punti sono quelli delle due rette di cui è unione. Se una conica non è riducibile, si dice che è irriducibile. Sia Γ la conica di equazione: a 11 x 2 + 2a12 x y + a 22 y 2 + 2a13 x t + 2a 23 y t + a 33 t 2 = 0. I suoi punti impropri sono determinati dal sistema: { a 11 x 2 + 2a 12 x y + a 22 y 2 + 2a 13 x t + 2a 23 y t + a 33 t 2 = 0 t = 0 { a 11 x 2 + 2a 12 x y + a 22 y 2 = 0 t = 0. 3 / 41
4 Se a 11 = a 12 = a 22 = 0, allora la conica è riducibile e contiene la retta impropria t = 0. Supponiamo a Dividiamo l equazione per y 2 : ( x ) 2 x a 11 y + 2a 12 y + a 22 = 0 t = 0. In questo caso otteniamo i punti impropri ( a 12 + a12 2 a 11a 22, a 11, 0) e ( a 12 a12 2 a 11a 22, a 11, 0). Se a 11 = 0, abbiamo: { 2a 12 x y + a 22 y 2 = 0 t = 0. e otteniamo i punti impropri (1, 0, 0) e (a 22, 2a 12, 0). 4 / 41
5 In ogni caso, si ottiene che i punti impropri di una conica che non contiene la retta impropria sono sempre 2 e sono: reali e distinti se a 2 12 a 11a 22 > 0 reali e coincidenti se a 2 12 a 11a 22 = 0 immaginari e coniugati se a 2 12 a 11a 22 < 0. Definizione Una conica irriducibile si dice: iperbole, se ha due punti impropri reali e distinti parabola, se ha due punti impropri reali e coincidenti ellisse, se ha due punti impropri immaginari e coniugati. 5 / 41
6 Osservazione Consideriamo la matrice: A = ( a11 a 12 a 12 a 22 ). Allora A = a 11 a 22 a 12 2 = (a 2 12 a 11a 22 ). Dunque, possiamo dire che una conica irriducibile è: un iperbole se A < 0 una parabola se A = 0 un ellisse se A > 0. 6 / 41
7 Fissiamo nel piano due sistemi di riferimento O, x, y, u e O, X, Y, u. Sia P = (x, y) un punto del piano. Se vogliamo passare da O, X, Y a O, x, y occorre effettuare una rototraslazione, cioè una composizione tra una rotazione e una traslazione: { x = X cos θ Y sen θ + a y = X sen θ + Y cos θ + b, dove O = (a, b) in O, x, y e θ è l angolo formato da i e I. y Y O I X θ O i x 7 / 41
8 Se: x = x y 1 e X = X Y 1, allora le equazioni del cambiamento di coordinate si possono scrivere nella forma: x = QX, con: Q = matrice della rototraslazione. cos θ sen θ a sen θ cos θ b / 41
9 Se a = b = 0, allora abbiamo una rotazione. y Y X O O I i θ x Le equazioni di una rotazione sono: { x = X cos θ Y sen θ y = X sen θ + Y cos θ. 9 / 41
10 Se θ = 0, allora abbiamo una traslazione. y Y O X O x Le equazioni di una traslazione sono: { x = X + a y = Y + b. 10 / 41
11 Teorema Data una conica Γ a coefficienti reali di equazione t xbx = 0, è sempre possibile effettuare una rototraslazione, di matrice Q, tale che Γ nel nuovo riferimento O, X, Y, u abbia una delle due forme: I) αx 2 + βy 2 = γ II) βy 2 = 2γX. Inoltre, dette B e A la matrice della conica e la sottomatrice dei termini di secondo grado in x e y, rispettivamente, e B e A le corrispondenti matrici per la conica in forma canonica, si ha: a) B e B hanno lo stesso determinante e lo stesso rango b) A e A sono simili, e, quindi, hanno lo stesso polinomio caratteristico, stesso determinante e stessa traccia. Osservazione Se: A = ( a11 a 12 a 12 a 22 ), allora Tr(A) = a 11 + a 22 è la traccia di A. 11 / 41
12 Definizione I numeri det(b), det(a), ρ(b), Tr(A) si dicono invarianti ortogonali, in quanto si mantengono inalterati dopo una rototraslazione. Teorema Sia data una conica Γ di equazione t xbx = 0. Allora: 1. Γ è spezzata in due rette coincidenti ρ(b) = 1 2. Γ è spezzata in due rette distinte ρ(b) = 2 3. Γ è irriducibile ρ(b) = / 41
13 Studio dell ellisse in forma canonica L equazione canonica dell ellisse reale è del tipo: x 2 a 2 + y 2 b 2 = 1. Essa rientra tra le coniche del tipo I αx 2 + βy 2 = γ, con α γ = 1 a 2 e β γ = 1 b 2. L equazione canonica dell ellisse immaginaria è: x 2 a 2 + y 2 b 2 = 1. Notiamo che per l ellisse reale Tr(A) B < 0, mentre per l ellisse immaginaria Tr(A) B > / 41
14 1. L origine O = (0, 0) è il centro di simmetria, perché se (α, β) Γ = ( α, β) Γ. 2. L asse x è asse di simmetria, perché se (α, β) Γ = (α, β) Γ. 3. L asse y è asse di simmetria, perché se (α, β) Γ = ( α, β) Γ. y ( α, β) (α, β) O x ( α, β) (α, β) 14 / 41
15 I vertici dell ellisse sono i punti che l ellisse ha in comune con i suoi assi di simmetria. Essi sono V 1 = (a, 0), V 2 = ( a, 0), V 3 = (0, b) e V 4 = (0, b). y V 3 V 2 O V 1 x V 4 15 / 41
16 Sia a > b. In tal caso, consideriamo i punti F 1 = (c, 0) e F 2 = ( c, 0), con c = a 2 b 2. F 1 e F 2 sono detti fuochi dell ellisse. Si dimostra che l ellisse si può ottenere come il luogo dei punti P = (x, y) del piano tali che: PF 1 + PF 2 = 2a. Le rette d 1 : x = a2 c e d 2 : x = a2 c sono dette direttrici relative ai fuochi F 1 e F 2. Sull asse maggiore vi sono i due fuochi. d 2 y d 1 F 2 O F 1 asse maggiore x 16 / 41
17 Proposizione I rapporti: PF 1 d(p, d 1 ) e PF 2 d(p, d 2 ) sono, al variare di P sull ellisse Γ, costanti e uguali a una costante e = c a, detta eccentricità dell ellisse. Inoltre si prova che e < 1, cioè: PF 1 d(p, d 1 ) = PF 2 d(p, d 2 ) = e = c a < 1 P Γ. 17 / 41
18 Se b > a, tutto si ripete in maniera analoga, solo che c = b 2 a 2, F 1 = (0, c) e F 2 = (0, c). Le direttrici sono le rette d 1 : y = b2 c e d 2 : y = b2. Inoltre, l ellisse è il luogo dei punti del piano tali che c PF 1 + PF 2 = 2b. y asse maggiore d 1 F 1 O x F 2 d 2 18 / 41
19 Studio dell iperbole in forma canonica L equazione canonica dell iperbole è del tipo: x 2 a 2 y 2 b 2 = 1. Essa rientra tra le coniche del tipo I αx 2 + βy 2 = γ, con α γ = 1 e a 2 β γ = 1. b 2 1. L origine O = (0, 0) è il centro di simmetria, perché se (α, β) Γ = ( α, β) Γ. 2. L asse x è asse di simmetria, perché se (α, β) Γ = (α, β) Γ. 3. L asse y è asse di simmetria, perché se (α, β) Γ = ( α, β) Γ. 19 / 41
20 L asse x è l unico dei due assi di simmetria che incontra l iperbole in due punti reali, V 1 = (a, 0) e V 2 = ( a, 0). Sono i due vertici dell iperbole e l asse x è detto asse trasverso. y V 2 O V 1 asse trasverso x 20 / 41
21 I punti impropri dell iperbole sono (1, b a, 0) e (1, b a, 0). Le rette che congiungono l origine con questi punti, cioè le rette y = b a x e y = b a x, cioè le due rette che congiungono il centro di simmetria con i punti impropri, sono dette asintoti dell iperbole e sono tangenti all iperbole nei punti impropri. Inoltre, gli assi di simmetria sono le bisettrici degli asintoti. asintoto y asintoto O x 21 / 41
22 Sia c = a 2 + b 2. I punti F 1 = (c, 0) e F 2 = ( c, 0) sono detti fuochi dell iperbole. Si dimostra che l iperbole si può ottenere come il luogo dei punti P = (x, y) del piano tali che: PF 1 PF 2 = 2a. Le rette d 1 : x = a2 c e d 2 : x = a2 c sono dette direttrici relative ai fuochi F 1 e F 2. Essi si trovano sull asse trasverso. d 2 y d 1 F 2 O F 1 asse trasverso x 22 / 41
23 Proposizione I rapporti: PF 1 d(p, d 1 ) e PF 2 d(p, d 2 ) sono, al variare di P sull iperbole Γ, costanti e uguali a una costante e = c a, detta eccentricità dell iperbole. Inoltre si prova che e > 1, cioè: PF 1 d(p, d 1 ) = PF 2 d(p, d 2 ) = e = c a > 1 P Γ. 23 / 41
24 Se l equazione dell iperbole è: x 2 a 2 y 2 b 2 = 1, allora i vertici sono i punti V 1 = (0, b) e V 2 = (0, b), l asse y è l asse trasverso, gli asintoti sono sempre le rette y = b a x e y = b a x, c = a 2 + b 2, i fuochi sono F 1 = (0, c) e F 2 = (0, c), le direttrici sono d 1 : y = b2 c e d 2 : y = b2 c e l eccentricità è e = c b. Inoltre, l iperbole è in tal caso il luogo dei punti P del piano tali che: PF 1 PF 2 = 2b. asse trasverso y V 1 O V 2 x 24 / 41
25 Definizione Un conica irriducibile si dice che è un iperbole equilatera se ha i punti impropri che individuano direzioni ortogonali. Proposizione La condizione Tr(A) = 0 caratterizza le coniche contenenti come parte la retta impropria oppure che hanno due punti impropri reali e in direzioni ortogonali. In particolare, le coniche irriducibili tali che Tr(A) = 0 sono tutte e sole iperboli equilatere. 25 / 41
26 Studio della parabola in forma canonica L equazione della parabola in forma canonica è y 2 = 2px. È una conica del tipo II βy 2 = 2γx, con p = γ β. 1. La parabola non ha centro di simmetria. 2. L asse x è asse di simmetria, perché se (α, β) Γ = (α, β) Γ. 3. L asse y è tangente alla parabola nell origine O = (0, 0). 4. L asse x incontra la parabola in O = (0, 0) e nel suo punto improprio. 5. Il punto O = (0, 0) è detto vertice e la retta passante per il vertice della parabola e ortogonale all asse di simmetria è tangente alla parabola nel vertice. y y p > 0 p < 0 O x O x 26 / 41
27 Il punto F = ( p 2, 0) è il fuoco della parabola e la retta d : x = p 2 è la direttrice. y d O F x L equazione della parabola y 2 = 2px si ottiene come il luogo dei punti P = (x, y) del piano tali che PF = d(p, d). Proposizione Il rapporto e = PF d(p,d) è costante per ogni punto P della parabola Γ e si chiama eccentricità, cioè: e = PF d(p, d) = 1 P Γ. 27 / 41
28 Circonferenze Una circonferenza è il luogo dei punti P = (x, y) del piano che distano r > 0 da un punto (α, β): (x α) 2 + (y β) 2 = r 2. r è il raggio e C = (α, β) è il centro della circonferenza, che ha equazione: x 2 + y 2 2αx 2βy + α 2 + β 2 γ 2 = 0. Le circonferenze, allora, sono coniche tali che a 11 = a 22 0 e a 12 = 0. Inoltre, se x 2 + y 2 + ax + by + c = 0 è una circonferenza, allora C = ( a 2, b 2 ) e r = a b2 4 c. Se a2 4 + b2 4 c > 0, la circonferenza è reale. Se a2 4 + b2 4 c = 0, la conica è spezzata in due rette immaginarie e coniugate aventi in comune il punto ( a 2, b 2 ) e la chiamiamo circonferenza di raggio nullo. Se a2 4 + b2 4 c < 0, la conica è irriducibile, ma è priva di punti reali: diremo che abbiamo una circonferenza immaginaria. 28 / 41
29 Le circonferenze hanno gli stessi punti impropri, (1, i, 0) e (1, i, 0), che vengono detti punti ciclici del piano. Proposizione Se una conica passa per i punti ciclici del piano, allora o contiene come parte la retta impropria oppure è una circonferenza. Riepilogando: se ρ(b) = 1, abbiamo una conica spezzata in due rette coincidenti; se ρ(b) = 2, abbiamo una conica spezzata in due rette distinte; se ρ(b) = 3, cioè se B 0, abbiamo una conica irriducibile. In tal caso: se A > 0, abbiamo un ellisse; essa sarà reale se Tr(A) B < 0, immaginaria se Tr(A) B > 0; se, inoltre, a 11 = a 22 0 e a 12 = 0, abbiamo una circonferenza; se A = 0, abbiamo una parabola; se A < 0, abbiamo un iperbole; se, inoltre, Tr(A) = 0, abbiamo un iperbole equilatera. 29 / 41
30 Centro e assi di simmetria Sia Γ una conica e supponiamo che sia un ellisse o un iperbole. Si può dimostrare che, se C = (a, b) è il centro di simmetria della conica, allora le sue coordinate verificano le condizioni: { a11 a + a 12 b + a 13 = 0 a 12 a + a 22 b + a 23 = 0, cioè sono soluzioni del seguente sistema associato alle prime due righe della matrice B: { a11 x + a 12 y + a 13 = 0 a 12 x + a 22 y + a 23 = 0. Inoltre, gli assi di simmetria sono le rette parallele agli autospazi associati alla matrice A e passano per il centro di simmetria C. Nel caso della parabola, gli autovalori della matrice A sono 0 e β, in quanto A = 0. In questo caso, si prova che l autospazio associato all autovalore 0 è una retta parallela all asse di simmetria. 30 / 41
31 Osservazione Per un iperbole o un ellisse avente a 12 = 0, gli assi di simmetria sono paralleli agli assi cartesiani e, ovviamente, passano per il centro di simmetria. Una parabola di equazione y = ax 2 + bx + c ha vertice V = ( b 2a, 4a ), fuoco F = ( b 2a, a ), direttrice y = 4a e asse di simmetria x = b 2a, dove = b2 4ac. Una parabola di equazione x = ay 2 + by + c ha vertice V = ( 4a, b 1 2a ), fuoco F = ( 4a, b 1+ 2a ), direttrice x = 4a e asse di simmetria y = b 2a, dove = b2 4ac. 31 / 41
32 Tangenza Definizione Data una conica Γ, diremo che una retta r è tangente a Γ in un suo punto P 0 se essa incontra Γ in due punti coincidenti in P 0. Teorema Data una conica Γ irriducibile di equazione t xbx = 0, sia P 0 un suo punto di coordinate x 0. Allora esiste la tangente a Γ in P 0 e la sua equazione è t x 0 Bx = / 41
33 Definizione Chiamiamo curva algebrica C di ordine n il luogo dei punti propri o impropri, reali o immaginari, che con le loro coordinate omogenee soddisfano un polinomio omogeneo F (x, y, t ) = 0 di grado n nelle variabili x, y, t. Osservazione Se F = F 1 n 1 F 2 n 2... F k n k, con F 1, F 2,..., F k irriducibili, allora la curva C è costituita dai punti di F 1 = 0 contati n 1 volte, dai punti F 2 = 0 contati n 2 volte,..., dai punti di F k = 0, contati n k volte. F 1 = 0, F 2 = 0,..., F k = 0 sono le componenti irriducibili della curva di equazione F = / 41
34 Teorema (Teorema di Bezout) Due curve algebriche C 1 e C 2 di ordini m e n si incontrano in m n punti oppure hanno una componente in comune. Osservazione Due coniche hanno in comune 4 punti oppure hanno in comune una retta. Teorema Dati 5 punti distinti nel piano, per questi punti passa una sola conica o ne passano infinite. Se ne passano infinite, almeno 4 dei 5 punti sono allineati. DIMOSTRAZIONE. 34 / 41
35 Fasci di coniche Definizione Date due coniche Γ 1 : f 1 = 0 e Γ 2 : f 2 = 0, chiamiamo fascio di coniche individuato da Γ 1 e Γ 2 la totalità delle coniche la cui equazione si ottiene dalla combinazione lineare λf 1 + µf 2 = 0, al variare di λ e µ non entrambi nulli. Osservazione Per determinare una conica del fascio è sufficiente determinare λ µ oppure µ λ. Definizione Un punto P Γ 1 Γ 2 è detto punto base del fascio. Osservazione Tutte le coniche del fascio passano per i punti base. Per un punto P 0 non base del fascio passa una sola conica del fascio. 35 / 41
36 Proposizione In un fascio di coniche λf 1 + µf 2 = 0 ci sono 3 coniche spezzate oppure tutte le coniche del fascio sono spezzate. DIMOSTRAZIONE. Teorema Un fascio di coniche è individuato da due sue coniche qualsiasi. 36 / 41
37 Coniche spezzate di un fascio Se un fascio di coniche è individuato da due coniche prive di rette in comune, i punti base del fascio sono 4, più o meno coincidenti, e le coniche spezzate appartenenti al fascio sono 3, più o meno coincidenti. 1. Punti base tutti distinti tra loro. In tal caso, le coniche spezzate distinte sono 3 e sono P 1 P 2 P 3 P 4, P 1 P 3 P 2 P 4 e P 1 P 4 P 2 P 3 : P 1 P 2 P 3 P 4 37 / 41
38 2. Tangenza: 2 dei 4 punti coincidenti tra loro. In questo caso le coniche del fascio hanno tutte la stessa retta tangente r in un punto P 1 P 2. Le coniche spezzate del fascio sono r P 3 P 4 e P 1 P 3 P 1 P 4, contata due volte nel computo delle coniche spezzate del fascio. P 1 P 2 retta tangente r P 3 P 4 P tangente alle coniche in P 38 / 41
39 3. Bitangenza: i 4 punti coincidono a due a due. In tal caso, le coniche del fascio hanno tutte la stessa retta tangente r in P 1 P 2 e la stessa retta tangente s in P 3 P 4. Le coniche spezzate del fascio sono r s e la conica spezzata in due rette coincidenti con P 1 P 3 (tale conica è contata due volte nel computo delle coniche spezzate.) P 1 P 2 retta tangente r rette tangenti alle due coniche in P 1 e P 3 P 3 P 4 retta tangente s P 3 P 1 39 / 41
40 4. Coniche che si osculano: 3 dei 4 punti coincidono. In tal caso le coniche hanno tutte la stessa retta tangente r in P 1 P 2 P 3. L unica conica spezzata del fascio è r P 1 P 4, contata 3 volte nel computo delle coniche spezzate: P 1 P 2 P 3 retta tangente r P 4 retta tangente in P 1 P 4 P 1 40 / 41
41 5. Coniche che si iperosculano: i 4 punti sono tutti coincidenti. In tal caso le coniche hanno tutte la stessa retta tangente r in P 1 P 2 P 3 P 4. L unica conica spezzata del fascio è quella spezzata in due rette coincidenti con r e tale conica è contata tre volte nel computo delle coniche spezzate: P 1 P 2 P 3 P 4 retta tangente r P retta tangente in P 41 / 41
Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u.
 Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Definizione Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee (x,
Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Definizione Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee (x,
Coniche in forma generale
 LE CONICHE Fissiamo nel piano un sistema di riferimento cartesiano ortogonaleo, x, y, u. Coniche in forma generale Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro
LE CONICHE Fissiamo nel piano un sistema di riferimento cartesiano ortogonaleo, x, y, u. Coniche in forma generale Una conica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro
Fissiamo nello spazio un sistema di riferimento cartesiano ortogonale O, x, y, z, u.
 Fissiamo nello spazio un sistema di riferimento cartesiano ortogonale O, x, y, z, u. Definizione Una quadriche è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee
Fissiamo nello spazio un sistema di riferimento cartesiano ortogonale O, x, y, z, u. Definizione Una quadriche è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate omogenee
Le quadriche. Fissiamo nello spazio un sistema di riferimento cartesiano ortogonale O, x, y, z, u.
 Le quadriche Fissiamo nello spazio un sistema di riferimento cartesiano ortogonale O, x, y, z, u. Definizione Una quadrica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate
Le quadriche Fissiamo nello spazio un sistema di riferimento cartesiano ortogonale O, x, y, z, u. Definizione Una quadrica è il luogo dei punti, propri o impropri, reali o immaginari, che con le loro coordinate
L algebra lineare nello studio delle coniche
 L algebra lineare nello studio delle coniche È possibile utilizzare le tecniche dell algebra lineare per studiare e classificare le coniche. Data l equazione generale di una conica, si considera la sua
L algebra lineare nello studio delle coniche È possibile utilizzare le tecniche dell algebra lineare per studiare e classificare le coniche. Data l equazione generale di una conica, si considera la sua
Cenni sulle coniche 1.
 1 Premessa Cenni sulle coniche 1. Corso di laurea in Ingegneria Civile ed Edile Università degli Studi di Palermo A.A. 2013/2014 prof.ssa Paola Staglianò (pstagliano@unime.it) Scopo della geometria analitica
1 Premessa Cenni sulle coniche 1. Corso di laurea in Ingegneria Civile ed Edile Università degli Studi di Palermo A.A. 2013/2014 prof.ssa Paola Staglianò (pstagliano@unime.it) Scopo della geometria analitica
Fasci di Coniche. Salvino Giuffrida. 2. Determinare e studiare il fascio Φ delle coniche che passano per A (1, 0) con tangente
 1 Fasci di Coniche Salvino Giuffrida 1. Determinare e studiare il fascio Φ delle coniche che passano per O = (0, 0), con tangente l asse y, e per i punti (1, 0), (1, ). Determinare vertice e asse della
1 Fasci di Coniche Salvino Giuffrida 1. Determinare e studiare il fascio Φ delle coniche che passano per O = (0, 0), con tangente l asse y, e per i punti (1, 0), (1, ). Determinare vertice e asse della
Un fascio di coniche è determinato da una qualsiasi coppia di sue coniche distinte.
 Piano proiettivo Conica: curva algebrica reale del II ordine. a 11 x 2 1 + 2a 12 x 1 x 2 + a 22 x 2 2 + 2a 13 x 1 x 3 + 2a 23 x 2 x 3 + a 33 x 2 3 = 0 x T A x = 0 Classificazione proiettiva delle coniche:
Piano proiettivo Conica: curva algebrica reale del II ordine. a 11 x 2 1 + 2a 12 x 1 x 2 + a 22 x 2 2 + 2a 13 x 1 x 3 + 2a 23 x 2 x 3 + a 33 x 2 3 = 0 x T A x = 0 Classificazione proiettiva delle coniche:
Coniche R. Notari 15 Aprile
 Coniche R. Notari 15 Aprile 2006 1 1. Notazioni. Proposizione 1 Ogni conica si rappresenta tramita un equazione algebrica di secondo grado della forma a 11 x 2 +2a 12 xy + a 22 y 2 + +2a 13 x + 2a 23 y
Coniche R. Notari 15 Aprile 2006 1 1. Notazioni. Proposizione 1 Ogni conica si rappresenta tramita un equazione algebrica di secondo grado della forma a 11 x 2 +2a 12 xy + a 22 y 2 + +2a 13 x + 2a 23 y
Classificazione delle coniche.
 Classificazione delle coniche Ora si vogliono studiare i luoghi geometrici rappresentati da equazioni di secondo grado In generale, non è facile riconoscere a prima vista di che cosa si tratta, soprattutto
Classificazione delle coniche Ora si vogliono studiare i luoghi geometrici rappresentati da equazioni di secondo grado In generale, non è facile riconoscere a prima vista di che cosa si tratta, soprattutto
1 Cambiamenti di coordinate nel piano.
 Cambiamenti di coordinate nel piano.. Coordinate cartesiane Coordinate cartesiane su una retta. Sia r una retta: dare un sistema di coordinate su r significa fissare un punto O di r e un vettore u = U
Cambiamenti di coordinate nel piano.. Coordinate cartesiane Coordinate cartesiane su una retta. Sia r una retta: dare un sistema di coordinate su r significa fissare un punto O di r e un vettore u = U
Geometria analitica: curve e superfici
 Geometria analitica: curve e superfici geometriche algebriche e matrici e isometrie Riduzione Invarianti Studio di coniche Intersezione con rette e tangenti in forma parametrica 006 Politecnico di Torino
Geometria analitica: curve e superfici geometriche algebriche e matrici e isometrie Riduzione Invarianti Studio di coniche Intersezione con rette e tangenti in forma parametrica 006 Politecnico di Torino
Formulario. Coordinate del punto medio M di un segmento di estremi A(x 1, y 1 ) e B(x 2, y 2 ): x1 + x y 2
 Formulario Componenti di un vettore di estremi A(x 1, y 1 e B(x 2, y 2 B A = AB = (x2 x 1 i + (y 2 y 1 j Distanza tra due punti A(x 1, y 1 e B(x 2, y 2 : AB = (x 2 x 1 2 + (y 2 y 1 2 Coordinate del punto
Formulario Componenti di un vettore di estremi A(x 1, y 1 e B(x 2, y 2 B A = AB = (x2 x 1 i + (y 2 y 1 j Distanza tra due punti A(x 1, y 1 e B(x 2, y 2 : AB = (x 2 x 1 2 + (y 2 y 1 2 Coordinate del punto
Dipartimento di Matematica Corso di laurea in Fisica Compito di Geometria assegnato il 1 Febbraio 2002
 Compito di Geometria assegnato il 1 Febbraio 2002 Trovare l equazione della conica irriducibile tangente all asse x nel punto A(2, 0), tangente all asse y e passante per i punti B(1, 1) e C(2, 2) Scrivere
Compito di Geometria assegnato il 1 Febbraio 2002 Trovare l equazione della conica irriducibile tangente all asse x nel punto A(2, 0), tangente all asse y e passante per i punti B(1, 1) e C(2, 2) Scrivere
Studio generale di una conica
 Studio generale di una conica Manlio De Domenico 19 Giugno 2003 Definizione 1 Si definisce conica C un equazione algebrica F (x 1, x 2, x 3 ) = 0 del secondo ordine omogenea. Detta A la matrice simmetrica
Studio generale di una conica Manlio De Domenico 19 Giugno 2003 Definizione 1 Si definisce conica C un equazione algebrica F (x 1, x 2, x 3 ) = 0 del secondo ordine omogenea. Detta A la matrice simmetrica
4. Sia Γ la conica che ha fuoco F (1, 1) e direttrice d : x y = 0, e che passa per il punto P (2, 1).
 Geometria Complementi ed esercizi sulle coniche 1 (a) Scrivere l equazione dell ellisse Γ che ha fuochi F 1 ( 1, 1), F (1, 1) e che passa per il punto P (1, 1) (b) Determinare il centro, gli assi e i vertici
Geometria Complementi ed esercizi sulle coniche 1 (a) Scrivere l equazione dell ellisse Γ che ha fuochi F 1 ( 1, 1), F (1, 1) e che passa per il punto P (1, 1) (b) Determinare il centro, gli assi e i vertici
II Università degli Studi di Roma
 Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
Versione preliminare gennaio TOR VERGATA II Università degli Studi di Roma Dispense di Geometria. Capitolo 3. 7. Coniche in R. Nel Capitolo I abbiamo visto che gli insiemi di punti P lineare di primo grado
CdL in Ingegneria Industriale (A-E e F-O)
 CdL in Ingegneria Industriale (A-E e F-O) Prova scritta di Algebra lineare e Geometria- Febbraio 06 Durata della prova: tre ore. È vietato uscire dall aula prima di aver consegnato definitivamente il compito.
CdL in Ingegneria Industriale (A-E e F-O) Prova scritta di Algebra lineare e Geometria- Febbraio 06 Durata della prova: tre ore. È vietato uscire dall aula prima di aver consegnato definitivamente il compito.
Prova scritta di Geometria - 16 Gennaio 2019
 Prova scritta di Geometria - 16 Gennaio 2019 COGNOME e NOME(stampatello): 1. Supponiamo di sapere che l invariante cubico di una conica è A 24, quello quadratico è α 00 3, e quello lineare è I 4. (a) Classificare
Prova scritta di Geometria - 16 Gennaio 2019 COGNOME e NOME(stampatello): 1. Supponiamo di sapere che l invariante cubico di una conica è A 24, quello quadratico è α 00 3, e quello lineare è I 4. (a) Classificare
Parte 12b. Riduzione a forma canonica
 Parte 2b. Riduzione a forma canonica A. Savo Appunti del Corso di Geometria 202-3 Indice delle sezioni. Coniche, 2. Esempio di riduzione, 4 3. Teoremi fondamentali, 6 4. Come determinare l equazione canonica,
Parte 2b. Riduzione a forma canonica A. Savo Appunti del Corso di Geometria 202-3 Indice delle sezioni. Coniche, 2. Esempio di riduzione, 4 3. Teoremi fondamentali, 6 4. Come determinare l equazione canonica,
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Coniche
 Analisi Matematica 1 e Matematica 1 Geometria Analitica: Coniche Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Coniche
Analisi Matematica 1 e Matematica 1 Geometria Analitica: Coniche Annalisa Amadori e Benedetta Pellacci amadori@uniparthenope.it pellacci@uniparthenope.it Università di Napoli Parthenope Contenuti Coniche
Didattica della Matematica per il triennio Geometria sintetica e geometria analitica
 Didattica della Matematica per il triennio Geometria sintetica e geometria analitica anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Didattica della Matematica
Didattica della Matematica per il triennio Geometria sintetica e geometria analitica anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Didattica della Matematica
H precedente. Procedendo come sopra, si costruisce la matrice del cambiamento di base
 Geometria analitica e algebra lineare, anno accademico 9/1 Commenti ad alcuni esercizi 17 Diagonalizzazione di matrici simmetriche Coniche Commenti ad alcuni degli esercizi proposti 17 Diagonalizzazione
Geometria analitica e algebra lineare, anno accademico 9/1 Commenti ad alcuni esercizi 17 Diagonalizzazione di matrici simmetriche Coniche Commenti ad alcuni degli esercizi proposti 17 Diagonalizzazione
1 Coniche. s (x, y, t ) (1) 1 (x, y, t )F r 2
 1 Coniche Studieremo le curve nel piano euclideo, cioè nel piano con un sistema di riferimento cartesiano ortogonale fissato, oppure nel completamento proiettivo di questo piano, ottenuto con l introduzione
1 Coniche Studieremo le curve nel piano euclideo, cioè nel piano con un sistema di riferimento cartesiano ortogonale fissato, oppure nel completamento proiettivo di questo piano, ottenuto con l introduzione
LEZIONE 23. ax 2 + bxy + cy 2 + dx + ey + f
 LEZIONE 23 23.1. Riduzione delle coniche a forma canonica. Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y a meno di costanti moltiplicative non nulle, diciamo
LEZIONE 23 23.1. Riduzione delle coniche a forma canonica. Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y a meno di costanti moltiplicative non nulle, diciamo
P z. OP x, OP y, OP z sono le proiezioni ortogonali di v sugli assi x, y, z, per cui: OP x = ( v i) i. k j. P x. OP z = ( v k) k
 Richiami di calcolo vettoriale Consideriamo il vettore libero v = OP. Siano P x, P y, P z le proiezioni ortogonali di P sui tre assi cartesiani. v è la diagonale del parallelepipedo costruito su OP x,
Richiami di calcolo vettoriale Consideriamo il vettore libero v = OP. Siano P x, P y, P z le proiezioni ortogonali di P sui tre assi cartesiani. v è la diagonale del parallelepipedo costruito su OP x,
Quadriche. R. Notari
 Quadriche R. Notari 1 1. Notazioni. Proposizione 1 Ogni quadrica si rappresenta tramite un equazione algebrica di secondo grado della forma a 11 x 2 + 2a 12 xy + a 22 y 2 + 2a 13 xz+ +2a 23 yz + a 33 z
Quadriche R. Notari 1 1. Notazioni. Proposizione 1 Ogni quadrica si rappresenta tramite un equazione algebrica di secondo grado della forma a 11 x 2 + 2a 12 xy + a 22 y 2 + 2a 13 xz+ +2a 23 yz + a 33 z
Corso di Matematica II
 Corso di Matematica II Università degli Studi della Basilicata Dipartimento di Scienze Corso di laurea in Chimica e in Scienze Geologiche A.A. 2014/15 dott.ssa Vita Leonessa Elementi di geometria analitica
Corso di Matematica II Università degli Studi della Basilicata Dipartimento di Scienze Corso di laurea in Chimica e in Scienze Geologiche A.A. 2014/15 dott.ssa Vita Leonessa Elementi di geometria analitica
GEOMETRIA svolgimento di uno scritto del 11 Gennaio 2012
 GEOMETRIA svolgimento di uno scritto del Gennaio ) Trovare una base per lo spazio delle soluzioni del seguente sistema omogeneo: x + y 5z = 3x y + z = x y + 8z =. Il sistema può essere scritto in forma
GEOMETRIA svolgimento di uno scritto del Gennaio ) Trovare una base per lo spazio delle soluzioni del seguente sistema omogeneo: x + y 5z = 3x y + z = x y + 8z =. Il sistema può essere scritto in forma
Soluzioni dello scritto di Geometria del 28 Maggio 2009
 Soluzioni dello scritto di Geometria del 8 Maggio 9 1) Trovare le equazioni del sottospazio V(w, x, y, z) R 4 generato dalle quaterne c 1 = (,,, 1) e c = (, 1, 1, ). ) Trovare una base per OGNI autospazio
Soluzioni dello scritto di Geometria del 8 Maggio 9 1) Trovare le equazioni del sottospazio V(w, x, y, z) R 4 generato dalle quaterne c 1 = (,,, 1) e c = (, 1, 1, ). ) Trovare una base per OGNI autospazio
Note di geometria analitica nel piano
 Note di geometria analitica nel piano e-mail: maurosaita@tiscalinet.it Versione provvisoria. Novembre 2015. 1 Indice 1 Punti e vettori spiccati dall origine 3 1.1 Coordinate......................................
Note di geometria analitica nel piano e-mail: maurosaita@tiscalinet.it Versione provvisoria. Novembre 2015. 1 Indice 1 Punti e vettori spiccati dall origine 3 1.1 Coordinate......................................
Ingegneria Civile. Compito di Geometria del 06/09/05. E assegnato l endomorfismo f : R 3 R 3 mediante le relazioni
 Ingegneria Civile. Compito di Geometria del 06/09/05 E assegnato l endomorfismo f : R 3 R 3 mediante le relazioni I f(,, 0) = (h +,h+, ) f(,, ) = (h,h, h) f(0,, ) = (,h, h) con h parametro reale. ) Studiare
Ingegneria Civile. Compito di Geometria del 06/09/05 E assegnato l endomorfismo f : R 3 R 3 mediante le relazioni I f(,, 0) = (h +,h+, ) f(,, ) = (h,h, h) f(0,, ) = (,h, h) con h parametro reale. ) Studiare
Vincenzo Aieta CONICHE, FASCI DI CONICHE
 Vincenzo Aieta CONICHE, FASCI DI CONICHE Le coniche 1 Teoria delle Coniche Il nome conica deriva dal semplice fatto che gli antichi Greci secando con un piano una conica a doppia falda ottenevano, a seconda
Vincenzo Aieta CONICHE, FASCI DI CONICHE Le coniche 1 Teoria delle Coniche Il nome conica deriva dal semplice fatto che gli antichi Greci secando con un piano una conica a doppia falda ottenevano, a seconda
Geometria analitica del piano
 Geometria analitica del piano dott.ssa Vita Leonessa Università degli Studi della Basilicata (27 marzo 2008) (Analisi) Matematica 2 CdL in Chimica, Biotecnologie, Scienze Geologiche Rette Fissato un sistema
Geometria analitica del piano dott.ssa Vita Leonessa Università degli Studi della Basilicata (27 marzo 2008) (Analisi) Matematica 2 CdL in Chimica, Biotecnologie, Scienze Geologiche Rette Fissato un sistema
Corso di Geometria Meccanica, Elettrotecnica Esercizi 11: soluzioni
 Corso di Geometria 0- Meccanica Elettrotecnica Esercizi : soluzioni Esercizio Scrivere la matrice canonica di ciascuna delle seguenti trasformazioni lineari del piano: a) Rotazione di angolo π b) Rotazione
Corso di Geometria 0- Meccanica Elettrotecnica Esercizi : soluzioni Esercizio Scrivere la matrice canonica di ciascuna delle seguenti trasformazioni lineari del piano: a) Rotazione di angolo π b) Rotazione
CdL in Ingegneria Gestionale e CdL in Ingegneria del Recupero Edilizio ed Ambientale
 CdL in Ingegneria Gestionale e CdL in Ingegneria del Recupero Edilizio ed Ambientale della prova scritta di Algebra Lineare e Geometria- Compito A- 8 Aprile 8 E assegnato l endomorfismo f : R 3 R 3 definito
CdL in Ingegneria Gestionale e CdL in Ingegneria del Recupero Edilizio ed Ambientale della prova scritta di Algebra Lineare e Geometria- Compito A- 8 Aprile 8 E assegnato l endomorfismo f : R 3 R 3 definito
Università di Catania Corso di laurea in Ingegneria Edile Architettura Svolgimento della prova scritta di Geometria assegnata l 8/2/2017
 Università di Catania Corso di laurea in Ingegneria Edile Architettura Svolgimento della prova scritta di Geometria assegnata l 8//07 a) Nello spazio siano dati i punti P (,, ) e Q(,, 4) e le rette: x
Università di Catania Corso di laurea in Ingegneria Edile Architettura Svolgimento della prova scritta di Geometria assegnata l 8//07 a) Nello spazio siano dati i punti P (,, ) e Q(,, 4) e le rette: x
Il punto di intersezione degli assi coordinati prende il nome di origine O degli assi
 GEOMETRIA ANALITICA PIANO CARTESIANO Ad ogni punto P del piano corrisponde una coppia di numeri sugli assi cartesiani. La coppia di numeri che indichiamo con (x,) prendono il nome di coordinate cartesiane
GEOMETRIA ANALITICA PIANO CARTESIANO Ad ogni punto P del piano corrisponde una coppia di numeri sugli assi cartesiani. La coppia di numeri che indichiamo con (x,) prendono il nome di coordinate cartesiane
1. conoscere le nozioni fondamentali della geometria analitica del piano e dello spazio
 Terzo modulo: Geometria analitica Obiettivi 1 conoscere le nozioni fondamentali della geometria analitica del piano e dello spazio interpretare geometricamente equazioni e sistemi algebrici di primo e
Terzo modulo: Geometria analitica Obiettivi 1 conoscere le nozioni fondamentali della geometria analitica del piano e dello spazio interpretare geometricamente equazioni e sistemi algebrici di primo e
Coordinate cartesiane e coordinate omogenee
 Coordinate cartesiane e coordinate omogenee Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Ad ogni punto P del piano possiamo associare le coordinate cartesiane (x, y),
Coordinate cartesiane e coordinate omogenee Fissiamo nel piano un sistema di riferimento cartesiano ortogonale O, x, y, u. Ad ogni punto P del piano possiamo associare le coordinate cartesiane (x, y),
X = x + 1. X = x + 1
 CONICHE. Esercizi Esercizio. Classificare, ridurre a forma canonica (completando i quadrati), e disegnare le seguenti coniche: γ : x y + x = 0; γ : x + 4x y + = 0; γ 3 : x + y + y + 0 = 0; γ 4 : x + y
CONICHE. Esercizi Esercizio. Classificare, ridurre a forma canonica (completando i quadrati), e disegnare le seguenti coniche: γ : x y + x = 0; γ : x + 4x y + = 0; γ 3 : x + y + y + 0 = 0; γ 4 : x + y
Formulario di Geometria Analitica a.a
 Formulario di Geometria Analitica a.a. 2006-2007 Dott. Simone Zuccher 23 dicembre 2006 Nota. Queste pagine potrebbero contenere degli errori: chi li trova è pregato di segnalarli all autore zuccher@sci.univr.it).
Formulario di Geometria Analitica a.a. 2006-2007 Dott. Simone Zuccher 23 dicembre 2006 Nota. Queste pagine potrebbero contenere degli errori: chi li trova è pregato di segnalarli all autore zuccher@sci.univr.it).
Esericizi Quadriche e Coniche nello spazio
 Esericizi Quadriche e Coniche nello spazio 1. In R 3 sia A = (1, 1, 0) e sia r la retta passante per A, parallela al piano x + y + z = 0 e complanare alla retta s di equazione cartesiana x + y z = 0 =
Esericizi Quadriche e Coniche nello spazio 1. In R 3 sia A = (1, 1, 0) e sia r la retta passante per A, parallela al piano x + y + z = 0 e complanare alla retta s di equazione cartesiana x + y z = 0 =
Coniche - risposte 1.9
 Coniche - risposte. CAMBI DI COORDINATE ) ) cosπ/) sinπ/). a. Rotazione di π/, la matrice di rotazione è = sinπ/) cosπ/) ) ) ) X = Y X = Quindi le formule sono: cioè: Y = X e inversamente Y = = Y X = b.
Coniche - risposte. CAMBI DI COORDINATE ) ) cosπ/) sinπ/). a. Rotazione di π/, la matrice di rotazione è = sinπ/) cosπ/) ) ) ) X = Y X = Quindi le formule sono: cioè: Y = X e inversamente Y = = Y X = b.
CdL in Ingegneria Gestionale
 CdL in Ingegneria Gestionale Risoluzione della prova scritta di Algebra lineare e geometria- 5 Febbraio 8 Si consideri l endomorfismo ϕ : R 3 R 3 definito da: con h parametro reale. I ϕ(x, y, z) = (x,
CdL in Ingegneria Gestionale Risoluzione della prova scritta di Algebra lineare e geometria- 5 Febbraio 8 Si consideri l endomorfismo ϕ : R 3 R 3 definito da: con h parametro reale. I ϕ(x, y, z) = (x,
COMPLEMENTI DEL CORSO DI MATEMATICA Anno Accademico 2012/2013 Prof. Francesca Visentin
 COMPLEMENTI DEL CORSO DI MATEMATICA Anno Accademico 0/03 Prof. Francesca Visentin CAPITOLO V ELEMENTI DI GEOMETRIA ANALITICA Riprendiamo alcune nozioni già date nel Capitolo II.. Coordinate cartesiane
COMPLEMENTI DEL CORSO DI MATEMATICA Anno Accademico 0/03 Prof. Francesca Visentin CAPITOLO V ELEMENTI DI GEOMETRIA ANALITICA Riprendiamo alcune nozioni già date nel Capitolo II.. Coordinate cartesiane
OLITECNICO DI MILANO I FACOLTÀ DI INGEGNERIA 1 APPELLO DI GEOMETRIA 19 GENNAIO 2009
 OLITECNICO DI MILANO I FACOLTÀ DI INGEGNERIA 1 APPELLO DI GEOMETRIA 19 GENNAIO 2009 Decidere se le seguenti affermazioni sono vere o false barrando le caselle opportune: Se le matrici A e B sono diagonalizzabili,
OLITECNICO DI MILANO I FACOLTÀ DI INGEGNERIA 1 APPELLO DI GEOMETRIA 19 GENNAIO 2009 Decidere se le seguenti affermazioni sono vere o false barrando le caselle opportune: Se le matrici A e B sono diagonalizzabili,
RIPASSO E APPROFONDIMENTO DI ARGOMENTI DEL TERZO ANNO
 RIPASSO E APPROFONDIMENTO DI ARGOMENTI DEL TERZO ANNO 1 La circonferenza. 2 La parabola. 3 L ellisse. L iperbole. 5 Le coniche. 6 Equazione generale di una conica. 7 Calcolo delle principali caratteristiche
RIPASSO E APPROFONDIMENTO DI ARGOMENTI DEL TERZO ANNO 1 La circonferenza. 2 La parabola. 3 L ellisse. L iperbole. 5 Le coniche. 6 Equazione generale di una conica. 7 Calcolo delle principali caratteristiche
Università di Pisa. Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare
 Università di Pisa Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare Cognome e Nome: Corso di studi: Anno di iscrizione: Numero di matricola: Scritto n. 1 del 16 Esercizio 1. Si studi
Università di Pisa Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare Cognome e Nome: Corso di studi: Anno di iscrizione: Numero di matricola: Scritto n. 1 del 16 Esercizio 1. Si studi
1 Ampliamento del piano e coordinate omogenee
 1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
Esercizi riepilogativi sulle coniche verso l esame di stato
 Esercizi riepilogativi sulle coniche verso l esame di stato n. 9 pag. 55 Sono date le curve α e β definite dalle seguenti relazioni: α : xy x y + 4 = 0 β : luogo dei punti P (k + ; 1 + k ), k R a) Dopo
Esercizi riepilogativi sulle coniche verso l esame di stato n. 9 pag. 55 Sono date le curve α e β definite dalle seguenti relazioni: α : xy x y + 4 = 0 β : luogo dei punti P (k + ; 1 + k ), k R a) Dopo
CLASSIFICAZIONE DELLE CONICHE AFFINI
 CLASSIFICAZIONE DELLE CONICHE AFFINI Pre-requisiti necessari. Elementi di geometria analitica punti e rette nel piano cartesiano, conoscenza delle coniche in forma canonica). Risoluzione di equazioni e
CLASSIFICAZIONE DELLE CONICHE AFFINI Pre-requisiti necessari. Elementi di geometria analitica punti e rette nel piano cartesiano, conoscenza delle coniche in forma canonica). Risoluzione di equazioni e
Università di Pisa. Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare
 Università di Pisa Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare Cognome e Nome: Corso di studi: Anno di iscrizione: Numero di matricola: Scritto n. 1 del 016 Esercizio 1. Si studi
Università di Pisa Corso di Laurea in Ingegneria Meccanica Geometria e Algebra Lineare Cognome e Nome: Corso di studi: Anno di iscrizione: Numero di matricola: Scritto n. 1 del 016 Esercizio 1. Si studi
PIANO CARTESIANO E RETTA
 PIANO CATESIANO E ETTA Distanza tra due punti: d(a, B) = (x A x B ) + (y A y B ) Distanza tra due punti su una retta di coefficiente angolare m: d(a, B) = x A x B + m Punto medio di un segmento: M = (
PIANO CATESIANO E ETTA Distanza tra due punti: d(a, B) = (x A x B ) + (y A y B ) Distanza tra due punti su una retta di coefficiente angolare m: d(a, B) = x A x B + m Punto medio di un segmento: M = (
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) CONICHE DI
 Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) CONICHE DI R. Docente: Prof. F. Flamini Esercizi Riepilogativi Svolti Esercizio
Universita degli Studi di Roma - "Tor Vergata" - Facolta Ingegneria Esercizi GEOMETRIA (Edile-Architettura e dell Edilizia) CONICHE DI R. Docente: Prof. F. Flamini Esercizi Riepilogativi Svolti Esercizio
CdL in Ingegneria Informatica (A-F), (G-Q)
 CdL in ngegneria nformatica (A-F), (G-Q) Prova scritta di Algebra Lineare e Geometria del giorno 31 Gennaio 2007 Sia V il sottospazio vettoriale di R 4 generato dai vettori v 1 = (2, 1, 2, 0), v 2 = (2,
CdL in ngegneria nformatica (A-F), (G-Q) Prova scritta di Algebra Lineare e Geometria del giorno 31 Gennaio 2007 Sia V il sottospazio vettoriale di R 4 generato dai vettori v 1 = (2, 1, 2, 0), v 2 = (2,
CLASSE Ingegneria Informatica (G-La)
 CLASSE ngegneria nformatica (G-La) Prova scritta di Algebra assegnata il 9 Novembre 2002 Durata della prova: due ore. Sia f : R 4 R 4 l endomorfismo definito dalle relazioni f (e 1 ) = v 1, f (e 2 ) =
CLASSE ngegneria nformatica (G-La) Prova scritta di Algebra assegnata il 9 Novembre 2002 Durata della prova: due ore. Sia f : R 4 R 4 l endomorfismo definito dalle relazioni f (e 1 ) = v 1, f (e 2 ) =
2 Forma canonica metrica delle ipequadriche
 26 Trapani Dispensa di Geometria, 1 Iperquadriche Sia A una matrice reale simmetrica n n, non nulla, sia b un vettore colonnna in R n e sia c R. L insieme delle soluzioni in R n dell equazione X t AX +
26 Trapani Dispensa di Geometria, 1 Iperquadriche Sia A una matrice reale simmetrica n n, non nulla, sia b un vettore colonnna in R n e sia c R. L insieme delle soluzioni in R n dell equazione X t AX +
Università degli Studi di Catania CdL in Ingegneria Civile e Ambientale
 CdL in ngegneria Civile e Ambientale Prova scritta di Algebra Lineare e Geometria del 26 gennaio 2018 Usare solo carta fornita dal Dipartimento di Matematica e nformatica, riconsegnandola tutta. 1) Siano
CdL in ngegneria Civile e Ambientale Prova scritta di Algebra Lineare e Geometria del 26 gennaio 2018 Usare solo carta fornita dal Dipartimento di Matematica e nformatica, riconsegnandola tutta. 1) Siano
Prova scritta di Algebra lineare e Geometria- 8 Settembre 2010
 CdL in Ingegneria d(el Recupero Edilizio ed Ambientale - - Ingegneria Edile-Architettura (A-L),(M-Z)- Ingegneria delle Telecomunicazioni - - Ingegneria Informatica (A-F), (R-Z) Prova scritta di Algebra
CdL in Ingegneria d(el Recupero Edilizio ed Ambientale - - Ingegneria Edile-Architettura (A-L),(M-Z)- Ingegneria delle Telecomunicazioni - - Ingegneria Informatica (A-F), (R-Z) Prova scritta di Algebra
1 Geometria analitica nel piano
 Lezioni di Geometria a.a. 2007-2008 cdl SIE prof. C. Franchetti 1 Geometria analitica nel piano 1.1 Distanza di due punti Siano P 1 = (x 1, y 1 ), P 2 = (x 2, y 2 ) due punti del piano, se d(p 1, P 2 )
Lezioni di Geometria a.a. 2007-2008 cdl SIE prof. C. Franchetti 1 Geometria analitica nel piano 1.1 Distanza di due punti Siano P 1 = (x 1, y 1 ), P 2 = (x 2, y 2 ) due punti del piano, se d(p 1, P 2 )
Algebra lineare. È assegnata l applicazione lineare f : R 3 R 3 definita da:
 Algebra lineare È assegnata l applicazione lineare f : R 3 R 3 definita da: al variare di h R. f (1, 1, 0) = (1, 1, 0) f (0, 1, 1) = (h, 0, h) f (1, 1, 1) = (1 + h, 2, 2h 2), 1) Studiare f al variare di
Algebra lineare È assegnata l applicazione lineare f : R 3 R 3 definita da: al variare di h R. f (1, 1, 0) = (1, 1, 0) f (0, 1, 1) = (h, 0, h) f (1, 1, 1) = (1 + h, 2, 2h 2), 1) Studiare f al variare di
Algebra lineare Geometria 1 15 luglio 2009
 Algebra lineare Geometria 1 15 luglio 2009 Esercizio 1. Nello spazio vettoriale reale R 3 [x] si considerino l insieme A k = {1 + x, k + (1 k)x 2, 1 + (k 1)x 2 + x 3 }, il vettore v k = k + kx x 3 e la
Algebra lineare Geometria 1 15 luglio 2009 Esercizio 1. Nello spazio vettoriale reale R 3 [x] si considerino l insieme A k = {1 + x, k + (1 k)x 2, 1 + (k 1)x 2 + x 3 }, il vettore v k = k + kx x 3 e la
a 11 a 12 a 13 x y 1 a 12 a 22 a 23 a 13 a 23 a 33 1 e sfruttando la notazione matriciale la (1) può essere riscritta come a 11 a 12 a 13 x a11 a A =
 Coniche Tutti sappiamo che intersecando un piano e un cono si ottengono delle sezioni che proiettate sul piano risultano essere una circonferenza, un ellisse, un iperbole o una parabola. Queste curve vengono
Coniche Tutti sappiamo che intersecando un piano e un cono si ottengono delle sezioni che proiettate sul piano risultano essere una circonferenza, un ellisse, un iperbole o una parabola. Queste curve vengono
~ E 2 (R) si determini l equazione cartesiana del
 In Esercizio 1 ~ E (R) si determini l equazione cartesiana del luogo dei punti equidistanti dal punto F=(1,) e dalla retta y=x. a) Si classifichi la conica così ottenuta; b) Si determini l asse e il vertice;
In Esercizio 1 ~ E (R) si determini l equazione cartesiana del luogo dei punti equidistanti dal punto F=(1,) e dalla retta y=x. a) Si classifichi la conica così ottenuta; b) Si determini l asse e il vertice;
1. Calcolare gli invarianti ortogonali e riconoscere le seguenti quadriche.
 Algebra Lineare e Geometria Analitica Politecnico di Milano Ingegneria Quadriche Esercizi 1. Calcolare gli invarianti ortogonali e riconoscere le seguenti quadriche. (a) x + y + z + xy xz yz 6x 4y + z
Algebra Lineare e Geometria Analitica Politecnico di Milano Ingegneria Quadriche Esercizi 1. Calcolare gli invarianti ortogonali e riconoscere le seguenti quadriche. (a) x + y + z + xy xz yz 6x 4y + z
RELAZIONI e CORRISPONDENZE
 RELAZIONI e CORRISPONDENZE Siano X e Y due insiemi non vuoti si chiama relazione tra X e Y un qualunque sottoinsieme del prodotto cartesiano: X x Y = {(x,y): x X, y Y} L insieme costituito dai primi (secondi)
RELAZIONI e CORRISPONDENZE Siano X e Y due insiemi non vuoti si chiama relazione tra X e Y un qualunque sottoinsieme del prodotto cartesiano: X x Y = {(x,y): x X, y Y} L insieme costituito dai primi (secondi)
CdL in Ingegneria Informatica (A-Faz), (Orp-Z) CdL in Ingegneria del Recupero Edilizio ed Ambientale
 Prova scritta di Geometria assegnata il 13 Dicembre 2003 Sia Si consideri l equazione AX = A t. 0 1 1 A = 1 1 5 R 3,3. 1 2 1 h 1) Determinare i valori di h per cui tale equazione ammette soluzioni. 2)
Prova scritta di Geometria assegnata il 13 Dicembre 2003 Sia Si consideri l equazione AX = A t. 0 1 1 A = 1 1 5 R 3,3. 1 2 1 h 1) Determinare i valori di h per cui tale equazione ammette soluzioni. 2)
Coniche Quadriche. Coniche e quadriche. A. Bertapelle. 9 gennaio A. Bertapelle Coniche e quadriche
 .. Coniche e quadriche A. Bertapelle 9 gennaio 2013 Cenni storici Appollonio di Perga (III a. C.) in Le coniche fu il primo a dimostrare che era possibile ottenere tutte le coniche (ellisse, parabola,
.. Coniche e quadriche A. Bertapelle 9 gennaio 2013 Cenni storici Appollonio di Perga (III a. C.) in Le coniche fu il primo a dimostrare che era possibile ottenere tutte le coniche (ellisse, parabola,
CdL in Ingegneria Informatica (A-F), (G-S)
 CdL in ngegneria nformatica (A-F), (G-S) Prova scritta di Algebra Lineare e Geometria del giorno 29 Gennaio 2008 Usare solo carta fornita dal Dipartimento di Matematica e nformatica, riconsegnandola tutta.
CdL in ngegneria nformatica (A-F), (G-S) Prova scritta di Algebra Lineare e Geometria del giorno 29 Gennaio 2008 Usare solo carta fornita dal Dipartimento di Matematica e nformatica, riconsegnandola tutta.
CONICHE. Esercizi Esercizio 1. Nel piano con riferimento cartesiano ortogonale Oxy sia data la conica C di equazione
 CONICHE Esercizi Esercizio 1. Nel piano con riferimento cartesiano ortogonale Oy sia data la conica C di equazione 7 2 + 2 3y + 5y 2 + 32 3 = 0. Calcolare le equazioni di una rototraslazione che riduce
CONICHE Esercizi Esercizio 1. Nel piano con riferimento cartesiano ortogonale Oy sia data la conica C di equazione 7 2 + 2 3y + 5y 2 + 32 3 = 0. Calcolare le equazioni di una rototraslazione che riduce
Geometria Anali-ca. DOCENTE: Vincenzo Pappalardo MATERIA: Matematica L IPERBOLE
 Geometria Anali-ca DOCENTE: Vincenzo Pappalardo MATERIA: Matematica L IPERBOLE INTRODUZIONE L iperbole fa parte di un insieme di curve (circonferenza, parabola, ellisse) chiamate coniche, perché si possono
Geometria Anali-ca DOCENTE: Vincenzo Pappalardo MATERIA: Matematica L IPERBOLE INTRODUZIONE L iperbole fa parte di un insieme di curve (circonferenza, parabola, ellisse) chiamate coniche, perché si possono
Corso di Matematica B - Ingegneria Informatica Testi di Esercizi. A1. Siano u, v, w vettori. Quali tra le seguenti operazioni hanno senso?
 A. Languasco - Esercizi Matematica B - 4. Geometria 1 A: Vettori geometrici Corso di Matematica B - Ingegneria Informatica Testi di Esercizi A1. Siano u, v, w vettori. Quali tra le seguenti operazioni
A. Languasco - Esercizi Matematica B - 4. Geometria 1 A: Vettori geometrici Corso di Matematica B - Ingegneria Informatica Testi di Esercizi A1. Siano u, v, w vettori. Quali tra le seguenti operazioni
25.1 Quadriche e loro riduzione a forma canonica
 Lezione 25 25.1 Quadriche e loro riduzione a forma canonica Fissiamo nello spazio un sistema di riferimento Oxyz e consideriamo un polinomio q(x, y, z) di grado 2 nelle tre variabili x, y, z amenodicostantimoltiplicativenon
Lezione 25 25.1 Quadriche e loro riduzione a forma canonica Fissiamo nello spazio un sistema di riferimento Oxyz e consideriamo un polinomio q(x, y, z) di grado 2 nelle tre variabili x, y, z amenodicostantimoltiplicativenon
Geometria Anali-ca. DOCENTE: Vincenzo Pappalardo MATERIA: Matematica LA PARABOLA
 Geometria Anali-ca DOCENTE: Vincenzo Pappalardo MATERIA: Matematica LA PARABOLA INTRODUZIONE La parabola fa parte di un insieme di curve (circonferenza, ellisse, iperbole) chiamate coniche, perché si possono
Geometria Anali-ca DOCENTE: Vincenzo Pappalardo MATERIA: Matematica LA PARABOLA INTRODUZIONE La parabola fa parte di un insieme di curve (circonferenza, ellisse, iperbole) chiamate coniche, perché si possono
Sullo svolgimento di una delle quattro versioni della prova scritta di Geometria analitica e algebra lineare del giorno 11 febbraio 2013.
 Sullo svolgimento di una delle quattro versioni della prova scritta di Geometria analitica e algebra lineare del giorno febbraio 0 x + y + z = 0 Stabilire se le due rette r, di equazioni cartesiane ed
Sullo svolgimento di una delle quattro versioni della prova scritta di Geometria analitica e algebra lineare del giorno febbraio 0 x + y + z = 0 Stabilire se le due rette r, di equazioni cartesiane ed
FACOLTA DI INGEGNERIA
 FACOLTA DI INGEGNERIA Corso di laurea in Ingegneria Telematica ed Ambiente e il Territorio Prova scritta di Algebra Lineare e Geometria assegnata il 9/09/004 - Durata della prova: due ore - Non si può
FACOLTA DI INGEGNERIA Corso di laurea in Ingegneria Telematica ed Ambiente e il Territorio Prova scritta di Algebra Lineare e Geometria assegnata il 9/09/004 - Durata della prova: due ore - Non si può
Università degli Studi di Catania CdL in Ingegneria Industriale
 CdL in ngegneria ndustriale Prova scritta di Algebra Lineare e Geometria del 27 gennaio 2014 Usare solo carta fornita dal Dipartimento di Matematica e nformatica, riconsegnandola tutta. È vietato consultare
CdL in ngegneria ndustriale Prova scritta di Algebra Lineare e Geometria del 27 gennaio 2014 Usare solo carta fornita dal Dipartimento di Matematica e nformatica, riconsegnandola tutta. È vietato consultare
Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 12/07/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI
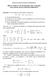 Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 12/07/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI Esercizio 1 Si consideri la conica affine d equazione 9x 2 + 6y 2 4xy 6x + 8y = 1 (1)
Corso di Laurea in Scienza dei Materiali PROVA SCRITTA DI GEOMETRIA DEL 12/07/2016 SOLUZIONE DEGLI ESERCIZI PROPOSTI Esercizio 1 Si consideri la conica affine d equazione 9x 2 + 6y 2 4xy 6x + 8y = 1 (1)
Calcolo Algebrico. Primo grado. ax 2 + bx + c = 0. Secondo grado. (a 0) Equazioni e disequazioni in una incognita e coefficienti reali: ax + b = 0
 Calcolo Algebrico Equazioni e disequazioni in una incognita e coefficienti reali: Primo grado ax + b = 0 (a 0) x = b a Secondo grado ax 2 + bx + c = 0 (a 0) Si hanno due soluzioni che possono essere reali
Calcolo Algebrico Equazioni e disequazioni in una incognita e coefficienti reali: Primo grado ax + b = 0 (a 0) x = b a Secondo grado ax 2 + bx + c = 0 (a 0) Si hanno due soluzioni che possono essere reali
LE CONICHE: RICHIAMI ED APPROFONDIMENTI
 LE CONICHE: RICHIAMI ED APPROFONDIMENTI Appunti presi dalle lezioni del Prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe B) October 12, 2002 1 Le coniche dal punto di vista analitico
LE CONICHE: RICHIAMI ED APPROFONDIMENTI Appunti presi dalle lezioni del Prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe B) October 12, 2002 1 Le coniche dal punto di vista analitico
Parte 12a. Trasformazioni del piano. Forme quadratiche
 Parte 12a Trasformazioni del piano Forme quadratiche A Savo Appunti del Corso di Geometria 2013-14 Indice delle sezioni 1 Trasformazioni del piano, 1 2 Cambiamento di coordinate, 8 3 Forme quadratiche,
Parte 12a Trasformazioni del piano Forme quadratiche A Savo Appunti del Corso di Geometria 2013-14 Indice delle sezioni 1 Trasformazioni del piano, 1 2 Cambiamento di coordinate, 8 3 Forme quadratiche,
Lezione 6 Richiami di Geometria Analitica
 1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
1 Piano cartesiano Lezione 6 Richiami di Geometria Analitica Consideriamo nel piano due rette perpendicolari che si intersecano in un punto O Consideriamo ciascuna di queste rette come retta orientata
CORSO ZERO DI MATEMATICA
 UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA GEOMETRIA ANALITICA NEL PIANO Dr. Erasmo Modica erasmo@galois.it LE COORDINATE CARTESIANE Quando si vuole fissare un sistema
UNIVERSITÀ DEGLI STUDI DI PALERMO FACOLTÀ DI ARCHITETTURA CORSO ZERO DI MATEMATICA GEOMETRIA ANALITICA NEL PIANO Dr. Erasmo Modica erasmo@galois.it LE COORDINATE CARTESIANE Quando si vuole fissare un sistema
CdL in Ingegneria Industriale (F-O)
 CdL in Ingegneria Industriale (F-O Prova scritta di Algebra lineare e Geometria- 0 Giugno 07 Durata della prova: tre ore. È vietato uscire dall aula prima di aver consegnato definitivamente il compito.
CdL in Ingegneria Industriale (F-O Prova scritta di Algebra lineare e Geometria- 0 Giugno 07 Durata della prova: tre ore. È vietato uscire dall aula prima di aver consegnato definitivamente il compito.
CdL in Ingegneria Informatica - Ingegneria Elettronica (P-Z) Ingegneria delle Telecomunicazioni
 CdL in Ingegneria Informatica - Ingegneria Elettronica (P-Z) Ingegneria delle Telecomunicazioni Prova scritta di Algebra lineare e Geometria- 9 Gennaio 3 Durata della prova: tre ore. È vietato uscire dall
CdL in Ingegneria Informatica - Ingegneria Elettronica (P-Z) Ingegneria delle Telecomunicazioni Prova scritta di Algebra lineare e Geometria- 9 Gennaio 3 Durata della prova: tre ore. È vietato uscire dall
PROVA SCRITTA DI GEOMETRIA 2 14 Febbraio 2017
 PROVA SCRITTA DI GEOMETRIA 2 14 Febbraio 2017 La prova orale deve essere sostenuta entro il 28 Febbraio 2017 A Fissato un sistema di riferimento cartesiano nello spazio si consideri la quadriche Q di equazione
PROVA SCRITTA DI GEOMETRIA 2 14 Febbraio 2017 La prova orale deve essere sostenuta entro il 28 Febbraio 2017 A Fissato un sistema di riferimento cartesiano nello spazio si consideri la quadriche Q di equazione
24.1 Coniche e loro riduzione a forma canonica
 Lezione 24 24. Coniche e loro riduzione a forma canonica Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y amenodicostantimoltiplicativenonnulle,diciamo ax
Lezione 24 24. Coniche e loro riduzione a forma canonica Fissiamo nel piano un sistema di riferimento Oxy e consideriamo un polinomio di grado 2 in x, y amenodicostantimoltiplicativenonnulle,diciamo ax
Università degli Studi di Catania CdL in Ingegneria Civile e Ambientale (A-L)
 Prova scritta di Algebra Lineare e Geometria del 26 gennaio 2017 Sia {( x11 x V = 12 x 13 x 21 x 22 x 23 ) R 2,3 x 11 + x 12 + x 13 = x 21 + x 22 + x 23 }. 1) Sia ϕ : V V l applicazione lineare definita
Prova scritta di Algebra Lineare e Geometria del 26 gennaio 2017 Sia {( x11 x V = 12 x 13 x 21 x 22 x 23 ) R 2,3 x 11 + x 12 + x 13 = x 21 + x 22 + x 23 }. 1) Sia ϕ : V V l applicazione lineare definita
formano una base B di R 3. Scrivere la matrice di passaggio dalla base B alla base canonica e dire se tale matrice è ortogonale.
 ) Mostrare che i 3 vettori v=, u=, w= 3 formano una base B di R 3. Scrivere la matrice di passaggio dalla base B alla base canonica e dire se tale matrice è ortogonale. ) Sia f : R 4 R 4 la seguente applicazione
) Mostrare che i 3 vettori v=, u=, w= 3 formano una base B di R 3. Scrivere la matrice di passaggio dalla base B alla base canonica e dire se tale matrice è ortogonale. ) Sia f : R 4 R 4 la seguente applicazione
[ ], classe. ( ) = 0 di grado n. [ ] di terne non nulle di. [ ] = x 1 x LE CONICHE DEL PIANO REALE
![[ ], classe. ( ) = 0 di grado n. [ ] di terne non nulle di. [ ] = x 1 x LE CONICHE DEL PIANO REALE [ ], classe. ( ) = 0 di grado n. [ ] di terne non nulle di. [ ] = x 1 x LE CONICHE DEL PIANO REALE](/thumbs/84/89684391.jpg) LE CONICHE DEL PIANO REALE 1. - IL PIANO PROIETTIVO REALE A) Coordinate omogenee Ad ogni punto P= x,y del piano R associamo una terna ordinata ( x 0, x 1, x ) non nulla in modo che: x = x 1 x 0 y = x x
LE CONICHE DEL PIANO REALE 1. - IL PIANO PROIETTIVO REALE A) Coordinate omogenee Ad ogni punto P= x,y del piano R associamo una terna ordinata ( x 0, x 1, x ) non nulla in modo che: x = x 1 x 0 y = x x
CdL in Ingegneria Informatica (Orp-Z)
 Prova scritta di Algebra Lineare e Geometria del giorno 1 Febbraio 2006 Sia f : R 4 R 4 l applicazione lineare definita dalla legge f (x, y, z, t) = (2x + (h + 3)y + (1 h)z + t, 2x + 5y + (h + 5)z + 2t,
Prova scritta di Algebra Lineare e Geometria del giorno 1 Febbraio 2006 Sia f : R 4 R 4 l applicazione lineare definita dalla legge f (x, y, z, t) = (2x + (h + 3)y + (1 h)z + t, 2x + 5y + (h + 5)z + 2t,
Studio generale di una quadrica
 Studio generale di una quadrica Manlio De Domenico 19 Giugno 2003 Definizione 1 Si definisce quadrica Q un equazione algebrica F (x 1, x 2, x 3, x 4 ) = 0 del secondo ordine omogenea. Detta A la matrice
Studio generale di una quadrica Manlio De Domenico 19 Giugno 2003 Definizione 1 Si definisce quadrica Q un equazione algebrica F (x 1, x 2, x 3, x 4 ) = 0 del secondo ordine omogenea. Detta A la matrice
1. Proprietà focali delle coniche
 1. Proprietà focali delle coniche Per questo argomento, vedere anche P. Maroscia, Introduzione alla geometria e all algebra lineare, Zanichelli, Appendice B. Ricordiamo che il fenomeno fisico della riflessione
1. Proprietà focali delle coniche Per questo argomento, vedere anche P. Maroscia, Introduzione alla geometria e all algebra lineare, Zanichelli, Appendice B. Ricordiamo che il fenomeno fisico della riflessione
Ripasso Formule sulle parabole:
 Ripasso Formule sulle parabole: Equazione generica: Y = ax 2 + bx + c a Apertura della parabola: 1/2p c Punto d incontro con l asse delle Y p Distanza focale: Fuoco direttrice (2 FV) Radici: Risoluzione
Ripasso Formule sulle parabole: Equazione generica: Y = ax 2 + bx + c a Apertura della parabola: 1/2p c Punto d incontro con l asse delle Y p Distanza focale: Fuoco direttrice (2 FV) Radici: Risoluzione
GEOMETRIA ANALITICA: LE CONICHE
 DIPARTIMENTO DI INGEGNERIA CIVILE PRECORSO DI MATEMATICA ANNO ACCADEMICO 2013-2014 ESERCIZI DI GEOMETRIA ANALITICA: LE CONICHE Esercizio 1: Fissato su un piano un sistema di riferimento cartesiano ortogonale
DIPARTIMENTO DI INGEGNERIA CIVILE PRECORSO DI MATEMATICA ANNO ACCADEMICO 2013-2014 ESERCIZI DI GEOMETRIA ANALITICA: LE CONICHE Esercizio 1: Fissato su un piano un sistema di riferimento cartesiano ortogonale
Appunti ed esercizi sulle coniche
 1 LA CIRCONFERENZA 1 Appunti ed esercizi sulle coniche Versione del 1 Marzo 011 1 La circonferenza Nel piano R, fissati un punto O = (a, b) e un numero r > 0, la circonferenza (o cerchio) C di centro O
1 LA CIRCONFERENZA 1 Appunti ed esercizi sulle coniche Versione del 1 Marzo 011 1 La circonferenza Nel piano R, fissati un punto O = (a, b) e un numero r > 0, la circonferenza (o cerchio) C di centro O
