ED AMPLIFICA GALILEO" PARTE I
|
|
|
- Ruggero Mari
- 8 anni fa
- Visualizzazioni
Transcript
1 FISICA/MENTE HUYGENS che "CORROBORA ED AMPLIFICA GALILEO" PARTE I Roberto Renzetti 0 - INTRODUZIONE E' a tutti noto che Galileo rappresenta in ambito scientifico il momento di transizione tra una tradizione magica, metafisica, legata all'autorità dei testi ad una età definita come moderna, nella quale si inaugura un diverso modo d'indagine della natura che risponde solo al metodo della verifica sperimentale di qualunque ipotesi e teoria introdotta. I lavori di Galileo rappresentano il compimento della nascita dell'intellettuale scientifico che è teorico e sperimentale, che sostituisce all'ingenua osservazione empirica un metodo semplice e complesso al medesimo tempo. Innanzitutto occorre un'idea, un pregiudizio, una teoria a priori, che guidi alcune osservazioni; si tratta poi di effettuare tali osservazioni in (1 of 57)23/02/
2 modo controllato, isolando ciò che si vuole studiare dal complesso delle complicazioni che la natura ci offre; ciò significa progettare un'esperienza nella quale siano ben individuate e misurabili le variabili da studiare; l'esperienza fornisce dei dati numerici che, di per sé, non vogliono dire nulla e che occorre quindi sottoporre a trattamento teorico; dall'analisi di tali dati con l'aiuto della matematica è possibile capire se il preconcetto ha una qualche conferma o se è da rigettare del tutto o in parte; ma il processo non si esaurisce qui perché, molto probabilmente, sorgeranno altre domande per rispondere alle quali occorrerà modificare l'esperienza o realizzarne un'altra o più al fine di affinare sempre più la conoscenza del particolare fenomeno che stiamo studiando; con l'accumularsi di dati, correzioni, cambiamenti di rotta, conferme, si è in grado di ricavare una qualche legge di comportamento del fenomeno in oggetto; tale legge ha sempre un carattere di provvisorietà: altre esperienze potranno confermarla e quindi renderla più attendibile ma si deve sapere che un particolare aspetto del fenomeno non ben evidenziato al momento del primo studio (per limiti della nostra teoria provvisoria o per la strumentazione a disposizione) può riservare risposte sperimentali in contrasto con la legge che abbiamo ricavato; tale contrasto può essere non sanabile e quindi richiedere la formulazione di nuove ipotesi eccetera, oppure può richiedere la formulazione di una teoria ed una legge più articolata che inglobi in sé quella già trovata come aspetto particolare. In tutto questo processo che è lento ed in quanto tale faticoso non debbono entrare spiegazioni tautologiche, nominalismi e tanto meno metafisiche. Lo scienziato credente, come certamente era Galileo, ha una visione superiore dell'ente Supremo supposto: grazie alla creazione ed alla sua magnanimità noi umani siamo dotati dell'intelletto, massima creazione di Dio, e del libero arbitrio con i quali ci è dato di poterci dedicare allo studio del mondo circostante, altro prodotto di Dio. Ma se, nel tentare di capire come funziona il mondo, introduciamo spiegazioni di tipo metafisico (ciò è un mistero, ciò è insondabile, questo è un miracolo, questa strada non è percorribile, questo non si può fare, le cose vanno così perché Dio lo vuole,...) allora facciamo una cosa diversa da quella indicataci da Galileo. Abbandoniamo il metodo sperimentale, che pur prevede un Dio che però non è attivo giorno per giorno a farci dei dispetti, e in qualche modo ripercorriamo se non tutte, alcune strade che fu faticosissimo abbandonare. In definitiva il metodo galileiano prescinde da un Dio onnipresente che tiene a balia il mondo circostante, dà grande fiducia all'intelletto dell'uomo nel tentare di comprendere sempre meglio i meccanismi più reconditi di funzionamento del mondo naturale. Tutto ciò non è banale per tentare di capire cosa è accaduto nel periodo di transizione che si può localizzare nell'età barocca. Ho in più lavori studiato (1) cosa accadeva in quell'epoca di grandi entusiasmi ma estremamente travagliata. Vi era una sorta di mondo antico che risucchiava gran parte delle grandi intelligenze, una melma magica e mistica che impediva il passo spedito e che avvolgeva almeno in parte molti tra i grandi personaggi di quel periodo. Quando noi studiamo la loro opera ci dobbiamo sempre confrontare con le semplificazioni di una facile divulgazione. Ognuno di tali personaggi è sistemato all'interno di una storia che si sviluppa in modo lineare con i contributi di ognuno che fanno da ulteriore scalino di una scalinata che sale, sale e salirà sempre. Non è così. La storia della scienza ci racconta di molti errori e passi indietro e, soprattutto, di personaggi che hanno dato importanti contributi che è stato difficile isolare da contesti farraginosi, contorti e soprattutto metafisici. (2 of 57)23/02/
3 Galileo, uno scienziato credente come accennato, studia la natura in modo meticoloso, passo passo. Non fa salti verso teorie complessive perché è fedele al metodo che si è imposto ed arriva fin dove il suo metodo gli consente. Ma Galileo teorizza anche il ruolo di Dio, o meglio della religione, nei processi di studio della natura: non deve entrare la metafisica nella spiegazione fisica. E Galileo su questo giocò la sua esistenza perché, se è vero che è famoso per ciò che ha fatto ed ha indicato come metodo anche in relazione alla metafisica che mai interviene nelle sue spiegazioni, è anche vero che questa posizione lo ha portato davanti al Tribunale dell'inquisizione. E' allora lecito chiedersi come si sono comportati coloro che hanno proseguito la sua opera, gli scienziati, almeno i più noti, che sono venuti dopo di lui. Anche qui ho già scritto molto (1) e la risposta, in senso lato, l'abbiamo già. Descartes, Pascal, Leibniz, Newton e molti altri, pur essendo noti come grandi scienziati ed alcuni, come Newton, considerati come suoi continuatori, non furono galileiani perché nella loro fisica sono presenti molti elementi metafisici. In tal senso, e qualche volta l'ho nominato ma solo nominato, emerge l'unico vero prosecutore del programma galileiano, Hans Christian Huygens. Un'altra osservazione è necessaria prima di iniziare. In Italia si non conosce Huygens se non per luoghi comuni e per un paio di cosette. Basta cercare nell'editoria un qualche libro, una qualche monografia che ce lo presenti. Esiste solo un libro della benemerita Alfonsina D'Elia (Christiaan Huygens, Una biografia intellettuale, FrancoAngeli, 1985). Purtroppo ho cercato questo libro dappertutto, anche il librerie antiquarie, ma non sono riuscito a trovarlo. Dall'indice che ho consultato in rete deve essere un gran bel lavoro ma, ripeto, è l'unica cosa esistente in Italia ed introvabile. Se si fa una qualche ricerca su internet negli USA, in UK, in Francia, in Olanda,... si trovano moltissime pubblicazioni scientifiche, testi originali, traduzioni, articoli di varia natura,.... Più in generale in questi Paesi internet è davvero una cosa importante per poter affrontare uno studio serio. Dalle parti nostre è mortificante, a cominciare dai siti delle varie università. A parte contatissime eccezioni, in rete non si trovano testi di classici. Sembra troppo informatizzare la nostra letteratura scientifica, uno sprecare tempo. Pubblicare poi ricerche, articoli, appare addirittura inutile. Così la dipendenza culturale da altri Paesi prosegue. Basterebbe solo fare un lavoro analogo a quello che è stato fatto in Francia con gallica... Mi rendo conto dell'inutilità delle cose che ho qui detto: l'italia è un Paese che manda via i suoi migliori cervelli e si affida continuamente alla mediocrità assoluta. 1 - HANS CHRISTIAAN HUYGENS: VITA ED OPERE Christiaan Huygens, secondo di cinque figli, nacque a l'aja (nell'allora nascente Olanda (2) ) nel 1629 da una famiglia calvinista dell'alta aristocrazia con solidi principi civili e morali. Suo padre, influente magistrato, diplomatico, (3 of 57)23/02/
4 consigliere del duca Guglielmo II D'Orange, uomo di cultura, cultore di matematiche ed anche poeta, era quel Constantijn Huygens de Zuylichem che più volte ospitò in casa l'amico Descartes e che aveva diverse entrature nel mondo della cultura, sia in Inghilterra che in Francia (era corrispondente di padre Mersenne (3) ). Sua madre, Susana van Baerle, morì quando Huygens aveva solo 8 anni. Tra le amicizie di famiglia occorre ricordare Rembrandt, e Spinoza, ma anche un personaggio meno rinomato ma forse più influente sul giovane Huygens, Antón van Leeuwenhoek, inventore del microscopio ed in grado di fabbricarsi piccole lenti, che ebbe modo di fare varie osservazioni con il giovane Christiaan. Fino ai 16 anni fu educato, dal padre e da istitutori privati, in casa perché diventasse diplomatico per la casa degli Orange. Mostrò subito particolari attitudini matematiche (4). Egli soleva dire: Il mondo è la mia patria, la scienza la mia religione. Durante il 1644 studiò matematica con Johan Jansz Stampioen (5), quindi passò a studiare legge nell'università di Leida (tra il 1645 ed il 1647) dove ebbe come professore uno dei più insigni matematici olandesi, Frans van Schooten (6). In questo periodo iniziò la sua fruttuosa e stimolante corrispondenza con Mersenne (7) che durò fino al 1648, anno della morte di quest'ultimo. Quindi continuò a studiare legge presso il Collegio Orange a Breda (tra il 1647 ed il 1649) dove ebbe un altro insigne matematico, l'inglese John Pell (8), come professore. Terminò i suoi studi in legge presso l'università francese di Angers (unica università francese aperta ai protestanti) dove ottenne il dottorato nel Intanto, nel 1649, aveva fatto un primo viaggio con una delegazione diplomatica in Danimarca. Sperava da lì di potersi recare a Stoccolma per incontrare Descartes ma le cattive condizioni del tempo glielo impedirono. Continuò con altri la visita in Danimarca e in giro per l'europa, arrivando fino a Roma. Durante questo viaggio ebbe modo di acquistare un libro di Grégoire de Saint Vincent, Opus geometricum quadraturae circuli et hyperbolae scritto nel La morte di Guglielmo II d'orange, nel 1650, fece cambiare indirizzo di vita ad Huygens, la carriera di diplomatico abortì prima di iniziare ed egli passò a dedicarsi a studi di matematica, ottica e meccanica. La stessa famiglia fu economicamente e politicamente ridimensionata. (4 of 57)23/02/
5 Huygens fu molto legato a Descartes e la cosa è testimoniata dai versi che egli scrisse nel 1650, in occasione della sua morte (9). (5 of 57)23/02/
6 Ma presto, con l'evolvere dei suoi studi e della sua personalità, fu molto duro con il filosofo francese, come egli stesso ci dice: Il signor Descartes aveva trovato il mezzo di far prendere le sue congetture e finzioni per verità. E capitava a coloro che leggevano i suoi Principes de philosophie qualche cosa di simile a coloro che leggono i romanzi che piacciono e fanno la medesima: impressione delle storie vere. La novità delle figure delle sue particelle e dei vortici vi fanno un grande piacere. Mi sembrava, quando io lessi quel libro di princìpi per la prima volta, che tutto andasse nel miglior modo possibile e credevo, quando vi trovavo qualche difficoltà, che fosse errore mio di comprendere bene il suo pensiero. Avevo appena 15 o 16 anni. Ma avendovi poi scoperto di tanto in (6 of 57)23/02/
7 tanto cose chiaramente false, ed altre poco verosimili, mi sono staccato molto bene dalla preoccupazione in cui mi ero trovato [citato da Dugas, in R. Taton] OSSERVAZIONI ASTRONOMICHE Le prime pubblicazioni di Huygens risalgono al 1651 ed al 1654 e sono di argomento matematico. Nel 1651 scrisse Cyclometriae, dove mostrò gli errori dei quattro metodi proposti da Grégoire de Saint Vincent, nel suo Opus geometricum, per risolvere la quadratura del cerchio. Sul medesimo tema tornò nel 1654 con il De Circuli Magnitudine Inventa, ma in modo più argomentato e completo affrontando altri problemi di quadratura e di cubatura (sferoidi e conoidi), risolvendo svariati problemi geometrici in forma algebrica, introducendo un metodo per ridurre le rettificazioni alle quadrature, studiando la cisoide, semplificando la regola che Descartes e Fermat avevano trovato per determinare le tangenti ed i massimi e minimi ad una curva. Il suo interesse era però anche rivolto alle attività manuali, così come aveva appreso nella sua prima educazione, quando, insieme agli studi di geometria e di musica, fu avviato alla costruzione di modelli meccanici. Così, tra il 1651 ed il 1654, mentre scriveva di matematica, rivolse la sua attenzione alla fabbricazione di lenti ed alla costruzione di telescopi. Apprese da studiosi e artigiani molte informazioni teoriche riguardo ai telescopi realizzati utilizzando più di due lenti, mettendo poi in pratica queste nozioni con la costruzione di lenti e telescopi. Intorno al 1654 sviluppò un modo originale di taglio e levigatura di lenti che lo portarono a telescopi di grande qualità ed anche di grandi dimensioni (uno di essi era lungo 5 metri). Diresse uno di tali telescopi, tra i migliori esistenti all'epoca, verso il cielo in cerca di eventuali lune di Marte (osservando tale pianeta, scoprì, come dirò più oltre, alcune macchie su di esso delle quali il primo disegno era stato realizzato nel 1636 dal napoletano Francesco Fontana), Venere e Saturno. Quest'ultimo pianeta lo incuriosiva particolarmente perché il suo aspetto, dalle osservazioni di Galileo, restava misterioso risultando (7 of 57)23/02/
8 I disegni di Galileo sulle sue osservazioni di Saturno tricorporeo. Dopo varie osservazioni, nel 1655, scoprì la prima luna di Saturno, Titano (10) e la natura della tricorporeità del pianeta, ma aspettò un anno prima di comunicare la sua scoperta perché voleva controllare molto bene le sue (8 of 57)23/02/
9 osservazioni. Nel frattempo, ad evitare che qualcuno gli togliesse la priorità delle (9 of 57)23/02/
10 scoperte, utilizzò anagrammi in latino composti di varie lettere che per loro trasposizione formavano la frase nascosta e li incideva sull'oculare del telescopio. L'anagramma per l'anello di Saturno era: aaaaaaa ccccc d eeeee g h iiiiiii llll mm nnnnnnnnn oooo pp q rr s ttttt uuuuu che sta per Annulo cingitur tenui, plano, numquam cohaerente ad eplicticam inclinato ("È circondato da un sottile anello piatto, che non lo tocca mai e che è inclinato rispetto all eclittica"), mentre quello per la scoperta di Titano era: aaaaa b ccc ddd eee h iiii l mm nn ooo q rrrrr ssssss ttt uuuuuuuuu x che sta per Saturno luna sua circumducitur diebus sexdecim, horas quatuor ("Saturno è accompagnato da una luna che gli gira intorno in 16 giorni e quattro ore"). Per la scoperta di Titano, Huygens ricevette le felicitazioni del grande astronomo ligure, Gian Domenico Cassini (che per la fama conquistatasi con le sue osservazioni a Bologna, nel 1669, venne chiamato a Parigi dal Re Sole, Luigi XIV, presso l'observatoire Royal, appena istituito). Disegno di Huygens rappresentante la Luna e Saturno (10 of 57)23/02/
11 (11 of 57)23/02/
12 Vari disegni di Huygens relativi alle sue osservazioni di Saturno. Spiegazione grafica di Huygens del perché, dalla Terra, le osservazioni danno immagini diverse dell'anello di Saturno (12 of 57)23/02/
13 Disegni di Huygens rappresentanti le grandezze di varie orbite planetarie confrontate con quelle della Luna intorno alla Terra (il piccolo disegno in basso). Questa illustrazione proviene dall'ultima opera di Huygens, Cosmotheoros, che discuterò più oltre. Egli non dette alcun nome al satellite di Saturno, lo chiamò semplicemente Luna Saturni. Le sue osservazioni proseguirono e nel 1656 riscoprì la nebulosa di Orione, già scoperta dal gesuita astronomo svizzero Jean-Baptiste Cysat (che fu allievo dello Scheiner delle macchie solari che ebbe varie controversie con Galileo)nel 1618, isolando varie stelle che la costituiscono (era la seconda nebulosa (13 of 57)23/02/
14 Il disegno di Orione fatto da Huygens osservata, dopo quella di Andromeda). Più tardi, nel 1659, pubblicò Systema Saturnium nella quale spiegava la tricorporeità di Saturno: si trattava di un anello piatto sottile, formato da rocce orbitanti, che circondava il pianeta inclinato sul piano dell'orbita, cambiando forma secondo determinate fasi e, soprattutto, non legato al pianeta in alcun punto: "Saturne est entourée d un anneau mince n'adhérant à l'astre en aucun point, et incliné sur l'écliptique". Per poter comprendere la vera natura delle singolari protuberanze, l'astronomo olandese adottò nelle osservazioni un nuovo telescopio da lui costruito avente una lunghezza focale circa doppia rispetto al primo e capace di raggiungere un centinaio di ingrandimenti. Nello stesso 1659 Christiaan Huygens misurò l'angolo che sottende Marte nel cielo e, attribuendo arbitrariamente un valore al diametro di questo pianeta, stimò che l'unità astronomica cioè la distanza media della Terra dal Sole, doveva essere di 160 milioni di chilometri, cioè sette volte maggiore di quella stimata da Kepler (ma un 10% più grande del suo valore reale che è di 149 milioni di chilometri). Tale misura non fu accettata ed anche lo stesso Huygens (14 of 57)23/02/
15 non la sostenne perché tutto dipendeva dall'arbitrarietà assunta per quel diametro di Marte (che per felice combinazione egli aveva indovinato). Altre osservazioni astronomiche di grande interesse sono dovute al nostro: fu lui che per primo parlò di atmosfera e nubi sul pianeta Venere; a lui si deve la scoperta di una macchia caratteristica su Marte, Syrtis Major, che gli permise di stabilire che anche quel pianeta aveva un moto di rotazione intorno al suo asse con una durata di circa 24 Disegni di Huygens della superficie di Marte. Il primo è del 28 novembre 1659; il secondo del 13 agosto 1672 (ore 22 e 30); il terzo del 17 maggio 1683 (ore 22 e 03) ore (11) ; fu ancora lui che, subito dopo che lo aveva fatto Robert Hooke, osservò la grande macchia rossa sul pianeta Giove. Naturalmente il giovane Huygens fu duramente attaccato da vari personaggi tra cui il gesuita Fabri. Solo nel 1665, quando tutti poterono disporre di migliori telescopi, la teoria di Huygens degli anelli di Saturno fu generalmente accettata, anche da Fabri. (15 of 57)23/02/
16 Il Sole, sullo sfondo, a confronto con le dimensioni di vari pianeti. Questa illustrazione proviene dall'ultima opera di Huygens, Cosmotheoros, che discuterò più oltre. Intanto nel 1655 si era recato per la prima volta a Parigi per informare i matematici e gli astronomi della città tra cui, Ismael Boulliau (12), Gassendi e Roberval, della scoperta della Luna Saturni. Tale viaggio e le subitanee entrature in ambienti colti fu reso possibile dalla fama che Mersenne gli aveva fatto precedere. Nel suo breve soggiorno parigino Huygens fu messo al corrente di nuovi filoni di ricerca matematica. Attraverso la corrispondenza tra Pascal e Fermat, (16 of 57)23/02/
17 venne a conoscenza del calcolo delle probabilità e, appena tornato in Olanda su insistenza di Pascal, scrisse un lavoro in proposito De Ratiociniis in Ludo Aleae (1657), che è il primo libro stampato sull'argomento, di una ottima fattura tanto che, mezzo secolo dopo, il padre del calcolo delle probabilità, Jacques Bernouilli lo pubblicò come introduzione al suo Ars Conjectandi (pubblicato postumo nel 1713). Nel 1656 Huygens confermò a Boulliau ed al gruppo dei matematici ed astronomi di Parigi le sue osservazioni sull'anello di Saturno OROLOGIO A PENDOLO Ma già da tempo Huygens, proprio per le sue osservazioni astronomiche, si era reso conto dell'enorme importanza della misura affidabile del tempo. Egli si era quindi messo al lavoro sul cammino che aveva aperto Galileo con la sua scoperta dell'isocronismo del pendolo. A tale proposito vi è una nota di Gliozzi [bibliografia n 16] che merita un cenno. Dice Gliozzi che il diplomatico Huygens padre aveva avuto un grande ruolo nei negoziati tra Galileo e gli Stati Generali d'olanda per l'acquisizione del metodo galileiano di misura della longitudine. Scriveva Galileo agli Stati Generali il 15 agosto 1636: Io ho un tal misuratore di tempo, che se si fabbricassero 4 o 6 di tali strumenti et si lasciassero scorrere troveremo (in confermazione della loro giustezza) che i tempi da quelli misurati et mostrati, non solamente d'hora in hora, ma di giorno in giorno et di mese in mese non differirebbero tra di loro né anco di un minuto secondo d'hora, tanto uniformemente camminano [citato da Gliozzi]. Il problema è se Huygens padre avesse conosciuto tali progetti di Galileo ed in particolare l'idea galileiana di applicazione del pendolo all'orologio. Huygens figlio ha sempre smentito anche se ha ammesso che la sua idea era la medesima di Galileo. In ogni caso, nel 1657, Huygens figlio aveva brevettato il primo orologio a pendolo che aumentò enormemente la precisione nella misura del tempo. Egli aveva incorporato al pendolo, che oscillava per un tempo limitato, il meccanismo di un orologio alimentato da pesi in caduta rallentata su una ruota dentata, in modo da mantenere l'oscillazione per tutto il tempo che tali pesi impiegavano nella loro caduta (13). La descrizione di tale strumento sarà data successivamente (17 of 57)23/02/
18 nell'horologium del L'idea di accoppiare meccanismi di orologi (che avevano una storia lunga, di circa 400 anni) con il pendolo era già stata di Galileo che non riuscì a realizzarla. Lo fece Huygens con l'invenzione di (18 of 57)23/02/
19 Ricostruzione da disegni di Viviani del pendolo di Galileo (Museum Victoria) un sistema meccanico che permetteva di mantenere per molto tempo le regolari oscillazioni del pendolo e di misurare intervalli di tempo relativamente piccoli (fino ad un secondo), lo scappamento. Si tratta di un sistema meccanico per trasformare il moto oscillatorio in moto rotatorio. L'energia a tale sistema, nell'orologio di Huygens, era fornita da una massa che, mediante una corda, si srotolava per gravità da un cilindro. (19 of 57)23/02/
20 La massa (il cilindro rosso in basso) è appesa ad una corda e, man mano che scende, fa ruotare il cilindro sovrapposto (in colore celeste) a cui è connessa una ruota dentata. Mediante gli ingranaggi sovrapposti, il moto viene trasferito alla piccola ruota dentata che si trova più in alto (in celeste). Su questa piccola ruota agisce il meccanismo dello scappamento ad ancora (in giallo) che fa muovere ritmicamente gli ingranaggi. In assenza di esso vi sarebbe una rotazione continua e veloce di tutte le ruote dentate fino a che la massa non arriva al suolo. Quell'ancora mossa dal pendolo che si trova a sinistra, oscilla con il pendolo in modo da bloccare con i suoi due denti per un breve istante (regolato dal periodo del pendolo) la piccola ruota celeste, una volta da un lato ed una da un altro come mostrato nella figura seguente. (20 of 57)23/02/
21 E' lo scatto dello scappamento da una parte e dall'altra che fa il classico rumore (il ticchettio) degli orologi. (21 of 57)23/02/
22 (22 of 57)23/02/
23 Disegno originale dall'horologium del 1658 dell'orologio di Huygens E' interessante osservare che il suo lavoro sul pendolo era in relazione con un lavoro matematico che Huygens aveva intrapreso su provocazione di Pascal e relativo alla cicloide. Il pendolo di Galileo era isocrono su piccole oscillazioni ed Huygens pensò che se la caratteristica di isocronia avesse potuto essere indipendente dall'ampiezza delle oscillazioni si sarebbe avuto a disposizione uno strumento molto utile. E pensò quindi (1659) di far oscillare un pendolo non più su archi di circonferenza ma secondo una cicloide per alcune proprietà della cicloide medesima. Se si dispongono due palline in posizioni contrapposte diverse su una guida a forma cicloidale, il tempo che esse impiegano per andare al punto più basso A della cicloide (vedi figura), da qualunque punto partano, è esattamente lo stesso e ciò vuol dire che si urteranno sempre in A. Tale proprietà della cicloide la fa chiamare curva tautocrona (dal greco tautos, lo stesso, e chronos, tempo). Ciò fa intendere che per avere un pendolo isocrono indipendentemente dall'ampiezza dell'oscillazione occorre farlo oscillare, come già detto, non lungo una circonferenza ma secondo una cicloide. Per realizzare ciò costruì due guide a forma di cicloide da applicare al punto di sospensione del pendolo. Si trattava di condizionare la traiettoria del pendolo facendo adagiare il filo di sospensione su due profili anch'essi a forma di arco di cicloide, perché tra le proprietà matematiche della cicloide vi è anche il fatto che la cicloide è l'evoluta di una identica cicloide. Con questi accorgimenti Huygens fu il primo a costruire un pendolo perfettamente isocrono che pensò subito di utilizzare alla misura della longitudine in mare. (23 of 57)23/02/
24 Schema di pendolo cicloide con due profili ad arco di cicloide nel punto di sospensione del pendolo medesimo Il disegno originale di Huygens (1657) del meccanismo per rendere cicloide il pendolo. (24 of 57)23/02/
25 Disegno di Huygens di un pendolo che oscilla tra due superfici cicloidali. Le due curve che scendono dal punto C sono cicloidi identiche. Quando il pendolo CA oscilla, la corda si avvolge intorno alle superfici e, come dimostrò Huygens, il bilanciere oscillando segue una cicloide identica a quelle che formano le superfici.. (25 of 57)23/02/
26 Realizzazione pratica del pendolo cicloide da parte di Huygens A questo punto si interseca una questione di grande importanza che, all'epoca, era all'ordine del giorno, soprattutto delle grandi potenze marittime, com'era l'olanda. Si tratta appunto del problema della misura della longitudine in mare, problema che aveva fatto bandire concorsi internazionali da corone come quelle di Spagna, di Francia, d'inghilterra e d'olanda. Già Galileo credeva di aver risolto la questione con metodi astronomici, mediante la misura della posizione dei satelliti di Giove. Con tale scoperta si propose alla Spagna ma le trattative non andarono in porto per ragioni economiche tra Spagna e Granducato di Toscana (quest'ultimo, per cedere Galileo alla Spagna aveva richiesto, tra l'altro, delle navi franche dalle colonie americane e la Spagna non aveva accettato). (26 of 57)23/02/
27 Huygens presenta a Luigi XIV il suo orologio a pendolo La realizzazione del pendolo cicloidale fece balenare ad Huygens l'idea di utilizzare questo particolare orologio per misure di longitudine, soprattutto nel mare, durante la navigazione oceanica. Sappiamo infatti che per dare la posizione di un oggetto sulla Terra, occorre disporre di due numeri, la sua latitudine e la sua longitudine. Sulla determinazione della latitudine non vi erano problemi, bastava misurare l'angolo che forniva l'altezza delle stelle rispetto all'orizzonte. Ma per determinare la longitudine serviva disporre a bordo di un orologio di grande precisione che avrebbe fornito l'ora del porto di partenza, mentre il sorgere e tramontare del Sole e delle stelle avrebbero fornito il tempo locale della nave. La differenza tra questi due tempi avrebbe dato la longitudine corrispondente alla posizione della nave. Huygens si dedicò a costruire orologi adatti a tale scopo che furono provati in mare tra il 1662 ed il 1686 dando risultati molto buoni nei primi viaggi ma deludendo in seguito. Nel 1665 realizzò anche un libro in olandese in cui vi erano le istruzioni d'uso di tali orologi per misurare la longitudine e tavole molto accurate con le quali fare gli aggiustamenti degli orologi per tener conto della lunghezza del giorno che non è esattamente di 24 ore, Kort Onderwys Aengaende Aengaende het Gebruyck Der Horologien Tot het vinden der Lenghten van Oost en West [1665] (Istruzioni d'uso degli orologi a pendolo per determinare la longitudine in mare, 1665). Per il buon funzionamento di tali orologi era sempre necessario tempo buono e mare calmo (soprattutto l'inclinazione della nave comprometteva la misura). Per risolvere il problema Huygens, negli anni (27 of 57)23/02/
28 seguenti, inventò la spirale del bilanciere che permetteva di fare a meno del pendolo (l'invenzione fu brevettata in Francia nel 1675) IN GIRO TRA FRANCIA ED INGHILTERRA Nel 1660 Huygens si recò a Parigi una seconda volta (ebbe qui dei contatti con Pascal e fu presentato al re Luigi XIV) e da lì, l'anno seguente (1661), passò in Inghilterra dove mostrò la tecnica che usava per la realizzazione di grandi lenti (a quel tempo i suoi telescopi erano i migliori e raggiungevano la lunghezza di 8 metri). Nel corso del breve soggiorno partecipò con gli astronomi inglesi all'osservazione del passaggio di Mercurio sul Sole. In quell'anno era al centro dell'interesse di fisici britannici la realizzazione della macchina da vuoto da parte di Otto von Guericke nel 1654 al perfezionamento della quale, oltre che lo stesso von Guericke, stava lavorando il già affermato Robert Boyle. Huygens fu coinvolto nelle discussioni e, tornato in Olanda (1661), ideò e realizzò vari esperimenti per perfezionare tale macchina. Nel 1663 Huygens si recò ancora a Parigi per questioni connesse ai suoi orologi marini e per cercare di proteggere questo brevetto anche in Inghilterra (14). Si rese conto di godere di grande fama in quella città ed ebbe offerte di importanti finanziamenti per le sue ricerche da Jean Baptiste Colbert, responsabile delle finanze di Luigi XIV. Un seguito di queste offerte si ebbe nel 1666 alla fondazione (28 of 57)23/02/
LA LEGGE DI GRAVITAZIONE UNIVERSALE
 GRAVIMETRIA LA LEGGE DI GRAVITAZIONE UNIVERSALE r La legge di gravitazione universale, formulata da Isaac Newton nel 1666 e pubblicata nel 1684, afferma che l'attrazione gravitazionale tra due corpi è
GRAVIMETRIA LA LEGGE DI GRAVITAZIONE UNIVERSALE r La legge di gravitazione universale, formulata da Isaac Newton nel 1666 e pubblicata nel 1684, afferma che l'attrazione gravitazionale tra due corpi è
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
I filosofi greci del IV secolo a.c. come Platone e Aristotele ritenevano che le stelle fossero oggetti celesti eterni e immutabili, che ruotavano
 Corso di Astronomia I filosofi greci del IV secolo a.c. come Platone e Aristotele ritenevano che le stelle fossero oggetti celesti eterni e immutabili, che ruotavano attorno alla Terra con orbite circolari.
Corso di Astronomia I filosofi greci del IV secolo a.c. come Platone e Aristotele ritenevano che le stelle fossero oggetti celesti eterni e immutabili, che ruotavano attorno alla Terra con orbite circolari.
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Il mistero dei muoni: perché arrivano sulla terra e cosa c entra la relatività del tempo e dello spazio?
 Il mistero dei muoni: perché arrivano sulla terra e cosa c entra la relatività del tempo e dello spazio? Carlo Cosmelli, Dipartimento di Fisica, Sapienza Università di Roma Abbiamo un problema, un grosso
Il mistero dei muoni: perché arrivano sulla terra e cosa c entra la relatività del tempo e dello spazio? Carlo Cosmelli, Dipartimento di Fisica, Sapienza Università di Roma Abbiamo un problema, un grosso
INTRODUZIONE I CICLI DI BORSA
 www.previsioniborsa.net 1 lezione METODO CICLICO INTRODUZIONE Questo metodo e praticamente un riassunto in breve di anni di esperienza e di studi sull Analisi Tecnica di borsa con specializzazione in particolare
www.previsioniborsa.net 1 lezione METODO CICLICO INTRODUZIONE Questo metodo e praticamente un riassunto in breve di anni di esperienza e di studi sull Analisi Tecnica di borsa con specializzazione in particolare
FISICA. Le forze. Le forze. il testo: 2011/2012 La Semplificazione dei Testi Scolastici per gli Alunni Stranieri IPSIA A.
 01 In questa lezione parliamo delle forze. Parliamo di forza quando: spostiamo una cosa; solleviamo un oggetto; fermiamo una palla mentre giochiamo a calcio; stringiamo una molla. Quando usiamo (applichiamo)
01 In questa lezione parliamo delle forze. Parliamo di forza quando: spostiamo una cosa; solleviamo un oggetto; fermiamo una palla mentre giochiamo a calcio; stringiamo una molla. Quando usiamo (applichiamo)
L'impulso di una forza che varia nel tempo
 Lezione 13 approfondimento pag.1 L'impulso di una forza che varia nel tempo Un riassunto di quel che sappiamo Riprendiamo in esame il solito carrellino che si trova sopra la rotaia a basso attrito. Se
Lezione 13 approfondimento pag.1 L'impulso di una forza che varia nel tempo Un riassunto di quel che sappiamo Riprendiamo in esame il solito carrellino che si trova sopra la rotaia a basso attrito. Se
Gli strumenti della geografia
 Gli strumenti della geografia La geografia studia lo spazio, cioè i tanti tipi di luoghi e di ambienti che si trovano sulla Terra. La geografia descrive lo spazio e ci spiega anche come è fatto, come vivono
Gli strumenti della geografia La geografia studia lo spazio, cioè i tanti tipi di luoghi e di ambienti che si trovano sulla Terra. La geografia descrive lo spazio e ci spiega anche come è fatto, come vivono
ESERCITAZIONE OSSERVARE UN ALBERO
 L esercizio richiesto consiste nella scelta di un albero e il suo monitoraggio/racconto al fine di sviluppare l osservazione attenta come mezzo per la conoscenza del materiale vegetale. L esercitazione
L esercizio richiesto consiste nella scelta di un albero e il suo monitoraggio/racconto al fine di sviluppare l osservazione attenta come mezzo per la conoscenza del materiale vegetale. L esercitazione
Come fare una scelta?
 Come fare una scelta? Don Alberto Abreu www.pietrscartata.com COME FARE UNA SCELTA? Osare scegliere Dio ha creato l uomo libero capace di decidere. In molti occasioni, senza renderci conto, effettuiamo
Come fare una scelta? Don Alberto Abreu www.pietrscartata.com COME FARE UNA SCELTA? Osare scegliere Dio ha creato l uomo libero capace di decidere. In molti occasioni, senza renderci conto, effettuiamo
La catena di assicurazione
 La catena di assicurazione A cosa serve la corda? A trattenere una eventuale caduta Solo questo? Che cosa succede al momento dell arresto di una caduta? L arrampicatore avverte uno strappo Quanto è violento
La catena di assicurazione A cosa serve la corda? A trattenere una eventuale caduta Solo questo? Che cosa succede al momento dell arresto di una caduta? L arrampicatore avverte uno strappo Quanto è violento
Scopri il piano di Dio: Pace e vita
 Scopri il piano di : Pace e vita E intenzione di avere per noi una vita felice qui e adesso. Perché la maggior parte delle persone non conosce questa vita vera? ama la gente e ama te! Vuole che tu sperimenti
Scopri il piano di : Pace e vita E intenzione di avere per noi una vita felice qui e adesso. Perché la maggior parte delle persone non conosce questa vita vera? ama la gente e ama te! Vuole che tu sperimenti
La Posta svizzera SecurePost SA, Oensingen
 La Posta svizzera SecurePost SA, Oensingen Il datore di lavoro Richard Mann Circa un anno e mezzo fa, nell ambito del progetto Integrazione di persone disabili presso la Posta, abbiamo assunto una nuova
La Posta svizzera SecurePost SA, Oensingen Il datore di lavoro Richard Mann Circa un anno e mezzo fa, nell ambito del progetto Integrazione di persone disabili presso la Posta, abbiamo assunto una nuova
www.andreatorinesi.it
 La lunghezza focale Lunghezza focale Si definisce lunghezza focale la distanza tra il centro ottico dell'obiettivo (a infinito ) e il piano su cui si forma l'immagine (nel caso del digitale, il sensore).
La lunghezza focale Lunghezza focale Si definisce lunghezza focale la distanza tra il centro ottico dell'obiettivo (a infinito ) e il piano su cui si forma l'immagine (nel caso del digitale, il sensore).
Apporti, Asporti e Regali
 Apporti, Asporti e Regali Collana: Ali d Amore N. 9 A Dilaila e alle anime candide dell Altra Dimensione A P P O R T I Gli apporti sono materializzazioni di oggetti, di animali, di piante o fiori, che
Apporti, Asporti e Regali Collana: Ali d Amore N. 9 A Dilaila e alle anime candide dell Altra Dimensione A P P O R T I Gli apporti sono materializzazioni di oggetti, di animali, di piante o fiori, che
LA FORZA E IL MOTO: ISACC NEWTON UN RE SCONTROSO
 WebQuest Studentessa Guidi Elisabetta Corso Laurea Scienze Formazione Primaria Università di Urbino Carlo Bo LA FORZA E IL MOTO: ISACC NEWTON UN RE SCONTROSO 1) INTRODUZIONE Il 1642 è un anno storico per
WebQuest Studentessa Guidi Elisabetta Corso Laurea Scienze Formazione Primaria Università di Urbino Carlo Bo LA FORZA E IL MOTO: ISACC NEWTON UN RE SCONTROSO 1) INTRODUZIONE Il 1642 è un anno storico per
OSCURI PREDATORI DI LUCE
 OSCURI PREDATORI DI LUCE LA CADUTA DI EUCLIDE IN UN BUCO NERO PAOLO DULIO DIPARTIMENTO DI MATEMATICA DI COSA PARLIAMO Ricerca e applicazioni I protagonisti di un viaggio fantastico Geometria dello spazio-tempo
OSCURI PREDATORI DI LUCE LA CADUTA DI EUCLIDE IN UN BUCO NERO PAOLO DULIO DIPARTIMENTO DI MATEMATICA DI COSA PARLIAMO Ricerca e applicazioni I protagonisti di un viaggio fantastico Geometria dello spazio-tempo
lo 2 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000
 Capittol lo 2 Visualizzazione 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000 Nel primo capitolo sono state analizzate le diverse componenti della finestra di Word 2000: barra del titolo, barra dei menu,
Capittol lo 2 Visualizzazione 2-1 - PERSONALIZZARE LA FINESTRA DI WORD 2000 Nel primo capitolo sono state analizzate le diverse componenti della finestra di Word 2000: barra del titolo, barra dei menu,
Helsana Assicurazioni SA, Lucerna
 Helsana Assicurazioni SA, Lucerna Il datore di lavoro Sandra Meier La signora F. è impiegata nella nostra azienda al servizio clienti. Lavora alla Helsana da oltre 20 anni. L ho conosciuta nel 2006 al
Helsana Assicurazioni SA, Lucerna Il datore di lavoro Sandra Meier La signora F. è impiegata nella nostra azienda al servizio clienti. Lavora alla Helsana da oltre 20 anni. L ho conosciuta nel 2006 al
9. Urti e conservazione della quantità di moto.
 9. Urti e conservazione della quantità di moto. 1 Conservazione dell impulso m1 v1 v2 m2 Prima Consideriamo due punti materiali di massa m 1 e m 2 che si muovono in una dimensione. Supponiamo che i due
9. Urti e conservazione della quantità di moto. 1 Conservazione dell impulso m1 v1 v2 m2 Prima Consideriamo due punti materiali di massa m 1 e m 2 che si muovono in una dimensione. Supponiamo che i due
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
GRUPPI DI INCONTRO per GENITORI
 Nell ambito delle attività previste dal servizio di Counseling Filosofico e di sostegno alla genitorialità organizzate dal nostro Istituto, si propone l avvio di un nuovo progetto per l organizzazione
Nell ambito delle attività previste dal servizio di Counseling Filosofico e di sostegno alla genitorialità organizzate dal nostro Istituto, si propone l avvio di un nuovo progetto per l organizzazione
L osservatorio è collocato all interno del Parco pineta tra Saronno e Varese. Attorno ad esso troviamo un incredibile distesa di alberi.
 L osservatorio L osservatorio è collocato all interno del Parco pineta tra Saronno e Varese. Attorno ad esso troviamo un incredibile distesa di alberi. All interno troviamo la sala conferenze e i vari
L osservatorio L osservatorio è collocato all interno del Parco pineta tra Saronno e Varese. Attorno ad esso troviamo un incredibile distesa di alberi. All interno troviamo la sala conferenze e i vari
LA DISTRIBUZIONE DI PROBABILITÀ DEI RITORNI AZIONARI FUTURI SARÀ LA MEDESIMA DEL PASSATO?
 LA DISTRIBUZIONE DI PROBABILITÀ DEI RITORNI AZIONARI FUTURI SARÀ LA MEDESIMA DEL PASSATO? Versione preliminare: 25 Settembre 2008 Nicola Zanella E-Mail: n.zanella@yahoo.it ABSTRACT In questa ricerca ho
LA DISTRIBUZIONE DI PROBABILITÀ DEI RITORNI AZIONARI FUTURI SARÀ LA MEDESIMA DEL PASSATO? Versione preliminare: 25 Settembre 2008 Nicola Zanella E-Mail: n.zanella@yahoo.it ABSTRACT In questa ricerca ho
1 Gli effetti della forza di Coriolis
 LA FORZA DI CORIOLIS di Giulio Mazzolini 2012 1 Gli effetti della forza di Coriolis È un effetto noto che i venti nell emisfero nord deviano sempre verso destra, invece nell emisfero sud deviano sempre
LA FORZA DI CORIOLIS di Giulio Mazzolini 2012 1 Gli effetti della forza di Coriolis È un effetto noto che i venti nell emisfero nord deviano sempre verso destra, invece nell emisfero sud deviano sempre
Bartoccini Marco 3 A
 Bartoccini Marco 3 A Le persone e le cose possono stare ferme oppure muoversi,e quando si muovono possono farlo a diverse velocità.il movimento si svolge nello spazio e nel tempo: esso infatti copre una
Bartoccini Marco 3 A Le persone e le cose possono stare ferme oppure muoversi,e quando si muovono possono farlo a diverse velocità.il movimento si svolge nello spazio e nel tempo: esso infatti copre una
Obbiettivo dell incontro: accompagnare i bambini verso la comprensione che per credere in Gesù dobbiamo amarlo e non dubitare mai del suo Amore
 Traccia: Obbiettivo dell incontro: accompagnare i bambini verso la comprensione che per credere in Gesù dobbiamo amarlo e non dubitare mai del suo Amore Per la preghiera: vedi in allegato. Sviluppo dell
Traccia: Obbiettivo dell incontro: accompagnare i bambini verso la comprensione che per credere in Gesù dobbiamo amarlo e non dubitare mai del suo Amore Per la preghiera: vedi in allegato. Sviluppo dell
PROMUOVERSI MEDIANTE INTERNET di Riccardo Polesel. 1. Promuovere il vostro business: scrivere e gestire i contenuti online» 15
 Indice Introduzione pag. 9 Ringraziamenti» 13 1. Promuovere il vostro business: scrivere e gestire i contenuti online» 15 1. I contenuti curati, interessanti e utili aiutano il business» 15 2. Le aziende
Indice Introduzione pag. 9 Ringraziamenti» 13 1. Promuovere il vostro business: scrivere e gestire i contenuti online» 15 1. I contenuti curati, interessanti e utili aiutano il business» 15 2. Le aziende
Nascita e morte delle stelle
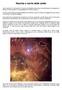 Nascita e morte delle stelle Se la materia che componeva l universo primordiale fosse stata tutta perfettamente omogenea e diffusa in modo uguale, non esisterebbero né stelle né pianeti. C erano invece
Nascita e morte delle stelle Se la materia che componeva l universo primordiale fosse stata tutta perfettamente omogenea e diffusa in modo uguale, non esisterebbero né stelle né pianeti. C erano invece
SENZA PAROLE. Illustrazione di Matteo Pericoli 2001
 SENZA PAROLE Illustrazione di Matteo Pericoli 2001 Agente di viaggio. Vedo che ha deciso per la Transiberiana. Ottima scelta. Un viaggio difficile, ma che le darà enormi soddisfazioni. Cliente. Mi preoccupa
SENZA PAROLE Illustrazione di Matteo Pericoli 2001 Agente di viaggio. Vedo che ha deciso per la Transiberiana. Ottima scelta. Un viaggio difficile, ma che le darà enormi soddisfazioni. Cliente. Mi preoccupa
Il riduttore di focale utilizzato è il riduttore-correttore Celestron f/ 6.3.
 LE FOCALI DEL C8 Di Giovanni Falcicchia Settembre 2010 Premessa (a cura del Telescope Doctor). Il Celestron C8 è uno Schmidt-Cassegrain, ovvero un telescopio composto da uno specchio primario concavo sferico
LE FOCALI DEL C8 Di Giovanni Falcicchia Settembre 2010 Premessa (a cura del Telescope Doctor). Il Celestron C8 è uno Schmidt-Cassegrain, ovvero un telescopio composto da uno specchio primario concavo sferico
La chimica e il metodo scientifico. Lezioni d'autore di Giorgio Benedetti
 La chimica e il metodo scientifico Lezioni d'autore di Giorgio Benedetti INTRODUZIONE (I) VIDEO INTRODUZIONE (II) VIDEO INTRODUZIONE (III) Fino alla fine del settecento, la manipolazione dei metalli, degli
La chimica e il metodo scientifico Lezioni d'autore di Giorgio Benedetti INTRODUZIONE (I) VIDEO INTRODUZIONE (II) VIDEO INTRODUZIONE (III) Fino alla fine del settecento, la manipolazione dei metalli, degli
Prove associate al percorso INVESTIGAZIONI SUL MODELLO PARTICELLARE
 Titolo: Prove associate al percorso INVESTIGAZIONI SUL MODELLO PARTICELLARE Autore: Elisabetta Caroti Percorsi didattici associati: 1. Investigazioni sul modello particellare AVVERTENZA: Le domande che
Titolo: Prove associate al percorso INVESTIGAZIONI SUL MODELLO PARTICELLARE Autore: Elisabetta Caroti Percorsi didattici associati: 1. Investigazioni sul modello particellare AVVERTENZA: Le domande che
MOCA. Modulo Candidatura. http://www.federscacchi.it/moca. moca@federscacchi.it. [Manuale versione 1.0 marzo 2013]
![MOCA. Modulo Candidatura. http://www.federscacchi.it/moca. moca@federscacchi.it. [Manuale versione 1.0 marzo 2013] MOCA. Modulo Candidatura. http://www.federscacchi.it/moca. moca@federscacchi.it. [Manuale versione 1.0 marzo 2013]](/thumbs/25/5308947.jpg) MOCA Modulo Candidatura http://www.federscacchi.it/moca moca@federscacchi.it [Manuale versione 1.0 marzo 2013] 1/12 MOCA in breve MOCA è una funzionalità del sito web della FSI che permette di inserire
MOCA Modulo Candidatura http://www.federscacchi.it/moca moca@federscacchi.it [Manuale versione 1.0 marzo 2013] 1/12 MOCA in breve MOCA è una funzionalità del sito web della FSI che permette di inserire
COME PARLARE DI DISLESSIA IN CLASSE.
 COME PARLARE DI DISLESSIA IN CLASSE. UNA METAFORA PER SPIEGARE I DSA La psicologa americana ANIA SIWEK ha sviluppato in anni di pratica professionale un modo semplice ed efficace di spiegare i DSA ai bambini,
COME PARLARE DI DISLESSIA IN CLASSE. UNA METAFORA PER SPIEGARE I DSA La psicologa americana ANIA SIWEK ha sviluppato in anni di pratica professionale un modo semplice ed efficace di spiegare i DSA ai bambini,
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
COME AVERE SUCCESSO SUL WEB?
 Registro 3 COME AVERE SUCCESSO SUL WEB? Guida pratica per muovere con successo i primi passi nel web MISURAZIONE ED OBIETTIVI INDEX 3 7 13 Strumenti di controllo e analisi Perché faccio un sito web? Definisci
Registro 3 COME AVERE SUCCESSO SUL WEB? Guida pratica per muovere con successo i primi passi nel web MISURAZIONE ED OBIETTIVI INDEX 3 7 13 Strumenti di controllo e analisi Perché faccio un sito web? Definisci
Lezione n 2 L educazione come atto ermeneutico (2)
 Lezione n 2 L educazione come atto ermeneutico (2) Riprendiamo l analisi interrotta nel corso della precedente lezione b) struttura dialogica del fatto educativo Per rispondere a criteri ermenutici, l
Lezione n 2 L educazione come atto ermeneutico (2) Riprendiamo l analisi interrotta nel corso della precedente lezione b) struttura dialogica del fatto educativo Per rispondere a criteri ermenutici, l
Indice. 1 Il monitoraggio del progetto formativo --------------------------------------------------------------- 3. 2 di 6
 LEZIONE MONITORARE UN PROGETTO FORMATIVO. UNA TABELLA PROF. NICOLA PAPARELLA Indice 1 Il monitoraggio del progetto formativo --------------------------------------------------------------- 3 2 di 6 1 Il
LEZIONE MONITORARE UN PROGETTO FORMATIVO. UNA TABELLA PROF. NICOLA PAPARELLA Indice 1 Il monitoraggio del progetto formativo --------------------------------------------------------------- 3 2 di 6 1 Il
UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA
 UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA Tutti gli anni, affrontando l argomento della divisibilità, trovavo utile far lavorare gli alunni sul Crivello di Eratostene. Presentavo ai ragazzi una
UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA Tutti gli anni, affrontando l argomento della divisibilità, trovavo utile far lavorare gli alunni sul Crivello di Eratostene. Presentavo ai ragazzi una
Plurilinguismo: dal mondo a casa nostra Poster 6
 1 Plurilingue?! Si, ma come? Spiegazioni Domande Risposte Corrette Note Non è assolutamente possibile dare una breve definizione scientifica che sia in grado di rendere la complessità del sistema di segni
1 Plurilingue?! Si, ma come? Spiegazioni Domande Risposte Corrette Note Non è assolutamente possibile dare una breve definizione scientifica che sia in grado di rendere la complessità del sistema di segni
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
Da dove nasce l idea dei video
 Da dove nasce l idea dei video Per anni abbiamo incontrato i potenziali clienti presso le loro sedi, come la tradizione commerciale vuole. L incontro nasce con una telefonata che il consulente fa a chi
Da dove nasce l idea dei video Per anni abbiamo incontrato i potenziali clienti presso le loro sedi, come la tradizione commerciale vuole. L incontro nasce con una telefonata che il consulente fa a chi
TEMPO TEMPO. Oggi la maestra ha chiesto ai bambini e alle bambine di pensare a una frase con la parola tempo. Quante idee diverse!
 TEMPO Oggi la maestra ha chiesto ai bambini e alle bambine di pensare a una frase con la parola tempo. Quante idee diverse! OGGI IL TEMPO È BRUTTO. PER FARE QUESTO DISEGNO HO IMPIEGATO TANTO TEMPO. TANTO
TEMPO Oggi la maestra ha chiesto ai bambini e alle bambine di pensare a una frase con la parola tempo. Quante idee diverse! OGGI IL TEMPO È BRUTTO. PER FARE QUESTO DISEGNO HO IMPIEGATO TANTO TEMPO. TANTO
DINAMICA DEL PUNTO MATERIALE E CONCETTO DI FORZA. Dinamica: studio delle forze che causano il moto dei corpi
 DINAMICA DEL PUNTO MATERIALE E CONCETTO DI FORZA Dinamica: studio delle forze che causano il moto dei corpi 1 Forza Si definisce forza una qualunque causa esterna che produce una variazione dello stato
DINAMICA DEL PUNTO MATERIALE E CONCETTO DI FORZA Dinamica: studio delle forze che causano il moto dei corpi 1 Forza Si definisce forza una qualunque causa esterna che produce una variazione dello stato
Dimostrare alla Scuola media: dal perché al rigore spontaneamente
 (Maria Cantoni, gennaio 2013). Un lavoro che viene da lontano e che continua oggi. Dimostrare alla Scuola media: dal perché al rigore spontaneamente Costruzione dei triangoli in prima media. Prima dei
(Maria Cantoni, gennaio 2013). Un lavoro che viene da lontano e che continua oggi. Dimostrare alla Scuola media: dal perché al rigore spontaneamente Costruzione dei triangoli in prima media. Prima dei
Relatività INTRODUZIONE
 Relatività INTRODUZIONE Un po di ordine Einstein, nel 1905, dopo aver inviato alcuni articoli alla rivista scientifica «Annalen der physik» diventa subito famoso, uno dei quali riguardava la relatività
Relatività INTRODUZIONE Un po di ordine Einstein, nel 1905, dopo aver inviato alcuni articoli alla rivista scientifica «Annalen der physik» diventa subito famoso, uno dei quali riguardava la relatività
da 2 a 5 giocatori, dai 10 anni in su, durata 30 minuti
 da 2 a 5 giocatori, dai 10 anni in su, durata 30 minuti OBIETTIVO Il vincitore è colui che, dopo due round di gioco, delle sue 11 ordinazioni, ne ha consegnate il maggior numero. CONTENUTO DELLA SCATOLA
da 2 a 5 giocatori, dai 10 anni in su, durata 30 minuti OBIETTIVO Il vincitore è colui che, dopo due round di gioco, delle sue 11 ordinazioni, ne ha consegnate il maggior numero. CONTENUTO DELLA SCATOLA
Come capire se la tua nuova iniziativa online avrà successo
 Come capire se la tua nuova iniziativa online avrà successo Ovvero: la regola dei 3mila Quando lanci un nuovo business (sia online che offline), uno dei fattori critici è capire se vi sia mercato per quello
Come capire se la tua nuova iniziativa online avrà successo Ovvero: la regola dei 3mila Quando lanci un nuovo business (sia online che offline), uno dei fattori critici è capire se vi sia mercato per quello
In questa lezione abbiamo ricevuto in studio il Dott. Augusto Bellon, Dirigente Scolastico presso il Consolato Generale d Italia a São Paulo.
 In questa lezione abbiamo ricevuto in studio il Dott. Augusto Bellon, Dirigente Scolastico presso il Consolato Generale d Italia a São Paulo. Vi consiglio di seguire l intervista senza le didascalie 1
In questa lezione abbiamo ricevuto in studio il Dott. Augusto Bellon, Dirigente Scolastico presso il Consolato Generale d Italia a São Paulo. Vi consiglio di seguire l intervista senza le didascalie 1
Quanta scienza in. una siringa?
 S.M.S Puecher Colombo Via G. Pizzigoni n 9 20156 Milano Tel. 0239215302 e-mail: colomboscuola@tiscali.it Quanta scienza in. una siringa? Classe: 3^A (sede Colombo) Anno scolastico: 2002/2003 Insegnante:
S.M.S Puecher Colombo Via G. Pizzigoni n 9 20156 Milano Tel. 0239215302 e-mail: colomboscuola@tiscali.it Quanta scienza in. una siringa? Classe: 3^A (sede Colombo) Anno scolastico: 2002/2003 Insegnante:
IL METODO PER IMPOSTARE E RISOLVERE I PROBLEMI DI FISICA (NB non ha nulla a che vedere con il metodo scientifico)
 IL METODO PER IMPOSTARE E RISOLVERE I PROBLEMI DI FISICA (NB non ha nulla a che vedere con il metodo scientifico) [nota: Nel testo sono riportate tra virgolette alcune domande che insegnanti e studenti
IL METODO PER IMPOSTARE E RISOLVERE I PROBLEMI DI FISICA (NB non ha nulla a che vedere con il metodo scientifico) [nota: Nel testo sono riportate tra virgolette alcune domande che insegnanti e studenti
Esame sezione Brevetti 2003-2004 Prova Pratica di meccanica
 Esame sezione Brevetti 2003-2004 Prova Pratica di meccanica OGGETVO: Brevettazione dl un perfezionamento riguardante I pressatori per mescolatori dl gomma Egregio dottore, Le invio una breve relazione
Esame sezione Brevetti 2003-2004 Prova Pratica di meccanica OGGETVO: Brevettazione dl un perfezionamento riguardante I pressatori per mescolatori dl gomma Egregio dottore, Le invio una breve relazione
Anche nel caso che ci si muova e si regga una valigia il lavoro compiuto è nullo: la forza è verticale e lo spostamento orizzontale quindi F s =0 J.
 Lavoro Un concetto molto importante è quello di lavoro (di una forza) La definizione di tale quantità scalare è L= F dl (unità di misura joule J) Il concetto di lavoro richiede che ci sia uno spostamento,
Lavoro Un concetto molto importante è quello di lavoro (di una forza) La definizione di tale quantità scalare è L= F dl (unità di misura joule J) Il concetto di lavoro richiede che ci sia uno spostamento,
Cenni di geografia astronomica. Giorno solare e giorno siderale.
 Cenni di geografia astronomica. Tutte le figure e le immagini (tranne le ultime due) sono state prese dal sito Web: http://www.analemma.com/ Giorno solare e giorno siderale. La durata del giorno solare
Cenni di geografia astronomica. Tutte le figure e le immagini (tranne le ultime due) sono state prese dal sito Web: http://www.analemma.com/ Giorno solare e giorno siderale. La durata del giorno solare
Casa di cura e di riposo per anziani di Gundeldingen, Basilea (BS)
 Casa di cura e di riposo per anziani di Gundeldingen, Basilea (BS) Werner Wassermann, datore di lavoro La signora L. lavora da noi da tanto tempo. È stata capo reparto e noi, ma anche gli altri collaboratori
Casa di cura e di riposo per anziani di Gundeldingen, Basilea (BS) Werner Wassermann, datore di lavoro La signora L. lavora da noi da tanto tempo. È stata capo reparto e noi, ma anche gli altri collaboratori
La valutazione nella didattica per competenze
 Nella scuola italiana il problema della valutazione delle competenze è particolarmente complesso, infatti la nostra scuola è tradizionalmente basata sulla trasmissione di saperi e saper fare ed ha affrontato
Nella scuola italiana il problema della valutazione delle competenze è particolarmente complesso, infatti la nostra scuola è tradizionalmente basata sulla trasmissione di saperi e saper fare ed ha affrontato
LA BIBBIA. composto da 46 libri, suddivisi in Pentateuco Storici Sapienziali Profetici 5 16 7 18
 GRUPPOQUINTAELEMENTARE Scheda 02 LA La Parola di Dio scritta per gli uomini di tutti i tempi Antico Testamento composto da 46 libri, suddivisi in Pentateuco Storici Sapienziali Profetici 5 16 7 18 Nuovo
GRUPPOQUINTAELEMENTARE Scheda 02 LA La Parola di Dio scritta per gli uomini di tutti i tempi Antico Testamento composto da 46 libri, suddivisi in Pentateuco Storici Sapienziali Profetici 5 16 7 18 Nuovo
Verifica sperimentale del principio di conservazione dell'energia meccanica totale
 Scopo: Verifica sperimentale del principio di conservazione dell'energia meccanica totale Materiale: treppiede con morsa asta millimetrata treppiede senza morsa con due masse da 5 kg pallina carta carbone
Scopo: Verifica sperimentale del principio di conservazione dell'energia meccanica totale Materiale: treppiede con morsa asta millimetrata treppiede senza morsa con due masse da 5 kg pallina carta carbone
Lezione 14: L energia
 Lezione 4 - pag. Lezione 4: L energia 4.. L apologo di Feynman In questa lezione cominceremo a descrivere la grandezza energia. Per iniziare questo lungo percorso vogliamo citare, quasi parola per parola,
Lezione 4 - pag. Lezione 4: L energia 4.. L apologo di Feynman In questa lezione cominceremo a descrivere la grandezza energia. Per iniziare questo lungo percorso vogliamo citare, quasi parola per parola,
Qui cade sua altezza
 Qui cade sua altezza Silvia Sbaragli N.R.D. Bologna DFA, SUPSI Locarno (Svizzera) Pubblicato in: Sbaragli S. (2010). Qui cade sua altezza. La Vita Scolastica. 18, 25-27. Nell insegnamento della matematica
Qui cade sua altezza Silvia Sbaragli N.R.D. Bologna DFA, SUPSI Locarno (Svizzera) Pubblicato in: Sbaragli S. (2010). Qui cade sua altezza. La Vita Scolastica. 18, 25-27. Nell insegnamento della matematica
MAPPA CONCETTUALE LA LEVA
 1 MAPPA CONCETTUALE LA LEVA Definizione Legge di equilibrio Storia I tre generi Leva vantaggiosa Leva indifferente Leva svantaggiosa 1 genere 2 genere 3 genere esempi esempi esempi esempi nel corpo umano
1 MAPPA CONCETTUALE LA LEVA Definizione Legge di equilibrio Storia I tre generi Leva vantaggiosa Leva indifferente Leva svantaggiosa 1 genere 2 genere 3 genere esempi esempi esempi esempi nel corpo umano
I libri di testo. Carlo Tarsitani
 I libri di testo Carlo Tarsitani Premessa Per accedere ai contenuti del sapere scientifico, ai vari livelli di istruzione, si usa comunemente anche un libro di testo. A partire dalla scuola primaria, tutti
I libri di testo Carlo Tarsitani Premessa Per accedere ai contenuti del sapere scientifico, ai vari livelli di istruzione, si usa comunemente anche un libro di testo. A partire dalla scuola primaria, tutti
Soluzione degli esercizi sul moto rettilineo uniformemente accelerato
 Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 00 Soluzione degli esercizi sul moto rettilineo uniformemente accelerato Esercizio. Un corpo parte da fermo con accelerazione
Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 00 Soluzione degli esercizi sul moto rettilineo uniformemente accelerato Esercizio. Un corpo parte da fermo con accelerazione
La pista del mio studio Riflettiamo sulla pista. Guida per l insegnante
 Riflettiamo sulla pista Guida per l insegnante Obiettivi educativi generali Compito di specificazione - possiede capacità progettuale - è in grado di organizzare il proprio tempo e di costruire piani per
Riflettiamo sulla pista Guida per l insegnante Obiettivi educativi generali Compito di specificazione - possiede capacità progettuale - è in grado di organizzare il proprio tempo e di costruire piani per
Esercizi sul moto rettilineo uniformemente accelerato
 Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 010 Esercizi sul moto rettilineo uniformemente accelerato Esercizio 1. Un corpo parte da fermo con accelerazione pari a
Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 010 Esercizi sul moto rettilineo uniformemente accelerato Esercizio 1. Un corpo parte da fermo con accelerazione pari a
Funzioni funzione dominio codominio legge argomento variabile indipendente variabile dipendente
 Funzioni In matematica, una funzione f da X in Y consiste in: 1. un insieme X detto dominio di f 2. un insieme Y detto codominio di f 3. una legge che ad ogni elemento x in X associa uno ed un solo elemento
Funzioni In matematica, una funzione f da X in Y consiste in: 1. un insieme X detto dominio di f 2. un insieme Y detto codominio di f 3. una legge che ad ogni elemento x in X associa uno ed un solo elemento
Salvatore Salamone. Manuale d istruzione per. Coppie che. Scoppiano QUALCOSA SI PUÒ FARE! ... tutto sommato un libro d amore
 Salvatore Salamone Manuale d istruzione per Coppie che Scoppiano QUALCOSA SI PUÒ FARE!... tutto sommato un libro d amore CAPITOLO 18 Voler avere ragione Spesso le coppie incontrano delle barriere insormontabili
Salvatore Salamone Manuale d istruzione per Coppie che Scoppiano QUALCOSA SI PUÒ FARE!... tutto sommato un libro d amore CAPITOLO 18 Voler avere ragione Spesso le coppie incontrano delle barriere insormontabili
Internet i vostri figli vi spiano! La PAROLA-CHIAVE: cacao Stralci di laboratorio multimediale
 Internet i vostri figli vi spiano! La PAROLA-CHIAVE: cacao Stralci di laboratorio multimediale Ins: nel laboratorio del Libro avevamo detto che qui, nel laboratorio multimediale, avremmo cercato qualcosa
Internet i vostri figli vi spiano! La PAROLA-CHIAVE: cacao Stralci di laboratorio multimediale Ins: nel laboratorio del Libro avevamo detto che qui, nel laboratorio multimediale, avremmo cercato qualcosa
Energia e Lavoro. In pratica, si determina la dipendenza dallo spazio invece che dal tempo
 Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
OSSERVAZIONI TEORICHE Lezione n. 4
 OSSERVAZIONI TEORICHE Lezione n. 4 Finalità: Sistematizzare concetti e definizioni. Verificare l apprendimento. Metodo: Lettura delle OSSERVAZIONI e risoluzione della scheda di verifica delle conoscenze
OSSERVAZIONI TEORICHE Lezione n. 4 Finalità: Sistematizzare concetti e definizioni. Verificare l apprendimento. Metodo: Lettura delle OSSERVAZIONI e risoluzione della scheda di verifica delle conoscenze
PLIDA Progetto Lingua Italiana Dante Alighieri Certificazione di competenza in lingua italiana
 PLIDA Progetto Lingua Italiana Dante Alighieri Certificazione di competenza in lingua italiana giugno 2011 PARLARE Livello MATERIALE PER L INTERVISTATORE 2 PLIDA Progetto Lingua Italiana Dante Alighieri
PLIDA Progetto Lingua Italiana Dante Alighieri Certificazione di competenza in lingua italiana giugno 2011 PARLARE Livello MATERIALE PER L INTERVISTATORE 2 PLIDA Progetto Lingua Italiana Dante Alighieri
La felicità per me è un sinonimo del divertimento quindi io non ho un obiettivo vero e proprio. Spero in futuro di averlo.
 Riflessioni sulla felicità.. Non so se sto raggiungendo la felicità, di certo stanno accadendo cose che mi rendono molto più felice degli anni passati. Per me la felicità consiste nel stare bene con se
Riflessioni sulla felicità.. Non so se sto raggiungendo la felicità, di certo stanno accadendo cose che mi rendono molto più felice degli anni passati. Per me la felicità consiste nel stare bene con se
Percezione della sicurezza sul lavoro in Toscana: il caso dei lavoratori immigrati nel settore agro-boschivo - ANOLF/CISL FOCUS GROUP
 Percezione della sicurezza sul lavoro in Toscana: il caso dei lavoratori immigrati nel settore agro-boschivo - ANOLF/CISL FOCUS GROUP PRESENTAZIONE DEL PROGETTO La CISL ha organizzato questo incontro perché
Percezione della sicurezza sul lavoro in Toscana: il caso dei lavoratori immigrati nel settore agro-boschivo - ANOLF/CISL FOCUS GROUP PRESENTAZIONE DEL PROGETTO La CISL ha organizzato questo incontro perché
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Le frasi sono state mescolate
 Roma o Venezia? 1 Questo percorso ti aiuterà a capire che cosa sia e come si costruisca un testo argomentativo Nella prossima pagina troverai un testo in cui ad ogni frase corrisponde un diverso colore.
Roma o Venezia? 1 Questo percorso ti aiuterà a capire che cosa sia e come si costruisca un testo argomentativo Nella prossima pagina troverai un testo in cui ad ogni frase corrisponde un diverso colore.
a. Legga questo primo brano e scelga il titolo corretto tra i tre proposti:
 Recupero TVI per matricole straniere a.a. 2010-11 Rosella Bozzone Costa - Lingua Italiana (13049 e 92020) Materiale 1b (Rg) TEST D INGRESSO Data Nome Cognome Matr.: Risultato della prova: PROVA DI COMPRENSIONE
Recupero TVI per matricole straniere a.a. 2010-11 Rosella Bozzone Costa - Lingua Italiana (13049 e 92020) Materiale 1b (Rg) TEST D INGRESSO Data Nome Cognome Matr.: Risultato della prova: PROVA DI COMPRENSIONE
I CIRCUITI ELETTRICI. Prima di tutto occorre mettersi d accordo anche sui nomi di alcune parti dei circuiti stessi.
 I CIRCUITI ELETTRICI Prima di tutto occorre mettersi d accordo anche sui nomi di alcune parti dei circuiti stessi. Definiamo ramo un tratto di circuito senza diramazioni (tratto evidenziato in rosso nella
I CIRCUITI ELETTRICI Prima di tutto occorre mettersi d accordo anche sui nomi di alcune parti dei circuiti stessi. Definiamo ramo un tratto di circuito senza diramazioni (tratto evidenziato in rosso nella
Nina Cinque. Guida pratica per organizzarla perfettamente in una sola settimana! Edizioni Lefestevere
 Nina Cinque Guida pratica per organizzarla perfettamente in una sola settimana! Edizioni Lefestevere TITOLO: FESTA DI COMPLEANNO PER BAMBINI: Guida pratica per organizzarla perfettamente in una sola settimana!
Nina Cinque Guida pratica per organizzarla perfettamente in una sola settimana! Edizioni Lefestevere TITOLO: FESTA DI COMPLEANNO PER BAMBINI: Guida pratica per organizzarla perfettamente in una sola settimana!
Teorie Etiche - Kant
 Teorie Etiche - Kant Gianluigi Bellin January 27, 2014 Tratto dalla Stanford Encyclopedia of Philosophy online alle voce Kant s Moral Philosophy. La filosofia morale di Immanuel Kant Immanuel Kant, visse
Teorie Etiche - Kant Gianluigi Bellin January 27, 2014 Tratto dalla Stanford Encyclopedia of Philosophy online alle voce Kant s Moral Philosophy. La filosofia morale di Immanuel Kant Immanuel Kant, visse
Corso di Laurea in Scienze della Formazione Primaria Università di Genova MATEMATICA Il
 Lezione 5:10 Marzo 2003 SPAZIO E GEOMETRIA VERBALE (a cura di Elisabetta Contardo e Elisabetta Pronsati) Esercitazione su F5.1 P: sarebbe ottimale a livello di scuola dell obbligo, fornire dei concetti
Lezione 5:10 Marzo 2003 SPAZIO E GEOMETRIA VERBALE (a cura di Elisabetta Contardo e Elisabetta Pronsati) Esercitazione su F5.1 P: sarebbe ottimale a livello di scuola dell obbligo, fornire dei concetti
6. La Terra. Sì, la terra è la tua casa. Ma che cos è la terra? Vediamo di scoprire qualcosa sul posto dove vivi.
 6. La Terra Dove vivi? Dirai che questa è una domanda facile. Vivo in una casa, in una certa via, di una certa città. O forse dirai: La mia casa è in campagna. Ma dove vivi? Dove sono la tua casa, la tua
6. La Terra Dove vivi? Dirai che questa è una domanda facile. Vivo in una casa, in una certa via, di una certa città. O forse dirai: La mia casa è in campagna. Ma dove vivi? Dove sono la tua casa, la tua
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1
 LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
1.6 Che cosa vede l astronomo
 1.6 Che cosa vede l astronomo Stelle in rotazione Nel corso della notte, la Sfera celeste sembra ruotare attorno a noi. Soltanto un punto detto Polo nord celeste resta fermo; esso si trova vicino a una
1.6 Che cosa vede l astronomo Stelle in rotazione Nel corso della notte, la Sfera celeste sembra ruotare attorno a noi. Soltanto un punto detto Polo nord celeste resta fermo; esso si trova vicino a una
INNOVATORE COLUI CHE SOGNA QUALCOSA DI DIVERSO, DI MIGLIORE PER TUTTI, ANDANDO OLTRE QUELLO CHE GIA ESISTE.
 LINEE DELL INTERVENTO DI GRAZIANO MALPASSI AL FIRST INNOVATION FORUMED a Civitanova Marche progetto WIDE INNOVATION IN MED finanziato dall Unione europea HO FONDATO L AZIENDA NEL 1984 ALL ETA DI 24 ANNI,
LINEE DELL INTERVENTO DI GRAZIANO MALPASSI AL FIRST INNOVATION FORUMED a Civitanova Marche progetto WIDE INNOVATION IN MED finanziato dall Unione europea HO FONDATO L AZIENDA NEL 1984 ALL ETA DI 24 ANNI,
La propagazione delle onde luminose può essere studiata per mezzo delle equazioni di Maxwell. Tuttavia, nella maggior parte dei casi è possibile
 Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
I tre pesci. (Favola araba)
 Favolaboratorio I tre pesci I tre pesci. (Favola araba) C'erano una volta tre pesci che vivevano in uno stagno: uno era intelligente, un altro lo era a metà e il terzo era stupido. La loro vita era quella
Favolaboratorio I tre pesci I tre pesci. (Favola araba) C'erano una volta tre pesci che vivevano in uno stagno: uno era intelligente, un altro lo era a metà e il terzo era stupido. La loro vita era quella
PROPULSORE A FORZA CENTRIFUGA
 PROPULSORE A FORZA CENTRIFUGA Teoria Il propulsore a forza centrifuga, è costituito essenzialmente da masse rotanti e rivoluenti attorno ad un centro comune che col loro movimento circolare generano una
PROPULSORE A FORZA CENTRIFUGA Teoria Il propulsore a forza centrifuga, è costituito essenzialmente da masse rotanti e rivoluenti attorno ad un centro comune che col loro movimento circolare generano una
Grandezze scalari e vettoriali
 Grandezze scalari e vettoriali 01 - Grandezze scalari e grandezze vettoriali. Le grandezze fisiche, gli oggetti di cui si occupa la fisica, sono grandezze misurabili. Altri enti che non sono misurabili
Grandezze scalari e vettoriali 01 - Grandezze scalari e grandezze vettoriali. Le grandezze fisiche, gli oggetti di cui si occupa la fisica, sono grandezze misurabili. Altri enti che non sono misurabili
Esercitazione 5 Dinamica del punto materiale
 Problema 1 Un corpo puntiforme di massa m = 1.0 kg viene lanciato lungo la superficie di un cuneo avente un inclinazione θ = 40 rispetto all orizzontale e altezza h = 80 cm. Il corpo viene lanciato dal
Problema 1 Un corpo puntiforme di massa m = 1.0 kg viene lanciato lungo la superficie di un cuneo avente un inclinazione θ = 40 rispetto all orizzontale e altezza h = 80 cm. Il corpo viene lanciato dal
Cosa ci può stimolare nel lavoro?
 a Cosa ci può stimolare nel lavoro? Quello dell insegnante è un ruolo complesso, in cui entrano in gioco diverse caratteristiche della persona che lo esercita e della posizione che l insegnante occupa
a Cosa ci può stimolare nel lavoro? Quello dell insegnante è un ruolo complesso, in cui entrano in gioco diverse caratteristiche della persona che lo esercita e della posizione che l insegnante occupa
Progetto La fisica nelle attrazioni Attrazione NIAGARA Dati Utili
 Progetto La fisica nelle attrazioni Attrazione NIAGARA Dati Utili Angolo di risalita = 25 Altezza massima della salita = 25,87 m Altezza della salita nel tratto lineare (fino all ultimo pilone di metallo)
Progetto La fisica nelle attrazioni Attrazione NIAGARA Dati Utili Angolo di risalita = 25 Altezza massima della salita = 25,87 m Altezza della salita nel tratto lineare (fino all ultimo pilone di metallo)
liste di liste di controllo per il manager liste di controllo per il manager liste di controllo per i
 liste di controllo per il manager r il manager liste di controllo per il manager di contr liste di liste di controllo per il manager i controllo trollo per il man liste di il man liste di controllo per
liste di controllo per il manager r il manager liste di controllo per il manager di contr liste di liste di controllo per il manager i controllo trollo per il man liste di il man liste di controllo per
Guida Strategica per gli Imprenditori
 Guida Strategica per gli Imprenditori Scopri la Formula atematica del Business 1 La Tavola degli Elementi del Business Come in qualsiasi elemento in natura anche nel Business è possibile ritrovare le leggi
Guida Strategica per gli Imprenditori Scopri la Formula atematica del Business 1 La Tavola degli Elementi del Business Come in qualsiasi elemento in natura anche nel Business è possibile ritrovare le leggi
4. Conoscere il proprio corpo
 4. Conoscere il proprio corpo Gli esseri viventi sono fatti di parti che funzionano assieme in modo diverso. Hanno parti diverse che fanno cose diverse. Il tuo corpo è fatto di molte parti diverse. Alcune
4. Conoscere il proprio corpo Gli esseri viventi sono fatti di parti che funzionano assieme in modo diverso. Hanno parti diverse che fanno cose diverse. Il tuo corpo è fatto di molte parti diverse. Alcune
16/05/2008. Continua sporadicamente ad occuparsi di matematica; muore tra le convulsioni, probabilmente per una lesione al cervello
 La probabilità Gli inizi della teoria della probabilità possono farsi risalire a Fermat e a un grande genio matematico che si dedicò invece al misticismo: Blaise (1623-1669) si dedicò alla matematica fin
La probabilità Gli inizi della teoria della probabilità possono farsi risalire a Fermat e a un grande genio matematico che si dedicò invece al misticismo: Blaise (1623-1669) si dedicò alla matematica fin
