Integrali di Riemann e di Cauchy
|
|
|
- Paolina Pellegrino
- 8 anni fa
- Visualizzazioni
Transcript
1 Integrali di Riemann e di Cauchy Gianni Gilardi Pavia, 14 novembre 1997 L integrale nell ambito delle teorie di Riemann e di Cauchy, fra loro equivalenti, può essere introdotto in vari modi e queste pagine sono dedicate a possibili definizioni. Per lo sviluppo della teoria rimandiamo invece a testi usuali di Analisi Matematica. Dapprima diamo le definizioni di integrabilità e di integrale secondo Riemann e secondo Cauchy operando una scelta fra le tante. Successivamente dimostriamo l equivalenza delle due teorie, presentiamo qualche variante alle definizioni date e commentiamo brevemente pregi e difetti delle varie impostazioni in relazione alle diverse esigenze di tipo didattico. Infine, nell Appendice, diamo la caratterizzazione di Vitali Lebesgue delle funzioni integrabili secondo Riemann. 1. Le definizioni fondamentali Precisiamo innanzi tutto il concetto di suddivisione di un intervallo chiuso e limitato. Definizione 1.1. Chiamiamo suddivisione dell intervallo [a, b] ogni sottoinsieme finito σ di [a, b] che contiene gli estremi a e b. Se σ è una suddivisione di [a, b], assumiamo le notazioni in modo che valgano le condizioni σ = {x 0,..., x n } e x k 1 < x k per k = 1,..., n. (1.1) La teoria dell integrazione secondo Riemann si basa sulla nozione di somma inferiore e di somma superiore e l integrabilità di una funzione richiede che l insieme delle somme inferiori e quello delle somme superiori costituiscano una coppia di classi contigue. Ricordiamo che due sottoinsiemi non vuoti A e B di R costituiscono una coppia di classi contigue quando valgono le due condizioni: i) per ogni a A e per ogni b B vale la disuguaglianza a b ; ii) per ogni ε > 0 esistono a A e b B tali che b a < ε. Ricordiamo inoltre che già la prima condizione, unita all ipotesi che i due insiemi A e B non sono vuoti, assicura l esistenza di almeno un elemento di separazione, cioè di un numero reale c tale che a c b per ogni a A e per ogni b B (questa affermazione, infatti, è una delle possibili formulazioni della completezza del campo dei numeri reali) e che la seconda condizione equivale al fatto che tale elemento di separazione è unico. Definizione 1.2. Siano f : [a, b] R una funzione limitata e {x 0,..., x n } una suddivisione di [a, b]. Chiamiamo somme inferiore e superiore di Riemann associate alla Le definizioni fondamentali 1
2 suddivisione data i due numeri reali S = n (x k x k 1 ) inf f e (x k 1,x k ) S = k=1 n (x k x k 1 ) sup k=1 (x k 1,x k ) f. (1.2) Osservazione 1.3. La Definizione 1.2 necessita dell ipotesi di limitatezza sulla funzione considerata, altrimenti le (1.2) potrebbero essere infinite. Di riflesso, la stessa ipotesi è necessaria nella definizione successiva di integrabilità e di integrale. Il caso più banale possibile è quello in cui f è una funzione costante. Detto c il valore assunto da f in tutti i punti di [a, b], si vede subito che, qualunque sia la suddivisione presa in esame, risulta S = S = (b a)c. In generale, invece, accade che le somme inferiore e superiore siano diverse fra loro e varino al variare della suddivisione. Considerata ad esempio la funzione f(x) = x 2, x [0, 1], se scegliamo la suddivisione {0, 1/2, 1} otteniamo S = (1/2 0) 0 + (1 1/2) 1/4 = 1/8 e S = (1/2 0) 1/4 + (1 1/2) 1 = 5/8 mentre la suddivisione {0, 1/4, 1/3, 1} fornisce altri valori di S e di S. Consideriamo ora l insieme di tutte le somme inferiori e l insieme di tutte le somme superiori ottenuti prendendo tutte le possibili suddivisioni dell intervallo (insiemi che saranno infiniti in generale ma non sempre) e ci chiediamo se essi costituiscono o meno una coppia di classi contigue secondo la definizione menzionata velocemente poco sopra. Ciò che si può dire è solo che essi sono non vuoti e verificano la prima delle due condizioni richieste, mentre la ii) può essere vera o falsa. Dunque è assicurata l esistenza di un elemento di separazione ma non la sua unicità. Definizione 1.4. Una funzione f : [a, b] R limitata è integrabile secondo Riemann se è unico il numero reale I compreso fra tutte le somme inferiori di f e tutte le somme superiori di f. Se f è integrabile secondo Riemann, l unico numero I nelle condizioni dette è chiamato integrale di Riemann di f. Si può poi dimostrare che si ottengono definizioni equivalenti di integrabilità e di integrale se si modifica la Definizione 1.2 prendendo nelle (1.2) gli estremi inferiori e superiori sui corrispondenti intervalli chiusi. La definizione di integrale secondo Cauchy, invece, fa riferimento alla nozione di somma di Cauchy e al comportamento delle somme di Cauchy all infittirsi della suddivisione. Una misura di quanto è fitta una suddivisione è il suo parametro di finezza introdotto nella definizione che segue. Definizione 1.5. Sia σ = {x 0,..., x n } una suddivisione di [a, b]. Chiamiamo parametro di finezza di σ il numero reale max (x k x k 1 ). k=1,...,n Le definizioni fondamentali 2
3 Ad esempio, il parametro di finezza della suddivisione {0, 1/4, 1/3, 1} di [0, 1] vale max {1/4 0, 1/3 1/4, 1 1/3} = max {1/4, 1/12, 2/3} = 2/3. Notiamo che, perché il parametro di finezza di una suddivisione sia piccolo, occorre che i punti di suddivisione siano numerosi. Tuttavia è chiaro che, anche se i punti di suddivisione sono numerosi, non è detto che il parametro di finezza sia piccolo. Definizione 1.6. Sia σ = {x 0,..., x n } una suddivisione di [a, b]. Un sottoinsieme σ di [a, b] è detto scelta di punti intermedi compatibile con σ quando esso è del tipo σ = {x 1,..., x n} con x k 1 < x k < x k per k = 1,..., n. (1.3) Definizione 1.7. Sia f : [a, b] R. Siano poi σ = {x 0,..., x n } una suddivisione di [a, b] e σ = {x 1,..., x n} una scelta di punti intermedi compatibile con σ. Chiamiamo somma di Cauchy di f associata a σ e a σ il numero reale S = n (x k x k 1 )f(x k). (1.4) k=1 Ancora, se f assume in tutti i punti di [a, b] uno stesso valore c, la somma di Cauchy vale (b a)c qualunque siano la suddivisione e la scelta dei punti intermedi, mentre nel caso generale la situazione è diversa. Considerata ad esempio la funzione f(x) = x 2, x [0, 1], con σ = {0, 1/2, 1} e σ = {1/4, 3/4} otteniamo S = (1/2 0) (1/4) 2 + (1 1/2) (3/4) 2 = 5/16 mentre altre scelte di σ e di σ porterebbero ad altri valori di S e, anzi, ciò avviene in generale cambiando anche solo la scelta σ dei punti intermedi. Definizione 1.8. Una funzione f : [a, b] R è integrabile secondo Cauchy se esiste un numero reale I verificante la condizione seguente: per ogni ε > 0 esiste δ > 0 tale che, per ogni suddivisione di [a, b] il cui parametro di finezza sia < δ e per ogni scelta di punti intermedi compatibile con la suddivisione considerata, la corrispondente somma di Cauchy S di f verifichi S I < ε. Per esprimere l integrabilità secondo Cauchy si usa dire che le somme di Cauchy di f convergono al tendere a 0 del parametro di finezza della suddivisione. Tuttavia questa frase è scorretta se l unica definizione di limite che si possiede riguarda funzioni di variabile reale, in quanto una somma di Cauchy dipende non solo dal valore del parametro di finezza della suddivisione considerata ma anche dalla suddivisione stessa e dalla scelta dei punti intermedi. Essa diventa invece perfettamente corretta se si generalizza opportunamente la nozione di limite. Si noti comunque che si è detto al tendere a 0 del parametro di finezza e non al tendere all infinito del numero dei punti di suddivisione. Le definizioni fondamentali 3
4 Proposizione 1.9. Sia f : [a, b] R integrabile secondo Cauchy. Allora il numero I nelle condizioni della definizione è unico. Dimostrazione. Ricalchiamo le classiche dimostrazioni dell unicità del limite di funzioni di variabile reale o di successioni anche se, come abbiamo osservato, la situazione è diversa. Per assurdo, sia J I nelle stesse condizioni di I e scegliamo ε = I J /2 nella Definizione 1.8: questa ci fornisce un numero δ > 0 (in realtà due numeri, dei quali scegliamo il più piccolo) tale che S I < ε e S J < ε per ogni suddivisione di [a, b] il cui parametro di finezza sia < δ e per ogni scelta di punti intermedi compatibile con la suddivisione considerata. Fissiamo dunque una suddivisione e una scelta di punti intermedi in queste condizioni: allora valgono contemporaneamente le due disuguaglianze S I < ε e S J < ε, dalle quali deduciamo I J < 2ε, contro la definizione di ε. Definizione Sia f : [a, b] R integrabile secondo Cauchy. Allora il numero I nelle condizioni della definizione è chiamato integrale di Cauchy di f. Si può dimostrare che si ottengono definizioni equivalenti di integrabilità e di integrale se si modifica la Definizione 1.6 prendendo nella (1.3) le disuguaglianze larghe anziché quelle strette. 2. Equivalenza delle due nozioni Il risultato centrale è il teorema successivo, che assicura che le funzioni integrabili secondo Riemann e secondo Cauchy sono le stesse e che anche i valori numerici dei corrispondenti integrali coincidono. In esso è sostanzialmente introdotta una terza nozione di integrabilità che, in analogia con quanto si usa dire nel caso dell integrabilità secondo Cauchy, viene espressa abitualmente con la frase: le somme di Riemann di f superiori e inferiori convergono allo stesso limite al tendere a 0 del parametro di finezza della suddivisione. Premettiamo un risultato preliminare, che afferma che l ambito in cui abbiamo dato la definizione di integrabilità secondo Cauchy è solo apparentemente più generale di quello delle funzioni limitate usato per l integrabilità secondo Riemann, e due lemmi tecnici. Proposizione 2.1. Ogni funzione integrabile secondo Cauchy è limitata. Dimostrazione. Denotiamo con I l integrale di Cauchy di f e scegliamo ad esempio ε = 1 nella Definizione 1.8: questa ci fornisce un numero δ > 0 tale che S I < 1 per ogni suddivisione di [a, b] il cui parametro di finezza sia < δ e per ogni scelta di punti intermedi compatibile con la suddivisione considerata, S denotando la corrispondente somma di Cauchy. Ora, per assurdo, supponiamo f non limitata, per fissare le idee non limitata superiormente, e costruiamo una suddivisione di [a, b] il cui parametro di finezza sia < δ e una scelta di punti intermedi compatibile con la suddivisione considerata tale che la corrispondente somma di Cauchy S verifichi la disuguaglianza opposta S I 1, arrivando in tal modo a una contraddizione. Precisamente, cerchiamo di realizzare la disuguaglianza S I + 1. (2.1) Equivalenza delle due nozioni 4
5 Scegliamo una suddivisione σ = {x 0,..., x n } di [a, b] il cui parametro di finezza sia < δ e determiniamo la scelta σ = {x 1,..., x n} di punti intermedi compatibile con σ come segue. Osserviamo che f non può essere limitata superiormente in tutti gli intervalli (x k 1, x k ) e, per semplificare le notazioni, supponiamo che f non sia limitata superiormente in (x 0, x 1 ). Scegliamo allora ad arbitrio x k in (x k 1, x k ) per k = 2,..., n e riserviamoci di determinare x 1 in modo da soddisfare la (2.1) per la corrispondente somma di Cauchy S. La (2.1) si esplicita in (x 1 x 0 )f(x 1) > S + I n (x k x k 1 )f(x k) e l unico parametro oramai a disposizione è x 1. Siccome la funzione f non è limitata superiormente in (x 0, x 1 ), esiste x 1 (x 0, x 1 ) che verifica la disuguaglianza richiesta. Lemma 2.2. Siano f : [a, b] R limitata e σ 1 e σ 2 due suddivisioni di [a, b] tali che σ 1 σ 2 e, per i = 1, 2, siano S,i e Si le somme inferiore e superiore di f associate a σ i. Allora valgono le disuguaglianze k=2 S 2 S 1 e S,2 S 1. Dimostrazione. Dimostriamo solo la prima disuguaglianza, dato che l altra è analoga. Detti x 0,..., x n i punti di σ 1, la suddivisione σ 2 contiene tutti i punti di σ 1 e altri eventuali, per cui possiamo assumere le notazioni come segue. Per k = 1,..., n denotiamo con y 0,k,..., y mk,k i punti di σ 2 che appartengono a [x k 1, x k ] ordinati in modo che y i 1,k < y i,k per i = 1,..., m k. In tal modo abbiamo le inclusioni e le uguaglianze (y i 1,k, y i,k ) (x k 1, x k ) per i = 1,..., m k e k = 1,..., n m k (y i,k y i 1,k ) = x k x k 1 per k = 1,..., n. i=1 Allora, per ogni k, vale la catena m k (y i,k y i 1,k ) sup f (y i 1,k,y i,k ) i=1 m k i=1 (y i,k y i 1,k ) sup (x k 1,x k ) e la disuguaglianza voluta segue sommando rispetto a k. f = (x k x k 1 ) sup (x k 1,x k ) Lemma 2.3. Una funzione f : [a, b] R limitata è integrabile secondo Riemann se e solo se per ogni ε > 0 esiste una suddivisione di [a, b] tale che le corrispondenti somme inferiore e superiore S e S verifichino la disuguaglianza S S < ε. f Equivalenza delle due nozioni 5
6 Dimostrazione. Chiaramente, se è verificata la condizione dell enunciato, l insieme di tutte le somme inferiori e quello di tutte le somme superiori costituiscono una coppia di classi contingue. Dunque l elemento di separazione è unico e f è integrabile secondo Riemann. Viceversa supponiamo f integrabile secondo Riemann e fissiamo ε > 0 ad arbitrio. Allora esistono due suddivisioni σ 1 e σ 2 di [a, b] tali che, dette S # e S # la somma superiore associata a σ 1 e, rispettivamente, la somma inferiore associata a σ 2, risulti S # S # < ε. Siano ora σ = σ 1 σ 2 e S e S le somme superiore e inferiore associate a σ. Grazie al lemma precedente abbiamo allora S S S # S # < ε. Teorema 2.4. Sia f : [a, b] R limitata. Allora sono equivalenti le condizioni f è integrabile secondo Riemann (2.2) f è integrabile secondo Cauchy (2.3) e ciascuna di esse equivale alla seguente: esiste un numero reale I tale che per ogni ε > 0 esista δ > 0 tale che, per ogni suddivisione di [a, b] avente parametro di finezza < δ, le corrispondenti somme superiore e inferiore di Riemann S e S verifichino le disuguaglianze S I < ε e I S < ε. Inoltre, in caso di integrabilità, i valori dei due integrali di f secondo Riemann e Cauchy coincidono fra loro e con il numero I, necessariamente unico, della terza condizione dell enunciato. Dimostrazione. Supponendo senz altro che f non sia la funzione identicamente nulla, denotiamo con ( ) la terza condizione dell enunciato e dimostriamo il teorema controllando che valgono le seguenti quattro implicazioni: i) se f è integrabile secondo Riemann, allora vale la ( ) se prendiamo come I l integrale di Riemann di f ; ii) se f verifica la ( ) con un certo I, allora f è integrabile secondo Riemann e I è il suo integrale; iii) se f è integrabile secondo Cauchy, allora vale la ( ) se prendiamo come I l integrale di Cauchy di f ; iv) se f verifica la ( ) con un certo I, allora f è integrabile secondo Cauchy e I è il suo integrale. Parte i) Supponiamo f integrabile secondo Riemann e denotiamo con I il corrispondente integrale. Dimostriamo che le somme di Riemann convergono a I al tendere a 0 del parametro di finezza, cioè, precisamente, che vale la ( ) con tale valore di I. Consideriamo tuttavia solo le somme superiori dato che il caso delle somme inferiori si tratta in modo perfettamente analogo. Fissiamo ε > 0 ad arbitrio. Chiamata {y 0,..., y m } una suddivisione di [a, b] tale che, detta S # la corrispondente somma superiore di Riemann, valga la disuguaglianza S # I < ε, definiamo δ = ε Mm Equivalenza delle due nozioni 6
7 ove M denota l estremo superiore di f in [a, b], che è strettamente positivo dato che f non è la funzione nulla. Sia ora {x 0,..., x n } una qualunque suddivisione di [a, b] avente parametro di finezza < δ e, denotando con S la corrispondente somma superiore di Riemann, dimostriamo che S I < 2ε. Poniamo per comodità M # i = sup f e Mk = sup f (y i 1,y i ) (x k 1,x k ) per i = 1,..., m e k = 1,..., n rispettivamente. Presentiamo ora l insieme K = {1,..., n} in cui varia k come unione di sottoinsiemi K, K 1,..., K m a due a due disgiunti come segue. Per i = 1,..., m denotiamo con K i l insieme degli indici k K tali che l intervallo (x k 1, x k ) sia incluso in (y i 1, y i ) e chiamiamo K l insieme degli indici restanti, cioè dei k K che non appartengono ad alcuno degli insiemi K i. Allora vale l uguaglianza S = m Mk (x k x k 1 ) + Mk (x k x k 1 ). k K i=1 k K i Ma abbiamo e per ogni i risulta Concludiamo perciò k K M k (x k x k 1 ) M k K i M k (x k x k 1 ) S ε + k K (x k x k 1 ) Mmδ = ε k K i M # i (x k x k 1 ) M # i (y i y i 1 ). m M # i (y i y i 1 ) = ε + S # I + 2ε. i=1 Parte ii) Supponiamo ora che valga la condizione ( ) con un certo I. Allora, in particolare, l insieme delle somme inferiori e quello delle somme superiori costituiscono una coppia di classi contigue con elemento separatore I. Dunque f è integrabile secondo Riemann e I è il suo integrale. Parte iii) Supponiamo ora che f sia integrabile secondo Cauchy e dimostriamo che la condizione ( ) vale se prendiamo come I l integrale di Cauchy di f. Sia infatti ε > 0 ad arbitrio e sia δ > 0 dato dalla Definizione 1.8. Sia poi σ = {x 0,..., x n } una qualunque suddivisione di [a, b] con parametro di finezza < δ e siano S e S le corrispondenti somme di Riemann inferiore e superiore. Considerate allora tutte le scelte σ = {x 1,..., x n} di punti intermedi compatibili con σ, abbiamo le disuguaglianze n (x k x k 1 )f(x k) > I ε e k=1 n (x k x k 1 )f(x k) < I + ε. k=1 Equivalenza delle due nozioni 7
8 Siccome i punti x k possono essere scelti ad arbitrio negli intervalli (x k 1, x k ) e indipendentemente fra loro, nelle due disuguaglianze possiamo passare agli estremi inferiori e, rispettivamente, superiori in ciascun termine della somma di Cauchy e dedurre S I ε e S I + ε. Parte iv) Supponiamo infine che f verifichi la condizione ( ) con un certo numero reale I e dimostriamo che f è integrabile secondo Cauchy verificando che possiamo prendere lo stesso valore di I nella Definizione 1.8. Sia infatti ε > 0 ad arbitrio e sia δ > 0 dato dall ipotesi. Se σ è una suddivisione con parametro di finezza < δ e σ è una scelta di punti intermedi compatibile con σ, per la somma di Cauchy S e per le somme di Riemann superiore e inferiore S e S valgono le disuguaglianze Ciò conclude la dimostrazione. I ε < S S S < I + ε. 3. Alcune varianti alle definizioni Le suddivisioni dell intervallo che intervengono nelle definizioni di integrabilità e di integrale che abbiamo dato sono completamente generiche. Si ottengono però definizioni equivalenti alle precedenti imponendo che le suddivisioni siano di qualche tipo particolare. Soffermiamoci sul caso delle suddivisioni che generano intervalli di uguale ampiezza e che chiamiamo uniformi. Definizione 3.1. uniforme quando Diciamo che la suddivisione σ = {x 0,..., x n } dell intervallo [a, b] è x k x k 1 = b a n per k = 1,..., n. Osservazione 3.2. Nelle condizioni e con le notazioni della definizione precedente il parametro di finezza di σ è dato semplicemente da (b a)/n. Dunque, se la suddivisione è uniforme, il suo parametro di finezza è piccolo se e solo se il numero dei punti di suddivisione è grande. Questa affermazione, anche se vaga e imprecisa, è tuttavia falsa per suddivisioni generiche, come abbiamo già sottolineato. A questo punto si potrebbero riscrivere i due paragrafi precedenti sostituendo il termine suddivisione con la locuzione suddivisione uniforme. A titolo esemplificativo vediamo le Definizioni 1.4 e 1.8 modificate in tal senso. Definizione 3.3. Una funzione f : [a, b] R limitata è integrabile secondo Riemann se è unico il numero reale I compreso fra tutte le somme inferiori di f associate a suddivisioni uniformi e tutte le somme superiori di f associate a suddivisioni uniformi. Se f è integrabile secondo Riemann, l unico numero I nelle condizioni dette è chiamato integrale di Riemann di f. Alcune varianti alle definizioni 8
9 Definizione 3.4. Una funzione f : [a, b] R è integrabile secondo Cauchy se esiste un numero reale I verificante la condizione seguente: per ogni ε > 0 esiste δ > 0 tale che, per ogni suddivisione uniforme di [a, b] il cui parametro di finezza sia < δ e per ogni scelta di punti intermedi compatibile con la suddivisione considerata, la corrispondente somma di Cauchy S di f verifichi S I < ε. Chiaramente, almeno per ora, c è una ambiguità, in quanto sono state date due definizioni diverse di integrabilità secondo Riemann e due definizioni diverse di integrabilità secondo Cauchy. Tuttavia l ambiguità è solo momentanea e apparente in quanto vale il risultato seguente: Teorema 3.5. Una funzione limitata è integrabile nel senso di una delle Definizioni 1.4, 1.8, 3.3 e 3.4 se e solo se essa è integrabile nel senso delle altre tre. Inoltre, in caso di integrabilità, i valori numerici degli integrali dati dalle rispettive teorie coincidono tutti fra loro. Dimostrazione. Ci limitiamo a un cenno. Controllando accuratamente tutti i passaggi visti a proposito dell equivalenza fra le Definizioni 1.4 e 1.8, si vede che nulla cambia se il termine suddivisione viene sostituito dalla locuzione suddivisione uniforme, con eccezione di un punto, relativo alla dimostrazione del Lemma 2.3: anche se σ 1 e σ 2 sono suddivisioni uniformi, la suddivisione σ = σ 1 σ 2 può non essere uniforme. Questo inconveniente, tuttavia, si supera immediatamente come segue: se le due suddivisioni σ 1 e σ 2 generano rispettivamente m e n intervalli, basta costruire σ suddividendo [a, b] in mn intervalli di uguale ampiezza. Allora σ include le due precedenti e la dimostrazione può proseguire inalterata. Ciò dimostra che le due Definizioni 3.3 e 3.4 sono equivalenti fra loro e all analoga della terza condizione dell enunciato del Teorema 2.4. Dunque, per concludere, basta verificare l equivalenza fra una qualunque delle condizioni di integrabilità di tipo vecchio e una qualunque di quelle di tipo nuovo. Dimostriamo che sono equivalenti le Definizioni 1.4 e 3.3 e che, in caso di integrabilità, anche i valori corrispondenti degli integrali coincidono. Siccome le somme considerate nella Definizione 3.3 sono particolari fra quelle prese nella Definizione 1.4, è chiaro che, se la funzione f in esame è integrabile nel senso di quest ultima e se I è il suo integrale, allora costituiscono a maggior ragione una coppia di classi contigue l insieme di tutte le somme inferiori e quello di tutte le somme superiori, le quali avranno poi ancora I come elemento separatore. Dunque f è integrabile nel senso della Definizione 1.4 e il suo integrale vale I. Sia ora f integrabile nel senso della Definizione 1.4 e sia I il suo integrale. Per dimostrare che f è integrabile anche nel senso della Definizione 3.3 e che il suo integrale vale I, basta mostrare che, per ogni ε > 0, esiste una suddivisione uniforme la cui somma superiore S verifichi la disuguaglianza S I < ε e analogamente per quanto riguarda le somme inferiori. Considerando solo il problema delle somme superiori, fissiamo ε > 0 ad arbitrio e imitiamo il procedimento seguito nella prima parte della dimostrazione del Teorema 2.4, anche questa volta supponendo che f non sia la funzione nulla e denotando con M l estremo superiore di f. Alcune varianti alle definizioni 9
10 la corrispon- Chiamata {y 0,..., y m } una suddivisione di [a, b] tale che, detta S # dente somma superiore di Riemann, valga la disuguaglianza S # I < ε, definiamo δ = ε Mm e scegliamo una suddivisione {x 0,..., x n } di [a, b], ora uniforme, avente parametro di finezza < δ. Denotando con S la corrispondente somma superiore di Riemann e procedendo esattamente come nella dimostrazione citata, si arriva senza difficoltà a dimostrare che S I < 2ε. Un altra variante che si può considerare relativamente alla teoria di Riemann riguarda l introduzione delle funzioni a scala nella definizione. Possiamo, anche in questo caso, prendere suddivisioni generiche oppure solo suddivisioni uniformi. Limitatamente alla prima delle due possibilità, ecco brevemente come si può procedere. Definizione 3.6. Diciamo che una funzione f : [a, b] R è a scala quando esiste una suddivisione {x 0,..., x n } di [a, b] tale che la funzione f sia costante su ciascuno degli intervalli (x k 1, x k ), k = 1,..., n. L integrale di una funzione a scala viene poi definito in modo elementare: se, con le notazioni della definizione, chiamiamo c 1,..., c n i valori costanti assunti da f nei vari intervalli della suddivisione, l integrale di f è, per definizione, il numero reale n (x k x k 1 )c k. (3.1) k=1 Notiamo però che tutto ciò andrebbe giustificato meglio in quanto la suddivisione di cui tratta la Definizione 3.6 non è unica: ad esempio una funzione costante può essere presentata in accordo con la definizione citata qualunque sia la suddivisione considerata. Occorrerebbe dunque dimostrare che il numero reale (3.1) non dipende dalla suddivisione scelta fra quelle ammissibili. Fatto ciò, una definizione, che si dimostra abbastanza facilmente essere equivalente alla Definizione 1.4, è la seguente: Definizione 3.7. Una funzione limitata f è integrabile quando è unico il numero reale I compreso fra gli integrali di tutte le funzioni a scala f e gli integrali di tutte le funzioni a scala f. Se f è integrabile, l unico numero I nelle condizioni dette è chiamato integrale di f. L ultima variante che prendiamo in considerazione riguarda l integrale secondo Cauchy e si riallaccia direttamente alla nozione di limite per successioni reali. Per semplificare il linguaggio introduciamo la notazione S(f; σ, σ ) (3.2) Alcune varianti alle definizioni 10
11 per la somma di Cauchy di f associata alla suddivisione σ e alla scelta σ di punti intermedi compatibile con σ. Definizione 3.8. Una funzione f : [a, b] R è integrabile quando esiste un numero reale I al quale convergono tutte le successioni {S(f; σ n, σ n)} di somme di Cauchy associate a suddivisioni σ n di [a, b] e a scelte σ n di punti intermedi verificanti le condizioni seguenti: i) per ogni n la scelta σ n di punti intermedi è compatibile con la suddivisione σ n ; ii) detto δ n il parametro di finezza della suddivisione σ n, la successione {δ n } tende a 0. Naturalmente si dimostra che il numero I è unico e lo si assume poi, per definizione, come valore dell integrale di f. Osserviamo che la condizione ii) della definizione precedente richiede che la suddivisione si infittisca indefinitamente. Essa, in particolare, impone che il numero dei punti di suddivisione diverga per n tendente all infinito, ma certamente pretende ben di più. Teorema 3.9. Una funzione f : [a, b] R è integrabile nel senso della Definizione 1.8 se e solo se essa è integrabile nel senso della Definizione 3.8. Inoltre, in caso di integrabilità, i valori numerici dei corrispondenti integrali coincidono. Dimostrazione. Sia f integrabile secondo la Definizione 1.8 e sia I il suo integrale. Verifichiamo che tutte le successioni di somme di Cauchy nelle condizioni della Definizione 3.8 convergono a I. Sia infatti {S(f; σ n, σ n)} una di esse. Fissato ε > 0 ad arbitrio, sia δ > 0 dato dalla Definizione 1.8. Siccome la successione {δ n } tende a 0, esiste un indice m tale che δ n < δ per ogni n > m. Per ogni n > m si ha allora anche S(f; σ n, σ n) I < ε. Supponiamo ora f integrabile nel senso della Definizione 3.8 con integrale I e dimostriamo che questo numero I soddisfa i requisiti della Definizione 1.8 ragionando per assurdo. Esista dunque un numero ε > 0, che fissiamo, tale che per ogni δ > 0 esistano una suddivisione σ con parametro di finezza < δ e una scelta σ di punti intermedi compatibile con σ tali che S(f; σ, σ ) I ε. Scegliendo in particolare δ = 1/n con n = 1, 2,..., costruiamo due successioni {σ n } e {σ n} nelle condizioni della Definizione 3.8 ma tali che S(f; σ n, σ n) I ε per ogni n. Allora la successione ottenuta di somme di Cauchy non può convergere a I e siamo arrivati a una contraddizione. 4. Qualche commento Ciò che abbiamo visto nei paragrafi precedenti assicura che è indifferente introdurre l integrale ricorrendo all una o all altra delle varie definizioni, che, infatti, sono tutte equivalenti fra loro. Notiamo in particolare ancora una volta che, grazie alla Proposizione 2.1, l ambito delle funzioni limitate in cui occorre impostare l integrazione secondo Riemann è solo apparentemente più ristretto di quello relativo alla teoria di Cauchy. La scelta della via da seguire è dunque dettata solo da motivi di opportunità e di carattere didattico, suggeriti dalle esigenze più disparate. Concorreranno infatti a determinare il percorso il tempo che si pensa di dedicare all argomento, l intenzione di spianare Qualche commento 11
12 la strada a generalizzazioni in varie direzioni, il numero di collegamenti che si vorrebbero sottolineare con altri punti importanti (teoria della misura, rapporti fra derivazione e integrazione, tecniche di calcolo, integrazione numerica, eccetera), il fatto che si intenda o meno sviluppare in modo rigoroso almeno una parte della teoria e, certo non ultimo, il confronto fra le difficoltà concettuali che offrono le varie impostazioni. Raccogliamo sotto forma di altrettante osservazioni alcuni dei numerosi commenti che si possono fare in proposito. Osservazione 4.1. La teoria di Riemann sfrutta in modo essenziale l ordinamento della retta reale come codominio della funzione: infatti già nella Definizione 1.2 è necessario saper eseguire il passaggio all estremo superiore e all estremo inferiore. Dunque non è possibile ridare una definizione formalmente identica nel caso in cui la funzione in esame assuma valori complessi oppure valori vettoriali. Nei due casi occorre separare le parti reale e immaginaria e, rispettivamente, considerare le varie componenti. Al contrario, la teoria di Cauchy sfrutta a livello del codominio solo la struttura metrica e le Definizioni 1.8 e 1.10 possono essere generalizzate senza difficoltà ad esempio al caso dei valori complessi e a quello dei valori vettoriali. Osservazione 4.2. La nozione di integrale di Cauchy si presta molto bene nelle interpretazioni che l integrale ha nelle varie applicazioni, ad esempio nel caso della definizione di lavoro di una forza in corrispondenza a un certo spostamento. Essa ha invece qualche difetto in relazione alla teoria della misura delle figure piane. Infatti, se è suggestiva l interpretazione geometrica dell integrale di Cauchy di una funzione f : [a, b] R non negativa come area del rettangoloide corrispondente, cioè dell insieme R(f) = {(x, y) R R : x [a, b], 0 y f(x)}, (4.1) in quanto le somme di Cauchy si interpretano come aree di plurirettangoli in qualche modo vicini al rettangoloide di f, non è evidente quale spunto dia la nozione vista alla generalizzazione al caso di una figura più complessa di un semplice rettangoloide. Al contrario, la teoria dell integrazione secondo Riemann si collega direttamente con la teoria della misura secondo Peano Jordan, che si applica a generiche figure piane limitate. Richiamiamo a questo proposito la definizione di misurabilità e di misura secondo Peano Jordan. Definiti i plurirettangoli come quei sottoinsiemi del piano rappresentabili come unione di un numero finito di rettangoli con i lati paralleli agli assi (inclusi i rettangoli degeneri che si riducono a segmenti o a punti) e definita la corrispondente misura per via elementare (con qualche difficoltà legata al fatto che è sì vero che un plurirettangolo può sempre essere presentato come unione di un numero finito di rettangoli a due a due disgiunti, ma che è altrettanto vero che tale rappresentazione non è unica), si passa alla misura dei sottoinsiemi limitati del piano mediante la definizione seguente: Definizione 4.3. Un sottoinsieme limitato S del piano è misurabile secondo Peano- Jordan quando è unico il numero A compreso fra le aree di tutti i plurirettangoli inclusi in S e le aree di tutti i plurirettangoli che includono S. In caso di misurabilità, l unico numero A nelle condizioni dette è chiamato area di S. Qualche commento 12
13 Osservato che il rettangoloide (4.1) di una funzione f è limitato se e solo se la funzione f è limitata, enunciamo senza dimostrarlo il risultato seguente: Teorema 4.4. Una funzione f : [a, b] R limitata e non negativa è integrabile secondo Riemann se e solo se il suo rettangoloide R(f) è misurabile secondo Peano- Jordan. Inoltre, in caso di integrabilità, il valore dell integrale della funzione coincide con l area di R(f). In quest ottica può apparire più naturale e opportuno premettere l integrazione delle funzioni a scala e introdurre l integrale di Riemann mediante la Definizione 3.7. Nel parallelismo con la teoria delle aree, se l integrale di una funzione limitata corrisponde alla nozione di area di un sottoinsieme limitato del piano, l integrale delle funzioni a scala corrisponde alla nozione di area di un plurirettangolo. Infatti il rettangoloide di una funzione a scala non negativa è un particolare plurirettangolo. Se si adotta questa via, sembra sensato prendere in considerazione tutte le suddivisioni e non solo quelle uniformi, altrimenti non sarebbe del tutto immediato (anche se sarebbe comunque facile) verificare che una generica funzione a scala è integrabile nel senso della Definizione 3.7. Osservazione 4.5. Il Teorema 4.4 suggerisce per l introduzione dell integrale una via alternativa che ha il pregio di dare grande risalto all aspetto geometrico. Introdotta la Definizione 4.3, si può definire l integrale di una funzione f limitata e non negativa come l area del suo rettangoloide R(f), affermando naturalmente, sempre per definizione, che f è integrabile o meno a seconda che R(f) sia misurabile o meno. Se poi f è una funzione limitata di segno qualunque, si può definirne l integrabilità e l integrale presentandola come differenza di funzioni limitate e non negative. La via più semplice consiste nel considerare la decomposizione canonica f = f + f, ove le funzioni f ±, dette parti positiva e negativa di f, sono definite dalle formule f + (x) = max {f(x), 0} e f (x) = max { f(x), 0}. Si dichiara allora f integrabile per definizione se e solo se entrambe le funzioni f ± sono integrabili nel senso della definizione relativa a funzioni non negative, il che equivale a richiedere che i due rettangoloidi R(f ± ) siano misurabili. L integrale di f viene poi definito per linearità come la differenza degli integrali di f + e di f. Se si segue questa via, risulta vero per definizione che l integrale di una funzione f vale la differenza delle aree di due figure collegate al grafico di f, i rettangoloidi R(f + ) e R(f ), i quali possono essere poi letti direttamente anche a partire dal grafico di f. Questo fatto, che andrebbe osservato comunque almeno a livello intuitivo, è di solito meno facile da giustificare rigorosamente in altre impostazioni. Osservazione 4.6. Anche se si abbandona per un attimo il piano logico deduttivo e si pensa invece di dare solo una presentazione descrittiva della nozione di integrale e delle sue proprietà senza pretendere di svolgere le dimostrazioni, la teoria di Riemann basata sulla Qualche commento 13
14 Definizione 1.4 richiede la nozione di estremo superiore. Questo però si evita se si adotta la variante di introdurre prima le funzioni a scala e di ricorrere alla Definizione 3.7. Notiamo poi che, se non si intendono dimostrare i teoremi successivi alla definizione di integrabilità secondo Riemann, non sarebbe nemmeno necessario disporre della nozione di coppia di classi contigue. Inoltre la teoria è svincolata dalla nozione di limite e, di conseguenza, può essere presentata anche prima di aver dato le definizioni di limite e di funzione continua (anche se prima o poi occorre collegare la continuità alla teoria dell integrazione). Al contrario, benché le Definizioni 1.8 e 1.10 non facciano esplicito riferimento alla nozione di limite, questa di fatto aleggia e sembra più che mai opportuno avere già trattato i limiti di funzioni di variabile reale. A conferma di questo fatto stanno la Definizione 3.8 e il Teorema 3.9. Tuttavia è chiaro che le difficoltà concettuali connesse con la definizione di limite (legate principalmente al numero di quantificatori che vi compaiono) si ritrovano a maggior ragione nella Definizione 1.8 e nelle sue varianti. A titolo esemplificativo descriviamo la struttura logica della Definizione 1.8 e la confrontiamo con quella della Definizione 1.4, evitando di esplicitare S, S e S in funzione di σ e di σ. L acquisizione da parte dell allievo delle definizioni di somme inferiore, superiore e di Cauchy, infatti, è comunque presupposta. La richesta di integrabilità secondo Cauchy è del tipo I : ε > 0 δ > 0 : σ σ ( α(σ, δ) β(σ, σ ) = γ(s, I, ε) ) ove i predicati α(σ, δ), β(σ, σ ) e γ(s, I, ε) significano rispettivamente σ ha parametro di finezza < δ, σ è compatibile con σ e S I < ε. L integrabilità secondo Riemann si schematizza invece in! I : S S λ(s, S, I) ove λ(s, S, I) significa S I S e il simbolo!, che sta a indicare l unicità, funge da quantificatore. La differenza di complessità logica è allora evidente. Osservazione 4.7. Se poi si vuole sviluppare un poco la teoria in modo perfettamente rigoroso, l integrazione secondo Riemann è più conveniente di quella di Cauchy. Confrontiamo infatti le due vie per quanto riguarda condizioni di integrabilità e di non integrabilità, in vista della dimostrazione di qualche risultato significativo della teoria e della costruzione di una funzione non integrabile. Nella teoria di Riemann una funzione è integrabile se e solo se costituiscono una coppia di classi contigue l insieme delle somme inferiori e l insieme delle somme superiori o, in modo equivalente, se è unico l elemento che le separa. Il modo più semplice per dimostrare l integrabilità di una funzione f è allora quello di verificare che per ogni ε > 0 esistono una somma inferiore S e una somma superiore S tali che S S < ε, mentre la via naturale per controllare che una funzione non è integrabile consiste nella costruzione di due elementi separatori fra le classi delle somme inferiori e superiori. Qualche commento 14
15 Ebbene tutto ciò è di solito realizzabile senza eccessive difficoltà, ad esempio nella dimostrazione dell integrabilità delle funzioni monotone e delle funzioni continue e della non integrabilità della funzione di Dirichlet. Vediamo invece che accade nell ambito della teoria di Cauchy. Per dimostrare che una funzione f è integrabile conviene in genere ricorrere alla classica condizione di Cauchy seguente: per ogni ε > 0 esiste δ > 0 tale che, per ogni coppia di suddivisioni σ 1 e σ 2 con parametro di finezza < δ e per ogni coppia di scelte σ 1 e σ 2 di punti intermedi compatibili con σ 1 e con σ 2 rispettivamente, le corrispondenti somme di Cauchy S 1 e S 2 verifichino la disuguaglianza S 1 S 2 < ε. Si noti però che tale condizione, che si dimostra essere necessaria e sufficiente per l integrabilità, non è di facile comprensione da parte degli allievi, essendo addirittura più complessa della condizione di Cauchy relativa alla convergenza di una successione. Per quanto riguarda la non integrabilità di una funzione, una via leggermente più semplice della negazione della condizione di Cauchy ora enunciata è quella che presentiamo. Essa, tuttavia, è legata alla Definizione 3.8 e il suo uso comporta che anche quanto espresso da questa seconda definizione sia stato introdotto, almeno come proprietà implicata dall integrabilità nel senso della Definizione 1.8. Se si costruiscono due successioni di somme di Cauchy, entrambe associate a suddivisioni e a scelte di punti intermedi verificanti le condizioni prescritte dalla Definizione 3.8 ma convergenti a due valori diversi, allora, chiaramente, la funzione in questione non può essere integrabile. Avvertiamo che l esistenza di una coppia di successioni in tali condizioni è anche necessaria per la non integrabilità. Osservazione 4.8. Torniamo sull equivalenza data dal Teorema 3.9 fra le Definizioni 1.8 e 3.8 e, per maggior completezza, riferiamoci anche al Teorema 3.5 per quanto riguarda l equivalenza fra le Definizioni 1.8 e 3.4. Ebbene le Definizioni 3.4 e 3.8 sono equivalenti alla Definizione 1.8 proprio perché in esse si è lasciata ampia libertà alle somme di Cauchy, soprattutto a livello delle scelte ammesse di punti intermedi. Infatti se si restringesse troppo la scelta, non si otterrebbe più una nozione di integrabilità equivalente a quella originaria e risulterebbero integrabili nel nuovo senso funzioni che nel senso vecchio integrabili non sono. Questa circostanza si presenta ad esempio se, nel definire l integrabilità di una funzione cercando di imitare la Definizione 3.8, si prendono in considerazione, con la notazione (3.2), solo le successioni {S(f; σ n, σ n)} di somme di Cauchy costruite come segue: per ogni n si assume come σ n la suddivisione uniforme in n intervalli e come σ n si assume sistematicamente la scelta dei punti medi degli intervalli generati da σ n, cioè x k = x k 1 + x k 2 per k = 1,..., n. Con una siffatta definizione risulterebbe integrabile in [0, 1] con integrale pari a 1 ogni funzione che nei razionali valesse 1, indipendentemente dal suo comportamento nei punti irrazionali, quindi anche la funzione di Dirichlet, notoriamente non integrabile. Se invece si affronta una situazione in cui non vi sono problemi di integrabilità, dato che è già noto che tutte le funzioni in gioco sono integrabili, e si è interessati solo ai valori degli integrali, allora la situazione è diversa e sarebbe perfettamente lecito riferirsi solo a somme di Cauchy di tipo molto particolare. Qualche commento 15
16 Questa circostanza si presenta ad esempio per l integrale delle funzioni continue o, più in generale, delle funzioni limitate con al massimo un numero finito di punti di discontinuità. Dunque, se ci si vuole limitare a questo caso e non si pretende di considerare funzioni di tipo più generale, è corretto definire l integrale di una funzione come il limite di una successione particolare di somme di Cauchy selezionata fra quelle della Definizione 3.8. Si possono, ad esempio, considerare solo suddivisioni uniformi e scegliere come punti intermedi i punti medi degli intervallini originati dalle suddivisioni considerate. Se così si procede, è però necessario enunciare un risultato che afferma l esistenza del limite in questione e sarebbe anche opportuno avvertire con un teorema che altre successioni di somme di Cauchy in condizioni analoghe convergono all integrale, ormai definito. 5. Appendice: caratterizzazione delle funzioni integrabili Come è ben noto, sono integrabili secondo Riemann le funzioni continue e, più in generale, le funzioni limitate con al massimo un numero finito di punti di discontinuità. Inoltre sono integrabili tutte le funzioni monotone, e queste possono avere anche un infinità numerabile di punti di discontinuità. Esistono poi funzioni integrabili, ad esempio in [0, 1], il cui insieme di discontinuità ha la cardinalità del continuo: è in queste condizioni, infatti, la funzione caratteristica dell insieme di Cantor. Infine, la funzione di Dirichlet, che è discontinua in ogni punto, non è integrabile in alcun intervallo. Queste brevi considerazioni suggeriscono che l integrabilità secondo Riemann di una funzione limitata deve essere in qualche modo legata a quanto è piccolo l insieme dei suoi punti di discontinuità. Il Teorema di Vitali Lebesgue che vogliamo presentare precisa la congettura e risolve completamente la questione. La dimostrazione che diamo sfrutta proprietà ben note della teoria della misura secondo Peano Jordan e della teoria della misura e dell integrazione secondo Lebesgue che enunciamo soltanto (le dimostrazioni si trovano in ogni testo specializzato). Altre affermazioni più specifiche, invece, verranno giustificate. La dimostrazione si basa, inoltre, su una caratterizzazione dei punti di continuità della funzione in esame e su una decomposizione opportuna della frontiera del suo rettangoloide. A questo scopo sono necessarie le nozioni di massimo e di minimo limite, che richiamiamo brevemente nel caso delle funzioni limitate. Ecco i risultati che enunciamo senza dimostrazione. Proposizione 5.1. Un sottoinsieme limitato del piano è misurabile secondo Peano- Jordan se e solo se la sua frontiera ha misura nulla secondo Peano Jordan. Proposizione 5.2. Siano f 1, f 2 : [a, b] R due funzioni integrabili secondo Lebesgue e tali che f 1 (x) f 2 (x) per ogni x [a, b]. Allora l insieme {(x, y) [a, b] R : f 1 (x) y f 2 (x)} è misurabile secondo Lebesgue e la sua misura vale b a (f 2 (x) f 1 (x)) dx. (5.1) Appendice: caratterizzazione delle funzioni integrabili 16
17 Proposizione 5.3. Sia f : [a, b] R una funzione non negativa e integrabile secondo Lebesgue. Allora l integrale di f è nullo se e solo se f è nulla quasi ovunque secondo Lebesgue, cioè se e solo se l insieme dei punti in cui f non si annulla ha misura nulla secondo Lebesgue. Ora, come abbiamo anticipato, richiamiamo le nozioni di massimo e di minimo limite. Definizione 5.4. Siano f : [a, b] R una funzione limitata e x (a, b). Definiamo lim sup f(t) = lim t x δ 0 + sup f(t) e lim inf 0< t x <δ t x f(t) = lim δ 0 + inf f(t). 0< t x <δ Se x = a o x = b le definizioni sono analoghe: si sostituisce l intorno di x di raggio δ con l intorno destro e sinistro rispettivamente. Notiamo che i secondi membri delle formule precedenti effettivamente esistono e sono finiti dato che le funzioni della variabile δ che vi compaiono sono monotone e limitate. Chiaramente, vale sempre la disuguaglianza lim inf t x f(t) lim sup f(t) e si dimostra che il limite lim t x f(t) esiste se e solo il massimo e il minimo limite coincidono. In tal caso il loro valore comune è anche il valore del limite. La caratterizzazione dei punti di continuità della funzione f e lo studio della frontiera del suo rettangoloide R(f) poggiano sulla costruzione delle funzioni e dell insieme che introduciamo nella definizione data di seguito. Definizione 5.5. Sia f : [a, b] R una funzione limitata. Definiamo le quattro funzioni f, f, f #, f # : [a, b] R ponendo per x [a, b] Definiamo poi l insieme t x f (x) = lim sup f(t) (5.2) t x f (x) = lim inf f(t) (5.3) t x f # (x) = max {f(x), f (x)} (5.4) f # (x) = min {f(x), f (x)}. (5.5) G(f) = { (x, y) R 2 : a x b, f # (x) y f # (x) }. (5.6) Dalle relazioni fra limite, massimo limite e minimo limite che abbiamo richiamato deduciamo immediatamente il risultato seguente: Proposizione 5.6. La funzione f è continua nel punto x se e solo se f # (x) = f # (x). Appendice: caratterizzazione delle funzioni integrabili 17
18 In particolare, se f è continua in [a, b], l insieme G(f) coincide con il grafico di f. In generale, invece, si può solo affermare che il grafico di f è incluso in G(f). Osserviamo inoltre che, grazie all ipotesi di limitatezza fatta su f e alla teoria generale dell integrazione, le quattro funzioni introdotte sono integrabili secondo Lebesgue. Lemma 5.7. Sia f : [a, b] R una funzione limitata non negativa. Allora la frontiera del rettangoloide R(f) è l unione dei tre segmenti e dell insieme G(f). {a} [0, f(a)], {b} [0, f(b)] e [a, b] {0} Dimostrazione. Siccome è chiaro che i tre segmenti dell enunciato sono inclusi nella frontiera del rettangoloide, basta controllare che un punto (x, y) tale che a < x < b e y > 0 (5.7) è di frontiera per R(f) se e solo se valgono le disuguaglianze f # (x) y f # (x). (5.8) Supponiamo che (x, y) verifichi le (5.7) e sia di frontiera per R(f) e dimostriamo che valgono le (5.8). Siano {(x n, y n)} e {(x n, y n)} due successioni di punti di R(f) e, rispettivamente, del complementare di R(f) convergenti a (x, y). Grazie alle (5.7) non è restrittivo supporre che per ogni n valgano le disuguaglianze a < x n < b, a < x n < b, 0 < y n f(x n) e y n > f(x n). (5.9) Inoltre, pur di passare a sottosuccessioni opportune, possiamo supporre che ciascuna delle due successioni {x n} e {x n} assuma solo il valore x per ogni n oppure solo valori diversi da x e diciamo che le successioni sono di tipo (a) o di tipo (b) nei due casi. Si hanno allora quattro combinazioni possibili. Supponiamo dapprima che entrambe le successioni siano di tipo (a). Allora y n f(x) < y n per ogni n, da cui y = f(x), e dunque le (5.8). Supponiamo ora che le due successioni siano di tipo (a) e (b) rispettivamente. Abbiamo allora y n f(x) per ogni n, da cui y f(x) ; d altra parte, passando al minimo limite nell ultima disuguaglianza delle (5.9), deduciamo y f (x). Dunque le (5.8) sono soddisfatte anche in questo caso. Se le due successioni sono di tipo (b) e (a) rispettivamente, si ragiona come nel caso precedente prendendo ora il massimo limite. Supponendo infine che entrambe le successioni {x n} e {x n} siano di tipo (b), passando al minimo e massimo limite nelle (5.9) deduciamo y f (x) e y f (x), da cui ancora le (5.8). Viceversa, nell ipotesi che valgano le (5.7) e le (5.8), dimostriamo che (x, y) è un punto della frontiera di R(f). Osserviamo subito che ogni punto (x, y) del grafico di f è di frontiera: infatti esso appartiene a R(f) e, contemporaneamente, è il limite della Appendice: caratterizzazione delle funzioni integrabili 18
19 successione {(x, y + 1/n)}, che è costituita da punti del complementare. Rimangono allora da considerare i punti verificanti le (5.7) e le (5.8) tali che y f(x) e a questo scopo distinguiamo tre casi. Supponiamo dapprima f # (x) = f(x). Allora f(x) y f (x) e y > f(x). In particolare (x, y) non appartiene a R(f) e dobbiamo vedere che esso è il limite di una successione {(x n, y n )} di punti di R(f). Come {x n } prendiamo una successione di numeri reali diversi da x convergente a x e tale che {f(x n )} converga a f (x) e definiamo y n = min {f(x n ), y}. Allora y n f(x n ), per cui (x n, y n ) R(f), e lim y n = min {f (x), y} = y. Supponiamo ora f # (x) = f(x). Allora f (x) y < f(x). In particolare (x, y) appartiene a R(f) e dobbiamo vedere che esso è il limite di una successione {(x n, y n )} di punti non appartenenti a R(f). Come {x n } prendiamo una successione di numeri reali diversi da x convergente a x e tale che {f(x n )} converga a f (x) e definiamo y n = max {f(x n ), y} + 1/n. Allora y n > f(x n ), per cui (x n, y n ) R(f), e lim y n = max {f (x), y} = y. Nel caso restante abbiamo f (x) < f(x) < f (x) e f (x) y f (x). Se y f(x), per cui (x, y) R(f), procediamo come nel secondo caso per costruire {(x n, y n )} ; se invece y > f(x), per cui (x, y) R(f), procediamo come nel primo. Lemma 5.8. Sia f : [a, b] R una funzione limitata. Allora l insieme G(f) definito dalla (5.6) è compatto. Dimostrazione. Sia M = sup f. Allora M f # (x) f # (x) M per ogni x [a, b], per cui G(f) è limitato. Occorre allora solo dimostrare che G(f) è anche chiuso. Sia {(x n, y n )} una successione di punti dell insieme G(f) convergente a un certo punto (x, y) : dobbiamo dedurre che (x, y) G(f). Chiaramente a x b. Per dimostrare le (5.8) fissiamo ε > 0 ad arbitrio. Per definizione di massimo e di minimo limite esiste un numero δ > 0, che fissiamo, tale che f (x) ε f(z) f (x) + ε per 0 < z x < δ. Deduciamo f # (x) ε f(z) f # (x) + ε per z x < δ. Ma per ogni n maggiore di un certo indice m risulta x n x < δ/2. Per n > m abbiamo allora f # (x) ε f(x n ) f # (x) + ε. (5.10) Per tali n abbiamo anche f # (x) ε f(t) f # (x) + ε per t x n < δ/2 e prendendo il minimo e il massimo limite per t x n deduciamo f # (x) ε f (x n ) f # (x) + ε e f # (x) ε f (x n ) f # (x) + ε. (5.11) Appendice: caratterizzazione delle funzioni integrabili 19
20 Combinando la (5.10), la (5.11) e l ipotesi su y n, otteniamo f # (x) ε f # (x n ) y n f # (x n ) f # (x) + ε per n > m. Passando al limite concludiamo e le (5.8) seguono dall arbitrarietà di ε. f # (x) ε y f # (x) + ε Lemma 5.9. Sia K una compatto del piano. Allora K ha misura nulla nel senso di Lebesgue se e solo se ha misura nulla nel senso di Peano Jordan. Dimostrazione. La misura esterna secondo Peano Jordan di un insieme piano limitato K e la sua misura esterna secondo Lebesgue sono definite come l estremo inferiore degli insiemi { i area(r i) : K i R i} ottenuti prendendo tutte le famiglie {R i }, rispettivamente finite e numerabili nei due casi, di rettangoli (aperti senza perdita di generalità) che ricoprono l insieme K considerato. Ora, se K è compatto, da ogni suo ricoprimento costituito da aperti si può estrarre un ricoprimento finito. Segue allora facilmente che, nel caso dei compatti, le due misure esterne secondo Peano Jordan e secondo Lebesgue coincidono, per cui affermare che una di esse è nulla equivale a dire che è nulla l altra. D altra parte gli insiemi di misura nulla sono gli insiemi di misura esterna nulla in ciascuna delle due teorie, da cui l affermazione dell enunciato. Possiamo finalmente dimostrare il risultato finale: Teorema Sia f : [a, b] R una funzione limitata. Allora f è integrabile secondo Riemann se e solo se l insieme dei suoi punti di discontinuità è un insieme di misura nulla secondo Lebesgue. Dimostrazione. Siccome f è limitata e, per ogni costante c, l integrabilità di f equivale a quella di f + c, non è restrittivo supporre f non negativa. Grazie al Teorema 4.4 e alla Proposizione 5.1, la funzione f è integrabile secondo Riemann se e solo se la frontiera del suo rettangoloide R(f) ha misura nulla secondo Peano Jordan. Tenendo conto dei Lemmi 5.7, 5.8 e 5.9, deduciamo che f è integrabile secondo Riemann se e solo se l insieme G(f) ha misura di Lebesgue nulla. D altra parte, grazie alla Proposizione 5.2, la misura di Lebesgue di G(f) vale b a ( f # (x) f # (x) ) dx (5.12) e siccome la funzione integranda è non negativa, deduciamo, grazie alla Proposizione 5.3, che l integrale (5.12) è nullo se e solo se l insieme dei punti in cui non è nulla la funzione integranda ha misura nulla secondo Lebesgue. Infine, per la Proposizione 5.6, l uguaglianza f # (x) = f # (x) vale se e solo se f è continua nel punto x considerato. Dunque l annullamento dell integrale (5.12), equivalente all integrabilità di f secondo Riemann, equivale anche al fatto che l insieme dei punti di discontinuità di f abbia misura nulla secondo Lebesgue. Appendice: caratterizzazione delle funzioni integrabili 20
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
u 1 u k che rappresenta formalmente la somma degli infiniti numeri (14.1), ordinati al crescere del loro indice. I numeri u k
 Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
19. Inclusioni tra spazi L p.
 19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Lezioni di Matematica 1 - I modulo
 Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
A i è un aperto in E. i=1
 Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
1 Applicazioni Lineari tra Spazi Vettoriali
 1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
L espressione torna invece sempre vera (quindi la soluzione originale) se cambiamo contemporaneamente il verso: 1 < 0.
 EQUAZIONI E DISEQUAZIONI Le uguaglianze fra espressioni numeriche si chiamano equazioni. Cercare le soluzioni dell equazione vuol dire cercare quelle combinazioni delle lettere che vi compaiono che la
EQUAZIONI E DISEQUAZIONI Le uguaglianze fra espressioni numeriche si chiamano equazioni. Cercare le soluzioni dell equazione vuol dire cercare quelle combinazioni delle lettere che vi compaiono che la
1 Giochi a due, con informazione perfetta e somma zero
 1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
1. Limite finito di una funzione in un punto
 . Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
. Limite finito di una funzione in un punto Consideriamo la funzione: f ( ) = il cui dominio risulta essere R {}, e quindi il valore di f ( ) non è calcolabile in =. Quest affermazione tuttavia non esaurisce
Sulla monotonia delle funzioni reali di una variabile reale
 Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Proof. Dimostrazione per assurdo. Consideriamo l insieme complementare di P nell insieme
 G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
5. La teoria astratta della misura.
 5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
x u v(p(x, fx) q(u, v)), e poi
 0.1. Skolemizzazione. Ogni enunciato F (o insieme di enunciati Γ) è equisoddisfacibile ad un enunciato universale (o insieme di enunciati universali) in un linguaggio estensione del linguaggio di F (di
0.1. Skolemizzazione. Ogni enunciato F (o insieme di enunciati Γ) è equisoddisfacibile ad un enunciato universale (o insieme di enunciati universali) in un linguaggio estensione del linguaggio di F (di
Corso di Analisi Matematica. Successioni e serie numeriche
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
Il principio di induzione e i numeri naturali.
 Il principio di induzione e i numeri naturali. Il principio di induzione è un potente strumento di dimostrazione, al quale si ricorre ogni volta che si debba dimostrare una proprietà in un numero infinito
Il principio di induzione e i numeri naturali. Il principio di induzione è un potente strumento di dimostrazione, al quale si ricorre ogni volta che si debba dimostrare una proprietà in un numero infinito
Le funzioni continue. A. Pisani Liceo Classico Dante Alighieri A.S. 2002-03. A. Pisani, appunti di Matematica 1
 Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8. Cognome:... Nome:... Matricola:...
 Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Serie numeriche. 1 Definizioni e proprietà elementari
 Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Limiti e continuità delle funzioni reali a variabile reale
 Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
Limiti e continuità delle funzioni reali a variabile reale Roberto Boggiani Versione 4.0 9 dicembre 2003 1 Esempi che inducono al concetto di ite Per introdurre il concetto di ite consideriamo i seguenti
APPUNTI DI MATEMATICA ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1)
 ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1) Un insieme è una collezione di oggetti. Il concetto di insieme è un concetto primitivo. Deve esistere un criterio chiaro, preciso, non ambiguo, inequivocabile,
ALGEBRA \ INSIEMISTICA \ TEORIA DEGLI INSIEMI (1) Un insieme è una collezione di oggetti. Il concetto di insieme è un concetto primitivo. Deve esistere un criterio chiaro, preciso, non ambiguo, inequivocabile,
La curva grafico della funzione, partendo dal punto A(a,f(a)), si snoda con continuità, senza interruzioni, fino ad approdare nel punto B(b,f(b)).
 Calcolo differenziale Il teorema di Rolle TEOREMA DI ROLLE Ipotesi f continua su [a, b] f derivabile per lo meno su (a,b) f(a) = f(b) Tesi Esiste almeno un punto c in (a, b) tale che Giustificazione con
Calcolo differenziale Il teorema di Rolle TEOREMA DI ROLLE Ipotesi f continua su [a, b] f derivabile per lo meno su (a,b) f(a) = f(b) Tesi Esiste almeno un punto c in (a, b) tale che Giustificazione con
Indice. 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo... 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità...
 Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
Indice 1 Introduzione alle Equazioni Differenziali 1 1.1 Esempio introduttivo............................. 1 1.2 Nomenclatura e Teoremi di Esistenza ed Unicità.............. 5 i Capitolo 1 Introduzione
Anno 3. Funzioni: dominio, codominio e campo di esistenza
 Anno 3 Funzioni: dominio, codominio e campo di esistenza 1 Introduzione In questa lezione parleremo delle funzioni. Ne daremo una definizione e impareremo a studiarne il dominio in relazione alle diverse
Anno 3 Funzioni: dominio, codominio e campo di esistenza 1 Introduzione In questa lezione parleremo delle funzioni. Ne daremo una definizione e impareremo a studiarne il dominio in relazione alle diverse
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
Prodotto libero di gruppi
 Prodotto libero di gruppi 24 aprile 2014 Siano (A 1, +) e (A 2, +) gruppi abeliani. Sul prodotto cartesiano A 1 A 2 definiamo l operazione (x 1, y 1 ) + (x 2, y 2 ) := (x 1 + x 2, y 1 + y 2 ). Provvisto
Prodotto libero di gruppi 24 aprile 2014 Siano (A 1, +) e (A 2, +) gruppi abeliani. Sul prodotto cartesiano A 1 A 2 definiamo l operazione (x 1, y 1 ) + (x 2, y 2 ) := (x 1 + x 2, y 1 + y 2 ). Provvisto
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
Esistenza di funzioni continue non differenziabili in alcun punto
 UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Corso di Analisi Matematica Serie numeriche
 Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
Ottimizazione vincolata
 Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI
 119 4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI Indice degli Argomenti: TEMA N. 1 : INSIEMI NUMERICI E CALCOLO
119 4 Dispense di Matematica per il biennio dell Istituto I.S.I.S. Gaetano Filangieri di Frattamaggiore EQUAZIONI FRATTE E SISTEMI DI EQUAZIONI Indice degli Argomenti: TEMA N. 1 : INSIEMI NUMERICI E CALCOLO
Analisi dei Dati 12/13 Esercizi proposti 3 soluzioni
 Analisi dei Dati 1/13 Esercizi proposti 3 soluzioni 0.1 Un urna contiene 6 palline rosse e 8 palline nere. Si estraggono simultaneamente due palline. Qual è la probabilità di estrarle entrambe rosse? (6
Analisi dei Dati 1/13 Esercizi proposti 3 soluzioni 0.1 Un urna contiene 6 palline rosse e 8 palline nere. Si estraggono simultaneamente due palline. Qual è la probabilità di estrarle entrambe rosse? (6
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
16. Vari modi di convergenza delle successioni di funzioni reali misurabili.
 16. Vari modi di convergenza delle successioni di funzioni reali misurabili. L argomento centrale di questa ultima parte del corso è lo studio in generale della convergenza delle successioni negli spazi
16. Vari modi di convergenza delle successioni di funzioni reali misurabili. L argomento centrale di questa ultima parte del corso è lo studio in generale della convergenza delle successioni negli spazi
l insieme Y è detto codominio (è l insieme di tutti i valori che la funzione può assumere)
 Che cos è una funzione? Assegnati due insiemi X e Y si ha una funzione elemento di X uno e un solo elemento di Y. f : X Y se esiste una corrispondenza che associa ad ogni Osservazioni: l insieme X è detto
Che cos è una funzione? Assegnati due insiemi X e Y si ha una funzione elemento di X uno e un solo elemento di Y. f : X Y se esiste una corrispondenza che associa ad ogni Osservazioni: l insieme X è detto
Lezione 1. Gli Insiemi. La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme:
 Lezione 1 Gli Insiemi La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme: degli iscritti ad un corso di laurea delle stelle in cielo dei punti di un piano
Lezione 1 Gli Insiemi La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme: degli iscritti ad un corso di laurea delle stelle in cielo dei punti di un piano
Università degli Studi di Catania A.A. 2012-2013. Corso di laurea in Ingegneria Industriale
 Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Moto uniforme sul toro bidimensionale
 4/3/06 Luigi Chierchia Moto uniforme sul toro bidimensionale 1. Il toro bidimensionale Denotiamo con R l insieme dei numeri reali e con Z l insieme dei numeri interi (con segno) {..., 2, 1, 0, 1, 2,...};
4/3/06 Luigi Chierchia Moto uniforme sul toro bidimensionale 1. Il toro bidimensionale Denotiamo con R l insieme dei numeri reali e con Z l insieme dei numeri interi (con segno) {..., 2, 1, 0, 1, 2,...};
Dipendenza dai dati iniziali
 Dipendenza dai dati iniziali Dopo aver studiato il problema dell esistenza e unicità delle soluzioni dei problemi di Cauchy, il passo successivo è vedere come le traiettorie di queste ultime dipendono
Dipendenza dai dati iniziali Dopo aver studiato il problema dell esistenza e unicità delle soluzioni dei problemi di Cauchy, il passo successivo è vedere come le traiettorie di queste ultime dipendono
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
Osservazioni sulla continuità per le funzioni reali di variabile reale
 Corso di Matematica, I modulo, Università di Udine, Osservazioni sulla continuità Osservazioni sulla continuità per le funzioni reali di variabile reale Come è noto una funzione è continua in un punto
Corso di Matematica, I modulo, Università di Udine, Osservazioni sulla continuità Osservazioni sulla continuità per le funzioni reali di variabile reale Come è noto una funzione è continua in un punto
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Applicazioni del calcolo differenziale allo studio delle funzioni
 Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
SERIE NUMERICHE. prof. Antonio Greco 6-11-2013
 SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
Funzioni funzione dominio codominio legge argomento variabile indipendente variabile dipendente
 Funzioni In matematica, una funzione f da X in Y consiste in: 1. un insieme X detto dominio di f 2. un insieme Y detto codominio di f 3. una legge che ad ogni elemento x in X associa uno ed un solo elemento
Funzioni In matematica, una funzione f da X in Y consiste in: 1. un insieme X detto dominio di f 2. un insieme Y detto codominio di f 3. una legge che ad ogni elemento x in X associa uno ed un solo elemento
MICROECONOMIA La teoria del consumo: Alcuni Arricchimenti. Enrico Saltari Università di Roma La Sapienza
 MICROECONOMIA La teoria del consumo: Alcuni Arricchimenti Enrico Saltari Università di Roma La Sapienza 1 Dotazioni iniziali Il consumatore dispone ora non di un dato reddito monetario ma di un ammontare
MICROECONOMIA La teoria del consumo: Alcuni Arricchimenti Enrico Saltari Università di Roma La Sapienza 1 Dotazioni iniziali Il consumatore dispone ora non di un dato reddito monetario ma di un ammontare
Parte 2. Determinante e matrice inversa
 Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
SPAZI METRICI. Uno spazio metrico X con metrica d si indica con il simbolo (X, d). METRICI 1
 SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale
 4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica,
Parte 3. Rango e teorema di Rouché-Capelli
 Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
Scelte in condizione di incertezza
 Scelte in condizione di incertezza Tutti i problemi di decisione che abbiamo considerato finora erano caratterizzati dal fatto che ogni possibile scelta dei decisori portava a un esito certo. In questo
Scelte in condizione di incertezza Tutti i problemi di decisione che abbiamo considerato finora erano caratterizzati dal fatto che ogni possibile scelta dei decisori portava a un esito certo. In questo
Serie numeriche e serie di potenze
 Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
+ P a n n=1 + X. a n = a m 3. n=1. m=4. Per poter dare un significato alla somma (formale) di infiniti termini, ricorriamo al seguente procedimento:
 Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
11) convenzioni sulla rappresentazione grafica delle soluzioni
 2 PARAGRAFI TRATTATI 1)La funzione esponenziale 2) grafici della funzione esponenziale 3) proprietá delle potenze 4) i logaritmi 5) grafici della funzione logaritmica 6) principali proprietá dei logaritmi
2 PARAGRAFI TRATTATI 1)La funzione esponenziale 2) grafici della funzione esponenziale 3) proprietá delle potenze 4) i logaritmi 5) grafici della funzione logaritmica 6) principali proprietá dei logaritmi
La Programmazione Lineare
 4 La Programmazione Lineare 4.1 INTERPRETAZIONE GEOMETRICA DI UN PROBLEMA DI PROGRAMMAZIONE LINEARE Esercizio 4.1.1 Fornire una rappresentazione geometrica e risolvere graficamente i seguenti problemi
4 La Programmazione Lineare 4.1 INTERPRETAZIONE GEOMETRICA DI UN PROBLEMA DI PROGRAMMAZIONE LINEARE Esercizio 4.1.1 Fornire una rappresentazione geometrica e risolvere graficamente i seguenti problemi
Scelta intertemporale: Consumo vs. risparmio
 Scelta intertemporale: Consumo vs. risparmio Fino a questo punto abbiamo considerato solo modelli statici, cioè modelli che non hanno una dimensione temporale. In realtà i consumatori devono scegliere
Scelta intertemporale: Consumo vs. risparmio Fino a questo punto abbiamo considerato solo modelli statici, cioè modelli che non hanno una dimensione temporale. In realtà i consumatori devono scegliere
Rette e curve, piani e superfici
 Rette e curve piani e superfici ) dicembre 2 Scopo di questo articolo è solo quello di proporre uno schema riepilogativo che metta in luce le caratteristiche essenziali delle equazioni di rette e curve
Rette e curve piani e superfici ) dicembre 2 Scopo di questo articolo è solo quello di proporre uno schema riepilogativo che metta in luce le caratteristiche essenziali delle equazioni di rette e curve
Probabilità discreta
 Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
F (x) = f(x) per ogni x I. Per esempio:
 Funzioni Primitive (Integrali Indefiniti) (l.v.) Pur essendo un argomento che fa parte del Calcolo Differenziale, molti autori inseriscono funzioni primitive nel capitolo sul Calcolo Integrale, in quanto
Funzioni Primitive (Integrali Indefiniti) (l.v.) Pur essendo un argomento che fa parte del Calcolo Differenziale, molti autori inseriscono funzioni primitive nel capitolo sul Calcolo Integrale, in quanto
Massimi e minimi vincolati di funzioni in due variabili
 Massimi e minimi vincolati di funzioni in due variabili I risultati principali della teoria dell ottimizzazione, il Teorema di Fermat in due variabili e il Test dell hessiana, si applicano esclusivamente
Massimi e minimi vincolati di funzioni in due variabili I risultati principali della teoria dell ottimizzazione, il Teorema di Fermat in due variabili e il Test dell hessiana, si applicano esclusivamente
Sulle funzioni di W 1,p (Ω) a traccia nulla
 Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 2011/2012
 Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
3.1 Successioni. R Definizione (Successione numerica) E Esempio 3.1 CAPITOLO 3
 CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
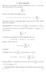 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
Algebra e Geometria. Ingegneria Meccanica e dei Materiali Sez (2) Ingegneria dell Automazione Industriale Sez (2)
 Algebra e Geometria Ingegneria Meccanica e dei Materiali Sez (2) Ingegneria dell Automazione Industriale Sez (2) Traccia delle lezioni che saranno svolte nell anno accademico 2012/13 I seguenti appunti
Algebra e Geometria Ingegneria Meccanica e dei Materiali Sez (2) Ingegneria dell Automazione Industriale Sez (2) Traccia delle lezioni che saranno svolte nell anno accademico 2012/13 I seguenti appunti
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Appunti sulla Macchina di Turing. Macchina di Turing
 Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
Macchina di Turing Una macchina di Turing è costituita dai seguenti elementi (vedi fig. 1): a) una unità di memoria, detta memoria esterna, consistente in un nastro illimitato in entrambi i sensi e suddiviso
CONVESSITÀ NELLA GEOMETRIA DEL TAXI DI MINKOWSKI
 CONVESSITÀ NELLA GEOMETRIA DEL TAXI DI MINKOWSKI ELISABETTA AVIZZANO NICOLETTA CAPOTORTO CHIARA CEROCCHI GIORGIO CICCARELLA IVAN COLAVITA EMANUELE DI CARO SERENA NUNZIATA AMANDA PISELLI ANDREA PIEPOLI
CONVESSITÀ NELLA GEOMETRIA DEL TAXI DI MINKOWSKI ELISABETTA AVIZZANO NICOLETTA CAPOTORTO CHIARA CEROCCHI GIORGIO CICCARELLA IVAN COLAVITA EMANUELE DI CARO SERENA NUNZIATA AMANDA PISELLI ANDREA PIEPOLI
LEZIONE 31. B i : R n R. R m,n, x = (x 1,..., x n ). Allora sappiamo che è definita. j=1. a i,j x j.
 LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
La funzione è continua nel suo dominio perchè y = f(x) è composizione di funzioni continue. Il punto x = 0 è un punto isolato per D f.
 FUNZIONI CONTINUE - ALCUNI ESERCIZI SVOLTI SIMONE ALGHISI 1. Continuità di una funzione Dati un insieme D R, una funzione f : D R e x 0 R, si è detto che f è continua in x 0 se sono soddisfatte le seguenti
FUNZIONI CONTINUE - ALCUNI ESERCIZI SVOLTI SIMONE ALGHISI 1. Continuità di una funzione Dati un insieme D R, una funzione f : D R e x 0 R, si è detto che f è continua in x 0 se sono soddisfatte le seguenti
LEZIONE 23. Esempio 23.1.3. Si consideri la matrice (si veda l Esempio 22.2.5) A = 1 2 2 3 3 0
 LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
LA FUNZIONE INTEGRALE
 LA FUNZIONE INTEGRALE MAGLIOCURIOSO & CAMILLO magliocurioso@hotmail.it Sommario. In questa breve dispensa ho semplicementrascritto in L A TEX il contenuto di questa discussione: http://www.matematicamente.it/forum/
LA FUNZIONE INTEGRALE MAGLIOCURIOSO & CAMILLO magliocurioso@hotmail.it Sommario. In questa breve dispensa ho semplicementrascritto in L A TEX il contenuto di questa discussione: http://www.matematicamente.it/forum/
Esponenziali elogaritmi
 Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
2 FUNZIONI REALI DI VARIABILE REALE
 2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
2 FUNZIONI REALI DI VARIABILE REALE 2.1 CONCETTO DI FUNZIONE Definizione 2.1 Siano A e B due insiemi. Una funzione (o applicazione) f con dominio A a valori in B è una legge che associa ad ogni elemento
Sui concetti di definizione, teorema e dimostrazione in didattica della matematica
 Liceo Scientifico Statale P. Paleocapa, Rovigo XX Settimana della Cultura Scientifica e Tecnologica 19 marzo 2010 Sui concetti di definizione, teorema e dimostrazione in didattica della matematica Prof.
Liceo Scientifico Statale P. Paleocapa, Rovigo XX Settimana della Cultura Scientifica e Tecnologica 19 marzo 2010 Sui concetti di definizione, teorema e dimostrazione in didattica della matematica Prof.
