Shading Rendering. IUAV dcp corso Disegno Digitale. Camillo Trevisan
|
|
|
- Pasquale Zani
- 8 anni fa
- Visualizzazioni
Transcript
1 Shading Rendering IUAV dcp corso Disegno Digitale Camillo Trevisan
2 Modelli di illuminazione Obiettivo: non tanto simulare il vero comportamento della luce, ma piuttosto riprodurre realisticamente l effetto che la luce ha sugli oggetti della scena. Il nostro occhio è sensibile anche a pochissimi fotoni e si adatta rapidamente a condizioni di luce molto diverse tra loro, anche se presenti contemporaneamente nella stessa scena. Nessuna tecnologia può, nemmeno lontanamente, avvicinarsi alla percezione umana. IUAV dcp corso Disegno digitale
3 Modelli di illuminazione Per mettere in luce le varie parti degli oggetti, individuare le ombre proprie e portate, dare profondità alla scena, è necessario usare un modello di illuminazione: un modello matematico che descrive, in modo più o meno semplificato, l interazione tra la luce e gli oggetti presenti nella scena. L illuminazione complessiva è data dalla somma di tre componenti di luce: Ambiente+Diffusa+Riflessa. L aspetto più critico è la resa della profondità: questa è, in realtà, un illusione ottica. IUAV dcp corso Disegno digitale
4 Luci Esistono vari tipi di luci: Direzionale (direction light) Puntiforme (point light) Spot (spot light) Area (area light) Volumetrica (volume light) Ambientale (ambient light) Queste possono essere ricondotte a due categorie di modelli di illuminazione: i modelli locali e i modelli globali. I primi descrivono in modo semplificato luci e interazioni di queste con gli oggetti in scena; i secondi considerano in modo più accurato le interazioni, comprendendo molti fenomeni trascurati dai primi modelli. IUAV dcp corso Disegno digitale
5 Assorbimento della luce che colpisce una superficie Angolo di riflessione uguale all angolo di incidenza (rispetto alla normale alla superficie) IUAV dcp corso Disegno digitale
6 Riflessione diffusa della luce IUAV dcp corso Disegno digitale
7 Shading Nella computer grafica, lo shading si riferisce al processo di alterare un colore di riferimento basandosi sull'angolo d'incidenza della luce e sulla distanza dalla sorgente, per raggiungere un effetto realistico. Lo shading è uno dei passi presenti nel processo di rendering e modifica il colore delle facce del modello tridimensionale basandosi anche sull'angolo formato dalla superficie rispetto al sole o ad altre sorgenti di luce. IUAV dcp corso Disegno digitale
8 Shading Teoricamente, due superfici parallele sono illuminate in modo identico da una sorgente posta a distanza infinita, come il sole. Anche se una delle due superfici è più distante dai nostri occhi, l illuminazione sembra identica. Molti algoritmi di shading e rendering implementano il Falloff che produce immagini che sembrano maggiormente realistiche senza la necessità di aggiungere altre luci per ottenere lo stesso effetto. L algoritmo fa sì che le facce più distanti dall osservatore appaiano più scure delle vicine, pur se parallele tra loro. IUAV dcp corso Disegno digitale
9 Equazione di rendering Per produrre una rappresentazione efficace dell'immagine, è necessario simulare la fisica della luce. Il modello matematico più astratto del comportamento della luce è l'equazione di rendering, basata sulla legge di conservazione dell'energia. Essa è un'equazione integrale, che calcola la luce in una certa posizione come la luce emessa in quella posizione sommata all'integrale della luce riflessa da tutti gli oggetti della scena che colpisce quel punto. Questa equazione infinita non può essere risolta con algoritmi finiti, quindi necessita di un approssimazione. IUAV dcp corso Disegno digitale
10 L equazione di rendering descrive il flusso di energia luminosa di una scena. E basata sulla fisica della luce e pertanto è teoricamente perfetta. I vari motori di rendering approssimano questa equazione in forma più o meno complessa mediante vari cortocircuiti e semplificazioni. La base fisica è la legge di conservazione dell energia, vale a dire che, sebbene possa essere trasformata e convertita da una forma all altra, la quantità totale di energia di un sistema isolato è una costante, ovvero il suo valore si mantiene immutato al passare del tempo. In una particolare posizione e direzione, la luce uscente (L o ) corrisponde alla somma della luce emessa (L e ) e di quella riflessa (L r ). La luce riflessa è la somma della luce entrante (L i ) da tutte le direzioni, moltiplicata per la superficie riflettente e per l angolo di incidenza. Due interessanti caratteristiche sono: la sua linearità (è composta solo di moltiplicazioni e addizioni), e la sua omogeneità spaziale (è la stessa in tutte le posizioni e direzioni). Unendo la luce uscente a quella entrante, attraverso un punto d'interazione, questa equazione rappresenta l'intero trasporto di luce presente nella scena. Tutti i più complessi algoritmi possono essere visti come soluzioni a particolari formulazioni di questa equazione. IUAV dcp corso Disegno digitale
11 In una particolare posizione e direzione, la luce uscente (L o ) corrisponde alla somma della luce emessa (L e ) e di quella riflessa. La luce riflessa è la somma della luce entrante (L i ) da tutte le direzioni, moltiplicata per la superficie riflettente e per l angolo di incidenza. IUAV dcp corso Disegno digitale
12 IUAV dcp corso Disegno digitale
13 I modelli di illuminazione più semplici considerano solo la luce che viaggia direttamente da una sorgente luminosa ad un oggetto: questa è chiamata illuminazione diretta. Il modo in cui la luce viene riflessa dall'oggetto può essere descritto da una funzione matematica, chiamata "funzione di distribuzione della riflessione bidirezionale" (bidirectional reflectance distribution function, BRDF), che tiene conto delle caratteristiche del materiale illuminato. La maggior parte dei sistemi di rendering semplifica ulteriormente e calcola l'illuminazione diretta come la somma di due componenti: diffusa e speculare. La componente diffusa, o Lambertiana, corrisponde alla luce che viene diffusa dall'oggetto in tutte le direzioni, quella speculare alla luce che si riflette sulla superficie dell'oggetto come su uno specchio. Il modello di riflessione di Phong aggiunge una terza componente, ambientale, che fornisce una simulazione semplice dell'illuminazione indiretta. IUAV dcp corso Disegno digitale
14 Con il termine bidirectional reflectance distribution function (BRDF) si intende una misura della distribuzione della riflettanza (la proporzione di luce incidente che una data superficie è in grado di riflettere). È una funzione a quattro dimensioni che definisce quanta luce è riflessa su una superficie opaca. La funzione considera la direzione della luce che arriva w i e quella che esce w o, entrambe rispetto alla normale alla superficie N. Questa funzione ritorna il rapporto tra la radianza (quantità di luce emessa, riflessa o trasmessa da una superficie di area unitaria) riflessa esistente lungo w o e l irradianza (o illuminanza, è la fluenza di radiazione elettromagnetica, ovvero la densità di corrente termica trasmessa per irraggiamento) incidente sulla superficie dalla direzionew i. Da notare che ogni direzione wè parametrizzata da due angoli: un azimuth e uno zenith (per questo ha quattro dimensioni). IUAV dcp corso Disegno digitale
15 Modello di riflessione di Phong Il modello di riflessione di Phong può essere visto come una semplificazione della più generica equazione di rendering, con il vantaggio di semplificare il calcolo del colore di un punto della superficie: - È un modello di riflessione locale, ovvero non considera riflessioni di secondo ordine, a differenza di quanto fatto dal ray tracing e dal radiosity. Al fine di compensare la perdita di parte della luce riflessa, un'ulteriore luce ambiente viene aggiunta alla scena. - Divide la riflessione in tre componenti: riflessione speculare, riflessione diffusiva e riflessione d'ambiente. IUAV dcp corso Disegno digitale
16 Rappresentazione del modello di riflessione di Phong In questa immagine, i colori "ambiente" e "diffuso" sono gli stessi. Da notare che l'intensità della componente diffusiva varia al variare della direzione della superficie, mentre la luce ambiente è costante. Il colore speculare è bianco, e riflette quasi tutta la luce entrante, ma solo in un limitato fascio di direzioni. IUAV dcp corso Disegno digitale
17 Definiamo per prima cosa, per ogni sorgente luminosa, le componenti i s e i d, che sono rispettivamente le intensità (spesso misurate in RGB) delle componenti speculare e diffusiva della luce. Una costante i a controlla la luce ambiente e viene calcolata come somma dei contributi forniti dalle varie sorgenti. Se definiamo, per ogni materiale: k s : costante di riflessione speculare, la percentuale riflessa di luce entrante; k d : costante di riflessione diffusiva, la percentuale di luce entrante che viene diffusa; k a : costante di riflessione d'ambiente, percentuale di riflessione della luce ambiente presente in ogni punto della scena; α: costante di lucentezza del materiale in questione, che decide in quale modo la luce viene riflessa. Definiamo inoltre lights come insieme di tutte le sorgenti di luce, N è la normale in questo punto, L è il vettore verso il punto luce considerato, R è la direzione di un raggio perfettamente riflesso (rappresentato con un vettore) e V è la direzione verso chi guarda (ad esempio una camera). Il valore di shading per ogni punto della superficie I p viene così calcolato: IUAV dcp corso Disegno digitale
18 IUAV dcp corso Disegno digitale
19 Il termine diffusivo non utilizza la direzione V (direzione verso la camera), dal momento che è costante in tutte le direzioni, inclusa la direzione della camera. Il termine speculare è grande se il vettore R (direzione raggio riflesso) è quasi allineato con V, valore ottenuto misurando il coseno dell'angolo formato tra di essi, ovvero il prodotto scalare dei vettori R e V. Quando α è grande, la superficie si presenta simile a uno specchio e la dimensione della riflessione sarà minima grazie all'alto valore del coseno che tende rapidamente a zero se i due vettori non sono allineati. Quando i colori sono rappresentati con valori RGB, questa equazione viene calcolata separatamente per ogni valore della terna. Quello di Phong è un modello di riflessione empirico, non basato sulla descrizione fisica dell'interazione di luce, ma piuttosto sull'osservazione informale. Phong osservò che le superfici altamente riflettenti creavano un riflesso piccolo, mentre l'intensità di quelle opache diminuiva in maniera più graduata. IUAV dcp corso Disegno digitale
20 Flat, Gouraud e Phong shading Il flat shading è la tecnica base usata nello shading di oggetti: colora ciascun poligono in relazione all angolo di incidenza della luce. Naturalmente evidenzia tutte le sfaccettature dell oggetto. Il Gouraud shading, che prende il nome da Henri Gouraud, serve per ottenere un graduato cambiamento di colore su superfici a basso numero di poligoni (low-polygon) senza dover ricorrere alla pesantezza computazionale del calcolo pixel per pixel. Gouraud pubblicò questa ricerca per la prima volta nel Il principio su cui si basa la tecnica di Gouraud è il seguente: viene fatta una stima della normale in ogni vertice di un modello 3D calcolando la media delle normali dei poligoni vi convergono. Partendo da queste stime si può utilizzare il modello di riflessione di Phong per calcolare l'intensità del colore nei vertici. Il colore dei vari pixel può essere trovato interpolando i valori calcolati nei vertici. IUAV dcp corso Disegno digitale
21 Gouraud shading I punti di forza e di debolezza del Gouraud shading risiedono entrambi nell'uso che esso fa dell'interpolazione. Interpolare i colori di vari pixel (conoscendone con precisione solo pochi) alleggerisce il calcolo rispetto a modelli più raffinati (come il Phong shading). Purtroppo, però, gli effetti di luce localizzati (come punti di riflettenza, ad esempio la riflessione di una sorgente di luce su di una sfera) non verranno renderizzati correttamente: se l'effetto è collocato al centro del poligono, senza raggiungere i vertici, non apparirà come risultato del rendering di Gouraud; se lo stesso effetto è collocato su di un vertice, verrà mostrato correttamente, ma verrà replicato in modo innaturale sui poligoni adiacenti. Il problema è facilmente riconoscibile se si renderizza una scena nella quale la sorgente di luce si muove, spostando la riflessione presente sull'oggetto in questione. Con il Gouraud shading si vedrebbe la riflessione allargarsi e stringersi continuamente, raggiungendo i picchi d'intensità nei vertici e sparendo al centro dei poligoni. IUAV dcp corso Disegno digitale
22 Esempio di shading Gouroud A sinistra. Sfera trattata con il Gouraud shading: da notare la scarsa accuratezza lungo i lati dei poligoni. A destra. La stessa sfera riprodotta con un alto numero di poligoni. IUAV dcp corso Disegno digitale
23 Phong shading La riflessione di Phong è un modello di illuminazione locale che può conferire un certo grado di realismo agli oggetti tridimensionali attraverso la combinazione di tre elementi: diffusione, riflessione e luce ambiente per ogni punto della superficie. Come metodo di rendering, il Phong Shading può essere visto come un miglioramento del Gouraud shading. Il problema principale del Gouraud Shading si ha quando la riflessione è vicina al centro di un grande triangolo. In pratica la riflessione non verrà mostrata, a causa dell'interpolazione di colori tra i vertici. Questo problema è stato corretto dal Phong shading. IUAV dcp corso Disegno digitale
24 Phong shading Siano dati tre vertici in due dimensioni (tre punti non allineati né coincidenti che definiscono un piano nello spazio e i tre vertici di un triangolo appartenente al piano), V 1, V 2 e V 3, e le normali alle superfici per ogni vertice: N 1, N 2 e N 3. Supponiamo che siano tutte di lunghezza unitaria (versori). A differenza del Gouraud shading, che interpola il colore lungo il triangolo, nel metodo di Phong si interpola linearmente la normale N lungo la superficie del triangolo, partendo dalle tre normali date. Questo calcolo viene effettuato per ogni pixel del triangolo. In ogni pixel si normalizza N (si fa in modo che N abbia valore unitario) e lo si usa all'interno del modello di riflessione di Phong per ottenere il colore da assegnare al pixel. E dunque necessario ricalcolare continuamente l angolo tra il Punto di Vista e il fascio di luce riflessa (R V, prodotto scalare). IUAV dcp corso Disegno digitale
25 Blinn-Phong shading Come appena visto, nel Phong shading è necessario calcolare per ciascuna faccia l angolo tra il Punto di Vista (V) e il fascio di luce riflessa (R). Se invece si calcola il vettore H bisettore dell angolo tra V e L, possiamo sostituire all angolo tra R e V quello tra N e H, dove N è la normale alla superficie. Questo angolo è la metà dell altro se V, L, N, R giacciono sullo stesso piano, ma la relazione si mantiene, sia pure approssimativamente, anche quando i vettori non giacciono sullo stesso piano, soprattutto se gli angoli sono piccoli. Il vantaggio del metodo consiste nel non dover calcolare l angolo per ogni faccia ma solo quello per ciascuna sorgente di luce, se V e L sono all infinito. IUAV dcp corso Disegno digitale
26 Blinn-Phong modificato Usare l angolo bisettore pone diversi problemi. Anzitutto di ordine matematico: distrugge la reciprocità di Helmholtz, vale a dire che non è più possibile ricostruire a ritroso il percorso dei raggi riflessi. In secondo luogo transizioni di luce molto dure tra pixel molto luminosi e molto scuri, con viste radenti, creano silhouette. Nel tempo sono state messe a punto molte varianti di questo algoritmo. IUAV dcp corso Disegno digitale
27 Oren-Nayar L algoritmo di Oren-Nayar si utilizza per superfici molto rugose, e dunque non Lambertiane (appartiene alla famiglia delle microfacet models, che trattano le superfici come un insieme di facce microscopiche). Un insieme numeroso di microfacce che descrivono superfici rugose viola la legge di Lambert, anzitutto perché, al variare dell angolo di vista, l insieme delle facce che vedono il PV sotto il medesimo angolo si modifica continuamente e fortemente e pertanto l apparenza della superficie è in funzione del Punto di Vista. Geometria delle microfacce. Esempio di superficie composta da microfacce. Direzione della normale A (con V normale alla macrosuperficie). Interazione tra le microfacce: interriflessioni, mascherature, shadowing. IUAV dcp corso Disegno digitale
28 Oren-Nayar Si assume che la superficie sia composta da cavità a V simmetriche e regolari, più piccole di un pixel, una volta proiettate. Ciascuna cavità è composta da due facce piane. La rugosità della superficie è data da una funzione di probabilità di distribuzione delle inclinazioni delle facce (in particolare si usa spesso una distribuzione Gaussiana). Ciascuna faccia usa una funzione di riflessione Lambertiana. Naturalmente minore è l inclinazione e maggiore è la vicinanza della superficie complessiva a quella Lambertiana e viceversa. IUAV dcp corso Disegno digitale
29 Illuminazione globale Gli oggetti sono in realtà bombardati da moltissime sorgenti luminose indirette: la luce rimbalza da un oggetto all'altro finché non perde energia. L'illuminazione globale indaga questo comportamento della radiazione luminosa. Come l'illuminazione diretta, essa comprende una componente diffusa ed una speculare. La riflessione reciproca diffusa riguarda la luce che colpisce un oggetto dopo averne già colpito un altro. Dal momento che questo ha assorbito una data lunghezza d'onda dello spettro della luce che lo ha colpito, la luce che respinge ha un colore diverso da quella da cui è illuminato. La riflessione reciproca speculare si manifesta generalmente con caustiche (ovvero con la concentrazione della radiazione luminosa in un punto da parte di una superficie speculare, come quella ottenibile dalla luce solare con una lente). IUAV dcp corso Disegno digitale
30 Algoritmi di illuminazione globale Gli algoritmi di Illuminazione globale vengono comunemente usati in computer grafica 3D per aggiungere un'illuminazione realistica alle scene. Alcuni di questi algoritmi tengono conto non solo della luce ricevuta direttamente da una sorgente di luce (illuminazione diretta), ma anche di quella riflessa, diffusa, o rifratta da altre superfici (illuminazione indiretta). Le immagini renderizzate con l'uso di algoritmi di illuminazione globale, spesso appaiono più realistiche rispetto a quelle che utilizzano solo l'illuminazione diretta. La loro computazione, però, è molto più lenta. Un approccio comune consiste nel calcolare l'illuminazione globale di una scena e memorizzare questa informazione in senso geometrico, ad esempio con la radiosity. I dati così salvati, possono essere usati per creare immagini da differenti punti di vista, generando così dei percorsi animati (walkthrough) senza dover ricalcolare continuamente l'illuminazione. IUAV dcp corso Disegno digitale
31 Algoritmi di illuminazione globale Radiosity, ray tracing, path tracing, ambient occlusion, e photon mapping sono esempi di algoritmi usati nel campo dell'illuminazione globale; alcuni possono essere combinati tra loro per ottenere risultati più rapidi, ma comunque accurati. Questi algoritmi modellano l'inter-riflessione diffusa, una parte molto importante dell'illuminazione globale. Buona parte di questi (esclusa la radiosity) modellano anche la riflessione speculare, il che li rende più precisi nella risoluzione dell'equazione di luce e fornisce un effetto più realistico alla scena. Gli algoritmi utilizzati per calcolare la distribuzione dell'energia luminosa tra superfici di una scena, sono strettamente correlati con le simulazioni di trasferimento di calore, risolte in ingegneria con l'uso del metodo degli elementi finiti. IUAV dcp corso Disegno digitale
32 Il metodo degli Elementi Finiti Il metodo degli elementi finiti è stato messo a punto per risolvere problemi di analisi strutturale e si applica a corpi che possono essere suddivisi in un gran numero di elementi di forma definita ed elementare e di dimensioni molto piccole rispetto al corpo stesso. Applicando lo stesso algoritmo a tutti gli elementi e risolvendo il problema per ciascun elemento, si giunge così alla soluzione del problema applicato all intero corpo. Ad esempio, dovendo calcolare, al variare della temperatura, la dilatazione di un oggetto metallico di forma complessa e anche composto di varie parti in leghe diverse tra loro e con temperature che variano nello spazio e nel tempo, lo si potrà suddividere in moltissimi piccoli cubi per i quali è semplice risolvere il problema del calcolo della dilatazione nel tempo. Sommando tra di loro gli effetti si troverà la soluzione complessiva. Naturalmente, più numerosi saranno i piccoli cubi che approssimano l oggetto, migliore sarà anche l accuratezza dell analisi. IUAV dcp corso Disegno digitale
33 Ray casting Il Ray casting usa il test di intersezione tra una semiretta e una superficie per risolvere vari problemi di computer grafica. Può riferirsi a: Un problema generale per determinare il primo oggetto intersecato da un raggio. Una tecnica per la rimozione delle superfici nascoste. Una variante non ricorsiva del Ray tracing che considera solo il raggio primario Un metodo diretto di volume rendering, il volume ray casting. IUAV dcp corso Disegno digitale
34 Ray casting Il Ray casting può essere considerato una versione veloce del Ray tracing, poiché non calcola la nuova direzione che un raggio di luce può assumere dopo aver intersecato una superficie nel suo viaggio verso l occhio dell osservatore. Questo comporta l impossibilità di calcolare accuratamente le riflessioni, le rifrazioni e il naturale falloff delle ombre. L algoritmo originale (Arthur Appel, 1968) consiste nel lanciare raggi dal punto di vista, uno al centro di ciascun pixel dell immagine da creare, per trovare il primo oggetto che lo interseca. Usando le proprietà del materiale e gli effetti di luce della scena, questo algoritmo può determinare lo shading degli oggetti in scena, usando un metodo di shading tradizionale. Un importante vantaggio del Ray casting è la sua capacità di trattare facilmente oggetti matematici non piani per i quali è semplice definire l intersezione con una retta: ad esempio, sfere, coni, cilindri. IUAV dcp corso Disegno digitale
35 Volume Ray casting Volume ray casting (anche noto come volumetric ray casting, volumetric ray tracing, volume ray marching) è una tecnica di rendering image-based, poiché calcola immagini 2D da una scena 3D. Comprende quattro passaggi: 1. Ray casting: per ciascun pixel è lanciato un raggio dal PV. 2. Sampling: si definiscono dei sampling points lungo la parte del raggio che si trova all interno del volume. IUAV dcp corso Disegno digitale
36 Volume Ray casting 3. Shading: per ciascun campione è calcolato il gradiente (vale a dire l orientamento della superficie entro il volume). I campioni sono quindi sottoposti a shading, in relazione all orientamento della loro superficie rispetto alle luci di scena. 4. Compositing: i colori dei campioni, ottenuti a partire dall equazione di rendering, sono composti e miscelati tra loro, a partire dal fondo, determinando il colore finale del pixel in elaborazione. IUAV dcp corso Disegno digitale
37 Ray tracing Come per il Ray casting la tecnica del Ray tracing (Turner Whitted, 1979) segue i raggi partendo dal Punto di Vista. Lavora tracciando, all inverso, il percorso che potrebbe aver seguito un raggio di luce prima di giungere al PV. Mentre la scena è attraversata dal raggio, sono calcolate la riflessione, la rifrazione e l assorbimento nel punto in cui il raggio stesso colpisce un qualsiasi oggetto. I precedenti algoritmi lanciavano anch essi il raggio dall'occhio verso la scena, ma i raggi non venivano più seguiti. Quando un raggio colpisce una superficie, può generare fino a tre nuovi tipi di raggio: riflessione, rifrazione e ombra. Un raggio riflesso continua nella direzione della riflessione a specchio su di una superficie lucida. A questo punto interagisce con altri oggetti della scena; il primo oggetto che colpisce sarà quello visto nel riflesso presente sull'oggetto originario. Il raggio rifratto viaggia attraverso il materiale trasparente in modo simile, con l'aggiunta che può entrare o uscire da un materiale. IUAV dcp corso Disegno digitale
38 Ray tracing Per evitare di tracciare tutti i raggi presenti in una scena, un raggio ombra viene usato per testare se la superficie sia visibile a una luce. Un raggio colpisce una superficie in un qualche punto. Se questo punto "vede" la luce, il raggio viene seguito fino alla sorgente. Se durante il tragitto si incontra un oggetto opaco, la superficie è in ombra e quella sorgente non contribuisce al calcolo del colore. IUAV dcp corso Disegno digitale
39 Ray tracing Svantaggi. Un grave svantaggio è dato dalle performance. Il raytracing itera tutto il procedimento per ogni nuovo pixel, trattando ogni raggio in modo separato. Questa separazione offre vantaggi, ad esempio la possibilità di spedire più raggi del necessario per ottenere l'antialiasing e migliorare la qualità dell'immagine. Nonostante gestisca accuratamente interriflessioni e rifrazioni, il Ray Tracing tradizionale non è necessariamente realistico. Il vero realismo si ottiene quando l'equazione di rendering è ben approssimata o completamente implementata. Il calcolo completo è normalmente impossibile date le risorse di computazione richieste. Il realismo di tutti i metodi di rendering, quindi, deve essere valutato in rapporto all'approssimazione dell'equazione e, nel caso del ray tracing, non è necessariamente il più realistico. Altri metodi, tra cui il photon mapping, sono basati sul ray tracing in alcune parti dell'algoritmo, e danno migliori risultati. IUAV dcp corso Disegno digitale
40 Photon mapping Il photon mapping è in grado di simulare la rifrazione della luce attraverso sostanze trasparenti, ad esempio il vetro o l'acqua, riflessioni reciproche tra oggetti illuminati e alcuni effetti causati da particelle come il fumo o il vapore acqueo. Il photon mapping è stato sviluppato dal ricercatore danese Henrik Wann Jensen. La prima fase consiste nel simulare l'emissione di fotoni (photon tracing, di solito più di ) dalle sorgenti di luce di scena e nel tracciamento, all'interno della scena stessa, di una mappa 3D di fotoni virtuali; la seconda fase consiste nel rendering della scena utilizzando le informazioni contenute nella mappa, precedentemente creata, per stimare la radianza riflessa sulle superfici della scena. Al contrario dei tradizionali algoritmi di rendering permette di calcolare con buona precisione effetti di luce quali caustiche, riflessioni e surface scattering, e pertanto risulta particolarmente utile nella produzione di immagini con elementi in cristallo o metallo o con materiali translucidi. IUAV dcp corso Disegno digitale
41 Ray Tracing classico Photon path IUAV dcp corso Disegno digitale
42 Photon mapping senza PM fotoni IUAV dcp corso Disegno digitale
43 Surface scattering In fisica la diffusione ottica (dispersione o scattering in inglese) si riferisce a un'ampia classe di fenomeni nei quali onde o particelle vengono deflesse (ovvero cambiano traiettoria) a causa della collisione con altre particelle o onde. La deflessione avviene in maniera disordinata e in buona misura casuale e per questo la diffusione si distingue dalla riflessione e dalla rifrazione, che invece cambiano le traiettorie in maniera regolare e determinata. Sono considerati processi di scattering solo le interazioni che non comportino rilevanti cessioni o guadagni di energia. Un esempio tipico è il colore bianco del latte o della farina o delle nuvole: in questo caso le particelle del latte o della farina, o le goccioline d'acqua delle nuvole, diffondono uniformemente tutte le lunghezze d onda della luce e, poiché il processo si ripete moltissime volte all'interno del mezzo, la direzione di provenienza della luce non è più riconoscibile e il mezzo assume un colore bianco. IUAV dcp corso Disegno digitale
44 Caustiche Le caustiche sono delle entità geometriche formate dalla concentrazione singolare di curve, che modellizzano approssimativamente il comportamento dei raggi luminosi focalizzati da lenti o specchi curvi, che danno luogo a delle zone molto luminose quando incontrano una superficie. IUAV dcp corso Disegno digitale
45 IUAV dcp corso Disegno digitale
46 IUAV dcp corso Disegno digitale
47 L algoritmo di Monte Carlo L algoritmo di Monte Carlo è un metodo numerico che viene utilizzato per trovare le soluzioni di problemi matematici che possono avere molte variabili e che non possono essere risolti facilmente per via diretta. Il metodo è usato per trarre stime attraverso simulazioni. Si basa su un algoritmo che genera una serie di numeri che seguono la distribuzione di probabilità che si suppone abbia il fenomeno da indagare. La simulazione Monte Carlo calcola una serie di realizzazioni possibili del fenomeno in esame, con il peso proprio della probabilità di tale evenienza, cercando di esplorare in modo denso tutto lo spazio dei parametri del fenomeno. Una volta calcolato questo campione casuale, la simulazione esegue delle misure delle grandezze di interesse su tale campione. La simulazione Monte Carlo è ben eseguita se il valore medio di queste misure sulle realizzazioni del sistema converge al valore vero. IUAV dcp corso Disegno digitale
48 L algoritmo di Monte Carlo Non c'è un solo metodo Monte Carlo: il termine descrive invece una classe di approcci molto utilizzati per una larga categoria di problemi. Tuttavia, questi approcci tendono a seguire un particolare schema: Definire un dominio di possibili dati in input. Generare input casuali dal dominio con una certa distribuzione di probabilità determinate. Eseguire un calcolo deterministico utilizzando i dati in ingresso (input). Aggregare i risultati dei calcoli singoli nel risultato finale. Un esempio particolare dell'utilizzo del metodo Monte Carlo è l'impiego del metodo nell'analisi scacchistica. Negli ultimi anni i più forti programmi scacchistici in commercio, implementano delle opzioni d'analisi che utilizzano la analisi Monte Carlo. Per valutare una posizione, si fanno giocare al computer migliaia di partite partendo dalla posizione da analizzare, facendo eseguire al PC mosse del tutto casuali o pseudocasuali (quindi scelte tra le mosse più logiche). La media dei risultati ottenuti in queste partite è un'indicazione plausibile della mossa migliore. Esempio del gioco della battaglia navale. IUAV dcp corso Disegno digitale
49 Ambient occlusion L'ambient occlusion è un metodo di shading che tiene conto dell'attenuazione luminosa in prossimità di volumi occlusi. Diversamente da metodi locali come il Phong shading, l'ambient occlusion è un metodo globale, cioè l'illuminazione di ogni punto è funzione della geometria della scena. Ad ogni modo è un'approssimazione grezza dell'intera illuminazione globale. L'aspetto generato dalla sola ambient occlusion è simile a quello di un oggetto in un giorno nuvoloso. Solitamente l'ambient occlusion viene calcolata tracciando raggi in ogni direzione dalla superficie. I raggi che raggiungono lo sfondo o il "cielo" aumentano la luminosità della superficie, mentre quelli che intercettano un altro oggetto non aggiungono alcuna illuminazione. Di conseguenza i punti circondati da molte altre geometrie vengono renderizzati in ombra, mentre i punti più liberi da ingombri risultano più chiari. Una buona caratteristica di questo metodo di shading è quella di offrire una migliore percezione della forma tridimensionale degli oggetti mostrati. IUAV dcp corso Disegno digitale
50 Ambient occlusion IUAV dcp corso Disegno digitale
51 Ambient occlusion IUAV dcp corso Disegno digitale
52 Ambient occlusion Texture mapping IUAV dcp corso Disegno digitale
53 Texture mapping IUAV dcp corso Disegno digitale
54 Texture mapping Per ciascun vertice del triangolo si assegnano le coordinate u,v nello spazio texture. Una texture è di norma definita in coordinate normalizzate [0,1]x[0,1] nello spazio parametrico della texture. Pertanto si definisce un mapping tra il triangolo e un triangolo della texture. Ciascun vertice (di ciascun triangolo) ha le sue coordinate u,v nello spazio texture. IUAV dcp corso Disegno digitale
55 Texture mapping IUAV dcp corso Disegno digitale
56 Texture mapping IUAV dcp corso Disegno digitale
57 Radiosity Radiosity è una tecnica di illuminazione globale che usa metodi degli elementi finiti per risolvere l equazione di rendering in scene composte da superfici perfettamente diffusive. Usa un meccanismo indiretto: anziché calcolare i percorsi della luce dalla fonte alle superfici, verifica quanta luce può vedere ciascuna porzione di superficie. La radiosity tiene conto solo dei percorsi che partono da una sorgente e vengono riflessi diffusivamente un certo numero di volte (anche zero) prima di colpire l'occhio. Come metodo di rendering, la radiosità venne presentata nel 1984 da ricercatori della Cornell University (C. Goral, K. E. Torrance, D. P. Greenberg and B. Battaile) in un articolo intitolato "Modeling the interaction of light between diffuse surfaces". IUAV dcp corso Disegno digitale
58 Radiosity L'inclusione di calcoli di radiosità nel processo di rendering spesso aggiunge realismo al risultato proprio per il modo con il quale simula il mondo reale. Consideriamo una semplice stanza. L'immagine in alto è stata generata con un normale renderer a illuminazione diretta. Esistono tre tipi di luce nella scena, scelte e collocate nel tentativo di creare la giusta illuminazione: luci spot con ombre (per creare l'illuminazione sul pavimento), luce d'ambiente (senza la quale il resto della stanza sarebbe al buio) e luci omnidirezionali senza ombra (per ridurre la piattezza della luce d'ambiente). L'immagine in basso è stata calcolata con l'uso di un algoritmo di radiosità. C'è una sola sorgente di luce, un'immagine del cielo posta all'esterno della stanza. La differenza è ben visibile. Ombre morbide sono visibili sul pavimento e vari effetti luminosi sono presenti nella stanza. Inoltre, il colore rosso del tappeto viene riflesso sui muri grigi, procurando un effetto realistico. Nessuno di questi effetti è stato creato ad arte, sono tutti frutto dell'algoritmo. IUAV dcp corso Disegno digitale
59 Radiosity La superficie della scena da visualizzare viene divisa in una o più superfici (patch) e l'algoritmo si occupa di una superficie alla volta. Per ogni passata dell'algoritmo viene calcolata la luce che una patch riceve dalle altre. Una parte della luce viene considerata assorbita, il resto viene riflesso nella scena per il prossimo passaggio dell'algoritmo. Uno dei comuni metodi per la risoluzione dell'equazione di radiosità viene definita shooting radiosity e risolve in modo iterativo sparando (da qui il nome) luce da una superficie a ogni passo dell algoritmo. Dopo la prima passata saranno illuminati solo gli oggetti che vedono la sorgente di luce. Dopo la seconda, altre superfici riceveranno la luce a causa del rimbalzo di quest'ultima sulle patch già illuminate. La scena acquisisce luminosità ad ogni passo, fino a raggiungere una stabilità, dovuta al quasi totale assorbimento della luce da parte delle patch. IUAV dcp corso Disegno digitale
60 Radiosity Il metodo si fonda sulla base della radiazione termica, visto che consiste nel calcolo dell'ammontare d'energia trasferito tra superfici. Per poter semplificare il calcolo si suppone che tutte le superfici siano perfettamente diffusive. Le superfici vengono solitamente discretizzate in un numero finito di quadrilateri o triangoli. Dopo questa frammentazione, l'ammontare dell energia trasferita può essere calcolato utilizzando la riflessività conosciuta delle patch, combinata con il fattore di forma delle due patch. Quest ultima quantità, adimensionale, viene calcolata partendo dall'orientamento delle due patch nello spazio 3D e può essere immaginata come la frazione della possibile area emittente della prima patch vista dalla seconda. L equazione è monocromatica e va pertanto ripetuta per ciascun colore primario. L algoritmo di base presenta alcuni problemi di visualizzazione, ad esempio sui bordi degli oggetti, causati da una discretizzazione delle superfici a volte rozza. Per migliorare la discretizzazione si adottano tecniche di discontinuity meshing che usano la conoscenza della visibilità reciproca degli oggetti per generare una discretizzazione più intelligente. IUAV dcp corso Disegno digitale
61 Ray tracing IUAV dcp corso Disegno digitale
62 Ray tracing + soft shadows IUAV dcp corso Disegno digitale
63 Ray tracing + soft shadows + caustics IUAV dcp corso Disegno digitale
64 Ray tracing + soft shadows + caustics + illuminaz. diffusa indiretta IUAV dcp corso Disegno digitale
65 Cinema 4D Esempi di rendering eseguiti con varie tecniche Illuminazione con luce infinita al 100%. Nessuna ombra. Il cubo presenta zone completamente non illuminate. Sembra fluttuare per la mancanza d'ombra riportata sul pavimento. E' evidente la mancanza di punti di riferimento spaziali. IUAV dcp corso Disegno digitale
66 Cinema 4D Esempi di rendering eseguiti con varie tecniche Illuminazione con luce infinita al 100%. Ombra morbida. Il cubo presenta zone non illuminate. L'ombra morbida colloca il cubo spazialmente nonostante la faccia opposta alla luce diretta sia completamente indistinta. IUAV dcp corso Disegno digitale
67 Cinema 4D Esempi di rendering eseguiti con varie tecniche Illuminazione con luce infinita al 100%. Ombra netta.. Il cubo presenta zone completamente non illuminate. L'ombra netta colloca il cubo spazialmente. IUAV dcp corso Disegno digitale
68 Cinema 4D Esempi di rendering eseguiti con varie tecniche Illuminazione con luce infinita al 100%. Ombra area. Il cubo presenta zone completamente non illuminate. L'ombra area colloca il cubo spazialmente e consente un maggiore realismo. Senza l'utilizzo di illuminazione globale sarebbe necessario inserire delle fonti di illuminazione aggiuntive per illuminare le zone in ombra. IUAV dcp corso Disegno digitale
69 Cinema 4D Esempi di rendering eseguiti con varie tecniche Global Illumination: IR. Diffusione: 1, Intensità primaria: 100%. Il cubo risulta ora ben illuminato. Le zone scure sono scomparse. Si nota una leggera ombreggiatura appena sotto il cubo dovuta alla smussatura dello stesso. Come si vede dal risultato, il cielo inserito emette radianza che è moltiplicata dalla Illuminazione Globale verso tutti gli oggetti presenti in scena. IUAV dcp corso Disegno digitale
70 Cinema 4D Esempi di rendering eseguiti con varie tecniche Global Illumination: IR. Diffusione: 2, Int. Prim.: 100%, second. 100% Aumentando la diffusione si aumentano i rimbalzi sulle superfici. Le zone d'ombra vengono schiarite dall'intensità secondaria. L'intensità primaria invece si potrà regolare per aumentare la luminosità delle superfici esposte direttamente alla fonte luminosa. Più si aumenta la diffusione e più l'immagine diverrà chiara IUAV dcp corso Disegno digitale
71 Cinema 4D Esempi di rendering eseguiti con varie tecniche Global Illumination: QMC. Diffusione: 1, Int. Prim.: 100%. 64 campioni Il metodo QMC è più brutale poiché - a differenza della IR che, grazie al prepass calcolava dei singoli punti (chiave di lettura dei chiaro-scuri) - interviene su ogni singolo pixel dell'immagine realizzando di fatto delle zone ombra più accentuate e definite anche se caratterizzate da una certa grana. IUAV dcp corso Disegno digitale
72 Cinema 4D Esempi di rendering eseguiti con varie tecniche Global Illumination: QMC. Diffusione: 1, Int. Prim.: 100%. 64 campioni Anche per il metodo Quasi- Monte Carlo aumentando la profondità diffusione aumenteremo la luminosità globale dell'immagine. IUAV dcp corso Disegno digitale
73 Cinema 4D Esempi di rendering eseguiti con varie tecniche Global Illumination: IR+QMC. Diff.: 2, Int. Prim.: 100%. 128 camp. E' un sistema che offre i vantaggi di entrambe le tecniche: perfetta per esterni per le ombre intense e definite e i piani bene illuminati. IUAV dcp corso Disegno digitale
74 Cinema 4D Esempi di rendering eseguiti con varie tecniche Global Illumination: campioni cielo. Intensità: 100%. 64 campioni. E' da utilizzarsi quando l'illuminazione è demandata solo alla presenza dell'oggetto Shader Cielo di Cinema 4D o all'oggetto Cielo Normale (quello presente in gestione luci). L'illuminazione proviene dall'alto (l oggetto da illuminare deve poggiare su di un piano). IUAV dcp corso Disegno digitale
75 Cinema 4D Esempi di rendering eseguiti con varie tecniche Global Illumination: campioni cielo. Intensità: 200%. 128 campioni. Aumentando l'intensità primaria si illumina maggiormente la scena. Maggiore è il numero dei campioni e minore sarà la grana presente nella scena. IUAV dcp corso Disegno digitale
Luci/Ombre. YAFARAY motore di rendering Open Source. Federico Frittelli aka fredfrittella. SUTURA-studio di progettazione.
 Luci/Ombre YAFARAY motore di rendering Open Source Federico Frittelli aka fredfrittella SUTURA-studio di progettazione LinuxDay, 2010 fredfrittella (SUTURA-studio di progettazione) Luci/Ombre 23 Ottobre
Luci/Ombre YAFARAY motore di rendering Open Source Federico Frittelli aka fredfrittella SUTURA-studio di progettazione LinuxDay, 2010 fredfrittella (SUTURA-studio di progettazione) Luci/Ombre 23 Ottobre
Interazione luce - materia
 Interazione luce - materia 1 Modelli di illuminazione Il modello di illuminazione descrive l interazione tra la luce e gli oggetti della scena Descrive i fattori che determinano il colore di un punto della
Interazione luce - materia 1 Modelli di illuminazione Il modello di illuminazione descrive l interazione tra la luce e gli oggetti della scena Descrive i fattori che determinano il colore di un punto della
IR(3): Illuminazione Globale
 IR(3): Illuminazione Globale Alessandro Martinelli alessandro.martinelli@unipv.it 21 Dicembre 2011 IR(3): Illuminazione Globale Illuminazione e Rendering: Principi di Illuminazione Rendering Real-Time
IR(3): Illuminazione Globale Alessandro Martinelli alessandro.martinelli@unipv.it 21 Dicembre 2011 IR(3): Illuminazione Globale Illuminazione e Rendering: Principi di Illuminazione Rendering Real-Time
Corso di Visione Artificiale. Radiometria. Samuel Rota Bulò
 Corso di Visione Artificiale Radiometria Samuel Rota Bulò Come vediamo? Teorie della visione Teoria emissionista Teoria emissionista (o visione tattile ): l'occhio emette un fascio di raggi che, viaggiando
Corso di Visione Artificiale Radiometria Samuel Rota Bulò Come vediamo? Teorie della visione Teoria emissionista Teoria emissionista (o visione tattile ): l'occhio emette un fascio di raggi che, viaggiando
RADIOSITY TUTORIAL. versione originale su: http://www.mvpny.com/radtutmv/radiositytut1mv.html
 RADIOSITY TUTORIAL La "Profondità Diffusione" che si imposta nella finesta Settaggi Radiosity (render- >parametri rendering->radiosity) stabilisce quante volte una fonte di illuminazione andrà a riflettersi
RADIOSITY TUTORIAL La "Profondità Diffusione" che si imposta nella finesta Settaggi Radiosity (render- >parametri rendering->radiosity) stabilisce quante volte una fonte di illuminazione andrà a riflettersi
Applicazioni 3D avanzate
 Azienda Ospedaliera Card. G. Panico Applicazioni 3D avanzate VR e segmentazione delle articolazioni: campi applicativi Indice Applicazioni 3D avanzate Articolazioni e grandi macchine 1. Definizioni 2.
Azienda Ospedaliera Card. G. Panico Applicazioni 3D avanzate VR e segmentazione delle articolazioni: campi applicativi Indice Applicazioni 3D avanzate Articolazioni e grandi macchine 1. Definizioni 2.
Ottica fisiologica (2): sistemi ottici
 Ottica fisiologica (2): sistemi ottici Corso di Principi e Modelli della Percezione Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it http://boccignone.di.unimi.it/pmp_2014.html
Ottica fisiologica (2): sistemi ottici Corso di Principi e Modelli della Percezione Prof. Giuseppe Boccignone Dipartimento di Informatica Università di Milano boccignone@di.unimi.it http://boccignone.di.unimi.it/pmp_2014.html
Illuminazione avanzata
 Informatica Grafica per le arti Illuminazione avanzata E' possibile applicare una bitmap ad una luce. Una luce a cui e' applicata una bitmap proietta l'immagine associata nello spazio. Marco Gribaudo marcog@di.unito.it
Informatica Grafica per le arti Illuminazione avanzata E' possibile applicare una bitmap ad una luce. Una luce a cui e' applicata una bitmap proietta l'immagine associata nello spazio. Marco Gribaudo marcog@di.unito.it
La propagazione delle onde luminose può essere studiata per mezzo delle equazioni di Maxwell. Tuttavia, nella maggior parte dei casi è possibile
 Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Raccomandazione del Parlamento europeo 18/12/2006 CLASSE PRIMA COMPETENZE ABILITÀ CONOSCENZE. Operare con i numeri
 COMPETENZA CHIAVE MATEMATICA Fonte di legittimazione Raccomandazione del Parlamento europeo 18/12/2006 CLASSE PRIMA COMPETENZE ABILITÀ CONOSCENZE L alunno utilizza il calcolo scritto e mentale con i numeri
COMPETENZA CHIAVE MATEMATICA Fonte di legittimazione Raccomandazione del Parlamento europeo 18/12/2006 CLASSE PRIMA COMPETENZE ABILITÀ CONOSCENZE L alunno utilizza il calcolo scritto e mentale con i numeri
Le luci. L'illuminazione diretta. Informatica Grafica per le arti. L'illuminazione diretta. L'illuminazione diretta. L'illuminazione diretta
 Informatica Grafica per le arti Per poter produrre delle immagini che diano il senso della tridimensionalita', i programmi di grafica 3D si servono di tecniche per simulare l'illuminazione degli oggetti
Informatica Grafica per le arti Per poter produrre delle immagini che diano il senso della tridimensionalita', i programmi di grafica 3D si servono di tecniche per simulare l'illuminazione degli oggetti
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
Il rendering fotorealistico. Conferimento ad oggetti 3D di un aspetto particolarmente fotorealistico
 Il rendering fotorealistico Conferimento ad oggetti 3D di un aspetto particolarmente fotorealistico Rendering fotorealistico Gli oggetti sottoposti a rendering devono essere facce 3D o essere tridimensionali.
Il rendering fotorealistico Conferimento ad oggetti 3D di un aspetto particolarmente fotorealistico Rendering fotorealistico Gli oggetti sottoposti a rendering devono essere facce 3D o essere tridimensionali.
Politecnico di Milano - Facoltà del design - Laboratorio di computer grafica C2 Michele Zannoni Giovanni Gigante Tutorial 05: Materiali in Maya
 Introduzione I materiali conferiscono un maggiore realismo alla scena. Un materiale descrive come un oggetto riflette o trasmette la luce. Le proprietà dei materiali sono strettamente associate a quelle
Introduzione I materiali conferiscono un maggiore realismo alla scena. Un materiale descrive come un oggetto riflette o trasmette la luce. Le proprietà dei materiali sono strettamente associate a quelle
ScuolaSI computer grafica 3d
 ScuolaSI computer grafica 3d pagina stampata dal sito ScuolaSI http://www.scuolasi.it pubblicato il 22/04/2011 Grafica - La computer grafica 3D è un ramo della computer grafica che basa la creazione di
ScuolaSI computer grafica 3d pagina stampata dal sito ScuolaSI http://www.scuolasi.it pubblicato il 22/04/2011 Grafica - La computer grafica 3D è un ramo della computer grafica che basa la creazione di
Università degli studi di Messina facoltà di Scienze mm ff nn. Progetto Lauree Scientifiche (FISICA) Prisma ottico
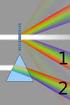
 Università degli studi di Messina facoltà di Scienze mm ff nn Progetto Lauree Scientifiche (FISICA) Prisma ottico Parte teorica Fenomenologia di base La luce che attraversa una finestra, un foro, una fenditura,
Università degli studi di Messina facoltà di Scienze mm ff nn Progetto Lauree Scientifiche (FISICA) Prisma ottico Parte teorica Fenomenologia di base La luce che attraversa una finestra, un foro, una fenditura,
Spline Nurbs. IUAV Disegno Digitale. Camillo Trevisan
 Spline Nurbs IUAV Disegno Digitale Camillo Trevisan Spline e Nurbs Negli anni 70 e 80 del secolo scorso nelle aziende si è iniziata a sentire l esigenza di concentrare in un unica rappresentazione gestita
Spline Nurbs IUAV Disegno Digitale Camillo Trevisan Spline e Nurbs Negli anni 70 e 80 del secolo scorso nelle aziende si è iniziata a sentire l esigenza di concentrare in un unica rappresentazione gestita
Fisica II - CdL Chimica. Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici
 Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici Ottica geometrica In ottica geometrica si analizza la formazione di immagini assumendo che la luce si propaghi in modo rettilineo
Formazione immagini Superfici rifrangenti Lenti sottili Strumenti ottici Ottica geometrica In ottica geometrica si analizza la formazione di immagini assumendo che la luce si propaghi in modo rettilineo
Librerie digitali. Video. Gestione di video. Caratteristiche dei video. Video. Metadati associati ai video. Metadati associati ai video
 Video Librerie digitali Gestione di video Ogni filmato è composto da più parti Video Audio Gestito come visto in precedenza Trascrizione del testo, identificazione di informazioni di interesse Testo Utile
Video Librerie digitali Gestione di video Ogni filmato è composto da più parti Video Audio Gestito come visto in precedenza Trascrizione del testo, identificazione di informazioni di interesse Testo Utile
Il campionamento. La digitalizzazione. Teoria e pratica. La rappresentazione digitale delle immagini. La rappresentazione digitale delle immagini
 ACQUISIZIONE ED ELABORAZIONE DELLE IMMAGINI Teoria e pratica La digitalizzazione La digitalizzazione di oggetti legati a fenomeni di tipo analogico, avviene attraverso due parametri fondamentali: Il numero
ACQUISIZIONE ED ELABORAZIONE DELLE IMMAGINI Teoria e pratica La digitalizzazione La digitalizzazione di oggetti legati a fenomeni di tipo analogico, avviene attraverso due parametri fondamentali: Il numero
Le texture. Informatica Grafica I. Le texture. Le texture. Le texture. Le texture. Le texture
 Informatica Grafica I Per rendere realistici gli oggetti modellati occorre definire accuratamente l'aspetto delle loro superfici. Il modo piu' semplice consiste nel sovrapporre immagini alle superfici.
Informatica Grafica I Per rendere realistici gli oggetti modellati occorre definire accuratamente l'aspetto delle loro superfici. Il modo piu' semplice consiste nel sovrapporre immagini alle superfici.
Le ombre in OpenGl. Daniele Varin LS Ing. Informatica Corso di Elementi di Grafica Digitale http://varindaniele.altervista.org
 Le ombre in OpenGl Daniele Varin LS Ing. Informatica Corso di Elementi di Grafica Digitale http://varindaniele.altervista.org Punto di partenza In OpenGl le luci non proiettano ombre 2 Perché si introducono
Le ombre in OpenGl Daniele Varin LS Ing. Informatica Corso di Elementi di Grafica Digitale http://varindaniele.altervista.org Punto di partenza In OpenGl le luci non proiettano ombre 2 Perché si introducono
All interno dei colori primari e secondari, abbiamo tre coppie di colori detti COMPLEMENTARI.
 Teoria del colore La teoria dei colori Gli oggetti e gli ambienti che ci circondano sono in gran parte colorati. Ciò dipende dal fatto che la luce si diffonde attraverso onde di diversa lunghezza: ad ogni
Teoria del colore La teoria dei colori Gli oggetti e gli ambienti che ci circondano sono in gran parte colorati. Ciò dipende dal fatto che la luce si diffonde attraverso onde di diversa lunghezza: ad ogni
Sommario Ottica geometrica... 2 Principio di Huygens-Fresnel... 4 Oggetto e immagine... 6 Immagine reale... 7 Immagine virtuale...
 IMMAGINI Sommario Ottica geometrica... 2 Principio di Huygens-Fresnel... 4 Oggetto e immagine... 6 Immagine reale... 7 Immagine virtuale... 9 Immagini - 1/11 Ottica geometrica È la branca dell ottica che
IMMAGINI Sommario Ottica geometrica... 2 Principio di Huygens-Fresnel... 4 Oggetto e immagine... 6 Immagine reale... 7 Immagine virtuale... 9 Immagini - 1/11 Ottica geometrica È la branca dell ottica che
28/05/2009. La luce e le sue illusioni ottiche
 La luce e le sue illusioni ottiche Cosa si intende per raggio luminoso? Immagina di osservare ad una distanza abbastanza elevata una sorgente di luce... il fronte d onda potrà esser approssimato ad un
La luce e le sue illusioni ottiche Cosa si intende per raggio luminoso? Immagina di osservare ad una distanza abbastanza elevata una sorgente di luce... il fronte d onda potrà esser approssimato ad un
Introduzione all analisi dei segnali digitali.
 Introduzione all analisi dei segnali digitali. Lezioni per il corso di Laboratorio di Fisica IV Isidoro Ferrante A.A. 2001/2002 1 Segnali analogici Si dice segnale la variazione di una qualsiasi grandezza
Introduzione all analisi dei segnali digitali. Lezioni per il corso di Laboratorio di Fisica IV Isidoro Ferrante A.A. 2001/2002 1 Segnali analogici Si dice segnale la variazione di una qualsiasi grandezza
Corso di Visione Artificiale. Immagini digitali. Samuel Rota Bulò
 Corso di Visione Artificiale Immagini digitali Samuel Rota Bulò Immagini digitali Un immagine viene generata dalla combinazione di una sorgente di energia e la riflessione o assorbimento di energia da
Corso di Visione Artificiale Immagini digitali Samuel Rota Bulò Immagini digitali Un immagine viene generata dalla combinazione di una sorgente di energia e la riflessione o assorbimento di energia da
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1
 LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
Capitolo 2 Caratteristiche delle sorgenti luminose In questo capitolo sono descritte alcune grandezze utili per caratterizzare le sorgenti luminose.
 Capitolo 2 Caratteristiche delle sorgenti luminose In questo capitolo sono descritte alcune grandezze utili per caratterizzare le sorgenti luminose. 2.1 Spettro di emissione Lo spettro di emissione di
Capitolo 2 Caratteristiche delle sorgenti luminose In questo capitolo sono descritte alcune grandezze utili per caratterizzare le sorgenti luminose. 2.1 Spettro di emissione Lo spettro di emissione di
Introduzione alla Computer Graphics
 Introduzione alla Computer Graphics Informatica Grafica CdLS a ciclo unico in Ingegneria Edile-Architettura a.a. 2008/09 Computer Graphics e Image Processing Image processing Insieme di teorie ed algoritmi
Introduzione alla Computer Graphics Informatica Grafica CdLS a ciclo unico in Ingegneria Edile-Architettura a.a. 2008/09 Computer Graphics e Image Processing Image processing Insieme di teorie ed algoritmi
LA GRAFICA E LA GEOMETRIA OPERATIVA
 LA GRAFICA E LA GEOMETRIA OPERATIVA La geometria operativa, contrariamente a quella descrittiva basata sulle regole per la rappresentazione delle forme geometriche, prende in considerazione lo spazio racchiuso
LA GRAFICA E LA GEOMETRIA OPERATIVA La geometria operativa, contrariamente a quella descrittiva basata sulle regole per la rappresentazione delle forme geometriche, prende in considerazione lo spazio racchiuso
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
SPC e distribuzione normale con Access
 SPC e distribuzione normale con Access In questo articolo esamineremo una applicazione Access per il calcolo e la rappresentazione grafica della distribuzione normale, collegata con tabelle di Clienti,
SPC e distribuzione normale con Access In questo articolo esamineremo una applicazione Access per il calcolo e la rappresentazione grafica della distribuzione normale, collegata con tabelle di Clienti,
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
Esecuzione: Ho indossato gli occhiali ( che funzionano come un prisma di vetro), quindi ho osservato una fonte di luce
 Esperimento 1: Dispersione della luce Materiali e strumenti: Occhiali speciali, luce Esecuzione: Ho indossato gli occhiali ( che funzionano come un prisma di vetro), quindi ho osservato una fonte di luce
Esperimento 1: Dispersione della luce Materiali e strumenti: Occhiali speciali, luce Esecuzione: Ho indossato gli occhiali ( che funzionano come un prisma di vetro), quindi ho osservato una fonte di luce
Laboratorio di Ottica, Spettroscopia, Astrofisica
 Università degli Studi di Palermo Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Fisica Progetto Lauree Scientifiche Laboratorio di Ottica, Spettroscopia, Astrofisica Antonio Maggio
Università degli Studi di Palermo Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea in Fisica Progetto Lauree Scientifiche Laboratorio di Ottica, Spettroscopia, Astrofisica Antonio Maggio
Nuovi toner HP ColorSphere
 Nuovi toner HP ColorSphere Nuove tecnologie e una speciale formulazione, frutto di oltre 20 anni di impegno nell'innovazione, garantiscono ai clienti HP risultati ottimali nella stampa laser a colori Troppo
Nuovi toner HP ColorSphere Nuove tecnologie e una speciale formulazione, frutto di oltre 20 anni di impegno nell'innovazione, garantiscono ai clienti HP risultati ottimali nella stampa laser a colori Troppo
Fisica II - CdL Chimica. La natura della luce Ottica geometrica Velocità della luce Dispersione Fibre ottiche
 La natura della luce Ottica geometrica Velocità della luce Dispersione Fibre ottiche La natura della luce Teoria corpuscolare (Newton) Teoria ondulatoria: proposta già al tempo di Newton, ma scartata perchè
La natura della luce Ottica geometrica Velocità della luce Dispersione Fibre ottiche La natura della luce Teoria corpuscolare (Newton) Teoria ondulatoria: proposta già al tempo di Newton, ma scartata perchè
Laboratorio di Progettazione 3M B. Fisica Tecnica. Calcolo del Fattore medio di luce diurna
 Laboratorio di Progettazione 3M B Fisica Tecnica Calcolo del Fattore medio di luce diurna Università degli Studi di Roma Tre Facoltà d Architettura A.A. 2011-2012 Il fattore di luce diurna Il Fattore di
Laboratorio di Progettazione 3M B Fisica Tecnica Calcolo del Fattore medio di luce diurna Università degli Studi di Roma Tre Facoltà d Architettura A.A. 2011-2012 Il fattore di luce diurna Il Fattore di
Animazioni 3D. Informatica Grafica I. Le basi dell'animazione 3D. Le basi dell'animazione 3D. Le basi dell'animazione 3D. Le basi dell'animazione 3D
 Informatica Grafica I Marco Gribaudo marcog@di.unito.it Animazioni 3D L'animazione 3D si basa sugli stessi principi dell'animazione tradizionale. Il filmato viene realizzato attraverso una sequenza di
Informatica Grafica I Marco Gribaudo marcog@di.unito.it Animazioni 3D L'animazione 3D si basa sugli stessi principi dell'animazione tradizionale. Il filmato viene realizzato attraverso una sequenza di
INFORMATICA E GRAFICA PER IL WEB
 INFORMATICA E GRAFICA PER IL WEB Psicologia e comunicazione A.A. 2013/2014 Università degli studi Milano-Bicocca docente: Diana Quarti INFORMATICA E GRAFICA PER IL WEB A.A. 2013/2014 docente: Diana Quarti
INFORMATICA E GRAFICA PER IL WEB Psicologia e comunicazione A.A. 2013/2014 Università degli studi Milano-Bicocca docente: Diana Quarti INFORMATICA E GRAFICA PER IL WEB A.A. 2013/2014 docente: Diana Quarti
www.andreatorinesi.it
 La lunghezza focale Lunghezza focale Si definisce lunghezza focale la distanza tra il centro ottico dell'obiettivo (a infinito ) e il piano su cui si forma l'immagine (nel caso del digitale, il sensore).
La lunghezza focale Lunghezza focale Si definisce lunghezza focale la distanza tra il centro ottico dell'obiettivo (a infinito ) e il piano su cui si forma l'immagine (nel caso del digitale, il sensore).
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
Misure di base su una carta. Calcoli di distanze
 Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
I CIRCUITI ELETTRICI. Prima di tutto occorre mettersi d accordo anche sui nomi di alcune parti dei circuiti stessi.
 I CIRCUITI ELETTRICI Prima di tutto occorre mettersi d accordo anche sui nomi di alcune parti dei circuiti stessi. Definiamo ramo un tratto di circuito senza diramazioni (tratto evidenziato in rosso nella
I CIRCUITI ELETTRICI Prima di tutto occorre mettersi d accordo anche sui nomi di alcune parti dei circuiti stessi. Definiamo ramo un tratto di circuito senza diramazioni (tratto evidenziato in rosso nella
Database. Si ringrazia Marco Bertini per le slides
 Database Si ringrazia Marco Bertini per le slides Obiettivo Concetti base dati e informazioni cos è un database terminologia Modelli organizzativi flat file database relazionali Principi e linee guida
Database Si ringrazia Marco Bertini per le slides Obiettivo Concetti base dati e informazioni cos è un database terminologia Modelli organizzativi flat file database relazionali Principi e linee guida
PROGETTO EM.MA PRESIDIO
 PROGETTO EM.MA PRESIDIO di PIACENZA Bentornati Il quadro di riferimento di matematica : INVALSI e TIMSS A CONFRONTO LE PROVE INVALSI Quadro di riferimento per la valutazione Quadro di riferimento per i
PROGETTO EM.MA PRESIDIO di PIACENZA Bentornati Il quadro di riferimento di matematica : INVALSI e TIMSS A CONFRONTO LE PROVE INVALSI Quadro di riferimento per la valutazione Quadro di riferimento per i
Lo spessimetro ( a cura di Elena Pizzinini)
 Lo spessimetro ( a cura di Elena Pizzinini) 1) Che cos è? Lo spessivetro è uno strumento (brevettato dalla ditta Saint Gobain) dal funzionamento piuttosto semplice che permette di misurare lo spessore
Lo spessimetro ( a cura di Elena Pizzinini) 1) Che cos è? Lo spessivetro è uno strumento (brevettato dalla ditta Saint Gobain) dal funzionamento piuttosto semplice che permette di misurare lo spessore
Ulteriori problemi di fisica e matematica
 Facoltà di Medicina e Chirurgia Università degli Studi di Firenze Agosto 2010 Ulteriori problemi di fisica e matematica Giovanni Romano Perché un raggio di luce proveniente dal Sole e fatto passare attraverso
Facoltà di Medicina e Chirurgia Università degli Studi di Firenze Agosto 2010 Ulteriori problemi di fisica e matematica Giovanni Romano Perché un raggio di luce proveniente dal Sole e fatto passare attraverso
ISTITUTO COMPRENSIVO MONTEGROTTO TERME SCUOLA PRIMARIA DISCIPLINA: MATEMATICA - CLASSE PRIMA OBIETTIVI DI APPRENDIMENTO
 PRIMA DELLA DISCIPLINA: MATEMATICA - CLASSE PRIMA L alunno si muove con sicurezza nel calcolo scritto e mentale con i numeri naturali. Legge e comprende testi che coinvolgono aspetti logici e matematici.
PRIMA DELLA DISCIPLINA: MATEMATICA - CLASSE PRIMA L alunno si muove con sicurezza nel calcolo scritto e mentale con i numeri naturali. Legge e comprende testi che coinvolgono aspetti logici e matematici.
Le immagini digitali. Le immagini digitali. Caterina Balletti. Caterina Balletti. Immagini grafiche. Trattamento di immagini digitali.
 1 Le immagini digitali Le immagini digitali Università IUAV di venezia Trattamento di immagini digitali immagini grafiche immagini raster immagini vettoriali acquisizione trattamento geometrico trattamento
1 Le immagini digitali Le immagini digitali Università IUAV di venezia Trattamento di immagini digitali immagini grafiche immagini raster immagini vettoriali acquisizione trattamento geometrico trattamento
Radiazione elettromagnetica
 Radiazione elettromagnetica Un onda e.m. e un onda trasversa cioe si propaga in direzione ortogonale alle perturbazioni ( campo elettrico e magnetico) che l hanno generata. Nel vuoto la velocita di propagazione
Radiazione elettromagnetica Un onda e.m. e un onda trasversa cioe si propaga in direzione ortogonale alle perturbazioni ( campo elettrico e magnetico) che l hanno generata. Nel vuoto la velocita di propagazione
Processo di rendering
 Processo di rendering Trasformazioni di vista Trasformazioni di vista Il processo di visione in tre dimensioni Le trasformazioni di proiezione 2 Rendering nello spazio 2D Il processo di rendering (visualizzazione)
Processo di rendering Trasformazioni di vista Trasformazioni di vista Il processo di visione in tre dimensioni Le trasformazioni di proiezione 2 Rendering nello spazio 2D Il processo di rendering (visualizzazione)
A.S. 2012-1013 CLASSE PRIMA SCUOLA PRIMARIA D ISTITUTO COMPETENZA CHIAVE EUROPEA DISCIPLINA
 ISTITUTO COMPRENSIVO STATALE di Scuola dell Infanzia, Scuola Primaria e Scuola Secondaria di 1 grado San Giovanni Teatino (CH) CURRICOLO A.S. 2012-1013 CLASSE PRIMA SCUOLA PRIMARIA OBIETTIVI DI Sviluppa
ISTITUTO COMPRENSIVO STATALE di Scuola dell Infanzia, Scuola Primaria e Scuola Secondaria di 1 grado San Giovanni Teatino (CH) CURRICOLO A.S. 2012-1013 CLASSE PRIMA SCUOLA PRIMARIA OBIETTIVI DI Sviluppa
Indice. pagina 2 di 10
 LEZIONE PROGETTAZIONE ORGANIZZATIVA DOTT.SSA ROSAMARIA D AMORE Indice PROGETTAZIONE ORGANIZZATIVA---------------------------------------------------------------------------------------- 3 LA STRUTTURA
LEZIONE PROGETTAZIONE ORGANIZZATIVA DOTT.SSA ROSAMARIA D AMORE Indice PROGETTAZIONE ORGANIZZATIVA---------------------------------------------------------------------------------------- 3 LA STRUTTURA
Il colore. IGEA 2006-07 7 febbraio 2007
 Il colore IGEA 2006-07 7 febbraio 2007 La luce Radiazione elettromagnetica 380 740 nanometri (790 480 THz) Percezione della luce /1 Organi sensoriali: Bastoncelli Molto sensibili (anche a un solo fotone:
Il colore IGEA 2006-07 7 febbraio 2007 La luce Radiazione elettromagnetica 380 740 nanometri (790 480 THz) Percezione della luce /1 Organi sensoriali: Bastoncelli Molto sensibili (anche a un solo fotone:
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Gestione della memoria centrale
 Gestione della memoria centrale Un programma per essere eseguito deve risiedere in memoria principale e lo stesso vale per i dati su cui esso opera In un sistema multitasking molti processi vengono eseguiti
Gestione della memoria centrale Un programma per essere eseguito deve risiedere in memoria principale e lo stesso vale per i dati su cui esso opera In un sistema multitasking molti processi vengono eseguiti
Prof. Gian Piero Pugliese Lezioni di Fisica
 Prof. Gian Piero Pugliese Lezioni di Fisica Il miraggio Fin dai tempi più remoti, il miraggio è stato un fenomeno che ha destano nell uomo paura e al tempo stesso meraviglia, proprio perché non conosciuto
Prof. Gian Piero Pugliese Lezioni di Fisica Il miraggio Fin dai tempi più remoti, il miraggio è stato un fenomeno che ha destano nell uomo paura e al tempo stesso meraviglia, proprio perché non conosciuto
Strutturazione logica dei dati: i file
 Strutturazione logica dei dati: i file Informazioni più complesse possono essere composte a partire da informazioni elementari Esempio di una banca: supponiamo di voler mantenere all'interno di un computer
Strutturazione logica dei dati: i file Informazioni più complesse possono essere composte a partire da informazioni elementari Esempio di una banca: supponiamo di voler mantenere all'interno di un computer
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
Amplificatori Audio di Potenza
 Amplificatori Audio di Potenza Un amplificatore, semplificando al massimo, può essere visto come un oggetto in grado di aumentare il livello di un segnale. Ha quindi, generalmente, due porte: un ingresso
Amplificatori Audio di Potenza Un amplificatore, semplificando al massimo, può essere visto come un oggetto in grado di aumentare il livello di un segnale. Ha quindi, generalmente, due porte: un ingresso
Tutorial 3DRoom. 3DRoom
 Il presente paragrafo tratta il rilievo di interni ed esterni eseguito con. L utilizzo del software è molto semplice ed immediato. Dopo aver fatto uno schizzo del vano si passa all inserimento delle diagonali
Il presente paragrafo tratta il rilievo di interni ed esterni eseguito con. L utilizzo del software è molto semplice ed immediato. Dopo aver fatto uno schizzo del vano si passa all inserimento delle diagonali
OTTICA TORNA ALL'INDICE
 OTTICA TORNA ALL'INDICE La luce è energia che si propaga in linea retta da un corpo, sorgente, in tutto lo spazio ad esso circostante. Le direzioni di propagazione sono dei raggi che partono dal corpo
OTTICA TORNA ALL'INDICE La luce è energia che si propaga in linea retta da un corpo, sorgente, in tutto lo spazio ad esso circostante. Le direzioni di propagazione sono dei raggi che partono dal corpo
Laboratorio di Fisica 3 Ottica 2. Studenti: Buoni - Giambastiani - Leidi Gruppo: G09
 Laboratorio di Fisica 3 Ottica 2 Studenti: Buoni - Giambastiani - Leidi Gruppo: G09 24 febbraio 2015 1 Lunghezza d onda di un laser He-Ne 1.1 Scopo dell esperienza Lo scopo dell esperienza è quello di
Laboratorio di Fisica 3 Ottica 2 Studenti: Buoni - Giambastiani - Leidi Gruppo: G09 24 febbraio 2015 1 Lunghezza d onda di un laser He-Ne 1.1 Scopo dell esperienza Lo scopo dell esperienza è quello di
SISTEMI DI NUMERAZIONE E CODICI
 SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
SISTEMI DI NUMERAZIONE E CODICI Il Sistema di Numerazione Decimale Il sistema decimale o sistema di numerazione a base dieci usa dieci cifre, dette cifre decimali, da O a 9. Il sistema decimale è un sistema
ELABORAZIONE DI DATI TRIDIMENSIONALI - RELAZIONE HOMEWORK 2
 DAVIDE ZANIN 1035601 ELABORAZIONE DI DATI TRIDIMENSIONALI - RELAZIONE HOMEWORK 2 SOMMARIO Elaborazione di dati tridimensionali - Relazione Homework 2... 1 Obiettivo... 2 Descrizione della procedura seguita...
DAVIDE ZANIN 1035601 ELABORAZIONE DI DATI TRIDIMENSIONALI - RELAZIONE HOMEWORK 2 SOMMARIO Elaborazione di dati tridimensionali - Relazione Homework 2... 1 Obiettivo... 2 Descrizione della procedura seguita...
3D e Realtà Virtuale
 3D e Realtà Virtuale Modello 3D La costruzione di un modello 3D, così come la realizzazione di un plastico tradizionale, necessita di grande precisione e attenzione conoscitiva. Tale modello convoglia
3D e Realtà Virtuale Modello 3D La costruzione di un modello 3D, così come la realizzazione di un plastico tradizionale, necessita di grande precisione e attenzione conoscitiva. Tale modello convoglia
Capitolo 4.2. Analisi tecnica: Fibonacci
 1 Capitolo 4.2 Analisi tecnica: Fibonacci 0 Contenuti ANALISI TECNICA: FIBONACCI L analisi di Fibonacci mira a identificare i potenziali livelli di supporto e di resistenza futuri basati sui trend dei
1 Capitolo 4.2 Analisi tecnica: Fibonacci 0 Contenuti ANALISI TECNICA: FIBONACCI L analisi di Fibonacci mira a identificare i potenziali livelli di supporto e di resistenza futuri basati sui trend dei
V= R*I. LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro.
 LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro. PREMESSA: Anche intuitivamente dovrebbe a questo punto essere ormai chiaro
LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro. PREMESSA: Anche intuitivamente dovrebbe a questo punto essere ormai chiaro
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Spettrofotometria. Le onde luminose consistono in campi magnetici e campi elettrici oscillanti, fra loro perpendicolari.
 Spettrofotometria. Con questo termine si intende l utilizzo della luce nella misura delle concentrazioni chimiche. Per affrontare questo argomento dovremo conoscere: Natura e proprietà della luce. Cosa
Spettrofotometria. Con questo termine si intende l utilizzo della luce nella misura delle concentrazioni chimiche. Per affrontare questo argomento dovremo conoscere: Natura e proprietà della luce. Cosa
LEZIONI CON I PAD Docente scuola secondaria IC Moglia Carla Casareggio Classi seconde 2014/2015 Proprietà triangoli e quadrilateri con Sketchometry
 LEZIONI CON I PAD Docente scuola secondaria IC Moglia Carla Casareggio Classi seconde 2014/2015 Proprietà triangoli e quadrilateri con Sketchometry La costruzione di figure geometriche al computer con
LEZIONI CON I PAD Docente scuola secondaria IC Moglia Carla Casareggio Classi seconde 2014/2015 Proprietà triangoli e quadrilateri con Sketchometry La costruzione di figure geometriche al computer con
Parte Seconda La Misura
 Il procedimento di misura è uno dei procedimenti fondamentali della conoscenza scientifica in quanto consente di descrivere quantitativamente una proprietà di un oggetto o una caratteristica di un fenomeno.
Il procedimento di misura è uno dei procedimenti fondamentali della conoscenza scientifica in quanto consente di descrivere quantitativamente una proprietà di un oggetto o una caratteristica di un fenomeno.
19 Il campo elettrico - 3. Le linee del campo elettrico
 Moto di una carica in un campo elettrico uniforme Il moto di una particella carica in un campo elettrico è in generale molto complesso; il problema risulta più semplice se il campo elettrico è uniforme,
Moto di una carica in un campo elettrico uniforme Il moto di una particella carica in un campo elettrico è in generale molto complesso; il problema risulta più semplice se il campo elettrico è uniforme,
TRAGUARDI PER LO SVILUPPO DELLE COMPETENZE AL TERMINE DELLA SCUOLA PRIMARIA
 SCUOLA PRIMARIA DI CORTE FRANCA MATEMATICA CLASSE QUINTA TRAGUARDI PER LO SVILUPPO DELLE COMPETENZE AL TERMINE DELLA SCUOLA PRIMARIA L ALUNNO SVILUPPA UN ATTEGGIAMENTO POSITIVO RISPETTO ALLA MATEMATICA,
SCUOLA PRIMARIA DI CORTE FRANCA MATEMATICA CLASSE QUINTA TRAGUARDI PER LO SVILUPPO DELLE COMPETENZE AL TERMINE DELLA SCUOLA PRIMARIA L ALUNNO SVILUPPA UN ATTEGGIAMENTO POSITIVO RISPETTO ALLA MATEMATICA,
Calcolo del Valore Attuale Netto (VAN)
 Calcolo del Valore Attuale Netto (VAN) Il calcolo del valore attuale netto (VAN) serve per determinare la redditività di un investimento. Si tratta di utilizzare un procedimento che può consentirci di
Calcolo del Valore Attuale Netto (VAN) Il calcolo del valore attuale netto (VAN) serve per determinare la redditività di un investimento. Si tratta di utilizzare un procedimento che può consentirci di
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
I motori di ricerca. Che cosa sono. Stefania Marrara Corso di Sistemi Informativi
 I motori di ricerca Stefania Marrara Corso di Sistemi Informativi a.a 2002/2003 Che cosa sono Un motore di ricerca è uno strumento per mezzo del quale è possibile ricercare alcuni termini (parole) all
I motori di ricerca Stefania Marrara Corso di Sistemi Informativi a.a 2002/2003 Che cosa sono Un motore di ricerca è uno strumento per mezzo del quale è possibile ricercare alcuni termini (parole) all
 1 Il Laser 2 Il laser quindi non è altro che una radiazione elettromagnetica, ovvero un'onda luminosa, avente particolari caratteristiche: deve essere composta da luce di una sola frequenza (monocromaticità).
1 Il Laser 2 Il laser quindi non è altro che una radiazione elettromagnetica, ovvero un'onda luminosa, avente particolari caratteristiche: deve essere composta da luce di una sola frequenza (monocromaticità).
INDAGINI TERMOGRAFICHE
 INDAGINI TERMOGRAFICHE INDAGO SRL Via Sestri 15/4 16154 GENOVA SESTRI Sede Operativa: Corso Italia 26-18012 Bordighera (IM) Tel/Fax: 0184-998536 Mail: info@indagosrl.it - indago@pec.it La termografia Per
INDAGINI TERMOGRAFICHE INDAGO SRL Via Sestri 15/4 16154 GENOVA SESTRI Sede Operativa: Corso Italia 26-18012 Bordighera (IM) Tel/Fax: 0184-998536 Mail: info@indagosrl.it - indago@pec.it La termografia Per
ESEMPIO 1: eseguire il complemento a 10 di 765
 COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
COMPLEMENTO A 10 DI UN NUMERO DECIMALE Sia dato un numero N 10 in base 10 di n cifre. Il complemento a 10 di tale numero (N ) si ottiene sottraendo il numero stesso a 10 n. ESEMPIO 1: eseguire il complemento
Lunghezza ocale. Donato Di Bello
 F Lunghezza ocale Donato Di Bello Cinepresa, telecamera, macchina fotografica: tre strumenti tecnologici che utilizziamo per registrare la realtà intorno a noi o per trasformare in immagini la nostra fantasia.
F Lunghezza ocale Donato Di Bello Cinepresa, telecamera, macchina fotografica: tre strumenti tecnologici che utilizziamo per registrare la realtà intorno a noi o per trasformare in immagini la nostra fantasia.
Analisi e diagramma di Pareto
 Analisi e diagramma di Pareto L'analisi di Pareto è una metodologia statistica utilizzata per individuare i problemi più rilevanti nella situazione in esame e quindi le priorità di intervento. L'obiettivo
Analisi e diagramma di Pareto L'analisi di Pareto è una metodologia statistica utilizzata per individuare i problemi più rilevanti nella situazione in esame e quindi le priorità di intervento. L'obiettivo
La lente singola rimane ancora in uso nelle macchine più economiche e, entro certi limiti, dà dei risultati accettabili.
 O.Welles usa in "Quarto potere" in modo magistrale la Profondità di Campo, in questo modo evita gli stacchi e un oggetto inquadrato riesce a mettere a ''fuoco'' anche ciò che c'è dietro - stesso uso magistrale
O.Welles usa in "Quarto potere" in modo magistrale la Profondità di Campo, in questo modo evita gli stacchi e un oggetto inquadrato riesce a mettere a ''fuoco'' anche ciò che c'è dietro - stesso uso magistrale
Percorsi, strategie e geometrie in gioco Complementi e spunti di lavoro Primaria e Secondaria Inferiore
 Percorsi, strategie e geometrie in gioco Complementi e spunti di lavoro Primaria e Secondaria Inferiore In queste note troverete suggerimenti e osservazioni per attività che traggono spunto dal problema
Percorsi, strategie e geometrie in gioco Complementi e spunti di lavoro Primaria e Secondaria Inferiore In queste note troverete suggerimenti e osservazioni per attività che traggono spunto dal problema
PROGRAMMA OPERATIVO NAZIONALE
 PROGRAMMA OPERATIVO NAZIONALE Fondo Sociale Europeo "Competenze per lo Sviluppo" Obiettivo C-Azione C1: Dall esperienza alla legge: la Fisica in Laboratorio Ottica geometrica Sommario 1) Cos è la luce
PROGRAMMA OPERATIVO NAZIONALE Fondo Sociale Europeo "Competenze per lo Sviluppo" Obiettivo C-Azione C1: Dall esperienza alla legge: la Fisica in Laboratorio Ottica geometrica Sommario 1) Cos è la luce
Creare superfici. Le superfici. Informatica Grafica ][ Le superfici. Le superfici. Le superfici. Le superfici
![Creare superfici. Le superfici. Informatica Grafica ][ Le superfici. Le superfici. Le superfici. Le superfici Creare superfici. Le superfici. Informatica Grafica ][ Le superfici. Le superfici. Le superfici. Le superfici](/thumbs/27/10902677.jpg) Informatica Grafica ][ Creare superfici Come visto nel corso di IG1, gli oggetti 3D vengono memorizzati attraverso le superfici che li delimitano. In Maya esistono 3 diverse classi di superfici: Marco
Informatica Grafica ][ Creare superfici Come visto nel corso di IG1, gli oggetti 3D vengono memorizzati attraverso le superfici che li delimitano. In Maya esistono 3 diverse classi di superfici: Marco
Domande a scelta multipla 1
 Domande a scelta multipla Domande a scelta multipla 1 Rispondete alle domande seguenti, scegliendo tra le alternative proposte. Cercate di consultare i suggerimenti solo in caso di difficoltà. Dopo l elenco
Domande a scelta multipla Domande a scelta multipla 1 Rispondete alle domande seguenti, scegliendo tra le alternative proposte. Cercate di consultare i suggerimenti solo in caso di difficoltà. Dopo l elenco
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Informatica grafica e Multimedialità. 4 Immagini grafiche
 Immagini raster e vettoriali Le immagini grafiche si distinguono in due classi differenti: immagini raster e immagini vettoriali. Le immagini raster, dette anche pittoriche o pixel-oriented, dividono l
Immagini raster e vettoriali Le immagini grafiche si distinguono in due classi differenti: immagini raster e immagini vettoriali. Le immagini raster, dette anche pittoriche o pixel-oriented, dividono l
CORRENTE ELETTRICA Intensità e densità di corrente sistema formato da due conduttori carichi a potenziali V 1 e V 2 isolati tra loro V 2 > V 1 V 2
 COENTE ELETTICA Intensità e densità di corrente sistema formato da due conduttori carichi a potenziali V 1 e V isolati tra loro V > V 1 V V 1 Li colleghiamo mediante un conduttore Fase transitoria: sotto
COENTE ELETTICA Intensità e densità di corrente sistema formato da due conduttori carichi a potenziali V 1 e V isolati tra loro V > V 1 V V 1 Li colleghiamo mediante un conduttore Fase transitoria: sotto
Rendering ed illuminazione
 Rendering ed illuminazione Dove si introduce un metodo per ottenere una immagine a partire da una descrizione degli oggetti tridimensionali e si presenta la legge fondamentale che governa l illuminazione.
Rendering ed illuminazione Dove si introduce un metodo per ottenere una immagine a partire da una descrizione degli oggetti tridimensionali e si presenta la legge fondamentale che governa l illuminazione.
RAPPRESENTAZIONE GRAFICA E ANALISI DEI DATI SPERIMENTALI CON EXCEL
 RAPPRESENTAZIONE GRAFICA E ANALISI DEI DATI SPERIMENTALI CON EXCEL 1 RAPPRESENTAZIONE GRAFICA Per l analisi dati con Excel si fa riferimento alla versione 2007 di Office, le versioni successive non differiscono
RAPPRESENTAZIONE GRAFICA E ANALISI DEI DATI SPERIMENTALI CON EXCEL 1 RAPPRESENTAZIONE GRAFICA Per l analisi dati con Excel si fa riferimento alla versione 2007 di Office, le versioni successive non differiscono
APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE
 APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE 1. Proporzionalità diretta e proporzionalità inversa Analizziamo le seguenti formule Peso Lordo = Peso Netto + Tara Ricavo = Utile + Costo Rata = Importo + Interesse
APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE 1. Proporzionalità diretta e proporzionalità inversa Analizziamo le seguenti formule Peso Lordo = Peso Netto + Tara Ricavo = Utile + Costo Rata = Importo + Interesse
Testo alla base del Pitgame redatto dal prof. Yvan Lengwiler, Università di Basilea
 Testo alla base del Pitgame redatto dal prof. Yvan Lengwiler, Università di Basilea Funzionamento di un mercato ben organizzato Nel Pitgame i giocatori che hanno poche informazioni private interagiscono
Testo alla base del Pitgame redatto dal prof. Yvan Lengwiler, Università di Basilea Funzionamento di un mercato ben organizzato Nel Pitgame i giocatori che hanno poche informazioni private interagiscono
LE FINESTRE E L ISOLAMENTO ACUSTICO
 LE FINESTRE E L ISOLAMENTO ACUSTICO Roberto Malatesta. William Marcone Ufficio Tecnico (giugno 2008) LA PROTEZIONE DAL RUMORE DEGLI EDIFICI, LA NORMATIVA NAZIONALE La maggior sensibilità delle persone
LE FINESTRE E L ISOLAMENTO ACUSTICO Roberto Malatesta. William Marcone Ufficio Tecnico (giugno 2008) LA PROTEZIONE DAL RUMORE DEGLI EDIFICI, LA NORMATIVA NAZIONALE La maggior sensibilità delle persone
MATEMATICA CLASSE PRIMA
 CLASSE PRIMA L alunno/a si muove con sicurezza nel calcolo scritto e mentale con i numeri naturali e sa valutare l opportunità di ricorrere a una calcolatrice. Contare oggetti o eventi, a voce e mentalmente,
CLASSE PRIMA L alunno/a si muove con sicurezza nel calcolo scritto e mentale con i numeri naturali e sa valutare l opportunità di ricorrere a una calcolatrice. Contare oggetti o eventi, a voce e mentalmente,
Illuminare il Progetto del Logo 3D
 ILLUMINAZIONE ILLUMINAZIONE 301 Illuminare il Progetto del Logo 3D Questa scena utilizza la luce di base e la filosofia delle luci di riempimento. Per accentuare le zone di massima luce degli oggetti metallici,
ILLUMINAZIONE ILLUMINAZIONE 301 Illuminare il Progetto del Logo 3D Questa scena utilizza la luce di base e la filosofia delle luci di riempimento. Per accentuare le zone di massima luce degli oggetti metallici,
