1. 4 ) 1 1 57 ) *) +) +0 + 5 1 + 6 +)46) 4 " 2 + 6. C E 1 B H =JEL + 6 +)46) 4 " 2 + 6 + J? HHA JA = F=??DAJJ HEIAHL=J =E? IK =J HE 241 +12) 1 +,1 1 1 + 1+0 37) 6 27 + 56)4 1 + 6 + 44 6 1 @E?=J HA 5E

. C E 1 B H =JEL 1. 4 ) 1 1 57 ) *) +) + 6 +)46) 7 1./ + J? HHA JA = F=??DAJJ HEIAHL=J =E? IK =J HE +0 + 5 1 + 6 +)46) 7 1./ 241 +12) 1 +,1 1 1 + 1+0 37) 6 + 56) 1 + 6 + 44 6 1 @E?=J HA 5E JAJE? @E +

. C E 1 B H =JEL + 61 + 44 61 + 7* 5 +1 2418)61 + 6 5 +1 ; 7 / + 6 5 +1.) 1 ; + 6 5 +1 /, + JE? HHA JE = F=??DAJJ HEIAHL=JE =E? IK =J HE 1. 4 ) 1 1 57 ) *) +) +0 + 5) 1 + 6 + 44 6 1 5481 1 + /)61 ) + 6

.CE 1BH=JEL +6 4,1)41 ) +57 +J?HHAJA =?IK HEIAHL=J =E?EAJE?IK=JHE 1.4)11 57) *)+) +0 +5 1 +6 +446 54811 +/)61 ) +6 +446 +,111 +1+0 )64 +,111 +1+0 *1.1+1 1 2)46) )4) 75 *1.1+1 1 2)46) )4) :64) 75 *1.1+1

! "## $"#%# $& ! # (.) (! + /!! ,&' 233-2452 ,'&.' " &'&!+!+ '! +7&+"! & &7&' ! 6 &&& &+ &' &'"%!& %!"!'!&!%!&& +'!7 '&!' %!" &&! +! 67 %!

! "## $"#%# $&!"# $%!&'&! # (") # ()# *+)#,!''')) -))) (.) (! + /!!,+# #) 0!&+) 0&&&#,&' (&# 1&) 233-2452 '($)'*$+,$*$((-$.//(' - &6)7%!7 (&!8 &6 &+'#7#7&!&&+ "79,'&.' " &'&!+!+ '! +7&+"! & &7&'!677 &&%!'8

Rappresentazione dell informazione

B Rappresentazione dell informazione {0, 1} 1475 1475 = 1 10 3 + 4 10 2 + 7 10 1 + 5 10 0 1475 1475 10 {0, 1, 2,..., 9} 5 B 2 β B β = {0, 1, 2,..., B 1} n b i β b n 1 b n 2 b 1 b 0 b n 1 B n 1 + b n 2

.CE 1BH=JEL 24/-66 )/41+674) 1FHAIA =CHE?A 1.4)11 57) *)+) 1 +)5,1..-46).741 5-,- +0- +5 1 24/-66 )/41+674) 767 +014/4).)41 +,111 -+1+0-6)55.155 6)55 8)41)*1- 5-4811 )++-5541.)+6)6181,1 612 )551+74)618

+0 241+12)1.CE 1BH=JEL +6 +446 *)+)41 E L=KJ= = HAIE@AJE A E L=KJ=AKH = HAIE@AJE 1.4)11 57) *)+) +5 1 +6 +446 *)+)41 74 8)76) +,111 +1+0 37)6 27 +56)4 1 +6 +446 1@E?=JHA 5EJAJE? @E +IJ 15+ )64 +,111 +1+0

Offerta Fuori Sede. Promotore Finanziario Nome e Cognome. Nr. Iscrizione Albo

1. 4 ) 1 1 57 ) *) +) Offerta Fuori Sede Promotore Finanziario Nome e Cognome Nr. Iscrizione Albo +0- + 5 1 + 6 + 44-6- 1? J? HHA JA K? JH=JJ? E GK= A = >=?= IL CA K IAHLE E @E?=II= FAH E? EA JA?KIJ @EI?A

FOGLIO INFORMATIVO FINANZIAMENTO ECOENERGY - IMPRESE

INFORMAZIONI SULLA BANCA Offerta Fuori Sede Promotore Finanziario Nome e Cognome Nr. Iscrizione Albo CHE COS È IL FINANZIAMENTO Foglio Informativo Finanziamento Ecoenergy Imprese SCHEDA N.5/bis (pag. 1

Energia. Costruttore Unità esterna Unità interna. Bassi consumi. Alti consumi

UNEP 7H UNEP 7HI UNEP 7HE 390 2.06 2.64 Potenza di kw 2.20 ABC EG UNEP 9H UNEP 9HI UNEP 9HE 520 2.50 2.40 Potenza di kw 2.85 ABC EG UNEP 12H UNEP 12HI UNEP 12HE 675 3.20 2.37 Potenza di kw 3.70 ABC EG

ID Sirea Codice Fiscale Cognome Nome Sesso Tipo Codice Fam./Conv. Data di nascita Stato revisione Conteggio Bilancio

37420936 0141I438 37418302 2829783 37381477 5802114 37396001 4603330 II II emmina 3184 01/08/2001 on ompletata 0 aschio 10826 29/03/1928 on ompletata 0 I aschio 5962 02/09/1958 on ompletata 0 I aschio

Chiusura lineare. N.B. A può essere indifferentemente un insieme, finito o no, o un sistema. Es.1. Es.2

Chiusura lineare Def. Sia A V (K) con A. Si dice copertura lineare (o chiusura lineare) di A, e si indica con L(A), l insieme dei vettori di V che risultano combinazioni lineari di un numero finito di

ASSESSORATO REGIONALE DELL INDUSTRIA

ASSESSORATO REGIONALE DELL INDUSTRIA ) >= AIA) AII= @H 2HAIE@A JA '! + K A@E) J=LE = E E?E= ) JE H ) CA = + F A JA? EJ=J @EHAJJEL # #! ) 2 1 5E?E E= *=H>=C E?DA A + F A JA? EJ=J @EHAJJEL # %! " )HJECE=

cod. IC8042 F 45 Ed. 06/12 Descrizione

. " # 15 6 ), 14 1+ ) * 1 15 6. 5 2 ) 4-2 ) 4 6 5 15 6 -, - 5 2 1- + - 5, - 4 - + 0 ) / - - 4 5 ) 6-6 - 1 15 6-15 6 ), - 4-2 7-5 6 5 1 / *., - + A? I K J= H A E ) 7 ) - 2 ) 4 6 1, 14 1+ ) * 1 1 = K = A

Cod. IC8043 F 90 Ed. 06/12. Descrizione

. ' 15 6 ), 14 1+ ) * 1 15 6. 5 2 ) 4-2 ) 4 6 5 15 6 -, - 5 2 1- + - 5, - 4 - + 0 ) / - - 4 5 ) 6-6 - 1 15 6-15 6 ), - 4-2 7-5 6 5 1 / *., - + A? I K J= H A E ) 7 ) - 2 ) 4 6 1, 14 1+ ) * 1 1 = K = A 2

Offerta Fuori Sede. Promotore Finanziario Nome e Cognome. Nr. Iscrizione Albo

1. 4 ) 1 1 57 ) *) +) Offerta Fuori Sede Promotore Finanziario Nome e Cognome Nr. Iscrizione Albo +0- + 5 1 + 6 +, 1 1 1 + J + @ E E K + J + HHA JA =FF IEJ= A JA HA= E =J FAH B H EHA = = + EA JA = = CAIJE

Schedulazione delle attività di un progetto in presenza di multi-calendari e di vincoli sulle risorse

Schedulazione delle attività di un progetto in presenza di multi-calendari e di vincoli sulle risorse Maria Silvia Pini Resp. accademico: Prof.ssa Francesca Rossi Università di Padova Attività FSE DGR

Posizionatore universale

Guida rapida 07.2002 QG EVE0109 A-(it) SRD960 Posizionatore universale Queste istruzioni sono un supporto per consentire una guida rapida al montaggio e alla messa in servizio del posizionatore. Per informazioni

.CE 1BH=JEL 7671 2-4 ) 4156476674)1-,1 1*11 ), 75 )*16)618 /)4)6161,) 126-+) 1.4)11 57) *)+) 1 +)5,1..-46).741 5-,- +0- +5 1 767 241+12)1 +,111 -+1+0- ! " # # # # # # # $ % % % - & & ' )) ) = FE=

Offerta Fuori Sede. Promotore Finanziario Nome e Cognome. Nr. Iscrizione Albo

1. 4 ) 1 1 57 ) *) +) Offerta Fuori Sede Promotore Finanziario Nome e Cognome Nr. Iscrizione Albo +0- + 5 1 + 6 + 44-6- 1? J? HHA JA K? JH=JJ? E GK= A = >=?= IL CA K IAHLE E @E?=II= FAH E? EA JA?KIJ @EI?A

Posizionatore universale

Guida rapida 07.2002 QG EVE0109 A-(it) SRD960 Posizionatore universale Queste istruzioni sono un supporto per consentire una guida rapida al montaggio e alla messa in servizio del posizionatore. Per informazioni

LABORATORIO DI PROGRAMMAZIONE E CALCOLO Docente E. Carlini A.A. 2012/13 Foglio di esercizi N.8 con la collaborazione di Andrea Pugliese

LABORATORIO DI PROGRAMMAZIONE E CALCOLO Docente E. Carlini A.A. / Foglio di esercizi N.8 con la collaborazione di Andrea Pugliese Dovete strutturare i programmi dei seguenti esercizi in funzioni ) (Metodo

LE STRUTTURE IN CEMENTO ARMATO: Predimensionamento di travi e pilastri

prof. Renato Giannini LE STRUTTURE IN CEMENTO ARMATO: Predimensionamento di travi e pilastri (arch. Lorena Sguerri) Il Telaio 1.80 4.00 2.40 3.00 3.25 Dato lo schema di un telaio come quello in figura,

LADDOMAT 21 Unità di riempimento

LADDOMAT 21 Unità di riempimento Nr. Art. 11 23 78 Manuale d istruzione e di installazione NOTA! I disegni del presente opuscolo descrivono solamente il principio di collegamento. Ciascuna installazione

" %$*!!! % &'(((((((((((((

!"#!$$! % &'(((((((( ) "#!$$! % &'((((((((( " %$*!!! % &'((((((((((((( !$ ! "#$ %!$ +!" #!$$! % ) " #!$$! %!$ " %$*!!! % INDICE INDICE DEI DOCUMENTI...3 CAPITOLO I...6 IL VIAGGIO: ARCHETIPO DELL INCONSCIO

Problemi di localizzazione impianti

Problemi di localizzazione impianti Laura Galli Dipartimento di Informatica Largo B. Pontecorvo 3, 56127 Pisa laura.galli@unipi.it http://www.di.unipi.it/~galli 2 Dicembre 2014 Ricerca Operativa 2 Laurea

Facoltà di Scienze MFN- Corso di laurea in Matematica ALGEBRA 2 - G.M. Piacentini Cattaneo- I. Damiani - GRUPPI- AZIONI DI GRUPPI-

Facoltà di Scienze MFN- Corso di laurea in Matematica ALGEBRA 2 - G.M. Piacentini Cattaneo- I. Damiani - GRUPPI- AZIONI DI GRUPPI- (1) (a) Determinare tutti i sottogruppi del gruppo dei quaternioni con

n a a a a n a a a a 2n a a a a 3n a m a m2 a m3 a M mn a a a n a m ( a a a a n ) m m n m n m n M mn < mn I n n 8 a ii 8i ; ; n >< >: a ij ij I 4 8i ; ; n 8j ; ; n a a a a a a a a a a a a a a a a 3 9 I

AFFIDABILITA DEI SISTEMI

AFFIDABILITA DEI SISTEMI STOCASTICI (complessi) Esercizio: Si assuma che i collegamenti tra una centrale elettrica e una città siano costituite da tre linee collegate in serie i cui tempi di funzionamento

Teoria dei Circuiti. Corso di. di analisi dei circuiti. Metodi sistematici. Università degli Studi di Pavia. Facoltà di Ingegneria

Università degli Studi di Pavia Facoltà di Ingegneria Corso di Teoria dei Circuiti di analisi dei circuiti METODO DEI POTENZILI DI NODO Si scelgano come incognite non le l tensioni di lato (legate da [M][]=),

Lezione 10 e 11, 26 Novembre e 3 Dicembre 2014

Lezione 0 e, 26 Novembre e 3 Dicembre 204 Elena Gaburro, elenagaburro@gmail.com Un applicazione per le curve di Bézier: i fonts Con il termine font si indica un tipo di carattere con uno stile e una forma

Modelli di Programmazione Lineare. PRTLC - Modelli

Modelli di Programmazione Lineare PRTLC - Modelli Schema delle esercitazioni Come ricavare la soluzione ottima Modelli Solver Come ricavare una stima dell ottimo Rilassamento continuo - generazione di

Miglioramento della mobilità articolare e dell allungamento muscolare

PROGRAMMA D EDUCAZIONE FISICA A.S. 2013/2014 CLASSE 1 As La classe ha partecipato al progetto Corso di nuoto Meda 8 Giugno 2014 PROGRAMMA D EDUCAZIONE FISICA A.S. 2012/2013 CLASSE 2 As La classe ha partecipato

Regione Lazio. Atti del Consiglio Regionale. 30/01/2014 - BOLLETTINO UFFICIALE DELLA REGIONE LAZIO - N. 9 Pag. 19 di 452

30/01/2014 - BOLLETTINO UFFICIALE DELLA REGIONE LAZIO - N. 9 Pag. 19 di 452 Regione Lazio Atti del Consiglio Regionale Deliberazione del Consiglio Regionale 2 ottobre 2013, n. 9 Regolamento del Monumento

Progetto di Reti di Telecomunicazione Modelli in Programmazione Lineare Problemi di Localizzazione

Progetto di Reti di Telecomunicazione Modelli in Programmazione Lineare Problemi di Localizzazione Posizionamento di antenne È dato un insieme A di possibili siti in cui installare antenne, a ciascuno

Offerta Fuori Sede. Promotore Finanziario Nome e Cognome. Nr. Iscrizione Albo

1. 4 ) 1 1 57 ) *) +) Offerta Fuori Sede Promotore Finanziario Nome e Cognome Nr. Iscrizione Albo +0- + 5 1 + 6 + 44-6- 1? J? HHA JA K? JH=JJ? E GK= A = >=?= IL CA K IAHLE E @E?=II= FAH E? EA JA?KIJ @EI?A

UNIVERSITÀ DEGLI STUDI DI SALERNO Svolgimento Prova scritta di Matematica II 09 Febbraio 2011

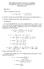UNIVERSITÀ DEGLI STUDI DI SALERNO Prova scritta di Matematica II 9 Febbraio Esercizio In R si considerino le due rette: t r : 5 y ; s : y t ; a) calcolare una base ortonormale di R a artire dai vettori

Parte 3: Gestione dei progetti, Shop scheduling

Parte : Gestione dei progetti, Shop scheduling Rappresentazione reticolare di un progetto Insieme di attività {,...,n} p i durata (nota e deterministica dell attività i) relazione di precedenza fra attività:

)7+1 27**1+16)41 +4,16 )1 +57)641 FAH EFHJE IE =@ AKH %# +4,161 245)1 4,1)41 ILLAEE )641.1)1)61 ).)1/1 KJKE?DEHCH=B=HE 51 +4,161 245)1 4,1)41 ILLAEE FAH EFHJE @= AKH =@ AKH!# 51 )641.1)1)61 ).)1/1 KJKE?DEHCH=B=HE

Soluzione sistemi lineari

Soluzione sistemi lineari Laboratorio di programmazione e calcolo Chimica e Tecnologie chimiche Pierluigi Amodio Dipartimento di Matematica Università di Bari Soluzione sistemi lineari p. / matrice diagonale

Informatica e diritto, Vol. XIV, 2005, n. 1-2, pp. 167-181

Informatica e diritto, Vol. XIV, 2005, n. 1-2, pp. 167-181 =@EIF E>E EJ @AE@=JE@A AFK>> E?DA= E EIJH= E E A + @E?A@A \= E EIJH= E A@ECEJ= A -4-56 *- 15)41 ] CEKIJ A FH @K?A JA? JE K=HA=F HHAIK AIF= A@A?EJJ=@E

"! # VINCENZO FOPPA SOCIETÀ COOPERATIVA SOCIALE - ONLUS $ $% $% &

!! "! # $ $% $% & ' '$$ & (()*+,#-./-0%( 1213202240#1213220,..5 6663((376663(83 ! " #$%&'(%)%&'*+**###%(),&-&+%,,.',,''%,,%)%,'%**+)*%#',('#/%*'%##%#%0'1%,%)&*0'#''.%)*(-%&,'.)%,.'))%2+%,*'/3 +#%&-%%(%%,,%)%**%*/%*%#%**'',*+%*%,&#%(%%,,%)%&'))%*+#4)%**'&'*%%*%#%,*)+0'.%)#5/.%'%#

SENATO DELLA REPUBBLICA

SET DELL REPLI X LEISLTR. 49/2 e DISE DI LEE pre l r el Ter (RLI) er l r el l e e Pre E (IRI P) l preve e S per l' fr 99 e bl ple per l r 99-992 IT LL PRESIDEZ IL LLI 99 TELL. 2 S preve el er el r e e

Un esempio di applicazione della PLI: il Sudoku

Un esempio di applicazione della PLI: il Sudoku 1/14 Risoluzione del Sudoku attraverso la PLI Nel seguito, si descrive come formulare il noto gioco del Sudoku come problema di programmazione lineare intera,

!"# $ # " # # $ % Formez- Centro di Formazione Studi 1

!"# #!! %&% '()*'**+ " # # % Formez- Centro di Formazione Studi 1 Indice 1 PRESENTAZIONE DELL ANALISI COMPARATIVA: LA SCELTA DEI MODELLI AMMINISTRATIVI 3 11 Il modello amministrativo Anglosassone 3 12

Fonti e strumenti statistici per la Comunicazione

Fonti e strumenti statistici per la Comunicazione Introduzione all analisi bivariata: il caso di caratteri qualitativi Prof.ssa Isabella Mingo A.A. 2018-2019 Che cosa è l analisi bivariata? E lo studio

Ricerca Operativa e Logistica

Ricerca Operativa e Logistica Dott. F.Carrabs e Dott.ssa M.Gentili A.A. 2011/2012 Lezione 10: Variabili e vincoli logici Variabili logiche Spesso nei problemi reali che dobbiamo affrontare ci sono dei

3 a 11 a a 1n a 21 a a 2n a 31 a a 3n. 5 a m1 a m2... a mn

Matrici n n n Nozioni fondamentali Algebra delle matrici Determinanti di matrici quadrate n Nozioni fondamentali Definizioni DEFINIZIONE MATRICE Detti m ed n due numeri interi positivi e considerati m

Calcolo scientifico. Prodotto Matrice per Matrice

Clolo sientifio Prodotto Mtrie per Mtrie Qul è l lgoritmo? for i=0,n- do for j=0,n- do ij =0 for k=0,n- do l mtrie C viene generlmente lolt omponente per omponente seondo un ordine prestilito ij = ij +

COMMISSIONE PROVINCIALE GIUDICANTE

MME RVE GUDE MU R. 33 9 2019 G U, W G, b, b, : D: : : E 7 G. 1820 U. b B R 4 M 2019. R. D R 73: -. R (U. b B R 4-0); - 50.00 (). R,. 1; -. R è 0,50. G U W G bb b : 9 2019 18.00 - V, 4 22100 M -. 031.5001688

Modelli di Programmazione Lineare e Programmazione Lineare Intera

Modelli di Programmazione Lineare e Programmazione Lineare Intera 1 Azienda Dolciaria Un azienda di cioccolatini deve pianificare la produzione per i prossimi m mesi. In ogni mese l azienda ha a disposizione

Reti simmetriche e calcolo parallelo

Reti simmetriche e calcolo parallelo Giorgio Gambosi Dipartimento di Matematica - Universita di Roma Tor Vergata Sistemi di calcolo parallelo 2 Composti da un insieme di unita di elaborazione, di elementi

ALGEBRE MATRICIALI E STRUTTURE DI RANGO: GEMELLAGGI E MATRIMONI

ALGEBRE MATRICIALI E STRUTTURE DI RANGO: GEMELLAGGI E MATRIMONI A U = {P = U U, diagonale} Popolazione in esame: 3 famiglie (allargate?) di algebre note ω-circolanti (ω C, ω = 1) 16 trasformate trigonometriche

8 - Analisi della deformazione

8 - Analisi della deformazione ü [A.a. - : ultima revisione 6 ottobre ] Esercizio n. Si supponga di voler conoscere sperimentalmente lo stato di deformazione in un punto M di un solido. A tal fine, si

Comune di Corigliano Calabro(CS) Indagini geognostiche, geotecniche in sito, prove di laboratorio e geofisiche eseguite per la realizzazione della banchina Nord e del piazzale retrostante il Porto di Corigliano

Alcuni Preliminari. Prodotto Cartesiano

Alcuni Preliminari Prodotto Cartesiano Dati due insiemi A e B, si definisce il loro prodotto cartesiano A x B come l insieme di tutte le coppie ordinate (a,b) con a! A e b! B. Es: dati A= {a,b,c} e B={,2,3}

Sistemi lineari. 2x 1 + x 2 x 3 = 2 x 1 x 2 + x 3 = 1 x 1 + 3x 2 2x 3 = 0. x 1 x 2 x 3

Sistemi lineari 2x 1 + x 2 x 3 = 2 x 1 x 2 + x 3 = 1 x 1 + 3x 2 2x 3 = 0 2 1 1 1 1 1 1 3 2 x 1 x 2 x 3 = 2 1 0 n j=1 a i,jx j = b i, i = 1,, n Ax = b A = (a i,j ) R n n matrice invertibile (det(a) 0) b

Introduzione e modellistica dei sistemi

Introduzione e modellistica dei sistemi Modellistica dei sistemi dinamici termici Elementi fondamentali Scrittura delle equazioni dinamiche Rappresentazione in variabili di stato Esempio di rappresentazione

Teoria dei Circuiti. Corso di. di analisi dei circuiti. Metodi sistematici. Università degli Studi di Pavia. Facoltà di Ingegneria

Università degli Studi di Pavia Facoltà di ngegneria Corso di Teoria dei Circuiti Metodi sistematici di analisi dei circuiti MTODO DLL CONT D MAGLA (MTODO DLL MAGL) DU CAS: A) Correnti di maglia = correnti

3 a 11 a a 1n a 21 a a 2n a 31 a a 3n ...

Matrici n n n n n Nozioni fondamentali Algebra delle matrici Determinanti di matrici quadrate Inversa di una matrice Rango di una matrice n Nozioni fondamentali Introduzione In questo capitolo affronteremo

ALGORITMI DI OTTIMIZZAZIONE M Esercizi Parte I

ALGORITMI DI OTTIMIZZAZIONE M Esercizi Parte I Esercizio 1 Dati n oggetti ed un contenitore, ad ogni oggetto j (j = 1,, n) sono associati un peso p j ed un costo c j (con p j e c j interi positivi). Si

MATCHING SU GRAFI E ALCUNE VARIANTI DEL PROBLEMA DEL MARIMONIO STABILE

UNIVERSITÀ À DEGLI STUDI ROMA TRE M.F.N. FACOLTÀ DI SCIENZE M.F.N. Tesi di Laurea in Matematica di Letizia Monaldi MATCHING SU GRAFI E ALCUNE VARIANTI DEL PROBLEMA DEL MARIMONIO STABILE Relatore Prof.

Trasformazioni 2D. Grande differenza rispetto alla grafica raster!

Trasformazioni 2D Il grande vantaggio della grafica vettoriale è che le immagini vettoriali descrivono entità matematiche È immediato manipolare matematicamente tali entità In quasi tutte le manipolazioni

Ottimizzazione nella gestione dei progetti Capitolo 4: la gestione dei costi (Programmazione multimodale): formulazioni

Ottimizzazione nella gestione dei progetti Capitolo 4: la gestione dei costi (Programmazione multimodale): formulazioni CARLO MANNINO Università di Roma La Sapienza Dipartimento di Informatica e Sistemistica

ESERCIZI SU SOTTOGRUPPI E QUOZIENTI. ESERCIZIO 1 Sia G un gruppo. Consideriamo il sottoinsieme (chiamato il centro di G)

ESERCIZI SU SOTTOGRUPPI E QUOZIENTI ESERCIZIO 1 Sia G u gruppo. Cosideriamo il sottoisieme (chiamato il cetro di G) Z(G) := {a G : ab = ba per ogi b G}. Dimostrare che Z(G) è u sottogruppo ormale di G.

Lo scopo della teoria dei determinanti è di definire una funzione. det : M n R. sia calcolabile facendo somme e prodotti delle entrate delle matrici

Determinanti 1 / 44 Lo scopo della teoria dei determinanti è di definire una funzione det : M n R chiamata determinante tale che: sia calcolabile facendo somme e prodotti delle entrate delle matrici det(a)

SENATO DELLA REPUBBLICA

SEA DELLA REPUBBLA LEGSLAURA. 96 / A 7 DSEG D LEGGE pr r r (GRA) r r B Prgr E (LG) B prv S pr fr 94 b pr pr r 94-96 UA ALLA PRESDEZA L SEEBRE 9 ABELLA. S prv r grr fr AESS. 7 SU EE AU DEL PAR AZALE DABRUZZ

! "#$!%#&'!#$!(#)'&'*! #&+'%#,! -.+'$$-/'.0!)'&! 12(+&3-&'!(-/.-41#0! 5#+'5#01-!

""#$%#&&#'()")*+,#"-$.")/0,1)23$4)$+),0"50$ "#$%#&'#$(#)'&'* #&+'%#, -.+'$$-/'.0)'& 12(+&3-&'(-/.-41#0 5#+'5#01-6$13.'125)2.'.012/.-07'%2.8#5'.+#$-.'$$9#))&'.8-5'.+28'$$#5#+'5#01# $#12.2(1'.:#.35'&-1#)&'7'&;#$'

Informatica e diritto, Vol. XIV, 2005, n. 1-2, pp. 147-166

Informatica e diritto, Vol. XIV, 2005, n. 1-2, pp. 147-166 =FK>> E?EJ JA A =JE?= A \E FE= J @A + @E?A@A \= E EIJH= E A@ECEJ= A ) /- /175-22- 4.1 5 )41 2HA AII=` =@EI?EF E =@A =FK>> E?EJ JA A =JE?= A +

Corso di Studi in Fisica. Geometria e Algebra Lineare II Prova scritta del 6 luglio 2009

Corso di Studi in Fisica Geometria e Algebra Lineare II Prova scritta del 6 luglio 009 Esercizio 1. Si considerino le matrici 3 1 1 3 1 1 A = 0 4 0, B = 3 1 3 1 1 3 0 a. (4 punti) Dimostrare che A e B

Un esempio di applicazione della programmazione lineare intera: il Sudoku

Un esempio di applicazione della programmazione lineare intera: il Sudoku Corso di Ricerca Operativa per il Corso di Laurea Magistrale in Ingegneria della Sicurezza: Trasporti e Sistemi Territoriali AA

file://c:\documents and Settings\g.brizzolari.POECO\Desktop\GUIDAMASTER.htm

Master Comunicazione Roma Master Media Roma Master Economia e Gestione della Comunicazio... Pagina 1 di 61 Username Password accedi '.!""! " # "!$"!!!! % % " "&& % '%!! ( # "'% ' " #" )))( (" ( " * + #

QPROVINCIA DI TORINO. Rapporto sulla Soddisfazione del Cliente Interno. febbraio 2000. Progetto Qualità La Soddisfazione del Cliente

GALLERIA DELLE ESPERIENZE Controllo di Gestione: Best Practices QPROVINCIA DI TORINO Gruppo di Lavoro Interfunzionale Progetto Qualità La Soddisfazione del Cliente Rapporto sulla Soddisfazione del Cliente

Elementi di Calcolo Matriciale

Corso di Lure in Disegno Industrile Corso di Metodi Numerici per il Design Lezione 7 Ottobre Elementi di Clcolo Mtricile F. Cliò Mtrici: Definizioni e Simbologi Lezione 7 Ottobre Elementi di Clcolo Mtricile

&&&&&,-#"&."&/(0"(&+%+&12&+3456&&&&& 7%)2&"&8%$"9"1"&8(:$(+%&1%/2&(&'(9(+"(&9:2+93(++"&0(;;;!"<"&*($(=(:=( >++?2

!"#"$%"&!"'&()*+',"--./'01)1+'#/,,"2./!"#$"%&'()($$" *"$(+% &&&&&,-#"&."&/(0"(&+%+&12&+3456&&&&& 7%)2&"&8%$"9"1"&8(:$(+%&1%/2&(&'(9(+"(&9:2+93(++"&0(;;;!"

Informatica e diritto, Vol. XIV, 2005, n. 1-2, pp. 135-145

Informatica e diritto, Vol. XIV, 2005, n. 1-2, pp. 135-145 =JH=I EIIE A@A @?K A J E B H =JE? E HK @A =F IJ=A AJJH E?=?AHJEBE?=J=,) 1- - )4 /17 5 )41 \E JH @K E A@A =@EI?EF E =IK =F IJ=A AJJH E?=?AHJEBE?=J=

INDICE SOMMARIO A.A. ASPETTI FORMALI ED ELEMENTI GENERALI... 1

INDICE SOMMARIO A.A. ASPETTI FORMALI ED ELEMENTI GENERALI.... 1 A.A.1 A.A.2 A.A.3 A.A.4 A.A.5 A.A.6. A.A.7 A.A.8 A.A.9 A.A.10 Verbalizzazione in data successiva alla riunione Legittimazione a richiedere

1 Insiemi e terminologia

1 Insiemi e terminologia Assumeremo come intuitiva la nozione di insieme e ne utilizzeremo il linguaggio come strumento per studiare collezioni di oggetti. Gli Insiemi sono generalmente indicati con le

Esercizi sul campo magnetico

www.francescozumbo.it Esercizi sul campo magnetico Forza magnetica, interazione tra correnti, spire, solenoidi, forza di Lorentz, moto di una particella carica immersa in un campo magnetico uniforme e

COMUNE DI SAN PIETRO AL NATISONE

REGIONE AUTONOMA FRIULI VENEZIA GIULIA PROVINCIA DI UDINE COMUNE DI SAN PIETRO AL NATISONE LAVORI DI RIQUALIFICAZIONE E VALORIZZAZIONE DEL COLLEGAMENTO PEDONALE TRA IL CENTRO STORICO DEL COMUNE E LA PASSERELLA

COMUNE DI CAGLIARI DOCUMENTO UNICO DI PROGRAMMAZIONE

COMUNE DI CAGLIARI DOCUMENTO UNICO DI PROGRAMMAZIONE 2016-2017-2018 !" #!!! $ %" &! # ' ( ') * $! ) + ) )! ( * )! *,! '- **.), #$, #/, *#.)), +#, 0#1 ) , 2# ( ), 3#1, 4#- ), 5#$ ) 6), #1 ), #$, # (!, *#1,

Offerta Fuori Sede. Promotore Finanziario Nome e Cognome. Nr. Iscrizione Albo

1. 4 ) 1 1 57 ) *) +) Offerta Fuori Sede Promotore Finanziario Nome e Cognome Nr. Iscrizione Albo +0- + 5 1 + 6 + 44-6- 1? J? HHA JA K? JH=JJ? E GK= A = >=?= IL CA K IAHLE E @E?=II= FAH E? EA JA?KIJ @EI?A

COMUNE DI BORGETTO (Città Metropolitana di Palermo)

OMU D BORGTTO à Mep e).y.. O, 4. V 518510821 Te. 091898109 e see. e@pe. u. e e e@ue. e.p. 2 ^ e R U.GG. U eee DTRMZO. / e,s /, /) Oe ee De e esee e Ree e essee Ree S e 5 ee201. Lue pes pe se eee. L O R

SPETT. ART WORK SRL 00179 ROMA. Fax 06.64463050. Responsabile Unico del Procedimento/Direttore dell' esecuzione contrattuale Geom.

MODULARIO P.C.I.( o P.C. o Modo 9 DIPARTIMENTO DELLA PROTEZIONE CIVILE UFFICIO V - AMMINISTRAZIONE E BILANCIO Servizio Politiche Contrattuali e p.c. SPETT. ART WORK SRL 00179 ROMA Fax 06.64463050 Responsabile

Introduzione al Vehicle Routing Problem

Introduzione al Vehicle Routing Problem Laboratorio di Strumenti di Ottimizzazione 2012-2013 Roberto Roberti roberto.roberti6@unibo.it 22 Maggio 2013 Il Vehicle Routing Problem (VRP) Problema di determinare

Università di Roma Tor Vergata Corso di Teoria dei Fenomeni Aleatori, AA 2012/13. Catene di Markov

Catene di Markov SISTEMI CASUALI DINAMICI (PROCESSI) - UN ESEMPIO: I GUASTI Frequenza dei guasti: N GUASTI 0 T N T 0 T! Catene di Markov SISTEMI CASUALI DINAMICI (PROCESSI) - UN ESEMPIO: I GUASTI Campionando

Introduzione allo Scilab Parte 4: matrici; esempi.

Introduzione allo Scilab Parte 4: matrici; esempi. Felice Iavernaro Dipartimento di Matematica Università di Bari http://dm.uniba.it/ iavernaro felix@dm.uniba.it 20 Giugno 2007 Felice Iavernaro (Univ.

Modelli di Programmazione Lineare

Capitolo 2 Modelli di Programmazione Lineare 2.1 Modelli di allocazione ottima di risorse Esercizio 2.1.1 Un industria manifatturiera può fabbricare 5 tipi di prodotti che indichiamo genericamente con

Probabilità condizionata e indipendenza stocastica

Capitolo 3 Probabilità condizionata e indipendenza stocastica 3.1 Considerazioniintroduttive Abbiamo trattato, finora, soltanto di probabilità di eventi che possono risultare Veri o Falsi. Tuttavia, il

Sistemi di equazioni lineari. la soluzione è unica se det(a) 0 e vale

Sistemi di equazioni lineari a 00 x 0 + a 01 x 1 + a 02 x 2 = b 0 a 10 x 0 + a 11 x 1 + a 12 x 2 = b 1 a 20 x 0 + a 21 x 1 + a 22 x 2 = b 2 Per N equazioni N 1 j=0 a ij x j = b i i = 0, N 1 la soluzione

)'t coniuge O figlio O genitore

A/ancato consenso Io sottoscritto R.o S-;f EL(. A e.(.., S. T l re { O Sindaco /;aias.sessore comunale l D Consigliere comunale, nato a _..._--=-=--=----------- il. {'.. Residente a e h~ fm T!7

2.1 Definizione di applicazione lineare. Siano V e W due spazi vettoriali su R. Un applicazione

Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza

Lezione Diagonalizzazione ortogonale per matrici simmetriche

Lezione 22 22. Diagonalizzazione ortogonale per matrici simmetriche La Proposizione 2. afferma che ogni matrice simmetrica reale è diagonalizzabile su R: ilrisultatoprincipalediquestasezioneèchelamatricechediagonalizzapuò

Gli elettroni nei cristalli

Gli lttroi i cristalli sio i ua disio: VVa fuzio d oda lttroica: dv risolvr l quazio di Schrödigr i rsza di u otzial riodico co si risolv il robla r il sigolo lttro: fi fuzio d oda ch riscchia la riodicità

n 260 del 26 agosto 2013

DELIBERAZIONE DEL DIRETTORE GENERALE n 260 del 26 agosto 2013 Oggetto: Acquisto autoveicoli in convenzione Consip e proroga contratti di noleggio autoveicoli. IL DIRETTORE GENERALE t:::,'~,':'~ ---::--.-

Offerta Fuori Sede. Promotore Finanziario Nome e Cognome. Nr. Iscrizione Albo

1. 4 ) 1 1 57 ) *) +) Offerta Fuori Sede Promotore Finanziario Nome e Cognome Nr. Iscrizione Albo +0- + 5 1 + 6 + 44-6- 1? J? HHA JA K? JH=JJ? E GK= A = >=?= IL CA K IAHLE E @E?=II= FAH E? EA JA?KIJ @EI?A

Risultati dell indagine sui costi di produzione del tabacco Bright e individuazione di best practice

Risultati dell indagine sui costi di produzione del tabacco Bright e individuazione di best practice Prof. Antonio Pierri 20 Aprile 2011 Dip. Scienze Economico-Estimative e degli Alimenti 1. Il campione