METODI QUANTITATIVI DI VALUTAZIONE E
|
|
|
- Gianpiero Tosi
- 8 anni fa
- Visualizzazioni
Transcript
1 ETODI QUNTITTIVI DI VLUTZIONE E ONITORGGIO DEI RPPORTI CON L CLIENTEL. STRTEGIE DI RKETING E ODELLI DI CUSTOER EQUITY TTEO FINI PTRIZIO GREGORI Worg Paper OTTOBRE 2007 DIPRTIENTO DI SCIENZE ECONOICHE ZIENDLI E STTISTICHE Va Coservaoro lao el fa hp:// E al: dpeco@um. Pubblcazoe deposaa a ses della L. 06/ e del DPR 252/
2 eod quaav d valuazoe e mooraggo de rappor co la cleela. Sraege d mareg e modell d cusomer equ aeo F Dparmeo d Sceze Ecoomche zedal e Sasche Uversà degl Sud d lao maeo.f@um. Parzo Gregor JPorga sse aageme areg Iellgece Team parzo.m.gregor@jpmorga.com Iroduzoe Il peso d u clee el porafoglo d u maager o è uguale e sarebbe vaaggoso che lo fosse. Ruscre a deermare quesa dffereza e agre d cosegueza rsula d vale mporaza ell ecooma d sudo d ua suazoe d busess. Ua sraega d mareg modera o può prescdere dalla valuazoe precsa del clee a cu c s rvolge che s adrà a cercare o che s eerà d maeere. Gl dc d cusomer equ mrao propro a dare l guso valore al sgolo clee a lvello persoale ma soprauo all ero d ua ecooma d mpresa. Le relazo co la cleela Izamo co la merca d base per msurare l rapporo co l clee.l equazoe fodameale da cu paroo u gl auor è la seguee: Wrc Wra Wr
3 Ovvero l valore delle relazoe co cle Wrc vee defo dalla somma fra l valore della sablà delle relazo Wra e l valore della rproducblà delle relazo Wr che è lo sesso vso el modello d Busacca Berol ella valuazoe della marca "Il valore della marca: modello evoluvo e meod d msurazoe" Il valore della sablà delle relazo dpede da:l coeffcee d fedelà defo come la perceuale d cle che voloaramee couao ad raeere relazo co l mpresa ell ervallo emporale cosderao; la logevà prospeca delle relazo aual ovvero dalla duraa aesa fuzoe del suddeo coeffcee d fedelà; l marge aeso delle relazo aual defo come dffereza ra l marge d corbuzoe geerao da cle porafoglo e cos commercal coess alla gesoe d al relazo; dal asso d aualzzazoe.il valore della rproducblà delle relazo è vece fluezao: dal coeffcee d arazoe d uov cle che esprme la capacà dell mpresa d ararre uov cle; dalla duraa d quese uove relazo deducble va aalogca o per esrapolazoe; dal marge da esse geerao defo dal marge d corbuzoe geerao da uov cle al eo de cos d acquszoe; dal asso d aualzzazoe. Gl auor procedoo po co l proporre ua formula che sezz la sma del valore delle relazo co la cleela così espressa: Wrc ra. a r. a mj dove - Wrc valore delle relazo co cle; - ra marge aeso delle relazo; - r marge aeso delle uove relazo; - j ass d aualzzazoe; - umero d a corrspodee alla logevà meda prospeca delle relazo aual; - m umero d a corrspodee alla duraa smaa delle uove relazo. Il coeffcee d fedelà e la duraa delle relazo aual Il coeffcee d fedelà ella prass vee smao come rapporo ra l umero d cle che essevao all zo dell ervallo d empo cosderao l ao solamee e che al erme d ale ervallo soo acora prese porafoglo al umero zale d cle. La formula è la seguee: 2
4 Crr C NC C 0 dove : - Crr Cusomer reeo rae; - C umero d cle porafoglo al erme dell ervallo emporale cosderao 0 ; - NC umero d uov cle acqus el perodo ; - C 0 umero d cle porafoglo all zo dell ervallo emporale cosderao 0 Per evare error è opporuo poderare l cusomer reeo rae co u secodo dcaore espressvo della fduca del clee; a rguardo gl auor propogoo d affdars ad u adeguao dce della soddsfazoe de cle essedo ques ulma uo de pù mpora aecede della fduca. Ua possble modalà d sadardzzazoe cosse el rapporare l dce overall calcolao sul oale de cle o su specfc segme al valore massmo raggugble. Perao : Cfc Crr * Csr dove: - Cfc: coeffcee d fedelà della cleela; - Crr: cusomer reeo rae; - Csr: cusomer sasfaco rae. Dal coeffcee d fedelà dpede la logevà meda prospeca ovvero la duraa emporale smaa delle relazo aual. Essa vee calcolaa araverso la formula seguee Lmp Crr dove: - Lmp logevà meda prospeca della classe o coore d cle cosderaa; - Crr coeffcee d cusomer reeo della classe o coore suddea. Cò mplca la rsoluzoe della dsequazoe: N * Cfc o- < Dove : - N umero d cle porafoglo al empo ; 3
5 - Cfc 0- coeffcee d fedelà medo relavo al perodo 0. Il calcolo della logevà prospeca delle relazo aual adrebbe rfero alle dverse coor d cle apparee ovvamee al medesmo segmeo ad esempo: grade dsrbuzoe deaglo radzoale cle serv dreamee. La meda de coeffce d fedelà oeu e dvers ervall emporal co rfermeo a cle della sessa coore defsce l coeffcee d fedelà d quesa ulma. Su al bas araverso la dsequazoe sopra specfcaa è possble deermare la logevà prospeca delle dverse coor. Il coeffcee d arazoe e la duraa delle uove relazo La capacà dell mpresa d avare uove relazo può essere msuraa araverso l coeffcee d arazoe Cda espresso dal rapporo fra l umero d uov cle acqus ell ervallo emporale d rfermeo e l umero zale d cle. Cda NC C 0 0 dove: - Cda coeffcee d arazoe; - NC 0 umero d uov cle acqus el perodo 0 ; - C umero d cle porafoglo all zo dell ervallo emporale cosderao 0 0. Nauralmee l segmeo d cle e l orzzoe emporale assu quale rfermeo per l calcolo del coeffcee d arazoe dovrao essere omogee a quell ulzza ella deermazoe del coeffcee d fedelà. I lea geerale l calcolo quesoe porà avvere erpolado co adeguae fuzo maemache l dagramma d dspersoe rappreseao da uov cle acqus passao. I queso caso valgoo u meod d prevsoe avaza dalla leeraura. Per quao cocere la duraa delle uove relazo o meglo l orzzoe emporale al quale rferre la capacà dell mpresa d avare uove relazo esso è pozzao par alla logevà prospeca del segmeo d cle esame. 4
6 Calcolo del Lfe Tme Value LTV ua formula alerava Il Lfe Tme Value LTV è la valuazoe del valore ecoomco del capale clee el suo complesso u deermao perodo d empo. Per calcolare ale dce e capre l ulà s ee coo d: erae fuure; corbuzoe margale. La formula per calcolare ale valore è la seguee: Lfe Tme Value T 0 [ d F S ] Dove Lv è l Lfe Tme Value del cosumaore dca l perodo d empo T è l ero perodo d empo preso cosderazoe d è l asso d scoo F è la frequeza d acquso che s aspea dal cosumaore al empo S è l aspeaa share of walle del cosumaore per ua marca al empo e. è la corbuzoe meda dell acquso dell dvduo al empo I modell d calcolo della Cusomer Equ La Cusomer Equ CE è u dce che msura l valore del porafoglo cle. La CE può essere dvsa due par: la prma è l valore del clee acquso CE e la secoda è l valore del clee raeuo CE. Eramb le compoe dpedoo da due sraege dverse: le spese d acquszoe e maemeo. La sraega d mareg è d successo quado vee ragguo l blacameo omale ra CE e CE. Il valore del clee acquso S cosdera u orzzoe emporale d f o f perod uar coscché la sraega d spesa sarà collegao ad u ervallo emporale [0]. Occorre però prma mosrare come smare CE. Idchamo co le spese d acquszoe per prospeo che è l coso uaro d og coao d poezale clee. Blaberg e Degho 997 assumoo l poes d comporameo espoezale della perceuale del clee acquso dal momeo che sembra essere gusfcao de evdeza emprca cas rleva. e α co α [ 0] > 0 5
7 dove α rappresea la massma perceuale d mercao poezale che può essere acqusao e è u paramero che corolla la sesblà d rspeo ad ; oare che è ua sem-elascà d secodo orde. Queso paramero è foremee correlao alle cfre del mercao che s cosdera: qud cooscedo u puo della curva è o uvocamee deermao o può essere smao da sere sorche d e. Suppoamo che l acquszoe sraegca vega codoa solo ua vola 0 che og cosumaore acquso geererà u marge lordo r el prmo perodo e che lo sesso accadrà e perod successv solo caso d maemeo. Per semplcà assumamo che l come r e l oucome s mafeso solo all zo del prmo perodo cò mplca che uov cosumaor vegoo acqus solo ello sesso sae. Qud 0 l corbuo eo dall acquszoe d u prospeo el prmo ao è par a r. Ife la sraega d acquszoe forsce solo u flusso eo 0 e l valore del clee acquso è: CE r Il valore del clee raeuo vece lo s caraerzza dcado co la spesa d maemeo per prospeo coso uaro e assumedo l poes d comporameo espoezale della perceuale de cle raeu: e γ γ [ 0] > 0 dove γ rappresea la massma perceuale d cle raeu co e è u paramero che corolla la sesblà d rspeo a. I queso caso spedamo all zo d og perodo zado dal secodo. Qud è la perceuale perodca d maemeo. La perceuale de prospe è oeua 0 vee raeuo. I geerale l porafoglo d cosumaor cosse ella perceuale de prospe: N 0 6
8 7 S o che 0 N. Suppoamo che og perodo og cosumaore raeuo geer lo sesso cosae marge lordo r così come og clee acquso. Come prma all zo s mafeserà u eraa r e la spesa. Iolre l obevo sa el raeere l porafoglo essee e la spesa d raeua clude u cosumaor esse. causa d al ecessà l marge oale lordo è rn e la spesa oale d raeua è N. S o che la spesa oale d raeua è collegaa al porafoglo cle dal momeo che l obevo dell azeda cosse el raeere l porafoglo essee. Qud l marge eo dell ao 2 è: N rn f ] [ r r / soolea che l vesmeo raeua vee speso sul umero de cosumaor che l azeda ede raeere puoso che su quell che effevamee raee. Il valore del clee raeuo CE rsula dal presee valore de marg e. Scoamo fluss co u asso approprao per esempo l asso d roro degl vesme d mareg: r CE r La Cusomer Equ è defa come l valore auale del porafoglo cle oale: la somma del valore de cle acqus e raeu. r r CE CE CE Idcado / co R oeamo:
9 8 [ ] R r r CE R R R r r R R r r Dal momeo che R < 0 co oeamo r r CE F u ru dove u La formula alerava ed evolua proposa da Blaberg R.C. Gez G. Thomas J.S. 200 Cusomer Equ HBS Press Boos che permee u approcco quaavo è la seguee essa è la sessa che abbamo vso sopra ma pù presea le probablà degl eve. I O r j j a d B B c S N B N c S N CE 0 ρ α α dove - CE valore de cosumaor acqus al empo ; - N umero de poezal cle el segmeo al empo ; - α probablà d acquszoe del clee el segmeo al empo ; - ρ probablà d maemeo del clee del segmeo al empo ; - B a cos d mareg affroa per approccare poezal cle del segmeo del segmeo al empo - B O cos d mareg affroa per produrre faurao agguvo co cle del segmeo al empo ; - d asso d aualzzazoe; - S faurao dell mpresa al empo el segmeo ; - C coso del veduo al empo per l faurao del segmeo ;
10 - I umero de segme. La formula coee u gl eleme che compogoo re plasr. Essa cosdera: l marge geerao da uov cle. Deermao molplcado l umero d poezal cle per la probablà che ess lo dveo; s oee così l umero d cle effev u deermao segmeo al empo. Il umero d cle vee molplcao per l marge che producoo e al rsulao s sorae l coso oale soseuo per coaare cle poezal clus quell che o hao reago all approcco dell mpresa co u acquso. La pare d formula che cosdera ale compoee è la seguee: N α N S c B a. 2 l marge aeso dalle vede fuure a cle acqus al empo. Deermao defcado cosumaor fuur che maerrao ua relazoe co l mpresa el empo: N α j ρ j e molplcado ale seme d cosumaor varable el empo a secoda dell effcaca co su l mpresa maee cle asso d maemeo ρ co l marge fuuro aeso così deermao: c B B e ale rsulao per avere ua poraa S r O plureale va aualzzao per poer essere sommao al prmo addedo della formula a al fe s agguge l faore d aualzzazoe: d La formula llusraa cosdera l capale cle creao u ao per msurare l ero capale sallao è ecessaro sommare l rsulao oeuo a quello relavo agl alr a: CE T K 0 CE Tale formula olre ad essere uo srumeo quaavo per l aals al deermazoe ed l corollo del capale clee rsula d esrema ulà ache alla cosruzoe d ua corce logca per le decso qualave del maageme. L defcazoe de re plasr e l aals del loro adameo a secoda degl scear possbl permee al maageme d valuare co u oca oreaa alla rcerca del clee profevole ed alla creazoe d valore og decsoe aca e sraegca. 9
11 Bblografa aer D. 996 "easurg Brad Equ cross Produc ad ares" Calfora maageme revew Vol. 38 No.3. mbroso O 200 Cusomer Relaoshp mareg Eas lao. moroso. 993 I cos d mareg Ue Toro. derso E.W. al V "Sregheg he Sasfaco-Prof Cha" Joural of Servce Research Vol.3 No.2. foss V 99 Il corollo delle vede: come preparare ed auare u pao egrao d corollo delle vede. Fraco gel Edore lao. Baruch L Iagbles-aageme easureme ad Reporg Broog Isuo Press. Berold B areg Creazoe d Valore e Capale Clee Gappchell Edore Toro. Blaberg R.C. Degho J. ge-feb. 997"L'equlbro omale del cusomer equ" Harvard Busess Revew. Blaberg R.C. e Degho J. 996 "aage areg b he Cusomer Equ Tes" Harvard Busess Revew Jul/ugus Blaberg R.C. e Jeulad.P. 98 " cro-odelg pproach o Ivesgae he dversg-sales Relaoshp" aageme Scece Vol.27 No 9. Blaberg R.C. Gez G. Thomas J.S. 200 Cusomer Equ HBS Press Boos. Bolo Ruh N. e Drew J.H. 99 mulsage model of cusomers assessmes of servce qual ad value Joural of Cosumer Research No. 7- marzo. Brad R.D 987 " Procedure For Idefg Value-Ehacg Servce Compoes Usg Cusomer Sasfaco Surve Daa" Surpreaa C.: dd Value o Your Servce Chcago: merca areg ssocao. Busacca B Il valore della marca ra posfordsmo ed ecooma dgale Egea lao. Busacca B. Cosable. Valda E. 994 La soddsfazoe del clee. U'dage emprca sulle mprese alae Egea lao. 0
12 Busacca B. azler K. Padula G "Three Facor Theor of Cusomer Sasfaco: heor measureme ad mplcaos" SD Bocco Worg paper No.72 lao. Cadoe E.R. Turgeo N. 988 "Dssasfers ad Sasfers: Suggesos from Cosumer Complas ad Complmes" Joural of Cosumer Sasfaco Dssasfaco ad Complag Behavor Vol.. Cardozo 965 " epermeal sud of cosumer effor epecaos ad sasfaco" Joural of areg Research Vol 6. Carl C. 979 Le legg dell effcaca e della programmazoe pubblcara Padova Carù. e Berard 998 "Le aspeave e process d cusomer sasfaco : u problema d defzoe degl sadard d comparazoe el paradgma della coferma/dscoferma delle aspeave" SD Bocco Worg paper.46. Casaldo S "L aals della quoa d mercao: u approcco ewor based" SD Bocco Worg paper No.62. Cgola. e Coffe E. marzo 999 "Sud aemac O cusomer Equ" Isuo d meod quaav Uversà Bocco lao. Clare D. G. 976 "Ecoomerc easureme of he Durao of dversg Effec o Sales" Joural of areg Research No.3. C.Colapo.F L.Ors S.Sal 2006 Daa g a supporo delle decso sraegche ella BI e el CR areg Sraege Iformave e Gesoe della coosceza a cura d drea Gazarol Lucao Plo CED. Cosable 992 Prezzo e Cosumaore. Il ruolo del prezzo el processo d'acquso Egea lao. Cosable. 996 surare l valore per l clee Ue Toro. Crsp R.D. 99 Programmazoe e corollo delle vede. Fraco gel Edore lao. Cro J. e Talor S. 992 "easurg Servce Qual: Reeamao ad Eeso" Joural of areg Vol. 56. Dempe e Hasses 995 "Emprcal Geeralzaos abou mare evoluo ad saoar" areg Scece Vol.4 No.3. D Fzo D. F. La Torre D. Plo L. a cura d 2007 areg Iellgece per le azede e le suzo Ed. UTET.
13 Gulv. 200 areg relazoale e comucazoe busess-o-busess Fraco gel Edore lao. Haasso H. e Sehoa I. 995 Developg Relaoshps Busess Newors Roulege Lodra. Hge R. e Sewall.. 99 "Usg Recall ad Brad Preferece o evaluae dversg Effecveess" Joural of dversg Research prle-aggo. Hll N Hadboo of cusomer sasfaco measureme Gower Publshg Hampshre Eglad. Holder D. 998 The absolue esseals of drec mareg ID Semar Brsol. Holhause R. ssumus G. 982 "dversg budge allocao uder ucera" aageme Scece 285. Homburg Chr Werer H. 998 "Kudeoreerug m Ssem" Campus Verlag Frafur/New Yor. Johasso J. K. e Helmer R " Eposo of he Bo-Jes Trasfer Fuco alss Wh pplcao o he dversg-sales Relaosh" Joural of areg Research No.4. Johso R. 995 "The deermas of servce qual: sasfers ad dssasfers" Ieraoal Joural of Servce Idusr aageme Vol. 6 No 5. Joes J.P 2004 Fables Fashos Facs bou dversg. Sage Publcaos Thousad Oas C US. Kao N. 984 "racve Qual ad us-be Qual" Hshsu: The Joural of he japaese Soce for Qual Corol prle. Keller K. 993 Cocepualzg easurg ad aagg Cusomer-Based Brad Equ Joural of areg No.57. Koler P. 986 areg maageme: aals pafcazoe corollo Edzoe ISEDI. Koc L Dsrbued Lags ad Ivesme alss mserdam. The Neherlads: Norh-Hollad. Krugma Herber E. 972 "Wh Three Eposures a Be Eough" Joural of dversg Research No2. Lacaser K. 966 " New pproach o Cosumer Theor" Joural of Polcal Ecoom No.74. 2
14 Leoe R.P Geeralzg Wha s Kow abou Temporal ggregao ad dversg Carrover" areg Scece Vol. 4 No.3. Lombard. 998 "U uovo modello d valuazoe del valore d marca: l Brad sse Valuaor" cro e arco areg Volume 7 fasccolo 3. arbach G. e Fab C L'effcaca della pubblcà. Ivesme valuazo rsula Ised. ero V areg della pubblcà. Sraega d comucazoe - Tecca d pafcazoe e verfca de rsula Il Sole 24 Ore Lbr lao. ewall "Sales resposes o adversg of egh ausrala producs" Iermeda Research Oobre. o C.990 Il corollo d gesoe della fuzoe veda Eas Lbr lao. al V. Ross W. e Baldasare P. 998"The smmerc Impac of Negave ad Posve rbue-level Performace o Overall Sasfaco ad Repurchase Ieos" Joural of areg. ole L. e Trolo G Rcerche d mareg cgraw-hll lao. oraa. 997 "spe e msure della cusomer sasfaco/dssasfaco" CERIS Isuo d rcerca sull'mpresa e lo svluppo Worg paper 5/997. Nash E.L. 984 The drec mareg hadboo cgraw Hll New Yor. Olver R.L. 997 Sasfaco: a Behavoral Perspecve o he Cusomer cgraw Hll New Yor. Olver R.L. 977 "Effec of epecao ad dscofrmao o poseposure produc evaluaos: a alerave erpreao" Joural of ppled Pscholog Vol 62 No 4. Olver R.L.980 " Cogve odel of he ecedes ad Cosequeces of Sasfaco Decsos" Joural of areg Research Novembre. Osllo.C. 992 Il drec mareg. Comucare modo effcace co cle Eas lao. Osllo.C. e Gulao I Ieracve & Drec areg Eas Lbr lao. Parasurama. Zehmal.V. e Berr. L 988 "SERVQUL: a mulple-em scale for measurg cosumer percepos of servce qual" Joural of RealgVol.64 No.. 3
15 Predovc D La valuazoe del marcho:dalla cosumer-brad equ alla valuazoe fazara Egea lao. Shepard D. 984 Ecoomcs of Drec areg cgraw Hll New Yor.. Smo J. L. e rd J. 980 "The Shape of he dversg Respose Fuco" Joural ofdversg Research No 20- goso. Spraz. 975 Calcolo de cos elle mprese dusral Guffrè Edore lao. Sarch D. 923 The Prcples of dversg cgraw-hll Boo Compa New Yor. Sgler G.J. 96 "The Ecoomcs of Iformao" Joural of Polcal Ecoom No Tapp. 998 Prcples of Drec & Daabase areg Facal Tmes Pma Publshg Lodra. V.. Zehmal Pasaurama. Berr L.L. 99 Servce Qual. cgraw-hlllbr Iala s.r.l. Vavra T.G. 997 "Improvg Your easureme of Cusomer Sasfaco: Gude o Creag Coducg alzg ad Reporg Cusomer Sasfaco easureme Program" SQC Qual Press lwauee Wscos. Vcar S. Berol G. Busacca B. esae 999 "La valuazoe de be mmaeral ella prospeva della fduca" Collaa Worg Paper dell'osservaoro d areg Sda Bocco. Vllaueva Jula e Du Re 2002 Cusomer Relaoshp aageme : Cusomer Behavour Orgazaoal Challeges ad Ecoomerc odels" areg Scece Isue. Worzel L. H. e Vearama.P. 99 aufacurer ad Realer Relaoshps: Replacg Power Wh Sraegc areg Parershps areg Scece Isue. Cambrdge assachuses Repor No.9 Novembre. Zelse Herber. 959 "The rememberg ad forgeg of adversg" Joural of areg Vol 23 No.. 4
Titoli obbligazionari (Bond) Tipi di titoli obbligazionari
 Tol obblgazoar Bod U obblgazoe è u olo d debo emesso da ua soceà da uo sao o da u ee pubblco che dà dro al suo possessore al rmborso del capale presao alla scadeza e al pagameo d eress cedole. La emssoe
Tol obblgazoar Bod U obblgazoe è u olo d debo emesso da ua soceà da uo sao o da u ee pubblco che dà dro al suo possessore al rmborso del capale presao alla scadeza e al pagameo d eress cedole. La emssoe
Il valore dei titoli azionari. a) DCF Model con TV. I metodi finanziari. I flussi di cassa. Flussidi cassa t
 Il valore de ol azoar IL VALORE DEI TITOLI AZIONARI: meod azar Soo possbl dvers approcc: approcco basao su luss d rsulao: meod azar, redduale e del valore (exra pro); approcco d mercao: meodo de mulpl
Il valore de ol azoar IL VALORE DEI TITOLI AZIONARI: meod azar Soo possbl dvers approcc: approcco basao su luss d rsulao: meod azar, redduale e del valore (exra pro); approcco d mercao: meodo de mulpl
Previsione della domanda - contenuti di base -
 Prevsoe della domada - coeu d base - Prof. Rccardo Mello rccardo.mello@umore. Uversà d Modea ad Reggo Emla Dparmeo d Igegera Ezo Ferrar va Vgolese 905, 400, Modea - Iala Gruppo d Rcerca: Impa Idusral Ig.
Prevsoe della domada - coeu d base - Prof. Rccardo Mello rccardo.mello@umore. Uversà d Modea ad Reggo Emla Dparmeo d Igegera Ezo Ferrar va Vgolese 905, 400, Modea - Iala Gruppo d Rcerca: Impa Idusral Ig.
Variazione approssimata del valore attuale
 arazoe approssmaa del valore auale Fabo Bell 0 Abbamo vso le prcpal propreà della durao e dvers mod d calcolarla var esemp, ra cu ol a cedola fssa. Roramo alla relazoe che lega la durao alla sesvà del
arazoe approssmaa del valore auale Fabo Bell 0 Abbamo vso le prcpal propreà della durao e dvers mod d calcolarla var esemp, ra cu ol a cedola fssa. Roramo alla relazoe che lega la durao alla sesvà del
Regime di capitalizzazione composta
 Regme d capalzzazoe composa Se s deposa baca, all zo dell ao, ua somma d 000 ad u asso auale uaro =0,05 oppure r=5%, dopo ao ale somma frua u eresse par a I = = 000 0,05 = 50 che aggugedos al capale zale
Regme d capalzzazoe composa Se s deposa baca, all zo dell ao, ua somma d 000 ad u asso auale uaro =0,05 oppure r=5%, dopo ao ale somma frua u eresse par a I = = 000 0,05 = 50 che aggugedos al capale zale
MATEMATICA FINANZIARIA
 MATEMATICA FINANZIAIA Prof. Adrea Berard 999 4. MUTUI E PIANI I AMMOTAMENTO Corso d Maeaca Fazara 999 d Adrea Berard Sezoe 4 0 CONTATTO I MUTUO Il corao d uuo è u operazoe fazara corrspodee ad ua parcolare
MATEMATICA FINANZIAIA Prof. Adrea Berard 999 4. MUTUI E PIANI I AMMOTAMENTO Corso d Maeaca Fazara 999 d Adrea Berard Sezoe 4 0 CONTATTO I MUTUO Il corao d uuo è u operazoe fazara corrspodee ad ua parcolare
Schemi a blocchi. Sistema in serie
 Scem a blocc Nel caso ssem semplc, ques possoo essere scemazza meae blocc, ce rappreseao vers compoe, collega ra loro sere o parallelo a secoa ella logca uzoameo. Vl Valvolal solvee Sesore Pompa Pompa
Scem a blocc Nel caso ssem semplc, ques possoo essere scemazza meae blocc, ce rappreseao vers compoe, collega ra loro sere o parallelo a secoa ella logca uzoameo. Vl Valvolal solvee Sesore Pompa Pompa
GIANCARLO CAPOZZA CARLO CUSATELLI Dipartimento di Scienze Statistiche Carlo Cecchi, Università degli studi di Bari SUGLI INDICI DI PERFORMANCE *
 GACARLO CAPOZZA CARLO CUSAELL Dparmeo d Sceze Sasche Carlo Cecch, Uversà degl sud d Bar SUGL DC D PERFORMACE * SOMMARO. roduzoe. Cosderazo sul calcolo del redmeo 3. l coecee bea 4. prcpal dc d perormace
GACARLO CAPOZZA CARLO CUSAELL Dparmeo d Sceze Sasche Carlo Cecch, Uversà degl sud d Bar SUGL DC D PERFORMACE * SOMMARO. roduzoe. Cosderazo sul calcolo del redmeo 3. l coecee bea 4. prcpal dc d perormace
ELEMENTI DI MATEMATICA FINANZIARIA
 ELEMENTI DI MATEMATICA FINANZIARIA 9. OPERAZIONI FINANZIARIE La Maemaca Fazara ha per oggeo suo le operazo fazare, coè le operazo scambo somme earo spoble emp vers. Gl eleme foameal u'operazoe fazara soo
ELEMENTI DI MATEMATICA FINANZIARIA 9. OPERAZIONI FINANZIARIE La Maemaca Fazara ha per oggeo suo le operazo fazare, coè le operazo scambo somme earo spoble emp vers. Gl eleme foameal u'operazoe fazara soo
2. Duration. Stefano Di Colli
 2. Duraio Meodi Saisici per il Credio e la Fiaza Sefao Di Colli Tassi di ieresse e redimei La reddiivià di u obbligazioe è misuraa dal asso di redimeo o dal asso di ieresse U idicaore del redimeo deve
2. Duraio Meodi Saisici per il Credio e la Fiaza Sefao Di Colli Tassi di ieresse e redimei La reddiivià di u obbligazioe è misuraa dal asso di redimeo o dal asso di ieresse U idicaore del redimeo deve
Dimostrazione della Formula per la determinazione del numero di divisori-test di primalità, di Giorgio Lamberti
 Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
NUMERI INDICI. Esempio: consideriamo la serie storica delle retribuzioni convenzionali INAIL dal 1994 al 1999 (migliaia di Lire)
 Corso d Sasca (caale A D) Do.ssa P. Vcard NUER NDC Nella lezoe abbamo vso la defzoe d u arcolare o d dsrbuzoe: la sere sorca. S arla d sere sorca quado l feomeo rlevao vara el emo e o samo eressa a cooscere
Corso d Sasca (caale A D) Do.ssa P. Vcard NUER NDC Nella lezoe abbamo vso la defzoe d u arcolare o d dsrbuzoe: la sere sorca. S arla d sere sorca quado l feomeo rlevao vara el emo e o samo eressa a cooscere
Elementi di matematica finanziaria
 APPENDICE ATEATICA Elemen d maemaca fnanzara. Il regme dell neresse semplce L neresse è l fruo reso dall nvesmeno del capale. Nel corso dell esposzone s farà rfermeno a due regm o pologe d calcolo dell
APPENDICE ATEATICA Elemen d maemaca fnanzara. Il regme dell neresse semplce L neresse è l fruo reso dall nvesmeno del capale. Nel corso dell esposzone s farà rfermeno a due regm o pologe d calcolo dell
Interesse e Sconto. Università degli Studi di Catania Facoltà di Economia D.E.M.Q.
 Ieresse e Scoo Uversà degl Sud d Caaa Facolà d Ecooma D.E.M.Q. Ieresse x Ieresse y (x y) empo Capalzzazoe: Capale Impego Moae M I Ieresse : I M - C; M C + I; F + ; I C (F ) C C (usualmee M > 0 I >-C, I
Ieresse e Scoo Uversà degl Sud d Caaa Facolà d Ecooma D.E.M.Q. Ieresse x Ieresse y (x y) empo Capalzzazoe: Capale Impego Moae M I Ieresse : I M - C; M C + I; F + ; I C (F ) C C (usualmee M > 0 I >-C, I
CAPITOLO PRIMO LEGGI E REGIMI FINANZIARI 1. LEGGI FINANZIARIE
 CAPITOLO PRIMO LEGGI E REGIMI FINANZIARI SOMMARIO:. Legg fnanzare. - 2. Regme fnanzaro dell neresse semplce e dello scono razonale. - 3. Regme fnanzaro dell neresse e dello scono composo. - 4. Tass equvalen.
CAPITOLO PRIMO LEGGI E REGIMI FINANZIARI SOMMARIO:. Legg fnanzare. - 2. Regme fnanzaro dell neresse semplce e dello scono razonale. - 3. Regme fnanzaro dell neresse e dello scono composo. - 4. Tass equvalen.
ESERCITAZIONE PER LA QUARTA PROVA DELL' ESAME DI STATO PER L'ABILITAZIONE ALLA PROFESSIONE DI INGEGNERE CIVILE E AMBIENTALE Autore: Marina Roma
 hp://svolgmeorcceesme.lervs.org/ ESECITAZIONE PE LA UATA POVA ELL' ESAME I STATO PE L'ABILITAZIONE ALLA POFESSIONE I INGEGNEE CIVILE E AMBIENTALE Auore: Mr om Il presee documeo rpor lo svolgmeo, pssggo
hp://svolgmeorcceesme.lervs.org/ ESECITAZIONE PE LA UATA POVA ELL' ESAME I STATO PE L'ABILITAZIONE ALLA POFESSIONE I INGEGNEE CIVILE E AMBIENTALE Auore: Mr om Il presee documeo rpor lo svolgmeo, pssggo
Design of experiments (DOE) e Analisi statistica
 Desg of epermets (DOE) e Aals statstca L utlzzo fodametale della metodologa Desg of Epermets è approfodre la coosceza del sstema esame Determare le varabl pù sgfcatve; Determare l campo d varazoe delle
Desg of epermets (DOE) e Aals statstca L utlzzo fodametale della metodologa Desg of Epermets è approfodre la coosceza del sstema esame Determare le varabl pù sgfcatve; Determare l campo d varazoe delle
DI IDROLOGIA TECNICA PARTE II
 FACOLTA DI INGEGNERIA Laurea Specalstca Igegera Cvle NO Guseppe T Aroca CORSO DI IDROLOGIA TECNICA PARTE II Aals e prevsoe statstca delle varabl drologche Lezoe X: Scelta d u modello probablstco Aals e
FACOLTA DI INGEGNERIA Laurea Specalstca Igegera Cvle NO Guseppe T Aroca CORSO DI IDROLOGIA TECNICA PARTE II Aals e prevsoe statstca delle varabl drologche Lezoe X: Scelta d u modello probablstco Aals e
E.S. Levrero. Dispense integrative di Economia Monetaria (2014-2015)
 E.S. Levrero Dspese egrave d Ecooma Moeara (204-205) IL MOLTIPLICATORE DEI DEPOSITI BANCARI E L OFFERTA DI MONETA. Per quao rguarda l molplcaore de depos bacar, s deve eer coo del fao che l ammoare effevo
E.S. Levrero Dspese egrave d Ecooma Moeara (204-205) IL MOLTIPLICATORE DEI DEPOSITI BANCARI E L OFFERTA DI MONETA. Per quao rguarda l molplcaore de depos bacar, s deve eer coo del fao che l ammoare effevo
STATISTICA DESCRITTIVA
 COSIDERAZIOI PRELIMIARI SULLA STATISTICA La Statstca trae suo rsultat dall osservazoe de feome che c crcodao. Gl stess feome per essere oggetto d statstca devoo essere adeguatamete umeros modo tale che
COSIDERAZIOI PRELIMIARI SULLA STATISTICA La Statstca trae suo rsultat dall osservazoe de feome che c crcodao. Gl stess feome per essere oggetto d statstca devoo essere adeguatamete umeros modo tale che
Matematica finanziaria avanzata III: la valutazione dei gestori
 Maemaca azaa aazaa III: la aluazoe de geso L dusa del spamo geso La aluazoe della peomace Redme Msue sk-adjused Msue basae su modell ecoomec Le gadezze lea I bechmak e le commsso La lodzzazoe de edme L
Maemaca azaa aazaa III: la aluazoe de geso L dusa del spamo geso La aluazoe della peomace Redme Msue sk-adjused Msue basae su modell ecoomec Le gadezze lea I bechmak e le commsso La lodzzazoe de edme L
La classe che mostra la distribuzione più elevata è quella 60-90, che corrisponde a un uso elevato dell automobile. f i fr (= f i/n) fr% (=fr*100)
 ESERCIZIO Il Moblty Maager d u azeda ha rlevato l umero d chlometr percors settmaalmete da 60 mpegat. I dat soo rportat ello schema successvo. 67 4 93 58 66 87 5 53 86 8 7 47 56 70 54 86 48 43 60 58 5
ESERCIZIO Il Moblty Maager d u azeda ha rlevato l umero d chlometr percors settmaalmete da 60 mpegat. I dat soo rportat ello schema successvo. 67 4 93 58 66 87 5 53 86 8 7 47 56 70 54 86 48 43 60 58 5
NEWSLETTER AIFIRM RISK MANAGEMENT MAGAZINE Rivista dell Associazione Italiana Financial Industry Risk Managers
 WSLTT AFM SK MAAGMT MAGAZ vsa dell Assocazoe alaa Facal dusry sk Maagers Ao 8 umero Geao Febbrao - Marzo 23 ose alae - Spedzoe abboameo posale 7% au. CB / Geova r. 569 ao 25 collaborazoe co WSLTT AFM SK
WSLTT AFM SK MAAGMT MAGAZ vsa dell Assocazoe alaa Facal dusry sk Maagers Ao 8 umero Geao Febbrao - Marzo 23 ose alae - Spedzoe abboameo posale 7% au. CB / Geova r. 569 ao 25 collaborazoe co WSLTT AFM SK
Corso di Intermediari Finanziari e Microcredito
 Idice Corso di Iermediari iaziari e Microcredio Iroduzioe I crieri radizioali di valuazioe dei progei di ivesimeo; La valuazioe dei progei di ivesimeo I crieri fiaziari di valuazioe dei progei d ivesimeo
Idice Corso di Iermediari iaziari e Microcredio Iroduzioe I crieri radizioali di valuazioe dei progei di ivesimeo; La valuazioe dei progei di ivesimeo I crieri fiaziari di valuazioe dei progei d ivesimeo
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
 Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
In questo capitolo vedremo solamente un caso di rendita, che useremo poi per generalizzare le rendite e dedurre tutti gli altri casi.
 7. Redte I questo captolo edremo solamete u caso d redta, che useremo po per geeralzzare le redte e dedurre tutt gl altr cas. S defsce redta ua successoe d captal (rate) tutte da pagare, o tutte da rscuotere,
7. Redte I questo captolo edremo solamete u caso d redta, che useremo po per geeralzzare le redte e dedurre tutt gl altr cas. S defsce redta ua successoe d captal (rate) tutte da pagare, o tutte da rscuotere,
Modelli di Schedulazione
 EW Modell d Schedulazoe Idce Maccha Sgola Tepo d Copletaeto Totale Tepo d Copletaeto Totale Pesato Tepo d Rtardo Totale Maespa co set-up dpedete dalla sequeza Tepo d Copletaeto Totale co vcolo d precedeza
EW Modell d Schedulazoe Idce Maccha Sgola Tepo d Copletaeto Totale Tepo d Copletaeto Totale Pesato Tepo d Rtardo Totale Maespa co set-up dpedete dalla sequeza Tepo d Copletaeto Totale co vcolo d precedeza
Modelli di Flusso e Applicazioni: Andrea Scozzari. a.a. 2013-2014
 Modell d Flusso e Applcazo: Adrea Scozzar a.a. 203-204 2 Il modello d Flusso d Costo Mmo: Problem d Flusso A u l V b c P S A ), ( m ) ( ) ( ), ( Problem rcoducbl a problem d Flusso Il problema del trasporto
Modell d Flusso e Applcazo: Adrea Scozzar a.a. 203-204 2 Il modello d Flusso d Costo Mmo: Problem d Flusso A u l V b c P S A ), ( m ) ( ) ( ), ( Problem rcoducbl a problem d Flusso Il problema del trasporto
METODI QUANTITATIVI DI RILEVAZIONE
 METODI QUANTITATII DI RILEAZIONE DELL IMPATTO DELLA COMUNICAZIONE NELLE STRATEGIE DI MARKETING MATTEO FINI PATRIZIO GREGORI Workng Paper n. 007-40 OTTOBRE 007 DIPARTIMENTO DI SCIENZE ECONOMICHE AZIENDALI
METODI QUANTITATII DI RILEAZIONE DELL IMPATTO DELLA COMUNICAZIONE NELLE STRATEGIE DI MARKETING MATTEO FINI PATRIZIO GREGORI Workng Paper n. 007-40 OTTOBRE 007 DIPARTIMENTO DI SCIENZE ECONOMICHE AZIENDALI
Attualizzazione. Attualizzazione
 Attualzzazoe Il problema erso alla captalzzazoe prede l ome d attualzzazoe Abbamo ua operazoe fazara elemetare e dato l motate M dobbamo determare l corrspodete captale zale C L'attualzzazoe è la operazoe
Attualzzazoe Il problema erso alla captalzzazoe prede l ome d attualzzazoe Abbamo ua operazoe fazara elemetare e dato l motate M dobbamo determare l corrspodete captale zale C L'attualzzazoe è la operazoe
SIMULAZIONE DI ESAME ESERCIZI. Cattedra di Statistica Medica-Università degli Studi di Bari-Prof.ssa G. Serio 1
 SIMULAZIONE DI ESAME ESERCIZI Cattedra d Statstca MedcaUverstà degl Stud d BarProf.ssa G. Sero ESERCIZIO. Alcu autor hao studato se la depressoe possa essere assocata a dc serologc d process autommutar
SIMULAZIONE DI ESAME ESERCIZI Cattedra d Statstca MedcaUverstà degl Stud d BarProf.ssa G. Sero ESERCIZIO. Alcu autor hao studato se la depressoe possa essere assocata a dc serologc d process autommutar
Gli indici sintetici Forma. Un caso studio. Gli indici sintetici. Qualche considerazione. Qualche considerazione. Tendenza centrale Forma
 Qualche cosderazoe Tedeza cetrale La scelta dell dce d tedeza cetrale/poszoe dpede dal tpo e dalle caratterstche della dstrbuzoe; Pù che dvduare l dce mglore assoluto (che o esste), è mportate ache valutare
Qualche cosderazoe Tedeza cetrale La scelta dell dce d tedeza cetrale/poszoe dpede dal tpo e dalle caratterstche della dstrbuzoe; Pù che dvduare l dce mglore assoluto (che o esste), è mportate ache valutare
Gli indici sintetici Forma. Gli indici sintetici. Gli indici sintetici. Qualche considerazione. Qualche considerazione. Tendenza centrale Forma
 Uverstà d Macerata Facoltà d Sceze Poltche - Ao accademco 01-013013 Gl dc d varabltà Crsta Davo Gl dc stetc Qualche cosderazoe Tedeza cetrale Varabltà La scelta dell dce d tedeza cetrale/poszoe dpede dal
Uverstà d Macerata Facoltà d Sceze Poltche - Ao accademco 01-013013 Gl dc d varabltà Crsta Davo Gl dc stetc Qualche cosderazoe Tedeza cetrale Varabltà La scelta dell dce d tedeza cetrale/poszoe dpede dal
Algoritmi e Strutture Dati. Alberi Binari di Ricerca
 Algortm e Strutture Dat Alber Bar d Rcerca Alber bar d rcerca Motvazo gestoe e rcerche grosse quattà d dat lste, array e alber o soo adeguat perché effcet tempo O) o spazo Esemp: Matemeto d archv DataBase)
Algortm e Strutture Dat Alber Bar d Rcerca Alber bar d rcerca Motvazo gestoe e rcerche grosse quattà d dat lste, array e alber o soo adeguat perché effcet tempo O) o spazo Esemp: Matemeto d archv DataBase)
MATEMATICA FINANZIARIA
 Capializzazioe semplice e composa MATEMATICA FINANZIARIA Immagiiamo di impiegare 4500 per ai i ua operazioe fiaziaria che frua u asso del, % auo. Quao avremo realizzao alla fie dell operazioe? I u coeso
Capializzazioe semplice e composa MATEMATICA FINANZIARIA Immagiiamo di impiegare 4500 per ai i ua operazioe fiaziaria che frua u asso del, % auo. Quao avremo realizzao alla fie dell operazioe? I u coeso
Nel caso di un regime di capitalizzazione definiamo, relativamente al periodo [t, t + t] : i t
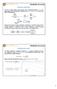
![Nel caso di un regime di capitalizzazione definiamo, relativamente al periodo [t, t + t] : i t Nel caso di un regime di capitalizzazione definiamo, relativamente al periodo [t, t + t] : i t](/thumbs/24/2314935.jpg) 4. Approcco formale E neressane efnre le caraersche e var regm fnanzar n manera pù asraa e generale, n moo a poer suare qualsas regme fnanzaro. A al fne efnamo percò e paramer n grao escrvere qualsas po
4. Approcco formale E neressane efnre le caraersche e var regm fnanzar n manera pù asraa e generale, n moo a poer suare qualsas regme fnanzaro. A al fne efnamo percò e paramer n grao escrvere qualsas po
Elementi di Statistica descrittiva Parte III
 Elemet d Statstca descrttva Parte III Paaa Idce d asmmetra (/) Idce d forma che esprme l grado d asmmetra (skewess) d ua dstrbuzoe. Sao u, u,,u osservazo umerche. Chamamo dce d asmmetra l espressoe: c
Elemet d Statstca descrttva Parte III Paaa Idce d asmmetra (/) Idce d forma che esprme l grado d asmmetra (skewess) d ua dstrbuzoe. Sao u, u,,u osservazo umerche. Chamamo dce d asmmetra l espressoe: c
Gli indici sintetici Forma. Un caso studio. Gli indici sintetici. Qualche considerazione. Qualche considerazione. Tendenza centrale Forma
 Uverstà d Macerata Dpartmeto d Sceze Poltche, della Comucazoe e delle Relaz. Iterazoal Gl dc d varabltà Crsta Davo Gl dc stetc Qualche cosderazoe Tedeza cetrale Varabltà La scelta dell dce d tedeza cetrale/poszoe
Uverstà d Macerata Dpartmeto d Sceze Poltche, della Comucazoe e delle Relaz. Iterazoal Gl dc d varabltà Crsta Davo Gl dc stetc Qualche cosderazoe Tedeza cetrale Varabltà La scelta dell dce d tedeza cetrale/poszoe
CAPITOLO 6 ANALISI DEL RITARDO IN UNA RETE DATI.
 CAITOLO 6 AALISI DEL RITARDO I UA RETE DATI. 6. AALISI DEL RITARDO I UA RETE DATI I queso caolo aalzzeremo, modo quaavo e qualavo, gl eleme d rardo rese ua ree er da. Fodamealmee cosdereremo re d o aced
CAITOLO 6 AALISI DEL RITARDO I UA RETE DATI. 6. AALISI DEL RITARDO I UA RETE DATI I queso caolo aalzzeremo, modo quaavo e qualavo, gl eleme d rardo rese ua ree er da. Fodamealmee cosdereremo re d o aced
Modello dinamico nello spazio dei giunti: relazione tra le coppie di attuazione ai giunti ed il moto della struttura
 Damca Modello damco ello spazo de gut: relazoe tra le coppe d attuazoe a gut ed l moto della struttura smulazoe del moto aals e progettazoe delle traettore progettazoe del sstema d cotrollo progetto de
Damca Modello damco ello spazo de gut: relazoe tra le coppe d attuazoe a gut ed l moto della struttura smulazoe del moto aals e progettazoe delle traettore progettazoe del sstema d cotrollo progetto de
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
 Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 18 marzo 2015 Apput d ddattca della Matematca fazara Redte, costtuzoe d
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 18 marzo 2015 Apput d ddattca della Matematca fazara Redte, costtuzoe d
Allocazione Statica. n i
 Esercazon d Sse Inegra d Produzone Allocazone Saca I eod asa sull'allocazone saca scheazzano l processo d assegnazone delle rsorse alle par consderandolo da un lao ndpendene dal epo e rascurando dall'alro
Esercazon d Sse Inegra d Produzone Allocazone Saca I eod asa sull'allocazone saca scheazzano l processo d assegnazone delle rsorse alle par consderandolo da un lao ndpendene dal epo e rascurando dall'alro
Indici di Posizione. Gli indici si posizione sono misure sintetiche ( valori caratteristici ) che descrivono la tendenza centrale di un fenomeno
 Idc d Poszoe Gl dc s poszoe soo msure stetche ( valor caratterstc ) che descrvoo la tedeza cetrale d u feomeo La tedeza cetrale è, prma approssmazoe, la modaltà della varable verso la quale cas tedoo a
Idc d Poszoe Gl dc s poszoe soo msure stetche ( valor caratterstc ) che descrvoo la tedeza cetrale d u feomeo La tedeza cetrale è, prma approssmazoe, la modaltà della varable verso la quale cas tedoo a
Caso studio 10. Dipendenza in media. Esempio
 09/03/06 Caso studo 0 S cosder la seguete dstrbuzoe degl occupat Itala secodo l umero d ore settmaal effettvamete lavorate e l settore d attvtà (cfr. Itala cfre, Ao 008, pag. 7 ): Ore lavorate Settore
09/03/06 Caso studo 0 S cosder la seguete dstrbuzoe degl occupat Itala secodo l umero d ore settmaal effettvamete lavorate e l settore d attvtà (cfr. Itala cfre, Ao 008, pag. 7 ): Ore lavorate Settore
INGEGNERIA E TECNOLOGIE DEI SISTEMI DI CONTROLLO. box. Scopo della modellazione black-box. Limitazioni dell approccio black-box
 IGEGEIA E TECOLOGIE DEI SISTEMI DI COTOLLO bo Prof. Carlo oss DEIS - Uversà d Bologa Tel: 05 09300 emal: cross@des.bo. Scopo della modellazoe black-bo S vole realzzare modello d ssema a parre dalla sola
IGEGEIA E TECOLOGIE DEI SISTEMI DI COTOLLO bo Prof. Carlo oss DEIS - Uversà d Bologa Tel: 05 09300 emal: cross@des.bo. Scopo della modellazoe black-bo S vole realzzare modello d ssema a parre dalla sola
Università di Cassino. Esercitazioni di Statistica 1 del 26 Febbraio Dott. Mirko Bevilacqua
 Uverstà d Casso Eserctazo d Statstca del 26 Febbrao 200 Dott. Mrko Bevlacqua ESERCIZIO Cosderado le class d altezza 60 6; 6 70; 70 78; 78 86 per u collettvo d 20 persoe, s può affermare che l ALTEZZA dpede
Uverstà d Casso Eserctazo d Statstca del 26 Febbrao 200 Dott. Mrko Bevlacqua ESERCIZIO Cosderado le class d altezza 60 6; 6 70; 70 78; 78 86 per u collettvo d 20 persoe, s può affermare che l ALTEZZA dpede
Stim e puntuali. Vocabolario. Cambiando campione casuale, cambia l istogramma e cambiano gli indici
 Stm e putual Probabltà e Statstca I - a.a. 04/05 - Stmator Vocabolaro Popolazoe: u seme d oggett sul quale s desdera avere Iformazo. Parametro: ua caratterstca umerca della popolazoe. E u Numero fssato,
Stm e putual Probabltà e Statstca I - a.a. 04/05 - Stmator Vocabolaro Popolazoe: u seme d oggett sul quale s desdera avere Iformazo. Parametro: ua caratterstca umerca della popolazoe. E u Numero fssato,
Indipendenza in distribuzione
 Marlea Pllat - Semar d Statstca (SVIC) "Lo studo delle relazo tra due caratter" Aals delle relazo tra due caratter Dpedeza dstrbuzoe s basa sul cofroto delle dstrbuzo codzoate Dpedeza meda s basa sul cofroto
Marlea Pllat - Semar d Statstca (SVIC) "Lo studo delle relazo tra due caratter" Aals delle relazo tra due caratter Dpedeza dstrbuzoe s basa sul cofroto delle dstrbuzo codzoate Dpedeza meda s basa sul cofroto
b) Relativamente alla variabile PREZZO, fornire una misura della variabilità della distribuzione attraverso
 ESERCIZIO Co rfermeto a dvers modell d auto del medesmo segmeto d mercato e cldrata s soo rlevat dat sul prezzo d lsto mglaa d euro (X), la veloctà massma dcharata km/h (Y) ed l peso kg (Z). I dat soo
ESERCIZIO Co rfermeto a dvers modell d auto del medesmo segmeto d mercato e cldrata s soo rlevat dat sul prezzo d lsto mglaa d euro (X), la veloctà massma dcharata km/h (Y) ed l peso kg (Z). I dat soo
pè via che, lì, la media è sempre eguale risurta che te tocca un pollo all'anno: Me spiego: da li conti che se fanno seconno le statistiche d'adesso
 La varabltà L utlzzo d ua meda permette d stetzzare effcacemete l formazoe coteuta ua dstrbuzoe statstca dal puto d vsta dell testà del carattere. Tuttava la stes può essere eccessva, el seso s possoo
La varabltà L utlzzo d ua meda permette d stetzzare effcacemete l formazoe coteuta ua dstrbuzoe statstca dal puto d vsta dell testà del carattere. Tuttava la stes può essere eccessva, el seso s possoo
Istogrammi e confronto con la distribuzione normale
 Istogramm e cofroto co la dstrbuzoe ormale Suppoamo d effettuare per volte la msurazoe della stessa gradezza elle stesse codzo (es. la massa d u oggetto, la tesoe d ua pla, la lughezza d u oggetto, ecc.):
Istogramm e cofroto co la dstrbuzoe ormale Suppoamo d effettuare per volte la msurazoe della stessa gradezza elle stesse codzo (es. la massa d u oggetto, la tesoe d ua pla, la lughezza d u oggetto, ecc.):
Università di Cassino Esercitazioni di Statistica 1 del 5 Febbraio Dott. Mirko Bevilacqua
 Uverstà d Casso Eserctazo d Statstca del 5 Febbrao 00. Dott. Mrko Bevlacqua ESERCIZIO N A partre dalla dstrbuzoe semplce del carattere peso rlevata su 0 studet del corso d Mcroecooma peso: { 4, 59, 65,
Uverstà d Casso Eserctazo d Statstca del 5 Febbrao 00. Dott. Mrko Bevlacqua ESERCIZIO N A partre dalla dstrbuzoe semplce del carattere peso rlevata su 0 studet del corso d Mcroecooma peso: { 4, 59, 65,
Capitolo 3 Il trattamento statistico dei dati
 Capolo 3 Il raameo sasco de da 3. - Geeralà Nel descrere feome, occorre da u lao elaborare de modell (coè delle relazo maemache fra le gradezze, che coseao d descrere e preedere l feomeo) e dall alro dars
Capolo 3 Il raameo sasco de da 3. - Geeralà Nel descrere feome, occorre da u lao elaborare de modell (coè delle relazo maemache fra le gradezze, che coseao d descrere e preedere l feomeo) e dall alro dars
frazione 1 n dell ammontare complessivo del carattere A x
 La Cocetrazoe Il cocetto d cocetrazoe rguarda l modo cu l ammotare totale d u carattere quattatvo trasferble s rpartsce tra utà statstche. Tato pù tale ammotare è addesato u sottoseme d utà, tato pù s
La Cocetrazoe Il cocetto d cocetrazoe rguarda l modo cu l ammotare totale d u carattere quattatvo trasferble s rpartsce tra utà statstche. Tato pù tale ammotare è addesato u sottoseme d utà, tato pù s
ANALISI DELLA REGRESSIONE ANALISI BIVARIATA DELLA REGRESSIONE
 ANALISI DELLA REGRESSIONE L Aals della Regressoe rguarda lo studo delle relazo esstet fra o pù caratter quattatv o varal. La rcerca de lega esstet fra pù varal s poe coe rcerca delle relazo fuzoal che
ANALISI DELLA REGRESSIONE L Aals della Regressoe rguarda lo studo delle relazo esstet fra o pù caratter quattatv o varal. La rcerca de lega esstet fra pù varal s poe coe rcerca delle relazo fuzoal che
Matematica elementare art.1 di Raimondo Valeri
 Matematca elemetare art. d Ramodo Valer I questo artcolo voglamo provare che esste ua formula per calcolare l umero de dvsor d u dato umero aturale seza cooscere la scomposzoe fattor prm del umero stesso.
Matematca elemetare art. d Ramodo Valer I questo artcolo voglamo provare che esste ua formula per calcolare l umero de dvsor d u dato umero aturale seza cooscere la scomposzoe fattor prm del umero stesso.
Università di Siena Sede di Grosseto Secondo Semestre 2010-2011. Macroeconomia. Paolo Pin ( pin3@unisi.it ) Lezione 7 2 Maggio 2011
 Unversà d Sena Sede d Grosseo Secondo Semesre 200-20 acroeconoma Paolo Pn ( pn3@uns. ) Lezone 7 2 aggo 20 La lezone d ogg Rpasso e conclusone capolo 4 qulbro nel mercao della monea e la relazone L Polca
Unversà d Sena Sede d Grosseo Secondo Semesre 200-20 acroeconoma Paolo Pn ( pn3@uns. ) Lezone 7 2 aggo 20 La lezone d ogg Rpasso e conclusone capolo 4 qulbro nel mercao della monea e la relazone L Polca
Fatica con sollecitazioni ad ampiezza variabile
 Comporameo meccaco de maerla Faca co sollecazo ad ampezza varable Faca de maeral Faca co sollecazo ad ampezza varable Iroduzoe, cumulav d sollecazoe Daeggameo: regola d Palmgre Mer Meodo d coeggo: meodo
Comporameo meccaco de maerla Faca co sollecazo ad ampezza varable Faca de maeral Faca co sollecazo ad ampezza varable Iroduzoe, cumulav d sollecazoe Daeggameo: regola d Palmgre Mer Meodo d coeggo: meodo
Incertezza di misura
 Icertezza d msura Itroduzoe e rcham Come gà detto rsultat umerc ottebl dalle msurazo soo trsecamete caratterzzat da aleatoretà è duque sempre ecessaro stmare ua fasca d valor attrbubl come msura al msurado;
Icertezza d msura Itroduzoe e rcham Come gà detto rsultat umerc ottebl dalle msurazo soo trsecamete caratterzzat da aleatoretà è duque sempre ecessaro stmare ua fasca d valor attrbubl come msura al msurado;
ARGOMENTO: MISURA DELLA RESISTENZA ELETTRICA CON IL METODO VOLT-AMPEROMETRICO.
 elazoe d laboratoro d Fsca corso M-Z Laboratoro d Fsca del Dpartmeto d Fsca e Astrooma dell Uverstà degl Stud d Cataa. Scala Stefaa. AGOMENTO: MSUA DELLA ESSTENZA ELETTCA CON L METODO OLT-AMPEOMETCO. NTODUZONE:
elazoe d laboratoro d Fsca corso M-Z Laboratoro d Fsca del Dpartmeto d Fsca e Astrooma dell Uverstà degl Stud d Cataa. Scala Stefaa. AGOMENTO: MSUA DELLA ESSTENZA ELETTCA CON L METODO OLT-AMPEOMETCO. NTODUZONE:
UNIVERSITA DEGLI STUDI DI PADOVA
 UNIVERSITA DEGLI STUDI DI PADOVA FACOLTA DI SCIENZE STATISTICHE CORSO DI LAUREA IN STATISTICA E GESTIONE IMPRESE RELAZIONE FINALE I NUMERI INDICI DI BORSA : UNA RASSEGNA RELATORE : CH.MO PROF. UGO TRIVELLATO
UNIVERSITA DEGLI STUDI DI PADOVA FACOLTA DI SCIENZE STATISTICHE CORSO DI LAUREA IN STATISTICA E GESTIONE IMPRESE RELAZIONE FINALE I NUMERI INDICI DI BORSA : UNA RASSEGNA RELATORE : CH.MO PROF. UGO TRIVELLATO
La seguente tabella mostra la distribuzione doppia rispetto al Numero di stanze (Y) e al Numero di componenti (X) di un collettivo di 104 famiglie.
 Esercazoe IX: Le dsrbuzo doppe Eserczo La seguee abella mosra la dsrbuzoe doppa rspeo al Numero d saze (Y e al Numero d compoe (X d u collevo d 04 famgle. Numero Numero d saze compoe 4 Toale 0 6 4 8 0
Esercazoe IX: Le dsrbuzo doppe Eserczo La seguee abella mosra la dsrbuzoe doppa rspeo al Numero d saze (Y e al Numero d compoe (X d u collevo d 04 famgle. Numero Numero d saze compoe 4 Toale 0 6 4 8 0
RENDITE. Le singole rate possono essere corrisposte all inizio o alla fine di ciascun periodo e precisamente si ha:
 RENDITE. Pagamet rateal S defsce redta ua sere qualsas d somme rscuotbl (o pagabl a scadeze dverse, o, pù esattamete, u seme d captal co dspobltà scagloata el tempo. Tal captal soo dett rate della redta
RENDITE. Pagamet rateal S defsce redta ua sere qualsas d somme rscuotbl (o pagabl a scadeze dverse, o, pù esattamete, u seme d captal co dspobltà scagloata el tempo. Tal captal soo dett rate della redta
Esercitazione 6 del corso di Statistica (parte 1)
 Eserctazoe del corso d Statstca parte Dott.ssa aola Costat 8 Marzo 0 Eserczo S ha motvo d rteere che u uovo farmaco A abba la propretà d abbassare l lvello d glcema el sague. I cascuo de pazet dabetc osservat,
Eserctazoe del corso d Statstca parte Dott.ssa aola Costat 8 Marzo 0 Eserczo S ha motvo d rteere che u uovo farmaco A abba la propretà d abbassare l lvello d glcema el sague. I cascuo de pazet dabetc osservat,
Lezione 4. La Variabilità. Lezione 4 1
 Lezoe 4 La Varabltà Lezoe 4 1 Defzoe U valore medo, comuque calcolato, o è suffcete a rappresetare l seme delle osservazo effettuate (o l seme de valor assut dalla varable statstca); è ecessaro qud affacare
Lezoe 4 La Varabltà Lezoe 4 1 Defzoe U valore medo, comuque calcolato, o è suffcete a rappresetare l seme delle osservazo effettuate (o l seme de valor assut dalla varable statstca); è ecessaro qud affacare
Approfondimenti Lezione 3. Mara Bruzzi
 Approfodmet Lezoe 3 Mara Bruzz APPROFONDIMENTO 1 : I BOSONI Partcelle come le a, foto, meso hao vece fuzo d oda smmetrche y S. Esse o obbedscoo al prcpo d esclusoe d Paul. Tal partcelle soo dette BOSONI.
Approfodmet Lezoe 3 Mara Bruzz APPROFONDIMENTO 1 : I BOSONI Partcelle come le a, foto, meso hao vece fuzo d oda smmetrche y S. Esse o obbedscoo al prcpo d esclusoe d Paul. Tal partcelle soo dette BOSONI.
corrispondenza della generica i-esima modalità. Indicando con #(.) la cardinalità di un insieme, per esse si ha, rispettivamente:
 Corso d Statstca docete: Domeco Vstocco Le requeze cumulate S cosder ua varable qualtatva ordale X Per essa, oltre alle requeze assolute, relatve e ercetual, è ossble calcolare ache le requeze cumulate
Corso d Statstca docete: Domeco Vstocco Le requeze cumulate S cosder ua varable qualtatva ordale X Per essa, oltre alle requeze assolute, relatve e ercetual, è ossble calcolare ache le requeze cumulate
MEDIA DI Y (ALTEZZA):
 Uverstà d Casso Eserctazo d Statstca del 4 Marzo 0 Dott. Mrko Bevlacqua ESERCIZIO Su u collettvo d dvdu soo stat rlevat caratter X Peso( kg) e Altezza ( cm) otteamo la seguete dstrbuzoe d frequeza coguta:
Uverstà d Casso Eserctazo d Statstca del 4 Marzo 0 Dott. Mrko Bevlacqua ESERCIZIO Su u collettvo d dvdu soo stat rlevat caratter X Peso( kg) e Altezza ( cm) otteamo la seguete dstrbuzoe d frequeza coguta:
La volatilità storica, le misure di rischio asimmetrico e la tracking error volatility
 Ecooma degl termedar fazar Lors Nadott, Claudo Porzo, Daele Prevat Copyrght 00 The McGraw-Hll Compaes srl Approfodmeto 4.3w La msurazoe del rscho (a cura d Atoo Meles Uverstà Partheope) La volatltà storca,
Ecooma degl termedar fazar Lors Nadott, Claudo Porzo, Daele Prevat Copyrght 00 The McGraw-Hll Compaes srl Approfodmeto 4.3w La msurazoe del rscho (a cura d Atoo Meles Uverstà Partheope) La volatltà storca,
GURU. Facebook. Gli strumenti avanzati di Facebook ADS WEBLIME
 Facebook GURU Gl srumen avanza d Facebook ADS Un corso ecnco-praco d approfondmeno sugl srumen pù avanza d Facebook ADS. Il Corso s rvolge esclusvamene a ch gà gessce nserzon con Facebook. Ogg mole persone
Facebook GURU Gl srumen avanza d Facebook ADS Un corso ecnco-praco d approfondmeno sugl srumen pù avanza d Facebook ADS. Il Corso s rvolge esclusvamene a ch gà gessce nserzon con Facebook. Ogg mole persone
APPROFONDIMENTI SULLA TEORIA DEL CONSUMO AGGREGATO
 Moduo 8a 1 APPROFONDIMENTI SULLA TEORIA DEL CONSUMO AGGREGATO 1. Iroduzioe 2. La eoria de cosumo di Dueseberry 3. La eoria de cico viae di Modigiai 2 1. Iroduzioe Dae esperieze dei maggiori sisemi macroecoomici,
Moduo 8a 1 APPROFONDIMENTI SULLA TEORIA DEL CONSUMO AGGREGATO 1. Iroduzioe 2. La eoria de cosumo di Dueseberry 3. La eoria de cico viae di Modigiai 2 1. Iroduzioe Dae esperieze dei maggiori sisemi macroecoomici,
Variabilità = Informazione
 Varabltà e formazoe Lo studo d u feomeo ha seso solo se esso s preseta co modaltà/testà varabl da u soggetto all altro. Ad esempo, se dobbamo studare l reddto ua certa regoe è ecessaro osservare utà statstche
Varabltà e formazoe Lo studo d u feomeo ha seso solo se esso s preseta co modaltà/testà varabl da u soggetto all altro. Ad esempo, se dobbamo studare l reddto ua certa regoe è ecessaro osservare utà statstche
Nozioni elementari di Analisi Matematica applicate alla Fisica Generale
 Nozioi elemeari di alisi Maemaica applicae alla Fisica Geerale Nozioe di iegrale ideiio La derivazioe può essere ierpreaa come ua regola che, per ogi uzioe assegaa (primiiva), ci permee di deermiare u
Nozioi elemeari di alisi Maemaica applicae alla Fisica Geerale Nozioe di iegrale ideiio La derivazioe può essere ierpreaa come ua regola che, per ogi uzioe assegaa (primiiva), ci permee di deermiare u
VALORE EFFICACE DEL VOLTAGGIO
 Fisica generale, a.a. /4 TUTOATO 8: ALO EFFC &CCUT N A.C. ALOE EFFCE DEL OLTAGGO 8.. La leura con un mulimero digiale del volaggio ai morsei di un generaore fornisce + in coninua e 5.5 in alernaa. Tra
Fisica generale, a.a. /4 TUTOATO 8: ALO EFFC &CCUT N A.C. ALOE EFFCE DEL OLTAGGO 8.. La leura con un mulimero digiale del volaggio ai morsei di un generaore fornisce + in coninua e 5.5 in alernaa. Tra
Analisi economica e valutazione delle alternative
 Aals ecoomca e valutazoe delle alteratve Ig. Lug Cucca (Ph.D.) Producto Egeerg Research WorkGROUP Dpartmeto d Tecologa Meccaca, Produzoe e Igegera Gestoale Uverstà d Palermo Ageda Elemet d calcolo ecoomco
Aals ecoomca e valutazoe delle alteratve Ig. Lug Cucca (Ph.D.) Producto Egeerg Research WorkGROUP Dpartmeto d Tecologa Meccaca, Produzoe e Igegera Gestoale Uverstà d Palermo Ageda Elemet d calcolo ecoomco
Struttura dei tassi per scadenza
 Sruura dei assi per scadenza /45-Unià 7. Definizione del modello ramie gli -coupon bonds preseni sul mercao Ipoesi di parenza Sul mercao sono preseni all isane ZCB che scadono fra,2,,n periodi Periodo:
Sruura dei assi per scadenza /45-Unià 7. Definizione del modello ramie gli -coupon bonds preseni sul mercao Ipoesi di parenza Sul mercao sono preseni all isane ZCB che scadono fra,2,,n periodi Periodo:
Tassi Equivalenti. Benedetto Matarazzo
 Tass Equval Bdo Maarazzo Corso d Maaca Fazara Rg fazar Oprazo fazar Irss Scoo Equvalz fazar Rg dll rss splc Rg dll rss coposo Rg dll rss acpao (scoo corcal Prcpal proprà d u qualsas rg fazaro Cofroo ra
Tass Equval Bdo Maarazzo Corso d Maaca Fazara Rg fazar Oprazo fazar Irss Scoo Equvalz fazar Rg dll rss splc Rg dll rss coposo Rg dll rss acpao (scoo corcal Prcpal proprà d u qualsas rg fazaro Cofroo ra
ERRATA CORRIGE. L intero contenuto del paragrafo 9.2.3 a pagina 47-48 del Capitolato tecnico Determinazione del Canone è sostituito come segue:
 Procedura aperta per l affdameto de servz tegrat, gestoal, operatv e d mautezoe multservzo tecologco da esegurs presso gl mmobl d propretà o uso alle Asl ed alle azede ospedalere della regoe Campaa ERRATA
Procedura aperta per l affdameto de servz tegrat, gestoal, operatv e d mautezoe multservzo tecologco da esegurs presso gl mmobl d propretà o uso alle Asl ed alle azede ospedalere della regoe Campaa ERRATA
EQUAZIONI ALLE RICORRENZE
 Esercizi di Fodameti di Iformatica 1 EQUAZIONI ALLE RICORRENZE 1.1. Metodo di ufoldig 1.1.1. Richiami di teoria Il metodo detto di ufoldig utilizza lo sviluppo dell equazioe alle ricorreze fio ad u certo
Esercizi di Fodameti di Iformatica 1 EQUAZIONI ALLE RICORRENZE 1.1. Metodo di ufoldig 1.1.1. Richiami di teoria Il metodo detto di ufoldig utilizza lo sviluppo dell equazioe alle ricorreze fio ad u certo
Università degli Studi di Milano Bicocca CdS ECOAMM Corso di Metodi Statistici per l Amministrazione delle Imprese CARTE DI CONTROLLO PER ATTRIBUTI
 Uverstà degl Stud d Mlao Bcocca CdS ECOAMM Corso d Metod Statstc per l Ammstrazoe delle Imprese CARTE DI CONTROLLO PER ATTRIBUTI 1. Carta d cotrollo per frazoe d o coform (carta U resposable d produzoe,
Uverstà degl Stud d Mlao Bcocca CdS ECOAMM Corso d Metod Statstc per l Ammstrazoe delle Imprese CARTE DI CONTROLLO PER ATTRIBUTI 1. Carta d cotrollo per frazoe d o coform (carta U resposable d produzoe,
Analisi dei Dati. La statistica è facile!!! Correlazione
 Aals de Dat La statstca è facle!!! Correlazoe A che serve la correlazoe? Mettere evdeza la relazoe esstete tra due varabl stablre l tpo d relazoe stablre l grado d tale relazoe stablre la drezoe d tale
Aals de Dat La statstca è facle!!! Correlazoe A che serve la correlazoe? Mettere evdeza la relazoe esstete tra due varabl stablre l tpo d relazoe stablre l grado d tale relazoe stablre la drezoe d tale
Analisi di dati vettoriali. Direzioni e orientazioni
 Aals d dat vettoral Drezo e oretazo I tal caso, dat soo msurat term d agol e spesso soo rfert al ord geografco (statstca crcolare) Soo rappresetat su ua crcofereza Dat d drezoe: flusso ua specfca drezoe,
Aals d dat vettoral Drezo e oretazo I tal caso, dat soo msurat term d agol e spesso soo rfert al ord geografco (statstca crcolare) Soo rappresetat su ua crcofereza Dat d drezoe: flusso ua specfca drezoe,
Lezione 3. Gruppi risolubili.
 Lezoe 3 Prerequst: Lezo 1 2 Class d cougo e cetralzzat rupp rsolubl I questo captolo troducamo ua ozoe che come vedremo seguto fuge da raccordo tra la teora de grupp e la teora de camp Defzoe 31 Dato u
Lezoe 3 Prerequst: Lezo 1 2 Class d cougo e cetralzzat rupp rsolubl I questo captolo troducamo ua ozoe che come vedremo seguto fuge da raccordo tra la teora de grupp e la teora de camp Defzoe 31 Dato u
( ) 2 i 1 X. n(n + 1) a) si determini se sono corretti; b) per quelli non corretti, si calcoli la distorsione d;
 ESERCIZIO 5. Sa (X, X,, X ) u campoe casuale geerato da ua v.c. X f(x; θ) per la quale è oto che E(X) θ e Var(X). S cosdero 3 stmator d θ: X ; X ; ( ) X 3 a) s determ se soo corrett; b) per quell o corrett,
ESERCIZIO 5. Sa (X, X,, X ) u campoe casuale geerato da ua v.c. X f(x; θ) per la quale è oto che E(X) θ e Var(X). S cosdero 3 stmator d θ: X ; X ; ( ) X 3 a) s determ se soo corrett; b) per quell o corrett,
Elementi di Matematica Finanziaria. Rendite e ammortamenti. Università Parthenope 1
 Elemet d Matematca Fazara Redte e ammortamet Uverstà Partheope 1 S chama redta ua successoe d captal da rscuotere (o da pagare) a scadeze determate S chamao rate della redta sgol captal da rscuotere (o
Elemet d Matematca Fazara Redte e ammortamet Uverstà Partheope 1 S chama redta ua successoe d captal da rscuotere (o da pagare) a scadeze determate S chamao rate della redta sgol captal da rscuotere (o
Le basi della valutazione secondo i cash flow. Aswath Damodaran
 Le basi della valuazione secondo i cash flow Aswah Damodaran Valuazione secondo i cash flow: le basi dell'approccio Valore = = n CF = 1 1+ r ( ) dove, n = anni di via dell'aivià CF = Cash flow nel periodo
Le basi della valuazione secondo i cash flow Aswah Damodaran Valuazione secondo i cash flow: le basi dell'approccio Valore = = n CF = 1 1+ r ( ) dove, n = anni di via dell'aivià CF = Cash flow nel periodo
Due distribuzioni, stessa media ma in quale delle due la media rappresenta, sintetizza meglio la situazione?
 Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 =3,6 5 5 38 40 45 63 63/5 =3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 =3,6 5 5 38 40 45 63 63/5 =3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
Processi periodici. Capitolo 2. 2.1 Modello. 2.1.1 Simboli. 2.1.2 Grafico dei processi. {τ 1,...,τ n } processi periodici
 3 Capolo 2 Process perodc 2. Modello 2.. Smbol {,...,τ n } process perodc τ,k sanza k-esma del processo φ fase d un processo (prmo empo d avazone) T perodo del processo r,k = φ +(k ) T k-esma avazone D
3 Capolo 2 Process perodc 2. Modello 2.. Smbol {,...,τ n } process perodc τ,k sanza k-esma del processo φ fase d un processo (prmo empo d avazone) T perodo del processo r,k = φ +(k ) T k-esma avazone D
Leasing: aspetti finanziari e valutazione dei costi
 Leasg: aspett fazar e valutazoe de cost Descrzoe Il leasg è u cotratto medate l quale ua parte (locatore), cede ad u altro soggetto (locataro), per u perodo d tempo prefssato, uo o pù be, sao ess mobl
Leasg: aspett fazar e valutazoe de cost Descrzoe Il leasg è u cotratto medate l quale ua parte (locatore), cede ad u altro soggetto (locataro), per u perodo d tempo prefssato, uo o pù be, sao ess mobl
Due distribuzioni, stessa media ma in quale delle due la media rappresenta, sintetizza meglio la situazione?
 Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 3,6 5 5 38 40 45 63 63/5 3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 3,6 5 5 38 40 45 63 63/5 3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
ammontare del carattere posseduto dalle i unità più povere.
 Eserctazoe VII: La cocetrazoe Eserczo Determare l rapporto d cocetrazoe d G del fatturato medo (espresso. d euro) d 8 mprese e rappresetare la curva d Lorez: 97 35 39 52 24 72 66 87 Eserczo apporto d cocetrazoe
Eserctazoe VII: La cocetrazoe Eserczo Determare l rapporto d cocetrazoe d G del fatturato medo (espresso. d euro) d 8 mprese e rappresetare la curva d Lorez: 97 35 39 52 24 72 66 87 Eserczo apporto d cocetrazoe
Costi della politica: Giudizio positivo per i sindaci, maglia nera per parlamentari e consiglieri regionali
 XXVI I IAssembl eaanci-larepubbl cadecomun Au onom apercamb ar e lpaese Lac l assepol c aec ad n Op n onsucos,r esponsab l àe mpegnodch gover nal e s uz on Cos della polca: Gudzo posvo per sndac, magla
XXVI I IAssembl eaanci-larepubbl cadecomun Au onom apercamb ar e lpaese Lac l assepol c aec ad n Op n onsucos,r esponsab l àe mpegnodch gover nal e s uz on Cos della polca: Gudzo posvo per sndac, magla
Introduzione (1) Introduzione (2) Prodotti e servizi sono realizzati per mezzo di processi produttivi.
 Iroduzioe () Ua defiizioe (geerale) del ermie qualià: qualià è l isieme delle caraerisiche di u eià (bee o servizio) che e deermiao la capacià di soddisfare le esigeze espresse ed implicie di chi la uilizza.
Iroduzioe () Ua defiizioe (geerale) del ermie qualià: qualià è l isieme delle caraerisiche di u eià (bee o servizio) che e deermiao la capacià di soddisfare le esigeze espresse ed implicie di chi la uilizza.
LA FUNZIONE DI VEROSIMIGLIANZA
 A FUNZIONE DI VEROSIMIGIANZA HA UN RUOO IMPORTANTE NEA PROCEDURE DI INFERENZA STATISTICA COME: ) METODO DI COSTRUZIONE DI STIMATORI (IN SITUAZIONI COMPESSE) ) METODO DI INDIVIDUAZIONE DI TEST UNIFORMEMENTE
A FUNZIONE DI VEROSIMIGIANZA HA UN RUOO IMPORTANTE NEA PROCEDURE DI INFERENZA STATISTICA COME: ) METODO DI COSTRUZIONE DI STIMATORI (IN SITUAZIONI COMPESSE) ) METODO DI INDIVIDUAZIONE DI TEST UNIFORMEMENTE
Rota Bulò Samuel 796408
 Roa Bulò Samuel 79648 ONNUO INRODUZION 4. osa soo le re eural 4. La mee umaa 4 NURON DI MULLOH-PIS 5. Modello euroe 5. p d fuzoe d aazoe 6.. resold fuco o Heasde fuco 6.. Pecese-lear fuco 6..3 Sgmod fuco
Roa Bulò Samuel 79648 ONNUO INRODUZION 4. osa soo le re eural 4. La mee umaa 4 NURON DI MULLOH-PIS 5. Modello euroe 5. p d fuzoe d aazoe 6.. resold fuco o Heasde fuco 6.. Pecese-lear fuco 6..3 Sgmod fuco
Contenuti. Facoltà di Economia. Scatterplot o diagramma a dispersione Analisi grafica della relazione tra due. francesco mola.
 Coteut Corso d Statstca Facoltà d Ecooma a.a. - fracesco mola Lezoe 9 Correlazoe leare Scatterplot e aals grafca L uso delle varabl stadardzzate La covaraza Il coeffcete d correlazoe leare d Bravas-Pearso
Coteut Corso d Statstca Facoltà d Ecooma a.a. - fracesco mola Lezoe 9 Correlazoe leare Scatterplot e aals grafca L uso delle varabl stadardzzate La covaraza Il coeffcete d correlazoe leare d Bravas-Pearso
La programmazione aggregata nella supply chain. La programmazione aggregata nella supply chain 1
 La programmazione aggregaa nella supply chain La programmazione aggregaa nella supply chain 1 Linea guida Il ruolo della programmazione aggregaa nella supply chain Il problema della programmazione aggregaa
La programmazione aggregaa nella supply chain La programmazione aggregaa nella supply chain 1 Linea guida Il ruolo della programmazione aggregaa nella supply chain Il problema della programmazione aggregaa
SCUOLA POLITECNICA IN ECONOMIA E ORGANIZZAZIONE VILFREDO PARETO MASTER IN E-BUSINESS CAPITAL BUDGETING
 CAPITAL BUDGETING VALUTAZIONE DI PROGETTI D INVESTIMENTO CON PREVISIONE DEI FLUSSI DI CASSA ATTESI: l impresa ivese moea oggi per oeere flussi moeari icremeali el fuuro.* PROGETTO: Ivesimeo i arezzaure
CAPITAL BUDGETING VALUTAZIONE DI PROGETTI D INVESTIMENTO CON PREVISIONE DEI FLUSSI DI CASSA ATTESI: l impresa ivese moea oggi per oeere flussi moeari icremeali el fuuro.* PROGETTO: Ivesimeo i arezzaure
Il valore delle. Argomenti. Domande chiave. Teoria della Finanza Aziendale Prof. Arturo Capasso A.A. 2005-2006
 - 4 Teoria della Finanza Aziendale rof. Aruro Capasso A.A. 5-6 Il valore delle A. azioni ordinarie - Argomeni Rendimeni richiesi rezzi delle azioni e ES Cash Flows e valore economico d impresa - 3 Domande
- 4 Teoria della Finanza Aziendale rof. Aruro Capasso A.A. 5-6 Il valore delle A. azioni ordinarie - Argomeni Rendimeni richiesi rezzi delle azioni e ES Cash Flows e valore economico d impresa - 3 Domande
Caso studio 12. Regressione. Esempio
 6/4/7 Caso studo Per studare la curva d domada d u bee che sta per essere trodotto sul mercato, s rlevao dat rguardat l prezzo mposto e l umero d pezz vedut 7 put vedta plota, ell arco d ua settmaa. I
6/4/7 Caso studo Per studare la curva d domada d u bee che sta per essere trodotto sul mercato, s rlevao dat rguardat l prezzo mposto e l umero d pezz vedut 7 put vedta plota, ell arco d ua settmaa. I
