L insieme N e l insieme Z Le cifre e i numeri Le quattro operazioni e le potenze in N Le espressioni La misura e i problemi
|
|
|
- Antonella Fedele
- 7 anni fa
- Visualizzazioni
Transcript
1 L nsm N l nsm Z L r numr L quttro oprzon l potnz n N L sprsson L msur prolm L r numr 1 Stls s l sunt rmzon sono vr o ls. SEZ. A l m n o p q 39 è un numro spr. 112 è un numro pr. In 79, 9 è un r. 10 è un r. Il prnt 1201 è Il sussvo è è vrso 3 s srv 3 3. S 1 < 5 llor, on N, può ssr 1, 2, 3, 4. Nl numro 488 l r 8 s vlor n s vlor untà. I numr ntr rltv spr mor 5 mnor +6 sono: 3, 1, +1, +3, +5. Con l r 2 4 s possono srvr solo sunt numr ntr u r: 24, 42, 22, 44. Nl numro 1033 l r 0 può ssr trlst. Du numr srtt on l stss r sono uul. Nl numro 7123 l r 1 vl 10. Nl sstm numrzon ml l r non nno un vlor sso. Nl sstm numrzon ml s usno solo 9 r. Un numro non può ssr ormto un sol r. l m n o p q Pré l ultm r, 9, è spr. Pré l ultm r, 2, è pr. Pré 9 è uno smol ust nl nostro sstm numrzon. Pré 1 0 sono r, 10 è un numro. Pré 1 è omprso ( ) mntr 5 è sluso (<). Pré 488 è uul 4 ntn, 8 n 8 untà. Onun ll u r può ssr un 2 o un 4. Pré 0 n qust poszon rpprsnt l ntn. S smpo onsrmo 21 12, pur vno l stss r, ss sono vrs n qunto l r uul oup poszon vrs. Pré l r 1 vl 100. Pré l vlor pn ll poszon. Pré smol, oè l r, sono 10: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. A smpo 4 è un r, m è n un numro rpprsnt 4 untà. 2 Sl l rspost stt. Il numro 3,014: è mor 3,2. è mor 3. è mor 3,14. Il numro 3,014 è ormto 3 untà, 0 m, 1 ntsmo, 4 mllsm, qun è mor 3 è ormto solo 3 untà, m è mnor 3,2 è ormto 3 untà 2 m, 3,14 è ormto 3 untà, 1 mo 4 ntsm. L rspost stt è qun. A. Clv - G. Pnzr ELI - L Sp 1
2 Szon A L nsm N l nsm Z L quttro oprzon l potnz n N 3 Stls s l sunt rmzon sono vr o ls. Il quoznt u numr nturl è smpr un numro nturl. S l vno è mor l vsor l quoznt è un numro nturl. S l vno è multplo l vsor l quoznt è un numro nturl. L sottrzon è l oprzon nvrs ll zon. Consrno smpo l vson 10 : 4 ottnmo 2,5 è un numro ml. Consrno smpr l vson 10 : 4, n u l vno 10 è mor l vsor 4, ottnmo 2,5 è un numro ml. Pr nzon, l multplo un numro lo ontn sttmnt. A smpo 12 2 = = 12. Sl l rspost stt. 4 Moltplno u numr nturl s ottn: smpr un numro nturl. n lun s prtolr un numro non è un numro nturl. volt un numro nturl, volt no. L rspost stt è pré s pnsmo l moltplzon om somm numr tutt uul nturl, l rsultto è surmnt un numro nturl. 5 L sottrzon tr u numr nturl à om rsultto: smpr un numro nturl. lun volt un numro nturl. m un numro nturl. L rspost stt è, ntt l rsultto è un numro nturl solo s l mnuno è mor l sottrno. 6 Stls s l sunt uulnz sono vr o ls = = = = = 71 0 : 8 = 0 8 : 0 = mpossl 1 5 = 1 6 : 1 1 : 6 L zon o ll proprtà ommuttv. L sottrzon non o ll proprtà ommuttv. Qulunqu numro moltplto pr 0 à om rsultto 0. 1 è l lmnto nutro ll moltplzon. Pré 0 8 = 0. Nssun numro moltplto pr 0 à om rsultto 8. 1 moltplto pr s stsso 5 volt à om rsultto 1. L vson non o ll proprtà ommuttv. 7 Srv l oprzon orrsponnt ll sunt rs. Azonr 9 l numro 23. Sottrrr 17 l numro 11. Clolr l multplo sono 4 8. Clolr l vson tr Sottrrr l numro 100 l numro 17 zonr l rsultto l numro 2. Dvr pr 7 l numro 56. Clolr l prootto ttor : : A. Clv - G. Pnzr ELI - L Sp 2
3 L quttro oprzon l potnz n N 8 Stls s l sunt rmzon sono vr o ls. l m n o p q r s t u v L potnz 0 2 è uul 0. L potnz 0 0 non sst. L potnz 5 1 è uul 1. L potnz 1 3 è uul 1. L potnz 7 2 è uul 14. L potnz 7 0 è uul 0. Pr l lvmnto potnz vl l proprtà ommuttv. 3 5 < > : 2 10 = = 30 4 (7 2 ) 3 = = : 5 3 = : 5 2 = : 4 0 = = 3 4 (5 2 ) 0 = = = 4 9 = : 4 = 100 : 4 = = = 25 l m n o p q r s t u Pré 0 2 = 0 0 = 0. Pré è un orm ntrmnt. On s lvt 1 è uul ll s stss. Pré 1 3 = = 1. Pré 7 2 = 7 7 = 49. Un qulunqu potnz on sponnt 0 pr rsultto 1. A smpo 2 3 = 8 m 3 2 = 9, qun Pré 3 5 = = = = 125, qun 3 5 > 5 3. Pré 5 0 = = 3, qun 5 0 < 3 1. Pré 6 10 : 2 10 = (6 : 2) 10 = Pré = (2 3 5) 4 = Pré (7 2 ) 3 = = 7 6. Pré 2 3 = = 8. Pré 5 3 : 5 3 = (5 : 5) 3 = 1 3. Pré 5 6 : 5 2 = = 5 4. Pré 4 0 : 4 0 = = 4 0 = 1. Pr l potnz non vl l proprtà ommuttv. Pré (5 2 ) 0 = = 5 0 = 1. Pré 1 lvto qulunqu sponnt à om rsultto smpr 1. Il prootto ll r è uul ll r l prootto. Il quoznt ll r è uul ll r l quoznt. v Intt 9 = 3, 16 = 4, 25 = Esprm on un sol potnz l rsultto ll sunt sprsson = 64 3 : 4 3 : 2 3 = 45 2 : 9 2 : 5 2 = 72 3 : = (4 3 2) 4 = 24 4 (64 : 4 : 2) 3 = (16 : 2) 3 = 8 3 (45 : 9 : 5) 2 = (5 : 5) 2 = 1 2 = 1 (72 : 9 2) 3 = (8 2) 3 = Applno l rol l prootto l rol l quoznt u r qurt, lol l vlor ll sunt sprsson : 5 = = = : : 2 = = = : 2 27 : 3 = = = : = = = 15 A. Clv - G. Pnzr ELI - L Sp 3
4 Szon A L nsm N l nsm Z L sprsson Rsolv l sunt sprsson vr tpolo : : 2 16 : = S rsolvono prm moltplzon vson, nll orn n u s trovno: = = {20 50 : [(40 5 6) + (6 8 33)] ( )} : 3 = S suono lol nll prnts ton, po nll qur nn nll r: = {20 50 : [(40 30) + (48 33)] (2 + 10)} : 3 = = {20 50 : [ ] 12} : 3 = = {20 50 : 25 12} : 3 = = { } : 3 = 6 : 3 = 2 13 ( ) : : 9 3 = Applmo l proprtà ll potnz, sussvmnt svluppmo l potnz, qun rsolvmo moltplzon vson, nll orn n u s trovno, nn zon sottrzon nll orn n u s trovno: = [(3 2) ] : (18 : 9) 3 = = [ ] : = = [36 24] : = = 12 : = = ( ) 2 : ( ) 3 : 3 4 = L sprsson ontn solo potnz l 3, qun pplmo l proprtà potnz on l stss s: = ( ) 2 : ( ) 3 : 3 4 = = (3 13 ) 2 : (3 7 ) 3 : 3 4 = = 3 26 : 3 21 : 3 4 = = 3 1 = 3 15 [16 3 (2 4 ) 2 : (4 2 ) 4 ] 3 [(2 4 ) 4 : 16 2 ] 3 : [ (2 3 ) 5 ] : (2 3 ) 3 = L potnz prsnt nno s 2, 4, 16, m 4 = = 2 4, qun trsormmo tutt l potnz n s 2: = [(2 4 ) 3 (2 4 ) 2 : (2 4 ) 4 ] 3 [(2 4 ) 4 : (2 4 ) 2 ] 3 : [(2 2 ) 2 (2 2 ) 3 (2 3 ) 5 ] : (2 3 ) 3 = = [ : 2 16 ] 3 [2 16 : 2 8 ] 3 : [ ] : 2 9 = = [ ] 3 [ ] 3 : [ ] : 2 9 = = [2 4 ] 3 [2 8 ] 3 : 2 25 : 2 9 = = : 2 25 : 2 9 = = = 2 2 = 4 A. Clv - G. Pnzr ELI - L Sp 4
5 L sprsson 16 ( ) : ( ) : ( ) 5 0 ( ) = Svluppmo tutt l potnz prsnt nl tsto: = ( ) : 1 + ( ) : (9 4) 1 ( ) = Esumo l oprzon prsnt nll prnts: = 8 : : = Esumo moltplzon vson: = = {[3 3 ( : 6 6 ) + ( ) 3] : } : [7 2 ( ) ] 2 = Esumo lol ontnut nll prnts ton no l prnz ll potnz pplno, ov è possl, l loro proprtà: = {[3 3 ( ) + ( ) 3] : 3 + 9} : [7 2 (25 8 3) ] 2 = = {[ ] : 3 + 9} : [ ] 2 = Esumo lol ontnut nll prnts qur: = {[ ] : 3 + 9} : [ ] 2 = = {[ ] : 3 + 9} : [ ] 2 = = {303 : 3 + 9} : = Esumo lol ontnut nll prnts r: = { } : = = 110 : = = = 4 L msur prolm 18 Stls s l sunt rmzon sono vr o ls. L tu ltzz è un rnzz. L lt uno sportvo è un rnzz. Il ro ll lun l lunzz l tuo to sono rnzz omon. L tmprtur l qunttà olo ontnut n un on non sono rnzz omon. In 2 mtr sono 200 ntmtr. Tr ltr qu psno 3 l. Un loo ronzo 100 m 3 (ps 8,95) ps 895 rmm. 30' =1800" 2 120' = 4 3 or =180 mnut Prto ll 12:30 rrvo stnzon ll 18:30, qun o pssto 4 or n vo. S può msurr n mtr o ntmtr. Pré non è msurl. Entrm s possono msurr on l stss untà msur. L tmprtur s msur n r ntr, l qunttà olo n ltr. Il ntmtro è l ntsm prt l mtro, qun n 1 mtro sono ontnut 100 ntmtr n 2 mtr sono 200 ntmtr. L ptà 3 ltr orrspon l volum 3 m 3 ssno l pso spo ll qu uul 1, l pso srà 3 l. 1 m 3 ronzo ps 8,95 moltplno pr 100 ottnmo 895. Pré 1 prmo orrspon 60 son. Pré 60' = 1, qun 120' = 2. Pré 1 or = 60 mnut m m = 6, qun o pssto 6 or n vo. A. Clv - G. Pnzr ELI - L Sp 5
6 Szon A L nsm N l nsm Z Rsolv sunt prolm. 19 Lu è srtto un orso nuoto 15 lzon. L lzon ostno omplssvmnt 112,50 uro on nrsso n psn 2,50 uro. Qunto spnrà n tutto Lu? L sprsson rsolutv è l sunt: (112,50 + 2,50 15) = (112, ,50) = Nll lot ll lss sono 32 volum. I romnz vvntur sono l trplo qull ntsnz. Qunt sono romnz vvntur ll lot? Qusto prolm s rsolv lmnt on l mtoo ro: romnz ntsnz: romnz vvntur (l trplo): totl volum (32): Qun 32 : 4 = 8 sono volum ntsnz, 8 3 = 24 sono volum vvntur. 21 L somm tr numr è 62; spno l prmo è l mtà l sono l trzo supr l sono 7, trmn tr numr. Usmo n n qusto so l mtoo ro: 1 o numro 2 o numro 7 3 o numro 1 o + 2 o + 3 o numro [(62 7) : 5] = 11 1 o numro (11 2) = 22 2 o numro (22 + 7) = 29 3 o numro 22 Un rvst sttmnl ost 2 uro ll op. In un nno sono 51 numr. Qunto s rsprm s, nv omprrl on sttmn, s sottosrv l onmnto ost 90 uro? Il prolm è rsolvl on un sprsson: (51 2) 90 = = 12 uro rsprmo ottnuto. A. Clv - G. Pnzr ELI - L Sp 6
Minimum Spanning Tree
 Mnmum Spnnn Tr Ivn Lns Dprtmnto Inormt Snz Innr Unvrstà Bolon vn.lns@ml.om ttp://www.s.uno.t/~lns/ Mnmum Spnnn Trs Introuzon Un prolm notvol mportnz: trmnr om ntronnttr vrs lmnt r loro mnmzzno rt vnol
Mnmum Spnnn Tr Ivn Lns Dprtmnto Inormt Snz Innr Unvrstà Bolon vn.lns@ml.om ttp://www.s.uno.t/~lns/ Mnmum Spnnn Trs Introuzon Un prolm notvol mportnz: trmnr om ntronnttr vrs lmnt r loro mnmzzno rt vnol
j Verso la scuola superiore Gli insiemi N, Z, Q, R
 j Vrso l suol suprior Gli insimi N, Z, Q, R Individu l rispost orrtt Un numro è divisor sondo di un numro s L oprzion è impossiil possiil in Z possiil in R Trdundo il tsto nll simologi mtmti si h ; pplindo
j Vrso l suol suprior Gli insimi N, Z, Q, R Individu l rispost orrtt Un numro è divisor sondo di un numro s L oprzion è impossiil possiil in Z possiil in R Trdundo il tsto nll simologi mtmti si h ; pplindo
Macchine non completamente specificate. Sintesi Sequenziale Sincrona Sintesi Comportamentale di Reti Sequenziali Sincrone
 Mhin non ompltmnt spifit Sintsi Squnzil Sinron Sintsi Comportmntl i Rti Squnzili Sinron Riuzion l numro gli stti pr Mhin Non Compltmnt Spifit Comptiilità Vrsion l 5/12/02 Sono mhin in ui pr lun onfigurzioni
Mhin non ompltmnt spifit Sintsi Squnzil Sinron Sintsi Comportmntl i Rti Squnzili Sinron Riuzion l numro gli stti pr Mhin Non Compltmnt Spifit Comptiilità Vrsion l 5/12/02 Sono mhin in ui pr lun onfigurzioni
6) Nel 1991 Carl Lewis ha stabilito il record del mondo dei 100 m percorrendoli in 9,86 s. Qual è la velocità media in km/h?
 1) L unità l SI pr l tmprtur l mss sono, rispttivmnt gri grmmi klvin kilogrmmi Clsius milligrmmi Clsius kilogrmmi klvin grmmi 2) Qul mtril ffon nll olio ( = 0,94 g/m 3 )? ghiio ( = 0,92 g/m 3 ) sughro
1) L unità l SI pr l tmprtur l mss sono, rispttivmnt gri grmmi klvin kilogrmmi Clsius milligrmmi Clsius kilogrmmi klvin grmmi 2) Qul mtril ffon nll olio ( = 0,94 g/m 3 )? ghiio ( = 0,92 g/m 3 ) sughro
Cammini minimi in un grafo orientato pesato. Un problema di percorso. Problemi di ottimizzazione
 Cmmn mnm n un gro orntto sto Algortm Dkstr Bllmn-For r l rolm l mmno mnmo sorgnt sngol Un rolm rorso Dt un m strl on stnz s. n lomtr un unto rtnz s tror rors ù r s sun ll ltr loltà Prolm ottmzzzon Prolm:
Cmmn mnm n un gro orntto sto Algortm Dkstr Bllmn-For r l rolm l mmno mnmo sorgnt sngol Un rolm rorso Dt un m strl on stnz s. n lomtr un unto rtnz s tror rors ù r s sun ll ltr loltà Prolm ottmzzzon Prolm:
FUNZIONI A DUE VARIABILI RICERCA DEI PUNTI DI MASSIMO E MINIMO
 Pg. Pro. Muro D Ettorr UNZIONI A DUE VARIABILI RICERCA DEI PUNTI DI MASSIMO E MINIMO PREMESSE DERIVATE PARZIALI DI UNA UNZIONE A DUE O PIU VARIABILI Dt un unzon d n vrbl z=... n s dc drvt przl l unzon
Pg. Pro. Muro D Ettorr UNZIONI A DUE VARIABILI RICERCA DEI PUNTI DI MASSIMO E MINIMO PREMESSE DERIVATE PARZIALI DI UNA UNZIONE A DUE O PIU VARIABILI Dt un unzon d n vrbl z=... n s dc drvt przl l unzon
Circuiti Sequenziali Macchine Non Completamente Specificate
 CEFRIEL Consorzio pr l Formzion l Rir in Inggnri ll Informzion Politnio i Milno Ciruiti Squnzili Mhin Non Compltmnt Spifit Introuzion Comptiilità Riuzion l numro gli stti Mtoo gnrl FSM non ompltmnt spifit
CEFRIEL Consorzio pr l Formzion l Rir in Inggnri ll Informzion Politnio i Milno Ciruiti Squnzili Mhin Non Compltmnt Spifit Introuzion Comptiilità Riuzion l numro gli stti Mtoo gnrl FSM non ompltmnt spifit
Sistemi e Tecnologie della Comunicazione
 Sstm olog dll Comuzo Complmt : sr trsformt d Fourr Formul d prostfrs L formul d prostfrs sprmoo l vlor d so o d somm d gol prodott d s d gol gol, vvrs: ( α β ) ( α ) ( β ) ( α ) ( β ) ( α β ) ( α ) ( β
Sstm olog dll Comuzo Complmt : sr trsformt d Fourr Formul d prostfrs L formul d prostfrs sprmoo l vlor d so o d somm d gol prodott d s d gol gol, vvrs: ( α β ) ( α ) ( β ) ( α ) ( β ) ( α β ) ( α ) ( β
Matematica. Sviluppo delle competenze 1-3 ciclo
 Mtmt Svluppo ll omptnz - lo Elmnt llo svluppo ll omptnz Imprssum Etor: Dprtmnto ll'uzon, ultur protzon ll'mnt Gron Ruro l prsnt oumnto: Ezon l 5.0.06 Immn oprtn: Alxy Klmntv/Hmr/Tnkstok Copyrt: Ttolr rtt
Mtmt Svluppo ll omptnz - lo Elmnt llo svluppo ll omptnz Imprssum Etor: Dprtmnto ll'uzon, ultur protzon ll'mnt Gron Ruro l prsnt oumnto: Ezon l 5.0.06 Immn oprtn: Alxy Klmntv/Hmr/Tnkstok Copyrt: Ttolr rtt
1 a. 1 b. Rappresenta i seguenti numeri su una retta orientata, scegliendo autonomamente una opportuna unità di misura. b 1
 Rpprsnt i sgunti numri su un rtt orintt, sglino utonommnt un opportun unità i misur. 0 0 f g 7 0 h 0 Si noti h il m..m i nomintori è 0, quini un slt opportun è siurmnt qull i utilizzr 0 qurtti om unità
Rpprsnt i sgunti numri su un rtt orintt, sglino utonommnt un opportun unità i misur. 0 0 f g 7 0 h 0 Si noti h il m..m i nomintori è 0, quini un slt opportun è siurmnt qull i utilizzr 0 qurtti om unità
Modelli equivalenti del BJT
 Modll ulnt dl JT Pr lo studo dll pplczon crcutl dl JT, s è rso opportuno formulr d modll ulnt dl dsposto ch srssro rpprsntr n modo connnt l suo comportmnto ll ntrno d crcut. A scond dl tpo d pplczon (mplfczon
Modll ulnt dl JT Pr lo studo dll pplczon crcutl dl JT, s è rso opportuno formulr d modll ulnt dl dsposto ch srssro rpprsntr n modo connnt l suo comportmnto ll ntrno d crcut. A scond dl tpo d pplczon (mplfczon
di Enzo Zanghì 1
 M@t_cornr d Enzo Zngì Intgrl ndfnto S dc c l funzon F () è un prmtv dll funzon f (), contnu nll'ntrvllo I s F '( ) f ( ) S un funzon mmtt n un ntrvllo I un prmtv, llor n mmtt nfnt c dffrscono tr loro mno
M@t_cornr d Enzo Zngì Intgrl ndfnto S dc c l funzon F () è un prmtv dll funzon f (), contnu nll'ntrvllo I s F '( ) f ( ) S un funzon mmtt n un ntrvllo I un prmtv, llor n mmtt nfnt c dffrscono tr loro mno
Sistemi lineari COGNOME... NOME... Classe... Data...
 Cpitolo Sistmi linri Risoluzion grfi lgri rifi pr l lss prim COGNOME............................... NOME............................. Clss.................................... Dt...............................
Cpitolo Sistmi linri Risoluzion grfi lgri rifi pr l lss prim COGNOME............................... NOME............................. Clss.................................... Dt...............................
Grandezze, funzioni empiriche e matematiche. 1 Stabilisci se le seguenti affermazioni sono vere o false.
 Grnzz unzioni Grnzz, unzioni mpirih mtmtih Grnzz irttmnt invrsmnt proporzionli Applizioni ll proporzionlità Grnzz, unzioni mpirih mtmtih Stilisi s l sunti rmzioni so vr o ls. SZ. I Un rnzz è vriil s ssum
Grnzz unzioni Grnzz, unzioni mpirih mtmtih Grnzz irttmnt invrsmnt proporzionli Applizioni ll proporzionlità Grnzz, unzioni mpirih mtmtih Stilisi s l sunti rmzioni so vr o ls. SZ. I Un rnzz è vriil s ssum
Problemi piani: L elemento triangolare a 3 nodi
 Prol pn: L lnto trngolr 3 nod Elnt dnsonl: stto d tnson pn In olt s, pr ssndo l oggtto d stdr n soldo ontno, l shtzzzon dl oportnto strttrl pò ssr ftt on n odllo ontno dnsonl, on n sffnt grdo d pprosszon.
Prol pn: L lnto trngolr 3 nod Elnt dnsonl: stto d tnson pn In olt s, pr ssndo l oggtto d stdr n soldo ontno, l shtzzzon dl oportnto strttrl pò ssr ftt on n odllo ontno dnsonl, on n sffnt grdo d pprosszon.
Minimizzazione degli Stati in una macchina a stati finiti
 Rti Loih Sintsi i rti squnzili sinron Minimizzzion li Stti in un mhin stti initi Proimnto: Spiih Dirmm li stti Tll li stti Minimizzzion li stti Coii li stti Tll ll trnsizioni Slt lmnti i mmori Tll ll itzioni
Rti Loih Sintsi i rti squnzili sinron Minimizzzion li Stti in un mhin stti initi Proimnto: Spiih Dirmm li stti Tll li stti Minimizzzion li stti Coii li stti Tll ll trnsizioni Slt lmnti i mmori Tll ll itzioni
Algoritmi e Strutture Dati
 Alortm su Gr: MST mmn mnm Mr Rt D Brrn, Emnul Mrll 1 1 Dprtmnto Mtmt Inormt Unvrstà Cmrno A.A. 00/0 Dnzon l prolm Prt I Mnmo Alro Roprnt Dnzon l prolm Mnmo lro roprnt S G = (V, E) un ro non orntto, onnsso
Alortm su Gr: MST mmn mnm Mr Rt D Brrn, Emnul Mrll 1 1 Dprtmnto Mtmt Inormt Unvrstà Cmrno A.A. 00/0 Dnzon l prolm Prt I Mnmo Alro Roprnt Dnzon l prolm Mnmo lro roprnt S G = (V, E) un ro non orntto, onnsso
Algoritmi e Strutture Dati
 Alortm su Gr: MST mmn mnm Mr Rt D Brrn, Emnul Mrll 1 1 Dprtmnto Mtmt Inormt Unvrstà Cmrno novmr 00 Prt I Mnmo Alro Roprnt Mnmo lro roprnt S G = (V, E) un ro non orntto, onnsso psto (w : E R è l unzon pso,
Alortm su Gr: MST mmn mnm Mr Rt D Brrn, Emnul Mrll 1 1 Dprtmnto Mtmt Inormt Unvrstà Cmrno novmr 00 Prt I Mnmo Alro Roprnt Mnmo lro roprnt S G = (V, E) un ro non orntto, onnsso psto (w : E R è l unzon pso,
Circuiti Nel progettare un circuito destinato a svolgere una certa funzione normalmente si hanno a disposizione i seguenti elementi:
 Ciruiti Nl progttr un iruito stinto svolgr un rt funzion normlmnt si hnno isposizion i sgunti lmnti: NODO )Uno o più sorgnti i f..m. not (ttri, gnrtor i tnsion) )Filo mtllio (onuttor) ) intrruttori )sistnz
Ciruiti Nl progttr un iruito stinto svolgr un rt funzion normlmnt si hnno isposizion i sgunti lmnti: NODO )Uno o più sorgnti i f..m. not (ttri, gnrtor i tnsion) )Filo mtllio (onuttor) ) intrruttori )sistnz
Albero di supporto di costo minimo
 Algortm Struttur Dat II Alro supporto osto mnmo Nl prolma lla struzon ll nrga lttra sono vrs as h vono rvr nrga a una ntral lttra. Pr rvr nrga, ogn asa v ssr ollgata alla ntral attravrso un ammno fatto
Algortm Struttur Dat II Alro supporto osto mnmo Nl prolma lla struzon ll nrga lttra sono vrs as h vono rvr nrga a una ntral lttra. Pr rvr nrga, ogn asa v ssr ollgata alla ntral attravrso un ammno fatto
Elettronica dei Sistemi Digitali Sintesi di porte logiche combinatorie fully CMOS
 Elttroni di Sistmi Digitli Sintsi di port logih omintori full CMOS Vlntino Lirli Diprtimnto di Tnologi dll Informzion Univrsità di Milno, 26013 Crm -mil: lirli@dti.unimi.it http://www.dti.unimi.it/ lirli
Elttroni di Sistmi Digitli Sintsi di port logih omintori full CMOS Vlntino Lirli Diprtimnto di Tnologi dll Informzion Univrsità di Milno, 26013 Crm -mil: lirli@dti.unimi.it http://www.dti.unimi.it/ lirli
a b }. L insieme Q è pertanto l insieme delle frazioni.
 I1. Insimisti I1.1 Insimi Il ontto i insim è un ontto primitivo, prtnto non n vin t un finizion rigoros. Si può ir, intuitivmnt, h un insim è un ollzion i oggtti pr ui vlgono lun proprità: Un lmnto i un
I1. Insimisti I1.1 Insimi Il ontto i insim è un ontto primitivo, prtnto non n vin t un finizion rigoros. Si può ir, intuitivmnt, h un insim è un ollzion i oggtti pr ui vlgono lun proprità: Un lmnto i un
Informatica 3. Informatica 3. LEZIONE 25: Algoritmi sui grafi. Lezione 25 - Modulo 1. Problema. Notazioni per il percorso più breve
 Informti Informti LZION : lgoritmi sui grfi Lzion - Moulo Moulo : Prolm l prorso più rv Moulo : Spnning tr osto minimo Prolm l prorso più rv Politnio i Milno - Prof. Sr omi Politnio i Milno - Prof. Sr
Informti Informti LZION : lgoritmi sui grfi Lzion - Moulo Moulo : Prolm l prorso più rv Moulo : Spnning tr osto minimo Prolm l prorso più rv Politnio i Milno - Prof. Sr omi Politnio i Milno - Prof. Sr
Funzione esponenziale e logaritmo. Proprietà di esponenziale e logaritmo.
 Funzion sponnzil ritmo. Proprità di sponnzil ritmo. 6. Funzion sponnzil ritmo. Proprità di sponnzil ritmo. Funzion sponnzil f ( ) fissto f : ( + ) è l bs dll funzion sponnzil d è fisst è l sponnt dll funzion
Funzion sponnzil ritmo. Proprità di sponnzil ritmo. 6. Funzion sponnzil ritmo. Proprità di sponnzil ritmo. Funzion sponnzil f ( ) fissto f : ( + ) è l bs dll funzion sponnzil d è fisst è l sponnt dll funzion
Esercitazioni di Elettrotecnica: circuiti in regime stazionario
 Maffucc: rcut n rgm stazonaro r- Unrstà dgl Stud d assno srctazon d lttrotcnca: crcut n rgm stazonaro ntono Maffucc r sttmbr Maffucc: rcut n rgm stazonaro r- Sr paralllo parttor S alcolar la rsstnza qualnt
Maffucc: rcut n rgm stazonaro r- Unrstà dgl Stud d assno srctazon d lttrotcnca: crcut n rgm stazonaro ntono Maffucc r sttmbr Maffucc: rcut n rgm stazonaro r- Sr paralllo parttor S alcolar la rsstnza qualnt
La contabilizzazione dei derivati: alcune problematiche
 Luc Frncsco Frncsch Dottor Commrcst Docnt Fnnz Aznd (Unvrstà Cttolc Mno) L contbzzzon d drvt: cun problmtch 12 mrzo 2009 Anno 2009 Strumnt fnnzr drvt -1- Agnd Crs d mrct fnnzr: problm dll modtà contbzzzon
Luc Frncsco Frncsch Dottor Commrcst Docnt Fnnz Aznd (Unvrstà Cttolc Mno) L contbzzzon d drvt: cun problmtch 12 mrzo 2009 Anno 2009 Strumnt fnnzr drvt -1- Agnd Crs d mrct fnnzr: problm dll modtà contbzzzon
Esercizi di matematica
 Esrizi i mtmti Gli srizi h trovi in qust pgin ti srvirnno pr vrifir h punto è l TUA prprzion in qust mtri: risponi solo ll omn S non risi risolvr qulh qusito, onsult i tuoi libri i tsto i tuoi qurni ll
Esrizi i mtmti Gli srizi h trovi in qust pgin ti srvirnno pr vrifir h punto è l TUA prprzion in qust mtri: risponi solo ll omn S non risi risolvr qulh qusito, onsult i tuoi libri i tsto i tuoi qurni ll
+ poligoni e l equivalenza di figure piane + triangoli + quadrilateri
 + poligoni + poligoni l quivlnz i figur pin + tringoli + quriltri + poligoni l quivlnz i figur pin 1 Stilisi s l sgunti ffrmzioni sono vr o fls. SEZ. E In un poligono i lti sono onsutivi u u. L somm gli
+ poligoni + poligoni l quivlnz i figur pin + tringoli + quriltri + poligoni l quivlnz i figur pin 1 Stilisi s l sgunti ffrmzioni sono vr o fls. SEZ. E In un poligono i lti sono onsutivi u u. L somm gli
Elementi dello sviluppo delle competenze
 Mtmt Elmnt llo svluppo ll omptnz Imprssum Etor: Dprtmnto ll'uzon, ultur protzon ll'mnt Gron Ruro l prsnt oumnto: Ezon l 5.0.06 Immn oprtn: Alxy Klmntv/Hmr/Tnkstok Copyrt: Ttolr rtt 'utor tutt l ltr rtt:
Mtmt Elmnt llo svluppo ll omptnz Imprssum Etor: Dprtmnto ll'uzon, ultur protzon ll'mnt Gron Ruro l prsnt oumnto: Ezon l 5.0.06 Immn oprtn: Alxy Klmntv/Hmr/Tnkstok Copyrt: Ttolr rtt 'utor tutt l ltr rtt:
Algebra + numeri relativi +l calcolo letterale Equazioni, disequazioni, problemi
 Algr + numri rltivi +l lolo lttrl Equzioni, isquzioni, prolmi + numri rltivi Rpprsnt on un numro rltivo l sgunti grnzz. SEZ. O g Altituin i 00 m sul livllo l mr. Trzo pino i un prhggio sottrrno. Prit i
Algr + numri rltivi +l lolo lttrl Equzioni, isquzioni, prolmi + numri rltivi Rpprsnt on un numro rltivo l sgunti grnzz. SEZ. O g Altituin i 00 m sul livllo l mr. Trzo pino i un prhggio sottrrno. Prit i
Minimizzazione degli Stati in una Rete Sequenziale Sincrona
 Minimizzzion gli Stti in un Rt Squnzil Sinron Murizio Plsi Murizio Plsi 1 Sintsi i Rti Squnzili Sinron Il proimnto gnrl i sintsi si svolg ni sgunti pssi: 1. Rlizzzion l igrmm gli stti prtir ll spifih l
Minimizzzion gli Stti in un Rt Squnzil Sinron Murizio Plsi Murizio Plsi 1 Sintsi i Rti Squnzili Sinron Il proimnto gnrl i sintsi si svolg ni sgunti pssi: 1. Rlizzzion l igrmm gli stti prtir ll spifih l
S kx. e che è dispari in quanto
 imulzion MIUR Esm di tto 09 - mtmtic Prolm f x 0, 0 i h immditmnt: 0 x 0 x f ' x 0 x lim f lim 0 lim f lim x x x x f 0 Il grfico riport l ndmnto; pplicndo ll curv l trslzion di vttor 0;, ovvro: x' x y
imulzion MIUR Esm di tto 09 - mtmtic Prolm f x 0, 0 i h immditmnt: 0 x 0 x f ' x 0 x lim f lim 0 lim f lim x x x x f 0 Il grfico riport l ndmnto; pplicndo ll curv l trslzion di vttor 0;, ovvro: x' x y
Totti, 37 anni da leggenda. Un monumento vivente. Scritto da Redazione Venerdì 27 Settembre 2013 08:39 - VALERIA META
 37 nni d lggnd Un monumnto vivnt Scritto d Rdzion VALERIA META Scrivrlo sull fccit Sn Pitro potv ffttivmnt smbrr irrivrnt pr qunto l omonimo inquino dl Vticno si si mostrto prson ll mno Così gli uguri
37 nni d lggnd Un monumnto vivnt Scritto d Rdzion VALERIA META Scrivrlo sull fccit Sn Pitro potv ffttivmnt smbrr irrivrnt pr qunto l omonimo inquino dl Vticno si si mostrto prson ll mno Così gli uguri
Corso di Automi e Linguaggi Formali Parte 3
 Esmpio Sdo il pumping lmm sist tl ch ogni prol di tin un sottostring non vuot ch puo ssr pompt o tglit rpprsntrl com Invc non in dv ssr in posso Corso di Automi Linguggi Formli Gnnio-Mrzo 2002 p.3/22 Corso
Esmpio Sdo il pumping lmm sist tl ch ogni prol di tin un sottostring non vuot ch puo ssr pompt o tglit rpprsntrl com Invc non in dv ssr in posso Corso di Automi Linguggi Formli Gnnio-Mrzo 2002 p.3/22 Corso
Rap a p p o p r o to o I n I c n r c em e e m n e t n al a e Def. rapporto incrementale nel punto x incremento h Nota:
 Rpporto Incrmntl α Δ Δy y m tnα y. Il rpporto incrmntl dll unzion nl punto rltivo d un incrmnto è il coicint nolr dll scnt l rico dll unzion ni punti di sciss d Not: Nll smpio rico è riportto > m, in nrl,
Rpporto Incrmntl α Δ Δy y m tnα y. Il rpporto incrmntl dll unzion nl punto rltivo d un incrmnto è il coicint nolr dll scnt l rico dll unzion ni punti di sciss d Not: Nll smpio rico è riportto > m, in nrl,
Simulazione di guasto. Introduzione. Simulazione di guasto. Simulazione dei circuiti digitali
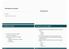 Introuzon M. Fvll Ennrn Dprtmnt n Frrr Introuzon Smulzon rut tl Smulzon n rut tl Prolm pplzon Alortm smulzon usto Srl Prlllo (ult prlll, tst prlll) Duttvo Conorrnt L smulzon rut tl puó vvnr vrs lvll: so
Introuzon M. Fvll Ennrn Dprtmnt n Frrr Introuzon Smulzon rut tl Smulzon n rut tl Prolm pplzon Alortm smulzon usto Srl Prlllo (ult prlll, tst prlll) Duttvo Conorrnt L smulzon rut tl puó vvnr vrs lvll: so
Analisi sistematica delle strutture. Rigidezza
 Anls sstemt elle strutture Rgezz u U x y v Trve nel pno v Vettore forze nol Vettore spostment nol θ u θ u U u V v Tre gr lertà per noo Due no per elemento x U θ u Se gr lertà per elemento V v tre rgezz
Anls sstemt elle strutture Rgezz u U x y v Trve nel pno v Vettore forze nol Vettore spostment nol θ u θ u U u V v Tre gr lertà per noo Due no per elemento x U θ u Se gr lertà per elemento V v tre rgezz
PROVINCIA DI TORINO SERVIZIO LOGISTICA PROGETTO DEFINITIVO-ESECUTIVO
 ALLEGATO: N. 1 PROVINCIA DI TORINO SERVIZIO LOGISTICA PROGETTO DEFINITIVO-ESECUTIVO MANUTENZIONE ORDINARIA E RIPARATIVA DEGLI EDIFICI PATRIMONIALI DESTINATI AD UFFICI DELLA PROVINCIA. IMPIANTI ELETTRICI
ALLEGATO: N. 1 PROVINCIA DI TORINO SERVIZIO LOGISTICA PROGETTO DEFINITIVO-ESECUTIVO MANUTENZIONE ORDINARIA E RIPARATIVA DEGLI EDIFICI PATRIMONIALI DESTINATI AD UFFICI DELLA PROVINCIA. IMPIANTI ELETTRICI
Corso di ordinamento - Sessione suppletiva - a.s. 2009-2010
 Corso di ordinmnto - Sssion suppltiv -.s. 9- PROBLEMA ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE SUPPLETIA Tm di: MATEMATICA. s. 9- Dt un circonrnz di cntro O rggio unitrio, si prndno
Corso di ordinmnto - Sssion suppltiv -.s. 9- PROBLEMA ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE SUPPLETIA Tm di: MATEMATICA. s. 9- Dt un circonrnz di cntro O rggio unitrio, si prndno
Costruiamo un aquilone SLED
 Costruimo un quon SLED Sgnr sul sgmnto cod du rifrimnti 3 cm dgli spigoli (vrso l'trno) poi sul bordo ntrior dll du li 11 cm dgli spigoli (vrso l'strno); qusto punto si dvono pplicr l du mnich sul bordo
Costruimo un quon SLED Sgnr sul sgmnto cod du rifrimnti 3 cm dgli spigoli (vrso l'trno) poi sul bordo ntrior dll du li 11 cm dgli spigoli (vrso l'strno); qusto punto si dvono pplicr l du mnich sul bordo
Test di autovalutazione
 UNITÀ LE FRAZIONI Tst Tst i utolutzion 0 0 0 0 0 0 0 0 0 0 00 n Il mio puntggio, in ntsimi, è n Risponi ogni qusito sgnno un sol ll ltrnti. n Conront l tu rispost on l soluzioni. n Color, prtno sinistr,
UNITÀ LE FRAZIONI Tst Tst i utolutzion 0 0 0 0 0 0 0 0 0 0 00 n Il mio puntggio, in ntsimi, è n Risponi ogni qusito sgnno un sol ll ltrnti. n Conront l tu rispost on l soluzioni. n Color, prtno sinistr,
ITALIA REPUBBLICA Francobolli nuovi
 ITALIA REPUBBLICA Fnll nuv n 113 A pt l l 6 6 ntsm ntsm Gnt Gnt ll ll fltl fltl l 8, l l 8, t vl l t pstl vl tln pstl sn mht u. Qull lfnum pp ll z stt qull ll Pst stt Itln. qull Qust ll llzn Pst Itln..Qust
ITALIA REPUBBLICA Fnll nuv n 113 A pt l l 6 6 ntsm ntsm Gnt Gnt ll ll fltl fltl l 8, l l 8, t vl l t pstl vl tln pstl sn mht u. Qull lfnum pp ll z stt qull ll Pst stt Itln. qull Qust ll llzn Pst Itln..Qust
Altezza canna > 3 mt / Chimney height >9,8 ft Diametro 25 cm oppure 25x25 cm o 20x30 cm / Diameter 9,8 In or 9,8x9,8 In or 7,8x11,8 In
 SH TNI / THNIL SPIITION r 95 o. NN095 NN UMRI (nst. ntrn) / HIMNY (or noor nstton) tzz nn > 5 mt / mny t >6,4 t mtro 5 m oppur 5x5 m / mtr 5,9 In or tzz nn > 4 mt / mny t >3, t mtro 0 m oppur 0x0 m / mtr
SH TNI / THNIL SPIITION r 95 o. NN095 NN UMRI (nst. ntrn) / HIMNY (or noor nstton) tzz nn > 5 mt / mny t >6,4 t mtro 5 m oppur 5x5 m / mtr 5,9 In or tzz nn > 4 mt / mny t >3, t mtro 0 m oppur 0x0 m / mtr
La pendenza m può essere ricavata derivando l equazione della semiellisse situata nel semipiano y 0 : a a
 Esm di Stto 7 sssion strordinri Prolm Utilizzndo l formul di sdoppimnto, l tngnt ll lliss nl punto ; x y x x y y x y Imponndo il pssggio pr (; ) si ottin: x ch, sostituito nll quzion dll lliss, prmtt di
Esm di Stto 7 sssion strordinri Prolm Utilizzndo l formul di sdoppimnto, l tngnt ll lliss nl punto ; x y x x y y x y Imponndo il pssggio pr (; ) si ottin: x ch, sostituito nll quzion dll lliss, prmtt di
Svolgimento di alcuni esercizi
 Svolgimnto di alcuni srcizi Si ha ch dal momnto ch / tnd a pr ch tnd a (la frazion formata da un numro, in qusto caso il numro, fratto una quantità ch tnd a ±, in qusto caso, tnd smpr a ) S facciamo tndr
Svolgimnto di alcuni srcizi Si ha ch dal momnto ch / tnd a pr ch tnd a (la frazion formata da un numro, in qusto caso il numro, fratto una quantità ch tnd a ±, in qusto caso, tnd smpr a ) S facciamo tndr
Lezione 3. F. Previdi - Automatica - Lez. 3 1
 Lzon 3. Movmno Equlbro F. Prv - Auomaca - Lz. 3 1 Schma lla lzon 1. Movmno ll usca un ssma LTI SISO. Movmno lbro movmno forzao 3. Equlbro un ssma LTI SISO 4. Guaagno saco un ssma LTI SISO F. Prv - Auomaca
Lzon 3. Movmno Equlbro F. Prv - Auomaca - Lz. 3 1 Schma lla lzon 1. Movmno ll usca un ssma LTI SISO. Movmno lbro movmno forzao 3. Equlbro un ssma LTI SISO 4. Guaagno saco un ssma LTI SISO F. Prv - Auomaca
Le basi del calcolo statistico
 L s dl clcolo sttstco qulro sttstco d prtcll su n stt possl: dscrzon dl sstm: ndvdur l stt possl mcrostt mdnt rltv numr quntc clcolr l nr dll -smo stto clcolr l dnrzon dll -smo stto clcolr l proltà d un
L s dl clcolo sttstco qulro sttstco d prtcll su n stt possl: dscrzon dl sstm: ndvdur l stt possl mcrostt mdnt rltv numr quntc clcolr l nr dll -smo stto clcolr l dnrzon dll -smo stto clcolr l proltà d un
L equazione del reticolo cristallino
 Chmc sc supror Modulo L quzo dl rtcolo crstllo Srgo Brutt Rchmo d mtmtc: l sr d ourr U quluqu uzo () può ssr rpprstt spso d Tylor purchè l uzo () s drzbl - volt : ( )!... Nl cso cu ()=g() s u uzo prodc
Chmc sc supror Modulo L quzo dl rtcolo crstllo Srgo Brutt Rchmo d mtmtc: l sr d ourr U quluqu uzo () può ssr rpprstt spso d Tylor purchè l uzo () s drzbl - volt : ( )!... Nl cso cu ()=g() s u uzo prodc
Aquadue Duplo Pag. 1
 Collgr il progrmmtor l ruintto. Pg. 1 4 5 6 TIME DY 4 5 6 STRT STOP CNCEL TIME DY lik! 4 5 6 STRT STOP CNCEL TIME DY Pr (o.): 8410 prir il moulo i progrmmzion prmno sui u pulsnti ltrli insrir un ttri llin
Collgr il progrmmtor l ruintto. Pg. 1 4 5 6 TIME DY 4 5 6 STRT STOP CNCEL TIME DY lik! 4 5 6 STRT STOP CNCEL TIME DY Pr (o.): 8410 prir il moulo i progrmmzion prmno sui u pulsnti ltrli insrir un ttri llin
App.Cap.II: Dettagli e sviluppi per il capitolo 2. App.Cap.II-1: Risposta di un sistema del primo ordine con ingresso a impulso.
 SCPC n C.II.C.II: Dgl svlu r l olo.c.ii-: sos un ssm l rmo orn on ngrsso mulso. () () δ () Pr l soluon onvn suvr l ss m n u r rsolvr u vrs E.D.O. Pr
SCPC n C.II.C.II: Dgl svlu r l olo.c.ii-: sos un ssm l rmo orn on ngrsso mulso. () () δ () Pr l soluon onvn suvr l ss m n u r rsolvr u vrs E.D.O. Pr
Matematica 15 settembre 2009
 Nom: Mtriol: Mtmti 5 sttmbr 2009 Non sono mmss loltrii. Pr l domnd rispost multipl, rispondr brrndo o rhindo hirmnt un un sol lttr. Pr l ltr domnd srivr l soluzion on svolgimnto ngli spzi prdisposti..
Nom: Mtriol: Mtmti 5 sttmbr 2009 Non sono mmss loltrii. Pr l domnd rispost multipl, rispondr brrndo o rhindo hirmnt un un sol lttr. Pr l ltr domnd srivr l soluzion on svolgimnto ngli spzi prdisposti..
Combattimento di Tancredi et Clorinda
 Trqut Tss (1544 1595) Clrd ' f '' Tncr d f ' Tst c g' B. c. TAn- LA- vl l' r pr Cmbtmnt Tncr t Clrd Libr ttv d dgli Tncr Cu Mnvr (1567 1643) Cl rd un h m s LA- 7 16 24 vr l pr. v d'n trr sp 3 2. 3 2 S
Trqut Tss (1544 1595) Clrd ' f '' Tncr d f ' Tst c g' B. c. TAn- LA- vl l' r pr Cmbtmnt Tncr t Clrd Libr ttv d dgli Tncr Cu Mnvr (1567 1643) Cl rd un h m s LA- 7 16 24 vr l pr. v d'n trr sp 3 2. 3 2 S
PROVINCIA DI TORINO SERVIZIO LOGISTICA PROGETTO DEFINITIVO-ESECUTIVO
 ALLEGATO: N. 3 PROVINCIA DI TORINO SERVIZIO LOGISTICA PROGETTO DEFINITIVO-ESECUTIVO MANUTENZIONE ORDINARIA E RIPARATIVA DEGLI EDIFICI PATRIMONIALI DESTINATI AD UFFICI DELLA PROVINCIA. AGGIORNAMENTO CENSIMENTO
ALLEGATO: N. 3 PROVINCIA DI TORINO SERVIZIO LOGISTICA PROGETTO DEFINITIVO-ESECUTIVO MANUTENZIONE ORDINARIA E RIPARATIVA DEGLI EDIFICI PATRIMONIALI DESTINATI AD UFFICI DELLA PROVINCIA. AGGIORNAMENTO CENSIMENTO
Una relazione R in un insieme A si dice relazione d'ordine (o ordinamento) se e solo se è riflessiva, antisimmetrica e transitiva.
 F0 RELZIONI D'ORDINE. Rlzioni 'orin Un rlzion R in un insim si i rlzion 'orin (o orinmnto) s solo s è rilssiv, ntisimmtri trnsitiv. Prsi u lmnti x, y, s R è un orinmnto in, si i h «x pr y» si sriv x y,
F0 RELZIONI D'ORDINE. Rlzioni 'orin Un rlzion R in un insim si i rlzion 'orin (o orinmnto) s solo s è rilssiv, ntisimmtri trnsitiv. Prsi u lmnti x, y, s R è un orinmnto in, si i h «x pr y» si sriv x y,
j Verso la scuola superiore Geometria euclidea e analitica
 j rso l suol suprior Gomtri uli nliti Ossrv l spzzt stilisi quli ll sgunti rmzioni sono vr quli ls. B D G E B è onsutivo B. DE è onsutivo G. B è onsutivo D. B è int D. B è onsutivo D. E è onsutivo G. Il
j rso l suol suprior Gomtri uli nliti Ossrv l spzzt stilisi quli ll sgunti rmzioni sono vr quli ls. B D G E B è onsutivo B. DE è onsutivo G. B è onsutivo D. B è int D. B è onsutivo D. E è onsutivo G. Il
LE SOLUZIONI. [Per definizione la concentrazione di una soluzione è il rapporto
 LE SOLUZIONI. Una soluzon (d un crto soluto n un crto solvnt dl pso d kg è concntrata al 0%. Calcolar la quanttà d solvnt (n kg ch s dv aggungr alla soluzon pr ottnr una nuova soluzon, concntrata al 0%.
LE SOLUZIONI. Una soluzon (d un crto soluto n un crto solvnt dl pso d kg è concntrata al 0%. Calcolar la quanttà d solvnt (n kg ch s dv aggungr alla soluzon pr ottnr una nuova soluzon, concntrata al 0%.
Studio di funzione. Pertanto nello studio di tali funzioni si esamino:
 Prof. Emnul ANDRISANI Studio di funzion Funzioni rzionli intr n n o... n n Crttristich: sono funzioni continu drivbili in tutto il cmpo rl D R quindi non sistono sintoti vrticli D R quindi non sistono
Prof. Emnul ANDRISANI Studio di funzion Funzioni rzionli intr n n o... n n Crttristich: sono funzioni continu drivbili in tutto il cmpo rl D R quindi non sistono sintoti vrticli D R quindi non sistono
Capitolo 1 - Misura e incertezza (parte I)
 Appunt d Msur lttrh Cptolo - Msur nrtzz (prt I) Mtod d msur... Inrtzz d msur... Il rsultto d un msur... 3 rror... 4 Propgzon dgl rror nll msur ndrtt... 5 smp... 6 Propgzon dll nrtzz nll msur ndrtt... 9
Appunt d Msur lttrh Cptolo - Msur nrtzz (prt I) Mtod d msur... Inrtzz d msur... Il rsultto d un msur... 3 rror... 4 Propgzon dgl rror nll msur ndrtt... 5 smp... 6 Propgzon dll nrtzz nll msur ndrtt... 9
CAVALLETTI UNIVERSALI PER SEGNALETICA STRADALE TEMPORANEA
 VLLTT UNVRSL PR SNLT STRL TMPRN LTZZ cm 200 LTZZ cm 160 L M N L1 PRTLR L RSVLT R S V LT P T R MNL UR L L1 - M N SRZN VLLTT 4 P M 200X65 VLLTT 4 P M 150X60 KT ULLNR VLLTT MPST 2 PZZ PR UR 392 393/ 240X60
VLLTT UNVRSL PR SNLT STRL TMPRN LTZZ cm 200 LTZZ cm 160 L M N L1 PRTLR L RSVLT R S V LT P T R MNL UR L L1 - M N SRZN VLLTT 4 P M 200X65 VLLTT 4 P M 150X60 KT ULLNR VLLTT MPST 2 PZZ PR UR 392 393/ 240X60
Le soluzioni della prova scritta di Matematica del 7 Febbraio 2014
 L soluzon dlla prova scrtta d Matmatca dl 7 Fbbrao. Sa data la unzon ln ln a. Trova l domno d. b. Scrv, splctamnt pr stso, qual sono gl ntrvall n cu è postva qull n cu è ngatva c. Dtrmna l vntual ntrszon
L soluzon dlla prova scrtta d Matmatca dl 7 Fbbrao. Sa data la unzon ln ln a. Trova l domno d. b. Scrv, splctamnt pr stso, qual sono gl ntrvall n cu è postva qull n cu è ngatva c. Dtrmna l vntual ntrszon
SICUREZZA SUL LAVORO SAFETY AT WORK SICUREZZA SUL LAVORO SAFETY AT WORK R 290 31 R 290 31
 SICUREZZA SUL LAVORO SAFETY AT WORK R 290 31 R 290 31 Sgnli i siurzz pr fontnll o i mrgnz pr l ontminzion UNI 7546/3. Symols for sfty signs-ys wshing - mrgny showr. 332 Normtiv in mtri i tutl ll slut siurzz
SICUREZZA SUL LAVORO SAFETY AT WORK R 290 31 R 290 31 Sgnli i siurzz pr fontnll o i mrgnz pr l ontminzion UNI 7546/3. Symols for sfty signs-ys wshing - mrgny showr. 332 Normtiv in mtri i tutl ll slut siurzz
pxty METODODIEUMINAHONEDIGAOSS .am#t:taaaexni:i / f,h;o sistema 3 2 ( seq LINEARE SISTEMAI. dinwgnitej DEFINIHONE dedric 3tttt= incognita)
 3tttt 4 METODODEUMNHONEDGOSS SSTEM LNERE 1) GENERL T DEFNHONE Unsstm lnr mxnsstm dm q ddrc n n ncogn m#ttxn µ mn tmzxzt mn n bm pxty x y7z 6to E sstm 2 4 ( tq ncogn) / f h;o sstm 3 2 ( sq dnwgnj DEFNZONE
3tttt 4 METODODEUMNHONEDGOSS SSTEM LNERE 1) GENERL T DEFNHONE Unsstm lnr mxnsstm dm q ddrc n n ncogn m#ttxn µ mn tmzxzt mn n bm pxty x y7z 6to E sstm 2 4 ( tq ncogn) / f h;o sstm 3 2 ( sq dnwgnj DEFNZONE
Ogni amante è guerrier Libro ottavo de madrigali
 4 Ottvi Rinuccini (1562 1621) Tnr I c ' Tnr II c g' 10 16 3 O- 3 B. c. 3 O- 3 3 3 t, t nch' 3 3 22 3 d, f n g. g s pr v, sl Ogni t r Libr ttv d mdg r; Qul fi f O nl t, pr v c tà, n cl t, t r ch'l dur g
4 Ottvi Rinuccini (1562 1621) Tnr I c ' Tnr II c g' 10 16 3 O- 3 B. c. 3 O- 3 3 3 t, t nch' 3 3 22 3 d, f n g. g s pr v, sl Ogni t r Libr ttv d mdg r; Qul fi f O nl t, pr v c tà, n cl t, t r ch'l dur g
SENATO DELLA REPUBBLIC
 SNAT DLLA RPUBBL X LGSLATURA N. 292 Ann DSGN D LGG p-ntt dl Mntr dl Tr GRA) d nrt l Mntr dl Bln dll Prrmmzn nm RMTA) V. Stmpt ntr n. 7) Apprvt dll mr d dptt nll dt dl 2 nvmbr 96 Trm dl Prdnt dll mr d dptt
SNAT DLLA RPUBBL X LGSLATURA N. 292 Ann DSGN D LGG p-ntt dl Mntr dl Tr GRA) d nrt l Mntr dl Bln dll Prrmmzn nm RMTA) V. Stmpt ntr n. 7) Apprvt dll mr d dptt nll dt dl 2 nvmbr 96 Trm dl Prdnt dll mr d dptt
Macchine non completamente specificate. Sintesi Sequenziale Sincrona Sintesi Comportamentale di Reti Sequenziali Sincrone
 Sintsi Squnzil Sinron Sintsi Comportmntl i Rti Squnzili Sinron Riuzion l numro gli stti pr Mhin Non Compltmnt Spiit Comptiilità Vrsion l 13/01/05 (Frrni( Antol) Mhin non ompltmnt spiit Sono mhin in ui
Sintsi Squnzil Sinron Sintsi Comportmntl i Rti Squnzili Sinron Riuzion l numro gli stti pr Mhin Non Compltmnt Spiit Comptiilità Vrsion l 13/01/05 (Frrni( Antol) Mhin non ompltmnt spiit Sono mhin in ui
ESTENSIONE ED EQUIVALENZA EQUIVALENZA DI POLIGONI
 ESTENSIONE ED EQUIVLENZ Supf pn mtt. Un supf pn mtt è un pt pno mtt un n us, oppu un pt pno omps t u o pù n us non s ntsno. Estnson un supf pn. I ontto - stnson un supf è un ontto pmtvo, om qu punto, tt,
ESTENSIONE ED EQUIVLENZ Supf pn mtt. Un supf pn mtt è un pt pno mtt un n us, oppu un pt pno omps t u o pù n us non s ntsno. Estnson un supf pn. I ontto - stnson un supf è un ontto pmtvo, om qu punto, tt,
T R I BU N A L E D I T R E V IS O A Z I E N D A LE. Pr e me s so
 1 T R I BU N A L E D I T R E V IS O BA N D O P E R L A C E S S IO N E C O M P E TI TI V A D EL C O M P E N D I O A Z I E N D A LE D E L C O N C O R D A T O PR EV E N T I V O F 5 Sr l i n l i q u i da z
1 T R I BU N A L E D I T R E V IS O BA N D O P E R L A C E S S IO N E C O M P E TI TI V A D EL C O M P E N D I O A Z I E N D A LE D E L C O N C O R D A T O PR EV E N T I V O F 5 Sr l i n l i q u i da z
Alberi di copertura minimi
 Albr d coprtur mnm Sommro Albr d coprtur mnm pr grf pst Algortmo d Kruskl Algortmo d Prm Albro d coprtur mnmo Un problm d notvol mportnz consst nl dtrmnr com ntrconnttr fr d loro dvrs lmnt mnmzzndo crt
Albr d coprtur mnm Sommro Albr d coprtur mnm pr grf pst Algortmo d Kruskl Algortmo d Prm Albro d coprtur mnmo Un problm d notvol mportnz consst nl dtrmnr com ntrconnttr fr d loro dvrs lmnt mnmzzndo crt
REGOLAMENTO (CE) n. 1223/2009 DEL PARLAMENTO EUROPEO E DEL CONSIGLIO del 30 novembre 2009 sui prodotti cosmetici
 22.12.2009 Gzztt uffl ll Unon urop L 342/59 REGOLAMENTO (CE) n. 1223/2009 DEL PARLAMENTO EUROPEO E DEL CONSIGLIO l 30 novmr 2009 su proott osmt (rfuson) (Tsto rlvnt fn l SEE) IL PARLAMENTO EUROPEO E IL
22.12.2009 Gzztt uffl ll Unon urop L 342/59 REGOLAMENTO (CE) n. 1223/2009 DEL PARLAMENTO EUROPEO E DEL CONSIGLIO l 30 novmr 2009 su proott osmt (rfuson) (Tsto rlvnt fn l SEE) IL PARLAMENTO EUROPEO E IL
PROVINCIA DI VERONA RENDICONTO ESERCIZIO 2012 ELENCO DEI RESIDUI ATTIVI E PASSIVI DISTINTI PER ANNO DI PROVENIENZA
 PROVINCIA DI VERONA RENDICONTO ESERCIZIO 2012 ELENCO DEI RESIDUI ATTIVI E PASSIVI DISTINTI PER ANNO DI PROVENIENZA 1 2 RIEPILOGO GENERALE RESIDUI ATTIVI CONSERVATI 3 4 Pgm. CPA0099R ***-----------------------------------------------------------***
PROVINCIA DI VERONA RENDICONTO ESERCIZIO 2012 ELENCO DEI RESIDUI ATTIVI E PASSIVI DISTINTI PER ANNO DI PROVENIENZA 1 2 RIEPILOGO GENERALE RESIDUI ATTIVI CONSERVATI 3 4 Pgm. CPA0099R ***-----------------------------------------------------------***
Matematica. Indice lezione. (Esercitazioni) dott. Francesco Giannino dott. Valeria Monetti. Funzione esponenziale
 Mtmtic (Esrcitzioni) Equzioni Disquzioni sponnzili - ritmich dott. Frncsco Ginnino dott. Vlri Montti Indic lzion Funzion sponnzil Equzioni disquzioni sponnzili Funzion ritmo Equzioni disquzioni ritmich
Mtmtic (Esrcitzioni) Equzioni Disquzioni sponnzili - ritmich dott. Frncsco Ginnino dott. Vlri Montti Indic lzion Funzion sponnzil Equzioni disquzioni sponnzili Funzion ritmo Equzioni disquzioni ritmich
Progetto di cinghie trapezoidali
 Progtto i cinghi trpzoili L cinghi trpzoili sono utilizzt frquntmnt pr l trsmission i potnz ntggi Bsso costo Smplicità i instllzion Cpcità i ssorbir vibrzioni torsionli picchi i coppi Svntggi Mncnz i sincronismo
Progtto i cinghi trpzoili L cinghi trpzoili sono utilizzt frquntmnt pr l trsmission i potnz ntggi Bsso costo Smplicità i instllzion Cpcità i ssorbir vibrzioni torsionli picchi i coppi Svntggi Mncnz i sincronismo
Esame di Matematica e Abilità Informatiche - Settembre Le soluzioni
 Esam d Matmatca Abltà Informatch - Sttmbr 03 L soluzon. Data la funzon f( ) a. trova l domno d f b. scrv, splctamnt pr stso, qual sono gl ntrvall n cu f() rsulta postva qull n cu rsulta ngatva c. dtrmna
Esam d Matmatca Abltà Informatch - Sttmbr 03 L soluzon. Data la funzon f( ) a. trova l domno d f b. scrv, splctamnt pr stso, qual sono gl ntrvall n cu f() rsulta postva qull n cu rsulta ngatva c. dtrmna
ANDAMENTO DELLA MORTALITA': TOSCANA E PROVINCIA DI AREZZO A CONFRONTO
 ANDAMENTO DELLA MORTALITA': TOSCANA E PROVINCIA DI AREZZO A CONFRONTO I numri riprtti nll tbll sn TASSI GREZZI, ciè il numr dgli vnti vrifictisi in un nn divis l pplzin mltiplict pr 1 Nl 9 si può ntr ch
ANDAMENTO DELLA MORTALITA': TOSCANA E PROVINCIA DI AREZZO A CONFRONTO I numri riprtti nll tbll sn TASSI GREZZI, ciè il numr dgli vnti vrifictisi in un nn divis l pplzin mltiplict pr 1 Nl 9 si può ntr ch
Esercizio 1. La matrice di controllabilità è: Studiare la controllabilità del sistema in figura le cui matrici A, b e c sono qui riportate.
 Gstvo Blfort Esr d otrollltà Ossrvltà Esro tdr l otrollltà dl sst fgr l tr, soo q rportt. (t) (t) Gstvo Blfort Esr d otrollltà Ossrvltà tr d otrollltà è: d, posto = +, s h dt l sst è dq opltt otrolll Gstvo
Gstvo Blfort Esr d otrollltà Ossrvltà Esro tdr l otrollltà dl sst fgr l tr, soo q rportt. (t) (t) Gstvo Blfort Esr d otrollltà Ossrvltà tr d otrollltà è: d, posto = +, s h dt l sst è dq opltt otrolll Gstvo
Bando Trasferimenti da altra sede e passaggi di corso di studio - A.A. 2015-16
 C Cr Sr rrr su 1 B rsr lr s pssgg rs su -.. 2015-16 Sr S l u l prvu sru (r. 5 l B) r. 1 l B sbls h pss prpr l su b slusv: ) gl su prv lr s h h l srz u rs su ll sss lss qull u s sr, qul ur h, ll s u prvg,
C Cr Sr rrr su 1 B rsr lr s pssgg rs su -.. 2015-16 Sr S l u l prvu sru (r. 5 l B) r. 1 l B sbls h pss prpr l su b slusv: ) gl su prv lr s h h l srz u rs su ll sss lss qull u s sr, qul ur h, ll s u prvg,
LICEO SCIENTIFICO SESSIONE STRAORDINARIA PROBLEMA 2
 www.mtfili.it LICEO SCIENTIFICO SESSIONE STRAORDINARIA 27 - PROBLEMA 2 L funzioni g, g 2, g, g 4 sono dfinit nl modo sgunt: g (x) = 2 x2 2 g 2 (x) = x g (x) = 2 π cos (π 2 x) ) g 4 (x) = ln( x ) Vrific
www.mtfili.it LICEO SCIENTIFICO SESSIONE STRAORDINARIA 27 - PROBLEMA 2 L funzioni g, g 2, g, g 4 sono dfinit nl modo sgunt: g (x) = 2 x2 2 g 2 (x) = x g (x) = 2 π cos (π 2 x) ) g 4 (x) = ln( x ) Vrific
... e. reie. sage* reep,----- fleura 4. rte,=mpagn-.ma sempre_,e nque NELNOMEDIBIO. elencoinfinitodi alimenti,enteessenze
 P. I scchtt rb 1000rntrutzzt ) r bon r 4 r ; d.0 r f 4 Ir s -41111 ) In t st f y u III N dt 10009-01092011 Dffuson 62000 Proctà Mns Vggd_10009_50_307.pdf Wb St www.so24or.com Pg 50 Dmns. 100 % NELNOMEDIBIO
P. I scchtt rb 1000rntrutzzt ) r bon r 4 r ; d.0 r f 4 Ir s -41111 ) In t st f y u III N dt 10009-01092011 Dffuson 62000 Proctà Mns Vggd_10009_50_307.pdf Wb St www.so24or.com Pg 50 Dmns. 100 % NELNOMEDIBIO
Laboratorio di Algoritmi e Strutture Dati Ingegneria e Scienze Informatiche - Cesena A.A
 Inggnri Sinz Informtih - Csn A.A. 3- iln@s.unio.it, pitro.iln@unio.it : psuooi Clol il osto l mmino minimo un vrti sorgnt s tutti i rstnti vrtii nl grfo. Clol un lro i oprtur i mmini minimi (shortst pth
Inggnri Sinz Informtih - Csn A.A. 3- iln@s.unio.it, pitro.iln@unio.it : psuooi Clol il osto l mmino minimo un vrti sorgnt s tutti i rstnti vrtii nl grfo. Clol un lro i oprtur i mmini minimi (shortst pth
Giornate Mondiali Onu dei Lavoratori Marittimi e degli Oceani, la 4a edizione della Omnibus
 Gornt Mondl Onu d Lvortor Mrttm dgl Ocn, l 4 dzon d Omnbus Sn Bndtto dl Tronto, 2018-05-28 Arrvt l IV dzon d clbrzon ngunt d Gornt Mondl ONU d Lvortor Mrttm dgl Ocn, n Ptrocno ONU cur d Omnbus Omns Onlus,
Gornt Mondl Onu d Lvortor Mrttm dgl Ocn, l 4 dzon d Omnbus Sn Bndtto dl Tronto, 2018-05-28 Arrvt l IV dzon d clbrzon ngunt d Gornt Mondl ONU d Lvortor Mrttm dgl Ocn, n Ptrocno ONU cur d Omnbus Omns Onlus,
S O L U Z I O N I + 100
 S O L U Z I O N I Nl 00 un farmaco vnva vnduto a 70 a) Nll pots ch ogn anno l przzo aumnt dl 3% rsptto all anno prcdnt quanto vrrbb a costar lo stsso farmaco nl 0? b) Supponamo ch l przzo dl farmaco nl
S O L U Z I O N I Nl 00 un farmaco vnva vnduto a 70 a) Nll pots ch ogn anno l przzo aumnt dl 3% rsptto all anno prcdnt quanto vrrbb a costar lo stsso farmaco nl 0? b) Supponamo ch l przzo dl farmaco nl
PROGRAMMA DI RIPASSO ESTIVO
 ISTITUTO TECNICO PER IL TURISMO EUROSCUOLA ISTITUTO TECNICO PER GEOMETRI BIANCHI SCUOLE PARITARIE PROGRAMMA DI RIPASSO ESTIVO CLASSI MATERIA PROF. QUARTA TURISMO Matmatica Andra Brnsco Làvor ANNO SCOLASTICO
ISTITUTO TECNICO PER IL TURISMO EUROSCUOLA ISTITUTO TECNICO PER GEOMETRI BIANCHI SCUOLE PARITARIE PROGRAMMA DI RIPASSO ESTIVO CLASSI MATERIA PROF. QUARTA TURISMO Matmatica Andra Brnsco Làvor ANNO SCOLASTICO
Pre sen ta zio ne. pri me espe rien ze, af fron ta te con in cer tez za e tal vol ta con scar sa
 2 P sn L m f qu n s p dl g qul, sp g v d c t cs dur t l dll sn d, g pr qu s lup p l s s fn qu s mz z, l p s u z z, pr r sr l t d f l m r n In l, l s m p, p sn, d l qu p s t s,. p m sp n z, f fn cr z l
2 P sn L m f qu n s p dl g qul, sp g v d c t cs dur t l dll sn d, g pr qu s lup p l s s fn qu s mz z, l p s u z z, pr r sr l t d f l m r n In l, l s m p, p sn, d l qu p s t s,. p m sp n z, f fn cr z l
CHIARA ZUCCHELLI. Florenzi, arriva il premio: contratto fino al 2016 e stipendio aumentato. Scritto da Redazione Giovedì 04 Ottobre 2012 07:31 -
 Flornzi rriv il prmio: contrtto fino l 2016 stipno umntto CHIARA ZUCCHELLI Il prmio più mritto rrivto Com nnuncito si d Sbtini si dl suo gnt Alssndro Lucci rrivto il rinnovo dl contrtto Alssndro Flornzi
Flornzi rriv il prmio: contrtto fino l 2016 stipno umntto CHIARA ZUCCHELLI Il prmio più mritto rrivto Com nnuncito si d Sbtini si dl suo gnt Alssndro Lucci rrivto il rinnovo dl contrtto Alssndro Flornzi
Cognome e Nome: Numero di Matricola: Spazio riservato alla correzione
 Cognom Nom: Numro di Matriola: Spazio risrvato alla orrzion 1 2 3 4 5 6 Total /18 /8 /20 20 /18 /16 /100 1. a) Indiar quali dll sgunti affrmazioni sono vr quali sono fals. 1. log(n n )= Θ((log n) n ) 2.
Cognom Nom: Numro di Matriola: Spazio risrvato alla orrzion 1 2 3 4 5 6 Total /18 /8 /20 20 /18 /16 /100 1. a) Indiar quali dll sgunti affrmazioni sono vr quali sono fals. 1. log(n n )= Θ((log n) n ) 2.
interazione forte il π ha una massa inferione al π violazione del numero lepto nico interazione debole conservazione dell'energia SI NO :
 Dir quali razioni sono possibili quali no. Nl caso siano possibili indicar l intrazion rsponsabil nl caso non lo siano, spigar prché. a) π π ν il π ha una massa infrion al π b) Λ p π ν violazion dl numro
Dir quali razioni sono possibili quali no. Nl caso siano possibili indicar l intrazion rsponsabil nl caso non lo siano, spigar prché. a) π π ν il π ha una massa infrion al π b) Λ p π ν violazion dl numro
Come Vendere AdWords. Programma Agenzie QUalificate AdWords
 Cm Vndr Prgrmm Agnz QUlfct 1 Pt frz PERTINENZA PERTINENZA Rggg Rggg clt clt nl nl mmnt mmnt tt tt mstr mstr gl gl nnc nnc ptnzl ptnzl clt clt mntr mntr stnn stnn ttvmnt ttvmnt crcnd crcnd 'ttvtà 'ttvtà
Cm Vndr Prgrmm Agnz QUlfct 1 Pt frz PERTINENZA PERTINENZA Rggg Rggg clt clt nl nl mmnt mmnt tt tt mstr mstr gl gl nnc nnc ptnzl ptnzl clt clt mntr mntr stnn stnn ttvmnt ttvmnt crcnd crcnd 'ttvtà 'ttvtà
Aquadue Duplo. Guida all utilizzo. click! NEW! ON! c. Collegare il programmatore al rubinetto.
 Collgr il progrmmtor l ruintto. quu Duplo Pg. Gui ll utilizzo DY DY DY lik! DY Pr quu Duplo volution (o.): 80 prir il moulo i progrmmzion prmno sui u pulsnti ltrli insrir un ttri llin. ppn ollgt l ttri,
Collgr il progrmmtor l ruintto. quu Duplo Pg. Gui ll utilizzo DY DY DY lik! DY Pr quu Duplo volution (o.): 80 prir il moulo i progrmmzion prmno sui u pulsnti ltrli insrir un ttri llin. ppn ollgt l ttri,
IL PRIVATE EQUITY IN ITALIA: PERFORMANCE E SCELTE DI COMPOSIZIONE DEL PORTAFOGLIO. Francesca Querci
 IL PRIVATE EQUITY IN ITALIA: PERFORMANCE E SCELTE DI COMPOSIZIONE DEL PORTAFOGLIO Frns Qur Rrtor Eonom l Intrmr Fnnzr Foltà Eonom Unvrstà l Stu Gnov Astrt Il ppr s pon l ottvo smnr l prormn onsut on tln
IL PRIVATE EQUITY IN ITALIA: PERFORMANCE E SCELTE DI COMPOSIZIONE DEL PORTAFOGLIO Frns Qur Rrtor Eonom l Intrmr Fnnzr Foltà Eonom Unvrstà l Stu Gnov Astrt Il ppr s pon l ottvo smnr l prormn onsut on tln
Esercizi Circuiti Resistivi
 srcizi Circuiti sistivi srcizio n isolvr il circuito in figur: v v v v 4 4 5 4 0 0Ω 5Ω 5Ω 4 5Ω Ω 5 v 5 5 4 () isolvr un circuito signific in gnrl dtrminr tnsioni corrnti in tutti i lti dl circuito. Trsformimo
srcizi Circuiti sistivi srcizio n isolvr il circuito in figur: v v v v 4 4 5 4 0 0Ω 5Ω 5Ω 4 5Ω Ω 5 v 5 5 4 () isolvr un circuito signific in gnrl dtrminr tnsioni corrnti in tutti i lti dl circuito. Trsformimo
Le P. Le Piagge. Le P. www.autoscuolalepiagge.it. Autoscuo. toscuola. la nostra passione al vostro servizio... ESAME DI GUIDA PATENTE B - FASE 1
 l l nostr psson l vostro srvzo... olzon sdl L ESAME DI GUIDA ATENTE B - FASE LEVE: ) Spostmnto sdl vnt/ndtro ) Spostmnto schnl vnt/ndtro ) spostmnto sdut lto/bsso L toscuol u A Il sdl v poszonto n modo
l l nostr psson l vostro srvzo... olzon sdl L ESAME DI GUIDA ATENTE B - FASE LEVE: ) Spostmnto sdl vnt/ndtro ) Spostmnto schnl vnt/ndtro ) spostmnto sdut lto/bsso L toscuol u A Il sdl v poszonto n modo
IV. L EQ. DI VAG MEDIANTE EQ. POLARE
 IV. L EQ. DI VAG MEDIANTE EQ. POLARE LA GEOMETRIA CON L EQ. PARAMETRICA DI VAG Euzion Polr C. IV Pg. 1 Essndo nll E. di Vg il vlor OA (dll'origin d un unto, d in gnrl tr unto unto) un vlor ssoluto, non
IV. L EQ. DI VAG MEDIANTE EQ. POLARE LA GEOMETRIA CON L EQ. PARAMETRICA DI VAG Euzion Polr C. IV Pg. 1 Essndo nll E. di Vg il vlor OA (dll'origin d un unto, d in gnrl tr unto unto) un vlor ssoluto, non
QUADRO ORARI FERROVIARI FERIALI UNIFICATI DA BARI VERSO MATERA, GRAVINA E POTENZA + TRATTA AVIGLIANO POTENZA
 QURO ORRI FRROVIRI FRILI UNIFITI RI VRSO MTR, GRVIN OTN + TRTT VIGLINO OTN RI RI S RI MOUGNO LO OLL INTTO GRUMO pp MLLITTO SRILLO LTMUR NUMRO TRNO s z : :5 :53 :55 :56 5: 5: 5: 5: 5: 5:3 5:6 5: 5:33 NUMRO
QURO ORRI FRROVIRI FRILI UNIFITI RI VRSO MTR, GRVIN OTN + TRTT VIGLINO OTN RI RI S RI MOUGNO LO OLL INTTO GRUMO pp MLLITTO SRILLO LTMUR NUMRO TRNO s z : :5 :53 :55 :56 5: 5: 5: 5: 5: 5:3 5:6 5: 5:33 NUMRO
Droga, il punto del comando provinciale dell'arma Mercoledì 06 Agosto 2014 16:59
 Drog, il pto comndo provcil l'arm Mrcoldì 06 Agosto 2014 16:59 REGGIO CALABRIA 6 go. - Costnt d cssnt è il controllo trritorio l zion rprssiv svolt i Crbiri nll provci Rggio Clbri nl consto ll produzion
Drog, il pto comndo provcil l'arm Mrcoldì 06 Agosto 2014 16:59 REGGIO CALABRIA 6 go. - Costnt d cssnt è il controllo trritorio l zion rprssiv svolt i Crbiri nll provci Rggio Clbri nl consto ll produzion
Campi elettromagnetici e salute
 Campi elettromagnetici e salute F r Pol pol @t n. t 1 Introduzione ``El ttrosmo '': nqu n m nto pro otto mp l ttr m n t n r t ll r z on pp rt n nt ll s z on non on zz nt (NIR) llo sp ttro l ttrom n t o;
Campi elettromagnetici e salute F r Pol pol @t n. t 1 Introduzione ``El ttrosmo '': nqu n m nto pro otto mp l ttr m n t n r t ll r z on pp rt n nt ll s z on non on zz nt (NIR) llo sp ttro l ttrom n t o;
Fig. 1. 1) La resistenza totale della bobina vale: (*) 2) Il modulo B del campo di induzione magnetica B r nel punto medio M della spira vale: L (*)
 Fcoltà di nggnri Prov Scritt di Fisic uglio 4 - Compito usito n. n un filo rttilino lungo fluisc un corrnt. Ad un distnz dl filo è post un oin, il cui punto mdio è ll stss quot dl punto mdio O dl filo.
Fcoltà di nggnri Prov Scritt di Fisic uglio 4 - Compito usito n. n un filo rttilino lungo fluisc un corrnt. Ad un distnz dl filo è post un oin, il cui punto mdio è ll stss quot dl punto mdio O dl filo.
SCPC Cap-VI: Trasformata di Laplace. T st + ε T. Di seguito, la F(s) indicherà la trasformata di Laplace della variabile f(t).
 SP p-vi: Tror pl VI: Tror pl VI-: Dzo D u uzo ou, :
SP p-vi: Tror pl VI: Tror pl VI-: Dzo D u uzo ou, :
test Di chimica per l accesso alle Facoltà UNiVersitarie
 tst i himia pr l asso all Faoltà UNiVrsitari il sistma priodio dgli lmnti il sistma priodio dgli lmnti 1. indiar qual di sgunti lmnti NoN è di transizion: a F zn as Cu Cr (Mdiina Chirurgia 2005) 2. indiar
tst i himia pr l asso all Faoltà UNiVrsitari il sistma priodio dgli lmnti il sistma priodio dgli lmnti 1. indiar qual di sgunti lmnti NoN è di transizion: a F zn as Cu Cr (Mdiina Chirurgia 2005) 2. indiar
