ANALISI MATEMATICA INGEGNERIA GESTIONALE PROF. GIACOMELLI ESEMPI DI ESERCIZI D ESAME
|
|
|
- Costanzo Rinaldi
- 7 anni fa
- Visualizzazioni
Transcript
1 ANALISI MATEMATICA INGEGNERIA GESTIONALE PROF. GIACOMELLI ESEMPI DI ESERCIZI D ESAME Contents. Numeri complessi. Funzioni: dominio, estremo superiore e inferiore, massimi e minimi 3. Successioni e serie 4 4. Limiti di funzioni 0 5. Funzioni dis)continue da R in R 6. Calcolo differenziale per funzioni da R in R 3 7. Applicazioni dei teoremi di de l Hopital e di Peano 7 8. Calcolo integrale per funzioni da R in R 9. Calcolo differenziale per funzioni da R in R 6 0. Integrali doppi 9. Equazioni differenziali ordinarie 3 Ultimo aggiornamento: febbraio 0 si prega di segnalare eventuali errori. Numeri complessi *) Data l equazione z i z + z = 4, determinarne se esistono) le soluzioni z C tali che z 3. Posto z = x + iy, si ha z i z + z = x y + ixy ix y + x + y = x y + ixy ), perciò le soluzioni devono verificare { x y = 4 xy ) = 0. Risolvendo la seconda equazione e sostituendo nella prima si ottiene { { y = 4 x oppure = 9/ x = 0 y = / ovvero z = 4i, z = 3/ + i/, z 3 = 3/ + i/. Poiché z = 6, z = 5/ e z 3 = 5/, le soluzioni che verificano la condizione richiesta sono z e z 3. *) Determinare purché esistano) le soluzioni z C della seguente equazione: z z) = 4i +.
2 Risposta: ± + i). *) Determinare le soluzioni in campo complesso delle seguenti equazioni: a) z 3 = i; b) z 3 = 5z. 05/06) a) Si ha i = e i π 4 +kπ, k Z. Perciò, posto z = re iθ, si ha e quindi le soluzioni sono z 3 = i r 3 e 3iθ = e i π 4 +kπ r = 6 e θ = 3 π 4 + kπ), k = 0,, z 0 = 6 e i π, b) Posto z = re iθ, si ha z = re iθ+kπ. Perciò e quindi le soluzioni sono z 3 = 5z r 3 e 3iθ = 5re iθ z = 6 e i 7π, z = 6 e i 5π 4. r = 0 oppure r = 5 e 4iθ = kπ z 0 = 0, z = 5, z = 5, z 3 = i 5, z 4 = i 5.. Funzioni: dominio, estremo superiore e inferiore, massimi e minimi *) Determinare il dominio naturale della funzione f : domf R R definita da fx) = x x. 06/07) Le condizioni sono x 0, { da cui segue che dom f = [, + ) \ x 0, x x 0,, 5+ 5 }. *) Determinare l estremo superiore, l estremo inferiore, gli eventuali punti di massimo locale e gli eventuali punti di minimo locale della funzione f : R R definita da fx) = x.
3 Il grafico della funzione è elementare: in figura, per x 0, il grafico qualitativo delle funzioni x x, x x, x x e x x, nell ordine. Dal grafico con calcoli banali) si deduce che x = ± sono punti di massimo locale, x = 0 e x = ± sono punti di minimo locale e assoluto), sup f = + e inf f = 0. *) Data la funzione f : [ 5, 3] R definita da fx) = 9 + x, x [ 5, 3], determinarne purché esistano) i punti di massimo locale, i punti di massimo assoluto, i punti di minimo locale e i punti di minimo assoluto. Il grafico qualitativo della funzione è elementare. Da esso si deduce che x = 9/ punto di minimo locale e assoluto, x = 3 punto di massimo locale e assoluto, x = 5 punto di massimo locale. *) Determinare l estremo superiore, l estremo inferiore, gli eventuali punti di massimo locale e gli eventuali punti di minimo locale della funzione f : R R definita da fx) = x 3. Dal grafico qualitativo, ottenuto per composizione di funzioni elementari, si deduce immediatamente che sup f = +, inf f = 0, x = 0 è punto di massimo locale e x = ± 3 sono punti di minimo locale e assoluto). *) Determinare l estremo superiore, l estremo inferiore, gli eventuali punti di massimo locale e gli eventuali punti di minimo locale della funzione f : [ 4, 3] R definita da { x + )x 3) se x > fx) = x + 3 se x. Il grafico della funzione è elementare; tracciandolo nell intervallo [ 4, 3] si ottiene che x = 4 e x = 3 sono punti di massimo locale, x = 3 e x = sono punti di minimo locale, sup f = 5 e inf f = 4. 05/06)
4 *) Determinare il dominio naturale, l estremo superiore, l estremo inferiore, gli eventuali punti di massimo locale e gli eventuali punti di minimo locale della funzione f :domf R definita da fx) = log x ). Risposta: domf =, 0) 4, + ). Dal grafico qualitativo, ottenibile per composizione di funzioni elementari, si deduce immediatamente che sup f = +, inf f =. Determinare estremo superiore, estremo inferiore ed eventuali massimi e minimi locali o assoluti della funzione f : R R definita da fx) = 3 x +. Dal grafico qualitativo della funzione, ottenibile per composizione di funzioni elementari come negli esercizi precedenti, si deduce immediatamente che sup f =, inf f = min f = 0 in x = ±/) e è un massimo locale in x = 0). 3. Successioni e serie *) Data la successione n + )! a n = n n, n!) calcolare a n+. n + a n a n+ = n + a n n + n + 3)! n n ) n!) n + ) n+ n + )!)n + )!) ) n n n + n + 3)n + ) = n + n + ) = 4 e. *) Sia {a n } n N una successione tale che a 0 > 0 e a n+ 3a n per ogni n N. a) Dimostrare che n + a n = + ; b) Mostrare con un contresempio che la conclusione in a) è falsa se non si assume che a 0 > 0. a) segue immediatamente da a n+ 3 n a 0, 05/06)
5 che dimostriamo per induzione: l affermazione è vera per n = 0; se è vera fino ad n, allora a n+ 3a n+ 3 3 n a 0 = 3 n+ a 0. b) Se a 0 = 0, la successione {a n } definita da a n = 0 per ogni n soddisfa tutte le ipotesi, ma il ite ovviamente è zero. *) Sia {a n } n N la successione ricorsiva definita da { an+ = a n n 0 a 0 = 4 ; a) utilizzando il principio di induzione, dimostrare che a n > 0 per ogni n N; b) determinare il carattere della serie n 3 a n. n=0 a) ) a 0 = 4 > 0; ) se a n > 0 allora a n+ = a n > 0. b) Poiché per a) la serie è a termini positivi, si può applicare il criterio del rapporto: ) 3 a n+ n + = = n + a n n + n, quindi la serie è convergente. *) Determinare la somma della serie k ). k + k= Risposta: 3/. 05/06) *) Dire se la seguente serie è convergente, divergente o irregolare: 3n)! nn!) 3. n= La serie è a termini positivi, quindi possiamo applicare il criterio del rapporto: poiché n + la serie è divergente. 3n+))! n+)n+)!) 3 = 3n)! n + nn!) 3 n3n + 3)3n + )3n + ) n + )n + ) 3 = 7 >, *) Al variare di x R, studiare il comportamento della serie e 3n n n n!) x. n= 05/06)
6 Utilizziamo il criterio del rapporto: n e 3n+) n+) n+) [n+)!] x e 3n n n Pertanto la serie converge per x [, + ). = n e 3 n + ) x n!) x 0 x > = e x = + x <. n + n ) n *) Determinare purché esistano) i valori di x R per i quali la seguente serie converge: x 7) k. k= Risposta: x 3, 4). *) Determinare se esistono) i valori di x R per i quali la seguente serie è convergente: ) n x x n= Risposta: ogni x R. *) Determinare i valori di x R per i quali la seguente serie è convergente: n )! n n+ x n. n= x [ e /4, e /4]. Determinare il carattere della serie k= k)! k! k k. Risposta: divergente a +. *) Determinare purché esistano) i valori di α 0, + ) per i quali la seguente serie converge: ) 5α k k+ k= k+ ) α ) 3/. k
7 Si ha k ) 5α ) 5α = = + o)) per k + k + k + k5α e ) α k + = + ) α = α + o)) per k +. k k k Pertanto k k+ k ) 5α k+ ) α ) 3/ = + o)) per k +. αk5α 3/ Per il criterio del confronto, la serie converge se e solo se 5α 3/ >, ovvero se e solo se α > /. *) Determinare se esistono) i valori di α R per i quali la seguente serie è convergente: n α + n 8 α 3n 6 sinn). n= La serie è a termini positivi. Per n +, si ha n α + o)) se α > 4 n α + n 8 α = n 4 se α = 4 n 8 α + o)) se α < 4 Quindi n α + n 8 α 3n 6 sinn) = 3 nα 6 + o)) se α > 4 3 n se α = 4 3 n α + o)) se α < 4 e 3n 6 sinn) = 3n 6 + o)). per n +. Dal criterio del confronto con le serie armoniche generalizzate) segue che la serie in esame è convergente se e solo se 3 < α < 5. *) Determinare se esistono) i valori di x R per i quali la seguente serie è convergente: ) 8n. n= n x + x Si ha, per le gerarchie di infiniti, 8n ) 8n = x ) + o)) se x > oppure x n x + n x + o)) se < x x per n +. Per confronto con la serie geometrica o con la serie armonica generalizzata), la serie converge se e solo se x > o x <.
8 *) Al variare del parametro α R, determinare il comportamento convergente, divergente o irregolare) della seguente serie: n α+8 n 7 + e. α )n n= Si tratta di una serie a termini positivi. Se α >, si ha n α+8 nα+8 n 7 + e α )n e α )n per n +. Poiché la serie n= nα+8 è convergente per ogni α > ad esempio per il criterio della e α )n radice), anche la serie in esame è convergente per α >. Se α, si ha Poiché la serie concludiamo che: n= n α+8 nα+8 n 7 + e α )n n 7 = n α per n +. n α è convergente se e solo se α >, ovvero α <, la serie in esame è { convergente per α, ), ) divergente a + per α [, ]. *) a) Al variare del parametro α 0, ), determinare nei casi in cui esiste) il seguente ite: ) n n + ; n α b) al variare del parametro α 0, ), determinare il comportamento convergente, divergente o irregolare) della seguente serie:. n= n α a) Si ha, per α 0, ), n α Quindi ) n = n + n α ) n ) n n α = e n log n α ) = e n α +o)) ) n per n. + α 0, ) = e / α = α, ). b) La serie diverge per ogni α 0, ) poiché, per a), la condizione necessaria non è soddisfatta. *) Al variare di α, ), studiare il carattere della serie n α + α. n n= 05/06)
9 Si tratta di una serie a termini positivi, quindi o converge o diverge a +. La condizione necessaria è sempre verificata: n α + α n = + α > 0 oppure α > α R. n Se α >, ovvero α, ) 3, ), si ha n α + α = n α n + o)), e la serie converge per il criterio del confronto asintotico. Se invece α [, 3], si ha n α + α n = n α + o)) e ancora per confronto asintotico la serie converge se α, 3]. Pertanto la serie converge per α, ), ) e diverge a + altrimenti. *) Determinare se esistono) i valori di α R per i quali la seguente serie è convergente: n= sinn 3 α ) n 4 α. Risposta: α < 3. *) a) Determinare, se esiste, il ite π ) x x arctan x ; 05/06) b) studiare la convergenza semplice e assoluta della serie π ) n ) arctann ). + log n n= Risposta: a) ; b) assolutamente convergente.
10 4. Limiti di funzioni *) Determinare il seguente ite: + 5 x 0 sin8x)) x. + Risposta: e 40. *) Determinare il seguente ite: ) x 0 + e 7x. ex Risposta:. *) Calcolare purché esista) il seguente ite: [ log4e x 4 x) log4x 6) ] x 4 + Ponendo y = x 4 e ricordando che e y = + y + oy) per y 0, si ottiene [ log4e x 4 x) log4x 6) ] = [log4e y y 4) log4y)] x 4 + y 0 + ) 3y + oy) = log y 0 + 4y ) 3 = log. 4 *) Determinare se esiste) ) log x x 0 3 log x + ) )) x). /x 3 Si ha ) log x 3 log x + ) ) x) /x 3 Perciò il ite vale. *) Determinare se esiste) x + = 3 x log x + ) ) x) 3 = x log + x 6x ) = x x 6x + ox 6x )) x 4 + 3x xx ) ) x + 9 = x + ox)) per x 0. x
11 Si ha x 4 + 3x xx ) x + 9 = x 4 + 3x x x ) + 9/x = x 4 + 3x x 4 x ) + 9 )) x + o x perciò il ite vale. = x + ox ) per x +, Per ogni α 0, + ) determinare purché esista) cos n α )) n. n + Risposta: 0 se α 0, /), e / se α = /, se α /, + ). *) In ciascuna delle seguenti situazioni, dire se è possibile determinare il ite e in tal caso calcolarlo: fx) gx) i) x 0 + x 4, dove fx) = ox ) e gx) = ox 4 ) per x 0 + ; ii) iii) x + fx) gx) x 4, dove fx) = ox ) e gx) = ox 4 ) per x + ; e fx) singx)), dove fx) = ox) e gx) = ox) per x 0 +. x 0 + x i) ii) iii) ox ) ox 4 ) ox ) x 0 + x 4 = x 0 + x 4 x + ox ) ox 4 ) x 4 = x + ox ) = x 0 + x ox 4 ) x 4 = 0; forma indeterminata ; x e fx) singx)) fx) gx)) + o)) ox) = = x 0 + x x 0 + x x 0 + x = 0. *) Determinare se esiste) l ordine di infinitesimo per x 0 + della funzione ) + x) sin x fx) = log + x) x. Si ha fx) = sin x log + x) x log + x) = x + ox))x + ox)) xlog + o)) = x log + ox) per x 0 +. Perciò l ordine di infinitesimo esiste e vale.
12 *) Sia fx) = x 4) /x. a) Determinare, se esiste, fx); x 0 + b) determinare, se esiste, l ordine di infinito o di infinitesimo di fx) per x 0 +. Si ha x 4 ) /x = e x log x4) = e x3 +o)) Perciò x 0 + fx) = 0 e quindi l ordine di infinitesimo è 3. per x 0 +. fx) = e x3 +o)) = x 3 + o)) per x 0 +, *) Determinare il dominio naturale e gli eventuali asintoti della seguente funzione: logx 3) fx) = log x 3 ). domf = 3/, ] 3 + e, + ). Asintoti verticali: x = 3/, x = 3 + e. Asintoto orizzontale: y = per x Funzioni dis)continue da R in R *) Sia f : R R definita da fx) = e x + arctgx 3 ), x R. a) Dimostrare che f è invertibile in R; b) determinare il dominio della funzione inversa f ; c) determinare se esiste) f ) ) si osservi che f0) = ). Per a), basta osservare che f x) = e x + 6x 4x 6 + > 0 x R; quindi f è strettamente crescente e perciò invertibile. Per b), ricordando che domf =imf, basta determinare imf. Poiché f è continua e monotona, e x, fx) = +, x + si conclude che domf =imf = π, + ). Per c), basta applicare il teorema di derivazione della funzione inversa: f ) ) = f f )) = f 0) =.
13 *) Determinare il valore del parametro a 0, + ) per il quale la funzione f : R R definita da { x a) se x < fx) = x + 5 se x è continua in x = ; per tale valore di a, determinare sup f e inf f. R R Risposta: a = 5; sup R f = +, inf R f = Calcolo differenziale per funzioni da R in R *) Determinare il dominio naturale, gli eventuali asintoti e gli eventuali punti critici della funzione ) fx) = log e x 3 x. domf =, log ) log, + ); x = log e x = log asintoti verticali, y = x asintoto obliquo per x +, y = x asintoto obliquo per x ; i punti critici sono x = log 3 e x = log 3. *) Determinare il valore della funzione fx) = e 3 cosx) nei suoi punti di flesso. Poiché f C R), i punti di flesso sono tutti e soli le soluzioni di f x) = 0. Si ha Perciò f x) = e 3 cosx) 6 sinx)), f x) = e 3 cosx) 36 sin x) cosx)) = 0. f x) = 0 3 sin x) = cosx) 3 3 cos x) = cosx) 37 cosx) = 6 37 l altra soluzione è inammissibile). Quindi il valore della funzione nei punti di flesso è e. *) Quanti sono i valori distinti di x [, + ) in cui la funzione si annulla? fx) = x + )x + ) logx + ) 4x + ) Sia x I = [, + ). Si ha fx) = x + )gx), gx) := x + ) logx + ) 4. Quindi fx) = 0 se e solo se x = oppure gx) = 0. Si ha g x) = logx + ) + 0 x + /e. In particolare g è strettamente crescente in I e g ) = 4. Perciò esiste un unico x, + ) tale che gx) = 0, e gli zeri di f in I sono complessivamente.
14 *) Determinare l estremo superiore e l estremo inferiore della funzione f : R R definita da fx) = ex 4x +. È possibile procedere in almeno) due modi. ) La funzione f è derivabile per ogni x R, e si ha Pertanto f è crescente in R. Quindi sup f = f x) = ex x) + 4x ) 0 per ogni x R. fx) = +, inf f = fx) = 0. x + x ) In alternativa allo studio della monotonia di f, si può osservare che fx) > 0 per ogni x R; quindi Imf) 0, + ), ovvero inf f [0, ) e sup f 0, ]. Poiché fx) + per x + e fx) 0 per x, si conclude che sup f = + e inf f = 0. *) Determinare l estremo superiore e l estremo inferiore della funzione f : R R definita da { 3e x se x 0 fx) = 3 e x se x < 0. Risposta: inf f = 5, sup f =. *) Determinare se esistono) i punti di massimo locale e i punti di minimo locale della seguente funzione: fx) = x 3 x +. Si ha fx) = { x 3 x + se x 3 3 x x + se x < 3 e quindi f x) = x +6x+ x +) se x > 3 x 6x x +) se x < 3. Dallo studio del segno della derivata si evince che f è crescente in, 3 0) e in 3, 3 + 0) e decrescente altrimenti. Perciò 3 ± 0 sono punti di massimo locale e x = 3 è punto di minimo locale. *) Data la funzione fx) = x 3 4 x +, determinarne i punti di massimo e minimo relativo e assoluto nell intervallo [, ].
15 Si ha Poiché si ottiene x 3 4 x x [ 3 4, ) fx) = 4 x 3 x x [, 3 4) 4 x 3 + x + x, ). 3x x 3 4, ) f x) = 3x x, 3 4) 3x + x, ), f crescente in 3, ) 3 4, ) f decrescente in, 3 ), 3 4). Quindi x =, x = / e x = sono punti di massimo locale, e x = / 3 e x = 3 4 sono punti di minimo locale. Per determinare gli estremi assoluti confrontiamo i valori: poiché f ) = 9 = 4 + > f ) = > f) = 4 5, x = è punto di massimo assoluto; analogamente, si ottiene che x = 3 4 è punto di minimo assoluto. *) [ Determinare i punti di massimo locale e i punti di minimo locale della funzione f : π 4, ] 3π 4 R definita da fx) = 0 sinx) cosx), x [ π 4, ] 3π 4. Si ha quindi Perciò x = π 4 e x = 3π 4 f x) = 0 cosx) + sinx) = cosx)sinx) + 5), f x) < 0 x > π per x [ π 4, ] 3π 4. sono punti di minimo locale, x = π è punto di massimo locale. *) Determinare, purché esistano, i punti di massimo locale e i punti di minimo locale della funzione f : 0, + ) R definita da fx) = 3x + x ) log8x)) x, x 0, + ). Risposta: x = 8 punto di massimo locale. *) Sia f : domf R la funzione definita da fx) = arctanx) x ; determinarne il dominio naturale, l estremo superiore, l estremo inferiore, gli eventuali punti di massimo locale e gli eventuali punti di minimo locale.
16 domf = R. Si ha quindi sup f = + e inf f =. Si ha quindi f x) = arctanx) x fx) =, x ± + x ) log, f x) > 0 se x, ), f x) = 0 se x = ±, f x) < 0 altrimenti; perciò f ha un punto di massimo locale in x = e un punto di minimo locale in x =. *) Determinare A R in modo tale che la funzione f : domf R definita da { x + ) 4 se x fx) = A arctgx + 3) se x < risulti continua nel suo dominio; per tale valore di A, determinare l estremo superiore, l estremo inferiore e gli eventuali punti di massimo e minimo locale e assoluto di f nel suo dominio. domf =, ], ed f C, ] \ { }) per le proprietà elementari delle funzioni continue. Si ha f C, ]) se e solo se In tal caso, si ha f ) = = fx) = A π x ) 4 A = 8 π. quindi: { 4x + ) f 3 < x x) = 8 π x+3) + x <, f crescente in, ) e in, ), f decrescente in, ). Pertanto x = è un punto di massimo locale, x = è un punto di minimo locale, e x = 0 è un punto di massimo locale. Poiché f ) = > f ) = 6, x = è in effetti un punto di massimo globale e sup f =. Poiché x fx) = 5 < f ) = 0, inf f = 5. *) a) Studiare la funzione ) fx) = log x x e tracciarne un grafico qualitativo nell ipotesi che il numero di flessi sia minimo. b) Utilizzando a), tracciare senza ulteriori calcoli un grafico qualitativo della funzione gx) = log x x domf =, + ), fx) = 0 se e solo se x = 3/, fx) + per x +, f strettamente decrescente in, ], fx) = log per ogni x [, + ). ). 05/06)
17 *) a) Studiare la funzione fx) = sin x 3 sin x + e tracciarne un grafico qualitativo nell ipotesi che il numero di flessi sia minimo. b) Utilizzando a), tracciare un grafico qualitativo della funzione gx) = fx) ; dire se la funzione gx) è derivabile nei punti x = π e x = 5π 6. 05/06) 7. Applicazioni dei teoremi di de l Hopital e di Peano *) Determinare se esiste) il seguente ite: 05/06) e cosx ) ) x 0 + x sinx)) Si ha cosx ) = x4 + o)), da cui e cosx) ) = e x4 +o)) = x4 + o)). Inoltre x sin x = 6 x3 + o)) da cui x sinx)) = 36 x6 + o)). Pertanto il ite vale. *) Determinare se esiste) il seguente ite: [ log x 0 x x) + log + x)) + x )] x. 05/06)
18 Si ha Pertanto x 0 log x) = x x + ox ), log + x)) = x + ox)) = x + ox ). [ log x x) + log + x)) + x )] x / x = x 0 x =. *) Determinare se esiste) il seguente ite: logx) + sin x) cos 3x 3) x + x ). Ponendo y = x 0 + per x +, si ottiene logx) + sin x) cos 3x 3) x + x ) log + y) + sin y) cos 3y) = y 0 + y y = y + oy )) y + oy )) 3 y + oy)) y 0 + y =. *) Determinare, purché esista, l ordine di infinito o di infinitesimo per x + della funzione f : 0, + ) R definita da fx) = 3 x log + 3 ). x Poiché log + y) = y y / + oy ) per y 0 e / 3 x 0 per x +, mediante la sostituzione y = / 3 x si ottiene ) ) /3 fx) = x /3 x /3 x /3 + ox /3 ) = + o)) per x +. x Perciò la funzione è infinitesima per x + e il suo ordine di infinitesimo è /3. *) Determinare purché esistano) i valori di α R per i quali il seguente ite è uguale a zero: x 3 x 0 + x 8α sinx). Si ha x 8α sin x = x 8α + o)) se 8α < x sinx) = x3 6 + o)) se 8α = x + o)) se 8α >. per x 0+.
19 Perciò x 3 x 8α sinx) = x 3 8α + o)) se 8α < 6 + o)) se 8α = x + o)) se 8α >. per x 0+. Poiché 3 8α > 0 se 8α <, si conclude che il ite è zero per ogni α /8. *) Determinare se esiste) sin3x) x 0 54x 3 cos3x) ) 8x 4. Risposta: /4. *) Determinare se esiste) il seguente ite: ) ) x 0 + x + x 3. log x) Risposta: +. *) Determinare il polinomio di Taylor di ordine di centro x 0 = della seguente funzione: ) πx 5 fx) = x + 3) cos. 3 Si ha f) = e da cui ) πx f 5 x) = cos x + 3) 5πx4 3 3 f ) = 0π 3. ) πx 5 sin 3 Pertanto T [f, x 0 ]x) = + 0π ) x ). 3 *) Determinare il polinomio di Taylor di ordine centrato in x = π/4 della seguente funzione: fx) = e tan x. Si ha f tan x x) = e f x) = e tan x cos x, Perciò fπ/4) =, f π/4) =, f π/4) = 8, e quindi T x) = + x π/4) + 4x π/4). cos 4 x + sin x cos 3 x ).
20 Determinare il polinomio di Taylor di ordine con centro in x = 0 della funzione fx) = log + x x ). Risposta: T x) = x 3x /. *) Sia fx) = e sin x ; a) utilizzando il teorema di de l Hôpital, calcolare il ite fx) x x 0 + x ; b) determinare il polinomio di Taylor di f di ordine 3 centrato in x = 0. a) Si ottiene: e sin x x x 0 + x? e sin x cos x? e sin x cos x sin x) = = = x 0 + x x 0 +. b) Dal calcolo precedente segue che T x) = x + x e che f x) = e sin x cos x sin x). Poiché f x) = e sin x cos 3 x 3 sin x cos x cos x), si conclude che f 0) = 0 e quindi T 3 x) = T x) + 6 f 0)x 3 = x + x. *) Determinare, purché esistano, i valori del parametro α R per i quali la serie k α+ e + ) ) k k è convergente. k= Si ha e Perciò + k ) k = e e k log+ k ) = e e +o))) k = e e )) = e + o)) + o + o)) = e + o)) k k k k α+ e + ) ) k k = e + o)) kα+ e quindi la serie è convergente se e solo se α >. k +o))) per k +, per k +. *) Determinare i valori del parametro α R per i quali la seguente serie è convergente: sinn α ) n α n 5α. + n= α > /4 e α < /3.
21 *) Calcolare x 5 sin4x 3 ) e x) dx. 8. Calcolo integrale per funzioni da R in R *) Calcolare coslogx )) dx. Per sostituzione, ponendo x = e y/ quindi y = logx )), si ottiene coslogx )) dx = e y/ cos y dy 05/06) che si integra per parti: e y/ cos y dy = e y/ sin y dy e y/ sin y dy = e y/ sin y + ey/ cos y e y/ cos y dy. 4 Pertanto ovvero e y/ cos y dy = 5 ey/ sin y + cos y) + C, coslogx )) dx = 5 x sinlogx )) + coslogx ))) + C. Ponendo y = x, e x dx = e y dy = ey + C = ex + C. Ponendo y = x 3, x 5 sin4x 3 )dx = 3 y sin4y)dy = y cos4y) + = sin4y) 4y cos4y)) + C 48 = 48 sin4x3 ) 4x 3 cos4x 3 )) + C. cos4y)dy Perciò x 5 sin4x 3 ) e x) dx = 48 sin4x3 ) 4x 3 cos4x 3 )) ex + C. *) Determinare le primitive della seguente funzione: fx) = e3x 6 + e 6x. Risposta: F x) = arctan e 3x 4 ) + C.
22 *) Determinare le primitive della seguente funzione: t 7 + 4t ) 3/ dt. Risposta: t ) 5/ + C. *) Calcolare 3π/4 π/ max { }, sinx) dx. Si ha, ponendo t = x, 3π/4 max { }, sinx) dx = π/ 3π/ π 7π/6 max { }, sint) dt = sint)dt π 4 3 = 4 π. 3π/ 7π/6 dt *) Calcolare 4 4 log + ) x La funzione integranda è pari. Perciò, ponendo t = x, si ottiene 4 log + ) 4 x dx = log + x ) dx 4 = dx. t log + t) dt = t log + t) 0 = 8 log 3 = 6 log 3. 0 t 0 + t dt t + ) dt + t *) Calcolare π/ π/3 sin x dx. Ponendo t =tanx/), si ottiene π/ π/3 sin x dx = / 3 t dt = log t / 3 = log 3.
23 *) Sia a) Calcolare F x) = x fx) = fs) ds; { 4x + per x 0 per x < 0. b) la funzione F è una primitiva della funzione f? a) Si ha F x) = { x ds = x se x 0 0 ds + x 0 4s + )ds = x + x se x > 0. b) no, poiché F x) non è derivabile in x = 0. *) Determinare se esistono) i punti di massimo locale e i punti di minimo locale della seguente funzione nell intervallo I: x 4 π ) 4 fx) = sin t dt, x I = [ 3, 3]. 0 La funzione è pari. Si ha Per x [0, 3] si ha x 3 0 e π ) f x) = 4x 3 sin x. π ) sin x > 0 x 0, ). Perciò, ricordando che f è pari, si ottiene che f è crescente in [ 3, ] e in [0, ] e decrescente in [, 0] e in [, 3]. Perciò x = ±3 e x = 0 sono punti di minimo locale, e x = ± sono punti di massimo locale. *) Sia f : R R definita da fx) = x 0 sint t) dt. Determinare se esiste) fx) x 0 x. Sono verificate le ipotesi del Teorema di de l Hôpital: perciò fx) x 0 x? sinx x) = x 0 x. *) a) Determinare purché esista) l ordine di infinitesimo per x 0 + della funzione f : R R definita da fx) = x 6 x6 + x 0 e t5 dt ;
24 b) calcolare purché esista) fx). x 0 + x 0 x 0 x a) Applicando, nell ordine, il Teorema di de l Hopital e il Teorema di Peano, si ottiene fx)? x 5 + e x 5 = x 0 + x α x 0 + αx α = x 0 + = x0 + ox 0 ) αx α se α =. Perciò l ordine di infinitesimo esiste ed è. b) Si può ad esempio procedere osservando che x 0 x 0 x = x 0 ) x = x 0 ) x + ox ) Perciò, utilizzando anche il punto a), si conclude che per x 0 +. x 0 + x 0 fx) x 0 x = x 0 + x + o)) x + o)) =. *) Calcolare, purché esista, il ite x 0 + x x 7 e t dt. Il ite non è una forma indeterminata in quanto x 0 + x 7 e t dt = 0 7 e t dt = C e C < 0 poiché la funzione integranda è sempre positiva in 0, 7). Perciò il ite esiste e vale. Si noti che, proprio perché la forma non è indeterminata, il Teorema di de l Hopital non è applicabile la sua applicazione condurrebbe alla conclusione errata che il ite valga ). *) Calcolare + 0 e x cos x dx.
25 Per parti, utilizzando l identità sin x = cos x: e x cos x dx = e x cos x e x cos x sin x dx = e x cos x sin x cos x) e x cos x sin x) dx = e x cos x sin x cos x) 4 e x cos x dx e x. Quindi ovvero + 0 e x cos x dx = 5 e x + cos x sin x cos x) + C, e x cos x dx = 3 5 x + 5 e x + cos x sin x cos x) = 3 5. *) Data la funzione 3 fx) = log x x )) : a) determinare il dominio naturale di f; b) determinare l equazione della retta tangente ad f nel punto, f)); c) determinare i valori del parametro α 0, ) per i quali la funzione fx)) 3α è integrabile in senso improprio in 3/, ). a) Si ha 3 x x ) > 0 x x 6 > 0 x, ), 3), x ) perciò domf =, ), 3). b) Si ha f) = 0 e f x) = 3 x ) 3 x x da cui f ) = 7/4; perciò la retta tangente ha equazione y = 7/4x ). c) La funzione è continua in [3/, ), quindi dobbiamo considerare solo il comportamento di f per x : per b), Perciò fx) = 7 4 x ) + o)) per x. fx)) 3α ) 3α 4 7 x) 3α per x, e dal criterio del confronto segue che fx)) 3α è integrabile in senso improprio in [3/, ) se e solo se α < /3., *) Determinare i valori di α R per i quali il seguente integrale improprio è convergente: arctanx) x + xα ) dx. 05/06)
26 La funzione è continua in [, + ), quindi dobbiamo solo considerarne il comportamento per x +, dove π arctanx) α < 0 x + xα ) x π / α = 0 per x +. 4x / π α > 0 x α+/ Quindi, per il criterio del confronto asintotico, l integrale è convergente se e solo se α+/ >, ovvero α /, + ). *) Determinare purché esistano) i valori di α 0, + ) per i quali il seguente integrale improprio converge: x ) 5α dx. x α ) 3/ La funzione integranda è continua in, ]. Poiché α > 0, si ha x α = + x )) α = αx ) + o)) per x e quindi x ) 5α x α ) = x 3/ )5α 3/ + o)) per x +. Perció, per il criterio del confronto asintotico, l integrale improprio converge se e solo se 5α 3/ >, ovvero se e solo se α > /0. *) Determinare purché esistano) i valori di α R per i quali il seguente integrale improprio converge: e 3α 5)x x α dx. Risposta: α, 5/3]. 9. Calcolo differenziale per funzioni da R in R *) Dire se esiste una funzione f : D R R che soddisfa le tre seguenti proprietà: - f C D); - f x) > 0 per ogni x D; - f non è monotona in D in caso affermativo fornire un esempio, in caso negativo motivare la risposta). Risposta: Si. La funzione fx) = /x verifica le proprietà richieste. 05/06) *) Sia f : domf R R definita da fx, y) = x logxy ) ; determinare l equazione del piano tangente al grafico di f nel punto,, f, )).
27 Si ha f, ) = e f x x, y) = x, f yx, y) = y x, y) dom f da cui f x, ) = 0 e f y, ) =. Perciò il piano tangente ha equazione z = y ) = 3 y. *) Determinare se esistono) i punti critici della seguente funzione: fx, y) = e y x 4y 7x). Si ha: { Perciò fx, y) = 0 f x x, y) = e y x 7x 4y 7) f y x, y) = e y x 4y 7xy + ). { 7x 4y = 7 y4y 7x) = da cui segue che l unico punto critico è 57/49, /7). { 7x 4y = 7 7y = *) Determinare i punti stazionari della funzione f : R R definita da fx, y) = y x y 3 x3. Risposta: 0, 0) e, /). *) Siano w =, ), v = w/ w e f : R R definita da fx, y) = xy arctanxy). Calcolare f, ). v Si ha v =, )/ 5 e Perciò fx, y) = ) y y + x y, xy x + x y. f, ) = f, ), v = 4 + /5, 4 /5),, ) = 3. v 5 5 *) Sia v =, )/ e sia f : R R definita da fx, y) = log + sin x )) x + y. Calcolare f v π, ).
28 Risposta: 3 π+. *) Fornire l esempio di una funzione f : R R che nel punto 0, 0) non è continua ma è derivabile nel punto 0, 0) lungo la direzione v = 5, ); verificare che la f prescelta soddisfa tali proprietà. La funzione fx) = non è continua in x = 0 in quanto ma è derivabile nella direzione v in quanto { se x > 0 e y = 0 0 altrimenti = 0 = f0, 0), x,y) 0,0) x>0,y=0 ft/ 5, t/ 5) f0, 0) = 0 = 0. t 0 t t 0 05/06) *) Determinare, se esistono, i punti di massimo e di minimo assoluto della funzione nell insieme fx, y) = x x + y) y 4y D = {x, y) R : x 0, y 0, x + y }. Si determinano anzitutto i punti stazionari: { { x3x + y) = 0 x = 0 y + x 4 = 0 y = { y = 3x oppure y + x 4 = 0. Sommando e due equazioni del secondo sistema e risolvendo l equazione risultante, si ottiene che i punti stazionari sono 0, ),, 3/) e 4, 6). Nessuno dei tre punti è interno a D; perciò i punti di massimo e minimo assoluto che esistono per il teorema di Weierstrass) si trovano sulla frontiera di D. Su x = 0 si ha f0, y) = y 4y che è decrescente per y [0, ]; su y = 0 si ha fx, 0) = x 3 che è crescente per x [0, ]; su x + y = si ha f y, y) = y) y 4y = 6y che è decrescente per y [0, ]. Combinando queste informazioni si conclude che, 0) è punto di massimo assoluto e 0, ) è punto di minimo assoluto. *) Sia f : R R definita da fx, y) = 3 x3 + 3 y3 + x y 4y ; determinare se esistono) i punti di massimo locale e i punti di minimo locale di f in R. Risposta: 0, ) punto di minimo locale, 0, ) punto di massimo locale 4, )/ 5 e 4, )/ 5 punti di sella). 05/06)
29 *) Determinare gli eventuali punti di massimo locale, di minimo locale e di sella della funzione f : R R definita da fx, y) = xx y)e x+y). Risposta: 0, 0) punto di sella, /, 3/) punto di minimo locale. 0. Integrali doppi *) Determinare l area del seguente insieme: D = {x, y) R : 5 x y 3}. Un grafico qualitativo elementare mostra che D è un triangolo di vertici 0, ),, 3),, 3). Quindi l area è 5. *) Determinare l area del seguente insieme: D = {x, y) R : y, x y 6 x}. Risposta: 5. *) Calcolare x + y dxdy, D = {x, y) R : x 0, y 0, x + y }. D Si ha x + y 0 in D. Perciò x + y dxdy = D = / y 0 / 0 = x + y)dx dy y) + y y ) dy *) Calcolare 05/06) x y dxdy, D = {x, y) R : x y e x y}. D
30 Si ha D x y dxdy = = x 0 0 = 60. x x y) dy dx = x x ) dx = 0 [ x y) ] y=x [ 3 x3 x4 + 5 x5 y=x ] x= x=0 dx *) Calcolare { } y dxdy, D = x, y) R : y x, y. D Si ha y se e solo se y 3. Quindi D si riscrive come dominio semplice come segue: { } D = x, y) R : y [, ], y x. Perciò D y dxdy = = = = y y dx dy y y )dy y + y)dy + y + ) y= 3 y3 = 7/6. y= y3 y)dy + 3 y ) y= 3 y3 y= *) Calcolare x dxdy, D = { x, y) R : 0 5x y x + 3 }. D Poiché 5x x + 3 x, si ha D = { x, y) R : x [0, ], 5x y x + 3 }. Pertanto x+3 x dxdy = x dy dx D = 0 0 = /. 5x 3x x) dx
31 *) Calcolare l area del seguente insieme: A = { x, y) R : x y 5 x }. A è simmetrico rispetto all asse x = 0; inoltre { } x 0 x 5 x x 3, { x 0 x 5 x } quindi A = {x, y) R : x [ 3, 3], x 5 x } lo studente verifichi per via grafica) e A = = 3 5 x 0 0 x 3 4dx + = ). dydx = 5 x 0 x dydx x x x, dydx 6 x )dx = ) ) *) Calcolare l area della seguente regione piana: D = {x, y) R : y 3 x 3 x)}. 05/06) Risposta: 3/0. *) Calcolare dove D x + y dxdy, D = { x, y) R : x 0, y 0, x + y 4 }. Passando in coordinate polari, si ha Perciò D D = {r cos θ, r sin θ) R : r, x + y dxdy = = = 7 3 π π/ π 3 r 3 π/ 3π/4 π/ = 7 3 ). r cos θ + sin θ drdθ cos θ + sin θ dθ sin θ + cos θ)dθ 7 3 π θ π}. π 3π/4 sin θ + cos θ)dθ
32 *) Sia D = {x, y) R : x 0, y 0, x + y } ; calcolare x + y D 4 dxdy. Risposta: 5π/64.. Equazioni differenziali ordinarie *) Determinare l integrale generale della seguente equazione differenziale ordinaria: z t) + zt) = e t log3e t + ). Si tratta di una EDO lineare del primo ordine. L equazione omogenea associata ha integrale generale z o t) = Ce t. Cerchiamo una soluzione particolare della forma z p t) = Ct)e t ; sostituendo si ottiene C t)e t = e t log3e t + ) C t) = e t log3e t + ). Integrando, Ct) = e t log3e t + ) dt y=et = = y log3y + ) log3y + ) dy 3y dy = y log3y + ) 3y + = y log3y + ) y + log3y + ) 3 = e t + 3 ) log3et + ) e t. Pertanto l integrale generale cercato è: zt) = Ce t + e t + 3 e 3t ) log3e t + ) e t, C R. ) dy 3y + *) Determinare l integrale generale dell equazione differenziale 05/06) y t) + y t) + yt) = sint). Le radici del polinomio caratteristico sono λ = ± i). Quindi l omogenea associata ha integrale generale y o t) = e t/ C cost/) + C sint/)). Cerchiamo una soluzione particolare con il metodo di somiglianza: da cui sostituendo si ottiene y p t) = A cos t + B sin t, A + B) cos t + B A) sin t = sin t A = 5 4, B = 5 8.
33 Pertanto l integrale generale è yt) = e t/ C cost/) + C sint/)) 5 cos t + sin t). 8 *) Determinare la soluzione dell equazione differenziale y t) + 8 y t) + 5 yt) = 0, t R tale che y0) = 0 e y 0) =. Risposta: yt) = 3 e 4t sin3t). *) a) Determinare l integrale generale dell equazione differenziale y t) y t) + yt) = te t ; b) tra le soluzioni ottenute al punto a) determinare, se esistono, quelle per le quali esiste t + yt). Si tratta di un equazione lineare del secondo ordine a coefficienti costanti non omogenea. Il polinomio caratteristico soddisfa λ λ + = 0 λ = ± i, quindi l omogenea associata ha integrale generale y o t) = e t A cos t+b sin t). Una soluzione particolare che si determina con il metodo di somiglianza) è data da y p t) = te t. Pertanto b) è verificata da tutte le soluzioni: a) : yt) = e t A cos t + B sin t + t), A, B R. e t A cos t + B sin t + t) = te t + o)) + per t + A, B R. Determinare l integrale generale della seguente equazione differenziale: y x) + 8y x) + 5yx) = cos x. Riposta: yx) = e 4x C cos3x) + C sin3x)) + 3 cos x + sin x)/80. *) Determinare l integrale generale della seguente equazione differenziale ordinaria: y x) y x) = e 3x. Ponendo y = z, si ottiene un equazione lineare del secondo ordine non omogenea a coefficienti costanti: z z = e 3x. L integrale generale dell omogenea associata è z o x) = Ae x + Be x. )
34 Per determinare una soluzione particolare si può utilizzare il metodo di variazione delle costanti. In alternativa, una soluzione particolare si ottiene con metodo ad-hoc: posto z p = Ce 3x, si ottiene Perciò l integrale generale di ) è Integrando, si ottiene la risposta: z p z p = 9C C)e 3x! = e 3x C = /7. zx) = z 0 x) + z p x) = Ae x + Be x + 7 e 3x. yx) = C e x + C e x + C 3 e 3x. *) a) Determinare l integrale generale dell equazione differenziale y + t + y = t + ; b) risolvere il problema di Cauchy y + t + y = t + y ) =. a) Si tratta di un equazione del primo ordine lineare. Risolvendo l omogenea per separazione di variabili, si ottiene y o t) = 0 oppure log y o t) = t + dt = t/ ) + dt = arctg t ) + C, C R 05/06) ovvero y o t) = C e arctg t/ ), C R. La soluzione particolare è immediata: y p t) = che si può ovviamente anche ottenere con il metodo di variazione delle costanti). Pertanto l integrale generale è yt) = + C e arctg t/ ), C R. b) La soluzione del problema di Cauchy deve verificare = + Ce arctg / ), da cui C = 0 e quindi yt) =. *) Determinare la soluzione yx) del seguente problema di Cauchy, specificandone il dominio massimale di esistenza: { y = y e /y sinx/) y0) = log. Per separazione di variabili: e /y + C = y e /y dx y = sinx/) dx = cosx/) + C,
35 ovvero e da y0) = log yx) = logcosx/) + C), segue C = /. Perciò yx) = logcosx/) /), il cui dominio naturale è D = {x R : cosx/) > /}; perciò il dominio massimale di esistenza della soluzione è π/3, π/3). *) Risolvere il problema di Cauchy { y t) = yt)3 + yt)) y0) = 6 specificando il dominio massimale di esistenza della soluzione. L integrale generale si determina per separazione di variabili: dy yy + 3) = 3 y ) = ) y y log y + 3 da cui ) yt) log = 3t + C yt) + 3 yt) yt) + 3 = Ke3t yt) = 3Ke3t, K R \ {0}, Ke3t a cui bisogna aggiungere le soluzioni costanti yt) = 0 e yt) = 3. Sostituendola condizione iniziale si ottiene K =, quindi la soluzione è yt) = 6e3t e 3t il cui intervallo massimale di esistenza è 3 log, ). *) Risolvere il seguente problema di Cauchy, determinando anche l intervallo massimale di esistenza della soluzione: { y = y 7y + y0) =. Risposta: yx) = 6e x 4)/e x ), I = log, + ). *) Determinare la soluzione yx) del seguente problema di Cauchy, specificandone l intervallo massimale di esistenza: y = y x y) = 3. Risposta: yx) = /3 + log x)), I =, e 3 ).
36 *) Risolvere il problema di Cauchy { y t) = t + tyt)) 05/06) y0) = specificando l intervallo massimale di esistenza della soluzione. ) π Risposta: yt) = tan 4 + t, t I = π/, ) π/.
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del
 ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del 3..7 TEMA Esercizio Calcolare l integrale log(3) 4 dx Svolgimento. Si ha log(3) 4 dx = (ponendo ex = t, per cui dx = dt/t) e = 4 3
ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del 3..7 TEMA Esercizio Calcolare l integrale log(3) 4 dx Svolgimento. Si ha log(3) 4 dx = (ponendo ex = t, per cui dx = dt/t) e = 4 3
Esonero di Analisi Matematica II (A)
 Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
Esonero di Analisi Matematica II (A) Ingegneria Edile, 8 aprile 3. Studiare la convergenza del seguente integrale improprio: + x log 3 x (x ) 3 dx.. Studiare la convergenza puntuale ed uniforme della seguente
ANALISI MATEMATICA I A.A. 02/03 PROVE SCRITTE E RISOLUZIONI
 ANALISI MATEMATICA I A.A. /3 PROVE SCRITTE E RISOLUZIONI L. GIACOMELLI, P. LORETI Contents I prova intermedia 5.. compito A 3 Risoluzioni 3 I prova intermedia 5.. compito B 5 Risoluzioni 6 I prova intermedia
ANALISI MATEMATICA I A.A. /3 PROVE SCRITTE E RISOLUZIONI L. GIACOMELLI, P. LORETI Contents I prova intermedia 5.. compito A 3 Risoluzioni 3 I prova intermedia 5.. compito B 5 Risoluzioni 6 I prova intermedia
Analisi Matematica I
 Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-7 Savona Tel. +39 9 264555 - Fax +39 9 264558 Analisi Matematica I Testi d esame e Prove parziali Analisi Matematica
Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-7 Savona Tel. +39 9 264555 - Fax +39 9 264558 Analisi Matematica I Testi d esame e Prove parziali Analisi Matematica
Soluzioni dello scritto di Analisi Matematica II - 10/07/09. C.L. in Matematica e Matematica per le Applicazioni
 Soluzioni dello scritto di Analisi Matematica II - /7/9 C.L. in Matematica e Matematica per le Applicazioni Proff. K. Payne, C. Tarsi, M. Calanchi Esercizio. a La funzione f è limitata e essendo lim fx
Soluzioni dello scritto di Analisi Matematica II - /7/9 C.L. in Matematica e Matematica per le Applicazioni Proff. K. Payne, C. Tarsi, M. Calanchi Esercizio. a La funzione f è limitata e essendo lim fx
Ingegneria civile - ambientale - edile
 Ingegneria civile - ambientale - edile Analisi - Prove scritte dal 7 Prova scritta del 9 giugno 7 Esercizio Determinare i numeri complessi z che risolvono l equazione Esercizio (i) Posto a n = n i z z
Ingegneria civile - ambientale - edile Analisi - Prove scritte dal 7 Prova scritta del 9 giugno 7 Esercizio Determinare i numeri complessi z che risolvono l equazione Esercizio (i) Posto a n = n i z z
Università di Roma Tor Vergata - Corso di Laurea in Ingegneria Analisi Matematica I - Prova scritta del 10 Luglio 2019
 Università di Roma Tor Vergata - Corso di Laurea in Ingegneria nalisi Matematica I - Prova scritta del 0 Luglio 09 Esercizio. [5 punti] Calcolare lo sviluppo di Taylor dell ordine n = 5 con centro x 0
Università di Roma Tor Vergata - Corso di Laurea in Ingegneria nalisi Matematica I - Prova scritta del 0 Luglio 09 Esercizio. [5 punti] Calcolare lo sviluppo di Taylor dell ordine n = 5 con centro x 0
Nozioni di base - Quiz - 2
 Nozioni di base - Quiz - Rispondere ai seguenti quesiti (una sola risposta è corretta).. L insieme delle soluzioni della disequazione (a) (0, ) (, + ) (x ) log(x) x + 0 è: (b) [, ] (c) (d) (e) (, + ) (0,
Nozioni di base - Quiz - Rispondere ai seguenti quesiti (una sola risposta è corretta).. L insieme delle soluzioni della disequazione (a) (0, ) (, + ) (x ) log(x) x + 0 è: (b) [, ] (c) (d) (e) (, + ) (0,
Calcolo I - Corso di Laurea in Fisica - 18 Giugno 2018 Soluzioni Scritto. f(x) = ( ln 1 + x + 1 ) =
 Calcolo I - Corso di Laurea in Fisica - 8 Giugno 08 Soluzioni Scritto ) Data la funzione fx) = ln + x + ) a) Calcolare il dominio, asintoti ed eventuali punti di non derivabilità; b) Calcolare, se esistono,
Calcolo I - Corso di Laurea in Fisica - 8 Giugno 08 Soluzioni Scritto ) Data la funzione fx) = ln + x + ) a) Calcolare il dominio, asintoti ed eventuali punti di non derivabilità; b) Calcolare, se esistono,
Esercizi riassuntivi per la prima prova di verifica di Analisi Matematica. n, n IN.
 Esercizi riassuntivi - B. Di Bella 1 Esercizi riassuntivi per la prima prova di verifica di Analisi Matematica 1. Sia A = n IN ] 1 n + 1, 1 [. n a) Determinare il derivato e l interno di A; b) stabilire
Esercizi riassuntivi - B. Di Bella 1 Esercizi riassuntivi per la prima prova di verifica di Analisi Matematica 1. Sia A = n IN ] 1 n + 1, 1 [. n a) Determinare il derivato e l interno di A; b) stabilire
Università degli Studi della Calabria Facoltà di Ingegneria. 17 luglio 2012
 Università degli Studi della Calabria Facoltà di Ingegneria Correzione della Seconda Prova Scritta di nalisi Matematica 7 luglio cura dei Prof. B. Sciunzi e L. Montoro. Seconda Prova Scritta di nalisi
Università degli Studi della Calabria Facoltà di Ingegneria Correzione della Seconda Prova Scritta di nalisi Matematica 7 luglio cura dei Prof. B. Sciunzi e L. Montoro. Seconda Prova Scritta di nalisi
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Esercitazioni di Matematica
 Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Secondo appello 2005/ Tema 1
 Secondo appello 2005/2006 - Tema Esercizio Risolvere l equazione di variabile complessa determinando le soluzioni in forma algebrica. Ponendo z = x + iy con x, y R, si ottiene z 2 + 2iz + 2 z = 0, () (x
Secondo appello 2005/2006 - Tema Esercizio Risolvere l equazione di variabile complessa determinando le soluzioni in forma algebrica. Ponendo z = x + iy con x, y R, si ottiene z 2 + 2iz + 2 z = 0, () (x
APPELLO X AM1C 17 SETTEMBRE 2009
 Cognome e nome APPELLO X AMC 7 SETTEMBRE 29 Esercizio. Sia f(x) = x arctan x + log( + x 2 ) (a) Determinarne: insieme di esistenza e di derivabilità, iti ed eventuali asintoti, eventuali massimi, minimi
Cognome e nome APPELLO X AMC 7 SETTEMBRE 29 Esercizio. Sia f(x) = x arctan x + log( + x 2 ) (a) Determinarne: insieme di esistenza e di derivabilità, iti ed eventuali asintoti, eventuali massimi, minimi
Analisi Matematica 1+2
 Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-700 Savona Tel. +39 09 264555 - Fax +39 09 264558 Ingegneria Gestionale Analisi Matematica +2 A.A 998/99 - Prove parziali
Università degli Studi di Genova Facoltà di Ingegneria - Polo di Savona via Cadorna 7-700 Savona Tel. +39 09 264555 - Fax +39 09 264558 Ingegneria Gestionale Analisi Matematica +2 A.A 998/99 - Prove parziali
APPELLO B AM1C 14 LUGLIO f(x) = xe 1
 Cognome e nome APPELLO B AM1C 14 LUGLIO 2009 Esercizio 1. Sia data la funzione f(x) = xe 1 log x. (a) Determinarne: insieme di esistenza e di derivabilità, limiti ed eventuali asintoti, eventuali massimi,
Cognome e nome APPELLO B AM1C 14 LUGLIO 2009 Esercizio 1. Sia data la funzione f(x) = xe 1 log x. (a) Determinarne: insieme di esistenza e di derivabilità, limiti ed eventuali asintoti, eventuali massimi,
TEMI D ESAME DI ANALISI MATEMATICA I
 TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea quadriennale) in Fisica a.a. 003/04 Prova scritta del 3 aprile 003 ] Siano a, c parametri reali. Studiare l esistenza e, in caso affermativo, calcolare
Matematica II prof. C.Mascia
 Corso di laurea in CHIMICA INDUSTRIALE Sapienza, Università di Roma Matematica II prof CMascia alcuni esercizi, parte, 7 marzo 25 Indice Testi degli esercizi 2 Svolgimento degli esercizi 4 Testi degli
Corso di laurea in CHIMICA INDUSTRIALE Sapienza, Università di Roma Matematica II prof CMascia alcuni esercizi, parte, 7 marzo 25 Indice Testi degli esercizi 2 Svolgimento degli esercizi 4 Testi degli
COGNOME... NOME... Matricola... Corso Prof... Esame di ANALISI MATEMATICA I - 28 Febbraio 2011, ore x e2x e 2x 1. f(x) = e 2x log(e 2x + 1) dx.
 Esame di ANALISI MATEMATICA I - 28 Febbraio 211, ore 8.3 A ESERCIZIO 1. (1 punti) Sia data la funzione f(x) = x e2x e 2x 1. (a) Determinarne il dominio e dimostrare che f si prolunga ad una funzione continua
Esame di ANALISI MATEMATICA I - 28 Febbraio 211, ore 8.3 A ESERCIZIO 1. (1 punti) Sia data la funzione f(x) = x e2x e 2x 1. (a) Determinarne il dominio e dimostrare che f si prolunga ad una funzione continua
CORSO DI LAUREA IN INFORMATICA ANALISI MATEMATICA I MODULO, I E II MODULO, II MODULO II PROVA SCRITTA DI GENNAIO 2006: SOLUZIONI
 CORSO DI LAUREA IN INFORMATICA ANALISI MATEMATICA I MODULO, I E II MODULO, II MODULO II PROVA SCRITTA DI GENNAIO 2006: SOLUZIONI Notiamo che lo studio delle funzioni assegnate f,..., f 4 si riduce a considerare
CORSO DI LAUREA IN INFORMATICA ANALISI MATEMATICA I MODULO, I E II MODULO, II MODULO II PROVA SCRITTA DI GENNAIO 2006: SOLUZIONI Notiamo che lo studio delle funzioni assegnate f,..., f 4 si riduce a considerare
Analisi Matematica 1 - a.a. 2017/ Quarto appello
 Analisi Matematica - a.a. 07/08 - Quarto appello Soluzione del test Test A E C B B C A D C C D Test B C B C E B A E E D B Test C A A D B E C A C D D Test D D B A A B E A E B D Soluzione della parte di
Analisi Matematica - a.a. 07/08 - Quarto appello Soluzione del test Test A E C B B C A D C C D Test B C B C E B A E E D B Test C A A D B E C A C D D Test D D B A A B E A E B D Soluzione della parte di
Analisi Matematica 1
 Michele Campiti Prove scritte di Analisi Matematica 1 Ingegneria Industriale a.a. 2011 2012 y f 1 g 0 x La funzione seno e la funzione esponenziale Raccolta delle tracce di Analisi Matematica 1 per Ingegneria
Michele Campiti Prove scritte di Analisi Matematica 1 Ingegneria Industriale a.a. 2011 2012 y f 1 g 0 x La funzione seno e la funzione esponenziale Raccolta delle tracce di Analisi Matematica 1 per Ingegneria
Prove scritte di Analisi I - Informatica
 Prove scritte di Analisi I - Informatica Prova scritta del 3 gennaio Esercizio Stabilire il comportamento delle seguenti serie: n= n + 3 sin n, n= ( ) n n + 3 sin n, n= (n)! (n!), n= n + n 9 n + n. Esercizio
Prove scritte di Analisi I - Informatica Prova scritta del 3 gennaio Esercizio Stabilire il comportamento delle seguenti serie: n= n + 3 sin n, n= ( ) n n + 3 sin n, n= (n)! (n!), n= n + n 9 n + n. Esercizio
Università degli Studi di Bergamo Facoltà di Ingegneria Matematica I Appello del 5 Febbraio 2007 Tema A
 Università degli Studi di Bergamo Facoltà di Ingegneria Matematica I Appello del 5 Febbraio 7 Tema A Cognome e Nome Matr... Disegnare un grafico approssimativo della funzione f() log( ). Indicare sul grafico
Università degli Studi di Bergamo Facoltà di Ingegneria Matematica I Appello del 5 Febbraio 7 Tema A Cognome e Nome Matr... Disegnare un grafico approssimativo della funzione f() log( ). Indicare sul grafico
Corso di Laurea in Ingegneria Edile Prova scritta dell esame di Analisi Matematica I (M-Z).C
 Analisi Matematica I (M-Z).C1 08-0-1997 1) Data la funzione h(x) = x log(x + 1 + x + x + ) + log(1 + ) determinarne il dominio D. Provare poi che h(x) > 0 x D ]0, + [, h(x) = 0 x = 0. ) Utilizzando i risultati
Analisi Matematica I (M-Z).C1 08-0-1997 1) Data la funzione h(x) = x log(x + 1 + x + x + ) + log(1 + ) determinarne il dominio D. Provare poi che h(x) > 0 x D ]0, + [, h(x) = 0 x = 0. ) Utilizzando i risultati
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione. Appello del
 ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del 9..8 NOTA: lo svolgimento del Tema contiene alcuni commenti di carattere generale. Esercizio Si consideri la funzione TEMA f := log
ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del 9..8 NOTA: lo svolgimento del Tema contiene alcuni commenti di carattere generale. Esercizio Si consideri la funzione TEMA f := log
Esercizi di prove scritte di Analisi Matematica I con schema di soluzione Paola Loreti. April 5, 2006
 Esercizi di prove scritte di Analisi Matematica I con schema di soluzione Paola Loreti April 5, 6 ESERCIZI. Studiare la convergenza della serie numerica al variare di γ IR.. Calcolare l integrale π n=
Esercizi di prove scritte di Analisi Matematica I con schema di soluzione Paola Loreti April 5, 6 ESERCIZI. Studiare la convergenza della serie numerica al variare di γ IR.. Calcolare l integrale π n=
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea (quadriennale) in Fisica a.a. 2002/03
 I seguenti quesiti ed il relativo svolgimento sono coperti dal diritto d autore, pertanto essi non possono essere sfruttati a fini commerciali o di pubblicazione editoriale senza autorizzazione esplicita
I seguenti quesiti ed il relativo svolgimento sono coperti dal diritto d autore, pertanto essi non possono essere sfruttati a fini commerciali o di pubblicazione editoriale senza autorizzazione esplicita
TEMI D ESAME DI ANALISI MATEMATICA I Corso di laurea in Fisica a.a.2001/02
 I seguenti quesiti ed il relativo svolgimento sono coperti dal diritto d autore, pertanto essi non possono essere sfruttati a fini commerciali o di pubblicazione editoriale senza autorizzazione esplicita
I seguenti quesiti ed il relativo svolgimento sono coperti dal diritto d autore, pertanto essi non possono essere sfruttati a fini commerciali o di pubblicazione editoriale senza autorizzazione esplicita
CODICE= Compiti di Analisi Matematica II per il Corso di Laurea in Ingegneria Edile A.A , Appelli 1, 2, 3 e 4
 Compiti di Analisi Matematica II per il Corso di Laurea in Ingegneria Edile A.A. 00-0, Appelli,, 3 e 4 Cognome: Nome: Matricola: CODICE = 33877 A B C D E 3 4 5 6 7 8 9 CODICE=33877 PARTE A. Lo sviluppo
Compiti di Analisi Matematica II per il Corso di Laurea in Ingegneria Edile A.A. 00-0, Appelli,, 3 e 4 Cognome: Nome: Matricola: CODICE = 33877 A B C D E 3 4 5 6 7 8 9 CODICE=33877 PARTE A. Lo sviluppo
Analisi Matematica 1
 Michele Campiti Prove scritte di Analisi Matematica Ingegneria Industriale aa 28 29 y f g x La funzione seno e la funzione esponenziale Raccolta delle tracce di Analisi Matematica per Ingegneria Industriale,
Michele Campiti Prove scritte di Analisi Matematica Ingegneria Industriale aa 28 29 y f g x La funzione seno e la funzione esponenziale Raccolta delle tracce di Analisi Matematica per Ingegneria Industriale,
ANALISI MATEMATICA 1 Commissione F. Albertini, V. Casarino e M. Motta Ingegneria Gestionale, Meccanica, Meccatronica, Vicenza
 TEMA f = 2 arctan 2) log e 2 αx α sin x + 2x + x 6 + x + n n 2 log n xe x dx al variare di a R x a e x dx Tempo: due ore e mezza Viene corretto solo ciò che è scritto sul foglio intestato È vietato tenere
TEMA f = 2 arctan 2) log e 2 αx α sin x + 2x + x 6 + x + n n 2 log n xe x dx al variare di a R x a e x dx Tempo: due ore e mezza Viene corretto solo ciò che è scritto sul foglio intestato È vietato tenere
Analisi Matematica 1
 Michele Campiti Prove scritte di Analisi Matematica 1 Ingegneria Industriale aa 2012 2013 y f 1 g 0 x La funzione seno e la funzione esponenziale Raccolta delle tracce di Analisi Matematica 1 per Ingegneria
Michele Campiti Prove scritte di Analisi Matematica 1 Ingegneria Industriale aa 2012 2013 y f 1 g 0 x La funzione seno e la funzione esponenziale Raccolta delle tracce di Analisi Matematica 1 per Ingegneria
Matematica A Corso di Laurea in Chimica. Prova scritta del Tema A
 Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
SOLUZIONI COMPITO del 1/02/2013 ANALISI MATEMATICA I - 9 CFU INGEGNERIA MECCANICA - INGEGNERIA ENERGETICA INGEGNERIA AMBIENTE e TERRITORIO TEMA A
 SOLUZIONI COMPITO del /0/0 ANALISI MATEMATICA I - 9 CFU INGEGNERIA MECCANICA - INGEGNERIA ENERGETICA INGEGNERIA AMBIENTE e TERRITORIO TEMA A Esercizio Osserviamo che la serie proposta è a termini di segno
SOLUZIONI COMPITO del /0/0 ANALISI MATEMATICA I - 9 CFU INGEGNERIA MECCANICA - INGEGNERIA ENERGETICA INGEGNERIA AMBIENTE e TERRITORIO TEMA A Esercizio Osserviamo che la serie proposta è a termini di segno
ANALISI MATEMATICA 1 Area dell Ingegneria dell Informazione
 ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del.. TEMA Esercizio. Sia f) = + 3) log + 3), D =] 3, + [. i) Determinare i iti di f agli estremi di D e gli eventuali asintoti; studiarne
ANALISI MATEMATICA Area dell Ingegneria dell Informazione Appello del.. TEMA Esercizio. Sia f) = + 3) log + 3), D =] 3, + [. i) Determinare i iti di f agli estremi di D e gli eventuali asintoti; studiarne
Analisi Matematica 1 Secondo appello
 Analisi Matematica 1 Secondo appello 11 febbraio 219 Testo A1 Consegnare solo questo foglio Prima parte: 2 punti per risposta corretta, 1 per ogni errore. Soglia minima 12/2. Seconda parte: Domande A e
Analisi Matematica 1 Secondo appello 11 febbraio 219 Testo A1 Consegnare solo questo foglio Prima parte: 2 punti per risposta corretta, 1 per ogni errore. Soglia minima 12/2. Seconda parte: Domande A e
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1
 Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 9 Gennaio 2018 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 9 Gennaio 2018 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Compito n. 1 (Gennaio 2013)
 Compito n. 1 (Gennaio 2013) PROBLEMA 1 Determinate le soluzioni (z, w), con z, w C, del sistema z + 2i zw z 6i = 0 z z 2w = 0. Ricavando dalla seconda equazione w = z z/2 e sostituendolo nella prima questa
Compito n. 1 (Gennaio 2013) PROBLEMA 1 Determinate le soluzioni (z, w), con z, w C, del sistema z + 2i zw z 6i = 0 z z 2w = 0. Ricavando dalla seconda equazione w = z z/2 e sostituendolo nella prima questa
Esercizi svolti. a 2 x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.
 Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;
![a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [; a) Il denominatore dev essere diverso da zero. Studiamo il trinomio x 2 5x + 6. Si ha: x 1,2 = 5 ± se x ], 2[ ]3, + [;](/thumbs/69/60588320.jpg) ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
ESERCIZIO - Data la funzione f (x) + x2 2x x 2 5x + 6, si chiede di: a) calcolare il dominio di f ; (2 punti) b) studiare la positività e le intersezioni con gli assi; (3 punti) c) stabilire se f ha asintoti
Esonero di Analisi Matematica I (A)
 Esonero di Analisi Matematica I A) Ingegneria Edile, 7 novembre 00 Michele Campiti) 1. Studiare il seguente ite: x π/ cos x 1 sin x) tan 3 x π ).. Calcolare le seguenti radici quarte: 3i 4 1 + i). Esonero
Esonero di Analisi Matematica I A) Ingegneria Edile, 7 novembre 00 Michele Campiti) 1. Studiare il seguente ite: x π/ cos x 1 sin x) tan 3 x π ).. Calcolare le seguenti radici quarte: 3i 4 1 + i). Esonero
Esame di Analisi Matematica Prova scritta del 9 giugno 2009
 Prova scritta del 9 giugno 2009 A1 Data la funzione f(x) = x2 3 e x, (f) determinare in base al grafico di f il numero delle soluzioni dell equazione f(x) = λ al variare di Calcolare un valore approssimato
Prova scritta del 9 giugno 2009 A1 Data la funzione f(x) = x2 3 e x, (f) determinare in base al grafico di f il numero delle soluzioni dell equazione f(x) = λ al variare di Calcolare un valore approssimato
Modulo di Matematica
 Università degli Studi di Udine Anno Accademico /3 Corso di Laurea in Biotecnologie Modulo di Matematica Esame del 9//3 N.B.: scrivere nome, cognome e numero di matricola su ogni foglio consegnato. Tempo
Università degli Studi di Udine Anno Accademico /3 Corso di Laurea in Biotecnologie Modulo di Matematica Esame del 9//3 N.B.: scrivere nome, cognome e numero di matricola su ogni foglio consegnato. Tempo
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005
 Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi I Ingegneria Chimica e Aerospaziale 1 o compitino
 1 o compitino 1 febbraio 215 1 Si consideri la funzione f : R R definita da { f) = 2 log se se = a) Si dimostri che f è continua e derivabile su tutto R b) Si dica se f ammette derivata seconda in ogni
1 o compitino 1 febbraio 215 1 Si consideri la funzione f : R R definita da { f) = 2 log se se = a) Si dimostri che f è continua e derivabile su tutto R b) Si dica se f ammette derivata seconda in ogni
Analisi Matematica 1 Soluzioni prova scritta n. 1
 Analisi Matematica Soluzioni prova scritta n Corso di laurea in Matematica, aa 008-009 5 giugno 009 Sia a n la successione definita per ricorrenza: a n+ 3 a n a 3 n, a 3 a n+ 3 a n a 3 n, a 3 a n+ 3 a
Analisi Matematica Soluzioni prova scritta n Corso di laurea in Matematica, aa 008-009 5 giugno 009 Sia a n la successione definita per ricorrenza: a n+ 3 a n a 3 n, a 3 a n+ 3 a n a 3 n, a 3 a n+ 3 a
Calcolo I - Corso di Laurea in Fisica - 18 Giugno 2019 Soluzioni Scritto. a) Calcolare il dominio, asintoti ed eventuali punti di non derivabilità;
 Calcolo I - Corso di Laurea in Fisica - 8 Giugno 209 Soluzioni Scritto Data la funzione fx = x 2 x 6 x /3 a Calcolare il dominio, asintoti ed eventuali punti di non derivabilità; b Calcolare, se esistono,
Calcolo I - Corso di Laurea in Fisica - 8 Giugno 209 Soluzioni Scritto Data la funzione fx = x 2 x 6 x /3 a Calcolare il dominio, asintoti ed eventuali punti di non derivabilità; b Calcolare, se esistono,
CORSO DI LAUREA IN INFORMATICA ANALISI MATEMATICA I MODULO, I E II MODULO, II MODULO. f 1 (x) = arctan(x2 7x + 12) x 2,
 CORSO DI LAUREA IN INFORMATICA ANALISI MATEMATICA I MODULO, I E II MODULO, II MODULO II PROVA SCRITTA DI GIUGNO 007: SOLUZIONI ESERCIZIO - Data la funzione f 1 (x) = arctan(x 7x + 1) x, 7x + 1 si chiede
CORSO DI LAUREA IN INFORMATICA ANALISI MATEMATICA I MODULO, I E II MODULO, II MODULO II PROVA SCRITTA DI GIUGNO 007: SOLUZIONI ESERCIZIO - Data la funzione f 1 (x) = arctan(x 7x + 1) x, 7x + 1 si chiede
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1
 Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 27 giugno 2017 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 27 giugno 2017 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
NOME:... MATRICOLA:... Corso di Laurea in Fisica, A.A. 2009/2010 Calcolo 1, Esame scritto del 19.01.2010
 NOME:... MATRICOLA:.... Corso di Laurea in Fisica, A.A. 009/00 Calcolo, Esame scritto del 9.0.00 Data la funzione fx = e /x x x +, a determinare il dominio massimale di f ; b trovare tutti gli asintoti
NOME:... MATRICOLA:.... Corso di Laurea in Fisica, A.A. 009/00 Calcolo, Esame scritto del 9.0.00 Data la funzione fx = e /x x x +, a determinare il dominio massimale di f ; b trovare tutti gli asintoti
Corsi di Laurea in Ingegneria Elettronica e Telecomunicazioni.
 Corsi di Laurea in Ingegneria Elettronica e Telecomunicazioni. Università di Pisa. Prima prova scritta di Analisi Matematica I. Soluzioni. Esercizio. Si consideri la successione c n ) n N definita dalla
Corsi di Laurea in Ingegneria Elettronica e Telecomunicazioni. Università di Pisa. Prima prova scritta di Analisi Matematica I. Soluzioni. Esercizio. Si consideri la successione c n ) n N definita dalla
Analisi Matematica 1 per IM - 11/02/2019. Tema 1 (parte di esercizi)
 Analisi Matematica per IM - /2/29 Cognome e Nome:....................................... Matricola:.................. Docente:.................. Tempo a disposizione: due ore. Il candidato, a meno che
Analisi Matematica per IM - /2/29 Cognome e Nome:....................................... Matricola:.................. Docente:.................. Tempo a disposizione: due ore. Il candidato, a meno che
Compitino di Analisi Matematica 1 Prima parte, Tema A Ingegneria Civile, Ambientale e Edile COGNOME: NOME: MATR.: RISPOSTE:
 Compitino di Analisi Matematica 1 Prima parte, Tema A Ingegneria Civile, Ambientale e Edile 20 maggio 2014 COGNOME: NOME: MATR.: RISPOSTE: A B C D E 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 X 9 X 10 X 1 Prima parte,
Compitino di Analisi Matematica 1 Prima parte, Tema A Ingegneria Civile, Ambientale e Edile 20 maggio 2014 COGNOME: NOME: MATR.: RISPOSTE: A B C D E 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 X 9 X 10 X 1 Prima parte,
APPELLO C AM1C 19 Gennaio f(x) = log( x + 2) x
 Esercizio 1. Sia data la funzione f(x) = log( x + 2) x (a )Determinarne: insieme di esistenza e di derivabilità, limiti ed eventuali asintoti, eventuali punti angolosi o di cuspide, eventuali massimi e
Esercizio 1. Sia data la funzione f(x) = log( x + 2) x (a )Determinarne: insieme di esistenza e di derivabilità, limiti ed eventuali asintoti, eventuali punti angolosi o di cuspide, eventuali massimi e
1) D0MINIO. Determinare il dominio della funzione f (x) = ln ( x 3 4x 2 3x). Deve essere x 3 4x 2 3x > 0. Ovviamente x 0.
 D0MINIO Determinare il dominio della funzione f ln 4 + Deve essere 4 + > 0 Ovviamente 0 Se > 0, 4 + 4 + quindi 0 < < > Se < 0, 4 + 4 4 e, ricordando che < 0, deve essere 4 < 0 dunque 7 < < 0 Il campo di
D0MINIO Determinare il dominio della funzione f ln 4 + Deve essere 4 + > 0 Ovviamente 0 Se > 0, 4 + 4 + quindi 0 < < > Se < 0, 4 + 4 4 e, ricordando che < 0, deve essere 4 < 0 dunque 7 < < 0 Il campo di
ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA
 ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA Prova scritta del 6 giugno 2004: soluzioni ESERCIZIO - Data la funzione f) 3 2 4 + 27 + 9 2 ) /3 4 + 27, + 9 si chiede
ANALISI MATEMATICA I MODULO, I e II MODULO, II MODULO CORSO DI LAUREA IN INFORMATICA Prova scritta del 6 giugno 2004: soluzioni ESERCIZIO - Data la funzione f) 3 2 4 + 27 + 9 2 ) /3 4 + 27, + 9 si chiede
Laurea triennale in Informatica - Corso B (M-Z) Prova scritta di Analisi Matematica Teoria
 13 giugno 2016 1. In base alla teoria studiata e giustificando la risposta, determinare (a) se la funzione f(x) = cos x è pari, dispari o nessuna delle due cose; x 5 (b) se la funzione g(x) = 2 x + x 3
13 giugno 2016 1. In base alla teoria studiata e giustificando la risposta, determinare (a) se la funzione f(x) = cos x è pari, dispari o nessuna delle due cose; x 5 (b) se la funzione g(x) = 2 x + x 3
NOME:... MATRICOLA:... Corso di Laurea in Fisica, A.A. 2008/2009 Calcolo 1, Esame scritto del f(x) = cos
 NOME:... MATRICOLA:.... Corso di Laurea in Fisica, A.A. 008/009 Calcolo, Esame scritto del 06.0.009 Consideriamo la funzione fx cos + x. a Determinare il dominio massimale di f. b Trovare tutti gli asintoti
NOME:... MATRICOLA:.... Corso di Laurea in Fisica, A.A. 008/009 Calcolo, Esame scritto del 06.0.009 Consideriamo la funzione fx cos + x. a Determinare il dominio massimale di f. b Trovare tutti gli asintoti
Modulo di Matematica
 Università degli Studi di Udine Anno Accademico 05/06 Corso di Laurea in Biotecnologie Modulo di Matematica Esame del 0/0/06 N.B.: scrivere nome, cognome e numero di matricola su ogni foglio consegnato.
Università degli Studi di Udine Anno Accademico 05/06 Corso di Laurea in Biotecnologie Modulo di Matematica Esame del 0/0/06 N.B.: scrivere nome, cognome e numero di matricola su ogni foglio consegnato.
ANALISI MATEMATICA 1 Commissione L. Caravenna, V. Casarino, S. Zoccante Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza
 ANALISI MATEMATICA Commissione L Caravenna, V Casarino, S Zoccante Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Nome, Cognome, numero di matricola: Vicenza, 7 Luglio 205 TEMA - parte B Esercizio
ANALISI MATEMATICA Commissione L Caravenna, V Casarino, S Zoccante Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Nome, Cognome, numero di matricola: Vicenza, 7 Luglio 205 TEMA - parte B Esercizio
1 Analisi mat. I - Esercizi del 13/10/99
 Analisi mat. I - Esercizi del //99 ES. Delle seguenti funzioni determinare: il dominio l immagine gli eventuali asintoti l insieme dove sono continue e quali siano estendibili per continuita. Determinare
Analisi mat. I - Esercizi del //99 ES. Delle seguenti funzioni determinare: il dominio l immagine gli eventuali asintoti l insieme dove sono continue e quali siano estendibili per continuita. Determinare
e 2x2 1 (x 2 + 2x 2) ln x
 Corso di laurea in Ingegneria delle Costruzioni A.A. 2016-17 Analisi Matematica - Esercitazione del 04-01-2017 Ripasso di alcuni argomenti in programma Gli esercizi sono divisi in più pagine, per separare
Corso di laurea in Ingegneria delle Costruzioni A.A. 2016-17 Analisi Matematica - Esercitazione del 04-01-2017 Ripasso di alcuni argomenti in programma Gli esercizi sono divisi in più pagine, per separare
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica I del c.
 Prova scritta di Analisi Matematica I del 22-5-2 - c. ) Provare che 3 3è irrazionale. 2) Provare che il grafico di f(x) =(x ) + 2 sin[(x ) ]:R \{} R ammette la retta di equazione x = come asintoto verticale.
Prova scritta di Analisi Matematica I del 22-5-2 - c. ) Provare che 3 3è irrazionale. 2) Provare che il grafico di f(x) =(x ) + 2 sin[(x ) ]:R \{} R ammette la retta di equazione x = come asintoto verticale.
Modulo di Matematica
 Università degli Studi di Udine nno ccademico 5/6 Corso di Laurea in Biotecnologie Modulo di Matematica Esame del 4/7/6 N.B.: scrivere nome, cognome e numero di matricola su ogni foglio consegnato. Tempo
Università degli Studi di Udine nno ccademico 5/6 Corso di Laurea in Biotecnologie Modulo di Matematica Esame del 4/7/6 N.B.: scrivere nome, cognome e numero di matricola su ogni foglio consegnato. Tempo
Università di Pisa - Corso di Laurea in Informatica Analisi Matematica A. Pisa, 12 giugno 2018 D) 73 60
 Università di Pisa - orso di Laurea in Informatica nalisi Matematica Pisa, giugno 08 Domanda + B e 3 D 6 e log lim x sin x x = x 0 + B Domanda La successione a n = n e n+ n e n non ha né massimo né minimo
Università di Pisa - orso di Laurea in Informatica nalisi Matematica Pisa, giugno 08 Domanda + B e 3 D 6 e log lim x sin x x = x 0 + B Domanda La successione a n = n e n+ n e n non ha né massimo né minimo
Pierpaolo Omari Maurizio Trombetta TEMI SVOLTI DI ANALISI MATEMATICA I
 Pierpaolo Omari Maurizio Trombetta TEMI SVOLTI DI ANALISI MATEMATICA I Trieste Udine giugno 005 Prefazione Questo volume raccoglie i temi assegnati alle prove d esame dei corsi di Analisi matematica I
Pierpaolo Omari Maurizio Trombetta TEMI SVOLTI DI ANALISI MATEMATICA I Trieste Udine giugno 005 Prefazione Questo volume raccoglie i temi assegnati alle prove d esame dei corsi di Analisi matematica I
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1
 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo. Tempo 0 minuti. Durante la prova non si può uscire dall aula. Non si possono consultare
Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo. Tempo 0 minuti. Durante la prova non si può uscire dall aula. Non si possono consultare
Seconda prova in itinere di Analisi Matematica 1 Ingegneria Elettronica. Politecnico di Milano. A.A. 2015/2016. Prof. M. Bramanti.
 Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 5/6. Prof. M. Bramanti Tema n 3 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Seconda prova in itinere di Analisi Matematica Ingegneria Elettronica. Politecnico di Milano Es. Punti A.A. 5/6. Prof. M. Bramanti Tema n 3 5 6 Tot. Cognome e nome (in stampatello) codice persona (o n
Argomento delle lezioni del corso di Analisi A.A
 Argomento delle lezioni del corso di Analisi A.A.2011-2012 30 gennaio 2012 Lezione 1-2 (5 ottobre 2011) Numeri naturali, interi, razionali. Definizione intuitiva dei reali attraverso la retta. Definizione
Argomento delle lezioni del corso di Analisi A.A.2011-2012 30 gennaio 2012 Lezione 1-2 (5 ottobre 2011) Numeri naturali, interi, razionali. Definizione intuitiva dei reali attraverso la retta. Definizione
MATEMATICA A Commissione Albertini, Mannucci, Motta, Zanella Ingegneria Gestionale, Meccanica, Meccatronica, Vicenza
 TEMA ( ) f() = log (determinare il dominio D; calcolare i limiti per che tende agli estremi finiti o infiniti z 4 + (3 + 6i)z + 5 + i = 0. ( + 3 ) α α (log + log + ) d. y = e y, y() = α. TEMA ( ) f() =
TEMA ( ) f() = log (determinare il dominio D; calcolare i limiti per che tende agli estremi finiti o infiniti z 4 + (3 + 6i)z + 5 + i = 0. ( + 3 ) α α (log + log + ) d. y = e y, y() = α. TEMA ( ) f() =
Facoltà di Scienze MM.FF.NN. Corso di Laurea in Matematica - A.A Prova scritta di Analisi Matematica II del c.1.
 Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Prova scritta di Analisi Matematica II del 14-07-1999 - c.1 1) Sia (d n ) una successione di numeri reali tali che inf d n > 0. Studiare il carattere della serie + n=1 al variare del parametro reale positivo
Prova in itinere di Matematica Pisa, 26 novembre 2005
 Università di Pisa - Corso di Laurea in Ingegneria Informatica Prova in itinere di Matematica Pisa, 26 novembre 25 Numero compito: 256 Tempo ora. Non si possono usare calcolatrici. Segnare le risposte
Università di Pisa - Corso di Laurea in Ingegneria Informatica Prova in itinere di Matematica Pisa, 26 novembre 25 Numero compito: 256 Tempo ora. Non si possono usare calcolatrici. Segnare le risposte
Esercizi di Analisi Matematica
 Università degli Studi di Udine Anno Accademico 00/ Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica e TWM Esercizi di Analisi Matematica Esercizi sul primo semestre del
Università degli Studi di Udine Anno Accademico 00/ Facoltà di Scienze Matematiche Fisiche e Naturali Corso di Laurea in Informatica e TWM Esercizi di Analisi Matematica Esercizi sul primo semestre del
Modulo di Matematica
 Università degli Studi di Udine Anno Accademico / Corso di Laurea in Biotecnologie Modulo di Matematica Esame del 9// N.B.: scrivere nome, cognome e numero di matricola su ogni foglio consegnato. Tempo
Università degli Studi di Udine Anno Accademico / Corso di Laurea in Biotecnologie Modulo di Matematica Esame del 9// N.B.: scrivere nome, cognome e numero di matricola su ogni foglio consegnato. Tempo
Corso di Laurea in Ingegneria Biomedica ed Elettronica Prima prova scritta di Analisi Matematica 1 del 18/12/2006
 Corso di Laurea in Ingegneria Biomedica ed Elettronica Prima prova scritta di Analisi Matematica del 8/2/26 () Fornire la definizione di derivata ed il suo significato geometrico. (2) Enunciare e dimostrare
Corso di Laurea in Ingegneria Biomedica ed Elettronica Prima prova scritta di Analisi Matematica del 8/2/26 () Fornire la definizione di derivata ed il suo significato geometrico. (2) Enunciare e dimostrare
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 2 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
Corso di Laurea in Ingegneria Biomedica ANALISI MATEMATICA 1. Prova scritta del 25 febbraio 2017 Fila 1.
 Corso di Laurea in Ingegneria Biomedica ANALISI MATEMATICA Prova scritta del 5 febbraio 07 Fila. Esporre il procedimento di risoluzione degli esercizi in maniera completa e leggibile.. (Punti 7) Posto
Corso di Laurea in Ingegneria Biomedica ANALISI MATEMATICA Prova scritta del 5 febbraio 07 Fila. Esporre il procedimento di risoluzione degli esercizi in maniera completa e leggibile.. (Punti 7) Posto
D Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica)
 COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. D Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
1) Studiare la natura dei seguenti integrali impropri: 2x2 1. x dx (c) e x + 1. log x. n n + 1 n (a) n=1. (b) n + log n n 2n 2 1.
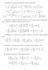 ) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
) Studiare la natura dei seguenti integrali impropri: 0 x 3 dx (b) + 2x2 2 x 2 + 2 dx (c) e x + 0 e x dx (g) (d) + 0 + 0 x( + x) dx x sin x x 2 dx (h) (e) 0 + log x x 2 dx (f) 2 log x dx x + log( + x 2
Analisi Matematica 1 - a.a. 2017/ Secondo appello
 Analisi Matematica - a.a. 27/28 - Secondo appello Soluzione del test Test A 2 3 4 5 6 7 8 9 D D A B C B A E D D Test B 2 3 4 5 6 7 8 9 B A C C B E D E A A Test C 2 3 4 5 6 7 8 9 A C B E E D C B B C Test
Analisi Matematica - a.a. 27/28 - Secondo appello Soluzione del test Test A 2 3 4 5 6 7 8 9 D D A B C B A E D D Test B 2 3 4 5 6 7 8 9 B A C C B E D E A A Test C 2 3 4 5 6 7 8 9 A C B E E D C B B C Test
Alcuni esercizi risolti da esami di anni passati
 Alcuni esercizi risolti da esami di anni passati Andrea Braides ( x. Calcolare, se esiste, il limite lim (x,y (, x + y log + y + x 3 y. x + y Dato che log( + s = s + o(s per s, abbiamo lim (x,y (, ( x
Alcuni esercizi risolti da esami di anni passati Andrea Braides ( x. Calcolare, se esiste, il limite lim (x,y (, x + y log + y + x 3 y. x + y Dato che log( + s = s + o(s per s, abbiamo lim (x,y (, ( x
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1
 Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 22 settembre 2017 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 22 settembre 2017 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
8.1. Esercizio. Determinare massimo e minimo delle seguenti funzioni nei corrispondenti intervalli: 2 x 4 x in [0, 1]; e x2 in [ 2, 2]
![8.1. Esercizio. Determinare massimo e minimo delle seguenti funzioni nei corrispondenti intervalli: 2 x 4 x in [0, 1]; e x2 in [ 2, 2] 8.1. Esercizio. Determinare massimo e minimo delle seguenti funzioni nei corrispondenti intervalli: 2 x 4 x in [0, 1]; e x2 in [ 2, 2]](/thumbs/91/107172861.jpg) ANALISI Soluzione esercizi 25 novembre 2011 8.1. Esercizio. Determinare massimo e minimo delle seguenti funzioni nei corrispondenti intervalli: 2 x 4 x in [0, 1]; e x2 in [ 2, 2] cos x cos x in [ 2π, 2π];
ANALISI Soluzione esercizi 25 novembre 2011 8.1. Esercizio. Determinare massimo e minimo delle seguenti funzioni nei corrispondenti intervalli: 2 x 4 x in [0, 1]; e x2 in [ 2, 2] cos x cos x in [ 2π, 2π];
Prova in itinere di Matematica Pisa, 26 novembre 2005
 Università di Pisa - Corso di Laurea in Ingegneria Informatica Prova in itinere di Matematica Pisa, 26 novembre 25 Numero compito: 256 Tempo ora. Non si possono usare calcolatrici. Segnare le risposte
Università di Pisa - Corso di Laurea in Ingegneria Informatica Prova in itinere di Matematica Pisa, 26 novembre 25 Numero compito: 256 Tempo ora. Non si possono usare calcolatrici. Segnare le risposte
1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: c) x + 1 d)x sin x.
 Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
Funzioni derivabili Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni: a)2x 5 b) x 3 x 4 c) x + 1 d)x sin x. 2) Scrivere l equazione della retta tangente
x + 1 2x], g(x) = x x + 2, h(x) = ln(x 1 2x 2 4x).
![x + 1 2x], g(x) = x x + 2, h(x) = ln(x 1 2x 2 4x). x + 1 2x], g(x) = x x + 2, h(x) = ln(x 1 2x 2 4x).](/thumbs/102/153351382.jpg) Funzioni Esercizio Siano f, g due funzioni definite da fx) = x x 2, gx) = ln x Trovare l insieme di definizione di f e g 2 Determinare le funzioni composte f g e g f, precisandone insieme di definizione
Funzioni Esercizio Siano f, g due funzioni definite da fx) = x x 2, gx) = ln x Trovare l insieme di definizione di f e g 2 Determinare le funzioni composte f g e g f, precisandone insieme di definizione
COGNOME... NOME... Matricola... Prof. Camporesi
 COGNOME... NOME... Matricola... Prof. Camporesi Esame di ANALISI MATEMATICA - 3 Febbraio 2010 A ESERCIZIO 1. (5 punti) 1. Verificare che z = 1 è una radice del polinomio P (z) = z 3 + ( 3 + 2i)z 2 + (2
COGNOME... NOME... Matricola... Prof. Camporesi Esame di ANALISI MATEMATICA - 3 Febbraio 2010 A ESERCIZIO 1. (5 punti) 1. Verificare che z = 1 è una radice del polinomio P (z) = z 3 + ( 3 + 2i)z 2 + (2
(ln 5)i 1 i. (c) (d) Scriviamo il numero complesso assegnato in forma algebrica:
 Primo parziale Test. L argomento principale del numero complesso (ln 5)i i è (a) 4 π (b) (c) (d) Scriviamo il numero complesso assegnato in forma algebrica: Risposta esatta a) ln 5 i i = ln 5 i( + i) i
Primo parziale Test. L argomento principale del numero complesso (ln 5)i i è (a) 4 π (b) (c) (d) Scriviamo il numero complesso assegnato in forma algebrica: Risposta esatta a) ln 5 i i = ln 5 i( + i) i
Prove d esame a.a , ,
 Prove d esame aa 4 5, 5 6, 6 7 Andrea Corli 6 gennaio 8 Sono qui raccolti i testi delle prove d esame assegnati negli aa 4 5, 5 6, 6 7, relativi al Corso di Analisi Matematica I (semestrale, crediti),
Prove d esame aa 4 5, 5 6, 6 7 Andrea Corli 6 gennaio 8 Sono qui raccolti i testi delle prove d esame assegnati negli aa 4 5, 5 6, 6 7, relativi al Corso di Analisi Matematica I (semestrale, crediti),
ANALISI MATEMATICA II-A. Prova scritta del 29/1/2010 TUTTE LE RISPOSTE DEVONO ESSERE MOTIVATE
 ANALISI MATEMATICA II-A CORSO DI LAUREA IN FISICA Prova scritta del 9//00 TUTTE LE RISPOSTE DEVONO ESSERE MOTIVATE Esercizio.(Punti 6) Calcolare il valore del seguente ite 0+ e cos. Esercizio.(Punti 6)
ANALISI MATEMATICA II-A CORSO DI LAUREA IN FISICA Prova scritta del 9//00 TUTTE LE RISPOSTE DEVONO ESSERE MOTIVATE Esercizio.(Punti 6) Calcolare il valore del seguente ite 0+ e cos. Esercizio.(Punti 6)
SCRITTO 02/07/18 - ANALISI MATEMATICA I
 SCRITTO 02/07/18 - ANALISI MATEMATICA I Esercizio 1. Determinare tutte le coppie z, w) C C tali che { zw = z 3 w 2 zw = 1 Soluzione: Dalla seconda equazione otteniamo che sia z che w non sono zero. Quindi
SCRITTO 02/07/18 - ANALISI MATEMATICA I Esercizio 1. Determinare tutte le coppie z, w) C C tali che { zw = z 3 w 2 zw = 1 Soluzione: Dalla seconda equazione otteniamo che sia z che w non sono zero. Quindi
Calcolo I - Corso di Laurea in Fisica - 19 Febbraio 2019 Soluzioni Scritto. a) Calcolare il dominio, asintoti ed eventuali punti di non derivabilità;
 Calcolo I - Corso di Laurea in Fisica - 9 Febbraio 209 Soluzioni Scritto ) Data la funzione fx) = arctanx + 4x 2 2 x + ) a) Calcolare il dominio, asintoti ed eventuali punti di non derivabilità; b) Calcolare,
Calcolo I - Corso di Laurea in Fisica - 9 Febbraio 209 Soluzioni Scritto ) Data la funzione fx) = arctanx + 4x 2 2 x + ) a) Calcolare il dominio, asintoti ed eventuali punti di non derivabilità; b) Calcolare,
A Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica)
 COGNOME NOME Matr. A Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. A Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
B Analisi Matematica 1 (Corso di Laurea in Informatica e Bioinformatica)
 COGNOME NOME Matr. B Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
COGNOME NOME Matr. B Firma dello studente Tempo: ore. Prima parte: test a risposta multipla. Una ed una sola delle 4 affermazioni è corretta. Indicatela con una croce. È consentita una sola correzione
PROVE SCRITTE DI ANALISI MATEMATICA I(N.O.), ANNO 2002/03
 PROVE SCRITTE DI ANALISI MATEMATICA I(N.O.), ANNO / Prova scritta del 6// Denotato con a il numero delle lettere del nome, si consideri la serie nx + cos nx a nx, per x IR, e si determini per quali valori
PROVE SCRITTE DI ANALISI MATEMATICA I(N.O.), ANNO / Prova scritta del 6// Denotato con a il numero delle lettere del nome, si consideri la serie nx + cos nx a nx, per x IR, e si determini per quali valori
1) D0MINIO FUNZIONE. Determinare il dominio della funzione f (x) = 4 x 2 4x + 3 x 2 6x + 8 Deve essere. x 2 6x + 5 (x 1) (x 5)
 ) DMINIO FUNZIONE Determinare il dominio della funzione f (x) = x x + x x + 8 x x + (x ) (x ) Deve essere = quindi x (, ] (, ] (, + ). x x + 8 (x ) (x ) Determinare il dominio della funzione f (x) = x
) DMINIO FUNZIONE Determinare il dominio della funzione f (x) = x x + x x + 8 x x + (x ) (x ) Deve essere = quindi x (, ] (, ] (, + ). x x + 8 (x ) (x ) Determinare il dominio della funzione f (x) = x
Elementi di analisi matematica
 Elementi di analisi matematica Prove in itinere dal 6 Prova in itinere del dicembre 6 Esercizio Si calcoli, se esiste, x ln( + sin x) sin x ln( + x). x + x sin x Esercizio Si descrivano le principali proprietà
Elementi di analisi matematica Prove in itinere dal 6 Prova in itinere del dicembre 6 Esercizio Si calcoli, se esiste, x ln( + sin x) sin x ln( + x). x + x sin x Esercizio Si descrivano le principali proprietà
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1
 Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 30 Gennaio 2018 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
Corso di Laurea in Ingegneria Informatica Prova di Analisi Matematica 1 30 Gennaio 2018 Scrivere subito nome e cognome e matricola sul foglio risposte e preparare il libretto sul banco per il controllo.
