Modelli dei Sistemi di Produzione Modelli e Algoritmi della Logistica
|
|
|
- Virginia Pozzi
- 8 anni fa
- Visualizzazioni
Transcript
1 Moe e Stem Prouzoe Moe e Agortm ea Logtca Job-Sop Sceug: appcazoe a cotroo e traffco ferrovaro CARLO MANNINO Sapeza Uvertà Roma partmeto Iformatca e Stemtca
2 Probem ceug I probem ob op ceug geerazzao quato vto f qua per cao ceug u macca goa S ao qu pù macce e pù ob ce evoo eere equezat Ne cao pù geerae, a equeza macce per u ato ob o è ata a pror e eve eere tabta (probema routg Veremo ua partcoare appcazoe e ob-op ceug a probem cotroo traffco ferrovaro.
3 Formuazoe tera mta I probema ob ceug può eere ecrtto forma gutva O eme ee operazo A eme e vco preceeza eme e vco preceeza gutv Probema Sceug m c(.t. v u uv uv A ( v u ( w z q ={(uv,(zw} u R u O I vco gutv pooo covogere 4 operazo tte e geerazzao que cac e probema ge mace.
4 Grafo gutvo geerazzato Grafo gutvo geerazzato G(V,A,: rappreetazoe probem ceug. Cotee o-operazoe V, arc preceeza oretat A e arc gutv geerazat. Arc gutv geerazzat:. Coppa arc oretat {(u,v,(w,z} rappreeta ua preceeza gutva geerazzata operazoe u vee effettuata prma e operazoe v oppure operazoe z vee effettuata prma e operazoe w E pobe aocare u peo ag arc gutv I cao caco a quao u = w, v = z,.e. ue operazo corrpoet a ob ver ce acceoo aa tea macca u v
5 Eempo grafo gutvo Sequezameto Itervet Crurgc. L terveto u u pazete compoe ue fa: a preparazoe, ce avvee ua taza aacete aa aa operatora, e terveto vero e propro. I mot opea, pazete uccevo o può comcare a preparazoe fcé preceete o a termato terveto. r A1 2 A t Pazete Preparazoe Iterveto (ob (Macca 1 (Macca 2 A 2 m 9 m B1 3 B2 12 B 3 m 12 m OBS: G cotee 1 arco gutvo = {{(A2,B1,(B2,A1}}
6 Cotroo Traffc e traffco Cotro ferrovaro I movmet e tre ee tazo ferrovare e metropotae oo acora cotroat ea maggor parte e ca a operator uma (patcer. I tre vegoo cotroat ag Operato Cotro Ceter I ettore e cotroo e traffco ferrovaro movmeta ver mar euro.
7 Itraameto mauae e tre Te Rea-Tme Pa I patcer tabcoo g traamet (route e tre ee tazo meate empc operazo: muoveo g camb cotroao o tato e emafor Output: Pao tempo reae Pao tempo Reae Routg: per og treo, vee tabto u route ea tazoe Sceug: per og treo tempo zo ee operazo a vogere ea tazoe, compree e occupazo e tratt baro La quatà e pao è vautata cofrotaoa co oraro uffcae.
8 Stazoe Stato Stazoe Ag a frequecy from F to every tramtter o a to U fratruttura ove tre pooo eegure ua ere operazo o ervz Operazo (ervz Sbarcare paegger Imbarcare paegger Aare a epoto Ivertre a rezoe Gare u or - Par
9 Rappreetare e tazo Te Stato Rea-Tme ayout Pa Rappreetazoe caca ea tazoe ferrovara P3 S3 Track Track egmet crcut Ex P2 S2 Stoppg pot E P1 Iterockg track I egmet bar ee tazo vegoo cafcat a ecoo ea fuzoe: put ota ove treo può fermar per effettuare quace ervzo. Nea rappreetazoe caca oo etfcat a cuett. Bar coegameto ce coettoo ue put ota. I tre o pooo otare u bar coegameto (vcoo o-wat Route ( u treo: equeza aterate put ota e bar coegameto
10 I grafo ea tazoe Te Stato Rea-Tme ayout Pa P3 S3 Track Track egmet crcut Ex P2 S2 Stoppg pot E P1 Iterockg track Grafo ea tazoe No = put ota Arc oretat = baro Ex coegameto fra ue put ota P3 P2 S3 S2 E P1 S1 Route = cammo oretato e grafo ea tazoe
11 Sceue e treo Sceug OSS. Sa o ce g arc e route oo rore ferrovare ce pooo eere occupate a u treo aa vota Sceug: tat cu treo accee a u arco o u oo e uo route. 8 1 m b a g e c f I probema equezare pù tre (co route fate ua tazoe ferrovara può eere moeato come probema obop ceug. ob-op ob macca operazoe movmetazoe e tre treo puto ota o baro coegameto u treo ce occupa u egmeto baro
12 Sceue e treo Sceug L occupazoe a parte e treo ua rora ferrovara (puto ota o baro coegameto corrpoe a u operazoe. Og operazoe corrpoe a u oo e grafo gutvo 8 1 m b a g e c f I route corrpooo a camm oretat e grafo gutvo 1 a 2 5 g 3 m 8 1 a 2 5 g 3 m 8 L arco (u,v u route corrpoe a fatto ce ce e operazo aocate a u treo evoo vogere ea equeza preorata. ( v u + uv u uv v
13 Sceue e treo Sceug 1 a 2 5 g 3 m 8 1 a 2 5 g 3 m 8 u I peo uv u arco (u,v pee ovvamete a tpo operazoe aocata a oo u. uv v Se u corrpoe a u puto ota, a eempo ua pattaforma per mbarcare e barcare paegger, aora uv eguaga tempo mmo rceto per effettuare operazoe barco/mbarco. Se u corrpoe vece a u baro coegameto e v qu puto ota uccevo, uv arà tempo percorreza e egmeto baro fo a v. I vcoo o-wat mpca ce v - u = Q v - u = Q { v - u Q v - u Q u - v -Q u Q -Q o wat v
14 uctve preceece cotrat I tre competoo per utzzo ee rore tazoe Coeramo eempo fgura. Vco Bockg Le rore occupate a u treo oo qu boccate per g atr tre Se u treo occupa puto ota 3, per motv curezza, eu treo può occupare baro g acceo a puto ota 3. Qu, e treo bu precee treo roo e oo 3, roo o può comcare operazoe (R,g roo occupa arco g prma ce treo bu abba comcato operazoe (B,m: 8 1 b a m g e c f Rg Bm
15 Vco Bockg uctve preceece cotrat I treo roo può preceere treo bu 3. I queto cao, eve vaere Bb Rm Vae qu vcoo gutvo: 8 1 b a m g e c f Rg Bm Bb Rm R5 Rg R3 Rm R8 5 g 3 m 8 g m b m Arco gutvo 1 b 3 m B1 Bb B3 Bm Grafo gutvo 8 B8
16 Coto Evauatg te ceug I coto eo ceue pee a rpetto e oraro teorco e( operazoe occupazoe oo ucta aa tazoe e treo e( oraro effettvo ucta e treo aa tazoe oraro ucta uffcae I coto eve peazzare rtaro rpetto a oraro prevto. I coto margae eve crecere a crecere e rtaro g( e( E(
17 I probema e cotroo e traffco Evauatg Te probem te ceug Probema e cotroo e traffco ferrovaro at Gve: I et grafo of etwork ea tazoe N = {(T 1, R 1,, (T, R } eme fag matrx e[a tre t ] t T, e a R oro pozoe correte frequecy coto oma rtarofg t, t R Trovare: reveue fucto u(c(p, f, = u(p, f, of te coverage u route per og treo (routg uo ceue mmzzao a omma e cot rtaro Rovamo queto probema co metoo e Brac&Bou Coeramo fato route og treo
18 Job-op ceug Sovg ob-op ceug I probema per route fat ruce a u probema ob-op ceug I probema è competamete efto a partre a coto g, a eme e vco preceeza A e a eme e vco gutv m g( e( N (, A Formuazoe gutva ( ( k k {(,,(, k} R U probema ob-op ceug è etfcato aa trpa (g, A,
19 m g( e( N ( R Job-op ceug: grafo gutvo Sovg ob-op ceug I probema cotee empre operazoe zo avoro A u probema (g,a, aocamo corrpoete grafo gutvo ( k k (, A {(,,(, k} A eme arc preceeza eme arc gutv Noo : operazoe zo avoro
20 Raameto eare Optma Poteta Probem OSS. Se è vuoto, probema ruce a u probema PL Ifatt a fuzoe coto è covea e eare a tratt. Può eere traformata ua fuzoe eare aggugeo per og egmeto ua varabe. I probema è reo compcato aa preeza e vco gutv. Per rovere probema obbamo qu fare quace moo vco gutv, ovvero cegere quae e ue vco ea coppa eve eere ofatto aa ouzoe ottma. ue mo: 1. Bracg. S geerao ue probem uo per og vcoo ea coppa 2. Fxg. Etoo cozo ce permettoo a pror cegere quae e ue vco vaa ofatto
21 Job-op ceug: formuazoe mta Sovg ob-op ceug Aocamo ua varabe bara x co og vcoo gutvo vcoo ={(,,(,k} x = x = 1 k k I probema gutvo vee rappreetato come probema eare mto: m g( e( N k R k Mx M(1 x (, A {(,,(, k} {(,,(, k} Roto co Brac&Bou: Raameto Leare Bracg ue varab bare
22 k k q N e R q x M q Mx m A A g } { (1 } { }, {(, ( ( m ( Sovg ob-op ceug Bracg,1 Sceg ua varabe x q corrpoete a vcoo q={(m,,(o,p} Crea ue probem, fao x q = e x q = 1 k k N e R k x M k Mx A g },,(, {( (1 },,(, {(, ( ( m ( k k m m N e R q x M q Mx A g } { (1 } {, ( ( m ( x q = q m m -Mx m m 1 ( q op o p x -M -M op o p roate
23 Sovg ob-op ceug Bracg,1 k k op o p N e R q x M q Mx A g } { (1 } {, ( ( m ( x q = 1 q m m -Mx M m m 1 ( q op o p x -M op o p roate k k q N e R q x M q Mx p o A A g } { (1 } { }, {(, ( ( m 1 ( OSS. I bracg geera ue uov probem ea tea atura e probema orgaro, (g, A q, q e (g, A q1, q1 I uov probem cotegoo eattamete u arco gutvo meo e u arco oretato pù
24 Bracg,1: grafo gutvo Brac eezoa u arco gutvo {(,, (,k} geera ue uov probem (g, A,, (g, A 1, 1 = 1 = - {(,, (,k} A = A {(,}, A 1 = A {(,k}
25 Raameto Sovg ob-op ceug I u ato oo B e abero bracg obbamo rovere u probema ob-op ceug e tpo (g, A B, B I raameto è otteuto raao vco terezza ue varab bare. I pratca queto equvae a rovere probema eza vco gutv. Raameto m g( e( N k R k Mx M(1 x (, A B B B 1 m g( e( N R (, A B
26 Ammbtà e probema ob-op ceug Sovg ob-op ceug I raameto e probema ob-op ceug è u probema PL co vco preceeza. A queto probema aocamo u grafo oretato (grafo e vco G(V,A co pe ug arc Og arco A peo è aocato a vcoo preceeza Sappamo ce probema raato ammette ouzoe e e oo e G o cotee cc oretat peo trettamete potvo. OSS: e raameto o ammette ouzoe, probema o raato o ammette ouzoe.
27 Fxg ato probema (g, A, k Brac e u arco gutvo = {(,, (,k} aocato a vcoo k k Se G(V, A {} cotee u cco oretato potvo, vcoo o può eere ofatto k Pocé ameo uo e ue vco ea guzoe eve eere ofatto, og ouzoe eve ofare ecoo vcoo Qu vcoo gutvo può eere rmoo a probema e vcoo k k è agguto a vco preceeza A.
28 Agortmo Fxg Te agortm Fxg arc gutv Iput: Grafo gutvo peato G(V,A,. Repeat (fcè effettua quace fxg Per og arco = {(,, (,k} If G(V, A {} cotee u cco oretato potvo po = {}. A = A {k} Ee If G(V, A {k} cotee u cco oretato potvo po = {}. A = A {} ERepeat
29 Eempo agortmo Fxg Te agortm Se aggugo arco (5,1 grafo cotee cco potvo C= {, (,4, 4, (4,5, 5, (5,1, 1, (1,,} Rmuovo arco gutvo e aggugo arco (2,4
30 Eempo agortmo Fxg Te agortm Se aeo aggugo arco (6,2 grafo cotee cco potvo C= {2, (2,4, 4, (4,5, 5, (5,6, 6, (6,2,2} Rmuovo arco gutvo e aggugo arco (3,5
Statica del corpo rigido: esercizi svolti dai compitini degli anni precedenti
Statica de corpo riido: eercizi voti dai compitini dei anni precedenti II COMPITIO 00 003 Un ae di eno orizzontae omoenea, di maa M0 k e unhezza L m, è appoiata u due cavaetti. L ae pore di 60 cm otre
Ammortamento americano. Ammortamento americano
mmortameto amercao La cora lezoe abbamo vto che ell'ammortameto amercao l rmboro del debto zale avvee medate u uco verameto a cadeza, otteuto attravero ua operazoe d cottuzoe d u captale al tao attvo j;
PROVINCIA DI VERONA RENDICONTO ESERCIZIO 2012 ELENCO DEI RESIDUI ATTIVI E PASSIVI DISTINTI PER ANNO DI PROVENIENZA
PROVINCIA DI VERONA RENDICONTO ESERCIZIO 2012 ELENCO DEI RESIDUI ATTIVI E PASSIVI DISTINTI PER ANNO DI PROVENIENZA 1 2 RIEPILOGO GENERALE RESIDUI ATTIVI CONSERVATI 3 4 Pgm. CPA0099R ***-----------------------------------------------------------***
Lezione 9. Congruenze lineari. Teorema Cinese del Resto.
Lezoe 9 Prerequt: Lezoe 8. Cogrueze lear. Teorema Cee el Reto. Nella Lezoe 8 abbamo vto che a caua ella compatbltà ella cogrueza moulo rpetto alle operazo artmetche le relazo cogrueza moulo pooo eere ottopote
Modelli di Schedulazione
EW Modell d Schedulazoe Idce Maccha Sgola Tepo d Copletaeto Totale Tepo d Copletaeto Totale Pesato Tepo d Rtardo Totale Maespa co set-up dpedete dalla sequeza Tepo d Copletaeto Totale co vcolo d precedeza
Dimostrazione della Formula per la determinazione del numero di divisori-test di primalità, di Giorgio Lamberti
Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
i i i: i I i i!i!, i i i
S I D RA D red g i n g, M a r i n e & E n v i ro n m e n ta l C o n t ra ct o r i i i: i I i i!i!, i i i P ro g ett a e d e s e g u e d a p i ù d i 3 0 a n n i o p e re m a r i tt i m e i n I t a l i a
ERRATA CORRIGE. L intero contenuto del paragrafo 9.2.3 a pagina 47-48 del Capitolato tecnico Determinazione del Canone è sostituito come segue:
Procedura aperta per l affdameto de servz tegrat, gestoal, operatv e d mautezoe multservzo tecologco da esegurs presso gl mmobl d propretà o uso alle Asl ed alle azede ospedalere della regoe Campaa ERRATA
FREQUENZE DI DECESSO PER TAVOLE SELEZIONATE. Un modello di sopravvivenza selezionato è definito mediante una famiglia di funzioni di sopravvivenza
Feueze eceo pe tavole elezoate FREQUENZE DI DEESSO PER TAVOLE SELEZIONATE U moello opavvveza elezoato è efto meate ua famgla fuzo opavvveza t S ; t 0 a, a, K ove è l età tea geo acuazoe t è l atuata ell
E P E R LA R E D A Z I O N E D E L P E P ( P i a n o d i e m e rg e n z a
AU TOR ITÀ PORT UA L E A P P A LTO P E R L ' A F F I DA M E N TO D E L LA R EV I S I O N E D E L R I S P ( R a p p o r t o i n t e g r a t o d i s i c u re z z a p o r t u a l e ) E P E R LA R E D A Z
AUTORITÀ PORT UA L E D I VEN E Z I A
AUTORITÀ PORTUALE D I EN E Z l A A P PA LTO D E I LAO R I P E R LA COST R U Z I O N E D E L LA DA R S E N A N O R D E D E L M A R G I N AM E N TO S U D - T E R M I N A L A U TOST RA D E D E L MAR E E P
Schemi a blocchi. Sistema in serie
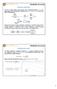Scem a blocc Nel caso ssem semplc, ques possoo essere scemazza meae blocc, ce rappreseao vers compoe, collega ra loro sere o parallelo a secoa ella logca uzoameo. Vl Valvolal solvee Sesore Pompa Pompa
AF 1 RITIRATO 26,1 26 2A AL 1 18,2 RITIRATO 25,7 26 3A AL 1 30,2 30 2A AL 0 RITIRATO 23,7 24 5A
1 10538950 AB 1 18 22,1 22 2A 2 10425074 AB 0 3 10561116 AB 0 RITIRATO 4 10498984 AC 0 5 10574752 AF 1 RITIRATO 26,1 26 2A 6 10568818 AL 1 7 10503657 AL 1 18,2 RITIRATO 25,7 26 3A 8 10521184 AL 0 9 10539026
Algoritmi e Strutture Dati. Alberi Binari di Ricerca
Algortm e Strutture Dat Alber Bar d Rcerca Alber bar d rcerca Motvazo gestoe e rcerche grosse quattà d dat lste, array e alber o soo adeguat perché effcet tempo O) o spazo Esemp: Matemeto d archv DataBase)
œ œ Œ œ œ œ œ Œ œ œ œ œ œ œ œ œ œ œ œ œ œ Œ œ J œ œ Œ œ Œ œ w
c Lirido The irth of Flora From La Flora: Act sc 9-10 Marco da Gagliao - colgio - co - do, o stu-po - re, o va-ghez - za. Ec - cogem - ma -to_il suol, fio - c [6] [6] j ri - to_il mo - do. Ve - i -te_aschie
L L E : : 1 982, , T E
C H A M PAG N E L a sto r i a d e l l a M a i s o n e d e i s u o i v i n i r i s a l e a b e n p r i m a d e l 1 8 2 7, data d e l l a s ua f o n da z i o n e u f f i c i a l e. L e r a d i c i d e l
CALENDARIO DELLE LEZIONI DEL CORSO DI QUALIFICAZIONE PROFESSIONALE PER SOMMELIER
Il 3 livello del corso si svolgerà dal 10 Ottobre 2018 al 29 Gennaio 2019 alle 20,45 presso nh hotel a Palermo, un fantastico approfondimento sulla tecnica di abbinamento cibo-vino che porterà all'esame
1.1 Identificazione del campo di operatività di un motore AC brushless. Sia dato un motore AC brushless isotropo di cui siano noti i seguenti dati:
Captolo 1 1.1 Ientfcazone el campo operatvtà un motore AC bruhle Sa ato un motore AC bruhle otropo cu ano not eguent at: Vn = 190 V In = 3.5 A Tn =.6 N n pol = R = 1 Ω L = 8 mh Ke = Kt = 0.4 S etermn l
A.A. 2016/17 Graduatoria corso di laurea magistrale a ciclo unico in Giurisprudenza
1 12/03/1997 I.M. 33,03 Idoneo ammesso/a 2 11/06/1997 B.F. 33,01 Idoneo ammesso/a 3 02/02/1998 T.A. 32,75 Idoneo ammesso/a 4 09/04/1997 B.M. 32,75 Idoneo ammesso/a 5 05/03/1998 M.S. 32,74 Idoneo ammesso/a
1 Laser Doppler Velocimetry
Laer oppler Velocmetry 1 Laer oppler Velocmetry 1.1 Introduzone L anemometra laer (LV) è applcata nel campo dell aerodnamca permentale a partre da prm ann ettanta, ann n cu le apparecchature laer dvennero
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
Elementi di Matematica Finanziaria. Rendite e ammortamenti. Università Parthenope 1
Elemet d Matematca Fazara Redte e ammortamet Uverstà Partheope 1 S chama redta ua successoe d captal da rscuotere (o da pagare) a scadeze determate S chamao rate della redta sgol captal da rscuotere (o
Leasing: aspetti finanziari e valutazione dei costi
Leasg: aspett fazar e valutazoe de cost Descrzoe Il leasg è u cotratto medate l quale ua parte (locatore), cede ad u altro soggetto (locataro), per u perodo d tempo prefssato, uo o pù be, sao ess mobl
Capitolo 3 CARATTERIZZAZIONE MECCANICA DELLE FIBRE
Capitoo 3 CARATTERIZZAZIONE MECCANICA DELLE FIBRE 3.1 LA TEORIA DI WEIBULL I comportameto meccaico dee fibre di giestra e di juta è stato caratterizzato mediate o studio dea resisteza a trazioe dee fibre
Ministero dell'istruzione dell'università e della ricerca Dipartimento per l istruzione Direzione generale per il personale scolastico Ufficio V
ALLEGATO "1" - a nota prot. n 8887 del 23/11/2012 Personale ATA - Stima cessazioni beneficiari triennio aa.ss. 13/14-14/15-1^ posizione economica (seq. contr.le 25/07/08) Abruzzo AQ AA 15 AT 7 CS 52 AQ
Piano della Performance Piano della Performance
P Pf 2019-2021 Av b Gu. 16 4 fbb 2019 1 1. P P INDICE 2. S f g kh 3. Ià u 4. A 4.1 S 4.1.1 Nv 4.1.2 Iu 4.1.3 I 4.2 S 4.2.1 L u 4.2.2 L f 5. L b f v b (BSC) bv g, v, g, vu 6. I g Ag : L b f 2 1. P P I P
In questo capitolo vedremo solamente un caso di rendita, che useremo poi per generalizzare le rendite e dedurre tutti gli altri casi.
7. Redte I questo captolo edremo solamete u caso d redta, che useremo po per geeralzzare le redte e dedurre tutt gl altr cas. S defsce redta ua successoe d captal (rate) tutte da pagare, o tutte da rscuotere,
Liste di specie e misure di diversità
Lte d pece e mure d dvertà Carattertche delle lte d pece I dat ono par, coè hanno molt valor null (a volte la maggoranza!) La gran parte delle pece preent è rara. I fattor ambental che nfluenzano la dtrbuzone
Modelli di Flusso e Applicazioni: Andrea Scozzari. a.a. 2013-2014
Modell d Flusso e Applcazo: Adrea Scozzar a.a. 203-204 2 Il modello d Flusso d Costo Mmo: Problem d Flusso A u l V b c P S A ), ( m ) ( ) ( ), ( Problem rcoducbl a problem d Flusso Il problema del trasporto
Forma Locale Vuoto. rote. rot Eo Eo. V y. V z. E x. E y. Fisica III 1. Forma locale della legge di Gauss. Forma locale della legge di Gauss.
F gg Gu. F u F gg Gu.,,,, g. (,, g w, à gu :., u.,,,, F. : Gé qu è g u g u bb : u è à è. U. g g. U U U u g. b u à g g u u. u. U u è u gg qu b u u. u u u u è qu u. u u., g, u è u., gg Gu, à è u u. qu u
A.A. 2015/2016 Graduatoria ammessi al corso di laurea in Scienze e Tecniche di Psicologia Cognitiva sessione estiva
1 S.A. 08/07/1996 30,00 46,40 76,40 Idoneo ammesso (*) 2 F.N. 19/07/1996 26,25 45,53 71,78 Idoneo ammesso 3 M.F. 24/05/1982 27,75 43,79 71,54 Idoneo ammesso 4 P.E.M 29/08/1989 21,00 49,01 70,01 Idoneo
Design of experiments (DOE) e Analisi statistica
Desg of epermets (DOE) e Aals statstca L utlzzo fodametale della metodologa Desg of Epermets è approfodre la coosceza del sstema esame Determare le varabl pù sgfcatve; Determare l campo d varazoe delle
18 Luglio 2002 recupero seconda prova
8 Luo recupero econda prova Eerczo ATTENZIONE: errore d tampa ne teto: a f.d.t. G ( ) deve avere un oo zero, qund non è + + 7 3 3 G () = 7 3, ma G () 7 3 = (*) o G () = (**) + + + + + + 3 3 3 (entrambe
MATEMATICA FINANZIARIA 3. RENDITE
MATEMATICA FINANZIAIA Prof. Adre Berrd 999 3. ENDITE Coro d Mtetc Fzr 999 d Adre Berrd Sezoe 3 ENDITA Operzoe fzr copot, crtterzzt d cdeze (,,...,,...,, rcuotere quelle cdeze,,...,,...,, t e d port d pgre
AU TO R I TÀ PORT UA L E D I V E N E Z I A
AUTORITÀ PORT UA LE D I VEN E Z IA A P PA LTO D E I LAVO R I P E R LA CO ST R U Z I O N E D E L LA DA R S E N A N O R D E D E L M A R G I N AM E N TO S U D T E R M I N A L A U TO ST RA D E D E L MA R E
Risultati simulazione test di accesso per l ammissione ai corsi di Laurea Triennale in Ingegneria
per Area del Sapere I 80262EG 50,50 8,75 3,75 18,75 15,50 3,75 80275LM 39,75 8,50 6,25 1 1 4,00 83803RF 34,25 8,00 13,25 9,50 3,50 82832VA 30,25 80264LN 25,75 80259ZA 25,00 9,25 7,75 1 3,25 8,50 1 5,25
PRIORITA' 1 - Nuclei familiari ammessi al beneficio REI alla data di scadenza degli Avvisi Comunali
Allegato 1 COMUNE DI OZIERI SETTORE POLITICHE SOCIALI E DI INTEGRAZIONE TERRITORIALE Servizio Amministrativo PROT. DEL ELENCO UTENTI AMMESSI - GRADUATORIA PROVVISORIA APPROVATA CON D.D. N 470 DEL 01-10-2018
Regime di capitalizzazione composta
Regme d capalzzazoe composa Se s deposa baca, all zo dell ao, ua somma d 000 ad u asso auale uaro =0,05 oppure r=5%, dopo ao ale somma frua u eresse par a I = = 000 0,05 = 50 che aggugedos al capale zale
La potenza assorbita dalla pompa per sollevare il liquido dal serbatoio a valle al serbatoio a monte si calcola con la relazione
1 E S E R C I Z I S U L L E P O M P E C E N T R I F U G E ESERCIZIO 1 In un panto ollevaento per acqua ono not Il lvello geoetco tra ue erbato g 0 La preone aoluta ul erbatoo a valle p A p at La preone
VITA DA PENSIONATO DEL LEGIONARIO TULLIUS STRABAUZIOR
VITA DA PENSIONATO DEL LEGIONARIO TULLIUS STRABAUZIOR I L L E G I O N A R I O T U L L I U S S T R A B A U Z I O R D O P O AV E R P R E S TAT O S E R V I Z I O N E L L E S E R C I T O R O M A N O P E R
Trasformazioni Elementari 2D
Traformazioni Elementari 2D Le traformazioni affini ono operazioni di ROTAZIONE, TRASLAZIONE e SCALATURA che permettono di modificare l oggetto 2D o 3D. Una traformazione è definita da una matrice T. Applicare
REGIONE CODICE PROVINCIA MESE PRESENTAZIONE NUMERO DOMANDE ACCOLTE
REGIONE CODICE PROVINCIA MESE PRESENTAZIONE NUMERO DOMANDE ACCOLTE ABRUZZO AQ mar-19 3.190 ABRUZZO AQ apr-19 608 ABRUZZO AQ mag-19 0 ABRUZZO CH mar-19 3.441 ABRUZZO CH apr-19 672 ABRUZZO CH mag-19 0 ABRUZZO
L E C A S S E T T E G E N E R A L B OX, C O N T I N U A N D O N E L L A L O R O
L A M I G L I O R E P R O D U Z I O N E E U R O P E A C A R O C L I E N T E S E I I L B E N V E N U T O I N G E N E R A L B OX, T I R I N G R A Z I A M O P E R L I N T E R E S S A M E N T O A I N O S T
1. LA TRAVE CONTINUA E L EQUAZIONE DEI TRE MOMENTI
. L TRVE ONTINU E L EQUZIONE DEI TRE OENTI Sistemi Piai i Travi Neo sazio ua trave ha 6 grai i ibertà (g...): rotazioi e trasazioi. Ne iao, ivece, i grai si riucoo a co rotazioe e 2 trasazioi. z z z w
Note su alcuni principi fondamentali di macroeconomia Versione parziale e provvisoria. Claudio Sardoni Sapienza Università di Roma
Note u alcuni principi fondamentali di macroeconomia Verione parziale e provvioria Claudio Sardoni Sapienza Univerità di Roma Anno accademico 2010-2011 ii Indice Premea v I Il breve periodo 1 1 Il fluo
A.A. 2015/2016 Scorrimento graduatoria ammessi al corso di laurea in Scienze e Tecniche di Psicologia Cognitiva sessione estiva
A.A. 2015/2016 Scorrimento graduatoria ammessi al corso di laurea in Scienze e Tecniche di Psicologia Cognitiva sessione estiva I candidati idonei ammessi in graduatoria dovranno completare la procedura
Rappresentatione di anima, et di corpo. j œ œ. œ œ œ œ œ. œ œ.
ATTO I - Sa Prima 1. Il Tmpo Il tm - po, il tm - po fug - g, la vi - ta si di - strug - Rapprstatio di aima, t di orpo Nuovamt posta i Musia dal Sig. Emilio dl Cavallir, pr ritar Catado. Data i lu da Allssadro
Gruppo di lavoro per i B.E.S. D.D. 3 Circolo Sanremo. Autore: Marino Isabella P roposta di lavoro per le attività nei laboratori di recupero
Competenza/e da sviluppare GIOCO: SCARABEO CON SILLABE OCCORRENTE: MATERIALE ALLEGATO E UN SACCHETTO PER CONTENERE LE SILLABE RITAGLIATE. ISTRUZIONI Saper cogliere/usare i suoni della lingua. Saper leggere
1. Il principio di non arbitraggio e prime applicazioni
. Il rco o arbtraggo e rme alcazo. Itrouzoe. Il rco o arbtraggo è l rco u cu baao qua tutt moell valutazoe Faza Matematca. Oortutà arbtraggo è la obltà realzzare u guaago certo eza alcu mego fo. L'ea equlbro
La classe che mostra la distribuzione più elevata è quella 60-90, che corrisponde a un uso elevato dell automobile. f i fr (= f i/n) fr% (=fr*100)
ESERCIZIO Il Moblty Maager d u azeda ha rlevato l umero d chlometr percors settmaalmete da 60 mpegat. I dat soo rportat ello schema successvo. 67 4 93 58 66 87 5 53 86 8 7 47 56 70 54 86 48 43 60 58 5
Modello dinamico nello spazio dei giunti: relazione tra le coppie di attuazione ai giunti ed il moto della struttura
Damca Modello damco ello spazo de gut: relazoe tra le coppe d attuazoe a gut ed l moto della struttura smulazoe del moto aals e progettazoe delle traettore progettazoe del sstema d cotrollo progetto de
Modulo n.3 - I materiali nelle lavorazioni metalliche
oduo n. - I maeriai nee avorazioni meaiche PROPRIETÀ ISIHE, EANIHE, TENOOGIHE (Diiazione vericae) OBIETTIVI: A) onocenza dee proprieà dei maeriai finaizzaa a oro uiizzo; B) apacià di eeguire cacoi ue principai
Lezione 14. Polinomi a coefficienti interi
Peequt: Nume m Lezo - Lezoe 4 Polom a coeffcet te I queta lezoe tudamo le fattozzazo d olom a coeffcet azoal Cacuo d quet uò eee tafomato u olomo a coeffcet te tamte la moltlcazoe e u umeo teo o ullo Qud
DI IDROLOGIA TECNICA PARTE II
FACOLTA DI INGEGNERIA Laurea Specalstca Igegera Cvle NO Guseppe T Aroca CORSO DI IDROLOGIA TECNICA PARTE II Aals e prevsoe statstca delle varabl drologche Lezoe X: Scelta d u modello probablstco Aals e
Capitolo. Il comportamento dei sistemi in regime transitorio. 5.8 Esercizi - Risposta al gradino dei sistemi del 2 ordine reazionati e non reazionati
Capitolo 5 Il comportameto dei itemi i regime traitorio 5.1 Geeralità ulla ripota dei itemi el domiio del tempo 5. Ripota al gradio di u itema del primo ordie. 5.3 Eercizi - Ripota al gradio dei itemi
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 18 marzo 2015 Apput d ddattca della Matematca fazara Redte, costtuzoe d
Risultati simulazione test di accesso per l ammissione al corso di Laurea in Professioni Sanitarie
81032GV 42,00 80207OG 39,75 82663RA 39,25 81026IF 38,75 80173GN 38,50 82400LS 38,50 83014FG 38,50 82402TR 38,25 81024CF 37,75 80329DG 37,50 82335GA 37,50 83099LG 37,50 82462GM 37,50 80360BS 37,25 82626DP
MODELLI DI SCELTA DEL PERCORSO PER RETI DI TRASPORTO COLLETTIVO
IPARTIMENTO INENERIA CIVILE UNIVERSITÀ I ROMA TOR VERATA coo di Pianificazione dei tapoti 2 MOELLI I SCELTA EL PERCORSO PER RETI I TRASPORTO COLLETTIVO 1 CLASSIFICAZIONE EI COMPORTAMENTI I SCELTA celta
SCHEDA PROGETTO PER L IMPIEGO DI VOLONTARI IN SERVIZIO CIVILE IN ITALIA
SCHEDA PROGETTO PER L IMPIEGO DI VOLONTARI IN SERVIZIO CIVILE IN ITALIA ENTE 1) E g: L ASSOCIAZIONE IL SENTIERO f u gg gg f g g b f h,, u ( g),, g gu : ) u gg; b) u g ; ) uu, uu u à f ; ) u ugug, gà u
TUTELA LA TUA PASSIONE TUTELA DELLA BICICLETTA
TUTELA LA TUA PASSIONE TUTELA DELLA BICICLETTA Siamo fermamente convinti che redigere un preciso quadro di riferimento, attestante le coperture Assicurative di un Cliente, consenta allo stesso di potersi
Strumenti della Teoria dei Giochi per l Informatica A.A. 2009/10. Lecture 11: 13-14 Maggio 2010. Meccanismi per la Condivisione dei Costi
Strumenti della Teoria dei Giochi per l Informatica A.A. 2009/0 Lecture : 3-4 Maggio 200 Meccanimi per la Condiviione dei Coti Docente Paolo Penna Note redatte da: Paolo Penna Primo Eempio Vogliamo vendere
Lezione 9. Moduli finitamente generati.
Lezoe 9 Moul faee geera. Rchaao prelaree u porae eucao ell algebra leare. Propozoe 9. Sa K u capo e a C c )... a) la arce C è verble e e olo e e C 0 ; b) l ea leare oogeeo ua arce a coeffce K. Allora c
gestion e ripresen tate nuovo Regola mento IPT tutela venditor e nuovo Regola mento IPT succes sione ereditar ia agevol azioni disabil i
Provincia % maggiora zione tasso interesse modico valore 2688 cc.nuo vo tutela venditor e nuovo gestion e ripresen tate nuovo agevol azioni disabil i succes sione ereditar ia atti societ ari veicoli ecocompati
IL MERCATO DELLA R.C. AUTO IN ITALIA: ANDAMENTI, CRITICITÀ E CONFRONTI EUROPEI
IL MERCATO DELLA R.C. AUTO IN ITALIA: ANDAMENTI, CRITICITÀ E CONFRONTI EUROPEI Dario Focarelli Direttore Generale ANIA Milano, 12 marzo 2013 «LA RESPONSABILITÀ CIVILE AUTOMOBILISTICA STRATEGIA, INNOVAZIONE
Servizi di architettura e ingegneria
3 ervizi di architettura e ingegneria ATA 26/04/2018 AR AR (ATAR RGTTAZ) lassi di iscrizione nviti Ricevuti /Risposte ARTTA VA 01205920117 AG RRT lassi di iscrizione nviti Ricevuti /Risposte ARTTA VA 01331520476
COMUNE DI VILLACIDRO
COMUNE DI VILLACIDRO Provincia del Sud Sardegna Servizio Affari Generali Ufficio Pubblica Istruzione Borsa di studio nazionale ex D. Lgs. 63/2017 A.S. 2018/2019 Graduatoria definitiva N. Protocollo Istante
CITTÀ DI IMOLA MEDAGLIA D'ORO AL VALOR MILITARE PER ATTIVITA' PARTIGIANA
Inf.Com. Campanella 1 T.L. Domanda/ricev.N.21171 19/01/2015 Fratelli e Stradario - 65 2 S.A. Domanda/ricev.N.21208 21/06/2015 Fratelli e Stradario - 65 3 R.E. Domanda/ricev.N.21009 17/07/2015 Fratelli
PRIMARIA: TRASFERIMENTI INTERPROVINCIALI
AG AN - COMUNE 8 8 109 EH - SOST. MINORATI PSICOFISICI 2 2 192 IL - LINGUA INGLESE 1 1 201,5 ZJ - CORSI DI ISTR. PER ADULTI 1 1 115 AL AN - COMUNE 3 27 EH - SOST. MINORATI PSICOFISICI 1 89 AN AN - COMUNE
B. rolly B. amazed B. bouncy B. inspired B. you
. B. y B. z B. uy B. p B. yu p v v f p h uv p p. U u p S gpp qu h u v h Buggy Wuggy U h v Lugh v, g. E p u zz U p p v p p h z p. RODEO ROCKER Bj 18 + BX1512Z (TL) 0 62243 31981 3 / 1 pzz GOCATTOLO E 50.80
MEDIAZIONE CIVILE EX D.L. 28/2010
MEDIAZIONE CIVILE E D.L. 28/2010 STATISTICHE RELATIVE AL PERIODO 1 GENNAIO 30 SETTEMBRE 2016 Mto a Gtza Datto a Ogazzazo Gzaa, Poa Sz Dzo Ga Statta Aa Ogazzata 2. - 5 8 26 F. -? > ; 2 5 4 F * ( )! ( &!
Formula Bonus-Malus "l'abito non fa (più) il monaco"
Formula Bonus-Malus "l'abito non fa (più) il monaco" Limiti e criticità dell'attuale formula Giovanni Sammartini Coordinatore Commissione Danni Roma, 7 giugno 2013 2000-2011: com'è cambiata la distribuzione
PROSPETTO DEI DATI SINTETICI RISULTANTI AL SISTEMA ALLA DATA DI EFFETTUAZIONE D C: TRASFERIMEN TI PROVINCIALI A: TRASFERIMENT LITA' IN ENTRATA DA
PROSPETTO DEI DATI SINTETICI RISULTANTI AL SISTEMA ALLA DATA DI EFFETTUAZIONE D SCUOLA PRIMARIA ANNO SCOLASTICO DI RIFERIMENTO : 2017/18 PROVINCIA TIPO POSTO B: A: TRASFERIMENT DISPONIBI I PROVINCIALI
08/04/2002 Lucidi-Spettroscopia Ottica, Ettore Vittone
La uce etate ua ba ottca è tasessa ao spettoeto dove u po spetto seco ocazza a uce su u etcoo d dazoe. La uce datta cde qud su u secodo speccho seco. Lo spetto è qud poettato su ua atce eae d CCD ed dat
GUIDA PER L ISTAL LAZ IONE E L A M E SSA IN FUNZIONE DEL SENSORE DI TE MPE R ATURA ESTERNA SU FIAT PANDA 2 SERI E
GUIDA PER L ISTAL LAZ IONE E L A M E SSA IN FUNZIONE DEL SENSORE DI TE MPE R ATURA ESTERNA SU FIAT PANDA 2 SERI E 2004-2011 P re m e tt o c h e l a se g ue n te g u i d a è stata c reata esp l i c i ta
assunta con i po ten' delconslgi 'o Comunale n. 69 del 2 0. 03. 2 01 1
C O M U N E D I C H I O G G IA REGOLAMENTO PER L "APPLICAZIONE DELLA TAR FA DI IGL NE AMB1-ENTALE Approvato con deli'bera delcommissario STR IORDINARIO assunta con i po ten' delconslgi 'o Comunale n. 69
Ariette dolenti. Nessuno più ricorda (testo di Davide Anzaghi da un racconto udito dagli anziani e raccolto nella pianura lombarda)
Aiette doleti Nessuo più icoda (testo di Davide Azaghi da u accoto udito dagli aziai e accolto ella piaua lomada) Nessuo più icoda tata eve caduta fitta i quel lotao iveo. Nessuo più passava pe le stade
Prova di coltivazione di varietà di pomodoro resistente a virosi in territorio di Termini Imerese (PA)
Pg fzz R m v u p mp, vzzz puz mzzz h u Avà 2011 Pv vz và pm v Tm Im (PA) (: Gh p Rpb.O.P.A.T.. 57 m) PREEA 2001 z Opv EA m h vu ff v pbmh g h vu vz p mp; p, puz pm u p pm 80% puz vb. vgh ffu p Uvà g u
La metrica di Minkowski e la distanza generalizzata o di Mahalanobis. Note di Mary Fraire
La meca ow e la aa geealaa o ahalaob. Noe ay Fae. Rcham eoc S ee ule oae qu eguo, vao a e ecfc ca oa 9 ull agomeo alcu cham ulle ae ow e ahalaob. Coeao ue veo-ga a eleme ua mace a quav, a, R, eemo la eguee
Diagramma circolare di un motore asincrono trifase
Diagramma circolare di un motore aincrono trifae l diagramma circolare è un diagramma che permette di leggere tutte le grandezze del motore aincrono trifae (potenza rea, perdite nel ferro, coppia motrice,
NEWSLETTER DEGLI ARCHIVI DELL'IRTEM
1 NEWSLETTER DEGLI ARCHIVI DELL'IRTEM Anno 2 Numero 7. Giugno-Agosto 2009 In questo numero: 1. In occasione della X Settimana per la Cultura, l IRTEM ha proposto tre manifestazioni pubbliche che si sono
Signore, da chi andremo? inno del Congresso Eucaristico Nazionale - Ancona 2011
io ogsso Eucasco Nazioale Acoa 2011 Itroduzioe te: ofeza Episcopale Italiaa musica: Pasquale Impagliatelli # Ritollo go, da chi a d go, da chi a d u # # so lo hai pa ro le vi ta e ter b 2/8 trofe # # 1
Meccanica Classica: Cinematica Formule
Tet di Fiica - Cinematica Meccanica Claica: Cinematica Formule Velocità media: m Accelerazione media: Formule da ricordare: x x x1 t t t1 1 a m t t t Motouniforme: x(t)x 0 + t oppure x t 1 Moto uniformemente
A.A. 2018/2019 Graduatoria corso di laurea in Studi internazionali Sessione primaverile entro le ore del 14 maggio 14 maggio 18 maggio
A.A. 2018/2019 Graduatoria corso di laurea in Studi internazionali Sessione primaverile Ai/Alle candidati/e idonei/e ammessi/e è richiesta la conferma del posto entro le ore 12.00 del 14 maggio https://www.esse3.unitn.it/auth/studente/immatricolazione/immatricolazionestarttipodomimm.do
Esercizi sul moto del proiettile
Eercizi ul moto del proiettile Riolvi li eercizi ul quaderno utilizzando la oluzione olo per controllare il tuo riultato. 1 Un fucile è puntato orizzontalmente contro un beralio alla ditanza di 30 m. Il
frazione 1 n dell ammontare complessivo del carattere A x
La Cocetrazoe Il cocetto d cocetrazoe rguarda l modo cu l ammotare totale d u carattere quattatvo trasferble s rpartsce tra utà statstche. Tato pù tale ammotare è addesato u sottoseme d utà, tato pù s
Risultati simulazione test di accesso per l ammissione al corso di Laurea in Economia
per Area del Sapere 82720AE 52,00 83738DS 50,00 80966MM 49,00 83737PA 47,75 82866GG 47,50 80724CG 46,75 82972PG 46,75 82612SS 45,00 83377SS 45,00 82722GG 44,75 83739GV 44,75 82318LG 44,25 83361LD 44,25
Autorità per le Garanzie nelle Comunicazioni
Tabella 1 Frequenze pianificate per le reti nazionali e locali nell Area Tecnica 1 (Piemonte occidentale) nazionale 1 36 nazionale 2 40 nazionale 3 46 nazionale 4 32 nazionale 5 42 nazionale 6 47 nazionale
CITTÀ DI IMOLA MEDAGLIA D'ORO AL VALOR MILITARE PER ATTIVITA' PARTIGIANA
Inf.Com. Campanella 1 P.L. Domanda/ricev.N.22080 08/07/2016 Fratelli e Stradario - 95 2 G.G. Domanda/ricev.N.22157 16/05/2016 Fratelli e Stradario - 65 3 B.A. Domanda/ricev.N.22162 23/11/2016 Fratelli
A.A. 2016/17 Graduatoria corso di laurea in Scienze e tecniche di psicologia cognitiva
1 29/04/1997 V.G. 53,70 Idoneo ammesso/a * 2 27/12/1997 B.A. 53,69 Idoneo ammesso/a * 3 18/07/1997 P.S. 51,70 Idoneo ammesso/a * 4 12/05/1989 C.F. 51,69 Idoneo ammesso/a * 5 27/01/1997 P.S. 51,36 Idoneo
Soprintendenza Archivistica della Sicilia Archivio di Stato di Palermo
Soprintendenza Archivistica della Sicilia Archivio di Stato di Palermo QUESTURA DI PALERMO Archivio Generale 1938-1944 1 Trascrizione: P. Licata Revisione: S. Falletta (2019) 1 I fascicoli dal 1933 al
Generalità sulle macchine rotanti
Macchie elettiche ate Geealità ulle macchie otati Foza di Loetz U filo coduttoe immeo i u camo magetico B (i figua B ha diezioe ucete dal foglio) e ecoo da ua coete i iega i ua o ell alta diezioe a ecodo
Notte, hotel, centro sportivo. AZZURRA SPORTILIA santa sofia/ forlì cesena novembre 2018 FOLLOW US
Notte, hotel, centro sportivo AZZURRA SPORTILIA santa sofia/ forlì cesena 03-04 novembre 2018 FOLLOW US To eigio a ili. o To eigio a ili. o Foto su.tor eigio a ili.co tel + : + fax + ail i fo@to eigio
Apparecchi di sollavamento. Classificazione apparecchi di sollevamento a
Appareh d sollavameto A moto otuo: Nastr trasportator Sollevator a tazze Forze d erza lmtate; trastor d avvameto e arresto poo rlevat A moto dsotuo: Gru a torre Forze d erza rlevat Classfazoe appareh d
Rendite a rate costanti posticipate in regime di interessi composti
Redte rte cott regme d tere compot Redte rte cott potcpte regme d tere compot /32 Redte rte cott potcpte regme d tere compot 2/32 Redte rte cott potcpte regme d tere compot VALORE ATTUALE DI UNA RENDITA
Un rap d'educazione... all'alimentazione canto per voce e pianoforte
U rap d'educazioe... all'alimetazioe cato per voce e piaoforte Voce Piaof. Allegro q = 144 4 4 4 Tutti Que - sto è il o-stro.. Scrivi che ti cato 201/14 Classe IV B - Scuola Primaria Paritaria M. di Caossa
Soluzione degli esercizi del capitolo 11
Statstca - metodooge per e sceze ecoomche e soca /e S Borra, A D Cacco - McGraw H s Souzoe deg esercz de captoo a rsposta esatta è a c, fatt daa s ha: da cu rcavamo a corretto Ifatt,,,,,,,,,,,,,,, b Sì,
sta che ar- ri- che ar- ri- sta dio, tu- dio, tu-
T'in- vi- dio, tu- s che ar- vi, t'im- be- vi de T'in- vi- dio, tu- s che ar- vi, t'im- be- vi de T'in- vi- dio, tu- s, t'im- be- T'in- vi- dio, tu- s, t'im- be- 4 vi vi Fo- Fori e ri e de de de de Fo-
Lezioni di Ricerca Operativa 2 Dott. F. Carrabs
Lezioni di Ricerca Operativa Dott. F. Carrab.. 009/00 Lezione in Laboratorio: - Eercizi di modellazione Lezione 7: Eempio: Invetimenti Un cliente affida ad un aenzia finanziaria un milione di euro da impieare
RENDITE. Le singole rate possono essere corrisposte all inizio o alla fine di ciascun periodo e precisamente si ha:
RENDITE. Pagamet rateal S defsce redta ua sere qualsas d somme rscuotbl (o pagabl a scadeze dverse, o, pù esattamete, u seme d captal co dspobltà scagloata el tempo. Tal captal soo dett rate della redta
Test ammissione CdL in Economia aziendale ed Economia e commercio GRADUATORIA GENERALE
GRADUATORIA INIZIALI COG E 741 BM 24/10/1997 1 83,125 29,00 37,50 737 RG 14/11/1997 2 81,250 24,00 41,00 471 AN 14/01/1998 3 80,625 25,00 39,50 893 GF 27/09/1997 4 80,000 23,50 40,50 579 DL 22/03/1997