LEZIONI DI STATISTICA
|
|
|
- Gennaro Gerardo Bellini
- 8 anni fa
- Visualizzazioni
Transcript
1 LEZIONI DI STATISTICA Lezione 1: Cenni di probabilita Diego di Bernardo Edito da Vincenza Maselli
2 CENNI DI PROBABILITÀ La probabilità è la teoria matematica alla base della statistica. DEFINIZIONI S SPAZIO DI CAMPIONI: insieme di tutti i possibili risultati di un esperimento. Esempi: DADO: MONETA: S = { 1,,3,4,5,6 } S = { testa,croce} MONETE: S={(testa,testa) (testa,croce) (croce,testa) (croce,croce)} X VARIABILE ALATORIA, valori di S x i è il valore assunto dalla v. a. X nell esperimento i. Viene anche chiamato realizzazione. X S può assumere uno dei PROBABILITÀ: { } s = x 1,x...,x N x i S P( X = x i ) [ 0,1] P ha le seguenti proprietà: 1. P(X = x 1 ) + P(X = x ) P(X = x n ) =1. N i=1 i,p(x = x i ) 0,1 P(X = x i ) [ ]
3 Esempi: S = { testa,croce} x i P( x i ) X S testa 1/ croce 1/ Due dadi: abbiamo bisogno di due variabili aleatorie { } S = 1,,3,4,5,6 X S Y S { } (X,Y) SxS = (1,1),(1,),(1,3)... (x i, y i ) 1 1 1/36 1 1/ / / / /36 1 1/36 P(X = x i,y = y i ) Osserviamo: P(X =1,Y = ) = 1 36 = = P(X =1)P(X = ) REGOLA 1: P(A,B) = P(A)P(B) SE E SOLO SE A e B sono INDIPENDENTI
4 Esempio: { } S = blu,verde,marrone X S v. a. colore occhio sinistro, Y S v. a. colore occhio destro P(X = blu) = P(X = verde) = P(X = marrone) = 1 3 P(X = marrone,y = marrone)? = P(X = marrone)p(y = marrone) = 1 9 è vero? Chiediamo: Nome X(o. s) Y(o. d.) 1) M M ) M M 3) M M P(X = marrone,y = marrone) =1 X ed Y non sono INDIPENDENTI REGOLA : P(A,B) = P(A)P(B / A) = P(B)P(A /B) P(X = marrone,y = marrone) = P(X = marrone)p(y = marrone / X = marrone) = 1/3*1 = 1/3 REGOLA 3: P(A oppure B) = P(A) + P(B) Esempio: DADO: S = 1,,3,4,5,6 { } X S P(X =1 oppure X = ) = P(X =1) + P(X =1) = = 1 3
5 CALCOLO DELLE PROBABILITÀ Se ho N possibili risultati nello spazio S tutti equiprobabili allora P(X = y i ) = 1 N POTENZA: N = n k numero di elementi di S per l unione di k esperimenti, dove ogni esperimento ha n possibili risultati. Esempio: Lancio di due dadi Ogni dado ha n = 6 possibili risultati, quindi per due (k=) dadi avrò N= 6 = 36 possibili risultati. Lancio di 3 dadi N = 6 3 Lancio di 3 monete N = 3 Definizione matematica: FATTORIALE n!= (n)(n 1)(n )...*1 Esempi: 3! = 3**1=6 10! = 10*9*8*7*6*5*4*3**1 100! = troppo grande!
6 COMBINAZIONI N = n! (n k)!k! combinazioni di k oggetti da n oggetti Esempio: k = coppie di topi n = 3 topi topo verde topo nero topo rosso 3! (3 )!! = 6 1* = PERMUTAZIONI N = n! (n k)! permutazione di k oggetti Esempio: Coppie di topi 3! (3 )! = 6 1 =
7 PERMUTAZIONI CON RIPETIZIONI POTENZA N = n k 3 =
8 DESCRIZIONE DI VARIABILE ALEATORIA X S X = x i S P( X = x i ) [ 0,1] v. a. P(X = x i ) = p i VALORE ATTESO O MEDIA PESATA µ x E(X) = p i x i N i=1 = P1x1+Px+ +PnXn Esempio: DADO S = { 1,,3,4,5,6 } X S E(X) = = 1 6 = 7 = 3,5 PROPRIETÀ DI LINEARITÀ: E(aX ± by) = ae(x) ± be(y) Esempio: somma di due dadi E(X + Y) = E(X) + E(Y) = 7
9 MEDIANA: X M M(X) = P(X = x i > x M ) = P(X = x i < x M ) Esempio: DADO a 7 facce X M = 4 S = { 1,,3,4,5,6,7 } P(x i > X M ) = P(x i = 5) + P(x i = 6) + P(x i = 7) = 3 7 P(x i < X M ) = P(x i =1) + P(x i = ) + P(x i = 3) = 3 7 Per gli spazi di S con N pari si usa la media dei valori centrali VARIANZA N σ VAR(X) = E[(X µ x x ) ] = p i (x i µ x ) i=1 µ x E(X) DEVIAZIONE STANDARD σ = x σ STD(X) = x VAR(X)
10 X Y STD(X) STD(Y) µ x µ y µ x µ y σ x = σ y X Y µx = µy µ x = µ y σ x σ y
11 PROPRIETÀ: VAR(aX + by) = a VAR(X) + b VAR(Y) + abe[(x µ x )(y µ y )] COV(X,Y) Se X, Y sono indipendenti COV(X,Y) = 0 STD X Y = X Y VAR(X) X + VAR(Y) Y STD(X + Y) STD(X) + STD(Y) STD(X ± Y) = VAR(X) + VAR(Y)
12 DISTRIBUZIONE DI PROBABILITÀ La funzione di probabilità può assumere diverse forme : P(X) UNIFORME P(X) v. a. discreta TRIANGOLARE Se X è un numero reale (es: misura dell espressione di un gene) f(x) b UNIFORME PARAMETRI a v.a. continua f(x) σ x PARAMETRI GAUSSIANA O NORMALE µ x
13 LEZIONI DI STATISTICA Lezione : Statistica Diego Di Bernardo Edito da Vincenza Maselli
14 STATISTICA Che cos è la statistica? A cosa serve? Esempio: Gene A: v.a. X P(X = x i ) Domanda: Il gene A è espresso oppure no nel topo wt? Quanto è espresso? Esperimento: è espresso? Quanto? Risposta classica SI oppure NO gene A = 4 Risposta statistica Si (96%) e NO (4%) gene A = 4,1 ± 0, INFERENZA STATISTICA: stima di P(X) dalle misure sperimentali Per dare la risposta statistica dobbiamo conoscere P(X). MA NON LA CONOSCIAMO! Come posso fare? Soluzione 1: Ripeto lo stesso esperimento molte volte, (L) Problema Devo fare troppi esperimenti P(X) 50% Numero di volte che il gene A è compreso tra 0 e 1 diviso il numero di esperimenti K/L 40% % 4% 1% 1% Gene A Soluzione : Cerco di stimare solo alcune proprietà di X, come la media E(X) e la varianza E[(X-E(X)) ]
15 STIMA DELLA MEDIA X v. a. P(X) X = { x 1, x,...,x n } Problema µ x = E(X) = P 1 x P n X n Non conosco P 1,P,,P n Soluzione: eseguo L misure di X e stimo µ x da queste L osservazioni: STIMA DELLA MEDIA ˆ µ x = a 1 + a a L L Perché è solo una stima? µ x = P 1 x 1 + P x P n X n Tutti i possibili valori di X, cioè gli elementi di S Nella stima invece conosco solo alcuni (L) degli elementi di S e non conosco P i che quindi assumo essere 1 L STIMA DELLA VARIANZA σ ˆ x = (a 1 ˆ µ x ) + (a ˆ µ x ) (a L ˆ µ x ) L 1 STIMA DELLA DEVIAZIONE STANDARD ˆ σ x = σ ˆ x
16 PROPRIETÀ ˆ µ x +y = ˆ µ x + ˆ µ y σ ˆ x +y = σ ˆ x + σ ˆ y
17 INFERENZA DELLA MEDIA ED INTERVALLI DI CONFIDENZA INTERVALLO DI CONFIDENZA: intervallo che contiene i valori più probabili della grandezza che ho stimato. 1. L misure dell espressione del gene A: a 1, a,, a L. STIMO la media 3. STIMO la varianza ˆ µ A = a 1 + a a L L σ A è la VERA VARIANZA dove µ A è la VERA MEDIA σ ˆ A = (a ˆ 1 µ A ) + (a ˆ µ A ) (a L ˆ µ A ) L 1 dove 4. Voglio trovare l intervallo che contiene i valori più probabili della vera media Come faccio? µ A cioè ˆ µ A ± K. STIMO la varianza di µ A : ˆ σ ˆ µ A = σ a1 +a +...+a L L per la proprietà additiva ˆ σ ˆ µ A σ a1 L = ˆ σ a L + ˆ ˆ σ al L = L σ ˆ A L σ = ˆ A L
18 ERRORE STANDARD: deviazione standard della stima della media σ σ ˆ µ ˆ A = ˆ A L OSSERVA: σ ˆ µ ˆ A σ ˆ A infatti σ ˆ A è la stima di σ A mentre σ ˆ µ ˆ A è la stima di σ ˆ µ A Se L è molto grande, ˆ σ ˆ µ A σ = ˆ A L = 0 mentre ˆ σ A = σ A Quindi più misure faccio, meno errore commetto nella stima di µ A REGOLA PRATICA: valori di ˆ σ ˆ µ A ± ˆ A L contiene circa il 96% dei possibili µ A. Cioè ho il 96% di probabilità che il VERO VALORE di cada in questo intervallo. µ A
19 Esempio Strumento di misura: GENE-O-MATIC S = { 1,,3,4,5,6,...,0} 1 = poco espresso 0 = molto espresso gene A quando è espresso P 1 =0.1 P =0.05 P 3 =0.1 P 4 =0.4 P 5 =0.0 P 0 =0. P 1 =numero di volte che uscito 1 / numero di misure P =numero di volte che uscito / numero di misure µ gene A =0.1*1+0.05*+ +0.*0=4.1 Strumento di misura: SUPER-GENE-O-MATIC non fa errori!!! S = { 1,,3,4,5,6,...,0} 1 = poco espresso 0 = molto espresso gene A quando è espresso P 1 =0 P =0 P 3 =0 P 4 =4 P 5 =0 P 0 =0 µ gene A =0*1+0*+0*3+1*4 +0*19+0*0=4
20 Esempio: espressione del gene A (in verde il primo esempio con L = in blu il secondo esempio con L = 3) stima MEDIA della X Controllo µ^ Y Trattamento = x = 14 = 7 ^ µ x = = = 14 stima della MEDIA stima VAR stima VAR stima STD stima STD ^ ^ µ x = = = 7 µ x = = = ^ (6 7) + (8 7) 1+ 1 ^ (10 14) + (18 14) σ x = = = σ x = = = ^ (6 7) + (8 7) + (7 7) 1+ 1 ^ (10 14) + (18 14) + (14 14) 3 σ x = = = 1 σ x = = = ^ σ x = 1.4 σ x = ^ σ x = 1 1 σ x = 16 4 ^ ^ errore standard σ^ µ^ = x =1 ^ σ µ x = = 4 ^ 3 errore standard ^ 1 ^ ^ ^ 16 σ µ x = = 0.6 σ µ x = = risultato 7±1 14±4 risultato 7±0.6 14±.3 Errore che faccio nello stimare la media
21 e il fold change? che errore faccio? Cioè qual è l errore standard? µ ˆ y µ ˆ x = 14 7 = ˆ σ µ ˆ y ˆ µ = ˆ y σ ˆ ˆ µ ˆ x µ x ˆ σ µ ˆ y µ x µ + ˆ x ˆ µ y = RISULTATO: ±0.64
22 LEZIONI DI STATISTICA Lezione 3: t-test Diego Di Bernardo Edito da Vincenza Maselli
23 Il gene a è espresso nel tessuto? t-test PROCEDURA PER IL t-test: TWO TAILEGDT-TEST (1) Eseguiamo L misure: a 1,a,...,a L () Calcoliamo la stima della media: ˆ µ A = a 1 + a a L L (3) Calcoliamo la stima della deviazione standard: σ ˆ A = (a 1 ˆ µ A ) + (a ˆ µ A ) (a L ˆ µ A ) L σ (4) Calcoliamo l errore standard: S.E.= ˆ A L (5) Formuliamo l ipotesi nulla: H 0 :µ 0 A = 0 (il gene non è espresso) (6) Calcoliamo la statistica t: t = µ ˆ 0 ( A µ A ) S.E. ( ) µ = ˆ 0 A µ A ˆ σ A L µ A = ˆ ˆ (7) Se t allora p 0.04 (il gene a è espresso con σ A L p 0.04) EXCEL BOX
24 CONFRONTO TRA DUE POPOLAZIONI t-test paired e unpaired t-test Problema: a 1,a,...,a N b 1,b,...,b N A B Esempio: misura dell espressione di un gene in due topi diversi, wt e ko IPOTESI NULLA: H : 0 µ = Ci sono 3 modi per affrontare il problema, a seconda dei casi: CASO 1. PAIRED t-test: si usa nel caso in cui le misure nei due esperimenti possono essere suddivisi in coppie. Quindi N = M. *** Esempio 1: Voglio sapere se un nuovo farmaco ha un effetto migliore rispetto ad uno tradizionale Esempio : voglio sapere se un gene è più espresso in un occhio trattato rispetto ad uno non trattato PROCEDURA PAIRED T-TEST: A µ Esempio: il gene di interesse non B varia, cioè non è diferenzialmente espresso nei due topi 1. Dalle L coppie di misure calcolo H 0 : µ Z = 0 Z 1 = a 1 b 1 Z = a b Z L = a L b L µ Z = µ A µ B = 0 µ A = µ B. 7. Come prima (con Z invece di A) EXCEL BOX
25 CASO 3. UNPAIRED t-test (VARIABILE DISEGUALE): si usa nel caso generale in cui ho due misure indipendenti. a 1,a,...,a N b 1,b,..,b M (gene nel topo wt) (gene nel topo ko) Assumo che σ A σ B H 0 : µ a = µ b µ a µ a = 0 = µ a b IPOTESI NULLA PROCEDURA UNPAIRED T-TEST (VARIANZA DISEGUALE) 1. Eseguo N misure. Calcolo la stima della media a 1,a,...,a N e M misure b 1,b,...,b M ˆ µ A = a + a a N N ˆ µ B = b + b b 1 M M ˆ µ A ˆ µ B = ˆ µ A B 3. Calcolo la deviazione standard σ ˆ A = (a ˆ µ 1 A ) + (a ˆ µ A ) (a L ˆ µ A ) N 1 σ ˆ B = (b ˆ µ + (b 1 B ) ˆ µ B ) (b M ˆ µ B ) M 1 4. Calcolo la deviazione standard di ˆ µ A ˆ µ B = ˆ µ A B (errore standard) σ ˆ σ ˆ µ ˆ A B = σ ˆ µ ˆ A + σ ˆ µ ˆ B = A N + σ ˆ B M 5. Calcolo della statistica t = ˆ µ ˆ µ ˆ µ A B σ ˆ A N + σ ˆ = A ˆ µ B S.E B A + S.E. B M
26 6. Se t allora p 0.04 Approssimativamente Meglio usare un programma tipo Excel EXCEL BOX ATTENZIONE: è meglio NON USARE MAI questo caso 3. L ipotesi di varianze diseguali è pericolosa, perché significa che le due popolazioni (cioè due set di misure) non sono confrontabili!
27 CASO. UNPAIRED T-TEST (VARIANZE UGUALI): si usa nelle stesse condizioni del caso 3, cioè due serie di misure indipendenti. ATTENZIONE usare SEMPRE questo al posto del caso 3! H 0 : µ a = µ b µ a µ a = 0 = µ a b Ipotesi nulla PROCEDURA UNPAIRED T-TEST (VARIANZE UGUALI) Come il caso 3 1. Eseguo N misure a 1,a,...,a N e M misure b 1,b,...,b M. Calcolo la stima della media ˆ µ A, ˆ µ B e ˆ µ A ˆ µ B = ˆ µ A B 3. Calcolo la deviazione standard σ ˆ A, σ ˆ B 4. Calcolo DELL ERRORE STANDARD COMBINATO, PSE (Pooled Standard Error) (N 1) σ ˆ µ ˆ A B = σ ˆ + (M 1) σ ˆ A B 1 N + M N + 1 M E un modo alternativo a quello del caso 3, ma molto più preciso se le varianze sono uguali. 5. Calcolo della statistica t = ˆ µ ˆ µ A B σ ˆ µ ˆ A B 6. Se t allora usiamo excel EXCEL BOX
28 LEZIONI DI STATISTICA Lezione 4: ANOVA Diego di Bernardo Edito da Vincenza Maselli
29 Riepilogo T-test 1) Il gene A è espresso nel topo wt? S.E. σ ˆ L STATISTICA T t = ˆ µ p 0,04 σ ˆ L 0 ˆ µ S.E. σ ˆ L IPOTESI NULLA H 0 : µ = 0 0 ˆ µ Più è grande questa distanza, più l ipotesi nulla è inattendibile, cioé più piccolo è il p-value ) Confronto tra due popolazioni (il gene A è differenzialmente espresso nel topo wt vs il topo ko) H 0 : µ wt = µ ko µ wt µ ko = 0 CASO ( il caso 3 non si usa mai) t = ˆ µ ˆ wt µ ko S.E. pooled S.E.pooled = ( N 1) σ ˆ wt + (M 1) σ ˆ ko N + M 1 N + 1 M 0 S.E wt ˆ µ wt S.E ko ˆ µ ko
30 S.E pooled 0 ˆ µ wt ˆ µ ko Per l ipotesi nulla S.E pooled 0 ˆ µ wt ˆ µ ko Più è grande questa distanza più è piccolo il p-value Cosa significa S.E. pooled? S.E.pooled = σ ˆ pooled = = a 1 µ ˆ wt ( N 1) σ ˆ wt + M 1 N M ( ) ˆ σ ko 1 N + 1 M ( ( N 1) a 1 µ ˆ wt ) ( a N µ ˆ wt ) N 1 a 1,...,a n gene A in wt b 1,...,b n gene B in ko ( ( ) b 1 µ ˆ ko ) ( b M µ ˆ ko ) + M 1 N + M ( ) ( a N ˆ ) + ( b 1 ˆ ) ( b M ˆ ) µ wt N + M µ ko µ ko M 1 Quindi σ ˆ pooled è la stima della deviazione standard usando tutte le misure. Se assumiamo che le varianze sono uguali nelle due popolazioni, allora si possono usare tutte le misure per avere una stima più precisa. =
31 ANOVA: ANalysis Of VAriance Si usa nel caso in cui si voglia confrontare la media in più di due popolazioni (nel caso di due popolazioni si usa il t-test). Esempio: il gene X è differenzialmente espresso tra un topo wt, un topo ko omozigote ed un topo ko eterozigote? oppure c è differenza tra 3 dosi diverse di farmaco nella valutazione della frequenza cardiaca? PERCHÈ NON SI FANNO TUTTI I POSSIBILI T-TEST? Usando tutte le possibili combinazioni di t-test aumento la probabilità di commettere un errore, Esempio: Topo a 5 occhi: o.s.s o.s o.c. o.d o.d.d a 1 b 1 c 1 d 1 e 1 a b c d e a 3 b 3 c 3 d 3 e 3 Facendo tutti I possibili t-test, cioè tutte le possibili combinazioni di due occhi da 5 si ha 5! N = = ( 5 )!! ( 1 3) ( 1 ) = 10 1 = 10 t-test. Se dico che un t-test è significativo quando p < 0.05, significa che acceto il 5% di probabilità di commettere un errore per ogni t-test.
32 Quindi su 10 t-test commetto 0.05*10 = 0.5 errori. Sei il topo avesse 10 10! occhi N sarebbe N = ( 10 )!! = = 45, cioè almeno 45*0.05 =.5 t-test saranno sbagliati.
33 Gene x nel topo wt Gene x nel topo ko omozigote Gene x nel topo ko eterozigote a 1,a,...,a N b 1,b,...,b M c 1,c,...,c L N misure M misure L misure ˆ ˆ ˆ µ wt µ o µ e ˆ µ wt ˆ µ o ˆ µ e ˆ µ wt ˆ µ e ˆ µ o ˆ µ wt ˆ µ e ˆ µ o IPOTESI NULLA: H 0 : ˆ µ wt = µ ˆ o = µ ˆ e Assumiamo uguale varianza Come caso del t-test LE MEDIE SONO UGUALI. L IPOTESI NULLA SARÀ RIFIUTATA SE ALMENO UNA MEDIA È DIVERSA DALLE ALTRE. L idea su cui si basa questa procedura è un confronto tra quanto variano le medie rispetto alla variazione delle misure. Cioè se le medie sono distanti tra loro rispetto agli S.E., allora H 0 verrà rifiutata con p value piccolo. Eseguo N misure c 1,c,...,c L a 1,a,...,a N, M misure b 1,b,...,b M ed L misure
34 Calcolo le stime delle medie: la media globale: e le stime delle deviazioni standard: ˆ µ wt = a a N N ˆ µ o = b b M M ˆ µ e = c c L L ˆ µ glo = a a N + b b M + c c L N + M + L σ ˆ wt, σ ˆ o, σ ˆ e Calcolo l errore standard combinato al quadrato (detto anche Mean Square Error MSE): ˆ σ µ ˆ glo = N 1 ( ) ( a N ˆ ) ( b 1 ˆ ) ( b M ˆ ) + ( c 1 ˆ ) ( c L ˆ ) = a 1 µ ˆ wt ( ) ˆ σ wt ( ) ˆ µ wt ( ) ˆ + M 1 σ o + L 1 N + M + L 3 σ e µ o N + M + L 3 1 N + 1 M + 1 L σ ˆ ˆ µ glo ci da un idea di quanto sono variabili le nostre misure. µ o µ e µ e 1 N + 1 M + 1 = L Un modo alternativo di calcolare σ ˆ ˆ µ glo quando H 0 è vera è calcolarlo direttamente dalle medie, invece che dalle misure: Mean Square For Treatments (MSTR): σ ˆ ˆ µ alt = N ( ˆ µ wt µ ˆ glo ) + M ( µ ˆ o ˆ µ glo ) + L( µ ˆ e µ ˆ glo ) N + 1 M + 1 L abbiamo usato la classica formula della varianza, ma pesata. ˆ σ ˆ µ alt ci da un idea di quanto sono variabili le misure. Calcoliamo la statistica σ F = ˆ ˆ µ alt se H ˆ 0 è vera allora σ ˆ µ glo ˆ σ ˆ µ alt σ ˆ = ˆ µ glo e quindi F = 1.
35 Più F > 1 più posso rifiutare H 0 con un p-value più piccolo. SE IL P-VALUE È SIGNIFICATIVO ( CIOÈ POSSO DIRE CHE NON È VERO CHE p 0.05) POSSO RIFIUTARE H0, ˆ µ wt = µ ˆ o = ˆ µ e MA NON SO DIRE SE TUTTE LE MEDIE SONO DIVERSE OPPURE SOLO UNA È DIVERSA DALLE ALTRE.
36 EXCEL BOX: TAVOLA DI ANOVA ANOVA: single factor alpha = 0.05 DATI wt o e VALORE DEL P-VALUE AL DI SOTTO DEL QUALE RIFIUTIAMO H 0 Source of variation Between groups Within groups ANOVA TABLE SS df MS F P Fcrit ˆ σ ˆ 3-1 µ alt ( N 1) ˆ + ( M 1) σ ˆ o + ( L 1) ˆ σ wt σ e N+M+L-3 SS df = MST R σ ˆ σ ˆ MST R MSE = ˆ ˆ µ alt µ glo p-value SS df = MSE Total somma somma valore di F per avere p =0.05
37 MULTIPLE HYPOTHESIS TESTING PROBLEM Esempio: micorarray con geni. Voglio i geni differenzialmente espressi. TRATTATO CONTROLLO 3 replicati 3 replicati 3 MA 3 MA Gene1 a 1,1,a 1,,...,a 1,0.000 b 1,1,b 1,,...,b 1,0.000 t-test t 1 Gene a,1,a,,...,a,0.000 b,1,b,,...,b,0.000 t-test t Gene0000 a 0.000,1,a 0.000,,...,a 0.000,0.000 b 0.000,1,b 0.000,,...,b 0.000,0.000 t-test t Faccio 0000 t-test. Assumo che ogni t-test è significativo se p 0.05 (probabilità del 5% di sbaglaire, cioè di dire che un gene è differenzialmente espresso quando non lo è). In uqesto modo commetto 0.05*0000=1000 errori, quindi sbaglio almeno 1000 geni
38 BONFERRONI CORRECTION E molto semplice. Vistoche un p<0.05 non e un criterio molto stringente quando eseguo molti t-test simultaneamente (come nel caso dei microrray) faccio una correzione: p bonferroni = α N dove α e il valore limite di p al di sotto del quale considero significativo il test (di solito α =0.05). N e il numero di t-test che eseguo simultaneamente (di solito N=numero di geni sul microarray). Quindi diro che il gene X e differenzialmente espresso se il suo p value e : p genex < p bonferroni = α N La Bonferroni correction funziona, ma e troppo stringente, cioe pochi gene risultano significativi, e molti sono scartati ingiustamente. False Discovery rate Un modo alternativo e calcolare una quantita chiamata FDR. Si calcola cosi, per ogni gene i nel microarray, prendiamo il suo valore p i e calcoliamo: FDR i = p i *K i N dove N e il numero di geni nel microarray e K i e il numero di gene che hanno un valore p minore di quello del gene in questione, cioe minore di p i.
39 FDR varia tra 0 e 1. Possiamo ora scegliere i geni in base al loro FDR invece che il valore p. Se ad esempio prendiamo tutti i geni con un FDR<0.1, di questi saranno veramente differenzialmente espressi solo il 90% (0.9) mentre il 10% (0.1) saranno falsi positivi. Se scegliamo FDR<0., allora dei geni selezionati l 80% saranno differenzialmente espressi, mentre il 0% (0.) saranno falsi positivi.
40 LEZIONI DI STATISTICA Lezione 5: Correlazione Lineare e Regressione Lineare Diego di Bernardo Edito da Vincenza Maselli
41 CORRELAZIONE LINEARE Si usa per capire se c è una associazione tra due variabili. Esempio 1. In un esperimento di microarray misuro la serie temporale di N geni (graf. 1). Voglio sapere quali geni si comportano allo stesso modo. Voglio sapere se c è un associazione tra il gene e il gene 1 e tra il gene e il gene 3 (graf ). Grafico t Grafico Gene 1 Gene 3 Osservando questi grafici si può dire che il gene e il gene 1 mostrano un associazione maggiore dei geni e 3, cioè I geni e 1 sono più
42 correlati dei geni e 3. È possibile quantificare questa associazione? Si può calcolare la significatività, ossia un p-value? Esempio. Data una serie di esperimenti di micorarray (ko, stress, drug treatment, etc..) si vogliono trovare dei geni che si comportano come il gene di interesse. (esempio gene della sordità): Gene 1 Gene Gene Per scoprire una correlazione o si osservano tutti i grafici o ci si affida più efficacemente al coefficiente di correlazione.
43 COEFFICIENTE DI CORRELAZIONE. Procedura per il calcolo di r (coefficiente di correlazione): gene 1: gene : a 1,a,...,a N b 1,b,...,b N STESSO NUMERO DI MISURE ˆ µ 1 = a + a a 1 N Calcolo la stima della media: N ˆ µ = b + b b N N (a Calcolo: r = 1 ˆ µ 1 )(b 1 ˆ µ )+...+ (a N ˆ µ 1 )(b N ˆ µ ) [(a 1 ˆ µ 1 ) (a N ˆ µ 1 ) ] (b 1 ˆ µ ) (b N ˆ µ ) Proprietà di r: r varia tra -1 e 1 r =1 r = -1 [ ] Vi ricorda qualcosa? Gene Gene Gene Gene Gene 1 Gene 1 r = 0 r = -0.8 Gene 1 Gene 1
44 r = 0.8 Gene 1 EXCEL BOX Posso sapere se l associazione tra i due geni è significativa? IPOTESI NULLA: H 0 : r = 0 I DUE GENI NON SONO CORRELATI Clacolo la statistica: t = r N 1 r Non chiedete perché Applico il classico t test che mi da il p-value: EXCEL BOX Attenzione! Va usato N- Esempio: Il gene 1 e il gene sono correlati: r = 0,76 p 0,05
45 ATTENZIONE: CORRELAZIONE NON IMPLICA CAUSALITÀ! Esempio: Cocktail Party Dopo un party alcune delle persone si ammalano. Un medico intervista le persone ammalate e misura il consumo di vino e di noccioline ed il livello dei sintomi. CORRELAZIONE CAUSALITÀ CORRELAZIONE Il medico trova che più vino le persone hanno bevuto più sono gravi i sintomi: cioè vino e sintomi sono correlati. r = 0,68 p 0,05 Consumo di vino
46 Questo porterebbe a pensare che sia stato il vino a causare la malattia. In realtà la causa sono le noccioline, le persone ammalate hanno mangiato più noccioline delle altre e di conseguenza hanno bevuto più vino!
47 SPEARMAN RANK-ORDER CORRELATION COEFFICIENT: r si può calcolare come prima e si può fare il t-test solo nell ipotesi che la distribuzione delle due variabili sia binormale: Gene 1 Gene Non sempre questo è vero, nei casi in cui non è vero si può procedere così: Procedura per il calcolo di r S : Spearman Correlation Coefficient Gene 1: Gene : a 1,a,...,a N b 1,b,...,b N Ordiniamo i valori in modo crescente, (facciamo il rank dei valori): Esempio: a 1 = 3,5 a =1, a 3 = 0,7 a 4 =,9 b 1 = 0,75 b = 0,7 b 3 = 0,4 b 4 =1, R a 3 = 0,7 1 a =1, a 4 =,9 3 a 1 = 3,5 4 S b 3 = 0,4 1 b = 0,7 b 1 = 0,75 3 b 4 =1, 4 R= rank gene 1 S = rank gene
48 Procediamo come prima ma invece di utilizzare a 1, b 1, etc usiamo R e S R ˆ = R + R R 1 N N ˆ S = S 1 + S S N N r S = ( r 1 R ˆ )( s 1 S ˆ )+...+ r N R ˆ ( r 1 R ˆ ) ( r N R ˆ [ ) ] s 1 ˆ ( )( s N S ˆ ) ( S ) ( s N S ˆ ) [ ] Calcoliamo EXCEL BOX t = r S N 1 r S Quando non usare la correlazione lineare: Gene Se otteniamo un grafico di questo tipo appare ovvio che non ha senso tentare di approssimare al curva ad una retta Bisogna sempre guardare i dati prima di farci qualcosa!!!
49 REGRESSIONE LINEARE Si usa per capire se c è una associazione tra una variabile (misura) ed un parametro di controllo. Esempio: Vettore inducibile Promotore inducibile dalla tetraciclina GFP GFP i = a TET i + b a =? b =? [tetraciclina] µl Vogliamo trovare la linea migliore che passa attraverso i punti. Il trucco è trovare la linea che passa più vicino ai miei punti. distanza GFP i GF ˆ P i a+ b(1µl) TET i
50 Cerco la linea che minimizza la somma al quadrato delle distanze, cioè che GFP i a btet i ( ) ( GFP N a btet N ) sia minima. Procedura per la regressione lineare y i = a+ bx i x 1, x,...,x N y 1,y,...,y N ˆ µ x ˆ µ y Clacolo b ˆ = x ˆ 1 a ˆ = ˆ µ y b ˆ ˆ µ x Errore standard di S.E. b = σ ˆ ˆ b ± S.E. b S xx ( )+...+ ( x N ˆ µ x )( y N ˆ µ y ) = S ( x 1 ˆ µ x ) ( x N ˆ µ x ) xx ( µ x ) y i ˆ µ y ˆ b σ ˆ = y a bx i i Posso testare l ipotesi nulla: H 0 : b = 0 ( ) ( y N a bx N ) EXCEL BOX N t = ˆ b S.E. b = b ˆ σ ˆ S xx p-value y i = a+ bx i Quanto è buona la linea? Residual sum of squares SS resid ( ) ( y N y ˆ N ) = y 1 y ˆ 1
51 Y ˆ y 1 Errore y 1 x i x Che relazione c è tra regressione lineare ed il coefficiente di correlazione? ( µ y ) ˆ y 1 R = y ˆ ˆ i y 1 ˆ r = R ( y N ˆ µ y ) = SS reg ( ) ( y N y ˆ N ) SS resid y ˆ EXCEL BOX LINREG(Y i :Y N ;X i :X N ;T RUE;TRUE) F =t TDIST( F i ; N-; )
52 LEZIONI DI STATISTICA Lezione 6: Metodi non parametrici Diego di Bernardo Edito da Vincenza Maselli
53 METODI NON-PARAMETRICI Tutto quello che abbiamo detto fino a questo punto è valido fino ad un certo punto, c è un piccolo imbroglio Abbiamo implicitamente assunto che le nostre misure avessero una distribuzione GAUSSIANA (o NORMALE). Che significa? Gene X Misure di espressione: a 1, a,,a N Gauss era sulla banconota da 10 marchi tedeschi I dati sono distribuiti come una gaussiana se l istogramma: E Simmetrico Ha forma a campana Max { a 1, a,,a N } Numero di volte che le nostre misure sono contenute in un questo intervallo Esempio: Gene X: 0,15 0,18 0, 0,14 0,0 0,31 0, ,1 0, 0,31 Se i dati non sono distribuiti come una gaussiana, TUTTO QUELLO CHE ABBIAMO DETTO NON È VALIDO! Cioè non possiamo fare t-test, anova, correlazione Cosa si può fare allora in questi casi? Imbroglio e me ne frego! (lo fanno in molti!!!)
54 Utilizzo metodi che non richiedono questa ipotesi.
55 WILCOXON SIGNED RANK Questo test è equivalente al t-test per una singola popolazione (T- DIST). Si usa per rispondere alla domanda: È LA MEDIA DELLA MIA MISURA DIVERSA DA ZERO? Esempio: è il gene X espresso nel topo wt? Procedura per il Wilcoxon Signed Rank: ho le mie misure (controllo che l istogramma sia più o meno simmetrico, non c è bisogno che sia a campana). H 0 : µ = 0 IPOTESI NULLA Calcoliamo ˆ µ x = a + a a 1 N N calcolo la differenza dei miei dati dalla media µ: d 1 = a 1 ˆ µ x d = a ˆ µ x d N = a N ˆ µ x calcolo i rank delle distanze: d 1 =1, ad esempio: se d = 0,8 d 3 =,4 d 4 = 0,9 li ordino dal più piccolo al più grande: R 1 = R( d 1 ) = 3 R = R( d ) = e quindi: R 3 = R d 3 ( ) = 4 ( ) =1 R 4 = R d 4 R 1,R,...,R N sono tutti numeri tra 1 e N d 4 < d < d1 < d3
56 calcolo la statistica d i > 0 S t = somma degli R i che hanno le differenze ( ) Osserva: N = N N +1 = R 1 + R R N Se la media µ = 0, cioè se H 0 è vera allora S t = N ( N +1 ) = R + R R 1 N 4 Esempio: x x x x x x x x x 0 x x x x x x x 0 Calcolo la σ di S t (perchè asumo che S t ha una distribuzione gaussiana, se uso un computer per fare i calcoli questa ipotesi non è necessaria). σ St = N ( N +1 )( N + ) 4 calcolo la statistica se Z > il p 0,04 Z = S t > N ( N +1 ) 4 ( ) S t < N N +1 4 S t N ( N +1 ) 4 = σ St S t N ( N +1 ) 4 N N +1 ( )( N + ) 4 oppure uso EXCEL EXCEL BOX Z > 0 Z < 0 *NORMDIST(Z) = p-value *(1-NORMDIST(Z)) = p-value
57 Se p 0,05 dico che espresso!!! H 0 : µ = 0 non è vera e quindi il mio gene è
58 MANN-WHITNEY TEST Si usa per confrontare la media tra due popolazioni. È l equivalente di un t-test. Esempio: è il gene X differenzialmente espresso in un topo wt e uno ko? a 1,a,...,a N b 1,b,...,b M wt ko PROCEDURA PER IL MANN-WITHNEY TEST: a 1,a,...,a N H 0 : µ A = µ B b 1,b,...,b M calcolo i rank R delle misure combinate cioè metto tutto assieme a 1,a,...,a N,b 1,b,...,b M. Ordino dal più piccolo al più grande e assegno i rank R 1,R,...R N +M Esempio: a 1 =1 a =,3 a 3 = 0,9 b 1 = 0,1 b =1,7 b 3 =1, R= b1 < a3 < a1 < b3 < b < a calcolo la statistica S A = soma degli R delle misure a Esempio: S A = R( a 1 )+ R( a )+ ( a 3 ) = =11 calcolo ( ) U A = S A N N +1
59 Esempio: U A =11 3 ( 3+1 ) U A varia tra 0 e NM =11 6 = 5 U A = 0 se tutte le misure a 1,a,...,a N sono sempre minori di b 1,b,...,b M U A = NM se a 1,a,...,a N sono sempre maggiori di b 1,b,...,b M Se H 0 è vera U A NM calcolo la statistica calcolo il p-value Z = U A NM NM M + N +1 ( ) 1 EXCEL BOX Z > 0 Z < 0 *NORMDIST(Z) = p-value *(1-NORMDIST(Z)) = p-value
60 KRUSKAL-WALLIS TEST Si usa per confrontare 3 o più popolazioni. È l equivalente dell ANOVA: Esempio: è il gene X differenzialmente espresso nel topo wt, O ed E? PROCEDURA PER IL KRUSKAL-WALLIS TEST: a 1,a,...,a N, b 1,b,...,b M c 1,c,...,c L Calcolo i rank delle misure combinatorie (come pr il MW test) R 1, R,...R N +M +L calcolo la media dei rank per le misure a, b e c, R a, R b e R c. calcolo la statistica H. 1 H = N + M + L calcolo il p-value ( )( N + M + L +1) NR a + MR ( b + LR c ) 3 N + M + L 1 ( ) EXCEL BOX CHIDIST(H,K) = p-value K = numero di popolazioni 1 (nel nostro esempio K = 3 1 = )
61 PARAMETRICI VERSO NON PARAMETRICI Parametrici Non Parametrici Singola Popolazione T-DIST WILCOXON SIGNED RANK Due Popolazioni T-TEST MANN-WHITNEY TEST Tre o più Popolazioni ANOVA KRUSKAL-WALLIS TEST Correlazione CORREL R PEARMAN RANK CORRELATION
Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B. Evento prodotto: Evento in cui si verifica sia A che B ; p(a&b) = p(a) x p(b/a)
 Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B Eventi indipendenti: un evento non influenza l altro Eventi disgiunti: il verificarsi di un evento esclude l altro Evento prodotto:
Probabilità condizionata: p(a/b) che avvenga A, una volta accaduto B Eventi indipendenti: un evento non influenza l altro Eventi disgiunti: il verificarsi di un evento esclude l altro Evento prodotto:
1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario:
 Esempi di domande risposta multipla (Modulo II) 1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario: 1) ha un numero di elementi pari a 5; 2) ha un numero di elementi
Esempi di domande risposta multipla (Modulo II) 1) Si consideri un esperimento che consiste nel lancio di 5 dadi. Lo spazio campionario: 1) ha un numero di elementi pari a 5; 2) ha un numero di elementi
Test statistici di verifica di ipotesi
 Test e verifica di ipotesi Test e verifica di ipotesi Il test delle ipotesi consente di verificare se, e quanto, una determinata ipotesi (di carattere biologico, medico, economico,...) è supportata dall
Test e verifica di ipotesi Test e verifica di ipotesi Il test delle ipotesi consente di verificare se, e quanto, una determinata ipotesi (di carattere biologico, medico, economico,...) è supportata dall
VARIABILI ALEATORIE CONTINUE
 VARIABILI ALEATORIE CONTINUE Se X è una variabile aleatoria continua, la probabilità che X assuma un certo valore x fissato è in generale zero, quindi non ha senso definire una distribuzione di probabilità
VARIABILI ALEATORIE CONTINUE Se X è una variabile aleatoria continua, la probabilità che X assuma un certo valore x fissato è in generale zero, quindi non ha senso definire una distribuzione di probabilità
LEZIONE n. 5 (a cura di Antonio Di Marco)
 LEZIONE n. 5 (a cura di Antonio Di Marco) IL P-VALUE (α) Data un ipotesi nulla (H 0 ), questa la si può accettare o rifiutare in base al valore del p- value. In genere il suo valore è un numero molto piccolo,
LEZIONE n. 5 (a cura di Antonio Di Marco) IL P-VALUE (α) Data un ipotesi nulla (H 0 ), questa la si può accettare o rifiutare in base al valore del p- value. In genere il suo valore è un numero molto piccolo,
Statistica. Lezione 6
 Università degli Studi del Piemonte Orientale Corso di Laurea in Infermieristica Corso integrato in Scienze della Prevenzione e dei Servizi sanitari Statistica Lezione 6 a.a 011-01 Dott.ssa Daniela Ferrante
Università degli Studi del Piemonte Orientale Corso di Laurea in Infermieristica Corso integrato in Scienze della Prevenzione e dei Servizi sanitari Statistica Lezione 6 a.a 011-01 Dott.ssa Daniela Ferrante
Elementi di Psicometria con Laboratorio di SPSS 1
 Elementi di Psicometria con Laboratorio di SPSS 1 12-Il t-test per campioni appaiati vers. 1.2 (7 novembre 2014) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
Elementi di Psicometria con Laboratorio di SPSS 1 12-Il t-test per campioni appaiati vers. 1.2 (7 novembre 2014) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
Elementi di Psicometria con Laboratorio di SPSS 1
 Elementi di Psicometria con Laboratorio di SPSS 1 29-Analisi della potenza statistica vers. 1.0 (12 dicembre 2014) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
Elementi di Psicometria con Laboratorio di SPSS 1 29-Analisi della potenza statistica vers. 1.0 (12 dicembre 2014) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
CAPITOLO 8 LA VERIFICA D IPOTESI. I FONDAMENTI
 VERO FALSO CAPITOLO 8 LA VERIFICA D IPOTESI. I FONDAMENTI 1. V F Un ipotesi statistica è un assunzione sulle caratteristiche di una o più variabili in una o più popolazioni 2. V F L ipotesi nulla unita
VERO FALSO CAPITOLO 8 LA VERIFICA D IPOTESI. I FONDAMENTI 1. V F Un ipotesi statistica è un assunzione sulle caratteristiche di una o più variabili in una o più popolazioni 2. V F L ipotesi nulla unita
Calcolo delle probabilità
 Calcolo delle probabilità Laboratorio di Bioinformatica Corso A aa 2005-2006 Statistica Dai risultati di un esperimento si determinano alcune caratteristiche della popolazione Calcolo delle probabilità
Calcolo delle probabilità Laboratorio di Bioinformatica Corso A aa 2005-2006 Statistica Dai risultati di un esperimento si determinano alcune caratteristiche della popolazione Calcolo delle probabilità
La variabile casuale Binomiale
 La variabile casuale Binomiale Si costruisce a partire dalla nozione di esperimento casuale Bernoulliano che consiste in un insieme di prove ripetute con le seguenti caratteristiche: i) ad ogni singola
La variabile casuale Binomiale Si costruisce a partire dalla nozione di esperimento casuale Bernoulliano che consiste in un insieme di prove ripetute con le seguenti caratteristiche: i) ad ogni singola
PROBABILITÀ - SCHEDA N. 2 LE VARIABILI ALEATORIE
 Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
Matematica e statistica: dai dati ai modelli alle scelte www.dima.unige/pls_statistica Responsabili scientifici M.P. Rogantin e E. Sasso (Dipartimento di Matematica Università di Genova) PROBABILITÀ -
Inferenza statistica. Statistica medica 1
 Inferenza statistica L inferenza statistica è un insieme di metodi con cui si cerca di trarre una conclusione sulla popolazione sulla base di alcune informazioni ricavate da un campione estratto da quella
Inferenza statistica L inferenza statistica è un insieme di metodi con cui si cerca di trarre una conclusione sulla popolazione sulla base di alcune informazioni ricavate da un campione estratto da quella
Elementi di Psicometria con Laboratorio di SPSS 1
 Elementi di Psicometria con Laboratorio di SPSS 1 10-Il test t per un campione e la stima intervallare (vers. 1.1, 25 ottobre 2015) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia,
Elementi di Psicometria con Laboratorio di SPSS 1 10-Il test t per un campione e la stima intervallare (vers. 1.1, 25 ottobre 2015) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia,
LEZIONE 3. Ing. Andrea Ghedi AA 2009/2010. Ing. Andrea Ghedi AA 2009/2010
 LEZIONE 3 "Educare significa aiutare l'animo dell'uomo ad entrare nella totalità della realtà. Non si può però educare se non rivolgendosi alla libertà, la quale definisce il singolo, l'io. Quando uno
LEZIONE 3 "Educare significa aiutare l'animo dell'uomo ad entrare nella totalità della realtà. Non si può però educare se non rivolgendosi alla libertà, la quale definisce il singolo, l'io. Quando uno
Test non parametrici. Test non parametrici. Test non parametrici. Test non parametrici
 Test non parametrici Test non parametrici Il test T di Student per uno o per due campioni, il test F di Fisher per l'analisi della varianza, la correlazione, la regressione, insieme ad altri test di statistica
Test non parametrici Test non parametrici Il test T di Student per uno o per due campioni, il test F di Fisher per l'analisi della varianza, la correlazione, la regressione, insieme ad altri test di statistica
Viene lanciata una moneta. Se esce testa vinco 100 euro, se esce croce non vinco niente. Quale è il valore della mia vincita?
 Viene lanciata una moneta. Se esce testa vinco 00 euro, se esce croce non vinco niente. Quale è il valore della mia vincita? Osserviamo che il valore della vincita dipende dal risultato dell esperimento
Viene lanciata una moneta. Se esce testa vinco 00 euro, se esce croce non vinco niente. Quale è il valore della mia vincita? Osserviamo che il valore della vincita dipende dal risultato dell esperimento
Statistica inferenziale
 Statistica inferenziale Popolazione e campione Molto spesso siamo interessati a trarre delle conclusioni su persone che hanno determinate caratteristiche (pazienti, atleti, bambini, gestanti, ) Osserveremo
Statistica inferenziale Popolazione e campione Molto spesso siamo interessati a trarre delle conclusioni su persone che hanno determinate caratteristiche (pazienti, atleti, bambini, gestanti, ) Osserveremo
Statistiche campionarie
 Statistiche campionarie Sul campione si possono calcolare le statistiche campionarie (come media campionaria, mediana campionaria, varianza campionaria,.) Le statistiche campionarie sono stimatori delle
Statistiche campionarie Sul campione si possono calcolare le statistiche campionarie (come media campionaria, mediana campionaria, varianza campionaria,.) Le statistiche campionarie sono stimatori delle
Statistica e biometria. D. Bertacchi. Variabili aleatorie. V.a. discrete e continue. La densità di una v.a. discreta. Esempi.
 Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Tasso di interesse e capitalizzazione
 Tasso di interesse e capitalizzazione Tasso di interesse = i = somma che devo restituire dopo un anno per aver preso a prestito un euro, in aggiunta alla restituzione dell euro iniziale Quindi: prendo
Tasso di interesse e capitalizzazione Tasso di interesse = i = somma che devo restituire dopo un anno per aver preso a prestito un euro, in aggiunta alla restituzione dell euro iniziale Quindi: prendo
Relazioni tra variabili
 Università degli Studi di Padova Facoltà di Medicina e Chirurgia Corso di Laurea in Medicina e Chirurgia - A.A. 009-10 Scuole di specializzazione in: Medicina Legale, Medicina del Lavoro, Igiene e Medicina
Università degli Studi di Padova Facoltà di Medicina e Chirurgia Corso di Laurea in Medicina e Chirurgia - A.A. 009-10 Scuole di specializzazione in: Medicina Legale, Medicina del Lavoro, Igiene e Medicina
RAPPRESENTAZIONE GRAFICA E ANALISI DEI DATI SPERIMENTALI CON EXCEL
 RAPPRESENTAZIONE GRAFICA E ANALISI DEI DATI SPERIMENTALI CON EXCEL 1 RAPPRESENTAZIONE GRAFICA Per l analisi dati con Excel si fa riferimento alla versione 2007 di Office, le versioni successive non differiscono
RAPPRESENTAZIONE GRAFICA E ANALISI DEI DATI SPERIMENTALI CON EXCEL 1 RAPPRESENTAZIONE GRAFICA Per l analisi dati con Excel si fa riferimento alla versione 2007 di Office, le versioni successive non differiscono
E naturale chiedersi alcune cose sulla media campionaria x n
 Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
Supponiamo che un fabbricante stia introducendo un nuovo tipo di batteria per un automobile elettrica. La durata osservata x i delle i-esima batteria è la realizzazione (valore assunto) di una variabile
Test d ipotesi. Statistica e biometria. D. Bertacchi. Test d ipotesi
 In molte situazioni una raccolta di dati (=esiti di esperimenti aleatori) viene fatta per prendere delle decisioni sulla base di quei dati. Ad esempio sperimentazioni su un nuovo farmaco per decidere se
In molte situazioni una raccolta di dati (=esiti di esperimenti aleatori) viene fatta per prendere delle decisioni sulla base di quei dati. Ad esempio sperimentazioni su un nuovo farmaco per decidere se
Capitolo 12 La regressione lineare semplice
 Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 12 La regressione lineare semplice Insegnamento: Statistica Corso di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara
Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 12 La regressione lineare semplice Insegnamento: Statistica Corso di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara
iovanella@disp.uniroma2.it http://www.disp.uniroma2.it/users/iovanella Verifica di ipotesi
 iovanella@disp.uniroma2.it http://www.disp.uniroma2.it/users/iovanella Verifica di ipotesi Idea di base Supponiamo di avere un idea del valore (incognito) di una media di un campione, magari attraverso
iovanella@disp.uniroma2.it http://www.disp.uniroma2.it/users/iovanella Verifica di ipotesi Idea di base Supponiamo di avere un idea del valore (incognito) di una media di un campione, magari attraverso
Esercitazione #5 di Statistica. Test ed Intervalli di Confidenza (per una popolazione)
 Esercitazione #5 di Statistica Test ed Intervalli di Confidenza (per una popolazione) Dicembre 00 1 Esercizi 1.1 Test su media (con varianza nota) Esercizio n. 1 Il calore (in calorie per grammo) emesso
Esercitazione #5 di Statistica Test ed Intervalli di Confidenza (per una popolazione) Dicembre 00 1 Esercizi 1.1 Test su media (con varianza nota) Esercizio n. 1 Il calore (in calorie per grammo) emesso
Facciamo qualche precisazione
 Abbiamo introdotto alcuni indici statistici (di posizione, di variabilità e di forma) ottenibili da Excel con la funzione Riepilogo Statistiche Facciamo qualche precisazione Al fine della partecipazione
Abbiamo introdotto alcuni indici statistici (di posizione, di variabilità e di forma) ottenibili da Excel con la funzione Riepilogo Statistiche Facciamo qualche precisazione Al fine della partecipazione
Metodi statistici per le ricerche di mercato
 Metodi statistici per le ricerche di mercato Prof.ssa Isabella Mingo A.A. 2014-2015 Facoltà di Scienze Politiche, Sociologia, Comunicazione Corso di laurea Magistrale in «Organizzazione e marketing per
Metodi statistici per le ricerche di mercato Prof.ssa Isabella Mingo A.A. 2014-2015 Facoltà di Scienze Politiche, Sociologia, Comunicazione Corso di laurea Magistrale in «Organizzazione e marketing per
Esercizi test ipotesi. Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010
 Esercizi test ipotesi Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Verifica delle ipotesi - Esempio quelli di Striscia la Notizia" effettuano controlli casuali per vedere se le pompe
Esercizi test ipotesi Prof. Raffaella Folgieri Email: folgieri@mtcube.com aa 2009/2010 Verifica delle ipotesi - Esempio quelli di Striscia la Notizia" effettuano controlli casuali per vedere se le pompe
VERIFICA DELLE IPOTESI
 VERIFICA DELLE IPOTESI Nella verifica delle ipotesi è necessario fissare alcune fasi prima di iniziare ad analizzare i dati. a) Si deve stabilire quale deve essere l'ipotesi nulla (H0) e quale l'ipotesi
VERIFICA DELLE IPOTESI Nella verifica delle ipotesi è necessario fissare alcune fasi prima di iniziare ad analizzare i dati. a) Si deve stabilire quale deve essere l'ipotesi nulla (H0) e quale l'ipotesi
Calcolo delle Probabilità
 Calcolo delle Probabilità Il calcolo delle probabilità studia i modelli matematici delle cosidette situazioni di incertezza. Molte situazioni concrete sono caratterizzate a priori da incertezza su quello
Calcolo delle Probabilità Il calcolo delle probabilità studia i modelli matematici delle cosidette situazioni di incertezza. Molte situazioni concrete sono caratterizzate a priori da incertezza su quello
L analisi dei rischi: l aspetto statistico Ing. Pier Giorgio DELLA ROLE Six Sigma Master Black Belt
 L analisi dei rischi: l aspetto statistico Ing. Pier Giorgio DELL ROLE Six Sigma Master lack elt Dicembre, 009 Introduzione Nell esecuzione dei progetti Six Sigma è di fondamentale importanza sapere se
L analisi dei rischi: l aspetto statistico Ing. Pier Giorgio DELL ROLE Six Sigma Master lack elt Dicembre, 009 Introduzione Nell esecuzione dei progetti Six Sigma è di fondamentale importanza sapere se
Università del Piemonte Orientale. Corsi di Specialità. Corso di Statistica Medica. Analisi dei dati quantitativi : Analisi della varianza
 Università del Piemonte Orientale Corsi di Specialità Corso di Statistica Medica Analisi dei dati quantitativi : Analisi della varianza Università del Piemonte Orientale Corso di laurea in biotecnologie
Università del Piemonte Orientale Corsi di Specialità Corso di Statistica Medica Analisi dei dati quantitativi : Analisi della varianza Università del Piemonte Orientale Corso di laurea in biotecnologie
La categoria «ES» presenta (di solito) gli stessi comandi
 Utilizzo delle calcolatrici FX 991 ES+ Parte II PARMA, 11 Marzo 2014 Prof. Francesco Bologna bolfra@gmail.com ARGOMENTI DELLA LEZIONE 1. Richiami lezione precedente 2.Calcolo delle statistiche di regressione:
Utilizzo delle calcolatrici FX 991 ES+ Parte II PARMA, 11 Marzo 2014 Prof. Francesco Bologna bolfra@gmail.com ARGOMENTI DELLA LEZIONE 1. Richiami lezione precedente 2.Calcolo delle statistiche di regressione:
Indici di dispersione
 Indici di dispersione 1 Supponiamo di disporre di un insieme di misure e di cercare un solo valore che, meglio di ciascun altro, sia in grado di catturare le caratteristiche della distribuzione nel suo
Indici di dispersione 1 Supponiamo di disporre di un insieme di misure e di cercare un solo valore che, meglio di ciascun altro, sia in grado di catturare le caratteristiche della distribuzione nel suo
Corso di Laurea in Scienze e Tecnologie Biomolecolari. NOME COGNOME N. Matr.
 Corso di Laurea in Scienze e Tecnologie Biomolecolari Matematica e Statistica II Prova di esame dell 11/1/2012 NOME COGNOME N. Matr. Rispondere alle domande nel modo più completo possibile, cercando di
Corso di Laurea in Scienze e Tecnologie Biomolecolari Matematica e Statistica II Prova di esame dell 11/1/2012 NOME COGNOME N. Matr. Rispondere alle domande nel modo più completo possibile, cercando di
OSSERVAZIONI TEORICHE Lezione n. 4
 OSSERVAZIONI TEORICHE Lezione n. 4 Finalità: Sistematizzare concetti e definizioni. Verificare l apprendimento. Metodo: Lettura delle OSSERVAZIONI e risoluzione della scheda di verifica delle conoscenze
OSSERVAZIONI TEORICHE Lezione n. 4 Finalità: Sistematizzare concetti e definizioni. Verificare l apprendimento. Metodo: Lettura delle OSSERVAZIONI e risoluzione della scheda di verifica delle conoscenze
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Elementi di Psicometria con Laboratorio di SPSS 1
 Elementi di Psicometria con Laboratorio di SPSS 1 5-Indici di variabilità (vers. 1.0c, 20 ottobre 2015) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
Elementi di Psicometria con Laboratorio di SPSS 1 5-Indici di variabilità (vers. 1.0c, 20 ottobre 2015) Germano Rossi 1 germano.rossi@unimib.it 1 Dipartimento di Psicologia, Università di Milano-Bicocca
Matematica Applicata. Probabilità e statistica
 Matematica Applicata Probabilità e statistica Fenomeni casuali Fenomeni che si verificano in modi non prevedibili a priori 1. Lancio di una moneta: non sono in grado di prevedere con certezza se il risultato
Matematica Applicata Probabilità e statistica Fenomeni casuali Fenomeni che si verificano in modi non prevedibili a priori 1. Lancio di una moneta: non sono in grado di prevedere con certezza se il risultato
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
3. Confronto tra medie di due campioni indipendenti o appaiati
 BIOSTATISTICA 3. Confronto tra medie di due campioni indipendenti o appaiati Marta Blangiardo, Imperial College, London Department of Epidemiology and Public Health m.blangiardo@imperial.ac.uk MARTA BLANGIARDO
BIOSTATISTICA 3. Confronto tra medie di due campioni indipendenti o appaiati Marta Blangiardo, Imperial College, London Department of Epidemiology and Public Health m.blangiardo@imperial.ac.uk MARTA BLANGIARDO
8 Elementi di Statistica
 8 Elementi di Statistica La conoscenza di alcuni elementi di statistica e di analisi degli errori è importante quando si vogliano realizzare delle osservazioni sperimentali significative, ed anche per
8 Elementi di Statistica La conoscenza di alcuni elementi di statistica e di analisi degli errori è importante quando si vogliano realizzare delle osservazioni sperimentali significative, ed anche per
L Analisi della Varianza ANOVA (ANalysis Of VAriance)
 L Analisi della Varianza ANOVA (ANalysis Of VAriance) 1 CONCETTI GENERALI Finora abbiamo descritto test di ipotesi finalizzati alla verifica di ipotesi sulla differenza tra parametri di due popolazioni
L Analisi della Varianza ANOVA (ANalysis Of VAriance) 1 CONCETTI GENERALI Finora abbiamo descritto test di ipotesi finalizzati alla verifica di ipotesi sulla differenza tra parametri di due popolazioni
La distribuzione Gaussiana
 Università del Piemonte Orientale Corso di Laurea in Biotecnologie Corso di Statistica Medica La distribuzione Normale (o di Gauss) Corso di laurea in biotecnologie - Corso di Statistica Medica La distribuzione
Università del Piemonte Orientale Corso di Laurea in Biotecnologie Corso di Statistica Medica La distribuzione Normale (o di Gauss) Corso di laurea in biotecnologie - Corso di Statistica Medica La distribuzione
2 CERTAMEN NAZIONALE DI PROBABILITA E STATISTICA FELICE FUSATO Fase di Istituto 15 febbraio 2011
 2 CERTAMEN NAZIONALE DI PROBABILITA E STATISTICA FELICE FUSATO Fase di Istituto 15 febbraio 2011 1) Non sfogliare questo fascicolo finché l insegnante non ti dice di farlo. 2) E ammesso l utilizzo di calcolatrici
2 CERTAMEN NAZIONALE DI PROBABILITA E STATISTICA FELICE FUSATO Fase di Istituto 15 febbraio 2011 1) Non sfogliare questo fascicolo finché l insegnante non ti dice di farlo. 2) E ammesso l utilizzo di calcolatrici
Esame di Statistica del 17 luglio 2006 (Corso di Laurea Triennale in Biotecnologie, Università degli Studi di Padova).
 Esame di Statistica del 17 luglio 2006 (Corso di Laurea Triennale in Biotecnologie, Università degli Studi di Padova). Cognome Nome Matricola Es. 1 Es. 2 Es. 3 Es. 4 Somma Voto finale Attenzione: si consegnano
Esame di Statistica del 17 luglio 2006 (Corso di Laurea Triennale in Biotecnologie, Università degli Studi di Padova). Cognome Nome Matricola Es. 1 Es. 2 Es. 3 Es. 4 Somma Voto finale Attenzione: si consegnano
STATISTICA IX lezione
 Anno Accademico 013-014 STATISTICA IX lezione 1 Il problema della verifica di un ipotesi statistica In termini generali, si studia la distribuzione T(X) di un opportuna grandezza X legata ai parametri
Anno Accademico 013-014 STATISTICA IX lezione 1 Il problema della verifica di un ipotesi statistica In termini generali, si studia la distribuzione T(X) di un opportuna grandezza X legata ai parametri
Corso di Psicometria Progredito
 Corso di Psicometria Progredito 3.1 Introduzione all inferenza statistica Prima Parte Gianmarco Altoè Dipartimento di Pedagogia, Psicologia e Filosofia Università di Cagliari, Anno Accademico 2013-2014
Corso di Psicometria Progredito 3.1 Introduzione all inferenza statistica Prima Parte Gianmarco Altoè Dipartimento di Pedagogia, Psicologia e Filosofia Università di Cagliari, Anno Accademico 2013-2014
RELAZIONE TRA VARIABILI QUANTITATIVE. Lezione 7 a. Accade spesso nella ricerca in campo biomedico, così come in altri campi della
 RELAZIONE TRA VARIABILI QUANTITATIVE Lezione 7 a Accade spesso nella ricerca in campo biomedico, così come in altri campi della scienza, di voler studiare come il variare di una o più variabili (variabili
RELAZIONE TRA VARIABILI QUANTITATIVE Lezione 7 a Accade spesso nella ricerca in campo biomedico, così come in altri campi della scienza, di voler studiare come il variare di una o più variabili (variabili
Probabilità discreta
 Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
= variazione diviso valore iniziale, il tutto moltiplicato per 100. \ Esempio: PIL del 2000 = 500; PIL del 2001 = 520:
 Fig. 10.bis.1 Variazioni percentuali Variazione percentuale di x dalla data zero alla data uno: x1 x 0 %x = 100% x 0 = variazione diviso valore iniziale, il tutto moltiplicato per 100. \ Esempio: PIL del
Fig. 10.bis.1 Variazioni percentuali Variazione percentuale di x dalla data zero alla data uno: x1 x 0 %x = 100% x 0 = variazione diviso valore iniziale, il tutto moltiplicato per 100. \ Esempio: PIL del
Statistica. Esercitazione 15. Alfonso Iodice D Enza iodicede@unicas.it. Università degli studi di Cassino. Statistica. A. Iodice
 Esercitazione 15 Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () 1 / 18 L importanza del gruppo di controllo In tutti i casi in cui si voglia studiare l effetto di un certo
Esercitazione 15 Alfonso Iodice D Enza iodicede@unicas.it Università degli studi di Cassino () 1 / 18 L importanza del gruppo di controllo In tutti i casi in cui si voglia studiare l effetto di un certo
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
PROGRAMMA SVOLTO NELLA SESSIONE N.
 Università C. Cattaneo Liuc, Corso di Statistica, Sessione n. 1, 2014 Laboratorio Excel Sessione n. 1 Venerdì 031014 Gruppo PZ Lunedì 061014 Gruppo AD Martedì 071014 Gruppo EO PROGRAMMA SVOLTO NELLA SESSIONE
Università C. Cattaneo Liuc, Corso di Statistica, Sessione n. 1, 2014 Laboratorio Excel Sessione n. 1 Venerdì 031014 Gruppo PZ Lunedì 061014 Gruppo AD Martedì 071014 Gruppo EO PROGRAMMA SVOLTO NELLA SESSIONE
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Corso di Laurea in Scienze e Tecnologie Biomolecolari. NOME COGNOME N. Matr.
 Corso di Laurea in Scienze e Tecnologie Biomolecolari Matematica e Statistica II Prova di esame del 18/7/2013 NOME COGNOME N. Matr. Rispondere ai punti degli esercizi nel modo più completo possibile, cercando
Corso di Laurea in Scienze e Tecnologie Biomolecolari Matematica e Statistica II Prova di esame del 18/7/2013 NOME COGNOME N. Matr. Rispondere ai punti degli esercizi nel modo più completo possibile, cercando
Tema A. 1.2. Se due eventi A e B sono indipendenti e tali che P (A) = 1/2 e P (B) = 2/3, si può certamente concludere che
 Statistica Cognome: Laurea Triennale in Biologia Nome: 26 luglio 2012 Matricola: Tema A 1. Parte A 1.1. Sia x 1, x 2,..., x n un campione di n dati con media campionaria x e varianza campionaria s 2 x
Statistica Cognome: Laurea Triennale in Biologia Nome: 26 luglio 2012 Matricola: Tema A 1. Parte A 1.1. Sia x 1, x 2,..., x n un campione di n dati con media campionaria x e varianza campionaria s 2 x
Piacenza, 10 marzo 2014 La preparazione della tesi di Laurea Magistrale
 Piacenza, 0 marzo 204 La preparazione della tesi di Laurea Magistrale ma questa statistica a che cosa serve? non vedo l ora di cominciare a lavorare per la tesi. e dimenticarmi la statistica!! il mio relatore
Piacenza, 0 marzo 204 La preparazione della tesi di Laurea Magistrale ma questa statistica a che cosa serve? non vedo l ora di cominciare a lavorare per la tesi. e dimenticarmi la statistica!! il mio relatore
Analisi di scenario File Nr. 10
 1 Analisi di scenario File Nr. 10 Giorgio Calcagnini Università di Urbino Dip. Economia, Società, Politica giorgio.calcagnini@uniurb.it http://www.econ.uniurb.it/calcagnini/ http://www.econ.uniurb.it/calcagnini/forecasting.html
1 Analisi di scenario File Nr. 10 Giorgio Calcagnini Università di Urbino Dip. Economia, Società, Politica giorgio.calcagnini@uniurb.it http://www.econ.uniurb.it/calcagnini/ http://www.econ.uniurb.it/calcagnini/forecasting.html
UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA
 UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA Tutti gli anni, affrontando l argomento della divisibilità, trovavo utile far lavorare gli alunni sul Crivello di Eratostene. Presentavo ai ragazzi una
UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA Tutti gli anni, affrontando l argomento della divisibilità, trovavo utile far lavorare gli alunni sul Crivello di Eratostene. Presentavo ai ragazzi una
Metodi statistici per l economia (Prof. Capitanio) Slide n. 9. Materiale di supporto per le lezioni. Non sostituisce il libro di testo
 Metodi statistici per l economia (Prof. Capitanio) Slide n. 9 Materiale di supporto per le lezioni. Non sostituisce il libro di testo 1 TEST D IPOTESI Partiamo da un esempio presente sul libro di testo.
Metodi statistici per l economia (Prof. Capitanio) Slide n. 9 Materiale di supporto per le lezioni. Non sostituisce il libro di testo 1 TEST D IPOTESI Partiamo da un esempio presente sul libro di testo.
Relazioni statistiche: regressione e correlazione
 Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
Corso di Laurea in Ingegneria Informatica e Automatica (A-O) Università di Roma La Sapienza
 Corso di Laurea in Ingegneria Informatica e Automatica (A-O) Università di Roma La Sapienza CALCOLO DELLE PROBABILITÀ E STATISTICA ESAME DEL 17/06/2015 NOME: COGNOME: MATRICOLA: Esercizio 1 Un sistema
Corso di Laurea in Ingegneria Informatica e Automatica (A-O) Università di Roma La Sapienza CALCOLO DELLE PROBABILITÀ E STATISTICA ESAME DEL 17/06/2015 NOME: COGNOME: MATRICOLA: Esercizio 1 Un sistema
Distribuzioni discrete
 Distribuzioni discrete Esercitazione 4 novembre 003 Distribuzione binomiale Si fa un esperimento (o prova): può manifestarsi un certo evento A con probabilità p oppure no (con probabilità q = p). La distribuzione
Distribuzioni discrete Esercitazione 4 novembre 003 Distribuzione binomiale Si fa un esperimento (o prova): può manifestarsi un certo evento A con probabilità p oppure no (con probabilità q = p). La distribuzione
PROBABILITA CONDIZIONALE
 Riferendoci al lancio di un dado, indichiamo con A l evento esce un punteggio inferiore a 4 A ={1, 2, 3} B l evento esce un punteggio dispari B = {1, 3, 5} Non avendo motivo per ritenere il dado truccato,
Riferendoci al lancio di un dado, indichiamo con A l evento esce un punteggio inferiore a 4 A ={1, 2, 3} B l evento esce un punteggio dispari B = {1, 3, 5} Non avendo motivo per ritenere il dado truccato,
matematica probabilmente
 IS science centre immaginario scientifico Laboratorio dell'immaginario Scientifico - Trieste tel. 040224424 - fax 040224439 - e-mail: lis@lis.trieste.it - www.immaginarioscientifico.it indice Altezze e
IS science centre immaginario scientifico Laboratorio dell'immaginario Scientifico - Trieste tel. 040224424 - fax 040224439 - e-mail: lis@lis.trieste.it - www.immaginarioscientifico.it indice Altezze e
Lineamenti di econometria 2
 Lineamenti di econometria 2 Camilla Mastromarco Università di Lecce Master II Livello "Analisi dei Mercati e Sviluppo Locale" (PIT 9.4) Aspetti Statistici della Regressione Aspetti Statistici della Regressione
Lineamenti di econometria 2 Camilla Mastromarco Università di Lecce Master II Livello "Analisi dei Mercati e Sviluppo Locale" (PIT 9.4) Aspetti Statistici della Regressione Aspetti Statistici della Regressione
ANALISI DELLE FREQUENZE: IL TEST CHI 2
 ANALISI DELLE FREQUENZE: IL TEST CHI 2 Quando si hanno scale nominali o ordinali, non è possibile calcolare il t, poiché non abbiamo medie, ma solo frequenze. In questi casi, per verificare se un evento
ANALISI DELLE FREQUENZE: IL TEST CHI 2 Quando si hanno scale nominali o ordinali, non è possibile calcolare il t, poiché non abbiamo medie, ma solo frequenze. In questi casi, per verificare se un evento
Analizza/Confronta medie. ELEMENTI DI PSICOMETRIA Esercitazione n. 7-8-9-107. Test t. Test t. t-test test e confronto tra medie chi quadrato
 Analizza/Confronta medie ELEMENTI DI PSICOMETRIA Esercitazione n. 7-8-9-107 t-test test e confronto tra medie chi quadrato C.d.L. Comunicazione e Psicologia a.a. 2008/09 Medie Calcola medie e altre statistiche
Analizza/Confronta medie ELEMENTI DI PSICOMETRIA Esercitazione n. 7-8-9-107 t-test test e confronto tra medie chi quadrato C.d.L. Comunicazione e Psicologia a.a. 2008/09 Medie Calcola medie e altre statistiche
Regressione Mario Guarracino Data Mining a.a. 2010/2011
 Regressione Esempio Un azienda manifatturiera vuole analizzare il legame che intercorre tra il volume produttivo X per uno dei propri stabilimenti e il corrispondente costo mensile Y di produzione. Volume
Regressione Esempio Un azienda manifatturiera vuole analizzare il legame che intercorre tra il volume produttivo X per uno dei propri stabilimenti e il corrispondente costo mensile Y di produzione. Volume
STATISTICA GIUSEPPE DE NICOLAO. Dipartimento di Informatica e Sistemistica Università di Pavia
 STATISTICA GIUSEPPE DE NICOLAO Dipartimento di Informatica e Sistemistica Università di Pavia SOMMARIO V.C. vettoriali Media e varianza campionarie Proprietà degli stimatori Intervalli di confidenza Statistica
STATISTICA GIUSEPPE DE NICOLAO Dipartimento di Informatica e Sistemistica Università di Pavia SOMMARIO V.C. vettoriali Media e varianza campionarie Proprietà degli stimatori Intervalli di confidenza Statistica
PROBABILITA MISURARE L INCERTEZZA Lanciamo due dadi, facciamo la somma dei punteggi ottenuti. Su quale numero mi conviene scommettere?
 Lanciamo due dadi, facciamo la somma dei punteggi ottenuti. Su quale numero mi conviene scommettere? Abbiamo visto nella lezione precedente che lo spazio degli eventi più idoneo a rappresentare l esperimento
Lanciamo due dadi, facciamo la somma dei punteggi ottenuti. Su quale numero mi conviene scommettere? Abbiamo visto nella lezione precedente che lo spazio degli eventi più idoneo a rappresentare l esperimento
Probabilità II Variabili casuali discrete
 Probabilità II Variabili casuali discrete Definizioni principali. Valore atteso e Varianza. Teorema di Bienaymé - Čebičev. V.C. Notevoli: Bernoulli e Binomiale. Concetto di variabile casuale Cos'è una
Probabilità II Variabili casuali discrete Definizioni principali. Valore atteso e Varianza. Teorema di Bienaymé - Čebičev. V.C. Notevoli: Bernoulli e Binomiale. Concetto di variabile casuale Cos'è una
Excel Terza parte. Excel 2003
 Excel Terza parte Excel 2003 TABELLA PIVOT Selezioniamo tutti i dati (con le relative etichette) Dati Rapporto tabella pivot e grafico pivot Fine 2 La tabella pivot viene messa di default in una pagina
Excel Terza parte Excel 2003 TABELLA PIVOT Selezioniamo tutti i dati (con le relative etichette) Dati Rapporto tabella pivot e grafico pivot Fine 2 La tabella pivot viene messa di default in una pagina
ANALISI DI CORRELAZIONE
 ANALISI DI CORRELAZIONE Esempio: Dati raccolti da n = 129 studenti di Pavia (A.A. 21/2) Altezza (cm) Peso (Kg) Voto Algebra e Geometria Voto Fisica I Valutare la correlazione delle seguenti coppie: Peso
ANALISI DI CORRELAZIONE Esempio: Dati raccolti da n = 129 studenti di Pavia (A.A. 21/2) Altezza (cm) Peso (Kg) Voto Algebra e Geometria Voto Fisica I Valutare la correlazione delle seguenti coppie: Peso
Abbiamo costruito il grafico delle sst in funzione del tempo (dal 1880 al 1995).
 ANALISI DI UNA SERIE TEMPORALE Analisi statistica elementare Abbiamo costruito il grafico delle sst in funzione del tempo (dal 1880 al 1995). Si puo' osservare una media di circa 26 C e una deviazione
ANALISI DI UNA SERIE TEMPORALE Analisi statistica elementare Abbiamo costruito il grafico delle sst in funzione del tempo (dal 1880 al 1995). Si puo' osservare una media di circa 26 C e una deviazione
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
PROBABILITA. Sono esempi di fenomeni la cui realizzazione non è certa a priori e vengono per questo detti eventi aleatori (dal latino alea, dado)
 L esito della prossima estrazione del lotto L esito del lancio di una moneta o di un dado Il sesso di un nascituro, così come il suo peso alla nascita o la sua altezza.. Il tempo di attesa ad uno sportello
L esito della prossima estrazione del lotto L esito del lancio di una moneta o di un dado Il sesso di un nascituro, così come il suo peso alla nascita o la sua altezza.. Il tempo di attesa ad uno sportello
La logica statistica della verifica (test) delle ipotesi
 La logica statistica della verifica (test) delle ipotesi Come posso confrontare diverse ipotesi? Nella statistica inferenziale classica vengono sempre confrontate due ipotesi: l ipotesi nulla e l ipotesi
La logica statistica della verifica (test) delle ipotesi Come posso confrontare diverse ipotesi? Nella statistica inferenziale classica vengono sempre confrontate due ipotesi: l ipotesi nulla e l ipotesi
MATEMATICA 2001. p = 4/6 = 2/3; q = 1-2/3 = 1/3. La risposta corretta è quindi la E).
 MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
PROVE D'ESAME DI CPS A.A. 2009/2010. 0 altrimenti.
 PROVE D'ESAME DI CPS A.A. 009/00 0/06/00 () (4pt) Olimpiadi, nale dei 00m maschili, 8 nalisti. Si sa che i 4 atleti nelle corsie centrali hanno probabilità di correre in meno di 0 secondi. I 4 atleti delle
PROVE D'ESAME DI CPS A.A. 009/00 0/06/00 () (4pt) Olimpiadi, nale dei 00m maschili, 8 nalisti. Si sa che i 4 atleti nelle corsie centrali hanno probabilità di correre in meno di 0 secondi. I 4 atleti delle
IL MODELLO CICLICO BATTLEPLAN
 www.previsioniborsa.net 3 Lezione METODO CICLICO IL MODELLO CICLICO BATTLEPLAN Questo modello ciclico teorico (vedi figura sotto) ci serve per pianificare la nostra operativita e prevedere quando il mercato
www.previsioniborsa.net 3 Lezione METODO CICLICO IL MODELLO CICLICO BATTLEPLAN Questo modello ciclico teorico (vedi figura sotto) ci serve per pianificare la nostra operativita e prevedere quando il mercato
LA STATISTICA si interessa del rilevamento, dell elaborazione e dello studio dei dati; studia ciò che accade o come è fatto un gruppo numeroso di
 STATISTICA LA STATISTICA si interessa del rilevamento, dell elaborazione e dello studio dei dati; studia ciò che accade o come è fatto un gruppo numeroso di oggetti; cerca, attraverso l uso della matematica
STATISTICA LA STATISTICA si interessa del rilevamento, dell elaborazione e dello studio dei dati; studia ciò che accade o come è fatto un gruppo numeroso di oggetti; cerca, attraverso l uso della matematica
Tabella iniziale con i dati. Malattia Malati Non malati Totale Test Positivo 183 Negativo 280 Totale 199 512. Calcolo i valori mancanti per differenza
 ESERCIZIO DI STATISTICA D.U. / simulazione di esame Esercizio 1: Per una malattia particolarmente grave viene sperimentato l utilizzo di una nuova tecnica radiologica allo scopo di identificare correttamente
ESERCIZIO DI STATISTICA D.U. / simulazione di esame Esercizio 1: Per una malattia particolarmente grave viene sperimentato l utilizzo di una nuova tecnica radiologica allo scopo di identificare correttamente
Cosa dobbiamo già conoscere?
 Cosa dobbiamo già conoscere? Insiemistica (operazioni, diagrammi...). Insiemi finiti/numerabili/non numerabili. Perché la probabilità? In molti esperimenti l esito non è noto a priori tuttavia si sa dire
Cosa dobbiamo già conoscere? Insiemistica (operazioni, diagrammi...). Insiemi finiti/numerabili/non numerabili. Perché la probabilità? In molti esperimenti l esito non è noto a priori tuttavia si sa dire
ANALISI DEI DATI EPIDEMIOLOGICI
 ANALISI DEI DATI EPIDEMIOLOGICI Cenni di statistica Che cosa è la statistica Statistica descrittiva e statistica inferenziale Test statistici di ipotesi Intervalli di confidenza Analisi stratificata TEST
ANALISI DEI DATI EPIDEMIOLOGICI Cenni di statistica Che cosa è la statistica Statistica descrittiva e statistica inferenziale Test statistici di ipotesi Intervalli di confidenza Analisi stratificata TEST
Probabilità e statistica
 Indice generale.probabilità ed eventi aleatori....come si può definire una probabilità....eventi equiprobabili....eventi indipendenti, eventi dipendenti....eventi incompatibili....eventi compatibili....probabilità
Indice generale.probabilità ed eventi aleatori....come si può definire una probabilità....eventi equiprobabili....eventi indipendenti, eventi dipendenti....eventi incompatibili....eventi compatibili....probabilità
Esercitazione n.2 Inferenza su medie
 Esercitazione n.2 Esercizio L ufficio del personale di una grande società intende stimare le spese mediche familiari dei suoi impiegati per valutare la possibilità di attuare un programma di assicurazione
Esercitazione n.2 Esercizio L ufficio del personale di una grande società intende stimare le spese mediche familiari dei suoi impiegati per valutare la possibilità di attuare un programma di assicurazione
Esercizi. Rappresentando le estrazioni con un grafo ad albero, calcolare la probabilità che:
 Esercizi Esercizio 4. Un urna contiene inizialmente 2 palline bianche e 4 palline rosse. Si effettuano due estrazioni con la seguente modalità: se alla prima estrazione esce una pallina bianca, la si rimette
Esercizi Esercizio 4. Un urna contiene inizialmente 2 palline bianche e 4 palline rosse. Si effettuano due estrazioni con la seguente modalità: se alla prima estrazione esce una pallina bianca, la si rimette
Un po di statistica. Christian Ferrari. Laboratorio di Matematica
 Un po di statistica Christian Ferrari Laboratorio di Matematica 1 Introduzione La statistica è una parte della matematica applicata che si occupa della raccolta, dell analisi e dell interpretazione di
Un po di statistica Christian Ferrari Laboratorio di Matematica 1 Introduzione La statistica è una parte della matematica applicata che si occupa della raccolta, dell analisi e dell interpretazione di
PROBABILITA CONDIZIONALE
 Riferendoci al lancio di un dado, indichiamo con A l evento esce un punteggio inferiore a 4 A ={1, 2, 3} B l evento esce un punteggio dispari B = {1, 3, 5} Non avendo motivo per ritenere il dado truccato,
Riferendoci al lancio di un dado, indichiamo con A l evento esce un punteggio inferiore a 4 A ={1, 2, 3} B l evento esce un punteggio dispari B = {1, 3, 5} Non avendo motivo per ritenere il dado truccato,
MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE. 23 novembre 2006
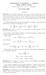 MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE PRIMO COMPITINO FILA B SOLUZIONI 3 novembre 006. Parte I Esercizio.. Al mercato della frutta i prezzi sono scontati rispetto ai prezzi nei supermercati.
MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE PRIMO COMPITINO FILA B SOLUZIONI 3 novembre 006. Parte I Esercizio.. Al mercato della frutta i prezzi sono scontati rispetto ai prezzi nei supermercati.
Confronto tra gruppi (campioni indipendenti)
 Confronto tra gruppi (campioni indipendenti) Campioni provenienti da una popolazione Normale con medie che possono essere diverse ma varianze uguali campioni: Test z or t sulla differenza tra medie 3,
Confronto tra gruppi (campioni indipendenti) Campioni provenienti da una popolazione Normale con medie che possono essere diverse ma varianze uguali campioni: Test z or t sulla differenza tra medie 3,
DISTRIBUZIONI DI VARIABILI CASUALI DISCRETE
 DISTRIBUZIONI DI VARIABILI CASUALI DISCRETE variabile casuale (rv): regola che associa un numero ad ogni evento di uno spazio E. variabile casuale di Bernoulli: rv che può assumere solo due valori (e.g.,
DISTRIBUZIONI DI VARIABILI CASUALI DISCRETE variabile casuale (rv): regola che associa un numero ad ogni evento di uno spazio E. variabile casuale di Bernoulli: rv che può assumere solo due valori (e.g.,
ORDINALI E NOMINALI LA PROBABILITÀ. Nell ambito della manifestazione di un fenomeno niente è certo, tutto è probabile.
 ORDINALI E NOMINALI LA PROBABILITÀ Statistica5 23/10/13 Nell ambito della manifestazione di un fenomeno niente è certo, tutto è probabile. Se si afferma che un vitello di razza chianina pesa 780 kg a 18
ORDINALI E NOMINALI LA PROBABILITÀ Statistica5 23/10/13 Nell ambito della manifestazione di un fenomeno niente è certo, tutto è probabile. Se si afferma che un vitello di razza chianina pesa 780 kg a 18
Metodi Matematici e Informatici per la Biologia----31 Maggio 2010
 Metodi Matematici e Informatici per la Biologia----31 Maggio 2010 COMPITO 4 (3 CREDITI) Nome: Cognome: Matricola: ISTRUZIONI Gli esercizi che seguono sono di tre tipi: Domande Vero/Falso: cerchiate V o
Metodi Matematici e Informatici per la Biologia----31 Maggio 2010 COMPITO 4 (3 CREDITI) Nome: Cognome: Matricola: ISTRUZIONI Gli esercizi che seguono sono di tre tipi: Domande Vero/Falso: cerchiate V o
