Soluzioni. Se l interallo avesse livello di confidenza 99%, al posto di 1,96 avremmo
|
|
|
- Battistina Moroni
- 7 anni fa
- Visualizzazioni
Transcript
1 Esercizio 1 Soluzioi 1. Ricordiamo che l ampiezza di u itervallo di cofideza è fuzioe della umerosità campioaria edellivellodicofideza. Aparità di tutto il resto, l ampiezza dimiuisce al crescere di eaumetaal crescere di 1 α. Quidi, se da 1 α =0, 9 si passa a 1 α=0,99 l ampiezza aumeta, ma per compesare questo aumeto possiamo far crescere. Sia R la variabile casuale che descrive il reddito di u abitate della cittadia. I base alle ipotesi del problema, R N(µ, σ )coσ ota. U itervallo di cofideza per µ al livello 9% co =100è σ σ x 1, 96, x +1, L ampiezza dell itervallo è 1, 96 σ 10 Se l iterallo avesse livello di cofideza 99%, al posto di 1,96 avremmo z 0,99 =, 76 e l ampiezza dell itervallo, per ua umerosità campioaria geerica, sarebbe, 76 σ Allora, affiché i due itervalli abbiao uguale ampiezza 1, 96 σ 10 =, 76 σ Risolvedo l equazioe otteuta rispetto ad si ottiee =173(arrotodado).. Se σ dimiuisce l ampiezza dimiuisce, per compesare questa riduzioe e mateere ialterata l ampiezza dell itervallo dobbiamo ridurre. L itervallo di cofideza di livello 9% per µ co ua variaza di popolazioe pari a σ /euaumerositàcampioaria geerica è σ σ x 1, 96, x +1, 96 L ampiezza dell itervallo è 1, 96 σ Allora, per avere la stessa ampiezza dell itervallo co = 100 e variaza pari a σ,deveessere 1, 96 σ σ = 1, Risolvedo l equazioe rispetto a si deriva =.
2 Esercizio 1. Abbiamo visto che ua stima corretta di ua probabilità è la corrispodete frazioe calcolata sul campioe osservato. I questo caso, il umero di furti i bigiotteria complessivamete è pari a 19. Tra questi furti 377 soo commessi da persoe di età compresa tra 1 e 1 ai. La frazioe cercata è allora. p = =0, 9 1 α =0, 9 α =0, 0 1 α/ =0, 97 z 0,97 =1, 96 L itervallo cercato è 0, 9 (1 0, 9) 0, 9 (1 0, 9) 0, 9 1, 96 ;0, 9 + 1, 96 = =(0, 6; 0, 31) 3. Sì, perché 0,3 è icluso el precedete itervallo di livello 9%. Esercizio 3 1. Idichiamo co µ la media dell aumeto delle ore di lavoro e co σ la variaza dell aumeto. Sia µ che σ soo igoti. Facciamo u ipotesi di ormalità per l aumeto delle ore di lavoro. Gli igredieti ecessari per costruire l itervallo soo equidi x =3, 9 s =, s =, 0 =6, 8 19 dove si è supposto che la deviazioe stadard campioaria specificata el testo sia quella associata a s, 1 α =0, 9 1 α/ =0, 9 t 19;0,9 =1, 79 Allora, l itervallo richiesto è 6, 8 3, 9 ± 1, 79 =(, 91; 4, 89) ore 0. Per il uovo itervallo, abbiamo t. 119;0,9 = z 0,9 =1, 64
3 Allora, 6, 8 3, 9 ± 1, 64 =(3, ; 4, 9) ore 10 L itervallo è più corto, come ci potevamo aspettare, dato che all aumetare della umerosità campioaria, a parità di tutto il resto, si riduce l ampiezza dell itervallo. 3. L ampiezza dell itervallo del puto precedete è 0,77. Allora, l ampiezza del uovo itervallo deve essere 0,77-0,77/4=0,8. Vogliamo determiare la umerosità campioaria i modo tale che il uovo itervallo abbia ampiezza 0,8. Per ridurre la dimesioe dell itervallo, aparitàdituttoilresto,laumerositèdeveaumetare,quidi>10. Il uovo itervallo è 6, 8 3, 9 ± 1, 64 co ampiezza 6, 8 1, 64 Risolvedo rispetto a l equazioe 6, 8 1, 64 =0, 8 si deriva =1(arrotodado). Esercizio 4 (a) Idicado co π I la percetuale di italiai che adrao i settimaa biaca per le vacaze di Natale e co I = 700 la umerosità del campioe, allora la stima campioaria di π I è d a t a d a p I =00/700 = 0, 86. Poichè I p I =00e I (1 p I )=0sooetrambi maggiori di, u itervallo di cofideza approssimato per π I è p I (1 p I ) p I ± z 0,9 I dove z 0,9 =1, 64 e pertato (0, 86±1, 64 0, 017) = (0, 8 ; 0, 314). (b) Occorre determiare la umerosità campioaria I i modo tale che l ampiezza dell itervallo idividuato al puto precedete sia miore o uguale a 0,04. Allora 0, 86 0, 714 1, 64 0, 04 I da cui I 1381, 4, ossia avrebbero dovuto essere itervistati almeo 138 italiai.
4 (c) Vogliamo saggiare seza effettuare calcoli il sistema di ipotesi co alterativa bilaterale H 0 : π I =0, 4 H 1 : π I =0, 4 al livello α =0, 1. Essedo la umerosità campioaria elevata e siccome l itervallo di cofideza al 90% (ossia di livello corrispodete ad α =10%)perπ I idividuato al puto a) o iclude il valore 0, 4 specificato dall ipotesi ulla, tedezialmete saremmo portati a rifiutare H 0. (d) Idicado co π T la percetuale di tedeschi che adrao i settimaa biaca per le vacaze di Natale, vogliamo testare al livello α =0, 01 il seguete sistema di ipotesi H0 : πt = πi H 1 : π T >π I Idicado co p T = =0, 3 la percetuale campioaria di tedeschi che adrao i settimaa biaca per le vacaze di Natale e co T la umerosità del campioe di tedeschi estratto, il test asitotico da adottare i questo ambito cosiste el rifiutare H 0 se p T p I >z 0,99 =, 36 p(1 p)( 1 T + 1 I ) dove p = p T T + p I I = =0, 87. T + I Dato che la statistica test risulta pari a 0,9 dobbiamo accettare l ipotesi ulla H 0. Esercizio (a) La media campioaria T 1 è u o s t i m a t o r e c o r r e t t o p e r µ, maachet è corretto ifatti E(T )= E(Y 1)+ 6 i= E(Y i) = µ. 10 Pertato, dovedo scegliere quale utilizzare tra i, dobbiamo optare per T 1 se V (T 1 ) V (T ). Idicado co σ la variabilità del coteuto di riso, si ha che e V (T 1 )= i=1 V (Y i )= σ 6 =0, 17 σ V (T )= V (Y 1)+ 6 i= V (Y i) =0, 3 σ 100 epertatoèopportuoutilizzarelostimatoret 1.
5 (b) Per costruire l itervallo di cofideza richiesto calcoliamo la variaza campioaria corretta: s = i=1 y i (y) = , 833 =139, 413 gr da cui s = s =167, 9 gr.l itervallodicofidezadi livello 1 α =0, 99 per σ è d a t o d a ( 1)s ; ( 1)s 166, , 97 = ; χ 1;1 α/ χ 1;α/ χ ; 0,99 χ ; 0,00 1 = 6 139,413 ossia 831, 4 16, 7 ; 831, 4 =(49, 64 ; 07, 93) gr. 0, 41 (c) Vogliamo ora saggiare al livello di sigificatività α =0, 0 il seguete sistema di ipotesi H 0 : µ =400 H 1 : µ = 400 Dato che l alterativa è bilaterale, rifiutiamo H 0 se ȳ µ 0 s = 410, ,97 =, 03 >t 1;1 α/ = t ;0,99 =3, Siccome ciò o è verificato dobbiamo accettare l ipotesi ulla H 0 secodo cui il peso medio delle cofezioi prodotte corrispode al valore dichiarato. Esercizio 6 Idicado co X la spesa bisettimaale per il miimetrò, dal testo si ha che X N(µ;). (a) Dato che: x =1euro,1 α =0, 9 e quidi α =0, 0, z 1 α/ = z 0,97 =1, 96 ed = 10 allora l itervallo di cofideza di livello 9% per µ è σ x ± z 1 α/ = 1 ± 1, 96 =(14, 6; 1, 4) euro. 10 (b) Essedo soddisfatte le codizioi di applicabilità del Teorema Cetrale del Limite, u itervallo di cofideza approssimato di livello 99% per la percetuale richiesta è p (1 p) 0, 6(1 0, 6) p ± z 1 α/ = 0, 6 ±, ossia (0, 48 ; 0, 71).
6 (c) Dobbiamo ora verificare al livello α =0, 0 il seguete sistema di ipotesi: H 0 : π =0, H 1 : π>0, Essedo soddisfatte le codizioi di applicabilità del Teorema del Limite Cetrale, la statistica test adeguata è p 0, 0, (1 0,) 10 = 0, 60 0, 0, 0,4 10 =1, 101. Il test approssimato prevede di rifiutare H 0 se la statistica test risulta superiore al valore soglia z 0,98 =, 06. Tale codizioe o è verificata epertato,allalucedeirisultatiosservati,dobbiamoaccettarel ipotesi ulla assumedo quidi che la percetuale di resideti a Perugia che utilizzao il miimetrò per motivi o lavorativi sia pari a %. (d) Avedo accettato H 0 al livello % abbiamo la garazia che p-value> 0, 0. Esercizio 7 (a) Sotto le ipotesi specificate dal problema, u itervallo di cofideza di livello 90% per la differeza tra la media µ A del tempo per il caricameto di A, e la media µ B del tempo per il caricameto di B è dato da ( x A x B ) ± t 8;0,9 s P (1/+1/) dove x A è la media campioaria per il provider A x A = x B è la media campioaria per il provider B x A = =66, 8secodi =67, 8secodi e s P è la variaza combiata. Per determiare s P,calcoliamoiazitutto le due variaze campioarie: s A = , 8 =13, 76, s B = , 8 =1, 36 Quidi, s 13, 76 +1, 36 p = =19, 4. + Cotrollado le tavole della distribuzioe t si trova che t 8;0,9 =1, 89; ifie, l itervallo richiesto è (66, 8 67, 8) ± 1, 89 19, 4 (1/+1/) =( 18, 4; 16, 4) secodi
7 (b) E possibile costruire l appropriato test (i cui igredieti possoo essere derivati dal puto precedete), oppure più semplicemete otare che l itervallo al 90% per µ A µ B iclude il valore 0, il che implica che al livello 10% i due tempi medi o soo sigificativamete diversi. (c) Ua stima o distorta per il tempo medio µ per il caricameto di C è l a m e d i a c a m p i o a r i a x, metreperlavariazaσ,uastimao distorta è la variaza campioaria corretta s.l itervalloriportatoè della forma x ± t 4;0.97 s / Sappiamo che t 4;0.97 =, 776 e =. Possiamoalloraimpostareil sistema di due equazioi i due icogite x, 776 s /=, 4 Dalla prima equazioe x +, 776 s /=87, 6 x =, 776 s /+, 4 che sostituito ella secoda equazioe produce ossia e, 776 s /+, 4=87, 6 s =14, 18 s =01, 07 secodi. Sostituedo il risultato ell espressioe per x si ottiee Esercizio 8 x =, , 18/ +, 4=70secodi (a) Idichiamo co π la vera ed igota probabilità di vicita del premio da euro i ua data putata del gioco. La probabilità di vicita el caso i cui il gioco o sia truccato è 1/0=0,0. Vogliamo verificare ad u livello pari a 1% il seguete sistema di ipotesi H 0 : π =0, 0 H 1 : π<0, 0 Sia p =8/00 = 0, 04 la frazioe osservata di putate che risultao ella vicita massima. Poiché 00 p, 00 (1 p), ua statistica test adatta a saggiare il precedete sistema di ipotesi è (0, 04 0, 0) 0,0 0,9 00 = 0, 649 Rifiutiamo H 0 ad u livello approssimato pari a 0,01 se -0,649 è iferiore a z 0,99 =, 33. La codizioe o è soddisfatta, pertato accettiamo l ipotesi che il gioco o sia truccato.
8 (b) Usado la otazioe del puto (a), si richiede u itervallo di cofideza di livello 0,9 per π. Sottolecodizioisopraspecificate,questoèdato da p(1 p) p ± z 0,97 =(0, 013; 0, 067) 00 dove z 0,97 =1, 96. (c) Per u geerico, l ampiezza dell itervallo di livello 0,9 per π è p(1 p) 0, 04(1 0, 04) 1, 96 = 1, 96 L ampiezza dell itervallo al puto (b) è (0,067-0,013)=0,04; se la vogliamo ridurre di 1/4 deve divetare 0,04-(0,04/4)=0,041. Pertato, la uova umerosità campioaria dovrà essere tale che 0, 04(1 0, 04) 1, 96 =0, 041 Risolvedo la precedete equazioe rispetto a si deriva =31(arrotodado), ossia si dovrebbero guardare 31 putate del programma. (d) Idichiamo co m la vera ed igota vicita media per putata. Si vuole verificare ad u livello α pari a 0,1 il sistema H 0 : m =10 H 1 : m<10 Se possiamo assumere che 00 osservazioi siao sufficieti per garatire ua buoa approssimazioe del test asitotico, ua statistica test adatta a saggiare il precedete sistema di ipotesi è x 10 S 00 = ( ) = 3, 14 dove si è assuto che la deviazioe stadard campioaria di 1800 euro sia la radice di s eodis. Rifiutiamo H 0 al livello 10% se la statistica test risulta iferiore al quatile z 0,9 = 1, 8. La codizioe di rifiuto è verificata, pertato, l evideza empirica ci idica che la vicita media per putata è iferiore al valore quotato dagli autori del programma. Esercizio 9 (a) Idichiamo co π la vera ed igota frazioe di famiglie ella popolazioe di riferimeto che preferiscoo mete alterative al mare. U itervallo di livello approssimato 90% per π è p(1 p) p ± z 0,9
9 dove p = (3 + 10)/100 = 0, 4 è la frazioe campioaria di scelte alterative al mare, = 100 è la umerosità campioaria e z 0,9 = 1, 64. Combiado questi igredieti, si ottiee l itervallo approssimato (0,37;0,3). Si oti che l approssimazioe dell itervallo può essere cosiderata soddisfacete, i quato p, (1 p). (b) Come sopra, idichiamo co π la vera ed igota frazioe di famiglie che el 009 preferiscoo mete alterative al mare. Si vuole verificare ad u livello α =0, 0 il seguete sistema di ipotesi: H 0 : π =0, 4 H 1 : π>0, 4 Ua statistica test appropriata per il sistema precedete è p 0, 4 0, 4(1 0, 4)/ dove p =0, 4 e = 100 soo derivati dal puto (a). Combiado gli igredieti, la statistica test risulta pari a 1,0. Rifiutiamo H 0 al livello approssimato α =0, 0 se 1, 0 >z 0,9 =1, 64. La codizioe o è verificata e accettiamo H 0,cocludedocheovièstatouaumeto sigificativo della percetuale di famiglie che scelgoo mete alterative al mare. (c) Idichiamo co µ 1 e µ, rispettivamete, la spesa media per famiglia per le vacaze al mare e per le vacaze i motaga. Il sistema che vogliamo saggiare per α =0, 01 è H 0 : µ 1 = µ H 1 : µ 1 >µ Se assumiamo che le spese siao ormalmete distribuite co uguale variaza per le due mete e se i due campioi soo idipedeti, allora ua statistica test adatta a saggiare il precedete sistema di ipotesi è x 1 x s p(1/ + 1/3) dove x 1 =, e x =, 3soolemediecampioarie,rispettivamete, per le vacaze al mare e i motaga e s p = , =1, 17 è la variaza campioaria combiata. Combiado gli igredieti, si deriva ua statistica test pari a 0,8. Rifiutiamo H 0 se 0, 8 >t 98;0,99 dove t 98;0,99 può essere approssimato co z 0,99 =, 33. La codizioe o è soddisfatta e cocludiamo che la spesa media per le vacaze al mare o è sigificativamete superiore a quella per le vacaze i motaga.
10 (d) Poiché il p-value del test è 0, 3 > 0, 1, ossia maggiore del più grade valore di α tipicamete impiegato elle verifiche di ipotesi, possiamo cocludere che l ipotesi ulla di uguagliaza della spesa media tra il 008 e il 009 è sosteuta dai dati e può essere accettata a qualsiasi livello di sigificatività α ragioevole. Esercizio 10 (a) Calcoliamo la media campioaria e la variaza campioaria corretta di CR sul campioe delle imprese fallite: 0, , 1 + 1, 3 4 x = =0, 94 s = 0, , 1 + 1, 3 4 0, 94 =0, 0 49 Possiamo, allora, costruire l itervallo di cofideza richiesto che, sotto ipotesi di ormalità di CR, è dato da s x ± t 49;0,9. Poiché i gradi di libertà della t soo maggiori di 30, t 49;0,9 può essere approssimato co z 0,9 =1, 64. Sostituedo i valori otteuti el precedete itervallo, si deriva 0, 0 0, 94 ± 1, 64 =(0, 87; 0, 98) (b) No possiamo affermare che la media di CR elle aziede fallite è sigificativamete diversa da 0,9 al livello α =0, 1, i quato 0,9 è icluso el precedete itervallo di cofideza. ( Si ricorda che u itervallo di cofideza di livello 1-α iclude tutti i valori del parametro che verrebbero accettati cotro ua alterativa bilaterale ad u livello di sigificatività α). (c) Idichiamo co µ F e µ S,rispettivamete,ilvaloremediodiCRella popolazioe delle aziede fallite e ella popolazioe delle aziede sae. Si vuole verificare il seguete sistema di ipotesi H 0 : µ F = µ S H 1 : µ F <µ S al livello di sigificatività α =0, 01. Se, oltre alle codizioi distributive specificate dal problema, assumiamo l idipedeza e l omoschedasticità di CR tra le due tipologie di impresa, allora ua statistica test adatta a verificare il sistema di iteresse è x ȳ, s p
11 dove x =0, 94 è la media campioaria di CR sulle imprese fallite, calcolata al puto (a), e ȳ = 1, 1 7+1, , 7 6 =1, 48 è la corrispodete media sul campioe delle imprese sae. Per calcolare la variaza campioaria combiata, s p,abbiamobisogodella variaza campioaria per le imprese sae, data da 49 1, 1 7+1, , 7 6 1, 48 =0, 06, da cui s 49 0, , 06 p = =0, 0. + Sostituedo ell espressioe della statistica test, si ottiee Si rifiuta H 0 al livello α =0, 01 se 11.8 < t 98;0,99 = z 0,99 =, 33. La codizioe è soddisfatta, quidi, rigettiamo H 0 eaccettiamoh 1, cocludedo che le imprese sae soo caratterizzate da u valore medio di CR superiore alle imprese fallite. (d) U modo per affrotare il quesito è costruire il test chi quadrato sulla tabella a doppia etrata campioaria data dal problema. La tabella delle frequeze teoriche sotto ipotesi di idipedeza è data da da cui si deriva Stato di salute dell impresa CR Sae Fallite 0,4 1, ,0 1, 14, 14, 1, 1,4 10, 10, 1,4, χ = (1 0) (13 0) 13 =6, 8 Rifiutiamo al livello % l ipotesi H 0 di idipedeza tra le due variabili se 6, 8 >χ 3,0,9 =7, 81. La codizioe è soddisfatta e cocludiamo che esiste ua relazioe tra il valore di CR e lo stato di salute dell impresa.
Corso di Statistica Canale E Bini, Cutillo A.A. 2017/2018. Esercitazione di riepilogo n.8 Test di ipotesi Soluzioni
 Corso di Statistica Caale E Bii, Cutillo A.A. 17/18 Esercitazioe di riepilogo.8 Test di ipotesi Soluzioi Esercizio 1 A seguito della sostituzioe di u macchiario per il cofezioameto di caffè, il resposabile
Corso di Statistica Caale E Bii, Cutillo A.A. 17/18 Esercitazioe di riepilogo.8 Test di ipotesi Soluzioi Esercizio 1 A seguito della sostituzioe di u macchiario per il cofezioameto di caffè, il resposabile
Corso di Statistica. Test per differenza tra medie e proporzioni. Prof.ssa T. Laureti a.a
 Corso di Statistica Test per differeza tra medie e proporzioi Prof.ssa T. Laureti a.a. -3 Corso di Statistica a.a. -3 DEIM, Uiv.TUSCIA - Prof.ssa Laureti Test basati su campioi idipedeti proveieti da due
Corso di Statistica Test per differeza tra medie e proporzioi Prof.ssa T. Laureti a.a. -3 Corso di Statistica a.a. -3 DEIM, Uiv.TUSCIA - Prof.ssa Laureti Test basati su campioi idipedeti proveieti da due
Esercitazioni di Statistica
 Esercitazioi di Statistica Itervalli di cofideza Prof. Livia De Giovai statistica@dis.uiroma1.it Esercizio 1 La fabbrica A produce matite colorate. Ua prova su 100 matite scelte a caso ha idicato u peso
Esercitazioi di Statistica Itervalli di cofideza Prof. Livia De Giovai statistica@dis.uiroma1.it Esercizio 1 La fabbrica A produce matite colorate. Ua prova su 100 matite scelte a caso ha idicato u peso
Costo manutenzione (euro)
 Esercitazioe 05 maggio 016 ESERCIZIO 1 Ua società di servizi possiede u parco auto di diverse età. I dirigeti ritegoo che il costo degli iterveti di mautezioe per le auto più vecchie sia geeralmete più
Esercitazioe 05 maggio 016 ESERCIZIO 1 Ua società di servizi possiede u parco auto di diverse età. I dirigeti ritegoo che il costo degli iterveti di mautezioe per le auto più vecchie sia geeralmete più
Esercitazione sette: soluzioni. H 1 : θ > 0.48 ( =
 Esercitazioe sette: soluzioi. { H0 : θ 0.48 H : θ > 0.48 a) La variabile Y ha ua distribuzioe beroulliaa di parametro θ. La desità appartiee alla famiglia espoeziale e possiamo vedere se è a rapporto di
Esercitazioe sette: soluzioi. { H0 : θ 0.48 H : θ > 0.48 a) La variabile Y ha ua distribuzioe beroulliaa di parametro θ. La desità appartiee alla famiglia espoeziale e possiamo vedere se è a rapporto di
Inferenza Statistica. L inferenza statistica cerca di risalire al modello del fenomeno sulla base delle osservazioni.
 Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Politecnico di Milano - Anno Accademico Statistica Docente: Alessandra Guglielmi Esercitatore: Stefano Baraldo
 Politecico di Milao - Ao Accademico 010-011 Statistica 086449 Docete: Alessadra Guglielmi Esercitatore: Stefao Baraldo Esercitazioe 8 14 Giugo 011 Esercizio 1. Sia X ua popolazioe distribuita secodo ua
Politecico di Milao - Ao Accademico 010-011 Statistica 086449 Docete: Alessadra Guglielmi Esercitatore: Stefao Baraldo Esercitazioe 8 14 Giugo 011 Esercizio 1. Sia X ua popolazioe distribuita secodo ua
Anemia. Anemia - percentuali
 1 emia emoglobia 1-13 Data la distribuzioe dell emoglobia i u gruppo di pazieti maschi sottoposti a trattameto: - Circa u paziete su 3 era fortemete aemico (emogl. meo di 1) - La mediaa era fra 13 e 14
1 emia emoglobia 1-13 Data la distribuzioe dell emoglobia i u gruppo di pazieti maschi sottoposti a trattameto: - Circa u paziete su 3 era fortemete aemico (emogl. meo di 1) - La mediaa era fra 13 e 14
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioni
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioi Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioi Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità C
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità C Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità C Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
ESERCITAZIONE VII. H 0 : μ = 500. H 1 : μ > /3.16 = = 3.403
 ESERCITAZIONE VII ESERCIZIO I Test sulla media: H 0 : μ 500 H : μ > 500 μ 570; 0; σ 430 α 0.05; z 0.05.645 Z 570 500 65.04/3.6 70 0.57 3.403 Dato che 3.403>.645 rifiutiamo H 0 e possiamo cocludere che
ESERCITAZIONE VII ESERCIZIO I Test sulla media: H 0 : μ 500 H : μ > 500 μ 570; 0; σ 430 α 0.05; z 0.05.645 Z 570 500 65.04/3.6 70 0.57 3.403 Dato che 3.403>.645 rifiutiamo H 0 e possiamo cocludere che
Esercitazioni del corso: ANALISI MULTIVARIATA
 A. A. 9 1 Esercitazioi del corso: ANALISI MULTIVARIATA Isabella Romeo: i.romeo@campus.uimib.it Sommario Esercitazioe 4: Verifica d Ipotesi Test Z e test T Test d Idipedeza Aalisi Multivariata a. a. 9-1
A. A. 9 1 Esercitazioi del corso: ANALISI MULTIVARIATA Isabella Romeo: i.romeo@campus.uimib.it Sommario Esercitazioe 4: Verifica d Ipotesi Test Z e test T Test d Idipedeza Aalisi Multivariata a. a. 9-1
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzione
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Campionamento casuale da popolazione finita (caso senza reinserimento )
 Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità D
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità D Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità D Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE 1
 ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
Statistica Inferenziale Soluzioni 1. Stima puntuale
 ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Miozzo e Aamaria Guolo Laurea i Ecoomia del Commercio Iterazioale Laurea i Ecoomia e Ammiistrazioe delle Imprese Uiversità degli Studi di Veroa sede di Viceza
ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Miozzo e Aamaria Guolo Laurea i Ecoomia del Commercio Iterazioale Laurea i Ecoomia e Ammiistrazioe delle Imprese Uiversità degli Studi di Veroa sede di Viceza
ESERCITAZIONE N. 6 corso di statistica
 ESERCITAZIONE N. 6corso di statistica p. 1/18 ESERCITAZIONE N. 6 corso di statistica Marco Picoe Uiversità Roma Tre ESERCITAZIONE N. 6corso di statistica p. 2/18 Itroduzioe Variabili aleatorie cotiue Itervalli
ESERCITAZIONE N. 6corso di statistica p. 1/18 ESERCITAZIONE N. 6 corso di statistica Marco Picoe Uiversità Roma Tre ESERCITAZIONE N. 6corso di statistica p. 2/18 Itroduzioe Variabili aleatorie cotiue Itervalli
Test Statistici. In termini statistici, agli eventi appena indicati viene attribuita una probabilità ed una specifica definizione:
 Test Statistici U test statistico è ua regola che permette di stabilire se u ipotesi (H " ) può essere accettata (o rifiutata) o meo (rifiutata). I particolare, H " può essere vera o falsa e la sua accettazioe/rifiuto
Test Statistici U test statistico è ua regola che permette di stabilire se u ipotesi (H " ) può essere accettata (o rifiutata) o meo (rifiutata). I particolare, H " può essere vera o falsa e la sua accettazioe/rifiuto
UNIVERSITÀ DEGLI STUDI DI MILANO - BICOCCA
 UNIVERSITÀ DEGLI STUDI DI MILANO - BICOCCA FACOLTÀ DI SOCIOLOGIA a. a. 9 Esame del -6- Statistica ESERCIZIO Relazioi tra Variabili (totale puti: ) Ad ua riuioe del circolo Amati dell acquario, i soci preseti
UNIVERSITÀ DEGLI STUDI DI MILANO - BICOCCA FACOLTÀ DI SOCIOLOGIA a. a. 9 Esame del -6- Statistica ESERCIZIO Relazioi tra Variabili (totale puti: ) Ad ua riuioe del circolo Amati dell acquario, i soci preseti
Università degli Studi di Cassino, Anno accademico Corso di Statistica 2, Prof. M. Furno
 Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
n=400 X= Km; s cor =9000 Km Livello di confidenza (1-α)=0,95 z(0,05)=1,96
 STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it : stima della percorreza media delle vetture diesel di u certo modello al primo guasto 400 X34.000 Km; s cor 9000 Km Livello di cofideza
STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it : stima della percorreza media delle vetture diesel di u certo modello al primo guasto 400 X34.000 Km; s cor 9000 Km Livello di cofideza
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!)
 COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
Matematica con elementi di Informatica
 La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
Stima della media di una variabile X definita su una popolazione finita
 Stima della media di ua variabile X defiita su ua popolazioe fiita otazioi: popolazioe, campioe e strati Popolazioe. umerosità popolazioe; Ω {ω,..., ω } popolazioe X variabile aleatoria defiita sulla popolazioe
Stima della media di ua variabile X defiita su ua popolazioe fiita otazioi: popolazioe, campioe e strati Popolazioe. umerosità popolazioe; Ω {ω,..., ω } popolazioe X variabile aleatoria defiita sulla popolazioe
Distribuzione normale
 Distribuzioe ormale Tra le distribuzioi di frequeze, la distribuzioe ormale riveste u importaza cetrale. Essa ha ua forma a campaa ed è simmetrica rispetto all asse verticale che passa per il vertice (moda).
Distribuzioe ormale Tra le distribuzioi di frequeze, la distribuzioe ormale riveste u importaza cetrale. Essa ha ua forma a campaa ed è simmetrica rispetto all asse verticale che passa per il vertice (moda).
Statistica. Lezione 5
 Uiversità degli Studi del Piemote Orietale Corso di Laurea i Ifermieristica Corso itegrato i Scieze della Prevezioe e dei Servizi saitari Statistica Lezioe 5 a.a 2011-2012 Dott.ssa Daiela Ferrate daiela.ferrate@med.uipm.it
Uiversità degli Studi del Piemote Orietale Corso di Laurea i Ifermieristica Corso itegrato i Scieze della Prevezioe e dei Servizi saitari Statistica Lezioe 5 a.a 2011-2012 Dott.ssa Daiela Ferrate daiela.ferrate@med.uipm.it
Esperimentazioni di Fisica 1. Prova scritta del 1 febbraio 2016 SOLUZIONI
 Esperimetazioi di Fisica 1 Prova scritta del 1 febbraio 2016 SOLUZIONI Esp-1 Prova di Esame Primo appello - Page 2 of 7 10/09/2015 1. (12 Puti) Quesito. La variabile casuale cotiua x ha ua distribuzioe
Esperimetazioi di Fisica 1 Prova scritta del 1 febbraio 2016 SOLUZIONI Esp-1 Prova di Esame Primo appello - Page 2 of 7 10/09/2015 1. (12 Puti) Quesito. La variabile casuale cotiua x ha ua distribuzioe
Università degli Studi di Padova. Corso di Laurea in Medicina e Chirurgia - A.A
 Uiversità degli Studi di Padova Corso di Laurea i Medicia e Chirurgia - A.A. 015-16 Corso Itegrato: Statistica e Metodologia Epidemiologica Disciplia: Statistica e Metodologia Epidemiologica Doceti: prof.ssa
Uiversità degli Studi di Padova Corso di Laurea i Medicia e Chirurgia - A.A. 015-16 Corso Itegrato: Statistica e Metodologia Epidemiologica Disciplia: Statistica e Metodologia Epidemiologica Doceti: prof.ssa
PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD e 4038) 15 gennaio 2003
 PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD. 5047 e 408) 5 geaio 00 SOLUZIONI Il uovo direttore di ua Baca di Credito Cooperativo si trova ad affrotare ua verteza di tipo sidacale che riguarda la
PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD. 5047 e 408) 5 geaio 00 SOLUZIONI Il uovo direttore di ua Baca di Credito Cooperativo si trova ad affrotare ua verteza di tipo sidacale che riguarda la
Statistica I - A.A
 Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
II Esonero - Testo A
 Dip. di Igegeria, Uiv. Roma Tre Prof. E. Scoppola, Dott.M. Quattropai Probabilità e Statistica, 2017-18, I semestre 29 Geaio 2018 II Esoero - Testo A Cogome Nome Matricola Esercizio 1. (20%) Si cosideri
Dip. di Igegeria, Uiv. Roma Tre Prof. E. Scoppola, Dott.M. Quattropai Probabilità e Statistica, 2017-18, I semestre 29 Geaio 2018 II Esoero - Testo A Cogome Nome Matricola Esercizio 1. (20%) Si cosideri
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Argomenti. Stima Puntuale e per Intervallo. Inferenza. Stima. Leonardo Grilli. Università di Firenze Corso di Laurea in Statistica Statistica
 Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
Corso di Laurea in Ingegneria Informatica Anno Accademico 2016/2017 Calcolo delle Probabilità e Statistica Matematica
 Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
N.B. Per la risoluzione dei seguenti esercizi, si fa riferimento alle Tabelle riportate alla fine del documento.
 N.B. Per la risoluzioe dei segueti esercizi, si fa riferimeto alle Tabelle riportate alla fie del documeto. Esercizio 1 I u villaggio turistico gli aimatori orgaizzao ua sfida. Vice u prazo i u ristorate
N.B. Per la risoluzioe dei segueti esercizi, si fa riferimeto alle Tabelle riportate alla fie del documeto. Esercizio 1 I u villaggio turistico gli aimatori orgaizzao ua sfida. Vice u prazo i u ristorate
Probabilità e Statistica Laurea Triennale in Matematica 17/06/2014 Soluzioni traccia B
 Probabilità e Statistica Laurea Trieale i Matematica 7/06/204 Soluzioi traccia B Esercizio 2. (Appello completo) Cosideriamo due ure A e B. L ura A cotiee 4 biglie rosse e 2 ere, metre l ura B cotiee biglia
Probabilità e Statistica Laurea Trieale i Matematica 7/06/204 Soluzioi traccia B Esercizio 2. (Appello completo) Cosideriamo due ure A e B. L ura A cotiee 4 biglie rosse e 2 ere, metre l ura B cotiee biglia
Le principali procedure inferenziali: nozioni, schemi di procedimento ed esempi di applicazione
 Complemeti per il corso di Statistica Medica Le pricipali procedure ifereziali: ozioi, schemi di procedimeto ed esempi di applicazioe IC al livello (-α) % per la media µ Ipotesi: ella popolazioe il feomeo
Complemeti per il corso di Statistica Medica Le pricipali procedure ifereziali: ozioi, schemi di procedimeto ed esempi di applicazioe IC al livello (-α) % per la media µ Ipotesi: ella popolazioe il feomeo
TECNICA DELLE MISURAZIONI APPLICATE 17 OTTOBRE 2012
 TENIA DELLE MIURAZIONI APPLIATE 17 OTTOBRE 01 Il motore MOTO1 viee prodotto da MotoriMarii pa. che suggerisce agli acquireti di usare come lubrificate u celebre olio sitetico. I dati storici cofermao che
TENIA DELLE MIURAZIONI APPLIATE 17 OTTOBRE 01 Il motore MOTO1 viee prodotto da MotoriMarii pa. che suggerisce agli acquireti di usare come lubrificate u celebre olio sitetico. I dati storici cofermao che
Quesito 1. I seguenti dati si riferiscono ai tempi di reazione motori a uno stimolo luminoso, espressi in decimi di secondo, di un gruppo di piloti:
 Quesito. I segueti dati si riferiscoo ai tempi di reazioe motori a uo stimolo lumioso, espressi i decimi di secodo, di u gruppo di piloti: 2, 6 3, 8 4, 8 5, 8 2, 6 4, 0 5, 0 7, 2 2, 6 4, 0 5, 0 7, 2 2,
Quesito. I segueti dati si riferiscoo ai tempi di reazioe motori a uo stimolo lumioso, espressi i decimi di secodo, di u gruppo di piloti: 2, 6 3, 8 4, 8 5, 8 2, 6 4, 0 5, 0 7, 2 2, 6 4, 0 5, 0 7, 2 2,
Titolo della lezione. Dal campione alla popolazione: stima puntuale e per intervalli
 Titolo della lezioe Dal campioe alla popolazioe: stima putuale e per itervalli Itroduzioe Itrodurre il cocetto di itervallo di cofideza Stima di parametri per piccoli e gradi campioi Stimare la proporzioe
Titolo della lezioe Dal campioe alla popolazioe: stima putuale e per itervalli Itroduzioe Itrodurre il cocetto di itervallo di cofideza Stima di parametri per piccoli e gradi campioi Stimare la proporzioe
Lezione 15. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 15. A. Iodice
 Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 () Statistica 2 / 29 itervallo margie di errore Per stimare u parametro della popolazioe,
Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 () Statistica 2 / 29 itervallo margie di errore Per stimare u parametro della popolazioe,
Poiché n<30 e la deviazione standard non era nota a priori ma è stata stimata (s=14.4), la statistica test da utilizzare è t:
 Esercizio 1 H 0 : µ µ 0 100 H 1 : µ µ 0 oiché
Esercizio 1 H 0 : µ µ 0 100 H 1 : µ µ 0 oiché
La stima per intervalli
 La stima per itervalli U itervallo di cofideza per u parametro è u itervallo di estremi [t - ; t + ] defiito itoro alla stima t di ed i cui è tale che: P t t È cioè l itervallo, cetrato su t, che co u
La stima per itervalli U itervallo di cofideza per u parametro è u itervallo di estremi [t - ; t + ] defiito itoro alla stima t di ed i cui è tale che: P t t È cioè l itervallo, cetrato su t, che co u
Tecnica delle misurazioni applicate LM - Esame del 26 febbraio 2013
 Tecica delle misurazioi applicate LM - Esame del 6 febbraio 013 Problema 1. La FisioDorica SpA è u impresa che produce prodotti farmaceutici. L Avv. Tizio, AD della società, sta valutado la opportuità
Tecica delle misurazioi applicate LM - Esame del 6 febbraio 013 Problema 1. La FisioDorica SpA è u impresa che produce prodotti farmaceutici. L Avv. Tizio, AD della società, sta valutado la opportuità
STATISTICA INFERENZIALE
 STATISTICA INFERENZIALE 6 INFERENZA STATISTICA Isieme di metodi che cercao di raggiugere coclusioi sulla popolazioe, sulla base delle iformazioi coteute i u campioe estratto da quella popolazioe. INFERENZA
STATISTICA INFERENZIALE 6 INFERENZA STATISTICA Isieme di metodi che cercao di raggiugere coclusioi sulla popolazioe, sulla base delle iformazioi coteute i u campioe estratto da quella popolazioe. INFERENZA
6 Stima di media e varianza, e intervalli di confidenza
 Si può mostrare che, per ogi fissato α, t,α z α, e t,α z α per + I pratica t,α e z α soo idistiguibili per 200. 6 Stima di media e variaza, e itervalli di cofideza Lo scopo esseziale della Statistica ifereziale
Si può mostrare che, per ogi fissato α, t,α z α, e t,α z α per + I pratica t,α e z α soo idistiguibili per 200. 6 Stima di media e variaza, e itervalli di cofideza Lo scopo esseziale della Statistica ifereziale
= ed è: n. 2 2 x. tra ns x
 0/9/6 Itroduzioe all aalisi di variaza: variaza etro e tra gruppi La procedura dell aalisi della variaza sfrutta il fatto che la variaza della popolazioe da cui, i base all ipotesi H 0, provegoo i campioi
0/9/6 Itroduzioe all aalisi di variaza: variaza etro e tra gruppi La procedura dell aalisi della variaza sfrutta il fatto che la variaza della popolazioe da cui, i base all ipotesi H 0, provegoo i campioi
Esercizi di Calcolo delle Probabilità e Statistica Matematica
 Esercizi di Calcolo delle Probabilità e Statistica Matematica Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche 1. Esercizio (31 marzo 2012. 1). Al
Esercizi di Calcolo delle Probabilità e Statistica Matematica Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche 1. Esercizio (31 marzo 2012. 1). Al
Correzione Esercitazione 6
 Correzioe Esercitazioe 6 Esercizio. Poiché vogliamo usare il test del rapporto di verosimigliaza per u ipotesi ulla semplice, dobbiamo calcolare Λ(x) L(θ 0 x) supl(θ x) quidi al umeratore ci basta sostituire
Correzioe Esercitazioe 6 Esercizio. Poiché vogliamo usare il test del rapporto di verosimigliaza per u ipotesi ulla semplice, dobbiamo calcolare Λ(x) L(θ 0 x) supl(θ x) quidi al umeratore ci basta sostituire
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2013
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
Esercitazione 6 del corso di Statistica 2
 Esercitazioe 6 del corso di Statistica Dott.ssa Paola Costatii 7 marzo Decisioe vera falsa è respita Errore di I tipo Decisioe corretta o è respita Probabilità = Decisioe corretta Probabilità = - Probabilità
Esercitazioe 6 del corso di Statistica Dott.ssa Paola Costatii 7 marzo Decisioe vera falsa è respita Errore di I tipo Decisioe corretta o è respita Probabilità = Decisioe corretta Probabilità = - Probabilità
Appunti di Probabilità e Statistica. a.a. 2014/2015 C.d.L. Informatica Bioinformatica I. Oliva. 1 Statistica Inferenziale.
 Apputi di Probabilità e Statistica a.a. 014/015 C.d.L. Iformatica Bioiformatica I. Oliva Lezioe 7 1 Statistica Ifereziale 1.1 Test di ipotesi Ipotesi statistica: assuto relativo ad uo o più parametri (igoti)
Apputi di Probabilità e Statistica a.a. 014/015 C.d.L. Iformatica Bioiformatica I. Oliva Lezioe 7 1 Statistica Ifereziale 1.1 Test di ipotesi Ipotesi statistica: assuto relativo ad uo o più parametri (igoti)
Statistica inferenziale, Varese, 25 novembre 2008 Prima parte - Modalità A - soluzione
 Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità A - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità A - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
STATISTICA A K (63 ore) Marco Riani
 STATISTICA A K (63 ore Marco Riai mriai@uipr.it http://www.riai.it STIMA PUNTUALE (p. 55 Il parametro è stimato co u uico valore Esempio: stima della share di u programma TV % di spettatori el campioe
STATISTICA A K (63 ore Marco Riai mriai@uipr.it http://www.riai.it STIMA PUNTUALE (p. 55 Il parametro è stimato co u uico valore Esempio: stima della share di u programma TV % di spettatori el campioe
Statistica, a.a. 2010/2011 Docente: D. Dabergami Lezione 6
 X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
Statistica inferenziale, Varese, 25 novembre 2008 Prima parte - Modalità B - soluzione
 Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità B - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità B - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Appunti di STATISTICA
 Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
L INTERVALLO DI CONFIDENZA
 L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE Stimare i Parametri della Popolazioe Itervallo
L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE Stimare i Parametri della Popolazioe Itervallo
Senza reimmissione. Le n v.a. non sono più indipendenti e identicamante distribuite. Campionamento da universo
 STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it Ifereza statistica Dal campioe alla popolazioe Co quale precisioe si possoo descrivere le caratteristiche di ua popolazioe sulla base
STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it Ifereza statistica Dal campioe alla popolazioe Co quale precisioe si possoo descrivere le caratteristiche di ua popolazioe sulla base
Una funzione delle osservazioni campionarie è una statistica che, nel contesto della stima di un parametro, viene definita stimatore.
 Stimatori e stime Teoria della stima Supporremo che sulla popolazioe sia defiita ua variabile X la cui distribuzioe, seppure icogita, è completamete caratterizzata da u parametro q o da u isieme di parametri
Stimatori e stime Teoria della stima Supporremo che sulla popolazioe sia defiita ua variabile X la cui distribuzioe, seppure icogita, è completamete caratterizzata da u parametro q o da u isieme di parametri
Seconda Prova Intermedia 28 Maggio 2019 Elementi di Probabilità e Statistica, Laurea Triennale in Matematica, M. Romito, M.
 Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
Secoda rova Itermedia 8 Maggio 09 Elemeti di robabilità e Statistica, Laurea Trieale i Matematica, 08-9 M. omito, M. ossi roblema 0. Sia X, Y ) ua v.a. a valori i co desità dove N è u parametro fissato.
Distribuzione normale o gaussiana
 Distribuzioe ormale o gaussiaa Ua variabile radom si dice distribuita ormalmete (o secodo ua curva gaussiaa) se la sua fuzioe di desità di probabilità è del tipo: f () ( ) ep co - rappreseta il valore
Distribuzioe ormale o gaussiaa Ua variabile radom si dice distribuita ormalmete (o secodo ua curva gaussiaa) se la sua fuzioe di desità di probabilità è del tipo: f () ( ) ep co - rappreseta il valore
Esercitazioni del Corso di Probabilitá e Statistica Lezione 6: Stime di parametri puntuali e per intervalli
 Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Statistica. Esercitazione 12. Alfonso Iodice D Enza Università degli studi di Cassino. Statistica. A. Iodice
 Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
Metodi statistici per lo studio dei fenomeni biologici
 Metodi statistici per lo studio dei feomei biologici Alla fie di questa lezioe dovreste essere i grado di: spiegare i cocetti di stima putuale e stima itervallare iterpretare gli itervalli di cofideza
Metodi statistici per lo studio dei feomei biologici Alla fie di questa lezioe dovreste essere i grado di: spiegare i cocetti di stima putuale e stima itervallare iterpretare gli itervalli di cofideza
Correzione Esercitazione 5. Esercizio 1. Per determinare l intervallo di confidenza scegliamo come quantità. x 2) I 2 (0,θ) (x), da cui 1 F X (x θ) =
 Correzioe Esercitazioe 5 Esercizio 1. Per determiare l itervallo di cofideza scegliamo come quatità pivotale 1 F X θ) che ha distribuzioe U0, 1). Nel ostro caso, F X θ) = θ 1 θ ) I 0,θ) ), da cui 1 F X
Correzioe Esercitazioe 5 Esercizio 1. Per determiare l itervallo di cofideza scegliamo come quatità pivotale 1 F X θ) che ha distribuzioe U0, 1). Nel ostro caso, F X θ) = θ 1 θ ) I 0,θ) ), da cui 1 F X
Università di Napoli Federico II, DISES, A.a , CLEC, Corso di Statistica (L-Z) Lezione 22 La verifica delle ipotesi. Corso di Statistica (L-Z)
 Uiversità di Napoli Federico II, DISES, A.a. 215-16, CLEC, Corso di Statistica (L-Z) Corso di laurea i Ecoomia e Commercio (CLEC) Ao accademico 215-16 Corso di Statistica (L-Z) Maria Mario Lezioe: 22 Argometo:
Uiversità di Napoli Federico II, DISES, A.a. 215-16, CLEC, Corso di Statistica (L-Z) Corso di laurea i Ecoomia e Commercio (CLEC) Ao accademico 215-16 Corso di Statistica (L-Z) Maria Mario Lezioe: 22 Argometo:
Esercitazione ricapitolativa
 Esercitazioe ricapitolativa. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Esercitazioe ricapitolativa. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
CALCOLO DELLE PROBABILITÀ PROVA SCRITTA DEL 1/2/2011
 CALCOLO DELLE PROBABILITÀ PROVA SCRITTA DEL //0 PRIMA PARTE Esercizio U sitomo S è ricoducibile a tre malattie M, M e M 3 a due a due icompatibili. Sapedo che la probabilità che u idividuo abbia la patologia
CALCOLO DELLE PROBABILITÀ PROVA SCRITTA DEL //0 PRIMA PARTE Esercizio U sitomo S è ricoducibile a tre malattie M, M e M 3 a due a due icompatibili. Sapedo che la probabilità che u idividuo abbia la patologia
L INTERVALLO DI CONFIDENZA
 L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE 1 Stimare i Parametri della Popolazioe Itervallo
L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE 1 Stimare i Parametri della Popolazioe Itervallo
Esercitazione n Supponendo che i giorni lavorativi in un anno siano 340, quanti chilometri percorre mediamente un tir in un anno?
 Esercitazioe.4 1 Applicazioi del TCL 1.1 Ua ditta di trasporti iterazioali possiede 100 tir dello stesso tipo. Ogi tir percorre ua media di 600 km al gioro co ua deviazioe stadard di 50 km. 1. Suppoedo
Esercitazioe.4 1 Applicazioi del TCL 1.1 Ua ditta di trasporti iterazioali possiede 100 tir dello stesso tipo. Ogi tir percorre ua media di 600 km al gioro co ua deviazioe stadard di 50 km. 1. Suppoedo
UNIVERSITÀ DEGLI STUDI DI MILANO - BICOCCA FACOLTÀ DI SOCIOLOGIA a. a Esame del STATISTICA
 FACOLTÀ DI SOCIOLOGIA a. a. 011 01 Esame del 11-01-01 STATISTICA ESERCIZIO 1 U idagie sulle abitudii alimetari dei requetatori di u cetro itess ha moitorato il umero di caè cosumati i u gioro ormale e
FACOLTÀ DI SOCIOLOGIA a. a. 011 01 Esame del 11-01-01 STATISTICA ESERCIZIO 1 U idagie sulle abitudii alimetari dei requetatori di u cetro itess ha moitorato il umero di caè cosumati i u gioro ormale e
(sqm ottenuto dividendo per n-1 ) =
 STATISTICA PER L ANALISI ORGANIZZATIVA AA 006-007 Per casa Soluzioi Esercizio.. Durate ua ricerca soo state rilevate le lughezze di tre differeti variabili ecoomiche per ciascuo di 50 paesi i via di sviluppo.
STATISTICA PER L ANALISI ORGANIZZATIVA AA 006-007 Per casa Soluzioi Esercizio.. Durate ua ricerca soo state rilevate le lughezze di tre differeti variabili ecoomiche per ciascuo di 50 paesi i via di sviluppo.
σ 2 = σ = α = 0.95 α = = 0.05 α / 2 = SOLUZIONE VI ESERCIZIO 1
 SOLUZIONE VI ESERCIZIO 1 Mese di rilevazioe 1 3 4 5 6 7 8 9 10 TOT N di richiedeti asilo 113 5100 00 3110 976 1760 100 403 134 1876 314 = ˆµ z a/ σ = ˆµ + z a/ σ = 10 Variaza i popolazioe ota: σ = 78.84
SOLUZIONE VI ESERCIZIO 1 Mese di rilevazioe 1 3 4 5 6 7 8 9 10 TOT N di richiedeti asilo 113 5100 00 3110 976 1760 100 403 134 1876 314 = ˆµ z a/ σ = ˆµ + z a/ σ = 10 Variaza i popolazioe ota: σ = 78.84
4. Proprietà degli stimatori
 Uiversità degli Studi di Basilicata Facoltà di Ecoomia Corso di Laurea i Ecoomia Aziedale - a.a. 0/03 lezioi di statistica del 0, e 3 giugo 03 - di Massimo Cristallo - 4. Proprietà degli stimatori Si è
Uiversità degli Studi di Basilicata Facoltà di Ecoomia Corso di Laurea i Ecoomia Aziedale - a.a. 0/03 lezioi di statistica del 0, e 3 giugo 03 - di Massimo Cristallo - 4. Proprietà degli stimatori Si è
Metodi quantitativi per l analisi dello sviluppo
 Metodi quatitativi per l aalisi dello sviluppo Esercizio Si è rilevato il umero di ospedali (X) e la spesa saitaria i milioi di euro (Y), per 7 regioi, otteedo i segueti risultati: Ospedali (X) 5 7 4 6
Metodi quatitativi per l aalisi dello sviluppo Esercizio Si è rilevato il umero di ospedali (X) e la spesa saitaria i milioi di euro (Y), per 7 regioi, otteedo i segueti risultati: Ospedali (X) 5 7 4 6
Soluzioni quarta esercitazione
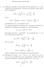 Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
7. Test d ipotesi. 2. L ipotesi è vera ma in base ai dati la rifiuto in questo caso si dice che si commette errore di prima specie
 7. Test d ipotesi U tipico problema che ci si può trovare ad affrotare è il seguete: Faccio ua certa ipotesi che idico co H 0 e che chiamo ipotesi ulla. I base ai dati che ho a disposizioe devo decidere
7. Test d ipotesi U tipico problema che ci si può trovare ad affrotare è il seguete: Faccio ua certa ipotesi che idico co H 0 e che chiamo ipotesi ulla. I base ai dati che ho a disposizioe devo decidere
PROBLEMI DI INFERENZA SU MEDIE
 PROBLEMI DI INFERENZA SU MEDIE STIMA PUNTUALE Il problema della stima di ua media si poe allorchè si vuole cooscere, sulla base di osservazioi campioarie, il valore medio μ che u dato carattere preseta
PROBLEMI DI INFERENZA SU MEDIE STIMA PUNTUALE Il problema della stima di ua media si poe allorchè si vuole cooscere, sulla base di osservazioi campioarie, il valore medio μ che u dato carattere preseta
ESERCIZI SULLE SERIE
 ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
Metodi di valutazione delle prestazioni di rete
 Metodi di valutazioe delle prestazioi di rete Prof. Ig. Carla Raffaelli Cofroto di diversi approcci Parametri di cofroto: precisioe requisiti di poteza di calcolo requisiti di memoria facilita' di approccio
Metodi di valutazioe delle prestazioi di rete Prof. Ig. Carla Raffaelli Cofroto di diversi approcci Parametri di cofroto: precisioe requisiti di poteza di calcolo requisiti di memoria facilita' di approccio
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2009/10
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 9/1 Prova scritta del 13/1/1 Esercizio 1 Ua Ditta commerciale guadaga ogi ao ua somma X, ove si puo assumere che X N(µ, σ ). Ogi ao la Ditta paga ua tassa fissa
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 9/1 Prova scritta del 13/1/1 Esercizio 1 Ua Ditta commerciale guadaga ogi ao ua somma X, ove si puo assumere che X N(µ, σ ). Ogi ao la Ditta paga ua tassa fissa
Stime puntuali. Statistica e biometria. D. Bertacchi. Stime puntuali. Intervalli di confidenza. Approfondiamo
 Abbiamo visto che, data ua v.a. X di cui o si cooscao valore atteso e variaza, tali umeri si possoo stimare putualmete el seguete modo: si prede u casuale X 1,...,X di v.a. aveti la stessa legge di X;
Abbiamo visto che, data ua v.a. X di cui o si cooscao valore atteso e variaza, tali umeri si possoo stimare putualmete el seguete modo: si prede u casuale X 1,...,X di v.a. aveti la stessa legge di X;
Alcuni concetti di statistica: medie, varianze, covarianze e regressioni
 A Alcui cocetti di statistica: medie, variaze, covariaze e regressioi Esistoo svariati modi per presetare gradi quatità di dati. Ua possibilità è presetare la cosiddetta distribuzioe, raggruppare cioè
A Alcui cocetti di statistica: medie, variaze, covariaze e regressioi Esistoo svariati modi per presetare gradi quatità di dati. Ua possibilità è presetare la cosiddetta distribuzioe, raggruppare cioè
ANalysis. Analisi della Varianza - ANOVA. Aprile, Aprile, Nel linguaggio delle variabili le operazioni fondamentali sono tre
 ANalsis Of VAriace Nel liguaggio delle variabili le operazioi fodametali soo tre Descrizioe Spiegazioe Iterpretazioe Descrizioe La relazioe tra variabili viee sitetizzata per meglio cogliere gli aspetti
ANalsis Of VAriace Nel liguaggio delle variabili le operazioi fodametali soo tre Descrizioe Spiegazioe Iterpretazioe Descrizioe La relazioe tra variabili viee sitetizzata per meglio cogliere gli aspetti
Esercizi con R. Corso Statistica corso avanzato A. A. 2013/2014
 Esercizi co R Corso Statistica corso avazato A. A. 203/204 Esercizio Due compagie di assicurazioe soo i cocorreza per stipulare polizze co = 000 clieti. Si suppoga che ogi cliete scelga tra le due società
Esercizi co R Corso Statistica corso avazato A. A. 203/204 Esercizio Due compagie di assicurazioe soo i cocorreza per stipulare polizze co = 000 clieti. Si suppoga che ogi cliete scelga tra le due società
14. TEORIA DEI TEST STATISTICI
 4. TEORIA DEI TEST STATISTICI 4. Geeralità sui test di sigificatività I dati campioari possoo essere utilizzati, oltre che per costruire l itervallo di cofideza di u parametro igoto, ache per verificare
4. TEORIA DEI TEST STATISTICI 4. Geeralità sui test di sigificatività I dati campioari possoo essere utilizzati, oltre che per costruire l itervallo di cofideza di u parametro igoto, ache per verificare
Campionamento e distribuzioni campionarie
 Campioameto e distribuzioi campioarie Approccio idu8vo Ruolo dell ifereza sta>s>ca Procedure ifereziali di uso comue (itervalli di cofideza e test delle ipotesi) Risulta> e decisioi che dipedoo dalla limitatezza
Campioameto e distribuzioi campioarie Approccio idu8vo Ruolo dell ifereza sta>s>ca Procedure ifereziali di uso comue (itervalli di cofideza e test delle ipotesi) Risulta> e decisioi che dipedoo dalla limitatezza
Lezione 4 Corso di Statistica. Francesco Lagona
 Lezioe 4 Corso di Statistica Fracesco Lagoa Uiversità Roma Tre F. Lagoa (fracesco.lagoa@uiroma3.it) 1 / 23 obiettivi della lezioe familiarizzare co il calcolo e le proprietà della media aritmetica familiarizzare
Lezioe 4 Corso di Statistica Fracesco Lagoa Uiversità Roma Tre F. Lagoa (fracesco.lagoa@uiroma3.it) 1 / 23 obiettivi della lezioe familiarizzare co il calcolo e le proprietà della media aritmetica familiarizzare
TEST STATISTICI. indica l ipotesi che il parametro della distribuzione di una variabile assume il valore 0
 TEST STATISTICI I dati campioari possoo essere utilizzati per verificare se ua certa ipotesi su ua caratteristica della popolazioe può essere riteuta verosimile o meo. Co il termie ipotesi statistica si
TEST STATISTICI I dati campioari possoo essere utilizzati per verificare se ua certa ipotesi su ua caratteristica della popolazioe può essere riteuta verosimile o meo. Co il termie ipotesi statistica si
Esame di Statistica A-Di Prof. M. Romanazzi
 1 Uiversità di Veezia Esame di Statistica A-Di Prof. M. Romaazzi 12 Maggio 2014 Cogome e Nome..................................... N. Matricola.......... Valutazioe Il puteggio massimo teorico di questa
1 Uiversità di Veezia Esame di Statistica A-Di Prof. M. Romaazzi 12 Maggio 2014 Cogome e Nome..................................... N. Matricola.......... Valutazioe Il puteggio massimo teorico di questa
Statistica Corso Base (Serale) Dott.ssa Cristina Mollica
 Statistica Corso Base (Serale) Dott.ssa Cristia Mollica cristia.mollica@uiroma1.it Idici di posizioe Esercizio 1: Data la seguete distribuzioe uitaria del carattere X 4 2 4 2 6 4 0 4 0 2 4 4 (1) calcolare
Statistica Corso Base (Serale) Dott.ssa Cristia Mollica cristia.mollica@uiroma1.it Idici di posizioe Esercizio 1: Data la seguete distribuzioe uitaria del carattere X 4 2 4 2 6 4 0 4 0 2 4 4 (1) calcolare
Prendere decisioni per un campione singolo
 Predere decisioi per u campioe sigolo 1 Ifereza statistica Il campo dell ifereza statistica riguarda i metodi utilizzati per predere decisioi o trarre coclusioi riguardo ua popolazioe. Questi metodi utilizzao
Predere decisioi per u campioe sigolo 1 Ifereza statistica Il campo dell ifereza statistica riguarda i metodi utilizzati per predere decisioi o trarre coclusioi riguardo ua popolazioe. Questi metodi utilizzao
Legge Gamma e Legge Chi quadro
 Legge Gamma e Legge Chi quadro Sia G ua variabile aleatoria di legge Gamma di parametri a e λ reali positivi, G Γ(a, λ, la cui fuzioe di desità è: f G (x = λa Γ(a e λx x a per x 0 dove Γ( è la fuzioe Gamma
Legge Gamma e Legge Chi quadro Sia G ua variabile aleatoria di legge Gamma di parametri a e λ reali positivi, G Γ(a, λ, la cui fuzioe di desità è: f G (x = λa Γ(a e λx x a per x 0 dove Γ( è la fuzioe Gamma
Proprietà asintotiche stimatori OLS e statistiche collegate
 Proprietà asitotiche stimatori OLS e statistiche collegate Eduardo Rossi 2 2 Uiversità di Pavia (Italy) Maggio 2014 Rossi Proprietà asitotiche Ecoometria - 2014 1 / 30 Sommario Risultati prelimiari Distribuzioe
Proprietà asitotiche stimatori OLS e statistiche collegate Eduardo Rossi 2 2 Uiversità di Pavia (Italy) Maggio 2014 Rossi Proprietà asitotiche Ecoometria - 2014 1 / 30 Sommario Risultati prelimiari Distribuzioe
Intervalli di Fiducia
 di Fiducia Itroduzioe per la media Caso variaza ota per la media Caso variaza o ota per i coefficieti di regressioe per la risposta media i per i coefficieti i di regressioe multilieare - Media aritmetica
di Fiducia Itroduzioe per la media Caso variaza ota per la media Caso variaza o ota per i coefficieti di regressioe per la risposta media i per i coefficieti i di regressioe multilieare - Media aritmetica
Elementi di statistica
 Elemeti di statistica La misura delle gradezze fisiche può essere effettuata direttamete o idirettamete. Se la misura viee effettuata direttamete si parla di misura diretta; se essa viee dedotta attraverso
Elemeti di statistica La misura delle gradezze fisiche può essere effettuata direttamete o idirettamete. Se la misura viee effettuata direttamete si parla di misura diretta; se essa viee dedotta attraverso
