I coefficienti delle incognite sono proporzionali fra loro ma NON coi termini noti, e il sistema è dunque IMPOSSIBILE (si dice anche: INCOMPATIBILE).
|
|
|
- Norma Ruggeri
- 7 anni fa
- Visualizzazioni
Transcript
1 RISOLUZIONI DEGLI ESERCIZI SUI SISTEMI DI 1 GRADO IMPOSSIBILI E INDETERMINATI Per ciascuno dei seguenti sistemi, stabilisci se è determinato, impossibile, o indeterminato. In caso di indeterminazione, stabilisci anche quali sono le soluzioni. 1) x+ y= 12 2x+ 2y= = I coefficienti delle incognite sono proporzionali fra loro ma NON coi termini noti, e il sistema è dunque IMPOSSIBILE (si dice anche: INCOMPATIBILE). In pratica, il 1 membro della 2a equazione è il doppio del 1 membro della 1a equazione: 2x+ 2y= 2( x+, MA il termine noto della 2a equazione NON è il doppio del termine noto della 1a equazione: , perciò le due equazioni sono INCOMPATIBILI, non possono essere verificate da una stessa coppia( xy, ): se una data coppia ( xy, ) verifica la 1a equazione, allora non potrà verificare anche la 2 a, e viceversa. Osserviamo che se si calcolasse il determinante D dei coefficienti delle incognite, lo si troverebbe uguale a 0: in effetti, TUTTI i sistemi lineari con tante equazioni quante incognite impossibili o indeterminati hanno D. 2) x+ y = 21 x+ y = 7 21 = = I coefficienti delle incognite sono proporzionali fra loro E ANCHE coi termini noti, e il sistema è INDETERMINATO. In pratica, il 1 membro della 1a equazione è il triplo del 1 membro della 2a equazione: x+ y = ( x+, e il termine noto della 1a equazione è ANCH'ESSO il triplo del termine noto della 2a equazione: 21 = 7, perciò le due equazioni sono sostanzialmente la ripetizione l'una dell'altra (semplificando per la 1a si otterrebbe la 2 a, moltiplicando per la 2a si otterrebbe la 1 a). E' come se si avesse 1 SOLA EQUAZIONE, e 1 sola equazione NON BASTA A DETERMINARE 2 INCOGNITE IN MODO UNICO, in quanto ne vincola, sì, i valori, ma lasciando aperte infinite possibilità. Insomma, sono soluzioni del sistema tutte le infinite coppie ( x, tali che x+ y = 7: ad esempio la coppia (0, 7), la (1, 6), la (2,5), la ( 1,8), la (0,5; 6,5), la (10, )... ossia tutte le infinite coppie ( x, tali che x y = 7 x oppure, il che è lo stesso, tali che x = 7 y y Osserviamo che se si calcolasse il determinante D dei coefficienti delle incognite, lo si troverebbe uguale a 0 : in effetti, TUTTI i sistemi lineari con tante equazioni quante incognite impossibili o indeterminati hanno D.
2 ) 4x 8y= = = tutti e tre i rapporti valgono 10x 20y I coefficienti delle incognite sono proporzionali fra loro E ANCHE coi termini noti, e il sistema è INDETERMINATO. E' come se si avesse 1SOLA EQUAZIONE (lo puoi vedere anche semplificando le due equazioni per 4 e per 10 rispettivamente: otterrai, nei due casi, la medesima equazione x 2y= ) e 1sola equazione NON BASTA A DETERMINARE 2 INCOGNITE IN MODO UNICO, in quanto ne vincola, sì, i valori, ma lasciando aperte infinite possibilità. Teniamo dunque una sola equazione a piacere, ad es. la 4x 8y= 12 che potrà essere semplificata in x 2y= : essa ci dice che sono soluzioni del sistema tutte le infinite coppie ( x, per cui x 2y= x= 2y+ ossia tutte le infnite coppie ( x, tali che (isolando x) y oppure, il che è lo stesso, tali che x (isolando. y = 2 x= 2y+ Prova a considerare il sistema y e a dare dei valori a y, calcolando poi i corrispondenti valori di x, e successivamente il sistema x y = 2 dando dei valori a x, e calcolando i corrispondenti valori di y: constaterai che nei due casi l'insieme delle infinite coppie ( xy, ) che si ottiene è esattamente il medesimo. Osserviamo che se si calcolasse il determinante D dei coefficienti delle incognite, lo si troverebbe uguale a 0 : in effetti, TUTTI i sistemi lineari con tante equazioni quante incognite impossibili o indeterminati hanno D. 4) 2( x+ = y+ 2x+ x y = y ( 12 x) 2x + 2y= y+ 2x + y = Facciamo i calcoli : x y= y 12+ x 4y= 12; y= x è dunque scomparsa ed entrambe le equazioni ci dicono che y deve valere : perciò x può essere mentre y deve valere, e sono soluzioni del sistema tutte e sole le coppie ( x,) con xarbitrario. Questa conclusione è ancora più evidente se si osserva che, rinunciando a mandar via le coppie di termini uguali a primo e a secondo membro, il nostro sistema potrebbe essere scritto sotto la forma 2 x 2 x + 2 y y = 0 ossia x + y = 0 x+ y= e infine x x y y= 12 0 x 4y= 12 ; 0 x+ y= da qui si vede molto bene che l'insieme delle soluzioni è appunto l'insieme delle infinite coppie ( xy, ) con Osserviamo che in questo sistema non ha senso considerare i rapporti fra i coeff. delle incognite, in quanto il rapporto fra i coefficienti della x ci darebbe l'operazione non eseguibile 0/0; tuttavia, se si calcolasse il determinante D dei coefficienti delle incognite, lo si troverebbe uguale a 0, il che conferma ciò che abbiamo più volte sottolineato : la caratteristica di TUTTI i sistemi lineari con tante equazioni quante incognite impossibili o indeterminati è di avere D. x y =
3 5) 2x y = 1 x 2y = 1 Qui se calcoliamo il determinante dei coefficienti delle incognite troveremo 2 1 D= = 4+ 1= quindi il sistema è "normale", o meglio "DETERMINATO" (l'aggettivo "determinato", "determinata" si utilizza per quei sistemi o quelle equazioni che hanno un numero finito e >0 di soluzioni; nel caso dei sistemi o delle equazioni di 1 grado, questo significa poi avere una e una sola soluzione). D'altronde, i coeff. delle incognite NON erano proporzionali. Si risolve con un metodo e si trova l'unica soluzione x = 1/ y = 1/ A PROPOSITO, ricorda che per "soluzione" di un sistema si intende una COPPIA (ordinata) di valori, se il sistema ha 2 incognite; una TERNA (ordinata) di valori, se il sistema ha incognite; ecc. Non devi dunque pensare che qui si abbiano2 soluzioni perché hai trovato un valore per x e un valore per y: UNA SOLUZIONE, perchè hai trovato UNA COPPIA ( x,. 6) 2 1 x+ y = : = : = 1: ( tutti e tre i rapporti valgono 4) x+ y = quindi i coefficienti delle incognite sonio proporzionalifra loro e coi termini noti, e il sistema è INDETERMINATO. 2 1 Si può tenere una sola equazione fra le due, ad esempio la x+ y = 1, 5 liberarla dai denominatori ottenendo 10x+ y = 15, e concludere che le soluzioni del sistema sono tutte le infinite coppie ( x, per cui 10x+ y = 15 ossia tutte le infinite coppie ( x, tali che 15 10x (isolando y = y oppure, il che è lo stesso, tali che 15 y (isolando x) x = 10 a a 10x+ y = 15 Anche, moltiplicando la l equazione per 15 e la 2 per 60 : 10 x+ y = 15 Le due equazioni coincidono, quindi si riducono a 1 SOLAEQUAZIONE Sono soluzioni del sistema tutte le infinite coppie ( x, per cui 10x+ y = 15 ossia tutte le infnite coppie ( x, tali che 15 10x (isolando y = y oppure, il che è lo stesso, tali che 15 y (isolando x) x = 10
4 7) x+ y = 2 ( x x+ y = 2 x+ y 2x = 2 x = 1 x y = 6 ( x+ x y = 6 x y 2x = 6 x = Il sistema è IMPOSSIBILE: la graffa di sistema equivale al conettivo logico ET (E, E CONTEMPORANEAMENTE)... ora, x non può essere uguale simultaneamente a 1 e a. Possiamo convincerci ancor meglio della correttezza di questa conclusione se procediamo nel modo seguente: x+ y = 2 ( x x+ y = 2 x+ y x+ x+ y y = 2 2x+ 0 y = 2 x y = 6 ( x+ x y = 6 x y x+ x y+ y = 6 2x+ 0 y = 6 La 1a equazione è verificata da tutte le coppie (1, con y, La 2a equazione è verificata da tutte le coppie (, con y. Esiste una coppia ( x, che verifichi contemporaneamente entrambe le equazioni? NO. Il sistema è dunque IMPOSSIBILE. 8) + y = 2 ( x 2( x+ = x+ 2y+ 1 x+ y = 2 x+ y 2x+ 2y = x+ 2y + 1 2x = 2 x = 1 x = 1 x = 1 y è dunque scomparsa ed entrambe le equazioni ci dicono che x deve valere 1: perciò sono soluzioni del sistema tutte e sole le coppie (1, con y arbitrario. Questa conclusione è ancora più evidente se si osserva che, volendo, il nostro sistema potrebbe essere scritto sotto la forma + y = 2 ( x 2( x+ = x+ 2y+ 1 x+ y = 2 x+ y 2x+ 2y = x+ 2y+ 1 x+ x+ y y = 2 2x x+ 2y 2y = 1 2x+ 0 y = 2 x+ 0 y = 1 La la equazione è verificata da tutte le coppie (1, con y, la 2a equazione... pure. Quindi le soluzioni del sistema sono tutte e sole le coppie ( xy, ) tali che x = 1 y
5 9) + y = ( y x) 2x y = ( y x) x+ y = y x 2x y = y+ x 4x ; x x y è dunque scomparsa ed entrambe le equazioni ci dicono che x deve valere 0 : perciò sono soluzioni del sistema tutte e sole le coppie (0, con y arbitrario. Questa conclusione è ancora più evidente se si osserva che, volendo, il nostro sistema potrebbe essere scritto sotto la forma + y = ( y x) 2x y = ( y x) x+ y = y x 2x y = y+ x x+ x+ y y 2x x y+ y 4x+ 0 y x+ 0 y La la equazione è verificata da tutte le coppie (0, con y, la 2a equazione... pure. Quindi le soluzioni del sistema sono tuttee sole le coppie ( xy, ) tali che x y 10) + 4y 5x 6y Il determinante D dei coefficienti delle incognite è diverso da 0 (D = 8): perciò il sistema è determinato. Risolvendo, si trova che la sua unica soluzione è la coppia y
6 11) + y+ 2z = 4 2x+ y+ z = 1 x+ 2y+ z Calcoliamo il determinante dei coefficienti delle incognite: = = 1 ( 2) 1 ( 6 ) + 2 ( 4 ) = D : dunque il sistema non è determinato, sarà impossibile o indeterminato. Vediamo. = 4 y 2z 2( 4 y 2z) + y + z = 1 ( 4 y 2z) + 2y + z = 4 y 2z 8 2y 4z + y + z = 1 12 y 6z + 2y + z = 4 y 2z y z = 7 y z = 7 x = 4 y 2z y + z = 7 y = 7 z x = 4 7+ z 2z = z e dunque = z y = 7 z SISTEMA INDETERMINATO: INFINITE SOLUZIONI z Avremmo anche potuto osservare fin da subito che LA TERZA EQUAZIONE E' LA SOMMA DELLE PRIME DUE, quindi è una CONSEGUENZA delle prime due e non ci dice niente di più rispetto a queste... la terza equazione può perciò scomparire e il sistema si riduce alle sole ( ) x+ y + 2z = 4 2x+ y + z = 1 da cui x = 4 y 2z x = 4 y 2z x = 4 y 2z 2 4 y 2z + y + z = 1 8 2y 4z + y + z = 1 y z = 7 x = 4 y 2z y + z = 7 y = 7 z x = 4 7+ z 2z = z e dunque = z y = 7 z SISTEMA INDETERMINATO z
7 12) + y+ z = 2x y+ z = 1 x 2y Calcoliamo ildeterminante dei coefficienti delle incognite: = = 1 ( 0+ 2) 1 ( 0 1) + 1 ( 4+ 1) = 2+ 1 = D : perciò il sistema non è determinato, sarà impossibile o indeterminato. Vediamo. = 2y 2y+ y+ z = 4y y+ z = 1 = 2y y+ z = y+ z = 1 e quindi le ultime due equazioni sono incompatibili, non possono essere verificate da una stessa coppia ( x, : il sistema è IMPOSSIBILE. D'altronde, proseguendo con sostituzione = 2y z = y y + y = 1 si otterrebbe una EQUAZIONE RISOLVENTE IMPOSSIBILE. A proposito: a) equazione risolvente (=con una sola incognita) impossibile sistema certamente impossibile b) equazione risolvente (=con una sola incognita) indeterminata sistema che di norma è indeterminato, ma non è certo: in casi eccezionali, che non si incontrano pressoché mai negli esercizi scolastici, la conclusionepotrebbe pure essere un'altra. Avremmo potuto renderci conto più rapidamente dell'impossibilità se avessimo sottratto, nel sistema iniziale, la prima equazione dalla seconda. (2) 2x y+ z = 1 (1) x+ y+ z = (2) (1) x 2y = 2 L'equazione così ottenuta è in contraddizione con la () x 2y da cui l'impossibilità. 1) y = 1/2 1 y x+ 6 = 8; x+ = 8; x x+ 6y = 8 (2) x 2 = 1 (1) y = 1/2 2 Il sistema ha dunque una e una sola soluzione; 1 6 d'altronde il determinante dei coefficienti delle incognite è diverso da 0: D = = 2 0 =
8 14) 22 ( x+ = y ( y 4x) x + y = 9 4x + 2y = y y + 4x indeterminata: verificata da valore della coppia ( xy, ) x + y = 9 La prima equazione non pone alcun vincolo alla coppia ( xy, ) ed è perciò ininfluente, si può tralasciare; resta solo laseconda equazione, che impone alla coppia ( xy, ) di soddisfare il vincolo x+ y= 9. Le soluzioni del sistema sono allora tutte e sole le coppie ( xy, ) tali che x+ y= 9, ossia tali che x y = 9 x oppure, il che è lo stesso, tali che x = 9 y y 15) ( x+ y+ 2) = x+ 8+ y 4x y = 2 x + y + 6= x + 8+ y impossibile 4x y = 2 La prima equazione è impossibile, cioè non è verificata da nessuna coppia ( x, : quindi, a maggior ragione, non può esistere nessuna coppia ( x, che verifichi contemporaneamente entrambe le equazioni. Il sistema è dunque IMPOSSIBILE. 16) 2( x 1= x+ y ( y x+ 1) 2( x+ = x+ y+ 1 ( y x) 2x 2y 1 = x + y y + x 1 indeterminata 2x + 2y = x + y + 1 y + x impossibile E' vero che la prima equazione è indeterminata, verificata da coppia ( x, ; tuttavia, la seconda equazione è impossibile, cioè non è verificata da nessuna coppia ( x, : quindi, a maggior ragione, non può esistere nessuna coppia ( x, che verifichi contemporaneamente entrambe le equazioni. Questo sistema è dunque IMPOSSIBILE.
9 Negli esercizi che seguono, è richiesto di determinare il valore del parametro in modo che il sistema non sia determinato, e di stabilire se, per quel valore, si ha impossibilità o indeterminazione. 17) 6x+ ay = 10 x 4y 6 a D = = 24 a 4 D se e solo se 24 a ; a = 8 In questo caso, il sistema diventa 6x 8y = 10 x 4y INDETERMINATO (la prima equazione non è altro che la seconda moltiplicata per 2) Anche: 6 a = 4 ( 6: = a :( 4) ) quando a = 24 (prodotto dei medi=prodotto degli estremi) cioè per a = 8 Più rapidamente: in 6x+ ay = 10 x 4y 6 è il doppio di ; il caso "speciale" si avrà allora quando anche a è il doppio di 4, quindi con a = 8.
10 18) kx + ( k 1) y 2x+ y = 4 k k 1 D= = k 2( k 1) = k 2k + 2= k+ 2 2 D se esolo se k+ 2; k = 2 In questo caso, il sistema diventa 2x y 2x+ y = 4 IMPOSSIBILE k k 1 Anche: = ( k: 2 = ( k 1) : ) 2 quando 2k 2 = k (prodotto dei medi=prodotto degli estremi) cioè per k = 2 19) bx y = 2 ( b 4) x+ y = b b 1 D = = b+ ( b 4) = 2b 4 b 4 1 D se e solo se 2b 4 ; b = 2 In questo caso, il sistema diventa 2x y = 2 2x + y = 2 INDETERMINATO (le equazioni sono opposte fra loro, quindi sono sostanzialmente la ripetizione l'una dell' altra) Anche: l'uguaglianza b 1 = b 4 1 è verificata con b = 2 Più rapidamente: in bx y = 2 ( b 4) x+ y = b i coefficienti di y sono opposti; il caso "speciale" si avrà nel caso siano simultaneamente opposti anche i coefficienti di x, ma a tale scopo occorre che si abbia b = ( b 4) equazione che è verificata quando b = 2.
11 20) + my = 6 2x+ ( m+ ) y = 4 m D= = m+ 9 2m= m+ 9 2 m + D se esolose m+ 9; m= 9 9y = 6 In questo caso, il sistema diventa 2 x 6 y = 4 INDETERMINATO (le due equazioni, semplificate, danno entrambe la medesima equazione x y = 2) Anche: m = 2 m + quando ( :2 = m:( m+ ) ) 2m= ( m+ ) (prodotto dei medi = prodotto degli estremi) cioè per m = 9 + my = 6 Più rapidamente: in 2 x+ ( m+ ) y = 4 èi/2di2; il caso "speciale" si avrà allora quando anche m= + 2 equazione che ha come soluzione m = 9. ( m ) 21) + y+ z = 2 hx + hz x y + z = h h h h 0 D= h 0 h = = 1 h ( h) = h h= Il sistema è dunque, per valore di h, sempre impossibile o indeterminato. Quando si avrà impossibilità e quando indeterminazione? Si potrebbe avviare la risoluzione con sostituzione perdomandarsi, una volta giunti all'equazione risolvente, per quali valori di m essa risulta impossibile e per quali indeterminata. Più rapidamente, se sommiamo la prima e la terza equazione otteniamo 2x+ 2z e confrontando questa equazione con la hx + hz capiremo subito che si ha indeterminazione con h = 2 e impossibilità con h 2.
Esercizi sui sistemi di equazioni lineari.
 Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
Esercizi sui sistemi di equazioni lineari Risolvere il sistema di equazioni lineari x y + z 6 x + y z x y z Si tratta di un sistema di tre equazioni lineari nelle tre incognite x, y e z Poichè m n, la
( 5) 2 = = = +1
 1 IDENTITA ED EQUAZIONI Consideriamo la seguente uguaglianza: ( 2x + 3) 2 = 4x 2 +12x + 9 Diamo alcuni valori arbitrari all incognita x e vediamo se l uguaglianza risulta vera. Per x = 1 si avrà: ( 2 1+
1 IDENTITA ED EQUAZIONI Consideriamo la seguente uguaglianza: ( 2x + 3) 2 = 4x 2 +12x + 9 Diamo alcuni valori arbitrari all incognita x e vediamo se l uguaglianza risulta vera. Per x = 1 si avrà: ( 2 1+
( 5) 2 = = = +1
 1 IDENTITA ED EQUAZIONI Consideriamo la seguente uguaglianza: ( 2x + 3) 2 = 4x 2 +12x + 9 Diamo alcuni valori arbitrari all incognita x e vediamo se l uguaglianza risulta vera. Per x = 1 si avrà: ( 2 1+
1 IDENTITA ED EQUAZIONI Consideriamo la seguente uguaglianza: ( 2x + 3) 2 = 4x 2 +12x + 9 Diamo alcuni valori arbitrari all incognita x e vediamo se l uguaglianza risulta vera. Per x = 1 si avrà: ( 2 1+
Equazioni lineari con due o più incognite
 Equazioni lineari con due o più incognite Siano date le uguaglianze: k 0; x + y = 6; 3a + b c = 8. La prima ha un termine incognito rappresentato dal simbolo letterale k; la seconda ha due termini incogniti
Equazioni lineari con due o più incognite Siano date le uguaglianze: k 0; x + y = 6; 3a + b c = 8. La prima ha un termine incognito rappresentato dal simbolo letterale k; la seconda ha due termini incogniti
SISTEMI DI 1 GRADO CON DUE EQUAZIONI IN DUE INCOGNITE
 Pagina 1 di 6 SISTEMI DI 1 GRADO CON DUE EQUAZIONI IN DUE INCOGNITE L insieme di due equazioni di primo grado in due incognite si dice SISTEMA DI 1 GRADO. La soluzione del sistema è ogni coppia di numeri
Pagina 1 di 6 SISTEMI DI 1 GRADO CON DUE EQUAZIONI IN DUE INCOGNITE L insieme di due equazioni di primo grado in due incognite si dice SISTEMA DI 1 GRADO. La soluzione del sistema è ogni coppia di numeri
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI
 SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
SISTEMI LINEARI: APPROFONDIMENTI ED ESEMPI Appunti presi dalle lezioni del prof. Nedo Checcaglini Liceo Scientifico di Castiglion Fiorentino (Classe 4B) January 17, 005 1 SISTEMI LINEARI Se a ik, b i R,
I sistemi di equazioni di primo grado
 I sistemi di equazioni di primo grado RIPASSIAMO INSIEME SISTEMI DI EQUAZIONI DI PRIMO GRADO Un sistema di equazioni di primo grado in due (o più) incognite è l insieme di due (o più) equazioni di primo
I sistemi di equazioni di primo grado RIPASSIAMO INSIEME SISTEMI DI EQUAZIONI DI PRIMO GRADO Un sistema di equazioni di primo grado in due (o più) incognite è l insieme di due (o più) equazioni di primo
Chi non risolve esercizi non impara la matematica.
 5.5 esercizi 9 Per trovare la seconda equazione ragioniamo così: la parte espropriata del primo terreno è x/00, la parte espropriata del secondo è y/00 e in totale sono stati espropriati 000 m, quindi
5.5 esercizi 9 Per trovare la seconda equazione ragioniamo così: la parte espropriata del primo terreno è x/00, la parte espropriata del secondo è y/00 e in totale sono stati espropriati 000 m, quindi
I sistemi lineari Prof. Walter Pugliese
 I sistemi lineari Prof. Walter Pugliese Le equazioni lineari in due incognite Un equazione nelle incognite x e y del tipo #$ + &' = ) dove *,,, - sono numeri reali è un equazione lineare in due incognite
I sistemi lineari Prof. Walter Pugliese Le equazioni lineari in due incognite Un equazione nelle incognite x e y del tipo #$ + &' = ) dove *,,, - sono numeri reali è un equazione lineare in due incognite
Le equazioni lineari
 Perchè bisogna saper risolvere delle equazioni? Perché le equazioni servono a risolvere dei problemi! Le equazioni lineari Un problema è una proposizione che richiede di determinare i valori di alcune
Perchè bisogna saper risolvere delle equazioni? Perché le equazioni servono a risolvere dei problemi! Le equazioni lineari Un problema è una proposizione che richiede di determinare i valori di alcune
Pagine di Algebra lineare. di premessa al testo Pagine di Geometria di Sara Dragotti. Parte terza: SISTEMI LINEARI
 Pagine di Algebra lineare di premessa al testo Pagine di Geometria di Sara Dragotti Parte terza: SISTEMI LINEARI 1. Definizioni Dato un campo K ed m 1 polinomi su K in n indeterminate di grado non superiore
Pagine di Algebra lineare di premessa al testo Pagine di Geometria di Sara Dragotti Parte terza: SISTEMI LINEARI 1. Definizioni Dato un campo K ed m 1 polinomi su K in n indeterminate di grado non superiore
Sistemi lineari (di I grado)
 Sistemi lineari (di I grado) Un sistema lineare è un insieme di equazioni lineari (di I grado), che devono essere verificate tutte contemporaneamente. Risolvere un sistema di equazioni vuol dire trovare
Sistemi lineari (di I grado) Un sistema lineare è un insieme di equazioni lineari (di I grado), che devono essere verificate tutte contemporaneamente. Risolvere un sistema di equazioni vuol dire trovare
Sistemi di equazioni
 Sistemi di equazioni 19 191 Equazione lineare in due incognite Definizione 191 Una equazione di primo grado (in n incognite) si chiama equazione lineare Problema 191 Determinare due numeri naturali la
Sistemi di equazioni 19 191 Equazione lineare in due incognite Definizione 191 Una equazione di primo grado (in n incognite) si chiama equazione lineare Problema 191 Determinare due numeri naturali la
SISTEMI DI DUE EQUAZIONI IN DUE INCOGNITE
 SISTEMI DI DUE EQUAZIONI IN DUE INCOGNITE Un equazione di primo grado in una incognita del tipo, con ha: una sola soluzione (equazione determinata) se nessuna soluzione (equazione impossibile) se tutte
SISTEMI DI DUE EQUAZIONI IN DUE INCOGNITE Un equazione di primo grado in una incognita del tipo, con ha: una sola soluzione (equazione determinata) se nessuna soluzione (equazione impossibile) se tutte
Appunti di matematica per le Scienze Sociali Parte 1
 Appunti di matematica per le Scienze Sociali Parte 1 1 Equazioni 1.1 Definizioni preliminari 1.1.1 Monomi Si definisce monomio ogni prodotto indicato di fattori qualsiasi, cioè uguali o diseguali, numerici
Appunti di matematica per le Scienze Sociali Parte 1 1 Equazioni 1.1 Definizioni preliminari 1.1.1 Monomi Si definisce monomio ogni prodotto indicato di fattori qualsiasi, cioè uguali o diseguali, numerici
Equazioni di secondo grado
 Equazioni di secondo grado Un equazione di secondo grado può sempre essere ridotta nella forma: a + bx + c 0 forma normale con a 0. Le lettere a, b, c sono rappresentano i coefficienti. Solo b e c possono
Equazioni di secondo grado Un equazione di secondo grado può sempre essere ridotta nella forma: a + bx + c 0 forma normale con a 0. Le lettere a, b, c sono rappresentano i coefficienti. Solo b e c possono
ax 1 + bx 2 + c = 0, r : 2x 1 3x = 0.
 . Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
. Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
Argomento 13 Sistemi lineari
 Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Sistemi lineari: definizioni Argomento Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto
Per equazione lineare nelle incognite x, y intendo un equazione del tipo. ax = b,
 Matematica II 161110 1 Equazioni lineari in una incognita Per equazione lineare nell incognita x intendo un equazione del tipo ax = b dove a b sono due costanti reali a e il coefficiente e b e il termine
Matematica II 161110 1 Equazioni lineari in una incognita Per equazione lineare nell incognita x intendo un equazione del tipo ax = b dove a b sono due costanti reali a e il coefficiente e b e il termine
EQUAZIONI DI PRIMO GRADO
 Cognome... Nome... Equazioni di primo grado EQUAZIONI DI PRIMO GRADO Un'equazione di primo grado e un'uguaglianza tra due espressioni algebriche di primo grado, vera solo per alcuni valori che si attribuiscono
Cognome... Nome... Equazioni di primo grado EQUAZIONI DI PRIMO GRADO Un'equazione di primo grado e un'uguaglianza tra due espressioni algebriche di primo grado, vera solo per alcuni valori che si attribuiscono
SISTEMI LINEARI. Prof.ssa R. Schettino Classe II a.s. 10/ 10/ 1111
 SISTEMI LINEARI Prof.ssa R. Schettino Classe II a.s. 10/ 10/ 1111 EQUAZIONE LINEARE IN DUE INCOGNITE 3x+7y=21-12x+6y-36=0 x-y+2=0 9y-21x+9=0 Con x e y si indicano le incognite delle equazioni Quali sono
SISTEMI LINEARI Prof.ssa R. Schettino Classe II a.s. 10/ 10/ 1111 EQUAZIONE LINEARE IN DUE INCOGNITE 3x+7y=21-12x+6y-36=0 x-y+2=0 9y-21x+9=0 Con x e y si indicano le incognite delle equazioni Quali sono
LE EQUAZIONI LINEARI LE IDENTITA ( )( ) 5. a Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a
 LE EQUAZIONI LINEARI 1 LE IDENTITA a b = ( a + b)( a b) () 1 a = a + a ( ) ( a + b) = a + ab + b () 3 Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a b = ( a+ b)( a b) È sempre vera qualunque
LE EQUAZIONI LINEARI 1 LE IDENTITA a b = ( a + b)( a b) () 1 a = a + a ( ) ( a + b) = a + ab + b () 3 Cosa hanno in comune le seguenti uguaglianze? Uguaglianza (1) a b = ( a+ b)( a b) È sempre vera qualunque
Note sull algoritmo di Gauss
 Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
Note sull algoritmo di Gauss 29 settembre 2009 Generalità Un sistema lineare di m equazioni in n incognite x,..., x n è un espressione del tipo: a x + a 2 x 2 + + a n x n = b a 2 x + a 22 x 2 + + a 2n
SISTEMI LINEARI MATRICI E SISTEMI 1
 MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
MATRICI E SISTEMI SISTEMI LINEARI Sistemi lineari e forma matriciale (definizioni e risoluzione). Teorema di Rouché-Capelli. Sistemi lineari parametrici. Esercizio Risolvere il sistema omogeneo la cui
Le equazioni e i sistemi di primo grado
 Le equazioni e i sistemi di primo grado prof. Roberto Boggiani Isiss Marco Minghetti 1 settembre 009 Sommario In questo documento verrà trattato in modo semplice e facilmente comprensibile la teoria delle
Le equazioni e i sistemi di primo grado prof. Roberto Boggiani Isiss Marco Minghetti 1 settembre 009 Sommario In questo documento verrà trattato in modo semplice e facilmente comprensibile la teoria delle
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI
 CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
CORSO DI ALGEBRA LINEARE Anno Accademico 2004/2005 Appunti su SISTEMI di EQUAZIONI LINEARI Lo studente ha forse già incontrato i sistemi di equazioni lineari alla scuola secondaria Con il termine equazione
Sistemi e problemi, Pag. 1\10 Prof. I. Savoia - Giugno 2011 SISTEMI E PROBLEMI
 Sistemi e problemi, Pag. 1\10 Prof. I. Savoia - Giugno 2011 SISTEMI E PROBLEMI Affrontare un problema richiede spesso l'uso di alcuni strumenti algebrici: fra essi vi sono i sistemi di equazioni. Infatti,
Sistemi e problemi, Pag. 1\10 Prof. I. Savoia - Giugno 2011 SISTEMI E PROBLEMI Affrontare un problema richiede spesso l'uso di alcuni strumenti algebrici: fra essi vi sono i sistemi di equazioni. Infatti,
Sistemi lineari di due equazioni in due incognite
 Sistemi lineari di due equazioni in due incognite Incognite Lettere (di solito X e Y) alle quali è possibile sostituire dei valori numerici Coppia ordinata Coppia (X;Y) di valori numerici, per la quale
Sistemi lineari di due equazioni in due incognite Incognite Lettere (di solito X e Y) alle quali è possibile sostituire dei valori numerici Coppia ordinata Coppia (X;Y) di valori numerici, per la quale
LEZIONE 2. ( ) a 1 x 1 + a 2 x a n x n = b, ove a j, b R sono fissati.
 LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
LEZIONE 2 2 Sistemi di equazioni lineari Definizione 2 Un equazione lineare nelle n incognite x, x 2,, x n a coefficienti reali, è un equazione della forma (2 a x + a 2 x 2 + + a n x n = b, ove a j, b
1. ESEMPI DI PROBLEMI A UNA INCOGNITA
 EQUAZIONI E PROBLEMI. ESEMPI DI PROBLEMI A UNA INCOGNITA PROBLEMA SVOLTO Per prender parte alla festa del primino ogni maschio deve pagare un biglietto da euro, ogni femmina un biglietto da euro. Si vendono
EQUAZIONI E PROBLEMI. ESEMPI DI PROBLEMI A UNA INCOGNITA PROBLEMA SVOLTO Per prender parte alla festa del primino ogni maschio deve pagare un biglietto da euro, ogni femmina un biglietto da euro. Si vendono
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof. Fabio Perroni. 3. Sistemi di equazioni lineari
 Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
Corso di GEOMETRIA Dipartimento di Ingegneria ed Architettura Università degli Studi di Trieste Prof Fabio Perroni 3 Sistemi di equazioni lineari Siano m, n N \ {}, sia K un campo Definizione a) Un sistema
LE EQUAZIONI Conoscenze
 LE EQUAZIONI Conoscenze 1. Completa. a. L identità è una... fra due... che è sempre..., qualunque sia... b. L equazione è una... fra due... che è... solo per... c. Due equazioni si dicono equivalenti se...
LE EQUAZIONI Conoscenze 1. Completa. a. L identità è una... fra due... che è sempre..., qualunque sia... b. L equazione è una... fra due... che è... solo per... c. Due equazioni si dicono equivalenti se...
RISOLVERE EQUAZIONI DI PRIMO GRADO INTERE
 Prof. Di Caprio 1 RISOLVERE EQUAZIONI DI PRIMO GRADO INTERE Introduzione In questa lezione impareremo a risolvere equazioni di primo grado intere. Esse sono molto utili principalmente per risolvere alcune
Prof. Di Caprio 1 RISOLVERE EQUAZIONI DI PRIMO GRADO INTERE Introduzione In questa lezione impareremo a risolvere equazioni di primo grado intere. Esse sono molto utili principalmente per risolvere alcune
SISTEMI LINEARI. x y + 2t = 0 2x + y + z t = 0 x z t = 0 ; S 3 : ; S 5x 2y z = 1 4x 7y = 3
 SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
SISTEMI LINEARI. Esercizi Esercizio. Verificare se (,, ) è soluzione del sistema x y + z = x + y z = 3. Trovare poi tutte le soluzioni del sistema. Esercizio. Scrivere un sistema lineare di 3 equazioni
Definizione: Due equazioni si dicono equivalenti se ammettono le stesse soluzioni.
 Facoltà di Medicina e Chirurgia Corso Zero di Matematica Gruppi: MC-MF3 / PS-MF3 II Lezione EQUAZIONI E SISTEMI Dr. E. Modica erasmo@galois.it www.galois.it IDENTITÀ ED EQUAZIONI Si consideri un uguaglianza
Facoltà di Medicina e Chirurgia Corso Zero di Matematica Gruppi: MC-MF3 / PS-MF3 II Lezione EQUAZIONI E SISTEMI Dr. E. Modica erasmo@galois.it www.galois.it IDENTITÀ ED EQUAZIONI Si consideri un uguaglianza
+2 3 = = =3 + =3 + =8 =15. Sistemi lineari. nelle stesse due incognite. + = + = = = Esempi + =5. Il sistema è determinato
 Sistemi di equazioni SISTEMI LINEARI Un sistema di equazioni è un insieme di equazioni per le quali si cercano eventuali soluzioni comuni. +=7 =1 Ognuna delle due equazioni ha infinite soluzioni. La coppia
Sistemi di equazioni SISTEMI LINEARI Un sistema di equazioni è un insieme di equazioni per le quali si cercano eventuali soluzioni comuni. +=7 =1 Ognuna delle due equazioni ha infinite soluzioni. La coppia
LEZIONE 3. a + b + 2c + e = 1 b + d + g = 0 3b + f + 3g = 2. a b c d e f g
 LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
LEZIONE 3 3.. Matrici fortemente ridotte per righe. Nella precedente lezione abbiamo introdotto la nozione di soluzione di un sistema di equazioni lineari. In questa lezione ci poniamo il problema di descrivere
Sistemi di 1 grado in due incognite
 Sistemi di 1 grado in due incognite Problema In un cortile ci sono polli e conigli: in totale le teste sono 7 e zampe 18. Quanti polli e quanti conigli ci sono nel cortile? Soluzione Indichiamo con e con
Sistemi di 1 grado in due incognite Problema In un cortile ci sono polli e conigli: in totale le teste sono 7 e zampe 18. Quanti polli e quanti conigli ci sono nel cortile? Soluzione Indichiamo con e con
ax 1 + bx 2 + c = 0, r : 2x 1 3x 2 + 1 = 0.
 . Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
. Rette in R ; circonferenze. In questo paragrafo studiamo le rette e le circonferenze in R. Ci sono due modi per descrivere una retta in R : mediante una equazione cartesiana oppure mediante una equazione
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito B 3/05/005 A. A. 004 005 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito B 3/05/005 A. A. 004 005 ) Risolvere il seguente sistema
Risoluzione di sistemi lineari
 Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
Risoluzione di sistemi lineari Teorema (Rouché-Capelli) Dato il sistema di m equazioni in n incognite Ax = b, con A M at(m, n) b R n x R n [A b] si ha che: matrice dei coefficienti, vettore dei termini
Prof. I. Savoia. SISTEMI LINEARI E RETTA (VERSIONE PROVVISORIA NON ULTIMATA)
 SISTEMI LINEARI E RETTA 1 Proprietà e rappresentazione grafica dei sistemi lineari. I sistemi lineari in due incognite sono insiemi di due equazioni di primo grado, nei qualiciascuna di esse rappresenta
SISTEMI LINEARI E RETTA 1 Proprietà e rappresentazione grafica dei sistemi lineari. I sistemi lineari in due incognite sono insiemi di due equazioni di primo grado, nei qualiciascuna di esse rappresenta
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA
 UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
UNIVERSITÀ DEGLI STUDI DI TERAMO FACOLTÀ DI SCIENZE POLITICHE CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA II Parziale - Compito C 3/5/25 A. A. 24 25 ) Risolvere il seguente sistema
Il teorema di Rouché-Capelli
 Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
Luciano Battaia Questi appunti (1), ad uso degli studenti del corso di Matematica (A-La) del corso di laurea in Commercio Estero dell Università Ca Foscari di Venezia, campus di Treviso, contengono un
y 5z = 7 y +8z = 10 +3z = 3
 Sistemi lineari Sistemi lineari in tre incognite; esempi tipici Tre equazioni incognite x, y, z Consideriamo il seguente sistema di tre equazioni lineari nelle tre x 2y +6z = 11 x +3y 11z = 18 2x 5y +20z
Sistemi lineari Sistemi lineari in tre incognite; esempi tipici Tre equazioni incognite x, y, z Consideriamo il seguente sistema di tre equazioni lineari nelle tre x 2y +6z = 11 x +3y 11z = 18 2x 5y +20z
LE EQUAZIONI (in rosso i risultati)
 LE EQUAZIONI (in rosso i risultati) 1. Completa. a. L identità è una...uguaglianza... fra due...espressioni letterali... che è sempre...vera..., qualunque sia... il valore delle lettere che vi figurano
LE EQUAZIONI (in rosso i risultati) 1. Completa. a. L identità è una...uguaglianza... fra due...espressioni letterali... che è sempre...vera..., qualunque sia... il valore delle lettere che vi figurano
Anno 2. Risoluzione di sistemi di primo grado in due incognite
 Anno Risoluzione di sistemi di primo grado in due incognite Introduzione In questa lezione impareremo alcuni metodi per risolvere un sistema di due equazioni in due incognite. Al termine di questa lezione
Anno Risoluzione di sistemi di primo grado in due incognite Introduzione In questa lezione impareremo alcuni metodi per risolvere un sistema di due equazioni in due incognite. Al termine di questa lezione
Sistemi lineari. a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2 : : : a m1 x 1 + a m2 x 2 +..
 Sistemi lineari: definizioni Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto termine
Sistemi lineari: definizioni Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto termine
Geometria BAER PRIMO CANALE Foglio esercizi 1
 Geometria BAER PRIMO CANALE Foglio esercizi 1 Esercizio 1. Risolvere le seguenti equazioni lineari nelle variabili indicate trovando una parametrizzazione dell insieme delle soluzioni. a) x + 5y = nelle
Geometria BAER PRIMO CANALE Foglio esercizi 1 Esercizio 1. Risolvere le seguenti equazioni lineari nelle variabili indicate trovando una parametrizzazione dell insieme delle soluzioni. a) x + 5y = nelle
Anno 2. Sistemi di grado superiore al primo in tre incognite
 Anno 2 Sistemi di grado superiore al primo in tre incognite 1 Introduzione In questa lezione verranno illustrati i metodi principali per la risoluzione di sistemi di grado superiore al primo in tre incognite.
Anno 2 Sistemi di grado superiore al primo in tre incognite 1 Introduzione In questa lezione verranno illustrati i metodi principali per la risoluzione di sistemi di grado superiore al primo in tre incognite.
IDENTITÀ ED EQUAZIONI
 IDENTITÀ ED EQUAZIONI Una identità è una eguaglianza tra due espressioni letterali che è verificata per qualsiasi valore attribuito alle lettere contenute nell espressione. Ad esempio le seguenti eguaglianze
IDENTITÀ ED EQUAZIONI Una identità è una eguaglianza tra due espressioni letterali che è verificata per qualsiasi valore attribuito alle lettere contenute nell espressione. Ad esempio le seguenti eguaglianze
Chi non risolve esercizi non impara la matematica.
 . esercizi Chi non risolve esercizi non impara la matematica.. esercizi + = + = + = 0 = + = 8 + = 0 = 8 8 = + 9 = 0 = + = = + = 0 = = + = 0 = 0 8 0 = 9 = 0 + = + = = 8 = 0 = = = + = 8 = 0 9 = 0 = = + 8
. esercizi Chi non risolve esercizi non impara la matematica.. esercizi + = + = + = 0 = + = 8 + = 0 = 8 8 = + 9 = 0 = + = = + = 0 = = + = 0 = 0 8 0 = 9 = 0 + = + = = 8 = 0 = = = + = 8 = 0 9 = 0 = = + 8
Esercizi svolti sui sistemi lineari
 Francesco Daddi - www.webalice.it/francesco.daddi Esercizi svolti sui sistemi lineari Esercizio 1. Risolvere il seguente sistema lineare al variare del parametro reale t: tx+(t 1)y + z =1 (t 1)y + tz =1
Francesco Daddi - www.webalice.it/francesco.daddi Esercizi svolti sui sistemi lineari Esercizio 1. Risolvere il seguente sistema lineare al variare del parametro reale t: tx+(t 1)y + z =1 (t 1)y + tz =1
3x 2 = 6. 3x 2 x 3 = 6
 Facoltà di Scienze Statistiche, Algebra Lineare 1 A, GParmeggiani LEZIONE 7 Sistemi lineari Scrittura matriciale di un sistema lineare Def 1 Un sistema di m equazioni ed n incognite x 1, x 2, x n, si dice
Facoltà di Scienze Statistiche, Algebra Lineare 1 A, GParmeggiani LEZIONE 7 Sistemi lineari Scrittura matriciale di un sistema lineare Def 1 Un sistema di m equazioni ed n incognite x 1, x 2, x n, si dice
ESERCIZI SVOLTI DI RIEPILOGO SU EQUAZIONI E DISEQUAZIONI IRRAZIONALI ALCUNI CONCETTI DI BASE SU EQUAZIONI E DISEQUAZIONI IRRAZIONALI
 ESERCIZI SVOLTI DI RIEPILOGO SU EQUAZIONI E DISEQUAZIONI IRRAZIONALI ALCUNI CONCETTI DI BASE SU EQUAZIONI E DISEQUAZIONI IRRAZIONALI EQUAZIONI IRRAZIONALI Una equazione si definisce irrazionale quando
ESERCIZI SVOLTI DI RIEPILOGO SU EQUAZIONI E DISEQUAZIONI IRRAZIONALI ALCUNI CONCETTI DI BASE SU EQUAZIONI E DISEQUAZIONI IRRAZIONALI EQUAZIONI IRRAZIONALI Una equazione si definisce irrazionale quando
Sistemi lineari. a 11 x 1 + a 12 x a 1n x n = b 1 a 21 x 1 + a 22 x a 2n x n = b 2 : : : a m1 x 1 + a m2 x 2 +..
 Sistemi lineari: definizioni Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto termine
Sistemi lineari: definizioni Sistemi lineari Un equazione nelle n incognite x,, x n della forma c x + + c n x n = b ove c,, c n sono numeri reali (detti coefficienti) e b è un numero reale (detto termine
Operazioni tra matrici e n-uple
 CAPITOLO Operazioni tra matrici e n-uple Esercizio.. Date le matrici 0 4 e dati λ = 5, µ =, si calcoli AB, BA, A+B, B A, λa+µb. Esercizio.. Per ognuna delle seguenti coppie di matrici A, B e scalari λ,
CAPITOLO Operazioni tra matrici e n-uple Esercizio.. Date le matrici 0 4 e dati λ = 5, µ =, si calcoli AB, BA, A+B, B A, λa+µb. Esercizio.. Per ognuna delle seguenti coppie di matrici A, B e scalari λ,
Lezione Sistemi di equazioni lineari
 Lezione. Sistemi di equazioni lineari Definizione. (Sistemi di equazioni lineari e loro soluzioni). Un equazione lineare nelle n incognite x,,...,x n acoefficientiink = R, èun equazionedellaforma a x +
Lezione. Sistemi di equazioni lineari Definizione. (Sistemi di equazioni lineari e loro soluzioni). Un equazione lineare nelle n incognite x,,...,x n acoefficientiink = R, èun equazionedellaforma a x +
Equazioni di primo grado
 Equazioni di primo grado 15 15.1 Identità ed equazioni Analizziamo le seguenti proposizioni: a ) cinque è uguale alla differenza tra sette e due ; b ) la somma di quattro e due è uguale a otto ; c ) il
Equazioni di primo grado 15 15.1 Identità ed equazioni Analizziamo le seguenti proposizioni: a ) cinque è uguale alla differenza tra sette e due ; b ) la somma di quattro e due è uguale a otto ; c ) il
ELETTRONICA E STRUMENTAZIONE PER INDAGINI BIOMEDICHE M ELETTRONICA 2 M BIOFISICA APPLICATA M INFORMATICA 2
 8058874 - ELETTRONICA E STRUMENTAZIONE PER INDAGINI BIOMEDICHE M-57 - ELETTRONICA M-59 - BIOFISICA APPLICATA M-58 - INFORMATICA Lezione n. 1i Equazioni (1) L identità è una eguaglianza tra due espressioni
8058874 - ELETTRONICA E STRUMENTAZIONE PER INDAGINI BIOMEDICHE M-57 - ELETTRONICA M-59 - BIOFISICA APPLICATA M-58 - INFORMATICA Lezione n. 1i Equazioni (1) L identità è una eguaglianza tra due espressioni
Soluzioni del Foglio 2 I sistemi lineari
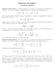 Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
Soluzioni del Foglio 2 I sistemi lineari Soluzione dell esercizio 1 Il sistema assegnato è un sistema di 2 equazioni in 2 incognite non omogeneo Le matrici incompleta e completa associate al sistema sono
EQUAZIONI DI II GRADO
 RICHIAMI SULLE EQUAZIONI DI PRIMO E SECONDO GRADO PROF.SSA ROSSELLA PISCOPO Indice 1 EQUAZIONI DI I GRADO --------------------------------------------------------------------------------------------------
RICHIAMI SULLE EQUAZIONI DI PRIMO E SECONDO GRADO PROF.SSA ROSSELLA PISCOPO Indice 1 EQUAZIONI DI I GRADO --------------------------------------------------------------------------------------------------
A titolo di esempio proponiamo la risoluzione del sistema sia con il metodo della matrice inversa sia con il metodo di Cramer.
 ) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
) Trovare le soluzioni del seguente sistema lineare: x+ y+ z = 3x y + z = 0 x + 5y 4z = 5 Osserviamo in primo luogo che il sistema dato è un sistema quadrato di tre equazioni in tre incognite, precisamente
Equazioni di primo grado ad un incognita. Identità
 Def: Equazioni di primo grado ad un incognita Identità Si dice IDENTITÀ un uguaglianza fra due espressioni letterali che è verificata per ogni valore attribuito alle lettere. 2a = 2a è un identità a =
Def: Equazioni di primo grado ad un incognita Identità Si dice IDENTITÀ un uguaglianza fra due espressioni letterali che è verificata per ogni valore attribuito alle lettere. 2a = 2a è un identità a =
Algebra Lineare (Matematica C.I.), 12.11.13. Sistemi di equazioni lineari. 1. Un equazione lineare in una incognita reale x e un equazione del tipo
 Algebra Lineare (Matematica C.I.), 12.11.13 Sistemi di equazioni lineari 1. Un equazione lineare in una incognita reale x e un equazione del tipo ax = b, dove a e b sono numeri reali dati; a e il coefficiente
Algebra Lineare (Matematica C.I.), 12.11.13 Sistemi di equazioni lineari 1. Un equazione lineare in una incognita reale x e un equazione del tipo ax = b, dove a e b sono numeri reali dati; a e il coefficiente
LE EQUAZIONI DI SECONDO GRADO
 LE EQUAZIONI DI SECONDO GRADO Definizione: un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza, si può scrivere nella forma, detta normale: ax + bx + c 0!!!!!con!a 0 Le lettere
LE EQUAZIONI DI SECONDO GRADO Definizione: un equazione è di secondo grado se, dopo aver applicato i principi di equivalenza, si può scrivere nella forma, detta normale: ax + bx + c 0!!!!!con!a 0 Le lettere
MODULO 3 TITOLO EQUAZIONI E DISEQUAZIONI ALGEBRICHE DI PRIMO GRADO FINALITA OBIETTIVI
 MODULO TITOLO FINALITA EQUAZIONI E DISEQUAZIONI ALGEBRICHE DI PRIMO GRADO Risoluzione delle equazioni e delle disequazioni algebriche di primo grado con una o più incognite e loro applicazioni PREREQUISITI
MODULO TITOLO FINALITA EQUAZIONI E DISEQUAZIONI ALGEBRICHE DI PRIMO GRADO Risoluzione delle equazioni e delle disequazioni algebriche di primo grado con una o più incognite e loro applicazioni PREREQUISITI
Equazioni di primo grado ad un incognita
 Equazioni di primo grado ad un incognita Identità Si dice IDENTITÀ un uguaglianza fra due espressioni letterali che è verificata per ogni valore attribuito alle lettere. 2 = 2 è un identità =3 2 3=2 3
Equazioni di primo grado ad un incognita Identità Si dice IDENTITÀ un uguaglianza fra due espressioni letterali che è verificata per ogni valore attribuito alle lettere. 2 = 2 è un identità =3 2 3=2 3
I sistemi di primo grado
 MATEMATICAperTUTTI 1 ESERCIZIO SVOLTO Un equazione che ha due incognite, x e y, salvo casi particolari, ha sempre infinite soluzioni rappresentate da tutte le coppie ðx, yþ che la soddisfano. Se di equazioni
MATEMATICAperTUTTI 1 ESERCIZIO SVOLTO Un equazione che ha due incognite, x e y, salvo casi particolari, ha sempre infinite soluzioni rappresentate da tutte le coppie ðx, yþ che la soddisfano. Se di equazioni
Esercitazione di Matematica sui problemi di 1 o grado in una e in due incognite
 Esercitazione di Matematica sui problemi di 1 o grado in una e in due incognite 1. In un triangolo rettangolo isoscele l'ipotenusa e il perimetro misurano rispettivamente 0 cm e 50 cm calcolare l'altezza
Esercitazione di Matematica sui problemi di 1 o grado in una e in due incognite 1. In un triangolo rettangolo isoscele l'ipotenusa e il perimetro misurano rispettivamente 0 cm e 50 cm calcolare l'altezza
1.1 Coordinate sulla retta e nel piano; rette nel piano
 1 Sistemi lineari 11 Coordinate sulla retta e nel piano; rette nel piano Coordinate sulla retta Scelti su una retta un primo punto O (origine) ed un diverso secondo punto U (unita ), l identificazione
1 Sistemi lineari 11 Coordinate sulla retta e nel piano; rette nel piano Coordinate sulla retta Scelti su una retta un primo punto O (origine) ed un diverso secondo punto U (unita ), l identificazione
Continuando con altri valori di x, constateremo che l uguaglianza x + x = 2x è sempre valida. Un uguaglianza di questo tipo si chiama identità.
 Consideriamo la frase: un numero più se stesso è uguale al suo doppio e traduciamola in termini matematici indicando un numero con la lettera : + = 2 Proviamo a verificarne la validità, sostituendo alla
Consideriamo la frase: un numero più se stesso è uguale al suo doppio e traduciamola in termini matematici indicando un numero con la lettera : + = 2 Proviamo a verificarne la validità, sostituendo alla
Esercizi svolti. risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale
 Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Esercizi svolti 1. Matrici e operazioni fra matrici 1.1 Date le matrici 1 2 1 6 A = B = 5 2 9 15 6 risolvere, se possibile, l equazione xa + B = O, essendo x un incognita reale Osservazione iniziale: qualunque
Liceo Scientifico Michelangelo - Forte dei Marmi. Esercizi sulla circonferenza svolti - Classe Terza
 Liceo Scientifico Michelangelo - Forte dei Marmi Esercizi sulla circonferenza svolti - Classe Terza Esercizio 0. Stabilire se le equazioni x + y x + 3y + e x + y x + 6y 3 rappresentano una circonferenza
Liceo Scientifico Michelangelo - Forte dei Marmi Esercizi sulla circonferenza svolti - Classe Terza Esercizio 0. Stabilire se le equazioni x + y x + 3y + e x + y x + 6y 3 rappresentano una circonferenza
Equazioni. Istituto San Gabriele 3 Liceo Scientifico 3 Liceo Scientifico sez. Scienze Applicate A.S. 2016/2017 Prof.
 Equazioni Istituto San Gabriele 3 Liceo Scientifico 3 Liceo Scientifico sez. Scienze Applicate A.S. 2016/2017 Prof. Andrea Pugliese Definizione ed esempi Un equazione è un uguaglianza tra due espressioni
Equazioni Istituto San Gabriele 3 Liceo Scientifico 3 Liceo Scientifico sez. Scienze Applicate A.S. 2016/2017 Prof. Andrea Pugliese Definizione ed esempi Un equazione è un uguaglianza tra due espressioni
Sistemi Lineari I. March 22, 2015
 Sistemi Lineari I March 22, 205 Sistemi lineari Nel seguito denoteremo con K il campo reale o il campo complesso e con K n l insieme delle n-uple ordinate di elementi di K Sia D un sottoinsieme di K n
Sistemi Lineari I March 22, 205 Sistemi lineari Nel seguito denoteremo con K il campo reale o il campo complesso e con K n l insieme delle n-uple ordinate di elementi di K Sia D un sottoinsieme di K n
Sistemi Lineari. Elisabetta Colombo. Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 200-20 2 a di o.0 4 Capelli Rango o Caratterisca : definizioni a di o.0 Un equazione nelle n incognite x,..., x n della forma dove
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 200-20 2 a di o.0 4 Capelli Rango o Caratterisca : definizioni a di o.0 Un equazione nelle n incognite x,..., x n della forma dove
Equazioni di primo grado ad un incognita
 Equazioni di primo grado ad un incognita Identità Si dice IDENTITÀ un uguaglianza fra due espressioni letterali che è verificata per ogni valore attribuito alle lettere. è un identità. Verificare un identità
Equazioni di primo grado ad un incognita Identità Si dice IDENTITÀ un uguaglianza fra due espressioni letterali che è verificata per ogni valore attribuito alle lettere. è un identità. Verificare un identità
GE110 Soluzioni Tutorato 7 a cura di Giordano Agostini, Giulia Salustri e Andrea Cattaneo
 GE110 Soluzioni Tutorato 7 a cura di Giordano Agostini, Giulia Salustri e Andrea Cattaneo Università degli studi Roma Tre, Corso di Laurea in Matematica Anno Accademico 2011/2012 1 Si determinino esplicitamente
GE110 Soluzioni Tutorato 7 a cura di Giordano Agostini, Giulia Salustri e Andrea Cattaneo Università degli studi Roma Tre, Corso di Laurea in Matematica Anno Accademico 2011/2012 1 Si determinino esplicitamente
Nome:. Data:. 1. Discutere la natura della conica di equazione
 Nome:. Data:. ISTRUZIONI. Riportare le soluzioni in bella copia negli spazi appositi sotto ciascun esercizio, usare eventualmente anche il retro del foglio. Non aggiungere altri fogli. La soluzione deve
Nome:. Data:. ISTRUZIONI. Riportare le soluzioni in bella copia negli spazi appositi sotto ciascun esercizio, usare eventualmente anche il retro del foglio. Non aggiungere altri fogli. La soluzione deve
SISTEMI LINEARI, METODO DI GAUSS
 SISTEMI LINEARI, METODO DI GAUSS Abbiamo visto che un sistema di m equazioni lineari in n incognite si può rappresentare in forma matriciale come A x = b dove: A è la matrice di tipo (m, n) dei coefficienti
SISTEMI LINEARI, METODO DI GAUSS Abbiamo visto che un sistema di m equazioni lineari in n incognite si può rappresentare in forma matriciale come A x = b dove: A è la matrice di tipo (m, n) dei coefficienti
Esercitazione di Matematica sui sistemi lineari 2 2 e 3 3
 Esercitazione di Matematica sui sistemi lineari e Esercizio 1. Risolvere i seguenti sistemi lineari : { 5x + y = 6 (a) x + y = 8 ; { x + 5y = 4 4x 7y =. Esercizio. sistemi: (a) { x + y = 6 x y = 1 ; {
Esercitazione di Matematica sui sistemi lineari e Esercizio 1. Risolvere i seguenti sistemi lineari : { 5x + y = 6 (a) x + y = 8 ; { x + 5y = 4 4x 7y =. Esercizio. sistemi: (a) { x + y = 6 x y = 1 ; {
Anno 3 Equazione dell'ellisse
 Anno Equazione dell'ellisse 1 Introduzione In questa lezione affronteremo una serie di problemi che ci chiederanno di determinare l equazione di un ellisse sotto certe condizioni. Al termine della lezione
Anno Equazione dell'ellisse 1 Introduzione In questa lezione affronteremo una serie di problemi che ci chiederanno di determinare l equazione di un ellisse sotto certe condizioni. Al termine della lezione
Secondo parziale di Matematica per l Economia lettere E-Z, a.a , compito A prof. Gianluca Amato
 Corso di Laurea in Economia e Management Secondo parziale di Matematica per l Economia lettere E-Z, a.a. 216 217, compito A prof. Gianluca Amato Regole generali Si svolga il primo esercizio e, a scelta
Corso di Laurea in Economia e Management Secondo parziale di Matematica per l Economia lettere E-Z, a.a. 216 217, compito A prof. Gianluca Amato Regole generali Si svolga il primo esercizio e, a scelta
SISTEMI ALGEBRICI DI SECONDO GRADO 1 PROPRIETA' DELLE SOLUZIONI ED EQUAZIONE IN FORMA DI PRODOTTO., x 2. = b+ Δ 2 a
 SISTEMI ALGEBRICI DI SECONDO GRADO 1 PROPRIETA' DELLE SOLUZIONI ED EQUAZIONE IN FORMA DI PRODOTTO Data una generica equazione di secondo grado a x +b x+c=0 con discriminante non negativo ( Δ=b 4 a c 0
SISTEMI ALGEBRICI DI SECONDO GRADO 1 PROPRIETA' DELLE SOLUZIONI ED EQUAZIONE IN FORMA DI PRODOTTO Data una generica equazione di secondo grado a x +b x+c=0 con discriminante non negativo ( Δ=b 4 a c 0
Appunti: il piano cartesiano. Distanza tra due punti
 ppunti: il piano cartesiano Distanza tra due punti Come determinare la distanza tra i punti ( ; ) e ( ; ): Se i due punti e hanno la stessa ascissa = allora (-3;1) (-3; 5) d()= d()= 1 5 4 4 Se i due punti
ppunti: il piano cartesiano Distanza tra due punti Come determinare la distanza tra i punti ( ; ) e ( ; ): Se i due punti e hanno la stessa ascissa = allora (-3;1) (-3; 5) d()= d()= 1 5 4 4 Se i due punti
Sistemi di equazioni lineari
 Sistemi di equazioni lineari Erica Boatto I.T.I.S. V.Volterra San Donà di Piave Piero Fantuzzi I.T.I.S. V.Volterra San Donà di Piave 6 febbraio 009 Sommario Indice 1 SISTEMI DI EQUAZIONI LINEARI 1.1 Introduzione...................................
Sistemi di equazioni lineari Erica Boatto I.T.I.S. V.Volterra San Donà di Piave Piero Fantuzzi I.T.I.S. V.Volterra San Donà di Piave 6 febbraio 009 Sommario Indice 1 SISTEMI DI EQUAZIONI LINEARI 1.1 Introduzione...................................
1 Ampliamento del piano e coordinate omogenee
 1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
FRAZIONI e NUMERI RAZIONALI
 FRAZIONI e NUMERI RAZIONALI Frazioni Come per i numeri naturali, anche per gli interi relativi si definisce l'operazione di divisione come operazione inversa della moltiplicazione: Divisione di numeri
FRAZIONI e NUMERI RAZIONALI Frazioni Come per i numeri naturali, anche per gli interi relativi si definisce l'operazione di divisione come operazione inversa della moltiplicazione: Divisione di numeri
Esercitazione n 6. Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (b)f(x, y) = 4y 4 16x 2 y + x
 Esercitazione n 6 1 Massimi e minimi di funzioni di più variabili Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (a)f(x, y) = x 3 + y 3 + xy (b)f(x, y) = 4y 4 16x
Esercitazione n 6 1 Massimi e minimi di funzioni di più variabili Esercizio 1: Determinare i punti di massimo e minimo relativo delle seguenti funzioni: (a)f(x, y) = x 3 + y 3 + xy (b)f(x, y) = 4y 4 16x
Rette e piani in R 3
 Rette e piani in R 3 In questa dispensa vogliamo introdurre in modo elementare rette e piani nello spazio R 3 (si faccia riferimento anche al testo Algebra Lineare di S. Lang). 1 Rette in R 3 Vogliamo
Rette e piani in R 3 In questa dispensa vogliamo introdurre in modo elementare rette e piani nello spazio R 3 (si faccia riferimento anche al testo Algebra Lineare di S. Lang). 1 Rette in R 3 Vogliamo
Equazioni parametriche di primo grado fratte - Esercizi svolti -
 Equazioni parametriche di primo grado fratte - Esercizi svolti - Carlo Alberini 15 novembre 2010 In queste poche pagine verranno risolti tre esercizi tratti dal libro di testo in adozione riguardanti alcune
Equazioni parametriche di primo grado fratte - Esercizi svolti - Carlo Alberini 15 novembre 2010 In queste poche pagine verranno risolti tre esercizi tratti dal libro di testo in adozione riguardanti alcune
Equazioni di Primo grado
 Equazioni di Primo grado Definizioni Si dice equazione di primo grado un uguaglianza tra due espressioni algebriche verificata solo per un determinato valore della variabile x, detta incognita. Si chiama
Equazioni di Primo grado Definizioni Si dice equazione di primo grado un uguaglianza tra due espressioni algebriche verificata solo per un determinato valore della variabile x, detta incognita. Si chiama
Identità ed equazioni
 Identità ed equazioni Un'identità è un'uguaglianza tra due espressioni letterali che è vera per qualsiasi valore numerico che si può attribuire alle lettere. (x + 2x = 3x è un'identità, perché sempre vera)
Identità ed equazioni Un'identità è un'uguaglianza tra due espressioni letterali che è vera per qualsiasi valore numerico che si può attribuire alle lettere. (x + 2x = 3x è un'identità, perché sempre vera)
Tempo a disposizione. 90 minuti. 1 [6 punti] Dimostrare che, per ogni n N, n 1, vale la disuguaglianza:
![Tempo a disposizione. 90 minuti. 1 [6 punti] Dimostrare che, per ogni n N, n 1, vale la disuguaglianza: Tempo a disposizione. 90 minuti. 1 [6 punti] Dimostrare che, per ogni n N, n 1, vale la disuguaglianza:](/thumbs/72/66437341.jpg) Dipartimento di Matematica e Informatica Anno Accademico 05-06 Corso di Laurea in Informatica (L-) Prova in itinere di Matematica Discreta ( CFU) Febbraio 06 A Tempo a disposizione. 90 minuti [6 punti]
Dipartimento di Matematica e Informatica Anno Accademico 05-06 Corso di Laurea in Informatica (L-) Prova in itinere di Matematica Discreta ( CFU) Febbraio 06 A Tempo a disposizione. 90 minuti [6 punti]
Precorso di Matematica
 UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTA DI ARCHITETTURA Precorso di Matematica Anna Scaramuzza Anno Accademico 2005-2006 4-10 Ottobre 2005 INDICE 1. ALGEBRA................................. 3 1.1 Equazioni
UNIVERSITÀ DEGLI STUDI ROMA TRE FACOLTA DI ARCHITETTURA Precorso di Matematica Anna Scaramuzza Anno Accademico 2005-2006 4-10 Ottobre 2005 INDICE 1. ALGEBRA................................. 3 1.1 Equazioni
I SISTEMI DI EQUAZIONI DI PRIMO GRADO
 I SISTEMI I EQUAZIONI I PRIMO GRAO Sistemi di primo grado con due o più equazioni in due o più incognite Numerici Letterali Interi Frazionari Interi Frazionari OBIETTIVI Le attività proposte in questa
I SISTEMI I EQUAZIONI I PRIMO GRAO Sistemi di primo grado con due o più equazioni in due o più incognite Numerici Letterali Interi Frazionari Interi Frazionari OBIETTIVI Le attività proposte in questa
3x + x 5x = x = = 4 + 3x ; che equivale, moltiplicando entrambi i membri per 2, a risolvere. 4x + 6 x = 4 + 3x.
 1 Soluzioni esercizi 1.1 Equazioni di 1 e grado Risolvere le seguenti equazioni di 1 grado: 1) 3x 5x = 1 x. Abbiamo: 3x + x 5x = 1 + x = 1 + 4 x = 5. ) x + 3 x = + 3x. Facciamo il m.c.m. : 4x + 6 x = 4
1 Soluzioni esercizi 1.1 Equazioni di 1 e grado Risolvere le seguenti equazioni di 1 grado: 1) 3x 5x = 1 x. Abbiamo: 3x + x 5x = 1 + x = 1 + 4 x = 5. ) x + 3 x = + 3x. Facciamo il m.c.m. : 4x + 6 x = 4
nota 1. Aritmetica sui numeri interi.
 nota 1. Aritmetica sui numeri interi. Numeri interi. Numeri primi. L algoritmo di Euclide per il calcolo del mcd. Equazioni diofantee di primo grado. Congruenze. Il Teorema Cinese del Resto. 1 0. Numeri
nota 1. Aritmetica sui numeri interi. Numeri interi. Numeri primi. L algoritmo di Euclide per il calcolo del mcd. Equazioni diofantee di primo grado. Congruenze. Il Teorema Cinese del Resto. 1 0. Numeri
