1. Proprietà della somma di matrici. 1. (A + B) + C = A + (B + C) qualunque. 2. A + B = B + A qualunque siano le matrici
|
|
|
- Iolanda Landi
- 7 anni fa
- Visualizzazioni
Transcript
1 Matrici R. Notari 1
2 1. Proprietà della somma di matrici 1. (A + B) + C = A + (B + C) qualunque siano le matrici A, B, C Mat(m, n; K). 2. A + B = B + A qualunque siano le matrici A, B Mat(m, n; K). 3. Sia O la matrice di tipo m n le cui entrate sono tutte nulle (matrice nulla). Allora A + O = A qualunque sia A Mat(m, n; K). 4. Sia A una matrice di tipo m n su K. La matrice A di tipo m n le cui entrate sono opposte a quelle di A, posizione per posizione (matrice opposta), è l unica matrice di tipo m n per cui A + ( A) = O. 2
3 2. Proprietà del prodotto scalare-matrice 1. x(ya) = y(xa) = (xy)a qualunque siano x, y K e qualunque sia A Mat(m, n; K). 2. 1A = A qualunque sia A Mat(m, n; K). 3. x(a + B) = xa + xb qualunque sia x K e qualunque siano A, B Mat(m, n; K). 4. (x+y)a = xa+ya qualunque siano x, y K e qualunque sia A Mat(m, n; K). Vale la Legga di Annullamento del prodotto scalare-matrice. Infatti abbiamo Proposizione 1 Sia x K, e sia A una matrice di tipo m n su K. Se O è la matrice nulla di tipo m n allora xa = O se, e solo se, x = 0 o A = O. 3
4 3. Proprietà della trasposizione 1. t ( t A) = A per ogni A Mat(m, n; K). 2. t (A+B) = t A+ t B qualunque siano A, B Mat(m, n; K). 3. t (xa) = x t A qualunque sia x K, e qualunque sia A Mat(m, n; K). 4
5 4. Matrici simmetriche ed antisimmetriche Teorema 2 L unica matrice quadrata di ordine n che è sia simmetrica sia antisimmetrica è la matrice nulla. Inoltre, data una matrice M quadrata di ordine n, esistono un unica matrice quadrata S di ordine n simmetrica ed un unica matrice A quadrata di ordine n antisimmetrica che verificano l uguaglianza M = S + A. 5
6 5. Proprietà del prodotto di matrici 1. Siano A, B, C tre matrici qualsiasi su K di tipo m n, n p, p q, rispettivamente. Allora (AB)C = A(BC). 2. Sia I p la matrice identica di ordine p. Allora, qualunque sia A Mat(m, n; K) si ha I m A = AI n = A. 3. Siano A, B Mat(m, n; K) e siano C, D Mat(n, p; K). Valgono le uguaglianze e (A + B)C = AC + BC A(C + D) = AC + AD. 6
7 4. Siano A, B matrici su K di tipo m n, n p, rispettivamente, e sia x K. Allora si ha x(ab) = (xa)b = A(xB). 5. Siano A, B matrici su K di tipo m n, n p, rispettivamente. Allora abbiamo t (AB) = t B t A. Non valgono la proprietà commutativa e la Legge di Annullamento del Prodotto di due matrici. 7
8 6. Operazioni elementari e rango Teorema 3 Data una matrice A su K di tipo m n, esiste una successione finita di operazioni elementari sulle righe che trasforma A in una matrice A di tipo m n ridotta per righe. Lemma 4 Sia A una matrice su K di tipo m n, e sia B una matrice ridotta per righe ottenuta da A con operazioni elementari sulle righe, ma senza usare scambi di righe. Allora la riga t esima di B è nulla se, e solo se, la riga t esima di A è combinazione lineare delle righe 1,..., t 1 di A. Teorema 5 Sia A una matrice su K di tipo m n, e siano B, C matrici di tipo m n ridotte per righe trasformando A con successioni diverse di operazioni elementari sulle righe di A. B e C hanno lo stesso numero di righe non nulle. 8
9 7. Teoremi sui determinanti Teorema 6 (di Laplace) Sia A una matrice quadrata di ordine n. Allora 1. Qualunque sia la riga i di A si ha a i1 A i1 + + a in A in = det(a). 2. Qualunque sia la colonna j di A si ha a 1j A 1j + + a nj A nj = det(a). 3. Scelte le due righe distinte i ed h di A si ha a i1 A h1 + + a in A hn = Scelte le due colonne distinte j e k di A si ha a 1j A 1k + + a nj A nk = 0. 9
10 Corollario 7 Sia A una matrice quadrata di ordine n. Allora det( t A) = det(a). Teorema 8 (di Binet) Siano A e B matrici quadrate di ordine n su K. Allora det(ab) = det(a) det(b). Corollario 9 Sia x K e sia A una matrice quadrata di ordine n. Allora det(xa) = x n det(a). 10
11 8. Determinante ed operazioni elementari Teorema 10 Sia A una matrice quadrata di ordine n su K, e siano A 1, A 2, A 3 le matrici ottenute da A effettuando l operazione elementare R i R h, R i ar i, R h R h + ar i, rispettivamente. Allora abbiamo ed infine det(a 1 ) = det(a), det(a 2 ) = a det(a), det(a 3 ) = det(a). 11
12 9. Determinante e rango Teorema 11 (di Kronecker) Sia A una matrice su K di tipo m n. Allora r(a) = p se, e solo se, esiste un minore di A di ordine p non nullo e tutti i minori di A di ordine p + 1 sono nulli, ossia, p è il massimo ordine di un minore non nullo di A. Corollario 12 Sia A una matrice quadrata di ordine n su K. Abbiamo che r(a) = n se, e solo se, det(a) 0. Inoltre, se r(a) = n, allora, detta A una matrice ridotta per righe ottenuta da A con sole operazioni elementari di tipo E1 ed E3, abbiamo che det(a) è uguale, a meno del segno, al prodotto degli elementi speciali di A. 12
MATRICI. 1. Esercizi
 MATICI Esercizio Siano A = 0, B = Esercizi 2, C = 0 2 2 Calcolare: a2a B; b3a + 2B 4C; c 2A + B + 2C 2B; d3b + 2(2A C (A + B + 2C isolvere, se possibile: ( 3X + 2(A X + B + 2(C + 2X = 0; (2 4A + 2(B +
MATICI Esercizio Siano A = 0, B = Esercizi 2, C = 0 2 2 Calcolare: a2a B; b3a + 2B 4C; c 2A + B + 2C 2B; d3b + 2(2A C (A + B + 2C isolvere, se possibile: ( 3X + 2(A X + B + 2(C + 2X = 0; (2 4A + 2(B +
MATRICI. Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: a 2 m. a n m) i j R, 1 i n, 1 j m.
 MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
MATRICI Matrici Una matrice A con n-righe e m-colonne, ad elementi reali, è una tabella con la seguente forma: 11 a 12 a 1 3 a 1m A=(a a 21 a 2 3 a 2m con a a n1 a n2 a n 3 a nm i j R, 1 i n, 1 j m. per
Lo scopo della teoria dei determinanti è di definire una funzione. det : M n R. sia calcolabile facendo somme e prodotti delle entrate delle matrici
 Determinanti 1 / 44 Lo scopo della teoria dei determinanti è di definire una funzione det : M n R chiamata determinante tale che: sia calcolabile facendo somme e prodotti delle entrate delle matrici det(a)
Determinanti 1 / 44 Lo scopo della teoria dei determinanti è di definire una funzione det : M n R chiamata determinante tale che: sia calcolabile facendo somme e prodotti delle entrate delle matrici det(a)
Corso di Geometria BIAR, BSIR Esercizi 2: soluzioni
 Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
Corso di Geometria 2- BIAR, BSIR Esercizi 2: soluzioni Esercizio Calcolare il determinante della matrice 2 3 : 3 2 a) con lo sviluppo lungo la prima riga, b) con lo sviluppo lungo la terza colonna, c)
RIDUZIONE E RANGO , C = 2 5 1
 MATRICI E SISTEMI RIDUZIONE E RANGO Riduzione di matrici (definizioni, trasformazioni elementari). Calcolo del rango e dell inversa (metodo di Gauss, metodo di Gauss-Jordan). 3 4 Esercizio Ridurre per
MATRICI E SISTEMI RIDUZIONE E RANGO Riduzione di matrici (definizioni, trasformazioni elementari). Calcolo del rango e dell inversa (metodo di Gauss, metodo di Gauss-Jordan). 3 4 Esercizio Ridurre per
PROBLEMA. Costruire matrici quadrate contenute. Fare i determinanti delle matrici quadrate contenute in A
 A = PROBLEMA 0 1 2 7 2 5 3 0 (2 4) Costruire matrici quadrate contenute in A (possibili solo matrici quadrate 2 2 e 1 1) Fare i determinanti delle matrici quadrate contenute in A Questo porta al concetto
A = PROBLEMA 0 1 2 7 2 5 3 0 (2 4) Costruire matrici quadrate contenute in A (possibili solo matrici quadrate 2 2 e 1 1) Fare i determinanti delle matrici quadrate contenute in A Questo porta al concetto
Geometria BIAR Esercizi 2
 Geometria BIAR 0- Esercizi Esercizio. a Si consideri il generico vettore v b R c (a) Si trovi un vettore riga x (x, y, z) tale che x v a (b) Si trovi un vettore riga x (x, y, z) tale che x v kb (c) Si
Geometria BIAR 0- Esercizi Esercizio. a Si consideri il generico vettore v b R c (a) Si trovi un vettore riga x (x, y, z) tale che x v a (b) Si trovi un vettore riga x (x, y, z) tale che x v kb (c) Si
Richiami di algebra delle matrici a valori reali
 Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Richiami di algebra delle matrici a valori reali Vettore v n = v 1 v 2. v n Vettore trasposto v n = (v 1, v 2,..., v n ) v n = (v 1, v 2,..., v n ) A. Pollice - Statistica Multivariata Vettore nullo o
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE. Giovanni Villani
 Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Corso di Matematica Generale M-Z Dipartimento di Economia Universitá degli Studi di Foggia ALGEBRA LINEARE Giovanni Villani Matrici Definizione 1 Si definisce matrice di tipo m n una funzione che associa
Elementi di Algebra Matriciale. (richiami)
 Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
Elementi di Algebra Matriciale Definizione di matrice (richiami) Matrice quadrata, diagonale, identità, triangolare, simmetrica Matrice trasposta Principali operazioni su matrici e vettori: somma, sottrazione,
Sui determinanti e l indipendenza lineare di vettori
 Sui determinanti e l indipendenza lineare di vettori 1 Si dice che m vettori v 1, v 2,,v m di R n sono linearmente indipendenti, se una loro combinazione lineare può dare il vettore nullo solo se i coefficienti
Sui determinanti e l indipendenza lineare di vettori 1 Si dice che m vettori v 1, v 2,,v m di R n sono linearmente indipendenti, se una loro combinazione lineare può dare il vettore nullo solo se i coefficienti
Il determinante. Calcolo del determinante di matrici particolari. matrici di ordine 2: sia. a11 a A = allora
 Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Calcolo del determinante di matrici particolari matrici di ordine 2: sia allora Esempio. [ ] a11 a A = 12, a 21 a 22 det A = a 11 a 22 a 21 a 12. Calcolare il determinante di [ ] 1 2 A =. 3 4 matrici di
Il prodotto tra matrici non è commutativo. Nelle notazioni precedenti, ponendo n = p e m = q si hanno:
 L anello delle matrici Esempio. Siano A = [ ] 0 1 3 0 2 1, B = 1 2 0 0 1 2 3 4, 1 0 calcolare AB e BA. Osservazioni Siano A Mat m,n (K) e B Mat p,q (K). Il prodotto AB è definito se n = p. Si ha AB Mat
L anello delle matrici Esempio. Siano A = [ ] 0 1 3 0 2 1, B = 1 2 0 0 1 2 3 4, 1 0 calcolare AB e BA. Osservazioni Siano A Mat m,n (K) e B Mat p,q (K). Il prodotto AB è definito se n = p. Si ha AB Mat
Si noti che la matrice trasposta A ha lo stesso determinante. Questa proprietà è generale;
 Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
Ottavio Serra Matrici e determinanti In questa nota estenderemo a matrici quadrate di ordine n qualsiasi il concetto di determinante introdotto nelle scuole secondarie per matrici di ordine 2 come tecnica
APPLICAZIONI. Im f = {b B a A tale che f (a) = b}.
 APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
APPLICAZIONI Diremo applicazione (o funzione) da un insieme A ad un insieme B una legge f che associa ad ogni elemento a A uno ed un solo elemento b B. Scriviamo f : A B e il corrispondente o immagine
Elementi di Algebra Lineare Il determinante
 Elementi di Algebra Lineare Cristina Turrini UNIMI - 2015/2016 Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 17 index 1 2 Sottomatrici e minori Cristina Turrini (UNIMI - 2015/2016)
Elementi di Algebra Lineare Cristina Turrini UNIMI - 2015/2016 Cristina Turrini (UNIMI - 2015/2016) Elementi di Algebra Lineare 1 / 17 index 1 2 Sottomatrici e minori Cristina Turrini (UNIMI - 2015/2016)
Algebra lineare. Laboratorio di programmazione e calcolo CdL in Chimica. Pierluigi Amodio
 Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
Algebra lineare Laboratorio di programmazione e calcolo CdL in Chimica Pierluigi Amodio Dipartimento di Matematica Università di Bari pierluigi.amodio@uniba.it http://dm.uniba.it/ amodio A.A. 2016/17 P.
VETTORI E MATRICI. Ing. Nicola Cappuccio 2014 U.F.5 ELEMENTI SCIENTIFICI ED ELETTRONICI APPLICATI AI SISTEMI DI TELECOMUNICAZIONI
 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 I VETTRORI E MATRICI (RICHIAMI) Ad ogni matrice quadrata a coefficienti reali è possibile associare un numero reale, detto determinante, calcolato
LeLing12: Ancora sui determinanti.
 LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
LeLing2: Ancora sui determinanti. Ārgomenti svolti: Sviluppi di Laplace. Prodotto vettoriale e generalizzazioni. Rango e determinante: i minori. Il polinomio caratteristico. Ēsercizi consigliati: Geoling
Determinanti. Definizione ed esempi. Definizione ed esempi. Proprietà dei determinanti Rango di matrici
 Introduzione S S S Rango di matrici Si dice sottomatrice d'una matrice data la matrice ottenuta selezionando un certo numero di righe e di colonne della matrice iniziale. Lezione 24.wpd 08/01/2011 XXIV
Introduzione S S S Rango di matrici Si dice sottomatrice d'una matrice data la matrice ottenuta selezionando un certo numero di righe e di colonne della matrice iniziale. Lezione 24.wpd 08/01/2011 XXIV
DETERMINANTE DI MATRICI QUADRATE
 DETERMINANTE DI MATRICI QUADRATE Definizioni e Proprietà 12 Novembre 2015 Pietro Pennestrì pennestri1694905@studentiuniroma1it Università di Roma Sapienza SOMMARIO 1 Introduzione 11 Cenni Storici 12 Definizione
DETERMINANTE DI MATRICI QUADRATE Definizioni e Proprietà 12 Novembre 2015 Pietro Pennestrì pennestri1694905@studentiuniroma1it Università di Roma Sapienza SOMMARIO 1 Introduzione 11 Cenni Storici 12 Definizione
LEZIONE 1 C =
 LEZIONE 1 11 Matrici a coefficienti in R Definizione 111 Siano m, n Z positivi Una matrice m n a coefficienti in R è un insieme di mn numeri reali disposti su m righe ed n colonne circondata da parentesi
LEZIONE 1 11 Matrici a coefficienti in R Definizione 111 Siano m, n Z positivi Una matrice m n a coefficienti in R è un insieme di mn numeri reali disposti su m righe ed n colonne circondata da parentesi
VETTORI E MATRICI. De nizione 1 Chiamiamo vettore x una n-pla ordinata di numeri reali. x 1 x 2. x n
 VETTORI E MATRICI De nizione 1 Chiamiamo vettore x una n-pla ordinata di numeri reali x 1 x. x n 5 L insieme di tutti i vettori con n componenti reali si indica con R n :I numeri reali si possono pensare
VETTORI E MATRICI De nizione 1 Chiamiamo vettore x una n-pla ordinata di numeri reali x 1 x. x n 5 L insieme di tutti i vettori con n componenti reali si indica con R n :I numeri reali si possono pensare
4. Richiami: sistemi lineari e matrici
 4 Richiami: sistemi lineari e matrici Vettori 4a Combinazioni lineari Indichiamo con R n l insieme delle n-uple ordinate di elementi di R, { } R n := x = (x 1, x 2,, x n ) x i R, i = 1,,n Si dice che x
4 Richiami: sistemi lineari e matrici Vettori 4a Combinazioni lineari Indichiamo con R n l insieme delle n-uple ordinate di elementi di R, { } R n := x = (x 1, x 2,, x n ) x i R, i = 1,,n Si dice che x
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Geometria BAER I canale Foglio esercizi 2 Esercizio 1. Calcolare il determinante e l inversa (quando esiste) della matrice ( ) cos θ sin θ R θ =, θ [0, 2π] sin θ cos θ Soluzione: Il determinante ( é cos
Algebra delle matrici
 Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
Algebra delle matrici Metodo di Gauss-Jordan per l inversione di una matrice. Nella lezione scorsa abbiamo visto che un modo per determinare l eventuale inversa di una matrice quadrata A consiste nel risolvere
, è Det(A) = a 11 a 22 a 12 a 21. ( il determinante della matrice che si ottiene da A. la 1 a riga e la 2 a colonna di A
 G Parmeggiani, 2/12/2013 Algebra Lineare 1 A, corso di laurea SGI, aa 2013/2014 Nota 4: Calcolo di determinanti Sia A una matrice quadrata di ordine n Il determinante di A è un numero che dipende da A
G Parmeggiani, 2/12/2013 Algebra Lineare 1 A, corso di laurea SGI, aa 2013/2014 Nota 4: Calcolo di determinanti Sia A una matrice quadrata di ordine n Il determinante di A è un numero che dipende da A
Capitolo 3 Matrici. Marco Robutti. Facoltà di ingegneria Università degli studi di Pavia. Anno accademico
 Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
Capitolo 3 Matrici Marco Robutti Facoltà di ingegneria Università degli studi di Pavia Anno accademico 2017-2018 Tutorato di geometria e algebra lineare Definizione (Matrice) Una matrice A M R (k, n) è
I determinanti. a11 a A = 12 a 21 a 22
 I determinanti. Queste note, basate sugli appunti delle lezioni, riepilogano rapidamente la definizione e le proprietà del determinante. Vengono inoltre illustrati i metodi di calcolo e alcune dimostrazioni.
I determinanti. Queste note, basate sugli appunti delle lezioni, riepilogano rapidamente la definizione e le proprietà del determinante. Vengono inoltre illustrati i metodi di calcolo e alcune dimostrazioni.
I sistemi lineari di n equazioni in n incognite
 I sistemi lineari I sistemi lineari di n equazioni in n incognite I sistemi lineari di n equazioni in n incognite, sono formati da equazioni di primo grado, in cui le incognite hanno tutte esponente uguale
I sistemi lineari I sistemi lineari di n equazioni in n incognite I sistemi lineari di n equazioni in n incognite, sono formati da equazioni di primo grado, in cui le incognite hanno tutte esponente uguale
G. Parmeggiani, 17/5/2018 Algebra Lineare, a.a. 2017/2018, numero di MATRICOLA PARI
 G Parmeggiani, 17/5/2018 Algebra Lineare, aa 2017/2018, Scuola di Scienze - Corsi di laurea: Studenti: Statistica per l economia e l impresa Statistica per le tecnologie e le scienze numero di MATRICOLA
G Parmeggiani, 17/5/2018 Algebra Lineare, aa 2017/2018, Scuola di Scienze - Corsi di laurea: Studenti: Statistica per l economia e l impresa Statistica per le tecnologie e le scienze numero di MATRICOLA
1 2 1 x = Quando sapremo calcolare i determinanti potremo ricavare:
 5 NOVEMBRE 2009 Esempio: Risolviamo il sistema: 3x + 2y + 4z = 1 2x y + z = 0 x + 2y + 3z = 1 1 2 4 3 1 4 3 2 1 0 1 1 2 0 1 2 1 0 1 2 3 1 1 3 1 2 1 x =, y =, z = 3 2 4 3 2 4 3 2 4 2 1 1 2 1 1 2 1 1 1 2
5 NOVEMBRE 2009 Esempio: Risolviamo il sistema: 3x + 2y + 4z = 1 2x y + z = 0 x + 2y + 3z = 1 1 2 4 3 1 4 3 2 1 0 1 1 2 0 1 2 1 0 1 2 3 1 1 3 1 2 1 x =, y =, z = 3 2 4 3 2 4 3 2 4 2 1 1 2 1 1 2 1 1 1 2
ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5. Indice. 2. Esercizi 5
 ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5 Indice 1. Principali definizioni 1 2. Esercizi 5 Operazioni con le matrici 1. Principali definizioni Ricordiamo le principali definizioni legate alle matrici a coefficienti
ALGEBRA LINEARE E GEOMETRIA: ESERCIZI 5 Indice 1. Principali definizioni 1 2. Esercizi 5 Operazioni con le matrici 1. Principali definizioni Ricordiamo le principali definizioni legate alle matrici a coefficienti
a + 2b + c 3d = 0, a + c d = 0 c d
 SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
SPAZI VETTORIALI 1. Esercizi Esercizio 1. Stabilire quali dei seguenti sottoinsiemi sono sottospazi: V 1 = {(x, y, z) R 3 /x = y = z} V = {(x, y, z) R 3 /x = 4} V 3 = {(x, y, z) R 3 /z = x } V 4 = {(x,
CORSO DI GEOMETRIA DETERMINANTE A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
CORSO DI GEOMETRIA DETERMINANTE AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Definizione induttiva di determinante 1 2 Caratterizzazione delle matrici quadrate di rango massimo 5 3 Regole di Laplace 6
MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI
 MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI LE MATRICI DEFINIZIONE: Una matrice è un insieme di numeri disposti su righe e colonne. 1 3 7 M = 2 5 1 M è
MATRICI E VETTORI APPROFONDIMENTO PER IL CORSO DI LABORATORIO DI INFORMATICA SARA POLTRONIERI LE MATRICI DEFINIZIONE: Una matrice è un insieme di numeri disposti su righe e colonne. 1 3 7 M = 2 5 1 M è
Argomento 12 Matrici
 Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
Argomento 2 Matrici 2 Vettori di R n eoperazioni I Vettore di R n : x =(x i ) i=n =(x i ) n i=,conx i R componenti di x I R n = spazio dei vettori reali a n componenti = spazio vettoriale reale n-dimensionale
Introduzione all algebra delle matrici. Appunti a cura di Lara Ercoli
 Introduzione all algebra delle matrici ppunti a cura di Lara Ercoli Indice Definizioni 3. Matrici particolari............................ 4 2 Operazioni con le matrici 8 2. Somma di matrici.............................
Introduzione all algebra delle matrici ppunti a cura di Lara Ercoli Indice Definizioni 3. Matrici particolari............................ 4 2 Operazioni con le matrici 8 2. Somma di matrici.............................
ALGEBRA LINEARE PARTE II
 DIEM sez. Matematica Finanziaria Marina Resta Università degli studi di Genova Dicembre 005 Indice PREMESSA INVERSA DI UNA MATRICE DETERMINANTE. DETERMINANTE DI MATRICI ELEMENTARI................. MATRICI
DIEM sez. Matematica Finanziaria Marina Resta Università degli studi di Genova Dicembre 005 Indice PREMESSA INVERSA DI UNA MATRICE DETERMINANTE. DETERMINANTE DI MATRICI ELEMENTARI................. MATRICI
Nozioni e notazioni: concetti primitivi di insieme, elemento ed appartenenza.
 Geometria I lezione del 30 settembre 2013 Presentazione del corso. Nozioni e notazioni: concetti primitivi di insieme, elemento ed appartenenza. Insiemi numerici: i numeri naturali, gli interi, i numeri
Geometria I lezione del 30 settembre 2013 Presentazione del corso. Nozioni e notazioni: concetti primitivi di insieme, elemento ed appartenenza. Insiemi numerici: i numeri naturali, gli interi, i numeri
Il determinante. a11 a A = 12 a 21 a 22
 Il determinante Queste note, basate sugli appunti delle lezioni, riepilogano rapidamente la definizione e le proprietà del determinante Vengono inoltre illustrati i metodi di calcolo e alcune dimostrazioni
Il determinante Queste note, basate sugli appunti delle lezioni, riepilogano rapidamente la definizione e le proprietà del determinante Vengono inoltre illustrati i metodi di calcolo e alcune dimostrazioni
Contenuti aggiuntivi su matrici e determinanti, Dimostrazioni del Capitolo 3
 Contenuti aggiuntivi su matrici e determinanti, Dimostrazioni del Capitolo 3 Dimostrazione 310 Sia W = L(C A ) K Osserviamo che S è una base di W Infatti S è indipendente, inoltre ogni vettore di W dipende
Contenuti aggiuntivi su matrici e determinanti, Dimostrazioni del Capitolo 3 Dimostrazione 310 Sia W = L(C A ) K Osserviamo che S è una base di W Infatti S è indipendente, inoltre ogni vettore di W dipende
LEZIONE i i 3
 LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 5 51 Determinanti In questo lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE i 0 3 Le sottomatrici 2 2 di A sono. 1 2 i i 3. Invece (
 LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 6 6 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
Richiami di Algebra Lineare Fabrizio Silvestri December 14, 010 Matrice Sia R il campo dei numeri reali. Si indica con R m n l insieme delle matrici ad elementi reali con m righe ed n colonne. Se A R n
Operazioni tra matrici. Moltiplicazione per uno Scalare Moltiplicare ogni elemento della matrice per lo scalare. Sia c = 3
 Operazioni tra matrici Definizione di matrice a ij è un elemento di A a ij è detto l elemento ij-esimo di A Moltiplicazione per uno Scalare Moltiplicare ogni elemento della matrice per lo scalare. Sia
Operazioni tra matrici Definizione di matrice a ij è un elemento di A a ij è detto l elemento ij-esimo di A Moltiplicazione per uno Scalare Moltiplicare ogni elemento della matrice per lo scalare. Sia
Algebra matriciale. Un algebra è un sistema di segni in cui sono definite delle operazioni Algebra scalare Algebra dei vettori Algebra matriciale
 Algebra matriciale Algebra Un algebra è un sistema di segni in cui sono definite delle operazioni Algebra scalare Algebra dei vettori Algebra matriciale In algebra matriciale un numero è chiamato scalare
Algebra matriciale Algebra Un algebra è un sistema di segni in cui sono definite delle operazioni Algebra scalare Algebra dei vettori Algebra matriciale In algebra matriciale un numero è chiamato scalare
Anno Accademico 2015/2016
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2015/2016 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2015/2016 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Capitolo 3. Determinante e rango Permutazioni
 Capitolo 3 Determinante e rango 303 Permutazioni Ricordiamo innanzitutto che, dato un insieme, l insieme S () delle applicazioni biunivoche da in sè stesso, può essere munito di una operazione, indicata
Capitolo 3 Determinante e rango 303 Permutazioni Ricordiamo innanzitutto che, dato un insieme, l insieme S () delle applicazioni biunivoche da in sè stesso, può essere munito di una operazione, indicata
Matrici. Prof. Walter Pugliese
 Matrici Prof. Walter Pugliese Le matrici Una matrice è un insieme di numeri reali organizzati in righe e colonne. Se n è il numero delle righe e m e il numero delle colonne si dice che la matrice è di
Matrici Prof. Walter Pugliese Le matrici Una matrice è un insieme di numeri reali organizzati in righe e colonne. Se n è il numero delle righe e m e il numero delle colonne si dice che la matrice è di
APPUNTI DI ALGEBRA LINEARE
 APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
APPUNTI DI ALGEBRA LINEARE. Definizione Si dice spazio vettoriale (sul campo dei numeri reali R) un insieme V per il quale siano definite l operazione interna di somma (che ad ogni coppia di vettori e
MATRICI E OPERAZIONI
 MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
MATRICI E SISTEMI MATRICI E OPERAZIONI Matrici, somma e prodotto (definizioni, esempi, non commutatività del prodotto, legge di annullamento del prodotto Potenze e inverse di matrici quadrate (definizioni
Sistemi lineari - Parte Seconda - Esercizi
 Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
Sistemi lineari - Parte Seconda - Esercizi Terminologia Operazioni elementari sulle righe. Equivalenza per righe. Riduzione a scala per righe. Rango di una matrice. Forma canonica per righe. Eliminazione
Le matrici. Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1.
 Le matrici Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1. Siano m, n N\{0}. Una matrice m n a coefficienti in K è una tabella di m n elementi di K disposti
Le matrici Sia K un campo con elemento neutro dell addizione 0 ed elemento neutro della moltiplicazione 1. Siano m, n N\{0}. Una matrice m n a coefficienti in K è una tabella di m n elementi di K disposti
Geometria BAER I canale Foglio esercizi 2
 Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
Geometria BAER I canale Foglio esercizi Esercizio. ( ) Data la matrice, determinare tutte le matrici X Mat( ) tali che AX = 0 e tutte le matrici Y Mat( ) tali che Y 0. ( ) ( ) ( ) x y x + z y + w Soluzione:
Terminiamo gli esercizi dell ultima lezione. (LUCIDI) Calcolare, se possibile, AC, CA, CH e HC. (LUCIDI)
 Terminiamo gli esercizi dell ultima lezione. (LUCIDI) Esempi Calcolare, se possibile, AC, CA, CH e HC. (LUCIDI) Osservazioni per le matrici quadrate a) Data A M n (K) è possibile definire ricorsivamente
Terminiamo gli esercizi dell ultima lezione. (LUCIDI) Esempi Calcolare, se possibile, AC, CA, CH e HC. (LUCIDI) Osservazioni per le matrici quadrate a) Data A M n (K) è possibile definire ricorsivamente
Esercizi di Algebra Lineare Determinanti
 Esercizi di Algebra Lineare Determinanti Anna M. Bigatti 3-6 dicembre 2012 Calcolo del determinante Proposizione 1. Alcune proprietà dei determinanti: (a) Il determinante del prodotto è il prodotto dei
Esercizi di Algebra Lineare Determinanti Anna M. Bigatti 3-6 dicembre 2012 Calcolo del determinante Proposizione 1. Alcune proprietà dei determinanti: (a) Il determinante del prodotto è il prodotto dei
A =, c d. d = ad cb. c d A =
 Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
Geometria e Algebra (II), 271112 1 Definizione D ora innanzi, al posto di dire matrice quadrata di tipo n n o matrice quadrata n n diremo matrice quadrata di ordine n o in breve matrice di ordine n Il
(V) (FX) L unione di due basi di uno spazio vettoriale è ancora una base dello spazio vettoriale.
 8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
8 gennaio 2009 - PROVA D ESAME - Geometria e Algebra T NOME: MATRICOLA: a=, b=, c= Sostituire ai parametri a, b, c rispettivamente la terzultima, penultima e ultima cifra del proprio numero di matricola
Corso di Matematica e Statistica 3 Algebra delle matrici. Una tabella rettangolare: la matrice. Una tabella rettangolare: la matrice
 Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
Pordenone Corso di Matematica e Statistica 3 Algebra delle UNIVERSITAS STUDIORUM UTINENSIS Giorgio T. Bagni Facoltà di Scienze della Formazione Dipartimento di Matematica e Informatica Università di Udine
Sistemi II. Sistemi II. Elisabetta Colombo
 Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
Corso di Approfondimenti di Matematica per Biotecnologie, Anno Accademico 2011-2012, http://users.mat.unimi.it/users/colombo/programmabio.html 1 2 3 con R.C.+ o 1.10 Rango massimo e determinante con R.C.+
il determinante che si ottiene da A, sopprimendo la i - esima riga e la j - esima colonna. Si definisce complemento algebrico dell'elemento a ij
 Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
Determinanti Sia data la matrice quadrata a... a n a a n =...... a... a n nn Chiamiamo determinante di il numero det o che ad essa viene associato. det = a a... a... a... a n n n... a nn Un generico elemento
MATRICI e DETERMINANTI. Prof.ssa Maddalena Dominijanni
 MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
MATRICI e DETERMINANTI Le matrici non sono altro che tabelle di elementi ordinati per righe e colonne. Se m = n la matrice si dice quadrata Matrice quadrata di ordine 3 Matrice rettangolare di tipo 2 3
GEOMETRIA I Prima Prova Intermedia 3 Novembre 2017
 Corso di Laurea in Fisica GEOMETRIA I Prima Prova Intermedia Novembre 017 Cognome: Nome: Matricola: PARTE 1 Test a risposta multipla Una ed una sola delle quattro affermazioni è corretta. Indicarla con
Corso di Laurea in Fisica GEOMETRIA I Prima Prova Intermedia Novembre 017 Cognome: Nome: Matricola: PARTE 1 Test a risposta multipla Una ed una sola delle quattro affermazioni è corretta. Indicarla con
Elementi di Algebra Lineare Applicazioni lineari
 Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 50 index Applicazioni lineari 1 Applicazioni lineari
Elementi di Algebra Lineare Applicazioni lineari Cristina Turrini UNIMI - 2016/2017 Cristina Turrini (UNIMI - 2016/2017) Elementi di Algebra Lineare 1 / 50 index Applicazioni lineari 1 Applicazioni lineari
Determinante. Sia M(n, n, K) lo spazio delle matrici quadrate n n a coefficienti in un campo K, vogliamo provare il seguente Teorema:
 Determinante 1 Proprieta Sia M(n, n, K) lo spazio delle matrici quadrate n n a coefficienti in un campo K, vogliamo provare il seguente Teorema: Theorem 1.1 Esiste un unica mappa F dallo spazio delle matrici
Determinante 1 Proprieta Sia M(n, n, K) lo spazio delle matrici quadrate n n a coefficienti in un campo K, vogliamo provare il seguente Teorema: Theorem 1.1 Esiste un unica mappa F dallo spazio delle matrici
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI A.A. 2018/2019 PROF. VALENTINA BEORCHIA
 CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
CORSO DI GEOMETRIA APPLICAZIONI LINEARI E MATRICI AA 2018/2019 PROF VALENTINA BEORCHIA INDICE 1 Matrici associate a un applicazione lineare 1 2 Cambiamenti di base 4 3 Diagonalizzazione 6 1 MATRICI ASSOCIATE
x n i sima pos. x, y = x T y = x i y i R. i=1
 1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
1 Elementi di Algebra Lineare In questo capitolo introduttivo al corso di Calcolo Numerico per la laurea triennale in Informatica, saranno presentate una serie di definizioni e proprietà di matrici e dei
Anno Accademico 2016/2017
 Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2016/2017 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Mod. 136/1 ALMA MATER STUDIORUM UNIVERSITÀ DI BOLOGNA Anno Accademico 2016/2017 Scuola di Scienze Corsi di Laurea o di Diploma Triennale in Matematica (nuovo ordinamento) Insegnamento Geometria I Docente
Equivalentemente, le colonne di A sono linearmente indipendenti se e solo se
 Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
Lezioni di Algebra Lineare. Versione novembre 2008 VI. Il determinante Il determinante det A di una matrice A, reale e quadrata, è un numero reale associato ad A. Dunque det è una funzione dall insieme
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia
 CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2015-16 Complementi ed Esercizi 1. AUTOVETTORI e AUTOVALORI di ENDOMORFISMI e MATRICI Una applicazione lineare avente per dominio e condominio lo stesso spazio vettoriale
CORSO DI ALGEBRA (M-Z) Prof. A. Venezia 2015-16 Complementi ed Esercizi 1. AUTOVETTORI e AUTOVALORI di ENDOMORFISMI e MATRICI Una applicazione lineare avente per dominio e condominio lo stesso spazio vettoriale
0.1 Soluzioni Foglio di esercizi 1: Matrici
 0.1 Soluzioni Foglio di esercizi 1: Matrici Esercizio 1 (dal Test di Autovalutazione 3/11/2015 M.Manaresi) Siano 1 1 1 1 A 2 2 0, B 1, 1 0 X M 3 (R) Si stabilisca per quali valori del parametro reale k
0.1 Soluzioni Foglio di esercizi 1: Matrici Esercizio 1 (dal Test di Autovalutazione 3/11/2015 M.Manaresi) Siano 1 1 1 1 A 2 2 0, B 1, 1 0 X M 3 (R) Si stabilisca per quali valori del parametro reale k
3 Soluzione di sistemi lineari
 3 Soluzione di sistemi lineari Prima di addentrarci nello studio dei metodi numerici, è doveroso introdurre le matrici e alcune strutture particolari di matrici nonchè alcuni concetti fondamentali quali
3 Soluzione di sistemi lineari Prima di addentrarci nello studio dei metodi numerici, è doveroso introdurre le matrici e alcune strutture particolari di matrici nonchè alcuni concetti fondamentali quali
Metodi e Modelli per l Ottimizzazione Combinatoria Problema dell assegnamento e matrici totalmente unimodulari
 Metodi e Modelli per l Ottimizzazione Combinatoria Problema dell assegnamento e matrici totalmente unimodulari L. De Giovanni G. Zambelli 1 Problema dell assegnamento Sia dato un grafo non orientato bipartito
Metodi e Modelli per l Ottimizzazione Combinatoria Problema dell assegnamento e matrici totalmente unimodulari L. De Giovanni G. Zambelli 1 Problema dell assegnamento Sia dato un grafo non orientato bipartito
PROGRAMMA del corso di. GEOMETRIA 1 - Algebra Lineare. Laurea Triennale in Matematica. Anno Accademico 2007/08. docente : Bruno Zimmermann
 PROGRAMMA del corso di GEOMETRIA 1 - Algebra Lineare Laurea Triennale in Matematica Anno Accademico 2007/08 docente : Bruno Zimmermann (Il presente programma è stato redatto sulla base degli appunti del
PROGRAMMA del corso di GEOMETRIA 1 - Algebra Lineare Laurea Triennale in Matematica Anno Accademico 2007/08 docente : Bruno Zimmermann (Il presente programma è stato redatto sulla base degli appunti del
Richiami di algebra delle matrici
 Richiami di algebra delle matrici (S. Terzi) 1. SPAZI VETTORIALI I. ALCUNE DEFINIZIONI 1) Definizione di spazio vettoriale Sia S un insieme di vettori di ordine n. S è detto spazio lineare se e' un insieme
Richiami di algebra delle matrici (S. Terzi) 1. SPAZI VETTORIALI I. ALCUNE DEFINIZIONI 1) Definizione di spazio vettoriale Sia S un insieme di vettori di ordine n. S è detto spazio lineare se e' un insieme
MATRICI E SISTEMI LINEARI
 1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
1 Rappresentazione di dati strutturati MATRICI E SISTEMI LINEARI Gli elementi di una matrice, detti coefficienti, possono essere qualsiasi e non devono necessariamente essere omogenei tra loro; di solito
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari
 Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
Elementi di Algebra Lineare Matrici e Sistemi di Equazioni Lineari Antonio Lanteri e Cristina Turrini UNIMI - 2016/2017 Antonio Lanteri e Cristina Turrini (UNIMI - 2016/2017 Elementi di Algebra Lineare
0.1 Soluzioni esercitazione IV, del 28/10/2008
 1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
1 0.1 Soluzioni esercitazione IV, del 28/10/2008 Esercizio 0.1.1. Risolvere, usando il teorema di Cramer, i seguenti sistemi lineari 2x + y + z = 0 x + 3z = 1 x y z = 1 kx + y z = 1 x y + 2z = 1 2x + 2y
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI
 CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # GEOMETRIA E ALGEBRA 009/0 Esercizio.. Dati i vettori di R : v (,, ), v (, 4, 6), v (,, 5), v 4 (,, 0) determinare se v 4 è combinazione
CORSO DI LAUREA IN INGEGNERIA DELLE TELECOMUNICAZIONI FOGLIO DI ESERCIZI # GEOMETRIA E ALGEBRA 009/0 Esercizio.. Dati i vettori di R : v (,, ), v (, 4, 6), v (,, 5), v 4 (,, 0) determinare se v 4 è combinazione
Lezione 4 - Esercitazioni di Algebra e Geometria - Anno accademico
 Trasformazioni elementari sulle matrici Data una matrice A K m,n definiamo su A le seguenti tre trasformazioni elementari: T : scambiare tra loro due righe (o due colonne) di A; T : sommare ad una riga
Trasformazioni elementari sulle matrici Data una matrice A K m,n definiamo su A le seguenti tre trasformazioni elementari: T : scambiare tra loro due righe (o due colonne) di A; T : sommare ad una riga
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2015 Rossi Algebra Lineare 2015 1 / 41 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2015 Rossi Algebra Lineare 2015 1 / 41 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
Vettori e matrici. Lorenzo Pareschi. Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara
 Vettori e matrici Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utentiunifeit/lorenzopareschi/ lorenzopareschi@unifeit Lorenzo Pareschi Univ Ferrara
Vettori e matrici Lorenzo Pareschi Dipartimento di Matematica & Facoltá di Architettura Universitá di Ferrara http://utentiunifeit/lorenzopareschi/ lorenzopareschi@unifeit Lorenzo Pareschi Univ Ferrara
Giuseppe Accascina. Note del corso di Geometria e Algebra
 Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 26-27 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Giuseppe Accascina Note del corso di Geometria e Algebra Corso di Laurea Specialistica in Ingegneria Gestionale Anno Accademico 26-27 ii Istruzioni per l uso Faremo spesso riferimento a ciò che è stato
Matrici e sistemi. Geometria. Matrici e operazioni tra matrici. Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante
 Geometria Matrici e sistemi Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante 2 2006 Politecnico di Torino 1 Matrici e sistemi Matrici: definizione e notazioni Somma e
Geometria Matrici e sistemi Operazioni elementari e riduzione Sistemi lineari Matrici invertibili Determinante 2 2006 Politecnico di Torino 1 Matrici e sistemi Matrici: definizione e notazioni Somma e
LEZIONE 4. Le sottomatrici 2 2 di A sono. Invece ( 1 3 non è sottomatrice di A.
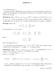 LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LEZIONE 4 4 Determinanti In questa lezione affronteremo da un punto di vista prettamente operativo la nozione di determinante, descrivendone le proprietà ed i metodi di calcolo, senza entrare nei dettagli
LeLing9: Prodotto tra matrici.
 Geometria Lingotto LeLing9: Prodotto tra matrici Ārgomenti svolti: Prodotto tra matrici Dimostrazione del teorema del rango L algebra delle matrici quadrate: Il prodotto tra matrici non e commutativo Rotazioni
Geometria Lingotto LeLing9: Prodotto tra matrici Ārgomenti svolti: Prodotto tra matrici Dimostrazione del teorema del rango L algebra delle matrici quadrate: Il prodotto tra matrici non e commutativo Rotazioni
Matrici e sistemi. Sistemi lineari. Invertibilità Matrici elementari Criteri di invertibilità Sistemi quadrati e Teorema di Cramer
 Sistemi lineari Invertibilità Matrici elementari Criteri di invertibilità Sistemi quadrati e Teorema di Cramer 2 2006 Politecnico di Torino 1 Prodotto tra matrici quadrate Date comunque A e B matrici quadrate
Sistemi lineari Invertibilità Matrici elementari Criteri di invertibilità Sistemi quadrati e Teorema di Cramer 2 2006 Politecnico di Torino 1 Prodotto tra matrici quadrate Date comunque A e B matrici quadrate
Autovalori e autovettori di una matrice quadrata
 Autovalori e autovettori di una matrice quadrata Data la matrice A M n (K, vogliamo stabilire se esistono valori di λ K tali che il sistema AX = λx ammetta soluzioni non nulle. Questo risulta evidentemente
Autovalori e autovettori di una matrice quadrata Data la matrice A M n (K, vogliamo stabilire se esistono valori di λ K tali che il sistema AX = λx ammetta soluzioni non nulle. Questo risulta evidentemente
PreCorso di Matematica - PCM Corso M-Z
 PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
PreCorso di Matematica - PCM Corso M-Z DOCENTE: M. Auteri Outline Docente: Auteri PreCorso di Matematica 2016 2 Definizione di matrice Una matrice (di numeri reali) è una tabella di m x n numeri disposti
a a 1n A = a n1... a nn a 11 x a 1n x n = b 1 a n1 x a nn x n = b n ] sono determinati. 2- La matrice A = [ a ij
![a a 1n A = a n1... a nn a 11 x a 1n x n = b 1 a n1 x a nn x n = b n ] sono determinati. 2- La matrice A = [ a ij a a 1n A = a n1... a nn a 11 x a 1n x n = b 1 a n1 x a nn x n = b n ] sono determinati. 2- La matrice A = [ a ij](/thumbs/102/154682810.jpg) Recupero. 2, Determinanti. 1. Determinanti Consideriamo una matrice A = a 11... a 1n.. a n1... a nn quadrata di ordine n ad elementi in R. Sappiamo che sono equivalenti la affermazioni 1- tutti i sistemi
Recupero. 2, Determinanti. 1. Determinanti Consideriamo una matrice A = a 11... a 1n.. a n1... a nn quadrata di ordine n ad elementi in R. Sappiamo che sono equivalenti la affermazioni 1- tutti i sistemi
1.1 Matrici a coefficienti in R. Vi sono alcuni casi particolari che vale la pena evidenziare:
 Lezione Matrici a coefficienti in R Definizione Siano m, n Z numeri interi positivi Una matrice m n acoefficientiinrèuninsiemedimn numeri reali disposti su m righe ed n colonne circondata da parentesi
Lezione Matrici a coefficienti in R Definizione Siano m, n Z numeri interi positivi Una matrice m n acoefficientiinrèuninsiemedimn numeri reali disposti su m righe ed n colonne circondata da parentesi
Determinante, autovalori e autovettori
 Determinante, autovalori e autovettori Lorenzo Pareschi Dipartimento di Matematica, Universitá di Ferrara http://wwwlorenzopareschicom lorenzopareschi@unifeit Lorenzo Pareschi (Univ Ferrara) Determinante,
Determinante, autovalori e autovettori Lorenzo Pareschi Dipartimento di Matematica, Universitá di Ferrara http://wwwlorenzopareschicom lorenzopareschi@unifeit Lorenzo Pareschi (Univ Ferrara) Determinante,
Applicazioni eliminazione di Gauss
 Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
Applicazioni eliminazione di Gauss. Premessa Nel seguito supporremo sempre di applicare il metodo di eliminazione di Gauss allo scopo di trasformare la matrice del sistema Ax = b in una matrice triangolare
Richiami di Algebra Lineare
 Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2012 Rossi Algebra Lineare 2012 1 / 59 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
Richiami di Algebra Lineare Eduardo Rossi Università degli Studi di Pavia Corso di Econometria Marzo 2012 Rossi Algebra Lineare 2012 1 / 59 Vettori Prodotto interno a : (n 1) b : (n 1) a b = a 1 b 1 +
( ) TEORIA DELLE MATRICI. A. Scimone a.s pag 1
 . Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
. Scimone a.s 1997 98 pag 1 TEORI DELLE MTRICI Dato un campo K, definiamo matrice ad elementi in K di tipo (m, n) un insieme di numeri ordinati secondo righe e colonne in una tabella rettangolare del tipo
