LA MODELLAZIONE DEL BILANCIO IDROLOGICO DI UN GHIACCIAIO: FONDAMENTI MODELLISTICI E TEST SU UN GHIACCIAIO TROPICALE
|
|
|
- Ortensia Angelini
- 8 anni fa
- Visualizzazioni
Transcript
1 XXX Convegno di Idraulica e Costruzioni Idrauliche - IDRA 2006 LA MODELLAZIONE DEL BILANCIO IDROLOGICO DI UN GHIACCIAIO: FONDAMENTI MODELLISTICI E TEST SU UN GHIACCIAIO TROPICALE Stefano Endrizzi 1, Riccardo Rigon 1 (1) Dipartimento di Ingegneria Civile e Ambientale, Università degli studi di Trento - Trento (IT) stefano.endrizzi@ing.unitn.it, riccardo.rigon@ing.unitn.it Parole chiave: Flussi suolo-atmosfera, Idrologia, Interazione suolo atmosfera, Neve, Glaciologia SOMMARIO Il modello idrologico distribuito fisicamente basato GEOtop è stato applicato per la prima volta ad un ghiacciaio per prevederne il bilancio idrologico. Il modello è in grado di stimare non solo la portata per una determinata sezione di chiusura, ma anche la distribuzione spazio-temporale della copertura nevosa, dell umidità del suolo, della temperatura della superficie, dei flussi termici, tenendo conto degli effetti topografici e della fisica della neve, e di altre variabili idrometeorologiche. In questo lavoro si discutono prevalentemente i fondamenti degli aspetti relativi all applicabilità del modello per un ghiacciaio, dei processi fisici che avvengono in presenza di neve e ghiaccio descritti nel modello e dei problemi che si presentano. E alla fine mostrata un applicazione preliminare ad un ghiacciaio tropicale (Zongo, Bolivia).
2 2 S.Endrizzi, R.Rigon 1 INTRODUZIONE GEOtop (Rigon et al., 2006) è un modello distribuito fisicamente basato del ciclo idrologico. La sua caratteristica principale è la risoluzione del sistema delle equazioni di bilancio di massa (equazione di Richards tridimensionale e varie schematizzazioni dei deflussi superficiali) e di energia (equazione del calore, solo in direzione verticale) in modo accoppiato per ogni singola cella della griglia regolare del modello digitale del terreno. Le equazioni sono risolte alle differenze finite discretizzando il suolo in layers di spessore variabile con la profondità. Il modello è stato concepito per essere un integrazione di un modello afflussi-deflussi di tipo tradizionale e di un Land Surface Model, in modo che possa non solo calcolare la portata di piena per una determinata sezione di chiusura del bacino, ma anche seguire l evoluzione nello spazio e nel tempo di un grande numero di variabili idrometeorologiche, delle quali sono rilevanti in questo studio l altezza della neve, la temperatura della superficie, i flussi di calore tra suolo e atmosfera. L evoluzione del manto nevoso e di un ghiacciaio è fortemente dipendente dagli scambi energetici con l atmosfera, che devono essere descritti con estremo dettaglio in quanto ogni errore si ripercuote immediatamente nei caratteri osservabili, come l altezza della neve e il volume del manto nevoso stesso. Un ghiacciaio di qualche chilometro quadrato di superficie, date le sue piccole dimensioni, è dunque un laboratorio naturale che permette di verificare l efficacia di un modello di scambi energetici con più facile controllabilità di quanto non avvenga in porzioni di territorio diversamente ricoperte. Prevedere l evoluzione del manto nevoso e delle superfici glacializzate è certamente utile a molti scopi applicative, in particolare per una corretta valutazione del volume della risorsa idrica disponibile al variare delle stagioni e nel corso degli anni, anche in presenza di cambiamenti climatici. 2 MODELLAZIONE DELLA NEVE Nel manto nevoso le equazioni di bilancio di massa e di energia si risolvono in modo accoppiato nello stesso modo in cui sono risolte nel suolo, sempre discretizzandole in un certo numero di layer. Tuttavia, visto che l acqua nella neve si muove principalmente per azione della gravità (Colbeck Anderson, 1982), l equazione del bilancio di massa liquida diventa molto più semplice: è monodimensionale e non ha più senso considerare la suzione. D altra parte l equazione del bilancio di energia si complica, in quanto è necessario prevedere il cambiamento di fase e definire le opportune variabili che descrivano lo stato energetico, oltre alla temperatura, il contenuto di ghiaccio e di acqua liquida nella neve. Una prima versione di GEOtop contenente l evoluzione del manto nevoso, come un unico layer, è presente in Zanotti et al. (2004). Successivamente la descrizione del manto nevoso è stata rivista ritenendo necessaria una rappresentazione multilayer della neve, come per il suolo. Il numero di layer che è stato implementato segue lo schema di Oleson et al. (2004). Per la neve le variabili di stato considerate sono, oltre alla temperatura (T), il contenuto adimensionale di ghiaccio (θ i ) e di acqua liquida (θ w ). A questi si aggiunge un ulteriore variabile che tiene conto dell età della neve, usata solo per calcolare l albedo (Tarboton e Luce, 1996). Le equazioni del bilancio di energia e di massa, per la fase liquida e per la fase solida, valide all interno del manto nevoso, sono le seguenti (tra parentesi le unità di misura usate nel modello):
3 3 La modellazione del bilancio idrologico di un ghiacciaio ( ) C "T "t + L "W f "T = " # "z k "T % ( + " Q wu w "z ' "z ) w = 1 #"W + "Q # w ) % ( Q * w "t "z ' w = k w +) r w % ( 1+) i +) r ' ) i = 1 #"W + "Q i % ( Q i = 0, * i "t "z ' (1-3) dove z è la coordinata verticale (m), con origine all interfaccia suolo-neve e positiva verso l alto, C la capacità termica volumetrica della neve (J K -1 m -3 ), t il tempo, L f il calore latente di fusione dell acqua (J kg -1 ), W (kg m -3 ) la massa di ghiaccio che scioglie (se positivo) oppure la massa d acqua che gela (se negativo), k la conducibilità termica della neve (W m -1 K -1 ), Q w la portata di acqua liquida (kg m -2 s -1 ), U w il contenuto di energia interna specifica dell acqua liquida (J kg -1 ), riferita all energia interna specifica del ghiaccio alla temperatura K, ρ w la densità dell acqua (1000 kg m -3 ), k w la conducibilità idraulica dell acqua nella neve (kg m -2 s -1 ) a saturazione, θ r il contenuto d acqua nella neve trattenuto per azione di forze capillari (normalmente tra 0.03 e 0.05 della porosità), ρi la densità del ghiaccio (917 kg m -3 ) e Q i la portata di ghiaccio (kg m -2 s -1 ), nulla in quanto si tratta di un mezzo solido. La continuità impone inoltre che " w + " i + " v =1 (4) dove θ v è il contenuto adimensionale di vapor d acqua. La capacità termica e la conducibilità termica sono calcolate come media pesata dei valori delle diverse fasi presenti (i pedici w, i e v si riferiscono rispettivamente alle fasi liquida, solida ed aeriforme): C = " w C w + " i C i + " v C v k = " w k w + " i k i + " v k v (5-6) Le equazioni (1), (2), (3) e (4) formano un sistema con 5 incognite (T, W, θ i, θ w e θ v ) che devono essere risolte contemporaneamente. Serve chiaramente un ulteriore equazione, per esempio un espressione che leghi il cambiamento di fase alla temperatura. Per ottenere questo risultato può essere usato il metodo della capacità termica apparente C a (Albert, 1983), applicato solitamente nei suoli ghiacciati, per cui il secondo secondo termine dell equazione (1) viene trasformato come segue: L f "W "t = L f "W "T "T "t (7) e poi inglobato nel primo termine che diventa "T C a "t = # % C + L f "W "T ( "T ' "t (8) Questa modellazione ha un elemento che può diventare critico da un punto di vista numerico. Infatti il cambiamento di fase di neve ad acqua e viceversa avviene quasi completamente alla temperatura di K. Questo produce valori molto elevati della derivata di W rispetto a T nell equazione (8) che deve invece essere regolarizzata. Nel modello invece si è quindi inserita la seguente relazione W " 0 se T = K ; W = 0 se T " K (9) In questo modo quando T = K il primo termine dell equazione (1) si annulla e T, rimanendo co-
4 4 S.Endrizzi, R.Rigon stante, non rientra più tra le incognite del problema. A sua volta se T K, W non è un incognita. Controlli sono necessari quando nell integrazione numerica T passa da valori inferiori a valori superiori a K e quando non sono più disponibili acqua da congelare o ghiaccio da sciogliere. All interfaccia suolo-neve (z = 0) e neve-atmosfera (z = D), dove D è l altezza del manto nevoso (m), vanno poste le condizioni al contorno: # % # % k "T "z k "T "z ( ' ( ' z= D z= 0 = )R n + H + L # "T = k soil % soil ( "z ' z= 0 (10-13) ( Q w ) z= D = P w ) E w ( Q i ) z= D = P i ) E i L equazione (10) esprime i flussi energetici tra atmosfera e neve: R n è la radiazione netta (W m 2 ), positiva se diretta verso la neve, H e L (W m 2 ) sono rispettivamente il flusso di calore sensibile e latenti, positivi se diretti verso l atmosfera. Tali flussi dipendono a loro volta anche dalla temperatura della superficie (T (D)), il che introduce un forte elemento di non linearità nel problema. L equazione (11) segue dalla continuità della temperatura nell interfaccia tra neve e suolo (k soil e T soil sono rispettivamente la conducibilità termica e la temperatura del suolo). Le equazioni (12) e (13) descrivono l alimentazione liquida e solida del manto nevoso: P w e P i (kg m 2 s 1 ) sono l intensità di precipitazione liquida e solida, E w ed E i (kg m 2 s 1 ) l intensità di evaporazione e sublimazione. Poiché di solito non vi sono misure dirette della precipitazione nevosa e risulta più spesso misurata la sola precipitazione totale, si discrimina la parte liquida da quella solida in base alla temperatura dell aria, come nella formula del U.S. Army Corps of Engineers (1956). L altezza della neve D viene modificata nel tempo tenendo conto della neve fresca accumulatasi, del metamorfismo distruttivo, gravitativo e di fusione: "D "t = P i # new F 1 F 2 F 3 (14) dove ρ new è la densità della neve fresca, per cui si utilizza una formula sperimentale dipendente dalla temperatura dell aria, F 1 è un termine che tiene conto del metamorfismo distruttivo, la compattazione che avviene per trasformazione dei cristalli di neve, F 2 tiene conto del metamorfismo gravitativo, la compattazione conseguente al peso della neve e F 3 è un indice del metamorfismo di fusione, pari a ( ) = % i( z) f z %t se F 3 = D # 0 % i z %t " i f ( z)dz ( ) < 0 ; f ( z) = 0 se ( ) % i z %t ' 0 (15) il che significa che l altezza della neve viene ridotta in modo proporzionale alla riduzione del contenuto di ghiaccio e che rimane invariata qualora ci sia un aumento del contenuto di ghiaccio per effetto di un rigelo. In questo modo è possibile simulare le croste di gelo-rigelo. Per le altre parametrizzazioni dell equazione (14) si è seguito Anderson (1976).
5 5 La modellazione del bilancio idrologico di un ghiacciaio 3 MODELLAZIONE DEL GHIACCIO Il ghiaccio è trattato come la neve, con la differenza che all interno di esso non si ammette un moto di filtrazione, ma si considera che la portata liquida uscente da ogni layer venga trasferita istantaneamente alla base del ghiacciaio dove diventa di fatto disponibile ad infiltrarsi nel suolo o a trasformarsi in deflusso superficiale. Anche se ciò costituisce una forte semplificazione, questo vuole rappresentare l effetto dei mulini e dei crepacci presenti nei ghiacciai, che permettono il trasferimento d acqua alla base in tempi molto più rapidi di quelli impiegati in un eventuale moto di filtrazione, comunque non possibile in quanto nel ghiacciaio i pori non sono interconnessi. Si trascura inoltre il runoff che avviene sulla superficie del ghiacciaio, che si assume verificarsi interamente alla base. Le equazioni precedenti valgono anche per il ghiacciaio, con le seguenti differenze: Nell equazione (2) Q w è sempre nullo, in quanto nel ghiacciaio non può verificarsi moto di filtrazione. La condizione al contorno (10) vale per il ghiacciaio qualora questo sia scoperto di neve. Qualora sia coperto di neve la continuità della temperatura impone un equazione del tipo della (11) alla base e alla superficie del ghiacciaio. Quando il ghiacciaio è scoperto valgono le condizioni al contorno (12) e (13), tuttavia il ghiacciaio non è mai alimentato da precipitazione liquida (pertanto P w è nullo) in quanto questa viene istantaneamente trasferita alla base del ghiacciaio, né da precipitazione solida (P i nullo), poiché questa contribuisce alla formazione di uno strato di neve. Quando invece il ghiacciaio è coperto da neve continuano a valere le (12) e (13), ma con valori nulli di E w e E i. Per risolvere le equazioni occorre valutare la profondità del ghiaccio. Inoltre rimane aperto il problema della trasformazione della neve in ghiaccio: deve essere definita una soglia di densità e di contenuto di ghiaccio, ma la determinazione di un valore preciso deve essere frutto di ricerche più approfondite della presente. 4 FLUSSI DI CALORE TRA GHIACCIO/NEVE/SUOLO E ATMOSFERA Gli scambi di calore con l atmosfera, presenti nella condizione al contorno (11), sono le forzanti del problema ed è necessaria pertanto una loro valutazione alquanto precisa. 4.1 Modellazione della radiazione La radiazione è normalmente l elemento fondamentale che determina lo scioglimento del manto nevoso. La radiazione netta R n (W m 2 ) è espressa dalla seguente formula (Rigon et al., 2006): R n = R SW,down ( 1" A) + # s R LW,down " R LW,up (16) dove R SW,down è la radiazione ad onde corte proveniente dall atmosfera, a sua volta suddivisa in radiazione diretta e diffusa, A è l albedo, R LW,down la radiazione ad onde lunghe proveniente dall atmosfera e R LW,up la radiazione ad onde lunghe emessa dal suolo (dalla neve neve o dal ghiaccio), considerato equivalente a un corpo grigio infinitamente profondo con temperatura uniforme e emissività ε s poco inferiore a 1 (0.99 per la neve). Pertanto: R LW,up = " s #T s 4 (17) dove σ è la costante di Stefan-Boltzmann e T s la temperatura della superficie (K). La radiazione ad onde corte può essere misurata in un punto, e poi estrapolata nell intero bacino usando
6 6 S.Endrizzi, R.Rigon questa formula: R SW,down = f " R LW,DIR,0 a" cos# a"v + R LW,DIR,0 (18) a 0 " cos# 0 a 0 " V 0 dove R LW,DIR,0 e R LW,DIFF,0 sono rispettivamente la radiazione diretta e diffusa misurate alla stazione meteorologica, a 0 e cosθ 0 l attenuazione atmosferica e il coseno dell angolo di incidenza dei raggi solari nel punto dove si trova la stazione (Iqbal, 1983), a e cosθ le stesse variabili in un generico punto del bacino, f un coefficiente che assume il valore di 0 o 1 a seconda che il punto sia in ombra o meno e V 0 l angolo di vista del cielo (sky view factor) alla stazione, cioè la frazione di cielo visibile nel punto (Blöschl et al., 1991), e V la stessa variabile in un punto generico. Gli algoritmi per calcolare V e f sono documentati in Bertoldi Rigon (2004). L angolo di incidenza tiene conto della topografia attraverso la pendenza e l esposizione, come da Iqbal (1983): cos" = cos# cos" z + sin# sin" z cos ( % ) (19) dove β è la pendenza, θ z l angolo zenitale (cioè l angolo tra il sole e lo zenit), che varia nel corso della giornata, ψ l azimut (la proiezione del raggio del sole su un piano orizzontale) e γ l aspetto (la proiezione su un piano orizzontale della normale alla superficie topografica). Gli angoli ψ e γ devono essere definiti rispetto alla medesima origine e devono avere lo stesso verso. Nel caso non siano disponibili misure di radiazione, si possono utilizzare formule di derivazione teorica per R LW,DIR,0 (Iqbal, 1983), che tuttavia presuppongono la presenza di cielo sereno, ma rimane problematico definire l attenuazione della copertura nuvolosa e la radiazione diffusa in assenza di specifiche misure. Esistono diverse formule di derivazione sperimentale (Iqbal, 1983), che utilizzano la copertura nuvolosa, dato di difficile reperibilità, soprattutto di notte. Grande problematicità pone anche la determinazione di R LW,down, per cui non esistono formule di derivazione teorica abbastanza precise. Normalmente essa si esprime come R LW,down = " ac #T a 4 f c (20) dove T a (K) è la temperatura dell aria misurata vicino alla superficie, ε ac un emissività atmosferica equivalente per cielo non coperto da nuvole e f c un coefficiente di attenuazione per la copertura nuvolosa. In letteratura sono reperibili diverse formule sperimentali che esprimono ε ac in funzione della temperatura e della pressione di vapore in aria (Brutsaert, 1975; Satterlund, 1979; Idso, 1981) e f c in funzione della copertura nuvolosa (Bolz, 1949), che tuttavia sono valide solo nelle condizioni sperimentali in cui sono state ricavate. Se non sono disponibili dati di copertura nuvolosa, questa può essere inferita dall escursione termica giornaliera (Bristow Campbell, 1984) oppure dal rapporto tra la radiazione diretta ad onde corte misurata e quella teorica in condizioni di cielo sereno, ma quest ultimo si può applicare solo di giorno. Pirazzini et al. (2000) hanno confrontato15 formule di ε ac e 6 formule di f c con misure effettuate nelle isole Svalbard e hanno ottenuto una notevole dispersione di risultati. L applicazione del modello ha mostrato inoltre come il bilancio di massa di un ghiacciaio manifesti una discreta sensibilità alle diverse formule. Un altro parametro chiave è l albedo (A) che viene calcolato per la neve secondo la teoria di Dickinson (1993), come funzione dell età della neve e dell altezza solare. L albedo del ghiacciaio scoperto può essere desunto da misure sperimentali e rientra normalmente tra 0.2 e 0.3 (Arnold et al., 1996).
7 7 La modellazione del bilancio idrologico di un ghiacciaio 4.2 Modellazione dei flussi turbolenti I flussi termici convettivi scambiati tra la superficie e l atmosfera H (flusso di calore sensibile, misurato in W m 2 ) ed E (flusso di vapor acqueo, misurato in kg m 2 s 1 ) sono principalmente trasportati per effetto della turbolenza, essendo normalmente trascurabile il trasporto molecolare, e sono espressi con una formula dipendente dal gradiente della grandezza trasportata: H = "c p UC h T s # T a E = "c p UC e q * T s ( ) (21) ( ) # q a ( ) (22) dove ρ è la densità dell aria (kg m 3 ), c p il calore specifico a pressione costante dell aria (J kg 1 K 1 ), U la velocità del vento (m s 1 ), q l umidità specifica a saturazione (kg kg -1 ), che dipende solo dalla temperatura, condizione che si suppone verificarsi subito sopra la superficie nevosa o di ghiaccio, e q a è l umidità specifica dell aria misurata alla quota in cui si misura la temperatura T a. Si suppone che avvenga sublimazione (cioè E i = E) quando T s è minore di K, evaporazione (E w = E) quando è maggiore o u- guale. Queste ultime vengono sono poi trasformate in flusso di calore latente L = L e E w + L s E i (23) dove L e e L i (J kg 1 ) sono rispettivamente il calore latente di evaporazione e di sublimazione dell acqua. C h e C e sono coefficienti di scambio turbolento che vengono calcolati usando la teoria della similarità di Monin-Obukhov (1954) (Garratt, 1992) basata sulle ipotesi che i flussi siano omogenei e quasi-stazionari, indipendenti dalla quota (come normalmente si suppone accada nello strato limite superficiale) e che gli effetti della scabrezza e dell altezza dello strato limite atmosferico siano completamente descritti dalla velocità d attrito u *. A rigore tale teoria è valida su una topografia piatta, o lentamente variabile, che è comunque piuttosto lontana da quella di un ghiacciaio. Tuttavia è normalmente applicata anche in questo contesto. I coefficienti C h e C e sono considerati uguali tra loro, assumendo, come si fa comunemente, che il trasferimento del calore sensibile tra superficie e atmosfera avvenga allo stesso modo del trasferimento di umidità. Secondo la presente teoria i profili di velocità, temperatura e umidità specifica sono i seguenti: + U = u* k ln " z % U # z 0U ' ( ) " z % " z U m # * ' + ) 0U %. - m ', # * /, T a " T s = #* k ln z ' h z ) " * h ' z h ) + * 0h '/. % z 0h ( % + ( h ) - % + ( 0 + q a " q * ( T s ) = Q* k ln # z # h z % ( " ) h # z h % ( + ) 0h. - z 0h ' * ' h % (, * '/ 0 (24) 1 (25) 0 (26) dove z U e z h sono rispettivamente le quote di misura della velocità del vento e della temperatura, z 0U e z 0h le scabrezze (roughness lengths) per la quantità di moto, il flusso di calore sensibile e il flusso di vapore, k la costante di Von Karman (0.41), Ψ h e Ψ m le funzioni di stabilità (sono usate le funzioni di Businger et al., 1971) θ, Q e Λ (lunghezza di Obukhov) sono i seguenti parametri scala:
8 8 S.Endrizzi, R.Rigon " * = H #c p u * Q * = E #u * = % u*2 T a kg" * (27) Il coefficiente di trasferimento C h si esprime nel modo seguente: C h = + " ln z % U # z 0U ' ( ) " z % " z - U m # * ' + ) 0U m, # * k 2 %. + " ' 0 ln z % " h z ' ( ) h % " - h ' + ) / # z 0h # * h, # z 0h * %. ' 0 / (28) Per la risoluzione numerica delle equazioni, partendo da un valore di Λ di primo tentativo, coerente con la stabilità (cioè maggiore di 0 se T s è minore di T a, minore di 0 in caso contrario) si risolvono le (26), (27) e (28) rispetto a u *, θ * e Q *. Si definisce a sua volta un nuovo valore di Λ e si itera fino a convergenza della lunghezza di Obukhov. La teoria di Monin-Obukhov applicata in questo modo presuppone che il limite della temperatura dell aria al tendere a 0 della distanza dalla superficie sia uguale alla temperatura del suolo T s, la skin temperature usata per i calcoli radiativi, e che questa sia lentamente variabile nel corso della giornata. Quest ultima ipotesi è piuttosto limitativa, in quanto T s manifesta una grande variabilità nel corso della giornata; tuttavia non sono stati effettuati test in numero sufficiente per verificare l accettabilità di tale ipotesi. L applicazione del metodo impone inoltre la spazializzazione della temperatura dell aria, dell umidità e della velocità del vento, noti solo per i punto dove sono localizzate le stazioni meteorologiche. 5 RISOLUZIONE NUMERICA L equazione (1) con le condizioni al contorno (11) e (12) è risolta alle differenze finite, discretizzando il dominio in layer di dimensioni crescenti con la profondità. Normalmente non si considerano più di 5 layer per la neve e 5 per il ghiaccio. Viene usato un metodo implicito che porta alla risoluzione di un sistema tridiagonale lineare, una volta linearizzati i termini di grado superiore al primo (Oleson et al., 2004). Per i dettagli si veda Endrizzi et al. (2006). Le equazioni (2), (3) e (14) sono risolte alle differenze finite con un metodo esplicito utilizzando la stessa discretizzazione usata per risolvere l equazione (1). 6 TEST DEL MODELLO CON APPLICAZIONE AL GHIACCIAIO DI ZONGO Si è fatta un applicazione preliminare di GEOtop cercando di riprodurre il bilancio idrologico del ghiacciaio di Zongo (Bolivia) nell anno idrologico 1 settembre agosto Questo ghiacciaio si estende per circa 2 km2 ad una quota compresa tra 4800 e 6000 m s.m.m. ed è localizzato a 16 gradi di latitudine sud, rientrando così tra i ghiacciai tropicali, per i quali non esistono stagioni di accumulo e di ablazione distinte come avviene per i ghiacciai alpini. Esiste invece una stagione secca e una umida che dipendono dall ENSO. Il ghiacciaio è ben monitorato dal 1991 all interno del progetto GREAT ICE del IRD (Institut de Recherche pour le Développement, Grenoble, Francia) ed è stato oggetto di altri studi idrologici (per esempio Francou et al., 1995). Oltre alla disponibilità dei dati meteorologici classici (temperatura, umidità relativa, velocità del vento) ogni 30 minuti, sono disponibili per il periodo considerato anche dati di radiazione ad onda corta e radiazione netta. Ciò ha permesso di inferire un dato di radiazione incidente ad onda lunga,
9 9 La modellazione del bilancio idrologico di un ghiacciaio senza ricorrere a formule sperimentali che potrebbero portare ad errori consistenti. Tutti i dati sono misurati in una stazione localizzata approssimativamente nel centro del ghiacciaio, per cui sono abbastanza rappresentativi. La temperatura è stata spazializzata stimando il gradiente termico dai dati di un altra stazione localizzata vicino alla fronte. Umidità e velocità del vento sono stati considerati uniformi nel ghiacciaio, anche se questo è un approssimazione abbastanza forte perché quasi mai il vento è uniforme. Per quanto riguarda il volume del ghiacciaio si sono fatte alcune ipotesi basate sulla conformazione topografica, ma la sua esatta riproduzione non è cruciale per l esperimento eseguito in quanto la variabile di interessa è la differenza di quota all inizio e alla fine dell anno idrologico, da cui si ricavano le perdite. La figura 1 riporta il bilancio annuale per fascie altimetriche effettuato con le misure (tratteggiato) e ricavato con il modello (continuo). Quest ultimo sottostima l accumulo nella parte elevata dove avviene anche accumulo da valanghe, come si nota dal massimo della curva sperimentale alla quota di circa 5600 m s.m.m.. Tuttavia nel complesso l accordo è abbastanza buono. La figura 2 mostra le componenti del bilancio idrologico secondo il modello: l alimentazione per precipitazioni (non è considerato l accumulo da valanghe), i volumi di ghiaccio e di neve sciolti e sublimati e il bilancio netto annuale per la neve e il ghiaccio. La sublimazione contribuisce a circa il 15% delle perdite della neve e a circa il 3% delle perdite del ghiaccio. Figura 1. Bilancio idrologico del ghiacciaio nell anno 1 settembre agosto 2001, ricavato dalle misure (tratteggiato) e dal modello (continuo). Il modello fornisce un accumulo netta di 213 mm, includendo sia la neve (accumulo di 678 mm) che il ghiaccio (perdita di 465 mm), quando dalle misure si è stimato un accumulo netto di 511 mm. La differenza è probabilmente in parte da attribuire ai volumi di accumulo per valanghe, in quanto riguardano la parte alta del ghiacciaio, in parte anche alle incertezze nei dati di temperatura (che sono stati estrapolati da dati misurati più in basso), di umidità e velocità del vento.
10 10 S.Endrizzi, R.Rigon Figura 2. Componenti del bilancio idrologico del ghiacciaio (compresa la copertura nevosa) secondo il modello. CONCLUSIONI Nonostante alcune incertezze nella descrizione di alcuni fenomeni fisici (radiazione ad onde lunghe, flussi turbolenti), il modello fornisce risultati abbastanza promettenti, in discreto accordo con i dati sperimentali. Ciò si giustifica probabilmente dal fatto che il peso maggiore nel bilancio di energia è esercitato dai termini radiativi, sia ad onde lunghe che ad onde corte, che nell applicazione sono stati inferiti direttamente da misure. Anche i flussi turbolenti hanno un ruolo nel bilancio, ma di peso minore. Ringraziamenti. Si ringraziano Joseph Tomasi, che ha svolto un periodo di studio all IRD in Bolivia e ha contribuito all applicazione del modello nella sua tesi di laurea, e l IRD per aver fornito i dati. BIBLIOGRAFIA M. Albert, Computer models for two-dimensional transient heat conduction, USA Cold Regions Research and Engineering Laboratory, (1983). E.A. Anderson, A point energy and mass balance model of a snow cover, Office of Hydrology National Weather Service, (1976). U.S. Army Corps of Engineers, Snow hydrology, Summary report of the snow investigations, U.S. Army Corps of Engineers, (1956). N. Arnold, I.C. Willis, M.J. Sharp, K.S. Richards, W.J. Lawson, A distributed surface energy balance model for a small valley glacier. I. Development and testing for Haut Glacier d Arolla, Valais, Switzerland, J. Glaciol. (1996), 42, pp G. Bertoldi, R. Rigon, GEOtop: A hydrological balance model. Technical description and program guide, Università di Trento E-Prints (2004). G. Blöschl, R. Kirnbauer, D. Gutknecht, Distribute snowmelt simulations in an Alpine catchment. 1. Model evaluation on the basis of snow cover patterns, Water Resour. Res. (1991), 27 (12), pp K.L. Bristow, G.S. Campbell, On the relationship between incoming solar radiation and the daily maximum and minimum temperature, Agricultural and Forset Meteorology (1984), 31, pp W. Brutsaert, On derivable formula for long-wave radiation from clear skies, Water Resour. Res. (1975), 11, pp H.M. Bolz, Die Abhaengigkeit der infraroten Gegenstrahlung von der Bewoelkung, Z. Meteorol (1949), 3, pp. 201-
11 11 La modellazione del bilancio idrologico di un ghiacciaio 203. J.A. Businger, J.C. Wyngaard, Y. Izumi, E.F. Bradley, Flux-profile relationship in the atmospheric surface layer, J. Atmos. Sci. (1971), 28, pp S.C. Colbeck, E.A. Anderson, The permeability of a melting snow cover, Water Resour. Res. (1982), 18 (4), pp R.E. Dickinson, A. Henderson-Sellers, P.J. Kennedy, Biosphere-Atmosphere transfer scheme (BATS), NCAR, (1993). S. Endrizzi, G. Bertoldi, R. Rigon, Technical description of GEOtop , in preparation (2006). B. Francou, P. Ribstein, R. Saracia, E. Tiriau, Monthly balance and water discharge of an inter-tropical glacier: Zongo Glacier, Cordillera Real, Bolivia, 16 S, Journal of Glaciology (1995), 41 (137), pp J.R. Garratt, The atmospheric boundary layer, Cambridge University Press, (1992). S.B. Idso, A set of equation for full spectrum and 8 to 14 µm and 10.5 to 12.5 µm thermal radiation from cloudless skies, Water Resour. Res. (1981), 17 (2), pp M. Iqbal, An introduction to solar radiation, Academic Press, (1983). A.S Monin, A.M. Obukhov, Basin turbulent mixing laws in the atmospheric boundary layer, Tr. Geofiz. Inst. Akad. Nauk. SSSR (1954), 24 (151), pp R. Pirazzini, M. Nardino, A. Orsini, F. Calzolari, T. Georgiadis, V. Levizzani, Parameterization of the downward longwave radiation from clear and cloudy skies at Ny Alesund (Svalbard), CNR-IBIMET, (2000). R. Rigon, G. Bertoldi, T. Over, GEOtop: A distributed hydrological model with coupled water and energy budgets, accettato per pubblicazione su Journal of Hydrometeorology, (2006). K.W. Oleson, Y. Dai, G. Bonan, M. Bosilovich, R. Dickinson, P. Dirmeyer, F. Hoffman, P. Houser, S. Levis, G. Niu, P. Thornton, M. Vertenstein, Z. Yang, X. Zeng, Technical description of the Community Land Model (CLM) NCAR, (2004). D.R. Satterlund, An improved equation for estimating longwave radiation from the atmosphere, Water Resour. Res. (1979), 15 (6), pp D.G. Tarboton, C.H. Luce, Utah energy balance snow accumulation and melt model (UEB). Computer model technical description and user s guide, Utah Water Research Laboratory and USDA Forest Service Intermountain Research Station, (1996). F. Zanotti, S. Endrizzi, G. Bertoldi, R. Rigon, The GEOtop snow module, Hydr. Proc. (2004), 18, pp
La propagazione delle onde luminose può essere studiata per mezzo delle equazioni di Maxwell. Tuttavia, nella maggior parte dei casi è possibile
 Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Elementi di ottica L ottica si occupa dello studio dei percorsi dei raggi luminosi e dei fenomeni legati alla propagazione della luce in generale. Lo studio dell ottica nella fisica moderna si basa sul
Termologia. Introduzione Scale Termometriche Espansione termica Capacità termica e calori specifici Cambiamenti di fase e calori latenti
 Termologia Introduzione Scale Termometriche Espansione termica Capacità termica e calori specifici Cambiamenti di fase e calori latenti Trasmissione del calore Legge di Wien Legge di Stefan-Boltzmann Gas
Termologia Introduzione Scale Termometriche Espansione termica Capacità termica e calori specifici Cambiamenti di fase e calori latenti Trasmissione del calore Legge di Wien Legge di Stefan-Boltzmann Gas
Transitori del primo ordine
 Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Il trasporto di materia. Principi di Ingegneria Chimica Ambientale
 Il trasporto di materia Principi di Ingegneria Chimica Ambientale 1 Considerazioni preliminari Il nostro studio sarà limitato a: miscele binarie miscele diluite (ossia in cui la frazione molare di uno
Il trasporto di materia Principi di Ingegneria Chimica Ambientale 1 Considerazioni preliminari Il nostro studio sarà limitato a: miscele binarie miscele diluite (ossia in cui la frazione molare di uno
IL PRE-PROCESSORE METEOROLOGICO CALMET-SMR. Una breve descrizione: caratteristiche, input, output, limiti
 IL PRE-PROCESSORE METEOROLOGICO CALMET-SMR Una breve descrizione: caratteristiche, input, output, limiti Meteorologia per la qualità dell aria la valutazione della qualità dell aria e in particolare l
IL PRE-PROCESSORE METEOROLOGICO CALMET-SMR Una breve descrizione: caratteristiche, input, output, limiti Meteorologia per la qualità dell aria la valutazione della qualità dell aria e in particolare l
STRUMENTO PER LA LOCALIZZAZIONE DI CAMPI EOLICI. Eolo-CISMA
 STRUMENTO PER LA LOCALIZZAZIONE DI CAMPI EOLICI Eolo-CISMA è un sistema di previsioni meteorologiche messo a punto da CISMA srl che ci permette di disporre di previsioni del potenziale eolico di un sito
STRUMENTO PER LA LOCALIZZAZIONE DI CAMPI EOLICI Eolo-CISMA è un sistema di previsioni meteorologiche messo a punto da CISMA srl che ci permette di disporre di previsioni del potenziale eolico di un sito
Metodologia di monitoraggio Impianti fotovoltaici
 Metodologia di monitoraggio Impianti fotovoltaici Per effettuare il monitoraggio degli impianti fotovoltaici è stato scelto il metodo di acquisizione dati proposto dal Dott. Ing. F. Spertino, Dott. Ing.
Metodologia di monitoraggio Impianti fotovoltaici Per effettuare il monitoraggio degli impianti fotovoltaici è stato scelto il metodo di acquisizione dati proposto dal Dott. Ing. F. Spertino, Dott. Ing.
Automazione Industriale (scheduling+mms) scheduling+mms. adacher@dia.uniroma3.it
 Automazione Industriale (scheduling+mms) scheduling+mms adacher@dia.uniroma3.it Introduzione Sistemi e Modelli Lo studio e l analisi di sistemi tramite una rappresentazione astratta o una sua formalizzazione
Automazione Industriale (scheduling+mms) scheduling+mms adacher@dia.uniroma3.it Introduzione Sistemi e Modelli Lo studio e l analisi di sistemi tramite una rappresentazione astratta o una sua formalizzazione
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
2. Leggi finanziarie di capitalizzazione
 2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
PRINCIPI DI TRASMISSIONE DEL CALORE
 PRINCIPI DI TRASMISSIONE DEL CALORE La trasmissione del calore può avvenire attraverso tre meccanismi: - Conduzione; - Convezione; - Irraggiamento; Nella conduzione la trasmissione del calore è riconducibile
PRINCIPI DI TRASMISSIONE DEL CALORE La trasmissione del calore può avvenire attraverso tre meccanismi: - Conduzione; - Convezione; - Irraggiamento; Nella conduzione la trasmissione del calore è riconducibile
Termodinamica: legge zero e temperatura
 Termodinamica: legge zero e temperatura Affrontiamo ora lo studio della termodinamica che prende in esame l analisi dell energia termica dei sistemi e di come tale energia possa essere scambiata, assorbita
Termodinamica: legge zero e temperatura Affrontiamo ora lo studio della termodinamica che prende in esame l analisi dell energia termica dei sistemi e di come tale energia possa essere scambiata, assorbita
VALORE DELLE MERCI SEQUESTRATE
 La contraffazione in cifre: NUOVA METODOLOGIA PER LA STIMA DEL VALORE DELLE MERCI SEQUESTRATE Roma, Giugno 2013 Giugno 2013-1 Il valore economico dei sequestri In questo Focus si approfondiscono alcune
La contraffazione in cifre: NUOVA METODOLOGIA PER LA STIMA DEL VALORE DELLE MERCI SEQUESTRATE Roma, Giugno 2013 Giugno 2013-1 Il valore economico dei sequestri In questo Focus si approfondiscono alcune
Complementi di Termologia. I parte
 Prof. Michele Giugliano (Dicembre 2) Complementi di Termologia. I parte N.. - Calorimetria. Il calore è una forma di energia, quindi la sua unità di misura, nel sistema SI, è il joule (J), tuttavia si
Prof. Michele Giugliano (Dicembre 2) Complementi di Termologia. I parte N.. - Calorimetria. Il calore è una forma di energia, quindi la sua unità di misura, nel sistema SI, è il joule (J), tuttavia si
CALORE. Compie lavoro. Il calore è energia. Temperatura e calore. L energia è la capacità di un corpo di compiere un lavoro
 Cos è il calore? Per rispondere si osservino le seguenti immagini Temperatura e calore Il calore del termosifone fa girare una girandola Il calore del termosifone fa scoppiare un palloncino Il calore del
Cos è il calore? Per rispondere si osservino le seguenti immagini Temperatura e calore Il calore del termosifone fa girare una girandola Il calore del termosifone fa scoppiare un palloncino Il calore del
Radiazione atmosferica
 Radiazione atmosferica Fondamenti di meteorologia e climatologia Trento, 28 Aprile 2015 Radiazione elettromagnetica La radiazione elettromagnetica puó essere vista come un insieme di onde che si propagano
Radiazione atmosferica Fondamenti di meteorologia e climatologia Trento, 28 Aprile 2015 Radiazione elettromagnetica La radiazione elettromagnetica puó essere vista come un insieme di onde che si propagano
Inserimento di distanze e di angoli nella carta di Gauss
 Inserimento di distanze e di angoli nella carta di Gauss Corso di laurea in Ingegneria per l Ambiente e il Territorio a.a. 2006-2007 Inserimento della distanza reale misurata nella carta di Gauss (passaggio
Inserimento di distanze e di angoli nella carta di Gauss Corso di laurea in Ingegneria per l Ambiente e il Territorio a.a. 2006-2007 Inserimento della distanza reale misurata nella carta di Gauss (passaggio
Simulazioni accoppiate 1D-3D per scenari d incendio
 Simulazioni accoppiate 1D-3D per scenari d incendio Applicazione a tunnel stradali e linee metropolitane Luca Iannantuoni Dipartimento di Energia - Politecnico di Milano 29 Ottobre 2009 Luca Iannantuoni
Simulazioni accoppiate 1D-3D per scenari d incendio Applicazione a tunnel stradali e linee metropolitane Luca Iannantuoni Dipartimento di Energia - Politecnico di Milano 29 Ottobre 2009 Luca Iannantuoni
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
La trasmittanza termica dell involucro edilizio - Introduzione. Le chiusure hanno il compito di: o Proteggere l interno dal clima esterno
 LA TRASMITTANZA TERMICA DI STRUTTURE OPACHE La trasmittanza termica dell involucro edilizio - Introduzione Le chiusure hanno il compito di: o Proteggere l interno dal clima esterno o Implementare le prestazioni
LA TRASMITTANZA TERMICA DI STRUTTURE OPACHE La trasmittanza termica dell involucro edilizio - Introduzione Le chiusure hanno il compito di: o Proteggere l interno dal clima esterno o Implementare le prestazioni
La nevicata eccezionale dell 11 marzo 2004
 La nevicata eccezionale dell 11 marzo 2004 Roberto Barbiero Introduzione Un intensa nevicata ha interessato nella giornata dell 11 marzo 2004 molte regioni del nord Italia. Dalle prime ore della notte
La nevicata eccezionale dell 11 marzo 2004 Roberto Barbiero Introduzione Un intensa nevicata ha interessato nella giornata dell 11 marzo 2004 molte regioni del nord Italia. Dalle prime ore della notte
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Soluzione. Calcolo la frequenza di Brunt-Väisälä: Γ Γ=0.0127. Calcolo il periodo: = 2 =494.7. Ricavo la velocità del vento: = =10000 494.7 =20.
 Problema 1 Uno flusso di aria secca scorre al di sopra di un terreno montano nel quale sono presenti due catene montuose parallele distanti 1 km nella direzione del vento. Il gradiente termico verticale
Problema 1 Uno flusso di aria secca scorre al di sopra di un terreno montano nel quale sono presenti due catene montuose parallele distanti 1 km nella direzione del vento. Il gradiente termico verticale
Pressione. Esempio. Definizione di pressione. Legge di Stevino. Pressione nei fluidi EQUILIBRIO E CONSERVAZIONE DELL ENERGIA NEI FLUIDI
 Pressione EQUILIBRIO E CONSERVAZIONE DELL ENERGIA NEI FLUIDI Cos è la pressione? La pressione è una grandezza che lega tra di loro l intensità della forza e l aerea della superficie su cui viene esercitata
Pressione EQUILIBRIO E CONSERVAZIONE DELL ENERGIA NEI FLUIDI Cos è la pressione? La pressione è una grandezza che lega tra di loro l intensità della forza e l aerea della superficie su cui viene esercitata
Prof. Ing. Andrea Giuseppe CAPODAGLIO. Prof. Ing. Arianna CALLEGARI
 RIDUZIONE IMPATTO AMBIENTALE CERTIFICATI DI VALIDAZIONE DIFFUSIONE DELLE EMISSIONI ODORIGENE DAL CANALE DI INGRESSO DELL IMPIANTO DI NOSEDO: STUDIO DIFFUSIONALE DI CONFRONTO TRA RISULTATI DEL SISTEMA ODOWATCH
RIDUZIONE IMPATTO AMBIENTALE CERTIFICATI DI VALIDAZIONE DIFFUSIONE DELLE EMISSIONI ODORIGENE DAL CANALE DI INGRESSO DELL IMPIANTO DI NOSEDO: STUDIO DIFFUSIONALE DI CONFRONTO TRA RISULTATI DEL SISTEMA ODOWATCH
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Corso di Componenti e Impianti Termotecnici LE RETI DI DISTRIBUZIONE PERDITE DI CARICO LOCALIZZATE
 LE RETI DI DISTRIBUZIONE PERDITE DI CARICO LOCALIZZATE 1 PERDITE DI CARICO LOCALIZZATE Sono le perdite di carico (o di pressione) che un fluido, in moto attraverso un condotto, subisce a causa delle resistenze
LE RETI DI DISTRIBUZIONE PERDITE DI CARICO LOCALIZZATE 1 PERDITE DI CARICO LOCALIZZATE Sono le perdite di carico (o di pressione) che un fluido, in moto attraverso un condotto, subisce a causa delle resistenze
ARTIFICIAL TORNADO. ovvero. la soluzione per generare energia elettrica in modo continuo e a costo nullo sfruttando un fenomeno della natura
 ARTIFICIAL TORNADO ovvero la soluzione per generare energia elettrica in modo continuo e a costo nullo sfruttando un fenomeno della natura 1 Il controllo del fenomeno tornado creato artificialmente, consente
ARTIFICIAL TORNADO ovvero la soluzione per generare energia elettrica in modo continuo e a costo nullo sfruttando un fenomeno della natura 1 Il controllo del fenomeno tornado creato artificialmente, consente
6.5. Risultati simulazioni sistema rifiuti e riscaldamento
 Capitolo 6 Risultati pag. 301 6.5. Risultati simulazioni sistema rifiuti e riscaldamento Come già detto nel paragrafo 5.8, i risultati riportati in questo paragrafo fanno riferimento alle concentrazione
Capitolo 6 Risultati pag. 301 6.5. Risultati simulazioni sistema rifiuti e riscaldamento Come già detto nel paragrafo 5.8, i risultati riportati in questo paragrafo fanno riferimento alle concentrazione
Modelli meteorologici
 Fondamenti di meteorologia e climatologia Cenni storici Vilhelm Bjerknes (1904): L evoluzione degli stati atmosferici é controllata da leggi fisiche, quindi condizioni necessarie e sufficienti per risolvere
Fondamenti di meteorologia e climatologia Cenni storici Vilhelm Bjerknes (1904): L evoluzione degli stati atmosferici é controllata da leggi fisiche, quindi condizioni necessarie e sufficienti per risolvere
Matematica 1 - Corso di Laurea in Ingegneria Meccanica
 Matematica 1 - Corso di Laurea in Ingegneria Meccanica Esercitazione su massimi e minimi vincolati 9 dicembre 005 Esercizio 1. Considerare l insieme C = {(x,y) R : (x + y ) = x } e dire se è una curva
Matematica 1 - Corso di Laurea in Ingegneria Meccanica Esercitazione su massimi e minimi vincolati 9 dicembre 005 Esercizio 1. Considerare l insieme C = {(x,y) R : (x + y ) = x } e dire se è una curva
Calcolo della trasmittanza di una parete omogenea
 Calcolo della trasmittanza di una parete omogenea Le resistenze liminari Rsi e Rse si calcolano, noti i coefficienti conduttivi (liminari) (o anche adduttanza) hi e he, dal loro reciproco. (tabella secondo
Calcolo della trasmittanza di una parete omogenea Le resistenze liminari Rsi e Rse si calcolano, noti i coefficienti conduttivi (liminari) (o anche adduttanza) hi e he, dal loro reciproco. (tabella secondo
Prof. Luigi Puccinelli IMPIANTI E SISTEMI AEROSPAZIALI SPAZIO
 Prof. Luigi Puccinelli IMPIANTI E SISTEMI AEROSPAZIALI SPAZIO CONTROLLO TERMICO Equilibrio termico 2 Al di fuori dell atmosfera la temperatura esterna non ha praticamente significato Scambi termici solo
Prof. Luigi Puccinelli IMPIANTI E SISTEMI AEROSPAZIALI SPAZIO CONTROLLO TERMICO Equilibrio termico 2 Al di fuori dell atmosfera la temperatura esterna non ha praticamente significato Scambi termici solo
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
Energia e Lavoro. In pratica, si determina la dipendenza dallo spazio invece che dal tempo
 Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Usando il pendolo reversibile di Kater
 Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
1. PREMESSA... 2 2. PARAMETRI IDROLOGICI DI PROGETTO... 3 3. VERIFICHE IDRAULICHE... 5
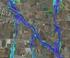 INDICE 1. PREMESSA... 2 2. PARAMETRI IDROLOGICI DI PROGETTO... 3 3. VERIFICHE IDRAULICHE... 5 PROGETTO ESECUTIVO 1/9 1. PREMESSA La presente relazione descrive gli aspetti idraulici connessi con lo smaltimento
INDICE 1. PREMESSA... 2 2. PARAMETRI IDROLOGICI DI PROGETTO... 3 3. VERIFICHE IDRAULICHE... 5 PROGETTO ESECUTIVO 1/9 1. PREMESSA La presente relazione descrive gli aspetti idraulici connessi con lo smaltimento
Pressione. www.easymaths.altervista.org. 01 - Pressione.
 Pressione 01 - Pressione La forza è una grandezza fisica caratterizzata dal fatto di essere in grado di modificare lo stato di moto di un corpo o di modificarne la struttura interna Supponiamo che una
Pressione 01 - Pressione La forza è una grandezza fisica caratterizzata dal fatto di essere in grado di modificare lo stato di moto di un corpo o di modificarne la struttura interna Supponiamo che una
Verranno descritti di seguito brevemente gli algoritmi di calcolo utilizzati per l interpretazione nei tre metodi inseriti all interno del programma.
 3. Teoria Verranno descritti di seguito brevemente gli algoritmi di calcolo utilizzati per l interpretazione nei tre metodi inseriti all interno del programma. 3.1 Metodo convenzionale (metodo del tempo
3. Teoria Verranno descritti di seguito brevemente gli algoritmi di calcolo utilizzati per l interpretazione nei tre metodi inseriti all interno del programma. 3.1 Metodo convenzionale (metodo del tempo
ALLEGATO 1 Analisi delle serie storiche pluviometriche delle stazioni di Torre del Lago e di Viareggio.
 ALLEGATO 1 Analisi delle serie storiche pluviometriche delle stazioni di Torre del Lago e di Viareggio. Per una migliore caratterizzazione del bacino idrologico dell area di studio, sono state acquisite
ALLEGATO 1 Analisi delle serie storiche pluviometriche delle stazioni di Torre del Lago e di Viareggio. Per una migliore caratterizzazione del bacino idrologico dell area di studio, sono state acquisite
LEGGE DI STEVIN (EQUAZIONE FONDAMENTALE DELLA STATICA DEI FLUIDI PESANTI INCOMPRIMIBILI) z + p / γ = costante
 IDRAULICA LEGGE DI STEVIN (EQUAZIONE FONDAMENTALE DELLA STATICA DEI FLUIDI PESANTI INCOMPRIMIBILI) z + p / γ = costante 2 LEGGE DI STEVIN Z = ALTEZZA GEODETICA ENERGIA POTENZIALE PER UNITA DI PESO p /
IDRAULICA LEGGE DI STEVIN (EQUAZIONE FONDAMENTALE DELLA STATICA DEI FLUIDI PESANTI INCOMPRIMIBILI) z + p / γ = costante 2 LEGGE DI STEVIN Z = ALTEZZA GEODETICA ENERGIA POTENZIALE PER UNITA DI PESO p /
CALCOLO ELETTRICO DELLE LINEE ELETTRICHE
 CALCOLO ELETTRICO DELLE LINEE ELETTRICHE Appunti a cura dell Ing. Stefano Usai Tutore del corso di ELETTROTECNICA per meccanici e chimici A. A. 2001/ 2002 e 2002/2003 Calcolo elettrico delle linee elettriche
CALCOLO ELETTRICO DELLE LINEE ELETTRICHE Appunti a cura dell Ing. Stefano Usai Tutore del corso di ELETTROTECNICA per meccanici e chimici A. A. 2001/ 2002 e 2002/2003 Calcolo elettrico delle linee elettriche
1. Introduzione. 2. Simulazioni elettromagnetiche per la misura del SAR
 Relazione Tecnica Analisi simulative e misure con termocamera relative al confronto tra l utilizzo di un telefono smartphone in assenza e in presenza di dispositivo distanziatore EWAD Annamaria Cucinotta
Relazione Tecnica Analisi simulative e misure con termocamera relative al confronto tra l utilizzo di un telefono smartphone in assenza e in presenza di dispositivo distanziatore EWAD Annamaria Cucinotta
6.1. Risultati simulazioni termovalorizzatore Osmannoro2000
 pag. 217 6. Risultati Di seguito si riportano i risultati relativi alle diverse simulazioni di diffusione atmosferica degli inquinanti effettuate. In particolare sono riportati i risultati sotto forma
pag. 217 6. Risultati Di seguito si riportano i risultati relativi alle diverse simulazioni di diffusione atmosferica degli inquinanti effettuate. In particolare sono riportati i risultati sotto forma
SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 2015
 SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 015 1. Indicando con i minuti di conversazione effettuati nel mese considerato, la spesa totale mensile in euro è espressa dalla funzione f()
SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 015 1. Indicando con i minuti di conversazione effettuati nel mese considerato, la spesa totale mensile in euro è espressa dalla funzione f()
COMPONENTI TERMODINAMICI APERTI
 CAPITOLO NONO COMPONENTI TERMODINAMICI APERTI Esempi applicativi Vengono di seguito esaminati alcuni componenti di macchine termiche che possono essere considerati come sistemi aperti A) Macchina termica
CAPITOLO NONO COMPONENTI TERMODINAMICI APERTI Esempi applicativi Vengono di seguito esaminati alcuni componenti di macchine termiche che possono essere considerati come sistemi aperti A) Macchina termica
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
RAPPORTO DI CALCOLO 110123-R-2522
 RAPPORTO DI CALCOLO Analisi FEM VALUTAZIONE NUMERICA DEL CONTRIBUTO ALLA RESISTENZA LIMINARE DI PARETE OPACA VERTICALE ED ORIZZONTALE DI VERNICE TERMORIFLETTENTE A BASSA EMISSIVITA (UNI EN ISO 6946:2008)
RAPPORTO DI CALCOLO Analisi FEM VALUTAZIONE NUMERICA DEL CONTRIBUTO ALLA RESISTENZA LIMINARE DI PARETE OPACA VERTICALE ED ORIZZONTALE DI VERNICE TERMORIFLETTENTE A BASSA EMISSIVITA (UNI EN ISO 6946:2008)
CAPACITÀ DI PROCESSO (PROCESS CAPABILITY)
 CICLO DI LEZIONI per Progetto e Gestione della Qualità Facoltà di Ingegneria CAPACITÀ DI PROCESSO (PROCESS CAPABILITY) Carlo Noè Università Carlo Cattaneo e-mail: cnoe@liuc.it 1 CAPACITÀ DI PROCESSO Il
CICLO DI LEZIONI per Progetto e Gestione della Qualità Facoltà di Ingegneria CAPACITÀ DI PROCESSO (PROCESS CAPABILITY) Carlo Noè Università Carlo Cattaneo e-mail: cnoe@liuc.it 1 CAPACITÀ DI PROCESSO Il
e-dva - eni-depth Velocity Analysis
 Lo scopo dell Analisi di Velocità di Migrazione (MVA) è quello di ottenere un modello della velocità nel sottosuolo che abbia dei tempi di riflessione compatibili con quelli osservati nei dati. Ciò significa
Lo scopo dell Analisi di Velocità di Migrazione (MVA) è quello di ottenere un modello della velocità nel sottosuolo che abbia dei tempi di riflessione compatibili con quelli osservati nei dati. Ciò significa
Guide d onda. Cerchiamo soluzioni caratterizzate da una propagazione lungo z
 GUIDE D ONDA Guide d onda Cerchiamo soluzioni caratterizzate da una propagazione lungo z Onde progressive e regressive Sostituendo nell equazione d onda ( essendo Valido anche per le onde regressive Equazione
GUIDE D ONDA Guide d onda Cerchiamo soluzioni caratterizzate da una propagazione lungo z Onde progressive e regressive Sostituendo nell equazione d onda ( essendo Valido anche per le onde regressive Equazione
Relazioni statistiche: regressione e correlazione
 Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
Esponenziali elogaritmi
 Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
Esponenziali elogaritmi Potenze ad esponente reale Ricordiamo che per un qualsiasi numero razionale m n prendere n>0) si pone a m n = n a m (in cui si può sempre a patto che a sia un numero reale positivo.
Idrostatica Correnti a pelo libero (o a superficie libera) Correnti in pressione. Foronomia
 Idrostatica Correnti a pelo libero (o a superficie libera) Correnti in pressione Foronomia In idrostatica era lecito trascurare l attrito interno o viscosità e i risultati ottenuti valevano sia per i liquidi
Idrostatica Correnti a pelo libero (o a superficie libera) Correnti in pressione Foronomia In idrostatica era lecito trascurare l attrito interno o viscosità e i risultati ottenuti valevano sia per i liquidi
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
IMPIANTI DI CLIMATIZZAZIONE: TERMODINAMICA DEI CICLI FRIGORIFERI AD ARIA ED ACQUA. Ing. Attilio Pianese (commissione Energia e Impianti)
 IMPIANTI DI CLIMATIZZAZIONE: TERMODINAMICA DEI CICLI FRIGORIFERI AD ARIA ED ACQUA Ing. Attilio Pianese (commissione Energia e Impianti) SCOPO DEGLI IMPIANTI DI CONDIZIONAMENTO Gli impianti di condizionamento
IMPIANTI DI CLIMATIZZAZIONE: TERMODINAMICA DEI CICLI FRIGORIFERI AD ARIA ED ACQUA Ing. Attilio Pianese (commissione Energia e Impianti) SCOPO DEGLI IMPIANTI DI CONDIZIONAMENTO Gli impianti di condizionamento
Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012
 Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012 Problema 1 Due carrelli A e B, di massa m A = 104 kg e m B = 128 kg, collegati da una molla di costante elastica k = 3100
Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012 Problema 1 Due carrelli A e B, di massa m A = 104 kg e m B = 128 kg, collegati da una molla di costante elastica k = 3100
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Corso di. Dott.ssa Donatella Cocca
 Corso di Statistica medica e applicata Dott.ssa Donatella Cocca 1 a Lezione Cos'è la statistica? Come in tutta la ricerca scientifica sperimentale, anche nelle scienze mediche e biologiche è indispensabile
Corso di Statistica medica e applicata Dott.ssa Donatella Cocca 1 a Lezione Cos'è la statistica? Come in tutta la ricerca scientifica sperimentale, anche nelle scienze mediche e biologiche è indispensabile
Stima della rifrattività radio superficiale in Sardegna
 Stima della rifrattività radio superficiale in Sardegna Ermanno Fionda (1), Fabrizio Pelliccia (2) (1) Fondazione Ugo Bordoni, Roma (I); ermanno@fub.it (2) Università di Perugia, Dip. di Ingegneria Elettronica
Stima della rifrattività radio superficiale in Sardegna Ermanno Fionda (1), Fabrizio Pelliccia (2) (1) Fondazione Ugo Bordoni, Roma (I); ermanno@fub.it (2) Università di Perugia, Dip. di Ingegneria Elettronica
Appendice III. Criteri per l utilizzo dei metodi di valutazione diversi dalle misurazioni in siti fissi
 Appendice III (articolo 5, comma 1 e art. 22 commi 5 e 7) Criteri per l utilizzo dei metodi di valutazione diversi dalle misurazioni in siti fissi 1. Tecniche di modellizzazione 1.1 Introduzione. In generale,
Appendice III (articolo 5, comma 1 e art. 22 commi 5 e 7) Criteri per l utilizzo dei metodi di valutazione diversi dalle misurazioni in siti fissi 1. Tecniche di modellizzazione 1.1 Introduzione. In generale,
Un po di statistica. Christian Ferrari. Laboratorio di Matematica
 Un po di statistica Christian Ferrari Laboratorio di Matematica 1 Introduzione La statistica è una parte della matematica applicata che si occupa della raccolta, dell analisi e dell interpretazione di
Un po di statistica Christian Ferrari Laboratorio di Matematica 1 Introduzione La statistica è una parte della matematica applicata che si occupa della raccolta, dell analisi e dell interpretazione di
RAPPORTO DI PROVA 110104 - R 0874
 RAPPORTO DI PROVA 110104 - R 0874 DETERMINAZIONE DEL CONTRIBUTO DI UNA VERNICE TERMICA A BASE CERAMICA SUI VALORI DI TRASMITTANZA DI PARETI INTONACATE, DELLA DITTA "ATRIA s.r.l." STABILIMENTO DI PARTANNA
RAPPORTO DI PROVA 110104 - R 0874 DETERMINAZIONE DEL CONTRIBUTO DI UNA VERNICE TERMICA A BASE CERAMICA SUI VALORI DI TRASMITTANZA DI PARETI INTONACATE, DELLA DITTA "ATRIA s.r.l." STABILIMENTO DI PARTANNA
Gas perfetti e sue variabili
 Gas perfetti e sue variabili Un gas è detto perfetto quando: 1. è lontano dal punto di condensazione, e quindi è molto rarefatto 2. su di esso non agiscono forze esterne 3. gli urti tra le molecole del
Gas perfetti e sue variabili Un gas è detto perfetto quando: 1. è lontano dal punto di condensazione, e quindi è molto rarefatto 2. su di esso non agiscono forze esterne 3. gli urti tra le molecole del
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Ottimizazione vincolata
 Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
Misure di base su una carta. Calcoli di distanze
 Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
LA TERMOGRAFIA SPETTRO ONDE ELETTROMAGNETICHE
 SPETTRO ONDE ELETTROMAGNETICHE La radiazione elettromagnetica è un mezzo di trasmissione dell energia sotto forma di onde aventi entrambe le componenti elettriche e magnetiche. La sequenza ordinata delle
SPETTRO ONDE ELETTROMAGNETICHE La radiazione elettromagnetica è un mezzo di trasmissione dell energia sotto forma di onde aventi entrambe le componenti elettriche e magnetiche. La sequenza ordinata delle
Come visto precedentemente l equazione integro differenziale rappresentativa dell equilibrio elettrico di un circuito RLC è la seguente: 1 = (1)
 Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Esercitazione N. 1 Misurazione di resistenza con metodo volt-amperometrico
 Esercitazione N. 1 Misurazione di resistenza con metodo volt-amperometrico 1.1 Lo schema di misurazione Le principali grandezze elettriche che caratterizzano un bipolo in corrente continua, quali per esempio
Esercitazione N. 1 Misurazione di resistenza con metodo volt-amperometrico 1.1 Lo schema di misurazione Le principali grandezze elettriche che caratterizzano un bipolo in corrente continua, quali per esempio
La scuola integra culture. Scheda3c
 Scheda3c Gli ELEMENTI DEL CLIMA che caratterizzano le condizioni meteorologiche di una regione sono: la temperatura, la pressione atmosferica, i venti, l umidità e le precipitazioni. La temperatura è data
Scheda3c Gli ELEMENTI DEL CLIMA che caratterizzano le condizioni meteorologiche di una regione sono: la temperatura, la pressione atmosferica, i venti, l umidità e le precipitazioni. La temperatura è data
V= R*I. LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro.
 LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro. PREMESSA: Anche intuitivamente dovrebbe a questo punto essere ormai chiaro
LEGGE DI OHM Dopo aver illustrato le principali grandezze elettriche è necessario analizzare i legami che vi sono tra di loro. PREMESSA: Anche intuitivamente dovrebbe a questo punto essere ormai chiaro
Idrogeologia. Velocità media v (m/s): nel moto permanente è inversamente proporzionale alla superficie della sezione. V = Q [m 3 /s] / A [m 2 ]
![Idrogeologia. Velocità media v (m/s): nel moto permanente è inversamente proporzionale alla superficie della sezione. V = Q [m 3 /s] / A [m 2 ] Idrogeologia. Velocità media v (m/s): nel moto permanente è inversamente proporzionale alla superficie della sezione. V = Q [m 3 /s] / A [m 2 ]](/thumbs/33/15874186.jpg) Idrogeologia Oltre alle proprietà indici del terreno che servono a classificarlo e che costituiscono le basi per utilizzare con facilità l esperienza raccolta nei vari problemi geotecnici, è necessario
Idrogeologia Oltre alle proprietà indici del terreno che servono a classificarlo e che costituiscono le basi per utilizzare con facilità l esperienza raccolta nei vari problemi geotecnici, è necessario
1. Distribuzioni campionarie
 Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Università degli Studi di Basilicata Facoltà di Economia Corso di Laurea in Economia Aziendale - a.a. 2012/2013 lezioni di statistica del 3 e 6 giugno 2013 - di Massimo Cristallo - 1. Distribuzioni campionarie
Forza. Forza. Esempi di forze. Caratteristiche della forza. Forze fondamentali CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA
 Forza CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA Cos è una forza? la forza è una grandezza che agisce su un corpo cambiando la sua velocità e provocando una deformazione sul corpo 2 Esempi
Forza CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA Cos è una forza? la forza è una grandezza che agisce su un corpo cambiando la sua velocità e provocando una deformazione sul corpo 2 Esempi
Note a cura di M. Martellini e M. Zeni
 Università dell Insubria Corso di laurea Scienze Ambientali FISICA GENERALE Lezione 6 Energia e Lavoro Note a cura di M. Martellini e M. Zeni Queste note sono state in parte preparate con immagini tratte
Università dell Insubria Corso di laurea Scienze Ambientali FISICA GENERALE Lezione 6 Energia e Lavoro Note a cura di M. Martellini e M. Zeni Queste note sono state in parte preparate con immagini tratte
TECNICA DELLE COSTRUZIONI: PROGETTO DI STRUTTURE LE FONDAZIONI
 LE FONDAZIONI Generalità sulle fondazioni Fondazioni dirette Plinti isolati Trave rovescia Esecutivi di strutture di fondazione Generalità Le opere di fondazione hanno il compito di trasferire le sollecitazioni
LE FONDAZIONI Generalità sulle fondazioni Fondazioni dirette Plinti isolati Trave rovescia Esecutivi di strutture di fondazione Generalità Le opere di fondazione hanno il compito di trasferire le sollecitazioni
Calcolatori Elettronici A a.a. 2008/2009
 Calcolatori Elettronici A a.a. 2008/2009 PRESTAZIONI DEL CALCOLATORE Massimiliano Giacomin Due dimensioni Tempo di risposta (o tempo di esecuzione): il tempo totale impiegato per eseguire un task (include
Calcolatori Elettronici A a.a. 2008/2009 PRESTAZIONI DEL CALCOLATORE Massimiliano Giacomin Due dimensioni Tempo di risposta (o tempo di esecuzione): il tempo totale impiegato per eseguire un task (include
Preparazione alle gare di II livello delle Olimpiadi della Fisica 2013
 Preparazione alle gare di II livello delle Olimpiadi della Fisica 01 Incontro su temi di termodinamica 14/1/01 Giuseppina Rinaudo - Dipartimento di Fisica dell Università di Torino Sommario dei quesiti
Preparazione alle gare di II livello delle Olimpiadi della Fisica 01 Incontro su temi di termodinamica 14/1/01 Giuseppina Rinaudo - Dipartimento di Fisica dell Università di Torino Sommario dei quesiti
Corso di Idrologia Applicata A.A. 2007-2008. Misure idrometriche. A. Cancelliere. Dipartimento di Ingegneria Civile e Ambientale Università di Catania
 Corso di Idrologia Applicata A.A. 2007-2008 Misure idrometriche A. Cancelliere Dipartimento di Ingegneria Civile e Ambientale Università di Catania PORTATA Volume liquido che attraversa una sezione normale
Corso di Idrologia Applicata A.A. 2007-2008 Misure idrometriche A. Cancelliere Dipartimento di Ingegneria Civile e Ambientale Università di Catania PORTATA Volume liquido che attraversa una sezione normale
Forze, leggi della dinamica, diagramma del. 28 febbraio 2009 (PIACENTINO - PREITE) Fisica per Scienze Motorie
 Forze, leggi della dinamica, diagramma del corpo libero 1 FORZE Grandezza fisica definibile come l' agente in grado di modificare lo stato di quiete o di moto di un corpo. Ci troviamo di fronte ad una
Forze, leggi della dinamica, diagramma del corpo libero 1 FORZE Grandezza fisica definibile come l' agente in grado di modificare lo stato di quiete o di moto di un corpo. Ci troviamo di fronte ad una
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
Modulo di Meccanica e Termodinamica
 Modulo di Meccanica e Termodinamica 1) Misure e unita di misura 2) Cinematica: + Moto Rettilineo + Moto Uniformemente Accelerato [+ Vettori e Calcolo Vettoriale] + Moti Relativi 3) Dinamica: + Forza e
Modulo di Meccanica e Termodinamica 1) Misure e unita di misura 2) Cinematica: + Moto Rettilineo + Moto Uniformemente Accelerato [+ Vettori e Calcolo Vettoriale] + Moti Relativi 3) Dinamica: + Forza e
Le funzioni continue. A. Pisani Liceo Classico Dante Alighieri A.S. 2002-03. A. Pisani, appunti di Matematica 1
 Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
1. PREMESSA 2. CALCOLI E VERIFICHE FOGNATURA ACQUE REFLUE
 1. PREMESSA La presente verifica idraulica fa riferimento alla precedente verifica allegata al progetto preliminare approvato con Deliberazione del Giunta Municipale n. 113 del 19.09.2011, con la quale
1. PREMESSA La presente verifica idraulica fa riferimento alla precedente verifica allegata al progetto preliminare approvato con Deliberazione del Giunta Municipale n. 113 del 19.09.2011, con la quale
La pista del mio studio Riflettiamo sulla pista. Guida per l insegnante
 Riflettiamo sulla pista Guida per l insegnante Obiettivi educativi generali Compito di specificazione - possiede capacità progettuale - è in grado di organizzare il proprio tempo e di costruire piani per
Riflettiamo sulla pista Guida per l insegnante Obiettivi educativi generali Compito di specificazione - possiede capacità progettuale - è in grado di organizzare il proprio tempo e di costruire piani per
DINAMICA DEL PUNTO MATERIALE E CONCETTO DI FORZA. Dinamica: studio delle forze che causano il moto dei corpi
 DINAMICA DEL PUNTO MATERIALE E CONCETTO DI FORZA Dinamica: studio delle forze che causano il moto dei corpi 1 Forza Si definisce forza una qualunque causa esterna che produce una variazione dello stato
DINAMICA DEL PUNTO MATERIALE E CONCETTO DI FORZA Dinamica: studio delle forze che causano il moto dei corpi 1 Forza Si definisce forza una qualunque causa esterna che produce una variazione dello stato
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
LA LEGGE DI GRAVITAZIONE UNIVERSALE
 GRAVIMETRIA LA LEGGE DI GRAVITAZIONE UNIVERSALE r La legge di gravitazione universale, formulata da Isaac Newton nel 1666 e pubblicata nel 1684, afferma che l'attrazione gravitazionale tra due corpi è
GRAVIMETRIA LA LEGGE DI GRAVITAZIONE UNIVERSALE r La legge di gravitazione universale, formulata da Isaac Newton nel 1666 e pubblicata nel 1684, afferma che l'attrazione gravitazionale tra due corpi è
I.T.C.G.T T. Acerbo - Pescara LABORATORIO DI FISICA A. S. 2009/10
 I.T.C.G.T T. Acerbo - Pescara LABORATORIO DI FISICA A. S. 2009/10 Cognome: D Ovidio Nome: Stefania Classe: 2 B Geometri Data: 04/12/2009 Gruppo: F. Illiceto; V. Ivanochko; M.C. Scopino; M.Terenzi N. pagine:
I.T.C.G.T T. Acerbo - Pescara LABORATORIO DI FISICA A. S. 2009/10 Cognome: D Ovidio Nome: Stefania Classe: 2 B Geometri Data: 04/12/2009 Gruppo: F. Illiceto; V. Ivanochko; M.C. Scopino; M.Terenzi N. pagine:
CLUB ALPINO ITALIANO COMMISSIONE CENTRALE MATERIALI E TECNICHE
 CLUB ALPINO ITALIANO COMMISSIONE CENTRALE MATERIALI E TECNICHE COMMISSIONE CENTRALE MATERIALI E TECNICHE Arco di Trento 31 ottobre 2004 a cura di Vittorio Bedogni ( CCMT - INA - INSA ) CONTENUTO : Introduzione
CLUB ALPINO ITALIANO COMMISSIONE CENTRALE MATERIALI E TECNICHE COMMISSIONE CENTRALE MATERIALI E TECNICHE Arco di Trento 31 ottobre 2004 a cura di Vittorio Bedogni ( CCMT - INA - INSA ) CONTENUTO : Introduzione
Luigi Piroddi piroddi@elet.polimi.it
 Automazione industriale dispense del corso 10. Reti di Petri: analisi strutturale Luigi Piroddi piroddi@elet.polimi.it Analisi strutturale Un alternativa all analisi esaustiva basata sul grafo di raggiungibilità,
Automazione industriale dispense del corso 10. Reti di Petri: analisi strutturale Luigi Piroddi piroddi@elet.polimi.it Analisi strutturale Un alternativa all analisi esaustiva basata sul grafo di raggiungibilità,
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Evapotraspirazione potenziale ETP
 Evapotraspirazione potenziale ETP Modello - calcolo dell evapotraspirazione Pagina 1 Calcolo dell'evapotraspirazione potenziale Il concetto di evapotraspirazione potenziale (ETP) espresso intorno al 1950
Evapotraspirazione potenziale ETP Modello - calcolo dell evapotraspirazione Pagina 1 Calcolo dell'evapotraspirazione potenziale Il concetto di evapotraspirazione potenziale (ETP) espresso intorno al 1950
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
CURVE DI LIVELLO. Per avere informazioni sull andamento di una funzione f : D IR n IR può essere utile considerare i suoi insiemi di livello.
 CURVE DI LIVELLO Per avere informazioni sull andamento di una funzione f : D IR n IR può essere utile considerare i suoi insiemi di livello. Definizione. Si chiama insieme di livello k della funzione f
CURVE DI LIVELLO Per avere informazioni sull andamento di una funzione f : D IR n IR può essere utile considerare i suoi insiemi di livello. Definizione. Si chiama insieme di livello k della funzione f
ENERGIA. Energia e Lavoro Potenza Energia cinetica Energia potenziale Principio di conservazione dell energia meccanica
 1 ENERGIA Energia e Lavoro Potenza Energia cinetica Energia potenziale Principio di conservazione dell energia meccanica 2 Energia L energia è ciò che ci permette all uomo di compiere uno sforzo o meglio
1 ENERGIA Energia e Lavoro Potenza Energia cinetica Energia potenziale Principio di conservazione dell energia meccanica 2 Energia L energia è ciò che ci permette all uomo di compiere uno sforzo o meglio
