Equazioni Differenziali alle Derivate Parziali del primo ordine semilineari
|
|
|
- Ada Sasso
- 7 anni fa
- Visualizzazioni
Transcript
1 Equazioni Differenziali alle Derivate Parziali el primo orine semilineari Analisi Matematica III C. Lattanzio B. Rubino 1 Teoria Per equazione ifferenziale alle erivate parziali el primo orine semilineare nelle variabili inipenenti (x, t) R 2 si intene un equazione ella forma: a(x, t)u t + b(x, t)u x = f(x, t, u), (1.1) ove la funzione incognita u = u(x, t) è una funzione a valori reali. Le funzioni a, b, f sono funzioni regolari, a esempio a, b C 1 (Ω) e f C 1 (Ω R), ove Ω R 2 è un aperto el piano (x, t). Una funzione u è soluzione ell equazione (1.1) in un aperto U Ω se verifica tale equazione puntualmente in U. Definiamo ora il problema i Cauchy per l equazione (1.1). Sia C una curva regolare contenuta in Ω i equazioni parametriche x = x 0 (σ), t = t 0 (σ). Definiamo problema i Cauchy il seguente sistema: a(x, t)u t + b(x, t)u x = f(x, t, u) (1.2) u(x 0 (σ), t 0 (σ)) = u 0 (σ) e u è soluzione i (1.2) in un aperto U Ω se verifica l equazione ifferenziale puntualmente in U e il ato iniziale in ogni punto ella curva C contenuto in U. Prima i iscutere l esistenza e l unicità elle soluzioni i (1.2), veiamo come eterminare tale soluzione in un esempio concreto. Esempio 1.1 Consieriamo l equazione ifferenziale alle erivate parziali u t + vu x = 0, (1.3) ove v > 0 è una costante, a cui aggiungiamo una conizione iniziale u(x, 0) = u 0 (x), (1.4) con u 0 funzione regolare. Associamo all equazione ifferenziale (1.3) il seguente sistema i equazioni ifferenziali orinarie: ẋ(s) = v (1.5) ṫ(s) = 1, 1
2 t x 0 x Figura 1: caratteristiche per l equazione (1.3) ove con inichiamo la erivata rispetto al parametro s. Le curve soluzioni i (1.5) sono ette curve caratteristiche per (1.3). Tale soluzione è fornita chiaramente a: x(s) = vs + x 0 + t 0, che, sceglieno per comoità (rispetto alla curva t = 0} in cui è assegnato il ato iniziale (1.4)) t 0 = 0, si può riscrivere, eliminano il parametro s, come x(t) = vt + x 0. (1.6) La (1.6) rappresenta pertanto la curva caratteristica che interseca in x 0 la curva t = 0} el ato iniziale. Tale curva risulta essere nel piano (x, t) una retta i penenza 1 o, equivalentemente, i velocità v (veere Figura 1). Sia v ora φ(t) = u(x(t), t) la soluzione i (1.3) calcolata lungo le caratteristiche (1.6). Dalla efinizie i caratteristica (sistema (1.5)), si ha: φ(t) = ẋ(t)u x (x(t), t) + u t (x(t), t) = vu x (x(t), t) + u t (x(t), t) = 0, vale a ire, la soluzione i (1.3) è costante lungo le caratteristiche (1.6). Quini, si può risolvere l equazione ifferenziale orinaria per φ e si ha: φ(t) = φ(0), 2
3 vale a ire u(vt + x 0, t) = u(x(t), t) = u(x(0), 0) = u 0 (x 0 ), utilizzano la (1.6) e la conizione iniziale (1.4). Per eterminare ora il valore ella soluzione u in un punto generico (x, t) el piano, basta eterminare il punto x 0 i intersezione tra la caratteristica passante per (x, t) e l asse t = 0}, cioè basta invertire la relazione x = vt + x 0 otteneno x 0 = x vt. In efinitiva, la soluzione i (1.3) (1.4) è ata a u(x, t) = u 0 (x vt), come è a questo punto facile convincersi anche per verifica iretta. La soluzione al tempo t è pertanto ottenuta traslano il grafico ella conizione iniziale u 0 ella quantità vt: questa proprietà giustifica la efinizione i velocità ata alla quantità v. In altre parole, le caratteristiche trasportano le informazioni al ato iniziale e le fanno viaggiare con velocità v (veere Figura 2). Nell Esempio 1.1 abbiamo visto come è utile introurre una opportuna famiglia i curve (le curve caratteristiche), che nel caso specifico risultano essere rette, lungo le quali l equazione ifferenziale ha una formulazione più semplice, formulazione che permette i risolvere esplicitamente il problema i Cauchy (1.3) (1.4) (nel caso esaminato, la soluzione risultava costante lungo le caratteristiche!!). In realtà, l utilizzo elle curve caratteristiche permette, anche nel caso generale (1.2), i arrivare a un teorema i esistenza e unicità elle soluzioni per tale problema i Cauchy. Definiamo allora curve caratteristiche per l equazione a(x, t)u t + b(x, t)u x = f(x, t, u) (1.7) le soluzioni el seguente sistema i equazioni ifferenziali orinarie: ẋ(s) = b(x(s), t(s)) ṫ(s) = a(x(s), t(s)). (1.8) Se calcoliamo la soluzione u i (1.7) lungo le soluzioni i (1.8), ossia consieriamo la funzione φ(s) = u(x(s), t(s)), si ha: φ(s) = ẋ(s)u x (x(s), t(s)) + ṫ(s)u t (x(s), t(s)) = a(x(s), t(s))u t (x(s), t(s)) + b(x(s), t(s))u x (x(s), t(s)) = f(x(s), t(s), u(x(s), t(s))) = ψ(s, φ(s)). 3
4 t x grafico ella soluzione per t=0 t v v x grafico ella soluzione per t=1 Figura 2: la soluzione i (1.3) (1.4) viaggia con velocità v Pertanto, lungo le caratteristiche, l equazione alle erivate parziali (1.7) si riscrive come un equazione ifferenziale orinaria: le caratteristiche sono efinite proprio in moo che il termine a sinistra in (1.7) iventi una erivata totale rispetto al parametro che escrive le caratteristiche stesse. Abbiamo quini riotto lo stuio un equazione alle erivate parziali allo stuio i equazioni ifferenziali orinarie e, meiante questo metoo, siamo in grao i eterminare la soluzione ell equazione (1.7), con ato iniziale u(x 0 (σ), t 0 (σ)) = u 0 (σ) (1.9) assegnato lungo una curva C (i equazioni parametriche (x 0 (σ), t 0 (σ))) regolare contenuta nel ominio Ω R 2 i efinizione el problema i Cauchy preso in consierazione. Come già osservato nell Esempio 1.1, per far sì che questo metoo sia efficace, le caratteristiche evono poter pescare informazioni alla curva el ato iniziale C e trasportarle in un aperto U Ω, nel quale otterremo la soluzione cercata. Pertanto, nel teorema i esistenza e unicità locali per (1.7) (1.9), ci aspettiamo una conizione i compatibi- 4
5 lità tra le caratteristiche ell equazione (1.7) e la scelta ella curva el ato iniziale C. Più precisamente, è naturale richieere che, in ogni punto ella curva C nel quale vogliamo costruire la soluzione locale el problema i Cauchy, la curva caratteristica e la curva C siano trasversali, cioè non abbiano la stessa tangente. Questo risultato è stabilito al teorema seguente. Teorema 1.2 Sia ato il problema i Cauchy (1.7) (1.9) per (x, t) Ω R 2, ove la curva iniziale C Ω è regolare e le funzioni a, b, f sono funzioni regolari elle loro variabili e tali che a(x, t) 2 +b(x, t) 2 0 per ogni (x, t) Ω. Sia (x 0, t 0 ) = (x 0 (σ 0 ), t 0 (σ 0 )) C un punto ella curva iniziale tale che C non sia caratteristica in (x 0, t 0 ) rispetto all equazione, vale a ire: a(x 0, t 0 ) x 0 σ b(x 0, t 0 ) t 0 σ=σ0 σ 0. (1.10) σ=σ0 Allora esiste un aperto U Ω, con (x 0, t 0 ) U, e un unica soluzione u = u(x, t) i (1.7) (1.9), che verifica (1.7) in ogni (x, t) U e (1.9) in ogni punto i C contenuto in U. Osservazione 1.3 Come abbiamo anticipato, per poter avere un risultato i esistenza e unicità per (1.7) (1.9), è necessario avere una conizione i trasversalità tra le caratteristiche stesse e la curva el ato iniziale C. Tale trasversalità è garantita alla conizione (1.10) el Teorema 1.2. Infatti, il vettore τ = (b(x 0, t 0 ), a(x 0, t 0 )) rappresenta il vettore tangente alla caratteristica nel punto (x 0, t 0 ) (si vea la efinizione ( elle caratteristiche tramite il sistema (1.8)), mentre il vettore ν 0 = t 0 σ, x ) 0 σ=σ0 σ è il vettore σ=σ0 normale alla curva iniziale C nel punto (x 0, t 0 ), esseno ( ortogonale al vetto- x 0 re tangente a tale curva, vale a ire il vettore T 0 = σ, t ) 0 σ=σ0 σ. σ=σ0 Pertanto, la conizione (1.10) in termini i tali vettori iventa τ, ν 0 = 0. In altre parole, il vettore tangente alla caratteristica non è ortogonale alla normale alla curva el ato iniziale C in (x 0, t 0 ), cioè la caratteristica e la curva el ato iniziale C non hanno la stessa tangente in (x 0, t 0 ) (veere la Figura 3). Esempio 1.4 Una classe i esempi fisicamente importanti è fornito al seguente problema i Cauchy: u t + b(x, t)u x = f(x, t, u) (1.11) u(x, 0) = u 0 (x), cioè problemi i Cauchy con ato assegnato lungo la curva t = 0} per equazioni ella forma (1.7) con a(x, t) = 1. In questo caso, l asse elle x 5
6 ν 0 τ T 0 curva iniziale C caratteristica Figura 3: interpretazione geometrica ella conizione (1.10) non è caratteristico rispetto all equazione consierata in ogni punto (x 0, 0). Infatti, il vettore normale a tale curva è ato, in ogni punto, a (0, 1) e pertanto la conizione (1.10) iventa: b(x 0, 0) 0 = 1 0. Osserviamo che lo stesso risultato si ottiene per equazioni con coefficiente a(x, t) 0 (e non necessariamente uguale a 1), in quanto in questo caso (1.10) iventa: a(x 0, 0) 1 + b(x 0, 0) 0 = a(x 0, 0) 0, ma, altra parte, tali equazioni si possono riconurre alla forma (1.11) semplicemente iviento per a(x, t). 2 Esercizi Esercizio 2.1 Determinare la soluzione el problema i Cauchy u t + tu x = u u(x, 0) = x 2. Risoluzione. Si tratta i una equazione alle erivate parziali in ue variabili lineare el prim orine con ato i Cauchy. Ne cerchiamo la soluzione u = u(x, t) con il metoo elle curve caratteristiche. 6
7 Le curve i tale equazione, una famiglia a un parametro, sono efinite al sistema inamico in (x, t) = (x(s), t(s)) ṫ = 1 ẋ = t, ẋ(t) = t, la cui soluzione, in forma cartesiana, è ata a x(t) = t2 2 + x 0, x 0 R. (2.1) Si osservi (Figura 4) che tutte le caratteristiche intersecano t = 0 e quini x 0 t Figura 4: Curve caratteristiche ell equazione alle erivate parziali ell Esercizio 2.1 pescano il ato per propagarlo su tutto il piano. Si ha poi u(x(t), t) = u(x(t), t), t a cui ( ) t 2 u 2 + x 0, t = u(x 0, 0)e t = x 2 0e t e visto che alla (2.1) si ha x 0 = x 0 (x, t) = x t2 2, si ottiene ( ) 2 u(x, t) = x t2 e t. 2 7
8 Lo stuente iligente può verificare che tale u = u(x, t) risolve effettivamente il problema i Cauchy proposto. Esercizio 2.2 Determinare la soluzione el problema i Cauchy u t + tu x = x u(x, 0) = x 2. Risoluzione. Si tratta i una equazione alle erivate parziali in ue variabili lineare el prim orine con ato i Cauchy. Ne cerchiamo la soluzione u = u(x, t) con il metoo elle curve caratteristiche. Le curve i tale equazione, una famiglia a un parametro, sono efinite al sistema inamico in (x, t) = (x(s), t(s)) ṫ = 1 ẋ = t, ẋ(t) = t, la cui soluzione, in forma cartesiana, è ata a x(t) = t2 2 + x 0, c R. (2.2) Si osservi (Figura 5) che tutte le caratteristiche intersecano t = 0 e quini pescano il ato per propagarlo su tutto il piano. Si ha poi t u(x(t), t) = x(t) = t2 2 + x 0, a cui ( ) t 2 u 2 + x 0, t = t3 6 + ct + u(x 0, 0) = t3 6 + ct + x2 0 e visto che alla (2.2) si ha x 0 = x 0 (x, t) = x t2 2, si ottiene ( ) ( ) 2 u(x, t) = t3 6 + x t2 t + x t2, 2 2 u(x, t) = x 2 + xt xt 2 t3 3 + t4 4. Lo stuente iligente può verificare che tale u = u(x, t) risolve effettivamente il problema i Cauchy proposto. 8
9 x 0 t Figura 5: Curve caratteristiche ell equazione alle erivate parziali ell Esercizio 2.2 Esercizio 2.3 Determinare la soluzione el problema i Cauchy u t + 2xtu x = u u(x, 0) = x. Risoluzione. Si tratta i una equazione alle erivate parziali in ue variabili lineare el prim orine con ato i Cauchy. Ne cerchiamo la soluzione u = u(x, t) con il metoo elle curve caratteristiche. Le curve caratteristiche i tale equazione, una famiglia a un parametro, sono efinite al sistema inamico in (x, t) = (x(s), t(s)) ṫ = 1 ẋ = 2xt, ẋ(t) = 2xt, la cui soluzione, in forma cartesiana, è ata a x(t) = x 0 e t2, x 0 R. (2.3) Si osservi (Figura 6) che tutte le caratteristiche intersecano t = 0 e quini pescano il ato per propagarlo su tutto il piano. Si ha poi u(x(t), t) = u(x(t), t), t 9
10 x 0 t Figura 6: Curve caratteristiche ell equazione alle erivate parziali ell Esercizio 2.3 a cui u ( ) x 0 e t2, t = u(x 0, 0)e t = x 0 e t e visto che alla (2.3) si ha x 0 = x 0 (x, t) = xe t2, si ottiene ( u(x, t) = xe t2) e t = xe t t2. Lo stuente iligente può verificare che tale u = u(x, t) risolve effettivamente il problema i Cauchy proposto. Esercizio 2.4 Determinare la soluzione el problema i Cauchy u t xu x = u + 1 u(x, 0) = x. Risoluzione. Si tratta i una equazione alle erivate parziali in ue variabili lineare el prim orine con ato i Cauchy. Ne cerchiamo la soluzione u = u(x, t) con il metoo elle curve caratteristiche. Le curve caratteristiche i tale equazione, una famiglia a un parametro, sono efinite al sistema inamico in (x, t) = (x(s), t(s)) ṫ = 1 ẋ = x, 10
11 ẋ(t) = x, la cui soluzione, in forma cartesiana, è ata a x(t) = x 0 e t, x 0 R. (2.4) Si osservi (Figura 7) che tutte le caratteristiche intersecano t = 0 e quini x 0 t Figura 7: Curve caratteristiche ell equazione alle erivate parziali ell Esercizio 2.4 pescano il ato per propagarlo su tutto il piano. Si ha poi a cui u(x(t), t) = u(x(t), t) + 1, t u ( x 0 e t, t ) = (u(x 0, 0) + 1)e t 1 = (x 0 + 1)e t 1 e visto che alla (2.4) si ha x 0 = x 0 (x, t) = xe t, si ottiene u(x, t) = ( xe t + 1 ) e t 1 = xe 2t + e t 1. Lo stuente iligente può verificare che tale u = u(x, t) risolve effettivamente il problema i Cauchy proposto. 11
12 Esercizio 2.5 Determinare la soluzione el problema i Cauchy u t + xu x = 0 1 per 0 x 1 u(x, 0) = 0 altrimenti. Risoluzione. Si tratta i una equazione alle erivate parziali in ue variabili lineare el prim orine con ato i Cauchy iscontinuo. Ne cerchiamo la soluzione u = u(x, t) con il metoo elle curve caratteristiche. Le curve caratteristiche i tale equazione, una famiglia a un parametro, sono efinite al sistema inamico in (x, t) = (x(s), t(s)) ṫ = 1 ẋ = x, ẋ(t) = x, la cui soluzione, in forma cartesiana, è ata a x(t) = x 0 e t, x 0 R. (2.5) Si osservi (Figura 8) che tutte le caratteristiche intersecano t = 0 e quini x 0 t Figura 8: Curve caratteristiche ell equazione alle erivate parziali ell Esercizio
13 pescano il ato per propagarlo su tutto il piano. Si ha poi a cui u(x(t), t) = 0, t u ( x 0 e t, t ) = u(x 0, 0) = 1 per 0 x altrimenti. e visto che alla (2.5) si ha x 0 = x 0 (x, t) = xe t, si ottiene 1 per 0 xe t 1 1 per 0 x e t u(x, t) = = 0 altrimenti 0 altrimenti. Lo stuente iligente può verificare che tale u = u(x, t) risolve effettivamente il problema i Cauchy proposto. È qui chiaro il meccanismo elle curve caratteristiche: il ato ell intervallo 0 x 1 viene propagato in tutti i punti in cui arrivano le curve caratteristiche che pescano in tale intervallo: poiché l equazione è omogenea e il ato costante, tale valore ella costante si propaga inalterata in tutta la regione i ipenenza. Esercizio 2.6 Determinare le curve caratteristiche per l equazione u t + xt 2 u x = xt 2 u e isegnarle sul piano (x, t). Successivamente, eterminare la soluzione el problema i Cauchy u t + xt 2 u x = xt 2 u u(x, 0) = x 3. Risoluzione. Si tratta i una equazione alle erivate parziali in ue variabili lineare el prim orine con ato i Cauchy. Le curve caratteristiche i tale equazione, una famiglia a un parametro, sono efinite al sistema inamico in (x, t) = (x(s), t(s)) ṫ = 1 ẋ = xt 2, la cui soluzione, in forma cartesiana, è ata a x(t) = x 0 e t3 /3, x 0 R. (2.6) Si osservi (Figura 9) che tutte le caratteristiche intersecano t = 0 e quini 13
14 x 0 t Figura 9: Curve caratteristiche ell equazione alle erivate parziali ell Esercizio 2.6 pescano il ato per propagarlo su tutto il piano. Si ha poi t u(x(t), t) = x(t)t2 u(x(t), t) = x 0 t 2 e t3 /3 u(x(t), t), a cui proceeno per separazioni i variabili, ( ) u x 0 e t3 /3, t = u(x 0, 0)e x 0 e x 0e t3 /3 = x 3 0e x 0 e x 0e t3 /3 e visto che alla (2.6) si ha x 0 = x 0 (x, t) = xe t3 /3, si ottiene u(x, t) = ( xe t3 /3 ) 3 e xe t3 /3 e x u(x, t) = x 3 e x 1 e t3 /3 t 3. Lo stuente iligente può verificare che tale u = u(x, t) risolve effettivamente il problema i Cauchy proposto. Esercizio 2.7 Utilizzano il metoo elle curve caratteristiche, eterminare la soluzione el problema i Cauchy u t + (2x 2t 3 )u x = x u(x, 0) = 2x. 14
15 Risoluzione. Si tratta i una equazione alle erivate parziali in ue variabili lineare el prim orine con ato i Cauchy. Ne cerchiamo la soluzione u = u(x, t) con il metoo elle curve caratteristiche. Le curve caratteristiche i tale equazione, una famiglia a un parametro, sono efinite al sistema inamico in (x, t) = (x(s), t(s)) ṫ = 1 ẋ = 2x 2t 3, ẋ(t) = 2x 2t 3. Si tratta i un equazione ifferenziale lineare el prim orine. La soluzione ell omogenea associata, ẋ(t) = 2x, è ata a x(t) = ce 2t, c R. (2.7) Per risolvere l equazione ifferenziale non omogenea proceiamo con il metoo ella variazione elle costanti: cerchiamo una soluzione el tipo x(t) = c(t)e 2t, a cui sostitueno nell equazione si ha ċe 2t = 2t 3. Perciò c(t) = 2t 3 e 2t t e proceeno ripetutamente con integrazione per parti, si ha c(t) =t 3 e 2t 3t 2 e 2t t = t 3 e 2t t2 e 2t 3te 2t t = (t t ) 3 t e 2t 2 e 2t t = ( t t t ) e 2t + c. (2.8) Sostitueno la (2.8) in (2.7), la soluzione ell equazione ifferenziale, perciò, in forma cartesiana, è ata a ( x(t) = t t t + 3 ) ( + x 0 3 ) e 2t, x 0 R. (2.9) 4 4 Si osservi (Figura 10) che tutte le caratteristiche intersecano t = 0 e quini pescano il ato per propagarlo su tutto il piano. Si ha poi ( u(x(t), t) = x(t) = t t 2 t t + 3 ) ( + x 0 3 ) e 2t,
16 x 0 t Figura 10: Curve caratteristiche ell equazione alle erivate parziali ell Esercizio 2.7 a cui integrano si ha u (t t t + 34 ( + x 0 3 ) ) e 2t, t 4 = t4 4 + t t t + x e 2t + u(x 0, 0) x = t4 4 + t t t + x e 2t + 2x 0 x e visto che alla (2.9) si ha ( x 0 = x 0 (x, t) = x t t2 3 2 t 3 ) e 2t , si ottiene u(x, t) = 3 ( x t t2 3 2 t 3 ) e 2t t4 4 + t t t + 1 ( x t t2 3 2 t 3 ), 4 u(x, t) = 3 2 ( x t t2 3 2 t 3 ) e 2t x t4. Lo stuente iligente può verificare che tale u = u(x, t) risolve effettivamente il problema i Cauchy proposto. 16
17 Esercizio 2.8 Utilizzano il metoo elle curve caratteristiche, eterminare la soluzione el problema i Cauchy u t 2xtu x = u + t u(x, 0) = 2x. Risoluzione. Si tratta i una equazione alle erivate parziali in ue variabili lineare el prim orine con ato i Cauchy. Le curve i tale equazione, una famiglia a un parametro, sono efinite al sistema inamico in (x, t) = (x(s), t(s)) ṫ = 1 ẋ = 2xt, ẋ(t) = 2xt, la cui soluzione, in forma cartesiana, è ata a x(t) = x 0 e t2, x 0 R. (2.10) Si osservi (Figura 11) che tutte le caratteristiche intersecano t = 0 e quini x 0 t Figura 11: Curve caratteristiche ell equazione alle erivate parziali ell Esercizio 2.8 pescano il ato per propagarlo su tutto il piano. Si ha poi u(x(t), t) = u(x(t), t) + t. (2.11) t 17
18 La (2.11) è un equazione ifferenziale lineare el prim orine el tipo y = y + t L equazione ifferenziale omogenea associata ha soluzione y(t) = αe t. Cerchiamo unque una soluzione ella non omogenea el tipo (metoo ella variazione elle costanti) y(t) = α(t)e t per cui sostitueno nell equazione si ha α = te t, e integrano una volta per parti si ottiene α(t) = te t e t. Sostitueno si ottiene infin y(t) = t 1 + αe t. Abbiamo perciò che le soluzioni i (2.11) sono ate a ( ) u x 0 e t2, t = t 1 + (u(x 0, 0) + 1)e t = t 1 + ( 2x 0 + 1)e t e visto che alla (2.10) si ha x 0 = x 0 (x, t) = xe t2, si ottiene ( u(x, t) = t xe t2) e t = t 1 + e t 2xe t+t2. Lo stuente iligente può verificare che tale u = u(x, t) risolve effettivamente il problema i Cauchy proposto. Esercizio 2.9 Utilizzano il metoo elle curve caratteristiche, eterminare la soluzione el problema i Cauchy u t + 3t 2 u x = x 2 u(x, 0) = sin x. Risoluzione. Si tratta i una equazione alle erivate parziali in ue variabili lineare el prim orine con ato i Cauchy. Le curve caratteristiche i tale equazione, una famiglia a un parametro, sono efinite al sistema inamico in (x, t) = (x(s), t(s)) ṫ = 1 ẋ = 3t 2, ẋ(t) = 3t 2, la cui soluzione, in forma cartesiana, è ata a x(t) = t 3 + x 0, x 0 R. (2.12) Si osservi (Figura 12) che tutte le caratteristiche intersecano t = 0 e quini 18
19 x 0 t Figura 12: Curve caratteristiche ell equazione alle erivate parziali ell Esercizio 2.9 pescano il ato per propagarlo su tutto il piano. Si ha poi a cui t u(x(t), t) = x(t)2 = t 6 + 2x 0 t 3 + x 2 0, u ( t 3 + x 0, t ) = t7 7 + x 0 2 t4 + x 2 0t + u(x 0, 0) = t7 7 + x 0 2 t4 + x 2 0t + sin x 0 e visto che alla (2.12) si ha x 0 = x 0 (x, t) = x t 3, si ottiene u(x, t) = 9 14 t7 3 2 xt4 + x 2 t + sin ( x t 3). Lo stuente iligente può verificare che tale u = u(x, t) risolve effettivamente il problema i Cauchy proposto. Esercizio 2.10 Utilizzano il metoo elle curve caratteristiche, eterminare la soluzione el problema i Cauchy u t + 2te x u x = e x u(x, 0) = x. La soluzione così trovata è globalmente efinita? 19
20 Risoluzione. Si tratta i una equazione alle erivate parziali in ue variabili lineare el prim orine con ato i Cauchy. Le curve i tale equazione, una famiglia a un parametro, sono efinite al sistema inamico in (x, t) = (x(s), t(s)) ṫ = 1 ẋ = 2te x, ẋ(t) = 2te x, a cui, proceeno per separazioni i variabili, si trova che la soluzione, in forma cartesiana, è ata a x(t) = log ( t 2 + c ), c R : t 2 + c > 0. Tenuto conto che è fonamentale che le caratteristiche peschino il ato su t = 0 per propagarlo, siamo perciò interessati solo a quelle caratteristiche efinite per t = 0, 0 < c = e x 0 e quini x(t) = log ( t 2 + e x 0 ), x 0 R. (2.13) È chiaro che tali curve caratteristiche non riempiono tutto il piano ma solo la regione e x t 2 > 0. Si ha poi x 0 t Figura 13: Curve caratteristiche ell equazione alle erivate parziali ell Esercizio 2.10 t u(x(t), t) = ex(t) = t 2 + e x 0, 20
21 a cui u ( log ( t 2 + e x 0 ), t ) = t3 3 + ex 0 t + u(x 0, 0) = t3 3 + ex 0 t + x 0 e visto che alla (2.13) si ha x 0 = x 0 (x, t) = log(e x t 2 ), si ottiene u(x, t) = 2 3 t3 + te x + log(e x t 2 ), efinita nella regione e x/2 < t < e x/2. La soluzione non è pertanto efinita globalmente. Lo stuente iligente può verificare che tale u = u(x, t) risolve effettivamente il problema i Cauchy proposto. Esercizio 2.11 Utilizzano il metoo elle curve caratteristiche, eterminare la soluzione el problema i Cauchy u t log(t + 1)u x = 2ut u(x, 0) = e x. Risoluzione. Si tratta i una equazione alle erivate parziali in ue variabili lineare el prim orine con ato i Cauchy il cui ominio i efinizione è il semipiano t > 1. Ne cerchiamo la soluzione u = u(x, t) con il metoo elle curve caratteristiche. Le curve i tale equazione, una famiglia a un parametro, sono efinite al sistema inamico in (x, t) = (x(s), t(s)) ṫ = 1 ẋ = log(1 + t), ẋ(t) = log(1 + t), la cui soluzione, in forma cartesiana, è ata a x(t) = (1 + t) log(1 + t) + t + x 0, x 0 R. (2.14) Si osservi (Figura 14) che tutte le caratteristiche intersecano t = 0 e quini pescano il ato per propagarlo su tutto il semipiano t > 1. Si ha poi u(x(t), t) = 2tu(x(t), t), t 21
22 x 1 0 t Figura 14: Curve caratteristiche ell equazione alle erivate parziali ell Esercizio 2.11 a cui u ( (1 + t) log(1 + t) + t + x 0, t) = u(x 0, 0)e t2 = e x 0 e t2 e visto che alla (2.14) si ha x 0 = x 0 (x, t) = x t + (1 + t) log(1 + t), si ottiene u(x, t) = e (x t+(1+t) log(1+t)+t2 ). Lo stuente iligente può verificare che tale u = u(x, t) risolve effettivamente il problema i Cauchy proposto. Esercizio 2.12 Utilizzano il metoo elle curve caratteristiche, eterminare la soluzione el problema i Cauchy u t + e t u x = x 2 u(x, 0) = x 1. Risoluzione. Si tratta i una equazione alle erivate parziali in ue variabili lineare el prim orine con ato i Cauchy. Le curve i tale equazione, una famiglia a un parametro, sono efinite al sistema inamico in (x, t) = (x(s), t(s)) ṫ = 1 ẋ = e t, 22
23 ẋ(t) = e t, la cui soluzione, in forma cartesiana, è ata a x(t) = e t + x 0 1, x 0 R. (2.15) Si osservi (Figura 15) che tutte le caratteristiche intersecano t = 0 e quini x 0 t Figura 15: Curve caratteristiche ell equazione alle erivate parziali ell Esercizio 2.12 pescano il ato per propagarlo su tutto il piano. Si ha poi a cui t u(x(t), t) = x(t)2 = e 2t + 2(x 0 1)e t + (x 0 1) 2, u ( e t + x 0 1, t ) = 1 2 e2t + 2(x 0 1)e t + (x 0 1) 2 t + u(x 0, 0) 1 2 2(x 0 1) = 1 2 e2t + 2(x 0 1)e t + (x 0 1) 2 t x e visto che alla (2.15) si ha x 0 = x 0 (x, t) = x e t + 1, si ottiene u(x, t) = 1 2 ( e 2t 1 ) + ( 2e t 1 ) ( x e t) + ( x e t) 2 t. Lo stuente iligente può verificare che tale u = u(x, t) risolve effettivamente il problema i Cauchy proposto. 23
24 Esercizio 2.13 Utilizzano il metoo elle curve caratteristiche, eterminare la soluzione el problema i Cauchy u t + (x + t 2 )u x = xu u(x, 0) = 1. Risoluzione. Si tratta i una equazione alle erivate parziali in ue variabili lineare el prim orine con ato i Cauchy. Le curve i tale equazione, una famiglia a un parametro, sono efinite al sistema inamico in (x, t) = (x(s), t(s)) ṫ = 1 ẋ = x + t 2, ẋ(t) = x + t 2. (2.16) La soluzione ell omogenea associata, x = x, è ata a x(t) = αe t ; cerchiamo una soluzione particolare ella non omogenea el tipo p(t) = a 0 + a 1 t + a 2 t 2 e sostitueno nella (2.16) 2 si trova p(t) = t 2 2t 2 a cui la soluzione generale ella (2.16) 2 x(t) = t 2 2t 2 + (x 0 + 2)e t, x 0 R. (2.17) Si osservi (Figura 16) che tutte le caratteristiche intersecano t = 0 e quini pescano il ato per propagarlo su tutto il piano. Si ha poi t u(x(t), t) = x(t)u(x(t), t) = ( t 2 2t 2 + (x 0 + 2)e t) u(x(t), t), a cui proceeno per separazione i variabili, u ( t 2 2t 2 + (x 0 + 2)e t, t ) = u(x 0, 0)e (x 0+2) e = e (x 0+2) e t3 3 t2 2t+(x 0 +2)e t t3 3 t2 2t+(x 0 +2)e t e visto che alla (2.17) si ha x 0 = x 0 (x, t) = ( x + t 2 + 2t + 2 ) e t 2, si ottiene u(x, t) = e (x+t2 +2t+2)e t e t3 3 t2 2t+x+t 2 +2t+2 per cui la soluzione el problema può essere scritta come u(x, t) = e t3 3 t2 2t+(1 e t )(x+t 2 +2t+2). Lo stuente iligente può verificare che tale u = u(x, t) risolve effettivamente il problema i Cauchy proposto., 24
25 x 0 t Figura 16: Curve caratteristiche ell equazione alle erivate parziali ell Esercizio 2.13 Esercizio 2.14 Utilizzano il metoo elle curve caratteristiche, eterminare la soluzione el problema i Cauchy u t + te t u x = 3x u(x, 0) = x + 3. Risoluzione. Si tratta i una equazione alle erivate parziali in ue variabili lineare el prim orine con ato i Cauchy. Le curve i tale equazione, una famiglia a un parametro, sono efinite al sistema inamico in (x, t) = (x(s), t(s)) ṫ = 1 ẋ = te t, ẋ(t) = te t, la cui soluzione, in forma cartesiana, è ata a x(t) = te t e t + x 0 + 1, x 0 R. (2.18) Si osservi (Figura 17) che tutte le caratteristiche intersecano t = 0 e quini pescano il ato per propagarlo su tutto il piano. Si ha poi t u(x(t), t) = 3x(t) = 3tet 3e t + 3(x 0 + 1), 25
26 x 0 t Figura 17: Curve caratteristiche ell equazione alle erivate parziali ell Esercizio 2.14 a cui u ( te t e t + x 0 + 1, t ) = 3te t 6e t + 3(x 0 + 1)t + u(x 0, 0) + 6 = 3te t 6e t + 3(x 0 + 1)t + x e visto che alla (2.18) si ha x 0 = x 0 (x, t) = x te t + e t 1, si ottiene u(x, t) = 3xt 3t 2 e t + 5te t 5e t + x + 8. Lo stuente iligente può verificare che tale u = u(x, t) risolve effettivamente il problema i Cauchy proposto. Esercizio 2.15 Utilizzano il metoo elle curve caratteristiche, eterminare la soluzione el problema i Cauchy u t + 5xt 2 u x = u + 2 u(x, 0) = x + 2. Risoluzione. Si tratta i una equazione alle erivate parziali in ue variabili lineare el prim orine con ato i Cauchy. Le curve i tale equazione, una famiglia a un parametro, sono efinite al sistema inamico in (x, t) = (x(s), t(s)) ṫ = 1 ẋ = 5xt 2, 26
27 ẋ(t) = 5xt 2, la cui soluzione, in forma cartesiana, è ata a x(t) = x 0 e 5 3 t3, x 0 R. (2.19) Si osservi (Figura 18) che tutte le caratteristiche intersecano t = 0 e quini x 0 t Figura 18: Curve caratteristiche ell equazione alle erivate parziali ell Esercizio 2.15 pescano il ato per propagarlo su tutto il piano. Si ha poi u(x(t), t) = u(x(t), t) + 2, t equazione ifferenziale el prim orine la cui soluzione è ata a ( ) u x 0 e 5 3 t3, t = (u(x 0, 0) + 2)e t 2 = (x 0 + 4)e t 2 e visto che alla (2.19) si ha x 0 = x 0 (x, t) = xe 5 3 t3, si ottiene u(x, t) = xe t 5 3 t3 + 4e t 2. Lo stuente iligente può verificare che tale u = u(x, t) risolve effettivamente il problema i Cauchy proposto. 27
28 Esercizio 2.16 Utilizzano il metoo elle curve caratteristiche, eterminare la soluzione el problema i Cauchy u t + (xt + t)u x = 4 u(x, 0) = 2x. Risoluzione. Si tratta i una equazione alle erivate parziali in ue variabili lineare el prim orine con ato i Cauchy. Le curve i tale equazione, una famiglia a un parametro, sono efinite al sistema inamico in (x, t) = (x(s), t(s)) ṫ = 1 ẋ = xt + t, ẋ(t) = xt + t, la cui soluzione, in forma cartesiana, è ata a x(t) = (x 0 + 1)e t2 /2 1, x 0 R. (2.20) Si osservi (Figura 19) che tutte le caratteristiche intersecano t = 0 e quini x 0 t Figura 19: Curve caratteristiche ell equazione alle erivate parziali ell Esercizio 2.16 pescano il ato per propagarlo su tutto il piano. Si ha poi u(x(t), t) = 4, t 28
29 equazione ifferenziale el prim orine la cui soluzione è ata a ( ) u (x 0 + 1)e t2 /2 1, t = 4t + u(x 0, 0) = 4t + 2x 0 e visto che alla (2.20) si ha x 0 = x 0 (x, t) = (x + 1)e t2 /2 1, si ottiene u(x, t) = 4t 2 + 2(x + 1)e t2 /2. Lo stuente iligente può verificare che tale u = u(x, t) risolve effettivamente il problema i Cauchy proposto. Esercizio 2.17 Utilizzano il metoo elle curve caratteristiche, eterminare la soluzione el problema i Cauchy u t + 3xt 5 u x = t 5 x + 2t u(x, 0) = x 3. Risoluzione. Si tratta i una equazione alle erivate parziali in ue variabili lineare el prim orine con ato i Cauchy. Le curve i tale equazione, una famiglia a un parametro, sono efinite al sistema inamico in (x, t) = (x(s), t(s)) ṫ = 1 ẋ = 3xt 5, ẋ(t) = 3xt 5, la cui soluzione, in forma cartesiana, è ata a x(t) = x 0 e t6 /2, x 0 R. (2.21) Si osservi (Figura 20) che tutte le caratteristiche intersecano t = 0 e quini pescano il ato per propagarlo su tutto il piano. Si ha poi a cui t u(x(t), t) = t5 x(t) + 2t = x 0 t 5 e t6 /2 + 2t, u ( ) x 0 e t6 /2, t = x 0 /2 3 et6 + t 2 + u(x 0, 0) x 0 3 = x 0 /2 3 et6 + t 2 + x 3 0 x 0 3 e visto che alla (2.21) si ha x 0 = x 0 (x, t) = xe t6 /2, si ottiene u(x, t) = x 3 + t2 + x 3 e 3 2 t6 x 3 e t6 /2. Lo stuente iligente può verificare che tale u = u(x, t) risolve effettivamente il problema i Cauchy proposto. 29
30 x 0 t Figura 20: Curve caratteristiche ell equazione alle erivate parziali ell Esercizio 2.17 Esercizio 2.18 Utilizzano il metoo elle curve caratteristiche, eterminare la soluzione el problema i Cauchy u t + (t + x)e t u x = xt u(x, 0) = x. Risoluzione. Si tratta i una equazione alle erivate parziali in ue variabili lineare el prim orine con ato i Cauchy. Le curve i tale equazione, una famiglia a un parametro, sono efinite al sistema inamico in (x, t) = (x(s), t(s)) ṫ = 1 ẋ = t + x, ẋ(t) = t + x, la cui soluzione, in forma cartesiana, è ata a x(t) = (x 0 + 1)e t 1 t, x 0 R. (2.22) Si osservi (Figura 21) che tutte le caratteristiche intersecano t = 0 e quini pescano il ato per propagarlo su tutto il piano. Si ha poi t u(x(t), t) = tx(t) = t ( (x 0 + 1)e t t 1 ) = (x 0 + 1)te t t t 2, 30
31 x 0 t Figura 21: Curve caratteristiche ell equazione alle erivate parziali ell Esercizio 2.18 a cui u ( (x 0 + 1)e t t 1, t ) = (x 0 + 1)(te t e t ) + u(x 0, 0) x 0 1 t2 2 t3 3 = (x 0 + 1)(te t e t ) 1 t2 2 t3 3 e visto che alla (2.18) si ha x 0 = x 0 (x, t) = e t (x + t + 1) 1, si ottiene u(x, t) = xt x + t e t (x + t + 1) t2 2 t3 3. Lo stuente iligente può verificare che tale u = u(x, t) risolve effettivamente il problema i Cauchy proposto. Esercizio 2.19 Determinare le curve caratteristiche per l equazione u t + (x + 2)u x = u + 2t e isegnarle sul piano (x, t). Successivamente, eterminare la soluzione el problema i Cauchy u t + (x + 2)u x = u + 2t u(x, 0) = x. 31
32 Risoluzione. Si tratta i una equazione alle erivate parziali in ue variabili lineare el prim orine con ato i Cauchy. Le curve i tale equazione, una famiglia a un parametro, sono efinite al sistema inamico in (x, t) = (x(s), t(s)) ṫ = 1 ẋ = x + 2, ẋ(t) = x + 2, la cui soluzione, in forma cartesiana, è ata a x(t) = (x 0 + 2)e t 2 x 0 R. (2.23) Si osservi (Figura 22) che tutte le caratteristiche intersecano t = 0 e quini x 0 t Figura 22: Curve caratteristiche ell equazione alle erivate parziali ell Esercizio 2.19 pescano il ato per propagarlo su tutto il piano. Si ha poi che l equazione alle erivate parziali lungo le caratteristiche iviene u(x(t), t) = u(x(t), t) + 2t, (2.24) t un equazione ifferenziale el prim orine non omogenea, y = y + 2t. Una sua soluzione particolare può essere ricercata tra i polinomi el prim orine, p(t) = a + bt, a cui sostitueno si trova p(t) = 2 2t. La 32
33 soluzione ell omogenea associata è invece y(t) = ke t. generale ell equazione (2.24) è ata a Perciò l integrale u ( (x 0 + 2)e t 2, t ) = (u(x 0, 0) + 2)e t 2 2t = (x 0 + 2)e t 2 2t e visto che alla (2.23) si ha x 0 = x 0 (x, t) = e t (x + 2) 2, si ottiene u(x, t) = ( e t (x + 2) ) e t 2 2t = x 2t. Lo stuente iligente può verificare facilmente che tale u = u(x, t) risolve effettivamente il problema i Cauchy proposto. Esercizio 2.20 Determinare le curve caratteristiche per l equazione u t + 2tx u x = 0 e isegnarle sul piano (x, t). Successivamente, eterminare la soluzione el problema i Cauchy u t + 2tx u x = 0 u(x, 0) = x. Risoluzione. Si tratta i una equazione alle erivate parziali in ue variabili lineare el prim orine con ato i Cauchy continuo ma non erivabile. Le curve i tale equazione, una famiglia a un parametro, sono efinite al sistema inamico in (x, t) = (x(s), t(s)) ṫ = 1 ẋ = 2tx, ẋ(t) = 2tx, la cui soluzione, in forma cartesiana, è ata a x(t) = x 0 e t2, x 0 R. (2.25) Si osservi (Figura 23) che tutte le caratteristiche intersecano t = 0 e quini pescano il ato per propagarlo su tutto il piano. Si ha poi a cui u(x(t), t) = 0, t u ( ) x 0 e t2, t = u(x 0, 0) = x 0 33
34 x 0 t Figura 23: Curve caratteristiche ell equazione alle erivate parziali ell Esercizio 2.20 e visto che alla (2.25) si ha x 0 = x 0 (x, t) = xe t2, si ottiene u(x, t) = xe t2 = x e t2. Lo stuente iligente può verificare che tale u = u(x, t) risolve effettivamente il problema i Cauchy proposto. Esercizio 2.21 Determinare la soluzione el problema i Cauchy u t + xu x = 2 + u u(x, 0) = x. Risoluzione. Si tratta i una equazione alle erivate parziali in ue variabili lineare el prim orine con ato i Cauchy. Le curve i tale equazione, una famiglia a un parametro, sono efinite al sistema inamico in (x, t) = (x(s), t(s)) ṫ = 1 ẋ = x, ẋ(t) = x, 34
35 x 0 t Figura 24: Curve caratteristiche ell equazione alle erivate parziali ell Esercizio 2.21 la cui soluzione, in forma cartesiana, è ata a x(t) = x 0 e t, x 0 R. (2.26) Si osservi (Figura 24) che tutte le caratteristiche intersecano t = 0 e quini pescano il ato per propagarlo su tutto il piano. Si ha poi a cui u(x(t), t) = 2 + u(x(t), t) t u ( x 0 e t, t ) = (u(x 0, 0) + 2)e t 2 = (x 0 + 2)e t 2 e visto che alla (2.26) si ha x 0 = x 0 (x, t) = xe t, si ottiene u(x, t) = ( xe t + 2 ) e t 2 = x + 2e t 2. Lo stuente iligente può verificare facilmente che tale u = u(x, t) risolve effettivamente il problema i Cauchy proposto. 35
11. Equazioni quasilineari del primo ordine
 11. Equazioni quasilineari el primo orine Una equazione quasilineare el primo orine in ue variabili è una espressione el tipo (1) a(x, y, u)u x + b(x, y, u)u y = c(x, y, u) ove x e y variano in un aperto
11. Equazioni quasilineari el primo orine Una equazione quasilineare el primo orine in ue variabili è una espressione el tipo (1) a(x, y, u)u x + b(x, y, u)u y = c(x, y, u) ove x e y variano in un aperto
Sistemi di due equazioni differenziali del primo ordine a coefficienti costanti
 Sistemi i ue equazioni ifferenziali el primo orine a coefficienti costanti Enrico Schlesinger In questo paragrafo si risolve il sistema i equazioni ifferenziali x ax + by () y cx + y ove x e y sono ue
Sistemi i ue equazioni ifferenziali el primo orine a coefficienti costanti Enrico Schlesinger In questo paragrafo si risolve il sistema i equazioni ifferenziali x ax + by () y cx + y ove x e y sono ue
= x + x 0 2x 0 per x x 0,
 Lezione el 17 ottobre. Derivate 1. Derivata i una funzione in un punto Definizione 1 Sia f una funzione efinita in un intorno I i un punto x 0. Per ciascun x I con x = x 0 consieriamo: l incremento a x
Lezione el 17 ottobre. Derivate 1. Derivata i una funzione in un punto Definizione 1 Sia f una funzione efinita in un intorno I i un punto x 0. Per ciascun x I con x = x 0 consieriamo: l incremento a x
12. Teoria qualitativa
 12. Teoria qualitativa Si esaminano le conizioni i regolarità per un campo vettoriale, che garantiscono esistenza e unicità ella soluzione per l equazione ifferenziale associata. La conizione i Lipschitz,
12. Teoria qualitativa Si esaminano le conizioni i regolarità per un campo vettoriale, che garantiscono esistenza e unicità ella soluzione per l equazione ifferenziale associata. La conizione i Lipschitz,
Meccanica Applicata Alle Macchine. Elementi di Meccanica Teorica ed Applicata
 Meccanica Applicata Alle Macchine (Ingegneria Energetica) Elementi i Meccanica Teorica e Applicata (Scienze per l Ingegneria) Università egli Stui i oma La Sapienza Una traccia egli argomenti el Corso
Meccanica Applicata Alle Macchine (Ingegneria Energetica) Elementi i Meccanica Teorica e Applicata (Scienze per l Ingegneria) Università egli Stui i oma La Sapienza Una traccia egli argomenti el Corso
E sem pi di E serci zi e Qui z d E sam e
 E sem pi i E serci zi e Qui z E sam e Eser cit azion i i Cont r olli Au t om at ici Quiz. Il segnale x(t), antitrasformata i Laplace i X(s) = s(s+a) : è nullo per t=0 [x(0) = 0]; ha erivata nulla per t=0
E sem pi i E serci zi e Qui z E sam e Eser cit azion i i Cont r olli Au t om at ici Quiz. Il segnale x(t), antitrasformata i Laplace i X(s) = s(s+a) : è nullo per t=0 [x(0) = 0]; ha erivata nulla per t=0
PDE lineari primo ordine
 PDE lineari primo ordine. Introduzione Un equazione lineare alle derivate parziali di primo ordine in R n é, indicato con x = x,..., x n }, un equazione della forma seguente: () n i= a i (x) u x i + b(x)
PDE lineari primo ordine. Introduzione Un equazione lineare alle derivate parziali di primo ordine in R n é, indicato con x = x,..., x n }, un equazione della forma seguente: () n i= a i (x) u x i + b(x)
ESERCITAZIONE DELL 11 DICEMBRE 2008 SOLUZIONI Corso di Matematica I per Geologia. dx dx dx sin x = (sin x)2 + (cos x) 2. (1)
 ESERCITAZIONE DELL DICEMBRE 008 SOLUZIONI Corso i Matematica I per Geologia A. Calcolare le erivate elle seguenti funzioni:. sin cos, sin 3, e sin 3 4 cos 3; +. log, log, arctan. Soluzioni.. Prima erivata.
ESERCITAZIONE DELL DICEMBRE 008 SOLUZIONI Corso i Matematica I per Geologia A. Calcolare le erivate elle seguenti funzioni:. sin cos, sin 3, e sin 3 4 cos 3; +. log, log, arctan. Soluzioni.. Prima erivata.
Complementi di Analisi Matematica e Statistica 04/07/ Testo e Soluzioni
 Complementi i Analisi Matematica e Statistica 04/07/016 - Testo e Soluzioni Parte A 1. Esercizio A1: Dati α, β, Si consieri la seguente serie i potenze: e αn n + 1 ( β)n. eterminare il raggio i convergenza
Complementi i Analisi Matematica e Statistica 04/07/016 - Testo e Soluzioni Parte A 1. Esercizio A1: Dati α, β, Si consieri la seguente serie i potenze: e αn n + 1 ( β)n. eterminare il raggio i convergenza
Esercitazioni del 18 marzo Calcolo della curvatura di un arco di curva regolare γ in R 3
 Esercitazioni el 18 marzo 2013 Calcolo ella curvatura i un arco i curva regolare γ in R 3 Consieriamo un arco i curva regolare γ, escritta analiticamente a una parametrizzazione α : I R 3, con I intervallo
Esercitazioni el 18 marzo 2013 Calcolo ella curvatura i un arco i curva regolare γ in R 3 Consieriamo un arco i curva regolare γ, escritta analiticamente a una parametrizzazione α : I R 3, con I intervallo
Curve in R n. Curve parametrizzate.
 Curve in R n Generalmente ci sono ue moi per escrivere una curva in R n, ovvero è possibile scrivere un equazione parametrica o un equazione cartesiana. Esempio: una retta in R 2 può essere escritta in
Curve in R n Generalmente ci sono ue moi per escrivere una curva in R n, ovvero è possibile scrivere un equazione parametrica o un equazione cartesiana. Esempio: una retta in R 2 può essere escritta in
Esercizi su Derivate parziali, differenziabilità e piani tangenti
 Esercizi su Derivate parziali, ifferenziabilità e piani tangenti 1. Per le funzioni che seguono, eterminare il graiente ella funzione ata nel punto inicato e l equazione el piano tangente al grafico ella
Esercizi su Derivate parziali, ifferenziabilità e piani tangenti 1. Per le funzioni che seguono, eterminare il graiente ella funzione ata nel punto inicato e l equazione el piano tangente al grafico ella
Una volgare introduzione alle EDO
 Una volgare introuzione alle EDO Tiziano Penati 1 Primitive Abbiamo già incontrato un esempio semplice i equazioni ifferenziali orinarie (EDO): il calcolo i primitive. Vale la pena infatti i ricorare che
Una volgare introuzione alle EDO Tiziano Penati 1 Primitive Abbiamo già incontrato un esempio semplice i equazioni ifferenziali orinarie (EDO): il calcolo i primitive. Vale la pena infatti i ricorare che
Nozioni elementari di calcolo differenziale e integrale
 Nozioni elementari i calcolo ifferenziale e integrale DIPARTIMENTO DI FISICA E INFN UNIVERSITÀ DEL SALENTO a.a. 013/014 L. Renna - Dipartimento i Fisica 1 Sommario 1 Funzioni... 3 Derivate... 4 3 Integrali...
Nozioni elementari i calcolo ifferenziale e integrale DIPARTIMENTO DI FISICA E INFN UNIVERSITÀ DEL SALENTO a.a. 013/014 L. Renna - Dipartimento i Fisica 1 Sommario 1 Funzioni... 3 Derivate... 4 3 Integrali...
Equazioni differenziali
 4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
Equazioni differenziali lineari del secondo ordine a coefficienti costanti
 Equazioni differenziali lineari del secondo ordine a coefficienti costanti 0.1 Introduzione Una equazione differenziale del secondo ordine è una relazione del tipo F (t, y(t), y (t), y (t)) = 0 (1) Definizione
Equazioni differenziali lineari del secondo ordine a coefficienti costanti 0.1 Introduzione Una equazione differenziale del secondo ordine è una relazione del tipo F (t, y(t), y (t), y (t)) = 0 (1) Definizione
Nome, Cognome: punti totali possibili, 50 punti corrispondono alla nota massima.
 Nome, Cognome:................................................................ 55 punti totali possibili, 5 punti corrisponono alla nota massima. 3 ottobre 23 ing. Ivan Furlan . Controllo i un oscillatore
Nome, Cognome:................................................................ 55 punti totali possibili, 5 punti corrisponono alla nota massima. 3 ottobre 23 ing. Ivan Furlan . Controllo i un oscillatore
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Terzo Appello 8 Settembre 2014
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Terzo Appello 8 Settembre 24 Cognome: Nome: Matricola: Compito A Es.: 9 punti Es.2: 8 punti Es.3: 8 punti Es.4: 8 punti Totale. Sia F la
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Terzo Appello 8 Settembre 24 Cognome: Nome: Matricola: Compito A Es.: 9 punti Es.2: 8 punti Es.3: 8 punti Es.4: 8 punti Totale. Sia F la
x = t y = t z = t 3 1 A = B = 1 2
 11/1/05 Teoria: Enunciare e discutere il teorema di Lagrange. Esercizio 1. Determinare l equazione cartesiana del piano passante per P 0 = (1,, 1) e contenente i vettori u = (,, ) e v = (1, 5, 4). Risposta
11/1/05 Teoria: Enunciare e discutere il teorema di Lagrange. Esercizio 1. Determinare l equazione cartesiana del piano passante per P 0 = (1,, 1) e contenente i vettori u = (,, ) e v = (1, 5, 4). Risposta
Syllabus di equazioni differenziali a derivate parziali
 Syllabus i equazioni ifferenziali a erivate parziali Equazioni Le tre famiglie più note i equazioni ifferenziali a erivate parziali sono le equazioni ellittiche, le equazioni paraboliche e le equazioni
Syllabus i equazioni ifferenziali a erivate parziali Equazioni Le tre famiglie più note i equazioni ifferenziali a erivate parziali sono le equazioni ellittiche, le equazioni paraboliche e le equazioni
5 DERIVATA. 5.1 Continuità
 5 DERIVATA 5. Continuità Definizione 5. Sia < a < b < +, f : (a, b) R e c (a, b). Diciamo che f è continua in c se sono verificate le ue conizioni: (i) c esiste (ii) = f(c) c Si osservi che nella efinizione
5 DERIVATA 5. Continuità Definizione 5. Sia < a < b < +, f : (a, b) R e c (a, b). Diciamo che f è continua in c se sono verificate le ue conizioni: (i) c esiste (ii) = f(c) c Si osservi che nella efinizione
Soluzione scritto 4 marzo 2011
 .. Esercizio. Scrivere ANALISI VETTORIALE Soluzione scritto 4 marzo l integrale generale dell equaz. y + y tan(t) =, π < t < π ; un integrale particolare dell equaz. y + y tan(t) = t cos(t); un integrale
.. Esercizio. Scrivere ANALISI VETTORIALE Soluzione scritto 4 marzo l integrale generale dell equaz. y + y tan(t) =, π < t < π ; un integrale particolare dell equaz. y + y tan(t) = t cos(t); un integrale
APPUNTI DI FISICA MATEMATICA A.A. 2014/15
 APPUNTI DI FISICA MATEMATICA A.A. 214/15 PARTE PRIMA: SISTEMI MECCANICI I Introuzione e richiami i cinematica In questa prima parte el corso si applicano metoi matematici rigorosi nell ambito i moelli
APPUNTI DI FISICA MATEMATICA A.A. 214/15 PARTE PRIMA: SISTEMI MECCANICI I Introuzione e richiami i cinematica In questa prima parte el corso si applicano metoi matematici rigorosi nell ambito i moelli
f(x) f(x 0 ) = m R ; (1.1) lim f(x) f(x 0 ) m(x x 0 ) lim (x x 0 ) f (n) (x 0 )
 I polinomi i Taylor Il resto i Peano Una funzione f efinita in un intorno i un punto x 0 si ice erivabile in x 0 se e solo se a sua volta la (1.1) equivale a lim f(x) f(x 0 ) x x 0 = m R ; (1.1) f(x) f(x
I polinomi i Taylor Il resto i Peano Una funzione f efinita in un intorno i un punto x 0 si ice erivabile in x 0 se e solo se a sua volta la (1.1) equivale a lim f(x) f(x 0 ) x x 0 = m R ; (1.1) f(x) f(x
Analisi Matematica 1, parte B Laurea in Matematica
 Analisi Matematica 1, parte B Laurea in Matematica Prima settimana Sia x una variabile reale efinita in un intorno bucato i 0 in seguito x enoterà un incremento infinitesimo). Una funzione R x) si ice
Analisi Matematica 1, parte B Laurea in Matematica Prima settimana Sia x una variabile reale efinita in un intorno bucato i 0 in seguito x enoterà un incremento infinitesimo). Una funzione R x) si ice
Lezione XII Analisi Formale
 SCENZA DE MATERAL Chimica Fisica Lezione X Analisi Formale Dr. Fabio Mavelli Dipartimento i Chimica Università egli Stui i Bari Analisi Cinetica Fenomenologica Analisi Cinetica Fenomenologica Meccanismo
SCENZA DE MATERAL Chimica Fisica Lezione X Analisi Formale Dr. Fabio Mavelli Dipartimento i Chimica Università egli Stui i Bari Analisi Cinetica Fenomenologica Analisi Cinetica Fenomenologica Meccanismo
Analisi Matematica III
 Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 1 giugno 4 (Cognome (Nome (Numero di matricola Esercizio 1 Si consideri la successione
Soluzioni verifica di Matematica 5 a E Liceo Scientifico - 17/10/2013
 Istituto Superiore XXV aprile Pontedera - Prof Francesco Daddi Soluzioni verifica di Matematica 5 a E Liceo Scientifico - 7/0/03 Esercizio Si consideri la funzione e x+ se x < f(x) = 0 se x = x x x se
Istituto Superiore XXV aprile Pontedera - Prof Francesco Daddi Soluzioni verifica di Matematica 5 a E Liceo Scientifico - 7/0/03 Esercizio Si consideri la funzione e x+ se x < f(x) = 0 se x = x x x se
Risoluzione del compito n. 5 (Luglio 2018/2)
 Risoluzione del compito n. 5 (Luglio 2018/2) PROBLEMA 1 Considerate il luogo di zeri S = {(x, y, z) R 3 : z 4+ x 2 + y 2 =0, 2x y + z =0}. a) Giustificando la risposta, dite se S è una curva liscia. b)
Risoluzione del compito n. 5 (Luglio 2018/2) PROBLEMA 1 Considerate il luogo di zeri S = {(x, y, z) R 3 : z 4+ x 2 + y 2 =0, 2x y + z =0}. a) Giustificando la risposta, dite se S è una curva liscia. b)
AM210/ : Tracce delle lezioni- Settimana XI
 AM21/213-14: Tracce elle lezioni- Settimana XI PROBLEMA DI CAUCHY Esistenza e unicitá locale, unicitá globale, soluzione massimale. Teorema i Picar locale) esistenza/unicitá locale in ipotesi Lip loc )
AM21/213-14: Tracce elle lezioni- Settimana XI PROBLEMA DI CAUCHY Esistenza e unicitá locale, unicitá globale, soluzione massimale. Teorema i Picar locale) esistenza/unicitá locale in ipotesi Lip loc )
(a) è chiuso; (b) il punto (1, 1/e) è punto di accumulazione di A; (c) è convesso.
 Cognome Nome Matricola Laurea Civ Amb Gest Inf Eln Tlc Mec Non scrivere qui 1 3 4 5 6 Università degli Studi di Parma Dipartimento di Ingegneria e Architettura Esame di Analisi Matematica Soluzioni AA
Cognome Nome Matricola Laurea Civ Amb Gest Inf Eln Tlc Mec Non scrivere qui 1 3 4 5 6 Università degli Studi di Parma Dipartimento di Ingegneria e Architettura Esame di Analisi Matematica Soluzioni AA
Equazioni differenziali
 4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
4 Equazioni differenziali Determinare le primitive di una funzione f(x) significa risolvere y (x) = f(x) dove l incognita è la funzione y(x). Questa equazione è un semplice esempio di equazione differenziale.
Equazioni differenziali
 Equazioni differenziali In un equazione differenziale l incognita da trovare è una funzione, di cui è data, dall equazione, una relazione con le sue derivate (fino ad un certo ordine) e la variabile libera:
Equazioni differenziali In un equazione differenziale l incognita da trovare è una funzione, di cui è data, dall equazione, una relazione con le sue derivate (fino ad un certo ordine) e la variabile libera:
11.1. Esercizio. Dato il numero complesso z = 2 + i 2, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8.
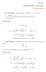 ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
ANALISI Soluzione esercizi gennaio 0.. Esercizio. Dato il numero complesso z = + i, calcolare z, z, scrivere la rappresentazione trigonometrica di z, calcolare z 8. z = i ( ) + ( ) =, π z = arg(z) = 4
Analisi Matematica 2. Michele Campiti. Prove scritte di. Ingegneria Industriale a.a
 Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
Michele Campiti Prove scritte di Analisi Matematica 2 Ingegneria Industriale a.a. 20 202 Grafico della funzione f(x, y) := sin(2x 2 y) cos(x 2y 2 ) in [ π/2, π/2] 2 Raccolta delle tracce di Analisi Matematica
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A Prof. G.Cupini
 ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A.2009-2010 - Prof. G.Cupini Equazioni differenziali ordinarie del primo ordine (lineari, a variabili separabili, di Bernoulli) ed
ANALISI MATEMATICA T-2 (C.d.L. Ing. per l ambiente e il territorio) A.A.2009-2010 - Prof. G.Cupini Equazioni differenziali ordinarie del primo ordine (lineari, a variabili separabili, di Bernoulli) ed
Equazioni della fisica matematica
 Equazioni ella fisica matematica Equazione i conservazione ella massa in fluioinamica Questo principio ella fisica si può scrivere come ρ = ρv n, t ove è una generica porzione i spazio occupata al fluio,
Equazioni ella fisica matematica Equazione i conservazione ella massa in fluioinamica Questo principio ella fisica si può scrivere come ρ = ρv n, t ove è una generica porzione i spazio occupata al fluio,
CORSO DI LAUREA in Fisica, aa 2017/18 (canale Pb-Z)
 CORSO DI LAUREA in Fisica, aa 2017/18 (canale Pb-Z) Equazioni lineari del II ordine a coefficienti costanti: questo è un richiamo dei risultati con altri esempi svolti. Il testo di riferimento è Bramanti
CORSO DI LAUREA in Fisica, aa 2017/18 (canale Pb-Z) Equazioni lineari del II ordine a coefficienti costanti: questo è un richiamo dei risultati con altri esempi svolti. Il testo di riferimento è Bramanti
1 x 2 y 2 dxdy D. 3 (1 ρ2 ) 3/2 = 1 3. = π 12.
 INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y = x e
INGEGNERIA CIVILE - AMBIENTE E TERRITORIO ANALISI MATEMATICA II SOLUZIONI DELLA PROVA SCRITTA DEL 19-6-15 ESERCIZIO 1 Calcolare 1 x y dxdy D dove D è il dominio piano delimitato dalla curva x + y = x e
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Seconda prova in itinere 31 gennaio 2011
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Seconda prova in itinere 3 gennaio Cognome: Nome: Matricola: Compito A Es. : 8 punti Es. : 8 punti Es. 3: 8 punti Es. 4: 8 punti Es. 5:
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Seconda prova in itinere 3 gennaio Cognome: Nome: Matricola: Compito A Es. : 8 punti Es. : 8 punti Es. 3: 8 punti Es. 4: 8 punti Es. 5:
Analisi Matematica III
 Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 7 gennaio 00 (Cognome) (Nome) (Numero di matricola) Esercizio Si consideri la successione
Università di Pisa - Corso di Laurea in Ingegneria Civile dell ambiente e territorio Analisi Matematica III Pisa, 7 gennaio 00 (Cognome) (Nome) (Numero di matricola) Esercizio Si consideri la successione
ESERCIZIO n.10. H 6cm d 2cm. d d d
 ESERCZO n.1 Data la sezione riportata in Figura, eterminare: a) gli assi principali centrali i inerzia; b) l ellisse principale centrale i inerzia; c) il nocciolo centrale i inerzia; ) i momenti i inerzia
ESERCZO n.1 Data la sezione riportata in Figura, eterminare: a) gli assi principali centrali i inerzia; b) l ellisse principale centrale i inerzia; c) il nocciolo centrale i inerzia; ) i momenti i inerzia
SIA DATO UN SOLENOIDE RETTILINEO DI LUNGHEZZA d, RAGGIO R e COSTITUITO DA N SPIRE.
 POBLEMA 11 SIA DATO UN SOLENOIDE ETTILINEO DI LUNGHEZZA, AGGIO e COSTITUITO DA N SPIE. A) DETEMINAE IL CAMPO MAGNETICO PODOTTO LUNGO L ASSE DEL SOLENOIDE. Un solenoie rettilineo è costituito a un filo
POBLEMA 11 SIA DATO UN SOLENOIDE ETTILINEO DI LUNGHEZZA, AGGIO e COSTITUITO DA N SPIE. A) DETEMINAE IL CAMPO MAGNETICO PODOTTO LUNGO L ASSE DEL SOLENOIDE. Un solenoie rettilineo è costituito a un filo
Esercizi proposti di Fondamenti di Automatica - Parte 2
 Esercizi proposti i Fonamenti i Automatica - Parte Febbraio 5 Es. Dimostrare che le matrici A, a elementi reali, e A D, a elementi complessi, sono simili. α ω α + ω A, A ω α D α ω Es. Calcolare e A t e
Esercizi proposti i Fonamenti i Automatica - Parte Febbraio 5 Es. Dimostrare che le matrici A, a elementi reali, e A D, a elementi complessi, sono simili. α ω α + ω A, A ω α D α ω Es. Calcolare e A t e
Matematica e Statistica
 Matematica e Statistica Prova d Esame (26/07/2010) Università di Verona - Laurea in Biotecnologie - A.A. 2009/10 1 Matematica e Statistica Prova d Esame di MATEMATICA (26/07/2010) Università di Verona
Matematica e Statistica Prova d Esame (26/07/2010) Università di Verona - Laurea in Biotecnologie - A.A. 2009/10 1 Matematica e Statistica Prova d Esame di MATEMATICA (26/07/2010) Università di Verona
DERIVATE DIREZIONALI ITERATE
 Analisi Matematica II, Anno Accaemico 206-207. Ingegneria Eile e Architettura Vincenzo M. Tortorelli FOGLIO DI TEORIA n. 0 SVILUPPI DI TAYLOR DERIVATE DIREZIONALI ITERATE Se v R è non nullo è efinito l
Analisi Matematica II, Anno Accaemico 206-207. Ingegneria Eile e Architettura Vincenzo M. Tortorelli FOGLIO DI TEORIA n. 0 SVILUPPI DI TAYLOR DERIVATE DIREZIONALI ITERATE Se v R è non nullo è efinito l
1 Ampliamento del piano e coordinate omogenee
 1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
1 Ampliamento del piano e coordinate omogenee Vogliamo dare una idea, senza molte pretese, dei concetti che stanno alla base di alcuni calcoli svolti nella classificazione delle coniche. Supponiamo di
Analisi Matematica A e B Soluzioni prova scritta parziale n. 4
 Analisi Matematica A e B Soluzioni prova scritta parziale n. Corso di laurea in Fisica, 08-09 7 aprile 09. Determinare le soluzioni u(x) dell equazione differenziale u + u u = sin x + ex + e x. Soluzione.
Analisi Matematica A e B Soluzioni prova scritta parziale n. Corso di laurea in Fisica, 08-09 7 aprile 09. Determinare le soluzioni u(x) dell equazione differenziale u + u u = sin x + ex + e x. Soluzione.
ESERCIZIO n.10. H 6cm d 2cm. d d d
 Esercizi svolti i geometria elle aree Alibrani U., Fuschi P., Pisano A., Sofi A. ESERCZO n.1 Data la sezione riportata in Figura, eterminare: a) gli assi principali centrali i inerzia; b) l ellisse principale
Esercizi svolti i geometria elle aree Alibrani U., Fuschi P., Pisano A., Sofi A. ESERCZO n.1 Data la sezione riportata in Figura, eterminare: a) gli assi principali centrali i inerzia; b) l ellisse principale
1 di 27 29/12/2018, 00:01
 Stuente: Data: Docente: Luciano Seta Corso: Metoi matematici per l'economia Attività: La erivazione prima parte 1. Trova la penenza ella curva nel punto assegnato. P A. 0 1 C. 1 3 D. 3 4. In quale punto
Stuente: Data: Docente: Luciano Seta Corso: Metoi matematici per l'economia Attività: La erivazione prima parte 1. Trova la penenza ella curva nel punto assegnato. P A. 0 1 C. 1 3 D. 3 4. In quale punto
Equazioni differenziali
 Capitolo 2 Equazioni differenziali I modelli matematici per lo studio di una popolazione isolata sono equazioni differenziali. Premettiamo dunque allo studio dei modelli di popolazioni isolate una breve
Capitolo 2 Equazioni differenziali I modelli matematici per lo studio di una popolazione isolata sono equazioni differenziali. Premettiamo dunque allo studio dei modelli di popolazioni isolate una breve
PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 2002
 PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 22 Prova scritta del 1/1/22 Si esamini la serie di funzioni: 1 log x (e n + n), definita per x IR. Si determini l insieme S in cui tale serie converge,
PROVE SCRITTE DI ANALISI MATEMATICA II (V.O.), ANNO 22 Prova scritta del 1/1/22 Si esamini la serie di funzioni: 1 log x (e n + n), definita per x IR. Si determini l insieme S in cui tale serie converge,
AM2: Tracce delle lezioni- X Settimana
 AM: Tracce delle lezioni- X Settimana EQUAZIONI DIFFERENZIALI ORDINARIE Equazioni differenziali lineari del I ordine Date le funzioni a(x), b(x) continue in (a, b) determinare, se esistono, le funzioni
AM: Tracce delle lezioni- X Settimana EQUAZIONI DIFFERENZIALI ORDINARIE Equazioni differenziali lineari del I ordine Date le funzioni a(x), b(x) continue in (a, b) determinare, se esistono, le funzioni
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/2017 EQUAZIONI DIFFERENZIALI 2
 Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/2017 EQUAZIONI DIFFERENZIALI 2 ESERCIZI CON SOLUZIONE 1. Risolvere il seguente problema di Cauchy: 1 2 1 2 L equazione differenziale
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/2017 EQUAZIONI DIFFERENZIALI 2 ESERCIZI CON SOLUZIONE 1. Risolvere il seguente problema di Cauchy: 1 2 1 2 L equazione differenziale
Analisi 4 - SOLUZIONI (compito del 29/09/2011)
 Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
Corso di laurea in Matematica Analisi 4 - SOLUZIONI compito del 9/09/0 Docente: Claudia Anedda Calcolare, tramite uno sviluppo in serie noto, la radice quinta di e la radice cubica di 9 Utilizzando la
Es. 1 Es. 2 Es. 3 Es. 4 Totale Teoria. Punteggi degli esercizi: Es.1: 8 punti; Es.2: 8 punti; Es.3: 8 punti; Es.4: 8 punti.
 Es. Es. Es. 3 Es. 4 Totale Teoria Analisi e Geometria Terzo appello 8 Settembre 4 Compito B Docente: Politecnico di Milano Ingegneria Industriale Cognome: Nome: Matricola: Punteggi degli esercizi: Es.:
Es. Es. Es. 3 Es. 4 Totale Teoria Analisi e Geometria Terzo appello 8 Settembre 4 Compito B Docente: Politecnico di Milano Ingegneria Industriale Cognome: Nome: Matricola: Punteggi degli esercizi: Es.:
Per determinare una soluzione particolare descriveremo un metodo che vale solo nel caso in cui la funzione f(x) abbia una forma particolare:
 42 Roberto Tauraso - Analisi 2 Ora imponiamo condizione richiesta: ( lim c e 4x + c 2 + c 3 e 2x cos(2x) + c 4 e 2x sin(2x) ) = 3. x + Il limite esiste se e solo c 3 = c 4 = perché le funzioni e 2x cos(2x)
42 Roberto Tauraso - Analisi 2 Ora imponiamo condizione richiesta: ( lim c e 4x + c 2 + c 3 e 2x cos(2x) + c 4 e 2x sin(2x) ) = 3. x + Il limite esiste se e solo c 3 = c 4 = perché le funzioni e 2x cos(2x)
Applicazioni chimiche dell integrazione sistemi di equazioni differenziali
 Applicazioni chimiche ell integrazione sistemi i equazioni ifferenziali Cinetica i reazione con intermeio Si consieri una reazione chimica el tipo: A + 2 B C che, segueno un meccanismo a ue step, procee
Applicazioni chimiche ell integrazione sistemi i equazioni ifferenziali Cinetica i reazione con intermeio Si consieri una reazione chimica el tipo: A + 2 B C che, segueno un meccanismo a ue step, procee
ESERCIZI DI ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 2006/2007
 ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
ESERCIZI I ANALISI II Ingegneria Civile e dei Trasporti (M-Z) a.a. 006/007 1 FUNZIONI IN UE VARIABILI (I parte) Insiemi di definizione eterminare gli insiemi di definizione delle seguenti funzioni in due
Esercizi su curvatura e torsione.
 Esercizi su curvatura e torsione. e-mail: maurosaita@tiscalinet.it Versione provvisoria, gennaio 016. 1 Indice 1 Curvatura e torsione 1.1 Curve parametrizzate alla lunghezza d arco................... 1.
Esercizi su curvatura e torsione. e-mail: maurosaita@tiscalinet.it Versione provvisoria, gennaio 016. 1 Indice 1 Curvatura e torsione 1.1 Curve parametrizzate alla lunghezza d arco................... 1.
12 gennaio Commenti esame di geometria - Ing. gestionale - a.a
 Questo documento riporta commenti, approfondimenti o metodi di soluzione alternativi per alcuni esercizi dell esame Ovviamente alcuni esercizi potevano essere risolti utilizzando metodi ancora diversi
Questo documento riporta commenti, approfondimenti o metodi di soluzione alternativi per alcuni esercizi dell esame Ovviamente alcuni esercizi potevano essere risolti utilizzando metodi ancora diversi
7. Equazioni differenziali
 18 Sezione 7. Equazioni differenziali 7. Equazioni differenziali [versione: 25/5/2012] Richiamo delle nozioni fondamentali In un equazione differenziale l incognita da determinare è una funzione (e non
18 Sezione 7. Equazioni differenziali 7. Equazioni differenziali [versione: 25/5/2012] Richiamo delle nozioni fondamentali In un equazione differenziale l incognita da determinare è una funzione (e non
Sistemi differenziali 2 2: esercizi svolti. 1 Sistemi lineari Stabilità nei sistemi lineari
 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Stabilità nei sistemi lineari 14 1 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Gli esercizi contrassegnati con il simbolo * presentano
Sistemi differenziali : esercizi svolti 1 Sistemi lineari Stabilità nei sistemi lineari 14 1 Sistemi differenziali : esercizi svolti 1 Sistemi lineari Gli esercizi contrassegnati con il simbolo * presentano
ε = ε = x TFA A048. Matematica applicata Incontro del 16 aprile 2014, ore 17-19
 TFA A048. Matematica applicata Incontro el 16 aprile 014, ore 17-19 Appunti i iattica ella matematica applicata all economia e alla finanza. Funzioni (i una variabile) utilizzate nello stuio ell Economia
TFA A048. Matematica applicata Incontro el 16 aprile 014, ore 17-19 Appunti i iattica ella matematica applicata all economia e alla finanza. Funzioni (i una variabile) utilizzate nello stuio ell Economia
Esercizi 2: Curve dello spazio Soluzioni
 Esercizi 2: Curve dello spazio Soluzioni. Esercizio Si consideri la curva (elica circolare): a α(t) = a sin t, t R, bt dove a >. a) Calcolare curvatura e torsione di α nel generico punto t. b) Determinare
Esercizi 2: Curve dello spazio Soluzioni. Esercizio Si consideri la curva (elica circolare): a α(t) = a sin t, t R, bt dove a >. a) Calcolare curvatura e torsione di α nel generico punto t. b) Determinare
COGNOME... NOME... Matricola... Corso Prof... Esame di ANALISI MATEMATICA II - 27 Gennaio cos x
 COGNOME... NOME... Matricola... Corso Prof.... Esame di ANALISI MATEMATICA II - 27 Gennaio 25 A ESERCIZIO. 4 punti) Verificare che la serie 7 2 cos x ) n è convergente per ogni x R, e calcolarne la somma.
COGNOME... NOME... Matricola... Corso Prof.... Esame di ANALISI MATEMATICA II - 27 Gennaio 25 A ESERCIZIO. 4 punti) Verificare che la serie 7 2 cos x ) n è convergente per ogni x R, e calcolarne la somma.
PARTICELLA LIBERA IN UNA DIMENSIONE. L equazione di Schrödinger per una particella libera in una dimensione è. t (x) = 2m t.
 4/ PARTICELLA LIBERA 09/0 PARTICELLA LIBERA IN UNA DIMENSIONE L equazione i Schröinger per una particella libera in una imensione è ) i ħ t ψ ˆp t x) = m ψ t x). Poiché Ĥ ) i πħ) exp / ħ px = p m ) i πħ)
4/ PARTICELLA LIBERA 09/0 PARTICELLA LIBERA IN UNA DIMENSIONE L equazione i Schröinger per una particella libera in una imensione è ) i ħ t ψ ˆp t x) = m ψ t x). Poiché Ĥ ) i πħ) exp / ħ px = p m ) i πħ)
Analisi Matematica B Soluzioni prova scritta parziale n. 4
 Analisi Matematica B Soluzioni prova scritta parziale n. 4 Corso di laurea in Fisica, 017-018 4 maggio 018 1. Risolvere il problema di Cauchy { u u sin x = sin(x), u(0) = 1. Svolgimento. Si tratta di una
Analisi Matematica B Soluzioni prova scritta parziale n. 4 Corso di laurea in Fisica, 017-018 4 maggio 018 1. Risolvere il problema di Cauchy { u u sin x = sin(x), u(0) = 1. Svolgimento. Si tratta di una
4.5 Equazioni differenziali lineari del secondo ordine non omogenee 159
 4.5 Equazioni differenziali lineari del secondo ordine non omogenee 159 Una volta stabilito che per ogni funzione continua f l equazione (4.23) è risolubile, ci interessa determinarne l integrale generale.
4.5 Equazioni differenziali lineari del secondo ordine non omogenee 159 Una volta stabilito che per ogni funzione continua f l equazione (4.23) è risolubile, ci interessa determinarne l integrale generale.
SOLUZIONI COMPITO A. Esercizio 1 Utilizzando la formula risolutiva per l equazioni di secondo grado, valida anche in campo complesso, otteniamo:
 SOLUZIONI COMPITO A Esercizio 1 Utilizzando la formula risolutiva per l equazioni di secondo grado, valida anche in campo complesso, otteniamo: z = i + i + i 3 In forma algebrica, otteniamo: = i + 1 +
SOLUZIONI COMPITO A Esercizio 1 Utilizzando la formula risolutiva per l equazioni di secondo grado, valida anche in campo complesso, otteniamo: z = i + i + i 3 In forma algebrica, otteniamo: = i + 1 +
FM1 - Equazioni differenziali e meccanica
 Corso di laurea in Matematica - Anno Accademico 2006/2007 FM1 - Equazioni differenziali e meccanica Prima prova d esonero (03-04-2006) CORREZIONE Esercizio 1. Lo spettro Σ(A) della matrice A si trova risolvendo
Corso di laurea in Matematica - Anno Accademico 2006/2007 FM1 - Equazioni differenziali e meccanica Prima prova d esonero (03-04-2006) CORREZIONE Esercizio 1. Lo spettro Σ(A) della matrice A si trova risolvendo
Test di autovalutazione
 Test i autovalutazione Marco Mougno Corso i laurea in Ingegneria per l Ambiente, le Risorse e il Territorio Facoltà i Ingegneria, Università i Firenze Via S. Marta 3, 5139 Firenze, Italia email: marco.mougno@unifi.it
Test i autovalutazione Marco Mougno Corso i laurea in Ingegneria per l Ambiente, le Risorse e il Territorio Facoltà i Ingegneria, Università i Firenze Via S. Marta 3, 5139 Firenze, Italia email: marco.mougno@unifi.it
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 29 settembre 2012
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9 settembre A) Data la funzione f(x, y) = { xy x se (x, y) (, ) se (x, y) = (, ), i) stabilire se risulta continua
Università degli Studi di Palermo Facoltà di Economia. Dipartimento di Scienze Economiche, Aziendali e Statistiche. Appunti del corso di Matematica
 Università egli Stui i Palermo Facoltà i Economia Dipartimento i Scienze Economice, Azienali e Statistice Appunti el corso i Matematica 08 - Derivate Anno Accaemico 2015/2016 M. Tumminello, V. Lacagnina,
Università egli Stui i Palermo Facoltà i Economia Dipartimento i Scienze Economice, Azienali e Statistice Appunti el corso i Matematica 08 - Derivate Anno Accaemico 2015/2016 M. Tumminello, V. Lacagnina,
19 Marzo Equazioni differenziali.
 19 Marzo 2019 Equazioni differenziali. Definizione 1. Si chiama equazione differenziale una relazione che coinvolge una o più derivate di una funzione incognita y(x), la funzione stessa, funzioni di x
19 Marzo 2019 Equazioni differenziali. Definizione 1. Si chiama equazione differenziale una relazione che coinvolge una o più derivate di una funzione incognita y(x), la funzione stessa, funzioni di x
Complementi di Analisi Matematica. Foglio di esercizi n.6 16/3/2018 (Aggiornamento del 6/4/2018)
 Complementi di Analisi Matematica. Foglio di esercizi n.6 16/3/2018 (Aggiornamento del 6/4/2018) Esercizio 1 Si consideri l insieme Esercizi sulla funzione implicita e superfici Z = {(x, y) R 2 2y xe y
Complementi di Analisi Matematica. Foglio di esercizi n.6 16/3/2018 (Aggiornamento del 6/4/2018) Esercizio 1 Si consideri l insieme Esercizi sulla funzione implicita e superfici Z = {(x, y) R 2 2y xe y
ESERCIZIO n.9. B 7cm H 3cm. b 3cm d 1cm. c 2cm. d d d
 ESERCZO n.9 Data la sezione cava riportata in Figura, eterminare: a) gli assi principali centrali i inerzia; ) l ellisse principale centrale i inerzia; c) il nocciolo centrale i inerzia; ) i momenti i
ESERCZO n.9 Data la sezione cava riportata in Figura, eterminare: a) gli assi principali centrali i inerzia; ) l ellisse principale centrale i inerzia; c) il nocciolo centrale i inerzia; ) i momenti i
Dinamica dei Sistemi Multicorpo Esempi di reti elettriche
 Dinamica ei Sistemi Multicorpo Esempi i reti elettriche Basilio Bona Dipartimento i Automatica e Informatica Politecnico i Torino versione provvisoria: 3 novembre 2003 1 Basilio Bona - Esempi i Sistemi
Dinamica ei Sistemi Multicorpo Esempi i reti elettriche Basilio Bona Dipartimento i Automatica e Informatica Politecnico i Torino versione provvisoria: 3 novembre 2003 1 Basilio Bona - Esempi i Sistemi
{ x + 2y = 3 αx + 2y = 1 αx + y = 0. f(x) = e x 2 +3x+4 x 5. f(x) = x 3 e 7x.
 0 Gennaio 006 Teoria: Definizione di derivata puntuale e suo significato geometrico Esercizio Determinare l equazione del piano contenente i vettori u = (,, 3 e v = (,, e passante per P o = (,, Scrivere
0 Gennaio 006 Teoria: Definizione di derivata puntuale e suo significato geometrico Esercizio Determinare l equazione del piano contenente i vettori u = (,, 3 e v = (,, e passante per P o = (,, Scrivere
CLASSE 5^ A LICEO SCIENTIFICO 27 Aprile 2017 Integrali
 CSSE 5^ ICEO SCIENTIFICO 7 prile 7 Integrali Problema Data la funzione, con, : etermina i coefficienti,, in moo che il punto ; sia un massimo relativo e la retta 36 sia asintoto obliquo; B esegui lo stuio
CSSE 5^ ICEO SCIENTIFICO 7 prile 7 Integrali Problema Data la funzione, con, : etermina i coefficienti,, in moo che il punto ; sia un massimo relativo e la retta 36 sia asintoto obliquo; B esegui lo stuio
appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a autore: Giovanni Alberti
 appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2013-14 autore: Giovanni Alberti Equazioni differenziali [versione: 22-12-2013] Richiamo delle nozioni fondamentali
appunti per il corso di Analisi Matematica I corso di laurea in Ingegneria Gestionale, a.a. 2013-14 autore: Giovanni Alberti Equazioni differenziali [versione: 22-12-2013] Richiamo delle nozioni fondamentali
y 3y + 2y = 1 + x x 2.
 Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 03-04 (dott.ssa Vita Leonessa) Esercizi svolti: Equazioni differenziali ordinarie. Risolvere
Università degli Studi della Basilicata Corsi di Laurea in Chimica / Scienze Geologiche Matematica II A. A. 03-04 (dott.ssa Vita Leonessa) Esercizi svolti: Equazioni differenziali ordinarie. Risolvere
Esercizi svolti di geometria delle aree Alibrandi U., Fuschi P., Pisano A., Sofi A. ESERCIZIO n.6
 ESERCZO n.6 Data la sezione riportata in Figura, eterminare: a) gli assi principali centrali i inerzia; b) l ellisse principale centrale i inerzia; c) il nocciolo centrale i inerzia. 6cm cm A#6 1 1. Determinazione
ESERCZO n.6 Data la sezione riportata in Figura, eterminare: a) gli assi principali centrali i inerzia; b) l ellisse principale centrale i inerzia; c) il nocciolo centrale i inerzia. 6cm cm A#6 1 1. Determinazione
ESERCIZI SULLE EQUAZIONI DIFFERENZIALI
 ESERCIZI SULLE EQUAZIONI DIFFERENZIALI 1. Generalità 1.1. Verifica delle soluzioni. Verificare se le funzioni date sono soluzioni delle equazioni differenziali. xy = 2y, y = 5x 2. y = x 2 + y 2, y = 1
ESERCIZI SULLE EQUAZIONI DIFFERENZIALI 1. Generalità 1.1. Verifica delle soluzioni. Verificare se le funzioni date sono soluzioni delle equazioni differenziali. xy = 2y, y = 5x 2. y = x 2 + y 2, y = 1
Equazioni differenziali
 Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 2 1 / 42 Equazioni differenziali Un equazione
Equazioni differenziali Hynek Kovarik Università di Brescia Analisi Matematica 2 Hynek Kovarik (Università di Brescia) Equazioni differenziali Analisi Matematica 2 1 / 42 Equazioni differenziali Un equazione
Risoluzione del compito n. 2 (Febbraio 2018/2)
 Risoluzione del compito n. 2 (Febbraio 218/2) PROBLEMA 1 Sia esiano Φ(t) (cost, sen t, t 2 ), f(x, y, z) z, g(x, y, z) t 2π ( y + x, y x, x 2 ). z a) Dite se Φ è una curva regolare; scrivete un equazione
Risoluzione del compito n. 2 (Febbraio 218/2) PROBLEMA 1 Sia esiano Φ(t) (cost, sen t, t 2 ), f(x, y, z) z, g(x, y, z) t 2π ( y + x, y x, x 2 ). z a) Dite se Φ è una curva regolare; scrivete un equazione
Equazioni differenziali del 2 ordine Prof. Ettore Limoli. Sommario. Equazione differenziale omogenea a coefficienti costanti
 Equazioni differenziali del 2 ordine Prof. Ettore Limoli Sommario Equazione differenziale omogenea a coefficienti costanti... 1 Equazione omogenea di esempio... 2 Equazione differenziale non omogenea a
Equazioni differenziali del 2 ordine Prof. Ettore Limoli Sommario Equazione differenziale omogenea a coefficienti costanti... 1 Equazione omogenea di esempio... 2 Equazione differenziale non omogenea a
y = cos x y = (y ) 2 + c : giustifichino le due affermazioni. y = y y = y 2 y = y(1 y) y = xy Applicazioni Equazioni delle cinetica chimica:
 Corso di laurea in Chimica Industriale Matematica II A.A. 2015/2016 Argomenti delle lezioni Giovedí 3 marzo - 2 ore. Richiami sulle equazioni e sui metodi utilizzati nel risolverle. Equazioni differenziali.
Corso di laurea in Chimica Industriale Matematica II A.A. 2015/2016 Argomenti delle lezioni Giovedí 3 marzo - 2 ore. Richiami sulle equazioni e sui metodi utilizzati nel risolverle. Equazioni differenziali.
Rette e piani nello spazio
 Rette e piani nello spazio Equazioni parametriche di una retta in R 3 : x(t) = x 0 + at r(t) : y(t) = y 0 + bt t R, parametro z(t) = z 0 + ct ovvero r(t) : X(t) = P 0 + vt, t R}, dove: P 0 = (x 0, y 0,
Rette e piani nello spazio Equazioni parametriche di una retta in R 3 : x(t) = x 0 + at r(t) : y(t) = y 0 + bt t R, parametro z(t) = z 0 + ct ovvero r(t) : X(t) = P 0 + vt, t R}, dove: P 0 = (x 0, y 0,
Curve parametrizzate. Esercizi. 1 Curve parametrizzate con parametri arbitrari. Curvatura. Torsione
 Curve parametrizzate. Esercizi Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria, gennaio 014. 1 1 Curve parametrizzate con parametri arbitrari. Curvatura. Torsione Qui di seguito si riporta
Curve parametrizzate. Esercizi Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria, gennaio 014. 1 1 Curve parametrizzate con parametri arbitrari. Curvatura. Torsione Qui di seguito si riporta
Analisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 2018
 nalisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 218 1) ia data la funzione f(x, y, z) = (x 2 + y 2 1) 2 + 8 a) tudiare l esistenza di massimi e minimi assoluti della funzione f nella
nalisi Matematica II - Ingegneria Meccanica/Energetica - 29 Gennaio 218 1) ia data la funzione f(x, y, z) = (x 2 + y 2 1) 2 + 8 a) tudiare l esistenza di massimi e minimi assoluti della funzione f nella
Analisi Matematica I per Ingegneria Gestionale, a.a Secondo compitino e primo appello, 12 gennaio 2017 Testi 1
 Secondo compitino e primo appello, gennaio 7 Testi Prima parte, gruppo.. Determinare l insieme di definizione della funzione arcsin(e ).. Determinare lo sviluppo di Taylor di ordine 4 (in ) della funzione
Secondo compitino e primo appello, gennaio 7 Testi Prima parte, gruppo.. Determinare l insieme di definizione della funzione arcsin(e ).. Determinare lo sviluppo di Taylor di ordine 4 (in ) della funzione
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica 2 del 19/06/2010 A
 Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9/6/ A ) ata la funzione f(x, y) x y log( + x + y ), a) stabilire dove risulta derivabile parzialmente nel suo
Corso di Laurea in Ingegneria Civile ed Ambientale Prova Scritta di Analisi Matematica del 9/6/ A ) ata la funzione f(x, y) x y log( + x + y ), a) stabilire dove risulta derivabile parzialmente nel suo
1 Equazioni Differenziali
 Equazioni Differenziali Un equazione differenziale è un equazione che esprime un legame tra una variabile indipendente x (o t, quando ci riferiamo al tempo) una variabile dipendente y o incognita che sta
Equazioni Differenziali Un equazione differenziale è un equazione che esprime un legame tra una variabile indipendente x (o t, quando ci riferiamo al tempo) una variabile dipendente y o incognita che sta
Analisi Matematica T-2 Ingegneria Edile Ravenna 2014/15
 Analisi Matematica T- Ingegneria Edile Ravenna 014/15 Maria Manfredini, Daniele Morbidelli Informazioni pratiche: Libro di riferimento: Bramanti, Pagani, Salsa, Analisi MAtematica, Seconda edizione, Zanichelli
Analisi Matematica T- Ingegneria Edile Ravenna 014/15 Maria Manfredini, Daniele Morbidelli Informazioni pratiche: Libro di riferimento: Bramanti, Pagani, Salsa, Analisi MAtematica, Seconda edizione, Zanichelli
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005
 Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Analisi Matematica 2 Ingegneria Gestionale Docenti: B. Rubino e R. Sampalmieri L Aquila, 21 marzo 2005 Prova orale il: Docente: Determinare, se esistono, il massimo ed il minimo assoluto della funzione
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 2 Secondo compito in itinere 30 Giugno 2016
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Giugno 6 Cognome: Nome: Matricola: Es.: 9 punti Es.: 9 punti Es.: 6 punti Es.4: 9 punti Totale. Si consideri
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Secondo compito in itinere Giugno 6 Cognome: Nome: Matricola: Es.: 9 punti Es.: 9 punti Es.: 6 punti Es.4: 9 punti Totale. Si consideri
Gruppo esercizi 1: Vettori e matrici [E.1] Date le due matrici e il vettore
![Gruppo esercizi 1: Vettori e matrici [E.1] Date le due matrici e il vettore Gruppo esercizi 1: Vettori e matrici [E.1] Date le due matrici e il vettore](/thumbs/74/70227812.jpg) Gruppo esercizi 1: Vettori e matrici [E.1] Date le due matrici e il vettore A = 1 2 0 0 2 1 B = 2 1 0 1 0 2 u = (1, 2, 1), 3 2 1 1 1 1 [E.2] Date le due matrici e il vettore A = 1 2 0 0 1 0 0 1 3 B = 1
Gruppo esercizi 1: Vettori e matrici [E.1] Date le due matrici e il vettore A = 1 2 0 0 2 1 B = 2 1 0 1 0 2 u = (1, 2, 1), 3 2 1 1 1 1 [E.2] Date le due matrici e il vettore A = 1 2 0 0 1 0 0 1 3 B = 1
