b) quando la biglia si ferma tutta la sua energia cinetica sara stata trasformata in energia potenziale della molla. Quindi
|
|
|
- Annibale Vaccaro
- 8 anni fa
- Visualizzazioni
Transcript
1 B C:\Didattica\SBAC_Fisica\Esercizi esame\sbac - problemi risolti-18jan2008.doc problema 1 Una biglia di massa m = 2 kg viene lasciata cadere (da ferma) da un'altezza h = 40 cm su di una molla avente una costante elastica k = 1960 N/m e una lunghezza (a riposo) L = 20 cm. Calcolare a) con quale velocita' v la biglia arriva a toccare la molla. b) la distanza dal muro alla quale la biglia si ferma. c) l'energia meccanica della biglia e quella della molla quando il sistema e' fermo. d) l'energia meccanica della biglia e quella della molla quando questa e' a distanza di 13 cm dal muro.. h A Risoluzione L a) quando la biglia tocca la molla avra' acquistato un'energia cinetica pari alla sua energia potenziale iniziale. Quindi, dal principio di conservazione dell'energia meccanica m g h = (1/2) m v 2 ottengo v = 2 g h = 2.80 m/s. b) quando la biglia si ferma tutta la sua energia cinetica sara stata trasformata in energia potenziale della molla. Quindi (1/2) m v 2 = (1/2) k x 2 dove x e' lo spostamento rispetto alla posizione di equilibrio della molla. Risolvendo, ottengo x = 2 g m h / k = 8.95 cm. Quindi, la distanza dal muro alla quale la biglia si ferma e' d = L - x = cm. c) quando la biglia e ferma la sua energia meccanica e zero ed e stata trasferita alla molla sotto forma di energia elastica. Quindi E mecc (biglia) = 0 E elast (molla) = m g h = 7.85 J d) quando la biglia si trova a distanza di 13 cm dal muro, e' ancora in movimento (si ferma a distanza di cm, vedi punto b), quindi solo parte della sua energia cinetica iniziale e' stata trasferita alla molla. La molla avra subito una compressione di x = L - 13cm = 7cm = 0.07 m Quindi la sua energia elastica sara' E elast (molla) = (1/2) k x 2 = 4.80 J Applicando il principio di conservazione dell'energia meccanica E ini =E fin, dove E ini = m g h E fin = E mecc (biglia) + E elast (molla) ottengo E mecc (biglia) = E fin - E elast (molla) = = 3.05 J 1
2 problema 2 Un blocco di ghiaccio di massa m=10 kg si trova inizialmente alla tempertura T= -50 o C in un contenitore aperto alla pressione atmosferica. Se il blocco viene scaldato con una sorgente di calore che eroga una potenza di P=1000 watt, quanto tempo sara' necessario per a) raggiungere la temperatura di 50 o C b) far evaporare tutto il liquido c) raggiungere la temperatura di 150 o C. d) quale sara' lo stato del sistema se il calore complessivamente cedutogli e' pari a Q tot =2x10 6 J dati: calore specifico del ghiaccio c ghi = 2090 J kg -1 o K -1 calore specifico dell'acqua c H20 = 4186 J kg -1 o K -1 calore specifico del vapore acqueo c vap = 2010 J kg -1 o K -1 calore latente di fusione del ghiaccio c fus = 3.33x10 5 J kg -1 calore latente di vaporizzazione dell'acqua c evap = 2.26x10 6 J kg -1 Risoluzione innanzitutto calcolo il calore necessario per le varie trasformazioni: Q1 (-50 a 0 o C) = c ghi m T = 1.045x10 6 J Q2 (fusione da 0 o C a 0 o C) = c fus m = 3.330x10 6 J Q3 (0 a 50 o C) = c H20 m T = 2.093x10 6 J Q4 (50 a 100 o C) = c H20 m T = 2.093x10 6 J Q5 (evaporazione da 100 o C a 100 o C) = c evap m = 2.260x10 7 J Q6 (100 a 150 o C) = c vap m T = 1.005x10 6 J a) per raggiungere i 50 o C occorre fornire il calore Q a =Q1+Q2+Q3=6.468x10 6 J. Il tempo necessario sara' quindi t a =Q a / P = 6.468x10 6 / 1000 J/W = 6468 s = 1.80 h. b) per far evaporare tutto il liquido occorre fornire il calore Q b =Q1+Q2+Q3+Q4+Q5=3.116x10 7 J. Il tempo necessario sara' quindi t b =Q b / P = 3.116x10 7 / 1000 J/W = s = 8.66 h c) per raggiungere i 150 o C occorre fornire il calore Q c =Q1+Q2+Q3+Q4+Q5+Q6=3.217x10 7 J. Il tempo necessario sara' quindi t c =Q c / P = 3.217x10 7 x10 7 / 1000 J/W = s = 8.93 h d) Il calore Q tot =2x10 6 J viene in parte utilizzato per scaldare il ghiaccio da -50 a 0 o C e in parte per scioglierlo. Quindi il calore disponibile per la fusione e' Q fus = Q tot - Q1 = 9.55x10 5 J. Questo calore servira' per fondere solo una parte del blocco, la cui massa m' e' pari a m' = Q fus / c fus = 9.55x10 5 J / 3.33x10 5 J = 2.87 kg. Il resto del blocco, ovvero = 7.13 kg, rimarra' sotto forma di ghiaccio. 2
3 problema 3 Una macchina fotografica utilizza un obiettivo con lunghezza focale F=50mm e apertura massima con diametro D=20 mm. La macchina viene utilizzata per fotografare da una distanza p=3 m un quadro divisionista di lunghezza L=1.20 m e altezza H=0.8 m, composto da puntini di colore rosso e verde distanti tra loro d=2 mm. Calcolare a) le dimensioni del quadro sul piano della p pellicola. b) la distanza fra i puntini sul piano della pellicola. c) le dimensioni dei puntini sul piano della L obj pellicola supponendo che la luce abbia una lunghezza d onda λ=0.5 µm. d) se la macchina e' utilizzata alla sua massima apertura (D=20mm), e' possibile distinguere i puntini sul piano della pellicola? e) quale e' l'apertura alla quale i puntini si sovrappongono? che colore avranno? q L imm Risoluzione a) Applicando la legge delle lenti, e sapendo che p=3m, posso trovare la distanza q tra la lente e la pellicola (1/p) + 1/q) = 1/F da cui trovo q = F p / (p - F) = mm. Quindi, sul piano della pellicola, l'immagine del quadro sara' ridotta di un fattore M=q/p=1.70x10-2.e avra' dimensioni L imm = L M = mm H imm = H M = mm b) La distanza d=2mm tra i puntini sara' ridotta dello stesso fattore M, e sara' d imm = d M = mm = µm c) Le dimensione dei puntini sono determinate dalla diffrazione della lente che ha un diametro D. Dalla legge della diffrazione, supponendo che la luce visibile ha una lunghezza d'onda λ=0.5 µm, la "dimensione" δ del singolo puntino e' δ ~ (λ / D ) q = 1.27 µm Quindi essendo δ < d imm i puntini sono risolti e i puntini rossi si vedono separati da quelli verdi. d) per far sovrapporre i puntini deve risultare δ > d imm, quindi D < λ q / d imm = 0.75 mm. 3
4 problema 4 Blaise Pascal fece una copia del barometro di Torricelli utilizzando del vino rosso di Bordeaux come liquido. La densita' del vino era x 10 3 kg/m 3 e la pressione atmosferica P 0 =1atm. Pascal ripete' l'esperimento due volte. La prima riusci' ad ottenere un vuoto perfetto sopra la colonna di vino, ma la seconda volta (forse un po' offuscato dal Bordeaux) fece untrare un po' di aria e la pressione residua fu pari a P 0 /3. Calcolare l'altezza h della colonna nei due casi. Risoluzione sia ρ =0.984 x 10 3 kg/m 3 la densita' del vino e P 0 =1atm = 1.013x10 5 N/m 2 la pressione atmosferica. Per la legge di Stevino: a) P 0 = ρ g h da cui h = P 0 / ρ g = m b) P 0 = ρ g h + P 0 /3 da cui h = (2/3)P 0 / ρ g = 7.00 m 4
5 problema 5 Una navetta viene lanciata con velocita' v 0 =20 m/s dalla prima gobba delle montagne russe che si trova ad una altezza h=20 m dal suolo. Se la rotaia e' priva di attrito, calcolare a) con quale velocita' arriva nel punto A b) con quale velocita' arriva nel punto B c) con quale velocita' arriva nel punto C d) a quale altezza H si ferma nel punto D D H Poiche' siamo in assenza di attrito, si puo' applicare il principio di conservazione dell'energia meccanica. L'energia meccanica iniziale E 0 e' data da E 0 =K 0 + U 0 = (1/2) m (v 0 ) 2 + m g h a) L'energia meccanica nel punto A e data da E A =K A + U A = (1/2) m (v A ) 2 + m g h A Applicando il principio di conservazione dell'energia meccanica E 0 =E A, poiche' h A =h, risulta v A = v 0 = 20 m/s b) L'energia meccanica nel punto B e data da E B =K B + U B = (1/2) m (v B ) 2 + m g h B Imponendo E 0 =E B, poiche' h B =h/2, risulta (v B ) 2 = (v 0 ) 2 +g h... da cui v B = m/s c) L'energia meccanica nel punto C e data da E C =K C + U C = (1/2) m (v C ) Imponendo E 0 =E C, ottengo (v C ) 2 = (v 0 ) 2 +2 g h da cui v C = m/s d) L'energia meccanica nel punto D e data da E D =K D + U D = 0 + m g H. Imponendo E 0 =E C, ottengo (1/2) m (v 0 ) 2 + m g h = m g H da cui ricavo H = h + (v 0 ) 2 / 2 g che corrisponde a H= 20 m m = m. 5
6 problema 6 Una sfera cava di ferro di massa 10 kg viene immersa in una vasca di acqua. Calcolare quanto deve essere il diametro della sfera affiche' la stessa non affondi (trascurando lo spessore della sfera) Se ripetete lo stesso esperimento sulla luna, sulla cui superficie la forza di gravita' e' circa 1/6 di quello sulla terra, trovereste lo stesso risultato? Se ripetete lo stesso esperimento con il mercurio al posto dell'acqua, cosa accade? dati: densita' dell'acqua ρ 0 = 1 g/cm 3 densita' del ferro ρ 1 = 7.9 g/cm 3 densita' del mercurio ρ 1 = 13.6 g/cm 3 La condizione di galleggiamento per la sfera e' che la sua densita' (media) sia minore o eguale a quella dell'acqua, poiché in questo caso la forza di gravita' che la spinge verso il basso e' controbilanciata dalla spinta di Archimede. La densita' della sfera cava (trascurando il peso dell'aria al suo interno) e' data dalla sua massa m diviso il suo volume v, ovvero ρ sfera = m (4 / 3) π r Uguagliando ρ 0 = ρ sfera =, posso ricavare r da cui risulta 3 r m 3 = ρ0 4 π 3. Numericamente r = 0.13 m, che corrisponde ad un diametro d = cm. b) basta osservare che il risultato non dipende da g. Quindi sulla luna il diametro della sfera sara' lo stesso. c) Il mercurio ha una densità' maggiore di quella del ferro di cui e' fatta la sfera. Quindi non e' necessario fare una sfera cava, anche una sfera di ferro piena galleggerà' sempre! 6
7 problema 7 Una imbarcazione a forma di parallelepipedo con la base S=5 m 2 e un altezza di H=1.80 m viene usata per traportare persone dall Africa alla Sicilia. Sapendo che mediamente una persona ha una massa m=60 kg e una densita di 1.05x10 3 kg/m 3, e che l imbarcazione ha una massa M=1300 kg, calcolare h a) il numero massimo di persone in modo da garantire un livello di sicurezza h=50 cm. b) Se a bordo ci sono 95 persone e si apre una falla che lascia entrare acqua ad una velocita di 0.5 litri/s, quanto tempo passera prima che l imabarcazione affondi? c) Sapendo che a bordo ci sono (pochi) salvagenti di volume v 0 =0.02 m 3, quante persone potranno salvarsi aggrappandosi a ciascun salvagente? d) Se ripetete la stessa traversata su un pianeta dove la forza di gravita' e' il doppio di quella sulla terra, trovereste lo stesso risultato? H a) La forza di archimede F A = v ρ g dipende dal volume di liquido spostato v che in questo caso e v = S (H-h)= 5 x 1.30 = 6.5 m 3. La forza F A deve controbilanciare la forza peso P = (M+Nm) g, da cui S (H-h) ρ g =(M+Nm) g Che risolta per N da vρ M N = = 86.7 persone m b) in questo caso h=0, V=SH e F A = V ρ g. La forza peso e invece P= (M+Nm+m H2O ). Uguagliando e risolvendo per m H2O, ottengo m H 2O = Vρ M Nm =2100 kg. Poiche la falla lascia entrare 0.5litri/s = 0.5kg/s, il tempo rimasto e 4200 s = 1.17 ore. c) la condizione di galleggiamento e che la densita media del salvagente + K persone sia uguale a quella dell acqua. I volume medio di una persona e v p = m/ρ p = m 3. La densita media del salvagente+ persone (trascurando la massa del salvagente), e ρ ave = (Km) / [v 0 + K v p ] ponendo ρ ave = ρ, e risolvendo per K, otteniamo v0ρ K = = 7persone v ( ρ ρ) p p a) basta osservare che il risultato non dipende da g. Quindi i risultati non cambiaranno e la tragedia si consumerebbe allo stesso modo. 7
8 problema 8 Il blocchetti A e B della figura hanno masse M A =10 Kg e M B =250 Kg. Il coefficiente di attrito statico µ s tre il blocchetto B e la superficie del tavolo e' µ s =0.2. Supponendo che la corda attaccata a B sia orizzontale, a) trovare il valore della tensione T della corda e della forza di attrito. b) trovare il valore massimo M A della massa del blocchetto A per cui il sistema e' in equilibrio. a) quando il sistema e' in equilbrio, la somma delle forze agenti sul punto di unione dei tre pezzi di corda deve essere nulla. Quindi, indicando con θ l'angolo di 30 gradi indicato in figura e con f att la forza di attrito sul blocchetto B, la condizione di equilibrio si scrive come asse y asse x T sin (θ) = g M A T cos (θ) = f att che corrisponde ad un sitema di due equazioni nelle dure incognite T e f att. Risolvendo ricavo f att = g M A [cos (θ) / sin (θ)] = N T = g M A / sin (θ) = N b) la forza massima di attrito esercitabile dal blocchetto B e' data da f max = µ s g M B = N. Quindi il valore massimo di M A per cui il sistema rimane in equilibrio si trova imponendo che f att = f max g M A [cos (θ) / sin (θ)] = µ s g M B che risolta rispetto a M A da' il risultato M A = µ s M B [sin (θ) / cos (θ)] = 28.9 kg. 8
9 problema 9 Un mongolfiera di diametro 20 m e' riempita con aria ad una temperatura T maggiore di quella ambiente T A =25 C. Sapendo che la massa della mongolfiera (cestello+pallone+corde+equipaggio) e' m=200 kg e che la densita' dell'aria a temperatura ambiente e' ρ A = 1.25 kg/m 3, a) quale deve essere la densita' dell'aria calda ρ perche' la mongolfiera si sollevi? b) A che temperatura deve essere l'aria interna al pallone della mongolfiera (usare la legge dei gas pefetti) c) Quanto calore Q bisogna fornire per raggiungere tale temperatura (calore specifico dell'aria c= J kg -1 C -1 ) a) Il volume del pallone e' V= (4/3) π r 3. Quindi V= m 3. La spinta di Archimede e' rivolta verso l'alto e e' data dal peso del volume del liquido spostato, quindi F Arch = M A g = ρ A V g dove per M A si intende la massa dell'aria spostata, cioe' quella a temperatura Ambiente. La forza di gravita' spinge verso il basso e agisce sia sull'aria calda che sulla zavorra. Quindi Fg = (M T + m) g = (ρ V + m) g dove per M T si intende la massa dell'aria calda che ha densita' ρ. Uguagliando, si ottiene ρ = ρ A - m/v che numericamente corrisponde a ρ = = 1.20 kg/m 3. b) Innanzitutto supponiamo che il volume del pallone non cambi e che la pressione dell'aria al suo interno rimanga sempre uguale a quella dell'aria esterna. Quindi, scaldando la temperatura interna, parte dell'aria calda uscira' all'esterno e la sua densita' diminuira'. Usando l'equazione di stato dei gas perfetti, se pressione e volume rimangono costanti al variare di T, l'unica variabile che puo' cambiare e' in numero di moli, ovvero la quantita' di aria contenuta del pallone. La densita' dell'aria scalera' quindi come ρ = ρ A (T A / T) Sostituendo ρ Α = 1.25 kg/m 3, ρ = 1.20 kg/m 3 e T A = K., si trova che T = K, ovvero T=37.42 C. c) La variazione di temperatura dell'aria e' T = = C. La sua massa e' M = ρ A V = kg. Quindi bisognera' fornire una quantita' di calore Q pari a Q= c M T = J kg -1 C kg C = 6.53 x 10 7 J 9
10 problema 10 Una pallina di massa m=4 kg viene lanciata in aria con una velocita' iniziale v 0 =15 m/s ad un angolo θ 0 =30 gradi. Calcolare a) L'altezza massima H raggiunta b) dopo quanto tempo ricade al terra c) La gittata R (distanza percorsa lungo l'asse x al momento della ricaduta. d) con quale velocita' ricade e) quale velocita' ha nel punto di massima altezza f) l'energia cinetica nel punto di massima altezza g) l'energia potenziale nel punto di massima altezza Innanzitutto considero indipendentemente I due moti lungo l asse x (moto rettilineo uniforme) e l asse y (moto uniformemente accelerato). Le rispettive velocita iniziali sono: v 0x = v 0 cosθ 0 = m/s v 0y = v 0 senθ 0 = 7.50 m/s a) L altezza H raggiunta puo essere trovata applicando il principio di conservazione dell energia meccanica per il moto lungo l asse y. Quindi m g h = (1/2) m v 2 2 (v 0y ) da cui ottengo H = = 2.87 m. 2g b) il tempo necessario a raggiungere tale altezza e dato dalla legge per la velocita in un moto uniformemente accelerato, ovvero v(t) = v 0y g t Poinche nel punto di massima altezza ho v(t)=0, ottengo t H =v 0y /g = 0.76 s. ovviamente il tempo necessario a ricadere e il doppio di quello per raggiungere H, quindi t R = 1.53 s. c) per tutto il moto parabolico, la pallina si muove lungo l asse x con velocita costante data da v 0x. Quindi al momento in cui ricade avra percorso tratto di strada dato da R = v 0x t R = m. d) ovviamente ricade con lo stesso modulo della velocita iniziale, ovvero v 0 =15 m/s, ma le cui componenti saranno (v x ) fin = (v 0x ) = m/s (v y ) fin = -(v 0y ) = m/s. Notare il cambio di segno nella componente y! e) la velocita alla massima altezza e data solo dalla componente x, cioe v H = (v 0x ) = m/s. f) l energia cinetica nel punto di massima altezza e (E cin ) H = (1/2)m(v H ) 2 = J g) l energia potenziale nel punto di massima altezza e (E pot ) H = m g H = J 10
11 problema 11 Un blocco di massa m = 5 kg viene lanciato lungo una pista orizzontale ad una velocita' v 0 = 16 m/s. La pista e' priva di attrito fino a quando il blocco raggiunge un livello piu' elevato di altezza h A = 3.5 m. A quel punto la pista presenta un coefficiente di attrito dinamico µ k = 0.4. Calcolare A a) con quale velocita' il blocco arriva nel punto A b) la distanza d percorsa c) l'energia meccanica del blocco nel punto A d) l'energia meccanica del blocco dopo che si e' fermato e) la velocita' v 0 minima affinche' il blocco arrivi nel punto A Poiche' nel tratto di strada fino al punto A, siamo in assenza di attrito, si puo' applicare il principio di conservazione dell'energia meccanica. Prendendo come quota di riferimento (U=0) quella iniziale del blocco, l''energia meccanica iniziale E 0 e' data solo dall'energia cinetica E 0 =K 0 + U 0 = (1/2) m (v 0 ) 2 = 640 J a) L'energia meccanica nel punto A e data da E A =K A + U A = (1/2) m (v A ) 2 + m g h A Applicando il principio di conservazione dell'energia meccanica (E 0 =E A ), si ha (1/2) m (v 0 ) 2 = (1/2) m (v A ) 2 + m g h A da cui (v A ) 2 = (v 0 ) 2-2 g h... Sapendo che h A = 3.5 m, si ottiene v A = m/s b) L'energia cinetica del corpo nel punto A viene dissipata tutta in calore a causa del lavoro (negativo) svolto dalla forza di attrito sul corpo in movimento. La forza di attrito e' f = µ N = µ m g e il lavoro e' dato da L attr = f d = µ m g d Quindi imponendo E A = L attr otteniamo (1/2) m (v A ) 2 = µ m g d che risolta per d da come risultato d = (v A ) 2 / (2 µ g ) da cui d = m c) L'energia meccanica del corpo nel punto A e' uguale a quella iniziale, quindi E A = 640 J d) L'energia meccanica del corpo dopo che si e' fermato e' solo quella potenziale, quindi E A = U A = m g h = J e) Affiche' il corpo arrivi in A (con velocita' nulla) la sua energia cinetica iniziale K 0 =(1/2) m (v 0 ) 2 deve essere sufficiente a fargli guadagnare un'energia potenziale U A =m g h. Quindi, imponendo (1/2) m (v 0 ) 2 > m g h trovo la condizione v 0 2 > 2 g h, che implica v 0 > 8.29 m/s. 11
12 problema 12 un blocco di massa m = 5 kg viene lanciato su di un piano inclinato (θ =30 o ) ad una velocita' iniziale v 0 = 8 m/s. In assenza di attrito calcolare: a) la distanza d percorsa b) la variazione dell'energia cinetica e potenziale del blocco al momento in cui si ferma. c) dopo quanto tempo il blocco ritorna al punto di partenza. OPZIONALE: Rispondere alle stesse domande a), b), c) nel caso in cui tra la superficie del piano e il blocco agisca un forza di attrito dinamico il cui coefficiente e' µ=0.12. Si indichino con i pedici 1 e 2 le posizioni iniziale e finale del blocchetto. L'energia meccanica nelle due posizioni e' E 1 =K 1 + U 1 = (1/2) m (v 0 ) posizione iniziale E 2 =K 2 + U 1 = 0 + m g h posizione finale a) -senza attrito. Applicando il principio di conservazione dell'energia meccanica E 1 =E 2, da cui v 0 d θ h = (v 0 ) 2 / 2 g = 3.26 m che trasformato in d [h = d sin(θ)] diviene d = 6.52 m b) -senza attrito. K = K 2 - K 1 = 0 - (1/2) m (v 0 ) 2 = -160 J U = U 2 - U 1 = m g h - 0 = 160 J notare che K+ U = 0 (conservazione E mecc ) c) -senza attrito. L'accelerazione cui e' sottoposto il blocco e' a = -g sin(θ) = m / s 2. (il segno - indica che a e' diretta in verso opposto a v 0 ). Dall'equazione per la velocita' del moto unif. de-celerato ( v = v 0 + a t), ponendo v=0, trovo t = v 0 / a = 1.63 s che corrisponde al tempo di sola andata. Per tornare al punto di partenza inpieghera' quindi t tot = 3.26 s. a') con attrito La forza di attrito e' f k = µ k N dove N=mg cos(θ) e la forza Normale. Quindi f k = µ k m g cos(θ). Il lavoro, ovvero l'energia dissipata per attrito e' L k = f k d = f k [h' / sin(θ)] = µ k m g h' [cos(θ) / sin(θ)] dove h' rappresenta la nuova altezza raggiunta. Applicando il principio di conservazione dell'energia meccanica e tenendo conto dell'energia dissipata in calore a causa dell'attrito E 1 - L k = E 2, (v ) 2 0 / 2g da cui ricavo h' = = 2.42 m che tradotto in d' = h' / sin(θ), da' il risultato d' = 4.84 m cos( θ) 1 + µ k sin( θ) b') con attrito K = K 2 - K 1 = 0 - (1/2) m (v 0 ) 2 = -160 J U = U 2 - U 1 = m g h' - 0 = J notare che K+ U 0 e che K = U + L k. c') con attrito L'accelerazione in salita e' a' = a - f k / m = -g [sin(θ) + µ k cos(θ)] = m/s 2. Quindi il tempo di andata e' t' = v 0 / a' = 1.21 s Per il viaggio di ritorno l' accelerazione e' diversa, a'' = g [sin(θ) - µ k cos(θ)] = m / s 2.In questo caso applico la legge d =(1/2) a''t 2, quindi t''=(2 d )/ a'' = 1.74 s. Complessivamente il tempo di andata e ritorno e t'+ t''= 2.95 s. 12
13 problema 13 Un blocco di massa m = 15 kg viene trascinato da una fune che forma un angolo θ=45 gradi rispetto al piano orizzontale ed esercita una tensione T = 180 N. Trascurando l'attrito, T a) descrivere il moto del blocco e calcolare la sua accelerazione b) calcolare la forza normale esercitata dal piano sul blocco c) cosa accade se la tensione della fune rimane la stessa, ma l'angolo diventa θ=60 gradi? f µ m θ Rispondere alle stesse domande nel caso in cui sia presente l'attrito con coeff. di attrito dinamico µ=0.20. (senza attrito) Applicando la II legge della dinamica lungo i due assi cartesiani, posso scrivere T cosθ = ma x T sinθ +N = mg asse x asse y da cui ottengo (nota: per θ = 45 gradi, cosθ = sinθ = 0.71) a, b) -senza attrito. a x = T cosθ / m = 180x 0.71 / 15 = 8.49 m/s 2 N = mg- T sinθ =15x x0.71= N c) -senza attrito. In questo caso, se usassi la formula di sopra, otterrei un valore negativo per la forza N, il che e' un assurdo. Questo vuol dire che la componente verticale della tensione diviene maggiore della forza peso e il blocco "decolla" accelerando verso l'alto! Infatti per θ=60 gradi sinθ =.0.87 e T sinθ > mg (180x0.87 = N > 15x9.81= N). Dunque in questo caso non esite forza nomale, esiste accelerazione lungo y e le equazioni del moto diventano T cosθ = ma x asse x T sinθ - mg = ma y asse y da cui a y = T sinθ /m g = 0.63 m/s 2. Ovviamente per a x vale la stessa equazione di sopra, per cui a x = T cosθ / m = 6.00 m/s 2. (con attrito) Applicando la II legge della dinamica nel caso T sinθ mg >0 (ovvero quando θ=45 ), T cosθ - µn = ma x T sinθ +N = mg asse x asse y risolvendo la seconda equazione trovo N = mg- T sinθ (che e' uguale al caso senza attrito) e inroducendola nella prima ricavo a x. a x = (T/m) [ cosθ - µ sinθ ] + µg = 5.88 m/s 2. se invece T sinθ mg <0 (ovvero quando θ=60 ), il blocco si solleva, non esiste ne N ne forza di attrito e tutto e come nel caso c) 13
14 problema 14 Un manometro a tubo aperto e' uno strumento che serve per misurare la pressione P di un gas contenuto all'interno di un serbatoio. Il manometro e' costituito da un tubo ad U contenete un liquido di densita' ρ. Un'estremita' del tubo e' collegata al serbatoio e l'altra e' aperta in atmosfera alla pressione P 0. Supponendo che il liquido sia mercurio (ρ = 13.6 g/cm 3 ) e che sia P 0 = 1 atm, calcolare a) l'altezza h nel caso in cui p=2.5 atm b) la pressione P nel caso in cui h = 0 c) Cosa accade se P=0.5 atm? Quanto vale h in questo caso? d) Supponiamo che inizialmente il gas abbia una pressione p=p 0 e si trovi a temperatura ambiente (t A =25 o C). Cosa accade se riscaldo il gas fino ad una temperatura di 100 o C? Quanto sara' h? (trascurare il volume del gas nel tubo). Risoluzione a) La pressione P all'interno del tubo e' maggiore della pressione atmosferica, quindi il liquido viene spinto verso l'alto fino ad un'altezza h tale da soddisfare la legge di Stevino da cui P = P 0 + ρ g h h = (P - P 0 ) / ρ g sapendo che 1atm = 1.013x10 5 N/m 2, g=9.81 m/s 2, ρ = 13.6x10 3 Kg/m 3, si ricava h = 1.14 m b) nel caso in cui h=0, chiaramente P=P 0. c) in questo caso P<P 0., quindi il livello del liquido nel ramo di destra del tubo sara' inferiore a quello di sinistra. Applicando sempre Stevino troviamo h = (P - P 0 ) / ρ g = m d) quando scaldo il gas, poiche' il suo volume e' costante, la pressione del gas aumentera'. Applicando la I legge di Gay-Lussac, si puo' ricavare la pressione P alla temperatura (assoluta) T data da P / T = P 0 / T A Sapendo che T A = o K, T= o K, si ottiene che P=1.25 P 0 = 1.27x10 5 Pascal. Applicando nuovamente Stevino, h = (P - P 0 ) / ρ g = 0.21 m 14
15 problema 15 1) Un carrello da montagne russe di massa m=500kg viene lanciato dal punto 1 posto ad una altezza h 1 =35m con velocita iniziale v 1 =3m/s. Supponendo che non ci sia attrito, calcolare a) le velocita nei punti 2, 3, 4. b) Le energie cinetiche nei punti 1,2,3,4 c) Le energie potenziali nei punti 1,2,3,4 d) Discutere qualitativamente cosa accade in presenza di attrito. e) Se la forza di attrito media e 1/10 del peso del carrello e la lunghezza della rotatia e d = 250m, con quale velocita il carrello arriva nel punto 4? Poiche' siamo in assenza di attrito, si puo' applicare il principio di conservazione dell'energia meccanica. L'energia meccanica iniziale E 1 e' data da v 1 E 1 =K 1 + U 1 = (1/2) m (v 1 ) 2 + m g h 1 = 1.74x10 5 J dove v 1 =3m/s e h 1 =35m rappresenta l altezza della posizione 1 rispetto a quella della posizione 2 (che prendiamo come riferimento di energia potenziale =0). a) L'energia meccanica nel punto 2, poiche h 2 =0, e data da E 2 =K 2 = (1/2) m (v 2 ) 2. Applicando il principio di conservazione dell'energia meccanica (E 1 =E 2,) si ha (1/2) m (v 1 ) 2 + m g h 1 = (1/2) m (v 2 ) 2 da cui (v 2 ) 2 = (v 1 ) 2 +2 g h 1 v 2 = m/s (1/2) m (v 1 ) 2 + m g h 1 = (1/2) m (v 3 ) 2 + m g h 3 da cui (v 3 ) 2 = (v 1 ) 2 +2 g (h 1 -h 3 ) v 3 = m/s (1/2) m (v 1 ) 2 + m g h 1 = (1/2) m (v 4 ) 2 + m g h 4 da cui (v 4 ) 2 = (v 1 ) 2 +2 g (h 1 -h 4 ) v 3 = m/s b) L'energia cinetica del carrello e data da K = (1/2) m (v) 2. Quindi nei vari punti risulta K 1 = (1/2) m (v 1 ) 2 = 2.25x10 3 J K 2 = (1/2) m (v 2 ) 2 = 1.74x10 5 J K 3 = (1/2) m (v 3 ) 2 = 3.66x10 4 J K 4 = (1/2) m (v 4 ) 2 = 1.00x10 5 J c) L'energia potenziale del carrello e data da U = m g h. Quindi nei vari punti risulta U 1 = m g h 1 = 1.72x10 5 J U 2 = m g h 2 = 0 J U 3 = m g h 3 = 1.37x10 5 J U 4 = m g h 4 = 7.36x10 4 J d) In presenza di attrito l energia meccanica non si conserva, ma in parte viene dissipata in calore. Di conseguenza, nei punti 2,3,4, il carrello avra energie cinetiche (e quindi velocita ) minori rispetto a quelle trovate nei casi a) e b). A seconda della forza di attrito e della distanza percorsa, potra capitare che il carrello non avra energia sufficiente a raggiungere il punto 3. In questo caso, il carrello oscillera nell avvallamento tra i punti 1 e 3, fino a fermarsi nel punto 2. e) Il lavoro compiuto dalla forza di attrito lungo il tragitto di d=250m sara dato da L att = F attr d = (mg/10) d = 1.23x10 5 J. Quindi l energia del carrello nel punto 4, sara E 4 = K 4 + U 4 = E 1.- L att = 1.74x x10 5 = 5.10 x10 4 J. Poiche tale energia e inferiore a quella potenziale U 4, se ne deduce che il carrello propbabilmente non arrivera al punto 4. Per essere certi di cio occorre sapere quanta strada ha percorso fino al punto 3, e controllare che in questo punto la sua energia residua sia maggiore dell energia potenziale del punto 3. 15
16 problema 16 Un pallone riempito di elio viene utilizzato per sollevare un carico di massa m carico =200Kg. Trascurando la massa del pallone vuoto e sapendo che le densita dell elio e ρ He =0.18 kg/m 3 mentre quella dell aria (sulla superficie terrstre) e ρ aria =1.29 kg/m 3, calcolare a) il diametro d del pallone affinche; questo inizi a sollevarsi. b) L accelerazione iniziale con cui sale se V=300m 3. c) L altezza massima al quale il pallore arriva sapendo che la densita dell aria diminuisce secondo la legge ρ(h)=1.29*(h/1000). [si usi il sistema mks]. a) Il volume del pallone e' La spinta di Archimede e' rivolta verso l'alto e e' data dal peso del volume delfluido (aria) spostato, quindi F( ) = F Arch = m aria g = ρ aria V g Dove V e il volume del pallone. La forza di gravita' spinge verso il basso e agisce sia sull'elio all interno del pallone che sul carico. Quindi F( ) = (m He + m c ) g = (ρ He V + m c ) g Uguagliando, si ottiene V = m c / ( ρ A - ρ He ) che numericamente corrisponde a V=180.2 m 3. Quindi, il diametro d del pallone e ricavabile dalla formula V= (4/3) π r 3, da cui d=7.01 m (d=2 r) b) In questo caso la spinta di archimede e maggiore del totale della forza peso e quindi la forza risultante verso l alto sara F( ) = (ρ aria -ρ He )V g- m c g Che numericamente corrisponde a Finire!!! 16
17 problema 17 Una comune tazza di vetro contiene V=200 cm 3 di liquido e ha una massa M=150g. Del te, che inizialmente e alla temperatura T 0 =95 o C, viene versato nella tazza e lasciato raffreddare. b) Supponendo che la temperatura iniziale della tazza sia quella ambiente (T A = o 25C) e che non ci sia dispersione di calore all esterno, quale sara le temperatura finale T f di tazza e te? c) Per raffreddare piu velocemente il te, viene messo nella tazza un cubetto di ghiaccio di massa m=20g a temperatura T 1 =0 o C. Quale sara la temperatura finale in questo caso? Dati: densita del te ρ te = 1 g/cm 3 calore specifico del te c te =4186 J Kg -1 o K -1 calore specifico del vetro c ve =840 J Kg -1 o K -1 calore latente di fusione del ghiaccio c fus =3.33x10 5 J/kg La massa di te versata nella tazza e data da m te = ρ te V = 1 (g/cm 3 ) 200 cm 3 = 200 g = 0.2 kg dove si e supposto che la densita del te sia uguale a quella dell acqua. a) Quando si versa il te, poiche quest ultimo e piu caldo della tazza, si avra un traferimento di calore dal te alla tazza; possiamo quindi scrivere che il te cedera una quantita di calore Q te data da Q te = c te m te (T 0 T f ) mentre la tazza acquistera una quantita di calore Q ve data da Q ve = c ve M (T f T A ) Nell ipotesi che non ci sia dispersione di calore, Q te = Q ve, quindi possiamo scrivere c te m te (T 0 T f ) = c ve M (T f T A ) da cui, risovendo rispetto a T f, otteniamo T f c = te m tet c m te 0 te + cvemt + c M ve A Inserendo i dati (espressi nel sistema MKS), otteniamo Tf = o C. Notare che in questa formula, essendo Tf una media pesata di T 0 e T A, e indifferente usare i gradi Celsius o Kelvin. b) In questo caso il calore ceduto dal te ( Q te ) servira per tre scopi: 1) far fondere il cubetto di ghiaccio di massa m=0.020 Kg. Tale calore Q 1 e dato da Q 1 (fusione da 0 o C a 0 o C) = c fus m = 3.33x10 5 (J/Kg) x (Kg) = 6.66 x10 3 J 2) elevare la temperatura del cubetto da 0 o C al suo valore finale. Questo richiede una quantita di calore Q 2 = c te m (T f 0) = c te m T f 3) elevare la temperatura della tazza di vetro, che richiede (come sopra riportato) Q ve. Quindi, se non c e dispersione, Q te = Q 1 + Q 2 + Q ve, il che implica c te m te (T 0 T f ) = c fus m + c te m T f + c ve M (T f T A ) risovendo rispetto a T f, otteniamo sostituendo, otteniamo T f = o C. T f c = te m c te T0 + cvem TA cfus m m + c M + c m te te ve te 17
18 problema 18 Un blocchetto di massa m = 5 kg viene lasciato cadere (da fermo) da un'altezza h = 4 m lungo un binario che presenta un tratto orizzontale di lunghezza d=2.2m. In fondo a tale tratto il blocchetto rimbaza indietro elasticamente e inverte la sua velocita senza cambiare la sua energia cinetica. Supponendo che non ci sia attrito, calcolare a) con quale velocita' v il blocchetto arriva nei punti A e in B. b) L energia cinetica e potenziale del blocchetto in A e B. c) Il tempo necessario per percorrere la distanza d in andata e ritorno. d) Rispondere alle stesse domande a,b,c nel caso in cui il (solo) tratto orizzontale presenti un attrito dinamico concoefficiente µ=0.2. d) Nel caso di attrito, quante volte il blocchetto percorrera il tratto di lunghezza d prima di fermarsi? h A d Risoluzione a) quando il blocchetto arriva nel punto A avra' acquistato un'energia cinetica pari alla sua energia potenziale iniziale. Quindi, dal principio di conservazione dell'energia meccanica m g h = (1/2) m v 2 da cui ottengo v = 2 g h = 8.86 m/s. Ovviamente, poiche siamo in assenza di attrito, lungo il tratto orizzontale il moto sara di tipo rettilineo uniforme e la sua velocita in B sara uguale a quella in A. b) In A e B il blocchetto avra la stessa energia cinetica e potenziale date da quando la biglia si ferma tutta la sua energia cinetica sara stata trasformata in energia potenziale della molla. Quindi Ep = 0 Ecin =(1/2) m v 2 = J c) Il tempo per percorrere il tratto orizzontale e t=d/v=0.45 s. 18
19 problema 19 La biglia A viene lanciata, al tempo t=0, su un piano orizzontale privo di attrito con velocita incognita v A. La biglia B si trova ad una altezza h=15 m rispetto alla biglia A e viene lanciata orizzontalmente con velocita v B =12 m/s in ritardo di un tempo t=5 s rispetto alla biglia A. Calcolare: a1) il tempo t 1 al quale la biglia B raggiunge il piano horizzontale e la distanza d 1 percorsa. b1) la velocita della biglia A affinche le due biglie si urtino come in figura. h v A v B x Supponiamo ora che le due biglie partano allo stesso tempo d t=0, la biglia B con velocita v B incognita, mentre la biglia A parta da ferma e si muova di moto uniformemente accelerato con a=2 m/s 2. Calcolare a2) il tempo t 2 al quale avviene l urto e la distanza d 2 percorsa dalla biglia A b2) la velocita v B affinche avvenga l urto Risoluzione a1) il tempo impiegato dalla biglia B per raggiunge terra e indipendente dalla sua velocita (orizzontale) v B e ricavabile dalla formula [h=(1/2) g (t B ) 2 ] da cui t B = 2 h / g = 1.75 s Quindi la biglia B raggiunge terra al tempo t 1 =t B + t = = 6.75 s. La distanza percorsa sara conseguentemente d 1 = v B t B = m. b1) la condizione per cui avvenga l urto e che la biglia A si trovi in x=d 1 al tempo t 1. Deve quindi risultare d 1 =v A t 1 da cui v A = d 1 / t 1 =3.11 m/s a2) l urto puo avvenire solo quando la biglia B raggiunge terra e questo e indipendente dalla sua velocita (orizzontale) v B. Quindi l urto avviene al tempo t 2 =t B = 1.75 s. La distanza percorsa dalla biglia A, che si muove di moto uniformente accerlearato, sara data dalla formula d 2 = (1/2) a (t 2 ) 2 = 3.06 m. b2) la condizione per cui avvenga l urto e che la biglia B abbia percorso una distanza orizzontale pari a d 2 nel tempo t 2. Deve quindi risultare d 2 =v B t 2 da cui v B = d 2 / t 2 =1.75 m/s 19
20 problema 20 Un corpo di massa m = 5 kg viene lanciato lungo una pista priva di attrito con velocita iniziale v 0 = 16 m/s. Rispetto alla posizione iniziale P 0, le altezze relative ai punti A,B,C,D,E sono h A = 3m, h B = -4m, h C = 7m, h D = -5m, h E = -2m. v 0 A C Calcolare B a) energia potenziale, energia cinetica e velocita in ciascun D punto. b) la velocita iniziale minima affiche il corpo raggiunga il punto E c) la velocita iniziale minima affinche il corpo superi la prima gobba A d) l intervallo di valori della velocita iniziale che permetta al corpo di superare la gobba A ma non la gobba C. Rispondere alle stesse domande se nel tratto tra i punti A e C la forza di attrito viene considerata costante pari a f=10 Newton. La lunghezza del tratto P 0 -A sia d 1 =10 m, mentre quella del tratto A-C sia d 2 =20 m P 0 E Risoluzione in assenz di attrito Se siamo in assenza di attrito, si puo' applicare il principio di conservazione dell'energia meccanica. Prendendo come quota di riferimento (U=0) quella iniziale del blocco, l''energia meccanica iniziale E 0 e' data solo dall'energia cinetica E 0 =K 0 + U 0 = (1/2) m (v 0 ) 2 = 640 J a) L'energia meccanica nei vari punti e E =K + U = (1/2) m (v) 2 + m g h. Quindi applicando il principio di conservazione dell'energia meccanica (E 0 =E), si ha (1/2) m (v 0 ) 2 = (1/2) m (v) 2 + m g h da cui v 2 = (v 0 ) g h e quindi v = (v ) 2gh. Per cui 0 v A = m/s U A = J K A = E 0 -U A = J... v C = m/s U A = J K A = E 0 -U A = J per trovare le energie cinetiche nei vari punti basta ora applicare la formula K = (1/2) m (v) 2, quindi... per trovare le energie potenzialoi nei vari punti basta ora applicare la formula U = m g h, quindi... b) La velocita iniziale minima per raggiungere il punto E e quella che fa arrivare il blocco nel punto C con velocita nulla, e quindi solo con energia potenziale U C =m g h C. Quindi, imponendo (1/2) m (v 0 ) 2 > m g h C trovo la condizione v 2 0 > 2 g h C, che implica v 0 > m/s. Risoluzione in presenza di attrito Il lavoro svolto dalla forza di attrito e Lattr = 20x10 = 200 J... da finire... 20
. Si determina quindi quale distanza viene percorsa lungo l asse y in questo intervallo di tempo: h = v 0y ( d
 Esercizio 1 Un automobile viaggia a velocità v 0 su una strada inclinata di un angolo θ rispetto alla superficie terrestre, e deve superare un burrone largo d (si veda la figura, in cui è indicato anche
Esercizio 1 Un automobile viaggia a velocità v 0 su una strada inclinata di un angolo θ rispetto alla superficie terrestre, e deve superare un burrone largo d (si veda la figura, in cui è indicato anche
Verifica sperimentale del principio di conservazione dell'energia meccanica totale
 Scopo: Verifica sperimentale del principio di conservazione dell'energia meccanica totale Materiale: treppiede con morsa asta millimetrata treppiede senza morsa con due masse da 5 kg pallina carta carbone
Scopo: Verifica sperimentale del principio di conservazione dell'energia meccanica totale Materiale: treppiede con morsa asta millimetrata treppiede senza morsa con due masse da 5 kg pallina carta carbone
28360 - FISICA MATEMATICA 1 A.A. 2014/15 Problemi dal libro di testo: D. Giancoli, Fisica, 2a ed., CEA Capitolo 6
 28360 - FISICA MATEMATICA 1 A.A. 2014/15 Problemi dal libro di testo: D. Giancoli, Fisica, 2a ed., CEA Capitolo 6 Lavoro, forza costante: W = F r Problema 1 Quanto lavoro viene compiuto dalla forza di
28360 - FISICA MATEMATICA 1 A.A. 2014/15 Problemi dal libro di testo: D. Giancoli, Fisica, 2a ed., CEA Capitolo 6 Lavoro, forza costante: W = F r Problema 1 Quanto lavoro viene compiuto dalla forza di
Esercitazione 5 Dinamica del punto materiale
 Problema 1 Un corpo puntiforme di massa m = 1.0 kg viene lanciato lungo la superficie di un cuneo avente un inclinazione θ = 40 rispetto all orizzontale e altezza h = 80 cm. Il corpo viene lanciato dal
Problema 1 Un corpo puntiforme di massa m = 1.0 kg viene lanciato lungo la superficie di un cuneo avente un inclinazione θ = 40 rispetto all orizzontale e altezza h = 80 cm. Il corpo viene lanciato dal
Problemi di dinamica del punto materiale (moto oscillatorio) A Sistemi di riferimento inerziali
 Problemi di dinamica del punto materiale (moto oscillatorio) A Sistemi di riferimento inerziali Problema n. 1: Un corpo puntiforme di massa m = 2.5 kg pende verticalmente dal soffitto di una stanza essendo
Problemi di dinamica del punto materiale (moto oscillatorio) A Sistemi di riferimento inerziali Problema n. 1: Un corpo puntiforme di massa m = 2.5 kg pende verticalmente dal soffitto di una stanza essendo
F S V F? Soluzione. Durante la spinta, F S =ma (I legge di Newton) con m=40 Kg.
 Spingete per 4 secondi una slitta dove si trova seduta la vostra sorellina. Il peso di slitta+sorella è di 40 kg. La spinta che applicate F S è in modulo pari a 60 Newton. La slitta inizialmente è ferma,
Spingete per 4 secondi una slitta dove si trova seduta la vostra sorellina. Il peso di slitta+sorella è di 40 kg. La spinta che applicate F S è in modulo pari a 60 Newton. La slitta inizialmente è ferma,
CONSERVAZIONE DELL ENERGIA MECCANICA
 CONSERVAZIONE DELL ENERGIA MECCANICA L introduzione dell energia potenziale e dell energia cinetica ci permette di formulare un principio potente e universale applicabile alla soluzione dei problemi che
CONSERVAZIONE DELL ENERGIA MECCANICA L introduzione dell energia potenziale e dell energia cinetica ci permette di formulare un principio potente e universale applicabile alla soluzione dei problemi che
MASSA VOLUMICA o DENSITA
 MASSA VOLUMICA o DENSITA Massa volumica di una sostanza: è la massa di sostanza, espressa in kg, che occupa un volume pari a 1 m 3 1 m 3 di aria ha la massa di 1,2 kg 1 m 3 di acqua ha la massa di 1000
MASSA VOLUMICA o DENSITA Massa volumica di una sostanza: è la massa di sostanza, espressa in kg, che occupa un volume pari a 1 m 3 1 m 3 di aria ha la massa di 1,2 kg 1 m 3 di acqua ha la massa di 1000
Forze, leggi della dinamica, diagramma del. 28 febbraio 2009 (PIACENTINO - PREITE) Fisica per Scienze Motorie
 Forze, leggi della dinamica, diagramma del corpo libero 1 FORZE Grandezza fisica definibile come l' agente in grado di modificare lo stato di quiete o di moto di un corpo. Ci troviamo di fronte ad una
Forze, leggi della dinamica, diagramma del corpo libero 1 FORZE Grandezza fisica definibile come l' agente in grado di modificare lo stato di quiete o di moto di un corpo. Ci troviamo di fronte ad una
Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012
 Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012 Problema 1 Due carrelli A e B, di massa m A = 104 kg e m B = 128 kg, collegati da una molla di costante elastica k = 3100
Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012 Problema 1 Due carrelli A e B, di massa m A = 104 kg e m B = 128 kg, collegati da una molla di costante elastica k = 3100
Lo spazio percorso in 45 secondi da un treno in moto con velocità costante di 130 km/h è: a) 2.04 km b) 6.31 km c) 428 m d) 1.
 L accelerazione iniziale di un ascensore in salita è 5.3 m/s 2. La forza di contatto normale del pavimento su un individuo di massa 68 kg è: a) 2.11 10 4 N b) 150 N c) 1.03 10 3 N Un proiettile viene lanciato
L accelerazione iniziale di un ascensore in salita è 5.3 m/s 2. La forza di contatto normale del pavimento su un individuo di massa 68 kg è: a) 2.11 10 4 N b) 150 N c) 1.03 10 3 N Un proiettile viene lanciato
Aprile (recupero) tra una variazione di velocità e l intervallo di tempo in cui ha luogo.
 Febbraio 1. Un aereo in volo orizzontale, alla velocità costante di 360 km/h, lascia cadere delle provviste per un accampamento da un altezza di 200 metri. Determina a quale distanza dall accampamento
Febbraio 1. Un aereo in volo orizzontale, alla velocità costante di 360 km/h, lascia cadere delle provviste per un accampamento da un altezza di 200 metri. Determina a quale distanza dall accampamento
Fisica Generale I (primo modulo) A.A. 2013-2014, 19 Novembre 2013
 Fisica Generale I (primo modulo) A.A. 203-204, 9 Novembre 203 Esercizio I. m m 2 α α Due corpi, di massa m = kg ed m 2 =.5 kg, sono poggiati su un cuneo di massa M m 2 e sono connessi mediante una carrucola
Fisica Generale I (primo modulo) A.A. 203-204, 9 Novembre 203 Esercizio I. m m 2 α α Due corpi, di massa m = kg ed m 2 =.5 kg, sono poggiati su un cuneo di massa M m 2 e sono connessi mediante una carrucola
Nome..Cognome.. Classe 4G 4 dicembre 2008. VERIFICA DI FISICA: lavoro ed energia
 Nome..Cognome.. Classe 4G 4 dicembre 8 VERIFIC DI FISIC: lavoro ed energia Domande ) Energia cinetica: (punti:.5) a) fornisci la definizione più generale possibile di energia cinetica, specificando l equazione
Nome..Cognome.. Classe 4G 4 dicembre 8 VERIFIC DI FISIC: lavoro ed energia Domande ) Energia cinetica: (punti:.5) a) fornisci la definizione più generale possibile di energia cinetica, specificando l equazione
Modulo di Meccanica e Termodinamica
 Modulo di Meccanica e Termodinamica 1) Misure e unita di misura 2) Cinematica: + Moto Rettilineo + Moto Uniformemente Accelerato [+ Vettori e Calcolo Vettoriale] + Moti Relativi 3) Dinamica: + Forza e
Modulo di Meccanica e Termodinamica 1) Misure e unita di misura 2) Cinematica: + Moto Rettilineo + Moto Uniformemente Accelerato [+ Vettori e Calcolo Vettoriale] + Moti Relativi 3) Dinamica: + Forza e
MECCANICA. 2. Un sasso cade da fermo da un grattacielo alto 100 m. Che distanza ha percorso dopo 2 secondi?
 MECCANICA Cinematica 1. Un oggetto che si muove di moto circolare uniforme, descrive una circonferenza di 20 cm di diametro e compie 2 giri al secondo. Qual è la sua accelerazione? 2. Un sasso cade da
MECCANICA Cinematica 1. Un oggetto che si muove di moto circolare uniforme, descrive una circonferenza di 20 cm di diametro e compie 2 giri al secondo. Qual è la sua accelerazione? 2. Un sasso cade da
2B LSSA Prof. Gariboldi a.s.14/15 Ripassare tutti gli argomenti come da programma e svolgere i seguenti esercizi
 COMPITI DELLE VACANZE PER IL RECUPERO DEL DEBITO 2B LSSA Prof. Gariboldi a.s.14/15 Ripassare tutti gli argomenti come da programma e svolgere i seguenti esercizi Moti 1) Scrivi la legge oraria del moto
COMPITI DELLE VACANZE PER IL RECUPERO DEL DEBITO 2B LSSA Prof. Gariboldi a.s.14/15 Ripassare tutti gli argomenti come da programma e svolgere i seguenti esercizi Moti 1) Scrivi la legge oraria del moto
Energia e Lavoro. In pratica, si determina la dipendenza dallo spazio invece che dal tempo
 Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Lavoro di una forza costante
 Lavoro ed energia Per spostare un oggetto o per sollevarlo dobbiamo fare un lavoro Il lavoro richiede energia sotto varie forme (elettrica, meccanica, ecc.) Se compio lavoro perdo energia Queste due quantità
Lavoro ed energia Per spostare un oggetto o per sollevarlo dobbiamo fare un lavoro Il lavoro richiede energia sotto varie forme (elettrica, meccanica, ecc.) Se compio lavoro perdo energia Queste due quantità
Corso di Laurea in Farmacia Verifica in itinere 3 dicembre 2014 TURNO 1
 Corso di Laurea in Farmacia Verifica in itinere 3 dicembre 2014 TURNO 1 COMPITO A Un blocco di massa m 1 = 1, 5 kg si muove lungo una superficie orizzontale priva di attrito alla velocità v 1 = 8,2 m/s.
Corso di Laurea in Farmacia Verifica in itinere 3 dicembre 2014 TURNO 1 COMPITO A Un blocco di massa m 1 = 1, 5 kg si muove lungo una superficie orizzontale priva di attrito alla velocità v 1 = 8,2 m/s.
Seminario didattico Ingegneria Elettronica. Lezione 5: Dinamica del punto materiale Energia
 Seminario didattico Ingegneria Elettronica Lezione 5: Dinamica del punto materiale Energia 1 Esercizio n 1 Un blocco di massa m = 2 kg e dimensioni trascurabili, cade da un altezza h = 0.4 m rispetto all
Seminario didattico Ingegneria Elettronica Lezione 5: Dinamica del punto materiale Energia 1 Esercizio n 1 Un blocco di massa m = 2 kg e dimensioni trascurabili, cade da un altezza h = 0.4 m rispetto all
Q 1 = +3 10-5 C carica numero 1 Q 2 = +4 10-5 C carica numero 2 forza esercitata tra le cariche distanza tra le cariche, incognita
 Problema n 1 A quale distanza, una dall'altra bisogna porre nel vuoto due cariche (Q 1 =3 10-5 C e Q 2 =4 10-5 C) perché esse esercitino una sull'altra la forza di 200 N? Q 1 = +3 10-5 C carica numero
Problema n 1 A quale distanza, una dall'altra bisogna porre nel vuoto due cariche (Q 1 =3 10-5 C e Q 2 =4 10-5 C) perché esse esercitino una sull'altra la forza di 200 N? Q 1 = +3 10-5 C carica numero
Esercitazione IX - Calorimetria
 Esercitazione IX - Calorimetria Esercizio 1 Un blocco di rame di massa m Cu = 5g si trova a una temperatura iniziale T i = 25 C. Al blocco viene fornito un calore Q = 120J. Determinare la temperatura finale
Esercitazione IX - Calorimetria Esercizio 1 Un blocco di rame di massa m Cu = 5g si trova a una temperatura iniziale T i = 25 C. Al blocco viene fornito un calore Q = 120J. Determinare la temperatura finale
1) Due grandezze fisiche si dicono omogenee se:
 1) Due grandezze fisiche si dicono omogenee se: A. Si possono moltiplicare tra loro B. Si possono dividere tra loro C. Ci possono sommare tra loro D. Sono divisibili per uno stesso numero 2) Un blocchetto
1) Due grandezze fisiche si dicono omogenee se: A. Si possono moltiplicare tra loro B. Si possono dividere tra loro C. Ci possono sommare tra loro D. Sono divisibili per uno stesso numero 2) Un blocchetto
Progetto La fisica nelle attrazioni Attrazione NIAGARA Dati Utili
 Progetto La fisica nelle attrazioni Attrazione NIAGARA Dati Utili Angolo di risalita = 25 Altezza massima della salita = 25,87 m Altezza della salita nel tratto lineare (fino all ultimo pilone di metallo)
Progetto La fisica nelle attrazioni Attrazione NIAGARA Dati Utili Angolo di risalita = 25 Altezza massima della salita = 25,87 m Altezza della salita nel tratto lineare (fino all ultimo pilone di metallo)
percorso fatto sul tratto orizzontale). Determinare il lavoro (minimo) e la potenza minima del motore per percorrere un tratto.
 Esercizio 1 Una pietra viene lanciata con una velocità iniziale di 20.0 m/s contro una pigna all'altezza di 5.0 m rispetto al punto di lancio. Trascurando ogni resistenza, calcolare la velocità della pietra
Esercizio 1 Una pietra viene lanciata con una velocità iniziale di 20.0 m/s contro una pigna all'altezza di 5.0 m rispetto al punto di lancio. Trascurando ogni resistenza, calcolare la velocità della pietra
Seconda Legge DINAMICA: F = ma
 Seconda Legge DINAMICA: F = ma (Le grandezze vettoriali sono indicate in grassetto e anche in arancione) Fisica con Elementi di Matematica 1 Unità di misura: Massa m si misura in kg, Accelerazione a si
Seconda Legge DINAMICA: F = ma (Le grandezze vettoriali sono indicate in grassetto e anche in arancione) Fisica con Elementi di Matematica 1 Unità di misura: Massa m si misura in kg, Accelerazione a si
9. Urti e conservazione della quantità di moto.
 9. Urti e conservazione della quantità di moto. 1 Conservazione dell impulso m1 v1 v2 m2 Prima Consideriamo due punti materiali di massa m 1 e m 2 che si muovono in una dimensione. Supponiamo che i due
9. Urti e conservazione della quantità di moto. 1 Conservazione dell impulso m1 v1 v2 m2 Prima Consideriamo due punti materiali di massa m 1 e m 2 che si muovono in una dimensione. Supponiamo che i due
Nome e Cognome. Nella copia da riconsegnare si scrivano solo il risultato numerico e la formula finale. Non riportare tutto il procedimento.
 Dipartimento di Scienze Agrarie, Alimentari e Agro-Ambientali: Corso di Fisica AA 13/14 Test di ammissione all'orale di Fisica. Appello del 16 Marzo 2015 Nome e Cognome Nella copia da riconsegnare si scrivano
Dipartimento di Scienze Agrarie, Alimentari e Agro-Ambientali: Corso di Fisica AA 13/14 Test di ammissione all'orale di Fisica. Appello del 16 Marzo 2015 Nome e Cognome Nella copia da riconsegnare si scrivano
Esercitazione VIII - Lavoro ed energia II
 Esercitazione VIII - Lavoro ed energia II Forze conservative Esercizio Una pallina di massa m = 00g viene lanciata tramite una molla di costante elastica = 0N/m come in figura. Ammesso che ogni attrito
Esercitazione VIII - Lavoro ed energia II Forze conservative Esercizio Una pallina di massa m = 00g viene lanciata tramite una molla di costante elastica = 0N/m come in figura. Ammesso che ogni attrito
2 R = mgr + 1 2 mv2 0 = E f
 Esercizio 1 Un corpo puntiforme di massa m scivola lungo la pista liscia di raggio R partendo da fermo da un altezza h rispetto al fondo della pista come rappresentato in figura. Calcolare: a) Il valore
Esercizio 1 Un corpo puntiforme di massa m scivola lungo la pista liscia di raggio R partendo da fermo da un altezza h rispetto al fondo della pista come rappresentato in figura. Calcolare: a) Il valore
DINAMICA DEL PUNTO MATERIALE E CONCETTO DI FORZA. Dinamica: studio delle forze che causano il moto dei corpi
 DINAMICA DEL PUNTO MATERIALE E CONCETTO DI FORZA Dinamica: studio delle forze che causano il moto dei corpi 1 Forza Si definisce forza una qualunque causa esterna che produce una variazione dello stato
DINAMICA DEL PUNTO MATERIALE E CONCETTO DI FORZA Dinamica: studio delle forze che causano il moto dei corpi 1 Forza Si definisce forza una qualunque causa esterna che produce una variazione dello stato
LEGGE DI STEVINO. La pressione non dipende dalla superficie della base del recipiente
 LA PRESSIONE NEI LIQUIDI DOVUTA ALLA FORZA PESO In condizioni di equilibrio la superficie libera di un liquido pesante deve essere piana ed orizzontale. Liquido di densitàρ Ogni strato orizzontale di liquido
LA PRESSIONE NEI LIQUIDI DOVUTA ALLA FORZA PESO In condizioni di equilibrio la superficie libera di un liquido pesante deve essere piana ed orizzontale. Liquido di densitàρ Ogni strato orizzontale di liquido
Statica e dinamica dei fluidi. A. Palano
 Statica e dinamica dei fluidi A. Palano Fluidi perfetti Un fluido perfetto e incomprimibile e indilatabile e non possiede attrito interno. Forza di pressione come la somma di tutte le forze di interazione
Statica e dinamica dei fluidi A. Palano Fluidi perfetti Un fluido perfetto e incomprimibile e indilatabile e non possiede attrito interno. Forza di pressione come la somma di tutte le forze di interazione
GIRO DELLA MORTE PER UN CORPO CHE SCIVOLA
 8. LA CONSERVAZIONE DELL ENERGIA MECCANICA IL LAVORO E L ENERGIA 4 GIRO DELLA MORTE PER UN CORPO CHE SCIVOLA Il «giro della morte» è una delle parti più eccitanti di una corsa sulle montagne russe. Per
8. LA CONSERVAZIONE DELL ENERGIA MECCANICA IL LAVORO E L ENERGIA 4 GIRO DELLA MORTE PER UN CORPO CHE SCIVOLA Il «giro della morte» è una delle parti più eccitanti di una corsa sulle montagne russe. Per
Forze Conservative. Il lavoro eseguito da una forza conservativa lungo un qualunque percorso chiuso e nullo.
 Lavoro ed energia 1. Forze conservative 2. Energia potenziale 3. Conservazione dell energia meccanica 4. Conservazione dell energia nel moto del pendolo 5. Esempio: energia potenziale gravitazionale 6.
Lavoro ed energia 1. Forze conservative 2. Energia potenziale 3. Conservazione dell energia meccanica 4. Conservazione dell energia nel moto del pendolo 5. Esempio: energia potenziale gravitazionale 6.
Proprieta meccaniche dei fluidi
 Proprieta meccaniche dei fluidi 1. Definizione di fluido: liquido o gas 2. La pressione in un fluido 3. Equilibrio nei fluidi: legge di Stevino 4. Il Principio di Pascal 5. Il barometro di Torricelli 6.
Proprieta meccaniche dei fluidi 1. Definizione di fluido: liquido o gas 2. La pressione in un fluido 3. Equilibrio nei fluidi: legge di Stevino 4. Il Principio di Pascal 5. Il barometro di Torricelli 6.
DINAMICA. 1. La macchina di Atwood è composta da due masse m
 DINAMICA. La macchina di Atwood è composta da due masse m e m sospese verticalmente su di una puleggia liscia e di massa trascurabile. i calcolino: a. l accelerazione del sistema; b. la tensione della
DINAMICA. La macchina di Atwood è composta da due masse m e m sospese verticalmente su di una puleggia liscia e di massa trascurabile. i calcolino: a. l accelerazione del sistema; b. la tensione della
Progetto La fisica nelle attrazioni Attrazione ISPEED
 Progetto La fisica nelle attrazioni Attrazione ISPEED Dati utili Lunghezza del treno: 8,8 m Durata del percorso: 55 s Lunghezza del percorso: 1200 m Massa treno a pieno carico: 7000 kg Altezza della prima
Progetto La fisica nelle attrazioni Attrazione ISPEED Dati utili Lunghezza del treno: 8,8 m Durata del percorso: 55 s Lunghezza del percorso: 1200 m Massa treno a pieno carico: 7000 kg Altezza della prima
ENERGIA. Energia e Lavoro Potenza Energia cinetica Energia potenziale Principio di conservazione dell energia meccanica
 1 ENERGIA Energia e Lavoro Potenza Energia cinetica Energia potenziale Principio di conservazione dell energia meccanica 2 Energia L energia è ciò che ci permette all uomo di compiere uno sforzo o meglio
1 ENERGIA Energia e Lavoro Potenza Energia cinetica Energia potenziale Principio di conservazione dell energia meccanica 2 Energia L energia è ciò che ci permette all uomo di compiere uno sforzo o meglio
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Test di autovalutazione Corso di Laurea in Tossicologia dell ambiente e degli alimenti
 Test di autovalutazione Corso di Laurea in Tossicologia dell ambiente e degli alimenti Quesito 1 Un punto materiale di massa 5 kg si muove di moto circolare uniforme con velocità tangenziale 1 m/s. Quanto
Test di autovalutazione Corso di Laurea in Tossicologia dell ambiente e degli alimenti Quesito 1 Un punto materiale di massa 5 kg si muove di moto circolare uniforme con velocità tangenziale 1 m/s. Quanto
LA FORZA. Il movimento: dal come al perché
 LA FORZA Concetto di forza Principi della Dinamica: 1) Principio d inerzia 2) F=ma 3) Principio di azione e reazione Forza gravitazionale e forza peso Accelerazione di gravità Massa, peso, densità pag.1
LA FORZA Concetto di forza Principi della Dinamica: 1) Principio d inerzia 2) F=ma 3) Principio di azione e reazione Forza gravitazionale e forza peso Accelerazione di gravità Massa, peso, densità pag.1
Preparazione alle gare di II livello delle Olimpiadi della Fisica 2013
 Preparazione alle gare di II livello delle Olimpiadi della Fisica 01 Incontro su temi di termodinamica 14/1/01 Giuseppina Rinaudo - Dipartimento di Fisica dell Università di Torino Sommario dei quesiti
Preparazione alle gare di II livello delle Olimpiadi della Fisica 01 Incontro su temi di termodinamica 14/1/01 Giuseppina Rinaudo - Dipartimento di Fisica dell Università di Torino Sommario dei quesiti
Verifica di Fisica- Energia A Alunno. II^
 Verifica di Fisica- Energia A Alunno. II^!!!!!!!!!!!!!! NON SARANNO ACCETTATI PER NESSUN MOTIVO ESERCIZI SVOLTI SENZA L INDICAZIONE DELLE FORMULE E DELLE UNITA DI MISURA!!!!!!!!!! 1-Il 31 ottobre ti rechi
Verifica di Fisica- Energia A Alunno. II^!!!!!!!!!!!!!! NON SARANNO ACCETTATI PER NESSUN MOTIVO ESERCIZI SVOLTI SENZA L INDICAZIONE DELLE FORMULE E DELLE UNITA DI MISURA!!!!!!!!!! 1-Il 31 ottobre ti rechi
Pressione. Esempio. Definizione di pressione. Legge di Stevino. Pressione nei fluidi EQUILIBRIO E CONSERVAZIONE DELL ENERGIA NEI FLUIDI
 Pressione EQUILIBRIO E CONSERVAZIONE DELL ENERGIA NEI FLUIDI Cos è la pressione? La pressione è una grandezza che lega tra di loro l intensità della forza e l aerea della superficie su cui viene esercitata
Pressione EQUILIBRIO E CONSERVAZIONE DELL ENERGIA NEI FLUIDI Cos è la pressione? La pressione è una grandezza che lega tra di loro l intensità della forza e l aerea della superficie su cui viene esercitata
19 Il campo elettrico - 3. Le linee del campo elettrico
 Moto di una carica in un campo elettrico uniforme Il moto di una particella carica in un campo elettrico è in generale molto complesso; il problema risulta più semplice se il campo elettrico è uniforme,
Moto di una carica in un campo elettrico uniforme Il moto di una particella carica in un campo elettrico è in generale molto complesso; il problema risulta più semplice se il campo elettrico è uniforme,
Soluzione degli esercizi sul moto rettilineo uniformemente accelerato
 Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 00 Soluzione degli esercizi sul moto rettilineo uniformemente accelerato Esercizio. Un corpo parte da fermo con accelerazione
Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 00 Soluzione degli esercizi sul moto rettilineo uniformemente accelerato Esercizio. Un corpo parte da fermo con accelerazione
Esercizi sul moto rettilineo uniformemente accelerato
 Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 010 Esercizi sul moto rettilineo uniformemente accelerato Esercizio 1. Un corpo parte da fermo con accelerazione pari a
Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 010 Esercizi sul moto rettilineo uniformemente accelerato Esercizio 1. Un corpo parte da fermo con accelerazione pari a
ESERCIZI CINEMATICA IN UNA DIMENSIONE
 ESERCIZI CINEMATICA IN UNA DIMENSIONE ES. 1 - Due treni partono da due stazioni distanti 20 km dirigendosi uno verso l altro rispettivamente alla velocità costante di v! = 50,00 km/h e v 2 = 100,00 km
ESERCIZI CINEMATICA IN UNA DIMENSIONE ES. 1 - Due treni partono da due stazioni distanti 20 km dirigendosi uno verso l altro rispettivamente alla velocità costante di v! = 50,00 km/h e v 2 = 100,00 km
1. calcolare l accelerazione del sistema e stabilire se la ruota sale o scende [6 punti];
![1. calcolare l accelerazione del sistema e stabilire se la ruota sale o scende [6 punti]; 1. calcolare l accelerazione del sistema e stabilire se la ruota sale o scende [6 punti];](/thumbs/24/2314490.jpg) 1 Esercizio Una ruota di raggio R = 15 cm e di massa M = 8 Kg può rotolare senza strisciare lungo un piano inclinato di un angolo θ 2 = 30 0, ed è collegato tramite un filo inestensibile ad un blocco di
1 Esercizio Una ruota di raggio R = 15 cm e di massa M = 8 Kg può rotolare senza strisciare lungo un piano inclinato di un angolo θ 2 = 30 0, ed è collegato tramite un filo inestensibile ad un blocco di
Moto sul piano inclinato (senza attrito)
 Moto sul piano inclinato (senza attrito) Per studiare il moto di un oggetto (assimilabile a punto materiale) lungo un piano inclinato bisogna innanzitutto analizzare le forze che agiscono sull oggetto
Moto sul piano inclinato (senza attrito) Per studiare il moto di un oggetto (assimilabile a punto materiale) lungo un piano inclinato bisogna innanzitutto analizzare le forze che agiscono sull oggetto
Una forza, per la fisica, compie un lavoro se provoca uno spostamento.
 Lavoro La forza è la causa del cambiamento di moto di un corpo (dinamica). Se la risultante di puù forze applicate ad un corpo è nulla il corpo è in equilibrio stabile (statica). Una forza può causare
Lavoro La forza è la causa del cambiamento di moto di un corpo (dinamica). Se la risultante di puù forze applicate ad un corpo è nulla il corpo è in equilibrio stabile (statica). Una forza può causare
Facoltà di Farmacia e Medicina - A.A. 2012-2013 12 giugno 2013 Scritto di Fisica (Compito A)
 Facoltà di Farmacia e Medicina - A.A. 2012-2013 12 giugno 2013 Scritto di Fisica (Compito A) Corso di Laurea: Laurea Magistrale in FARMACIA Nome: Matricola Canale: Cognome: Aula: Docente: Riportare sul
Facoltà di Farmacia e Medicina - A.A. 2012-2013 12 giugno 2013 Scritto di Fisica (Compito A) Corso di Laurea: Laurea Magistrale in FARMACIA Nome: Matricola Canale: Cognome: Aula: Docente: Riportare sul
distanza percorsa in 12s x-x 0 =v i t+1/2 at 2 =(70/3.6)*12 +1/2*(-1.41)*12 2 =1.3*10 2 m
 Alcuni esercizi di cinematica 1. Una macchina ha una velocita` v i =70km/h quando inizia a frenare e dopo 90m la velocita` si è ridotta a v f = 40km/h. Si chiede di calcolare l accelerazione che supponiamo
Alcuni esercizi di cinematica 1. Una macchina ha una velocita` v i =70km/h quando inizia a frenare e dopo 90m la velocita` si è ridotta a v f = 40km/h. Si chiede di calcolare l accelerazione che supponiamo
Lunedì 20 dicembre 2010. Docente del corso: prof. V. Maiorino
 Lunedì 20 dicembre 2010 Docente del corso: prof. V. Maiorino Se la Terra si spostasse all improvviso su un orbita dieci volte più lontana dal Sole rispetto all attuale, di quanto dovrebbe variare la massa
Lunedì 20 dicembre 2010 Docente del corso: prof. V. Maiorino Se la Terra si spostasse all improvviso su un orbita dieci volte più lontana dal Sole rispetto all attuale, di quanto dovrebbe variare la massa
EQUAZIONE DI STATO e LEGGI DEI GAS esercizi risolti Classi quarte L.S.
 EQUAZIONE DI STATO e LEGGI DEI GAS esercizi risolti Classi quarte L.S. In questa dispensa verrà riportato lo svolgimento di alcuni esercizi inerenti l'equazione di stato dei gas perfetti e le principali
EQUAZIONE DI STATO e LEGGI DEI GAS esercizi risolti Classi quarte L.S. In questa dispensa verrà riportato lo svolgimento di alcuni esercizi inerenti l'equazione di stato dei gas perfetti e le principali
Cap 3.1- Prima legge della DINAMICA o di Newton
 Parte I Cap 3.1- Prima legge della DINAMICA o di Newton Cap 3.1- Prima legge della DINAMICA o di Newton 3.1-3.2-3.3 forze e principio d inerzia Abbiamo finora studiato come un corpo cambia traiettoria
Parte I Cap 3.1- Prima legge della DINAMICA o di Newton Cap 3.1- Prima legge della DINAMICA o di Newton 3.1-3.2-3.3 forze e principio d inerzia Abbiamo finora studiato come un corpo cambia traiettoria
FAM. 1. Sistema composto da quattro PM come nella tabella seguente
 Serie 11: Meccanica IV FAM C. Ferrari Esercizio 1 Centro di massa: sistemi discreti Determina il centro di massa dei seguenti sistemi discreti. 1. Sistema composto da quattro PM come nella tabella seguente
Serie 11: Meccanica IV FAM C. Ferrari Esercizio 1 Centro di massa: sistemi discreti Determina il centro di massa dei seguenti sistemi discreti. 1. Sistema composto da quattro PM come nella tabella seguente
28360 - FISICA MATEMATICA 1 A.A. 2014/15 Problemi dal libro di testo: D. Giancoli, Fisica, 2a ed., CEA Capitolo 6
 28360 - FISICA MATEMATICA A.A. 204/5 Problemi dal libro di testo: D. Giancoli, Fisica, 2a ed., CEA Capitolo 6 Energia potenziale Problema 26 Una molla ha una costante elastica k uguale a 440 N/m. Di quanto
28360 - FISICA MATEMATICA A.A. 204/5 Problemi dal libro di testo: D. Giancoli, Fisica, 2a ed., CEA Capitolo 6 Energia potenziale Problema 26 Una molla ha una costante elastica k uguale a 440 N/m. Di quanto
 ELEMENTI DI IDROSTATICA IDROSTATICA L'idrostatica (anche detta fluidostatica) è una branca della meccanica dei fluidi che studiailiquidi liquidiin instato statodi diquiete quiete. Grandezze caratteristiche
ELEMENTI DI IDROSTATICA IDROSTATICA L'idrostatica (anche detta fluidostatica) è una branca della meccanica dei fluidi che studiailiquidi liquidiin instato statodi diquiete quiete. Grandezze caratteristiche
F 2 F 1. r R F A. fig.1. fig.2
 N.1 Un cilindro di raggio R = 10 cm e massa M = 5 kg è posto su un piano orizzontale scabro (fig.1). In corrispondenza del centro del cilindro è scavata una sottilissima fenditura in modo tale da ridurre
N.1 Un cilindro di raggio R = 10 cm e massa M = 5 kg è posto su un piano orizzontale scabro (fig.1). In corrispondenza del centro del cilindro è scavata una sottilissima fenditura in modo tale da ridurre
Anche nel caso che ci si muova e si regga una valigia il lavoro compiuto è nullo: la forza è verticale e lo spostamento orizzontale quindi F s =0 J.
 Lavoro Un concetto molto importante è quello di lavoro (di una forza) La definizione di tale quantità scalare è L= F dl (unità di misura joule J) Il concetto di lavoro richiede che ci sia uno spostamento,
Lavoro Un concetto molto importante è quello di lavoro (di una forza) La definizione di tale quantità scalare è L= F dl (unità di misura joule J) Il concetto di lavoro richiede che ci sia uno spostamento,
TEORIA CINETICA DEI GAS
 TEORIA CINETICA DEI GAS La teoria cinetica dei gas è corrispondente con, e infatti prevede, le proprietà dei gas. Nella materia gassosa, gli atomi o le molecole sono separati da grandi distanze e sono
TEORIA CINETICA DEI GAS La teoria cinetica dei gas è corrispondente con, e infatti prevede, le proprietà dei gas. Nella materia gassosa, gli atomi o le molecole sono separati da grandi distanze e sono
2. L ENERGIA MECCANICA
 . L ENERGIA MECCANICA.1 Il concetto di forza La forza può essere definita come «azione reciproca tra corpi che ne altera lo stato di moto o li deforma: essa é caratterizzata da intensità direzione e verso».
. L ENERGIA MECCANICA.1 Il concetto di forza La forza può essere definita come «azione reciproca tra corpi che ne altera lo stato di moto o li deforma: essa é caratterizzata da intensità direzione e verso».
a t Esercizio (tratto dal problema 5.10 del Mazzoldi)
 1 Esercizio (tratto dal problema 5.10 del Mazzoldi) Una guida semicircolare liscia verticale di raggio = 40 cm è vincolata ad una piattaforma orizzontale che si muove con accelerazione costante a t = 2
1 Esercizio (tratto dal problema 5.10 del Mazzoldi) Una guida semicircolare liscia verticale di raggio = 40 cm è vincolata ad una piattaforma orizzontale che si muove con accelerazione costante a t = 2
2. La disequazione 9 (3x 2 + 2) > 16 (x - 3) è soddisfatta: A) sempre B) solo per x < 0 C) solo per x > 2/3 D) mai E) solo per x < 2/3
 MATEMATICA 1. Per quali valori di x è x 2 > 36? A) x > - 6 B) x < - 6, x > 6 C) - 6 < x < 6 D) x > 6 E) Nessuno 2. La disequazione 9 (3x 2 + 2) > 16 (x - 3) è soddisfatta: A) sempre B) solo per x < 0 C)
MATEMATICA 1. Per quali valori di x è x 2 > 36? A) x > - 6 B) x < - 6, x > 6 C) - 6 < x < 6 D) x > 6 E) Nessuno 2. La disequazione 9 (3x 2 + 2) > 16 (x - 3) è soddisfatta: A) sempre B) solo per x < 0 C)
Note di fisica. Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria, luglio 2012. 1 Quantità di moto.
 Note di fisica. Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria, luglio 2012. Indice 1 Quantità di moto. 1 1.1 Quantità di moto di una particella.............................. 1 1.2 Quantità
Note di fisica. Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria, luglio 2012. Indice 1 Quantità di moto. 1 1.1 Quantità di moto di una particella.............................. 1 1.2 Quantità
Appunti sul galleggiamento
 Appunti sul galleggiamento Prof.sa Enrica Giordano Corso di Didattica della fisica 1B a.a. 2006/7 Ad uso esclusivo degli studenti frequentanti, non diffondere senza l autorizzazione della professoressa
Appunti sul galleggiamento Prof.sa Enrica Giordano Corso di Didattica della fisica 1B a.a. 2006/7 Ad uso esclusivo degli studenti frequentanti, non diffondere senza l autorizzazione della professoressa
MOTO DI UNA CARICA IN UN CAMPO ELETTRICO UNIFORME
 6. IL CONDNSATOR FNOMNI DI LTTROSTATICA MOTO DI UNA CARICA IN UN CAMPO LTTRICO UNIFORM Il moto di una particella carica in un campo elettrico è in generale molto complesso; il problema risulta più semplice
6. IL CONDNSATOR FNOMNI DI LTTROSTATICA MOTO DI UNA CARICA IN UN CAMPO LTTRICO UNIFORM Il moto di una particella carica in un campo elettrico è in generale molto complesso; il problema risulta più semplice
Capitolo 03 LA PRESSIONE ATMOSFERICA. 3.1 Esperienza del Torricelli 3.2 Unità di misura delle pressioni
 Capitolo 03 LA PRESSIONE ATMOSFERICA 3.1 Esperienza del Torricelli 3.2 Unità di misura delle pressioni 12 3.1 Peso dell aria I corpi solidi hanno un loro peso, ma anche i corpi gassosi e quindi l aria,
Capitolo 03 LA PRESSIONE ATMOSFERICA 3.1 Esperienza del Torricelli 3.2 Unità di misura delle pressioni 12 3.1 Peso dell aria I corpi solidi hanno un loro peso, ma anche i corpi gassosi e quindi l aria,
L'impulso di una forza che varia nel tempo
 Lezione 13 approfondimento pag.1 L'impulso di una forza che varia nel tempo Un riassunto di quel che sappiamo Riprendiamo in esame il solito carrellino che si trova sopra la rotaia a basso attrito. Se
Lezione 13 approfondimento pag.1 L'impulso di una forza che varia nel tempo Un riassunto di quel che sappiamo Riprendiamo in esame il solito carrellino che si trova sopra la rotaia a basso attrito. Se
CONSERVAZIONE DELL'ENERGIA MECCANICA esercizi risolti Classi terze L.S.
 CONSERVAZIONE DELL'ENERGIA MECCANICA esercizi risolti Classi terze L.S. In questa dispensa verrà riportato lo svolgimento di alcuni esercizi inerenti il principio di conservazione dell'energia meccanica,
CONSERVAZIONE DELL'ENERGIA MECCANICA esercizi risolti Classi terze L.S. In questa dispensa verrà riportato lo svolgimento di alcuni esercizi inerenti il principio di conservazione dell'energia meccanica,
Relazione di laboratorio di fisica-chimica. Studiare il moto di un carrellino con il marcatempo
 Relazione di laboratorio di fisica-chimica Studiare il moto di un carrellino con il marcatempo Prima parte. Il moto rettilineo uniforme. Scopo esperimento. Verificare se un carrellino, lanciato lungo una
Relazione di laboratorio di fisica-chimica Studiare il moto di un carrellino con il marcatempo Prima parte. Il moto rettilineo uniforme. Scopo esperimento. Verificare se un carrellino, lanciato lungo una
Esempio Esame di Fisica Generale I C.d.L. ed.u. Informatica
 Esempio Esame di Fisica Generale I C.d.L. ed.u. Informatica Nome: N.M.: 1. 1d (giorno) contiene all incirca (a) 8640 s; (b) 9 10 4 s; (c) 86 10 2 s; (d) 1.44 10 3 s; (e) nessuno di questi valori. 2. Sono
Esempio Esame di Fisica Generale I C.d.L. ed.u. Informatica Nome: N.M.: 1. 1d (giorno) contiene all incirca (a) 8640 s; (b) 9 10 4 s; (c) 86 10 2 s; (d) 1.44 10 3 s; (e) nessuno di questi valori. 2. Sono
CAFFE` Il segreto è nel fisico
 CAFFE` Il segreto è nel fisico Preparata la macchina del caffè, e messala sul fuoco: L acqua raggiunge rapidamente la temperatura di ebollizione (100 C). Lo spazio del serbatoio lasciato libero viene occupato
CAFFE` Il segreto è nel fisico Preparata la macchina del caffè, e messala sul fuoco: L acqua raggiunge rapidamente la temperatura di ebollizione (100 C). Lo spazio del serbatoio lasciato libero viene occupato
Il potenziale a distanza r da una carica puntiforme è dato da V = kq/r, quindi è sufficiente calcolare V sx dovuto alla carica a sinistra:
 1. Esercizio Calcolare il potenziale elettrico nel punto A sull asse di simmetria della distribuzione di cariche in figura. Quanto lavoro bisogna spendere per portare una carica da 2 µc dall infinito al
1. Esercizio Calcolare il potenziale elettrico nel punto A sull asse di simmetria della distribuzione di cariche in figura. Quanto lavoro bisogna spendere per portare una carica da 2 µc dall infinito al
LE TORRI: DISCOVERY e COLUMBIA
 LE TORRI: DISCOVERY e COLUMBIA Osservazioni e misure a bordo Le tue sensazioni e l accelerometro a molla 1) Nelle due posizioni indicate dalle frecce indica le sensazioni ricevute rispetto al tuo peso
LE TORRI: DISCOVERY e COLUMBIA Osservazioni e misure a bordo Le tue sensazioni e l accelerometro a molla 1) Nelle due posizioni indicate dalle frecce indica le sensazioni ricevute rispetto al tuo peso
Dinamica II Lavoro di una forza costante
 Dinamica II Lavoro di una forza costante Se il punto di applicazione di una forza subisce uno spostamento ed esiste una componente della forza che sia parallela allo spostamento, la forza compie un lavoro.
Dinamica II Lavoro di una forza costante Se il punto di applicazione di una forza subisce uno spostamento ed esiste una componente della forza che sia parallela allo spostamento, la forza compie un lavoro.
Prova Scritta Completa-Fisica 9 CFU Corso di Laurea in Tossicologia dell ambiente e degli alimenti Novembre 2013
 Prova Scritta Completa-Fisica 9 CFU Corso di Laurea in Tossicologia dell ambiente e degli alimenti Novembre 2013 Quesito 1 Due cubi A e B costruiti con lo stesso legno vengono trascinati sullo stesso pavimento.
Prova Scritta Completa-Fisica 9 CFU Corso di Laurea in Tossicologia dell ambiente e degli alimenti Novembre 2013 Quesito 1 Due cubi A e B costruiti con lo stesso legno vengono trascinati sullo stesso pavimento.
Lunghezza Massa Peso Volume Capacità Densità Peso specifico Superficie Pressione Forza Lavoro Potenza
 Misurare una grandezza La Grandezza 1. La grandezza è una caratteristica misurabile. Lunghezza Massa Peso Volume Capacità Densità Peso specifico Superficie Pressione Forza Lavoro Potenza 2. Misurare una
Misurare una grandezza La Grandezza 1. La grandezza è una caratteristica misurabile. Lunghezza Massa Peso Volume Capacità Densità Peso specifico Superficie Pressione Forza Lavoro Potenza 2. Misurare una
Stati di aggregazione della materia unità 2, modulo A del libro
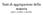 Stati di aggregazione della materia unità 2, modulo A del libro Gli stati di aggregazione della materia sono tre: solido, liquido e gassoso, e sono caratterizzati dalle seguenti grandezze: Quantità --->
Stati di aggregazione della materia unità 2, modulo A del libro Gli stati di aggregazione della materia sono tre: solido, liquido e gassoso, e sono caratterizzati dalle seguenti grandezze: Quantità --->
GAS. I gas si assomigliano tutti
 I gas si assomigliano tutti Aeriforme liquido solido GAS Descrizione macroscopica e microscopica degli stati di aggregazione della materia Fornendo energia al sistema, le forze di attrazione tra le particelle
I gas si assomigliano tutti Aeriforme liquido solido GAS Descrizione macroscopica e microscopica degli stati di aggregazione della materia Fornendo energia al sistema, le forze di attrazione tra le particelle
Esercizi e Problemi di Termodinamica.
 Esercizi e Problemi di Termodinamica. Dr. Yves Gaspar March 18, 2009 1 Problemi sulla termologia e sull equilibrio termico. Problema 1. Un pezzetto di ghiaccio di massa m e alla temperatura di = 250K viene
Esercizi e Problemi di Termodinamica. Dr. Yves Gaspar March 18, 2009 1 Problemi sulla termologia e sull equilibrio termico. Problema 1. Un pezzetto di ghiaccio di massa m e alla temperatura di = 250K viene
IL FORMULARIO DI FISICA PER LE CLASSI DI 3 E 4 LICEO SCIENTIFICO Di Pietro Aceti
 IL FORMULARIO DI FISICA PER LE CLASSI DI 3 E 4 LICEO SCIENTIFICO Di Pietro Aceti ATTENZIONE Quest opera è stata scritta con l intenzione di essere un comodo strumento di ripasso, essa non dà informazioni
IL FORMULARIO DI FISICA PER LE CLASSI DI 3 E 4 LICEO SCIENTIFICO Di Pietro Aceti ATTENZIONE Quest opera è stata scritta con l intenzione di essere un comodo strumento di ripasso, essa non dà informazioni
ESERCIZI SULLA DILATAZIONE TERMICA
 ESERCIZI SULLA DILATAZIONE TERMICA Esercizio n. 1 Di quanto varia la lunghezza di una sbarra di ferro che ha, a 0 C, una lunghezza di 20 m se fosse portata alla temperatura di 50 C? (coefficiente di dilatazione
ESERCIZI SULLA DILATAZIONE TERMICA Esercizio n. 1 Di quanto varia la lunghezza di una sbarra di ferro che ha, a 0 C, una lunghezza di 20 m se fosse portata alla temperatura di 50 C? (coefficiente di dilatazione
v = 4 m/s v m = 5,3 m/s barca
 SOLUZIONI ESERCIZI CAPITOLO 2 Esercizio n.1 v = 4 m/s Esercizio n.2 v m = 5,3 m/s = 7 minuti e 4 secondi Esercizio n.3 Usiamo la seguente costruzione grafica: fiume 1 km/h barca 7 km/h La velocità della
SOLUZIONI ESERCIZI CAPITOLO 2 Esercizio n.1 v = 4 m/s Esercizio n.2 v m = 5,3 m/s = 7 minuti e 4 secondi Esercizio n.3 Usiamo la seguente costruzione grafica: fiume 1 km/h barca 7 km/h La velocità della
COMPONENTI TERMODINAMICI APERTI
 CAPITOLO NONO COMPONENTI TERMODINAMICI APERTI Esempi applicativi Vengono di seguito esaminati alcuni componenti di macchine termiche che possono essere considerati come sistemi aperti A) Macchina termica
CAPITOLO NONO COMPONENTI TERMODINAMICI APERTI Esempi applicativi Vengono di seguito esaminati alcuni componenti di macchine termiche che possono essere considerati come sistemi aperti A) Macchina termica
Cosa determina il moto? Aristotele pensava che occorresse uno sforzo per mantenere un corpo in movimento. Galileo non era d'accordo.
 Introduzione Cosa determina il moto? Aristotele pensava che occorresse uno sforzo per mantenere un corpo in movimento. Galileo non era d'accordo. riassunto Cosa determina il moto? Forza - Spinta di un
Introduzione Cosa determina il moto? Aristotele pensava che occorresse uno sforzo per mantenere un corpo in movimento. Galileo non era d'accordo. riassunto Cosa determina il moto? Forza - Spinta di un
VERIFICA A ALUNNO. CLASSE I^. DATA...
 VERIFICA A ALUNNO. CLASSE I^. DATA... N.B. SCHEMATIZZARE LA SITUAZIONE CON UN DISEGNO IN TUTTI GLI ESERCIZI INDICARE TUTTE LE FORMULE E TUTTE LE UNITA DI MISURA NEI CALCOLI 1-Quando spingi un libro di
VERIFICA A ALUNNO. CLASSE I^. DATA... N.B. SCHEMATIZZARE LA SITUAZIONE CON UN DISEGNO IN TUTTI GLI ESERCIZI INDICARE TUTTE LE FORMULE E TUTTE LE UNITA DI MISURA NEI CALCOLI 1-Quando spingi un libro di
Lezione 14: L energia
 Lezione 4 - pag. Lezione 4: L energia 4.. L apologo di Feynman In questa lezione cominceremo a descrivere la grandezza energia. Per iniziare questo lungo percorso vogliamo citare, quasi parola per parola,
Lezione 4 - pag. Lezione 4: L energia 4.. L apologo di Feynman In questa lezione cominceremo a descrivere la grandezza energia. Per iniziare questo lungo percorso vogliamo citare, quasi parola per parola,
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
E 0 = E 1 2 + E 0. 2 = E h. = 3.2kV / m. 2 1 x. κ 1. κ 2 κ 1 E 1 = κ 2 E 2. = κ 1 E 1 x ε 0 = 8
 Solo Ingegneria dell Informazione e Ingegneria dell Energia (Canale 2 e DM 59) Problema Due condensatori piani C e C, uguali ad armature quadrate separate dalla distanza, sono connessi in parallelo. Lo
Solo Ingegneria dell Informazione e Ingegneria dell Energia (Canale 2 e DM 59) Problema Due condensatori piani C e C, uguali ad armature quadrate separate dalla distanza, sono connessi in parallelo. Lo
CALORE. Compie lavoro. Il calore è energia. Temperatura e calore. L energia è la capacità di un corpo di compiere un lavoro
 Cos è il calore? Per rispondere si osservino le seguenti immagini Temperatura e calore Il calore del termosifone fa girare una girandola Il calore del termosifone fa scoppiare un palloncino Il calore del
Cos è il calore? Per rispondere si osservino le seguenti immagini Temperatura e calore Il calore del termosifone fa girare una girandola Il calore del termosifone fa scoppiare un palloncino Il calore del
Termologia. Introduzione Scale Termometriche Espansione termica Capacità termica e calori specifici Cambiamenti di fase e calori latenti
 Termologia Introduzione Scale Termometriche Espansione termica Capacità termica e calori specifici Cambiamenti di fase e calori latenti Trasmissione del calore Legge di Wien Legge di Stefan-Boltzmann Gas
Termologia Introduzione Scale Termometriche Espansione termica Capacità termica e calori specifici Cambiamenti di fase e calori latenti Trasmissione del calore Legge di Wien Legge di Stefan-Boltzmann Gas
Complementi di Termologia. I parte
 Prof. Michele Giugliano (Dicembre 2) Complementi di Termologia. I parte N.. - Calorimetria. Il calore è una forma di energia, quindi la sua unità di misura, nel sistema SI, è il joule (J), tuttavia si
Prof. Michele Giugliano (Dicembre 2) Complementi di Termologia. I parte N.. - Calorimetria. Il calore è una forma di energia, quindi la sua unità di misura, nel sistema SI, è il joule (J), tuttavia si
Concetto di forza. 1) Principio d inerzia
 LA FORZA Concetto di forza Pi Principi ii dll della Dinamica: i 1) Principio d inerzia 2) F=ma 3) Principio di azione e reazione Forza gravitazionale i e forza peso Accelerazione di gravità Massa, peso,
LA FORZA Concetto di forza Pi Principi ii dll della Dinamica: i 1) Principio d inerzia 2) F=ma 3) Principio di azione e reazione Forza gravitazionale i e forza peso Accelerazione di gravità Massa, peso,
FISICA. Le forze. Le forze. il testo: 2011/2012 La Semplificazione dei Testi Scolastici per gli Alunni Stranieri IPSIA A.
 01 In questa lezione parliamo delle forze. Parliamo di forza quando: spostiamo una cosa; solleviamo un oggetto; fermiamo una palla mentre giochiamo a calcio; stringiamo una molla. Quando usiamo (applichiamo)
01 In questa lezione parliamo delle forze. Parliamo di forza quando: spostiamo una cosa; solleviamo un oggetto; fermiamo una palla mentre giochiamo a calcio; stringiamo una molla. Quando usiamo (applichiamo)
DINAMICA, LAVORO, ENERGIA. G. Roberti
 DINAMICA, LAVORO, ENERGIA G. Roberti 124. Qual è il valore dell'angolo che la direzione di una forza applicata ad un corpo deve formare con lo spostamento affinché la sua azione sia frenante? A) 0 B) 90
DINAMICA, LAVORO, ENERGIA G. Roberti 124. Qual è il valore dell'angolo che la direzione di una forza applicata ad un corpo deve formare con lo spostamento affinché la sua azione sia frenante? A) 0 B) 90
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
