Fig Struttura elementare del motore in corrente continua
|
|
|
- Raffaello Poggi
- 8 anni fa
- Visualizzazioni
Transcript
1 4 MACCHINA IN CORRENTE CONTINUA 4.1 Suu schm lmn P compn l pncpo funzonmno ll mcchn n con connu (m.c.c.) fccmo fmno ll suu lmn nc n Fg A φ 2 B Fg Suu lmn l moo n con connu Fg Pcoso l flusso cczon o so è l po pol sln. Su pol sono ol l bobn ch compongono l olgmno cmpo o cczon. Tl olgmno è pcoso con connu gn l flusso cczon (o cmpo) l moo, nco con φ. Quso flusso è po szono, coè l su confguzon spzl (mpp) s fss nl mpo. Inchmo con l ss mgnco (fsso) l flusso cczon. Sul oo, clnco, mmgnmo spos un sol sp (olgmno lmn) l cu smà 1 2 fnno cpo u lmll, loo sol soll l oo (coè uono ssm ll sp). lmll sono n cono lco con u spzzol (nc con A B), ch sono nc soll con lo so nu n psson sull lmll mn moll. spzzol pmono cc lcmn, l fmno fsso so, ll olgmno sposo sul oo (qu compos ll unc sp) o olgmno mu. Inchmo con l ss mgnco ll olgmno mu, concn con l ss ll sp 1-2 fssmo msu l ngolo ozon l ss l zon ng ll ss. o schm ll mcchn n con connu è nco nll sgun Fg Vso n mn ssm conson lomccnco l mcchn n con connu poss u po lch (gl olgmn cczon mu) so l qul ns ponz lc (n mn pooo nson con mos) un po Cp.4 MCC suu (2001) 31/03/
2 50 Cp. 4 Mcchn n con connu mccnc (l ss ozon) so l qul ns ponz mccnc n mn pooo locà ozon copp. In bs s l fluss ponz s può l funzonmno gno oppu moo com lluso nl sguo. Concomn ll connzon ulzz nll scu ll quzon ll qulbo nmco nll fnzon l pno copp locà consmo pos l ponz nl funzonmno moo, coè ponz lc nn ponz mccnc uscn (copp locà conco). cczon mu ss ozon Fg Schm lmn ll mcchn n con connu 4.2 Pncpo funzonmno Funzonmno gno In quso po funzonmno n fon ponz lc (P) ll olgmno cczon ponz mccnc (Pm) ll ss ozon, s ccogl ponz lc (P) sull olgmno mu. mcchn n con connu s compo gno (o nmo) può ss ulzzo p lmn un cco (nco n fgu ll ssnz Rc). P fss l, consmo l suu lmn l m.c.c. nll qul un moo pmo m (ll sno) n ozon l oo ( s. nl so cscn ϑ) mn s lmn l cczon con un gno n connu Funzonmno gno uoo Anlzzmo ppm l cso n cu l olgmno mu s po ( 0) coè l funzonmno gno uoo 1, Fg sp oo concn un p l flusso gno ll cczon. A sguo ll ozon l flusso concno con l sp s gn un nson no ch n bs ll gg Fy sc con l connzon ll ulzzo (C..U) fonsc: 1 Rspo l fgu, s s scuno l p p o nlzon, nl funzonmno gno uoo s à, gm, C Pm 0.
3 Pncpo funzonmno 51 0 P P 0 Rc Pm C, Fg Funzonmno gno uoo AB E φˆ π 2π φ 12 Fg Tnson no nll sp lmn φ 12 (4.1) Il flusso concno sà mssmo ngo p 0, nullo p π/2. Ipozzno un nmno snusol s può sc: cu: φ φˆ cos (4.2) 12 ( ) φˆ sn φˆ sn (4.3) P P Rc Pm C,
4 52 Cp. 4 Mcchn n con connu Fg Funzonmno gno cco S chmmo AB l nson ccol sull spzzol, n bs ll ozon l oo s hnno l sgun suzon cono 2 : - n (0,π) s hnno con: A 1, B 2, cu: AB 12 - n (π,2π) con s nono: A 2, B 1, cu: AB nson ccol l spzzol ppsn l nson no nll olgmno mu ( AB), l cu nmno, poo nll fgu pcn, è qun po connuo, nl snso unpol lo mo (E) non nullo, Fg S oss pno com, con l ssm collo lmll spzzol s lzz un commuo n go sfom un ln n un connu. Inumn, snno l numo sp è possbl on nson pù connu, pcmn cosn, com cc n moo l Funzonmno gno cco Vmo o cos succ nl funzonmno cco (Fg. 4.6), quno coè n chuso l nuo qun flusc un con nll olgmno mu. (0,π) C C 1() φ φ A 2() φ φ A 2(-) B R c 1(-) B R c ( π,2π) Fg Gnzon l flusso mu nl funzonmno gno Con fmno ll Fg. 4.7, n bs l sgno ll nson no s h ch p (0,π) l smo 1 h ponzl mggo ll smo 2, pno nl ccuo sno cco l con flusc 1 (pun ll fcc) so 2 (co ll fcc) 3. P ffo qus con s gn un flusso mu o n so opposo ll ss mgnzzzon (). P (π,2π) l suzon s n, coè 2 h ponzl mggo 1, m l so ll con è lo ssso qun nch l zon l flusso mu. 2 S scuno l poszon lm 0,π 2π. 3 Concomn ll connzon l gno (C..G.) nll olgmno mu l con flusc l moso ponzl mno so qullo ponzl mggo.
5 Pncpo funzonmno 53 φ φ Fg Fluss cczon mu con un sol sp mu In sosnz, l flusso mu è o smp nl smpno s ll fgu, è llno conco con l flusso cczon p 0 2π, llno sco p π non llno nll mnn poszon. succss Fg. 4.8 llus quso spo, mno n luc com, l uo ll sp, l so ll con s smp uscn p l conuo suo nl smpno supo, nn p l conuo suo nl smpno nfo. Il sulo è un copp lomgnc (C) ch n f uo l sp n moo lln (nl so conco) l flusso mu con l flusso cczon. Tl copp sà n moo oppos l moo l oo 4, à l nmno qulo nco n Fg. 4.9 nlogo ll nson no (lo mssmo quno u fluss sono ppncol loo). Pno, p ffo l commuo spzzol lmll, è possbl slupp un copp connu, nl snso l lo mo (Cm) non nullo. Esnno l numo sp s on un copp smp pù cosn. A smpo, nll Fg. 4.10, Fg Fg è lluso l cso (smp lmn) un mcchn con u sp 5. C C m 0 π 2π Fg Copp poo con un sol sp mu 4 Concomn ll conzon o copp locà sono sco nl funzonmno gno. 5 Quso cso può ss compso ossno ch l scon sp è sfs π/2 spo l pm, l lmll s snono nch p π/2.
6 54 Cp. 4 Mcchn n con connu π/ Fg Suu lmn con u sp mu 3-4 π/ E 0 π/4 π/2 π 3π/2 2π Fg Tnson no nl m.c.c con u sp mu C Cm 0 π/2 π 3π/2 2π Fg Copp poo nl m.c.c con u sp mu φ φ π/2 Fg Fluss cczon mu con u sp mu (gno)
7 Pncpo funzonmno Funzonmno moo P P Pm C, Fg Funzonmno moo Nl funzonmno moo (Fg. 4.14) s lmnno gl olgmn cczon mu (ngss) s c n usc ponz mccnc ll ss l moo soo fom copp locà ozon. In pcol, spo l cso l funzonmno gno, l so ll con mu () è opposo 6. Cò uol ch l flusso mu è o nch sso n moo opposo, spo l cso l funzonmno gno 7. φ φ Fg Fluss cczon mu con u sp mu (moo) D consgunz, nch l copp lomgnc ch n f uo l sp oo p lln fluss mu cczon h so opposo spo l cso l funzonmno nmo, cus un momno ozon nll su sss zon (l nmno n funzon ll ngolo è lo ssso l cso funzonmno nmo). 6 Concomn ll connzon ll ulzzo (C..U.) nll olgmno mu l con flusc l moso ponzl mggo so qullo ponzl mno 7 In pcol l flusso mu è o smp nl smpno sns ll fgu.
8 56 Cp. 4 Mcchn n con connu (0,π) C C φ φ 1() φ A 2(-) B 2() φ A 1(-) B (π,2π) Fg Gnzon l flusso mu nl funzonmno moo Espolno gfcmn un mcchn con un numo lo sp, l flusso mu sà fsso π/2 g spo l flusso cczon, l con n conuo oo nno so conco con l flusso (consno l funzonmno moo o nmo) l spzzol snno spos n quu (zon q chm ss nuo) spo l flusso cczon, sgnfc l collgmno conuo ch nsno n qus poszon 8. ppsnzon schmc ll mcchn n con connu nl funzonmno moo è llus n Fg π/2 q Fg Rppsnzon un m.c.c. funzonn moo 8 Con l sposzon, nll mcchn l l spzzol ccolgono l mssm nson no nll olgmno mu. Inol, un l commuzon u lmll succss, l spzzol ngono coo-ccu conuo n qul l nson no l flusso cczon è cc null, lmno l con coo.
9 Dmnzon l mollo l puno s ccu ccopp Dmnzon l mollo l puno s ccu ccopp Abbmo so ch l funzonmno l collo spzzol lmll f sì ch l olgmno mu, bnché composo conuo on qun sogg nson no l flusso cczon, gn su ol un flusso mu cosnmn o scono l ss q. Quso funzonmno ss nuo n b conszon quno s ogl mn l mollo nlco ll mcchn n con connu p l moo gnl ccu mgncmn ccopp. A l scopo, con fmno ll ppsnzon n Fg. 4.17, mmgnmo ch conmn quno cc nll mcchn l l spzzol uono sollmn l oo. D consgunz, l ss mgnco q ll olgmno mu uoà con l ngolo. Scmo qun l quzon p gl olgmn cczon mu succssmn mo cono l fo ch, nll mcchn l, l poszon ll ss q è fss n π/ Equzon lch quzon lch gl olgmn sono: ψ R ψ M olgmno mu ψ R ψ M olgmno cczon In ss, coffcn uo muu nuzon psn nll spsson fluss nno sgun nmn qul n funzon 10 : Inunz pop ll olgmno cczon: ( ) cosn Inunz pop ll olgmno mu: () q 0 π/2 π 3π/2 2π Fg Anmno qulo ll nunz pop ll olgmno mu 9 Con quso pocmno è possbl ulzz l moo gnl p l scu ll quzon n un suu lomgnc n ccu sul oo sullo so, nno cono po qulmn l funzonmno l collo. 10 Suppomo p smplcà po snusol gl nmn poc ll nunz.
10 58 Cp. 4 Mcchn n con connu Inunz muu gl olgmn mu cczon: M() M ( ) G sn G 0 π/2 π 3π/2 2π -G Fg Anmno qulo ll nunz muu mu cczon D l nmno s uc quno sgu: - l ll nunz pop ll olgmno cczon spo l poszon è smp ncmn null; - l ll nunz pop ll olgmno mu spo l poszon è null n cosponnz π/2 o l nunz h un mnmo; - l ll nunz muu spo l poszon è l po (Fg. 4.20): M G cos M G 0 π/2 π 3π/2 2π -G Fg Anmno qulo ll ll nunz muu mu cczon l suo lo clcolo n π/2 l: M G Sosuno l spsson fluss concn nll quzon ll nson gl olgmn s on: π 2
11 Dmnzon l mollo l puno s ccu ccopp 59 2 π M M M R ) ( 2 π M M M R ) ( sosuno l spsson coffcn nu ll loo clcol n π/2 s h: G R q G R I mn l po zon ll poszon nl mpo sono s sn nll quzon mu cczon n quno: - nll quzon mu, ppsn l locà l l flusso cczon l bobn mu; ffmn, ss conc con l locà ozon l oo ; - nll quzon cczon, ppsn l locà l l flusso mu l bobn cmpo; l locà è null, n quno l bobn cmpo sono fm spo l flusso mu. Pno, ll pcn conszon, ponno p comoà q, s ongono l sgun quzon lch ll mcchn n con connu: G R nson mu (4.4) R nson cczon (4.5) Consno nch l quzon fluss, s è sol fn: φ flusso mu 11 (4.6) φ flusso cczon (4.7) cu s o nch: G R φ nson mu (4.8) 11 Tl flusso conc con l flusso popo mu.
12 60 Cp. 4 Mcchn n con connu φ R nson cczon (4.9) Nll quzon ll nson mu, l mn popozonl ll locà ozon ppsn l nson no, ch consno l lgm (4.7) flusso con cczon s può sc: G k φ nson no (4.10) no fno l coffcn 12 : ( ) G k G φ (4.11) Espsson ll copp P quno gu l copp lomgnc, nl cso un suu lomgnc con un olgmno sullo so (1) uno sul oo (2) s l spsson gnl: C ( ) M( ) ( ) Pocno com l pgfo pcn, s può spclzz l spsson p l mcchn n con connu consno l lo ll coffcn nu n π/2. Sosuno 1 2 s h: 1 C 2 ll qul s c mmmn: 2 ( ) M ( ) 1 2 ( ) 2 π 2 C G (4.12) In bs ll (4.7) (4.11), l copp lomgnc s può nch sc n funzon l flusso cczon ll con mu: C k φ (4.13) Rppsnzon ccul quzon lch l spsson ll copp, nsm ll quzon qulbo mccnco, fnscono l mollo lomgnco ll mcchn n con connu. ppsnzon ccul ssoc è llus n Fg Il coffcn k sul cosn n pos lnà l ccuo mgnco.
13 Ts ppnmno 61 R () _ c() () () _ () c() R () () _ Fg Rppsnzon ccul ll mcchn n con connu Ts ppnmno 1) Dsc l suu bs un mcchn n con connu. 2) Dsc l collo lmll spzzol. 3) Dsgn lo schm lmn un mcchn n c.c. nuno l po ponz lc mccnc. 4) Dsc l funzonmno ll mcchn n c.c. nmo moo. Dsgn fluss ponz ngl olgmn cczon mu p u p funzonmno. 5) Cos s nn p nson nll olgmno mu? Rcn l nmno nl funzonmno nmo uoo p l mcchn con un sol sp mu. 6) Dsc l gnzon l flusso mu nl funzonmno moo ll mcchn con un sol sp mu. 7) Dsc l pncpo gnzon ll copp nl funzonmno moo. Rcn l nmno qulo p l mcchn con un sol sp mu. 8) Dsgn l suu un mcchn con pù sp mu nl funzonmno moo gno, pcsno l so ll con n conuo. 9) Rc l mollo lco l moo n c.c. p ll nls ccu mgncmn ccopp. 10) Rc l spsson ll copp lomgnc p ll spsson gnl p ccu mgncmn ccopp. 11) Espm l mollo lco l copp n mn flusso oppu con cczon. 12) Espm l nson no n mn flusso oppu con cczon. 13) Dsgn lo schm ccul un mcchn n con connu.
14 62 Cp. 4 Mcchn n con connu Inc ll fgu Fg Suu lmn l moo n con connu Fg Pcoso l flusso cczon Fg Schm lmn ll mcchn n con connu Fg Funzonmno gno uoo Fg Tnson no nll sp lmn Fg Funzonmno gno cco Fg Gnzon l flusso mu nl funzonmno gno Fg Fluss cczon mu con un sol sp mu Fg Copp poo con un sol sp mu Fg Suu lmn con u sp mu Fg Tnson no nl m.c.c con u sp mu Fg Copp poo nl m.c.c con u sp mu Fg Fluss cczon mu con u sp mu (gno) Fg Funzonmno moo Fg Fluss cczon mu con u sp mu (moo) Fg Gnzon l flusso mu nl funzonmno moo Fg Rppsnzon un m.c.c. funzonn moo Fg Anmno qulo ll nunz pop ll olgmno mu Fg Anmno qulo ll nunz muu mu cczon Fg Anmno qulo ll ll nunz muu mu cczon Fg Rppsnzon ccul ll mcchn n con connu INDICE 4 Mcchn n con connu Suu schm lmn Pncpo funzonmno Funzonmno gno Funzonmno gno uoo Funzonmno gno cco Funzonmno moo Dmnzon l mollo l puno s ccu ccopp Equzon lch Espsson ll copp Rppsnzon ccul...60 Ts ppnmno...61 Inc ll fgu...62 INDICE...62
MACCHINE ROTANTI A CORRENTE ALTERNATA:
 ACCHIE OTATI A COETE ATEATA: GEEAITA Inouzon l pn polo ngono noo l nozon h onnono l'nl l funzonno ll hn on on ln. T l pozon pol è l l o fol o ol o nno lun n phé onn un on unf l funzonno n g zono no. T
ACCHIE OTATI A COETE ATEATA: GEEAITA Inouzon l pn polo ngono noo l nozon h onnono l'nl l funzonno ll hn on on ln. T l pozon pol è l l o fol o ol o nno lun n phé onn un on unf l funzonno n g zono no. T
c r e a t i v i t à O G G I
 9 c mp us l pnso co p l succsso dll pop znd o dll pop ognzzzon To d Cy Tody d. Byb R. Vullngs UNA MENTE CREATVA ESERCTATE LE VSTRE ABLTA CREATVE! Esmn com un l, l pnso co d f sczo p mnn l popo cllo n fom.
9 c mp us l pnso co p l succsso dll pop znd o dll pop ognzzzon To d Cy Tody d. Byb R. Vullngs UNA MENTE CREATVA ESERCTATE LE VSTRE ABLTA CREATVE! Esmn com un l, l pnso co d f sczo p mnn l popo cllo n fom.
Aletti Borsa Protetta Certificate. Sentirsi al sicuro.
 Al Bos Po Cfc Sns l scuo Al Cfc T pomo dov d solo non uscs d v Lo sumno fnnzo ch consn d lzz un sg d nvsmno ch pnsv nccssbl Quso è Al Cfc Bnc Al, vo p dzon soddsf nch l sgnz pù sofsc dgl nvso, m dsposzon
Al Bos Po Cfc Sns l scuo Al Cfc T pomo dov d solo non uscs d v Lo sumno fnnzo ch consn d lzz un sg d nvsmno ch pnsv nccssbl Quso è Al Cfc Bnc Al, vo p dzon soddsf nch l sgnz pù sofsc dgl nvso, m dsposzon
5 DINAMICA DEI MOTORI A C.C. 5.1 Introduzione. 5.2 Modello dinamico della macchina a c.c. R a L a. + ia(t) R e + va(t) cr(t) ωr(t) φ (5.
 5 NM E MOTO.. 5. nouzon l gm noo moo c.c. è czzo gnzz, lch ch mccnch, bl nl mpo. Eo è conppoo l funzonmno n gm pmnn, czzo nc gnzz con nl mpo. l funzonmno noo fc nl pggo un conzon gm un l (un pco mpo è
5 NM E MOTO.. 5. nouzon l gm noo moo c.c. è czzo gnzz, lch ch mccnch, bl nl mpo. Eo è conppoo l funzonmno n gm pmnn, czzo nc gnzz con nl mpo. l funzonmno noo fc nl pggo un conzon gm un l (un pco mpo è
Aletti Bonus Certificate. Ti premia anche quando non te lo aspetti.
 Al Bonus Cfc T pm nch qundo non lo sp Al Cfc T pomo dov d solo non uscs d v Lo sumno fnnzo ch consn d lzz un sg d nvsmno ch pnsv nccssbl Quso è Al Cfc Bnc Al, vo p dzon soddsf nch l sgnz pù sofsc dgl nvso,
Al Bonus Cfc T pm nch qundo non lo sp Al Cfc T pomo dov d solo non uscs d v Lo sumno fnnzo ch consn d lzz un sg d nvsmno ch pnsv nccssbl Quso è Al Cfc Bnc Al, vo p dzon soddsf nch l sgnz pù sofsc dgl nvso,
ALLEGATO 4 al Disciplinare di gara DICHIARAZIONE DI OFFERTA ECONOMICA. Procedura per l affidamento della gestione del
 Allgo 4 ALLEGAT 4 l Disciplin di g DICHIARAZINE DI FFERTA ECNMICA Pocdu p l idmno dll gsion dl «Svizio di css vo dll Isiuo Compnsivo PISSASC I» p il innio 01/01/2014 31/12/2016 (Schm di o: compil su c
Allgo 4 ALLEGAT 4 l Disciplin di g DICHIARAZINE DI FFERTA ECNMICA Pocdu p l idmno dll gsion dl «Svizio di css vo dll Isiuo Compnsivo PISSASC I» p il innio 01/01/2014 31/12/2016 (Schm di o: compil su c
SCHEDA DI PROGRAMMAZIONE DISCIPLINARE TRIENNIO
 CERTIFICAZIONE QUALITÀ SCHEDA DI PROGRAMMAZIONE DISCIPLINARE TRIENNIO.. 2014-2015 INDIRIZZO ECONOMICO E TURISTICO DISCIPLINA RELIGIONE Lo n l n l coo à o go l gn copnz pcfch: vlpp n o no cco n ponl pogo
CERTIFICAZIONE QUALITÀ SCHEDA DI PROGRAMMAZIONE DISCIPLINARE TRIENNIO.. 2014-2015 INDIRIZZO ECONOMICO E TURISTICO DISCIPLINA RELIGIONE Lo n l n l coo à o go l gn copnz pcfch: vlpp n o no cco n ponl pogo
Teoria delle opzioni e Prodotti strutturati
 L FIME a.a. 8-9 9 oa ll ozon Poo suua Gogo Consgl gogo.onsgl@unbg. Uff 58 vmno m:.-3. Pogamma. Mao ll ozon ona va. oa ll ozon 3. nh valuazon 4. Hgng 5. Inggna fnanzaa 6. Pou numh 7. Dvavs sass Ozon Pou
L FIME a.a. 8-9 9 oa ll ozon Poo suua Gogo Consgl gogo.onsgl@unbg. Uff 58 vmno m:.-3. Pogamma. Mao ll ozon ona va. oa ll ozon 3. nh valuazon 4. Hgng 5. Inggna fnanzaa 6. Pou numh 7. Dvavs sass Ozon Pou
ICOM IC-F30 ICOM IC-F31 ICOM IC-F3062 EMC Whisper / Ward. Blocco tasti / Fonia / Selettiva. Composizione selettiva da inviare lungo lungo
 CROCE ROSSA ITALIANA Como d Pmnov ICOM IC-F30 ICOM IC-F31 ICOM IC-F3062 EMC Whp / Wd Bocco / Fon / Sv Cmbo cn T numc Compozon v d nv ungo ungo T numc Chm b Chm v 1 Codc Idnfcv Cn CRI FVG Udn 33 00 00 Pmnov
CROCE ROSSA ITALIANA Como d Pmnov ICOM IC-F30 ICOM IC-F31 ICOM IC-F3062 EMC Whp / Wd Bocco / Fon / Sv Cmbo cn T numc Compozon v d nv ungo ungo T numc Chm b Chm v 1 Codc Idnfcv Cn CRI FVG Udn 33 00 00 Pmnov
SISTEMI ELETTRICI DI POTENZA
 G. SUPETI UG OEISTIC EI SISTEI EETTOECCNICI ggo 00 SISTEI EETTICI I POTENZ g. 7 SISTEI EETTICI I POTENZ COPONENTI S coo olo lm f mmc, bl co o zl. No coo l omool. S co u fmo gl Pk comu czzo locà ω o cm
G. SUPETI UG OEISTIC EI SISTEI EETTOECCNICI ggo 00 SISTEI EETTICI I POTENZ g. 7 SISTEI EETTICI I POTENZ COPONENTI S coo olo lm f mmc, bl co o zl. No coo l omool. S co u fmo gl Pk comu czzo locà ω o cm
SCHEDA DI PROGRAMMAZIONE DISCIPLINARE
 SCHEDA DI PROGRAMMAZIONE DISCIPLINARE.. 2014-2015 DISCIPLINA : STORIA BIENNIO COORDINATRICE: Pof. Glon Cnp PROFILO IN USCITA A CONCLUSIONE DEL PERCORSO BIENNALE, IN TERMINI DI ABILITA E COMPETENZE Al n
SCHEDA DI PROGRAMMAZIONE DISCIPLINARE.. 2014-2015 DISCIPLINA : STORIA BIENNIO COORDINATRICE: Pof. Glon Cnp PROFILO IN USCITA A CONCLUSIONE DEL PERCORSO BIENNALE, IN TERMINI DI ABILITA E COMPETENZE Al n
MACCHINA SINCRONA MODELLO NELLE VARIABILI DI FASE
 G. SUPE UG OES E SSE EEOE l H SO g. 7 H SO OEO EE SE o o ll cch co è clco. Sullo o oo olg cou ugul o c lugo l o oo ch gl gc, b,c oo o lc loo. u coucoo gl olg cl, collg llo. l oo l o cch co. l ollo clco
G. SUPE UG OES E SSE EEOE l H SO g. 7 H SO OEO EE SE o o ll cch co è clco. Sullo o oo olg cou ugul o c lugo l o oo ch gl gc, b,c oo o lc loo. u coucoo gl olg cl, collg llo. l oo l o cch co. l ollo clco
Allegato n. 13. Fac simile REGISTRO DI MANUTENZIONE COMUNE DI LIVORNO
 Allgo n. 13 Fc sl REGISTRO DI MANUTENZIONE COMUNE DI LIVORNO REGISTRO DI MANUTENZIONE COME SI USA IL REGISTRO DI MANUTENZIONE ORDINARIA Il psn gso vuol ss uno suno suppoo ll Vos và p s ch l zzu cqus sno
Allgo n. 13 Fc sl REGISTRO DI MANUTENZIONE COMUNE DI LIVORNO REGISTRO DI MANUTENZIONE COME SI USA IL REGISTRO DI MANUTENZIONE ORDINARIA Il psn gso vuol ss uno suno suppoo ll Vos và p s ch l zzu cqus sno
CITTÀ DI IMOLA MEDAGLIA D'ORO AL VALOR MILITARE PER ATTIVITA' PARTIGIANA
 Inf.Com. Campanella 1 T.L. Domanda/ricev.N.21171 19/01/2015 Fratelli e Stradario - 65 2 S.A. Domanda/ricev.N.21208 21/06/2015 Fratelli e Stradario - 65 3 R.E. Domanda/ricev.N.21009 17/07/2015 Fratelli
Inf.Com. Campanella 1 T.L. Domanda/ricev.N.21171 19/01/2015 Fratelli e Stradario - 65 2 S.A. Domanda/ricev.N.21208 21/06/2015 Fratelli e Stradario - 65 3 R.E. Domanda/ricev.N.21009 17/07/2015 Fratelli
SCHEDA DI PROGRAMMAZIONE DISCIPLINARE TRIENNIO
 Sch Pogzon Tnno SCHEDA DI PROGRAMMAZIONE DISCIPLINARE TRIENNIO.. 2014-2015 INDIRIZZO: Anzon, Fnnz Mkng ARTICOLAZIONE: S nfov znl DISCIPLINA: Infoc PROFILO IN USCITA A CONCLUSIONE DEL PERCORSO QUINQUENNALE
Sch Pogzon Tnno SCHEDA DI PROGRAMMAZIONE DISCIPLINARE TRIENNIO.. 2014-2015 INDIRIZZO: Anzon, Fnnz Mkng ARTICOLAZIONE: S nfov znl DISCIPLINA: Infoc PROFILO IN USCITA A CONCLUSIONE DEL PERCORSO QUINQUENNALE
LA DOMANDA DI TRASPORTO CARATTERIZZAZIONE E MODELLI (Capitolo 2)
 Fcolà d Inggnr - Unvrsà d Bologn nno ccdmco: 00/ TECNIC ED ECONOMI DEI TSPOTI Docn: Mrno Lup L DOMND DI TSPOTO CTTEIZZZIONE E MODELLI (Cpolo Modll d domnd - Modllo d domnd dscrvo (o non compormnl: non
Fcolà d Inggnr - Unvrsà d Bologn nno ccdmco: 00/ TECNIC ED ECONOMI DEI TSPOTI Docn: Mrno Lup L DOMND DI TSPOTO CTTEIZZZIONE E MODELLI (Cpolo Modll d domnd - Modllo d domnd dscrvo (o non compormnl: non
Facoltà di Ingegneria 2 a prova in itinere di Fisica II Compito A
 Fcolà Ingegne pov n nee Fsc II.6. Compo A Eseczo n. Un cvo cossle nefno è cosuo un flo conuoe clnco ggo n ccono un gun conuce, clnc, cossle l flo, spessoe scule e ggo ex (ve nche l sezone). Il flo neno
Fcolà Ingegne pov n nee Fsc II.6. Compo A Eseczo n. Un cvo cossle nefno è cosuo un flo conuoe clnco ggo n ccono un gun conuce, clnc, cossle l flo, spessoe scule e ggo ex (ve nche l sezone). Il flo neno
Risultati esame scritto Fisica 2-26/06/2018 orali: 05/07/2018 alle ore presso aula O
 isui sm scio isic - 6/6/8 oi: 5/7/8 o.3 psso u O gi suni ssi vision o scio sono pgi i psnsi i giono 'o mico voo 5767 6 mm. isv 5446 4 988 3 mmsso 8535 6 mm. isv 846 4 7867 mmsso 754 8 mmsso 976 3 857 6
isui sm scio isic - 6/6/8 oi: 5/7/8 o.3 psso u O gi suni ssi vision o scio sono pgi i psnsi i giono 'o mico voo 5767 6 mm. isv 5446 4 988 3 mmsso 8535 6 mm. isv 846 4 7867 mmsso 754 8 mmsso 976 3 857 6
SCHEDA DI PROGRAMMAZIONE DISCIPLINARE TRIENNIO
 SCHEDA DI PROGRAMMAZIONE DISCIPLINARE TRIENNIO INDIRIZZO TURISMO.. 2014-15 DISCIPLINA Dcpln ch znl PROFILO IN USCITA A CONCLUSIONE DEL PERCORSO QUINQUENNALE, IN TER- MINI DI ABILITA E COMPETENZE (n b ll
SCHEDA DI PROGRAMMAZIONE DISCIPLINARE TRIENNIO INDIRIZZO TURISMO.. 2014-15 DISCIPLINA Dcpln ch znl PROFILO IN USCITA A CONCLUSIONE DEL PERCORSO QUINQUENNALE, IN TER- MINI DI ABILITA E COMPETENZE (n b ll
SCHEDA DI PROGRAMMAZIONE DISCIPLINARE
 SCHEDA DI PROGRAMMAZIONE DISCIPLINARE.. 2015/2016 DISCIPLINA MATEMATICA APPLICATA INDIRIZZO TURISMO FINALITÀ DELLA DISCIPLINA L c è n lo no nzl p n copnon nv ll là ll'lo, n p logcn con co, czzo n fo nà
SCHEDA DI PROGRAMMAZIONE DISCIPLINARE.. 2015/2016 DISCIPLINA MATEMATICA APPLICATA INDIRIZZO TURISMO FINALITÀ DELLA DISCIPLINA L c è n lo no nzl p n copnon nv ll là ll'lo, n p logcn con co, czzo n fo nà
Risultati simulazione test di accesso per l ammissione al corso di Laurea in Professioni Sanitarie
 81032GV 42,00 80207OG 39,75 82663RA 39,25 81026IF 38,75 80173GN 38,50 82400LS 38,50 83014FG 38,50 82402TR 38,25 81024CF 37,75 80329DG 37,50 82335GA 37,50 83099LG 37,50 82462GM 37,50 80360BS 37,25 82626DP
81032GV 42,00 80207OG 39,75 82663RA 39,25 81026IF 38,75 80173GN 38,50 82400LS 38,50 83014FG 38,50 82402TR 38,25 81024CF 37,75 80329DG 37,50 82335GA 37,50 83099LG 37,50 82462GM 37,50 80360BS 37,25 82626DP
T R I BU N A L E D I T R E V IS O A Z I E N D A LE. Pr e me s so
 1 T R I BU N A L E D I T R E V IS O BA N D O P E R L A C E S S IO N E C O M P E TI TI V A D EL C O M P E N D I O A Z I E N D A LE D E L C O N C O R D A T O PR EV E N T I V O F 5 Sr l i n l i q u i da z
1 T R I BU N A L E D I T R E V IS O BA N D O P E R L A C E S S IO N E C O M P E TI TI V A D EL C O M P E N D I O A Z I E N D A LE D E L C O N C O R D A T O PR EV E N T I V O F 5 Sr l i n l i q u i da z
SCHEDA DI PROGRAMMAZIONE DISCIPLINARE
 SCHEDA DI PROGRAMMAZIONE DISCIPLINARE.. 2013/2014 DISCIPLINA MATEMATICA APPLICATA INDIRIZZO ITER FINALITÀ DELLA DISCIPLINA L c è n lo no nzl p n copnon nv ll là ll'lo, n p logcn con co, czzo n fo nà cll.
SCHEDA DI PROGRAMMAZIONE DISCIPLINARE.. 2013/2014 DISCIPLINA MATEMATICA APPLICATA INDIRIZZO ITER FINALITÀ DELLA DISCIPLINA L c è n lo no nzl p n copnon nv ll là ll'lo, n p logcn con co, czzo n fo nà cll.
LE 10 REGOLE D ORO DELLA BUONA DIGESTIONE INDICATE DA
 ACQUA E TERME DI ULIVETO PISA LE 10 REGOLE D ORO DELLA BUONA DIGESTIONE INDICATE DA LE 10 REGOLE D ORO DELLA BUONA DIGESTIONE 1. ASSUMI UNA DIETA VARIA, RICCA DI FIBRE E CIBI GENUINI, SECONDO LO SCHEMA
ACQUA E TERME DI ULIVETO PISA LE 10 REGOLE D ORO DELLA BUONA DIGESTIONE INDICATE DA LE 10 REGOLE D ORO DELLA BUONA DIGESTIONE 1. ASSUMI UNA DIETA VARIA, RICCA DI FIBRE E CIBI GENUINI, SECONDO LO SCHEMA
Ogni amante è guerrier Libro ottavo de madrigali
 4 Ottvi Rinuccini (1562 1621) Tnr I c ' Tnr II c g' 10 16 3 O- 3 B. c. 3 O- 3 3 3 t, t nch' 3 3 22 3 d, f n g. g s pr v, sl Ogni t r Libr ttv d mdg r; Qul fi f O nl t, pr v c tà, n cl t, t r ch'l dur g
4 Ottvi Rinuccini (1562 1621) Tnr I c ' Tnr II c g' 10 16 3 O- 3 B. c. 3 O- 3 3 3 t, t nch' 3 3 22 3 d, f n g. g s pr v, sl Ogni t r Libr ttv d mdg r; Qul fi f O nl t, pr v c tà, n cl t, t r ch'l dur g
A.A. 2016/17 Graduatoria corso di laurea magistrale a ciclo unico in Giurisprudenza
 1 12/03/1997 I.M. 33,03 Idoneo ammesso/a 2 11/06/1997 B.F. 33,01 Idoneo ammesso/a 3 02/02/1998 T.A. 32,75 Idoneo ammesso/a 4 09/04/1997 B.M. 32,75 Idoneo ammesso/a 5 05/03/1998 M.S. 32,74 Idoneo ammesso/a
1 12/03/1997 I.M. 33,03 Idoneo ammesso/a 2 11/06/1997 B.F. 33,01 Idoneo ammesso/a 3 02/02/1998 T.A. 32,75 Idoneo ammesso/a 4 09/04/1997 B.M. 32,75 Idoneo ammesso/a 5 05/03/1998 M.S. 32,74 Idoneo ammesso/a
SCHEDA DI PROGRAMMAZIONE DISCIPLINARE
 SCHEDA DI PROGRAMMAZIONE DISCIPLINARE.. 2014/2015 DISCIPLINA MATEMATICA APPLICATA INDIRIZZO ITER FINALITÀ DELLA DISCIPLINA L c è n lo no nzl p n copnon nv ll là ll'lo, n p logcn con co, czzo n fo nà cll.
SCHEDA DI PROGRAMMAZIONE DISCIPLINARE.. 2014/2015 DISCIPLINA MATEMATICA APPLICATA INDIRIZZO ITER FINALITÀ DELLA DISCIPLINA L c è n lo no nzl p n copnon nv ll là ll'lo, n p logcn con co, czzo n fo nà cll.
della 1 furto, 6 sospettati, 1 solo colpevole (forse) Graziella Tarter e Monja Tait I libri-gioco per allenarsi nei dettati alla scuola primaria
 g n I m Gz T Mnj T n g Im I b-gc p ns n scu pm Qus nuv s ppn un ppcc ngu sc vs u, cn scz ch p sb un cqus n unm cnc scu gu. O bbn sun sgn, bmbn s nnn scv cmn u p nuv sgnfc scnscu. I vum hnn un v cmpssà
g n I m Gz T Mnj T n g Im I b-gc p ns n scu pm Qus nuv s ppn un ppcc ngu sc vs u, cn scz ch p sb un cqus n unm cnc scu gu. O bbn sun sgn, bmbn s nnn scv cmn u p nuv sgnfc scnscu. I vum hnn un v cmpssà
Legge regionale 2 agosto 2013, n. 45
 Dzn n D Cnnz Cn c Lgg gn g 013 n. 45 Invn gn fnnz n fv fmg v n ffcà cn cn g c. bn Uffc n. 39 m 07.0.013 gg 45 v CONRIBUI gn fmg n c c cnbu fv fg nuv n cc n ff v 70000 g un num; c 3 cnbu fv fmg num (mn
Dzn n D Cnnz Cn c Lgg gn g 013 n. 45 Invn gn fnnz n fv fmg v n ffcà cn cn g c. bn Uffc n. 39 m 07.0.013 gg 45 v CONRIBUI gn fmg n c c cnbu fv fg nuv n cc n ff v 70000 g un num; c 3 cnbu fv fmg num (mn
Europei calcio: l Italia delle seconde linee non convince
 Euop cco: I d scond n non convnc Euop cco. Con cmb qus u squd spo pm du p. G uomsm sno. Mo sopuo Suo non gnscono movmn gus. Insgn n d g unco mpo zzuo. L Ind vnc con mo. Euop cco. Pm d qus sfd, M n O N
Euop cco: I d scond n non convnc Euop cco. Con cmb qus u squd spo pm du p. G uomsm sno. Mo sopuo Suo non gnscono movmn gus. Insgn n d g unco mpo zzuo. L Ind vnc con mo. Euop cco. Pm d qus sfd, M n O N
ESTENSIONE ED EQUIVALENZA EQUIVALENZA DI POLIGONI
 ESTENSIONE ED EQUIVLENZ Supf pn mtt. Un supf pn mtt è un pt pno mtt un n us, oppu un pt pno omps t u o pù n us non s ntsno. Estnson un supf pn. I ontto - stnson un supf è un ontto pmtvo, om qu punto, tt,
ESTENSIONE ED EQUIVLENZ Supf pn mtt. Un supf pn mtt è un pt pno mtt un n us, oppu un pt pno omps t u o pù n us non s ntsno. Estnson un supf pn. I ontto - stnson un supf è un ontto pmtvo, om qu punto, tt,
3) DIFFUSIONE DELLA LUCE E SPETTROSCOPIA RAMAN
 DIFFUSION DLLA LU STTROSOIA RAAN La uso lla lu a pa u aomo quval al sgu posso (l aomo è l lvllo : (A Assobmo u oo quza vo oa k passaggo allo sao ao aua (sao al o msso u oo quza vo oa k. Oppu: (B msso u
DIFFUSION DLLA LU STTROSOIA RAAN La uso lla lu a pa u aomo quval al sgu posso (l aomo è l lvllo : (A Assobmo u oo quza vo oa k passaggo allo sao ao aua (sao al o msso u oo quza vo oa k. Oppu: (B msso u
MECCANICA STATICA CINEMATICA DINAMICA
 MECCANICA STATICA CINEMATICA DINAMICA CINEMATICA DESCRIVE IL MOTO INDIPENDENTEMENTE DALLE CAUSE CHE LO PRODUCONO O LO MODIFICANO DINAMICA STUDIA IL MOTO IN RELAZIONE ALLE CAUSE (FORZE) CHE LO PRODUCONO
MECCANICA STATICA CINEMATICA DINAMICA CINEMATICA DESCRIVE IL MOTO INDIPENDENTEMENTE DALLE CAUSE CHE LO PRODUCONO O LO MODIFICANO DINAMICA STUDIA IL MOTO IN RELAZIONE ALLE CAUSE (FORZE) CHE LO PRODUCONO
ConsigliStrategici. Errata. ConsigliGenerali. CarteDiceria: LimiteStivanelPorto: Pirati: Mercanti: NazionalitadelCapitano
 DmndFqun V n Qu ndun d h d n TUTT ununu m u n hnnh nn n u u n S hnnh nn n u u n ì h n nun à u num d u n A n Snbb d u u m ndu n u n N pup n p p nd b m n O d m qu nd n n dr d n md n mp d nè u n np u qu nd
DmndFqun V n Qu ndun d h d n TUTT ununu m u n hnnh nn n u u n S hnnh nn n u u n ì h n nun à u num d u n A n Snbb d u u m ndu n u n N pup n p p nd b m n O d m qu nd n n dr d n md n mp d nè u n np u qu nd
TRATTATO CHE ISTITUISCE LA C.E. Allegato 1)
 TRATTATO CHE ISTITUISCE LA C.E. Ago 1) Ago 2) GIURISPRUDENZA COMUNITARIA Ago 3) BIBLIOGRAFIA Gmbno G * Cobn G. L nomv u ng mpn : 3 o 1) Obbgo d u u voo I G o n d I ng. 2 / 1 / 19 79p. 7 2
TRATTATO CHE ISTITUISCE LA C.E. Ago 1) Ago 2) GIURISPRUDENZA COMUNITARIA Ago 3) BIBLIOGRAFIA Gmbno G * Cobn G. L nomv u ng mpn : 3 o 1) Obbgo d u u voo I G o n d I ng. 2 / 1 / 19 79p. 7 2
UNIVERSITA' CATTOLICA DEL SACRO CUORE
 Rpg vutzn p Cs Lu Ann ccmc 010/011 S Bsc Fctà FACOLTA' DI SCIENZE ATEATICHE,FISICHE E NATURALI Cs Lu ATEATICA (L) Dt stzn t 10/0/011 UNIERSITA' CATTOLICA DEL SACRO CUORE utzn ssfzn g stunt (Lgg 0/1) Rpg
Rpg vutzn p Cs Lu Ann ccmc 010/011 S Bsc Fctà FACOLTA' DI SCIENZE ATEATICHE,FISICHE E NATURALI Cs Lu ATEATICA (L) Dt stzn t 10/0/011 UNIERSITA' CATTOLICA DEL SACRO CUORE utzn ssfzn g stunt (Lgg 0/1) Rpg
Combattimento di Tancredi et Clorinda
 Trqut Tss (1544 1595) Clrd ' f '' Tncr d f ' Tst c g' B. c. TAn- LA- vl l' r pr Cmbtmnt Tncr t Clrd Libr ttv d dgli Tncr Cu Mnvr (1567 1643) Cl rd un h m s LA- 7 16 24 vr l pr. v d'n trr sp 3 2. 3 2 S
Trqut Tss (1544 1595) Clrd ' f '' Tncr d f ' Tst c g' B. c. TAn- LA- vl l' r pr Cmbtmnt Tncr t Clrd Libr ttv d dgli Tncr Cu Mnvr (1567 1643) Cl rd un h m s LA- 7 16 24 vr l pr. v d'n trr sp 3 2. 3 2 S
SCHEDA DI PROGRAMMAZIONE DISCIPLINARE
 Pno Lvoo Docn SCHEDA DI PROGRAMMAZIONE DISCIPLINARE.. 2014/15 DISCIPLINA INFORMATICA PROFILO IN USCITA A CONCLUSIONE DEL PERCORSO QUINQUENNALE, IN TERMINI DI ABILITA E COMPETENZE Ulzz gl n l nfoch nll
Pno Lvoo Docn SCHEDA DI PROGRAMMAZIONE DISCIPLINARE.. 2014/15 DISCIPLINA INFORMATICA PROFILO IN USCITA A CONCLUSIONE DEL PERCORSO QUINQUENNALE, IN TERMINI DI ABILITA E COMPETENZE Ulzz gl n l nfoch nll
graduatoria FASCIA 1 estrazione al 28/06/2018
 graduatoria FASCIA 1 estrazione al 28/06/2018 Nome POSIZIONE ESITO STRUTTURA BC 1 AMMESSO STACCIABURATTA (nido 7.30/16.30) BC 2 AMMESSO STACCIABURATTA (nido 7.30-13.30) AC 3 AMMESSO LA GIRANDOLA (7.30-16.30)
graduatoria FASCIA 1 estrazione al 28/06/2018 Nome POSIZIONE ESITO STRUTTURA BC 1 AMMESSO STACCIABURATTA (nido 7.30/16.30) BC 2 AMMESSO STACCIABURATTA (nido 7.30-13.30) AC 3 AMMESSO LA GIRANDOLA (7.30-16.30)
FABBISOGNO FINANZIARIO E LIMITI PER L'ACQUISTO DEI BUONI PASTO PER IL PERSONALE CIVILE - ANNO Allegato A Pagina 1 di 8
 CO. OVV. U' OVVGO S OVV. umero L SS SSGZ. O 100 1 O FSUU OO O 100 1 O FSUU OO O 1 1 F 11.132 65.990,50 101 10 CO FO O OL 101 10 CO FO O OL 2 5 1 F 53.460 308.571,12 102 10 O FSUU OL 102 10 O FSUU OL 5
CO. OVV. U' OVVGO S OVV. umero L SS SSGZ. O 100 1 O FSUU OO O 100 1 O FSUU OO O 1 1 F 11.132 65.990,50 101 10 CO FO O OL 101 10 CO FO O OL 2 5 1 F 53.460 308.571,12 102 10 O FSUU OL 102 10 O FSUU OL 5
Circuiti del II ordine. Contengono due elementi dinamici Il loro comportamento è rappresentato da un equazione differenziale del II ordine.
 rcu l II orn onngono u lmn nmc Il loro compormno è rpprsno un quzon ffrnzl l II orn. rcuo sr uonomo KT Drno rornno Occorr conoscr c..: I,? I V I V λ λ, λ ± Equzon crrsc λ, α α ± α [ s ] Frqunz lbr o nurl
rcu l II orn onngono u lmn nmc Il loro compormno è rpprsno un quzon ffrnzl l II orn. rcuo sr uonomo KT Drno rornno Occorr conoscr c..: I,? I V I V λ λ, λ ± Equzon crrsc λ, α α ± α [ s ] Frqunz lbr o nurl
Lezione 3. F. Previdi - Automatica - Lez. 3 1
 Lzon 3. Movmno Equlbro F. Prv - Auomaca - Lz. 3 1 Schma lla lzon 1. Movmno ll usca un ssma LTI SISO. Movmno lbro movmno forzao 3. Equlbro un ssma LTI SISO 4. Guaagno saco un ssma LTI SISO F. Prv - Auomaca
Lzon 3. Movmno Equlbro F. Prv - Auomaca - Lz. 3 1 Schma lla lzon 1. Movmno ll usca un ssma LTI SISO. Movmno lbro movmno forzao 3. Equlbro un ssma LTI SISO 4. Guaagno saco un ssma LTI SISO F. Prv - Auomaca
Campi Elettromagnetici e Circuiti I Circuiti del secondo ordine
 Facolà Inggnra Unrsà gl su Paa orso Laura Trnnal n Inggnra Elronca Informaca amp Elromagnc rcu I rcu l scono orn amp Elromagnc rcu I a.a. 3/4 Prof. Luca Prrgrn rcu l scono orn, pag. ommaro Dfnzon rcuo
Facolà Inggnra Unrsà gl su Paa orso Laura Trnnal n Inggnra Elronca Informaca amp Elromagnc rcu I rcu l scono orn amp Elromagnc rcu I a.a. 3/4 Prof. Luca Prrgrn rcu l scono orn, pag. ommaro Dfnzon rcuo
FABBISOGNO FINANZIARIO E LIMITI PER L'ACQUISTO DEI BUONI PASTO PER IL PERSONALE CIVILE - ANNO Allegato A Pagina 1 di 10
 FBBSOGO FZO L L'CQUSO BUO SO L SOL CVL - O F.. CO. O U' O (in ordine alfabetico) S O CO. OVV. U' OVVGO S OVV. OULZO cod.. L SS SSGZ. O 100 1 O FSUU OO O 100 1 O FSUU OO O 1 1 F 11.132 65.990,50 101 10
FBBSOGO FZO L L'CQUSO BUO SO L SOL CVL - O F.. CO. O U' O (in ordine alfabetico) S O CO. OVV. U' OVVGO S OVV. OULZO cod.. L SS SSGZ. O 100 1 O FSUU OO O 100 1 O FSUU OO O 1 1 F 11.132 65.990,50 101 10
( x) n x. 0 altrove = 1. f n. g n
 co : L sm d Co l o d Vl. Ism d Co: Cosdo [ ] sddvdo l sm l cossco C [ /] U [/ ] o d ovo l oo oo C [ /9] U [/9 /] U [/ 7/9] U [8/9 ] Io l ocdmo s h ch: C C C */ C 4*/9 C / L sm d Co: I o d Vl: C C chso
co : L sm d Co l o d Vl. Ism d Co: Cosdo [ ] sddvdo l sm l cossco C [ /] U [/ ] o d ovo l oo oo C [ /9] U [/9 /] U [/ 7/9] U [8/9 ] Io l ocdmo s h ch: C C C */ C 4*/9 C / L sm d Co: I o d Vl: C C chso
CITTA' DI ALGHERO PROVINCIA DI SASSARI - SETTORE V - QUALITA' DELLA VITA II AMBITO POLITICHE DI AFFIANCAMENTO E DI SOSTEGNO ALLE FAMIGLIE
 1 A.N. 01/01/1958 11 2 A.F. 07/05/1966 13 3 A.C. 07/10/1941 17 4 A.S. 05/12/1987 11 5 A.A. 14/03/1978 11 6 A.T. 22/12/1959 11 7 A.D. 18/09/1983 10 8 A.C. 17/06/1941 17 9 A.M. 11/05/1975 11 10 B.A. 15/08/1972
1 A.N. 01/01/1958 11 2 A.F. 07/05/1966 13 3 A.C. 07/10/1941 17 4 A.S. 05/12/1987 11 5 A.A. 14/03/1978 11 6 A.T. 22/12/1959 11 7 A.D. 18/09/1983 10 8 A.C. 17/06/1941 17 9 A.M. 11/05/1975 11 10 B.A. 15/08/1972
PROVINCIA DI VERONA RENDICONTO ESERCIZIO 2012 ELENCO DEI RESIDUI ATTIVI E PASSIVI DISTINTI PER ANNO DI PROVENIENZA
 PROVINCIA DI VERONA RENDICONTO ESERCIZIO 2012 ELENCO DEI RESIDUI ATTIVI E PASSIVI DISTINTI PER ANNO DI PROVENIENZA 1 2 RIEPILOGO GENERALE RESIDUI ATTIVI CONSERVATI 3 4 Pgm. CPA0099R ***-----------------------------------------------------------***
PROVINCIA DI VERONA RENDICONTO ESERCIZIO 2012 ELENCO DEI RESIDUI ATTIVI E PASSIVI DISTINTI PER ANNO DI PROVENIENZA 1 2 RIEPILOGO GENERALE RESIDUI ATTIVI CONSERVATI 3 4 Pgm. CPA0099R ***-----------------------------------------------------------***
ALLE ORE I CANDIDATI DOVRANNO PRESENTARSI NELL'AULA INDICATA MUNITI DI DOCUMENTO DI IDENTITA'
 TEST DI INGRESSO 10 APRILE 2015 DISLOCAZIONE AULE (Test valido per: Giurisprudenza; Interfacce e Tecnologie della Comunicazione; Scienze e Tecniche di Psicologia Cognitiva; Servizio Sociale; Sociologia;
TEST DI INGRESSO 10 APRILE 2015 DISLOCAZIONE AULE (Test valido per: Giurisprudenza; Interfacce e Tecnologie della Comunicazione; Scienze e Tecniche di Psicologia Cognitiva; Servizio Sociale; Sociologia;
Appendice 1. Richiami su sistemi dinamici e sulle equazioni differenziali lineari
 A. Mo, Uvà Bolog Elocc T-A, A.A. / Ac. chm m mc ll qzo ffzl l m lgco-ffzl. Eqzo o qzo c. olzo ll qzo o l l mo o. Ecczo co cczo ol. olzo ml. Eqzo cc co mo. o l o foz co go zo co o zo. là m l mo o. Com oo
A. Mo, Uvà Bolog Elocc T-A, A.A. / Ac. chm m mc ll qzo ffzl l m lgco-ffzl. Eqzo o qzo c. olzo ll qzo o l l mo o. Ecczo co cczo ol. olzo ml. Eqzo cc co mo. o l o foz co go zo co o zo. là m l mo o. Com oo
Note sull elettrostatica
 . Mffucc: Not su ttosttc. 1. 11/1 Unstà g tu Cssno Not su ttosttc pof. ntono Mffucc www.ocnt.uncs.t/ntono_mffucc V.1. - nomb 1 1 . Mffucc: Not su ttosttc. 1. 11/1. Mffucc: Not su ttosttc. 1. 11/1 1. Conctt
. Mffucc: Not su ttosttc. 1. 11/1 Unstà g tu Cssno Not su ttosttc pof. ntono Mffucc www.ocnt.uncs.t/ntono_mffucc V.1. - nomb 1 1 . Mffucc: Not su ttosttc. 1. 11/1. Mffucc: Not su ttosttc. 1. 11/1 1. Conctt
FABBISOGNO FINANZIARIO E LIMITI PER L'ACQUISTO DEI BUONI PASTO PER IL PERSONALE CIVILE - ANNO Allegato A Pagina 1 di 6
 CO. OVV. U' OVVGO S OVV. cod. L SS SSGZ. O 100 1 O FSUU OO O 100 1 O FSUU OO O 1 1 F 9.724 57.643,87 101 10 CO FO O OL 101 10 CO FO O OL 5 1 F 33.580 193.823,76 102 10 O FSUU OL 102 10 O FSUU OL 1 5 1
CO. OVV. U' OVVGO S OVV. cod. L SS SSGZ. O 100 1 O FSUU OO O 100 1 O FSUU OO O 1 1 F 9.724 57.643,87 101 10 CO FO O OL 101 10 CO FO O OL 5 1 F 33.580 193.823,76 102 10 O FSUU OL 102 10 O FSUU OL 1 5 1
L inizio: il problema del colore. *1660 Newton studia la rifrazione e scopre gli spettri. sviluppo storico della spettroscopia
 svlupp s dll spsp L nz: l plm dl l Il l è nnu nll lu n p? *66 Nwn sud l fzn sp l sp f l l è nnu nll lu uv d dv pvn l l dll fmm? *75 Mlvll sp l sp h dsv l ll dll fmm sd f l l è nnu nh n p? *8 Hshl sp l
svlupp s dll spsp L nz: l plm dl l Il l è nnu nll lu n p? *66 Nwn sud l fzn sp l sp f l l è nnu nll lu uv d dv pvn l l dll fmm? *75 Mlvll sp l sp h dsv l ll dll fmm sd f l l è nnu nh n p? *8 Hshl sp l
Risultati simulazione test di accesso per l ammissione al corso di Laurea in Economia
 per Area del Sapere 82720AE 52,00 83738DS 50,00 80966MM 49,00 83737PA 47,75 82866GG 47,50 80724CG 46,75 82972PG 46,75 82612SS 45,00 83377SS 45,00 82722GG 44,75 83739GV 44,75 82318LG 44,25 83361LD 44,25
per Area del Sapere 82720AE 52,00 83738DS 50,00 80966MM 49,00 83737PA 47,75 82866GG 47,50 80724CG 46,75 82972PG 46,75 82612SS 45,00 83377SS 45,00 82722GG 44,75 83739GV 44,75 82318LG 44,25 83361LD 44,25
I vettori. Grandezze scalari: Grandezze vettoriali
 I etto Gndee scl: engono defnte dl loo loe numeco esemp: lunghe d un segmento, e d un fgu pn, tempetu d un copo, ecc. Gndee ettol engono defnte, olte che dl loo loe numeco, d un deone e d un eso esemp:
I etto Gndee scl: engono defnte dl loo loe numeco esemp: lunghe d un segmento, e d un fgu pn, tempetu d un copo, ecc. Gndee ettol engono defnte, olte che dl loo loe numeco, d un deone e d un eso esemp:
SCHEDA DI PROGRAMMAZIONE DISCIPLINARE
 P.O.F. 2013-2014 SCHEDA DI PROGRAMMAZIONE DISCIPLINARE.. 2013/2014 DISCIPLINA MATEMATICA APPLICATA INDIRIZZI AFM colzon SIA RIM IGEA TRIENNIO FINALITÀ DELLA DISCIPLINA L c è n lo no nzl p n copnon nv ll
P.O.F. 2013-2014 SCHEDA DI PROGRAMMAZIONE DISCIPLINARE.. 2013/2014 DISCIPLINA MATEMATICA APPLICATA INDIRIZZI AFM colzon SIA RIM IGEA TRIENNIO FINALITÀ DELLA DISCIPLINA L c è n lo no nzl p n copnon nv ll
OSCILLATORE SINUSOIDALE A RETROAZIONE POSITIVA REALIZZATO CON AMPLIFICATORE OPERAZIONALE
 OSIATOE SINUSOIDAE A ETOAZIONE POSITIVA EAIZZATO ON AMPIFIATOE OPEAZIONAE I m h è pno zz pobb un nuov ouzon. Non è o ovo nu d m n n né n ; dov ndvdu quh fmno o d un b vzon. d è mu qundo vondo zz, uzzndo
OSIATOE SINUSOIDAE A ETOAZIONE POSITIVA EAIZZATO ON AMPIFIATOE OPEAZIONAE I m h è pno zz pobb un nuov ouzon. Non è o ovo nu d m n n né n ; dov ndvdu quh fmno o d un b vzon. d è mu qundo vondo zz, uzzndo
di Enzo Zanghì 1
 M@t_cornr d Enzo Zngì Intgrl ndfnto S dc c l funzon F () è un prmtv dll funzon f (), contnu nll'ntrvllo I s F '( ) f ( ) S un funzon mmtt n un ntrvllo I un prmtv, llor n mmtt nfnt c dffrscono tr loro mno
M@t_cornr d Enzo Zngì Intgrl ndfnto S dc c l funzon F () è un prmtv dll funzon f (), contnu nll'ntrvllo I s F '( ) f ( ) S un funzon mmtt n un ntrvllo I un prmtv, llor n mmtt nfnt c dffrscono tr loro mno
Rivelazione su singolo impulso
 Rivlio su sigolo imulso RRSN DE Uivsià i Rom L Si Rivlio oi ll cisio Sism smio i cisio bii: il v ci u iosi: bsglio ss: sgl icvuo solo isubo bsglio s: sgl icvuo sgl uil iù isubo M: Sio gli vi M : bsglio
Rivlio su sigolo imulso RRSN DE Uivsià i Rom L Si Rivlio oi ll cisio Sism smio i cisio bii: il v ci u iosi: bsglio ss: sgl icvuo solo isubo bsglio s: sgl icvuo sgl uil iù isubo M: Sio gli vi M : bsglio
Risultati simulazione test di accesso per l ammissione ai corsi di Laurea Triennale in Ingegneria
 per Area del Sapere I 80262EG 50,50 8,75 3,75 18,75 15,50 3,75 80275LM 39,75 8,50 6,25 1 1 4,00 83803RF 34,25 8,00 13,25 9,50 3,50 82832VA 30,25 80264LN 25,75 80259ZA 25,00 9,25 7,75 1 3,25 8,50 1 5,25
per Area del Sapere I 80262EG 50,50 8,75 3,75 18,75 15,50 3,75 80275LM 39,75 8,50 6,25 1 1 4,00 83803RF 34,25 8,00 13,25 9,50 3,50 82832VA 30,25 80264LN 25,75 80259ZA 25,00 9,25 7,75 1 3,25 8,50 1 5,25
Prodotto. Fascio tubiero ad U su piastra estraibile Esercizio (P max. / T max.): 12 bar / 95 C
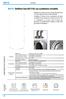 V1X Pootto V1X - ollto Inox ISI 16 con scmbto stbl ollto n cco Inox ISI 16 l ozon lo stocco c Cl Snt. Il bollto è otto no scmbto clo stbl fsco tbo n cco Inox ISI 16. o scmbto è cvto vso l bsso vn l olfzon
V1X Pootto V1X - ollto Inox ISI 16 con scmbto stbl ollto n cco Inox ISI 16 l ozon lo stocco c Cl Snt. Il bollto è otto no scmbto clo stbl fsco tbo n cco Inox ISI 16. o scmbto è cvto vso l bsso vn l olfzon
Sistemi trifase. Parte 2. www.die.ing.unibo.it/pers/mastri/didattica.htm (versione del 16-12-2013) Potenza assorbita da un carico trifase (1)
 Ssm rfas ar www.d.ng.unbo./prs/masr/ddaca.hm rson dl 6--0 onza assorba da un carco rfas Un gnrco carco rfas può ssr consdrao un doppo bpolo du por Sclo un rmnal d rfrmno, s può sprmr la ponza sanana assorba
Ssm rfas ar www.d.ng.unbo./prs/masr/ddaca.hm rson dl 6--0 onza assorba da un carco rfas Un gnrco carco rfas può ssr consdrao un doppo bpolo du por Sclo un rmnal d rfrmno, s può sprmr la ponza sanana assorba
Oltre i principi di Kirchhoff verso una trattazione elettromagnetica Kirchhoff prevederebbe che appena chiuso l
 O pcp d Kchh s n z mgnc Kchh pd ch ppn chs scss snnmn n cn n s s cn ns n mp s ssm ch cn s gn sn sss mg. km 3 n- n O pcp d Kchh s n z mgnc Kchh pd ch ppn chs scss snnmn n cn n s s cn ns n mp s ssm ch cn
O pcp d Kchh s n z mgnc Kchh pd ch ppn chs scss snnmn n cn n s s cn ns n mp s ssm ch cn s gn sn sss mg. km 3 n- n O pcp d Kchh s n z mgnc Kchh pd ch ppn chs scss snnmn n cn n s s cn ns n mp s ssm ch cn
SOSTEGNO AGLI ALUNNI CON DISABILITÀ (D.M. 30 settembre 2011) A.A. 2018/2019
 ELENCO AMMESSI TEST PRELIMINARE CORSI DI SPECIALIZZAZIONE PER LE ATTIVITÀ DI SOSTEGNO AGLI ALUNNI CON DISABILITÀ (D.M. 30 settembre 2011) A.A. 2018/2019 TUTTI I CANDIDATI SONO AMMESSI CON RISERVA IN ATTESA
ELENCO AMMESSI TEST PRELIMINARE CORSI DI SPECIALIZZAZIONE PER LE ATTIVITÀ DI SOSTEGNO AGLI ALUNNI CON DISABILITÀ (D.M. 30 settembre 2011) A.A. 2018/2019 TUTTI I CANDIDATI SONO AMMESSI CON RISERVA IN ATTESA
LE MATERICHE PRIMA SEZIONE (VERDE) - I QUADRATI - SEZIONE TURCHESE - GLI ORIZZONTALI - SEZIONE GIALLA - I VERTICALI - SEZIONE ROSSA
 L LOGO SUDDVSO N 4 GND SZON P FLN L ONSULZON P SZON (VD) L Sono opere uniche in quanto la riproduzione artistica su tela è arricchita dalla mano esperta di pittori, per restituire all opera riprodotta
L LOGO SUDDVSO N 4 GND SZON P FLN L ONSULZON P SZON (VD) L Sono opere uniche in quanto la riproduzione artistica su tela è arricchita dalla mano esperta di pittori, per restituire all opera riprodotta
AF 1 RITIRATO 26,1 26 2A AL 1 18,2 RITIRATO 25,7 26 3A AL 1 30,2 30 2A AL 0 RITIRATO 23,7 24 5A
 1 10538950 AB 1 18 22,1 22 2A 2 10425074 AB 0 3 10561116 AB 0 RITIRATO 4 10498984 AC 0 5 10574752 AF 1 RITIRATO 26,1 26 2A 6 10568818 AL 1 7 10503657 AL 1 18,2 RITIRATO 25,7 26 3A 8 10521184 AL 0 9 10539026
1 10538950 AB 1 18 22,1 22 2A 2 10425074 AB 0 3 10561116 AB 0 RITIRATO 4 10498984 AC 0 5 10574752 AF 1 RITIRATO 26,1 26 2A 6 10568818 AL 1 7 10503657 AL 1 18,2 RITIRATO 25,7 26 3A 8 10521184 AL 0 9 10539026
A.A. 2016/17 Graduatoria corso di laurea in Scienze e tecniche di psicologia cognitiva
 1 29/04/1997 V.G. 53,70 Idoneo ammesso/a * 2 27/12/1997 B.A. 53,69 Idoneo ammesso/a * 3 18/07/1997 P.S. 51,70 Idoneo ammesso/a * 4 12/05/1989 C.F. 51,69 Idoneo ammesso/a * 5 27/01/1997 P.S. 51,36 Idoneo
1 29/04/1997 V.G. 53,70 Idoneo ammesso/a * 2 27/12/1997 B.A. 53,69 Idoneo ammesso/a * 3 18/07/1997 P.S. 51,70 Idoneo ammesso/a * 4 12/05/1989 C.F. 51,69 Idoneo ammesso/a * 5 27/01/1997 P.S. 51,36 Idoneo
Divisione di Polizia Amministrativa Sociale e dell Immigrazione
 Divisione di Polizia Amministrativa Sociale e dell Immigrazione Polizia di Stato ELENCO PORTO D ARMI E NULLA OSTA PRONTI DA RITIRARE COMMISSARIATO CC DI RESIDENZA NR. PROTOCOLLO AIELLO D.S. AIELLO D.S.
Divisione di Polizia Amministrativa Sociale e dell Immigrazione Polizia di Stato ELENCO PORTO D ARMI E NULLA OSTA PRONTI DA RITIRARE COMMISSARIATO CC DI RESIDENZA NR. PROTOCOLLO AIELLO D.S. AIELLO D.S.
ID_PRATIC C A OGN N OM OME
 1 1188866 MV 2171 86,20 1 2 1190598 AV 2171 82,10 1 3 1188568 BC 2171 79,80 1 4 1191133 NP 2171 79,40 1 5 1192227 PR 2171 78,70 1 6 1188924 SA 2171 77,90 1 7 1175747 MG 2171 77,60 1 8 1191497 ZF 2171 76,80
1 1188866 MV 2171 86,20 1 2 1190598 AV 2171 82,10 1 3 1188568 BC 2171 79,80 1 4 1191133 NP 2171 79,40 1 5 1192227 PR 2171 78,70 1 6 1188924 SA 2171 77,90 1 7 1175747 MG 2171 77,60 1 8 1191497 ZF 2171 76,80
Aletti Up&Up Certificate. Salire. Anche quando gli altri scendono.
 Al Up&Up Cfc Sl Anch qundo gl l scndono Al Cfc T pomo dov d solo non uscs d v Lo sumno fnnzo ch consn d lzz un sg d nvsmno ch pnsv nccssbl Quso è Al Cfc Bnc Al, vo p dzon soddsf nch l sgnz pù sofsc dgl
Al Up&Up Cfc Sl Anch qundo gl l scndono Al Cfc T pomo dov d solo non uscs d v Lo sumno fnnzo ch consn d lzz un sg d nvsmno ch pnsv nccssbl Quso è Al Cfc Bnc Al, vo p dzon soddsf nch l sgnz pù sofsc dgl
PIANO COMUNALE DI PROTEZIONE CIVILE
 C VNZ SVZO POZON CV PNO COMUN POZON CV SCHO UCO C VNZ SVZO POZON CV PNO COMUN POZON CV, PNO POSSB SCN SCHO UCO, OVVO SCZON POSSB FF S SU UOMO SU NFSUU VFCS UN FNOMNO CMOSO, VU QU SNO ZON NPN P FFON MGNZ
C VNZ SVZO POZON CV PNO COMUN POZON CV SCHO UCO C VNZ SVZO POZON CV PNO COMUN POZON CV, PNO POSSB SCN SCHO UCO, OVVO SCZON POSSB FF S SU UOMO SU NFSUU VFCS UN FNOMNO CMOSO, VU QU SNO ZON NPN P FFON MGNZ
Elenco candidati preselezione - Comune di Padova-4
 CONCORSO PUBBLICO, PER ESAMI, A TEMPO INDETERMINATO PER N. 28 POSTI DI EDUCATORE ASILO NIDO DI CUI N. 4 PART-TIME, CATEGORIA C ELENCO CANDIDATI CHE DEVONO SOSTENERE LA PRESELEZIONE IL GIORNO 1 AGOSTO 2019
CONCORSO PUBBLICO, PER ESAMI, A TEMPO INDETERMINATO PER N. 28 POSTI DI EDUCATORE ASILO NIDO DI CUI N. 4 PART-TIME, CATEGORIA C ELENCO CANDIDATI CHE DEVONO SOSTENERE LA PRESELEZIONE IL GIORNO 1 AGOSTO 2019
App.Cap.II: Dettagli e sviluppi per il capitolo 2. App.Cap.II-1: Risposta di un sistema del primo ordine con ingresso a impulso.
 SCPC n C.II.C.II: Dgl svlu r l olo.c.ii-: sos un ssm l rmo orn on ngrsso mulso. () () δ () Pr l soluon onvn suvr l ss m n u r rsolvr u vrs E.D.O. Pr
SCPC n C.II.C.II: Dgl svlu r l olo.c.ii-: sos un ssm l rmo orn on ngrsso mulso. () () δ () Pr l soluon onvn suvr l ss m n u r rsolvr u vrs E.D.O. Pr
ALL. 1 - GRADUATORIA DEFINITIVA
 ALLEGATO 1 GRADUATORIA ASSEGNAZIONE CONTRIBUTI ALLE FAMIGLIE (VOUCHER) A PARZIALE COPERTURA DEL COSTO DI FREQUENZA ATTIVITA' ESTIVE 2019 (ALLEGATO 1) N. INIZIALI GENITORE INIZIALI FIGLIO/A NUMERO PROT.
ALLEGATO 1 GRADUATORIA ASSEGNAZIONE CONTRIBUTI ALLE FAMIGLIE (VOUCHER) A PARZIALE COPERTURA DEL COSTO DI FREQUENZA ATTIVITA' ESTIVE 2019 (ALLEGATO 1) N. INIZIALI GENITORE INIZIALI FIGLIO/A NUMERO PROT.
1 - Nuovo servizio CZ POINT con biglietteria concerti, eventi sportivi, teatri etc.
 N. 0 - Mzo 2009 Pzz ll Pc, 3 58014 Mncno (GR) Tl. Fx 0564 628390 www.c.n -ml: nfo@c.n C INIZIATIVE 1 - Nuovo svzo CZ POINT con bgl conc, vn spov, c. 2 - Psnzon lb con uo ll nno. 3 - Pomozon su gocol Nl
N. 0 - Mzo 2009 Pzz ll Pc, 3 58014 Mncno (GR) Tl. Fx 0564 628390 www.c.n -ml: nfo@c.n C INIZIATIVE 1 - Nuovo svzo CZ POINT con bgl conc, vn spov, c. 2 - Psnzon lb con uo ll nno. 3 - Pomozon su gocol Nl
Componenti dinamici. Carica e flusso. Si considera un bipolo e si indicano con v(t) e i(t) la sua tensione e la sua corrente
 omponen nmc.e.ng.unbo./pers/msr/c.hm ersone el --3 rc e flusso S conser un bpolo e s ncno con e l su ensone e l su correne Defnzone: crc ssoc ll correne q q Unà msur: coulomb Defnzone: flusso ssoco ll
omponen nmc.e.ng.unbo./pers/msr/c.hm ersone el --3 rc e flusso S conser un bpolo e s ncno con e l su ensone e l su correne Defnzone: crc ssoc ll correne q q Unà msur: coulomb Defnzone: flusso ssoco ll
3.1 Ridisegnando il circuito senza incroci e applicando la trasformazione triangolo-stella si ottengono gli schemi seguenti.
 . dsegnndo l crcuto senz ncroc e pplcndo l trsformzone trngolostell s ottengono gl schem seguent. Ω Ω eq Ω Ω Ω Ω Ω Ω eq Ω Ω Ω Ω eq Ω eq // Ω. S trsform l stell edenzt n rosso n un trngolo (le resstenze
. dsegnndo l crcuto senz ncroc e pplcndo l trsformzone trngolostell s ottengono gl schem seguent. Ω Ω eq Ω Ω Ω Ω Ω Ω eq Ω Ω Ω Ω eq Ω eq // Ω. S trsform l stell edenzt n rosso n un trngolo (le resstenze
TRASFORMATE DI LAPLACE
 TASOMATE D APACE rorm lc co rormr l quzo rzl quzo lgbrch mlco l l crcu mc lr. l moo ll rorm lc grlzz l moo or: zché clcolr l ro rm gr uol, co l rorm lc omo rcvr l ro coml u cl gr molo ù grl ch olr ll uo
TASOMATE D APACE rorm lc co rormr l quzo rzl quzo lgbrch mlco l l crcu mc lr. l moo ll rorm lc grlzz l moo or: zché clcolr l ro rm gr uol, co l rorm lc omo rcvr l ro coml u cl gr molo ù grl ch olr ll uo
Bando Trasferimenti da altra sede e passaggi di corso di studio - A.A. 2015-16
 C Cr Sr rrr su 1 B rsr lr s pssgg rs su -.. 2015-16 Sr S l u l prvu sru (r. 5 l B) r. 1 l B sbls h pss prpr l su b slusv: ) gl su prv lr s h h l srz u rs su ll sss lss qull u s sr, qul ur h, ll s u prvg,
C Cr Sr rrr su 1 B rsr lr s pssgg rs su -.. 2015-16 Sr S l u l prvu sru (r. 5 l B) r. 1 l B sbls h pss prpr l su b slusv: ) gl su prv lr s h h l srz u rs su ll sss lss qull u s sr, qul ur h, ll s u prvg,
ufficio show room scrittura ufficio elettronica hi-tech/accessori agende/calendari ombrelli borse
 how room cur uffco lonc h-ch/cco gnd/clnd ombrll bor uffco 38 l quozon ono ogg obl gumn ggornmn d mco c/orzon gg bmbo mr ugn uo clln bbgmno r S4068 d r bloccho un connor n c con bloccho n cr nn f. m ul
how room cur uffco lonc h-ch/cco gnd/clnd ombrll bor uffco 38 l quozon ono ogg obl gumn ggornmn d mco c/orzon gg bmbo mr ugn uo clln bbgmno r S4068 d r bloccho un connor n c con bloccho n cr nn f. m ul
SCHEDA DI PROGRAMMAZIONE DISCIPLINARE TRIENNIO
 Sch Pogzon Bnno P.O.F. ITCT BORDONI SCHEDA DI PROGRAMMAZIONE DISCIPLINARE TRIENNIO INDIRIZZO TURISTICO.. 2016/17 DISCIPLINA : ARTE E TERRITORIO PROFILO IN USCITA A CONCLUSIONE DEL PERCORSO QUINQUENNALE,
Sch Pogzon Bnno P.O.F. ITCT BORDONI SCHEDA DI PROGRAMMAZIONE DISCIPLINARE TRIENNIO INDIRIZZO TURISTICO.. 2016/17 DISCIPLINA : ARTE E TERRITORIO PROFILO IN USCITA A CONCLUSIONE DEL PERCORSO QUINQUENNALE,
al sistema GHS fabbricanti e agli impo
 hm d p h E m f n n md l ssm GHS nuv z l v n p Infmzn m m dsn h d p p l zzn d p. fbbn gl mp GHS l nuv ssm glblmn unfm d zn d pl GHS è l nm d Glblly Hmnzd Sysm f Cssfn nd Lbllng f Chmls, l nuv ssm d ssfzn
hm d p h E m f n n md l ssm GHS nuv z l v n p Infmzn m m dsn h d p p l zzn d p. fbbn gl mp GHS l nuv ssm glblmn unfm d zn d pl GHS è l nm d Glblly Hmnzd Sysm f Cssfn nd Lbllng f Chmls, l nuv ssm d ssfzn
SCHEDA DI PROGRAMMAZIONE DISCIPLINARE TRIENNIO
 SCHEDA DI PROGRAMMAZIONE DISCIPLINARE TRIENNIO.. 2013-2014 INDIRIZZO IGEA ITER CLASSI QUINTE DISCIPLINA SECONDA E TERZA LINGUA COMUNITARIA- TEDESCO PROFILO IN USCITA A CONCLUSIONE DEL PERCORSO QUINQUENNALE
SCHEDA DI PROGRAMMAZIONE DISCIPLINARE TRIENNIO.. 2013-2014 INDIRIZZO IGEA ITER CLASSI QUINTE DISCIPLINA SECONDA E TERZA LINGUA COMUNITARIA- TEDESCO PROFILO IN USCITA A CONCLUSIONE DEL PERCORSO QUINQUENNALE
APPLICAZIONI DELL INTEGRALE DEFINITO
 APPLICAZIONI DELL INTEGRALE DEFINITO Clolo d d dom p om d Ahmd Clolo d volum - volum d gu d ozo Lughzz d u o d uv Clolo dll d sup d voluzo 5 Igl mpop o glzz 6 Applzo dl lolo gl ll s To ll pm p CALCOLO
APPLICAZIONI DELL INTEGRALE DEFINITO Clolo d d dom p om d Ahmd Clolo d volum - volum d gu d ozo Lughzz d u o d uv Clolo dll d sup d voluzo 5 Igl mpop o glzz 6 Applzo dl lolo gl ll s To ll pm p CALCOLO
VectorWorks. Differenze fra la versione International e la versione in italiano
 7150 Rvw Dv, Club, MD 21046 Tlf: 410.290.5114 Fx: 410.290.8050 www.s. VWs è u Ns N Dsbu slusv l Il: VWs Dffz f l vs Il l vs l vs l, è suu lu, s u uz ll vs Il, è lu ls, u vs s l z ( s u) l l us ù sl uv.
7150 Rvw Dv, Club, MD 21046 Tlf: 410.290.5114 Fx: 410.290.8050 www.s. VWs è u Ns N Dsbu slusv l Il: VWs Dffz f l vs Il l vs l vs l, è suu lu, s u uz ll vs Il, è lu ls, u vs s l z ( s u) l l us ù sl uv.
Esperienza n 8:Determinazione del calore specifico di un corpo
 Espz 8:Dzo dl lo spfo d u opo Spo: o Eul (N ol 4549 v.o.) v Noo (N ol 458656 v.o.) Sopo dll spz Qus spz h lo sopo d d l lo spfo d u opo vso l uso dl loo dll solz. Su ulzz P l'spz soo s ulzz sgu su: -U
Espz 8:Dzo dl lo spfo d u opo Spo: o Eul (N ol 4549 v.o.) v Noo (N ol 458656 v.o.) Sopo dll spz Qus spz h lo sopo d d l lo spfo d u opo vso l uso dl loo dll solz. Su ulzz P l'spz soo s ulzz sgu su: -U
A.A. 2018/19 Graduatoria corso di laurea in Viticoltura ed Enologia Sessione estiva di agosto
 I/le idonei/e ammessi/e nella graduatoria del corso di laurea indicato come seconda scelta dovranno procedere con disponibili con i/le che hanno ottenuto un punteggio superiore alla soglia, l ammissione
I/le idonei/e ammessi/e nella graduatoria del corso di laurea indicato come seconda scelta dovranno procedere con disponibili con i/le che hanno ottenuto un punteggio superiore alla soglia, l ammissione
ANNO 2007 IMPORTO TOTALE ANNUO 68,12 L. 62/2000 68,12 L. 62/2000 68,12 L. 62/2000 68,12 L. 62/2000 68,12 L. 62/2000
 N. 1 COGNOME NOME 2 RC 3 PM 4 RP 5 NU GD FINALITA' DEL BENEFICIO CONCESSO IMPORTO TOTALE ANNUO RIFERIMENTI LEGISLATIVI 6 AV 7 PD 8 KN 9 AL 10 AR 11 TG 12 LD 13 GL 14 DD 15 DL 16 BM 17 BM 18 BE 19 AM 20
N. 1 COGNOME NOME 2 RC 3 PM 4 RP 5 NU GD FINALITA' DEL BENEFICIO CONCESSO IMPORTO TOTALE ANNUO RIFERIMENTI LEGISLATIVI 6 AV 7 PD 8 KN 9 AL 10 AR 11 TG 12 LD 13 GL 14 DD 15 DL 16 BM 17 BM 18 BE 19 AM 20
Giornata di studi UNIVERSITA DEGLI STUDI LINK CAMPUS UNIVERSITY. ROMA Via Nomentana, SETTEMBRE 2013 ore 08.30/19.30
 LS Vè nv G n S u L nv n nm pu n L p à mm n f u u p nm à, Cm C uz n, h mvnn,p Rm C z n S n Ann S m n L u C n u u ì C C m ò n n m pu L v uz n n m n m nn D num m p p n p nf m p S P : 6 8 m : @un nk Un v à
LS Vè nv G n S u L nv n nm pu n L p à mm n f u u p nm à, Cm C uz n, h mvnn,p Rm C z n S n Ann S m n L u C n u u ì C C m ò n n m pu L v uz n n m n m nn D num m p p n p nf m p S P : 6 8 m : @un nk Un v à
CITTÀ DI IMOLA MEDAGLIA D'ORO AL VALOR MILITARE PER ATTIVITA' PARTIGIANA
 Inf.Com. Campanella 1 P.L. Domanda/ricev.N.22080 08/07/2016 Fratelli e Stradario - 95 2 G.G. Domanda/ricev.N.22157 16/05/2016 Fratelli e Stradario - 65 3 B.A. Domanda/ricev.N.22162 23/11/2016 Fratelli
Inf.Com. Campanella 1 P.L. Domanda/ricev.N.22080 08/07/2016 Fratelli e Stradario - 95 2 G.G. Domanda/ricev.N.22157 16/05/2016 Fratelli e Stradario - 65 3 B.A. Domanda/ricev.N.22162 23/11/2016 Fratelli
SCHEDA DI PROGRAMMAZIONE DISCIPLINARE TRIENNIO
 P.O.F. ITCT BORDONI SCHEDA DI PROGRAMMAZIONE DISCIPLINARE TRIENNIO INDIRIZZO Tco ARTICOLAZIONE.. 2014/2015 DISCIPLINA A Too PROFILO IN USCITA A CONCLUSIONE DEL PERCORSO QUINQUENNALE [-p l nzzo: pn l ocno:
P.O.F. ITCT BORDONI SCHEDA DI PROGRAMMAZIONE DISCIPLINARE TRIENNIO INDIRIZZO Tco ARTICOLAZIONE.. 2014/2015 DISCIPLINA A Too PROFILO IN USCITA A CONCLUSIONE DEL PERCORSO QUINQUENNALE [-p l nzzo: pn l ocno:
Sistemi trifase. www.die.ing.unibo.it/pers/mastri/didattica.htm (versione del 30-10-2012) Sistemi trifase
 Ssm rfas www.d.ng.unbo./prs/masr/ddaca.hm vrson dl 0-0-0 Ssm rfas l rasporo la dsrbuzon d nrga lrca avvngono n prvalnza pr mzzo d ln rfas Un ssma rfas è almnao mdan gnraor a r rmnal rapprsnabl mdan rn
Ssm rfas www.d.ng.unbo./prs/masr/ddaca.hm vrson dl 0-0-0 Ssm rfas l rasporo la dsrbuzon d nrga lrca avvngono n prvalnza pr mzzo d ln rfas Un ssma rfas è almnao mdan gnraor a r rmnal rapprsnabl mdan rn
Giornate Mondiali Onu dei Lavoratori Marittimi e degli Oceani, la 4a edizione della Omnibus
 Gornt Mondl Onu d Lvortor Mrttm dgl Ocn, l 4 dzon d Omnbus Sn Bndtto dl Tronto, 2018-05-28 Arrvt l IV dzon d clbrzon ngunt d Gornt Mondl ONU d Lvortor Mrttm dgl Ocn, n Ptrocno ONU cur d Omnbus Omns Onlus,
Gornt Mondl Onu d Lvortor Mrttm dgl Ocn, l 4 dzon d Omnbus Sn Bndtto dl Tronto, 2018-05-28 Arrvt l IV dzon d clbrzon ngunt d Gornt Mondl ONU d Lvortor Mrttm dgl Ocn, n Ptrocno ONU cur d Omnbus Omns Onlus,
A.A. 2015/2016 Graduatoria ammessi al corso di laurea in Scienze e Tecniche di Psicologia Cognitiva sessione estiva
 1 S.A. 08/07/1996 30,00 46,40 76,40 Idoneo ammesso (*) 2 F.N. 19/07/1996 26,25 45,53 71,78 Idoneo ammesso 3 M.F. 24/05/1982 27,75 43,79 71,54 Idoneo ammesso 4 P.E.M 29/08/1989 21,00 49,01 70,01 Idoneo
1 S.A. 08/07/1996 30,00 46,40 76,40 Idoneo ammesso (*) 2 F.N. 19/07/1996 26,25 45,53 71,78 Idoneo ammesso 3 M.F. 24/05/1982 27,75 43,79 71,54 Idoneo ammesso 4 P.E.M 29/08/1989 21,00 49,01 70,01 Idoneo
LA DIVERSITÀ FUNZIONALE
 OPO OCO N FUNZON Mauro pezzi docente di Psicologia Generale e pplicata OPO OCO N Mauro pezzi (docente di Psicologia Generale e pplicata) GNOCO Mauro pezzi docente di Psicologia Generale e pplicata OPO
OPO OCO N FUNZON Mauro pezzi docente di Psicologia Generale e pplicata OPO OCO N Mauro pezzi (docente di Psicologia Generale e pplicata) GNOCO Mauro pezzi docente di Psicologia Generale e pplicata OPO
Servizio Politiche attive per il lavoro Servizio Formazione professionale
 Graduatoria provinciale integrata Bando di avviamento a selezione, riservato a lavoratori disabili, c/o Azienda ULSS 12 veneziana per n. 12 posti di Coadiutore amministrativo cat. B, a tempo indeterminato
Graduatoria provinciale integrata Bando di avviamento a selezione, riservato a lavoratori disabili, c/o Azienda ULSS 12 veneziana per n. 12 posti di Coadiutore amministrativo cat. B, a tempo indeterminato
Protezione al fuoco di pareti non caricate EN 1364-1
 Pozon al foco d pa non caca vson 1.0 Pncp gnal Qsa noma dscv pncp gnal p la dmnazon dlla ssnza al foco d pa non poan. Campon d pova L oggo dlla noma è la vfca d alcn paam lva s n povno sposo al foco n
Pozon al foco d pa non caca vson 1.0 Pncp gnal Qsa noma dscv pncp gnal p la dmnazon dlla ssnza al foco d pa non poan. Campon d pova L oggo dlla noma è la vfca d alcn paam lva s n povno sposo al foco n
al Braglia! Campagna Abbonamenti Stagione Sportiva 2013/2014
 V l Bgl! g bb g v 213/214 2 g bb g v 213/214 BBNMN P BUNM UÀ 1.25 BUNM LL 1.5 BUNM P BUN B F BUN P 7 42 28 8 21 PXYZ BUN P v B PLNM 38 225 14 8 21 F N LL 23 145 125 8 21 G H L M N Q GN P N NN.GV. NN UN
V l Bgl! g bb g v 213/214 2 g bb g v 213/214 BBNMN P BUNM UÀ 1.25 BUNM LL 1.5 BUNM P BUN B F BUN P 7 42 28 8 21 PXYZ BUN P v B PLNM 38 225 14 8 21 F N LL 23 145 125 8 21 G H L M N Q GN P N NN.GV. NN UN
Il prisma Interferenza costruttiva solo quando l angolo di incidenza è tale che ', cioè. Spettroscopia e Interferenza. Risoluzione del Prisma
 Spscpa nfnza P sua un sp s ulzza quas sp l fnn ll nfnza. Nl sgu sò c a scna l nu fasc luns ch s fann nf l nfazn spal vna pù n vn a è cunqu sp cnnua nlla fgua nfnza pa lla luc. bba vs ch nl cas l psa c
Spscpa nfnza P sua un sp s ulzza quas sp l fnn ll nfnza. Nl sgu sò c a scna l nu fasc luns ch s fann nf l nfazn spal vna pù n vn a è cunqu sp cnnua nlla fgua nfnza pa lla luc. bba vs ch nl cas l psa c
Test di autovalutazione
 UNITÀ 2 GLI ELEMENTI FONMENTLI ELL GEOMETRI T T i uovluzion 0 10 20 30 40 0 0 70 80 90 100 n Il mio punggio, in nimi, è 1 2 3 Ov l figu gn l uni popoizion o. ppin L. ppin l. ppin l. ppin l ppin l. l ppin.
UNITÀ 2 GLI ELEMENTI FONMENTLI ELL GEOMETRI T T i uovluzion 0 10 20 30 40 0 0 70 80 90 100 n Il mio punggio, in nimi, è 1 2 3 Ov l figu gn l uni popoizion o. ppin L. ppin l. ppin l. ppin l ppin l. l ppin.
