B1.3 Analisi armonica del sistema biella-manovella
|
|
|
- Giovanni Catalano
- 8 anni fa
- Visualizzazioni
Transcript
1 .3 Analisi armonica del sistema biella-manovella Meccanica, Macchine ed Energia articolazione Meccanica e Meccatronica 3 Giuseppe Anzalone, Paolo Bassignana, Giuseppe Brafa Musicoro Copyright Ulrico Hoepli Editore S.p.A. poliglotta Componente armonica GB: Harmonic component F: Composante harmonique D: Teilschwingung richiamo La formula che pone in relazione la pulsazione con la frequenza è la seguente: ω = 2 π f. Lo studio che ha condotto alla formulazione approssimata della velocità (4Form. 1.6) e dell accelerazione del piede di biella (4Form. 1.7) è stato condotto utilizzando equazioni semplificate nelle quali sono stati trascurati alcuni termini. È pur sempre possibile sviluppare le derivate dello spostamento x, operando a partire dalla formulazione completa (4Form. 1.3), senza trascurare nessun fattore, onde ricavare formule esatte per la velocità e soprattutto per l accelerazione. Per ovviare alle difficoltà concettuali causate dalla presenza della radice quadrata all interno della parentesi tonda nella [1.3], è possibile sostituire la radice quadrata mediante uno sviluppo in serie di potenze. Poiché: λ sen ϑ è riconducibile alla seguente funzione generale: (1 + x) a in cui la variabile indipendente x è pari al prodotto (-λ 2 sen 2 ϑ) e l esponente a è pari a 1/2. Sviluppando (1 + x) a in serie di Mc Laurin e tralasciando i passaggi relativi allo sviluppo in serie e alle successive operazioni di derivazione, per i quali si rimanda a testi specialistici, si perviene alla seguente formulazione dell accelerazione del piede di biella: a p = ω 2 r(cos ϑ + A 2 cos 2 ϑ + A 4 cos 4 ϑ + A 6 cos 6 ϑ + A 8 cos 8 ϑ + ) in cui l angolo ϑ può essere sostituito con il prodotto della pulsazione ω per la variabile tempo t: a p = ω 2 r(cos ω t + A 2 cos 2 ω t + A 4 cos 4 ω t + + A 6 cos 6 ω t + A 8 cos 8 ω t + ) [1.10] L accelerazione del piede di biella si presenta in forma di serie, i cui termini sinusoidali sono detti componenti armoniche. Attraverso una rigorosa procedura matematica si è ottenuta la [1.10], che costituisce l espressione esatta per l accelerazione del piede di biella, le cui caratteristiche sono riportate di seguito. Essa si presenta sotto forma di somma di infinite funzioni coseno che differiscono fra loro per ampiezza e pulsazione. La prima delle funzioni coseno, avente ampiezza A 1 unitaria e pulsazione ω pari alla velocità angolare dell albero, è detta componente fondamentale o del primo ordine. La seconda delle funzioni coseno, avente ampiezza A 2 e pulsazione pari al doppio della velocità angolare dell albero, è detta componente del secondo ordine. La terza delle funzioni coseno, avente ampiezza A 4 e pulsazione pari al quadruplo della velocità angolare dell albero, è detta componente del quarto ordine; per le componenti di ordine superiore si procede 1
2 richiamo Lo studio delle frequenze proprie dei corpi è analizzato nella Unità didattica A1. utilizzando lo stesso principio, per cui si avranno componenti del sesto ordine, dell ottavo ordine e così via. Tranne la componente fondamentale, tutte le componenti armoniche hanno ordine pari: ciò si nota dal fatto che in esse la pulsazione ω è moltiplicata per un numero multiplo di 2. Le ampiezze A 2, A 4, A 6 sono dette coefficienti armonici e decrescono all aumentare dell ordine: A 2 > A 4 > A 6 > A 8 > Di norma solo i primi due termini hanno importanza nello studio dei fenomeni vibratori (specie nello studio dinamico del sistema biellamanovella), poiché l ampiezza delle componenti armoniche si riduce man mano che si prendono in considerazione gli ordini più elevati. Le armoniche di ordine elevato non sono tuttavia trascurabili, qualora una di esse risulti in fase con la frequenza propria di alcuni organi appartenenti al macchinario e che entrano in risonanza quando sono eccitati dalla componente con frequenza uguale a quella dell organo. L insieme delle frequenze delle diverse armoniche generate nel moto alterno del piede di biella, induce nei vari organi sottoposti a vibrazione uno stato di sollecitazione che causa l affaticamento della struttura. La formulazione semplificata dell accelerazione del piede di biella (4Form. 1.7) si ottiene dalla formulazione completa (4Form. 1.10), di cui rappresenta un caso particolare. È sufficiente prendere in considerazione i primi due termini della serie (4Form. 1.10), aventi ampiezze A 1 = 1 e A 2 = λ, per ottenere esattamente la [1.7]. Anche la forza d inerzia si presenta in forma di somma di infinite funzioni coseno; essa è ottenuta moltiplicando l accelerazione (4Form. 1.10) per la massa m p applicata nel piede di biella. Le componenti più importanti per l esecuzione del calcolo strutturale della biella sono la componente fondamentale e la componente di secondo ordine. Esempio Una pompa alternativa monocilindrica funziona a regime, alla frequenza di rotazione n = 1800 giri/min. Calcolare i valori delle pulsazioni relative alle componenti dell accelerazione al piede di biella del primo, del secondo, del quarto, del sesto e dell ottavo ordine. Soluzione Si calcola per prima la velocità angolare a cui corrisponde la pulsazione dell armonica fondamentale ω I : ω cui corrisponde la frequenza f I : I 2π n 2π 1800 = = = 188, f I I ω 188, 5 = = = 30 Hz 2π 2π La pulsazione della componente del secondo ordine vale il doppio rispetto rad s 2
3 a quella della componente fondamentale: ω cui corrisponde la frequenza f II : II I rad = 2ω = 2 188, 5 = 377 s Meccanica, Macchine ed Energia articolazione Meccanica e Meccatronica 3 Giuseppe Anzalone, Paolo Bassignana, Giuseppe Brafa Musicoro Copyright Ulrico Hoepli Editore S.p.A. f II II ω 377 = = = 60 Hz 2π 2π La pulsazione della componente del quarto ordine vale il doppio rispetto a quella del secondo: ω cui corrisponde la frequenza f IV : IV II rad = 2ω = = 754 f IV IV ω 754 = = = 120 Hz 2π 2π La pulsazione della componente del sesto ordine vale il sestuplo rispetto a quella della componente fondamentale: ω VI cui corrisponde la frequenza f VI : I = 6ω = 6 188, 5 = 1131 f VI VI ω 1131 = = = 180 Hz 2π 2π La pulsazione della componente dell ottavo ordine vale il doppio rispetto a quella del quarto: ω cui corrisponde la frequenza f VIII : = 2ω = = 1508 s rad s VIII IV rad f VIII VIII ω 1508 = = = 240 Hz 2π 2π Analisi sperimentale dell accelerazione del piede di biella È possibile effettuare il percorso inverso a quello della somma delle componenti armoniche appena descritto, grazie al teorema formulato dal matematico Jean Baptiste Fourier, per il quale: una qualsiasi funzione periodica, non importa quanto complessa, può essere decomposta nella somma di un numero infinito di componenti sinusoidali, aventi diverse ampiezze e con le frequenze correlate fra loro. s 3
4 poliglotta Spettro delle frequenze GB: Frequency spectrum F: Spectre de fréquences D: Frequenzspektrum richiamo Le apparecchiature in grado di scomporre un segnale di natura acustica o vibrazionale nelle sue componenti armoniche sono dette Sound Intensity Analyzer o Fast Fourier Transformer (FFT). Fig. 1.7 Analisi spettrografica dell accelerazione del piede di biella: a) schema teorico; b) risultato sperimentale. poliglotta Vibrazione GB: Vibration F: Vibration D: Schwingung L insieme delle componenti armoniche di una vibrazione costituisce lo spettro delle frequenze. Osservazione: su questo principio si basano i rilevamenti sperimentali eseguiti applicando accelerometri su macchinari vibranti, allo scopo di prelevare segnali proporzionali all accelerazione complessiva; tale segnale viene amplificato e inviato ad apparecchiature in grado di decodificarlo e scomporlo nelle sue componenti armoniche. È possibile rappresentare lo spettro riportando le ampiezze delle componenti su un grafico, in cui sull asse delle ascisse sono indicate le frequenze, anziché il tempo o l angolo di rotazione; pertanto il grafico in dominio di tempo diventa un grafico in dominio di frequenza, evidenziando il valore dell ampiezza di ciascuna componente armonica. Nella figura 1.7a si riporta lo spettro in dominio di frequenza per l accelerazione del piede di biella, in cui sono state prese in considerazione le componenti fino al quarto ordine. Il grafico indicato nella figura 1.7b corrisponde a un rilievo sperimentale con l accelerometro posto, per esempio, sulla testata di un motore monocilindrico in funzione, dotato quindi di un solo meccanismo biella-manovella; anche in questo caso sono stati riportati i contributi delle componenti comprese tra il primo e il quarto ordine. Dal confronto fra i due grafici, rispettivamente teorico e sperimentale, tracciati nella figura 1.7, emergono diverse considerazioni: si conferma il ruolo preponderante svolto dall armonica fondamentale e, in percentuale minore, da quella del secondo ordine; l ampiezza dall armonica fondamentale e quella del secondo ordine stanno fra loro nel rapporto λ; gli spettri indicano il decadere dei contributi delle funzioni al crescere del loro ordine, soprattutto per gli ordini superiori al secondo; le ampiezze rilevate per via sperimentale sono di poco superiori a quelle teoriche: ciò è dovuto alle componenti vibrazionali generate all atto della combustione, che si propagano attraverso la struttura e che vengono percepite dal sensore e poi trasmesse lungo la catena di misura; lo spettro rilevato per via sperimentale evidenzia anche la presenza delle ampiezze di ordine dispari, seppure di bassa entità: anche queste sono generate dalla combustione. 4
5 richiamo I motori a V, aventi l angolo fra le due bancate pari a 60, sono detti motori a V stretto o a V scalato (4Fig.1.28). Fig Imbiellaggio per: a) motore bicilindrico a V di 90 ; b) motore bicilindrico contrapposto; c) motore bicilindrico boxer, di produzione BMW. Motori e compressori con cilindri a V e contrapposti La ripartizione dei cilindri a V consiste nello sdoppiamento del basamento in due bancate parallele e inclinate; il numero dei cilindri viene suddiviso a metà per ciascuna bancata. Tale architettura è molto diffusa quando è presente un elevato numero di cilindri (per esempio nei motori con otto e più cilindri), mentre è meno diffusa nei motori a due e a sei cilindri. Il vantaggio che ne deriva consiste essenzialmente nel contenimento dell ingombro longitudinale dell albero e del motore in generale. Infatti la lunghezza di un basamento formato da un certo numero di cilindri in linea è pari alla somma degli alesaggi di ciascun cilindro più gli spessori di parete fra un cilindro e l altro. Suddividendo i cilindri alternativamente su due bancate affiancate si ottiene una macchina di forma più compatta: infatti all aumento delle dimensioni trasversali segue una riduzione di ingombro longitudinale, poiché le due bancate sono affiancate e ciascuna occupa circa la metà della lunghezza del basamento unico. A questo punto è opportuno montare due bielle per manovella, collegate con pistoni operanti il primo in una bancata, il secondo nell altra; in tal modo si sono ridotti sia l ingombro in longitudinale del basamento sia la lunghezza complessiva dell albero; l angolo fra le due bancate è scelto fra pochi valori, principalmente 60, 90 e 120. Nei motori bicilindrici a V l albero a gomiti presenta una sola manovella su cui sono montate affiancate entrambe le bielle, consentendo di ottenere una buona riduzione degli ingombri in senso assiale unitamente a un elevata rigidezza torsionale (4Fig.1.25a). Si tratta di un architettura adottata frequentemente sia nei motori motociclistici sia nei compressori. Con riferimento allo schema rappresentato nella figura 1.25a è possibile notare la presenza di un abbondante contrappeso, il cui asse di simmetria è in linea con l asse del cilindro destro, proprio quando il pistone 5
6 Fig Compressore bicilindrico a V di 90, modello XLE, di produzione Ingersoll-Rand. destro si trova al PMS. Quest ultimo è dimensionato in modo da controbilanciare al 100% sia la forza alterna del primo ordine, agente sul pistone destro, sia la forza centrifuga dell albero. Nella suddetta configurazione, inoltre, il pistone sinistro si trova esattamente a metà della sua corsa, e la sua forza alterna del primo ordine vale 0. Eseguendo una rotazione oraria di 90 le parti si invertono; il pistone destro si trova a metà corsa (quindi la sua forza alterna del primo ordine è nulla); il pistone sinistro si trova al PMI, pertanto la forza alterna del primo ordine è massima ma del tutto controbilanciata dal contrappeso: in questa seconda configurazione esso si dispone con l asse di simmetria allineato all asse del cilindro sinistro. Si può affermare che adottando l architettura a due cilindri a V di 90 mediante contrappesatura si ottiene la completa equilibratura delle forze alterne del primo ordine. Un interessante variante consiste nell aumentare l angolo fra i due cilindri fino a 180, così che le loro posizioni siano contrapposte. L albero a gomiti è ora formato da due manovelle pure contrapposte, in modo che entrambi i pistoni giungano contemporaneamente al PMS, condizione necessaria per il funzionamento regolare dei bicilindrici a quattro tempi (4Fig.1.25b). L albero a gomiti è analogo a quello impiegato nelle pompe e nei compressori. Nella figura 1.25c è riportata la vista in elevazione del motore motociclistico bicilindrico contrapposto R 1100 S, di produzione BMW, in cui è posto in evidenza il pistone destro al PMS e un contrappeso a mannaia: tale contrappeso più un secondo ribaltato di 180 servono per assicurare l equilibratura dinamica dell albero (4Fig.1.18b). Nella figura 1.26 è riportato il compressore modello XLE, di produzione Ingersoll-Rand, avente due cilindri a
7 Fig Cilindri a V: a) compressore tricilindrico a W, di produzione Ingersoll-Rand; b) motore quadricilindrico Honda a V di 90. poliglotta Imbardata, beccheggio GB: Yaw, pitch F: Lacet, galop D: Gieren, Stampfen Si possono osservare le valvole (1), il pistone (2), il passaggio dell aria proveniente dal primo stadio (3), l interrefrigeratore (4), il vano separatore di condensa (5), due intercapedini di passaggio dell acqua di raffreddamento (6), la flangia di fissaggio del cilindro di alta pressione all incastellatura (7), la superficie di scorrimento della testa a croce in materiale antifrizione (8) e l indicatore del livello dell olio (9). Nella figura 1.27a è raffigurato il compressore modello T 30, di produzione Ingersoll-Rand, avente tre cilindri a doppia V: tale soluzione è detta a W. Poco diffusa è la soluzione a quattro cilindri a V, usata su alcuni modelli motociclistici, come riportato in sezione nella figura 1.27b, in cui sono posti in evidenza i pistoni e le bielle della prima manovella, orientati fra loro a 90, dietro ai quali vi sono le due cascate di ingranaggi, una per bancata, di comando delle due coppie di assi a camme della distribuzione. La soluzione a V trova un vasto campo di applicazione nei motori a sei cilindri. Nell esempio illustrato nella figura 1.28 l albero motore ha sei manovelle orientate fra loro a 60, presentandosi come un doppio motore tricilindrico simmetrico: pertanto quando un pistone di una bancata giunge al PMS, anche nell altra bancata si ha un pistone al PMS. Questa proprietà rende la successione delle combustioni molto regolare, tuttavia, venendo a mancare il piano mediano di simmetria, nasce uno squilibrio nelle coppie centrifughe. In tal modo sorgono due momenti squilibrati: il primo è orientato secondo un asse verticale che determina un moto vibratorio di imbardata; il secondo è orientato sull asse orizzontale, perpendicolare all asse dell albero motore, che determina un moto vibratorio di beccheggio, per la cui equilibratura si deve ricorrere alle contrappesature. 7
8 Fig Motore Duratec V6 da 2544 cc di produzione Ford: a) sezione trasversale; b) vista in esploso con il basamento a V, l albero motore e i semigusci, il sottobasamento e la coppa dell olio. Fig Albero a gomiti a otto cilindri a V, di 90 per un motore a quattro tempi: a) schema; b) vista frontale. Nei motori a otto, dieci, dodici e più cilindri l architettura a V permette di dimezzare il numero di manovelle: per esempio, nei motori a otto cilindri l albero motore si presenta con solo quattro manovelle orientate fra di loro a 90, con due bielle su ciascun perno di manovella, realizzando un ingombro longitudinale notevolmente ridotto (Figg e 1.29). Osservazione: nel caso del motore 8V la numerazione prevede che, osservando il motore dal lato della puleggia, il cilindro 1 sia il primo della bancata sinistra e che il cilindro 5 sia il primo della bancata destra. Anche nel motore 8V sono presenti due momenti squilibrati: il primo è orientato secondo un asse verticale, mentre il secondo è orientato secondo un asse orizzontale, perpendicolare all asse dell albero motore, per la cui equilibratura è necessario ricorrere alle contrappesature. Osservazione: l architettura a otto cilindri a V di 90 è usata anche per le auto da competizione, come per esempio la monoposto Ferrari 248 F1 di Formula 1, destinata a disputare il campionato 2006: il motore ha una cilindrata di 2398 cc, ha 32 valvole ed eroga una potenza di circa 720 CV. Nella figura 1.30 sono riportate le sezioni longitudinale e trasversale del motore automobilistico 8V a 90 a ciclo Otto, di produzione Daimler Benz, che equipaggia l autovettura Mercedes 300. In particolare è possibile osservare l albero a gomiti cruciforme (22), la biella (21), il pistone (49) e il basamento (17). 8
9 Fig Motore M119 per l autovettura Mercedes 300: a) sezione longitudinale; b) sezione trasversale (archivio Mercedes-Benz). Si riportano i seguenti dati tecnici: ciclo di lavoro: iniezione di benzina a quattro tempi; potenza nominale: KAT 240 kw/326 CV (normativa 80/1269/CEE); coppia nominale: KAT 480 N m (normativa 80/1269/CEE); numero dei cilindri: 8 rapporto alesaggio/corsa: 96,5/85,0 mm; cilindrata totale effettiva: 4973 cm 3. 1 Occhio di sospensione 2 Dispositivo di regolazione albero a camme 3 Catena a rulli doppia 4 Coperchio testa cilindri 5 Cappuccio candela 6 Filtro aria 7 Albero a camme agente sulle valvole di scarico 8 Albero a camme agente sulle valvole di aspirazione 9 Valvola di aspirazione 10 Valvola di scarico 11 Distributore carburante 12 Regolatore di pressione carburante 13 Tiranteria di regolazione 14 Valvola d iniezione 15 Tubo di mandata acqua di riscaldamento Ritorno acqua di riscaldamento 17 Basamento 18 Anello di tenuta 19 Cappello cuscinetto di banco 20 Corona dentata del volano 21 Biella 22 Albero motore 23 Interruzione indicazione livello olio 24 Valvola di sovrappressione olio 25 Pompa olio 26 Smorzatore di vibrazioni 27 Catena a rulli singola (azionamento pompa olio) 28 Ventilatore a giunto viscoso 29 Pompa acqua 30 Ventilatore 31 Distributore alta tensione 32 Manicotto entrata acqua Canale olio 34 Bocchettone dell olio 35 Tubo di aspirazione 36 Misuratore masse d aria a filo caldo (HLM) 37 Tubazione ricircolo gas di scarico 38 Parte inferiore tubo di aspirazione 39 Supporto albero a camme 40 Punteria idraulica 42 Collettore di scarico 42 Canale principale olio 43 Supporto motore 44 Foro di compensazione della pressione 45 Asta controllo livello olio 46 Trasduttore di pressione 47 Tubo radiatore olio 48 Filtro olio 49 Pistone 50 Testa cilindri 9
10 Fig Imbiellaggio completo per il motore 8V dell autovettura Ferrari, modello 360 Modena (per cortesia Ferrari Image Service). Fig Motore a 12 cilindri a V a 60, per l autovettura Ferrari F 50 (per cortesia Ferrari Image Service): a) albero a gomiti; b) imbiellaggio completo. In diverse applicazioni, per ragioni di semplicità di lavorazione e di elevata rigidità, l albero motore degli 8V presenta le quattro manovelle complanari, esattamente come nel caso del motore quadricilindrico: questa è la soluzione adottata in molti motori Ferrari 8V di 90, come il motore dell autovettura modello 360 Modena, il cui albero è riportato nella figura Nella figura 1.32 sono riportate due immagini dell albero del motore a 12 cilindri a V di 60, dell autovettura Ferrari F 50. L albero presenta sei manovelle e sette supporti ed è analogo all albero di un motore a quattro tempi a sei cilindri in linea, illustrato nella figura
11 Fig Sezione trasversale del motore della vettura FERRARI 458 Italia (per cortesia Ferrari Image Service). richiamo Il sistema formato da alberi ausiliari rotanti è detto Lanchester Harmonic Balancer, dal nome dell inventore. Nella figura 1.33 è riportata la sezione del motore della vettura Ferrari 458 Italia. La vettura è una berlinetta a due posti che monta un motore 8V di 90 in posizione posteriore/longitudinale. Il motore ha la cilindrata di 4499 cc e sviluppa la potenza massima di 570 CV alla frequenza di rotazione di 9000 giri/min. La coppia massima vale 540 Nm al regime di 6000 giri/min. Equilibratura mediante alberi ausiliari contrappesati L evoluzione raggiunta dalla tecnica motoristica nel corso degli anni Ottanta e Novanta ha consentito di raggiungere regimi di rotazione sempre più elevati, in modo da ottenere elevate prestazioni da cilindrate minori e con architetture semplificate come lo schema a quattro cilindri e a quattro tempi. L aumento dei regimi di potenza massima ha richiesto l esecuzione di interventi volti al miglioramento del comfort e dell affidabilità degli organi, costringendo all adozione di misure di contenimento delle vibrazioni emesse dal motore e in particolare dagli organi alterni. Relativamente ai problemi legati all equilibratura del motore a quattro cilindri, il principale difetto consiste nello squilibrio delle forze alterne del secondo ordine. La soluzione adottata da molti costruttori consiste nel realizzare dei contrappesi rotanti a velocità doppia rispetto a quella dell albero motore, sistemando all interno del basamento due alberi paralleli all albero motore, ma rotanti a velocità doppia. Tali alberi sono muniti di masse 11
12 eccentriche, generando forze centrifughe rotanti in grado di controbilanciare gli effetti delle forze alterne squilibrate del secondo ordine. Il principio di funzionamento è illustrato nella figura Meccanica, Macchine ed Energia articolazione Meccanica e Meccatronica 3 Giuseppe Anzalone, Paolo Bassignana, Giuseppe Brafa Musicoro Copyright Ulrico Hoepli Editore S.p.A. Fig Sistema di equilibratura delle forze alterne d inerzia del secondo ordine mediante alberi ausiliari: a) pistone al PMI; le masse degli alberi ausiliari sono rivolte verso il basso; b) manovella a 45 ; le masse degli alberi ausiliari sono orizzontali; c) manovella a 90 ; le masse degli alberi ausiliari sono rivolte verso l alto; d) manovella al PMI; le masse degli alberi ausiliari sono rivolte verso il basso. richiamo L albero ausiliario rotante nello stesso verso dell albero motore è detto corotante, quello rotante in verso opposto è detto controrotante. Due alberi gemelli, che portano ciascuno una massa eccentrica, ruotano a velocità doppia rispetto all albero motore, il primo nello stesso senso dell albero motore, mentre il secondo in senso opposto. Quando il pistone è al PMS, i due contrappesi sono rivolti verso il basso, con le due forze centrifughe pari ciascuna alla metà della forza alterna d inerzia del secondo ordine: le tre forze appaiono quindi in equilibrio (4Fig.1.34a). Quando l albero motore ha compiuto una rotazione di 45, la forza alterna d inerzia del secondo ordine è nulla (4Fig.1.34b); i due alberi ausiliari hanno compiuto una rotazione di 90, dato che ruotano a velocità doppia; le due masse eccentriche si trovano in posizioni opposte, per cui le due forze centrifughe risultano opposte. Facendo compiere all albero motore altri 45, il pistone ha effettuato circa metà corsa in discesa, mentre la forza alterna d inerzia del secondo ordine è orientata verso il basso, avendo raggiunto il suo valore massimo negativo: le due masse centrifughe hanno compiuto un altro mezzo giro e si trovano ora rivolte verso l alto, equilibrando il sistema (4Fig.1.34c). 12
13 Fig Motore a quattro cilindri munito di due alberi ausiliari per l equilibratura della forze alterne d inerzia del secondo ordine. Si analizza infine la configurazione in cui il pistone è al PMI: dopo una rotazione complessiva di 180, la forza alterna d inerzia del secondo ordine ha compiuto un ciclo completo, raggiungendo di nuovo il valore massimo positivo; anche gli alberi ausiliari hanno compiuto una rotazione completa, per cui i due contrappesi sono di nuovo rivolti verso il basso: le tre forze pertanto si annullano (4Fig.1.34d). Nella figura 1.35 viene illustrato il montaggio e l azionamento mediante cinghia bidentata dei due alberi ausiliari. Si noti come i due alberi ausiliari sono posizionati ad altezza diversa rispetto all albero motore, allo scopo di generare anche una coppia di riequilibrio, per annullare l effetto rollio dovuto alle spinte laterali dei pistoni sulle pareti. Nei motori monocilindrici e bicilindrici spesso si ricorre alla pratica dell albero controrotante singolo per bilanciare gli squilibri del primo ordine: in tal modo, malgrado la complicazione costruttiva introdotta, si opera un alleggerimento della contrappesatura dell albero motore, riducendo le inerzie dell imbiellaggio e gli ingombri radiali. La figura 1.36 riporta due immagini del motore Rotax V 990, che equipaggia la moto Aprilia RSV Si tratta di un motore bicilindrico a V stretto di 60, con due assi a camme per ciascuna testata. È possibile osservare lo schema della trasmissione del moto dall albero motore ai quattro assi a camme, mediante due catene, una anteriore e una posteriore, con interposto un ingranaggio riduttore con rapporto 2:1. Anche il moto dell albero controrotante laterale di equilibrio delle forze alterne del primo ordine viene trasmesso da un ingranaggio, in questo caso con rapporto 1:1 (4Fig.1.36b). 13
14 Fig Motore bicilindrico Rotax V 990, con un albero ausiliario per l equilibratura della forze alterne d inerzia del primo ordine: a) vista a motore semismontato; b) schema della trasmissione del moto agli organi interni. Si osserva inoltre la parte di propulsore su metà basamento con in primo piano, da sinistra verso destra, la trasmissione primaria, l albero motore a gomito unico, con le due bielle e con il contrappeso a mannaia; sulla destra è collocato l albero controrotante con il suo contrappeso in evidenza (4Fig.1.36a). Il motore bicilindrico Twin-Air che equipaggia la vettura Fiat 500 presenta le due manovelle allineate, secondo lo schema già descritto nella figura Esso ha l albero motore in ghisa con quattro contrappesi (anziché un unico contrappeso centrale a mannaia, come raffigurato nella figura 1.17) e poggia su tre supporti di banco. All estremità dell albero lato volano si osserva la presenza di una ruota dentata (4Fig. 1.37a) che ingrana con la rispettiva ruota compagna posta sull albero controrotante, con rapporto di trasmissione unitario: l albero controrotante ruota quindi alla stessa velocità dell albero motore ma in senso opposto (4Fig. 1.37b); tale albero porta due masse eccentriche di estremità (4Fig. 1.37c) per equilibrare le forze alterne del primo ordine che, per la [1.9], su un singolo pistone valgono F i I = m P ω 2 r cos ϑ. 14
15 Fig Albero motore e albero controrotante del motore Twin Air (FPT Fiat Powertrain Technologies); a) vista dell albero motore con in evidenza i supporti di banco (1), i perni di biella (2) e il semianello di rasamento per la regolazione del gioco assiale; b) schema dell insieme formato dall albero motore (3) con relativo imbiellaggio e dall albero controrotante (1) con le sue masse di bilanciamento (2); c) albero controrotante con in evidenza le masse eccentriche a mannaia. Fig Contrappesatura di una maschetta dell albero a gomiti del motore Twin Air e scomposizione della forza centrifuga parziale F mc applicata sul singolo contrappeso; in figura compare anche la forza alterna del primo ordine F i I applicata nel piede di biella P Da notare come l albero controrotante sia stato dimensionato per equilibrare le forze alterne del primo ordine solo al 50%, mentre il restante 50% viene equilibrato dai quattro contrappesi presenti sull albero motore: ne consegue che i quattro contrappesi assolvono alla duplice funzione di equilibrare sia le forze centrifughe sia le forze d inerzia del primo ordine, ma quest ultime solo al 50%. In altri termini, è come se ciascun contrappeso fosse formato da due masse contigue, una per bilanciare le forze centrifughe, l altra per equilibrare parte delle forze alterne d inerzia del primo ordine. La maggiorazione così ottenuta ha come conseguenza la migrazione del baricentro al di fuori dell asse di rotazione, con la conseguente perdita dell equilibratura statica, perdita che tuttavia viene compensata dal benefico effetto di bilanciare parzialmente le forze d inerzia: questa soluzione è detta sovraequilibratura. Nello schema delle forze rappresentato nella figura 1.38 si nota la presenza della forza alterna del primo ordine F i I applicata sul piede di biella con direzione assiale e della quota parte della forza centrifuga che si origina nel contrappeso, destinata esclusivamente a equilibrare la forza alterna: questa quota parte è indicata con la sigla F mc ; tale forza parziale, concentrata nel baricentro del singolo contrappeso, può essere scomposta in due componenti, di cui una assiale di valore F a = m c ω 2 r c cos ϑ, orientata in figura verso destra, l altra normale all asse, di valore Fn = m c ω 2 r c sen ϑ. Scegliendo opportunamente la geometria del contrappeso, si ha che F a = ¼ F i I e ricordando che i contrappesi sono due per ogni manovella, si è ottenuta l equilibratura al 50% della forza alterna d inerzia del primo ordine. 3 15
16 richiamo L operazione di disaccoppiamento comporta un grosso vantaggio dal punto di vista del comfort vibrazionale, essendo i tamponi in gomma molto più rigidi in verticale (nella direzione del peso e dei sobbalzi della vettura) che in orizzontale. Pertanto l effetto di filtraggio di una vibrazione orizzontale risulta molto più efficace. Fig Motore a tre cilindri in linea orizzontali, modello BMW K 75, con un albero ausiliario per l equilibratura delle coppie causate dalle forze alterne d inerzia del primo ordine. Osservazione: si noti come la funzione cosϑ compaia in entrambe le formule, in quella della F i I come pure in quella della F a : da ciò si deduce che l equilibratura apportata dai contrappesi si realizza con un effetto continuativo e costante, cioè, sempre al 50% di F i I per qualunque valore istantaneo dell angolo ϑ di rotazione dell albero. La componente normale F n evidenziata nella figura 1.38 non prende parte in alcun modo al fenomeno dell equilibratura. Pertanto risulta totalmente squilibrata e va a scaricarsi sui tamponi in gomma della sospensione del motopropulsore, come già visto in precedenza nella figura 1.4 in cui il motore è montato su vettura con l asse del cilindro verticale. In tale caso, la condizione di squilibrio dovuto alle forze alterne assiali verticali, destinata a scuotere il motopropulsore in verticale, nel senso della gravità, è stata ruotata di 90 ed ora agisce in senso orizzontale: questo effetto è noto come disaccoppiamento. Nella figura 1.39 si possono osservare diversi organi interni del motore K 75, di produzione BMW, tra cui l albero motore a tre cilindri e l albero controrotante laterale, per equilibrare le coppie dovute alle forze alterne del primo ordine. Questa soluzione consente di raggiungere un livello elevato di equilibratura complessiva. 16
17 L Unità didattica in breve b1 Velocità e accelerazione del piede di biella Meccanica, Macchine ed Energia articolazione Meccanica e Meccatronica 3 Giuseppe Anzalone, Paolo Bassignana, Giuseppe Brafa Musicoro Copyright Ulrico Hoepli Editore S.p.A. Il sistema biella-manovella è un meccanismo articolato che trasforma il moto alternativo in rotatorio o viceversa. Esso è costituito dalla manovella di lunghezza r e dalla biella di lunghezza l; i punti principali sono il bottone di manovella B, il piede di biella P e i punti estremi della corsa, detti punto morto superiore PMS e punto morto inferiore PMI. Il sistema biella-manovella viene descritto inoltre dalle seguenti grandezze cinematiche: lo spostamento x del piede di biella, quotato a partire dal PMS; l angolo β formato dall asse della biella con l asse del cilindro; l angolo ϑ, corrispondente allo spostamento angolare della manovella. Il parametro λ, detto lunghezza ridotta della biella, è pari al rapporto fra il raggio r di manovella e la lunghezza l della biella. Nelle macchine motrici il sistema biella-manovella trasforma la forza di compressione F g, agente sulla biella, in momento motore agente sull albero; tale forza è costituita dalla pressione p esercitata dai gas in combustione, moltiplicata per l area di base del cilindro di alesaggio A. Nelle macchine operatrici il momento motore M che agisce sull albero e proviene da un motore esterno si trasforma in forza motrice agente alla base della biella, destinata a trasformarsi a sua volta in pressione sul fluido in pompaggio. La forza esercitata dai gas F g viene scomposta in due componenti: la componente F b si scarica lungo la biella sul bottone di manovella B; la componente F n, normale all asse del cilindro, si scarica sul basamento. Per determinare la velocità v p del piede di biella si esegue la derivata dello spazio x rispetto all angolo di manovella e la si moltiplica per la velocità angolare. La velocità media v m è proporzionale alla corsa e alla frequenza di rotazione: in campo motoristico essa assume valori compresi tra 8 20 m/s. Per determinare l accelerazione si esegue la derivata della velocità del piede di biella rispetto alla variabile angolare, moltiplicata per la velocità angolare. Conviene semplificare la formula della velocità trascurando i termini meno influenti sul risultato: in tal caso la velocità e l accelerazione sono costituite dalla somma di due funzioni trigonometriche, di cui la prima ha pulsazione ω, mentre la seconda ha pulsazione 2 ω, essendo la pulsazione ω pari alla velocità angolare dell albero. La sinusoide con pulsazione ω è detta componente armonica fondamentale, o del primo ordine; la sinusoide con pulsazione doppia, pari a 2 ω, è detta componente armonica del secondo ordine; è possibile ottenere la risultante sommando punto a punto le due sinusoidi. Forze alterne d inerzia del primo e del secondo ordine Per calcolare la forza alterna d inerzia agente sul piede di biella si moltiplica l accelerazione a p del piede di biella per la massa m p applicata nel piede medesimo. La forza così trovata ha andamento periodico, è costante come direzione (orientata secondo l asse x), alterna come verso 17
18 e varia periodicamente come ampiezza. Adottando la procedura di calcolo semplificata, tale forza può essere considerata come la somma di due componenti: una forza alterna F i I del primo ordine e una forza alterna F i II del secondo ordine. Nel tempo in cui la manovella compie una rotazione, la forza del primo ordine compie un onda completa, mentre la forza del secondo ordine ne compie due, poiché ha pulsazione doppia. Analisi armonica del sistema biella-manovella Eseguendo la derivata della velocità del piede di biella, senza trascurare nessun fattore, e servendosi dello strumento matematico dello sviluppo in serie di Mc Laurin si perviene alla formulazione esatta e completa dell accelerazione del piede di biella in serie, i cui termini sinusoidali sono detti componenti armoniche. L accelerazione è pari a una somma di infinite funzioni coseno che differiscono fra loro per ampiezza e pulsazione. La prima delle funzioni coseno, avente ampiezza A 1 e pulsazione ω pari alla velocità angolare dell albero, è detta componente fondamentale o del primo ordine. La seconda delle funzioni coseno, avente ampiezza A 2 e pulsazione pari al doppio della velocità angolare dell albero, è detta componente del secondo ordine. La terza delle funzioni coseno che compare nello sviluppo in serie, avente ampiezza A 4 e pulsazione pari al quadruplo della velocità angolare dell albero, è detta componente del quarto ordine; per le componenti di ordine superiore si procede utilizzando lo stesso principio, per cui si avranno componenti del sesto ordine, dell ottavo ordine e così via. Tranne la componente fondamentale, tutte le componenti armoniche hanno ordine pari. Il rilievo sperimentale della vibrazione dovuta al sistema biella-manovella conferma quanto trovato per via teorica. Lo spettro delle frequenze è un grafico su cui sono riportate le am piez ze delle componenti, in funzione delle frequenze ricavate mediante l analisi armonica. Equilibratura del sistema biella-manovella Attraverso l albero a gomito, detto anche albero a manovelle, la biella scambia la forze motrici con l esterno; esso è formato da campate in numero proporzionale al numero dei cilindri. La campata è costituita da due bracci di manovella paralleli, detti maschette, e da un perno di manovella parallelo all asse di rotazione, sul quale è montata la testa di biella. Le campate possono essere fra loro adiacenti oppure separate da un perno, detto perno di banco, coassiale con l asse di rotazione dell albero. Ogni perno di banco poggia su un supporto di banco con interposto un cuscinetto di strisciamento. Il bloccaggio dell albero sui supporti avviene mediante ponticelli muniti di semigusci, detti cappelli di banco. Nei motori endotermici l angolo di orientamento fra le manovelle è scelto in modo da distribuire simmetricamente le masse, regolarizzando la coppia motrice e ottenendo la successione delle fasi utili nei cilindri con 18
19 intervalli uguali. Nelle macchine operatrici è fondamentale distribuire le masse con regolarità. Nei motori bicilindrici a quattro tempi le manovelle sono orientate a 360 ; nei compressori e nelle pompe bicilindriche e nei motori quadricilindrici a quattro tempi le manovelle sono orientate a 180. Un albero rotante è detto già di per sé staticamente (dinamicamente) equilibrato se non necessita dell aggiunta di contrappesi per raggiungere lo stato di equilibratura statica (dinamica). Si raggiunge l equilibratura dinamica di un corpo rotante nel caso in cui la risultante dei momenti dovuti alle forze centrifughe, riferiti a un punto qualunque dell asse, risulti uguale a 0. Un albero è in condizione di equilibratura dinamica se, essendo già equilibrato staticamente, ammette un piano di simmetria perpendicolare all asse di rotazione. Ciò è ottenuto automaticamente sia per l albero a gomito a una sola manovella sia per l albero del motore bicilindrico a quattro tempi. L albero a gomito del motore bicilindrico a due tempi ha le forze centrifughe uguali, parallele e con versi opposti, formanti una coppia; pertanto, per equilibrare tale coppia occorre applicare due contrappesi. Per quanto concerne l equilibratura delle forze alterne d inerzia vale la seguente regola: nessuna delle due componenti alterne d inerzia può essere completamente equilibrata con la sola applicazione di contrappesi sull albero a gomito. Bilanciando la forza alterna d inerzia del primo ordine mediante contrappeso si crea uno squilibrio agente in senso perpendicolare all asse della corsa. Nella maggioranza dei casi, infatti, è preferibile raggiungere solo un equilibratura parziale della forza alterna d inerzia del primo ordine. Fra le infinite componenti armoniche, la forza alterna del secondo ordine, avente frequenza doppia rispetto alla frequenza dell albero, per essere equilibrata richiede una forza opposta rotante a velocità doppia rispetto a quella dell albero motore. Da queste considerazioni derivano le seguenti regole: né le forze né le coppie del secondo ordine sono equilibrabili parzialmente attraverso contrappesi posti sull albero a gomito; non è possibile formulare relazioni fra lo stato di equilibratura dell albero e quello delle forze e delle coppie del secondo ordine. Esistono comunque alcuni tipi di imbiellaggi completamente equilibrati come forze alterne del primo e del secondo ordine, senza dovere ricorrere a contrappesi o a altri dispositivi, come l imbiellaggio a sei cilindri per motori a quattro tempi. Si esegue lo studio dell equilibratura dei carichi alterni tracciando un diagramma circolare: se la distribuzione dei raggi che rappresentano le forze di uno stesso ordine presenta una simmetria, si deduce che la somma vettoriale delle forze è pari al vettore nullo e la macchina risulta equilibrata relativamente a quell ordine specifico. Gli alberi motore a due cilindri e a quattro tempi sono squilibrati sulle forze alterne e centrifughe; gli alberi motore a quattro cilindri e a quattro tempi sono squilibrati sulle forze alterne del secondo ordine: tale squilibrio viene annullato ricorrendo a una coppia di alberi ausiliari, uno controrotante e uno corotante, che ruotano a velocità doppia di quella dell albero. Gli alberi motore a cinque cilindri sono invece equilibrati sulle forze alterne del primo e del secondo ordine. 19
20 PROBLEMI DI RIEPilogo b1 1. Calcolare l angolo di orientamento delle manovelle per un motore a sei cilindri a due tempi. Meccanica, Macchine ed Energia articolazione Meccanica e Meccatronica 3 Giuseppe Anzalone, Paolo Bassignana, Giuseppe Brafa Musicoro Copyright Ulrico Hoepli Editore S.p.A. 2. La lunghezza della biella misurata fra l asse del piede e l asse della testa per il motore a quattro cilindri e a quattro tempi, modello M41 di produzione BMW, vale l = 130 mm. La corsa vale C = 82,8 mm. Ipotizzando che la pressione dei gas valga p = 10 bar quando la biella e la manovella sono in quadratura, calcolare il momento motore istantaneo nella suddetta configurazione. 3. Calcolare il tratto di corsa, misurato a partire dal PMS, descritto dal piede di biella quando l angolo di manovella passa da ϑ = 0 a ϑ = π/4. La corsa vale C = 140 mm, mentre la lunghezza ridotta della biella vale λ = 0, Un motore motociclistico monocilindrico ha un accelerazione massima al piede di biella pari ad a p = m/s 2, alla frequenza di rotazione n = 7600 giri/min. Sapendo che la corsa vale C = 62,6 mm, calcolare la lunghezza ridotta della biella. 5. Una pompa alternativa monocilindrica funziona a regime alla frequenza di rotazione n = 1200 giri/min. Calcolare i valori delle pulsazioni e delle frequenze relative alle componenti dell accelerazione al piede di biella del primo, del secondo, del quarto, del sesto e dell ottavo ordine. 6. Calcolare le forze alterne del primo e del secondo ordine al PMS, agenti sul piede di biella di un motore ad accensione per compressione camionistico, la cui corsa vale C = 150 mm, mentre la lunghezza della biella misura l = 250 mm e funziona alla frequenza di rotazione n = 2200 giri/min. La massa concentrata al piede della singola biella vale m p = 7,5 kg. 7. Un motore ha la corsa che vale C = 58 mm. La forza alterna d inerzia del secondo ordine vale F i II = 3200 N, quando ruota alla velocità n = 8000 giri/min. La lunghezza ridotta della biella vale λ = 0,24. Calcolare la massa m p concentrata al piede di biella. 8. Un motore marino a due tempi e sei cilindri ha il raggio di manovella r = 300 mm e la lunghezza ridotta della biella λ = 0,282. Il rapporto corsa/alesaggio vale C/A = 1,14, mentre la frequenza di rotazione vale n = 200 giri/min. La massa m p concentrata al piede di biella è m p = 1350 kg. Calcolare l alesaggio, la lunghezza della biella e la forza alterna d inerzia agente sul piede di biella al PMS. 9. Un motore motociclistico a tre cilindri ha alesaggio A = 53,4 mm, corsa C = 52 mm, lunghezza della biella l = 118 mm e frequenza di rotazione n = giri/min. Determinare la cilindrata e l accelerazione a p al piede di biella al PMS e al PMI. 20
CANDIDATO: William Berardi. RELATORE: Prof. Ing. Luca Piancastelli
 Alma Mater Studiorum Università di Bologna Facoltà di Ingegneria Corso di laurea in Ingegneria Meccanica A.A. 2010/2011 - Sessione III CANDIDATO: William Berardi RELATORE: Prof. Ing. Luca Piancastelli
Alma Mater Studiorum Università di Bologna Facoltà di Ingegneria Corso di laurea in Ingegneria Meccanica A.A. 2010/2011 - Sessione III CANDIDATO: William Berardi RELATORE: Prof. Ing. Luca Piancastelli
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
CORSO DI IMPIANTI DI PROPULSIONE NAVALE
 ACCADEMIA NAVALE 1 ANNO CORSO APPLICATIVO GENIO NAVALE CORSO DI IMPIANTI DI PROPULSIONE NAVALE Lezione 09 Motori diesel lenti a due tempi A.A. 2011 /2012 Prof. Flavio Balsamo Nel motore a due tempi l intero
ACCADEMIA NAVALE 1 ANNO CORSO APPLICATIVO GENIO NAVALE CORSO DI IMPIANTI DI PROPULSIONE NAVALE Lezione 09 Motori diesel lenti a due tempi A.A. 2011 /2012 Prof. Flavio Balsamo Nel motore a due tempi l intero
Classificazione delle pompe. Pompe rotative volumetriche POMPE ROTATIVE. POMPE VOLUMETRICHE si dividono in... VOLUMETRICHE
 Classificazione delle pompe Pompe rotative volumetriche POMPE VOLUMETRICHE si dividono in... POMPE ROTATIVE VOLUMETRICHE Pompe rotative volumetriche Principio di funzionamento Le pompe rotative sono caratterizzate
Classificazione delle pompe Pompe rotative volumetriche POMPE VOLUMETRICHE si dividono in... POMPE ROTATIVE VOLUMETRICHE Pompe rotative volumetriche Principio di funzionamento Le pompe rotative sono caratterizzate
 Funzionamento del motore 4 tempi I componenti fondamentali del motore 4 tempi I componenti ausiliari del motore 4 tempi La trasmissione del moto Le innovazioni motoristiche L influenza dell aerodinamica
Funzionamento del motore 4 tempi I componenti fondamentali del motore 4 tempi I componenti ausiliari del motore 4 tempi La trasmissione del moto Le innovazioni motoristiche L influenza dell aerodinamica
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
La propulsione Informazioni per il PD
 Informazioni per il PD 1/10 Compito Come funziona un automobile? Gli alunni studiano i diversi tipi di propulsione (motore) dell auto e imparano qual è la differenza tra un motore diesel e uno a benzina.
Informazioni per il PD 1/10 Compito Come funziona un automobile? Gli alunni studiano i diversi tipi di propulsione (motore) dell auto e imparano qual è la differenza tra un motore diesel e uno a benzina.
PROBLEMA 1. Soluzione. Indicare quattro requisiti fondamentali che un fluido frigorigeno deve possedere: 1) 2) 3) 4)
 PROBLEMA 1 Indicare quattro requisiti fondamentali che un fluido frigorigeno deve possedere: 1) 2) 3) 4) Deve possedere un elevato calore latente, cioè, deve evaporare asportando molto calore dall ambiente
PROBLEMA 1 Indicare quattro requisiti fondamentali che un fluido frigorigeno deve possedere: 1) 2) 3) 4) Deve possedere un elevato calore latente, cioè, deve evaporare asportando molto calore dall ambiente
Disegno di Macchine. corso per I anno della laurea in ing. meccanica Docente: ing. Francesca Campana
 Disegno di Macchine corso per I anno della laurea in ing. meccanica Docente: ing. Francesca Campana Lezione n 4 Componentistica di base: alberi, trasmissione per cinghie e catene, giunti Alberi Appunti
Disegno di Macchine corso per I anno della laurea in ing. meccanica Docente: ing. Francesca Campana Lezione n 4 Componentistica di base: alberi, trasmissione per cinghie e catene, giunti Alberi Appunti
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Valutazioni di massima sui motori a combustione interna
 Valutazioni di massima sui motori a combustione interna Giulio Cazzoli v 1.0 Maggio 2014 Indice Elenco dei simboli 3 1 Motore ad accensione comandata 4 1.1 Dati........................................
Valutazioni di massima sui motori a combustione interna Giulio Cazzoli v 1.0 Maggio 2014 Indice Elenco dei simboli 3 1 Motore ad accensione comandata 4 1.1 Dati........................................
Aprile (recupero) tra una variazione di velocità e l intervallo di tempo in cui ha luogo.
 Febbraio 1. Un aereo in volo orizzontale, alla velocità costante di 360 km/h, lascia cadere delle provviste per un accampamento da un altezza di 200 metri. Determina a quale distanza dall accampamento
Febbraio 1. Un aereo in volo orizzontale, alla velocità costante di 360 km/h, lascia cadere delle provviste per un accampamento da un altezza di 200 metri. Determina a quale distanza dall accampamento
DIMENSIONAMENTO DEL MARTINETTO PER RICIRCOLO DI SFERE
 DIMENSIONAMENTO DEL MARTINETTO PER RICIRCOLO DI SFERE Per un corretto dimensionamento del martinetto a ricircolo di sfere è necessario operare come segue: definizione dei dati del dell applicazione (A)
DIMENSIONAMENTO DEL MARTINETTO PER RICIRCOLO DI SFERE Per un corretto dimensionamento del martinetto a ricircolo di sfere è necessario operare come segue: definizione dei dati del dell applicazione (A)
FISICA DELLA BICICLETTA
 FISICA DELLA BICICLETTA Con immagini scelte dalla 3 SB PREMESSA: LEGGI FISICHE Velocità periferica (tangenziale) del moto circolare uniforme : v = 2πr / T = 2πrf Velocità angolare: ω = θ / t ; per un giro
FISICA DELLA BICICLETTA Con immagini scelte dalla 3 SB PREMESSA: LEGGI FISICHE Velocità periferica (tangenziale) del moto circolare uniforme : v = 2πr / T = 2πrf Velocità angolare: ω = θ / t ; per un giro
Programmazione modulare a.s. 2015-2016 Disciplina: Meccanica
 Programmazione modulare a.s. 2015-2016 Disciplina: Meccanica Classe: 5 Meccanica Docente prof. Angelo Rinaldi Ore settimanali previste: 4 ore ro totale di ore 4x33=132 ore Libro di testo Corso di Meccanica
Programmazione modulare a.s. 2015-2016 Disciplina: Meccanica Classe: 5 Meccanica Docente prof. Angelo Rinaldi Ore settimanali previste: 4 ore ro totale di ore 4x33=132 ore Libro di testo Corso di Meccanica
Introduzione ai Motori a Combustione Interna
 IPS Mario Carrara Guastalla (RE) Tecnologie e Tecniche di Installazione e Manutenzione Docente: Prof. Matteo Panciroli Introduzione ai Motori a Combustione Interna 1 Classificazione delle macchine MACCHINE
IPS Mario Carrara Guastalla (RE) Tecnologie e Tecniche di Installazione e Manutenzione Docente: Prof. Matteo Panciroli Introduzione ai Motori a Combustione Interna 1 Classificazione delle macchine MACCHINE
APPUNTI SUL CAMPO MAGNETICO ROTANTE
 APPUTI UL CAPO AGETICO ROTATE Campo agnetico Rotante ad una coppia polare Consideriamo la struttura in figura che rappresenta la vista, in sezione trasversale, di un cilindro cavo, costituito da un materiale
APPUTI UL CAPO AGETICO ROTATE Campo agnetico Rotante ad una coppia polare Consideriamo la struttura in figura che rappresenta la vista, in sezione trasversale, di un cilindro cavo, costituito da un materiale
STUDIO DI MASSIMA DI UN DIESEL AD ALTE PRESTAZIONI
 Università degli Studi di Bologna FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA MECCANICA Elaborato Finale di Laurea in Laboratorio di CAD STUDIO DI MASSIMA DI UN DIESEL AD ALTE PRESTAZIONI Candidato
Università degli Studi di Bologna FACOLTA DI INGEGNERIA CORSO DI LAUREA IN INGEGNERIA MECCANICA Elaborato Finale di Laurea in Laboratorio di CAD STUDIO DI MASSIMA DI UN DIESEL AD ALTE PRESTAZIONI Candidato
GRANDEZZE SINUSOIDALI
 GRANDEE SINUSOIDALI INDICE -Grandezze variabili. -Grandezze periodiche. 3-Parametri delle grandezze periodiche. 4-Grandezze alternate. 5-Grandezze sinusoidali. 6-Parametri delle grandezze sinusoidali.
GRANDEE SINUSOIDALI INDICE -Grandezze variabili. -Grandezze periodiche. 3-Parametri delle grandezze periodiche. 4-Grandezze alternate. 5-Grandezze sinusoidali. 6-Parametri delle grandezze sinusoidali.
Forma d onda rettangolare non alternativa.
 Forma d onda rettangolare non alternativa. Lo studio della forma d onda rettangolare è utile, perché consente di conoscere il contenuto armonico di un segnale digitale. FIGURA 33 Forma d onda rettangolare.
Forma d onda rettangolare non alternativa. Lo studio della forma d onda rettangolare è utile, perché consente di conoscere il contenuto armonico di un segnale digitale. FIGURA 33 Forma d onda rettangolare.
Motori endotermici I MOTORI ENDOTERMICI. Corso di Laurea Scienze e Tecnologie Agrarie
 Corso di Laurea Scienze e Tecnologie Agrarie Motori endotermici Dipartimento Ingegneria del Territorio - Università degli Studi di Sassari I MOTORI ENDOTERMICI Il motore converte l energia termica del
Corso di Laurea Scienze e Tecnologie Agrarie Motori endotermici Dipartimento Ingegneria del Territorio - Università degli Studi di Sassari I MOTORI ENDOTERMICI Il motore converte l energia termica del
Idrostatica Correnti a pelo libero (o a superficie libera) Correnti in pressione. Foronomia
 Idrostatica Correnti a pelo libero (o a superficie libera) Correnti in pressione Foronomia In idrostatica era lecito trascurare l attrito interno o viscosità e i risultati ottenuti valevano sia per i liquidi
Idrostatica Correnti a pelo libero (o a superficie libera) Correnti in pressione Foronomia In idrostatica era lecito trascurare l attrito interno o viscosità e i risultati ottenuti valevano sia per i liquidi
Esercitazione 5 Dinamica del punto materiale
 Problema 1 Un corpo puntiforme di massa m = 1.0 kg viene lanciato lungo la superficie di un cuneo avente un inclinazione θ = 40 rispetto all orizzontale e altezza h = 80 cm. Il corpo viene lanciato dal
Problema 1 Un corpo puntiforme di massa m = 1.0 kg viene lanciato lungo la superficie di un cuneo avente un inclinazione θ = 40 rispetto all orizzontale e altezza h = 80 cm. Il corpo viene lanciato dal
Forza. Forza. Esempi di forze. Caratteristiche della forza. Forze fondamentali CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA
 Forza CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA Cos è una forza? la forza è una grandezza che agisce su un corpo cambiando la sua velocità e provocando una deformazione sul corpo 2 Esempi
Forza CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA Cos è una forza? la forza è una grandezza che agisce su un corpo cambiando la sua velocità e provocando una deformazione sul corpo 2 Esempi
LA CORRENTE ELETTRICA CONTINUA
 LA CORRENTE ELETTRICA CONTINUA (Fenomeno, indipendente dal tempo, che si osserva nei corpi conduttori quando le cariche elettriche fluiscono in essi.) Un conduttore metallico è in equilibrio elettrostatico
LA CORRENTE ELETTRICA CONTINUA (Fenomeno, indipendente dal tempo, che si osserva nei corpi conduttori quando le cariche elettriche fluiscono in essi.) Un conduttore metallico è in equilibrio elettrostatico
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
CIRCUITI OLEODINAMICI ELEMENTARI
 CIRCUITI OLEODINAMICI ELEMENTARI Un esame sistematico dei circuiti completi, anche se limitato a pochi tipi di macchine e di attrezzature, sarebbe estremamente complesso e vasto. Il raggiungimento del
CIRCUITI OLEODINAMICI ELEMENTARI Un esame sistematico dei circuiti completi, anche se limitato a pochi tipi di macchine e di attrezzature, sarebbe estremamente complesso e vasto. Il raggiungimento del
Corso di Componenti e Impianti Termotecnici LE RETI DI DISTRIBUZIONE PERDITE DI CARICO LOCALIZZATE
 LE RETI DI DISTRIBUZIONE PERDITE DI CARICO LOCALIZZATE 1 PERDITE DI CARICO LOCALIZZATE Sono le perdite di carico (o di pressione) che un fluido, in moto attraverso un condotto, subisce a causa delle resistenze
LE RETI DI DISTRIBUZIONE PERDITE DI CARICO LOCALIZZATE 1 PERDITE DI CARICO LOCALIZZATE Sono le perdite di carico (o di pressione) che un fluido, in moto attraverso un condotto, subisce a causa delle resistenze
Forze, leggi della dinamica, diagramma del. 28 febbraio 2009 (PIACENTINO - PREITE) Fisica per Scienze Motorie
 Forze, leggi della dinamica, diagramma del corpo libero 1 FORZE Grandezza fisica definibile come l' agente in grado di modificare lo stato di quiete o di moto di un corpo. Ci troviamo di fronte ad una
Forze, leggi della dinamica, diagramma del corpo libero 1 FORZE Grandezza fisica definibile come l' agente in grado di modificare lo stato di quiete o di moto di un corpo. Ci troviamo di fronte ad una
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza A.A. 2007/08
 UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica Tolleranze
UNIVERSITÀ DEGLI STUDI DI PADOVA Facoltà di Ingegneria sede di Vicenza Corso di Disegno Tecnico Industriale per il Corso di Laurea triennale in Ingegneria Meccanica e in Ingegneria Meccatronica Tolleranze
Dispositivo di conversione di energia elettrica per aerogeneratori composto da componenti commerciali.
 Sede legale: Viale Vittorio Veneto 60, 59100 Prato P.IVA /CF 02110810971 Sede operativa: Via del Mandorlo 30, 59100 Prato tel. (+39) 0574 550493 fax (+39) 0574 577854 Web: www.aria-srl.it Email: info@aria-srl.it
Sede legale: Viale Vittorio Veneto 60, 59100 Prato P.IVA /CF 02110810971 Sede operativa: Via del Mandorlo 30, 59100 Prato tel. (+39) 0574 550493 fax (+39) 0574 577854 Web: www.aria-srl.it Email: info@aria-srl.it
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
A. Maggiore Appunti dalle lezioni di Meccanica Tecnica
 Il giunto idraulico Fra i dispositivi che consentono di trasmettere potenza nel moto rotatorio, con la possibilità di variare la velocità relativa fra movente e cedente, grande importanza ha il giunto
Il giunto idraulico Fra i dispositivi che consentono di trasmettere potenza nel moto rotatorio, con la possibilità di variare la velocità relativa fra movente e cedente, grande importanza ha il giunto
Impianti di propulsione navale
 Motori diesel 4T Sistemi per ridurre la fumosità e le emissioni La sempre più continua attenzione alle problematiche ambientali e l inasprirsi di alcune normative regionali in tema di fumosità ed emissioni,
Motori diesel 4T Sistemi per ridurre la fumosità e le emissioni La sempre più continua attenzione alle problematiche ambientali e l inasprirsi di alcune normative regionali in tema di fumosità ed emissioni,
Esercizio 20 - tema di meccanica applicata e macchine a fluido- 2002
 Esercizio 0 - tema di meccanica applicata e macchine a fluido- 00 er regolare il regime di rotazione di un gruppo elettrogeno, viene calettato sull albero di trasmissione del motore un volano in ghisa.
Esercizio 0 - tema di meccanica applicata e macchine a fluido- 00 er regolare il regime di rotazione di un gruppo elettrogeno, viene calettato sull albero di trasmissione del motore un volano in ghisa.
Transitori del primo ordine
 Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Politecnico di Bari I Facoltà di Ingegneria Corso di Laurea Specialistica in Ingegneria Meccanica ENERGIA EOLICA
 Politecnico di Bari I Facoltà di Ingegneria Corso di Laurea Specialistica in Ingegneria Meccanica ENERGIA EOLICA turbine eoliche ad asse verticale VAWT A.A. 2008/09 Energie Alternative Prof.B.Fortunato
Politecnico di Bari I Facoltà di Ingegneria Corso di Laurea Specialistica in Ingegneria Meccanica ENERGIA EOLICA turbine eoliche ad asse verticale VAWT A.A. 2008/09 Energie Alternative Prof.B.Fortunato
METODO PER LA DESCRIZIONE DEL CAMPO MAGNETICO ROTANTE
 Ing. ENRICO BIAGI Docente di Tecnologie elettrice, Disegno, Progettazione ITIS A. Volta - Perugia ETODO PER LA DESCRIZIONE DEL CAPO AGNETICO ROTANTE Viene illustrato un metodo analitico-grafico per descrivere
Ing. ENRICO BIAGI Docente di Tecnologie elettrice, Disegno, Progettazione ITIS A. Volta - Perugia ETODO PER LA DESCRIZIONE DEL CAPO AGNETICO ROTANTE Viene illustrato un metodo analitico-grafico per descrivere
1 A DISEGNO PROGETTAZIONE ORGANIZZAZIONE INDUSTRIALE. T n. =C, con C = 366 ed n = 0.25, Motore
 Disegno, Progettazione ed rganizzazione Industriale esame 03 DISEGN PRGETTZINE RGNIZZZINE INDUSTRILE Sessione ordinaria 03 L albero di trasmissione rappresentato in figura trasmette una potenza P = 5 kw
Disegno, Progettazione ed rganizzazione Industriale esame 03 DISEGN PRGETTZINE RGNIZZZINE INDUSTRILE Sessione ordinaria 03 L albero di trasmissione rappresentato in figura trasmette una potenza P = 5 kw
Sistema di diagnosi CAR TEST
 Data: 30/09/09 1 di 7 Sistema di diagnosi CAR TEST Il sistema di diagnosi CAR TEST venne convenientemente utilizzato per: - verificare che la scocca di un veicolo sia dimensionalmente conforme ai disegni
Data: 30/09/09 1 di 7 Sistema di diagnosi CAR TEST Il sistema di diagnosi CAR TEST venne convenientemente utilizzato per: - verificare che la scocca di un veicolo sia dimensionalmente conforme ai disegni
STUDIO DI MASSIMA DI UN MOTORE DIESEL A DUE TEMPI AD INIEZIONE DIRETTA PER USO AERONAUTICO
 STUDIO DI MASSIMA DI UN MOTORE DIESEL A DUE TEMPI AD INIEZIONE DIRETTA PER USO AERONAUTICO Relatore: Prof. Ing.. L. Piancastelli Correlatori: Prof. Ing.. F. Persiani Prof. Ing.. A. Liverani Candidato:
STUDIO DI MASSIMA DI UN MOTORE DIESEL A DUE TEMPI AD INIEZIONE DIRETTA PER USO AERONAUTICO Relatore: Prof. Ing.. L. Piancastelli Correlatori: Prof. Ing.. F. Persiani Prof. Ing.. A. Liverani Candidato:
a) Il campo di esistenza di f(x) è dato da 2x 0, ovvero x 0. Il grafico di f(x) è quello di una iperbole -1 1
 LE FUNZIONI EALI DI VAIABILE EALE Soluzioni di quesiti e problemi estratti dal Corso Base Blu di Matematica volume 5 Q[] Sono date le due funzioni: ) = e g() = - se - se = - Determina il campo di esistenza
LE FUNZIONI EALI DI VAIABILE EALE Soluzioni di quesiti e problemi estratti dal Corso Base Blu di Matematica volume 5 Q[] Sono date le due funzioni: ) = e g() = - se - se = - Determina il campo di esistenza
LEGGE DI STEVIN (EQUAZIONE FONDAMENTALE DELLA STATICA DEI FLUIDI PESANTI INCOMPRIMIBILI) z + p / γ = costante
 IDRAULICA LEGGE DI STEVIN (EQUAZIONE FONDAMENTALE DELLA STATICA DEI FLUIDI PESANTI INCOMPRIMIBILI) z + p / γ = costante 2 LEGGE DI STEVIN Z = ALTEZZA GEODETICA ENERGIA POTENZIALE PER UNITA DI PESO p /
IDRAULICA LEGGE DI STEVIN (EQUAZIONE FONDAMENTALE DELLA STATICA DEI FLUIDI PESANTI INCOMPRIMIBILI) z + p / γ = costante 2 LEGGE DI STEVIN Z = ALTEZZA GEODETICA ENERGIA POTENZIALE PER UNITA DI PESO p /
COMPOSIZIONE E FUNZIONAMENTO DEL MOTORE QUATTRO TEMPI(4-Stroke)
 COMPOSIZIONE E FUNZIONAMENTO DEL MOTORE QUATTRO TEMPI(4-Stroke) Salve a tutti. In questa recensione spiegherò la composizione e il funzionamento del motore a scoppio Quattro Tempi, in inglese 4-stroke.
COMPOSIZIONE E FUNZIONAMENTO DEL MOTORE QUATTRO TEMPI(4-Stroke) Salve a tutti. In questa recensione spiegherò la composizione e il funzionamento del motore a scoppio Quattro Tempi, in inglese 4-stroke.
La caratteristica meccanica rappresenta l'andamento della coppia motrice C in
 MOTORI CORRENTE ALTERNATA: CARATTERISTICA MECCANICA La caratteristica meccanica rappresenta l'andamento della coppia motrice C in funzione della velocità di rotazione del rotore n r Alla partenza la C
MOTORI CORRENTE ALTERNATA: CARATTERISTICA MECCANICA La caratteristica meccanica rappresenta l'andamento della coppia motrice C in funzione della velocità di rotazione del rotore n r Alla partenza la C
bensì una tendenza a ruotare quando vengono applicate in punti diversi di un corpo
 Momento di una forza Nella figura 1 è illustrato come forze uguali e contrarie possono non produrre equilibrio, bensì una tendenza a ruotare quando vengono applicate in punti diversi di un corpo esteso.
Momento di una forza Nella figura 1 è illustrato come forze uguali e contrarie possono non produrre equilibrio, bensì una tendenza a ruotare quando vengono applicate in punti diversi di un corpo esteso.
Trasportatori a nastro
 Trasportatori a nastro Realizzano un trasporto di tipo continuo, in orizzontale o in pendenza, di materiali alla rinfusa e di carichi concentrati leggeri. incastellatura di sostegno Trasporti interni 1
Trasportatori a nastro Realizzano un trasporto di tipo continuo, in orizzontale o in pendenza, di materiali alla rinfusa e di carichi concentrati leggeri. incastellatura di sostegno Trasporti interni 1
Esercitazione di Laboratorio - Leve di 1-2 - 3 genere TITOLO ESERCITAZIONE: VERIFICA DELLE LEGGI DELLE LEVE
 TITOLO ESERCITAZIONE: VERIFICA DELLE LEGGI DELLE LEVE PREREQUISITI RICHIESTI PER LO SVOLGIMENTO DELL ATTIVITÀ DI LABORATORIO L alunno deve conoscere la definizione di forza, la definizione di momento.
TITOLO ESERCITAZIONE: VERIFICA DELLE LEGGI DELLE LEVE PREREQUISITI RICHIESTI PER LO SVOLGIMENTO DELL ATTIVITÀ DI LABORATORIO L alunno deve conoscere la definizione di forza, la definizione di momento.
RUOTE DENTATE. Introduzione
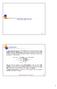 RUOTE DENTATE 362 Introduzione Le ruote dentate costituiscono un sistema affidabile per la trasmissione del moto tra assi paralleli, incidenti e sghembi. La trasmissione avviene per spinta dei denti della
RUOTE DENTATE 362 Introduzione Le ruote dentate costituiscono un sistema affidabile per la trasmissione del moto tra assi paralleli, incidenti e sghembi. La trasmissione avviene per spinta dei denti della
BILANCIAMENTO. 8-1 Bilanciamento statico di un rotore
 8 BILANCIAMENTO Come si è visto al capitolo 7-3.3, quando il baricentro di un rotore non coincide con l asse di rotazione possono insorgere fenomeni vibratori di entità rilevante, talvolta tali, in condizioni
8 BILANCIAMENTO Come si è visto al capitolo 7-3.3, quando il baricentro di un rotore non coincide con l asse di rotazione possono insorgere fenomeni vibratori di entità rilevante, talvolta tali, in condizioni
Lezione IX - 19/03/2003 ora 8:30-10:30 - Ciclo di Carnot, Otto, Diesel - Originale di Spinosa Alessandro.
 Lezione IX - 9/03/003 ora 8:30-0:30 - Ciclo di Carnot, Otto, Diesel - Originale di Spinosa Alessandro. Ciclo di Carnot Si consideri una macchina termica semplice che compie trasformazioni reversibili,
Lezione IX - 9/03/003 ora 8:30-0:30 - Ciclo di Carnot, Otto, Diesel - Originale di Spinosa Alessandro. Ciclo di Carnot Si consideri una macchina termica semplice che compie trasformazioni reversibili,
Relazioni statistiche: regressione e correlazione
 Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
Relazioni statistiche: regressione e correlazione È detto studio della connessione lo studio si occupa della ricerca di relazioni fra due variabili statistiche o fra una mutabile e una variabile statistica
Modellistica e Simulazione del Comportamento Dinamico di Beccheggio di un Trattore Agricolo
 Università degli Studi di Modena e Reggio Emilia Facoltà di Ingegneria Modellistica e Simulazione del Comportamento Dinamico di Beccheggio di un Trattore Agricolo Relatore: Prof. Roberto Zanasi Correlatori:
Università degli Studi di Modena e Reggio Emilia Facoltà di Ingegneria Modellistica e Simulazione del Comportamento Dinamico di Beccheggio di un Trattore Agricolo Relatore: Prof. Roberto Zanasi Correlatori:
Moto circolare uniforme
 Moto circolare uniforme 01 - Moto circolare uniforme. Il moto di un corpo che avviene su una traiettoria circolare (una circonferenza) con velocità (in modulo, intensità) costante si dice moto circolare
Moto circolare uniforme 01 - Moto circolare uniforme. Il moto di un corpo che avviene su una traiettoria circolare (una circonferenza) con velocità (in modulo, intensità) costante si dice moto circolare
bipolari, quando essi, al variare del tempo, assumono valori sia positivi che negativi unipolari, quando essi non cambiano mai segno
 Parametri dei segnali periodici I segnali, periodici e non periodici, si suddividono in: bipolari, quando essi, al variare del tempo, assumono valori sia positivi che negativi unipolari, quando essi non
Parametri dei segnali periodici I segnali, periodici e non periodici, si suddividono in: bipolari, quando essi, al variare del tempo, assumono valori sia positivi che negativi unipolari, quando essi non
DFP 13 100/112 ID POMPE A PALETTE A CILINDRATA FISSA SERIE 20 PRINCIPIO DI FUNZIONAMENTO CARATTERISTICHE TECNICHE SIMBOLO IDRAULICO.
 3 00/ ID DFP POMPE A PALETTE A CILINDRATA FISSA PRINCIPIO DI FUNZIONAMENTO Le pompe DFP sono pompe a palette a cilindrata fissa, realizzate in quattro diverse grandezze, divise a loro volta in cinque dimensioni
3 00/ ID DFP POMPE A PALETTE A CILINDRATA FISSA PRINCIPIO DI FUNZIONAMENTO Le pompe DFP sono pompe a palette a cilindrata fissa, realizzate in quattro diverse grandezze, divise a loro volta in cinque dimensioni
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
 Elementi di macchine 9 Elementi di macchine Generalità La costruzione di una macchina si basa anche sull utilizzo di componenti commerciali normalizzati; tali componenti possono essere impiegati come reperiti
Elementi di macchine 9 Elementi di macchine Generalità La costruzione di una macchina si basa anche sull utilizzo di componenti commerciali normalizzati; tali componenti possono essere impiegati come reperiti
Multipurpose All Terrain Vehicle
 FRESIA F18 4X4 Multipurpose All Terrain Vehicle Mezzo Speciale per Trasporto Materiale Logistico in condizioni estreme su ogni tipo di terreno 4 Ruote Motrici 4 Ruote Sterzanti L F18 4x4 è un veicolo leggero
FRESIA F18 4X4 Multipurpose All Terrain Vehicle Mezzo Speciale per Trasporto Materiale Logistico in condizioni estreme su ogni tipo di terreno 4 Ruote Motrici 4 Ruote Sterzanti L F18 4x4 è un veicolo leggero
ESTRATTO ATTUATORE CON VITE SENZA FINE PER TRAIETTORIE NON LINEARI E ALZACRISTALLI REALIZZATO CON IL MEDESIMO
 ESTRATTO ATTUATORE CON VITE SENZA FINE PER TRAIETTORIE NON LINEARI E ALZACRISTALLI REALIZZATO CON IL MEDESIMO vittorio.scialla@strumentiperleaziende.com Attuatore per traiettorie non lineari dotato di
ESTRATTO ATTUATORE CON VITE SENZA FINE PER TRAIETTORIE NON LINEARI E ALZACRISTALLI REALIZZATO CON IL MEDESIMO vittorio.scialla@strumentiperleaziende.com Attuatore per traiettorie non lineari dotato di
Progetto e costruzione di macchine Joseph E. Shigley, Charles R. Mischke, Richard G. Budynas Copyright 2005 The McGraw-Hill Companies srl
 Copyright 2005 The Companies srl Esercizi aggiuntivi capitolo 13 Analisi 13-4 Un pignone cilindrico a denti dritti di 21 denti ingrana con una ruota da 28 denti. Il passo diametrale è di 3 denti/in e l
Copyright 2005 The Companies srl Esercizi aggiuntivi capitolo 13 Analisi 13-4 Un pignone cilindrico a denti dritti di 21 denti ingrana con una ruota da 28 denti. Il passo diametrale è di 3 denti/in e l
I.T.I.S. «G. MARCONI» - PADOVA Via Manzoni, 80 Tel.: 049.80.40.211 Fax 049.80.40.277 e-mail: marconi@provincia.padova.it ww.itismarconipadova.
 PAG. 1/5 I.T.I.S. «G. MARCONI» - PADOVA Via Manzoni, 80 Tel.: 049.80.40.211 Fax 049.80.40.277 e-mail: marconi@provincia.padova.it ww.itismarconipadova.it DIPARTIMANTO DI MECCANICA E MACCHINE A FLUIDO Rev.
PAG. 1/5 I.T.I.S. «G. MARCONI» - PADOVA Via Manzoni, 80 Tel.: 049.80.40.211 Fax 049.80.40.277 e-mail: marconi@provincia.padova.it ww.itismarconipadova.it DIPARTIMANTO DI MECCANICA E MACCHINE A FLUIDO Rev.
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare
 L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
14.4 Pompe centrifughe
 14.4 Pompe centrifughe Le pompe centrifughe sono molto diffuse in quanto offrono una notevole resistenza all usura, elevato numero di giri e quindi facile accoppiamento diretto con i motori elettrici,
14.4 Pompe centrifughe Le pompe centrifughe sono molto diffuse in quanto offrono una notevole resistenza all usura, elevato numero di giri e quindi facile accoppiamento diretto con i motori elettrici,
Minicorso Regole di Disegno Meccanico
 Parte 3 Minicorso Regole di Disegno Meccanico di Andrea Saviano Tolleranze dimensionali di lavorazione Accoppiamenti mobili, stabili e incerti Giochi e interferenze Posizione della zona di tolleranza e
Parte 3 Minicorso Regole di Disegno Meccanico di Andrea Saviano Tolleranze dimensionali di lavorazione Accoppiamenti mobili, stabili e incerti Giochi e interferenze Posizione della zona di tolleranza e
. Si determina quindi quale distanza viene percorsa lungo l asse y in questo intervallo di tempo: h = v 0y ( d
 Esercizio 1 Un automobile viaggia a velocità v 0 su una strada inclinata di un angolo θ rispetto alla superficie terrestre, e deve superare un burrone largo d (si veda la figura, in cui è indicato anche
Esercizio 1 Un automobile viaggia a velocità v 0 su una strada inclinata di un angolo θ rispetto alla superficie terrestre, e deve superare un burrone largo d (si veda la figura, in cui è indicato anche
Disegno di Macchine. Lezione n 7 Componentistica di base: alberi. corso per I anno della laurea in ing. meccanica Docente: ing.
 Disegno di Macchine corso per I anno della laurea in ing. meccanica Docente: ing. Francesca Campana Lezione n 7 Componentistica di base: alberi Introduzione ai componenti di macchine I componenti meccanici
Disegno di Macchine corso per I anno della laurea in ing. meccanica Docente: ing. Francesca Campana Lezione n 7 Componentistica di base: alberi Introduzione ai componenti di macchine I componenti meccanici
Come visto precedentemente l equazione integro differenziale rappresentativa dell equilibrio elettrico di un circuito RLC è la seguente: 1 = (1)
 Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
19 Il campo elettrico - 3. Le linee del campo elettrico
 Moto di una carica in un campo elettrico uniforme Il moto di una particella carica in un campo elettrico è in generale molto complesso; il problema risulta più semplice se il campo elettrico è uniforme,
Moto di una carica in un campo elettrico uniforme Il moto di una particella carica in un campo elettrico è in generale molto complesso; il problema risulta più semplice se il campo elettrico è uniforme,
9. Urti e conservazione della quantità di moto.
 9. Urti e conservazione della quantità di moto. 1 Conservazione dell impulso m1 v1 v2 m2 Prima Consideriamo due punti materiali di massa m 1 e m 2 che si muovono in una dimensione. Supponiamo che i due
9. Urti e conservazione della quantità di moto. 1 Conservazione dell impulso m1 v1 v2 m2 Prima Consideriamo due punti materiali di massa m 1 e m 2 che si muovono in una dimensione. Supponiamo che i due
Energia e Lavoro. In pratica, si determina la dipendenza dallo spazio invece che dal tempo
 Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
INTEGRATORE E DERIVATORE REALI
 INTEGRATORE E DERIVATORE REALI -Schemi elettrici: Integratore reale : C1 R2 vi (t) R1 vu (t) Derivatore reale : R2 vi (t) R1 C1 vu (t) Elenco componenti utilizzati : - 1 resistenza da 3,3kΩ - 1 resistenza
INTEGRATORE E DERIVATORE REALI -Schemi elettrici: Integratore reale : C1 R2 vi (t) R1 vu (t) Derivatore reale : R2 vi (t) R1 C1 vu (t) Elenco componenti utilizzati : - 1 resistenza da 3,3kΩ - 1 resistenza
LA CORRENTE ELETTRICA
 L CORRENTE ELETTRIC H P h Prima che si raggiunga l equilibrio c è un intervallo di tempo dove il livello del fluido non è uguale. Il verso del movimento del fluido va dal vaso a livello maggiore () verso
L CORRENTE ELETTRIC H P h Prima che si raggiunga l equilibrio c è un intervallo di tempo dove il livello del fluido non è uguale. Il verso del movimento del fluido va dal vaso a livello maggiore () verso
 Motori commerciali Tra le varie applicazioni del motore Stirling, esistono anche motori commerciali, realizzati e testati in laboratorio. Tra questi possiamo illustrarne alcuni: Stirling Power System V160
Motori commerciali Tra le varie applicazioni del motore Stirling, esistono anche motori commerciali, realizzati e testati in laboratorio. Tra questi possiamo illustrarne alcuni: Stirling Power System V160
Usando il pendolo reversibile di Kater
 Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Dimensionamento delle strutture
 Dimensionamento delle strutture Prof. Fabio Fossati Department of Mechanics Politecnico di Milano Lo stato di tensione o di sforzo Allo scopo di caratterizzare in maniera puntuale la distribuzione delle
Dimensionamento delle strutture Prof. Fabio Fossati Department of Mechanics Politecnico di Milano Lo stato di tensione o di sforzo Allo scopo di caratterizzare in maniera puntuale la distribuzione delle
Scelta e verifica dei motori elettrici per gli azionamenti di un mezzo di trazione leggera
 Scelta e verifica dei motori elettrici per gli azionamenti di un mezzo di trazione leggera Si consideri un convoglio ferroviario per la trazione leggera costituito da un unità di trazione, la quale è formata
Scelta e verifica dei motori elettrici per gli azionamenti di un mezzo di trazione leggera Si consideri un convoglio ferroviario per la trazione leggera costituito da un unità di trazione, la quale è formata
Grandezze scalari e vettoriali
 Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
Università di Roma Tor Vergata
 Università di oma Tor Vergata Facoltà di Ingegneria Dipartimento di Ingegneria Industriale Corso di: TEMOTECNIC 1 IMPINTI DI ISCLDMENTO D CQU: DIMENSIONMENTO Ing. G. Bovesecchi gianluigi.bovesecchi@gmail.com
Università di oma Tor Vergata Facoltà di Ingegneria Dipartimento di Ingegneria Industriale Corso di: TEMOTECNIC 1 IMPINTI DI ISCLDMENTO D CQU: DIMENSIONMENTO Ing. G. Bovesecchi gianluigi.bovesecchi@gmail.com
Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012
 Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012 Problema 1 Due carrelli A e B, di massa m A = 104 kg e m B = 128 kg, collegati da una molla di costante elastica k = 3100
Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012 Problema 1 Due carrelli A e B, di massa m A = 104 kg e m B = 128 kg, collegati da una molla di costante elastica k = 3100
F S V F? Soluzione. Durante la spinta, F S =ma (I legge di Newton) con m=40 Kg.
 Spingete per 4 secondi una slitta dove si trova seduta la vostra sorellina. Il peso di slitta+sorella è di 40 kg. La spinta che applicate F S è in modulo pari a 60 Newton. La slitta inizialmente è ferma,
Spingete per 4 secondi una slitta dove si trova seduta la vostra sorellina. Il peso di slitta+sorella è di 40 kg. La spinta che applicate F S è in modulo pari a 60 Newton. La slitta inizialmente è ferma,
Il Campionameto dei segnali e la loro rappresentazione. 1 e prende il nome frequenza di
 Il Campionameto dei segnali e la loro rappresentazione Il campionamento consente, partendo da un segnale a tempo continuo ovvero che fluisce con continuità nel tempo, di ottenere un segnale a tempo discreto,
Il Campionameto dei segnali e la loro rappresentazione Il campionamento consente, partendo da un segnale a tempo continuo ovvero che fluisce con continuità nel tempo, di ottenere un segnale a tempo discreto,
FONDAMENTI DI CONTROLLI AUTOMATICI Ingegneria Meccanica. http://web.ing.unimo.it/~lbiagiotti/fondamenticontrolli1415.html SISTEMI ELEMENTARI
 FONDAMENTI DI CONTROLLI AUTOMATICI Ingegneria Meccanica http://web.ing.unimo.it/~lbiagiotti/fondamenticontrolli1415.html SISTEMI ELEMENTARI Ing. e-mail: luigi.biagiotti@unimore.it http://www.dii.unimore.it/~lbiagiotti
FONDAMENTI DI CONTROLLI AUTOMATICI Ingegneria Meccanica http://web.ing.unimo.it/~lbiagiotti/fondamenticontrolli1415.html SISTEMI ELEMENTARI Ing. e-mail: luigi.biagiotti@unimore.it http://www.dii.unimore.it/~lbiagiotti
Q 1 = +3 10-5 C carica numero 1 Q 2 = +4 10-5 C carica numero 2 forza esercitata tra le cariche distanza tra le cariche, incognita
 Problema n 1 A quale distanza, una dall'altra bisogna porre nel vuoto due cariche (Q 1 =3 10-5 C e Q 2 =4 10-5 C) perché esse esercitino una sull'altra la forza di 200 N? Q 1 = +3 10-5 C carica numero
Problema n 1 A quale distanza, una dall'altra bisogna porre nel vuoto due cariche (Q 1 =3 10-5 C e Q 2 =4 10-5 C) perché esse esercitino una sull'altra la forza di 200 N? Q 1 = +3 10-5 C carica numero
Stagisti: Bottaini Federico, Konica Francesco Tutor aziendali: Calistri Cesare, Ferri Leonardo Tutor scolastico: Carosella Vincenzo
 Stagisti: Bottaini Federico, Konica Francesco Tutor aziendali: Calistri Cesare, Ferri Leonardo Tutor scolastico: Carosella Vincenzo 1 Prefazione Lo scopo principale di queste cabine è quello di ottenere
Stagisti: Bottaini Federico, Konica Francesco Tutor aziendali: Calistri Cesare, Ferri Leonardo Tutor scolastico: Carosella Vincenzo 1 Prefazione Lo scopo principale di queste cabine è quello di ottenere
28360 - FISICA MATEMATICA 1 A.A. 2014/15 Problemi dal libro di testo: D. Giancoli, Fisica, 2a ed., CEA Capitolo 6
 28360 - FISICA MATEMATICA 1 A.A. 2014/15 Problemi dal libro di testo: D. Giancoli, Fisica, 2a ed., CEA Capitolo 6 Lavoro, forza costante: W = F r Problema 1 Quanto lavoro viene compiuto dalla forza di
28360 - FISICA MATEMATICA 1 A.A. 2014/15 Problemi dal libro di testo: D. Giancoli, Fisica, 2a ed., CEA Capitolo 6 Lavoro, forza costante: W = F r Problema 1 Quanto lavoro viene compiuto dalla forza di
Cuscinetti a strisciamento e a rotolamento
 Cuscinetti a strisciamento e a rotolamento La funzione dei cuscinetti a strisciamento e a rotolamento è quella di interporsi tra organi di macchina in rotazione reciproca. Questi elementi possono essere
Cuscinetti a strisciamento e a rotolamento La funzione dei cuscinetti a strisciamento e a rotolamento è quella di interporsi tra organi di macchina in rotazione reciproca. Questi elementi possono essere
Nome..Cognome.. Classe 4G 4 dicembre 2008. VERIFICA DI FISICA: lavoro ed energia
 Nome..Cognome.. Classe 4G 4 dicembre 8 VERIFIC DI FISIC: lavoro ed energia Domande ) Energia cinetica: (punti:.5) a) fornisci la definizione più generale possibile di energia cinetica, specificando l equazione
Nome..Cognome.. Classe 4G 4 dicembre 8 VERIFIC DI FISIC: lavoro ed energia Domande ) Energia cinetica: (punti:.5) a) fornisci la definizione più generale possibile di energia cinetica, specificando l equazione
Laboratorio di Fisica 3 Ottica 2. Studenti: Buoni - Giambastiani - Leidi Gruppo: G09
 Laboratorio di Fisica 3 Ottica 2 Studenti: Buoni - Giambastiani - Leidi Gruppo: G09 24 febbraio 2015 1 Lunghezza d onda di un laser He-Ne 1.1 Scopo dell esperienza Lo scopo dell esperienza è quello di
Laboratorio di Fisica 3 Ottica 2 Studenti: Buoni - Giambastiani - Leidi Gruppo: G09 24 febbraio 2015 1 Lunghezza d onda di un laser He-Ne 1.1 Scopo dell esperienza Lo scopo dell esperienza è quello di
IL RISPARMIO ENERGETICO E GLI AZIONAMENTI A VELOCITA VARIABILE L utilizzo dell inverter negli impianti frigoriferi.
 IL RISPARMIO ENERGETICO E GLI AZIONAMENTI A VELOCITA VARIABILE L utilizzo dell inverter negli impianti frigoriferi. Negli ultimi anni, il concetto di risparmio energetico sta diventando di fondamentale
IL RISPARMIO ENERGETICO E GLI AZIONAMENTI A VELOCITA VARIABILE L utilizzo dell inverter negli impianti frigoriferi. Negli ultimi anni, il concetto di risparmio energetico sta diventando di fondamentale
MOTO DI UNA CARICA IN UN CAMPO ELETTRICO UNIFORME
 6. IL CONDNSATOR FNOMNI DI LTTROSTATICA MOTO DI UNA CARICA IN UN CAMPO LTTRICO UNIFORM Il moto di una particella carica in un campo elettrico è in generale molto complesso; il problema risulta più semplice
6. IL CONDNSATOR FNOMNI DI LTTROSTATICA MOTO DI UNA CARICA IN UN CAMPO LTTRICO UNIFORM Il moto di una particella carica in un campo elettrico è in generale molto complesso; il problema risulta più semplice
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
Fondamenti di Trasporti. Meccanica della Locomozione Utilizzazione della potenza a bordo
 Università di Catania Facoltà di Ingegneria Corso di Laurea in Ingegneria Civile AA 1011 1 Fondamenti di Trasporti Meccanica della Locomozione Utilizzazione della potenza a bordo Giuseppe Inturri Dipartimento
Università di Catania Facoltà di Ingegneria Corso di Laurea in Ingegneria Civile AA 1011 1 Fondamenti di Trasporti Meccanica della Locomozione Utilizzazione della potenza a bordo Giuseppe Inturri Dipartimento
Pressione. Esempio. Definizione di pressione. Legge di Stevino. Pressione nei fluidi EQUILIBRIO E CONSERVAZIONE DELL ENERGIA NEI FLUIDI
 Pressione EQUILIBRIO E CONSERVAZIONE DELL ENERGIA NEI FLUIDI Cos è la pressione? La pressione è una grandezza che lega tra di loro l intensità della forza e l aerea della superficie su cui viene esercitata
Pressione EQUILIBRIO E CONSERVAZIONE DELL ENERGIA NEI FLUIDI Cos è la pressione? La pressione è una grandezza che lega tra di loro l intensità della forza e l aerea della superficie su cui viene esercitata
Anglo Belgian Corporation (ABC) è uno dei principali costruttori di motori diesel a
 Anglo Belgian Corporation (ABC) è uno dei principali costruttori di motori diesel a media velocità d Europa. L azienda ha quasi un secolo di esperienza in motori affidabili e poteni. Originariamente, la
Anglo Belgian Corporation (ABC) è uno dei principali costruttori di motori diesel a media velocità d Europa. L azienda ha quasi un secolo di esperienza in motori affidabili e poteni. Originariamente, la
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Regole della mano destra.
 Regole della mano destra. Macchina in continua con una spira e collettore. Macchina in continua con due spire e collettore. Macchina in continua: schematizzazione di indotto. Macchina in continua. Schematizzazione
Regole della mano destra. Macchina in continua con una spira e collettore. Macchina in continua con due spire e collettore. Macchina in continua: schematizzazione di indotto. Macchina in continua. Schematizzazione
Introduzione al Campionamento e
 Introduzione al Campionamento e all analisi analisi in frequenza Presentazione basata sul Cap.V di Introduction of Engineering Experimentation, A.J.Wheeler, A.R.Ganj, Prentice Hall Campionamento L'utilizzo
Introduzione al Campionamento e all analisi analisi in frequenza Presentazione basata sul Cap.V di Introduction of Engineering Experimentation, A.J.Wheeler, A.R.Ganj, Prentice Hall Campionamento L'utilizzo
