Le leggi dei gas. Capitolo Le leggi di Boyle e di Gay-Lussac. Massimo Banfi
|
|
|
- Ferdinando Casali
- 8 anni fa
- Visualizzazioni
Transcript
1 Cap. 1 - Le leggi dei gas Capitolo 1 Le leggi dei gas 1.1. Le leggi di Boyle e di Gay-Lussac Lo stato termodinamico di un gas è perfettamente noto quando si conoscano i valori delle tre variabili P, V, (pressione, volume e temperatura). A differenza dei solidi e dei liquidi, quindi, le variazioni di pressione in funzione della temperatura non sono più trascurabili. I primi studi quantitativi delle proprietà dei gas si basano su esperienze che hanno inizio attorno alla metà del 1600 e che proseguono con alterne fortune fino a gran parte dell 800. Per limitare la complessità del problema affrontato, l indagine sperimentale avviene inizialmente tenendo costante a turno una delle tre grandezze in gioco e studiando la dipendenza esistente tra le altre due. Si presentano così tre situazioni fondamentali che andiamo ad analizzare. La legge di Boyle ( = costante) Consideriamo un tubo ad U parzialmente riempito di mercurio. Le due estremità sono aperte e a contatto con l atmosfera esterna. In questa situazione il livello del liquido si attesta alla stessa quota in entrambi i rami, essendo uguale la pressione che si sviluppa sulle due colonnine di liquido. L esperimento deve svolgersi a temperatura costante. Provvediamo ora a tappare il tubo di sinistra (figura 1), e introduciamo un certo quantitativo di mercurio nel ramo di destra. La nuova situazione di equilibrio che si viene a creare è ora contraddistinta da un netto dislivello del liquido presente nei due rami, perché all incremento di pressione causato dal mercurio aggiunto a destra fa resistenza la pressione dell aria intrappolata nel tubo di sinistra, il cui volume tende inevitabilmente a diminuire. Poiché le due grandezze in gioco sono fa
2 Cap. 1 - Le leggi dei gas cilmente misurabili, si nota immediatamente come esse siano legate da una proporzionalità inversa dove il loro prodotto rimane costante. Questa relazione prende il nome di legge di Boyle: 1 PV = cost Una trasformazione termodinamica che, come la precedente, avviene a temperatura costante si dice trasformazione isoterma. Fig.1 La legge di Boyle: all aumentare della pressione P diminuisce il volume V del gas racchiuso nel ramo di sinistra. La prima legge di Gay-Lussac (P = cost) Consideriamo ora un recipiente cilindrico chiuso superiormente da un pistone mobile che contenga un volume iniziale V 0 di gas. Manteniamo costante la pressione esercitata dall esterno dovuta, in questo caso, al contributo congiunto dell atmosfera e del peso dello stesso pistone. Se ora aumentiamo la temperatura del gas riscaldando il contenitore con un fornellino da laboratorio, si può facilmente notare il fenomeno (già noto) della dilatazione termica: il gas si espande e va ad occupare un nuovo volume V 1. Ricordiamo che il tasso di espansione assume un valore costante per tutti i gas (in quanto l influenza delle forze molecolari di coesione è nulla) e che il fenomeno è già stato interpretato nel capitolo precedente dalla relazione: V = V 0 (1 + α t) dove t è la temperatura espressa in gradi Celsius, V 0 è il volume alla temperatura di 0 C e la costante α = 1/ 7,15 assume lo stesso valore per tutti i gas. Questa espressione è detta prima legge di Gay-Lussac. Una trasformazione a pressione costante si chiama isobara. La seconda legge di Gay-Lussac (V = cost) Ripetiamo ora la stessa esperienza mantenendo costante il volume V 0 del gas durante il processo di riscaldamento. Perché ciò avvenga, siamo costretti ad aggiungere dei pesi sopra la superficie del pistone mobile in modo che la sua posizione rimanga inalterata. Questo vuol dire che dobbiamo contrastare un aumento di pressione del gas che si manifesta all aumentare della sua temperatura. L espressione algebrica che interpreta il fenomeno è nota con il nome di seconda legge di Gay- Lussac ed è espressa dalla seguente relazione: P = P 0 (1 + α t) dove P 0 è la pressione misurata alla temperatura di zero gradi Celsius e α = 1/ 7,15. 1 Oltre che al fisico irlandese Robert Boyle ( ), la legge deve la sua attuale formulazione anche agli studi pressoché contemporanei del francese Edme Mariotte ( ). Per questo motivo in molti testi è ricordata come legge di Boyle Mariotte. - -
3 Cap. 1 - Le leggi dei gas Una trasformazione di questo tipo si chiama isocora (o isovolumica ). Figura Prima legge di Gay-Lussac: a pressione P costante, esiste una proporzionalità lineare tra il volume V di un gas e la sua temperatura t (espressa in gradi Celsius). Figura Seconda legge di Gay-Lussac: a volume V costante, esiste una proporzionalità lineare tra la temperatura t (espressa in gradi Celsius) di un gas e la sua pressione P. Se riportiamo in un piano cartesiano le tre leggi dei gas, con le grandezze opportune sui due assi, il loro andamento risulta essere di ancor più facile lettura. Figura 4 Le tre leggi dei gas rappresentate nel piano cartesiano. La prima legge di Gay-Lussac è spesso citata con il nome di legge di Volta Gay-Lussac per il contributo dato dal fisico italiano Alessandro Volta ( ). Con motivazioni analoghe, la seconda legge è in genere ricordata come legge di Charles Gay-Lussac, essendo Jacques Charles un fisico francese di fine Settecento ( ). - -
4 Cap. 1 - Le leggi dei gas 1.. La scala Kelvin (o scala assoluta ) Le due leggi di Gay-Lussac mettono in luce un aspetto sperimentale di notevole importanza che viene notato dal fisico e ingegnere irlandese William homson, (nominato barone con il nome di Lord Kelvin) solo nel Kelvin si accorge che estrapolando le due relazioni di Gay-Lussac a temperature molto basse (ben al disotto di quelle ottenibili per via sperimentale con le tecniche del tempo) e supponendo che la legge di Gay-Lussac continui a valere anche per queste situazioni e- streme, la retta rappresentata nel piano cartesiano interseca l asse delle ascisse nel punto t = -7,15 C. Alla luce di questa osservazione, per valori di temperatura ancora minori la pressione e il volume del gas dovrebbero addirittura assumere segno algebrico negativo, il che però non ha nessun significato reale. Kelvin si convince così che il valore di -7,15 C deve rappresentare una sorta di temperatura limite, forse nemmeno raggiungibile nella realtà dei fatti, e lo pone come punto di zero di una nuova scala termometrica che, a differenza di quella Celsius, non si fonda su una definizione di comodo (il comportamento dell acqua nei suoi passaggi di stato), ma su una più oggettiva proprietà della materia: l esistenza in Natura di una temperatura limite impossibile da superare Nasce così la scala assoluta di temperatura, detta anche scala Kelvin: per questioni di comodità operativa l ampiezza del grado rimane numericamente uguale al grado Celsius, e il punto di zero, detto zero assoluto, viene posto a -7,15 C. Le temperature assolute sono contraddistinte dalla lettera (maiuscola) e il simbolo è la lettera K (e non K!!!!). La relazione algebrica che lega la scala Kelvin a quella Celsius è quindi: = t + 75,1 oppure, in modo analogo t = - 7,15 Figura 5 Estrapolando le leggi di Gay-Lussac a temperatura molto basse, si nota come la retta intersechi l asse delle ascisse nel punto t= -7,15 C sotto il quale il volume (o la pressione) di un gas dovrebbero assumere valori negativi. Kelvin suppose che tale temperatura estrema dovesse essere considerata come la più bassa raggiungibile in Natura e che quindi costituisse una sorta di zero assoluto. L introduzione della temperatura assoluta consente di riscrivere le due leggi di Gay-Lussac in un modo più semplice, trasformandole in due proporzionalità dirette. Nel 00 un gruppo di fisici guidati dal premio Nobel Wolfgang Ketterle riuscirono a raffreddare una piccola nube di atomi di sodio fino ad una temperatura di pochi miliardesimi di kelvin, quindi appena sopra lo zero assoluto!!! - 4 -
5 Cap. 1 - Le leggi dei gas Consideriamo la prima legge e sostituiamo alla temperatura Celsius quella Kelvin: V = V α Nell ultimo passaggio si è sostituito 7,15 con 0, che rappresenta la temperatura assoluta dello zero Celsius. Si può allora scrivere: V V 0 = 1 7,15 7,15 + 7,15 7,15 0 (1+ t ) = V0 [1+ ( 7,15) ] = V0 [ ] = V0 0 0 che è una proporzionalità diretta tra il volume V e la temperatura assoluta. In modo analogo si può procedere con la seconda legge di Gay-Lussac: P = P α 1 7,15 7,15 + 7,15 7,15 0 (1+ t ) = P0 [1+ ( 7,15) ] = P0 [ ] = P0 0 e anche in questo caso la relazione assume la forma di una proporzionalità diretta tra pressione P e temperatura assoluta ; in un piano cartesiano essa è rappresentata da una retta passante per l origine P P 0 = 0 Figura 6 Utilizzando la temperatura assoluta le leggi di Gay-Lussac diventano delle proporzionalità dirette tra V e, e tra P e. 1.. L equazione di stato dei gas perfetti In termodinamica lo stato di un sistema è descritto da un punto di vista macroscopico quando siano noti i valori di pressione, temperatura e volume. Affinché tale descrizione sia realmente possibile, il sistema deve trovarsi in uno stato di equilibrio termodinamico, cioè in una condizione che rimane stazionaria finché non intervengono cause e- sterne a modificarla: in tale situazione P, V e assumono lo stesso valore in tutti i punti del sistema, oltre a non cambiare nel tempo
6 Cap. 1 - Le leggi dei gas L equilibrio termodinamico prevede: l equilibrio termico (assenza di scambi di calore con l esterno) equilibrio meccanico (assenza di forze non bilanciate che agiscono sul sistema) equilibrio chimico (assenza di reazioni chimiche o trasformazioni di fase in atto) Le leggi dei gas che abbiamo finora considerato rappresentano delle trasformazioni termodinamiche che coinvolgono due variabili alla volta: la terza, a rotazione, rimane costante. Se questa impostazione rappresenta sicuramente un approccio semplificato al problema, è anche vero che molte situazioni reali coinvolgono tutte e tre la variabili di stato contemporaneamente. Abbiamo quindi la necessità di dedurre una espressione di carattere più generale. Vediamo come fare. La legge di Boyle ci informa che il prodotto pressione-volume rimane costante. E anche sì vero che le due leggi di Gay-Lussac dimostrano come entrambe le grandezze P, V dipendono dalla temperatura assoluta secondo una proporzionalità diretta. Possiamo quindi fondere queste due informazioni in una unica proporzione: PV Se poi, in via generale, consideriamo n moli di gas, è evidente come sia la pressione che il volume siano direttamente proporzionali al quantitativo di gas studiato. Per cui è ragionevole scrivere: PV n Per trasformare queste considerazioni in una vera e propria equazione è ora sufficiente introdurre la giusta costante di proporzionalità. Se chiamiamo R tale costante, possiamo allora scrivere la relazione che prende il nome di equazione di stato dei gas perfetti: PV = n R Per determinare numericamente R ragioniamo in questo modo: il suo valore deve essere costante per ogni valore delle tre variabili P, V e. Se consideriamo ora n = 1 mole di un qualunque gas in condizioni normali, sappiamo che il suo volume è sempre V =,414 litri. Quindi, in questa situazione: P = 1 atm = Pa = 7,15 K V =,414 litri =, m Sostituendo i valori numerici, si ottiene la cosiddetta costante universale dei gas: R = 8,1 J mol -1 K -1. A volte risulta più comodo esprimere R in unità di misura che non appartengono al Sistema Internazionale S.I. perché capita frequentemente di trovare problemi in cui il volume di un gas è misurato in litri e la pressione in atmosfere. In tal caso, eseguite le opportune equivalenze, si ha: R = 0,081 litri atm mol -1 K -1 Infine, è molto utile sapere che, a seconda delle esigenze, l equazione di stato dei gas perfetti può anche essere scritta in modo completamente diverso. Se consideriamo il fatto che il numero n di moli è dato dal rapporto tra il numero totale di molecole N e il numero di Avogadro N A (numero di molecole in una mole), otteniamo: PV = (N/N A ) R Introduciamo ora una nuova costante universale, detta costante di Boltzmann, così definita: k = R (N/N A ) = 1, J/K - 6 -
7 Cap. 1 - Le leggi dei gas L equazione di stato dei gas perfetti assume allora la forma: PV = N k Un gas che segua perfettamente queste leggi si dice gas perfetto Il gas perfetto e l ipotesi atomica della materia Il gas perfetto rappresenta un modello ideale di gas, di fatto inesistente in Natura, che risponde ai seguenti requisiti teorici: le molecole sono puntiformi, perfettamente rigide e di dimensioni trascurabili le forze intermolecolari sono assenti gli urti delle molecole tra di loro, e delle molecole con la parete del contenitore, sono perfettamente elastici per cui vale sempre la conservazione dell energia. Il comportamento di un gas reale differisce in misura più o meno marcata da quello di un gas perfetto, ma in particolari situazioni le differenze risultano di piccola entità. Ciò avviene soprattutto quando il gas reale: è rarefatto si trova a temperatura lontana dal punto di liquefazione. In questa situazione, infatti, le singole molecole sono mediamente molto lontane tra loro: da ciò ne consegue che le forze di coesione sono praticamente nulle e le dimensioni reali delle molecole sono trascurabili rispetto a quelle dello spazio che le contiene, per cui in prima approssimazione i requisiti richiesti dal modello teorico risultano ragionevolmente soddisfatti. L'aria, per esempio, può considerarsi un gas perfetto nei limiti di errore dell'1% alla temperatura ambiente e per pressioni fino a 5 atmosfere: lo stesso margine d'errore vale considerando la pressione di una atmosfera e la temperatura fino a - 95 ºC. Con queste premesse, possiamo applicare le leggi dei gas anche a situazioni reali commettendo errori veramente trascurabili. Figura 7 Moto browniano di una particella di polline sull acqua. Il modello di gas perfetto si fonda sull ipotesi che la materia abbia una struttura atomica e molecolare. Al giorno d oggi nessuna affermazione sembrerebbe essere più ovvia di questa, ma per grande parte dell Ottocento l esistenza degli atomi era considerata dalla stragrande maggioranza degli scienziati una ipotesi senza senso. Sicuramente non giocava a favore di questa teoria la difficoltà di dimostrarne sperimentalmente la correttezza: atomi e molecole non si mostravano troppo facilmente all analisi sperimentale. A dire il vero, una esperienza cruciale in questo senso era stata compiuta casualmente nel 187 dal botanico inglese Robert Brown il quale, studiando con un rudimentale microscopio delle piccole particelle di polline disperse sulla superficie di un liquido, si rese conto che queste non rimanevano - 7 -
8 Cap. 1 - Le leggi dei gas ferme ma si muovevano in continuazione e in modo molto disordinato dirigendosi da tutte le parti, invertendo spesso in modo brusco e casuale la loro direzione di moto. Questo fenomeno prese il nome di moto Browniano e costituiva di fatto la prova sperimentale a favore dell ipotesi atomica della materia: le particelle di polline venivano infatti colpite in continuazione dalle molecole d acqua su cui esse si appoggiavano e spinte da questi urti caotici in tutte le direzioni. L ipotesi atomica si impose con grande difficoltà: per la dimostrazione definitiva della sua correttezza occorrerà aspettare i primi anni del Novecento e i lavori di Jean Baptiste Perrin ed Albert Einstein La teoria cinetica dei gas: la pressione Nonostante la profonda diffidenza nei confronti della teoria atomica della materia, non mancano alcuni scienziati che nella seconda metà dell Ottocento fondano su di essa, e con estremo successo, l interpretazione dei concetti di pressione e di temperatura di un gas. I risultati più eclatanti sono ottenuti da Ludwig Boltzmann ( ) e James Clerk Maxwell ( ). Consideriamo un gas perfetto contenuto in un recipiente di forma cubica di lato L. Cerchiamo ora di dare una interpretazione quantitativa alla definizione di pressione come misura del numero di urti delle molecole contro le pareti del recipiente che contiene il gas. L urto di una singola particella, considerata puntiforme e perfettamente rigida, è di tipo elastico e conserva sia la quantità di moto che l energia. Consideriamo, per iniziare, solo il moto lungo la direzione x. Nel momento dell urto la parete del recipiente esercita una forza F x sulla particella come predetto dal teorema dell impulso. Prendendo come positiva la direzione di moto verso destra, e in riferimento alla figura 8, posso scrivere: F x t = q x = - mv x (+mv x ) = -mv x La componente y della quantità di moto si conserva nell urto, per cui F y t = q y = 0 Per il principio di azione e reazione, la particella eserciterà una forza uguale e contraria sulla parete del recipiente, a cui corrisponde un impulso pari a: F x t = q x = + mv x Dopo l urto la molecola inverte la sua componente x della velocità e torna indietro. Figura 8 Nell urto di una molecola del gas contro la parete X del recipiente, la componente y della quantità di moto si conserva, la componente x inverte il segno algebrico. rascurando le forze di coesione tra le singole molecole e supponendo che gli eventuali urti tra esse siano solo ed esclusivamente di tipo elastico, il modulo della velocità rimane costante non essendoci perdita di energia. La molecola si muove quindi di moto rettilineo uniforme lungo il lato L del cubo con velocità v x = L/ t - 8 -
9 Cap. 1 - Le leggi dei gas colpisce la parete opposta del contenitore, inverte il suo moto e torna a colpire la prima parete che abbiamo considerato dopo un tempo t = L/v x Sostituendo nell espressione precedente ed esplicitando rispetto alla forza F x si ottiene: F x =mv x/ L = mv x/ L Poiché le molecole sono molte, dovremo sommare la forza esercitata nell urto sulla stessa parete da tutte le particelle del gas. Ricordando poi che la pressione è definita come F/S, nel nostro caso F x /L, posto il volume del contenitore uguale a V = L, possiamo scrivere: mv x Px = = L L mv V x Ragionando in modo analogo per le pareti poste lungo le altre due direzioni y e z, otteniamo: mv y Py = = L L mv V y mv z Pz = = L L mv V z Dobbiamo ora introdurre una considerazione di tipo statistico per affermare che le pressioni sulle pareti sono in media uguali in ogni direzione: questa ipotesi porta a risultati corretti a causa del grandissimo numero di molecole coinvolte, per la casualità degli urti e per la evidente simmetria del fenomeno che non ha motivo di presentare delle direzioni privilegiate. Così facendo, però, rinunciamo a determinare in modo preciso quello che avviene ad ogni molecola e, in un certo senso, ci accontentiamo di introdurre considerazioni di tipo statistico sulle proprietà medie delle molecole. Ma la straordinaria concordanza tra i risultati predetti dalla teoria e i valori misurati sperimentalmente ci rassicura sulla correttezza del procedimento. La pressione totale del gas ha (in media) un valore pari a quello misurato su ogni parete. Possiamo quindi scrivere: P P = x + P y V + P z mv x + mv y + mv z m = = ( + + ) = m v x v y v z V V V v dove, l ultima espressione in parentesi non è altro che il modulo al quadrato del vettore velocità v scritto in tre dimensioni. Si è inoltre supposto che le molecole del gas abbiano tutte quante la stessa massa m. Moltiplicando a numeratore e a denominatore per il numero totale N di molecole e indicando con M la massa totale del gas ( M = Nm) possiamo anche scrivere: 1 M PV = N v Abbiamo già detto dell impossibilità pratica di misurare il vettore velocità di ogni molecola e quindi della necessità di introdurre concetti di tipo statistico. Seguendo questa linea di pensiero (nuova per la fisica), definiamo la grandezza velocità quadratica media v qm come la radice quadrata del valore medio dei quadrati delle velocità delle particelle appartenenti al sistema che si sta studiando. In simboli, se le molecole sono N si ha: - 9 -
10 Cap. 1 - Le leggi dei gas v v qm = N Per cui è immediato ottenere la seguente (conclusiva) equazione: 1 PV = M v qm Risulta così dimostrato il legame tra la pressione di un gas e la velocità delle sue molecole e, in definitiva, la conseguente proporzionalità con il numero di urti di queste sulle pareti del recipiente che le contiene La teoria cinetica dei gas: la temperatura assoluta La teoria cinetica dei gas ci aiuta a dimostrare anche l affermazione secondo la quale la temperatura assoluta non é altro che una misura dello stato di agitazione termica delle molecole. Nel modello di gas perfetto le molecole sono considerate puntiformi: quindi, quando ci riferisce alla loro velocità, si intende unicamente la velocità di traslazione delle stesse e si trascura, come diretta conseguenza, ogni tipo di rotazione. Ciò è sicuramente vero per molecole monoatomiche, mentre in tutti gli altri casi i risultati che ora andremo ad ottenere dovranno essere modificati. Non bisogna poi dimenticare che il concetto di velocità è qui da intendersi in senso statistico e quindi coincide con quello di velocità quadratica media calcolata su tutte le molecole del gas (come spiegato nel paragrafo precedente). L energia cinetica media di traslazione di una singola molecola risulta allora espressa dalla seguente relazione di tipo statistico: E cin media = ½ m v qm dove abbiamo qui attribuito alla molecola di massa m la velocità quadratica media v qm. Ricordiamo ora che valgono le equazioni: PV = Nk PV 1 = M v qm 1 = Nmv qm N = mv qm = N E cin media per cui, uguagliando i membri, si ottiene: / N E cin media = Nk e infine E = k cin media espressione che dimostra in modo evidente il legame tra la temperatura assoluta di un gas e l energia cinetica media delle sue molecole
11 Cap. 1 - Le leggi dei gas Grazie a questa equazione, assume così un preciso significato fisico anche il concetto di temperatura assoluta, finora legato solo all esistenza di un limite di natura rappresentato dallo zero assoluto: la temperatura diventa quella grandezza macroscopica che consente una valutazione quantitativa dell energia cinetica molecolare L equipartizione dell energia Le molecole monoatomiche sono state finora considerate come punti materiali senza dimensione. Questo vuol dire che il moto di una qualunque di queste particelle può essere solo di traslazione (un punto non ruota) e che quindi è completamente rappresentato scomponendolo vettorialmente lungo tre soli assi: x, y e z. In virtù di questo fatto si dice che ad una molecola monoatomica competono tre gradi di libertà. Un molecola biatomica, oltre a traslare lungo le tre direzioni x, y e z, può anche ruotare attorno a due assi. In tutto, quindi, la descrizione del suo moto è riconducibile a cinque gradi di libertà. Una molecola triatomica (o anche poliatomica, la situazione è la stessa), oltre a traslare può ruotare attorno a tre assi e quindi possiede in tutto sei gradi di libertà. L intuizione di Boltzmann e Maxwell fu quella di supporre che il quantitativo di energia cinetica che compete ad ogni grado di libertà di una molecola dovesse essere (in media) sempre uguale. Analizzando il risultato ottenuto nel paragrafo precedente per le sole molecole monoatomiche (quindi con tre gradi di libertà), per il quale avevamo ottenuto: E = k cin media ci si convinse che ad ogni grado di libertà dovesse corrispondere un quantitativo di energia cinetica pari a ½ k. In tal modo si arriva alle seguenti conclusioni: E cin media = 5/ k E cin media = 6/ k = k molecole biatomiche molecole triatomiche (e poliatomiche) 1.8. La distribuzione delle velocità: la curva di Maxwell Nei paragrafi precedenti abbiamo associato ad ogni molecola non la sua reale velocità (impossibile da conoscere per ovvie limitazioni sperimentali) ma una grandezza statistica detta velocità quadratica media, univocamente definita attraverso la temperatura del gas. E importante non dimenticare il significato dichiaratamente statistico di tale grandezza: nella realtà dei fatti, ad una fissata temperatura, ci saranno molecole con velocità sia superiore che inferiore rispetto a tale valore. Fu Maxwell il primo ad ottenere una espressione matematica corretta della distribuzione delle velocità delle molecole di un gas in condizioni di equilibrio a temperatura fissata e costante. Vediamo innanzitutto di chiarire il concetto di distribuzione. Quando si studia un sistema caratterizzato da un numero molto grande di costituenti come le persone di una nazione (o le molecole di un gas, ovviamente) può anche non essere di alcuna utilità sapere quante persone, ad esempio, hanno oggi 18 anni. ale indagine escluderebbe tutti coloro che hanno 18 anni e 1 giorno, 18 anni e due mesi, e così via ma potrebbe essere certamente più utile sapere quanti oggi hanno una età compresa tra 18 e 19 anni, tra 19 e 0 anni, tra 60 e 61 anni Una analisi di questo tipo, che for
12 Cap. 1 - Le leggi dei gas nisce una risposta per valori della variabile appartenenti ad una data serie di intervalli, si dice distribuzione. Maxwell applicò questi concetti allo studio delle velocità delle molecole di un gas e, per ogni temperatura fissata, ottenne una curva come quella rappresentata in figura 9. In ascisse è riportato il valore del modulo delle velocità (sempre positivo per definizione), e in ordinata il numero di molecole che hanno una velocità appartenente ad prefissato intervallo v + v. Il vertice della curva corrisponde alla velocità più probabile v p. La velocità media v m e la velocità quadratica media v qm risultano avere un valore leggermente superiore. L area sottesa dalla curva rappresenta il numero totale di particelle del gas. Aumentando la temperatura il picco della curva si sposta verso destra: le velocità più probabili e medie delle molecole tendono ad aumentare. La curva, invece, tende ad appiattirsi in quanto la sua area deve rimanere costante (perché è costante il numero N delle molecole del gas). Le conclusioni teoriche di Maxwell saranno pienamente dimostrate per via sperimentale da Otto Stern nel 190. L ipotesi atomica della materia viene coronata da un completo successo e la meccanica statistica fa il suo ingresso nel mondo della fisica. Figura 9 (sopra) Distribuzione delle velocità delle molecole di un gas perfetto a temperatura fissata. (sotto) Aumentando la temperatura, il picco della curva si sposta verso destra e la curva si appiattisce
13 Cap. 1 - Le leggi dei gas Indice Capitolo Le leggi dei gas Le leggi di Boyle e di Gay-Lussac La scala Kelvin (o scala assoluta ) L equazione di stato dei gas perfetti Il gas perfetto e l ipotesi atomica della materia La teoria cinetica dei gas: la pressione La teoria cinetica dei gas: la temperatura assoluta L equipartizione dell energia La distribuzione delle velocità: la curva di Maxwell
LO STATO GASSOSO. Proprietà fisiche dei gas Leggi dei gas Legge dei gas ideali Teoria cinetico-molecolare dei gas Solubilità dei gas nei liquidi
 LO STATO GASSOSO Proprietà fisiche dei gas Leggi dei gas Legge dei gas ideali Teoria cinetico-molecolare dei gas Solubilità dei gas nei liquidi STATO GASSOSO Un sistema gassoso è costituito da molecole
LO STATO GASSOSO Proprietà fisiche dei gas Leggi dei gas Legge dei gas ideali Teoria cinetico-molecolare dei gas Solubilità dei gas nei liquidi STATO GASSOSO Un sistema gassoso è costituito da molecole
Gas perfetti e sue variabili
 Gas perfetti e sue variabili Un gas è detto perfetto quando: 1. è lontano dal punto di condensazione, e quindi è molto rarefatto 2. su di esso non agiscono forze esterne 3. gli urti tra le molecole del
Gas perfetti e sue variabili Un gas è detto perfetto quando: 1. è lontano dal punto di condensazione, e quindi è molto rarefatto 2. su di esso non agiscono forze esterne 3. gli urti tra le molecole del
Cenni di Teoria Cinetica dei Gas
 Cenni di Teoria Cinetica dei Gas Introduzione La termodinamica descrive i sistemi termodinamici tramite i parametri di stato (p, T,...) Sufficiente per le applicazioni: impostazione e progettazione di
Cenni di Teoria Cinetica dei Gas Introduzione La termodinamica descrive i sistemi termodinamici tramite i parametri di stato (p, T,...) Sufficiente per le applicazioni: impostazione e progettazione di
GAS. I gas si assomigliano tutti
 I gas si assomigliano tutti Aeriforme liquido solido GAS Descrizione macroscopica e microscopica degli stati di aggregazione della materia Fornendo energia al sistema, le forze di attrazione tra le particelle
I gas si assomigliano tutti Aeriforme liquido solido GAS Descrizione macroscopica e microscopica degli stati di aggregazione della materia Fornendo energia al sistema, le forze di attrazione tra le particelle
LABORATORIO DI CHIMICA GENERALE E INORGANICA
 UNIVERSITA DEGLI STUDI DI MILANO Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea Triennale in Chimica CORSO DI: LABORATORIO DI CHIMICA GENERALE E INORGANICA Docente: Dr. Alessandro Caselli
UNIVERSITA DEGLI STUDI DI MILANO Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea Triennale in Chimica CORSO DI: LABORATORIO DI CHIMICA GENERALE E INORGANICA Docente: Dr. Alessandro Caselli
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
I.T.C.G.T T. Acerbo - Pescara LABORATORIO DI FISICA A. S. 2009/10
 I.T.C.G.T T. Acerbo - Pescara LABORATORIO DI FISICA A. S. 2009/10 Cognome: D Ovidio Nome: Stefania Classe: 2 B Geometri Data: 04/12/2009 Gruppo: F. Illiceto; V. Ivanochko; M.C. Scopino; M.Terenzi N. pagine:
I.T.C.G.T T. Acerbo - Pescara LABORATORIO DI FISICA A. S. 2009/10 Cognome: D Ovidio Nome: Stefania Classe: 2 B Geometri Data: 04/12/2009 Gruppo: F. Illiceto; V. Ivanochko; M.C. Scopino; M.Terenzi N. pagine:
Ripasso sulla temperatura, i gas perfetti e il calore
 Ripasso sulla temperatura, i gas perfetti e il calore Prof. Daniele Ippolito Liceo Scientifico Amedeo di Savoia di Pistoia La temperatura Fenomeni non interpretabili con le leggi della meccanica Dilatazione
Ripasso sulla temperatura, i gas perfetti e il calore Prof. Daniele Ippolito Liceo Scientifico Amedeo di Savoia di Pistoia La temperatura Fenomeni non interpretabili con le leggi della meccanica Dilatazione
Energia e Lavoro. In pratica, si determina la dipendenza dallo spazio invece che dal tempo
 Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Gas e gas perfetti. Marina Cobal - Dipt.di Fisica - Universita' di Udine 1
 Gas e gas perfetti 1 Densita Densita - massa per unita di volume Si misura in g/cm 3 ρ = M V Bassa densita Alta densita Definizione di Pressione Pressione = Forza / Area P = F/A unita SI : 1 Nt/m 2 = 1
Gas e gas perfetti 1 Densita Densita - massa per unita di volume Si misura in g/cm 3 ρ = M V Bassa densita Alta densita Definizione di Pressione Pressione = Forza / Area P = F/A unita SI : 1 Nt/m 2 = 1
9. Urti e conservazione della quantità di moto.
 9. Urti e conservazione della quantità di moto. 1 Conservazione dell impulso m1 v1 v2 m2 Prima Consideriamo due punti materiali di massa m 1 e m 2 che si muovono in una dimensione. Supponiamo che i due
9. Urti e conservazione della quantità di moto. 1 Conservazione dell impulso m1 v1 v2 m2 Prima Consideriamo due punti materiali di massa m 1 e m 2 che si muovono in una dimensione. Supponiamo che i due
EQUAZIONE DI STATO e LEGGI DEI GAS esercizi risolti Classi quarte L.S.
 EQUAZIONE DI STATO e LEGGI DEI GAS esercizi risolti Classi quarte L.S. In questa dispensa verrà riportato lo svolgimento di alcuni esercizi inerenti l'equazione di stato dei gas perfetti e le principali
EQUAZIONE DI STATO e LEGGI DEI GAS esercizi risolti Classi quarte L.S. In questa dispensa verrà riportato lo svolgimento di alcuni esercizi inerenti l'equazione di stato dei gas perfetti e le principali
Termodinamica. Sistema termodinamico. Piano di Clapeyron. Sistema termodinamico. Esempio. Cosa è la termodinamica? TERMODINAMICA
 Termodinamica TERMODINAMICA Cosa è la termodinamica? La termodinamica studia la conversione del calore in lavoro meccanico Prof Crosetto Silvio 2 Prof Crosetto Silvio Il motore dell automobile trasforma
Termodinamica TERMODINAMICA Cosa è la termodinamica? La termodinamica studia la conversione del calore in lavoro meccanico Prof Crosetto Silvio 2 Prof Crosetto Silvio Il motore dell automobile trasforma
Complementi di Termologia. I parte
 Prof. Michele Giugliano (Dicembre 2) Complementi di Termologia. I parte N.. - Calorimetria. Il calore è una forma di energia, quindi la sua unità di misura, nel sistema SI, è il joule (J), tuttavia si
Prof. Michele Giugliano (Dicembre 2) Complementi di Termologia. I parte N.. - Calorimetria. Il calore è una forma di energia, quindi la sua unità di misura, nel sistema SI, è il joule (J), tuttavia si
GLI STATI DI AGGREGAZIONE DELLA MATERIA. Lo stato gassoso
 GLI STATI DI AGGREGAZIONE DELLA MATERIA Lo stato gassoso Classificazione della materia MATERIA Composizione Struttura Proprietà Trasformazioni 3 STATI DI AGGREGAZIONE SOLIDO (volume e forma propri) LIQUIDO
GLI STATI DI AGGREGAZIONE DELLA MATERIA Lo stato gassoso Classificazione della materia MATERIA Composizione Struttura Proprietà Trasformazioni 3 STATI DI AGGREGAZIONE SOLIDO (volume e forma propri) LIQUIDO
GIROSCOPIO. Scopo dell esperienza: Teoria fisica. Verificare la relazione: ω p = bmg/iω
 GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
GIROSCOPIO Scopo dell esperienza: Verificare la relazione: ω p = bmg/iω dove ω p è la velocità angolare di precessione, ω è la velocità angolare di rotazione, I il momento principale d inerzia assiale,
Esempi di funzione. Scheda Tre
 Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE
 APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE 1. Proporzionalità diretta e proporzionalità inversa Analizziamo le seguenti formule Peso Lordo = Peso Netto + Tara Ricavo = Utile + Costo Rata = Importo + Interesse
APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE 1. Proporzionalità diretta e proporzionalità inversa Analizziamo le seguenti formule Peso Lordo = Peso Netto + Tara Ricavo = Utile + Costo Rata = Importo + Interesse
LA MOLE : UN UNITA DI MISURA FONDAMENTALE PER LA CHIMICA
 LA MOLE : UN UNITA DI MISURA FONDAMENTALE PER LA CHIMICA Poiché è impossibile contare o pesare gli atomi o le molecole che formano una qualsiasi sostanza chimica, si ricorre alla grandezza detta quantità
LA MOLE : UN UNITA DI MISURA FONDAMENTALE PER LA CHIMICA Poiché è impossibile contare o pesare gli atomi o le molecole che formano una qualsiasi sostanza chimica, si ricorre alla grandezza detta quantità
TEORIA CINETICA DEI GAS
 TEORIA CINETICA DEI GAS La teoria cinetica dei gas è corrispondente con, e infatti prevede, le proprietà dei gas. Nella materia gassosa, gli atomi o le molecole sono separati da grandi distanze e sono
TEORIA CINETICA DEI GAS La teoria cinetica dei gas è corrispondente con, e infatti prevede, le proprietà dei gas. Nella materia gassosa, gli atomi o le molecole sono separati da grandi distanze e sono
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
Temperatura. V(t) = Vo (1+at) Strumento di misura: termometro
 I FENOMENI TERMICI Temperatura Calore Trasformazioni termodinamiche Gas perfetti Temperatura assoluta Gas reali Principi della Termodinamica Trasmissione del calore Termoregolazione del corpo umano Temperatura
I FENOMENI TERMICI Temperatura Calore Trasformazioni termodinamiche Gas perfetti Temperatura assoluta Gas reali Principi della Termodinamica Trasmissione del calore Termoregolazione del corpo umano Temperatura
p atm 1. V B ; 2. T B ; 3. W A B 4. il calore specifico a volume costante c V
 1 Esercizio (tratto dal Problema 13.4 del Mazzoldi 2) Un gas ideale compie un espansione adiabatica contro la pressione atmosferica, dallo stato A di coordinate, T A, p A (tutte note, con p A > ) allo
1 Esercizio (tratto dal Problema 13.4 del Mazzoldi 2) Un gas ideale compie un espansione adiabatica contro la pressione atmosferica, dallo stato A di coordinate, T A, p A (tutte note, con p A > ) allo
L E L E G G I D E I G A S P A R T E I
 L E L E G G I D E I G A S P A R T E I Variabili di stato Equazioni di stato Legge di Boyle Pressione, temperatura, scale termometriche Leggi di Charles/Gay-Lussac Dispense di Chimica Fisica per Biotecnologie
L E L E G G I D E I G A S P A R T E I Variabili di stato Equazioni di stato Legge di Boyle Pressione, temperatura, scale termometriche Leggi di Charles/Gay-Lussac Dispense di Chimica Fisica per Biotecnologie
Capitolo 10 Il primo principio 113
 Capitolo 10 Il primo principio 113 QUESITI E PROBLEMI 1 Tenuto conto che, quando il volume di un gas reale subisce l incremento dv, il lavoro compiuto dalle forze intermolecolari di coesione è L = n 2
Capitolo 10 Il primo principio 113 QUESITI E PROBLEMI 1 Tenuto conto che, quando il volume di un gas reale subisce l incremento dv, il lavoro compiuto dalle forze intermolecolari di coesione è L = n 2
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
Unità di misura. Perché servono le unità di misura nella pratica di laboratorio e in corsia? Le unità di misura sono molto importanti
 Unità di misura Le unità di misura sono molto importanti 1000 è solo un numero 1000 lire unità di misura monetaria 1000 unità di misura monetaria ma il valore di acquisto è molto diverso 1000/mese unità
Unità di misura Le unità di misura sono molto importanti 1000 è solo un numero 1000 lire unità di misura monetaria 1000 unità di misura monetaria ma il valore di acquisto è molto diverso 1000/mese unità
Nome..Cognome.. Classe 4G 4 dicembre 2008. VERIFICA DI FISICA: lavoro ed energia
 Nome..Cognome.. Classe 4G 4 dicembre 8 VERIFIC DI FISIC: lavoro ed energia Domande ) Energia cinetica: (punti:.5) a) fornisci la definizione più generale possibile di energia cinetica, specificando l equazione
Nome..Cognome.. Classe 4G 4 dicembre 8 VERIFIC DI FISIC: lavoro ed energia Domande ) Energia cinetica: (punti:.5) a) fornisci la definizione più generale possibile di energia cinetica, specificando l equazione
Le funzioni continue. A. Pisani Liceo Classico Dante Alighieri A.S. 2002-03. A. Pisani, appunti di Matematica 1
 Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
LA CORRENTE ELETTRICA Prof. Erasmo Modica erasmo@galois.it
 LA CORRENTE ELETTRICA Prof. Erasmo Modica erasmo@galois.it L INTENSITÀ DELLA CORRENTE ELETTRICA Consideriamo una lampadina inserita in un circuito elettrico costituito da fili metallici ed un interruttore.
LA CORRENTE ELETTRICA Prof. Erasmo Modica erasmo@galois.it L INTENSITÀ DELLA CORRENTE ELETTRICA Consideriamo una lampadina inserita in un circuito elettrico costituito da fili metallici ed un interruttore.
Stati di aggregazione della materia unità 2, modulo A del libro
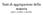 Stati di aggregazione della materia unità 2, modulo A del libro Gli stati di aggregazione della materia sono tre: solido, liquido e gassoso, e sono caratterizzati dalle seguenti grandezze: Quantità --->
Stati di aggregazione della materia unità 2, modulo A del libro Gli stati di aggregazione della materia sono tre: solido, liquido e gassoso, e sono caratterizzati dalle seguenti grandezze: Quantità --->
Preparazione alle gare di II livello delle Olimpiadi della Fisica 2013
 Preparazione alle gare di II livello delle Olimpiadi della Fisica 01 Incontro su temi di termodinamica 14/1/01 Giuseppina Rinaudo - Dipartimento di Fisica dell Università di Torino Sommario dei quesiti
Preparazione alle gare di II livello delle Olimpiadi della Fisica 01 Incontro su temi di termodinamica 14/1/01 Giuseppina Rinaudo - Dipartimento di Fisica dell Università di Torino Sommario dei quesiti
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
SOMMARIO. 13.1 I radicali pag. 3. 13.2 I radicali aritmetici pag. 5. 13.3 Moltiplicazione e divisione fra radicali aritmetici pag.
 SOMMARIO CAPITOLO : I RADICALI. I radicali pag.. I radicali aritmetici pag.. Moltiplicazione e divisione fra radicali aritmetici pag.. Potenza di un radicale aritmetico pag.. Trasporto di un fattore esterno
SOMMARIO CAPITOLO : I RADICALI. I radicali pag.. I radicali aritmetici pag.. Moltiplicazione e divisione fra radicali aritmetici pag.. Potenza di un radicale aritmetico pag.. Trasporto di un fattore esterno
Termologia. Introduzione Scale Termometriche Espansione termica Capacità termica e calori specifici Cambiamenti di fase e calori latenti
 Termologia Introduzione Scale Termometriche Espansione termica Capacità termica e calori specifici Cambiamenti di fase e calori latenti Trasmissione del calore Legge di Wien Legge di Stefan-Boltzmann Gas
Termologia Introduzione Scale Termometriche Espansione termica Capacità termica e calori specifici Cambiamenti di fase e calori latenti Trasmissione del calore Legge di Wien Legge di Stefan-Boltzmann Gas
Termodinamica: legge zero e temperatura
 Termodinamica: legge zero e temperatura Affrontiamo ora lo studio della termodinamica che prende in esame l analisi dell energia termica dei sistemi e di come tale energia possa essere scambiata, assorbita
Termodinamica: legge zero e temperatura Affrontiamo ora lo studio della termodinamica che prende in esame l analisi dell energia termica dei sistemi e di come tale energia possa essere scambiata, assorbita
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Pressione. Esempio. Definizione di pressione. Legge di Stevino. Pressione nei fluidi EQUILIBRIO E CONSERVAZIONE DELL ENERGIA NEI FLUIDI
 Pressione EQUILIBRIO E CONSERVAZIONE DELL ENERGIA NEI FLUIDI Cos è la pressione? La pressione è una grandezza che lega tra di loro l intensità della forza e l aerea della superficie su cui viene esercitata
Pressione EQUILIBRIO E CONSERVAZIONE DELL ENERGIA NEI FLUIDI Cos è la pressione? La pressione è una grandezza che lega tra di loro l intensità della forza e l aerea della superficie su cui viene esercitata
Gas. Vapore. Forma e volume del recipiente in cui è contenuto. un gas liquido a temperatura e pressione ambiente. microscopico MACROSCOPICO
 Lo Stato Gassoso Gas Vapore Forma e volume del recipiente in cui è contenuto. un gas liquido a temperatura e pressione ambiente MACROSCOPICO microscopico bassa densità molto comprimibile distribuzione
Lo Stato Gassoso Gas Vapore Forma e volume del recipiente in cui è contenuto. un gas liquido a temperatura e pressione ambiente MACROSCOPICO microscopico bassa densità molto comprimibile distribuzione
Una soluzione è un sistema omogeneo (cioè costituito da una sola fase, che può essere liquida, solida o gassosa) a due o più componenti.
 Una soluzione è un sistema omogeneo (cioè costituito da una sola fase, che può essere liquida, solida o gassosa) a due o più componenti. Solvente (componente presente in maggior quantità) SOLUZIONE Soluti
Una soluzione è un sistema omogeneo (cioè costituito da una sola fase, che può essere liquida, solida o gassosa) a due o più componenti. Solvente (componente presente in maggior quantità) SOLUZIONE Soluti
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
13 La temperatura - 8. Il gas perfetto
 La mole e l equazione del gas perfetto Tutto ciò che vediamo intorno a noi è composto di piccolissimi grani, che chiamiamo «molecole». Per esempio, il ghiaccio, l acqua liquida e il vapore acqueo sono
La mole e l equazione del gas perfetto Tutto ciò che vediamo intorno a noi è composto di piccolissimi grani, che chiamiamo «molecole». Per esempio, il ghiaccio, l acqua liquida e il vapore acqueo sono
UNIVERSITÀ DEGLI STUDI DI TERAMO
 UNIVERSITÀ DEGLI STUDI DI TERAMO CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA (Classe 7) Corso di Matematica per l Economia (Prof. F. Eugeni) TEST DI INGRESSO Teramo, ottobre 00 SEZIONE
UNIVERSITÀ DEGLI STUDI DI TERAMO CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA (Classe 7) Corso di Matematica per l Economia (Prof. F. Eugeni) TEST DI INGRESSO Teramo, ottobre 00 SEZIONE
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
L'ENTROPIA. Lezioni d'autore
 L'ENTROPIA Lezioni d'autore Un video : Clic Un altro video : Clic La funzione di distribuzione delle velocità (I) Nel grafico accanto sono riportati i numeri delle molecole di un gas, suddivise a seconda
L'ENTROPIA Lezioni d'autore Un video : Clic Un altro video : Clic La funzione di distribuzione delle velocità (I) Nel grafico accanto sono riportati i numeri delle molecole di un gas, suddivise a seconda
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 2014
 Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
LE LEGGI DEI GAS. Dalle prime teorie cinetiche dei gas simulazioni della dinamica molecolare. Lezioni d'autore
 LE LEGGI DEI GAS Dalle prime teorie cinetiche dei gas simulazioni della dinamica molecolare. Lezioni d'autore alle Un video : Clic Un altro video : Clic Un altro video (in inglese): Clic Richiami sulle
LE LEGGI DEI GAS Dalle prime teorie cinetiche dei gas simulazioni della dinamica molecolare. Lezioni d'autore alle Un video : Clic Un altro video : Clic Un altro video (in inglese): Clic Richiami sulle
Proprieta meccaniche dei fluidi
 Proprieta meccaniche dei fluidi 1. Definizione di fluido: liquido o gas 2. La pressione in un fluido 3. Equilibrio nei fluidi: legge di Stevino 4. Il Principio di Pascal 5. Il barometro di Torricelli 6.
Proprieta meccaniche dei fluidi 1. Definizione di fluido: liquido o gas 2. La pressione in un fluido 3. Equilibrio nei fluidi: legge di Stevino 4. Il Principio di Pascal 5. Il barometro di Torricelli 6.
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
28360 - FISICA MATEMATICA 1 A.A. 2014/15 Problemi dal libro di testo: D. Giancoli, Fisica, 2a ed., CEA Capitolo 6
 28360 - FISICA MATEMATICA 1 A.A. 2014/15 Problemi dal libro di testo: D. Giancoli, Fisica, 2a ed., CEA Capitolo 6 Lavoro, forza costante: W = F r Problema 1 Quanto lavoro viene compiuto dalla forza di
28360 - FISICA MATEMATICA 1 A.A. 2014/15 Problemi dal libro di testo: D. Giancoli, Fisica, 2a ed., CEA Capitolo 6 Lavoro, forza costante: W = F r Problema 1 Quanto lavoro viene compiuto dalla forza di
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
Esercitazione X - Legge dei gas perfetti e trasformazioni
 Esercitazione X - Legge dei gas perfetti e trasformazioni termodinamiche Formulario Il primo principio della termodinamica afferma che la variazione dell energia interna di un sistema U è uguale alla somma
Esercitazione X - Legge dei gas perfetti e trasformazioni termodinamiche Formulario Il primo principio della termodinamica afferma che la variazione dell energia interna di un sistema U è uguale alla somma
Quantità di moto. Per un corpo puntiforme possiamo definire la grandezza vettoriale quantità di moto come il prodotto m v.
 Quantità di moto Per un corpo puntiforme possiamo definire la grandezza vettoriale quantità di moto come il prodotto m v. La seconda legge di Newton può essere scritta con la quantità di moto: d Q F =
Quantità di moto Per un corpo puntiforme possiamo definire la grandezza vettoriale quantità di moto come il prodotto m v. La seconda legge di Newton può essere scritta con la quantità di moto: d Q F =
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare
 L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
L EQUILIBRIO UNIVERSALE dalla meccanica celeste alla fisica nucleare Cap.4 giroscopio, magnetismo e forza di Lorentz teoria del giroscopio Abbiamo finora preso in considerazione le condizionidi equilibrio
C V. gas monoatomici 3 R/2 5 R/2 gas biatomici 5 R/2 7 R/2 gas pluriatomici 6 R/2 8 R/2
 46 Tonzig La fisica del calore o 6 R/2 rispettivamente per i gas a molecola monoatomica, biatomica e pluriatomica. Per un gas perfetto, il calore molare a pressione costante si ottiene dal precedente aggiungendo
46 Tonzig La fisica del calore o 6 R/2 rispettivamente per i gas a molecola monoatomica, biatomica e pluriatomica. Per un gas perfetto, il calore molare a pressione costante si ottiene dal precedente aggiungendo
bensì una tendenza a ruotare quando vengono applicate in punti diversi di un corpo
 Momento di una forza Nella figura 1 è illustrato come forze uguali e contrarie possono non produrre equilibrio, bensì una tendenza a ruotare quando vengono applicate in punti diversi di un corpo esteso.
Momento di una forza Nella figura 1 è illustrato come forze uguali e contrarie possono non produrre equilibrio, bensì una tendenza a ruotare quando vengono applicate in punti diversi di un corpo esteso.
. Si determina quindi quale distanza viene percorsa lungo l asse y in questo intervallo di tempo: h = v 0y ( d
 Esercizio 1 Un automobile viaggia a velocità v 0 su una strada inclinata di un angolo θ rispetto alla superficie terrestre, e deve superare un burrone largo d (si veda la figura, in cui è indicato anche
Esercizio 1 Un automobile viaggia a velocità v 0 su una strada inclinata di un angolo θ rispetto alla superficie terrestre, e deve superare un burrone largo d (si veda la figura, in cui è indicato anche
Fondamenti e didattica di Matematica Finanziaria
 Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
Vademecum studio funzione
 Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
Come visto precedentemente l equazione integro differenziale rappresentativa dell equilibrio elettrico di un circuito RLC è la seguente: 1 = (1)
 Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Transitori Analisi nel dominio del tempo Ricordiamo che si definisce transitorio il periodo di tempo che intercorre nel passaggio, di un sistema, da uno stato energetico ad un altro, non è comunque sempre
Metodi statistici per le ricerche di mercato
 Metodi statistici per le ricerche di mercato Prof.ssa Isabella Mingo A.A. 2014-2015 Facoltà di Scienze Politiche, Sociologia, Comunicazione Corso di laurea Magistrale in «Organizzazione e marketing per
Metodi statistici per le ricerche di mercato Prof.ssa Isabella Mingo A.A. 2014-2015 Facoltà di Scienze Politiche, Sociologia, Comunicazione Corso di laurea Magistrale in «Organizzazione e marketing per
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
LA TERMOLOGIA. studia le variazioni di dimensione di un corpo a causa di una
 LA TERMOLOGIA La termologia è la parte della fisica che si occupa dello studio del calore e dei fenomeni legati alle variazioni di temperatura subite dai corpi. Essa si può distinguere in: Termometria
LA TERMOLOGIA La termologia è la parte della fisica che si occupa dello studio del calore e dei fenomeni legati alle variazioni di temperatura subite dai corpi. Essa si può distinguere in: Termometria
REAZIONI ORGANICHE Variazioni di energia e velocità di reazione
 REAZIONI ORGANICHE Variazioni di energia e velocità di reazione Abbiamo visto che i composti organici e le loro reazioni possono essere suddivisi in categorie omogenee. Per ottenere la massima razionalizzazione
REAZIONI ORGANICHE Variazioni di energia e velocità di reazione Abbiamo visto che i composti organici e le loro reazioni possono essere suddivisi in categorie omogenee. Per ottenere la massima razionalizzazione
Trasformazioni Geometriche 1 Roberto Petroni, 2011
 1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
ENERGIA. Energia e Lavoro Potenza Energia cinetica Energia potenziale Principio di conservazione dell energia meccanica
 1 ENERGIA Energia e Lavoro Potenza Energia cinetica Energia potenziale Principio di conservazione dell energia meccanica 2 Energia L energia è ciò che ci permette all uomo di compiere uno sforzo o meglio
1 ENERGIA Energia e Lavoro Potenza Energia cinetica Energia potenziale Principio di conservazione dell energia meccanica 2 Energia L energia è ciò che ci permette all uomo di compiere uno sforzo o meglio
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
L analisi dei dati. Capitolo 4. 4.1 Il foglio elettronico
 Capitolo 4 4.1 Il foglio elettronico Le più importanti operazioni richieste dall analisi matematica dei dati sperimentali possono essere agevolmente portate a termine da un comune foglio elettronico. Prenderemo
Capitolo 4 4.1 Il foglio elettronico Le più importanti operazioni richieste dall analisi matematica dei dati sperimentali possono essere agevolmente portate a termine da un comune foglio elettronico. Prenderemo
Le equazioni. Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete.
 Le equazioni Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete. Definizione e caratteristiche Chiamiamo equazione l uguaglianza tra due espressioni algebriche,
Le equazioni Diapositive riassemblate e rielaborate da prof. Antonio Manca da materiali offerti dalla rete. Definizione e caratteristiche Chiamiamo equazione l uguaglianza tra due espressioni algebriche,
Modulo di Meccanica e Termodinamica
 Modulo di Meccanica e Termodinamica 1) Misure e unita di misura 2) Cinematica: + Moto Rettilineo + Moto Uniformemente Accelerato [+ Vettori e Calcolo Vettoriale] + Moti Relativi 3) Dinamica: + Forza e
Modulo di Meccanica e Termodinamica 1) Misure e unita di misura 2) Cinematica: + Moto Rettilineo + Moto Uniformemente Accelerato [+ Vettori e Calcolo Vettoriale] + Moti Relativi 3) Dinamica: + Forza e
GRANDEZZE SINUSOIDALI
 GRANDEE SINUSOIDALI INDICE -Grandezze variabili. -Grandezze periodiche. 3-Parametri delle grandezze periodiche. 4-Grandezze alternate. 5-Grandezze sinusoidali. 6-Parametri delle grandezze sinusoidali.
GRANDEE SINUSOIDALI INDICE -Grandezze variabili. -Grandezze periodiche. 3-Parametri delle grandezze periodiche. 4-Grandezze alternate. 5-Grandezze sinusoidali. 6-Parametri delle grandezze sinusoidali.
Energia nelle reazioni chimiche. Lezioni d'autore di Giorgio Benedetti
 Energia nelle reazioni chimiche Lezioni d'autore di Giorgio Benedetti VIDEO Introduzione (I) L energia chimica è dovuta al particolare arrangiamento degli atomi nei composti chimici e le varie forme di
Energia nelle reazioni chimiche Lezioni d'autore di Giorgio Benedetti VIDEO Introduzione (I) L energia chimica è dovuta al particolare arrangiamento degli atomi nei composti chimici e le varie forme di
a) Il campo di esistenza di f(x) è dato da 2x 0, ovvero x 0. Il grafico di f(x) è quello di una iperbole -1 1
 LE FUNZIONI EALI DI VAIABILE EALE Soluzioni di quesiti e problemi estratti dal Corso Base Blu di Matematica volume 5 Q[] Sono date le due funzioni: ) = e g() = - se - se = - Determina il campo di esistenza
LE FUNZIONI EALI DI VAIABILE EALE Soluzioni di quesiti e problemi estratti dal Corso Base Blu di Matematica volume 5 Q[] Sono date le due funzioni: ) = e g() = - se - se = - Determina il campo di esistenza
Cap 3.1- Prima legge della DINAMICA o di Newton
 Parte I Cap 3.1- Prima legge della DINAMICA o di Newton Cap 3.1- Prima legge della DINAMICA o di Newton 3.1-3.2-3.3 forze e principio d inerzia Abbiamo finora studiato come un corpo cambia traiettoria
Parte I Cap 3.1- Prima legge della DINAMICA o di Newton Cap 3.1- Prima legge della DINAMICA o di Newton 3.1-3.2-3.3 forze e principio d inerzia Abbiamo finora studiato come un corpo cambia traiettoria
Forze, leggi della dinamica, diagramma del. 28 febbraio 2009 (PIACENTINO - PREITE) Fisica per Scienze Motorie
 Forze, leggi della dinamica, diagramma del corpo libero 1 FORZE Grandezza fisica definibile come l' agente in grado di modificare lo stato di quiete o di moto di un corpo. Ci troviamo di fronte ad una
Forze, leggi della dinamica, diagramma del corpo libero 1 FORZE Grandezza fisica definibile come l' agente in grado di modificare lo stato di quiete o di moto di un corpo. Ci troviamo di fronte ad una
Note di fisica. Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria, luglio 2012. 1 Quantità di moto.
 Note di fisica. Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria, luglio 2012. Indice 1 Quantità di moto. 1 1.1 Quantità di moto di una particella.............................. 1 1.2 Quantità
Note di fisica. Mauro Saita e-mail: maurosaita@tiscalinet.it Versione provvisoria, luglio 2012. Indice 1 Quantità di moto. 1 1.1 Quantità di moto di una particella.............................. 1 1.2 Quantità
Slide Cerbara parte1 5. Le distribuzioni teoriche
 Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
Slide Cerbara parte1 5 Le distribuzioni teoriche I fenomeni biologici, demografici, sociali ed economici, che sono il principale oggetto della statistica, non sono retti da leggi matematiche. Però dalle
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
QUESITI DI FISICA RISOLTI A LEZIONE TERMODINAMICA
 QUESITI DI FISICA RISOLTI A LEZIONE TERMODINAMICA Un recipiente contiene gas perfetto a 27 o C, che si espande raggiungendo il doppio del suo volume iniziale a pressione costante. La temperatura finale
QUESITI DI FISICA RISOLTI A LEZIONE TERMODINAMICA Un recipiente contiene gas perfetto a 27 o C, che si espande raggiungendo il doppio del suo volume iniziale a pressione costante. La temperatura finale
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
Gas, liquidi, solidi. Tutti i gas, tranne l'elio, solidificano a basse temperature (alcuni richiedono anche alte pressioni).
 Gas, liquidi, solidi Tutti i gas raffreddati liquefano Tutti i gas, tranne l'elio, solidificano a basse temperature (alcuni richiedono anche alte pressioni). Sostanza T L ( C) T E ( C) He - -269 H 2-263
Gas, liquidi, solidi Tutti i gas raffreddati liquefano Tutti i gas, tranne l'elio, solidificano a basse temperature (alcuni richiedono anche alte pressioni). Sostanza T L ( C) T E ( C) He - -269 H 2-263
Definire la potenza e ricordare l unità di misura della potenza. Definire l energia e la sua unità di misura. Enunciare il teorema delle forze vive
 Programmazione per competenze: Istituto scolastico Classe Riferimento ai documenti programmatici Liceo scientifico, indirizzo scienze applicate II Competenza N 3.2, Asse scientifico tecnologico Analizzare
Programmazione per competenze: Istituto scolastico Classe Riferimento ai documenti programmatici Liceo scientifico, indirizzo scienze applicate II Competenza N 3.2, Asse scientifico tecnologico Analizzare
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Complementi di Analisi per Informatica *** Capitolo 2. Numeri Complessi. e Circuiti Elettrici. a Corrente Alternata. Sergio Benenti 7 settembre 2013
 Complementi di Analisi per nformatica *** Capitolo 2 Numeri Complessi e Circuiti Elettrici a Corrente Alternata Sergio Benenti 7 settembre 2013? ndice 2 Circuiti elettrici a corrente alternata 1 21 Circuito
Complementi di Analisi per nformatica *** Capitolo 2 Numeri Complessi e Circuiti Elettrici a Corrente Alternata Sergio Benenti 7 settembre 2013? ndice 2 Circuiti elettrici a corrente alternata 1 21 Circuito
Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012
 Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012 Problema 1 Due carrelli A e B, di massa m A = 104 kg e m B = 128 kg, collegati da una molla di costante elastica k = 3100
Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012 Problema 1 Due carrelli A e B, di massa m A = 104 kg e m B = 128 kg, collegati da una molla di costante elastica k = 3100
3. Stato gassoso. Al termine dell unità didattica si dovranno raggiungere i seguenti obiettivi:
 3. Stato gassoso. Al termine dell unità didattica si dovranno raggiungere i seguenti obiettivi:. Descrivere le caratteristiche e il comportamento del gas a livello microscopico.. Definire pressione temperatura
3. Stato gassoso. Al termine dell unità didattica si dovranno raggiungere i seguenti obiettivi:. Descrivere le caratteristiche e il comportamento del gas a livello microscopico.. Definire pressione temperatura
LEZIONE 7. Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2. 2, x3 +2x +3.
 7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
Transitori del primo ordine
 Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Università di Ferrara Corso di Elettrotecnica Transitori del primo ordine Si consideri il circuito in figura, composto da un generatore ideale di tensione, una resistenza ed una capacità. I tre bipoli
Temperatura e Calore
 Temperatura e Calore 1 Temperatura e Calore Stati di Aggregazione Temperatura Scale Termometriche Dilatazione Termica Il Calore L Equilibrio Termico La Propagazione del Calore I Passaggi di Stato 2 Gli
Temperatura e Calore 1 Temperatura e Calore Stati di Aggregazione Temperatura Scale Termometriche Dilatazione Termica Il Calore L Equilibrio Termico La Propagazione del Calore I Passaggi di Stato 2 Gli
3. Le Trasformazioni Termodinamiche
 3. Le Trasformazioni Termodinamiche Lo stato termodinamico di un gas (perfetto) è determinato dalle sue variabili di stato: ressione, olume, Temperatura, n moli ffinché esse siano determinate è necessario
3. Le Trasformazioni Termodinamiche Lo stato termodinamico di un gas (perfetto) è determinato dalle sue variabili di stato: ressione, olume, Temperatura, n moli ffinché esse siano determinate è necessario
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
