FISICA TECNICA 1 (CCS Ing.Meccanica La Spezia)
|
|
|
- Dante Pucci
- 8 anni fa
- Visualizzazioni
Transcript
1 DISPENSE DEL CORSO FISICA TECNICA 1 (CCS Ing.Meccanica La Spezia) Prof. Annalisa MARCHITTO Prof. Giovanni TANDA Anno Accademico Settembre 2006
2 CAPITOLO 1. TERMOMETRIA La termodinamica presuppone, rispetto alla meccanica, la definizione di una nuova grandezza fisica denominata temperatura. Empiricamente questa grandezza è legata alla sensazione di caldo e di freddo indotta dal contatto con il corpo in oggetto. Mediante questo metodo soggettivo è possibile però stabilire soltanto tra due corpi quale sia il più caldo e quale il più freddo, e ciò in un campo limitato di temperature. Un metodo di determinazione più oggettivo può fare ricorso ad un termoscopio, ovvero un tubo capillare contenente un liquido che si dilata (o contrae) al contatto con il misurando. Per definire quantitativamente la temperatura, occorre tarare il termoscopio (ovvero trasformarlo in un termometro). Ad esempio si può immergere il termoscopio nel ghiaccio fondente, marcando il livello indicato dal liquido nel capillare e successivamente nei vapori dell acqua bollente (alla pressione di Pa, ovvero bar), ripetendo l operazione precedente. La distanza tra le due tacche potrà essere suddivisa in 100 intervalli equidistanti (gradi centigradi), assegnando il valore 0 alla tacca inferiore (h g ) e 100 alla tacca superiore (h v ). La scala potrà essere estrapolata al di fuori dell intervallo Per misurare la temperatura di un corpo, si mette il termometro in contatto termico con il corpo e si guarda, atteso un certo tempo (per consentire il raggiungimento dell equilibrio termico tra corpo e termometro) a quale altezza h x si porta il liquido. La temperatura t x del corpo risulterà: t x = 100 (h x -h g )/(h v -h g ), C L altezza di un liquido che si dilata o contrae non è l unica proprietà di un corpo funzione della temperatura. Efficienti termometri possono essere realizzati utilizzando la resistenza elettrica di un filo conduttore, il volume di un gas a pressione costante, la pressione di un gas a volume costante, etc. La temperatura può anche essere definita senza ricorrere a due valori di riferimento, ma soltanto ad uno. Ad esempio, se X è il valore della proprietà scelta per misurare la temperatura, si ha: T x = a X Ove a è una costante arbitraria, il cui valore può essere fissato ricorrendo ad un'unica temperatura di riferimento. Si è convenuto di fissare a=273.16/x 0 in corrispondenza del punto triplo dell acqua (0.01 C), in cui si avrà X=X 0. La temperatura del punto triplo nella nuova scala (Kelvin) sarà quindi T 0 = K. Si avrà pertanto: T x = (X/X 0 ) Il valore di fa coincidere l intervallo tra due temperature espresso in C all intervallo tra le medesime temperature in K. In particolare si avrà: T (K) = t ( C) La temperatura T x precedentemente definita prende il nome di temperatura assoluta. Per determinare T x si può utilizzare un gas all interno di un ampolla (e quindi a volume costante). Si avrà in tal caso: T P = (p/p 0 ) ove p e p 0 sono le pressioni del gas alla temperatura T P che si vuole misurare e alla temperatura del punto triplo. Se p 0 è molto piccolo (ovvero il gas nell ampolla è molto rarefatto), il rapporto p/p 0 non dipende dalla natura chimica del gas. 2
3 CAPITOLO 2. SISTEMI TERMODINAMICI Un sistema termodinamico è costituito da una quantità costante di materia oppure da una porzione di spazio delimitato dall esterno per mezzo di confini reali o ideali (volume di controllo). Un sistema chiuso non consente scambi di massa con l esterno (figura 2.1a). Un sistema aperto permette il deflusso di massa attraverso una o più sezioni di passaggio (figura 2.1b). Il sistema, chiuso o aperto, può avere interazioni con l esterno. Con questo termine si intendono scambi di calore e/o lavoro. Un sistema che non ha scambi di calore e lavoro viene detto isolato. Figura 2.1 La definizione di un certo numero di grandezze identifica lo stato termodinamico di un sistema in equilibrio meccanico, termico e chimico (in condizioni diverse dall equilibrio, queste grandezze non sono uniformi all interno del sistema e sono difficilmente definibili). Le grandezze che definiscono lo stato di un sistema possono essere intensive, quando non dipendono dalla massa del sistema (ad esempio pressione, temperatura e volume specifico) oppure estensive, quando sono proporzionali alla massa (ad esempio il volume). Come si vedrà, calore e lavoro non sono grandezze di stato. In generale, per una data sostanza le grandezze (o funzioni) di stato non sono indipendenti tra loro. Per stabilire il numero di grandezze necessarie e sufficienti a definire lo stato termodinamico di un sistema si ricorre alla regola delle fasi: il numero N di grandezze indipendenti è dato da: N = 2 + n f ove n è il numero di componenti indipendenti e f è il numero delle fasi indipendenti. Ad esempio, in un gas o in un liquido (sostanze monofasi per cui f=1) di una sostanza ad un componente (n=1) come l aria o l acqua, si ottiene N=2. Precisando pertanto pressione e temperatura verrà definito univocamente lo stato termodinamico della sostanza, mentre le altre grandezze di stato potranno essere dedotte dalla conoscenza di pressione e temperatura (ad esempio il volume specifico v lo si ottiene attraverso l equazione di stato della sostanza, come si vedrà in seguito). Nel caso di una miscela di acqua e zucchero, n=2, f=1 (ogni componente è presente in una sola fase) e N=3, ovvero lo stato è definito, ad esempio da pressione temperatura e concentrazione (massa di zucchero nell unità di massa d acqua). Nel caso di un liquido in equilibrio col suo vapore, si ha n=1 e f=2 da cui deriva N=1; in tale caso la pressione non è indipendente dalla temperatura; tuttavia, per definire lo stato termodinamico occorrerà conoscere anche il rapporto tra la massa di una fase rapportata alla massa totale (titolo) non conteggiata nella regola delle fasi. Si è detto che un sistema termodinamico può interagire con l esterno mediante scambi di calore e lavoro. A seguito di queste interazioni il sistema si trasforma. Le trasformazioni lente sono dette quasi statiche, esse sono caratterizzate da graduali variazioni delle proprietà di stato (che si mantengono uniformi nel sistema) e possono essere percorse nei due sensi, ovvero sono reversibili. Le trasformazioni reali non sono quasi mai reversibili. Un tipico esempio di trasformazione irreversibile è una trasformazione spontanea (ad esempio il deflusso d aria da un palloncino che si sgonfia). 3
4 CAPITOLO 3. CALORE E LAVORO Si è parlato di interazioni di tipo calore e lavoro. Per chiarire il concetto di calore, si può ricorrere ad un dispositivo chiamato calorimetro di Bunsen, costituito da un recipiente a pareti adiabatiche (che non permettono lo scambio di calore) riempito da ghiaccio ed acqua in equilibrio. All interno del calorimetro è collocata una provetta a pareti conduttrici. Se nella provetta è collocato un corpo a temperatura maggiore di 0 C, parte del ghiaccio si scioglierà ed il livello di acqua e ghiaccio nel calorimetro scenderà leggermente (poiché il ghiaccio occupa un volume maggiore dell acqua). La differenza di livello è proporzionale alla quantità di calore ceduta dal corpo al calorimetro. Prima dell avvento del Sistema Internazionale di Misura, la quantità di calore veniva misurata con la kcal (kilocaloria) definita come la quantità di calore ceduta da 1 kg d acqua per diminuire di 1 C la propria temperatura (precisamente nel passare da 15.5 a 14.5 C). Si consideri ora un cilindro contenente un gas ed un pistone in grado di muoversi all interno del cilindro. Se p indica la pressione che dall esterno agisce sul pistone di sezione A, la forza F=pxA che agisce sul pistone provoca uno spostamento dh dello stesso ed una variazione dv del volume totale del gas. Il lavoro elementare scambiato sarà dato da: dl * = p A dh =p dv e dividendo per la massa m del gas dl = pdv che rappresenta l espressione del lavoro meccanico durante una trasformazione infinitesima. Occorrerà aggiungere che tale espressione vale a rigore per trasformazioni quasi-statiche, per le quali il sistema (gas nel cilindro) vede cambiare le proprie funzioni di stato in maniera lenta ed in modo uniforme. Le interazioni calore e lavoro, come detto in precedenza, non sono funzioni di stato (non ha senso parlare di calore o lavoro posseduto dai corpi, al contrario di temperatura e pressione, ad esempio) ed il loro valore dipende dalla modalità della trasformazione termodinamica. Una funzione (o proprietà) di stato F(x,y) può essere espressa, in forma differenziale, nel seguente modo: df = ( F/ x) y dx + ( F/ y) x dy df rappresenta il differenziale esatto della funzione F qui dipendente dalle variabili x e y. Affinché sia dichiarato esatto occorre che le derivate parziali di F rispetto ad x e y siano definite in un dominio semplicemente connesso, siano funzioni continue e derivabili e che soddisfino la relazione: [( F/ y) x / x] y = [( F/ x) y / y] x Se il differenziale di una funzione F è esatto, allora l integrale di df tra due punti qualsiasi (x 1,y 1 ) e (x 2,y 2 ) dipende solo dagli estremi. Poiché gli scambi di calore e lavoro, dipendono non solo dagli estremi degli stati termodinamici ma anche dalla modalità della trasformazione, allora i differenziali dq e dl non sono esatti (e a tal fine andrebbero indicati come δq e δl). Nella termodinamica agli scambi di calore e lavoro vengono assegnati dei segni convenzionali. In particolare, viene assunto positivo il calore scambiato dall esterno verso il sistema e negativo il calore rilasciato dal sistema verso l esterno; viceversa, è dichiarato positivo il lavoro fatto dal sistema sull esterno e negativo il lavoro scambiato in direzione esterno-sistema. Esercizio 3.1: Descrivere alcuni esempi di trasformazioni, reversibili e irreversibili, accompagnate da interazioni con l esterno ( scambio di calore e/o scambio di lavoro). (a) Se si scalda una massa d acqua contenuta in una pentola, ponendola in successione su fornelli isotermi caratterizzati da temperature sempre crescenti da T=T 1 sino a T=T 2 (procedendo per piccoli salti di temperatura T, come rappresentato in figura 3.1a), la trasformazione 1-2 4
5 corrispondente sarà quasi-statica e potrà essere tracciata sul piano p-t come un segmento rettilineo; poiché le variazioni di volume dell acqua nella fase di riscaldamento sono modeste, si concretizza solo uno scambio di calore (e non di lavoro) con l esterno. Nel caso irreversibile si pone la pentola su un fornello a gas e la si riscalda: la trasformazione reale conseguente non può essere tracciata in maniera continua sui piani termodinamici. (b) Se sul pistone mobile di un cilindro contenente un gas (e collocato su un termostato, ovvero un sistema a temperatura costante) vengono posti in lenta successione dei pesi in modo da esercitare una pressione sempre maggiore sul gas (figura 3.1b), la trasformazione conseguente 1-2 è quasi statica (con scambio di lavoro) e può essere tracciata da un tratto inclinato(e continuo) sul piano p-v; per adeguarsi alla temperatura T del termostato, il gas è soggetto ad uno scambio di calore col termostato. Se la compressione non è graduale ma brusca, la trasformazione è tipicamente irreversibile e non può essere tracciata mediante una linea continua sui piani termodinamici. Figura 3.1 Le trasformazioni, come già detto, sono dovute alle interazioni tra il sistema e l esterno e sono accompagnate da variazioni delle proprietà di stato. Se lo stato finale coincide con lo stato iniziale, si è in presenza di una trasformazione chiusa o ciclica, diversamente la trasformazione è detta aperta. Empiricamente si è constatato che in una trasformazione ciclica, il calore ed il lavoro scambiati dal sistema che esegue il ciclo con l esterno soddisfano la relazione J Q L = 0 Avendo considerato Q ed L con i segni attribuiti dalla convenzione. La relazione precedente prende il nome di enunciato di Mejer è può essere descritta facendo riferimento alla seguente esperienza: in una provetta contenente acqua è immerso un mulinello girevole attorno ad un asse (figura 3.2); il mulinello è posto in rotazione trasferendo del lavoro L (in quantità nota e misurabile) dall esterno al sistema (costituito dall acqua nella provetta); ponendo la provetta in un calorimetro, si osserva che l acqua cede una quantità di calore Q al calorimetro proporzionale al lavoro ricevuto. La costante J di proporzionalità è pari a L/Q=4186 J/kcal. L equivalenza di Mejer consente di esprimere calore e lavoro nelle medesime unità di misura (J). In tal caso si può scrivere: Q L = 0 Figura 3.2 5
6 CAPITOLO 4. PRIMO PRINCIPIO DELLA TERMODINAMICA 4.1 Primo principio per sistemi chiusi Si consideri un sistema chiuso, costituito da un gas contenuto in un cilindro con pistone (v. esempio di figura 2.1 a). Si supponga di trasferire del calore dall esterno al sistema: sperimentalmente si osserva una espansione del gas con conseguente spostamento del pistone e quindi con una quantità di lavoro fatto sull esterno. Lo stato finale 2 non coincide con lo stato iniziale 1; per riportare il sistema nello stato 1 occorre ancora procedere con scambi di calore e/o lavoro con l esterno. L esperienza dimostra che, in qualunque trasformazione ciclica effettuata sul sistema, la somma algebrica degli scambi di calore eguaglia la somma algebrica degli scambi di lavoro, ovvero (ΣQ * - ΣL * ) ciclo = 0 oppure (dq * -dl * ) tr.chiusa = 0 Da un punto di vista matematico, se l integrale di una funzione lungo una linea chiusa è nullo, allora la funzione integranda è un differenziale esatto (infatti la differenza tra i valori estremi della funzione è pari a zero). Se si indica de = dq * - dl * allora de rappresenta un differenziale esatto ed E una nuova funzione di stato chiamata energia del sistema. Con riferimento all unità di massa, l energia specifica e (=E/m) sarà espressa, in forma differenziale, da: de = dq dl L energia posseduta dal sistema può essere associata alla sua posizione (potenziale) o al suo moto (cinetica) o al suo stato termodinamico (energia interna termodinamica, u). Escludendo i termini potenziali e cinetici (ovvero per sistemi a baricentro fermo), si ha: du = dq dl ove i vari termini sono riferiti all unità di massa (e pertanto espressi in J/kg o kj/kg). Le relazioni (dq-dl) tr.chiusa = 0 dq dl = de ( o du) Q L = e = e 2 e 1 (in termini infinitesimi) (in termini finiti) sono le espressioni matematiche del I principio della termodinamica. Esercizio 4.1: valutare (a) lo scambio di lavoro in una trasformazione senza scambio di calore (adiabatica) e (b) lo scambio di calore in una trasformazione senza scambio di lavoro. (a) In una trasformazione adiabatica, Q=0 e quindi il lavoro è espresso dalla variazione di energia interna col segno cambiato (L= u). (b) In una trasformazione senza scambio di lavoro, si ottiene invece che la differenza di energia interna corrisponde allo scambio di calore(q= u). Le precedenti considerazioni si applicano a trasformazioni anche non reversibili. 6
7 4.2 Primo principio per sistemi aperti Si consideri ora un sistema aperto, delimitato da un volume di controllo (V.C.), come raffigurato in figura 4.1. Si ammetta l esistenza di una sezione di entrata e di una sezione di uscita per il deflusso del fluido. Si assumano le proprietà termodinamiche e cinetiche uniformemente distribuite lungo le sezioni di ingresso/uscita (ipotesi monodimensionale). Figura 4.1 Se con dm e si indica la porzione elementare di massa entrante nel tempo infinitesimo dτ e con dm u la massa elementare uscente nel medesimo intervallo di tempo, allora la legge di conservazione della massa imporrà che: (massa nel V.C. all istante τ) = (massa nel V.C. all istante τ+dτ) e cioè m(τ) + dm e = m(τ+dτ) + dm u ovvero, dopo semplici passaggi dm/dτ = m e m u ove m = V ρdv, (con ρ = 1/v, densità o massa volumica del sistema) è la massa contenuta nel volume di controllo ad un determinato istante di tempo, mentre m e ed m u rappresentano le portate massiche in entrata ed in uscita. La massa elementare entrante dm e (nel tempo dτ) è pari a ρ e dv e, ove dv e ne rappresenta il volume elementare, esprimibile come il prodotto tra la sezione di passaggio A e e la dimensione dh e del pacchetto fluido. La portata m e risulterà quindi esprimibile come m e = dm e /dτ = ρ e A e (dh e /dτ) = ρ e A e w e e analogamente m u = ρ u A u w u Nel caso di regime stazionario (proprietà che non variano nel tempo), si ha m = cost., ovvero la portata massica entrante eguaglia la portata massica uscente. In queste circostanze, dalla costanza della portata deriva l equazione di CONTINUITA della portata: ρ e A e w e = ρ u A u w u da cui d(ρaw) = 0 ovvero d(aw/v) = 0 ove w è la velocità del fluido, ortogonale alla sezione di passaggio di area A. Si supponga ora che il V.C. sia interessato da interazioni con l esterno. Si indichino con Q * e con L * gli scambi complessivi di calore e lavoro. In regime stazionario, la portata entrante m vedrà modificare il proprio stato termodinamico dalle condizioni 1 (in entrata) alle condizioni 2 (in 7
8 uscita). Precisamente, per effetto del I principio, per la massa m, transitata attraverso il V.C. nell intervallo temporale τ, varrà la seguente relazione: Q * - L * = E ovvero Q L = e in relazione all unità di massa (e= E / m). Indicando con e 1 l energia in entrata e con e 2 l energia in uscita, si avrà e 1 = (1/2)w 1 2 +g z 1 + u 1 e 2 = (1/2)w 2 2 +g z 2 + u 2 (in presenza di un deflusso di massa non si potranno trascurare i termini energetici macroscopici, associati alla posizione z e alla velocità w). Per sostituzione, si ottiene: Q L = (1/2)(w w 1 2 ) + g (z 2 z 1 ) + (u 2 - u 1 ) Si conviene a questo punto scindere il lavoro totale L scambiato tra le sezioni 1 e 2 in due termini: il lavoro esterno netto L e, scambiato attraverso i confini del V.C. impermeabili al passaggio di massa ed il lavoro di pulsione L p, connesso al deflusso della massa attraverso le sezioni di ingresso ed uscita: L = L e + L p Il lavoro di pulsione è l azione dinamica risultante tra il lavoro fatto dall esterno sul sistema per convogliare nel V.C. la massa entrante ed il lavoro fatto dal sistema sull esterno che accompagna la massa uscente. Come tale, il lavoro di pulsione non può essere utilizzato concretamente nei sistemi ingegneristici. Si valuti ora l ammontare di tale lavoro di pulsione: l azione dinamica associata alla massa dm e entrante sarà pari a (p e xa e ), ove A e è l area della sezione d ingresso; all azione dinamica p e xa e, segue uno spostamento della massa elementare dm e pari a dh e : il lavoro fatto dall esterno sul sistema per far entrare la massa dm e nel volume di controllo sarà quindi dato da p e A e dh e ovvero da p e dv e (ossia da p e v e, con v e pari a dv e /dm e ). Conseguentemente, il lavoro effettuato dal sistema per far uscire la massa dm u sarà p u v u. Il lavoro di pulsione sarà quindi espresso da L p = p u v u p e v e e, in termini differenziali, dl p = d(pv) Pertanto, il lavoro totale scambiato in una trasformazione elementare di tipo reversibile sarà: dl = pdv e sarà nullo nel caso di confine tra sistema ed esterno INDILATABILE (dv=0) mentre il lavoro esterno netto scambiato in una trasformazione elementare reversibile sarà 8
9 dl e = pdv d(pv) = vdp Si noti che nel caso reale, non è sufficiente che il sistema (o il volume di controllo) sia indilatabile (dv=0), ma occorre anche che sia INDEFORMABILE (ad esempio, la rotazione di un elica all interno di un volume di controllo che non si dilata dà luogo ad uno scambio di lavoro tra l esterno ed il sistema perché quest ultimo si deforma per effetto del moto dell elica). Sostituendo al lavoro totale la somma tra il lavoro esterno netto ed il lavoro di pulsione, il I principio della termodinamica per un volume di controllo (sistemi aperti) in regime stazionario si scriverà nel seguente modo: Q L e = (1/2)(w w 1 2 ) + g (z 2 z 1 ) + (h 2 - h 1 ) ove le condizioni d entrata sono qui indicate col pedice 1 e quelle d uscita con il pedice 2. La funzione h = u + pv si chiama entalpia (specifica, in quanto riferita all unità di massa) del sistema ed è misurata in J/kg o kj/kg. Moltiplicando per la massa del sistema, si avrà ovviamente H = m h [J o kj]. Si noti che, a differenza di quanto ottenuto per un sistema chiuso, gli stati 1 e 2 si riferiscono qui alle due sezioni di ingresso e uscita, mentre in precedenza indicavano due stati termodinamici in successione temporale. In termini differenziali, si ha: dq dl e = (1/2)dw 2 + gdz + dh Le relazioni precedentemente scritte fanno riferimento all unità di massa. Moltiplicando ogni termine per la massa defluente in un dato intervallo di tempo (ovvero per la portata m costante), si ha: q l e = (1/2) m (w w 1 2 ) +m g (z 2 z 1 ) +m (h 2 - h 1 ), ove q ed l e rappresentano il flusso termico e la potenza meccanica scambiati (espressi in J/s ovvero in W o kw). 4.3 Calore specifico Se si rapporta la quantità di calore Q * scambiata da un corpo di data massa m alla riduzione (o aumento) di temperatura conseguente, si ottiene il calore specifico c= (dq * /m)/dt= dq/dt. Poiché lo scambio di calore elementare dq * può avvenire secondo diverse modalità, per definire in maniera univoca c occorre precisare il tipo di trasformazione che accompagna lo scambio termico. Si distinguono di solito due calori specifici, c v e c p, rispettivamente a volume costante e a pressione costante: c v = [(dq * /m)/dt] v=cost. = (dq/dt) v=cost. c p = [(dq * /m)/dt] P=cost. = (dq/dt) P=cost. 9
10 In una trasformazione reversibile, il calore specifico generico c = dq/dt, misurato in J/kgK (o kj/kgk), vale: c = (du + pdv) /dt = (dh pdv vdp +pdv)/dt = (dh vdp)/dt e sviluppando i differenziali esatti du (in funzione di dt e dv) e dh (in funzione di dt e dp): du(t,v) = ( u/ T) v dt + ( u/ v) T dv dh(t,p) = ( h/ T) p dt + ( h/ p) T dp da cui c = ( u/ T) v + [( u/ v) T +p](dv/dt) = ( h/ T) p + [( h/ p) T v](dp/dt) Ora, nel caso di trasformazione a v=cost., si avrà c v = ( u/ T) v mentre per p= cost. segue che c p = ( h/ T) p Per alcune sostanze (solidi e liquidi) i calori specifici c v e c p praticamente coincidono (ovvero c è una modesta influenza del tipo di trasformazione associata allo scambio di calore) e si possono indicare genericamente con c. Esercizio 4.2: In un recipiente a pareti adiabatiche vengono mescolati 0.3 kg di acqua alla temperatura di 20 C con 0.7 kg di acqua alla temperatura di 80 C. Il calore specifico c dell acqua vale kj/kgk. Qual è la temperatura finale di equilibrio? Il bilancio termico impone che il calore ceduto dalla massa più calda sia interamente acquisito da quella più fredda. Quindi se t f è la temperatura finale di equilibrio, con t 1 =20 C (m 1 =0.3 kg) e t 2 =80 C (m 2 =0.7 kg), si ha: c m 1 (t f t 1 ) = c m 2 (t 2 t f ) ossia t f = (m 1 t 1 + m 2 t 2 )/(m 1 +m 2 )= 62 C. Si noti che in questo caso la conoscenza del valore di c non è necessaria ai fini della risoluzione del problema. 10
11 CAPITOLO 5. SECONDO PRINCIPIO DELLA TERMODINAMICA 5.1 Enunciati del secondo principio Il II principio delle termodinamica può essere formulato in vari modi. Storicamente si ricordano i postulati di Lord Kelvin e Clausius. Lord Kelvin: In una trasformazione ciclica è impossibile ottenere, come unico risultato finale, la trasformazione in lavoro del calore sottratto da una sola sorgente a temperatura uniforme (il concetto di sorgente a temperatura uniforme verrà chiarito nel seguito del corso) Clausius: In una trasformazione ciclica è impossibile ottenere, come unico risultato finale, il passaggio di una certa quantità di calore da una sorgente più fredda ad una sorgente più calda (equivale ad affermare che non si può trasferire spontaneamente del calore da temperature più basse a temperature più alte). Si noti che il solo I principio non escludeva quelle possibilità esplicitamente negate dal II principio. L esemplificazione grafica delle macchine impossibili secondo Kelvin e Clausius è schematizzata in figura 5.1. Figura 5.1 Il II principio può anche essere enunciato per mezzo di una nuova funzione di stato denominata entropia. Considerando un sistema chiuso soggetto ad una trasformazione ciclica, si osserva sperimentalmente che la somma degli scambi di calore con l esterno (assunti con il loro segno attribuito dalla convenzione) rapportati alla temperatura alla quale si concretizzano è sempre negativa: (dq/t) trasf.chiusa < 0 Nel caso di trasformazioni reversibili, la precedente relazione ammette un eccezione: (dq/t) trasf.chiusa rev. = 0 In base all analisi matematica, se si somma alla funzione integranda (dq/t) una quantità positiva ds i (o al limite nulla nel caso di trasformazione reversibile) tale da annullare la diseguaglianza, allora la funzione ds = dq/t + ds i 11
12 rappresenterà un differenziale esatto ed s (detta entropia specifica, misurata in J/kgK o kj/kgk) sarà una funzione di stato. Moltiplicando per la massa m del sistema si otterrà l entropia S = m s, misurata in J/K o kj/k. Pertanto l enunciato matematico del II principio della termodinamica sarà il seguente: trasformazioni chiuse: (dq/t) < 0 (dq/t) = 0, rev. trasformazioni aperte infinitesime: ds = dq/t + ds i ds = dq/t, rev. trasformazioni aperte finite: s 2 s 1 = dq/t + s i s 2 s 1 = dq/t, rev. Il termine s i rappresenta la produzione entropica associata alle irreversibilità, sempre maggiore di zero o al limite nulla. Una relazione analoga può essere sviluppata per i sistemi aperti con deflusso di massa. Considerando ancora il regime stazionario (massa uscente pari alla massa entrante nell unità di tempo): s 2 s 1 = V.C. dq/t + s i,v.c. dove l integrale e la produzione entropica si riferiscono qui al volume di controllo e non al lasso di tempo che intercorre tra i due stati 1 (ingresso) e 2 (uscita). Esercizio 5.1: valutare le variazioni di entropia per trasformazioni adiabatiche reversibili e irreversibili e per trasformazioni isoterme reversibili. In una trasformazione adiabatica reversibile dq=0 (adiabatica) ed inoltre dq=tds (reversibile). Ne segue che ds=0, ovvero s=costante: la trasformazione è isoentropica. Diversamente, in una adiabatica irreversibile, dq/t + ds i = ds, ovvero ds = ds i >0; l entropia è destinata a crescere essendo ds i sempre positivo. In una trasformazione isoterma dt=0, se reversibile dq/t = ds. Integrando tra gli estremi della trasformazione, si ha: Q/T = s, ovvero la variazione d entropia eguaglia il rapporto tra il calore scambiato e la temperatura assoluta alla quale avviene lo scambio di calore. 5.2 Relazioni tra grandezze termodinamiche I due principi della termodinamica consentono di ottenere due utili relazioni tra le grandezze termodinamiche: du = dq pdv = Tds pdv dh = du + d(pv) = du + pdv + vdp = Tds + vdp Pur avendo scelto di operare secondo una trasformazione reversibile (dq=tds), il risultato finale ottenuto du = Tds pdv dh = Tds + vdp 12
13 mette in relazione tra loro funzioni di stato e loro variazioni. Pertanto le suddette relazioni possono essere considerate valide anche per trasformazioni reali e, come si vedrà, esse stanno alla base dei procedimenti di valutazione delle proprietà termodinamiche delle sostanze. Due ulteriori funzioni di stato impiegate nella termodinamica sono la funzione di Helmotz f v (detta energia libera) e la funzione di Gibbs f p (detta entalpia libera): f v = u Ts f p = h Ts Introducendo i rispettivi differenziali esatti: df v = du Tds sdt = pdv sdt df p = dh Tds sdt = vdp sdt Ricordando le proprietà delle funzioni di stato, si ottiene: du(s,v) = ( u/ s) v ds + ( u/ v) s dv = Tds pdv dh(s,p) = ( h/ s) p ds + ( h/ p) s dp = Tds + vdp da cui: ( u/ s) v = T ( u/ v) s = p ( h/ s) p = T ( h/ p) s = v ed in base all uguaglianza delle derivate miste, si ottiene: ( T/ v) s = ( p/ s) v ( T/ p) s = ( v/ s) p direttamente dalle relazioni per du e dh, e: ( p/ T) v = ( s/ v) T ( v/ T) p = ( s/ p) T dalle relazioni per df v e df p. Le quattro ultime formule prendono il nome di relazioni di Maxwell e risultano particolarmente utili nella costruzione delle funzioni di stato s, h, ed u per le sostanze al variare delle proprietà p, v e T. 13
14 CAPITOLO 6. GAS IDEALI 6.1 Equazione di stato Sinora ci si è soffermati sulle proprietà che identificano uno stato termodinamico e sulle relazioni tra dette proprietà, senza specificare la natura della sostanza costituente il sistema termodinamico. Ora si cominceranno ad applicare i concetti suesposti a sostanze aventi un particolare rilievo nell ambito della termodinamica tecnica, in quanto impiegate in processi tecnici di interesse ingegneristico. Verranno innanzitutto presi in esame i cosiddetti gas ideali (o perfetti), gas che seguono una particolare (e semplice) equazione di stato che lega tra loro le variabili termodinamiche fondamentali p, v e T. Tale relazione è la seguente: p V = n R T ove n è il numero di moli (unità di sostanza che corrisponde ad un definito numero di molecole di gas) e R assume i connotati di una costante universale pari a 8314 J/kmol K. In pratica ogni mole di gas perfetto, ad una data pressione p e temperatura T, occupa lo stesso volume V (precisamente 22.4 m 3 per 1 kmol a Pa e K). Introducendo la massa molecolare M = m/n (massa di una mole), si ottiene: p V = m (R/M) T ovvero p V = m R T p v = R T con R costante particolare del gas. Ad esempio, per l aria M = kg/kmol, da cui R = 287 J/kgK; per l ossigeno M=32 kg/kmol, R=259.8 J/kgK, sempre nell ipotesi di poter considerare questi due gas allo stato ideale. Il comportamento di gas ideale è tipico di un gas molto rarefatto; nella pratica, tale modello rappresenta abbastanza bene i gas a pressione relativamente bassa e temperatura relativamente alta e comunque tutti quei gas che sono lontani dalle condizioni di liquefazione. Nel caso dell aria nelle condizioni ambientali di pressione e temperatura non troppo inferiore a quella ambientale, il modello di gas ideale funziona abbastanza bene. 6.2 Proprietà termodinamiche Per i gas ideali si può dimostrare che l energia interna e l entalpia dipendono solo dalla temperatura. Ricordando che du = Tds pdv e sviluppando s in funzione di T e v ds= ( s/ v) T dv + ( s/ T) v dt si ottiene 14
FONDAMENTI CHIMICO FISICI DEI PROCESSI IL SECONDO E IL TERZO PRINCIPIO DELLA TERMODINAMICA
 FONDAMENTI CHIMICO FISICI DEI PROCESSI IL SECONDO E IL TERZO PRINCIPIO DELLA TERMODINAMICA LE MACCHINE TERMICHE Sono sistemi termodinamici che trasformano il calore in lavoro. Operano ciclicamente, cioè
FONDAMENTI CHIMICO FISICI DEI PROCESSI IL SECONDO E IL TERZO PRINCIPIO DELLA TERMODINAMICA LE MACCHINE TERMICHE Sono sistemi termodinamici che trasformano il calore in lavoro. Operano ciclicamente, cioè
Termodinamica. Sistema termodinamico. Piano di Clapeyron. Sistema termodinamico. Esempio. Cosa è la termodinamica? TERMODINAMICA
 Termodinamica TERMODINAMICA Cosa è la termodinamica? La termodinamica studia la conversione del calore in lavoro meccanico Prof Crosetto Silvio 2 Prof Crosetto Silvio Il motore dell automobile trasforma
Termodinamica TERMODINAMICA Cosa è la termodinamica? La termodinamica studia la conversione del calore in lavoro meccanico Prof Crosetto Silvio 2 Prof Crosetto Silvio Il motore dell automobile trasforma
Il lavoro nelle macchine
 Il lavoro nelle macchine Corso di Impiego industriale dell energia Ing. Gabriele Comodi I sistemi termodinamici CHIUSO: se attraverso il contorno non c è flusso di materia in entrata ed in uscita APERTO:
Il lavoro nelle macchine Corso di Impiego industriale dell energia Ing. Gabriele Comodi I sistemi termodinamici CHIUSO: se attraverso il contorno non c è flusso di materia in entrata ed in uscita APERTO:
QUESITI DI FISICA RISOLTI A LEZIONE TERMODINAMICA
 QUESITI DI FISICA RISOLTI A LEZIONE TERMODINAMICA Un recipiente contiene gas perfetto a 27 o C, che si espande raggiungendo il doppio del suo volume iniziale a pressione costante. La temperatura finale
QUESITI DI FISICA RISOLTI A LEZIONE TERMODINAMICA Un recipiente contiene gas perfetto a 27 o C, che si espande raggiungendo il doppio del suo volume iniziale a pressione costante. La temperatura finale
Termodinamica: legge zero e temperatura
 Termodinamica: legge zero e temperatura Affrontiamo ora lo studio della termodinamica che prende in esame l analisi dell energia termica dei sistemi e di come tale energia possa essere scambiata, assorbita
Termodinamica: legge zero e temperatura Affrontiamo ora lo studio della termodinamica che prende in esame l analisi dell energia termica dei sistemi e di come tale energia possa essere scambiata, assorbita
CHIMICA GENERALE MODULO
 Corso di Scienze Naturali CHIMICA GENERALE MODULO 6 Termodinamica Entalpia Entropia Energia libera - Spontaneità Relatore: Prof. Finelli Mario Scienza che studia i flussi energetici tra un sistema e l
Corso di Scienze Naturali CHIMICA GENERALE MODULO 6 Termodinamica Entalpia Entropia Energia libera - Spontaneità Relatore: Prof. Finelli Mario Scienza che studia i flussi energetici tra un sistema e l
Gas, liquidi, solidi. Tutti i gas, tranne l'elio, solidificano a basse temperature (alcuni richiedono anche alte pressioni).
 Gas, liquidi, solidi Tutti i gas raffreddati liquefano Tutti i gas, tranne l'elio, solidificano a basse temperature (alcuni richiedono anche alte pressioni). Sostanza T L ( C) T E ( C) He - -269 H 2-263
Gas, liquidi, solidi Tutti i gas raffreddati liquefano Tutti i gas, tranne l'elio, solidificano a basse temperature (alcuni richiedono anche alte pressioni). Sostanza T L ( C) T E ( C) He - -269 H 2-263
Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012
 Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012 Problema 1 Due carrelli A e B, di massa m A = 104 kg e m B = 128 kg, collegati da una molla di costante elastica k = 3100
Prova scritta di Fisica Generale I Corso di studio in Astronomia 22 giugno 2012 Problema 1 Due carrelli A e B, di massa m A = 104 kg e m B = 128 kg, collegati da una molla di costante elastica k = 3100
Complementi di Termologia. I parte
 Prof. Michele Giugliano (Dicembre 2) Complementi di Termologia. I parte N.. - Calorimetria. Il calore è una forma di energia, quindi la sua unità di misura, nel sistema SI, è il joule (J), tuttavia si
Prof. Michele Giugliano (Dicembre 2) Complementi di Termologia. I parte N.. - Calorimetria. Il calore è una forma di energia, quindi la sua unità di misura, nel sistema SI, è il joule (J), tuttavia si
CALCOLO DELL'ENERGIA INTERNA
 CALCOLO DELL'ENERGIA INTERNA Enrico Valenti Matricola 145442 29 novembre ore 10,30-12,30 ( trasformazione a temperatura costante ) U 0 = 0 J energia ( J ) p 0 = 1 bar pressione ( Pa ) T 0 = 273 K temperatura
CALCOLO DELL'ENERGIA INTERNA Enrico Valenti Matricola 145442 29 novembre ore 10,30-12,30 ( trasformazione a temperatura costante ) U 0 = 0 J energia ( J ) p 0 = 1 bar pressione ( Pa ) T 0 = 273 K temperatura
Fisica Generale 1 per Chimica Formulario di Termodinamica e di Teoria Cinetica
 Fisica Generale 1 per Chimica Formulario di Termodinamica e di Teoria Cinetica Termodinamica Equazione di Stato: p = pressione ; V = volume ; T = temperatura assoluta ; n = numero di moli ; R = costante
Fisica Generale 1 per Chimica Formulario di Termodinamica e di Teoria Cinetica Termodinamica Equazione di Stato: p = pressione ; V = volume ; T = temperatura assoluta ; n = numero di moli ; R = costante
LEGGI DEI GAS / CALORI SPECIFICI. Introduzione 1
 LEGGI DEI GAS / CALORI SPECIFICI Introduzione 1 1 - TRASFORMAZIONE ISOBARA (p = costante) LA PRESSIONE RIMANE COSTANTE DURANTE TUTTA LA TRASFORMAZIONE V/T = costante (m, p costanti) Q = m c p (Tf - Ti)
LEGGI DEI GAS / CALORI SPECIFICI Introduzione 1 1 - TRASFORMAZIONE ISOBARA (p = costante) LA PRESSIONE RIMANE COSTANTE DURANTE TUTTA LA TRASFORMAZIONE V/T = costante (m, p costanti) Q = m c p (Tf - Ti)
Lezione estd 29 pagina 1. Argomenti di questa lezione (esercitazione) Iniziare ad affrontare esercizi di termodinamica
 Lezione estd 29 pagina 1 Argomenti di questa lezione (esercitazione) Iniziare ad affrontare esercizi di termodinamica Lezione estd 29 pagina 2 Esercizio 3, 5 luglio 2005 Una macchina di Carnot produce
Lezione estd 29 pagina 1 Argomenti di questa lezione (esercitazione) Iniziare ad affrontare esercizi di termodinamica Lezione estd 29 pagina 2 Esercizio 3, 5 luglio 2005 Una macchina di Carnot produce
Esercizi di Fisica Tecnica 2013-2014. Termodinamica
 Esercizi di Fisica Tecnica 2013-2014 Termodinamica TD1 In un sistema pistone-cilindro, 1 kg di gas ( = 1,29 ed R * = 190 J/(kg K)) si espande da 5 bar e 90 C ad 1 bar. Nell'ipotesi che la trasformazione
Esercizi di Fisica Tecnica 2013-2014 Termodinamica TD1 In un sistema pistone-cilindro, 1 kg di gas ( = 1,29 ed R * = 190 J/(kg K)) si espande da 5 bar e 90 C ad 1 bar. Nell'ipotesi che la trasformazione
Energia e Lavoro. In pratica, si determina la dipendenza dallo spazio invece che dal tempo
 Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
Energia e Lavoro Finora abbiamo descritto il moto dei corpi (puntiformi) usando le leggi di Newton, tramite le forze; abbiamo scritto l equazione del moto, determinato spostamento e velocità in funzione
9. TRASFORMAZIONI TERMODINAMICHE E CICLI REALI
 9. TRASFORMAZIONI TERMODINAMICHE E CICLI REALI 9. Introduzione I processi termodinamici che vengono realizzati nella pratica devono consentire la realizzazione di uno scambio di energia termica o di energia
9. TRASFORMAZIONI TERMODINAMICHE E CICLI REALI 9. Introduzione I processi termodinamici che vengono realizzati nella pratica devono consentire la realizzazione di uno scambio di energia termica o di energia
BILANCI DI ENERGIA. Capitolo 2 pag 70
 BILANCI DI ENERGIA Capitolo 2 pag 70 BILANCI DI ENERGIA Le energie in gioco sono di vario tipo: energia associata ai flussi entranti e uscenti (potenziale, cinetica, interna), Calore scambiato con l ambiente,
BILANCI DI ENERGIA Capitolo 2 pag 70 BILANCI DI ENERGIA Le energie in gioco sono di vario tipo: energia associata ai flussi entranti e uscenti (potenziale, cinetica, interna), Calore scambiato con l ambiente,
Una soluzione è un sistema omogeneo (cioè costituito da una sola fase, che può essere liquida, solida o gassosa) a due o più componenti.
 Una soluzione è un sistema omogeneo (cioè costituito da una sola fase, che può essere liquida, solida o gassosa) a due o più componenti. Solvente (componente presente in maggior quantità) SOLUZIONE Soluti
Una soluzione è un sistema omogeneo (cioè costituito da una sola fase, che può essere liquida, solida o gassosa) a due o più componenti. Solvente (componente presente in maggior quantità) SOLUZIONE Soluti
Secondo principio della Termodinamica
 Secondo principio della Termodinamica Enunciato di Kelvin Enunciato di Clausius Ciclo di Carnot Entropia Antonio Pierro Per consigli, suggerimenti, eventuali errori o altro potete scrivere una email a
Secondo principio della Termodinamica Enunciato di Kelvin Enunciato di Clausius Ciclo di Carnot Entropia Antonio Pierro Per consigli, suggerimenti, eventuali errori o altro potete scrivere una email a
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Temperatura. V(t) = Vo (1+at) Strumento di misura: termometro
 I FENOMENI TERMICI Temperatura Calore Trasformazioni termodinamiche Gas perfetti Temperatura assoluta Gas reali Principi della Termodinamica Trasmissione del calore Termoregolazione del corpo umano Temperatura
I FENOMENI TERMICI Temperatura Calore Trasformazioni termodinamiche Gas perfetti Temperatura assoluta Gas reali Principi della Termodinamica Trasmissione del calore Termoregolazione del corpo umano Temperatura
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
p atm 1. V B ; 2. T B ; 3. W A B 4. il calore specifico a volume costante c V
 1 Esercizio (tratto dal Problema 13.4 del Mazzoldi 2) Un gas ideale compie un espansione adiabatica contro la pressione atmosferica, dallo stato A di coordinate, T A, p A (tutte note, con p A > ) allo
1 Esercizio (tratto dal Problema 13.4 del Mazzoldi 2) Un gas ideale compie un espansione adiabatica contro la pressione atmosferica, dallo stato A di coordinate, T A, p A (tutte note, con p A > ) allo
I DIAGRAMMA DI MOLLIER E TABELLE DEL VAPOR D'ACQUA
 I DIAGRAMMA DI MOLLIER E TABELLE DEL VAPOR D'ACQUA DIAGRAMMA DI MOLLIER DEL VAPORE D'ACQUA RAPPRESENTA I VALORI DELLE VARIABILI TERMODINAMICHE DEL VAPOR D'ACQUA IN UN PIANO h (ASSE Y) / s (ASSE X) h =
I DIAGRAMMA DI MOLLIER E TABELLE DEL VAPOR D'ACQUA DIAGRAMMA DI MOLLIER DEL VAPORE D'ACQUA RAPPRESENTA I VALORI DELLE VARIABILI TERMODINAMICHE DEL VAPOR D'ACQUA IN UN PIANO h (ASSE Y) / s (ASSE X) h =
3. Le Trasformazioni Termodinamiche
 3. Le Trasformazioni Termodinamiche Lo stato termodinamico di un gas (perfetto) è determinato dalle sue variabili di stato: ressione, olume, Temperatura, n moli ffinché esse siano determinate è necessario
3. Le Trasformazioni Termodinamiche Lo stato termodinamico di un gas (perfetto) è determinato dalle sue variabili di stato: ressione, olume, Temperatura, n moli ffinché esse siano determinate è necessario
LABORATORIO DI CHIMICA GENERALE E INORGANICA
 UNIVERSITA DEGLI STUDI DI MILANO Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea Triennale in Chimica CORSO DI: LABORATORIO DI CHIMICA GENERALE E INORGANICA Docente: Dr. Alessandro Caselli
UNIVERSITA DEGLI STUDI DI MILANO Facoltà di Scienze Matematiche, Fisiche e Naturali Corso di Laurea Triennale in Chimica CORSO DI: LABORATORIO DI CHIMICA GENERALE E INORGANICA Docente: Dr. Alessandro Caselli
L E L E G G I D E I G A S P A R T E I
 L E L E G G I D E I G A S P A R T E I Variabili di stato Equazioni di stato Legge di Boyle Pressione, temperatura, scale termometriche Leggi di Charles/Gay-Lussac Dispense di Chimica Fisica per Biotecnologie
L E L E G G I D E I G A S P A R T E I Variabili di stato Equazioni di stato Legge di Boyle Pressione, temperatura, scale termometriche Leggi di Charles/Gay-Lussac Dispense di Chimica Fisica per Biotecnologie
Gas perfetti e sue variabili
 Gas perfetti e sue variabili Un gas è detto perfetto quando: 1. è lontano dal punto di condensazione, e quindi è molto rarefatto 2. su di esso non agiscono forze esterne 3. gli urti tra le molecole del
Gas perfetti e sue variabili Un gas è detto perfetto quando: 1. è lontano dal punto di condensazione, e quindi è molto rarefatto 2. su di esso non agiscono forze esterne 3. gli urti tra le molecole del
Preparazione alle gare di II livello delle Olimpiadi della Fisica 2013
 Preparazione alle gare di II livello delle Olimpiadi della Fisica 01 Incontro su temi di termodinamica 14/1/01 Giuseppina Rinaudo - Dipartimento di Fisica dell Università di Torino Sommario dei quesiti
Preparazione alle gare di II livello delle Olimpiadi della Fisica 01 Incontro su temi di termodinamica 14/1/01 Giuseppina Rinaudo - Dipartimento di Fisica dell Università di Torino Sommario dei quesiti
ENERGIA INTERNA ENERGIA INTERNA SPECIFICA. e = E/m = cv T ENTALPIA. H = E + pv ENTALPIA SPECIFICA. h = H/m = cp T h = e + pv = e + p/d L-1
 L - SISTEMI APERTI ENERGIA INTERNA E = n Cv T E = m cv T (Cv molare = J/kmol C) (cv massico = J/kg C) ENERGIA INTERNA SPECIFICA e = E/m = cv T ENTALPIA H = E + pv H = n Cp T H = m cp T (Cp molare = J/kmol
L - SISTEMI APERTI ENERGIA INTERNA E = n Cv T E = m cv T (Cv molare = J/kmol C) (cv massico = J/kg C) ENERGIA INTERNA SPECIFICA e = E/m = cv T ENTALPIA H = E + pv H = n Cp T H = m cp T (Cp molare = J/kmol
Seconda legge della termodinamica
 Seconda legge della termodinamica In natura tutti i processi devono soddisfare il principio di conservazione dell energia (e quindi anche la a legge della termodinamica) ma non tutti i processi che conservano
Seconda legge della termodinamica In natura tutti i processi devono soddisfare il principio di conservazione dell energia (e quindi anche la a legge della termodinamica) ma non tutti i processi che conservano
EQUAZIONE DI STATO e LEGGI DEI GAS esercizi risolti Classi quarte L.S.
 EQUAZIONE DI STATO e LEGGI DEI GAS esercizi risolti Classi quarte L.S. In questa dispensa verrà riportato lo svolgimento di alcuni esercizi inerenti l'equazione di stato dei gas perfetti e le principali
EQUAZIONE DI STATO e LEGGI DEI GAS esercizi risolti Classi quarte L.S. In questa dispensa verrà riportato lo svolgimento di alcuni esercizi inerenti l'equazione di stato dei gas perfetti e le principali
LA TERMOLOGIA. studia le variazioni di dimensione di un corpo a causa di una
 LA TERMOLOGIA La termologia è la parte della fisica che si occupa dello studio del calore e dei fenomeni legati alle variazioni di temperatura subite dai corpi. Essa si può distinguere in: Termometria
LA TERMOLOGIA La termologia è la parte della fisica che si occupa dello studio del calore e dei fenomeni legati alle variazioni di temperatura subite dai corpi. Essa si può distinguere in: Termometria
Formulario di Fisica Tecnica Matteo Guarnerio 1
 Formulario di Fisica Tecnica Matteo Guarnerio 1 CONVENZIONI DI NOTAZIONE Calore scambiato da 1 a 2. Calore entrante o di sorgente. Calore uscente o ceduto al pozzo. CONVERSIONI UNITÀ DI MISURA PIÙ FREQUENTI
Formulario di Fisica Tecnica Matteo Guarnerio 1 CONVENZIONI DI NOTAZIONE Calore scambiato da 1 a 2. Calore entrante o di sorgente. Calore uscente o ceduto al pozzo. CONVERSIONI UNITÀ DI MISURA PIÙ FREQUENTI
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
Proprieta meccaniche dei fluidi
 Proprieta meccaniche dei fluidi 1. Definizione di fluido: liquido o gas 2. La pressione in un fluido 3. Equilibrio nei fluidi: legge di Stevino 4. Il Principio di Pascal 5. Il barometro di Torricelli 6.
Proprieta meccaniche dei fluidi 1. Definizione di fluido: liquido o gas 2. La pressione in un fluido 3. Equilibrio nei fluidi: legge di Stevino 4. Il Principio di Pascal 5. Il barometro di Torricelli 6.
Le macchine termiche e il secondo principio della termodinamica
 Le macchine termiche e il secondo principio della termodinamica ) Definizione di macchina termica È sperimentalmente verificato che nel rispetto del primo principio della termodinamica (ovvero della conservazione
Le macchine termiche e il secondo principio della termodinamica ) Definizione di macchina termica È sperimentalmente verificato che nel rispetto del primo principio della termodinamica (ovvero della conservazione
COMPONENTI TERMODINAMICI APERTI
 CAPITOLO NONO COMPONENTI TERMODINAMICI APERTI Esempi applicativi Vengono di seguito esaminati alcuni componenti di macchine termiche che possono essere considerati come sistemi aperti A) Macchina termica
CAPITOLO NONO COMPONENTI TERMODINAMICI APERTI Esempi applicativi Vengono di seguito esaminati alcuni componenti di macchine termiche che possono essere considerati come sistemi aperti A) Macchina termica
Termologia. Introduzione Scale Termometriche Espansione termica Capacità termica e calori specifici Cambiamenti di fase e calori latenti
 Termologia Introduzione Scale Termometriche Espansione termica Capacità termica e calori specifici Cambiamenti di fase e calori latenti Trasmissione del calore Legge di Wien Legge di Stefan-Boltzmann Gas
Termologia Introduzione Scale Termometriche Espansione termica Capacità termica e calori specifici Cambiamenti di fase e calori latenti Trasmissione del calore Legge di Wien Legge di Stefan-Boltzmann Gas
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
~ Copyright Ripetizionando - All rights reserved ~ http://ripetizionando.wordpress.com STUDIO DI FUNZIONE
 STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
STUDIO DI FUNZIONE Passaggi fondamentali Per effettuare uno studio di funzione completo, che non lascia quindi margine a una quasi sicuramente errata inventiva, sono necessari i seguenti 7 passaggi: 1.
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
5. FLUIDI TERMODINAMICI
 5. FLUIDI TERMODINAMICI 5.1 Introduzione Un sistema termodinamico è in genere rappresentato da una quantità di una determinata materia della quale siano definibili le proprietà termodinamiche. Se tali
5. FLUIDI TERMODINAMICI 5.1 Introduzione Un sistema termodinamico è in genere rappresentato da una quantità di una determinata materia della quale siano definibili le proprietà termodinamiche. Se tali
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
RICHIAMI DI TERMOCHIMICA
 CAPITOLO 5 RICHIAMI DI TERMOCHIMICA ARIA TEORICA DI COMBUSTIONE Una reazione di combustione risulta completa se il combustibile ha ossigeno sufficiente per ossidarsi completamente. Si ha combustione completa
CAPITOLO 5 RICHIAMI DI TERMOCHIMICA ARIA TEORICA DI COMBUSTIONE Una reazione di combustione risulta completa se il combustibile ha ossigeno sufficiente per ossidarsi completamente. Si ha combustione completa
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
Esercizi di Macroeconomia per il corso di Economia Politica
 Esercizi di Macroeconomia per il corso di Economia Politica (Gli esercizi sono suddivisi in base ai capitoli del testo di De Vincenti) CAPITOLO 3. IL MERCATO DEI BENI NEL MODELLO REDDITO-SPESA Esercizio.
Esercizi di Macroeconomia per il corso di Economia Politica (Gli esercizi sono suddivisi in base ai capitoli del testo di De Vincenti) CAPITOLO 3. IL MERCATO DEI BENI NEL MODELLO REDDITO-SPESA Esercizio.
Temperatura termodinamica assoluta
 Temperatura termodinamica assoluta Nuova definizione di temperatura Si sceglie come punto fisso fondamentale il punto triplo dell acqua, al quale si attribuisce la temperatura T 3 = 273.16 K. Per misurare
Temperatura termodinamica assoluta Nuova definizione di temperatura Si sceglie come punto fisso fondamentale il punto triplo dell acqua, al quale si attribuisce la temperatura T 3 = 273.16 K. Per misurare
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
Bruno Jannamorelli, traduzione ed edizione critica La potenza motrice del fuoco di Sadi Carnot, Cuen 1996, pp. 19 e 20. 2
 LA LEZIONE Lo studio di una macchina termica ideale [ ] Si può paragonare molto bene la potenza motrice del calore a quella di una cascata d acqua: entrambe hanno un massimo che non si può superare, qualunque
LA LEZIONE Lo studio di una macchina termica ideale [ ] Si può paragonare molto bene la potenza motrice del calore a quella di una cascata d acqua: entrambe hanno un massimo che non si può superare, qualunque
9. Urti e conservazione della quantità di moto.
 9. Urti e conservazione della quantità di moto. 1 Conservazione dell impulso m1 v1 v2 m2 Prima Consideriamo due punti materiali di massa m 1 e m 2 che si muovono in una dimensione. Supponiamo che i due
9. Urti e conservazione della quantità di moto. 1 Conservazione dell impulso m1 v1 v2 m2 Prima Consideriamo due punti materiali di massa m 1 e m 2 che si muovono in una dimensione. Supponiamo che i due
ENERGIA. Energia e Lavoro Potenza Energia cinetica Energia potenziale Principio di conservazione dell energia meccanica
 1 ENERGIA Energia e Lavoro Potenza Energia cinetica Energia potenziale Principio di conservazione dell energia meccanica 2 Energia L energia è ciò che ci permette all uomo di compiere uno sforzo o meglio
1 ENERGIA Energia e Lavoro Potenza Energia cinetica Energia potenziale Principio di conservazione dell energia meccanica 2 Energia L energia è ciò che ci permette all uomo di compiere uno sforzo o meglio
GAS. I gas si assomigliano tutti
 I gas si assomigliano tutti Aeriforme liquido solido GAS Descrizione macroscopica e microscopica degli stati di aggregazione della materia Fornendo energia al sistema, le forze di attrazione tra le particelle
I gas si assomigliano tutti Aeriforme liquido solido GAS Descrizione macroscopica e microscopica degli stati di aggregazione della materia Fornendo energia al sistema, le forze di attrazione tra le particelle
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
LA MACCHINA FRIGORIFERA E LA POMPA DI
 asdf LA MACCHINA FRIGORIFERA E LA POMPA DI CALORE 12 March 2012 Il ciclo di Carnot... "al contrario" Nell'articolo dedicato alla macchina termica, avevamo visto nel finale la macchina di Carnot e il ciclo
asdf LA MACCHINA FRIGORIFERA E LA POMPA DI CALORE 12 March 2012 Il ciclo di Carnot... "al contrario" Nell'articolo dedicato alla macchina termica, avevamo visto nel finale la macchina di Carnot e il ciclo
Temperatura e Calore
 Temperatura e Calore 1 Temperatura e Calore Stati di Aggregazione Temperatura Scale Termometriche Dilatazione Termica Il Calore L Equilibrio Termico La Propagazione del Calore I Passaggi di Stato 2 Gli
Temperatura e Calore 1 Temperatura e Calore Stati di Aggregazione Temperatura Scale Termometriche Dilatazione Termica Il Calore L Equilibrio Termico La Propagazione del Calore I Passaggi di Stato 2 Gli
2. Leggi finanziarie di capitalizzazione
 2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
2. Leggi finanziarie di capitalizzazione Si chiama legge finanziaria di capitalizzazione una funzione atta a definire il montante M(t accumulato al tempo generico t da un capitale C: M(t = F(C, t C t M
FACOLTÀ DI INGEGNERIA. 2. Exergia. Roberto Lensi
 Roberto Lensi 2. Exergia Pag. 1 UNIVERSITÀ DEGLI STUDI DI PISA FACOLTÀ DI INGEGNERIA 2. Exergia Roberto Lensi DIPARTIMENTO DI ENERGETICA Anno Accademico 2002-03 Roberto Lensi 2. Exergia Pag. 2 REVERSIBILITÀ
Roberto Lensi 2. Exergia Pag. 1 UNIVERSITÀ DEGLI STUDI DI PISA FACOLTÀ DI INGEGNERIA 2. Exergia Roberto Lensi DIPARTIMENTO DI ENERGETICA Anno Accademico 2002-03 Roberto Lensi 2. Exergia Pag. 2 REVERSIBILITÀ
Forza. Forza. Esempi di forze. Caratteristiche della forza. Forze fondamentali CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA
 Forza CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA Cos è una forza? la forza è una grandezza che agisce su un corpo cambiando la sua velocità e provocando una deformazione sul corpo 2 Esempi
Forza CONCETTO DI FORZA E EQUILIBRIO, PRINCIPI DELLA DINAMICA Cos è una forza? la forza è una grandezza che agisce su un corpo cambiando la sua velocità e provocando una deformazione sul corpo 2 Esempi
GLI STATI DI AGGREGAZIONE DELLA MATERIA. Lo stato gassoso
 GLI STATI DI AGGREGAZIONE DELLA MATERIA Lo stato gassoso Classificazione della materia MATERIA Composizione Struttura Proprietà Trasformazioni 3 STATI DI AGGREGAZIONE SOLIDO (volume e forma propri) LIQUIDO
GLI STATI DI AGGREGAZIONE DELLA MATERIA Lo stato gassoso Classificazione della materia MATERIA Composizione Struttura Proprietà Trasformazioni 3 STATI DI AGGREGAZIONE SOLIDO (volume e forma propri) LIQUIDO
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
LEZIONE 7. Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2. 2, x3 +2x +3.
 7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
Nome..Cognome.. Classe 4G 4 dicembre 2008. VERIFICA DI FISICA: lavoro ed energia
 Nome..Cognome.. Classe 4G 4 dicembre 8 VERIFIC DI FISIC: lavoro ed energia Domande ) Energia cinetica: (punti:.5) a) fornisci la definizione più generale possibile di energia cinetica, specificando l equazione
Nome..Cognome.. Classe 4G 4 dicembre 8 VERIFIC DI FISIC: lavoro ed energia Domande ) Energia cinetica: (punti:.5) a) fornisci la definizione più generale possibile di energia cinetica, specificando l equazione
PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA
 Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
Macchine termiche. Alla fine di ogni ciclo il fluido ripassa per lo stesso stato.
 Macchine termiche In una macchina termica - ad esempio un motore - un fluido (il vapore delle vecchie locomotive, la miscela del motore a scoppio) esegue qualche tipo di ciclo termodinamico. Alla fine
Macchine termiche In una macchina termica - ad esempio un motore - un fluido (il vapore delle vecchie locomotive, la miscela del motore a scoppio) esegue qualche tipo di ciclo termodinamico. Alla fine
Idrostatica Correnti a pelo libero (o a superficie libera) Correnti in pressione. Foronomia
 Idrostatica Correnti a pelo libero (o a superficie libera) Correnti in pressione Foronomia In idrostatica era lecito trascurare l attrito interno o viscosità e i risultati ottenuti valevano sia per i liquidi
Idrostatica Correnti a pelo libero (o a superficie libera) Correnti in pressione Foronomia In idrostatica era lecito trascurare l attrito interno o viscosità e i risultati ottenuti valevano sia per i liquidi
Studio di funzioni ( )
 Studio di funzioni Effettuare uno studio qualitativo e tracciare un grafico approssimativo delle seguenti funzioni. Si studi in particolare anche la concavità delle funzioni e si indichino esplicitamente
Studio di funzioni Effettuare uno studio qualitativo e tracciare un grafico approssimativo delle seguenti funzioni. Si studi in particolare anche la concavità delle funzioni e si indichino esplicitamente
Energia potenziale elettrica
 Energia potenziale elettrica Simone Alghisi Liceo Scientifico Luzzago Novembre 2013 Simone Alghisi (Liceo Scientifico Luzzago) Energia potenziale elettrica Novembre 2013 1 / 14 Ripasso Quando spingiamo
Energia potenziale elettrica Simone Alghisi Liceo Scientifico Luzzago Novembre 2013 Simone Alghisi (Liceo Scientifico Luzzago) Energia potenziale elettrica Novembre 2013 1 / 14 Ripasso Quando spingiamo
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Fondamenti e didattica di Matematica Finanziaria
 Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
Esercizi di Fisica Generale
 Esercizi di Fisica Generale 2. Temodinamica prof. Domenico Galli, dott. Daniele Gregori, prof. Umberto Marconi dott. Alessandro Tronconi 27 marzo 2012 I compiti scritti di esame del prof. D. Galli propongono
Esercizi di Fisica Generale 2. Temodinamica prof. Domenico Galli, dott. Daniele Gregori, prof. Umberto Marconi dott. Alessandro Tronconi 27 marzo 2012 I compiti scritti di esame del prof. D. Galli propongono
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
CORRENTE ELETTRICA Intensità e densità di corrente sistema formato da due conduttori carichi a potenziali V 1 e V 2 isolati tra loro V 2 > V 1 V 2
 COENTE ELETTICA Intensità e densità di corrente sistema formato da due conduttori carichi a potenziali V 1 e V isolati tra loro V > V 1 V V 1 Li colleghiamo mediante un conduttore Fase transitoria: sotto
COENTE ELETTICA Intensità e densità di corrente sistema formato da due conduttori carichi a potenziali V 1 e V isolati tra loro V > V 1 V V 1 Li colleghiamo mediante un conduttore Fase transitoria: sotto
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
Esercizi e Problemi di Termodinamica.
 Esercizi e Problemi di Termodinamica. Dr. Yves Gaspar March 18, 2009 1 Problemi sulla termologia e sull equilibrio termico. Problema 1. Un pezzetto di ghiaccio di massa m e alla temperatura di = 250K viene
Esercizi e Problemi di Termodinamica. Dr. Yves Gaspar March 18, 2009 1 Problemi sulla termologia e sull equilibrio termico. Problema 1. Un pezzetto di ghiaccio di massa m e alla temperatura di = 250K viene
Stati di aggregazione della materia unità 2, modulo A del libro
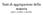 Stati di aggregazione della materia unità 2, modulo A del libro Gli stati di aggregazione della materia sono tre: solido, liquido e gassoso, e sono caratterizzati dalle seguenti grandezze: Quantità --->
Stati di aggregazione della materia unità 2, modulo A del libro Gli stati di aggregazione della materia sono tre: solido, liquido e gassoso, e sono caratterizzati dalle seguenti grandezze: Quantità --->
Usando il pendolo reversibile di Kater
 Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
Usando il pendolo reversibile di Kater Scopo dell esperienza è la misurazione dell accelerazione di gravità g attraverso il periodo di oscillazione di un pendolo reversibile L accelerazione di gravità
PSICROMETRIA DELL ARIA UMIDA
 PSICROMETRIA DELL ARIA UMIDA 1. PROPRIETÀ TERMODINAMICHE DEI GAS PERFETTI Un modello di comportamento interessante per la termodinamica è quello cosiddetto d i gas perfetto. Il gas perfetto è naturalmente
PSICROMETRIA DELL ARIA UMIDA 1. PROPRIETÀ TERMODINAMICHE DEI GAS PERFETTI Un modello di comportamento interessante per la termodinamica è quello cosiddetto d i gas perfetto. Il gas perfetto è naturalmente
LO STATO GASSOSO. Proprietà fisiche dei gas Leggi dei gas Legge dei gas ideali Teoria cinetico-molecolare dei gas Solubilità dei gas nei liquidi
 LO STATO GASSOSO Proprietà fisiche dei gas Leggi dei gas Legge dei gas ideali Teoria cinetico-molecolare dei gas Solubilità dei gas nei liquidi STATO GASSOSO Un sistema gassoso è costituito da molecole
LO STATO GASSOSO Proprietà fisiche dei gas Leggi dei gas Legge dei gas ideali Teoria cinetico-molecolare dei gas Solubilità dei gas nei liquidi STATO GASSOSO Un sistema gassoso è costituito da molecole
a t Esercizio (tratto dal problema 5.10 del Mazzoldi)
 1 Esercizio (tratto dal problema 5.10 del Mazzoldi) Una guida semicircolare liscia verticale di raggio = 40 cm è vincolata ad una piattaforma orizzontale che si muove con accelerazione costante a t = 2
1 Esercizio (tratto dal problema 5.10 del Mazzoldi) Una guida semicircolare liscia verticale di raggio = 40 cm è vincolata ad una piattaforma orizzontale che si muove con accelerazione costante a t = 2
LA CORRENTE ELETTRICA Prof. Erasmo Modica erasmo@galois.it
 LA CORRENTE ELETTRICA Prof. Erasmo Modica erasmo@galois.it L INTENSITÀ DELLA CORRENTE ELETTRICA Consideriamo una lampadina inserita in un circuito elettrico costituito da fili metallici ed un interruttore.
LA CORRENTE ELETTRICA Prof. Erasmo Modica erasmo@galois.it L INTENSITÀ DELLA CORRENTE ELETTRICA Consideriamo una lampadina inserita in un circuito elettrico costituito da fili metallici ed un interruttore.
Capitolo 10 Il primo principio 113
 Capitolo 10 Il primo principio 113 QUESITI E PROBLEMI 1 Tenuto conto che, quando il volume di un gas reale subisce l incremento dv, il lavoro compiuto dalle forze intermolecolari di coesione è L = n 2
Capitolo 10 Il primo principio 113 QUESITI E PROBLEMI 1 Tenuto conto che, quando il volume di un gas reale subisce l incremento dv, il lavoro compiuto dalle forze intermolecolari di coesione è L = n 2
UNIVERSITÀ DEGLI STUDI DI TERAMO
 UNIVERSITÀ DEGLI STUDI DI TERAMO CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA (Classe 7) Corso di Matematica per l Economia (Prof. F. Eugeni) TEST DI INGRESSO Teramo, ottobre 00 SEZIONE
UNIVERSITÀ DEGLI STUDI DI TERAMO CORSO DI LAUREA IN ECONOMIA BANCARIA FINANZIARIA ED ASSICURATIVA (Classe 7) Corso di Matematica per l Economia (Prof. F. Eugeni) TEST DI INGRESSO Teramo, ottobre 00 SEZIONE
Esercitazione X - Legge dei gas perfetti e trasformazioni
 Esercitazione X - Legge dei gas perfetti e trasformazioni termodinamiche Formulario Il primo principio della termodinamica afferma che la variazione dell energia interna di un sistema U è uguale alla somma
Esercitazione X - Legge dei gas perfetti e trasformazioni termodinamiche Formulario Il primo principio della termodinamica afferma che la variazione dell energia interna di un sistema U è uguale alla somma
CALORE. Compie lavoro. Il calore è energia. Temperatura e calore. L energia è la capacità di un corpo di compiere un lavoro
 Cos è il calore? Per rispondere si osservino le seguenti immagini Temperatura e calore Il calore del termosifone fa girare una girandola Il calore del termosifone fa scoppiare un palloncino Il calore del
Cos è il calore? Per rispondere si osservino le seguenti immagini Temperatura e calore Il calore del termosifone fa girare una girandola Il calore del termosifone fa scoppiare un palloncino Il calore del
Il mercato di monopolio
 Il monopolio Il mercato di monopolio Il monopolio è una struttura di mercato caratterizzata da 1. Un unico venditore di un prodotto non sostituibile. Non ci sono altre imprese che possano competere con
Il monopolio Il mercato di monopolio Il monopolio è una struttura di mercato caratterizzata da 1. Un unico venditore di un prodotto non sostituibile. Non ci sono altre imprese che possano competere con
Definizione di sorgente di calore e di macchina termica
 34 Unità Didattica N 19C I principi della ermodinamica Definizione di sorgente di calore e di macchina termica Sorgente di calore è un corpo ( o un sistema di corpi ) a temperatura costante che ha la proprietà
34 Unità Didattica N 19C I principi della ermodinamica Definizione di sorgente di calore e di macchina termica Sorgente di calore è un corpo ( o un sistema di corpi ) a temperatura costante che ha la proprietà
I.T.C.G.T T. Acerbo - Pescara LABORATORIO DI FISICA A. S. 2009/10
 I.T.C.G.T T. Acerbo - Pescara LABORATORIO DI FISICA A. S. 2009/10 Cognome: D Ovidio Nome: Stefania Classe: 2 B Geometri Data: 04/12/2009 Gruppo: F. Illiceto; V. Ivanochko; M.C. Scopino; M.Terenzi N. pagine:
I.T.C.G.T T. Acerbo - Pescara LABORATORIO DI FISICA A. S. 2009/10 Cognome: D Ovidio Nome: Stefania Classe: 2 B Geometri Data: 04/12/2009 Gruppo: F. Illiceto; V. Ivanochko; M.C. Scopino; M.Terenzi N. pagine:
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 2014
 Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Definiamo Entalpia la funzione: DH = DU + PDV. Variando lo stato del sistema possiamo misurare la variazione di entalpia: DU = Q - PDV.
 Problemi Una mole di molecole di gas ideale a 292 K e 3 atm si espandono da 8 a 20 L e a una pressione finale di 1,20 atm seguendo 2 percorsi differenti. Il percorso A è un espansione isotermica e reversibile;
Problemi Una mole di molecole di gas ideale a 292 K e 3 atm si espandono da 8 a 20 L e a una pressione finale di 1,20 atm seguendo 2 percorsi differenti. Il percorso A è un espansione isotermica e reversibile;
Applicazioni del calcolo differenziale allo studio delle funzioni
 Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
C V. gas monoatomici 3 R/2 5 R/2 gas biatomici 5 R/2 7 R/2 gas pluriatomici 6 R/2 8 R/2
 46 Tonzig La fisica del calore o 6 R/2 rispettivamente per i gas a molecola monoatomica, biatomica e pluriatomica. Per un gas perfetto, il calore molare a pressione costante si ottiene dal precedente aggiungendo
46 Tonzig La fisica del calore o 6 R/2 rispettivamente per i gas a molecola monoatomica, biatomica e pluriatomica. Per un gas perfetto, il calore molare a pressione costante si ottiene dal precedente aggiungendo
LEGGE GAS PERFETTI. Gas perfetto è governato dalla legge: PV=nRT=(N/NA) RT. kb=1.38*10-23 (J/K) cost Boltzmann
 LEGGE GAS PERFETTI Gas perfetto è governato dalla legge: PV=nRT=(N/NA) RT PV=NkBT dove kb=r/na kb=1.38*10-23 (J/K) cost Boltzmann TEORIA CINETICA DEI GAS Scopo: legame tra quantità macroscopiche e microscopiche
LEGGE GAS PERFETTI Gas perfetto è governato dalla legge: PV=nRT=(N/NA) RT PV=NkBT dove kb=r/na kb=1.38*10-23 (J/K) cost Boltzmann TEORIA CINETICA DEI GAS Scopo: legame tra quantità macroscopiche e microscopiche
STUDIO DI UNA FUNZIONE
 STUDIO DI UNA FUNZIONE OBIETTIVO: Data l equazione Y = f(x) di una funzione a variabili reali (X R e Y R), studiare l andamento del suo grafico. PROCEDIMENTO 1. STUDIO DEL DOMINIO (CAMPO DI ESISTENZA)
STUDIO DI UNA FUNZIONE OBIETTIVO: Data l equazione Y = f(x) di una funzione a variabili reali (X R e Y R), studiare l andamento del suo grafico. PROCEDIMENTO 1. STUDIO DEL DOMINIO (CAMPO DI ESISTENZA)
7 Applicazioni ulteriori
 7 Applicazioni ulteriori 7 Applicazioni ulteriori 7.1 Strutture con maglie chiuse 7.1.1 Analisi cinematica Si consideri la struttura in figura 7.1: i gradi di libertà sono pari a l =3n c v =3 0 3 = 0,
7 Applicazioni ulteriori 7 Applicazioni ulteriori 7.1 Strutture con maglie chiuse 7.1.1 Analisi cinematica Si consideri la struttura in figura 7.1: i gradi di libertà sono pari a l =3n c v =3 0 3 = 0,
Ripasso sulla temperatura, i gas perfetti e il calore
 Ripasso sulla temperatura, i gas perfetti e il calore Prof. Daniele Ippolito Liceo Scientifico Amedeo di Savoia di Pistoia La temperatura Fenomeni non interpretabili con le leggi della meccanica Dilatazione
Ripasso sulla temperatura, i gas perfetti e il calore Prof. Daniele Ippolito Liceo Scientifico Amedeo di Savoia di Pistoia La temperatura Fenomeni non interpretabili con le leggi della meccanica Dilatazione
