CALCOLO COMBINATORIO E PROBABILITA
|
|
|
- Geronimo Caselli
- 8 anni fa
- Visualizzazioni
Transcript
1 CALCOLO COMBINATORIO E PROBABILITA Con calcolo combinatorio si indica quel settore della matematica che studia i possibili modi di raggruppare ed ordinare oggetti presi da un insieme assegnato, con l obiettivo finale di contare il numero dei possibili raggruppamenti od ordinamenti; permette quindi di rispondere alle domande del tipo «in quanti modi?» oppure «quanti sono?». Col termine probabilità si indica la possibilità che un certo evento si verifichi, cioè che diventi realtà. La regola operativa per calcolare la probabilità che un dato evento (E) si verifichi è: P E = casi favorevoli casi possibili Dove per contare i casi favorevoli all evento e i casi possibili, è a volte necessario ricorrere al calcolo combinatorio.
2 Calcolo combinatorio: definizioni e regole di calcolo. Fattoriale di un numero: il fattoriale di un numero naturale n, che si scrive n!, è dato dal valore di quel numero moltiplicato per tutti gli interi precedenti fino ad arrivare a 1: n! = n(n-1)(n-2) 1. Per esempio, 5! = 5x4x3x2x1= 120
3 Supponiamo di avere n elementi (persone, numeri, lettere, caramelle un qualsiasi gruppo di oggetti), e di dover creare dei gruppi con questi elementi. Per esempio: in quanti modi possono sedersi sei persone a tavola? In quanti modi posso estrarre a caso due persone perché siano rappresentanti di classe? Quanti numeri di 5 cifre tutte dispari ci sono? Se lancio una moneta 20 volte, in quanti modi posso ottenere 10 volte croce? Per rispondere, bisogna innanzi tutto tenere conto di alcune caratteristiche fondamentali dei gruppi che dobbiamo creare, che portano a identificare diverse regole di calcolo. Tali caratteristiche sono: Devo selezionare solo alcuni elementi da quel gruppo, oppure li devo considerare tutti? L ordine degli elementi del gruppo è importante oppure no? Cioè, un gruppo con gli stessi elementi in ordine diverso, è un gruppo effettivamente diverso? E possibile che all interno di un gruppo un elemento venga ripetuto?
4 PERMUTAZIONI (considero tutti gli n elementi) DISPOSIZIONI (k elementi su n, l ordine conta) COMBINAZIONI (k elementi su n, l ordine non conta) semplici: n! semplici: n! n k! semplici: n! k! n k! con ripetizione: n! r 1! r 2! r 3! con ripetizione: n k con ripetizione: (n + k 1)! k! n 1!
5 Quindi, per decidere che forma usare, i dobbiamo porre alcune domande: DEVO UTILIZZARE TUTTI GLI n ELEMENTI DELL INSIEME? NO. Possono essere disposizioni o combinazioni. L ORDINE CONTA? SI. Allora sono permutazioni. POSSO RIPETERE GLI ELEMENTI? SI: sono disposizioni. POSSO RIPETERE GLI ELEMENTI? NO: sono combinazioni. POSSO RIPETERE GLI ELEMENTI? Una volta riconosciuto se si tratta di combinazioni, disposizioni o permutazioni, devo sempre chiedermi se posso ripetere gli elementi (con ripetizione) oppure no (semplici).
6 PERMUTAZIONI (considero tutti gli n elementi) DISPOSIZIONI (k elementi su n, l ordine conta) COMBINAZIONI (k elementi su n, l ordine non conta) In quanti modi possono sedersi 6 persone su 6 poltrone al cinema? In quanti modi tre persone possono alternarsi sul podio, in un gara con 10 partecipanti? In quanti modi posso estrarre a caso due persone per un interrogazione? Quanti sono gli anagrammi della parola MATEMATICA? Quanti numeri di 5 cifre dispari ci sono? In quanti modi posso distribuire 10 caramelle uguali a tre bambini?
7 Teoremi sulla probabilità Consideriamo solo eventi indipendenti (cioè il verificarsi dell uno non influenza il verificarsi dell altro) ed equiprobabili (non ci sono casi truccati o che si possono verificare con più facilità). Intersezione di due eventi: è la probabilità che due eventi si verifichino contemporaneamente: un evento E anche l altro (per esempio, pescare da un mazzo una figura di picche): P E 1 E 2 = P(E 1 ) P(E 2 ) Unione di due eventi: è la probabilità che si verifichi un evento OPPURE un altro (esempio, roulette: rosso o pari): P E 1 E 2 = P E 1 + P E 2 P(E 1 E 2 ) (se due eventi non possono verificarsi insieme sono incompatibili es: sia rosso che nero)
8 Evento complementare Un evento E si definisce complementare di E se il verificarsi di uno esclude che si verifichi l altro, e l unione di E ed E è la somma di tutti i casi possibili. Esempio: evento E = lancio un dado ed esce 4 evento E = lancio un dado ed esce 1, oppure 2, oppure 3, oppure 5, oppure 6 = non esce 4. P E = 1 P(E) utile perché a volte è più facile calcolare la probabilità dell evento complementare.
9 In un vassoio ci sono 100 caramelle: 35 all arancia, 33 alla menta e 32 al limone. Se ne estraggo una, che probabilità c è che non sia alla menta? E = menta E = non menta P E = P E = = = = 0,67 Oppure: non menta = 35+32=67 P E = non menta =
10 Se lancio una moneta 6 volte, quante probabilità ho di fare esattamente 4 volte testa? Casi possibili Qual è l insieme di partenza? Quello che contiene gli esiti di ogni lancio: testa o croce. n = 2. Devo prendere tutti gli elementi? No, potrei avere solo teste o solo croci. L ordine conta? Si, perché l evento testa croce è diverso da croce testa. Posso ripetere? Si, può venire più volte testa o croce. sono disposizioni con ripetizione, n k = 2 6 = 64
11 Se lancio una moneta 6 volte, quante probabilità ho di fare esattamente 4 volte testa? Casi favorevoli Qual è l insieme di partenza? Stavolta è quello che contiene il numero di teste e di croci richiesto: 4 teste e 2 croci. Devo considerare tutti i suoi elementi? Si, per fare 6 lanci devo considerarli tutti e 6 (TTTTCC). L ordine conta? Si. Posso ripetere? Si, perché ho 4 elementi uguali (T) e 2 elementi uguali (C). sono permutazioni con ripetizione: 6! = 6 5 4! 2!4! 2 4! = 15
12 A questo punto, P(4T) = 15 Questo vale per ogni esercizio di questo genere: Casi possibili su n lanci: n k = 2 lanci/monete ; Casi favorevoli alla richiesta: num. lanci! num. teste! numcroci! 64 Analogamente, se si tratta di lanciare un dado varie volte, il numero di casi possibili è n k = 6 lanci Infatti i 6 numeri che fanno parte dell insieme «esito del lancio» si possono ripetere e possono non uscire tutti. I casi favorevoli dipendono dalla richiesta.
13 Tirando contemporaneamente 5 dadi con facce numerate da 1 a 6, qual è la probabilità di ottenere 5 numeri pari? 1 10 ; 1 25 ; 1 32 ; 1 6 ; (1 6 )5 Ogni lancio è indipendente dal precedente e dal successivo. Quindi, devo considerare la probabilità che in un lancio esca un numero pari: essa è ½. Poi, considero che la richiesta è un caso di intersezione di eventi: pari nel primo lancio E nel secondo E nel terzo quindi la probabilità richiesta è: = 1 32 E se avessi voluto usare casi favorevoli / casi possibili sui 5 lanci, ricavandoli usando il calcolo combinatorio? So che i casi possibili sono 6 numero.lanci, però NON posso calcolare i casi favorevoli, perché devo considerare di scegliere 5 elementi su 3 dei 6 in maniera selettiva. Però posso comunque rispondere: noti i casi possibili, escludo l ultima perché troppo bassa, la prima e la seconda perché 10 e 25 non sono multipli di 6 5, e resta la scelta fra due, ma 1/6 è troppo alta.
14 Determinare quante sono le parole di 7 lettere (anche prive di senso) che si possono formare usando solo le lettere A, C, G, T. devo usare tutti gli n elementi (le lettere)? No, niente nel testo lo rende obbligatorio. AAATTGG andrebbe bene. l ordine conta? Si, perché la parola TAAATGG è diversa dalla precedente pur avendo gli stessi elementi. posso ripetere? Si, altrimenti con 4 lettere mai potrei formare una parola di 7! DISPOSIZIONI CON RIPETIZIONE, n k = 4 7 Attenzione: n = 4, sono gli elementi (le lettere) dell insieme di partenza, e k=7, elementi dei gruppi che formo.
15 Tredici persone si stringono la mano. Ciascuna stringe la mano a tutte le altre. Quante sono le strette di mano totali? 13; 78; 26; 156; 169. come prima cosa escludiamo 13 e 26 (sono poche, se consideriamo che una persona stringe 12 mani). escludiamo anche 169, che è 13x13: se ogni persona stringe 12 mani, 13x13 è troppo. devo considerare tutti gli elementi? No, perché le strette avvengono fra due persone alla volta. n = 13, k = 2. l ordine conta? No: la stretta fra me e paolo e quella fra paolo e me non sono due strette diverse, ma la stessa stretta che va considerata una volta sola. posso ripetere un elemento? No, perché vorrebbe dire che una persona stringe la mano a se stessa. COMBINAZIONI SEMPLICI n! k! n k! = 13! 2! 11! = ! 2 11! = = 13 6 = 78 2
16 Quanti sono i numeri naturali di 4 cifre dispari distinte? 20; 5; 60; 625; 120 devo considerare tutti gli n elementi? No. Infatti, le cifre dispari sono 5 (1,3,5,7,9), se formo numeri di 4 cifre una resta esclusa. l ordine conta? Si! Il numero 7539 è diverso dal numero 5937! posso ripetere gli elementi? No. Lo dice chiaramente il testo: cifre distinte. DISPOSIZIONI SEMPLICI: n! n k! = 5! 5 4! = 5! 1! = = 120
17 Lanciando contemporaneamente due dadi regolari a 6 facce, qual è la probabilità che la somma sia 4? i casi favorevoli sono solo tre: 2+2, 3+1, 1+3 i casi possibili sono 6 n.lanci = 6 2 : infatti, lanciare due dadi contemporaneamente è la stessa cosa che lanciarne uno due volte. Allora P E = 3 36 = 1 12 I casi favorevoli potevo contarli solo a mano, perché la richiesta (somma 4) rendeva specifiche le possibilità di esito.
18 Da un mazzo di 40 carte (10 picche, 10 fiori, 10 cuori, 10 quadri) se ne estraggono 3. Qual è la probabilità di avere tre carte di fiori, se non rimetto le carte estratte nel mazzo? 3 ; 9 ; ; 7 10 ; La probabilità di ottenere nella prima estrazione la carta di fiori è = 1 4. La probabilità che nella seconda estrazione esca una carta di fiori è 9 39 (non ho rimesso la carta nel mazzo). La probabilità che nella terza estrazione esca una carta di fiori è 8 38 = 4 19 (non ho rimesso la carta nel mazzo). La probabilità richiesta è un intersezione delle tre: stesso seme nella prima E nella seconda E nella terza estrazione: = = 3 247
19 4 italiani, 3 francesi e 5 tedeschi devono sedersi ad uno stesso tavolo. Le persone di stessa nazionalità devono rimanere vicine. In quanti modi si può fare? Devo tenere in considerazione che devo lasciare vicine persone della stessa nazionalità. Quindi mi chiedo: in quanti modi possono sedersi all interno dello stesso gruppo? Devo tenere tutti gli elementi (persone), e non posso ripetere un elemento (persona!), quindi sono permutazioni semplici: Italiani 4!, francesi 3!, Tedeschi 5! In quanti modi posso sistemare i tre gruppi? 3! (sono sempre disposizioni semplici). gruppi di nazionalità x rotazione dei gruppi = 4! 3! 5! x(3!)
20 Logica proposizionale La logica proposizionale si propone di formalizzare e quindi analizzare i ragionamenti che, nel nostro linguaggio naturale, possono es25/03/2014sere formulati ricorrendo ad affermazioni (quindi niente esclamazioni, domande, ecc.) composte fra loro usando particelle come: e, o, sia...sia, né né, ma non, o...o, e/o. Non possiamo prendere in considerazioni frasi dal significato ambiguo o soggettivo.
21 «Il cioccolato con le nocciole è più buono del cioccolato bianco» «Pioverà domani?» «Il fratello di Marco è più alto di Luca» Solo l ultima è una proposizione, cioè una affermazione che descrive un fatto a cui è possibile attribuire un valore di verità. Attraverso la logica possiamo attribuire (o no) valore di verità ad affermazioni complesse a partire dalla verità di quelle più semplici che le compongono.
22 Gli elementi che fanno parte di un sistema logico sono essenzialmente di due tipi: Atomi (o oggetti), che possono essere numeri, frasi, o altri oggetti, nei quali non vogliamo, o non possiamo, distinguere elementi più semplici. Predicati: i predicati esprimono proprietà che uno o più atomi possono avere.
23 I vari elementi del sistema possono essere collegati tra loro mediante i seguenti operatori: (non importa il simbolo, ma il significato!!) CONNETTIVI LOGICI: = uguaglianza negazione (non) congiunzione (e) disgiunzione (o) implicazione (se, allora) QUANTIFICATORI: Ǝ esiste almeno uno Ǝ! esiste un solo per ogni Attenzione: Dire TUTTI non ammette eccezioni. Dire NESSUNO non ammette eccezioni. «alcuni», «quasi tutti», «quasi nessuno», «qualcuno» ammettono eccezioni.
24 NEGAZIONE: Data una proposizione, la sua negazione è la proposizione che è vera quando essa è falsa e viceversa. Proposizione: «tutti i gatti sono neri» Negazione: «non tutti i gatti sono neri», «c è almeno un gatto non nero», «nessun gatto è nero». NB: per negare, mi basta una eccezione.
25 CONGIUNZIONE: date due proposizioni, la congiunzione è la proposizione che è vera quando entrambe sono vere e falsa altrimenti. «per essere ammessi al concorso, bisogna essere diplomati E maggiorenni» «per poter salire sulla giostra, è necessario essere più alti di 1,50m E avere più di 10 anni»
26 IMPLICAZIONE (condizioni necessarie, condizioni sufficienti) Se «A», allora «B»: A B (cioè «A» implica «B») A condizione sufficiente per B B condizione necessaria per A «A» se e solo se «B»: A B (cioè «A» implica «B» e viceversa) A condizione necessaria e sufficiente per B
27 CONDIZIONE SUFFICIENTE: A è sufficiente per B equivale a dire che "se A è vera, allora B è vera", oppure che "ogni qualvolta si avvera A, si avvera anche B". Mi basta avere A per sapere che c è B, ma B potrebbe esserci anche senza A. CONDIZIONE NECESSARIA: B è necessaria per A se vale la formulazione "se B non è vera, allora A non è vera". Se ho A, sono sicura di avere anche B, dato che A senza B non c è. «essere padre» implica essere «biologicamente maschio»: A condizione sufficiente per B B condizione necessaria per A Essere padre è condizione sufficiente per essere biologicamente maschio. Essere biologicamente maschio è condizione necessaria per essere padre. B può esserci senza A: si può essere «biologicamente maschio» senza «essere padre». Essere biologicamente maschio non è condizione sufficiente per essere padre.
28 CONDIZIONE SUFFICIENTE: A è sufficiente per B equivale a dire che "se A è vera, allora B è vera", oppure che "ogni qualvolta si avvera A, si avvera anche B". Mi basta avere A per sapere che c è B, ma B potrebbe esserci anche senza A. CONDIZIONE NECESSARIA: B è necessaria per A se vale la formulazione "se B non è vera, allora A non è vera". Se ho A, sono sicura di avere anche B, dato che A senza B non c è. «essere modenese» implica «essere emiliano»: Essere modenese è condizione sufficiente per essere emiliano. Essere emiliano è condizione necessaria per essere modenese. Posso essere emiliano senza essere modenese «essere emiliano» implica essere «modenese»: è FALSA! Essere emiliano non è condizione sufficiente per essere modenese. Essere modenese non è condizione sufficiente per essere emiliano
29 Condizione sufficiente, ma non necessaria, affinché al Liceo Pitagora l'anno scolastico si concluda con una festa è che le interrogazioni terminino entro la fine del mese di maggio. Determinare quale delle seguenti situazioni è INCOMPATIBILE con l'affermazione precedente. A) Nel 2008 le interrogazioni sono terminate a marzo, e poi non c'è stata la festa B) Nel 2006 uno studente è stato interrogato il 4 giugno, e poi c'è stata la festa C) Nel 2003 uno studente è stato interrogato il 4 giugno, e poi non c'è stata la festa D) Nel 2010 uno studente è stato interrogato il 3 aprile, e poi non c'è stata la festa E) Da quando esiste il Liceo Pitagora la festa c'è stata ad anni alterni cosa significa sufficiente ma non necessaria? sufficiente: se «concludo le interrogazioni a maggio» è vera, «faccio la festa» è vera. Ogni volta che le interrogazioni si concludono a maggio, la festa c è. non necessaria: se «concludo le interrogazioni a maggio» è falsa, «faccio la festa» può essere vera o falsa. (infatti, se fosse necessaria, non concludere le interrogazioni implicherebbe non fare la festa, ma dato che NON è necessaria, non so con certezza cosa accade se le interrogazioni non sono concluse). ALLORA LA RISPOSTA CORRETTA E LA A.
30 Quale di questi ragionamenti è corretto da un punto di vista deduttivo: A) Carlo frequenta la prima elementare. La maggioranza dei bambini che frequentano la prima elementare ha sei anni, quindi Carlo ha sei anni Errata. La maggior parte non vuol dire tutti, Carlo potrebbe essere nella minoranza. B) Carlo ha 4 anni. I bambini sopra 4 anni sono biondi. Quindi Carlo non è biondo Errata. Non so nulla sui bambini sotto ai 4 anni. C) Carlo ha 4 anni. I bambini di 4 anni sono tutti biondi. Quindi Carlo è biondo. Corretta. Se «tutti» sono biondi, Carlo non è un eccezione, ed è biondo. D) Carlo ha 4 anni. I bambini sopra 4 anni non sono biondi. Quindi Carlo è biondo. Errata. Non so nulla sui bambini sotto ai 4 anni E) se Carlo avesse sei anni e frequentasse la prima elementare, e se tutti gli altri bambini di quella classe fossero biondi, Carlo sarebbe biondo. Errata. «tutti gli altri» non è «tutti in generale», quindi Carlo potrebbe essere un eccezione.
31 INSIEMISTICA Dati gli insiemi A e B, possiamo definire: Intersezione di A e B: gli elementi in comune fra A e B. (esempio: A = donne, B = biondi: intersezione = donne bionde) Unione di A e B: gli elementi di A più gli elementi di B (quelli di solo A + quelli di solo B + quelli che appartengono all intersezione). (donne more + uomini biondi + donne bionde) Differenza fra A e B: gli elementi che appartengono ad A ma NON a B. (donne more) A e B sono disgiunti se non hanno elementi comuni. (A= donne B =pennuti)
32 Identificare le proposizioni semplici contenute in quelle più complesse. Identificare le implicazioni. «non tutti» = «alcuni», quindi «non tutti» è incompatibile con «tutti», e anche con «nessuno». Per abbattere una certezza basta una sola eccezione: per negare tutti, e nessuno mi basta almeno uno. Controllare che la risposta che consideriamo esatta corrisponda a tutte le implicazioni e renda vere tutte le proposizioni semplici (compatibilità). Concentrarsi sulle richieste. Controllare con dei controesempi la risposta che consideriamo esatta. Attenzione ai giri di parole.
33 A quale delle seguenti affermazioni equivale la frase: Non tutti i miopi portano gli occhiali? A) Nessun miope porta gli occhiali B) Tutti i miopi portano gli occhiali C) Non vi è un miope che non porti gli occhiali D) C è almeno un miope che non porta gli occhiali E) Tutti i miopi evitano di portare gli occhiali «non tutti» = «alcuni lo fanno e altri no» Quindi, non lo fanno tutti: la B non va bene, e neanche la C, che dice la stessa cosa. Però alcuni lo fanno, e allora la A non va bene. La E è uguale alla A. Quella corretta è la D.
34 Alberto, Carlo, Roberto, Paolo e Sergio sono nati in cinque città diverse: Amsterdam, Cagliari, Roma, Pavia, Siracusa. Alberto e Sergio mentono sempre mentre Paolo non mente mai. (queste sono proposizioni vere) Alberto afferma di essere nato ad Amsterdam e che Sergio è nato a Siracusa. Paolo afferma di essere nato a Pavia e riferisce che Alberto gli ha detto di essere nato a Cagliari. Dove può essere nato Alberto? Alberto: «sono nato ad Amsterdam» FALSA Alberto NON è nato ad Amsterdam. Paolo: «sono nato a Pavia e Alberto mi dice di essere nato a Cagliari» VERA Alberto NON è nato a Cagliari; Alberto NON è nato a Pavia. Alberto può essere nato a Siracusa o a Roma
35 Paolo è così amico di Giuseppe e di Claudio che quando lui va alle feste ci vanno anche i suoi due amici. Data la frase precedente, quale delle seguenti affermazioni è certamente vera? A) Ieri c era una festa alla quale Paolo non è andato, quindi anche Giuseppe e Claudio non c erano B) Ieri Claudio è andato ad una festa, quindi c è andato anche Paolo C) Giuseppe e Claudio ieri erano ad una festa, quindi c era anche Paolo D) Paolo ieri è andato ad una festa, quindi sicuramente c erano anche Giuseppe e Claudio E) Giuseppe ieri era ad una festa, quindi sicuramente c è andato anche Claudio Cosa so: «Paolo alla festa» implica «Giuseppe e Claudio alla festa» Cosa significa: Se Paolo è a una festa ci sono i suoi amici. (Paolo condizione sufficiente) COERENTE CON D. Se non ci sono Giuseppe e Claudio, non c è Paolo (G&C condizioni necessarie, se loro non ci sono vuol dire che lui non c è) Se Paolo non c è, non posso sapere se ci sono Claudio e Giuseppe: vanno sempre alle feste quando c è lui, ma non sappiamo cosa fanno quando lui non c è. (Paolo non è condizione necessaria, G&C non sono sufficienti). ESCLUDO LA A, LA B e LA C Non posso sapere cosa fanno Claudio e Giuseppe uno rispetto all altro. ESCLUDO LA E LA RISPOSTA CORRETTA E LA D.
36 In un cinema ci sono 200 spettatori: 40 sono italiani, 50 sono donne, e 60 preferiscono i film di genere fantasy. Sulla base di queste informazioni, di quanti spettatori si può affermare con certezza che sono allo stesso tempo italiani, donne e amanti del genere fantasy? A) Di cinquanta B) Di cento C) Di nessuno D) Di dieci E) Di quaranta la richiesta è: quanti sono gli elementi che di sicuro appartengono all intersezione dei tre insiemi (italiani, donne e amanti del fantasy). Prima di tutto devo quindi chiedermi se tale intersezione esiste obbligatoriamente (con certezza!); devo cioè domandarmi se esiste almeno una possibilità che gli insiemi siano disgiunti (niente certezza) oppure se tale possibilità non esiste < 200, quindi è possibile che i tre insiemi non abbiano elementi in comune; cioè non è obbligatorio che l intersezione esista. Data la richiesta «con certezza», LA RISPOSTA CORRETTA E LA C. se avessero chiesto «al massimo di quanti si può affermare che potrebbero..», la risposta sarebbe stata 40 (cioè tutti gli italiani sono anche donne che amano il fantasy. Non di più perché non ci sono abbastanza italiani)
37 In un cinema ci sono 100 spettatori: 40 sono italiani, 50 sono donne, e 60 preferiscono i film di genere fantasy. Sulla base di queste informazioni, di quanti spettatori si può affermare con certezza che sono allo stesso tempo italiani, donne e amanti del genere fantasy? A) Di cinquanta B) Di cento C) Di nessuno D) Di dieci E) Di quaranta > 100, quindi (al contrario di prima) sono sicura che ci sono persone con più di una caratteristica. Quindi, per capire se è possibile che non esista l intersezione richiesta (è quello che esclude la certezza) devo chiedermi se è possibile che un insieme sia disgiunto dall unione degli altri due (due caratteristiche ma non tre) = 100, quindi può essere che dei 40 italiani nessuno ami il fantasy, e quindi l intersezione non esiste con certezza < 100, quindi può essere che dei 40 italiani nessuno sia donna, e quindi l intersezione non esiste con certezza > 100, quindi almeno 10 persone sono donne che amano il fantasy. Però, supponendo che siano 10, restano 90 persone che hanno solo una caratteristica, e il 40 italiani possono essere fra questi. LA RISPOSTA ESATTA E ANCORA LA C.
38 In un cinema ci sono 70 spettatori: 40 sono italiani, 50 sono donne, e 60 preferiscono i film di genere fantasy. Sulla base di queste informazioni, di quanti spettatori si può affermare con certezza che sono allo stesso tempo italiani, donne e amanti del genere fantasy? A) Di cinquanta B) Di cento C) Di nessuno D) Di dieci E) Di quaranta > 70, quindi sono sicura che ci sono persone con più di una caratteristica. Quindi, per capire se è possibile che non esista l intersezione richiesta (è quello che esclude la certezza) devo chiedermi se è possibile che un insieme sia disgiunto dall unione degli altri due (due caratteristiche ma non tre) = 100, quindi per rispettare il vincolo di 70 persone, posso dire che (almeno) 30 sono italiani che amano il fantasy. supponiamo quindi che 30 persone abbiano due caratteristiche: ne restano 40 che ne hanno una sola. ipotizzando che queste 40 siano tutte donne (ragioniamo sempre al limite), per arrivare a 50 ne restano comunque 10 che devono ricadere nelle 30 persone che sono italiane e amano il fantasy. LA RISPOSTA ESATTA E LA D. (al minimo, con certezza, 10. potrebbero essere di più, potrei avere 40 donne italiane che amano il fantasy e i restanti 30 non italiani, ma non posso saperlo.)
39 Tutti i piccioni mangiano le fave alcuni uccelli non mangiano le fave dunque... non sono piccioni. S individui il CORRETTO COMPLETAMENTO del sillogismo: A) le fave B) alcuni uccelli C) alcuni piccioni D) alcune fave E) tutti gli uccelli Non è un piccione chi non mangia le fave, perché tutti i piccioni le mangiano. Chi non mangia le fave? Alcuni uccelli. Allora «alcuni uccelli non sono piccioni». La B. A e D non hanno senso. Le fave non sono piccioni e non sono uccelli, sono quelle che vengono mangiate. Anche la C non ha senso, i piccioni sono piccioni. La E è sbagliata perché sono solo alcuni, gli uccelli che non mangiano fave, non tutti.
40 Mario è nato martedì 8 febbraio. Stella è nata mercoledì 8 marzo, nello stesso anno. Di quale anno potrebbe trattarsi? A) 1976 B) 1973 C) 1970 D) 1979 E) 1982 La risposta è legata al fatto che l anno sia bisestile o meno. Infatti, quando febbraio ha 28 giorni (multiplo di 7) i giorni della settimana hanno, a marzo, gli stessi numeri progressivi. Quindi, in un anno NON bisestile, a martedì 8 febbraio segue martedì 8 marzo. Se invece i giorni sono 29, si avrà mercoledì 8 marzo. Quale di questi anni è bisestile, quindi? Un anno è bisestile se il suo numero è divisibile per 4, con l'eccezione degli anni secolari (quelli divisibili per 100) che non sono divisibili per 400. A questo punto, l unico divisibile per 4 è 1976.
41 Quando prende il treno, Carlo arriva sempre in ritardo a destinazione. Quale delle seguenti affermazioni può essere dedotta dalla frase precedente? A) Carlo è arrivato in ritardo, quindi ha preso il treno B) Carlo è arrivato in orario, quindi non ha preso il treno C) Carlo non ha preso il treno, quindi è arrivato in ritardo D) Carlo è arrivato in orario, quindi ha preso il treno E) Carlo non ha preso il treno, quindi è arrivato in orario L affermazione mi dice che: «prendere il treno» è condizione sufficiente per «ritardo». Non è però necessaria: Carlo arriva sempre in ritardo se è in treno, ma può arrivare in ritardo anche in altri casi ( quando, non solo quando ). la A e la E non vanno bene perché presuppongono il treno come condizione «necessaria» al ritardo. la C e la D sono in contraddizione con l affermazione, quindi le escludo. quella corretta è la B.
42 Si legga la seguente cronaca elettorale: A ha conseguito il 36,4% dei voti, mentre in lieve flessione rispetto alle elezioni del 2005 appare B (fermo al 28,5); C ha quasi raddoppiato i consensi (20,9) e D, al battesimo delle urne, si attesta al 14,2. Quale è l'unico risultato delle elezioni del 2005 che sia compatibile col quadro appena delineato? A) A 18,3 - B 41,4 - C 40, 3 B) A 63,3 - B 26,2 - C 10,5 C) A 58,3 - B 30,7 - C 11,0 D) A 43,3 - B 30,3 - C 10,9 - D 15,5 E) A 36,4 - B 32,4 - C 20,7 - D 10.5 Le informazioni utili (cioè di confronto col 2005) sono solo tre: Nel 2005 D non c era. escludo D ed E C ha quasi raddoppiato, quindi nel 2005 deve aver ottenuto poco più del 10,45%. escludo la A, restano B e C B ha leggermente diminuito rispetto al C.
43 Ad una festa partecipano 8 studenti, i quali complessivamente possiedono 17 cellulari. Determinare quale delle seguenti affermazioni è sicuramente vera. A) Almeno un ragazzo possiede almeno 3 cellulari B) C'è un unico ragazzo che possiede almeno 3 cellulari C) Almeno un ragazzo possiede esattamente 3 cellulari D) C'è un unico ragazzo che possiede esattamente 3 cellulari E) Nessun ragazzo possiede più di 3 cellulari Valutiamo il caso più estremo: un ragazzo ha tutti e i 17 i cellulari. Essendo possibile, escludo la E. Distribuiamoli considerano il numero minimo di cellulari ciascuno se li distribuiamo equamente : sono in 8, ne hanno 2 a testa, e un solo ragazzo ne ha 3. Ovviamente, potrebbe poi succedere che qualcuno ne abbia solo uno o nessuno: in questo caso, o più di una persona ne ha 3, o una persona ne ha più di tre. In ognuno di questi casi, almeno una persona ne ha 3 come minimo, e questa è l unica cosa che posso dire con certezza. Questo è compatibile con la A, che è in effetti la risposta corretta. Non posso dire «uno solo ne ha almeno 3» (B), perché potrebbe essere Questo esclude anche la D (uno solo esattamente 3) Non posso dire «almeno uno ESATTAMENTE 3» (C) perché potrebbe essere Questo esclude anche la E, di nuovo. (nessuno più di tre). ricordare che basta una eccezione a demolire una affermazione. «certezza logica» non è per forza «la cosa più sensata». Anzi
44 L analisi dei risultati di un test ha evidenziato che, per ognuna delle 70 domande proposte, c'è stato almeno un candidato che ha fornito la risposta corretta. Determinare quale delle seguenti situazioni è compatibile con questa analisi. A) Tutti hanno risposto in maniera errata alla domanda 47 B) Esiste un candidato che ha risposto in maniera errata a tutte le domande C) Nessuno ha fornito una risposta alla domanda 53 D) Nessuno ha risposto correttamente alla domanda 70 E) Almeno due domande hanno ricevuto risposte errate da parte di tutti i concorrenti Rendiamo più semplice l affermazione: «per ogni domanda, c è stata almeno una risposta corretta» (che NON vuol dire «ogni candidato ha dato almeno una risposta corretta») A, C, D non sono compatibili perché affermano che una domanda non abbia avuto risposta corretta. E non è compatibile perché comporta che addirittura due o più domande non abbiano avuto neanche una risposta corretta. B invece è compatibile, perché un candidato può aver sbagliato tutto, questo non da informazioni su cosa hanno fatto gli altri: è possibile che le altrui risposte comprendano almeno una risposta corretta per ogni domanda.
45 Di solito Laura pota le rose nel mese di novembre, ma lo scorso anno ha dimenticato di farlo. Ha aspettato, invece, che terminasse il gelo invernale per poi potarle nel mese di marzo. Quest estate Laura ha avuto la più abbondante fioritura di rose che si fosse mai vista nel suo giardino. Quindi, il gelo fa bene alle rose. Quale delle seguenti risposte costituisce il passaggio logico errato nel brano precedente? A) Si presuppone che il gelo abbia causato l abbondante fioritura di rose B) Si presuppone che non ci siano gelate nel mese di marzo C) Si presuppone che le rose debbano essere potate D) Si presuppone sulla base di un solo caso che una tarda potatura faccia bene a tutte le piante in generale E) Si presuppone che il mese di novembre e il mese di marzo siano gli unici mesi in cui si può effettuare la potatura Analizziamole tutte, e vediamo quali sono, innanzi tutto, passaggi logici davvero fatti nel testo. A «QUINDI il gelo fa bene alle rose» è una deduzione del testo, ma è corretta? B non è vero, ha aspettato che salisse la temperatura e poi le ha potate a marzo. Non c è scritto «dato che a marzo non ci sono gelate». C parla di un abitudine di Laura, ma non dice che lo fa perché «si deve». D non si fa collegamento fra il ritardo e la potatura, né si parla di altre piante. Però, il fatto che un solo caso non basta per una deduzione logica è vero, e supporta la scelta della A. E non è vero, e in fatti si specifica che Laura lo fa «di solito» a novembre, una sua abitudine e non una condizione obbligatoria. E anche marzo è casuale, dopo il gelo.
Test sul calcolo della probabilità
 Test sul calcolo della probabilità 2 Test sul calcolo della probabilità Test sul calcolo della probabilità. La probabilità p di un evento E, quando si indica con E il suo complementare, è : a) 0 se E è
Test sul calcolo della probabilità 2 Test sul calcolo della probabilità Test sul calcolo della probabilità. La probabilità p di un evento E, quando si indica con E il suo complementare, è : a) 0 se E è
Esercizi di Calcolo delle Probabilita (I)
 Esercizi di Calcolo delle Probabilita (I) 1. Si supponga di avere un urna con 15 palline di cui 5 rosse, 8 bianche e 2 nere. Immaginando di estrarre due palline con reimmissione, si dica con quale probabilità:
Esercizi di Calcolo delle Probabilita (I) 1. Si supponga di avere un urna con 15 palline di cui 5 rosse, 8 bianche e 2 nere. Immaginando di estrarre due palline con reimmissione, si dica con quale probabilità:
Calcolo delle probabilità
 Calcolo delle probabilità Laboratorio di Bioinformatica Corso A aa 2005-2006 Statistica Dai risultati di un esperimento si determinano alcune caratteristiche della popolazione Calcolo delle probabilità
Calcolo delle probabilità Laboratorio di Bioinformatica Corso A aa 2005-2006 Statistica Dai risultati di un esperimento si determinano alcune caratteristiche della popolazione Calcolo delle probabilità
Primi esercizi per gli studenti del corso di Statistica ed Elementi di Probabilita
 Primi esercizi per gli studenti del corso di Statistica ed Elementi di Probabilita NOTA 1 Gli esercizi sono presi da compiti degli scorsi appelli, oppure da testi o dispense di colleghi. A questi ultimi
Primi esercizi per gli studenti del corso di Statistica ed Elementi di Probabilita NOTA 1 Gli esercizi sono presi da compiti degli scorsi appelli, oppure da testi o dispense di colleghi. A questi ultimi
Analisi dei Dati 12/13 Esercizi proposti 3 soluzioni
 Analisi dei Dati 1/13 Esercizi proposti 3 soluzioni 0.1 Un urna contiene 6 palline rosse e 8 palline nere. Si estraggono simultaneamente due palline. Qual è la probabilità di estrarle entrambe rosse? (6
Analisi dei Dati 1/13 Esercizi proposti 3 soluzioni 0.1 Un urna contiene 6 palline rosse e 8 palline nere. Si estraggono simultaneamente due palline. Qual è la probabilità di estrarle entrambe rosse? (6
Probabilità discreta
 Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
Probabilità discreta Daniele A. Gewurz 1 Che probabilità c è che succeda...? Una delle applicazioni della combinatoria è nel calcolo di probabilità discrete. Quando abbiamo a che fare con un fenomeno che
Calcolo delle Probabilità
 Calcolo delle Probabilità Il calcolo delle probabilità studia i modelli matematici delle cosidette situazioni di incertezza. Molte situazioni concrete sono caratterizzate a priori da incertezza su quello
Calcolo delle Probabilità Il calcolo delle probabilità studia i modelli matematici delle cosidette situazioni di incertezza. Molte situazioni concrete sono caratterizzate a priori da incertezza su quello
Ulteriori problemi di fisica e matematica
 Facoltà di Medicina e Chirurgia Università degli Studi di Firenze Agosto 2010 Ulteriori problemi di fisica e matematica Giovanni Romano Perché un raggio di luce proveniente dal Sole e fatto passare attraverso
Facoltà di Medicina e Chirurgia Università degli Studi di Firenze Agosto 2010 Ulteriori problemi di fisica e matematica Giovanni Romano Perché un raggio di luce proveniente dal Sole e fatto passare attraverso
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Per poter affrontare il problema abbiamo bisogno di parlare di probabilità (almeno in maniera intuitiva). Analizziamo alcune situazioni concrete.
 Parliamo di probabilità. Supponiamo di avere un sacchetto con dentro una pallina rossa; posso aggiungere tante palline bianche quante voglio, per ogni pallina bianca che aggiungo devo pagare però un prezzo
Parliamo di probabilità. Supponiamo di avere un sacchetto con dentro una pallina rossa; posso aggiungere tante palline bianche quante voglio, per ogni pallina bianca che aggiungo devo pagare però un prezzo
(concetto classico di probabilità)
 Probabilità matematica (concetto classico di probabilità) Teoria ed esempi Introduzione Il calcolo delle probabilità è la parte della matematica che si occupa di prevedere, sulla base di regole e leggi
Probabilità matematica (concetto classico di probabilità) Teoria ed esempi Introduzione Il calcolo delle probabilità è la parte della matematica che si occupa di prevedere, sulla base di regole e leggi
Esercizi di Probabilità e Statistica
 Esercizi di Probabilità e Statistica Samuel Rota Bulò 19 marzo 2007 Spazi di probabilità finiti e uniformi Esercizio 1 Un urna contiene due palle nere e una rossa. Una seconda urna ne contiene una bianca
Esercizi di Probabilità e Statistica Samuel Rota Bulò 19 marzo 2007 Spazi di probabilità finiti e uniformi Esercizio 1 Un urna contiene due palle nere e una rossa. Una seconda urna ne contiene una bianca
Una sperimentazione. Probabilità. Una previsione. Calcolo delle probabilità. Nonostante ciò, è possibile dire qualcosa.
 Una sperimentazione Probabilità Si sta sperimentando l efficacia di un nuovo farmaco per il morbo di Parkinson. Duemila pazienti partecipano alla sperimentazione: metà di essi vengono trattati con il nuovo
Una sperimentazione Probabilità Si sta sperimentando l efficacia di un nuovo farmaco per il morbo di Parkinson. Duemila pazienti partecipano alla sperimentazione: metà di essi vengono trattati con il nuovo
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA. Esercizi su eventi, previsioni e probabilità condizionate
 CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su eventi, previsioni e probabilità condizionate Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi su eventi, previsioni e probabilità condizionate Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability
Matematica Applicata. Probabilità e statistica
 Matematica Applicata Probabilità e statistica Fenomeni casuali Fenomeni che si verificano in modi non prevedibili a priori 1. Lancio di una moneta: non sono in grado di prevedere con certezza se il risultato
Matematica Applicata Probabilità e statistica Fenomeni casuali Fenomeni che si verificano in modi non prevedibili a priori 1. Lancio di una moneta: non sono in grado di prevedere con certezza se il risultato
Si considerino gli eventi A = nessuno studente ha superato l esame e B = nessuno studente maschio ha superato l esame. Allora A c B è uguale a:
 TEST DI AUTOVALUTAZIONE - SETTIMANA 2 I diritti d autore sono riservati. Ogni sfruttamento commerciale non autorizzato sarà perseguito. Metodi statistici per la biologia 1 Parte A 1.1 Si considerino gli
TEST DI AUTOVALUTAZIONE - SETTIMANA 2 I diritti d autore sono riservati. Ogni sfruttamento commerciale non autorizzato sarà perseguito. Metodi statistici per la biologia 1 Parte A 1.1 Si considerino gli
Esercizio 1 Dato il gioco ({1, 2, 3}, v) con v funzione caratteristica tale che:
 Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
Teoria dei Giochi, Trento, 2004/05 c Fioravante Patrone 1 Teoria dei Giochi Corso di laurea specialistica: Decisioni economiche, impresa e responsabilità sociale, A.A. 2004/05 Soluzioni degli esercizi
Soluzione degli esercizi sul moto rettilineo uniformemente accelerato
 Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 00 Soluzione degli esercizi sul moto rettilineo uniformemente accelerato Esercizio. Un corpo parte da fermo con accelerazione
Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 00 Soluzione degli esercizi sul moto rettilineo uniformemente accelerato Esercizio. Un corpo parte da fermo con accelerazione
UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA
 UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA Tutti gli anni, affrontando l argomento della divisibilità, trovavo utile far lavorare gli alunni sul Crivello di Eratostene. Presentavo ai ragazzi una
UNA LEZIONE SUI NUMERI PRIMI: NASCE LA RITABELLA Tutti gli anni, affrontando l argomento della divisibilità, trovavo utile far lavorare gli alunni sul Crivello di Eratostene. Presentavo ai ragazzi una
Esercizi sul moto rettilineo uniformemente accelerato
 Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 010 Esercizi sul moto rettilineo uniformemente accelerato Esercizio 1. Un corpo parte da fermo con accelerazione pari a
Liceo Carducci Volterra - Classe 3 a B Scientifico - Francesco Daddi - 8 novembre 010 Esercizi sul moto rettilineo uniformemente accelerato Esercizio 1. Un corpo parte da fermo con accelerazione pari a
Logica Numerica Approfondimento 1. Minimo Comune Multiplo e Massimo Comun Divisore. Il concetto di multiplo e di divisore. Il Minimo Comune Multiplo
 Logica Numerica Approfondimento E. Barbuto Minimo Comune Multiplo e Massimo Comun Divisore Il concetto di multiplo e di divisore Considerato un numero intero n, se esso viene moltiplicato per un numero
Logica Numerica Approfondimento E. Barbuto Minimo Comune Multiplo e Massimo Comun Divisore Il concetto di multiplo e di divisore Considerato un numero intero n, se esso viene moltiplicato per un numero
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE
 APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE 1. Proporzionalità diretta e proporzionalità inversa Analizziamo le seguenti formule Peso Lordo = Peso Netto + Tara Ricavo = Utile + Costo Rata = Importo + Interesse
APPUNTI SU PROBLEMI CON CALCOLO PERCENTUALE 1. Proporzionalità diretta e proporzionalità inversa Analizziamo le seguenti formule Peso Lordo = Peso Netto + Tara Ricavo = Utile + Costo Rata = Importo + Interesse
Capitolo 4 Probabilità
 Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 4 Probabilità Insegnamento: Statistica Corso di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara Docenti: Dott.
Levine, Krehbiel, Berenson Statistica II ed. 2006 Apogeo Capitolo 4 Probabilità Insegnamento: Statistica Corso di Laurea Triennale in Economia Facoltà di Economia, Università di Ferrara Docenti: Dott.
Corso di Matematica. Corso di Laurea in Farmacia, Facoltà di Farmacia. Università degli Studi di Pisa. Maria Luisa Chiofalo.
 Corso di Matematica Corso di Laurea in Farmacia, Facoltà di Farmacia Università degli Studi di Pisa Maria Luisa Chiofalo Scheda 18 Esercizi svolti sul calcolo delle probabilità I testi degli esercizi sono
Corso di Matematica Corso di Laurea in Farmacia, Facoltà di Farmacia Università degli Studi di Pisa Maria Luisa Chiofalo Scheda 18 Esercizi svolti sul calcolo delle probabilità I testi degli esercizi sono
Siamo così arrivati all aritmetica modulare, ma anche a individuare alcuni aspetti di come funziona l aritmetica del calcolatore come vedremo.
 DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
DALLE PESATE ALL ARITMETICA FINITA IN BASE 2 Si è trovato, partendo da un problema concreto, che con la base 2, utilizzando alcune potenze della base, operando con solo addizioni, posso ottenere tutti
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
Esercizi. Rappresentando le estrazioni con un grafo ad albero, calcolare la probabilità che:
 Esercizi Esercizio 4. Un urna contiene inizialmente 2 palline bianche e 4 palline rosse. Si effettuano due estrazioni con la seguente modalità: se alla prima estrazione esce una pallina bianca, la si rimette
Esercizi Esercizio 4. Un urna contiene inizialmente 2 palline bianche e 4 palline rosse. Si effettuano due estrazioni con la seguente modalità: se alla prima estrazione esce una pallina bianca, la si rimette
Tasso di interesse e capitalizzazione
 Tasso di interesse e capitalizzazione Tasso di interesse = i = somma che devo restituire dopo un anno per aver preso a prestito un euro, in aggiunta alla restituzione dell euro iniziale Quindi: prendo
Tasso di interesse e capitalizzazione Tasso di interesse = i = somma che devo restituire dopo un anno per aver preso a prestito un euro, in aggiunta alla restituzione dell euro iniziale Quindi: prendo
Cosa dobbiamo già conoscere?
 Cosa dobbiamo già conoscere? Insiemistica (operazioni, diagrammi...). Insiemi finiti/numerabili/non numerabili. Perché la probabilità? In molti esperimenti l esito non è noto a priori tuttavia si sa dire
Cosa dobbiamo già conoscere? Insiemistica (operazioni, diagrammi...). Insiemi finiti/numerabili/non numerabili. Perché la probabilità? In molti esperimenti l esito non è noto a priori tuttavia si sa dire
OSSERVAZIONI TEORICHE Lezione n. 4
 OSSERVAZIONI TEORICHE Lezione n. 4 Finalità: Sistematizzare concetti e definizioni. Verificare l apprendimento. Metodo: Lettura delle OSSERVAZIONI e risoluzione della scheda di verifica delle conoscenze
OSSERVAZIONI TEORICHE Lezione n. 4 Finalità: Sistematizzare concetti e definizioni. Verificare l apprendimento. Metodo: Lettura delle OSSERVAZIONI e risoluzione della scheda di verifica delle conoscenze
Corso di ELEMENTI DI STATISTICA Alcuni problemi di probabilità, con soluzioni
 Corso di ELEMENTI DI STATISTICA Alcuni problemi di probabilità, con soluzioni Si tratta di problemi elementari, formulati nel linguaggio ordinario Quindi, per ogni problema la suluzione proposta è sempre
Corso di ELEMENTI DI STATISTICA Alcuni problemi di probabilità, con soluzioni Si tratta di problemi elementari, formulati nel linguaggio ordinario Quindi, per ogni problema la suluzione proposta è sempre
Test d ipotesi. Statistica e biometria. D. Bertacchi. Test d ipotesi
 In molte situazioni una raccolta di dati (=esiti di esperimenti aleatori) viene fatta per prendere delle decisioni sulla base di quei dati. Ad esempio sperimentazioni su un nuovo farmaco per decidere se
In molte situazioni una raccolta di dati (=esiti di esperimenti aleatori) viene fatta per prendere delle decisioni sulla base di quei dati. Ad esempio sperimentazioni su un nuovo farmaco per decidere se
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
CENTRO PRISTEM-UNIVERSITÀ BOCCONI
 CENTRO PRISTEM-UNIVERSITÀ BOCCONI 1 Compleanni e ritardi Carla ha festeggiato il suo compleanno di domenica, il 28 marzo, con due giorni di ritardo rispetto alla data esatta. Milena è nata (in un altro
CENTRO PRISTEM-UNIVERSITÀ BOCCONI 1 Compleanni e ritardi Carla ha festeggiato il suo compleanno di domenica, il 28 marzo, con due giorni di ritardo rispetto alla data esatta. Milena è nata (in un altro
CALCOLO COMBINATORIO
 CALCOLO COMBINATORIO 1 Modi di formare gruppi di k oggetti presi da n dati 11 disposizioni semplici, permutazioni Dati n oggetti distinti a 1,, a n si chiamano disposizioni semplici di questi oggetti,
CALCOLO COMBINATORIO 1 Modi di formare gruppi di k oggetti presi da n dati 11 disposizioni semplici, permutazioni Dati n oggetti distinti a 1,, a n si chiamano disposizioni semplici di questi oggetti,
Calcolo combinatorio
 Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.S.: Ingegneria Civile-Architettonico, Ingegneria Civile-Strutturistico Calcolo combinatorio Ines Campa e Marco Longhi Probabilità e Statistica
Probabilità e Statistica Esercitazioni a.a. 2009/2010 C.d.L.S.: Ingegneria Civile-Architettonico, Ingegneria Civile-Strutturistico Calcolo combinatorio Ines Campa e Marco Longhi Probabilità e Statistica
= variazione diviso valore iniziale, il tutto moltiplicato per 100. \ Esempio: PIL del 2000 = 500; PIL del 2001 = 520:
 Fig. 10.bis.1 Variazioni percentuali Variazione percentuale di x dalla data zero alla data uno: x1 x 0 %x = 100% x 0 = variazione diviso valore iniziale, il tutto moltiplicato per 100. \ Esempio: PIL del
Fig. 10.bis.1 Variazioni percentuali Variazione percentuale di x dalla data zero alla data uno: x1 x 0 %x = 100% x 0 = variazione diviso valore iniziale, il tutto moltiplicato per 100. \ Esempio: PIL del
A) 30 minuti B) 15 minuti C) 40 minuti D) 60 minuti E) 120 minuti
 Due auto si trovano ad una distanza iniziale di 60 chilometri. Partono contemporaneamente andando l una verso l altra, la prima ad una velocità costante di 70 km/h e la seconda di 50 km/h. Dopo quanto
Due auto si trovano ad una distanza iniziale di 60 chilometri. Partono contemporaneamente andando l una verso l altra, la prima ad una velocità costante di 70 km/h e la seconda di 50 km/h. Dopo quanto
La prof.ssa SANDRA VANNINI svolge da diversi anni. questo percorso didattico sulle ARITMETICHE FINITE.
 La prof.ssa SANDRA VANNINI svolge da diversi anni questo percorso didattico sulle ARITMETICHE FINITE. La documentazione qui riportata è ricavata dalla trascrizione dei lucidi che vengono prodotti dall
La prof.ssa SANDRA VANNINI svolge da diversi anni questo percorso didattico sulle ARITMETICHE FINITE. La documentazione qui riportata è ricavata dalla trascrizione dei lucidi che vengono prodotti dall
PROBABILITA CONDIZIONALE
 Riferendoci al lancio di un dado, indichiamo con A l evento esce un punteggio inferiore a 4 A ={1, 2, 3} B l evento esce un punteggio dispari B = {1, 3, 5} Non avendo motivo per ritenere il dado truccato,
Riferendoci al lancio di un dado, indichiamo con A l evento esce un punteggio inferiore a 4 A ={1, 2, 3} B l evento esce un punteggio dispari B = {1, 3, 5} Non avendo motivo per ritenere il dado truccato,
Probabilità e statistica
 Indice generale.probabilità ed eventi aleatori....come si può definire una probabilità....eventi equiprobabili....eventi indipendenti, eventi dipendenti....eventi incompatibili....eventi compatibili....probabilità
Indice generale.probabilità ed eventi aleatori....come si può definire una probabilità....eventi equiprobabili....eventi indipendenti, eventi dipendenti....eventi incompatibili....eventi compatibili....probabilità
COMPITO DI MATEMATICA FINANZIARIA 8 Febbraio 2013. - Come cambia il REA atteso se l'obbligazione sarà ancora in vita dopo le prime tre estrazioni?
 UNIVERSITA DEGLI STUDI DI URBINO (Sede di Fano) COMPITO DI MATEMATICA FINANZIARIA 8 Febbraio 2013 1) L'impresa Gamma emette 250 obbligazioni il cui VN unitario è pari a 100. Il rimborso avverrà tramite
UNIVERSITA DEGLI STUDI DI URBINO (Sede di Fano) COMPITO DI MATEMATICA FINANZIARIA 8 Febbraio 2013 1) L'impresa Gamma emette 250 obbligazioni il cui VN unitario è pari a 100. Il rimborso avverrà tramite
IGiochidiArchimede-SoluzioniBiennio 22 novembre 2006
 PROGETTO OLIMPII I MTEMTI U.M.I. UNIONE MTEMTI ITLIN SUOL NORMLE SUPERIORE IGiochidirchimede-Soluzioniiennio novembre 006 Griglia delle risposte corrette Problema Risposta corretta E 4 5 6 7 8 9 E 0 Problema
PROGETTO OLIMPII I MTEMTI U.M.I. UNIONE MTEMTI ITLIN SUOL NORMLE SUPERIORE IGiochidirchimede-Soluzioniiennio novembre 006 Griglia delle risposte corrette Problema Risposta corretta E 4 5 6 7 8 9 E 0 Problema
12. Le date possono essere scritte in forma numerica usando le otto cifre. Per esempio, il 19 gennaio 2005 può essere scritto come 19-01-2005.
 Logica matematica 12. Le date possono essere scritte in forma numerica usando le otto cifre. Per esempio, il 19 gennaio 2005 può essere scritto come 19-01-2005. In quale anno cadrà la prossima data nella
Logica matematica 12. Le date possono essere scritte in forma numerica usando le otto cifre. Per esempio, il 19 gennaio 2005 può essere scritto come 19-01-2005. In quale anno cadrà la prossima data nella
PLIDA Progetto Lingua Italiana Dante Alighieri Certificazione di competenza in lingua italiana
 PLIDA Progetto Lingua Italiana Dante Alighieri Certificazione di competenza in lingua italiana giugno 2011 PARLARE Livello MATERIALE PER L INTERVISTATORE 2 PLIDA Progetto Lingua Italiana Dante Alighieri
PLIDA Progetto Lingua Italiana Dante Alighieri Certificazione di competenza in lingua italiana giugno 2011 PARLARE Livello MATERIALE PER L INTERVISTATORE 2 PLIDA Progetto Lingua Italiana Dante Alighieri
Esercizi di calcolo combinatorio
 CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi di calcolo combinatorio Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability di Sheldon Ross, quinta
CORSO DI CALCOLO DELLE PROBABILITÀ E STATISTICA Esercizi di calcolo combinatorio Nota: Alcuni esercizi sono tradotti, più o meno fedelmente, dal libro A first course in probability di Sheldon Ross, quinta
Schemi delle Lezioni di Matematica Generale. Pierpaolo Montana
 Schemi delle Lezioni di Matematica Generale Pierpaolo Montana Al-giabr wa al-mukabalah di Al Khuwarizmi scritto approssimativamente nel 820 D.C. Manuale arabo da cui deriviamo due nomi: Algebra Algoritmo
Schemi delle Lezioni di Matematica Generale Pierpaolo Montana Al-giabr wa al-mukabalah di Al Khuwarizmi scritto approssimativamente nel 820 D.C. Manuale arabo da cui deriviamo due nomi: Algebra Algoritmo
PROBABILITA. Sono esempi di fenomeni la cui realizzazione non è certa a priori e vengono per questo detti eventi aleatori (dal latino alea, dado)
 L esito della prossima estrazione del lotto L esito del lancio di una moneta o di un dado Il sesso di un nascituro, così come il suo peso alla nascita o la sua altezza.. Il tempo di attesa ad uno sportello
L esito della prossima estrazione del lotto L esito del lancio di una moneta o di un dado Il sesso di un nascituro, così come il suo peso alla nascita o la sua altezza.. Il tempo di attesa ad uno sportello
Esercizi sul calcolo delle probabilità
 Esercizi sul calcolo delle probabilità Svolti e da svolgere (per MAR 13 marzo) Dati due eventi A e B dello spazio campionario Ω. Si sappia che P(A c )=0,3 P(B)=0,4 e P(A B c )=0,5 si determinino le probabilità
Esercizi sul calcolo delle probabilità Svolti e da svolgere (per MAR 13 marzo) Dati due eventi A e B dello spazio campionario Ω. Si sappia che P(A c )=0,3 P(B)=0,4 e P(A B c )=0,5 si determinino le probabilità
Intervista a Gabriela Stellutti, studentessa di italiano presso la Facoltà di Lettere dell Università di São Paulo (FFLCH USP).
 In questa lezione abbiamo ricevuto Gabriella Stellutti che ci ha parlato delle difficoltà di uno studente brasiliano che studia l italiano in Brasile. Vi consiglio di seguire l intervista senza le didascalie
In questa lezione abbiamo ricevuto Gabriella Stellutti che ci ha parlato delle difficoltà di uno studente brasiliano che studia l italiano in Brasile. Vi consiglio di seguire l intervista senza le didascalie
Esempi di algoritmi. Lezione III
 Esempi di algoritmi Lezione III Scopo della lezione Implementare da zero algoritmi di media complessità. Verificare la correttezza di un algoritmo eseguendolo a mano. Imparare a valutare le prestazioni
Esempi di algoritmi Lezione III Scopo della lezione Implementare da zero algoritmi di media complessità. Verificare la correttezza di un algoritmo eseguendolo a mano. Imparare a valutare le prestazioni
matematica probabilmente
 IS science centre immaginario scientifico Laboratorio dell'immaginario Scientifico - Trieste tel. 040224424 - fax 040224439 - e-mail: lis@lis.trieste.it - www.immaginarioscientifico.it indice Altezze e
IS science centre immaginario scientifico Laboratorio dell'immaginario Scientifico - Trieste tel. 040224424 - fax 040224439 - e-mail: lis@lis.trieste.it - www.immaginarioscientifico.it indice Altezze e
Alcune nozioni di base di Logica Matematica
 Alcune nozioni di base di Logica Matematica Ad uso del corsi di Programmazione I e II Nicola Galesi Dipartimento di Informatica Sapienza Universitá Roma November 1, 2007 Questa é una breve raccolta di
Alcune nozioni di base di Logica Matematica Ad uso del corsi di Programmazione I e II Nicola Galesi Dipartimento di Informatica Sapienza Universitá Roma November 1, 2007 Questa é una breve raccolta di
1 Giochi a due, con informazione perfetta e somma zero
 1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
Predicati e Quantificatori
 Predicati e Quantificatori Limitazioni della logica proposizionale! Logica proposizionale: il mondo è descritto attraverso proposizioni elementari e loro combinazioni logiche! I singoli oggetti cui si
Predicati e Quantificatori Limitazioni della logica proposizionale! Logica proposizionale: il mondo è descritto attraverso proposizioni elementari e loro combinazioni logiche! I singoli oggetti cui si
MATEMATICA 2001. p = 4/6 = 2/3; q = 1-2/3 = 1/3. La risposta corretta è quindi la E).
 MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
Laboratorio di Pedagogia Sperimentale. Indice
 INSEGNAMENTO DI LABORATORIO DI PEDAGOGIA SPERIMENTALE LEZIONE III INTRODUZIONE ALLA RICERCA SPERIMENTALE (PARTE III) PROF. VINCENZO BONAZZA Indice 1 L ipotesi -----------------------------------------------------------
INSEGNAMENTO DI LABORATORIO DI PEDAGOGIA SPERIMENTALE LEZIONE III INTRODUZIONE ALLA RICERCA SPERIMENTALE (PARTE III) PROF. VINCENZO BONAZZA Indice 1 L ipotesi -----------------------------------------------------------
Guardiamo ora però la cosa da un altro punto di vista analizzando il seguente grafico a forma di torta. La torta in 5 parti
 L EQUIVALENZA FRA I NUMERI RAZIONALI (cioè le frazioni), I NUMERI DECIMALI (quelli spesso con la virgola) ED I NUMERI PERCENTUALI (quelli col simbolo %). Ora vedremo che ogni frazione (sia propria, che
L EQUIVALENZA FRA I NUMERI RAZIONALI (cioè le frazioni), I NUMERI DECIMALI (quelli spesso con la virgola) ED I NUMERI PERCENTUALI (quelli col simbolo %). Ora vedremo che ogni frazione (sia propria, che
PROBABILITA CONDIZIONALE
 Riferendoci al lancio di un dado, indichiamo con A l evento esce un punteggio inferiore a 4 A ={1, 2, 3} B l evento esce un punteggio dispari B = {1, 3, 5} Non avendo motivo per ritenere il dado truccato,
Riferendoci al lancio di un dado, indichiamo con A l evento esce un punteggio inferiore a 4 A ={1, 2, 3} B l evento esce un punteggio dispari B = {1, 3, 5} Non avendo motivo per ritenere il dado truccato,
A = { escono 2 teste e due croci (indipendentemente dall ordine) } B = { al primo tiro esce testa }.
 ESERCIZI ELEMENTARI DI CALCOLO DELLE PROBABILITÀ Teorema della somma 1) Giocando alla roulette, calcolare la probabilità che su una estrazione esca: a) Un numero compreso tra 6 e 12 (compresi) oppure maggiore
ESERCIZI ELEMENTARI DI CALCOLO DELLE PROBABILITÀ Teorema della somma 1) Giocando alla roulette, calcolare la probabilità che su una estrazione esca: a) Un numero compreso tra 6 e 12 (compresi) oppure maggiore
da 2 a 5 giocatori, dai 10 anni in su, durata 30 minuti
 da 2 a 5 giocatori, dai 10 anni in su, durata 30 minuti OBIETTIVO Il vincitore è colui che, dopo due round di gioco, delle sue 11 ordinazioni, ne ha consegnate il maggior numero. CONTENUTO DELLA SCATOLA
da 2 a 5 giocatori, dai 10 anni in su, durata 30 minuti OBIETTIVO Il vincitore è colui che, dopo due round di gioco, delle sue 11 ordinazioni, ne ha consegnate il maggior numero. CONTENUTO DELLA SCATOLA
1. Calcolare la probabilità che estratte a caso ed assieme tre carte da un mazzo di 40, fra di esse vi sia un solo asso, di qualunque seme.
 Esercizi difficili sul calcolo delle probabilità. Calcolare la probabilità che estratte a caso ed assieme tre carte da un mazzo di, fra di esse vi sia un solo asso, di qualunque seme. Le parole a caso
Esercizi difficili sul calcolo delle probabilità. Calcolare la probabilità che estratte a caso ed assieme tre carte da un mazzo di, fra di esse vi sia un solo asso, di qualunque seme. Le parole a caso
Dall italiano al linguaggio della logica proposizionale
 Dall italiano al linguaggio della logica proposizionale Dall italiano al linguaggio della logica proposizionale Enunciati atomici e congiunzione In questa lezione e nelle successive, vedremo come fare
Dall italiano al linguaggio della logica proposizionale Dall italiano al linguaggio della logica proposizionale Enunciati atomici e congiunzione In questa lezione e nelle successive, vedremo come fare
MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE. 23 novembre 2006
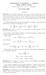 MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE PRIMO COMPITINO FILA B SOLUZIONI 3 novembre 006. Parte I Esercizio.. Al mercato della frutta i prezzi sono scontati rispetto ai prezzi nei supermercati.
MATEMATICA E STATISTICA CORSO B PROF. MARCO ABATE PRIMO COMPITINO FILA B SOLUZIONI 3 novembre 006. Parte I Esercizio.. Al mercato della frutta i prezzi sono scontati rispetto ai prezzi nei supermercati.
Macroeconomia, Esercitazione 2. 1 Esercizi. 1.1 Moneta/1. 1.2 Moneta/2. 1.3 Moneta/3. A cura di Giuseppe Gori (giuseppe.gori@unibo.
 acroeconomia, Esercitazione 2. A cura di Giuseppe Gori (giuseppe.gori@unibo.it) 1 Esercizi. 1.1 oneta/1 Sapendo che il PIL reale nel 2008 è pari a 50.000 euro e nel 2009 a 60.000 euro, che dal 2008 al
acroeconomia, Esercitazione 2. A cura di Giuseppe Gori (giuseppe.gori@unibo.it) 1 Esercizi. 1.1 oneta/1 Sapendo che il PIL reale nel 2008 è pari a 50.000 euro e nel 2009 a 60.000 euro, che dal 2008 al
Terza Edizione Giochi di Achille (13-12-07) - Olimpiadi di Matematica Soluzioni Categoria M1 (Alunni di prima media)
 Il Responsabile coordinatore dei giochi: Prof. Agostino Zappacosta Chieti tel. 087 65843 (cell.: 340 47 47 95) e-mail:agostino_zappacosta@libero.it Terza Edizione Giochi di Achille (3--07) - Olimpiadi
Il Responsabile coordinatore dei giochi: Prof. Agostino Zappacosta Chieti tel. 087 65843 (cell.: 340 47 47 95) e-mail:agostino_zappacosta@libero.it Terza Edizione Giochi di Achille (3--07) - Olimpiadi
Soluzione dell esercizio del 2 Febbraio 2004
 Soluzione dell esercizio del 2 Febbraio 2004 1. Casi d uso I casi d uso sono riportati in Figura 1. Figura 1: Diagramma dei casi d uso. E evidenziato un sotto caso di uso. 2. Modello concettuale Osserviamo
Soluzione dell esercizio del 2 Febbraio 2004 1. Casi d uso I casi d uso sono riportati in Figura 1. Figura 1: Diagramma dei casi d uso. E evidenziato un sotto caso di uso. 2. Modello concettuale Osserviamo
Corso di Laurea in Scienze e Tecnologie Biomolecolari. NOME COGNOME N. Matr.
 Corso di Laurea in Scienze e Tecnologie Biomolecolari Matematica e Statistica II Prova di esame del 18/7/2013 NOME COGNOME N. Matr. Rispondere ai punti degli esercizi nel modo più completo possibile, cercando
Corso di Laurea in Scienze e Tecnologie Biomolecolari Matematica e Statistica II Prova di esame del 18/7/2013 NOME COGNOME N. Matr. Rispondere ai punti degli esercizi nel modo più completo possibile, cercando
Rappresentare i nessi logici con gli insiemi
 Rappresentare i nessi logici con gli insiemi È un operazione molto utile in quesiti come quello nell Esempio 1, in cui gruppi di persone o cose vengono distinti in base a delle loro proprietà. Un elemento
Rappresentare i nessi logici con gli insiemi È un operazione molto utile in quesiti come quello nell Esempio 1, in cui gruppi di persone o cose vengono distinti in base a delle loro proprietà. Un elemento
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Errori più comuni. nelle prove scritte
 Errori più comuni nelle prove scritte Gli errori più frequenti, e reiterati da chi sostiene diverse prove, sono innanzi tutto meta-errori, cioè errori che non riguardano tanto l applicazione delle tecniche,
Errori più comuni nelle prove scritte Gli errori più frequenti, e reiterati da chi sostiene diverse prove, sono innanzi tutto meta-errori, cioè errori che non riguardano tanto l applicazione delle tecniche,
IL MODELLO CICLICO BATTLEPLAN
 www.previsioniborsa.net 3 Lezione METODO CICLICO IL MODELLO CICLICO BATTLEPLAN Questo modello ciclico teorico (vedi figura sotto) ci serve per pianificare la nostra operativita e prevedere quando il mercato
www.previsioniborsa.net 3 Lezione METODO CICLICO IL MODELLO CICLICO BATTLEPLAN Questo modello ciclico teorico (vedi figura sotto) ci serve per pianificare la nostra operativita e prevedere quando il mercato
Cenni sul calcolo combinatorio
 Cenni sul calcolo combinatorio Disposizioni semplici Le disposizioni semplici di n elementi distinti di classe k con kn sono tutti i gruppi di k elementi scelti fra gli n, che differiscono per almeno un
Cenni sul calcolo combinatorio Disposizioni semplici Le disposizioni semplici di n elementi distinti di classe k con kn sono tutti i gruppi di k elementi scelti fra gli n, che differiscono per almeno un
Statistica e biometria. D. Bertacchi. Variabili aleatorie. V.a. discrete e continue. La densità di una v.a. discreta. Esempi.
 Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Maschere a Venezia VERO O FALSO
 45 VERO O FALSO CAP I 1) Altiero Ranelli è il direttore de Il Gazzettino di Venezia 2) Altiero Ranelli ha trovato delle lettere su MONDO-NET 3) Colombina è la sorella di Pantalone 4) La sera di carnevale,
45 VERO O FALSO CAP I 1) Altiero Ranelli è il direttore de Il Gazzettino di Venezia 2) Altiero Ranelli ha trovato delle lettere su MONDO-NET 3) Colombina è la sorella di Pantalone 4) La sera di carnevale,
VINCERE AL BLACKJACK
 VINCERE AL BLACKJACK Il BlackJack è un gioco di abilità e fortuna in cui il banco non può nulla, deve seguire incondizionatamente le regole del gioco. Il giocatore è invece posto continuamente di fronte
VINCERE AL BLACKJACK Il BlackJack è un gioco di abilità e fortuna in cui il banco non può nulla, deve seguire incondizionatamente le regole del gioco. Il giocatore è invece posto continuamente di fronte
Università per Stranieri di Siena Livello A2
 Unità 17 Il Centro Territoriale Permanente In questa unità imparerai: a comprendere testi che danno informazioni sui Centri Territoriali Permanenti per l istruzione e la formazione in età adulta parole
Unità 17 Il Centro Territoriale Permanente In questa unità imparerai: a comprendere testi che danno informazioni sui Centri Territoriali Permanenti per l istruzione e la formazione in età adulta parole
LA STATISTICA NEI TEST INVALSI
 LA STATISTICA NEI TEST INVALSI 1 Prova Nazionale 2011 Osserva il grafico seguente che rappresenta la distribuzione percentuale di famiglie per numero di componenti, in base al censimento 2001. Qual è la
LA STATISTICA NEI TEST INVALSI 1 Prova Nazionale 2011 Osserva il grafico seguente che rappresenta la distribuzione percentuale di famiglie per numero di componenti, in base al censimento 2001. Qual è la
Guida all uso di Java Diagrammi ER
 Guida all uso di Java Diagrammi ER Ver. 1.1 Alessandro Ballini 16/5/2004 Questa guida ha lo scopo di mostrare gli aspetti fondamentali dell utilizzo dell applicazione Java Diagrammi ER. Inizieremo con
Guida all uso di Java Diagrammi ER Ver. 1.1 Alessandro Ballini 16/5/2004 Questa guida ha lo scopo di mostrare gli aspetti fondamentali dell utilizzo dell applicazione Java Diagrammi ER. Inizieremo con
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
SIMULAZIONE TEST INVALSI
 SIMULAZIONE TEST INVALSI STATISTICA E PROBABILITA Nel sacchetto A ci sono 4 palline rosse e 8 nere mentre nel sacchetto B ci sono 4 palline rosse e 6 nere. a. Completa correttamente la seguente frase inserendo
SIMULAZIONE TEST INVALSI STATISTICA E PROBABILITA Nel sacchetto A ci sono 4 palline rosse e 8 nere mentre nel sacchetto B ci sono 4 palline rosse e 6 nere. a. Completa correttamente la seguente frase inserendo
Probabilità Calcolo combinatorio, probabilità elementare, probabilità condizionata, indipendenza, th delle probabilità totali, legge di Bayes
 Sessione Live #3 Settimana dal 7 all 11 marzo 2003 Probabilità Calcolo combinatorio, probabilità elementare, probabilità condizionata, indipendenza, th delle probabilità totali, legge di Bayes Lezioni
Sessione Live #3 Settimana dal 7 all 11 marzo 2003 Probabilità Calcolo combinatorio, probabilità elementare, probabilità condizionata, indipendenza, th delle probabilità totali, legge di Bayes Lezioni
Amore in Paradiso. Capitolo I
 4 Amore in Paradiso Capitolo I Paradiso. Ufficio dei desideri. Tanti angeli vanno e vengono nella stanza. Arriva un fax. Lo ha mandato qualcuno dalla Terra, un uomo. Quando gli uomini vogliono qualcosa,
4 Amore in Paradiso Capitolo I Paradiso. Ufficio dei desideri. Tanti angeli vanno e vengono nella stanza. Arriva un fax. Lo ha mandato qualcuno dalla Terra, un uomo. Quando gli uomini vogliono qualcosa,
Ins. Zanella Classe seconda. Problemi moltiplicativi
 Ins. Zanella Classe seconda Problemi moltiplicativi FOGLI DI CARTA OGGI IN CLASSE SIAMO IN 23 ALUNNI. LA MAESTRA DA AD OGNI ALUNNO 3 FOGLI. DISEGNA QUESTA SITUAZIONE, IN MODO CHE SI CAPISCA QUANTI FOGLI
Ins. Zanella Classe seconda Problemi moltiplicativi FOGLI DI CARTA OGGI IN CLASSE SIAMO IN 23 ALUNNI. LA MAESTRA DA AD OGNI ALUNNO 3 FOGLI. DISEGNA QUESTA SITUAZIONE, IN MODO CHE SI CAPISCA QUANTI FOGLI
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
Ancora sull indipendenza. Se A e B sono indipendenti allora lo sono anche
 Ancora sull indipendenza Se A e B sono indipendenti allora lo sono anche A e B Ā e B Ā e B Sfruttiamo le leggi di De Morgan Leggi di De Morgan A B = Ā B A B = Ā B P (Ā B) = P (A B) = 1 P (A B) = 1 (P (A)
Ancora sull indipendenza Se A e B sono indipendenti allora lo sono anche A e B Ā e B Ā e B Sfruttiamo le leggi di De Morgan Leggi di De Morgan A B = Ā B A B = Ā B P (Ā B) = P (A B) = 1 P (A B) = 1 (P (A)
G iochi con le carte 1
 Giochi con le carte 1 PREPARAZIONE E DESCRIZIONE DELLE CARTE L insegnante prepara su fogli A3 e distribuisce agli allievi le fotocopie dei tre diversi tipi di carte. Invita poi ciascun allievo a piegare
Giochi con le carte 1 PREPARAZIONE E DESCRIZIONE DELLE CARTE L insegnante prepara su fogli A3 e distribuisce agli allievi le fotocopie dei tre diversi tipi di carte. Invita poi ciascun allievo a piegare
Un modello matematico di investimento ottimale
 Un modello matematico di investimento ottimale Tiziano Vargiolu 1 1 Università degli Studi di Padova Liceo Scientifico Benedetti Venezia, giovedì 30 marzo 2011 Outline 1 Investimento per un singolo agente
Un modello matematico di investimento ottimale Tiziano Vargiolu 1 1 Università degli Studi di Padova Liceo Scientifico Benedetti Venezia, giovedì 30 marzo 2011 Outline 1 Investimento per un singolo agente
8. Qual è la probabilità di estrarre da un mazzo di 40 carte napoletane una figura?
 www.matematicamente.it Probabilità 1 Calcolo delle probabilità Cognome e nome: Classe Data 1. Quali affermazioni sono vere? A. Un evento impossibile ha probabilità 1 B. Un vento certo ha probabilità 0
www.matematicamente.it Probabilità 1 Calcolo delle probabilità Cognome e nome: Classe Data 1. Quali affermazioni sono vere? A. Un evento impossibile ha probabilità 1 B. Un vento certo ha probabilità 0
lettera raccomandata. Ecco alcune parole ed espressioni che possono aiutarti a capire meglio il testo.
 Unità 12 Inviare una raccomandata CHIAVI In questa unità imparerai: a comprendere testi che danno informazioni su come inviare una raccomandata parole relative alle spedizioni postali e all invio di una
Unità 12 Inviare una raccomandata CHIAVI In questa unità imparerai: a comprendere testi che danno informazioni su come inviare una raccomandata parole relative alle spedizioni postali e all invio di una
Logica deduttiva, applicazioni avanzate
 Logica deduttiva, applicazioni avanzate 1. Se si assume la verità delle proposizioni se l ornitorinco fa le uova, allora non è un mammifero e l ornitorinco è un mammifero deve di conseguenza essere vera
Logica deduttiva, applicazioni avanzate 1. Se si assume la verità delle proposizioni se l ornitorinco fa le uova, allora non è un mammifero e l ornitorinco è un mammifero deve di conseguenza essere vera
I loro clienti si dedicano maggiormente alle slot e ai gratta&vinci, come mostrato nel grafico sottostante:
 REPORT GIOCO D AZZARDO Come MOVIMENTO NO SLOT in questi mesi abbiamo somministrato ai gestori dei locali, bar, tabacchi e sale slot un questionario per cercare di capire il fenomeno dell azzardo nella
REPORT GIOCO D AZZARDO Come MOVIMENTO NO SLOT in questi mesi abbiamo somministrato ai gestori dei locali, bar, tabacchi e sale slot un questionario per cercare di capire il fenomeno dell azzardo nella
LA MOLTIPLICAZIONE IN CLASSE SECONDA
 LA MOLTIPLICAZIONE IN CLASSE SECONDA Rossana Nencini, 2013 Le fasi del lavoro: 1. Proponiamo ai bambini una situazione reale di moltiplicazione: portiamo a scuola una scatola di biscotti (. ) e diamo la
LA MOLTIPLICAZIONE IN CLASSE SECONDA Rossana Nencini, 2013 Le fasi del lavoro: 1. Proponiamo ai bambini una situazione reale di moltiplicazione: portiamo a scuola una scatola di biscotti (. ) e diamo la
informazioni che si può leggere bene, chiaro con caratteri di scrittura simile a quelli usati nella stampa, ma scritti a mano chi riceve una lettera
 Unità 12 Inviare una raccomandata In questa unità imparerai: a comprendere testi che danno informazioni su come inviare una raccomandata parole relative alle spedizioni postali e all invio di una raccomandata
Unità 12 Inviare una raccomandata In questa unità imparerai: a comprendere testi che danno informazioni su come inviare una raccomandata parole relative alle spedizioni postali e all invio di una raccomandata
a) Determinare i numeri indice a base fissa del fatturato con base 2007=100 e commentare i risultati ottenuti per gli anni 2008 e 2012
 ESERCIZIO 1 Nella tabella che segue sono riportate le variazioni percentuali, rispetto all anno precedente, del fatturato di un azienda. Sulla base dei dati contenuti in tabella a) Determinare i numeri
ESERCIZIO 1 Nella tabella che segue sono riportate le variazioni percentuali, rispetto all anno precedente, del fatturato di un azienda. Sulla base dei dati contenuti in tabella a) Determinare i numeri
