P 210, , ,618 m C 88, , ,405 m D 57, , ,835 m C 114, , ,437 m B
|
|
|
- Eleonora Orlando
- 8 anni fa
- Visualizzazioni
Transcript
1 ESERCIZI SVOLTI DI TOPOGRAFIA PROF. ING. PIANTONI ALDO 1. si deve determinare la pendenza tra due punti P e Q, che rappresentano gli estremi di una strada rettilinea. Poiché non si è riusciti ad individuare un punto dal quale siano visibili contemporaneamente i due punti, sono state effettuate, con un teodolite a graduazione destrorsa integrato da distanziometro ad onde, due stazioni celerimetriche collegate tra loro in modo indiretto. I dati rilevati sono i seguenti. stazione Punto collimato C.O. C.V. Distanza inclinata A H=1.705 P 210, , ,618 m C 88, , ,405 m D 57, , ,835 m C 114, , ,437 m B D 154, , ,585 m H=1.644 Q 246, , ,606m Si assuma, per i calcoli altimetrici, un altezza del prisma pari a 1,500m, k=0,12 e R= m. Con i dati forniti nel libretto delle misure si determinano innanzi tutto le distanze orizzontali AP= sen = m AC= sen = m AD= sen = m BC = sen = m BD= sen = m BQ= sen = m Per risolvere la parte planimetrica conviene determinare le coordinate di P e Q nel sistema di riferimento celerimetrico con origine in A, adottando il procedimento del collegamento di Porro. Le coordinate del punto P possono essere determinate subito, poiché tale punto è stato collimato direttamente da A: x p =AP senθ AP = sen = m y p =AP cosθ AP = cos = m si procede col calcolo dell angolo di disorientamento tra le due stazioni, calcolando le coordinate dei due punti C e D nei due sistemi di riferimento
2 Sistema di riferimento con origine in A x C =AC senθ AC = sen = m y C =AC cosθ AC = cos = m x D =AD senθ AD = sen = m y D =AD cosθ AD = cos = m x D - x C θ CD =ARCTAN = y D - y C Sistema di riferimento con origine in B x C =BC senθ BC = sen = m y C =BC cosθ BC = cos = m x D =BD senθ BD = sen = m y D =BD cosθ BD = cos = m x D - x C θ CD =ARCTAN = y D - y C L angolo di disorientamento tra le due stazioni è pari alla differenza dei due azimut ε=θ CD - θ CD = le coordinate del punto Q, nel sistema di riferimento con origine in A valgono: x Q = x C +CB senθ CB + BQ senθ BQ = x C +CB sen(θ' CB - ε ) + BQ sen(θ' BQ - ε ) = sen ( ) sen ( ) = m y Q = y C +CB cosθ CB + BQ cosθ BQ = y C +CB cos(θ' CB - ε ) + BQ cos(θ' BQ - ε ) = cos( ) cos ( ) = m per controllo, si ripete il calcolo delle coordinate di Q, utilizzando il percorso ADBQ anziché ACBQ: x Q = x D +DB senθ DB + BQ senθ BQ = x D +DB sen(θ' DB - ε ) + BQ sen(θ' BQ - ε ) = 242, sen ( ) sen ( ) = m y Q = y D +DB cosθ DB + BQ cosθ BQ = y D +DB cos(θ' DB - ε ) + BQ cos(θ' BQ - ε ) = cos( ) cos ( ) = m che, in pratica, coincidono con quelle calcolate precedentemente. La distanza tra i punti P e Q risulta quindi: PQ= w (x Q - x P ) 2 + (y Q - y P ) 2 = m Anche la parte altimetrica può essere risolta considerando i percorsi PACBQ e PADBQ. I dislivelli misurati si calcolano con la formula della livellazione trigonometrica: AP = h A - h P + AP cot φ AP + (1-k) AP 2 /2R = 15,121 AC = h A - h P + AC cot φ AC + (1-k) AC 2 /2R = AD = h A - h P + AD cot φ AD + (1-k) AD 2 /2R = BC = h B - h P + BC cot φ BC + (1-k) BC 2 /2R = BD = h B - h P + BD cot φ BD + (1-k) BD 2 /2R = BQ = h B - h P + BQ cot φ BQ + (1-k) BQ 2 /2R = utilizzando il percorso PACBQ si ottiene il seguente dislivello PQ: ricordando che PA= - AP PQ = PA + AC + CB + BQ = = m utilizzando invece il percorso PADBQ si ottiene: PQ = PA + AD + DB + BQ = = m
3 si adotta come valore più attendibile del dislivello la media aritmetica dei due valori PQ = ( )/2 = m la pendenza della strada vale dunque: p PQ = / = = % 2. determinare le coordinate planimetriche e la quota del punto P, dal quale si sono collimati, con un teodolite centesimale destrorso, i tre punti A, B e C di coordinate note: A( ; ) B( ; ) C( ; ) stazione Punto collimato C.O. C.V. A gon gon P B gon gon h=1.609m C gon gon Si assuma, per il calcolo della quota, k=0,14; R=6.377 Km; Q A =188,766, Q B =189,215, Q C =201,545 Gli angoli orizzontali che le proiezioni delle linee di collimazione formano tra loro valgono: α=(pb) - (PA)= = gon β= (PC) - (PA) = = gon dalla sequenza con cui si succedono gli angoli di direzione, il punto P non può che stare a sinistra della spezzata ABC; infatti, se il punto P fosse a destra, gli angoli di direzione dovrebbero aumentare da C verso A, mentre si verifica il contrario. Stabilita dunque la posizione di P è possibile effettuare la costruzione grafica, che permette di stabilire una soluzione approssimata del problema. Dalle coordinate di A e di B si ricava la distanza e l'azimut tra tali punti AB= w q ( ) 2 + ( ) 2 r = m θ AB =arctan q( )/( )r+200= gon
4 tracciata la circonferenza passante per P, A e B, detto H il punto di intersezione con il segmento PC, si ha, visto che gli angoli AHB e BAH sono uguali agli angoli α, β Le coordinate di H valgono quindi: AH=AB/senα x sen(α+β) = m x H = x A +AH senθ AH = x A +AH sen(θ AB + β ) = m y H = y A +AH cosθ AH = y A +AH cos(θ AH + β) = m Dalle coordinate di H si ottiene: θ HC = θ PC = arctan q( )/( )r+200 = θ PA = θ PC - (α+β ) = gon θ AP = θ PA + 200= gon da cui si possono calcolare gli elementi incogniti del triangolo ABP: Che permette di calcolare le coordinate di P BAP=θ AP -θ AB = = gon PBA= 200-(α + BAP) = gon PA= AB/senα x senpba = m X P = x A +PA senθ AP = sen = m Y P = y A +PA cosθ AP = cos = m Per risolvere il problema altimetrico è necessario calcolare le distanze dei vertici B e C dal punto P: PB= wq( ) 2 + ( ) 2 r = PC= wq( ) 2 + ( ) 2 r = I tre dislivelli misurati valgono quindi: R+Q PA = h P + PA cot ϕ PA + (1-k) PA 2 /2R = R R+Q PB = h P + PB cot ϕ PB + (1-k) PB 2 /2R = R R+Q PC = h P + PC cot ϕ PC + (1-k) PC 2 /2R = R La quota del punto P può quindi essere determinata in tre modi diversi a seconda che si consideri come riferimento rispettivamente il punto A, B o C: Q' P =Q A + AP = Q A - PA = = Q" P =Q B + BP = Q B - PB = = Q'" P =Q C + CP = Q C - PC = = Come quota potrà quindi essere assunta la media aritmetica Qp=
5 3. determinare l area compensata della particella rilevata Operazioni di campagna Per ogni punto collimato si sono determinate le distanze orizzontali, utilizzando un nastro metrico d'acciaio, e gli angoli orizzontali. Gli angoli verticali non sono stati letti, poiché non è stata presa in considerazione la parte altimetrica del rilievo. Sono state prefissate sia la tolleranza angolare sia quella lineare, che devono essere superiori ai rispettivi errori di chiusura: tα = 4 c e3 =6.9 c t l = 0.02en l LIBRETTO DELLE MISURE stazione Punto collimato Cerchio orizzontale Distanza orizzontale g m g m g m g m g g m g m g m g g g g La planimetria dell'appezzamento, con i punti rilevati, è riportata nella figura.
6 Calcolo dell'area con compensazione empirica Si esegue dapprima il calcolo della poligonale, mediante compensazione empirica. Gli angoli al vertice risultano: α = 121,583-77,543 = 44,040 g β=399, ,583 = 78,069 g γ = = 77,837 g Si procede quindi con la compensazione angolare degli angoli interni: ε α = 44, , , = 199, = 0,054 g che risulta inferiore alla tolleranza angolare prefissata: ta = 4 c w3 = 6,9 c > 5,4 c e pertanto si può procedere con la compensazione angolare. Poiché la somma degli angoli misurati è risultata minore di 200 g, si dovrà aggiungere a ciascun angolo misurato 1/3 dell'errore di chiusura angolare εα: αc = 44, ,018 = 44,058 g
7 βc = 78, ,018 = 78,087 g γc = 77, ,018 =77,855 g Si possono ora calcolare gli azimut, assumendo un sistema di riferimento avente origine nel punto 100 e asse delle ordinate diretto lungo l'origine del cerchio orizzontale in tale stazione; θ = 121,583 g θ = θ βc +200= g θ = θ γc -200= g Per controllo: θ = θ αc -200= g Si procede con la compensazione lineare, calcolando le coordinate parziali provvisorie: sono le proiezioni dei lati sugli assi (x 200 ) 100 = d sen θ = 23,151 m (x 300 ) 200 = d sen θ = -0,086 m (x 100 ) 300 = d sen θ = -23,049 m (y 200 ) 100 = d cos θ = -8,164 m (y 300 ) 200 = d cos θ = 16,625 m (y 100 ) 300 = d cos θ = - 8,493 m Gli errori di chiusura lineare, rispettivamente lungo X e lungo Y, si ricavano facendo la somma: delle coordinate parziali: e x = n(xj)i = 23,151-0,086-23,049 = 0,016 m e y = n(yj)i = -8, ,65-8,493 = -0,032 m Si ricava quindi l'errore lineare complessivo, confrontandolo con la tolleranza lineare: ε L = e(ε 2 x + ε 2 y)= 0,036 m < t L = 0,02 e65,737 =. 0,162 m Poiché la verifica è soddisfatta, si può procedere con la compensazione lineare; si calcolano dapprima gli errori unitari:
8 ux= εx / n (xj)i = 3, (x 200 ) 100 = (x 200 ) u x (x 200 ) 100 = 23,143 m (x 300 ) 200 = (x 300 ) u x (x 300 ) 200 = -0,086 m (x 100 ) 300 = (x 100 ) u x (x 100 ) 300 = -23,057 m uy= εy / n (yj)i = - 9, (y 200 ) 100 = (x 200 ) u x (y 200 ) 100 = -8,156 m (y 300 ) 200 = (x 300 ) u y (y 300 ) 200 = 16,641 m (y 100 ) 300 = (x 100 ) u y (y 100 ) 300 = - 8,485 m Le coordinate compensate delle tre stazioni valgono quindi: x 100 = 0,000 m x 200 = x 100 +(x 200 ) 100 = m x 300 = x 200 +(x 300 ) 200 = 23,057 m y 100 = 0,000 m y 200 = y 100 +(y 200 ) 100 = -8,156 m y 300 = y 200 +(y 300 ) 200 = 8,845 m Si ricavano ora le coordinate dei quattro vertici dell'appezzamento, partendo dalle coordinate compensate della poligonale e facendo la media aritmetica dei punti iper-determinati: x 101 = x 100 +d sen θ =0, ,400 sen 8,801 = 1,709 m y 101 = y 100 +d cos θ =0, ,400 cos 8,801 = 12,282 m x' 102 = x 100 +d sen θ =0, ,868 sen 198,201 = 0,364 m y' 102 = y 100 +d cos θ =0, ,868 cos 198,201 = -12,863 m x" 102 = x 200 +d sen θ =23, ,235 sen 287,011 = 0,390 m y" 102 = y 200 +d cos θ = -8, ,235 cos 287,011 = -12,864 m x 102= ( x' 102+ x" 102)/2 = 0,377 y 102= ( y' 102+ y" 102)/2 = -12,864 x' 201 = x 200 +d sen θ = 23,143+ 6,679 sen 79,518 = 29,479 m y' 201 = y 200 +d cos θ = -8, ,679 cos 79,518 = -6,044 m x" 201 = x 300 +d sen θ =23, ,859 sen 173,528 = 29,463 m y" 201 = y 300 +d cos θ = 8, ,859 cos 173,528 = -6,023 m
9 x 201= ( x' 201+ x" 201)/2 = 29,471 m y 201= ( y' 201+ y" 201)/2 = -6,034 x 301 = x 300 +d sen θ = 23,057+ 4,395 sen 348,724 = 19,888 m y 301 = y 300 +d cos θ = 8, ,395 cos 348,724 = 11,530 m Avendo determinato le coordinate dei vertici, si può ora calcolare l'area compensata dell'appezzamento racchiuso dalla poligonale applicando la formula di Gauss: A =1/2 ny i (X i-l - X i+ l) =1/2[12,282 (19,888-0,377) - 12,864 (1,709-29,471) - 6,034 (0,377-19,888)+11,350 (29,471-1,709)] =517,3 m 2 4. il quadrilatero ABCD è stato rilevato con un tacheometro centesimale destrorso determinando i seguenti elementi stazione Punto collimato Cerchio orizzontale Distanza orizzontale D 0,000 gon 66,153 gon A B 135,456 gon 98,389 gon C 31,558 gon 115,444 gon B A 377,165 gon 98,387 gon Dividere il quadrilatero in tre parti, proporzionali ai numeri 3,5 4,5 3,2 con due dividenti parallele al lato CD, in modo che l'area proporzionale a 3,5 contenga tale lato, mediante le distanze dei loro estremi dai vertici C e D Dal libretto delle misure si ricavano gli angoli in A e in B e la distanza media AB: α=(ab)-(cd)=135,456 gon β=(bc)-(ba) = 54,393 gon AB= (98, ,387)/2= 98,388 m dapprima risolviamo il quadrilatero ABCD, scomponendolo nei due triangoli ABD e BDC.
10 TRIANGOLO ADB BD= w AB 2 + AD 2-2AB AD cos α = 144,697 m Per determinare l'angolo β 1 possiamo applicare il teorema dei seni, poichè α è ottuso β 1 = arcsen (sen α / BD x AD)= 25,373 gon δ 1 = α - β 1 = 39,171 gon A (ABD) = 1/2 ABxAD sen α= 2762,52 m 2 TRIANGOLO BDC β2 = β - β1 = gon CD = w BD 2 + BC 2-2BD BC COSβ 2 =65,323 m γ = arccos q(bc 2 + CD 2 - BD 2 ) /(2BC CD) r = 114,228 gon δ 2 = γ - β 2 = 56,752 gon δ = δ 1 + δ 2 = 95, 923 gon A (BDC) = 1/2 BDxBC sen β2 = 3676,81 m 2 Si può ora determinare l'area del quadrilatero ABCD e delle parti frazionate A(ABCD)= A(ABD) + A(BDC) = 6439,33 m 2 A 1 = 3,5/(3, + 4,5 + 3,2 ) xa(abcd) = 2012,29 A 2 = 4,5/(3, + 4,5 + 3,2 ) xa(abcd) = 2587,23 A 3 = A(ABCD) - A1 - A2 = 1839,81 Applichiamo ora la formula del trapezio alla prima superficie CDMN MN = w CD 2-2A 1 (cotγ +cotδ) = 70,169 m h= 2A 1 / (CD+MN) = 29,703 m CM = h/senγ = 30,461 m DN = h/senδ = 29,764 m In modo analogo si procede per determinare la posizione della dividente PQ, salvo verificare in questo caso che il punto Q ricada all'interno del segmento DA (altrimenti si deve procedere partendo dalla terza superficie) PQ = w CD 2-2(A 1 + A 2 )(cotγ +cotδ) = 75,947 m h 2 = 2(A 1 + A 2 )/ (CD+PQ) = 65,117 m CP = h 2 /senγ = 65,777 m DN = h 2 /senδ = 65,250 m < AD=66,153 m
11 5. la bisettrice CM divide il triangolo ABC in due parti aventi la seguente valenza unitaria: triangolo ACM: v 1 =5,00 /m 2 triangolo BCM: v 2 = 7,00 /m 2 la posizione degli estremi P e Q delle due nuove dividenti uscenti dal vertice C che dividono il triangolo in tre parti di uguale valore, conoscendo i seguenti dati c= 158,42 m α = 42,615 β= 38,744 applicando il teorema dei seni, determiniamo gli elementi incogniti del triangolo γ= (α+β) = 98,641 b= c/senγ x senβ = 100,284 m a= c/senγ x senα = 108,493 m e la bisettrice che divide le superfici a diversa valenza : b CM = sen (α+γ/2) sen α = 67,938 m il valore complessivo dell'appezzamento ABC è quindi v T = A(ACM)x5,00 + A(BCM)x7,00 = 1/2(bx5,00 + ax7,00)cm sen γ/2 = ,28 pertanto ciascuna delle parti derivate dovrà avere un valore pari ad 1/3 di quello totale, che diviso per il valore unitario della parte corrispondente fornisce la relativa area A (ACQ) = v 1 /5,00 = ,09/5,00 = 2165,4 m 2 A (BCP) = v 2 /7,00 = ,09/7,00 = 1546,7 m 2 AQ= 2A(ACQ)/(b senα) = 63,783 m BP= 2A(BCP)/(a senβ) = 45,559 m
12 6. due appezzamenti di terreno contigui, appartenenti a due distinti proprietari, hanno la parte di confine in comune rappresentata dalla spezzata ABCD. Uno degli appezzamenti è rappresentato dalla poligonale ABCDE; i confini dell'altro appezzamento sono rappresentati in corrispondenza del punto A dal prolungamento del lato EA ed in corrispondenza del punto D dal prolungamento del lato ED. I due proprietari desiderano sostituire alla spezzata ABCD un nuovo confine rettilineo, parallelo alla direzione AD, in modo da realizzare la condizione di compenso delle aree aggiunte e sottratte ai due proprietari. Gli elementi misurati con un tacheometro destrorso sono raccolti nel seguente libretto di campagna. stazione Punto collimato Cerchio orizzontale Distanza orizzontale E 44,9074 g - A B 143,7116 g 109,003 A 0,0000 g - B C 84,3715 g - B 0,0000 g 156,374 C D 315,3065 g 85,606 C 0,0000 g - D E 35,6848 g - Determinare la posizione della nuova dividente Si ricavano innanzi tutto dal libretto di campagna gli angoli al vertice (vedi figura): α= (AB) - (AE) = 98,8042 g β = (CD) - (CB) = 315,3065 g γ = (BC) - (BA) = 84,3715 g δ = (DE) - (DC) = 35,6848 g II problema può essere risolto in due modi diversi: imponendo che l'area ceduta da un proprietario sia equivalente a quella acquisita dallo stesso, oppure calcolando l'area di un appezzamento di terreno fittizio che contenga la spezzata da rettificare e imponendo la stessa area all'appezzamento col confine rettificato. Generalmente la prima soluzione è conveniente quando la spezzata da rettificare è formata da solo due lati, mentre conviene la seconda soluzione quando la spezzata ha più di due lati. In quest'ultimo caso è opportuno calcolare l'area dell'appezzamento fittizio mediante la formula di Gauss; infatti, se il poligono è intrecciato, abbiamo visto nella prima unità che tale formula fornisce già la differenza tra l'area percorsa in senso antiorario e quella percorsa in senso orario. Per rendersi conto dei vantaggi della seconda soluzione rispetto alla prima, con una spezzata di soli tre lati, come in questo caso, si presentano qui di seguito entrambe le soluzioni. Prima modalità Congiunto A con D, e indicato con P il punto di intersezione col lato BC, si nota dalla figura che se le aree dei due triangoli ABP e PCD fossero uguali, il lato AD sarebbe la dividente cercata. Se invece dovesse prevalere l'area ABP sull'area PCD, si dovrà spostare il confine AD verso B, parallelamente a se stesso, in modo che l'area del trapezio AA'D'D risulti uguale all'eccedenza dell'area ABP rispetto all'area PCD. Viceversa, se dovesse risultare maggiore l'area del triangolo PCD, il confine AD dovrà essere spostato verso C. Ricaviamo dunque le aree dei due triangoli staccati dal lato AD. Considerato il triangolo ABC, del quale si conoscono due lati e l'angolo compreso, si ha: AC = eab 2 + BC 2-2 AB BCcos β = 167,479 m
13 AC 2 + BC 2 - AB 2 ACB = arccos = 43,4982 g 2 AC BC CAB = β - ACB = 72,1303 g Considerando ora il triangolo ACD: ACD = ACB + (400 - δ) = 128,1917 g AD = wac 2 + CD 2-2 AC CD cos ACD = 218,323 m CD 2 + AD 2 - AC 2 ADC = arccos = 48,7531 g 2 CD AD CAD = ACD - ADC = 23,0552 g Si possono pertanto ricavare le aree dei due triangoli, applicando la formula : A(PCD) = 1/2 CD 2 ( senbcd senadc ) / sen (BCD + ADC) = 2.851,21 m 2 A(ABP) = 1/2 AB 2 ( sendab senβ ) / sen (DAB + β) = 4.641,15 m 2 essendo DAB = CAB - CAD = 49,0751 g. L'area del triangolo ABP risulta dunque più grande di quella del triangolo PCD di: = 4.641, ,21 = 1.789,94 m 2 Tale area dovrà essere restituita al proprietario dell'appezzamento ABCDE, mediante il trapezio A'ADD'. Si ricavano quindi ì due angoli adiacenti alla base AD di tale trapezio: DAA' = α + DAB = 150,2709 g ADD' = δ - ADC = 115,5621 g Per cui, applicando la formula del trapezio: Valtezza del trapezio si ricava dalla formula inversa dell'area: A'D' = wad 2-2 (cot DAA' + cot ADD') = 228,404 m h = 2 /(AD + A'D') = 8,014 m Per cui le distanze cercate risultano:
14 AA'= h/sen DAA' = 11,381 m DD' = h/ sen ADD' = 8,259 m Seconda modalità Per calcolare l'area del poligono intrecciato ABCD si devono determinare le coordinate dei vertici della poligonale ABCD. Allo scopo si assume un sistema di assi avente origine in A ed asse delle ordinate diretto lungo AE (v. figura). Gli azimut della poligonale si ricavano con la formula di trasporto: θab = α = 98,8042 g θbc = θ AB + β = 383,1757 g θcd = θbc + γ = 98,4822 g Poiché le distanze sono note si possono subito ricavare le coordinate dei vertici: X B = AB senθab = 108,984 m Xc =X B + BC sen θbc = 68,138 m X D = Xc + CD sen θcd = 153,720 m Y B = AB cos θab = 2,047 m Yc = Y B + BC cos θbc = 152,992 m Y D = Yc + CD cos θcd = 155,033 m Dalle coordinate, applicando la formula di Gauss, si può ricavare direttamente l'area del poligono intrecciato. Si noti che se l'area risulterà positiva significherà che l'area del triangolo ABP (numerato in senso antiorario) prevale su quella del triangolo PCR = 1/2 [2,047(0-68,138) + 152,992(108, ,720) + 155,033(68,138 - O)] = 1.789,95 m 2 il risultato è positivo, uguale a quello ricavato nelta prima modalità. Ciò sta ad indicare quindi che il lato AD dovrà essere spostato verso il vertice B (si noti come il numero di passaggi risulti inferiore rispetto alla precedente soluzione). Per applicare la formula del trapezio si devono prima determinare la base AD e i due angoli adiacenti; si ha: AD = w (x D 2 + y D 2 ) = 218,323 m A'AD = θ AD = arctan (x D /y D ) = 150,2707 g ADD' = δ - θ DC + θ DA = 115,5625 g e quindi: A'D' = w (AD 2-2 (cotdaa' +cotadd') )= 228,404 m L'altezza del trapezio si ricava dalla formula inversa dell'area: h =2 / (AD+A'D')= 8,014 m
15 e, procedendo come nel caso precedente: AA' = h/sen DAA' = 11,381 m DD' = h/senadd' = 8,259 m 7. Un appezzamento di terreno di forma quadrilatera ABCD è individuato altimetricamente dalle due falde ABC e ACD. Conoscendo le coordinate e le quote dei vertici: A(O; O; 5,456) B(35,466; - 15,443; 7,554) C(81,466; - 5,455; 5,649) D(12,455; 33,566; 6,876) si determini il volume di terreno necessario per realizzare lo spianamento nei seguenti casi: a) piano orizzontale a quota 5,000 m; b) piano orizzontale a quota 10,000 m. SQLUZlONE Caso a Determiniamo le quote rosse nei vertici per stabilire se si tratta di spianamento di sferro, riporto o misto (vedi figura): r A = 5,000-5,456 = - 0,456 m r B = 5,000-7,554 = - 2,554 m r C = 5,000-5,649 = - 0,649 m r D = 5,000-6,876 = - 1,876 m Dato che tutte le quote rosse sono negative, lo spianamento sarà completamente di sferro. Per calcolare il volume necessario, calcoliamo le aree delle due falde con la formula di Gauss: A(ABC) =1/2 n y i (x i-1 -x i+1 ) = 1/2[y B (-x c ) + y c (x B )] = 532,31 m 2 A(ACD) =1/2 n y i (x i-1 -x i+1 ) = 1/2[y C (-x D ) + y D (x C )] = 1.401,21 m 2
16 Il volume di sterro risulta quindi (ignorando i segni meno delle quote rosse, tutti negativi): Caso b V st = A(ABC) (r A + r B + r C )/3 + A(ACD) (r A + r C + r D )/3= 649, ,34 = 2.041,58 m 3 In questo caso lo spianamento è di solo riporto, poiché le quote rosse sono tutte positive: r A = 10,000-5,456= 4,544 m r B = 10,000-7,554 = 2,446 m r C = 10,000-5,649 = 4,351 m r D = 10,000-6,876 = 3,124 m Il volume di riporto totale.risulta: Vrip = A(ABC) (r A + r B + r C )/3+ A (ACD) (r A + r C + r D )/3= 2.012, ,71 = 7.626,02m 3
17 ESAME DI STATO PER GEOMETRI - ANNO 1998 La proprietà fondiaria quadrilatera di vertici 1324, per motivi di successione testamentaria, deve essere divisa in due parti equivalenti. I benefici ari decidono di realizzare il frazionamento con una dividente MN parallela al lato U e convengono, altresì, che quella dividente rappresenti l'asse di un canale per uso irriguo, di comune proprietà. Il tecnico preposto all'espletamento dell'incarico professionale decide, indipendentemente dalle coordinate cartografiche planimetriche lette sugli atti catastali, di ridefinire la geometria di quel fondo mediante un opportuno rilevamento, i cui risultati, comprensivi delle quote, conseguenti alle misurazioni e ai relativi calcoli, sono qui riportati. X1= 236,80 m y 1= 172,40 m Q1=201,OO m X2 =576,10 m Y2 =368,40 m Q2 =207,90 m X3 = 616,00 m Y3= 960,10 m Q3=202,80 m X4 = 208,50 m Y4=840,20 m Q4= 191,10 m Le due falde piane 124 e 234 definiscono l'orografia del fondo. L'asse del canale sarà costituito da un'unica livelletta con quota rossa uguale a zero nel punto N, e con pendenza negativa da N verso M. TI valore di essa sarà scelto dal candidato che fisserà anche la larghezza del fondo del canale e le scarpe delle sue sponde. Il candidato, dopo aver determinato le distanze 1M e 2N (M sulla 14, N sulla 23), disegni, per la definizione di quel progetto, la planimetria della proprietà fondiaria e del frazionamento, il profilo longitudinale lungo l'asse del canale e un congruo numero di sezioni trasversali adottando opportunamente le scale di rappresentazione. Determinazione della nuova dividente Per il disegno della planimetria, assumiamo che le coordinate assegnate siano riferite ad un sistema di assi avente l'asse X come asse delle ascisse e l'asse Y come asse delle ordinate, non essendo specificato nel testo che si tratta di coordinate catastali. I Si calcola innanzi tutto l'area A T dell'intero appezzamento 1234, metà della quale dovrà essere assegnata alle due parti i derivate. Poiché si dispone delle coordinate dei vertici, risulta più pratico applicare la formula di Gauss :
18 A T = ny i (X i-1 - X i+i ) = m 2 Essendo la nuova dividente parallela al lato 12 si applica il problema del trapezio, calcolando dapprima la lunghezza della base 12 e i due angoli adiacenti: 12 = w (X 2 - X l ) 2 + (Y 2 - Y 1 ) 2 = 391,84 m α = θ 12 - θ gon = 69,3481 gon essendo: β = θ 23 - θ gon = 137,6345 gon θ 12 = arctan (X 2 ) 1 /(Y 2 ) 1 = 66,6519 gon θ. 14 = arctan (X 4 ) 1 /(Y 4 ) gon = 397,3037 gon θ 23 = arctan (X 3 ) 2 /(Y 3 ) 2 = 4,2864 gon θ 21 = θ gon = 266,6519 gon Applicando ora la formula risolutiva del problema del trapezio, si ottiene la lunghezza della nuova dividente: MN = w (1-2) 2-2A T ( cot α + cot β )= 434,03 m Ricavando ora l'altezza del trapezio dalla formula dell'area si possono determinare le distanze richieste dal tema: h = 2A T / (1-2) + MN)=283,62m 1M =h/sen α= 320,00 m 2N = h/sen β= 341,59 m Nella figura 1 è riportata la planimetria della proprietà con indicazione della nuova dividente.
19 Determinazione della pendenza del canale Calcoliamo dapprima le quote del terreno in corrispondenza dell'asse del canale (punti M ed N), tenuto conto che l'appezzamento di terreno è costituito dalle due falde piane 124 e 234. Si conviene di indicare con Q le quote del terreno e con q quelle di progetto. Q N = Q 2 + 2N (Q 3 -Q 2 )/ 23 =204,96 m Q M = Q 1 + 1M (Q 4 -Q 1 )/ 14 =196,26 m essendo: 23 =w q (X 3 - X 2 ) 2 + (Y 3 - Y 2 ) 2 r = 593,04m 14 =w q (X 4 - X 1 ) 2 + (Y 4 - Y 1 ) 2 r = 668,40m Prima di determinare la pendenza di progetto è necessario calcolare la quota del terreno nel punto P di intersezione della congiungente 24 con l'asse del canale. Si ha: 4P = 4M/ senmp4 = 311,76 m δ1 = θ 41 - θ 42 = 39,4412 gon MP = 4M/ sen (α+δ1) sen δ1= 204,25m Q p = Q 4 +4P (Q 2 -Q 4 )/ (24)= 199,86 m Per la scelta ottimale della pendenza, trattandosi di un canale ad uso irriguo, si dovrebbe utilizzare un valore compreso tra 0,06 e 0,10%, affinché la velocità dell'acqua non risulti troppo elevata, per evitare fenomeni di erosione delle sponde e del fondo. Tale valore risulta però in disaccordo con la pendenza massima della congiungente MN (si noti che si tratta di una spezzata, appartenendo a due falde diverse), che risulta pari rispettivamente a:
20 tratto NP: (199,86-204,96)/229,79= -2,22% tratto PM: (196,26-199,86)/204,25= -1,76% Le pendenze del terreno sono molto elevate per la realizzazione di un canale ad uso irriguo, tali comunque da richiedere la realizzazione di particolari accorgimenti costruttivi del canale. Continuiamo comunque nello svolgimento dell' esercizio assumendo che il canale in progetto rappresenti il tronco di un canale irriguo avente larghezza del fondo di 2 m, profondità iniziale di 2 m e pendenza uniforme del 2,3% (valore esagerato dal punto di vista idraulico, ma tale da mantenere una profondità minima di 2 m e non ottenere un canale pensile). In tali ipotesi le quote di progetto di fondo del canale risultano: q N = Q N - 2,0 = 202,96 m q M = q N - MN. 0,023 = 192,98 m. q P =q M + MP. 0,023 = 197,68 m Le differenze tra le quote del progetto e quelle del terreno (quote rosse), corrispondenti alla profondità del canale rispetto al piano campagna risultano quindi: r N = 202,96-204,96 = - 2,00 m r M = 192,98-196,26 = - 3,28 m r p = 197,68-199,86 = - 2,18 m Per il disegno delle sezioni trasversali, è necessario determinare la pendenza del terreno perpendicolarmente all'asse del canale. Tale pendenza risulterà diversa a seconda che si considerino le falde piane 124 o 234. Per il calcolo si I mandino
21 da M e da N le perpendicolari all'asse del canale, fino ad intersecare in R ed S rispettivamente i lati 12 e 34. Si determinano quindi le distanze di tali punti dai vertici 1 e 3. Per il triangolo M1R: 1R = 1M. cos α = 148,19m MR = 1M. Sen α = 283,63 m E per il triangolo SN3: SN3 = β = 37,6345 gon S3N = θ 34 - θ 32 = 77,4962 gon 3S = 3N/ sen (SN3 + S3N) x sen SN3 = (23-2N)/sen (SN3 + S3N) x sensn3 = 114,20m NS= 3N/sen (SN3 + S3N) x sen S3N = 242,73 m Le quote dei punti R ed S risultano pertanto: Q R = Q 1 + 1R (Q 2 -Q 1 )/ 12= 203,61 m Q S = Q 3 + 3S (Q 4 -Q 3 )/ 34= 198,83 m Le pendenze del terreno perpendicolarmente all'asse del canale p 1 e p 2 risultano quindi, rispettivamente nelle due falde 124 e 234: P 1 = (Q M - Q R )/ MR= -2,59% P 2 = (Q s - Q N )/NS= -2,53% Nelle figure 3, 4 e 5 riportiamo le tre sezioni trasversali ritenute più rappresentative, effettuate rispettivamente in corrispondenza dei punti N, P e M. Si è assunto come riferimento per il tracciamento delle sezioni quello relativo al senso di scorrimento dell'acqua, in modo che la destra della sezione corrisponda alla destra idraulica. Per completare il tracciamento delle sezioni si è ipotizzato che la pendenza del terreno oltre le falde sia costante, in quanto non si hanno dati a disposizione per calcolarla.
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ELEMENTI DI TOPOGRAFIA - ESERCIZI
 ELEMENTI I TOPOGRFI ESERIZI 1. ato il quadrilatero, i cui vertici si seguono in senso antiorario, di cui si conoscono le coordinate dei vertici e rispetto a un sistema di assi ortogonali: E = 23,55 m N
ELEMENTI I TOPOGRFI ESERIZI 1. ato il quadrilatero, i cui vertici si seguono in senso antiorario, di cui si conoscono le coordinate dei vertici e rispetto a un sistema di assi ortogonali: E = 23,55 m N
ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA.
 ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA. Prerequisiti I radicali Risoluzione di sistemi di equazioni di primo e secondo grado. Classificazione e dominio delle funzioni algebriche Obiettivi minimi Saper
ELEMENTI DI GEOMETRIA ANALITICA: LA RETTA. Prerequisiti I radicali Risoluzione di sistemi di equazioni di primo e secondo grado. Classificazione e dominio delle funzioni algebriche Obiettivi minimi Saper
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 2004
 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 004 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1 Sia f la funzione definita da: f
ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO 004 Il candidato risolva uno dei due problemi e 5 dei 10 quesiti in cui si articola il questionario. PROBLEMA 1 Sia f la funzione definita da: f
LE SEZIONI TRASVERSALI
 LE SEZIONI TRASVERSALI Rappresentano l intersezione del corpo stradale e del terreno con un piano verticale e normale all asse stradale. Vengono eseguite in corrispondenza di ciascun picchetto d asse.
LE SEZIONI TRASVERSALI Rappresentano l intersezione del corpo stradale e del terreno con un piano verticale e normale all asse stradale. Vengono eseguite in corrispondenza di ciascun picchetto d asse.
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA
 Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
3. Sia g(x) = 4. Si calcoli l area del triangolo mistilineo ROS, ove l arco RS appartiene al grafico di f(x) o, indifferentemente, di g(x).
 Esame liceo Scientifico : ordinamento Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario. PROBLEMI Problema. Sia ABCD un quadrato di lato, P un punto di AB e γ la circonferenza
Esame liceo Scientifico : ordinamento Il candidato risolva uno dei due problemi e risponda a 5 quesiti del questionario. PROBLEMI Problema. Sia ABCD un quadrato di lato, P un punto di AB e γ la circonferenza
Corso di ordinamento Sessione straordinaria - a.s. 2009-2010 ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE STRAORDINARIA
 Sessione straordinaria - a.s. 9- ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE STRAORDINARIA Tema di: MATEMATICA a.s. 9- Svolgimento a cura di Nicola De Rosa Il candidato risolva uno
Sessione straordinaria - a.s. 9- ESAME DI STATO DI LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE STRAORDINARIA Tema di: MATEMATICA a.s. 9- Svolgimento a cura di Nicola De Rosa Il candidato risolva uno
Maturità Scientifica PNI, sessione ordinaria 2000-2001
 Matematica per la nuova maturità scientifica A. Bernardo M. Pedone Maturità Scientifica PNI, sessione ordinaria 000-00 Problema Sia AB un segmento di lunghezza a e il suo punto medio. Fissato un conveniente
Matematica per la nuova maturità scientifica A. Bernardo M. Pedone Maturità Scientifica PNI, sessione ordinaria 000-00 Problema Sia AB un segmento di lunghezza a e il suo punto medio. Fissato un conveniente
Parte Seconda. Geometria
 Parte Seconda Geometria Geometria piana 99 CAPITOLO I GEOMETRIA PIANA Geometria: scienza che studia le proprietà delle figure geometriche piane e solide, cioè la forma, l estensione e la posizione dei
Parte Seconda Geometria Geometria piana 99 CAPITOLO I GEOMETRIA PIANA Geometria: scienza che studia le proprietà delle figure geometriche piane e solide, cioè la forma, l estensione e la posizione dei
GEOMETRIA DELLE MASSE
 1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
1 DISPENSA N 2 GEOMETRIA DELLE MASSE Si prende in considerazione un sistema piano, ossia giacente nel pian x-y. Un insieme di masse posizionato nel piano X-Y, rappresentato da punti individuati dalle loro
RETTE, PIANI, SFERE, CIRCONFERENZE
 RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
RETTE, PIANI, SFERE, CIRCONFERENZE 1. Esercizi Esercizio 1. Dati i punti A(1, 0, 1) e B(, 1, 1) trovare (1) la loro distanza; () il punto medio del segmento AB; (3) la retta AB sia in forma parametrica,
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Trasformazioni Geometriche 1 Roberto Petroni, 2011
 1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
1 Trasformazioni Geometriche 1 Roberto etroni, 2011 Trasformazioni Geometriche sul piano euclideo 1) Introduzione Def: si dice trasformazione geometrica una corrispondenza biunivoca che associa ad ogni
Forze come grandezze vettoriali
 Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
Forze come grandezze vettoriali L. Paolucci 23 novembre 2010 Sommario Esercizi e problemi risolti. Per la classe prima. Anno Scolastico 2010/11 Parte 1 / versione 2 Si ricordi che la risultante di due
CORSO DI LAUREA IN INGEGNERIA.
 CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 4 GEOMETRIA E ALGEBRA LINEARE 2010/11 Esercizio 4.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
CORSO DI LAUREA IN INGEGNERIA. FOGLIO DI ESERCIZI 4 GEOMETRIA E ALGEBRA LINEARE 2010/11 Esercizio 4.1 (2.2). Determinare l equazione parametrica e Cartesiana della retta dello spazio (a) Passante per i
Insegnamento di Fondamenti di Infrastrutture viarie
 Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione generale del moto
Insegnamento di Fondamenti di Infrastrutture viarie Territorio ed infrastrutture di trasporto La meccanica della locomozione: questioni generali Il fenomeno dell aderenza e l equazione generale del moto
r.berardi COSTRUZIONI GEOMETRICHE
 r.berardi COSTRUZIONI Costruzioni geometriche di base perpendicolari Pag.. 2 OVALI Pag. 12 Bisettrice e divisione Pag. 3 angoli COSTRUZIONE POLIGONI RACCORDI GRAFICI DATO IL LATO Triangolo equilatero,
r.berardi COSTRUZIONI Costruzioni geometriche di base perpendicolari Pag.. 2 OVALI Pag. 12 Bisettrice e divisione Pag. 3 angoli COSTRUZIONE POLIGONI RACCORDI GRAFICI DATO IL LATO Triangolo equilatero,
Rette e piani con le matrici e i determinanti
 CAPITOLO Rette e piani con le matrici e i determinanti Esercizio.. Stabilire se i punti A(, ), B(, ) e C(, ) sono allineati. Esercizio.. Stabilire se i punti A(,,), B(,,), C(,, ) e D(4,,0) sono complanari.
CAPITOLO Rette e piani con le matrici e i determinanti Esercizio.. Stabilire se i punti A(, ), B(, ) e C(, ) sono allineati. Esercizio.. Stabilire se i punti A(,,), B(,,), C(,, ) e D(4,,0) sono complanari.
Inserimento di distanze e di angoli nella carta di Gauss
 Inserimento di distanze e di angoli nella carta di Gauss Corso di laurea in Ingegneria per l Ambiente e il Territorio a.a. 2006-2007 Inserimento della distanza reale misurata nella carta di Gauss (passaggio
Inserimento di distanze e di angoli nella carta di Gauss Corso di laurea in Ingegneria per l Ambiente e il Territorio a.a. 2006-2007 Inserimento della distanza reale misurata nella carta di Gauss (passaggio
Collegio dei Geometri di Bergamo I.S.I.S. Quarenghi
 Collegio dei Geometri di Bergamo I.S.I.S. Quarenghi Corso di preparazione agli Esami di abilitazione alla libera professione di Geometra Sessione 009 TOPOGRAFIA Docente Ing. Aldo Piantoni Come misuriamo
Collegio dei Geometri di Bergamo I.S.I.S. Quarenghi Corso di preparazione agli Esami di abilitazione alla libera professione di Geometra Sessione 009 TOPOGRAFIA Docente Ing. Aldo Piantoni Come misuriamo
APPUNTI DI MATEMATICA GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1)
 GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1) Un ente (geometrico) è un oggetto studiato dalla geometria. Per descrivere gli enti vengono utilizzate delle definizioni. Una definizione è una
GEOMETRIA \ GEOMETRIA EUCLIDEA \ GEOMETRIA DEL PIANO (1) Un ente (geometrico) è un oggetto studiato dalla geometria. Per descrivere gli enti vengono utilizzate delle definizioni. Una definizione è una
MATEMATICA 2001. p = 4/6 = 2/3; q = 1-2/3 = 1/3. La risposta corretta è quindi la E).
 MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
MATEMATICA 2001 66. Quale fra le seguenti affermazioni è sbagliata? A) Tutte le funzioni ammettono la funzione inversa B) Una funzione dispari è simmetrica rispetto all origine C) Una funzione pari è simmetrica
Misure di base su una carta. Calcoli di distanze
 Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Misure di base su una carta Calcoli di distanze Per calcolare la distanza tra due punti su una carta disegnata si opera nel modo seguente: 1. Occorre identificare la scala della carta o ricorrendo alle
Liceo G.B. Vico Corsico
 Liceo G.B. Vico Corsico Classe: 3A Materia: MATEMATICA Insegnante: Nicola Moriello Testo utilizzato: Bergamini Trifone Barozzi: Manuale blu.0 di Matematica Moduli S, L, O, Q, Beta ed. Zanichelli 1) Programma
Liceo G.B. Vico Corsico Classe: 3A Materia: MATEMATICA Insegnante: Nicola Moriello Testo utilizzato: Bergamini Trifone Barozzi: Manuale blu.0 di Matematica Moduli S, L, O, Q, Beta ed. Zanichelli 1) Programma
15 febbraio 2010 - Soluzione esame di geometria - 12 crediti Ingegneria gestionale - a.a. 2009-2010 COGNOME... NOME... N. MATRICOLA...
 15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
15 febbraio 010 - Soluzione esame di geometria - 1 crediti Ingegneria gestionale - a.a. 009-010 COGNOME.......................... NOME.......................... N. MATRICOLA............. La prova dura
LE FUNZIONI MATEMATICHE
 ALGEBRA LE FUNZIONI MATEMATICHE E IL PIANO CARTESIANO PREREQUISITI l l l l l conoscere il concetto di insieme conoscere il concetto di relazione disporre i dati in una tabella rappresentare i dati mediante
ALGEBRA LE FUNZIONI MATEMATICHE E IL PIANO CARTESIANO PREREQUISITI l l l l l conoscere il concetto di insieme conoscere il concetto di relazione disporre i dati in una tabella rappresentare i dati mediante
Percorsi di matematica per il ripasso e il recupero
 Giacomo Pagina Giovanna Patri Percorsi di matematica per il ripasso e il recupero 2 per la Scuola secondaria di secondo grado UNITÀ CAMPIONE Edizioni del Quadrifoglio à t i n U 1 Sistemi di primo grado
Giacomo Pagina Giovanna Patri Percorsi di matematica per il ripasso e il recupero 2 per la Scuola secondaria di secondo grado UNITÀ CAMPIONE Edizioni del Quadrifoglio à t i n U 1 Sistemi di primo grado
a) Si descriva, internamente al triangolo, con centro in B e raggio x, l arco di circonferenza di π π
 PROBLEMA Il triangolo rettangolo ABC ha l ipotenusa AB = a e l angolo CAB =. a) Si descriva, internamente al triangolo, con centro in B e raggio, l arco di circonferenza di estremi P e Q rispettivamente
PROBLEMA Il triangolo rettangolo ABC ha l ipotenusa AB = a e l angolo CAB =. a) Si descriva, internamente al triangolo, con centro in B e raggio, l arco di circonferenza di estremi P e Q rispettivamente
Simulazione seconda prova (Tema assegnato all esame di stato per l'abilitazione alla professione di geometra, 1998)
 Simulazione seconda prova (Tema assegnato all esame di stato per l'abilitazione alla professione di geometra, 998) IL TEA La proprietà fondiaria uadrilatera di vertici 3, per motivi di successione testamentaria,
Simulazione seconda prova (Tema assegnato all esame di stato per l'abilitazione alla professione di geometra, 998) IL TEA La proprietà fondiaria uadrilatera di vertici 3, per motivi di successione testamentaria,
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
ESERCIZIO GUIDA (spostamento)
 ESERCIZIO GUIDA (spostamento) Due terreni, uno di forma triangolare ABC e l altro di forma quadrilatera ABDE confinano tra loro con il lato AB. Si conoscono: AB=,90m AC=5,440m BC=36,04m Il punto E si trova
ESERCIZIO GUIDA (spostamento) Due terreni, uno di forma triangolare ABC e l altro di forma quadrilatera ABDE confinano tra loro con il lato AB. Si conoscono: AB=,90m AC=5,440m BC=36,04m Il punto E si trova
Disegno in quadretti le parti da calcolare; se capisco quanto vale un quadretto è fatta.
 CLASSE III C RECUPERO GEOMETRIA AREA PERIMETRO POLIGONI Disegno in quadretti le parti da calcolare; se capisco quanto vale un quadretto è fatta. ES: se ho fatto questo disegno e so che 1 quadretto vale
CLASSE III C RECUPERO GEOMETRIA AREA PERIMETRO POLIGONI Disegno in quadretti le parti da calcolare; se capisco quanto vale un quadretto è fatta. ES: se ho fatto questo disegno e so che 1 quadretto vale
Prof. Silvio Reato Valcavasia Ricerche. Il piano cartesiano
 Il piano cartesiano Per la rappresentazione di grafici su di un piano si utilizza un sistema di riferimento cartesiano. Su questo piano si rappresentano due rette orientate (con delle frecce all estremità
Il piano cartesiano Per la rappresentazione di grafici su di un piano si utilizza un sistema di riferimento cartesiano. Su questo piano si rappresentano due rette orientate (con delle frecce all estremità
B. Vogliamo determinare l equazione della retta
 Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
Esempi di funzione. Scheda Tre
 Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Scheda Tre Funzioni Consideriamo una legge f che associa ad un elemento di un insieme X al più un elemento di un insieme Y; diciamo che f è una funzione, X è l insieme di partenza e X l insieme di arrivo.
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Anna Montemurro. 2Geometria. e misura
 Anna Montemurro Destinazione Matematica 2Geometria e misura GEOMETRIA E MISURA UNITÀ 11 Le aree dei poligoni apprendo... 11. 1 FIGURE PIANE EQUIVALENTI Consideriamo la figura A. A Le figure B e C
Anna Montemurro Destinazione Matematica 2Geometria e misura GEOMETRIA E MISURA UNITÀ 11 Le aree dei poligoni apprendo... 11. 1 FIGURE PIANE EQUIVALENTI Consideriamo la figura A. A Le figure B e C
MAPPE DI KARNAUGH. Nei capitoli precedenti si è visto che è possibile associare un circuito elettronico o elettrico ad una funzione logica.
 MAPPE DI KARNAUGH 1. Generalità Nei capitoli precedenti si è visto che è possibile associare un circuito elettronico o elettrico ad una funzione logica. E ovvio che più semplice è la funzione e più semplice
MAPPE DI KARNAUGH 1. Generalità Nei capitoli precedenti si è visto che è possibile associare un circuito elettronico o elettrico ad una funzione logica. E ovvio che più semplice è la funzione e più semplice
Grandezze scalari e vettoriali
 Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
Grandezze scalari e vettoriali Esempio vettore spostamento: Esistono due tipi di grandezze fisiche. a) Grandezze scalari specificate da un valore numerico (positivo negativo o nullo) e (nel caso di grandezze
LA RETTA. Retta per l'origine, rette orizzontali e verticali
 Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
Retta per l'origine, rette orizzontali e verticali LA RETTA Abbiamo visto che l'equazione generica di una retta è del tipo Y = mx + q, dove m ne rappresenta la pendenza e q il punto in cui la retta incrocia
Anno 5 Funzioni inverse e funzioni composte
 Anno 5 Funzioni inverse e funzioni composte 1 Introduzione In questa lezione impareremo a definire e ricercare le funzioni inverse e le funzioni composte. Al termine di questa lezione sarai in grado di:
Anno 5 Funzioni inverse e funzioni composte 1 Introduzione In questa lezione impareremo a definire e ricercare le funzioni inverse e le funzioni composte. Al termine di questa lezione sarai in grado di:
ESERCIZI DI TOPOGRAFIA per gli Allievi Istituto per Geometri. rel. 0.1. Esercizi di Topografia distribuzione gratuita 1/6
 ESERCIZI DI TOPOGRAFIA per gli Allievi Istituto per Geometri rel. 0.1 Esercizi di Topografia distribuzione gratuita 1/6 Indice generale ANNO 3...3 1.1 - Esercizi pratica calcolatrice...3 1.2 - Esercizi
ESERCIZI DI TOPOGRAFIA per gli Allievi Istituto per Geometri rel. 0.1 Esercizi di Topografia distribuzione gratuita 1/6 Indice generale ANNO 3...3 1.1 - Esercizi pratica calcolatrice...3 1.2 - Esercizi
PERCORSO ESTIVO PER STUDENTI CON DEBITO FORMATIVO IN TOPOPGRAFIA
 I. I. S."MOREA-VIVARELLI" ----- FABRIANO ********************************************************* sez. COSTRUZIONI AMBIENTE TERRITORIO - a.s.2013/2014 corso di TOPOGRAFIA prof. FABIO ANDERLINI nella classe
I. I. S."MOREA-VIVARELLI" ----- FABRIANO ********************************************************* sez. COSTRUZIONI AMBIENTE TERRITORIO - a.s.2013/2014 corso di TOPOGRAFIA prof. FABIO ANDERLINI nella classe
7 Applicazioni ulteriori
 7 Applicazioni ulteriori 7 Applicazioni ulteriori 7.1 Strutture con maglie chiuse 7.1.1 Analisi cinematica Si consideri la struttura in figura 7.1: i gradi di libertà sono pari a l =3n c v =3 0 3 = 0,
7 Applicazioni ulteriori 7 Applicazioni ulteriori 7.1 Strutture con maglie chiuse 7.1.1 Analisi cinematica Si consideri la struttura in figura 7.1: i gradi di libertà sono pari a l =3n c v =3 0 3 = 0,
LEZIONI DI TOPOGRAFIA
 Prof. Ing. Paolo Saija LEZIONI DI TOPOGRAFIA (Appunti per l esame di abilitazione alla professione di Geometra) Anno 2006 II a Edizione 1 SOMMARIO LA TOPOGRAFIA Grandezze geometriche e unità di misura
Prof. Ing. Paolo Saija LEZIONI DI TOPOGRAFIA (Appunti per l esame di abilitazione alla professione di Geometra) Anno 2006 II a Edizione 1 SOMMARIO LA TOPOGRAFIA Grandezze geometriche e unità di misura
Geometria analitica di base (prima parte)
 SAPERE Al termine di questo capitolo, avrai appreso: come fissare un sistema di riferimento cartesiano ortogonale il significato di equazione di una retta il significato di coefficiente angolare di una
SAPERE Al termine di questo capitolo, avrai appreso: come fissare un sistema di riferimento cartesiano ortogonale il significato di equazione di una retta il significato di coefficiente angolare di una
Formule trigonometriche
 Formule trigonometriche C. Enrico F. Bonaldi 1 Formule trigonometriche In trigonometria esistono delle formule fondamentali che permettono di calcolare le funzioni goniometriche della somma di due angoli
Formule trigonometriche C. Enrico F. Bonaldi 1 Formule trigonometriche In trigonometria esistono delle formule fondamentali che permettono di calcolare le funzioni goniometriche della somma di due angoli
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Kangourou della Matematica 2014 finale nazionale italiana Mirabilandia, 12 maggio 2014
 Kangourou della Matematica 2014 finale nazionale italiana Mirabilandia, 12 maggio 2014 LIVELLO STUDENT K,M N CD BC A S1. (5 punti ) In figura si vede una circonferenza della quale i segmenti AB, BC e CD
Kangourou della Matematica 2014 finale nazionale italiana Mirabilandia, 12 maggio 2014 LIVELLO STUDENT K,M N CD BC A S1. (5 punti ) In figura si vede una circonferenza della quale i segmenti AB, BC e CD
CONI, CILINDRI, SUPERFICI DI ROTAZIONE
 CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
CONI, CILINDRI, SUPERFICI DI ROTAZIONE. Esercizi x + z = Esercizio. Data la curva x, calcolare l equazione del cilindro avente γ y = 0 come direttrice e con generatrici parallele al vettore v = (, 0, ).
Verranno descritti di seguito brevemente gli algoritmi di calcolo utilizzati per l interpretazione nei tre metodi inseriti all interno del programma.
 3. Teoria Verranno descritti di seguito brevemente gli algoritmi di calcolo utilizzati per l interpretazione nei tre metodi inseriti all interno del programma. 3.1 Metodo convenzionale (metodo del tempo
3. Teoria Verranno descritti di seguito brevemente gli algoritmi di calcolo utilizzati per l interpretazione nei tre metodi inseriti all interno del programma. 3.1 Metodo convenzionale (metodo del tempo
Come si indica un punto? Un punto si indica (distingue) con una lettera maiuscola dell alfabeto italiano.
 Il punto Il punto è un elemento geometrico fondamentale privo di dimensioni ed occupa solo una posizione. Come si indica un punto? Un punto si indica (distingue) con una lettera maiuscola dell alfabeto
Il punto Il punto è un elemento geometrico fondamentale privo di dimensioni ed occupa solo una posizione. Come si indica un punto? Un punto si indica (distingue) con una lettera maiuscola dell alfabeto
la restituzione prospettica da singolo fotogramma
 la restituzione prospettica da singolo fotogramma arch. francesco guerini francesco.guerini@gmail.com politecnico di Milano, Facoltà di Architettura e Società Laboratorio di Rappresentazione 1 Prof. Andrea
la restituzione prospettica da singolo fotogramma arch. francesco guerini francesco.guerini@gmail.com politecnico di Milano, Facoltà di Architettura e Società Laboratorio di Rappresentazione 1 Prof. Andrea
LIVELLO STUDENT S1. S2. S3. S4. S5. S6.
 LIVELLO STUDENT S1. (5 punti ) La figura mostra due quadrati uguali che hanno in comune esattamente un vertice. È possibile precisare la misura dell'angolo ABC? S2. (7 punti ) Negli usuali fogli (rettangolari)
LIVELLO STUDENT S1. (5 punti ) La figura mostra due quadrati uguali che hanno in comune esattamente un vertice. È possibile precisare la misura dell'angolo ABC? S2. (7 punti ) Negli usuali fogli (rettangolari)
La trigonometria prima della trigonometria. Maurizio Berni
 La trigonometria prima della trigonometria Maurizio Berni 9 maggio 2010 Negli istituti tecnici agrari la trigonometria viene affrontata: nella seconda classe in Disegno e Topografia (risoluzione di triangoli
La trigonometria prima della trigonometria Maurizio Berni 9 maggio 2010 Negli istituti tecnici agrari la trigonometria viene affrontata: nella seconda classe in Disegno e Topografia (risoluzione di triangoli
Anno 4 I Triangoli qualsiasi
 Anno 4 I Triangoli qualsiasi 1 Introduzione In questa lezione descriveremo i triangoli qualunque. Enunceremo i teoremi su questi triangoli e illustreremo le loro applicazioni. Al termine della lezione
Anno 4 I Triangoli qualsiasi 1 Introduzione In questa lezione descriveremo i triangoli qualunque. Enunceremo i teoremi su questi triangoli e illustreremo le loro applicazioni. Al termine della lezione
la funzione è definita la funzione non è definita Si osservi, infatti, che la radice di un numero negativo non esiste nel campo dei numeri reali.
 1 y 4 CAMPO DI ESISTENZA. Poiché data è una irrazionale con indice di radice pari, il cui radicando è un polinomio, essa risulta definita solo per i valori della per i quali il radicando è positivo, ovvero
1 y 4 CAMPO DI ESISTENZA. Poiché data è una irrazionale con indice di radice pari, il cui radicando è un polinomio, essa risulta definita solo per i valori della per i quali il radicando è positivo, ovvero
13. Campi vettoriali
 13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
13. Campi vettoriali 1 Il campo di velocità di un fluido Il concetto di campo in fisica non è limitato ai fenomeni elettrici. In generale il valore di una grandezza fisica assegnato per ogni punto dello
Punti notevoli di un triangolo
 Punti notevoli dei triangoli (UbiLearning). - 1 Punti notevoli di un triangolo Particolarmente importanti in un triangolo sono i punti dove s intersecano specifici segmenti, rette o semirette (Encyclopedia
Punti notevoli dei triangoli (UbiLearning). - 1 Punti notevoli di un triangolo Particolarmente importanti in un triangolo sono i punti dove s intersecano specifici segmenti, rette o semirette (Encyclopedia
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 2014
 Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
0. Piano cartesiano 1
 0. Piano cartesiano Per piano cartesiano si intende un piano dotato di due assi (che per ragioni pratiche possiamo scegliere ortogonali). Il punto in comune ai due assi è detto origine, e funziona da origine
0. Piano cartesiano Per piano cartesiano si intende un piano dotato di due assi (che per ragioni pratiche possiamo scegliere ortogonali). Il punto in comune ai due assi è detto origine, e funziona da origine
Teoria in sintesi 10. Attività di sportello 1, 24 - Attività di sportello 2, 24 - Verifica conclusiva, 25. Teoria in sintesi 26
 Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
Indice L attività di recupero 6 Funzioni Teoria in sintesi 0 Obiettivo Ricerca del dominio e del codominio di funzioni note Obiettivo Ricerca del dominio di funzioni algebriche; scrittura del dominio Obiettivo
LE GEOMETRIE NON EUCLIDEE FRA CULTURA, STORIA E DIDATTICA DELLA MATEMATICA. Dario Palladino (Università di Genova)
 LE GEOMETRIE NON EUCLIDEE FRA CULTURA, STORIA E DIDATTICA DELLA MATEMATICA Dario Palladino (Università di Genova) Seconda parte Momenti della storia dei tentativi di dimostrazione del V postulato di Euclide
LE GEOMETRIE NON EUCLIDEE FRA CULTURA, STORIA E DIDATTICA DELLA MATEMATICA Dario Palladino (Università di Genova) Seconda parte Momenti della storia dei tentativi di dimostrazione del V postulato di Euclide
LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 2006/2007 SIMULAZIONE DI II PROVA - A
 LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 6/7 SIMULAZIONE DI II PROVA - A Tempo a disposizione: cinque ore E consentito l uso della calcolatrice non programmabile. Non è consentito uscire dall aula
LICEO SCIENTIFICO STATALE G.GALILEI CATANIA A.S. 6/7 SIMULAZIONE DI II PROVA - A Tempo a disposizione: cinque ore E consentito l uso della calcolatrice non programmabile. Non è consentito uscire dall aula
SEZIONI. Introduzione
 SEIONI 128 Introduzione Sezionare un solido significa tagliarlo secondo una superficie ideale in modo da mostrare il volume interno del solido stesso. Nella maggior parte dei casi l elemento secante è
SEIONI 128 Introduzione Sezionare un solido significa tagliarlo secondo una superficie ideale in modo da mostrare il volume interno del solido stesso. Nella maggior parte dei casi l elemento secante è
DIVISIONE DELLE AREE - ESERCIZI
 ESERCIZIO N.2 DIVISIONE DELLE AREE - ESERCIZI ESERCIZIO N.1 AB=80,34 m AC=144,86 m a=63 c,7261 Il terreno va suddiviso in tre parti S 1, S 2, S 3 direttamente proporzionali ai coefficienti m 1 =2,5 m 2
ESERCIZIO N.2 DIVISIONE DELLE AREE - ESERCIZI ESERCIZIO N.1 AB=80,34 m AC=144,86 m a=63 c,7261 Il terreno va suddiviso in tre parti S 1, S 2, S 3 direttamente proporzionali ai coefficienti m 1 =2,5 m 2
ESERCIZI CINEMATICA IN UNA DIMENSIONE
 ESERCIZI CINEMATICA IN UNA DIMENSIONE ES. 1 - Due treni partono da due stazioni distanti 20 km dirigendosi uno verso l altro rispettivamente alla velocità costante di v! = 50,00 km/h e v 2 = 100,00 km
ESERCIZI CINEMATICA IN UNA DIMENSIONE ES. 1 - Due treni partono da due stazioni distanti 20 km dirigendosi uno verso l altro rispettivamente alla velocità costante di v! = 50,00 km/h e v 2 = 100,00 km
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
FASCI DI RETTE. scrivere la retta in forma esplicita: 2y = 3x + 4 y = 3 2 x 2. scrivere l equazione del fascio di rette:
 FASCI DI RETTE DEFINIZIONE: Si chiama fascio di rette parallele o fascio improprio [erroneamente data la somiglianza effettiva con un fascio!] un insieme di rette che hanno tutte lo stesso coefficiente
FASCI DI RETTE DEFINIZIONE: Si chiama fascio di rette parallele o fascio improprio [erroneamente data la somiglianza effettiva con un fascio!] un insieme di rette che hanno tutte lo stesso coefficiente
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
GIOCHI A SQUADRE. 30 marzo 2012
 Centro Pristem Università Bocconi GIOCHI A SQUADRE 30 marzo 2012 1. La campestre Carla, Milena, Anna, Fausta e Debora hanno partecipato alla corsa campestre della loro classe. Carla e Anna non hanno vinto.
Centro Pristem Università Bocconi GIOCHI A SQUADRE 30 marzo 2012 1. La campestre Carla, Milena, Anna, Fausta e Debora hanno partecipato alla corsa campestre della loro classe. Carla e Anna non hanno vinto.
Similitudine e omotetia nella didattica della geometria nella scuola secondaria di primo grado di Luciano Porta
 Similitudine e omotetia nella didattica della geometria nella scuola secondaria di primo grado di Luciano Porta Il concetto di similitudine è innato: riconosciamo lo stesso oggetto se è più o meno distante
Similitudine e omotetia nella didattica della geometria nella scuola secondaria di primo grado di Luciano Porta Il concetto di similitudine è innato: riconosciamo lo stesso oggetto se è più o meno distante
STUDIO DI UNA FUNZIONE
 STUDIO DI UNA FUNZIONE OBIETTIVO: Data l equazione Y = f(x) di una funzione a variabili reali (X R e Y R), studiare l andamento del suo grafico. PROCEDIMENTO 1. STUDIO DEL DOMINIO (CAMPO DI ESISTENZA)
STUDIO DI UNA FUNZIONE OBIETTIVO: Data l equazione Y = f(x) di una funzione a variabili reali (X R e Y R), studiare l andamento del suo grafico. PROCEDIMENTO 1. STUDIO DEL DOMINIO (CAMPO DI ESISTENZA)
S.C.S. - survey CAD system 4 - PARTICELLE
 4 - PARTICELLE Il menu PARTICELLE gestisce la creazione di nuove particelle mediante diversi problemi relativi alla divisione di aree. È possibile impostare l orientamento della dividente, generarla parallela
4 - PARTICELLE Il menu PARTICELLE gestisce la creazione di nuove particelle mediante diversi problemi relativi alla divisione di aree. È possibile impostare l orientamento della dividente, generarla parallela
Le scale di riduzione
 Le scale di riduzione Le dimensioni di un oggetto, quando sono troppo grandi perché siano riportate sul foglio da disegno, si riducono in scala. Scala 1 a 200 (si scrive 1 : 200) rappresenta una divisione.
Le scale di riduzione Le dimensioni di un oggetto, quando sono troppo grandi perché siano riportate sul foglio da disegno, si riducono in scala. Scala 1 a 200 (si scrive 1 : 200) rappresenta una divisione.
PLANIMETRIA E PROFILO INSIEME
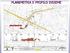 PLANIMETRIA E PROFILO INSIEME planimetria profili 11 RELAZIONE TRA PLANIMETRIA E PROFILO La correlazione tra andamento planimetrico e altimetrico è molto stretta; variazioni del primo incidono subito sul
PLANIMETRIA E PROFILO INSIEME planimetria profili 11 RELAZIONE TRA PLANIMETRIA E PROFILO La correlazione tra andamento planimetrico e altimetrico è molto stretta; variazioni del primo incidono subito sul
b) Il luogo degli estremanti in forma cartesiana è:
 Soluzione della simulazione di prova del 9/5/ PROBLEMA È data la funzione di equazione: k f( ). a) Determinare i valori di k per cui la funzione ammette punti di massimo e minimo relativi. b) Scrivere
Soluzione della simulazione di prova del 9/5/ PROBLEMA È data la funzione di equazione: k f( ). a) Determinare i valori di k per cui la funzione ammette punti di massimo e minimo relativi. b) Scrivere
Studio di funzioni ( )
 Studio di funzioni Effettuare uno studio qualitativo e tracciare un grafico approssimativo delle seguenti funzioni. Si studi in particolare anche la concavità delle funzioni e si indichino esplicitamente
Studio di funzioni Effettuare uno studio qualitativo e tracciare un grafico approssimativo delle seguenti funzioni. Si studi in particolare anche la concavità delle funzioni e si indichino esplicitamente
Lenti sottili/1. Menisco convergente. Menisco divergente. Piano convessa. Piano concava. Biconcava. Biconvessa. G. Costabile
 Lenti sottili/1 La lente è un sistema ottico costituito da un pezzo di materiale trasparente omogeneo (vetro, policarbonato, quarzo, fluorite,...) limitato da due calotte sferiche (o, più generalmente,
Lenti sottili/1 La lente è un sistema ottico costituito da un pezzo di materiale trasparente omogeneo (vetro, policarbonato, quarzo, fluorite,...) limitato da due calotte sferiche (o, più generalmente,
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
ABCD è un parallelogrammo 90. Dimostrazione
 EQUISCOMPONIBILITÀ Problema G2.360.1 È dato il parallelogrammo ABCD: dai vertici A e B si conducano le perpendicolari alla retta del lato CD e siano rispettivamente E e F i piedi di tali perpendicolari
EQUISCOMPONIBILITÀ Problema G2.360.1 È dato il parallelogrammo ABCD: dai vertici A e B si conducano le perpendicolari alla retta del lato CD e siano rispettivamente E e F i piedi di tali perpendicolari
Categoria Student Per studenti degli ultimi due anni della scuola secondaria di secondo grado
 Categoria Student Per studenti degli ultimi due anni della scuola secondaria di secondo grado. Risposta A). Il triangolo ABC ha la stessa altezza del triangolo AOB ma base di lunghezza doppia (il diametro
Categoria Student Per studenti degli ultimi due anni della scuola secondaria di secondo grado. Risposta A). Il triangolo ABC ha la stessa altezza del triangolo AOB ma base di lunghezza doppia (il diametro
SOLUZIONE DEL PROBLEMA 1 CORSO SPERIMENTALE P.N.I. 2014
 SOLUZIONE DEL PROBLEMA 1 CORSO SPERIMENTALE P.N.I. 01 1. Determiniamo l espressione analitica di g() dividendo il suo dominio in intervalli. La circonferenza di diametro AO ha equazione (+) + = + + = 0
SOLUZIONE DEL PROBLEMA 1 CORSO SPERIMENTALE P.N.I. 01 1. Determiniamo l espressione analitica di g() dividendo il suo dominio in intervalli. La circonferenza di diametro AO ha equazione (+) + = + + = 0
GEOGEBRA I OGGETTI GEOMETRICI
 GEOGEBRA I OGGETTI GEOMETRICI PROPRIETA : Finestra Proprietà (tasto destro mouse sull oggetto) Fondamentali: permette di assegnare o cambiare NOME, VALORE, di mostrare nascondere l oggetto, di mostrare
GEOGEBRA I OGGETTI GEOMETRICI PROPRIETA : Finestra Proprietà (tasto destro mouse sull oggetto) Fondamentali: permette di assegnare o cambiare NOME, VALORE, di mostrare nascondere l oggetto, di mostrare
Vertici opposti. Fig. C6.1 Definizioni relative ai quadrilateri.
 6. Quadrilateri 6.1 efinizioni Un poligono di 4 lati è detto quadrilatero. I lati di un quadrilatero che hanno un vertice in comune sono detti consecutivi. I lati di un quadrilatero non consecutivi tra
6. Quadrilateri 6.1 efinizioni Un poligono di 4 lati è detto quadrilatero. I lati di un quadrilatero che hanno un vertice in comune sono detti consecutivi. I lati di un quadrilatero non consecutivi tra
Geoute. Versione 8.01 Gestione dati da Stazioni Totali PENTAX. GUIDO VERONESI S.r.l.
 Geoute Versione 8.01 Gestione dati da Stazioni Totali PENTAX GUIDO VERONESI S.r.l. Via Caselle, 46 40068 San Lazzaro di S. (BOLOGNA) +39 (051) 454733-453229 Fax +39 (051) 453181 Web site: www.veronesi.org
Geoute Versione 8.01 Gestione dati da Stazioni Totali PENTAX GUIDO VERONESI S.r.l. Via Caselle, 46 40068 San Lazzaro di S. (BOLOGNA) +39 (051) 454733-453229 Fax +39 (051) 453181 Web site: www.veronesi.org
( x) ( x) 0. Equazioni irrazionali
 Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
Equazioni irrazionali Definizione: si definisce equazione irrazionale un equazione in cui compaiono uno o più radicali contenenti l incognita. Esempio 7 Ricordiamo quanto visto sulle condizioni di esistenza
La curva grafico della funzione, partendo dal punto A(a,f(a)), si snoda con continuità, senza interruzioni, fino ad approdare nel punto B(b,f(b)).
 Calcolo differenziale Il teorema di Rolle TEOREMA DI ROLLE Ipotesi f continua su [a, b] f derivabile per lo meno su (a,b) f(a) = f(b) Tesi Esiste almeno un punto c in (a, b) tale che Giustificazione con
Calcolo differenziale Il teorema di Rolle TEOREMA DI ROLLE Ipotesi f continua su [a, b] f derivabile per lo meno su (a,b) f(a) = f(b) Tesi Esiste almeno un punto c in (a, b) tale che Giustificazione con
I TRIANGOLI Un triangolo è un poligono con tre lati e tre angoli.
 I TRIANGOLI Un triangolo è un poligono con tre lati e tre angoli. In ogni triangolo un lato è sempre minore della somma degli altri due e sempre maggiore della loro differenza. Relazione fra i lati di
I TRIANGOLI Un triangolo è un poligono con tre lati e tre angoli. In ogni triangolo un lato è sempre minore della somma degli altri due e sempre maggiore della loro differenza. Relazione fra i lati di
SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 2015
 SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 015 1. Indicando con i minuti di conversazione effettuati nel mese considerato, la spesa totale mensile in euro è espressa dalla funzione f()
SOLUZIONE DEL PROBLEMA 1 TEMA DI MATEMATICA ESAME DI STATO 015 1. Indicando con i minuti di conversazione effettuati nel mese considerato, la spesa totale mensile in euro è espressa dalla funzione f()
DIVISIONE DELLE AREE - ESERCIZI ESERCIZIO N.1
 ESERCIZIO N.2 ESERCIZIO N.1 AB=80,34 m AC=144,86 m a=63 c,7261 Il terreno va suddiviso in tre parti S 1, S 2, S 3 direttamente proporzionali ai coefficienti m 1 =2,5 m 2 =3 m 3 =4 con due dividenti uscenti
ESERCIZIO N.2 ESERCIZIO N.1 AB=80,34 m AC=144,86 m a=63 c,7261 Il terreno va suddiviso in tre parti S 1, S 2, S 3 direttamente proporzionali ai coefficienti m 1 =2,5 m 2 =3 m 3 =4 con due dividenti uscenti
Geogebra. Numero lati: Numero angoli: Numero diagonali:
 TRIANGOLI Geogebra IL TRIANGOLO 1. Fai clic sull icona Ic2 e nel menu a discesa scegli Nuovo punto : fai clic all interno della zona geometria e individua il punto A. Fai di nuovo clic per individuare
TRIANGOLI Geogebra IL TRIANGOLO 1. Fai clic sull icona Ic2 e nel menu a discesa scegli Nuovo punto : fai clic all interno della zona geometria e individua il punto A. Fai di nuovo clic per individuare
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1
 LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
LA TRASMISSIONE DELLE INFORMAZIONI QUARTA PARTE 1 I CODICI 1 IL CODICE BCD 1 Somma in BCD 2 Sottrazione BCD 5 IL CODICE ECCESSO 3 20 La trasmissione delle informazioni Quarta Parte I codici Il codice BCD
Nicola De Rosa, Liceo scientifico di ordinamento sessione suppletiva 2011, matematicamente.it
 Nicola De Rosa, Liceo scientifico di ordinamento sessione suppletiva, matematicamente.it PROBLEMA Data una semicirconferenza di diametro AB =, si prenda su di essa un punto P e sia M la proiezione di P
Nicola De Rosa, Liceo scientifico di ordinamento sessione suppletiva, matematicamente.it PROBLEMA Data una semicirconferenza di diametro AB =, si prenda su di essa un punto P e sia M la proiezione di P
Le trasformazioni geometriche
 Le trasformazioni geometriche Le trasformazioni geometriche Le trasformazioni affini del piano o affinità Le similitudini Le isometrie Le traslazioni Le rotazioni Le simmetrie assiale e centrale Le omotetie
Le trasformazioni geometriche Le trasformazioni geometriche Le trasformazioni affini del piano o affinità Le similitudini Le isometrie Le traslazioni Le rotazioni Le simmetrie assiale e centrale Le omotetie
PARTICOLARI COSTRUTTIVI MURATURA ARMATA POROTON
 PARTICOLARI COSTRUTTIVI MURATURA ARMATA POROTON La muratura armata rappresenta un sistema costruttivo relativamente nuovo ed ancora non molto conosciuto e le richieste di chiarimenti sulle modalità di
PARTICOLARI COSTRUTTIVI MURATURA ARMATA POROTON La muratura armata rappresenta un sistema costruttivo relativamente nuovo ed ancora non molto conosciuto e le richieste di chiarimenti sulle modalità di
I teoremi di Euclide e di Pitagora
 I teoremi di Euclide e di Pitagora In questa dispensa vengono presentati i due teoremi di Euclide ed il teorema di Pitagora, fondamentali per affrontare diverse questioni sui triangoli rettangoli. I teoremi
I teoremi di Euclide e di Pitagora In questa dispensa vengono presentati i due teoremi di Euclide ed il teorema di Pitagora, fondamentali per affrontare diverse questioni sui triangoli rettangoli. I teoremi
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
