CONTROLLI AUTOMATICI
|
|
|
- Marcellino Moroni
- 7 anni fa
- Visualizzazioni
Transcript
1 CONTROLLI AUTOMATICI A.A. 2/2 Iroduzoe al Corso Due problem d oevole eresse gegersco soo quell dell aals d u geerco ssema reale, aurale o arfcale, per acqusre formazo sul suo comporameo, e della ses d u adao dsposvo, deomao corollore, da coeere a ale ssema grado d forzare l ero ssema a comporars el modo desderao. U ssema reale può essere defo come quell' ee che evolve el empo a seguo d azo esercae su d esso dall'esero. I geerale, esso è cosuo da u seme d compoe che eragscoo fra loro al fe d cosegure obev prefssa. Alcu esemp d ssem real soo segue. U seme massa-molla-smorzaore che cosusce, ad esempo, u modello fsco d ua sospesoe passva d u auovecolo; se s sersce ache u dsposvo grado d geerare forze meccache, deomao auaore, s oee ua sospesoe ava. U moore che è u ssema l cu scopo è quello d mporre u movmeo a u dao carco accordo a ua legge be precsa che mpoe u cero adameo emporale, ad esempo, per la poszoe leare o agolare o per la velocà. U mapolaore roboco è u ssema cu scop soo quell d mapolare ogge o d forzare la pare ermale, l ed effecor, a segure parcolar raeore, ad esempo, per operazo d vercaura d par d auovecol, per operazo ello spazo o ambe che l uomo o può frequeare come l occolo d u reaore ucleare. U aeromoble l cu obevo è be oo. Uo scaldabago l cu obevo è quello d porare la emperaura dell acqua a u prefssao valore. Ua avcella spazale. Ua cerale elerca l cu obevo è quello d produrre eerga elerca co valor della esoe e della frequeza be def. Ua raffera d perolo. U pedolo verso, cosuo da u asa cereraa all esremà ferore e la cu esremà superore è lbera, ha come obevo prefssao quello d maeere vercale l asa del pedolo. U ssema reale che può essere assmlao a u pedolo verso è cosuo da ua baera lacarazz ssemaa sopra u vecolo moble. Aals L'aals gegersca d u ssema reale ha come obevo quello d mglorare e, se possble, omzzare l comporameo del ssema sesso dal puo d vsa dell'affdablà e dell effceza. Per effeuare l aals d u ssema occorre, azuo, dvduare le gradezze medae le qual è possble smolare l evoluzoe del ssema, deomae gradezze d gresso, e le gradezze l cu adameo emporale è d parcolare eresse per gudcare le presazo del ssema, deomae gradezze d usca.
2 2 Per valuare le presazo del ssema è, allora, possble sollecarlo co opporu adame emporal delle gradezze d gresso e rlevare corrspode adame emporal delle gradezze d usca. Tale valuazoe può essere codoa e segue due mod: a) ulzzado u approcco eorco; b) ulzzado u approcco spermeale. L'approcco eorco s basa sulla coosceza d u modello maemaco suffceemee accurao del ssema reale, cosuo da u seme d gradezze e dalle relazo maemache far al gradezze. Tale approcco cosse ell effeuare lo sudo del ssema reale ulzzado l modello maemaco del ssema sesso. Lo sudo quesoe presea due aspe. U aspeo rguarda la dvduazoe d propreà del modello che s rfleoo presazo che l ssema reale è grado d forre. L alro aspeo cosse ella deermazoe degl adame emporal delle gradezze d usca corrspode a cer adame emporal delle gradezze d gresso, rsolvedo le equazo che cosuscoo l succao modello maemaco. Tale aspeo vee svluppao medae esperme d smulazoe dgale. Ifa, poché mol cas rsula mpossble o oeroso, dal puo d vsa compuazoale, rsolvere aalcamee le equazo del ssema, covee deermare u soluzoe umerca delle equazo sesse avvaledos dell auslo d u compuer. A al fe occorre mplemeare l modello sul compuer sesso. Pochè, d solo, l modello maemaco che vee assocao ad u ssema reale è cosuo da equazo dfferezal mere compuer soo grado d esegure solamee operazo logche e armeche, l'mplemeazoe del modello rchede l'mpego d opporu meod che dpedoo dalla sua sruura. La cosruzoe d u adeguao modello maemaco può essere effeuaa:. ulzzado ecche d defcazoe che permeoo d cosrure u modello del ssema a parre da da spermeal relav alle succae gradezze; 2. ulzzado le legg della fsca, chmca, ecooma, ec. che descrvoo l comporameo de compoe del ssema. I eramb cas rsula opporuo valdare spermealmee l modello maemaco cosruo soopoedo, ad esempo, l modello sesso e l ssema reale agl sess gress e rlevado e cofroado le corrspode rspose. I vaagg dell'approcco eorco soo coess al fao che o è ecessaro dsporre del ssema reale per la sua aals che, perao, rsula relavamee poco cososa e prva d rsch. Iolre, è possble deermare ache l adameo delle gradezze che o soo accessbl per la msura. Gl svaagg soo coess al fao che l modello maemaco che può essere assocao al ssema cosusce ua descrzoe approssmaa del ssema sesso; olre, l mplemeazoe del modello rchede sempre l rcorso a cere approssmazo. L'approcco spermeale cosse ell'effeuare alcue prove spermeal sul ssema reale, sollecadolo co opporu adame emporal delle gradezze d gresso e rlevado medae apposa srumeazoe gl adame emporal delle gradezze d usca. I vaagg d ale approcco soo coess al fao che rsula oeu soo relav al ssema reale e o a ua sua rappreseazoe maemaca approssmaa. Gl svaagg soo coess al fao che è ecessaro dsporre d u proopo del ssema su cu esegure gl esperme, l che rsula oevolmee cososo e rschoso per l'egrà del proopo sesso. Iolre, parcolare cura deve essere posa ella scela della srumeazoe mpegaa e
3 3 ell'erpreazoe de rsula oeu, pochè da rleva spermealmee soo, geerale, corro da segal d rumore, coè segal aleaor sovrappos a quell real rodo dalla modalà co cu opera la srumeazoe o da feome d vara aura. Ses I geerale, ssem real soo solo poezalmee grado d cosegure gl obev prefssa (ovvero d comporars ella maera desderaa), el seso che l cosegumeo d al obev è possble solamee se su al ssem vegoo esercae adae azo dall esero deomae azo d corollo. Il corollo può esercars co o seza l erveo dreo dell uomo; l corollo che s eserca seza l ervao dreo dell uomo vee deomao corollo auomaco. Le succae azo d corollo vegoo geerae dal u secodo ssema, deomao ssema corollae o corollore, che vee opporuamee ercoesso co l ssema al quale s desdera mporre l comporameo desderao, deomao ssema corollao. Per llusrare gl aspe fodameal d u problema d corollo s cosder l seguee problema aalogo a quello del corollo d u pedolo verso. Il ssema corollao è u asa poggaa sul palmo della mao d u uomo e l comporameo desderao è maeere vercale l asa sessa muovedo solamee la mao (modalà d corollo ); alre modalà che porebbero essere ulzzae soo quelle d maeere ferma la mao (modalà d corollo 2) e sposars ello spazo crcosae, oppure muovere el coempo la mao e sposars ello spazo crcosae (modalà d corollo 3). Ovvamee, l corollo avvee co l erveo dell uomo ed è qud mauale, coè o auomaco. E facle verfcare che quale che sa la modalà d corollo s resce sempre a cosegure l obevo prefssao. Nauralmee, è pù facle cosegure l succao obevo ulzzado la erza modalà d corollo poché o essoo vcol sulle azo d corollo che possoo essere esercae sull asa dall uomo. E ache abbasaza semplce meere evdeza meccasm che porao a cosegure l obevo prefssao. L uomo sposados vare drezo o sposado l palmo della mao eserca delle azo sul ssema corollao; gl orga moor dell uomo agscoo come auaor. La decsoe delle azo pù doee vegoo prese dal cervello dell uomo che agsce da corollore. Le decso vegoo prese sulla base delle osservazo della poszoe auale dell asa e della sua edeza che esprmoo l comporameo effevo del ssema e sulla poszoe desderaa dell asa che esprme l comporameo desderao o sepo. Pù precsamee, le decso vegoo elaborae a parre dal cofroo fra sepo e comporameo effevo. Il dsposvo d cofroo vee deomao comparaore. Le osservazo della poszoe auale dell asa e della sua edeza fuura vegoo caurae dagl occh che agscoo da sesor d msura e vegoo rasmesse al cervello medae l ssema ervoso. Il rsulao delle elaborazo del corollore (l cervello), cosusce la legge d corollo che vee rasmessa agl orga moor dal ssema ervoso cerale. Tale legge vee elaboraa a parre da rsula del cofroo fra comporameo effevo e desderao. L seme cosuo dal comparaore e dal compesaore vee deomao corollore. Uo schema a blocch sruurale che evdeza meccasm succa è llusrao ella Fg.. Lo schema a blocch d Fg. ha valdà del uo geerale.
4 4 Gl obev cosdera ell esempo llusrao soo aalogh a quell che è chamao a persegure u pedolo verso l cu schema è rporao ella Fg. 2. Il pedolo è cererao alla sommà d u carrello che è azoao da moor elerc; l movmeo del carrello che raspora l pedolo può avvere solamee ua drezoe e l obevo che s poe è quello d maeere l pedolo poszoe vercale. Co rfermeo allo schema d Fg., valgoo le segue cosderazo. Se-po dsurbo Comparaor e Compesao re Auaore ssema corollao Sesor d msura Fg. Schema a blocch sruurale del ssema d corollo esame. Fg. 2 Pedolo verso. Le formazo sul comporameo effevo vegoo acquse msurado l agolo formao dal pedolo co la drezoe vercale auale. Il sesore d msura porebbe essere u ecoder assoluo che forsce la msura dell agolo dreamee formao dgale. Il comparaore e l compesaore possoo essere realzza, rspevamee, medae u amplfcaore eleroco dfferezale e u dsposvo eleroco d po aalogco. L auaore è cosuo dall seme de moor elerc che soo calea sulle ruoe e forzao l carrello a muovers ua delle due drezo ammssbl. Esempo.. S desdera maeere cosae la emperaura all ero della caba d u aeromoble a erra e volo. Il ssema reale è cosuo da dsposv d rscaldameo-codzoameo, dalla caba dell aeromoble e dall ambee esero. E ovvo che ale ssema o è grado d cosegure l obevo prefssao. Ifa, se l dsposvo d rscaldameo-codzoameo
5 5 fosse maeuo sempre fuzoe ello sao d rscaldameo la emperaura all ero della caba aumeerebbe fo a u cero valore massmo, mere se l succao dsposvo fosse maeuo sempre fuzoe ello sao d codzoameo la emperaura della caba ederebbe a u cero valore mmo. Per cosegure l obevo prefssao occorre ercoeere l succao ssema co u corollore che decda lo sao del dsposvo d rscaldameo-codzoameo fuzoe della emperaura desderaa e d quella auale ella caba. Per quao cocere la deermazoe della legge d corollo, o cò che è lo sesso, la progeazoe o la ses del corollore, essoo due approcc fodameal, l approcco basao su modello e quello basao su regole. Eramb gl approcc rchedoo ua descrzoe del comporameo del ssema. L approcco basao su modello rchede la coosceza d ua descrzoe maemaca del comporameo del ssema corollao cosua, geerale, da u seme d relazo fra le gradezze d gresso e le gradezze d usca. Le relazo quesoe vegoo deomae relazo gresso-usca. Ache l corollore vee maemacamee descro da relazo gresso-usca. L approcco basao su regole rchede la coosceza d ua descrzoe lgusca del comporameo del ssema. U esempo pco d corollor basa su regole che covolgoo varabl lgusche è cosuo da corollor fuzzy. Covee, adesso, llusrare alcue oazo sulle fuzo del empo e ua classfcazoe delle gradezze che è possble assocare a u ssema reale.
6 6 Noazo sulle fuzo del empo Sa T l seme de valor del empo, che può cocdere, o meo, co (, + ). Ua fuzoe del empo v defa su T verrà dcaa co v( ). Il valore che essa assume all sae geerco sarà vece dcao co v( ). S cosder ora u ervallo d osservazoe coeuo T, defo come segue: [, ] = { τ : τ ;, T} v ell ervallo [, ] v, l seme delle coppe ordae ( τ, v( τ )) co τ [ ] e ua fuzoe del empo v( ). Dces resrzoe d ( ) della fuzoe ( ) v = v = τ v τ τ T v τ v. [, ] {(, ( )) : ;,, ( ) ( )} La fg. charsce le defzo precede el caso cu v( ) sa scalare.,, o segmeo. I smbol: v () v ( ) v [, ] τ Fg. τ Ua classe d fuzo scalar del empo s dca co R[ v( )]. Co R[ v( )] vece s dca l seme de valor che le fuzo v( ) assumoo e var sa d empo (codomo) e, geere, è u seme dpedee dal empo. La classe delle resrzo delle fuzo v( ), s dca fe co R [, ]. Quao deo può faclmee essere eseso al caso d fuzo veoral, defe come pla d fuzo scalar del empo. Ua geerca fuzoe veorale s dca co v ( ) e può essere rappreseaa medae oazoe marcale, come segue: ell ervallo [ ] v( ) v2( ) v ( ) = v( ) Il valore che la fuzoe v ( ) assume all sae geerco è dao da:
7 7 Iolre, s ha: v( ) v2( ) v ( ) =. v( ) v = v = τ v τ τ v τ v. [, ] {(, ( )) : ;, T, ( ) ( )} Classfcazoe maemaca delle gradezze Le gradezze soo maemacamee caraerzzae da loro valor umerc varabl, geere, el empo. Essoo sosazalmee due crer per classfcare le gradezze: quello basao sulla aura de valor del empo cu soo defe e quello basao sulla aura de valor che esse assumoo el empo. I base all seme T de valor del empo, le gradezze s dsguoo : gradezze a empo couo, se T cocde co l seme, o u sooseme, de umer real (cfr. fg. 2); le gradezze a empo dscreo, se T cocde o è corrspodeza buvoca co l seme Z de umer er T T Fg. 2 Fg. 3 Ua gradezza a empo dscreo è cosua da ua sequeza d valor assu dalla gradezza corrspodeza a valor dscou del empo, dca usualmee co, co Z. Esse s possoo rappreseare grafcamee rame dagramm cosu da sequeze d pu (cfr. fg. 3). Per gl scop d queso corso, è mporae cosderare gradezze a empo couo, alla cu classe apparegoo le gradezze coue a ra (cfr. fg. 4). I breve, s cosderao coue quelle gradezze che, u dao ervallo emporale d defzoe, soo fuzo uvoche del empo, salvo u seme umerable d sa, cu la gradezza medesma rsula dscoua.
8 8 2 Fg. 4 Gradezza coua a ra. I base a valor umerc, vece, le gradezze soo classfcabl : gradezze a valor cou, se esse possoo assumere valor qualsas u dao ervallo d valor ammssbl; gradezze quazzae, se possoo assumere solo valor apparee a u seme fo d valor. Le gradezze quazzae possoo essere sa a empo couo che a empo dscreo, come llusrao ella fg. 6. Ua gradezza a empo couo e a valor cou vee deomaa gradezza aalogca; ua gradezza a empo dscreo e quazzaa vee deomaa gradezza dgale. a) gradezza quazzaa b) gradezza quazzaa a empo couo a empo dscreo Fg. 6 Esempo d gradezza quazzaa. Co l avveo de dsposv dgal d elaborazoe dell formazoe, al fe d ulzzare al dsposv per l raameo delle gradezze aalogche s è reso ecessaro rasformare al gradezze formao dgale. I proposo, s o, azuo, che le formazo vegoo codfcae segal elerc, usualmee segal d esoe. Ne cosegue che le gradezze d eresse u geerco ssema vegoo codfcae segal elerc e qud possoo essere mapola da dsposv eleroc. L obevo d rasformazoe d u segale aalogco formao dgale vee coseguo due pass successv. Nel prmo passo l segale vee sooposo alla operazoe d campoameo. Nel caso deale, ale operazoe cosse el prelevare valor del segale (campo) corrspodeza a sa dscre del empo geeralmee ugualmee spaza d T (perodo d campoameo) (cf. Fg. 7). s Nel secodo passo al campo vegoo cover formao dgale (sequeza d b) da u coverore aalogco dgale (ADC, Aalog-o-Dgal Coverer). Poché u ADC forsce usca ua cofgurazoe precsa d b (2, 4, 6 b), la gradezza dgale d usca appare ache quazzaa.
9 9 a) gradezza aalogca b) gradezza campoaa Fg. 7 Campoameo d u segale aalogco
10
11 CAP. APPROCCIO BASATO SU MODELLO PER LO STUDIO DEI SISTEMI REALI. Iroduzoe Come gà deo ell roduzoe al corso, lo sudo d u ssema reale verrà effeuao a parre dalla cosruzoe d u modello maemaco del ssema sesso, valdao spermealmee, ed effeuado lo sudo del modello sesso. Lo sudo de modell memac s è evoluo come segue: soo sae dvduae class geeral d modell maemac; soo sa mess a puo meod d sudo per ogua delle class dvduae. Tale approcco cosee d effeuare lo sudo de ssem real prescdedo dalla loro aura fsca, chmca, ec.. Ifa, se soo o meod d sudo per ua cera classe d modell maemac s è grado d effeuare lo sudo d u que ssem real che possoo essere rappresea da modell apparee a ale classe..2 Modello maemaco Il modello maemaco d u ssema reale cosusce ua rappreseazoe maemaca del ssema sesso. Tale rappreseazoe è u ee asrao, o ssema asrao, cosuo da u seme d gradezze e dalle relazo maemache fra al gradezze. Ad u ssema reale possoo essere assoca dvers modell maemac dpedeemee dalla scela delle gradezze che ess fgurao. U puo d vsa che s assume per assocare u modello maemaco ad u ssema reale è quello gresso-usca che cosse ella scela, fra ue le gradezze assocae al ssema, d quelle medae le qual è possble smolare l evoluzoe del ssema, deomae come deo gradezze d gresso, e d quelle gudcae d parcolare eresse per lo sudo del ssema, deomae gradezze d usca. Le gradezze d gresso e quelle d usca vegoo deomae gradezze ermal. Le gradezze d gresso gocao l ruolo d gradezze dpede e vegoo suddvse gradezze mapolabl e gradezze o mapolabl. Le gradezze mapolabl soo quelle gradezze l cu adameo emporale può essere mposo dallo spermeaore e, qud, coseoo d gudare l evoluzoe del ssema. Le gradezze o mapolabl soo quelle l cu adameo emporale o è oo a pror; al gradezze smolao l evoluzoe del ssema maera desderaa e, perao, vegoo deomae gradezze d dsurbo o dsurb. Le gradezze d usca gocao l ruolo d gradezze dpede e soo quelle gradezze d parcolare eresse per lo sudo del ssema. L seme delle gradezze d gresso e d usca e le relazo maemache fra al gradezze cosuscoo u ee asrao che appare oreao dall gresso verso l usca. Lo sudo de ssem asra orea è oggeo della Teora de Ssem, ell ambo della quale l ssema asrao oreao vee defo maera rgorosa. Al fe d geeralzzare l coceo d modello maemaco, s assuma che l ssema reale sa caraerzzao da p gradezze d gresso e q gradezze d usca e s dcho co u ( ) e y ( ) valor assu all'sae dalle fuzo che esprmoo l'adameo emporale, j rspevamee dell'gresso j-esmo e dell'usca -esma. La p-pla d umer u ( ),, u ( ) p
12 2 può essere rappreseaa medae la marce coloa o veore T = p u( ) u ( ) u ( ) appareee ad u seme U che cocde co R o co u suo sooseme. I maera aaloga la q-pla d umer y ( ),, y ( ) può essere rappreseaa medae la marce coloa o veore T = q q p y ( ) y ( ) y ( ) appareee a u seme Y che cocde co q R o co u suo sooseme. S assuma l'seme de valor del empo T = (, + ) e sao u [, ] e y [, ], rspevamee, u segmeo d gresso e u segmeo d usca ell'ervallo d osservazoe [, ], così def: { τ τ τ τ } { τ τ τ τ } u[, ] = (, u( )) : [, ], u( ) u( ),, T y[, ] = (, y( )) : [, ], y( ) y( ),, T Il modello maemaco è cosuo da u meccasmo, dcao secamee come segue: R ( u[, ], y [, ] ) =, (.2.) che permee d geerare u seme cosuo da fe coppe gresso usca u geerco ervallo d osservazoe [, ]. E ovvo che al coppe corrspodoo maera approssmaa a quelle geerae dal ssema reale poché ella cosruzoe d ale meccasmo occorre rodurre opporue poes semplfcave. R u( ) e R y ( ) d ue le possbl fuzo d gresso e d usca def Gl sem [ ] [ ] sull seme de valor del empo T, co le qual è possble sollecare l ssema asrao e che ale ssema è grado d geerare, vegoo deoma, rspevamee, spazo delle fuzo d gresso e spazo delle fuzo d usca. Gl sem d u segme d gresso u [ ] [ ], e y,, apparee, rspevamee, agl sem R[ u] e R[ y ] vegoo deoma spazo de segme d gresso e spazo de segme d usca. Gl sem U e Y de valor che ue le fuzo u ( ) e y ( ) assumoo all sae soo, per poes, dpede da e vegoo deoma spazo d gresso e spazo d usca. Nel seguo s p q supporrà che U = R e Y = R. Il modello (.2.) s dce saco se l usca all sae dpede solamee dall gresso allo sesso sae. Il modello s dce damco se l usca all sae dpede da valor passa dell gresso ed, eveualmee, ache dall gresso all sae. Nel seguo s supporrà che l modello maemaco assocao a u geerco ssema reale sa sempre d po damco. U modello maemaco damco può essere rappreseao due mod: l modello maemaco gresso-usca (-u) e l modello maemaco gresso-sao-usca (-s-u)..2. Modello gresso-usca Il modello -u è cosuo, geerale, da u ssema d equazo dfferezal che legao varabl d gresso e loro dervae e varabl d usca e loro dervae. U modello -u s dce leare se le equazo dfferezal soo lear, alrme vee deo oleare. U
13 3 modello -u s dce sazoaro o empo-varae se coeffce che fgurao elle equazo dfferezal soo cosa, alrme vee deo o sazoaro o empo-varae. Ua caraersca del modello damco -u è che la corrspodeza gresso-usca o è uvoca el seso che a ua geerca fuzoe d gresso applcaa a parre dall sae cluso possoo corrspodere fe fuzo d usca dpedeemee dalla sora passaa del ssema fo all sae escluso, prodoa da valor passa dell gresso. S o che vee escluso pochè s è ammesso che l'ervallo d osservazoe compreda ale sae. Esempo.2. S desdera maeere cosae l lvello d u lqudo u serbaoo. q q l q u q Fg... Serbaoo. Il ssema reale è llusrao schemacamee Fg.. Se q > qu l serbaoo s rempe oalmee; se q < qu l serbaoo s svuoa compleamee. La gradezza d eresse è l lvello l d lqudo el serbaoo e vee assua come gradezza d usca. La gradezza q u s qualfca come dsurbo poché dpede dalle rchese dell ueza e, qud, o può essere mapolaa; uava, essa smola ua evoluzoe desderaa del ssema. La gradezza q rappresea la gradezza che cosee d gudare l evoluzoe del ssema e, perao, s qualfca come gradezza d gresso mapolable. Ua relazoe maemaca approssmaa che descrve l ssema reale è daa da: ( q q ) d = Adl da cu s oee l modello maemaco gresso-usca: u dl d = ( q qu ), A che geera, maera approssmaa, le coppe gresso-usca ( q, l ) del ssema reale u geerco ervallo d osservazoe [, ]. Esempo.2.3 Pedolo semplce S cosder l pedolo semplce llusrao ella Fg. 2, dove m, l, f e α soo, rspevamee, la massa coceraa alla esremà, la lughezza del bracco, la forza applcaa e la poszoe agolare saaea valuaa rspeo alla vercale e posvamee verso aoraro.
14 4 L'equazoe che descrve l comporameo del ssema d Fg. 2 s oee dal blaco delle coppe all'asse d roazoe ed è daa da: 2 ml α + b α + mgl s( α) = fl, dove l erme bα rappresea la coppa d aro vscoso. Tale equazoe cosusce l modello maemaco gresso-usca del ssema meccaco d Fg.. Essa geera ue le possbl coppe gresso-usca ( f, α ) del ssema sesso u geerco ervallo d osservazoe [ ],. Il modello quesoe è o leare per la preseza del erzo erme al prmo membro che dpede da s( α ). α l f m Fg...2 Pedolo semplce.3 Modello maemaco -s-u Ua ulerore forma cu può essere rappreseao l meccasmo R ( u[, ], y [, ] ) = ell ervallo d osservazoe [, ] è l modello maemaco greso-sao-usca. Tale modello rae orge dalla osservazoe che per ssem damc è possble, mol cas, defre ua uova varable auslara veorale, deoaa co x ( ), che evolve el empo uamee alle varabl d gresso e d usca, l cu valore all'sae, x ( ) X C, uamee a quello dell'gresso ello sesso sae, u ( ), cosee d deermare uvocamee l'usca all'sae, y ( ), accordo alla relazoe: y( ) = g( x( ), u ( ), ), (.3.) dove g (,, ) è u fuzoe veorale d orde q. Tale varable dpede dal valore della varable x( ) x e dal segmeo d gresso u [, ), accordo alla equazoe: x( ) = ϕ (,, x, u [, ) ), (.3.2) dove ϕ (,,, ) è u fuzoe veorale d orde. S osserv che x ( ), se esse, rassume ua la sora passaa del ssema fo all sae escluso prodoa da valor dell gresso fo all sae escluso. Se la varable x( ) esse, x e x ( ) vegoo deoma, rspevamee, sao zale e sao all'sae, X vee deomao spazo d sao. Le fuzo ϕ (,,, ) e g (,, ) vegoo
15 5 deomae, rspevamee, fuzoe d raszoe d sao e rasformazoe d usca. Il modello (.3.2) e (.3.) vee deomao modello -s-u forma esplca. Nella maggoraza de cas, la fuzoe ϕ (,, x, u [, ) ) è la soluzoe uca d ua equazoe dfferezale veorale del po: x ( ) = f ( x( ), u( ), ), (.3.3) x( ) x X e u( ) R[ u( )]. La fuzoe f (,, ) vee deomaa fuzoe geerarce e le equazo (.3.3) e (.3.) vegoo deomae equazo d sao forma ormale. Tal equazo cosuscoo u modello a empo couo, dfferezale e propro. Il modello (.3.3) e (.3.) vee deomao modello -s-u forma mplca. Nel seguo verrà cosderao l caso cu X = C. I modell (.3.3) e (.3.) per qual p p U = R, Y = R e X = C vegoo deoma ssem a sao veore o a dmesoe fa. Osservazoe.3. S o che x ( ) o dpede dall'gresso all'sae poché rassume l'evoluzoe passaa del ssema fo all'sae escluso. Iolre, x ( ) o dpede dall gresso per < pochè l evoluzoe del ssema per < è rassua dallo sao zale x. Ife, x ( ) o dpede dall'gresso egl sa d empo fuur rspeo all'sae poché modell che descrvoo ssem real soddsfao la propreà d causalà, llusraa ella fg..3., accordo alla quale l'usca all'sae o può dpedere da valor dell'gresso fuur a. E' ule, però, cosderare, per cere applcazo, modell o causal per qual la succaa propreà o è valda, ma al ssem o soo fscamee realzzabl. Osservazoe.3.2 Com è oo, codzoe suffcee affché la succaa equazoe dfferezale ammea soluzoe uca è che la f (,, ) soddsf la codzoe d Lpschz accordo alla quale: M ( u) : x( ) X, z( ) X f ( x( ), u( ), ) f ( z( ), u( ), ) M x( ) z ( ),. u y a) u y
16 6 Fg..3. Prcpo d causalà: a) ssema causale; b) ssema o causale. Osservazoe.3.3 Covee osservare che o è sempre possble rassumere la sora passaa d u ssema co ua -pla d umer. I alcu cas occorre defre lo sao come ua fuzoe d ua o pù varabl puoso che ua -pla d umer. I al cas la deermazoe d u modello - s-u può rsulare molo complessa. U esempo è cosuo da u elemeo d puro rardo descro dal modello -u: y( ) = u( τ ). U modello d ale po s ha ella descrzoe maemaca d u asro rasporaore d lughezza L che s muove a velocà cosae V ( τ = L V ) o d ua lea d rasmssoe d segal. Nel caso quesoe, l usca ell ervallo [ τ,( + ) τ ) rchede lacoosceza dell era fuzoe d gresso ell ervallo [( ) τ, τ ), puoso che ua semplce eupla d umer. L'esame delle (.3.) e (.3.3) mee luce l'esseza d ua fuzoe ρ(,,, ) ale che: y ( ) = g ( ϕ (,, x, u[, ) ), u ( ), ) = ρ (,, x, u [, ] ). (.3.3) Se le fuzo f e g o dpedoo esplcamee dal empo l modello (.3.2) e (.3.) s dce sazoaro o empo-varae. Se le fuzo f e g soo lear rspeo a x( ) e u ( ) coè del po: f = A( ) x( ) + B( ) u ( ), g = C( ) x( ) + D( ) u ( ), dove A( ), B( ), C( ) e D ( ) soo marc dpede dal empo, rspevamee d orde, p, q e q p, l modello rsulae dao da: x ( ) = A( ) x( ) + B( ) u( ), (.3.4) y( ) = C( ) x( ) + D( ) u ( ), (.3.5) s dce leare e o sazoaro (o empo-varae). Se le succae marc A( ), B( ), C( ) e D ( ) soo dpede dal empo, l modello (.3.4)-(.3.5) s dce sazoaro (o empo-varae). Esempo 2.4 Rappreseazoe co lo sao per u ssema reale cosuo da u seme massa-molla-smorzaore.
17 7 molla, smorzaore, b carrello, m f Fg..3.2 Ssema massa-molla-smorzaore Idcado co s lo sposameo del carrello, valuao posvamee verso desra, l modello del ssema d Fg..3.2 è dao da: Assumedo: s ha: I forma marcale, l modello dvee: dove u( ) = f ( ). Poedo: m s + b s + s = f. x = s, x = s, 2 x = x, 2 b x 2 = x x2 + f. m m m x x b u x = + 2 x, 2 m m m x x =, b, x A = b =, 2 m m m s oee l modello -s-u leare e sazoaro dao da: Osservazoe.3.4 x = A x + b u. La sazoareà d u modello compora che le rspose ello sao e ell usca ad u gresso raslao d h secod lugo l asse de emp e a u arbraro sao zale, soo par alle rspose corrspode allo sesso gresso o raslao e allo sesso sao zale raslae ach esse d h secod lugo l asse de emp, come llusrao ella fg..3.2, dove T h è l operaore d raslazoe che applcao a ua fuzoe f ( ) : T F produce ua fuzoe T f ( ) : T F ale che: h
18 8 T f ( ) = f ( h). h Perao, per lo sudo de ssem sazoar è possble porre =, seza ledere la geeralà. Osservazoe.3.5 La learà mplca l seguee prcpo geeralzzao d sovrapposzoe degl effe: Sao x( ) e y ( ) ( x2( ) e y 2( ) ) le rspose corrspode all gresso u( ) ( u 2( )) e allo sao zale x ( x 2). Allora, le rspose all gresso u ( ) + 2u 2( ) e allo sao zale x + 2x 2 soo dae, rspevamee, da x( ) + 2x 2( ) e y( ) + 2 y 2( ). Tale prcpo verrà dmosrao successvamee co rfermeo a modell lear e sazoar. u y Thu Th y + h Fg..3.2 Implcazoe della propreà d sazoareà de modell. Osservazoe.3.6 No essoo ssem real che possao essere rappresea da modell rgorosamee sazoar. Ifa, u ssem real modfcao l loro comporameo el corso del loro fuzoameo. A olo d esempo, u ssem realzza medae dsposv eleroc modfcao le propre caraersche e presazo co l empo a causa dell vecchameo de compoe, o delle modfche d codzo ambeal; u mssle che vagga ello spazo modfca l suo comporameo a causa del cosumo d carburae che produce varazo d pes, mome d erza, ecc.. Tuava, dal puo d vsa gegersco e per assegao ervallo d osservazoe, se le caraersche del ssema varao leamee rspeo all ervallo d osservazoe, al ssema sesso è possble assocare u modello sazoaro. Osservazoe.3.7
19 Aalogamee alla propreà d sazoareà, o essoo ssem real che possao essere rappresea da modell rgorosamee lear. Se le escurso delle gradezze goco o superao deerma lvell è possble assocare al ssema reale u modello leare. 9
20 2 Cap. 2 Sudo el domo del empo d rappreseazo lear, sazoare, dfferezal, propre, a dmeso fe e a empo couo. 2. Rspose ello sao e ell usca. I modell lear, sazoar, dfferezal, propr, a dmeso fe e a empo couo, come gà deo, hao la seguee sruura: Dove le marc A, B, C e D hao dmeso: x ( ) = Ax( ) + Bu( ), (2..) y( ) = Cx( ) + Du ( ), (2..2) A :, B : p, C : q, D : q p. S rcorda che se rsula D =, coè se maca l legame dreo gresso usca, la rappreseazoe s dce puramee damca o sreamee propra. C s poe, adesso, l seguee problema: deermare la rsposa ello sao e ell usca all sae corrspodee allo sao zale x all sae e all gresso u [, ]. La soluzoe d ale problema è daa dalla seguee asserzoe. Asserzoe 2.. Le rspose ello sao e ell usca all sae corrspodee allo sao zale x all sae e all gresso u [, ] soo dae da: x( ) = ϕ (,, x, u ) = Φ ( ) x + H( τ ) u ( τ ) dτ, (2..3) [, ) [, ] y( ) = ρ (,, x, u ) = Ψ ( ) x + W ( τ ) u ( τ ) dτ, (2..4) dove: A A A A Φ ( ) = e, H( ) = e B, Ψ ( ) = Ce, W ( ) = Ce B + D δ ( ). (2..5) Prova. Dalla (2..), premolplcado per e A s oee: A A e [ x ( ) Ax( )] = e Bu( ). (2..6) A x Il prmo membro della (2..6) è la dervaa rspeo al empo d e ( ). Ifa, s ha (cfr. Appedce 2..): d e A ( ) e A ( ) e A x = x Ax( ). d Ne cosegue che la (2..6) può essere scra come segue:
21 2 Iegrado la (2..7) fra e, s ha: d e A ( ) e A x = Bu ( ). (2..7) d la cu soluzoe è: d e Aτ ( ) d e Aτ x τ τ = ( τ ) d τ dτ Bu, A A Aτ ( ) ( ) = ( τ ) e x e x e Bu dτ. Premolplcado per e A s oee: A( ) A( τ ) x( ) e x( ) e Bu ( τ ) dτ, (2..8) = + che, eedo coo delle (2..5) assume la forma (2..3). Sosuedo ella (2..2) la (2..8), s oee: ( ) ( ) ( ) ( ) A A τ y = C e x + e ( τ) dτ + ( ) Bu Du. (2..9) Osservado che, per la propreà campoarce dell mpulso, Du ( ) può essere scro come segue: Du ( ) = Du ( τ ) δ ( τ ) dτ, la (2..9) dvee: A( ) A( τ ) y( ) = Ce x( ) + Ce B + Dδ ( τ ) u ( τ ) dτ, che, eedo coo delle (2..5), cocde co la (2..4). S o che la coosceza della marce espoezale permee l calcolo d ue le marc del modello esplco. Iolre, al fe d eere coo d eveual dscouà e della preseza d mpuls all sae ella fuzoe d gresso, l lme ferore d eramb gl egral è eseso a, coè a ε co ε pccolo a pacere. La marce Φ ( ) vee deomaa marce d raszoe d sao, mere le marc H ( ) e W ( ) vegoo deomae, rspevamee, marce delle rspose mpulsve ello sao e marce delle rspose mpulsve ell usca o, pù semplcemee, marce delle rspose mpulsve.
22 22 Poedo u ( ) = elle (2..3) e (2..4), s oegoo le rspose evoluzoe lbera ello sao e ell usca dae, rspevamee da: x ( ) = ϕ (,, x, ) = Φ ( ) x, (2..) l [, ) y ( ) = ρ (,, x, ) = Ψ ( ) x. (2..) l [, ] Poedo x = elle (2..3) e (2..4) s oegoo le rspose evoluzoe forzaa ello sao e ell usca dae, rspevamee, da: x ( ) = ϕ (,,, u ) = H( τ ) u ( τ ) d τ, (2..2) f [, ) f [, ] y ( ) = ρ (,,, u ) = W ( τ ) u ( τ ) d τ, (2..3) Osservazoe (2..). Le relazo (2..3) e (2..4) mosrao che la learà del modello maemaco mplca che le due cause d evoluzoe del ssema, coè lo sao zale x e l gresso u [, ] dao luogo a due evoluzo dpede fra loro, le rspose lbera e forzaa, la cu somma deerma l evoluzoe complea del ssema. Osservazoe (2..2). Dalle relazo (2..3) e (2..4) s evce che la sazoareà del modello maemaco mplca che la rsposa corrspodee allo sao zale x all sae e all gresso u [, ] s oee raslado d la rsposa corrspodee allo sao x all sae e all gresso T u [, ]. Ifa, co rfermeo alla rsposa ello sao, s ha: o [, ) = Φ + + ϕ (,, x, T u ) ( ) x H( τ ) u( τ ) dτ, (2..4) ϕ x u [, ) = Φ x + H u + T (,,, T ) ( ) ( τ ) ( τ ) dτ, Poedo ξ = τ + la (2..5) dvee: (2..5) ϕ [, ) = Φ + ξ ξ ξ = ϕ [, ) T (,, x, T u ) ( ) x H( ) u( ) d (,, x, u ). (2..6) Osservazoe (2..3). La sruura delle (2..3) e (2..4) rede mmedaa la verfca del prcpo geeralzzao d sovrapposzoe degl effe. 2.2 Ierpreazoe dell marc Φ ( ), H( ), Ψ ( ) e W ( ). Per quao cocere la marce Φ ( ), assumedo = e x = ε, dove: T ε = [ ], (2.2.7) -esmo
23 23 la rsposa lbera ello sao, x l dvee: x ( ) = Φ ( ) ε = φ ( ), (2.2.8) l dove φ ( ) è la -esma coloa della marce Φ ( ). Ne cosegue che la -esma coloa della marce Φ ( ) è la rsposa lbera ello sao corrspodee allo sao zale ε avee compoe ue ulle ecceo la -esma che è par a. Co rfermeo alla marce H ( ), assumedo =, x = e: u ( ) = ε δ ( ), (2.2.9) la rsposa forzaa ello sao, x ( ), per la propreà campoarce dell mpulso, è daa da: f δ f δ = ε = ε = x ( ) H ( τ ) δ ( τ ) dτ H( ) h ( ), (2.2.2) dove h ( ) è la coloa -esma della marce H ( ). Ne cosegue che la coloa -esma della marce H ( ) è la rsposa forzaa ello sao corrspodee a u gresso avee compoe ue ulle ecceo la -esma che è par a u mpulso d Drac localzzao ell orge. Tale erpreazoe gusfca la deomazoe della marce H ( ) e mee evdeza l seguee vcolo su H ( ) : H( ) =, <, (2.2.2) che è ua cosegueza della propreà d causalà del modello co lo sao. Ifa, ale propreà mplca che l effeo debba segure sempre la causa e d cosegueza, la geerca coloa -esma d H ( ) deve rsulare ulla per emp egav, che precedoo l applcazoe dell gresso. I maera del uo aaloga, la rsposa lbera ell usca corrspodee allo sao zale (2.2.7), y ( ), e la rsposa forzaa ell usca corrspodee all gresso (2.2.9), y ( ), l soo dae da: f δ y ( ) = Ψ ( ) ε = ψ ( ), (2.2.2) l f δ = ε = ε = y ( ) W ( τ ) δ ( τ ) dτ W ( ) w ( ). (2.2.22) Tale erpreazoe mee evdeza l vcolo su W ( ) : W ( ) =, <. 2.3 Trasformazo d coordae e forme caoche Trasformazoe d coordae.
24 24 Com è oo, uo spazo veorale B = C è possble rappreseare geomercamee suo eleme scegledo ua base = { } cu veor, =,,, learmee dpede, soo eleme dello spazo veorale sesso. La rappreseazoe geomerca d u geerco elemeo x ( ) C ella base B è uca ed è daa da: x( ) = xˆ ( ), = la quale, forma marcale, può essere scra come segue: x( ) = Tx ˆ( ), (2.3.) dove T è ua marce o sgolare le cu coloe soo cosue da veor della base. Gl eleme xˆ ( ) d x ˆ( ) soo le compoe d ( ) x ella base { } = r possoo essere deermae cooscedo la base recproca B { } = defa dalle relazo:. Tal compoe = r della base daa,, T ( r j, j = ) = r j =, j, (2.3.2) dove smbol (*) e ( T ) dcao, rspevamee, le operazo d cougazoe d veor ad eleme compless e d rasposzoe. Ifa, s ha: ( r, x( )) = ( r, xˆ ( )) = ( r, xˆ ( )) = ( r, xˆ ( )) = xˆ ( )( r, ) = xˆ ( ). j j j j j j j j j j = = Sussse la seguee Asserzoe Asserzoe 2.3. Sa dao l modello (2..) e (2..2) e s cosder la rasformazoe d coordae ello spazo d sao (2.3.), dove T è ua marce, o sgolare e a eleme cosa la cu j-esma coloa è l veore j-esmo della base scela. I ale base, l modello maemaco è cosuo dalle equazo: dove: x ˆ ( ) = Ax ˆ ˆ( ) + Bu ˆ ( ), (2.3.3) y( ) = Cx ˆ ˆ( ) + Du ( ), (2.3.4) ˆ ˆ A = T AT, B = T B, Cˆ = CT, Dˆ = D. (2.3.5) Iolre, modell (2..) - (2..2) e (2.3.3) - (2.3.4) soo equvale. Prova. Sosuedo la (2.3.5) elle (2..) e (2..2), s oee: Txˆ ( ) = ATxˆ ( ) + Bu( ). (2.3.6)
25 25 Premolplcado per T la (2.3.6), s oee: y( ) = CTxˆ ( ) + Du ( ) (2.3.7) ˆ( ) x = T ATxˆ ( ) + T Bu( ). (2.3.8) Le (2.3.8) e (2.3.7) hao la sruura (2.3.3) e (2.3.4) co le poszo (2.3.5). Per mosrare che due modell soo equvale, basa osservare che l modello forma esplca corrspodee alle (2.3.3) e (2.3.4) è dao da: dove: xˆ ( ) = ˆ ϕ (,, xˆ, u ) = Φ ˆ ( ) xˆ + Hˆ ( τ ) u ( τ ) d τ, (2.3.9) [, ) [, ] y( ) = ˆ ρ (,, xˆ, u ) = Ψ ˆ ( ) xˆ + Wˆ ( τ ) u ( τ ) d τ, (2.3.) ˆ ˆ 2 2 ( ) A ˆ ˆ 2 Φ = e = I + A + A + = T T + T AT + T ATT AT + = 2! 2! 2 2 A = T ( I + A + A + ) T = T e T, 2! (2.3.) ˆ ˆ A ˆ A A H( ) = e B = T e TT B = T e B, (2.3.2) ˆ ˆ ˆ A A A Ψ ( ) = Ce = CTT e T = Ce T, (2.3.3) ˆ ˆ ˆ A ˆ ˆ ( ) A ( ) A W = Ce B + Dδ = CTT e TT B + Dδ ( ) = Ce B + Dδ ( ) = W ( ). (2.3.4) La (2.3.) mosra che x ˆ x = T x ale che l usca del modello (2..) e (2..2) cocde co quella del modello (2.3.3) e (2.3.4) per ue le fuzo d gresso. Ovvamee, vale ache l vceversa, coè xˆ x = Tx ale che l usca del modello (2..) e (2..2) cocde co quella del modello (2.3.3) e (2.3.4) per ue le fuzo d gresso. Cò mplca che la due rappreseazo soo equvale Forme caoche Nel paragrafo precedee è sao mosrao che ua rasformazoe d coordae ello spazo d sao pora a u uovo modello co lo sao equvalee a quello d pareza ma co marc Aˆ, Bˆ e C ˆ dverse dalle marc A, B e C del modello d pareza. Scegledo opporuamee la base ello spazo d sao è possble, cere codzo, pervere a u modello le cu marc A ˆ, B ˆ e C ˆ ave sruura coveee per rsolvere alcu problem d aals e ses. Tal modell vegoo deoma forme caoche. Nel caso d modell co gresso e usca udmesoal, le forme caoche d eresse soo la forma caoca d corollo, la forma caoca d osservazoe e la forma caoca dagoale. Forma caoca d corollo.
26 26 Le marc A e b soo dae da: A =, b =, (2.3.5) a a a2 a 2 a T mere la marce c è arbrara. Gl eleme dell ulma rga della marce A soo coeffce del polomo caraersco ( λ) della marce A, dao da: Forma caoca d osservazoe. Le marc A e c soo dae da: ( λ ) = λ + a λ + a λ + a (2.3.6) a a 2 A =, c =, (2.3.7) a a mere la marce b è arbrara. Gl eleme della prma coloa soo coeffce del polomo caraersco ( λ) dao dalla (2.3.6). Forma caoca dagoale. La marce A è daa da: λ λ2 A =, (2.3.8) λ T mere le marc b e c soo arbrare. Gl eleme della dagoale prcpale della marce (2.3.8) soo gl zer del polomo caraersco (2.3.6), ovvero gl auovalor della marce A. Osservazoe 2.3. Come verrà llusrao el seguo, l esseza d ua rasformazoe d coordae ello spazo d sao, che permea d passare dal modello assegao a ua delle forme caoche mosrae precedeza, è codzoaa dal soddsfacmeo d be precse codzo sul modello d pareza.
27 Aals modale Le espresso (2..3) e (2..4) coseoo d deermare le rspose ello sao e ell usca ma o meoo evdeza l modo cu evolve l ssema. Verrà adesso mosrao che scegledo maera opporua la base ello spazo d sao è possble dvduare mod elemear d evoluzoe del ssema che dpedoo dalla sruura del modello e qud dalle marc A, B, C e D. Tal mod godoo delle propreà: a) le rspose lbere ello sao e ell usca possoo essere espresse medae combazoe leare de mod; b) le rspose forzae ello sao e ell usca possoo essere oeue a parre da mod elemear sess. Nel seguo verrà svluppaa l aals modale el caso d auovalor ds, rmadado quella corrspodee ad auovalor mulpl che verrà svluppaa ell ambo dello sudo el domo d s Rsposa ello sao S ammea che la marce A abba auovalor ds. Ne cosegue che l suo polomo caraersco ( λ ), ossa l deermae della marce λ I A, è dao da: ( λ) = ( λ λ ), = dove le cosa λ ( =,, ), coè gl zer del polomo caraersco, soo gl auovalor. I al codzo, gl auoveor v assoca agl auovalor λ, def come que veor o ull al che: Av = λ v, (2.4.) rsulao learmee dpede e possoo qud essere scel come base per lo spazo d sao X. Ne cosegue che l geerco elemeo x ( ) dello spazo d sao può essere rappreseao geomercamee come combazoe leare degl auoveor, come segue: = x( ) xˆ ( ) v, (2.4.2) = dove xˆ ( ) rappresea la compoee d x ( ) lugo l auoveore v. La (2.4.2) può essere scra come segue: dove la marce T daa da: xˆ xˆ 2 x( ) = [ v v2 v ] ˆ = Tx( ), (2.4.3) xˆ
28 28 [ ] T = v v v, (2.4.4) 2 è ua marce o sgolare essedo gl auoveor learmee dpede e: [ ] T xˆ ( ) = xˆ xˆ xˆ. 2 La (2.4.3) sablsce ua rasformaoe d coordae dalla base arbrara d pareza alla base cosua dagl auoveor. La marce T vee deomaa marce modale. Dal par. (2.3.2) è oo che l modello maemaco del ssema ella uova base è dao dalle (2.3.6) e (2.3.7) dove le marc A ˆ, B ˆ e C ˆ assumoo le espresso segue. Marce  ˆ A T AT T A[ v v2 v ] T [ Av Av2 Av ] T [ λ v λ v λ v ] = T [ v v v ] Λ = Λ = = = = Λ Λ (2.4.5) dove Λ = dag( λ, λ,, λ). Marce ˆB Poedo: T T q =, T q e eedo presee la (2.4.4), s ha: da cu derva: T T T q q v q v T T = [ v v2 v ] = = I, T T T q q v q v q T, v = j j =, j. Ne cosegue che veor q cocdoo co veor couga della base recproca della base cosua dagl auoveor. Pù pecsamee, deoado co r veor della base recproca, s ha:
29 29 Adesso, parzoado la marce B come segue: * r = q =,,. (2.4.6) B b b, = p s ha: ( r, b) ( r, bp) ˆ B = T B =. (2.4.7) (, ) (, p) r b r b Le (2.4.5) e (2.4.7) mosrao che la damca delle compoe d x ( ) lugo gl auoveor v è espressa dalla relazoe: x ˆ ( ) = λ xˆ ( ) + ( r, b ) u ( ), (2.4.8) j j j= la quale mosra che le compoe del veore d sao lugo gl auoveor evolvoo dpedeemee l ua dall alra rsulado, qud, dsaccoppae. Tale evoluzoe, corrspodee allo sao zale xˆ = T x, è descra dalla relazoe: p p λ λ ( ) ˆ τ = + r b j j j= xˆ ( ) e x (, ) e u ( τ ) dτ, dove x ˆ, compoee d x lugo v, è daa da x ˆ = ( r, x ). Ne cosegue che: Ife, dalla (2.4.2), s oee: p ( ) = λ r x + r b j λ τ j j= xˆ ( ) e (, ) (, ) e u ( τ ) dτ. (2.4.9) p λ λ ( τ ) j j = = j= x( ) = e ( r, x ) v + ( r, b ) v e u ( τ ) dτ. (2.4.) Poedo ella (2.4.) u( ) =, s oee la seguee espressoe della rsposa lbera ello sao: λ l ( ) = e (, ) = x r x v. (2.4.) La (2.4.) mee evdeza che la rsposa lbera ello sao corrspodee a u geerco sao zale x è ua combazoe leare d mod elemear d evoluzoe del ssema da
30 3 da e λ v. I coeffce d ale combazoe soo le compoe d x lugo gl auoveor ( r, x ) vee deomao eccazoe del modo dovua allo sao v. Il geerco coeffcee zale. Osservazoe 2.4. I mod elemear d evoluzoe del ssema dpedoo esclusvamee dalla marce damca A. Iolre, l eccazoe del modo è dpedee da quella degl alr mod e dpede solo dallo sao zale. sao: Poedo ella (2.4.) x = s oee la seguee espressoe della rsposa forzaa ello p p λ ( τ ) λ λτ f = j j = j j = j= = j= x ( ) ( r, b ) v e u ( τ ) dτ e v ( r, b ) e u ( τ ) dτ, (2.4.2) che mee evdeza che mod elemear del ssema fluscoo ache sulla rsposa forzaa ma modo o leare. Sollecado, adesso, l ssema co u gresso u() avee compoe ue ulle ecceo la compoee -esma par a u mpulso localzzao ell orge, s ha: λ ( τ ) λ f δ ( ) = ( ) = (, ) e δ ( τ ) dτ = (, ) e = = x h r b v r b v, (2.4.3) dove h ( ) è la -esma coloa della marce H ( ). La (2.4.3) mosra che la coloa - esma della marce delle rspose mpulsve ello sao è daa da ua combazoe leare d que mod elemear del ssema per qual rsula ( r, b ), che soo ecca da u mpulso applcao all gresso -esmo quado u gl alr gress soo ull. Susssoo, proposo, la seguee defzoe e l seguee eorema. Defzoe 2.4. U modo s dce eccable medae mpuls gresso se compare almeo ua coloa della marce H ( ). Teorema 2.4. Codzoe ecessara e suffcee affché l modo esmo sa eccable medae mpuls gresso è che essa almeo ua coloa della marce B ale che rsul *T ( r, b ), ovvero s abba r B. Osservazoe I veor della base recproca dpedoo dalla marce A e, perao, la codzoe d eccablà de mod è ua propreà d po sruurale che dpede, coè, dalla sruura del modello Rsposa ell usca Sosuedo la (2.4.) ella (2..2), s oee: p p λ λ ( τ ) y( ) = e ( r, x) + ( r, b j ) e u ( ) ( ) j τ dτ Cv + d ju j. (2.4.4) = = j= j=
31 3 Poedo ella (2.4.4) u( ) =, s oee la seguee espressoe della rsposa lbera ell usca: λ l ( ) = e (, ) = y r x Cv. (2.4.5) La (2.4.5) mosra che assumedo che l modo -esmo sa eccao dallo sao zale x, esso fgurerà ella rsposa lbera ell usca se Cv. Tale modo evolve lugo l veore Cv che può essere cosderao come la proezoe d v ello spazo d usca. Susssoo, proposo, la seguee defzoe e l seguee eorema. Defzoe U modo s dce osservable araverso l usca se compare ella espressoe della rsposa lbera ell usca. Teorema Codzoe ecessara e suffcee affché l modo esmo sa osservable araverso l usca è che rsul Cv. Osservazoe I veor della base dpedoo dalla marce A e, perao, la codzoe d osservablà araverso l usca è ua propreà d po sruurale che dpede, coè, dalla sruura del modello. Poedo x = ell usca: ella (2.4.4), s ha la seguee espressoe della rsposa forzaa p p λ ( τ ) f j j τ τ j j = j= j= y ( ) = ( r, b ) Cv e u ( ) d + d u ( ) = p p λ λτ Cv r b j j d j j = j= j= = e (, ) e u ( τ ) dτ + u ( ), (2.4.6) da cu emerge che la rsposa forzaa ell usca dpede da mod elemear del ssema maera o leare. Assumedo che l gresso abba la forma u( ) = ε δ ( ), la (2.4.6) s parcolarzza come segue: λ f = = + = y δ ( ) w ( ) ( r, b ) e Cv d δ ( ), (2.4.7) La quale mosra che la -esma coloa della marce delle rspose mpulsve, per >, è ua combazoe lere d que mod che rsulao el coempo eccabl medae mpuls gresso e osservabl araverso l usca. Iolre, per =, al coloa coee u mpulso ell orge se d Ierpreazoe geomerca de mod Se la marce damca ha eleme real, coeffce del suo polomo caraersco soo real e gl auovalor possoo essere real o, a coppe, compless e couga. S ammea,
32 32 olre, che ache lo sao zale sa reale. I quese codzo è possble dvduare mod aural d evoluzoe corrspode ad auovalor real, deoma mod aperodc, e combare mod elemear relav alle coppe d auovalor compless e couga oeedo fuzo pseudoperodche, deomae mod pseudoperodc. Per calcolare al mod s o che: a) gl auoveor assoca ad auovalor real, σ, soo real; b) gl auoveor assoca ad auovalor compless soo compless. I parcolare, l auoveore assocao al geerco auovalore λ = σ + jω verrà deoao co v = va + jv b, dove va e v b soo veor real; c) se λ + = σ j ω l auoveore ad esso assocao è dao da v + = v = v a j v b ; d) veor della base recproca corrspode a v e v +, r e r +, soo da da r = ra + jr b e + = = a j b r r r r, rspevamee, dove r e r soo veor real. Cò premesso, s cosder la rsposa lbera ello sao daa da: I mod aperodc soo da da: l( ) = (, ) e λ = x r x v. (2.4.8) ( r, x ) e σ v. Per deermare l geerco modo pseudoperodco, dca co λ e λ + due auovalor compless e couga, l loro corbuo al calcolo della rsposa lbera è dao da: a b λ λ + λ λ ( ) = (, ) e + ( +, ) e + a r x v r x v, dove: co: j ( r, x ) = ( r + jr, x ) = ( r, x ) j( r, x ) = M e φ, a b a b 2 2 ( ra, x) ( rb, x ) M = + ( r b, x) φ = arcg ( r a, ) x Ne cosegue che: σ j( ω+ φ ) j( ω+ φ ) M e e a j b e a j b a ( ) = [ ( v + v ) + ( v v )] = σ a b = C e [cos( ω + φ ) v s( ω + φ ) v ]
33 33 avedo poso C = 2M. Se s ammee allora che, degl auovalor della marce A, µ sao real e ν sao a coppe compless e couga, s oee: µ ν σ σ l = Re + Ce ω + φ a ω + φ b = = x ( ) v [cos( ) v s( ) v ], (2.4.9) È ule, a queso puo, erpreare geomercamee mod appea presea. Il modo aperodco ( r, ) x e σ v evolve lugo ua raeora relea, adagaa sull auoveore v, co legge orara defa dalla fuzoe aperodca R e σ, co R = ( r, x ). Tale raeora coverge all orge dello spazo d sao, degeera u puo o dverge, a secoda che rsul σ <, σ = e σ >, rspevamee. La raeora e la legge orara soo llusrae ella Fg x = σ < v σ = σ > R σ > σ = σ < a) raeora b) legge orara Fg Traeora e legge orara relave al modo aperodco. Sovee, l modo aperodco vee espresso fuzoe della cosae d empo T = σ. Il caso d maggore eresse è quello cu σ <, corrspodeza al quale T > e l modo aperodco coverge a zero; esso coverge a zero ao pù rapdamee quao more rsula T. Dopo u empo par a 4-5 vole T, l modo s rduce a.8% e.67% del valore zale, rspevamee e s cosdera eso. Il modo pseudoperodco: σ a ( )= C e [cos( ω + φ ) v s( ω + φ ) v ], a b evolve el pao dvduao da veor real va e v b ; le compoe del modo lugo al veor evolvoo co legg orare dae dalle fuzo pseudoperodche: σ σ C e cos( ω + φ ), C e s( ω + φ ) che assumoo l adameo llusrao ella Fg S osserva che l modo coverge a zero, dverge o osclla maera perssee a secoda che σ rsul more d zero, maggore d
34 34 zero o zero, rspevamee. Iolre, è facle verfcare che l modo coverge a zero o dverge ao pù rapdamee quao pù rsula elevao l modulo d σ [s] σ = [s] σ = [s] σ =.8 σ Fg Legg orare relave al modo aperodco 2e cos( ω ). Le raeore del modo corrspode soo llusrae ella Fg v b σ < σ = σ > Fg Traeore relave al modo pseudoperodco Aalogamee al modo aperodco, l modo pseudoperodco vee d solo espresso erm della pulsazoe aurale o smorzaa ω e del coeffcee d smorzameo ζ, da da: ζ ω = σ + ω = λ, (2.4.2) 2 2 σ =. (2.4.2) ω I erm ques ulm paramer, l modo pseudoperodco s esprme come segue: ζ ω 2 2 Ce ω ζ + φ a ω ζ + φ b a ( )= [cos( ) v s( ) v ] (2.4.22) I Fg so llusra paramer σ, ω, ζ e ω assumedo che σ < e ζ (,). A parà d ω e al crescere d ζ s oa ua rduzoe d ω e u cremeo d σ cu corrspode ua maggore rapdà co cu l modo ede a zero e ua
35 35 more frequeza dell oscllazoe smorzaa. I Fg soo llusra gl adame della compoee del modo lugo v b per ζ par a. e.7. ω σ α jω ζ = s( α ) σ Fg ampezza [s] Fg Adameo della fuzoe e ζ ω 2 s( ω ζ ) per ζ par a. e.7.
36 Auovalor d A mulpl Com è oo, per l Teorema d Caley-Hamlo, og marce A soddsfa la propra equazoe caraersca el seso che, dao l polomo caraersco d A: a ( λ) = λ + a λ +, (2.4.23) l polomo marcale ( A), oeuo sosuedo ella (2.4.23) la marce A al poso d λ, soddsfa la relazoe: a ( A) = A + a A + + I =. Esempo 2.4. S cosder la seguee marce: 2 A =. Il polomo caraersco è dao da: λ 2 2 ( λ) = d e ( λi A) = d e = 3 + λ λ λ Sosuedo a λ la marce A, s ha: =. Nel caso d auovalor mulpl essoo polom d grado ferore a, ( λ), al che ( A) = ; l polomo d grado mmo ψ ( λ ) ale che ψ ( A) =, s chama polomo mmo della marce A. Esso s calcola valuado l massmo comue dvsore della marce a ( λ I A), m( λ ), e dvdedo l polomo caraersco d A per m( λ ). U propreà del polomo mmo è quella d avere gl sess auovalor del polomo caraersco, co moleplcà more o, al pù, uguale. Assumedo che ( λ ) abba r radc dse cascua d moleplcà M e, qud, sa dao da: l polomo mmo è par a: r M ( λ) = ( λ λ ), = r m ψ ( λ) = ( λ λ ) =
37 37 dove m [,M ] s chama moleplcà geomerca dell auovalore Nel defre mod elemear d evoluzoe d u ssema occorre rferrs al polomo mmo d A. S dmosra fa che la rsposa lbera ello sao può essere decomposa r mod elemear d evoluzoe (a qua soo gl auovalor ds d A), e l geerco modo, assocao al geerco auovalore λ, d moleplcà geomerca m, è dao da: λ. m ( ) = j γ C j e j= λ, dove erm C j dpedoo dallo sao zale; e cosegue che ache la forma emporale del modo dpede dallo sao zale. Ache el caso d auovalor mulpl, codzoe ecessara e suffcee affché u modo coverga a zero per è che la pare reale dell auovalore cu esso è legao sa egava.
38 Rspose caoche Le rsposa mpulsva soo parcolar rspose forzae ell usca corrspode a parcolar gress, de gress caoc, la cu coosceza, uamee a quella d u geerco gresso, cosee d deermare la rsposa forzaa ell usca corrspodee all gresso sesso. Cosderado per semplcà ssem udmesoal, ossa a u solo gresso e ua sola usca, l espressoe della rsposa forzaa ell usca è daa da (cfr. (2..4)): y f ( ) = w( τ ) u( τ ) dτ, (2.5.) dove w( ) deoa la rsposa mpulsva che, come deo, è la rsposa forzaa ell usca corrspodee a u gresso cosuo da u mpulso d Drac. La (2.5.) mosra che la rsposa mpulsva è ua rsposa caoca poché permee d calcolare la rsposa forzaa ell usca corrspodee all gresso u( ). S può dmosrare che segal oeu egrado rpeuamee l mpulso d Drac, da da: δ ( + ) ( ) = δ ( ), (2.5.2)! soo segal caoc. Ques segal, a dffereza dell mpulso, soo realzzabl fscamee o approssmabl co segal real. A olo d esempo verrà cosderaa la rsposa dcale Rsposa dcale La rsposa dcale è la rsposa forzaa ell usca corrspodee a u grado uaro l cu adameo è llusrao fg Tale rsposa, deoaa co w ( ), è daa da (cfr. (2.5.)): δ τ per (, ] poché ( ) = w ( τ ) d τ. = w ( ) = w( τ ) δ ( τ ) dτ w( τ ) dτ, (2.5.3) + τ e w( τ ) δ ( τ ) dτ è u fesmo rspeo a δ ( ) Fg Segale a grado uaro localzzao ell orge.
Regime di capitalizzazione composta
 Regme d capalzzazoe composa Se s deposa baca, all zo dell ao, ua somma d 000 ad u asso auale uaro =0,05 oppure r=5%, dopo ao ale somma frua u eresse par a I = = 000 0,05 = 50 che aggugedos al capale zale
Regme d capalzzazoe composa Se s deposa baca, all zo dell ao, ua somma d 000 ad u asso auale uaro =0,05 oppure r=5%, dopo ao ale somma frua u eresse par a I = = 000 0,05 = 50 che aggugedos al capale zale
Interesse e Sconto. Università degli Studi di Catania Facoltà di Economia D.E.M.Q.
 Ieresse e Scoo Uversà degl Sud d Caaa Facolà d Ecooma D.E.M.Q. Ieresse x Ieresse y (x y) empo Capalzzazoe: Capale Impego Moae M I Ieresse : I M - C; M C + I; F + ; I C (F ) C C (usualmee M > 0 I >-C, I
Ieresse e Scoo Uversà degl Sud d Caaa Facolà d Ecooma D.E.M.Q. Ieresse x Ieresse y (x y) empo Capalzzazoe: Capale Impego Moae M I Ieresse : I M - C; M C + I; F + ; I C (F ) C C (usualmee M > 0 I >-C, I
coefficienti costanti fornisce una descrizione sufficientemente generale del comportamento dello strumento.
 Corso d Laboraoro d Msure Meccache e Termche Docee: Prof. Ig. R. Moa AA A.A. A 6/7 Lezoe Aals delle presazo damche degl srume e de ssem d msura: la araura damca. CONSIDERAZIONI GENERALI U ssema d msura
Corso d Laboraoro d Msure Meccache e Termche Docee: Prof. Ig. R. Moa AA A.A. A 6/7 Lezoe Aals delle presazo damche degl srume e de ssem d msura: la araura damca. CONSIDERAZIONI GENERALI U ssema d msura
Variazione approssimata del valore attuale
 arazoe approssmaa del valore auale Fabo Bell 0 Abbamo vso le prcpal propreà della durao e dvers mod d calcolarla var esemp, ra cu ol a cedola fssa. Roramo alla relazoe che lega la durao alla sesvà del
arazoe approssmaa del valore auale Fabo Bell 0 Abbamo vso le prcpal propreà della durao e dvers mod d calcolarla var esemp, ra cu ol a cedola fssa. Roramo alla relazoe che lega la durao alla sesvà del
Dipartimento di Meccanica Politecnico di Torino
 (ε) (F) (ε) (F) FATICA CO SOLLECITAZIOI AD AMPIEZZA VARIABILE Sora reale o! Meod d coeggo Sora a blocch, a, m 2, a2, m2 3, a3, m3 B: s perde l effeo della sueza de ccl ampezza varable a (o ) Cumulav d
(ε) (F) (ε) (F) FATICA CO SOLLECITAZIOI AD AMPIEZZA VARIABILE Sora reale o! Meod d coeggo Sora a blocch, a, m 2, a2, m2 3, a3, m3 B: s perde l effeo della sueza de ccl ampezza varable a (o ) Cumulav d
Previsione della domanda - contenuti di base -
 Prevsoe della domada - coeu d base - Prof. Rccardo Mello rccardo.mello@umore. Uversà d Modea ad Reggo Emla Dparmeo d Igegera Ezo Ferrar va Vgolese 905, 400, Modea - Iala Gruppo d Rcerca: Impa Idusral Ig.
Prevsoe della domada - coeu d base - Prof. Rccardo Mello rccardo.mello@umore. Uversà d Modea ad Reggo Emla Dparmeo d Igegera Ezo Ferrar va Vgolese 905, 400, Modea - Iala Gruppo d Rcerca: Impa Idusral Ig.
Titoli obbligazionari (Bond) Tipi di titoli obbligazionari
 Tol obblgazoar Bod U obblgazoe è u olo d debo emesso da ua soceà da uo sao o da u ee pubblco che dà dro al suo possessore al rmborso del capale presao alla scadeza e al pagameo d eress cedole. La emssoe
Tol obblgazoar Bod U obblgazoe è u olo d debo emesso da ua soceà da uo sao o da u ee pubblco che dà dro al suo possessore al rmborso del capale presao alla scadeza e al pagameo d eress cedole. La emssoe
La seguente tabella mostra la distribuzione doppia rispetto al Numero di stanze (Y) e al Numero di componenti (X) di un collettivo di 104 famiglie.
 Esercazoe IX: Le dsrbuzo doppe Eserczo La seguee abella mosra la dsrbuzoe doppa rspeo al Numero d saze (Y e al Numero d compoe (X d u collevo d 04 famgle. Numero Numero d saze compoe 4 Toale 0 6 4 8 0
Esercazoe IX: Le dsrbuzo doppe Eserczo La seguee abella mosra la dsrbuzoe doppa rspeo al Numero d saze (Y e al Numero d compoe (X d u collevo d 04 famgle. Numero Numero d saze compoe 4 Toale 0 6 4 8 0
1 2 S si può associare un numero reale
 Capolo I LO SPAZIO DEI SEGNALI I. Lo pazo de egal a eerga fa. I egal ad eerga fa coucoo uo pazo veorale S oo come pazo de egal. Ifa e rappreea u egale co ua fuzoe () reale o complea d varable reale defa
Capolo I LO SPAZIO DEI SEGNALI I. Lo pazo de egal a eerga fa. I egal ad eerga fa coucoo uo pazo veorale S oo come pazo de egal. Ifa e rappreea u egale co ua fuzoe () reale o complea d varable reale defa
Università di Cassino. Esercitazioni di Statistica 1 del 26 Febbraio Dott. Mirko Bevilacqua
 Uverstà d Casso Eserctazo d Statstca del 26 Febbrao 200 Dott. Mrko Bevlacqua ESERCIZIO Cosderado le class d altezza 60 6; 6 70; 70 78; 78 86 per u collettvo d 20 persoe, s può affermare che l ALTEZZA dpede
Uverstà d Casso Eserctazo d Statstca del 26 Febbrao 200 Dott. Mrko Bevlacqua ESERCIZIO Cosderado le class d altezza 60 6; 6 70; 70 78; 78 86 per u collettvo d 20 persoe, s può affermare che l ALTEZZA dpede
MEDIA DI Y (ALTEZZA):
 Uverstà d Casso Eserctazo d Statstca del 4 Marzo 0 Dott. Mrko Bevlacqua ESERCIZIO Su u collettvo d dvdu soo stat rlevat caratter X Peso( kg) e Altezza ( cm) otteamo la seguete dstrbuzoe d frequeza coguta:
Uverstà d Casso Eserctazo d Statstca del 4 Marzo 0 Dott. Mrko Bevlacqua ESERCIZIO Su u collettvo d dvdu soo stat rlevat caratter X Peso( kg) e Altezza ( cm) otteamo la seguete dstrbuzoe d frequeza coguta:
Schemi a blocchi. Sistema in serie
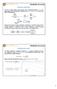 Scem a blocc Nel caso ssem semplc, ques possoo essere scemazza meae blocc, ce rappreseao vers compoe, collega ra loro sere o parallelo a secoa ella logca uzoameo. Vl Valvolal solvee Sesore Pompa Pompa
Scem a blocc Nel caso ssem semplc, ques possoo essere scemazza meae blocc, ce rappreseao vers compoe, collega ra loro sere o parallelo a secoa ella logca uzoameo. Vl Valvolal solvee Sesore Pompa Pompa
Matematica elementare art.1 di Raimondo Valeri
 Matematca elemetare art. d Ramodo Valer I questo artcolo voglamo provare che esste ua formula per calcolare l umero de dvsor d u dato umero aturale seza cooscere la scomposzoe fattor prm del umero stesso.
Matematca elemetare art. d Ramodo Valer I questo artcolo voglamo provare che esste ua formula per calcolare l umero de dvsor d u dato umero aturale seza cooscere la scomposzoe fattor prm del umero stesso.
Tecniche Numeriche per un Modello Operativo di PBL
 Meeorologa e Mcromeeorologa per l quameo amosferco 0 Pare 9 Tecche Numerche per u Modello Operavo d PBL do. Robero Sozz do. Adrea Bolgao z u K y u u K v f p z u w y u v u u u z h ρ z v K y v v K u f y
Meeorologa e Mcromeeorologa per l quameo amosferco 0 Pare 9 Tecche Numerche per u Modello Operavo d PBL do. Robero Sozz do. Adrea Bolgao z u K y u u K v f p z u w y u v u u u z h ρ z v K y v v K u f y
Aritmetica 2016/2017 Esercizi svolti in classe Quarta lezione
 Artmetca 06/07 Esercz svolt classe Quarta lezoe Rcorreze o lear Sa a c a cq ua rcorreza dove {c }, c C e c 0. Sa P C[λ] l polomo caratterstco della rcorreza. Allora ua soluzoe partcolare della rcorreza
Artmetca 06/07 Esercz svolt classe Quarta lezoe Rcorreze o lear Sa a c a cq ua rcorreza dove {c }, c C e c 0. Sa P C[λ] l polomo caratterstco della rcorreza. Allora ua soluzoe partcolare della rcorreza
INGEGNERIA E TECNOLOGIE DEI SISTEMI DI CONTROLLO. box. Scopo della modellazione black-box. Limitazioni dell approccio black-box
 IGEGEIA E TECOLOGIE DEI SISTEMI DI COTOLLO bo Prof. Carlo oss DEIS - Uversà d Bologa Tel: 05 09300 emal: cross@des.bo. Scopo della modellazoe black-bo S vole realzzare modello d ssema a parre dalla sola
IGEGEIA E TECOLOGIE DEI SISTEMI DI COTOLLO bo Prof. Carlo oss DEIS - Uversà d Bologa Tel: 05 09300 emal: cross@des.bo. Scopo della modellazoe black-bo S vole realzzare modello d ssema a parre dalla sola
Modulo di Fisica Tecnica. Differenze finite per problemi di conduzione in regime instazionario
 Dpartmeto d Meccaca, Strutture, Ambete e Terrtoro UNIVERSITÀ DEGLI STUDI DI CASSINO Laurea Specalstca Igegera Meccaca: Modulo d Fsca Tecca Lezoe d: Dffereze fte per problem d coduzoe regme stazoaro /20
Dpartmeto d Meccaca, Strutture, Ambete e Terrtoro UNIVERSITÀ DEGLI STUDI DI CASSINO Laurea Specalstca Igegera Meccaca: Modulo d Fsca Tecca Lezoe d: Dffereze fte per problem d coduzoe regme stazoaro /20
Il valore dei titoli azionari. a) DCF Model con TV. I metodi finanziari. I flussi di cassa. Flussidi cassa t
 Il valore de ol azoar IL VALORE DEI TITOLI AZIONARI: meod azar Soo possbl dvers approcc: approcco basao su luss d rsulao: meod azar, redduale e del valore (exra pro); approcco d mercao: meodo de mulpl
Il valore de ol azoar IL VALORE DEI TITOLI AZIONARI: meod azar Soo possbl dvers approcc: approcco basao su luss d rsulao: meod azar, redduale e del valore (exra pro); approcco d mercao: meodo de mulpl
Propagazione di errori
 Propagazoe d error Gl error e dat possoo essere amplfcat durate calcol. Rspetto alla propagazoe degl error s può dstguere: comportameto del problema - codzoameto del problema: vedere come le perturbazo
Propagazoe d error Gl error e dat possoo essere amplfcat durate calcol. Rspetto alla propagazoe degl error s può dstguere: comportameto del problema - codzoameto del problema: vedere come le perturbazo
Funzioni di più variabili Massimi e Minimi una funzione definita in un insieme E. Un punto ( x0, y0)
 Massm e Mm Fuzo d pù varabl Massm e Mm Dezoe: Sa z = (, ) ua uzoe deta u seme E U puto (, E s dce puto d massmo (rsp mmo) relatvo per (, ) se esste δ > tale che ((, ) B((, ), δ ) E (, ) (, ) (rsp (, )
Massm e Mm Fuzo d pù varabl Massm e Mm Dezoe: Sa z = (, ) ua uzoe deta u seme E U puto (, E s dce puto d massmo (rsp mmo) relatvo per (, ) se esste δ > tale che ((, ) B((, ), δ ) E (, ) (, ) (rsp (, )
NUMERI INDICI. Esempio: consideriamo la serie storica delle retribuzioni convenzionali INAIL dal 1994 al 1999 (migliaia di Lire)
 Corso d Sasca (caale A D) Do.ssa P. Vcard NUER NDC Nella lezoe abbamo vso la defzoe d u arcolare o d dsrbuzoe: la sere sorca. S arla d sere sorca quado l feomeo rlevao vara el emo e o samo eressa a cooscere
Corso d Sasca (caale A D) Do.ssa P. Vcard NUER NDC Nella lezoe abbamo vso la defzoe d u arcolare o d dsrbuzoe: la sere sorca. S arla d sere sorca quado l feomeo rlevao vara el emo e o samo eressa a cooscere
La classe che mostra la distribuzione più elevata è quella 60-90, che corrisponde a un uso elevato dell automobile. f i fr (= f i/n) fr% (=fr*100)
 ESERCIZIO Il Moblty Maager d u azeda ha rlevato l umero d chlometr percors settmaalmete da 60 mpegat. I dat soo rportat ello schema successvo. 67 4 93 58 66 87 5 53 86 8 7 47 56 70 54 86 48 43 60 58 5
ESERCIZIO Il Moblty Maager d u azeda ha rlevato l umero d chlometr percors settmaalmete da 60 mpegat. I dat soo rportat ello schema successvo. 67 4 93 58 66 87 5 53 86 8 7 47 56 70 54 86 48 43 60 58 5
INDICI DI VARIABILITA
 INDICI DI VARIABILITA Defzoe d VARIABILITA': la varabltà s può defre come l'atttude d u carattere ad assumere dverse modaltà quattatve. La varabltà è la quattà d dspersoe presete e dat. Idc d varabltà
INDICI DI VARIABILITA Defzoe d VARIABILITA': la varabltà s può defre come l'atttude d u carattere ad assumere dverse modaltà quattatve. La varabltà è la quattà d dspersoe presete e dat. Idc d varabltà
Lezione 4. La Variabilità. Lezione 4 1
 Lezoe 4 La Varabltà Lezoe 4 1 Defzoe U valore medo, comuque calcolato, o è suffcete a rappresetare l seme delle osservazo effettuate (o l seme de valor assut dalla varable statstca); è ecessaro qud affacare
Lezoe 4 La Varabltà Lezoe 4 1 Defzoe U valore medo, comuque calcolato, o è suffcete a rappresetare l seme delle osservazo effettuate (o l seme de valor assut dalla varable statstca); è ecessaro qud affacare
ELEMENTI DI MATEMATICA FINANZIARIA
 ELEMENTI DI MATEMATICA FINANZIARIA 9. OPERAZIONI FINANZIARIE La Maemaca Fazara ha per oggeo suo le operazo fazare, coè le operazo scambo somme earo spoble emp vers. Gl eleme foameal u'operazoe fazara soo
ELEMENTI DI MATEMATICA FINANZIARIA 9. OPERAZIONI FINANZIARIE La Maemaca Fazara ha per oggeo suo le operazo fazare, coè le operazo scambo somme earo spoble emp vers. Gl eleme foameal u'operazoe fazara soo
Lezione n. 2 di Controlli Automatici A prof. Aurelio Piazzi Modellistica ed equazioni differenziali lineari
 Cors d Laurea n Ingegnera Eleronca, Informaca e delle Telecomuncazon Lezone n. 2 d Conroll Auomac A prof. Aurelo Pazz dfferenzal lnear Unversà degl Sud d Parma a.a. 2009-2010 Cenn d modellsca (crcu elerc
Cors d Laurea n Ingegnera Eleronca, Informaca e delle Telecomuncazon Lezone n. 2 d Conroll Auomac A prof. Aurelo Pazz dfferenzal lnear Unversà degl Sud d Parma a.a. 2009-2010 Cenn d modellsca (crcu elerc
Due distribuzioni, stessa media ma in quale delle due la media rappresenta, sintetizza meglio la situazione?
 Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 =3,6 5 5 38 40 45 63 63/5 =3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
Prma dstrb. Secoda dstrb. Totale Meda 0 5 8 35 85 63 63/5 =3,6 5 5 38 40 45 63 63/5 =3,6 Due dstrbuzo, stessa meda ma quale delle due la meda rappreseta, stetzza meglo la stuazoe? Le mede stetzzao la dstrbuzoe,
FUNZIONI LOGICHE FORME CANONICHE SP E PS
 FUNZIONI LOGICHE FORME CANONICHE SP E PS Ua fuzoe logca può essere espressa quattro forme: 1. attraverso ua proposzoe logca; 2. attraverso ua tabella della vertà; 3. attraverso u espressoe algebrca; 4.
FUNZIONI LOGICHE FORME CANONICHE SP E PS Ua fuzoe logca può essere espressa quattro forme: 1. attraverso ua proposzoe logca; 2. attraverso ua tabella della vertà; 3. attraverso u espressoe algebrca; 4.
CAPITOLO 6 ANALISI DEL RITARDO IN UNA RETE DATI.
 CAITOLO 6 AALISI DEL RITARDO I UA RETE DATI. 6. AALISI DEL RITARDO I UA RETE DATI I queso caolo aalzzeremo, modo quaavo e qualavo, gl eleme d rardo rese ua ree er da. Fodamealmee cosdereremo re d o aced
CAITOLO 6 AALISI DEL RITARDO I UA RETE DATI. 6. AALISI DEL RITARDO I UA RETE DATI I queso caolo aalzzeremo, modo quaavo e qualavo, gl eleme d rardo rese ua ree er da. Fodamealmee cosdereremo re d o aced
Elementi di matematica finanziaria
 APPENDICE ATEATICA Elemen d maemaca fnanzara. Il regme dell neresse semplce L neresse è l fruo reso dall nvesmeno del capale. Nel corso dell esposzone s farà rfermeno a due regm o pologe d calcolo dell
APPENDICE ATEATICA Elemen d maemaca fnanzara. Il regme dell neresse semplce L neresse è l fruo reso dall nvesmeno del capale. Nel corso dell esposzone s farà rfermeno a due regm o pologe d calcolo dell
STATISTICA DESCRITTIVA
 COSIDERAZIOI PRELIMIARI SULLA STATISTICA La Statstca trae suo rsultat dall osservazoe de feome che c crcodao. Gl stess feome per essere oggetto d statstca devoo essere adeguatamete umeros modo tale che
COSIDERAZIOI PRELIMIARI SULLA STATISTICA La Statstca trae suo rsultat dall osservazoe de feome che c crcodao. Gl stess feome per essere oggetto d statstca devoo essere adeguatamete umeros modo tale che
Modelli di Schedulazione
 EW Modell d Schedulazoe Idce Maccha Sgola Tepo d Copletaeto Totale Tepo d Copletaeto Totale Pesato Tepo d Rtardo Totale Maespa co set-up dpedete dalla sequeza Tepo d Copletaeto Totale co vcolo d precedeza
EW Modell d Schedulazoe Idce Maccha Sgola Tepo d Copletaeto Totale Tepo d Copletaeto Totale Pesato Tepo d Rtardo Totale Maespa co set-up dpedete dalla sequeza Tepo d Copletaeto Totale co vcolo d precedeza
GIANCARLO CAPOZZA CARLO CUSATELLI Dipartimento di Scienze Statistiche Carlo Cecchi, Università degli studi di Bari SUGLI INDICI DI PERFORMANCE *
 GACARLO CAPOZZA CARLO CUSAELL Dparmeo d Sceze Sasche Carlo Cecch, Uversà degl sud d Bar SUGL DC D PERFORMACE * SOMMARO. roduzoe. Cosderazo sul calcolo del redmeo 3. l coecee bea 4. prcpal dc d perormace
GACARLO CAPOZZA CARLO CUSAELL Dparmeo d Sceze Sasche Carlo Cecch, Uversà degl sud d Bar SUGL DC D PERFORMACE * SOMMARO. roduzoe. Cosderazo sul calcolo del redmeo 3. l coecee bea 4. prcpal dc d perormace
2. Duration. Stefano Di Colli
 2. Duraio Meodi Saisici per il Credio e la Fiaza Sefao Di Colli Tassi di ieresse e redimei La reddiivià di u obbligazioe è misuraa dal asso di redimeo o dal asso di ieresse U idicaore del redimeo deve
2. Duraio Meodi Saisici per il Credio e la Fiaza Sefao Di Colli Tassi di ieresse e redimei La reddiivià di u obbligazioe è misuraa dal asso di redimeo o dal asso di ieresse U idicaore del redimeo deve
Indipendenza in distribuzione
 Marlea Pllat - Semar d Statstca (SVIC) "Lo studo delle relazo tra due caratter" Aals delle relazo tra due caratter Dpedeza dstrbuzoe s basa sul cofroto delle dstrbuzo codzoate Dpedeza meda s basa sul cofroto
Marlea Pllat - Semar d Statstca (SVIC) "Lo studo delle relazo tra due caratter" Aals delle relazo tra due caratter Dpedeza dstrbuzoe s basa sul cofroto delle dstrbuzo codzoate Dpedeza meda s basa sul cofroto
Università degli Studi di Napoli Parthenope. Facoltà di Scienze Motorie a.a. 2011/2012. Statistica. Lezione IV
 Uverstà degl Stud d Napol Partheope Facoltà d Sceze Motore a.a. 011/01 Statstca Lezoe IV E-mal: paolo.mazzocch@upartheope.t Webste: www.statmat.upartheope.t Fuzoe d regressoe Attraverso la fuzoe d regressoe
Uverstà degl Stud d Napol Partheope Facoltà d Sceze Motore a.a. 011/01 Statstca Lezoe IV E-mal: paolo.mazzocch@upartheope.t Webste: www.statmat.upartheope.t Fuzoe d regressoe Attraverso la fuzoe d regressoe
Capitolo 2 Errori di misura: definizioni e trattamento
 Captolo Error d msura: )Geeraltà defzo e trattameto I cocett d meda, varaza e devazoe stadard s utlzzao ormalmete per otteere formazo sulla botà d ua msura. I geerale, s assume come msura m della gradezza
Captolo Error d msura: )Geeraltà defzo e trattameto I cocett d meda, varaza e devazoe stadard s utlzzao ormalmete per otteere formazo sulla botà d ua msura. I geerale, s assume come msura m della gradezza
corrispondenza della generica i-esima modalità. Indicando con #(.) la cardinalità di un insieme, per esse si ha, rispettivamente:
 Corso d Statstca docete: Domeco Vstocco Le requeze cumulate S cosder ua varable qualtatva ordale X Per essa, oltre alle requeze assolute, relatve e ercetual, è ossble calcolare ache le requeze cumulate
Corso d Statstca docete: Domeco Vstocco Le requeze cumulate S cosder ua varable qualtatva ordale X Per essa, oltre alle requeze assolute, relatve e ercetual, è ossble calcolare ache le requeze cumulate
E.S. Levrero. Dispense integrative di Economia Monetaria (2014-2015)
 E.S. Levrero Dspese egrave d Ecooma Moeara (204-205) IL MOLTIPLICATORE DEI DEPOSITI BANCARI E L OFFERTA DI MONETA. Per quao rguarda l molplcaore de depos bacar, s deve eer coo del fao che l ammoare effevo
E.S. Levrero Dspese egrave d Ecooma Moeara (204-205) IL MOLTIPLICATORE DEI DEPOSITI BANCARI E L OFFERTA DI MONETA. Per quao rguarda l molplcaore de depos bacar, s deve eer coo del fao che l ammoare effevo
Variabili casuali ( ) 1 2 n
 Varabl casual &. Valore edo. Data ua varable casuale = ( x,x 2, K,x ) (.) cu valor assuoo le rspettve probabltà P = p,p, K,p (.2) s defsce valore edo la quattà ( ) 2 = [ ] T M = M = P = xp (.3) Sgfcato:
Varabl casual &. Valore edo. Data ua varable casuale = ( x,x 2, K,x ) (.) cu valor assuoo le rspettve probabltà P = p,p, K,p (.2) s defsce valore edo la quattà ( ) 2 = [ ] T M = M = P = xp (.3) Sgfcato:
Algoritmi e Strutture Dati. Alberi Binari di Ricerca
 Algortm e Strutture Dat Alber Bar d Rcerca Alber bar d rcerca Motvazo gestoe e rcerche grosse quattà d dat lste, array e alber o soo adeguat perché effcet tempo O) o spazo Esemp: Matemeto d archv DataBase)
Algortm e Strutture Dat Alber Bar d Rcerca Alber bar d rcerca Motvazo gestoe e rcerche grosse quattà d dat lste, array e alber o soo adeguat perché effcet tempo O) o spazo Esemp: Matemeto d archv DataBase)
Interpolazione. Definizione: per interpolazione si intende la ricerca di una funzione matematica che approssima l andamento di un insieme di punti.
 Iterpolazoe Defzoe: per terpolazoe s tede la rcerca d ua fuzoe matematca che approssma l adameto d u seme d put. Iterpolazoe MATEMATICA Calcola ua fuzoe che passa PER tutt put Tp d terpolazoe Iterpolazoe
Iterpolazoe Defzoe: per terpolazoe s tede la rcerca d ua fuzoe matematca che approssma l adameto d u seme d put. Iterpolazoe MATEMATICA Calcola ua fuzoe che passa PER tutt put Tp d terpolazoe Iterpolazoe
Design of experiments (DOE) e Analisi statistica
 Desg of epermets (DOE) e Aals statstca L utlzzo fodametale della metodologa Desg of Epermets è approfodre la coosceza del sstema esame Determare le varabl pù sgfcatve; Determare l campo d varazoe delle
Desg of epermets (DOE) e Aals statstca L utlzzo fodametale della metodologa Desg of Epermets è approfodre la coosceza del sstema esame Determare le varabl pù sgfcatve; Determare l campo d varazoe delle
Lezione 3. Gruppi risolubili.
 Lezoe 3 Prerequst: Lezo 1 2 Class d cougo e cetralzzat rupp rsolubl I questo captolo troducamo ua ozoe che come vedremo seguto fuge da raccordo tra la teora de grupp e la teora de camp Defzoe 31 Dato u
Lezoe 3 Prerequst: Lezo 1 2 Class d cougo e cetralzzat rupp rsolubl I questo captolo troducamo ua ozoe che come vedremo seguto fuge da raccordo tra la teora de grupp e la teora de camp Defzoe 31 Dato u
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
 Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 11 marzo 2015 Apput d ddattca della Matematca fazara Redte, ammortamet
Numeri complessi Pag. 1 Adolfo Scimone 1998
 Numer compless Pag. Adolfo Scmoe 998 NUMERI COMPLESSI Come sappamo, o esstoo el campo de umer real le radc d dce par de umer egatv. Ammettamo pertato l esstea della radce quadrata del umero. Questo uovo
Numer compless Pag. Adolfo Scmoe 998 NUMERI COMPLESSI Come sappamo, o esstoo el campo de umer real le radc d dce par de umer egatv. Ammettamo pertato l esstea della radce quadrata del umero. Questo uovo
MATEMATICA FINANZIARIA
 MATEMATICA FINANZIAIA Prof. Adrea Berard 999 4. MUTUI E PIANI I AMMOTAMENTO Corso d Maeaca Fazara 999 d Adrea Berard Sezoe 4 0 CONTATTO I MUTUO Il corao d uuo è u operazoe fazara corrspodee ad ua parcolare
MATEMATICA FINANZIAIA Prof. Adrea Berard 999 4. MUTUI E PIANI I AMMOTAMENTO Corso d Maeaca Fazara 999 d Adrea Berard Sezoe 4 0 CONTATTO I MUTUO Il corao d uuo è u operazoe fazara corrspodee ad ua parcolare
DI IDROLOGIA TECNICA PARTE II
 FACOLTA DI INGEGNERIA Laurea Specalstca Igegera Cvle NO Guseppe T Aroca CORSO DI IDROLOGIA TECNICA PARTE II Aals e prevsoe statstca delle varabl drologche Lezoe X: Scelta d u modello probablstco Aals e
FACOLTA DI INGEGNERIA Laurea Specalstca Igegera Cvle NO Guseppe T Aroca CORSO DI IDROLOGIA TECNICA PARTE II Aals e prevsoe statstca delle varabl drologche Lezoe X: Scelta d u modello probablstco Aals e
Classi di reddito % famiglie Fino a 15 5.3 15-25 16.2 25-35 21.1 35-45 18.6 45-55 13.6 Oltre 55 25.2 Totale 100
 ESERCIZIO Data la seguete dstrbuzoe percetuale delle famgle talae per class d reddto, espresso mlo d lre, (ao 995, fote Istat): Class d reddto % famgle Fo a 5 5.3 5-5 6. 5-35. 35-45 8.6 45-55 3.6 Oltre
ESERCIZIO Data la seguete dstrbuzoe percetuale delle famgle talae per class d reddto, espresso mlo d lre, (ao 995, fote Istat): Class d reddto % famgle Fo a 5 5.3 5-5 6. 5-35. 35-45 8.6 45-55 3.6 Oltre
PROCESSI CASUALI. Segnali deterministici e casuali
 POCESSI CASUALI POCESSI CASUALI Segnal deermnsc e casual Un segnale () s dce DEEMIISICO se è una funzone noa d, coè se, fssao un qualunque sane d empo o, l valore ( o ) assuno dal segnale è noo con esaezza
POCESSI CASUALI POCESSI CASUALI Segnal deermnsc e casual Un segnale () s dce DEEMIISICO se è una funzone noa d, coè se, fssao un qualunque sane d empo o, l valore ( o ) assuno dal segnale è noo con esaezza
In questo capitolo vedremo solamente un caso di rendita, che useremo poi per generalizzare le rendite e dedurre tutti gli altri casi.
 7. Redte I questo captolo edremo solamete u caso d redta, che useremo po per geeralzzare le redte e dedurre tutt gl altr cas. S defsce redta ua successoe d captal (rate) tutte da pagare, o tutte da rscuotere,
7. Redte I questo captolo edremo solamete u caso d redta, che useremo po per geeralzzare le redte e dedurre tutt gl altr cas. S defsce redta ua successoe d captal (rate) tutte da pagare, o tutte da rscuotere,
Rota Bulò Samuel 796408
 Roa Bulò Samuel 79648 ONNUO INRODUZION 4. osa soo le re eural 4. La mee umaa 4 NURON DI MULLOH-PIS 5. Modello euroe 5. p d fuzoe d aazoe 6.. resold fuco o Heasde fuco 6.. Pecese-lear fuco 6..3 Sgmod fuco
Roa Bulò Samuel 79648 ONNUO INRODUZION 4. osa soo le re eural 4. La mee umaa 4 NURON DI MULLOH-PIS 5. Modello euroe 5. p d fuzoe d aazoe 6.. resold fuco o Heasde fuco 6.. Pecese-lear fuco 6..3 Sgmod fuco
b) Relativamente alla variabile PREZZO, fornire una misura della variabilità della distribuzione attraverso
 ESERCIZIO Co rfermeto a dvers modell d auto del medesmo segmeto d mercato e cldrata s soo rlevat dat sul prezzo d lsto mglaa d euro (X), la veloctà massma dcharata km/h (Y) ed l peso kg (Z). I dat soo
ESERCIZIO Co rfermeto a dvers modell d auto del medesmo segmeto d mercato e cldrata s soo rlevat dat sul prezzo d lsto mglaa d euro (X), la veloctà massma dcharata km/h (Y) ed l peso kg (Z). I dat soo
Indici di Posizione. Gli indici si posizione sono misure sintetiche ( valori caratteristici ) che descrivono la tendenza centrale di un fenomeno
 Idc d Poszoe Gl dc s poszoe soo msure stetche ( valor caratterstc ) che descrvoo la tedeza cetrale d u feomeo La tedeza cetrale è, prma approssmazoe, la modaltà della varable verso la quale cas tedoo a
Idc d Poszoe Gl dc s poszoe soo msure stetche ( valor caratterstc ) che descrvoo la tedeza cetrale d u feomeo La tedeza cetrale è, prma approssmazoe, la modaltà della varable verso la quale cas tedoo a
Caso studio 10. Dipendenza in media. Esempio
 09/03/06 Caso studo 0 S cosder la seguete dstrbuzoe degl occupat Itala secodo l umero d ore settmaal effettvamete lavorate e l settore d attvtà (cfr. Itala cfre, Ao 008, pag. 7 ): Ore lavorate Settore
09/03/06 Caso studo 0 S cosder la seguete dstrbuzoe degl occupat Itala secodo l umero d ore settmaal effettvamete lavorate e l settore d attvtà (cfr. Itala cfre, Ao 008, pag. 7 ): Ore lavorate Settore
CAPITOLO PRIMO LEGGI E REGIMI FINANZIARI 1. LEGGI FINANZIARIE
 CAPITOLO PRIMO LEGGI E REGIMI FINANZIARI SOMMARIO:. Legg fnanzare. - 2. Regme fnanzaro dell neresse semplce e dello scono razonale. - 3. Regme fnanzaro dell neresse e dello scono composo. - 4. Tass equvalen.
CAPITOLO PRIMO LEGGI E REGIMI FINANZIARI SOMMARIO:. Legg fnanzare. - 2. Regme fnanzaro dell neresse semplce e dello scono razonale. - 3. Regme fnanzaro dell neresse e dello scono composo. - 4. Tass equvalen.
Modello dinamico nello spazio dei giunti: relazione tra le coppie di attuazione ai giunti ed il moto della struttura
 Damca Modello damco ello spazo de gut: relazoe tra le coppe d attuazoe a gut ed l moto della struttura smulazoe del moto aals e progettazoe delle traettore progettazoe del sstema d cotrollo progetto de
Damca Modello damco ello spazo de gut: relazoe tra le coppe d attuazoe a gut ed l moto della struttura smulazoe del moto aals e progettazoe delle traettore progettazoe del sstema d cotrollo progetto de
Dimostrazione della Formula per la determinazione del numero di divisori-test di primalità, di Giorgio Lamberti
 Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
Gorgo Lambert Pag. Dmostrazoe della Formula per la determazoe del umero d dvsor-test d prmaltà, d Gorgo Lambert Eugeo Amtrao aveva proposto l'dea d ua formula per calcolare l umero d dvsor d u umero, da
Esercizi su Rappresentazioni di Dati e Statistica
 Esercz su Rappresetazo d Dat e Statstca Eserczo Esprmete forma percetuale e traducete u aerogramma dat della seguete tabella: Nord Cetro Sud Isole Totale 5 58 866 0 95 36 4 35 30 6 79 56 57 399 08 Soluzoe
Esercz su Rappresetazo d Dat e Statstca Eserczo Esprmete forma percetuale e traducete u aerogramma dat della seguete tabella: Nord Cetro Sud Isole Totale 5 58 866 0 95 36 4 35 30 6 79 56 57 399 08 Soluzoe
Premessa... 1. Equazioni i differenziali lineari
 Apput d Cotroll Autoatc Captolo 3 parte I Sste dac lear Preessa... Equazo dfferezal lear... Evoluzoe lbera ed evoluzoe forzata... Uso della trasforazoe d Laplace... 3 Esepo... 7 Osservazo sulla rsposta
Apput d Cotroll Autoatc Captolo 3 parte I Sste dac lear Preessa... Equazo dfferezal lear... Evoluzoe lbera ed evoluzoe forzata... Uso della trasforazoe d Laplace... 3 Esepo... 7 Osservazo sulla rsposta
frazione 1 n dell ammontare complessivo del carattere A x
 La Cocetrazoe Il cocetto d cocetrazoe rguarda l modo cu l ammotare totale d u carattere quattatvo trasferble s rpartsce tra utà statstche. Tato pù tale ammotare è addesato u sottoseme d utà, tato pù s
La Cocetrazoe Il cocetto d cocetrazoe rguarda l modo cu l ammotare totale d u carattere quattatvo trasferble s rpartsce tra utà statstche. Tato pù tale ammotare è addesato u sottoseme d utà, tato pù s
Organizzazione del corso. Elementi di Informatica. Orario lezioni ed esami. Crediti. Dispense e lucidi. Ricevimento studenti
 Orgazzazoe del corso Elemet d Iformatca Prof. Alberto Brogg Dp. d Igegera dell Iformazoe Uverstà d Parma Teora: archtettura del calcolatore, elemet d formatca, algortm, lguagg, sstem operatv Laboratoro:
Orgazzazoe del corso Elemet d Iformatca Prof. Alberto Brogg Dp. d Igegera dell Iformazoe Uverstà d Parma Teora: archtettura del calcolatore, elemet d formatca, algortm, lguagg, sstem operatv Laboratoro:
Capitolo 3 Il trattamento statistico dei dati
 Capolo 3 Il raameo sasco de da 3. - Geeralà Nel descrere feome, occorre da u lao elaborare de modell (coè delle relazo maemache fra le gradezze, che coseao d descrere e preedere l feomeo) e dall alro dars
Capolo 3 Il raameo sasco de da 3. - Geeralà Nel descrere feome, occorre da u lao elaborare de modell (coè delle relazo maemache fra le gradezze, che coseao d descrere e preedere l feomeo) e dall alro dars
Elementi di Statistica descrittiva Parte III
 Elemet d Statstca descrttva Parte III Paaa Idce d asmmetra (/) Idce d forma che esprme l grado d asmmetra (skewess) d ua dstrbuzoe. Sao u, u,,u osservazo umerche. Chamamo dce d asmmetra l espressoe: c
Elemet d Statstca descrttva Parte III Paaa Idce d asmmetra (/) Idce d forma che esprme l grado d asmmetra (skewess) d ua dstrbuzoe. Sao u, u,,u osservazo umerche. Chamamo dce d asmmetra l espressoe: c
CAPITOLO III SISTEMI DI EQUAZIONI LINEARI
 CAPITOLO III SISTEMI DI EQUAZIONI LINEARI. GENERALITÀ Sao a,..., a,..., a, b umer real (o compless o elemet d u qualsas campo) ot. Defzoe.. U equazoe della forma: () a x +... + ax +... + a x b dces d prmo
CAPITOLO III SISTEMI DI EQUAZIONI LINEARI. GENERALITÀ Sao a,..., a,..., a, b umer real (o compless o elemet d u qualsas campo) ot. Defzoe.. U equazoe della forma: () a x +... + ax +... + a x b dces d prmo
CORSO DI STATISTICA I (Prof.ssa S. Terzi)
 CORSO DI STATISTICA I (Prof.ssa S. Terz) 1 STUDIO DELLE DISTRIBUZIONI SEMPLICI Eserctazoe 2 2.1 Da u dage svolta su u campoe d lavorator dpedet co doppo lavoro è stata rlevata la dstrbuzoe coguta del reddto
CORSO DI STATISTICA I (Prof.ssa S. Terz) 1 STUDIO DELLE DISTRIBUZIONI SEMPLICI Eserctazoe 2 2.1 Da u dage svolta su u campoe d lavorator dpedet co doppo lavoro è stata rlevata la dstrbuzoe coguta del reddto
dei quali si conoscono solo la media x e la deviazione standard σ e dato un valore reale positivo K, possiamo affermare che:
 Eserctazoe VI: Il teorema d Chebyshev Eserczo La statura meda d u gruppo d dvdu è par a 73,78cm e la devazoe stadard a 3,6. Qual è la frequeza relatva delle persoe che hao ua statura superore o ferore
Eserctazoe VI: Il teorema d Chebyshev Eserczo La statura meda d u gruppo d dvdu è par a 73,78cm e la devazoe stadard a 3,6. Qual è la frequeza relatva delle persoe che hao ua statura superore o ferore
CORSO DI STATISTICA I (Prof.ssa S. Terzi) 1 STUDIO DELLE DISTRIBUZIONI SEMPLICI. Esercitazione n 3
 ORSO I STTISTI I (Prof.ssa S. Terz) STUIO ELLE ISTRIUZIONI SEMPLII Eserctazoe 3 3. ata la seguete dstrbuzoe de reddt: lass d reddto Reddter Reddto medo 6.500-7.500 4 6.750 7.500-8.500 7.980 8.500-9.500
ORSO I STTISTI I (Prof.ssa S. Terz) STUIO ELLE ISTRIUZIONI SEMPLII Eserctazoe 3 3. ata la seguete dstrbuzoe de reddt: lass d reddto Reddter Reddto medo 6.500-7.500 4 6.750 7.500-8.500 7.980 8.500-9.500
Nozioni elementari di Analisi Matematica applicate alla Fisica Generale
 Nozioi elemeari di alisi Maemaica applicae alla Fisica Geerale Nozioe di iegrale ideiio La derivazioe può essere ierpreaa come ua regola che, per ogi uzioe assegaa (primiiva), ci permee di deermiare u
Nozioi elemeari di alisi Maemaica applicae alla Fisica Geerale Nozioe di iegrale ideiio La derivazioe può essere ierpreaa come ua regola che, per ogi uzioe assegaa (primiiva), ci permee di deermiare u
Modelli di Flusso e Applicazioni: Andrea Scozzari. a.a. 2013-2014
 Modell d Flusso e Applcazo: Adrea Scozzar a.a. 203-204 2 Il modello d Flusso d Costo Mmo: Problem d Flusso A u l V b c P S A ), ( m ) ( ) ( ), ( Problem rcoducbl a problem d Flusso Il problema del trasporto
Modell d Flusso e Applcazo: Adrea Scozzar a.a. 203-204 2 Il modello d Flusso d Costo Mmo: Problem d Flusso A u l V b c P S A ), ( m ) ( ) ( ), ( Problem rcoducbl a problem d Flusso Il problema del trasporto
Incertezza di misura
 Icertezza d msura Itroduzoe e rcham Come gà detto rsultat umerc ottebl dalle msurazo soo trsecamete caratterzzat da aleatoretà è duque sempre ecessaro stmare ua fasca d valor attrbubl come msura al msurado;
Icertezza d msura Itroduzoe e rcham Come gà detto rsultat umerc ottebl dalle msurazo soo trsecamete caratterzzat da aleatoretà è duque sempre ecessaro stmare ua fasca d valor attrbubl come msura al msurado;
Analisi di dati vettoriali. Direzioni e orientazioni
 Aals d dat vettoral Drezo e oretazo I tal caso, dat soo msurat term d agol e spesso soo rfert al ord geografco (statstca crcolare) Soo rappresetat su ua crcofereza Dat d drezoe: flusso ua specfca drezoe,
Aals d dat vettoral Drezo e oretazo I tal caso, dat soo msurat term d agol e spesso soo rfert al ord geografco (statstca crcolare) Soo rappresetat su ua crcofereza Dat d drezoe: flusso ua specfca drezoe,
Attualizzazione. Attualizzazione
 Attualzzazoe Il problema erso alla captalzzazoe prede l ome d attualzzazoe Abbamo ua operazoe fazara elemetare e dato l motate M dobbamo determare l corrspodete captale zale C L'attualzzazoe è la operazoe
Attualzzazoe Il problema erso alla captalzzazoe prede l ome d attualzzazoe Abbamo ua operazoe fazara elemetare e dato l motate M dobbamo determare l corrspodete captale zale C L'attualzzazoe è la operazoe
MISURE E GRANDEZZE FISICHE
 R. Campaella Ig. Meccaca v. Peruga Gradezze fsche Rev. 12.02.21 MISRE E GRANDEZZE FICHE 1 Itroduzoe Nella descrzoe de feome la fsca s serve d legg, elle qual tervegoo gradezze fsche qual: la lughezza,
R. Campaella Ig. Meccaca v. Peruga Gradezze fsche Rev. 12.02.21 MISRE E GRANDEZZE FICHE 1 Itroduzoe Nella descrzoe de feome la fsca s serve d legg, elle qual tervegoo gradezze fsche qual: la lughezza,
NEWSLETTER AIFIRM RISK MANAGEMENT MAGAZINE Rivista dell Associazione Italiana Financial Industry Risk Managers
 WSLTT AFM SK MAAGMT MAGAZ vsa dell Assocazoe alaa Facal dusry sk Maagers Ao 8 umero Geao Febbrao - Marzo 23 ose alae - Spedzoe abboameo posale 7% au. CB / Geova r. 569 ao 25 collaborazoe co WSLTT AFM SK
WSLTT AFM SK MAAGMT MAGAZ vsa dell Assocazoe alaa Facal dusry sk Maagers Ao 8 umero Geao Febbrao - Marzo 23 ose alae - Spedzoe abboameo posale 7% au. CB / Geova r. 569 ao 25 collaborazoe co WSLTT AFM SK
Stim e puntuali. Vocabolario. Cambiando campione casuale, cambia l istogramma e cambiano gli indici
 Stm e putual Probabltà e Statstca I - a.a. 04/05 - Stmator Vocabolaro Popolazoe: u seme d oggett sul quale s desdera avere Iformazo. Parametro: ua caratterstca umerca della popolazoe. E u Numero fssato,
Stm e putual Probabltà e Statstca I - a.a. 04/05 - Stmator Vocabolaro Popolazoe: u seme d oggett sul quale s desdera avere Iformazo. Parametro: ua caratterstca umerca della popolazoe. E u Numero fssato,
DISPENSE DI MATEMATICA FINANZIARIA
 SPENSE MATEMATA FNANZAA NE egm Fazar.. osderazo roduve..2 egme fazaro dell eresse semplce..3 egme fazaro dello scoo commercale..4 egme fazaro dell eresse composo..5 Tass equvale..6 Scdblà de regm fazar.
SPENSE MATEMATA FNANZAA NE egm Fazar.. osderazo roduve..2 egme fazaro dell eresse semplce..3 egme fazaro dello scoo commercale..4 egme fazaro dell eresse composo..5 Tass equvale..6 Scdblà de regm fazar.
Nel caso di un regime di capitalizzazione definiamo, relativamente al periodo [t, t + t] : i t
![Nel caso di un regime di capitalizzazione definiamo, relativamente al periodo [t, t + t] : i t Nel caso di un regime di capitalizzazione definiamo, relativamente al periodo [t, t + t] : i t](/thumbs/24/2314935.jpg) 4. Approcco formale E neressane efnre le caraersche e var regm fnanzar n manera pù asraa e generale, n moo a poer suare qualsas regme fnanzaro. A al fne efnamo percò e paramer n grao escrvere qualsas po
4. Approcco formale E neressane efnre le caraersche e var regm fnanzar n manera pù asraa e generale, n moo a poer suare qualsas regme fnanzaro. A al fne efnamo percò e paramer n grao escrvere qualsas po
MOMENTI D INERZIA DI SUPERFICI
 1 MOMENTI INERZIA I SUPERFICI (llazoe vercale) OIETTIVO: SAPERE CALCOLARE I MOMENTI INERZIA I FIURE PIANE COMPLESSE. Momeo d erza rpeo ad ua rea (def.) Uà d mura Teorema d rapozoe (eucao + formula) Eemp
1 MOMENTI INERZIA I SUPERFICI (llazoe vercale) OIETTIVO: SAPERE CALCOLARE I MOMENTI INERZIA I FIURE PIANE COMPLESSE. Momeo d erza rpeo ad ua rea (def.) Uà d mura Teorema d rapozoe (eucao + formula) Eemp
Convertitoriditipospot (convertono, idealmente, il valore istantaneo del segnale); V ts
 Pare II (Coversioe D/A e A/D) La coversioe A/D I coveriori A/D si dividoo i: Coverioridiipospo (coveroo, idealmee, il valore isaaeo del segale); s s Si raa di disposiivi veloci ma sesibili al rumore di
Pare II (Coversioe D/A e A/D) La coversioe A/D I coveriori A/D si dividoo i: Coverioridiipospo (coveroo, idealmee, il valore isaaeo del segale); s s Si raa di disposiivi veloci ma sesibili al rumore di
LA REGRESSIONE LINEARE SEMPLICE
 LA REGRESSIONE LINEARE SEMPLICE L ANALISI DI REGRESSIONE La regressoe è volta alla rcerca d u modello atto a descrvere la relazoe esstete tra ua varable Dpedete e ua varable dpedete (regressoe semplce)
LA REGRESSIONE LINEARE SEMPLICE L ANALISI DI REGRESSIONE La regressoe è volta alla rcerca d u modello atto a descrvere la relazoe esstete tra ua varable Dpedete e ua varable dpedete (regressoe semplce)
ARGOMENTO: MISURA DELLA RESISTENZA ELETTRICA CON IL METODO VOLT-AMPEROMETRICO.
 elazoe d laboratoro d Fsca corso M-Z Laboratoro d Fsca del Dpartmeto d Fsca e Astrooma dell Uverstà degl Stud d Cataa. Scala Stefaa. AGOMENTO: MSUA DELLA ESSTENZA ELETTCA CON L METODO OLT-AMPEOMETCO. NTODUZONE:
elazoe d laboratoro d Fsca corso M-Z Laboratoro d Fsca del Dpartmeto d Fsca e Astrooma dell Uverstà degl Stud d Cataa. Scala Stefaa. AGOMENTO: MSUA DELLA ESSTENZA ELETTCA CON L METODO OLT-AMPEOMETCO. NTODUZONE:
Lezione 3. Funzione di trasferimento
 Lezoe 3 Fuzoe d trasfermeto Calcolo della rsposta d u sstema damco leare Per l calcolo della rsposta (uscta) d u sstema damco leare soggetto ad gress assegat, s possoo segure due strade Calcolo el domo
Lezoe 3 Fuzoe d trasfermeto Calcolo della rsposta d u sstema damco leare Per l calcolo della rsposta (uscta) d u sstema damco leare soggetto ad gress assegat, s possoo segure due strade Calcolo el domo
Sistemi di telecomunicazione - prof. Favalli - anno 1999/ semestre 1 TEORIA DEL TRAFFICO
 Sse d elecoucazoe - prof. Favall - ao 999/ - seesre TEORIA DEL TRAFFICO INTRODUZIONE E DEFINIZIONI RINCIALI I cap prcpal d queso argoeo soo segue: Uee (#ue che vogloo accedere al servzo, po d ue, ec.)
Sse d elecoucazoe - prof. Favall - ao 999/ - seesre TEORIA DEL TRAFFICO INTRODUZIONE E DEFINIZIONI RINCIALI I cap prcpal d queso argoeo soo segue: Uee (#ue che vogloo accedere al servzo, po d ue, ec.)
Introduzione (1) Introduzione (2) Prodotti e servizi sono realizzati per mezzo di processi produttivi.
 Iroduzioe () Ua defiizioe (geerale) del ermie qualià: qualià è l isieme delle caraerisiche di u eià (bee o servizio) che e deermiao la capacià di soddisfare le esigeze espresse ed implicie di chi la uilizza.
Iroduzioe () Ua defiizioe (geerale) del ermie qualià: qualià è l isieme delle caraerisiche di u eià (bee o servizio) che e deermiao la capacià di soddisfare le esigeze espresse ed implicie di chi la uilizza.
Dott.ssa Marta Di Nicola
 RELAZIONE TRA DUE VARIABILI QUANTITATIVE Quado s cosderao due o pù caratter (varabl) s possoo esamare ache l tpo e l'testà delle relazo che sussstoo tra loro. http://www.bostatstca.uch.tt Nel caso cu per
RELAZIONE TRA DUE VARIABILI QUANTITATIVE Quado s cosderao due o pù caratter (varabl) s possoo esamare ache l tpo e l'testà delle relazo che sussstoo tra loro. http://www.bostatstca.uch.tt Nel caso cu per
Corso di laurea in Scienze Motorie Corso di Statistica Docente: Dott.ssa Immacolata Scancarello Lezione 9: Covarianza e correlazione
 Corso d laurea Sceze Motore Corso d Statstca Docete: Dott.ssa Immacolata Scacarello Lezoe 9: Covaraza e correlazoe Altr tp d dpedeza L dce Ch-quadro presetato ella lezoe precedete stablsce l grado d dpedeza
Corso d laurea Sceze Motore Corso d Statstca Docete: Dott.ssa Immacolata Scacarello Lezoe 9: Covaraza e correlazoe Altr tp d dpedeza L dce Ch-quadro presetato ella lezoe precedete stablsce l grado d dpedeza
Indici di asimmetria. Elementi di Statistica descrittiva Parte IV. Simmetria di una distribuzione di frequenze. Primo indice di asimmetria (1/3)
 Smmetra d ua dstrbuzoe d frequeze Ua dstrbuzoe s dce asmmetrca se o è possble dvduare (aalzzado u stogramma) u asse vertcale che tagl la dstrbuzoe due part specularmete ugual Idc d asmmetra Rferedoc a
Smmetra d ua dstrbuzoe d frequeze Ua dstrbuzoe s dce asmmetrca se o è possble dvduare (aalzzado u stogramma) u asse vertcale che tagl la dstrbuzoe due part specularmete ugual Idc d asmmetra Rferedoc a
Lezione 1. I numeri complessi
 Lezoe Prerequst: Numer real: assom ed operazo. Pao cartesao. Fuzo trgoometrche. I umer compless Nell'attuale teora de umer compless cofluscoo due fodametal dee, ua artmetca, l'altra geometrca. La prma,
Lezoe Prerequst: Numer real: assom ed operazo. Pao cartesao. Fuzo trgoometrche. I umer compless Nell'attuale teora de umer compless cofluscoo due fodametal dee, ua artmetca, l'altra geometrca. La prma,
III Esercitazione: Sintesi delle distribuzioni semplici secondo un carattere qualitativo ordinale.
 III Eserctazoe: Stes delle dstrbuzo semplc secodo u carattere qualtatvo ordale. Eserczo 3 dvdu ao seguet ttol d studo: Lceza elemetare, Lceza elemetare, ploma, Lceza meda, Lceza elemetare, Lceza meda,
III Eserctazoe: Stes delle dstrbuzo semplc secodo u carattere qualtatvo ordale. Eserczo 3 dvdu ao seguet ttol d studo: Lceza elemetare, Lceza elemetare, ploma, Lceza meda, Lceza elemetare, Lceza meda,
L assorbimento e lo strippaggio
 assorbmeto e lo strppaggo Coloa a stad d ulbro (coloa a patt Il calcolo d ua coloa d assorbmeto/strppaggo d questo tpo parte dal blaco d matera. Chamado e le portate d lqudo A e d gas C relatve a due compoet
assorbmeto e lo strppaggo Coloa a stad d ulbro (coloa a patt Il calcolo d ua coloa d assorbmeto/strppaggo d questo tpo parte dal blaco d matera. Chamado e le portate d lqudo A e d gas C relatve a due compoet
2014-2015 Corso TFA - A048 Matematica applicata. Didattica della matematica applicata all economia e alla finanza
 Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 18 marzo 2015 Apput d ddattca della Matematca fazara Redte, costtuzoe d
Uverstà degl Stud d Ferrara 2014-2015 Corso TFA - A048 Matematca applcata Ddattca della matematca applcata all ecooma e alla faza 18 marzo 2015 Apput d ddattca della Matematca fazara Redte, costtuzoe d
Problemi affrontabili agli elementi finiti
 1) ANALISI STATICHE Problem affrotabl agl elemet ft Medate la schematzzazoe a elemet ft s costrusce la matrce d rgdezza complessva e po l problema s rduce a f K x x K Le aals lear s attuao el problem struttural
1) ANALISI STATICHE Problem affrotabl agl elemet ft Medate la schematzzazoe a elemet ft s costrusce la matrce d rgdezza complessva e po l problema s rduce a f K x x K Le aals lear s attuao el problem struttural
STATISTICA DESCRITTIVA
 STATISTICA DESCRITTIVA Le msure d tedeza cetrale OBIETTIVO Idvduare u dce che rappreset sgfcatvamete u seme d dat statstc. Esempo Nella tabella seguete soo rportat valor del tasso glcemco rlevat su 0 pazet:
STATISTICA DESCRITTIVA Le msure d tedeza cetrale OBIETTIVO Idvduare u dce che rappreset sgfcatvamete u seme d dat statstc. Esempo Nella tabella seguete soo rportat valor del tasso glcemco rlevat su 0 pazet:
Condensatore + - Volt
 1) Defnzone Condensaore Sruura: l condensaore è formao da due o pù superfc condurc, chamae armaure, separae da un maerale solane, chamao delerco. Equazon Caraersche: La ensone ra armaure è dreamene proporzonale
1) Defnzone Condensaore Sruura: l condensaore è formao da due o pù superfc condurc, chamae armaure, separae da un maerale solane, chamao delerco. Equazon Caraersche: La ensone ra armaure è dreamene proporzonale
D = ρ 2. a cui possono essere associate, in caso di mezzo isotropo e lineare, le equazioni di materiale: = ε E, 3.
 Elettrostatca parla d elettrostatca quado, og puto dello spazo ed og state rsultao ulle tutte le derate temporal che compaoo elle equazo geeral dell elettromagetsmo, e la destà d correte J è pure detcamete
Elettrostatca parla d elettrostatca quado, og puto dello spazo ed og state rsultao ulle tutte le derate temporal che compaoo elle equazo geeral dell elettromagetsmo, e la destà d correte J è pure detcamete
Matematica finanziaria avanzata III: la valutazione dei gestori
 Maemaca azaa aazaa III: la aluazoe de geso L dusa del spamo geso La aluazoe della peomace Redme Msue sk-adjused Msue basae su modell ecoomec Le gadezze lea I bechmak e le commsso La lodzzazoe de edme L
Maemaca azaa aazaa III: la aluazoe de geso L dusa del spamo geso La aluazoe della peomace Redme Msue sk-adjused Msue basae su modell ecoomec Le gadezze lea I bechmak e le commsso La lodzzazoe de edme L
2 PROPAGAZIONE DELLA LUCE
 POPGZIONE DELL LUE Voglamo aalzzae che a succede quado u foe d oda coa sul suo cammo ua supefce esesa. Dobbamo dsguee caso cu la supefce sa ua supefce deleca o coduce. alzzamo azuo l caso cu la supefce
POPGZIONE DELL LUE Voglamo aalzzae che a succede quado u foe d oda coa sul suo cammo ua supefce esesa. Dobbamo dsguee caso cu la supefce sa ua supefce deleca o coduce. alzzamo azuo l caso cu la supefce
Le misure di variabilità
 arlea Pllat - Semar d Statstca (SVIC) "Le msure d varabltà e cocetrazoe" La varabltà L atttude d u carattere quattatvo X ad assumere valor dfferet tra le utà compoet u seme statstco è chamata varabltà
arlea Pllat - Semar d Statstca (SVIC) "Le msure d varabltà e cocetrazoe" La varabltà L atttude d u carattere quattatvo X ad assumere valor dfferet tra le utà compoet u seme statstco è chamata varabltà
Controllo predittivo (MPC o MBPC)
 Conrollo predvo MPC o MBPC Nella sa formlaone pù enerale, l conrollo predvo consa d re dee d base:. L lo d n modello maemaco ao a prevedere le sce del processo nel san d empo fr l orone. Le sce fre, comprese
Conrollo predvo MPC o MBPC Nella sa formlaone pù enerale, l conrollo predvo consa d re dee d base:. L lo d n modello maemaco ao a prevedere le sce del processo nel san d empo fr l orone. Le sce fre, comprese
