Analisi Matematica 3 appunti
|
|
|
- Sebastiano Piccolo
- 8 anni fa
- Visualizzazioni
Transcript
1 Corso di Laurea in Statistica Matematica e trattamento Informatico dei Dati Analisi Matematica 3 appunti Francesca Astengo Università di Genova, A.A. 20/202
2
3 Indice Capitolo. Serie numeriche. Brevi richiami sulle successioni 2. Le serie numeriche 2 3. Serie a termini non negativi 8 4. Approssimazioni Approssimazione dal criterio integrale Approssimazione dal criterio del rapporto/radice 6 5. Serie assolutamente convergenti 7 6. Serie di Leibniz 8 7. Esercizi 2 Capitolo 2. Serie di funzioni 23. Tipi di convergenza 23.. Convergenza puntuale Convergenza uniforme Serie di potenze Raggio di convergenza Continuità della somma di una serie di potenze Derivabilità e integrazione per serie di potenze Esempi Serie di Taylor Convergenza di una serie di Taylor Esercizi 40 Capitolo 3. Calcolo differenziale per funzioni di più variabili reali 43. Limiti e continuità 47.. Intorni e punti di accumulazione Definizione di limite Calcolo di limiti Continuità Derivabilità e differenziabilità Derivate direzionali Piani in R 3 iperpiani in R n Differenziabilità Derivazione della funzione composta Derivate di ordine successivo Ricerca di massimi e minimi, relativi e assoluti, punti sella 7 6. Estremi vincolati Esercizi 84 i
4 8. Complementi su gradiente e curve di livello, n = 2 87 Capitolo 4. Calcolo integrale per funzioni di più variabili reali 9. Il calcolo di volumi 9 2. Teorema di cambiamento di variabili Complementi sulle funzioni a valori vettoriali Invertibilità e matrice Jacobiana Integrali impropri (con n = 2) Domini non limitati Funzioni non limitate superiormente Integrali n-dimensionali Coordinate cilindriche in R Volume di un solido di rotazione Coordinate sferiche in R Coordinate sferiche in R n Integrazione impropria in R n La funzione Gamma di Eulero Area e volume delle sfere in R n Esercizi 25 Argomenti di anni passati 27 Appendice A. I numeri complessi 29. Rappresentazione geometrica dei numeri complessi Il Teorema fondamentale dell algebra Radici ennesime di un numero complesso Alcuni comandi Maple Esercizi 37 Appendice B. Equazioni differenziali e alle differenze 39. Equazioni differenziali Equazioni differenziali del primo ordine a variabili separabili Equazioni differenziali lineari del primo ordine Il problema di Cauchy Il metodo di Eulero Equazioni differenziali del secondo ordine, lineari, omogenee,a coefficienti costanti Alcuni comandi Maple Equazioni alle differenze Generalità Equazioni alle differenze lineari a coefficienti costanti di ordine Equazioni alle differenze lineari a coefficienti costanti di ordine Esercizi 69 Equazioni differenziali 69 Equazioni alle differenze 7 Riferimenti bibliografici 73 ii
5 CAPITOLO Serie numeriche. Brevi richiami sulle successioni Ricordiamo che una successione reale è una funzione definita da N, eventualmente privato di un numero finito di elementi, a R. a 2 a a Solitamente si indica una successione con la lista dei suoi valori: (a n ) n N. Il valore a n si chiama n-esimo termine della successione. Graficamente possiamo rappresentare una successione come in figura. Una successione importante in probabilità è la successione geometrica di parametro p, con 0 < p <. In formule, è la successione i cui termini sono p n con n. Pensate di lanciare ripetutamente una moneta e che la probabilità che esca testa in un singolo lancio sia p. Ovviamente il risultato di un lancio non influenza il successivo. Il termine p n rappresenta la probabilità di avere esattamente n volte testa in n lanci consecutivi. Sia (a n ) n N una successione e sia ϕ : N N una successione di numeri naturali strettamente crescente. Indichiamo con n k = ϕ(k). Allora la successione (a nk ) k N si chiama successione estratta o sottosuccessione della successione data. In pratica, questo significa scegliere, senza variarne l ordine, infiniti termini della successione di partenza, immagazzinandoli in una nuova lista. Ad esempio, immaginiamo di scegliere per primo il termine a 2 e immagazziniamo questo valore come primo termine ponendo b = a 2. Ora operiamo una seconda scelta; sono a nostra disposizione tutti i termini a partire da a 3 ; scegliamo ad esempio a 0 e poniamo b 2 = a 0. Ora operiamo una terza scelta; sono a nostra disposizione tutti i termini a partire da a ; scegliamo ad esempio a 20 e poniamo b 3 = a 20. E così via. La successione estratta è la b,b 2,b 3,... Esempio.. Sia (a n ) n N la successione definita da a n = cos(nπ/4). Come lista di elementi la successione è, 2 2,0, 2 2,, 2,0, 2,, 2,0, Sia n k = 2k. Allora l estratta, cosiddetta di posto pari è la successione,0,,0,,0,...
6 2 Capitolo Se invece n k = 2k + stiamo considerando la cosiddetta estratta di posto dispari, ovvero la successione: 2 2, 2 2, 2, 2, 2, Supponiamo ora che lim a n = l. n Ovviamente selezionando infiniti termini dallasuccessione (a n ) n N, purchési rispettil ordine, non si varia il carattere della successione, ossia anche lim a n n k = l. In figura, immaginiamo di scegliere dalla successione (a n ) n N (che converge a 0) i termini circolettati di verde Anche i termini circolettati di verde tendono a zero. Può invece succedere che una successione non abbia limite, mentre una sua estratta lo abbia. Una successione che non ha limite è a n = cos(nπ/4) definita nell esempio.. Considerate n k = 2 + 4k. È facile controllare che (a nk ) k N è la successione costantemente nulla, quindi convergente (a 0). In sintesi: se (a n ) n N è una successione che ha limite l (finito o infinito) allora il limite di una sua qualsiasi estratta è ancora uguale a l. 2. Le serie numeriche Per comodità, solitamente in quanto segue le successioni saranno definite su N\{0}, ossia a partire da.
7 .2 Le serie numeriche 3 Data una successione (a n ) n, possiamo formare un altra successione, che indicheremo solitamente con (s n ) n, delle somme parziali o delle ridotte, dove s = a s n = n a k = a + +a n. k= Il termine s n, in cui sommiamo i primi n termini della successione (a n ), si chiama ridotta di ordine n. Graficamente, possiamo pensare alla ridotta di ordine n, ad esempio 3, come all area della regione disegnata nella figura a sinistra (o equivalentemente in quella a destra): è la somma di tre rettangoli, tutti di base e altezze rispettivamente a,a 2,a 3. Al solito, i pallini rossi indicano il grafico della successione Ora immaginiamo di voler sapere se continuando a sommare le aree di questi rettangoli otteniamo un poligono di area finita oppure no. Un altra motivazione allo studio delle somme infinite deriva dalla probabilità. Pensiamo di comprare ogni anno un biglietto della lotteria. Se la lotteria stampa e vende un milione di biglietti ogni anno, la probabilità che il nostro venga estratto è pari a p = 0 6 (supponendo che la lotteria sia onesta, ossia che tutti i biglietti abbiano la stessa probabilità di essere estratti). La probabilità di vincere esattamente la prima volta che acquistiamo il biglietto è ovviamente p; di perdere il primo anno ma vincere il secondo anno è più piccola e precisamente ( p)p; al terzo anno è ( p) 2 p; e così via, la probabilità di prima vincita all ennesimo anno è ( p) n p. Quindi la probabilità che si vinca entro l ennesimo anno è la somma di tali probabilità. In formule, T è la variabile aleatoria che misura l anno in cui si vince e abbiamo detto che P(T = n) = ( p) n p P(T n) = n ( p) k p. k= Come è facile controllare, la probabilità di aver vinto entro l ennesimo anno aumenta. Supponendo di continuare imperterriti a tentare la sorte, ci chiediamo cosa può accadere quando n diventa molto grande.
8 4 Capitolo Ci accorgeremo di un risultato sorprendente: sicuramente vinceremo. Il problema è il tempo medio di attesa per la vincita (ossia il valore atteso di T) che è E(T) = + np(t = n) = + n( p) n p. Scopriremo che è finito, ma pari a un milione di anni (il che dovrebbe bastare a sconsigliare dallo spendere i soldi del biglietto). Definizione.. Sia data una successione reale (a n ) n. Una serie è una somma formale + a n. Si dice che questa serie è convergente e ha per somma s R se la successione delle ridotte (s n ) converge a s. Se la successione delle ridotte diverge, anche la serie si dice divergente. Se la successione delle ridotte non ha limite, la serie si dice indeterminata. Non tutte le successioni in generale partono dall indice. Se abbiamo una successione che parte dall indice p, con p N della forma (a n ) n p, la serie + a n ha lo stesso significato di + b n, dove b n = a p+n. Esempio.2. La serie geometrica di ragione : si consideri la successione definita da 2 La serie geometrica di ragione 2 è + a n = 2 n n N. n=0 (.) s = a 0 = s 2 = + 2 n=p = +. La successione delle ridotte è data da 2 n 2 n... s n = n k= 2 = n n 2 n. Più in generale, dato x R, possiamo considerare la serie geometrica di ragione x, data da + x n = + x n, dove, se x = 0, poniamo 0 0 =. n=0 È facile notare che, nel caso x =, la successione delle ridotte è s n = n, pertanto divergente. Quindi la serie geometrica di ragione diverge a +. Se invece x, allora n s n = k=0 x n = xn x. Quindi, ricordando che se x < si ha lim n + x n = 0, otteniamo che la serie geometrica di ragione x, con x <, è convergente e ha per somma. Inoltre, se x >, allora si x k=0
9 .2 Le serie numeriche 5 ha lim n + x n = +, quindi la serie geometrica di ragione x, con x >, è positivamente divergente. Se invece x, la successione (x n ) non ha limite, quindi la serie geometrica di ragione x, con x, è indeterminata. Riassumendo: se < x < x + x n = + se x n=0 indeterminata se x. Esempio.3. Le serie telescopiche. Studiare la convergenza di + =. Quindi la ridotta di ordine n diventa n(n+) n n+ n n ( s n = k(k +) = k ) k + k= ( = 2 = ) + k= ( 2 3 ) + ( 3 4 ) + + ( n ) n+. Si noti che n(n+). n+ Quindi la serie data è convergente e ha somma. Questo esempio è il prototipo di una classe di serie che si chiamano serie telescopiche. Una serie che si possa scrivere come + (b n b n+ ), dove (b n ) è una successione reale si dice telescopica. Per una tale serie la ridotta di ordine n risulta n (b k b k+ ) = b b n+, k= perché tutti gli altri addendi si elidono. Quindi, se esiste finito lim n + b n = l, la serie telescopica è convergente e ha somma b l. Teorema.4 (Condizione necessaria per la convergenza). Sia + a n una serie convergente. Allora lim a n = 0. n + Dimostrazione. Sia l R la somma della serie, ovvero, detta (s n ) la successione delle ridotte, si ha lim n + s n = l. Ma allora a n = s n s n n + l l = 0.
10 6 Capitolo Questo criterio ci aiuta a stabilire facilmente quando una serie non converge, come nel prossimo esempio. In quello successivo invece vediamo che ci possono essere serie non convergenti il cui termine generale è infinitesimo. Esempio.5. Dire se è convergente + nsin ( n). Siccome la serie data non converge. lim nsin n + ( n ) = Esempio.6. La serie armonica: si consideri la successione definita da a n = n n =,2,... La serie armonica è + n. Notiamo che potrebbe essere una serie convergente, perché lim n + = 0. Tuttavia, questo n potrebbe non essere sufficiente. Mostriamo che la serie armonica diverge. La successione delle ridotte è data da s = a = s 2 = + n... s n = 2 k. La successione delle ridotte è monotona crescente, quindi o diverge positivamente o converge. Notiamo che a n è la restrizione ai naturali della funzione reale f(x) =, di cui sappiamo x calcolare primitive e quindi integrali definiti. Usiamo ora il criterio del confronto per i limiti, confrontando la ridotta di ordine n (area gialla) con un opportuno integrale definito di f, ragionando come in figura: k= n k= n+ k dx = log(n+) x Ne segue che lim n + ovvero la serie armonica diverge. n k= k lim log(n+) = +, n +
11 .2 Le serie numeriche 7 Il carattere di una serie (convergenza, divergenza, indeterminazione) rimane lo stesso se si alterano i termini corrispondenti a un numero finito di indici, perché le ridotte, da un certo ordine in poi, differiranno per una costante. Ad esempio, consideriamo la successione b n = 0 se n = 0,,...,0; b n = /2 n altrimenti. Essa differisce dalla successione geometrica di ragione /2 per i primi termini. Chiamiamo (σ n ) la successione delle ridotte di (b n ) e (s n ) la successione delle ridotte della geometrica di ragione /2 come nella formula (.). Ovviamente, σ n = s n s n + 2 e quindi + b n ha lo stesso carattere di + n=0 invece sono diverse) n=0 s = = (Le somme delle due serie + 2 n Data la serie (convergente o no) + a n, chiamiamo resto n esimo la serie r n = + k=n+ a k n 0. n=0 e + b 2 n n n=0 Questa serie coincide, tranne che per i primi n termini, con la serie data, quindi ha lo stesso carattere di + a n. Proposizione.7. Se la serie numerica + a n è convergente, allora la successione (r n ) n dei resti n esimi è infinitesima. Dimostrazione. Sias Rlasommadellaserienumerica + a n. Siccomelasuccessione delle ridotte (s n ) converge a s, si ha r n = + k=n+ a k = s s n n + 0. Dalla linearità dell operazione di limite si ricavano facilmente le seguenti proprietà: () se + a n e + b n sono serie convergenti e hanno somma s a e s b rispettivamente, allora anche + (a n +b n ) è convergente e la sua somma è s a +s b ;
12 8 Capitolo (2) se c R e + a n è una serie convergente di somma s a, allora + ca n è convergente e la sua somma è cs a ; (3) se + a n e + b n sono serie positivamente divergenti, allora anche + (a n + b n ) è positivamente divergente; (4) se c > 0 e + a n è una serie positivamente divergente, allora + ca n è positivamente divergente; (5) se c < 0e + divergente. a n èuna serie positivamente divergente, allora + ca n ènegativamente 3. Serie a termini non negativi Una serie + a n si dice a termini non negativi se a n 0 per ogni n. Per una tale serie, la successione delle ridotte è sempre crescente, perché per ogni n n+ n s n+ = a k = a k +a n+ s n. k= k= Quindi, siccome una successione crescente ammette sempre limite (o diverge a + oppure, se è superiormente limitata, converge all estremo superiore sup n s n ), le serie a termini non negativi non possono essere indeterminate. Nel prossimo teorema mettiamo in relazione la convergenza dell integrale improprio di una funzione f su [,+ ) con la convergenza della serie di termine generale f(n), n in N. Teorema.8 (Criterio integrale). Sia f : [,+ ) R una funzione positiva e decrescente. Allora: i) la serie + f(n) è convergente se e solo se l integrale improprio + f(x)dx è convergente; ii) la serie + f(n) è divergente se e solo se l integrale improprio + f(x)dx è divergente. Dimostrazione. Siccome f è decrescente, per ogni k =,2,... si ha f(k +) f(x) f(k) x [k,k +] f(k +) Ne ricaviamo che n+ f(x)dx = n k+ f(x)dx k= k k= k+ k n f(k) f(x)dx f(k).
13 .3 Serie a termini non negativi 9 e che n n n f(k) = f(k +) k=2 k= k= Geometricamente la situazione è quella in figura: k+ f(x)dx = n k f(x)dx. n f(x)dx k= n f(k) n f(k) n k=2 f(x)dx Concludiamo ora con il criterio del confronto per i limiti. Esempio.9. La serie armonica generalizzata è una serie del tipo +, dove α è un n α numero reale positivo. Per ogni valore di α è una serie a termini positivi e abbiamo già visto che per α = la serie risulta divergente. Con il criterio integrale è facile notare che la serie armonica generalizzata + è convergente se e solo se lo è l integrale improprio + n α dx e quindi, come abbiamo visto lo scorso x α anno se e solo se α >. Un altro criterio importante è il seguente. Teorema.0 (Criterio del confronto). Siano (a n ) n e (b n ) n due successioni tali che 0 a n b n n. Allora: i) se la serie + b n è convergente, allora anche la serie + a n è convergente; ii) se la serie + a n è divergente, allora anche la serie + b n è divergente. Dimostrazione. Nelle nostre ipotesi è facile e graficamente ovvio che valga la diseguaglianza n n a k b k. k= k=
14 0 Capitolo In figura, abbiamo indicato con un pallino rosso il graficodellasuccessione (a n ) n N econunquadratoblu il grafico della successione (b n ) n N. Il confronto tra le somme delle aree dei rettangoli generati dalle due successioni fornisce la diseguaglianza cercata: l area della regione tratteggiata è banalmente maggiore o uguale all area della regione gialla. Nel caso i) basta controllare che la successione delle ridotte di (a n ) è superiormente limitata, il che segue facilmente da n n + a k b k che è la somma (un numero finito) della serie. k= k= Nel caso ii) basta notare che quindi lim n + k= n b k = +. Esempio.. La serie + k= b k 2+sin n n n k= a k } {{ } + n k= b k è (positivamente) divergente, perché è a termini non negativi e inoltre ciascun termine si minora con il rispettivo termine della serie armonica, che è divergente: n 2+sinn + n e n n = +. Questo criterio funziona anche se la maggiorazione è vera da un certo punto in poi, in particolare se le successioni (a n ) n e (b n ) n hanno lo stesso comportamento all infinito. In particolare: Corollario.2 (Criterio del confronto asintotico). Siano (a n ) n e (b n ) n due successioni a termini non negativi e sia a n = O(b n ) per n +. i) Se la serie + b n è convergente allora anche la serie + a n è convergente. ii) Se la serie + a n è divergente allora anche la serie + b n è divergente. In particolare se esiste finito e non nullo il lim n + a n b n il carattere delle due serie è lo stesso.
15 .3 Serie a termini non negativi Esempio.3. La serie + Inoltre la serie + ( cos n) è convergente. Infatti è a termini non negativi. è convergente e vale n 2 cos n 2n 2 per n +. Esempio.4. La serie + + n 2 è convergente e vale è convergente. Infatti è a termini non negativi. Inoltre la serie n! ( ) n! = o n 2 per n +. Corollario.5 (Criterio dell ordine di infinitesimo). Sia (a n ) n una successione a termini non negativi e infinitesima di ordine α > 0. i) Se α > allora la serie + a n è convergente; ii) Se 0 < α allora la serie + a n è divergente. Esempio.6. Nel caso in cui a n = o(/n) però per ogni α > si abbia n α = o(a n ) questi criteri non dicono nulla. Le serie e hanno entrambe queste proprietà, ma nlogn nlog 2 n sono una divergente e l altra convergente (come si può facilmente vedere usando il criterio integrale). Teorema.7 (Criterio del rapporto). Sia (a n ) n N una successione a termini positivi tale che esista a n+ lim = l. n + a n i) Se l <, allora la serie + n=0 ii) se l >, allora la serie + n=0 a n è convergente e lim n + a n = 0; a n è divergente e lim n + a n = +.
16 2 Capitolo Dimostrazione. Analizziamo il caso i). Sia l < m <. Da un certo N in poi si ha a N+ < ma N a N+2 < ma N+ < m 2 a N a N+3 < ma N+2 < m 3 a N. a N+k < m k a N con k = 0,,... Maalloradauncertopuntoinpoiitermini sonodominatidaitermini diunaseriegeometrica di ragione m <, quindi convergente. Allora per il criterio del confronto la serie di partenza è convergente e quindi lim n + a n = 0. Con analoghi ragionamenti si prova ii). Infatti, se l > M >. Da un certo N in poi si ha a N+ > M a N a N+2 > M a N+ > M 2 a N a N+3 > M a N+2 > M 3 a N. a N+k > M k a N con k = 0,,... Ma allorada uncerto punto inpoi i termini sono minoratidai termini di una serie geometrica di ragione M >, quindi il termine generale è positivamente divergente e la serie di partenza è positivamente divergente. Esempio.8. Nel caso in cui l =, il criterio del rapporto non permette di concludere nulla. Si considerino ad esempio le serie armoniche generalizzate con α = e α = 2. Una è divergente, l altra è convergente, ma per entrambe il limite del rapporto è. Esempio.9. La serie esponenziale. Per quali x > 0 è convergente la serie + x n n=0 n!? Vedremo in seguito che questa serie è convergente per ogni x in R e la sua somma è e x. Sia a n = xn n! ; allora a n > 0 e possiamo applicare il criterio del rapporto: a n+ a n = x n+ (n+)! x n n! La serie esponenziale è convergente per ogni x > 0. Osserviamo che in particolare per ogni x > 0 vale = x 0 x > 0. n+ lim n + x n n! = 0. Questo fatto è banale quando x, ma per x > no; il limite precedente ci fa osservare che per n + l ordine di infinito di n! è maggiore di quello di x n.
17 .3 Serie a termini non negativi 3 Ilcriteriodelrapportononsiusaquandoa n èunafunzionerazionaledin, perchésiotterrebbe l =. Può essere utile soprattutto quando ci sono i fattoriali. Esempio.20. Dire se converge + n! n n n=0 n! n n. Si tratta di una serie a termini positivi. Proviamo col criterio del rapporto: (n+)! ( ) a n+ (n+) = n+ n n n ( n = (n+) a n (n+) = = n+ n+ n+ ) n e <. Quindi la serie data è convergente. Questo dice anche che lim n + n! n n = 0, ossia che l ordine di infinito del fattoriale è minore di quello di n n. Analogo al criterio del rapporto è il Teorema.2 (Criterio della radice). Sia (a n ) n N una successione a termini non negativi tale che esista n an = l. lim n + i) Se l <, allora la serie + a n è convergente; n=0 ii) se l >, allora la serie + a n è divergente. n=0 Esempio.22. Dire se è convergente + ( n. logn) È una serie a termini non negativi; inoltre n=2 ( ) n ( ) n = 0. logn logn Allora la serie di partenza è convergente per il criterio della radice. a Si noti che se esiste lim n+ n + a n = l, allora anche lim n n + a n = l. Infatti, se il limite del rapporto è l, fissiamo ε > 0. Allora esiste N tale che per n = N +p con p = 0,,... vale (l ε) p a N < a n < (l+ε) p a N. Quindi sempre per n = N +p con p = 0,,... vale ((l ε) p a N ) /n < n a n < ((l+ε) p a N ) /n. Passando al limite per p + nella precedente relazione otteniamo a sinistra l ε e a destra l+ε. Ne segue che definitivamente l 2ε n a n l+2ε. Per l arbitrarietà di ε > 0, lim n + n a n = l.
18 4 Capitolo Anche qui nel caso l = non si può dire nulla (usare le serie armoniche generalizzate come nel criterio del rapporto). 4. Approssimazioni In generale, calcolare la somma di una serie convergente è un problema abbastanza difficile, tranne in alcuni casi particolari (serie geometriche, telescopiche). È quindi utile saper approssimare la somma di una serie. Vedremo due casi in cui è facile trovare l approssimazione della somma: quello di serie che si possono trattare col criterio integrale e quello di serie che si possono trattare col criterio del rapporto Approssimazione dal criterio integrale. Supponiamo di voler approssimare a n, dove a n è della forma a n = f(n) con f : [,+ ) R una funzione positiva, decrescente di integrale improprio + f(x) dx convergente (come nel criterio integrale). Allora la serie + f(n) è convergente. Desideriamo stimare la sua somma s a meno di un errore E (ad esempio E = 0 2 ). Inizialmente possiamo pensare di troncare la somma a un certo indice N, da determinare, e trattare il resto N esimo come errore. In formule: + f(n) = N f(n) } {{ } ridotta, s N che dà l approssimazione Ricordando che, come nel criterio integrale, + N+ f(x)dx s s N = + + n=n+ + n=n+ f(n) } {{ } resto, che per N opportuno deve essere<e f(n) + N f(x)dx,. abbiamo che s N + + f(x)dx s s N + + N+ N f(x)dx. Abbiamo così determinato un intervallo di ampiezza N+ N f(x)dx in cui si trova la somma s della serie. Se prendiamo il punto medio di questo intervallo, avremo una approssimazione s N della somma della serie (migliore di quella che potrebbe darci s N).
19 .4 Approssimazioni 5 Riassumendo, se poniamo s N = s N + (I 2 N+ +I N ) allora l errore commesso è s s N (I 2 N I N+ ). I N = + N f(x)dx s N +I N+ s N s N +I N Occorre determinare N in modo che questo sia minore di E (ad es. 0 2 ). Esempio.23. Approssimare a meno di 0 4 la somma di + Usiamo il trucchetto precedente. Si ha I N = e la stima fornita da N s N dà un errore dell ordine di (I 2 N I N+ ) =. Abbiamo < 2N(N+) 2N(N+) 0 4 ad esempio per N = 7. Con Maple possiamo scrivere una variazione dei comandi n 2. > ridotta:=convert(sum(/k^2,k=..7),float); > int_infinito:=n->/n; > approssimazione:=ridotta+0.5*(int_infinito(7)+int_infinito(72)); Il risultato che otteniamo è.6449, con quindi due cifre decimali esatte. Notiamo che il metodo ingenuo di usare solo la stima dall alto fornita dal criterio integrale ci avrebbe obbligati a molte iterazioni in più: siccome si tratta di una serie a termini positivi e convergente, possiamo approssimare (per difetto) la somma della serie con una opportuna ridotta di ordine N. Il problema è determinare N in modo che l errore commesso sia più piccolo di 0 4. In formule: + n 2 = N n 2 } {{ } ridotta, che dà l approssimazione + +. n 2 n=n+ } {{ } resto, che per N opportuno deve essere<0 4 Cerchiamo allora di determinare N, in modo che il resto sia minore di 0 4. La stima dall alto del criterio integrale ci dice che 0 + n=n+ + n dx 2 N x = 2 N. Pertanto N dovrà essere scelto abbastanza grande, in modo che N < 0 4, quindi almeno N = 000.
20 6 Capitolo 4.2. Approssimazione dal criterio del rapporto/radice. Vediamo come approssimarela somma di serie positive la cui convergenza si può determinare con il criterio del rapporto o della radice o, più in generale, serie il cui termine generale a n soddisfa, almeno definitivamente, una stima del tipo 0 a n Kr n, con K > 0, 0 < r <. Possiamo pensare di fissare un certo errore E o precisione della stima, troncare la serie a un certo indice N, da determinare, e trattare il resto come errore. In formule: + a n = N a n } {{ } ridotta, s N che dà l approssimazione + + n=n+ a n } {{ } resto, che per N opportuno deve essere<e In questo caso il resto della serie può essere stimata tramite una serie geometrica. Più precisamente: 0 s s N = + n=n+ + = K a n n=n+ = KrN+ r. + n=n+ Kr n r n = Kr N+ + n=0 r n. Bisognerà quindi determinare N in modo che KrN+ r Esempio.24. Approssimare a meno di 0 4 la somma di + somma di questa serie è e. Si ha per n 2 n! = 2 n = 2 Dobbiamo quindi determinare N in modo che e possiamo prendere N = 5. 2 ( 2 sia minore dell errore richiesto. n=0 3 n 22 2 = 2 ) N+ 2 < 0 4. Come già anticipato, la n! ( ) n. 2 La somma della serie richiesta è quindi approssimabile, a meno di 0 4 con 5 n=0 =.782. n! Da notare è che la velocità con cui questa serie converge a e è molto interessante, soprattutto se paragonata con la velocità con cui la successione b n = ( + n )n tende (crescendo) a e. Con lo stesso numero di iterazioni: b 5 = , non ha nemmeno una cifra decimale esatta. La prima cifra decimale esatta fa capolino dopo 74 passi b 74 =
21 .5 Serie assolutamente convergenti 7 5. Serie assolutamente convergenti Cosa possiamo dire se una serie ha termini di segno variabile? Ci sono alcune serie che sono facilmente trattabili e sono quelle assolutamente convergenti. Definizione.2. Una serie + a n si dice assolutamente convergente se è convergente la serie + a n. La loro importanza è dovuta in parte al seguente criterio e alle sue conseguenze. Teorema.25. Se una serie è assolutamente convergente, allora essa è convergente. Dimostrazione. Si ha a n a n a n, quindi 0 a n + a n 2 a n. Poiché 2 a n è termine generale di una serie convergente, allora per il criterio del confronto anche + (a n + a n ) è convergente, diciamo a l. Chiamiamo l la somma di + a n. Si ha n a k = k= n (a k + a k ) k= n k= a k n + l l, ovvero la serie + a n è convergente. Esempio.26. La serie + sinn n 2 perché sinn n 2 n 2 e la serie + è convergente. Infatti essa è assolutamente convergente, è convergente. n 2 Esempio.27. La serie esponenziale + n=0 x n n! è assolutamente convergente per ogni x in R. Infatti è banalmente convergente se x = 0. D altra parte, usando il criterio del rapporto, è facile concludere che + x n è convergente per ogni x. n! n=0 Combinando il Teorema.25, il Corollario.5 e l esempio.9 delle serie armoniche generalizzate otteniamo l usatissimo
22 8 Capitolo Teorema.28 (Criterio dell ordine di infinitesimo). Sia (a n ) n N una successione infinitesima di ordine α. Se α >, allora la serie + a n è assolutamente convergente. n=0 Esempio.29. La serie + generale log(+ n ) n ( log(+ n ) n) è assolutamente convergente, perché il termine è infinitesimo di ordine 2 per n +. Un esempio di serie convergente ma non assolutamente convergente è nella prossima sezione. Ovviamente non si tratta di una serie a termini non negativi. Le serie assolutamente convergenti sono soprattutto famose all interno delle serie convergenti, perché la loro somma non varia quando permutiamo l ordine degli addendi (anche infiniti addendi). Senza addentrarci maggiormente nell argomento, qui precisiamo solo che riordinando in maniera opportuna i termini di una serie convergente ma non assolutamente convergente si può ottenere una nuova serie con somma diversa dalla serie di partenza. Anzi, comunque fissato l(reale o anche infinito) è possibile trovare un opportuno riordinamento che abbia l come somma (se l = ±+ si intende che il riordinamento diverge positivamente o negativamente). E è anche possibile riordinare in modo da ottenere una serie indeterminata. Ciò comunque esula dagli scopi di questo corso. 6. Serie di Leibniz Una serie di Leibniz o serie a segni alterni è una serie che si può scrivere nella forma + ( ) n a n con a n > 0 n (oppure anche + ( ) n a n ). Teorema.30. Sia (a n ) una successione non negativa, decrescente, infinitesima. Allora la serie + ( ) n a n converge. Inoltre, se s è la somma della serie e (s n ) la successione delle ridotte, si ha 0 s s n a n+ se n è pari a n+ s s n 0 se n è dispari
23 .6 Serie di Leibniz 9 Dimostrazione. Consideriamo i casi in cui abbiamo un numero dispari di addendi, ad esempio 2m e 2m+. Si ha s 2m+ = s 2m +( ) 2m a 2m +( ) 2m a 2m+ = s 2m a 2m +a 2m+ s 2m, perché, siccome la successione (a n ) è decrescente, a 2m+ a 2m 0. Questo vuol dire che la successione (s 2m+ ) è decrescente. Analogamente, se consideriamo i casi in cui abbiamo un numero pari di addendi, ad esempio 2m e 2m+2, si ha s 2m+2 = s 2m +a 2m+ a 2m+2 s 2m. Questo vuol dire che la successione (s 2m ) è crescente. Inoltre, siccome (a n ) è non negativa, s 2m s 2m +a 2m+ = s 2m+ s 2m...s. Nel disegno vediamo il grafico della successione (s n ) con le proprietà che abbiamo appena stabilito: s s 3 s 2m s 2m+ s s 2m+2 s 2m s 4 s m 2m 2m+ 2m+2 In particolare, (s 2m ) è crescente e limitata dall alto da s, mentre (s 2m+ ) è decrescente e limitata dal basso da s 2 ; comunque entrambe sono convergenti. Sia s = lim m + s 2m. Allora, siccome (a n ) è infinitesima, anche Infine s 2m s s 2m+ per ogni m da cui lim s 2m+ = lim s 2m +a 2m+ = s. m + m + 0 s s 2m s 2m+ s 2m = a 2m+ 0 s 2m+ s s 2m+ s 2m+2 = a 2m+2.
24 20 Capitolo Quindi per n pari oppure dispari 0 s s n a n+ n + 0, ovvero + ( ) n a n = lim s n = s. n + n=0 Esempio.3. + ( ) n è una serie convergente per il criterio appena visto. Si noti n che non è assolutamente convergente e che il termine generale è un infinitesimo di ordine uno. Qualora si desideri determinarne la somma a meno di 0 3, è sufficiente ricordare che la ridotta di ordine n approssima la somma della serie a meno di. Pertanto occorre n+ prendere n = 00 e, a meno di 0 3, la somma della serie è 0,693. Tale approssimazione è per difetto. La somma di questa serie si potrebbe calcolare con un po di fatica e è log2. Tuttavia la velocità di convergenza è molto lenta e questo non fornisce un buon metodo per approssimare log2. Esempio.32. La proprietà di decrescenza della successione (a n ) è fondamentale. Si consideri ad esempio la serie a segni alterni = ( ) n a n dove a n = { /k se n = 2k è pari /k 2 se n = 2k è dispari È facile vedere che lim n + a n = 0 e che (a n ) non è decrescente. Mostriamo che la serie non converge guardando le somme parziali di ordine pari. s 2n = 2n k= a k = n k= n k 2 k, n + k= perché la serie + diverge e la serie + n converge. n 2
25 .7 Esercizi 2 ) Dire se sono convergenti le seguenti serie: n=0 n+5 n 3 2n+3 ; ne n; + n 4 + n! ; + n 2n ; 7. Esercizi + ( ) n + 2 n n ; +n! (+n)! ; 2 n+ n n ; n=0 + +( ) n n ; sin ; n 2 + n=2 + + n=2 log 3 n ; π n +5. (log(logn)) n, + ( ) n log ; n+ 2) Dire se le seguenti serie sono convergenti e eventualmente approssimarne la somma a meno di n n! ; ( ) n + ( ) n. n 3 n 3) Dire se sono convergenti e eventualmente calcolare la somma di n; 3+2 n 2 n+2 ; + (2n )(2n+) ; + n=2 logn. 4) Per quali x in R sono assolutamente convergenti o convergenti o divergenti le seguenti serie + + (x 5) n n3 n ; + n=0 (n+) 2 ( x x+2 ) n ; + n=0 x n n+ ; (4x+) n n 3.
26
27 CAPITOLO 2 Serie di funzioni Una serie di funzioni è un espressione del tipo + oppure f n + f n (x) dove le f n sono funzioni di una variabile reale a valori reali e hanno un dominio comune I. In questo corso ci occuperemo essenzialmente di un tipo di serie di funzioni: le serie di potenze (e le serie di Taylor).. Tipi di convergenza Osserviamo che se x è fissato in I, allora la successione (f n (x)) n è una successione numerica. Possiamo quindi chiederci se, per x fissato in I, la serie numerica + f n (x) è convergente. Per tutte le x in I per cui la serie numerica + f n (x) è convergente, si definisce una nuova funzione, la funzione somma... Convergenza puntuale. Una prima definizione di convergenza è quindi la seguente. Definizione 2.. Siano f n funzioni reali di variabile reale con comune dominio I. Si dice che la serie di funzioni + f n converge puntualmente in un insieme D I se per ogni x in D la serie numerica + f n(x) è convergente. La funzione f definita da f(x) = + f n (x) x D è la funzione somma. L insieme D si dice insieme di convergenza puntuale della serie di funzioni + f n. Proprietà. Siccome la serie dei resti n esimi ha lo stesso carattere della serie di partenza, la successione r n (x) = + k=n+ 23 f k (x)
28 24 Capitolo 2 è ben definita per ogni x in D, insieme di convergenza puntuale della serie di funzioni data. Inoltre per ogni x in D fissato, r n (x) = f(x) s n (x) n + 0. Dalla definizione di limite, questo vuol dire che comunque siano fissati x in D e ε > 0 esiste unindicen (chepuò dipenderesia daxsiada ε)talecheper ognin N si abbia r n (x) < ε. Proprietà. Dalla condizione necessaria per la convergenza di una serie numerica (Teorema.4), ricaviamo che l insieme di convergenza puntuale è contenuto nell insieme dei punti x tali che (f n (x)) n è infinitesima: D {x I : lim n + f n(x) = 0}. La nozione di convergenza puntuale è però poco interessante, perché non permette di trasferire proprietà delle funzioni f n alla funzione somma. Ad esempio la somma di una serie di funzioni continue potrebbe non essere continua. Esempio 2.. Consideriamo (x n x n+ ) vi ricordo che 0 0 = per convenzione. n=0 In questo esempio, le funzioni f n sono le funzioni definite su I = R da f n (x) = x n x n+ x R. Per x fissato, abbiamo una serie telescopica, per cui n x < s n (x) = (x k x k+ ) = x 0 x n = x n 0 x = k=0 non converge x, x >. Quindi la funzione somma f è definita su D = (,] e f(x) = { x < 0 x =. Nonostante tutte le funzioni f n siano continue in D, la funzione f non è continua in D..2. Convergenza uniforme. È quindi opportuno sostituire la nozione di convergenza puntuale con una più forte, la convergenza uniforme.
29 2. Tipi di convergenza 25 Definizione 2.2. Siano f n funzioni reali di variabilereale concomune dominio I. Supponiamo che la serie di funzioni + f n converga puntualmente in D I alla funzione somma f. Si dice che la serie di funzioni + f n converge uniformemente in D D alla sua somma se lim sup{ s n(x) f(x) : x D } = 0 n + In simboli s n = n k= f k f. D Proprietà. Possiamo riscrivere la condizione di uniforme convergenza facendo intervenire il resto lim sup{ r n(x) : x D } = 0. n + Dalla definizione di limite, questo vuol dire che comunque sia fissato ε > 0 esiste un indice N (che può dipendere da ε) tale che per ogni n N si abbia r n (x) < ε per ogni x in D. Si ha quindi un uniformità rispetto a x in D per la scelta di tale indice N. Proposizione 2.2 (Continuità e convergenza uniforme). Siano f n funzioni continue in un punto x 0 di I per ogni n e sia + f n uniformemente convergente in I a f. Allora f è continua in x 0. Dimostrazione. Sia ε > 0 fissato. Siccome la serie + f n converge uniformemente a f in I, si trova un indice N tale che sup{ s n (x) f(x) : x I} < ε n N. Siccome la somma finita di funzioni continue è continua, esiste un intorno U di x 0 tale che per ogni x in U I si abbia Ne ricaviamo quindi che per ogni x in U I s N (x) s N (x 0 ) < ε. f(x) f(x 0 ) f(x) s N (x) + s N (x) s N (x 0 ) + s N (x 0 ) f(x 0 ) 2sup{ s n (x) f(x) : x I}+ s N (x) s N (x 0 ) < 3ε. Una proprietà importante sullo scambio tra serie e integrale è l oggetto della seguente proposizione, di cui vediamo solo l enunciato.
30 26 Capitolo 2 Proposizione 2.3 (Integrazione per serie). Siano f n funzioni Riemann integrabili su un intervallo chiuso e limitato [a,b] per ogni n e sia + f n uniformemente convergente in [a,b] alla somma f. Allora f è Riemann integrabile su [a,b] e b ( b + ) + b f(t)dt = f n (t) dt = f n (t)dt. a a k= k= a In particolare la Proposizione 2.3 ci permette di concludere che per ogni x,x 0 in [a,b] si ha n x x f n (t)dt x 0 x [a,b] f(t)dt. x 0 k= In altre parole, detta F n la primitiva di f n che vale 0 in un punto x 0 e F la primitiva di f che vale 0 nello stesso punto x 0 si ha n F k F, [a,b] k= brevemente: la serie delle primitive (che si annullano nello stesso punto) è la primitiva (nulla nello stesso punto) della serie. Proposizione 2.4 (Derivazione per serie). Siano f n funzioni di classe C su un intervallo I e sia + f n puntualmente convergente in I alla somma f. Supponiamo che + f n sia uniformemente convergente in I a g. Allora f è di classe C in I e f = g. Dimostrazione. Notiamo che per ogni n e per ogni x,x 0 in I per il Teorema fondamentale del calcolo integrale vale quindi f n (x) = f n (x 0 )+ n f n (x) = k= x n f n (x 0 )+ k= x 0 f n (t)dt, n k= x x 0 f n (t)dt. Siccome la serie + f n converge puntualmente in I a f, si ha n f k (x) f(x) x I n + k= (e quindi anche x 0 ). Siccome la serie + f n è uniformemente convergente a g in I, per la Proposizione 2.3 di integrazione per serie vale n x x + x f n(t)dt f n(t)dt = g(t)dt x n + 0 x 0 k= x 0 k=
31 2. Tipi di convergenza 27 Quindi f(x) = f(x 0 )+ x x 0 g(t)dt x I. Per la Proposizione 2.2 la funzione g è continua. Quindi dal Teorema fondamentale del calcolo integrale deduciamo che f è derivabile e f = g, ossia f è C. La Proposizione 2.4 afferma quindi che (per una serie di funzioni derivabili, puntualmente convergente, con serie delle derivate uniformemente convergente) si possono scambiare l operazione di serie e quella di derivata: ( + ) f (x) = f n (x) = + f n (x). Purtroppo non è semplice stabilire la convergenza uniforme, specialmente se non conosciamo la funzione somma di una serie data. Una condizione necessaria per la convergenza uniforme è la seguente (si confronti con il Teorema.4). Teorema 2.5 (Condizione necessaria per la convergenza uniforme). Sia + f n una serie di funzioni convergente uniformemente in D. Allora lim sup{ f n(x) : x D} = 0. n + Dimostrazione. Sia f la funzione somma della serie, ovvero, detta (s n ) la successione delle ridotte, si ha lim n + sup{ s n (x) f(x) : x D} = 0. Ma allora 0 sup{ f n (x) : x D} = sup{ s n (x) s n (x) : x D} sup{ s n (x) f(x) : x D}+sup{ f(x) s n (x) : x D} n + 0. Un modo facile di controllare la convergenza uniforme è il cosiddetto test di Weierstrass. Il vantaggio è che permette di concludere positivamente sulla convergenza uniforme di una serie di funzioni senza conoscerne la somma.
32 28 Capitolo 2 Teorema 2.6 (Test di Weierstrass). Siano f n : I R. Se f n (x) M n per ogni x in I e la serie numerica + M n è convergente, allora la serie di funzioni + f n converge uniformemente in I. Dimostrazione. Si ha sup{ s n (x) f(x) : x D} = sup{ r n (x) : x D} sup{ + k=n+ + k=n+ M k. f k (x) : x D} Siccome + M n è convergente, per la Proposizione.7, il suo resto n esimo tende a zero, quindi 0 sup{ s n (x) f(x) : x D} Esempio 2.7. La serie di funzioni + x n n 2 n 2 + k=n+ M k n + 0. x n è uniformemente convergente in [,], perché n2 e + n 2 è convergente. Esempio 2.8. La serie esponenziale e x = + x n è puntualmente convergente in R, non è n! uniformemente convergente in R, ma lo è sui sottointervalli chiusi e limitati. Infatti { } x n + sup n! : x [ A,A] An A n e n! n! è convergente, da cui n k= x k k! e x. (Vedremo in seguito che la somma è e x.) [ A,A] Non è uniformemente convergente in R perché non è soddisfatta la condizione necessaria del Teorema 2.5: { } x n sup{ f n (x) : x R} = sup : x R = +. n! Esempio 2.9. Sia f(x) = + n=0 n 2 x 2 +.
33 2.2 Serie di potenze 29 Determiniamo il dominio di f e diciamo se f è continua. Per x reale poniamo f n (x) =. Quando x = 0 il termine generale non è infinitesimo, n 2 x 2 + perché f n (0) = per ogni n. Quindi 0 non è nell insieme di convergenza puntuale ovvero nel dominio di f. Quando x 0 il termine generale f n (x) è un infinitesimo di ordine 2, quindi la serie risulta essere assolutamente convergente. In particolare la serie di funzioni data è convergente puntualmente in (,0) (0,+ ), che è il dominio di f. La serie non è uniformemente convergente su (,0) (0,+ ), perché non è soddisfatta la condizione necessaria del Teorema 2.5: { } sup{ f n (x) : x 0} = sup n 2 x 2 + : x 0 = n. Tuttavia è uniformemente convergente in ogni sottoinsieme della forma (, A] [A, + ) per ogni A > 0. Infatti, possiamo usare il test di Weierstrass: { } sup n 2 x 2 + : x A + = e n 2 A 2 + n 2 A 2 + è convergente. Dalla Proposizione 2.2 deduciamo che f è continua in (, A] [A,+ ) per ogni A > 0. Se fissiamo un punto x 0 nel dominio di f, cioè prendiamo x 0 0, allora x 0 apparterrà a un opportuno intervallo della forma (, A] [A,+ ) e quindi f risulta continua in x 0. Siccome f è continua in ogni punto del suo dominio, f è continua. Ci sono fondamentalmente due ragioni per considerare le serie di funzioni: da una parte sono uno strumento per definire nuove funzioni e studiarne le proprietà, d altra parte si può voler scrivere una funzione nota come sovrapposizione di funzioni più semplici, ad esempio, allo scopo di integrare o derivare per serie. Nella prossima sezione ci occupiamo di un tipo particolare di serie di funzioni: le serie di potenze. 2. Serie di potenze Una serie di potenze centrate nel numero reale x 0 è una serie della forma con a n R. + n=0 a n (x x 0 ) n,
34 30 Capitolo 2 Si tratta di una serie di funzioni, in cui f n (x) = a n (x x 0 ) n. I numeri a n si chiamano i coefficienti della serie di potenze, x 0 si chiama centro della serie di potenze. In particolare sono serie di potenze centrate in 0 le serie della forma (2.) + n=0 a n x n A meno della traslazione t = x x 0, ci possiamo ricondurre a avere una serie della forma ovvero una serie centrata in 0. + n=0 a n (x x 0 ) n = + n=0 a n t n Per semplicità quindi ci limitiamo a considerare il caso x 0 = 0. Il risultato fondamentale per le serie di potenze riguarda la forma dell insieme di convergenza assoluta. Possiamo subito notare che quando x = 0 la serie (2.) contiene solo un termine non nullo, il primo: a 0 (ricordate la convenzione 0 0 = ). Quindi la serie (2.) è convergente nel suo centro è lì ha somma a 0. Teorema 2.0. Se la serie di potenze + a n x n converge nel punto x = p 0, allora essa converge puntualmente assolutamente nei punti dell intervallo ( p, p ). n=0 Dimostrazione. Per ipotesi la serie converge per x = p. Quindi il suo termine generale, per x = p, deve essere infinitesimo, in particolare sarà limitato da una costante M: lim a np n = 0 a n p n M n N. n + Supponiamo ora che x sia un punto dell intervallo ( p, p ). Allora q = x / p < e per ogni n n 0 a n x n = a n p n x p M q n. Siccome la serie q n geometrica di parametro q < è convergente, per il criterio del confronto converge la serie a n x n. Una conseguenza importante di questo teorema è che se la serie di potenze + a n x n non converge nel punto x = p, allora non converge in tutti i punti x tali che x > p. Infatti, se per assurdo convergesse in p, con p > p, allora sarebbe convergente anche nei punti dell intervallo I = ( p, p ). Siccome p è in questo intervallo e in p la serie non converge, abbiamo trovato un assurdo. Abbiamo così provato che n=0
35 2.2 Serie di potenze 3 Corollario 2.. Se la serie di potenze + a n x n non converge nel punto x = p 0, allora essa non converge in ogni punto al di fuori dell intervallo [ p, p ]. n=0 2.. Raggio di convergenza. Da quanto visto deduciamo che l insieme di convergenza puntuale della serie di potenze + a n x n centrata in 0 è un intervallo (simmetrico, se non ci n=0 occupiamo degli estremi) di centro 0. All interno di tale intervallo si ha convergenza assoluta. Analogamente, l insieme di convergenza puntuale della serie di potenze + a n (x x 0 ) n centrata in x 0 è un intervallo di centro x 0 e all interno di tale intervallo si ha convergenza assoluta. Nei prossimi esempi osserviamo che l intervallo di convergenza puntuale può ridursi al solo centro, può essere tutto R, può essere limitato, chiuso o aperto (anche solo da un lato). Esempio 2.2. La serie + n!x n converge solo per x = 0. Infatti per ogni x 0 il termine n=0 generale non è infinitesimo: Esempio 2.3. La serie esponenziale + convergenza è (, + ). lim n + n! x n = +. Esempio 2.4. La serie geometrica + x n converge in (,). n=0 n=0 n=0 x n n! converge per ogni x reale, quindi l intervallo di La serie + n=0 x n n converge in [,). La serie + ( ) n xn n n=0 converge in (,]. La serie + n=0 x n converge in [,]. n2 La semiampiezza del più grande intervallo in cui la serie converge costituisce il raggio di convergenza. Precisamente:
36 32 Capitolo 2 Definizione 2.3. Data una serie di potenze + a n x n, si dice raggio di convergenza il { sup x : la serie n=0 + n=0 } a n x n converge. Da quanto detto, ogni serie di potenze centrata in 0 si può inquadrare in uno dei tre casi seguenti. n=0 ) La serie di potenze + a n x n converge solo per x = 0 e quindi ha raggio di convergenza 0. 2) La serie di potenze + n=0 a n x n converge per ogni x in un intervallo della forma ( ρ,ρ), con ρ > 0, e non converge se x > ρ. In questo caso ρ è il raggio di convergenza. Si noti che per x = ρ la serie può avere qualsiasi comportamento. 3) La serie di potenze + a n x n converge per ogni x reale; in questo caso il raggio di convergenza è +. n=0 Il problema è ora come determinare il raggio di convergenza della serie di potenze + a n x n. Dai criteri del rapporto e della radice per serie numeriche (Teoremi.7 e.2) applicati alla serie + a n x n discendono immediatamente i seguenti risultati. n=0 n=0 Teorema 2.5. Sia + a n x n una serie di potenze, con a n 0 per ogni n e sia n=0 a n+ lim = l. n + a n Se 0 < l < + allora il raggio di convergenza è ρ = /l. Se l = + allora il raggio di convergenza è ρ = 0. Se l = 0 allora il raggio di convergenza è ρ = +.
37 2.2 Serie di potenze 33 Teorema 2.6. Sia + a n x n una serie di potenze e sia n=0 lim n + n an = l. Se 0 < l < + allora il raggio di convergenza è ρ = /l. Se l = + allora il raggio di convergenza è ρ = 0. Se l = 0 allora il raggio di convergenza è ρ = Continuità della somma di una serie di potenze. Mostriamo ora che in sottointervalli chiusi e limitati contenuti all interno dell intervallo di convergenza si ha anche convergenza uniforme. Teorema 2.7. Sia + a n x n una serie di potenze con raggio di convergenza ρ > 0 (anche n=0 + ). Allora + a n x n converge uniformemente in ogni intervallo della forma n=0 0 < r < ρ se ρ R + [ r,r] ( ρ,ρ) r > 0 se ρ = +. Dimostrazione. Occupiamoci del caso in cui ρ non sia +. Il caso ρ = + è analogo. Se x r si ha a n x n a n r n n. Dalla definizione di raggio di convergenza, sappiamo che quando r < ρ la serie numerica + n=0 a n r n èassolutamenteconvergente. AlloraadoperandoiltestdiWeierstrass(Teorema2.6) possiamo concludere che la serie + a n x n converge uniformemente in [ r,r]. n=0 Corollario 2.8. Sia f la somma di una serie di potenze centrate in 0 e con raggio di convergenza ρ. Allora f è continua in ( ρ,ρ). Dimostrazione. Sia x un punto di ( ρ,ρ) e sia h tale che x h. Siccome la serie di potenze converge uniformemente in [ h, h] e le potenze sono funzioni continue, per la Proposizione 2.2 su continuità e convergenza uniforme, f risulta continua in x. Per l arbitrarietà di x otteniamo la tesi.
38 34 Capitolo 2 Osserviamo che può esserci convergenza uniforme in tutti i sottointervalli contenuti nell intervallo di convergenza senza esserci convergenza uniforme in tutto l intervallo di convergenza. Esempio 2.9. La serie geometrica + x n ha raggio di convergenza e il suo intervallo di n=0 convergenza è (, ). C è convergenza uniforme nei sottointervalli della forma [ r, r] con r <, ma non c è convergenza uniforme su (,), perché non è soddisfatta la condizione necessaria del Teorema 2.5 lim n + sup{ x n : x (,)} = lim =. n + Tuttavia, se in un estremo dell intervallo di convergenza la serie di potenze è convergente, allora l intervallo di convergenza uniforme (e quindi l intervallo di continuità della funzione somma) è più grande. È il significato del seguente criterio, che non dimostriamo. Teorema 2.20 (Abel). Sia + a n x n una serie di potenze con raggio di convergenza ρ > 0 finito. Allora n=0 se la serie converge in x = ρ, allora la serie è uniformemente convergente in [ r,ρ] per ogni 0 < r < ρ e quindi la funzione somma è continua in ( ρ,ρ]; se la serie converge in x = ρ, allora la serie è uniformemente convergente in [ ρ,r] per ogni 0 < r < ρ e quindi la funzione somma è continua in [ ρ,ρ); se la serie converge in x = ±ρ, allora la serie è uniformemente convergente in [ ρ,ρ] e quindi la funzione somma è continua in [ ρ,ρ] Derivabilità e integrazione per serie di potenze. Dai Teoremi 2.3 e 2.4 seguono facilmente i seguenti criteri (con estremi inclusi o esclusi a seconda dei casi). Teorema 2.2 (Integrazione per serie della somma di una serie di potenze). Sia ρ > 0 il raggio di convergenza della serie di potenze + a n x n e sia f la sua somma. Allora x 0 f(t)dt = + n=0 In particolare, per ogni a,b ( ρ,ρ) si ha b a f(t)dt = n=0 a n n+ xn+ x ( ρ,ρ). + n=0 a n n+ (bn+ a n+ ).
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Serie numeriche e serie di potenze
 Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
Serie numeriche e serie di potenze Sommare un numero finito di numeri reali è senza dubbio un operazione che non può riservare molte sorprese Cosa succede però se ne sommiamo un numero infinito? Prima
Corso di Analisi Matematica Serie numeriche
 Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
Corso di Analisi Matematica Serie numeriche Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 25 1 Definizione e primi esempi 2 Serie a
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
+ P a n n=1 + X. a n = a m 3. n=1. m=4. Per poter dare un significato alla somma (formale) di infiniti termini, ricorriamo al seguente procedimento:
 Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
Capitolo 3 Serie 3. Definizione Sia { } una successione di numeri reali. Ci proponiamo di dare significato, quando possibile, alla somma a + a 2 +... + +... di tutti i termini della successione. Questa
u 1 u k che rappresenta formalmente la somma degli infiniti numeri (14.1), ordinati al crescere del loro indice. I numeri u k
 Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
SERIE NUMERICHE. prof. Antonio Greco 6-11-2013
 SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
Matematica e Statistica
 Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
Matematica e Statistica Prova d esame (0/07/03) Università di Verona - Laurea in Biotecnologie - A.A. 0/3 Matematica e Statistica Prova di MATEMATICA (0/07/03) Università di Verona - Laurea in Biotecnologie
I appello - 24 Marzo 2006
 Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
Quesiti di Analisi Matematica A
 Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
Quesiti di Analisi Matematica A Presentiamo una raccolta di quesiti per la preparazione alla prova orale del modulo di Analisi Matematica A. Per una buona preparazione é consigliabile rispondere ad alta
Capitolo 1 ANALISI COMPLESSA
 Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Serie numeriche. 1 Definizioni e proprietà elementari
 Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
SIMULAZIONE TEST ESAME - 1
 SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
Università degli Studi di Catania A.A. 2012-2013. Corso di laurea in Ingegneria Industriale
 Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
Università degli Studi di Catania A.A. 2012-2013 Corso di laurea in Ingegneria Industriale Corso di Analisi Matematica I (A-E) (Prof. A.Villani) Elenco delle dimostrazioni che possono essere richieste
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
3.1 Successioni. R Definizione (Successione numerica) E Esempio 3.1 CAPITOLO 3
 CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
CAPITOLO 3 Successioni e serie 3. Successioni Un caso particolare di applicazione da un insieme numerico ad un altro insieme numerico è quello delle successioni, che risultano essere definite nell insieme
Esercizi svolti. 1. Si consideri la funzione f(x) = 4 x 2. a) Verificare che la funzione F(x) = x 2 4 x2 + 2 arcsin x è una primitiva di
 Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
Esercizi svolti. Si consideri la funzione f() 4. a) Verificare che la funzione F() 4 + arcsin è una primitiva di f() sull intervallo (, ). b) Verificare che la funzione G() 4 + arcsin π è la primitiva
1 Alcuni criteri di convergenza per serie a termini non negativi
 Alcuni criteri di convergenza per serie a termini non negativi (Criterio del rapporto.) Consideriamo la serie a (.) a termini positivi (ossia a > 0, =, 2,...). Supponiamo che esista il seguente ite a +
Alcuni criteri di convergenza per serie a termini non negativi (Criterio del rapporto.) Consideriamo la serie a (.) a termini positivi (ossia a > 0, =, 2,...). Supponiamo che esista il seguente ite a +
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
Schemi delle Lezioni di Matematica Generale. Pierpaolo Montana
 Schemi delle Lezioni di Matematica Generale Pierpaolo Montana A volte i fenomeni economici che ci interessano non variano con continuitá oppure non possono essere osservati con continuitá, ma solo a intervalli
Schemi delle Lezioni di Matematica Generale Pierpaolo Montana A volte i fenomeni economici che ci interessano non variano con continuitá oppure non possono essere osservati con continuitá, ma solo a intervalli
Corso di Analisi Matematica. Successioni e serie numeriche
 a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
a.a. 2011/12 Laurea triennale in Informatica Corso di Analisi Matematica Successioni e serie numeriche Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità
19. Inclusioni tra spazi L p.
 19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
FUNZIONE REALE DI UNA VARIABILE
 FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
FUNZIONE REALE DI UNA VARIABILE Funzione: legge che ad ogni elemento di un insieme D (Dominio) tale che D R, fa corrispondere un elemento y R ( R = Codominio ). f : D R : f () = y ; La funzione f(): A
Corso di Analisi Matematica. Polinomi e serie di Taylor
 a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Polinomi e serie di Taylor Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in
 Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Intorni Fissato un punto sull' asse reale, si definisce intorno del punto, un intervallo aperto contenente e tutto contenuto in Solitamente si fa riferimento ad intorni simmetrici =, + + Definizione: dato
Sulla monotonia delle funzioni reali di una variabile reale
 Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Proof. Dimostrazione per assurdo. Consideriamo l insieme complementare di P nell insieme
 G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
LEZIONE 7. Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2. 2, x3 +2x +3.
 7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
7 LEZIONE 7 Esercizio 7.1. Quale delle seguenti funzioni è decrescente in ( 3, 0) e ha derivata prima in 3 che vale 0? x 3 3 + x2 2 6x, x3 +2x 2 6x, 3x + x2 2, x3 +2x +3. Le derivate sono rispettivamente,
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Una ricetta per il calcolo dell asintoto obliquo. Se f(x) è asintotica a mx+q allora abbiamo f(x) mx q = o(1), da cui (dividendo per x) + o(1), m =
 Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Esercizi di Analisi Matematica I
 Esercizi di Analisi Matematica I Andrea Corli e Alessia Ascanelli gennaio 9 Indice Introduzione iii Nozioni preliminari. Fattoriali e binomiali..................................... Progressioni..........................................
Esercizi di Analisi Matematica I Andrea Corli e Alessia Ascanelli gennaio 9 Indice Introduzione iii Nozioni preliminari. Fattoriali e binomiali..................................... Progressioni..........................................
Funzioni. Parte prima. Daniele Serra
 Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
Funzioni Parte prima Daniele Serra Nota: questi appunti non sostituiscono in alcun modo le lezioni del prof. Favilli, né alcun libro di testo. Sono piuttosto da intendersi a integrazione di entrambi. 1
INTEGRALI DEFINITI. Tale superficie viene detta trapezoide e la misura della sua area si ottiene utilizzando il calcolo di un integrale definito.
 INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
INTEGRALI DEFINITI Sia nel campo scientifico che in quello tecnico si presentano spesso situazioni per affrontare le quali è necessario ricorrere al calcolo dell integrale definito. Vi sono infatti svariati
Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata, Matematica
 DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
DIPARTIMENTO DI MATEMATICA Università degli Studi di Trento Via Sommarive - Povo (TRENTO) Raccolta degli Scritti d Esame di ANALISI MATEMATICA U.D. 1 assegnati nei Corsi di Laurea di Fisica, Fisica Applicata,
Statistica e biometria. D. Bertacchi. Variabili aleatorie. V.a. discrete e continue. La densità di una v.a. discreta. Esempi.
 Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Iniziamo con definizione (capiremo fra poco la sua utilità): DEFINIZIONE DI VARIABILE ALEATORIA Una variabile aleatoria (in breve v.a.) X è funzione che ha come dominio Ω e come codominio R. In formule:
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 2014
 Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Proposta di soluzione della prova di matematica Liceo scientifico di Ordinamento - 14 Problema 1 Punto a) Osserviamo che g (x) = f(x) e pertanto g () = f() = in quanto Γ è tangente all asse delle ascisse,
Applicazioni del calcolo differenziale allo studio delle funzioni
 Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
Capitolo 9 9.1 Crescenza e decrescenza in piccolo; massimi e minimi relativi Sia y = f(x) una funzione definita nell intervallo A; su di essa non facciamo, per ora, alcuna particolare ipotesi (né di continuità,
CONTINUITÀ E DERIVABILITÀ Esercizi proposti. 1. Determinare lim M(sinx) (M(t) denota la mantissa di t)
 CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi proposti 1. Determinare lim M(sin) (M(t) denota la mantissa di t) kπ/ al variare di k in Z. Ove tale limite non esista, discutere l esistenza dei limiti laterali. Identificare
CONTINUITÀ E DERIVABILITÀ Esercizi risolti
 CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
CONTINUITÀ E DERIVABILITÀ Esercizi risolti. Determinare kπ/ [cos] al variare di k in Z. Ove tale ite non esista, discutere l esistenza dei iti laterali. Identificare i punti di discontinuità della funzione
Le funzioni continue. A. Pisani Liceo Classico Dante Alighieri A.S. 2002-03. A. Pisani, appunti di Matematica 1
 Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
Le funzioni continue A. Pisani Liceo Classico Dante Alighieri A.S. -3 A. Pisani, appunti di Matematica 1 Nota bene Questi appunti sono da intendere come guida allo studio e come riassunto di quanto illustrato
POLITECNICO di BARI - A.A. 2012/2013 Corso di Laurea in INGEGNERIA Informatica e dell Automazione
 POLITECNICO di BARI - A.A. 0/03 Corso di Laurea in INGEGNERIA Informatica e dell Automazione Problema Sia f :[0, +[! R una funzione continua. La funzione composta g() =f(kk) è c o n t i n u a? Problema
POLITECNICO di BARI - A.A. 0/03 Corso di Laurea in INGEGNERIA Informatica e dell Automazione Problema Sia f :[0, +[! R una funzione continua. La funzione composta g() =f(kk) è c o n t i n u a? Problema
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
Docente: Anna Valeria Germinario. Università di Bari. A.V.Germinario (Università di Bari) Analisi Matematica ITPS 1 / 22
 Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
Laurea in Informatica e Tecnologie per la Produzione del Software Corso di Analisi Matematica Calcolo differenziale e approssimazioni, formula di Taylor Docente: Anna Valeria Germinario Università di Bari
Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R
 Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Studio di funzione Per studio di funzione intendiamo un insieme di procedure che hanno lo scopo di analizzare le proprietà di una funzione f ( x) R R : allo scopo di determinarne le caratteristiche principali.
Lezione 9: Cambio di base
 Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Matematica 1 - Corso di Laurea in Ingegneria Meccanica
 Matematica 1 - Corso di Laurea in Ingegneria Meccanica Esercitazione su massimi e minimi vincolati 9 dicembre 005 Esercizio 1. Considerare l insieme C = {(x,y) R : (x + y ) = x } e dire se è una curva
Matematica 1 - Corso di Laurea in Ingegneria Meccanica Esercitazione su massimi e minimi vincolati 9 dicembre 005 Esercizio 1. Considerare l insieme C = {(x,y) R : (x + y ) = x } e dire se è una curva
Consideriamo due polinomi
 Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
Capitolo 3 Il luogo delle radici Consideriamo due polinomi N(z) = (z z 1 )(z z 2 )... (z z m ) D(z) = (z p 1 )(z p 2 )... (z p n ) della variabile complessa z con m < n. Nelle problematiche connesse al
I appello - 26 Gennaio 2007
 Facoltà di Ingegneria - Corso di Laurea in Ing. Informatica e delle Telecom. A.A.006/007 I appello - 6 Gennaio 007 Risolvere gli esercizi motivando tutte le risposte. (N.B. il quesito teorico è obbligatorio)
Facoltà di Ingegneria - Corso di Laurea in Ing. Informatica e delle Telecom. A.A.006/007 I appello - 6 Gennaio 007 Risolvere gli esercizi motivando tutte le risposte. (N.B. il quesito teorico è obbligatorio)
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
Applicazioni lineari
 Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
Anno 4 Grafico di funzione
 Anno 4 Grafico di funzione Introduzione In questa lezione impareremo a disegnare il grafico di una funzione reale. Per fare ciò è necessario studiare alcune caratteristiche salienti della funzione che
Anno 4 Grafico di funzione Introduzione In questa lezione impareremo a disegnare il grafico di una funzione reale. Per fare ciò è necessario studiare alcune caratteristiche salienti della funzione che
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
NOME:... MATRICOLA:... Scienza dei Media e della Comunicazione, A.A. 2007/2008 Analisi Matematica 1, Esame scritto del 08.02.2008. x 1.
 NOME:... MATRICOLA:.... Scienza dei Media e della Comunicazione, A.A. 007/008 Analisi Matematica, Esame scritto del 08.0.008 Indicare per quali R vale la seguente diseguaglianza : + >. Se y - - è il grafico
NOME:... MATRICOLA:.... Scienza dei Media e della Comunicazione, A.A. 007/008 Analisi Matematica, Esame scritto del 08.0.008 Indicare per quali R vale la seguente diseguaglianza : + >. Se y - - è il grafico
La curva grafico della funzione, partendo dal punto A(a,f(a)), si snoda con continuità, senza interruzioni, fino ad approdare nel punto B(b,f(b)).
 Calcolo differenziale Il teorema di Rolle TEOREMA DI ROLLE Ipotesi f continua su [a, b] f derivabile per lo meno su (a,b) f(a) = f(b) Tesi Esiste almeno un punto c in (a, b) tale che Giustificazione con
Calcolo differenziale Il teorema di Rolle TEOREMA DI ROLLE Ipotesi f continua su [a, b] f derivabile per lo meno su (a,b) f(a) = f(b) Tesi Esiste almeno un punto c in (a, b) tale che Giustificazione con
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 2011/2012
 Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
7 - Esercitazione sulle derivate
 7 - Esercitazione sulle derivate Luigi Starace gennaio 0 Indice Dimostrare il teorema 5.5.3.a................................................b............................................... Dimostrazioni.a
7 - Esercitazione sulle derivate Luigi Starace gennaio 0 Indice Dimostrare il teorema 5.5.3.a................................................b............................................... Dimostrazioni.a
F (x) = f(x) per ogni x I. Per esempio:
 Funzioni Primitive (Integrali Indefiniti) (l.v.) Pur essendo un argomento che fa parte del Calcolo Differenziale, molti autori inseriscono funzioni primitive nel capitolo sul Calcolo Integrale, in quanto
Funzioni Primitive (Integrali Indefiniti) (l.v.) Pur essendo un argomento che fa parte del Calcolo Differenziale, molti autori inseriscono funzioni primitive nel capitolo sul Calcolo Integrale, in quanto
Diario del corso di Analisi Matematica 1 (a.a. 2015/16)
 Diario del corso di Analisi Matematica (a.a. 205/6) 4 settembre 205 ( ora) Presentazione del corso. 6 settembre 205 (2 ore) Numeri naturali, interi, razionali, reali. 2 non è razionale. Introduzione alle
Diario del corso di Analisi Matematica (a.a. 205/6) 4 settembre 205 ( ora) Presentazione del corso. 6 settembre 205 (2 ore) Numeri naturali, interi, razionali, reali. 2 non è razionale. Introduzione alle
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
COGNOME e NOME: FIRMA: MATRICOLA:
 Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti,
Anno Accademico 04/ 05 Corsi di Analisi Matematica I Proff. A. Villani, R. Cirmi e F. Faraci) Prova d Esame del giorno 6 febbraio 05 Prima prova scritta compito A) Non sono consentiti formulari, appunti,
Successioni di funzioni reali
 E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
B. Vogliamo determinare l equazione della retta
 Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
Risoluzione quesiti ordinamento Quesito N.1 Indicata con α la misura dell angolo CAB, si ha che: 1 Area ( ABC ) = AC AB sinα = 3 sinα π 3 sinα = 3 sinα = 1 α = Il triangolo è quindi retto in A. La misura
PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA
 Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
Simulazione 01/15 ANNO SCOLASTICO 01/15 PROBLEMI TRADIZIONALI SIMULAZIONE DELLA PROVA DI MATEMATICA DELL ESAME DI STATO PER IL LICEO SCIENTIFICO Il candidato risolva uno dei due problemi Problema 1 Nella
SVILUPPO IN SERIE DI FOURIER. Prof. Attampato Daniele
 SVILUPPO IN SERIE DI FOURIER Prof. Attampato Daniele SVILUPPO IN SERIE DI UNA FUNZIONE Uno dei problemi più frequenti in matematica è legato alla necessità di approssimare una funzione. Uno degli strumenti
SVILUPPO IN SERIE DI FOURIER Prof. Attampato Daniele SVILUPPO IN SERIE DI UNA FUNZIONE Uno dei problemi più frequenti in matematica è legato alla necessità di approssimare una funzione. Uno degli strumenti
Alcuni complementi sulle successioni
 Alcuni complementi sulle successioni 1 (Teorema del confronto) Siano {a n } e {b n } due successioni regolari tali che si abbia a n b n n N. (1) Allora: a n b n. (2) Dim. Sia L = a n ed L = b n. Se L =
Alcuni complementi sulle successioni 1 (Teorema del confronto) Siano {a n } e {b n } due successioni regolari tali che si abbia a n b n n N. (1) Allora: a n b n. (2) Dim. Sia L = a n ed L = b n. Se L =
4 3 4 = 4 x 10 2 + 3 x 10 1 + 4 x 10 0 aaa 10 2 10 1 10 0
 Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
Rappresentazione dei numeri I numeri che siamo abituati ad utilizzare sono espressi utilizzando il sistema di numerazione decimale, che si chiama così perché utilizza 0 cifre (0,,2,3,4,5,6,7,8,9). Si dice
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
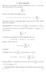 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
Capitolo 13: L offerta dell impresa e il surplus del produttore
 Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
Capitolo 13: L offerta dell impresa e il surplus del produttore 13.1: Introduzione L analisi dei due capitoli precedenti ha fornito tutti i concetti necessari per affrontare l argomento di questo capitolo:
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI
 APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
APPUNTI DI MATEMATICA LE FRAZIONI ALGEBRICHE ALESSANDRO BOCCONI Indice 1 Le frazioni algebriche 1.1 Il minimo comune multiplo e il Massimo Comun Divisore fra polinomi........ 1. Le frazioni algebriche....................................
EQUAZIONI non LINEARI
 EQUAZIONI non LINEARI Francesca Pelosi Dipartimento di Matematica, Università di Roma Tor Vergata CALCOLO NUMERICO e PROGRAMMAZIONE http://www.mat.uniroma2.it/ pelosi/ EQUAZIONI non LINEARI p.1/44 EQUAZIONI
EQUAZIONI non LINEARI Francesca Pelosi Dipartimento di Matematica, Università di Roma Tor Vergata CALCOLO NUMERICO e PROGRAMMAZIONE http://www.mat.uniroma2.it/ pelosi/ EQUAZIONI non LINEARI p.1/44 EQUAZIONI
2 Argomenti introduttivi e generali
 1 Note Oltre agli esercizi di questa lista si consiglia di svolgere quelli segnalati o assegnati sul registro e genericamente quelli presentati dal libro come esercizio o come esempio sugli argomenti svolti
1 Note Oltre agli esercizi di questa lista si consiglia di svolgere quelli segnalati o assegnati sul registro e genericamente quelli presentati dal libro come esercizio o come esempio sugli argomenti svolti
Analisi Complessa. Prova intermedia del 7 novembre 2002 - Soluzioni. (z 11 1) 11 1 = 0.
 Analisi Complessa Prova intermedia del 7 novembre 2002 - Soluzioni Esercizio. Si consideri l equazione z 0. Quante soluzioni distinte esistono in C? Quante di esse sono contenute all interno del disco
Analisi Complessa Prova intermedia del 7 novembre 2002 - Soluzioni Esercizio. Si consideri l equazione z 0. Quante soluzioni distinte esistono in C? Quante di esse sono contenute all interno del disco
La distribuzione Normale. La distribuzione Normale
 La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
La Distribuzione Normale o Gaussiana è la distribuzione più importante ed utilizzata in tutta la statistica La curva delle frequenze della distribuzione Normale ha una forma caratteristica, simile ad una
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
Analisi Mat. 1 - Ing. Inform. - Soluzioni del compito del 23-3-06
 Analisi Mat. - Ing. Inform. - Soluzioni del compito del 3-3-6 Sia p il polinomio di quarto grado definito da pz = z 4. Sia S il settore circolare formato dai numeri complessi che hanno modulo minore o
Analisi Mat. - Ing. Inform. - Soluzioni del compito del 3-3-6 Sia p il polinomio di quarto grado definito da pz = z 4. Sia S il settore circolare formato dai numeri complessi che hanno modulo minore o
Programmazione Matematica classe V A. Finalità
 Finalità Acquisire una formazione culturale equilibrata in ambito scientifico; comprendere i nodi fondamentali dello sviluppo del pensiero scientifico, anche in una dimensione storica, e i nessi tra i
Finalità Acquisire una formazione culturale equilibrata in ambito scientifico; comprendere i nodi fondamentali dello sviluppo del pensiero scientifico, anche in una dimensione storica, e i nessi tra i
Insiemi di livello e limiti in più variabili
 Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
Capitolo 2. Serie Numeriche
 Capitolo 2 Serie Numeriche Iniziamo ricordando la nozione di successione e le operazioni definibili tra successioni. Questo permetterà di poter definire, con una certa semplicità la nozione di somma infinita
Capitolo 2 Serie Numeriche Iniziamo ricordando la nozione di successione e le operazioni definibili tra successioni. Questo permetterà di poter definire, con una certa semplicità la nozione di somma infinita
Il concetto di valore medio in generale
 Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
Il concetto di valore medio in generale Nella statistica descrittiva si distinguono solitamente due tipi di medie: - le medie analitiche, che soddisfano ad una condizione di invarianza e si calcolano tenendo
1 Giochi a due, con informazione perfetta e somma zero
 1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
LEZIONE 23. Esempio 23.1.3. Si consideri la matrice (si veda l Esempio 22.2.5) A = 1 2 2 3 3 0
 LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
Vademecum studio funzione
 Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
Vademecum studio funzione Campo di Esistenza di una funzione o dominio: Studiare una funzione significa determinare gli elementi caratteristici che ci permettono di disegnarne il grafico, a partire dalla
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Parte 2. Determinante e matrice inversa
 Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione:
 Verso l'esame di Stato Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione: y ln 5 6 7 8 9 0 Rappresenta il campo di esistenza determinato
Verso l'esame di Stato Definisci il Campo di Esistenza ( Dominio) di una funzione reale di variabile reale e, quindi, determinalo per la funzione: y ln 5 6 7 8 9 0 Rappresenta il campo di esistenza determinato
ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA
 ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA Francesco Bottacin Padova, 24 febbraio 2012 Capitolo 1 Algebra Lineare 1.1 Spazi e sottospazi vettoriali Esercizio 1.1. Sia U il sottospazio di R 4 generato dai
ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA Francesco Bottacin Padova, 24 febbraio 2012 Capitolo 1 Algebra Lineare 1.1 Spazi e sottospazi vettoriali Esercizio 1.1. Sia U il sottospazio di R 4 generato dai
Facoltà di Dipartimento di Ingegneria Elettrica e dell'informazione anno accademico 2014/15 Registro lezioni del docente SPORTELLI LUIGI
 Facoltà di Dipartimento di Ingegneria Elettrica e dell'informazione anno accademico 2014/15 Registro lezioni del docente SPORTELLI LUIGI Attività didattica ANALISI MATEMATICA [2000] Periodo di svolgimento:
Facoltà di Dipartimento di Ingegneria Elettrica e dell'informazione anno accademico 2014/15 Registro lezioni del docente SPORTELLI LUIGI Attività didattica ANALISI MATEMATICA [2000] Periodo di svolgimento:
ESAME DI STATO DI LICEO SCIENTIFICO CORSO SPERIMENTALE P.N.I. 2004
 ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
ESAME DI STAT DI LICE SCIENTIFIC CRS SPERIMENTALE P.N.I. 004 Il candidato risolva uno dei due problemi e 5 dei 0 quesiti in cui si articola il questionario. PRBLEMA Sia la curva d equazione: ke ove k e
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
SUCCESSIONI NUMERICHE Una funzione reale di una variabile reale f di dominio A è una legge che ad ogni x A associa un numero reale che denotiamo con f(x). Se A = N, la f è detta successione di numeri reali.
Studio di funzioni ( )
 Studio di funzioni Effettuare uno studio qualitativo e tracciare un grafico approssimativo delle seguenti funzioni. Si studi in particolare anche la concavità delle funzioni e si indichino esplicitamente
Studio di funzioni Effettuare uno studio qualitativo e tracciare un grafico approssimativo delle seguenti funzioni. Si studi in particolare anche la concavità delle funzioni e si indichino esplicitamente
Numeri Complessi. 4. Ricordando che, se z è un numero complesso, zz è un numero reale, mettere sotto la forma. z 2 + 2z + 2 = 0. z 2 + 2z + 6 = 0.
 Numeri Complessi. Siano z = + i e z 2 = i. Calcolare z + z 2, z z 2, z z 2 e z z 2. 2. Siano z = 2 5 + i 2 e z 2 = 5 2 2i. Calcolare z + z 2, z z 2, z z 2 e z z 2. 3. Ricordando che, se z è un numero complesso,
Numeri Complessi. Siano z = + i e z 2 = i. Calcolare z + z 2, z z 2, z z 2 e z z 2. 2. Siano z = 2 5 + i 2 e z 2 = 5 2 2i. Calcolare z + z 2, z z 2, z z 2 e z z 2. 3. Ricordando che, se z è un numero complesso,
SOLUZIONE DEL PROBLEMA 1 CORSO SPERIMENTALE P.N.I. 2014
 SOLUZIONE DEL PROBLEMA 1 CORSO SPERIMENTALE P.N.I. 01 1. Determiniamo l espressione analitica di g() dividendo il suo dominio in intervalli. La circonferenza di diametro AO ha equazione (+) + = + + = 0
SOLUZIONE DEL PROBLEMA 1 CORSO SPERIMENTALE P.N.I. 01 1. Determiniamo l espressione analitica di g() dividendo il suo dominio in intervalli. La circonferenza di diametro AO ha equazione (+) + = + + = 0
