Introduzione alla Trasformata di Fourier
|
|
|
- Sibilla Berardino
- 7 anni fa
- Visualizzazioni
Transcript
1 Corso di Laura Magisral in Chimica A.A. 3-4 Sproscopi Magnich Inroduzion alla Trasformaa di Fourir La Trasformaa di Fourir è usaa in moli divrsi campi: dalla analisi di sgnali lrici, alla analisi dll immagini di suoni, all cnich srumnali in Chimica, ra l quali la spromria FT-IR la spromria FT-NMR. È inolr alla bas dll analisi di fnomni di diffrazion di raggi X in crisallografia. In gnral moli fnomni fisici sono fondai su vibrazioni d ond. Spsso l ossrvabil fisica è l innsià di una grandzza fisica (luc, nsion o alro) in funzion dl mpo (o dllo spazio). In qusi fnomni è fondamnal conoscr non solo l ampizz ma anch l frqunz dll oscillazioni ch producono i sgnali ossrvai. Pr conoscr quali siano qus frqunz si fa ricorso alla Analisi di Fourir di dai rgisrai. La rasformaa di Fourir ssnzialmn è uno srumno ch consn di analizzar una funzion f(, qual può ssr un sgnal lrico ch varia nl mpo, sulla bas dll su componni in frqunza cioè di funzioni sno cosno di divrsa frqunza. La rasformaa di Fourir indica quali sono i psi (l innsià) dll divrs componni in frqunza. In quso snso rapprsna l snsion dllo sviluppo in sri di Fourir a funzioni non priodich. In gnral una coppia di funzioni F( f( può ssr collgaa da sprssioni dlla forma sgun: F f K( k, ( Eq. dov la funzion K(k, vin da nuclo o krnl di rasformazion. La funzion F( vin da rasformaa ingral dlla funzion f( mdian il nuclo K(k,. L oprazion dscria dalla q. vin alvola dscria com mappaura dlla funzion f( dfinia nllo spazio su una funzion F( dfinia nllo spazio k. E imporan noar ch l variabili k hanno dimnsioni rciproch. Così pr smpio, s ha la dimnsion dl mpo, k ha l dimnsioni dlla frqunza. Oppur s è una disanza, ad s.la diffrnza di cammino oico di un inrfromro, k è l invrso di una disanza, cioè un numro d onda. Si dfinisc rasformaa di Fourir dlla funzion f( la funzion F( così onua : πik f F( Eq. dov i è l unià immaginaria. In quso caso il krnl è -iπk. Si dfinisc la rasformaa invrsa com: πik f F( dk Eq. 3 Dall formul di Eulro, ch dfiniscono un sponnzial complsso in bas a funzioni rigonomrich: ia cos( A) + isin( A) Eq. 4 si oin ch la rasformaa di Fourir può ssr dfinia com: F ( f cos( k i f sin(πk π Eq. 5 Si dfinisc la rasformaa cosno com: Auor: Lornzo Franco Pagina di 3
2 Corso di Laura Magisral in Chimica A.A. 3-4 Sproscopi Magnich la rasformaa sno com: da cui F c ( f cos(π k Eq. 6 F s ( f sin(π k Eq. 7 F( F ( if ( Eq. 8 c s Una funzion è dfinia pari o dispari s valgono l sguni rlazioni: Pari g g ( Eq. 9 P P Dispari g g ( Eq. D D Una funzion gnrica di variabil ral può ssr sprssa com somma di funzioni pari dispari: dov si abbia: g g f g g Eq. P D P + D [ f + f ( ] [ f f ( ] L funzioni g P g D possono ssr, in gnral, funzioni complss. Eq. Pr l funzioni pari dispari valgono l sguni rlazioni: Funzion pari : g P dk Eq. 3 Funzion dispari: g D Eq. 4 I prodoi di funzioni pari dispari rispano l sguni rgol: Pari Pari Pari Pari Dispari Dispari Dispari Dispari Pari Sapndo ch la funzion cosno è pari la funzion sno è dispari, si ricava ch la rasformaa di Fourir di una funzion gnrica f(g P (+g D ( è sprimibil com: Auor: Lornzo Franco Pagina di 3
3 Corso di Laura Magisral in Chimica A.A. 3-4 Sproscopi Magnich F( g cos( k + i g sin(πk p D ) π Eq. 5 N consgu ch una funzion pari ha una rasformaa pari d una funzion dispari ha una rasformaa dispari. La ablla sgun riassum l proprià dll rasforma di Fourir in bas all cararisich dlla funzion da rasformar: FUNZIONE Ral pari Ral dispari Immaginaria pari Complssa pari Complssa dispari Ral d asimmrica Immaginaria d asimmrica Par ral pari d immaginaria dispari Par ral dispari d immaginaria pari Pari Dispari TRASFORMATA Ral pari Immaginaria dispari Immaginaria pari Complssa pari Complssa dispari Complssa d asimmrica Complssa d asimmrica Ral Immaginaria Pari Dispari PROPRIETÀ DELLE TRASFORMATE DI FOURIER Proprià di scaling: Sia a una cosan ral d F( la rasformaa di f(. La rasformaa di f(a è: } f ( a πik f ( β ) a k F a a β πik α dβ Eq. 6 Dov β a. Dalla quazion scria sopra si si vd ch, s la larghzza di una funzion vin diminuia la sua innsià è mannua cosan (cioè si passa da f( a f(a ), la sua rasformaa divna più ampia mno innsa (si passa da F( ad /a*f(k/a) ). In modo simil si oin: a f a πik F( ak ) Eq. 7 Auor: Lornzo Franco Pagina 3 di 3
4 Corso di Laura Magisral in Chimica A.A. 3-4 Sproscopi Magnich Proprià di shifing S è una cosan ral d F( sia la rasformaa di f(, si ha ch: { f ( )} f ( ) f ( β ) πi k F( πi k πik πik ( β + ) f ( β ) dβ πikβ dβ Eq. 8 Dov β-. Si vd com la rasformaa di una funzion raslaa f(- è la rasformaa dlla funzion original moliplicaa pr un faor di fas (l sponnzial complsso). Analogamn, s la raslazion avvin nl dominio k, la rasformaa invrsa produc una funzion in moliplicaa pr un faor sponnzial. ESEMPI Nl sguio vngono indicai alcuni smpi, ra i più imporani, di coppi di funzioni lga da una rasformaa di Fourir. La doppia frccia ni grafici indica ch l du funzioni rapprsna sono lga da una rasformaa dira (frccia a dsra) d invrsa (frccia a sinisra). Funzion Cosan Sia daa una funzion f(c, dov C è una cosan. La sua Trasformaa d Fourir è: } C C C πik πik cos(πk i sin(πk Eq. 9 il scondo ingral val zro (la funzion sno è dispari). Il primo ingral non ha significao a mno ch si inrpri nll ambio dlla oria dll disribuzioni. In quso ambio si ricava ch l ingral è pari alla funzion di Dirac: Auor: Lornzo Franco Pagina 4 di 3
5 Corso di Laura Magisral in Chimica A.A. 3-4 Sproscopi Magnich } C C πik Cδ ( cos(πk Eq. Dov δ( è una funzion di Dirac dfinia nl puno k. Il risulao ci mosra ch un sgnal coninuo (una cosan) è cosiuio da una sola componn in frqunza, prcisamn la frqunza zro Funzion cosan Trasformaa di Fourir K Funzion Impulso (funzion di Dirac) S la funzion f( è la funzion di Dirac: f Aδ ricordando ch la fondamnal proprià dlla funzion di Dirac è: Eq. ( ) f f ( ) ( δ Eq. si oin ch la sua rasformaa di Fourir è: } F( Cδ C C πik Eq. 3 Cioè la rasformaa di una funzion impulso è una cosan. Nll ambio dlla analisi di sgnali quso risulao indica ch una funzion di duraa infiniamn brv ha un connuo spral ch includ u l frqunz in modo ugual. Quso risulao è alla bas dlla spromria ad impulsi, dov si ccia un campion mdian un impulso srmamn brv di radiazion, ch conin una ampia banda di frqunz, in modo da cciar u l rasizioni prmss nl campion. Tano più brv è l impulso ano più ampia sarà la banda cciaa. Auor: Lornzo Franco Pagina 5 di 3
6 Corso di Laura Magisral in Chimica A.A. 3-4 Sproscopi Magnich Fuunzion Dla di Dirac Trasformaa di Fourir -5 5 X Funzion Cosno -5 5 La rasformaa di Fourir di una funzion cosno è una funzion dla di Dirac (uno picco infiniamn sro) in corrispondnza dl valor dlla frqunza dll oscillazion dl cosno. Essndo la funzion cosno una funzion ral pari, la rasformaa sarà ral pari, quindi vi sarà un picco a + v d uno a v. f Acos(πv A A } F( δ ( k v ) + δ ( k + v ) Eq. 4 Funzion Cosno 6 Trasformaa di Fourir (par ral) K Funzion Sno: Pr drminar la rasformaa di Fourir dlla funzion sno si possono applicar l considrazioni sull proprià dll rasforma dscri prima: proprià di shif di parià. f Asin(πv A A } F( i δ ( k v ) + i δ ( k + v ) Eq. 5 Com si vd la rasformaa dlla funzion sno è una funzion immaginaria dispari: Auor: Lornzo Franco Pagina 6 di 3
7 Corso di Laura Magisral in Chimica A.A. 3-4 Sproscopi Magnich Funzion Sno - - Trasformaa di Fourir (par immaginaria) K Funzion Gaussiana: Una funzion gaussiana normalizzaa ha la forma: f La rasformaa di Fourir di una gaussiana è: α α Eq. 6 π } F( α π π k α α π α α πik cos(πk Eq. 7 Gaussiana Trasformaa di Fourir k Si vd com la rasformaa di una Gaussiana (funzion ral pari) è ancora una funzion Gaussiana (ral pari) nllo spazio dlla variabil k. Si noi ch la larghzza dlla funzion Gaussiana è invrsamn proporzional ni du domini k. Quindi, ano più larga è la funzion f(, ano più sra sarà la funzion rasformaa F(: Auor: Lornzo Franco Pagina 7 di 3
8 Corso di Laura Magisral in Chimica A.A. 3-4 Sproscopi Magnich Funzion Esponnzial Esaminiamo la funzion sponnzial dfinia com: La rasformaa di Fourir di qusa funzion è f α A Eq. 8 } F( A A A α + iπk A α + iπk Aα α + 4π k α i πk α πik α i πk Aπk i α + 4π k Eq. 9 La funzion F( è una funzion complssa prché la f( è ral. La par ral dlla F( è una funzion Lornziana: Funzion Esponnzial Trasformaa di Fourir par Ral Par Immaginaria -5 5 k Auor: Lornzo Franco Pagina 8 di 3
9 Corso di Laura Magisral in Chimica A.A. 3-4 Sproscopi Magnich Funzion Scaola ( bocar ) Si considri la funzion rangolar: è una funzion ch val zro al di fuori dlla rgion dfinia dai limii l +l. All inrno di qusa rgin assum un valor cosan, drminao dalla condizion di normalizzazion (il suo ingral su uo il dominio di sia pari ad ): la funzion val quindi /l all inrno dlla rgion. Qusa funzion vin spsso indicaa com funzion bocar. -l +l La rasformaa di Fourir di qusa funzion è (si noi ch la rasformaa sno non compar ssndo la f( una funzion pari): } F( l l l cos(πk sin(πkl ) πkl cos(πk La funzion risulan sin(/, indicaa col nom di funzion sinc(, è rapprsnaa nlla figura sgun: Eq Funzion riangolo Sia daa la funzion riangolo, così dfinia: La rasformaa di Fourir di qusa funzion è: -5 5 K pr > l pr < l l f Eq. 3 Auor: Lornzo Franco Pagina 9 di 3
10 Corso di Laura Magisral in Chimica A.A. 3-4 Sproscopi Magnich } F( l f cos(πk l sin(πkl ) πkl sinc (πkl ) iπk Eq. 3 CONVOLUZIONE Si dfinisc la convoluzion ra du funzioni g( d f( il sgun ingral: y f g( f ( ) g( ) d ( Eq. 33 dov d sono dfini nllo ssso dominio. La convoluzion ra l du funzioni (indicaa soliamn da un simbolo qual * ) rapprsna la sovrapposizion dlla funzion g( riflssa aorno all ass y raslaa di, con la funzion f(. Il risulao è una funzion y( ch è una mscolanza di g con f. La convoluzion di du funzioni è un conco ch dscriv un fnomno piuoso gnral nlla acquisizion di dai sprimnali. Infai scondo la oria di rsponsi linari, dao un sisma soggo ad uno simolo, si dfinisc la funzion f( com lo simolo la funzion g( com la funzion risposa dl sisma. In paricolar g( è l oupu s lo simolo è rapprsnao da un impulso. In gnral, la risposa in uscia (l oupu) di un sisma è la convoluzion ra f( g(. Ad smpio in una misura sprofoomrica, la funzion ingrsso è rapprsnaa dallo spro vro, la funzion risposa è una funzion gradino la cui larghzza è daa dalla risoluzion srumnal, ad smpio daa dalla larghzza dlla fndiura in uscia da un monocromaor. S la risoluzion srumnal è bassa rispo alla larghzza di picchi sproscopici, lo spro misurao è lo spro vro convoluo con la risposa srumnal. L ffo final è un allargamno di picchi sprali, con vnual prdia di risoluzion. Pr illusrar il conco di convoluzion vin prsnao un smpio. Siano f() g() l du funzioni mosra ni grafici sguni: f() g() Pr onr l ingral di convoluzion occorr considrar il prodoo di f() d g(-). Qus ulima funzion è la funzion g() riflssa aorno all ass y raslaa di : g() g(-) f() Auor: Lornzo Franco Pagina di 3 g(-) g(-)
11 Corso di Laura Magisral in Chimica A.A. 3-4 Sproscopi Magnich Nlla figura mosraa sopra si ha ch, pr il valor di considrao, f()*g(-) quindi la convoluzion val zro. Pr valori di divrsi, si ongono valori dlla convoluzion divrsi da zro, com visualizzao nlla figura sgun: Di paricolar inrss è la convoluzion di una funzion qualsiasi con una funzion Dla di Dirac f(δ(- ). ( ) g( d y f * g( ) δ Eq. 34 applicando l q., nlla prcdn quazion, si oin: y f * g( g( ) Eq. 35 ( Quindi la convoluzion di una funzion qualsiasi con una funzion di Dirac localizzaa in è la funzion sssa raslaa di. Torma di convoluzion Il orma di convoluzion sabilisc ch la rasformaa di Fourir dlla convoluzion di du funzioni è il prodoo dlla rasformaa di Fourir dll du funzioni. In forma splicia, s F( è la rasformaa di f(, G( è la rasformaa di g( y() è la convoluzion ra f( g( val la sgun rlazion: Auor: Lornzo Franco Pagina di 3
12 Corso di Laura Magisral in Chimica A.A. 3-4 Sproscopi Magnich g( } F( G( Eq. 36 Val anch il sgun orma: La rasformaa di Fourir di un prodoo di funzioni è la convoluzion ra l rasforma. g( } F( * G( Eq. 37 Qus ulimo orma è di fondamnal imporanza pr dminar la rasformaa di alcun funzioni complica. Un caso molo comun si rova nlla sproscopia NMR. Il sgnal fisicamn misurao (il FID) è cosiuio da una somma di oscillazioni di frqunza pari all frqunz di risonanza di ui i nucli in sam, la cui innsià dcad nl mpo. Si raa di oscillazioni smorza; nlla forma più smplic (una sola frqunza di risonanza) si può scrivr la funzion dipndn dal mpo com: f ( ) T cos(π v ) Eq. 38 dov ν è la frqunza di risonanza T è il mpo di rilassamno rasvrsal. Lo spro NMR, ssndo la rasformaa di Fourir di qusa funzion, è la convoluzion di una funzion Lornziana (rasformaa dll sponnzial) di una Dla di Dirac cnraa su ν (rasformaa dlla funzion cosno). Pr quano do prima, la convoluzion di qus du funzioni risula in una Lornziana cnraa sulla frqunza ν. Quando sono prsni più nucli con divrs frqunz di risonanza, si aggiungono rmini oscillani al FID di consgunza alri picchi cioè funzioni Lornzian nllo spro. Una ulrior applicazion dl orma sprsso dalla q. 37 si ha considrando ch i sgnali misurai in sproscopia (FID o inrfrogramma) in ralà non sono misurai pr un mpo (FID) o un riardo di cammino (Inrfrogramma) infinii. Il risulao è ch il sgnal ralmn misurao è rapprsnabil dal prodoo di un FID o Infrogramma pr la funzion bocar dfinia prima, di snsion pari al mpo (spazio) di misura. Di consgunza la rasformaa di Fourir di quso prodoo è la convoluzion ra la funzion sinc (rasformaa dlla funzion bocar lo spro vro. Si ongono di picchi ch hanno dll band larali oscillani causa dalla funzion sinc. Quso fnomno alvola impdisc la lura corra di uno spro. Pr liminar quso inconvnin si usa moliplicar il FID o l inrfrogramma pr un alra funzion (un sponnzial, una funzion riangolo, una gaussiana cc.) ch rnd lo spro mno soggo a qusi arfai. Uno svanaggio è ch alvola l righ sprali si allargano scapio dlla risoluzion. L funzioni usa pr corrggr la forma dl FID o dll inrfrogramma sono d funzioni finsra. Auor: Lornzo Franco Pagina di 3
13 Corso di Laura Magisral in Chimica A.A. 3-4 Sproscopi Magnich Auor: Lornzo Franco Pagina 3 di 3
Esercizi sulla CONVOLUZIONE
 Esrcizi sulla CONVOLUZIONE 1 INTRODUZIONE Si ricorda ch la convoluzion ra du sgnali x(), rali o complssi, indicaa simbolicamn com: C xy () = x() * è daa indiffrnmn dall du sprssioni: C xy () = C xy ()
Esrcizi sulla CONVOLUZIONE 1 INTRODUZIONE Si ricorda ch la convoluzion ra du sgnali x(), rali o complssi, indicaa simbolicamn com: C xy () = x() * è daa indiffrnmn dall du sprssioni: C xy () = C xy ()
Esercizi sulla CONVOLUZIONE INTRODUZIONE. x(t)y( τ - t)dt. x(τ - t)y(t)dt
 INTRODUZIONE Si ricorda ch la convoluzion ra du sgnali x() y(), rali o complssi, indicaa simbolicamn com: C xy () = x() * y() è daa indiffrnmn dall du sprssioni: Esrcizi sulla CONVOLUZIONE C xy () = C
INTRODUZIONE Si ricorda ch la convoluzion ra du sgnali x() y(), rali o complssi, indicaa simbolicamn com: C xy () = x() * y() è daa indiffrnmn dall du sprssioni: Esrcizi sulla CONVOLUZIONE C xy () = C
Richiami su numeri complessi
 Richiami su numri complssi Insim C di numri complssi E' l'insim dll coppi ordina di numri rali = Z R j Z I ; Z R, Z I R Z = Z R, Z I j Δ = (0,1) unià immaginaria Si noi ch C conin R; in paricolar linsim
Richiami su numri complssi Insim C di numri complssi E' l'insim dll coppi ordina di numri rali = Z R j Z I ; Z R, Z I R Z = Z R, Z I j Δ = (0,1) unià immaginaria Si noi ch C conin R; in paricolar linsim
Appendice Analisi in frequenza dei segnali
 Appndic Analisi in rqunza di sgnali - Appndic Analisi in rqunza di sgnali - Sgnali priodici Sviluppo in sri di Fourir Un sgnal è priodico nl mpo quando si rip ogni scondi. Si vda, com smpio, il sgnal in
Appndic Analisi in rqunza di sgnali - Appndic Analisi in rqunza di sgnali - Sgnali priodici Sviluppo in sri di Fourir Un sgnal è priodico nl mpo quando si rip ogni scondi. Si vda, com smpio, il sgnal in
Autovalori complessi e coniugati
 Auovalori complssi coniugai Noazioni A A α ω ω α λ λ λ α + jω, λ α jω, maric ad lmni rali α + jω, maric diagonal ad lmni complssi α jω L du marici A A hanno gli sssi auovalori λ, λ. aa una gnrica maric
Auovalori complssi coniugai Noazioni A A α ω ω α λ λ λ α + jω, λ α jω, maric ad lmni rali α + jω, maric diagonal ad lmni complssi α jω L du marici A A hanno gli sssi auovalori λ, λ. aa una gnrica maric
Laurea triennale in BIOLOGIA A. A
 Laura rinnal in BIOLOGIA A. A. 3-4 4 CHIMICA Vn 8 novmbr 3 Lzioni di Chimica Fisica Cinica chimica: razioni paralll razioni conscuiv Effo dlla mpraura sulla cosan di vlocià Prof. Anonio Toffoli Chimica
Laura rinnal in BIOLOGIA A. A. 3-4 4 CHIMICA Vn 8 novmbr 3 Lzioni di Chimica Fisica Cinica chimica: razioni paralll razioni conscuiv Effo dlla mpraura sulla cosan di vlocià Prof. Anonio Toffoli Chimica
Sistemi lineari a tempo continuo. Un sistema lineare analogico, in generale tempo variante, caratterizzato da una risposta
 Capiolo V SISTEMI LIERI CO IGRESSI LETORI Sisi linari a po coninuo V. - Cararizzazion nl doinio dl po. Un sisa linar analogico, in gnral po arian, cararizzao da una risposa ipulsia daa da h (, ) rasfora
Capiolo V SISTEMI LIERI CO IGRESSI LETORI Sisi linari a po coninuo V. - Cararizzazion nl doinio dl po. Un sisa linar analogico, in gnral po arian, cararizzao da una risposa ipulsia daa da h (, ) rasfora
Determinare il dominio di una funzione
 Drminar il dominio di una funzion CHE COSA SONO LE FUNZON. Una funzion = f( è una rlazion ch lga du grandzz (variabili: la variabil vin chiamaa variabil indipndn, mnr la variabil dipndn. Pr smpio la rlazion
Drminar il dominio di una funzion CHE COSA SONO LE FUNZON. Una funzion = f( è una rlazion ch lga du grandzz (variabili: la variabil vin chiamaa variabil indipndn, mnr la variabil dipndn. Pr smpio la rlazion
Serie di Fourier a tempo continuo. La rappresentazione dei segnali nel dominio della frequenza. Jean Baptiste Joseph Fourier (1768 1830 )
 Sri di Fourir a mpo coninuo La rapprsnazion di sgnali nl dominio dlla frqunza Jan Bapis Josph Fourir (768 83 ) Fourir sviluppò la oria mamaica dl calor uilizzando funzioni rigonomrich (sni cosni), ch noi
Sri di Fourir a mpo coninuo La rapprsnazion di sgnali nl dominio dlla frqunza Jan Bapis Josph Fourir (768 83 ) Fourir sviluppò la oria mamaica dl calor uilizzando funzioni rigonomrich (sni cosni), ch noi
Segnali e sistemi nel dominio della frequenza
 oria di sgnali Sgnali sismi nl dominio dlla rqunza EORIA DEI SEGNALI LAUREA IN INGEGNERIA DELL INORMAZIONE Sommario Sgnali mpo coninuo priodici Sri di ourir Sgnali mpo coninuo apriodici rasormaa di ourir
oria di sgnali Sgnali sismi nl dominio dlla rqunza EORIA DEI SEGNALI LAUREA IN INGEGNERIA DELL INORMAZIONE Sommario Sgnali mpo coninuo priodici Sri di ourir Sgnali mpo coninuo apriodici rasormaa di ourir
Integrale di sin t/t e varianti
 Ingral di sin / variani Annalisa Massaccsi dicmbr Ingral di sin / In rifrimno all s. 7 dl VII gruppo di srcizi, com già viso ad srciazion, vogliamo dimosrar ch sin / d R. Ossrvazion. Ossrviamo innanziuo
Ingral di sin / variani Annalisa Massaccsi dicmbr Ingral di sin / In rifrimno all s. 7 dl VII gruppo di srcizi, com già viso ad srciazion, vogliamo dimosrar ch sin / d R. Ossrvazion. Ossrviamo innanziuo
Modello di Einstein. Stato eccitato. Stato fondamentale
 Modllo di Einsin Il modllo di Einsin dscriv in manira fnomnoloica d a livllo microscopico i procssi di l inrazion ra la r..m. maria ch porano ai fnomni di assorbimno d mission radiaiva. Il sisma modllo
Modllo di Einsin Il modllo di Einsin dscriv in manira fnomnoloica d a livllo microscopico i procssi di l inrazion ra la r..m. maria ch porano ai fnomni di assorbimno d mission radiaiva. Il sisma modllo
Teoria dei Sistemi - A.A. 2003/2004
 ANAISI ODAE DEI SISTEI INEARI A TEPO CONTINUO Dr. Crisian Scchi ARSconrol ab Univrsià di odna Rggio Emilia Il movimno di un sisma TI & ( A( + Bu( y( C( + Du( Formula di agrang ( A A( τ + Bu( τ dτ A I +
ANAISI ODAE DEI SISTEI INEARI A TEPO CONTINUO Dr. Crisian Scchi ARSconrol ab Univrsià di odna Rggio Emilia Il movimno di un sisma TI & ( A( + Bu( y( C( + Du( Formula di agrang ( A A( τ + Bu( τ dτ A I +
INGEGNERIA CIVILE E AMBIENTALE ESERCITAZIONI DI ANALISI C SETTIMANA 7 DEFINIZIONE: FUNZIONE DIFFERENZIABILE IN UN PUNTO.
 DEFINIZIONE: FUNZIONE DIFFERENZIABILE IN UN PUNTO Sia A un apro di : sis un vor ab, al ch,, f A Prso, A si dic ch f è diffrnziabil in,, 0, 0 0 0 f f a b 0 si pon df, a, b f Si dimosra ch a, b,, quindi
DEFINIZIONE: FUNZIONE DIFFERENZIABILE IN UN PUNTO Sia A un apro di : sis un vor ab, al ch,, f A Prso, A si dic ch f è diffrnziabil in,, 0, 0 0 0 f f a b 0 si pon df, a, b f Si dimosra ch a, b,, quindi
Facoltà di Economia. Equazioni differenziali Lineari ed Applicazioni Economiche
 Facolà di Economia Equazioni diffrnziali Linari d Applicazioni Economich prof. EQUAZIONI DIFFERENZIALI LINEARI APPLICAZIONI ECONOMICHE EQUAZIONI DIFFERENZIALI DEL PRIMO ORDINE LINEARI Quso ipo di quazioni
Facolà di Economia Equazioni diffrnziali Linari d Applicazioni Economich prof. EQUAZIONI DIFFERENZIALI LINEARI APPLICAZIONI ECONOMICHE EQUAZIONI DIFFERENZIALI DEL PRIMO ORDINE LINEARI Quso ipo di quazioni
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/2017 FUNZIONI INTEGRALI
 Univrsià Carlo Caano Inggnria gsional Analisi mamaica aa 6/7 FUNZIONI INTEGRALI ESERCIZI CON SOLUZIONE 6 ) Daa la funzion F d a) calcolar F, F ', '' F ; b) scrivr l quazion dlla ra angn nl puno ; c) scrivr
Univrsià Carlo Caano Inggnria gsional Analisi mamaica aa 6/7 FUNZIONI INTEGRALI ESERCIZI CON SOLUZIONE 6 ) Daa la funzion F d a) calcolar F, F ', '' F ; b) scrivr l quazion dlla ra angn nl puno ; c) scrivr
[ ] [ ] [ ] [ ] lim. x 1 3 R. lim. lim. lim. lim. lim. lim 5 R. lim. Calcola i seguenti limiti risolvendo le eventuali forme di indeterminazione
![[ ] [ ] [ ] [ ] lim. x 1 3 R. lim. lim. lim. lim. lim. lim 5 R. lim. Calcola i seguenti limiti risolvendo le eventuali forme di indeterminazione [ ] [ ] [ ] [ ] lim. x 1 3 R. lim. lim. lim. lim. lim. lim 5 R. lim. Calcola i seguenti limiti risolvendo le eventuali forme di indeterminazione](/thumbs/92/110333272.jpg) Educnica.i Calcolo di ii Calcola i sguni ii risolvndo l vnuali form di indrminazion Esrcizio no. Esrcizio no. Soluzion a pag.8 Soluzion a pag.8 [ ] Esrcizio no. Esrcizio no. Esrcizio no. lg Esrcizio no.6
Educnica.i Calcolo di ii Calcola i sguni ii risolvndo l vnuali form di indrminazion Esrcizio no. Esrcizio no. Soluzion a pag.8 Soluzion a pag.8 [ ] Esrcizio no. Esrcizio no. Esrcizio no. lg Esrcizio no.6
Circuiti dinamici. Introduzione. (versione del ) Circuiti resistivi e circuiti dinamici
 ircuii dinamici nroduzion www.di.ing.unibo.i/prs/masri/didaica.m (vrsion dl --3) ircuii rsisivi circuii dinamici ircuii rsisivi: circuii formai solo da componni rsisivi l quazioni dl circuio cosiuiscono
ircuii dinamici nroduzion www.di.ing.unibo.i/prs/masri/didaica.m (vrsion dl --3) ircuii rsisivi circuii dinamici ircuii rsisivi: circuii formai solo da componni rsisivi l quazioni dl circuio cosiuiscono
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2017/2018 FUNZIONI INTEGRALI
 Univrsià Carlo Caano Inggnria gsional Analisi mamaica aa 7/8 FUNZIONI INTEGRALI ESERCIZI CON SOLUZIONE 6 ) Daa la funzion F d a) calcolar F, F ', '' F ; b) scrivr l quazion dlla ra angn nl puno ; c) scrivr
Univrsià Carlo Caano Inggnria gsional Analisi mamaica aa 7/8 FUNZIONI INTEGRALI ESERCIZI CON SOLUZIONE 6 ) Daa la funzion F d a) calcolar F, F ', '' F ; b) scrivr l quazion dlla ra angn nl puno ; c) scrivr
Innanzitutto, dalla descrizione data nel testo dell esercizio possiamo scrivere:
 Corso di conomia Poliica II (HZ) /0/202 Soluzion srcizio Innanziuo, dalla dscrizion daa nl so dll srcizio possiamo scrivr: i * 0,06, 5. a) Sappiamo ch il asso di apprzzamno/dprzzamno dlla mona nazional
Corso di conomia Poliica II (HZ) /0/202 Soluzion srcizio Innanziuo, dalla dscrizion daa nl so dll srcizio possiamo scrivr: i * 0,06, 5. a) Sappiamo ch il asso di apprzzamno/dprzzamno dlla mona nazional
Lezione 15 (BAG cap. 14) Le aspettative: nozioni di base
 Lzion 5 (BAG cap. 4) L aspaiv: nozioni di bas Corso di Macroconomia Prof. Guido Ascari, Univrsià di Pavia Il asso di inrss in rmini di mona è do asso di inrss nominal Il asso di inrss in rmini di bni è
Lzion 5 (BAG cap. 4) L aspaiv: nozioni di bas Corso di Macroconomia Prof. Guido Ascari, Univrsià di Pavia Il asso di inrss in rmini di mona è do asso di inrss nominal Il asso di inrss in rmini di bni è
Spettro di densità di potenza e rumore termico
 Spro di dnsià di ponza rumor rmico lcomunicazioni pr l rospazio. Lombardo DI, Univ. di Roma La Sapinza Spro di dnsià di onza- roprià sprali: rasormaa di Fourir RSFORM DI FOURIR NI-RSFORM DI FOURIR S s
Spro di dnsià di ponza rumor rmico lcomunicazioni pr l rospazio. Lombardo DI, Univ. di Roma La Sapinza Spro di dnsià di onza- roprià sprali: rasormaa di Fourir RSFORM DI FOURIR NI-RSFORM DI FOURIR S s
Esercizi per il corso Matematica clea
 Esrcizi pr il corso Mamaica cla Danil Rilli anno accadmico 8/9 Lzion : Ingrali Esrcizi svoli. Provar, usando il cambio di variabil ch:. Dimosrar ch. Ingrando pr pari dimosrar ch + = + = 6 sin(π) = π Svolgimno.
Esrcizi pr il corso Mamaica cla Danil Rilli anno accadmico 8/9 Lzion : Ingrali Esrcizi svoli. Provar, usando il cambio di variabil ch:. Dimosrar ch. Ingrando pr pari dimosrar ch + = + = 6 sin(π) = π Svolgimno.
La spettroscopia di risonanza magnetica nucleare - NMR
 Corso di Laura agistral in Chimica Industrial A.A: 3/4 La spttroscopia di risonanza magntica nuclar - R La spttroscopia di Risonanza agntica uclar (R) si basa sulla intrazion tra una radiazion lttromagntica
Corso di Laura agistral in Chimica Industrial A.A: 3/4 La spttroscopia di risonanza magntica nuclar - R La spttroscopia di Risonanza agntica uclar (R) si basa sulla intrazion tra una radiazion lttromagntica
Corsi di Laurea in Fisica, Fisica ed Astrofisica
 Corsi di Laura in Fisica, Fisica d Asrofisica Analisi A.A. 007-008 - Foglio 1 1.1. Esrcizio. Sudiar la coninuià in R dlla funzion sn(x y) x + y s y > 0, y ln(1 + x ) s y 0. La funzion è chiaramn coninua
Corsi di Laura in Fisica, Fisica d Asrofisica Analisi A.A. 007-008 - Foglio 1 1.1. Esrcizio. Sudiar la coninuià in R dlla funzion sn(x y) x + y s y > 0, y ln(1 + x ) s y 0. La funzion è chiaramn coninua
Modello AD-AS. Mercato del lavoro. Mercato dei beni. Mercati finanziari
 Modllo AD-AS Mrcao dl lavoro Equilibrio di mdio priodo su Mrcao di bni Mrcai finanziari.b. A un dao asso di disoccupazion corrispond un dao livllo dlla produzion (assumndo funzion di produzion =): U u
Modllo AD-AS Mrcao dl lavoro Equilibrio di mdio priodo su Mrcao di bni Mrcai finanziari.b. A un dao asso di disoccupazion corrispond un dao livllo dlla produzion (assumndo funzion di produzion =): U u
Istituzioni di Matematica I (Chimica) canale A-L 14 febbraio 2014 Soluzioni
 Esrcizio. Isiuzioni di Mamaica I (Chimica) canal A-L 4 fbbraio 204 i) Si sudi la funzion Soluzioni f(x) = arcan ( log x x ) s n disgni il grafico, solo pr por rispondr all sguni domand: ii) pr quali α
Esrcizio. Isiuzioni di Mamaica I (Chimica) canal A-L 4 fbbraio 204 i) Si sudi la funzion Soluzioni f(x) = arcan ( log x x ) s n disgni il grafico, solo pr por rispondr all sguni domand: ii) pr quali α
Oscillazioni e onde. Oscillatore armonico. x( t) e sostituendo nell equazione originale si ha. dx dt. x cos infatti. Periodo del moto armonico T
 No il k:\scuola\corsi\corso isica\ond\oscillaori aronico sorzao orzaodoc Crao il 5// 87 Dinsion il: 86 b ndra Zucchini Elaborao il 5// all or 885, salao il 5// 87 sapao il 5// 88 Wb: hp://digilandrioli/prozucchini
No il k:\scuola\corsi\corso isica\ond\oscillaori aronico sorzao orzaodoc Crao il 5// 87 Dinsion il: 86 b ndra Zucchini Elaborao il 5// all or 885, salao il 5// 87 sapao il 5// 88 Wb: hp://digilandrioli/prozucchini
Compito di Matematica sul problema di Cauchy e sulle equazioni differenziali ordinarie del 2º ordine. [1]
![Compito di Matematica sul problema di Cauchy e sulle equazioni differenziali ordinarie del 2º ordine. [1] Compito di Matematica sul problema di Cauchy e sulle equazioni differenziali ordinarie del 2º ordine. [1]](/thumbs/88/115203540.jpg) Compio di Mamaica sul problma di Cauch sull quazioni diffrnziali ordinari dl º ordin [] Esrcizio Spigar la formulazion, il significao com si procd alla risoluzion dl problma di Cauch pr EDO dl º ordin
Compio di Mamaica sul problma di Cauch sull quazioni diffrnziali ordinari dl º ordin [] Esrcizio Spigar la formulazion, il significao com si procd alla risoluzion dl problma di Cauch pr EDO dl º ordin
Corso di Macroeconomia
 Corso di Macroconomia LE ASPETTATIVE: NOZIONI DI BASE. Tassi di inrss nominali rali Il asso di inrss in rmini di mona è chiamao asso di inrss nominal. Il asso di inrss sprsso in rmini di bni è chiamao
Corso di Macroconomia LE ASPETTATIVE: NOZIONI DI BASE. Tassi di inrss nominali rali Il asso di inrss in rmini di mona è chiamao asso di inrss nominal. Il asso di inrss sprsso in rmini di bni è chiamao
9. Eventuali Punti di non derivabilità: Punti angolosi, cuspidi e flessi a tangente verticale. 10. Derivata seconda (calcolo)
 Capisaldi:. Insim di sisnza Sudio di una funzion.. Evnuali simmri pari, dispari, priodicià. Grafico riconducibil. Inrszioni con gli assi 4. Sgno dlla funzion [f 0] 5. Limii alla fronira dll insim di dfinizion
Capisaldi:. Insim di sisnza Sudio di una funzion.. Evnuali simmri pari, dispari, priodicià. Grafico riconducibil. Inrszioni con gli assi 4. Sgno dlla funzion [f 0] 5. Limii alla fronira dll insim di dfinizion
9. Eventuali Punti di non derivabilità: Punti angolosi, cuspidi e flessi a tangente verticale. 10.Derivata seconda (calcolo)
 Capisaldi:. Insim di sisnza Sudio di una funzion.. Evnuali simmri pari, dispari, priodicià. Grafico riconducibil. Inrszioni con gli assi. Sgno dlla funzion [f 0] 5. Limii alla fronira dll insim di dfinizion
Capisaldi:. Insim di sisnza Sudio di una funzion.. Evnuali simmri pari, dispari, priodicià. Grafico riconducibil. Inrszioni con gli assi. Sgno dlla funzion [f 0] 5. Limii alla fronira dll insim di dfinizion
ESERCITAZIONE N 12 SIMULAZIONE DI UN SISTEMA DI ATTESA M/M/1
 ESERCITAZIONE N 12 SIMULAZIONE DI UN SISTEMA DI ATTESA M/M/1 Toria dll cod La oria dll cod comprnd lo sudio mamaico dll cod o sismi d'asa. La formazion dll lin di asa è un fnomno comun ch si vrifica ogni
ESERCITAZIONE N 12 SIMULAZIONE DI UN SISTEMA DI ATTESA M/M/1 Toria dll cod La oria dll cod comprnd lo sudio mamaico dll cod o sismi d'asa. La formazion dll lin di asa è un fnomno comun ch si vrifica ogni
INTRODUZIONE. P.Galeotti A.A.2003/04 - Segnali 1
 INTRODUZIONE I sgnali sono nai com srumno di comunicazion fin dall'anichia` pr smpio sgnali luminosi o sonori; l'uso dl lgrafo l alfabo Mors ` dl 85 n sgna la nascia modrna. Ora i sgnali lrici sono alla
INTRODUZIONE I sgnali sono nai com srumno di comunicazion fin dall'anichia` pr smpio sgnali luminosi o sonori; l'uso dl lgrafo l alfabo Mors ` dl 85 n sgna la nascia modrna. Ora i sgnali lrici sono alla
Introduzione ai Circuiti Elettronici
 Inroduzion ai Circuii Elronici Sommario Naura di Sgnali Analogici Digiali Bipoli Bipoli Elmnari Connion di Bipoli Analii di Circuii Linari Tmpo-Invariani Equazioni diffrnziali Faori Funzion di Trafrimno
Inroduzion ai Circuii Elronici Sommario Naura di Sgnali Analogici Digiali Bipoli Bipoli Elmnari Connion di Bipoli Analii di Circuii Linari Tmpo-Invariani Equazioni diffrnziali Faori Funzion di Trafrimno
Induzione magnetica. Capitolo. 1. Autoinduzione
 Capiolo nduzion magnica B. Auoinduzion La forza lromoric indoa rapprsna il lavoro pr unià di carica svolo dall forz ch gnrano la corrn indoa. Essa è lgaa alla variazion dl flusso magnico F concanao al
Capiolo nduzion magnica B. Auoinduzion La forza lromoric indoa rapprsna il lavoro pr unià di carica svolo dall forz ch gnrano la corrn indoa. Essa è lgaa alla variazion dl flusso magnico F concanao al
Correnti di linea e tensioni concatenate
 Sismi Trifas Sismi rifas l rasporo la disribuzion di nrgia lrica avvngono in prvalnza pr mzzo di lin rifas Un sisma rifas è alimnao mdian gnraori a r rminali rapprsnabili mdian rn di gnraori sinusoidali
Sismi Trifas Sismi rifas l rasporo la disribuzion di nrgia lrica avvngono in prvalnza pr mzzo di lin rifas Un sisma rifas è alimnao mdian gnraori a r rminali rapprsnabili mdian rn di gnraori sinusoidali
Massa M. dt Il modello dinamico del sistema nel dominio del tempo continuo è espresso dal secondo principio della dinamica: j.
 EEI E: AA E ZATE VI Un carrllo di massa è riidamn collao ad uno smorzaor iscoso, ralizzao rami un pison c si muo un cildro connn dl liquido cararizzao dal coffic di iscosià, c produc l ffo di una forza
EEI E: AA E ZATE VI Un carrllo di massa è riidamn collao ad uno smorzaor iscoso, ralizzao rami un pison c si muo un cildro connn dl liquido cararizzao dal coffic di iscosià, c produc l ffo di una forza
Corso di Analisi: Algebra di Base. 3^ Lezione
 Corso di Analisi: Algbra di Bas ^ Lzion Disquazioni algbrich. Disquazioni di. Disquazioni di. Disquazioni faoriali. Disquazioni biquadraich. Disquazioni binomi. Disquazioni fra. Sismi di disquazioni. Allgao
Corso di Analisi: Algbra di Bas ^ Lzion Disquazioni algbrich. Disquazioni di. Disquazioni di. Disquazioni faoriali. Disquazioni biquadraich. Disquazioni binomi. Disquazioni fra. Sismi di disquazioni. Allgao
Macroeconomia. Laura Vici. laura.vici@unibo.it. www.lauravici.com/macroeconomia LEZIONE 22. Rimini, 19 novembre 2014
 Macroconomia Laura Vici laura.vici@unibo.i www.lauravici.com/macroconomia LEZIONE 22 Rimini, 19 novmbr 2014 Macroconomia 362 I mrcai finanziari in conomia apra Dao ch l acquiso o la vndia di aivià finanziari
Macroconomia Laura Vici laura.vici@unibo.i www.lauravici.com/macroconomia LEZIONE 22 Rimini, 19 novmbr 2014 Macroconomia 362 I mrcai finanziari in conomia apra Dao ch l acquiso o la vndia di aivià finanziari
Il ruolo delle aspettative in economia
 Capiolo XV. Il ruolo dll aspaiv in conomia . Tassi di inrss nominali rali Il asso di inrss in rmini di mona è chiamao asso di inrss nominal. Il asso di inrss sprsso in rmini di bni è chiamao asso di inrss
Capiolo XV. Il ruolo dll aspaiv in conomia . Tassi di inrss nominali rali Il asso di inrss in rmini di mona è chiamao asso di inrss nominal. Il asso di inrss sprsso in rmini di bni è chiamao asso di inrss
Analisi dei Sistemi. Soluzione del compito del 26 Giugno ÿ(t) + (t 2 1)y(t) = 6u(t T ). 2 x1 (t) 0 1
 Analisi di Sistmi Soluzion dl compito dl 26 Giugno 23 Esrcizio. Pr i du sistmi dscritti dai modlli sgunti, individuar l proprità strutturali ch li carattrizzano: linar o non linar, stazionario o tmpovariant,
Analisi di Sistmi Soluzion dl compito dl 26 Giugno 23 Esrcizio. Pr i du sistmi dscritti dai modlli sgunti, individuar l proprità strutturali ch li carattrizzano: linar o non linar, stazionario o tmpovariant,
Lezione 11. Controllo predittivo a minima varianza. F. Previdi - Controlli Automatici - Lez. 11 1
 Lion. onrollo prdiivo a minima variana F. Prvidi - onrolli uomaici - L. Schma dlla lion. Inroduion. smpio splicaivo 3. smpio splicaivo 4. Soluion dl problma gnral (modlli RMX) F. Prvidi - onrolli uomaici
Lion. onrollo prdiivo a minima variana F. Prvidi - onrolli uomaici - L. Schma dlla lion. Inroduion. smpio splicaivo 3. smpio splicaivo 4. Soluion dl problma gnral (modlli RMX) F. Prvidi - onrolli uomaici
Aspettative. In questa lezione: Discutiamo di previsioni sulle variabili future, e di aspettative. Definiamo tassi di interesse nominale e reale.
 Aspaiv In qusa lzion: Discuiamo di prvisioni sull variabili fuur, di aspaiv. Dfiniamo assi di inrss nominal ral. Ridfiniamo lo schma IS-LM con inflazion. 198 Imporanza dll Aspaiv L dcisioni rlaiv a consumo
Aspaiv In qusa lzion: Discuiamo di prvisioni sull variabili fuur, di aspaiv. Dfiniamo assi di inrss nominal ral. Ridfiniamo lo schma IS-LM con inflazion. 198 Imporanza dll Aspaiv L dcisioni rlaiv a consumo
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2017/2018 PRIMITIVE E INTEGRALI DEFINITI
 Univrsià Carlo Caano Inggnria gsional nalisi mamaia aa 7/8 PRIMITIVE E INTEGRLI DEFINITI ESERCIZI CON SOLUZIONE Calolar i sguni ingrali indfinii: ) d ; ) d ; ) d ; ) os sin d ; 6 ) d SOLUZIONI ) La funzion
Univrsià Carlo Caano Inggnria gsional nalisi mamaia aa 7/8 PRIMITIVE E INTEGRLI DEFINITI ESERCIZI CON SOLUZIONE Calolar i sguni ingrali indfinii: ) d ; ) d ; ) d ; ) os sin d ; 6 ) d SOLUZIONI ) La funzion
SVOLGIMENTO. 2 λ = b S
 RELAZIONE Dimnsionar sol d anima dl longhron d il rivsimno dl bordo di aacco, in una szion disan 4 m dalla mzzria, pr un ala monolonghron di un vlivolo avn l sguni cararisich: - pso oal W 4700 N - suprfici
RELAZIONE Dimnsionar sol d anima dl longhron d il rivsimno dl bordo di aacco, in una szion disan 4 m dalla mzzria, pr un ala monolonghron di un vlivolo avn l sguni cararisich: - pso oal W 4700 N - suprfici
Lezione 21 (BAG cap. 19) Regimi di cambio. Corso di Macroeconomia Prof. Guido Ascari, Università di Pavia
 Lzion 21 (BAG cap. 19) Rgimi di cambio Corso di Macroconomia Prof. Guido Ascari, Univrsià di Pavia Il capiolo si occupa Aggiusamno nl mdio priodo d ffi di una svaluazion Crisi dl asso di cambio Tasso di
Lzion 21 (BAG cap. 19) Rgimi di cambio Corso di Macroconomia Prof. Guido Ascari, Univrsià di Pavia Il capiolo si occupa Aggiusamno nl mdio priodo d ffi di una svaluazion Crisi dl asso di cambio Tasso di
RUMORE TERMICO - SOLUZIONI
 UMOE EMICO - SOLUZIONI Nl circuio in i. è una rsisnza rumorosa alla mpraura assolua L è un induanza. Si uol drminar il alor quadraico mdio dlla corrn i ch scorr all inrno dll induor. Da un puno di isa
UMOE EMICO - SOLUZIONI Nl circuio in i. è una rsisnza rumorosa alla mpraura assolua L è un induanza. Si uol drminar il alor quadraico mdio dlla corrn i ch scorr all inrno dll induor. Da un puno di isa
Formule generali di carica e scarica dei condensatori in un circuito RC
 Formul gnrali di aria saria di ondnsaori in un iruio A ura di ugnio Amirano onnuo dll ariolo:. Inroduzion........ 2 2. aria saria di un ondnsaor..... 2 3. Formula gnral pr nsioni fiss..... 4 4. Formula
Formul gnrali di aria saria di ondnsaori in un iruio A ura di ugnio Amirano onnuo dll ariolo:. Inroduzion........ 2 2. aria saria di un ondnsaor..... 2 3. Formula gnral pr nsioni fiss..... 4 4. Formula
PROVA SCRITTA DI FONDAMENTI DI AUTOMATICA A.A. 2004/ gennaio 2005 TESTO E SOLUZIONE
 PROVA SCRITTA DI FONDAMENTI DI AUTOMATICA A.A. 24/25 2 gnnaio 25 TESTO E SOLUZIONE Esrcizio In rifrimnto allo schma a blocchi in figura. s3 r y 2 s2 s y K Domanda.. Dtrminar una ralizzazion in quazioni
PROVA SCRITTA DI FONDAMENTI DI AUTOMATICA A.A. 24/25 2 gnnaio 25 TESTO E SOLUZIONE Esrcizio In rifrimnto allo schma a blocchi in figura. s3 r y 2 s2 s y K Domanda.. Dtrminar una ralizzazion in quazioni
Analisi Matematica 3 (Fisica e Astronomia) Esercizi sulle equazioni differenziali ordinarie lineari
 Analisi Mamaica Fisica Asronomia Esrcizi sull quazioni diffrnziali ordinari linari Risolvr i sguni problmi sull quazioni diffrnziali linari a Risolvr x y y in du modi Vi sono soluzioni dfini su uo R? b
Analisi Mamaica Fisica Asronomia Esrcizi sull quazioni diffrnziali ordinari linari Risolvr i sguni problmi sull quazioni diffrnziali linari a Risolvr x y y in du modi Vi sono soluzioni dfini su uo R? b
I APPELLO (& II ESONERO) DI SEGNALI E SISTEMI 05 giugno 2017
 I PPELLO (& II ESONERO) DI SEGNLI E SISTEMI 05 giugno 017 Esrcizio 1. [+ punti] SOLO PER CHI SOSTIENE L PROV COMPLET Si considri il modllo ingrsso/uscita LTI causal dscritto dalla sgunt quazion diffrnzial:
I PPELLO (& II ESONERO) DI SEGNLI E SISTEMI 05 giugno 017 Esrcizio 1. [+ punti] SOLO PER CHI SOSTIENE L PROV COMPLET Si considri il modllo ingrsso/uscita LTI causal dscritto dalla sgunt quazion diffrnzial:
P.M. Azzoni, Strumenti e misure per l ingegneria meccanica - copyright 2006, Hoepli, Milano.
 Capiolo 4 No sull amplificaor oprazional 7 4. NOTE ULL AMPLIFICATORE OPERAZIONALE 4. LIMITI FIICI DELL AMPLIFICATORE OPERAZIONALE Il comporamno dll amplificaor a circuio chiuso, dscrio ni capioli prcdni,
Capiolo 4 No sull amplificaor oprazional 7 4. NOTE ULL AMPLIFICATORE OPERAZIONALE 4. LIMITI FIICI DELL AMPLIFICATORE OPERAZIONALE Il comporamno dll amplificaor a circuio chiuso, dscrio ni capioli prcdni,
17. Le soluzioni dell equazione di Schrödinger approfondimento
 7. soluzon dll quazon d Scrödngr approfondmno Gl sa ms Il gao d Scrödngr è l pù famoso sao mso dlla MQ. E una parclla un po spcal, prcé è un oggo macroscopco d cu s dscu l comporamno quansco. E anc una
7. soluzon dll quazon d Scrödngr approfondmno Gl sa ms Il gao d Scrödngr è l pù famoso sao mso dlla MQ. E una parclla un po spcal, prcé è un oggo macroscopco d cu s dscu l comporamno quansco. E anc una
Capitolo 8. La curva di Phillips, il tasso naturale di disoccupazione e l inflazione
 Capiolo 8. La curva di Phillips, il asso naural di disoccupazion l inflazion 1. Inflazion, inflazion asa disoccupazion Inflazion disoccupazion ngli Sai Unii, 1900-1960. = (1931 1939) Duran il priodo 1900-1960,
Capiolo 8. La curva di Phillips, il asso naural di disoccupazion l inflazion 1. Inflazion, inflazion asa disoccupazion Inflazion disoccupazion ngli Sai Unii, 1900-1960. = (1931 1939) Duran il priodo 1900-1960,
Lezione 5. Sistemi di trasmissione numerica. Gianluca Reali
 Lzion 5 Sismi di rasmission numrica Gianluca ali Ingrazion dll diaposiiv di S. Cacopardi Schma gnral di un sisma rasmissivo numrico Informazion digial Informazion analogica Campionam. Codr CM Quanizz.
Lzion 5 Sismi di rasmission numrica Gianluca ali Ingrazion dll diaposiiv di S. Cacopardi Schma gnral di un sisma rasmissivo numrico Informazion digial Informazion analogica Campionam. Codr CM Quanizz.
Sollecitazioni semplici La torsione
 Sollciazioni smlici La orsion Considrazioni inroduiv Un lmno sruural è soggo a sollciazion di orsion quando su di sso agiscono du momni uguali d oosi giacni su un iano rndicolar al suo ass longiudinal
Sollciazioni smlici La orsion Considrazioni inroduiv Un lmno sruural è soggo a sollciazion di orsion quando su di sso agiscono du momni uguali d oosi giacni su un iano rndicolar al suo ass longiudinal
Sistemi dinamici lineari del 1 ordine
 Appuni di onrolli Auomaici Simi dinamici linari dl ordin Inroduzion... ipoa al gradino uniario... ipoa alla rampa... Empio...3 Empio...4 INTODUZIONE Si dfinic ima (lmnar) dl primo ordin un ima (linar mpo-invarian)
Appuni di onrolli Auomaici Simi dinamici linari dl ordin Inroduzion... ipoa al gradino uniario... ipoa alla rampa... Empio...3 Empio...4 INTODUZIONE Si dfinic ima (lmnar) dl primo ordin un ima (linar mpo-invarian)
Il processo inverso della derivazione si chiama integrazione.
 Ingral Indinio l Anidrivaa Il prosso invrso dlla drivazion si hiama ingrazion. Noa la variazion isanana di una grandzza p.s. la vloià è nssario sapr om si ompora al grandzza isan pr isan p.s. la posizion.
Ingral Indinio l Anidrivaa Il prosso invrso dlla drivazion si hiama ingrazion. Noa la variazion isanana di una grandzza p.s. la vloià è nssario sapr om si ompora al grandzza isan pr isan p.s. la posizion.
E stato dimostrato sperimentalmente che la rapidità con cui una famiglia di nuclei radioattivi decade dipende da una legge di natura statistica.
 5. La lgg dl dcadino radioaivo Il nuro di nucli naurali arificiali oggi conosciui sono circa 700 di cui solo circa 70 sono qulli sabili. I nucli insabili ndono a rasforarsi sponanan in alr spci nuclari
5. La lgg dl dcadino radioaivo Il nuro di nucli naurali arificiali oggi conosciui sono circa 700 di cui solo circa 70 sono qulli sabili. I nucli insabili ndono a rasforarsi sponanan in alr spci nuclari
Esame di Teoria dei Segnali
 Esam di Toria di Sgnali April Esrcizio Daa una variabil alaoria con dnsià di probabilià com in igura, drminar la dnsià di probabiià la disribuzion di probabilià dlla variabil alaoria onua mdian la sgun
Esam di Toria di Sgnali April Esrcizio Daa una variabil alaoria con dnsià di probabilià com in igura, drminar la dnsià di probabiià la disribuzion di probabilià dlla variabil alaoria onua mdian la sgun
Progetto di cinghie trapezoidali
 Progo i cinghi rapzoiali L cinghi rapzoiali sono uilizza rqunmn pr la rasmission i ponza Vanaggi Basso coso Smplicià i insallazion Capacià i assorbir vibrazioni orsionali picchi i coppia Svanaggi Mancanza
Progo i cinghi rapzoiali L cinghi rapzoiali sono uilizza rqunmn pr la rasmission i ponza Vanaggi Basso coso Smplicià i insallazion Capacià i assorbir vibrazioni orsionali picchi i coppia Svanaggi Mancanza
Teoria dei Segnali. La Convoluzione (esercizi) parte prima
 Teoria dei Segnali La Convoluzione (esercizi) pare prima 1 Si ricorda che la convoluzione ra due segnali x() e y(), reali o complessi, indicaa simbolicamene come: C xy () = x() * y() è daa indifferenemene
Teoria dei Segnali La Convoluzione (esercizi) pare prima 1 Si ricorda che la convoluzione ra due segnali x() e y(), reali o complessi, indicaa simbolicamene come: C xy () = x() * y() è daa indifferenemene
LIMITI. 6. Esempi di riepilogo. 7. Limite per eccesso e per difetto 8. Limiti fondamentali. Nota bene 1. Nota bene 2
 LIITI Limit inito in un punto Limit ininito in un punto 3 Limit inito all ininito 4 Limit ininito all ininito 5 Limiti da dstra da sinistra Nota bn 6 Esmpi di ripilogo Nota bn 7 Limit pr ccsso pr ditto
LIITI Limit inito in un punto Limit ininito in un punto 3 Limit inito all ininito 4 Limit ininito all ininito 5 Limiti da dstra da sinistra Nota bn 6 Esmpi di ripilogo Nota bn 7 Limit pr ccsso pr ditto
La valutazione finanziaria
 STUDIO BERETTA DOTTTARELLI TTARELLI DOTTORI COMMERCIALISTI ASSOCIATI Srgio Bra La valuazion finanziaria Prmssa Il valor dl capial conomico vin simao considrando i flussi di cassa prodoi in fuuro dall imprsa
STUDIO BERETTA DOTTTARELLI TTARELLI DOTTORI COMMERCIALISTI ASSOCIATI Srgio Bra La valuazion finanziaria Prmssa Il valor dl capial conomico vin simao considrando i flussi di cassa prodoi in fuuro dall imprsa
Ingegneria dei Sistemi Elettrici_3c (ultima modifica 22/03/2010)
 Inggnria di Sistmi Elttrici_3c (ultima modifica /03/00) Enrgia Forz lttrostatich P F + + Il lavoro richisto nl vuoto pr portar una carica lntamnt, (prché possano ritnrsi trascurabili sia l nrgia cintica
Inggnria di Sistmi Elttrici_3c (ultima modifica /03/00) Enrgia Forz lttrostatich P F + + Il lavoro richisto nl vuoto pr portar una carica lntamnt, (prché possano ritnrsi trascurabili sia l nrgia cintica
LABORATORIO DI FISICA INGEGNERIA "La Sapienza"
 ABOATOO D FSA NGEGNEA "a Sapinza" Prof. A. Sciubba APPOSSMAZONE NEAE o sudio di un qualsiasi sisma fisico richid una prima fas di modllizzazion nlla qual si crca di schmaizzar il fnomno in sudio in rmini
ABOATOO D FSA NGEGNEA "a Sapinza" Prof. A. Sciubba APPOSSMAZONE NEAE o sudio di un qualsiasi sisma fisico richid una prima fas di modllizzazion nlla qual si crca di schmaizzar il fnomno in sudio in rmini
Errore standard di misurazione. Calcolare l intervallo del punteggio vero
 Error sandard di misurazion Calcolar l inrvallo dl punggio vro Problmi di prcision La prsnza noa dll rror di misura rnd incro il significao dl punggio onuo. L andibilià dl s ci informa di quano rror di
Error sandard di misurazion Calcolar l inrvallo dl punggio vro Problmi di prcision La prsnza noa dll rror di misura rnd incro il significao dl punggio onuo. L andibilià dl s ci informa di quano rror di
I sensori di spostamento
 I snsori di sposamno Mol grandzz (prssion, mpraura, forza, acclrazion, c.) vngono rasforma in uno sposamno, prima di ssr convri in un sgnal lrico. 1 I ponziomri i p p i o i p I ponziomri sono snsori di
I snsori di sposamno Mol grandzz (prssion, mpraura, forza, acclrazion, c.) vngono rasforma in uno sposamno, prima di ssr convri in un sgnal lrico. 1 I ponziomri i p p i o i p I ponziomri sono snsori di
ESERCIZI di TEORIA dei SEGNALI. La Correlazione
 ESERCIZI di TEORI dei SEGNLI La Correlazione Correlazione Si definisce correlazione (o correlazione incrociaa o cross-correlazione) ra i due segnali di energia, in generale complessi, x() e y() la quanià:
ESERCIZI di TEORI dei SEGNLI La Correlazione Correlazione Si definisce correlazione (o correlazione incrociaa o cross-correlazione) ra i due segnali di energia, in generale complessi, x() e y() la quanià:
ECONOMIA POLITICA II - ESERCITAZIONE 4 Parità dei tassi d interesse IS-LM in economia aperta
 CONOMIA POLITICA II - SRCITAZION 4 Parià i assi inrss IS-LM in conomia apra srcizio Suppon ch all sro il asso i inrss sia l 5.5% ch l aual asso i cambio nominal sia pari a.5. a) Nl caso in cui ci si aspi
CONOMIA POLITICA II - SRCITAZION 4 Parià i assi inrss IS-LM in conomia apra srcizio Suppon ch all sro il asso i inrss sia l 5.5% ch l aual asso i cambio nominal sia pari a.5. a) Nl caso in cui ci si aspi
Dispense del corso di Processi e Impianti Chimici. Corso di Laurea Specialistica in Chimica Industriale. Docente Guido Sassi
 Dispns dl corso di rocssi Ipiani hiici orso di Laura Spcialisica in hiica Indusrial Docn Guido Sassi Facolà di Scinz Maaich Fisich Naurali Univrsià di Torino aori 3 aori oogni isori con razioni coplss...
Dispns dl corso di rocssi Ipiani hiici orso di Laura Spcialisica in hiica Indusrial Docn Guido Sassi Facolà di Scinz Maaich Fisich Naurali Univrsià di Torino aori 3 aori oogni isori con razioni coplss...
Phillips (1958): Correlazione negativa stabile tra variazione percentuale dei salari monetari e il tasso di disoccupazione (Dati UK, )
 INFLAZIONE E DISOCCUAZIONE: INTRODUZIONE hillips (958): Corrlazion ngaiva sabil ra variazion prcnal di salari monari il asso di disoccpazion (Dai UK, 86-957) Samlson Solow (960): confrmano il rislao di
INFLAZIONE E DISOCCUAZIONE: INTRODUZIONE hillips (958): Corrlazion ngaiva sabil ra variazion prcnal di salari monari il asso di disoccpazion (Dai UK, 86-957) Samlson Solow (960): confrmano il rislao di
SISTEMI LINEARI TEMPO INVARIANTI. Fondamenti Segnali e Trasmissione
 SISTEMI LINEARI TEMPO INVARIANTI Fondameni Segnali e Trasmissione Definizione di sisema Sisema: Da un puno di visa fisico e un disposiivo ce modifica un segnale (), deo ingresso, generando il segnale y(),
SISTEMI LINEARI TEMPO INVARIANTI Fondameni Segnali e Trasmissione Definizione di sisema Sisema: Da un puno di visa fisico e un disposiivo ce modifica un segnale (), deo ingresso, generando il segnale y(),
Teoria dei segnali terza edizione
 eoria dei segnali Capiolo 4 Sisemi monodimensionali a empo coninuo SOLUZIONI DEGLI ESERCIZI Soluzione dell esercizio 4. Il segnale x () coniene le requenza = and = 7 / ( ) = 3.5 / quindi, disorsioni di
eoria dei segnali Capiolo 4 Sisemi monodimensionali a empo coninuo SOLUZIONI DEGLI ESERCIZI Soluzione dell esercizio 4. Il segnale x () coniene le requenza = and = 7 / ( ) = 3.5 / quindi, disorsioni di
Blanchard, Macroeconomia, Il Mulino 2009 Capitolo VIII. Il tasso naturale di disoccupazione e la curva di Phillips. Capitolo VIII.
 Capiolo VIII. Il asso naral di disoccpazion la crva di Phillips Capiolo VIII. Il asso naral di disoccpazion la crva di Phillips Capiolo VIII. Il asso naral di disoccpazion la crva di Phillips 1. Inflazion,
Capiolo VIII. Il asso naral di disoccpazion la crva di Phillips Capiolo VIII. Il asso naral di disoccpazion la crva di Phillips Capiolo VIII. Il asso naral di disoccpazion la crva di Phillips 1. Inflazion,
ELETTROMAGNETISMO APPLICATO ALL'INGEGNERIA ELETTRICA ED ENERGETICA_3B (ultima modifica 17/10/2017) Energia e Forze elettrostatiche R 12 F Q 2
 + ELETTOMAGNETISMO APPLICATO ALL'INGEGNEIA ELETTICA ED ENEGETICA_B (ultima modifica 7/0/07) Enrgia Forz lttrostatich F Una carica positiva posta in un punto P a distanza da una carica positiva fissa ch
+ ELETTOMAGNETISMO APPLICATO ALL'INGEGNEIA ELETTICA ED ENEGETICA_B (ultima modifica 7/0/07) Enrgia Forz lttrostatich F Una carica positiva posta in un punto P a distanza da una carica positiva fissa ch
LA TRASFORMATA DI FOURIER: PROPRIETA ED ESEMPI. 1 Fondamenti TLC
 LA TRASFORMATA DI FOURIER: PROPRIETA ED ESEMPI Fondameni TLC Propriea della () LINEARITA : la della combinazione lineare (somma pesaa) di due segnali e uguale alla combinazione lineare delle dei due segnali.
LA TRASFORMATA DI FOURIER: PROPRIETA ED ESEMPI Fondameni TLC Propriea della () LINEARITA : la della combinazione lineare (somma pesaa) di due segnali e uguale alla combinazione lineare delle dei due segnali.
Il circuito RLC serie
 l circui sri S si aggiung un indur al circui si in un circui sri. Sia l induanza cfficin di auinduzin dll indur Prviam a rislvr il circui ci a rvar la crrn ch l aravrsa quand è ccia da una srgn sinusidal.
l circui sri S si aggiung un indur al circui si in un circui sri. Sia l induanza cfficin di auinduzin dll indur Prviam a rislvr il circui ci a rvar la crrn ch l aravrsa quand è ccia da una srgn sinusidal.
I criteri di resistenza (o teorie della rottura) definiscono un legame tra lo stato tensionale e la sua pericolosità.
 6-0 6- I critri di rsistnza (o tori dlla rottura) dfiniscono un lgam tra lo stato tnsional la sua pricolosità. Ogni stato tnsional può ssr rapprsntato da una funzion scalar dll tnsioni principali ch può
6-0 6- I critri di rsistnza (o tori dlla rottura) dfiniscono un lgam tra lo stato tnsional la sua pricolosità. Ogni stato tnsional può ssr rapprsntato da una funzion scalar dll tnsioni principali ch può
Corso di Laurea in Ingegneria Elettronica ANALISI E TRASMISSIONE DEI SEGNALI
 Corso di Laura in Inggnria Elttronica NLISI E TRSMISSIONE DEI SEGNLI Soluzioni prova scritta dl /6/ Esrcizio Si considrino i du sgnali x ( t) = sinc( t / T) x( t) = sinc( t / T ) i) Si trovi l sprssion
Corso di Laura in Inggnria Elttronica NLISI E TRSMISSIONE DEI SEGNLI Soluzioni prova scritta dl /6/ Esrcizio Si considrino i du sgnali x ( t) = sinc( t / T) x( t) = sinc( t / T ) i) Si trovi l sprssion
Diagonalizzazione delle forme quadratiche
 Diagonaliaion dll form uadraich Illusrrmo ora du modi pr diagonaliar una forma uadraica (o uivalnmn una forma bilinar Modo dl complamno dl uadrao Quso modo consis in una succssion di passaggi algbrici
Diagonaliaion dll form uadraich Illusrrmo ora du modi pr diagonaliar una forma uadraica (o uivalnmn una forma bilinar Modo dl complamno dl uadrao Quso modo consis in una succssion di passaggi algbrici
Il candidato risolva uno dei due problemi e 5 dei 10 quesiti scelti nel questionario.
 LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE STRAORDINARIA Il candidao risolva uno di du problmi 5 di qusii scli nl qusionario. N. D Rosa, La prova di mamaica pr il lico PROBLEMA Sia daa una circonfrnza
LICEO SCIENTIFICO CORSO DI ORDINAMENTO SESSIONE STRAORDINARIA Il candidao risolva uno di du problmi 5 di qusii scli nl qusionario. N. D Rosa, La prova di mamaica pr il lico PROBLEMA Sia daa una circonfrnza
TRASFORMATA DI FOURIER DI DISTRIBUZIONI
 TRASFORMATA DI FOURIER DI DISTRIBUZIONI Tue le proprieà vise per la rasformaa di Fourier sono applicabili alle funzioni dello spazio S. Queso permee di rasferire le sesse proprieà alle disribuzioni di
TRASFORMATA DI FOURIER DI DISTRIBUZIONI Tue le proprieà vise per la rasformaa di Fourier sono applicabili alle funzioni dello spazio S. Queso permee di rasferire le sesse proprieà alle disribuzioni di
03. Le oscillazioni meccaniche. 03 d. Le onde stazionarie
 03. 03 d. L ond stazionari 03. Contnuti : la fnomnologia, il formalismo ral qullo complsso, il principio di sovrapposizion l analisi spttral. slid#3 Pitagora Samo 570-495 a.c. Jan Baptist Josph Fourir
03. 03 d. L ond stazionari 03. Contnuti : la fnomnologia, il formalismo ral qullo complsso, il principio di sovrapposizion l analisi spttral. slid#3 Pitagora Samo 570-495 a.c. Jan Baptist Josph Fourir
I criteri di resistenza (o teorie della rottura) definiscono un legame tra lo stato tensionale e la sua pericolosità.
 6-0 6- I critri di rsistnza (o tori dlla rottura) dfiniscono un lgam tra lo stato tnsional la sua pricolosità. Ogni stato tnsional può ssr rapprsntato da una funzion scalar dll tnsioni principali ch può
6-0 6- I critri di rsistnza (o tori dlla rottura) dfiniscono un lgam tra lo stato tnsional la sua pricolosità. Ogni stato tnsional può ssr rapprsntato da una funzion scalar dll tnsioni principali ch può
Sistema di comunicazione
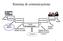 Sisma di comunicazion Sgnal rasduor rasmior rasmior rasduor Sgnal Sgnal lrico Sgnal lrico adaao al canal Canal di comunicazion rumor Sgnal lrico Sgnal lrico adaao al canal rumor Cosa dov sudiar Inroduzion
Sisma di comunicazion Sgnal rasduor rasmior rasmior rasduor Sgnal Sgnal lrico Sgnal lrico adaao al canal Canal di comunicazion rumor Sgnal lrico Sgnal lrico adaao al canal rumor Cosa dov sudiar Inroduzion
11 Funzioni iperboliche
 11 Funzioni iprbolich 11.1 L funzioni iprbolich: dfinizioni grafici L funzioni iprbolich sono particolari combinazioni di di. Hanno numros applicazioni nl campo dll inggnria si prsntano in modo dl tutto
11 Funzioni iprbolich 11.1 L funzioni iprbolich: dfinizioni grafici L funzioni iprbolich sono particolari combinazioni di di. Hanno numros applicazioni nl campo dll inggnria si prsntano in modo dl tutto
SOLUZIONE PROBLEMA 1 SOLUZIONE PROBLEMA 1 1
 SOLUZIONE PROBLEMA 1 1 SOLUZIONE PROBLEMA 1 1. Studiamo la funzion q ( = at, ssndo a b costanti rali con a >. Il dominio dlla funzion è tutto R la funzion è ovunqu continua. Il grafico dlla funzion non
SOLUZIONE PROBLEMA 1 1 SOLUZIONE PROBLEMA 1 1. Studiamo la funzion q ( = at, ssndo a b costanti rali con a >. Il dominio dlla funzion è tutto R la funzion è ovunqu continua. Il grafico dlla funzion non
Lezione 6. Stabilità e matrice A nei sistemi LTI. F.Previdi - Fondamenti di Automatica - Lez. 6
 Lzion 6. Sabilià maric A ni imi LTI F.Prvidi - Fondamni di Auomaica - Lz. 6 Schma dlla lzion A. Sudio dlla maric pr. Tormi ulla abilià di imi LTI. Rgion di ainoica abilià. Criri di abilià baai ulla maric
Lzion 6. Sabilià maric A ni imi LTI F.Prvidi - Fondamni di Auomaica - Lz. 6 Schma dlla lzion A. Sudio dlla maric pr. Tormi ulla abilià di imi LTI. Rgion di ainoica abilià. Criri di abilià baai ulla maric
TIPI TIPI DI DI DECADIMENTO RADIOATTIVO --ALFA
 TIPI TIPI DI DI DECDIMENTO RDIOTTIVO --LF LF Dcadimnto alfa: il nuclo instabil mtt una particlla alfa (), ch è composta da du protoni du nutroni (un nuclo di 4 H), quindi una particlla carica positivamnt.
TIPI TIPI DI DI DECDIMENTO RDIOTTIVO --LF LF Dcadimnto alfa: il nuclo instabil mtt una particlla alfa (), ch è composta da du protoni du nutroni (un nuclo di 4 H), quindi una particlla carica positivamnt.
Equazioni differenziali ordinarie
 4/11/015 Equazioni diffrnziali ordinari Equazioni diffrnziali ordinari Equazioni diffrnziali dl 1 ordin a variabili sparabili, Equazioni diffrnziali linari dl 1 ordin Equazioni diffrnziali dl 1 ordin non
4/11/015 Equazioni diffrnziali ordinari Equazioni diffrnziali ordinari Equazioni diffrnziali dl 1 ordin a variabili sparabili, Equazioni diffrnziali linari dl 1 ordin Equazioni diffrnziali dl 1 ordin non
lim β α e detto infinitesimo una qualsiasi quantita tendente a zero quando una dati due infinitesimi α e β non esiste
 Infinitsimi dtto infinitsimo una qualsiasi quantita tndnt a zro quando una opportuna variabil tnd ad assumr un dtrminato valor dati du infinitsimi α β α β non sono paragonabili tra loro s il lim β α non
Infinitsimi dtto infinitsimo una qualsiasi quantita tndnt a zro quando una opportuna variabil tnd ad assumr un dtrminato valor dati du infinitsimi α β α β non sono paragonabili tra loro s il lim β α non
SISTEMI LINEARI TEMPO INVARIANTI
 SISTEMI LINEARI TEMPO INVARIANTI Fondameni di Segnali e Trasmissione Sisema: Definizione di Sisema Da un puno di visa fisico e un disposiivo ce modifica un segnale, deo ingresso, generando il segnale,
SISTEMI LINEARI TEMPO INVARIANTI Fondameni di Segnali e Trasmissione Sisema: Definizione di Sisema Da un puno di visa fisico e un disposiivo ce modifica un segnale, deo ingresso, generando il segnale,
Esercizio 1 Approssimare il seguente integrale con la formula di Gauss a tre nodi (n=2)
 Esrcizi su intgrazion numrica sistmi linari Approssimar il sgunt intgral con la formula di Gauss a tr nodi (n) x cos xdx Si considri il sistma Applicando il mtodo di Eulro implicito con h π /( ω), quanto
Esrcizi su intgrazion numrica sistmi linari Approssimar il sgunt intgral con la formula di Gauss a tr nodi (n) x cos xdx Si considri il sistma Applicando il mtodo di Eulro implicito con h π /( ω), quanto
PRIMI ESERCIZI SULLE FUNZIONI DERIVABILI. (1) Applicando la definizione di derivata, calcolare la derivata in x = 0 delle funzioni:
 PRIMI ESERCIZI SULLE FUNZIONI DERIVABILI VALENTINA CASARINO Esrcizi pr il corso di Analisi Matmatica (Inggnria Gstional, dll Innovazion dl Prodotto, Mccanica Mccatronica, Univrsità dgli studi di Padova)
PRIMI ESERCIZI SULLE FUNZIONI DERIVABILI VALENTINA CASARINO Esrcizi pr il corso di Analisi Matmatica (Inggnria Gstional, dll Innovazion dl Prodotto, Mccanica Mccatronica, Univrsità dgli studi di Padova)
TRASFORMATA DI FOURIER. Trasformata di Fourier: definizione
 Si può arrivar allo sviluppo i sri di Fourir ach pr sgali apriodici? RASFORMAA DI FOURIER rasormaa di Fourir: diizio Dao u sgal apriodico, sso può ssr scrio mdia la ormula dov d d L du quazioi si chiamao
Si può arrivar allo sviluppo i sri di Fourir ach pr sgali apriodici? RASFORMAA DI FOURIER rasormaa di Fourir: diizio Dao u sgal apriodico, sso può ssr scrio mdia la ormula dov d d L du quazioi si chiamao
