4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale
|
|
|
- Gina Marchi
- 8 anni fa
- Visualizzazioni
Transcript
1 4 Quarta lezione: Spazi di Banach e funzionali lineari. Spazio duale Spazi Metrici Ricordiamo che uno spazio metrico è una coppia (X, d) dove X è un insieme e d : X X [0, + [ è una funzione, detta metrica, che gode delle seguenti proprietà 1. d(x, y) = 0 x = y; 2. d(x, y) = d(y, x) x, y X; 3. d(x, y) d(x, z) + d(z, y) x, y, z X (disuguaglianza triangolare). Esempio 4.1 Su ogni insieme X la funzione { 0 se x = y d(x, y) = 1 se x y è una metrica (detta metrica banale). Esempio 4.2 Su R n la funzione d(x, y) = n x i y i 2 è una metrica (detta metrica euclidea). Esempio 4.3 Su R n le funzioni d 1 (x, y) = sono metriche. i=1 n x i y i d 2 (x, y) = max{ x i y i : i = 1,..., n} i=1 In uno spazio metrico (X, d) l insieme S(x 0, r) = {x X : d(x, x 0 ) = r}, x 0 X, r > 0 è la superficie sferica (o sfera) di raggio r, mentre l insieme B(x 0, r) = {x X : d(x, x 0 ) < r}, x 0 X, r > 0 è la palla aperta di centro x 0 e raggio r. In uno spazio metrico le famiglie {B(x, r) : x X, r > 0}, {B(x, r) : x X, r > 0, r Q}, {B(x, 1/n) : x X, n N} 21
2 sono sistemi fondamentali di intorni e pertanto ne individuano la topologia. Ciò implica in particolare che ogni spazio metrico soddisfa al primo assioma di numerabilità. Ad una metrica è quindi sempre associata una topologia, ma non viceversa, cioè esistono topologie che non sono descrivibili da una metrica, cioè non sono metrizzabili. Inoltre metriche diverse possono individuare la stessa topologia, e in tal caso si dicono topologicamente equivalenti. Per esempio le metriche d 1 e d 2 dell Esempio 4.3 inducono entrambe la topologia euclidea, cioè definiscono gli stessi insiemi aperti. Per dimostrare che due metriche d 1 e d 2 sono equivalenti basta mostrare che per ogni palla B(x, ε 1 ) di (X, d 1 ) esiste una palla B(x, ε 2 ) di (X, d 2 ) contenuta in B(x, ε 1 ) e viceversa. Esercizio 4.4 Disegnare le palle di centro 0 e raggio 1 in (R 2, d 1 ) e in (R 2, d 2 ). Esempio 4.5 Nella metrica banale dell esempio 4.1 si ha B(x 0, r) = { {x0 } se r 1 X se r = 1 Esercizio 4.6 Scrivere le definizioni di successione convergente, di funzione continua e sequenzialmente continua in uno spazio metrico (X, d) e ricordare che, poichè gli spazi metrici soddisfano al primo assioma di numerabilità allora la continuità equivale alla continuità sequenziale. Spazi normati Ricordiamo che uno spazio normato (su R) è una coppia (X, ) dove X è uno spazio vettoriale su R e : X [0, + [ è una funzione, detta normaa, che gode delle seguenti proprietà 1. x = 0 x = 0; 2. λx = λ x λ R, x X; 3. x + y x + y x, y X. Una norma su X induce sempre una metrica d(x, y) = x y e pertanto definisce una topologia. La norma di un punto x rappresenta dunque la sua distanza dall origine mentre la norma di un vettore rappresenta la sua lunghezza. Esempio 4.7 In R n la norma x = ( n i=1 22 x 2 ) 1/2 i
3 induce la metrica euclidea ed è pertanto detta norma euclidea. inducono la stessa topologia (ma non la stessa metrica) sono n x i e max{ x i : i = 1,..., n}. i=1 Esempio 4.8 Sia Ω un sottoinsieme aperto di R n. La funzione f 1 = f(x) dx Ω Altre norme che è una norma nello spazio delle funzioni sommabili L 1 (Ω) (è importante, qui, affinchè valga la prima proprietà della norma, identificare funzioni che differiscono su insiemi di misura nulla). Questa è una norma anche nello spazio delle funzioni continue a supporto compatto C c (Ω). La funzione f = sup f(x) x Ω è una norma nello spazio B(Ω) delle funzioni limitate su Ω, ma non lo è in L 1 (Ω). è una norma in C c (Ω), o anche in C k c (Ω), mentre un altra norma in C 1 c (Ω) è la seguente f 1, = f + f. Definizione 4.9 Due norme 1 e 2 sullo stesso spazio X si dicono equivalenti se inducono la stessa topologia. È subito visto che due norme sono equivalenti se e solo se generano metriche equivalenti, cioè, dette 1 e 2 le due norme, se e solo se esistono due costanti positive c e C tali che c x 1 x 2 C x 1 per ogni x X. Esercizio 4.10 Mostrare che nello spazio C 1 0 ([0, 1]) delle funzioni C1 ([0, 1]) tali che u(0) = u(1) = 0, le norme u e u 1, = u + u sono equivalenti. Poichè u u + u = u 1, basta mostrare che esiste una costante c > 0 tale che (infatti in tal caso si avrebbe e pertanto u(x) x 0 c c u u 1+c u 1, u ). Per provarlo basta osservare che u(x) = u (t) dt x u (t) dt sup t [0,1] La tesi segue dunque passando al sup sugli x [0, 1]. condizione u(1) = 0 non è stata utilizzata. u (t) dt = u. Concludiamo osservando che la 23
4 Funzionali lineari. Spazio duale Osserviamo che la convergenza debole introdotta nella lezione precedente è la convergenza più debole che rende continui tutti i prodotti scalari con funzioni di L 2. Per il teorema di rappresentazione di Riesz, d altra parte, i prodotti scalari sono esattamente tutte e sole le funzioni lineari e fortemente continue L 2 R. Possiamo quindi dire che la convergenza debole è la più debole tra le convergenze che rendono continue tutte le applicazioni lineari e fortemente continue L 2 R. La trasposizione topologica di questo concetto conduce alla nozione di topologia debole. Poiché le funzioni lineari e continue giocano un ruolo essenziale ricordiamo alcune cose fondamentali su di esse. Quando il dominio X è R n vale la seguente proposizione. Proposizione 4.11 Una funzione f : R n R è lineare se e solo se è un prodotto scalare, cioè se e solo se esiste a R n tale che f(x) = a, x per ogni x R n. Dimostrazione Se f(x) = a, x, allora è ovviamente lineare. Viceversa, supponiamo che f sia lineare e non identicamente nulla (altrimenti basta prendere a = 0). In tal caso ker f = {x R n : f(x) = 0} = R n. Sia dunque x 0 ker f tale che f(x 0 ) 0. Consideriamo il vettore x f(x) f(x 0 ) x 0 e osserviamo che, per la linearità Dunque x f(x) f(x 0 ) x 0 ker f e quindi f(x f(x) f(x 0 ) x 0) = 0 x f(x) f(x 0 ) x 0, x 0 = 0 da cui, sviluppando il prodotto scalare a primo membro, si ottiene f(x) = f(x 0) x 0 2 x 0, x. Come conseguenza in R n tutte le applicazioni lineari sono continue, perché tutte le lineari sono prodotti scalari e se f(x) = a, x allora, per Cauchy-Schwarz, si ha f(x) a x e quindi f è continua (lipschitziana) per la topologia della norma. A differenza di R n, in spazi vettoriali di dimensione infinita esistono sempre funzioni lineari f : X R non continue. Diamo subito un esempio. Esempio 4.12 Consideriamo lo spazio delle funzioni continue C([ 1, 1]) con la morma u 1 = 1 1 u dt. La funzione δ 0 : C([ 1, 1]) R ϕ δ 0 (ϕ) = ϕ(0) 24
5 è lineare (ovviamente) ma non è continua. Si consideri infatti la successione di funzioni ϕ n C([ 1, 1]) tale che ϕ n (0) = 1 e ϕ(x) = 0 per ogni x 1/n e prolungata linearmente su [ 1, 1]. Si ha ϕ 1 = 1/n 1/n ϕ(x) dx = 1/n 0 per n. Si dunque ϕ n 0 in morma. Ora, se δ 0 fosse continua allora si avrebbe δ 0 (ϕ n ) δ 0 (0) ma questo non è possibile perché δ 0 (ϕ n ) = 1 per ogni n mentre δ 0 (0) = 0. Per la disuguaglianza di Schwarz d altra parte i prodotti scalari sono continui. Abbiamo già ricordato, infatti, che se il dominio X è uno spazio di Hilbert allora vale il seguente teorema di rappresentazione di Riesz, la cui dimostrazione procede essenzialmente come quella in cui X = R n. Teorema 4.13 Sia X uno spazio di Hilbert. f : X R è lineare e continua se e solo se è un prodotto scalare, cioè se e solo se esiste a X tale che f(x) = a, x per ogni x X. Osserviamo che se X = L 2 allora il teorema di Riesz dice che ogni funzionale F : L 2 R lineare e fortemente continuo ammette la rappresentazione integrale F (u) = g(x)u(x) dx dove g è un opportuna funzione di L 2 e si tratta quindi di un teorema di rappresentazione integrale. Se X è solamente uno spazio vettoriale normato, ma in cui la norma non proviene da un prodotto scalare, vale il risultato seguente. Proposizione 4.14 Sia (X, ) uno spazio normato e f : X R, una funzione lineare. f è continua se e solo se esiste una costante L > 0 tale che (4.1) f(x) L x per ogni x X. Dimostrazione L unica parte non banale è. Supponiamo dunque f continua. In particolare f è continua in 0, cioè ε > 0 δ ε > 0 : x < δ f(x) < ε. In particolare, in corrispondenza ad ε = 1 esiste δ > 0 tale che x < δ f(x) < 1. Sia x qualunque, diverso da 0. Preso x = δx 2 x si ha x = δ 2 < δ e pertanto f(x) < 1. Ma d altra parte f(x) = δf(x ) 2 x e perciò f(x ) x < 2 δ = L. 25
6 Osservazione 4.15 Anche negli spazi normati le funzioni lineari e continue sono lipschitziane. Dato uno spazio normato (X, ), un altro importante esempio di spazio normato che si può costruire a partire da X è il cosiddetto spazio duale di X, X, costituito da tutte le funzioni lineari e continue ϕ : X R, con le usuali operazioni di somma di funzioni e di prodotto di una funzione con un numero reale. Una norma in questo spazio è data dalla più piccole costante per cui vale la (4.1), cioè (4.2) ϕ X = sup{ ϕ(x) : x X, x 0} x = sup{ ϕ(x) : x X, x 1} = sup{ ϕ(x) : x X, x = 1}, dove l ultima uguaglianza segue osservando che per la linearità ϕ(0) = 0 e 0 < x 1 ϕ(x) ϕ(x/ x ). Con questa definizione e usando la notazione ϕ, x := ϕ(x) si può quindi scrivere ϕ, x ϕ x. Teorema di Hahn-Banach Negli spazi normati ogni funzione lineare e continua definita su un sottospazio si può estendere ad una funzione lineare e continua su tutto lo spazio senza incrementarne la norma. Teorema 4.16 Sia X uno spazio vettoriale normato e M un sottospazio di X (cioè un sottoinsieme di X chiuso rispetto alla somma e al prodotto per uno scalare). Sia f : M R una funzione lineare e continua. Esiste una funzione lineare e continua f : X R tale che 1. f(x) = f(x) x M; 2. f = f. La dimostrazione di questo teorema (che non faremo) fa uso dell Assioma della Scelta. Una sua importante conseguenza è la seguente formula duale della (4.2) ϕ, x x = max{ : ϕ X } ϕ = max{ ϕ, x : ϕ X, ϕ = 1} x X. Infatti, se x = 0 la formula è vera. Supponiamo x 0. Siccome ϕ, x ϕ x allora ϕ, x sup{ : ϕ X } x. ϕ 26
7 La formula sarà dunque provata se dimostreremo che esiste ϕ X tale che (4.3) ϕ = x e ϕ, x = x 2. A tal scopo sia M = {tx : t R} il sottospazio di X generato da x. Su questo sottospazio consideriamo la funzione lineare e continua ϕ(tx) = t x 2 ; questa funzione per il momento è definita solo su M e soddisfa le (4.3). Ma per il Teorema di Hahn-Banach essa si può prolungare su tutto X ad una ϕ che soddisfa ancora le condizioni (4.3). Spazi metrici completi Sia (X, d) uno spazio metrico. Definizione 4.17 Una successione (x n ) di elementi di X si dice di Cauchy se per ogni ε > 0 esiste n ε N tale che d(x n, x m ) < ε per ogni n, m > n ε. Si dimostra facilmente che ogni successione convergente è anche di Cauchy. Il viceversa non è vero, in generale. Per esempio è falso in Q come sottospazio topologico di R con la metrica euclidea. Quello che comunque si riesce a dimostrare in generale è che ogni successione di Cauchy è limitata (procedere come in Analisi 1). Definizione 4.18 Uno spazio metrico X si dice completo se ogni successione di Cauchy è convergente ad un punto di X. Esempio 4.19 R con la metrica euclidea è completo, mentre Q non lo è. Gli spazi normati che sono completi rispetto alla metrica indotta dalla norma si dicono spazi di Banach. Esempio 4.20 ( L 1 (Ω), 1 ) è uno spazio di Banach. Se Ω è compatto ( C(Ω), ) e ( C 1 (Ω), 1, ) sono spazi di Banach. Esercizio 4.21 Mostrare che 1. ( C 1 ([0, 1]), ) è normato ma non è completo. 2. C c (Ω) con la norma 1 o con la norma non è completo. Proposizione 4.22 Sia X uno spazio vettoriale normato. 7 X con la norma duale è di Banach. 7 Anche non completo. 27
8 Dimostrazione Dimostriamo che X è completo. Sia dunque (T n ) una successione di Cauchy in X, cioè per ogni ε > 0 esiste n ε N tale che T m T n < ε per ogni m, n > n ε. Per definizione di norma duale allora per ogni x X con x 1 si ha anche T m x T n x < ε. Ne consegue che per tali x la successione (T n x) n è di Cauchy in R e quindi è convergente (R è completo). Detto T x il suo limite è banale verificare che T è lineare. Basta ora provare che T n T 0, perché da ciò segue anche che T è continua. Infatti, essendo allora T x T x T n x + T n x T T T n + T n e poichè la successione ( T n ) è limitata (essendo di Cauchy) allora si ha che T <, cioè T è continua. Proviamo dunque che T n T 0. Avendosi T x T n x T x T m x + T m x T n x T x T m x + T m T n x, e poiché il primo membro è indipendente da m, allora passando al limite per m si ottiene che T T n < ε n > n ε e quindi la tesi. Completamento di uno spazio metrico Se uno spazio metrico non è completo, come ad esempio (Q, ), lo si può completare immergendolo isometricamente in uno spazio completo, come ad esempio (R, ). L esistenza e l unicità (a meno di isometrie) del completamento è garantita dal Teorema del Completamento (cfr. per esempio [3], pag. 182). Riferimenti bibliografici [1] H. Brezis, Analyse fonctionnelle. Théorie et applications., Masson, Paris, [2] G. Buttazzo, Semicontinuity, relaxation and integral representation in the calculus of variations, Pitman Res. Notes Math. Ser., vol. 207, Longman, Harlow, [3] V. Checcucci, A. Tognoli, and E. Vesentini, Lezioni di topologia generale, Feltrinelli, Milano, [4] G. Dal Maso, An introduction to Γ-convergence, Birkhäuser, Boston, [5] E. Giusti, Analisi matematica 2, Boringhieri. [6] W. Rudin, Analisi reale e complessa, Boringhieri. 28
SPAZI METRICI. Uno spazio metrico X con metrica d si indica con il simbolo (X, d). METRICI 1
 SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
SPAZI METRICI Nel piano R 2 o nello spazio R 3 la distanza fra due punti è la lunghezza, o norma euclidea, del vettore differenza di questi due punti. Se p = (x, y, z) è un vettore in coordinate ortonormali,
Per lo svolgimento del corso risulta particolarmente utile considerare l insieme
 1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
1. L insieme R. Per lo svolgimento del corso risulta particolarmente utile considerare l insieme R = R {, + }, detto anche retta reale estesa, che si ottiene aggiungendo all insieme dei numeri reali R
19. Inclusioni tra spazi L p.
 19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
19. Inclusioni tra spazi L p. Nel n. 15.1 abbiamo provato (Teorema 15.1.1) che, se la misura µ è finita, allora tra i corispondenti spazi L p (µ) si hanno le seguenti inclusioni: ( ) p, r ]0, + [ : p
Esistenza di funzioni continue non differenziabili in alcun punto
 UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
UNIVERSITÀ DEGLI STUDI DI CAGLIARI FACOLTÀ DI SCIENZE MATEMATICHE, FISICHE E NATURALI CORSO DI LAUREA IN MATEMATICA Esistenza di funzioni continue non differenziabili in alcun punto Relatore Prof. Andrea
6 Sesta lezione: Compattezza sequenziale nelle topologie deboli. Dualità e convergenze deboli negli spazi L p.
 6 Sesta lezione: Compattezza sequenziale nelle topologie deboli. Dualità e convergenze deboli negli spazi L p. Metrizzabilità delle topologie deboli Anche se le topologie deboli non sono mai metrizzabili,
6 Sesta lezione: Compattezza sequenziale nelle topologie deboli. Dualità e convergenze deboli negli spazi L p. Metrizzabilità delle topologie deboli Anche se le topologie deboli non sono mai metrizzabili,
A i è un aperto in E. i=1
 Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
Proposizione 1. A è aperto se e solo se A c è chiuso. Dimostrazione. = : se x o A c, allora x o A = A o e quindi esiste r > 0 tale che B(x o, r) A; allora x o non può essere di accumulazione per A c. Dunque
10. Insiemi non misurabili secondo Lebesgue.
 10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
10. Insiemi non misurabili secondo Lebesgue. Lo scopo principale di questo capitolo è quello di far vedere che esistono sottoinsiemi di R h che non sono misurabili secondo Lebesgue. La costruzione di insiemi
3 Terza lezione. Il metodo diretto del Calcolo delle Variazioni
 3 Terza lezione. Il metodo diretto del Calcolo delle Variazioni Coercività Definizione 3.1 Una funzione F : X R si dice coerciva (risp. sequenzialmente coerciva) se per ogni t R esiste un sottoinsieme
3 Terza lezione. Il metodo diretto del Calcolo delle Variazioni Coercività Definizione 3.1 Una funzione F : X R si dice coerciva (risp. sequenzialmente coerciva) se per ogni t R esiste un sottoinsieme
Ottimizazione vincolata
 Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
Ottimizazione vincolata Ricordiamo alcuni risultati provati nella scheda sulla Teoria di Dini per una funzione F : R N+M R M di classe C 1 con (x 0, y 0 ) F 1 (a), a = (a 1,, a M ), punto in cui vale l
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI
 CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
CAPITOLO 16 SUCCESSIONI E SERIE DI FUNZIONI Abbiamo studiato successioni e serie numeriche, ora vogliamo studiare successioni e serie di funzioni. Dato un insieme A R, chiamiamo successione di funzioni
LEZIONE 31. B i : R n R. R m,n, x = (x 1,..., x n ). Allora sappiamo che è definita. j=1. a i,j x j.
 LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
LEZIONE 31 31.1. Domini di funzioni di più variabili. Sia ora U R n e consideriamo una funzione f: U R m. Una tale funzione associa a x = (x 1,..., x n ) U un elemento f(x 1,..., x n ) R m : tale elemento
Spazi lineari - PARTE II - Felice Iavernaro. Dipartimento di Matematica Università di Bari. 9 e 16 Marzo 2007
 Spazi lineari - PARTE II - Felice Iavernaro Dipartimento di Matematica Università di Bari 9 e 16 Marzo 2007 Felice Iavernaro (Univ. Bari) Spazi lineari 9-16/03/2007 1 / 17 Condizionamento dei sistemi lineari
Spazi lineari - PARTE II - Felice Iavernaro Dipartimento di Matematica Università di Bari 9 e 16 Marzo 2007 Felice Iavernaro (Univ. Bari) Spazi lineari 9-16/03/2007 1 / 17 Condizionamento dei sistemi lineari
Sulle funzioni di W 1,p (Ω) a traccia nulla
 Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
Sulle funzioni di W 1,p () a traccia nulla Sia u W 1,p (R n ) e supponiamo che il supp u, essendo un aperto di R n. Possiamo approssimare u con una successione di funzioni C il cui supporto è contenuto
Applicazioni lineari
 Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
Applicazioni lineari Esempi di applicazioni lineari Definizione. Se V e W sono spazi vettoriali, una applicazione lineare è una funzione f: V W tale che, per ogni v, w V e per ogni a, b R si abbia f(av
x 1 + x 2 3x 4 = 0 x1 + x 2 + x 3 = 0 x 1 + x 2 3x 4 = 0.
 Problema. Sia W il sottospazio dello spazio vettoriale R 4 dato da tutte le soluzioni dell equazione x + x 2 + x = 0. (a. Sia U R 4 il sottospazio dato da tutte le soluzioni dell equazione Si determini
Problema. Sia W il sottospazio dello spazio vettoriale R 4 dato da tutte le soluzioni dell equazione x + x 2 + x = 0. (a. Sia U R 4 il sottospazio dato da tutte le soluzioni dell equazione Si determini
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 2011/2012
 Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
Analisi Matematica 2 per Matematica Esempi di compiti, primo semestre 211/212 Ricordare: una funzione lipschitziana tra spazi metrici manda insiemi limitati in insiemi limitati; se il dominio di una funzione
1 Applicazioni Lineari tra Spazi Vettoriali
 1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
1 Applicazioni Lineari tra Spazi Vettoriali Definizione 1 (Applicazioni lineari) Si chiama applicazione lineare una applicazione tra uno spazio vettoriale ed uno spazio vettoriale sul campo tale che "!$%!
1 Serie di Taylor di una funzione
 Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
Analisi Matematica 2 CORSO DI STUDI IN SMID CORSO DI ANALISI MATEMATICA 2 CAPITOLO 7 SERIE E POLINOMI DI TAYLOR Serie di Taylor di una funzione. Definizione di serie di Taylor Sia f(x) una funzione definita
1.1. Spazi metrici completi
 SPAZI METRICI: COMPLETEZZA E COMPATTEZZA Note informali dalle lezioni 1.1. Spazi metrici completi La nozione di convergenza di successioni è centrale nello studio degli spazi metrici. In particolare è
SPAZI METRICI: COMPLETEZZA E COMPATTEZZA Note informali dalle lezioni 1.1. Spazi metrici completi La nozione di convergenza di successioni è centrale nello studio degli spazi metrici. In particolare è
Sulla monotonia delle funzioni reali di una variabile reale
 Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Liceo G. B. Vico - Napoli Sulla monotonia delle funzioni reali di una variabile reale Prof. Giuseppe Caputo Premetto due teoremi come prerequisiti necessari per la comprensione di quanto verrà esposto
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8. Cognome:... Nome:... Matricola:...
 Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Prova parziale di Geometria e Topologia I - 5 mag 2008 (U1-03, 13:30 16:30) 1/8 Cognome:................ Nome:................ Matricola:................ (Dare una dimostrazione esauriente di tutte le
Esercizi su lineare indipendenza e generatori
 Esercizi su lineare indipendenza e generatori Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V uno spazio vettoriale su K Cose da ricordare Definizione Dei vettori v,,v
Esercizi su lineare indipendenza e generatori Per tutto il seguito, se non specificato esplicitamente K indicherà un campo e V uno spazio vettoriale su K Cose da ricordare Definizione Dei vettori v,,v
RICHIAMI SULLE MATRICI. Una matrice di m righe e n colonne è rappresentata come
 RICHIAMI SULLE MATRICI Una matrice di m righe e n colonne è rappresentata come A = a 11 a 12... a 1n a 21 a 22... a 2n............ a m1 a m2... a mn dove m ed n sono le dimensioni di A. La matrice A può
RICHIAMI SULLE MATRICI Una matrice di m righe e n colonne è rappresentata come A = a 11 a 12... a 1n a 21 a 22... a 2n............ a m1 a m2... a mn dove m ed n sono le dimensioni di A. La matrice A può
LEZIONE 16. Proposizione 16.1.2. Siano V e W spazi vettoriali su k = R, C. Se f: V W
 LEZIONE 16 16.1. Applicazioni lineari iniettive e suriettive. Ricordo le seguenti due definizioni valide per applicazioni di qualsiasi tipo ϕ: X Y fra due insiemi. L applicazione ϕ si dice iniettiva se
LEZIONE 16 16.1. Applicazioni lineari iniettive e suriettive. Ricordo le seguenti due definizioni valide per applicazioni di qualsiasi tipo ϕ: X Y fra due insiemi. L applicazione ϕ si dice iniettiva se
LEZIONE 17. B : kn k m.
 LEZIONE 17 17.1. Isomorfismi tra spazi vettoriali finitamente generati. Applichiamo quanto visto nella lezione precedente ad isomorfismi fra spazi vettoriali di dimensione finita. Proposizione 17.1.1.
LEZIONE 17 17.1. Isomorfismi tra spazi vettoriali finitamente generati. Applichiamo quanto visto nella lezione precedente ad isomorfismi fra spazi vettoriali di dimensione finita. Proposizione 17.1.1.
Equazioni differenziali ordinarie
 Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
Equazioni differenziali ordinarie Denis Nardin January 2, 2010 1 Equazioni differenziali In questa sezione considereremo le proprietà delle soluzioni del problema di Cauchy. Da adesso in poi (PC) indicherà
LE FUNZIONI A DUE VARIABILI
 Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
Capitolo I LE FUNZIONI A DUE VARIABILI In questo primo capitolo introduciamo alcune definizioni di base delle funzioni reali a due variabili reali. Nel seguito R denoterà l insieme dei numeri reali mentre
LEZIONE 23. Esempio 23.1.3. Si consideri la matrice (si veda l Esempio 22.2.5) A = 1 2 2 3 3 0
 LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
LEZIONE 23 231 Diagonalizzazione di matrici Abbiamo visto nella precedente lezione che, in generale, non è immediato che, data una matrice A k n,n con k = R, C, esista sempre una base costituita da suoi
EQUAZIONI DIFFERENZIALI. 1. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x 2 log t (d) x = e t x log x (e) y = y2 5y+6
 EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
EQUAZIONI DIFFERENZIALI.. Trovare tutte le soluzioni delle equazioni differenziali: (a) x = x log t (d) x = e t x log x (e) y = y 5y+6 (f) y = ty +t t +y (g) y = y (h) xy = y (i) y y y = 0 (j) x = x (k)
Parte 6. Applicazioni lineari
 Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
Parte 6 Applicazioni lineari A Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Applicazioni fra insiemi, 2 Applicazioni lineari tra spazi vettoriali, 2 3 Applicazioni lineari da R n a R
Funzioni in più variabili
 Funzioni in più variabili Corso di Analisi 1 di Andrea Centomo 27 gennaio 2011 Indichiamo con R n, n 1, l insieme delle n-uple ordinate di numeri reali R n4{(x 1, x 2,,x n ), x i R, i =1,,n}. Dato X R
Funzioni in più variabili Corso di Analisi 1 di Andrea Centomo 27 gennaio 2011 Indichiamo con R n, n 1, l insieme delle n-uple ordinate di numeri reali R n4{(x 1, x 2,,x n ), x i R, i =1,,n}. Dato X R
Matematica generale CTF
 Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Successioni numeriche 19 agosto 2015 Definizione di successione Monotonìa e limitatezza Forme indeterminate Successioni infinitesime Comportamento asintotico Criterio del rapporto per le successioni Definizione
Lezione 6. Divisibilità e divisori. Teorema di divisione euclidea. Algoritmo delle divisioni successive.
 Lezione 6 Prerequisiti: L'insieme dei numeri interi. Lezione 5. Divisibilità e divisori. Teorema di divisione euclidea. Algoritmo delle divisioni successive. Questa è la prima lezione dedicata all'anello
Lezione 6 Prerequisiti: L'insieme dei numeri interi. Lezione 5. Divisibilità e divisori. Teorema di divisione euclidea. Algoritmo delle divisioni successive. Questa è la prima lezione dedicata all'anello
Lezioni di Matematica 1 - I modulo
 Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
Lezioni di Matematica 1 - I modulo Luciano Battaia 16 ottobre 2008 Luciano Battaia - http://www.batmath.it Matematica 1 - I modulo. Lezione del 16/10/2008 1 / 13 L introduzione dei numeri reali si può
Parte 3. Rango e teorema di Rouché-Capelli
 Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
Parte 3. Rango e teorema di Rouché-Capelli A. Savo Appunti del Corso di Geometria 203-4 Indice delle sezioni Rango di una matrice, 2 Teorema degli orlati, 3 3 Calcolo con l algoritmo di Gauss, 6 4 Matrici
APPLICAZIONI LINEARI
 APPLICAZIONI LINEARI Esercizi Esercizio 1. Sia f: R 3 R 2 (x, y, z) (x + 2y + z, y + z). (1) Verificare che f è lineare. (2) Determinare una base di ker(f) e stabilire se f è iniettiva. (3) Calcolare w
APPLICAZIONI LINEARI Esercizi Esercizio 1. Sia f: R 3 R 2 (x, y, z) (x + 2y + z, y + z). (1) Verificare che f è lineare. (2) Determinare una base di ker(f) e stabilire se f è iniettiva. (3) Calcolare w
4. Operazioni binarie, gruppi e campi.
 1 4. Operazioni binarie, gruppi e campi. 4.1 Definizione. Diremo - operazione binaria ovunque definita in A B a valori in C ogni funzione f : A B C - operazione binaria ovunque definita in A a valori in
1 4. Operazioni binarie, gruppi e campi. 4.1 Definizione. Diremo - operazione binaria ovunque definita in A B a valori in C ogni funzione f : A B C - operazione binaria ovunque definita in A a valori in
x (x i ) (x 1, x 2, x 3 ) dx 1 + f x 2 dx 2 + f x 3 dx i x i
 NA. Operatore nabla Consideriamo una funzione scalare: f : A R, A R 3 differenziabile, di classe C (2) almeno. Il valore di questa funzione dipende dalle tre variabili: Il suo differenziale si scrive allora:
NA. Operatore nabla Consideriamo una funzione scalare: f : A R, A R 3 differenziabile, di classe C (2) almeno. Il valore di questa funzione dipende dalle tre variabili: Il suo differenziale si scrive allora:
8 Ottava lezione: Spazi di Sobolev
 8 Ottava lezione: Spazi di Sobolev Definizioni e proprietà topologiche Per tutta la lezione, se non altrimenti specificato, tutte le derivate si intendono in senso distribuzionale, Ω indicherà un sottoinsieme
8 Ottava lezione: Spazi di Sobolev Definizioni e proprietà topologiche Per tutta la lezione, se non altrimenti specificato, tutte le derivate si intendono in senso distribuzionale, Ω indicherà un sottoinsieme
2.1 Definizione di applicazione lineare. Siano V e W due spazi vettoriali su R. Un applicazione
 Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Capitolo 2 MATRICI Fra tutte le applicazioni su uno spazio vettoriale interessa esaminare quelle che mantengono la struttura di spazio vettoriale e che, per questo, vengono dette lineari La loro importanza
Parte 2. Determinante e matrice inversa
 Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
Parte. Determinante e matrice inversa A. Savo Appunti del Corso di Geometria 013-14 Indice delle sezioni 1 Determinante di una matrice, 1 Teorema di Cramer (caso particolare), 3 3 Determinante di una matrice
APPLICAZIONI LINEARI
 APPLICAZIONI LINEARI 1. Esercizi Esercizio 1. Date le seguenti applicazioni lineari (1) f : R 2 R 3 definita da f(x, y) = (x 2y, x + y, x + y); (2) g : R 3 R 2 definita da g(x, y, z) = (x + y, x y); (3)
APPLICAZIONI LINEARI 1. Esercizi Esercizio 1. Date le seguenti applicazioni lineari (1) f : R 2 R 3 definita da f(x, y) = (x 2y, x + y, x + y); (2) g : R 3 R 2 definita da g(x, y, z) = (x + y, x y); (3)
Dipendenza dai dati iniziali
 Dipendenza dai dati iniziali Dopo aver studiato il problema dell esistenza e unicità delle soluzioni dei problemi di Cauchy, il passo successivo è vedere come le traiettorie di queste ultime dipendono
Dipendenza dai dati iniziali Dopo aver studiato il problema dell esistenza e unicità delle soluzioni dei problemi di Cauchy, il passo successivo è vedere come le traiettorie di queste ultime dipendono
Prodotto libero di gruppi
 Prodotto libero di gruppi 24 aprile 2014 Siano (A 1, +) e (A 2, +) gruppi abeliani. Sul prodotto cartesiano A 1 A 2 definiamo l operazione (x 1, y 1 ) + (x 2, y 2 ) := (x 1 + x 2, y 1 + y 2 ). Provvisto
Prodotto libero di gruppi 24 aprile 2014 Siano (A 1, +) e (A 2, +) gruppi abeliani. Sul prodotto cartesiano A 1 A 2 definiamo l operazione (x 1, y 1 ) + (x 2, y 2 ) := (x 1 + x 2, y 1 + y 2 ). Provvisto
risulta (x) = 1 se x < 0.
 Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Questo file si pone come obiettivo quello di mostrarvi come lo studio di una funzione reale di una variabile reale, nella cui espressione compare un qualche valore assoluto, possa essere svolto senza necessariamente
Parte 2. Metodi Matematici per la Meccanica Quantistica. Spazi di pre-hilbert e spazi di Hilbert. Gianpiero CATTANEO
 Parte Metodi Matematici per la Meccanica Quantistica Spazi di pre-hilbert e spazi di Hilbert Gianpiero CATTANEO 10 giugno 008 Indice I - Spazi con Prodotto Interno e Spazi di Hilbert 5 1 Spazi con Prodotto
Parte Metodi Matematici per la Meccanica Quantistica Spazi di pre-hilbert e spazi di Hilbert Gianpiero CATTANEO 10 giugno 008 Indice I - Spazi con Prodotto Interno e Spazi di Hilbert 5 1 Spazi con Prodotto
5. La teoria astratta della misura.
 5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
5. La teoria astratta della misura. 5.1. σ-algebre. 5.1.1. σ-algebre e loro proprietà. Sia Ω un insieme non vuoto. Indichiamo con P(Ω la famiglia di tutti i sottoinsiemi di Ω. Inoltre, per ogni insieme
Appunti sul corso di Complementi di Matematica - prof. B.Bacchelli. 03 - Equazioni differenziali lineari omogenee a coefficienti costanti.
 Appunti sul corso di Complementi di Matematica - prof. B.Bacchelli 03 - Equazioni differenziali lineari omogenee a coefficienti costanti. Def. Si dice equazione differenziale lineare del secondo ordine
Appunti sul corso di Complementi di Matematica - prof. B.Bacchelli 03 - Equazioni differenziali lineari omogenee a coefficienti costanti. Def. Si dice equazione differenziale lineare del secondo ordine
1 Giochi a due, con informazione perfetta e somma zero
 1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
1 Giochi a due, con informazione perfetta e somma zero Nel gioco del Nim, se semplificato all estremo, ci sono due giocatori I, II e una pila di 6 pedine identiche In ogni turno di gioco I rimuove una
G. Pareschi ALGEBRE DI BOOLE. 1. Algebre di Boole
 G. Pareschi ALGEBRE DI BOOLE 1. Algebre di Boole Nel file precedente abbiamo incontrato la definizione di algebra di Boole come reticolo: un algebra di Boole e un reticolo limitato, complementato e distributivo.
G. Pareschi ALGEBRE DI BOOLE 1. Algebre di Boole Nel file precedente abbiamo incontrato la definizione di algebra di Boole come reticolo: un algebra di Boole e un reticolo limitato, complementato e distributivo.
Proof. Dimostrazione per assurdo. Consideriamo l insieme complementare di P nell insieme
 G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
G Pareschi Principio di induzione Il Principio di Induzione (che dovreste anche avere incontrato nel Corso di Analisi I) consente di dimostrare Proposizioni il cui enunciato è in funzione di un numero
Il metodo diretto del Calcolo delle Variazioni
 Capitolo 3 Il metodo diretto del Calcolo delle Variazioni Coercività Definizione 3.1 Una funzione F : X R si dice coerciva (risp. sequenzialmente coerciva) se per ogni t R esiste un sottoinsieme compatto
Capitolo 3 Il metodo diretto del Calcolo delle Variazioni Coercività Definizione 3.1 Una funzione F : X R si dice coerciva (risp. sequenzialmente coerciva) se per ogni t R esiste un sottoinsieme compatto
1. PRIME PROPRIETÀ 2
 RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
RELAZIONI 1. Prime proprietà Il significato comune del concetto di relazione è facilmente intuibile: due elementi sono in relazione se c è un legame tra loro descritto da una certa proprietà; ad esempio,
Forme bilineari e prodotti scalari. Definizione Dato lo spazio vettoriale V (K) sul campo K, una funzione. b :
 Forme bilineari e prodotti scalari Definizione Dato lo spazio vettoriale V (K) sul campo K, una funzione b : { V V K ( v, w) b( v, w), si dice forma bilineare su V se per ogni u, v, w V e per ogni k K:
Forme bilineari e prodotti scalari Definizione Dato lo spazio vettoriale V (K) sul campo K, una funzione b : { V V K ( v, w) b( v, w), si dice forma bilineare su V se per ogni u, v, w V e per ogni k K:
Capitolo 1 ANALISI COMPLESSA
 Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Capitolo 1 ANALISI COMPLESSA 1 1.4 Serie in campo complesso 1.4.1 Serie di potenze Una serie di potenze è una serie del tipo a k (z z 0 ) k. Per le serie di potenze in campo complesso valgono teoremi analoghi
Insiemi di livello e limiti in più variabili
 Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
Insiemi di livello e iti in più variabili Insiemi di livello Si consideri una funzione f : A R, con A R n. Un modo per poter studiare il comportamento di una funzione in più variabili potrebbe essere quello
3 GRAFICI DI FUNZIONI
 3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
3 GRAFICI DI FUNZIONI Particolari sottoinsiemi di R che noi studieremo sono i grafici di funzioni. Il grafico di una funzione f (se non è specificato il dominio di definizione) è dato da {(x, y) : x dom
Dimensione di uno Spazio vettoriale
 Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Capitolo 4 Dimensione di uno Spazio vettoriale 4.1 Introduzione Dedichiamo questo capitolo ad un concetto fondamentale in algebra lineare: la dimensione di uno spazio vettoriale. Daremo una definizione
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria).
 Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
Politecnico di Milano. Facoltà di Ingegneria Industriale. Corso di Analisi e Geometria 2. Sezione D-G. (Docente: Federico Lastaria). Aprile 20 Indice Serie numeriche. Serie convergenti, divergenti, indeterminate.....................
STRUTTURE ALGEBRICHE
 STRUTTURE ALGEBRICHE Operazioni in un insieme Sia A un insieme non vuoto; una funzione f : A A A si dice operazione binaria (o semplicemente operazione), oppure legge di composizione interna. Per definizione
STRUTTURE ALGEBRICHE Operazioni in un insieme Sia A un insieme non vuoto; una funzione f : A A A si dice operazione binaria (o semplicemente operazione), oppure legge di composizione interna. Per definizione
ESERCIZI SVOLTI. 1) Dimostrare che l insieme. non è ricorsivo. Soluzione: Definiamo l insieme
 ESERCIZI SVOLTI 1) Dimostrare che l insieme Allora notiamo che π non è vuoto perché la funzione ovunque divergente appartiene all insieme avendo per dominio l insieme. Inoltre π non coincide con l insieme
ESERCIZI SVOLTI 1) Dimostrare che l insieme Allora notiamo che π non è vuoto perché la funzione ovunque divergente appartiene all insieme avendo per dominio l insieme. Inoltre π non coincide con l insieme
TOPOLOGIA ALBERTO SARACCO
 TOPOLOGIA ALBERTO SARACCO Abstract. Le presenti note saranno il più fedeli possibile a quanto detto a lezione. I testi consigliati sono Jänich [1], Kosniowski [2] e Singer- Thorpe [3]. Un ottimo libro
TOPOLOGIA ALBERTO SARACCO Abstract. Le presenti note saranno il più fedeli possibile a quanto detto a lezione. I testi consigliati sono Jänich [1], Kosniowski [2] e Singer- Thorpe [3]. Un ottimo libro
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI
 FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
FUNZIONI ELEMENTARI - ESERCIZI SVOLTI 1) Determinare il dominio delle seguenti funzioni di variabile reale: (a) f(x) = x 4 (c) f(x) = 4 x x + (b) f(x) = log( x + x) (d) f(x) = 1 4 x 5 x + 6 ) Data la funzione
ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA
 ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA Francesco Bottacin Padova, 24 febbraio 2012 Capitolo 1 Algebra Lineare 1.1 Spazi e sottospazi vettoriali Esercizio 1.1. Sia U il sottospazio di R 4 generato dai
ESERCIZI DI ALGEBRA LINEARE E GEOMETRIA Francesco Bottacin Padova, 24 febbraio 2012 Capitolo 1 Algebra Lineare 1.1 Spazi e sottospazi vettoriali Esercizio 1.1. Sia U il sottospazio di R 4 generato dai
Capitolo 2. Operazione di limite
 Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Capitolo 2 Operazione di ite In questo capitolo vogliamo occuparci dell operazione di ite, strumento indispensabile per scoprire molte proprietà delle funzioni. D ora in avanti riguarderemo i domini A
Facoltà di Dipartimento di Ingegneria Elettrica e dell'informazione anno accademico 2014/15 Registro lezioni del docente SPORTELLI LUIGI
 Facoltà di Dipartimento di Ingegneria Elettrica e dell'informazione anno accademico 2014/15 Registro lezioni del docente SPORTELLI LUIGI Attività didattica ANALISI MATEMATICA [2000] Periodo di svolgimento:
Facoltà di Dipartimento di Ingegneria Elettrica e dell'informazione anno accademico 2014/15 Registro lezioni del docente SPORTELLI LUIGI Attività didattica ANALISI MATEMATICA [2000] Periodo di svolgimento:
f(x) = 1 x. Il dominio di questa funzione è il sottoinsieme proprio di R dato da
 Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Data una funzione reale f di variabile reale x, definita su un sottoinsieme proprio D f di R (con questo voglio dire che il dominio di f è un sottoinsieme di R che non coincide con tutto R), ci si chiede
Algebra Lineare e Geometria
 Algebra Lineare e Geometria Corso di Laurea in Ingegneria Elettronica A.A. 2013-2014 Prova d esame del 16/06/2014. 1) a) Determinare la matrice associata all applicazione lineare T : R 3 R 4 definita da
Algebra Lineare e Geometria Corso di Laurea in Ingegneria Elettronica A.A. 2013-2014 Prova d esame del 16/06/2014. 1) a) Determinare la matrice associata all applicazione lineare T : R 3 R 4 definita da
IL CALCOLO VETTORIALE (SUPPLEMENTO AL LIBRO)
 IL CALCOLO VETTORIALE SUPPLEMENTO AL LIBRO CLAUDIO BONANNO Contents. Campi di vettori e operatori 2. Il lavoro di un campo di vettori 5 2.. Lavoro e campi conservativi 6 2.2. Lavoro e campi irrotazionali:
IL CALCOLO VETTORIALE SUPPLEMENTO AL LIBRO CLAUDIO BONANNO Contents. Campi di vettori e operatori 2. Il lavoro di un campo di vettori 5 2.. Lavoro e campi conservativi 6 2.2. Lavoro e campi irrotazionali:
CONCETTO DI LIMITE DI UNA FUNZIONE REALE
 CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
CONCETTO DI LIMITE DI UNA FUNZIONE REALE Il limite di una funzione è uno dei concetti fondamentali dell'analisi matematica. Tramite questo concetto viene formalizzata la nozione di funzione continua e
Successioni di funzioni reali
 E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
E-school di Arrigo Amadori Analisi I Successioni di funzioni reali 01 Introduzione. In questo capitolo applicheremo i concetti di successione e di serie alle funzioni numeriche reali. Una successione di
Corso di Calcolo Numerico
 Corso di Calcolo Numerico Dottssa MC De Bonis Università degli Studi della Basilicata, Potenza Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica Corso di Calcolo Numerico - Dottssa MC De Bonis
Corso di Calcolo Numerico Dottssa MC De Bonis Università degli Studi della Basilicata, Potenza Facoltà di Ingegneria Corso di Laurea in Ingegneria Meccanica Corso di Calcolo Numerico - Dottssa MC De Bonis
Università di Trieste Facoltà d Ingegneria. Esercitazioni per la preparazione della prova scritta di Matematica 3 Dott.
 Università di Trieste Facoltà d Ingegneria. Esercitazioni per la preparazione della prova scritta di Matematica 3 Dott. Franco Obersnel Lezione 19: campi vettoriali e formule di Gauss-Green nel piano.
Università di Trieste Facoltà d Ingegneria. Esercitazioni per la preparazione della prova scritta di Matematica 3 Dott. Franco Obersnel Lezione 19: campi vettoriali e formule di Gauss-Green nel piano.
I appello - 24 Marzo 2006
 Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
Facoltà di Ingegneria - Corso di Laurea in Ing. Energetica e Gestionale A.A.2005/2006 I appello - 24 Marzo 2006 Risolvere gli esercizi motivando tutte le risposte. I.) Studiare la convergenza puntuale,
EQUAZIONI DIFFERENZIALI Esercizi svolti. y = xy. y(2) = 1.
 EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
EQUAZIONI DIFFERENZIALI Esercizi svolti 1. Determinare la soluzione dell equazione differenziale (x 2 + 1)y + y 2 =. y + x tan y = 2. Risolvere il problema di Cauchy y() = 1 2 π. 3. Risolvere il problema
Equazioni alle differenze finite (cenni).
 AL 011. Equazioni alle differenze finite (cenni). Sia a n } n IN una successione di numeri reali. (Qui usiamo la convenzione IN = 0, 1,,...}). Diremo che è una successione ricorsiva o definita per ricorrenza
AL 011. Equazioni alle differenze finite (cenni). Sia a n } n IN una successione di numeri reali. (Qui usiamo la convenzione IN = 0, 1,,...}). Diremo che è una successione ricorsiva o definita per ricorrenza
Esercizi svolti su serie di Fourier
 Esercizi svolti su serie di Fourier Esercizio. (Onda quadra. Determinare i coefficienti di Fourier della funzione x [, f(x = x [, prolungata a una funzione -periodica su R (d ora in poi denoteremo con
Esercizi svolti su serie di Fourier Esercizio. (Onda quadra. Determinare i coefficienti di Fourier della funzione x [, f(x = x [, prolungata a una funzione -periodica su R (d ora in poi denoteremo con
I tre concetti si possono descrivere in modo unitario dicendo che f e iniettiva, suriettiva, biiettiva se e solo se per ogni b B l equazione
 Lezioni del 29 settembre e 1 ottobre. 1. Funzioni iniettive, suriettive, biiettive. Sia f : A B una funzione da un insieme A ad un insieme B. Sia a A e sia b = f (a) B l elemento che f associa ad a, allora
Lezioni del 29 settembre e 1 ottobre. 1. Funzioni iniettive, suriettive, biiettive. Sia f : A B una funzione da un insieme A ad un insieme B. Sia a A e sia b = f (a) B l elemento che f associa ad a, allora
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora:
 Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
Iniziamo con un esercizio sul massimo comun divisore: Esercizio 1. Sia d = G.C.D.(a, b), allora: G.C.D.( a d, b d ) = 1 Sono state introdotte a lezione due definizioni importanti che ricordiamo: Definizione
Basi di matematica per il corso di micro
 Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
Basi di matematica per il corso di micro Microeconomia (anno accademico 2006-2007) Lezione del 21 Marzo 2007 Marianna Belloc 1 Le funzioni 1.1 Definizione Una funzione è una regola che descrive una relazione
SIMULAZIONE TEST ESAME - 1
 SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
SIMULAZIONE TEST ESAME - 1 1. Il dominio della funzione f(x) = log (x2 + 1)(4 x 2 ) (x 2 2x + 1) è: (a) ( 2, 2) (b) ( 2, 1) (1, 2) (c) (, 2) (2, + ) (d) [ 2, 1) (1, 2] (e) R \{1} 2. La funzione f : R R
MATEMATICA. { 2 x =12 y 3 y +8 x =0, si pone il problema di trovare, se esistono, un numero x ed un numero y che risolvano entrambe le equazioni.
 MATEMATICA. Sistemi lineari in due equazioni due incognite. Date due equazioni lineari nelle due incognite x, y come ad esempio { 2 x =12 y 3 y +8 x =0, si pone il problema di trovare, se esistono, un
MATEMATICA. Sistemi lineari in due equazioni due incognite. Date due equazioni lineari nelle due incognite x, y come ad esempio { 2 x =12 y 3 y +8 x =0, si pone il problema di trovare, se esistono, un
SUCCESSIONI NUMERICHE
 SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
SUCCESSIONI NUMERICHE Definizione: Si chiama successione numerica una funzione definita su IN a valori in IR, cioè una legge che associa ad ogni intero n un numero reale a n. Per abuso di linguaggio, si
Serie numeriche. 1 Definizioni e proprietà elementari
 Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
Serie numeriche Definizioni e proprietà elementari Sia { } una successione, definita per ogni numero naturale n n. Per ogni n n, consideriamo la somma s n degli elementi della successione di posto d s
SERIE NUMERICHE. prof. Antonio Greco 6-11-2013
 SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
SERIE NUMERICHE prof. Antonio Greco 6--203 Indice Motivazioni........... 3 Definizione........... 3 Errore tipico........... 3 Un osservazione utile...... 3 Condizione necessaria...... 4 Serie armonica.........
I polinomi 1; x;x 2 ;x 3 sono linearmente indipendenti; infatti. 0= 1 1+ 2 x+ 3 x 2 + 4 x 3 =) 1 = 2 == 4 =0
 ASPETTI TEORICI Spazio vettoriale Un insieme qualunque di inniti elementi V = fv i g si dice uno spazio vettoriale sull'insieme dei numeri reali R se: { E possibile denire un'operazione binaria fra gli
ASPETTI TEORICI Spazio vettoriale Un insieme qualunque di inniti elementi V = fv i g si dice uno spazio vettoriale sull'insieme dei numeri reali R se: { E possibile denire un'operazione binaria fra gli
Una ricetta per il calcolo dell asintoto obliquo. Se f(x) è asintotica a mx+q allora abbiamo f(x) mx q = o(1), da cui (dividendo per x) + o(1), m =
 Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Una ricetta per il calcolo dell asintoto obliquo Se f() è asintotica a m+q allora abbiamo f() m q = o(1), da cui (dividendo per ) m = f() q + 1 f() o(1) = + o(1), mentre q = f() m = o(1). Dunque si ha
Corso di Analisi Numerica
 Corso di Laurea in Ingegneria Informatica Corso di Analisi Numerica 8 - METODI ITERATIVI PER I SISTEMI LINEARI Lucio Demeio Dipartimento di Scienze Matematiche 1 Norme e distanze 2 3 4 Norme e distanze
Corso di Laurea in Ingegneria Informatica Corso di Analisi Numerica 8 - METODI ITERATIVI PER I SISTEMI LINEARI Lucio Demeio Dipartimento di Scienze Matematiche 1 Norme e distanze 2 3 4 Norme e distanze
Lezione 9: Cambio di base
 Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Lezione 9: Cambio di base In questa lezione vogliamo affrontare uno degli argomenti piu ostici per lo studente e cioè il cambio di base all interno di uno spazio vettoriale, inoltre cercheremo di capire
Analisi Complessa. Prova intermedia del 7 novembre 2002 - Soluzioni. (z 11 1) 11 1 = 0.
 Analisi Complessa Prova intermedia del 7 novembre 2002 - Soluzioni Esercizio. Si consideri l equazione z 0. Quante soluzioni distinte esistono in C? Quante di esse sono contenute all interno del disco
Analisi Complessa Prova intermedia del 7 novembre 2002 - Soluzioni Esercizio. Si consideri l equazione z 0. Quante soluzioni distinte esistono in C? Quante di esse sono contenute all interno del disco
Corrispondenze e funzioni
 Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Corrispondenze e funzioni L attività fondamentale della mente umana consiste nello stabilire corrispondenze e relazioni tra oggetti; è anche per questo motivo che il concetto di corrispondenza è uno dei
Fondamenti e didattica di Matematica Finanziaria
 Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
Fondamenti e didattica di Matematica Finanziaria Silvana Stefani Piazza dell Ateneo Nuovo 1-20126 MILANO U6-368 silvana.stefani@unimib.it 1 Unità 9 Contenuti della lezione Operazioni finanziarie, criterio
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica.
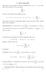 8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
8. Serie numeriche Assegnata la successione di numeri complessi {a 1, a 2, a 3,...} si considera con il nome di serie numerica la nuova successione {s n } definita come s 1 = a 1, s 2 = a 1 + a 2, s 3
Funzioni con dominio in R n
 0.1 Punti e vettori di R n Politecnico di Torino. Funzioni con dominio in R n Nota Bene: delle lezioni. Questo materiale non deve essere considerato come sostituto Molto spesso risulta che una quantita
0.1 Punti e vettori di R n Politecnico di Torino. Funzioni con dominio in R n Nota Bene: delle lezioni. Questo materiale non deve essere considerato come sostituto Molto spesso risulta che una quantita
CRITERI DI CONVERGENZA PER LE SERIE. lim a n = 0. (1) s n+1 = s n + a n+1. (2) CRITERI PER LE SERIE A TERMINI NON NEGATIVI
 Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
Il criterio più semplice è il seguente. CRITERI DI CONVERGENZA PER LE SERIE Teorema(condizione necessaria per la convergenza). Sia a 0, a 1, a 2,... una successione di numeri reali. Se la serie a k è convergente,
u 1 u k che rappresenta formalmente la somma degli infiniti numeri (14.1), ordinati al crescere del loro indice. I numeri u k
 Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Capitolo 4 Serie numeriche 4. Serie convergenti, divergenti, indeterminate Data una successione di numeri reali si chiama serie ad essa relativa il simbolo u +... + u +... u, u 2,..., u,..., (4.) oppure
Lezione 1. Gli Insiemi. La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme:
 Lezione 1 Gli Insiemi La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme: degli iscritti ad un corso di laurea delle stelle in cielo dei punti di un piano
Lezione 1 Gli Insiemi La nozione di insieme viene spesso utilizzata nella vita di tutti i giorni; si parla dell insieme: degli iscritti ad un corso di laurea delle stelle in cielo dei punti di un piano
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE
 LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
LE SUCCESSIONI 1. COS E UNA SUCCESSIONE La sequenza costituisce un esempio di SUCCESSIONE. Ecco un altro esempio di successione: Una successione è dunque una sequenza infinita di numeri reali (ma potrebbe
OGNI SPAZIO VETTORIALE HA BASE
 1 Mimmo Arezzo OGNI SPAZIO VETTORIALE HA BASE CONVERSAZIONE CON ALCUNI STUDENTI DI FISICA 19 DICEMBRE 2006 2 1 Preliminari Definizione 1.0.1 Un ordinamento parziale (o una relazione d ordine parziale)
1 Mimmo Arezzo OGNI SPAZIO VETTORIALE HA BASE CONVERSAZIONE CON ALCUNI STUDENTI DI FISICA 19 DICEMBRE 2006 2 1 Preliminari Definizione 1.0.1 Un ordinamento parziale (o una relazione d ordine parziale)
11 Undicesima lezione: Coercività e semicontinuità di funzionali integrali
 11 Undicesima lezione: Coercività e semicontinuità di funzionali integrali In questa lezione torniamo a considerare problemi di minimo per funzionali integrali del tipo (11.1) f(x, u(x), u(x)) dx. dove
11 Undicesima lezione: Coercività e semicontinuità di funzionali integrali In questa lezione torniamo a considerare problemi di minimo per funzionali integrali del tipo (11.1) f(x, u(x), u(x)) dx. dove
