= y h. m x0 (h) = y Q y P x Q x P. f(x 0 + h) f(x 0 )
|
|
|
- Gianluca Beretta
- 7 anni fa
- Visualizzazioni
Transcript
1 ESERCIZI DI MATEMATICA: SCHEDA n.1 su derivate: la definzione Classe 5B Sc.Soc. Data: Teoria in sintesi. Data una funzione y = f(x) denita intorno ad x 0 (ovverosia il dominio contiene un intervallo aperto I contenente x 0 ) e assegnato l'incremento convenzionalmente positivo R della variabile indipendente (sucientemente piccolo ancé x 0 + I) si ciama rapporto incrementale di punto iniziale x 0 e incremento il rapporto: m x0 () = y Q y P x Q x P = y x = f(x 0 + ) f(x 0 ). tale rapporto incrementale (ce dipende da x 0 e oltre ce dalla specica funzione f) è un numero ce rappresenta la pendenza (= il coeciente angolare) della retta secante il graco della funzione e passante per i punti del graco di f aventi di ascissa x 0 e x 0 +, cioè P (x 0, f(x 0 )) e Q(x 0 +, f(x 0 + )). Se l'incremento viene lasciato generico, il rapporto incrementale m x0 () = f(x 0 + ) f(x 0 ) è una funzione di (denita in un intorno di 0, zero escluso); a senso pertanto provare a calcolare: lim m f(x 0 + ) f(x 0 ) x 0 (), cioè lim. 0 0 Se tale limite esiste ed è nito esso si ciama derivata della funzione in x 0 e si indica con f (x 0 ) (si tratta quindi di un numero) e quindi: f (x 0 ) = lim 0 f(x 0 + ) f(x 0 ). Le derivata della funzione in x 0 rappresenta la pendenza (= il coeciente angolare) della retta tangente t x0 al graco della funzione nel punto di ascissa x 0, cioè in P (x 0, f(x 0 )). Tale retta a dunque equazione: t x0 : y f(x 0 ) = f (x 0 ) (x x 0 ). Esercizio 1: Scrivi il rapporto incrementale m x0 () della funzione y = f(x) assegnata relativo al punto iniziale x 0 assegnato e all'incremento indicato della variabile indipendente; negli esercizi contrassegnati con determina ance l'equazione della retta secante il graco della funzione, passante per i punti P (x 0, f(x 0 ) e Q(x 0 +, f(x 0 + )). (1) f(x) = x 2 1; x 0 = 1; = 2 R 1 (2) = 4; retta secante y = 4x 4 1
2 (2) f(x) = x 2; x 0 = 4; = 1 R 4 ( 1) = 2 1 (3) f(x) = 1 2x + 1 ; x 0 = 2; = 3 R 2 (3) = 55 2 ; retta secante y = 2 55 x (4) f(x) = 2 3x 4 ; x 0 = 1; = 2 R 1 ( 2) = Esercizio 2: Scrivi il rapporto incrementale m x0 () della funzione y = f(x) assegnata relativo al punto iniziale x 0 assegnato e all'incremento ( 0) generico della variabile indipendente. (1) f(x) = x 2 1; x 0 = 1 R 1 () = + 2 (2) f(x) = 3x 1; x 0 = 1 R 1 () = (3) f(x) = x 2 x 2 ; x 0 = 2 R 2 () = 1 (+2) 2 (4) f(x) = log 3 (x 2 1); x 0 = 2 R 2 () = log 3 (2 +4+3) 1 Esercizio 3: Mediante l'uso diretto della denizione, calcola il valore della derivata f (x 0 ) delle seguenti funzioni nel punto x 0 assegnato. (1) f(x) = x 2 1; x 0 = 1 f (1) = 2 (2) f(x) = x x 2 ; x 0 = 1 f (1) = 2 (3) f(x) = x; x 0 = 4 f (4) = 1 4 (4) f(x) = 2x 3 + x 2 4x 1; x 0 = 0 f (0) = 4 Esercizio 4: Determina l'equazione della retta tangente t x0 al graco della funzione y = f(x) nel suo punto di ascissa x 0. (si tratta delle stesse funzioni e dello stesso punto x 0 del gruppo di esercizi precedenti). (1) f(x) = x 2 1; x 0 = 1 t 1 : y = 2x 2 (2) f(x) = x x 2 ; x 0 = 1 t 1 : y = 2x + 1 (3) f(x) = x; x 0 = 4 t 4 : y = 1 4 x + 1 (4) f(x) = 2x 3 + x 2 4x 1; x 0 = 0 t 0 : y = 4x 1
3 ESERCIZI DI MATEMATICA: SCHEDA n.2 su derivate Il calcolo della funzione derivata mediante le regole di derivazione: funzioni elementari Classe VB SC Data: Teoria in sintesi. derivate delle funzioni elementari: funzione y = f(x) funzione derivatay = f (x) funzione potenza y = x n y = nx n 1 funzione logaritmica y = log b x y = 1 x ln b funzione esponenziale y = a x y = a x ln a casi particolari: funzione y = f(x) funzione derivata y = f (x) funzione costante y = k y = 0 funzione prima potenza y = x y = 1 funzione seconda potenza y = x 2 y = 2x funzione terza potenza y = x 3 y = 3x 2 funzione radice quadrata y = x y = 1 2 x funzione logaritmo naturale y = ln x y = 1 x funzione esponenziale, base e y = e x y = e x regole di derivazioni funzioni e operazioni: funzione funzione derivata moltiplicazione per una costante f(x) = k g(x) f (x) = k g (x) somma algebrica di funzioni f(x) = (x) ± g(x) f (x) = (x) ± g (x) prodotto di funzioni f(x) = (x) g(x) f (x) = (x) g(x) + (x) g (x) quoziente di funzioni f(x) = n(x) d(x) f (x) = n (x) d(x) n(x) d (x) [d(x)] 2 Nota e = è un numero irrazionale; i logaritmi in base e sono detti logaritmi naturali ed indicati semplicemente con ln anzicé log e ; la funzione esponenziale con base e non a un nome particolare, ma spesso, soprattutto in ambito informatico è spesso indicata con y = exp(x) anzicé con y = e x.
4 ESERCIZI DI MATEMATICA: SCHEDA n.3 su derivate: la definzione Classe VB SC Data: Teoria in sintesi. Data una funzione y = f(x) denita intorno ad x 0 (ovverosia il dominio contiene un intervallo aperto I contenente x 0 ) e assegnato l'incremento R della variabile indipendente (sucientemente piccolo ancé x 0 + I) si ciama rapporto incrementale di punto iniziale x 0 e incremento il rapporto m x0 () = y Q y P x Q x P = y x = f(x 0 + ) f(x 0 ). Tale rapporto incrementale (ce dipende da x 0 e oltre ce dalla specica funzione f) è un numero ce rappresenta la pendenza (= il coeciente angolare) della retta secante il graco della funzione e passante per i punti del graco di f aventi di ascissa x 0 e x 0 +, cioè P (x 0, f(x 0 )) e Q(x 0 +, f(x 0 + )). Se l'incremento viene lasciato generico, il rapporto incrementale: m x0 () = f(x 0 + ) f(x 0 ) è una funzione di (denita in un intorno di 0, zero escluso); a senso pertanto provare a calcolare: lim m f(x 0 + ) f(x 0 ) x 0 () = lim. 0 0 Se tale limite esiste ed è nito esso si ciama derivata della funzione in x 0 e si indica con f (x 0 ) (si tratta quindi di un numero) e quindi: f f(x 0 + ) f(x 0 ) (x 0 ) = lim 0 se tale limite esiste nito. Le derivata della funzione in x 0 rappresenta la pendenza (= il coeciente angolare) della retta tangente t x0 funzione nel punto di ascissa x 0, cioè in P (x 0, f(x 0 )). Tale retta a dunque equazione: al graco della t x0 : y f(x 0 ) = f (x 0 ) (x x 0 ) Esercizio 1: USO DIRETTO DELLA DEFINIZIONE: Mediante l'uso diretto della denizione, calcola il valore della derivata f (x 0 ) delle seguenti funzioni nel punto x 0 assegnato; determina ance l'equazione della retta tangente t al graco della funzione y = f(x) nel punti di ascissa x 0. [1] f(x) = 2x 2 + x 3; x 0 = 1 [2] f(x) = x2 x 2 ; x 0 = 3 [3] f(x) = x 3 + 2; x 0 = 7 f (1) = 2 f (1) = 2 f (1) = 2 Esercizio 2: USO DIRETTO DELLA DEFINIZIONE TEORIA: Mediante l'uso diretto della denizione, calcola il valore della derivata f (x 0 ) delle seguenti funzioni nel punto x 0 generico. [1] f(x) = x [2] f(x) = 1 x f (x) = 1 2 (x) f (x) = 1 x 2 [3] f(x) = 5x 2 f (x) = 10x Esercizio 3: USO DELLE REGOLE DI DERIVAZIONE E DELLA CONOSCENZA DELLA FUNZIONE DERIVATA DI FUNZIONI ELEMENTARI: utilizzando non la denizione, ma le regole di derivazione e la tabella delle derivate delle funzioni elementari, determina la funzione derivata y = f (x) delle seguenti funzioni. [1] f(x) = 4 x + 2x 2 1 [2] f(x) = e x + ln x 3x 4 [3] f(x) = 2 4 x + 4 log 2 x 2x 3 [4] f(x) = 6x 3 3x 2 x + 3
5 ESERCIZI DI MATEMATICA: SCHEDA n.4 su derivate: calcolo della derivata del prodotto/quoziente di funzioni; applicazione alla ricerca degli intervalli di monotonia e dei punti di massimo e minimo relativo Classe VB SC Data: Teoria in sintesi Indiciamo con D[f(x)] la funzione derivata di f(x): (1) la (funzione) derivata del prodotto di due funzioni: D[f(x) g(x)] = D[f(x)] g(x) + f(x) D[g(x)] [ ] f(x) D[f(x)] g(x) f(x) D[g(x)] (2) la (funzione) derivata del quoziente di due funzioni: D = g(x) g 2 (x) Denizione di punto stazionario (o punto a tangente orizzontale): data una funzione y = f(x), ogni punto x 0 del domino della funzione in cui la derivata esiste e vale zero, cioè f (x 0 ) = 0, è detto punto stazionario (o punto a tangente orizzontale). Denizione di punto di massimo relativo (interno) e di massimo relativo: sia x 0 un punto del dominio interno al dominio di una funzione (cioè non un estremo del dominio) ; se vale f(x) f(x 0 ) per tutti i valori di x intorno ad x 0 (cioè per tutti gli x appartenenti ad un intervallino aperto contente x 0 ) allora x 0 è detto punto di massimo relativo; il valore f(x 0 ) ce la funzione assume in x 0 è detto massimo relativo. Denizione di punto di minimo relativo (interno) e di minimo relativo: sia x 0 un punto del dominio interno al dominio di una funzione (cioè non un estremo del dominio) ; se vale f(x) f(x 0 ) per tutti i valori di x intorno ad x 0 (cioè per tutti gli x appartenenti ad un intervallino aperto contente x 0 ) allora x 0 è detto punto di minimo relativo; il valore f(x 0 ) ce la funzione assume in x 0 è detto minimo relativo. In generale i punti di massimo/minimo relativi sono detti estremanti relativi (interni); i massimi e i mininimi relativi sono detti estremi relativi. (1) Teorema: punti stazionari ed estremanti relativi: se x 0 è estremante relativo (interno) e la funzione è derivabile in x 0, allora f (x 0 ) = 0, cioè x 0 è un punto stazionario. Nota: non vale il viceversa: esistono punti stazionari ce non sono estremanti relativi: essi sono detti punti di esso a tangente orizzontale. Nota: un punto può essere un estremante relativo ma in esso può non esistere la derivata. (2) Teorema: Intervalli di monotonia e segno della derivata: se una funzione è derivabile in tutti i punti di un intervallo aperto I e si a f(x) > 0 per tutti gli x I, allora su tale intervallo la funzione è crescente, cioè x 1 > x 2 f(x 1 ) > f(x 2 ). (3) Teorema: Intervalli di monotonia e segno della derivata: se una funzione è derivabile in tutti i punti di un intervallo aperto I e si a f(x) < 0 per tutti gli x I, allora su tale intervallo la funzione è decrescente, cioè x 1 > x 2 f(x 1 ) < f(x 2 ). Nota: non vale il viceversa: ad esempio esistono funzioni ce sono crescenti su un intervallo, ma ce non anno la derivata positiva su tutti i punti di tale intervallo (la derivata al più può essere nulla in qualce punto, nei punti di esso a tangente orizzontale) e comunque un funzione potrebbe essere crescente/decrescente su tutti i punti di un intervallo, ma la derivata su alcuni punti potrebbe non esistere (punti di non derivabilità). Esercizi: Esercizio 1: CALCOLO DELLA (FUNZIONE) DERIVATA DI UN PRODOTTO/QUOZIENTE: calcola la derivata delle seguenti funzioni (ove compaiono il prodotto/quoziente di funzioni elementari (o della somma di funzioni elementari) (1) y = x ln x (2) y = 4 x e x (3) y = 2x2 + 1 x 3 (4) y = (log x + 3x 2 ) 2 x (5) y = x2 + e x x ln x (6) y = x3 ln x 2x 3
6 (7) y = 3x x 1 Esercizio 2: RICERCA DEI PUNTI STAZIONARI: determina tutti i punti stazionari delle seguenti funzioni. RICERCA DEGLI INTERVALLI DI MONOTONIA: determina gli intervalli di monotonia delle seguenti funzioni funzioni (prima occorre trovare il dominio). (1) y = 2 3 x x2 2x + 9 f (1) = 2 (2) y = x 2 e x f (1) = 2 (3) y = 8 ln x x 2 f (1) = 2 (4) y = x + 4 2x 3 (5) y = x + 1 x 2 2 f (1) = 2 f (1) = 2
7 SCHEDA n.5 su derivate: Derivazione di una funzione composta (o funzione di funzione) Classe VB SC Data: Teoria in sintesi La derivata di una funzione composta o funzione di funzione f = g (x) = g((x)) è = g () (x) dove la prima derivata è eseguita rispetto alla funzione e non rispetto alla variabile x, come negli esempi ce seguono: g(x) (x) f(x) = g (x) = g((x)) f (x) = g () (x) x x 3 + 5x (x) = x3 + 5x (x) 1 (x) = 2 x 3 + 5x (3x2 + 10x) x 10 3x 2 2x + 7 [(x)] 10 = (3x 2 2x + 7) 10 10[(x)] 9 (x) = 10(3x 2 2x + 7) 9 (6x 2) e x 2x 4 1 e (x) = e 2x4 3x 3 e (x) (x) = e 2x4 3x 3 (8x 3 9x 2 ) Vediamo ora l'applicazione a casi più generali: funzione elementare derivata funzione elementare funzione composta derivata funzione composta g(x) g (x) f(x) = g((x)) = g (x) f (x) = g () (x) x n n x n 1 f(x) = [(x)] n f (x) = n [(x)] n 1 (x) x 2 2 x f(x) = [(x)] 2 f (x) = 2 (x) (x) x 3 3 x 2 f(x) = [(x)] 3 f (x) = 3 [(x)] 2 (x) x 1 2 x f(x) = (x) f (x) = 1 2 (x) (x) log b x 1 x ln b f(x) = log b [(x)] f (x) = 1 (x) ln b (x) ln x 1 x f(x) = ln[(x)] f (x) = 1 (x) (x) a x a x ln a f(x) = a (x) f (x) = a (x) ln a (x) e x e x e (x) e (x) (x) Esercizi: Esercizio 1: LA DEFINIZIONE DI DERIVATA: calcola mediante la denizione la derivata delle seguenti funzioni nel punto x 0 indicato; determina l'equazione esplicita della retta tangente t al graco della funzione nel punto P di ascissa x 0. a) f(x) = x 2 + 3; x 0 = 1 f (1) = 1 2 f t : y = 1 2 x b) f(x) = x 2 x 2 ; x 0 = 2 f (1) = 1 4 t : y = 1 4 x 1 2 Esercizio 2: LA DERIVATA DELLA FUNZIONE COMPOSTA: ricordando ce Esercizio 3: determina la funzione derivata delle seguenti funzioni composte: (1) y = x y = x x 2 +1 (2) y = ln(2x 2 3x + 1) y = (3) y = e 2x 1 x 4x 3 2x 2 3x+1 y = e 2x 1 x 1 x 2 (4) y = x ln(x 2 + 1) y = ln(x 2 + 1) + 2x2 x 2 +1 (5) y = ln(3x 2) + 2 y = ln(3x 2)+2 3x 2
8 (6) y = e x x y = 3 2 ex x x (7) y = x(1 e x ) y = e x (x 1) + 1 Esercizio 4: PUNTI STAZIONARI E INTERVALLI DI MONOTONIA; PUNTI ESTREMANTI RELATIVI; ESTRE- MI RELATIVI: dopo aver determinato il dominio D delle funzioni assegnate, determina punti stazionari ed intervalli di monotonia; determina i punti di max e min relativo e i max e min relativi. (1) y = x x D = R, punti staz.= { 1, +1}, f 1 < x < 1, f x < 1 x > 1; x = 1 punto di minimo relativo; y = 1 2 di massimo relativo; y = 2 1 massimo relativo; (2) y = ln(x 2 + x + 1) minimo relativo; x = 1 punto D = R, punti staz.= { 1 2 }, f x > 1 2, f x < 1 2 ; x = 1 2 punto di minimo relativo; y = ln ( 34 ) = 0.29 minimo relativo (3) y = e x x 2 D = R \ {2}, f mai, f x < 2 x > 2; Esercizio 5: determina per quali valori del parametro reale m la seguente funzione cubica y = x 3 +mx 2 +(2m+9)x+3 è decrescente su tutto R (e non presenta punti stazionari). 3 < m < 9 Esercizio 6: RICERCA DEI PUNTI STAZIONARI: determina tutti i punti stazionari delle seguenti funzioni e determina gli intervalli di monotonia delle seguenti funzioni funzioni (prima occorre trovare il dominio). (1) y = 2 3 x x2 2x + 9 (2) y = x 2 e x (3) y = 8 ln x x 2 (4) y = x + 4 2x 3 (5) y = x + 1 x 2 2
9 Classe VB SC SCHEDA n.6 su (applicazioni delle) derivate: ESERCIZI PER VERIFICA/SIMULAZIONE III PROVA DI APRILE Data: Teoria: il teorema degli zeri delle funzioni continue: sia f una funzione reale di variabile reale denita sull'intervallo [a, b] e ivi continua; se f(a) > 0 e f(b) < 0 (o viceversa f(a) < 0 e f(b) > 0) allora esiste c ]a, b[ tale ce f(c) = 0 (un tale valore del dominio è detto zero della funzione; il teorema pertanto ci dà una condizione suciente (ma non necessaria, percé?) per l'esistenza di uno zero di una funzione continua). Teoria: il teorema degli zeri delle funzioni continue: caso particolare: sia f una funzione reale di variabile reale denita su R e continua; se f(x) = + e lim f(x) = (o viceversa lim f(x) = e lim f(x) = + ) allora esiste c R tale ce f(c) = 0. lim x + x x + x ESERCIZI: LO STUDIO COMPLETO DI FUNZIONE: studia le seguenti funzioni determinando dominio segno ed eventuali intersezioni con asse x eventuale intersezione con asse y limiti agli estremi del dominio (punti disc., asintoti verticali e orizzontali) derivata zeri e segno della derivata (punti stazionari, intervalli di monotonia, punti di max e min relativo, max e min relativi) codominio Esercizio 1: y = (x + 3) e x Informazione assegnata (ce non saresti in grado di ottenere senza l'utilizzo del Teorema di De L'Hopital f(x) = [+ 0] = [F I] = 0 lim x + alcune risposte: f(x) > 0 x > 3, f(x) < 0 x < 3; f (x) = ( x 2)e x ; x = 2 punto stazionario e max relativo e assoluto; y = e 2 = 7.4 max relativo e assoluto; f crescente su ], 2[. Domanda extra: si stabilisca al variare di k R quante soluzioni a l'equazione (x + 3) e x = k Esercizio 2: y = x 3 3x + 7 Nota: si salti lo studio del segno della funzione. alcune risposte: punti stazionari x = 1; x = 1 Domanda extra: si stabilisca al variare di k R quante soluzioni a l'equazione x 3 3x + 7 = k Domanda extra: si dimostri ce esiste uno zero c per f e lo si approssimi a meno di un'unità. Utilizzando questo valore cosa diresti ora relativamente allo studio del segno? Esercizio 3: y = ln(x) 1 2 x2 Nota: si salti inizialmente lo studio del segno della funzione. Informazione assegnata (ce non saresti in grado di ottenere senza l'utilizzo del Teorema di De L'Hopital f(x) = [+ ] = [F I] = lim x + alcune risposte: punto di max x = 1 Domanda extra: si dimostri f(x) < 0 per tutti i valori di x del dominio della funzione. Esercizio 4: y = x2 x + 1 x 2 + x + 1 alcune risposte: punti stazionari x = 1; x = 1
10 SIMULAZIONE 1 DELLA TERZA PROVA Classe VB SC Sceda 3 Mercoledì 10 giugno 2009 (1) QUESITO 1: Dopo aver ricordato (teoria)..., il candidato consideri le tre seguenti funzioni; tutte e tre sono denite intorno al punto x = 1, ma x = 1 non fa parte del dominio naturale di nessuna di esse; utilizzando lo spazio a disposizione, il candidato classici il punto di discontinuità x = 1. (a) f(x) = 3x2 x 2 x 1 (b) g(x) = x log 2 (x + 7) se x > 1 (c) (x) = 8 se x < 1 x 3
11 (2) QUESITO 2: Dopo aver ricordato (teoria)..., il candidato consideri la funzione y = e x2 +4x avente R come dominio naturale; di essa si ciede di determinare, utilizzando lo spazio a disposizione (a) la funzione derivata prima; (b) l'equazione della retta tangente t nel punto P del graco della funzione di ascissa x = 0; (c) gli intervalli di monotonia della funzione; (d) i punti estremanti relativi e gli estremi relativi. Cognome:
12 VERIFICA DI MATEMATICA Classe VB SC Data: venerdì 17 aprile 2009 Cognome: NORME: è consentito l'uso della calcolatrice; non saltate troppi passaggi per evitare malintesi. consegnato denitivamente la verica). Punteggi: massimo 10+2 Non è consentito uscire dall'aula durante la prova (a meno di aver (1) ESERCIZIO 0: [Punti 1.00] Riporta la denizione di derivata di una funzione in un punto (a parole e in simboli); nota non on ciesto il signicato geometrico o altro, ma semplicemente la denizione. (2) ESERCIZIO 1: Mediante l'uso diretto della denizione, calcola il valore della derivata f (x 0 ) delle seguenti funzioni nel punto x 0 assegnato; determina ance l'equazione della retta tangente t al graco della funzione y = f(x) nel punti di ascissa x 0. (a) [Punti 1.50] f(x) = 1 x 2 ; x 0 = 2 (b) [Punti 1.50] f(x) = x + 3; x 0 = 1 (3) ESERCIZIO 2: USO DELLE REGOLE DI DERIVAZIONE: utilizzando non la denizione, ma le regole di derivazione e la tabella delle derivate delle funzioni elementari, determina la funzione derivata y = f (x) delle seguenti funzioni. (a) [Punti 1.50] f(x) = x ln x x (4) ESERCIZIO 3: RICERCA DEI PUNTI STAZIONARI E DEGLI INTERVALLI DI MONOTONIA: determina tutti i punti stazionari delle seguenti funzioni (stabilisci se sono punti di massimo o minimo relativo o altro; non è riciesto il calcolo del max/min relativo) e determina gli intervalli di monotonia delle seguenti funzioni funzioni (tieni conto del fatto ce ce per le prime due funzioni il dominio è D = R laddove per la terza esso è D = {x R x > 0} ). (a) [Punti 1.50] y = x 3 3x 2 (b) [Punti 1.50] y = (2x 1) e x (c) [Punti 1.50] y = x 2 ln x (5) ESERCIZIO EXTRA: [Punti 2.00] dopo aver rapidamente disegnato un graco qualitativo della funzione y = x 3 3x 2 determina al variare di k R quante soluzioni a l'equazione x 3 3x 2 ). Nota: per disegnare un graco qualitativo della funzione y = x 3 3x 2 sfrutterai le informazioni trovate nell'esercizio precedente, (ma dovrai ance calcolare i max e min relativi) oltre a dominio e ai limiti (istantanei) agli estremi del dominio; invece, pur essendo non dicili da trovare, puoi evitare di trovare intersezioni con l'asse x e segno visto ce non sono necessari per lo svolgimento dell'esercizio.
Derivate e studio di funzioni di una variabile
 Derivate e studio di funzioni di una variabile Paolo Montanari Appunti di Matematica Derivate e studio di funzioni 1 Rapporto incrementale e derivata Sia f(x) una funzione definita in un intervallo X R
Derivate e studio di funzioni di una variabile Paolo Montanari Appunti di Matematica Derivate e studio di funzioni 1 Rapporto incrementale e derivata Sia f(x) una funzione definita in un intervallo X R
QUESITI DI ANALISI Derivate versione senza graci
 QUESITI DI ANALISI Derivate versione senza graci Dai la denizione di derivata di una funzione f(x) in un punto x 0, illustra il suo signicato geometrico e serviti di tale denizione per dimostrare che f
QUESITI DI ANALISI Derivate versione senza graci Dai la denizione di derivata di una funzione f(x) in un punto x 0, illustra il suo signicato geometrico e serviti di tale denizione per dimostrare che f
DERIVATA DI UNA FUNZIONE REALE. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR.
 DERIVATA DI UNA FUNZIONE REALE 1. Definizioni. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR. DEFINIZIONE 1. Sia x 0 un elemento di I. Per ogni x (I \ {x 0 }) consideriamo
DERIVATA DI UNA FUNZIONE REALE 1. Definizioni. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR. DEFINIZIONE 1. Sia x 0 un elemento di I. Per ogni x (I \ {x 0 }) consideriamo
Richiami sullo studio di funzione
 Richiami sullo studio di funzione Per studiare una funzione y = f() e disegnarne un grafico approssimativo, possiamo procedere in ordine secondo i seguenti passi:. determinare il campo di esistenza (o
Richiami sullo studio di funzione Per studiare una funzione y = f() e disegnarne un grafico approssimativo, possiamo procedere in ordine secondo i seguenti passi:. determinare il campo di esistenza (o
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler)
 Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
CALCOLO DIFFERENZIALE per Informatica Programma aa 2011/12, canale A-L.
 CALCOLO DIFFERENZIALE per Informatica Programma aa 2011/12, canale A-L. I numeri dei capitoli e dei paragra si riferiscono al testo consigliato: R.A. Adams: Calcolo dierenziale 1. Funzioni di una variabile,
CALCOLO DIFFERENZIALE per Informatica Programma aa 2011/12, canale A-L. I numeri dei capitoli e dei paragra si riferiscono al testo consigliato: R.A. Adams: Calcolo dierenziale 1. Funzioni di una variabile,
Mauro Saita Grafici qualitativi di funzioni reali di variabile reale
 Mauro Saita Grafici qualitativi di funzioni reali di variabile reale Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Ottobre 2017 1 Indice 1 Qual è il grafico della
Mauro Saita Grafici qualitativi di funzioni reali di variabile reale Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Ottobre 2017 1 Indice 1 Qual è il grafico della
Studio del segno delle derivate. Lezione 11 del 6/12/2018
 Studio del segno delle derivate Lezione 11 del 6/12/2018 Segno della derivata prima Data una funzione f(x) derivabile in un intervallo I, allora se f x > 0 x I allora la funzione f(x) è strettamente crescente
Studio del segno delle derivate Lezione 11 del 6/12/2018 Segno della derivata prima Data una funzione f(x) derivabile in un intervallo I, allora se f x > 0 x I allora la funzione f(x) è strettamente crescente
Studio di funzione. numeri.altervista.org
 Studio di funzione 1. Determinazione del campo di esistenza CONDIZIONE DI ESISTENZA intera: FUNZIONE RAZIONALE se è del tipo f(x)=p(x) dove P(x) e' un polinomio nella variabile x --------------------------------------------------------------------
Studio di funzione 1. Determinazione del campo di esistenza CONDIZIONE DI ESISTENZA intera: FUNZIONE RAZIONALE se è del tipo f(x)=p(x) dove P(x) e' un polinomio nella variabile x --------------------------------------------------------------------
SIMULAZIONE TERZA PROVA DOMANDE CHIUSE CAMPO DI ESISTENZA. 4 è: x 6x. = è:
 SIMULAZIONE TERZA PROVA DOMANDE CHIUSE CAMPO DI ESISTENZA Il campo di esistenza della funzione f() = 4 + a) ± b) c) d) > - + Il campo di esistenza della funzione f() = + a) b) -, - c) - < - d) > - Campo
SIMULAZIONE TERZA PROVA DOMANDE CHIUSE CAMPO DI ESISTENZA Il campo di esistenza della funzione f() = 4 + a) ± b) c) d) > - + Il campo di esistenza della funzione f() = + a) b) -, - c) - < - d) > - Campo
Giovanni Rapisarda. Derivata di una funzione. df dx. Sia. una funzione definita in un intervallo. Fissato un punto
 Derivata di una funzione Sia una funzione definita in un intervallo a, b R. Fissato un punto appartenente allinsieme di definizione della funzione, sia P (, f ( )) il punto di ascissa appartenente al grafico
Derivata di una funzione Sia una funzione definita in un intervallo a, b R. Fissato un punto appartenente allinsieme di definizione della funzione, sia P (, f ( )) il punto di ascissa appartenente al grafico
1. Mercoledì 07/03/2018, ore: 2(2) Introduzione e presentazione del corso. Richiami: i numeri naturali, interi, razionali e reali.
 Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: May 17, 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: May 17, 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA
 ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
PENDENZA (ripasso classe II)
 PENDENZA (ripasso classe II) Vediamo di definire quantitativamente il concetto di pendenza. Già ritroviamo la pendenza indicata in percentuale nei cartelli di pericolo nelle strade di montagna. La definizione
PENDENZA (ripasso classe II) Vediamo di definire quantitativamente il concetto di pendenza. Già ritroviamo la pendenza indicata in percentuale nei cartelli di pericolo nelle strade di montagna. La definizione
1 è l estremo inferiore della funzione (inf f = 1 R) e quindi la funzione è limitata inferiormente
 f x = x 2 1 allora Im f = [ 1, + ) 1 è l estremo inferiore della funzione (inf f = 1 R) e quindi la funzione è limitata inferiormente + è l estremo superiore della funzione (sup f = + R) e quindi la funzione
f x = x 2 1 allora Im f = [ 1, + ) 1 è l estremo inferiore della funzione (inf f = 1 R) e quindi la funzione è limitata inferiormente + è l estremo superiore della funzione (sup f = + R) e quindi la funzione
3. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE.
 3. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso y = f(x) rappresenta l evoluzione di un fenomeno al passare del tempo x.se siamo interessati a sapere con che rapidità il fenomeno
3. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso y = f(x) rappresenta l evoluzione di un fenomeno al passare del tempo x.se siamo interessati a sapere con che rapidità il fenomeno
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler)
 Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f è crescente nell intervallo (a, b) se
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f è crescente nell intervallo (a, b) se
Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile
 Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 41 1 Derivata
Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 41 1 Derivata
Teoremi fondamentali dell'analisi Matematica versione 1
 Teoremi fondamentali dell'analisi Matematica versione 1 Roberto Boggiani 7 novembre 2012 1 Richiami di geometria analitica Dalla geometria analitica sulla retta sappiamo che dati due punti del piano A(x
Teoremi fondamentali dell'analisi Matematica versione 1 Roberto Boggiani 7 novembre 2012 1 Richiami di geometria analitica Dalla geometria analitica sulla retta sappiamo che dati due punti del piano A(x
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler)
 Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler)
 Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
Retta Tangente. y retta tangente. retta secante y = f(x) f(x )
 Retta Tangente f(x ) y P retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x x quando P tende a P 0 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0, f(x 0 ))
Retta Tangente f(x ) y P retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x x quando P tende a P 0 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0, f(x 0 ))
a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre gli zeri di f e studiarne il segno.
 1 ESERCIZI CON SOLUZIONE DETTAGLIATA Esercizio 1. Si consideri la funzione f(x) = e x 3e x +. a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre
1 ESERCIZI CON SOLUZIONE DETTAGLIATA Esercizio 1. Si consideri la funzione f(x) = e x 3e x +. a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre
1. Mercoledì 07/03/2018, ore: 2(2) Introduzione e presentazione del corso. Richiami: i numeri naturali, interi, razionali e reali.
 Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: 28 maggio 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: 28 maggio 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
DERIVATE. Equazione della retta tangente al grafico di f nel suo punto P(x 0 ;y 0 ):
 DERIVATE La derivata di una funzione in un punto c, quando esiste, rappresenta il coefficiente angolare della retta tangente al grafico della funzione nel suo punto di ascissa c: f ( c) = Df ( c) = m tg
DERIVATE La derivata di una funzione in un punto c, quando esiste, rappresenta il coefficiente angolare della retta tangente al grafico della funzione nel suo punto di ascissa c: f ( c) = Df ( c) = m tg
LICEO SCIENTIFICO STATALE G. MARCONI FOGGIA
 LICEO SCIENTIFICO STATALE G. MARCONI FOGGIA PROGRAMMA DI MATEMATICA Classe VB Anno Scolastico 014-015 Insegnante: Prof.ssa La Salandra Incoronata 1 Nozioni di topologia su Intervalli; Estremo superiore
LICEO SCIENTIFICO STATALE G. MARCONI FOGGIA PROGRAMMA DI MATEMATICA Classe VB Anno Scolastico 014-015 Insegnante: Prof.ssa La Salandra Incoronata 1 Nozioni di topologia su Intervalli; Estremo superiore
Esame di MATEMATICA CORSO BASE del
 Esame di MATEMATICA CORSO BASE del Cognome Matricola Nome Esercizio. Si consideri il seguente sistema x 3y + z =5 x ky +z = k kx y z = Si trovino il numero delle soluzioni al variare del parametro k e
Esame di MATEMATICA CORSO BASE del Cognome Matricola Nome Esercizio. Si consideri il seguente sistema x 3y + z =5 x ky +z = k kx y z = Si trovino il numero delle soluzioni al variare del parametro k e
Esercitazioni di Matematica
 Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
Università degli Studi di Udine Anno Accademico 009/00 Facoltà di Agraria Corsi di Laurea in VIT e STAL Esercitazioni di Matematica novembre 009 Trovare le soluzioni della seguente disequazione: x + +
y retta tangente retta secante y = f(x)
 Retta tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Retta tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
LICEO CLASSICO ANDREA DA PONTEDERA
 ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classe 5A PROGRAMMA DI MATEMATICA svolto fino al 15 aprile (evidenziate in giallo le aggiunte rispetto al file precedente) Intervallo limitato
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classe 5A PROGRAMMA DI MATEMATICA svolto fino al 15 aprile (evidenziate in giallo le aggiunte rispetto al file precedente) Intervallo limitato
Concavità verso il basso (funzione concava) Si dice che in x0 il grafico della funzione f(x) abbia la concavità rivolta verso il basso, se esiste
 CONCAVITA E CONVESSITA DI UNA FUNZIONE. FLESSI. SCHEMA GENERALE PER LO STUDIO DI FUNZIONE. FUNZIONI RAZIONALI E IRRAZIONALI INTERE E FRATTE. TEOREMA DI DE L HOSPITAL CON APPLICAZIONI AI LIMITI. 1 Concavit{
CONCAVITA E CONVESSITA DI UNA FUNZIONE. FLESSI. SCHEMA GENERALE PER LO STUDIO DI FUNZIONE. FUNZIONI RAZIONALI E IRRAZIONALI INTERE E FRATTE. TEOREMA DI DE L HOSPITAL CON APPLICAZIONI AI LIMITI. 1 Concavit{
y x y x A (x 1,y 1 ) = (c, f(c)) B(x 2,y 2 ) = (c+h, f(c+h)) m =
 DERIVATA DI UNA FUNZIONE IN UN PUNTO SIGNIFICATO GEOMETRICO. EQUAZIONE DELLA RETTA TANGENTE AL GRAFICO NEL PUNTO DI TANGENZA. REGOLE DI DERIVAZIONE. CONTINUITA E DERIVABILITA PUNTI DI NON DERIVABILITA
DERIVATA DI UNA FUNZIONE IN UN PUNTO SIGNIFICATO GEOMETRICO. EQUAZIONE DELLA RETTA TANGENTE AL GRAFICO NEL PUNTO DI TANGENZA. REGOLE DI DERIVAZIONE. CONTINUITA E DERIVABILITA PUNTI DI NON DERIVABILITA
I.T.T.L. BUCCARI CAGLIARI PROGRAMMA DI MATEMATICA E COMPLEMENTI DOCENTE: PODDA GIAMPAOLO
 I.T.T.L. BUCCARI CAGLIARI ANNO SCOLASTICO 2017/201 8 CLASSE II I E PROGRAMMA DI MATEMATICA E COMPLEMENTI DOCENTE: PODDA GIAMPAOLO IL PIANO CARTESIANO L ascissa di un punto su una retta: la distanza di
I.T.T.L. BUCCARI CAGLIARI ANNO SCOLASTICO 2017/201 8 CLASSE II I E PROGRAMMA DI MATEMATICA E COMPLEMENTI DOCENTE: PODDA GIAMPAOLO IL PIANO CARTESIANO L ascissa di un punto su una retta: la distanza di
1. Mercoledì 07/03/2018, ore: 2(2) Introduzione e presentazione del corso. Richiami: i numeri naturali, interi, razionali e reali.
 Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: 7 giugno 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: 7 giugno 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
Docente: Analisi e Geometria 1 Prima Prova 22 Novembre 2016 Compito F Cognome: Nome: Matricola:
 Es. 1 Es. 2 Es. Teoria: Totale Numero di iscrizione alla prova scritta: Docente: Analisi e Geometria 1 Prima Prova 22 Novembre 2016 Compito F Cognome: Nome: Matricola: Punteggi: Es.1: 7; Es.2: 7; Es.:
Es. 1 Es. 2 Es. Teoria: Totale Numero di iscrizione alla prova scritta: Docente: Analisi e Geometria 1 Prima Prova 22 Novembre 2016 Compito F Cognome: Nome: Matricola: Punteggi: Es.1: 7; Es.2: 7; Es.:
Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile
 Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di Bari) Analisi Matematica
Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di Bari) Analisi Matematica
ANALISI MATEMATICA 1 Commissione L. Caravenna, V. Casarino, S. Zoccante Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza
 ANALISI MATEMATICA Commissione L Caravenna, V Casarino, S Zoccante Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Nome, Cognome, numero di matricola: Vicenza, 7 Luglio 205 TEMA - parte B Esercizio
ANALISI MATEMATICA Commissione L Caravenna, V Casarino, S Zoccante Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Nome, Cognome, numero di matricola: Vicenza, 7 Luglio 205 TEMA - parte B Esercizio
Elenco moduli Argomenti Strumenti / Testi Letture / Metodi. partecipazione degli alunni. 2 Completamento equazioni e disequazioni.
 Pagina 1 di 5 DISCIPLINA: MATEMATICA E LABORATORIO INDIRIZZO: IGEA CLASSE: IV FM DOCENTE : Cornelio Terreni Elenco moduli Argomenti Strumenti / Testi Letture / Metodi 1 Matematica RIPASSO e COMPLETAMENTO:
Pagina 1 di 5 DISCIPLINA: MATEMATICA E LABORATORIO INDIRIZZO: IGEA CLASSE: IV FM DOCENTE : Cornelio Terreni Elenco moduli Argomenti Strumenti / Testi Letture / Metodi 1 Matematica RIPASSO e COMPLETAMENTO:
Studiamo adesso il comportamento di f(x) alla frontiera del dominio. Si. x 0 lim f(x) = lim. x 2 +
 Esercizi del 2//09. Data la funzione f(x) = ln(x 2 2x) (a) trovare il dominio, gli eventuali asintoti e gli intervalli in cui la funzione cresce o decresce. Disegnare il grafico della funzione. (b) Scrivere
Esercizi del 2//09. Data la funzione f(x) = ln(x 2 2x) (a) trovare il dominio, gli eventuali asintoti e gli intervalli in cui la funzione cresce o decresce. Disegnare il grafico della funzione. (b) Scrivere
Calcolo Differenziale. Corsi di Laurea in Tecniche di Radiologia ecc... A.A Analisi Matematica - Calcolo Differenziale - p.
 Calcolo Differenziale Corsi di Laurea in Tecniche di Radiologia ecc... A.A. 2010-2011 - Analisi Matematica - Calcolo Differenziale - p. 1/33 Velocità istantanea Percorriamo il tratto di strada tra Udine
Calcolo Differenziale Corsi di Laurea in Tecniche di Radiologia ecc... A.A. 2010-2011 - Analisi Matematica - Calcolo Differenziale - p. 1/33 Velocità istantanea Percorriamo il tratto di strada tra Udine
Programmazione disciplinare: Matematica 5 anno
 Programmazione disciplinare: Matematica 5 anno Modulo 1/Ripasso: Funzione reale di variabile reale CONTENUTI Funzione fra due insiemi. Funzione reale di variabile reale: definizione e classificazione.
Programmazione disciplinare: Matematica 5 anno Modulo 1/Ripasso: Funzione reale di variabile reale CONTENUTI Funzione fra due insiemi. Funzione reale di variabile reale: definizione e classificazione.
MATEMATICA MATURITA LINGUISTICA. Istituto Paritario A.Ruiz Istituto Paritario A.Ruiz
 MATEMATICA MATURITA LINGUISTICA Istituto Paritario A.Ruiz Istituto Paritario A.Ruiz 1 MATEMATICA MATURITA LINGUISTICA 1. CLASSIFICAZIONE FUNZIONI FUNZIONI ALGEBRICHE (in cui compaiono le quattro operazioni):
MATEMATICA MATURITA LINGUISTICA Istituto Paritario A.Ruiz Istituto Paritario A.Ruiz 1 MATEMATICA MATURITA LINGUISTICA 1. CLASSIFICAZIONE FUNZIONI FUNZIONI ALGEBRICHE (in cui compaiono le quattro operazioni):
PROGRAMMA DIDATTICO CONSUNTIVO CLASSE 4 DI UDA1: RICHIAMI E COMPLEMENTI UDA2: ESPONENZIALI E LOGARITMI. Docente Disciplina
 PROGRAMMA DIDATTICO CONSUNTIVO CLASSE 4 DI Docente Disciplina LEGATO ANTONELLA MATEMATICA UDA1: RICHIAMI E COMPLEMENTI Periodo: settembre Equazioni e disequazioni con i valori assoluti; Equazioni e disequazioni
PROGRAMMA DIDATTICO CONSUNTIVO CLASSE 4 DI Docente Disciplina LEGATO ANTONELLA MATEMATICA UDA1: RICHIAMI E COMPLEMENTI Periodo: settembre Equazioni e disequazioni con i valori assoluti; Equazioni e disequazioni
ISTITUTO ISTRUZIONE SECONDARIA SUPERIORE. Leonardo da Vinci. Martina Franca ANNO SCOLASTICO 2015/2016
 ISTITUTO ISTRUZIONE SECONDARIA SUPERIORE Leonardo da Vinci Martina Franca ANNO SCOLASTICO 2015/2016 Disciplina: MATEMATICA APPLICATA Classe : 3 ^ A A.F.M. Docente : Prof. GIANGASPERO Francesco Testo :
ISTITUTO ISTRUZIONE SECONDARIA SUPERIORE Leonardo da Vinci Martina Franca ANNO SCOLASTICO 2015/2016 Disciplina: MATEMATICA APPLICATA Classe : 3 ^ A A.F.M. Docente : Prof. GIANGASPERO Francesco Testo :
Istituzioni di Matematiche quarta parte
 Istituzioni di Matematiche quarta parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 22 index Derivate 1 Derivate 2 Teoremi
Istituzioni di Matematiche quarta parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 22 index Derivate 1 Derivate 2 Teoremi
Lo studio di funzione. 18 febbraio 2013
 Lo studio di funzione 18 febbraio 2013 1 Indice 1 Lo studio di funzione 3 1.1 Dominio di funzioni......................... 3 1.1.1 Domini di funzioni elementari............... 3 1.1.2 Funzioni composte,
Lo studio di funzione 18 febbraio 2013 1 Indice 1 Lo studio di funzione 3 1.1 Dominio di funzioni......................... 3 1.1.1 Domini di funzioni elementari............... 3 1.1.2 Funzioni composte,
è vietato consultare libri, appunti,...etc e lasciare l aula prima della conclusione della prova
 Facoltà di Agraria - Anno Accademico 2009-2010 24 febbraio 2010 1) L equazione 2x 3 3x 2 12x + 7 = 0 ha a)1 radice reale e 2 complesse b)nessuna radice reale c)2 radici reali ed 1 complessa d)3 radici
Facoltà di Agraria - Anno Accademico 2009-2010 24 febbraio 2010 1) L equazione 2x 3 3x 2 12x + 7 = 0 ha a)1 radice reale e 2 complesse b)nessuna radice reale c)2 radici reali ed 1 complessa d)3 radici
Argomento 7 - Studi di funzioni Soluzioni Esercizi
 Argomento 7 - Studi di funzioni Soluzioni Esercizi Sol. E. 7. f() = log + 4 Insieme di definizione : Limiti : 4 log + = + 0 + (confronto tra infiniti in cui prevale la potenza) 4 log + = log = + + + Notiamo
Argomento 7 - Studi di funzioni Soluzioni Esercizi Sol. E. 7. f() = log + 4 Insieme di definizione : Limiti : 4 log + = + 0 + (confronto tra infiniti in cui prevale la potenza) 4 log + = log = + + + Notiamo
Retta Tangente. y retta tangente. retta secante y = f(x) f(x )
 Retta Tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Retta Tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Osservazione: ogni informazione ricavata va inserita immediatamente nel grafico.
 1. Dominio 2. Limiti => eventuali asintoti 3. Studio del segno (opzionale) Osservazione: ogni informazione ricavata va inserita immediatamente nel grafico. Se x x0 f(x) = ± x = x 0 asintoto verticale Se
1. Dominio 2. Limiti => eventuali asintoti 3. Studio del segno (opzionale) Osservazione: ogni informazione ricavata va inserita immediatamente nel grafico. Se x x0 f(x) = ± x = x 0 asintoto verticale Se
Conoscenze. L operazione di divisione (la divisione di due polinomi) - La divisibilità fra polinomi (la regola di Ruffini, il teorema. del resto.
 Classe: TERZA (Liceo Artistico) Pagina 1 / 2 della Matematica La scomposizione dei polinomi in fattori primi L operazione di divisione (la divisione di due polinomi) - La divisibilità fra polinomi (la
Classe: TERZA (Liceo Artistico) Pagina 1 / 2 della Matematica La scomposizione dei polinomi in fattori primi L operazione di divisione (la divisione di due polinomi) - La divisibilità fra polinomi (la
4. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE.
 4. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso rappresenta l evoluzione di un fenomeno al passare del tempo. Se siamo interessati a sapere con che rapidità il fenomeno si evolve
4. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso rappresenta l evoluzione di un fenomeno al passare del tempo. Se siamo interessati a sapere con che rapidità il fenomeno si evolve
Esempi di QUESITI sulle derivate con risoluzione
 Esempi di QUESITI sulle derivate con risoluzione 1 Sia data una funzione f(x) continua nel punto x 0 : allora essa è anche derivabile in x 0? Se invece l'ipotesi prevede che f(x) è derivabile in x 0, si
Esempi di QUESITI sulle derivate con risoluzione 1 Sia data una funzione f(x) continua nel punto x 0 : allora essa è anche derivabile in x 0? Se invece l'ipotesi prevede che f(x) è derivabile in x 0, si
Istituzioni di matematica
 Istituzioni di matematica TUTORATO 2 - Soluzioni Mercoledì 28 novembre 2018 Esercizio 1. Studiare la seguente funzione e tracciarne il graco f(x) = x 3 3x 2 - Il dominio di denizione è l'insieme D = R
Istituzioni di matematica TUTORATO 2 - Soluzioni Mercoledì 28 novembre 2018 Esercizio 1. Studiare la seguente funzione e tracciarne il graco f(x) = x 3 3x 2 - Il dominio di denizione è l'insieme D = R
Modulo di Matematica
 Università degli Studi di Udine nno ccademico 5/6 Corso di Laurea in Biotecnologie Modulo di Matematica Esame del 4/7/6 N.B.: scrivere nome, cognome e numero di matricola su ogni foglio consegnato. Tempo
Università degli Studi di Udine nno ccademico 5/6 Corso di Laurea in Biotecnologie Modulo di Matematica Esame del 4/7/6 N.B.: scrivere nome, cognome e numero di matricola su ogni foglio consegnato. Tempo
Richiami di matematica
 corso di Economia Politica I (sede di San Benedetto del Tronto) Nota Lo scopo di queste pagine è sostanzialmente quello di richiamare l attenzione degli studenti su alcuni strumenti analitici utili per
corso di Economia Politica I (sede di San Benedetto del Tronto) Nota Lo scopo di queste pagine è sostanzialmente quello di richiamare l attenzione degli studenti su alcuni strumenti analitici utili per
Lezione 18 (8 gennaio) Limiti
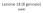 Lezione 18 (8 gennaio) Limiti Ripasso f x = ln 3 x 1 D = (1, + ) ln 3 x 1 + x 1 = ln 3 1 + 1 = ln 3 = ln(+ ) = + 0 + ln 3 x + x 1 = ln 3 + 1 = ln 3 + = ln(0+ ) = 1 Esempi di forme indeterminate x + x3
Lezione 18 (8 gennaio) Limiti Ripasso f x = ln 3 x 1 D = (1, + ) ln 3 x 1 + x 1 = ln 3 1 + 1 = ln 3 = ln(+ ) = + 0 + ln 3 x + x 1 = ln 3 + 1 = ln 3 + = ln(0+ ) = 1 Esempi di forme indeterminate x + x3
SYLLABUS DI ANALISI 5B DON BOSCO
 SYLLABUS DI ANALISI 5B DON BOSCO 2016-17 Si precisa che, con questo syllabus, l intenzione non è quella di ridurre l apprendimento della matematica allo studio mnemonico di una serie di procedure. Al contrario,
SYLLABUS DI ANALISI 5B DON BOSCO 2016-17 Si precisa che, con questo syllabus, l intenzione non è quella di ridurre l apprendimento della matematica allo studio mnemonico di una serie di procedure. Al contrario,
Liceo Scientifico Paritario R. Bruni Padova, loc. Ponte di Brenta, 15/01/2019. Verifica scritta di Matematica Classe V
 Liceo Scientifico Paritario R. Bruni Padova, loc. Ponte di Brenta, 15/01/2019 Verifica scritta di Matematica Classe V Soluzione Risolvi 4 degli 8 quesiti proposti. Ogni quesito vale 25 p.ti. 1. Un corpo
Liceo Scientifico Paritario R. Bruni Padova, loc. Ponte di Brenta, 15/01/2019 Verifica scritta di Matematica Classe V Soluzione Risolvi 4 degli 8 quesiti proposti. Ogni quesito vale 25 p.ti. 1. Un corpo
Programmazione disciplinare: Matematica 5 anno
 Programmazione disciplinare: Matematica 5 anno CONTENUTI RISULTATI DI APPRENDIMENTO (Competenze) CONOSCENZE ABILITA TEMPI (settimane) Funzione fra due insiemi. di Saper riconoscere se una relazione è anche
Programmazione disciplinare: Matematica 5 anno CONTENUTI RISULTATI DI APPRENDIMENTO (Competenze) CONOSCENZE ABILITA TEMPI (settimane) Funzione fra due insiemi. di Saper riconoscere se una relazione è anche
14. Studio grafico completo di funzioni
 14. Studio grafico completo di funzioni Davide Catania davide.catania@unibs.it Esercitazioni di Analisi Matematica 1 Studio elementare di funzioni (1) Trova il dominio. data f (x) (2) Studia la simmetria
14. Studio grafico completo di funzioni Davide Catania davide.catania@unibs.it Esercitazioni di Analisi Matematica 1 Studio elementare di funzioni (1) Trova il dominio. data f (x) (2) Studia la simmetria
FUNZIONI REALI DI UNA VARIABILE REALE
 FUNZIONI REALI DI UNA VARIABILE REALE INTERVALLI Per definire il campo di esistenza (o dominio) di una funzione reale di variabile reale y=f()si devono indicare talvolta insiemi di numeri reali che su
FUNZIONI REALI DI UNA VARIABILE REALE INTERVALLI Per definire il campo di esistenza (o dominio) di una funzione reale di variabile reale y=f()si devono indicare talvolta insiemi di numeri reali che su
Programma svolto a.s. 2017/2018 Classe 1H Materia: Matematica Docente: De Rossi Francesco
 Classe 1H Materia: Matematica Docente: De Rossi Francesco - Matematica multimediale. bianco Vol 1 Autori: M. Bergamini, G. Barozzi Casa Editrice: Zanichelli codice ISBN 978888334671 Capitolo 1 Insiemi
Classe 1H Materia: Matematica Docente: De Rossi Francesco - Matematica multimediale. bianco Vol 1 Autori: M. Bergamini, G. Barozzi Casa Editrice: Zanichelli codice ISBN 978888334671 Capitolo 1 Insiemi
Matematica per Economia Finanza e Management
 School of Economics and Management Matematica per Economia Finanza e Management A.A. 2018/2019 Annuale Prof. Paolo Crespi E-mail Office pcrespi@liuc.it Piano Terra Antistante Torre Phone +39-0331.572418
School of Economics and Management Matematica per Economia Finanza e Management A.A. 2018/2019 Annuale Prof. Paolo Crespi E-mail Office pcrespi@liuc.it Piano Terra Antistante Torre Phone +39-0331.572418
Matematica per Economia Finanza e Management
 School of Economics and Management Matematica per Economia Finanza e Management A.A. 2018/2019 Annuale Prof. Paolo Crespi E-mail Office pcrespi@liuc.it Piano Terra Antistante Torre Phone +39-0331.572418
School of Economics and Management Matematica per Economia Finanza e Management A.A. 2018/2019 Annuale Prof. Paolo Crespi E-mail Office pcrespi@liuc.it Piano Terra Antistante Torre Phone +39-0331.572418
Matematica con elementi di statistica ESERCIZI sui limiti Corso di Laurea in Biotecnologie - anno acc. 2014/2015
 Calcolare i seguenti iti. Esercizio 1. Esercizio 2. Esercizio 3. Esercizio 4. Matematica con elementi di statistica ESERCIZI sui iti Corso di Laurea in Biotecnologie - anno acc. 2014/2015 Esercizi 6: iti
Calcolare i seguenti iti. Esercizio 1. Esercizio 2. Esercizio 3. Esercizio 4. Matematica con elementi di statistica ESERCIZI sui iti Corso di Laurea in Biotecnologie - anno acc. 2014/2015 Esercizi 6: iti
Matematica. Tutorato Attivo: Derivate. Alessio Bianchi. Matematica 20 maggio 2017
 Matematica Tutorato Attivo: Derivate Alessio Bianchi email: alessio.bianchi02@universitadipavia.it Home page: https://bianchiunipv.wordpress.com/ Matematica 20 maggio 2017 Alessio Bianchi Tutorato Attivo:
Matematica Tutorato Attivo: Derivate Alessio Bianchi email: alessio.bianchi02@universitadipavia.it Home page: https://bianchiunipv.wordpress.com/ Matematica 20 maggio 2017 Alessio Bianchi Tutorato Attivo:
Istituto d Istruzione Superiore A. Tilgher Ercolano (Na)
 Premessa Istituto d Istruzione Superiore A. Tilgher Ercolano (Na) Questa breve trattazione non vuole costituire una guida completa ed esauriente sull argomento, ma vuole fornire solamente i concetti fondamentali
Premessa Istituto d Istruzione Superiore A. Tilgher Ercolano (Na) Questa breve trattazione non vuole costituire una guida completa ed esauriente sull argomento, ma vuole fornire solamente i concetti fondamentali
RAPPORTO INCREMENTALE E DERIVATA PRIMA. Agg Tutorial di Paola Barberis
 RAPPORTO INCREMENTALE E DERIVATA PRIMA Agg 2017 - Tutorial di Paola Barberis Come misurare la CRESCITA MEDIA di una funzione fra due punti A e B? introduzione A=(1;3) Incremento orizzontale B=(4;5) y=f(x)
RAPPORTO INCREMENTALE E DERIVATA PRIMA Agg 2017 - Tutorial di Paola Barberis Come misurare la CRESCITA MEDIA di una funzione fra due punti A e B? introduzione A=(1;3) Incremento orizzontale B=(4;5) y=f(x)
Esame di MATEMATICA CORSO BASE del
 Esame di MATEMATICA CORSO BASE del Cognome Matricola Nome Esercizio 1. Si consideri il seguente sistema 2x 3y + z =5 x ky +2z = k kx y z = 1 Si trovino il numero delle soluzioni al variare del parametro
Esame di MATEMATICA CORSO BASE del Cognome Matricola Nome Esercizio 1. Si consideri il seguente sistema 2x 3y + z =5 x ky +2z = k kx y z = 1 Si trovino il numero delle soluzioni al variare del parametro
Matematica per Economia Finanza e Management
 School of Economics and Management Matematica per Economia Finanza e Management A.A. 2015/2016 Annuale Prof. Paolo Crespi E-mail Office pcrespi@liuc.it Piano Terra Antistante Torre Phone +39-0331.572418
School of Economics and Management Matematica per Economia Finanza e Management A.A. 2015/2016 Annuale Prof. Paolo Crespi E-mail Office pcrespi@liuc.it Piano Terra Antistante Torre Phone +39-0331.572418
Esercizi svolti. a 2 x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.
 Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Esercizi svolti 1. Sia sin(x ) f(x) = x ( 1 + x 1 ) se x > 0 a x + 3 se x 0; determinare a in modo che f risulti continua nel suo dominio.. Scrivere l equazione della retta tangente nel punto di ascissa
Coordinate Cartesiane nel Piano
 Coordinate Cartesiane nel Piano O = (0,0) origine degli assi x ascissa, y ordinata sistemi monometrici: stessa unità di misura sui due assi x, y sistemi dimetrici: unità di misura diverse sui due assi
Coordinate Cartesiane nel Piano O = (0,0) origine degli assi x ascissa, y ordinata sistemi monometrici: stessa unità di misura sui due assi x, y sistemi dimetrici: unità di misura diverse sui due assi
LA DERIVATA DI UNA FUNZIONE. Prof Giovanni Ianne
 LA ERIVATA I UNA FUNZIONE Pro. Giovanni Ianne /22 Come si determina la retta tangente a una curva in un punto P? Per una circonerenza, la tangente è la retta che interseca la curva solo in P. IL PROBLEMA
LA ERIVATA I UNA FUNZIONE Pro. Giovanni Ianne /22 Come si determina la retta tangente a una curva in un punto P? Per una circonerenza, la tangente è la retta che interseca la curva solo in P. IL PROBLEMA
Lezione 4 (8/10/2014)
 Lezione 4 (8/10/2014) Esercizi svolti a lezione Nota 1. Teorema del valore intermedio: Se la funzione f(x) è continua in [a,b] e si a: f(a) < k (f(a) > k), f(b) > k (f(b) < k) allora esiste almeno un punto
Lezione 4 (8/10/2014) Esercizi svolti a lezione Nota 1. Teorema del valore intermedio: Se la funzione f(x) è continua in [a,b] e si a: f(a) < k (f(a) > k), f(b) > k (f(b) < k) allora esiste almeno un punto
e 2x2 1 (x 2 + 2x 2) ln x
 Corso di laurea in Ingegneria delle Costruzioni A.A. 2016-17 Analisi Matematica - Esercitazione del 04-01-2017 Ripasso di alcuni argomenti in programma Gli esercizi sono divisi in più pagine, per separare
Corso di laurea in Ingegneria delle Costruzioni A.A. 2016-17 Analisi Matematica - Esercitazione del 04-01-2017 Ripasso di alcuni argomenti in programma Gli esercizi sono divisi in più pagine, per separare
I TEOREMI DEL CALCOLO DIFFERENZIALE
 I TEOREMI DEL CALCOLO DIFFERENZIALE 1. DEFINIZIONI. TEOREMI DEL CALCOLO DIFFERENZIALE.1 TEOREMA DELL ESTREMANTE LOCALE. TEOREMI DI ROLLE, CAUCHY, LAGRANGE.3 TEOREMI CONSEGUENTI AL T. DI LAGRANGE 3. DETERMINAZIONE
I TEOREMI DEL CALCOLO DIFFERENZIALE 1. DEFINIZIONI. TEOREMI DEL CALCOLO DIFFERENZIALE.1 TEOREMA DELL ESTREMANTE LOCALE. TEOREMI DI ROLLE, CAUCHY, LAGRANGE.3 TEOREMI CONSEGUENTI AL T. DI LAGRANGE 3. DETERMINAZIONE
1. Teorema del valor medio D ora in poi ciascun intervallo considerato verra tacitamente assunto non ridotto
 Lezione del 22 ottobre. 1. Teorema del valor medio D ora in poi ciascun intervallo considerato verra tacitamente assunto non ridotto ad un punto. Data una funzione f definita su un intervallo [a, b], derivabile
Lezione del 22 ottobre. 1. Teorema del valor medio D ora in poi ciascun intervallo considerato verra tacitamente assunto non ridotto ad un punto. Data una funzione f definita su un intervallo [a, b], derivabile
Matematica per Economia Finanza e Management
 School of Economics and Management Matematica per Economia Finanza e Management A.A. 2017/2018 Annuale Prof. Paolo Crespi E-mail Office pcrespi@liuc.it Piano Terra Antistante Torre Phone +39-0331.572418
School of Economics and Management Matematica per Economia Finanza e Management A.A. 2017/2018 Annuale Prof. Paolo Crespi E-mail Office pcrespi@liuc.it Piano Terra Antistante Torre Phone +39-0331.572418
4.3 Teoremi sulle funzioni derivabili
 4.3 Teoremi sulle funzioni derivabili Teorema (di Fermat) Sia : [, ] ℝ una funzione derivabile in (, ) e si un punto di massimo o minimo (relativo o assoluto) per. Allora 0 si dice anche che è un punto
4.3 Teoremi sulle funzioni derivabili Teorema (di Fermat) Sia : [, ] ℝ una funzione derivabile in (, ) e si un punto di massimo o minimo (relativo o assoluto) per. Allora 0 si dice anche che è un punto
Per cominciare, osserviamo che f si ottiene traslando di 2, nella direzione negativa dell asse x, la funzione. g(x) = x e x
 Studi di funzione 1) Studiare la funzione definita da f(x) = x + 2 e (x+2). Per cominciare, osserviamo che f si ottiene traslando di 2, nella direzione negativa dell asse x, la funzione g(x) = x e x cioè
Studi di funzione 1) Studiare la funzione definita da f(x) = x + 2 e (x+2). Per cominciare, osserviamo che f si ottiene traslando di 2, nella direzione negativa dell asse x, la funzione g(x) = x e x cioè
Programma svolto a.s. 2018/2019 Classe 1H Materia: Matematica Docente: De Rossi Francesco
 Programma svolto a.s. 2018/2019 Classe 1H Materia: Matematica Docente: De Rossi Francesco - Matematica multimediale. bianco Vol 1 Autori: M. Bergamini, G. Barozzi Casa Editrice: Zanichelli codice ISBN
Programma svolto a.s. 2018/2019 Classe 1H Materia: Matematica Docente: De Rossi Francesco - Matematica multimediale. bianco Vol 1 Autori: M. Bergamini, G. Barozzi Casa Editrice: Zanichelli codice ISBN
Lezioni di Matematica 1 - I modulo
 Lezioni di Matematica 1 - I modulo Luciano Battaia 14 novembre 2008 L. Battaia - http://www.batmath.it Matematica 1 - I mod. Lezione del 14/11/2008 1 / 22 Cr-decr-max-min Esempio 1 Esempio 2 Esempio 3
Lezioni di Matematica 1 - I modulo Luciano Battaia 14 novembre 2008 L. Battaia - http://www.batmath.it Matematica 1 - I mod. Lezione del 14/11/2008 1 / 22 Cr-decr-max-min Esempio 1 Esempio 2 Esempio 3
Matematica classe 5 C a.s. 2012/2013
 Matematica classe 5 C a.s. 2012/2013 Asintoti e grafici 1) Una funzione y = f(x) gode delle seguenti caratteristiche: D / 4, y 0 se x 0 x 2, lim, 3. Rappresentare un grafico qualitativo della funzione.
Matematica classe 5 C a.s. 2012/2013 Asintoti e grafici 1) Una funzione y = f(x) gode delle seguenti caratteristiche: D / 4, y 0 se x 0 x 2, lim, 3. Rappresentare un grafico qualitativo della funzione.
STUDIO DEL GRAFICO DI UNA FUNZIONE
 STUDIO DEL GRAFICO DI UNA FUNZIONE 1 Richiami Teorema 1 (Test di monotonia). Sia f : (a, b) R una funzione derivabile. Allora f è monotona crescente (risp. decrescente) in (a, b) se e solo se f () 0 (risp.
STUDIO DEL GRAFICO DI UNA FUNZIONE 1 Richiami Teorema 1 (Test di monotonia). Sia f : (a, b) R una funzione derivabile. Allora f è monotona crescente (risp. decrescente) in (a, b) se e solo se f () 0 (risp.
Lezione 11 (30 novembre)
 Lezione 11 (30 novembre) Teorema di De l Hopital Massimi e minimi assoluti e relativi Funzioni limitate superiormente e inferiormente Legame tra derivata prima e crescita e decrescita della funzione Derivata
Lezione 11 (30 novembre) Teorema di De l Hopital Massimi e minimi assoluti e relativi Funzioni limitate superiormente e inferiormente Legame tra derivata prima e crescita e decrescita della funzione Derivata
12/10/05 (2 ore): Esercizi vari sull ellisse, iperbole, parabola. Disequazioni in due variabili. Equazione dell iperbole equilatera. Esempi.
 Università degli Studi di Trento Facolta di Scienze Cognitive Corso di Laurea in Scienze e Tecniche di Psicologia Cognitiva Applicata Corso di Analisi Matematica - a.a. 2005/06 Docente: Prof. Anneliese
Università degli Studi di Trento Facolta di Scienze Cognitive Corso di Laurea in Scienze e Tecniche di Psicologia Cognitiva Applicata Corso di Analisi Matematica - a.a. 2005/06 Docente: Prof. Anneliese
e verificare che la parabola e la funzione 2 logaritmica hanno la stessa tangente in A 2,0
 UNIVERSITÀ DEGLI STUDI DI VERONA CORSO DI LAUREA IN SCIENZE E TECNOLOGIE VITICOLE ED ENOLOGICHE Esame di MATEMATICA (A) San Floriano, /0/07 Informazioni personali Si prega di indicare il proprio nome,
UNIVERSITÀ DEGLI STUDI DI VERONA CORSO DI LAUREA IN SCIENZE E TECNOLOGIE VITICOLE ED ENOLOGICHE Esame di MATEMATICA (A) San Floriano, /0/07 Informazioni personali Si prega di indicare il proprio nome,
Retta Tangente. y retta tangente. retta secante y = f(x) f(x )
 Retta Tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Retta Tangente f(x ) 1 y P 1 retta secante y = f(x) y retta tangente y = f(x) f(x ) 0 P 0 f(x ) 0 P 0 O x 0 x 1 x quando P tende a P 0 1 O x 0 x Consideriamo una funzione continua f. Siano P 0 = (x 0,
Corso di Analisi Matematica. Calcolo differenziale
 a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Calcolo differenziale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Calcolo differenziale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
Matematica A Corso di Laurea in Chimica. Prova scritta del Tema A
 Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
Matematica A Corso di Laurea in Chimica Prova scritta del 7..6 Tema A P) Data la funzione f(x) = ex+ x determinarne (a) campo di esistenza; (b) zeri e segno; (c) iti agli estremi del campo di esistenza
Quesito 1 (1/0/-0.25 punti)
 NOME COGNOME Politecnico di Milano Analisi Matematica 1 Anno Accademico 2017-2018 Prof. Ettore Lanzarone Prima prova in itinere 15 novembre 2017 Parte A: punteggio 6/0; soglia minima per passare la prova
NOME COGNOME Politecnico di Milano Analisi Matematica 1 Anno Accademico 2017-2018 Prof. Ettore Lanzarone Prima prova in itinere 15 novembre 2017 Parte A: punteggio 6/0; soglia minima per passare la prova
Analisi Matematica 1 (prof. G. Cupini) (CdS Astronomia - Univ. Bologna) REGISTRO DELLE LEZIONI A.A
 Analisi Matematica 1 (prof. G. Cupini) (CdS Astronomia - Univ. Bologna) REGISTRO DELLE LEZIONI A.A.2015-2016 22 SETTEMBRE 2015 3 ore 14-17 Insiemi e operazioni tra insiemi. Numeri reali. Assiomi dei numeri
Analisi Matematica 1 (prof. G. Cupini) (CdS Astronomia - Univ. Bologna) REGISTRO DELLE LEZIONI A.A.2015-2016 22 SETTEMBRE 2015 3 ore 14-17 Insiemi e operazioni tra insiemi. Numeri reali. Assiomi dei numeri
Politecnico di Milano Ingegneria Industriale Analisi e Geometria 1 Primo compito in itinere 21 Novembre 2016
 Politecnico di Milano Ingegneria Industriale Analisi e Geometria Primo compito in itinere Novembre 0 Cognome: Nome: Matricola: Compito A T: 5 punti T: punti Totale Es: 7 punti Es: 7 punti Es: 0 punti Totale
Politecnico di Milano Ingegneria Industriale Analisi e Geometria Primo compito in itinere Novembre 0 Cognome: Nome: Matricola: Compito A T: 5 punti T: punti Totale Es: 7 punti Es: 7 punti Es: 0 punti Totale
Università degli Studi di Cagliari Dipartimento di Matematica e Informatica Corso di Laurea in Chimica. Matematica 2.
 Università degli Studi di Cagliari Dipartimento di Matematica e Informatica Corso di Laurea in Chimica Matematica 2 9 Maggio 2018 Schema Lezione numero 15 Outiline Regola di derivazione delle funzioni
Università degli Studi di Cagliari Dipartimento di Matematica e Informatica Corso di Laurea in Chimica Matematica 2 9 Maggio 2018 Schema Lezione numero 15 Outiline Regola di derivazione delle funzioni
Derivate. Rette per uno e per due punti. Rette per uno e per due punti
 Introduzione Rette per uno e per due punti Rette per uno e per due punti Rette secanti e tangenti Derivata d una funzione in un punto successive Derivabilità a destra e a sinistra Rette per uno e per due
Introduzione Rette per uno e per due punti Rette per uno e per due punti Rette secanti e tangenti Derivata d una funzione in un punto successive Derivabilità a destra e a sinistra Rette per uno e per due
PROGRAMMA DI MATEMATICA APPLICATA Classe III SIA sez. A A.S. 2015/2016
 PROGRAMMA DI MATEMATICA APPLICATA Classe III SIA sez. A A.S. 2015/2016 LE DISEQUAZIONI 1. Le disequazioni di primo e secondo grado 2. Le disequazioni di grado superiore al secondo e le disequazioni fratte
PROGRAMMA DI MATEMATICA APPLICATA Classe III SIA sez. A A.S. 2015/2016 LE DISEQUAZIONI 1. Le disequazioni di primo e secondo grado 2. Le disequazioni di grado superiore al secondo e le disequazioni fratte
Le Funzioni. Modulo Esponenziali Logaritmiche. Prof.ssa Maddalena Dominijanni
 Le Funzioni Modulo Esponenziali Logaritmiche Definizione di modulo o valore assoluto Se x è un generico numero reale, il suo modulo o valore assoluto è: x = x se x 0 -x se x
Le Funzioni Modulo Esponenziali Logaritmiche Definizione di modulo o valore assoluto Se x è un generico numero reale, il suo modulo o valore assoluto è: x = x se x 0 -x se x
