STUDIO di FUNZIONE. c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 1
|
|
|
- Teresa Federici
- 7 anni fa
- Visualizzazioni
Transcript
1 STUDIO di FUNZIONE c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 1
2 Punti di estremo: punto di massimo assoluto Def. Sia 0 dom(f) = D. Si dice che 0 è un punto di massimo assoluto per f se f( 0 ) f() dom(f) ovvero f( 0 ) è il massimo dell insieme immagine di f: f( 0 ) = maf() = ma(im(f)). D f( 0 ) im(f) f( 0 ) im(f) dom(f) 0 dom(f) 0 c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 2
3 Punto di massimo relativo Def. Sia 0 dom(f). Si dice che 0 è un punto di massimo relativo per f se esiste un intorno I( 0 ) del punto 0 tale che f( 0 ) f() f( 0 ) I( 0 ) dom(f). f( 0 ) I( 0 ) 0 0 I( 0 ) c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 3
4 Punto di minimo assoluto Sia 0 dom(f) = D. Si dice che 0 è un punto di minimo assoluto per f se f( 0 ) f() dom(f) ovvero f( 0 ) è il minimo dell insieme immagine di f: f( 0 ) = minf() = min(im(f)). D im(f) im(f) 0 0 f( 0 ) dom(f) f( 0 ) dom(f) c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 4
5 Punto di minimo relativo Def. Sia 0 dom(f). Si dice che 0 è un punto di minimo relativo per f se esiste un intorno I( 0 ) del punto 0 tale che f( 0 ) f() I( 0 ) dom(f). f( 0 ) 0 f( 0 ) I( 0 ) I( 0 ) 0 c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 5
6 Osservazioni 1 Per definire i punti di estremo NON abbiamo utilizzato il concetto di derivata, ma solo il confronto dei valori = f(). 2 I punti di massimo relativo e minimo relativo sono detti punti di estremo relativo, mentre i punti di massimo e minimo assoluto sono detti punti di estremo assoluto. 3 Un punto di estremo assoluto è anche punto di estremo relativo, il viceversa non è sempre vero. 4 In un punto di massimo o minimo relativo la funzione può non essere derivabile. 5 Punti angolosi e punti di cuspide sono sempre punti di massimo o di minimo relativo c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 6
7 Punti stazionari (o critici) Def. Un punto 0 dom(f) si dice punto stazionario (o punto critico) per f, se: - f è derivabile in 0 e - f ( 0 ) = 0, ovvero la tangente ad f in 0 è una retta orizzontale Oss. Per definire un punto stazionario serve la definizione di derivata prima. c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 7
8 Esempi Tutti punti di massimo relativo e assoluto. 2 punti angolosi e 1 punto stazionario c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 8
9 Derivata di f agli estremi di un intervallo Se f è definita solo in un intorno sinistro di 0 ed esiste f ( 0) si assume che f sia derivabile in 0 e si definisce f ( 0 ) = f ( 0). (es. f (b) = f (b).) a b Se f è definita solo in un intorno destro di 0 ed esiste f +( 0 ) si assume che f sia derivabile in 0 e si definisce f ( 0 ) = f +( 0 ). (es. f (a) = f +(a)) c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 9
10 Teorema dei punti stazionari di Fermat Sia f definita in un intorno I r ( 0 ) del punto 0 e derivabile in 0. Se 0 è un punto di massimo o minimo relativo per f allora f ( 0 ) = 0, ovvero 0 è un punto stazionario per f. (La dimostrazione sarà svolta nella lezione successiva.) 0 a b a 0 b f NON è derivabile in 0 f è derivabile in 0 0 NON è punto stazionario 0 è punto stazionario In entrambi i casi 0 è un punto di minimo relativo c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 10
11 Ricerca dei punti di estremo I punti di estremo di una funzione vanno ricercati tra i punti dom(f) che sono: punti di non derivabilità (punti angolosi e cuspidi) estremi finiti (in R) del dominio. punti stazionari, f ( 0 ) = 0 (per il teorema di Fermat) =punto di non derivabilità 0 =estremo (in R) del dominio 0 =punto stazionario c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 11
12 Legame fra crescenza/decrescenza e f () Ricordiamo la def. di funzione crescente: Sia I il dominio di una funzione f reale a valori reali, oppure un intervallo contenuto nel dominio di f. Def. La funzione f si dice monotona crescente su I se 1, 2 I, 1 < 2 f( 1 ) f( 2 ). Def. La funzione f si dice monotona strettamente crescente su I se 1, 2 I, 1 < 2 f( 1 ) < f( 2 ). f( 2 ) f( 1 ) = f( 2 ) f( 1 ) I I Risulta impossibile verificare la crescenza e decrescenza di f() mediante la definizione: dovremmo verificare la propr. per infinite coppie di punti! c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 12
13 Criterio del segno della derivata prima Teorema. Sia I dom(f) un intervallo e sia f derivabile su I. Allora f () 0, I f è crescente su I e f () > 0, I f è strettamente crescente su I. (La dimostrazione sarà svolta la lezione successiva) =f() =f () segno derivata.m c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 13
14 f strett. crescente f () > 0 Esempio. f() = 3 +1 è strettamente crescente su R, ma f (0) = 0, ovvero f strett. crescente. non implica f () > c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 14
15 Crescenza/decrescenza e punti di estremo Corollario Sia f derivabile sull intervallo I e sia 0 punto stazionario interno ad I. Se f () 0 < 0 e f () 0 > 0 allora 0 è punto di ma relativo per f (figura a sinistra). Se f () 0 < 0 e f () 0 > 0 allora 0 è punto di min relativo per f (figura a destra) = 0 è p.to di ma. rel = 0 è p.to di min. rel. c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 15
16 Derivata seconda Def. Se f è derivabile in 0, si dice che f è derivabile due volte in 0 e si pone f ( 0 ) := (f ) ( 0 ). f ( 0 ) è detta derivata seconda di f in 0. La funzione che associa ad il valore f (), ove questo sia definito, è detta funzione derivata seconda. Es. f() = , f () = 6 12 f () = , c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 16
17 Convessità e concavità Consideriamo la funzione f(), definita in un intorno del punto 0 e l equazione della retta t tangente ad f nel punto 0 dom(f): t : = t() = f ( 0 )( 0 )+f( 0 ). Def. La funzione f si dice convessa (o volge la concavità verso l alto) in 0 se esiste un intorno I r ( 0 ) di 0 tale che: I r ( 0 ) f() t() e si dice strettamente convessa in 0 se f() > t() 0. = f() = t() 0 c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 17
18 Def. La funzione f si dice concava in 0 se esiste un intorno I r ( 0 ) di 0 tale che: I r ( 0 ) f() t() e si dice strettamente concava in 0 se f() < t() 0. = t() = f() 0 Def. Sia I un intervallo e f derivabile su I. f si dice convessa (risp. concava) su I, se è convessa (risp. concava) in ogni punto di I. c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 18
19 Criterio del segno della derivata seconda Teorema. Se f è una funzione derivabile due volte su I, si ha: f () 0, I f è convessa su I. e f () > 0, I = f è strettamente convessa su I. Osservazione. Se f è strettamente convessa su I, non è detto che f () > 0 su I. Es.: f() = 4. In = 0 si ha f (0) = 0 ed f strettamente convessa su tutto R. c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 19
20 Punti di flesso Def. Sia f una funzione definita e derivabile in un intorno del punto 0. Il punto 0 si dice punto di flesso per f se esiste un intorno sinistro di 0 in cui f è concava ed esiste un intorno destro di 0 in cui f è convessa o, viceversa, se esiste un intorno sinistro di 0 in cui f è convessa ed esiste un intorno destro di 0 in cui f è concava. 0 Oss. Un punto di flesso 0 per cui si ha f ( 0 ) = 0 è detto punto di flesso a tangente orizzontale, mentre un punto di flesso 0 per cui si ha f ( 0 ) 0 è detto punto di flesso a tangente obliqua. 0 c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 20
21 Studio di funzione completo Obiettivo: disegnare il grafico di una funzione = f(). Passi da seguire. 1. Determinare il dom(f) 2. Determinare eventuali simmetrie e periodicità. 3. Determinare possibili asintoti (verticali, orizzontali, obliqui) [questo vuol dire calcolare i limiti di f agli estremi del dominio]. 4. Individuare eventuali punti di discontinuità. 5. Calcolare la derivata prima e determinare il suo dominio, individuando e classificando eventuali punti di non derivabilità. 6. Studiare il segno della derivata prima per individuare dove la funzione è crescente/decrescente. Determinare, se esistono, i punti di estremo della funzione. 7. Calcolare la derivata seconda di f. 8. Studiare il segno della derivata seconda per individuare dove la funzione è convessa/concava. Determinare, se esistono, i punti di flesso della funzione. 9. DISEGNARE IL GRAFICO DI = f() c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 21
22 Riferimenti bibliografici: Canuto Tabacco, Sez. 6.4, 6.7, 6.8, 6.9, Esercizi: Svolgere i vari passi dello studio di funzione per le funzioni elementari viste. Fare lo studio delle seguenti funzioni: 1. f() = f() = log() 3. f() = log() 4. f() = e 1/2 5. f() = e 1/ c Paola Gervasio - Analisi Matematica 1 - A.A. 16/17 Studio di funzione cap6b.pdf 22
STUDIO di FUNZIONE. c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Studio di funzione cap6b.pdf 1
 STUDIO di FUNZIONE c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Studio di funzione cap6b.pdf 1 Punti di estremo: punto di massimo assoluto Def. Sia 0 dom(f) = D. Si dice che 0 è un punto di massimo
STUDIO di FUNZIONE c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Studio di funzione cap6b.pdf 1 Punti di estremo: punto di massimo assoluto Def. Sia 0 dom(f) = D. Si dice che 0 è un punto di massimo
Gli asintoti di una funzione sono rette, quindi possono essere: rette verticali o rette orizzontali o rette oblique.
 Asintoti Gli asintoti di una funzione sono rette, quindi possono essere: rette verticali o rette orizzontali o rette oblique. Asintoti verticali Sia 0 punto di accumulazione per dom(f). La retta = 0 è
Asintoti Gli asintoti di una funzione sono rette, quindi possono essere: rette verticali o rette orizzontali o rette oblique. Asintoti verticali Sia 0 punto di accumulazione per dom(f). La retta = 0 è
Esercizi di Analisi Matematica 1, utili per la preparazione all esame scritto - Seconda parte SOLUZIONI
 Esercizi di Analisi Matematica Esercizi di Analisi Matematica, utili per la preparazione all esame scritto - Seconda parte SOLUZIONI Es. Per ognuna delle seguenti figure, dire se la curva nel piano cartesiano
Esercizi di Analisi Matematica Esercizi di Analisi Matematica, utili per la preparazione all esame scritto - Seconda parte SOLUZIONI Es. Per ognuna delle seguenti figure, dire se la curva nel piano cartesiano
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler)
 Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
STUDIO DEL GRAFICO DI UNA FUNZIONE
 STUDIO DEL GRAFICO DI UNA FUNZIONE 1 Richiami Teorema 1 (Test di monotonia). Sia f : (a, b) R una funzione derivabile. Allora f è monotona crescente (risp. decrescente) in (a, b) se e solo se f () 0 (risp.
STUDIO DEL GRAFICO DI UNA FUNZIONE 1 Richiami Teorema 1 (Test di monotonia). Sia f : (a, b) R una funzione derivabile. Allora f è monotona crescente (risp. decrescente) in (a, b) se e solo se f () 0 (risp.
4.3 Teoremi sulle funzioni derivabili
 4.3 Teoremi sulle funzioni derivabili Teorema (di Fermat) Sia : [, ] ℝ una funzione derivabile in (, ) e si un punto di massimo o minimo (relativo o assoluto) per. Allora 0 si dice anche che è un punto
4.3 Teoremi sulle funzioni derivabili Teorema (di Fermat) Sia : [, ] ℝ una funzione derivabile in (, ) e si un punto di massimo o minimo (relativo o assoluto) per. Allora 0 si dice anche che è un punto
Per cominciare, osserviamo che f si ottiene traslando di 2, nella direzione negativa dell asse x, la funzione. g(x) = x e x
 Studi di funzione 1) Studiare la funzione definita da f(x) = x + e (x+). Per cominciare, osserviamo che f si ottiene traslando di, nella direzione negativa dell asse x, la funzione g(x) = x e x cioè abbiamo
Studi di funzione 1) Studiare la funzione definita da f(x) = x + e (x+). Per cominciare, osserviamo che f si ottiene traslando di, nella direzione negativa dell asse x, la funzione g(x) = x e x cioè abbiamo
CONTINUITA. c Paola Gervasio - Analisi Matematica 1 - A.A. 2018/19 Limiti di funzioni - Funzioni continue cap3b.pdf 1
 CONTINUITA c Paola Gervasio - Analisi Matematica - A.A. 208/9 Limiti di funzioni - Funzioni continue cap3b.pdf Ricordiamo la definizione di limite lim 0 f () = l R: I ε (l), I δ ( 0 ) : dom(f ) I δ ( 0
CONTINUITA c Paola Gervasio - Analisi Matematica - A.A. 208/9 Limiti di funzioni - Funzioni continue cap3b.pdf Ricordiamo la definizione di limite lim 0 f () = l R: I ε (l), I δ ( 0 ) : dom(f ) I δ ( 0
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler)
 Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f è crescente nell intervallo (a, b) se
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f è crescente nell intervallo (a, b) se
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler)
 Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
La derivata. variabile indipendente x. Definiamo f := f(x) f(x 0 ) l incremento (positivo o negativo) della variabile dipendente.
 La derivata Sia f : domf R R; sia x 0 domf, f sia definita in I r (x 0 ) e sia x I r (x 0 ). ments Definiamo x := x x 0 l incremento (positivo o negativo) della f(x 0 ) + x + x) variabile indipendente
La derivata Sia f : domf R R; sia x 0 domf, f sia definita in I r (x 0 ) e sia x I r (x 0 ). ments Definiamo x := x x 0 l incremento (positivo o negativo) della f(x 0 ) + x + x) variabile indipendente
Concavità verso il basso (funzione concava) Si dice che in x0 il grafico della funzione f(x) abbia la concavità rivolta verso il basso, se esiste
 CONCAVITA E CONVESSITA DI UNA FUNZIONE. FLESSI. SCHEMA GENERALE PER LO STUDIO DI FUNZIONE. FUNZIONI RAZIONALI E IRRAZIONALI INTERE E FRATTE. TEOREMA DI DE L HOSPITAL CON APPLICAZIONI AI LIMITI. 1 Concavit{
CONCAVITA E CONVESSITA DI UNA FUNZIONE. FLESSI. SCHEMA GENERALE PER LO STUDIO DI FUNZIONE. FUNZIONI RAZIONALI E IRRAZIONALI INTERE E FRATTE. TEOREMA DI DE L HOSPITAL CON APPLICAZIONI AI LIMITI. 1 Concavit{
Studio del segno delle derivate. Lezione 11 del 6/12/2018
 Studio del segno delle derivate Lezione 11 del 6/12/2018 Segno della derivata prima Data una funzione f(x) derivabile in un intervallo I, allora se f x > 0 x I allora la funzione f(x) è strettamente crescente
Studio del segno delle derivate Lezione 11 del 6/12/2018 Segno della derivata prima Data una funzione f(x) derivabile in un intervallo I, allora se f x > 0 x I allora la funzione f(x) è strettamente crescente
Corso di Analisi Matematica
 Corso di Laurea in Ingegneria Edile Corso di CONVESSITÀ Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Derivata seconda Se la derivata (prima) di una funzione è definita
Corso di Laurea in Ingegneria Edile Corso di CONVESSITÀ Lucio Demeio Dipartimento di Ingegneria Industriale e delle Scienze Matematiche Derivata seconda Se la derivata (prima) di una funzione è definita
DERIVATA DI UNA FUNZIONE REALE. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR.
 DERIVATA DI UNA FUNZIONE REALE 1. Definizioni. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR. DEFINIZIONE 1. Sia x 0 un elemento di I. Per ogni x (I \ {x 0 }) consideriamo
DERIVATA DI UNA FUNZIONE REALE 1. Definizioni. In quanto segue denoteremo con I un intervallo di IR e con f una funzione di I in IR. DEFINIZIONE 1. Sia x 0 un elemento di I. Per ogni x (I \ {x 0 }) consideriamo
Soluzioni degli Esercizi per il Corso di Istituzioni di Matematica. x2 1 x x + 7 ; d) f (x) =
 Soluzioni degli Esercizi per il Corso di Istituzioni di Matematica 1 La retta tangente al grafico di f nel punto ( 0, f( 0 ha equazione y = f( 0 + f ( 0 ( 0. a y = 2; b y = log 2 (e( 1; c y = 1 2 + 1 4
Soluzioni degli Esercizi per il Corso di Istituzioni di Matematica 1 La retta tangente al grafico di f nel punto ( 0, f( 0 ha equazione y = f( 0 + f ( 0 ( 0. a y = 2; b y = log 2 (e( 1; c y = 1 2 + 1 4
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler)
 Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
Calcolo differenziale 2: Massimi e minimi. Studio di una funzione. (M.S.Bernabei & H. Thaler) Studio di una funzione Funzioni crescenti e decrescenti Una funzione f é crescente nell intervallo (a, b) se
Lo studio di funzione. 18 febbraio 2013
 Lo studio di funzione 18 febbraio 2013 1 Indice 1 Lo studio di funzione 3 1.1 Dominio di funzioni......................... 3 1.1.1 Domini di funzioni elementari............... 3 1.1.2 Funzioni composte,
Lo studio di funzione 18 febbraio 2013 1 Indice 1 Lo studio di funzione 3 1.1 Dominio di funzioni......................... 3 1.1.1 Domini di funzioni elementari............... 3 1.1.2 Funzioni composte,
Per cominciare, osserviamo che f si ottiene traslando di 2, nella direzione negativa dell asse x, la funzione. g(x) = x e x
 Studi di funzione 1) Studiare la funzione definita da f(x) = x + 2 e (x+2). Per cominciare, osserviamo che f si ottiene traslando di 2, nella direzione negativa dell asse x, la funzione g(x) = x e x cioè
Studi di funzione 1) Studiare la funzione definita da f(x) = x + 2 e (x+2). Per cominciare, osserviamo che f si ottiene traslando di 2, nella direzione negativa dell asse x, la funzione g(x) = x e x cioè
STUDIO DI FUNZIONI pag. 1
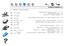 STUDIO DI FUNZIONI pag. Dominio e ricerca asintoti.0. f () = 6 +.0. f () =.0.3 f () = 3.0. () = log( 5 6) + [ dom () = R \ { ±} [ dom () = R \ {, 3} f ; asintoti verticali in = e = 3; asintoto orizzontale
STUDIO DI FUNZIONI pag. Dominio e ricerca asintoti.0. f () = 6 +.0. f () =.0.3 f () = 3.0. () = log( 5 6) + [ dom () = R \ { ±} [ dom () = R \ {, 3} f ; asintoti verticali in = e = 3; asintoto orizzontale
Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile
 Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 41 1 Derivata
Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Laurea in Informatica e Comunicazione Digitale A.A. 2013/2014 Università di Bari ICD (Bari) Analisi Matematica 1 / 41 1 Derivata
Dominio di f ed eventuali simmetrie: Il dominio di f è definito dall insieme degli x R che verificano le condizioni:
 Studi di funzione 5) Studiare la funzione definita da f() = arcsin ( ) + 3 2 +. Dominio di f ed eventuali simmetrie: Il dominio di f è definito dall insieme degli R che verificano le condizioni: () : +,
Studi di funzione 5) Studiare la funzione definita da f() = arcsin ( ) + 3 2 +. Dominio di f ed eventuali simmetrie: Il dominio di f è definito dall insieme degli R che verificano le condizioni: () : +,
3. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE.
 3. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso y = f(x) rappresenta l evoluzione di un fenomeno al passare del tempo x.se siamo interessati a sapere con che rapidità il fenomeno
3. CALCOLO DIFFERENZIALE PER FUNZIONI DI UNA VARIABILE REALE. Molto spesso y = f(x) rappresenta l evoluzione di un fenomeno al passare del tempo x.se siamo interessati a sapere con che rapidità il fenomeno
SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7
 SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7 Esercizio. Funzione da studiare: log( 3).. Dominio: dobbiamo richiedere che il denominatore non si annulli e che il logaritmo sia ben definito. Quindi le condizioni
SOLUZIONE DEGLI ESERCIZI DEL FOGLIO N. 7 Esercizio. Funzione da studiare: log( 3).. Dominio: dobbiamo richiedere che il denominatore non si annulli e che il logaritmo sia ben definito. Quindi le condizioni
MATEMATICA. a.a. 2014/15
 MATEMATICA a.a. 2014/15 3. DERIVATE E STUDIO DI FUNZIONE (II parte): Massimi, minimi e derivata prima. Flessi e derivata seconda. Schema per lo studio qualitativo completo di una funzione y=f(x) Crescenza
MATEMATICA a.a. 2014/15 3. DERIVATE E STUDIO DI FUNZIONE (II parte): Massimi, minimi e derivata prima. Flessi e derivata seconda. Schema per lo studio qualitativo completo di una funzione y=f(x) Crescenza
Corso di Analisi Matematica. Calcolo differenziale
 a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Calcolo differenziale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
a.a. 2013/14 Laurea triennale in Informatica Corso di Analisi Matematica Calcolo differenziale Avvertenza Questi sono appunti informali delle lezioni, che vengono resi disponibili per comodità degli studenti.
ESERCITAZIONE 6: STUDIO DI FUNZIONI
 ESERCITAZIONE 6: STUDIO DI FUNZIONI Tiziana Raparelli 31/03/009 1 ESERCIZI ESERCIZIO 1 Studiare le seguenti funzioni, discuterne l uniforme continuità e tracciarne un grafico qualitativo. (a) f() = log(
ESERCITAZIONE 6: STUDIO DI FUNZIONI Tiziana Raparelli 31/03/009 1 ESERCIZI ESERCIZIO 1 Studiare le seguenti funzioni, discuterne l uniforme continuità e tracciarne un grafico qualitativo. (a) f() = log(
Algebra dei limiti. quando l espressione a secondo membro è definita (non si hanno forme indeterminate), si ha. lim. f (x)
 Algebra dei limiti Teorema. Se lim f () = l R e lim g() = m R, allora, 0 0 quando l espressione a secondo membro è definita (non si hanno forme indeterminate), si ha lim (f () + g()) = lim f () + lim g()
Algebra dei limiti Teorema. Se lim f () = l R e lim g() = m R, allora, 0 0 quando l espressione a secondo membro è definita (non si hanno forme indeterminate), si ha lim (f () + g()) = lim f () + lim g()
14. Studio grafico completo di funzioni
 14. Studio grafico completo di funzioni Davide Catania davide.catania@unibs.it Esercitazioni di Analisi Matematica 1 Studio elementare di funzioni (1) Trova il dominio. data f (x) (2) Studia la simmetria
14. Studio grafico completo di funzioni Davide Catania davide.catania@unibs.it Esercitazioni di Analisi Matematica 1 Studio elementare di funzioni (1) Trova il dominio. data f (x) (2) Studia la simmetria
Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile
 Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di Bari) Analisi Matematica
Laurea in Informatica Corso di Analisi Matematica Calcolo differenziale per funzioni di una variabile Docente: Anna Valeria Germinario Università di Bari A.V.Germinario (Università di Bari) Analisi Matematica
Analisi Matematica 1 - a.a. 2017/ Quarto appello
 Analisi Matematica - a.a. 07/08 - Quarto appello Soluzione del test Test A E C B B C A D C C D Test B C B C E B A E E D B Test C A A D B E C A C D D Test D D B A A B E A E B D Soluzione della parte di
Analisi Matematica - a.a. 07/08 - Quarto appello Soluzione del test Test A E C B B C A D C C D Test B C B C E B A E E D B Test C A A D B E C A C D D Test D D B A A B E A E B D Soluzione della parte di
Programmazione disciplinare: Matematica 5 anno
 Programmazione disciplinare: Matematica 5 anno Modulo 1/Ripasso: Funzione reale di variabile reale CONTENUTI Funzione fra due insiemi. Funzione reale di variabile reale: definizione e classificazione.
Programmazione disciplinare: Matematica 5 anno Modulo 1/Ripasso: Funzione reale di variabile reale CONTENUTI Funzione fra due insiemi. Funzione reale di variabile reale: definizione e classificazione.
LICEO STATALE CARLO TENCA? MILANO
 LICEO STATALE CARLO TENCA? MILANO P. I. 80126370156 Cod. Mecc. MIPM11000D Bastioni di Porta Volta,16 20121 Milano Tel. 02.6551606 Fax 02.6554306 C. F. 80126370156 - Cod. Mecc. MIPM11000D Email: mipm11000d@istruzione.it
LICEO STATALE CARLO TENCA? MILANO P. I. 80126370156 Cod. Mecc. MIPM11000D Bastioni di Porta Volta,16 20121 Milano Tel. 02.6551606 Fax 02.6554306 C. F. 80126370156 - Cod. Mecc. MIPM11000D Email: mipm11000d@istruzione.it
Def. L unico elemento y Y associato ad un elemento x domf si dice immagine. di x attraverso f e si scrive y = f(x) (oppure f : x y = f(x)).
 FUNZIONI Siano X e due insiemi. Def. Una funzione f definita in X a valori in è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in. Def. L insieme è detto codominio di
FUNZIONI Siano X e due insiemi. Def. Una funzione f definita in X a valori in è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in. Def. L insieme è detto codominio di
ANALISI MATEMATICA I per Ingegneria Aerospaziale - A.A Diario delle lezioni. Mercoledì 2 ottobre 2013 (2 ore)
 c Andrea Dall Aglio - Analisi Matematica: Diario delle lezioni - 8 novembre 0 ANALISI MATEMATICA I per Ingegneria Aerospaziale - A.A. 0-04 Diario delle lezioni Questo è un indice degli argomenti trattati
c Andrea Dall Aglio - Analisi Matematica: Diario delle lezioni - 8 novembre 0 ANALISI MATEMATICA I per Ingegneria Aerospaziale - A.A. 0-04 Diario delle lezioni Questo è un indice degli argomenti trattati
SOLUZIONI 3. f (x) = (x 2 1) 2/3 e x. (x 2 1) 2/3 e x 0 x R. x 4/3 e x = e 4/3 log x e x
 Domanda Si consideri la funzione SOLUZIONI f x = x 2 2/ e x. Determinare il campo di esistenza, il segno, i iti alla frontiera e gli eventuali asintoti. Classificare gli eventuali punti di discontinuità
Domanda Si consideri la funzione SOLUZIONI f x = x 2 2/ e x. Determinare il campo di esistenza, il segno, i iti alla frontiera e gli eventuali asintoti. Classificare gli eventuali punti di discontinuità
FUNZIONI. y Y. Def. L insieme Y è detto codominio di f. Es. Siano X = R, Y = R e f : x y = 1 x associo il suo inverso). (ad un numero reale
 FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al più un elemento in Y. X Y Def. L insieme Y è detto codominio
FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al più un elemento in Y. X Y Def. L insieme Y è detto codominio
Def. L insieme Y è detto codominio di f. Es. Siano X = R, Y = R e f : x y = 1 x. (ad un numero reale associo. il suo inverso). 2 2/3... e... 0.
 FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in Y. PSfrag replacements X Y Def. L
FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in Y. PSfrag replacements X Y Def. L
1. Mercoledì 07/03/2018, ore: 2(2) Introduzione e presentazione del corso. Richiami: i numeri naturali, interi, razionali e reali.
 Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: May 17, 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: May 17, 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre gli zeri di f e studiarne il segno.
 1 ESERCIZI CON SOLUZIONE DETTAGLIATA Esercizio 1. Si consideri la funzione f(x) = e x 3e x +. a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre
1 ESERCIZI CON SOLUZIONE DETTAGLIATA Esercizio 1. Si consideri la funzione f(x) = e x 3e x +. a) Determinare il dominio, i limiti agli estremi del dominio e gli eventuali asintoti di f. Determinare inoltre
Mauro Saita Grafici qualitativi di funzioni reali di variabile reale
 Mauro Saita Grafici qualitativi di funzioni reali di variabile reale Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Ottobre 2017 1 Indice 1 Qual è il grafico della
Mauro Saita Grafici qualitativi di funzioni reali di variabile reale Per commenti o segnalazioni di errori scrivere, per favore, a: maurosaita@tiscalinet.it Ottobre 2017 1 Indice 1 Qual è il grafico della
Istituzioni di Matematiche quarta parte
 Istituzioni di Matematiche quarta parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 22 index Derivate 1 Derivate 2 Teoremi
Istituzioni di Matematiche quarta parte anno acc. 2012/2013 Univ. degli Studi di Milano Cristina Turrini (Univ. degli Studi di Milano) Istituzioni di Matematiche 1 / 22 index Derivate 1 Derivate 2 Teoremi
Programmazione disciplinare: Matematica 5 anno
 Programmazione disciplinare: Matematica 5 anno CONTENUTI RISULTATI DI APPRENDIMENTO (Competenze) CONOSCENZE ABILITA TEMPI (settimane) Funzione fra due insiemi. di Saper riconoscere se una relazione è anche
Programmazione disciplinare: Matematica 5 anno CONTENUTI RISULTATI DI APPRENDIMENTO (Competenze) CONOSCENZE ABILITA TEMPI (settimane) Funzione fra due insiemi. di Saper riconoscere se una relazione è anche
ISTITUZIONI DI ANALISI MATEMATICA Commissione P. Mannucci, A. Sommariva, a.a Corsi di laurea in Scienze Statistiche
 ISTITUZIONI DI ANALISI MATEMATICA Commissione P. Mannucci, A. Sommariva, a.a. 4- Corsi di laurea in Scienze Statistiche 4 febbraio TEMA Esercizio 8 punti) Si consideri la funzione ) e f) = arctan e a)
ISTITUZIONI DI ANALISI MATEMATICA Commissione P. Mannucci, A. Sommariva, a.a. 4- Corsi di laurea in Scienze Statistiche 4 febbraio TEMA Esercizio 8 punti) Si consideri la funzione ) e f) = arctan e a)
Esercitazione 6 - Soluzioni
 Esercitazione 6 - Soluzioni Francesco Davì 9 novembre 01 Soluzioni esercizio 1 (a) Dominio: Il dominio della funzione è D f = R, in quanto la funzione è definita R o, equivalentemente, (, + ). Intersezioni
Esercitazione 6 - Soluzioni Francesco Davì 9 novembre 01 Soluzioni esercizio 1 (a) Dominio: Il dominio della funzione è D f = R, in quanto la funzione è definita R o, equivalentemente, (, + ). Intersezioni
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA
 ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classi 5A-5B PROGRAMMA DI MATEMATICA PRIMA PARTE Intervallo limitato di numeri reali Dati due numeri reali a e b, con a
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/2017
 Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/201 Primitive quasi elementari = + 1 = ln + = + + 1 sin = cos+ cos = sin + 1 + " = arctan + = arcsin+ &1 " Tecnica di integrazione
Università Carlo Cattaneo Ingegneria gestionale Analisi matematica a.a. 2016/201 Primitive quasi elementari = + 1 = ln + = + + 1 sin = cos+ cos = sin + 1 + " = arctan + = arcsin+ &1 " Tecnica di integrazione
Esercizio 1. f (x) = e 8x x2 14 ***
 Esercizio Studiare la funzione f () = e 8 () *** Soluzione Insieme di definizione La funzione è definita in X = (, + ) Intersezioni con gli assi essendo γ il grafico della funzione. Inoltre: X, f () >
Esercizio Studiare la funzione f () = e 8 () *** Soluzione Insieme di definizione La funzione è definita in X = (, + ) Intersezioni con gli assi essendo γ il grafico della funzione. Inoltre: X, f () >
STUDIO DI UNA FUNZIONE INTEGRALE. Z x. ln t ln t 2 2 dt. f(x) =
 STUDIO DI UNA FUNZIONE INTEGRALE Studiamo la funzione f di una variabile reale, a valori in R, definitada. Il dominio di f. f() = Z Denotiamo con g la funzione integranda. Allora g(t) = numeri reali tali
STUDIO DI UNA FUNZIONE INTEGRALE Studiamo la funzione f di una variabile reale, a valori in R, definitada. Il dominio di f. f() = Z Denotiamo con g la funzione integranda. Allora g(t) = numeri reali tali
Modulo o "valore assoluto"
 Modulo o "valore assoluto" Dato x R definiamo modulo o valore assoluto di x il numero reale positivo x se x 0 x = x se x < 0 Sfrag replacements Es. 5 è 5. 2.34 è 2.34 Dal punto di vista geometrico x rappresenta
Modulo o "valore assoluto" Dato x R definiamo modulo o valore assoluto di x il numero reale positivo x se x 0 x = x se x < 0 Sfrag replacements Es. 5 è 5. 2.34 è 2.34 Dal punto di vista geometrico x rappresenta
10 - Applicazioni del calcolo differenziale
 Università degli Studi di Palermo Facoltà di Economia CdS Sviuppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 10 - Applicazioni del calcolo differenziale Anno Accademico 2015/2016
Università degli Studi di Palermo Facoltà di Economia CdS Sviuppo Economico e Cooperazione Internazionale Appunti del corso di Matematica 10 - Applicazioni del calcolo differenziale Anno Accademico 2015/2016
1. Mercoledì 07/03/2018, ore: 2(2) Introduzione e presentazione del corso. Richiami: i numeri naturali, interi, razionali e reali.
 Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: 28 maggio 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: 28 maggio 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
STUDIO DI FUNZIONI pag. 1
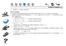 STUDIO DI FUNZIONI pag. Dominio e ricerca asintoti REGOLA GENERALE. Individuare il dominio della unzione, cioè l insieme dei valori reali per cui () è ancora un valore reale.. Studiare i iti della unzione
STUDIO DI FUNZIONI pag. Dominio e ricerca asintoti REGOLA GENERALE. Individuare il dominio della unzione, cioè l insieme dei valori reali per cui () è ancora un valore reale.. Studiare i iti della unzione
40 ESERCIZI SUL CALCOLO DIFFERENZIALE ECONCETTICOLLEGATI
 40 ESERCIZI SUL CALCOLO DIFFERENZIALE ECONCETTICOLLEGATI Derivate parziali e piani tangenti Scrivere l equazione del piano tangente al grafico delle funzioni: f(, y) = (y ) + log nel punto = y = y + f(,
40 ESERCIZI SUL CALCOLO DIFFERENZIALE ECONCETTICOLLEGATI Derivate parziali e piani tangenti Scrivere l equazione del piano tangente al grafico delle funzioni: f(, y) = (y ) + log nel punto = y = y + f(,
Tema 1: esercizi. 1. Studiare la funzione seguente e tracciarne un grafico qualitativo. + = Soluzione 1) Dominio x ( ) { }
 Tema : esercizi. Studiare la funzione seguente e tracciarne un grafico qualitativo. ) Dominio ( ) { } R \ f Dom ) Intersezione con gli assi impossibile per il dominio ± e si ottiene ancora ( ) ; e ( )
Tema : esercizi. Studiare la funzione seguente e tracciarne un grafico qualitativo. ) Dominio ( ) { } R \ f Dom ) Intersezione con gli assi impossibile per il dominio ± e si ottiene ancora ( ) ; e ( )
Teorema di sostituzione o del limite di funzioni composte
 Teorema di sostituzione o del limite di funzioni composte Questo teorema serve per calcolare il limite di funzioni composte sfruttando limiti fondamentali o altri limiti già noti. TEOREMA. Se esiste lim
Teorema di sostituzione o del limite di funzioni composte Questo teorema serve per calcolare il limite di funzioni composte sfruttando limiti fondamentali o altri limiti già noti. TEOREMA. Se esiste lim
Sia y = f(x) definita in un intervallo I. x 0 è punto di massimo assoluto. x 0 è punto di minimo assoluto. x 0 è punto di massimo relativo o locale se
 PUNTI ESTREMANTI E PUNTI STAZIONARI. MASSIMI E MINIMI ASSOLUTI E RELATIVI. TEOREMI DI FERMAT, ROLLE E LAGRANGE. CONDIZIONI NECESSARIE E SUFFICIENTI PER MASSIMI E MINIMI RELATIVI. PROBLEMI DI MASSIMO E
PUNTI ESTREMANTI E PUNTI STAZIONARI. MASSIMI E MINIMI ASSOLUTI E RELATIVI. TEOREMI DI FERMAT, ROLLE E LAGRANGE. CONDIZIONI NECESSARIE E SUFFICIENTI PER MASSIMI E MINIMI RELATIVI. PROBLEMI DI MASSIMO E
Corso di laurea in Geologia Istituzioni di matematiche Esercizi n. 1617/2/5
 Corso di laurea in Geologia Istituzioni di matematiche Esercizi n. 1617//5 Determinare il grafico delle funzioni sotto indicate, rispondendo, per quando possibile, ai seguenti punti: Dove è definita la
Corso di laurea in Geologia Istituzioni di matematiche Esercizi n. 1617//5 Determinare il grafico delle funzioni sotto indicate, rispondendo, per quando possibile, ai seguenti punti: Dove è definita la
Esercizi proposti. x b) f(x) = 2. Determinare i punti di non derivabilità delle funzioni
 Esercizi proposti 1. Calcolare la derivata prima f () per le seguenti funzioni: a) f() = c) f() = ( 1 + 1 b) f() = 1 arctan ) d) f() = cos ( ( + ) 5) e) f() = 1 + sin 1 f) f() = arcsin 1. Determinare i
Esercizi proposti 1. Calcolare la derivata prima f () per le seguenti funzioni: a) f() = c) f() = ( 1 + 1 b) f() = 1 arctan ) d) f() = cos ( ( + ) 5) e) f() = 1 + sin 1 f) f() = arcsin 1. Determinare i
FUNZIONI. y Y. Def. L insieme Y è detto codominio di f. Es. Siano X = R, Y = R e f : x y = 1 x associo il suo inverso). (ad un numero reale
 FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in Y. X Y Def. L insieme Y è detto codominio
FUNZIONI Siano X e Y due insiemi. Def. Una funzione f definita in X a valori in Y è una corrispondenza (una legge) che associa ad ogni elemento X al piú un elemento in Y. X Y Def. L insieme Y è detto codominio
Analisi Matematica per Informatici Esercitazione 10 a.a
 Analisi Matematica per Informatici Esercitazione a.a. 6-7 Dott. Simone Zuccher 7 Febbraio 7 Nota. Queste pagine potrebbero contenere degli errori: chi li trova è pregato di segnalarli all autore (zuccher@sci.univr.it).
Analisi Matematica per Informatici Esercitazione a.a. 6-7 Dott. Simone Zuccher 7 Febbraio 7 Nota. Queste pagine potrebbero contenere degli errori: chi li trova è pregato di segnalarli all autore (zuccher@sci.univr.it).
Analisi Matematica 1 - a.a. 2017/ Primo appello
 Analisi Matematica - a.a. 7/8 - Primo appello Soluzione del test Test A 3 4 5 6 7 8 9 C E E C D E A B B D Test B 3 4 5 6 7 8 9 A A B E B B C D E A Test C 3 4 5 6 7 8 9 B D C A E D E C D C Test D 3 4 5
Analisi Matematica - a.a. 7/8 - Primo appello Soluzione del test Test A 3 4 5 6 7 8 9 C E E C D E A B B D Test B 3 4 5 6 7 8 9 A A B E B B C D E A Test C 3 4 5 6 7 8 9 B D C A E D E C D C Test D 3 4 5
Studio di una funzione razionale fratta
 Studio di una funzione razionale fratta Nella figura è rappresentata la funzione 1. Quale tra gli insiemi proposti è il suo CDE? 2. La funzione presenta un asintoto verticale di equazione... x = 0 x =
Studio di una funzione razionale fratta Nella figura è rappresentata la funzione 1. Quale tra gli insiemi proposti è il suo CDE? 2. La funzione presenta un asintoto verticale di equazione... x = 0 x =
Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 25 Gennaio Studio di Funzione
 Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 25 Gennaio 2017 Studio di Funzione 1. Si consideri la funzione reale di variabile reale così definita f() = 2 + 4. (a) Determinare
Esercitazioni di Matematica Generale A.A. 2016/2017 Pietro Pastore Lezione del 25 Gennaio 2017 Studio di Funzione 1. Si consideri la funzione reale di variabile reale così definita f() = 2 + 4. (a) Determinare
Matematica Lezione 19
 Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 19 Sonia Cannas 6/12/2018 Derivata di una funzione composta Derivata di una funzione composta La derivata di una funzione composta
Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 19 Sonia Cannas 6/12/2018 Derivata di una funzione composta Derivata di una funzione composta La derivata di una funzione composta
DERIVATE. Equazione della retta tangente al grafico di f nel suo punto P(x 0 ;y 0 ):
 DERIVATE La derivata di una funzione in un punto c, quando esiste, rappresenta il coefficiente angolare della retta tangente al grafico della funzione nel suo punto di ascissa c: f ( c) = Df ( c) = m tg
DERIVATE La derivata di una funzione in un punto c, quando esiste, rappresenta il coefficiente angolare della retta tangente al grafico della funzione nel suo punto di ascissa c: f ( c) = Df ( c) = m tg
Istituto Tecnico Statale per il Turismo "Francesco Algarotti" Classe: 3 Sez. A A. S. 2018/19 PROGRAMMA DI MATEMATICA
 Classe: 3 Sez. A A. S. 2018/19 Libro di testo: Bergamini Trifone Barozzi Matematica.bianco (2 vol.) Bergamini Trifone Barozzi Matematica.rosso (vol. 3s) Volume 2 Ripasso. Scomposizione in fattori primi
Classe: 3 Sez. A A. S. 2018/19 Libro di testo: Bergamini Trifone Barozzi Matematica.bianco (2 vol.) Bergamini Trifone Barozzi Matematica.rosso (vol. 3s) Volume 2 Ripasso. Scomposizione in fattori primi
1. Mercoledì 07/03/2018, ore: 2(2) Introduzione e presentazione del corso. Richiami: i numeri naturali, interi, razionali e reali.
 Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: 7 giugno 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
Registro delle lezioni di MATEMATICA 2 Corso di Laurea in Chimica 6 CFU - A.A. 2017/2018 docente: Francesco Demontis ultimo aggiornamento: 7 giugno 2018 1. Mercoledì 07/03/2018, 9 11. ore: 2(2) Introduzione
Istituto Tecnico Statale per il Turismo "Francesco Algarotti" Classe: 3 Sez. A A. S. 2017/18 PROGRAMMA DI MATEMATICA
 Classe: 3 Sez. A A. S. 2017/18 Libro di testo: Bergamini Trifone Barozzi Matematica.bianco (2 vol.) Bergamini Trifone Barozzi Matematica.rosso (vol. 3s) Volume 2 Ripasso. Scomposizione in fattori primi
Classe: 3 Sez. A A. S. 2017/18 Libro di testo: Bergamini Trifone Barozzi Matematica.bianco (2 vol.) Bergamini Trifone Barozzi Matematica.rosso (vol. 3s) Volume 2 Ripasso. Scomposizione in fattori primi
12/10/05 (2 ore): Esercizi vari sull ellisse, iperbole, parabola. Disequazioni in due variabili. Equazione dell iperbole equilatera. Esempi.
 Università degli Studi di Trento Facolta di Scienze Cognitive Corso di Laurea in Scienze e Tecniche di Psicologia Cognitiva Applicata Corso di Analisi Matematica - a.a. 2005/06 Docente: Prof. Anneliese
Università degli Studi di Trento Facolta di Scienze Cognitive Corso di Laurea in Scienze e Tecniche di Psicologia Cognitiva Applicata Corso di Analisi Matematica - a.a. 2005/06 Docente: Prof. Anneliese
MASSIMI, MINIMI E FLESSI
 MASSIMI, MINIMI E FLESSI N.B. Se f(x) è continua in [a;b], esistono sicuramente M e m (Teor. di Weierstrass) I punti di massimo e di minimo relativi si chiamano anche punti estremanti relativi di f(x).
MASSIMI, MINIMI E FLESSI N.B. Se f(x) è continua in [a;b], esistono sicuramente M e m (Teor. di Weierstrass) I punti di massimo e di minimo relativi si chiamano anche punti estremanti relativi di f(x).
Matematica Lezione 20
 Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 20 Sonia Cannas 7/12/2018 Applicazioni delle derivate: calcolo dei iti Le derivate permettono di calcolare i iti che presentano le
Università di Cagliari Corso di Laurea in Farmacia Matematica Lezione 20 Sonia Cannas 7/12/2018 Applicazioni delle derivate: calcolo dei iti Le derivate permettono di calcolare i iti che presentano le
Facoltà di Scienze MFN, Università di Cagliari Analisi Matematica 1 (Informatica), a.a. 2007/08. Insiemi numerici: sup A, inf A
 Facoltà di Scienze MFN, Università di Cagliari Analisi Matematica 1 (Informatica, a.a. 2007/08 Esercizi: Parte 1 Insiemi numerici: sup A, inf A 1. Verificare se A, nel caso sia non vuoto, è limitato superiormente,
Facoltà di Scienze MFN, Università di Cagliari Analisi Matematica 1 (Informatica, a.a. 2007/08 Esercizi: Parte 1 Insiemi numerici: sup A, inf A 1. Verificare se A, nel caso sia non vuoto, è limitato superiormente,
Esercizi su serie numeriche, integrali ed equazioni differenziali utili per la preparazione all esame scritto 1
 Esercizi di Analisi Matematica Paola Gervasio Esercizi su serie numeriche, integrali ed equazioni differenziali utili per la preparazione all esame scritto Es Determinare il carattere delle seguenti serie
Esercizi di Analisi Matematica Paola Gervasio Esercizi su serie numeriche, integrali ed equazioni differenziali utili per la preparazione all esame scritto Es Determinare il carattere delle seguenti serie
LICEO CLASSICO ANDREA DA PONTEDERA
 ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classe 5A PROGRAMMA DI MATEMATICA svolto fino al 15 aprile (evidenziate in giallo le aggiunte rispetto al file precedente) Intervallo limitato
ISTITUTO SUPERIORE XXV APRILE LICEO CLASSICO ANDREA DA PONTEDERA classe 5A PROGRAMMA DI MATEMATICA svolto fino al 15 aprile (evidenziate in giallo le aggiunte rispetto al file precedente) Intervallo limitato
Esercizi di Matematica per le Scienze Studio di funzione
 Esercizi di Matematica per le Scienze Studio di funzione A.M. Bigatti e G. Tamone Esercizi Studio di funzione Esercizio 1. Disegnare il grafico di una funzione continua f che soddisfi tutte le seguenti
Esercizi di Matematica per le Scienze Studio di funzione A.M. Bigatti e G. Tamone Esercizi Studio di funzione Esercizio 1. Disegnare il grafico di una funzione continua f che soddisfi tutte le seguenti
ANALISI MATEMATICA 1 Commissione L. Caravenna, V. Casarino, S. Zoccante Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza
 ANALISI MATEMATICA Commissione L Caravenna, V Casarino, S Zoccante Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Nome, Cognome, numero di matricola: Vicenza, 7 Luglio 205 TEMA - parte B Esercizio
ANALISI MATEMATICA Commissione L Caravenna, V Casarino, S Zoccante Ingegneria Gestionale, Meccanica e Meccatronica, Vicenza Nome, Cognome, numero di matricola: Vicenza, 7 Luglio 205 TEMA - parte B Esercizio
LICEO SCIENTIFICO STATALE A. Einstein
 LICEO SCIENTIFICO STATALE A. Einstein PROGRAMMA CONSUNTIVO MATEMATICA Classe V L Anno Scolastico 2017-2018 Docente: prof. Barbara Veronesi Ore di insegnamento: 4 settimanali Analisi matematica 1. Ripasso
LICEO SCIENTIFICO STATALE A. Einstein PROGRAMMA CONSUNTIVO MATEMATICA Classe V L Anno Scolastico 2017-2018 Docente: prof. Barbara Veronesi Ore di insegnamento: 4 settimanali Analisi matematica 1. Ripasso
Università degli Studi di Siena Correzione Prova intermedia di Matematica Generale (A.A ) 12 novembre 2016 Compito 1
 Università degli Studi di Siena Correzione Prova intermedia di Matematica Generale (A.A. 7) novembre Compito ) ) L'espressione è equivalente a quindi sse ovvero, ma non può essere un numero negativo e
Università degli Studi di Siena Correzione Prova intermedia di Matematica Generale (A.A. 7) novembre Compito ) ) L'espressione è equivalente a quindi sse ovvero, ma non può essere un numero negativo e
PROGRAMMA SVOLTO A. S. 2015/ 2016
 Nome docente BORGNA Giorgio Materia insegnata MATEMATICA Classe V G manutenzione e assistenza tecnica numero ore di insegnamento svolte ore complessive di insegnamento 3 33 di cui in compresenza di cui
Nome docente BORGNA Giorgio Materia insegnata MATEMATICA Classe V G manutenzione e assistenza tecnica numero ore di insegnamento svolte ore complessive di insegnamento 3 33 di cui in compresenza di cui
1 è l estremo inferiore della funzione (inf f = 1 R) e quindi la funzione è limitata inferiormente
 f x = x 2 1 allora Im f = [ 1, + ) 1 è l estremo inferiore della funzione (inf f = 1 R) e quindi la funzione è limitata inferiormente + è l estremo superiore della funzione (sup f = + R) e quindi la funzione
f x = x 2 1 allora Im f = [ 1, + ) 1 è l estremo inferiore della funzione (inf f = 1 R) e quindi la funzione è limitata inferiormente + è l estremo superiore della funzione (sup f = + R) e quindi la funzione
Analisi Matematica T1 - A.A prof.g.cupini CdL Ingegneria Edile Università di Bologna REGISTRO DELLE LEZIONI
 Analisi Matematica T1 - A.A.2011-2012 - prof.g.cupini CdL Ingegneria Edile Università di Bologna REGISTRO DELLE LEZIONI (Grazie agli studenti del corso che comunicheranno omissioni o errori) 27 SETTEMBRE
Analisi Matematica T1 - A.A.2011-2012 - prof.g.cupini CdL Ingegneria Edile Università di Bologna REGISTRO DELLE LEZIONI (Grazie agli studenti del corso che comunicheranno omissioni o errori) 27 SETTEMBRE
Funzioni derivabili (V. Casarino)
 Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Funzioni derivabili (V. Casarino) Esercizi svolti 1) Applicando la definizione di derivata, calcolare la derivata in = 0 delle funzioni: a) 5 b) 3 4 c) + 1 d) sin. ) Scrivere l equazione della retta tangente
Appunti di Matematica 5 - Derivate - Derivate. Considero una funzione e sia e definita in un intorno completo di.
 Derivate Definizione di derivata di f(x) in x D o f Considero una funzione e sia e definita in un intorno completo di. Consideriamo il rapporto (detto rapporto incrementale ) È evidente che il rapporto
Derivate Definizione di derivata di f(x) in x D o f Considero una funzione e sia e definita in un intorno completo di. Consideriamo il rapporto (detto rapporto incrementale ) È evidente che il rapporto
Limiti di funzioni a +
 Limiti di funzioni a + Consideriamo una funzione = f() reale a variabile reale, di dominio D R. Sia f definita in un intorno di +. Def. La funzione f tende al limite l R per tendente a + e si scrive se
Limiti di funzioni a + Consideriamo una funzione = f() reale a variabile reale, di dominio D R. Sia f definita in un intorno di +. Def. La funzione f tende al limite l R per tendente a + e si scrive se
FUNZIONI REALI DI UNA VARIABILE REALE
 FUNZIONI REALI DI UNA VARIABILE REALE INTERVALLI Per definire il campo di esistenza (o dominio) di una funzione reale di variabile reale y=f()si devono indicare talvolta insiemi di numeri reali che su
FUNZIONI REALI DI UNA VARIABILE REALE INTERVALLI Per definire il campo di esistenza (o dominio) di una funzione reale di variabile reale y=f()si devono indicare talvolta insiemi di numeri reali che su
Argomento 7 - Studi di funzioni Soluzioni Esercizi
 Argomento 7 - Studi di funzioni Soluzioni Esercizi Sol. E. 7. f() = log + 4 Insieme di definizione : Limiti : 4 log + = + 0 + (confronto tra infiniti in cui prevale la potenza) 4 log + = log = + + + Notiamo
Argomento 7 - Studi di funzioni Soluzioni Esercizi Sol. E. 7. f() = log + 4 Insieme di definizione : Limiti : 4 log + = + 0 + (confronto tra infiniti in cui prevale la potenza) 4 log + = log = + + + Notiamo
Analisi Matematica I Primo Appello ( ) - Fila 1
 Analisi Matematica I Primo Appello (4-11-003) - Fila 1 1. Determinare la retta tangente alla funzione f() = (1 + ) 1+ in = 0. R. f(0) = 1, mentre la derivata è f () = ( e (1+) log(1+)) ( ) = e (1+) log(1+)
Analisi Matematica I Primo Appello (4-11-003) - Fila 1 1. Determinare la retta tangente alla funzione f() = (1 + ) 1+ in = 0. R. f(0) = 1, mentre la derivata è f () = ( e (1+) log(1+)) ( ) = e (1+) log(1+)
ANALISI MATEMATICA I (Versione A) - 24 Novembre 2000 RISOLUZIONE. = 4x 2 + 8x 3 + o(x 3 )
 ANALISI MATEMATICA I (Versione A) - 4 Novembre 000 RISOLUZIONE ESERCIZIO 1. Data la funzione = (e x 1) log(1 + 4x ) : 1. Calcolare lo sviluppo di ordine 3 di MacLaurin di. Scriviamo gli sviluppi di ordine
ANALISI MATEMATICA I (Versione A) - 4 Novembre 000 RISOLUZIONE ESERCIZIO 1. Data la funzione = (e x 1) log(1 + 4x ) : 1. Calcolare lo sviluppo di ordine 3 di MacLaurin di. Scriviamo gli sviluppi di ordine
Argomento 6 Derivate
 Argomento 6 Derivate Derivata in un punto Definizione 6. Data una funzione f definita su un intervallo I e 0 incrementale di f in 0 di incremento h = 0 = il rapporto I, si chiama rapporto per = 0 + h =
Argomento 6 Derivate Derivata in un punto Definizione 6. Data una funzione f definita su un intervallo I e 0 incrementale di f in 0 di incremento h = 0 = il rapporto I, si chiama rapporto per = 0 + h =
Scheda elaborata dalla prof.ssa Biondina Galdi Docente di Matematica
 Tutorial - Studio di una funzione reale di variabile reale f : x R y = f (x) R Una funzione può essere: - 1 - algebrica ( razionale o irrazionale, intera o fratta) Classificare la trascendentale ( esponenziale,
Tutorial - Studio di una funzione reale di variabile reale f : x R y = f (x) R Una funzione può essere: - 1 - algebrica ( razionale o irrazionale, intera o fratta) Classificare la trascendentale ( esponenziale,
dato da { x i }; le rette verticali passanti per
 Schema riepilogativo per lo studio di una funzione reale di una var. reale. Studio grafico-analitico delle funzioni reali di variabile reale y = f ( Sequenza dei passi utili allo studio di una funzione
Schema riepilogativo per lo studio di una funzione reale di una var. reale. Studio grafico-analitico delle funzioni reali di variabile reale y = f ( Sequenza dei passi utili allo studio di una funzione
Analisi e Geometria 1 Politecnico di Milano Ingegneria
 Analisi e Geometria Politecnico di Milano Ingegneria Esercizi Funzioni. Calcolare la derivata delle funzioni: (a f( = ln tg cos sin (b f( = + ln( + +. Dimostrare che la funzione è costante a tratti. 3.
Analisi e Geometria Politecnico di Milano Ingegneria Esercizi Funzioni. Calcolare la derivata delle funzioni: (a f( = ln tg cos sin (b f( = + ln( + +. Dimostrare che la funzione è costante a tratti. 3.
Punti di estremo e Teorema di Fermat
 Punti di estremo e Teorema di Fermat Nello studio di una funzione, le derivate sono (tra le altre cose) uno strumento utile per la determinazione di intervalli di monotonia e puntidiestremo. Definizione.
Punti di estremo e Teorema di Fermat Nello studio di una funzione, le derivate sono (tra le altre cose) uno strumento utile per la determinazione di intervalli di monotonia e puntidiestremo. Definizione.
ISTITUZIONI DI MATEMATICHE ( M.M. Porzio ) Foglio di esercizi n. 1: Limiti di funzioni e continuitá
 ISTITUZIONI DI MATEMATICHE ( M.M. Porzio ) Foglio di esercizi n. : Limiti di funzioni e continuitá a) Calcolare, se esistono, i seguenti limiti di funzioni: ( ) 5x. lim 3 x 8 +4x+ x +. lim x 5 4+x +x 3
ISTITUZIONI DI MATEMATICHE ( M.M. Porzio ) Foglio di esercizi n. : Limiti di funzioni e continuitá a) Calcolare, se esistono, i seguenti limiti di funzioni: ( ) 5x. lim 3 x 8 +4x+ x +. lim x 5 4+x +x 3
Istituzioni di Matematica I
 Istituzioni di Matematica I Le soluzioni proposte costituiscono solo una traccia di possibili soluzioni (lo studente deve giustificare i vari risultati), possono esserci altri modi, altrettanto corretti,
Istituzioni di Matematica I Le soluzioni proposte costituiscono solo una traccia di possibili soluzioni (lo studente deve giustificare i vari risultati), possono esserci altri modi, altrettanto corretti,
