RAPPRESENTAZIONE PROBABILISTICA DI UN CAMPIONE CASUALE SEMPLICE
|
|
|
- Daniella Calabrese
- 7 anni fa
- Visualizzazioni
Transcript
1 INFERENZA STATISTICA La Statistica Ifereziale studia come estedere i risultati e le coclusioi che provegoo dall aalisi di u campioe di osservazioi alla popolazioe a cui il campioe appartiee. Vi soo molteplici motivi per ricorrere ad ua idagie campioaria: costi di u idagie cesuaria; tempi prolugati di u idagie cesuaria; l osservazioe è distruttiva; i moltissimi casi, la popolazioe di riferimeto è virtuale eifiita. 1
2 IL CAMPIONAMENTO Si ituisce che il campioe deve essere rappresetativo della popolazioe di riferimeto e quidi libero da qualsiasi elemeto soggettivo. Esistoo vari metodi di campioameto (Teciche di Campioameto), ma oi cosidereremo solo il campioameto casuale: leuitàstatistichecheetrao afarpartedelcampioesooestratteimodocasuale dalla popolazioe di riferimeto. Se le estrazioi delle uità statistiche che etrao el campioe soo idipedeti si parla di campioe casuale semplice. Affichéleestrazioisiaoidipedeti se la popolazioe è fiita le estrazioi devoo essere co reiserimeto se la popolazioe è ifiita oppure se la popolazioe è molto più ampia della umerosità del campioe, le estrazioi possoo essere co o seza reiserimeto Nel seguito ci limiteremo a cosiderare campioi casuali semplici, che verrao abbreviati co c.c.s. 2
3 RAPPRESENTAZIONE PROBABILISTICA DI UN CAMPIONE CASUALE SEMPLICE Suppoiamo di estrarre a caso ua uità dalla popolazioe di riferimeto e di osservare su di essa la caratteristica di iteresse. Sia x il valore osservato sull uità. Aprioririspetto all esperimeto, ossia prima dell estrazioe dell uità e della rilevazioe della caratteristica, o siamo i grado di prevedere quale valore osserveremo. Pertato, x è la realizzazioe di ua variabile casuale X la cui distribuzioe di probabilità descrive quali soo i valori che possoo essere assuti dalla caratteristica su u uità estratta a caso e co quale probabilità (se X è discreta) o desità (se X è cotiua ) verrao osservati. Geeralizziamo il ragioameto da ua sola uità a uità, per otteere u c.c.s. di dimesioe. Se x 1,x 2,...,x soo le osservazioi umeriche raccolte sulle uità estratte, ciascua è la realizzazioe di ua variabile casuale. Più precisamete, x 1 è l a r e a l i z z a - zioe della variabile casuale X 1 che descrive il risultato che osserveremo sulla prima uità estratta, x 2 è l a r e a l i z - zazioe della variabile casuale X 2 che descrive il risultato che osserveremo sulla secoda uità estratta e così via. 3
4 Trattadosi di repliche della variabile X queste variabili soo ideticamete distribuite, tutte co la stessa distribuzioe di X. Ioltre,essedoleestrazioiidipedeti, le variabili stesse soo idipedeti. I sitesi, PRIMA di effettuare l osservazioe, u c.c.s. può essere rappresetato da ua pla di variabilicasuali, X 1,X 2,...,X, i.i.d.; DOPO aver effettuato l osservazioe, u c.c.s. è rappresetabile da ua pla di valori, x 1,x 2,..., x,ciascuorealizzazioediuavariabilecasuale. Esempio 1 Suppoiamo di voler studiare l altezza della popolazioe italiaa. Estraiamo u c.c.s. di dimesioe 8, osservado le segueti altezze (i cm): x 1 =170,x 2 =181,x 3 =189,x 4 =160, x 5 =182,x 6 =171,x 7 =158,x 8 =186 Questi valori soo realizzazioi di altrettate variabili casuali, X 1,...,X 8,i.i.d.chedescrivooilc.c.s.prima di fare l osservazioe. La distribuzioe di caratteristiche atropometriche è spesso approssimabile co ua distribuzioe gaussiaa. È quidi ragioevole assumere che X N(µ, σ 2 ), dove X è la variabile casuale che descrive l osservazioe su ua geerica uità estratta a caso. Aalogamete, X 1,...,X soo i.i.d. co distribuzioe N(µ, σ 2 ). 4
5 I questo esempio, µ = E(X) =E(X i )èl igota altezza media della popolazioe italiaa e σ 2 = V (X) = V (X i )èl igota variaza dell altezza ella popolazioe italiaa. Quidi, etrambi i parametri della ormale, µ e σ 2,rappresetaodellequatitàdiiteressedellapopolazioe di riferimeto e soo igoti. Potremmo pesare di stimare le igote quatità di popolazioe, µ e σ 2,colecorrispodetiquatitàcampioarie: x =175cm e s 2 =10, 85 2 Tuttavia, se ripetessimo l esperimeto ed estraessimo u uovo c.c.s. di 8 idividui otterremmo, i geerale, altezze diverse dalle precedeti e quidi stime diverse delle quatità di popolazioe. Ci domadiamo, pertato, quato soo accurate le stime della media e della variaza dell altezza della popolazioe italiaa? possiamo idividuare u itervallo di valori ragioevoli per µ eperσ 2? i base ai risultati otteuti, è ragioevole affermare, ad esempio, che l altezza media della popolazioe italiaa è superiore a 170 cm? Esempio 2 U idustria che produce pompe idrauliche acquista guarizioi i plastica da u foritore. Per garatire la qualità delle pompe prodotte, l idustria ha la ecessità di verificare quale è la percetuale di guarizioi acquistate che soo difettose. A questo fie, si estraggoo casualmete 20 guarizioi tra quelle acquistate e per ciascua si 5
6 verifica la coformità alle specifiche, otteedo i segueti risultati x 1 =0,x 2 =0,x 3 =0,x 4 =0,x 5 =0,x 6 =1,x 7 =0, x 8 =0,x 9 =0,x 10 =0,x 11 =0,x 12 =0,x 13 =0,x 14 =0, x 15 =1,x 16 =0,x 17 =0,x 18 =0,x 19 =0,x 20 =0 dove 0= o difettosa, 1= difettosa. Si oti che la popolazioe di riferimeto è costituita da tutte le guarizioi acquistate, preseti e future (popolazioe virtuale ). Prima di estrarre il campioe o siamo i grado di prevedere i risultati, per cui ciascua x i può essere vista come realizzazioe di ua variabile casuale X i,co X 1,X 2,...,X 20 i.i.d.. Poiché il risultato è dicotomico (difettosa/o difettosa), è aturale assumere X i Be(π). I questo esempio, π = P (X i =1)rappreseta la frazioe di guarizioi difettose ell itera popolazioe (virtuale) di riferimeto, ed è igota. Come ell Esempio 1, ache i questo cotesto il parametro della distribuzioe delle X i è u a q u a t i t à d i i t e r e s s e d e l l a popolazioe: è da π, cheèpossibilegiudicarelaqualità delle guarizioi acquistate. Sembra ragioevole stimare l igoto π tramite la corrispodete frazioe campioaria di pezzi difettosi, ossia tramite p = 20 i=1 x i 20 = 2 20 =0, 1 Tuttavia, se ripetessimo il campioameto, estraedo u uovo c.c.s. di dimesioe 20, potremmo otteere u 6
7 umero differete di pezzi difettosi e quidi ua stima differete. Le domade che ci poiamo soo allora Quato accurata è la ostra valutazioe della vera, ma igota frazioe di guarizioi difettose acquistate? Possiamo idividuare u itervallo di valori ragioevoli per π? Se l idustria foritrice ha garatito ua percetuale di guarizioi difettose o superiore a 5%, metre il campioe e cotiee 10%, ci soo elemeti per cotestare la foritura e chiedere il risarcimeto? Esempio 3 Per valutare l uso di uo sportello bacomat, è stato rilevato il umero di utilizzi su u campioe di 10 giori scelti casualmete, otteedo i segueti valori x 1 =10,x 2 =6,x 3 =5,x 4 =7,x 5 =7, x 6 =6,x 7 =7,x 8 =8,x 9 =11,x 10 =9 Si oti che, come ell Esempio 2, la popolazioe di riferimeto è ifiita e virtuale, essedo costituita da tutti igioripassati,presetiefuturi. Segliutilizzitrai vari giori soo tra loro idipedeti e o vi è stato essu cambiameto sistematico durate il periodo della rilevazioe, le variabili casuali X 1,...,X 10,dicuile10 osservazioi campioarie soo realizzazioi, possoo essere assute i.i.d.. I aggiuta, trattadosi di coteggi, potrebbe essere ragioevole assumere X i Po(λ). I 7
8 questo esempio, λ = E(X i )rappresetailumeromedio gioraliero di utilizzi del bacomat ella popolazioe di iteresse ed è igoto. Acheiquestocaso,ilparametro della distribuzioe delle X i è u a q u a t i t à d i i t e r e s s e della popolazioe: tramite λ è p o s s i b i l e v a l u t a r e l u s o d e l bacomat. Èragioevolestimarel igotoλ attraverso la corrispodete media campioaria x =7, 6. Siamo, però, cosapevoli che se predessimo u uovo campioe di 10 giori otterremmo valori diversi e quidi ua media diversa. Pertato, valgoo le usuali cosiderazioi: quato affidabile è la ostra stima? possiamo idetificare u itervallo di valori ragioevoli per λ? idaticampioaridaosostego,adesempio,all ipotesi che il umero medio gioraliero di utilizzi sia iferiore a 10? 8
9 IFONDAMENTIDELL INFERENZA STATISTICA (PARAMETRICA) Itreesempivistihaoicomuealcuecaratteristiche che costituiscoo i fodameti dell Ifereza Statistica (parametrica). Dato u c.c.s. di osservazioi x 1,x 2,...,x,ogix i è realizzazioe di ua variabile casuale X i. Le variabili X 1,X 2,...,X soo i.i.d. co ua fuzioe di probabilità (se le X i soo discrete) o di desità (se le X i soo cotiue) che idicheremo i modo geerico co f(x). La fuzioe f(x) dipededauoopiùparametri igoti che rappresetao caratteristiche di iteresse della popolazioe di riferimeto. Nell Esempio 1, X i N(µ, σ 2 )eiparametriigoti soo µ e σ 2,cherappresetao,rispettivamete, la media e la variaza dell altezza della popolazioe italiaa: f(x) = 1 σ 2π exp { 1 2σ2(x µ)2 } x IR Nell Esempio 2, X i Be(π) eilparametroigotoè π che rappreseta la frazioe di guarizioi difettose ella popolazioe di tutte le guarizioi acquistate: f(x) =π x (1 π) 1 x, x =0oppure1 Nell Esempio 3, X i Po(λ) eilparametroigoto è λ che rappreseta il umero medio gioraliero di 9
10 utilizzi del bacomat ella popolazioe costituita da tutti i giori: f(x) = e λ λ x, x =0, 1, 2,... x! Obiettivo dell Ifereza Statistica è utilizzare le osservazioi campioarie per risalire al vero valore dei parametri igoti e da qui alla distribuzioe di probabilità del feomeo di iteresse. Ad esempio, ell Esempio 2, variado π (0, 1) si geera ua famiglia di distribuzioi beroulliae di parametro π. Attraversoidati,sivuoleidetificare il vero valore di π edaquestolaveradistribuzioe di probabilità delle X i. 10
11 Le domade a cui l Ifereza Statistica cerca di dare ua risposta rietrao i 3 pricipali categorie 1. Si vuole stimare il vero valore dei parametri igoti i base alle osservazioi del campioe e capire quato accurata è la stima proposta (STIMA PUN- TUALE). 2. Si vuole idetificare u isieme di valori ragioevoli per i parametri igoti (STIMA INTERVALLA- RE). 3. Si formula u ipotesi sul vero valore dei parametri igoti e si vuole verificare se tale ipotesi è vera oppure o, i base alle osservazioi capioarie. (VERI- FICA DI IPOTESI). 11
12 LE STATISTICHE CAMPIONARIE: IL CASO DELLA MEDIA CAMPIONARIA Prediamo u c.c.s. x 1,x 2,...,x,realizzazioedella -pla di variabili casuali X 1, X 2,..., X,i.i.d.. Suppoiamo di voler fare ifereza sulla media igota di popolazioe (o, i geerale, del feomeo di iteresse) che idichiamo co m = E(X i ). Ua scelta aturale è stimare m tramite la corrispodete media campioaria: x = 1 x i Tuttavia, ogi c.c.s. di dimesioe produce potezialmete u valore diverso di x. Poichéleosservazioix i soo realizzazioi delle variabili casuali X i,lastessamedia x può essere vista come la realizzazioe della variabile casuale X = 1 X i. La distribuzioe di probabilità di X,chiamatadistribuzioe campioaria, rappresetaladistribuzioedelle medie campioarie di tutti i c.c.s. di dimesioe estraibili dalla popolazioe di riferimeto. I altre parole, la distribuzioe di X determia il modo i cui la media campioaria x varia passado da u c.c.s. di dimesioe all altro. i=1 i=1 12
13 Popolazioe Camp.4 Camp.5 x 4 x 5 Camp.1 x 1 Camp.3 x 3 Camp.2 x 2 Esempio 4 Suppoiamo che la ostra popolazioe di riferimeto sia u ura co 3 pallie umerate da 1 a 3 e idichiamo co X la variabile casuale che descrive il valore di ua pallia estratta casualmete dall ura. Prediamo =2. Tuttiipossibilic.c.s. didimesioe 2soo(estrazioicoreiserimeto):(1,2),(2,1),(1,3), (3,1), (2,3), (3,2), (1,1), (2,2), (3,3). Poiamo X 1 =valore della prima pallia estratta, X 2 =valore della secoda pallia estratta e X =(X 1 + X 2 )/2 13
14 La distribuzioe campioaria di X è valori di X 1 1,5 2 2,5 3 Tot probabilità 1/9 2/9 3/9 2/9 1/9 1 Ad esempio, la probabilità di osservare u c.c.s. tale che x =2è3/9(ossialaprobabilitàdiestrarre(2,2)o(1,3) o(3,1)). N.B.: La media di popolazioe è m = E(X 1 )=E(X 2 )= 2. Esempio 1 Riprediamo l Esempio 1 e suppoiamo che µ =170cm e σ 2 =15 2 (ma media e variaza di popolazioe soo i geerale igote). Sappiamo che X 1,...,X 8 soo i.i.d. co distribuzioe N(µ =170;σ 2 =15 2 ). Per oti risultati della probabilità, la distribuzioe campioaria di X è (si cofroti co pag. 101 della Probabilità) X = 1 8 ) X i N (170, i=1 Pertato, la probabilità, per esempio, di osservare u campioe per il quale x <175 è ( ) P ( X <175) = Φ 15/ =0,
15 LE STATISTICHE CAMPIONARIE Quato visto per X può essere esteso a qualuque altra fuzioe di X 1,...,X. I geerale, si defiisce STATISTICA CAMPIO- NARIA ua qualsiasi fuzioe T = g(x 1,X 2,...,X ) delle variabili casuali X 1,...,X che geerao i dati. Essedo fuzioe di variabili casuali, T stessa è ua variabile casuale dotata di ua propria distribuzioe di probabilità, chiamata distribuzioe campioaria. Sul campioe effettivamete osservato x 1,x 2,...,x, T avrà come realizzazioe il valore umerico t = g(x 1,x 2,...,x )(sipesiallarelazioetralavariabile casuale X elamediaumerica x). La media campioaria è u esempio di statistica campioaria. U altro esempio molto importate di statistica campioaria è la variaza campioaria S 2 = 1 (X i X) 2 i=1 la cui realizzazioe sul c.c.s. effettivamete osservato è s 2 = 1 (x i x) 2. i=1 15
16 Esempio 4 Riprediamo l esempio di ua popolazioe costituita da u ura co 3 pallie umerate da 1 a 3. Ricordiamo che tutti i possibili c.c.s di dimesioe 2soo: (1,2),(2,1),(1,3),(3,1),(2,3),(3,2),(1,1), (2,2), (3,3). La distribuzioe campioaria della variaza campioaria S 2 = 1 { (X1 2 X) 2 +(X 2 X) 2} è valori di S 2 0 0,25 1 Tot probabilità 3/9 4/9 2/9 1 Ad esempio, la probabilità di estrarre u c.c.s tale che s 2 =0è3/9(èlaprobabilitàdiestrarreo(1,1) o(2,2)o(3,3)). 16
17 LA STIMA PUNTUALE Sulla base di u c.c.s. di osservazioi, l obiettivo è idetificare il vero valore del parametro igoto i modo putuale, ossia attraverso u uico valore. I modo formale, il problema della stima putuale può ricodursi alla scelta di ua statistica campioaria t = g(x 1,...,x )chequatifichiilverovaloredelparametro igoto. La statistica campioaria t usata per stimare il parametro igoto è chiamata STIMA. La variabile casuale T = g(x 1,...,X ), di cui t è l a r e a l i z z a z i o e s u l campioe effettivamete estratto, viee chiamata STI- MATORE. Lostimatoreèquidiuavariabilecasuale dotata di ua sua distribuzioe campioaria. Esistoo metodi geerali di stima putuale che permettoo di costruire stimatori/stime per parametri di iteresse i qualuque situazioe. Tuttavia, iizieremo ad affrotare il problema della stima putuale i modo semplice, usado criteri di ragioevolezza. 1. Se vogliamo stimare ua media di popolazioe, m = E(X i ), è ragioevole usare come stima la media campioaria x, cheèrealizzazioedellostimatore X. È quello che abbiamo fatto ell Esempio 1 per stimare µ, l altezzamediadegliitaliai,otteedocome stima x =175cm. 2. Se vogliamo stimare la variaza di popolazioe, v 2 = V (X i ), è ragioevole usare come stima la variaza campioaria s 2, che è realizzazioe dello stimato- 17
18 re S 2. Èquellocheabbiamofattoell Esempio1 per stimare σ 2,lavariazadell altezzadegliitaliai, otteedo come stima s 2 =10, Se vogliamo stimare ua probabilità π di successo i ua popolazioe beroulliaa (ossia, X i Be(π)), è ragioevole usare come stima la frazioe di successi el campioe p p = 1 x i i=1 che è realizzazioe dello stimatore p = 1 X i. i=1 Èquellocheabbiamofattoell Esempio2,otteedo la stima p=0,1. N.B.: Per la frazioe campioaria di successi, si userà la stessa otazioe per la variabile casuale (lo stimatore) e per la sua realizzazioe (la stima). Soo tutti e tre stimatori/stime suggeriti dal buo seso, ma hao qualche proprietà? Il puto fodametale è che lavoriamo co stime, ossia approssimazioi del vero valore; per questo vorremmo sapere quato buoa è la stima? quato grade è l errore di approssimazioe? 18
19 Rispoderemo a queste domade teedo coto che uo stimatore è ua variabile casuale co ua sua distribuzioe di probabilità (la distribuzioe campioaria). Le proprietà dello stimatore possoo, quidi, essere studiate aalizzado le caratteristiche della sua distribuzioe campioaria, come il valore atteso, la variaza, ecc.. Questo è oto come il pricipio del campioameto ripetuto i base al quale si valutao le proprietà di uo stimatore pesado ad ipotetiche repliche del campioameto. Si ragioa, cioè, come se si estraessero tutti i c.c.s.di dimesioe dalla popolazioe di riferimeto, esuciascuodiessisicalcolasseuauovastima. Viee poi studiato il comportameto complessivo di tutte le stime otteute, le quali soo realizzazioi della stessa variabile casuale, lo stimatore. Di fatto l esperimeto o viee replicato, ma si ragioa come se lo fosse. Di seguito, vediamo le più importati proprietà formali che possoo essere richieste ad uo stimatore. 19
20 PROPRIETA DEGLI STIMATORI: 1) L ERRORE QUADRATICO MEDIO Idichiamo geericamete co θ il parametro igoto che vogliamo stimare (ad esempio, θ = µ o θ = π, ecc.) e co T lo stimatore di θ (ad esempio, T = X o T = p, ecc.). Suppoiamo che T 1 e T 2 siao due stimatori per lo stesso parametro igoto θ, le cui fuzioi di desità di probabilità soo rappresetate el grafico sottostate; quale dei due preferireste? T 2 f(t) T θ t 20
21 Idealmete, vorremmo che la distribuzioe campioaria dello stimatore T di θ fosse il più possibile cocetrata attoro a θ stesso. Se così fosse, ifatti, qualuque sia il c.c.s. estratto, la stima t o potrebbe discostarsi molto da θ. Per esempio, el caso molto irrealistico che T = θ co probabilità 1, avremmo la certezza che qualuque sia il c.c.s. estratto la stima t sia esattamete uguale al parametro da stimare θ. Ua quatità che viee frequetemete utilizzata per misurare la cocetrazioe della distribuzioe di T attoro a θ è l ERRORE QUADRATICO ME- DIO (EQM) defiito come EQM(T )=E [ (T θ) 2]. Poiché (T θ) 2 può essere iterpretato come ua distaza di T da θ, EQMèladistazamediadaθ. I altre parole, EQM misura di quato i media le realizzazioi di T su tutti i possibili c.c.s. di dimesioe estraibili dalla popolazioe di riferimeto distao da θ. U valore piccolo di EQM implica che qualuque sia il c.c.s. di dimesioe estratto dalla popolazioe, co alta probabilità, la stima t sarà vicia a θ. Èauspicabile,pertato,scegliereuostimatoreco EQM piccolo. I particolare, tra due stimatori T 1 e T 2 dello stesso parametro θ, dovremmoscegliere quello co EQM più piccolo. 21
22 L EQM può essere scomposto el modo seguete: Ifatti, EQM(T )=V (T )+[E(T ) θ] 2 E[(T θ) 2 ]=E(T 2 +θ 2 2θT) =E(T 2 )+θ 2 2θE(T )= = E(T 2 ) [E(T )] 2 +[E(T )] 2 + θ 2 2θE(T )= La quatità = V (T )+[E(T ) θ] 2. E(T ) θ è c h i a m a t a DISTORSIONE dello stimatore T. Pertato, l EQM può essere espresso come EQM(T )=[distorsioe(t )] 2 + V (T ) Le due compoeti dell EQM soo 1. la distorsioe di T,cheèlegataallaposizioe della distribuzioe di T ; 2. la variabilità della distribuzioe di T. Per avere uo stimatore co EQM piccolo possiamo lavorare su etrambe le compoeti. Iizieremo cosiderado la distorsioe. 22
23 PROPRIETA DEGLI STIMATORI: 2) LA CORRETTEZZA Suppoiamo che T 1 e T 2 siao due stimatori per lo stesso parametro igoto θ, le cui fuzioi di desità di probabilità soo rappresetate el grafico sottostate; quale dei due preferireste? T 2 T 1 0 f(t) 0 θ t Uo stimatore T per θ è d e t t o corretto o o distorto se E(T )=θ, ossia se la distorsioe E(T ) θ è p a r i a 0. 23
24 La distribuzioe campioaria di uo stimatore corretto è cetrata attoro a θ. La correttezza di uo stimatore garatisce che la media delle stime otteute su tutti i c.c.s. di dimesioe che possiamo estrarre dalla popolazioe sia uguale al parametro igoto. Seppure la correttezza è ua proprietà auspicabile, essa forisce solo delle garazie i media e o ci assicura che la stima otteuta sul c.c.s. effettivamete estratto sia uguale a θ (o ache solo vicia). 24
25 ESEMPI DI STIMATORI CORRETTI E NON CORRETTI 1. La media campioaria X è sempre uo stimatore corretto per la media di popolazioe m = E(X i ). Dimostrazioe: Dato m = E(X i ), per ogi i = 1,...,,siha ( ) E( X) X X =E = m = m Esempio 4 La correttezza della media campioaria è u risultato geerale. Tuttavia, per fissare le idee, riprediamo l esempio dell ura co 3 pallie umerate da 1 a 3 e verifichiamo per questo caso specifico per via diretta la o distorsioe di X. La media di popolazioe è m = 2 = E(X 1 ) = E(X 2 ). Usado la distribuzioe campioaria di X specificata apag.12,abbiamo E( X) = , , =2 Si oti però che se avessimo estratto il campioe (1,1) la stima di m sarebbe stata x = La frazioe campioaria di successi p è u o s t i m a t o r e corretto della frazioe π di successi ella popolazioe. 25
26 Dimostrazioe: Segue dalla correttezza della media campioaria, otado che p stessa è ua media di variabili casuali Be(π), ciascua co valore atteso π. 3. La variaza campioaria S 2 o è uo stimatore corretto della variaza di popolazioe v 2. Sia x 1,...,x u c.c.s. da ua popolazioe di media m evariazav 2,ossiaE(X i )=mev(x i )=v 2, per ogi i =1,...,.Allora, E(S 2 )=E [ 1 ] (X i X) 2 = E i=1 = 1 ( 1 E(Xi 2 ) E( X 2 ) i=1 ) Xi 2 X 2 = Teedo coto del fatto che E(X 2 i )=V (X i)+[e(x i )] 2 = v 2 +m 2 e, aalogamete, E( X 2 )=V ( X)+[E( X)] 2, si ha i=1 E(S 2 )= 1 (v2 + m 2 ) { V ( X)+[E( X)] 2}. Sappiamo ioltre che E( X) =m e ( ) V ( X) X X =V = v2 da cui { } v E(S 2 )=v 2 + m m2 = v2 = 1 v2. 26
27 Èfacile correggere S 2 i modo da derivare uo stimatore corretto di v 2. Per i precedeti risultati, ifatti, lo stimatore S 2 = S 2 1 = 1 (X i 1 X) 2 è t a l e c h e ( E(S 2 )=E S 2 i=1 ) = E(S 2 ) 1 1 = v2. S 2 è c h i a m a t a variaza campioaria corretta. Idicheremo la realizzazioe campioaria di S 2 co s 2. Ad esempio, ell Esempio 1, la variaza campioaria corretta osservata è s 2 =10, /7 = 134, 54 27
28 L EQM PER STIMATORI CORRETTI Si oti che se T è u o s t i m a t o r e c o r r e t t o d i θ, allora EQM(T )=V (T ) elaqualitàdellostimatorepuòsemplicemeteessere valutata i base alla sua variaza. Esempio 5 Valutiamo l EQM della media campioaria X come stimatore di ua media di popolazioe m = E(X i ). Abbiamo visto che la media campioaria è uo stimatore corretto di m, quidi ( ) EQM( X) =V ( X) X X =V = 1 2 v2 = v2 dove v 2 = V (X i )èlavariazadipopolazioe. Si oti che l EQM decresce al crescere di. Ialtre parole, più grade è il campioe e meglio si comporta lo stimatore. Èquestauacodizioechedeveessere soddisfatta da u qualuque stimatore sesato. Se T 1 e T 2 soo etrambi stimatori corretti per θ, i base al criterio dell EQM, tra i due è preferibile quello co variaza più piccola. Esempio 6 Cosideriamo T 1 = X 1 e T 2 = X come stimatori per ua media m = E(X i )dipopolazioe. Soo etrambi stimatori corretti, ifatti E(T 1 ) = E(X 1 )=m, ma EQM(T 1 )=V (T 1 )=V (X 1 )=v 2 28
29 edall Esempio5sappiamoche EQM(T 2 )=V ( X) = v2, dove v 2 = V (X i ). Da cui si deduce che, per ogi 1, EQM(T 1 ) EQM(T 2 )echet 2 è p r e f e r i b i l e a T 1. Ua parte della Statistica Ifereziale (la Teoria ottimale) si dedica a idetificare per ciascu problema di stima lo stimatore migliore, ossia co EQM più piccolo. No etreremo ei dettagli della Teoria ottimale, ci limitiamo a dire (seza dimostrazioe) che se il c.c.s. x 1,...,x è t r a t t o d a u a popolazioe ormale, ossiax i N(µ, σ 2 )perogi i =1,...,,alloralamediacampioaria X ela variaza campioaria corretta S 2 soo gli stimatori ottimali, rispettivamete, per µ e σ 2,ella classe degli stimatori corretti; se il c.c.s. x 1,...,x è t r a t t o d a u a popolazioe beroulliaa, ossiax i Be(π) per ogi i =1,...,,alloralafrazioecampioaria di successi p è l o s t i m a t o r e o t t i m a l e d i π ella classe degli stimatori corretti. 29
30 PROPRIETÀ DEGLISTIMATORI: 3) LA CONSISTENZA Trae i problemi di stima molto semplici, è i geerale difficile idetificare uo stimatore co proprietà di ottimalità, ad esempio, o distorto e/o co EQM miimo. Questo ha idotto gli statistici ad aalizzare le proprietà asitotiche degli stimatori, ossia come si comporta la distribuzioe campioaria dello stimatore per. Verificare le proprietà di uo stimatore per o è u mero esercizio teorico: l idea di base è che ua proprietà asitotica sarà almeo approssimativamete soddisfatta i campioi di dimesioe fiita, purché sufficietemete gradi. La cosisteza è u a d e l l e pricipali proprietà asitotiche che possoo essere richieste ad uo stimatore. Per sottolieare la dipedeza dalla umerosità campioaria,idichiamolostimatorecot = g(x 1,...,X ). Idealmete, si vorrebbe che T θ, per (se il campioe è così grade da coprire l itera popolazioe, dovremmo essere i grado di quatificare le quatità di popolazioe di iteresse i modo esatto). Tuttavia, o possiamo applicare l usuale defiizioe di limite, perché T o è ua successioe umerica, besì ua successioe di variabile casuali. Abbiamo, 30
31 per questo, bisogo di ua defiizioe di covergeza diversa. Il problema viee risolto richiededo che, al crescere di, ladistribuzioecampioariadit si cocetri sempre di più attoro a θ. Più precisamete, uo stimatore T di θ si dice cosistete se lim EQM(T )= lim E[(T θ) 2 ]=0 I sostaza, uo stimatore è cosistete se la sua accuratezza migliora all aumetare della umerosità campioaria, sio a divetare perfetta. 31
32 Se T è u o s t i m a t o r e c o r r e t t o d i θ,alloraeqm(t )= V (T )elostimatoreècosistetese lim V (T )=0, Esempio 6 Riprediamo gli stimatori T 1 = X 1 e T 2 = X per ua media di popolazioe m. MetreT 2 è u o s t i m a t o r e cosistete, dato che EQM(T 2 )= v2 0, per, T 1 o è uo stimatore cosistete, poiché EQM(T 1 )=v 2 0, per. dove v 2 è l a v a r i a z a d i p o p o l a z i o e. Per gli stimatori X, S 2 e p si ha la media campioaria X è u o s t i m a t o r e c o s i - stete per ua media di popolazioe m = E(X i ), sia che la popolazioe sia gaussiaa che o gaussiaa. Segue dagli sviluppi dell Esempio 6. la variaza campioaria corretta S 2 è u o s t i m a - tore cosistete per ua variaza di popolazioe v 2 = V (X i ), sia che la popolazioe sia gaussiaa che o gaussiaa (o dimostrato). la frazioe campioaria di successi p è u o s t i - matore cosistete per ua probabilità π. Segue dagli sviluppi per la media campioaria, ricordado che p stesso è ua media di variabili beroulliae. 32
33 Esercizio (per casa) Siao X 1,...,X i.i.d. co distribuzioe N(µ, σ 2 ). Dati i due stimatori di µ T 1 =0, 9X 1 +0, 1 ( 1 1 ) X i i=2, T 2 = X 1 + X 2 1. dimostrare che soo etrambi stimatori corretti per µ; 2. calcolare l EQM di etrambi gli stimatori; 3. verificare se soo stimatori cosisteti. 33
34 SINTESI DELLE PROPRIETÀ DI X, S 2 e p 1. LA MEDIA CAMPIONARIA La media campioaria X = 1 i=1 X i co X 1,...,X i.i.d. tali che E(X i ) = m e V (X i )=v 2,èuostimatorecorrettoecosistete per m. IlsuoEQMè EQM( X) =V ( X) = v2 che forisce ua misura dell accuratezza di X come stimatore di m. Sev 2 o è ota, l EQM può essere valutato sostituedo v 2 co s 2. Se X 1,...,X soo i.i.d. N(µ, σ 2 ), allora X è ache lo stimatore migliore (co EQM più piccolo) tra tutti gli stimatori corretti di µ. Per oti risultati della probabilità (si veda pag. 101 della Probabilità), vale ioltre ) X N (µ, σ2 Se il campioe ha umerosità grade, allora, per il teorema del limite cetrale, qualuque sia la distribuzioe (o gaussiaa) delle variabili X i X = X X N (m, v2 dove m = E(X i )ev 2 = V (X i )(sicofrotico pag. 114 della Probabilità). 34 )
35 2. LA FRAZIONE CAMPIONARIA DI SUCCESSI La frazioe campioaria di successi p = 1 X i, i=1 co X 1,...,X i.i.d. tali che X i Be(π), è uo stimatore corretto e cosistete di ua probabilità di successo π. Èachelostimatoreco il più piccolo EQM ella classe degli stimatori corretti di π. IlsuoEQMè π(1 π) EQM(p) =V (p) = che si deriva facilmete dall EQM di X sostituedo la variaza geerica v 2 co V (X i )=π(1 π). L EQM può essere valutato sostituedo a π la sua stima p. Per il teorema del limite cetrale, per grade vale ( ) π(1 π) p N π,, (si cofroti co pag. 115 della Probabilità). 3. LA VARIANZA CAMPIONARIA CORRETTA La variaza campioaria corretta S 2 = 1 (X i 1 X) 2 = 1 S2 i=1 co X 1,...,X i.i.d. tali che E(X i ) = m e V (X i )=v 2,èuostimatorecorrettoecosistete per v 2. (No viee precisato l EQM, perché o utilizzato el seguito). 35
36 Se X 1,...,X soo i.i.d. N(µ, σ 2 ), allora S 2 è ache lo stimatore migliore (co EQM più piccolo) tra tutti gli stimatori corretti di σ 2.Ioltre, ( 1)S 2 σ 2 (risultato o dimostrato) χ
37 UN METODO GENERALE DI STIMA PUNTUALE: IL METODO DEI MOMENTI Gli stimatori X, p e S 2 soo stati proposti sulla base di criteri di ragioevalezza, ma è importate poter disporre di metodi geerali di costruzioe di stimatori, applicabili, i liea di pricipio, a qualuque problema di stima e per qualuque parametro. Esistoo diversi metodi geerali per la stima putuale. Noi copriremo uo solo di questi, il metodo dei mometi. Sia x 1,...,x u c.c.s. e θ il parametro da stimare. Il primo passo del metodo dei mometi cosiste el determiare E(X i )chesaràigeeraleuafuzioe di θ. Al secodo passo, si risolve rispetto a θ l equazioe E(X i )= x. La soluzioe dell equazioe, che idichiamo co θ, è la stima co il metodo dei mometi di θ. L idea di base del metodo dei mometi è eguagliare la media teorica (ache chiamata mometo primo teorico) E(X i )allacorrispodetemediacampioaria x edaquestaequazioederivareuastimaper θ. 37
38 Esempio 1 Se vogliamo stimare l altezza media degli italiai µ, i base al metodo dei mometi, dovremmo risolvere rispetto a µ l equazioe E(X i )=µ = x =175, otteedo la stima µ = x =175. Esempio 2 Se vogliamo stimare la frazioe π di guarizioi difettose ell itera popolazioe, i base al metodo dei mometi dovremmo risolvere rispetto a π l equazioe E(X i )=π = x = p =0, 1 dove si tiee coto del fatto che, essedo le x i realizzazioi di variabili casuali beroulliae, x = p. La stima co il metodo dei mometi di π è q u i d i π = p =0, 1. Esempio 3 Se vogliamo stimare il umero medio gioraliero di utilizzi del bacomat λ, i base al metodo dei mometi dovremmo risolvere rispetto a λ l equazioe E(X i )=λ = x =7, 6. La stima co il metodo dei mometi di λ è q u i d i λ = x =7, 6. Esempio 7 Èstatoosservataladuratadi15lampadiescelte casualmete tra quelle prodotte da ua fabbrica. La durata media delle 15 lampadie del campioe è 38
39 x =65ore. Sipuòipotizzarecheladuratadelle lampadie abbia distribuzioe espoeziale di parametro λ igoto. Si vuole stimare λ. Co queste ipotesi le variabili casuali che descrivoo il campioe, X 1,...,X 15,sooi.i.d. Exp(λ). Applicado il metodo dei mometi, si ottiee ua stima putuale per λ risolvedo l equazioe E(X i )=1/λ = x =65. La stima co il medoto dei mometi per λ è q u i d i λ =1/ x =1/65. Il metodo dei mometi è applicabile ache al caso i cui si debbao stimare due o più parametri igoti. Vediamo il caso di due parametri. Suppoiamo che la distribuzioe delle X i dipeda da due parametri igoti, θ 1 e θ 2,chedevooessere stimati. Al primo passo il metodo dei mometi richiede il calcolo di E(X i )ee(x 2 i )chesarao,i geerale, fuzioi di θ 1 e θ 2. Al secodo passo, si risolve rispetto a θ 1 e θ 2 il sistema di equazioi { E(X i )= x E(X 2 i )= 1 i=1 x2 i Le soluzioi del sistema, θ 1 e θ 2,soolestimecoil metodo dei mometi di θ 1 e θ 2,rispettivamete. L idea di base è acora eguagliare le medie teoriche, E(X i )ee(xi 2 ), co la corrispodeti medie campioarie. Lo stesso meccaismo può essere applicato 39
40 apiùdidueparametri. Ilomedelmetododeriva dal fatto che E(X j )èachechiamatoilmometo j-esimo di X i. Esempio 1 Nell esempio sull altezza degli italiai, sia la media di popolazioe µ che la variaza di popolazioe σ 2 soo igote e devoo essere stimate dalle osservazioi. Applicado il metodo dei mometi, abbiamo che E(X i )=µ e E(X 2 i )=σ2 + µ 2 erisolvedorispetto a µ e σ 2 il sistema di equazioi { µ = x σ 2 + µ 2 = 1 i=1 x2 i si ottego le stime µ = x =175e σ 2 = s 2 =10, 85 2, rispettivamete, per µ e σ 2.Lestimecoilmetodo dei mometi della media e della variaza di popolazioe soo quidi la media campioaria e la variaza campioaria o corretta, rispettivamete. Proprietà del metodo dei mometi: Èumetodomoltosempliceequasisempreapplicabile co campioi casuali semplici. Produce stimatori cosisteti, ma o ecessariamete corretti e/o ottimali (co EQM miimo). Può produrre stimatori corretti e/o ottimali, ma le due proprietà o soo garatite e devoo essere verificate caso per caso. 40
41 STIMA INTERVALLARE L obiettivo della stima itervallare è idetificare, sullabase delle osservazioi del campioe, u itervallo di valori che, co u certo grado di attedibilità, cotega l igoto parametro di popolazioe θ. Esempio 2 Avevamo otteuto la stima putuale p =0, 1. Possiamo dire che l itervallo (0,05,0,15) è u itervallo di valori ragioevoli per π, laverafrazioediguarizioidifettose ella popolazioe? quali garazie ci dà questo itervallo di icludere π? GLI INTERVALLI DI CONFIDENZA Il problema di idividuare u itervallo di valori ragioevoli per u parametro θ igoto può essere affrotato trovado due statistiche campioarie, T I = g I (X 1,...,X ) e T S = g S (X 1,...,X ), tali che P (T I θ T S )=1 α dove α è u v a l o r e p r e fi s s a t o. I questo modo, la probabilità che θ sia icluso ell itervallo (T I,T S )è1 α. L itervallo (T I,T S )vieechiamatoitervallo di cofideza di livello 1-α odilivello(1-α) 100% per θ. 41
42 CONSIDERAZIONI 1. α è la probabilità che l itervallo di cofideza o icluda θ e, idealmete, vorremmo che fosse più piccola possibile. Ma attezioe, se poessimo α = 0, l itervallo dovrebbe compredere tutti i valori che possoo essere assuti da θ equestoitervalloo ha alcua utilità pratica. I geerale, più piccolo è α più ampio è l itervallo di cofideza, idetificado così i modo meo preciso dove si colloca θ. Esisteu trade-off tra la garazia di icludere θ elaprecisioe dell itervallo. Come compromesso, tipicamete si sceglie α [0, 01; 0, 1]. 2. Essedo T I e T S due variabili casuali, ache l itervallo (T I,T S ) è c a s u a l e. Dopo aver osservato il c.c.s. x 1,...,x avremo che t I = g I (x 1,...,x )e t S = g S (x 1,...,x )soolerealizzazioieffettivamete osservate di T I e T S.Pertato,l itervallodi cofideza osservato (t I,t S )oèpiùcasuale,ma umerico. 3. No è corretto dire che l itervallo umerico (t I,t S ) cotiee θ co probabilità 1 α. Questaaffermazioe vale solo per l itervallo casuale (T I,T S ). Richiamado il pricipio del campioameto ripetuto, la corretta iterpretazioe di u itervallo di cofideza di livello 1 α è l a s e g u e t e. S e r i p e t i a m o i l c a m - pioameto e su tutti i possibili c.c.s. di dimesioe calcoliamo u uovo itervallo osservato (t I,t S ), allora (1 α) 100% di questi cotiee θ. Tuttavia, sul sigolo campioe effettivamete estratto o possiamo sapere se cotega θ oppure o. 42
43 METODI DI COSTRUZIONI DI INTERVALLI DI CONFIDENZA Esistoo varie procedure di costruzioe di itervalli di cofideza per u parametro θ di popolazioe igoto. I geerale, esse si fodao sui segueti passi. 1. Si sceglie il livello di cofideza 1 α. 2. Si idetifica uo stimatore T di θ. 3. Si cerca ua fuzioe di T ediθ, Q(T,θ)(quatità pivotale), la cui distribuzioe di probabilità sia completamete ota. 4. Se q α/2 e q 1 α/2 soo, rispettivamete, i quatili α/2 e1 α/2 diq(t,θ), allora P (q α/2 Q(T,θ) q 1 α/2 )=1 α 5. Isolado θ all itero della disuguagliaza, si deriva u itervallo di cofideza per θ. 43
44 ESEMPI DI INTERVALLI DI CONFIDENZA 1. INTERVALLI DI CONFIDENZA PER I PARAMETRI DI UNA POPOLAZIONE NORMALE Sia x 1,x 2,...,x u c.c.s. da ua popolazioe ormale, ossia X 1, X 2,..., X soo i.i.d. co distribuzioe N(µ, σ 2 ). INTERVALLO DI CONFIDENZA PER µ CASO CON σ 2 NOTA Suppoiamo di cooscere σ 2,lavariazadipopolazioe, ma di o cooscere µ, lamediadi popolazioe. Vogliamo costruire u itervallo di cofideza di livello 1 α per µ. Sappiamo che ) X N (µ, σ2 da cui Allora, P X µ σ 2 z 1 α/2 X µ σ 2 N(0, 1). z 1 α/2 =1 α 44
45 ricordado che z α/2 = z 1 α/2.ora,isoladoµ si ottiee ( ) σ 2 P X z 1 α/2 µ }{{ X σ 2 + z 1 α/2 =1 α }}{{ } T I T S Allora, u itervallo di cofideza di livello 1 α per la media µ quado la variaza σ 2 è o t a è ( ) σ 2 X z 1 α/2, X σ 2 + z 1 α/2 opiùbrevemete ( ) σ 2 X ± z 1 α/2 L ampiezza dell itervallo è σ 2 2z 1 α/2 Aparitàdituttoilresto,alcresceredi l ampiezza dell itervallo dimiuisce, ossia l itervallo diveta più preciso. A parità di tutto il resto, se dimiuisce α, z 1 α/2 aumeta e quidi l ampiezza dell itervallo aumeta. A parità di tutto il resto, se dimiuisce σ 2,dimiuiscel ampiezza dell itervallo. L itervallo umerico, basato sulle osservazioi x 1,..., x,realizzazioedell itervallocasuale trovato è ( ) σ 2 x ± z 1 α/2 dove x è la media calcolata sul campioe estratto. 45
46 Esempio 8 Si suppoga che il peso (i kg) di certe cofezioi abbia distribuzioe ormale di media µ igota e deviazioe stadard pari a 2,5kg. Su u campioe casuale di 100 cofezioi è stato calcolato u peso medio di 11,5kg. Si costruisca u itervallo di cofideza di livello 95% per µ. E chiaro dal testo che la variaza σ 2 può cosiderarsi ota e pari a 2,5 2 kg 2.Sitrattaalloradi usare l espressioe per l itervallo di cofideza per µ appea trovata: ( ) σ 2 x ± z 1 α/2 I questo caso x =11, 5kg 1 α =0, 95 e quidi α =0, 05 z 1 α/2 = z 0,975 =1, 96 =100 L itervallo di cofideza (umerico) di livello 95% per µ è ( ) 2, , 5 ± 1, 96 =(11, 02kg; 11, 98kg) 100 Iterpretazioe... 46
47 CASO CON σ 2 IGNOTA Siamo ella stessa situazioe di prima, ma suppoiamo ora che sia µ che σ 2 siao igoti. Il ostro parametro di iteresse rimae la media di popolazioe µ e, i particolare, vogliamo costruire u itervallo di cofideza per µ. Nel caso precedete abbiamo usato la quatità X µ σ 2 N(0, 1) per costruire l itervallo per µ. Oraperòσ 2 o è o t a e q u e s t a q u a t i t à o è d i r e t t a m e t e u t i - lizzabile. Possiamo procedere i questo modo: stimare σ 2 tramite il suo stimatore corretto S 2 e sostituire questo stimatore all itero della precedete quatità, otteedo X µ S 2 t 1 Ifatti, X e S 2 soo idipedeti (o dimostrato). Ioltre, X µ = ( X µ) ( X σ µ)/ = t 1, ( 1)σ 2 ( 1)σ 2 S 2 S 2 ( 1)σ 2 S 2 ( 1) dato che il umeratore dell ultima frazioe ha di- N(0, 1) e al deomiatore abbiamo stribuzioe χ 2 1 /( 1). 47
48 P Da questo risultato, si ha che P t 1;1 α/2 X µ S 2 t 1;1 α/2 =1 α teedo coto del fatto che t 1;α/2 = t 1,1 α/2. Ora, isolado µ, siottiee S X 2 t 1;1 α/2 µ X S + t 2 1;1 α/2 =1 α }{{}}{{} T I T S Allora, u itervallo di cofideza per µ di livello 1 α, quadoacheσ 2 o è ota, è S X 2 t 1;1 α/2, X S + t 2 1;1 α/2 o, più brevemete, X ± t 1;1 α/2 S 2 Si oti che, valedo S 2 = S 2 /( 1), l itervallo otteuto è equivalete a ( ) S 2 X ± t 1;1 α/2 1 dove S 2 la variaza campioaria o corretta. 48
49 L itervallo umerico, basato sulle osservazioi x 1,..., x,corrispodeteall itervallocasuale trovato è s x ± t 2 1;1 α/2 dove x e s 2 soo, rispettivamete, la media e la variaza corretta calcolate sul campioe. Si ricordi ifie, che, per sufficietemete grade, diciamo maggiore di 31, possiamo approssimare t 1;1 α/2 co z 1 α/2. 49
50 Esempio 9 Ua macchia è stata predisposta per riempire bottiglie di olio dal coteuto omiale di 1 litro. Si sa che la macchia commette degli errori i fase di riempimeto e che la quatità effettivamete versata su ciascua bottiglia segue ua distribuzioe gaussiaa. La macchia viee fermata e cotrollata ogi qualvolta si verifica che la media gioraliera esce dai limiti di ±5 ml. Se l osservazioe per u dato gioro viee fatta solo su u campioe di 10 bottiglie, otteedo i segueti dati (i litri) 1, 000 0, 998 1, 003 1, 002 0, 999 0, 997 0, 999 1, 001 1, 000, 1, 010 utilizzare i dati per vedere se la macchia deve essere fermata trovado u itervallo di cofideza al 99% per la media gioraliera. Poichè gli errori el riempimeto soo ormalmete distribuiti, possiamo vedere le 10 osservazioi x 1, x 2,..., x 10 come u c.c.s. da ua N(µ, σ 2 ), dove µ rappreseta la media della quatità di olio versata elle bottiglie. Sia µ che σ 2 soo igote. Vogliamo costruire u itervallo di cofideza di livello 0,99 per µ. Calcoliamo gli igredieti dell itervallo di cofideza. x =1, 0009 litri s 2 =0, litri 2 50
51 1 α =0, 99 α =0, 01 α/2 =0, α/2 =0, 995 t 9;0,995 =3, 2498 L itervallo cercato è ( ) 0, , , , 2498 ;1, , 2498 = =(0, 99614; 1, 00466) litri I base all itervallo otteuto, fermeremmo la macchia? La tolleraza è ±5mlsulcoteutoomiale di 1 lt, ossia riteiamo la macchia fuori cotrollo se la media gioraliera esce al di fuori dell itervallo (0,995,1,005) lt. I base all itervallo otteuto, la media gioraliera cade all itero dei limiti di tolleraza equidiofermeremmolamacchia. 51
52 INTERVALLO DI CONFIDENZA PER σ 2 Spostiamo ora l iteresse da µ, cheèstatoilpara- metro di iteresse ei precedeti itervalli, a σ 2,la variaza della popolazioe. Vogliamo costruire u itervallo di cofideza di livello 1 α per σ 2,quado ache µ è i g o t o. Così come la media campioaria X è s t a t o i l p u t o di parteza per costruire u itervallo di cofideza per µ, lavariazacampioaria(ellasuaversioe corretta) S 2 è i l p u t o d i p a r t e z a p e r c o s t r u i r e u itervallo di cofideza per σ 2. Sappiamo che, per ua popolazioe ormale, Pertato, ( P ( 1)S 2 σ 2 χ 2 1;α/2 ( 1)S 2 σ 2 χ 2 1 χ 2 1;1 α/2 ) =1 α Ora isoliamo σ 2,otteedo ( ) ( 1)S 2 P χ 2 σ 2 ( 1)S 2 1;1 α/2 χ 2 1;α/2 =1 α Allora, u itervallo di cofideza di livello 1 α per σ 2 è ( ) ( 1)S 2 χ 2, ( 1)S 2 1;1 α/2 χ 2 1;α/2 52
53 Se volessimo u itervallo per σ piuttosto che per σ 2 basterà predere la radice quadrata di etrambi gli estremi: Ifatti, = P P ( ( 1)S 2 χ 2, 1;1 α/2 ( ( 1)S 2 χ 2 1;1 α/2 ( ( 1)S 2 χ 2 1;1 α/2 ) ( 1)S 2 χ 2 1;α/2 ) σ 2 ( 1)S 2 = σ χ 2 1;α/2 ) ( 1)S 2 χ 2 1;α/2 =1 α 53
54 Esempio 10 Ua uova terapia è stata sperimetata su u campioe di 12 pazieti e i tempi di guarigioe osservati soo stati (i giori) (a) Assumedo ua distribuzioe ormale per il tempo di guarigioe, trovare u itervallo di cofideza di livello 95% per il tempo medio di guarigioe dei pazieti sottoposti a terapia. Le 12 osservazioi rappresetao u c.c.s. da N(µ, σ 2 ), co µ e σ 2 etrambi igoti. I particolare, µ è i l t e m p o m e d i o ( i g i o r i ) d i g u a r i g i o e per il quale vogliamo costruire u itervallo di cofideza. Gli igredieti dell itervallo soo da cui x =24, 67 giori s 2 =53, 39 s 2 = S2 12 =58, α =0, 95 α =0, 05 1 α/2 =0, 975 t 11;0,975 =2, 2 L itervallo cercato è ( ) 58, 24 24, 67 ± 2, 2 =(19, 82; 29, 52) giori 12 54
55 (b) Si dia u itervallo di cofideza al 90% per la variaza σ 2 1 α =0, 9 α =0, 1 1 α/2 =0, 95 α/2 =0, 05 χ 2 11;0,05 =4, 57 χ 2 11,0,95 =19, 68 L itervallo cercato per σ 2 è ( ) 11 58, , 24 ; =(32, 55; 140, 18) 19, 68 4, 57 55
56 2. INTERVALLO DI CONFIDENZA APPROS- SIMATO PER UNA PROBABILITÀ Sia x 1,x 2,...,x u c.c.s. da ua popolazioe beroulliaa, ossia X 1,X 2,...,X soo i.i.d. Be(π). P ( No coosciamo la probabilità π di successo ella popolazioe e vogliamo costruire u itervallo di cofideza per π di livello 1 α. Partiamoda p = 1 X i i=1 che sappiamo essere uo stimatore ottimale per π. Sappiamo ioltre che, per grade, ( ) π(1 π) p N π, Allora, da cui P z 1 α/2 p π π(1 π) p π π(1 π) Ora, isolado π, otteiamo p z 1 α/2 π(1 π) N(0, 1) z 1 α/2 = p p + z 1 α/2 π(1 π) 1 α ) = 1 α 56
57 da cui u itervallo di cofideza di livello approssimato 1 α per π è ( ) π(1 π) π(1 π) p z 1 α/2,p+ z 1 α/2 Il problema è che o cooscedo π o siamo i grado di calcolare π(1 π)/. Tuttavia, poiché stiamo lavorado co gradi campioi, possiamo sostituire a π il suo stimatore cosistete p otteedo l itervallo ( p(1 p) p(1 p) p z 1 α/2,p+ z 1 α/2 Il corrispodete itervallo umerico si ottiee poedo p uguale alla frazioe osservata di successi el campioe. OSSERVAZIONE: Affiché l approssimazioe risulti buoa, dovremmo avere π, (1 π) 5, ma o cooscedo π, possiamo verificare se p, (1 p) 5. Dobbiamo avere quidi a disposizioe almeo 10 osservazioi, di cui almeo 5 successi e 5 isuccessi. ) 57
58 Esempio 11 Il direttore di ua baca di ua piccola città itede ivestigare la proporzioe di depositati che vegoo pagati mesilmete. Per compiere tale studio vegoo scelti i modo casuale 200 depositati e di questi 23 affermao di essere pagati mesilmete. Stimare la vera proporzioe di depositati della baca pagati mesilmete e costruire u itervallo di cofideza di livello 90% per tale proporzioe. Abbiamo due modi equivaleti di vedere il problema. 1. Osserviamo 200 valori, x 1,..., x 200,co { 1 se l i-esimo cliete è pagato mesilmete x i = 0 se l i-esimo cliete o è pagato mesilmete 23 x i soo uguali a 1 e x i soo uguali a 0. I questo caso abbiamo u c.c.s di dimesioe 200 da Be(π). 2. Osserviamo u uico valore x = 23 da ua Bi(200,π). Qualuque sia il modo di iterpretare l idagie, sappiamo che p = =0, 115 = frazioe di successi osservati è ua stima della frazioe π ella popolazioe. 58
59 Per costruire l itervallo di cofideza, 1 α =0, 9 α =0, 1 1 α/2 =0, 95 z 0,95 =1, 64 L itervallo di cofideza cercato è ( ) 0, 115(1 0, 115) 0, 115(1 0, 115) 0, 115 1, 64, (0, , = =(0, 082; 0, 158) 59
60 3. INTERVALLO DI CONFIDENZA APPROS- SIMATO PER LA MEDIA DI UNA PO- POLAZIONE NON-NORMALE Sia x 1,...,x u c.c.s. da ua popolazioe di media m evariazav 2,ossiaE(X i )=m e V (X i )=v 2 per ogi i =1,...,. Si vuole costruire u itervallo di cofideza di livello 1 α per m. I geerale, per poter costruire tale itervallo è ecessario cooscere la distribuzioe delle X i che o è però qui specificata. Tuttavia, se è grade, geeralizzadoquatovistoperπ, è possibile costruire u itervallo che abbia almeo livello approssimato 1 α, usadoargometazioi asitotiche. Ifatti, per il teorema del limite cetrale, per grade, si ha che ) X N (m, v2 da cui X m v2 / N (0, 1). e P ( z 1 α/2 X ) m v2 / z 1 α/2 = 1 α. Isolado m all itero della disuguagliaza, si deriva ( P X z1 α/2 v2 / m X + z 1 α/2 v2 /) = 1 α, 60
61 equidiuitervallodicofidezadilivelloapprossimato 1 α per m per gradi campioi è dato da ( X z1 α/2 v2 /, X + z 1 α/2 v2 /). Se, come spesso accade, v 2 o è oto, poiché stiamo lavorado co gradi campioi, possiamo sostituirlo co il suo stimatore cosistete S 2,otteedo l itervallo ( X z1 α/2 S 2 /, X + z 1 α/2 S 2 /). Il corrispodete itervallo umerico è ( ) x z 1 α/2 s 2 /, x + z 1 α/2 s 2 /. N.B.: L espressioe dell itervallo otteuto per v 2 oto è l a s t e s s a d i q u e l l o p e r u a p o p o l a z i o e o r m a - le. Tuttavia, el caso di ua popolazioe ormale l itervallo ha esatto livello 1 α idipedetemete dalla umerosità campioaria, metre el caso di ua popolazioe o-ormale l itervallo ha livello approssimato 1 α solo i gradi campioi. La qualità dell approssimazioe migliora co la dimesioe del campioe. L itervallo di cofideza otteuto per π è u c a - so particolare di questa procedura, i cui X = p e, sfruttado il fatto che per ua popolazioe beroulliaa v 2 = π(1 π), lo stimatore utilizzato per v 2 o è S 2,besìp(1 p). 61
62 Esempio 12 Si è iteressati a studiare il reddito medio mesile delle famiglie di u certo paese. A questo scopo si estrae u campioe di 196 famiglie il cui reddito medio mesile risulta pari a x =1864eurocovariaza campioaria corretta pari a s 2 =141, 61. Si costruisca u itervallo di cofideza di livello 1 α =0, 95 per il reddito medio mesile della popolazioe. La distribuzioe del reddito è geeralmete caratterizzata da ua forte asimmetria positiva, determiata dalla preseza di pochi redditi molto elevati. Per questo o è ragioevole assumere che le X i siao ormalmete distribuite. Tuttavia, essedo la umerosità campioaria piuttosto elevata possiamo ricorrere ad argometi asitotici e utilizzare l itervallo approssimato (1864 ± z 0, , 61/196 ) =(1865, 67; 1862, 33). 62
63 4. INTERVALLO DI CONFIDENZA PER LA DIFFERENZA DELLE MEDIE DI DUE POPOLAZIONI NORMALI Suppoiamo di voler cofrotare due popolazioi i relazioe ad u feomeo di iteresse. Ad esempio, vogliamo cofrotare il reddito delle famiglie italiae co il reddito delle famiglie fracesi, oppure la redditività di ua strategia aziedale A cotro la redditività di ua strategia B. A questo fie prediamo due c.c.s.: x 1,x 2,...,x 1 dalla popolazioe I y 1,y 2,...,y 2 dalla popolazioe II esuppoiamoche x 1,x 2,...,x 1 siao realizzazioi di X 1,X 2,...,X 1 i.i.d. N(µ 1,σ1 2); y 1,y 2,...,y 2 siao realizzazioi di Y 1,Y 2,...,Y 2 i.i.d. N(µ 2,σ2); 2 eiduecampioisiaotraloroidipedeti. Ad esempio, per cofrotare il reddito dei fracesi eilredditodegliitaliai,prediamo 1 famiglie fracesi e e osserviamo il reddito e 2 famiglie italiae e e osserviamo il reddito. Quidi assumiamo che sia per i fracesi che per gli italiai il reddito sia ormalmete distribuito, ma co medie e variaze che possoo essere diverse. Siamo iteressati a cofrotare il livello medio del feomeo elle due popolazioi, ossia µ 1 e µ 2 (ad esempio, il reddito medio dei fracesi cotro il reddi- 63
64 to medio degli italiai) e, per questo, costruiamo u itervallo di cofideza per µ 1 µ 2. CASO CON VARIANZE NOTE Suppoiamo iizialmete che σ 2 1 e σ 2 2 siao ote. Il puto di parteza per costruire u itervallo di cofideza per µ 1 µ 2 è l a d i ff e r e z a t r a l e d u e medie campioarie Sappiamo che e X Ȳ = X N Ȳ N i=1 X i ( µ 1, σ2 1 1 ) ( ) µ 2, σ2 2 2 i=1 Y i BREVE RICHIAMO DI PROBABILITA Se X N(µ 1,σ 2 1 )ey N(µ 2,σ 2 2 )idipedeti, allora, ax + by N(aµ 1 + bµ 2,a 2 σ b2 σ 2 2 ) Dal richiamo di probabilità, ) X (µ Ȳ N 1 µ 2, σ2 1 + σ
65 e Allora, ( X Ȳ ) (µ 1 µ 2 ) N(0, 1) σ σ2 2 2 P z 1 α/2 ( X Ȳ ) (µ 1 µ 2 ) z 1 α/2 =1 α σ σ2 1 2 Se isoliamo µ 1 µ 2,otteiamo P ( X Ȳ ) z σ1 2 1 α/2 + σ2 2 µ 1 µ ( X Ȳ )+z 1 α/2 σ1 2 + σ =1 α Abbiamo quidi otteuto l itervallo di cofideza di livello 1 α per µ 1 µ 2,cheèdatoda ( X Ȳ ) ± z σ1 2 1 α/2 + σ2 2 1 Il corrispodete itervallo umerico, si ottiee sostituedo alle variabili casuali X e Ȳ le medie campioarie osservate x e ȳ. 2 65
66 Esempio 13 Per valutare la diversità della preparazioe degli studeti di due corsi di laurea A e B della facoltà di Ecoomia, 50 studeti del corso A e 100 studeti del corso B vegoo sottoposti ad u test. Gli studeti del corso A e B ottegoo u puteggio medio di 3 e 2,5, rispettivamete. Si suppoga ioltre che le variabili casuali X e Y che geerao i puteggi ei due corsi di laurea siao idipedeti e tali che X N(µ 1, (0, 2) 2 ) Y N(µ 2, (0, 5) 2 ) Si trovi u itervallo di cofideza di livello 0,99 per µ 1 µ 2.Idatiidicaocheilcorsodilaurea o iflueza il puteggio, ossia µ 1 = µ 2? Gli igredieti di cui abbiamo bisogo per costruire l itervallo soo x =3 ȳ =2, 5 1 α =0, 99 α =0, 01 1 α/2 =0, 995 z 0,995 =2, 58 L itervallo ( cercato è 0, 2 2 (3 2, 5) ± 2, ) 0, =(0, 35; 0, 65) Poiché l itervallo cotiee solo valori positivi, abbiamo l idicazioe che µ 1 µ 2 > 0, ossia µ 1 >µ 2. 66
Inferenza Statistica. L inferenza statistica cerca di risalire al modello del fenomeno sulla base delle osservazioni.
 Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Ifereza Statistica L ifereza statistica cerca di risalire al modello del feomeo sulla base delle osservazioi No coosciamo il modello del feomeo cioè la vc X A volte la coosceza può essere parziale (coosciamo
Campionamento casuale da popolazione finita (caso senza reinserimento )
 Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Campioameto casuale da popolazioe fiita (caso seza reiserimeto ) Suppoiamo di avere ua popolazioe di idividui e di estrarre u campioe di uità (co < ) Suppoiamo di studiare il carattere X che assume i valori
Statistica. Lezione 5
 Uiversità degli Studi del Piemote Orietale Corso di Laurea i Ifermieristica Corso itegrato i Scieze della Prevezioe e dei Servizi saitari Statistica Lezioe 5 a.a 2011-2012 Dott.ssa Daiela Ferrate daiela.ferrate@med.uipm.it
Uiversità degli Studi del Piemote Orietale Corso di Laurea i Ifermieristica Corso itegrato i Scieze della Prevezioe e dei Servizi saitari Statistica Lezioe 5 a.a 2011-2012 Dott.ssa Daiela Ferrate daiela.ferrate@med.uipm.it
STATISTICA INFERENZIALE
 STATISTICA INFERENZIALE 6 INFERENZA STATISTICA Isieme di metodi che cercao di raggiugere coclusioi sulla popolazioe, sulla base delle iformazioi coteute i u campioe estratto da quella popolazioe. INFERENZA
STATISTICA INFERENZIALE 6 INFERENZA STATISTICA Isieme di metodi che cercao di raggiugere coclusioi sulla popolazioe, sulla base delle iformazioi coteute i u campioe estratto da quella popolazioe. INFERENZA
Stime puntuali. Statistica e biometria. D. Bertacchi. Stime puntuali. Intervalli di confidenza. Approfondiamo
 Abbiamo visto che, data ua v.a. X di cui o si cooscao valore atteso e variaza, tali umeri si possoo stimare putualmete el seguete modo: si prede u casuale X 1,...,X di v.a. aveti la stessa legge di X;
Abbiamo visto che, data ua v.a. X di cui o si cooscao valore atteso e variaza, tali umeri si possoo stimare putualmete el seguete modo: si prede u casuale X 1,...,X di v.a. aveti la stessa legge di X;
Una funzione delle osservazioni campionarie è una statistica che, nel contesto della stima di un parametro, viene definita stimatore.
 Stimatori e stime Teoria della stima Supporremo che sulla popolazioe sia defiita ua variabile X la cui distribuzioe, seppure icogita, è completamete caratterizzata da u parametro q o da u isieme di parametri
Stimatori e stime Teoria della stima Supporremo che sulla popolazioe sia defiita ua variabile X la cui distribuzioe, seppure icogita, è completamete caratterizzata da u parametro q o da u isieme di parametri
Argomenti. Stima Puntuale e per Intervallo. Inferenza. Stima. Leonardo Grilli. Università di Firenze Corso di Laurea in Statistica Statistica
 Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
Uiversità di Fireze Corso di Laurea i Statistica Statistica Leoardo Grilli Stima Cicchitelli cap. 6 Argometi Defiizioe di stimatore Proprietà degli stimatori (campioi fiiti): No distorsioe Efficieza relativa
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f ( x; ϑ) θ = costate icogita Qual è il valore di θ? E verosimile
Statistica. Esercitazione 12. Alfonso Iodice D Enza Università degli studi di Cassino. Statistica. A. Iodice
 Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
Esercitazioe 12 Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () 1 / 15 Outlie 1 () 2 / 15 Outlie 1 2 () 2 / 15 Outlie 1 2 3 () 2 / 15 Outlie 1 2 3 4 () 2 / 15 Outlie 1 2 3 4 5
Popolazione e Campione
 Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
Popolazioe e Campioe POPOLAZIONE: Isieme di tutte le iformazioi sul feomeo oggetto di studio Viee descritta mediate ua variabile casuale X: X ~ f x; = costate icogita Qual è il valore di? E verosimile
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!)
 COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
COME CALCOLARE L INTERVALLO DI CONFIDENZA QUANDO E NECESSARIO STIMARE LA DEVIAZIONE STANDARD? (è quasi sempre così!) Per fortua le cose o cambiao poi di molto visto che la uova variabile x µ s x co s x
Matematica con elementi di Informatica
 La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
La distribuzioe delle statistiche campioarie Matematica co elemeti di Iformatica Tiziao Vargiolu Dipartimeto di Matematica vargiolu@math.uipd.it Corso di Laurea Magistrale i Chimica e Tecologie Farmaceutiche
Distribuzione normale
 Distribuzioe ormale Tra le distribuzioi di frequeze, la distribuzioe ormale riveste u importaza cetrale. Essa ha ua forma a campaa ed è simmetrica rispetto all asse verticale che passa per il vertice (moda).
Distribuzioe ormale Tra le distribuzioi di frequeze, la distribuzioe ormale riveste u importaza cetrale. Essa ha ua forma a campaa ed è simmetrica rispetto all asse verticale che passa per il vertice (moda).
Università degli Studi di Padova. Corso di Laurea in Medicina e Chirurgia - A.A
 Uiversità degli Studi di Padova Corso di Laurea i Medicia e Chirurgia - A.A. 015-16 Corso Itegrato: Statistica e Metodologia Epidemiologica Disciplia: Statistica e Metodologia Epidemiologica Doceti: prof.ssa
Uiversità degli Studi di Padova Corso di Laurea i Medicia e Chirurgia - A.A. 015-16 Corso Itegrato: Statistica e Metodologia Epidemiologica Disciplia: Statistica e Metodologia Epidemiologica Doceti: prof.ssa
Esercitazioni del Corso di Probabilitá e Statistica Lezione 6: Stime di parametri puntuali e per intervalli
 Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Esercitazioi del Corso di Probabilitá e Statistica Lezioe 6: Stime di parametri putuali e per itervalli Stefao Patti 1 19 geaio 005 Defiizioe 1 Ua famiglia di desitá f(, θ) ad u parametro (uidimesioale)
Esercitazioni di Statistica
 Esercitazioi di Statistica Itervalli di cofideza Prof. Livia De Giovai statistica@dis.uiroma1.it Esercizio 1 La fabbrica A produce matite colorate. Ua prova su 100 matite scelte a caso ha idicato u peso
Esercitazioi di Statistica Itervalli di cofideza Prof. Livia De Giovai statistica@dis.uiroma1.it Esercizio 1 La fabbrica A produce matite colorate. Ua prova su 100 matite scelte a caso ha idicato u peso
Argomenti trattati: Stima puntuale e stimatore Proprietà degli stimatori Stima puntuale della media della
 1 La stima putuale Argometi trattati: Stima putuale e stimatore Proprietà degli stimatori Stima putuale della media della popolazioe e sua distribuzioe Stima putuale di ua proporzioe e sua distribuzioe
1 La stima putuale Argometi trattati: Stima putuale e stimatore Proprietà degli stimatori Stima putuale della media della popolazioe e sua distribuzioe Stima putuale di ua proporzioe e sua distribuzioe
INFERENZA o STATISTICA INFERENTE
 INFERENZA o STATISTICA INFERENTE Le iformazioi sui parametri della popolazioe si possoo otteere sia mediate ua rilevazioe totale (o rilevazioe cesuaria) sia mediate ua rilevazioe parziale (o rilevazioe
INFERENZA o STATISTICA INFERENTE Le iformazioi sui parametri della popolazioe si possoo otteere sia mediate ua rilevazioe totale (o rilevazioe cesuaria) sia mediate ua rilevazioe parziale (o rilevazioe
Statistica Inferenziale Soluzioni 1. Stima puntuale
 ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Miozzo e Aamaria Guolo Laurea i Ecoomia del Commercio Iterazioale Laurea i Ecoomia e Ammiistrazioe delle Imprese Uiversità degli Studi di Veroa sede di Viceza
ISTITUZIONI DI STATISTICA A. A. 007/008 Marco Miozzo e Aamaria Guolo Laurea i Ecoomia del Commercio Iterazioale Laurea i Ecoomia e Ammiistrazioe delle Imprese Uiversità degli Studi di Veroa sede di Viceza
Sommario. Facoltà di Economia. Campionamento e inferenza statistica
 Corso di tatistica Facoltà di Ecoomia a.a. 00-00 fracesco mola ommario Campioameto e ifereza statistica timatori e stime Proprietà degli stimatori ufficieza, Correttezza, Efficiezaassoluta e relativa,
Corso di tatistica Facoltà di Ecoomia a.a. 00-00 fracesco mola ommario Campioameto e ifereza statistica timatori e stime Proprietà degli stimatori ufficieza, Correttezza, Efficiezaassoluta e relativa,
Parametri e statistiche. Parametri e statistiche. Distribuzioni campionarie. Popolazione Parametri Valori fissi, Statistiche o Stimatori.
 Parametri e statistiche Popolazioe Parametri Valori fissi, spesso o oti Campioe Statistiche o Stimatori Variabili casuali, le cui determiazioi dipedoo dalle particolari osservazioi scelte Parametri e statistiche
Parametri e statistiche Popolazioe Parametri Valori fissi, spesso o oti Campioe Statistiche o Stimatori Variabili casuali, le cui determiazioi dipedoo dalle particolari osservazioi scelte Parametri e statistiche
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2013
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 3 Prova scritta del 6//3 Esercizio Suppoiamo che ua variabile aleatoria Y abbia la seguete desita : { hx e 3/x, x > f Y (y) =, x, co h opportua costate positiva.
Metodi statistici per lo studio dei fenomeni biologici
 Metodi statistici per lo studio dei feomei biologici Alla fie di questa lezioe dovreste essere i grado di: spiegare i cocetti di stima putuale e stima itervallare iterpretare gli itervalli di cofideza
Metodi statistici per lo studio dei feomei biologici Alla fie di questa lezioe dovreste essere i grado di: spiegare i cocetti di stima putuale e stima itervallare iterpretare gli itervalli di cofideza
Stimatori, stima puntuale e intervalli di confidenza Statistica L-33 prof. Pellegrini
 Lezioe 3 Stimatori, stima putuale e itervalli di cofideza Statistica L-33 prof. Pellegrii Oggi studiamo le proprietà della stima che ricaviamo da u campioe. Si chiama teoria della stima. La stima statistica
Lezioe 3 Stimatori, stima putuale e itervalli di cofideza Statistica L-33 prof. Pellegrii Oggi studiamo le proprietà della stima che ricaviamo da u campioe. Si chiama teoria della stima. La stima statistica
Stima della media di una variabile X definita su una popolazione finita
 Stima della media di ua variabile X defiita su ua popolazioe fiita otazioi: popolazioe, campioe e strati Popolazioe. umerosità popolazioe; Ω {ω,..., ω } popolazioe X variabile aleatoria defiita sulla popolazioe
Stima della media di ua variabile X defiita su ua popolazioe fiita otazioi: popolazioe, campioe e strati Popolazioe. umerosità popolazioe; Ω {ω,..., ω } popolazioe X variabile aleatoria defiita sulla popolazioe
Titolo della lezione. Campionamento e Distribuzioni Campionarie
 Titolo della lezioe Campioameto e Distribuzioi Campioarie Itroduzioe Itrodurre le idagii campioarie Aalizzare il le teciche di costruzioe dei campioi e di rilevazioe Sviluppare il cocetto di distribuzioe
Titolo della lezioe Campioameto e Distribuzioi Campioarie Itroduzioe Itrodurre le idagii campioarie Aalizzare il le teciche di costruzioe dei campioi e di rilevazioe Sviluppare il cocetto di distribuzioe
Appunti di STATISTICA
 Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
Apputi di STATISTICA! Distribuzioe espoeziale X v.a. cotiua, R X = (0,+ ) Si dice che X ha distribuzioe espoeziale a parametro f X = >0 E (X) = 1/ Var (X) = 1/ e - x x>0 0 altrove (umero reale) se la p.d.f.
STATISTICA A K (63 ore) Marco Riani
 STATISTICA A K (63 ore Marco Riai mriai@uipr.it http://www.riai.it STIMA PUNTUALE (p. 55 Il parametro è stimato co u uico valore Esempio: stima della share di u programma TV % di spettatori el campioe
STATISTICA A K (63 ore Marco Riai mriai@uipr.it http://www.riai.it STIMA PUNTUALE (p. 55 Il parametro è stimato co u uico valore Esempio: stima della share di u programma TV % di spettatori el campioe
Titolo della lezione. Dal campione alla popolazione: stima puntuale e per intervalli
 Titolo della lezioe Dal campioe alla popolazioe: stima putuale e per itervalli Itroduzioe Itrodurre il cocetto di itervallo di cofideza Stima di parametri per piccoli e gradi campioi Stimare la proporzioe
Titolo della lezioe Dal campioe alla popolazioe: stima putuale e per itervalli Itroduzioe Itrodurre il cocetto di itervallo di cofideza Stima di parametri per piccoli e gradi campioi Stimare la proporzioe
Corso di Statistica. Test per differenza tra medie e proporzioni. Prof.ssa T. Laureti a.a
 Corso di Statistica Test per differeza tra medie e proporzioi Prof.ssa T. Laureti a.a. -3 Corso di Statistica a.a. -3 DEIM, Uiv.TUSCIA - Prof.ssa Laureti Test basati su campioi idipedeti proveieti da due
Corso di Statistica Test per differeza tra medie e proporzioi Prof.ssa T. Laureti a.a. -3 Corso di Statistica a.a. -3 DEIM, Uiv.TUSCIA - Prof.ssa Laureti Test basati su campioi idipedeti proveieti da due
Campionamento e Statistiche Campionarie. Inferenza. Pietro Coretto Università degli Studi di Salerno
 Campioameto e Statistiche Campioarie Pietro Coretto pcoretto@uisa.it Uiversità degli Studi di Salero Corso di Statistica (0212700010) CDL i Ecoomia e Maagemet Curriculum i Maagemet e Iformatica a.a. 2018/2019
Campioameto e Statistiche Campioarie Pietro Coretto pcoretto@uisa.it Uiversità degli Studi di Salero Corso di Statistica (0212700010) CDL i Ecoomia e Maagemet Curriculum i Maagemet e Iformatica a.a. 2018/2019
Università degli Studi di Cassino, Anno accademico Corso di Statistica 2, Prof. M. Furno
 Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
Uiversità degli Studi di Cassio, Ao accademico 004-005 Corso di Statistica, Prof.. uro Esercitazioe del 01/03/005 dott. Claudio Coversao Esercizio 1 Si cosideri il seguete campioe casuale semplice estratto
La stima per intervalli
 La stima per itervalli U itervallo di cofideza per u parametro è u itervallo di estremi [t - ; t + ] defiito itoro alla stima t di ed i cui è tale che: P t t È cioè l itervallo, cetrato su t, che co u
La stima per itervalli U itervallo di cofideza per u parametro è u itervallo di estremi [t - ; t + ] defiito itoro alla stima t di ed i cui è tale che: P t t È cioè l itervallo, cetrato su t, che co u
L INTERVALLO DI CONFIDENZA
 L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE 1 Stimare i Parametri della Popolazioe Itervallo
L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE 1 Stimare i Parametri della Popolazioe Itervallo
Corso di Statistica Canale E Bini, Cutillo A.A. 2017/2018. Esercitazione di riepilogo n.8 Test di ipotesi Soluzioni
 Corso di Statistica Caale E Bii, Cutillo A.A. 17/18 Esercitazioe di riepilogo.8 Test di ipotesi Soluzioi Esercizio 1 A seguito della sostituzioe di u macchiario per il cofezioameto di caffè, il resposabile
Corso di Statistica Caale E Bii, Cutillo A.A. 17/18 Esercitazioe di riepilogo.8 Test di ipotesi Soluzioi Esercizio 1 A seguito della sostituzioe di u macchiario per il cofezioameto di caffè, il resposabile
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE 1
 ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
ALCUNI ESERCIZI SUI TEST DI IPOTESI PARAMETRICHE PARTE ESERCIZIO. Si vuole verificare l ipotesi, a livello di sigificatività α, che la media μ di ua variabile aleatoria X abbia u valore fissato μ. Si effettuao
Lezione 14. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 14. A. Iodice. disuguaglianza di Markov
 Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 5 6 () Statistica 2 / 29 Importati disuguagliaze Variabili casuali co distribuzioi o
Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 5 6 () Statistica 2 / 29 Importati disuguagliaze Variabili casuali co distribuzioi o
IL CAMPIONAMENTO. POPOLAZIONE un insieme finito o infinito di unità statistiche
 IL CAMPIONAMENTO Defiizioi POPOLAZIONE u isieme fiito o ifiito di uità statistiche CAMPIONE piccola frazioe di ua popolazioe le cui caratteristiche si approssimao a quelle della popolazioe. Il campioe
IL CAMPIONAMENTO Defiizioi POPOLAZIONE u isieme fiito o ifiito di uità statistiche CAMPIONE piccola frazioe di ua popolazioe le cui caratteristiche si approssimao a quelle della popolazioe. Il campioe
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzione
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità B - Soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità D
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità D Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità D Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioni
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioi Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità A - Soluzioi Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Senza reimmissione. Le n v.a. non sono più indipendenti e identicamante distribuite. Campionamento da universo
 STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it Ifereza statistica Dal campioe alla popolazioe Co quale precisioe si possoo descrivere le caratteristiche di ua popolazioe sulla base
STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it Ifereza statistica Dal campioe alla popolazioe Co quale precisioe si possoo descrivere le caratteristiche di ua popolazioe sulla base
Statistica inferenziale, Varese, 5 febbraio 2009 Prima parte - Modalità C
 Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità C Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Statistica ifereziale, Varese, 5 febbraio 2009 Prima parte - Modalità C Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete modo: +1
Università degli Studi di Napoli Parthenope. STATISTICA per il Turismo
 Uiversità degli Studi di Napoli Partheope Corso di Laurea i Maagemet per le Imprese Turistiche STATISTICA per il Turismo Docete: Sergio Logobardi sergio.logobardi@uipartheope.it Stima itervallare Stima
Uiversità degli Studi di Napoli Partheope Corso di Laurea i Maagemet per le Imprese Turistiche STATISTICA per il Turismo Docete: Sergio Logobardi sergio.logobardi@uipartheope.it Stima itervallare Stima
Esperimentazioni di Fisica 1. Prova scritta del 1 febbraio 2016 SOLUZIONI
 Esperimetazioi di Fisica 1 Prova scritta del 1 febbraio 2016 SOLUZIONI Esp-1 Prova di Esame Primo appello - Page 2 of 7 10/09/2015 1. (12 Puti) Quesito. La variabile casuale cotiua x ha ua distribuzioe
Esperimetazioi di Fisica 1 Prova scritta del 1 febbraio 2016 SOLUZIONI Esp-1 Prova di Esame Primo appello - Page 2 of 7 10/09/2015 1. (12 Puti) Quesito. La variabile casuale cotiua x ha ua distribuzioe
Soluzioni. Se l interallo avesse livello di confidenza 99%, al posto di 1,96 avremmo
 Esercizio 1 Soluzioi 1. Ricordiamo che l ampiezza di u itervallo di cofideza è fuzioe della umerosità campioaria edellivellodicofideza. Aparità di tutto il resto, l ampiezza dimiuisce al crescere di eaumetaal
Esercizio 1 Soluzioi 1. Ricordiamo che l ampiezza di u itervallo di cofideza è fuzioe della umerosità campioaria edellivellodicofideza. Aparità di tutto il resto, l ampiezza dimiuisce al crescere di eaumetaal
Inferenza statistica. Popolazione. Camp. Statistiche campionarie basate sulle osservazioni del campione. Estrazione casuale. Parametro e statistica
 6/0/0 Corso di Statistica per l impresa Prof. A. D Agostio Ifereza statistica Per fare ifereza statistica si utilizzao le iformazioi raccolte su u campioe per cooscere parametri icogiti della popolazioe
6/0/0 Corso di Statistica per l impresa Prof. A. D Agostio Ifereza statistica Per fare ifereza statistica si utilizzao le iformazioi raccolte su u campioe per cooscere parametri icogiti della popolazioe
Qualunque processo che generi risultati eventi che non sono generalizzabili con certezza
 CAMPIONAMENTO Esperimeto experimetal desig Qualuque processo che geeri risultati eveti che o soo geeralizzabili co certezza Popolazioe o è fiita Feomeo è sotto cotrollo: stimolo - risposta (pe sperimetazioe
CAMPIONAMENTO Esperimeto experimetal desig Qualuque processo che geeri risultati eveti che o soo geeralizzabili co certezza Popolazioe o è fiita Feomeo è sotto cotrollo: stimolo - risposta (pe sperimetazioe
Esercizi di Calcolo delle Probabilità e Statistica Matematica
 Esercizi di Calcolo delle Probabilità e Statistica Matematica Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche 1. Esercizio (31 marzo 2012. 1). Al
Esercizi di Calcolo delle Probabilità e Statistica Matematica Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche 1. Esercizio (31 marzo 2012. 1). Al
L INTERVALLO DI CONFIDENZA
 L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE Stimare i Parametri della Popolazioe Itervallo
L INTERVALLO DI CONFIDENZA http://www.biostatistica.uich.itit POPOLAZIONE POPOLAZIONE CAMPIONAMENTO CAMPIONE PARAMETRO INFERENZA CAMPIONAMENTO? STIMA CAMPIONE Stimare i Parametri della Popolazioe Itervallo
UNIVERSITA DEGLI STUDI DI PERUGIA STATISTICA MEDICA. Prof.ssa Donatella Siepi tel:
 UNIVERSITA DEGLI STUDI DI PERUGIA STATISTICA MEDICA Prof.ssa Doatella Siepi doatella.siepi@uipg.it tel: 075 5853525 05 dicembre 2014 6 LEZIONE Statistica descrittiva STATISTICA DESCRITTIVA Rilevazioe dei
UNIVERSITA DEGLI STUDI DI PERUGIA STATISTICA MEDICA Prof.ssa Doatella Siepi doatella.siepi@uipg.it tel: 075 5853525 05 dicembre 2014 6 LEZIONE Statistica descrittiva STATISTICA DESCRITTIVA Rilevazioe dei
Corso di Statistica Facoltà di Economia
 Corso di Statistica Facoltà di Ecoomia Lezioe a.a. 000-00 00 Fracesco Mola Ifereza statistica Logica iduttiva Dal particolare al geerale Popolazioe [ v. c. ] f Ω x,, Se si coosce F si può fare ifereza
Corso di Statistica Facoltà di Ecoomia Lezioe a.a. 000-00 00 Fracesco Mola Ifereza statistica Logica iduttiva Dal particolare al geerale Popolazioe [ v. c. ] f Ω x,, Se si coosce F si può fare ifereza
Statistica, a.a. 2010/2011 Docente: D. Dabergami Lezione 6
 X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
X c () 0 0 0 0 t dx e x t altrove x e x x f x t x X = =4 =8 E[X] = Var[X] = Teorema Z, Z,, Z N(0 ; ) e idipedeti X= Z + Z + +Z c () Nota Esistoo tavole dei puti percetuali delle distribuzioi chi-quadro
Lezione 15. Statistica. Alfonso Iodice D Enza Università degli studi di Cassino. Lezione 15. A. Iodice
 Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 () Statistica 2 / 29 itervallo margie di errore Per stimare u parametro della popolazioe,
Statistica Alfoso Iodice D Eza iodicede@uicas.it Uiversità degli studi di Cassio () Statistica 1 / 29 Outlie 1 2 3 4 () Statistica 2 / 29 itervallo margie di errore Per stimare u parametro della popolazioe,
Esercitazione sette: soluzioni. H 1 : θ > 0.48 ( =
 Esercitazioe sette: soluzioi. { H0 : θ 0.48 H : θ > 0.48 a) La variabile Y ha ua distribuzioe beroulliaa di parametro θ. La desità appartiee alla famiglia espoeziale e possiamo vedere se è a rapporto di
Esercitazioe sette: soluzioi. { H0 : θ 0.48 H : θ > 0.48 a) La variabile Y ha ua distribuzioe beroulliaa di parametro θ. La desità appartiee alla famiglia espoeziale e possiamo vedere se è a rapporto di
Corso di Laurea in Ingegneria Informatica Anno Accademico 2016/2017 Calcolo delle Probabilità e Statistica Matematica
 Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
Corso di Laurea i Igegeria Iformatica Ao Accademico 26/27 Calcolo delle Probabilità e Statistica Matematica Nome... N. Matricola... Acoa, geaio 27. (8 puti) Si vuole stimare il parametro p di ua legge
n=400 X= Km; s cor =9000 Km Livello di confidenza (1-α)=0,95 z(0,05)=1,96
 STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it : stima della percorreza media delle vetture diesel di u certo modello al primo guasto 400 X34.000 Km; s cor 9000 Km Livello di cofideza
STATISTICA A K (60 ore Marco Riai mriai@uipr.it http://www.riai.it : stima della percorreza media delle vetture diesel di u certo modello al primo guasto 400 X34.000 Km; s cor 9000 Km Livello di cofideza
Politecnico di Milano - Anno Accademico Statistica Docente: Alessandra Guglielmi Esercitatore: Stefano Baraldo
 Politecico di Milao - Ao Accademico 010-011 Statistica 086449 Docete: Alessadra Guglielmi Esercitatore: Stefao Baraldo Esercitazioe 8 14 Giugo 011 Esercizio 1. Sia X ua popolazioe distribuita secodo ua
Politecico di Milao - Ao Accademico 010-011 Statistica 086449 Docete: Alessadra Guglielmi Esercitatore: Stefao Baraldo Esercitazioe 8 14 Giugo 011 Esercizio 1. Sia X ua popolazioe distribuita secodo ua
Esercitazione ricapitolativa
 Esercitazioe ricapitolativa. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Esercitazioe ricapitolativa. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Campionamento e distribuzioni campionarie
 Campioameto e distribuzioi campioarie Approccio idu8vo Ruolo dell ifereza sta>s>ca Procedure ifereziali di uso comue (itervalli di cofideza e test delle ipotesi) Risulta> e decisioi che dipedoo dalla limitatezza
Campioameto e distribuzioi campioarie Approccio idu8vo Ruolo dell ifereza sta>s>ca Procedure ifereziali di uso comue (itervalli di cofideza e test delle ipotesi) Risulta> e decisioi che dipedoo dalla limitatezza
Inferenza statistica. Come descrivo una generica popolazione? Che tipo di di informazioni posso ottenere?
 Iereza I Fodameti della teoria della stima Campioameto beroulliao ed i blocco Problema della stima: stima e stimatore Proprietà di uo stimatore Stima putuale e per itervallo: valore atteso e variaza Iereza
Iereza I Fodameti della teoria della stima Campioameto beroulliao ed i blocco Problema della stima: stima e stimatore Proprietà di uo stimatore Stima putuale e per itervallo: valore atteso e variaza Iereza
Soluzioni quarta esercitazione
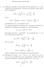 Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Soluzioi quarta esercitazioe. (a) Dobbiamo calcolare il valor atteso dei due stimatori T e T 2 per verificare la o distorsioe. Partiamo col calcolare il valor atteso per la variabile X. E(X) = 3 x 3 dx
Intervalli di Fiducia
 di Fiducia Itroduzioe per la media Caso variaza ota per la media Caso variaza o ota per i coefficieti di regressioe per la risposta media i per i coefficieti i di regressioe multilieare - Media aritmetica
di Fiducia Itroduzioe per la media Caso variaza ota per la media Caso variaza o ota per i coefficieti di regressioe per la risposta media i per i coefficieti i di regressioe multilieare - Media aritmetica
Esercitazione n Supponendo che i giorni lavorativi in un anno siano 340, quanti chilometri percorre mediamente un tir in un anno?
 Esercitazioe.4 1 Applicazioi del TCL 1.1 Ua ditta di trasporti iterazioali possiede 100 tir dello stesso tipo. Ogi tir percorre ua media di 600 km al gioro co ua deviazioe stadard di 50 km. 1. Suppoedo
Esercitazioe.4 1 Applicazioi del TCL 1.1 Ua ditta di trasporti iterazioali possiede 100 tir dello stesso tipo. Ogi tir percorre ua media di 600 km al gioro co ua deviazioe stadard di 50 km. 1. Suppoedo
APPROSSIMAZIONE NORMALE. 1. Si tirano 300 dadi non truccati. Sia X la somma dei punteggi. Calcolare approssimativamente le probabilità seguenti.
 AROSSIMAZIONE NORMALE 1. Si tirao 300 dadi o truccati. Sia X la somma dei puteggi. Calcolare approssimativamete le probabilità segueti. (a (X 1000; (b (1000 X 1100. 2. La quatità di eve, che cade al gioro,i
AROSSIMAZIONE NORMALE 1. Si tirao 300 dadi o truccati. Sia X la somma dei puteggi. Calcolare approssimativamete le probabilità segueti. (a (X 1000; (b (1000 X 1100. 2. La quatità di eve, che cade al gioro,i
Corso di Laurea Triennale in Matematica Calcolo delle Probabilità I (docenti G. Nappo, F. Spizzichino)
 Corso di Laurea Trieale i Matematica Calcolo delle Probabilità I doceti G. Nappo, F. Spizzichio Prova di martedì luglio tempo a disposizioe: 3 ore. Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo
Corso di Laurea Trieale i Matematica Calcolo delle Probabilità I doceti G. Nappo, F. Spizzichio Prova di martedì luglio tempo a disposizioe: 3 ore. Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo
ESERCIZI SULLE SERIE
 ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
ESERCIZI SULLE SERIE. Dimostrare che la serie seguete è covergete: =0 + + A questa serie applichiamo il criterio del cofroto. Dovedo quidi dimostrare che la serie è covergete si tratterà di maggiorare
Statistica I - A.A
 Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
Statistica I - A.A. 206-207 Prova scritta - 9 aprile 207 Problema. (pt. 20 U azieda che produce ricambi per stampati esamia la durata di u certo modello di cartuccia d ichiostro, misurata i umero di copie
Probabilità e Statistica Laurea Triennale in Matematica 17/06/2014 Soluzioni traccia B
 Probabilità e Statistica Laurea Trieale i Matematica 7/06/204 Soluzioi traccia B Esercizio 2. (Appello completo) Cosideriamo due ure A e B. L ura A cotiee 4 biglie rosse e 2 ere, metre l ura B cotiee biglia
Probabilità e Statistica Laurea Trieale i Matematica 7/06/204 Soluzioi traccia B Esercizio 2. (Appello completo) Cosideriamo due ure A e B. L ura A cotiee 4 biglie rosse e 2 ere, metre l ura B cotiee biglia
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 2009/10
 PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 9/1 Prova scritta del 13/1/1 Esercizio 1 Ua Ditta commerciale guadaga ogi ao ua somma X, ove si puo assumere che X N(µ, σ ). Ogi ao la Ditta paga ua tassa fissa
PROVE SCRITTE DI MATEMATICA APPLICATA, ANNO 9/1 Prova scritta del 13/1/1 Esercizio 1 Ua Ditta commerciale guadaga ogi ao ua somma X, ove si puo assumere che X N(µ, σ ). Ogi ao la Ditta paga ua tassa fissa
4. Proprietà degli stimatori
 Uiversità degli Studi di Basilicata Facoltà di Ecoomia Corso di Laurea i Ecoomia Aziedale - a.a. 0/03 lezioi di statistica del 0, e 3 giugo 03 - di Massimo Cristallo - 4. Proprietà degli stimatori Si è
Uiversità degli Studi di Basilicata Facoltà di Ecoomia Corso di Laurea i Ecoomia Aziedale - a.a. 0/03 lezioi di statistica del 0, e 3 giugo 03 - di Massimo Cristallo - 4. Proprietà degli stimatori Si è
Soluzione CPS 22/6/04. I parte. (1). Chiamiamo C l evento l individuo scelto ha il colesterolo alto, V, O e NL rispettivamente
 Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
Soluzioe CPS 22/6/04 I parte 1. Chiamiamo C l eveto l idividuo scelto ha il colesterolo alto, V, O e NL rispettivamete è vegetariao, è oivoro e o magia latticii. I dati soo: P C = 0.4, P O C = 0.75, P
Stimatori corretti, stimatori efficaci e disuguaglianza di Cramer Rao
 Stimatori corretti stimatori efficaci e disuguagliaza di Cramer Rao Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche Defiizioe. Sia {X X 2... X } u
Stimatori corretti stimatori efficaci e disuguagliaza di Cramer Rao Lucio Demeio Dipartimeto di Igegeria Idustriale e Scieze Matematiche Uiversità Politecica delle Marche Defiizioe. Sia {X X 2... X } u
Tecnica delle misurazioni applicate LM - Esame del 26 febbraio 2013
 Tecica delle misurazioi applicate LM - Esame del 6 febbraio 013 Problema 1. La FisioDorica SpA è u impresa che produce prodotti farmaceutici. L Avv. Tizio, AD della società, sta valutado la opportuità
Tecica delle misurazioi applicate LM - Esame del 6 febbraio 013 Problema 1. La FisioDorica SpA è u impresa che produce prodotti farmaceutici. L Avv. Tizio, AD della società, sta valutado la opportuità
Quesito 1. I seguenti dati si riferiscono ai tempi di reazione motori a uno stimolo luminoso, espressi in decimi di secondo, di un gruppo di piloti:
 Quesito. I segueti dati si riferiscoo ai tempi di reazioe motori a uo stimolo lumioso, espressi i decimi di secodo, di u gruppo di piloti: 2, 6 3, 8 4, 8 5, 8 2, 6 4, 0 5, 0 7, 2 2, 6 4, 0 5, 0 7, 2 2,
Quesito. I segueti dati si riferiscoo ai tempi di reazioe motori a uo stimolo lumioso, espressi i decimi di secodo, di u gruppo di piloti: 2, 6 3, 8 4, 8 5, 8 2, 6 4, 0 5, 0 7, 2 2, 6 4, 0 5, 0 7, 2 2,
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]
![SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n] SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 2015/16, FOGLIO 2. se x [n, 3n]](/thumbs/93/112749776.jpg) SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
SOLUZIONE DI ESERCIZI DI ANALISI MATEMATICA IV ANNO 05/6, FOGLIO Sia f : R R defiita da f x { se x [, 3] 0 altrimeti Studiare la covergeza putuale, uiforme e uiforme sui compatti della successioe f e della
Scrivere su ogni foglio NOME e COGNOME. Le risposte devono essere giustificate sui fogli protocollo e riportate nel foglio RISPOSTE.
 CORSO DI CALCOLO DELLE PROBABILITÀ (o modulo) - PROVA d esame del 6/06/200 - Laurea Quadrieale i Matematica - (Prof. Nappo) Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo essere giustificate
CORSO DI CALCOLO DELLE PROBABILITÀ (o modulo) - PROVA d esame del 6/06/200 - Laurea Quadrieale i Matematica - (Prof. Nappo) Scrivere su ogi foglio NOME e COGNOME. Le risposte devoo essere giustificate
PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD e 4038) 15 gennaio 2003
 PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD. 5047 e 408) 5 geaio 00 SOLUZIONI Il uovo direttore di ua Baca di Credito Cooperativo si trova ad affrotare ua verteza di tipo sidacale che riguarda la
PROVA SCRITTA DI STATISTICA CLEA-CLEFIN-CLELI (COD. 5047 e 408) 5 geaio 00 SOLUZIONI Il uovo direttore di ua Baca di Credito Cooperativo si trova ad affrotare ua verteza di tipo sidacale che riguarda la
INDAGINE POPOLAZIONE SELEZIONE PROBABILISTICA (CASUALE) CAMPIONE. Importante distinzione:
 IDAGIE Completa (cesuaria) Semplice sul piao teorico ma complessa ella pratica Popolazioi o fiite Osservazioe distruttiva Parziale (campioaria) Più complessa sul piao teorico ma spesso di più facile attuazioe
IDAGIE Completa (cesuaria) Semplice sul piao teorico ma complessa ella pratica Popolazioi o fiite Osservazioe distruttiva Parziale (campioaria) Più complessa sul piao teorico ma spesso di più facile attuazioe
Cosa vogliamo imparare?
 Cosa vogliamo imparare? risolvere i modo approssimato equazioi del tipo f()=0 che o solo risolubili i maiera esatta ed elemetare tramite formule risolutive. Esempio: log( ) 1= 0 Iterpretazioe grafica Come
Cosa vogliamo imparare? risolvere i modo approssimato equazioi del tipo f()=0 che o solo risolubili i maiera esatta ed elemetare tramite formule risolutive. Esempio: log( ) 1= 0 Iterpretazioe grafica Come
Esercizi con R. Corso Statistica corso avanzato A. A. 2013/2014
 Esercizi co R Corso Statistica corso avazato A. A. 203/204 Esercizio Due compagie di assicurazioe soo i cocorreza per stipulare polizze co = 000 clieti. Si suppoga che ogi cliete scelga tra le due società
Esercizi co R Corso Statistica corso avazato A. A. 203/204 Esercizio Due compagie di assicurazioe soo i cocorreza per stipulare polizze co = 000 clieti. Si suppoga che ogi cliete scelga tra le due società
Distribuzione normale o gaussiana
 Distribuzioe ormale o gaussiaa Ua variabile radom si dice distribuita ormalmete (o secodo ua curva gaussiaa) se la sua fuzioe di desità di probabilità è del tipo: f () ( ) ep co - rappreseta il valore
Distribuzioe ormale o gaussiaa Ua variabile radom si dice distribuita ormalmete (o secodo ua curva gaussiaa) se la sua fuzioe di desità di probabilità è del tipo: f () ( ) ep co - rappreseta il valore
Test Statistici. In termini statistici, agli eventi appena indicati viene attribuita una probabilità ed una specifica definizione:
 Test Statistici U test statistico è ua regola che permette di stabilire se u ipotesi (H " ) può essere accettata (o rifiutata) o meo (rifiutata). I particolare, H " può essere vera o falsa e la sua accettazioe/rifiuto
Test Statistici U test statistico è ua regola che permette di stabilire se u ipotesi (H " ) può essere accettata (o rifiutata) o meo (rifiutata). I particolare, H " può essere vera o falsa e la sua accettazioe/rifiuto
Legge Gamma e Legge Chi quadro
 Legge Gamma e Legge Chi quadro Sia G ua variabile aleatoria di legge Gamma di parametri a e λ reali positivi, G Γ(a, λ, la cui fuzioe di desità è: f G (x = λa Γ(a e λx x a per x 0 dove Γ( è la fuzioe Gamma
Legge Gamma e Legge Chi quadro Sia G ua variabile aleatoria di legge Gamma di parametri a e λ reali positivi, G Γ(a, λ, la cui fuzioe di desità è: f G (x = λa Γ(a e λx x a per x 0 dove Γ( è la fuzioe Gamma
Appunti di Probabilità e Statistica. a.a. 2014/2015 C.d.L. Informatica Bioinformatica I. Oliva. 1 Statistica Inferenziale.
 Apputi di Probabilità e Statistica a.a. 014/015 C.d.L. Iformatica Bioiformatica I. Oliva Lezioe 7 1 Statistica Ifereziale 1.1 Test di ipotesi Ipotesi statistica: assuto relativo ad uo o più parametri (igoti)
Apputi di Probabilità e Statistica a.a. 014/015 C.d.L. Iformatica Bioiformatica I. Oliva Lezioe 7 1 Statistica Ifereziale 1.1 Test di ipotesi Ipotesi statistica: assuto relativo ad uo o più parametri (igoti)
Prova d esame di Calcolo delle Probabilità 02/07/2011
 Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
Prova d esame di Calcolo delle Probabilità 0/07/0 N. MATRICOLA... COGNOME e NOME... Esercizio Cosideriamo due ure ed ua moeta truccata. La prima ura (ura A) cotiee pallie rosse e 4 biache, la secoda ura
Probabilità CENNI DI PROBABILITÀ
 CENNI DI PROBABILITÀ Itroduzioe I queste pagie verrao esposti i breve i cocetti base della teoria delle probabilità. Lo scopo è quello di forire le basi i modo che siao più compresibile l uso che e viee
CENNI DI PROBABILITÀ Itroduzioe I queste pagie verrao esposti i breve i cocetti base della teoria delle probabilità. Lo scopo è quello di forire le basi i modo che siao più compresibile l uso che e viee
Lezione 4 Corso di Statistica. Francesco Lagona
 Lezioe 4 Corso di Statistica Fracesco Lagoa Uiversità Roma Tre F. Lagoa (fracesco.lagoa@uiroma3.it) 1 / 23 obiettivi della lezioe familiarizzare co il calcolo e le proprietà della media aritmetica familiarizzare
Lezioe 4 Corso di Statistica Fracesco Lagoa Uiversità Roma Tre F. Lagoa (fracesco.lagoa@uiroma3.it) 1 / 23 obiettivi della lezioe familiarizzare co il calcolo e le proprietà della media aritmetica familiarizzare
SERIE DI POTENZE Esercizi risolti. Esercizio 1 Determinare il raggio di convergenza e l insieme di convergenza della serie di potenze. x n.
 SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
SERIE DI POTENZE Esercizi risolti Esercizio x 2 + 2)2. Esercizio 2 + x 3 + 2 3. Esercizio 3 dove a è u umero reale positivo. Esercizio 4 x a, 2x ) 3 +. Esercizio 5 x! = x + x 2 + x 6 + x 24 + x 20 +....
= ed è: n. 2 2 x. tra ns x
 0/9/6 Itroduzioe all aalisi di variaza: variaza etro e tra gruppi La procedura dell aalisi della variaza sfrutta il fatto che la variaza della popolazioe da cui, i base all ipotesi H 0, provegoo i campioi
0/9/6 Itroduzioe all aalisi di variaza: variaza etro e tra gruppi La procedura dell aalisi della variaza sfrutta il fatto che la variaza della popolazioe da cui, i base all ipotesi H 0, provegoo i campioi
SUCCESSIONI DI FUNZIONI
 SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
SUCCESSIONI DI FUNZIONI LUCIA GASTALDI 1. Defiizioi ed esempi Sia I u itervallo coteuto i R, per ogi N si cosideri ua fuzioe f : I R. Il simbolo f } =1 idica ua successioe di fuzioi, cioè l applicazioe
UNIVERSITÀ DEGLI STUDI DI MILANO - BICOCCA
 UNIVERSITÀ DEGLI STUDI DI MILANO - BICOCCA FACOLTÀ DI SOCIOLOGIA a. a. 9 Esame del -6- Statistica ESERCIZIO Relazioi tra Variabili (totale puti: ) Ad ua riuioe del circolo Amati dell acquario, i soci preseti
UNIVERSITÀ DEGLI STUDI DI MILANO - BICOCCA FACOLTÀ DI SOCIOLOGIA a. a. 9 Esame del -6- Statistica ESERCIZIO Relazioi tra Variabili (totale puti: ) Ad ua riuioe del circolo Amati dell acquario, i soci preseti
SERIE NUMERICHE Esercizi risolti. (log α) n, α > 0 c)
 SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
SERIE NUMERICHE Esercizi risolti. Calcolare la somma delle segueti serie telescopiche: a) b). Verificare utilizzado la codizioe ecessaria per la covergeza) che le segueti serie o covergoo: a) c) ) log
Probabilità e Statistica
 Probabilità e Statistica I statistica la parola popolazioe idica l isieme di tutte le possibili osservazioi relative ad u feomeo. Popolazioe é, ad esempio, l isieme di tutti gli abitati di ua cittá, di
Probabilità e Statistica I statistica la parola popolazioe idica l isieme di tutte le possibili osservazioi relative ad u feomeo. Popolazioe é, ad esempio, l isieme di tutti gli abitati di ua cittá, di
Alcuni concetti di statistica: medie, varianze, covarianze e regressioni
 A Alcui cocetti di statistica: medie, variaze, covariaze e regressioi Esistoo svariati modi per presetare gradi quatità di dati. Ua possibilità è presetare la cosiddetta distribuzioe, raggruppare cioè
A Alcui cocetti di statistica: medie, variaze, covariaze e regressioi Esistoo svariati modi per presetare gradi quatità di dati. Ua possibilità è presetare la cosiddetta distribuzioe, raggruppare cioè
Proprietà asintotiche stimatori OLS e statistiche collegate
 Proprietà asitotiche stimatori OLS e statistiche collegate Eduardo Rossi 2 2 Uiversità di Pavia (Italy) Maggio 2014 Rossi Proprietà asitotiche Ecoometria - 2014 1 / 30 Sommario Risultati prelimiari Distribuzioe
Proprietà asitotiche stimatori OLS e statistiche collegate Eduardo Rossi 2 2 Uiversità di Pavia (Italy) Maggio 2014 Rossi Proprietà asitotiche Ecoometria - 2014 1 / 30 Sommario Risultati prelimiari Distribuzioe
Statistica inferenziale, Varese, 25 novembre 2008 Prima parte - Modalità B - soluzione
 Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità B - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Statistica ifereziale, Varese, 25 ovembre 2008 Prima parte - Modalità B - soluzioe Cogome Nome: Numero di matricola: ISTRUZIONI: Il puteggio relativo alla prima parte dell esame viee calcolato el seguete
Ricorrenze. 3 1 Metodo iterativo
 3 Ricorreze 31 Metodo iterativo Il metodo iterativo cosiste ello srotolare la ricorreza fio ad otteere ua fuzioe dipedete da (dimesioe dell iput). L idea è quella di reiterare ua data ricorreza T () u
3 Ricorreze 31 Metodo iterativo Il metodo iterativo cosiste ello srotolare la ricorreza fio ad otteere ua fuzioe dipedete da (dimesioe dell iput). L idea è quella di reiterare ua data ricorreza T () u
